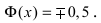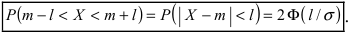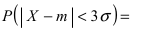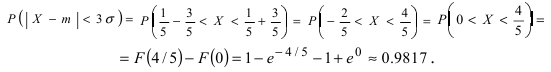Содержание:
Нормальный закон распределения:
Нормальный закон распределения имеет плотность вероятности
где
График функции плотности вероятности (2.9.1) имеет максимум в точке 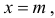

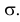
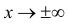
Помимо геометрического смысла, параметры нормального закона распределения имеют и вероятностный смысл. Параметр 
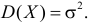
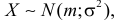

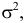
где 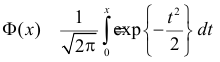
Значения функции 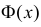
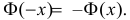
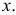
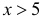
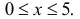
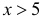
Если 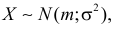
Пример:
Случайная величина X имеет нормальный закон распределения 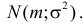
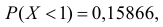
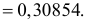
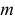
Решение. Воспользуемся формулой (2.9.2):
Так как 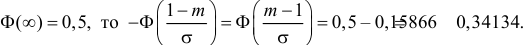
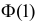
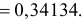
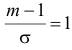
Аналогично 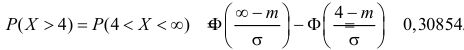
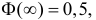
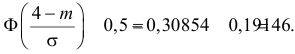
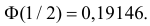
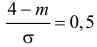
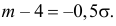
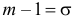
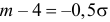
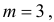
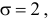
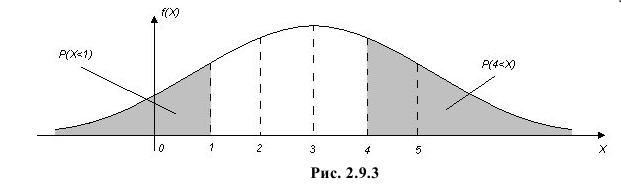
График функции плотности вероятности этого закона распределения изображен на рис. 2.9.3.
Ответ.
Пример:
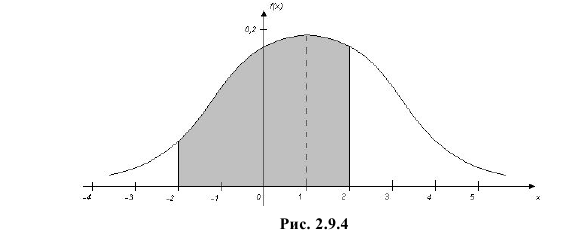
Ошибка измерения X имеет нормальный закон распределения, причем систематическая ошибка равна 1 мк, а дисперсия ошибки равна 4 мк2. Какова вероятность того, что в трех независимых измерениях ошибка ни разу не превзойдет по модулю 2 мк?
Решение. По условиям задачи 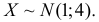
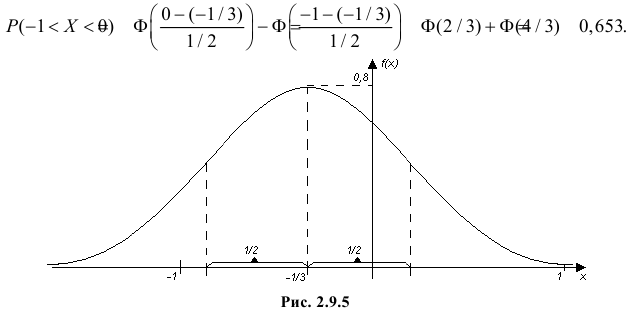
Вычисленная вероятность численно равна заштрихованной площади на рис. 2.9.4.
Каждое измерение можно рассматривать как независимый опыт. Поэтому по формуле Бернулли (2.6.1) вероятность того, что в трех независимых измерениях ошибка ни разу не превзойдет 2 мк, равна
Ответ.
Пример:
Функция плотности вероятности случайной величины X имеет вид
Требуется определить коэффициент 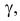
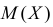
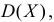
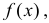
Замечание. Если каждый закон распределения из некоторого семейства законов распределения имеет функцию распределения , 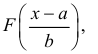
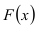
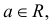
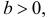
Решение. Так как (2.9.4) функция плотности вероятности, то интеграл от нее по всей числовой оси должен быть равен единице:
Преобразуем выражение в показателе степени, выделяя полный квадрат:
Тогда (2.9.5) можно записать в виде
Сделаем замену переменных так, чтобы 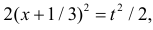
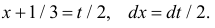
Умножим и разделим левую часть равенства на 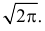
Так как 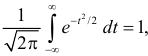
Поэтому
Последняя запись означает, что случайная величина имеет нормальный закон распределения с параметрами 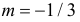
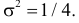
Ответ.
Пример:
Цех на заводе выпускает транзисторы с емкостью коллекторного перехода 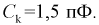
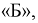
Решение.
Статистическими исследованиями в цеху установлено, что 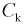
Чтобы вычислить количество транзисторов, попадающих в группу 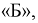
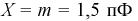
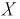
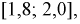
Для расчета этой вероятности надо построить математическую модель. Экспериментальные данные говорят о том, что нормальное распределение можно принять в качестве математической модели. Эмпирическая оценка (установлена статистическими исследованиями в цеху) среднего значения
дает 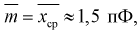
Обозначая 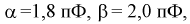
Тогда количество транзисторов 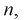
Нормальное распределение и его свойства
Если выйти на улицу любого города и случайным образом выбранных прохожих спросить о том, какой у них рост, вес, возраст, доход, и т.п., а потом построить график любой из этих величин, например, роста… Но не будем спешить, сначала посмотрим, как можно построить такой график.
Сначала, мы просто запишем результаты своего исследования. Потом, мы отсортируем всех людей по группам, так чтобы каждый попал в свой диапазон роста, например, «от 180 до 181 включительно».
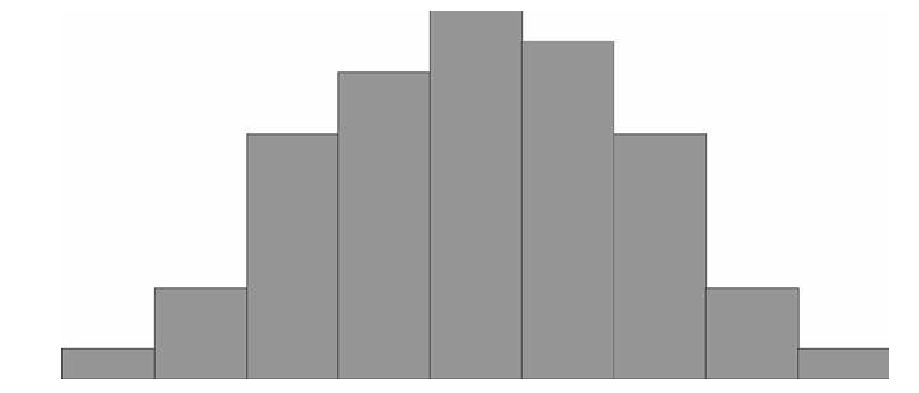
После этого мы должны посчитать количество людей в каждой подгруппе-диапазоне, это будет частота попадания роста жителей города в данный диапазон. Обычно эту часть удобно оформить в виде таблички. Если затем эти частоты построить по оси у, а диапазоны отложить по оси х, можно получить так называемую гистограмму, упорядоченный набор столбиков, ширина которых равна, в данном случае, одному сантиметру, а длина будет равна той частоте, которая соответствует каждому диапазону роста. Если
Вам попалось достаточно много жителей, то Ваша схема будет выглядеть примерно так:
Дальше можно уточнить задачу. Каждый диапазон разбить на десять, жителей рассортировать по росту с точностью до миллиметра. Диаграмма станет глаже, но уменьшится по высоте, «оплывет» вниз, т.к. в каждом маленьком диапазоне количество жителей уменьшается. Чтобы избежать этого, просто увеличим масштаб по вертикальной оси в 10 раз. Если гипотетически повторить эту процедуру несколько раз, будет вырисовываться та знаменитая колоколообразная фигура, которая характерна для нормального (или Гауссова) распределения. В результате, относительная частота встречаемости каждого конкретного диапазона роста может быть посчитана как отношение площади «ломтика» кривой, приходящегося на этот диапазон к площади подо всей кривой. Стандартизированные кривые нормального распределения, значения функций которых приводятся в таблицах книг по статистике, всегда имеют суммарную площадь под кривой равную единице. Это связано с тем, что, как Вы помните из курса теории вероятности, вероятность достоверного события всегда равна 100% (или единице), а для любого человека иметь хоть какое-то значение роста — достоверное событие. А вот вероятность того, что рост произвольного человека попадет в определенный выбранный нами диапазон, будет зависеть от трех факторов.
Во-первых, от величины такого диапазона — чем точнее наши требования, тем меньше вероятности, что нам повезет.
Во-вторых, от того, насколько «популярен» выбранный нами рост. Напомним, что мода — самое часто встречающееся значение роста. Кстати для нормального распределения мода, медиана и среднее значение совпадают. Кривая нормального распределения симметрична относительно среднего значения.
И, в-третьих, вероятность попадания роста в определенный диапазон зависит от характеристики рассеивания случайной величины. Отчасти это связано с единицами измерения (представьте, что мы бы измеряли людей в дюймах, а не в миллиметрах, но сами люди и их рост были бы теми же). Но дело не только в этом. Просто некоторые процессы кучнее группируются возле среднего значения, в то время как другие более разбросаны.
Например, рост собак и рост домашних кошек имеют разный разброс значений, их кривые нормального распределения будут выглядеть по-разному (напомним еще раз, что площадь под обеими кривыми будет единичной).
Так, кривая для роста кошек будет более узкой и высокой, а для роста собак кривая будет ниже и шире. Для характеристики разброса конечного ряда данных в прошлом разделе мы использовали величину среднего квадратического отклонения. Аналогичная величина используется для характеристики кривой нормального распределения. Она обозначается буквой s и называется в этом случае стандартным отклонением. Это очень важная величина для кривой нормального распределения. Кривая нормального распределения полностью задана, если известно среднее значение 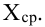
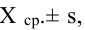
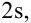
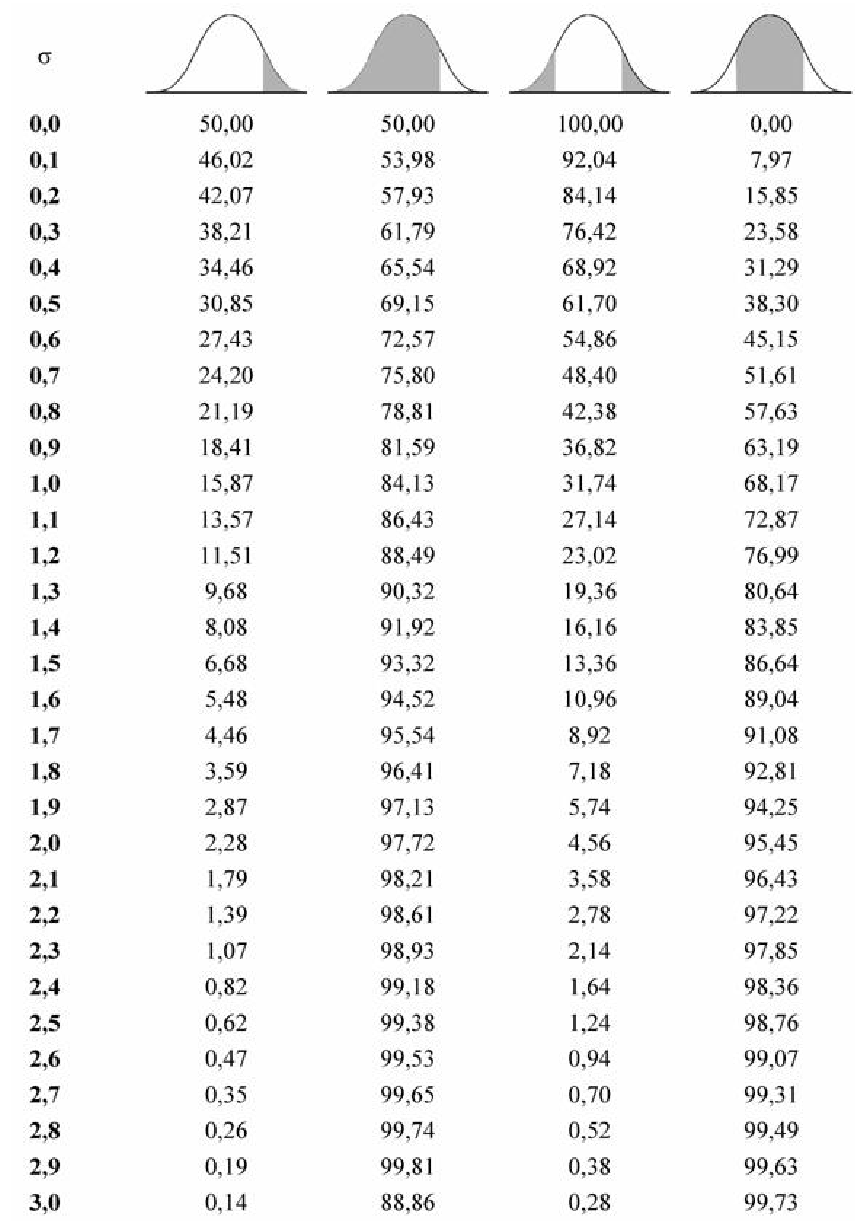
Для вычисления других значений вероятности, которые могут Вам понадобиться, можно воспользоваться приведенной таблицей:
Таблица вероятности попадания случайной величины в отмеченный (заштрихованный) диапазон
Нормальный закон распределения
Нормальный закон распределения случайных величин, который иногда называют законом Гаусса или законом ошибок, занимает особое положение в теории вероятностей, так как 95 % изученных случайных величин подчиняются этому закону. Природа этих случайных величин такова, что их значение в проводимом эксперименте связано с проявлением огромного числа взаимно независимых случайных факторов, действие каждого из которых составляет малую долю их совокупного действия. Например, длина детали, изготавливаемой на станке с программным управлением, зависит от случайных колебаний резца в момент отрезания, от веса и толщины детали, ее формы и температуры, а также от других случайных факторов. По нормальному закону распределения изменяются рост и вес мужчин и женщин, дальность выстрела из орудия, ошибки различных измерений и другие случайные величины.
Определение: Случайная величина X называется нормальной, если она подчиняется нормальному закону распределения, т.е. ее плотность распределения задается формулой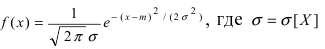
Приведенная дифференциальная функция распределения удовлетворяет всем свойствам плотности вероятности, проверим, например, свойство 4.:
Выясним геометрический смысл параметров 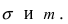
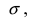
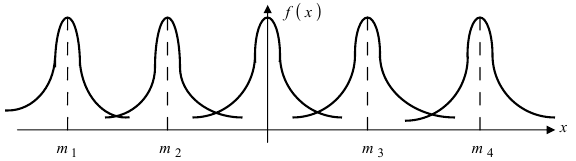
Рис. 8. Изменение графика плотности вероятности в зависимости от изменения математического ожидания при фиксированном значении средне-квадратичного отклонения. Из рисунка видно, кривая 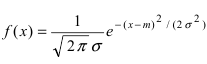
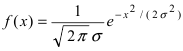
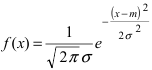
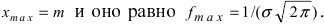
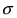
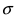
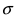
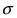
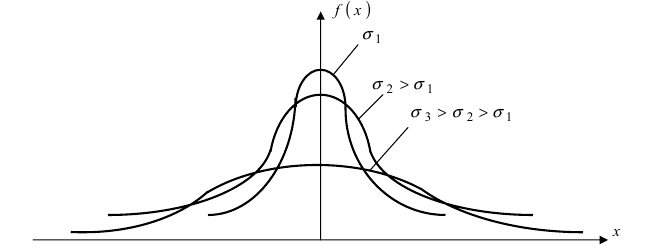
Рис. 9. Изменение графика плотности вероятности в зависимости от изменения средне-квадратичного отклонения при фиксированном значении математического ожидания.
Интегральная функция нормального распределения имеет вид:
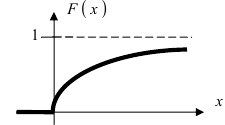
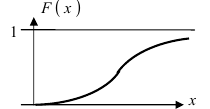
График функции распределения имеет вид (Рис. 10):
Рис. 10. Графика интегральной функции распределения нормальной случайной величины.
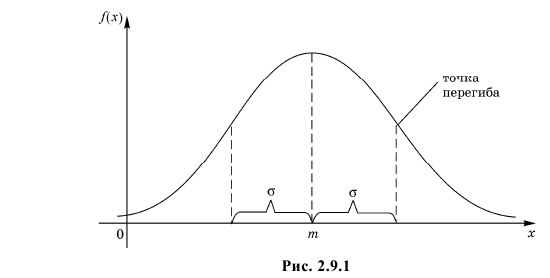
Вероятность попадания нормальной случайной величины в заданный интервал
Пусть требуется определить вероятность того, что нормальная случайная величина попадает в интервал 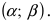
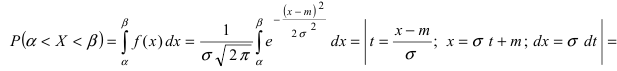
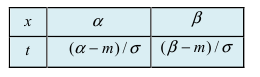
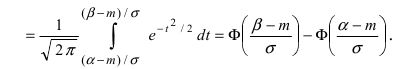
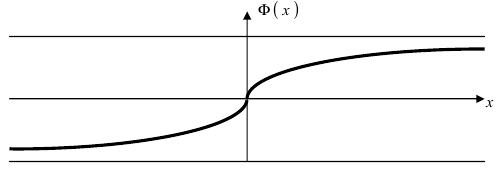
Рассмотрим основные свойства функции Лапласа Ф(х):
- Ф(0) = 0 — график функции Лапласа проходит через начало координат.
- Ф (-х) = — Ф(х) — функция Лапласа является нечетной функцией, поэтому
- таблицы для функции Лапласа приведены только для неотрицательных значений аргумента.
— график функции Лапласа имеет горизонтальные асимптоты
Следовательно, график функции Лапласа имеет вид (Рис. 11):
Рис. 11. График функции Лапласа.
Пример №1
Закон распределения нормальной случайной величины X имеет вид: 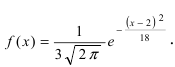
Решение:
Согласно условиям задачи 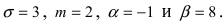
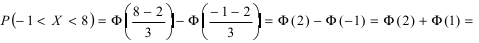
Вычисление вероятности заданного отклонения
Вычисление вероятности заданного отклонения. Правило 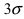
Если интервал, в который попадает нормальная случайная величина X, симметричен относительно математического ожидания 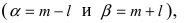
Данная формула показывает, что отклонение случайной величины Х от ее математического ожидания на заданную величину l равна удвоенному значению функции Лапласа от отношения / к среднему квадратичному отклонению. Если положить 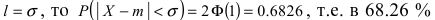
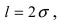
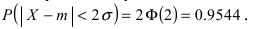
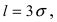
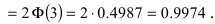
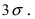
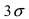
Показательный закон распределения
Определение: Закон распределения, определяемый фу нкцией распределения:
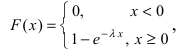
График экспоненциального закона распределения имеет вид (Рис. 12):
Рис. 12. График функции распределения для случая экспоненциального закона.
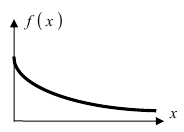
Дифференциальная функция распределения (плотность вероятности) имеет вид: 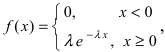
Рис. 13. График плотности вероятности для случая экспоненциального закона.
Пример №2
Случайная величина X подчиняется дифференциальной функции распределения 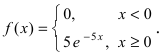
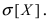
Решение:
Интегральная функция распределения 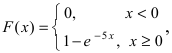
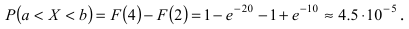
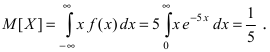
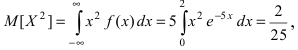
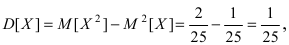
отклонение 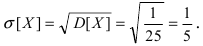
- Основные законы распределения вероятностей
- Асимптотика схемы независимых испытаний
- Функции случайных величин
- Центральная предельная теорема
- Повторные независимые испытания
- Простейший (пуассоновский) поток событий
- Случайные величины
- Числовые характеристики случайных величин
Случайной
погрешностью измерения называется
составляющая погрешности, изменяющаяся
случайным образом (по знаку и значению)
при повторных измерениях одной и той
же физической величины, проведенных
с одинаковой тщательностью. Примеры
распределения случайных величин
Способы
нахождения значений случайной величины
зависят от вида функции ее распределения.
Однако на практике такие функции, как
правило, неизвестны. Если же случайный
характер результатов наблюдений
обусловлен погрешностями измерений,
то полагают, что наблюдения имеют
нормальное
распределение.
Это обусловлено тем, что погрешности
измерений складываются из большого
числа небольших возмущений, ни одно из
которых не является преобладающим.
Согласно же центральной
предельной теореме
сумма бесконечно большого числа взаимно
независимых бесконечно малых случайных
величин с любыми распределениями имеет
нормальное
распределение.
Нормальное распределение для
случайной
величиных
с
математическим ожиданием
и
дисперсиейs
имеет вид:
Реально даже воздействие
ограниченного числа возмущений приводит
к нормальному распределению результатов
измерений и их погрешностей. В
настоящее время наиболее полно разработан
математический аппарат именно для
случайных величин, имеющих нормальное
распределение. Если же предположение
о нормальности распределения отвергается,
то статистическая обработка наблюдений
существенно усложняется и в таком
случае невозможно рекомендовать общую
методику статистической обработки
наблюдений. Часто даже не известно,
какая характеристика распределения
может служить оценкой истинного значения
измеряемой величины.
Выше приведено
аналитическое выражение нормального
распределения для случайной измеряемой
величины х.
Переход к нормальному
распределению случайных погрешностей
осуществляется
переносом центра распределений ви
откладывания по оси абсцисс погрешности.
Нормальное
распределение характеризуется двумя
парамет-рами: математическим ожиданием
m1
и
средним квадратическим отклонением
σ.
При многократных измерениях
несмещенной, состоятельной и эффективной
оценкой m1
для группы из n
наблюдений является среднее арифметическое
:
.
Нужно
сказать, что среднее арифметическое
дает оценку математического ожидания
результата наблюдений и может бытьоценкой
истинного (действительного) значения
измеряемой
величины только после
исключения
систематических погрешностей.
Оценка
S
среднего квадратического отклонения
(СКО) дается
формулой:
Эта
оценка характеризуетрассеяние
единичных результатов измерений в ряду
равноточных измерений одной и той же
величины около их среднего значения.
Другими оценками рассеяния результатов
в ряду измерений являются размах
(разница между наибольшим и наименьшим
значением), модуль средней
арифметической погрешности
(арифметическая сумма погрешностей,
деленная на число измерений) и
доверительная граница погрешности
(подробно рассматривается ниже).
СКО
является наиболее удобной характеристикой
погрешности в случае ее дальнейшего
преобразования. Например, для нескольких
некоррелированных слагаемых СКО суммы
определяется по
формуле:
.
Оценка
S характеризует рассеяние единичных
результатов наблюдений относительно
среднего значения, то есть в случае,
если мы за результат измерений примем
отдельный исправленный результат
наблюдений. Если же в качестве результата
измерений принимается среднее
арифметическое, то СКО этого среднегоопределяется
по формуле:Нормальное
распределение погрешностей имеет
следующиесвойства:
-
симметричность,
т.е. погрешности, одинаковые по величине,
но противоположные по знаку,
встречаются одинаково часто; -
математическое
ожидание случайной погрешности равно
нулю; -
малые
погрешности более вероятны, чем большие; -
чем
меньше s, тем меньше рассеяние результатов
наблюдений и больше вероятность малых
погрешностей.
Доверительные
интервалы
Приведенные
выше оценки параметров распределения
случайных величин в виде среднего
арифметического для оценки математического
ожидания и СКО для оценки дисперсии
называются точечными
оценками,
так как они выражаются одним числом.
Однако в некоторых случаях знание
точечной оценки является недостаточным.
Наиболее корректной и наглядной оценкой
случайной погрешности измерений
является оценка с помощью доверительных
интервалов.
Симметричный интервал в границами
± Δх(Р)
называется доверительным
интервалом случайной
погрешности с довери-тельной вероятностью
Р,
если площадь кривой распределения
между абсциссами –Δх
и
+Δх
составляет Р-ю
часть всей площади под кривой плотности
распределения вероятностей. При
нормировке всей площади на единицу Р
представляет часть этой площади в долях
единицы (или в процентах). Другими
словами, в интервале от -Dх(Р)
до +Dх(Р)
с заданной вероятностью Р
встречаются Р×100%
всех возможных значений случайной
погрешности.
Доверительный интервал
для нормального распределения находится
по формуле:
где
коэффициентt
зависит от доверительной вероятности
Р.
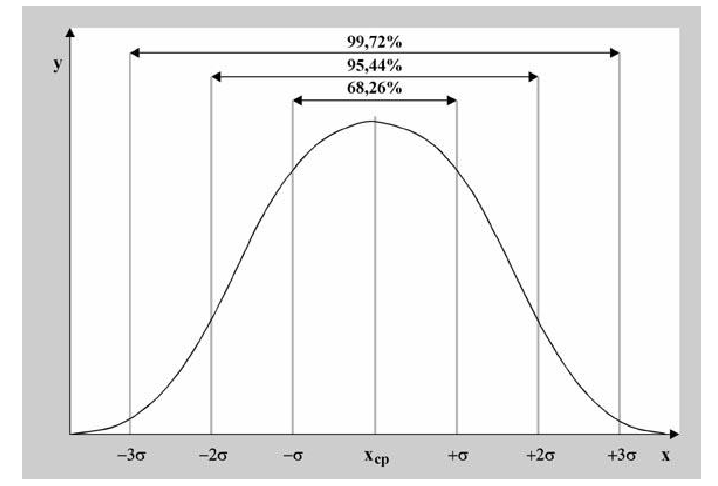
Для
нормального распределения существуют
следующие соотношения между доверительными
интервалами и доверительной вероятностью:
1s (Р=0,68), 2s (Р= 0,95), 3s (Р= 0,997), 4s (Р=0,999).
Доверительные
вероятности для выражения результатов
измерений и погрешностей в различных
областях науки и техники принимаются
равными. Так, в технических измерениях
принята доверительная вероятность
0,95. Лишь для особо точных и ответственных
измерений принимают более высокие
доверительные вероятности. В метрологии
используют, как правило, доверитель-ные
вероятности 0,97, в исключительных случаях
0,99. Необходимо отметить, что точность
измерений должна соответствовать
поставленной измерительной задаче.
Излишняя точность ведет к неоправданному
расходу средств. Недостаточная точность
измерений может привести к принятию
по его результатам ошибочных решений
с самыми непредсказуемыми последствиями,
вплоть до серьезных материальных потерь
или катастроф.
При
проведении многократных измерений
величины х,
подчиняющейся нормальному распределению,
доверительный интервал может быть
построен для любой доверительной
вероятности по формуле:
гдеtq–
коэффициент Стьюдента, зависящий от
числа наблюдений n
и выбранной доверительной вероятности
Р.
Он определяется с помощью таблицы
q-процентных
точек распределения Стьюдента, которая
имеет два параметра: k
= n
– 1 и q=
1 – P;
–
оценка среднего квадратического
отклонения среднего арифметического.
Доверительный
интервал для погрешностиDх(Р)
позволяет построить доверительный
интервал для истинного (действительного)
значения измеряемой величины ,
оценкой которой является среднее
арифметическое
.
Истинное значение измеряемой величины
находится с доверительной вероятностью
Р внутри интервала:.
Доверительный интервал позволяет
выяснить, насколько может измениться
полученная в результате данной серии
измерений оценка измеряемой величины
при проведении повторной серии измерений
в тех же условиях. Необходимо отметить,
что доверительные интервалы строят
длянеслучайных
величин,
значения которых неизвестны. Такими
являются истинное значение измеряемой
величины и средние квадратические
отклонения. В то же время оценки этих
величин, получаемые в результате
обработки данных наблюдений, являются
случайными величинами.
Недостатком
доверительных интервалов при оценке
случай-ных погрешностей является то,
что при произвольно выбираемых
доверительных вероятностях нельзя
суммировать несколько погреш-ностей,
т.к. доверительный интервал суммы не
равен сумме довери-тельных интервалов.
Суммируются
дисперсии независимых случай-ных
величин:
Då
= åDi.
То есть, для возможности суммирования
составляющие случайной погрешности
должны быть представлены своими СКО,
а не предельными или доверительными
погрешностями.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
30)Нормальный закон распределения случайных погрешностей. Функция Лапласа. Распределение Стьюдента.
Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности
Нормальный закон распределения также называется законом Гаусса.
Нормальный закон распределения занимает центральное место в теории вероятностей. Это обусловлено тем, что этот закон проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. К нормальному закону приближаются все остальные законы распределения.
Нормальный закон распределения имеет плотность распределения
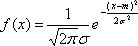
где m и s>0 некоторые числовые параметры. В разделе «Предельные теоремы теории вероятностей.» будут обсуждены причины, в силу которых нормальный закон распределения играет важную
роль в теории вероятностей и ее приложениях.
х. Легко убедиться, что кривая, определяемая функцией распределения (*), имеет максимум в точке x=m, а точки перегиба отстоят от точки x=m на расстоянии s и при 
В зависимости от величины параметров кривая плотности вероятности имеет различный вид и поэтому правильнее было бы говорить о семействе нормальных законов распределения (на рис. 10 показана зависимость формы кривой распределения от величины s при фиксированном m).
Нормальный закон распределения относится к непрерывной случайной величине. И тесно связан с таким понятием как функция Лапласа. Она нужна для нахождения вероятности
Функцию Лапласа и данную таблицу чаще всего изучают на втором курсе университета, при изучении математики и теории вероятности, если Вам в данной теме, что-то не понятно, то Вы всегда можете задать вопрос на нашем форуме, мы будем рады вам помочь. Пользуйтесь нашим сайтом и таблицей на здоровье.
При разных значениях t; F(–t) = –F(t) (функция нормального распределения).
Источник
32.Нормальное распределение случайных погрешностей измерений и их оценка.
Случайной погрешностью измерения называется составляющая погрешности, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях одной и той же физической величины, проведенных с одинаковой тщательностью. Примеры распределения случайных величин
Способы нахождения значений случайной величины зависят от вида функции ее распределения. Однако на практике такие функции, как правило, неизвестны. Если же случайный характер результатов наблюдений обусловлен погрешностями измерений, то полагают, что наблюдения имеют нормальное распределение. Это обусловлено тем, что погрешности измерений складываются из большого числа небольших возмущений, ни одно из которых не является преобладающим. Согласно же центральной предельной теореме сумма бесконечно большого числа взаимно независимых бесконечно малых случайных величин с любыми распределениями имеет нормальное распределение. Нормальное распределение для 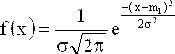
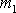

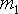
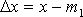
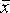
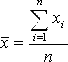
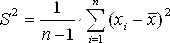
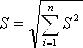
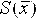
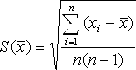
симметричность, т.е. погрешности, одинаковые по величине, но противоположные по знаку, встречаются одинаково часто;
математическое ожидание случайной погрешности равно нулю;
малые погрешности более вероятны, чем большие;
чем меньше s, тем меньше рассеяние результатов наблюдений и больше вероятность малых погрешностей.
Приведенные выше оценки параметров распределения случайных величин в виде среднего арифметического для оценки математического ожидания и СКО для оценки дисперсии называются точечными оценками, так как они выражаются одним числом. Однако в некоторых случаях знание точечной оценки является недостаточным. Наиболее корректной и наглядной оценкой случайной погрешности измерений является оценка с помощью доверительных интервалов. Симметричный интервал в границами ± Δх(Р) называется доверительным интервалом случайной погрешности с довери-тельной вероятностью Р, если площадь кривой распределения между абсциссами –Δх и +Δх составляет Р-ю часть всей площади под кривой плотности распределения вероятностей. При нормировке всей площади на единицу Р представляет часть этой площади в долях единицы (или в процентах). Другими словами, в интервале от -Dх(Р) до +Dх(Р) с заданной вероятностью Р встречаются Р×100% всех возможных значений случайной погрешности. Доверительный интервал для нормального распределения находится по формуле: 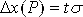
Доверительные вероятности для выражения результатов измерений и погрешностей в различных областях науки и техники принимаются равными. Так, в технических измерениях принята доверительная вероятность 0,95. Лишь для особо точных и ответственных измерений принимают более высокие доверительные вероятности. В метрологии используют, как правило, доверитель-ные вероятности 0,97, в исключительных случаях 0,99. Необходимо отметить, что точность измерений должна соответствовать поставленной измерительной задаче. Излишняя точность ведет к неоправданному расходу средств. Недостаточная точность измерений может привести к принятию по его результатам ошибочных решений с самыми непредсказуемыми последствиями, вплоть до серьезных материальных потерь или катастроф.
При проведении многократных измерений величины х, подчиняющейся нормальному распределению, доверительный интервал может быть построен для любой доверительной вероятности по формуле: 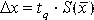
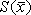
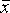
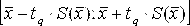
Источник
Глава 2 Элементы теории ошибок
2.1 Случайная величина
Гистограммы.
Свойства распределений.
Из определения функции w ( x ) следует, что вероятность получить в результате эксперимента величину x в диапазоне от a до b можно найти, вычислив интеграл:
Согласно определению вероятности, сумма вероятностей для всех возможных случаев всегда равна единице. Поэтому интеграл распределения w ( x ) по всей области значений x (то есть суммарная площадь под графиком w ( x ) ) равен единице:
Среднее и дисперсия.
Вычислим среднее по построенной гистограмме. Если размер корзин h достаточно мал, все измерения в пределах одной корзины можно считать примерно одинаковыми. Тогда среднее арифметическое всех результатов можно вычислить как
Переходя к пределу, получим следующее определение среднего значения случайной величины:
Доверительный интервал.
2.2 Нормальное распределение
Доказательство теоремы довольно громоздко и мы его не приводим (его можно найти в любом учебнике по теории вероятностей). Остановимся кратко на том, что такое нормальное распределение и его основных свойствах.
Плотность нормального распределения выражается следующей формулой:
Доверительные вероятности.
Вычислим некоторые доверительные вероятности ( 2.4 ) для нормально распределённых случайных величин.
Вероятность того, что результат отдельного измерения x окажется в пределах x ¯ ± σ оказывается равна
Вероятность отклонения в пределах x ¯ ± 2 σ :
а в пределах x ¯ ± 3 σ :
Сравнение результатов измерений.
Теперь мы можем дать количественный критерий для сравнения двух измеренных величин или двух результатов измерения одной и той же величины.
2.3 Независимые величины
Таким образом, при сложении независимых величин их погрешности складываются среднеквадратичным образом.
Эти обстоятельства важны при планирования эксперимента: как правило, величина, измеренная наименее точно, вносит наибольший вклад в погрешность конечного результата. При этом, пока не устранены наиболее существенные ошибки, бессмысленно гнаться за повышением точности измерения остальных величин.
2.4 Погрешность среднего
Если < x i >есть набор независимых измерений одной и той же физической величины, то мы можем, применяя результат ( 2.7 ) предыдущего параграфа, записать
поскольку под корнем находится n одинаковых слагаемых. Отсюда с учётом =Z/n» display=»inline»> ⟨ x ⟩ = Z / n получаем
Подчеркнём отличия между σ x и >» display=»inline»> σ ⟨ x ⟩ :
2.5 Результирующая погрешность опыта
Предположим для простоты, что измеряемая величина в принципе может быть определена сколь угодно точно, так что можно говорить о некотором её «истинном» значении x ист (иными словами, погрешность результата связана в основном именно с процессом измерения). Назовём полной погрешностью измерения среднеквадратичное значения отклонения от результата измерения от «истинного»:
Причём случайную составляющую можно считать независимой от систематической. В таком случае из ( 2.7 ) находим:
Таким образом, для получения максимального значения полной погрешности некоторого измерения нужно квадратично сложить максимальную систематическую и случайную погрешности.
Если измерения проводятся многократно, то согласно ( 2.8 ) случайная составляющая погрешности может быть уменьшена, а систематическая составляющая при этом остаётся неизменной:
Отсюда следует важное практическое правило (см. также обсуждение в п. 2.3 ): если случайная погрешность измерений в 2–3 раза меньше предполагаемой систематической, то нет смысла проводить многократные измерения в попытке уменьшить погрешность всего эксперимента. В такой ситуации измерения достаточно повторить 2–3 раза — чтобы убедиться в повторяемости результата, исключить промахи и проверить, что случайная ошибка действительно мала. В противном случае повторение измерений может иметь смысл до тех пор, пока погрешность среднего >=frac<sigma_><sqrt>» display=»inline»> σ ⟨ x ⟩ = σ x n не станет меньше систематической.
2.6 Обработка косвенных измерений
Косвенными называют измерения, полученные в результате расчётов, использующих результаты прямых (то есть «непосредственных») измерений физических величин. Сформулируем основные правила пересчёта погрешностей при косвенных измерениях.
2.6.1 Случай одной переменной
В качестве «наилучшего» приближения для y используем значение функции при «наилучшем» x :
Пример. Для y = 1 / x имеем ε 1 / x = ε x — при обращении величины сохраняется её относительная погрешность.
2.6.2 Случай многих переменных
Для нахождения погрешности σ u воспользуемся свойством, известным из математического анализа, — малые приращения гладких функции многих переменных складываются линейно, то есть справедлив принцип суперпозиции малых приращений:
| σ u 2 = f x ′ 2 σ x 2 + f y ′ 2 σ y 2 + … | (2.11) |
Это и есть искомая общая формула пересчёта погрешностей при косвенных измерениях.
Остановимся на некоторых важных частных случаях формулы ( 2.11 ).
По итогам данного раздела можно дать следующие практические рекомендации.
При этом, как следует из ( 2.13 ), особое внимание следует уделять измерению величин, возводимых при расчётах в степени с большими показателями. А при сложных функциональных зависимостях имеет смысл детально проанализировать структуру формулы ( 2.11 ): если вклад от некоторой величины в общую погрешность мал, нет смысла гнаться за высокой точностью её измерения, и наоборот, точность некоторых измерений может оказаться критически важной.
Источник
Законы распределения случайных величин
ЛЕКЦИЯ 4.
Случайные погрешности измерений и способы их описания.
При выполнении повторных измерений одной и той же величины легко убедиться, что результаты отдельных измерений отличаются друг от друга. Это объясняется действием случайных погрешностей. Случайные погрешности вызываются большим числом причин, действующих независимо друг от друга. Их нельзя исключить опытным путем, но их влияние на результат измерения можно оценить, проведя ряд наблюдений одной и той же величины. Результат измерения всегда содержит как систематическую DС, так и случайную погрешности, т.е. 
Систематическая погрешность 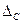

Случайная погрешность 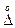

Математическое ожидание погрешности равно математическому ожиданию систематической составляющей погрешности, так как математическое ожидание случайной погрешности всегда равно нулю:

Законы распределения случайных величин
Полным описанием случайной величины, а, следовательно, и погрешности является ее закон распределения. Этим законом распределения и определяется характер появления различных результатов отдельных измерений в ряду наблюдений.
В практике электрических измерений встречаются различные законы распределения. Это равномерное (прямоугольное) распределение, нормальное распределение Гаусса, распределение c 2 (хи-квадрат), распределение t-Стьюдента и др. Одним из наиболее распространенных законов распределения погрешностей является нормальный закон (Гаусса), который базируется на центральной предельной теореме теории вероятностей, согласно которой нормальное распределение плотности вероятности имеет сумма бесконечно большого числа бесконечно малых случайных возмущений с любыми распределениями. Применительно к измерениям это означает, что нормальное распределение случайных погрешностей возникает тогда, когда на результат измерения действует множество случайных возмущений и ни одно из которых не является преобладающим. Практически, суммарное воздействие даже сравнительно небольшого числа возмущений приводит к закону распределения результатов и погрешностей измерений, близкому к нормальному. Закон нормального распределения имеет фундаментальное значение для теории обработки результатов измерений. Он позволяет вести расчеты даже тогда, когда действительный закон неизвестен.
Математически нормальное распределение случайных погрешностей может быть представлено формулой


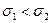
Из этих кривых видно, что чем меньше s, тем чаще встречаются малые случайные погрешности, т.е. тем точнее выполнены измерения. Кривые симметричны относительно оси ординат, так как положительные и отрицательные погрешности встречаются одинаково часто.
Основные характеристики законов распределения.
Основными характеристиками являются математическое ожидание и дисперсия.
Математическое ожиданиеряда наблюдений есть величина, относительно которой рассеиваются результаты отдельных измерений. Если систематическая погрешность отсутствует, и разброс результатов отдельных измерений обусловлен только случайной погрешностью, то математическим ожиданием такого ряда наблюдений будет истинное значение измеряемой величины. Если же результаты отдельных измерений кроме случайной погрешности содержат постоянную систематическую погрешность, то математическое ожидание ряда наблюдений будет смещено от истинного значения измеряемой величины на значение систематической погрешности.
ДисперсияD ряда наблюдений характеризует степень рассеивания (разброса) результатов отдельных наблюдений вокруг математического ожидания. Чем меньше дисперсия, тем меньше разброс отдельных результатов, тем точнее выполнены измерения. Следовательно, дисперсия может служить характеристикой точности проведенных измерений. Однако, дисперсия выражается в единицах в квадрате измеряемой величины. Поэтому в качестве характеристики точности ряда наблюдений наиболее часто применяют среднее квадратическое отклонение результата наблюдения (СКО) s, равное корню квадратному из дисперсии с положительным знаком и выражаемое в единицах измеряемой величины. Среднее квадратическое отклонение, отнесенное к значению измеряемой величины, может быть выражено в относительных единицах или процентах.
Источник
Нормальный закон распределения погрешностей
Для характеристики свойств случайной величины в теории вероятности используется понятие закона распределения вероятностей случайной величины. Различают две формы описания закона распределения: интегральную и дифференциальную. В метрологии используют преим. Дифференциальную – закон распределения плотности вероятностей случайной величины.
| Номер интервала | |||||
| nk | |||||
| nk/n | 0,1 | 0,2 | 0,36 | 0,22 | 0,12 |
При бесконечном повторении и увеличении n ступенчатая кривая перейдет в плавную кривую f(x) – кривая плотности распределения вероятности случайной величины.(Или r)
Числовые характеристики распределений:
1. Математическое ожидание (среднее арифметическое):

2. Среднее квадратичное отклонение (СКО) или рассеивание единичных результатов и дисперсияч:
где D – дисперсия.
Качество и точность измерений тем выше, чем меньше СКО, тем меньше вероятность рассеивания результатов наблюдений D.
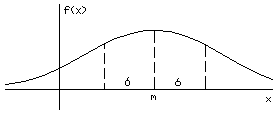
Рис 1.12. Графики нормального закона распределения плотности вероятности случайных погрешностей
Чаще начало координат совмещают с центром распрелделения.
В аналитической форме закон нормального закона распределения записывают:
f(x)= 
где s – среднеквадратическое отклонение(СКО), характеризующее точность выполненных измерений (чем меньше s, тем выше точность). По мере уменьшения s рассеяние случайных погрешностей D относительно центра их распределения, (в данном случае относительно значения D= 0) уменьшается. На рис. 1.12 изображены кривые нормального распределения случайных погрешностей для различных значений среднеквадратичного отклонения. Из рисунка видно, что по мере увеличения среднеквадратического отклонения распределение все более и более расплывается, вероятность появления больших значений погрешностей возрастает, а вероятность меньших погрешностей сокращается, т.е. увеличивается рассеивание результатов наблюдений.
На графике плотности вероятности для конкретного СКО (см. рис. 1.12) вероятность численно равна площади S заштрихованной фигуры, ограниченной функцией r(D), отрезком оси D от –DГ1 до DГ1 и ординатами r(–DГ1), r(DГ1). Чем шире заданный интервал погрешностей, тем больше площадь S, т.е. больше вероятность попадания случайных погрешностей измерений D в этот интервал. Для интервала (–¥,+¥) вероятность R(–¥ £ D £ +¥) =1.
Более универсальным методом является оценки погрешности с использованием доверительных интервалов: На графике норм. распределения отложены интервалы с границами ±s ±2s и т.д.
Доверительные вероятности для этих интервалов в таб. В технике принят 99% уровень надежности, т.е. границы ±3s.
Источник

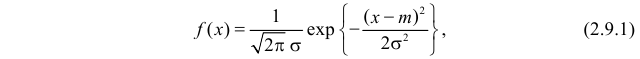
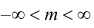
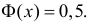
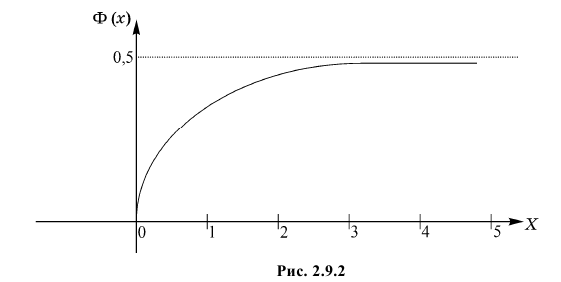
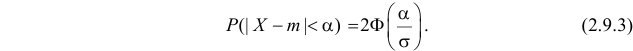
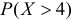
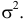
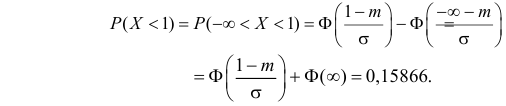
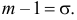
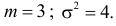
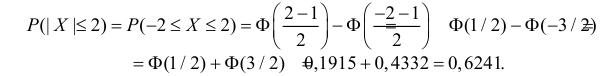
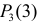
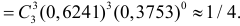
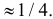
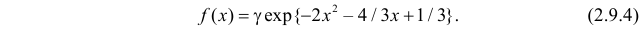
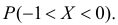
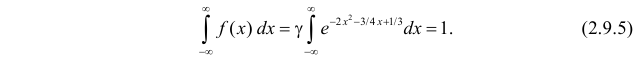
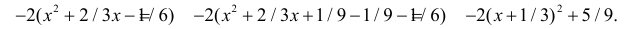
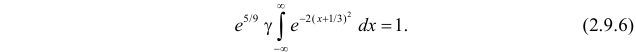

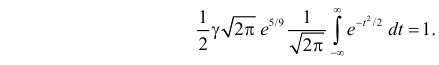

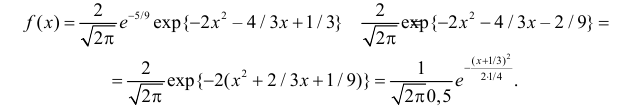
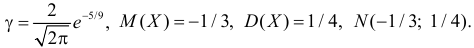
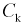
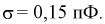
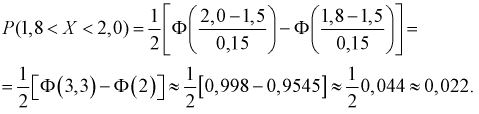
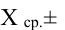
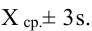
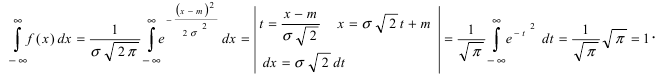
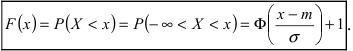
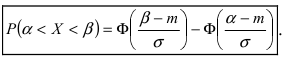
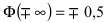 — график функции Лапласа имеет горизонтальные асимптоты
— график функции Лапласа имеет горизонтальные асимптоты