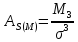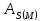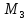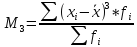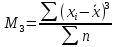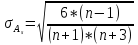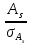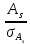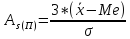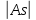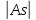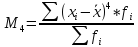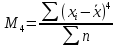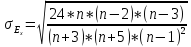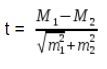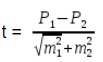Показатели,
характеризующие форму распределения.
Понятие
нормального распределения
Что
такое статистическое распределение
данных.
Статистическим
распределением данных
называют
перечень вариантов и соответствующих
им частот или относительных частот.
Основная
задача анализа вариационных рядов –
это выявление подлинной закономерности
распределения.
Первое
представление о характере распределения
данных в изучаемой совокупности можно
получить при построении гистограммы
или полигона частот.
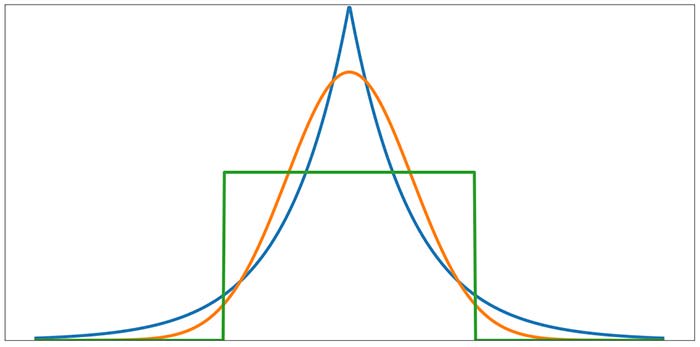
Если
увеличить объем совокупности и уменьшить
интервал группировки, изобразить эти
данные графически, по полигон (гистограмма)
распределения все более будут приближаться
к некоторой плавной линии, носящей
название кривой распределения (красная
линия на рисунке).
Различают
следующие разновидности кривых
распределения:
-
одновершинные
кривые:-
симметричные,
-
умеренно
асимметричные -
крайне
асимметричные;
-
-
многовершинные
кривые.
Для
однородных совокупностей, как правило,
характерны одновершинные распределения.
Многовершинность свидетельствует о
неоднородности изучаемой совокупности.
Появление двух и более вершин делает
необходимой перегруппировку данных с
целью выделения более однородных групп.
Если
Ваше распределение получится похожим
на симметричный холм, то оно называется
нормальным распределением. Нормальным
такое распределение называется потому,
что оно очень часто встречалось в
естественнонаучных исследованиях и
казалось «нормой» всякого массового
случайного проявления признаков.
Нормальное распределение часто
встречается в природе и в общественных
явлениях. Доказано, что нормальное
распределение получается в результате
воздействия многих независящих друг
от друга факторов. Несмотря на это не
все распределения, которые встречаются
в жизни, являются нормальными.
Свойства
нормального распределения
Как
уже неоднократно отмечалось, часто
пользуются типом распределения, которое
называется нормальным. Нормальное
распределение можно построить по
формуле.
Особенности
кривой нормального распределения:
-
кривая
симметрична и имеет максимум в точке,
соответствующей значению
(среднее значение признака) = Ме (медиана)
= Мо (мода); -
кривая
асимптотически приближается к оси
абсцисс, продолжаясь в обе стороны до
бесконечности (чем больше отдельные
значения X отклоняются от X , тем реже
они встречаются); -
коэффициенты
асимметрии и эксцесса для кривой
нормального распределения равны нулю; -
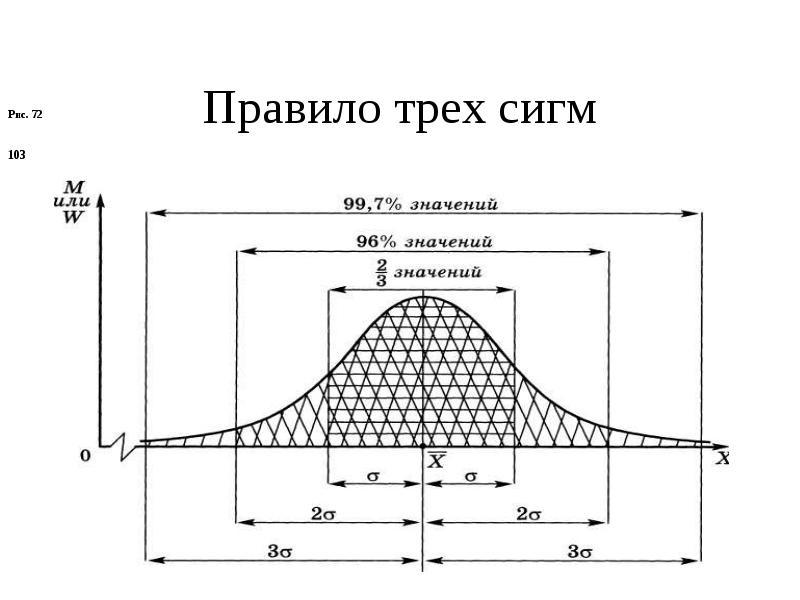
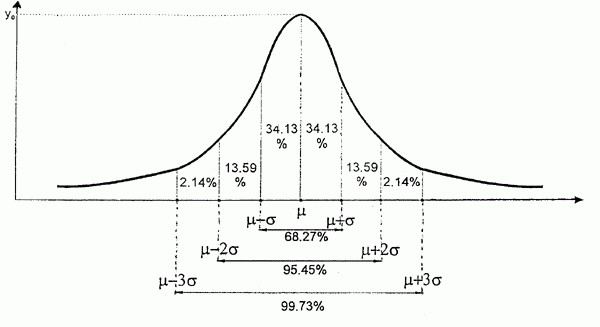
ПРАВИЛО
ТРЕХ СИГМ
-
68%
всех наблюдений лежат в диапазоне ±1
стандартное отклонение ()
от среднего значения (),
-
диапазон
±2 стандартных отклонения ()
от среднего значения ()
содержит 95% значений, -
а
диапазон ±3 стандартных отклонения
()
от среднего значения ()
содержит 99,7% значений.
Многие
методы исследования, которые будут
рассмотрены в дальнейшем, требуют
нормального распределения анализируемых
переменных.
Показатели,
характеризующие форму распределения
Форму
распределения хорошо видно на рисунке,
но для анализа нужны конкретные значения.
Кроме того, очень редко встречаются
абсолютно нормальные распределения,
преобладающее большинство распределений,
встречающихся при анализе природных и
общественных процессов, являются
чуть-чуть не нормальными. Поэтому для
выяснения
общего характера распределения необходимо
оценить его однородность
и вычислить показатели формы распределения
(показатель асимметрии и эксцесс).
Определение
симметричности распределения
(коэффициент
ассиметрии)
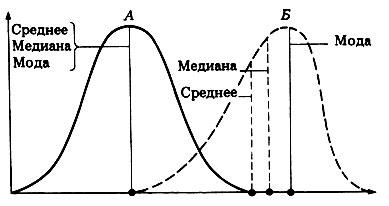
Для
симметричных распределений среднее
значение признака, мода и медиана равны
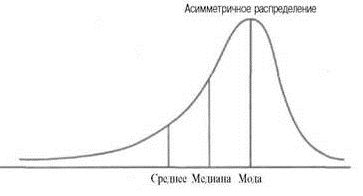
(на
рисунке А – симметричное распределение,
Б – ассиметричное распределение).
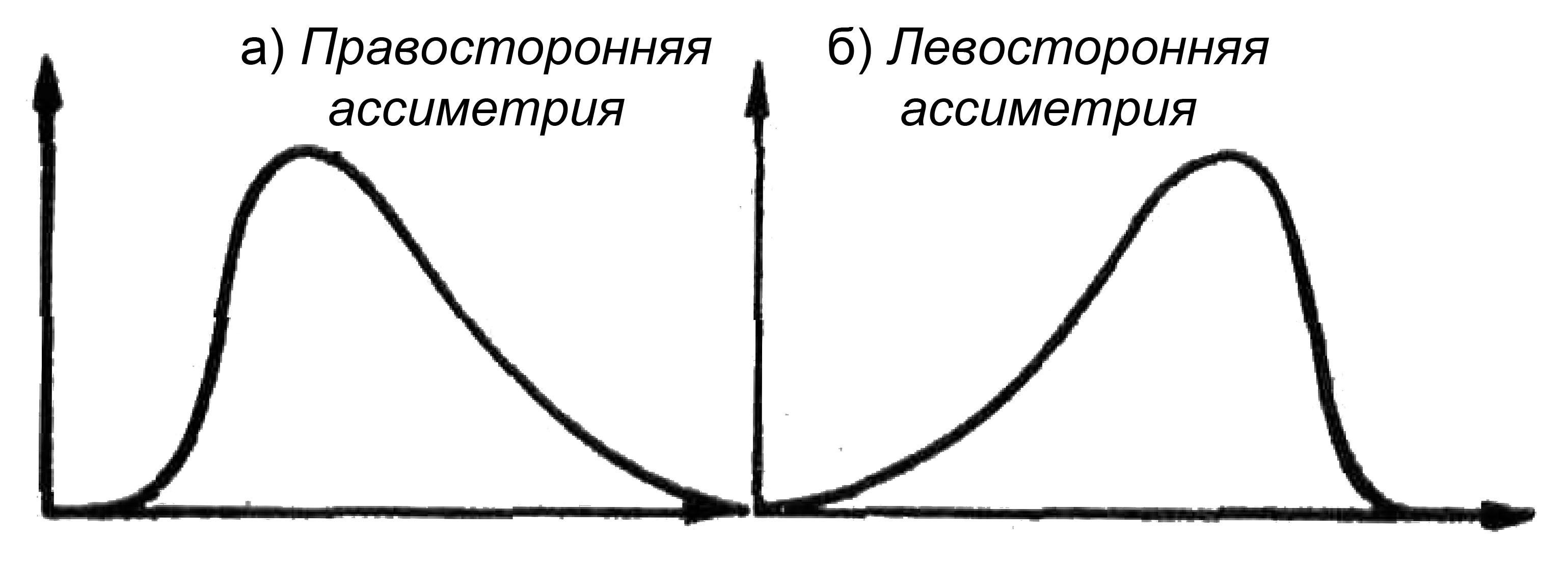
Кроме
симметричных распределений, различают
распределения с левосторонней и с
правосторонней ассиметрией.
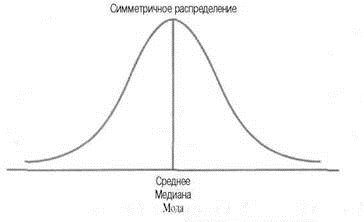
А)
Симметричное распределение
(
= Ме = Мо);
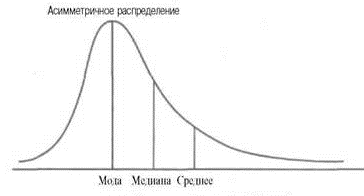
Б)
Распределение с правосторонней
ассиметрией (
Ме > Мо);
в)
Распределение с левосторонней
ассиметрией (
Ме < Мо);
Для
оценки симметричности распределения
используют коэффициенты ассиметрии:
-
Моментный
коэффициент ассиметрии
С
помощью этого показателя измеряют не
только направление ассиметрии, но и
степень скошенности или ассиметричности
распределения.
– моментный
коэффициент ассиметрии
– центральный
момент третьего порядка
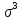
среднеквадратическое отклонение в кубе
(для
вариационного ряда)
(для
несгруппированных данных)
В
симметричных распределениях
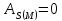
Если 
то асимметрия правосторонняя
и относительно максимальной ординаты
вытянута в сторону правая ветвь; если ,
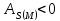
то асимметрия левосторонняя (на
графике это соответствует вытянутости
в сторону левой ветви).
Степень
существенности асимметрии можно оценить
с помощью средней квадратической ошибки
коэффициента асимметрии, которая зависит
от объема изучаемой совокупности и
рассчитывается по формуле:
где
n — число единиц совокупности.
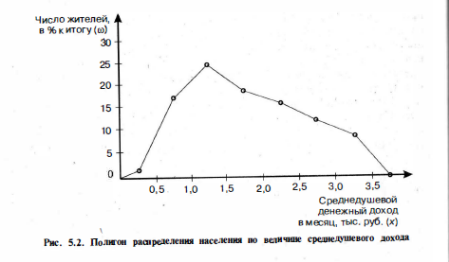
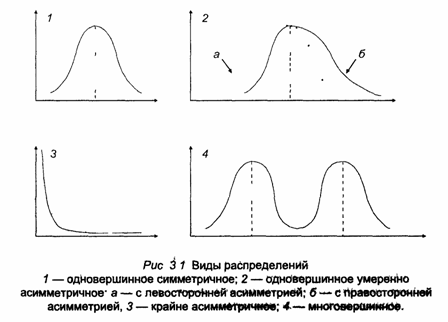
Если
отношение
>3,
асимметрия считается существенной
и распределение нельзя считать нормальным;
если
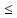
то асимметрия признается несущественной,
вызванной влиянием случайных обстоятельств,
а распределение
признается умеренно симметричным и
приближенным к нормальному распределению
Основной
недостаток моментного коэффициента
асимметрии заключается в том, что его
величина зависит от наличия в совокупности
резко выделяющихся единиц. Для таких
совокупностей этот коэффициент
малопригоден,
-
структурный
коэффициент ассиметрии Пирсона
или
Значение
коэффициентов Пирсона может быть
положительным или отрицательным.
Если
As>0,
то распределение с правосторонней
асимметрией,
Если
As<0
— с левосторонней ассиметрией.
Если
< 0.25, то ассиметрия считается
незначительной.
Если
0.25
< 0.5, то ассиметрия считается умеренной.
Если
0.5, то ассиметрия считается существенной.
Структурные
коэффициенты асимметрии характеризуют
ассиметричность только в центральной
части распределения, т. е. для основной
массы единиц, и в отличие от моментного
коэффициента не зависят от крайних
значений признака.
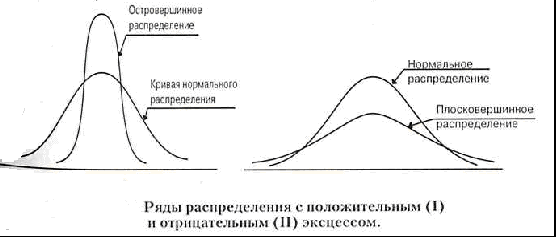
Эксцесс
(показатель, характеризующий «крутизну»
распределения)
Другим
свойством рядов распределения является
эксцесс (Ex).
Под
эксцессом понимают островершинность
или плосковершинность распределения
по сравнению с нормальным распределением
при той же силе вариации.
Другими
словами, эксцесс — это отклонение вершины
эмпирического распределения вверх или
вниз от вершины кривой нормального
распределения.
При
этом эксцесс определяется только для
симметричных и умеренно асимметричных
распределений.
Наиболее
точно эксцесс (Ex)
определяется по формуле с использованием
центрального момента четвертого
порядка:
(для
вариационного ряда)
(для
несгруппированных данных)
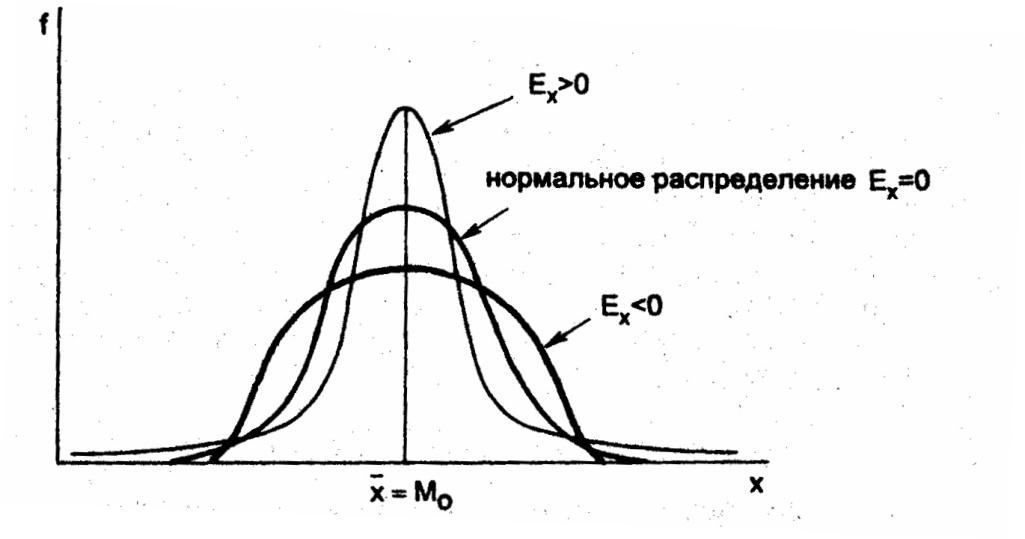
Для
нормальных распределений Ex=0.
Распределения более островершинные,
чем нормальные, обладают положительным
эксцессом (Ех > 0), более плосковершинные
— отрицательным (Ех < 0).
Положительный
эксцесс свидетельствует о том, что в
совокупности есть слабоварьирующее по
данному признаку «ядро», а в плосковершинных
распределениях такого «ядра» нет и
единицы рассеяны по всем значениям
признака более равномерно.
Чтобы
оценить существенность эксцесса
распределения, рассчитывают
среднеквадратическую ошибку эксцесса.
Среднеквадратическая
ошибка эксцесса (σEх)
рассчитывается по формуле:
где п –
число наблюдений
Если
отношение
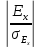
то отклонение от нормального можно
считать существенным и распределение
нельзя считать нормальным; если
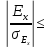
то отклонение признается несущественным,
а распределение
признается приближенным к нормальному
распределению.
Хотя
показатели асимметрии и эксцесса
характеризуют непосредственно лишь
форму распределения признака в пределах
изучаемой совокупности, но их определение
имеет не только описательное значение.
Часто асимметрия и эксцесс дают
определенные указания для дальнейшего
исследования социально-экономических
явлений. Так появление значительного
отрицательного эксцесса может указывать
на качественную неоднородность
исследуемой совокупности. Кроме того,
эти показатели позволяют сделать вывод
о возможности применения данного
эмпирического распределения к типу
кривых нормального распределения.
4
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Нормальное распределение
Время на прочтение
7 мин
Количество просмотров 37K

Автор статьи: Виктория Ляликова
Нормальный закон распределения или закон Гаусса играет важную роль в статистике и занимает особое положение среди других законов. Вспомним как выглядит нормальное распределение
где a -математическое ожидание, — среднее квадратическое отклонение.
Тестирование данных на нормальность является достаточно частым этапом первичного анализа данных, так как большое количество статистических методов использует тот факт, что данные распределены нормально. Если выборка не подчиняется нормальному закону, тогда предположении о параметрических статистических тестах нарушаются, и должны использоваться непараметрические методы статистики
Нормальное распределение естественным образом возникает практически везде, где речь идет об измерении с ошибками. Например, координаты точки попадания снаряда, рост, вес человека имеют нормальный закон распределения. Более того, центральная предельная теорема вообще утверждает, что сумма большого числа слагаемых сходится к нормальной случайной величине, не зависимо от того, какое было исходное распределение у выборки. Таким образом, данная теорема устанавливает условия, при которых возникает нормальное распределение и нарушение которых ведет к распределению, отличному от нормального.
Можно выделить следующие этапы проверки выборочных значений на нормальность
-
Подсчет основных характеристик выборки. Выборочное среднее, медиана, коэффициенты асимметрии и эксцесса.
-
Графический. К этому методу относится построение гистограммы и график квантиль-квантиль или кратко QQ
-
Статистические методы. Данные методы вычисляют статистику по данным и определяют, какая вероятность того, что данные получены из нормального распределения
При нормальном распределении, которое симметрично, значения медианы и выборочного среднего будут одинаковы, значения эксцесса равно 3, а асимметрии равно нулю. Однако ситуация, когда все указанные выборочные характеристики равны именно таким значениям, практически не встречается. Поэтому после этапа подсчета выборочных характеристик можно переходить к графическому представлению выборочных данных.
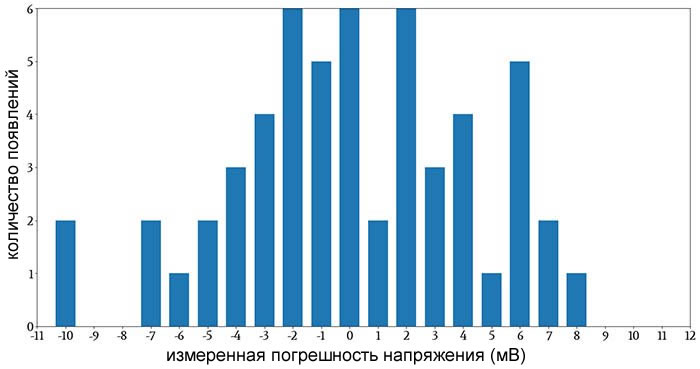
Гистограмма позволяет представить выборочные данные в графическом виде – в виде столбчатой диаграммы, где данные делятся на заранее определенное количество групп. Вид гистограммы дает наглядное представление функции плотности вероятности некоторой случайной величины, построенной по выборке.
График QQ (квантиль-квантиль) является графиком вероятностей, который представляет собой графический метод сравнения двух распределений путем построения их квантилей. QQ график сравнивает наборы данных теоретических и выборочных (эмпирических) распределений. Если два сравниваемых распределения подобны, тогда точки на графике QQ будут приблизительно лежать на линии y=x. Основным шагом в построении графика QQ является расчет или оценка квантилей.
Существует множество статистических тестов, которые можно использовать для проверки выборочных значений на нормальность. Каждый тест использует разные предположения и рассматривает разные аспекты данных.
Чтобы применять статистические критерии сформулируем задачу. Выдвигаются две гипотезы H0 и H1, которые утверждают
H0 — Выборка подчиняется нормальному закону распределения
H1 — Выборка не подчиняется нормальному распределению
Установи уровень значимости alpha=0,05.
Теперь задача состоит в том, чтобы на основании какого-то критерия отвергнуть или принять основную нулевую гипотезу при уровне значимости
Критерий Шапиро-Уилка
Критерий Шапиро-Уилка основан на отношении оптимальной линейной несмещенной оценки дисперсии к ее обычной оценке методом максимального правдоподобия. Статистика критерия имеет вид
Числитель является квадратом оценки среднеквадратического отклонения Ллойда. Коэффициенты и критические
значения статистики являются табулированными значениями. Если
, то нулевая гипотеза нормальности распределения отклоняется на уровне значимости
.
В Python функция содержится в библиотеке scipy.stats и возвращает как статистику, рассчитанную тестом, так и значение p. В Python можно использовать выборку до 5000 элементов. Интерпретация вывода осуществляется следующим образом
Если значение , тогда принимается гипотеза H0, в противном случае, т.е. если,
, тогда принимается гипотеза H1, т.е. что выборка не подчиняется нормальному закону.
Критерий Д’Агостино
В данном критерии в качестве статистики для проверки нормальности распределения используется отношение оценки Даутона для стандартного отклонения к выборочному стандартному отклонению, оцененному методом максимального правдоподобия
В качестве статистики критерия Д’Агостино используется величина
значение которой рассчитывается на основе центральной предельной теоремы, которая утверждает, что при
гдестандартная нормальная случайная величина.
Критические значения являются табулированными значениями. Гипотеза нормальности принимается, если значение статистики лежит в интервале критических значений. Данный критерий показывает хорошую мощность против большого спектра альтернатив, по мощности немного уступая критерию Шапиро-Уилка.
В Python функция normaltest() также содержится в библиотеке scipy.stats и возвращает статистику теста и значение p. Интерпретация результата аналогична результатам в критерии Шапиро-Уилка.
Критерий согласия— Пирсона
Данный критерий является одним из наиболее распространенных критериев проверки гипотез о виде закона распределения и позволяет проверить значимость расхождения эмпирических (наблюдаемых) и теоретических (ожидаемых) частот. Таким образом, данный критерий позволяет проверить гипотезу о принадлежности наблюдаемой выборки некоторому теоретическому закону. Можно сказать, что критерий является универсальным, так как позволяет проверить принадлежность выборочных значений практическому любому закону распределения.
Для решения задачи используется статистика — Пирсона
где — эмпирические частоты (подсчитывается число элементов выборки, попавших в интервал),
— теоретические частоты. Подсчитывается критическое значение
. Если
, отклоняется гипотеза о принадлежности выборки нормальному распределению и принимается, если
.
Теперь перейдем к практической части. Для демонстрации функций будем использовать Dataset, взятый с сайта kaggle.com по прогнозированию инсульта по 11 клиническим характеристикам.
Загружаем необходимые библиотеки
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as npЗагружаем датасет
data_healthcares = pd.read_csv('E:/vika/healthcare-dataset-stroke-data.csv')Набор состоит из 5110 строк и 12 столбцов.
Посмотрим на основные характеристики, каждого признака.data_healthcares.describe()
Из данных характеристик можно увидеть, что есть пропущенные значения в показателях индекс массы тела. Посчитаем количество пропущенных значений.
Если бы нам необходимо было делать модель для прогноза, то пропущенные значения bmi являются достаточно большой проблемой, в которой возникает вопрос как их восстановить. Поэтому будем предполагать, что значения столбца bmi (индекс массы тела) подчиняются нормальному закону распределения (предварительно был построен график распределения, поэтому сделано такое предположение). Но так как, на данный момент, у нас нет необходимости в построении модели для прогноза, то удалим все пропущенные значения
new_data=data_healthcares.dropna()
Теперь можем приступать к проверке выборочных значений показателя bmi на нормальность. Вычислим основные выборочные характеристики
|
Выборочная характеристика |
Код в python |
Значение характеристики |
|
Выборочное среднее |
new_data.bmi.mean() |
28,89 |
|
Выборочная медиана |
new_data.bmi.median() |
28,1 |
|
Выборочная мода |
new_data.bmi.mode() |
28,7 |
|
Выборочное среднеквадратическое отклонение |
new_data.bmi.std() |
7.854066729680458 |
|
Выборочный коэффициент асиметрии |
new_data.bmi.skew() |
1.0553402052962928 |
|
Выборочный эксцесс |
new_data.bmi.kurtosis() |
3.362659165623678 |
После вычислений основных характеристик мы видим, что выборочное среднее и медиана можно сказать принимают одинаковые значения и коэффициент эксцесса равен 3. Но, к сожалению коэффициент асимметрии равен 1, что вводить нас в некоторое замешательство, т.е. мы уже можем предположить, что значения bmi не подчиняются нормальному закону. Продолжим исследования, перейдем к построению графиков.
Строим гистограмму
fig = plt.figure
fig,ax= plt.subplots(figsize=(7,7))
sns.distplot(new_data.bmi,color='red',label='bmi',ax=ax)
plt.show()Гистограмма достаточно хорошо напоминает нормальное распределение, кроме конечно, небольшого выброса справа, но смотрим дальше. Тут скорее, можно предположить, что значения bmi подчиняются распределению .
Строим QQ график. В python есть отличная функция qqplot(), содержащаяся в библиотеке statsmodel, которая позволяет строить как раз такие графики.
from statsmodels.graphics.gofplots import qqplot
from matplotlib import pyplot
qqplot(new_data.bmi, line=’s’)
Pyplot.showЧто имеем из графика QQ? Наши выборочные значений имеют хвосты слева и справа, и также в правом верхнем углу значения становятся разреженными.
На основе данных графика можно сделать вывод, что значения bmi не подчиняются нормальному закону распределения. Рядом приведен пример QQ графика распределения хи-квадрат с 8 степенями свободы из выборки в 1000 значений.
Для примера построим график QQ для выборки из нормального распределения с такими же показателями стандартного отклонения и среднего, как у bmi.
std=new_data.bmi.std() # вычисляем отклонение
mean=new_data.bmi.mean() #вычисляем среднее
Z=np.random.randn(4909)*std+mean # моделируем нормальное распределение
qqplot(Z,line='s') # строим график
pyplot.show()Продолжим исследования. Перейдем к статистическим критериям. Будем использовать критерий Шапиро-Уилка и Д’Агостино, чтобы окончательно принять или опровергнуть предположение о нормальном распределении. Для использования критериев подключим библиотеки
from scipy.stats import shapiro
from scipy.stats import normaltest
shapiro(new_data.bmi)
ShapiroResult(statistic=0.9535483717918396, pvalue=6.623218133972133e-37)
Normaltest(new_data.bmi)
NormaltestResult(statistic=1021.1795052962864, pvalue=1.793444363882936e-222)После применения двух тестов мы имеем, что значение p-value намного меньше заданного критического значения alpha , значит выборочные значения не принадлежат нормальному закону.
Конечно, мы рассмотрели не все тесты на нормальности, которые существуют. Какие можно дать рекомендации по проверке выборочных значений на нормальность. Лучше использовать все возможные варианты, если они уместны.
На этом все. Еще хочу порекомендовать бесплатный вебинар, который 15 июня пройдет на платформе OTUS в рамках запуска курса Математика для Data Science. На вебинаре расскажут про несколько часто используемых подходов в анализе данных, а также разберут, какие математические идеи работают у них под капотом и почему эти подходы вообще работают так, как нам нужно. Регистрация на вебинар доступна по этой ссылке.
Понятие параметрических тестов, ассиметрии и эксцесса
Добавлено 30 августа 2020 в 22:13
В данной статье представлены важные категории логически выводимых статистических тестов и обсуждаются параметры описательной статистики, относящиеся к нормальному распределению.
Добро пожаловать в нашу серию статей о статистике в электротехнике. Ранее мы рассмотрели статистический анализ и описательный анализ в электротехнике, а затем обсудили среднее отклонение, стандартное отклонение и дисперсию в обработке сигналов.
Затем мы рассмотрели компенсацию размера выборки при расчетах стандартного отклонения и то, как стандартное отклонение связано со среднеквадратичными значениями.
Теперь мы перешли к исследованию нормального распределения в электротехнике, в частности, как понимать гистограммы, вероятность и кумулятивную функцию распределения нормально распределенных данных. Данная статья расширяет это обсуждение, касаясь параметрических тестов, асимметрии и эксцесса.
Когда нормальное распределение не выглядит нормальным
В предыдущих статьях мы рассмотрели нормальное распределение (также известное как распределение Гаусса) как идеализированное математическое распределение и как гистограмму, полученную из эмпирических данных. Если измеряемое явление характеризуется нормальным распределением значений, форма гистограммы по мере увеличения размера выборки будет всё больше похожа на колоколообразную (гауссову) кривую.
Однако это приводит нас к интересному вопросу: как мы узнаем, что явление характеризуется нормальным распределением значений?
Если у нас есть большой объем данных, мы можем просто посмотреть на гистограмму и сравнить ее с гауссовой кривой. Однако с меньшими наборами данных ситуация будет сложнее. Даже если мы анализируем базовый процесс, который действительно создает нормально распределенные данные, гистограммы, созданные из небольших наборов данных, могут оставлять место для сомнений.
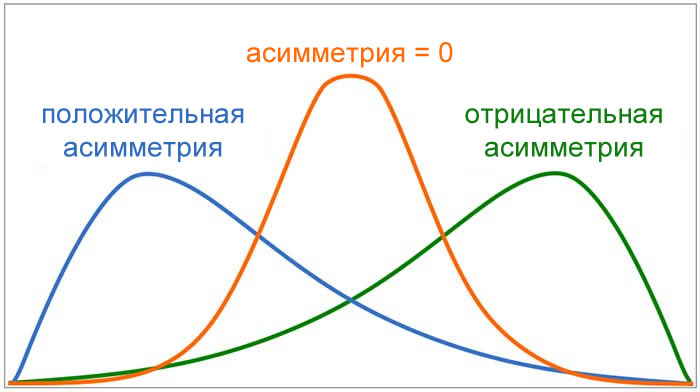
В данной статье мы обсудим два описательных статистических показателя (асимметрию и эксцесс), которые помогут нам определить, соответствуют ли наши данные нормальному распределению. Однако сначала я хочу изучить связанный с этим вопрос: почему нас волнует, соответствует ли набор данных нормальному распределению? Существуют различные статистические методы, помогающие нам анализировать и интерпретировать данные, и некоторые из этих методов относятся к категории статистических выводов. Мы часто используем слово «тест», когда говорим о статистической процедуре вывода, и эти тесты могут быть параметрическими или непараметрическими. Различие между параметрическими и непараметрическими тестами заключается в характере данных, к которым применяется тест. Когда набор данных демонстрирует распределение, которое в достаточной степени согласуется с нормальным распределением, можно использовать параметрические тесты. Когда данные не распределены нормально, мы переходим к непараметрическим тестам. Примерами параметрических тестов являются парный t-критерий, односторонний дисперсионный анализ (ANOVA) и коэффициент корреляции Пирсона. Непараметрическими альтернативами этим критериям являются, соответственно, критерий знаковых рангов Уилкоксона, критерий Краскела–Уоллиса и ранговая корреляция Спирмена. Если вас смущает эта терминология параметрический/непараметрический, вот объяснение: параметр – это характеристика всей генеральной совокупности (совокупности значений), например, средний рост всех канадцев или стандартное отклонение выходных напряжений, генерируемых всеми микросхемами эталонного напряжения REF100 (я придумал эту модель микросхемы). Обычно мы не можем знать параметр с уверенностью потому, что наши данные представляют собой только выборку из генеральной совокупности. Однако мы можем произвести оценку параметра, вычислив соответствующее статистическое значение на основе выборки. Параметрические тесты основываются на предположениях, связанных с нормальностью распределения генеральной совокупности, и параметрами, которые характеризуют это распределение. Когда данные не распределены нормально, мы не можем делать такие предположения, и, следовательно, мы должны использовать непараметрические тесты. Если существуют непараметрические тесты и их можно применять независимо от нормальности распределения, зачем утруждать себя определением, является ли распределение нормальным? Давайте, просто применим непараметрический тест и покончим с этим! Есть простая причина, по которой мы избегаем непараметрических тестов, когда данные достаточно нормальны: параметрические тесты, как правило, более эффективны. «Эффективность» в статистическом смысле означает, насколько эффективно тест обнаружит взаимосвязь между переменными (если эта взаимосвязь существует). Мы можем сделать любой тип тестов более эффективным, увеличив размер выборки, но для того, чтобы получить наилучшую информацию из имеющихся данных, мы по возможности используем параметрические тесты. Мы можем попытаться определить, демонстрируют ли эмпирические данные неопределенно нормальное распределение, просто взглянув на гистограмму. Однако, чтобы решить, является ли распределение достаточно нормальным, чтобы оправдать использование параметрических тестов, нам могут потребоваться дополнительные аналитические методы. Один из этих методов – вычислить асимметрию набора данных. Нормальное распределение идеально симметрично относительно среднего, и, таким образом, любое отклонение от идеальной симметрии указывает на некоторую степень ненормальности измеренного распределения. На следующем рисунке представлены примеры асимметричных форм распределения. Асимметрия может представляться положительным или отрицательным числом (или нулем). Распределения, симметричные относительно среднего значения, такие как нормальное распределение, имеют нулевую асимметрию. Распределение, которое «наклоняется» вправо, имеет отрицательную асимметрию, а распределение, которое «наклоняется» влево, имеет положительную асимметрию. Как правило, значения асимметрии, которые находятся в пределах ±1 от асимметрии нормального распределения, указывают на достаточную нормальность для использования параметрических тестов. Мы используем эксцесс, чтобы количественно оценить тенденцию явления создавать значения, далекие от среднего. Существуют различные способы описания информации, которую эксцесс передает о наборе данных: «хвостатость» (обратите внимание, что значения, далекие от среднего, находятся в хвостах распределения), «величина хвоста» или «вес хвоста» и «островершинность» (последнее несколько проблематично, потому что эксцесс напрямую не измеряет остроту или гладкость). Нормальное распределение имеет значение эксцесса 3. Следующая диаграмма дает общее представление о том, как эксцесс больше или меньше 3 соответствует формам ненормального распределения. Оранжевая кривая – нормальное распределение. Обратите внимание, что синяя кривая по сравнению с оранжевой кривой имеет большую «величину хвоста», то есть большую массу вероятности в хвостах. Эксцесс синей кривой, которая называется распределением Лапласа, равен 6. Зеленая кривая называется равномерным распределением; вы можете видеть, что хвосты отсутствуют. Эксцесс равномерного распределения равен 1,8. Как и в случае асимметрии, общее правило состоит в том, что эксцесс в пределах ±1 от эксцесса нормального распределения указывает на достаточную нормальность. Конечно, о параметрических тестах, асимметрии и эксцессе можно сказать гораздо больше, но я думаю, что мы рассмотрели достаточно материала для вводной статьи. Обобщим вышесказанное: АсимметрияНормальное распределение / Гауссово распределениеПараметрический тестСтатистикаСтатистический анализЭксцессПараметрические и непараметрические тесты
Почему «параметрический» и «непараметрический»?
Зачем заморачиваться с параметрическими тестами?
Оценка нормальности: асимметрия и эксцесс
Асимметрия
Эксцесс
Заключение
Теги
Коэффициент асимметрии. Эксцесс распределения
Краткая теория
При изучении распределений, отличных от нормального,
возникает необходимость количественно оценить это различие. С этой целью вводят
специальные характеристики, в частности асимметрию и эксцесс. Для нормального
распределения эти характеристики равны нулю. Поэтому если для изучаемого
распределения асимметрия и эксцесс имеют небольшие значения, то можно
предположить близость этого распределения к нормальному.
Наоборот, большие значения асимметрии и эксцесса указывают на значительное
отклонение от нормального.
Асимметрией теоретического распределения называют отношение
центрального момента третьего порядка к кубу среднего квадратического
отклонения:
Коэффициент асимметрии характеризует скошенность
распределения по отношению к математическому ожиданию. Асимметрия положительна,
если «длинная часть» кривой распределения расположена справа от математического
ожидания; асимметрия отрицательна, если «длинная часть» кривой расположена слева
от математического ожидания.
На рисунке показаны две кривые распределения: I и II. Кривая I имеет
положительную (правостороннюю) асимметрию
,
а кривая II – отрицательную (левостороннюю)
.
Кроме вышеописанного коэффициента, для характеристики асимметрии
рассчитывают также показатель асимметрии Пирсона:
Коэффициент асимметрии Пирсона характеризует асимметрию только в
центральной части распределения, поэтому более распространенным и более точным
является коэффициент асимметрии, рассчитанный на основе центрального момента третьего
порядка.
Для оценки «крутости», т. е. большего или меньшего подъема кривой
теоретического распределения по сравнению с нормальной кривой, пользуются
характеристикой — эксцессом.
Эксцессом (или коэффициентом эксцесса) случайной величины
называется число:
Число 3 вычитается из отношения
потому, что для наиболее часто встречающегося
нормального распределения отношение
.
Кривые, более островершинные, чем нормальная,
обладают положительным эксцессом, более плосковершинные — отрицательным
эксцессом.
Примеры решения задач
Задача 1
Для заданного
вариационного ряда вычислить коэффициенты асимметрии и эксцесса.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Составим расчетную
таблицу
Средняя:
Найдем моду — варианту, которой соответствует наибольшая частота.
Дисперсия:
Среднее квадратическое
отклонение:
Коэффициент асимметрии Пирсона:
Коэффициент асимметрии можно найти по формуле:
Центральный момент
3-го порядка:
Получаем:
Эксцесс можно найти по формуле:
Центральный момент
4-го порядка:
Получаем:
Задача 2
Для заданного
вариационного ряда (см. условие задачи 1) вычислить коэффициенты асимметрии и
эксцесса методом произведений, используя условные моменты.
Решение
Составим расчетную таблицу
Перейдем к условным вариантам
В качестве ложного нуля возьмем
3-ю варианту
0
Условные варианты вычислим по
формуле:
где
4
(разность между соседними вариантами)
Условный момент 1-го порядка:
Средняя:
Условный момент 2-го порядка:
Дисперсия:
Среднее квадратическое
отклонение:
Коэффициент асимметрии можно найти
по формуле:
Условный момент 3-го порядка:
Центральный момент 3-го порядка:
Получаем:
Эксцесс можно найти по формуле:
Условный момент 4-го порядка:
Центральный момент 4-го порядка:
Получаем:
Весь смысл выборочной совокупности в том, чтоб по ней можно было судить о генеральной совокупности, для этого выборка должна быть репрезентативной. Репрезентативность достигается в том числе достаточным количеством наблюдений (n).
Параметры распределения
Важнейшие параметры распределения случайной величины Х являются — математическое ожидание µ (Мген) и дисперсия σ2.
- Математическое ожидание (Х) — среднее значение случайной величины при стремлении количества выборок к бесконечности.
- Среднеквадратичное отклонение (σ2) — показатель рассеивания значений случайной величины относительно ей математического ожидания.
Распределения бывают непрерывными и дискретными. Наиболее известно из непрерывних распределений — нормальное.
Характеристики нормального распределения
- Совпадение средней арифметической (М), медианы (Ме) и моды (Мо).
- Чем больше величина отклоняется от среднего значения, тем меньше частота его встречаемости.
Пример нормального распределения
Первичные величины, характеризующие распределение
- Средняя арифметическая (М)
- Среднее квадратичное отклонение (σ2)
- Коэффициент вариации
- Коэффициент асимметрии — показатель отклонения распределения в левую и правую сторону по оси абсцесс. Если больше влево — левосторонняя или отрицательная. Если вправо — правосторонняя положительная.
- Эксцесс — мера сглаженности. Если близко к 0, то форма распределения близка к нормальному виду. Если > 0 — то форма остроконечная. Если < 0 — форма плосковершинная. Норма эксцесса от -1 до +1.
Вид графика в зависимости от значения коэффициента асимметрии
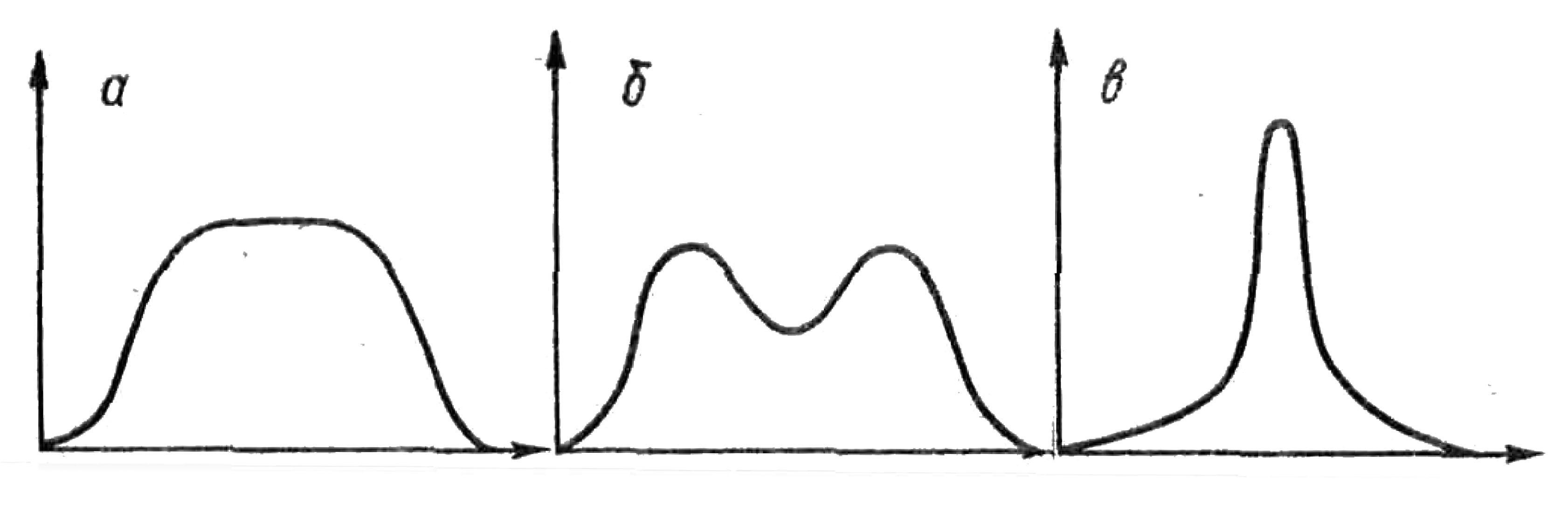
Вид графика в зависимости от эксцесса
а,б — отрицательные эксцессы
в — положительный
Значение нормального распределения
Если нормальное распределение, для обработки используют параметрические методы математической статистики для расчёта достоверности различий между выборками:
- Критерий Стьюдента (t)
- Критерий Фишера (F)
- Коэффициент корреляции Пирсона (r)
Если кривая распределения отлична от нормальной, используют методы непараметрической статистики, расчёт достоверности разности по
- Критерию Манна-Уитни (U)
- Коэффициенту ранговой корреляции Спирмена (p)
Альтернативное (дихотомическое) распределение
Параметр математического ожидания выражает относительную величину (долю) единиц совокупности, не которые обладают изученным признаком (Р). Доля совокупности, не обладающая признаком, обозначается q.
Как правило, q = 10 - P.
Дисперсия в таком случае: Рв = nx/nв
Ошибки репрезентативности
- Ошибка выборочного наблюдения (mвн) — разность между значением параметра в генеральной совокупности и его выборочным значением.
Для среднего значения mвн = | Мген - Мв |; для доли: mвн = | Рген - Рв |.
- Средняя ошибка (m) — величина, выражающая среднее квадратичное отклонение выборочной средней от математического ожидания:
m = √(σ2/n) - Соотношение дисперсий между выборочной и генеральной совокупностями:
σ2=σ2в × n/(n-1)
При достаточно больших выборках (n) можно считать, что σ2=σ2в
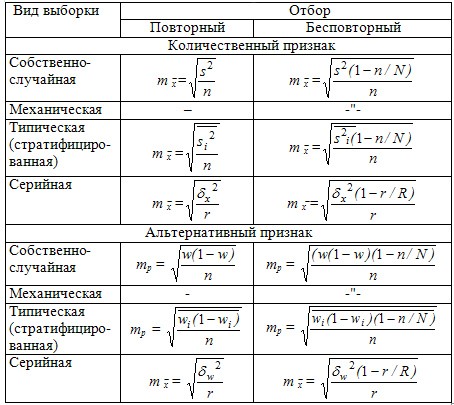
Расчёт средней ошибки (m) для разных видов выборок
На практике чаще используются следующие формулы
- Расчёт ошибки репрезентативности средней арифметической (mM):
mM=σ/√n - Расчёт ошибки репрезентативности относительной величины (mp):
mp=√(P*q / n)
где P — относительная величина (проценты, промилле и т.д.)
q — доля единиц совокупности с альтернативным признаком (1-Р или 100-Р или 1000-Р) в зависимости от основания, на которое рассчитан коэффициент
n — численность выборки
- Если в испытании объём выборки менее 30, то n уменьшается на 1:
(n-1)
Вероятность безошибочного прогноза
В медицинских исследований достаточная вероятность — 95-99%. В некоторых случаях должный прогноз — 99,7%.
Определённой вероятности безошибочного прогноза соответствует величина предельной ошибки случайной выборки (Δ).
Δ = t × m
где t — доверительный коэффициент (критерий Стьюдента)
m — средняя ошибка выборки
Вероятность прогноза (р) при значении критерия Стьюдента (t)
| t | p |
|---|---|
| < 1.96 | < 0.95 |
| 2 | 0.954 |
| 2.5 | 0.988 |
| 3 | 0.997 |
| 3.5 | 0.999 |
- Предельная ошибка выборки:
Δ = t × √( σ2 ÷ n) - Необходимая численность выборки:
n = t2 × σ2 ÷ Δ2
Для определения достоверности различий между двумя показателями или средними величинами при малом числе наблюдений (n ≤ 30, в каждой группе) критерий достоверности оценивается по таблице значений t-критерия Стьюдента по числу степеней свободы/ При этом число степеней свободы определяется, как n´= n1 + n2 - 2.
| Число степеней свободы, n´ | Значение t-критерия Стьюдента при p=0.05 |
|---|---|
| 1 | 12.706 |
| 2 | 4.303 |
| 3 | 3.182 |
| 4 | 2.776 |
| 5 | 2.571 |
| 6 | 2.447 |
| 7 | 2.365 |
| 8 | 2.306 |
| 9 | 2.262 |
| 10 | 2.228 |
| 11 | 2.201 |
| 12 | 2.179 |
| 13 | 2.160 |
| 14 | 2.145 |
| 15 | 2.131 |
| 16 | 2.120 |
| 17 | 2.110 |
| 18 | 2.101 |
| 19 | 2.093 |
| 20 | 2.086 |
| 21 | 2.080 |
| 22 | 2.074 |
| 23 | 2.069 |
| 24 | 2.064 |
| 25 | 2.060 |
| 26 | 2.056 |
| 27 | 2.052 |
| 28 | 2.048 |
| 29 | 2.045 |
| 30 | 2.042 |
| 31 | 2.040 |
| 32 | 2.037 |
| 33 | 2.035 |
| 34 | 2.032 |
| 35 | 2.030 |
| 36 | 2.028 |
| 37 | 2.026 |
| 38 | 2.024 |
| 40-41 | 2.021 |
| 42-43 | 2.018 |
| 44-45 | 2.015 |
| 46-47 | 2.013 |
| 48-49 | 2.011 |
| 50-51 | 2.009 |
| 52-53 | 2.007 |
| 54-55 | 2.005 |
| 56-57 | 2.003 |
| 58-59 | 2.002 |
| 60-61 | 2.000 |
| 62-63 | 1.999 |
| 64-65 | 1.998 |
| 66-67 | 1.997 |
| 68-69 | 1.995 |
| 70-71 | 1.994 |
| 72-73 | 1.993 |
| 74-75 | 1.993 |
| 76-77 | 1.992 |
| 78-79 | 1.991 |
| 80-89 | 1.990 |
| 90-99 | 1.987 |
| 100-119 | 1.984 |
| 120-139 | 1.980 |
| 140-159 | 1.977 |
| 160-179 | 1.975 |
| 180-199 | 1.973 |
| 200 | 1.972 |
| ∞ | 1.960 |
Оценка достоверности разности величин
Для средних величин:
Для относительных величин:
где М1 и М2, Р1 и Р2 — статистические величины, полученные при проведении выборочных исследований;
m1 и m2; — их ошибки репрезентативности; t — коэффициент достоверности.





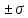 )
)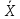 ),
),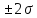 )
) )
)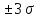 )
)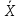 )
)