Содержание:
Нормальный закон распределения:
Нормальный закон распределения имеет плотность вероятности
где
График функции плотности вероятности (2.9.1) имеет максимум в точке 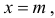

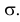
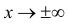
Помимо геометрического смысла, параметры нормального закона распределения имеют и вероятностный смысл. Параметр 
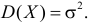
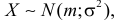

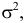
где 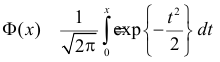
Значения функции 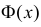
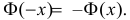
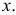
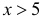
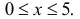
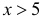
Если 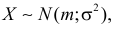
Пример:
Случайная величина X имеет нормальный закон распределения 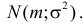
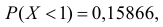
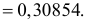
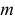
Решение. Воспользуемся формулой (2.9.2):
Так как 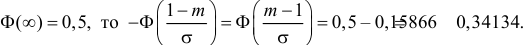
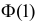
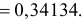
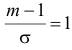
Аналогично 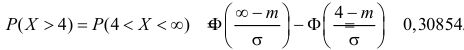
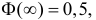
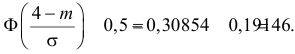
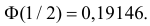
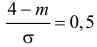
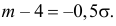
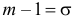
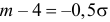
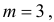
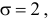
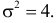
График функции плотности вероятности этого закона распределения изображен на рис. 2.9.3.
Ответ.
Пример:
Ошибка измерения X имеет нормальный закон распределения, причем систематическая ошибка равна 1 мк, а дисперсия ошибки равна 4 мк2. Какова вероятность того, что в трех независимых измерениях ошибка ни разу не превзойдет по модулю 2 мк?
Решение. По условиям задачи 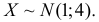
Вычисленная вероятность численно равна заштрихованной площади на рис. 2.9.4.
Каждое измерение можно рассматривать как независимый опыт. Поэтому по формуле Бернулли (2.6.1) вероятность того, что в трех независимых измерениях ошибка ни разу не превзойдет 2 мк, равна
Ответ.
Пример:
Функция плотности вероятности случайной величины X имеет вид
Требуется определить коэффициент 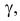
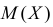
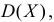
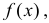
Замечание. Если каждый закон распределения из некоторого семейства законов распределения имеет функцию распределения , 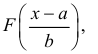
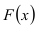
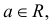
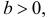
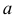
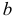
Решение. Так как (2.9.4) функция плотности вероятности, то интеграл от нее по всей числовой оси должен быть равен единице:
Преобразуем выражение в показателе степени, выделяя полный квадрат:
Тогда (2.9.5) можно записать в виде
Сделаем замену переменных так, чтобы 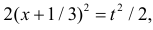
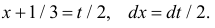
Умножим и разделим левую часть равенства на 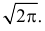
Так как 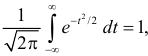
Поэтому
Последняя запись означает, что случайная величина имеет нормальный закон распределения с параметрами 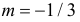
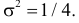
Ответ.
Пример:
Цех на заводе выпускает транзисторы с емкостью коллекторного перехода 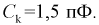
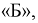
Решение.
Статистическими исследованиями в цеху установлено, что 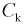
Чтобы вычислить количество транзисторов, попадающих в группу 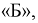
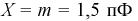
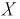
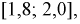
Для расчета этой вероятности надо построить математическую модель. Экспериментальные данные говорят о том, что нормальное распределение можно принять в качестве математической модели. Эмпирическая оценка (установлена статистическими исследованиями в цеху) среднего значения
дает 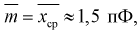
Обозначая 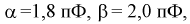
Тогда количество транзисторов 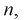
Нормальное распределение и его свойства
Если выйти на улицу любого города и случайным образом выбранных прохожих спросить о том, какой у них рост, вес, возраст, доход, и т.п., а потом построить график любой из этих величин, например, роста… Но не будем спешить, сначала посмотрим, как можно построить такой график.
Сначала, мы просто запишем результаты своего исследования. Потом, мы отсортируем всех людей по группам, так чтобы каждый попал в свой диапазон роста, например, «от 180 до 181 включительно».
После этого мы должны посчитать количество людей в каждой подгруппе-диапазоне, это будет частота попадания роста жителей города в данный диапазон. Обычно эту часть удобно оформить в виде таблички. Если затем эти частоты построить по оси у, а диапазоны отложить по оси х, можно получить так называемую гистограмму, упорядоченный набор столбиков, ширина которых равна, в данном случае, одному сантиметру, а длина будет равна той частоте, которая соответствует каждому диапазону роста. Если
Вам попалось достаточно много жителей, то Ваша схема будет выглядеть примерно так:
Дальше можно уточнить задачу. Каждый диапазон разбить на десять, жителей рассортировать по росту с точностью до миллиметра. Диаграмма станет глаже, но уменьшится по высоте, «оплывет» вниз, т.к. в каждом маленьком диапазоне количество жителей уменьшается. Чтобы избежать этого, просто увеличим масштаб по вертикальной оси в 10 раз. Если гипотетически повторить эту процедуру несколько раз, будет вырисовываться та знаменитая колоколообразная фигура, которая характерна для нормального (или Гауссова) распределения. В результате, относительная частота встречаемости каждого конкретного диапазона роста может быть посчитана как отношение площади «ломтика» кривой, приходящегося на этот диапазон к площади подо всей кривой. Стандартизированные кривые нормального распределения, значения функций которых приводятся в таблицах книг по статистике, всегда имеют суммарную площадь под кривой равную единице. Это связано с тем, что, как Вы помните из курса теории вероятности, вероятность достоверного события всегда равна 100% (или единице), а для любого человека иметь хоть какое-то значение роста — достоверное событие. А вот вероятность того, что рост произвольного человека попадет в определенный выбранный нами диапазон, будет зависеть от трех факторов.
Во-первых, от величины такого диапазона — чем точнее наши требования, тем меньше вероятности, что нам повезет.
Во-вторых, от того, насколько «популярен» выбранный нами рост. Напомним, что мода — самое часто встречающееся значение роста. Кстати для нормального распределения мода, медиана и среднее значение совпадают. Кривая нормального распределения симметрична относительно среднего значения.
И, в-третьих, вероятность попадания роста в определенный диапазон зависит от характеристики рассеивания случайной величины. Отчасти это связано с единицами измерения (представьте, что мы бы измеряли людей в дюймах, а не в миллиметрах, но сами люди и их рост были бы теми же). Но дело не только в этом. Просто некоторые процессы кучнее группируются возле среднего значения, в то время как другие более разбросаны.
Например, рост собак и рост домашних кошек имеют разный разброс значений, их кривые нормального распределения будут выглядеть по-разному (напомним еще раз, что площадь под обеими кривыми будет единичной).
Так, кривая для роста кошек будет более узкой и высокой, а для роста собак кривая будет ниже и шире. Для характеристики разброса конечного ряда данных в прошлом разделе мы использовали величину среднего квадратического отклонения. Аналогичная величина используется для характеристики кривой нормального распределения. Она обозначается буквой s и называется в этом случае стандартным отклонением. Это очень важная величина для кривой нормального распределения. Кривая нормального распределения полностью задана, если известно среднее значение 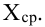
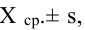
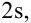
Для вычисления других значений вероятности, которые могут Вам понадобиться, можно воспользоваться приведенной таблицей:
Таблица вероятности попадания случайной величины в отмеченный (заштрихованный) диапазон
Нормальный закон распределения
Нормальный закон распределения случайных величин, который иногда называют законом Гаусса или законом ошибок, занимает особое положение в теории вероятностей, так как 95 % изученных случайных величин подчиняются этому закону. Природа этих случайных величин такова, что их значение в проводимом эксперименте связано с проявлением огромного числа взаимно независимых случайных факторов, действие каждого из которых составляет малую долю их совокупного действия. Например, длина детали, изготавливаемой на станке с программным управлением, зависит от случайных колебаний резца в момент отрезания, от веса и толщины детали, ее формы и температуры, а также от других случайных факторов. По нормальному закону распределения изменяются рост и вес мужчин и женщин, дальность выстрела из орудия, ошибки различных измерений и другие случайные величины.
Определение: Случайная величина X называется нормальной, если она подчиняется нормальному закону распределения, т.е. ее плотность распределения задается формулой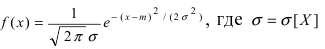
Приведенная дифференциальная функция распределения удовлетворяет всем свойствам плотности вероятности, проверим, например, свойство 4.:
Выясним геометрический смысл параметров 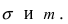
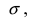
Рис. 8. Изменение графика плотности вероятности в зависимости от изменения математического ожидания при фиксированном значении средне-квадратичного отклонения. Из рисунка видно, кривая 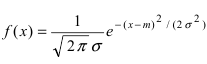
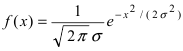
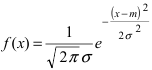
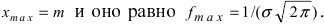
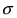
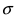
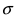
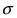
Рис. 9. Изменение графика плотности вероятности в зависимости от изменения средне-квадратичного отклонения при фиксированном значении математического ожидания.
Интегральная функция нормального распределения имеет вид:
График функции распределения имеет вид (Рис. 10):
Рис. 10. Графика интегральной функции распределения нормальной случайной величины.
Вероятность попадания нормальной случайной величины в заданный интервал
Пусть требуется определить вероятность того, что нормальная случайная величина попадает в интервал 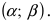
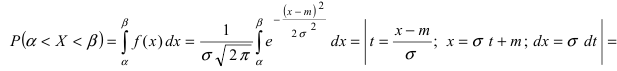
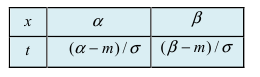
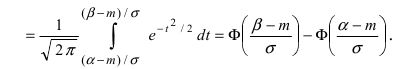
Рассмотрим основные свойства функции Лапласа Ф(х):
- Ф(0) = 0 — график функции Лапласа проходит через начало координат.
- Ф (-х) = — Ф(х) — функция Лапласа является нечетной функцией, поэтому
- таблицы для функции Лапласа приведены только для неотрицательных значений аргумента.
— график функции Лапласа имеет горизонтальные асимптоты
Следовательно, график функции Лапласа имеет вид (Рис. 11):
Рис. 11. График функции Лапласа.
Пример №1
Закон распределения нормальной случайной величины X имеет вид: 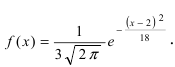
Решение:
Согласно условиям задачи 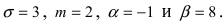
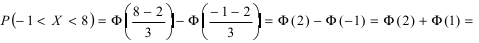
Вычисление вероятности заданного отклонения
Вычисление вероятности заданного отклонения. Правило 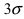
Если интервал, в который попадает нормальная случайная величина X, симметричен относительно математического ожидания 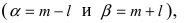
Данная формула показывает, что отклонение случайной величины Х от ее математического ожидания на заданную величину l равна удвоенному значению функции Лапласа от отношения / к среднему квадратичному отклонению. Если положить 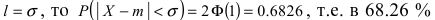
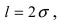
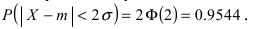
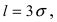
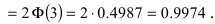
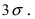
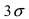
Показательный закон распределения
Определение: Закон распределения, определяемый фу нкцией распределения:
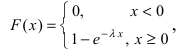
График экспоненциального закона распределения имеет вид (Рис. 12):
Рис. 12. График функции распределения для случая экспоненциального закона.
Дифференциальная функция распределения (плотность вероятности) имеет вид: 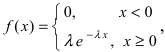
Рис. 13. График плотности вероятности для случая экспоненциального закона.
Пример №2
Случайная величина X подчиняется дифференциальной функции распределения 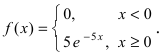
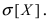
Решение:
Интегральная функция распределения 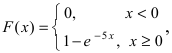
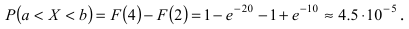
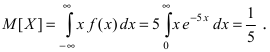
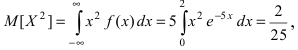
отклонение 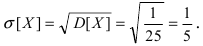
- Основные законы распределения вероятностей
- Асимптотика схемы независимых испытаний
- Функции случайных величин
- Центральная предельная теорема
- Повторные независимые испытания
- Простейший (пуассоновский) поток событий
- Случайные величины
- Числовые характеристики случайных величин
Случайной
погрешностью измерения называется
составляющая погрешности, изменяющаяся
случайным образом (по знаку и значению)
при повторных измерениях одной и той
же физической величины, проведенных
с одинаковой тщательностью. Примеры
распределения случайных величин
Способы
нахождения значений случайной величины
зависят от вида функции ее распределения.
Однако на практике такие функции, как
правило, неизвестны. Если же случайный
характер результатов наблюдений
обусловлен погрешностями измерений,
то полагают, что наблюдения имеют
нормальное
распределение.
Это обусловлено тем, что погрешности
измерений складываются из большого
числа небольших возмущений, ни одно из
которых не является преобладающим.
Согласно же центральной
предельной теореме
сумма бесконечно большого числа взаимно
независимых бесконечно малых случайных
величин с любыми распределениями имеет
нормальное
распределение.
Нормальное распределение для
случайной
величиных
с
математическим ожиданием
и
дисперсиейs
имеет вид:
Реально даже воздействие
ограниченного числа возмущений приводит
к нормальному распределению результатов
измерений и их погрешностей. В
настоящее время наиболее полно разработан
математический аппарат именно для
случайных величин, имеющих нормальное
распределение. Если же предположение
о нормальности распределения отвергается,
то статистическая обработка наблюдений
существенно усложняется и в таком
случае невозможно рекомендовать общую
методику статистической обработки
наблюдений. Часто даже не известно,
какая характеристика распределения
может служить оценкой истинного значения
измеряемой величины.
Выше приведено
аналитическое выражение нормального
распределения для случайной измеряемой
величины х.
Переход к нормальному
распределению случайных погрешностей
осуществляется
переносом центра распределений ви
откладывания по оси абсцисс погрешности.
Нормальное
распределение характеризуется двумя
парамет-рами: математическим ожиданием
m1
и
средним квадратическим отклонением
σ.
При многократных измерениях
несмещенной, состоятельной и эффективной
оценкой m1
для группы из n
наблюдений является среднее арифметическое
:
.
Нужно
сказать, что среднее арифметическое
дает оценку математического ожидания
результата наблюдений и может бытьоценкой
истинного (действительного) значения
измеряемой
величины только после
исключения
систематических погрешностей.
Оценка
S
среднего квадратического отклонения
(СКО) дается
формулой:
Эта
оценка характеризуетрассеяние
единичных результатов измерений в ряду
равноточных измерений одной и той же
величины около их среднего значения.
Другими оценками рассеяния результатов
в ряду измерений являются размах
(разница между наибольшим и наименьшим
значением), модуль средней
арифметической погрешности
(арифметическая сумма погрешностей,
деленная на число измерений) и
доверительная граница погрешности
(подробно рассматривается ниже).
СКО
является наиболее удобной характеристикой
погрешности в случае ее дальнейшего
преобразования. Например, для нескольких
некоррелированных слагаемых СКО суммы
определяется по
формуле:
.
Оценка
S характеризует рассеяние единичных
результатов наблюдений относительно
среднего значения, то есть в случае,
если мы за результат измерений примем
отдельный исправленный результат
наблюдений. Если же в качестве результата
измерений принимается среднее
арифметическое, то СКО этого среднегоопределяется
по формуле:Нормальное
распределение погрешностей имеет
следующиесвойства:
-
симметричность,
т.е. погрешности, одинаковые по величине,
но противоположные по знаку,
встречаются одинаково часто; -
математическое
ожидание случайной погрешности равно
нулю; -
малые
погрешности более вероятны, чем большие; -
чем
меньше s, тем меньше рассеяние результатов
наблюдений и больше вероятность малых
погрешностей.
Доверительные
интервалы
Приведенные
выше оценки параметров распределения
случайных величин в виде среднего
арифметического для оценки математического
ожидания и СКО для оценки дисперсии
называются точечными
оценками,
так как они выражаются одним числом.
Однако в некоторых случаях знание
точечной оценки является недостаточным.
Наиболее корректной и наглядной оценкой
случайной погрешности измерений
является оценка с помощью доверительных
интервалов.
Симметричный интервал в границами
± Δх(Р)
называется доверительным
интервалом случайной
погрешности с довери-тельной вероятностью
Р,
если площадь кривой распределения
между абсциссами –Δх
и
+Δх
составляет Р-ю
часть всей площади под кривой плотности
распределения вероятностей. При
нормировке всей площади на единицу Р
представляет часть этой площади в долях
единицы (или в процентах). Другими
словами, в интервале от -Dх(Р)
до +Dх(Р)
с заданной вероятностью Р
встречаются Р×100%
всех возможных значений случайной
погрешности.
Доверительный интервал
для нормального распределения находится
по формуле:
где
коэффициентt
зависит от доверительной вероятности
Р.
Для
нормального распределения существуют
следующие соотношения между доверительными
интервалами и доверительной вероятностью:
1s (Р=0,68), 2s (Р= 0,95), 3s (Р= 0,997), 4s (Р=0,999).
Доверительные
вероятности для выражения результатов
измерений и погрешностей в различных
областях науки и техники принимаются
равными. Так, в технических измерениях
принята доверительная вероятность
0,95. Лишь для особо точных и ответственных
измерений принимают более высокие
доверительные вероятности. В метрологии
используют, как правило, доверитель-ные
вероятности 0,97, в исключительных случаях
0,99. Необходимо отметить, что точность
измерений должна соответствовать
поставленной измерительной задаче.
Излишняя точность ведет к неоправданному
расходу средств. Недостаточная точность
измерений может привести к принятию
по его результатам ошибочных решений
с самыми непредсказуемыми последствиями,
вплоть до серьезных материальных потерь
или катастроф.
При
проведении многократных измерений
величины х,
подчиняющейся нормальному распределению,
доверительный интервал может быть
построен для любой доверительной
вероятности по формуле:
гдеtq–
коэффициент Стьюдента, зависящий от
числа наблюдений n
и выбранной доверительной вероятности
Р.
Он определяется с помощью таблицы
q-процентных
точек распределения Стьюдента, которая
имеет два параметра: k
= n
– 1 и q=
1 – P;
–
оценка среднего квадратического
отклонения среднего арифметического.
Доверительный
интервал для погрешностиDх(Р)
позволяет построить доверительный
интервал для истинного (действительного)
значения измеряемой величины ,
оценкой которой является среднее
арифметическое
.
Истинное значение измеряемой величины
находится с доверительной вероятностью
Р внутри интервала:.
Доверительный интервал позволяет
выяснить, насколько может измениться
полученная в результате данной серии
измерений оценка измеряемой величины
при проведении повторной серии измерений
в тех же условиях. Необходимо отметить,
что доверительные интервалы строят
длянеслучайных
величин,
значения которых неизвестны. Такими
являются истинное значение измеряемой
величины и средние квадратические
отклонения. В то же время оценки этих
величин, получаемые в результате
обработки данных наблюдений, являются
случайными величинами.
Недостатком
доверительных интервалов при оценке
случай-ных погрешностей является то,
что при произвольно выбираемых
доверительных вероятностях нельзя
суммировать несколько погреш-ностей,
т.к. доверительный интервал суммы не
равен сумме довери-тельных интервалов.
Суммируются
дисперсии независимых случай-ных
величин:
Då
= åDi.
То есть, для возможности суммирования
составляющие случайной погрешности
должны быть представлены своими СКО,
а не предельными или доверительными
погрешностями.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Нормальным называют распределение вероятностей непрерывной случайной величины
, плотность которого имеет вид:
где
–
математическое ожидание,
–
среднее квадратическое отклонение
.
Вероятность того, что
примет
значение, принадлежащее интервалу
:
где
– функция Лапласа:
Вероятность того, что абсолютная
величина отклонения меньше положительного числа
:
В частности, при
справедливо
равенство:
Асимметрия, эксцесс,
мода и медиана нормального распределения соответственно равны:
, где
Правило трех сигм
Преобразуем формулу:
Положив
. В итоге получим
если
, и, следовательно,
, то
то есть вероятность того, что
отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонение, равна 0,9973.
Другими словами, вероятность того,
что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна
0,0027. Это означает, что лишь в 0,27% случаев так может произойти. Такие
события исходя из принципа невозможности маловероятных
событий можно считать практически невозможными. В этом и состоит
сущность правила трех сигм: если случайная величина распределена нормально, то
абсолютная величина ее отклонения от математического ожидания не превосходит
утроенного среднего квадратического отклонения.
На практике правило трех сигм
применяют так: если распределение изучаемой случайной величины неизвестно, но
условие, указанное в приведенном правиле, выполняется, то есть основание
предполагать, что изучаемая величина распределена нормально; в противном случае
она не распределена нормально.
Смежные темы решебника:
- Таблица значений функции Лапласа
- Непрерывная случайная величина
- Показательный закон распределения случайной величины
- Равномерный закон распределения случайной величины
Пример 2
Ошибка
высотометра распределена нормально с математическим ожиданием 20 мм и средним
квадратичным отклонением 10 мм.
а) Найти
вероятность того, что отклонение ошибки от среднего ее значения не превзойдет 5
мм по абсолютной величине.
б) Какова
вероятность, что из 4 измерений два попадут в указанный интервал, а 2 – не
превысят 15 мм?
в)
Сформулируйте правило трех сигм для данной случайной величины и изобразите
схематично функции плотности вероятностей и распределения.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
а) Вероятность того, что случайная величина, распределенная по
нормальному закону, отклонится от среднего не более чем на величину
:
В нашем
случае получаем:
б) Найдем
вероятность того, что отклонение ошибки от среднего значения не превзойдет 15
мм:
Пусть событие
– ошибки 2
измерений не превзойдут 5 мм и ошибки 2 измерений не превзойдут 0,8664 мм
– ошибка не
превзошла 5 мм;
– ошибка не
превзошла 15 мм
в)
Для заданной нормальной величины получаем следующее правило трех сигм:
Ошибка высотометра будет лежать в интервале:
Функция плотности вероятностей:
График плотности распределения нормально распределенной случайной величины
Функция распределения:
График функции
распределения нормально распределенной случайной величины
Задача 1
Среднее
количество осадков за июнь 19 см. Среднеквадратическое отклонение количества
осадков 5 см. Предполагая, что количество осадков нормально-распределенная
случайная величина найти вероятность того, что будет не менее 13 см осадков.
Какой уровень превзойдет количество осадков с вероятностью 0,95?
Задача 2
Найти
закон распределения среднего арифметического девяти измерений нормальной
случайной величины с параметрами m=1.0 σ=3.0. Чему равна вероятность того, что
модуль разности между средним арифметическим и математическим ожиданием
превысит 0,5?
Указание:
воспользоваться таблицами нормального распределения (функции Лапласа).
Задача 3
Отклонение
напряжения в сети переменного тока описывается нормальным законом
распределения. Дисперсия составляет 20 В. Какова вероятность при изменении
выйти за пределы требуемых 10% (22 В).
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 4
Автомат
штампует детали. Контролируется длина детали Х, которая распределена нормально
с математическим ожиданием (проектная длинна), равная 50 мм. Фактическая длина
изготовленных деталей не менее 32 и не более 68 мм. Найти вероятность того, что
длина наудачу взятой детали: а) больше 55 мм; б) меньше 40 мм.
Задача 5
Случайная
величина X распределена нормально с математическим ожиданием a=10и средним
квадратическим отклонением σ=5. Найти
интервал, симметричный относительно математического ожидания, в котором с
вероятностью 0,9973 попадает величина Х в результате испытания.
Задача 6
Заданы
математическое ожидание ax=19 и среднее квадратическое отклонение σ=4
нормально распределенной случайной величины X. Найти: 1) вероятность
того, что X примет значение, принадлежащее интервалу (α=15;
β=19); 2) вероятность того, что абсолютная величина отклонения значения
величины от математического ожидания окажется меньше δ=18.
Задача 7
Диаметр
выпускаемой детали – случайная величина, распределенная по нормальному закону с
математическим ожиданием и дисперсией, равными соответственно 10 см и 0,16 см2.
Найти вероятность того, что две взятые наудачу детали имеют отклонение от
математического ожидания по абсолютной величине не более 0,16 см.
Задача 8
Ошибка
прогноза температуры воздуха есть случайная величина с m=0,σ=2℃. Найти вероятность
того, что в течение недели ошибка прогноза трижды превысит по абсолютной
величине 4℃.
Задача 9
Непрерывная
случайная величина X распределена по нормальному
закону: X∈N(a,σ).
а) Написать
плотность распределения вероятностей и функцию распределения.
б) Найти
вероятность того, что в результате испытания случайная величина примет значение
из интервала (α,β).
в) Определить
приближенно минимальное и максимальное значения случайной величины X.
г) Найти
интервал, симметричный относительно математического ожидания a, в котором с
вероятностью 0,98 будут заключены значения X.
a=5; σ=1.3;
α=4; β=6
Задача 10
Производится измерение вала без
систематических ошибок. Случайные ошибки измерения X
подчинены нормальному закону с σx=10. Найти вероятность того, что измерение будет
произведено с ошибкой, превышающей по абсолютной величине 15 мм.
Задача 11
Высота
стебля озимой пшеницы — случайная величина, распределенная по нормальному закону
с параметрами a = 75 см, σ = 1 см. Найти вероятность того, что высота стебля:
а) окажется от 72 до 80 см; б) отклонится от среднего не более чем на 0,5 см.
Задача 12
Деталь,
изготовленная автоматом, считается годной, если отклонение контролируемого
размера от номинала не превышает 10 мм. Точность изготовления деталей
характеризуется средним квадратическим отклонением, при данной технологии
равным 5 мм.
а)
Считая, что отклонение размера детали от номинала есть нормально распределенная
случайная величина, найти долю годных деталей, изготовляемых автоматом.
б) Какой
должна быть точность изготовления, чтобы процент годных деталей повысился до
98?
в)
Написать выражение для функции плотности вероятности и распределения случайной
величины.
Задача 13
Диаметр
детали, изготовленной цехом, является случайной величиной, распределенной по
нормальному закону. Дисперсия ее равна 0,0001 см, а математическое ожидание –
2,5 см. Найдите границы, симметричные относительно математического ожидания, в
которых с вероятностью 0,9973 заключен диаметр наудачу взятой детали. Какова
вероятность того, что в серии из 1000 испытаний размер диаметра двух деталей
выйдет за найденные границы?
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 14
Предприятие
производит детали, размер которых распределен по нормальному закону с
математическим ожиданием 20 см и стандартным отклонением 2 см. Деталь будет
забракована, если ее размер отклонится от среднего (математического ожидания)
более, чем на 2 стандартных отклонения. Наугад выбрали две детали. Какова вероятность
того, что хотя бы одна из них будет забракована?
Задача 15
Диаметры
деталей распределены по нормальному закону. Среднее значение диаметра равно d=14 мм
, среднее квадратическое
отклонение σ=2 мм
. Найти вероятность того,
что диаметр наудачу взятой детали будет больше α=15 мм и не меньше β=19 мм; вероятность того, что диаметр детали
отклонится от стандартной длины не более, чем на Δ=1,5 мм.
Задача 16
В
электропечи установлена термопара, показывающая температуру с некоторой
ошибкой, распределенной по нормальному закону с нулевым математическим
ожиданием и средним квадратическим отклонением σ=10℃. В момент когда термопара
покажет температуру не ниже 600℃, печь автоматически отключается. Найти
вероятность того, что печь отключается при температуре не превышающей 540℃ (то
есть ошибка будет не меньше 30℃).
Задача 17
Длина
детали представляет собой нормальную случайную величину с математическим
ожиданием 40 мм и среднеквадратическим отклонением 3 мм. Найти:
а)
Вероятность того, что длина взятой наугад детали будет больше 34 мм и меньше 43
мм;
б)
Вероятность того, что длина взятой наугад детали отклонится от ее
математического ожидания не более, чем на 1,5 мм.
Задача 18
Случайное
отклонение размера детали от номинала распределены нормально. Математическое
ожидание размера детали равно 200 мм, среднее квадратическое отклонение равно
0,25 мм, стандартами считаются детали, размер которых заключен между 199,5 мм и
200,5 мм. Из-за нарушения технологии точность изготовления деталей уменьшилась
и характеризуется средним квадратическим отклонением 0,4 мм. На сколько
повысился процент бракованных деталей?
Задача 19
Случайная
величина X~N(1,22). Найти P{2
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 20
Заряд пороха для охотничьего ружья
должен составлять 2,3 г. Заряд отвешивается на весах, имеющих ошибку
взвешивания, распределенную по нормальному закону со средним квадратическим
отклонением, равным 0,2 г. Определить вероятность повреждения ружья, если максимально
допустимый вес заряда составляет 2,8 г.
Задача 21
Заряд
охотничьего пороха отвешивается на весах, имеющих среднеквадратическую ошибку
взвешивания 150 мг. Номинальный вес порохового заряда 2,3 г. Определить
вероятность повреждения ружья, если максимально допустимый вес порохового
заряда 2,5 г.
Задача 21
Найти
вероятность попадания снарядов в интервал (α1=10.7; α2=11.2).
Если случайная величина X распределена по
нормальному закону с параметрами m=11;
σ=0.2.
Задача 22
Плотность
вероятности распределения случайной величины имеет вид
Найти
вероятность того, что из 3 независимых случайных величин, распределенных по
данному закону, 3 окажутся на интервале (-∞;5).
Задача 23
Непрерывная
случайная величина имеет нормальное распределение. Её математическое ожидание
равно 12, среднее квадратичное отклонение равно 2. Найти вероятность того, что
в результате испытания случайная величина примет значение в интервале (8,14)
Задача 24
Вероятность
попадания нормально распределенной случайной величины с математическим
ожиданием m=4 в интервал (3;5) равна 0,6. Найти дисперсию данной случайной
величины.
Задача 25
В
нормально распределенной совокупности 17% значений случайной величины X
меньше 13% и 47% значений случайной величины X
больше 19%. Найти параметры этой совокупности.
Задача 26
Студенты
мужского пола образовательного учреждения были обследованы на предмет
физических характеристик и обнаружили, что средний рост составляет 182 см, со
стандартным отклонением 6 см. Предполагая нормальное распределение для роста,
найдите вероятность того, что конкретный студент-мужчина имеет рост более 185
см.

Дискретная СВ Х имеет геометрическое распределение, принимает значения 0, 1, … , ∞ с вероятностями
p( X = i) = pi = qi p ,
где p – параметр распределения (0 ≤ p ≤ 1), q = 1 – p.
Числовые характеристики геометрического распределения:
Дискретная значения 0, 1, … ,
m X = q / p , D X = q / p 2 .
СВ X имеет биномиальное распределение, если она принимает n со следующими вероятностями:
|
p(X =i) = p = |
n! |
piqn−i |
(7.2) |
|
i |
i!(n −i)! |
, |
|
где n, p – параметры распределения (0 ≤ p ≤1), q=1 – p. Числовые характеристики биномиального распределения:
m X = n p , D X = n q p .
Дискретная СВ Х имеет распределение Пуассона, если она принимает значения 0, 1, … , ∞ со следующими вероятностями:
|
p(X =i) = p = ai |
e−a |
(7.3) |
|
i |
i! |
, |
|
где a – параметр распределения (a > 0). |
||
|
Числовые характеристики пуассоновской СВ: |
||
|
m X = a , D X |
= a . |
Непрерывная СВ Х имеет равномерное распределение, если ее плотность вероятности в некотором интервале [а; b] постоянна, т.е. если все значения X в этом интервале равновероятны:
0, x <
f ( x ) = 1
b − a
0, x >
|
a , |
0 , x |
< a , |
||||||
|
− a |
||||||||
|
, a ≤ x ≤ b , F ( x ) = |
x |
, a |
≤ |
x ≤ |
b , |
|||
|
(7.4) |
||||||||
|
a |
||||||||
|
b. |
b |
− |
||||||
|
1, x |
> b . |
|||||||
Числовые характеристики равномерно распределенной СВ:
|
m X = |
a + b |
, D X |
= |
( b − a ) 2 |
. |
|
|
2 |
1 2 |
|||||
Непрерывная СВ T, принимающая только положительные значения, имеет экспоненциальное распределение, если ее плотность вероятности и функция распределения равны
|
λ e |
− λ t |
, t |
≥ 0 , |
− e |
−λt |
, t ≥ 0, |
||||
|
f (t ) = |
1 |
(7.5) |
||||||||
|
0 , t < 0 , |
F(t) = |
0, t < 0, |
||||||||
где λ – параметр распределения (λ > 0).

Числовые характеристики экспоненциальной СВ:
m T = 1 / λ , D T = 1 / λ 2 .
Непрерывная СВ Х имеет нормальное распределение, если ее плотность вероятности и функция распределения равны
|
f (x ) = |
1 |
exp − |
(x − m)2 |
F ( x ) = |
0 .5 + Φ |
x − m |
, |
||||||||
|
2 |
, |
(7.6) |
|||||||||||||
|
σ 2π |
2σ |
σ |
|||||||||||||
|
где m, σ – параметры распределения ( σ >0), |
|||||||||||||||
|
1 |
x |
t2 |
|||||||||||||
|
Φ(x) = |
∫e− |
dt — функция Лапласа. |
|||||||||||||
|
2 |
|||||||||||||||
|
2π |
|||||||||||||||
|
0 |
Значения функции Лапласа приведены в приложении. При использовании таблицы значений функции Лапласа следует учитывать, что Φ(–x) = –Φ(x),
Φ(0) = 0, Φ(∞) = 0,5.
Числовые характеристики нормальной СВ:
m X = m , D X = σ 2 ,
|
I [ k / 2 ] |
m |
k −2 i |
(σ |
/ 2) |
i |
|||||||
|
αk ( x) = k ! ∑ |
, |
|||||||||||
|
(k − 2i)!i ! |
||||||||||||
|
i =0 |
||||||||||||
|
0 , k − нечетное, |
||||||||||||
|
µ |
( x ) = |
2 k / 2 |
||||||||||
|
k |
k ! |
σ |
||||||||||
|
, k − четное. |
||||||||||||
|
( k / 2 ) ! |
2 |
Пример 7.1. Время безотказной работы аппаратуры является случайной величиной Х, распределенной по экспоненциальному закону. Среднее время безотказной работы 100 ч. Найти вероятность того, что аппаратура проработает больше среднего времени.
Решение. Так как среднее время безотказной работы, т.е. математическое ожидание, равно 100 ч, то параметр λ экспоненциального закона будет равен λ = 1 / m X = 1 / 100 = 0, 01 . Искомая вероятность
p(X > mX ) = p(100 < X < ∞) =1− F(100) = e−1 ≈ 0,368.
Пример 7.2. Для замера напряжения используются специальные датчики. Определить среднюю квадратическую ошибку датчика, если он не имеет систематических ошибок, а случайные распределены по нормальному закону и с вероятностью 0,8 не выходят за пределы ±0,2.
Решение. Из условия задачи следует, что p(-0,2<X<0,2) = 0,8. Так как распределение ошибок нормальное, а математическое ожидание m равно 0 (систематические ошибки отсутствуют), то
р{–0,2 < X < 0,2} = Ф(–0,2 / σ) – Ф(0,2 / σ) = 2Ф(0,2 / σ) = 0,8.
По таблице функции Лапласа находим аргумент 0,2/ σ =1,28, откуда
σ = 0,2 / 1,28 = 1,0156.

ЗАДАЧИ
7.1. По каналу связи пересылается пакет информации до тех пор, пока он не будет передан без ошибок. Вероятность искажения пакета равна 0,1, найти среднее количество попыток передать пакет.
Ответ: 1,11.
7.2. При работе прибора в случайные моменты времени возникают неисправности. Количество неисправностей, возникающих за определенный промежуток времени, подчиняется закону Пуассона. Среднее число неисправностей за сутки равно двум. Определить вероятность того, что: а) за двое суток не будет ни одной неисправности; б) в течение суток возникнет хотя бы одна неисправность; в) за неделю работы прибора возникнет не более трех неисправностей.
Ответ: а) 0,018; б) 0,865; в) 0,004.
7.3. Шкала рычажных весов имеет цену деления 1 г. При измерении массы отсчет делается с точностью до целого деления с округлением в ближайшую сторону. Какова вероятность того, что абсолютная ошибка определения массы: а) не превысит величины среднего квадратического отклонения возможных ошибок определения массы; б) будет заключена между
значениями σX и2σX .
|
Ответ: а) |
1 |
; б) 1 − |
1 |
. |
|
|
3 |
3 |
||||
7.4. Среднее время работы электронного модуля равно 700 ч. Определить время безотказной работы модуля с надежностью 0,8.
Ответ: 140 ч.
7.5. Сообщение передается последовательностью амплитудномодулированных импульсов с заданным шагом квантования ∆ (∆ – наименьшая разность амплитуд импульсов). На сообщение накладываются шумы, распределенные по нормальному закону N(0, σ). Если мгновенное значение шума превышает половину шага квантования, то при передаче сообщения возникает ошибка. Определить, при каком минимально допустимом шаге квантования ∆ вероятность ошибки из-за шумов не превысит 0,1.
Ответ: 3,4 σ.
7.6. СВ X – ошибка измерительного прибора – распределена нормально с дисперсией 16 мВ2. Систематическая ошибка прибора отсутствует. Вычислить вероятность того, что в пяти независимых измерениях ошибка: а) превысит по модулю 6 мВ не более трех раз; б) хотя бы один раз окажется в интервале
(0,5; 3,5) мВ.
Ответ: а) 0,999; б) 0,776.
8. ФУНКЦИИ ОДНОГО СЛУЧАЙНОГО АРГУМЕНТА
Рассмотрим функцию одного случайного аргумента Y = ϕ(X). Если X – непрерывная случайная величина, то плотность вероятности g(y) величины Y определяется по формуле
|
k |
|||||
|
g( y) = ∑ f (ψ j ( y)) |
ψ′j ( y) |
, |
(8.1) |
||
|
j=1 |
где f(х) – плотность вероятности величины X; ψj(y) – функции, обратные функции ϕ(x);
k – число обратных функций для данного y.
Весь диапазон значений Y необходимо разбить на интервалы, в которых число k обратных функций постоянно, и определить вид g(y) по формуле (8.1) для каждого интервала.
Если X – дискретная случайная величина, принимающая значения xi, то величина Y будет принимать дискретные значения yi = ϕ(xi) с вероятностями
p(yi) = p(xi).
Числовые характеристики функции Y = ϕ(X) одного случайного аргумента
Xопределяются по формулам:
–начальные моменты
|
∑n |
ϕ k ( xi ) pi |
для ДСВ |
|||
|
i =1 |
; |
(8.2) |
|||
|
α k ( y ) = M [Y k ] = M [ϕ k ( x)] = |
∞ |
||||
|
∫ ϕ k ( x) f ( x)dx для НСВ |
|||||
|
– математическое ожидание |
−∞ |
||||
|
m y = M [Y ] = M [ϕ (x )] = α1 ( x ) ; |
(8.3) |
||||
|
– центральные моменты |
|||||
|
n |
|||||
|
∑(ϕ( xi ) − m y )k pi |
для ДСВ |
||||
|
i=1 |
; |
(8.4) |
|||
|
µk ( y) = M[(Y − mY )k ] = |
∞ |
||||
|
∫ (ϕ( x) − my )k f ( x)dx для НСВ |
|||||
|
−∞ |
|||||
|
– дисперсия |
|||||
|
DY =µ2(y) =M[(Y −mY )2]=α2(y)−mY2 . |
(8.5) |
Пример 8.1. Определить плотность вероятности величины Y = X2, если X – случайная величина, равномерно распределенная на интервале [–1, 2].
Решение. Так как Х равномерно распределена в интервале [–1, 2], то ее
|
плотность вероятности равна (7.4): |
−1≤ x ≤ 2, |
|
1/3, |
|
|
f (x) = |
x < −1, x > 2. |
|
0, |

Построим график величины Y = X2 для x в интервале [–1, 2] и в зависимости от числа k обратных функций выделим следующие интервалы для
|
Y (рис. 8.1): |
k = 0, |
|||||||||||||||||||||||||||||
|
[–∞, 0[ |
||||||||||||||||||||||||||||||
|
[0, 1] |
k = 2, |
|||||||||||||||||||||||||||||
|
]1, 4] |
k = 1, |
|||||||||||||||||||||||||||||
|
]4, +∞] |
k = 0. |
|||||||||||||||||||||||||||||
|
Так как на интервалах [–∞, 0[ и ]4, +∞] |
||||||||||||||||||||||||||||||
|
обратная функция не существует, то для этих |
||||||||||||||||||||||||||||||
|
интервалов g(y) = 0. |
||||||||||||||||||||||||||||||
|
В интервале [0, 1] две обратные функции: |
||||||||||||||||||||||||||||||
|
ψ1(y) = + y и ψ2(y) = – y . |
||||||||||||||||||||||||||||||
|
По формуле (8.1) получим |
||||||||||||||||||||||||||||||
|
g( y) = fx (ψ1( y)) |
ψ1′( y) |
+ fx (ψ2( y)) |
ψ2′ ( y) |
= |
||||||||||||||||||||||||||
|
= fx ( y ) |
1 |
+ fx |
(− y ) |
1 |
= |
1 |
. |
|||||||||||||||||||||||
|
2 |
||||||||||||||||||||||||||||||
|
y |
2 |
y |
3 |
y |
||||||||||||||||||||||||||
|
В интервале ]1, 4] одна обратная функция |
||||||||||||||||||||||||||||||
|
ψ1(y) = + |
y , следовательно, |
|||||||||||||||||||||||||||||
|
g( y) = fx (ψ1( y)) |
ψ1′( y) |
= fx ( |
y ) |
1 |
= |
1 |
. |
Рис. 8.1 |
||||||||||||||||||||||
|
2 |
y |
6 |
y |
|||||||||||||||||||||||||||
|
Таким образом, плотность вероятности величины Y равна |
||||||||||||||||||||||||||||||
|
0, |
y < 0, |
|||||||||||||||||||||||||||||
|
1 |
||||||||||||||||||||||||||||||
|
0 ≤ y ≤1, |
||||||||||||||||||||||||||||||
|
y |
, |
|||||||||||||||||||||||||||||
|
3 |
||||||||||||||||||||||||||||||
|
g ( y) = |
1 |
|||||||||||||||||||||||||||||
|
, |
1 < y ≤ 4, |
|||||||||||||||||||||||||||||
|
6 |
y |
|||||||||||||||||||||||||||||
|
y > 4. |
||||||||||||||||||||||||||||||
|
0, |
||||||||||||||||||||||||||||||
Пример 8.2 Случайная величина X равномерно распределена от –1 до +1. Определить математическое ожидание и дисперсию величины Y = X2.
Решение. Плотность вероятности СВ X равна
0,5, −1 ≤ x ≤1, f (x) =
0 , x < −1, x >1.
Вычислим математическое ожидание Y по формуле (8.3):
|
m y = M [X 2 ] = ∫1 |
x 2 0, 5dx = |
1 . |
|
−1 |
3 |
Дисперсию Dy рассчитаем по формуле (8.5):
|
Dy = M[( X 2 )2 ] − mY2 = ∫1 |
(x2 )2 0,5dx − my2 = |
4 |
. |
|
|
45 |
||||
|
−1 |

ЗАДАЧИ
8.1. Определить плотность вероятности величины Y = lnX, если X – случайная величина, равномерно распределенная на интервале (1, 3).
|
0, 5e |
y |
, 0 |
≤ y < ln 3, |
||
|
Ответ: |
g ( y ) = |
||||
|
0 , y < 0, y > ln 3 . |
8.2. Определить плотность вероятности величины Y = |X|, если X – случайная равномерно распределенная величина со следующими характеристиками mx = 1, Dx = 1, и вычислить вероятность того, что р{1 ≤ Y < 2}.
|
0, y < 0, y > 2, 73, |
|||||
|
1 |
|||||
|
Ответ: g( y) = |
, 0 |
≤ y < 0, 73, |
|||
|
3 |
|||||
|
1 |
, 0, 73 ≤ y ≤ 2, 73. |
||||
|
2 3 |
|||||
р{1 ≤ Y < 2} = 0,445.
8.3. Случайная величина X равномерно распределена от 0 до 1. Определить математическое ожидание и дисперсию величины Y = X – 0,2 .
Ответ: mY = 0,34; DY = 0,0574.
8.4. Точка U, изображающая объект на круглом экране радиолокатора, распределена равномерно в пределах круга единичного радиуса. Найти дисперсию расстояния Y от точки U до центра экрана.
Ответ: DY = 1/18.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Тема: Задача по теор веру, определить СКО (Прочитано 2222 раз)
0 Пользователей и 1 Гость просматривают эту тему.
Ребята, помогите срочно решить задачу по теор веру…
Итоговая работа на сессии
Ошибка Х измерительного прибора распределена нормально. Систематической ошибки прибор не имеет (mx=0). Каким должно быть среднее квадратическое отклонение Qx ( сигма), чтобы с вероятностью не меньшей 0,9 ошибка измерения не превышала 20 микрометров по модулю?
« Последнее редактирование: 20 Января 2012, 10:36:38 от Asix »
Всегда пожалуйста, только Вы забыли сообщить, какая помощь нужна. Видимо, кусок сообщения, где Вы рассказываете, как решали задачу и что не получается, куда-то потерялся.
К сожалению, я не могу написать ход решения, т к не понимаю, как можно сделать
Поэтому и обращаюсь за помощью к вам.
Знаю только что ответ должен получиться : Qx<12.2(мкм)
натолкните на умные мысли пожалуйста.
Всё просто: изучаете по учебнику, что такое нормальное распределение, как считаются вероятности для него, и задачка сразу решается.
Измерительный прибор работает без систематических ошибок.doc
Зарегистрируйся в два клика и получи неограниченный доступ к материалам, а также
промокод
на новый заказ в Автор24. Это бесплатно.
Условие
Измерительный прибор работает без систематических ошибок (работа измерительного прибора без систематических ошибок означает, что mx=0). Известно, что вероятность ошибки измерения, превышающей по абсолютной величине 7, равна 0,08. Пусть случайная величина X- это величина ошибки измерения. Предполагается, что случайная величина X нормально распределена, найти:
а) приближенное значение дисперсии;
б) вероятность того, что ошибка измерения не превысит ε=4;
в) вероятность того, что ошибка измерения изменяется от α=-4 до β=6.
Решение
А) Для случайной величины Х имеещей нормальный закон распределения с параметрами mx и σx справедливо:
Px-mx≤ε=Фε σx, где Фt=12π-∞xe- t22dt-функция Лапласа.
По условию задачи вероятность ошибки измерения, превышающей по абсолютной величине 7, равна 0,08
. Тогда вероятность противоположного события (вероятность того, что случайная величина Х не превышает по абсолютной величине 7, равна 1-0,08=0,92. Имеем:
Px-0≤7=Ф7 σx=0,92⇒7 σx≈5⇒ σx≈7 5=1,4.
Тогда искомая дисперсия приближенно равна: Dx=σx2≈1,96.
б) вероятность того, что ошибка измерения не превысит ε=4:
Px-0≤4=Ф4 1,4≈Ф2,857≈0,4979..
в) вероятность того, что ошибка измерения изменяется от α=-4 до β=6 найдем по формуле:
Pα≤Х≤β=Фβ-mxσx-Фα-mxσx.
P-4≤Х≤6=Ф61,4-Ф-41,4≈Ф4,286-Ф-2,857=
≈0,499997+0,4979≈0,998.
Ответ
50% решения задач недоступно для прочтения
Закажи персональное решение задач. Эксперты
напишут качественную работу за 30 минут! ⏱️
Макеты страниц
Ошибки измерений и способ наименьших квадратов
9.1.21. Ошибки измерений и нормальный закон распределения.
Измерения всегда сопровождаются ошибками. Различают ошибки двух основных видов: систематические и случайные. Систематические ошибки имеют определенные причины, которые искажают измерение всегда в одном направлении и часто на постоянную величину. Они возникают за счет неисправности или плохой регулировки приборов, за счет ошибок в эталонах, из-за плохого выполнения технологии и т. д. Во многих случаях можно найти причины таких ошибок и устранить их.
Случайные ошибки неопределенны, и причина их неизвестна. Свое незнание причины ошибок мы обычно маскируем, говоря, что их порождает случай. А это просто означает, что их можно приписать большому количеству причин, действующих в любом направлении и создающих каждая свою погрешность. Такие случайные ошибки можно учитывать статистическими методами.
Существует еще одна категория ошибок, о которой будет кратко сказано в п. 9.1.27; это категория отдельных промахов, происходящих по однократной вине экспериментатора, например, если он по рассеянности один раз неправильно считает показания со шкалы измерительного прибора. В этом случае мы имеем дело с анормальным результатом измерения. Существует простое правилу, позволяющее исключить из таблицы результатов измерений ошибки этой категории.
Мы займемся в основном категорией случайных ошибок. Допустим, что имеется несколько в одинаковой степени надежных измерений физической величины, истинное значение которой равно 


Это чисто случайные ошибки.
Мы не знаем точного значения величины X и не можем определить ее на опыте, так как всякое измерение, сделанное для ее определения, искажается ошибкой. Обозначим через X наиболее вероятное значение величины 
Рассмотрим величины

Величины 

Положим




где 
Вычертим кривые Гаусса при двух различных значениях мерь; точности 



Вероятность того, что ошибка будет заключаться между 

Измерительный прибор не имеет систематической ошибки. Случайные ошибки распределены по нормальному закону, и с
Измерительный прибор не имеет систематической ошибки. Случайные ошибки распределены по нормальному закону, и с вероятностью 0,8 они не превосходят по абсолютной величине 12 мм. Найти среднюю квадратическую ошибку.
Используем нормальный закон и следующую формулу, таблицу значений функции Лапласа Ф(х):
px-a<δ=2Фδσ;
0.8=2Ф12σ;1.62=12σ;σ=7.407 мм.
Ответ: 7,407 мм.
- Измерительный прибор работает без систематических ошибок (работа измерительного прибора без систематических ошибок означает, что
- Измерить и записать результат измерения активной мощности Р = U·I·cosφ, рассеиваемой на нагрузке Zнагр.;
— - Измеряется мощность трехфазного тока двумя ваттметрами. Какова наибольшая погрешность измерения, если стрелка первого ваттметра
- Измеряется напряжение в виде периодической последовательности прямоугольных импульсов с параметрами: длительность импульсов τ, период
- Измеряется напряжение переменного тока.
Дано.
Цифровой вольтметр:
— предел измерения Uк = 200 B;
— измеренное - Измеряется размер некоторой детали, затем из генеральной совокупности берется выборка объемом n=8. Зная, что
- Измеряется электрическое сопротивление постоянному току (рисунок).
Получено:
UV =(5,00±0,50) мВ; Р=1
IA=(2,60±0,25) мА; Р=1
RV=
Записать результат измерения сопротивления - Измерительный канал включает в себя термометр сопротивления типа 150М и вторичный прибор со шкалой
- Измерительный механизм (ИМ) магнитоэлектрической системы расситан на ток и Iии напряжение Uи и имеет
- Измерительный механизм (ИМ) магнитоэлектрической системы рассчитан на ток Iи=15 мA и напряжение Uи=75 мB
- Измерительный механизм (ИМ) магнитоэлектрической системы рассчитан на ток Iи=25 мA и напряжение Uи=100 мB
- Измерительный механизм (ИМ) магнитоэлектрической системы рассчитан на ток Iи=25 мA и напряжение Uи=75 мB
- Измерительный механизм (ИМ) магнитоэлектрической системы рассчитан на ток Iи=7,5 мA и напряжение Uи=75 мB
- Измерительный прибор (ИП) магнитоэлектрической системы рассчитан на ток IП и напряжение UП и имеет

Дискретная СВ Х имеет геометрическое распределение, принимает значения 0, 1, … , ∞ с вероятностями
p( X = i) = pi = qi p ,
где p – параметр распределения (0 ≤ p ≤ 1), q = 1 – p.
Числовые характеристики геометрического распределения:
Дискретная значения 0, 1, … ,
m X = q / p , D X = q / p 2 .
СВ X имеет биномиальное распределение, если она принимает n со следующими вероятностями:
|
p(X =i) = p = |
n! |
piqn−i |
(7.2) |
|
i |
i!(n −i)! |
, |
|
где n, p – параметры распределения (0 ≤ p ≤1), q=1 – p. Числовые характеристики биномиального распределения:
m X = n p , D X = n q p .
Дискретная СВ Х имеет распределение Пуассона, если она принимает значения 0, 1, … , ∞ со следующими вероятностями:
|
p(X =i) = p = ai |
e−a |
(7.3) |
|
i |
i! |
, |
|
где a – параметр распределения (a > 0). |
||
|
Числовые характеристики пуассоновской СВ: |
||
|
m X = a , D X |
= a . |
Непрерывная СВ Х имеет равномерное распределение, если ее плотность вероятности в некотором интервале [а; b] постоянна, т.е. если все значения X в этом интервале равновероятны:
0, x <
f ( x ) = 1
b − a
0, x >
|
a , |
0 , x |
< a , |
||||||
|
− a |
||||||||
|
, a ≤ x ≤ b , F ( x ) = |
x |
, a |
≤ |
x ≤ |
b , |
|||
|
(7.4) |
||||||||
|
a |
||||||||
|
b. |
b |
− |
||||||
|
1, x |
> b . |
|||||||
Числовые характеристики равномерно распределенной СВ:
|
m X = |
a + b |
, D X |
= |
( b − a ) 2 |
. |
|
|
2 |
1 2 |
|||||
Непрерывная СВ T, принимающая только положительные значения, имеет экспоненциальное распределение, если ее плотность вероятности и функция распределения равны
|
λ e |
− λ t |
, t |
≥ 0 , |
− e |
−λt |
, t ≥ 0, |
||||
|
f (t ) = |
1 |
(7.5) |
||||||||
|
0 , t < 0 , |
F(t) = |
0, t < 0, |
||||||||
где λ – параметр распределения (λ > 0).

Числовые характеристики экспоненциальной СВ:
m T = 1 / λ , D T = 1 / λ 2 .
Непрерывная СВ Х имеет нормальное распределение, если ее плотность вероятности и функция распределения равны
|
f (x ) = |
1 |
exp − |
(x − m)2 |
F ( x ) = |
0 .5 + Φ |
x − m |
, |
||||||||
|
2 |
, |
(7.6) |
|||||||||||||
|
σ 2π |
2σ |
σ |
|||||||||||||
|
где m, σ – параметры распределения ( σ >0), |
|||||||||||||||
|
1 |
x |
t2 |
|||||||||||||
|
Φ(x) = |
∫e− |
dt — функция Лапласа. |
|||||||||||||
|
2 |
|||||||||||||||
|
2π |
|||||||||||||||
|
0 |
Значения функции Лапласа приведены в приложении. При использовании таблицы значений функции Лапласа следует учитывать, что Φ(–x) = –Φ(x),
Φ(0) = 0, Φ(∞) = 0,5.
Числовые характеристики нормальной СВ:
m X = m , D X = σ 2 ,
|
I [ k / 2 ] |
m |
k −2 i |
(σ |
/ 2) |
i |
|||||||
|
αk ( x) = k ! ∑ |
, |
|||||||||||
|
(k − 2i)!i ! |
||||||||||||
|
i =0 |
||||||||||||
|
0 , k − нечетное, |
||||||||||||
|
µ |
( x ) = |
2 k / 2 |
||||||||||
|
k |
k ! |
σ |
||||||||||
|
, k − четное. |
||||||||||||
|
( k / 2 ) ! |
2 |
Пример 7.1. Время безотказной работы аппаратуры является случайной величиной Х, распределенной по экспоненциальному закону. Среднее время безотказной работы 100 ч. Найти вероятность того, что аппаратура проработает больше среднего времени.
Решение. Так как среднее время безотказной работы, т.е. математическое ожидание, равно 100 ч, то параметр λ экспоненциального закона будет равен λ = 1 / m X = 1 / 100 = 0, 01 . Искомая вероятность
p(X > mX ) = p(100 < X < ∞) =1− F(100) = e−1 ≈ 0,368.
Пример 7.2. Для замера напряжения используются специальные датчики. Определить среднюю квадратическую ошибку датчика, если он не имеет систематических ошибок, а случайные распределены по нормальному закону и с вероятностью 0,8 не выходят за пределы ±0,2.
Решение. Из условия задачи следует, что p(-0,2<X<0,2) = 0,8. Так как распределение ошибок нормальное, а математическое ожидание m равно 0 (систематические ошибки отсутствуют), то
р{–0,2 < X < 0,2} = Ф(–0,2 / σ) – Ф(0,2 / σ) = 2Ф(0,2 / σ) = 0,8.
По таблице функции Лапласа находим аргумент 0,2/ σ =1,28, откуда
σ = 0,2 / 1,28 = 1,0156.

ЗАДАЧИ
7.1. По каналу связи пересылается пакет информации до тех пор, пока он не будет передан без ошибок. Вероятность искажения пакета равна 0,1, найти среднее количество попыток передать пакет.
Ответ: 1,11.
7.2. При работе прибора в случайные моменты времени возникают неисправности. Количество неисправностей, возникающих за определенный промежуток времени, подчиняется закону Пуассона. Среднее число неисправностей за сутки равно двум. Определить вероятность того, что: а) за двое суток не будет ни одной неисправности; б) в течение суток возникнет хотя бы одна неисправность; в) за неделю работы прибора возникнет не более трех неисправностей.
Ответ: а) 0,018; б) 0,865; в) 0,004.
7.3. Шкала рычажных весов имеет цену деления 1 г. При измерении массы отсчет делается с точностью до целого деления с округлением в ближайшую сторону. Какова вероятность того, что абсолютная ошибка определения массы: а) не превысит величины среднего квадратического отклонения возможных ошибок определения массы; б) будет заключена между
значениями σX и2σX .
|
Ответ: а) |
1 |
; б) 1 − |
1 |
. |
|
|
3 |
3 |
||||
7.4. Среднее время работы электронного модуля равно 700 ч. Определить время безотказной работы модуля с надежностью 0,8.
Ответ: 140 ч.
7.5. Сообщение передается последовательностью амплитудномодулированных импульсов с заданным шагом квантования ∆ (∆ – наименьшая разность амплитуд импульсов). На сообщение накладываются шумы, распределенные по нормальному закону N(0, σ). Если мгновенное значение шума превышает половину шага квантования, то при передаче сообщения возникает ошибка. Определить, при каком минимально допустимом шаге квантования ∆ вероятность ошибки из-за шумов не превысит 0,1.
Ответ: 3,4 σ.
7.6. СВ X – ошибка измерительного прибора – распределена нормально с дисперсией 16 мВ2. Систематическая ошибка прибора отсутствует. Вычислить вероятность того, что в пяти независимых измерениях ошибка: а) превысит по модулю 6 мВ не более трех раз; б) хотя бы один раз окажется в интервале
(0,5; 3,5) мВ.
Ответ: а) 0,999; б) 0,776.
8. ФУНКЦИИ ОДНОГО СЛУЧАЙНОГО АРГУМЕНТА
Рассмотрим функцию одного случайного аргумента Y = ϕ(X). Если X – непрерывная случайная величина, то плотность вероятности g(y) величины Y определяется по формуле
|
k |
|||||
|
g( y) = ∑ f (ψ j ( y)) |
ψ′j ( y) |
, |
(8.1) |
||
|
j=1 |
где f(х) – плотность вероятности величины X; ψj(y) – функции, обратные функции ϕ(x);
k – число обратных функций для данного y.
Весь диапазон значений Y необходимо разбить на интервалы, в которых число k обратных функций постоянно, и определить вид g(y) по формуле (8.1) для каждого интервала.
Если X – дискретная случайная величина, принимающая значения xi, то величина Y будет принимать дискретные значения yi = ϕ(xi) с вероятностями
p(yi) = p(xi).
Числовые характеристики функции Y = ϕ(X) одного случайного аргумента
Xопределяются по формулам:
–начальные моменты
|
∑n |
ϕ k ( xi ) pi |
для ДСВ |
|||
|
i =1 |
; |
(8.2) |
|||
|
α k ( y ) = M [Y k ] = M [ϕ k ( x)] = |
∞ |
||||
|
∫ ϕ k ( x) f ( x)dx для НСВ |
|||||
|
– математическое ожидание |
−∞ |
||||
|
m y = M [Y ] = M [ϕ (x )] = α1 ( x ) ; |
(8.3) |
||||
|
– центральные моменты |
|||||
|
n |
|||||
|
∑(ϕ( xi ) − m y )k pi |
для ДСВ |
||||
|
i=1 |
; |
(8.4) |
|||
|
µk ( y) = M[(Y − mY )k ] = |
∞ |
||||
|
∫ (ϕ( x) − my )k f ( x)dx для НСВ |
|||||
|
−∞ |
|||||
|
– дисперсия |
|||||
|
DY =µ2(y) =M[(Y −mY )2]=α2(y)−mY2 . |
(8.5) |
Пример 8.1. Определить плотность вероятности величины Y = X2, если X – случайная величина, равномерно распределенная на интервале [–1, 2].
Решение. Так как Х равномерно распределена в интервале [–1, 2], то ее
|
плотность вероятности равна (7.4): |
−1≤ x ≤ 2, |
|
1/3, |
|
|
f (x) = |
x < −1, x > 2. |
|
0, |

Построим график величины Y = X2 для x в интервале [–1, 2] и в зависимости от числа k обратных функций выделим следующие интервалы для
|
Y (рис. 8.1): |
k = 0, |
|||||||||||||||||||||||||||||
|
[–∞, 0[ |
||||||||||||||||||||||||||||||
|
[0, 1] |
k = 2, |
|||||||||||||||||||||||||||||
|
]1, 4] |
k = 1, |
|||||||||||||||||||||||||||||
|
]4, +∞] |
k = 0. |
|||||||||||||||||||||||||||||
|
Так как на интервалах [–∞, 0[ и ]4, +∞] |
||||||||||||||||||||||||||||||
|
обратная функция не существует, то для этих |
||||||||||||||||||||||||||||||
|
интервалов g(y) = 0. |
||||||||||||||||||||||||||||||
|
В интервале [0, 1] две обратные функции: |
||||||||||||||||||||||||||||||
|
ψ1(y) = + y и ψ2(y) = – y . |
||||||||||||||||||||||||||||||
|
По формуле (8.1) получим |
||||||||||||||||||||||||||||||
|
g( y) = fx (ψ1( y)) |
ψ1′( y) |
+ fx (ψ2( y)) |
ψ2′ ( y) |
= |
||||||||||||||||||||||||||
|
= fx ( y ) |
1 |
+ fx |
(− y ) |
1 |
= |
1 |
. |
|||||||||||||||||||||||
|
2 |
||||||||||||||||||||||||||||||
|
y |
2 |
y |
3 |
y |
||||||||||||||||||||||||||
|
В интервале ]1, 4] одна обратная функция |
||||||||||||||||||||||||||||||
|
ψ1(y) = + |
y , следовательно, |
|||||||||||||||||||||||||||||
|
g( y) = fx (ψ1( y)) |
ψ1′( y) |
= fx ( |
y ) |
1 |
= |
1 |
. |
Рис. 8.1 |
||||||||||||||||||||||
|
2 |
y |
6 |
y |
|||||||||||||||||||||||||||
|
Таким образом, плотность вероятности величины Y равна |
||||||||||||||||||||||||||||||
|
0, |
y < 0, |
|||||||||||||||||||||||||||||
|
1 |
||||||||||||||||||||||||||||||
|
0 ≤ y ≤1, |
||||||||||||||||||||||||||||||
|
y |
, |
|||||||||||||||||||||||||||||
|
3 |
||||||||||||||||||||||||||||||
|
g ( y) = |
1 |
|||||||||||||||||||||||||||||
|
, |
1 < y ≤ 4, |
|||||||||||||||||||||||||||||
|
6 |
y |
|||||||||||||||||||||||||||||
|
y > 4. |
||||||||||||||||||||||||||||||
|
0, |
||||||||||||||||||||||||||||||
Пример 8.2 Случайная величина X равномерно распределена от –1 до +1. Определить математическое ожидание и дисперсию величины Y = X2.
Решение. Плотность вероятности СВ X равна
0,5, −1 ≤ x ≤1, f (x) =
0 , x < −1, x >1.
Вычислим математическое ожидание Y по формуле (8.3):
|
m y = M [X 2 ] = ∫1 |
x 2 0, 5dx = |
1 . |
|
−1 |
3 |
Дисперсию Dy рассчитаем по формуле (8.5):
|
Dy = M[( X 2 )2 ] − mY2 = ∫1 |
(x2 )2 0,5dx − my2 = |
4 |
. |
|
|
45 |
||||
|
−1 |

ЗАДАЧИ
8.1. Определить плотность вероятности величины Y = lnX, если X – случайная величина, равномерно распределенная на интервале (1, 3).
|
0, 5e |
y |
, 0 |
≤ y < ln 3, |
||
|
Ответ: |
g ( y ) = |
||||
|
0 , y < 0, y > ln 3 . |
8.2. Определить плотность вероятности величины Y = |X|, если X – случайная равномерно распределенная величина со следующими характеристиками mx = 1, Dx = 1, и вычислить вероятность того, что р{1 ≤ Y < 2}.
|
0, y < 0, y > 2, 73, |
|||||
|
1 |
|||||
|
Ответ: g( y) = |
, 0 |
≤ y < 0, 73, |
|||
|
3 |
|||||
|
1 |
, 0, 73 ≤ y ≤ 2, 73. |
||||
|
2 3 |
|||||
р{1 ≤ Y < 2} = 0,445.
8.3. Случайная величина X равномерно распределена от 0 до 1. Определить математическое ожидание и дисперсию величины Y = X – 0,2 .
Ответ: mY = 0,34; DY = 0,0574.
8.4. Точка U, изображающая объект на круглом экране радиолокатора, распределена равномерно в пределах круга единичного радиуса. Найти дисперсию расстояния Y от точки U до центра экрана.
Ответ: DY = 1/18.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Макеты страниц
Ошибки измерений и способ наименьших квадратов
9.1.21. Ошибки измерений и нормальный закон распределения.
Измерения всегда сопровождаются ошибками. Различают ошибки двух основных видов: систематические и случайные. Систематические ошибки имеют определенные причины, которые искажают измерение всегда в одном направлении и часто на постоянную величину. Они возникают за счет неисправности или плохой регулировки приборов, за счет ошибок в эталонах, из-за плохого выполнения технологии и т. д. Во многих случаях можно найти причины таких ошибок и устранить их.
Случайные ошибки неопределенны, и причина их неизвестна. Свое незнание причины ошибок мы обычно маскируем, говоря, что их порождает случай. А это просто означает, что их можно приписать большому количеству причин, действующих в любом направлении и создающих каждая свою погрешность. Такие случайные ошибки можно учитывать статистическими методами.
Существует еще одна категория ошибок, о которой будет кратко сказано в п. 9.1.27; это категория отдельных промахов, происходящих по однократной вине экспериментатора, например, если он по рассеянности один раз неправильно считает показания со шкалы измерительного прибора. В этом случае мы имеем дело с анормальным результатом измерения. Существует простое правилу, позволяющее исключить из таблицы результатов измерений ошибки этой категории.
Мы займемся в основном категорией случайных ошибок. Допустим, что имеется несколько в одинаковой степени надежных измерений физической величины, истинное значение которой равно 


Это чисто случайные ошибки.
Мы не знаем точного значения величины X и не можем определить ее на опыте, так как всякое измерение, сделанное для ее определения, искажается ошибкой. Обозначим через X наиболее вероятное значение величины 
Рассмотрим величины

Величины 

Положим




где 
Вычертим кривые Гаусса при двух различных значениях мерь; точности 



Вероятность того, что ошибка будет заключаться между 

Любые измерения всегда производятся с какими-то погрешностями, связанными с ограниченной точностью измерительных приборов, неправильным выбором, и погрешностью метода измерений, физиологией экспериментатора, особенностями измеряемых объектов, изменением условий измерения и т.д. Поэтому в задачу измерения входит нахождение не только самой величины, но и погрешности измерения, т.е. интервала, в котором вероятнее всего находится истинное значение измеряемой величины. Например, при измерении отрезка времени t секундомером с ценой деления 0,2 с можно сказать, что истинное значение его находится в интервале от с до
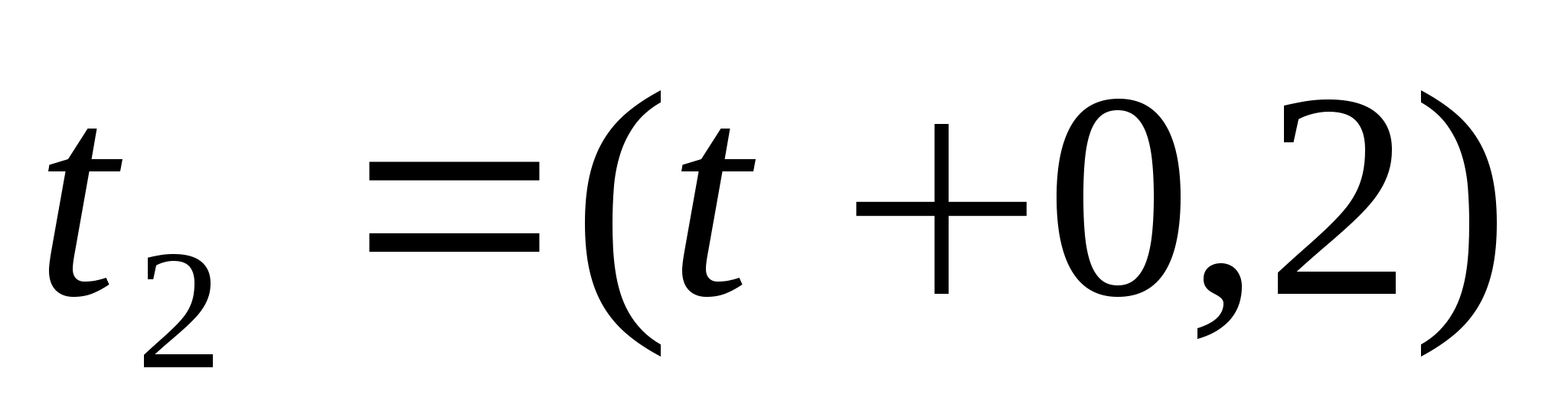
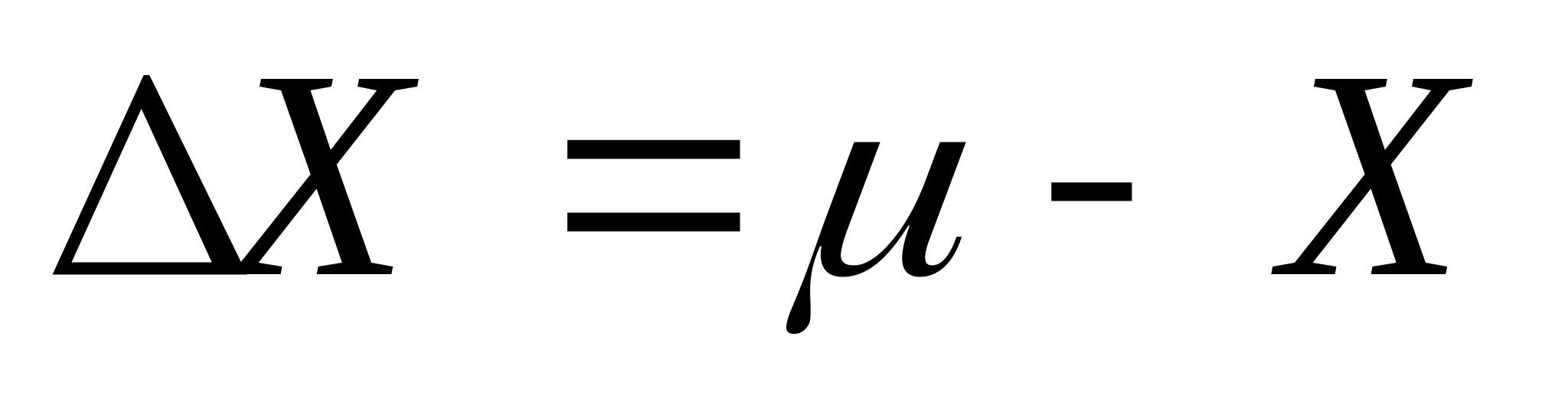
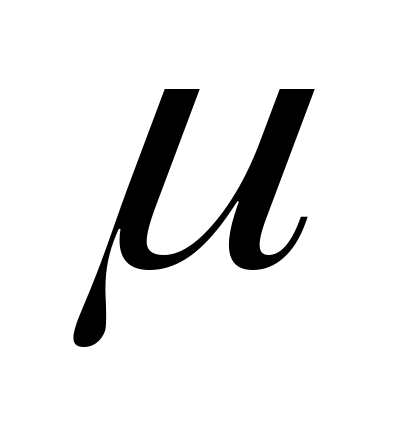
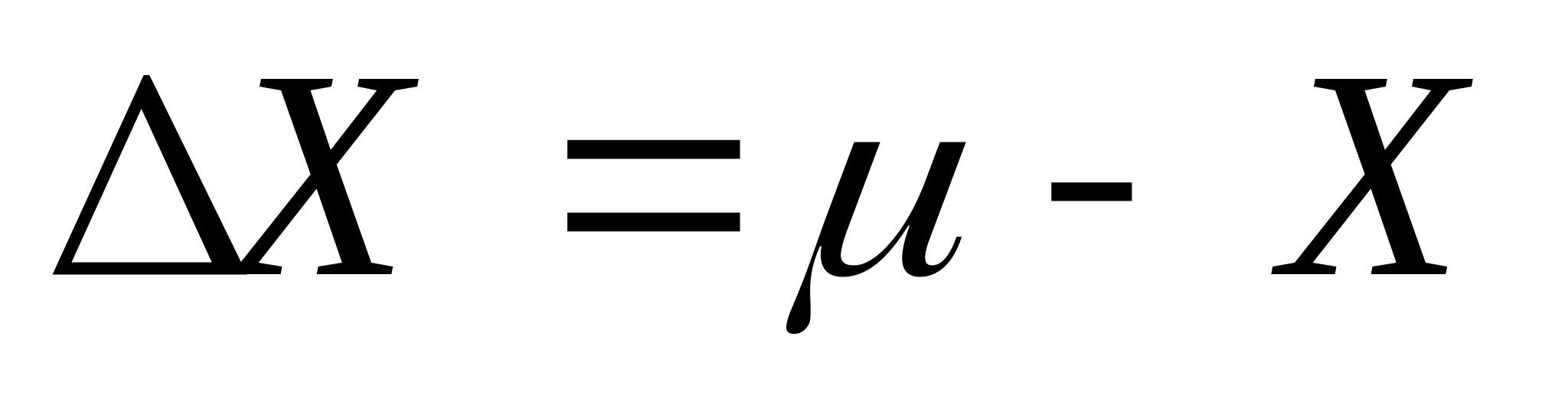
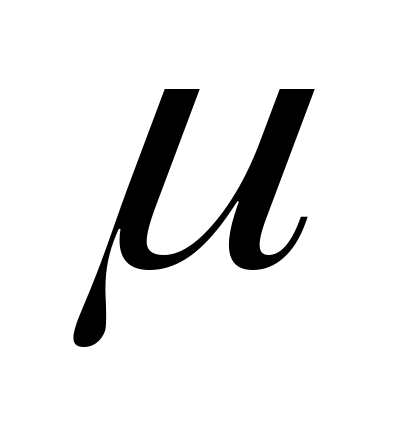
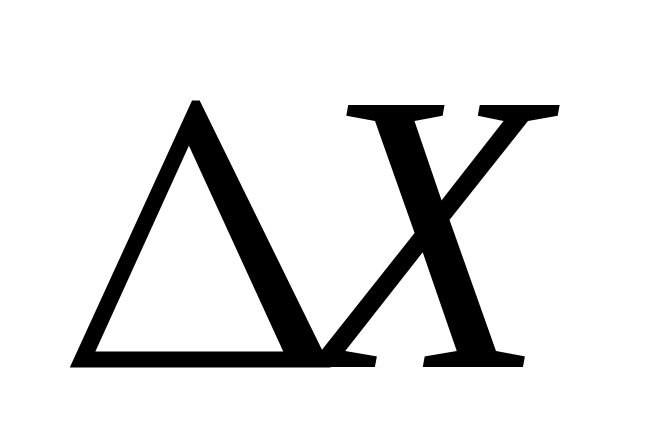
(ошибкой) измерения, а выражение
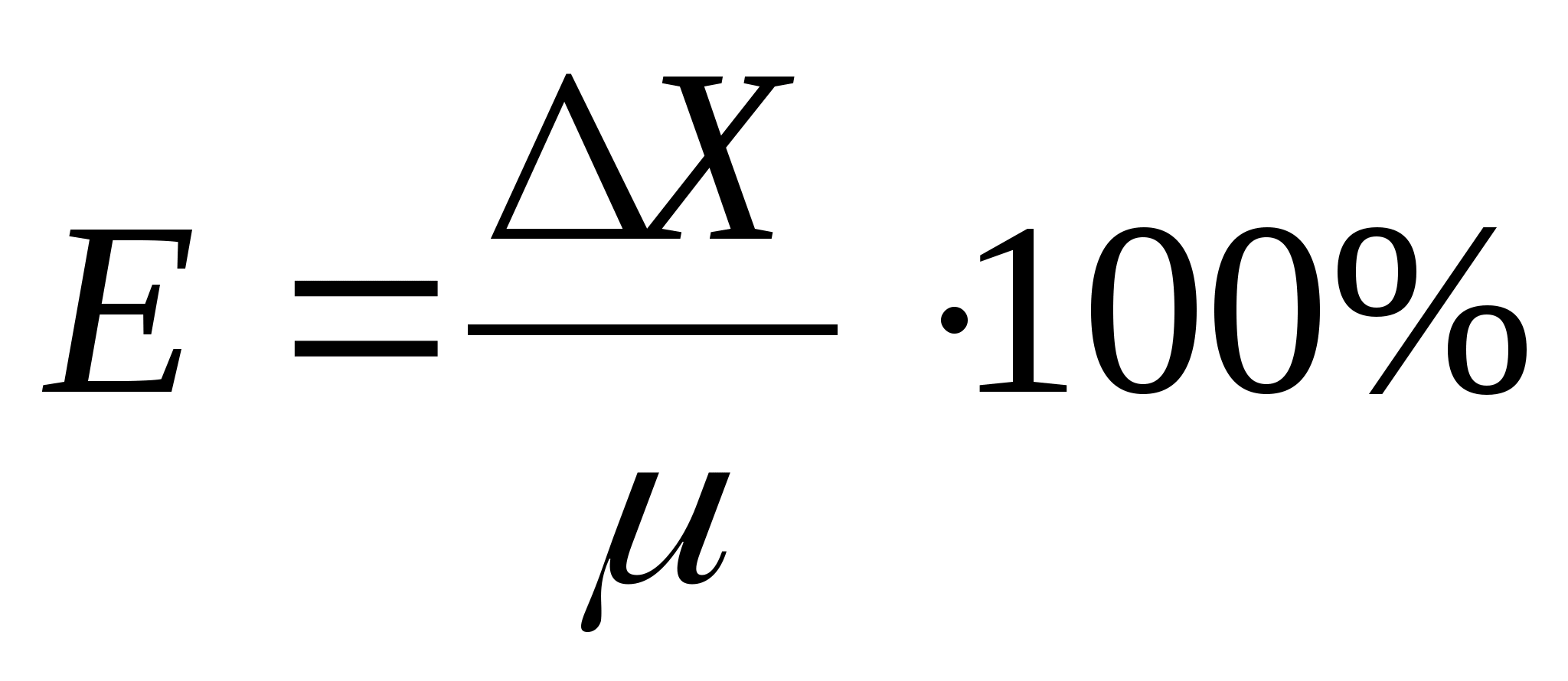
Вполне естественно стремление экспериментатора произвести всякое измерение с наибольшей достижимой точностью, однако такой подход не всегда целесообразен. Чем точнее мы хотим измерить ту ил иную величину, тем сложнее приборы мы должны использовать, тем больше времени потребуют эти измерения. Поэтому точность окончательного результата должна соответствовать цели проводимого эксперимента. Теория погрешностей дает рекомендации, как следует вести измерения и как обрабатывать результаты, чтобы величина погрешности была минимальной.
Все возникающие при измерениях погрешности обычно разделяют на три типа – систематические, случайные и промахи, или грубые ошибки.
Систематические погрешности
обусловлены ограниченной точностью изготовления приборов (приборные погрешности), недостатками выбранного метода измерений, неточностью расчетной формулы, неправильной установкой прибора и т.д. Таким образом, систематические погрешности вызываются факторами, действующими одинаковым образом при многократном повторении одних и тех же измерений. Величина этой погрешности систематически повторяется либо изменяется по определенному закону. Некоторые систематические ошибки могут быть исключены (на практике этого всегда легко добиться) путем изменения метода измерений, введение поправок к показаниям приборов, учета постоянного влияния внешних факторов.
Хотя систематическая (приборная) погрешность при повторных измерениях дает отклонение измеряемой величины от истинного значения в одну сторону, мы никогда не знаем в какую именно. Поэтому приборная погрешность записывается с двойным знаком
Случайные погрешности
вызываются большим числом случайных причин (изменением температуры, давления, сотрясения здания и т.д.), действия которых на каждое измерение различно и не может быть заранее учтено. Случайные погрешности происходят также из-за несовершенства органов чувств экспериментатора. К случайным погрешностям относятся и погрешности обусловленные свойствами измеряемого объекта.
Исключить случайны погрешности отдельных измерений невозможно, но можно уменьшить влияние этих погрешностей на окончательный результат путем проведения многократных измерений. Если случайная погрешность окажется значительно меньше приборной (систематической), то нет смысла дальше уменьшать величину случайной погрешности за счет увеличения числа измерений. Если же случайная погрешность больше приборной, то число измерений следует увеличить, чтобы уменьшить значение случайной погрешности и сделать ее меньше или одного порядка с погрешностью прибора.
Промахи, или грубые ошибки,
— это неправильные отсчеты по прибору, неправильная запись отсчета и т.п. Как правило, промахи, обусловленные указанными причинами хорошо заметны, так как соответствующие им отсчеты резко отличаются от других отсчетов. Промахи должны быть устранены путем контрольных измерений. Таким образом, ширину интервала в котором лежат истинные значения измеряемых величин, будут определять только случайные и систематические погрешности.
2
. Оценка систематической (приборной) погрешности
При прямых измерениях
значение измеряемой величины отсчитывается непосредственно по шкале измерительного прибора. Ошибка в отсчете может достигать нескольких десятых долей деления шкалы. Обычно при таких измерениях величину систематической погрешности считают равной половине цены деления шкалы измерительного прибора. Например, при измерении штангенциркулем с ценой деления 0,05 мм величина приборной погрешности измерения принимают равной 0,025 мм.
Цифровые измерительные приборы дают значение измеряемых ими величин с погрешностью, равной значению одной единицы последнего разряда на шкале прибора. Так, если цифровой вольтметр показывает значение20,45 мВ, то абсолютная погрешность при измерении равна
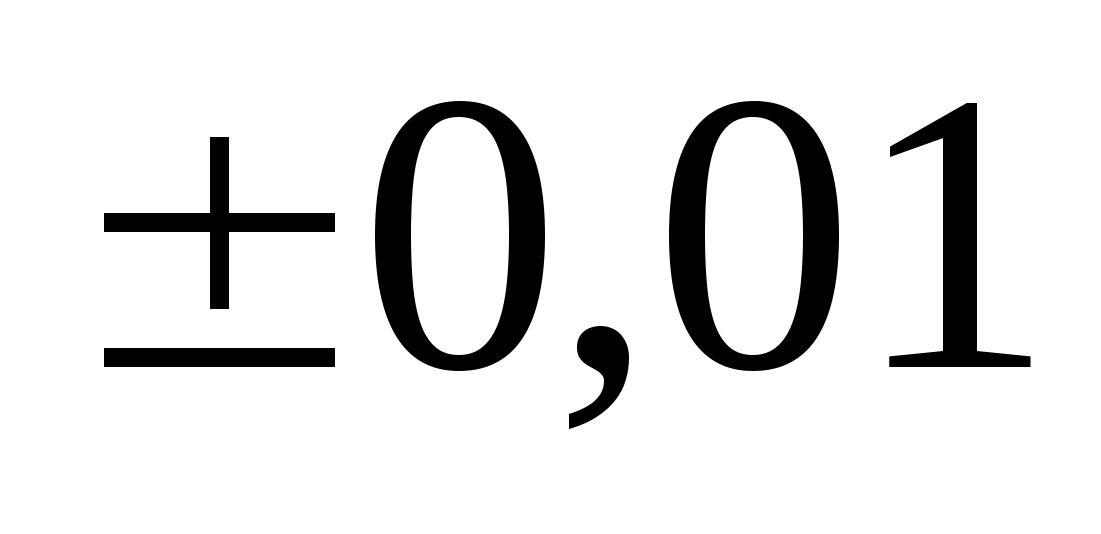
Систематические погрешности возникают и при использовании постоянных величин, определяемых из таблиц. В подобных случаях погрешность принимается равной половине последнего значащего разряда. Например, если в таблице значение плотности стали дается величиной, равной 7,9∙10 3 кг/м 3 , то абсолютная погрешность в этом случае равна
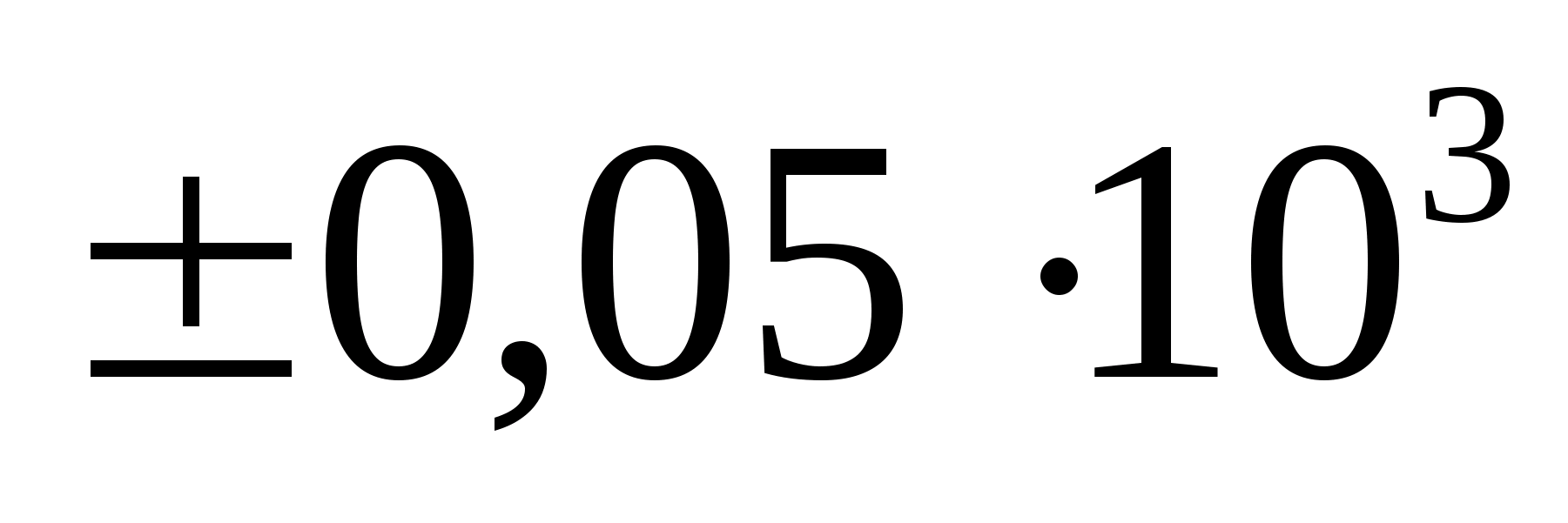
Некоторые особенности в расчете приборных погрешностей электроизмерительных приборов будут рассмотрены ниже.
При определении систематической (приборной) погрешности косвенных измерений
функциональной величины
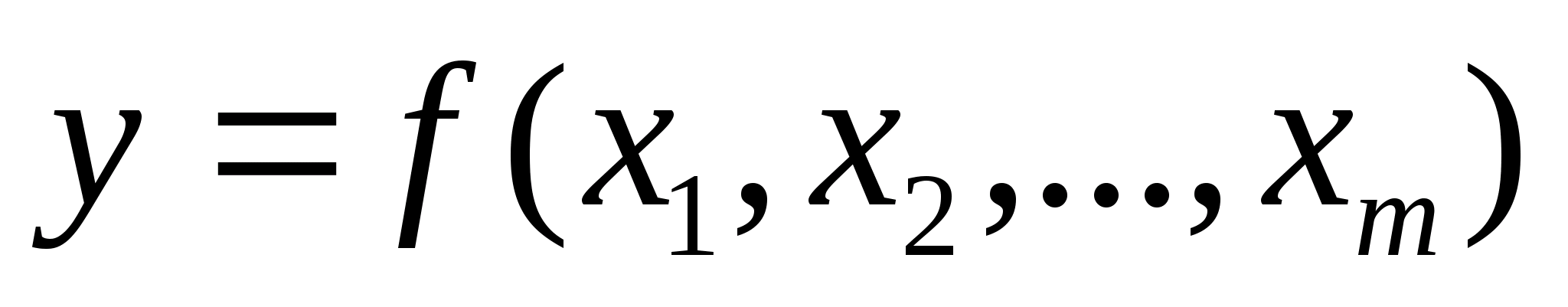
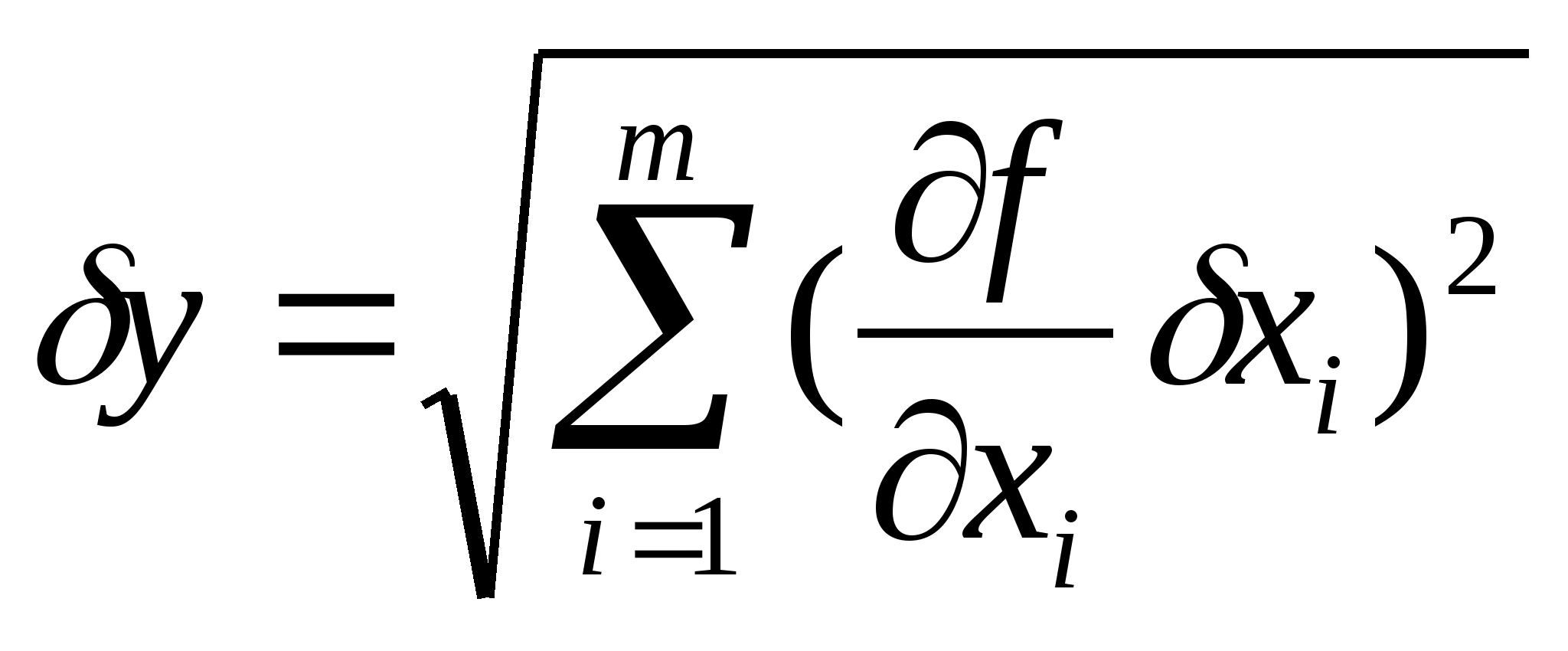
где 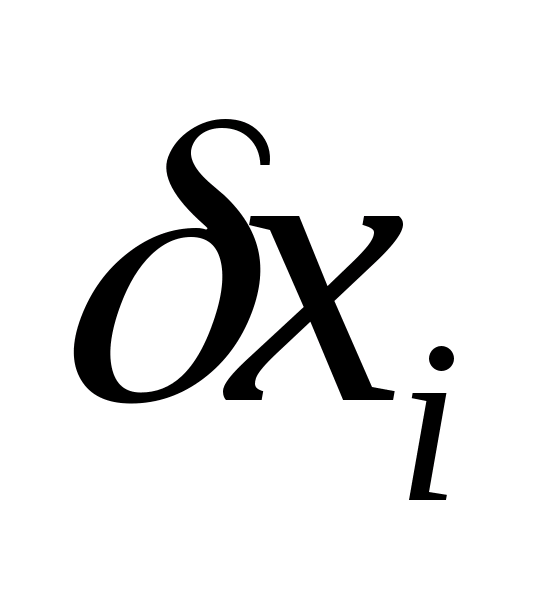
(ошибкой) измерения, а выражение
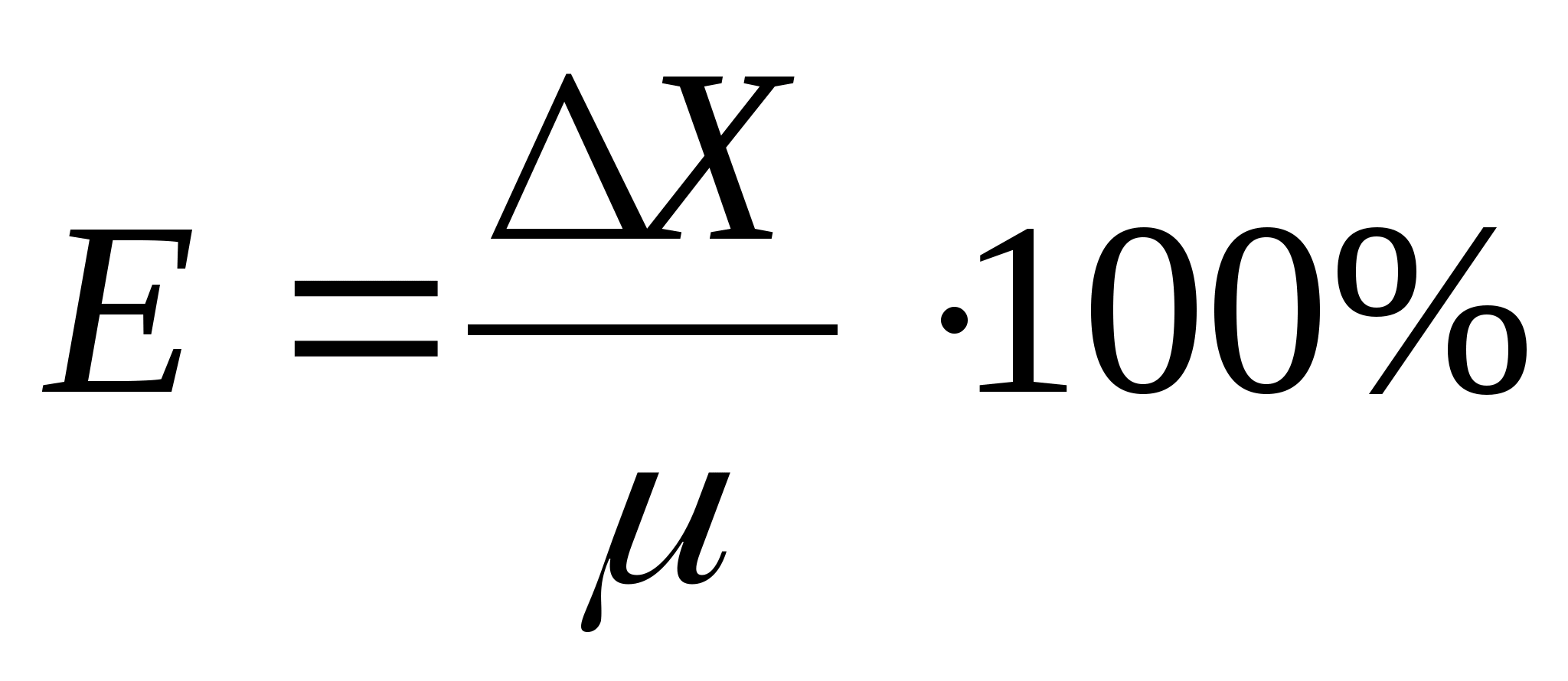
Вполне естественно стремление экспериментатора произвести всякое измерение с наибольшей достижимой точностью, однако такой подход не всегда целесообразен. Чем точнее мы хотим измерить ту ил иную величину, тем сложнее приборы мы должны использовать, тем больше времени потребуют эти измерения. Поэтому точность окончательного результата должна соответствовать цели проводимого эксперимента. Теория погрешностей дает рекомендации, как следует вести измерения и как обрабатывать результаты, чтобы величина погрешности была минимальной.
Все возникающие при измерениях погрешности обычно разделяют на три типа – систематические, случайные и промахи, или грубые ошибки.
Систематические погрешности
обусловлены ограниченной точностью изготовления приборов (приборные погрешности), недостатками выбранного метода измерений, неточностью расчетной формулы, неправильной установкой прибора и т.д. Таким образом, систематические погрешности вызываются факторами, действующими одинаковым образом при многократном повторении одних и тех же измерений. Величина этой погрешности систематически повторяется либо изменяется по определенному закону. Некоторые систематические ошибки могут быть исключены (на практике этого всегда легко добиться) путем изменения метода измерений, введение поправок к показаниям приборов, учета постоянного влияния внешних факторов.
Хотя систематическая (приборная) погрешность при повторных измерениях дает отклонение измеряемой величины от истинного значения в одну сторону, мы никогда не знаем в какую именно. Поэтому приборная погрешность записывается с двойным знаком
Случайные погрешности
вызываются большим числом случайных причин (изменением температуры, давления, сотрясения здания и т.д.), действия которых на каждое измерение различно и не может быть заранее учтено. Случайные погрешности происходят также из-за несовершенства органов чувств экспериментатора. К случайным погрешностям относятся и погрешности обусловленные свойствами измеряемого объекта.
Исключить случайны погрешности отдельных измерений невозможно, но можно уменьшить влияние этих погрешностей на окончательный результат путем проведения многократных измерений. Если случайная погрешность окажется значительно меньше приборной (систематической), то нет смысла дальше уменьшать величину случайной погрешности за счет увеличения числа измерений. Если же случайная погрешность больше приборной, то число измерений следует увеличить, чтобы уменьшить значение случайной погрешности и сделать ее меньше или одного порядка с погрешностью прибора.
Промахи, или грубые ошибки,
— это неправильные отсчеты по прибору, неправильная запись отсчета и т.п. Как правило, промахи, обусловленные указанными причинами хорошо заметны, так как соответствующие им отсчеты резко отличаются от других отсчетов. Промахи должны быть устранены путем контрольных измерений. Таким образом, ширину интервала в котором лежат истинные значения измеряемых величин, будут определять только случайные и систематические погрешности.
2
. Оценка систематической (приборной) погрешности
При прямых измерениях
значение измеряемой величины отсчитывается непосредственно по шкале измерительного прибора. Ошибка в отсчете может достигать нескольких десятых долей деления шкалы. Обычно при таких измерениях величину систематической погрешности считают равной половине цены деления шкалы измерительного прибора. Например, при измерении штангенциркулем с ценой деления 0,05 мм величина приборной погрешности измерения принимают равной 0,025 мм.
Цифровые измерительные приборы дают значение измеряемых ими величин с погрешностью, равной значению одной единицы последнего разряда на шкале прибора. Так, если цифровой вольтметр показывает значение20,45 мВ, то абсолютная погрешность при измерении равна
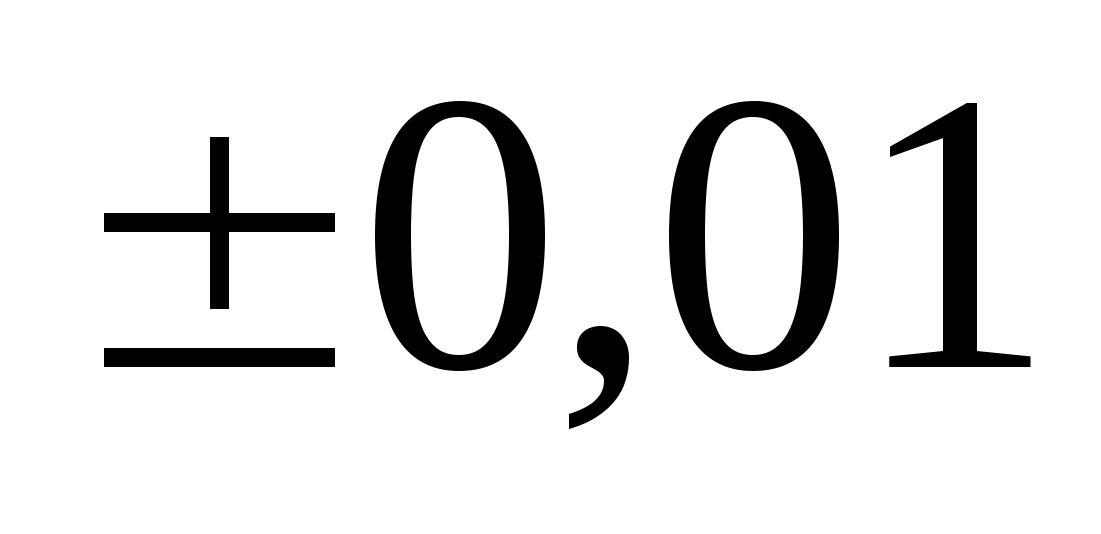
Систематические погрешности возникают и при использовании постоянных величин, определяемых из таблиц. В подобных случаях погрешность принимается равной половине последнего значащего разряда. Например, если в таблице значение плотности стали дается величиной, равной 7,9∙10 3 кг/м 3 , то абсолютная погрешность в этом случае равна
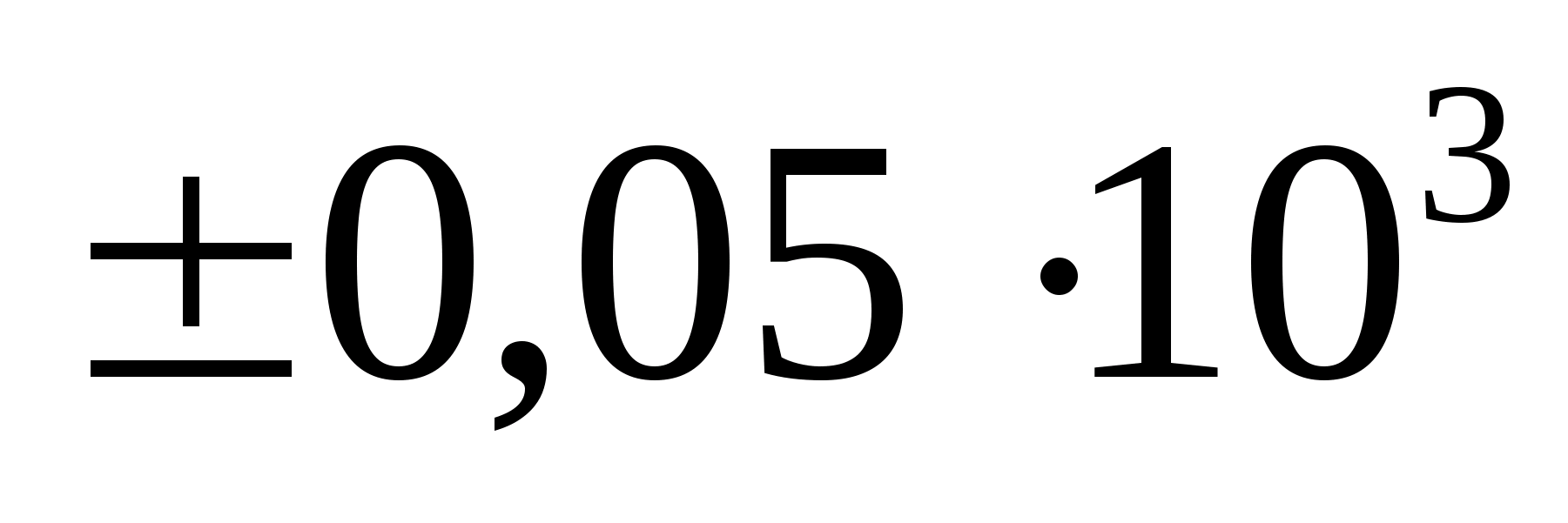
Некоторые особенности в расчете приборных погрешностей электроизмерительных приборов будут рассмотрены ниже.
При определении систематической (приборной) погрешности косвенных измерений
функциональной величины
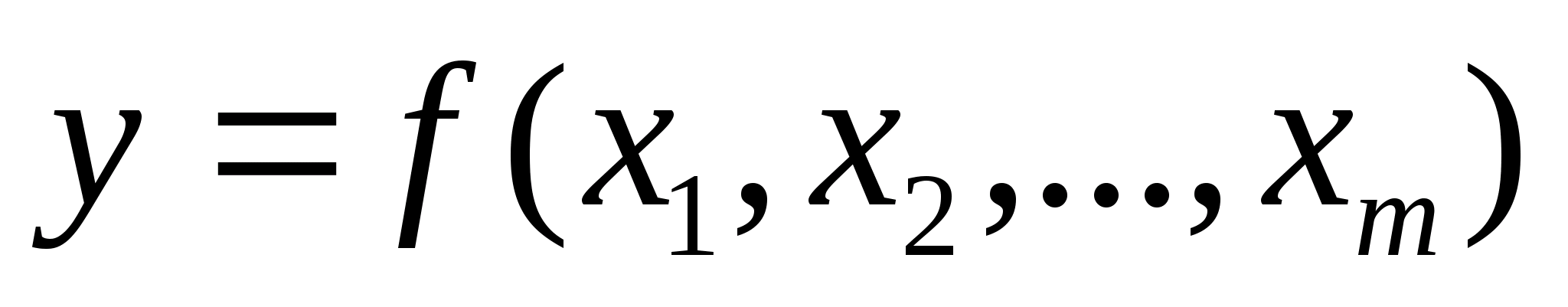
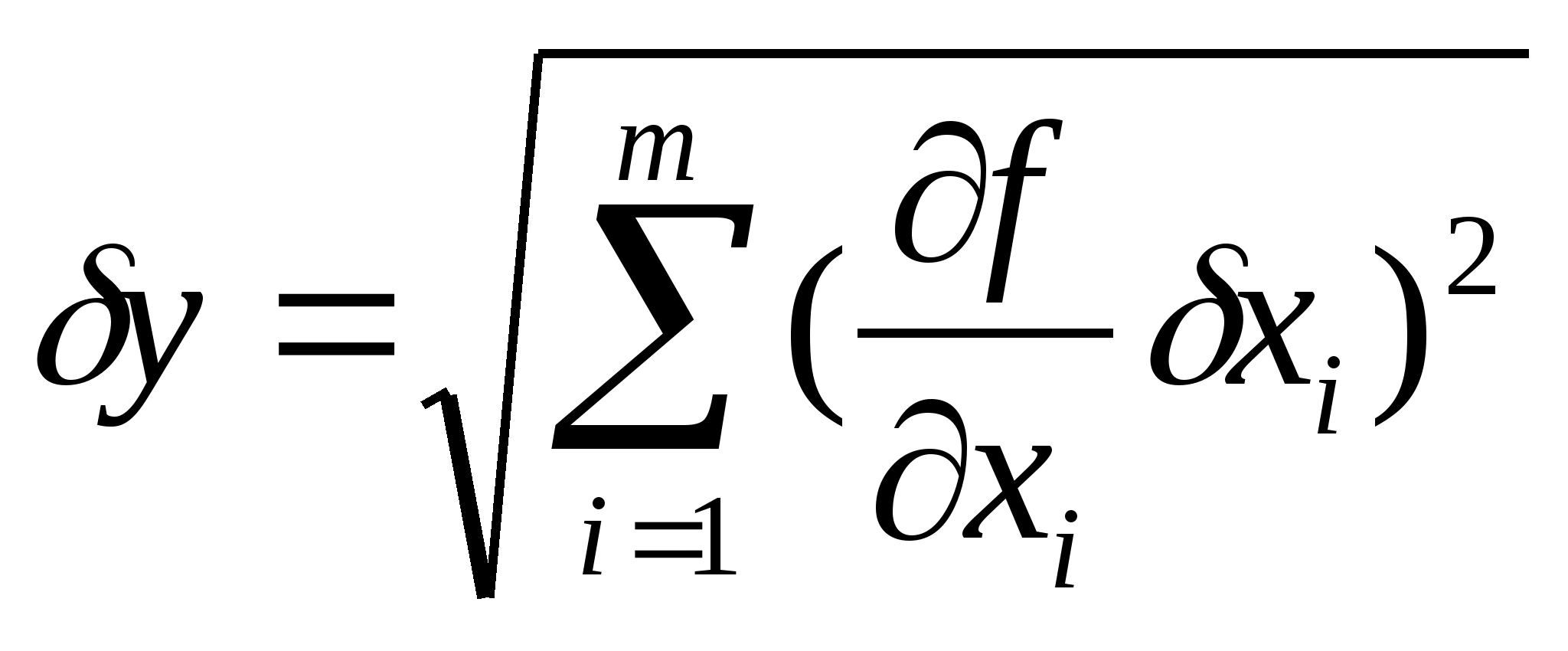
где 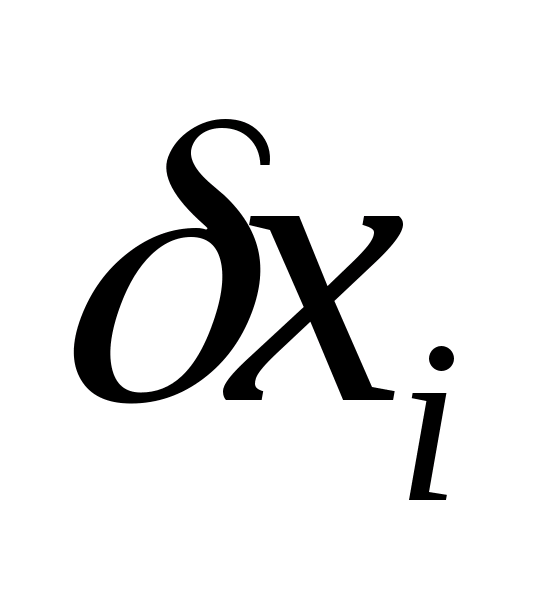
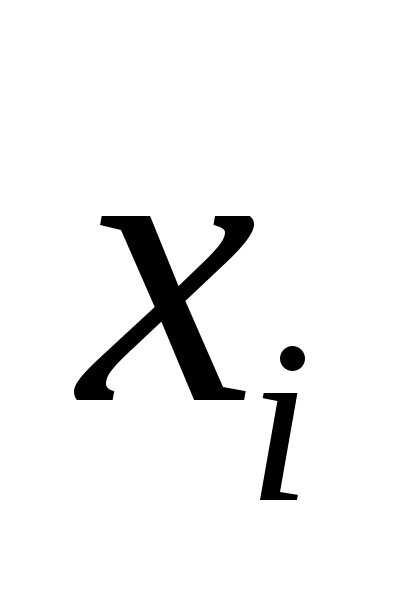
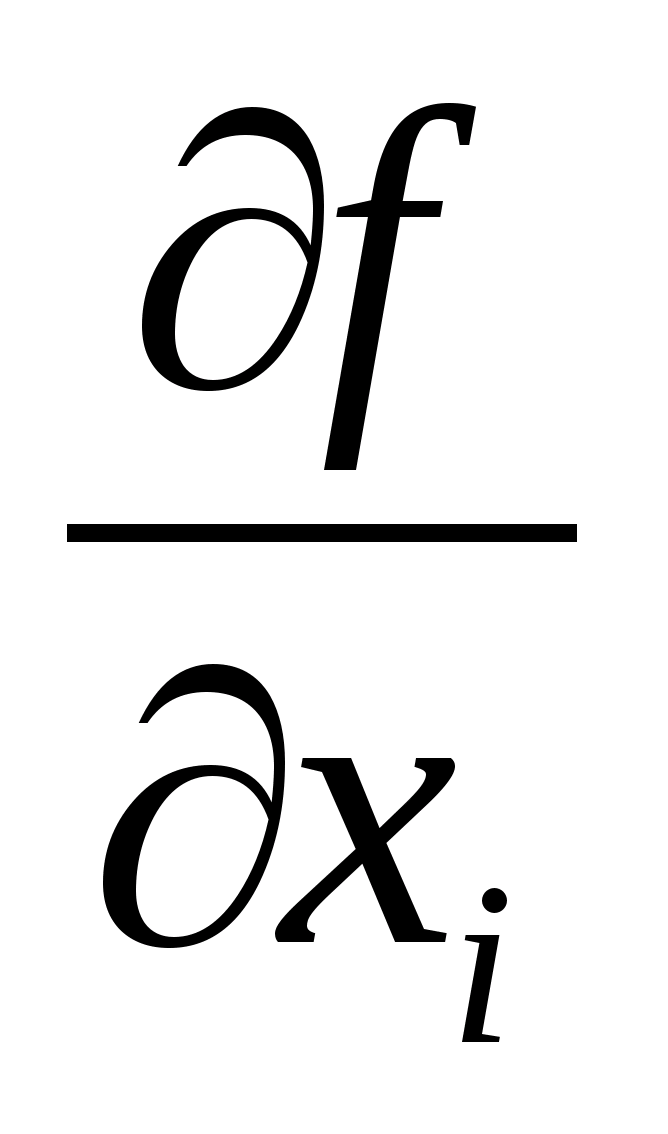
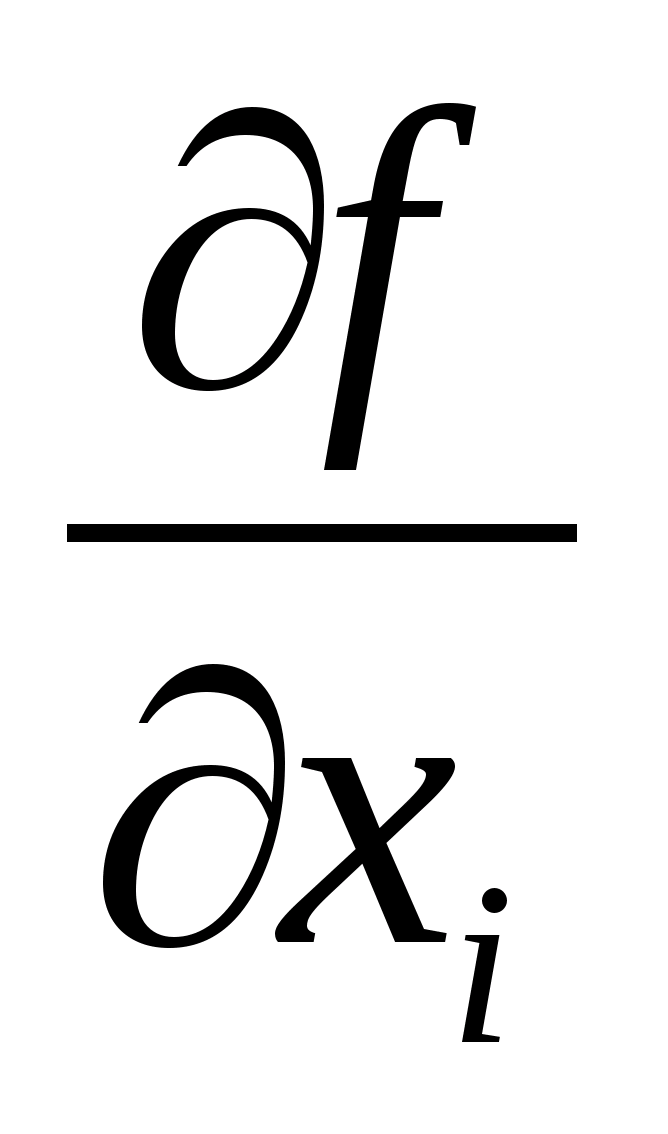
В качестве примера, получим формулу для расчета систематической погрешности при измерении объема цилиндра. Формула вычисления объема цилиндра имеет вид
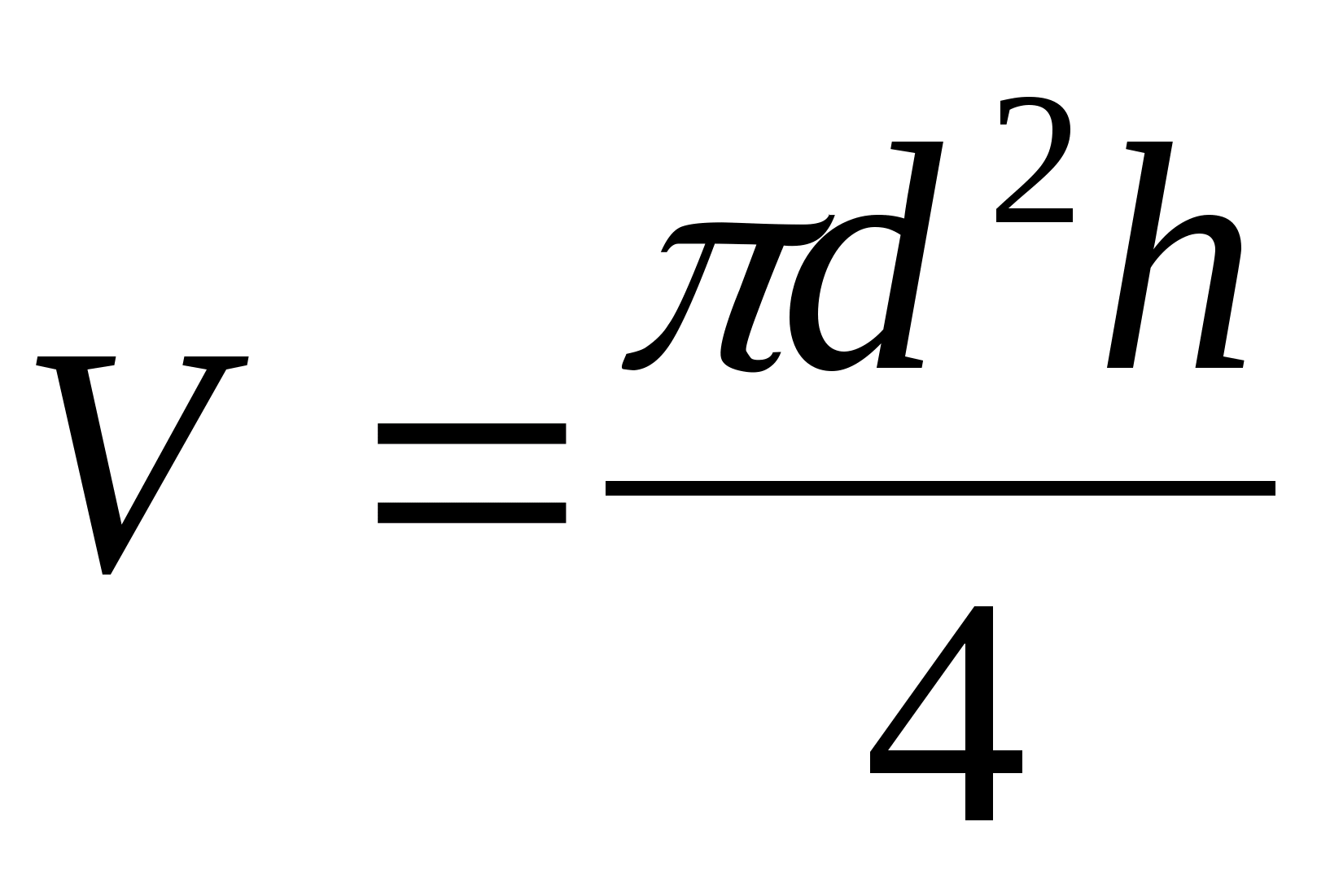
Частные производные по переменным d
и
h
будут равны
Таким образом, формула для определения абсолютной систематической погрешности при измерении объема цилиндра в соответствии с (2. ..) имеет следующий вид
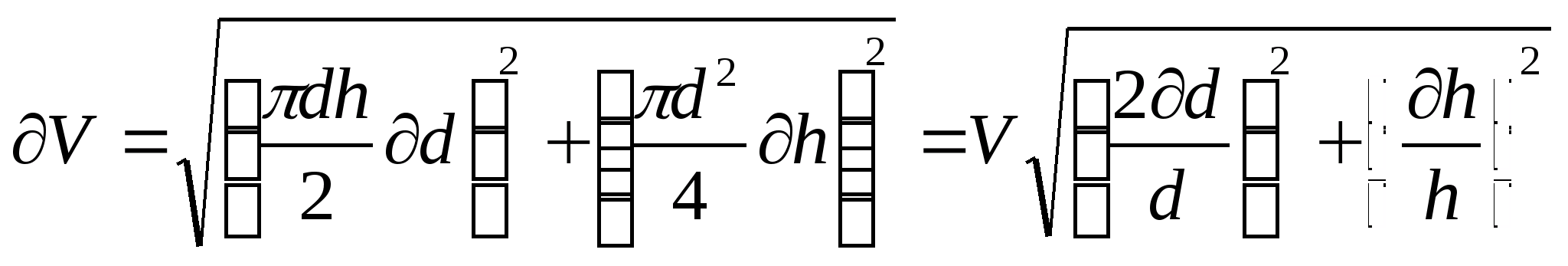
где
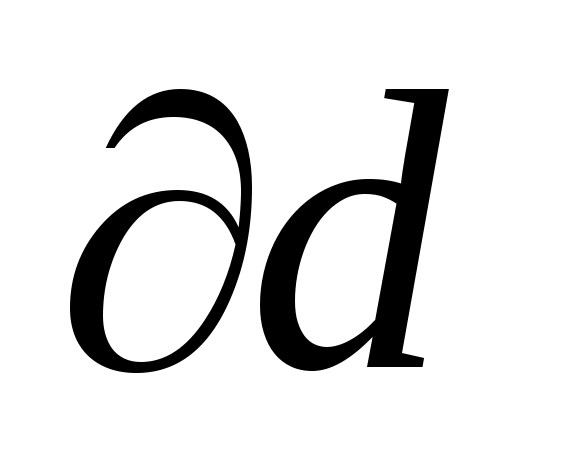

3. Оценка случайной погрешности.
Доверительный интервал и доверительная вероятность

Частные производные по переменным d
и
h
будут равны
Таким образом, формула для определения абсолютной систематической погрешности при измерении объема цилиндра в соответствии с (2. ..) имеет следующий вид
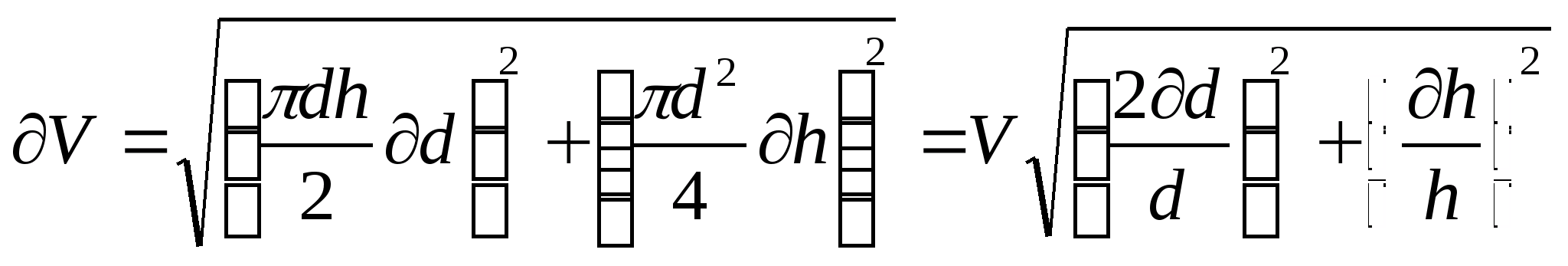
где
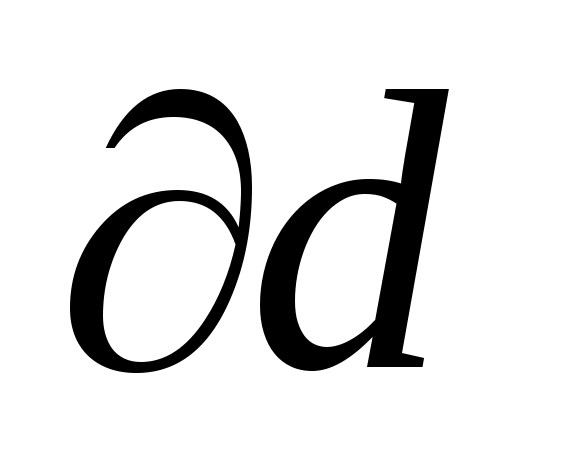

3. Оценка случайной погрешности.
Доверительный интервал и доверительная вероятность
Ля подавляющего большинства простых измерений достаточно хорошо выполняется так называемый нормальный закон случайных погрешностей (закон Гаусса)
, выведенный из следующих эмпирических положений.
погрешности измерений могут принимать непрерывный ряд значений;
при большом числе измерений погрешности одинаковой величины, но разного знака встречаются одинаково часто,
чем больше величина случайной погрешности, тем меньше вероятность ее появления.
График нормального закона распределения Гаусса представлен на рис.1. Уравнение кривой имеет вид
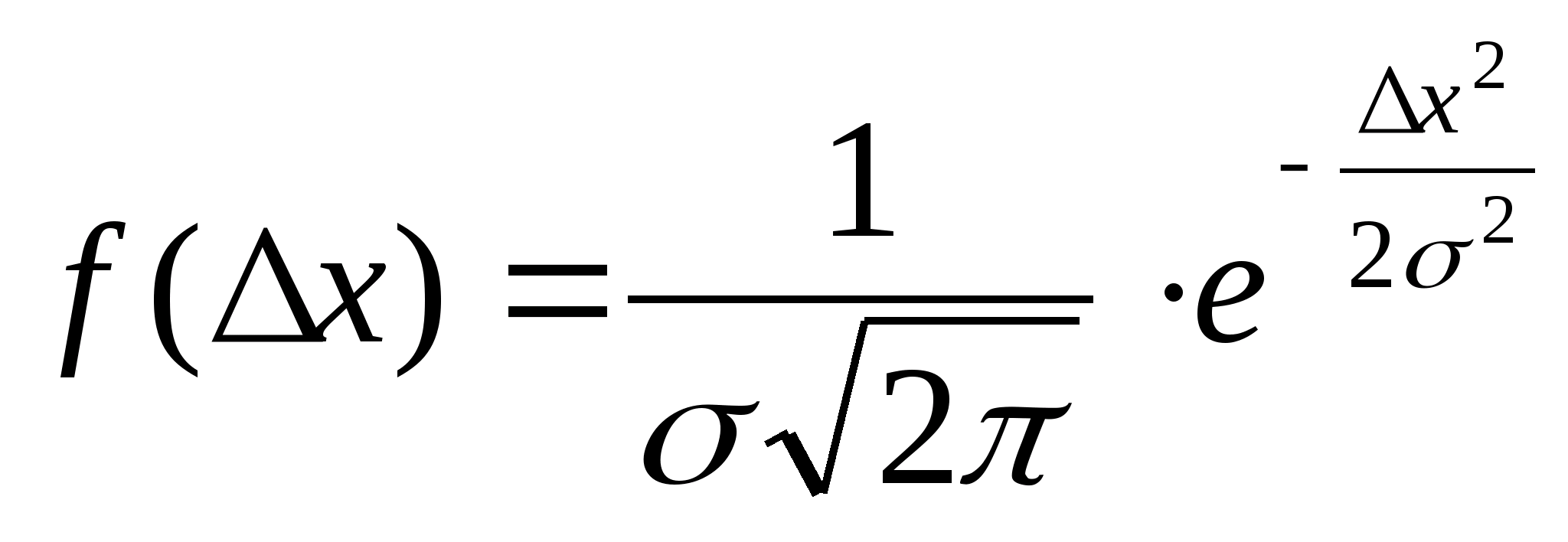
где
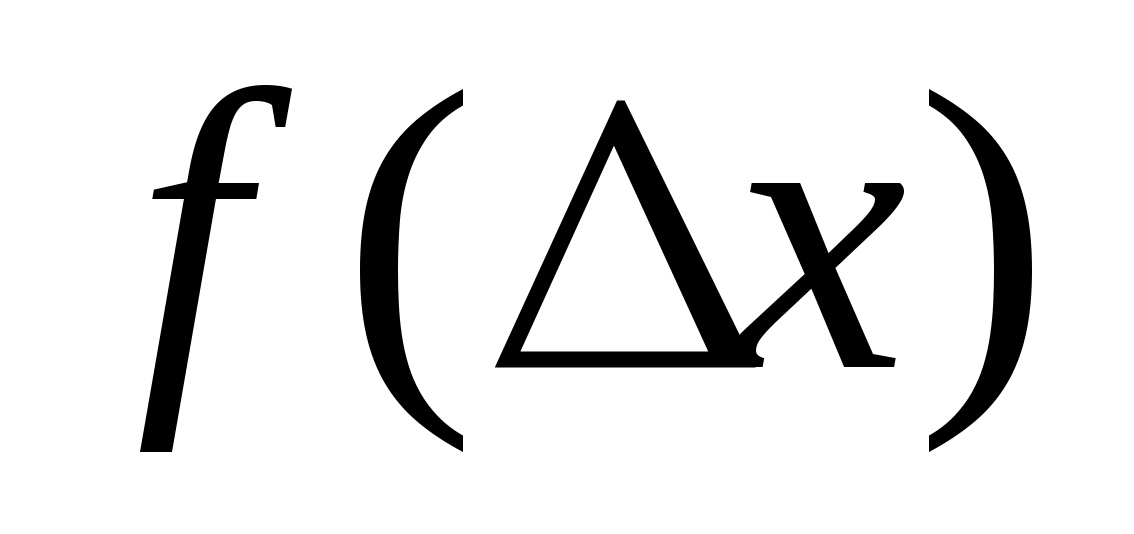
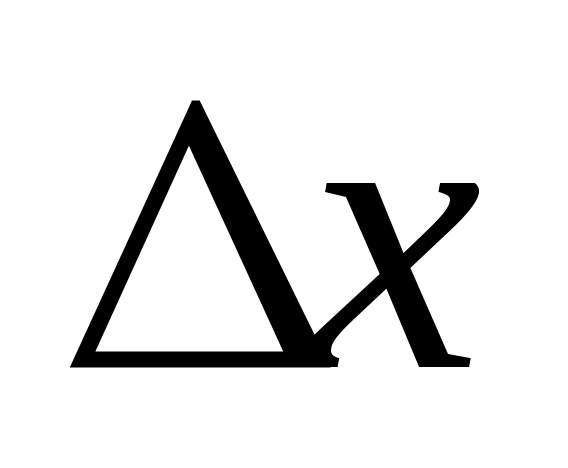
Величина σ не является случайной величиной и характеризует процесс измерений. Если условия измерений не изменяются, то σ остается постоянной величиной. Квадрат этой величины называют дисперсией измерений.
Чем меньше дисперсия, тем меньше разброс отдельных значений и тем выше точность измерений.
Точное значение средней квадратичной ошибки σ, как и истинное значение измеряемой величины, неизвестно. Существует так называемая статистическая оценка этого параметра, в соответствии с которой средняя квадратичная ошибка равняется средней квадратичной ошибке среднего арифметического 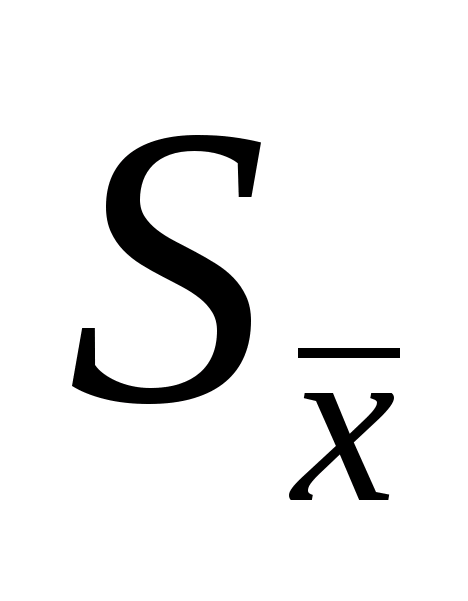
где
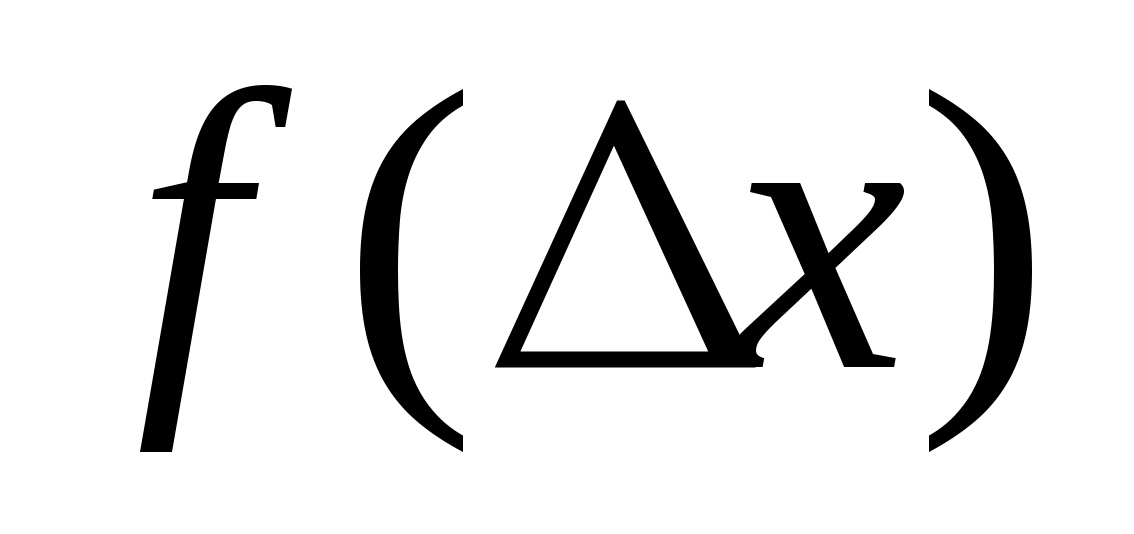
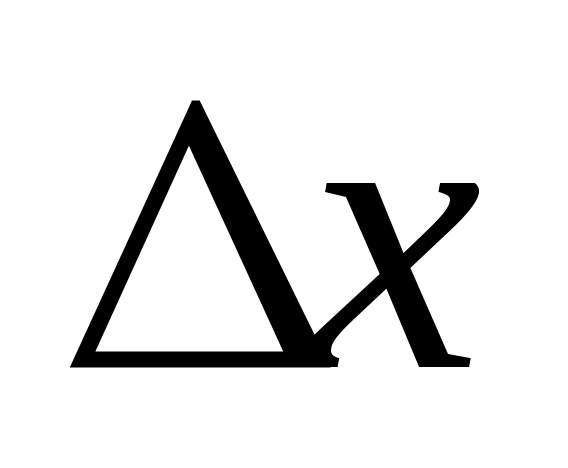
Величина σ не является случайной величиной и характеризует процесс измерений. Если условия измерений не изменяются, то σ остается постоянной величиной. Квадрат этой величины называют дисперсией измерений.
Чем меньше дисперсия, тем меньше разброс отдельных значений и тем выше точность измерений.
Точное значение средней квадратичной ошибки σ, как и истинное значение измеряемой величины, неизвестно. Существует так называемая статистическая оценка этого параметра, в соответствии с которой средняя квадратичная ошибка равняется средней квадратичной ошибке среднего арифметического 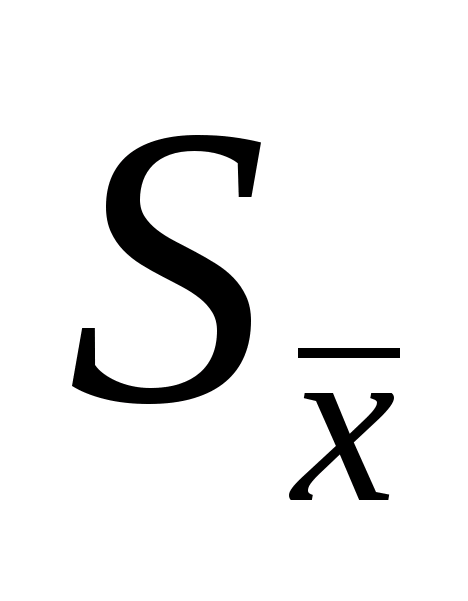

где 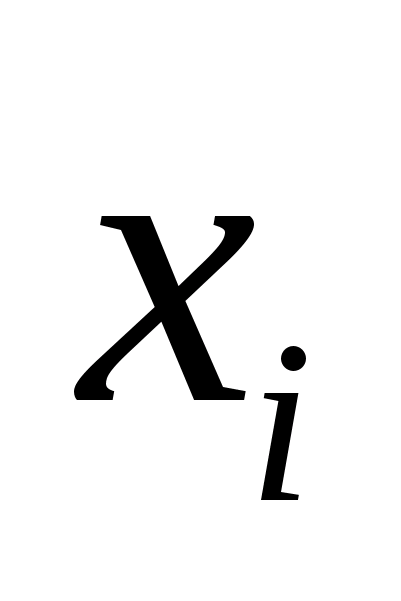
где 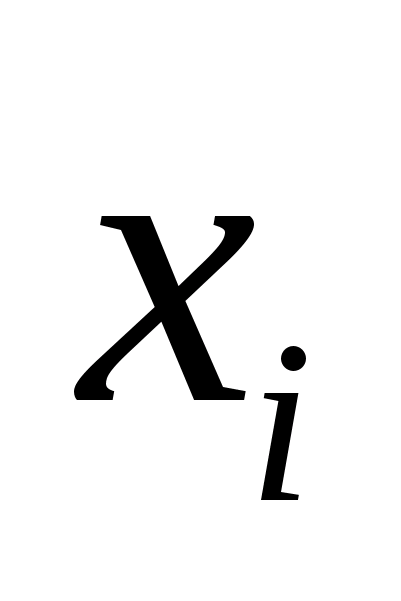
-го измерения; 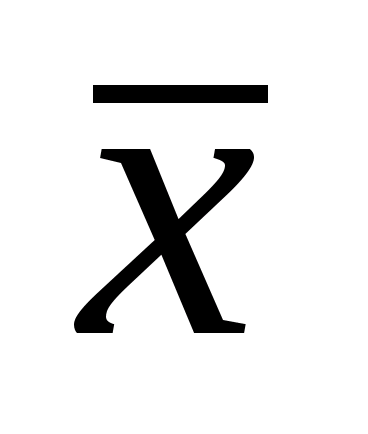
– число измерений.
Чем больше число измерений, тем меньше и тем больше оно приближается к σ. Если истинное значение измеряемой величины μ, ее среднее арифметическое значение, полученное в результате измерений , а случайная абсолютная погрешность , то результат измерений запишется в виде
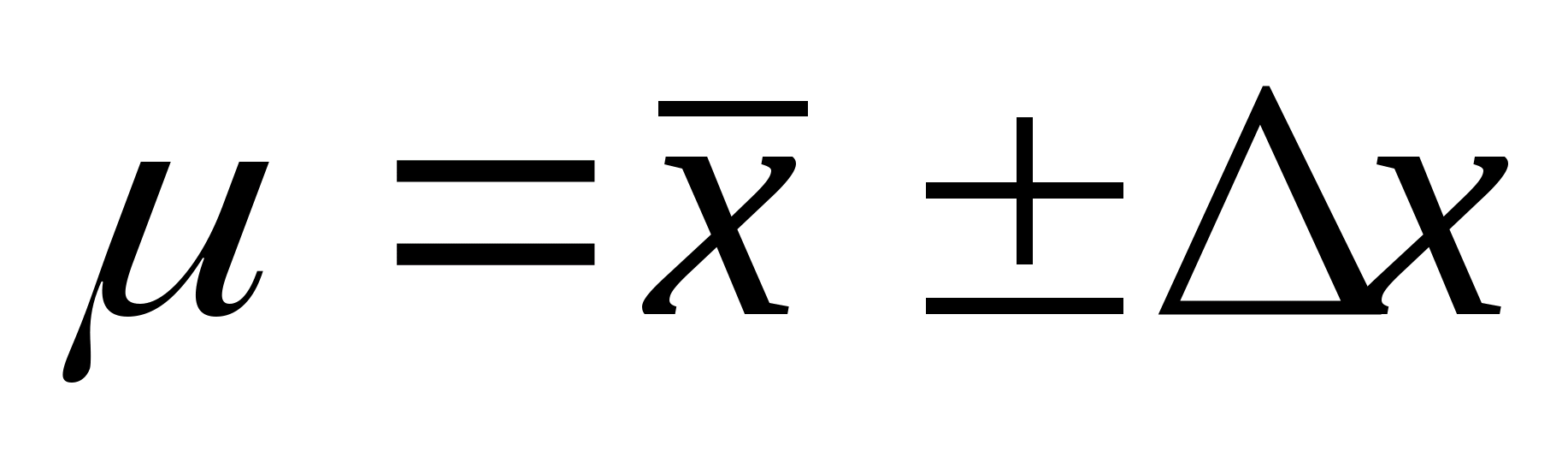
Интервал значений от
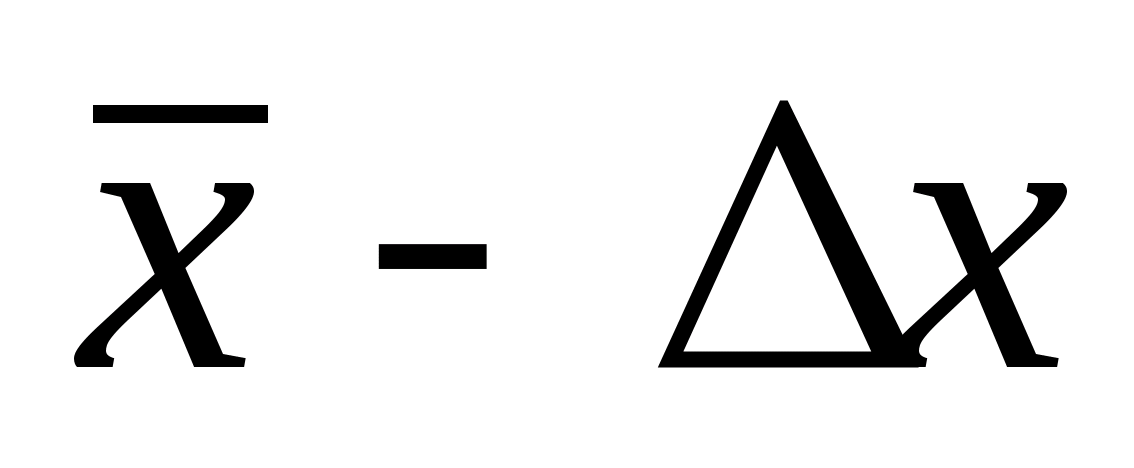
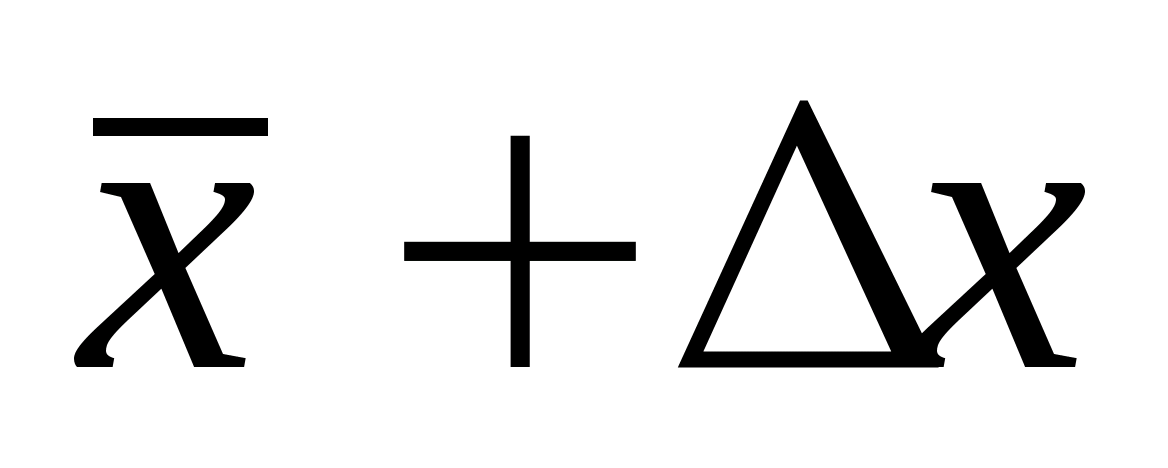
Поскольку является случайной величиной, то истинное значение попадает в доверительный интервал с вероятностью α, которая называется доверительной вероятностью,
или надежностью
измерений. Эта величина численно равна площади заштрихованной криволинейной трапеции. (см. рис.)
Все это справедливо для достаточно большого числа измерений, когда близка к σ. Для отыскания доверительного интервала и доверительной вероятности при небольшом числе измерений, с которым мы имеем дело в ходе выполнения лабораторных работ, используется распределение вероятностей Стьюдента.
Это распределение вероятностей случайной величины 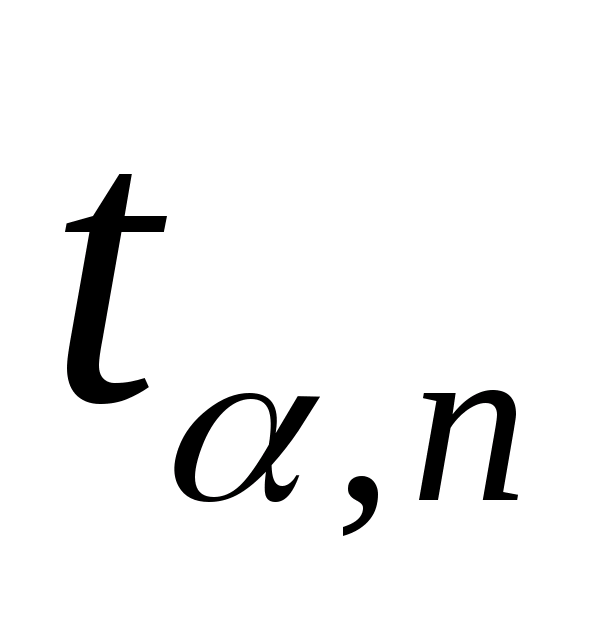
– число измерений.
Чем больше число измерений, тем меньше и тем больше оно приближается к σ. Если истинное значение измеряемой величины μ, ее среднее арифметическое значение, полученное в результате измерений , а случайная абсолютная погрешность , то результат измерений запишется в виде
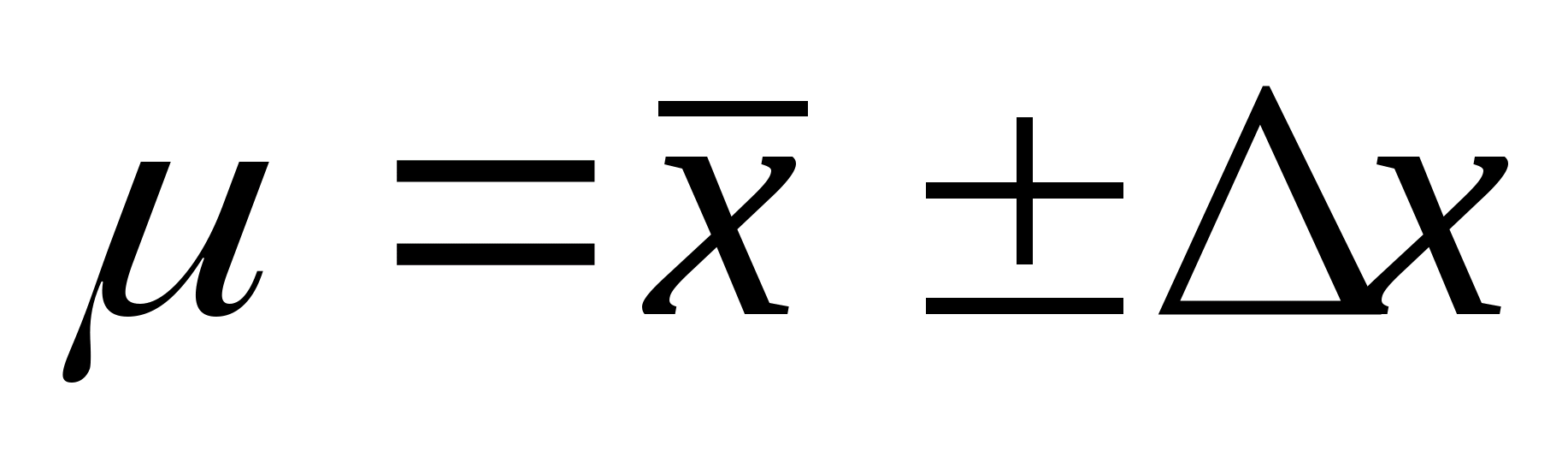
Интервал значений от
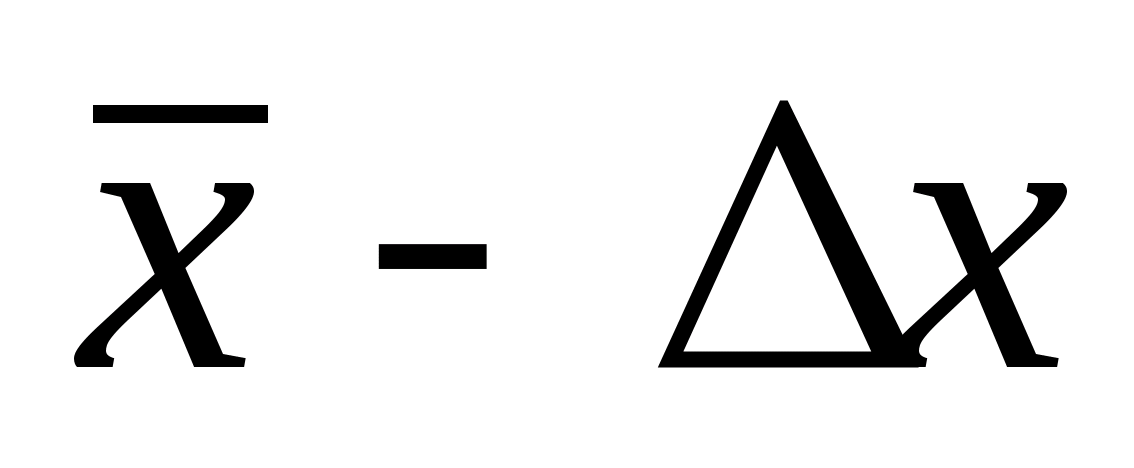
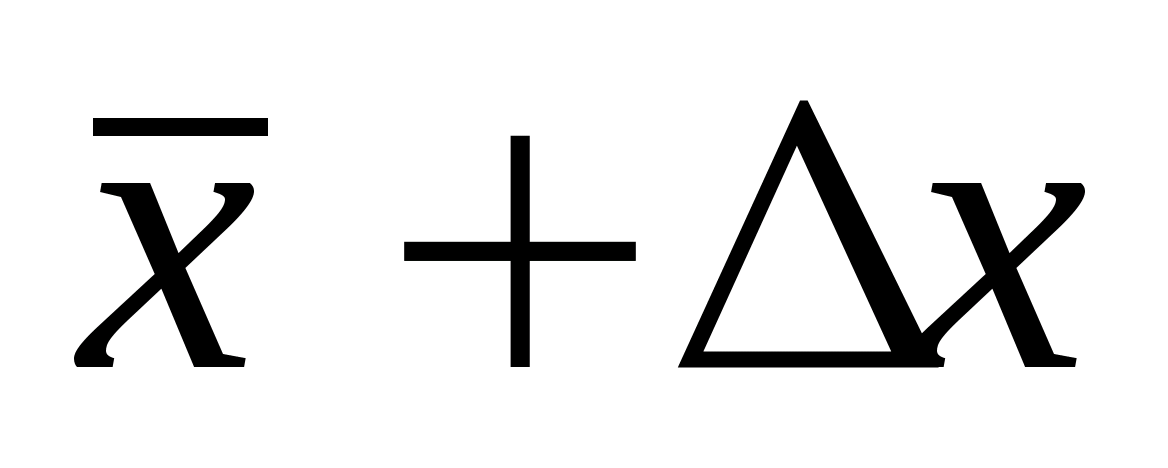
Поскольку является случайной величиной, то истинное значение попадает в доверительный интервал с вероятностью α, которая называется доверительной вероятностью,
или надежностью
измерений. Эта величина численно равна площади заштрихованной криволинейной трапеции. (см. рис.)
Все это справедливо для достаточно большого числа измерений, когда близка к σ. Для отыскания доверительного интервала и доверительной вероятности при небольшом числе измерений, с которым мы имеем дело в ходе выполнения лабораторных работ, используется распределение вероятностей Стьюдента.
Это распределение вероятностей случайной величины 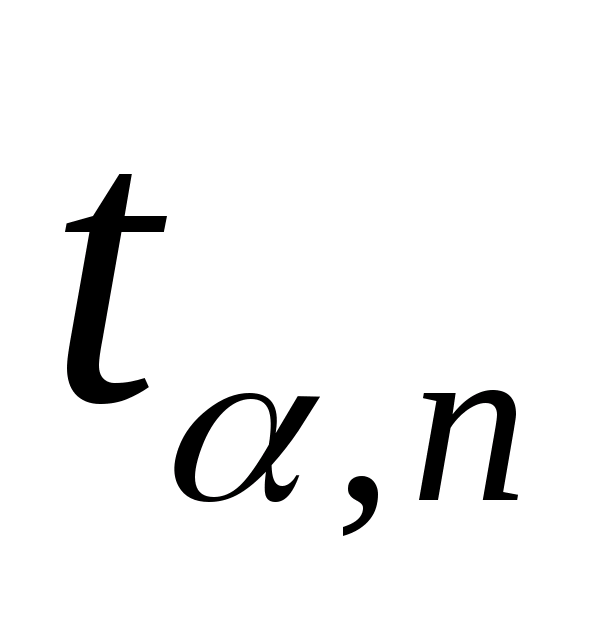
, дает значение доверительного интервала в долях средней квадратичной ошибки среднего арифметического .
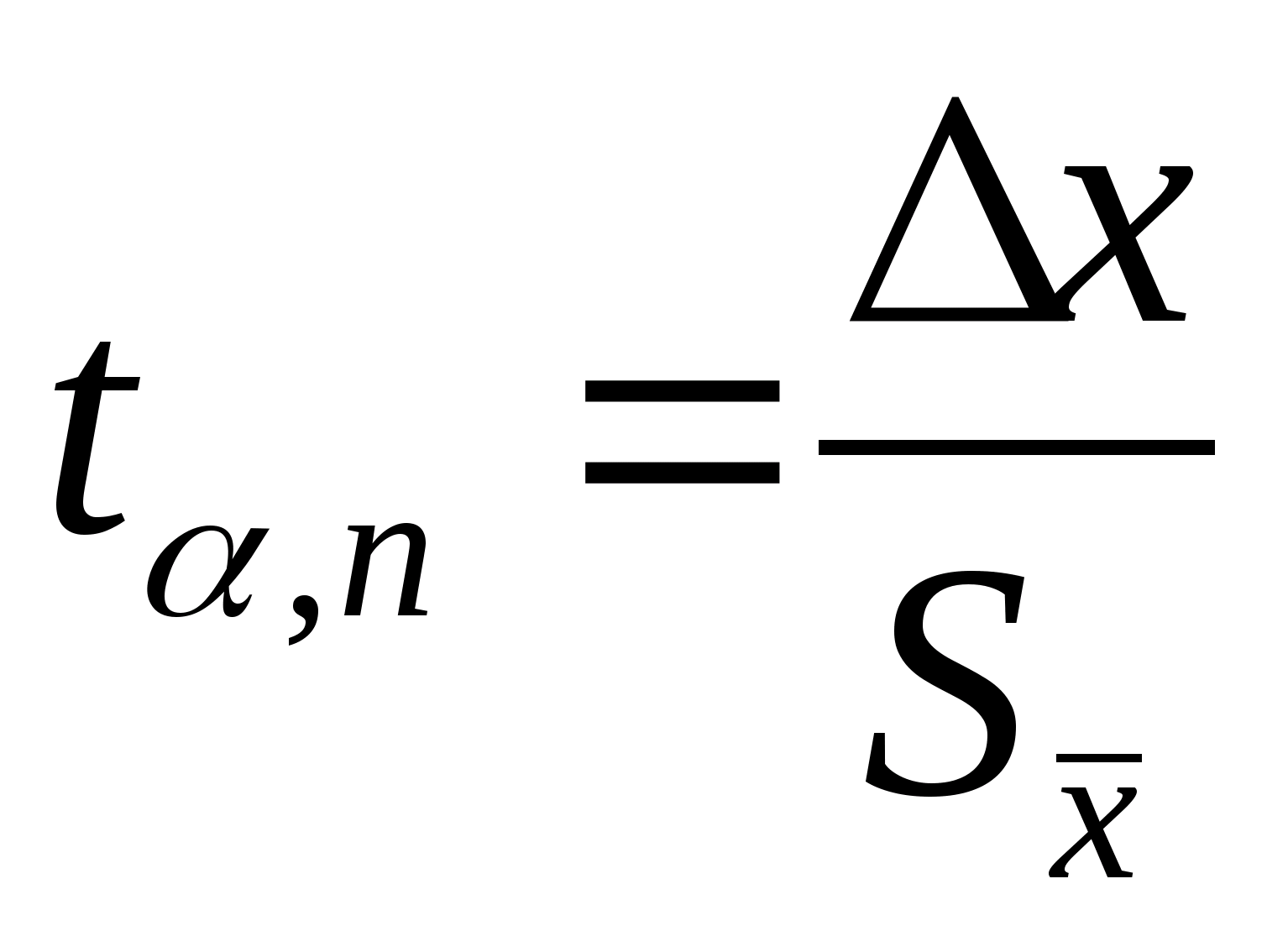
Распределение вероятностей этой величины не зависит от σ 2 , а существенно зависит от числа опытов n
.
С увеличением числа опытов n
распределение Стьюдента стремится к распределению Гаусса.
Функция распределения табулирована (табл.1). Значение коэффициента Стьюдента находится на пересечении строки, соответствующей числу измерений n
, и столбца, соответствующего доверительной вероятности α
Таблица 1.
Пользуясь данными таблицы, можно:
определить доверительный интервал, задаваясь определенной вероятностью;
выбрать доверительный интервал и определить доверительную вероятность.
При косвенных измерениях среднюю квадратичную ошибку среднего арифметического значения функции вычисляют по формуле
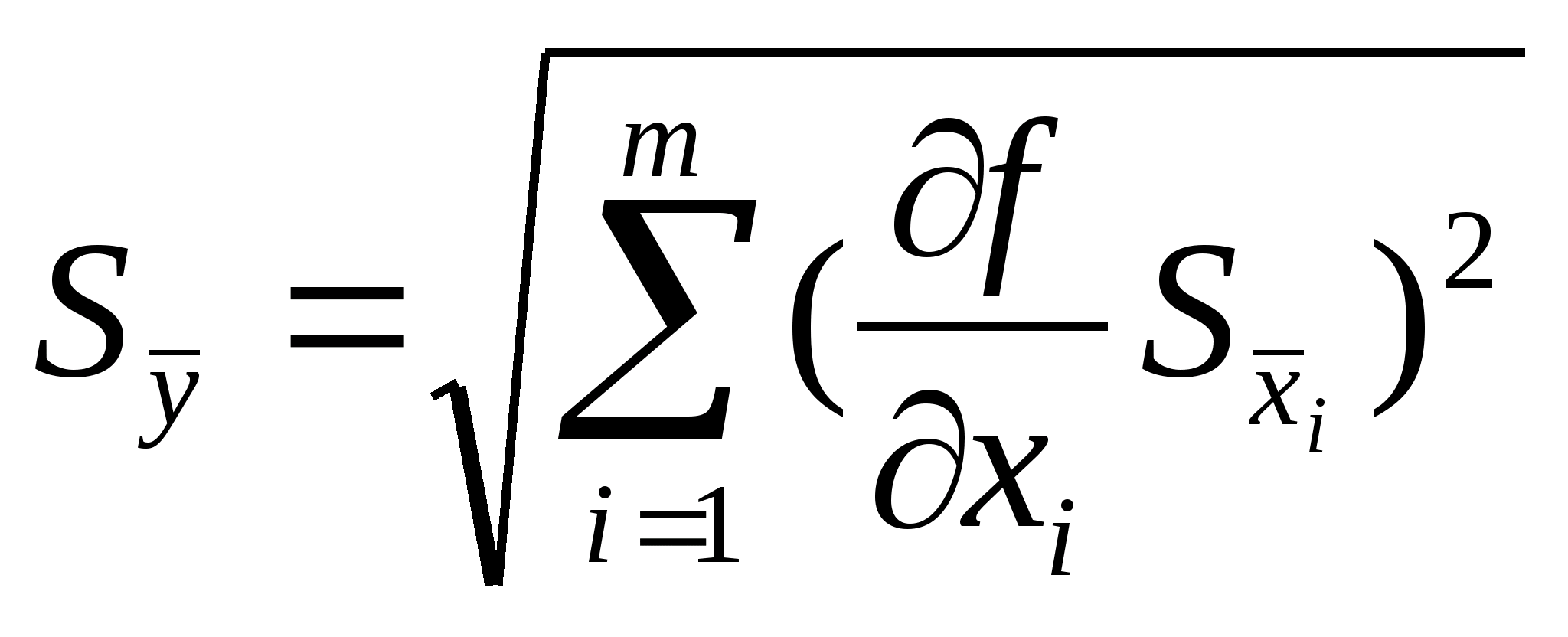
Доверительный интервал и доверительная вероятность определяются так же, как и в случае прямых измерений.
Оценка суммарной погрешности измерений. Запись окончательного результата.
Суммарную погрешность результата измерений величины Х
будем определять как среднее квадратичное значение систематической и случайной погрешностей
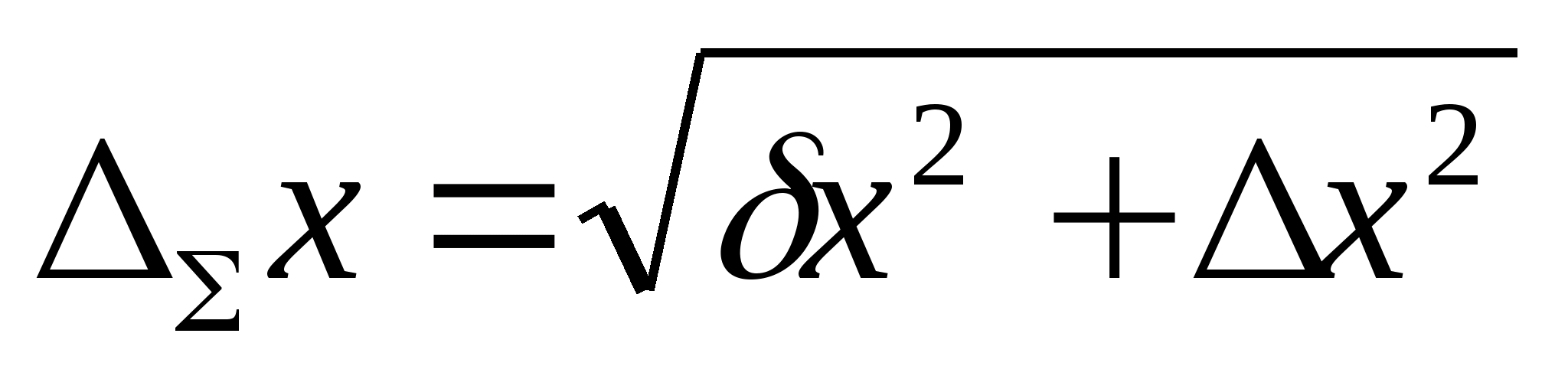
где δх –
приборная погрешность, Δх
– случайная погрешность.
В качестве Х может быть как непосредственно, так и косвенно измеряемая величина.
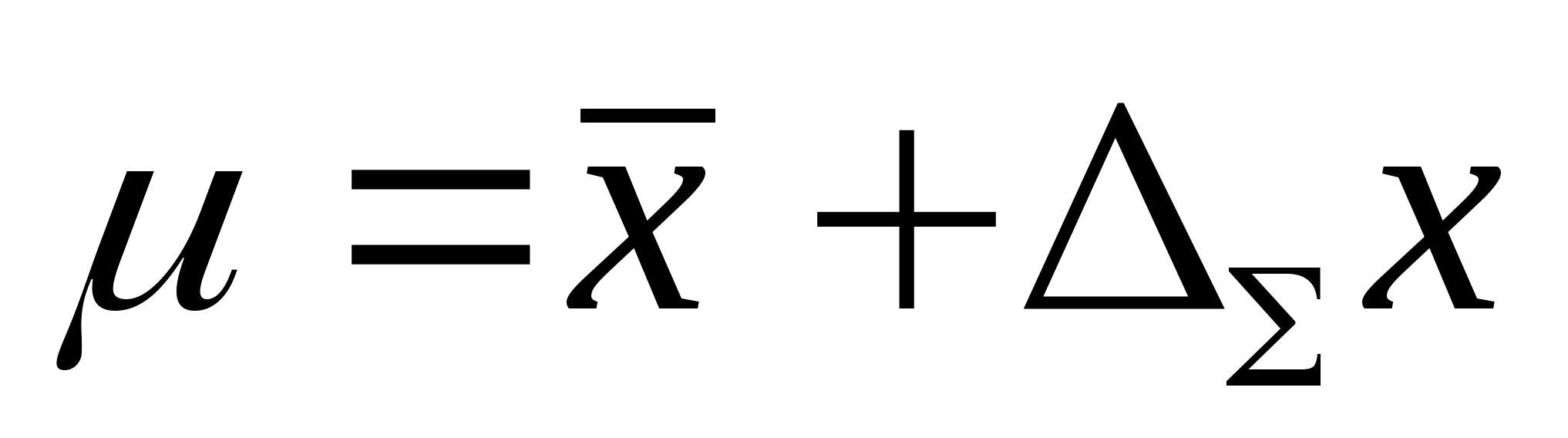
(7)
Следует иметь в виду, что сами формулы теории ошибок справедливы для большого число измерений. Поэтому значение случайной, а следовательно, и суммарной погрешности определяется при малом n
с большой ошибкой. При вычислении Δх
при числе измерений
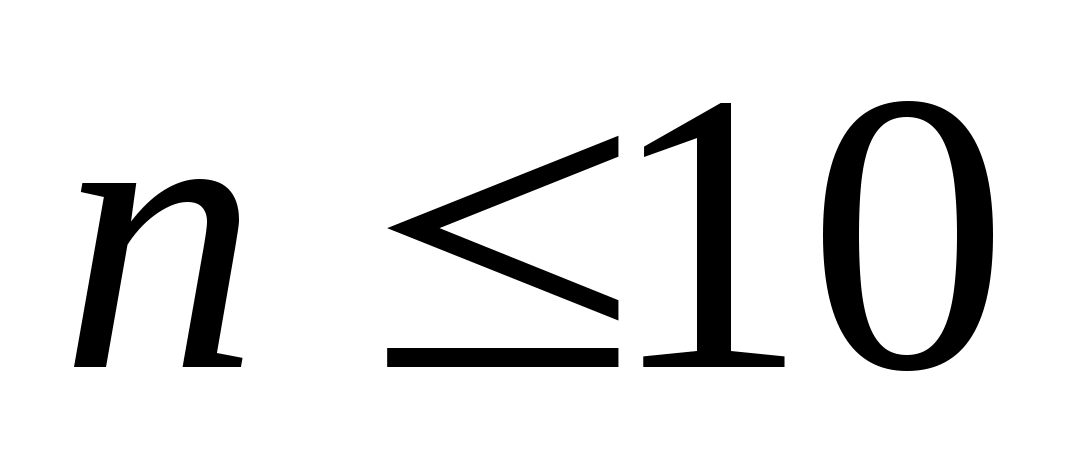
= 0,042, то отбрасываем 2 и пишем Δх
=0,04, а если Δх
=0,123, то пишем Δх
=0,12.
Число разрядов результата и суммарной погрешности должно быть одинаковым. Поэтому среднее арифметическое погрешности должно быть одинаковым. Поэтому среднее арифметическое вычисляется вначале на один разряд больше, чем измерение, а при записи результата его значение уточняется до числа разрядов суммарной ошибки.
4. Методика расчета погрешностей измерений.
Погрешности прямых измерений
При обработке результатов прямых измерений рекомендуется принять следующий порядок выполнение операций.
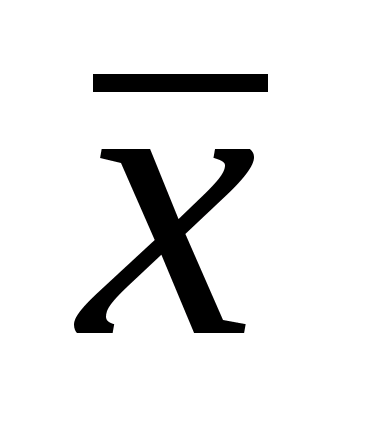
Распределение вероятностей этой величины не зависит от σ 2 , а существенно зависит от числа опытов n
.
С увеличением числа опытов n
распределение Стьюдента стремится к распределению Гаусса.
Функция распределения табулирована (табл.1). Значение коэффициента Стьюдента находится на пересечении строки, соответствующей числу измерений n
, и столбца, соответствующего доверительной вероятности α
Таблица 1.
Пользуясь данными таблицы, можно:
определить доверительный интервал, задаваясь определенной вероятностью;
выбрать доверительный интервал и определить доверительную вероятность.
При косвенных измерениях среднюю квадратичную ошибку среднего арифметического значения функции вычисляют по формуле
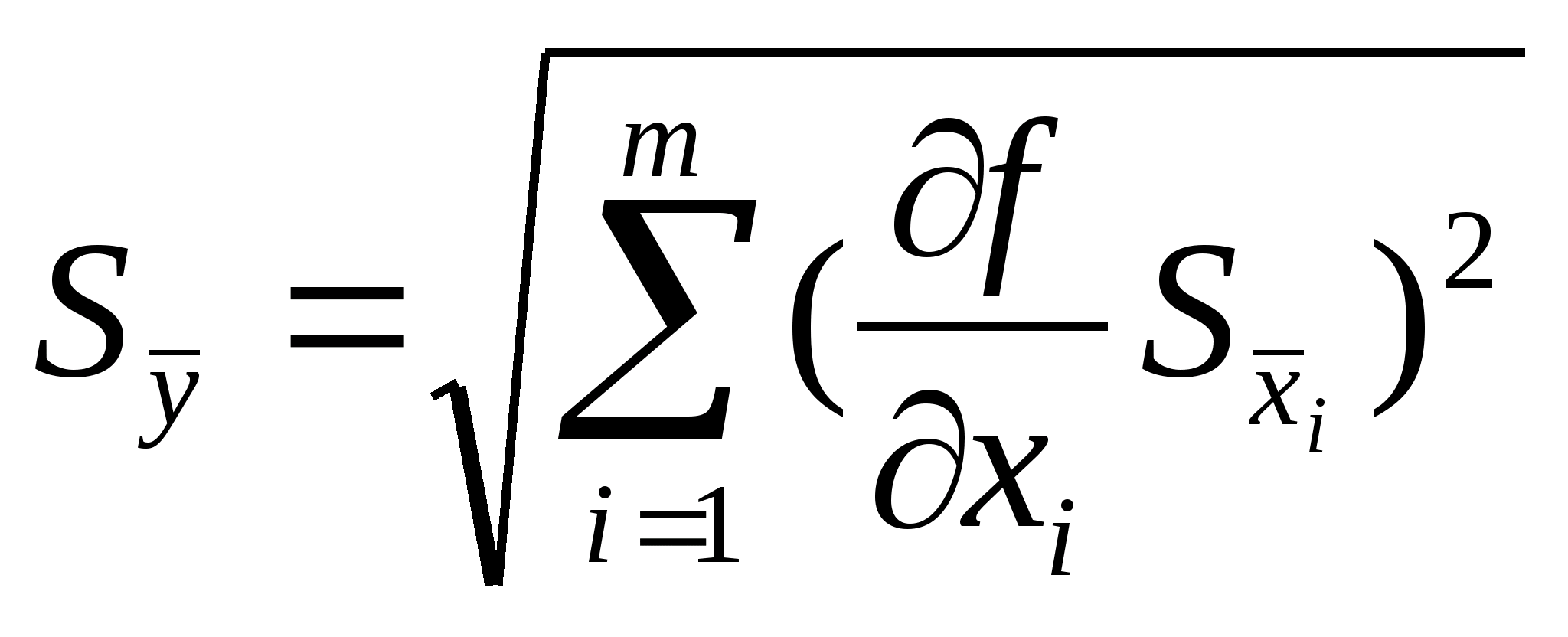
Доверительный интервал и доверительная вероятность определяются так же, как и в случае прямых измерений.
Оценка суммарной погрешности измерений. Запись окончательного результата.
Суммарную погрешность результата измерений величины Х
будем определять как среднее квадратичное значение систематической и случайной погрешностей
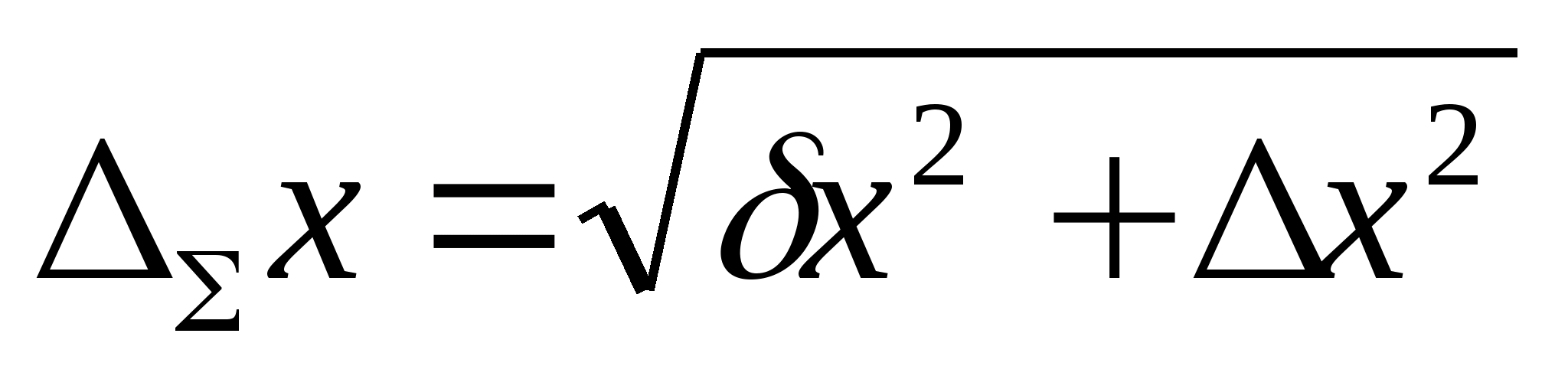
где δх –
приборная погрешность, Δх
– случайная погрешность.
В качестве Х может быть как непосредственно, так и косвенно измеряемая величина.
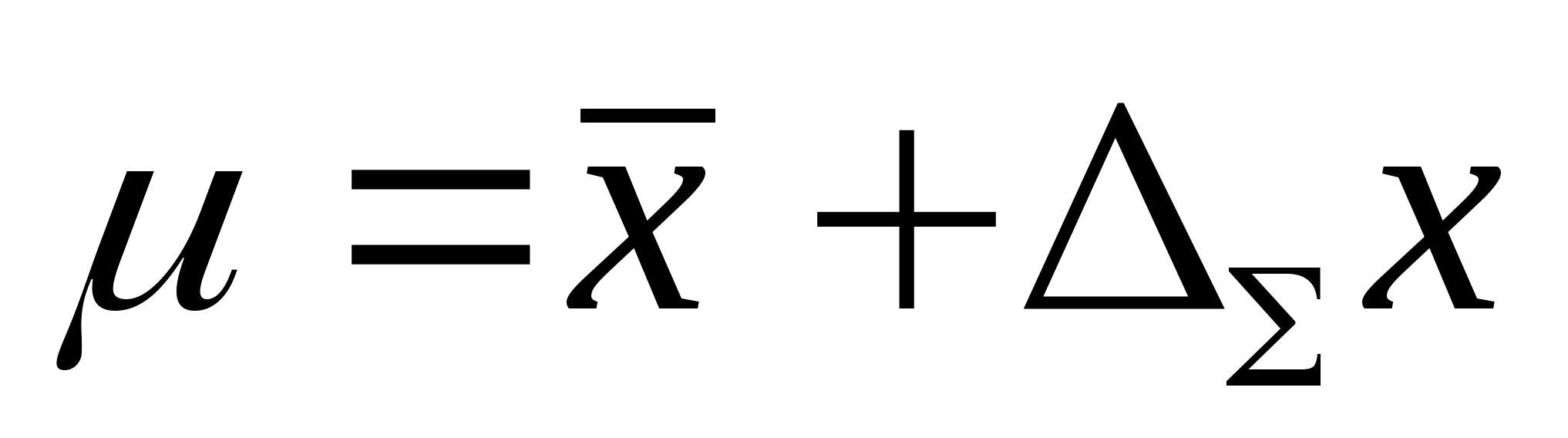
(7)
Следует иметь в виду, что сами формулы теории ошибок справедливы для большого число измерений. Поэтому значение случайной, а следовательно, и суммарной погрешности определяется при малом n
с большой ошибкой. При вычислении Δх
при числе измерений
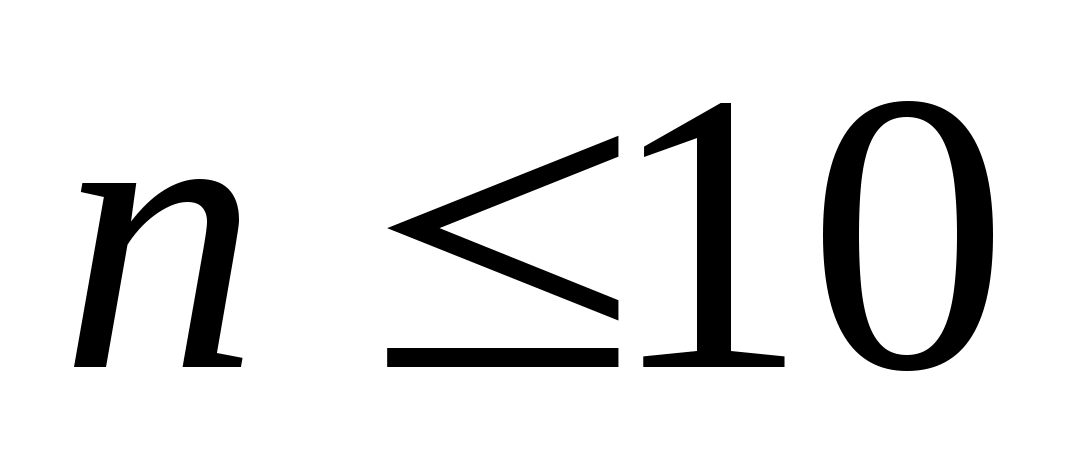
= 0,042, то отбрасываем 2 и пишем Δх
=0,04, а если Δх
=0,123, то пишем Δх
=0,12.
Число разрядов результата и суммарной погрешности должно быть одинаковым. Поэтому среднее арифметическое погрешности должно быть одинаковым. Поэтому среднее арифметическое вычисляется вначале на один разряд больше, чем измерение, а при записи результата его значение уточняется до числа разрядов суммарной ошибки.
4. Методика расчета погрешностей измерений.
Погрешности прямых измерений
При обработке результатов прямых измерений рекомендуется принять следующий порядок выполнение операций.
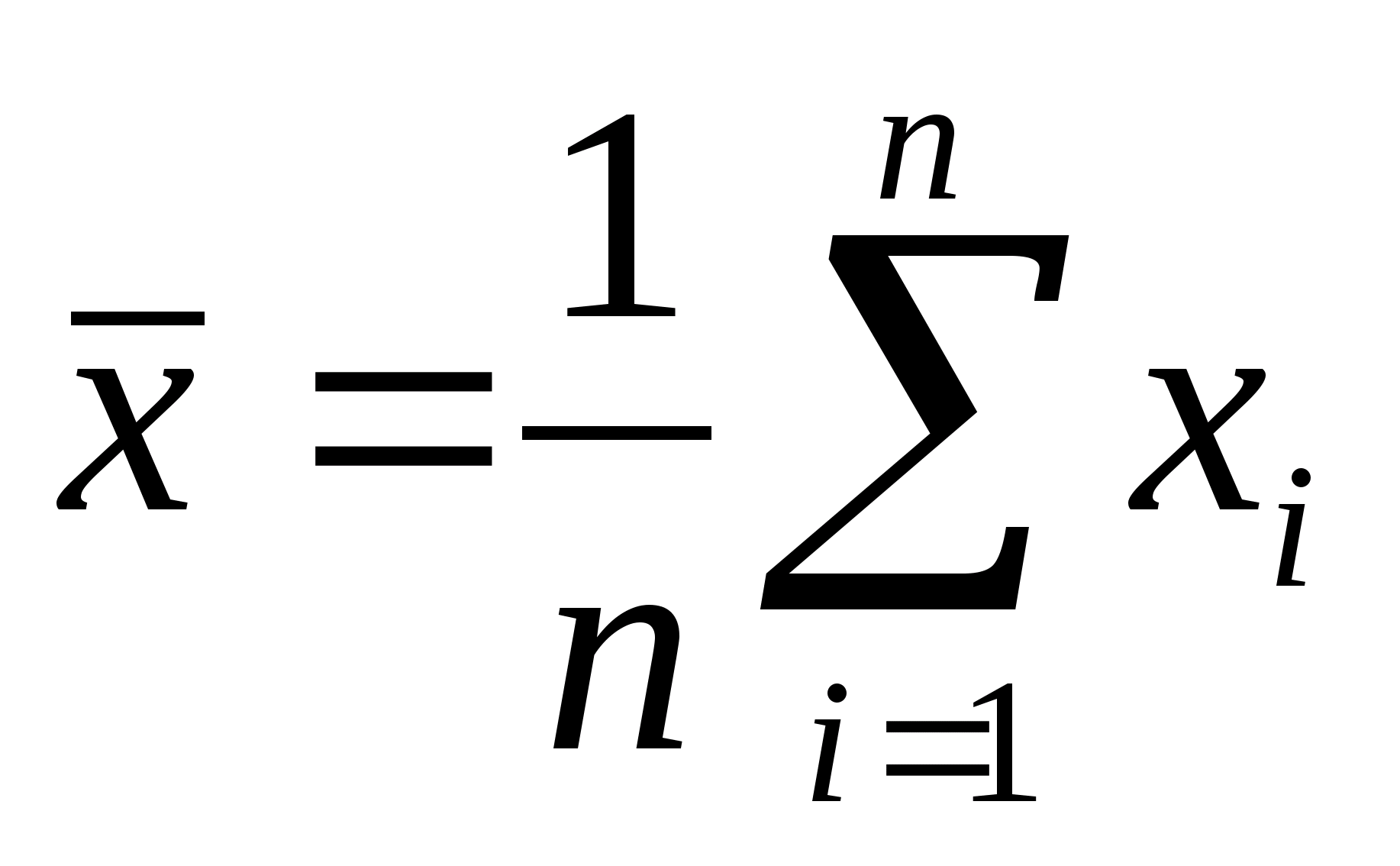
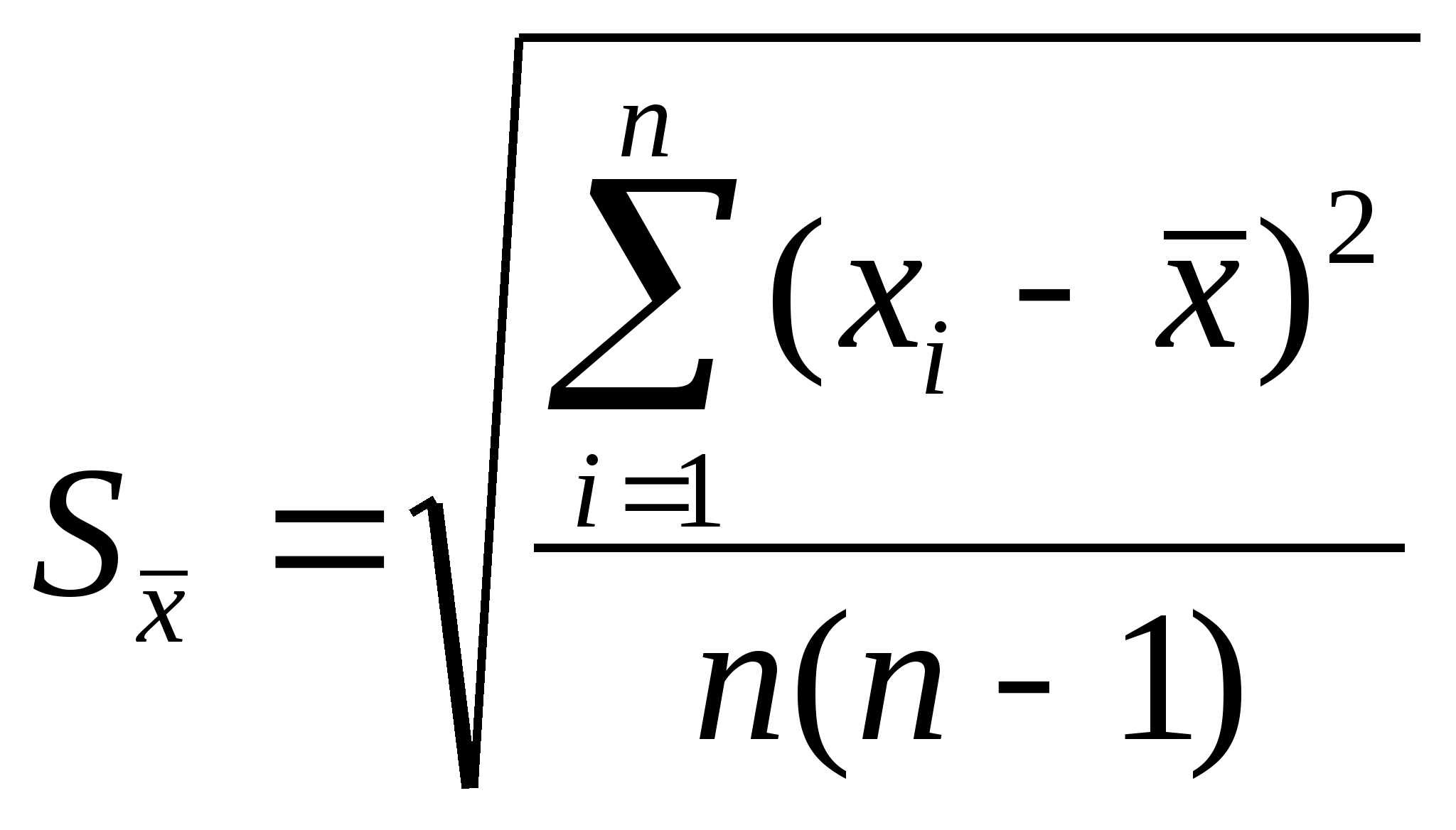
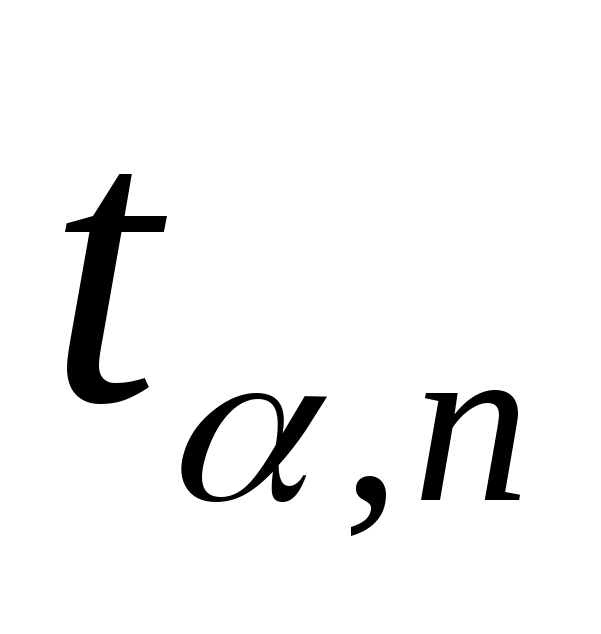
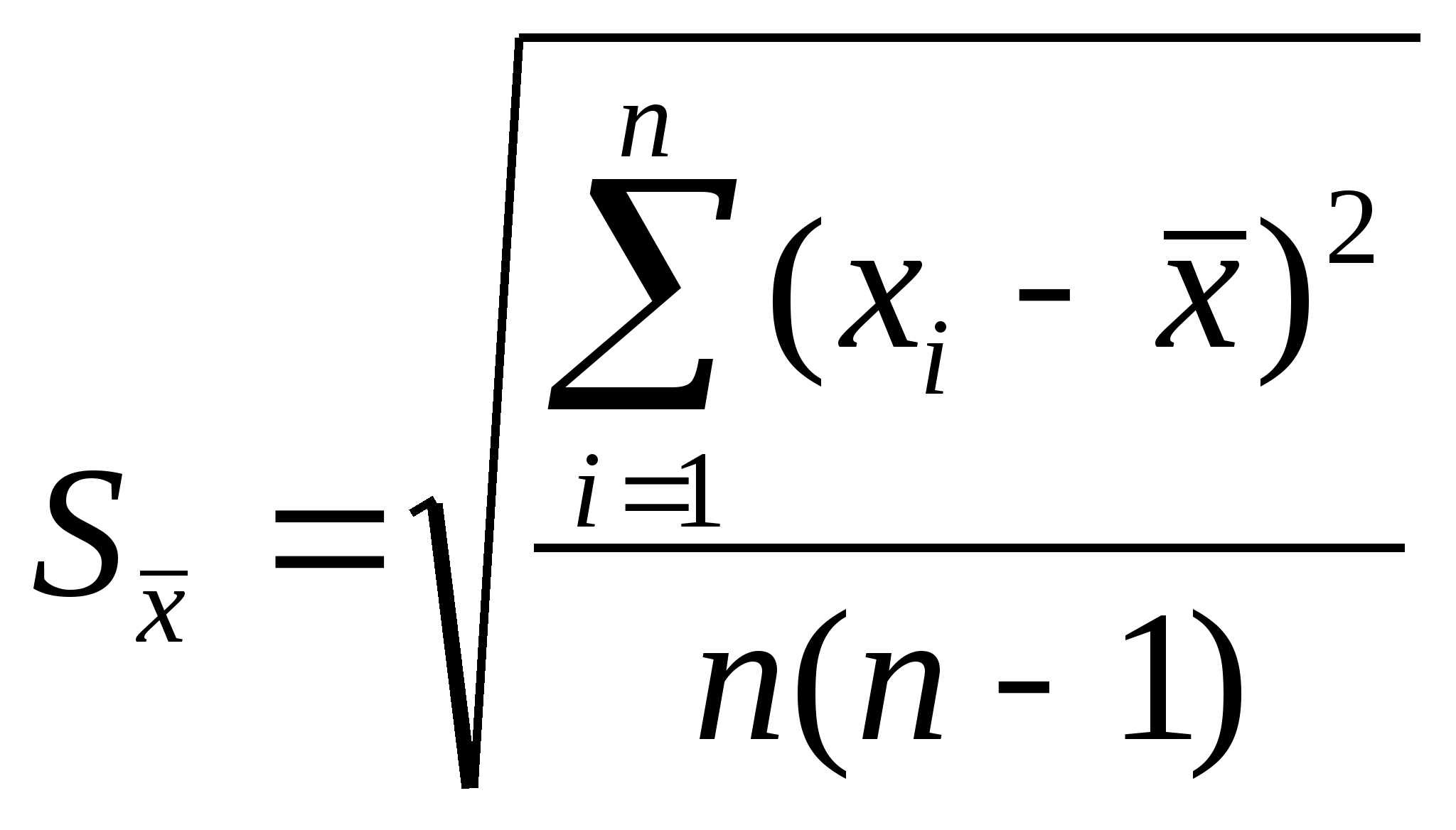
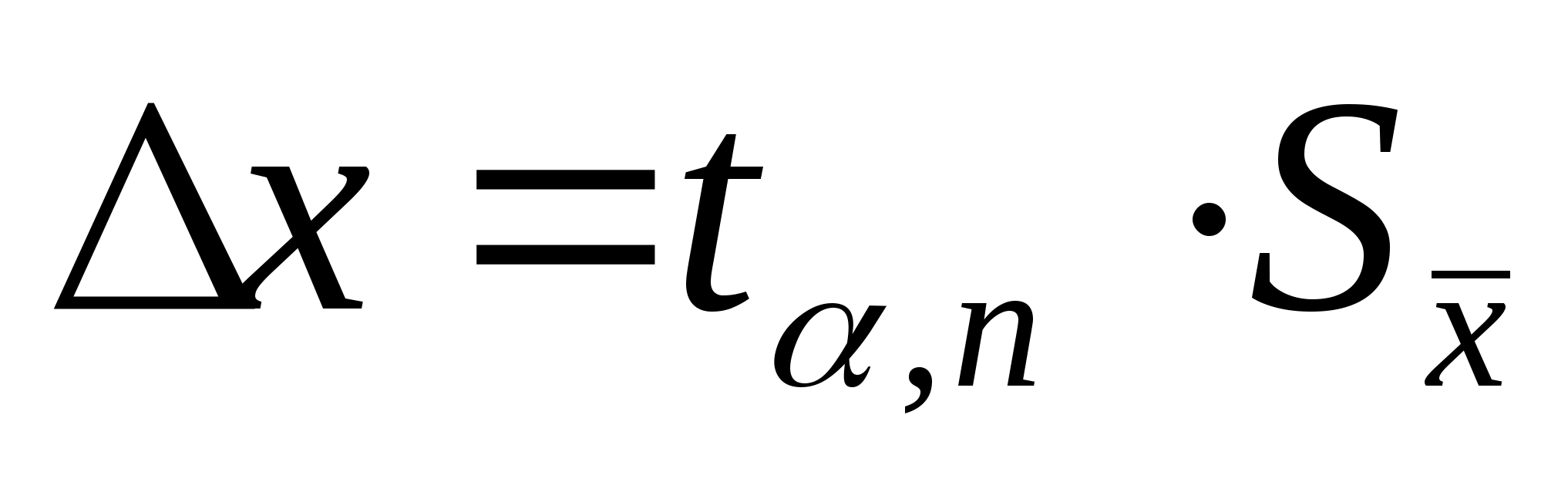
Определяется суммарная погрешность
Оценивается относительная погрешность результата измерений
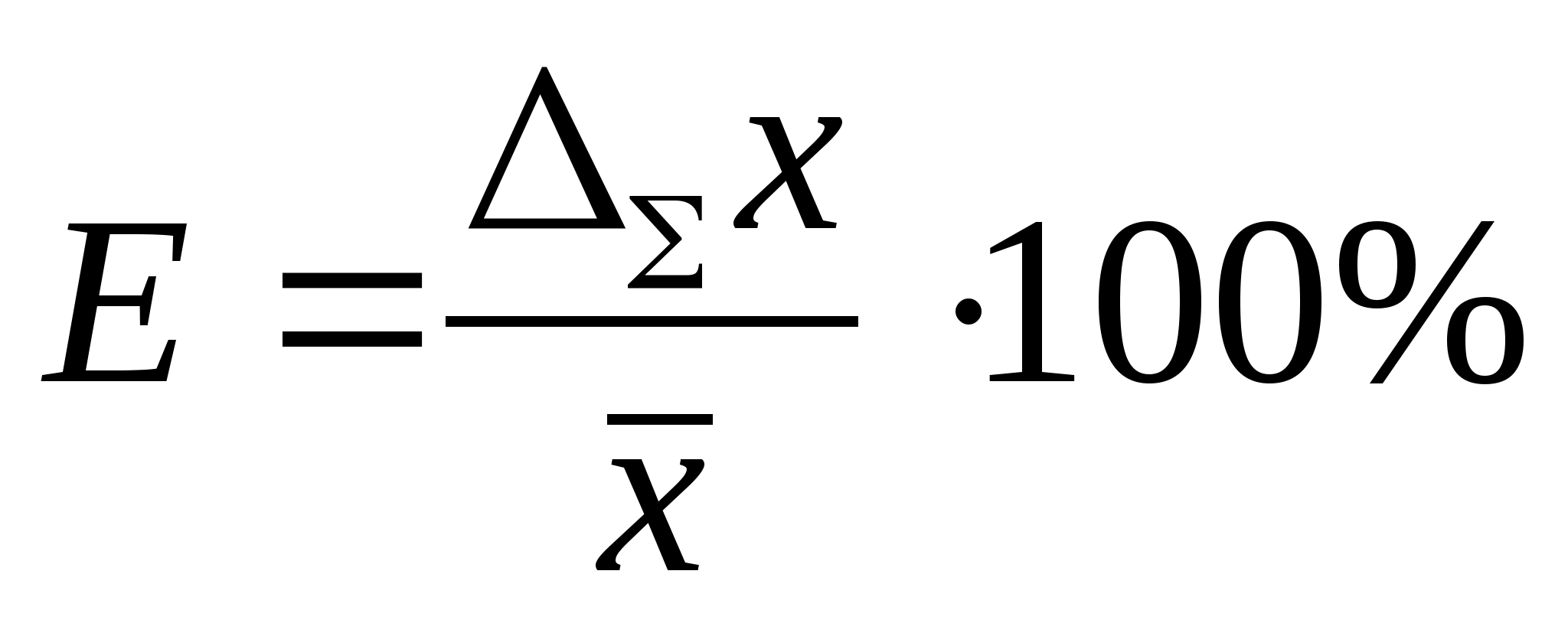
Записывается окончательный результат в виде
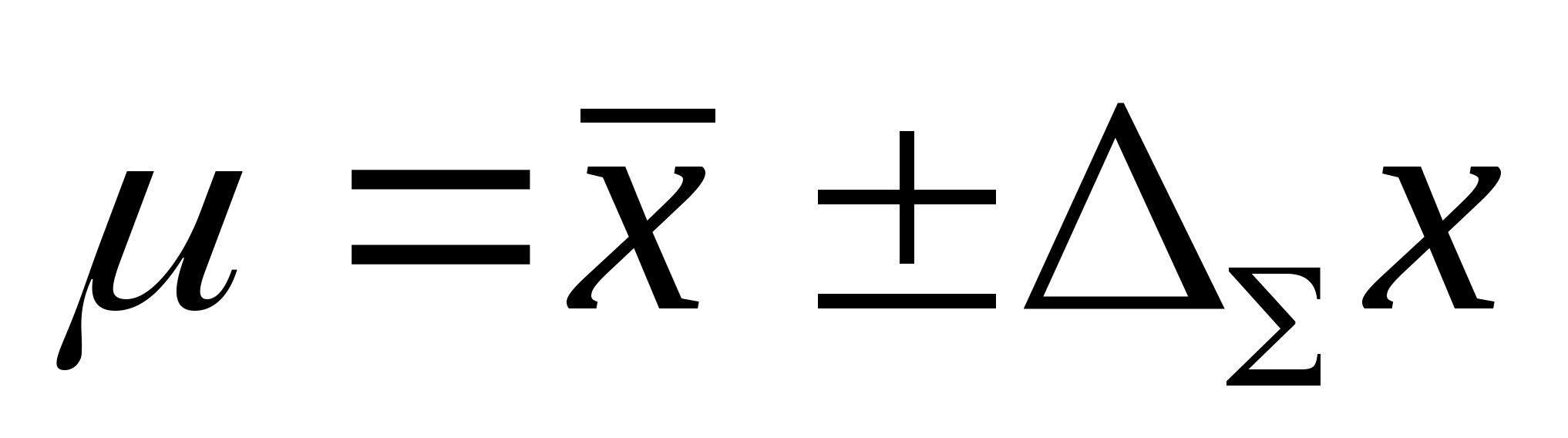
5. Погрешность косвенных измерений
При оценке истинного значения косвенно измеряемой величины , являющейся функцией других независимых величин

Первый способ
используется, если величина y
определяется при различных условиях опыта. В этом случае для каждого из значений вычисляется
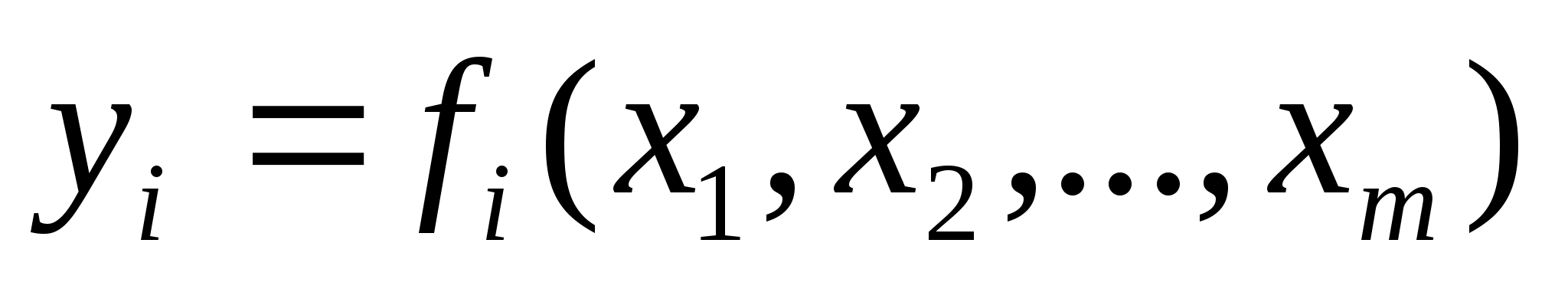
i
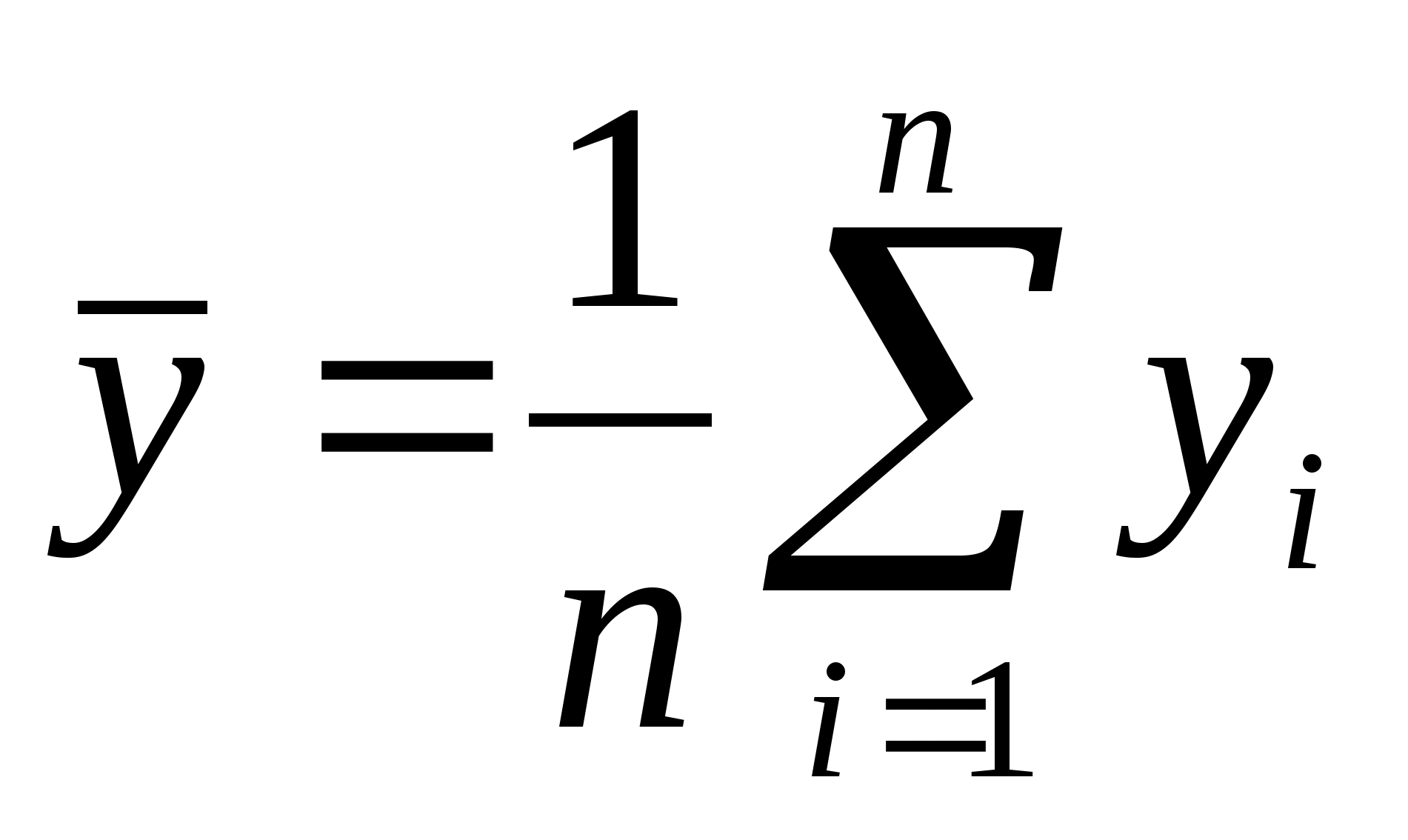
Систематическая (приборная) погрешность находится на основании известных приборных погрешностей всех измерений по формуле. Случайная погрешность в этом случае определяется как ошибка прямого измерения.
Второй способ
применяется, если данная функция y
определяется несколько раз при одних и тех же измерений. В этом случае величина рассчитывается по средним значениям . В нашем лабораторном практикуме чаще используется второй способ определения косвенно измеряемой величины y
.
Систематическая (приборная) погрешность, как и при первом способе, находится на основании известных приборных погрешностей всех измерений по формуле
Для нахождения случайной погрешности косвенного измерения вначале рассчитываются средние квадратичные ошибки среднего арифметического отдельных измерений. Затем находится средняя квадратичная ошибка величины y
.
Задание доверительной вероятности α, нахождение коэффициента Стьюдента , определение случайной и суммарной ошибок осуществляются так же, как и в случае прямых измерений. Аналогичным образом представляется результат всех расчетов в виде
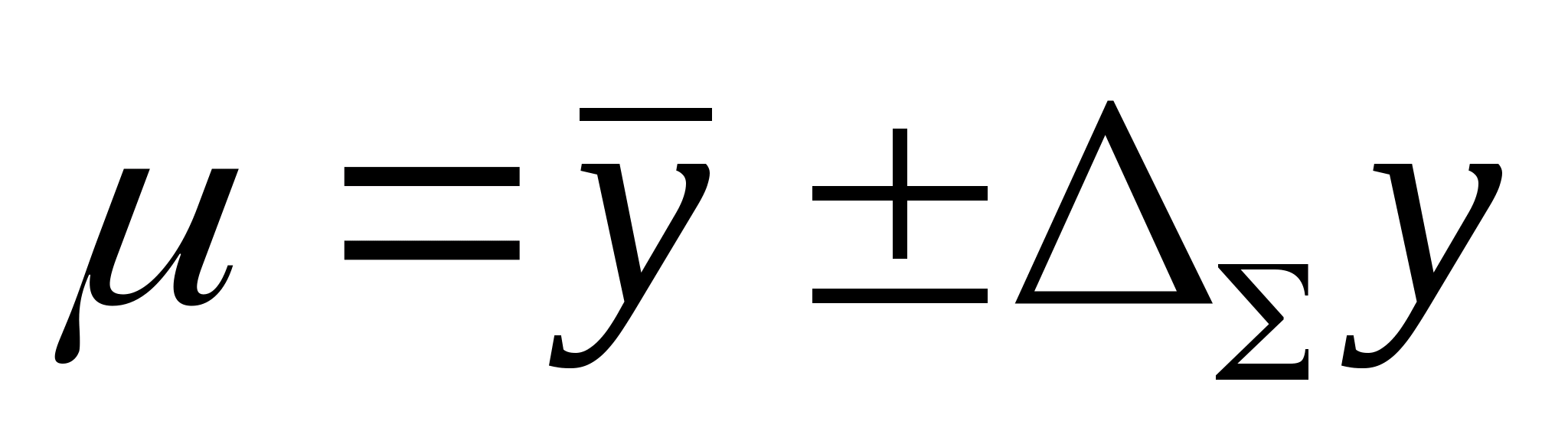
6. Пример оформления лабораторной работы
Лабораторная работа №1
ОПРЕДЕЛЕНИЕ ОБЪЕМА ЦИЛИНДРА
Принадлежности:
штангенциркуль с ценой деления 0,05 мм, микрометр с ценой деления 0,01 мм, цилиндрическое тело.
Цель работы:
ознакомление с простейшими физическими измерениями, определение объема цилиндра, расчет погрешностей прямых и косвенных измерений.
Порядок выполнения работы
Провести не менее 5 раз измерения штангенциркулем диаметра цилиндра, а микрометром его высоту.
Расчетная формула для вычисления объема цилиндра
где d – диаметр цилиндра; h – высота.
Результаты измерений
Таблица 2.
|
№ измерения |
||||||
Наличие случайных погрешностей в результате при повторении измерений в неизменных условиях эксперимента объясняется самой природой этих погрешностей. Строго говоря, условия не остаются неизменными и их колебания вызывают непостоянство результата, т.е. случайные погрешности всегда будут присутствовать в результате измерений.
Характером проявления случайной погрешности определяется и способ их учета. Учесть влияние случайных погрешностей на результат измерения можно только путем анализа всей совокупности случайных погрешностей.
Случайная погрешность считается случайной величиной, и поэтому ее оценивают методами математической статистики и теории вероятности. Наиболее полной характеристикой случайной погрешности является закон распределения, представляющий собой зависимость вероятности появления случайной погрешности от величины этой погрешности. Большинство результатов измерений содержит случайную погрешность, подчиняющуюся нормальному закону распределения:
где W
(D) – плотность вероятности случайной погрешности отдельного измерения , это отклонение может быть вычислено для каждого измерения. Следует помнить, что сумма отклонений результата измерений от среднего значения равна нулю, а сумма их квадратов минимальна. Эти свойства используются при обработке результатов измерений для контроля правильности вычислений;
s – параметр, характеризующий степень случайного разброса результатов отдельных измерений относительно истинного значения Х0, называют средним квадратическим отклонением случайной величины измерения;
Математическое ожидание результатов наблюдений.
S – являются точечными оценками случайной погрешности.
При случайных погрешностях результат каждого измерения Х
i
будет отличаться от истинного значения Х0
измеряемой величины:
.
Определяется суммарная погрешность
Оценивается относительная погрешность результата измерений
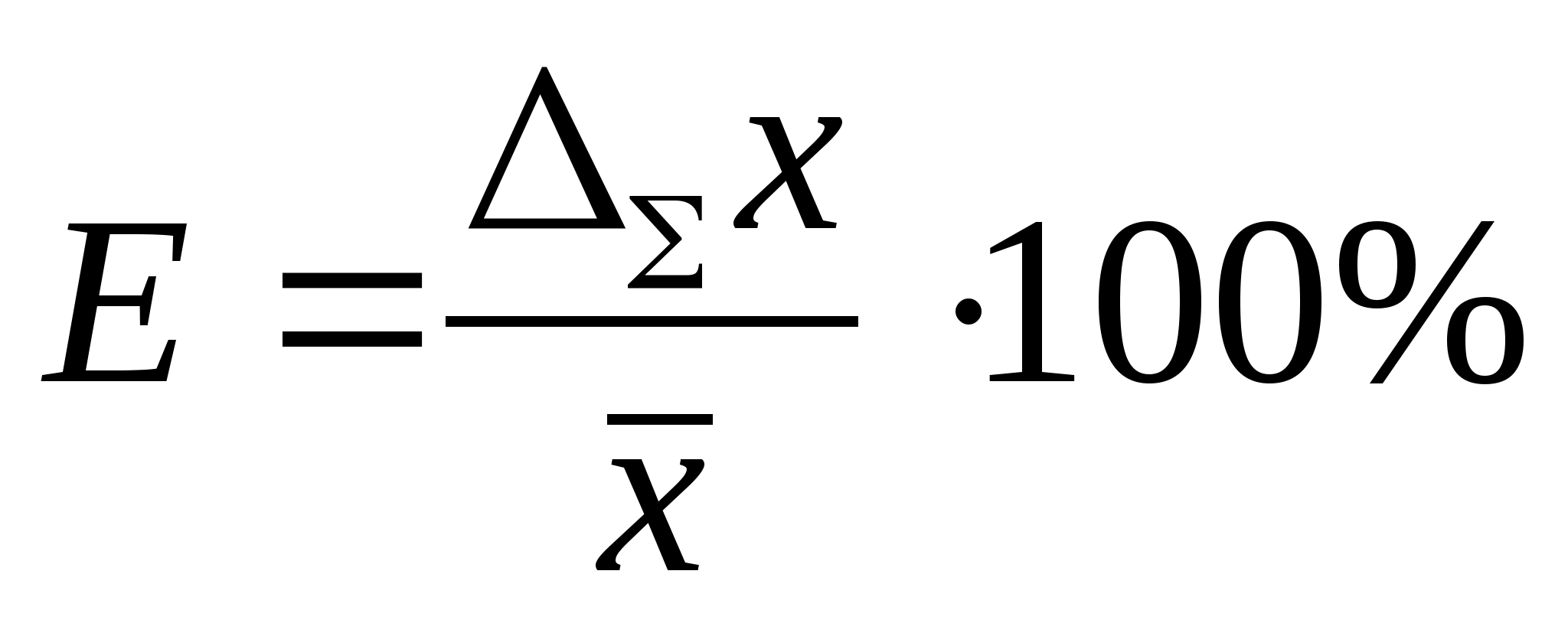
Записывается окончательный результат в виде
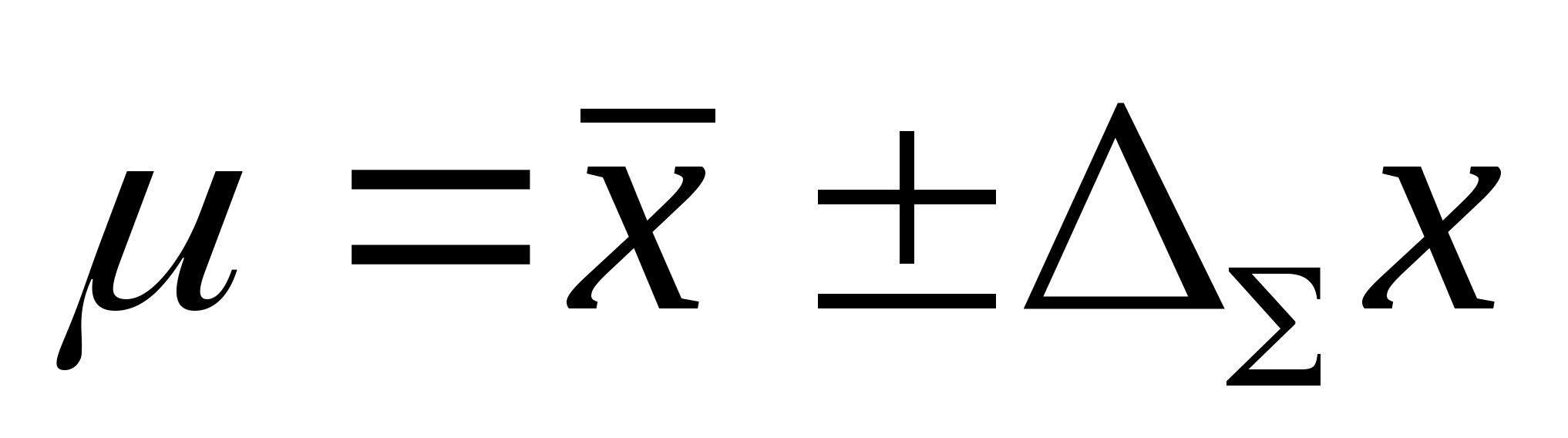
5. Погрешность косвенных измерений
При оценке истинного значения косвенно измеряемой величины , являющейся функцией других независимых величин

Первый способ
используется, если величина y
определяется при различных условиях опыта. В этом случае для каждого из значений вычисляется
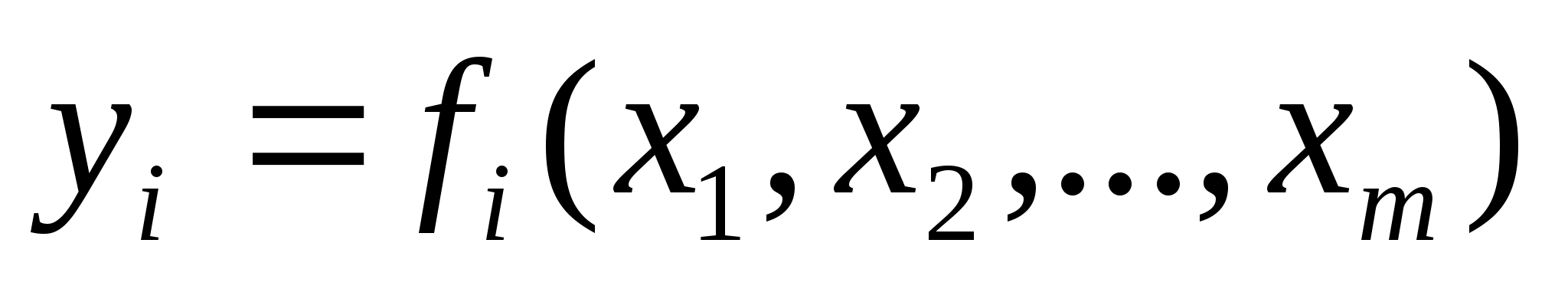
i
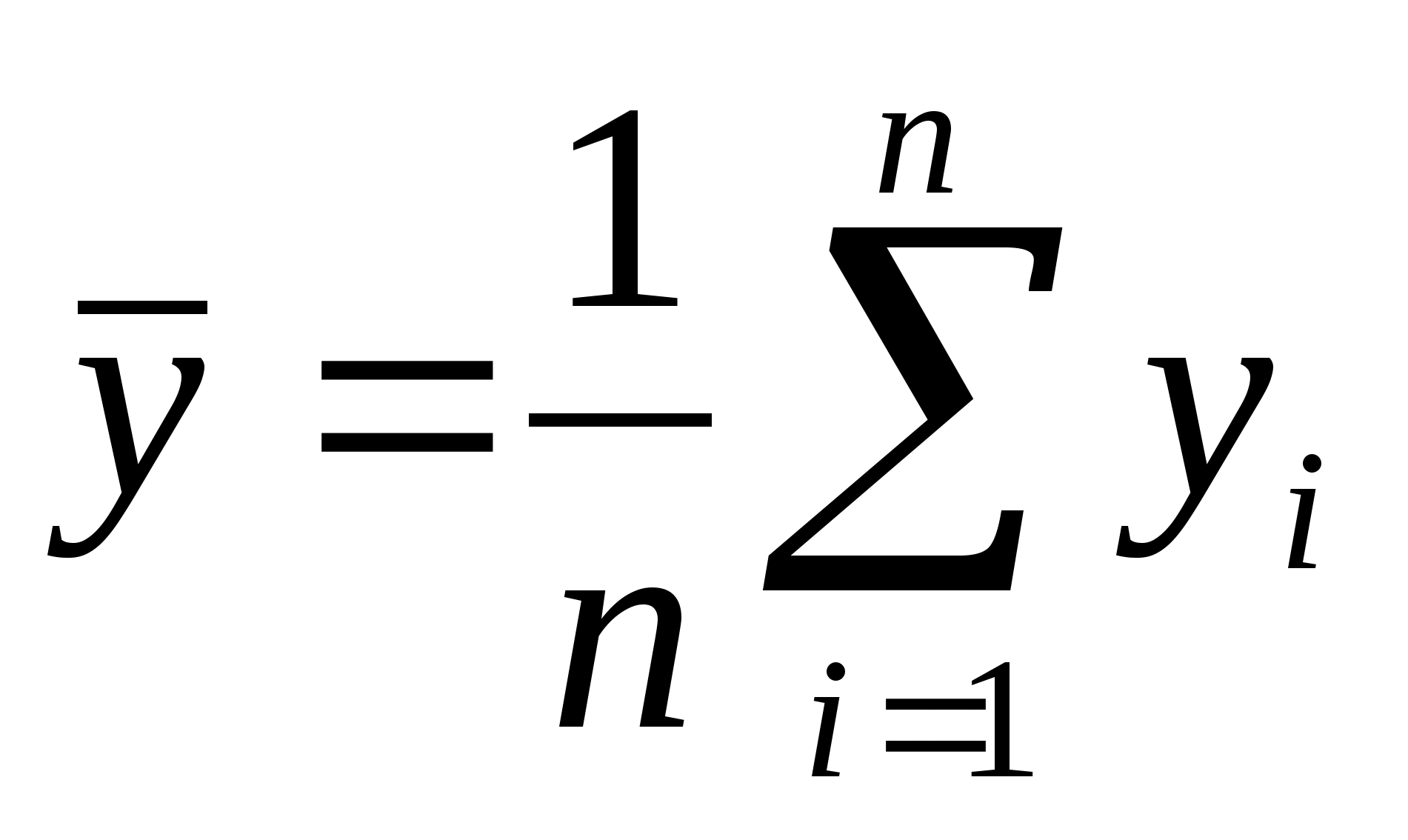
Систематическая (приборная) погрешность находится на основании известных приборных погрешностей всех измерений по формуле. Случайная погрешность в этом случае определяется как ошибка прямого измерения.
Второй способ
применяется, если данная функция y
определяется несколько раз при одних и тех же измерений. В этом случае величина рассчитывается по средним значениям . В нашем лабораторном практикуме чаще используется второй способ определения косвенно измеряемой величины y
.
Систематическая (приборная) погрешность, как и при первом способе, находится на основании известных приборных погрешностей всех измерений по формуле
Для нахождения случайной погрешности косвенного измерения вначале рассчитываются средние квадратичные ошибки среднего арифметического отдельных измерений. Затем находится средняя квадратичная ошибка величины y
.
Задание доверительной вероятности α, нахождение коэффициента Стьюдента , определение случайной и суммарной ошибок осуществляются так же, как и в случае прямых измерений. Аналогичным образом представляется результат всех расчетов в виде
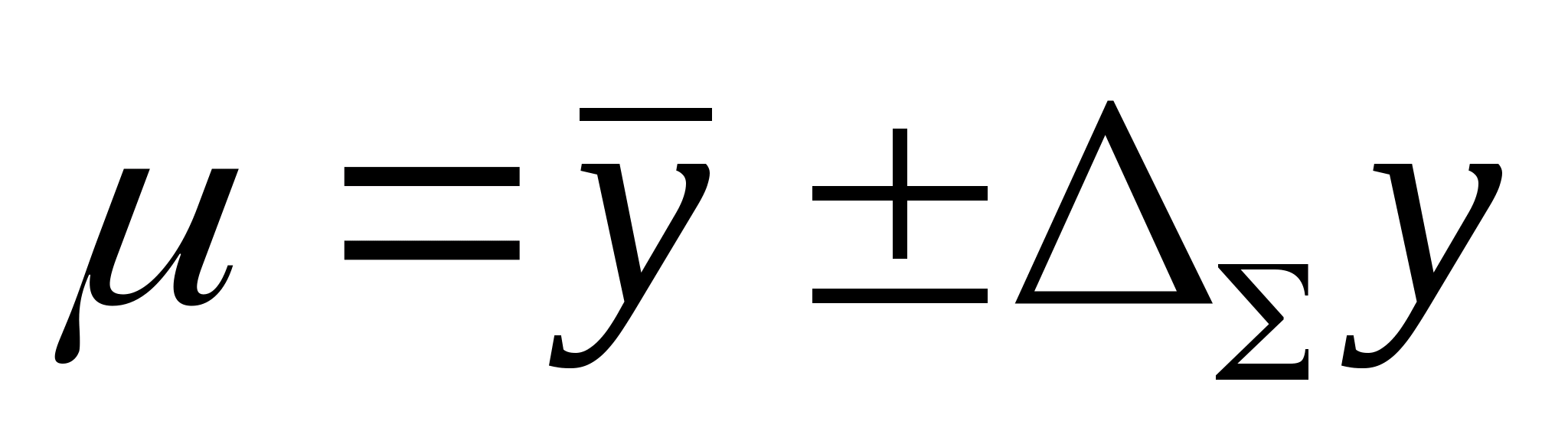
6. Пример оформления лабораторной работы
Лабораторная работа №1
ОПРЕДЕЛЕНИЕ ОБЪЕМА ЦИЛИНДРА
Принадлежности:
штангенциркуль с ценой деления 0,05 мм, микрометр с ценой деления 0,01 мм, цилиндрическое тело.
Цель работы:
ознакомление с простейшими физическими измерениями, определение объема цилиндра, расчет погрешностей прямых и косвенных измерений.
Порядок выполнения работы
Провести не менее 5 раз измерения штангенциркулем диаметра цилиндра, а микрометром его высоту.
Расчетная формула для вычисления объема цилиндра
где d – диаметр цилиндра; h – высота.
Результаты измерений
Таблица 2.
|
№ измерения |
||||||
Наличие случайных погрешностей в результате при повторении измерений в неизменных условиях эксперимента объясняется самой природой этих погрешностей. Строго говоря, условия не остаются неизменными и их колебания вызывают непостоянство результата, т.е. случайные погрешности всегда будут присутствовать в результате измерений.
Характером проявления случайной погрешности определяется и способ их учета. Учесть влияние случайных погрешностей на результат измерения можно только путем анализа всей совокупности случайных погрешностей.
Случайная погрешность считается случайной величиной, и поэтому ее оценивают методами математической статистики и теории вероятности. Наиболее полной характеристикой случайной погрешности является закон распределения, представляющий собой зависимость вероятности появления случайной погрешности от величины этой погрешности. Большинство результатов измерений содержит случайную погрешность, подчиняющуюся нормальному закону распределения:
где W
(D) – плотность вероятности случайной погрешности отдельного измерения , это отклонение может быть вычислено для каждого измерения. Следует помнить, что сумма отклонений результата измерений от среднего значения равна нулю, а сумма их квадратов минимальна. Эти свойства используются при обработке результатов измерений для контроля правильности вычислений;
s – параметр, характеризующий степень случайного разброса результатов отдельных измерений относительно истинного значения Х0, называют средним квадратическим отклонением случайной величины измерения;
Математическое ожидание результатов наблюдений.
S – являются точечными оценками случайной погрешности.
При случайных погрешностях результат каждого измерения Х
i
будет отличаться от истинного значения Х0
измеряемой величины:
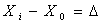
Эту разность называют случайной погрешностью отдельного измерения (результата наблюдения).
Истинное значение Х0
неизвестно, поэтому на практике его заменяют наиболее достоверным значением измеряемой величины, определяемым на основании экспериментальных данных.
Если проводить серию измерений исследуемой величины и определить среднее арифметическое значение, то оно является наиболее достоверным значением измеряемой величины. При вычислении среднего арифметического большого числа измерений погрешности отдельных измерений, имеющие разный знак, взаимно компенсируются.
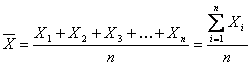
где n – число измерений.
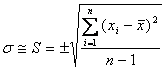
где n – число измерений.
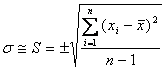
где xi
– численный результат отдельного измерения;
n – число измерений.
Характер кривых, описываемых (4.5), показан на рисунке 4.1а для трёх значений s. Функция (4.5) графически изображается колоколообразной кривой, симметричной относительно ординат, асимптотически приближающейся к оси абсцисс. Максимум этой кривой получается в точке D=0, а величина этого максимума . Как видно из рисунка 4.1, чем меньше s, тем уже кривая и, следовательно, реже встречаются большие отклонения, т.е. тем точнее выполняются измерения.
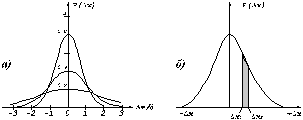
Рисунок 4.1
Вероятность появления погрешности в пределах между D1 и D2
определяется площадью заштрихованного участка на рис. 4.1 б
, т.е. определённым интегралом от функции W
(D):
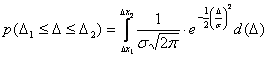
Значения интеграла вычислены для различных пределов и сведены в таблицы. Интеграл, вычисленный для пределов D1=–¥ и D2=+¥, равен единице, т. е. вероятность появления случайной погрешности в интервале от –¥ до +¥ равна единице.
Из таблиц, приведенных в математических справочниках, следует что:
(4.9)
Значения интеграла вычислены для различных пределов и сведены в таблицы. Интеграл, вычисленный для пределов D1=–¥ и D2=+¥, равен единице, т. е. вероятность появления случайной погрешности в интервале от –¥ до +¥ равна единице.
Из таблиц, приведенных в математических справочниках, следует что:

Таким образом, с вероятностью 0,683 случайные погрешности измерения не выходят за пределы ±s. С вероятностью 0,997 случайная погрешность находится в пределах ±3s, т.е. только 3 измерения из 1000 могут дать погрешность, превышающую ±3s. Это соотношение называется законом трёх сигм.
Так как на практике число измерений не превышает нескольких десятков, то появление погрешности равной ±3s , маловероятно. Поэтому погрешность ±3s считается максимально возможной случайной погрешностью. Погрешности более ±3s считаются промахами и при обработке результатов измерений не учитываются.
В теории случайных погрешностей вводится также понятие о среднем квадратическом отклонении среднего арифметического (средняя квадратическая погрешность результата измерений)

где t
α(n) —
табулированный коэффициент распределения Стъюдента, который зависит от доверительной вероятности a и числа измерений n, значения которого можно найти в математических справочниках.
Доверительную вероятность и доверительный интервал называют интервальными оценками.
Случайные погрешности и критерии их оценки.
Случайная погрешность — это погрешность, изменяющаяся случайным образом при повторном определении одной и той же физической величины с помощью одной и той же измерительной аппаратуры при неизменных внешних условиях. Случайные погрешности вызываются большим количеством факторов, воздействия которых столь незначительны, что их нельзя выделить и учесть в отдельности.
Случайные погрешности могут возникнуть из-за погрешности округления при отсчете показаний, нестабильности переходного сопротивления в контактах коммутирующих устройств, нестабильности напряжения источника питания, влияния электромагнитных полей пылинки, воздушные течения и других влияющих величин. Но истинное значение измеряемой величины заключено в интервале от минимального до максимального результатов измерения.
Случайную погрешность нельзя исключить в каждом из результатов измерений. Но с помощью многократных наблюдений, а также используя методы теории вероятности и математической статистики, можно учесть их влияние на оценку истинного значения измеряемой величины. Это позволяет определить значение измеряемой величины со значительно меньшей погрешностью, чем погрешности отдельных измерений (наблюдений).
Наиболее полной характеристикой случайной величины является закон ее распределения. Различают две формы описания закона распределения: интегральную и дифференциальную. В метрологии принято использовать, в основном, дифференциальную форму.
Дифференциальный закон распределения можно определить через построение гистограммы. Для этого необходимо произвести n независимых наблюдений. При этом каждое наблюдение, возможно, отличается от предыдущего, так как содержит случайную погрешность. Следует разбить интервал между наибольшим и наименьшим измеренными значениями на ряд равных интервалов шириной Δх. По результатам подсчетов строится график: на ось абсцисс наносятся значения результатов наблюдений и обозначаются границы интервалов, на ось ординат – относительная частота попаданий в интервал.
Если устремить число измерений к бесконечности, а интервал h —
к нулю, то гистограмма переходит в пределе в непрерывную кривую, которая является кривой распределения погрешностей. При некоторых условиях, которые обычно выполняются при проведении измерений, эта кривая представляет собой график функции Гаусса (нормальное распределение), имеющей следующий вид:
|
где t Доверительную вероятность и доверительный интервал называют интервальными оценками. Случайные погрешности и критерии их оценки. Случайная погрешность — это погрешность, изменяющаяся случайным образом при повторном определении одной и той же физической величины с помощью одной и той же измерительной аппаратуры при неизменных внешних условиях. Случайные погрешности вызываются большим количеством факторов, воздействия которых столь незначительны, что их нельзя выделить и учесть в отдельности. Случайные погрешности могут возникнуть из-за погрешности округления при отсчете показаний, нестабильности переходного сопротивления в контактах коммутирующих устройств, нестабильности напряжения источника питания, влияния электромагнитных полей пылинки, воздушные течения и других влияющих величин. Но истинное значение измеряемой величины заключено в интервале от минимального до максимального результатов измерения. Случайную погрешность нельзя исключить в каждом из результатов измерений. Но с помощью многократных наблюдений, а также используя методы теории вероятности и математической статистики, можно учесть их влияние на оценку истинного значения измеряемой величины. Это позволяет определить значение измеряемой величины со значительно меньшей погрешностью, чем погрешности отдельных измерений (наблюдений). Наиболее полной характеристикой случайной величины является закон ее распределения. Различают две формы описания закона распределения: интегральную и дифференциальную. В метрологии принято использовать, в основном, дифференциальную форму. Дифференциальный закон распределения можно определить через построение гистограммы. Для этого необходимо произвести n независимых наблюдений. При этом каждое наблюдение, возможно, отличается от предыдущего, так как содержит случайную погрешность. Следует разбить интервал между наибольшим и наименьшим измеренными значениями на ряд равных интервалов шириной Δх. По результатам подсчетов строится график: на ось абсцисс наносятся значения результатов наблюдений и обозначаются границы интервалов, на ось ординат – относительная частота попаданий в интервал. Если устремить число измерений к бесконечности, а интервал h —
Основными числовыми характеристиками случайной погрешности являются математическое ожидание М(Δ), дисперсия D и среднее квадратическое отклонение σ . Дисперсия, т.е. средняя квадратическая погрешность отдельного измерения применяется лишь для оценки точности применяемого метода измерений. А средняя арифметическая погрешность обозначает оценку отклонения среднего арифметического отклонения от истинного значения искомой величины. Чем больше число опытов, тем ближе значение среднего арифметического отклонения к истинному значению искомой величины. Вероятность того, что истинное значение измеряемой величины попадет взаданный интервал, называется доверительной вероятностью, или коэффициентом доверия Р, а соответствующий интервал, определяемый величиной абсолютной погрешности – доверительным интервалом. Достоверность результата при данном количестве измерений можно увеличить, уменьшая его точность, т. е. расширяя доверительный интервал. Случайную погрешность рассчитывают по формуле ε = ± t S(х), где ε – доверительные границы случайной погрешности результата измерений t – коэффициент Стьюдента, определяемый по заданным значениям доверительной вероятности Р и числу измерений n. Таким образом, для характеристики величины случайной погрешности необходимо задать два числа: саму погрешность и доверительную вероятность, позволяющую оценить степень надежности полученного результата. Необходимая степень надежности определяется спецификой производимых измерений. Доверительная вероятность должна быть, например, очень высокой при контроле размеров деталей самолетов и достаточно низкой при аналогичном контроле деталей ручной тележки. При большинстве обычных измерений можно ограничиться доверительной вероятностью 0,9 или 0,95, если не требуется более высокая степень надежности. Вывод Реально даже воздействие ограниченного числа возмущений приводит к нормальному распределению результатов измерений и их погрешностей. В настоящее время наиболее полно разработан математический аппарат именно для случайных величин, имеющих нормальное распределение. Если же предположение о нормальности распределения отвергается, то статистическая обработка наблюдений существенно усложняется и в таком случае невозможно рекомендовать общую методику статистической обработки наблюдений. Часто даже не известно, какая характеристика распределения может служить оценкой истинного значения измеряемой величины. Выше приведено аналитическое выражение нормального распределения для случайной измеряемой величины х
Нормальное распределение характеризуется двумя парамет-рами: математическим ожиданием m При многократных измерениях несмещенной, состоятельной и эффективной оценкой m
Нормальное распределение характеризуется двумя парамет-рами: математическим ожиданием m При многократных измерениях несмещенной, состоятельной и эффективной оценкой m
Нужно сказать, что среднее арифметическое дает оценку математического ожидания результата наблюдений и может быть оценкой истинного (действительного) значения Оценка S Эта оценка характеризует рассеяние Другими оценками рассеяния результатов в ряду измерений являются размах СКО является наиболее удобной характеристикой погрешности в случае ее дальнейшего преобразования. Например, для нескольких некоррелированных слагаемых СКО суммы определяется по формуле:
Оценка S характеризует рассеяние единичных результатов наблюдений относительно среднего значения, то есть в случае, если мы за результат измерений примем отдельный исправленный результат наблюдений. Если же в качестве результата измерений принимается среднее арифметическое, то СКО этого среднего
Нормальное распределение погрешностей имеет следующие свойства симметричность, математическое ожидание случайной погрешности равно нулю; малые погрешности более вероятны, чем большие; чем меньше , тем меньше рассеяние результатов наблюдений и больше вероятность малых погрешностей. Другим распространенным в метрологии распределением случайной величины является равномерное распределение Дифференциальная функция равномерного распределения имеет вид: f f При нормировке площади кривой распределения на единицу, получаем, что с(х Р
Кроме рассмотренных примеров распределений случайных величин существуют и другие важные для практического использования распределения дискретных случайных величин, например, биномиальное распределение и распределение Пуассона 4.5.5 Доверительные интервалы Приведенные выше оценки параметров распределения случайных величин в виде среднего арифметического для оценки математического ожидания и СКО для оценки дисперсии называются точечными оценками Симметричный интервал в границами ± Δх(Р) Доверительный интервал для нормального распределения находится по формуле: где коэффициент t Для нормального распределения существуют следующие соотношения между доверительными интервалами и доверительной вероятностью: 1 (Р=0,68), 2 (Р= 0,95), 3 (Р= 0,997), 4 (Р=0,999). Доверительные вероятности для выражения результатов измерений и погрешностей в различных областях науки и техники принимаются равными. Так, в технических измерениях принята доверительная вероятность 0,95. Лишь для особо точных и ответственных измерений принимают более высокие доверительные вероятности. В метрологии используют, как правило, доверитель-ные вероятности 0,97, в исключительных случаях 0,99. Необходимо отметить, что точность измерений должна соответствовать поставленной измерительной задаче. Излишняя точность ведет к неоправданному расходу средств. Недостаточная точность измерений может привести к принятию по его результатам ошибочных решений с самыми непредсказуемыми последствиями, вплоть до серьезных материальных потерь или катастроф. При проведении многократных измерений величины х где t Доверительный интервал для погрешности Недостатком доверительных интервалов при оценке случай-ных погрешностей является то, что при произвольно выбираемых доверительных вероятностях нельзя суммировать несколько погреш-ностей, т.к. доверительный интервал суммы не равен сумме довери-тельных интервалов. 4.6 Систематические погрешности Обнаружение и исключение систематических погрешностей представляет собой сложную задачу, требующую глубокого анализа всей совокупности результатов наблюдений, используемых средств, методов и условий измерений. При этом необходимо отметить, что устранение систематических погрешностей осуществляется не путем математической обработки результатов наблюдений, а применением соответствующих методов измерений Существуют некоторые специальные приемы проведения измерений Исключение Замещение Компенсация Наблюдения через период Измерения одной величины несколькими независимыми методами Измерения одной величины несколькими приборами Систематические погрешности устраняются путем введения поправок, Поправки для учета влияющих величин Так как полностью исключить систематические погрешности невозможно, то возникает задача оценивания границ или других параметров этих погрешностей. Как правило, систематическая погрешность результата измерения оценивается по ее состав-ляющим В связи с этим возникает задача суммирования если известна оценка границ погрешности, то ее распределение следует считать равномерным; если же известна оценка СКО погрешности, распределение следует считать нормальным Применение этого правила позволяет статистически суммировать составляющие систематической погрешности. В соответствии с ним при отсутствии дополнительной информации неисключенные остатки систематической погрешности рассматриваются как случайные величины, имеющие равномерное распределение Границы неисключенной систематической погрешности где Нужно сказать, что среднее арифметическое дает оценку математического ожидания результата наблюдений и может быть оценкой истинного (действительного) значения Оценка S Эта оценка характеризует рассеяние Другими оценками рассеяния результатов в ряду измерений являются размах СКО является наиболее удобной характеристикой погрешности в случае ее дальнейшего преобразования. Например, для нескольких некоррелированных слагаемых СКО суммы определяется по формуле:
Оценка S характеризует рассеяние единичных результатов наблюдений относительно среднего значения, то есть в случае, если мы за результат измерений примем отдельный исправленный результат наблюдений. Если же в качестве результата измерений принимается среднее арифметическое, то СКО этого среднего
Нормальное распределение погрешностей имеет следующие свойства симметричность, математическое ожидание случайной погрешности равно нулю; малые погрешности более вероятны, чем большие; чем меньше , тем меньше рассеяние результатов наблюдений и больше вероятность малых погрешностей. Другим распространенным в метрологии распределением случайной величины является равномерное распределение Дифференциальная функция равномерного распределения имеет вид: f f При нормировке площади кривой распределения на единицу, получаем, что с(х Р
Кроме рассмотренных примеров распределений случайных величин существуют и другие важные для практического использования распределения дискретных случайных величин, например, биномиальное распределение и распределение Пуассона 4.5.5 Доверительные интервалы Приведенные выше оценки параметров распределения случайных величин в виде среднего арифметического для оценки математического ожидания и СКО для оценки дисперсии называются точечными оценками Симметричный интервал в границами ± Δх(Р) Доверительный интервал для нормального распределения находится по формуле: где коэффициент t Для нормального распределения существуют следующие соотношения между доверительными интервалами и доверительной вероятностью: 1 (Р=0,68), 2 (Р= 0,95), 3 (Р= 0,997), 4 (Р=0,999). Доверительные вероятности для выражения результатов измерений и погрешностей в различных областях науки и техники принимаются равными. Так, в технических измерениях принята доверительная вероятность 0,95. Лишь для особо точных и ответственных измерений принимают более высокие доверительные вероятности. В метрологии используют, как правило, доверитель-ные вероятности 0,97, в исключительных случаях 0,99. Необходимо отметить, что точность измерений должна соответствовать поставленной измерительной задаче. Излишняя точность ведет к неоправданному расходу средств. Недостаточная точность измерений может привести к принятию по его результатам ошибочных решений с самыми непредсказуемыми последствиями, вплоть до серьезных материальных потерь или катастроф. При проведении многократных измерений величины х где t Доверительный интервал для погрешности Недостатком доверительных интервалов при оценке случай-ных погрешностей является то, что при произвольно выбираемых доверительных вероятностях нельзя суммировать несколько погреш-ностей, т.к. доверительный интервал суммы не равен сумме довери-тельных интервалов. 4.6 Систематические погрешности Обнаружение и исключение систематических погрешностей представляет собой сложную задачу, требующую глубокого анализа всей совокупности результатов наблюдений, используемых средств, методов и условий измерений. При этом необходимо отметить, что устранение систематических погрешностей осуществляется не путем математической обработки результатов наблюдений, а применением соответствующих методов измерений Существуют некоторые специальные приемы проведения измерений Исключение Замещение Компенсация Наблюдения через период Измерения одной величины несколькими независимыми методами Измерения одной величины несколькими приборами Систематические погрешности устраняются путем введения поправок, Поправки для учета влияющих величин Так как полностью исключить систематические погрешности невозможно, то возникает задача оценивания границ или других параметров этих погрешностей. Как правило, систематическая погрешность результата измерения оценивается по ее состав-ляющим В связи с этим возникает задача суммирования если известна оценка границ погрешности, то ее распределение следует считать равномерным; если же известна оценка СКО погрешности, распределение следует считать нормальным Применение этого правила позволяет статистически суммировать составляющие систематической погрешности. В соответствии с ним при отсутствии дополнительной информации неисключенные остатки систематической погрешности рассматриваются как случайные величины, имеющие равномерное распределение Границы неисключенной систематической погрешности где При числе слагаемых меньших или равных 3 значения суммируются арифметически по модулю. Если же суммировать НСП арифметически при любом числе слагаемых, то полученная оценка будет хотя и надежной, но завышенной. Доверительную вероятность для вычисления границ неисключенной систематической погрешности принимают той же, что при вычислении доверительных границ случайной погрешности. 4.7 Методы обработки результатов прямых измерений Основные положения методов обработки результатов прямых измерений с многократными наблюдениями определены в ГОСТ 8.207-76. За результат измерения принимают среднее арифмети-ческое Следует отметить, что иногда в литературе вместо термина результат При статистической обработке групп результатов наблюдений следует выполнять следующие операции Исключить из каждого наблюдения известную систематическую погрешность и получить исправленный результат отдельного наблюдения x Вычислить среднее арифметическое исправленных результатов наблюдений, принимаемое за результат измерения: Т группы наблюдений: Проверить наличие грубых погрешностей
Проверить наличие грубых погрешностей
арифметического) Проверить гипотезу о нормальности распределения результатов наблюдений. Существуют различные приближенные методы проверки нормальности распределения результатов наблюдений. Некоторые из них приведены в ГОСТ 8.207-76. При числе наблюдений меньше 15 в соответствии с этим ГОСТ принадлежность их к нормальному распределению не проверяют. Доверительные границы случайной погрешности определяют лишь в том случае, если заранее известно, что результаты наблюдений принадлежат этому распределению. Приближенно о характере распределения можно судить, построив гистограмму результатов наблюдений. Математические методы проверки нормальности распределения рассматриваются в специальной литературе. Вычислить доверительные границы случайной погрешности (случайной составляющей погрешности) результата измерения где t Если
Коэффициент К вычисляют по эмпирической формуле:
Доверительная вероятность для вычисления Проверить гипотезу о нормальности распределения результатов наблюдений. Существуют различные приближенные методы проверки нормальности распределения результатов наблюдений. Некоторые из них приведены в ГОСТ 8.207-76. При числе наблюдений меньше 15 в соответствии с этим ГОСТ принадлежность их к нормальному распределению не проверяют. Доверительные границы случайной погрешности определяют лишь в том случае, если заранее известно, что результаты наблюдений принадлежат этому распределению. Приближенно о характере распределения можно судить, построив гистограмму результатов наблюдений. Математические методы проверки нормальности распределения рассматриваются в специальной литературе. Вычислить доверительные границы случайной погрешности (случайной составляющей погрешности) результата измерения где t Если
Коэффициент К вычисляют по эмпирической формуле:
Доверительная вероятность для вычисления Погрешность от применения последней формулы для композиции равномерного (для НСП) и нормального (для случайной погрешности) распределений достигает 12 % при доверительной вероятности 0,99. 9. Записать результат измерений. Написание результата измерений предусмотрено в двух вариантах, так как следует различать измерения, когда получение значения измеряемой величины является конечной целью, и измерения, результаты которых будут использоваться для дальнейших вычислений или анализа. В
где – результат измерения. Во втором случае должны быть известны характеристики составляющих погрешности измерения – оценка среднего квадратического отклонения результата измерения , границы НСП , число выполненных наблюдений Погрешность от применения последней формулы для композиции равномерного (для НСП) и нормального (для случайной погрешности) распределений достигает 12 % при доверительной вероятности 0,99. 9. Записать результат измерений. Написание результата измерений предусмотрено в двух вариантах, так как следует различать измерения, когда получение значения измеряемой величины является конечной целью, и измерения, результаты которых будут использоваться для дальнейших вычислений или анализа. В
где – результат измерения. Во втором случае должны быть известны характеристики составляющих погрешности измерения – оценка среднего квадратического отклонения результата измерения , границы НСП , число выполненных наблюдений Если границы НСП вычислены в соответствии с п.4.6, то дополнительно указывают доверительную вероятность Р. Оценки , и производные от их величины могут быть выражены как в абсолютной форме, то есть в единицах измеряемой величины, так и относительной, то есть как отношение абсолютного значения данной величины к результату измерения. При этом вычисления по формулам настоящего раздела следует проводить с использованием величин, выраженных только в абсолютной или в относительной форме. 4.8 Однократные измерения В технике большинство измерений являются однократ-ными Случайная составляющая погрешности не может быть рассчитана по результатам измерения, хотя она неявно присутствует в нем. В качестве оценки случайной составляющей погрешности Оценку систематических погрешностей Основные этапы Учитывается систематическая погрешность прибора. Оценивается систематическая погрешность метода измерений. Оцениваются по документации на прибор дополнительные систематические погрешности, обусловленные влияющими величинами. Из отсчета прибора исключаются все известные система-тические погрешности (в соответствии с пп. 1, 2, 3) и опреде-ляется исправленный результат измерения, который содержит НСП и случайные составляющие погрешности. Оцениваются границы i составляющих НСП, распределение которых принимается равномерным. Ими могут быть, например, погрешности эталонов при поверке СИ, погрешности поправок и т.п. После этого определяются границы суммарной НСП по приведенным выше формулам. Предварительно перед использованием прибора определяется коэффициент вариации оценка случайной погрешности, которая используется при последующих однократных измерениях с прибором. Сопоставляются оценки НСП и случайной погрешности по критериям предыдущего раздела и при возможности пренебрежения какой-либо из них определяются границы погрешности результата Если необходимо учитывать обе составляющие, то в качестве границы погрешности результата измерения На практике часто встречаются измерения, для которых нет необходимости точно оценивать погрешность. В таких измерениях в качестве результата принимают значение отсчета х Мокров стандартизация и сертификацияУчебное пособие Человека “Дубна” Кафедра “Биофизика 3. СЛУЧАЙНЫЕ 3.1. Понятие При а) погрешность б) в Сказанное Теория Теория Исходя Случайные Присутствие Таким где Если границы НСП вычислены в соответствии с п.4.6, то дополнительно указывают доверительную вероятность Р. Оценки , и производные от их величины могут быть выражены как в абсолютной форме, то есть в единицах измеряемой величины, так и относительной, то есть как отношение абсолютного значения данной величины к результату измерения. При этом вычисления по формулам настоящего раздела следует проводить с использованием величин, выраженных только в абсолютной или в относительной форме. 4.8 Однократные измерения В технике большинство измерений являются однократ-ными Случайная составляющая погрешности не может быть рассчитана по результатам измерения, хотя она неявно присутствует в нем. В качестве оценки случайной составляющей погрешности Оценку систематических погрешностей Основные этапы Учитывается систематическая погрешность прибора. Оценивается систематическая погрешность метода измерений. Оцениваются по документации на прибор дополнительные систематические погрешности, обусловленные влияющими величинами. Из отсчета прибора исключаются все известные система-тические погрешности (в соответствии с пп. 1, 2, 3) и опреде-ляется исправленный результат измерения, который содержит НСП и случайные составляющие погрешности. Оцениваются границы i составляющих НСП, распределение которых принимается равномерным. Ими могут быть, например, погрешности эталонов при поверке СИ, погрешности поправок и т.п. После этого определяются границы суммарной НСП по приведенным выше формулам. Предварительно перед использованием прибора определяется коэффициент вариации оценка случайной погрешности, которая используется при последующих однократных измерениях с прибором. Сопоставляются оценки НСП и случайной погрешности по критериям предыдущего раздела и при возможности пренебрежения какой-либо из них определяются границы погрешности результата Если необходимо учитывать обе составляющие, то в качестве границы погрешности результата измерения На практике часто встречаются измерения, для которых нет необходимости точно оценивать погрешность. В таких измерениях в качестве результата принимают значение отсчета х Мокров стандартизация и сертификацияУчебное пособие Человека “Дубна” Кафедра “Биофизика 3. СЛУЧАЙНЫЕ 3.1. Понятие При а) погрешность б) в Сказанное Теория Теория Исходя Случайные Присутствие Таким где Случайные P( 1)=F( 1), либо P( 1 2)=F( 2)–F( 1)/ Функция В 3.2. Нормальное Большинство
где: Нормальное Математическое Мерой где: Нормальное Математическое Мерой
где где Дисперсия
СКО
т.е. Нормальное Иногда
Для
3.3. Точечные Повторив При Оценка
СКО
т.е. Нормальное Иногда
Для
3.3. Точечные Повторив При Оценка
Оценка Оценка Оценка Существуют Для
Оценка и *Среднее
При
В а) случайные б) дисперсия При
Оценка и *Среднее
При
В а) случайные б) дисперсия При
Для
где
Для
где Для
Вывод:
Вывод:
Таким
Таким
Вывод: Итог Что 3.4. Оценка Представление В Ранее, Доверительный Предположим, P[(X–t p )Q(X+t p )]=2Ф(t p) Это Половина Проведение Вывод: Итог Что 3.4. Оценка Представление В Ранее, Доверительный Предположим, P[(X–t p )Q(X+t p )]=2Ф(t p) Это Половина Проведение P[(–t p ) Q (+t p )]=2Ф(t p)–1. где
Полученный
Половина называется Итог
Запись 3.5 Оценка Вычисляемая
Приклад Електронним 1) оцінити Полученный
Половина называется Итог
Запись 3.5 Оценка Вычисляемая
Приклад Електронним 1) оцінити 2) визначити 3) оцінити
4) оцінити
5) оцінити
6) оцінити Розв’язання 1) Результат
2) Визначаємо
4) оцінити
5) оцінити
6) оцінити Розв’язання 1) Результат
2) Визначаємо
Возможно, вам также будет интересно:
Подписаться
авторизуйтесь
0 комментариев
Старые
|

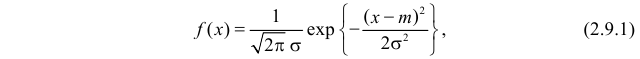
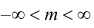
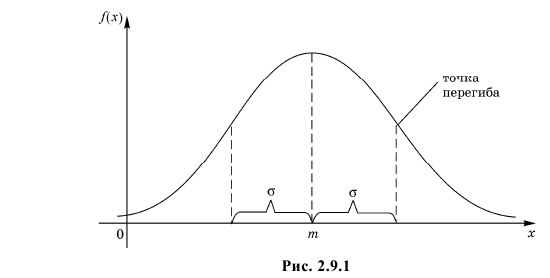
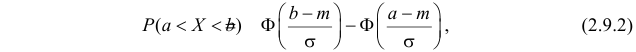
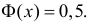
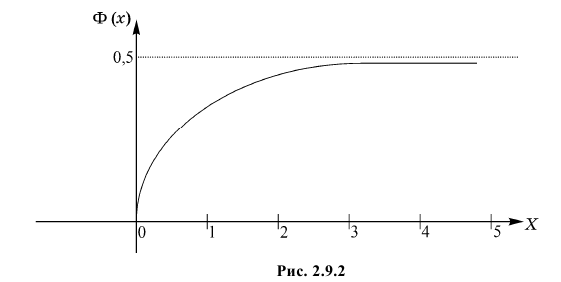
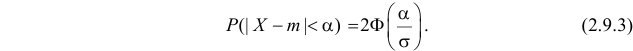
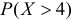
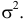
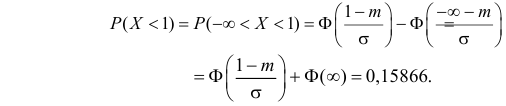
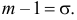
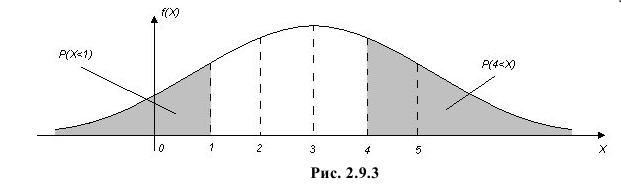
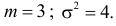
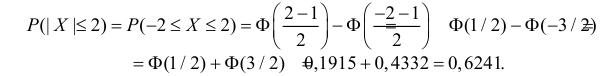
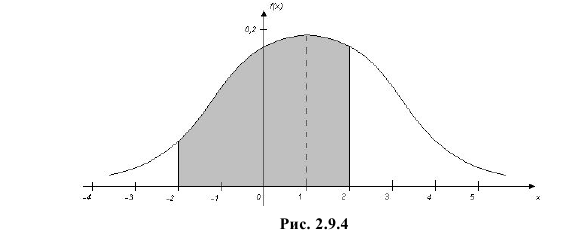
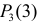
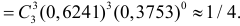
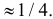
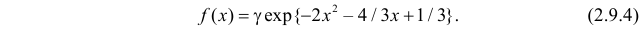
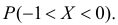
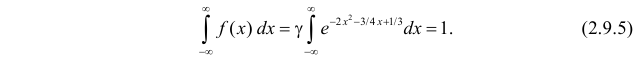
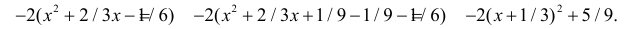
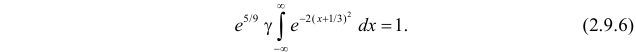

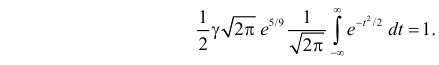

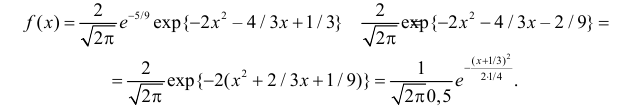
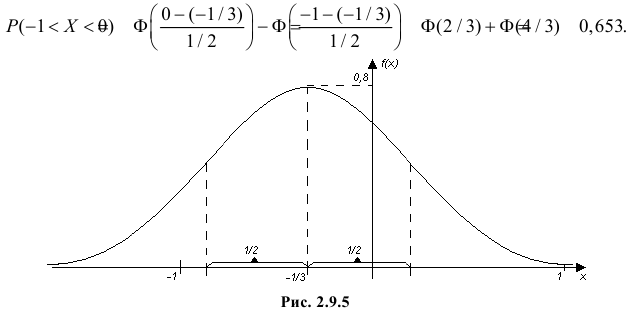
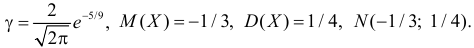
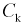
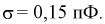
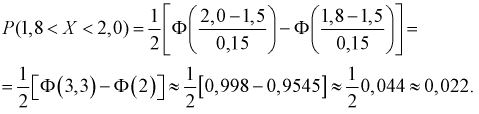
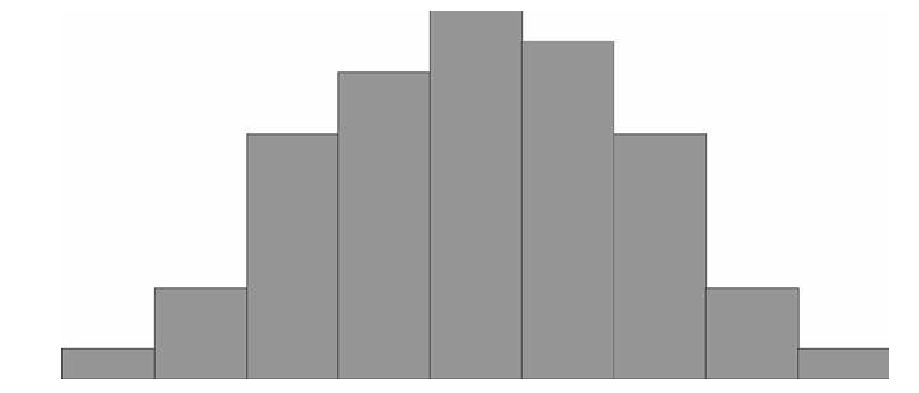
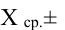
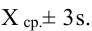
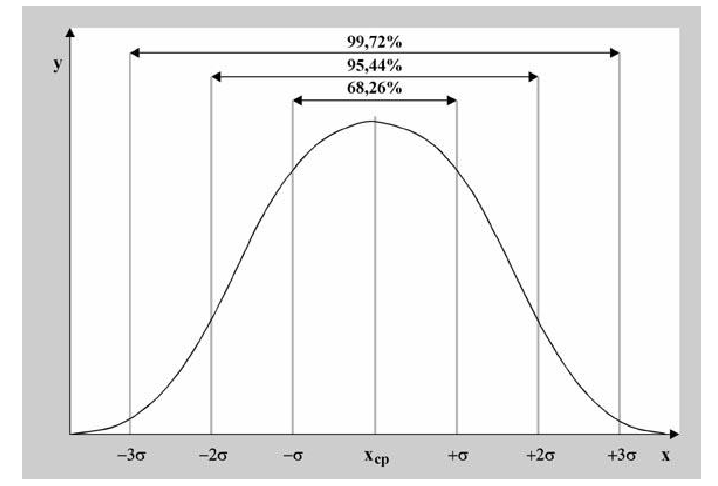
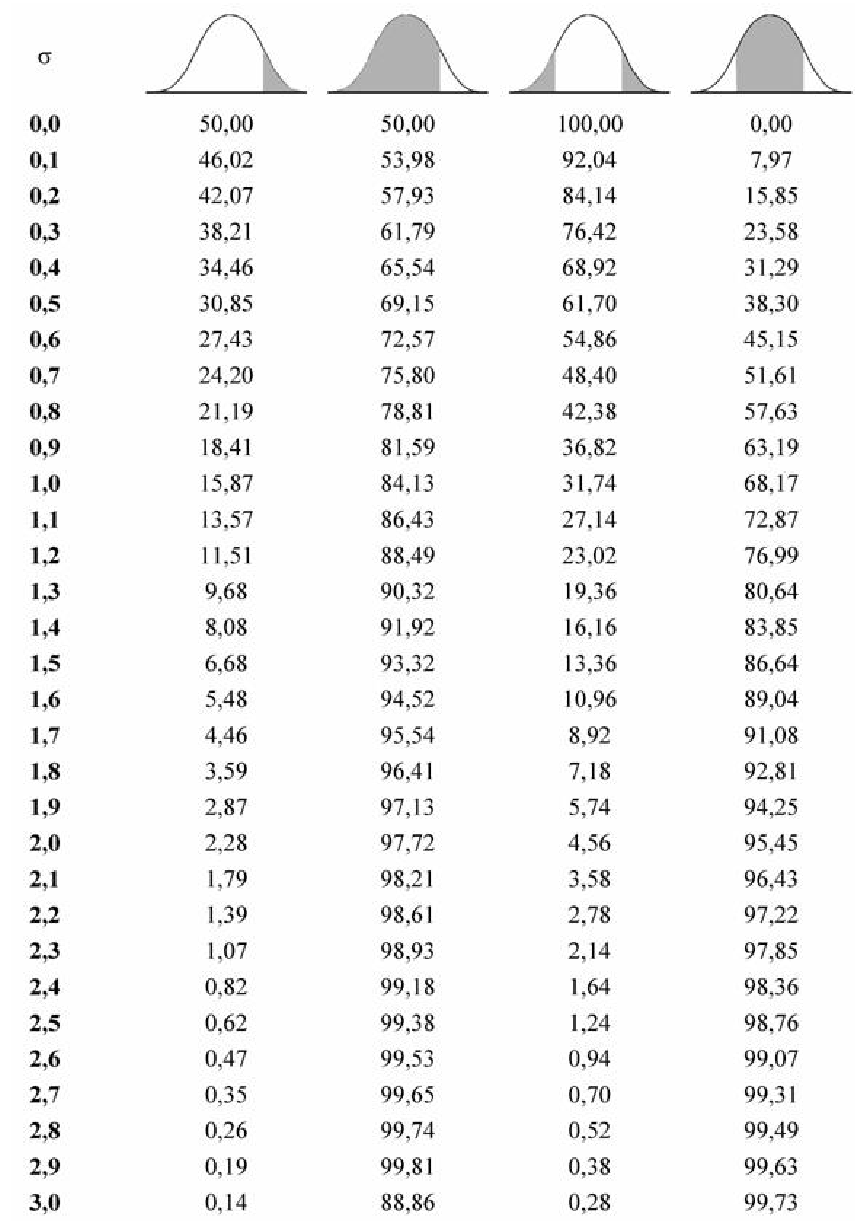
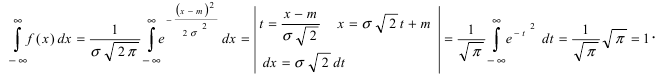
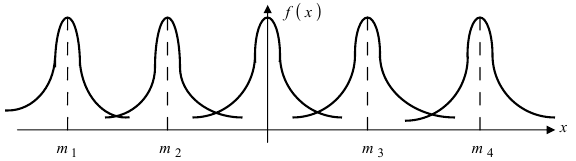
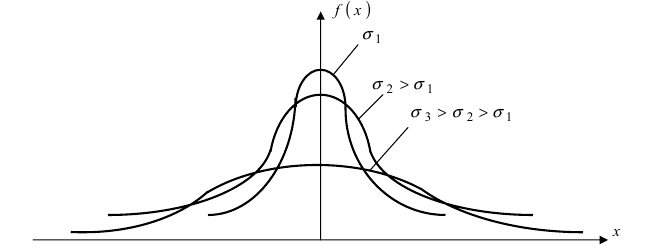
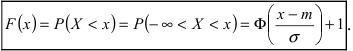
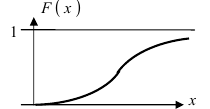
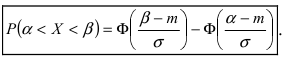
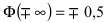 — график функции Лапласа имеет горизонтальные асимптоты
— график функции Лапласа имеет горизонтальные асимптоты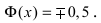
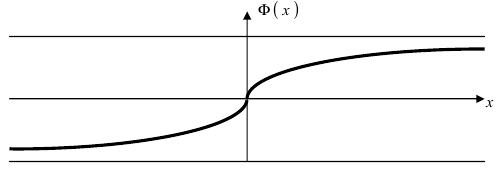
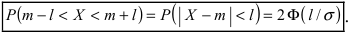
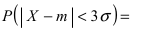
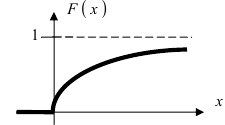
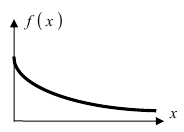
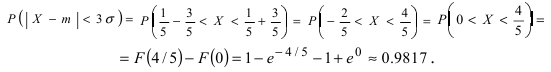









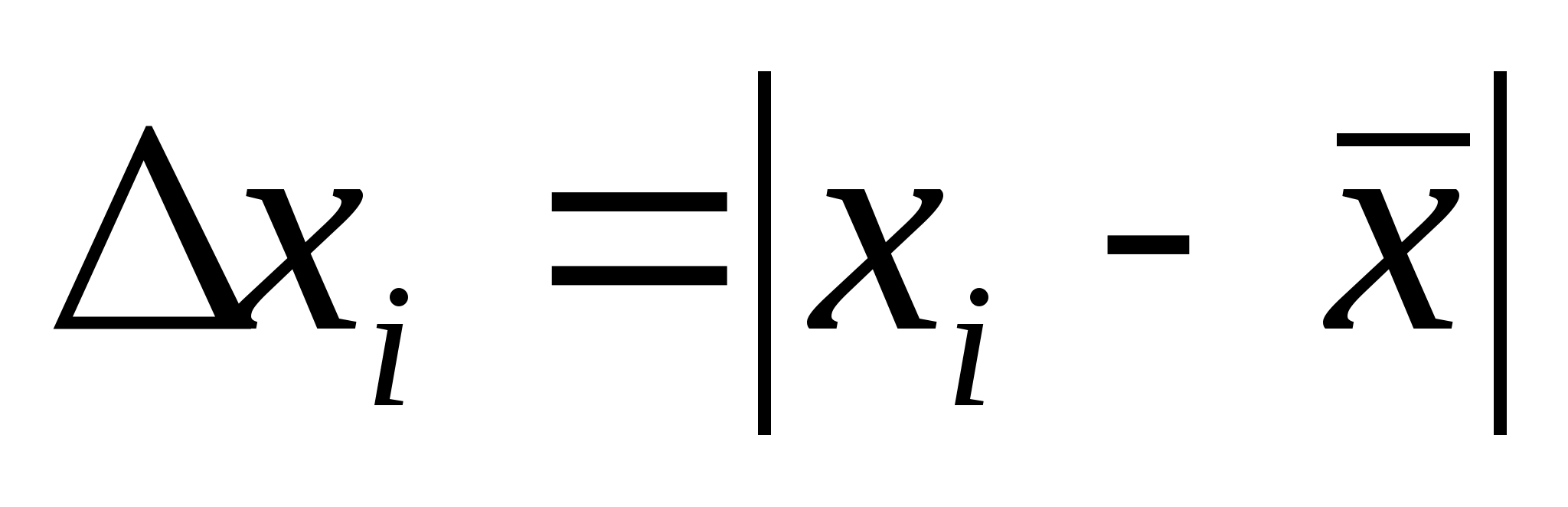
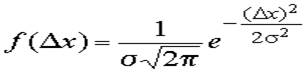 (4.11)+D — доверительным интервалом. Обычно его выражают в долях средней квадратической погрешности
(4.11)+D — доверительным интервалом. Обычно его выражают в долях средней квадратической погрешности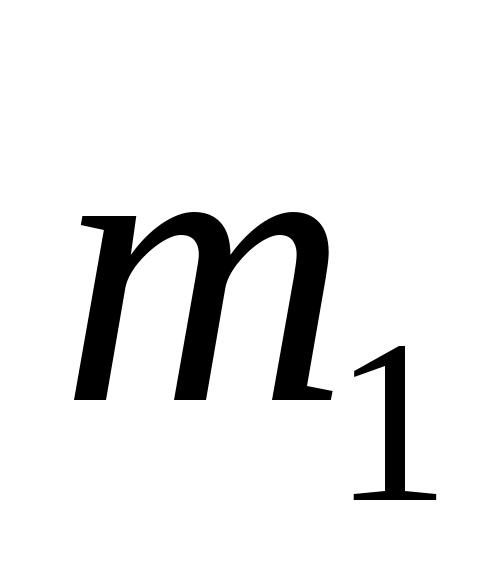 и откладывания по оси абсцисс погрешности
и откладывания по оси абсцисс погрешности 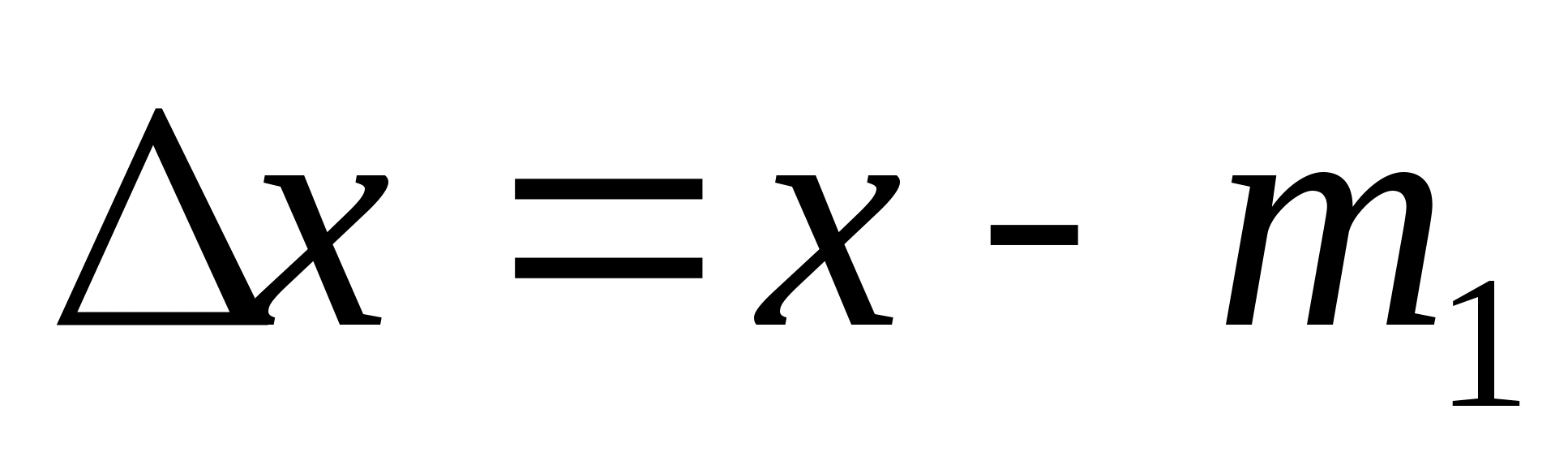 .
.
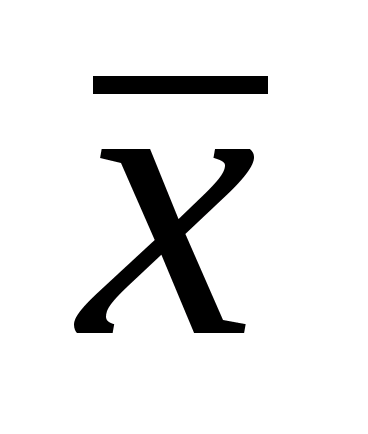 и откладывания по оси абсцисс погрешности
и откладывания по оси абсцисс погрешности  .
.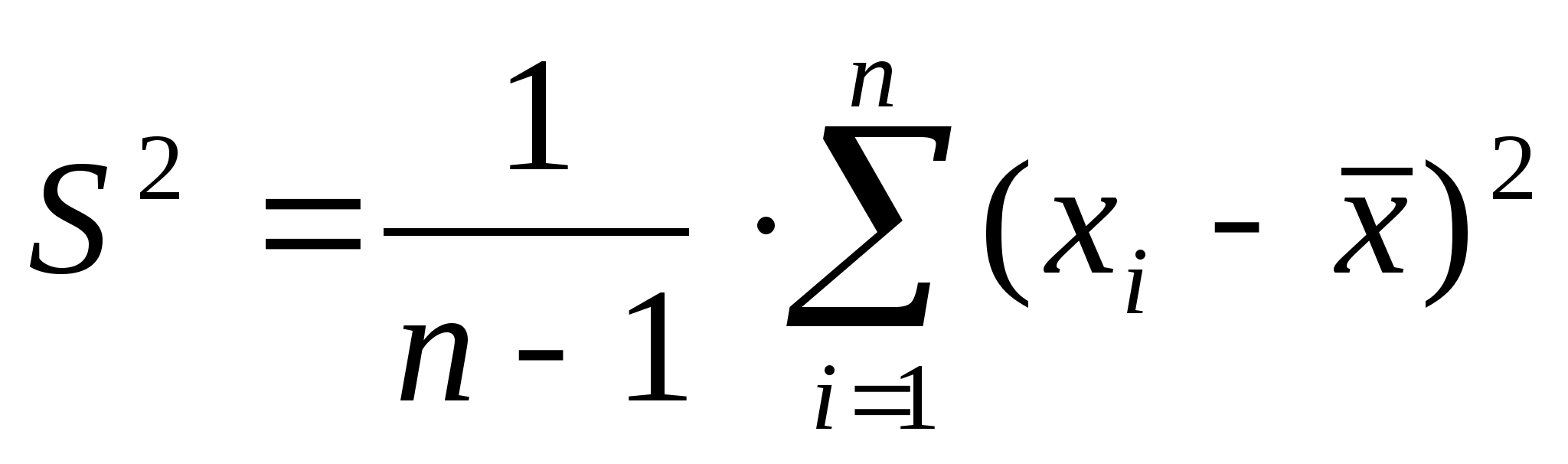
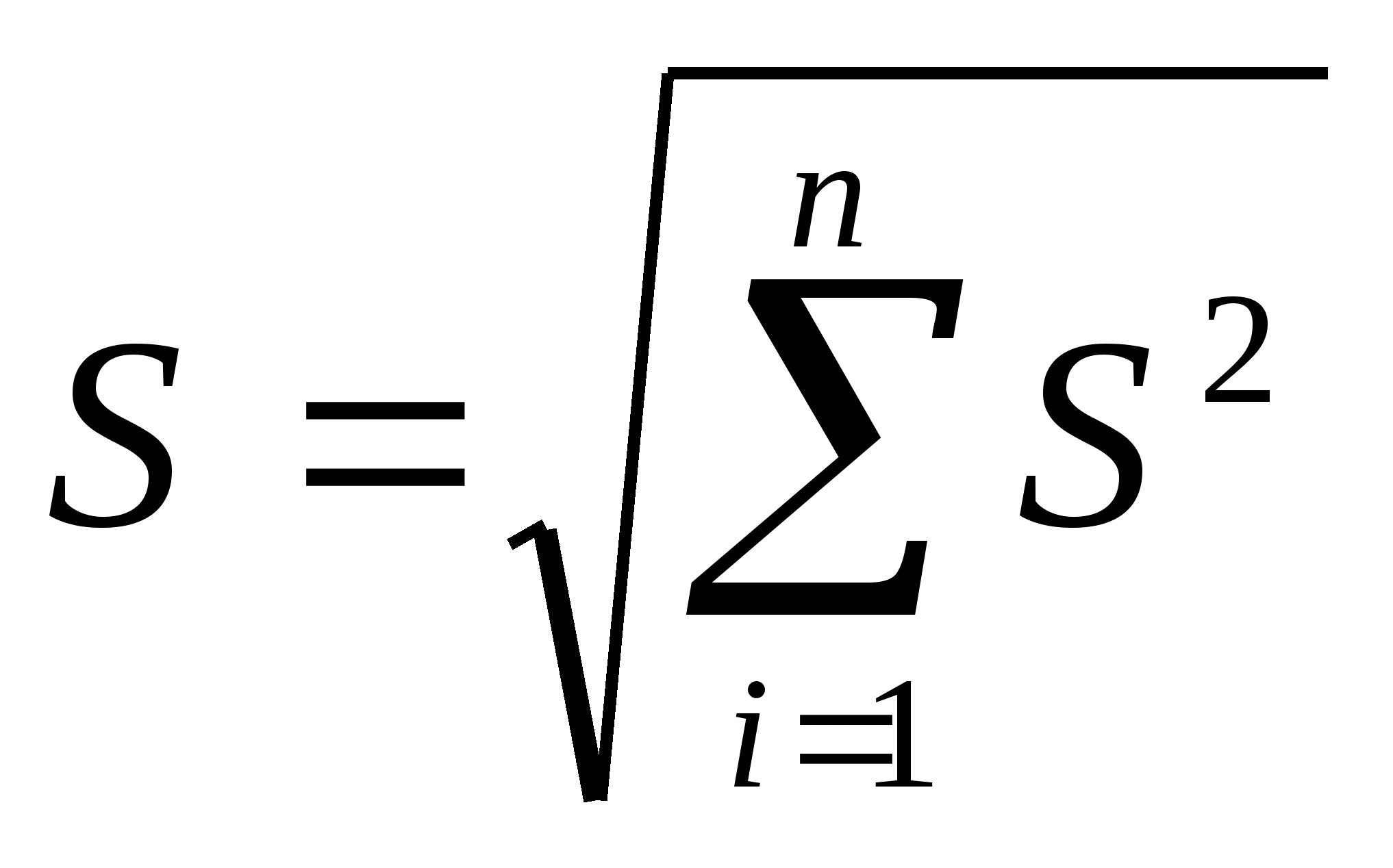 .
.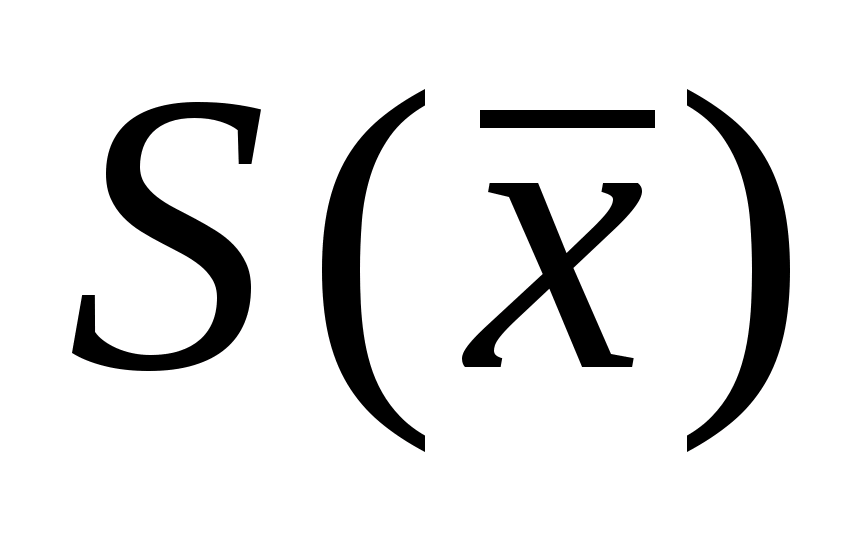 определяется по формуле:
определяется по формуле: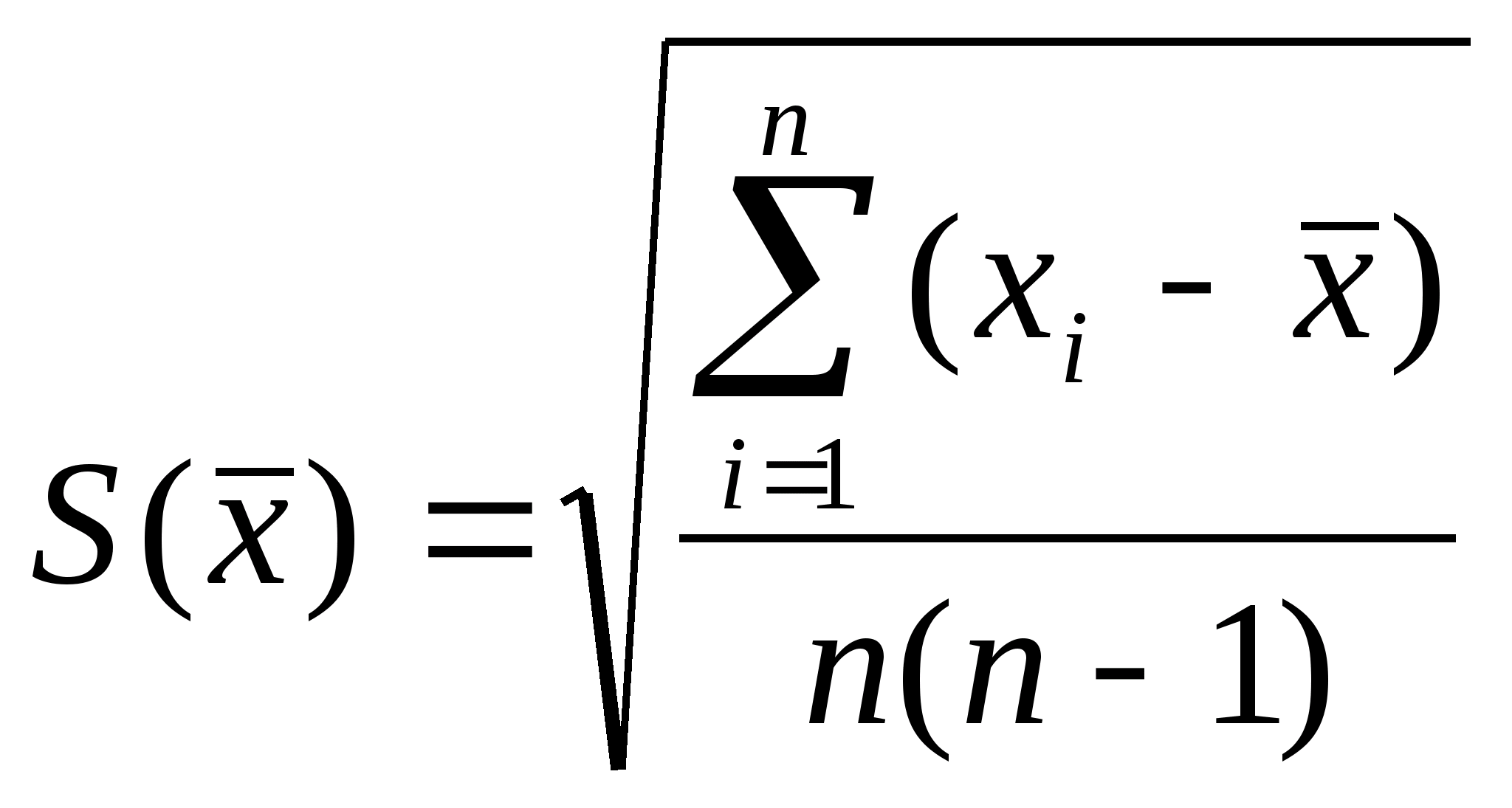
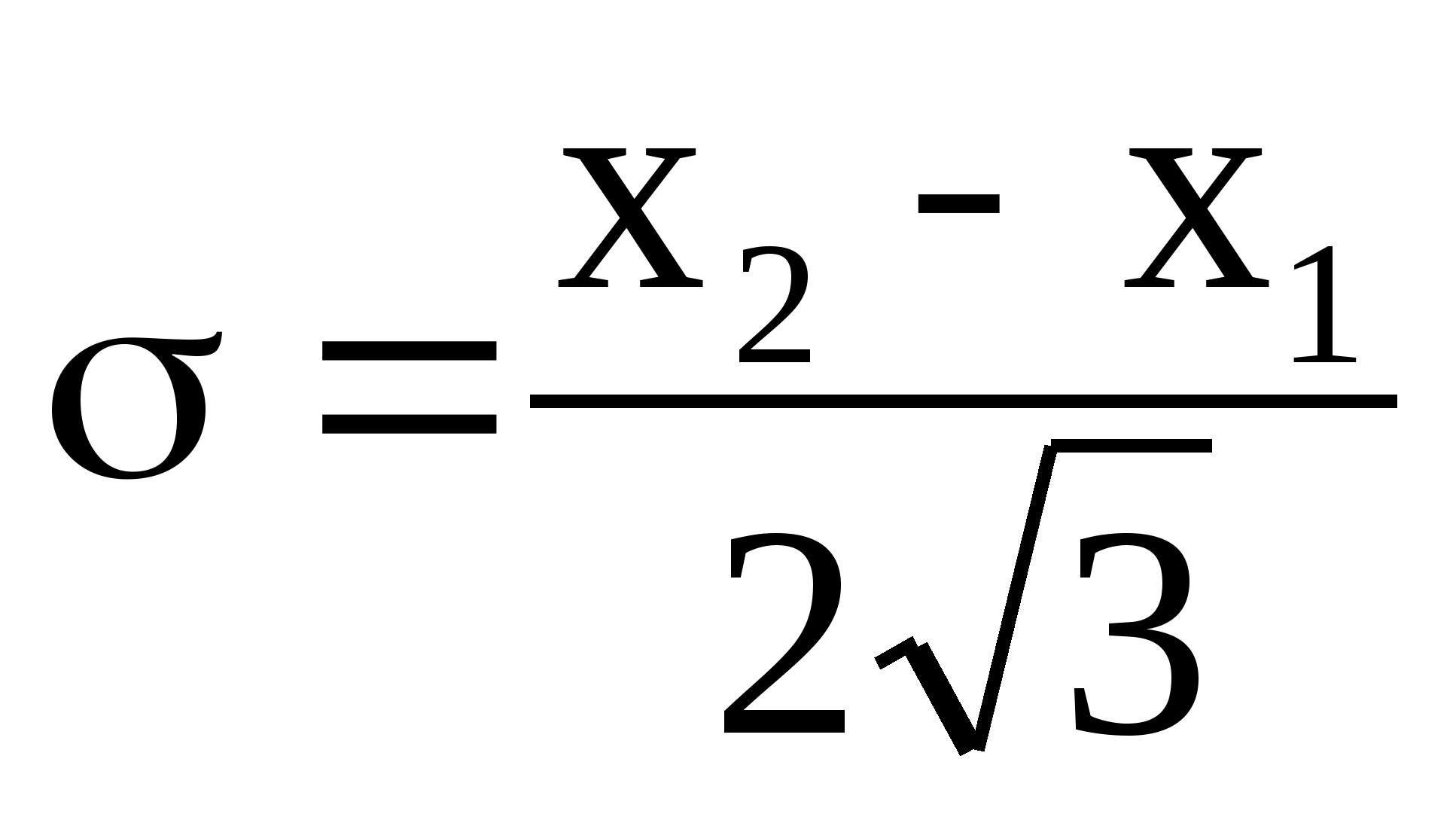 авномерное распределение характеризуется математичес-ким ожиданием
авномерное распределение характеризуется математичес-ким ожиданием 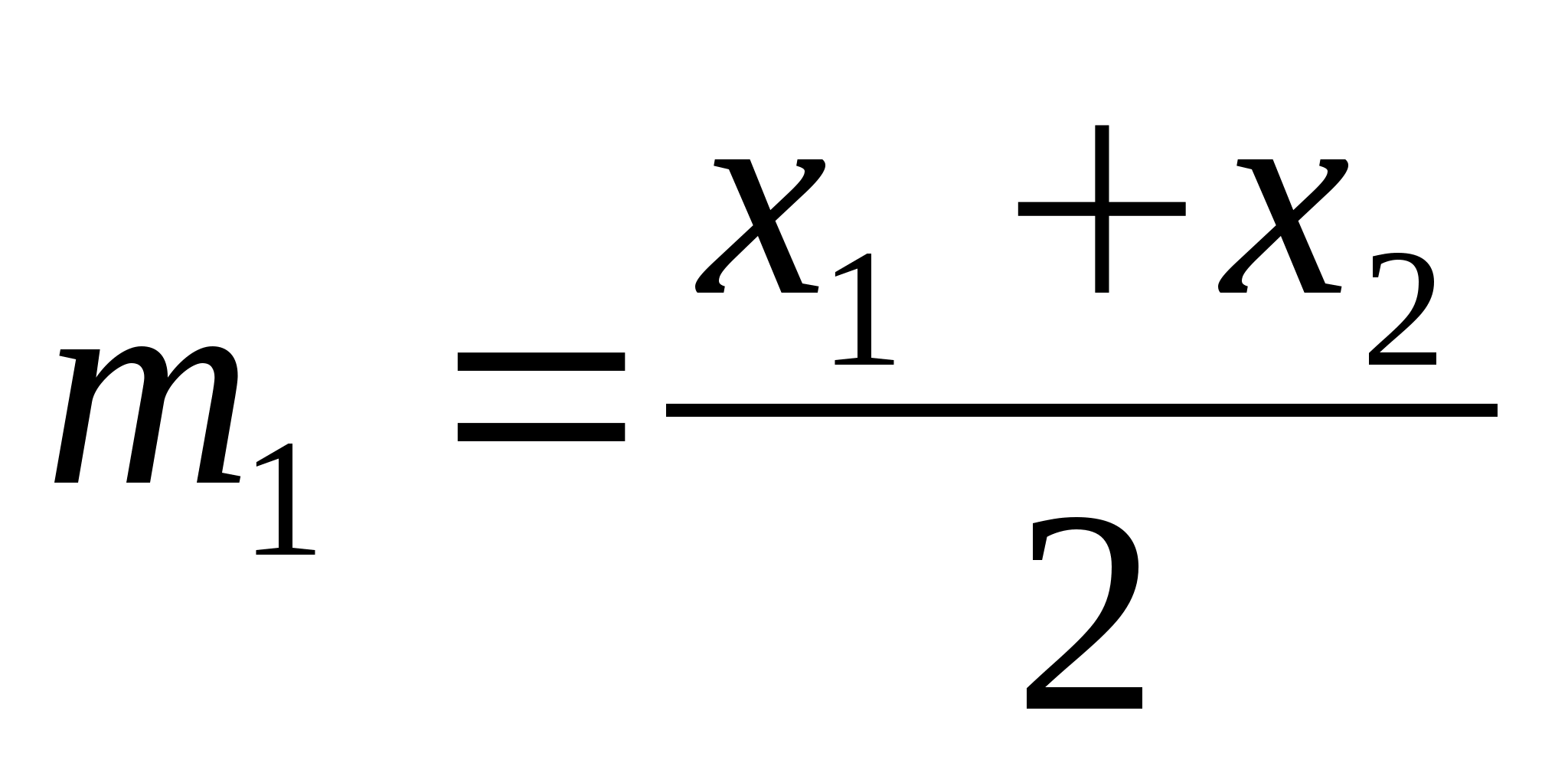 , дисперсией
, дисперсией 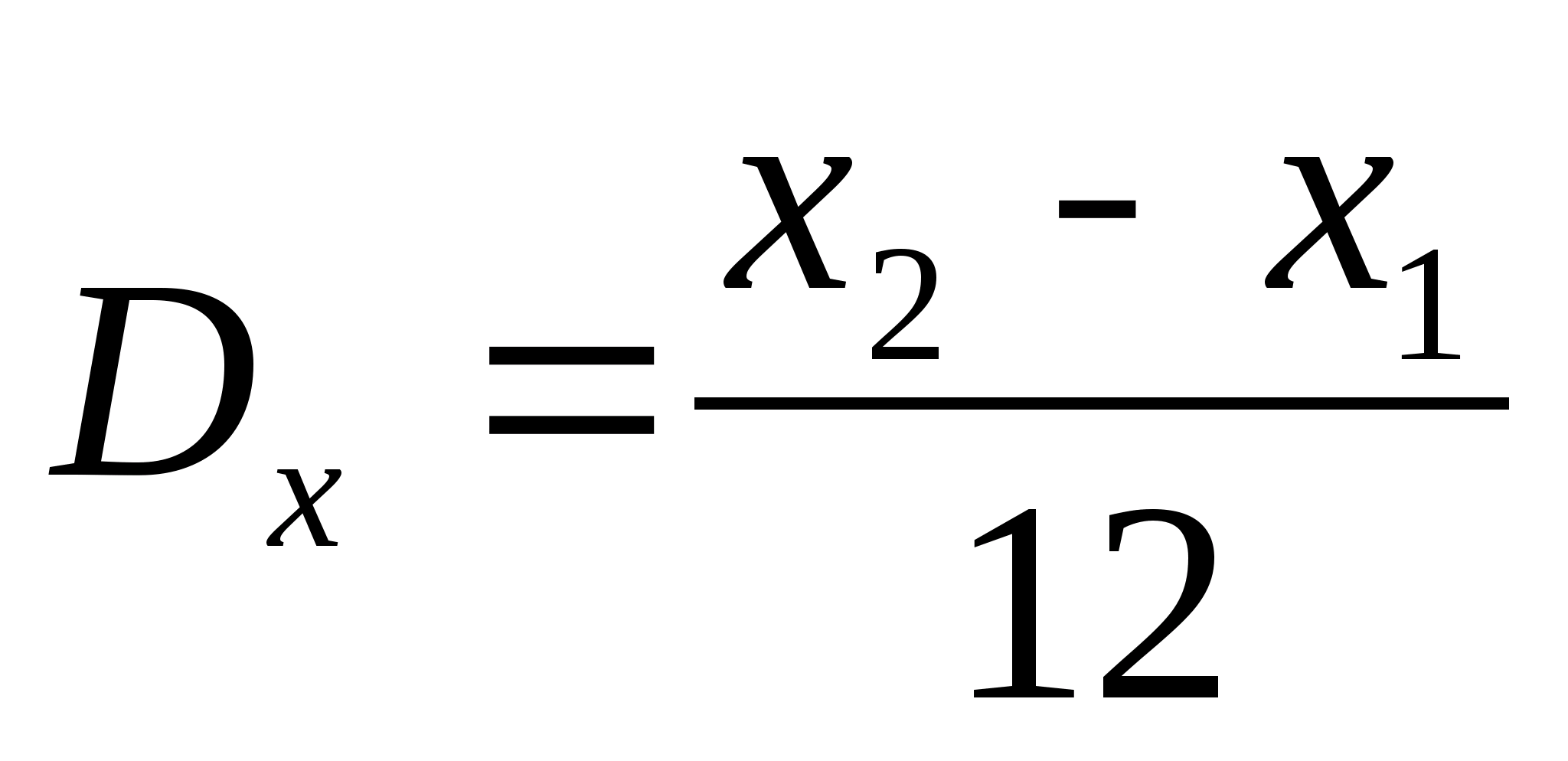 или СКО.
или СКО.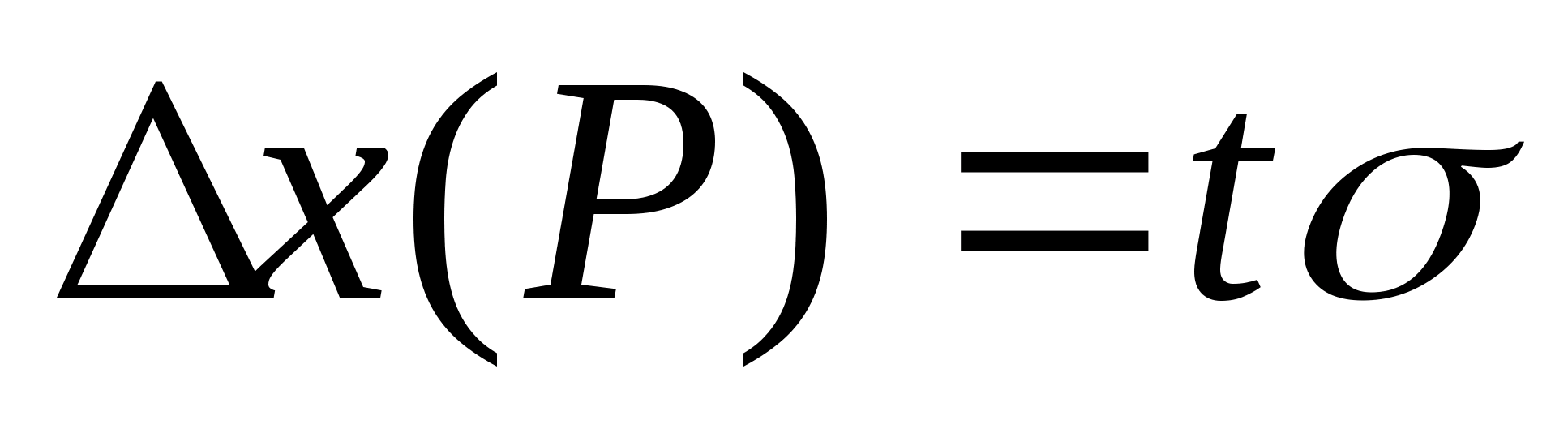
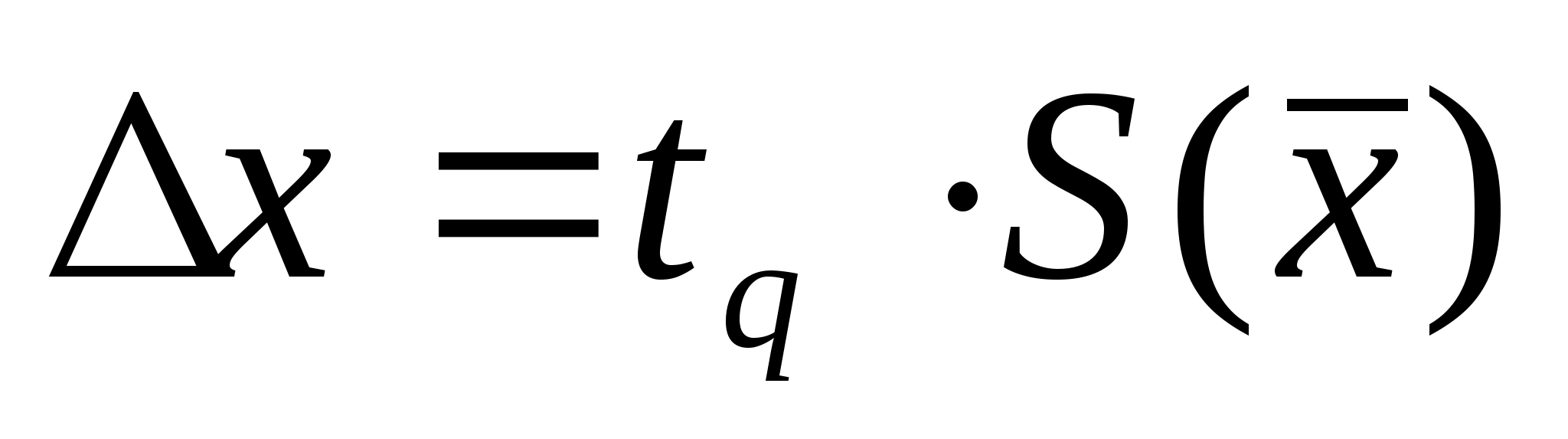
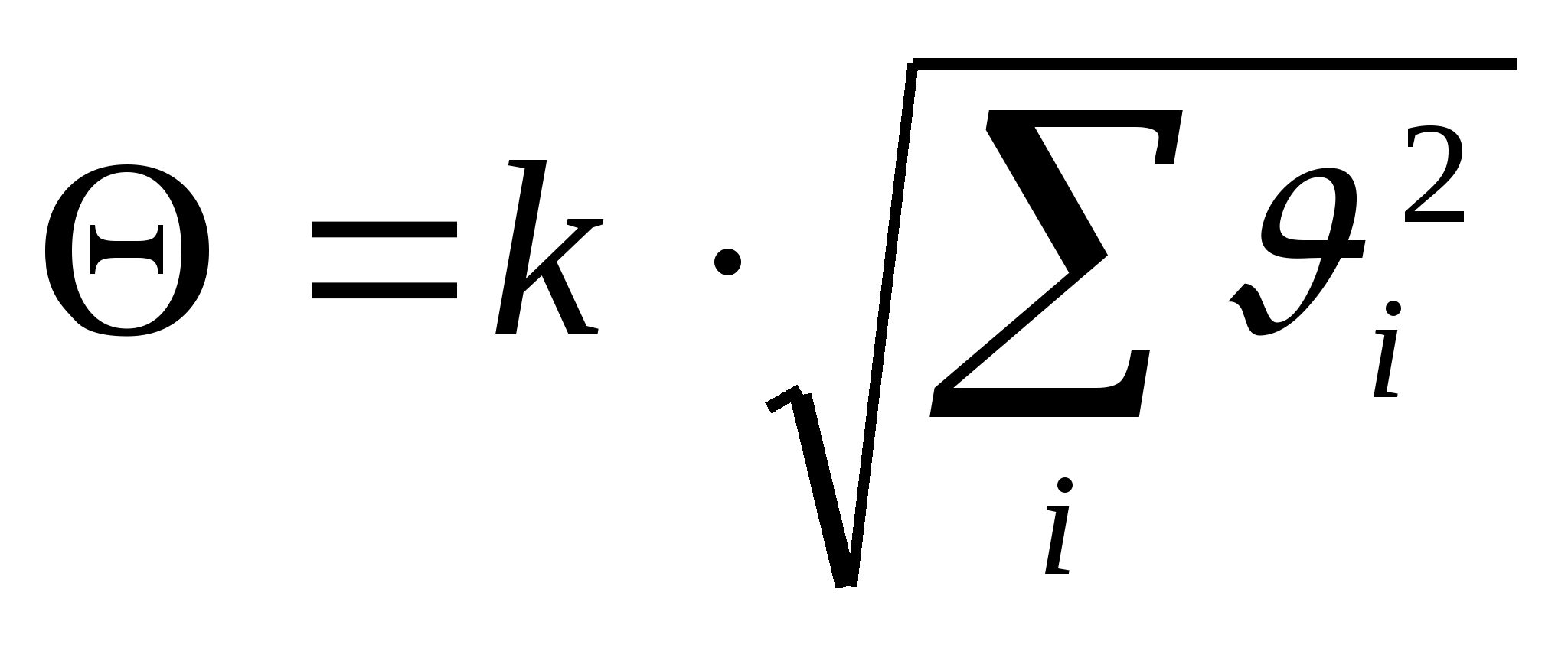
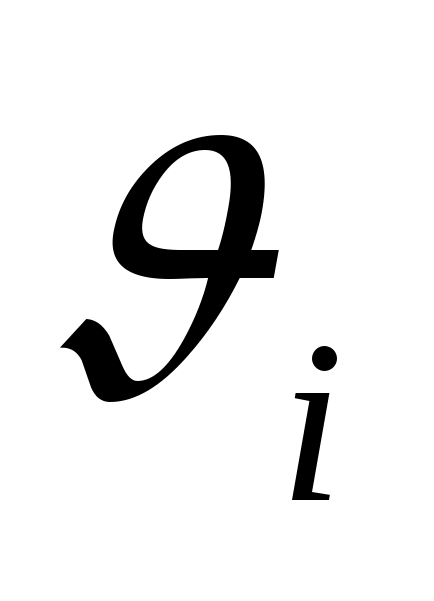 .
.
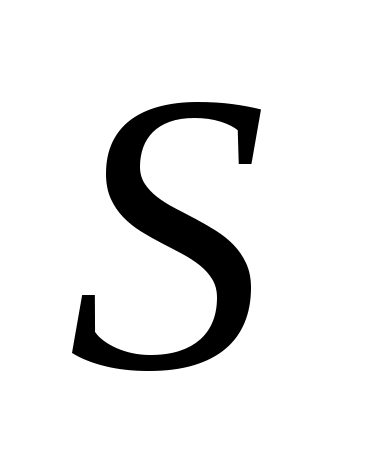
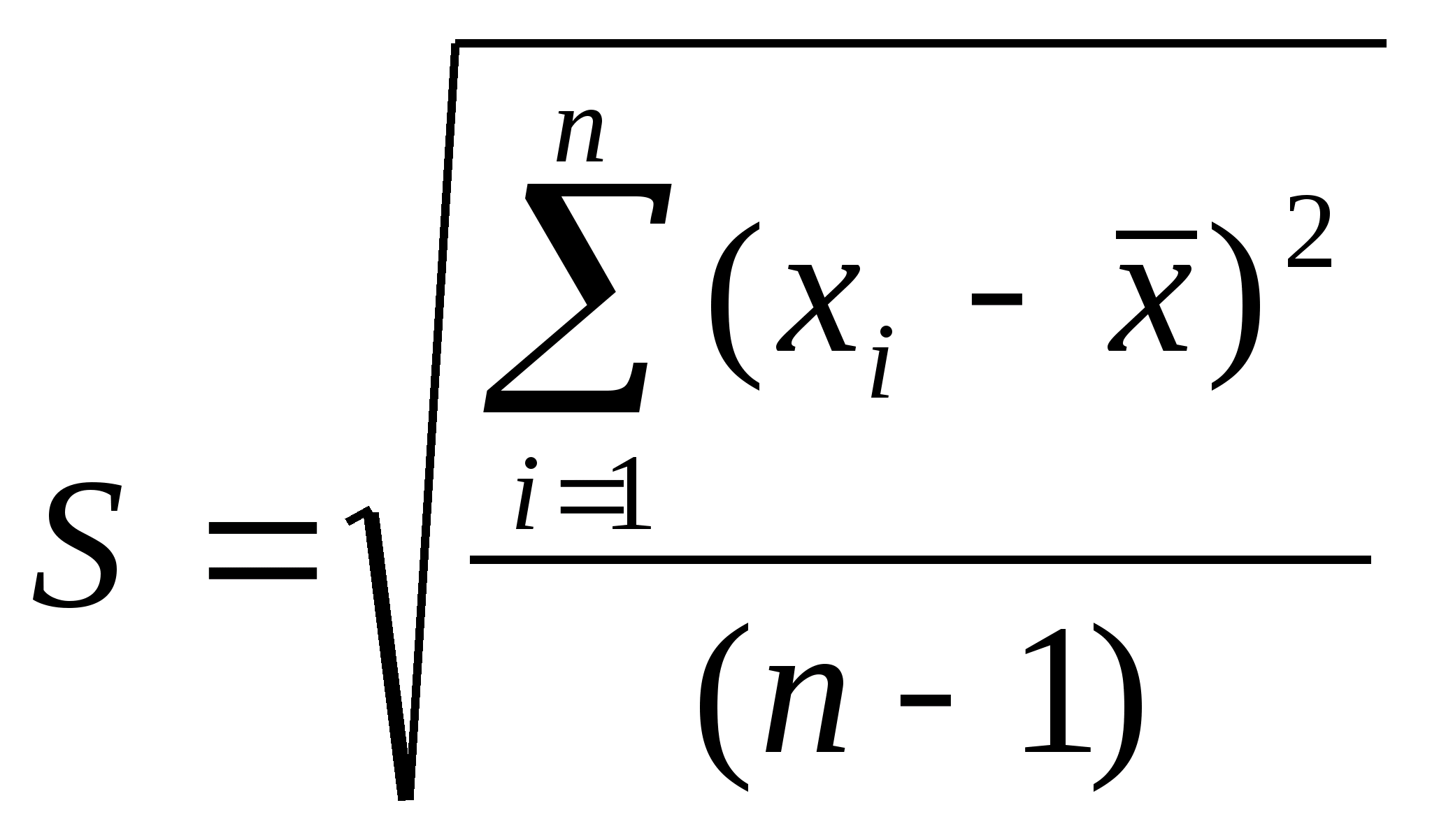
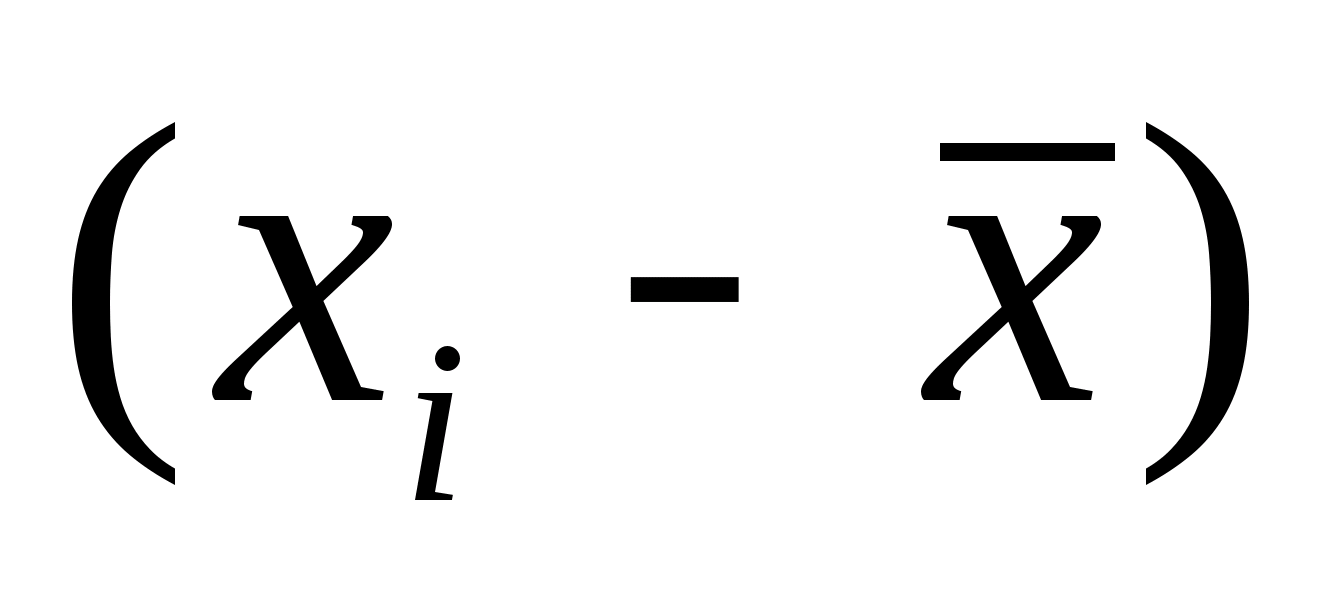 , которые выходят за пределы 3S
, которые выходят за пределы 3S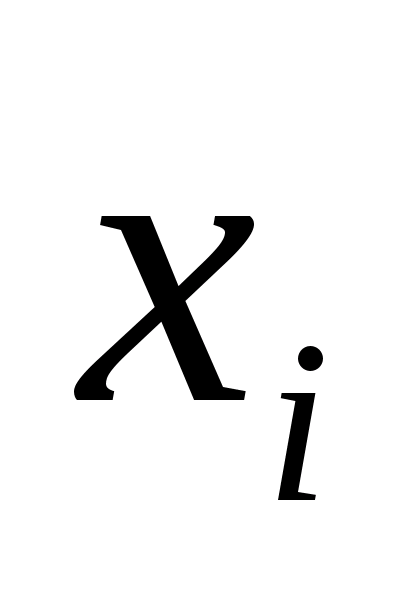
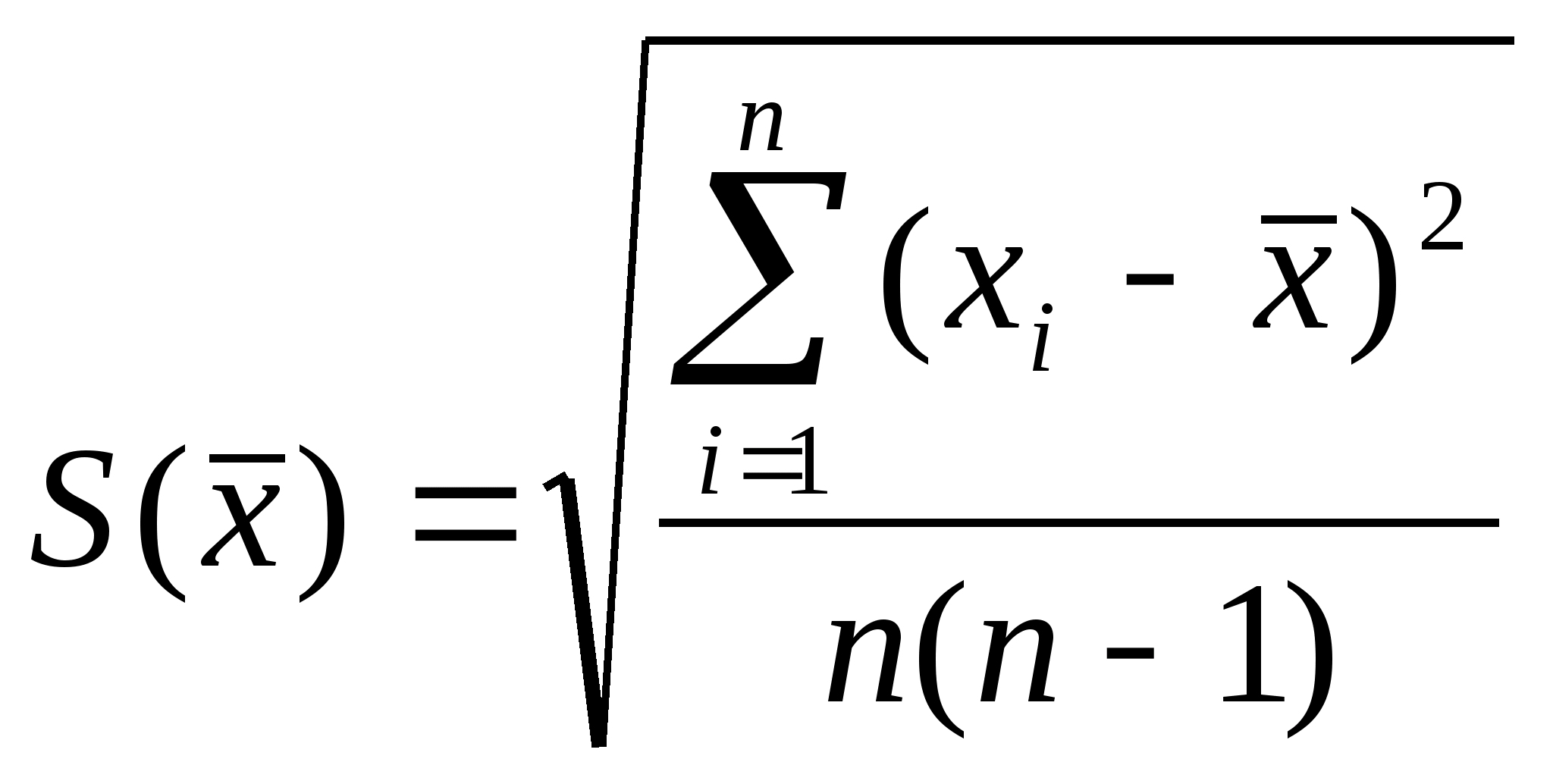
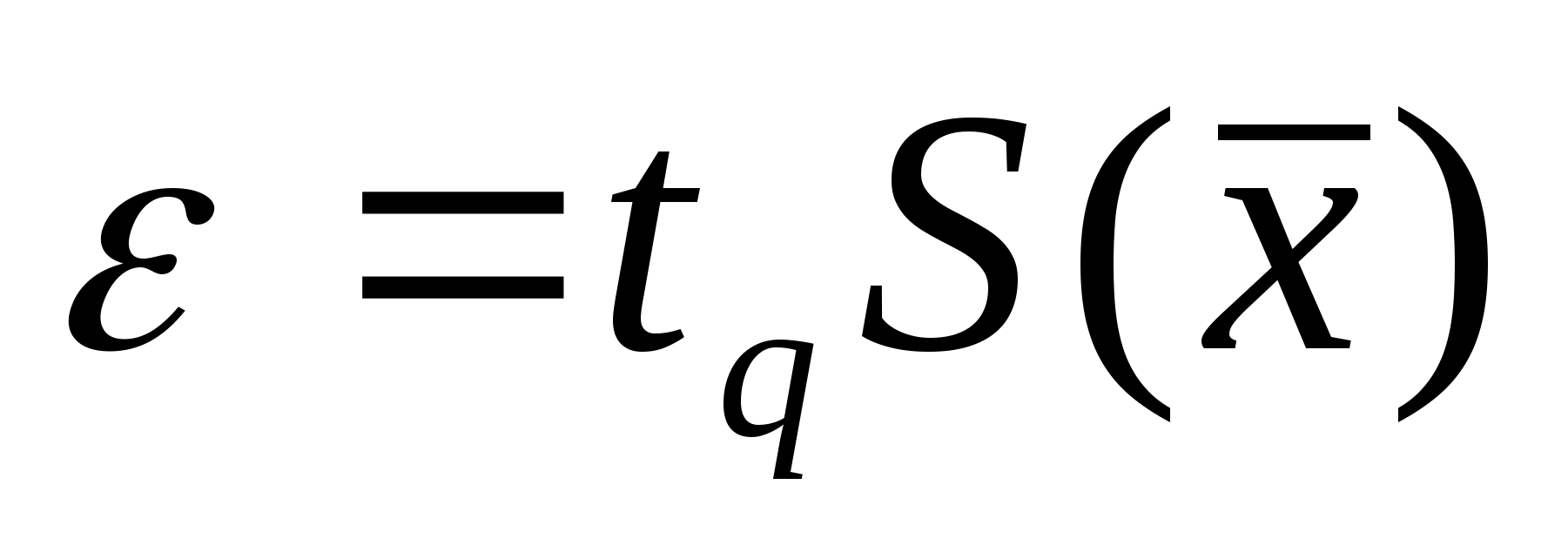
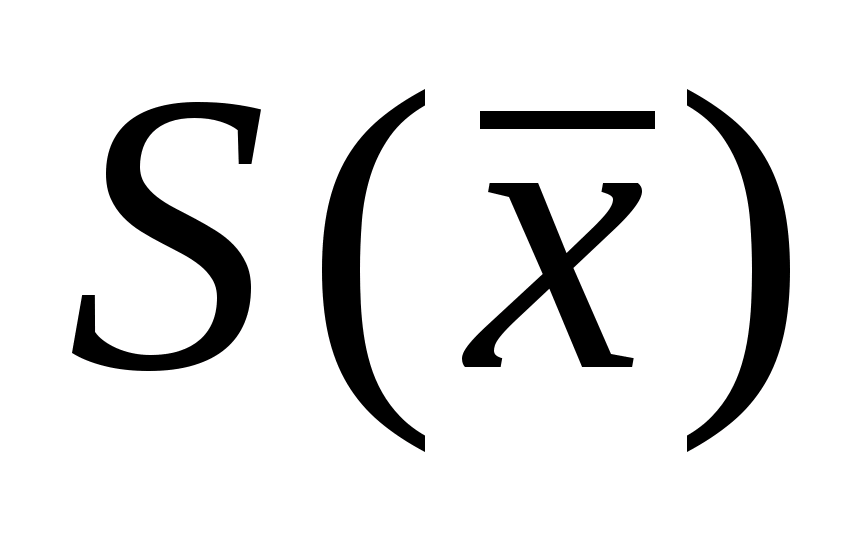
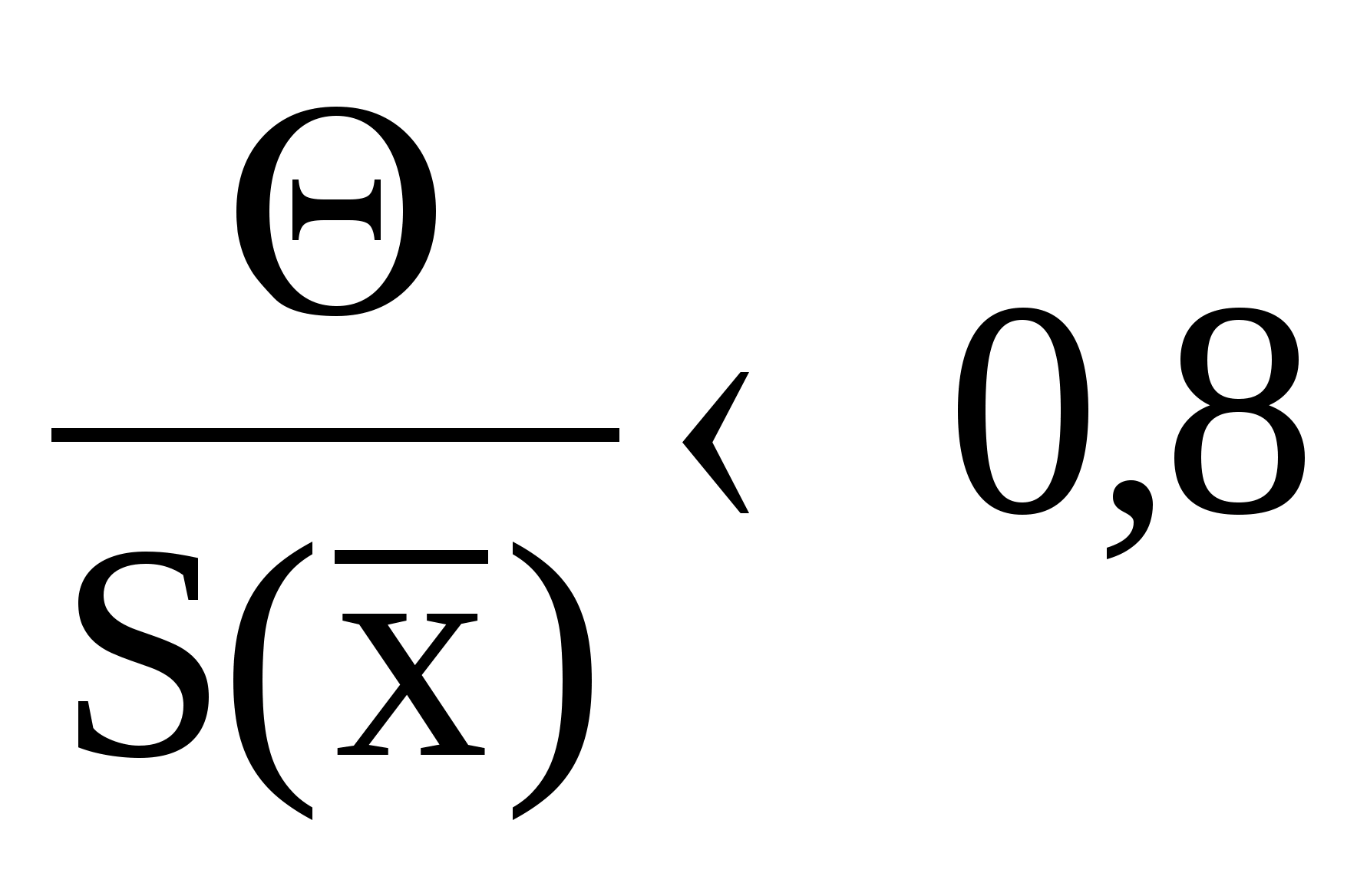 , то НСП по сравнению со случайными погрешностя-ми пренебрегают, и граница погрешности результата
, то НСП по сравнению со случайными погрешностя-ми пренебрегают, и граница погрешности результата 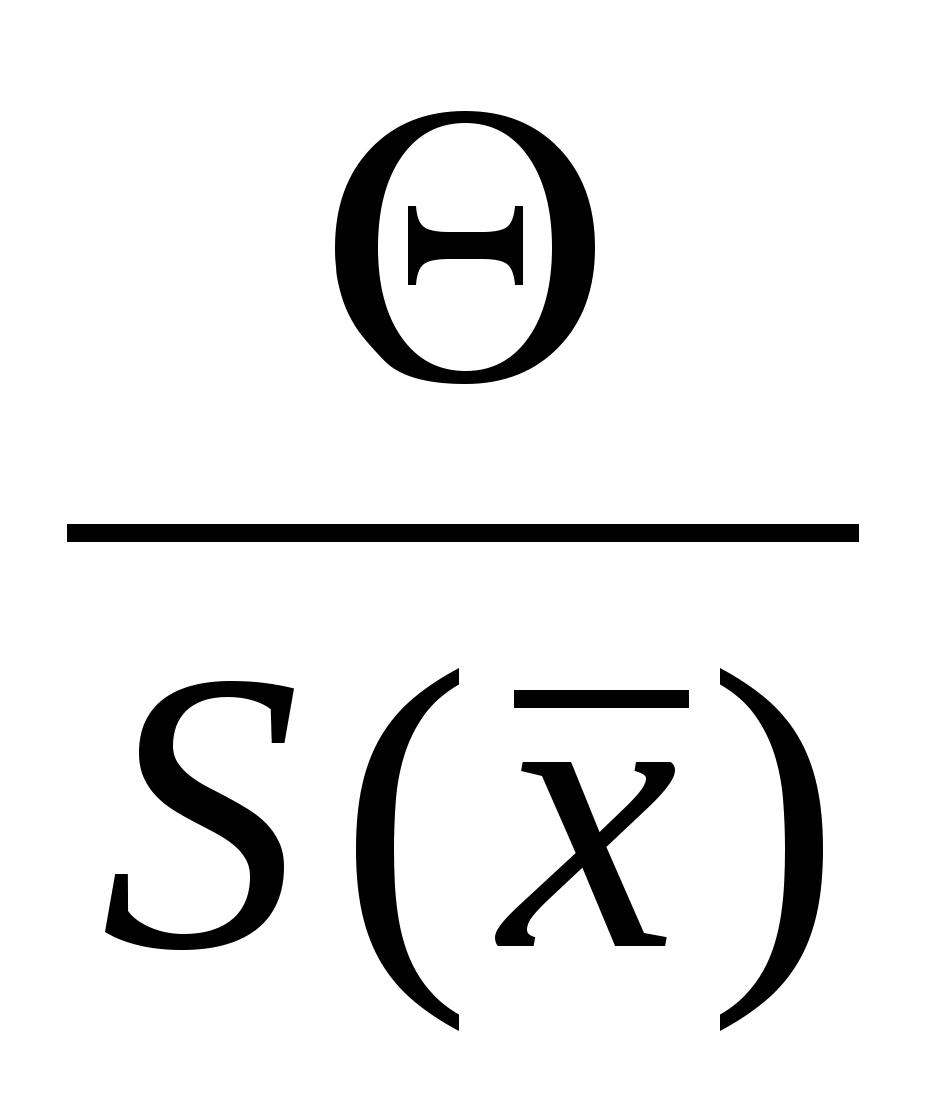 8, то случайной погрешностью можно пренебречь и граница погрешности результата
8, то случайной погрешностью можно пренебречь и граница погрешности результата 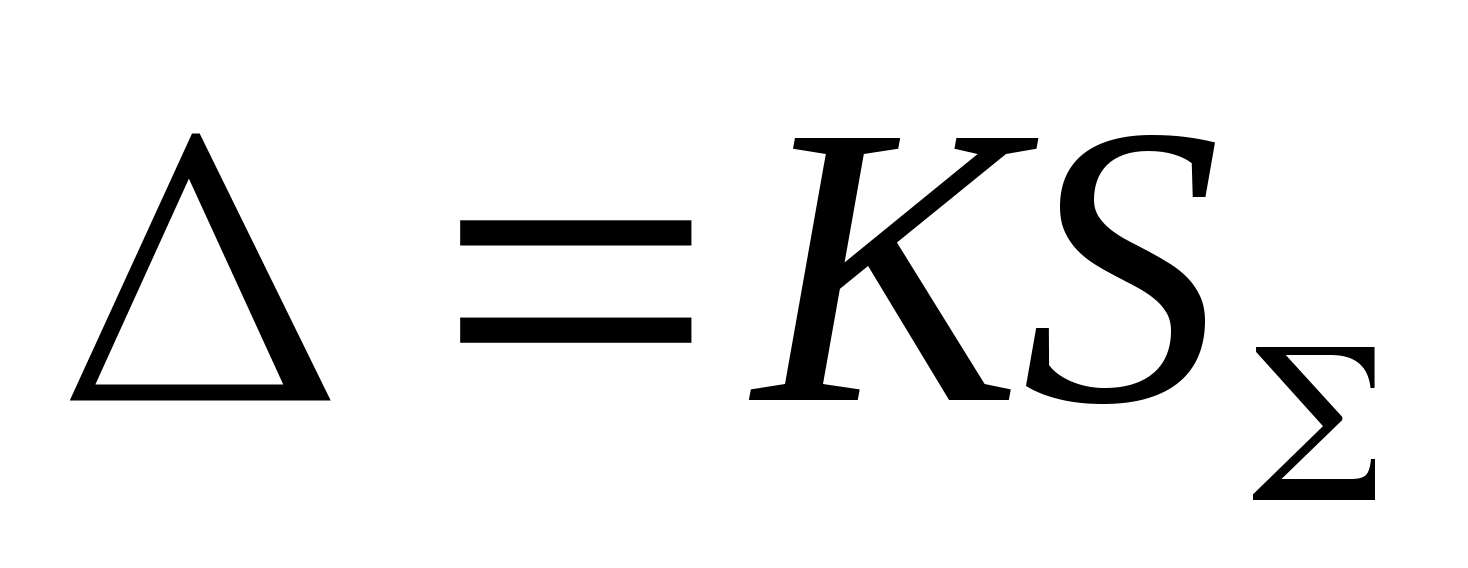 , где К
, где К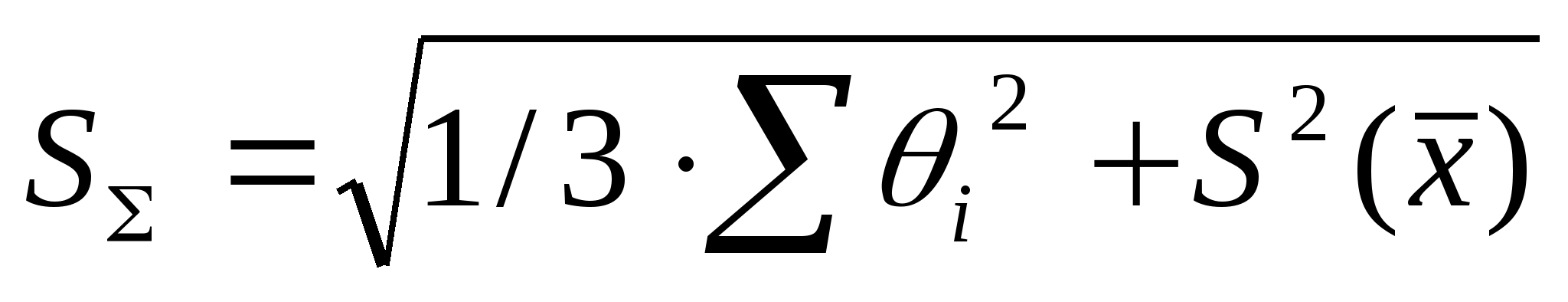 .
.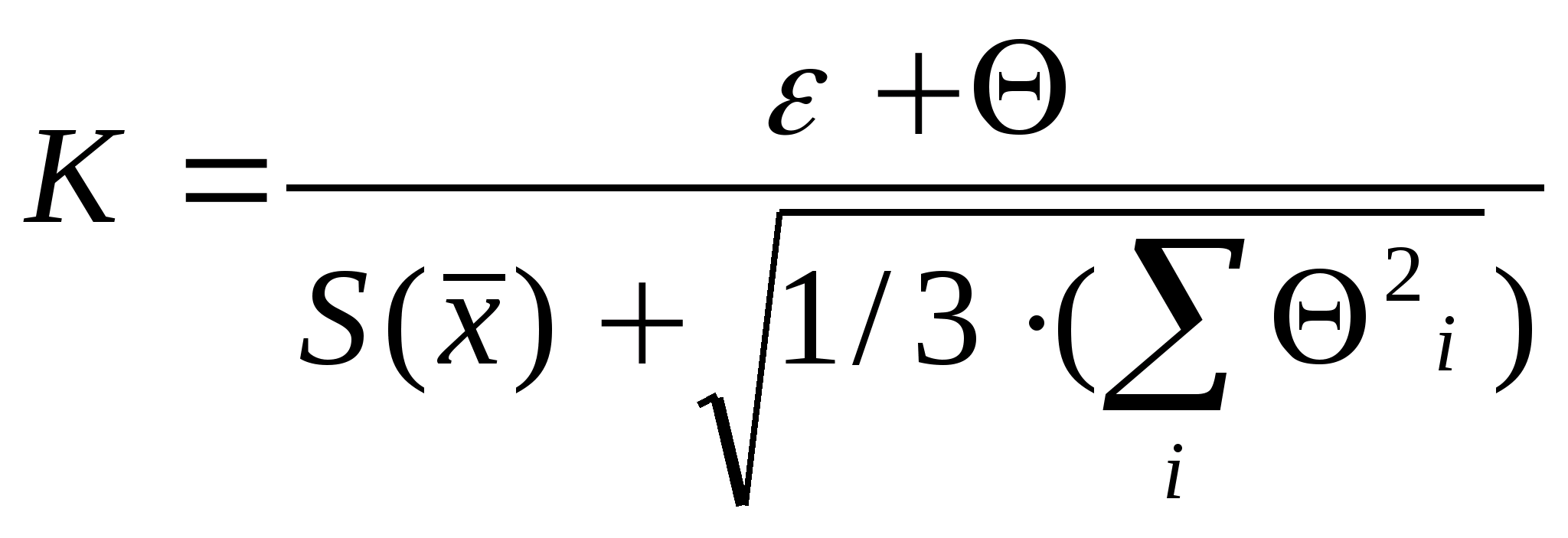 .
.
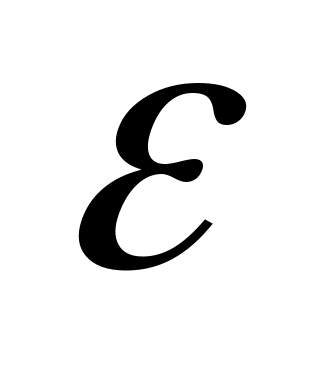 должна быть одной и той же.
должна быть одной и той же.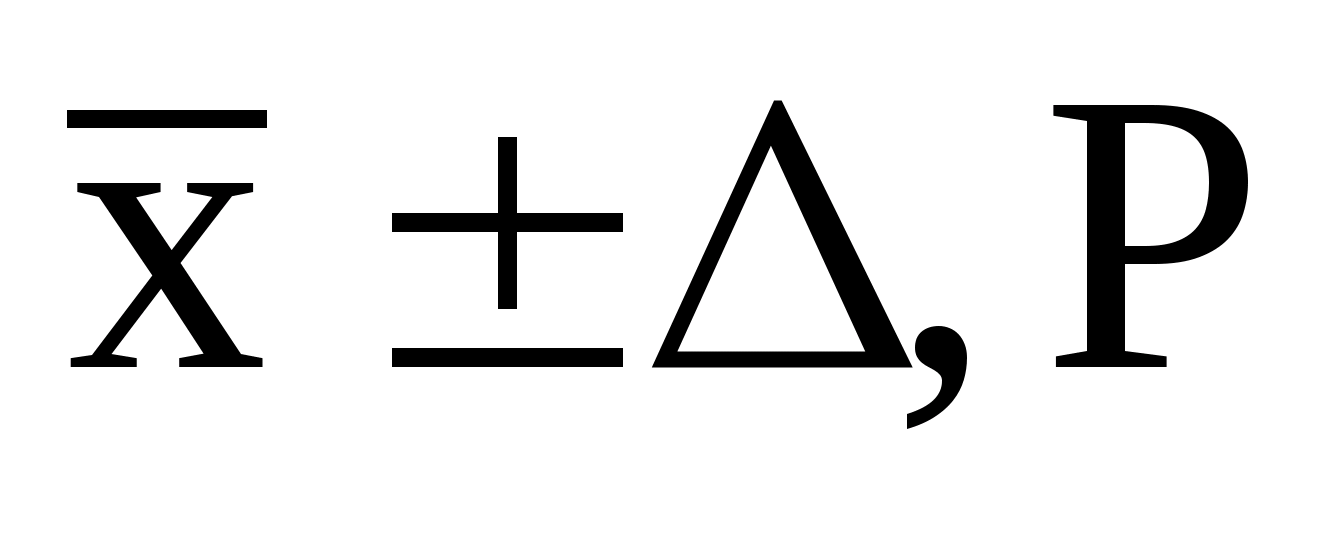 первом случае достаточно знать общую погрешность результата измерения и при симметричной доверительной погреш-ности результаты измерений представляют в форме: , где
первом случае достаточно знать общую погрешность результата измерения и при симметричной доверительной погреш-ности результаты измерений представляют в форме: , где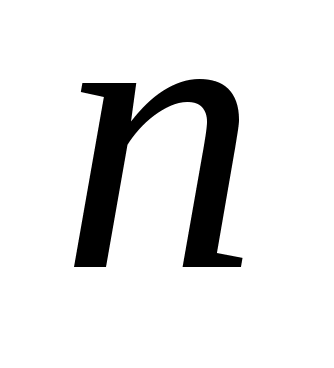 должна быть одной и той же.
должна быть одной и той же.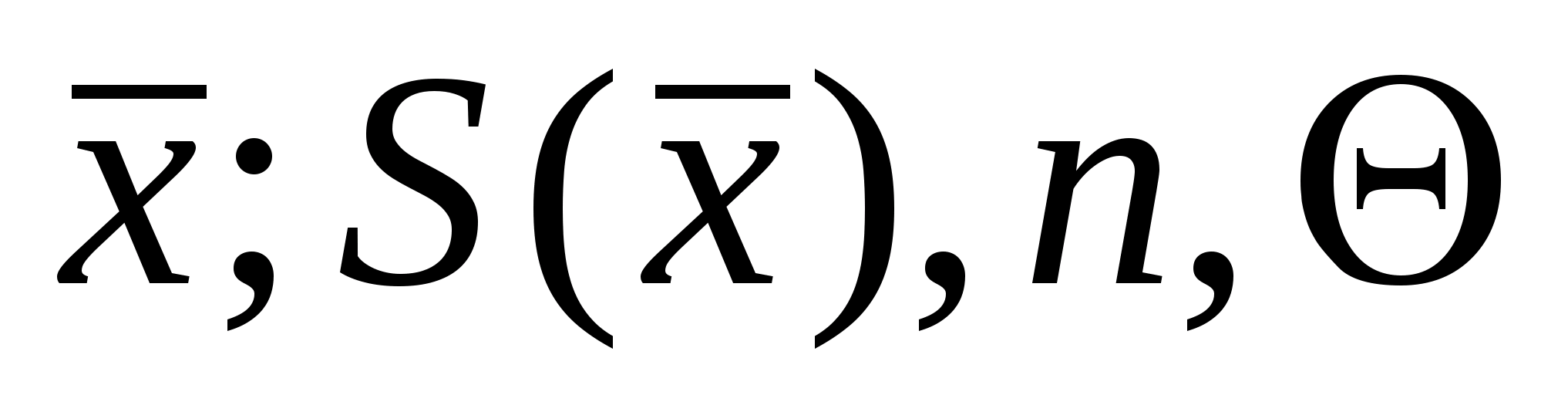
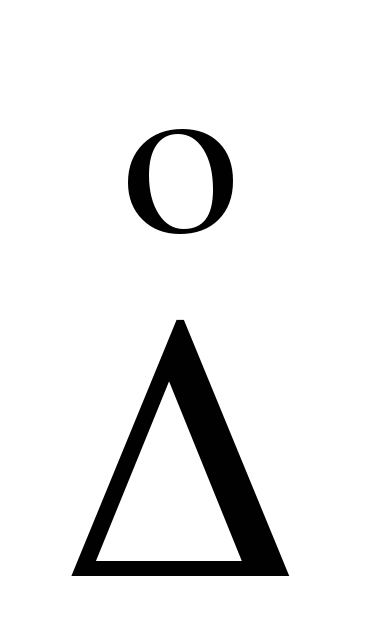
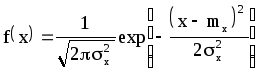 ,
, ,
, ,
,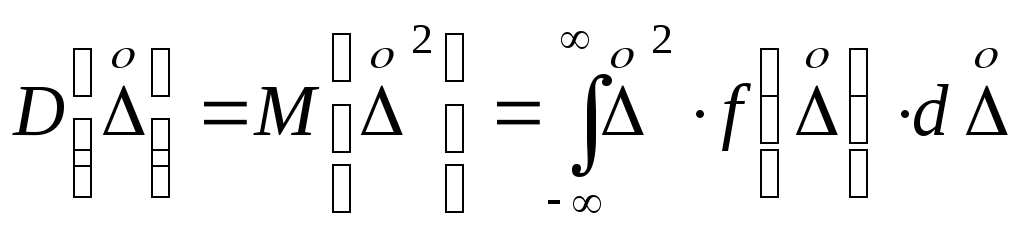 ,
,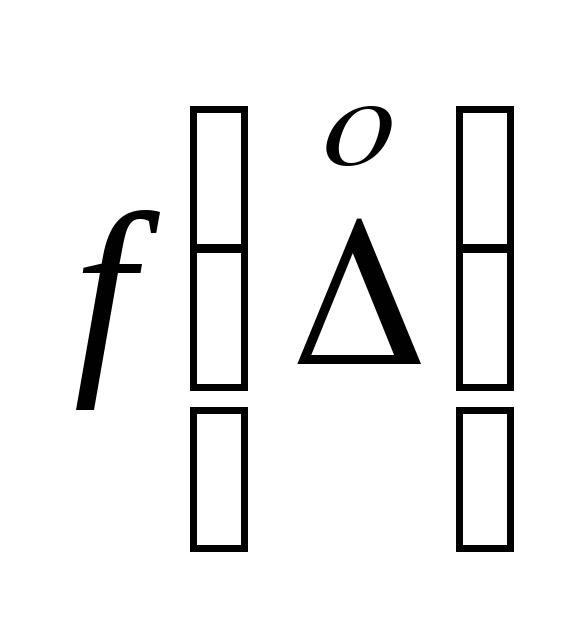 ,
,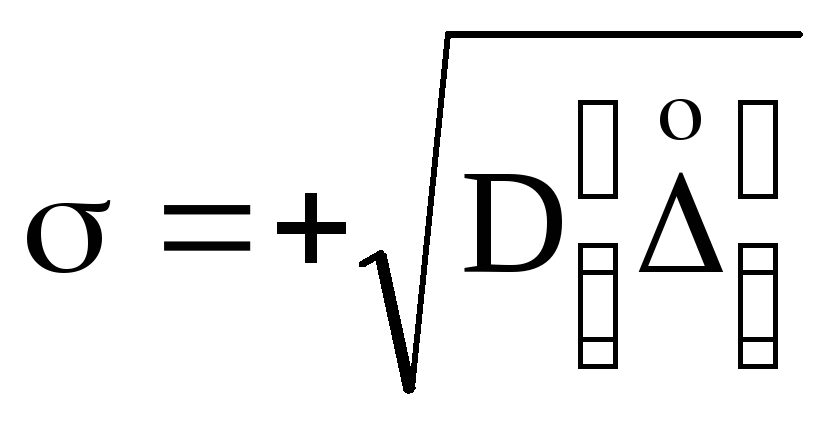 .
.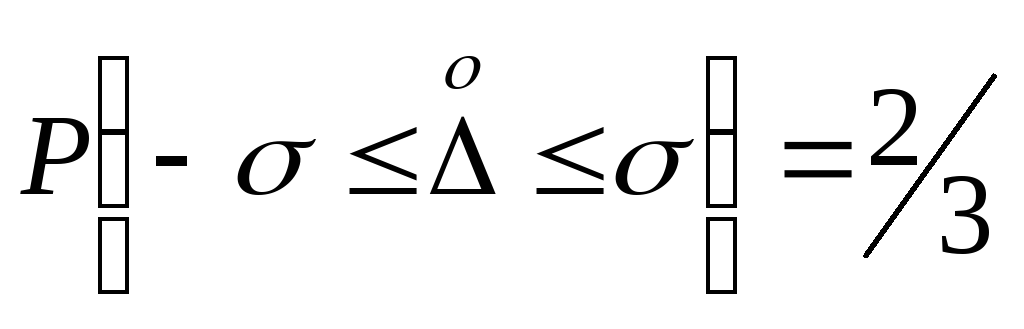 ,
,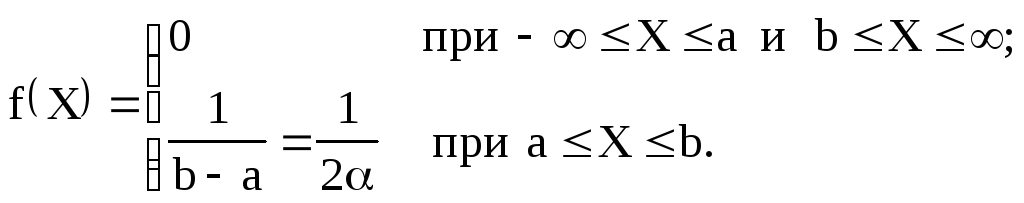 ,
,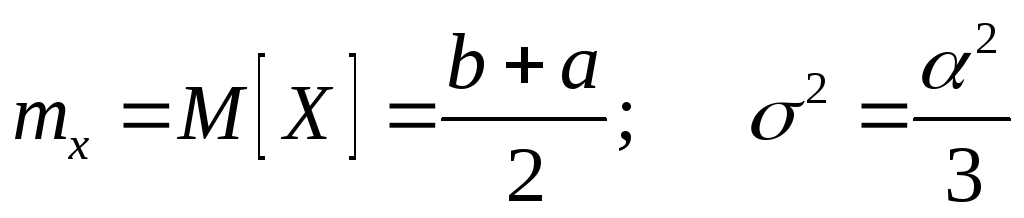 .
.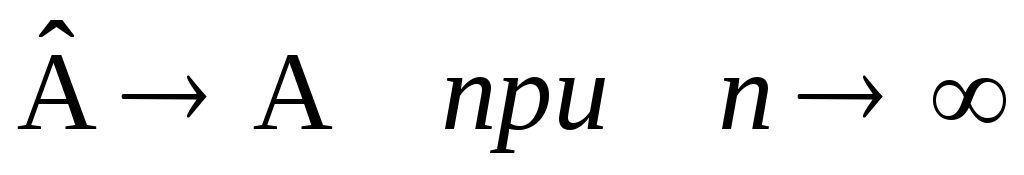 (гдеА –
(гдеА – .
.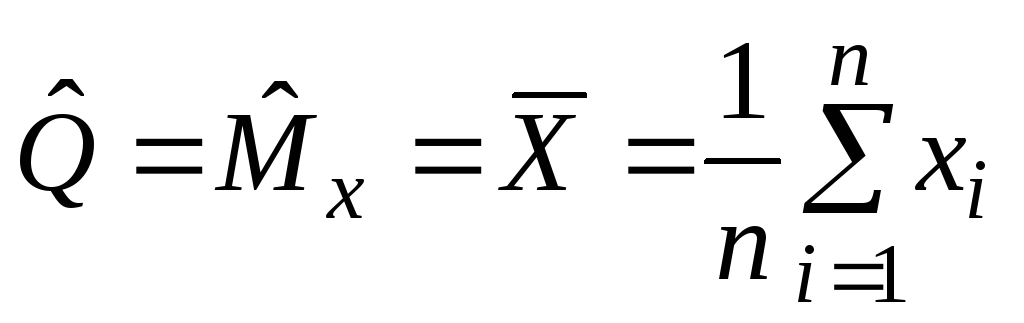 ;
;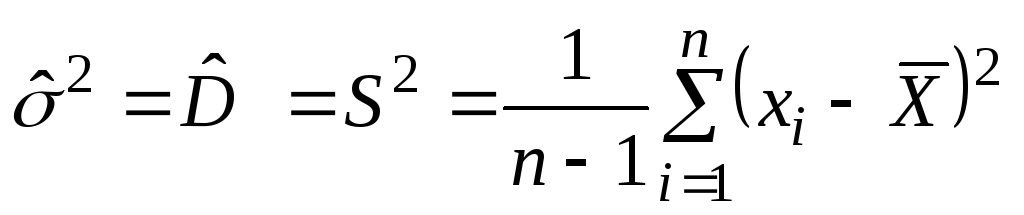 .
.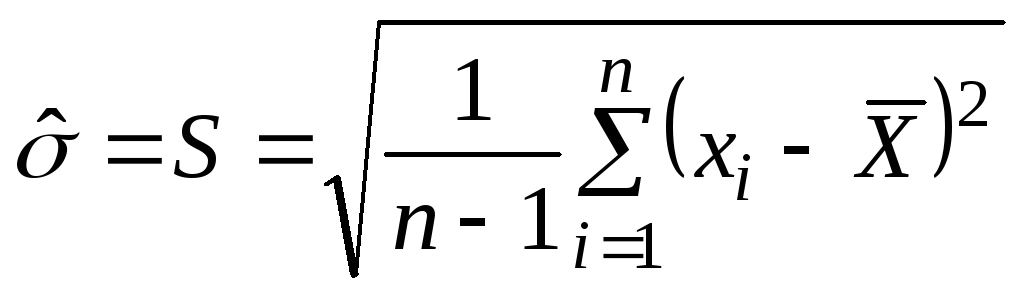
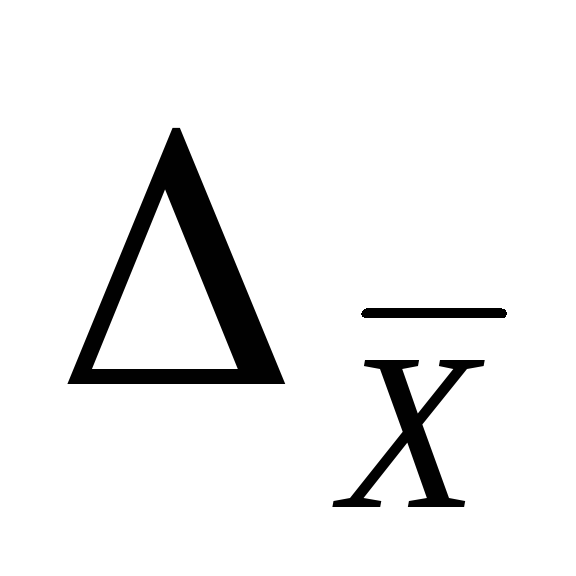 ,
,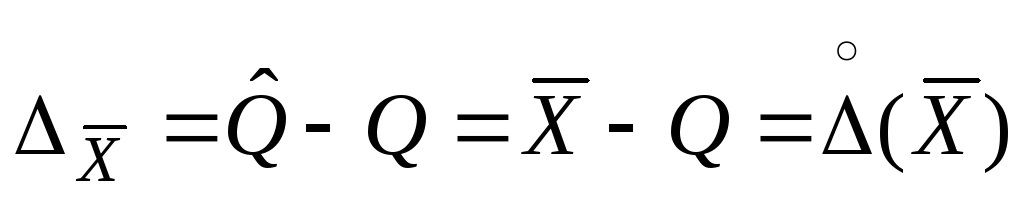 .
.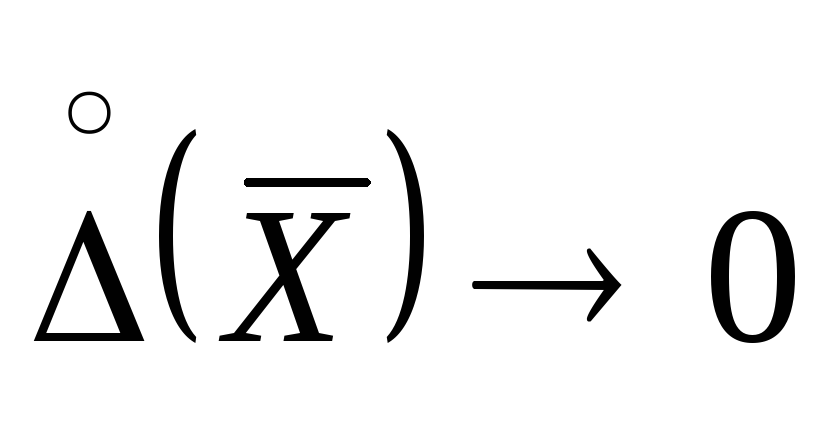 .
.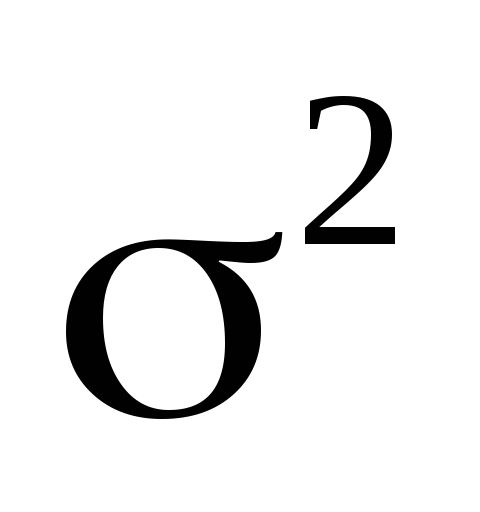 ;
;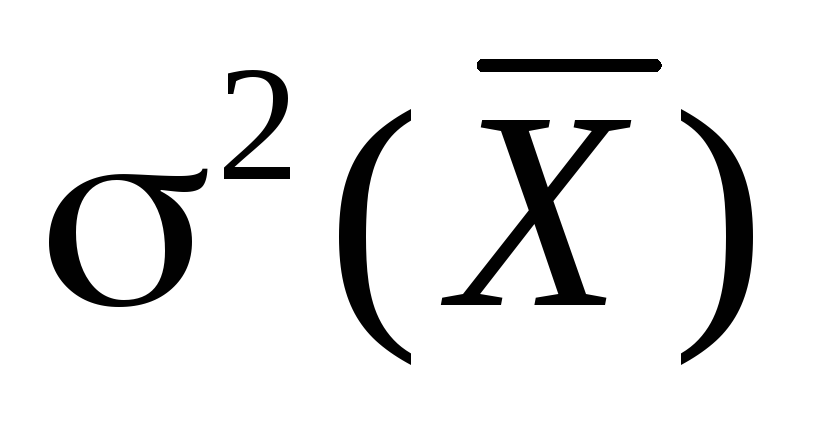 :
: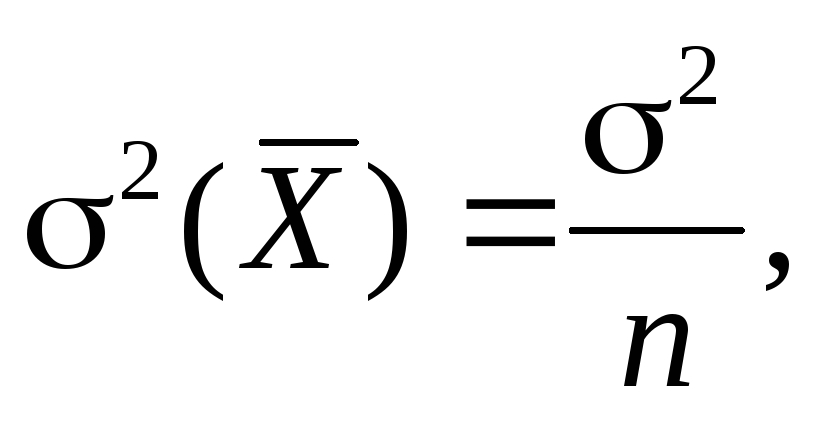 n
n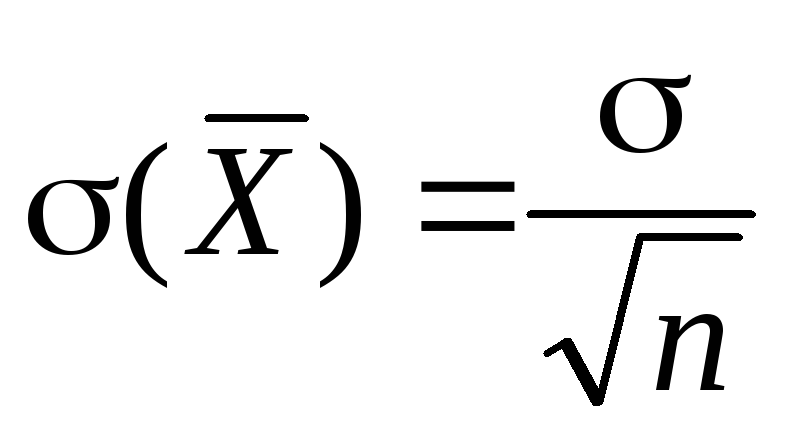 ,
,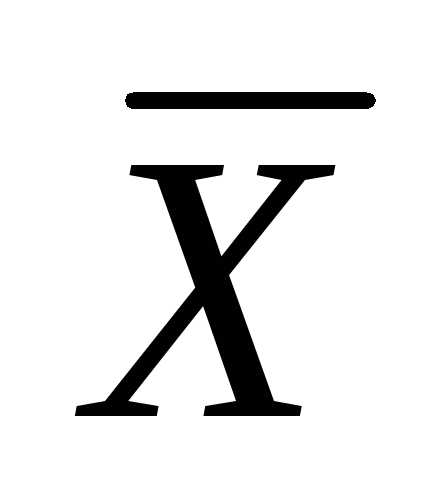 :
: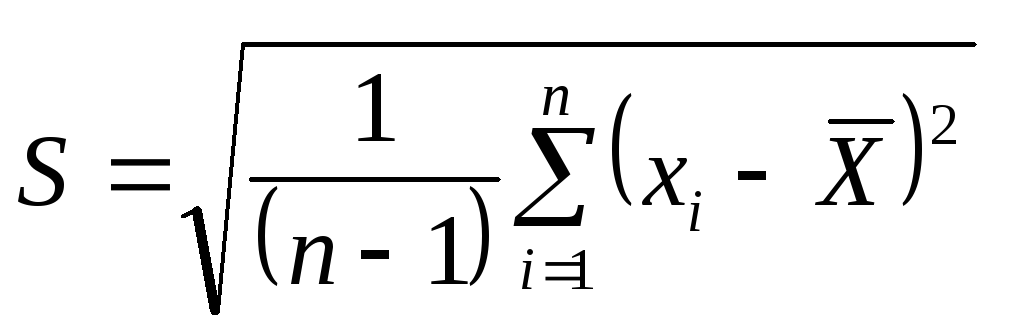 и
и
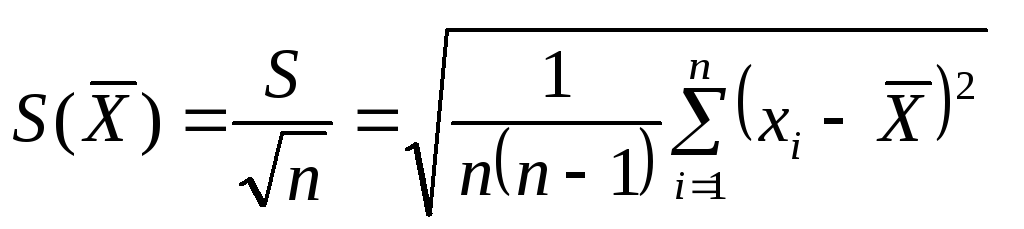 .
.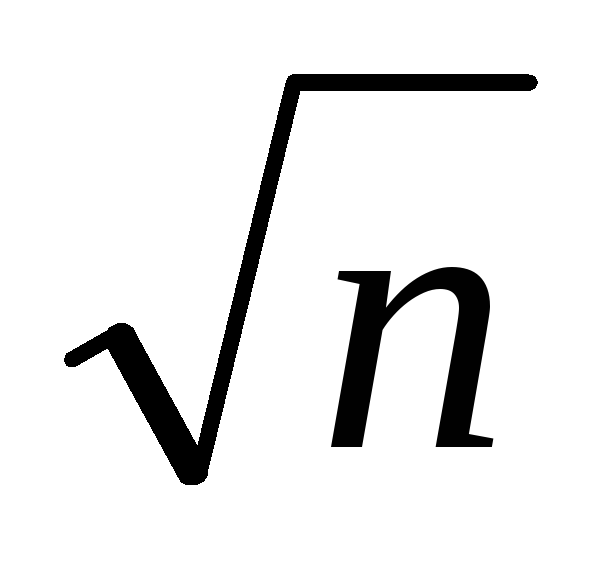 раз.
раз. раз меньшее.
раз меньшее.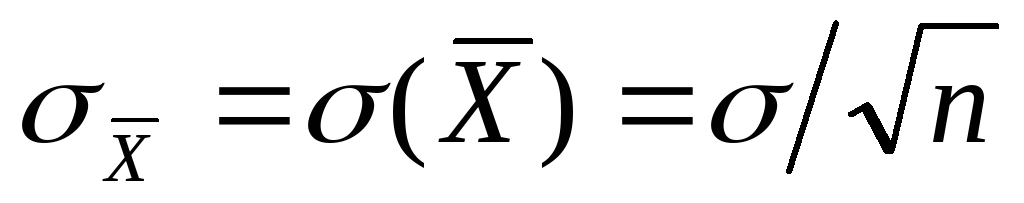 —
—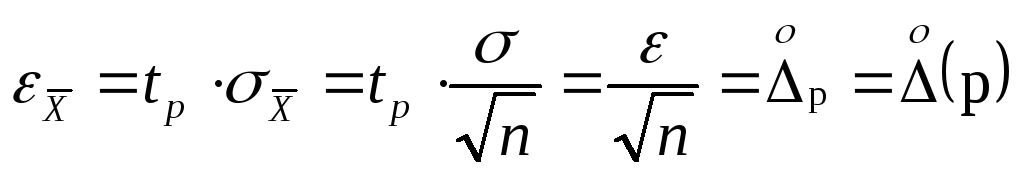
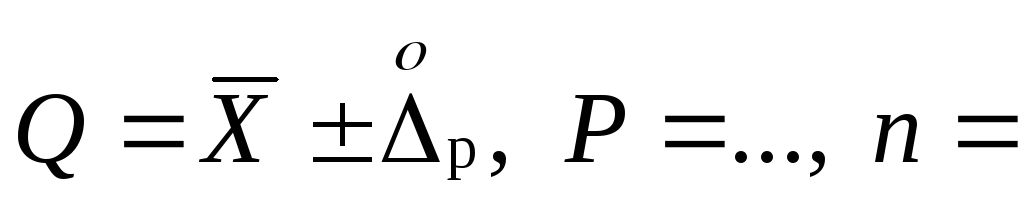 ….
…. »,
», —
—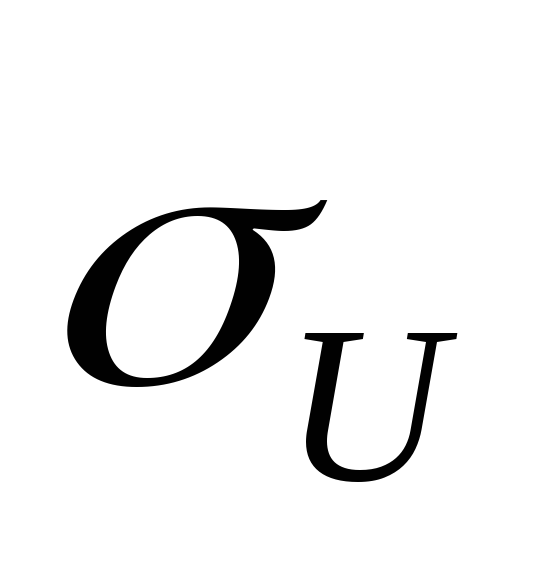 та СКВ результату багаторазового
та СКВ результату багаторазового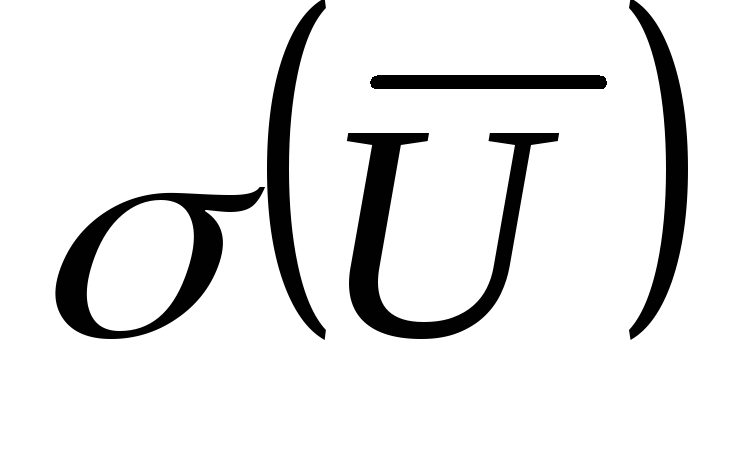 ;
;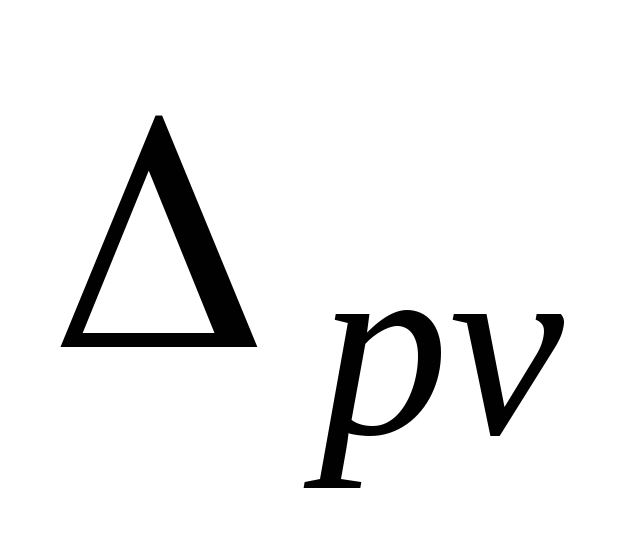 ;межу відносної похибки
;межу відносної похибки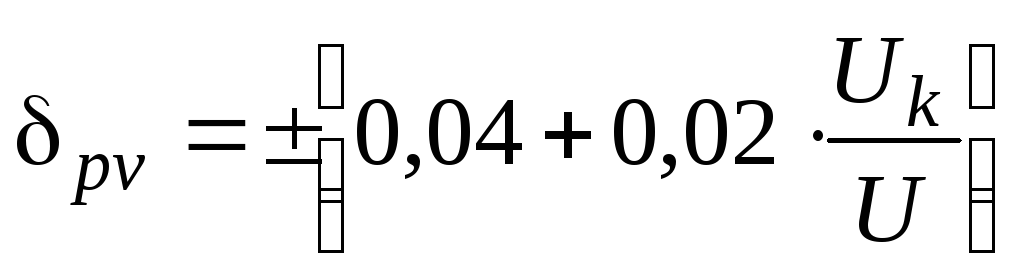 ;
; ;
;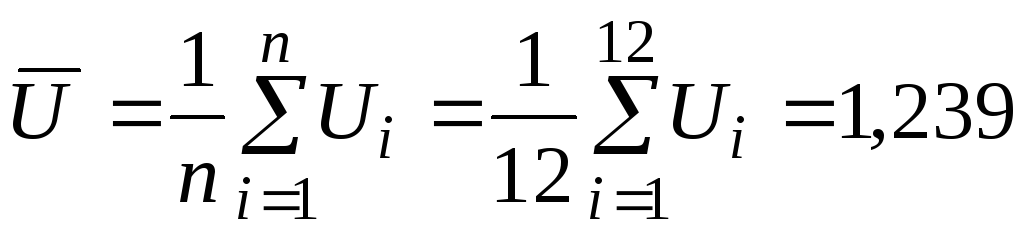 В.
В. та СКВ результату багаторазового
та СКВ результату багаторазового