Недостающим элементом формулы предельной ошибки

σ²

∆

∆²

(N-1)

σ²

∆

+∆²

(N-1)

σ²

∆

∆²

(N-1)

Репрезентативность
результатов выборочного наблюдения
зависит от

вариации
признака и объема выборки

определения
границ объекта исследования

времени
проведения наблюдения

продолжительности
проведения наблюдения

наличии
высокого уровня вариации признака

изучении
качественных характеристик явлений

малой
выборке

уточнении
данных сплошного наблюдения

Cредняя
ошибка случайной повторной выборки …
, если ее объем увеличить в 4 раза

уменьшится
в 2 раза

увеличится
в 4 раза

уменьшится
в 4 раза

не
изменится

t

t²

n²

n

N

вариацию
признака

тес
ноту связи между двумя факторами

среднюю
величину всех возможных расхождений
выборочной и генеральной средней

Среднее
значение признака

темп
роста

Под
выборочным наблюдением понимают:

сплошное
наблюдение всех единиц совокупности

несплошное
наблюдение части единиц совокупности

несплошное
наблюдение части единиц совокупности,
отобранных случайным способом

наблюдение
за единицами совокупности в определенные
моменты времени

обследование
наиболее крупных единиц изучаемой
совокупности

Недостающим
элементом в формуле дисперсии доли для
генеральной совокупности является

р

m

M

W

Пропорция
отбора в выборочную совокупность при
механической выборке определяется:

соотношением
объемов выборочной и генеральной
совокупностей

уровнем
вероятности

методом
отбора

Способ
собственно-случайного отбора в выборочную
совокупность заключается в отборе из
генеральной совокупности:

каждой
десятой единицы совокупности

без
какой либо системности

в
зависимости от уровня вероятности

Необходимая
численность серийной выборки при
бесповторном отборе определяется по
формуле:

+

Для
оценки результатов малой выборки
пользуются :

критерием
Фишера

критерием
Стъюдента

ничем
не пользуются

Недостающим
элементов в формуле предельной ошибки
выборки для доли при бесповторном отборе
является:

n

N

W

σ

Для
получения предельной ошибки выборки
необходимо умножить среднюю ошибку
выборки на:

коэффициент
доверия

численность
выборочной совокупности

численность
генеральной совокупности

По
формуле
определяется ошибка выборки:

средняя повторная

средняя
бесповторная

предельная повторная

предельная
бесповторная

При случайном
бесповторном отборе средняя ошибка
выборки определяется по формуле:

+

Выборка называется
малой, если ее объем составляет менее:

40
единиц

30 Единиц

100 единиц

150 единиц

Выборка
заключающаяся в отборе единиц из общего
списка единиц генеральной совокупности
через равные интервалы в соответствии
с установленным процентом отбора
называется:

типической

механической

случайной повторной

Для
использования выборочной совокупности
для дальнейшего анализа развития
социально-экономического явления
необходимо, чтобы разница между средним
значением генеральной совокупности и
средним значением выборочной совокупности
была не более ошибки выборки:

средней

индивидуальной

предельной

генеральной

Тема 6. Методы изучения взаимосвязи социально-экономических явлений

Между различными
явлениями и их признаками выделяют два
типа связей:

функциональная и
жестко детерминированная

функциональная
и статистическая

стохастически
детерминированная и вероятностная

Функциональной
называется связь, при которой:

каждому
значению признака-фактора соответствует
вполне определенное значение
результативного признака

каждому
значению признака-фактора соответствует
распределение значений результативного
признака

В
зависимости от направления действия
функциональные и статистические связи
могут быть:

прямолинейные и
криволинейные

прямые
и обратные

однофакторные и
многофакторные

По аналитическому
выражению функциональные и статистические
связи могут быть:

прямолинейные
и криволинейные

прямые и обратные

однофакторные
и многофакторные

По
количеству факторов, действующих на
результативный признак статистические
связи могут быть:

прямолинейные и
криволинейные

прямые и обратные

однофакторные
и многофакторные

Линейный коэффициент
корреляции может быть:

как
положительной, так и отрицательной
величиной

только положительной
величиной

только отрицательной
величиной

В линейном уравнении
коэффициент регрессии (а) показывает:

тесноту связи

долю дисперсии
«у», зависимую от «х»

на
сколько в среднем изменится «у» при
изменении «х» на одну единицу

ошибку коэффициента
корреляции

на сколько %
изменится «у» при изменении «х» на 1 %

С помощью
корреляционного анализа можно:

измерить
тесноту связи между варьирующими
признаками

установить степень
влияния независимых переменных на
зависимую

С помощью
регрессионного анализа можно:

измерить тесноту
связи между варьирующими признаками

установить
степень влияния независимых переменных
на зависимую

С
помощью коэффициентов ассоциации и
контингенции устанавливается связь
между признаками:

только количественными

только
качественными

количественными
и качественными

Коэффициенты
ассоциации и контингенции изменяются:

от 0 до 1

от
-1 до +1

от
-1 до 0

Коэффициенты
взаимной сопряжённости Пирсона и Чупрова
изменяются:

от
0 до 1

от -1 до +1

от
-1 до 0

Коэффициенты
корреляции рангов Фехнера и Спирмена
изменяются:

от
0 до 1

от
-1 до +1

от
-1 до 0

Коэффициент
эластичности показывает:

тесноту связи

долю дисперсии
«у», зависимую от «х»

на
сколько в среднем изменится «у» при
изменении «х» на одну единицу

ошибку коэффициента
корреляции

на
сколько % изменится «у» при изменении
«х» на 1 %

Коэффициент
корреляциирангов Кендалла изменяется:

от 0 до 1

от
-1 до +1

от
-1 до 0

Тесноту связи
между альтернативными признаками можно
оценить

непараметрическими
методами через:

коэффициенты
ассоциации и контингенции

показатели взаимной
сопряженности Пирсона и Чупрова

коэффициент
корреляции рангов Кендалла

Для аналитического
выражения нелинейной связи между
факторами используется формула:

+

r_xy=
0,982

r_xy=-
-0,991

r_xy=
0,870

r_xy=
0,982

r_xy=-
-0,991

r_xy=
0,870

Эмпирическое
корреляционное отношение представляет
собой корень квадратный из отношения
… дисперсии(й)

средней
из групповых дисперсий к общей

межгрупповой
дисперсии к общей

межгрупповой
дисперсии к средней из групповых

средней
из групповых дисперсий к межгрупповой

Теснота
связи двух признаков при нелинейной
зависимости определяется по формуле

+

Корреляционный
анализ используется для изучения

взаимосвязи
явлений

развития
явления во времени

структуры
явлений

Тесноту
связи между двумя альтернативными
признаками можно измерить с помощью
коэффициентов

знаков
Фехнера

корреляции
рангов Спирмена

ассоциации
и контингенции

Парный
коэффициент корреляции показывает
тесноту

линейной
зависимости между двумя признаками на
фоне действия остальных, входящих в
модель

линейной
зависимости между двумя признаками при
исключении влияния остальных, входящих
в модель

связи
между результативным признаком и
остальными, включенными в модель

нелинейной
зависимости между двумя признаками

Парный
коэффициент корреляции может принимать
значения

от
0 до 1

от
-1 до 0

от
-1 до +1

Коэффициент
детерминации может принимать значения

от
0 до 1

от
-1 до 0

от
-1 до +1

В
результате проведения регрессионного
анализа получают функцию, описывающую
… показателей

взаимосвязь

соотношение

структуру

темпы
роста

темпы
прироста

Прямолинейная
связь между факторами исследуется с
помощью уравнения регрессии

+

С
помощью коэффициентов Спирмена и Чупрова
устанавливается связь между признаками:

только количественными

только качественными

количественными
и качественными

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Прямолинейная регрессия, ее коэффициент и уравнение

ПРЯМОЛИНЕЙНАЯ РЕГРЕССИЯ, ЕЕ КОЭФФИЦИЕНТ И УРАВНЕНИЕ

При линейном типе связи между двумя изучаемыми признаками кроме расчета корреляций применяется расчет коэффициента регрессии.

В случае прямолинейной корреляционной связи каждому из изменений одного признака соответствует вполне определенное изменение другого признака. Однако коэффициент корреляции показывает эту связь лишь в относительных величинах — в долях единицы. С помощью же регрессионного анализа эту величину связи получают в именованных единицах. Та величина, на которую в среднем изменяется первый признак при изменении второго на единицу измерения, называется коэффициентом регрессии.

В отличие от корреляционного регрессионный анализ дает более широкую информацию, поскольку вычислением двух коэффициентов регрессии Rx/y и Rу/х возможно определить как зависимость первого признака от второго, так и второго от первого. Выражение регрессионной связи с помощью уравнения позволяет по определенному значению одного признака установить значение другого признака.

Коэффициент регрессии R представляет собой произведение коэффициента корреляции на отношение квадратических отклонений, вычисленных для каждого признака. Рассчитывается он по формуле

Rx/y = r ´

где, R — коэффициент регрессии; SХ — среднее квадратическое отклонение первого признака, который изменяется в связи с изменением второго; SУ — среднее квадратическое отклонение второго признака в связи с изменением которого изменяется первый признак; r — коэффициент корреляции между этими признаками; х — функция; у — аргумент.

По этой формуле определяется величина значения х при изменении у на единицу измерения. При необходимости обратного расчета можно найти величину у при изменении х на единицу измерения по формуле:

Rу/х = r ´

В этом случае активная роль в изменении одного признака по отношению к другому меняется, по сравнению с предыдущей формулой аргумент становится функцией и наоборот. Величины SX и SY принимаются в именованном выражении.

Между значениями г и R имеется четкая взаимосвязь, выражающаяся в том, что произведение регрессии х по у на регрессию у по х равно квадрату коэффициента корреляции, т. е.

Это свидетельствует, что коэффициент корреляции представляет собой среднюю геометрическую из обоих значений коэффициентов регрессии данной выборки. Данная формула может быть использована для проверки правильности расчетов.

При обработке цифрового материала на счетных машинах могут применяться развернутые формулы коэффициента регрессии:

Rx/y =;

Rx/y =

Для коэффициента регрессии может быть рассчитана его ошибка репрезентативности. Ошибка коэффициента регрессии равна ошибке коэффициента корреляции, умноженной на отношение квадратических отношений:

SR = ´Sr = ´

Критерий достоверности коэффициента регрессии вычисляется по обычной формуле:

tR =

в итоге он равен критерию достоверности коэффициента корреляции:

tR = = = = tr

Достоверность величины tR устанавливается по таблице Стьюдента при n = n — 2, где n — число пар наблюдений.

Предположим, что при расчете коэффициента корреляции между уровнем яйценоскости и массой яиц:

было установлено, что r = -0,46;

для показателя яйценоскости: = 102; S = 7,0; n = 40

для показателя массы яйца: = 56,68; S = 1,94;n = 40

регрессия первого признака по второму равна:

Rx/y = ´(-0,46) = 3,61´(-0,46) = -1,66

Это означает, что увеличение массы яйца на 1 г в данной популяции кур сопровождается уменьшением яйценоскости за 5 мес. на 1,66 яйцо.

Ry/x = ´(-0,46) = 0,277´(-0,46) = -0,127

показывает, что повышение яйценоскости на 1 яйцо за 5-месячный период в данной популяции кур сопровождается уменьшением средней массы яиц на 0,127 г.

По формуле взаимозависимости r и R можно проверить правильность расчета:

(-1,66) ´ (-0,127) = 0,210; (-0,46)2 = 0,210.

Ошибка коэффициента регрессии Rx/y = равна

SR = ´Sr = ´

SR = 3,61´= 3,61´= 3,61´0,144 = 0,52

Критерий достоверности Rx/y равен

tR = = 3,19

По таблице Стьюдента стандартные значения t для n = 38 равны 2,0-2,7-3,6. Следовательно, рассчитанный коэффициент регрессии достоверен при Р ³ 0,99.

Более глубокий анализ связи двух признаков может быть сделан на основе расчета уравнения прямолинейной регрессии. Сущность коэффициента прямолинейной регрессии, показывающей насколько второй признак отклоняется от своей средней, если первый отклоняется от своей средней на единицу измерения, можно выразить формулой

Преобразуя это уравнение, получаем рабочую формулу прямолинейной регрессии. Обозначаем Ry/x через b:

Обозначаем = а, следовательно

В этом уравнении х является аргументом, у — его функцией. Уравнение показывает взаимоотношение между аргументом и функцией, именно то взаимоотношение признаков, которое и образует коэффициент регрессии. По этой формуле, зная значения аргумента (х) можно определить значение его функции (у) без непосредственного ее измерения.

В рассмотренном выше примере были вычислены коэффициенты корреляции и регрессии между уровнем яйценоскости и массой яиц у кур. Если принять яйценоскость кур за аргумент, можно составить следующее уравнение прямолинейной регрессии:

;

а = 56,6,127) ´ 102 = 56,68 + 12,95 – 69,63; а = 69,63

у = 69,63 + (-0,127) ´ x = 69,63 – 0,127 ´ x

Таким образом, для того, чтобы установить, какая масса яйца может соответствовать тому или иному уровню яйценоскости, нужно умножить показатель яйценоскости на коэффициент 0,127 и вычесть это произведение из числа 69,63. На основе этого уравнения можно заранее рассчитать значение функций для каждого значения аргумента. Таким образом, в частности в данном примере, можно составить ряд, показывающий регрессионные зависимости яйценоскости и массы яиц в данной популяции кур.

Теоретический ряд регрессии между признаками яйценоскости кур

Основы линейной регрессии

Что такое регрессия?

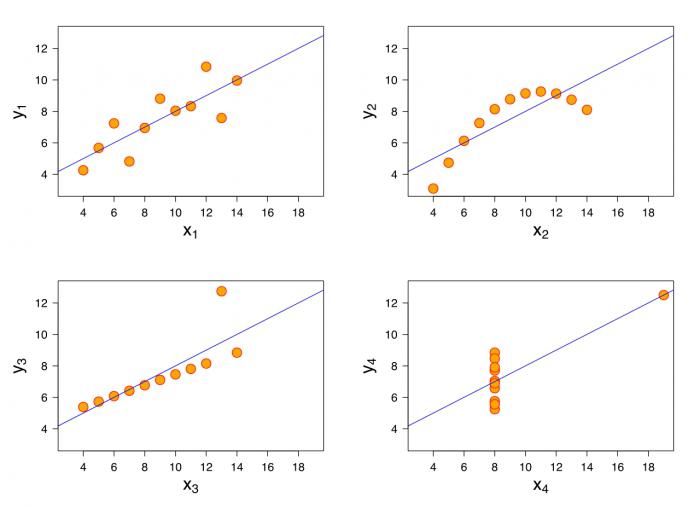
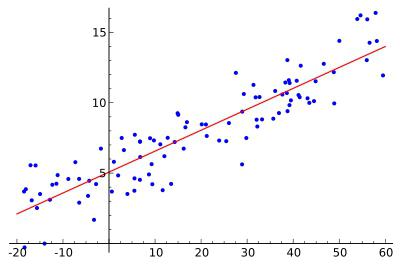
Разместим точки на двумерном графике рассеяния и скажем, что мы имеем линейное соотношение, если данные аппроксимируются прямой линией.

Если мы полагаем, что y зависит от x, причём изменения в y вызываются именно изменениями в x, мы можем определить линию регрессии (регрессия y на x), которая лучше всего описывает прямолинейное соотношение между этими двумя переменными.

Статистическое использование слова «регрессия» исходит из явления, известного как регрессия к среднему, приписываемого сэру Френсису Гальтону (1889).

Он показал, что, хотя высокие отцы имеют тенденцию иметь высоких сыновей, средний рост сыновей меньше, чем у их высоких отцов. Средний рост сыновей «регрессировал» и «двигался вспять» к среднему росту всех отцов в популяции. Таким образом, в среднем высокие отцы имеют более низких (но всё-таки высоких) сыновей, а низкие отцы имеют сыновей более высоких (но всё-таки довольно низких).

Линия регрессии

Математическое уравнение, которое оценивает линию простой (парной) линейной регрессии:

x называется независимой переменной или предиктором.

Y – зависимая переменная или переменная отклика. Это значение, которое мы ожидаем для y (в среднем), если мы знаем величину x, т.е. это «предсказанное значение y»

• a – свободный член (пересечение) линии оценки; это значение Y, когда x=0 (Рис.1).
• b – угловой коэффициент или градиент оценённой линии; она представляет собой величину, на которую Y увеличивается в среднем, если мы увеличиваем x на одну единицу.
• a и b называют коэффициентами регрессии оценённой линии, хотя этот термин часто используют только для b.

Парную линейную регрессию можно расширить, включив в нее более одной независимой переменной; в этом случае она известна как множественная регрессия.

Рис.1. Линия линейной регрессии, показывающая пересечение a и угловой коэффициент b (величину возрастания Y при увеличении x на одну единицу)

Метод наименьших квадратов

Мы выполняем регрессионный анализ, используя выборку наблюдений, где a и b – выборочные оценки истинных (генеральных) параметров, α и β , которые определяют линию линейной регрессии в популяции (генеральной совокупности).

Наиболее простым методом определения коэффициентов a и b является метод наименьших квадратов (МНК).

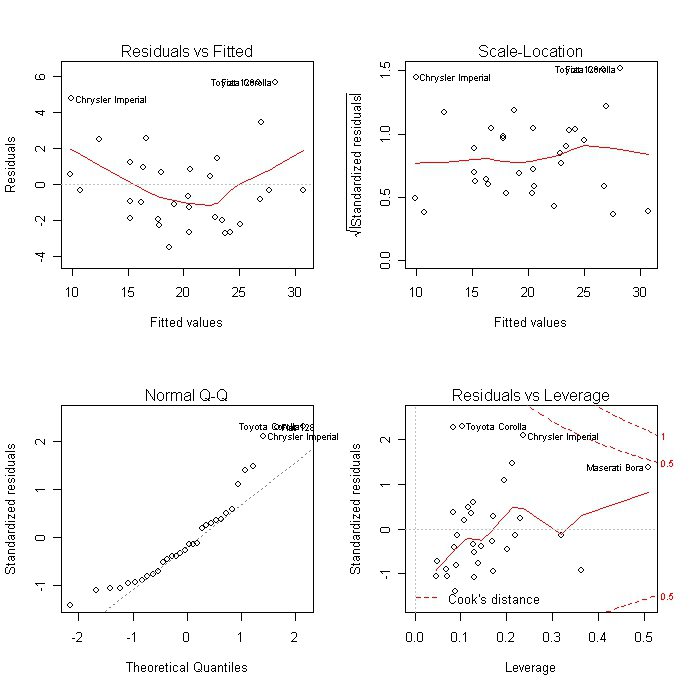
Подгонка оценивается, рассматривая остатки (вертикальное расстояние каждой точки от линии, например, остаток = наблюдаемому y – предсказанный y, Рис. 2).

Линию лучшей подгонки выбирают так, чтобы сумма квадратов остатков была минимальной.

Рис. 2. Линия линейной регрессии с изображенными остатками (вертикальные пунктирные линии) для каждой точки.

Предположения линейной регрессии

Итак, для каждой наблюдаемой величины остаток равен разнице и соответствующего предсказанного Каждый остаток может быть положительным или отрицательным.

Можно использовать остатки для проверки следующих предположений, лежащих в основе линейной регрессии:

• Между и существует линейное соотношение: для любых пар данные должны аппроксимировать прямую линию. Если нанести на двумерный график остатки, то мы должны наблюдать случайное рассеяние точек, а не какую-либо систематическую картину.

• Остатки нормально распределены с нулевым средним значением;

• Остатки имеют одну и ту же вариабельность (постоянную дисперсию) для всех предсказанных величин Если нанести остатки против предсказанных величин от мы должны наблюдать случайное рассеяние точек. Если график рассеяния остатков увеличивается или уменьшается с увеличением то это допущение не выполняется;

Если допущения линейности, нормальности и/или постоянной дисперсии сомнительны, мы можем преобразовать или и рассчитать новую линию регрессии, для которой эти допущения удовлетворяются (например, использовать логарифмическое преобразование или др.).

Аномальные значения (выбросы) и точки влияния

«Влиятельное» наблюдение, если оно опущено, изменяет одну или больше оценок параметров модели (т.е. угловой коэффициент или свободный член).

Выброс (наблюдение, которое противоречит большинству значений в наборе данных) может быть «влиятельным» наблюдением и может хорошо обнаруживаться визуально, при осмотре двумерной диаграммы рассеяния или графика остатков.

И для выбросов, и для «влиятельных» наблюдений (точек) используют модели, как с их включением, так и без них, обращают внимание на изменение оценки (коэффициентов регрессии).

При проведении анализа не стоит отбрасывать выбросы или точки влияния автоматически, поскольку простое игнорирование может повлиять на полученные результаты. Всегда изучайте причины появления этих выбросов и анализируйте их.

Гипотеза линейной регрессии

При построении линейной регрессии проверяется нулевая гипотеза о том, что генеральный угловой коэффициент линии регрессии β равен нулю.

Если угловой коэффициент линии равен нулю, между и нет линейного соотношения: изменение не влияет на

Для тестирования нулевой гипотезы о том, что истинный угловой коэффициент равен нулю можно воспользоваться следующим алгоритмом:

Вычислить статистику критерия, равную отношению , которая подчиняется распределению с степенями свободы, где стандартная ошибка коэффициента

,

— оценка дисперсии остатков.

Обычно если достигнутый уровень значимости нулевая гипотеза отклоняется.

Можно рассчитать 95% доверительный интервал для генерального углового коэффициента :

где процентная точка распределения со степенями свободы что дает вероятность двустороннего критерия

Это тот интервал, который содержит генеральный угловой коэффициент с вероятностью 95%.

Для больших выборок, скажем, мы можем аппроксимировать значением 1,96 (то есть статистика критерия будет стремиться к нормальному распределению)

Оценка качества линейной регрессии: коэффициент детерминации R 2

Из-за линейного соотношения и мы ожидаем, что изменяется, по мере того как изменяется , и называем это вариацией, которая обусловлена или объясняется регрессией. Остаточная вариация должна быть как можно меньше.

Если это так, то большая часть вариации будет объясняться регрессией, а точки будут лежать близко к линии регрессии, т.е. линия хорошо соответствует данным.

Долю общей дисперсии , которая объясняется регрессией называют коэффициентом детерминации, обычно выражают через процентное соотношение и обозначают R 2 (в парной линейной регрессии это величина r 2 , квадрат коэффициента корреляции), позволяет субъективно оценить качество уравнения регрессии.

Разность представляет собой процент дисперсии который нельзя объяснить регрессией.

Нет формального теста для оценки мы вынуждены положиться на субъективное суждение, чтобы определить качество подгонки линии регрессии.

Применение линии регрессии для прогноза

Можно применять регрессионную линию для прогнозирования значения по значению в пределе наблюдаемого диапазона (никогда не экстраполируйте вне этих пределов).

Мы предсказываем среднюю величину для наблюдаемых, которые имеют определенное значение путем подстановки этого значения в уравнение линии регрессии.

Итак, если прогнозируем как Используем эту предсказанную величину и ее стандартную ошибку, чтобы оценить доверительный интервал для истинной средней величины в популяции.

Повторение этой процедуры для различных величин позволяет построить доверительные границы для этой линии. Это полоса или область, которая содержит истинную линию, например, с 95% доверительной вероятностью.

Подобным образом можно рассчитать более широкую область, внутри которой, как мы ожидаем, лежит наибольшее число (обычно 95%) наблюдений.

Простые регрессионные планы

Простые регрессионные планы содержат один непрерывный предиктор. Если существует 3 наблюдения со значениями предиктора P , например, 7, 4 и 9, а план включает эффект первого порядка P , то матрица плана X будет иметь вид

а регрессионное уравнение с использованием P для X1 выглядит как

Если простой регрессионный план содержит эффект высшего порядка для P , например квадратичный эффект, то значения в столбце X1 в матрице плана будут возведены во вторую степень:

а уравнение примет вид

Y = b 0 + b 1 P 2

Сигма -ограниченные и сверхпараметризованные методы кодирования не применяются по отношению к простым регрессионным планам и другим планам, содержащим только непрерывные предикторы (поскольку, просто не существует категориальных предикторов). Независимо от выбранного метода кодирования, значения непрерывных переменных увеличиваются в соответствующей степени и используются как значения для переменных X . При этом перекодировка не выполняется. Кроме того, при описании регрессионных планов можно опустить рассмотрение матрицы плана X , а работать только с регрессионным уравнением.

Пример: простой регрессионный анализ

Этот пример использует данные, представленные в таблице:

Рис. 3. Таблица исходных данных.

Данные составлены на основе сравнения переписей 1960 и 1970 в произвольно выбранных 30 округах. Названия округов представлены в виде имен наблюдений. Информация относительно каждой переменной представлена ниже:

Рис. 4. Таблица спецификаций переменных.

Задача исследования

Для этого примера будут анализироваться корреляция уровня бедности и степень, которая предсказывает процент семей, которые находятся за чертой бедности. Следовательно мы будем трактовать переменную 3 ( Pt_Poor ) как зависимую переменную.

Можно выдвинуть гипотезу: изменение численности населения и процент семей, которые находятся за чертой бедности, связаны между собой. Кажется разумным ожидать, что бедность ведет к оттоку населения, следовательно, здесь будет отрицательная корреляция между процентом людей за чертой бедности и изменением численности населения. Следовательно мы будем трактовать переменную 1 ( Pop_Chng ) как переменную-предиктор.

Просмотр результатов

Коэффициенты регрессии

Рис. 5. Коэффициенты регрессии Pt_Poor на Pop_Chng.

На пересечении строки Pop_Chng и столбца Парам. не стандартизованный коэффициент для регрессии Pt_Poor на Pop_Chng равен -0.40374 . Это означает, что для каждого уменьшения численности населения на единицу, имеется увеличение уровня бедности на .40374. Верхний и нижний (по умолчанию) 95% доверительные пределы для этого не стандартизованного коэффициента не включают ноль, так что коэффициент регрессии значим на уровне p . Обратите внимание на не стандартизованный коэффициент, который также является коэффициентом корреляции Пирсона для простых регрессионных планов, равен -.65, который означает, что для каждого уменьшения стандартного отклонения численности населения происходит увеличение стандартного отклонения уровня бедности на .65.

Распределение переменных

Коэффициенты корреляции могут стать существенно завышены или занижены, если в данных присутствуют большие выбросы. Изучим распределение зависимой переменной Pt_Poor по округам. Для этого построим гистограмму переменной Pt_Poor .

Рис. 6. Гистограмма переменной Pt_Poor.

Как вы можете заметить, распределение этой переменной заметно отличается от нормального распределения. Тем не менее, хотя даже два округа (два правых столбца) имеют высокий процент семей, которые находятся за чертой бедности, чем ожидалось в случае нормального распределения, кажется, что они находятся «внутри диапазона.»

Рис. 7. Гистограмма переменной Pt_Poor.

Это суждение в некоторой степени субъективно. Эмпирическое правило гласит, что выбросы необходимо учитывать, если наблюдение (или наблюдения) не попадают в интервал (среднее ± 3 умноженное на стандартное отклонение). В этом случае стоит повторить анализ с выбросами и без, чтобы убедиться, что они не оказывают серьезного эффекта на корреляцию между членами совокупности.

Диаграмма рассеяния

Если одна из гипотез априори о взаимосвязи между заданными переменными, то ее полезно проверить на графике соответствующей диаграммы рассеяния.

Рис. 8. Диаграмма рассеяния.

Диаграмма рассеяния показывает явную отрицательную корреляцию ( -.65 ) между двумя переменными. На ней также показан 95% доверительный интервал для линии регрессии, т.е., с 95% вероятностью линия регрессии проходит между двумя пунктирными кривыми.

Критерии значимости

Рис. 9. Таблица, содержащая критерии значимости.

Критерий для коэффициента регрессии Pop_Chng подтверждает, что Pop_Chng сильно связано с Pt_Poor , p .

На этом примере было показано, как проанализировать простой регрессионный план. Была также представлена интерпретация не стандартизованных и стандартизованных коэффициентов регрессии. Обсуждена важность изучения распределения откликов зависимой переменной, продемонстрирована техника определения направления и силы взаимосвязи между предиктором и зависимой переменной.

Уравнение регрессии. Уравнение множественной регрессии

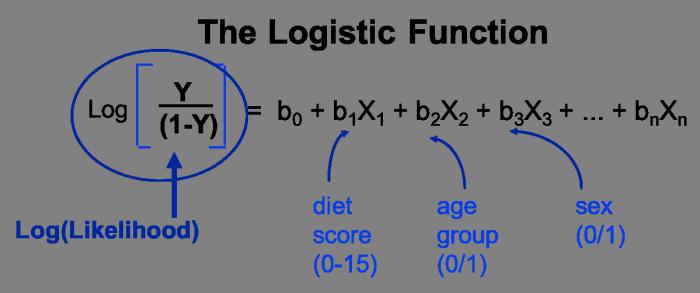
Во время учебы студенты очень часто сталкиваются с разнообразными уравнениями. Одно из них – уравнение регрессии — рассмотрено в данной статье. Такой тип уравнения применяется специально для описания характеристики связи между математическими параметрами. Данный вид равенств используют в статистике и эконометрике.

Определение понятия регрессии

В математике под регрессией подразумевается некая величина, описывающая зависимость среднего значения совокупности данных от значений другой величины. Уравнение регрессии показывает в качестве функции определенного признака среднее значение другого признака. Функция регрессии имеет вид простого уравнения у = х, в котором у выступает зависимой переменной, а х – независимой (признак-фактор). Фактически регрессия выражаться как у = f (x).

Какие бывают типы связей между переменными

В общем, выделяется два противоположных типа взаимосвязи: корреляционная и регрессионная.

Первая характеризуется равноправностью условных переменных. В данном случае достоверно не известно, какая переменная зависит от другой.

Если же между переменными не наблюдается равноправности и в условиях сказано, какая переменная объясняющая, а какая – зависимая, то можно говорить о наличии связи второго типа. Для того чтобы построить уравнение линейной регрессии, необходимо будет выяснить, какой тип связи наблюдается.

Виды регрессий

На сегодняшний день выделяют 7 разнообразных видов регрессии: гиперболическая, линейная, множественная, нелинейная, парная, обратная, логарифмически линейная.

Гиперболическая, линейная и логарифмическая

Уравнение линейной регрессии применяют в статистике для четкого объяснения параметров уравнения. Оно выглядит как у = с+т*х+Е. Гиперболическое уравнение имеет вид правильной гиперболы у = с + т / х + Е. Логарифмически линейное уравнение выражает взаимосвязь с помощью логарифмической функции: In у = In с + т* In x + In E.

Множественная и нелинейная

Два более сложных вида регрессии – это множественная и нелинейная. Уравнение множественной регрессии выражается функцией у = f(х₁ , х₂ . х_с)+E. В данной ситуации у выступает зависимой переменной, а х – объясняющей. Переменная Е — стохастическая, она включает влияние других факторов в уравнении. Нелинейное уравнение регрессии немного противоречиво. С одной стороны, относительно учтенных показателей оно не линейное, а с другой стороны, в роли оценки показателей оно линейное.

Обратные и парные виды регрессий

Обратная – это такой вид функции, который необходимо преобразовать в линейный вид. В самых традиционных прикладных программах она имеет вид функции у = 1/с + т*х+Е. Парное уравнение регрессии демонстрирует взаимосвязь между данными в качестве функции у = f (x) + Е. Точно так же, как и в других уравнениях, у зависит от х, а Е — стохастический параметр.

Понятие корреляции

Это показатель, демонстрирующий существование взаимосвязи двух явлений или процессов. Сила взаимосвязи выражается в качестве коэффициента корреляции. Его значение колеблется в рамках интервала [-1;+1]. Отрицательный показатель говорит о наличии обратной связи, положительный – о прямой. Если коэффициент принимает значение, равное 0, то взаимосвязи нет. Чем ближе значение к 1 – тем сильнее связь между параметрами, чем ближе к 0 – тем слабее.

Методы

Корреляционные параметрические методы могут оценить тесноту взаимосвязи. Их используют на базе оценки распределения для изучения параметров, подчиняющихся закону нормального распределения.

Параметры уравнения линейной регрессии необходимы для идентификации вида зависимости, функции регрессионного уравнения и оценивания показателей избранной формулы взаимосвязи. В качестве метода идентификации связи используется поле корреляции. Для этого все существующие данные необходимо изобразить графически. В прямоугольной двухмерной системе координат необходимо нанести все известные данные. Так образуется поле корреляции. Значение описывающего фактора отмечаются вдоль оси абсцисс, в то время как значения зависимого – вдоль оси ординат. Если между параметрами есть функциональная зависимость, они выстраиваются в форме линии.

В случае если коэффициент корреляции таких данных будет менее 30 %, можно говорить о практически полном отсутствии связи. Если он находится между 30 % и 70 %, то это говорит о наличии связей средней тесноты. 100 % показатель – свидетельство функциональной связи.

Нелинейное уравнение регрессии так же, как и линейное, необходимо дополнять индексом корреляции (R).

Корреляция для множественной регрессии

Коэффициент детерминации является показателем квадрата множественной корреляции. Он говорит о тесноте взаимосвязи представленного комплекса показателей с исследуемым признаком. Он также может говорить о характере влияния параметров на результат. Уравнение множественной регрессии оценивают с помощью этого показателя.

Для того чтобы вычислить показатель множественной корреляции, необходимо рассчитать его индекс.

Метод наименьших квадратов

Данный метод является способом оценивания факторов регрессии. Его суть заключается в минимизировании суммы отклонений в квадрате, полученных вследствие зависимости фактора от функции.

Парное линейное уравнение регрессии можно оценить с помощью такого метода. Этот тип уравнений используют в случае обнаружения между показателями парной линейной зависимости.

Параметры уравнений

Каждый параметр функции линейной регрессии несет определенный смысл. Парное линейное уравнение регрессии содержит два параметра: с и т. Параметр т демонстрирует среднее изменение конечного показателя функции у, при условии уменьшения (увеличения) переменной х на одну условную единицу. Если переменная х – нулевая, то функция равняется параметру с. Если же переменная х не нулевая, то фактор с не несет в себе экономический смысл. Единственное влияние на функцию оказывает знак перед фактором с. Если там минус, то можно сказать о замедленном изменении результата по сравнению с фактором. Если там плюс, то это свидетельствует об ускоренном изменении результата.

Каждый параметр, изменяющий значение уравнения регрессии, можно выразить через уравнение. Например, фактор с имеет вид с = y – тх.

Сгруппированные данные

Бывают такие условия задачи, в которых вся информация группируется по признаку x, но при этом для определенной группы указываются соответствующие средние значения зависимого показателя. В таком случае средние значения характеризуют, каким образом изменяется показатель, зависящий от х. Таким образом, сгруппированная информация помогает найти уравнение регрессии. Ее используют в качестве анализа взаимосвязей. Однако у такого метода есть свои недостатки. К сожалению, средние показатели достаточно часто подвергаются внешним колебаниям. Данные колебания не являются отображением закономерности взаимосвязи, они всего лишь маскируют ее «шум». Средние показатели демонстрируют закономерности взаимосвязи намного хуже, чем уравнение линейной регрессии. Однако их можно применять в виде базы для поиска уравнения. Перемножая численность отдельной совокупности на соответствующую среднюю можно получить сумму у в пределах группы. Далее необходимо подбить все полученные суммы и найти конечный показатель у. Чуть сложнее производить расчеты с показателем суммы ху. В том случае если интервалы малы, можно условно взять показатель х для всех единиц (в пределах группы) одинаковым. Следует перемножить его с суммой у, чтобы узнать сумму произведений x на у. Далее все суммы подбиваются вместе и получается общая сумма ху.

Множественное парное уравнение регрессии: оценка важности связи

Как рассматривалось ранее, множественная регрессия имеет функцию вида у = f (x₁,x₂,…,x_m)+E. Чаще всего такое уравнение используют для решения проблемы спроса и предложения на товар, процентного дохода по выкупленным акциям, изучения причин и вида функции издержек производства. Ее также активно применяют в самых разнообразным макроэкономических исследованиях и расчетах, а вот на уровне микроэкономики такое уравнение применяют немного реже.

Основной задачей множественной регрессии является построение модели данных, содержащих огромное количество информации, для того чтобы в дальнейшем определить, какое влияние имеет каждый из факторов по отдельности и в их общей совокупности на показатель, который необходимо смоделировать, и его коэффициенты. Уравнение регрессии может принимать самые разнообразные значения. При этом для оценки взаимосвязи обычно используется два типа функций: линейная и нелинейная.

Линейная функция изображается в форме такой взаимосвязи: у = а₀ + a₁х₁ + а₂х₂,+ . + a_mx_m. При этом _а2, a_m, считаются коэффициентами «чистой» регрессии. Они необходимы для характеристики среднего изменения параметра у с изменением (уменьшением или увеличением) каждого соответствующего параметра х на одну единицу, с условием стабильного значения других показателей.

Нелинейные уравнения имеют, к примеру, вид степенной функции у=ах₁ b1 х₂ b2 . x_m bm . В данном случае показатели b₁, b₂. b_m – называются коэффициентами эластичности, они демонстрируют, каким образом изменится результат (на сколько %) при увеличении (уменьшении) соответствующего показателя х на 1 % и при стабильном показателе остальных факторов.

Какие факторы необходимо учитывать при построении множественной регрессии

Для того чтобы правильно построить множественную регрессию, необходимо выяснить, на какие именно факторы следует обратить особое внимание.

Необходимо иметь определенное понимание природы взаимосвязей между экономическими факторами и моделируемым. Факторы, которые необходимо будет включать, обязаны отвечать следующим признакам:

• Должны быть подвластны количественному измерению. Для того чтобы использовать фактор, описывающий качество предмета, в любом случае следует придать ему количественную форму.
• Не должна присутствовать интеркорреляция факторов, или функциональная взаимосвязь. Такие действия чаще всего приводят к необратимым последствиям – система обыкновенных уравнений становится не обусловленной, а это влечет за собой ее ненадежность и нечеткость оценок.
• В случае существования огромного показателя корреляции не существует способа для выяснения изолированного влияния факторов на окончательный результат показателя, следовательно, коэффициенты становятся неинтерпретируемыми.

Методы построения

Существует огромное количество методов и способов, объясняющих, каким образом можно выбрать факторы для уравнения. Однако все эти методы строятся на отборе коэффициентов с помощью показателя корреляции. Среди них выделяют:

• Способ исключения.
• Способ включения.
• Пошаговый анализ регрессии.

Первый метод подразумевает отсев всех коэффициентов из совокупного набора. Второй метод включает введение множества дополнительных факторов. Ну а третий – отсев факторов, которые были ранее применены для уравнения. Каждый из этих методов имеет право на существование. У них есть свои плюсы и минусы, но они все по-своему могут решить вопрос отсева ненужных показателей. Как правило, результаты, полученные каждым отдельным методом, достаточно близки.

Методы многомерного анализа

Такие способы определения факторов базируются на рассмотрении отдельных сочетаний взаимосвязанных признаков. Они включают в себя дискриминантный анализ, распознание обликов, способ главных компонент и анализ кластеров. Кроме того, существует также факторный анализ, однако он появился вследствие развития способа компонент. Все они применяются в определенных обстоятельствах, при наличии определенных условий и факторов.

Прямолинейная связь между факторами исследуется с помощью уравнения регрессии . .

Что такое статистика?

Статистика – это одна из общественных наук, имеющая своей целью сбор, упорядочивание и анализ соответствия числового представления факторов, относящихся к самым разнообразным массовым явлениям. Это учение о системе показателей количественных характеристик, дающих представление об общественных явлениях в народном хозяйстве и в целом по всем отраслям.

Статистика – одна из форм практической деятельности людей, цель которой сбор, обработка и анализ массовых данных о тех или иных социально-экономических явлений.

Статистика – различный ряд числовых данных, характеризующих различные стороны жизни государства.

Статистика – это общественная наука, изучающая количественную сторону качественно-определённых социально-экономических явлений и процессов, их структуру и распределение, размещение в пространстве, движение во времени, выявляя действие количественных закономерностей в конкретных условиях места и времени.

2. Виды несплошного статистического наблюдения:

· Наблюдение основного массива

3. Дискретные признаки группировок для построения дискретных вариационных рядов распределения:

4. Соответствие между видами относительных величин:

5. Мода в ряду распределения = .. :

Медиана в ряду распределения = .

6. Формулы для расчета дисперсии признака:

7. Формулы для расчета индекса фиксированного (постоянного) состава:

8. Индекс структурных сдвигов = .... % (с точностью до 0,1 %), если индекс постоянного состава = 101,05 %, индекс переменного состава = 100,58 %.

9. Индекс изменения средней цены товара «А» (индекс цен переменного состава) =… %(с точностью до 0,1 %) при условии:

10. Средний гармонический индекс ценисчисляется с использованием индивидуальных индексов .

11. Ряд динамики характеризует:

12. По формуле определяется…

13. Наиболее тесную связь показывает коэффициент корреляции…

Линейный коэффициент корреляции

Линейный коэффициент корреляции показывает тесноту . .

и направление связи (в случае наличия между ними линейной зависимости)

15. Под выборочным наблюдением понимают:

Несплошное обследование, при котором признаки регистрируются у отдельных единиц изучаемой совокупности, отобранных с использованием специальных методов.

16. Недостающим элементом формулы предельной ошибки случайной выборки при бесповоротном отборе является:

Единица, имеющая центр экономического интереса на экономической территории страны, — это.

Институциональные единицы, основной функцией которых является производство товаров для продажи по ценам, позволяющим получать прибыль, относятся к сектору . .

Использование материальных оборотных средств характеризуется показателями . .

Стоимость воспроизводства основных фондов в современных условиях характеризует их . стоимость.

Что является предметом статистики?

22. Способы статистического наблюдения (в зависимости от источника сведений):

23. Непрерывные признаки группировок для построения интервальных вариационных рядов распределения:

24. Относительная величина планового задания по выпуску продукции (с точностью до 0,1 %) = . %, если план выполнен на 104 %, а прирост выпуска продукции по сравнению с прошлым годом составил 7 %.

25. Сумма отклонений индивидуальных значений признака от их средней арифметической . нуля(ю)

Дисперсия альтернативного признака . .

27. Формула среднего гармонического индекса цен:

28. Индекс изменения себестоимости газовых плит в ноябре по сравнению с сентябрем = . % (с точностью до 0,1%) если известно, что в октябре она была меньше, чем в сентябре на 2 %, а в ноябре меньше, чем в октябре на 3,3%

29. Индекс физического объема по предприятию в целом =… %(с точностью до 0,1%) при условии:

Агрегатные индексы цен Пааше строятся .

Средний уровень моментного ряда динамики с равными временными промежутками исчисляется по формуле средней .

Среднегодовой темп роста исчисляется по формулам . .

В результате проведения регрессионного анализа получают функцию, описывающую . показателей

д) темпы прироста.

Прямолинейная связь между факторами исследуется с помощью уравнения регрессии . .

35. При проведении выборочного наблюдения определяют:

36. Недостающим элементом формулы расчета объема выборки при бесповоротном отборе (оценивается среднее значение признака)