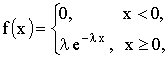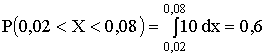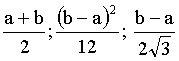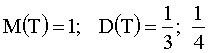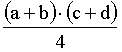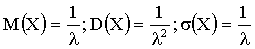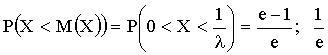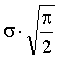Найти вероятность того что ошибка превзойдет - ErrorsMaster.ru - большая энциклопедия ошибок и их решений

Нормальным называют распределение вероятностей непрерывной случайной величины

, плотность которого имеет вид:

где

–
математическое ожидание,

–
среднее квадратическое отклонение

Вероятность того, что

примет
значение, принадлежащее интервалу

где

– функция Лапласа:

Вероятность того, что абсолютная
величина отклонения меньше положительного числа

В частности, при

справедливо
равенство:

Асимметрия, эксцесс,
мода и медиана нормального распределения соответственно равны:

, где

Правило трех сигм

Преобразуем формулу:

Положив

. В итоге получим

если

, и, следовательно,

, то

то есть вероятность того, что
отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонение, равна 0,9973.

Другими словами, вероятность того,
что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна
0,0027. Это означает, что лишь в 0,27% случаев так может произойти. Такие
события исходя из принципа невозможности маловероятных
событий можно считать практически невозможными. В этом и состоит
сущность правила трех сигм: если случайная величина распределена нормально, то
абсолютная величина ее отклонения от математического ожидания не превосходит
утроенного среднего квадратического отклонения.

На практике правило трех сигм
применяют так: если распределение изучаемой случайной величины неизвестно, но
условие, указанное в приведенном правиле, выполняется, то есть основание
предполагать, что изучаемая величина распределена нормально; в противном случае
она не распределена нормально.

Смежные темы решебника:

Таблица значений функции Лапласа
Непрерывная случайная величина
Показательный закон распределения случайной величины
Равномерный закон распределения случайной величины

Пример 2

Ошибка
высотометра распределена нормально с математическим ожиданием 20 мм и средним
квадратичным отклонением 10 мм.

а) Найти
вероятность того, что отклонение ошибки от среднего ее значения не превзойдет 5
мм по абсолютной величине.

б) Какова
вероятность, что из 4 измерений два попадут в указанный интервал, а 2 – не
превысят 15 мм?

в)
Сформулируйте правило трех сигм для данной случайной величины и изобразите
схематично функции плотности вероятностей и распределения.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

а) Вероятность того, что случайная величина, распределенная по
нормальному закону, отклонится от среднего не более чем на величину

В нашем
случае получаем:

б) Найдем
вероятность того, что отклонение ошибки от среднего значения не превзойдет 15
мм:

Пусть событие

– ошибки 2
измерений не превзойдут 5 мм и ошибки 2 измерений не превзойдут 0,8664 мм

– ошибка не
превзошла 5 мм;

– ошибка не
превзошла 15 мм

в)
Для заданной нормальной величины получаем следующее правило трех сигм:

Ошибка высотометра будет лежать в интервале:

Функция плотности вероятностей:

График плотности распределения нормально распределенной случайной величины

Функция распределения:

График функции
распределения нормально распределенной случайной величины

Задача 1

Среднее
количество осадков за июнь 19 см. Среднеквадратическое отклонение количества
осадков 5 см. Предполагая, что количество осадков нормально-распределенная
случайная величина найти вероятность того, что будет не менее 13 см осадков.
Какой уровень превзойдет количество осадков с вероятностью 0,95?

Задача 2

Найти
закон распределения среднего арифметического девяти измерений нормальной
случайной величины с параметрами m=1.0 σ=3.0. Чему равна вероятность того, что
модуль разности между средним арифметическим и математическим ожиданием
превысит 0,5?

Указание:
воспользоваться таблицами нормального распределения (функции Лапласа).

Задача 3

Отклонение
напряжения в сети переменного тока описывается нормальным законом
распределения. Дисперсия составляет 20 В. Какова вероятность при изменении
выйти за пределы требуемых 10% (22 В).

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 4

Автомат
штампует детали. Контролируется длина детали Х, которая распределена нормально
с математическим ожиданием (проектная длинна), равная 50 мм. Фактическая длина
изготовленных деталей не менее 32 и не более 68 мм. Найти вероятность того, что
длина наудачу взятой детали: а) больше 55 мм; б) меньше 40 мм.

Задача 5

Случайная
величина X распределена нормально с математическим ожиданием a=10и средним
квадратическим отклонением σ=5. Найти
интервал, симметричный относительно математического ожидания, в котором с
вероятностью 0,9973 попадает величина Х в результате испытания.

Задача 6

Заданы
математическое ожидание a_x=19 и среднее квадратическое отклонение σ=4
нормально распределенной случайной величины X. Найти: 1) вероятность
того, что X примет значение, принадлежащее интервалу (α=15;
β=19); 2) вероятность того, что абсолютная величина отклонения значения
величины от математического ожидания окажется меньше δ=18.

Задача 7

Диаметр
выпускаемой детали – случайная величина, распределенная по нормальному закону с
математическим ожиданием и дисперсией, равными соответственно 10 см и 0,16 см².
Найти вероятность того, что две взятые наудачу детали имеют отклонение от
математического ожидания по абсолютной величине не более 0,16 см.

Задача 8

Ошибка
прогноза температуры воздуха есть случайная величина с m=0,σ=2℃. Найти вероятность
того, что в течение недели ошибка прогноза трижды превысит по абсолютной
величине 4℃.

Задача 9

Непрерывная
случайная величина X распределена по нормальному
закону: X∈N(a,σ).

а) Написать
плотность распределения вероятностей и функцию распределения.

б) Найти
вероятность того, что в результате испытания случайная величина примет значение
из интервала (α,β).

в) Определить
приближенно минимальное и максимальное значения случайной величины X.

г) Найти
интервал, симметричный относительно математического ожидания a, в котором с
вероятностью 0,98 будут заключены значения X.

a=5; σ=1.3;
α=4; β=6

Задача 10

Производится измерение вала без
систематических ошибок. Случайные ошибки измерения X
подчинены нормальному закону с σ_x=10. Найти вероятность того, что измерение будет
произведено с ошибкой, превышающей по абсолютной величине 15 мм.

Задача 11

Высота
стебля озимой пшеницы — случайная величина, распределенная по нормальному закону
с параметрами a = 75 см, σ = 1 см. Найти вероятность того, что высота стебля:
а) окажется от 72 до 80 см; б) отклонится от среднего не более чем на 0,5 см.

Задача 12

Деталь,
изготовленная автоматом, считается годной, если отклонение контролируемого
размера от номинала не превышает 10 мм. Точность изготовления деталей
характеризуется средним квадратическим отклонением, при данной технологии
равным 5 мм.

а)
Считая, что отклонение размера детали от номинала есть нормально распределенная
случайная величина, найти долю годных деталей, изготовляемых автоматом.

б) Какой
должна быть точность изготовления, чтобы процент годных деталей повысился до
98?

в)
Написать выражение для функции плотности вероятности и распределения случайной
величины.

Задача 13

Диаметр
детали, изготовленной цехом, является случайной величиной, распределенной по
нормальному закону. Дисперсия ее равна 0,0001 см, а математическое ожидание –
2,5 см. Найдите границы, симметричные относительно математического ожидания, в
которых с вероятностью 0,9973 заключен диаметр наудачу взятой детали. Какова
вероятность того, что в серии из 1000 испытаний размер диаметра двух деталей
выйдет за найденные границы?

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 14

Предприятие
производит детали, размер которых распределен по нормальному закону с
математическим ожиданием 20 см и стандартным отклонением 2 см. Деталь будет
забракована, если ее размер отклонится от среднего (математического ожидания)
более, чем на 2 стандартных отклонения. Наугад выбрали две детали. Какова вероятность
того, что хотя бы одна из них будет забракована?

Задача 15

Диаметры
деталей распределены по нормальному закону. Среднее значение диаметра равно d=14 мм
, среднее квадратическое
отклонение σ=2 мм
. Найти вероятность того,
что диаметр наудачу взятой детали будет больше α=15 мм и не меньше β=19 мм; вероятность того, что диаметр детали
отклонится от стандартной длины не более, чем на Δ=1,5 мм.

Задача 16

В
электропечи установлена термопара, показывающая температуру с некоторой
ошибкой, распределенной по нормальному закону с нулевым математическим
ожиданием и средним квадратическим отклонением σ=10℃. В момент когда термопара
покажет температуру не ниже 600℃, печь автоматически отключается. Найти
вероятность того, что печь отключается при температуре не превышающей 540℃ (то
есть ошибка будет не меньше 30℃).

Задача 17

Длина
детали представляет собой нормальную случайную величину с математическим
ожиданием 40 мм и среднеквадратическим отклонением 3 мм. Найти:

а)
Вероятность того, что длина взятой наугад детали будет больше 34 мм и меньше 43
мм;

б)
Вероятность того, что длина взятой наугад детали отклонится от ее
математического ожидания не более, чем на 1,5 мм.

Задача 18

Случайное
отклонение размера детали от номинала распределены нормально. Математическое
ожидание размера детали равно 200 мм, среднее квадратическое отклонение равно
0,25 мм, стандартами считаются детали, размер которых заключен между 199,5 мм и
200,5 мм. Из-за нарушения технологии точность изготовления деталей уменьшилась
и характеризуется средним квадратическим отклонением 0,4 мм. На сколько
повысился процент бракованных деталей?

Задача 19

Случайная
величина X~N(1,2²). Найти P{2

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 20

Заряд пороха для охотничьего ружья
должен составлять 2,3 г. Заряд отвешивается на весах, имеющих ошибку
взвешивания, распределенную по нормальному закону со средним квадратическим
отклонением, равным 0,2 г. Определить вероятность повреждения ружья, если максимально
допустимый вес заряда составляет 2,8 г.

Задача 21

Заряд
охотничьего пороха отвешивается на весах, имеющих среднеквадратическую ошибку
взвешивания 150 мг. Номинальный вес порохового заряда 2,3 г. Определить
вероятность повреждения ружья, если максимально допустимый вес порохового
заряда 2,5 г.

Задача 21

Найти
вероятность попадания снарядов в интервал (α₁=10.7; α₂=11.2).
Если случайная величина X распределена по
нормальному закону с параметрами m=11;
σ=0.2.

Задача 22

Плотность
вероятности распределения случайной величины имеет вид

Найти
вероятность того, что из 3 независимых случайных величин, распределенных по
данному закону, 3 окажутся на интервале (-∞;5).

Задача 23

Непрерывная
случайная величина имеет нормальное распределение. Её математическое ожидание
равно 12, среднее квадратичное отклонение равно 2. Найти вероятность того, что
в результате испытания случайная величина примет значение в интервале (8,14)

Задача 24

Вероятность
попадания нормально распределенной случайной величины с математическим
ожиданием m=4 в интервал (3;5) равна 0,6. Найти дисперсию данной случайной
величины.

Задача 25

В
нормально распределенной совокупности 17% значений случайной величины X
меньше 13% и 47% значений случайной величины X
больше 19%. Найти параметры этой совокупности.

Задача 26

Студенты
мужского пола образовательного учреждения были обследованы на предмет
физических характеристик и обнаружили, что средний рост составляет 182 см, со
стандартным отклонением 6 см. Предполагая нормальное распределение для роста,
найдите вероятность того, что конкретный студент-мужчина имеет рост более 185
см.

Источник

Нормальный закон распределения имеет плотность вероятности

f (x) =	1		ì	(x — m)	2	ü
	exp í—		ý	,	(2.9.1)
		2s2
	2p s	î		þ

где –¥ < m < ¥ и s > 0 –– некоторые параметры.

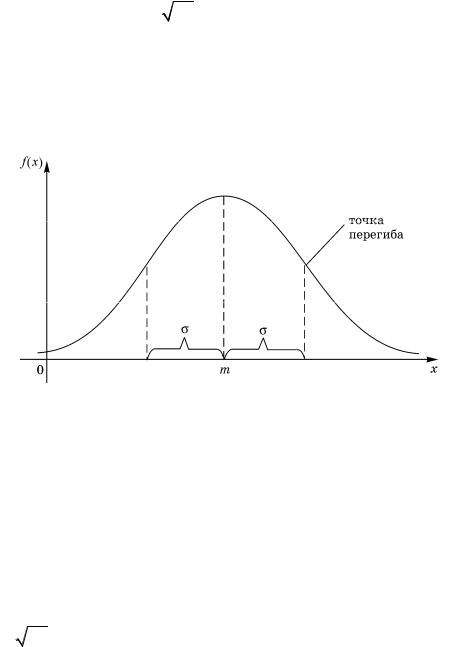
График функции плотности вероятности(2.9.1) имеет максимум в точке х = m , а точки перегиба отстоят от точкиm на расстояние s. При х ® ±¥ функция (2.9.1) асимптотически приближается к нулю(ее график изображен на рис. 2.9.1).

Рис. 2.9.1

Помимо геометрического смысла, параметры нормального закона распределения имеют и вероятностный смысл. Параметр m равен

математическому

ожиданию

нормально

распределенной

случайной

величины,

дисперсия D( X ) = s2 .

Если

X : N (m;s2 ),

т.е. X

имеет

нормальный закон распределения с параметрами m и s2, то

Р(а <

Х < =b)

æ b — m ö

æ a — m ö

Fç

— Fç

÷ ,

(2.9.2)

òexp=

где F(x)

í—

ý dt

–– функция Лапласа.

Значения

функции F(x) можно

найти

по

таблице(см. прил., табл.

П2). Функция

Лапласа нечетна, т.е. F(—x)= –F(x). Поэтому ее

таблица

дана только для неотрицательныхх. График функции Лапласа изображен

на рис. 2.9.2. При

значениях х > 5

она практически остается постоянной.

Поэтому в таблице даны значения функции

только

0для£ х £ 5. При

значениях х > 5 можно считать, что F(x) = 0,5.

Рис. 2.9.2

Если X : N (m;s2 ), то


		æ a ö
	Р(\| X — m \|< a) =2Fç			÷.		(2.9.3)

		è s ø
Пример	2.49. Случайная величинаX	имеет	нормальный закон
распределения	N (m;s2 ) . Известно, что	P( X <1) = 0,15866, а P( X > 4) =
= 0,30854. Найти значения параметров m и s2.
Решение. Воспользуемся формулой (2.9.2):
	æ1 — m ö	æ	-¥ — m ö
P( X <1) = P(-¥ < X <1) = Fç		÷	— Fç	=	÷

	è	s ø	è	s	ø

æ1 — m ö

=Fç ÷ + F(¥) = 0,15866.

è s ø

Так как F(¥) = 0,5,	æ1 — m ö	æ m —1ö	= 0,5 – 0,15866=	0,34134. По
то -Fç		÷	= Fç		÷
s	s
	è	ø	è	ø

таблице функции		Лапласа(см. прил., табл.	П2)	находим,	что	F(1) =
= 0,34134. Поэтому		m —1	=1 или m – 1 = s.
	s

Аналогично				æ	¥ — m ö	æ	4 — m ö
P( X > 4) = P(4 < X < ¥) =Fç		÷	— Fç	=	÷	0,30854.
s
				è	ø	è	s	ø

Так как F(¥) = 0,5,	æ 4 — m ö	0,5 –= 0,30854 0,19146= . По таблице
то Fç		÷
s
	è	ø

функции Лапласа (см.	прил., табл. П2)	находим, что F(1 / 2) = 0,19146.
Поэтому	4 — m	= 0,5	или m – 4 = –0,5s.	Из системы двух уравнений
s

m – 1 = s и m – 4 = –0,5s находим, что m = 3 , а s = 2 , т.е. s2 = 4. Итак, случайная величина X имеет нормальный закон распределенияN(3;4).

График функции плотности вероятности этого закона распределения изображен на рис. 2.9.3.

Ответ. m = 3 ; s2 = 4.

							Рис. 2.9.3
	Задача	2.49.	Случайная	величинаX	имеет	нормальный закон
распределения N (m;s2 ) . Известно, что:
	а) для нечетных вариантов P( X < =a)	a, а P( X < =b)	b;
	б) для четных вариантов P( X < =a) a, а P( X > =b)	b.
	Найдите значения	параметровm и	s2.	Сделайте	эскиз	функции
плотности вероятности	при найденных	значениях	параметров. Найдите
P( X 2 < 4). (См. пример 2.49 и исходные данные.)
	Исходные данные к задаче 2.49.
№	a		a	b		b		№	a	a		b		b
1	–2		0,0668	3		0,8413		16	–1/2	0,4013	2		0,1587
2	–1		0,1587	5		0,0227		17	5	0,6915	2		0,1587
3	–1		0,4332	4		0,8413		18	5	0,6915	2		0,8413
4	0		0,1587	6		0,0227		19	2	0,0227	8		0,8413
5	–2		0,1587	1		0,6915		20	2	0,0227	8		0,1587
6	2		0,8413	–1		0,6915		21	3	0,1587	12		0,9773
7	1		0,1587	5		0,8413		22	3	0,1587	4,5		0,6915
8	1		0,1587	5		0,1587		23	0	0,3085	6		0,8413
9	–6		0,0227	3		0,8413		24	0	0,3085	6		0,6915
10	3		0,1587	6		0,0227		25	–2	0,1587	4		0,6915
11	–3		0,1587	0		0,6915		26	–2	0,1587	4		0,3085
12	–3		0,1587	0		0,3085		27	2	0,5000	4		0,6915
13	0		0,3446	5		0,7258		28	4	0,6915	2		0,5000
14	–1/2		0,4013	2		0,8413		29	–3	0,1587	0		0,9773
15	–3		0,1587	0		0,0227		30	0	0,3446	5		0,2742

Пример 2.50. Ошибка измеренияX имеет нормальный закон распределения, причем систематическая ошибка равна1 мк, а дисперсия ошибки равна 4 мк2. Какова вероятность того, что в трех независимых измерениях ошибка ни разу не превзойдет по модулю 2 мк?

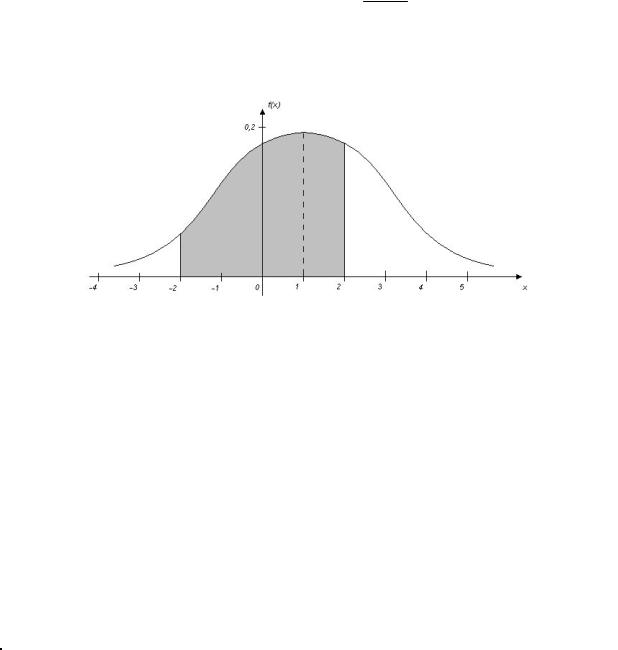
Решение. По условиям задачиX ~ N (1;4). Вычислим сначала вероятность того, что в одном измерении ошибка не превзойдет2 мк. По формуле (2.9.2)

P(\| X \|£	2) = P(—2 £	X £	æ 2 —1 ö	æ	—2 —1	ö
2) = Fç			÷	— Fç	=	÷	F(1 / 2)	— F(—3 / 2)=

			è		2 ø	è	2	ø
	= F(1 / 2) + F(3 / 2)	=0,1915 + 0, 4332 = 0, 6241.

Вычисленная вероятность численно равна заштрихованной площади на рис. 2.9.4.

Рис. 2.9.4

Каждое измерение можно рассматривать как независимый .опыт Поэтому по формуле Бернулли(2.6.1) вероятность того, что в трех независимых измерениях ошибка ни разу не превзойдет 2 мк, равна P3 (3) =

= C33 (0,6241)3 (0,3753)0 »1 / 4.

Ответ. »1 / 4.

Задача 2.50. Ошибка измеренияX имеет нормальный закон распределения N (m;s2 ) . Найдите вероятность того, что при измерении ошибка по модулю не превысит v. Изобразите найденную вероятность на рисунке. Найдите вероятность того, что в n независимых измерениях ошибка измерения k раз превзойдет v. (См. пример 2.50 и исходные данные.)

Исходные данные к задаче 2.50.

№	m	s2	v	n	k	№	m	s2	v	n	k	№	m	s2	v	n	k
1	–1	4	2	4	1	11	2	2,25	3	4	1	21	–1	9	3	3	1
2	2	9	3	3	1	12	0,5	4	2	3	1	22	2	2,25	2	3	1
3	1	4	3	4	2	13	2	9	3	4	1	23	0,5	4	3	4	1
4	2	4	3	3	1	14	0,5	9	3	4	2	24	0,5	6,25	4	3	1
5	–1	16	5	4	1	15	–1	4	3	4	2	25	2	9	3	4	2
6	2	4	4	3	1	16	0,5	4	3	4	1	26	0,5	9	4	3	1
7	1	2,25	3	3	1	17	0,5	16	3	3	1	27	1,5	4	3	3	2

8	–1	9	2	4	1	18	2	9	3	4	1	28	–2	9	3	4	1
9	2	9	3	3	1	19	0,5	4	2	4	2	29	0	4	3	4	2
10	1	4	3	4	2	20	0,5	2,25	3	3	1	30	0	9	4	3	1

Пример 2.51. Функция плотности вероятности случайной величины

X имеет вид
f (x) = gexp{—2x2 – 4 / 3x +1 / 3}.	(2.9.4)

Требуется определить коэффициентg, найти M ( X ) и D( X ) , определить тип закона распределения, нарисовать график функции f (x) , вычислить вероятность P(—1 < X < 0).

	Замечание.	Если	каждый закон распределения из некоторого
семейства	законов	распределения	имеет	функцию	распределения
æ x — a ö		где F (x) –– фиксированная
F ç			÷	,	функция	распределения,	a Î R,
b
è	ø
b > 0,	то		говорят,	что эти	законы распределенияпринадлежат к	одному

виду или типу распределений. Параметр a называют параметром сдвига, b –

– параметром масштаба.

Решение. Так как (2.9.4) функция плотности вероятности, то интеграл от нее по всей числовой оси должен быть равен единице:

¥¥

ò	f (x) dx = g ò e—2 x2 —3/4 x+1/3dx =1.	(2.9.5)
-¥	-¥

Преобразуем выражение в показателе степени, выделяя полный квадрат:

—2(x2 + 2 / 3x —1=/ 6) —2(x2 + 2 / 3x +1 / 9 —1 / 9 —1=/ 6) —2( x +1 / 3)2 + 5 / 9.

Тогда (2.9.5) можно записать в виде

e5/9 g ò e—2( x+1/3)2 dx =1.

(2.9.6)

-¥

Сделаем

замену

переменных

,такчтобы

2(x +1 / 3)2 = t 2 / 2, т..е

x +1 / 3 = t / 2,

dx = dt / 2.

Пределы интегрирования при этом останутся

прежними. Тогда (2.9.6) преобразуется к виду

e5/9 g ò e—t 2 /2

=1.

-¥

Умножим и разделим левую часть равенства на

. Получим равенство

e5/9

ò e—t2 /2 dt =1.

-¥

Так как 1 ò e—t2 /2 dt =1, как интеграл по всей числовой оси от

2p -¥

функции

плотности

вероятности

стандартного

нормального

закона

распределения N(0,1), то приходим к выводу, что

g =

e—5/9 .

Поэтому

f (x) =

e—5/9 exp{—2x2

– 4 / 3x +1 / 3}

exp{= —2x2 — 4 / 3x – 2 / 9} =

exp{—2(x2 + 2 / 3x +1 / 9)} =

( x+1/3)2

2×1/4 .

—

0,5

Последняя

запись

означает, что

случайная

величина

имеет

нормальный

закон

распределения

параметрамиm = —1 / 3 и s2 =1 / 4.

График функции плотности вероятности этого закона изображен на .рис

2.9.5. Распределение случайной величиныX принадлежит к семейству

нормальных законов распределения. По формуле (2.9.2)

P(—1 < X < 0)=

æ 0 — (—1 / 3) ö

æ —1

— (—1 / 3)

F(2 / 3)

+ F(4= / 3) 0,653.

Fç

— F

ç=

1 / 2

						Рис. 2.9.5
Ответ. g =		2		е—5/9 ,	M ( X ) = —1 / 3,	D( X ) =1 / 4, N (—1 / 3; 1 / 4).

2p

Задача 2.51. Функция плотности вероятности случайной величиныX
имеет вид					f (x) = gexp{ax2 + bx + c}.

Найдите	коэффициент g, M ( X ),	D( X ) , определите	тип закона
распределения,	нарисуйте	график функции f (x) . Вычислите	P(\| x \|< 2).

(См. пример 2.51 и исходные данные.)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Говорят, что СВ X имеет равномерное распределение на участке от a до b, если ее плотность f(x) на этом участке постоянна, то есть

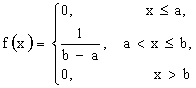
Например, производится измерение какой-то величины с помощью прибора с грубыми делениями; в качестве приближенного значения измеряемой величины берется ближайшее целое. СВ X — ошибка измерения распределена равномерно на участке 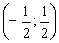, так как ни одно из значений случайной величины ничем не предпочтительнее других.

Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью

где 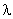— постоянная положительная величина.

Примером непрерывной случайной величины, распределенной по показательному закону, может служить время между появлениями двух последовательных событий простейшего потока.

Часто длительность времени безотказной работы элементы имеет показательное распределение, функция распределения которого
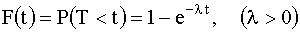
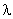
определяет вероятность отказа элемента за время длительностью t.

— интенсивность отказов (среднее число отказов в единицу времени).

Нормальный закон распределения (иногда называемый законом Гаусса) играет исключительно важную роль в теории вероятностей и занимает среди других законов распределения особое положение. Плотность распределения нормального закона имеет вид

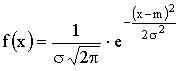
где m — математическое ожидание,

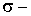
— среднее квадратическое отклонение X.

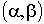
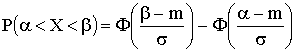
Вероятность того, что нормально распределенная СВ X примет значение, принадлежащее интервалу , вычисляется по формуле: ,

где Ф(X) — функция Лапласа. Ее значения определяются из таблицы приложения учебника по теории вероятностей.

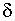
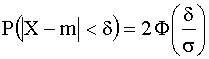
Вероятность того, что отклонение нормально распределенной случайной величины X от математического ожидания по абсолютной величине меньше заданного положительного числа , вычисляется по формуле

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

ПРИМЕР 13.2.41. Цена одного деления шкалы амперметра равна 0,1 А. Показания округляются до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана ошибка, превышающая 0,02 А.

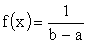
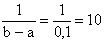
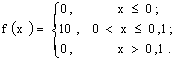
Решение. Ошибку округления можно рассматривать как СВ X, которая распределена равномерно в интервале между двумя соседними делениями. Плотность равномерного распределения , где (b-a) — длина интервала, в котором заключены возможные значения X. В рассматриваемой задаче эта длина равна 0,1. Поэтому . Итак, .

Ошибка отсчета превысит 0,02, если она будет заключена в интервале (0,02; 0,08). По формуле 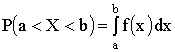имеем

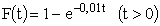
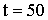
ПРИМЕР 13.2.42. Длительность времени безотказной работы элемента имеет показательное распределение . Найти вероятность того, что за время длительностью часов:

а) элемент откажет;

б) элемент не откажет.

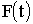
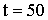
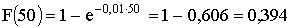
Решение. а) Функция определяет вероятность отказа элемента за время длительностью t, поэтому, подставив , получим вероятность отказа: .

б) События «элемент откажет» и «элемент не откажет» — противоположные, поэтому вероятность того, что элемент не откажет .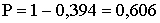

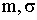
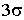
ПРИМЕР 13.2.43. Случайная величина X распределена нормально с параметрами . Найти вероятность того, что СВ X отклонится от своего математического ожидания m больше, чем на .

Решение.

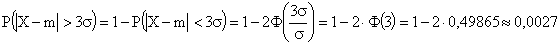
Эта вероятность очень мала, то есть такое событие можно считать практически невозможным (можно ошибиться примерно в трех случаях из 1000). Это и есть “правило трех сигм”: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.

ПРИМЕР 13.2.44. Математическое ожидание и среднее квадратического отклонение нормально распределенной случайной величины соответственно равны 10 и 2. Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале (12, 14).

Решение.Для нормально распределенной величины

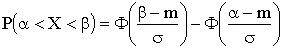
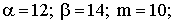
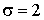
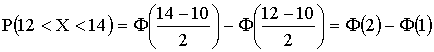
Подставив , получим

По таблице находим .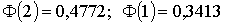

Искомая вероятность .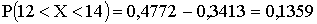

Примеры и задачи для самостоятельного решения

Решить задачи, используя формулы расчета вероятности для непрерывных случайных величин и их характеристик

3.2.9.1. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X, распределенной равномерно в интервале (a,b).

Отв.:

3.2.9.2. Поезда метрополитена идут регулярно с интервалом 2 мин. Пассажир выходит на платформу в случайный момент времени. Найти плотность распределения СВ T — времени, в течение которого ему придется ждать поезда; . Найти вероятность того, что ждать придется не больше полминуты.

Отв.:

3.2.9.3. Минутная стрелка электрических часов перемещается скачком в конце каждой минуты. Найти вероятность того, что в данное мгновение часы покажут время, которое отличается от истинного не более чем на 20 с.

Отв.:2/3

3.2.9.4. Случайная величина X распределена равномерно на участке (a,b). Найти вероятность того, что в результате опыта она отклонится от своего математического ожидания больше, чем на .

Отв.:0

3.2.9.5. Случайные величины X и Y независимы и распределены равномерно: X — в интервале (a,b), Y — в интервале (c,d). Найти математическое ожидание произведения XY.

Отв.:

3.2.9.6. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение показательно распределенной случайной величины.

Отв.:

3.2.9.7. Написать плотность и функцию распределения показательного закона, если параметр .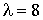

Отв.:,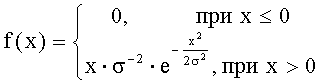

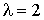
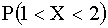
3.2.9.8. Случайная величина имеет показательное распределение с параметром . Найти .

Отв.:0,233

3.2.9.9. Время безотказной работы элемента распределено по показательному закону 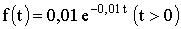, где t — время, ч. Найти вероятность того, что элемент проработает безотказно 100 ч.

Отв.:0,37

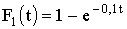
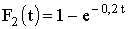
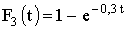
3.2.9.10. Испытывают три элемента, которые работают независимо один от другого. Длительность времени безотказной работы элементов распределена по показательному закону: для первого элемента ; для второго ; для третьего элемента . Найти вероятность того, что в интервале времени (0; 5) ч. откажут: а) только один элемент; б) только два элемента; в) все три элемента.

Отв.: а)0,292; б)0,466; в)0,19

3.2.9.11. Доказать, что если непрерывная случайная величина распределена по показательному закону, то вероятность того, что X примет значение меньшее математического ожидания M(X), не зависит от величины параметра 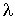; б) найти вероятность того, что X > M(X).

Отв.:

3.2.9.12. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины соответственно равны 20 и 5. Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале (15; 25).

Отв.: 0,6826

3.2.9.13. Производится взвешивание некоторого вещества без систематических ошибок. Случайные ошибки взвешивания подчинены нормальному закону со средним квадратическим отклонением 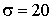г. Найти вероятность того, что а) взвешивание будет произведено с ошибкой, не превосходящей по абсолютной величине 10г; б) из трех независимых взвешиваний ошибка хотя бы одного не превзойдет по абсолютной величине 4г.

Отв.:

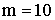
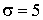
3.2.9.14. Случайная величина X распределена нормально с математическим ожиданием и средним квадратическим отклонением . Найти интервал, симметричный относительно математического ожидания, в который с вероятностью 0,9973 попадет величина X в результате испытания.

Отв.:(-5,25)

3.2.9.15. Завод изготовляет шарики для подшипников, номинальный диаметр которых равен 10 мм, а фактический диаметр случаен и распределен по нормальному закону с 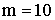мм и мм. При контроле бракуются все шарики, не проходящие через круглое отверстие с диаметром 10,7 мм и все, проходящие через круглое отверстие с диаметром 9,3 мм. Найти процент шариков, которые будут браковаться.

Отв.:8,02%

3.2.9.16. Автомат штампует детали. Контролируется длина детали X, которая распределена нормально с проектной длиной (математическим ожиданием), равным 50 мм. Фактически длина изготовленных деталей не менее 32 и не более 68 мм. Найти вероятность того, что длина наудачу взятой детали: а) больше 55 мм; б) меньше 40 мм.

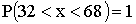
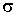
Указание: Из равенства предварительно найти .

Отв.:а)0,0823; б)0,0027

3.2.9.17. Коробки с шоколадом упаковываются автоматически; их средняя масса равна 1,06 кг. Найти дисперсию, если 5% коробок имеют массу меньше 1 кг. Предполагается, что масса коробок распределена по нормальному закону.

Отв.:0,00133

3.2.9.18. Бомбардировщик, пролетевший вдоль моста, длина которого 30 м и ширина 8 м, сбросил бомбы. Случайные величины X и Y (расстояние от вертикальной и горизонтальной осей симметрии моста до места падения бомбы) независимы и распределены нормально со средними квадратическими отклонениями, соответственно равными 6 и 4 м, и математическими ожиданиями, равными нулю. Найти: а) вероятность попадания в мост одной брошенной бомбы; б) вероятность разрушения моста, если сброшены две бомбы, причем известно, что для разрушения моста достаточно одного попадания.

Отв.:

3.2.9.19. В нормально распределенной совокупности 11% значений X меньше 0,5 и 8% значений X больше 5,8. Найти параметры m и 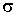данного распределения.

Отв.:3; 2

3.2.9.20. В нормально распределенной совокупности 25% значений X меньше -5,38 и 10% значений X больше 4,44. Найти параметры m и 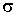данного распределения.

Отв.: -2; 5

3.2.9.21. Масса арбуза некоторого сорта – нормально распределенная случайная величина с m=5 кг и 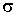=0,5 кг. Какова вероятность того, что в партии весом в 10 т находится не менее 1900 и не более 2100 арбузов?

Отв.: 0,3863

3.2.9.22. Найти математическое ожидание случайной величины Х, которая подчиняется закону распределения Рэлея:
,
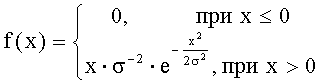
где 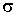> 0 – параметр.

Отв.:

3.2.9.23. В некоторых странах действует закон о налогообложении, который распространяется на тех частных предпринимателей, годовой доход которых превосходит некоторый установленный законом уровень x0. Считая, что годовой доход наудачу выбранного лица, облагаемого налогом, является случайной величиной Х, распределенной по закону Парето
,
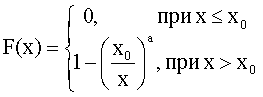
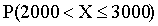
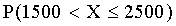
с параметрами a=4, x0=1000, найти D(X) и сравнить вероятности и .

Отв.: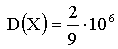; 0,05; 0,17

3.2.9.24. Найти M(X) случайной величины Х, которая подчиняется закону распределения Парето, если ее функция распределения имеет вид: ,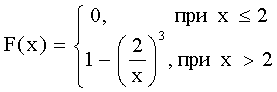

и выяснить, вероятность какого события выше P(X < M(X)) или P(X > M(X)).

Отв.: M(X)=3; P(X < M(X))=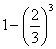; P(X > M(X))=

Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >

Источник

Условие

4. Случайные ошибки измерения подчинены нормальному закону со средним квадратическим отклонением сигма =1 мм и математическим ожиданием а = 0. Найти вероятность того, что из двух независимых наблюдений ошибка хотя бы одного из них не превзойдет по абсолютной величине 1,28 мм.

Отв. 0,96.

математика ВУЗ
11053

Решение

★

Пусть случайная величина Х — ошибка измерения.

Так как вероятность отклонения нормально распределенной случайной величины Х от ее математического ожидания а по абсолютной величине меньше заданного положительного числа ε вычисляется по формуле:
P(|X-a| < ε) =2Ф(ε/σ)
и
по условию
σ=1
a=0
ε=1,28
ε/σ=1,28
Ф(1,28/1)=Ф(1,28)=0,3997 ( см. приложение),
то
вероятность ошибки в одном наблюдении
2Ф(ε/σ)=2*Ф(1,28)=2*0,3997=0,7994
p=0,7994

Найдем вероятность противоположного события:, что ошибка превзойдет 1,28 мм
q=1 — p =1 — 0,7994 = 0,2006

Вероятность того, что ошибка превзойдет 1,28 в двух испытаниях
q*q=q^2=0,2006^2≈0,04

Тогда вероятность того, что из двух независимых испытаний ошибка [b] хотя бы в одном из них [/b] не превзойдет 1,28
равна
1-q^2=1-0,2006^2≈1-0,04=0,96
О т в е т. 0,96

Написать комментарий

Источник