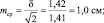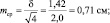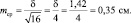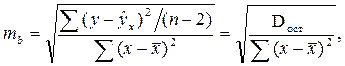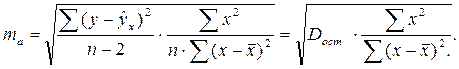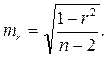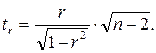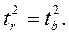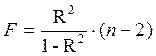Найти стандартную ошибку и доверительный интервал

Стандартная ошибка измерения: определение и пример

Когда нам нужно получить одно число в качестве оценки параметра совокупности, мы используем точечную оценку. Тем не менее, из-за ошибки выборки, точечная оценка не будет в точности равняться параметру совокупности при любом размере данной выборки.

Часто, вместо точечной оценки, более полезным подходом будет найти диапазон значений, в рамках которого, как мы ожидаем, может находится значение искомого параметра с заданным уровнем вероятности.

Этот подход называется интервальной оценкой параметра (англ. ‘interval estimate of parameter’), а доверительный интервал выполняет роль этого диапазона значений.

Определение доверительного интервала.

Доверительный интервал (англ. ‘confidence interval’) представляет собой диапазон, для которого можно утверждать, с заданной вероятностью (1 — alpha ), называемой степенью доверия (или степенью уверенности, англ. ‘degree of confidence’), что он будет содержать оцениваемый параметр.

Этот интервал часто упоминается как (100 (1 — alpha)% ) доверительный интервал для параметра.

Конечные значения доверительного интервала называются нижним и верхним доверительными пределами (или доверительными границами или предельной погрешностью, англ. ‘lower/upper confidence limits’).

В этом чтении, мы имеем дело только с двусторонними доверительными интервалами — доверительные интервалами, для которых мы вычисляем и нижние и верхние пределы.

Доверительные интервалы часто дают либо вероятностную интерпретацию, либо практическую интерпретацию.

При вероятностной интерпретации, мы интерпретируем 95%-ный доверительный интервал для среднего значения совокупности следующим образом.

При повторяющейся выборке, 95% таких доверительных интервалов будут, в конечном счете, включать в себя среднее значение совокупности.

Например, предположим, что мы делаем выборку из совокупности 1000 раз, и на основании каждой выборки мы построим 95%-ный доверительный интервал, используя вычисленное выборочное среднее.

Из-за случайного характера выборок, эти доверительные интервалы отличаются друг от друга, но мы ожидаем, что 95% (или 950) этих интервалов включают неизвестное значение среднего по совокупности.

На практике мы обычно не делаем такие повторяющиеся выборки. Поэтому в практической интерпретации, мы утверждаем, что мы 95% уверены в том, что один 95%-ный доверительный интервал содержит среднее по совокупности.

Мы вправе сделать это заявление, потому что мы знаем, что 95% всех возможных доверительных интервалов, построенных аналогичным образом, будут содержать среднее по совокупности.

Доверительные интервалы, которые мы обсудим в этом чтении, имеют структуры, подобные описанной ниже базовой структуре.

Построение доверительных интервалов.

Доверительный интервал (100 (1 — alpha)% ) для параметра имеет следующую структуру.

Величину (Фактор надежности) (times) (Cтандартная ошибка) иногда называют точностью оценки (англ. ‘precision of estimator’). Большие значения этой величины подразумевают более низкую точность оценки параметра совокупности.

Самый базовый доверительный интервал для среднего значения по совокупности появляется тогда, когда мы делаем выборку из нормального распределения с известной дисперсией. Фактор надежности в данном случае на основан стандартном нормальном распределении, которое имеет среднее значение, равное 0 и дисперсию 1.

Стандартная нормальная случайная величина обычно обозначается как (Z). Обозначение (z_alpha ) обозначает такую точку стандартного нормального распределения, в которой (alpha) вероятности остается в правом хвосте.

Например, 0.05 или 5% возможных значений стандартной нормальной случайной величины больше, чем ( z_{0.05} = 1.65 ).

Предположим, что мы хотим построить 95%-ный доверительный интервал для среднего по совокупности, и для этой цели, мы сделали выборку размером 100 из нормально распределенной совокупности с известной дисперсией (sigma^2) = 400 (значит, (sigma) = 20).

Мы рассчитываем выборочное среднее как ( overline X = 25 ). Наша точечная оценка среднего по совокупности, таким образом, 25.

Если мы перемещаем 1.96 стандартных отклонений выше среднего значения нормального распределения, то 0.025 или 2.5% вероятности остается в правом хвосте. В силу симметрии нормального распределения, если мы перемещаем 1.96 стандартных отклонений ниже среднего, то 0.025 или 2.5% вероятности остается в левом хвосте.

В общей сложности, 0.05 или 5% вероятности лежит в двух хвостах и 0.95 или 95% вероятности лежит между ними.

---

Таким образом, ( z_{0.025} = 1.96) является фактором надежности для этого 95%-ного доверительного интервала. Обратите внимание на связь (100 (1 — alpha)% ) для доверительного интервала и (z_{alpha/2}) для фактора надежности.

Стандартная ошибка среднего значения выборки, заданная Формулой 1, равна:

( sigma_{overline X} = 20 Big / sqrt{100} = 2 )

Доверительный интервал, таким образом, имеет нижний предел:

( overline X — 1.96 sigma_{overline X} ) = 25 — 1.96(2) = 25 — 3.92 = 21.08.

Верхний предел доверительного интервала равен:

( overline X + 1.96sigma_{overline X} ) = 25 + 1.96(2) = 25 + 3.92 = 28.92

95%-ный доверительный интервал для среднего по совокупности охватывает значения от 21.08 до 28.92.

Доверительные интервалы для среднего по совокупности (нормально распределенная совокупность с известной дисперсией).

Доверительный интервал (100 (1 — alpha)% ) для среднего по совокупности ( mu ), когда мы делаем выборку из нормального распределения с известной дисперсией ( sigma^2 ) задается формулой:

( Large dst overline X pm z_{alpha /2}{sigma over sqrt n}  ) (Формула 4)

Факторы надежности для наиболее часто используемых доверительных интервалов приведены ниже.

Факторы надежности для доверительных интервалов на основе стандартного нормального распределения.

Мы используем следующие факторы надежности при построении доверительных интервалов на основе стандартного нормального распределения:

Эти факторы надежности подчеркивают важный факт о всех доверительных интервалах. По мере того, как мы повышаем степень доверия, доверительный интервал становится все шире и дает нам менее точную информацию о величине, которую мы хотим оценить.

«Чем уверенней мы хотим быть, тем меньше мы должны быть уверены»

см. Freund и Williams (1977), стр. 266.

На практике, допущение о том, что выборочное распределение выборочного среднего, по меньшей мере, приблизительно нормальное, часто является обоснованным, либо потому, что исходное распределение приблизительно нормальное, либо потому что мы имеем большую выборку и поэтому к ней применима центральная предельная теорема.

Однако, на практике, мы редко знаем дисперсию совокупности. Когда дисперсия генеральной совокупности неизвестна, но выборочное среднее, по меньшей мере, приблизительно нормально распределено, у нас есть два приемлемых пути чтобы вычислить доверительные интервалы для среднего значения совокупности.

---

Вскоре мы обсудим более консервативный подход, который основан на t-распределении Стьюдента (t-распределение, для краткости).

Распределение статистики (t) называется t-распределением Стьюдента (англ. «Student’s t-distribution») из-за псевдонима «Студент» (Student), использованного британским математиком Уильямом Сили Госсеттом, который опубликовал свою работу в 1908 году.

В финансовой литературе, это наиболее часто используемый подход для статистической оценки и проверки статистических гипотез, касающихся среднего значения, когда дисперсия генеральной совокупности не известна, как для малого, так и для большого размер выборки.

Второй подход к доверительным интервалам для среднего по совокупности, основанного на стандартном нормальном распределении, — это z-альтернатива (англ. ‘z-alternative’). Он может быть использован только тогда, когда размер выборки является большим (в общем случае, размер выборки 30 или больше, можно считать большим).

В отличии от доверительного интервала, приведенного в Формуле 4, этот доверительный интервал использует стандартное отклонение выборки (s) при вычислении стандартной ошибки выборочного среднего (по Формуле 2).

Доверительные интервалы для среднего по совокупности — z-альтернатива (большая выборка, дисперсия совокупности неизвестна).

Доверительный интервал (100 (1 — alpha)% ) для среднего по совокупности ( mu ) при выборке из любого распределения с неизвестной дисперсией, когда размер выборки большой, задается формулой:

( Large dst overline X pm z_{alpha /2}{s over sqrt n} ) (Формула 5)

Поскольку этот тип доверительного интервала применяется довольно часто, мы проиллюстрируем его вычисление в Примере 4.

Пример (4) расчета доверительного интервала для среднего по совокупности коэффициентов Шарпа с использованием z-статистики.

Предположим, что инвестиционный аналитик делает случайную выборку акций взаимных фондов США и рассчитывает средний коэффициент Шарпа.

[см. также: CFA — Коэффициент Шарпа]

Размер выборки равен 100, а средний коэффициент Шарпа составляет 0.45. Выборка имеет стандартное отклонение 0.30.

Рассчитайте и интерпретируйте 90-процентный доверительный интервал для среднего по совокупности всех акций взаимных фондов США с использованием фактора надежности на основе стандартного нормального распределения.

---

Фактор надежности для 90-процентного доверительного интервала, как указано ранее, составляет ( z_{0.05} = 1.65 ).

Доверительный интервал будет равен:

( begin{aligned} & overline X pm z_{0.05}{s over sqrt n } \ &= 0.45 pm 1.65{0.30 over sqrt {100}} \ &= 0.45 pm 1.65(0.03) = 0.45 pm 0.0495   end{aligned} )

Доверительный интервал охватывает значения 0.4005 до 0.4995, или от 0.40 до 0.50, с округлением до двух знаков после запятой. Аналитик может сказать с 90-процентной уверенностью, что интервал включает среднее по совокупности.

В этом примере аналитик не делает никаких конкретных предположений о распределении вероятностей, характеризующем совокупность. Скорее всего, аналитик опирается на центральную предельную теорему для получения приближенного нормального распределения для выборочного среднего.

Как показывает Пример 4, даже если мы не уверены в характере распределения совокупности, мы все еще можем построить доверительные интервалы для среднего по совокупности, если размер выборки достаточно большой, поскольку можем применить центральную предельную теорему.

Концепция степеней свободы.

Обратимся теперь к консервативной альтернативе и используем t-распределение Стьюдента, чтобы построить доверительные интервалы для среднего по совокупности, когда дисперсия генеральной совокупности не известна.

Для доверительных интервалов на основе выборок из нормально распределенных совокупностей с неизвестной дисперсией, теоретически правильный фактор надежности основан на t-распределении. Использование фактора надежности, основанного на t-распределении, имеет важное значение для выборок небольшого размера.

Применение фактора надежности (t) уместно, когда дисперсия генеральной совокупности неизвестна, даже если у нас есть большая выборка и мы можем использовать центральную предельную теорему для обоснования использования фактора надежности (z). В этом случае большой выборки, t-распределение обеспечивает более консервативные (широкие) доверительные интервалы.

t-распределение является симметричным распределением вероятностей и определяется одним параметром, известным как степени свободы (DF, от англ. ‘degrees of freedom’). Каждое значение для числа степеней свободы определяет одно распределение в этом семействе распределений.

Далее мы сравним t-распределения со стандартным нормальным распределением, но сначала мы должны понять концепцию степеней свободы. Мы можем сделать это путем изучения расчета выборочной дисперсии.

Формула 3 дает несмещенную оценку выборочной дисперсии, которую мы используем. Выражение в знаменателе, ( n — 1 ), означающее размер выборки минус 1, это число степеней свободы при расчете дисперсии совокупности с использованием Формулы 3.

Мы также используем ( n — 1 ) как число степеней свободы для определения факторов надежности на основе распределения Стьюдента. Термин «степени свободы» используются, так как мы предполагаем, что в случайной выборке наблюдения отобраны независимо друг от друга. Числитель выборочной дисперсии, однако, использует выборочное среднее.

---

Каким образом использование выборочного среднего влияет на количество наблюдений, отобранных независимо, для формулы выборочной дисперсии?

При выборке размера 10 и среднем значении в 10%, к примеру, мы можем свободно отобрать только 9 наблюдений. Независимо от отобранных 9 наблюдений, мы всегда можем найти значение для 10-го наблюдения, которое дает среднее значение, равное 10%. С точки зрения формулы выборочной дисперсии, здесь есть 9 степеней свободы.

Учитывая, что мы должны сначала вычислить выборочное среднее от общего числа (n) независимых наблюдений, только (n — 1) наблюдений могут быть отобраны независимо друг от друга для расчета выборочной дисперсии.

Концепция степеней свободы часто применяется в финансовой статистике, и вы встретите ее в последующих чтениях.

t-распределение Стьюдента.

Предположим, что мы делаем выборку из нормального распределения.

Коэффициент (z = (overline X — mu) Big / (sigma big / sqrt n) ) нормально распределен со средним значением 0 и стандартным отклонением 1, однако, коэффициент (t = (overline X — mu) Big / (s big / sqrt n) ) следует t-распределению со средним 0 и (n — 1) степеней свободы.

Коэффициент (t) не является нормальным, поскольку представляет собой отношение двух случайных величин, выборочного среднего и стандартного отклонения выборки.

Определение стандартной нормальной случайной величины включает в себя только одну случайную величину, выборочное среднее. По мере увеличения степеней свободы, однако, t-распределение приближается к стандартному нормальному распределению.

На Рисунке 1 показано стандартное нормальное распределение и два t-распределения, одно с DF = 2 и одно с DF = 8.

Рисунок (1) t-распределение Стьюдента по сравнению со стандартным нормальным распределением.

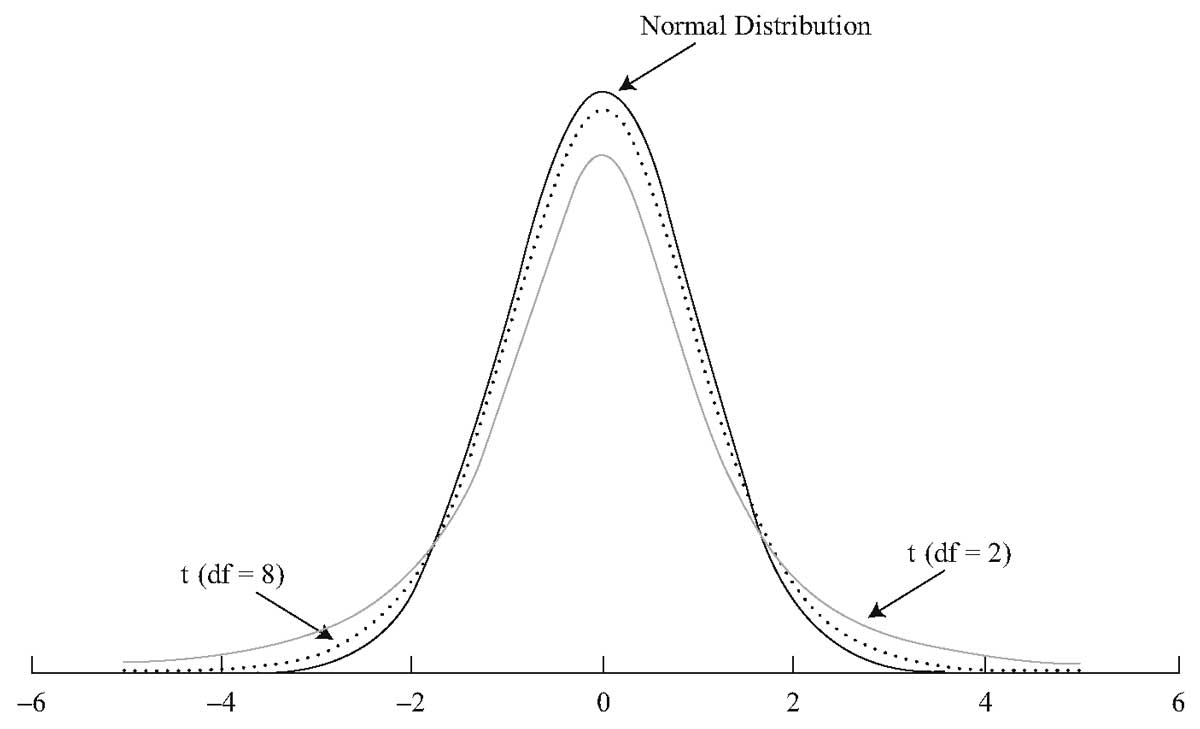
Из трех распределений, показанных на Рисунке 1, стандартное нормальное распределение имеет хвосты, которые стремятся к нулю быстрее, чем хвосты двух t-распределений. t-распределение симметрично распределено вокруг среднего нулевого значения, так же как и нормальное распределение.

По мере увеличения степеней свободы, t-распределение приближается к стандартному нормальному распределению. t-распределение с DF = 8 ближе к стандартному нормальному, чем t-распределение с DF = 2.

Помимо области плюс и минус четырех стандартных отклонений от среднего значения, остальная область под стандартным нормальным распределением, как представляется, близка к 0. Однако, оба t-распределения содержать некоторую площадь под каждой кривой за пределом четырех стандартных отклонений.

t-распределения имеют более толстые хвосты, но хвосты t-распределения Стьюдента с DF = 8 сильнее напоминают хвосты нормального распределения. По мере увеличения степеней свободы, хвосты распределения Стьюдента становятся менее толстыми.

Для часто используемых значений распределения Стьюдента составлены таблицы. Например, для каждой степени свободы (t_{0.10}), (t_{0.05}), (t_{0.025}), (t_{0.01}) и (t_{0.005}) значения будут такими, что соответственно, 0.10, 0.05, 0.025, 0.01 и 0.005 вероятности останется в правом хвосте для заданного числа степеней свободы.

Значения (t_{0.10}), (t_{0.05}), (t_{0.025}), (t_{0.01}) и (t_{0.005}) также называют односторонними критическими значениями t на значимых уровнях 0.10, 0.05, 0.025, 0.01 и 0.005, для указанного числа степеней свободы.

Например,

Приведем форму доверительных интервалов для среднего по совокупности, используя распределение Стьюдента.

Доверительные интервалы для среднего по совокупности (дисперсия совокупности неизвестна) — t-распределение.

Если мы делаем выборку из генеральной совокупности с неизвестной дисперсией и соблюдается одно из перечисленных ниже условий:

• выборка является большой, или
• выборка небольшая, но совокупность имеет нормальное распределение, или приблизительно нормально распределена,

то доверительный интервал (100 (1 — alpha)% ) для среднего совокупности ( mu ) задается формулой:

Пример 5 использует данные Примера 4, но применяет t-статистику, а не z-статистику, чтобы рассчитать доверительный интервал для среднего значения совокупности коэффициентов Шарпа.

Пример (5) расчета доверительного интервала для среднего по совокупности коэффициентов Шарпа с использованием t-статистики.

Как и в Примере 4, инвестиционный аналитик стремится вычислить 90-процентный доверительный интервал для среднего по совокупности коэффициентов Шарпа, основанных на случайной выборке из 100 взаимных фондов США.

Выборочное среднее коэффициентов Шарпа составляет 0.45, а выборочное стандартное отклонение — 0.30.

Теперь, признав, что дисперсия генеральной совокупности распределения коэффициентов Шарпа неизвестна, аналитик решает вычислить доверительный интервал, используя теоретически правильную t-статистику.

Поскольку размер выборки равен 100, DF = 99. Используя таблицу степеней свободы, мы находим, что (t_{0.05}) = 1.66.

Этот фактор надежности немного больше, чем фактор надежности (z_{0.05}) = 1.65, который был использован в Примере 4.

Доверительный интервал будет:

( begin{aligned} & overline X pm t_{0.05}{s over sqrt n } \  &= 0.45 pm 1.66{0.30 over sqrt {100}} \ &= 0.45 pm 1.66(0.03) = 0.45 pm 0.0498   end{aligned} )

Доверительный интервал охватывает значения 0.4002 до 0.4998, или 0.40 до 0.50, с двумя знаками после запятой. При округлении до двух знаков после запятой, доверительный интервал не изменился по сравнению с Примером 4.

В Таблице 3 приведены различные факторы надежности, которые мы использовали.

Таблица 3. Основы для расчета факторов надежности.

Выборка из:	Статистика для выборки малого размера	Статистика для выборки большого размера
Нормальное распределение с известной дисперсией	(z)	(z)
Нормальное распределение с неизвестной дисперсией	(t)	(t)*
Ненормальное распределение с известной дисперсией	недоступно	(z)
Ненормальное распределение с неизвестной дисперсией	недоступно	(t)*

* Использование (z) также приемлемо.

2.1. Стандартное отклонение среднего выборочного значения (ошибка среднего) и доверительный интервал

Результаты измерений обычно показывают с так называемой «средней статистической ошибкой средней величины» и для нашего случая (см. табл. 1.1) это будет запись: «высота сеянцев в опыте составила 5,0 ± 0,28 см». Словосочетание «средняя статистическая ошибка» обычно сокращают до названия «ошибка среднего» или просто «ошибка», обозначают буквой m и определяют по очень простой формуле. Для итогов упомянутой таблицы, где расчеты по 25 высотам дали значение δ = 1,42 см, эта ошибка составит:

(2.1)

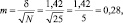
где δ –	стандартное отклонение;
N –	число наблюдений или объем выборки, шт.

Если объем выборки взять 100 шт., то ошибка снизится в 2 раза: 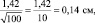а если увеличить до 10000 шт., то в 10 раз, до 0,014 см.

Рассмотрим эту «среднюю статистическую ошибку» (далее просто ошибка) подробно, так как именно в ней скрыто понимание того, что называют статистическим мышлением. Интуитивно мы понимаем, что малая выборка дает большую ошибку, т.е. неточное определение среднего значения. Последний термин настолько привычен, что мы даже не задумываемся о том, что его правильное и полное название «среднее выборочное значение», т.е. среднее, определяемое в некоторой выборке. И выборки могут быть очень разные по численности. Начнем с самых малых. Например, что произойдет с ошибкой, если объем выборки сократить до 2 измерений? Такие выборки бывают, например, в почвенных исследованиях, когда каждое измерение достается дорогой ценой. Для этого вернемся к рис. 1.1. На нем стандартное отклонение ±δ, которое отражает разброс значений вокруг среднего в левую и правую сторону в виде холма, наблюдается при объеме выборки 1 шт. В этом случае ошибка среднего выборочного значения будет равна стандартному отклонению: m = δ = 1,42. С увеличением N ошибка уменьшается:

при объеме выборки N = 2 ошибка будет

при объеме выборки N = 4 ошибка будет

при объеме выборки N = 16 ошибка будет

Важно понять, что ряд распределения частот этих выборочных средних будет постепенно как бы съеживаться и приближаться к центру, где находится так называемое «генеральное» среднее. Поясним, что в математике генеральное среднее значение называется математическим ожиданием и его обозначают буквой «М». Например, это может быть средняя высота, рассчитанная по всем измеренным в теплице сеянцам, или среднее число семян в 1 шишке у дерева после подсчета семян во всех собранных с дерева шишках (50, 100, 500 и т.д., т.е. весьма небольшая генеральная совокупность). Распределение частот значений выборочных средних, которых может быть множество, будет иметь форму такого же холма, как и распределение единичных значений на рис. 1.1. При этом, если выборка будет из 1 шт., то холм будет в точности таким же, но при выборках из 2 шт. 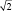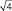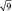его форма съежится в  = в 1,41 раза; при выборках из 4 шт. –
в  = в 2 раза; при выборках из 9 шт. – в  = в 3 раза и т.д.

Для этих сокращающихся рядов распределения выборочных средних можно рассчитать свое, особое стандартное отклонение. Вероятно, чтобы не путать его со СТАНДОТКЛ, его стали называть по-другому, т.е. «средней статистической ошибкой средней величины». Чем больше по объему выборки, тем короче ряд распределения средних значений этих выборок с его «хвостами» в левую и правую сторону, и тем меньше величина этого особого стандартного отклонения. Закон распределения частот выборочных средних точно такой же, и имеет те же свойства: в пределах ±2m находится 95 % всех значений выборочных средних, в пределах ±3m – 99,5 %, а в пределах ±4m находится 100 % всех значений xср. Форма этого распределения меняется от пологой при малых выборках до очень крутой, вплоть до «схлопывания» в центре при выборках большого объема, когда ошибка среднего стремится к нулю.

Здесь следует пояснить, что, на наш взгляд, словосочетание «средняя статистическая ошибка средней величины», сокращаемое до «ошибки среднего значения» или просто до «ошибки», вводит нас в некоторое заблуждение, так как мы привыкли со школы, что ошибки надобно исправлять. Более правильным, вместо слов «ошибка среднего значения», будет использование слов «стандартное отклонение выборочных средних значений от генерального среднего». Не случайно математики выбрали для обозначения величины этого отклонения букву «m», а для обозначения генерального среднего (математического ожидания) – букву «М». Слова для объяснения этих сложных явлений могут быть разными, но и у математиков, и у биологов есть единодушие в понимании статистического смысла, лежащего за этими буквенными символами. Вообще, лучше было бы ввести некий иной термин вместо слов «ошибка» или «отклонение», так как они изначально имеют в нашем сознании иной смысл; на наш взгляд, более всего подходит слово «скачок» (чем сильнее отскакивает выборочное среднее от генерального среднего, тем реже оно встречается). Но так уж получилось, что не нашлось нейтрального (иностранного) слова, и слово «ошибка» традиционно используют, и мы также будем его использовать; важно понимать его иной, чем в обыденном употреблении, математический и статистический смысл.

Для самого точного определения средней высоты сеянцев нужно измерять все растения в питомнике, и тогда мы получим «генеральное среднее значение». Но так не делают, а измеряют несколько сотен растений в разных местах и этого бывает достаточно для определения среднего выборочного значения с приемлемой точностью. В нашем примере при 100 растениях ошибка его определения составит 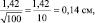а ее отнесение к средней высоте сеянцев 5,0 см, выражаемое в %, дает нам так называемую точность опыта: 0,14/5,0×100 = 2,8 %. В биологии точность опыта ±2–3 % считается высокой, ±5 % – достаточной, а ±6–7 % – пониженной, но это весьма упрощенное представление о планировании эксперимента.

Вообще, точность опыта не самоцель; гораздо важнее сократить численность (объем) выборки до минимума. Представим себе, что средняя высота сеянцев xср = 5,0 см, а ее ±δ = 1,42 см, рассмотренные выше, получены при измерении 1000 растений потомства сосны, например, из Кунгура. Поделив ±δ на корень из 1000 получаем ошибку опыта m = ±0,045 см. Далее получаем точность опыта

Р = m/xср×100 = 0,045/5,0×100 = 0,9 %.

Точность получилась очень высокой. Но в питомнике есть потомства и из других мест и такой уровень точности совершенно не нужен, так как нужно узнать еще высоты сеянцев, например, из Очера, Осы, Добрянки и других районов. Если выборку из 1 тыс. растений снижать, то будет увеличиваться ошибка в определении средней высоты. И нужно найти приемлемую величину такой ошибки, которая позволит нам, тем не менее, уверенно утверждать, что это потомство растет быстрее, либо медленнее других. Причем происхождений может быть несколько сотен и минимизация выборок крайне важна, так как масштабы работ ограничены физическими возможностями бригады селекционеров. Следовательно, надо сокращать объем выборки. Как это сделать правильно?

Рассмотрим два потомства. Первое – это упомянутые сеянцы происхождением из Кунгура (хср1), второе – сеянцы из Кизела с хср2 = 6,0 см и δ2 = ± 1,0 см (превышение высоты на 20 %). Надо это превышение доказать. При выборках из 100 растений ранее определенная ошибка m1 была равна 0,14 см, вторая ошибка m2 после расчетов по формуле (2.1) составит 0,1 см. По закону нормального распределения 99,5 % всех возможных значений этих средних хср1 и хср2 будут в пределах «плюс-минус три ошибки», что можно показать графически (рис. 2.1) или в виде формул:

хср1 ± 3m1 = 5,0 ± 3×0,14 = 5,0 ± 0,4 см

и

хср2 ± 3m2 = 6,0 ± 3×0,1 = 6,0 ± 0,3 см.

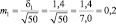
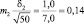
Возможные теоретические значения средних в генеральной совокупности не перекрывают друг друга, значит, различие достоверно. А если сократить выборки до 50 сеянцев? Тогда и  и пределы колебаний возможных значений средних будут:

хср1 ± 3m1 = 5,0 ± 3×0,20 = 5,0 ± 0,6 см;

хср2 ± 3m2 = 6,0 ± 3×0,14 = 6,0 ± 0,3 см.

Рис. 2.1. Средние значения по выборкам из 100 растений и их тройные ошибки (пределы возможных значений выборочных средних в 99,5 % случаев)

Снова вынесем эти пределы на график (рис. 2.2).

Рис. 2.2. Средние значения при N = 50 растений и их тройные ошибки

Как видим, пределы сблизились и если еще сократить выборки, то они перекроются. Можно ли далее снижать объем выборки?

Можно, но здесь вступает в силу так называемое условие безошибочного прогноза. Мы это условие задали на уровне 99,5 % и для этого взяли ±3m для распределения ошибок. Но можно взять уровень пониже, с пределами ±2δ (уровень 95 %) и даже с пределами ±1,7δ (уровень 90 %).

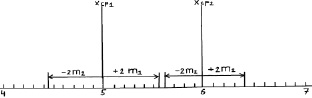
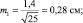
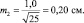
При выборках из 25 штук сеянцев, получаем две ошибки: Тогда пределы значений для этих двух выборочных средних для уровня прогноза в 95 % будут:

хср1 ± 2m1 = 5,0 ± 2×0,28 = 5,0 ± 0,56 см;

хср2 ± 2m2 = 6,0 ± 2×0,20 = 6,0 ± 0,40 см.

Выносим эти пределы опять на график (рис. 2.3).

Рис. 2.3. Средние значения при N = 25 растений и их двойные ошибки (пределы возможных значений средних в 95 % случаев)

Как видим, просвет все еще есть, и поэтому между возможными значениями средних высот сеянцев в других выборках из происхождений Кунгур и Кизел различия будут опять доказаны. Но уровень доказательства понизился до 95 %, и для 5 % оставшихся случаев нет гарантии, что различия будут иметь место при выборке из 25 растений. Их может и не быть, но эту вероятность в 5 % мы допускаем.

Стандартное
отклонение для оценки обозначается S_e
и рассчитывается по формуле
среднеквадратичного отклонения:

.

Величина стандартного
отклонения характеризует точность
прогноза.

Вариант
5. Возвращаясь к данным нашего примера,
рассчитаем значение S_e:

Предположим,
необходимо оценить значение Y для
конкретного значения независимой
переменной, например, спрогнозировать
объем продаж при затратах на рекламу в
объеме 10 тыс. долл. Обычно при этом также
требуется оценить степень достоверности
результата, одним из показателей которого
является доверительный интервал для
Y.

Граница доверительного
интервала для Y при заданной величине
X рассчитывается следующим образом:

где
Х_p
– выбранное значение независимой
переменной, на основе которого выполняется
прогноз. Обратите внимание: t – это
критическое значение текущего уровня
значимости. Например, для уровня
значимости, равного 0,025 (что соответствует
уровню доверительности двухстороннего
критерия, равному 95%) и числа степеней
свободы, равного 10, критическое значение
t равно 2, 228 (см. Приложение II). Как можно
увидеть, доверительный интервал – это
интервал, ограниченный с двух сторон
граничными значениями предсказания
(зависимой переменной).

Вариант
6. Для нашего примера расходов на рекламу
в размере 10 тыс. долл. интервал предсказания
зависимой переменной (объема продаж) с
уровнем доверительности в 95% находится
в пределах [10,5951; 21,8361]. Его границы
определяются следующим образом (обратите
внимание, что в Варианте 2 Y’=16,2156):

Из приведенного
расчета имеем: для заданных расходов
на рекламу в объеме 10 тыс. долл., объем
продаж изменяется в диапазоне от 10,5951
до 21,8361 тыс. долл. При этом:
10,5951=16,2156-5,6205 и 21,8361=16,2156+5,6205.

3. Стандартное отклонение для коэффициента регрессии Sb и t-статистика

Значения
стандартного отклонения для коэффициентов
регрессии S_b
и значение статистики тесно взаимосвязаны.
S_b
рассчитываются как

Или в сокращенной
форме:

S_b
задает интервал, в который попадают.
Все возможные значения коэффициента
регрессии. t-статистика
(или t-значение)
– мера статистической значимости
влияния независимой переменной Х на
зависимую переменную Y
определяется путем деления оценки
коэффициента b
на его стандартное отклонение S_b.
Полученное значение затем сравнивается
с табличным (см. табл. В Приложении II).

Таким
образом, t-статистика
показывает, насколько велики величина
стандартного отклонения для коэффициента
регрессии (насколько оно больше нуля).
Практика показывает, что любое t-значение,
не принадлежащее интервалу [-2;2], является
приемлемым. Чем выше t-значение,
тем выше достоверность коэффициента
(т.е. точнее прогноз на его основе). Низкое
t-значение
свидетельствует о низкой прогнозирующей
силе коэффициента регрессии.

Вариант
7. S_b
для нашего примера равно:

t-статистика
определяется:

Так
как t=3,94>2,
можно заключить,
что
коэффициент
b
является
статистически
значимым.
Как
отмечалось раньше,
табличное
критическое
значение (уровень отсечения)
для 10 степеней свободы равно
2,228
(см.
табл.
в
Приложении
11).

Обратите
внимание:

—
t-значения
играют большую
роль для коэффициентов
множественной регрессии
(множественная
модель описывается
с помощью
нескольких
коэффициентов
b);

—
R²
характеризует
общее согласие (всего
«леса»
невязок
на
диаграмме
разброса),
в
то время как
t-значение
характеризует
отдельную
независимую переменную
(отдельное
«дерево»
невязок).

В
общем случае
табличное
t-значение
для
заданных
числа
степеней свободы и уровня
значимости используется,
чтобы:

—
установить
диапазон
предсказания:
верхнюю
и нижнюю границы
для прогнозируемого
значения при заданном значении
независимой
переменной;

-установить
доверительные
интервалы
для
коэффициентов
регрессии;

—
определить
уровень
отсечения
для t-теста.

РЕГРЕССИОННЫЙ
АНАЛИЗ С ПРИМЕНЕНИЕМ ЭЛЕКТРОННЫХ ТАБЛИЦ
MS EXCEL

Электронные
таблицы,
такие
как Excel,
имеют
встроенную
процедуру
регрессионного
анализа,
легкую
в
применении.

Регрессионный
анализ
с помощью
MS Ехсеl
требует
выполнения
следующих
действий:

—
выберите
пункт
меню
«Сервис
— Надстройки»;

—
в
появившемся
окне отметьте
галочкой
надстройку
Analysis
ToolPak
–
VBA нажмите
кнопку
ОК.

Если
в списке Analysis
ToolPak
—
VВА
отсутствует,
выйдите
из MS Ехсеl
и добавьте эту надстройку,
воспользовавшись
программой
установки Мiсrosоft
Office.
Затем
запустите Ехсеl
снова
и повторите
эти действия.
Убедившись,
что
надстройка
Analysis
ToolPak
—
VВА
доступна,
запустите
инструмент
регрессионного
анализа,
выполнив
следующие
действия:

—
выберите
пункт меню «Сервис
—
Анализ»
данных;

—
в появившемся окне выберите
пункт
«Регрессия»
и
нажмите
кнопку
ОК.
На
рисунке 16.3
показано окно ввода данных для
регрессионного
анализа.

Рисунок 16.3 – Окно
ввода данных для регрессионного анализа

Таблица
16.2
показывает
выходной
результат
регрессии,
содержащий
описанные
выше статистические
данные.

Примечание:
для
того чтобы получить
поточечный
график
(ХY график),
используйте
«Мастер
Диаграмм»
MS
Excel.

Получаем:
Y’
= 10,5386
+ 0,563197
Х (d
виде
Y’
=
а
+
bХ)
с R²=0,608373=60,84%.

Все
полученные
данные
ответствуют
данным,
рассчитанным
вручную.

Таблица 16.2 –
Результаты регрессионного анализа

в
электронных таблицах MS
Excel

Вывод итогов
Регрессионная статистика
Множественный R	0,7800
R-квадрат	0,6084
Нормированный R-квадрат	0,5692
Стандартная ошибка	2,3436
Наблюдения	12
Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия	1	85,3243	85,3243	15,5345	0,0028
Остаток	10	54,9257	5,4926
Итого	11	140,2500
	Коэффи-циенты	Стандарт-ная ошибка	t-статистика	Р- значение*	Нижние 95%	Верхние 95%
Свободный член	10,5836	2,1796	4,8558	0,0007	5,7272	15,4401
Линейный коэффициент	0,563197	0,1429	3,9414	0,0028	0,2448	0,8816
*Р – значение для переменной X, равное 0,0028 показывает, что истинное значение переменной коэффициента с 0,28%-ной вероятностью равна нулю, что предполагает высокую точность прогнозируемого значения, равного 0б563197.

Таблица
16.3 показывает выходной результат
регрессии, полученный с применением
популярного программного обеспечения
Minitab
для статистического анализа.

Таблица
16.3 – Результаты регрессионного анализа
Minitab

Анализ регрессии Уравнение регрессии: FO=10,6+0,563DLH
Прогнозируемые параметры	Коэффициент	Стандартное отклонение	t-значение	P
Константа	10,584	2,180	4,86	0,000
DLH	0,5632	0,1429	3,94	0,003
s=2,344	R-квадрат=60,8%	R-квадрат (нормированный)=56,9%
Анализ отклонений
Показатель	DF	SS	MS	F	P
Регрессия	1	85,324	85,324	15,53	0,003
Отклонение	10	54,926	5,493
Итого	11	140,250

ВЫВОДЫ

C
помощью регрессионного анализа
устанавливается
зависимость
между
изменениями
независимых
переменных
и
значениями зависимой
переменной.
Регрессионный
анализ
— популярный
метод для прогнозирования
продаж.
В
этой
главе обсуждался
широко
распространенный
способ
оценки значений,
так
называемый
метод
наименьших
квадратов.
Метод
наименьших
квадратов
рассматривался
применительно
к
модели
простой
регрессии
Y
=
а
+ bх.
Обсуждались
различные
статистические
коэффициенты,
характеризующие
добротность
и надежность
уравнения
(согласие
модели)
и помогающие установить
доверительный
интервал.

Показано
применение
электронных
таблиц MS Ехсеl для
проведения
регрессионного
анализа
шаг за шагом.
С
помощью электронных
таблиц
можно не только составить
уравнение
регрессии,
но
и рассчитать статистические
коэффициенты.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Расчет доверительных интервалов и прогнозов для линейного уравнения регрессии

Как правило, в линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его параметров.Показатели корреляционной связи, вычисленные по ограничен­ной совокупности (по выборке), являются лишь оценками той или иной статистической закономерности, поскольку в любом парамет­ре сохраняется элемент не полностью погасившейся случайности, присущей индивидуальным значениям признаков. Поэтому необхо­дима статистическая оценка степени точности и надежности пара­метров корреляции. Под надежностью здесь понимается вероятность того, что значение проверяемого параметра не равно нулю, не вклю­чает в себя величины противоположных знаков.

Вероятностная оценка параметров корреляции производится по общим правилам проверки статистических гипотез, разработанным математической статистикой, в частности путем сравнения оцени­ваемой величины со средней случайной ошибкой оценки. Для ко­эффициента парной регрессии b средняя ошибка оценки вычисля­ется как:

где D_ост – остаточная дисперсия на одну степень свободы.

Для нашего примера величина стандартной ошибки коэффициента регрессии составила:

.

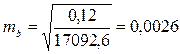
Для оценки того, насколько точные значения показателей могут отличаться от рассчитанных, осуществляется построение доверительных интервалов. Они определяют пределы, в которых лежат точные значения определяемых показателей с заданной степенью точности, соответствующей заданному уровню значимости α (α – вероятность отвергнуть правильную гипотезу при условии, что она верна, обычно принимается равной 0,05 или 0,01).

Для оценки статистической значимости коэффициента линейной регрессии и линейного коэффициента парной корреляции, а также для расчета доверительных интервалов b, применяется t – критерий Стьюдента.

Для оценки существенности коэффициента регрессии его величина сравнивается с его стандартной ошибкой, т.е. определяется фактическое значение t-критерия Стьюдента: 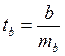, которое затем сравнивается с табличным значением при определенном уровне значимости а и числе степеней свободы (n — 2).

В рассматриваемом примере фактическое значение t-критерия для коэффициента регрессии составило:

.

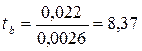
Этот же результат получим, извлекая квадратный корень из найденного F-критерия, т.е.

.

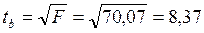
Действительно, справедливо равенство .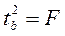

При 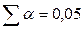(для двустороннего критерия) и числе степеней свободы 13 табличное значение t_b=2,16. Так как фактическое значение t‑критерия превышает табличное, то, следовательно, гипотезу о несущественности коэффициента регрессии можно отклонить.

Для расчета доверительных интервалов для параметров a и b уравнения линейной регрессии определяем предельную ошибку ∆ для каждого показателя:

Формулы для расчета доверительных интервалов имеют вид:

Если границы интервала имеют разные знаки, т.е. в эти границы попадает ноль, то оцениваемый параметр принимается нулевым.

Доверительный интервал для коэффициента регрессии определяется как 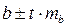. Для коэффициента регрессии b в примере 95%-ные границы составят:

0,022 ± 2,16·0,0026 = 0,022 ± 0,0057, т.е.

Поскольку коэффициент регрессии в эконометрических исследованиях имеет четкую экономическую интерпретацию, то доверительные границы интервала для коэффициента регрессии не должны содержать противоречивых результатов, например, -10 ≤ b ≤ 40. Такого рода запись указывает, что истинное значение коэффициента регрессии одновременно содержит положительные и отрицательные величины и даже ноль, чего не может быть.

Стандартная ошибка параметра а определяется по формуле:

Процедура оценивания существенности данного параметра не отличается от рассмотренной выше для коэффициента регрессии; вычисляется t-критерий: 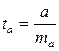, его величина сравнивается с табличным значением при df = n — 2 степенях свободы. В нашем примере m_a составила 0,032.

Значимость линейного коэффициента корреляции проверяется на основе величины ошибки коэффициента корреляции m_r:

Фактическое значение t-критерия Стьюдента определяется как

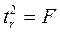
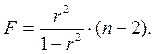
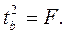
Данная формула свидетельствует, что в парной линейной регрессии , ибо, как уже указывалось, Кроме того, Следовательно,

Таким образом, проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.

В рассматриваемом примере t_r совпало с t_b. Величина t_r =8,37 значительно превышает табличное значение 2,16 при а=0,05. Следовательно, коэффициент корреляции существенно отличен от нуля и зависимость является достоверной.

Прогноз, полученный подстановкой в уравнение регрессии ожи­даемого значения фактора, называют точечным прогнозом. Вероят­ность точной реализации такого прогноза крайне мала. Необходимо сопроводить его значением средней ошибки прогноза или довери­тельным интервалом прогноза с достаточно большой вероятностью.

Точечный прогноз заключается в получении прогнозного значения y_p, которое определяется путем подстановки в уравнение регрессии

соответствующего прогнозного значения x_p:

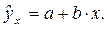
Интервальный прогноз заключается в построении доверительного интервала прогноза, т.е. верхней и нижней границы y_pmin, y_pmax интервала, содержащего точную величину для прогнозного значения
(y_pmin 2 – индекс детерминации;

n – число наблюдений;

m – число параметров при переменных х.

Величина m характеризует число степеней свободы для факторной суммы квадратов, а (n – m — 1) – число степеней свободы для остаточной суммы квадратов.

Для степенной функции 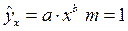и формула F – критерия примет тот же вид, что и при линейной зависимости:

Для параболы второй степени y=a + b·x + c·x 2 + ε m=2 и .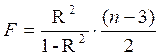

Для оценки качества построенной модели используется также средняя ошибка аппроксимации. Фактические значения результативного признака отличаются от теоретических, рассчитанных по уравнению регрессии, т.е. у и . Чем меньше это отличие, тем ближе теоретические значения подходят к эмпирическим данным, лучше качество модели. Величина отклонений фактических и расчетных значений результативного признака (у— ) по каждому наблюдению представляет собой ошибку аппроксимации. Их число соответствует объему совокупности. В отдельных случаях ошибка аппроксимации может оказаться равной нулю. Для сравнения берутся величины отклонений, выраженные в процентах к фактическим значениям. Так, если для первого наблюдения у=20, а для второго у=50, ошибка аппроксимации составит 25% для первого наблюдения и 20% — для второго.

Поскольку (у— ) может быть как величиной положительной, так и отрицательной, то ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю.

Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации как среднюю арифметическую простую:

.

Для нашего примера представим расчет средней ошибки аппроксимации в таблице 4.

Пример нахождения доверительных интервалов коэффициентов регрессии

1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.

2. Постройте уравнение зависимости экспорта нефти от цены на нефть.

3. Рассчитайте среднюю ошибку аппроксимации и коэффициент детерминации. Оценить статистическую значимость параметров регрессии и уравнения в целом.

4. Оцените полученные результаты, выводы оформите в аналитической записке.

Таблица 5

Цена нефти марки Urals (Россия), долл/барр.

Экспорт нефти и нефтепродуктов, млн.т.

Решение:

Уравнение имеет вид y = ax + b
1. Параметры уравнения регрессии.
Средние значения

Связь между признаком Y фактором X сильная и прямая
Уравнение регрессии

x	y	x 2	y 2	x ∙ y	y(x)	(y- y ) 2	(y-y(x)) 2	(x-x p ) 2
119	298.12	14161	88875.53	35476.28	219.63	232120.8	6160.56	24362.01
203	481.03	41209	231389.86	97649.09	521.16	89328.76	1610.26	5196.01
281	539.12	78961	290650.37	151492.72	801.15	57979.42	68658.51	35.01
305	653.57	93025	427153.74	199338.85	887.3	15961.59	54628.94	895.01
381	987.66	145161	975472.28	376298.46	1160.11	43160.41	29738.57	11218.34
363	1252.85	131769	1569633.12	454784.55	1095.5	223673.03	24760.35	7729.34
389	1276.88	151321	1630422.53	496706.32	1188.83	246980.01	7753.57	12977.01
387	1396.70	149769	1950770.89	540522.9	1181.65	380430.93	46248.04	12525.34
315	952.03	99225	906361.12	299889.45	923.19	29625.58	831.49	1593.34
217	619.96	47089	384350.4	134531.32	571.41	25583.74	2356.85	3373.67
149	384.40	22201	147763.36	57275.6	327.32	156427.5	3258.23	15897.01
192	516.59	36864	266865.23	99185.28	481.67	69336.98	1219.24	6902.84
3301	9358.91	1010755	8869708.45	2943150.82	9358.91	1570608.75	247224.62	102704.92

По таблице Стьюдента находим Tтабл
T_табл (n-m-1;a) = (10;0.05) = 1.812
Поскольку Tнабл > Tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициента корреляции статистически — значим.

Анализ точности определения оценок коэффициентов регрессии

S _a = 0.4906
Доверительные интервалы для зависимой переменной

Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X = 1
(-587.75;179.86)
Проверка гипотез относительно коэффициентов линейного уравнения регрессии
1) t-статистика

Статистическая значимость коэффициента регрессии a подтверждается (7.32>1.812)

Статистическая значимость коэффициента регрессии b не подтверждается (1.46 Fkp, то коэффициент детерминации статистически значим.

Доверительные интервалы для зависимой переменной

Уравнение тренда имеет вид y = at 2 + bt + c
1. Находим параметры уравнения методом наименьших квадратов.
Система уравнений

Для наших данных система уравнений имеет вид (см. таблицу).

Получаем a₀ = -11.37, a₁ = 88.47, a₂ = 2151.09
Уравнение тренда: y = -11.37t 2 +88.47t+2151.09
Оценим качество уравнения тренда с помощью ошибки абсолютной аппроксимации.

Поскольку ошибка больше 15%, то данное уравнение не желательно использовать в качестве тренда
Средние значения

т.е. в 87.35 % случаев влияет на изменение данных. Другими словами — точность подбора уравнения тренда — высокая

t	y	t 2	y 2	x ∙ y	y(t)	(y-y cp ) 2	(y-y(t)) 2	(t-t p ) 2	(y-y(t)) : y	t 3	t 4	t 2 y
1	2225.3	1	4951960.09	2225.3	2228.19	65.6099	8.352	16	6431.117	1	1	2225.3
2	2254.9	4	5084574.01	4509.8	2282.55	462.25	764.5225	9	62347.985	8	16	9019.6
3	2332.3	9	5439623.29	6996.9	2314.17	9781.21	328.6969	4	42284.599	27	81	20990.7
4	2365.8	16	5597009.64	9463.2	2323.05	17529.76	1827.5625	1	101137.95	64	256	37852.8
5	2295.4	25	5268861.16	11477	2309.19	3844	190.1641	0	31653.566	125	625	57385
6	2303.9	36	5307955.21	13823.4	2272.59	4970.25	980.3161	1	72135.109	216	1296	82940.4
7	2166.7	49	4694588.89	15166.9	2213.25	4448.89	2166.9025	4	100859.885	343	2401	106168.3
8	2080.4	64	4328064.16	16643.2	2131.17	23409	2577.5929	9	105621.908	512	4096	133145.6
9	2075.9	81	4309360.81	18683.1	2026.35	24806.25	2455.2025	16	102860.845	729	6561	168147.9
45	20100.6	285	44981997.26	98988.8	20100.51	89317.2199	11299.312	60	625332.964	4050	30666	1235751.2

2. Анализ точности определения оценок параметров уравнения тренда.

Анализ точности определения оценок параметров уравнения тренда

S _a = 4.8518
Доверительные интервалы для зависимой переменной

По таблице Стьюдента находим Tтабл
T_табл (n-m-1;a) = (7;0.05) = 1.895
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и t = 6
2151.09 + 88.47*6 + -11.37*6₂ — 1.895*39.911 ; 2151.09 + 88.47*6 + -11.37*6₂ — 1.895*39.911
(-55.3814;95.8814)
Интервальный прогноз.
Определим среднеквадратическую ошибку прогнозируемого показателя.

где L — период упреждения; у_n+L — точечный прогноз по модели на (n + L)-й момент времени; n — количество наблюдений во временном ряду; Sy — стандартная ошибка прогнозируемого показателя; T_табл — табличное значение критерия Стьюдента для уровня значимости а и для числа степеней свободы, равного n — 2.
Точечный прогноз, t = 10: y(10) = -11.37*10 2 + 88.47* + 2151.09 = 1898.79
K₁ = 247.4924
1898.79 — 247.4924 = 1651.2976 ; 1898.79 + 247.4924 = 2146.2824
t = 10: (1651.2976;2146.2824)
Точечный прогноз, t = 11: y(11) = -11.37*11 2 + 88.47* + 2151.09 = 1748.49
K₂ = 261.9213
1748.49 — 261.9213 = 1486.5687 ; 1748.49 + 261.9213 = 2010.4113
t = 11: (1486.5687;2010.4113)
Точечный прогноз, t = 12: y(12) = -11.37*12 2 + 88.47* + 2151.09 = 1575.45
K₃ = 278.0099
1575.45 — 278.0099 = 1297.4401 ; 1575.45 + 278.0099 = 1853.4599
t = 12: (1297.4401;1853.4599)
Точечный прогноз, t = 13: y(13) = -11.37*13 2 + 88.47* + 2151.09 = 1379.67
K₄ = 295.4871
1379.67 — 295.4871 = 1084.1829 ; 1379.67 + 295.4871 = 1675.1571
t = 13: (1084.1829;1675.1571)
Точечный прогноз, t = 14: y(14) = -11.37*14 2 + 88.47* + 2151.09 = 1161.15
K₅ = 314.1213
1161.15 — 314.1213 = 847.0287 ; 1161.15 + 314.1213 = 1475.2713
t = 14: (847.0287;1475.2713)
3. Проверка гипотез относительно коэффициентов линейного уравнения тренда.
1) t-статистика. Критерий Стьюдента.

Статистическая значимость коэффициента уравнения подтверждается

Статистическая значимость коэффициента тренда подтверждается
Доверительный интервал для коэффициентов уравнения тренда
Определим доверительные интервалы коэффициентов тренда, которые с надежность 95% будут следующими (t_табл=1.895):
(a — t_табл·S_a; a + t_табл·S_a)
(-20.5642;-2.1758)
(b — t _табл·S_b; b + t_таблS·_b)
(36.7313;140.2087)
2) F-статистика. Критерий Фишера.

Fkp = 5.32
Поскольку F > Fkp, то коэффициент детерминации статистически значим
4. Тест Дарбина-Уотсона на наличие автокорреляции остатков для временного ряда.

y	y(x)	e i = y-y(x)	e 2	(e i — e i-1 ) 2
2225.3	2228.19	-2.89	8.3521	0
2254.9	2282.55	-27.65	764.5225	613.0576
2332.3	2314.17	18.13	328.6969	2095.8084
2365.8	2323.05	42.75	1827.5625	606.1444
2295.4	2309.19	-13.79	190.1641	3196.7716
2303.9	2272.59	31.31	980.3161	2034.01
2166.7	2213.25	-46.55	2166.9025	6062.1796
2080.4	2131.17	-50.77	2577.5929	17.8084
2075.9	2026.35	49.55	2455.2025	10064.1024
11299.3121	24689.8824

Критические значения d₁ и d₂ определяются на основе специальных таблиц для требуемого уровня значимости a, числа наблюдений n и количества объясняющих переменных m.
Не обращаясь к таблицам, можно пользоваться приблизительным правилом и считать, что автокорреляция остатков отсутствует, если 1.5

Задача №3. Расчёт параметров регрессии и корреляции с помощью Excel

По территориям региона приводятся данные за 200Х г.

Номер региона	Среднедушевой прожиточный минимум в день одного трудоспособного, руб., х	Среднедневная заработная плата, руб., у
1	78	133
2	82	148
3	87	134
4	79	154
5	89	162
6	106	195
7	67	139
8	88	158
9	73	152
10	87	162
11	76	159
12	115	173

Задание:

1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.

2. Рассчитайте параметры уравнения линейной регрессии

.

3. Оцените тесноту связи с помощью показателей корреляции и детерминации.

4. Дайте с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.

5. Оцените с помощью средней ошибки аппроксимации качество уравнений.

6. Оцените с помощью F-критерия Фишера статистическую надёжность результатов регрессионного моделирования.

7. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости .

8. Оцените полученные результаты, выводы оформите в аналитической записке.

Решение:

Решим данную задачу с помощью Excel.

1. Сопоставив имеющиеся данные х и у, например, ранжировав их в порядке возрастания фактора х, можно наблюдать наличие прямой зависимости между признаками, когда увеличение среднедушевого прожиточного минимума увеличивает среднедневную заработную плату. Исходя из этого, можно сделать предположение, что связь между признаками прямая и её можно описать уравнением прямой. Этот же вывод подтверждается и на основе графического анализа.

Чтобы построить поле корреляции можно воспользоваться ППП Excel. Введите исходные данные в последовательности: сначала х, затем у.

Выделите область ячеек, содержащую данные.

Затем выберете: Вставка / Точечная диаграмма / Точечная с маркерами как показано на рисунке 1.

Рисунок 1 Построение поля корреляции

Анализ поля корреляции показывает наличие близкой к прямолинейной зависимости, так как точки расположены практически по прямой линии.

2. Для расчёта параметров уравнения линейной регрессии
воспользуемся встроенной статистической функцией ЛИНЕЙН.

1) Откройте существующий файл, содержащий анализируемые данные;
2) Выделите область пустых ячеек 5×2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики.
3) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
4) В окне Категория выберете Статистические, в окне функция – ЛИНЕЙН. Щёлкните по кнопке ОК как показано на Рисунке 2;

Рисунок 2 Диалоговое окно «Мастер функций»

5) Заполните аргументы функции:

Известные значения у – диапазон, содержащий данные результативного признака;

Известные значения х – диапазон, содержащий данные факторного признака;

Константа – логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0;

Статистика – логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения.

Щёлкните по кнопке ОК;

Рисунок 3 Диалоговое окно аргументов функции ЛИНЕЙН

6) В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу , а затем на комбинацию клавиш + + .

Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:

Значение коэффициента b	Значение коэффициента a
Стандартная ошибка b	Стандартная ошибка a
Коэффициент детерминации R 2	Стандартная ошибка y
F-статистика	Число степеней свободы df
Регрессионная сумма квадратов

Остаточная сумма квадратов

Рисунок 4 Результат вычисления функции ЛИНЕЙН

Получили уровнение регрессии:

Делаем вывод: С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.

3. Коэффициент детерминации означает, что 52% вариации заработной платы (у) объясняется вариацией фактора х – среднедушевого прожиточного минимума, а 48% — действием других факторов, не включённых в модель.

По вычисленному коэффициенту детерминации можно рассчитать коэффициент корреляции: .

Связь оценивается как тесная.

4. С помощью среднего (общего) коэффициента эластичности определим силу влияния фактора на результат.

Для уравнения прямой средний (общий) коэффициент эластичности определим по формуле:

Средние значения найдём, выделив область ячеек со значениями х, и выберем Формулы / Автосумма / Среднее, и то же самое произведём со значениями у.

Рисунок 5 Расчёт средних значений функции и аргумент

Таким образом, при изменении среднедушевого прожиточного минимума на 1% от своего среднего значения среднедневная заработная плата изменится в среднем на 0,51%.

С помощью инструмента анализа данных Регрессия можно получить:
— результаты регрессионной статистики,
— результаты дисперсионного анализа,
— результаты доверительных интервалов,
— остатки и графики подбора линии регрессии,
— остатки и нормальную вероятность.

Порядок действий следующий:

1) проверьте доступ к Пакету анализа. В главном меню последовательно выберите: Файл/Параметры/Надстройки.

2) В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.

3) В окне Надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.

• Если Пакет анализа отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор, чтобы выполнить поиск.

• Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да, чтобы установить его.

4) В главном меню последовательно выберите: Данные / Анализ данных / Инструменты анализа / Регрессия, а затем нажмите кнопку ОК.

5) Заполните диалоговое окно ввода данных и параметров вывода:

Входной интервал Y – диапазон, содержащий данные результативного признака;

Входной интервал X – диапазон, содержащий данные факторного признака;

Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;

Константа – ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;

Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;

6) Новый рабочий лист – можно задать произвольное имя нового листа.

Затем нажмите кнопку ОК.

Рисунок 6 Диалоговое окно ввода параметров инструмента Регрессия

Результаты регрессионного анализа для данных задачи представлены на рисунке 7.

Рисунок 7 Результат применения инструмента регрессия

5. Оценим с помощью средней ошибки аппроксимации качество уравнений. Воспользуемся результатами регрессионного анализа представленного на Рисунке 8.

Рисунок 8 Результат применения инструмента регрессия «Вывод остатка»

Составим новую таблицу как показано на рисунке 9. В графе С рассчитаем относительную ошибку аппроксимации по формуле:

Рисунок 9 Расчёт средней ошибки аппроксимации

Средняя ошибка аппроксимации рассчитывается по формуле:

Качество построенной модели оценивается как хорошее, так как не превышает 8 – 10%.

6. Из таблицы с регрессионной статистикой (Рисунок 4) выпишем фактическое значение F-критерия Фишера:

Поскольку при 5%-ном уровне значимости, то можно сделать вывод о значимости уравнения регрессии (связь доказана).

8. Оценку статистической значимости параметров регрессии проведём с помощью t-статистики Стьюдента и путём расчёта доверительного интервала каждого из показателей.

Выдвигаем гипотезу Н₀ о статистически незначимом отличии показателей от нуля:

.

для числа степеней свободы

На рисунке 7 имеются фактические значения t-статистики:

t-критерий для коэффициента корреляции можно рассчитать двумя способами:

I способ:

где – случайная ошибка коэффициента корреляции.

Данные для расчёта возьмём из таблицы на Рисунке 7.

II способ:

Фактические значения t-статистики превосходят табличные значения:

Поэтому гипотеза Н₀ отклоняется, то есть параметры регрессии и коэффициент корреляции не случайно отличаются от нуля, а статистически значимы.

Доверительный интервал для параметра a определяется как

Для параметра a 95%-ные границы как показано на рисунке 7 составили:

Доверительный интервал для коэффициента регрессии определяется как

Для коэффициента регрессии b 95%-ные границы как показано на рисунке 7 составили:

Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью параметры a и b, находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля.

7. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:

Тогда прогнозное значение прожиточного минимума составит:

Ошибку прогноза рассчитаем по формуле:

где

Дисперсию посчитаем также с помощью ППП Excel. Для этого:

1) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.

2) В окне Категория выберете Статистические, в окне функция – ДИСП.Г. Щёлкните по кнопке ОК.

3) Заполните диапазон, содержащий числовые данные факторного признака. Нажмите ОК.

Рисунок 10 Расчёт дисперсии

Получили значение дисперсии

Для подсчёта остаточной дисперсии на одну степень свободы воспользуемся результатами дисперсионного анализа как показано на Рисунке 7.

Доверительные интервалы прогноза индивидуальных значений у при с вероятностью 0,95 определяются выражением:

Интервал достаточно широк, прежде всего, за счёт малого объёма наблюдений. В целом выполненный прогноз среднемесячной заработной платы оказался надёжным.

Условие задачи взято из: Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2003. – 192 с.: ил.