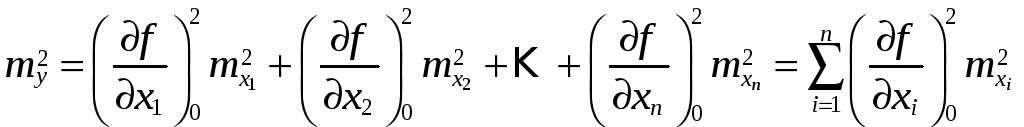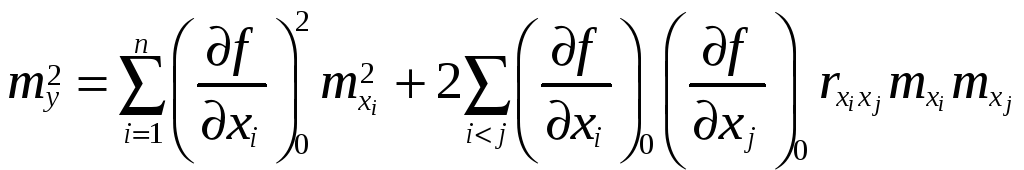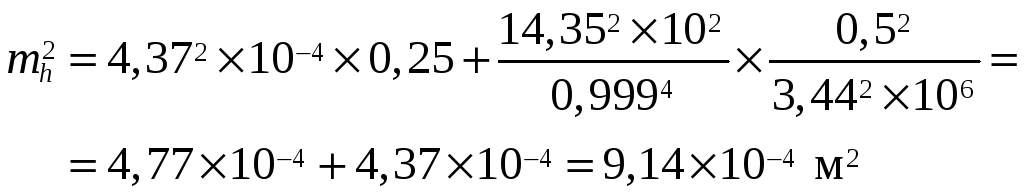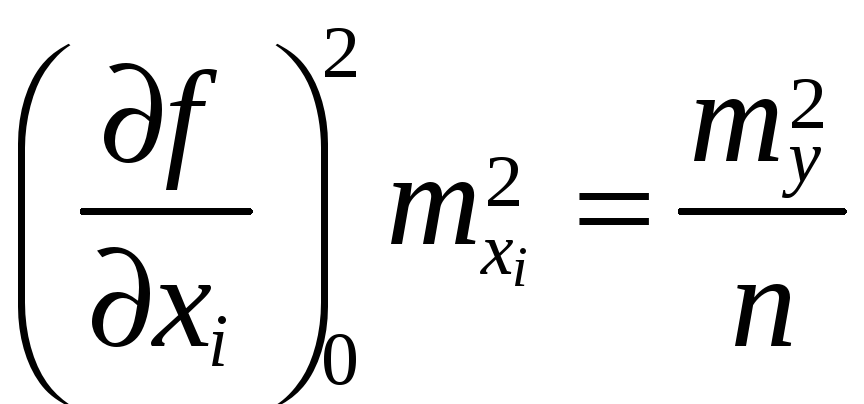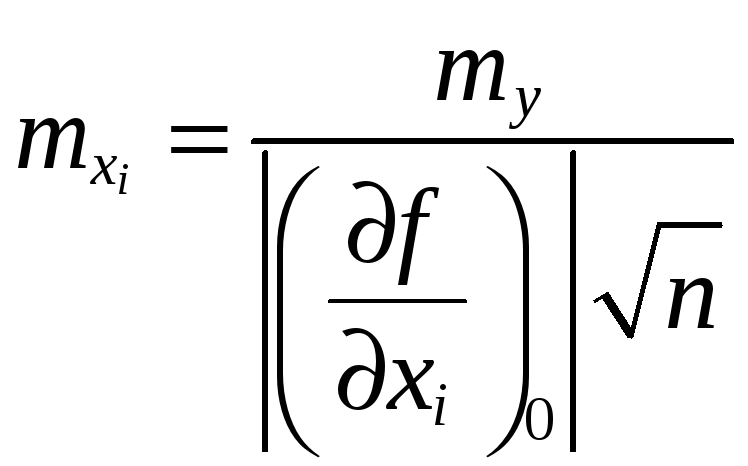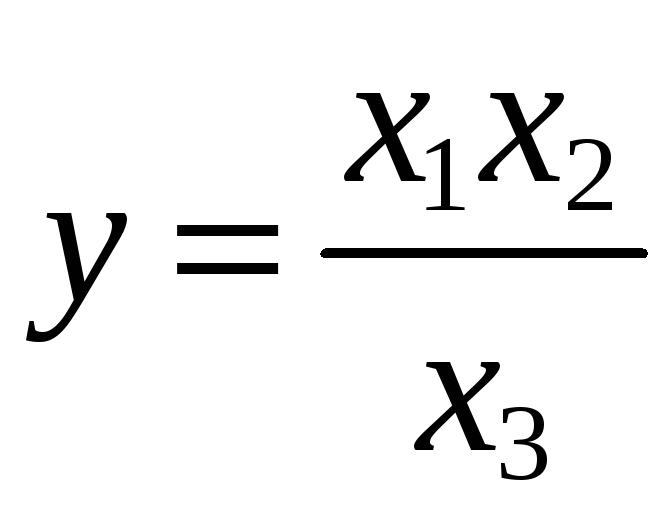Найти среднюю квадратическую ошибку превышения - ErrorsMaster.ru - большая энциклопедия ошибок и их решений

Беспалый Н.П., Ахонина Л.И.

Геодезия часть 2 Учебное пособие для студентов геодезических специальностей вузов Донецк 1999

2.6 Точность нивелирования

Под точностью нивелирования понимается средняя квадратическая ошибка определения одного превышения (на одной станции) — m_h и средняя квадратическая ошибка определения превышения на 1 км нивелирного хода — m_км.

При предрасчете этих ошибок необходимо вычислить, прежде всего, среднюю квадратическую ошибку определения отсчета по рейке (ошибку взгляда).

На точность отсчета по рейке наиболее существенно будут влиять источники ошибок, связанные со зрительной трубой и рейкой:

— недостаточная разрешающая способность трубы — m_рс

— ошибка установки визирной оси в горизонтальное положение — m_y

— ошибка дециметровых делений рейки — m_дел

— ошибка округлений отсчета по рейке — m_o.

Эти элементарные ошибки будут зависеть от типа нивелира и реек, а также от длины визирного луча.

Так как указанные источники ошибок действуют независимо, то согласно формулам (2.26), (2.36), (2.34) средняя квадратическая ошибка взгляда будет определяться формулой:

. (2.37)

Численные значения элементарных ошибок определяются по ранее полученным формулам.

Для нивелирования III кл. при применении нивелира и реек с характеристиками:

 = 15”, Г = 30^х, t = 10 мм

и длине визирного луча S = 75 мм в соответствии с формулами (2.26), (2.34), (2.36), будем иметь:

мм;

мм.

При этих численных значениях элементарных ошибок, средняя квадратическая ошибка отсчета по рейке будет равна m_взл = 1.1 мм.

Превышение на станции вычисляется из отсчетов по задней и передней рейкам по черной (h = а₁ — b₁) и красной (h = а₂ — b₂) сторонам реек и из них берется среднее значение т.е.

Принимая ошибки отсчета по рейкам одинаковыми m_а1 = m_b1 = m_а2 = m_b2 = m_взл на основании теории ошибок измерений имеем

мм.

По ГОСТ.10528-90 m_hдля точных нивелиров не должна превышать 2.0мм.

При расчете этой ошибки действие некоторых ошибок не учтено: наклон реек, несоблюдение главного условия, вертикальные перемещения реек и нивелира, влияние внешних факторов, т.е. учтены только некоторые ошибки прибора.

В нивелирном ходе длиной 1 км надо сделать n станций. Пусть расстояние между рейками на станции по ходу нивелирование равно 150м. Тогда

Ошибка превышения на 1 км хода будет вычислена по формуле

мм. (2.38)

где m_h – средняя квадратическая ошибка превышения на станций.

Подставим вычисленные ранее значения m_h и n в формулу (2.38).

m_км = 1,1= 2,9мм

Предельная ошибка (или предельная невязка) суммы превышений на 1 км нивелирного хода равна

, мм. (2.39)

Если m_км=2.9мм, то f_h(_пред)=3х2.9=8.7мм.

Если длина хода L км, то

, мм. (2.40)

Для рассматриваемого примера: f_h(_пред)=3х2.9=8.7,мм

При нивелировании в прямом и обратном направлении секции длиной в L км (между реперами) образуется замкнутый ход длиной 2L: поэтому

Если принять f_h(пред) равным не 3m_км, а равным удвоенной средней квадратической ошибке, т.е.

мм,

то предельная ошибка (невязка) суммы превышений двойного нивелирного хода длиной L км будет равна

Аналогично можно рассчитать точность нивелирования IV класса.

Приведенные расчеты имеют теоретическое значение. В практической деятельности надо руководствоваться требованиями инструкции [5], которой устанавливаются невязки нивелирных ходов III класса равными 10мм, а IV класса — 20 мм.

Источник

В геодезии часто
искомые величины находят в результате
вычислений, как функции измеренных
величин (аргументов). Очевидно, что
ошибка функции будет зависеть как от
ошибок измерения аргументов, так и от
вида функции.

2.1 Средняя квадратическая ошибка функции

Пусть дана функция

где
величины
—
измерены независимо. Известны их средние
квадратические ошибки .

Средняя квадратическая
ошибка функции (2.1) вычисляется по
формуле:

Если
величины

коррелированы, т.е. коэффициенты попарной
корреляционной связи отличны от нуля,

,
то средняя квадратическая ошибка функции
вычисляется по формуле:

где

—
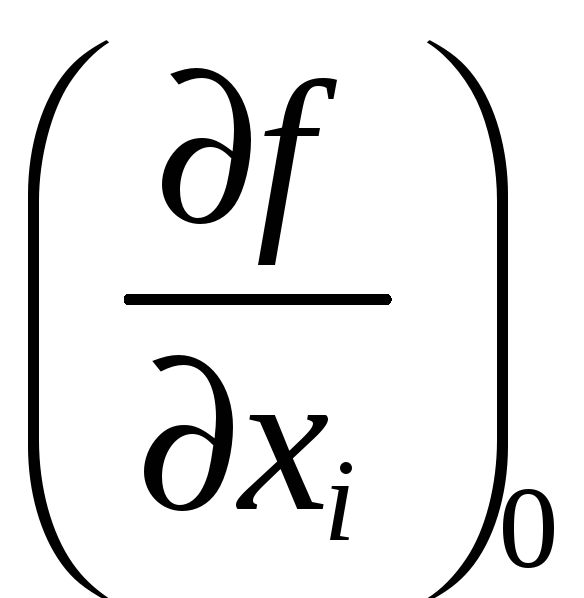
частные производные функции, взятые по
точным значениям величин Х_i,
но вычисленные по их приближённым
значениям, в качестве которых принимают
измеренные значения х_i,
близкие к точным значениям.

Предрасчёт
ожидаемой средней квадратической ошибки
функции по формулам и называют
решением прямой
задачи теории ошибок.

Задача 2.1.
В треугольнике измерены два угла,
известны их средние квадратические
ошибки ,

.
Найти среднюю квадратическую ошибку
третьего угла, вычисленного по двум
измеренным.

Решение.
Составляем функцию
;
имеем:

;

—
точное
число; x₁ и x₂ —
независимо измеренные углы.

Тогда по формуле
имеем:

;

Задача 2.2.
Определить среднюю квадратическую
ошибку превышения, вычисленного по
формуле ,
где S —
горизонтальное проложение,  —
угол наклона. Известно, что
;

;

Решение.
Находим

и по формуле его среднюю квадратическую
ошибку m_h:

^{^}⁾,

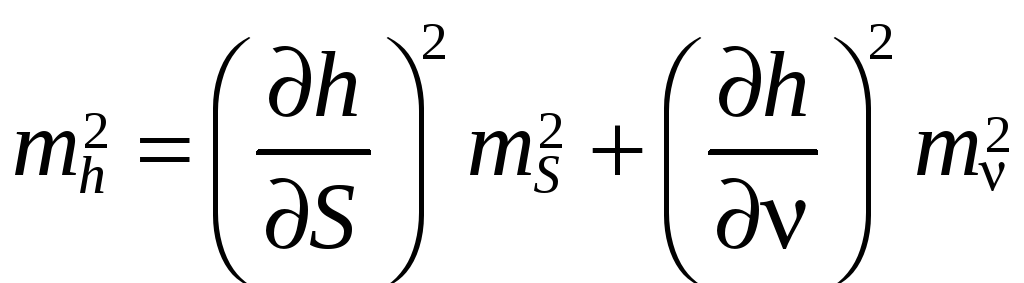
где

;

Тогда

;

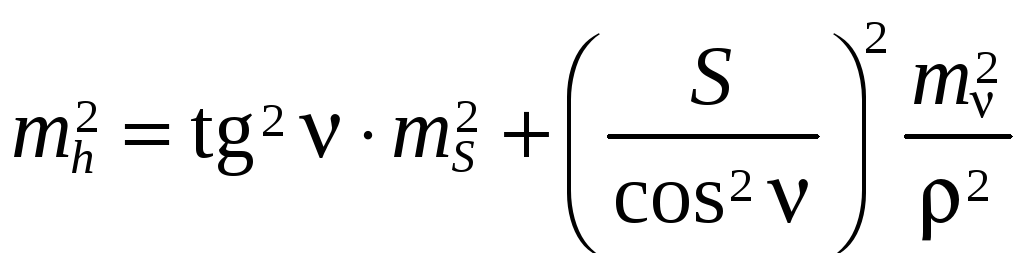
Известно,
что величина m_h
должна быть получена с двумя (или тремя,
если число начинается с единицы) значащими
цифрами. Чтобы это требование обеспечить,
необходимо в промежуточных вычислениях
по формуле удерживать в числах на
одну значащую цифру больше, т.е. оставлять
три (или четыре) значащие цифры, а сами
числа следует представлять в стандартной
форме. Например, число 0,04366²
необходимо записать так:
;
число 3438²
следует записать так:
.
Такие действия позволят упростить
вычисления по формуле и, кроме того,
дадут представление о величине влияния
каждого источника ошибок на общую
среднюю квадратическую ошибку функции.

С учётом сказанного
выше находим:

По результатам
вычислений видно, что влияние линейных
и угловых ошибок измерений в данной
задаче примерно одинаково. Окончательно
получаем:

Ответ:

При
решении обратной
задачи теории ошибок —
расчёте
точности измерений аргументов по
заданной средней квадратической ошибке
функции — применяют так называемый
принцип
равных влияний, требование
которого состоит в том, чтобы влияние
каждого источника ошибок на общую ошибку
функции было одинаковым.

Так из формулы
следует:

Все
находят из решения уравнений .

Задачи
для контроля.
Найти средние квадратические ошибки
следующих функций независимо измеренных
величин:

;

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Собрание уникальных книг, учебных материалов и пособий, курсов лекций и отчетов по геодезии, литологии, картированию, строительству, бурению, вулканологии и т.д.
Библиотека собрана и рассчитана на инженеров, студентов высших учебных заведений по соответствующим специальностям. Все материалы собраны из открытых источников.

Средняя квадратическая погрешность функции измеренных величин.

В практике геодезических измерений определяемые величины обычно являются функциями других, непосредственно измеряемых величин. Рассмотрим функцию u независимых переменных x, y, z, …

u = f (x,y,z…). (5.5)

Продифференцируем функцию (5.5) по всем переменным и заменим дифференциалы du, dx, dy, dz, …. погрешностями Du, Dx, Dy, Dz, ….

Получили выражение случайной погрешности Du в зависимости от случайной комбинации погрешностей Dx, Dy, Dz, …. Положим, что имеем n таких комбинаций, которым соответствует n выражений:

(i = 1, 2, …, n)

Возведем полученные выражения в квадрат, сложим и разделим на n:

где квадратными скобками обозначены суммы.

Устремим число комбинаций в бесконечность (n ® ¥) и, воспользовавшись выражениями (5.4) и (5.3), получим: , , , , , , . И окончательно

. И окончательно

(5.6)

Итак, квадрат средней квадратической погрешности функции общего вида равен сумме квадратов произведений частных производных по каждой переменной, умноженных на их средние квадратические погрешности.

Частные случаи.

1. Функция u является суммой переменных x , y, z:

u = x + y + z.

В этом случае =1, =1, =1, =1. Следовательно

=1. Следовательно

=+++.

2. Функция u является разностью переменных x и y:

u = x — y.

В этом случае .

2. Функция u является разностью переменных x и y:

u = x — y.

В этом случае =1, =-1. Следовательно

=-1. Следовательно

=++.

3. Функция u имеет вид:

u = k× x,

где k – постоянный множитель. Теперь = k, поэтому = k, поэтому = k²× и

m_u = k× m_x.

4. Функция u является линейной функцией от x, y, z, …:

u = k₁ x + k₂ y + k₃ z …,

где k_i постоянные множители. Теперь частные производные равны и

m_u = k× m_x.

4. Функция u является линейной функцией от x, y, z, …:

u = k₁ x + k₂ y + k₃ z …,

где k_i постоянные множители. Теперь частные производные равны =k₁, = k₂, = k₂, = k₃. Поэтому

Рассмотрим примеры.

Пример 1. Определить среднюю квадратическую погрешность превышения, вычисленного по горизонтальному расстоянию d=124,16 м и углу наклона n=2°16´, если m_d= 0,06 м, а m_n = 1´.

Превышение вычисляют по формуле

h = d tgν.

Продифференцируем формулу по переменным d и n: