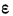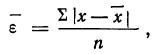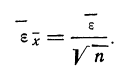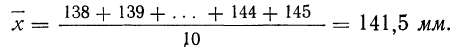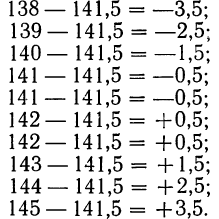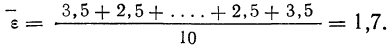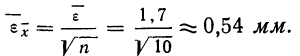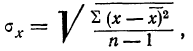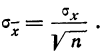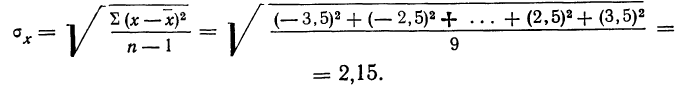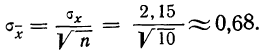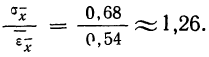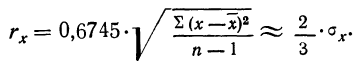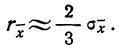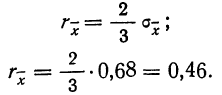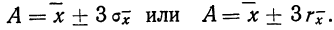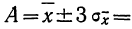После
выполненных измерений всегда необходимо
оценить их точность. Оценку точности
можно сделать только тогда, когда есть
повторные или избыточные измерения.
Существуют различные критерии точности.
Наиболее удобным и естественным критерием
является дисперсия D
, характеризующая меру рассеяния
результатов измерений. Поскольку на
практике число повторных измерений
всегда конечно, приходится ограничиваться
приближенным значением ее, носящим
название оценки дисперсии. Она
вычисляется по формуле
(13)
где 1
, 2 , … , n
-случайные погрешности в результатах
измерений одной и той же величины. В
математической статистике доказывается,
что оценка (13) является состоятельной,
эффективной и несмещенной. Определенным
неудобством в использовании этой оценки
является её квадратическая размерность
по сравнению с результатами измерений.
Для избежания этого неудобства используют
критерий точности
или
(14)
носящей название
средней квадратической погрешности.
Она обладает рядом достоинств.
I. При
числе измерений n
9 величина т изменяется очень мало
и, следовательно, значение т близко
к её теоретическому аналогу — стандарту
. При числе
измерений n<9 критерий
точности т следует считать
ненадёжным.
2. Из
опыта установлено, что в ряду, состоящем
из 1000 измерений, лишь три случайные
погрешности превосходят величину 3m.
Следовательно, её можно принять за
предельную погрешность Δпред
, т.е.
Δпред = 3m
.
Величина
3m и является тем
пределом, о котором речь шла в первом
свойстве случайных погрешностей.
Предельная погрешность играет важную
роль при установлении допусков в
различных нормативных документах,
так как 3m принимают
за допустимую погрешность Δдоп
, т.е.
Δдоп = Δпред = 3m
.
При
увеличении числа измерений надёжность
найденной по формуле (14) погрешности
возрастает. В теории погрешностей
измерений доказывается, что погрешность
тm определения
самой погрешности приближённо можно
найти по формуле
В
заключение подчеркнем, что погрешность
m служит критерием
точности одного измерения, характерного
для всей группы выполненных измерений
3.3. Формула Бесселя
Критерий
точности m, введённый
по формуле (14), на практике имеет
ограниченное применение, так как
случайные погрешности Δi
остаются неизвестными. Для той же самой
средней квадратической погрешности
m можно вывести
формулу с использованием арифметической
средины x0
(15)
где vi
= li
– x0 ,
x0 = (l1
+ l2 + …
+ ln)/n
, li
– результаты измерений. Формула (15)
носит название формулы Бесселя и
применяется на практике для оценки
точности.
3.4. Средняя квадратическая погрешность функций измеренных величин
Выше
был рассмотрен вопрос об оценке точности
непосредственно измеренных величин.
На практике часто для получения
интересующей нас величины измеряют
другие величины, а нужную нам величину
затем вычисляют по известным аналитическим
формулам. При этом, естественно,
неизбежные случайные погрешности в
непосредственно измеренных величинах
повлияют на точность окончательного
результата. Возникает задача
нахождения средней квадратической
погрешности этого окончательного
результата как функции погрешностей
отдельных измерений. Например, для
определения площади фигуры, имеющей
форму прямоугольника, измеряют его
стороны а и b,
а затем вычисляют площадь S
= a·b
. Погрешности в измеренных сторонах тa
и mb
могут быть найдены по формуле (15). Они
внесут некоторую погрешность в
найденное значение площади S.
Определению погрешностей функций
измеренных величин и посвящается данный
раздел.
В самом
общем виде функция многих независимых
переменных имеет вид f(х,
у, z,…, t).
Погрешности mx
, my
, mz
, … , mt
известны заранее или вычислены из
многократных измерений по формуле
Бесселя. В теории погрешностей измерений
доказывается, что средняя квадратическая
погрешность mf
функции f будет равна
(16)
где
суть частные
производные,
конечно, при условии
их существования. Применим общую формулу
(16) для вычисления погрешностей некоторых
частных видов функций.
1. f
= kx ( k
= Const);
тогда
или (17)
-
f
= k1x
+ k2y
+ k3z
+ … + knt
;
тогда
(18)
В
рассмотренном нами примере вычисления
площади
и
Применим
формулу (18) для вычисления средней
квадратической погрешности среднего
арифметического
и найдем
П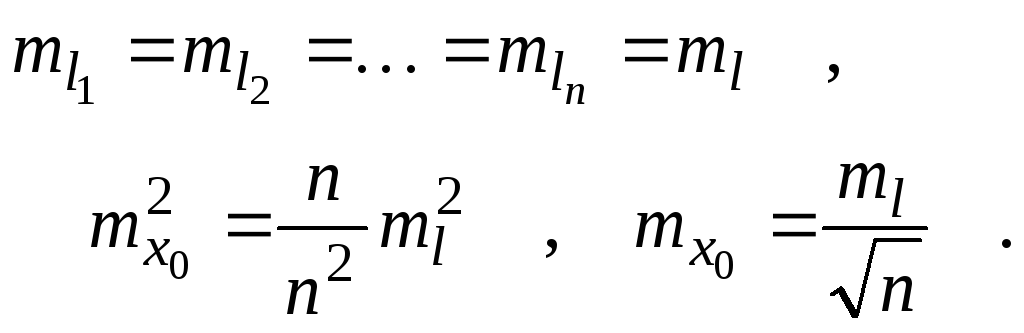
каждое измерение li
выполнено с одинаковой точностью ml
, т.е.
(19)
Как
и следовало ожидать, точность среднего
арифметического оказалась
выше точности одного измерения ml
, причем выше в раз.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Ошибки измерения: Опыт убеждает, что измерения объектов не могут быть произведены абсолютно точно и каждое конкретное измерение дает лишь, как правило, приближенное значение величины явления, истинное значение которой (A) нам неизвестно. Ошибки измерения (
Рассмотрим такие измерения, которые производятся одним наблюдателем, одним и тем же инструментом, в одинаковых условиях, т. е. равноточные измерения.
Различают два вида ошибок измерения:
- систематические ошибки, т. е. такие, которые при данных условиях проведения измерения имеют вполне определенное значение (например, ошибка измерительного прибора);
- случайные — такие, которые являются результатом взаимодействия большого числа незначительных в отдельности факторов и имеют в каждом отдельном случае различные значения.
Задача математической статистики — предусмотреть возможность возникновения систематических ошибок и добиться их ликвидации или сведения к минимуму.
Случайные ошибки измерения обладают рядом свойств: при большом числе измерений крупные ошибки встречаются реже мелких и число положительных ошибок примерно равно числу отрицательных, вследствие чего сумма всех ошибок близка к нулю.
Если ошибки получаются весьма малыми по сравнению с величиной явления, то ими просто пренебрегают или считаются с наибольшей возможной ошибкой, чтобы обезопасить себя от влияния случайной неточности.
В теории ошибок изучаются те ошибки, которые, являясь, с одной стороны, ошибками случайного характера, по своему абсолютному значению настолько велики, что ими пренебречь нельзя, а с другой стороны, для них существует закон, позволяющий установить зависимость между величиной ошибки и вероятностью ее появления. Закон случайных ошибок, полученный Гауссом, состоит в том, что случайные ошибки подчиняются закону нормального распределения.
Средняя ошибка сводного результата измерения
Принимая за действительное значение измеряемой величины при равноточном измерении среднюю арифметическую из всех результатов n измерений, можно охарактеризовать точность одного измерения с помощью средней арифметической из абсолютных величин значений ошибок:
где n — число измерений, х — численное значение отдельных измерений, 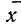
За меру точности соответствия принятой средней арифметической 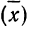
Пример 1. Произведено 10-кратное измерение размера детали (в мм), давшее следующие, расположенные в возрастающем порядке результаты: 138; 139; 140; 141; 141; 142; 142; 143; 144; 145.
Охарактеризуем сначала точность одного измерения, т. е. вычислим среднюю арифметическую из абсолютных значений ошибок. Для этой цели вычислим среднюю арифметическую из результатов измерений:
Найдем ошибки измерения:
Следовательно:
Теперь можно вычислить среднюю ошибку сводного результата измерения:
Значит, мерой точности соответствия 141,5 мм истинной величине размера детали является средняя ошибка, равная 0,54 мм.
Средняя квадратическая ошибка
Если в качестве меры точности одного измерения принять не среднюю арифметическую из абсолютных значений ошибок (средняя ошибка), а среднюю квадратическую из ошибок измерений, т. е.
то средняя квадратическая ошибка найденной средней арифметической из ошибок измерения вычисляется по формуле:
Между средней -квадратической ошибкой и средней ошибкой сводного результата измерения существует связь: 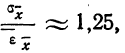
Пример 2. Используя данные предыдущего примера, находим меру точности одного измерения, т. е. среднюю квадратическую ошибку:
Затем исчисляем среднюю квадратическую ошибку найденной средней арифметической, равной 141,5 мм:
Сопоставляя среднюю квадратическую ошибку сводного результата измерения со средней ошибкой, получаем:
Вероятная ошибка
За меру точности одного измерения иногда принимают вероятную ошибку:
Тогда в качестве вероятной ошибки сводного результата измерения используют соотношение:
Пример 3. Используя данные предыдущих примеров, находим вероятную ошибку сводного результата измерения:
Наиболее вероятные границы сводных результатов измерения
Математическое ожидание случайной ошибки равно нулю. В качестве значения измеряемой величины применяется средняя арифметическая всех измерений (если они равноточны). Использование отклонений результатов измерений (х) от средней из них 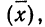
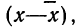
Для этой цели используют удвоенную или утроенную среднюю квадратическую ошибку сводного результата измерения или его вероятную ошибку и получают:
Найденные границы неизвестной истинной величины в случае, если ошибки подчинены нормальному закону распределения Гаусса (чаще всего так и бывает), соблюдаются с большой вероятностью (0,997 и 0,954).
Пример 4. По данным предыдущих примеров находим границы истинного значения размера детали 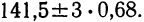
- Методы математической статистики
- Комбинаторика — правила, формулы и примеры
- Классическое определение вероятности
- Геометрические вероятности
- Законы распределения случайных величин
- Дисперсионный анализ
- Математическая обработка динамических рядов
- Корреляция — определение и вычисление
4
ЗАДАЧА 2.7.
Вариант 1. Измерительный прибор не имеет систематической ошибки, а средняя квадратическая ошибка равна 75. Какова вероятность, что ошибка измерения не превзойдет по абсолютной величине 45 (закон распределения — нормальный)?
Вариант 2. Точность изготовления деталей характеризуется систематической ошибкой 2 мм, а случайное отклонение распределено по нормальному закону со средней квадратической ошибкой 10 мм. Какова вероятность, что отклонение длины изделия от стандарта находится в пределах от 8 до 12 мм?
Вариант 3. Систематическая ошибка высотомера равна нулю, а случайные ошибки распределены по нормальному закону. Какую среднюю квадратическую ошибку должен иметь высотомер, чтобы с вероятностью 0,95 ошибка измерения высоты по абсолютной величине была меньше 50 м?
Вариант 4. Каким должен быть допуск отклонения размера детали от номинала, чтобы с вероятностью 0,9 отклонение было допустимым, если систематическая ошибка отклонения отсутствует, а средняя квадратическая равна 25 мм (закон распределения — нормальный)?
Вариант 5. Деталью высшего качества считается такая, у которой отклонение размера от номинала не превосходит по абсолютной величине 4,3 мк. Случайное отклонение распределено по нормальному закону. Найти среднюю квадратическую ошибку, если систематическая ошибка равна нулю, а вероятность того, что деталь высшего качества равна 0,99.
Вариант 6. Систематическая ошибка измерительного прибора равна нулю. Случайные ошибки распределены по нормальному закону. Найти среднюю квадратическую ошибку, если ошибка измерения не превосходит по абсолютной величине 0,5 с вероятностью 0,95.
Вариант 7. Деталь, изготовленная автоматом, считается годной, если отклонение ξ контролируемого размера от номинала не превышает 8 мм. Точность изготовления деталей характеризуется среднеквадратическим отклонением, равным 4мм. Считая, что случайная величина ξ распределена нормально, выяснить, сколько процентов годных деталей изготавливает автомат.
Вариант 8. Стандартный вес производимых на заводе болванок составляет 1 т., а отклонение распределено по нормальному закону со средней квадратической ошибкой 0,05т. Систематическая ошибка отсутствует. В каком интервале с вероятностью 0,99 находится вес болванки?
Вариант 9. Радиолокационная станция при измерении дальности дает систематическую ошибку 5 м., средняя квадратическая ошибка равна 10 м. Найти вероятность того, что случайная ошибка не превосходит по абсолютной величине 17 м. Закон распределения нормальный.
Вариант 10. Измерительный прибор не имеет систематической ошибки. Случайные ошибки распределены по нормальному закону, и с вероятностью 0,8 они не превосходят по абсолютной величине 12 мм. Найти среднюю квадратическую ошибку.
Вариант 11. Автомат по нарезанию гвоздей длиной 80 мм в нормальном режиме имеет случайную ошибку, распределенную по нормальному закону. Систематическая ошибка отсутствует, средняя квадратическая ошибка равна 0,5 мм. В каком интервале с вероятностью 0,999 будет находиться длина гвоздя?
Вариант 12. Прибор, контролирующий напряжение, имеет случайную ошибку в показаниях, распределенную по нормальному закону. Систематическая ошибка отсутствует. Случайная ошибка по абсолютной величине не превосходит 15В с вероятностью 0,8. Найти среднюю квадратическую ошибку.
Вариант 13. Деталь принимается ОТК, если ее диаметр отклоняется по абсолютной величине от стандартного не более чем на 2 мм. Отклонение — случайная величина, распределенная по нормальному ‘закону с систематической ошибкой 0,5 мм и среднеквадратическим отклонением 1 мм. Найти вероятность того, что деталь принимается.
Вариант 14. При испытании орудия отклонение снаряда по дальности распределено по нормальному закону с математическим ожиданием, равным нулю, и среднеквадратическим отклонением, равным 25 м. Найти вероятность того, что отклонение по дальности по абсолютной величине не превосходит 12 м.
Вариант 15. Максимальная скорость самолетов определенного типа распределена по нормальному закону с математическим ожиданием 420м/с и среднеквадратическим отклонением 25 м/с. Найти вероятность того, что при испытаниях самолета этого типа его максимальная скорость будет изменяться от 390 м/с до 440 м/с.
Вариант 16. Глубина моря измеряется прибором, систематическая ошибка которого равна нулю, а случайная распределена по нормальному закону. Найти среднеквадратическое отклонение, если при определении глубины ошибка с вероятностью 0,95 составит не более 15 м.
Вариант 17. Среднее значение расстояния до ориентира равно 1250 м. Средняя квадратическая ошибка измерения прибора Е=40 м, систематическая ошибка отсутствует. С вероятностью 0,999 определить максимальную ошибку измерения расстояния.
Вариант 18. Срок службы электрической лампы является случайной величиной, распределенной по нормальному закону с средним квадратическим отклонением 15 ч. Найти математическое ожидание, если с вероятностью 0,99 срок службы лампы более 300 ч.
Вариант 19. Время изготовления детали распределено по нормальному закону с математическим ожиданием 5,8с и среднеквадратическим отклонением 1,9с. Какова вероятность, что для изготовления детали потребуется от 5 до 7с?
Вариант 20. Рассеивание скорости снаряда подчинено нормальному распределению и с вероятностью 0,95 не превосходит по абсолютной величине 2 м/с. Найти отклонение рассеивания. Систематическая ошибка отсутствует.
Вариант 21. При измерении заряда электрона ошибки распределены по нормальному закону, и измерения не имеют систематической ошибки. Найти с вероятностью 0.99 максимальную по абсолютной величине ошибку, если средняя квадратическая ошибка равна 0,05 абсолютных электростатических единиц.
Вариант 22. Измерения дальномера не имеют систематической ошибки, а случайные ошибки распределены нормально. Найти среднюю квадратическую ошибку, если при определении дальности цели абсолютная величина ошибки с вероятностью 0,9 не превосходит 15 м.
Вариант 23. При испытании регистрируется время выхода из строя прибора, которое является случайной величиной, распределенной по нормальному закону с математическим ожиданием 400ч и среднеквадратическим отклонением 50ч. Найти вероятность того, что прибор проработает безотказно от 300 до 500ч.
Вариант 24. Отклонение размера детали от номинала подчинено нормальному закону. Систематической ошибки нет. С вероятностью 0,95 отклонение по абсолютной величине не превышает 2мк. Найти среднеквадратическую ошибку.
Вариант 25. Отклонение диаметров валиков от заданных размеров подчинено нормальному закону без систематической ошибки и со средней квадратической ошибкой 5мк. Найти вероятность того, что отклонение по абсолютной величине не превысит 10мк.
Вариант 26. Отклонение размера изделия от номинала распределено по нормальному закону с нулевой систематической ошибкой. Найти среднюю квадратическую ошибку. если вероятность того, что абсолютная величина отклонения не превышает 5 мм. равна 0,95.
Вариант 27. Прибор для измерения высоты имеет систематическую ошибку 15 м и среднюю квадратическую ошибку 10 м. Найти вероятность того, что ошибка по абсолютной величине не превзойдет 20 м. Закон распределения ошибок нормальный.
Вариант 28. При стрельбе из орудия отклонение от цели по дальности подчиняется нормальному закону, систематической ошибки нет. Найти среднеквадратическое отклонение, если с вероятностью 0,94 абсолютная величина отклонения дальности не превосходит 5 метров.
Вариант 29. Средняя квадратическая ошибка измерения длины
детали раина 0,5мк. Систематическая ошибка отсутствует. Найти наибольшую по абсолютной величине ошибку, которую можно допустить с вероятностью 0,9. (Закон распределения нормальный).
Вариант 30. Скорость лодки — случайная величина, распределенная нормально с математическим ожиданием 10 км/ч и среднеквадратическим отклонением 5 км/ч. Найти вероятность того, что скорость будет не менее 8 км/ч и не более 15 км/ч.