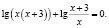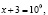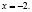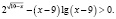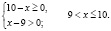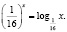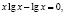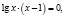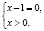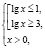1
Решение линейных уравнений. Поймай ошибку (7 класс)
2
Презентация составлена учителем математики МОУ «СОШ» п. Аджером Корткеросского района Республики Коми Мишариной Альбиной Геннадьевной
3
А. Нивен
4
Повторим правила: 1. Решить уравнение – это значит найти все его корни или доказать, что их нет. 2. Число Х, которое превращает данное уравнение в верное числовое равенство, называется решением (корнем) уравнения.
5
Найди ошибку: Решить уравнение 3 х – (х + 5) = 11 Решение 3 х – х + 5 = 11 2 х = х = 6 х = 6 : 2 =3 Ответ: 3 Правильное решение 3 х – (х + 5) = 11 3 х – х – 5 = 11 3 х – х = х = 16 х = 16 : 2 = 8 Ответ: 8
6
Найди ошибку. Решить уравнение -7(3 х+1)+15=2(3 -10 х)-2 Решение -21 х+7+15=6-20 х х+20 х = х = -26 х = 26 Ответ: 26 Правильное решение -7(3 х+1)+15=2(3 -10 х) х = х – х+20 х = х = — 4 х = 4 Ответ: 4
7
Найди ошибку. Решить уравнение 5(х-4)-3 = 7 + 2(х+3) Решение 5 х = х х – 2 х = х = 48 х = 42 : 3 = 16 Ответ: 16 Правильное решение 5(х-4)-3 = 7 + 2(х+3) 5 х = х х – 2 х = х = 36 х = 36 : 3 = 12 Ответ: 12
8
Найди ошибку. Решить уравнение -5,6(х-3)+2,1 х=-2,5 х+10 Решение -5,6 х +15,8+2,1 х=-2,5 х+10 -5,6 х+2,1 х+2,5 х=-15, ,1 х = -5,8 х = 58 Ответ: 58 Правильное решение -5,6(х-3)+2,1 х=-2,5 х+10 -5,6 х +16,8+2,1 х=-2,5 х+10 -5,6 х+2,1 х+2,5 х=-16,8+10 -х = -6,8 х = 6,8 Ответ: 6,8
9
Найди ошибку. Решить уравнение 8 х – 5 = 3 х – 4 Решение 8 х – 3 х = — 5 – 4 5 х = — 9 х = — 9 : 5 х = 1,8 Ответ: 1,8 Правильное решение 8 х – 5 = 3 х – 4 8 х – 3 х = 5 – 4 5 х = 1 х = 1 : 5 х = 0,2 Ответ: 0,2
10
Найди ошибку. Решить уравнение 0,2 – 2(х+1) = 0,4 х Решение 0,2 – 2 х – 2 = 0,4 х -2 х + 0,4 х = 0, ,6 х = 2,2 х = — (2,2:1,6)=-(22:16)= = -11/8 Ответ: — 11/8 Правильное решение 0,2 – 2(х+1) = 0,4 х 0,2 – 2 х – 2 = 0,4 х — 2 х – 0,4 х = — 0, ,4 х = 1,8 х = — (1,8:2,4)=-(18:24)=-¾ Ответ: — 0,75
11
Найди ошибку. Решить уравнение 22 х – 6 = х Решение 22 х + 3 х = х = 15 х = 25 : 15 = 5/3 Ответ: 5/3 Правильное решение 22 х – 6 = х 22 х + 3 х = х = 15 х = 15:25 = 3/5 Ответ: 0,6
12
Урок по теме «Работа над ошибками» 7 класс
Цели урока
- Развивать у учащихся критическое мышление, навыки самостоятельной работы, культуру математической речи.
- Способствовать развитию мыслительных операций (сравнения, абстрагирования, обобщения, конкретизации, анализа, синтеза);
- Закрепить знания и умения учащихся при решении задач составлением уравнений, нестандартных задач;
Оборудование:
1. Компьютер
2. Мультимедийный проектор
3. Лист заданий
Тип урока: коррекция и систематизация знаний
Ход урока.
- Вступительное слово учителя. Постановка цели урока.
Два человека стоят у подножия красивейшей горы. Один думает:
«Хочется приблизиться к этой красоте, но вдруг я упаду. Нет, не пойду»
А другой размышляет: «Страшно, опасно, но даже если я упаду, встану,
поднимусь и снова пойду вперед, навстречу прекрасному».
Какова мораль? Ошибся, оступился, исправляй ошибку и двигайся вперед.
Наш урок сегодня обычен. Главная его цель: проанализировать ошибки,
допущенные в контрольной работе по теме «Решение уравнений» и
скорректировать знания по теме.
- Работа по теме урока
I. Напомните:
— Что называется уравнением? (Равенство, содержащее букву)
— Что значит решить уравнение? (Решить уравнение – значит найти все его корни или доказать, что корней нет)
— Что такое корень уравнения? (Корнем уравнения называется число, при подстановке которого в уравнение получается верное равенство)
— Сформулируйте правило переноса слагаемых из одной части в другую.
II. На доске: устно: письменно:
Дима: 1/6х = 18 (у) 6х – (2х – 5) = 2 (3х – 2)
Рита: 7х + 11,9 = 0
Сережа: 6х – (2х -5) = 2 (2х – 4)
Юлиана: 5х – (7х + 7) = 9
Вадим: 8х – (2х + 4) = 2 (3х – 2)
Саша: 3х – 0,5 = 2х + 1,3
Дана – консультант
Никита, Рита, Саша решают задачу:
Саша решил две задачи за 35 мин. Первую задачу он решал на 7 мин. дольше, чем вторую. Сколько мин Саша решал вторую задачу?
III. Прочитать задачу по краткой записи (на доске), составить уравнение и решить задачу:
Навага — ?
Треска — ?, в 1,5 раз больше наваги всего 520 тонн
Окунь — ? на 16 тонн больше трески
На базе хранится 520 тонн рыбы. При этом трески в 1,5 раза больше, чем наваги. Окуня на 16 тонн больше, чем трески. Сколько тонн трески, наваги и окуня находится на складе?
уравнения?
- Работа в тетрадях и у доски
Юлиана (у доски)
- 2х – 15 = 3х – 7 (-8)
- у + 6 = 2у – 5 (11)
Сережа (у доски)
1. 4у – 10 = -6у (1)
- 3х +2 = 6х + 2 (0)
Вадим (у доски)
- 2(1,1 – 5у) = 6у – 1 (0,2)
- 29 – 13х = 17 – 3х (1,2)
Ряд у окна
1. 7х – 18 = 3х + 22 (10)
2. 0,3х – 17 = -1,4х (10)
Ряд к двери
1. 1,3х + 2,5 = 0,3х – 1,5 (-4)
2. 18 – 5у = 6у – 15 (3)
- Необычная задача
Отцу 32 года, сыну 5 лет. Через сколько лет отец будет в 10 раз старше сына?
(решить самостоятельно, сделать вывод)
(Решение.
Обозначим искомый срок через х. Спустя х лет отцу будет (32 + х) лет, сыну (5 + х) лет.
Так как отец должен быть в 10 раз старше сына, то получим уравнение 32 + х = 10(5 + х). Решив его, получаем: х = -2).
Итак, через минус два года. Как вы это можете объяснить?
(Через «минус 2 года» означает «два года назад»).
4. Самостоятельная работа с последующей самопроверкой (10 мин)
Решите уравнение:
I. а) 12х – 21 = 11х + 2(3х + 2); б) 5х – 4(2х – 1) = 2(2х – 5);
в) 0,4 (х – 1,2) + 1,6 = — 2; г) 10х – 2,5(0,6х – 3) = — 1.
II. а) (х + 5) / 6 =(3 – х) /4 б) (1,5х -3,6) / 5 = (- 2,4 + х) / 2
III. а) (3х + 3)(6 – 2х) = 0; б) (2х – 4)(х + 5) = 0;
в) (4х – 8)(х + 3) = 0; г) (х – 2)(2х + 6) = 0;
IV. а) 5х = 3х*х – х; б) 2х *х = 10х.
V. При каких значениях буквенной переменной уравнение
(6 – 4х) / (х – 4) = 0 не имеет корней?
(самооценки по самостоятельной работе)
- Математические фокусы – задача из занимательной алгебры Перельмана (если останется время)
Задумайте число, прибавьте 2, умножьте на 3, отнимите 5, отнимите задуманное число, умножьте на 2, отнимите 1, сообщите окончательный результат. Я легко угадаю, какое число было задумано. Как? Это задание на дом.
(Решение.
Составим таблицу:
|
Задумайте число |
х |
|
Прибавьте 2 |
х + 2 |
|
Умножьте результат на 3 |
3(х + 2) = 3х + 6 |
|
Отнимите 5 |
3х + 6 – 5 = 3х + 1 |
|
Отнимите задуманное число |
3х + 1 – х = 2х + 1 |
|
Умножьте на 2 |
2(2х + 1) = 4х + 2 |
|
Отнимите 1 |
4х + 2 – 1 = 4х + 1 |
Пусть, например, в результате операций получилось число 33, тогда необходимо решить уравнение: 4х + 1 = 33.) О других способах отгадывать числа можно узнать из книги Я.И. Перельмана «Занимательная алгебра».
- Итог урока (2 мин)
|
Посмотрите на уравнение: 4х + 2х *х = 10х |
|
|
Встречались с ним ранее? |
нет |
|
Попробуем решить |
|
|
Какие правила мы применяем при решении уравнений? |
Перенос слагаемых c переменной в одну сторону, а известных слагаемых в другую сторону |
|
Что получилось? |
4х + 2х *х — 10х = 0 |
|
Что заметили? |
Можно привести подобные слагаемые |
|
2х*х -6х = 0 |
|
|
Что общего у каждого из слагаемых? |
общий множитель х |
|
Что с ним можно сделать? |
2х(х – 3) = 0 |
|
Назовите корни |
0 или 3 |
Если вы стоите у подножия горы и видите, какая прекрасная перед вами открывается панорама, не стойте на месте, поднимитесь хотя бы на несколько шагов и красоты преумножатся.
Сегодня мы познакомились с Я.И. Перельманом.
(Учитель сообщает ребятам отметки, заработанные ими на уроке).
- Задание на дом.
Составить уравнение по задаче (текст на столах), найти информацию по Перельману, решить из самостоятельной работы то, что не успели решить.
Проверочная работа по теме « Решение линейных уравнений» 6 класс.
При выполнении проверочной работы ученик допустил ошибки в решении некоторых уравнений. Постарайся найти ошибки . Запиши правильное решение справа, напротив той строки, в которой, по твоему мнению, находится ошибка.
Выбери тип ошибки :
В- вычислительная,
С- раскрытие скобок,
П— перенос слагаемых из одной части равенства в другую часть.
Напротив строки, где, по твоему мнению, допущена ошибка поставьте букву, соответствующую типу ошибки «В», «П», «С» и запишите правильное преобразование.
По окончании выполнения работы проверь правильность своих ответов по образцам, выданным учителем. Затем приступайте к выполнению самостоятельной работы выбранного вами уровня сложности.
|
1) —5,2а = 10,4; |
||
|
а= 10,4:(-5,2); |
||
|
а= -2. |
||
|
2) -12+х=-24,4; |
||
|
х = 24,4-12; |
||
|
х = 12,4. |
||
|
3) 3х – 18 = 6х – 12; |
||
|
3х + 6х = 18 – 12; |
||
|
9х = 6; |
||
|
х = |
||
|
х = |
||
|
4) 5(2у-1,2) = 4,3у-0,3; |
||
|
10у- 6 = 4,3у-0,3; |
||
|
10у — 4,3у = 6 -0,3; |
||
|
5,7у = 5,7; у=5,7:5,7; |
||
|
У=0,1. |
||
|
5) -18+ 4( х-1,5) = 9+ 7х; |
||
|
-18+ 4х-1,5 = 9+7х; |
||
|
-18 -1,5 -9 = 7х+4х; |
||
|
-11х=28,5; |
||
|
х= — |
||
|
х= — |
||
|
х= — |
||
|
6) 2-(8а+2,7)+(-3а-8)=13,3; |
||
|
2-8а-2,7-3а-8=14,3; |
||
|
-11а=13,3 +8,7; |
||
|
-11а=22; |
||
|
а=-2. |
Выполни устный анализ выполнения своей работы.
Реши уравнения выбранного уровня сложности.
5-6 баллов — «3», 7-9 баллов – «4», 10-12 баллов –«5».
1 вариант 2 вариант
1) -5х -1 = 4; 1) -3Х+6=-9;
2) -5х + 2 = -10х; 2) 9Х+14= -6Х+5;
3) -6 – 4х = -9х – 4,5; 3) -1,5Х+2,5=-5,5Х+12,5;
2 уровень(2 балла) 2 уровень(2 балла)
1) 4( 2 -3х) = -7х + 10; 1) 7(4+5Х)= -15Х-28;
2) -4( -7 -0,6Х) = -9,6Х – 6; 2) -2х+1-3(Х-4)=4(3-Х)+4;
3) 6,5(а+3)-5 = -6,5а + 14,5; 3) 0,9(4у-2)=0,5(3у-4)+4,4;
3 уровень ( 3 балла). 3 уровень( 3 балла)
1) 8+Х= 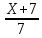
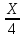
2) 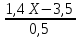
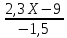
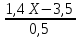
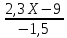
2 вариант
|
1) -4,3Х=12,9; Х= 12,9: (-4,3); Х= 3,3. |
||
|
2) -13 + а=-15,2; а = 15,2-13; а= 2,2. |
||
|
3) 6 -2Х = 3Х -10; -2Х -3 = -10 -6; -5Х = -16; Х = 3,2. |
||
|
4) 6( 5 – 3Х) = — 8Х-5; 30-3Х = -8Х -5; -3Х +8Х=-5-30; 5Х = -35; Х=-7. |
||
|
5) 6 — 18 – 7Х = 3Х; -7Х-3Х=-18; -10Х=-18; Х= 1,8. |
||
|
6) -5а-5+5(а-5)=-(5-а)-4: -5а-5+5а-25=-5+а-4; -5а+5а+а=5+25-5-4; а = 21. |
«Проблематика решений уравнений в 5-7 классах»
статья по математике (5, 6, 7 класс)
Краткий очерк о проблеммах в уравнениях с которыми сталкиваются учащиеся в 5-7 классах.
Скачать:
| Вложение | Размер |
|---|---|
| problematika_resheniy_uravneniy_v_5-7_klassah.docx | 23.1 КБ |
Предварительный просмотр:
ПРОБЛЕМАТИКА РЕШЕНИЙ УРАВНЕНИЙ В 5-7 КЛАССАХ.
В.А. Егорова
ГБОУ СОШ №411 «Гармония» с углубленным изучением английского языка Петродворцового района Санкт-Петербурга, Санкт-Петербург
E-mail: EgorovaVika96@mail.ru
Ключевые слова: уравнение, линейное уравнение, корень, неизвестное, правила, перенос, знаки, равенство, сумма, разность, вычитаемое, уменьшаемое, делитель, делимое, множитель, произведение, частное, слагаемое.
Аннотация. В работе рассмотрены проблемы решений уравнений в пятых, шестых и седьмых классах. Описаны необходимые знания, умения, навыки. Рассказано об особенностях уравнений в каждом из классов. Описана сложность адаптации детей к уравнениям в седьмых классах. Предложен способ объяснения «переноса» через знак равенства. Решены примеры уравнений самими обучающимися. Проведен анализ системы решения уравнений по траектории пятых-седьмых классов.
Уравнения всегда занимали ведущую роль в курсе изучения математики в школе, не даром на них отводят много учебного времени. Известно всем, если ребёнка научить решать уравнения, то большинство задач для него станут по силам. Даже те задачи, которые вызывали сложности в понимании и решении, с уравнением принимают облегченное значение. Но прежде, чем переходить к задачам, необходимо сформировать навык решения линейных уравнений.
Уравнения – это равенство, содержащее неизвестное число, которое надо найти. Корень – число, при подстановке которого в уравнение, получаем верное равенство. Поиск корня уравнения является решением уравнения . Удивительно, но эти определения учащиеся узнают в первом классе, последующие четыре года, закрепляют полученные знания. В итоге, мы получаем, что курс математики в пятых и шестых классах вновь повторяет изученные правила для поиска корней уравнения. Единственное отличие, это сложность самих уравнений. Получается, чтобы решать уравнения необходимо и достаточно знать около шести правил для нахождения неизвестного (слагаемого, вычитаемого, уменьшаемого, делителя, делимого, множителя). В помощь детям на данном этапе нам нужно предложить следующие схемы:
К сожалению, опытным путем известно, дети, которые отлично выучили правила, не могут их применять при отсутствии понимания расположения объектов в уравнении и их названиях. В целом для пятого класса достаточно знать правил и «названия» чисел в примерах.
Шестой класс добавляет сложности в решений уравнений тем, что появляются отрицательные числа. Необходимо чёткое понимание знаков перед числами. Нужно добиться запоминания, что перед числом всегда есть свой знак или Здесь сразу встает вопрос перед преподавателем, как теперь строить решение уравнений. Через уже известные правила или начинать объяснять детям перенос чисел за знак равенства. Так как появление отрицательных чисел уже само по себе является стрессом для учеников, то путь наименьшего сопротивления – вернуться к известным правилам. (Заметим, что всё зависит от способностей учеников. Нельзя предлагать другие способы решения, если дети не в силах их освоить.) Но возвращение к правилам вызовут трудности в старшем классе с пониманием «переноса числа через знак», поэтому важным является момент обсуждения другого способа решения. Возможно, уже в шестом классе ученики возьмут этот способ на вооружение!
Рассмотрим пример . Ученики пятых/шестых классов скажут:
- является неизвестным уменьшаемым;
- Чтобы найти неизвестное уменьшаемое , надо к разности прибавить вычитаемое ;
- – неизвестный множитель ;
- Чтобы найти неизвестный множитель , надо произведение разделить на известный множитель ;
Ученики решают уравнения через правила, они не заметят, что у числа 25 знак при переносе через знак «равно» поменялся на противоположный. На это стоит обращать внимание уже в шестом классе, чтобы в последующем им было легче ориентироваться.
Седьмой класс несет новые усложнения материала. Самым главным является то, к примеру неизвестное ( ) уже может стоять в обеих частях уравнения и на данном этапе воспользоваться правилами у учеников нет возможности. Появляется перенос чисел через знак равенства, появляются ошибки. Чтобы ошибок было меньше необходимо работать с ними больше, если начинать говорить о переносе раньше, чем в седьмом классе, то осознание действия происходит раньше.
Рассмотрим уравнение: Как можно заметить, тут несколько неизвестных и применить правило пятого/шестого класса достаточно проблематично. Здесь, как две аксиомы даются советы учителей:
- Неизвестные в одну сторону уравнения, известные в другую.
- При переносе числа через знак равенства его знак меняется на противоположный.
Представим ход решения глазами учеников:
- Переношу неизвестные влево, известные вправо. необходимо перенести влево, вправо.
- неизвестный множитель , чтобы его найти надо произведение разделить на известный множитель .
Видим, что на последнем этапе ученики седьмых классов всё же используют правила, которые изучали до этого. Если они не доведены до автоматизма, то необходимо вновь их выучить.
Есть интересный способ объяснения переноса через знак равенства через «уравнивание» частей. Важным здесь является то, что надо объяснить главный смысл уравнения. Уравнение — значит равенство левой и правой части, а если мы прибавляем к левой части какое-то число, то обязаны прибавить его же и к правой! Рассмотрим уравнение, но постараемся подвести мысль к «уравниванию» частей.
У детей сформировано понятие уравнения вида: , где число. То есть, они привыкли что слева (с одной стороны) должно оставаться неизвестное. Что сейчас мешает нам? Конечно, . А что необходимо сделать, чтобы этого числа не было в левой части? Прибавить ему противоположное, а если мы прибавляем к левой части, то обязаны прибавить и к правой части уравнение тоже самое число.
Этот ход для учеников более понятен и математически обоснован. Его можно сравнить с чашами весов. Где мы добавляем гирю на одну сторону и, чтобы привести весы в равновесие, нам необходимо столько же прибавить и на вторую сторону. И когда этот механизм уже осознан, можно говорить о сокращении записи и подметить тот факт, что справа число 25 отличается тем, что имеет перед собой знак . А значит перенос через знак равенства меняет знак перед числом на противоположный.
Как мы с вами могли заметить, уравнения идут красной нитью по всем классам. С каждым годом усложняя какую-то часть. Необходимо знать о сложностях в изучении данной темы, чтобы знать обходы и способы избегания ошибок. Самое главное в любом классе — это объяснение материала, основанное уже на изученном материале или общеизвестных фактах, подкрепленных экспериментами. Всегда необходимо давать немного больше для размышления ученикам, немного больше, чем предусмотрено программой. Тогда в будущем будет легче самим детям, не говоря уже о преподавателях.
1. Петерсон Л.Г. Учебник «Математика. 1 класс» Издательство «С-инфо».
2. Программы для общеобразовательных учреждений. Алгебра 7 – 9 классы. Составитель Бурмистрова Т.А. – М: Просвещение, 2008.
3. Алгебра 7 класс. 12 сентября. Решение линейных уравнений #2. Развивающее обучение на уроках математики и во внеклассной работе. Андреев Андрей Андреевич. Режим доступа: https://www.youtube.com/watch?v=a0Yd0tejekg
4. Математика. Рабочие программы. Предметная линия учебников «Сферы». 5–6 классы : пособие для учителей общеобразоват. организаций / [Е.А. Бунимович, Л.В. Кузнецова, С.С. Минаева и др.]. — 3-е изд. — М. : Просвещение, 2014.
5. Федеральный компонент государственного стандарта основного общего образования по математике
По теме: методические разработки, презентации и конспекты
Презентапция к уроку математики по теме «Решение уравнений»в 5, 6 классах
Презентация составлена к уроку математики в 5,6 классах (класс — комплект) малокомплектной школы по проблеме разновозрастного убучения в сельской малокомплектной школе.
Способы решения уравнений высших степеней. 8 класс
Данную презентацию использую при решении уравнений высших степеней в 8 классе. Решать квадратные уравнения школьники научились по формулам, а если уравнение выше второй степени? Есть ли алгоритм.
Конспект урока. Тема: «Решение уравнений высших степеней» 8 класс
Полное описание урока. Как решать уравнения выше второго порядка? Есть ли алгоритм решения? На эти и другие вопросы отвечает данный материал.
Презентация по теме «Решение уравнений. Раскрытие скобок», 6 класс
Презентация по теме «Решение уравнений. Раскрытие скобок», 6 класс.
Урок-защита проектов «Решение уравнений высших степеней» 9 класс
Конспект урока по алгебре в 9 классе «Решение уравнений высших степеней», на котором учащиеся защищали свои проекты.Презентации учащихся: Решение биквадратных уравнений, Решение возвратных уравнений, .
Элективный курс «Нестандартные методы решения уравнений и неравенств» 11 класс
Настоящая программа составлена для выпускников 11 класса и рассчитана на 35 часов в год (1 час в неделю). Программа состо.
Контрольная работа по теме «Решение уравнений второй степени» (9 класс)
В контрольну работу включены системы уравнений второй степени, для решения которых используются различные методы. Контольная работа составлена для базового уровня сложности. Представлены 2 варианта ра.
math4school.ru
Ошибки в уравнениях
При выполнении контрольных, тестовых и экзаменационных работ по математике учащиеся решают самые разнообразные уравнения, отличающиеся по тематике и по сложности. Разобрать все ошибки, которые при этом допускаются, не представляется возможным. Ниже предлагаются примеры лишь наиболее распространенных ошибок и анализ ситуаций, в которых эти ошибки допускаются.
Потеря корней
При решении уравнений из-за выполнения нетождественных преобразований может произойти либо потеря корней , либо появление посторонних корней .
При выполнении нетождественных преобразований в процессе решения уравнения может произойти сужение области допустимых значений неизвестного , а значит, корни могут оказаться потерянными.
K Упражнение. Решить уравнение lg (x – 10) 2 + lg x 2 = 2lg 24 .
L Неправильное решение.
2lg (x – 10) + 2lg x = 2lg 24,
Произвели проверку и убедились, что все корни удовлетворяют данному уравнению.
Комментарий . Из-за неправильного применения формул произошло сужение области допустимых значений неизвестного.
J Правильное решение.
Ответ: –2; 4; 6 и 12.
При делении обеих частей уравнения на выражение, содержащее неизвестное , могут быть потеряны корни, которые обращают эти выражения в ноль.
K Упражнение 1. Решить уравнение 3 х ( х 2 – 2 х – 3) = 9 ( х 2 – 2 х – 3) .
L Неправильное решение.
Разделим обе части уравнения на квадратный трехчлен, записанный в скобках, и получим:
J Правильное решение.
Перенесем правую часть исходного уравнения влево и вынесем общий множитель за скобки:
K Упражнение 2. Решить уравнение lg 2 x – lg x = 0 .
L Неправильное решение.
Разделим обе части уравнения на lg x и получим:
J Правильное решение.
Необходимо помнить, что обычно легче исключить посторонний корень, чем найти потерянный.
Посторонние корни
При решении уравнений существуют два диаметрально противоположных мнения относительно полученного результата. Одни считают, что проверка должна производиться всегда, другие считают ее необязательной. На самом деле проверка полученных корней в одних случаях является обязательной и является частью решения уравнения, а в других случаях в проверке необходимости нет.
Проверка полученного решения уравнения обычно делается с целью исключения посторонних корней, которые чаще всего появляются в результате нетождественных преобразований, приводящих к расширению области допустимых значений переменного. Рассмотрим далее некоторые случаи появления посторонних корней.
Это может случиться при умножении обеих частей дробного уравнения на выражение, содержащее неизвестную величину .
K Упражнение. Решить уравнение
| 5 – x | – | 5 + 3х | = 0 . |
| x – 1 | x 2 – 1 |
L Неправильное решение.
Умножим все члены уравнения на х 2 – 1 и получим:
Комментарий . Был приобретен посторонний корень х = 1, в чем можно убедиться с помощью проверки .
J Правильный ответ: х = 0.
Появление посторонних корней может быть вызвано сокращением дроби на множитель, содержащий неизвестную величину .
K Упражнение. Решить уравнение
L Неправильное решение.
Заметим, что х 2 – 81 = (x – 9) (x + 9) и произведем сокращение дроби на x – 9 . Имеем:
Комментарий . Был приобретен посторонний корень х = 9 .
J Правильный ответ: решений нет.
Приведение подобных слагаемых с неизвестным в знаменателе, в том случае, если они взаимно уничтожаются, также может привести к приобретению постороннего корня.
K Упражнение. Решить уравнение
| 2 | + х 2 – | 2 | – 4х = 0 . |
| 3х 2 | 3х 2 |
L Неправильное решение.
После приведения подобных слагаемых получим:
Комментарий . Был приобретен посторонний корень х = 0 .
J Правильный ответ: 4 .
Заметим, что аналогичная ситуация может сложиться и для слагаемых, содержащих переменную под знаком корня или под знаком логарифма.
Очень часто посторонние корни появляются при возведении в четную степень обеих частей уравнения . Рассмотрим следующее иррациональное уравнение и на его примере – процесс появления посторонних корней.
K Упражнение. Решить уравнение √ х + 3 + √ 7 – х = 2 .
L Неправильное решение.
И число –2 , и число 6 содержатся в области допустимых значений переменной х , значит, являются решениями исходного уравнения.
Комментарий . Оба корня посторонние и были приобретены в процессе решения. Как же это произошло? Дело вот в чем. В процессе решения с помощью возведения в квадрат и элементарных преобразований мы перешли от уравнения
Последнему уравнению число –2 удовлетворяет, после подстановки получаем верное равенство 1 = 1 . Предыдущее же уравнение при подстановке –2 дает ложное равенство 1 = –1 , которое стало верным именно в результате возведения в квадрат, ведь 1 2 = (–1) 2 . Число –2 является корнем второго уравнения, для первого – посторонний корень. А вот число 6 не является корнем ни одного из них.
Шестерка выходит на арену при переходе от уравнения
которое уже имеет один корень –2 , к уравнению
Теперь возведение в квадрат превращает ложное равенство 2 = –2 в истинное равенство 4 = 4 , которые соответствуют этим уравнениям для случая х = 6 . Для последнего уравнения 6 – истинный корень, а для предпоследнего – ложный. И вот, путем преобразований мы получаем уравнение
для которого числа –2 и 6 — самые настоящие корни, а для исходного — посторонние. Два раза мы применяли возведение в квадрат и каждый раз приобретали посторонний корень, каждый из которых благополучно преодолел фильтр ОДЗ. В данном случае проверка обязательна.
J Правильный ответ: решений нет.
Необходимо помнить, что если область допустимых значений неизвестного найдена и при решении уравнения получены корни, принадлежащие ей, то проверка корней не нужна, только если при этом в процессе решения все преобразования были тождественными.
Если при решении уравнения используется тот факт, что произведение равно нулю, когда хотя бы один из множителей равен нулю , прежде чем писать ответ, необходимо убедиться, что все найденные корни удовлетворяют условию.
K Упражнение. Решить уравнение ( x – 5) (х + 2) √ х – 3 = 0 .
L Неправильное решение.
Перейдем от данного уравнения у совокупности уравнений:
Комментарий . Число –2 обращает подкоренное выражение х – 3 в отрицательное число, а значит не может быть корнем уравнения.
J Правильный ответ: 5 и 3 .
Часто причиной изменения множества корней уравнения во время его преобразования является применение равенств, правая и левая части которых имеют разные области определения . Таких равенств много, вот некоторые из них:
| tg ( x + y ) = | tg x + tg y |
| 1 – tg x · tg y |
| sin 2 x = | 2 tg x |
| 1 + tg 2 x |
В каждом из этих равенств область определения выражения, стоящего в правой части, является подмножеством области выражения, стоящего в левой части. Поэтому использование этих равенств слева направо может привести к потере корней, а справа налево – к появлению посторонних корней .
L Неправильное решение.
так как х ≥ 3 , то |х – 1| = х – 1 и
Комментарий . Применение формулы √ х · y = √ х · √ y привело к потере корня x = 1 . И вот почему. Исходное уравнение имеет область допустимых значений <1>∪[3; +∞) , а вот уже ОДЗ уравнения (left| x-1right|cdot sqrt=x-1) – только [3; +∞) , что и привело к потере 1 .
Можем порекомендовать возвести обе части исходного уравнения в квадрат. Это может привести к появлению посторонних корней, избавиться от которых проверкой, как правило, проще, чем заниматься поисками потерянных корней.
J Правильное решение.
(left(x-1 right)^2cdot left(x-3 right)=left(x-1 right)^2;)
(left(x-1 right)^2cdot left(x-3 right)-left(x-1 right)^2=0;)
(left(x-1 right)^2cdot left(x-4 right)=0;)
Проверкой убеждаемся, что оба корня действительные.
Ошибки, связанные с заменой переменной
При решении некоторых уравнений достаточно удачным является метод замены переменной . Но применение этого метода учащиеся осуществляют не всегда правильно.
Так необходимо помнить, что при наличии нескольких степеней заменять новой переменной надо ту, у которой показатель наименьший .
K Упражнение. Решить уравнение (5 left(x-3 right)^<1/4>-6=left(x-3 right)^<1/2>.)
L Неправильное решение.
Сделав замену ( left(x-3 right)^<1/2>=t), считают, что ( left(x-3 right)^<1/4>=t^2) и уравнение переписывают в виде 5t 2 – t – 6 = 0 , после чего, конечно, верный результат уже не получить.
J Правильное решение.
Верный результат можно получить, сделав замену ( left(x-3 right)^<1/4>=t), тогда ( left(x-3 right)^<1/2>=t^2) с продолжением:
Правильно сделав замену и верно найдя значение вспомогательной переменной, учащиеся часто допускают ошибку, используя не то равенство, которым вспомогательная переменная вводилась .
K Упражнение. Решить уравнение х + 4 √ x – 5 = 0 .
L Неправильное решение.
Комментарий . После нахождения значений вспомогательной переменной t для нахождения х следовало использовать подстановку √ x = t , а не x = t 2 .
J Правильное решение.
При решении иррациональных уравнений учащиеся чаще всего применяют метод возведения в соответствующую степень. В результате этого решения иррациональных уравнений получаются громоздкими и не всегда доводятся до конца .
K Упражнение. Решить уравнение (x^2-4x-sqrt<2x^2-8x+12>=6.)
L Неправильное (нерациональное) решение.
Чаще всего данное уравнение начинают решать так:
Нередко продолжения решения не следует, так как с полученным уравнением четвертой степени справится не каждый.
Комментарий . В качестве альтернативы можно предложить способ введения новой переменной.
J Правильное решение.
и исходное уравнение принимает вид:
А дальше все просто:
Комментарий . Числа –2 и 6 не подвергались проверке осознанно. В данном случае после возведения в квадрат не могли появиться посторонние корни, так как и квадратный корень, и подкоренное выражение после возведения в квадрат заведомо равны положительным числам.
Ошибки, связанные с использованием модуля
При решении уравнений, в тех случаях, когда необходимо использовать понятия модуля и арифметического корня , допускаются серьезные ошибки, связанные либо с незнанием, либо с непониманием этих понятий.
K Упражнение 1. Решить уравнение (sqrt=9.)
L Неправильное решение.
J Правильное решение.
K Упражнение 2. Решить уравнение (sqrt<(x+3)^2>=x+3.)
L Неправильное решение.
Ответ: корнем данного уравнения является любое действительное число.
J Правильное решение.
Учитывая, что решение уравнений, содержащих модуль, часто вызывает затруднения, приведем полное и развернутое решение одного из таких уравнений.
K Упражнение. Решить уравнение |x – 3| + |x –4| = 1 .
J Правильное решение.
Находим нули модулей, для |х – 3| это 3 , для |x – 4| это 4 , и разбиваем ими область допустимых значений неизвестного на числовые промежутки:
На каждом из этих промежутков исходное уравнение принимает свой вид.
1) при х ∈ (–∞; 3) исходное уравнение принимает вид:
так как 3 ∉ (–∞; 3 ) , то на этом промежутке решений нет;
2) при х ∈ [3; 4) исходное уравнение принимает вид:
что является истинным тождеством; значит, каждое число рассматриваемого промежутка [3; 4) является решением уравнения;
3) при х ∈ [4; +∞) исходное уравнение принимает вид:
так как 4 ∈ [4; +∞) , то 4 – корень уравнения.
Так как [3; 4)∪ <4>= [3; 4] , то корнями исходного уравнения являются все числа числового промежутка [3; 4] .
Подбор корней без обоснования
К ошибочным решениям можно отнести и верный подбор корня заданного уравнения, иногда просто угадывание, без доказательства его единственности .
K Упражнение. Решить уравнение х (х + 1) (х + 2) (х + 3) = 24 .
L Неправильное решение.
Подбором находят корень х = 1 из разложения 24 = 1 · 2 · 3 · 4.
Комментарий . Был подобран корень х = 1 , но не обнаружен еще один корень х = –4 , который соответствует разложению 24 = –4 · (–3) · (–2) · (–1) . Но даже если и второй корень успешно подобран, но не обосновано отсутствие других корней, то считать такое решение уравнения правильным нельзя.
J Правильное решение.
введем новую переменную x 2 + 3х + 1 = t , тогда
1) x 2 + 3х + 1 = –5, x 2 + 3х + 6 = 0, решений нет;
Наиболее распространенным методом доказательства единственности корня нестандартного уравнения является использование свойства монотонности входящих в уравнение функций . Часто при этом используется производная.
K Упражнение. Решить уравнение x 11 + 5х – 6 = 0 .
L Неправильное решение.
Методом подбора находим корень уравнения х = 1 .
Комментарий . Не приведено обоснование единственности подобранного корня уравнения.
J Правильное решение.
Корень х = 1 легко угадывается, а производная левой части равна 11x 10 + 5 и положительна на всей числовой оси. Отсюда следует монотонность функции у = x 11 + 5х – 6 , что и доказывает единственность подобранного корня.
Ошибки в логарифмических и показательных уравнениях
Для решения логарифмических и показательных уравнений используются специальные приемы, основанные на свойствах логарифмов и степеней. Рассмотрим связанные с применением этих приемов ошибки.
При решении уравнений, которые можно свести к равенству степеней с одинаковыми основаниями или с одинаковыми показателями , не всегда делаются правильные выводы.
K Упражнение 1. Решить уравнение (log7 x) 1 /3 = 1 .
L Неправильное решение.
Так как при одинаковых основаниях показатели не равны, то равенство степеней невозможно, а, значит, корней нет.
Ответ: корней нет.
J Правильное решение.
Возведем в куб обе части уравнения, тогда
K Упражнение 2. Решить уравнение (х + 5) х 2 + х – 2 = 1 .
L Неправильное решение.
Комментарий . Потерян корень х = –4 . Избежать этого можно было и при данном способе решения уравнения, если учесть, что степень равна 1 не только в случае нулевого показателя, но и в случае основания равного 1 при произвольном показателе. И тогда в дополнение к приведенному решению имеем:
J Правильное решение.
Прологарифмируем обе части уравнения по некоторому основанию, например 10, при условии х > 5 , тогда
Необходимо помнить, что:
из равенства степеней, основания которых равны единице, не следует обязательное равенство показателей этих степеней;
степенно–показательное уравнение предпочтительно решать путем логарифмирования.
При решении логарифмических уравнений часто приходится применять свойства логарифмов с одинаковыми основаниями . При применении этих свойств учащиеся часто допускают ошибки.
L Неправильное решение.
Комментарий . В решении допущены две серьезные ошибки: во-первых, произведение логарифмов двух чисел заменено логарифмом произведения этих чисел; во-вторых, при решении уравнения 3х 2 = 81x потерян корень х = 0 (этот корень, конечно, не является корнем исходного уравнения, что не оправдывает его потерю).
J Правильное решение.
K Упражнение 2. Решить уравнение lg x 2 = 4 .
L Неправильное решение.
J Правильное решение 1.
2lg |x| = 4; lg | x| = 2; |x| = 100; x = ±100.
J Правильное решение 2.
lg x 2 = lg 10000; x 2 = 10000; x = ±100.
Большие затруднения у многих учащихся возникают при выполнении действий над логарифмами с разными основаниями , так как учащиеся либо не умеют пользоваться соответствующими формулами, либо не знают их.
Следует помнить, что переход к логарифму с другим основанием может привести как к приобретению посторонних корней, так и к потере корней .
K Упражнение 1. Решить уравнение (left(log_5 +2 right)<log _<5>>^2 ;x=0.)
L Неправильное решение.
(left(1 +2 log _<5>xright)log _<5>x=0;)
Комментарий . Преобразование логарифма с основание х в логарифм с основанием 5 привело к появлению постороннего корня, так как произошло расширение ОДЗ.
J Правильное решение.
Приведенное выше решение следует дополнить указанием области допустимых значений неизвестного в исходном уравнении. Это объединение числовых промежутков (0; 1)∪(1; +∞) . И указанием того факта, что 1 ∉ (0; 1)∪(1; +∞) , а, значит, не является корнем.
K Упражнение 2. Решить уравнение (20log_<4x>sqrt+ 7log_<16x>x^3-3log _x^2=0.)
L Неправильное решение.
Комментарий . В приведенном решении потерян корень, и вот почему. Был выполнен переход к логарифму с основанием х . Это вызвало изменения в ОДЗ неизвестного. Одно из таких изменений – это х ≠ 1 . Поэтому число 1 , как возможный корень исходного уравнения, следует рассмотреть отдельно.
J Правильное решение.
Приведенное выше решение нужно дополнить лишь проверкой того, не является ли 1 корнем уравнения. Подставляем 1 в исходное уравнение и убеждаемся, что 1 – корень.
Ошибки в тригонометрических уравнениях
Выделение в отдельный подраздел тригонометрических уравнений связано стем, что при их решении применяются не только алгебраические методы. Рассмотрим наиболее типичные ошибки, которые допускают учащиеся при решении тригонометрических уравнений.
Часто можно встретить неправильную запись решения тригонометрического уравнения или лишь частное решение .
Как избежать типичных ошибок, возникающих при выполнении заданий ЕГЭ по математике
Дземяшкевич Е.В., преподаватель математики
(Факультет довузовской подготовки ТулГУ)
Чтобы подготовиться к ЕГЭ по математике, необходимо уже сегодня перестать комплексовать и паниковать перед предстоящим единым экзаменом. Уже сейчас можно сказать, что на ЕГЭ можно получить вполне приличное количество баллов: время для форсированной подготовки еще не потеряно. Конечно, ЕГЭ — это не легко и просто, но и не безнадежно. Важно, чтобы школьник сам честно сформулировал для себя планируемый результат обучения. Это вовсе не означает, что выпускник, наметивший себе «3», может получить только «3» и не более, напротив, ориентируясь на намеченный результат, может и должен получить на один балл выше. Ученики, ориентированные на получение «4», должны помнить, что если постараться, то можно получить и «5».
Но не всегда так получается. Возможны ошибки при решении заданий, недостатки при подготовке, которые приводят к низким результатам ЕГЭ.
Для устранения недостатков в подготовке учеников к ЕГЭ по математике, необходимо совершенствовать процесс преподавания: активнее включать в учебный процесс идеи дифференцированного обучения; использовать практические разработки по индивидуализации обучения (создание индивидуальных модулей обучения), учитывать рекомендации психологов по организации усвоения и пр.).
Поговорим подробнее об ошибках, которые возможны при выполнении заданий ЕГЭ. Рассмотрим важные темы, встречающиеся на экзамене по математике.
| Тема | Ошибки | Рекомендации |
|---|---|---|
| преобразование иррациональных выражений | При кажущейся простоте этого задания, решаемость его далека от 100%. Сложно заставить себя при выполнении этих заданий сделать проверку. Казалось бы, все свойства действий с корнями просты. Вроде всё просто. Только не все выпускники могут вычислить или, не обращая внимания на степень корня, извлекают корень квадратный. | Не торопясь, выполнить все действия на черновике (обязательно записать все этапы решения). |
| преобразование показательных выражений | Выполнить проверку показательного выражения сложно | Не торопясь, выполнить все действия на черновике (обязательно записать все этапы решения); можно составить аналогичное задание и попытаться найти закономерность. |
| преобразование логарифмических выражений | Особенность темы заключается в том, что большинство одиннадцатиклассников узнают о логарифмах только в ноябре-декабре. Времени на «присвоение знаний» нет. Многие выпускники бояться решать задания с логарифмами, несмотря на то, что все свойства логарифмов они знают. Самое сложное при выполнении этих заданий – выполнить проверку. | Не торопясь, выполнить все действия на черновике (обязательно записать все этапы решения). |
| линейные уравнения | Решают все, правда, если a 0. Как только уравнение решается автоматически, возможны ошибки. Например, . Что это? Невнимательность? Досадная ошибка? | При решении линейных уравнений никто не застрахован от ошибок. Обязательно выполняем проверку. |
| квадратные уравнения | Очень большой процент ошибок приходится на квадратные уравнения. Ошибки начинаются с вычисления дискриминанта. В формулах для вычисления корней есть ошибки для –b и 2a. Не стоит упоминать про формулу «четного коэффициента» — много ошибок, особенно у сильных учеников. Важно повторить теорему Виета. | Не стоит пренебрегать проверкой корней с помощью теоремы Виета или подстановкой: она занимает меньше времени, чем полная проверка всего решения сложного задания. |
| дробно-рациональные уравнения | Школьники решают очень тяжело. Серьезные проблемы возникают при решении такого уравнения: даже записывая такое формальное условие- знаменатель не равен нулю – они о нем тут же забывают. | Чтобы избежать многих ошибок, проверка нужна обязательно: подстановка и удовлетворение условию «знаменатель не равен нулю». Обязательно включать в каждую домашнюю работу хотя бы одно задание на решение дробно рационального уравнения |
| рациональные неравенства | Линейные: чаще всего при делении на отрицательное число, неравенство вида: |
© Факультет довузовской подготовки Тульского государственного университета
300012, город Тула, проспект Ленина, 84, кор. 8, 3-й учебный корпус ТулГУ
(4872) 25-46-83, 25-46-84, 717-535
Тульский государственный университет
300012, город Тула, проспект Ленина, 92
(4872) 33-24-10, 35-34-44
Приемная комиссия ТулГУ: (4872) 332-332
Для того, чтобы мы могли качественно предоставить Вам услуги, мы используем cookies, которые сохраняются на Вашем компьютере (сведения о местоположении; ip-адрес; источник, откуда пришел на сайт пользователь, эта же информация используется для обработки статистических данных использования сайта посредством интернет-сервисов Google Analytics и Яндекс.Метрика). Продолжая использовать сайт, Вы соглашаетесь на использовании cookies. Отключить cookies Вы можете в настройках своего браузера.
http://math4school.ru/oshibki_v_uravnenijah.html
http://fdp.tsu.tula.ru/useful/TrainingMathematicEGE
math4school.ru
Ошибки в системах уравнений
Системы уравнений с двумя переменными – один из самых распространенных видов упражнений в математических тестах, письменных работах и экзаменах различных уровней. Если система решена правильно, то ответ не зависит от выбранного метода решения. Но ошибки, допускаемые учащимися при решении систем, часто связаны не только с решением, а и с неправильной формой записи .
K Упражнение. Решить систему уравнений:
L Неправильная запись.
[begin log _<2>xy=5, \ frac=frac<1><2>; end begin log _<2>xy=5, \ y=2x; end begin log _<2>2x^2=5, \ y=2x; end begin 2x^2=2^5, \ y=2x; end begin x^2=16, \ y=2x; end begin x=pm 4, \ y=2x; end begin x=pm 4, \ y=pm 8. end]
Комментарий . Использованная при записи ответа форма записи, как правило, подразумевает четыре пары чисел:
тогда как в действительности эта система имеет только два решения:
Справедливости ради, следует сказать, что действительно, иногда под записью (±4; ±8) понимают только пары
используют запись (±4; ∓8) . С этих позиций ответ (±4; ±8) является верным. Не будучи уверенным в правильной трактовке ваших записей, следует избегать подобных двойственностей.
J Правильный ответ.
K Упражнение. Решить систему уравнений
L Неправильное решение.
Комментарий . При решении системы методом извлечения корня из обеих частей уравнений следует рассмотреть совокупность систем уравнений, решение которой, в данном случае, даст четыре решения.
J Правильное решение.
Ответ: (2,5; –0,5), (0,5; –2,5), (–0,5; 2,5) и (–2,5; 0,5) .
Статья. Проблемы, типичные ошибки учащихся, допускаемые при решении уравнений и неравенств.
Задание «Проблемы, типичные ошибки учащихся»
Вспоминается расхожая истина – умные люди учатся на чужих ошибках. В математике приходится учиться, в основном, на собственных ошибках. Если ученик не ошибается, то он не учится. Ошибка – вещь необходимая и полезная. Нужно лишь правильно относиться к ошибке, правильно ее использовать.
Обидно получать плохие оценки из-за ошибок «на ровном месте». Глупые ошибки – проблема многих учеников: случайная потеря знака, скобки, необоснованное изменение чисел, пропуски переменных и всевозможные ляпы. Сами ученики порой не могут объяснить, чем вызваны эти ошибки.
Решая уравнения и неравенства учащиеся допускают типичные ошибки:
· Незнание правил, определений, формул.
· Непонимание правил, определений, формул.
· Неумение применять правила, определения, формулы.
· Неверное применение формул.
· Невнимательное чтение условия и вопроса задания.
· Раскрытие скобок и применение формул сокращенного умножения.
Какие же проблемы, трудности общего характера возникают у учащихся при изучении математики ( их несомненно можно отнести и к трудностям, которые возникают у уч-ся при изучении темы «Уравнения и неравенства»):
· Пропуски занятий приводят к незнанию материала, пробелам в знаниях.
· Поверхностное, невдумчивое восприятие нового материала приводят к непониманию его.
· Недостаточная мозговая деятельность приводит к неумению применять правила, определения и формулы .
· Неряшливый, неаккуратный почерк ученика приводит к досадным ошибкам . Учащиеся не всегда сами понимают, что именно они написали.
· Усталость . Чрезмерная нагрузка и недостаточный сон приводит к снижению внимания, скорости мышления и, как следствие, к многочисленным ошибкам.
· Кратковременное или полное переключение внимания с одной деятельности на другую (учебную или внеучебную) приводит к утрате только что воспринятого материала, приходится все начинать сначала.
· Скорость работы. Низкая скорость выполнения мыслительных операций часто мешает ученику контролировать себя и это может стать еще одной причиной ошибки. «Зависание» с какой-нибудь одной частью задания удаляет из «оперативной памяти» информацию о другой, в которой допускается не вынужденная ошибка. Скорость работы определяется физиологией конкретного школьника и навыками выполнения тех или иных операций.
· Мотивация. Следствие низкой мотивации – потеря внимания и ошибка.
Ошибки, допускаемые обучающимися при решении уравнений и неравенств, самые разнообразные: от неверного оформления решения до ошибок логического характера.
1. Самая типичная ошибка состоит в том, что учащиеся при решении уравнений и неравенств без дополнительных пояснений используют преобразования, нарушающие равносильность, что приводит к потере корней и появлению посторонних корней.
Предлагаю на конкретных примерах рассмотреть ошибки подобного рода и определить способы их предупреждения и исправления, но прежде всего хочу обратить внимание на следующую мысль: не надо бояться приобрести посторонние корни, их можно отбросить путем проверки ,надо бояться потерять корни.
а) Решить уравнение:
log3(5 – x) = 3 – log3(–1 – x).
Это уравнение учащиеся очень часто решают следующим образом.
log3(5 – x) = 3 – log3(–1 – x), log3(5 – x) + log3(–1 – x) = 3, log3((5 – x)( –1 – x)) = 3, (5 – x)( –1 – x) = 33, x2 – 4x – 32 = 0,
Учащиеся часто, не проводя дополнительных рассуждений, записывают оба числа в ответ. Но как показывает проверка, число x = 8 не является корнем исходного уравнения, так как при x = 8 левая и правая части уравнения теряют смысл. Проверка показывает, что число x = –4 является корнем заданного уравнения.
б) Решить уравнение
Область определения исходного уравнения задается системой
Для решения заданного уравнения перейдем к логарифму по основанию x, получим
Мы видим, что левая и правая части этого последнего уравнения при x = 1 не определены, но это число является корнем исходного уравнения (убедиться в этом можно путем непосредственной подстановки). Таким образом, формальный переход к новому основанию привел к потере корня. Чтобы избежать потери корня x = 1, следует указать, что новое основание должно быть положительным числом, отличным от единицы, и рассмотреть отдельно случай x = 1.
2. Целая группа ошибок, вернее сказать недочетов, состоит в том, что учащиеся не уделяют должного внимания нахождению области определения уравнений, хотя именно она в ряде случаев есть ключ к решению.
3. Типичной ошибкой учащихся является то, что они не владеют на нужном уровне определениями понятий, формулами, формулировками теорем, алгоритмами. Хочу подтвердить сказанное следующим примером.
Ученик предлагает следующее ошибочное решение этого уравнения:
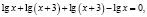
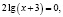
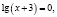
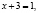
Поверка показывает, что х = –2 не является корнем исходного уравнения.
Напрашивается вывод, что заданное уравнение корней не имеет.
Однако это не так. Выполнив подстановку х = –4 в заданное уравнение, мы можем убедиться, что это корень.
Предлагаю проанализировать, почему произошла потеря корня.
В исходном уравнении выражения х и х + 3 могут быть одновременно оба отрицательными или оба положительными, но при переходе к уравнению 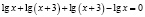
Чтобы избежать потери корня, можно поступить следующим образом: перейти в исходном уравнении от логарифма суммы к логарифму произведения. Возможно в этом случае появление посторонних корней, но от них, путем подстановки, можно освободиться.
4. Многие ошибки, допускаемые при решении уравнений и неравенств, являются следствием того, что учащиеся очень часто пытаются решать задачи по шаблону, то есть привычным путем. Предлагаю рассмотреть это на следующем примере.
Попытка решать это неравенство привычными алгоритмическими способами не приведет к ответу. Решение здесь должно состоять в оценке значений каждого слагаемого левой части неравенства на области определения неравенства.
Найдем область определения неравенства:
Для всех x из промежутка (9;10] выражение 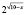
Для всех x из промежутка (9;10] выражение ( x – 9) имеет положительные значения, а выражение lg(x – 9) имеет значения отрицательные или ноль, тогда выражение
– (x – 9) lg(x – 9) положительно или равно нулю.
Окончательно имеем x ∈ (9;10]. Хочу заметить, что при таких значениях переменной каждое слагаемое, стоящее в левой части неравенства, положительно (второе слагаемое может быть равно нулю), а значит их сумма всегда больше нуля. Следовательно, решением исходного неравенства является промежуток (9;10].
5. Одна из ошибок связана с графическим решением уравнений.
Некоторые учащиеся, решая это уравнение графически (хочу отметить, что его другими элементарными способами решить нельзя), получают лишь один корень (он является абсциссой точки, лежащей на прямой y = x), ибо графики функций
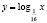
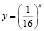
это графики взаимно обратных функций.
На самом деле исходное уравнение имеет три корня: один из них является абсциссой точки, лежащей на биссектрисе первого координатного угла y = x, другой корень 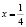
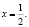
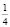
Этот пример удачно иллюстрирует следующий вывод: графическое решение уравнения f(x) = g(x) “безупречно”, если обе функции «разномонотонны» (одна из них возрастает, а другая – убывает), и недостаточно математически корректно в случае одномонотонных функций (обе либо одновременно убывают, либо одновременно возрастают).
6. Ряд типичных ошибок связан с тем, что учащиеся не совсем корректно решают уравнения и неравенства на основе функционального подхода. Остановлюсь на типичных ошибки такого рода.
а) Решить уравнение x х = x.
Функция, стоящая в левой части уравнения, – показательно-степенная и раз так, то на основание степени следует наложить такие ограничения: x > 0, x ≠ 1. Прологарифмируем обе части заданного уравнения:
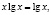
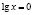
Откуда имеем x = 1.
Логарифмирование не привело к сужению области определения исходного уравнения. Но тем не менее произошла потеря двух корней уравнения; непосредственным усмотрением мы находим, что x = 1 и x = –1 являются корнями исходного уравнения.
7. При решении неравенств с помощью подстановки мы всегда сначала решаем новое неравенство относительно новой переменной, и лишь в его решении делаем переход к старой переменной.
Школьники очень часто ошибочно делают обратный переход раньше.Этого делать не следует.
8.Хочу привести пример еще одной ошибки, связанной с решением неравенств.
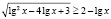
Привожу ошибочное решение, которое очень часто предлагают учащиеся.
Возведем обе части исходного неравенства в квадрат. Будем иметь:
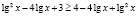
откуда получаем неверное числовое неравенство 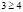
Однако полученный вывод неверен, например, при х = 1000 имеем
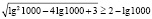
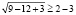
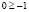
Полученное числовое неравенство верно, а значит х = 1000 является решением.
Значит, заданное неравенство имеет решение, и, следовательно, приведенное выше решение ошибочно.
Привожу правильное решение. Найдем область определения исходного неравенства. Она задается системой
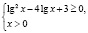
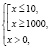
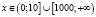
Ясно, что на интервале (10;1000) нет решений, ибо левая часть заданного неравенства при любом х из этого интервала не имеет смысла.
Рассмотрим два случая.
а) 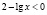
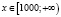
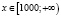
б) 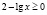
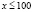
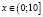
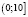
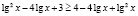
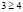
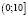
Ответ: 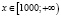
9. Типичная ошибка при решении уравнений, неравенств и их систем состоит в том, что неверно преобразовываются выражения.
Большинство ошибок напрямую не связаны с наличием или отсутствием знаний, хотя доведение некоторых вычислительных операций до автоматизма несколько снижает вероятность их появления.
Необходимо осуществлять процесс обучения правилам с помощью специальной модели с использованием приема, активизирующего рефлексивную деятельность учащихся по предупреждению и исправлению ошибок, которые возникают в результате формального усвоения правил.
Самостоятельная работа учащихся над ошибками обеспечивает более осознанный их анализ и анализ собственных действий по решению конкретной задачи, что оказывает благоприятное влияние на качество получаемых знаний и стимулирует развитие логического мышления.
Пример неосознанного применения алгоритма: получив уравнение sin x = 1,2, ученик автоматически ищет его корни по хорошо известной формуле, не обращая внимания на недопустимые значения sin x .
Для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля. Выработке навыков самоконтроля помогает и приём приближённой оценки ожидаемого результата.
Каждый учитель знает, что планомерное и систематическое повторение и есть основной помощник в ликвидации пробелов, а, следовательно, и ошибок.
Систематические проверки чужих записей формируют у ученика привычку критически относиться к своему решению. Для этого подходят задания типа «найди ошибку в решении». Процесс отыскания и исправления ошибок самими учащимися под руководством учителя можно сделать поучительным для учащихся.
Для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля. Эти навыки состоят из двух частей:
а) умения обнаружить ошибку;
б) умения её объяснить и исправить.
В процессе обучения применяются несколько приёмов самоконтроля, которые помогают обнаружить допущенные ошибки и своевременно их исправить. К ним относятся:
· проверка вычисления и тождественного преобразования путём выполнения обратного действия или преобразования;
· проверка правильности решения задач путём составления и решения задач, обратных к данной;
· оценка результата решения задачи с точки зрения здравого смысла;
· проверка аналитического решения графическим способом.
Способы исправления и предупреждения ошибок
Свести ошибки к минимуму способствуют следующие профилактические меры:
- Тексты письменных заданий должны быть удобными для восприятия: грамотно сформулированными, хорошо читаемыми.
- Активная устная отработка основных ЗУН, регулярный разбор типичных ошибок.
- При объяснении нового материала предугадать ошибку и подобрать систему заданий на отработку правильного усвоения понятия. Акцентировать внимание на каждом элементе формулы, выполнение разнотипных заданий позволит свести ошибочность к минимуму.
- Подбирать задания, вызывающие интерес, формирующие устойчивое внимание.
- Прочному усвоению (а значит, отсутствию ошибок) способствуют правила, удобные для запоминания, четкие алгоритмы, следуя которым заведомо придешь к намеченной цели.
Каждый учитель знает, что планомерное и систематическое повторение и есть основной помощник в ликвидации пробелов, а, следовательно, и ошибок. В математике, как ни в какой другой науке, особенно сильна взаимосвязь материала. Изучение и понимание последующего невозможно без знания предыдущего, отсюда неизбежность повторения на каждом уроке. При объяснении нового материала следует использовать ряд определений и теорем, которые были изучены ранее.
Задания с ошибками по темам: «Уравнения», «Системы уравнений». Книга для учащихся.
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Муниципальное автономное общеобразовательное учреждение
Туендатская основная общеобразовательная школа
Учебно-методическое пособие по математике
для учителей и учащихся средней школы
Автор: Кара Светлана Ивановна,
Многолетний опыт работы учителем математики показывает, что поговорка «на ошибках учатся» на практике не «работает». При выполнении математических заданий и упражнений учащиеся, допуская ошибки, их не замечают и вовремя не исправляют.
Анализируя учебники математики, обращаем внимание на то, что в них достаточно много образцов решения различных заданий, но совсем нет рекомендаций о том, какие ошибки мы можем допустить при выполнении математических упражнений. Поэтому вопрос о том, как учиться без ошибок, как научиться находить собственные ошибки в решениях, является актуальным и требует исследования.
Для пробного исследования были выбраны математические понятия – уравнения, приводящиеся к линейным (далее уравнения) и системы линейных уравнений (далее системы уравнений). Считаем, что эти понятия являются основными в алгебре. Предметом исследования будут ошибки, которые допускают учащиеся, когда решают уравнения и системы уравнений.
На основании детального анализа теоретического материала по проблеме исследования, можно предположить, что при решении уравнений и систем уравнений можно допустить ошибки в тех преобразованиях, которые мы выполняем, решая их.
Для подтверждения данного предположения были составлены анкеты с целью опроса учащихся: анкета – опрос, анкета – уравнение, анкета – система уравнений. В опросе приняли участие 20 учащихся (7, 8, 9 классы) МАОУ Туендатская ООШ.
Проанализировав результаты анкетирования, мы получили следующий результат.
В основном все старшеклассники считают, что они умеют решать уравнения и системы уравнений (70%). Но при этом отмечают, что без ошибок могут решать уравнения только 25% опрошенных учащихся и системы уравнений — 15%. Находить, же ошибки в собственных решениях могут, по мнению ребят 40% опрошенных, и 45% учащихся с помощью учителя или его подсказки. И абсолютно все ребята хотят решать без ошибок.
Во второй анкете учащимся было предложено решить уравнение
Анализ результатов показал, что ошибки допускаются в преобразованиях:
Раскрытие скобок (30%).
Перенос членов уравнения из одной части уравнения в другую(30%).
Приведение подобных слагаемых (40%).
Деление обеих частей уравнения на одно и то же число, отличное от нуля (20%).
Вычислительные ошибки (30%).
В третьей анкете было предложено учащимся решить систему уравнений несколькими способами: методом подстановки, методом сложения, графическим методом и методом сравнения.
Анализ результатов показал, что ошибки допускаются в преобразованиях:
При решении методом подстановки – при выражении одной переменной через другую (35%); при решении уравнения (30%); при записи ответа (15%).
При решении методом сложения – при умножении обеих частей уравнения на одно и то же число (20%); при сложении или вычитании равенств (10%); при решении уравнения (30%); при подстановке найденного числового значения для одной переменной в выражение для нахождения значения другой переменной (25%).
При решении графическим методом – при выражении одной переменной через другую (35%); при построении графика линейной зависимости (30%); при нахождении решения системы уравнений по графической иллюстрации (20%).
При решении методом сравнения – при выражении одной переменной через другую (35%); при решении уравнения с дробными коэффициентами (30%); при подстановке найденного числового значения одной переменной в выражение для нахождения значения другой переменной (25%).
Таким образом, мы получили подтверждение того, что ошибки учащиеся допускают в преобразованиях при решении уравнений и систем уравнений. При этом не умеют находить ошибки в собственных решениях (60%) опрошенных или находят их с помощью подсказки (40%), но все обучающиеся хотят быть успешными по математике и решать без ошибок.
Как же научиться находить ошибки и использовать их с пользой для дела? Думаем, что способы поиска ошибок в готовых решениях частично помогут решить данную проблему.
С этой целью было разработано учебно-методическое пособие для учителей и учащихся, в котором представлены серии заданий по темам: «Уравнения» и «Системы уравнений» с ошибками в тех преобразованиях, которые мы используем при решении данного класса задач. Задания оформили как книгу для учащихся «Найди ошибку», в которую вошли различные уравнения и системы уравнений с ошибками. Эту книгу можно использовать для того, чтобы научиться находить ошибки и контролировать свои учебно-предметные действия.
источники:
http://znanio.ru/media/statya_problemy_tipichnye_oshibki_uchaschihsya_dopuskaemye_pri_reshenii_uravnenij_i_neravenstv-173622
http://infourok.ru/zadaniya-s-oshibkami-po-temam-uravneniya-sistemi-uravneniy-kniga-dlya-uchaschihsya-3932760.html

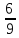 ;
;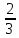 .
.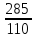 ;
;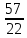 ;
;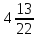 .
.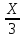 =
=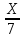 ;
;