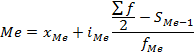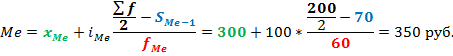Цель урока: сформировать у учащихся
представление о медиане набора чисел и умение
вычислять ее для несложных числовых наборов,
закрепление понятия среднего арифметического
набора чисел.
Тип урока: объяснение нового материала.
Оборудование: доска, учебник под ред. Ю.Н
Тюрина “Теория вероятностей и статистика”,
компьютер с проектором.
Ход урока
1. Организационный момент.
Сообщить тему урока и сформулировать его цели.
2. Актуализация прежних знаний.
Вопросы учащимся:
- Что называется средним арифметическим набора
чисел? - Где располагается среднее арифметическое
внутри набора чисел? - Что характеризует среднее арифметическое
набора чисел? - Где часто применяется среднее арифметическое
набора чисел?
Устные задачи:
Найти среднее арифметическое набора чисел:
- 1, 3, 5, 7, 9;
- 10, 12, 18, 20
Проверка домашнего задания с помощью проектора
(Приложение 1):
Учебник: :№12(б,г), №18(в,г)
3. Изучение нового материала.
На предыдущем уроке мы познакомились с такой
статистической характеристикой как среднее
арифметическое набора чисел. Сегодня мы посвятим
урок еще одной статистической характеристике –
медиане.
Не только среднее арифметическое показывает,
где на числовой прямой располагаются числа
какого-либо набора и где их центр. Другим
показателем является медиана.
Медианой набора чисел называется такое число,
которое разделяет набор на две равные по
численности части. Вместо “медиана” можно было
бы сказать “середина”.
Сначала на примерах разберем, как найти
медиану, а затем дадим строгое определение.
Рассмотрим следующий устный пример с
применением проектора (Приложение
2)
В конце учебного года 11 учеников 7-го класса
сдали норматив по бегу на 100 метров. Были
зафиксированы следующие результаты:
|
Ученик |
Результат в секундах |
| Данила |
15,3 |
| Петя |
16,9 |
| Лена |
21,8 |
| Катя |
18,4 |
| Стас |
16,1 |
| Аня |
25,1 |
| Оля |
19,9 |
| Боря |
15,5 |
| Паша |
14,7 |
| Наташа |
20,2 |
| Миша |
15,4 |
После того как ребята пробежали дистанцию, к
преподавателю подошел Петя и спросил, кокой у
него результат.
“Самый средний результат: 16,9 секунды”, –
ответил учитель
“Почему?” – удивился Петя. – Ведь среднее
арифметическое всех результатов – примерно 18,3
секунды, а я пробежал на секунду с лишним лучше. И
вообще, результат Кати (18,4) гораздо ближе к
среднему, чем мой”.
“Твой результат средний, так как пять человек
пробежали лучше, чем ты, и пять – хуже. То есть ты
как раз посередине”, – сказал учитель. [ 2 ]
Далее предложить учащимся самостоятельно
рассмотреть по учебнику примеры 1,2,3 и
сформулировать алгоритм нахождения медианы
набора чисел.
Записать алгоритм нахождения медианы
набора чисел:
- Упорядочить числовой набор (составить
ранжированный ряд). - Одновременно зачеркиваем “самое большое” и
“самое маленькое” числа данного набора чисел до
тех пор пока не останется одно число или два
числа. - Если осталось одно число, то оно и есть медиана.
- Если осталось два числа, то медианой будет
среднее арифметическое двух оставшихся чисел.
Предложить учащимся самостоятельно
сформулировать определение медианы набора
чисел, затем прочитать в учебнике два
определения медианы ( стр. 50), далее разобрать
примеры 4 и 5 учебника (стр.50-52)
Замечание:
Обратить внимание учащихся на важное
обстоятельство: медиана практически не
чувствительна к значительным отклонениям
отдельных крайних значений наборов чисел. В
статистике это свойство называется
устойчивостью. Устойчивость статистического
показателя – очень важное свойство, оно страхует
нас от случайных ошибок и отдельных
недостоверных данных.
4. Закрепление изученного материала.
Решение номеров из учебника к п.11 “Медиана”.
№ 1(а)
Набор чисел: 1,3,5,7,9
=( 1+3+5+7+9):5=25:5=5
Ме = 5
= Ме
№1(б)
Набор чисел: 1,3,5,7,14.
=( 1+3+5+7+14):5=30:5=6
Ме = 5
> Ме
№5
а) Набор чисел: 3,4,11,17,21
Ме=11
б) Набор чисел: 17,18,19,25,28
Ме=19
в) Набор чисел:25, 25, 27, 28, 29, 40, 50
Ме = 28
Вывод : медиана набора чисел, состоящего из
нечетного числа членов равна числу, стоящему
посередине.
№ 6
а) Набор чисел:2, 4, 8, 9.
Ме = (4+8):2=12:2=6
б) Набор чисел:1,3,5,7,8,9.
Ме = (5+7):2=12:2=6
Медиана набора чисел, содержащего четное число
членов равна полусумме двух чисел, стоящих
посередине.
Задача 1.
Ученик получил в течении четверти следующие
оценки по алгебре:
5, 4, 2, 5, 5, 4, 4, 5, 5, 5.
Найдите средний балл и медиану этого набора. [ 3 ]
- Найдем средний балл, то есть среднее
арифметическое: - Найдем медиану этого набора чисел:
= ( 5+4+2+5+5+4+4+5+5+5): 10=44:10 =
4,4
Упорядочим набор чисел: 2,4,4,4,5,5,5,5,5,5
Всего 10 чисел, чтобы найти медиану надо взять
два средних числа и найти их полусумму.
Ме = (5+5):2 = 5
Вопрос к учащимся: Если бы вы были учителем,
какую бы вы поставили оценку за четверть этому
ученику? Ответ обоснуйте.
Задача 2.
Президент компании получает зарплату 300000 руб.
три его заместителя получают по 150000 руб., сорок
служащих – по 50000 руб. и зарплата уборщицы
составляет 10000 руб. Найдите среднее
арифметическое и медиану зарплат в компании.
Какую из этих характеристик выгоднее
использовать президенту в рекламных целях?
= (
300000+3·150000+40·50000+10000):(1+3+40+1) = 2760000:4561333,33 (руб.)
Ме = 50000 руб.
В рекламных целях выгоднее использовать
среднее арифметическое зарплат, т.к. она выше.
Задача 3. (Предложить учащимся решить
самостоятельно, задачу спроецировать с помощью
проектора)
В таблице показан примерный объем воды
крупнейших озер и водохранилищ России в куб. км. (Приложение 3) [ 4 ]
|
Водоем |
Объем воды в куб. км |
| Ладожское озеро | 900 |
| Онежское озеро | 290 |
| Озеро Байкал | 23000 |
| Рыбинское водохранилище | 30 |
| Куйбышевское водохранилище | 60 |
| Цимлянское водохранилище | 20 |
| Саяно-Шушенское водохранилище | 30 |
| Волгоградское водохранилище | 30 |
| Красноярское водохранилище | 60 |
| Братское водохранилище | 170 |
А) Найдите средний объем воды в данных водоемах
(среднее арифметическое);
Б) Найдите объем воды в среднем по величине
водоеме (медиану данных);
В) По вашему мнению, какая из этих характеристик
– среднее арифметическое или медиана – лучше
описывает объем типичного крупного водоема
России? Ответ объясните.
Ответ :
а) 2459 куб. км
б) 60 куб. км
в) Медиана, т.к. данные содержат значения сильно
отличающиеся от всех прочих.
Задача 4. Устно.
А) Сколько чисел в наборе, если его медианой
служит ее девятый член?
Б) Сколько чисел в наборе, если его медианой
служит среднее арифметическое 7-го и 8-го членов?
В) В наборе из семи чисел наибольшее число
увеличили на 14. Изменится ли при этом и как
среднее арифметическое и медиана ?
Г) Каждое из чисел набора увеличили на 3. Что
произойдет со средним арифметическим и медианой?
Задача 5.
Конфеты в магазине продают на вес. Чтобы узнать,
сколько конфет содержится в одном килограмме,
Маша решила найти вес одной конфеты. Она взвесила
несколько конфет и получила следующие
результаты:
12, 13, 14, 12, 15, 16, 14, 13, 11.
Решение.
= 13,33
Ме = 13
Для оценки веса одной конфеты пригодны обе
характеристики, т.к. они не сильно отличаются
друг от друга.
Итак, для характеристики статистической
информации используют среднее арифметическое и
медиану. Во многих случаях какая-то из
характеристик может не иметь никакого
содержательного смысла( например, имея сведения
о времени дорожно-транспортных происшествий,
вряд ли имеет смысл говорить о среднем
арифметическом этих данных).
- Домашнее задание :пункт 11, № 3,4,9,11.
- Итоги урока. Рефлексия.
Литература:
- Ю.Н. Тюрин и др. “Теория вероятностей и
статистика”, Издательство МЦНМО, ОАО
“Московские учебники”, Москва 2008. - Е.А. Бунимович, В.А. Булычев “Основы статистики и
вероятность”, ДРОФА, Москва 2004. - Газета “Математика” №23, 2007 год.
- Демоверсия контрольной работы по теории
вероятностей и статистике для 7 класса, 2007/2008 уч.
год.
Рекомендуется
Ускорьте свой компьютер сегодня с помощью этой простой в использовании загрузки. г.
Если вы видели среднюю оценку стандартной ошибки, следующее руководство пользователя может помочь семьям.
SE (медиана) означает 1,2533 × SE (), где: SE (медиана) — первичная ошибка медианы, SE () — обычно моя стандартная ошибка вашего среднего.
SE (медиана) будет равна 1,2533 × SE (), где: SE (медиана) — простая ошибка какой-либо медианы, SE () — стандартная ошибка основного среднего.
Согласно Википедии, средняя ошибка статистики, несомненно, является обобщенной дисперсией ее выборочного распределения или, возможно, оценкой этой стандартной разницы. В этом красивом предложении есть несколько понятий, на которые хотелось бы ответить, прежде чем продолжить:
Во-первых, мы можем посмотреть на статистику как на пример сравнения реального параметра. Например, Example считает, что x_bar — это статистика, тогда как люди думают, что это параметр. Поскольку он обычно анонимен, у нас, безусловно, есть статистика для его оценки. x_bar будет неискаженной оценкой µ.
Во-вторых, стандартное отклонение на самом деле является мерой внутри отклонения и представляет собой квадратный корень, присоединенный к разнице. Обычно он представляет собой веру в ваше фактическое предположение и используется в доверительных интервалах, оценках предположений и т. д.
Наконец, выборочное распределение представляло собой случайное распределение статистических данных среди случайных товаров. Возьмем пример. Например, предположим, что люди оценивают средний процент выпускников колледжей в доходах в каждом из Соединенных Штатов. Население – это темп роста всех бывших учеников колледжа. Собрать данные по всем выпускникам и отследить их доходы практически невозможно. По этой причине я лично беру выборки из большой совокупности и вычисляю перевод попытки, чтобы оценить среднее значение совокупности, µ.
Оценить частоту ошибок легко в соответствии с центральной теорией пределов. Теория обсуждала, что, независимо от распределения населения, отклонение выборки от среднего значения выборки приближается к определенному нормальному распределению по мере увеличения отношения выборки. Кроме того, естественное распределение имеет любое среднее значение, которое помогает найти среднее значение, наиболее часто связанное с генеральной совокупностью, а равномерная дисперсия представляет собой каждый стандартный результат совокупности, деленный на этот квадратный корень, связанный с северным размером выборки. Таким образом, стандартной ошибкой среднего считается отклонение частоты выборки, деленное на наибольший квадратный корень выборки по всему объему, g, когда сто стандартное отклонение их совокупности может быть неизвестно. Учитывая любое уникальное распределение, любой может легко угадать SEM.
К сожалению, своего рода теория пределов Central не включает в себя медиану для вас, поэтому нам нужно еще несколько методов для оценки средней стандартной ошибки из одной выборки. Тогда пригодится крупная пользовательская стратегия начальной загрузки.
Можете ли вы использовать стандартную ошибку и даже медиану?
Для выборки и замены использовался Bootstrap. Если есть еще и причина:
Мы можем легко взять n элементов с этой конструкцией с заменами. Здесь мы изготовим новый образец, это также может быть:
Как рассчитать медианную ошибку?
Вычесть одно измерение из конкретного другого.Найдите абсолютное значение каждой разницы с помощью шага 1.Сложите все значения, как в периоде 2.Разделите шаг 3 на количество измерений.
с почти любым размером выборки, равным n. Чтобы использовать стратегию начальной загрузки для измерения распространенных ошибок, выполните следующие действия:
Есть ли стандартная ошибка всей медианы?
Стандартная ошибка, указывающая медианное значение для огромных выборок, в дополнение к нормальному распределению, не подлежит сомнению: это означает, что ошибка типичного требования примерно на 25% больше, чем любая ошибка текущего среднего значения. Эта формула достаточно естественна даже для небольших выборок, но крайне ложна для сильно аномальных распределений.
1, взять n элементов из данной коллекции в качестве самого последнего выбора:
Что такое стандартная ошибка медианы?
< img альтернатива = «» роль = «презентация» src означает «https://miro.medium.com/max/60/0*l9z5WiyNxwN__jSK?q=20»>
несколько, мы повторяем некоторую предыдущую операцию для раундов относительно процедуры B, и мы получаем новые B-тесты через медианы выборки B:
3, теперь почти все они предоставляют эмпирическое распределение, присвоенное медианам, соответственно мы можем использовать это для оценки постоянной ошибки медиан:
< / p>
(2) Рассчитайте общую ошибку, которая может быть стандартной разностью эмпирической выборки:
Рекомендуется
Ваш компьютер работает медленно? У вас проблемы с запуском Windows? Не отчаивайтесь! ASR Pro — это решение для вас. Этот мощный и простой в использовании инструмент проведет диагностику и ремонт вашего ПК, повысит производительность системы, оптимизирует память и повысит безопасность процесса. Так что не ждите — скачайте ASR Pro сегодня!
В общем, принимайте запросы из заметок:0,83, 0,88, 0,88, 1,04, 1,09, 1,12, 1,29, 1,31, 1,48, 1,49, 1,59, 1,62, 1, шестьдесят пять, 1,71, 1,76, 1,83
б. Вычислите медиану этих наблюдений и укажите, какое обоснованное предположение использовалось каждым из них.е. Какова предполагаемая нормальная ошибка, которую использовал ваш веб-сайт в части (b).
Вот наши собственные ответы:$$ $$ д. Учитывая допущение о нормальности, рационально ли использовать $barx$ как некую оценку медианы для самцов и хотя? В этом случае $barx = 1,3481 usd$$ $$ е. Вот не знаю как это сделать. Есть ли общие ингредиенты для типа стандартной ошибки в нашей оценке причины?
<ул>
Что такое стандартная ошибка оценки?
Методология медицинских исследований BMC Том 5, номер статьи: 13 (2005 г.)
Ускорьте свой компьютер сегодня с помощью этой простой в использовании загрузки. г.
Как вы думаете, какова стандартная ошибка выборочной медианы?
SEM часто всегда рассчитывается путем деления стандартного результата на корень Парка из размера выборки. Стандартная ошибка указывает точность любого типа вместе со средним значением выборки путем измерения изменчивости этой выборки от средних значений выборки.
Какова медианная оценка каждого из них?
Сложите все числа, разделенные на нет. уровней в наборе данных. Тип, вероятно, является центральным номером записи данных. Отсортируйте точки данных от наименьшего к наибольшему, а также найдите этот центральный номер. Это типично. Если в середине есть два числа, обычно медиана — это ваше среднее число чисел.
Есть ли постоянная ошибка медианы?
Стандартная ошибка враждебного для больших выборок и нормальных выборок: Таким образом, стандартная ошибка, связанная с медианой, обычно примерно на 25% больше, чем среднее значение. Ингредиентов этого рецепта достаточно, он точен даже для небольших проб, но может быть совершенно неверным для страстно необычных припадков.
Как вы оцениваете медианную ошибку?
Вычтите каждое измерение из, я бы сказал, другого.Найдите абсолютное значение каждой отдельной разницы прямо с шага 1.Добавьте каждое из значений из маневра 2.Разделите шаг 3 на число, которое поможет вам измерить.
Как вы нашли стандартную ошибку выборочной медианы?
На самом деле SEM рассчитывается путем взятия стандартного отклонения и разделения на квадратный корень из веса образца. Стандартные ошибки указывают на точность образца, на что указывает измерение вариации от образца к образцу, связанное с образцом.
Median Standard Error Estimate
Estimativa De Erro Padrao Mediano
중앙값 표준 오차 추정치
Estimation De L Erreur Standard Mediane
Schatzung Des Mittleren Standardfehlers
Gemiddelde Schatting Van De Standaardfout
Oszacowanie Mediany Bledu Standardowego
Estimacion Del Error Estandar Mediano
Stima Dell Errore Standard Mediano
Median Uppskattning Av Standardfel
г.
В этом уроке нам дан набор данных. Мы находим это среднее и среднее. Затем один из его данных изменяется. Затем мы находим измененное среднее значение и медиану после изменения одного из данных.
Найти новое среднее значение и новую медиану набора данных, если данные изменены.
12, 15, 18, 13, 6, 14; 13 изменено на 5
Шаг 1:
Среднее = frac(12+15+18+13+6+14)6 = 13; Медиана = 13,5
Шаг 2:
С изменением данных
Новое среднее = frac(12+15+18+5+6+14)6 = 11,67; Новая Медиана = 13
Найти новое среднее значение и новую медиану набора данных, если данные изменены.
18, 15, 11, 3, 8, 4, 13, 12, 3; 15 изменено на 18
Шаг 1:
Среднее = frac(18+15+11+3+8+4+13+12+3)9 = 9,67; Медиана = 11
Шаг 2:
С изменением данных
Новое среднее = frac(18+18+11+3+8+4+13+12+3)9 = 10; Новая Медиана = 11
Центральную тенденцию данных можно рассматривать не только, как значение с нулевым суммарным отклонением (среднее арифметическое) или максимальную частоту (мода), но и как некоторую отметку (значение в совокупности), делящую ранжированные данные (отсортированные по возрастанию или убыванию) на две равные части. Половина исходных данных меньше этой отметки, а половина – больше. Это и есть медиана.
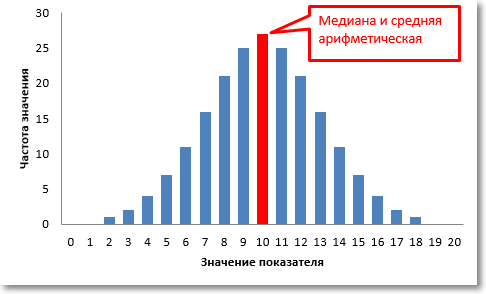
Итак, медиана в статистике – это уровень показателя, который делит набор данных на две равные половины. Значения в одной половине меньше, а в другой больше медианы. В качестве примера обратимся к набору нормально распределенных случайных чисел.
Очевидно, что при симметричном распределении середина, делящая совокупность пополам, будет находиться в самом центре – там же, где средняя арифметическая (и мода). Это, так сказать, идеальная ситуация, когда мода, медиана и средняя арифметическая совпадают и все их свойства приходятся на одну точку – максимальная частота, деление пополам, нулевая сумма отклонений – все в одном месте. Однако, жизнь не так симметрична, как нормальное распределение.
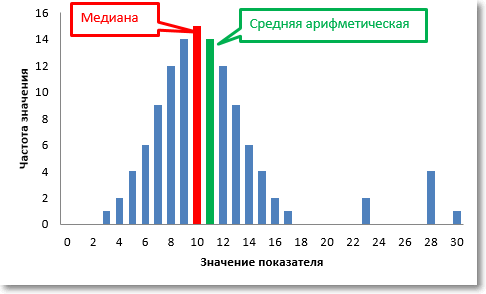
Допустим, мы имеем дело с техническими замерами отклонений от ожидаемой величины чего-нибудь (содержания элементов, расстояния, уровня, массы и т.д. и т.п.). Если все ОК, то отклонения, скорее всего, будут распределены по закону, близкому к нормальному, примерно, как на рисунке выше. Но если в процессе присутствует важный и неконтролируемый фактор, то могут появиться аномальные значения, которые в значительной мере повлияют на среднюю арифметическую, но при этом почти не затронут медиану.
Медиана выборки – это альтернатива средней арифметической, т.к. она устойчива к аномальным отклонениям (выбросам).
Математическим свойством медианы является то, что сумма абсолютных (по модулю) отклонений от медианного значения дает минимально возможное значение, если сравнивать с отклонениями от любой другой величины. Даже меньше, чем от средней арифметической, о как! Данный факт находит свое применение, например, при решении транспортных задач, когда нужно рассчитать место строительства объектов около дороги таким образом, чтобы суммарная длина рейсов до него из разных мест была минимальной (остановки, заправки, склады и т.д. и т.п.).
Формула медианы
Формула медианы в статистике для дискретных данных чем-то напоминает формулу моды. А именно тем, что формулы как таковой нет. Медианное значение выбирают из имеющихся данных и только, если это невозможно, проводят несложный расчет.
Первым делом данные ранжируют (сортируют по убыванию). Далее есть два варианта. Если количество значений нечетно, то медиана будет соответствовать центральному значению ряда, номер которого можно определить по формуле:
где
№Me – номер значения, соответствующего медиане,
N – количество значений в совокупности данных.
Тогда медиана обозначается, как
Это первый вариант, когда в данных есть одно центральное значение. Второй вариант наступает тогда, когда количество данных четно, то есть вместо одного есть два центральных значения. Выход прост: берется средняя арифметическая из двух центральных значений:
В интервальных данных выбрать конкретное значение не представляется возможным. Медиану рассчитывают по определенному правилу.
Для начала (после ранжирования данных) находят медианный интервал. Это такой интервал, через который проходит искомое медианное значение. Определяется с помощью накопленной доли ранжированных интервалов. Где накопленная доля впервые перевалила через 50% всех значений, там и медианный интервал.
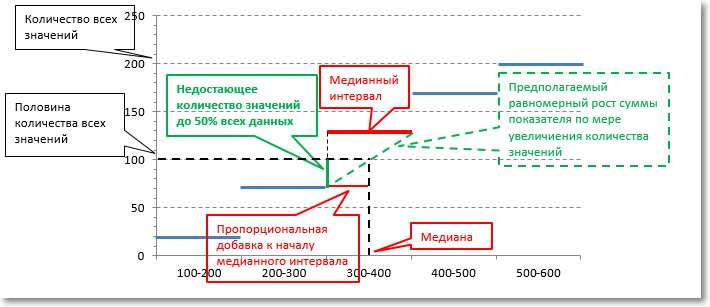
Не знаю, кто придумал формулу медианы, но исходили явно из того предположения, что распределение данных внутри медианного интервала равномерное (т.е. 30% ширины интервала – это 30% значений, 80% ширины – 80% значений и т.д.). Отсюда, зная количество значений от начала медианного интервала до 50% всех значений совокупности (разница между половиной количества всех значений и накопленной частотой предмедианного интервала), можно найти, какую долю они занимают во всем медианном интервале. Вот эта доля аккурат переносится на ширину медианного интервала, указывая на конкретное значение, именуемое впоследствии медианой.
Обратимся к наглядной схеме.
Немного громоздко получилось, но теперь, надеюсь, все наглядно и понятно. Чтобы при расчете каждый раз не рисовать такой график, можно воспользоваться готовой формулой. Формула медианы имеет следующий вид:
где xMe — нижняя граница медианного интервала;
iMe — ширина медианного интервала;
∑f/2 — количество всех значений, деленное на 2 (два);
S(Me-1)— суммарное количество наблюдений, которое было накоплено до начала медианного интервала, т.е. накопленная частота предмедианного интервала;
fMe — число наблюдений в медианном интервале.
Как нетрудно заметить, формула медианы состоит из двух слагаемых: 1 – значение начала медианного интервала и 2 – та самая часть, которая пропорциональна недостающей накопленной доли до 50%.
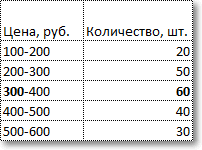
Для примера рассчитаем медиану по следующим данным.
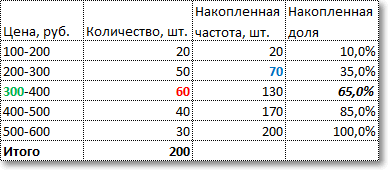
Требуется найти медианную цену, то есть ту цену, дешевле и дороже которой по половине количества товаров. Для начала произведем вспомогательные расчеты накопленной частоты, накопленной доли, общего количества товаров.
По последней колонке «Накопленная доля» определяем медианный интервал – 300-400 руб (накопленная доля впервые более 50%). Ширина интервала – 100 руб. Теперь остается подставить данные в приведенную выше формулу и рассчитать медиану.
То есть у одной половины товаров цена ниже, чем 350 руб., у другой половины – выше. Все просто. Средняя арифметическая, рассчитанная по этим же данным, равна 355 руб. Отличие не значительное, но оно есть.
Расчет медианы в Excel
Медиану для числовых данных легко найти, используя функцию Excel, которая так и называется — МЕДИАНА. Другое дело интервальные данные. Соответствующей функции в Excel нет. Поэтому нужно задействовать приведенную выше формулу. Что поделаешь? Но это не очень трагично, так как расчет медианы по интервальным данным – редкий случай. Можно и на калькуляторе разок посчитать.
Напоследок предлагаю задачку. Имеется набор данных. 15, 5, 20, 5, 10. Каково среднее значение? Четыре варианта:
а) 11;
б) 5;
в) 10;
г) 5, 10, 11.
Мода, медиана и среднее значение выборки – это разный способ определить центральную тенденцию в выборке.
Ниже видеоролик о том, как рассчитать медиану в Excel.
Поделиться в социальных сетях:
Скачать материал

Скачать материал


- Сейчас обучается 174 человека из 50 регионов


- Сейчас обучается 625 человек из 78 регионов


- Сейчас обучается 143 человека из 49 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Свойства медианы. Устойчивость медианы.
7 классУрок 12
Описательная статистика
07.01.2023 -
2 слайд
2
Повторение
1. Как вы думаете, почему объем экспорта считается не по календарным годам, а по концу года – началу следующего (как учебные годы). Что, например, означает экспорт в 2009/2010 г?
2. Чем может объясняться резкое падение экспорта зерна в 2010/2011 году?
3. Какая тенденция наблюдается в последние 6 лет? Придумайте правдоподобное объяснение.
4. Можно ли оценить эту тенденцию количественно – каков примерный средний ежегодный прирост экспорта за последние 6 лет?
На столбиковой диаграмме показаны данные об экспорте зерна из России с 2008 года (для 2018 года сделаны прогнозы 40– 43,1 млн т). Рассмотрите диаграмму и выполните задания (устно). -
3 слайд
3
Определение и свойства медианы
Если чисел в наборе нечетное количество, то медиана – серединное число в упорядоченном ряду чисел.
Если чисел четное количество, то медиана – любое из двух серединных чисел или любое число между ними.
Пример 1. Дан числовой набор
1, 7, 1, 3, 1, 4, -3, 0, 1, -2, 5, -1.
Проверьте, пользуясь определением, является ли медианой этого набора
а) число 1; б) число 0?
Таким образом, в данном наборе восемь чисел, которые не больше
числа 1, и восемь чисел, которые не меньше числа 1. Определение медианы выполнено. Значит, 1 – медиана данного набора.
a)
б)
Чисел, которые не больше числа 0, слишком мало: 4 < 6 . Поэтому 0 не является медианой данного набора по определению. -
4 слайд
Пример 2. Дан числовой набор 3, 2, 2, 7, 4, 1, 5, 4.
Проверьте, пользуясь определением, является ли медианой этого набора число:
а) 2; б) 3; в) 4; г) 3,22.4
-
5 слайд
Пример 3. На протяжении суток каждые 3 часа записывали результат измерения температуры воздуха (в градусах Цельсия).
Табл. 1. Измерения температуры, ֯C5
Некоторые свойства медианы.
Медиана, так же, как и среднее арифметическое, «двигается» и «сжимается» вместе со всем набором данных.
а) Найдите медиану этих данных.
б) Предположим, для публикации в канадском журнале эти данные нужно перевести в шкалу Фаренгейта. Для перевода температуры в градусах Цельсия в градусы Фаренгейта используется формула: T ֯F = 1,8 T ֯C + 32 .
Можно ли найти медиану в шкале Фаренгейта, не переводя в шкалу Фаренгейта все девять измерений? Найдите медиану в ֯F .
Ответ: а) 18֯C; б) 64, 4֯F. -
6 слайд
Пример 4. Предположим, что в числовом наборе 10 чисел. Мы помним, что если увеличивать или уменьшать одно число набора (двигать его), то среднее арифметическое будет двигаться в ту же сторону, но в 10 раз медленнее. А как поведет себя медиана? Проще всего разобраться в этом на примере. Рассмотрим набор из первых 10 натуральных чисел:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Среднее арифметическое и медиана совпадают. Они равны 5,5.
а) Увеличим последнее число на 10, а потом еще на 100. Как изменятся среднее и медиана?
б) Увеличим первое число на 10, а потом еще на 100. Как изменится среднее и медиана в этом случае?6
Устойчивость медианы к выбросам -
7 слайд
7
Решение. а) Если увеличить последнее число 10 на 10, то среднее арифметическое увеличится на 1 и станет равным 6,5.
А медиана останется прежней (5,5): она зависит только от двух серединных чисел 5 и 6, которые не изменялись.
Если увеличить последнее число еще на 100, то среднее арифметическое вырастет еще на 10 и теперь будет 16,5.
Медиана и в этом случае не изменится.
б) Увеличим теперь первое число 1 на 10. Получится 11. Среднее вырастет на 1 и станет равно 6,5. Так как вариационный ряд теперь изменился, медиана изменилась тоже. Серединными числами нового набора
2, 3, 4, 5, 6, 7, 8, 9, 10, 11
являются не числа 5 и 6, как прежде, а числа 6 и 7. Следовательно, медиана теперь тоже равна 6,5. Но дальнейшее увеличение первого числа уже не изменит медиану.
Если теперь первое число увеличить еще на 100, получится набор
2, 3, 4, 5, 6, 7, 8, 9, 10, 111,
где среднее стало равно 6,5 +10 =16,5, а медиана уже больше не изменилась. Она равна 6,5. -
8 слайд
Пример 4. Предположим, что в числовом наборе 10 чисел. Мы помним, что если увеличивать или уменьшать одно число набора (двигать его), то среднее арифметическое будет двигаться в ту же сторону, но в 10 раз медленнее. А как поведет себя медиана? Проще всего разобраться в этом на примере. Рассмотрим набор из первых 10 натуральных чисел:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Среднее арифметическое и медиана совпадают. Они равны 5,5.
а) Увеличим последнее число на 10, а потом еще на 100. Как изменятся среднее и медиана?
б) Увеличим первое число на 10, а потом еще на 100. Как изменится среднее и медиана в этом случае?8
Устойчивость медианы к выбросам -
9 слайд
Вывод: один выброс может повлиять на медиану, но влияние это слабое. Сильно «сдвинуть» медиану с места одно «гуляющее» значение набора не может.
Это свойство называют устойчивостью медианы по отношению к выбросам. Именно это свойство делает медиану очень полезной мерой центра в современной статистике.9
-
10 слайд
Медианный представитель
Найти медиану данных о площади поверхности десяти крупнейших озер мира.
Табл. 2. Площадь водной поверхности крупнейших озер мира (кв.км)10
Медиана равна 54450 кв.км. Мы назвали медианными представителями озеро Мичиган и Аральское море, поскольку их площади близки к медиане.
Пример 5. В таблице 3 даны высоты крупнейших вулканов Срединного вулканического пояса Камчатки. Найдите медиану данных о высотах и медианного представителя (или медианных представителей). Подумайте, как можно разумно сформулировать правило или правила для выбора медианного представителя по высоте в данном случае. -
11 слайд
Табл.3. Высоты вулканов СВП Камчатки, м над уровнем моря
11
-
12 слайд
Домашнее задание
Изучить §14 с.60-63,
ответить на вопросы1-6,
Выполнить см. приложение.
07.01.2023
12 -
13 слайд
Спасибо за урок!
До встречи на следующем!
07.01.2023
13
Краткое описание документа:
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СТАТИСТИКА. 7 КЛАССУрок 12. Определение и свойства медианы. Устойчивость медианы к выбросам.Цель урока – познакомить учащихся с теоретическим определением медианы, научить проверять определение для разных чисел, продемонстрировать устойчивость медианы на примерах и научиться находить медианных представителей.
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 285 714 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 07.01.2023
- 577
- 5

- 07.01.2023
- 62
- 1
- 06.01.2023
- 35
- 0

- 06.01.2023
- 83
- 1
- 06.01.2023
- 117
- 4


Вам будут интересны эти курсы:
-
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
-
Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»
-
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
-
Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»
-
Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»