На каком образном примере рассматривается модель переменные ошибки

В статистике , ошибки-в-переменных модели или измерения модели ошибок являются регрессионные модели , которые учитывают ошибок измерения в независимых переменных . Напротив, стандартные модели регрессии предполагают, что эти регрессоры были точно измерены или наблюдались без ошибок; как таковые, эти модели учитывают только ошибки в зависимых переменных или ответах.

В случае, когда некоторые регрессоры были измерены с ошибками, оценка, основанная на стандартном предположении, приводит к непоследовательным оценкам, что означает, что оценки параметров не стремятся к истинным значениям даже в очень больших выборках. Для простой линейной регрессии эффект заключается в занижении коэффициента, известном как смещение затухания . В нелинейных моделях направление смещения, вероятно, будет более сложным.

Мотивирующий пример

Рассмотрим простую модель линейной регрессии вида

где обозначает истинный, но ненаблюдаемый регрессор . Вместо этого мы наблюдаем это значение с ошибкой:

где предполагается, что ошибка измерения не зависит от истинного значения .

Если ‘s просто регрессируют на ‘ s (см. Простую линейную регрессию ), то оценка коэффициента наклона будет

который сходится по мере неограниченного увеличения размера выборки :

Вариации неотрицательны, так что в пределе оценка меньше по величине, чем истинное значение , эффект, который статистики называют ослаблением или разбавлением регрессии . Таким образом, «наивная» оценка методом наименьших квадратов несовместима в этой настройке. Однако оценщик является последовательным оценщиком параметра, необходимого для наилучшего линейного предиктора данного : в некоторых приложениях это может быть то, что требуется, а не оценка « истинного » коэффициента регрессии, хотя это предполагает, что дисперсия ошибки в наблюдении остаются исправленными. Это непосредственно следует из результата, приведенного непосредственно выше, и того факта, что коэффициент регрессии, связывающий ‘s с фактически наблюдаемыми ‘ s, в простой линейной регрессии определяется выражением

Именно этот коэффициент, а не тот, который потребовался бы для построения предиктора на основе наблюдаемого, подверженного шуму.

Можно утверждать, что почти все существующие наборы данных содержат ошибки разной природы и величины, поэтому систематическая ошибка ослабления встречается очень часто (хотя при многомерной регрессии направление систематической ошибки неоднозначно). Джерри Хаусман видит в этом железный закон эконометрики : «Величина оценки обычно меньше ожидаемой».

Технические характеристики

Обычно модели ошибок измерения описываются с использованием подхода скрытых переменных . Если переменная отклика и наблюдаются значения регрессоров, то предполагается , существуют какие — то скрытые переменные и которые следуют «истинной» в модели функциональной зависимости , и таким образом, что наблюдаемые величины их шумные наблюдения:

где находятся в модели параметры и те регрессоры , которые предполагаются свободными от ошибок (например , когда линейная регрессия содержит перехват, регрессор что соответствует константе , безусловно , не имеет «ошибки измерений»). В зависимости от спецификации эти безошибочные регрессоры могут или не могут рассматриваться отдельно; в последнем случае просто предполагается, что соответствующие элементы в матрице дисперсии s равны нулю.

Переменные , , все наблюдали , что означает , что статистик обладает набором данных из статистических единиц , которые следуют за процесс генерирования данных , описанными выше; латентные переменные , , и не наблюдается , однако.

Эта спецификация не охватывает все существующие модели ошибок в переменных. Например, в некоторых из них функция может быть непараметрической или полупараметрической. Другие подходы моделируют отношения между и как распределительные, а не функциональные, то есть они предполагают, что условно on следует за определенным (обычно параметрическим) распределением.

Терминология и предположения

• Наблюдаемая переменная может называться манифестом , индикатором или косвенной переменной .
• Ненаблюдаемая переменная может быть названа скрытой или истинной переменной. Его можно рассматривать либо как неизвестную константу (в этом случае модель называется функциональной моделью ), либо как случайную величину (соответственно структурную модель ).
• Связь между ошибкой измерения и скрытой переменной можно моделировать по-разному:
  
  • Классические ошибки : ошибки не зависят от скрытой переменной. Это наиболее распространенное предположение, оно подразумевает, что ошибки вносятся измерительным устройством и их величина не зависит от измеряемого значения.
  • Независимость от среднего : ошибки равны нулю для каждого значения скрытого регрессора. Это менее ограничительное предположение, чем классическое, поскольку оно допускает наличие гетероскедастичности или других эффектов в ошибках измерения.
  • Ошибки Берксона :ошибки не зависят от наблюдаемого регрессора x . Это предположение имеет очень ограниченную применимость. Одним из примеров являются ошибки округления: например, если возраст человека * является непрерывной случайной величиной , тогда как наблюдаемый возраст усекается до следующего наименьшего целого числа, тогда ошибка усечения приблизительно не зависит от наблюдаемого возраста . Другая возможность связана с экспериментом с фиксированным планом: например, если ученый решает провести измерение в определенный заранее определенный момент времени, скажем, в, тогда реальное измерение может произойти при каком-то другом значении(например, из-за конечного времени реакции ), и такая ошибка измерения обычно не зависит от «наблюдаемого» значения регрессора.
  • Ошибки неправильной классификации : частный случай фиктивных регрессоров . Если это индикатор определенного события или состояния (например, лицо мужского / женского пола, какое-либо лечение было / не предоставлено и т. Д.), То ошибка измерения в таком регрессоре будет соответствовать неправильной классификации, аналогичной типу I и типу II. ошибки в статистическом тестировании. В этом случае ошибка может принимать только 3 возможных значения, а ее условное распределение моделируется двумя параметрами:, и . Необходимым условием идентификации является то , что ошибочная классификация не должна происходить «слишком часто». (Эту идею можно обобщить на дискретные переменные с более чем двумя возможными значениями.)

Линейная модель

Первыми были изучены линейные модели ошибок в переменных, вероятно, потому, что линейные модели были так широко использованы и они легче нелинейных. В отличие от стандартной регрессии методом наименьших квадратов (OLS), расширение ошибок в регрессии переменных (EiV) с простого случая на многомерный не так просто.

Простая линейная модель

Простая линейная модель ошибок в переменных уже была представлена ​​в разделе «мотивация»:

где все переменные скалярны . Здесь α и β представляют собой интересующие параметры, а σ _ε и σ _{η —} стандартные отклонения членов ошибки — являются мешающими параметрами . «Истинный» регрессор x * рассматривается как случайная величина ( структурная модель), не зависящая от ошибки измерения η ( классическое допущение).

Эта модель идентифицируемой в двух случаях: (1) либо латентный регрессор х * является не нормально распределены , (2) или х * имеет нормальное распределение, но ни ε _т , ни η _т делимы нормальным распределением. То есть параметры α , β могут быть последовательно оценены из набора данных без какой-либо дополнительной информации, при условии, что скрытый регрессор не является гауссовским.

До того, как этот результат идентифицируемости был установлен, статистики пытались применить метод максимального правдоподобия , предполагая, что все переменные являются нормальными, а затем пришли к выводу, что модель не идентифицирована. Предлагаемое решение заключалось в том, чтобы предположить, что некоторые параметры модели известны или могут быть оценены из внешнего источника. К таким методам оценки относятся:

• Регрессия Деминга — предполагается, что отношение δ = σ² _ε / σ² _η известно. Это может быть подходящим, например, когда ошибки в y и x вызваны измерениями, а точность измерительных устройств или процедур известна. Случай, когда δ = 1, также известен как ортогональная регрессия .
• Регрессия с известным коэффициентом надежности λ = σ² _∗ / ( σ² _η + σ² _∗ ), где σ² _∗ — дисперсия скрытого регрессора. Такой подход может быть применим, например, когда доступны повторяющиеся измерения одного и того же устройства, или когда коэффициент надежности известен из независимого исследования. В этом случае непротиворечивая оценка наклона равна оценке методом наименьших квадратов, деленной на λ .
• Регрессия с известным σ² _η может произойти, если источник ошибок в x известен и их дисперсия может быть вычислена. Это может включать ошибки округления или ошибки, вносимые измерительным устройством. Когда известно σ² _η, мы можем вычислить коэффициент надежности как λ = ( σ² _x — σ² _η ) / σ² _x и свести проблему к предыдущему случаю.

Новые методы оценки, которые не предполагают знания некоторых параметров модели, включают:

Многопараметрическая линейная модель

Модель с несколькими переменными выглядит точно так же, как простая линейная модель, только на этот раз β , η _t , x _t и x * _t являются векторами k × 1.

В случае, когда ( ε _t , η _t ) совместно нормально, параметр β не идентифицируется тогда и только тогда, когда существует невырожденная  блочная матрица k × k [ a A ], где a — вектор k × 1, такой что a′x *  распределяется нормально и независимо от  A′x * . В случае, когда ε _t , η _t1 , …, η _tk взаимно независимы, параметр  β  не идентифицируется тогда и только тогда, когда в дополнение к указанным выше условиям некоторые ошибки могут быть записаны как сумма двух независимых переменных один из которых нормальный.

Некоторые из методов оценивания многомерных линейных моделей:

Нелинейные модели

Общая модель нелинейных ошибок измерения принимает форму

Здесь функция g может быть параметрической или непараметрической. Когда функция g параметрическая, она будет записана как g (x *, β) .

Для общего векторного регрессора x * условия идентифицируемости модели неизвестны. Однако в случае скаляра x * модель идентифицируется, если только функция g не имеет «логарифмически экспоненциальную» форму.

а скрытый регрессор x * имеет плотность

где константы A, B, C, D, E, F могут зависеть от a, b, c, d .

Несмотря на этот оптимистичный результат, в настоящее время не существует методов оценки нелинейных моделей ошибок в переменных без какой-либо посторонней информации. Однако есть несколько методов, которые используют некоторые дополнительные данные: либо инструментальные переменные, либо повторные наблюдения.

Методы инструментальных переменных

Повторные наблюдения

В этом подходе доступны два (или, может быть, более) повторных наблюдения регрессора x * . Оба наблюдения содержат собственные ошибки измерения, однако эти ошибки должны быть независимыми:

где x * ⊥ η ₁ ⊥ η ₂ . Переменные η ₁ , η ₂ не обязательно должны быть одинаково распределены (хотя, если они являются эффективными оценками, их можно немного улучшить). С помощью только этих двух наблюдений можно последовательно оценить функцию плотности x *, используя технику деконволюции Котлярского .

Рекомендации

дальнейшее чтение

• Догерти, Кристофер (2011). «Стохастические регрессоры и ошибки измерения» . Введение в эконометрику (Четвертое изд.). Издательство Оксфордского университета. С. 300–330. ISBN 978-0-19-956708-9.
• Кмента, Ян (1986). «Оценка с недостаточными данными» . Элементы эконометрики (второе изд.). Нью-Йорк: Макмиллан. С.  346–391 . ISBN 978-0-02-365070-3.
• Шеннах, Сюзанна . «Погрешность измерения в нелинейных моделях — обзор» . Серия рабочих документов Cemmap . Cemmap . Проверено 6 февраля 2018 года .

Внешние ссылки

• Исторический обзор линейной регрессии с ошибками в обеих переменных , Дж. В. Гиллард, 2006 г.
• Лекция по эконометрики (тема: стохастические регрессоров и ошибки измерения) на YouTube с помощью Mark Thoma .

Модели регрессии с учетом возможных ошибок в независимых переменных

В статистике, модели ошибок в переменных или модели ошибок измерения — это модели регрессии, которые учитывают ошибки измерения в независимых переменных. Напротив, стандартные регрессионные модели предполагают, что эти регрессоры были точно измерены или наблюдались без ошибок; как таковые, эти модели учитывают только ошибки в зависимых переменных или ответах.

Иллюстрация разбавления регрессии (или смещения ослабления) с помощью диапазона оценок регрессии в ошибках: модели без переменных. Две линии регрессии (красные) ограничивают диапазон возможностей линейной регрессии. Неглубокий наклон получается, когда независимая переменная (или предиктор) находится на абсциссе (ось x). Более крутой наклон получается, когда независимая переменная находится на ординате (ось y). По соглашению с независимой переменной на оси x получается более пологий наклон. Зеленые контрольные линии — это средние значения в пределах произвольных интервалов по каждой оси. Обратите внимание, что более крутые оценки регрессии зеленого и красного цвета более согласуются с меньшими ошибками в переменной оси Y.

В случае, когда некоторые регрессоры были измерены с ошибками, оценка, основанная на стандартном предположении, приводит к несогласованным 61>оценок, что означает, что оценки параметров не стремятся к истинным значениям даже в очень больших выборках. Для простой линейной регрессии эффект заключается в занижении коэффициента, известном как смещение затухания. В нелинейных моделях направление смещения, вероятно, будет более сложным.

Содержание

• 1 Мотивационный пример
• 2 Спецификация
  • 2.1 Терминология и предположения
• 3 Линейный модель
  • 3.1 Простая линейная модель
  • 3.2 Многопараметрическая линейная модель
• 4 Нелинейные модели
  • 4.1 Методы инструментальных переменных
  • 4.2 Повторные наблюдения
• 5 Ссылки
• 6 Дополнительная литература
• 7 Внешние ссылки

Пример мотивации

Рассмотрим простую модель линейной регрессии вида

yt = α + β xt ∗ + ε t, t = 1,…, T, { displaystyle y_ { t} = альфа + бета x_ {t} ^ {*} + varepsilon _ {t} ,, quad t = 1, ldots, T,}

где xt ∗ { displaystyle x_ {t} ^ {*}}обозначает истинный, но ненаблюдаемый регрессор. Вместо этого мы наблюдаем это значение с ошибкой:

xt = xt ∗ + η t { displaystyle x_ {t} = x_ {t} ^ {*} + eta _ {t} ,}

где ошибка измерения η t { displaystyle eta _ {t}}считается независимой от истинного значения xt ∗ { displaystyle x_ {t} ^ {*}}.

Если yt { displaystyle y_ {t}}‘s просто регрессируют на xt { displaystyle x_ {t}}′ s ( см. простая линейная регрессия ), тогда оценка коэффициента наклона будет

β ^ = 1 T ∑ t = 1 T (xt — x ¯) (yt — y ¯) 1 T ∑ t = 1 T (xt — x ¯) 2, { displaystyle { hat { beta}} = { frac {{ tfrac {1} {T}} sum _ {t = 1} ^ {T} (x_ {t} — { bar {x}}) (y_ {t} — { bar {y}})} {{ tfrac {1} {T}} sum _ {t = 1} ^ {T} (x_ {t} — { bar {x}}) ^ {2}}} ,,}

который сходится по мере увеличения размера выборки T { displaystyle T}без граница:

β ^ → p Cov ⁡ [xt, yt] Var ⁡ [xt] = β σ x ∗ 2 σ x ∗ 2 + σ η 2 = β 1 + σ η 2 / σ x ∗ 2. { displaystyle { hat { beta}} { xrightarrow {p}} { frac { operatorname {Cov} [, x_ {t}, y_ {t} ,]} { operatorname {Var} [ , x_ {t} ,]}} = { frac { beta sigma _ {x ^ {*}} ^ {2}} { sigma _ {x ^ {*}} ^ {2} + sigma _ { eta} ^ {2}}} = { frac { beta} {1+ sigma _ { eta} ^ {2} / sigma _ {x ^ {*}} ^ {2}} } ,.}

Варианты неотрицательны, так что в пределе оценка меньше по величине, чем истинное значение β { displaystyle beta}, эффект, который статистики называют ослаблением или разбавлением регрессии. Таким образом, «наивная» оценка методом наименьших квадратов несовместима в этой настройке. Однако оценщик является последовательным оценщиком параметра, необходимого для наилучшего линейного предиктора y { displaystyle y}при x { displaystyle x}: в некоторых приложениях это может быть то, что требуется, а не оценка «истинного» коэффициента регрессии, хотя это предполагает, что дисперсия ошибок при наблюдении x ∗ { displaystyle x ^ {*}}остается неизменным. Это следует непосредственно из результата, приведенного непосредственно выше, и того факта, что коэффициент регрессии, связывающий yt { displaystyle y_ {t}}′ s с фактически наблюдаемым xt { displaystyle x_ {t}}′ s в простой линейной регрессии задается как

β x = Cov ⁡ [xt, yt] Var ⁡ [xt]. { displaystyle beta _ {x} = { frac { operatorname {Cov} [, x_ {t}, y_ {t} ,]} { operatorname {Var} [, x_ {t} , ]}}.}

Именно этот коэффициент, а не β { displaystyle beta}, необходим для построения предиктора y { displaystyle y}на основе наблюдаемого x { displaystyle x}, подверженного шуму.

Можно утверждать, что почти все существующие наборы данных содержат ошибки разной природы и величины, так что смещение затухания встречается очень часто (хотя в многомерной регрессии направление смещения неоднозначно). Джерри Хаусман видит в этом железный закон эконометрики: «Величина оценки обычно меньше ожидаемой».

Спецификация

Обычно модели ошибок измерения описываются с использованием подход скрытых переменных. Если y { displaystyle y}— это переменная ответа, а x { displaystyle x}— наблюдаемые значения регрессоров, то предполагается, что существуют некоторые скрытые переменные y ∗ { displaystyle y ^ {*}}и x ∗ { displaystyle x ^ {*}}, которые соответствуют «истинному» модели. функциональная связь g (⋅) { displaystyle g ( cdot)}, и такие, что наблюдаемые величины являются их зашумленными наблюдениями:

{y ∗ = g (Икс *, вес | θ), Y = Y * + ε, Икс = Икс * + η, { Displaystyle { begin {cases} y ^ {*} = g (x ^ {*} !, ш , | , theta), \ y = y ^ {*} + varepsilon, \ x = x ^ {*} + eta, end {ases}}

где θ { displaystyle theta}— параметр модели и w { displaystyle w}— те регрессоры, которые считаются безошибочными (для пример, когда линейная регрессия содержит точку пересечения, регрессор, который соответствует константе, безусловно, не имеет «ошибок измерения»). В зависимости от спецификации эти безошибочные регрессоры могут или не могут рассматриваться отдельно; в последнем случае просто предполагается, что соответствующие элементы в матрице дисперсии элементов η { displaystyle eta}равны нулю.

Переменные y { displaystyle y}, x { displaystyle x}, w { displaystyle w}все наблюдаются, что означает, что статистик обладает a набор данных из n { displaystyle n}статистических единиц {yi, xi, wi} i = 1,…, n { displaystyle left {y_ {i}, x_ {i}, w_ {i} right } _ {i = 1, dots, n}}, которые следуют описанному процессу создания данных над; скрытые переменные x ∗ { displaystyle x ^ {*}}, y ∗ { displaystyle y ^ {*}}, ε { displaystyle varepsilon}и η { displaystyle eta}, однако, не соблюдаются.

Эта спецификация не охватывает все существующие модели ошибок в переменных. Например, в некоторых из них функция g (⋅) { displaystyle g ( cdot)}может быть непараметрической или полупараметрической. Другие подходы моделируют связь между y ∗ { displaystyle y ^ {*}}и x ∗ { displaystyle x ^ {*}}как распределительную. функционала, то есть они предполагают, что y ∗ { displaystyle y ^ {*}}условно на x ∗ { displaystyle x ^ {*}}следует определенному (обычно параметрическому) распределению.

Терминология и предположения

• Наблюдаемая переменная x { displaystyle x}может называться манифестом, индикатором или прокси-переменной.
• ненаблюдаемой переменной x ∗ { displaystyle x ^ {*}}можно назвать скрытой или истинной переменной. Его можно рассматривать либо как неизвестную константу (в этом случае модель называется функциональной моделью), либо как случайную величину (соответственно структурную модель).
• Связь между погрешностью измерения η { displaystyle eta}и скрытую переменную x ∗ { displaystyle x ^ {*}}можно моделировать разными способами:
  • Классический ошибки: η ⊥ x ∗ { displaystyle eta perp x ^ {*}}ошибки не зависят от скрытой переменной. Это наиболее распространенное допущение, оно подразумевает, что ошибки вносятся измерительным устройством и их величина не зависит от измеряемого значения.
  • Независимость от среднего: E ⁡ [η | x ∗] = 0, { displaystyle operatorname {E} [ eta | x ^ {*}] , = , 0,}ошибки равны нулю в среднем для каждого значения скрытого регрессор. Это менее ограничительное предположение, чем классическое, поскольку оно допускает наличие гетероскедастичности или других эффектов в ошибках измерения.
  • Ошибки Берксона : η ⊥ x, { displaystyle eta , perp , x,}ошибки не зависят от наблюдаемого регрессора x. Это предположение имеет очень ограниченную применимость. Одним из примеров являются ошибки округления: например, если возраст человека * является непрерывной случайной величиной, тогда как наблюдаемый возраст усекается до следующего наименьшего целого числа, тогда ошибка усечения приблизительно не зависит от наблюдаемого возраста.. Другая возможность связана с экспериментом с фиксированным планом: например, если ученый решает провести измерение в определенный заранее определенный момент времени x { displaystyle x}, скажем, при x = 10 s { displaystyle x = 10s}, тогда реальное измерение может произойти при некотором другом значении x ∗ { displaystyle x ^ {*}}(например, из-за к ее конечному времени реакции), и такая ошибка измерения обычно не зависит от «наблюдаемого» значения регрессора.
  • Ошибки неправильной классификации: особый случай, используемый для фиктивных регрессоров. Если x ∗ { displaystyle x ^ {*}}является индикатором определенного события или состояния (например, лицо мужского / женского пола, какое-либо лечение предоставлено / нет и т. Д.), то ошибка измерения в таком регрессоре будет соответствовать неверной классификации, аналогичной ошибкам типа I и типа II при статистическом тестировании. В этом случае ошибка η { displaystyle eta}может принимать только 3 возможных значения, а ее распределение зависит от x ∗ { displaystyle x ^ {*}}моделируется двумя параметрами: α = Pr ⁡ [η = — 1 | x ∗ = 1] { displaystyle alpha = operatorname {Pr} [ eta = -1 | x ^ {*} = 1]}и β = Pr ⁡ [η = 1 | x ∗ = 0] { displaystyle beta = operatorname {Pr} [ eta = 1 | x ^ {*} = 0]}. Необходимым условием идентификации является то, что α + β < 1 {displaystyle alpha +beta <1}, то есть ошибочная классификация не должна происходить «слишком часто». (Эта идея может быть обобщена на дискретные переменные с более чем двумя возможными значениями.)

Линейная модель

Линейные модели ошибок в переменных были изучены первыми, вероятно потому, что были линейные модели так широко используются, и они проще нелинейных. В отличие от стандартной регрессии по методу наименьших квадратов (OLS), расширение ошибок в регрессии переменных (EiV) с простого случая на многомерный не так просто.

Простая линейная модель

Простая линейная модель ошибок в переменных уже была представлена ​​в разделе «мотивация»:

{yt = α + β xt ∗ + ε t, xt знак равно xt * + η t, { displaystyle { begin {cases} y_ {t} = alpha + beta x_ {t} ^ {*} + varepsilon _ {t}, \ x_ {t} = x_ {t} ^ {*} + eta _ {t}, end {cases}}}

где все переменные скалярны. Здесь α и β представляют собой интересующие параметры, тогда как σ ε и σ η — стандартные отклонения членов ошибки — являются мешающими параметрами. «Истинный» регрессор x * рассматривается как случайная величина (структурная модель), не зависящая от ошибки измерения η (классическое предположение).

Эта модель идентифицируема в двух случаях: (1) либо скрытый регрессор x * не нормально распределен, (2) или x * имеет нормальное распределение, но ни ε t, ни η t не делятся на нормальное распределение. То есть параметры α, β можно последовательно оценить на основе набора данных (xt, yt) t = 1 T { displaystyle scriptstyle (x_ {t}, , y_ {t}) _ {t = 1} ^ {T}}без какой-либо дополнительной информации, при условии, что скрытый регрессор не является гауссовским.

Перед тем, как этот результат идентифицируемости был установлен, статистики пытались применить метод максимального правдоподобия, предполагая, что все переменные являются нормальными, а затем пришли к выводу, что модель не идентифицирована. Предлагаемое решение состояло в том, чтобы предположить, что некоторые параметры модели известны или могут быть оценены из внешнего источника. К таким методам оценки относятся

• регрессия Деминга — предполагается, что отношение δ = σ² ε / σ² η известно. Это может быть подходящим, например, когда ошибки в y и x вызваны измерениями, и точность измерительных устройств или процедур известна. Случай, когда δ = 1, также известен как ортогональная регрессия.
• Регрессия с известным коэффициентом надежности λ = σ² ∗ / (σ² η + σ² ∗), где σ² ∗ — дисперсия скрытого регрессора. Такой подход может быть применим, например, когда доступны повторяющиеся измерения одного и того же устройства, или когда коэффициент надежности известен из независимого исследования. В этом случае согласованная оценка наклона равна оценке методом наименьших квадратов, деленной на λ.
• Регрессия с известным σ² η может произойти, если источник ошибок в x известен и их дисперсию можно рассчитать. Это может включать ошибки округления или ошибки, вносимые измерительным устройством. Когда известно σ² η, мы можем вычислить коэффициент надежности как λ = (σ² x — σ² η) / σ² x и уменьшить проблема с предыдущим случаем.

Более новые методы оценки, которые не предполагают знания некоторых параметров модели, включают

• Метод моментов — оценку GMM на основе третьего — ( или соединение более высокого порядка кумулянтов наблюдаемых переменных. Коэффициент наклона можно оценить по формуле

  β ^ = K ^ (n 1, n 2 + 1) K ^ (n 1 + 1, n 2), n 1, n 2>0, { displaystyle { hat { beta}} = { frac {{ hat {K}} (n_ {1}, n_ {2} +1)} {{ hat {K}} (n_ {1} + 1, n_ {2 })}}, quad n_ {1}, n_ {2}>0,}

  где (n 1,n2) такие, что K (n 1 + 1, n 2) — совместный кумулянт из (x, y) — не равен нулю. В случае, когда третий центральный момент скрытого регрессора x * не равен нулю, формула сводится к

  β ^ = 1 T ∑ T = 1 T (xt — x ¯) (yt — y ¯) 2 1 T ∑ t = 1 T (xt — x ¯) 2 (yt — y ¯). { displaystyle { hat { beta}} = { frac {{ tfrac {1} {T}} sum _ {t = 1} ^ {T} (x_ {t} — { bar {x}}) (y_ { t} — { bar {y}}) ^ {2}} {{ tfrac {1} {T}} sum _ {t = 1} ^ {T} (x_ {t} — { bar {x }}) ^ {2} (y_ {t} — { bar {y}})}} .}

• Инструментальные переменные — регрессия, требующая некоторых дополнительных переменных данных z, назывались инструменты, были в наличии. Эти переменные не должны быть коррелированы с ошибками в уравнении для зависимой переменной (действительны), и они также должны быть коррелированы (релевантны) с истинными регрессорами x *. Если такие переменные могут быть найдены, то оценка принимает вид
  β ^ = 1 T ∑ t = 1 T (zt — z ¯) (yt — y ¯) 1 T ∑ t = 1 T (zt — z ¯) (xt — x ¯). { displaystyle { hat { beta}} = { frac {{ tfrac {1} {T}} sum _ {t = 1} ^ {T} (z_ {t} — { bar {z}) }) (y_ {t} — { bar {y}})} {{ tfrac {1} {T}} sum _ {t = 1} ^ {T} (z_ {t} — { bar { z}}) (x_ {t} — { bar {x}})}} .}

Многопараметрическая линейная модель

Многопараметрическая модель выглядит точно так же, как простая линейная модель, только на этот раз β, η t, x t и x * t являются векторами k × 1.

{y t = α + β ′ x t ∗ + ε t, x t = x t ∗ + η t. { displaystyle { begin {case} y_ {t} = alpha + beta ‘x_ {t} ^ {*} + varepsilon _ {t}, \ x_ {t} = x_ {t} ^ {* } + eta _ {t}. end {cases}}}

В случае, когда (ε t,ηt) совместно нормально, параметр β не идентифицируется тогда и только тогда, когда существует неособое k Блочная матрица × k [a A] (где a — вектор k × 1) такая, что a′x * распределяется нормально и независимо от A′x *. В случае, когда ε t, η t1,…, η tk являются взаимно независимыми, параметр β не идентифицируется тогда и только тогда, когда дополнительно В приведенных выше условиях некоторые ошибки могут быть записаны как сумма двух независимых переменных, одна из которых является нормальной.

Некоторые из методов оценки для многомерных линейных моделей:

• Всего наименьших квадратов равно расширение регрессии Деминга на многопараметрическую настройку. Когда все k + 1 компоненты вектора (ε, η) имеют равные дисперсии и независимы, это эквивалентно запуску ортогональной регрессии y по вектору x, то есть регрессии, которая минимизирует сумму квадратов расстояний между точек (y t,xt) и k-мерной гиперплоскости «наилучшего соответствия».
• Оценка метода моментов может быть построена на основе моментных условий E [z t · (y t — α — β’x t)] = 0, где (5k + 3) -мерный вектор инструментов z t определяется как

  zt = (1 zt 1 ′ zt 2 ′ zt 3 ′ zt 4 ′ zt 5 ′ zt 6 ′ zt 7 ′) ′, где zt 1 = xt ∘ xtzt 2 = xtytzt 3 = yt 2 zt 4 = xt ∘ xt ∘ xt — 3 (E ⁡ [xtxt ′] ∘ I k) xtzt 5 = xt ∘ xtyt — 2 (E ⁡ [ytxt ′] ∘ I k) xt — yt (E ⁡ [xtxt ′] ∘ I k) ι kzt 6 = xtyt 2 — E ⁡ [yt 2] xt — 2 yt E ⁡ [xtyt] zt 7 = yt 3 — 3 yt E ⁡ [yt 2] { displaystyle { begin {align} z_ {t} = left (1 z_ {t1} ‘ z_ {t2}’ z_ {t3} ‘ z_ { t4} ‘ z_ {t5}’ z_ {t6} ‘ z_ {t7}’ right) ‘, quad { text {where}} \ z_ {t1} = x_ {t} circ x_ { t} \ z_ {t2} = x_ {t} y_ {t} \ z_ {t3} = y_ {t} ^ {2} \ z_ {t4} = x_ {t} circ x_ {t} circ x_ {t} -3 { big (} operatorname {E} [x_ {t} x_ {t} ‘] circ I_ {k} { big)} x_ {t} \ z_ {t5} = x_ {t} circ x_ {t} y_ {t} -2 { big (} operatorname {E} [y_ {t} x_ {t} ‘] circ I_ {k} { big)} x_ { t} -y_ {t} { big (} operatorname {E} [x_ {t} x_ {t} ‘] circ I_ {k} { big)} iota _ {k} \ z_ {t6 } = x_ {t} y_ {t} ^ {2} — operatorname {E} [y_ {t} ^ {2}] x_ {t} -2y_ {t} operatorname {E} [x_ {t} y_ {t}] \ z_ {t7} = y_ {t} ^ {3} -3y_ {t} operatorname {E} [y_ {t} ^ {2}] end {align}}}

  где ∘ { displaystyle circ}обозначает произведение Адамара матриц, а переменные x t, y t были предварительно лишенный смысла. Авторы метода предлагают использовать модифицированную оценку IV Фуллера..

  Этот метод может быть расширен для использования моментов выше третьего порядка, если необходимо, и для учета переменных, измеренных без ошибок.

• Подход инструментальных переменных требует поиска дополнительных переменных данных z t, которые будут служить инструментами для неверно измеренных регрессоров x t. Этот метод является наиболее простым с точки зрения реализации, однако его недостаток в том, что он требует сбора дополнительных данных, что может быть дорогостоящим или даже невозможным. Когда инструменты найдены, оценщик принимает стандартную форму

  β ^ = (X ′ Z (Z ′ Z) — 1 Z ′ X) — 1 X ′ Z (Z ′ Z) — 1 Z ′ y. { displaystyle { hat { beta}} = { big (} X’Z (Z’Z) ^ {- 1} Z’X { big)} ^ {- 1} X’Z (Z’Z) ^ {- 1} Z’y.}

Нелинейные модели

Общая модель нелинейных ошибок измерения принимает вид

{yt = g (xt ∗) + ε t, xt = xt ∗ + η t. { displaystyle { begin {cases} y_ {t} = g (x_ {t} ^ {*}) + varepsilon _ {t}, \ x_ {t} = x_ {t} ^ {*} + eta _ {t}. end {ases}}}

Здесь функция g может быть параметрической или непараметрической. Если функция g параметрическая, она будет записана как g (x *, β).

Для общего векторного регрессора x * условия для модели идентифицируемости неизвестны. Однако в случае скаляра x * модель идентифицируется, если функция g не имеет «логарифмически экспоненциальную» форму

g (x ∗) = a + b ln ⁡ (ecx ∗ + d) { displaystyle g ( x ^ {*}) = a + b ln { big (} e ^ {cx ^ {*}} + d { big)}}

и скрытый регрессор x * имеет плотность

fx ∗ (Икс) = {А е — В е С Икс + CD Икс (е С Икс + Е) — F, если d>0, А е — В х 2 + С х, если d = 0 { displaystyle f_ {x ^ { *}} (x) = { begin {cases} Ae ^ {- Be ^ {Cx} + CDx} (e ^ {Cx} + E) ^ {- F}, { text {if}} d>0 \ Ae ^ {- Bx ^ {2} + Cx} { text {if}} d = 0 end {cases}}}

где константы A, B, C, D, E, F могут зависеть от a, b, c, d.

Несмотря на этот оптимистичный результат, на данный момент не существует методов оценки нелинейных моделей ошибок в переменных без какой-либо посторонней информации. Однако существует несколько методов, которые используют некоторые дополнительные данные: r инструментальные переменные или повторные наблюдения.

Методы инструментальных переменных

• Метод моделирования моментов Ньюи для параметрических моделей — требует наличия дополнительного набора наблюдаемых переменных-предикторов z t, так что истинный регрессор может быть выражается как

  xt ∗ = π 0 ′ zt + σ 0 ζ t, { displaystyle x_ {t} ^ {*} = pi _ {0} ‘z_ {t} + sigma _ {0} zeta _ {t},}

  где π 0 и σ 0 — (неизвестные) постоянные матрицы, а ζ t ⊥ z t. Коэффициент π 0 можно оценить с помощью стандартной наименьших квадратов регрессии x по z. Распределение ζ t неизвестно, однако мы можем смоделировать его как принадлежащее к гибкому параметрическому семейству — ряду Эджворта :

  f ζ (v; γ) = ϕ (v) ∑ j Знак равно 1 J γ jvj { displaystyle f _ { zeta} (v; , gamma) = phi (v) , textstyle sum _ {j = 1} ^ {J} ! Gamma _ {j } v ^ {j}}

  где ϕ — стандартное нормальное распределение.

  Смоделированные моменты могут быть рассчитаны с использованием алгоритма выборки по важности : сначала мы генерируем несколько случайных величин {v ts ~ ϕ, s = 1,…, S, t = 1,…, T} из стандартного нормального распределения, тогда мы вычисляем моменты в t-м наблюдении как

  mt (θ) = A (zt) 1 S ∑ s = 1 SH (xt, yt, zt, vts; θ) ∑ J знак равно 1 J γ jvtsj, { displaystyle m_ {t} ( theta) = A (z_ {t}) { frac {1} {S}} sum _ {s = 1} ^ {S} H (x_ {t}, y_ {t}, z_ {t}, v_ {ts}; theta) sum _ {j = 1} ^ {J} ! Gamma _ {j} v_ { ts} ^ {j},}

  где θ = (β, σ, γ), A — просто некоторая функция инструментальных переменных z, а H — двухкомпонентный вектор моментов

  H 1 (xt, yt, zt, vts; θ) = yt — g (π ^ ′ zt + σ vts, β), H 2 (xt, yt, zt, vts; θ) = ztyt — (π ^ ′ zt + σ vts) g (π ^ ′ zt + σ vts, β) { displaystyle { begin {выровнено} H_ {1} (x_ {t}, y_ {t}, z_ {t}, v_ {ts}; theta) = y_ {t} -g ({ hat { pi}} ‘z_ {t} + sigma v_ {ts}, beta), \ H_ {2} (x_ {t}, y_ {t}, z_ {t}, v_ {ts}; theta) = z_ {t} y_ {t} — ({ hat { pi}} ‘z_ {t} + sigma v_ {ts}) g ({ hat { pi}}’ z_ {t} + sigma v_ {ts}, beta) end {выровнено}} }

  С помощью моментных функций m t можно применить стандартный метод GMM для оценки неизвестного параметра θ.

Повторные наблюдения

В этом подходе два ( или, может быть, больше) доступны повторные наблюдения регрессора x *. Оба наблюдения содержат собственные ошибки измерения, однако эти ошибки должны быть независимыми:

{x 1 t = xt ∗ + η 1 t, x 2 t = xt ∗ + η 2 t, { displaystyle { begin { case} x_ {1t} = x_ {t} ^ {*} + eta _ {1t}, \ x_ {2t} = x_ {t} ^ {*} + eta _ {2t}, end {случаи }}}

где x * ⊥ η 1 ⊥ η 2. Переменные η 1, η 2 не обязательно должны быть одинаково распределены (хотя, если они являются эффективностью средства оценки, можно немного улучшить). С помощью только этих двух наблюдений можно согласованно оценить функцию плотности x *, используя метод Котлярского деконволюции.

• Метод условной плотности Ли для параметрических моделей. Уравнение регрессии может быть записано в терминах наблюдаемых переменных как

  E ⁡ [y t | x t] = ∫ g (x t ∗, β) f x ∗ | Икс (xt * | xt) dxt *, { displaystyle Operatorname {E} [, y_ {t} | x_ {t} ,] = int g (x_ {t} ^ {*}, beta) f_ {x ^ {*} | x} (x_ {t} ^ {*} | x_ {t}) dx_ {t} ^ {*},}

  где можно было бы вычислить интеграл, если бы мы знали функция условной плотности ƒ x * | x ​​. Если эта функция может быть известна или оценена, тогда проблема превращается в стандартную нелинейную регрессию, которую можно оценить, например, с помощью метода NLLS.. Предположим для простоты, что η 1, η 2 одинаково распределены, эта условная плотность может быть вычислена как

  f ^ x ∗ | Икс (Икс * | Икс) знак равно е ^ Икс * (Икс *) е ^ Икс (Икс) ∏ J = 1 КФ ^ η J (xj — xj *), { Displaystyle { Hat {f}} _ {х ^ {*} | x} (x ^ {*} | x) = { frac {{ hat {f}} _ {x ^ {*}} (x ^ {*})} {{ hat {f }} _ {x} (x)}} prod _ {j = 1} ^ {k} { hat {f}} _ { eta _ {j}} { big (} x_ {j} -x_ {j} ^ {*} { big)},}

  где с небольшим злоупотреблением обозначениями x j обозначает j-й компонент вектора.. Все плотности в этой формуле могут можно оценить с помощью обращения эмпирических характеристических функций. В частности,

  φ ^ η j (v) = φ ^ xj (v, 0) φ ^ xj ∗ (v), где φ ^ xj (v 1, v 2) = 1 T ∑ t = 1 T eiv 1 x 1 tj + iv 2 x 2 tj, φ ^ xj ∗ (v) = exp ⁡ ∫ 0 v ∂ φ ^ xj (0, v 2) / ∂ v 1 φ ^ xj (0, v 2) dv 2, φ ^ x (u) = 1 2 T ∑ t = 1 T (eiu ′ x 1 t + eiu ′ x 2 t), φ ^ x ∗ (u) = φ ^ x (u) ∏ j = 1 k φ ^ η j (uj). { displaystyle { begin {align} { hat { varphi}} _ { eta _ {j}} (v) = { frac {{ hat { varphi}} _ {x_ {j}} (v, 0)} {{ hat { varphi}} _ {x_ {j} ^ {*}} (v)}}, quad { text {where}} { hat { varphi}} _ {x_ {j}} (v_ {1}, v_ {2}) = { frac {1} {T}} sum _ {t = 1} ^ {T} e ^ {iv_ {1} x_ {1tj } + iv_ {2} x_ {2tj}}, \ { hat { varphi}} _ {x_ {j} ^ {*}} (v) = exp int _ {0} ^ {v} { frac { partial { hat { varphi}} _ {x_ {j}} (0, v_ {2}) / partial v_ {1}} {{ hat { varphi}} _ {x_ {j }} (0, v_ {2})}} dv_ {2}, \ { hat { varphi}} _ {x} (u) = { frac {1} {2T}} sum _ { t = 1} ^ {T} { Big (} e ^ {iu’x_ {1t}} + e ^ {iu’x_ {2t}} { Big)}, quad { hat { varphi}} _ {x ^ {*}} (u) = { frac {{ hat { varphi}} _ {x} (u)} { prod _ {j = 1} ^ {k} { hat { varphi}} _ { eta _ {j}} (u_ {j})}}. end {align}}}

  Чтобы инвертировать эту характеристическую функцию, нужно применить обратное преобразование Фурье с обрезкой параметр C необходим для обеспечения числовой устойчивости. Например:

  f ^ x (x) = 1 (2 π) k ∫ — C C ⋯ ∫ — C C e — i u ′ x φ ^ x (u) d u. { displaystyle { hat {f}} _ {x} (x) = { frac {1} {(2 pi) ^ {k}}} int _ {- C} ^ {C} cdots int _ {- C} ^ {C} e ^ {- iu’x} { hat { varphi}} _ {x} (u) du.}

• Оценка Шеннаха для параметрического линейного входа -параметрическая нелинейная модель в переменных. Это модель вида
  {yt = ∑ j = 1 k β jgj (xt ∗) + ∑ j = 1 ℓ β k + jwjt + ε t, x 1 t = xt ∗ + η 1 T, Икс 2 T знак равно XT * + η 2 T, { Displaystyle { begin {case} Y_ {t} = textstyle sum _ {j = 1} ^ {k} beta _ {j} g_ {j } (x_ {t} ^ {*}) + sum _ {j = 1} ^ { ell} beta _ {k + j} w_ {jt} + varepsilon _ {t}, \ x_ {1t } = x_ {t} ^ {*} + eta _ {1t}, \ x_ {2t} = x_ {t} ^ {*} + eta _ {2t}, end {cases}}}

  где w t представляет переменные, измеренные без ошибок. Регрессор x * здесь является скалярным (метод может быть расширен и на случай вектора x *).. Если бы не ошибки измерения, это была бы стандартная линейная модель с оценка

  β ^ = (E ^ [ξ t ξ t ′]) — 1 E ^ [ξ tyt], { displaystyle { hat { beta}} = { big (} { hat { operatorname {E}}} [, xi _ {t} xi _ {t} ‘,] { big)} ^ {- 1} { hat { operatorname {E}}} [, xi _ {t} y_ {t} ,],}

  где

  ξ t ′ = (g 1 (xt ∗), ⋯, gk (xt ∗), w 1, t, ⋯, wl, t). { displaystyle xi _ {t} ‘= (g_ {1} (x_ {t} ^ {*}), cdots, g_ {k} (x_ {t} ^ {*}), w_ {1, t }, cdots, w_ {l, t}).}

  Оказывается, все ожидаемые значения в этой формуле можно оценить с помощью того же трюка с деконволюцией. В частности, для типичной наблюдаемой w t (которая может быть 1, w 1t,…, w ℓ t или y t) и некоторой функции h (которая может представлять любые g j или g igj) имеем

  E ⁡ [wth (xt ∗)] = 1 2 π ∫ — ∞ ∞ φ h ( — и) ψ вес (и) ду, { Displaystyle OperatorName {E} [, w_ {t} h (x_ {t} ^ {*}) ,] = { гидроразрыва {1} {2 pi }} int _ {- infty} ^ { infty} varphi _ {h} (- u) psi _ {w} (u) du,}

  где φ h — преобразование Фурье h (x *), но с использованием того же соглашения, что и для характеристических функций,

  φ h (u) = ∫ eiuxh (x) dx { displaystyle varphi _ {h} (u) = int e ^ {iux} h (x) dx},

  и

  ψ w (u) = E ⁡ [wteiux ∗] = E ⁡ [wteiux 1 t] E ⁡ [ eiux 1 t] ехр ⁡ ∫ 0 ui E ⁡ [x 2 teivx 1 t] E ⁡ [eivx 1 t] dv { displaystyle psi _ {w} (u) = operatorname {E} [, w_ {t } e ^ {iux ^ {*}} ,] = { frac { operatorname {E} [w_ {t} e ^ {iux_ {1t}}]} { operatorname {E} [e ^ {iux_ { 1t}}]}} exp int _ {0} ^ {u} i { frac { operatorname {E} [x_ {2t} e ^ {ivx_ {1t}}]} { operatorname {E} [e ^ {ivx_ {1t}}]}} dv}

  Результирующая оценка β ^ { displaystyle scriptstyle { hat { beta}}}согласован и асимптотически нормален.

• Оценка Шеннаха для непараметрической модели. Стандартная оценка Надарая – Ватсона для непараметрической модели принимает вид

  g ^ (x) = E ^ [yt K h (xt ∗ — x)] E ^ [K h (xt ∗ — x)], { displaystyle { hat {g}} (x) = { frac {{ hat { operatorname {E}}} [, y_ {t} K_ {h} (x_ {t} ^ { *} — x) ,]} {{ hat { operatorname {E}}} [, K_ {h} (x_ {t} ^ {*} — x) ,]}},}

  для подходящего выбора ядра K и пропускной способности h. Оба ожидания здесь можно оценить с помощью того же метода, что и в предыдущем методе.

Ссылки

Дополнительная литература

• Dougherty, Christopher (2011). «Стохастические регрессоры и ошибки измерения». Введение в эконометрику (Четвертое изд.). Издательство Оксфордского университета. С. 300–330. ISBN 978-0-19-956708-9 .
• Кмента, янв (1986). «Оценка с недостаточными данными». Элементы эконометрики (Второе изд.). Нью-Йорк: Макмиллан. С. 346–391. ISBN 978-0-02-365070-3 .
• Шеннах, Сюзанна. «Погрешность измерения в нелинейных моделях — обзор». Серия рабочих документов Cemmap. Cemmap. Получено 6 февраля 2018 г.

Внешние ссылки

• Исторический обзор линейной регрессии с ошибками в обеих переменных, J.W. Гиллард 2006
• Лекция по эконометрике (тема: Стохастические регрессоры и ошибка измерения) на YouTube, автор Марк Тома.

4. 
Использование
предварительной информации о значениях некоторых параметров. Иногда значения некоторых неизвестных параметров
модели могут быть определены по пробным выборочным наблюдениям, тогда
мультиколлинеарность может быть устранена путем установления значений параметра
у одной коррелирующих переменных. Ограниченность метода – в сложности получения
предварительных значений параметров с высокой точностью.

5. 
Преобразование переменных. Для устранения мультиколлинеарности можно
преобразовать переменные, например, путем линеаризации или получения
относительных показателей, а также перехода от номинальных к реальным
показателям (особенно в макроэкономических исследованиях).

При построении модели множественной регрессии с точки
зрения обеспечения ее высокого качества возникают следующие вопросы:

1. 
Каковы признаки качественной
модели?

2. 
Какие ошибки спецификации могут
быть?

3. 
Каковы последствия ошибок
спецификации?

4. 
Какие существуют методы
обнаружения и устранения ошибок спецификации?

Рассмотрим основные признаки качественной модели
множественной регрессии:

1. 
Простота. Из двух моделей примерно одинаковых статистических
свойств более качественной является та, которая содержит меньше переменных, или
же более простая по аналитической форме.

2. 
Однозначность. Метод вычисления коэффициентов должен быть одинаков
для любых наборов данных.

3. 
Максимальное соответствие. Этот признак говорит о том, что основным критерием
качества модели является коэффициент детерминации, отражающий объясненную
моделью вариацию зависимой переменной. Для практического использования выбирают
модель, для которой расчетное значение F-критерия для
коэффициента детерминации б четыре раза больше табличного.

4. 
Согласованность с теорией. Получаемые значения коэффициентов должны быть
интерпретируемы с точки зрения экономических явлений и процессов. К примеру,
если строится линейная регрессионная модель спроса на товар, то соответствующий
коэффициент при цене товара должен быть отрицательным.

5. 
Хорошие прогнозные качества.
Обязательным условием построения
качественной модели является возможность ее использования для прогнозирования.

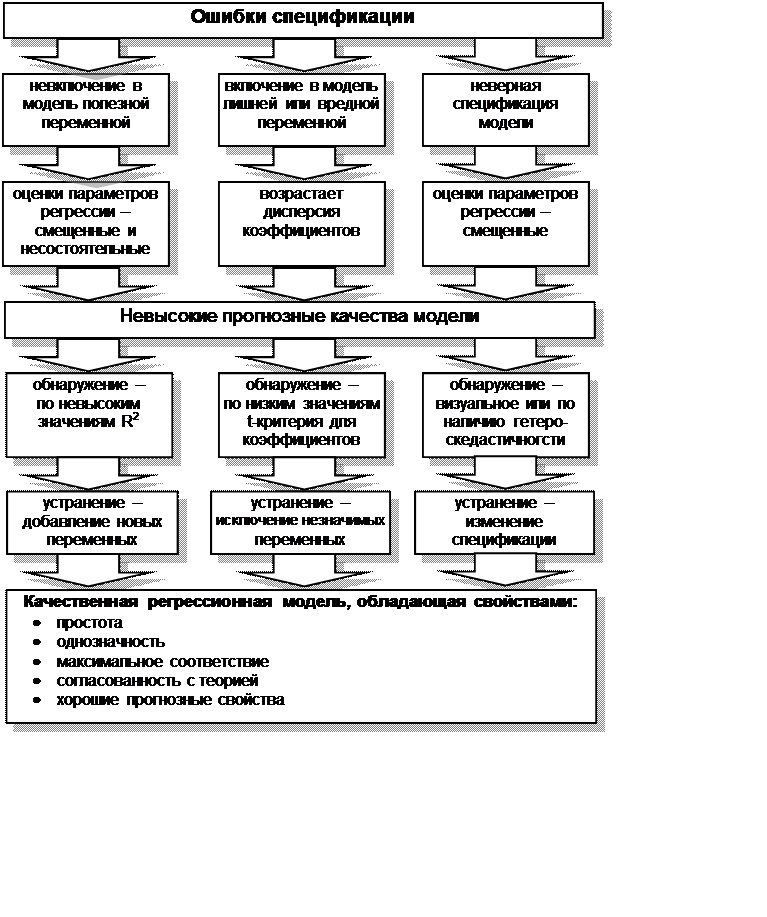
Одной из основных ошибок, допускаемых при построении
регрессионной модели, является ошибка спецификации (рис. 4.3).
Под ошибкой спецификации понимается неправильный выбор функциональной формы
модели или набора объясняющих переменных.

Различают следующие виды ошибок спецификации:

1. 
Невключение в модель полезной
(значимой) переменной.

2. 
Добавление в модель лишней
(незначимой) переменной

3. 
Выбор неправильной функциональной
формы модели

Последствия ошибки первого вида (невключение в
модель значимой переменной) заключаются в том, что полученные по МНК оценки
параметров являются смещенными и несостоятельными, а значение коэффициента
детерминации значительно снижаются.

При добавлении в модель лишней переменной
(ошибка второго вида) ухудшаются статистические свойства оценок
коэффициентов, возрастают их дисперсии, что ухудшает прогнозные качества модели
и затрудняет содержательную интерпретацию параметров, однако по сравнению с
другими ошибками ее последствия менее серьезны.

Если же осуществлен неверный выбор
функциональной формы модели, то есть допущена ошибка третьего вида, то
получаемые оценки будут смещенными, качество модели в целом и отдельных
коэффициентов будет невысоким. Это может существенно сказаться на прогнозных
качествах модели.

Ошибки спецификации первого вида можно обнаружить только
по невысокому качеству модели, низким значениям R².

Обнаружение ошибок спецификации второго вида, если лишней
является только одна переменная, осуществляется на основе расчета t — статистики для коэффициентов. При лишней переменной коэффициент
будет статистически незначим.

Иллюстрация разбавления регрессии (или смещения ослабления) с помощью диапазона оценок регрессии в ошибках: модели без переменных. Две линии регрессии (красные) ограничивают диапазон возможностей линейной регрессии. Неглубокий наклон получается, когда независимая переменная (или предиктор) находится на абсциссе (ось x). Более крутой наклон получается, когда независимая переменная находится на ординате (ось y). По соглашению с независимой переменной на оси x получается более пологий наклон. Зеленые контрольные линии — это средние значения в пределах произвольных интервалов по каждой оси. Обратите внимание, что более крутые оценки регрессии зеленого и красного цвета более согласуются с меньшими ошибками в переменной оси Y.

В случае, когда некоторые регрессоры были измерены с ошибками, оценка, основанная на стандартном предположении, приводит к несогласованным 61>оценок, что означает, что оценки параметров не стремятся к истинным значениям даже в очень больших выборках. Для простой линейной регрессии эффект заключается в занижении коэффициента, известном как смещение затухания. В нелинейных моделях направление смещения, вероятно, будет более сложным.

Содержание

• 1 Мотивационный пример
• 2 Спецификация
  • 2.1 Терминология и предположения
• 3 Линейный модель
  • 3.1 Простая линейная модель
  • 3.2 Многопараметрическая линейная модель
• 4 Нелинейные модели
  • 4.1 Методы инструментальных переменных
  • 4.2 Повторные наблюдения
• 5 Ссылки
• 6 Дополнительная литература
• 7 Внешние ссылки

Пример мотивации

Рассмотрим простую модель линейной регрессии вида

yt = α + β xt ∗ + ε t, t = 1,…, T, { displaystyle y_ { t} = альфа + бета x_ {t} ^ {*} + varepsilon _ {t} ,, quad t = 1, ldots, T,}

где xt ∗ { displaystyle x_ {t} ^ {*}}обозначает истинный, но ненаблюдаемый регрессор. Вместо этого мы наблюдаем это значение с ошибкой:

xt = xt ∗ + η t { displaystyle x_ {t} = x_ {t} ^ {*} + eta _ {t} ,}

где ошибка измерения η t { displaystyle eta _ {t}}считается независимой от истинного значения xt ∗ { displaystyle x_ {t} ^ {*}}.

Если yt { displaystyle y_ {t}}‘s просто регрессируют на xt { displaystyle x_ {t}}′ s ( см. простая линейная регрессия ), тогда оценка коэффициента наклона будет

β ^ = 1 T ∑ t = 1 T (xt — x ¯) (yt — y ¯) 1 T ∑ t = 1 T (xt — x ¯) 2, { displaystyle { hat { beta}} = { frac {{ tfrac {1} {T}} sum _ {t = 1} ^ {T} (x_ {t} — { bar {x}}) (y_ {t} — { bar {y}})} {{ tfrac {1} {T}} sum _ {t = 1} ^ {T} (x_ {t} — { bar {x}}) ^ {2}}} ,,}

который сходится по мере увеличения размера выборки T { displaystyle T}без граница:

β ^ → p Cov ⁡ [xt, yt] Var ⁡ [xt] = β σ x ∗ 2 σ x ∗ 2 + σ η 2 = β 1 + σ η 2 / σ x ∗ 2. { displaystyle { hat { beta}} { xrightarrow {p}} { frac { operatorname {Cov} [, x_ {t}, y_ {t} ,]} { operatorname {Var} [ , x_ {t} ,]}} = { frac { beta sigma _ {x ^ {*}} ^ {2}} { sigma _ {x ^ {*}} ^ {2} + sigma _ { eta} ^ {2}}} = { frac { beta} {1+ sigma _ { eta} ^ {2} / sigma _ {x ^ {*}} ^ {2}} } ,.}

Варианты неотрицательны, так что в пределе оценка меньше по величине, чем истинное значение β { displaystyle beta}, эффект, который статистики называют ослаблением или разбавлением регрессии. Таким образом, «наивная» оценка методом наименьших квадратов несовместима в этой настройке. Однако оценщик является последовательным оценщиком параметра, необходимого для наилучшего линейного предиктора y { displaystyle y}при x { displaystyle x}: в некоторых приложениях это может быть то, что требуется, а не оценка «истинного» коэффициента регрессии, хотя это предполагает, что дисперсия ошибок при наблюдении x ∗ { displaystyle x ^ {*}}остается неизменным. Это следует непосредственно из результата, приведенного непосредственно выше, и того факта, что коэффициент регрессии, связывающий yt { displaystyle y_ {t}}′ s с фактически наблюдаемым xt { displaystyle x_ {t}}′ s в простой линейной регрессии задается как

β x = Cov ⁡ [xt, yt] Var ⁡ [xt]. { displaystyle beta _ {x} = { frac { operatorname {Cov} [, x_ {t}, y_ {t} ,]} { operatorname {Var} [, x_ {t} , ]}}.}

Именно этот коэффициент, а не β { displaystyle beta}, необходим для построения предиктора y { displaystyle y}на основе наблюдаемого x { displaystyle x}, подверженного шуму.

Можно утверждать, что почти все существующие наборы данных содержат ошибки разной природы и величины, так что смещение затухания встречается очень часто (хотя в многомерной регрессии направление смещения неоднозначно). Джерри Хаусман видит в этом железный закон эконометрики: «Величина оценки обычно меньше ожидаемой».

Спецификация

Обычно модели ошибок измерения описываются с использованием подход скрытых переменных. Если y { displaystyle y}— это переменная ответа, а x { displaystyle x}— наблюдаемые значения регрессоров, то предполагается, что существуют некоторые скрытые переменные y ∗ { displaystyle y ^ {*}}и x ∗ { displaystyle x ^ {*}}, которые соответствуют «истинному» модели. функциональная связь g (⋅) { displaystyle g ( cdot)}, и такие, что наблюдаемые величины являются их зашумленными наблюдениями:

{y ∗ = g (Икс *, вес | θ), Y = Y * + ε, Икс = Икс * + η, { Displaystyle { begin {cases} y ^ {*} = g (x ^ {*} !, ш , | , theta), \ y = y ^ {*} + varepsilon, \ x = x ^ {*} + eta, end {ases}}

где θ { displaystyle theta}— параметр модели и w { displaystyle w}— те регрессоры, которые считаются безошибочными (для пример, когда линейная регрессия содержит точку пересечения, регрессор, который соответствует константе, безусловно, не имеет «ошибок измерения»). В зависимости от спецификации эти безошибочные регрессоры могут или не могут рассматриваться отдельно; в последнем случае просто предполагается, что соответствующие элементы в матрице дисперсии элементов η { displaystyle eta}равны нулю.

Переменные y { displaystyle y}, x { displaystyle x}, w { displaystyle w}все наблюдаются, что означает, что статистик обладает a набор данных из n { displaystyle n}статистических единиц {yi, xi, wi} i = 1,…, n { displaystyle left {y_ {i}, x_ {i}, w_ {i} right } _ {i = 1, dots, n}}, которые следуют описанному процессу создания данных над; скрытые переменные x ∗ { displaystyle x ^ {*}}, y ∗ { displaystyle y ^ {*}}, ε { displaystyle varepsilon}и η { displaystyle eta}, однако, не соблюдаются.

Эта спецификация не охватывает все существующие модели ошибок в переменных. Например, в некоторых из них функция g (⋅) { displaystyle g ( cdot)}может быть непараметрической или полупараметрической. Другие подходы моделируют связь между y ∗ { displaystyle y ^ {*}}и x ∗ { displaystyle x ^ {*}}как распределительную. функционала, то есть они предполагают, что y ∗ { displaystyle y ^ {*}}условно на x ∗ { displaystyle x ^ {*}}следует определенному (обычно параметрическому) распределению.

Терминология и предположения

• Наблюдаемая переменная x { displaystyle x}может называться манифестом, индикатором или прокси-переменной.
• ненаблюдаемой переменной x ∗ { displaystyle x ^ {*}}можно назвать скрытой или истинной переменной. Его можно рассматривать либо как неизвестную константу (в этом случае модель называется функциональной моделью), либо как случайную величину (соответственно структурную модель).
• Связь между погрешностью измерения η { displaystyle eta}и скрытую переменную x ∗ { displaystyle x ^ {*}}можно моделировать разными способами:
  • Классический ошибки: η ⊥ x ∗ { displaystyle eta perp x ^ {*}}ошибки не зависят от скрытой переменной. Это наиболее распространенное допущение, оно подразумевает, что ошибки вносятся измерительным устройством и их величина не зависит от измеряемого значения.
  • Независимость от среднего: E ⁡ [η | x ∗] = 0, { displaystyle operatorname {E} [ eta | x ^ {*}] , = , 0,}ошибки равны нулю в среднем для каждого значения скрытого регрессор. Это менее ограничительное предположение, чем классическое, поскольку оно допускает наличие гетероскедастичности или других эффектов в ошибках измерения.
  • Ошибки Берксона : η ⊥ x, { displaystyle eta , perp , x,}ошибки не зависят от наблюдаемого регрессора x. Это предположение имеет очень ограниченную применимость. Одним из примеров являются ошибки округления: например, если возраст человека * является непрерывной случайной величиной, тогда как наблюдаемый возраст усекается до следующего наименьшего целого числа, тогда ошибка усечения приблизительно не зависит от наблюдаемого возраста.. Другая возможность связана с экспериментом с фиксированным планом: например, если ученый решает провести измерение в определенный заранее определенный момент времени x { displaystyle x}, скажем, при x = 10 s { displaystyle x = 10s}, тогда реальное измерение может произойти при некотором другом значении x ∗ { displaystyle x ^ {*}}(например, из-за к ее конечному времени реакции), и такая ошибка измерения обычно не зависит от «наблюдаемого» значения регрессора.
  • Ошибки неправильной классификации: особый случай, используемый для фиктивных регрессоров. Если x ∗ { displaystyle x ^ {*}}является индикатором определенного события или состояния (например, лицо мужского / женского пола, какое-либо лечение предоставлено / нет и т. Д.), то ошибка измерения в таком регрессоре будет соответствовать неверной классификации, аналогичной ошибкам типа I и типа II при статистическом тестировании. В этом случае ошибка η { displaystyle eta}может принимать только 3 возможных значения, а ее распределение зависит от x ∗ { displaystyle x ^ {*}}моделируется двумя параметрами: α = Pr ⁡ [η = — 1 | x ∗ = 1] { displaystyle alpha = operatorname {Pr} [ eta = -1 | x ^ {*} = 1]}и β = Pr ⁡ [η = 1 | x ∗ = 0] { displaystyle beta = operatorname {Pr} [ eta = 1 | x ^ {*} = 0]}. Необходимым условием идентификации является то, что α + β < 1 {displaystyle alpha +beta <1}, то есть ошибочная классификация не должна происходить «слишком часто». (Эта идея может быть обобщена на дискретные переменные с более чем двумя возможными значениями.)

Линейная модель

Линейные модели ошибок в переменных были изучены первыми, вероятно потому, что были линейные модели так широко используются, и они проще нелинейных. В отличие от стандартной регрессии по методу наименьших квадратов (OLS), расширение ошибок в регрессии переменных (EiV) с простого случая на многомерный не так просто.

Простая линейная модель

Простая линейная модель ошибок в переменных уже была представлена ​​в разделе «мотивация»:

{yt = α + β xt ∗ + ε t, xt знак равно xt * + η t, { displaystyle { begin {cases} y_ {t} = alpha + beta x_ {t} ^ {*} + varepsilon _ {t}, \ x_ {t} = x_ {t} ^ {*} + eta _ {t}, end {cases}}}

где все переменные скалярны. Здесь α и β представляют собой интересующие параметры, тогда как σ ε и σ η — стандартные отклонения членов ошибки — являются мешающими параметрами. «Истинный» регрессор x * рассматривается как случайная величина (структурная модель), не зависящая от ошибки измерения η (классическое предположение).

Эта модель идентифицируема в двух случаях: (1) либо скрытый регрессор x * не нормально распределен, (2) или x * имеет нормальное распределение, но ни ε t, ни η t не делятся на нормальное распределение. То есть параметры α, β можно последовательно оценить на основе набора данных (xt, yt) t = 1 T { displaystyle scriptstyle (x_ {t}, , y_ {t}) _ {t = 1} ^ {T}}без какой-либо дополнительной информации, при условии, что скрытый регрессор не является гауссовским.

Перед тем, как этот результат идентифицируемости был установлен, статистики пытались применить метод максимального правдоподобия, предполагая, что все переменные являются нормальными, а затем пришли к выводу, что модель не идентифицирована. Предлагаемое решение состояло в том, чтобы предположить, что некоторые параметры модели известны или могут быть оценены из внешнего источника. К таким методам оценки относятся

• регрессия Деминга — предполагается, что отношение δ = σ² ε / σ² η известно. Это может быть подходящим, например, когда ошибки в y и x вызваны измерениями, и точность измерительных устройств или процедур известна. Случай, когда δ = 1, также известен как ортогональная регрессия.
• Регрессия с известным коэффициентом надежности λ = σ² ∗ / (σ² η + σ² ∗), где σ² ∗ — дисперсия скрытого регрессора. Такой подход может быть применим, например, когда доступны повторяющиеся измерения одного и того же устройства, или когда коэффициент надежности известен из независимого исследования. В этом случае согласованная оценка наклона равна оценке методом наименьших квадратов, деленной на λ.
• Регрессия с известным σ² η может произойти, если источник ошибок в x известен и их дисперсию можно рассчитать. Это может включать ошибки округления или ошибки, вносимые измерительным устройством. Когда известно σ² η, мы можем вычислить коэффициент надежности как λ = (σ² x — σ² η) / σ² x и уменьшить проблема с предыдущим случаем.

Более новые методы оценки, которые не предполагают знания некоторых параметров модели, включают

• Метод моментов — оценку GMM на основе третьего — ( или соединение более высокого порядка кумулянтов наблюдаемых переменных. Коэффициент наклона можно оценить по формуле

  β ^ = K ^ (n 1, n 2 + 1) K ^ (n 1 + 1, n 2), n 1, n 2>0, { displaystyle { hat { beta}} = { frac {{ hat {K}} (n_ {1}, n_ {2} +1)} {{ hat {K}} (n_ {1} + 1, n_ {2 })}}, quad n_ {1}, n_ {2}>0,}

  где (n 1,n2) такие, что K (n 1 + 1, n 2) — совместный кумулянт из (x, y) — не равен нулю. В случае, когда третий центральный момент скрытого регрессора x * не равен нулю, формула сводится к

  β ^ = 1 T ∑ T = 1 T (xt — x ¯) (yt — y ¯) 2 1 T ∑ t = 1 T (xt — x ¯) 2 (yt — y ¯). { displaystyle { hat { beta}} = { frac {{ tfrac {1} {T}} sum _ {t = 1} ^ {T} (x_ {t} — { bar {x}}) (y_ { t} — { bar {y}}) ^ {2}} {{ tfrac {1} {T}} sum _ {t = 1} ^ {T} (x_ {t} — { bar {x }}) ^ {2} (y_ {t} — { bar {y}})}} .}

• Инструментальные переменные — регрессия, требующая некоторых дополнительных переменных данных z, назывались инструменты, были в наличии. Эти переменные не должны быть коррелированы с ошибками в уравнении для зависимой переменной (действительны), и они также должны быть коррелированы (релевантны) с истинными регрессорами x *. Если такие переменные могут быть найдены, то оценка принимает вид
  β ^ = 1 T ∑ t = 1 T (zt — z ¯) (yt — y ¯) 1 T ∑ t = 1 T (zt — z ¯) (xt — x ¯). { displaystyle { hat { beta}} = { frac {{ tfrac {1} {T}} sum _ {t = 1} ^ {T} (z_ {t} — { bar {z}) }) (y_ {t} — { bar {y}})} {{ tfrac {1} {T}} sum _ {t = 1} ^ {T} (z_ {t} — { bar { z}}) (x_ {t} — { bar {x}})}} .}

Многопараметрическая линейная модель

Многопараметрическая модель выглядит точно так же, как простая линейная модель, только на этот раз β, η t, x t и x * t являются векторами k × 1.

{y t = α + β ′ x t ∗ + ε t, x t = x t ∗ + η t. { displaystyle { begin {case} y_ {t} = alpha + beta ‘x_ {t} ^ {*} + varepsilon _ {t}, \ x_ {t} = x_ {t} ^ {* } + eta _ {t}. end {cases}}}

В случае, когда (ε t,ηt) совместно нормально, параметр β не идентифицируется тогда и только тогда, когда существует неособое k Блочная матрица × k [a A] (где a — вектор k × 1) такая, что a′x * распределяется нормально и независимо от A′x *. В случае, когда ε t, η t1,…, η tk являются взаимно независимыми, параметр β не идентифицируется тогда и только тогда, когда дополнительно В приведенных выше условиях некоторые ошибки могут быть записаны как сумма двух независимых переменных, одна из которых является нормальной.

Некоторые из методов оценки для многомерных линейных моделей:

• Всего наименьших квадратов равно расширение регрессии Деминга на многопараметрическую настройку. Когда все k + 1 компоненты вектора (ε, η) имеют равные дисперсии и независимы, это эквивалентно запуску ортогональной регрессии y по вектору x, то есть регрессии, которая минимизирует сумму квадратов расстояний между точек (y t,xt) и k-мерной гиперплоскости «наилучшего соответствия».
• Оценка метода моментов может быть построена на основе моментных условий E [z t · (y t — α — β’x t)] = 0, где (5k + 3) -мерный вектор инструментов z t определяется как

  zt = (1 zt 1 ′ zt 2 ′ zt 3 ′ zt 4 ′ zt 5 ′ zt 6 ′ zt 7 ′) ′, где zt 1 = xt ∘ xtzt 2 = xtytzt 3 = yt 2 zt 4 = xt ∘ xt ∘ xt — 3 (E ⁡ [xtxt ′] ∘ I k) xtzt 5 = xt ∘ xtyt — 2 (E ⁡ [ytxt ′] ∘ I k) xt — yt (E ⁡ [xtxt ′] ∘ I k) ι kzt 6 = xtyt 2 — E ⁡ [yt 2] xt — 2 yt E ⁡ [xtyt] zt 7 = yt 3 — 3 yt E ⁡ [yt 2] { displaystyle { begin {align} z_ {t} = left (1 z_ {t1} ‘ z_ {t2}’ z_ {t3} ‘ z_ { t4} ‘ z_ {t5}’ z_ {t6} ‘ z_ {t7}’ right) ‘, quad { text {where}} \ z_ {t1} = x_ {t} circ x_ { t} \ z_ {t2} = x_ {t} y_ {t} \ z_ {t3} = y_ {t} ^ {2} \ z_ {t4} = x_ {t} circ x_ {t} circ x_ {t} -3 { big (} operatorname {E} [x_ {t} x_ {t} ‘] circ I_ {k} { big)} x_ {t} \ z_ {t5} = x_ {t} circ x_ {t} y_ {t} -2 { big (} operatorname {E} [y_ {t} x_ {t} ‘] circ I_ {k} { big)} x_ { t} -y_ {t} { big (} operatorname {E} [x_ {t} x_ {t} ‘] circ I_ {k} { big)} iota _ {k} \ z_ {t6 } = x_ {t} y_ {t} ^ {2} — operatorname {E} [y_ {t} ^ {2}] x_ {t} -2y_ {t} operatorname {E} [x_ {t} y_ {t}] \ z_ {t7} = y_ {t} ^ {3} -3y_ {t} operatorname {E} [y_ {t} ^ {2}] end {align}}}

  где ∘ { displaystyle circ}обозначает произведение Адамара матриц, а переменные x t, y t были предварительно лишенный смысла. Авторы метода предлагают использовать модифицированную оценку IV Фуллера..

  Этот метод может быть расширен для использования моментов выше третьего порядка, если необходимо, и для учета переменных, измеренных без ошибок.

• Подход инструментальных переменных требует поиска дополнительных переменных данных z t, которые будут служить инструментами для неверно измеренных регрессоров x t. Этот метод является наиболее простым с точки зрения реализации, однако его недостаток в том, что он требует сбора дополнительных данных, что может быть дорогостоящим или даже невозможным. Когда инструменты найдены, оценщик принимает стандартную форму

  β ^ = (X ′ Z (Z ′ Z) — 1 Z ′ X) — 1 X ′ Z (Z ′ Z) — 1 Z ′ y. { displaystyle { hat { beta}} = { big (} X’Z (Z’Z) ^ {- 1} Z’X { big)} ^ {- 1} X’Z (Z’Z) ^ {- 1} Z’y.}

Нелинейные модели

Общая модель нелинейных ошибок измерения принимает вид

{yt = g (xt ∗) + ε t, xt = xt ∗ + η t. { displaystyle { begin {cases} y_ {t} = g (x_ {t} ^ {*}) + varepsilon _ {t}, \ x_ {t} = x_ {t} ^ {*} + eta _ {t}. end {ases}}}

Здесь функция g может быть параметрической или непараметрической. Если функция g параметрическая, она будет записана как g (x *, β).

Для общего векторного регрессора x * условия для модели идентифицируемости неизвестны. Однако в случае скаляра x * модель идентифицируется, если функция g не имеет «логарифмически экспоненциальную» форму

g (x ∗) = a + b ln ⁡ (ecx ∗ + d) { displaystyle g ( x ^ {*}) = a + b ln { big (} e ^ {cx ^ {*}} + d { big)}}

и скрытый регрессор x * имеет плотность

fx ∗ (Икс) = {А е — В е С Икс + CD Икс (е С Икс + Е) — F, если d>0, А е — В х 2 + С х, если d = 0 { displaystyle f_ {x ^ { *}} (x) = { begin {cases} Ae ^ {- Be ^ {Cx} + CDx} (e ^ {Cx} + E) ^ {- F}, { text {if}} d>0 \ Ae ^ {- Bx ^ {2} + Cx} { text {if}} d = 0 end {cases}}}

где константы A, B, C, D, E, F могут зависеть от a, b, c, d.

Несмотря на этот оптимистичный результат, на данный момент не существует методов оценки нелинейных моделей ошибок в переменных без какой-либо посторонней информации. Однако существует несколько методов, которые используют некоторые дополнительные данные: r инструментальные переменные или повторные наблюдения.

Методы инструментальных переменных

• Метод моделирования моментов Ньюи для параметрических моделей — требует наличия дополнительного набора наблюдаемых переменных-предикторов z t, так что истинный регрессор может быть выражается как

  xt ∗ = π 0 ′ zt + σ 0 ζ t, { displaystyle x_ {t} ^ {*} = pi _ {0} ‘z_ {t} + sigma _ {0} zeta _ {t},}

  где π 0 и σ 0 — (неизвестные) постоянные матрицы, а ζ t ⊥ z t. Коэффициент π 0 можно оценить с помощью стандартной наименьших квадратов регрессии x по z. Распределение ζ t неизвестно, однако мы можем смоделировать его как принадлежащее к гибкому параметрическому семейству — ряду Эджворта :

  f ζ (v; γ) = ϕ (v) ∑ j Знак равно 1 J γ jvj { displaystyle f _ { zeta} (v; , gamma) = phi (v) , textstyle sum _ {j = 1} ^ {J} ! Gamma _ {j } v ^ {j}}

  где ϕ — стандартное нормальное распределение.

  Смоделированные моменты могут быть рассчитаны с использованием алгоритма выборки по важности : сначала мы генерируем несколько случайных величин {v ts ~ ϕ, s = 1,…, S, t = 1,…, T} из стандартного нормального распределения, тогда мы вычисляем моменты в t-м наблюдении как

  mt (θ) = A (zt) 1 S ∑ s = 1 SH (xt, yt, zt, vts; θ) ∑ J знак равно 1 J γ jvtsj, { displaystyle m_ {t} ( theta) = A (z_ {t}) { frac {1} {S}} sum _ {s = 1} ^ {S} H (x_ {t}, y_ {t}, z_ {t}, v_ {ts}; theta) sum _ {j = 1} ^ {J} ! Gamma _ {j} v_ { ts} ^ {j},}

  где θ = (β, σ, γ), A — просто некоторая функция инструментальных переменных z, а H — двухкомпонентный вектор моментов

  H 1 (xt, yt, zt, vts; θ) = yt — g (π ^ ′ zt + σ vts, β), H 2 (xt, yt, zt, vts; θ) = ztyt — (π ^ ′ zt + σ vts) g (π ^ ′ zt + σ vts, β) { displaystyle { begin {выровнено} H_ {1} (x_ {t}, y_ {t}, z_ {t}, v_ {ts}; theta) = y_ {t} -g ({ hat { pi}} ‘z_ {t} + sigma v_ {ts}, beta), \ H_ {2} (x_ {t}, y_ {t}, z_ {t}, v_ {ts}; theta) = z_ {t} y_ {t} — ({ hat { pi}} ‘z_ {t} + sigma v_ {ts}) g ({ hat { pi}}’ z_ {t} + sigma v_ {ts}, beta) end {выровнено}} }

  С помощью моментных функций m t можно применить стандартный метод GMM для оценки неизвестного параметра θ.

Повторные наблюдения

В этом подходе два ( или, может быть, больше) доступны повторные наблюдения регрессора x *. Оба наблюдения содержат собственные ошибки измерения, однако эти ошибки должны быть независимыми:

{x 1 t = xt ∗ + η 1 t, x 2 t = xt ∗ + η 2 t, { displaystyle { begin { case} x_ {1t} = x_ {t} ^ {*} + eta _ {1t}, \ x_ {2t} = x_ {t} ^ {*} + eta _ {2t}, end {случаи }}}

где x * ⊥ η 1 ⊥ η 2. Переменные η 1, η 2 не обязательно должны быть одинаково распределены (хотя, если они являются эффективностью средства оценки, можно немного улучшить). С помощью только этих двух наблюдений можно согласованно оценить функцию плотности x *, используя метод Котлярского деконволюции.

• Метод условной плотности Ли для параметрических моделей. Уравнение регрессии может быть записано в терминах наблюдаемых переменных как

  E ⁡ [y t | x t] = ∫ g (x t ∗, β) f x ∗ | Икс (xt * | xt) dxt *, { displaystyle Operatorname {E} [, y_ {t} | x_ {t} ,] = int g (x_ {t} ^ {*}, beta) f_ {x ^ {*} | x} (x_ {t} ^ {*} | x_ {t}) dx_ {t} ^ {*},}

  где можно было бы вычислить интеграл, если бы мы знали функция условной плотности ƒ x * | x ​​. Если эта функция может быть известна или оценена, тогда проблема превращается в стандартную нелинейную регрессию, которую можно оценить, например, с помощью метода NLLS.. Предположим для простоты, что η 1, η 2 одинаково распределены, эта условная плотность может быть вычислена как

  f ^ x ∗ | Икс (Икс * | Икс) знак равно е ^ Икс * (Икс *) е ^ Икс (Икс) ∏ J = 1 КФ ^ η J (xj — xj *), { Displaystyle { Hat {f}} _ {х ^ {*} | x} (x ^ {*} | x) = { frac {{ hat {f}} _ {x ^ {*}} (x ^ {*})} {{ hat {f }} _ {x} (x)}} prod _ {j = 1} ^ {k} { hat {f}} _ { eta _ {j}} { big (} x_ {j} -x_ {j} ^ {*} { big)},}

  где с небольшим злоупотреблением обозначениями x j обозначает j-й компонент вектора.. Все плотности в этой формуле могут можно оценить с помощью обращения эмпирических характеристических функций. В частности,

  φ ^ η j (v) = φ ^ xj (v, 0) φ ^ xj ∗ (v), где φ ^ xj (v 1, v 2) = 1 T ∑ t = 1 T eiv 1 x 1 tj + iv 2 x 2 tj, φ ^ xj ∗ (v) = exp ⁡ ∫ 0 v ∂ φ ^ xj (0, v 2) / ∂ v 1 φ ^ xj (0, v 2) dv 2, φ ^ x (u) = 1 2 T ∑ t = 1 T (eiu ′ x 1 t + eiu ′ x 2 t), φ ^ x ∗ (u) = φ ^ x (u) ∏ j = 1 k φ ^ η j (uj). { displaystyle { begin {align} { hat { varphi}} _ { eta _ {j}} (v) = { frac {{ hat { varphi}} _ {x_ {j}} (v, 0)} {{ hat { varphi}} _ {x_ {j} ^ {*}} (v)}}, quad { text {where}} { hat { varphi}} _ {x_ {j}} (v_ {1}, v_ {2}) = { frac {1} {T}} sum _ {t = 1} ^ {T} e ^ {iv_ {1} x_ {1tj } + iv_ {2} x_ {2tj}}, \ { hat { varphi}} _ {x_ {j} ^ {*}} (v) = exp int _ {0} ^ {v} { frac { partial { hat { varphi}} _ {x_ {j}} (0, v_ {2}) / partial v_ {1}} {{ hat { varphi}} _ {x_ {j }} (0, v_ {2})}} dv_ {2}, \ { hat { varphi}} _ {x} (u) = { frac {1} {2T}} sum _ { t = 1} ^ {T} { Big (} e ^ {iu’x_ {1t}} + e ^ {iu’x_ {2t}} { Big)}, quad { hat { varphi}} _ {x ^ {*}} (u) = { frac {{ hat { varphi}} _ {x} (u)} { prod _ {j = 1} ^ {k} { hat { varphi}} _ { eta _ {j}} (u_ {j})}}. end {align}}}

  Чтобы инвертировать эту характеристическую функцию, нужно применить обратное преобразование Фурье с обрезкой параметр C необходим для обеспечения числовой устойчивости. Например:

  f ^ x (x) = 1 (2 π) k ∫ — C C ⋯ ∫ — C C e — i u ′ x φ ^ x (u) d u. { displaystyle { hat {f}} _ {x} (x) = { frac {1} {(2 pi) ^ {k}}} int _ {- C} ^ {C} cdots int _ {- C} ^ {C} e ^ {- iu’x} { hat { varphi}} _ {x} (u) du.}

• Оценка Шеннаха для параметрического линейного входа -параметрическая нелинейная модель в переменных. Это модель вида
  {yt = ∑ j = 1 k β jgj (xt ∗) + ∑ j = 1 ℓ β k + jwjt + ε t, x 1 t = xt ∗ + η 1 T, Икс 2 T знак равно XT * + η 2 T, { Displaystyle { begin {case} Y_ {t} = textstyle sum _ {j = 1} ^ {k} beta _ {j} g_ {j } (x_ {t} ^ {*}) + sum _ {j = 1} ^ { ell} beta _ {k + j} w_ {jt} + varepsilon _ {t}, \ x_ {1t } = x_ {t} ^ {*} + eta _ {1t}, \ x_ {2t} = x_ {t} ^ {*} + eta _ {2t}, end {cases}}}

  где w t представляет переменные, измеренные без ошибок. Регрессор x * здесь является скалярным (метод может быть расширен и на случай вектора x *).. Если бы не ошибки измерения, это была бы стандартная линейная модель с оценка

  β ^ = (E ^ [ξ t ξ t ′]) — 1 E ^ [ξ tyt], { displaystyle { hat { beta}} = { big (} { hat { operatorname {E}}} [, xi _ {t} xi _ {t} ‘,] { big)} ^ {- 1} { hat { operatorname {E}}} [, xi _ {t} y_ {t} ,],}

  где

  ξ t ′ = (g 1 (xt ∗), ⋯, gk (xt ∗), w 1, t, ⋯, wl, t). { displaystyle xi _ {t} ‘= (g_ {1} (x_ {t} ^ {*}), cdots, g_ {k} (x_ {t} ^ {*}), w_ {1, t }, cdots, w_ {l, t}).}

  Оказывается, все ожидаемые значения в этой формуле можно оценить с помощью того же трюка с деконволюцией. В частности, для типичной наблюдаемой w t (которая может быть 1, w 1t,…, w ℓ t или y t) и некоторой функции h (которая может представлять любые g j или g igj) имеем

  E ⁡ [wth (xt ∗)] = 1 2 π ∫ — ∞ ∞ φ h ( — и) ψ вес (и) ду, { Displaystyle OperatorName {E} [, w_ {t} h (x_ {t} ^ {*}) ,] = { гидроразрыва {1} {2 pi }} int _ {- infty} ^ { infty} varphi _ {h} (- u) psi _ {w} (u) du,}

  где φ h — преобразование Фурье h (x *), но с использованием того же соглашения, что и для характеристических функций,

  φ h (u) = ∫ eiuxh (x) dx { displaystyle varphi _ {h} (u) = int e ^ {iux} h (x) dx},

  и

  ψ w (u) = E ⁡ [wteiux ∗] = E ⁡ [wteiux 1 t] E ⁡ [ eiux 1 t] ехр ⁡ ∫ 0 ui E ⁡ [x 2 teivx 1 t] E ⁡ [eivx 1 t] dv { displaystyle psi _ {w} (u) = operatorname {E} [, w_ {t } e ^ {iux ^ {*}} ,] = { frac { operatorname {E} [w_ {t} e ^ {iux_ {1t}}]} { operatorname {E} [e ^ {iux_ { 1t}}]}} exp int _ {0} ^ {u} i { frac { operatorname {E} [x_ {2t} e ^ {ivx_ {1t}}]} { operatorname {E} [e ^ {ivx_ {1t}}]}} dv}

  Результирующая оценка β ^ { displaystyle scriptstyle { hat { beta}}}согласован и асимптотически нормален.

• Оценка Шеннаха для непараметрической модели. Стандартная оценка Надарая – Ватсона для непараметрической модели принимает вид

  g ^ (x) = E ^ [yt K h (xt ∗ — x)] E ^ [K h (xt ∗ — x)], { displaystyle { hat {g}} (x) = { frac {{ hat { operatorname {E}}} [, y_ {t} K_ {h} (x_ {t} ^ { *} — x) ,]} {{ hat { operatorname {E}}} [, K_ {h} (x_ {t} ^ {*} — x) ,]}},}

  для подходящего выбора ядра K и пропускной способности h. Оба ожидания здесь можно оценить с помощью того же метода, что и в предыдущем методе.

Ссылки

Дополнительная литература

• Dougherty, Christopher (2011). «Стохастические регрессоры и ошибки измерения». Введение в эконометрику (Четвертое изд.). Издательство Оксфордского университета. С. 300–330. ISBN 978-0-19-956708-9 .
• Кмента, янв (1986). «Оценка с недостаточными данными». Элементы эконометрики (Второе изд.). Нью-Йорк: Макмиллан. С. 346–391. ISBN 978-0-02-365070-3 .
• Шеннах, Сюзанна. «Погрешность измерения в нелинейных моделях — обзор». Серия рабочих документов Cemmap. Cemmap. Получено 6 февраля 2018 г.

Внешние ссылки

• Исторический обзор линейной регрессии с ошибками в обеих переменных, J.W. Гиллард 2006
• Лекция по эконометрике (тема: Стохастические регрессоры и ошибка измерения) на YouTube, автор Марк Тома.

4. 
Использование
предварительной информации о значениях некоторых параметров. Иногда значения некоторых неизвестных параметров
модели могут быть определены по пробным выборочным наблюдениям, тогда
мультиколлинеарность может быть устранена путем установления значений параметра
у одной коррелирующих переменных. Ограниченность метода – в сложности получения
предварительных значений параметров с высокой точностью.

5. 
Преобразование переменных. Для устранения мультиколлинеарности можно
преобразовать переменные, например, путем линеаризации или получения
относительных показателей, а также перехода от номинальных к реальным
показателям (особенно в макроэкономических исследованиях).

При построении модели множественной регрессии с точки
зрения обеспечения ее высокого качества возникают следующие вопросы:

1. 
Каковы признаки качественной
модели?

2. 
Какие ошибки спецификации могут
быть?

3. 
Каковы последствия ошибок
спецификации?

4. 
Какие существуют методы
обнаружения и устранения ошибок спецификации?

Рассмотрим основные признаки качественной модели
множественной регрессии:

1. 
Простота. Из двух моделей примерно одинаковых статистических
свойств более качественной является та, которая содержит меньше переменных, или
же более простая по аналитической форме.

2. 
Однозначность. Метод вычисления коэффициентов должен быть одинаков
для любых наборов данных.

3. 
Максимальное соответствие. Этот признак говорит о том, что основным критерием
качества модели является коэффициент детерминации, отражающий объясненную
моделью вариацию зависимой переменной. Для практического использования выбирают
модель, для которой расчетное значение F-критерия для
коэффициента детерминации б четыре раза больше табличного.

4. 
Согласованность с теорией. Получаемые значения коэффициентов должны быть
интерпретируемы с точки зрения экономических явлений и процессов. К примеру,
если строится линейная регрессионная модель спроса на товар, то соответствующий
коэффициент при цене товара должен быть отрицательным.

5. 
Хорошие прогнозные качества.
Обязательным условием построения
качественной модели является возможность ее использования для прогнозирования.

Одной из основных ошибок, допускаемых при построении
регрессионной модели, является ошибка спецификации (рис. 4.3).
Под ошибкой спецификации понимается неправильный выбор функциональной формы
модели или набора объясняющих переменных.

Различают следующие виды ошибок спецификации:

1. 
Невключение в модель полезной
(значимой) переменной.

2. 
Добавление в модель лишней
(незначимой) переменной

3. 
Выбор неправильной функциональной
формы модели

Последствия ошибки первого вида (невключение в
модель значимой переменной) заключаются в том, что полученные по МНК оценки
параметров являются смещенными и несостоятельными, а значение коэффициента
детерминации значительно снижаются.

При добавлении в модель лишней переменной
(ошибка второго вида) ухудшаются статистические свойства оценок
коэффициентов, возрастают их дисперсии, что ухудшает прогнозные качества модели
и затрудняет содержательную интерпретацию параметров, однако по сравнению с
другими ошибками ее последствия менее серьезны.

Если же осуществлен неверный выбор
функциональной формы модели, то есть допущена ошибка третьего вида, то
получаемые оценки будут смещенными, качество модели в целом и отдельных
коэффициентов будет невысоким. Это может существенно сказаться на прогнозных
качествах модели.

Ошибки спецификации первого вида можно обнаружить только
по невысокому качеству модели, низким значениям R².

Обнаружение ошибок спецификации второго вида, если лишней
является только одна переменная, осуществляется на основе расчета t — статистики для коэффициентов. При лишней переменной коэффициент
будет статистически незначим.

Рис. 4.3 Ошибки спецификации и свойства качественной
регрессионной модели

«Хорошая» аналитическая модель должна удовлетворять двум, зачастую противоречивым, требованиям — как можно лучше соответствовать данным и при этом быть удобной для интерпретации пользователем. Действительно, повышение соответствия модели данным как правило связано с её усложнением (в случае регрессии — увеличением числа входных переменных модели). А чем сложнее модель, тем ниже её интерпретируемость.

Поэтому при выборе между простой и сложной моделью последняя должна значимо увеличивать соответствие модели данным чтобы оправдать рост сложности и соответствующее снижение интерпретируемости. Если это условие не выполняется, то следует выбрать более простую модель.

Таким образом, чтобы оценить, насколько повышение сложности модели значимо увеличивает её точность, необходимо использовать аппарат оценки качества регрессионных моделей. Он включает в себя следующие меры:

• Среднеквадратичная ошибка (MSE).
• Корень из среднеквадратичной ошибки (RMSE).
• Среднеквадратичная ошибка в процентах (MSPE).
• Средняя абсолютная ошибка (MAE).
• Средняя абсолютная ошибка в процентах (MAPE).
• Cимметричная средняя абсолютная процентная ошибка (SMAPE).
• Средняя абсолютная масштабированная ошибка (MASE)
• Средняя относительная ошибка (MRE).
• Среднеквадратичная логарифмическая ошибка (RMSLE).
• Коэффициент детерминации R-квадрат.
• Скорректированный коэффициент детеминации.

Прежде чем перейти к изучению метрик качества, введём некоторые базовые понятия, которые нам в этом помогут. Для этого рассмотрим рисунок.

Наклонная прямая представляет собой линию регрессии с переменной, на которой расположены точки, соответствующие предсказанным значениям выходной переменной widehat{y} (кружки синего цвета). Оранжевые кружки представляют фактические (наблюдаемые) значения y . Расстояния между ними и линией регрессии — это ошибка предсказания модели y-widehat{y} (невязка, остатки). Именно с её использованием вычисляются все приведённые в статье меры качества.

Горизонтальная линия представляет собой модель простого среднего, где коэффициент при независимой переменной x равен нулю, и остаётся только свободный член b, который становится равным среднему арифметическому фактических значений выходной переменной, т.е. b=overline{y}. Очевидно, что такая модель для любого значения входной переменной будет выдавать одно и то же значение выходной — overline{y}.

В линейной регрессии такая модель рассматривается как «бесполезная», хуже которой работает только «случайный угадыватель». Однако, она используется для оценки, насколько дисперсия фактических значений y относительно линии среднего, больше, чем относительно линии регрессии с переменной, т.е. насколько модель с переменной лучше «бесполезной».

MSE

Среднеквадратичная ошибка (Mean Squared Error) применяется в случаях, когда требуется подчеркнуть большие ошибки и выбрать модель, которая дает меньше именно больших ошибок. Большие значения ошибок становятся заметнее за счет квадратичной зависимости.

Действительно, допустим модель допустила на двух примерах ошибки 5 и 10. В абсолютном выражении они отличаются в два раза, но если их возвести в квадрат, получив 25 и 100 соответственно, то отличие будет уже в четыре раза. Таким образом модель, которая обеспечивает меньшее значение MSE допускает меньше именно больших ошибок.

MSE рассчитывается по формуле:

MSE=frac{1}{n}sumlimits_{i=1}^{n}(y_{i}-widehat{y}_{i})^{2},

где n — количество наблюдений по которым строится модель и количество прогнозов, y_{i} — фактические значение зависимой переменной для i-го наблюдения, widehat{y}_{i} — значение зависимой переменной, предсказанное моделью.

Таким образом, можно сделать вывод, что MSE настроена на отражение влияния именно больших ошибок на качество модели.

Недостатком использования MSE является то, что если на одном или нескольких неудачных примерах, возможно, содержащих аномальные значения будет допущена значительная ошибка, то возведение в квадрат приведёт к ложному выводу, что вся модель работает плохо. С другой стороны, если модель даст небольшие ошибки на большом числе примеров, то может возникнуть обратный эффект — недооценка слабости модели.

RMSE

Корень из среднеквадратичной ошибки (Root Mean Squared Error) вычисляется просто как квадратный корень из MSE:

RMSE=sqrt{frac{1}{n}sumlimits_{i=1}^{n}(y_{i}-widehat{y_{i}})^{2}}

MSE и RMSE могут минимизироваться с помощью одного и того же функционала, поскольку квадратный корень является неубывающей функцией. Например, если у нас есть два набора результатов работы модели, A и B, и MSE для A больше, чем MSE для B, то мы можем быть уверены, что RMSE для A больше RMSE для B. Справедливо и обратное: если MSE(A)<MSE(B), то и RMSE(A)<RMSE(B).

Следовательно, сравнение моделей с помощью RMSE даст такой же результат, что и для MSE. Однако с MSE работать несколько проще, поэтому она более популярна у аналитиков. Кроме этого, имеется небольшая разница между этими двумя ошибками при оптимизации с использованием градиента:

frac{partial RMSE}{partial widehat{y}_{i}}=frac{1}{2sqrt{MSE}}frac{partial MSE}{partial widehat{y}_{i}}

Это означает, что перемещение по градиенту MSE эквивалентно перемещению по градиенту RMSE, но с другой скоростью, и скорость зависит от самой оценки MSE. Таким образом, хотя RMSE и MSE близки с точки зрения оценки моделей, они не являются взаимозаменяемыми при использовании градиента для оптимизации.

Влияние каждой ошибки на RMSE пропорционально величине квадрата ошибки. Поэтому большие ошибки оказывают непропорционально большое влияние на RMSE. Следовательно, RMSE можно считать чувствительной к аномальным значениям.

MSPE

Среднеквадратичная ошибка в процентах (Mean Squared Percentage Error) представляет собой относительную ошибку, где разность между наблюдаемым и фактическим значениями делится на наблюдаемое значение и выражается в процентах:

MSPE=frac{100}{n}sumlimits_{i=1}^{n}left ( frac{y_{i}-widehat{y}_{i}}{y_{i}} right )^{2}

Проблемой при использовании MSPE является то, что, если наблюдаемое значение выходной переменной равно 0, значение ошибки становится неопределённым.

MSPE можно рассматривать как взвешенную версию MSE, где вес обратно пропорционален квадрату наблюдаемого значения. Таким образом, при возрастании наблюдаемых значений ошибка имеет тенденцию уменьшаться.

MAE

Cредняя абсолютная ошибка (Mean Absolute Error) вычисляется следующим образом:

MAE=frac{1}{n}sumlimits_{i=1}^{n}left | y_{i}-widehat{y}_{i} right |

Т.е. MAE рассчитывается как среднее абсолютных разностей между наблюдаемым и предсказанным значениями. В отличие от MSE и RMSE она является линейной оценкой, а это значит, что все ошибки в среднем взвешены одинаково. Например, разница между 0 и 10 будет вдвое больше разницы между 0 и 5. Для MSE и RMSE, как отмечено выше, это не так.

Поэтому MAE широко используется, например, в финансовой сфере, где ошибка в 10 долларов должна интерпретироваться как в два раза худшая, чем ошибка в 5 долларов.

MAPE

Средняя абсолютная процентная ошибка (Mean Absolute Percentage Error) вычисляется следующим образом:

MAPE=frac{100}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y_{i}} right |}{left | y_{i} right |}

Эта ошибка не имеет размерности и очень проста в интерпретации. Её можно выражать как в долях, так и в процентах. Если получилось, например, что MAPE=11.4, то это говорит о том, что ошибка составила 11.4% от фактического значения.

SMAPE

Cимметричная средняя абсолютная процентная ошибка (Symmetric Mean Absolute Percentage Error) — это мера точности, основанная на процентных (или относительных) ошибках. Обычно определяется следующим образом:

SMAPE=frac{100}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y_{i}} right |}{(left | y_{i} right |+left | widehat{y}_{i} right |)/2}

Т.е. абсолютная разность между наблюдаемым и предсказанным значениями делится на полусумму их модулей. В отличие от обычной MAPE, симметричная имеет ограничение на диапазон значений. В приведённой формуле он составляет от 0 до 200%. Однако, поскольку диапазон от 0 до 100% гораздо удобнее интерпретировать, часто используют формулу, где отсутствует деление знаменателя на 2.

Одной из возможных проблем SMAPE является неполная симметрия, поскольку в разных диапазонах ошибка вычисляется неодинаково. Это иллюстрируется следующим примером: если y_{i}=100 и widehat{y}_{i}=110, то SMAPE=4.76, а если y_{i}=100 и widehat{y}_{i}=90, то SMAPE=5.26.

Ограничение SMAPE заключается в том, что, если наблюдаемое или предсказанное значение равно 0, ошибка резко возрастет до верхнего предела (200% или 100%).

MASE

Средняя абсолютная масштабированная ошибка (Mean absolute scaled error) — это показатель, который позволяет сравнивать две модели. Если поместить MAE для новой модели в числитель, а MAE для исходной модели в знаменатель, то полученное отношение и будет равно MASE. Если значение MASE меньше 1, то новая модель работает лучше, если MASE равно 1, то модели работают одинаково, а если значение MASE больше 1, то исходная модель работает лучше, чем новая модель. Формула для расчета MASE имеет вид:

MASE=frac{MAE_{i}}{MAE_{j}}

MASE симметрична и устойчива к выбросам.

MRE

Средняя относительная ошибка (Mean Relative Error) вычисляется по формуле:

MRE=frac{1}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y}_{i}right |}{left | y_{i} right |}

Несложно увидеть, что данная мера показывает величину абсолютной ошибки относительно фактического значения выходной переменной (поэтому иногда эту ошибку называют также средней относительной абсолютной ошибкой, MRAE). Действительно, если значение абсолютной ошибки, скажем, равно 10, то сложно сказать много это или мало. Например, относительно значения выходной переменной, равного 20, это составляет 50%, что достаточно много. Однако относительно значения выходной переменной, равного 100, это будет уже 10%, что является вполне нормальным результатом.

Очевидно, что при вычислении MRE нельзя применять наблюдения, в которых y_{i}=0.

Таким образом, MRE позволяет более адекватно оценить величину ошибки, чем абсолютные ошибки. Кроме этого она является безразмерной величиной, что упрощает интерпретацию.

RMSLE

Среднеквадратичная логарифмическая ошибка (Root Mean Squared Logarithmic Error) представляет собой RMSE, вычисленную в логарифмическом масштабе:

RMSLE=sqrt{frac{1}{n}sumlimits_{i=1}^{n}(log(widehat{y}_{i}+1)-log{(y_{i}+1}))^{2}}

Константы, равные 1, добавляемые в скобках, необходимы чтобы не допустить обращения в 0 выражения под логарифмом, поскольку логарифм нуля не существует.

Известно, что логарифмирование приводит к сжатию исходного диапазона изменения значений переменной. Поэтому применение RMSLE целесообразно, если предсказанное и фактическое значения выходной переменной различаются на порядок и больше.

R-квадрат

Перечисленные выше ошибки не так просто интерпретировать. Действительно, просто зная значение средней абсолютной ошибки, скажем, равное 10, мы сразу не можем сказать хорошая это ошибка или плохая, и что нужно сделать чтобы улучшить модель.

В этой связи представляет интерес использование для оценки качества регрессионной модели не значения ошибок, а величину показывающую, насколько данная модель работает лучше, чем модель, в которой присутствует только константа, а входные переменные отсутствуют или коэффициенты регрессии при них равны нулю.

Именно такой мерой и является коэффициент детерминации (Coefficient of determination), который показывает долю дисперсии зависимой переменной, объяснённой с помощью регрессионной модели. Наиболее общей формулой для вычисления коэффициента детерминации является следующая:

R^{2}=1-frac{sumlimits_{i=1}^{n}(widehat{y}_{i}-y_{i})^{2}}{sumlimits_{i=1}^{n}({overline{y}}_{i}-y_{i})^{2}}

Практически, в числителе данного выражения стоит среднеквадратическая ошибка оцениваемой модели, а в знаменателе — модели, в которой присутствует только константа.

Главным преимуществом коэффициента детерминации перед мерами, основанными на ошибках, является его инвариантность к масштабу данных. Кроме того, он всегда изменяется в диапазоне от −∞ до 1. При этом значения близкие к 1 указывают на высокую степень соответствия модели данным. Очевидно, что это имеет место, когда отношение в формуле стремится к 0, т.е. ошибка модели с переменными намного меньше ошибки модели с константой. R^{2}=0 показывает, что между независимой и зависимой переменными модели имеет место функциональная зависимость.

Когда значение коэффициента близко к 0 (т.е. ошибка модели с переменными примерно равна ошибке модели только с константой), это указывает на низкое соответствие модели данным, когда модель с переменными работает не лучше модели с константой.

Кроме этого, бывают ситуации, когда коэффициент R^{2} принимает отрицательные значения (обычно небольшие). Это произойдёт, если ошибка модели среднего становится меньше ошибки модели с переменной. В этом случае оказывается, что добавление в модель с константой некоторой переменной только ухудшает её (т.е. регрессионная модель с переменной работает хуже, чем предсказание с помощью простой средней).

На практике используют следующую шкалу оценок. Модель, для которой R^{2}>0.5, является удовлетворительной. Если R^{2}>0.8, то модель рассматривается как очень хорошая. Значения, меньшие 0.5 говорят о том, что модель плохая.

Скорректированный R-квадрат

Основной проблемой при использовании коэффициента детерминации является то, что он увеличивается (или, по крайней мере, не уменьшается) при добавлении в модель новых переменных, даже если эти переменные никак не связаны с зависимой переменной.

В связи с этим возникают две проблемы. Первая заключается в том, что не все переменные, добавляемые в модель, могут значимо увеличивать её точность, но при этом всегда увеличивают её сложность. Вторая проблема — с помощью коэффициента детерминации нельзя сравнивать модели с разным числом переменных. Чтобы преодолеть эти проблемы используют альтернативные показатели, одним из которых является скорректированный коэффициент детерминации (Adjasted coefficient of determinftion).

Скорректированный коэффициент детерминации даёт возможность сравнивать модели с разным числом переменных так, чтобы их число не влияло на статистику R^{2}, и накладывает штраф за дополнительно включённые в модель переменные. Вычисляется по формуле:

R_{adj}^{2}=1-frac{sumlimits_{i=1}^{n}(widehat{y}_{i}-y_{i})^{2}/(n-k)}{sumlimits_{i=1}^{n}({overline{y}}_{i}-y_{i})^{2}/(n-1)}

где n — число наблюдений, на основе которых строится модель, k — количество переменных в модели.

Скорректированный коэффициент детерминации всегда меньше единицы, но теоретически может принимать значения и меньше нуля только при очень малом значении обычного коэффициента детерминации и большом количестве переменных модели.

Сравнение метрик

Резюмируем преимущества и недостатки каждой приведённой метрики в следующей таблице:

Мера	Сильные стороны	Слабые стороны
MSE	Позволяет подчеркнуть большие отклонения, простота вычисления.	Имеет тенденцию занижать качество модели, чувствительна к выбросам. Сложность интерпретации из-за квадратичной зависимости.
RMSE	Простота интерпретации, поскольку измеряется в тех же единицах, что и целевая переменная.	Имеет тенденцию занижать качество модели, чувствительна к выбросам.
MSPE	Нечувствительна к выбросам. Хорошо интерпретируема, поскольку имеет линейный характер.	Поскольку вклад всех ошибок отдельных наблюдений взвешивается одинаково, не позволяет подчёркивать большие и малые ошибки.
MAPE	Является безразмерной величиной, поэтому её интерпретация не зависит от предметной области.	Нельзя использовать для наблюдений, в которых значения выходной переменной равны нулю.
SMAPE	Позволяет корректно работать с предсказанными значениями независимо от того больше они фактического, или меньше.	Приближение к нулю фактического или предсказанного значения приводит к резкому росту ошибки, поскольку в знаменателе присутствует как фактическое, так и предсказанное значения.
MASE	Не зависит от масштаба данных, является симметричной: положительные и отрицательные отклонения от фактического значения учитываются одинаково. Устойчива к выбросам. Позволяет сравнивать модели.	Сложность интерпретации.
MRE	Позволяет оценить величину ошибки относительно значения целевой переменной.	Неприменима для наблюдений с нулевым значением выходной переменной.
RMSLE	Логарифмирование позволяет сделать величину ошибки более устойчивой, когда разность между фактическим и предсказанным значениями различается на порядок и выше	Может быть затруднена интерпретация из-за нелинейности.
R-квадрат	Универсальность, простота интерпретации.	Возрастает даже при включении в модель бесполезных переменных. Плохо работает когда входные переменные зависимы.
R-квадрат скорр.	Корректно отражает вклад каждой переменной в модель.	Плохо работает, когда входные переменные зависимы.

В данной статье рассмотрены наиболее популярные меры качества регрессионных моделей, которые часто используются в различных аналитических приложениях. Эти меры имеют свои особенности применения, знание которых позволит обоснованно выбирать и корректно применять их на практике.

Однако в литературе можно встретить и другие меры качества моделей регрессии, которые предлагаются различными авторами для решения конкретных задач анализа данных.

Другие материалы по теме:

Отбор переменных в моделях линейной регрессии

Репрезентативность выборочных данных

Логистическая регрессия и ROC-анализ — математический аппарат