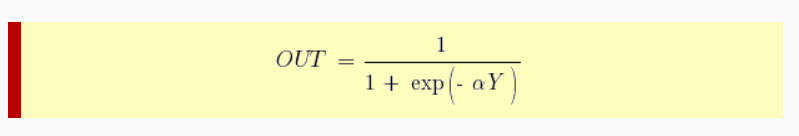Цель
модификации алгоритма обратного
распространения ошибки – повысить
оперативность обучения ИНС. В основу
модификации была положена идея «упругого
распространения», впервые реализованная
в одноименном алгоритме Rpгop
(Resilent
Propogation
– «упругое распространение») [105]. Суть
идеи Rpгop
состоит в использовании знаков частных
производных для подстройки весовых
коэффициентов. Для определения величины
коррекции используется следующее
правило:
, (4.22)
где
,
а
.
Если
на текущем шаге частная производная по
соответствующему весу wij изменила
знак, то из этого следует, что последнее
изменение было большим и алгоритм
проскочил локальный минимум. Следовательно,
величину изменения необходимо уменьшить
на
и
вернуть предыдущее значение весового
коэффициента, то есть сделать «откат»
на величину
.
Если
знак частной производной не изменился,
то нужно увеличить величину коррекции
на
для
достижения более быстрой сходимости.
В результате проведенных экспериментов
(т.е эмпирическим путем) установлено,
что целесообразно выбирать
=1,2,
а
=0,5.
Начальные значения для всех
устанавливались равными 0,1. Для вычисления
значения коррекции весов использовалось
следующее правило:
. (4.23)
Если
производная положительна, т. е. ошибка
возрастает, то весовой коэффициент
уменьшается на величину коррекции, в
противном случае – увеличивается.
Затем
веса подстраивались в соответствии с
выражением:
. (4.24)
Блок-схема
данного алгоритма приведена на рис.
4.24.
Блоки
1,9 используются для пуска и остановки
процесса обратного распространения
ошибок.
В блоке 2 реализован
ввод исходных данных.
Блок
3 обеспечивает инициализацию значений
величин коррекции
.
В
блоке 4 предъявляются все примеры из
выборки и вычисляются частные производные.
Блок
5 рассчитывает новые значения
по формулам (4.22) и (4.23).
В
блоке 6 реализуется корректировка весов
в соответствии с выражением (4.24).
Блок
7 проверяет условие останова данного
процесса. Если условие останова не
выполняется, то управление передается
блоку 4. В противном случае управление
передается блоку 8.
В блоке 8 реализован
вывод полученных результатов.
Совокупность
проведенных экспериментов (более
200), показала, что данный алгоритм
сходится почти в 6 раз быстрее, чем
стандартный алгоритм обратного
распространения ошибок.
-
4.12. Эвристическая оптимизация функционирования алгоритма обратного распространения ошибки
Эвристическая
оптимизация функционирования алгоритма
обратного распространения ошибки,
улучшающая его производительность,
проводилась по таким аспектам, как:
—
выбор режима обучения;
—
максимизация информативности;
—
выбор функции активации;
—
выбор целевых значений функции активации;
—
выбор начальных значений синаптических
весов и пороговых значений;
—
реализация обучения по подсказке;
—
управление параметрами скорости обучения
нейронов.
При
выборе режима обучения было установлено,
что последовательный режим обучения
методом обратного распространения
(использующий последовательное
предоставление примеров эпохи с
обновлением весов на каждом шаге) в
вычислительном плане оказался значительно
быстрее. Это особенно сказалось при
достаточно большом и избыточном обучающем
множестве данных. Причиной этого является
тот факт, что избыточные данные вызывают
вычислительные проблемы при оценке
Якобиана, необходимого для пакетного
режима.
Процедура
максимизации информативности строилась
на следующем правиле: «Каждый обучающий
пример, предоставляемый алгоритму
обратного распространения, должен
выбираться из соображений наибольшей
информационной насыщенности в области
решаемой задачи». С этой целью
использовались, во-первых, примеры,
вызывающие наибольшие ошибки обучения,
и, во-вторых, примеры, которые радикально
отличались от ранее использованных.
Кроме того, при подаче примеров соблюдался
случайный порядок
их следования.
При
выборе функции активации, в интересах
повышения оперативности обучения ИНС,
предпочтение было отдано антисимметричной
функции.
Функция
активации
называется антисимметричной (т.е. четной
функцией cвoeгo apгyмeнтa), если выполняется
условие:
, (4.25)
что
показано на рис. 4.25, а.
Стандартная
логистическая функция не удовлетворяет
этому условию (рис. 4.25, б).
Известным
примером антисимметричной функции
активации является сигмоидальная
нелинейная функция гиперболического
тангенса:
, (4.26)
где
а
и b
— константы. В результате проведенных
экспериментов установлено,
что приемлемыми значениями для констант
а и b
являются следующие [130]: а = 1,7159, b
= 2/3.
Определенная
таким образом функция гиперболического
тангенса имеет ряд полезных свойств.
Например,
(1)
= 1 и
(-1)
= -1.
Кроме
того, в начале координат тaнгeнс угла
наклона (т.е. эффективный угoл) функции
активации близок к единице:
(0) = аb
= 1,7159 х 2/3 = 1,1424.
Вторая
производная
( v)
достигает свoeгo максимального значения
при v
= 1.
Для
выбора целевых значений функции активации
важно, чтобы они выбирались из области
значений сигмоидальной функции активации.
Более точно, желаемый отклик
dj
нейрона j
выходного слоя многослойного персептрона
должен быть смещен на
некоторую
величину
от границы области значений функции
активации в сторону ее
внутренней
части. В противном случае алгоритм
обратного распространения будет
модифицировать свободные па раметры
сети, устремляя их в бесконечность,
замедляя таким образом процесс обучения
и доводя скрытые нейроны до предела
насыщения. В качестве примера рассмотрим
антисимметричную функцию активации,
показанную на рис. 4.25, а. Для предельного
значения +а
выберем dj
= а
—
.
Аналогично, для предельного значения
-a
установим dj
= a +
,
где
соответствующая положительная константа.
Для выбранного ранее значения а
= 1,7159
установим
=
0,7159.
В этом случае желаемый отклик dj
будет находиться в диапазоне от 1 до +1
(см. рис. 4.25, а).
При
выборе начальных значений синаптических
весов и пороговых значений сети
учитывались следующие правила.
Если
синаптические веса принимают большие
начальные значения, то нейроны быстрее
достигнут режима насыщения. Если такое
случится, то локальные градиенты
алгоритма обратного распространения
будут принимать малые значения, что, в
свою очередь, вызовет торможение процесса
обучения.
Если
же синаптическим весам присвоить малые
начальные значения, алгоритм будет
очень вяло работать в окрестности начала
координат поверхности ошибок. В частности,
это верно для случая антисимметричной
функции активации, такой как гиперболический
тангенс. К сожалению, начало координат
является седловой точкой, т.е. стационарной
точкой, где, образующие поверхности
ошибок вдоль одной оси, имеют положительный
градиент, а вдоль другой — отрицательный.
Поэтому при выборе начальных значений
использовались средние величины. Для
примера рассмотрим многослойный
персептрон, в котором в качестве функции
активации используется гиперболический
тангенс. Пусть пороговое значение,
применяемое к нейронам сети, равно нулю.
Исходя из этого индуцированное локальное
поле нейрона j
можно выразить следующим образом:
. (4.27)
Предположим,
что входные значения, передаваемые
нейронам сети, имеют нулевое среднее
значение и дисперсию, равную единице,
т.е
для
всех i,
для
всех i.
Далее предположим,
что входные сигналы некоррелированны:
и
синаптические веса выбраны из множества
равномерно распределенных чисел с
нулевым средним:
,
и дисперсией:
для
всех пар (j,i).
Следовательно,
математическое ожидание и дисперсию
индуцированного локальнoгo поля можно
выразить так:
(4.28)
где
m
— число синаптических связей нейрона.
На
основании этого результата можно описать
хорошую стратегию инициализации
синаптических весов таким образом,
чтобы стандартное отклонение
индуцировaннoгo локального поля нейрона
лежало в переходной области между
линейной частью сигмоидальной функции
активации и областью насыщения. Например,
для случая гиперболического тангeнca с
параметрами а
и b
(см. определение функции) эта цель
достигается при
в
(4.28). Исходя из этого получим [105]
. (4.29)
Таким
образом, желательно, чтобы равномерное
распределение, из котopoгo выбираются
исходные значения синаптических весов,
имело нулевое среднее значение и
дисперсию, обратную корню квадратному
из количества синаптических связей
нейрона.
Изначально
обучение ИНС реализуется на множестве
примеров, что связано с аппроксимацией
неизвестной функции отображения входного
сигнала на выходной. В процессе обучения
из примеров извлекается информация о
функции f(.)
и строится некоторая аппроксимация
этой функциональной зависимости. Процесс
обучения на примерах можно обобщить,
что и сделано, при добавлении обучения
по подсказке, которое реализуется путем
предоставления некоторой априорной
информации о функции f(.).
Такая информация может включать свойства
инвариантности, симметрии и прочие
знания о функции f
(.),
которые можно использовать для ускорения
поиска ее аппроксимации и, что более
важно, для повышения качества конечной
оценки.
Использование
соотношения (4.28) является одним из
примеров тaкoгo подхода.
При
управлении параметрами скорости обучения
нейронов учитывалось следующее.
Теоретически все нейроны многослойного
персептрона должны обучаться с одинаковой
скоростью. На практике оказалось, что
последние слои ИНС имеют более высокие
значения локальных градиентов, чем
начальные. Поэтому параметру скорости
обучения
назначались меньшие значения для
последних слоев сети и большие для
первых. Кроме того, чтобы время обучения
для всех нейронов сети было примерно
одинаковым, нейроны с большим числом
входов имели меньшее значение параметра
обучения, чем нейроны с малым количеством
входов. Величина назначаемого параметра
скорости обучения для каждого нейрона
была обратно пропорциональна квадратному
корню из суммы eгo синаптических связей.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
A modified error backpropagation algorithm for complex-value neural networks
Xiaoming Chen et al.
Int J Neural Syst.
2005 Dec.
Abstract
The complex-valued backpropagation algorithm has been widely used in fields of dealing with telecommunications, speech recognition and image processing with Fourier transformation. However, the local minima problem usually occurs in the process of learning. To solve this problem and to speed up the learning process, we propose a modified error function by adding a term to the conventional error function, which is corresponding to the hidden layer error. The simulation results show that the proposed algorithm is capable of preventing the learning from sticking into the local minima and of speeding up the learning.
Similar articles
-
A fast and convergent stochastic MLP learning algorithm.
Sakurai A.
Sakurai A.
Int J Neural Syst. 2001 Dec;11(6):573-83. doi: 10.1142/S0129065701000977.
Int J Neural Syst. 2001.PMID: 11852440
-
New learning automata based algorithms for adaptation of backpropagation algorithm parameters.
Meybodi MR, Beigy H.
Meybodi MR, et al.
Int J Neural Syst. 2002 Feb;12(1):45-67. doi: 10.1142/S012906570200090X.
Int J Neural Syst. 2002.PMID: 11852444
-
Stability analysis of a three-term backpropagation algorithm.
Zweiri YH, Seneviratne LD, Althoefer K.
Zweiri YH, et al.
Neural Netw. 2005 Dec;18(10):1341-7. doi: 10.1016/j.neunet.2005.04.007. Epub 2005 Aug 30.
Neural Netw. 2005.PMID: 16135404
-
Nonlinear complex-valued extensions of Hebbian learning: an essay.
Fiori S.
Fiori S.
Neural Comput. 2005 Apr;17(4):779-838. doi: 10.1162/0899766053429381.
Neural Comput. 2005.PMID: 15829090
Review.
-
Deep learning.
LeCun Y, Bengio Y, Hinton G.
LeCun Y, et al.
Nature. 2015 May 28;521(7553):436-44. doi: 10.1038/nature14539.
Nature. 2015.PMID: 26017442
Review.
Cited by
-
Biologically inspired intelligent decision making: a commentary on the use of artificial neural networks in bioinformatics.
Manning T, Sleator RD, Walsh P.
Manning T, et al.
Bioengineered. 2014 Mar-Apr;5(2):80-95. doi: 10.4161/bioe.26997. Epub 2013 Dec 16.
Bioengineered. 2014.PMID: 24335433
Free PMC article.Review.
-
A new method for diagnosis of cirrhosis disease: complex-valued artificial neural network.
Ozbay Y.
Ozbay Y.
J Med Syst. 2008 Oct;32(5):369-77. doi: 10.1007/s10916-008-9142-z.
J Med Syst. 2008.PMID: 18814493
MeSH terms
LinkOut — more resources
-
Full Text Sources
- Atypon
Статья опубликована в выпуске журнала № 2 за 2019 год. [ на стр. 258-262 ]
Аннотация:В статье исследуется эвристическое улучшение алгоритма обратного распространения ошибки с использованием пакетного режима обучения.
Алгоритм обратного распространения ошибки является одним из самых распространенных алгоритмов обучения нейронных сетей. Использование его сопряжено с рядом сложностей, главная из которых – обеспечение приемлемой способности к обобщению нейронной сети. Способность к обобщению полученных знаний является одним из важнейших свойств нейронной сети и заключается в генерации нейронной сетью ожидаемых значений на данных, не участвующих непосредственно в процессе обучения. Однако использование зашумленных и ошибочных данных может привести к переобучению и снижению способности к обобщению обученной нейронной сети.
Рассматриваемые в статье вопросы являются важной частью процесса обучения нейронных сетей. Предложенный метод дает возможность более эффективно рассчитывать значения целевой функции, лежащей в основе алгоритма обратного распространения ошибки, а также игнорировать ошибочные значения в данных для обучения, исключая их на ранних стадиях обучения. Кроме то-го, метод позволяет использовать для обучения нейронных сетей неоднородные выборки данных, а также учитывать при обучении априорную информацию о ценности отдельных примеров.
В статье приведен алгоритм работы данного метода. Использование метода позволит повысить точность работы нейронной сети для задач классификации и аппроксимации.
Abstract:The paper describes heuristic modification of backpropagation algorithm using for remote batching.
The backpropagation algorithm is a common algorithm for neural network training. It causes some difficulties. The main problem is enabling the generalizing of a neural network. The ability of general-izing is a most important characteristics of a neural network. It assumes that a neural produces antici-pated values on data that is not a part of a training process. However, using of noisy data causes re-training and decreasing of a generalizing ability of a neural network.
The problems considered in the paper are an important part of a neural network training process. The paper describes a method to use objective functions effectively. The proposed method allows more effective calculating of the values of a goal function that is a base of the backpropagation algorithm. It also ignores failure values in training data and excludes them at earlier stages. In addition, the method allows using heterogeneous data samples for training neural networks, as well as taking into account prior information on the significance of some examples when training.
The paper describes the algorithm of the proposed method. The method will improve the accuracy of a neural network for classification and regression tasks.
Размер шрифта:
Шрифт:
В статье представлен метод отбора примеров в обучающую выборку с учетом их влияния на процесс обучения сети. Показано, что в задаче обучения сети с учителем при использовании пакетного режима [1] скорость обучения и качество работы обученной нейронной сети зависят от величины ошибки на выходе, обусловленной не только уровнем обученности сети, но и характеристиками обучающей выборки: типичностью примеров, их количеством для различных исходов, а также достоверностью. Целью работы является повышение качества обучения сети за счет оценки обучающего множества и формирования обучающей выборки.
Обучение нейронной сети – это процесс минимизации в пространстве обучаемых параметров функции оценки. При использовании метода обратного распространения ошибки корректировка синаптической карты весов нейронной сети выполняется после подачи всех обучающих примеров по усредненному значению градиента целевой функции, формулируемой в виде квадратичной суммы разностей между фактическими и ожидаемыми значениями выходных сигналов [2]:
, (1)
где y – выходное значение нейронной сети; d – желаемое значение выхода; m – количество нейронов в выходном слое; k – номер нейрона в выходном слое.
Основная идея рассматриваемого в данной работе подхода состоит в том, что используемые для обучения примеры должны получать весовые коэффициенты, улучшающие нейронную сеть, полученную в процессе обучения.
Необходимость использования весов примеров при обучении может быть обусловлена следующими причинами:
1) один из примеров плохо обучается;
2) число примеров разных классов в обучающем множестве сильно отличается;
3) примеры в обучающем множестве имеют различную достоверность [3].
Первая причина актуальна в случае, когда имеется априорная информация о значимости примера и необходимо, чтобы нейронная сеть научилась его воспринимать. Однако в силу своих особенностей пример не учитывается при обучении нейронной сети обычными методами.
Вторая причина актуальна для случая, когда в обучающей выборке есть классы, число примеров которых мало по сравнению с другими классами. В пакетном режиме обучения ошибка, рассчитанная по этим примерам, может потеряться в суммарной ошибке по всей выборке, в результате чего такие примеры могут быть проигнорированы. Ошибка по этим примерам останется большой, и нейронная сеть не научится их воспринимать. По этой причине существует критика пакетного режима обучения. Так, в работе [4] показывается преимущество online-обучения в контексте объема вычислений, осуществляемых в процессе обучения. Однако последовательный режим обучения не решает данную проблему. Еще одним подходом, используемым для решения данной проблемы, является уменьшение размеров нейронной сети. В работе [5] доказана несостоятельность данного метода.
Третья причина актуальна при наличии в данных ошибочных значений – выбросов, которые могут давать большую ошибку. Пытаясь научиться воспринимать такие значения, нейронная сеть может ухудшить свою способность к обобщению [6].
Для решения проблемы, вызванной первой и второй причинами, обучающим примерам необходимо присвоить весовые коэффициенты. Они будут использоваться при расчете ошибки обучения E и усиливать вклад выбранных примеров в суммарную ошибку обучения.
Для решения третьей проблемы в работе [7] предложена редукция данных, основанная на ограничении диапазона значений признака, однако при данном подходе существует вероятность исключения значимых примеров.
Учитывая все перечисленные особенности, становится очевидной необходимость более эффективного представления обучающей выборки.
Так, в работе [8] предлагается задавать пороговое значение ошибки, при превышении которого пример не должен рассматриваться. Более гибкий подход реализован в Lazy training (ленивое обучение) [9], однако этот алгоритм предназначен исключительно для задач классификации. Его основная идея заключается в том, что для коррекции весов используются только те наблюдения, которые были классифицированы неправильно. Помимо узкой направленности, этот алгоритм имеет и другие недостатки. Для решения проблемы, вызван- ной третьей причиной, необходим алгоритм, учитывающий описанные недостатки.
Основная идея рассматриваемого подхода состоит в том, что обучающие примеры, ошибки по которым оказываются слишком большими, не должны участвовать в обучении нейронной сети. Однако задание граничного значения ошибки, разделяющего исходное множество на используемые и неиспользуемые примеры, неэффективно. Если использовать для обучения часть примеров, то ошибка выхода по ним будет постепенно уменьшаться. При этом ошибка на неиспользуемых примерах может расти. Таким образом, использование граничного значения может привести к следующему эффекту. Если ошибка, полученная на рассматриваемом примере, меньше заданного значения, то при следующей итерации этот пример не будет использован. При этом ошибка по этому примеру может вырасти и снова преодолеть установленную границу. При очередной итерации данный пример опять будет использован в обучающей выборке. В результате нейронная сеть перестанет обучаться.
Для избежания подобного эффекта предложено использовать два граничных значения ошибки обучения: нижнее (E1) и верхнее (E2), которые определяют три области и являются функцией количества циклов обучения. Для каждого примера в зависимости от значения ошибки E и его положения относительно значений E1 и E2 принимается решение о выборе значения весового коэффициента:
— E < E1 – пример не усиливается весовым коэффициентом (получает весовой коэффициент, равный единице);
— E1 < E < E2 – пример усиливается весовым коэффициентом;
— E > E2 – пример игнорируется (получает нулевой весовой коэффициент).
Весовые коэффициенты рассчитываются индивидуально для каждого примера на каждом шаге обучения.
В начале процесса обучения используются все имеющиеся примеры. Поскольку нейронная сеть перед началом обучения инициализируется случайными значениями, распределение ошибок по используемым примерам равномерно. При этом ошибки по всем примерам не превышают значение E2. В процессе обучения нейронной сети ошибка обучения приобретает нормальный вид распределения. У большинства примеров ошибка стремится к нулю, у части примеров она остается большой. Попав в интервал E1 < E < E2, пример получает весовой коэффициент и ошибка по нему начинает уменьшаться быстрее.
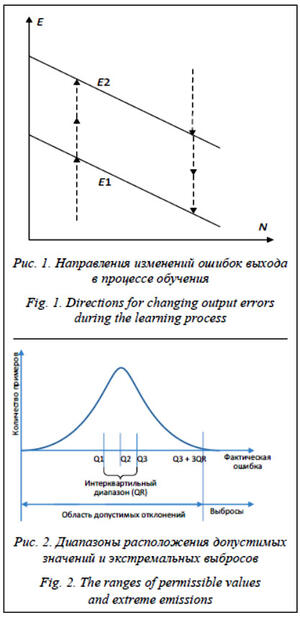
Как только ошибка примера пересекает границу E1, он получает единичный коэффициент. Если при дальнейшем обучении ошибка примера превысит E1, он снова получит усиливающий весовой коэффициент. Если ошибка примера превысила значение E2, то пример считается выбросом и не участвует в дальнейшем обучении. Направления изменений ошибок показаны пунктирными стрелками на рисунке 1.
Граничные значения E1 и E2 рассчитываются на каждом шаге обучения сети. Для расчета значений E1 и E2 используется критерий, основанный на интерквартильном размахе. Метод основан на вычислении трех квартилей, делящих данные на четыре равные группы по ошибке обучения. Интерквартильный размах [10] считается как разность между первой и третьей квартилями:
IQR = Q3 – Q1. (2)
Значения E1 и E2 рассчитываются следующим образом:
E1 = Q1, (3)
E2 = Q3 + QR. (4)
На рисунке 2 показана схема, выражающая эти определения.
Предложенная реализация алгоритма обучения позволяет избежать переобучения нейронной сети, связанного с чрезмерным стремлением достичь нулевой ошибки. При этом данный алгоритм в большей степени учитывает свойства малочисленных групп примеров, чем стандартный алгоритм. Блок-схема алгоритма изображена на рисунке 3.
Таким образом, алгоритм будет следующим.
Шаг 1. Формируем обучающую выборку, используя все обучающее множество.
Шаг 2. Вычисляем значение среднего градиента для предоставленной выборки.
Шаг 3. Выполняем корректировку весов нейронной сети.
Шаг 4. Устанавливаем веса примерам, используя данные об ошибках выхода. Для этого создается матрица, содержащая флаг для каждого наблюдения. Если ошибка, соответствующая наблюдению, меньше значения ошибки E1, этому наблюдению ставится единичный коэффициент. Если ошибка больше значения ошибки E2, наблюдению ставится нулевой коэффициент. Если ошибка находится в диапазоне E1–E2, наблюдению ставится усиливающий коэффициент.
Шаг 5. Используя полученный набор флагов, разделяем выборку на две части: используемую для следующего уточнения весов нейронной сети и игнорируемую.
Шаг 6. Создаем новую обучающую выборку для следующей итерации.
Шаг 7. Возвращаемся к шагу 2.

Литература
1. Дьяконов В.П., Круглов В.В. MATLAB 6.5 SP1/7/7 SP1/7 SP2 + Simulink 5/6. Инструменты искусственного интеллекта и биоинформатики. М.: Солон-Пресс, 2006. 456 с.
2. Оссовский С. Нейронные сети для обработки информации; [пер. с польск. И.Д. Рудинского]. М.: Финансы и статистика, 2004. 344 с.
3. Миркес Е.М. Нейроинформатика. Красноярск: Изд-во КГТУ, 2002. 347 с.
4. Царегородцев В.Г. Общая неэффективность использования суммарного градиента выборки при обучении нейронной сети // Нейроинформатика и ее приложения: матер. XIII Всерос. семинара. 2004. С. 145–151.
5. Царегородцев В.Г. Редукция размеров нейросети не приводит к повышению обобщающей способности // Нейроинформатика и ее приложения: матер. XII Всерос. семинара. Красноярск, 2004. С. 163–165.
6. Хайкин С. Нейронные сети: полный курс; [пер. с англ. Н.Н. Куссуль, А.Ю. Шелестова]. М.: Вильямс, 2006. 1104 с.
7. Царегородцев В.Г. Оптимизация предобработки данных для обучаемой нейросети: критерии оптимальности предобработки // Междунар. конф. по нейрокибернетике: сб. докл. Ростов н/Д, 2005. Т. 2. С. 64–67.
8. Xiao-Ping Zhang. Thresholding neural network for adaptive noise reduction. Proc. IEEE Transactions on Neural Networks, 2001, vol. 12, no. 3, pp. 567–584.
9. Rimer M.E., Anderson T.L. and Martinez T.R. Improving backpropagation ensembles through lazy training. Proc. IEEE IJCNN’01, 2001, pp. 2007–2112.
10. Певзнер М.З. Систематизация, статистический анализ данных, контроль и управление производственными процессами. Киров: Изд-во ВятГУ, 2012. 165 с.
References
- Dyakonov V.P., Kruglov V.V. MatLab 6.5 SP1/7/7 SP1/7 SP2 + Simulink 5/6. Artificial Intelligence and Bioinformatics Tools. Moscow, Solon-Press, 2006, 456 p.
- Asowsky S. Neural Networks for Information Processing. Moscow, Finansy i statistika Publ., 2004,
344 p. - Mirkes Е.М. Neuroinformatics. Krasnoyarsk, 2002, 347 p.
- Tsaregorodtsev V.G. The overall inefficient use of a sample total gradient when training a neural network. Proc. 13th All-Russ. Workshop “Neuroinformatics and Its Applications”. Krasnoyarsk, 2004,
pp. 145–151 (in Russ.). - Tsaregorodtsev V.G. Reducing of neural network sizes does not lead to an increasing generalization ability. Proc. 13th All-Russ. Workshop “Neuroinformatics and Its Applications”. Krasnoyarsk, 2004,
pp. 163–165 (in Russ.). - Khaykin S. Neural Networks: a Comprehensive Foundation. 2nd ed., Moscow, Vilyams Press, 2006. 1104 p.
- Tsaregorodtsev V.G. Optimization of data preprocessing for a trained neural network: preprocessing optimality criteria. Proc. 14th Intern. Conf. on Neurocybernetics. Rostov-on-Don, 2005, vol. 2, pp. 64–67
(in Russ.). - Xiao-Ping Zhang. Thresholding neural network for adaptive noise reduction. Proc. IEEE Trans. on Neural Networks. 2001, vol. 12, no. 3, pp. 567–584.
- Rimer M.E., Anderson T.L., Martinez T.R. Improving backpropagation ensembles through lazy training. Proc. IEEE Intern. Joint Conf. on Neural Networks IJCNN’01. 2001, pp. 2007–2112.
- Pevzner M.Z. Systematization, Statistical Data Analysis, Control and Management of Manufacturing Processes. Kirov: VyatGU Press, 2012, 165 p.
Применение алгоритма обратного распространения ошибки — один из известных методов, используемых для глубокого обучения нейронных сетей прямого распространения (такие сети ещё называют многослойными персептронами). Этот метод относят к методу обучения с учителем, поэтому требуется задавать в обучающих примерах целевые значения. В этой статье мы рассмотрим, что собой представляет метод обратного распространения ошибки, как он реализуется, каковы его плюсы и минусы.
Сегодня нейронные сети прямого распространения используются для решения множества сложных задач. Если говорить об обучении нейронных сетей методом обратного распространения, то тут пользуются двумя проходами по всем слоям нейросети: прямым и обратным. При выполнении прямого прохода осуществляется подача входного вектора на входной слой сети, после чего происходит распространение по нейронной сети от слоя к слою. В итоге должна осуществляться генерация набора выходных сигналов — именно он, по сути, является реакцией нейронной сети на этот входной образ. При прямом проходе все синаптические веса нейросети фиксированы. При обратном проходе все синаптические веса настраиваются согласно правил коррекции ошибок, когда фактический выход нейронной сети вычитается из желаемого, что приводит к формированию сигнала ошибки. Такой сигнал в дальнейшем распространяется по сети, причём направление распространения обратно направлению синаптических связей. Именно поэтому соответствующий метод и называют алгоритмом с обратно распространённой ошибкой. Синаптические веса настраивают с целью наибольшего приближения выходного сигнала нейронной сети к желаемому.
Общее описание алгоритма обратного распространения ошибки
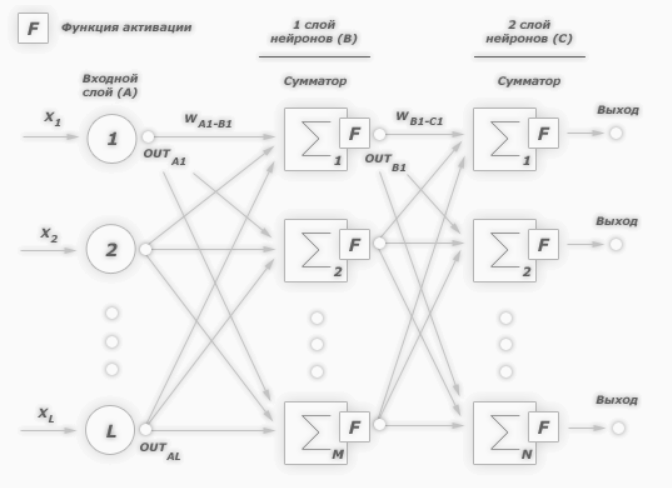
К примеру, нам надо обучить нейронную сеть по аналогии с той, что представлена на картинке ниже. Естественно, задачу следует выполнить, применяя алгоритм обратного распространения ошибки:
В многослойных персептронах в роли активационной функции обычно применяют сигмоидальную активационную функция, в нашем случае — логистическую. Формула:
Причём «альфа» здесь означает параметр наклона сигмоидальной функции. Меняя его, мы получаем возможность строить функции с разной крутизной.
Сигмоид может сужать диапазон изменения таким образом, чтобы значение OUT лежало между нулем и единицей. Нейронные многослойные сети характеризуются более высокой представляющей мощностью, если сравнивать их с однослойными, но это утверждение справедливо лишь в случае нелинейности. Нужную нелинейность и обеспечивает сжимающая функция. Но на практике существует много функций, которые можно использовать. Говоря о работе алгоритма обратного распространения ошибки, скажем, что для этого нужно лишь, чтобы функция была везде дифференцируема, а данному требованию как раз и удовлетворяет сигмоид. У него есть и дополнительное преимущество — автоматический контроль усиления. Если речь идёт о слабых сигналах (OUT близко к нулю), то кривая «вход-выход» характеризуется сильным наклоном, дающим большое усиление. При увеличении сигнала усиление падает. В результате большие сигналы будут восприниматься сетью без насыщения, а слабые сигналы будут проходить по сети без чрезмерного ослабления.
Цель обучения сети
Цель обучения нейросети при использовании алгоритма обратного распространения ошибки — это такая подстройка весов нейросети, которая позволит при приложении некоторого множества входов получить требуемое множество выходов нейронов (выходных нейронов). Можно назвать эти множества входов и выходов векторами. В процессе обучения предполагается, что для любого входного вектора существует целевой вектор, парный входному и задающий требуемый выход. Эту пару называют обучающей. Работая с нейросетями, мы обучаем их на многих парах.
Также можно сказать, что алгоритм использует стохастический градиентный спуск и продвигается в многомерном пространстве весов в направлении антиградиента, причём цель — это достижение минимума функции ошибки.
При практическом применении метода обучение продолжают не до максимально точной настройки нейросети на минимум функции ошибки, а пока не будет достигнуто довольно точное его приближение. С одной стороны, это даёт возможность уменьшить количество итераций обучения, с другой — избежать переобучения нейронной сети.
Пошаговая реализация метода обратного распространения ошибки
Необходимо выполнить следующие действия:
1. Инициализировать синаптические веса случайными маленькими значениями.
2. Выбрать из обучающего множества очередную обучающую пару; подать на вход сети входной вектор.
3. Выполнить вычисление выходных значений нейронной сети.
4. Посчитать разность между выходом нейросети и требуемым выходом (речь идёт о целевом векторе обучающей пары).
5. Скорректировать веса сети в целях минимизации ошибки.
6. Повторять для каждого вектора обучающего множества шаги 2-5, пока ошибка обучения нейронной сети на всём множестве не достигнет уровня, который является приемлемым.
Виды обучения сети по методу обратного распространения
Сегодня существует много модификаций алгоритма обратного распространения ошибки. Возможно обучение не «по шагам» (выходная ошибка вычисляется, веса корректируются на каждом примере), а «по эпохам» в offline-режиме (изменения весовых коэффициентов происходит после подачи на вход нейросети всех примеров обучающего множества, а ошибка обучения neural сети усредняется по всем примерам).
Обучение «по эпохам» более устойчиво к выбросам и аномальным значениям целевой переменной благодаря усреднению ошибки по многим примерам. Зато в данном случае увеличивается вероятность «застревания» в локальных минимумах. При обучении «по шагам» такая вероятность меньше, ведь применение отдельных примеров создаёт «шум», «выталкивающий» алгоритм обратного распространения из ям градиентного рельефа.
Преимущества и недостатки метода
К плюсам можно отнести простоту в реализации и устойчивость к выбросам и аномалиям в данных, и это основные преимущества. Но есть и минусы:
• неопределенно долгий процесс обучения;
• вероятность «паралича сети» (при больших значениях рабочая точка функции активации попадает в область насыщения сигмоиды, а производная величина приближается к 0, в результате чего коррекции весов почти не происходят, а процесс обучения «замирает»;
• алгоритм уязвим к попаданию в локальные минимумы функции ошибки.
Значение метода обратного распространения
Появление алгоритма стало знаковым событием и положительно отразилось на развитии нейросетей, ведь он реализует эффективный с точки зрения вычислительных процессов способ обучения многослойного персептрона. В то же самое время, было бы неправильным сказать, что алгоритм предлагает наиболее оптимальное решение всех потенциальных проблем. Зато он действительно развеял пессимизм относительно машинного обучения многослойных машин, который воцарился после публикации в 1969 году работы американского учёного с фамилией Минский.
Источники:
— «Алгоритм обратного распространения ошибки»;
— «Back propagation algorithm».
Нейронные сети обучаются с помощью тех или иных модификаций градиентного спуска, а чтобы применять его, нужно уметь эффективно вычислять градиенты функции потерь по всем обучающим параметрам. Казалось бы, для какого-нибудь запутанного вычислительного графа это может быть очень сложной задачей, но на помощь спешит метод обратного распространения ошибки.
Открытие метода обратного распространения ошибки стало одним из наиболее значимых событий в области искусственного интеллекта. В актуальном виде он был предложен в 1986 году Дэвидом Э. Румельхартом, Джеффри Э. Хинтоном и Рональдом Дж. Вильямсом и независимо и одновременно красноярскими математиками С. И. Барцевым и В. А. Охониным. С тех пор для нахождения градиентов параметров нейронной сети используется метод вычисления производной сложной функции, и оценка градиентов параметров сети стала хоть сложной инженерной задачей, но уже не искусством. Несмотря на простоту используемого математического аппарата, появление этого метода привело к значительному скачку в развитии искусственных нейронных сетей.
Суть метода можно записать одной формулой, тривиально следующей из формулы производной сложной функции: если $f(x) = g_m(g_{m-1}(ldots (g_1(x)) ldots))$, то $frac{partial f}{partial x} = frac{partial g_m}{partial g_{m-1}}frac{partial g_{m-1}}{partial g_{m-2}}ldots frac{partial g_2}{partial g_1}frac{partial g_1}{partial x}$. Уже сейчас мы видим, что градиенты можно вычислять последовательно, в ходе одного обратного прохода, начиная с $frac{partial g_m}{partial g_{m-1}}$ и умножая каждый раз на частные производные предыдущего слоя.
Backpropagation в одномерном случае
В одномерном случае всё выглядит особенно просто. Пусть $w_0$ — переменная, по которой мы хотим продифференцировать, причём сложная функция имеет вид
$$f(w_0) = g_m(g_{m-1}(ldots g_1(w_0)ldots)),$$
где все $g_i$ скалярные. Тогда
$$f'(w_0) = g_m'(g_{m-1}(ldots g_1(w_0)ldots))cdot g’_{m-1}(g_{m-2}(ldots g_1(w_0)ldots))cdotldots cdot g’_1(w_0)$$
Суть этой формулы такова. Если мы уже совершили forward pass, то есть уже знаем
$$g_1(w_0), g_2(g_1(w_0)),ldots,g_{m-1}(ldots g_1(w_0)ldots),$$
то мы действуем следующим образом:
-
берём производную $g_m$ в точке $g_{m-1}(ldots g_1(w_0)ldots)$;
-
умножаем на производную $g_{m-1}$ в точке $g_{m-2}(ldots g_1(w_0)ldots)$;
-
и так далее, пока не дойдём до производной $g_1$ в точке $w_0$.
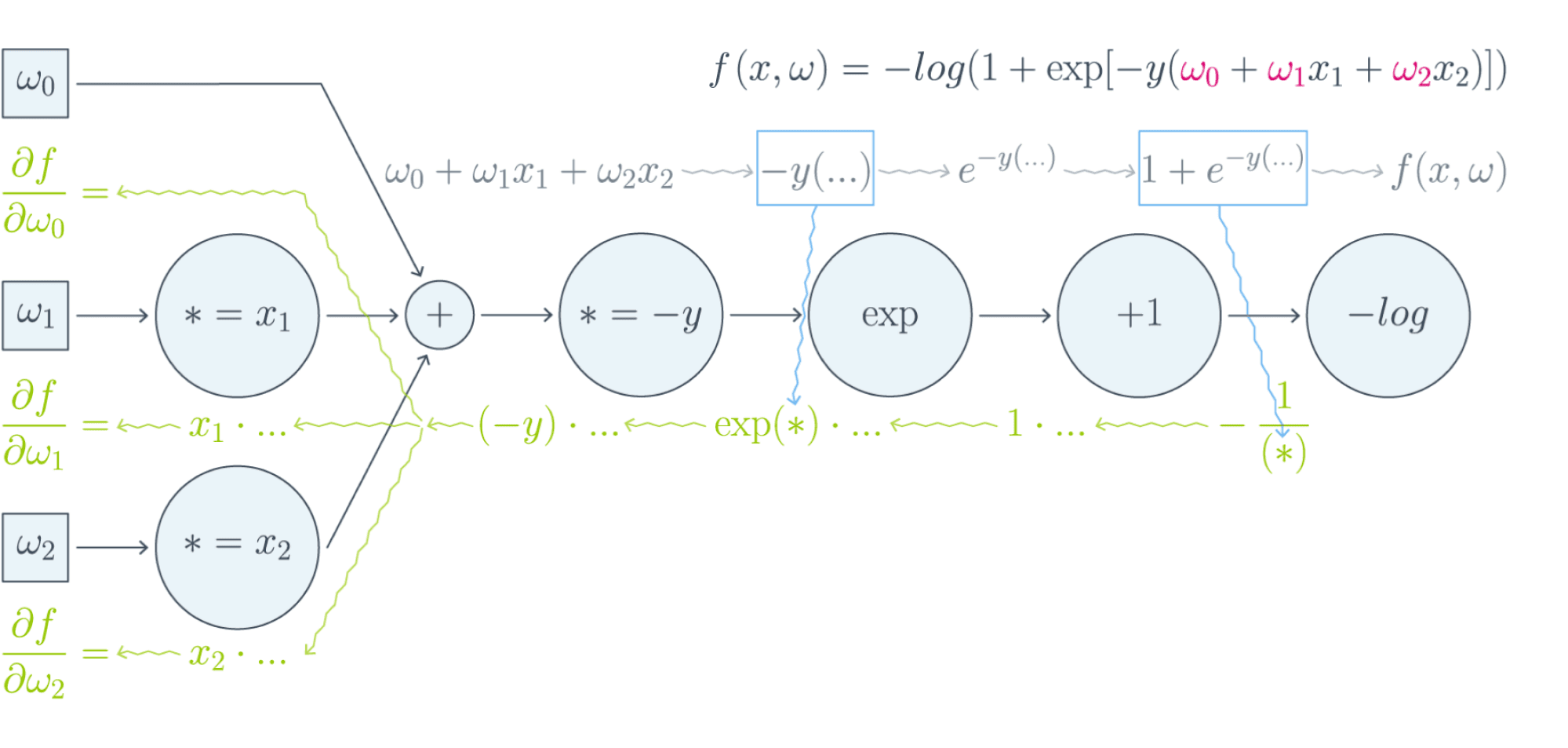
Проиллюстрируем это на картинке, расписав по шагам дифференцирование по весам $w_i$ функции потерь логистической регрессии на одном объекте (то есть для батча размера 1):
Собирая все множители вместе, получаем:
$$frac{partial f}{partial w_0} = (-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
$$frac{partial f}{partial w_1} = x_1cdot(-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
$$frac{partial f}{partial w_2} = x_2cdot(-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
Таким образом, мы видим, что сперва совершается forward pass для вычисления всех промежуточных значений (и да, все промежуточные представления нужно будет хранить в памяти), а потом запускается backward pass, на котором в один проход вычисляются все градиенты.
Почему же нельзя просто пойти и начать везде вычислять производные?
В главе, посвящённой матричным дифференцированиям, мы поднимаем вопрос о том, что вычислять частные производные по отдельности — это зло, лучше пользоваться матричными вычислениями. Но есть и ещё одна причина: даже и с матричной производной в принципе не всегда хочется иметь дело. Рассмотрим простой пример. Допустим, что $X^r$ и $X^{r+1}$ — два последовательных промежуточных представления $Ntimes M$ и $Ntimes K$, связанных функцией $X^{r+1} = f^{r+1}(X^r)$. Предположим, что мы как-то посчитали производную $frac{partialmathcal{L}}{partial X^{r+1}_{ij}}$ функции потерь $mathcal{L}$, тогда
$$frac{partialmathcal{L}}{partial X^{r}_{st}} = sum_{i,j}frac{partial f^{r+1}_{ij}}{partial X^{r}_{st}}frac{partialmathcal{L}}{partial X^{r+1}_{ij}}$$
И мы видим, что, хотя оба градиента $frac{partialmathcal{L}}{partial X_{ij}^{r+1}}$ и $frac{partialmathcal{L}}{partial X_{st}^{r}}$ являются просто матрицами, в ходе вычислений возникает «четырёхмерный кубик» $frac{partial f_{ij}^{r+1}}{partial X_{st}^{r}}$, даже хранить который весьма болезненно: уж больно много памяти он требует ($N^2MK$ по сравнению с безобидными $NM + NK$, требуемыми для хранения градиентов). Поэтому хочется промежуточные производные $frac{partial f^{r+1}}{partial X^{r}}$ рассматривать не как вычисляемые объекты $frac{partial f_{ij}^{r+1}}{partial X_{st}^{r}}$, а как преобразования, которые превращают $frac{partialmathcal{L}}{partial X_{ij}^{r+1}}$ в $frac{partialmathcal{L}}{partial X_{st}^{r}}$. Целью следующих глав будет именно это: понять, как преобразуется градиент в ходе error backpropagation при переходе через тот или иной слой.
Вы спросите себя: надо ли мне сейчас пойти и прочитать главу учебника про матричное дифференцирование?
Встречный вопрос. Найдите производную функции по вектору $x$:
$$f(x) = x^TAx, Ain Mat_{n}{mathbb{R}}text{ — матрица размера }ntimes n$$
А как всё поменяется, если $A$ тоже зависит от $x$? Чему равен градиент функции, если $A$ является скаляром? Если вы готовы прямо сейчас взять ручку и бумагу и посчитать всё, то вам, вероятно, не надо читать про матричные дифференцирования. Но мы советуем всё-таки заглянуть в эту главу, если обозначения, которые мы будем дальше использовать, покажутся вам непонятными: единой нотации для матричных дифференцирований человечество пока, увы, не изобрело, и переводить с одной на другую не всегда легко.
Мы же сразу перейдём к интересующей нас вещи: к вычислению градиентов сложных функций.
Градиент сложной функции
Напомним, что формула производной сложной функции выглядит следующим образом:
$$left[D_{x_0} (color{#5002A7}{u} circ color{#4CB9C0}{v}) right](h) = color{#5002A7}{left[D_{v(x_0)} u right]} left( color{#4CB9C0}{left[D_{x_0} vright]} (h)right)$$
Теперь разберёмся с градиентами. Пусть $f(x) = g(h(x))$ – скалярная функция. Тогда
$$left[D_{x_0} f right] (x-x_0) = langlenabla_{x_0} f, x-x_0rangle.$$
С другой стороны,
$$left[D_{h(x_0)} g right] left(left[D_{x_0}h right] (x-x_0)right) = langlenabla_{h_{x_0}} g, left[D_{x_0} hright] (x-x_0)rangle = langleleft[D_{x_0} hright]^* nabla_{h(x_0)} g, x-x_0rangle.$$
То есть $color{#FFC100}{nabla_{x_0} f} = color{#348FEA}{left[D_{x_0} h right]}^* color{#FFC100}{nabla_{h(x_0)}}g$ — применение сопряжённого к $D_{x_0} h$ линейного отображения к вектору $nabla_{h(x_0)} g$.
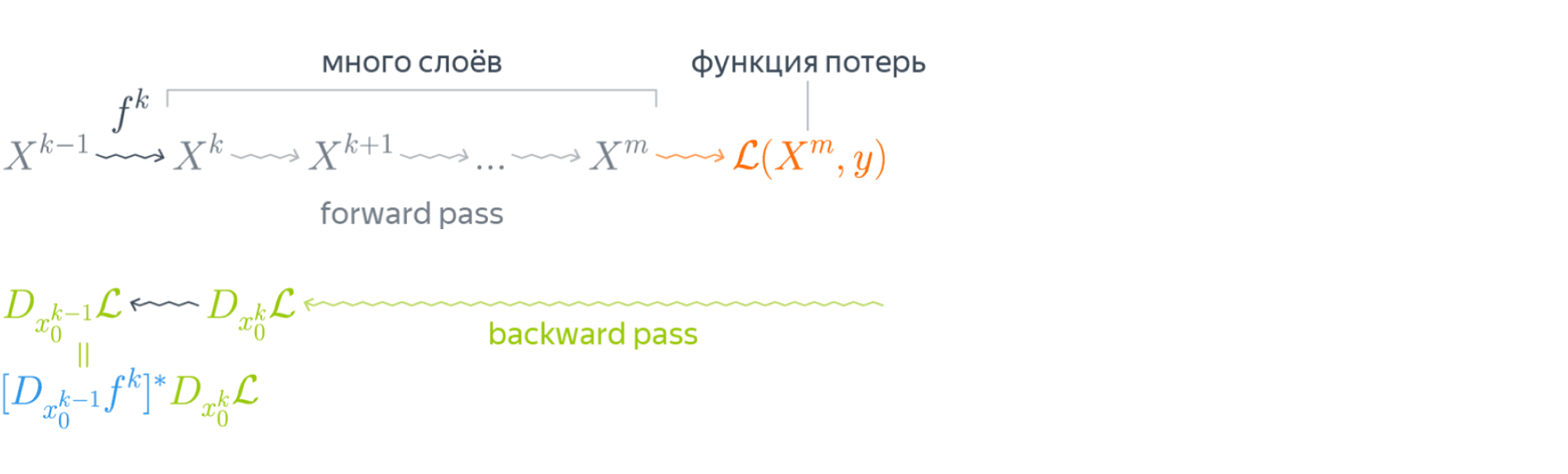
Эта формула — сердце механизма обратного распространения ошибки. Она говорит следующее: если мы каким-то образом получили градиент функции потерь по переменным из некоторого промежуточного представления $X^k$ нейронной сети и при этом знаем, как преобразуется градиент при проходе через слой $f^k$ между $X^{k-1}$ и $X^k$ (то есть как выглядит сопряжённое к дифференциалу слоя между ними отображение), то мы сразу же находим градиент и по переменным из $X^{k-1}$:
Таким образом слой за слоем мы посчитаем градиенты по всем $X^i$ вплоть до самых первых слоёв.
Далее мы разберёмся, как именно преобразуются градиенты при переходе через некоторые распространённые слои.
Градиенты для типичных слоёв
Рассмотрим несколько важных примеров.
Примеры
-
$f(x) = u(v(x))$, где $x$ — вектор, а $v(x)$ – поэлементное применение $v$:
$$vbegin{pmatrix}
x_1 \
vdots\
x_N
end{pmatrix}
= begin{pmatrix}
v(x_1)\
vdots\
v(x_N)
end{pmatrix}$$Тогда, как мы знаем,
$$left[D_{x_0} fright] (h) = langlenabla_{x_0} f, hrangle = left[nabla_{x_0} fright]^T h.$$
Следовательно,
$$
left[D_{v(x_0)} uright] left( left[ D_{x_0} vright] (h)right) = left[nabla_{v(x_0)} uright]^T left(v'(x_0) odot hright) =\
$$$$
= sumlimits_i left[nabla_{v(x_0)} uright]_i v'(x_{0i})h_i
= langleleft[nabla_{v(x_0)} uright] odot v'(x_0), hrangle.
,$$где $odot$ означает поэлементное перемножение. Окончательно получаем
$$color{#348FEA}{nabla_{x_0} f = left[nabla_{v(x_0)}uright] odot v'(x_0) = v'(x_0) odot left[nabla_{v(x_0)} uright]}$$
Отметим, что если $x$ и $h(x)$ — это просто векторы, то мы могли бы вычислять всё и по формуле $frac{partial f}{partial x_i} = sum_jbig(frac{partial z_j}{partial x_i}big)cdotbig(frac{partial h}{partial z_j}big)$. В этом случае матрица $big(frac{partial z_j}{partial x_i}big)$ была бы диагональной (так как $z_j$ зависит только от $x_j$: ведь $h$ берётся поэлементно), и матричное умножение приводило бы к тому же результату. Однако если $x$ и $h(x)$ — матрицы, то $big(frac{partial z_j}{partial x_i}big)$ представлялась бы уже «четырёхмерным кубиком», и работать с ним было бы ужасно неудобно.
-
$f(X) = g(XW)$, где $X$ и $W$ — матрицы. Как мы знаем,
$$left[D_{X_0} f right] (X-X_0) = text{tr}, left(left[nabla_{X_0} fright]^T (X-X_0)right).$$
Тогда
$$
left[ D_{X_0W} g right] left(left[D_{X_0} left( ast Wright)right] (H)right) =
left[ D_{X_0W} g right] left(HWright)=\
$$ $$
= text{tr}, left( left[nabla_{X_0W} g right]^T cdot (H) W right) =\
$$ $$
=
text{tr} , left(W left[nabla_{X_0W} (g) right]^T cdot (H)right) = text{tr} , left( left[left[nabla_{X_0W} gright] W^Tright]^T (H)right)
$$Здесь через $ast W$ мы обозначили отображение $Y hookrightarrow YW$, а в предпоследнем переходе использовалось следующее свойство следа:
$$
text{tr} , (A B C) = text{tr} , (C A B),
$$где $A, B, C$ — произвольные матрицы подходящих размеров (то есть допускающие перемножение в обоих приведённых порядках). Следовательно, получаем
$$color{#348FEA}{nabla_{X_0} f = left[nabla_{X_0W} (g) right] cdot W^T}$$
-
$f(W) = g(XW)$, где $W$ и $X$ — матрицы. Для приращения $H = W — W_0$ имеем
$$
left[D_{W_0} f right] (H) = text{tr} , left( left[nabla_{W_0} f right]^T (H)right)
$$Тогда
$$
left[D_{XW_0} g right] left( left[D_{W_0} left(X astright) right] (H)right) = left[D_{XW_0} g right] left( XH right) =
$$ $$
= text{tr} , left( left[nabla_{XW_0} g right]^T cdot X (H)right) =
text{tr}, left(left[X^T left[nabla_{XW_0} g right] right]^T (H)right)
$$Здесь через $X ast$ обозначено отображение $Y hookrightarrow XY$. Значит,
$$color{#348FEA}{nabla_{X_0} f = X^T cdot left[nabla_{XW_0} (g)right]}$$
-
$f(X) = g(softmax(X))$, где $X$ — матрица $Ntimes K$, а $softmax$ — функция, которая вычисляется построчно, причём для каждой строки $x$
$$softmax(x) = left(frac{e^{x_1}}{sum_te^{x_t}},ldots,frac{e^{x_K}}{sum_te^{x_t}}right)$$
В этом примере нам будет удобно воспользоваться формализмом с частными производными. Сначала вычислим $frac{partial s_l}{partial x_j}$ для одной строки $x$, где через $s_l$ мы для краткости обозначим $softmax(x)_l = frac{e^{x_l}} {sum_te^{x_t}}$. Нетрудно проверить, что
$$frac{partial s_l}{partial x_j} = begin{cases}
s_j(1 — s_j), & j = l,
-s_ls_j, & jne l
end{cases}$$Так как softmax вычисляется независимо от каждой строчки, то
$$frac{partial s_{rl}}{partial x_{ij}} = begin{cases}
s_{ij}(1 — s_{ij}), & r=i, j = l,
-s_{il}s_{ij}, & r = i, jne l,
0, & rne i
end{cases},$$где через $s_{rl}$ мы обозначили для краткости $softmax(X)_{rl}$.
Теперь пусть $nabla_{rl} = nabla g = frac{partialmathcal{L}}{partial s_{rl}}$ (пришедший со следующего слоя, уже известный градиент). Тогда
$$frac{partialmathcal{L}}{partial x_{ij}} = sum_{r,l}frac{partial s_{rl}}{partial x_{ij}} nabla_{rl}$$
Так как $frac{partial s_{rl}}{partial x_{ij}} = 0$ при $rne i$, мы можем убрать суммирование по $r$:
$$ldots = sum_{l}frac{partial s_{il}}{partial x_{ij}} nabla_{il} = -s_{i1}s_{ij}nabla_{i1} — ldots + s_{ij}(1 — s_{ij})nabla_{ij}-ldots — s_{iK}s_{ij}nabla_{iK} =$$
$$= -s_{ij}sum_t s_{it}nabla_{it} + s_{ij}nabla_{ij}$$
Таким образом, если мы хотим продифференцировать $f$ в какой-то конкретной точке $X_0$, то, смешивая математические обозначения с нотацией Python, мы можем записать:
$$begin{multline*}
color{#348FEA}{nabla_{X_0}f =}\
color{#348FEA}{= -softmax(X_0) odot text{sum}left(
softmax(X_0)odotnabla_{softmax(X_0)}g, text{ axis = 1}
right) +}\
color{#348FEA}{softmax(X_0)odot nabla_{softmax(X_0)}g}
end{multline*}
$$
Backpropagation в общем виде
Подытожим предыдущее обсуждение, описав алгоритм error backpropagation (алгоритм обратного распространения ошибки). Допустим, у нас есть текущие значения весов $W^i_0$ и мы хотим совершить шаг SGD по мини-батчу $X$. Мы должны сделать следующее:
- Совершить forward pass, вычислив и запомнив все промежуточные представления $X = X^0, X^1, ldots, X^m = widehat{y}$.
- Вычислить все градиенты с помощью backward pass.
- С помощью полученных градиентов совершить шаг SGD.
Проиллюстрируем алгоритм на примере двуслойной нейронной сети со скалярным output’ом. Для простоты опустим свободные члены в линейных слоях.
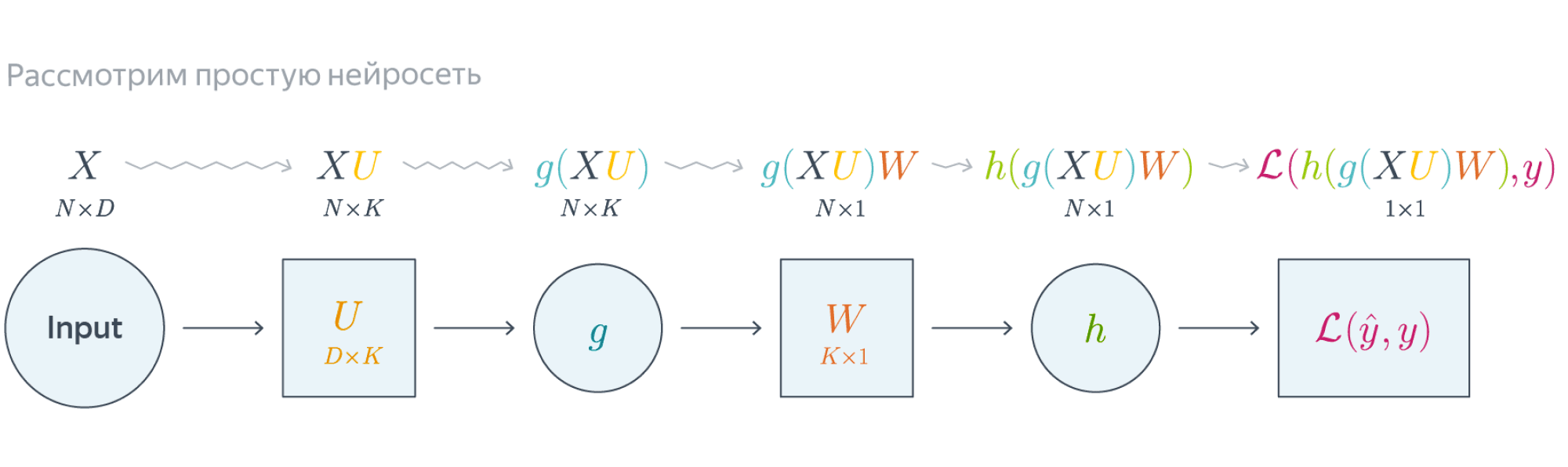
$$nabla_{W_0}mathcal{L} = nabla_{W_0}{left({vphantom{frac12}mathcal{L}circ hcircleft[Wmapsto g(XU_0)Wright]}right)}=$$
$$=g(XU_0)^Tnabla_{g(XU_0)W_0}(mathcal{L}circ h) = underbrace{g(XU_0)^T}_{ktimes N}cdot
left[vphantom{frac12}underbrace{h’left(vphantom{int_0^1}g(XU_0)W_0right)}_{Ntimes 1}odot
underbrace{nabla_{hleft(vphantom{int_0^1}g(XU_0)W_0right)}mathcal{L}}_{Ntimes 1}right]$$
Итого матрица $ktimes 1$, как и $W_0$
$$nabla_{U_0}mathcal{L} = nabla_{U_0}left(vphantom{frac12}
mathcal{L}circ hcircleft[Ymapsto YW_0right]circ gcircleft[ Umapsto XUright]
right)=$$
$$=X^Tcdotnabla_{XU^0}left(vphantom{frac12}mathcal{L}circ hcirc [Ymapsto YW_0]circ gright) =$$
$$=X^Tcdotleft(vphantom{frac12}g'(XU_0)odot
nabla_{g(XU_0)}left[vphantom{in_0^1}mathcal{L}circ hcirc[Ymapsto YW_0right]
right)$$
$$=ldots = underset{Dtimes N}{X^T}cdotleft(vphantom{frac12}
underbrace{g'(XU_0)}_{Ntimes K}odot
underbrace{left[vphantom{int_0^1}left(
underbrace{h’left(vphantom{int_0^1}g(XU_0)W_0right)}_{Ntimes1}odotunderbrace{nabla_{h(vphantom{int_0^1}gleft(XU_0right)W_0)}mathcal{L}}_{Ntimes 1}
right)cdot underbrace{W^T}_{1times K}right]}_{Ntimes K}
right)$$
Итого $Dtimes K$, как и $U_0$
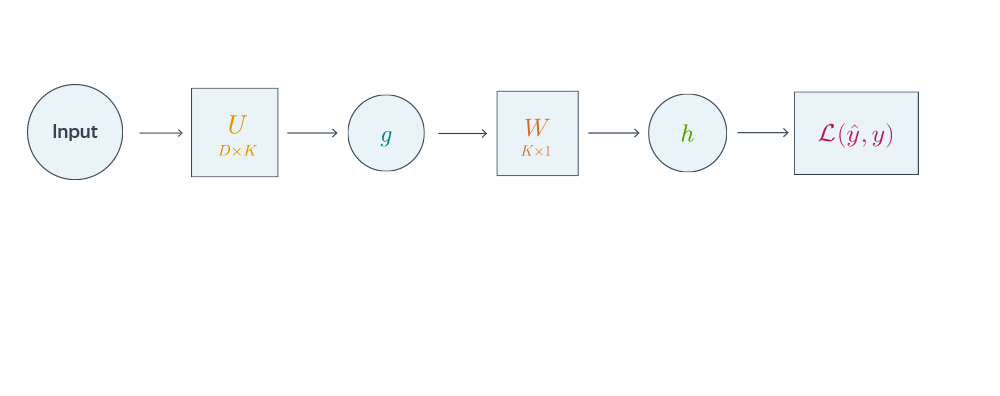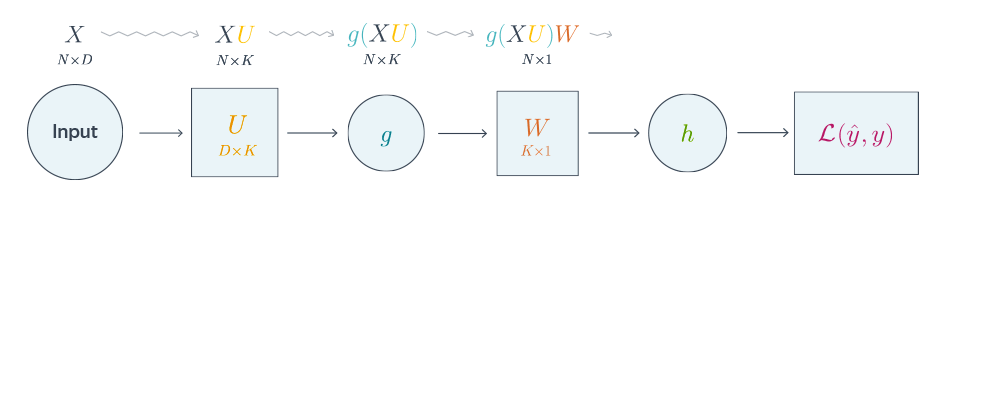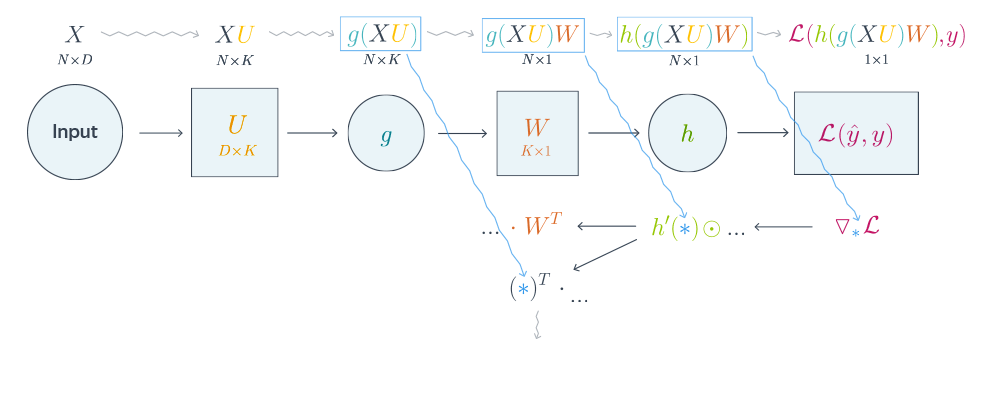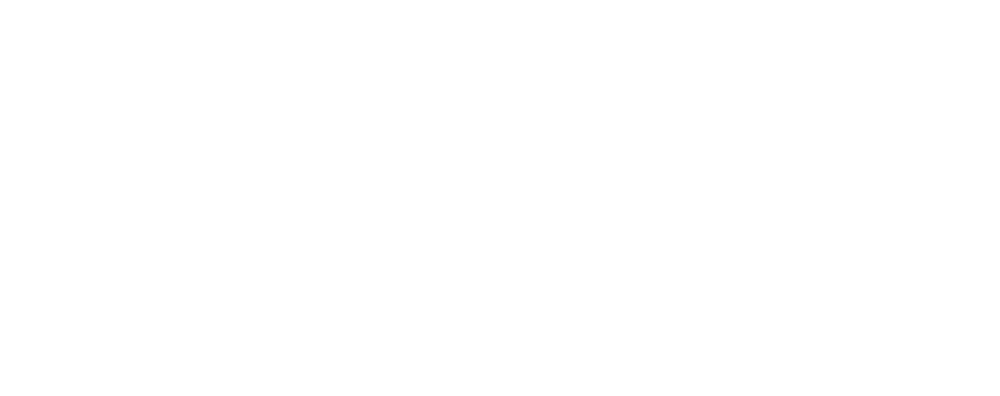
Схематически это можно представить следующим образом:
Backpropagation для двуслойной нейронной сети
Подробнее о предыдущих вычисленияхЕсли вы не уследили за вычислениями в предыдущем примере, давайте более подробно разберём его чуть более конкретную версию (для $g = h = sigma$).
Рассмотрим двуслойную нейронную сеть для классификации. Мы уже встречали ее ранее при рассмотрении линейно неразделимой выборки. Предсказания получаются следующим образом:
$$
widehat{y} = sigma(X^1 W^2) = sigmaBig(big(sigma(X^0 W^1 )big) W^2 Big).
$$
Пусть $W^1_0$ и $W^2_0$ — текущее приближение матриц весов. Мы хотим совершить шаг по градиенту функции потерь, и для этого мы должны вычислить её градиенты по $W^1$ и $W^2$ в точке $(W^1_0, W^2_0)$.
Прежде всего мы совершаем forward pass, в ходе которого мы должны запомнить все промежуточные представления: $X^1 = X^0 W^1_0$, $X^2 = sigma(X^0 W^1_0)$, $X^3 = sigma(X^0 W^1_0) W^2_0$, $X^4 = sigma(sigma(X^0 W^1_0) W^2_0) = widehat{y}$. Они понадобятся нам дальше.
Для полученных предсказаний вычисляется значение функции потерь:
$$
l = mathcal{L}(y, widehat{y}) = y log(widehat{y}) + (1-y) log(1-widehat{y}).
$$
Дальше мы шаг за шагом будем находить производные по переменным из всё более глубоких слоёв.
-
Градиент $mathcal{L}$ по предсказаниям имеет вид
$$
nabla_{widehat{y}}l = frac{y}{widehat{y}} — frac{1 — y}{1 — widehat{y}} = frac{y — widehat{y}}{widehat{y} (1 — widehat{y})},
$$где, напомним, $ widehat{y} = sigma(X^3) = sigmaBig(big(sigma(X^0 W^1_0 )big) W^2_0 Big)$ (обратите внимание на то, что $W^1_0$ и $W^2_0$ тут именно те, из которых мы делаем градиентный шаг).
-
Следующий слой — поэлементное взятие $sigma$. Как мы помним, при переходе через него градиент поэлементно умножается на производную $sigma$, в которую подставлено предыдущее промежуточное представление:
$$
nabla_{X^3}l = sigma'(X^3)odotnabla_{widehat{y}}l = sigma(X^3)left( 1 — sigma(X^3) right) odot frac{y — widehat{y}}{widehat{y} (1 — widehat{y})} =
$$$$
= sigma(X^3)left( 1 — sigma(X^3) right) odot frac{y — sigma(X^3)}{sigma(X^3) (1 — sigma(X^3))} =
y — sigma(X^3)
$$ -
Следующий слой — умножение на $W^2_0$. В этот момент мы найдём градиент как по $W^2$, так и по $X^2$. При переходе через умножение на матрицу градиент, как мы помним, умножается с той же стороны на транспонированную матрицу, а значит:
$$
color{blue}{nabla_{W^2_0}l} = (X^2)^Tcdot nabla_{X^3}l = (X^2)^Tcdot(y — sigma(X^3)) =
$$$$
= color{blue}{left( sigma(X^0W^1_0) right)^T cdot (y — sigma(sigma(X^0W^1_0)W^2_0))}
$$Аналогичным образом
$$
nabla_{X^2}l = nabla_{X^3}lcdot (W^2_0)^T = (y — sigma(X^3))cdot (W^2_0)^T =
$$$$
= (y — sigma(X^2W_0^2))cdot (W^2_0)^T
$$ -
Следующий слой — снова взятие $sigma$.
$$
nabla_{X^1}l = sigma'(X^1)odotnabla_{X^2}l = sigma(X^1)left( 1 — sigma(X^1) right) odot left( (y — sigma(X^2W_0^2))cdot (W^2_0)^T right) =
$$$$
= sigma(X^1)left( 1 — sigma(X^1) right) odotleft( (y — sigma(sigma(X^1)W_0^2))cdot (W^2_0)^T right)
$$ -
Наконец, последний слой — это умножение $X^0$ на $W^1_0$. Тут мы дифференцируем только по $W^1$:
$$
color{blue}{nabla_{W^1_0}l} = (X^0)^Tcdot nabla_{X^1}l = (X^0)^Tcdot big( sigma(X^1) left( 1 — sigma(X^1) right) odot (y — sigma(sigma(X^1)W_0^2))cdot (W^2_0)^Tbig) =
$$$$
= color{blue}{(X^0)^Tcdotbig(sigma(X^0W^1_0)left( 1 — sigma(X^0W^1_0) right) odot (y — sigma(sigma(X^0W^1_0)W_0^2))cdot (W^2_0)^Tbig) }
$$
Итоговые формулы для градиентов получились страшноватыми, но они были получены друг из друга итеративно с помощью очень простых операций: матричного и поэлементного умножения, в которые порой подставлялись значения заранее вычисленных промежуточных представлений.
Автоматизация и autograd
Итак, чтобы нейросеть обучалась, достаточно для любого слоя $f^k: X^{k-1}mapsto X^k$ с параметрами $W^k$ уметь:
- превращать $nabla_{X^k_0}mathcal{L}$ в $nabla_{X^{k-1}_0}mathcal{L}$ (градиент по выходу в градиент по входу);
- считать градиент по его параметрам $nabla_{W^k_0}mathcal{L}$.
При этом слою совершенно не надо знать, что происходит вокруг. То есть слой действительно может быть запрограммирован как отдельная сущность, умеющая внутри себя делать forward pass и backward pass, после чего слои механически, как кубики в конструкторе, собираются в большую сеть, которая сможет работать как одно целое.
Более того, во многих случаях авторы библиотек для глубинного обучения уже о вас позаботились и создали средства для автоматического дифференцирования выражений (autograd). Поэтому, программируя нейросеть, вы почти всегда можете думать только о forward-проходе, прямом преобразовании данных, предоставив библиотеке дифференцировать всё самостоятельно. Это делает код нейросетей весьма понятным и выразительным (да, в реальности он тоже бывает большим и страшным, но сравните на досуге код какой-нибудь разухабистой нейросети и код градиентного бустинга на решающих деревьях и почувствуйте разницу).
Но это лишь начало
Метод обратного распространения ошибки позволяет удобно посчитать градиенты, но дальше с ними что-то надо делать, и старый добрый SGD едва ли справится с обучением современной сетки. Так что же делать? О некоторых приёмах мы расскажем в следующей главе.