Коды для контроля и исправления ошибок - ErrorsMaster.ru - большая энциклопедия ошибок и их решений

Корректирующие коды «на пальцах»

Время на прочтение
11 мин

Количество просмотров 63K

Корректирующие (или помехоустойчивые) коды — это коды, которые могут обнаружить и, если повезёт, исправить ошибки, возникшие при передаче данных. Даже если вы ничего не слышали о них, то наверняка встречали аббревиатуру CRC в списке файлов в ZIP-архиве или даже надпись ECC на планке памяти. А кто-то, может быть, задумывался, как так получается, что если поцарапать DVD-диск, то данные всё равно считываются без ошибок. Конечно, если царапина не в сантиметр толщиной и не разрезала диск пополам.

Как нетрудно догадаться, ко всему этому причастны корректирующие коды. Собственно, ECC так и расшифровывается — «error-correcting code», то есть «код, исправляющий ошибки». А CRC — это один из алгоритмов, обнаруживающих ошибки в данных. Исправить он их не может, но часто это и не требуется.

Давайте же разберёмся, что это такое.

Для понимания статьи не нужны никакие специальные знания. Достаточно лишь понимать, что такое вектор и матрица, как они перемножаются и как с их помощью записать систему линейных уравнений.

Внимание! Много текста и мало картинок. Я постарался всё объяснить, но без карандаша и бумаги текст может показаться немного запутанным.

Каналы с ошибкой

Разберёмся сперва, откуда вообще берутся ошибки, которые мы собираемся исправлять. Перед нами стоит следующая задача. Нужно передать несколько блоков данных, каждый из которых кодируется цепочкой двоичных цифр. Получившаяся последовательность нулей и единиц передаётся через канал связи. Но так сложилось, что реальные каналы связи часто подвержены ошибкам. Вообще говоря, ошибки могут быть разных видов — может появиться лишняя цифра или какая-то пропасть. Но мы будем рассматривать только ситуации, когда в канале возможны лишь замены нуля на единицу и наоборот. Причём опять же для простоты будем считать такие замены равновероятными.

Ошибка — это маловероятное событие (а иначе зачем нам такой канал вообще, где одни ошибки?), а значит, вероятность двух ошибок меньше, а трёх уже совсем мала. Мы можем выбрать для себя некоторую приемлемую величину вероятности, очертив границу «это уж точно невозможно». Это позволит нам сказать, что в канале возможно не более, чем $k$ ошибок. Это будет характеристикой канала связи.

Для простоты введём следующие обозначения. Пусть данные, которые мы хотим передавать, — это двоичные последовательности фиксированной длины. Чтобы не запутаться в нулях и единицах, будем иногда обозначать их заглавными латинскими буквами ( $A$ , $B$ , $C$ , …). Что именно передавать, в общем-то неважно, просто с буквами в первое время будет проще работать.

Кодирование и декодирование будем обозначать прямой стрелкой (), а передачу по каналу связи — волнистой стрелкой (). Ошибки при передаче будем подчёркивать.

Например, пусть мы хотим передавать только сообщения $A=0$ и $B=1$ . В простейшем случае их можно закодировать нулём и единицей (сюрприз!):

$begin{aligned} A &to 0,\ B &to 1. end{aligned}$

Передача по каналу, в котором возникла ошибка будет записана так:

Цепочки нулей и единиц, которыми мы кодируем буквы, будем называть кодовыми словами. В данном простом случае кодовые слова — это $0$ и $1$ .

Код с утроением

Давайте попробуем построить какой-то корректирующий код. Что мы обычно делаем, когда кто-то нас не расслышал? Повторяем дважды:

$begin{aligned} A &to 00,\ B &to 11. end{aligned}$

Правда, это нам не очень поможет. В самом деле, рассмотрим канал с одной возможной ошибкой:

Какие выводы мы можем сделать, когда получили $01$ ? Понятно, что раз у нас не две одинаковые цифры, то была ошибка, но вот в каком разряде? Может, в первом, и была передана буква $B$ . А может, во втором, и была передана $A$ .

То есть, получившийся код обнаруживает, но не исправляет ошибки. Ну, тоже неплохо, в общем-то. Но мы пойдём дальше и будем теперь утраивать цифры.

$begin{aligned} A &to 000,\ B &to 111. end{aligned}$

Проверим в деле:

Получили $010$ . Тут у нас есть две возможности: либо это $B$ и было две ошибки (в крайних цифрах), либо это $A$ и была одна ошибка. Вообще, вероятность одной ошибки выше вероятности двух ошибок, так что самым правдоподобным будет предположение о том, что передавалась именно буква $A$ . Хотя правдоподобное — не значит истинное, поэтому рядом и стоит вопросительный знак.

Если в канале связи возможна максимум одна ошибка, то первое предположение о двух ошибках становится невозможным и остаётся только один вариант — передавалась буква $A$ .

Про такой код говорят, что он исправляет одну ошибку. Две он тоже обнаружит, но исправит уже неверно.

Это, конечно, самый простой код. Кодировать легко, да и декодировать тоже. Ноликов больше — значит передавался ноль, единичек — значит единица.

Если немного подумать, то можно предложить код исправляющий две ошибки. Это будет код, в котором мы повторяем одиночный бит 5 раз.

Расстояния между кодами

Рассмотрим поподробнее код с утроением. Итак, мы получили работающий код, который исправляет одиночную ошибку. Но за всё хорошее надо платить: он кодирует один бит тремя. Не очень-то и эффективно.

И вообще, почему этот код работает? Почему нужно именно утраивать для устранения одной ошибки? Наверняка это всё неспроста.

Давайте подумаем, как этот код работает. Интуитивно всё понятно. Нолики и единички — это две непохожие последовательности. Так как они достаточно длинные, то одиночная ошибка не сильно портит их вид.

Пусть мы передавали $000$ , а получили $001$ . Видно, что эта цепочка больше похожа на исходные $000$ , чем на $111$ . А так как других кодовых слов у нас нет, то и выбор очевиден.

Но что значит «больше похоже»? А всё просто! Чем больше символов у двух цепочек совпадает, тем больше их схожесть. Если почти все символы отличаются, то цепочки «далеки» друг от друга.

Можно ввести некоторую величину , равную количеству различающихся цифр в соответствующих разрядах цепочек $alpha$ и $beta$ . Эту величину называют расстоянием Хэмминга. Чем больше это расстояние, тем меньше похожи две цепочки.

Например, , так как все цифры в соответствующих позициях равны, а вот .

Расстояние Хэмминга называют расстоянием неспроста. Ведь в самом деле, что такое расстояние? Это какая-то характеристика, указывающая на близость двух точек, и для которой верны утверждения:

Расстояние между точками неотрицательно и равно нулю только, если точки совпадают.
Расстояние в обе стороны одинаково.
Путь через третью точку не короче, чем прямой путь.

Достаточно разумные требования.

Математически это можно записать так (нам это не пригодится, просто ради интереса посмотрим):

Предлагаю читателю самому убедиться, что для расстояния Хэмминга эти свойства выполняются.

Окрестности

Таким образом, разные цепочки мы считаем точками в каком-то воображаемом пространстве, и теперь мы умеем находить расстояния между ними. Правда, если попытаться сколько нибудь длинные цепочки расставить на листе бумаги так, чтобы расстояния Хэмминга совпадали с расстояниями на плоскости, мы можем потерпеть неудачу. Но не нужно переживать. Всё же это особое пространство со своими законами. А слова вроде «расстояния» лишь помогают нам рассуждать.

Пойдём дальше. Раз мы заговорили о расстоянии, то можно ввести такое понятие как окрестность. Как известно, окрестность какой-то точки — это шар определённого радиуса с центром в ней. Шар? Какие ещё шары! Мы же о кодах говорим.

Но всё просто. Ведь что такое шар? Это множество всех точек, которые находятся от данной не дальше, чем некоторое расстояние, называемое радиусом. Точки у нас есть, расстояние у нас есть, теперь есть и шары.

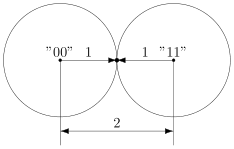
Так, скажем, окрестность кодового слова $000$ радиуса 1 — это все коды, находящиеся на расстоянии не больше, чем 1 от него, то есть отличающиеся не больше, чем в одном разряде. То есть это коды:

Да, вот так странно выглядят шары в пространстве кодов.

А теперь посмотрите. Это же все возможные коды, которые мы получим в канале в одной ошибкой, если отправим $000$ ! Это следует прямо из определения окрестности. Ведь каждая ошибка заставляет цепочку измениться только в одном разряде, а значит удаляет её на расстояние 1 от исходного сообщения.

Аналогично, если в канале возможны две ошибки, то отправив некоторое сообщение $x$ , мы получим один из кодов, который принадлежит окрестности $x$ радиусом 2.

Тогда всю нашу систему декодирования можно построить так. Мы получаем какую-то цепочку нулей и единиц (точку в нашей новой терминологии) и смотрим, в окрестность какого кодового слова она попадает.

Сколько ошибок может исправить код?

Чтобы код мог исправлять больше ошибок, окрестности должны быть как можно шире. С другой стороны, они не должны пересекаться. Иначе если точка попадёт в область пересечения, непонятно будет, к какой окрестности её отнести.

В коде с удвоением между кодовыми словами $00$ и $11$ расстояние равно 2 (оба разряда различаются). А значит, если мы построим вокруг них шары радиуса 1, то они будут касаться. Это значит, точка касания будет принадлежать обоим шарам и непонятно будет, к какому из них её отнести.

Именно это мы и получали. Мы видели, что есть ошибка, но не могли её исправить.

Что интересно, точек касания в нашем странном пространстве у шаров две — это коды $01$ и $10$ . Расстояния от них до центров равны единице. Конечно же, в обычно геометрии такое невозможно, поэтому рисунки — это просто условность для более удобного рассуждения.

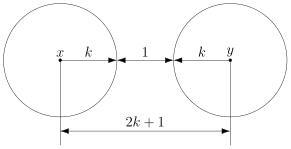
В случае кода с утроением, между шарами будет зазор.

Минимальный зазор между шарами равен 1, так как у нас расстояния всегда целые (ну не могут же две цепочки отличаться в полутора разрядах).

В общем случае получаем следующее.

Этот очевидный результат на самом деле очень важен. Он означает, что код с минимальным кодовым расстоянием $d_{min}$ будет успешно работать в канале с $k$ ошибками, если выполняется соотношение

$d_{min} geqslant 2k+1.$

Полученное равенство позволяет легко определить, сколько ошибок будет исправлять тот или иной код. А сколько код ошибок может обнаружить? Рассуждения такие же. Код обнаруживает $k$ ошибок, если в результате не получится другое кодовое слово. То есть, кодовые слова не должны находиться в окрестностях радиуса $k$ других кодовых слов. Математически это записывается так:

$d_{min}geqslant k + 1.$

Рассмотрим пример. Пусть мы кодируем 4 буквы следующим образом.

$begin{aligned} A to 10100,\ B to 01000,\ C to 00111,\ D to 11011.\ end{aligned}$

Чтобы найти минимальное расстояние между различными кодовыми словами, построим таблицу попарных расстояний.

	A	B	C	D
A	—	3	3	4
B	3	—	4	3
C	3	4	—	3
D	4	3	3	—

Минимальное расстояние $d_{min}=3$ , а значит , откуда получаем, что такой код может исправить до $k=1$ ошибок. Обнаруживает же он две ошибки.

Рассмотрим пример:

Чтобы декодировать полученное сообщение, посмотрим, к какому символу оно ближе всего.

$begin{aligned} A:, d(10110, 10100) &= 1,\ B:, d(10110, 01000) &= 4,\ C:, d(10110, 00111) &= 2,\ D:, d(10110, 11011) &= 3. end{aligned}$

Минимальное расстояние получилось для символа $A$ , значит вероятнее всего передавался именно он:

Итак, этот код исправляет одну ошибку, как и код с утроением. Но он более эффективен, так как в отличие от кода с утроением здесь кодируется уже 4 символа.

Таким образом, основная проблема при построении такого рода кодов — так расположить кодовые слова, чтобы они были как можно дальше друг от друга, и их было побольше.

Для декодирования можно было бы использовать таблицу, в которой указывались бы все возможные принимаемые сообщения, и кодовые слова, которым они соответствуют. Но такая таблица получилась бы очень большой. Даже для нашего маленького кода, который выдаёт 5 двоичных цифр, получилось бы варианта возможных принимаемых сообщений. Для более сложных кодов таблица будет значительно больше.

Попробуем придумать способ коррекции сообщения без таблиц. Мы всегда сможем найти полезное применение освободившейся памяти.

Интерлюдия: поле GF(2)

Для изложения дальнейшего материала нам потребуются матрицы. А при умножении матриц, как известно мы складываем и перемножаем числа. И тут есть проблема. Если с умножением всё более-менее хорошо, то как быть со сложением? Из-за того, что мы работаем только с одиночными двоичными цифрами, непонятно, как сложить 1 и 1, чтобы снова получилась одна двоичная цифра. Значит вместо классического сложения нужно использовать какое-то другое.

Введём операцию сложения как сложение по модулю 2 (хорошо известный программистам XOR):

$begin{aligned} 0 + 0 &= 0,\ 0 + 1 &= 1,\ 1 + 0 &= 1,\ 1 + 1 &= 0. end{aligned}$

Умножение будем выполнять как обычно. Эти операции на самом деле введены не абы как, а чтобы получилась система, которая в математике называется полем. Поле — это просто множество (в нашем случае из 0 и 1), на котором так определены сложение и умножение, чтобы основные алгебраические законы сохранялись. Например, чтобы основные идеи, касающиеся матриц и систем уравнений по-прежнему были верны. А вычитание и деление мы можем ввести как обратные операции.

Множество из двух элементов с операциями, введёнными так, как мы это сделали, называется полем Галуа GF(2). GF — это Galois field, а 2 — количество элементов.

У сложения есть несколько очень полезных свойств, которыми мы будем пользоваться в дальнейшем.

Это свойство прямо следует из определения.

А в этом можно убедиться, прибавив $y$ к обеим частям равенства. Это свойство, в частности означает, что мы можем переносить в уравнении слагаемые в другую сторону без смены знака.

Проверяем корректность

Вернёмся к коду с утроением.

$begin{aligned} A &to 000,\ B &to 111. end{aligned}$

Для начала просто решим задачу проверки, были ли вообще ошибки при передаче. Как видно, из самого кода, принятое сообщение будет кодовым словом только тогда, когда все три цифры равны между собой.

Пусть мы приняли вектор-строку $x$ из трёх цифр. (Стрелочки над векторами рисовать не будем, так как у нас почти всё — это вектора или матрицы.)

Математически равенство всех трёх цифр можно записать как систему:

$left{ begin{aligned} x_1 &= x_2,\ x_2 &= x_3. end{aligned} right.$

Или, если воспользоваться свойствами сложения в GF(2), получаем

$left{ begin{aligned} x_1 + x_2 &= 0,\ x_2 + x_3 &= 0. end{aligned} right.$

Или

$left{ begin{aligned} 1cdot x_1 + 1cdot x_2 + 0cdot x_3 &= 0,\ 0cdot x_1 + 1cdot x_2 + 1cdot x_3 &= 0. end{aligned} right.$

В матричном виде эта система будет иметь вид

где

$H = begin{pmatrix} 1 & 1 & 0\ 0 & 1 & 1 end{pmatrix}.$

Транспонирование здесь нужно потому, что $x$ — это вектор-строка, а не вектор-столбец. Иначе мы не могли бы умножать его справа на матрицу.

Будем называть матрицу $H$ проверочной матрицей. Если полученное сообщение — это корректное кодовое слово (то есть, ошибки при передаче не было), то произведение проверочной матрицы на это сообщение будет равно нулевому вектору.

Умножение на матрицу — это гораздо более эффективно, чем поиск в таблице, но у нас на самом деле есть ещё одна таблица — это таблица кодирования. Попробуем от неё избавиться.

Кодирование

Итак, у нас есть система для проверки

$left{ begin{aligned} x_1 + x_2 &= 0,\ x_2 + x_3 &= 0. end{aligned} right.$

Её решения — это кодовые слова. Собственно, мы систему и строили на основе кодовых слов. Попробуем теперь решить обратную задачу. По системе (или, что то же самое, по матрице $H$ ) найдём кодовые слова.

Правда, для нашей системы мы уже знаем ответ, поэтому, чтобы было интересно, возьмём другую матрицу:

$H = begin{pmatrix} 1 & 0 & 1 & 0 & 0 \ 0 & 1 & 1 & 0 & 1\ 0 & 0 & 0 & 1 & 1 end{pmatrix}.$

Соответствующая система имеет вид:

$left{ begin{aligned} x_1 + x_3 &= 0,\ x_2 + x_3 + x_5 &= 0,\ x_4 + x_5 &= 0. end{aligned} right.$

Чтобы найти кодовые слова соответствующего кода нужно её решить.

В силу линейности сумма двух решений системы тоже будет решением системы. Это легко доказать. Если $a$ и $b$ — решения системы, то для их суммы верно

что означает, что она тоже — решение.

Поэтому если мы найдём все линейно независимые решения, то с их помощью можно получить вообще все решения системы. Для этого просто нужно найти их всевозможные суммы.

Выразим сперва все зависимые слагаемые. Их столько же, сколько и уравнений. Выражать надо так, чтобы справа были только независимые. Проще всего выразить .

Если бы нам не так повезло с системой, то нужно было бы складывая уравнения между собой получить такую систему, чтобы какие-то три переменные встречались по одному разу. Ну, или воспользоваться методом Гаусса. Для GF(2) он тоже работает.

Итак, получаем:

$left{ begin{aligned} x_1 &= x_3,\ x_2 &= x_3 + x_5,\ x_4 &= x_5. end{aligned} right.$

Чтобы получить все линейно независимые решения, приравниваем каждую из зависимых переменных к единице по очереди.

$begin{aligned} x_3=1, x_5=0:quad x_1=1, x_2=1, x_4=0 Rightarrow x^{(1)} = (1, 1, 1, 0, 0),\ x_3=0, x_5=1:quad x_1=0, x_2=1, x_4=1 Rightarrow x^{(2)} = (0, 1, 0, 1, 1). end{aligned}$

Всевозможные суммы этих независимых решений (а именно они и будут кодовыми векторами) можно получить так:

$a_1 x^{(1)}+a_2 x^{(2)},$

где равны либо нулю или единице. Так как таких коэффициентов два, то всего возможно $2^2=4$ сочетания.

Но посмотрите! Формула, которую мы только что получили — это же снова умножение матрицы на вектор.

$(a_1, a_2)cdot begin{pmatrix} 1 & 1 & 1 & 0 & 0 \ 0 & 1 & 0 & 1 & 1 end{pmatrix} = aG.$

Строчки здесь — линейно независимые решения, которые мы получили. Матрица $G$ называется порождающей. Теперь вместо того, чтобы сами составлять таблицу кодирования, мы можем получать кодовые слова простым умножением на матрицу:

Найдём кодовые слова для этого кода. (Не забываем, что длина исходных сообщений должна быть равна 2 — это количество найденных решений.)

$begin{aligned} 00 &to 00000,\ 01 &to 01011,\ 10 &to 11100,\ 11 &to 10111. end{aligned}$

Итак, у нас есть готовый код, обнаруживающий ошибки. Проверим его в деле. Пусть мы хотим отправить 01 и у нас произошла ошибка при передаче. Обнаружит ли её код?

$a=01 to aG=01011 rightsquigarrow x=01underline{1}11 to Hx^T = (110)^T neq 0.$

А раз в результате не нулевой вектор, значит код заподозрил неладное. Провести его не удалось. Ура, код работает!

Для кода с утроением, кстати, порождающая матрица выглядит очень просто:

Подобные коды, которые можно порождать и проверять матрицей называются линейными (бывают и нелинейные), и они очень широко применяются на практике. Реализовать их довольно легко, так как тут требуется только умножение на константную матрицу.

Ошибка по синдрому

Ну хорошо, мы построили код обнаруживающий ошибки. Но мы же хотим их исправлять!

Для начала введём такое понятие, как вектор ошибки. Это вектор, на который отличается принятое сообщение от кодового слова. Пусть мы получили сообщение $x$ , а было отправлено кодовое слово $v$ . Тогда вектор ошибки по определению

Но в странном мире GF(2), где сложение и вычитание одинаковы, будут верны и соотношения:

$begin{aligned} v &= x + e,\ x &= v + e. end{aligned}$

В силу особенностей сложения, как читатель сам может легко убедиться, в векторе ошибки на позициях, где произошла ошибка будет единица, а на остальных ноль.

Как мы уже говорили раньше, если мы получили сообщение $x$ с ошибкой, то . Но ведь векторов, не равных нулю много! Быть может то, какой именно ненулевой вектор мы получили, подскажет нам характер ошибки?

Назовём результат умножения на проверочную матрицу синдромом:

И заметим следующее

Это означает, что для ошибки синдром будет таким же, как и для полученного сообщения.

Разложим все возможные сообщения, которые мы можем получить из канала связи, по кучкам в зависимости от синдрома. Тогда из последнего соотношения следует, что в каждой кучке будут вектора с одной и той же ошибкой. Причём вектор этой ошибки тоже будет в кучке. Вот только как его узнать?

А очень просто! Помните, мы говорили, что у нескольких ошибок вероятность ниже, чем у одной ошибки? Руководствуясь этим соображением, наиболее правдоподобным будет считать вектором ошибки тот вектор, у которого меньше всего единиц. Будем называть его лидером.

Давайте посмотрим, какие синдромы дают всевозможные 5-элементные векторы. Сразу сгруппируем их и подчеркнём лидеров — векторы с наименьшим числом единиц.

В принципе, для корректирования ошибки достаточно было бы хранить таблицу соответствия синдрома лидеру.

Обратите внимание, что в некоторых строчках два лидера. Это значит для для данного синдрома два паттерна ошибки равновероятны. Иными словами, код обнаружил две ошибки, но исправить их не может.

Лидеры для всех возможных одиночных ошибок находятся в отдельных строках, а значит код может исправить любую одиночную ошибку. Ну, что же… Попробуем в этом убедиться.

$a=01 to aG=01011 rightsquigarrow x=01underline{1}11 to s(x)=Hx^T = (110)^T to e=(00100).$

Вектор ошибки равен , а значит ошибка в третьем разряде. Как мы и загадали.

Ура, всё работает!

Что же дальше?

Чтобы попрактиковаться, попробуйте повторить рассуждения для разных проверочных матриц. Например, для кода с утроением.

Логическим продолжением изложенного был бы рассказ о циклических кодах — чрезвычайно интересном подклассе линейных кодов, обладающим замечательными свойствами. Но тогда, боюсь, статья уж очень бы разрослась.

Если вас заинтересовали подробности, то можете почитать замечательную книжку Аршинова и Садовского «Коды и математика». Там изложено гораздо больше, чем представлено в этой статье. Если интересует математика кодирования — то поищите «Теория и практика кодов, контролирующих ошибки» Блейхута. А вообще, материалов по этой теме довольно много.

Надеюсь, когда снова будет свободное время, напишу продолжение, в котором расскажу про циклические коды и покажу пример программы для кодирования и декодирования. Если, конечно, почтенной публике это интересно.

Источник

Для
того, чтобы код исправлял ошибки,
необходимо увеличить его минимальное
кодовое расстояние.

Пример.
Трёхразрядный код состоит из двух
допустимых комбинаций 000 и 111. В случае
одиночной ошибки для первого кодового
набора возможные кодовые наборы
001,010,100, для второго – 011,101,110. У каждого
допустимого кодового набора “свои”
недопустимые кодовые наборы. Его
минимальное кодовое расстояние d_min
равно 3.

Если
ошибка одиночная, то удается определить
её местоположение и исправить её, так
как каждая ошибка приводит к недопустимому
кодовому набору, соответствующему
только одному из допустимых кодовых
наборов.

Определение.
Код называется
кодом с исправлением ошибок, если всегда
из неправильного кодового набора можно
получить правильный кодовый набор
(например, коды Хэмминга).

Если
d_min= 3, то любая
одиночная ошибка переводит допустимый
кодовый набор в недопустимый, находящийся
на расстоянии, равном 1, от исходного
кодового набора, и на расстоянии, равном
2, от любого другого допустимого кодового
набора. Поэтому в коде с d_min= 3 можно
исправить любую одиночную ошибку или
обнаружить любую двойную ошибку. Если
d_min= 4, то можно
исправить любую одиночную ошибку и
обнаружить любую двойную или обнаружить
тройную ошибку.

Основное
свойство кода – возможность обнаруживать
и выделять местоположение ошибочных
разрядов. Когда местоположение ошибки
определено, то осуществляют замену
ошибочного разряда на его дополнение.

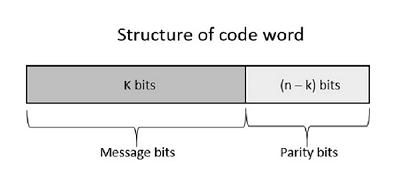
5.2.1. Основные принципы построения кодов Хэмминга с исправлением ошибок

К
каждому набору из m
информационных разрядов (сообщению)
присоединяются k
разрядов p₁,
p₂,
…p_k
проверки на чётность.
Каждому
из (m+k)
присваивается десятичное значение
позиции, начиная со значения 1 для
старшего разряда и кончая значением
(m+k)
для младшего разряда.
Производится
k
проверок на чётность числа единиц в
выбранных разрядах каждого кодового
набора. Результат каждой проверки на
чётность записывается как 1 или 0 в
зависимости от того, обнаружена ошибка
или нет.
По
результатам проверок строится двоичное
число c_k
_…
c₂c₁,
равное десятичному значению, присвоенному
местоположению ошибочного разряда,
если произошла ошибка, и нулю при её
отсутствии. Это число называется номером
позиции ошибочного разряда.

Число
разрядов k
должно быть достаточно большим для
указания положения любой из (m+k)
возможных одиночных ошибок. Так как
m+k+1-количество
возможных событий, 2^k
– максимальное количество кодовых
комбинаций, то k
должно удовлетворять неравенству 2^k
m+k+1.

Определим
максимальное значение m
для заданного количества k.Обозначим
количество разрядов в коде n=
m+k.

Таблица 15

n	1	2…3	4…7	8…15	16…31	32…63
m	0	0…1	1…4	4…11	11…26	26…57
k	1	2…2	3…3	4…4	5…5	6…6

Определим
теперь позиции, которые необходимо
проверить в каждой из k
проверок. Если в кодовой комбинации
ошибок нет, то контрольное число двоичное
c_k_…
c₂c₁содержит
только 0. Если в первом разряде контрольного
числа стоит 1, то в результате первой
проверки обнаружена ошибка.

Таблица 16

№ позиции возможной ошибки	Двоичный эквивалент
0	00000
1	00001
2	00010
3	00011
4	00100
5	00101
6	00110
7	00111
8	01000
9	01001

Окончание
таблицы 16

№ позиции возможной ошибки	Двоичный эквивалент
10	01010
11	01011
12	01100
13	01101
14	01110
15	01111
16	10000
17	10001
18	10010
…	…

Из
табл. 16 двоичных эквивалентов для номера
позиции возможной ошибки видно, что в
первую проверяемую группу разрядов
входят 1,3,5,7,9, 11,13,15, 17 и т.д., во вторую –
2,3,6,7,10,11,14,15,18 и т.д.

Таблица
17

Проверка	Проверяемые разряды
1	1,3,5,7,9, 11,13,15, 17 …
2	2,3,6,7,10,11,14,15,18 …
3	4,5,6,7, 12,13,14, 15 …
4	8,9,10,11, 12,13,14, 15 …
…	…

Разряды,
номера которых кратны степеням 2:
1,2,4,8,16…, встречаются в каждой проверяемой
группе один раз. Удобно использовать
эти разряды в качестве контрольных, а
остальные – информационных разрядов.

Пример.
Пусть исходное сообщение 00111. Количество
информационных разрядов m=5.
Количество контрольных разрядов k=4.
Длина кода Хэмминга равна 9. Построим
код Хэмминга для исходного сообщения.

Номер позиции	1	2	3	4	5	6	7	8	9
Исходное сообщение			0		0	1	1		1
1-я контрольная группа	0		0		0		1		1
2-я контрольная группа		0	0			1	1
3-я контрольная группа				0	0	1	1
4-я контрольная группа								1	1
Код Хэмминга	0	0	0	0	0	1	1	1	1

Код
Хэмминга для десятичных цифр в
двоично-десятичном коде 8421 приведен в
табл. 18.

Таблица
18

Десятичная цифра	p₁	p₂	m₁	p₃	m₂	m₃	m₄
0	0	0	0	0	0	0	0
1	1	1	0	1	0	0	1
2	0	1	0	1	0	1	0
3	1	0	0	0	0	1	1
4	1	0	0	1	1	0	0
5	0	1	0	0	1	0	1
6	1	1	0	0	1	1	0
7	0	0	0	1	1	1	1
8	1	1	1	0	0	0	0
9	0	0	1	1	0	0	1

Рассмотрим
способ выявления положения ошибки и её
исправления.

Пример.
Пусть передана последовательность
1000011. Из-за ошибки в третьем разряде
принято сообщение 1010011. Положение ошибки
можно определить, выполняя 3 проверки
на четность.

Номер позиции	1	2	3	4	5	6	7	c_i
Сообщение	1	0	1	0	0	1	1
1-я проверка на четность	1		1		0		1	1
2-я проверка на четность		0	1			1	1	1
3-я проверка на четность				0	0	1	1	0
Исправленное сообщение	1	0	0	0	0	1	1

Полученный
номер позиции c₃c₂c₁=
011, т.е. ошибка в третьем разряде.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Аннотация: Контроль по четности, CRC, алгоритм Хэмминга. Введение в коды Рида-Соломона: принципы, архитектура и реализация. Метод коррекции ошибок FEC (Forward Error Correction).

Каналы передачи данных ненадежны (шумы, наводки и т.д.), да и само оборудование обработки информации работает со сбоями. По этой причине важную роль приобретают механизмы детектирования ошибок. Ведь если ошибка обнаружена, можно осуществить повторную передачу данных и решить проблему. Если исходный код по своей длине равен полученному коду, обнаружить ошибку передачи не предоставляется возможным. Можно, конечно, передать код дважды и сравнить, но это уже двойная избыточность.

Простейшим способом обнаружения ошибок является контроль по четности. Обычно контролируется передача блока данных ( М бит). Этому блоку ставится в соответствие кодовое слово длиной N бит, причем N>M. Избыточность кода характеризуется величиной 1-M/N. Вероятность обнаружения ошибки определяется отношением M/N (чем меньше это отношение, тем выше вероятность обнаружения ошибки, но и выше избыточность).

При передаче информации она кодируется таким образом, чтобы с одной стороны характеризовать ее минимальным числом символов, а с другой – минимизировать вероятность ошибки при декодировании получателем. Для выбора типа кодирования важную роль играет так называемое расстояние Хэмминга.

Пусть А и Б — две двоичные кодовые последовательности равной длины. Расстояние Хэмминга между двумя этими кодовыми последовательностями равно числу символов, которыми они отличаются. Например, расстояние Хэмминга между кодами 00111 и 10101 равно 2.

Можно показать, что для детектирования ошибок в n битах схема кодирования требует применения кодовых слов с расстоянием Хэмминга не менее N + 1. Можно также показать, что для исправления ошибок в N битах необходима схема кодирования с расстоянием Хэмминга между кодами не менее 2N + 1. Таким образом, конструируя код, мы пытаемся обеспечить расстояние Хэмминга между возможными кодовыми последовательностями большее, чем оно может возникнуть из-за ошибок.

Широко распространены коды с одиночным битом четности. В этих кодах к каждым М бит добавляется 1 бит, значение которого определяется четностью (или нечетностью) суммы этих М бит. Так, например, для двухбитовых кодов 00, 01, 10, 11 кодами с контролем четности будут 000, 011, 101 и 110. Если в процессе передачи один бит будет передан неверно, четность кода из М+1 бита изменится.

Предположим, что частота ошибок ( BER – Bit Error Rate) равна р = 10^-4. В этом случае вероятность передачи 8 бит с ошибкой составит 1 – (1 – p)⁸ = 7,9 х 10^-4. Добавление бита четности позволяет детектировать любую ошибку в одном из переданных битах. Здесь вероятность ошибки в одном из 9 битов равна 9p(1 – p)⁸. Вероятность же реализации необнаруженной ошибки составит 1 – (1 – p)⁹ – 9p(1 – p)⁸ = 3,6 x 10^-7. Таким образом, добавление бита четности уменьшает вероятность необнаруженной ошибки почти в 1000 раз. Использование одного бита четности типично для асинхронного метода передачи. В синхронных каналах чаще используется вычисление и передача битов четности как
для строк, так и для столбцов передаваемого массива данных. Такая схема позволяет не только регистрировать, но и исправлять ошибки в одном из битов переданного блока.

Контроль по четности достаточно эффективен для выявления одиночных и множественных ошибок в условиях, когда они являются независимыми. При возникновении ошибок в кластерах бит метод контроля четности неэффективен, и тогда предпочтительнее метод вычисления циклических сумм ( CRC — Cyclic Redundancy Check). В этом методе передаваемый кадр делится на специально подобранный образующий полином. Дополнение остатка от деления и является контрольной суммой.

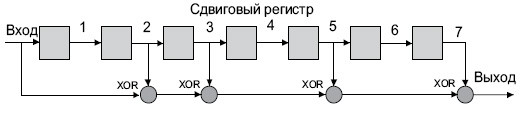
В Ethernet вычисление CRC производится аппаратно. На
рис.
4.1 показан пример реализации аппаратного расчета CRC для образующего полинома R(x) = 1 + x² + x³ + x⁵ + x⁷. В этой схеме входной код приходит слева.

Рис.
4.1.
Схема реализации расчета CRC

Эффективность CRC для обнаружения ошибок на многие порядки выше простого контроля четности. В настоящее время стандартизовано несколько типов образующих полиномов. Для оценочных целей можно считать, что вероятность невыявления ошибки в случае использования CRC, если ошибка на самом деле имеет место, равна (1/2)^r, где r — степень образующего полинома.

Таблица
4.1.

CRC -12	x¹² + x¹¹ + x³ + x² + x¹ + 1
CRC -16	x¹⁶ + x¹⁵ + x² + 1
CRC -CCITT	x¹⁶ + x¹² + x⁵ + 1

4.1. Алгоритмы коррекции ошибок

Исправлять ошибки труднее, чем их детектировать или предотвращать. Процедура коррекции ошибок предполагает два совмещеных процесса: обнаружение ошибки и определение места (идентификации сообщения и позиции в сообщении). После решения этих двух задач исправление тривиально — надо инвертировать значение ошибочного бита. В наземных каналах связи, где вероятность ошибки невелика, обычно используется метод детектирования ошибок и повторной пересылки фрагмента, содержащего дефект. Для спутниковых каналов с типичными для них большими задержками системы коррекции ошибок становятся привлекательными. Здесь используют коды Хэмминга или коды свертки.

Код Хэмминга представляет собой блочный код, который позволяет выявить и исправить ошибочно переданный бит в пределах переданного блока. Обычно код Хэмминга характеризуется двумя целыми числами, например, (11,7), используемыми при передаче 7-битных ASCII-кодов. Такая запись говорит, что при передаче 7-битного кода используется 4 контрольных бита (7 + 4 = 11). При этом предполагается, что имела место ошибка в одном бите и что ошибка в двух или более битах существенно менее вероятна. С учетом этого исправление ошибки осуществляется с определенной вероятностью. Например, пусть возможны следующие правильные коды (все они, кроме первого и последнего, отстоят друг от друга на расстояние Хэмминга 4):

00000000

11110000

00001111

11111111

При получении кода 00000111 нетрудно предположить, что правильное значение полученного кода равно 00001111. Другие коды отстоят от полученного на большее расстояние Хэмминга.

Рассмотрим пример передачи кода буквы s = 0x073 = 1110011 с использованием кода Хэмминга (11,7). Таблица 4.2.

Таблица
4.2.

Позиция бита	11	10	9	8	7	6	5	4	3	2	1
Значение бита	1	1	1	*	0	0	1	*	1	*	*

Символами * помечены четыре позиции, где должны размещаться контрольные биты. Эти позиции определяются целой степенью 2 (1, 2, 4, 8 и т.д.). Контрольная сумма формируется путем выполнения операции XoR (исключающее ИЛИ) над кодами позиций ненулевых битов. В данном случае это 11, 10, 9, 5 и 3. Вычислим контрольную сумму:

11=	1011
10=	1010
09=	1001
05=	0101
03=	0011
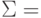	1110

Таким образом, приемник получит код

Позиция бита	11	10	9	8	7	6	5	4	3	2	1
Значение бита	1	1	1	1	0	0	1	1	1	1	0

Просуммируем снова коды позиций ненулевых битов и получим нуль;

11=	1011
10=	1010
09=	1001
08=	1000
05=	0101
04=	0100
03=	0011
02=	0010
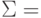	0000

Ну а теперь рассмотрим два случая ошибок в одном из битов посылки, например в бите 7 (1 вместо 0) и в бите 5 (0 вместо 1). Просуммируем коды позиций ненулевых битов еще раз:

Таблица
4.3.

11=	1011
10=	1010
09=	1001
08=	1000
07=	0111
05=	0101
04=	0100
03=	0011
02=	0010
	0111

11=	1011
10=	1010
09=	1001
08=	1000
04=	0100
03=	0011
02=	0010
	0001

В обоих случаях контрольная сумма равна позиции бита, переданного с ошибкой. Теперь для исправления ошибки достаточно инвертировать бит, номер которого указан в контрольной сумме. Понятно, что если ошибка произойдет при передаче более чем одного бита, код Хэмминга при данной избыточности окажется бесполезен.

В общем случае код имеет N = M + C бит и предполагается, что не более чем один бит в коде может иметь ошибку. Тогда возможно N+1 состояние кода (правильное состояние и n ошибочных). Пусть М = 4, а N = 7, тогда слово-сообщение будет иметь вид: M4, M3, M2, C3, M1, C2, C1. Теперь попытаемся вычислить значения С1, С2, С3. Для этого используются уравнения, где все операции представляют собой сложение по модулю 2:

С1 = М1 + М2 + М4
С2 = М1 + М3 + М4
С3 = М2 + М3 + М4

Для определения того, доставлено ли сообщение без ошибок, вычисляем следующие выражения (сложение по модулю 2):

С11 = С1 + М4 + М2 + М1
С12 = С2 + М4 + М3 + М1
С13 = С3 + М4 + М3 + М2

Результат вычисления интерпретируется следующим образом:

Таблица
4.4.

C11	C12	C13	Значение
1	2	4	Позиция бит
0	0	0	Ошибок нет
0	0	1	Бит С3 неверен
0	1	0	Бит С2 неверен
0	1	1	Бит M3 неверен
1	0	0	Бит С1 неверен
1	0	1	Бит M2 неверен
1	1	0	Бит M1 неверен
1	1	1	Бит M4 неверен

Описанная схема легко переносится на любое число n и М.

Число возможных кодовых комбинаций М помехоустойчивого кода делится на n классов, где N — число разрешенных кодов. Разделение на классы осуществляется так, чтобы в каждый класс вошел один разрешенный код и ближайшие к нему (по расстоянию Хэмминга ) запрещенные коды. В процессе приема данных определяется, к какому классу принадлежит пришедший код. Если код принят с ошибкой, он заменяется ближайшим разрешенным кодом. При этом предполагается, что кратность ошибки не более q_m.

В теории кодирования существуют следующие оценки максимального числа N n -разрядных кодов с расстоянием D.

d=1	n=2ⁿ
d=2	n=2^n-1
d=3	N 2ⁿ/(1 + n)
d = 2q + 1	(для кода Хэмминга это неравенство превращается в равенство)

В случае кода Хэмминга первые k разрядов используются в качестве информационных, причем

K = n – log(n + 1), откуда следует (логарифм по основанию 2), что k может принимать значения 0, 1, 4, 11, 26, 57 и т.д., это и определяет соответствующие коды Хэмминга (3,1); (7,4); (15,11); (31,26); (63,57) и т.д.

Обобщением кодов Хэмминга являются циклические коды BCH (Bose-Chadhuri-hocquenghem). Эти коды имеют широкий выбор длин и возможностей исправления ошибок.

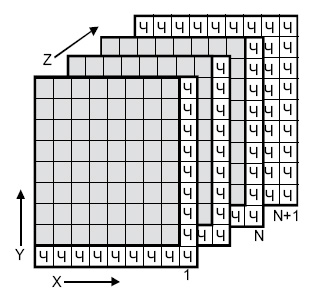
Одной из старейших схем коррекции ошибок является двух-и трехмерная позиционная схема (
рис.
4.2). Для каждого байта вычисляется бит четности (бит <Ч>, направление Х). Для каждого столбца также вычисляется бит четности (направление Y. Производится вычисление битов четности для комбинаций битов с координатами (X,Y) (направление Z, слои с 1 до N ). Если при транспортировке будет искажен один бит, он может быть найден и исправлен по неверным битам четности X и Y. Если же произошло две ошибки в одной из плоскостей, битов четности данной плоскости недостаточно. Здесь поможет плоскость битов четности N+1.
Таким образом, на 512 передаваемых байтов данных пересылается около 200 бит четности.

Рис.
4.2.
Позиционная схема коррекции ошибок

Источник

схема управления ошибками в данных по зашумленным каналам связи

В вычислениях, телекоммуникации, теория информации и теория кодирования, код исправления ошибок, иногда код исправления ошибок, (ECC ) используется для контроля ошибок в данных по ненадежным или зашумленным каналам связи. Основная идея заключается в том, что отправитель кодирует сообщение с помощью избыточной информации в форме ECC. Избыточность позволяет получателю обнаруживать ограниченное количество ошибок, которые могут возникать в любом месте сообщения, и часто исправлять эти ошибки без повторной передачи. Американский математик Ричард Хэмминг был пионером в этой области в 1940-х годах и изобрел первый исправляющий ошибки код в 1950 году: код Хэмминга (7,4).

ECC контрастирует с обнаружением ошибок. в том, что обнаруженные ошибки можно исправить, а не просто обнаружить. Преимущество состоит в том, что системе, использующей ECC, не требуется обратный канал для запроса повторной передачи данных при возникновении ошибки. Обратной стороной является то, что к сообщению добавляются фиксированные накладные расходы, что требует более высокой полосы пропускания прямого канала. Таким образом, ECC применяется в ситуациях, когда повторные передачи являются дорогостоящими или невозможными, например, при односторонних каналах связи и при передаче на несколько приемников в многоадресной передаче. Соединения с длительной задержкой также выигрывают; в случае спутника, вращающегося вокруг Урана, повторная передача из-за ошибок может вызвать задержку в пять часов. Информация ECC обычно добавляется к запоминающим устройствам для восстановления поврежденных данных, широко используется в модемах и используется в системах, где основной памятью является память ECC.

Обработка ЕСС в приемнике может применяться к цифровому потоку битов или к демодуляции несущей с цифровой модуляцией. В последнем случае ECC является неотъемлемой частью начального аналого-цифрового преобразования в приемнике. Декодер Витерби реализует алгоритм мягкого решения для демодуляции цифровых данных из аналогового сигнала, искаженного шумом. Многие кодеры / декодеры ECC также могут генерировать сигнал с коэффициентом ошибок по битам (BER), который можно использовать в качестве обратной связи для точной настройки аналоговой приемной электроники.

Максимальная доля ошибок или отсутствующих битов, которые могут быть исправлены, определяется конструкцией кода ECC, поэтому разные коды исправления ошибок подходят для разных условий. Как правило, более сильный код вызывает большую избыточность, которую необходимо передавать с использованием доступной полосы пропускания, что снижает эффективную скорость передачи данных при одновременном улучшении принимаемого эффективного отношения сигнал / шум. Теорема кодирования с шумом канала из Клод Шеннон отвечает на вопрос о том, какая полоса пропускания остается для передачи данных при использовании наиболее эффективного кода, который сводит вероятность ошибки декодирования к нулю. Это устанавливает границы теоретической максимальной скорости передачи информации канала с некоторым заданным базовым уровнем шума. Однако это доказательство неконструктивно и, следовательно, не дает представления о том, как создать код, обеспечивающий производительность. После многих лет исследований некоторые современные системы ECC сегодня очень близки к теоретическому максимуму.

Содержание

1 Прямое исправление ошибок
2 Как это работает
3 Усреднение шума для уменьшения количества ошибок
4 Типы ECC
5 Кодовая скорость и компромисс между надежностью и скоростью передачи данных
6 Составные коды ECC для повышения производительности
7 Проверка четности с низкой плотностью (LDPC)
8 Турбо-коды
9 Локальное декодирование и тестирование кодов
10 Чередование
- 10.1 Пример
- 10.2 Недостатки чередования
11 Программное обеспечение для кодов исправления ошибок
12 Список кодов исправления ошибок
13 См. Также
14 Ссылки
15 Дополнительная литература
16 Внешние ссылки

Прямое исправление ошибок

В электросвязи, теории информации и теории кодирования, прямое исправление ошибок (FEC ) или канальное кодирование — это метод, используемый для контроля ошибок в передаче данных по ненадежным или зашумленным каналам связи. Основная идея заключается в том, что отправитель кодирует сообщение с помощью избыточного способа, чаще всего с помощью ECC.

Избыточность позволяет получателю обнаруживать ограниченное количество ошибок, которые могут возникнуть в любом месте сообщения, и часто исправлять эти ошибки без повторной передачи. FEC дает приемнику возможность исправлять ошибки без необходимости использования обратного канала для запроса повторной передачи данных, но за счет фиксированной более высокой полосы пропускания прямого канала. Поэтому FEC применяется в ситуациях, когда повторные передачи являются дорогостоящими или невозможными, например, при односторонних каналах связи и при передаче на несколько приемников в многоадресной передаче. Информация FEC обычно добавляется к запоминающим устройствам (магнитным, оптическим и твердотельным / флэш-накопителям) для восстановления поврежденных данных, широко используется в модемах, используется в системах, где первичной памятью является память ECC, и в ситуациях широковещательной передачи, когда приемник не имеет возможности запрашивать повторную передачу или это может вызвать значительную задержку. Например, в случае спутника, вращающегося вокруг Урана, повторная передача из-за ошибок декодирования может вызвать задержку не менее 5 часов.

Обработка FEC в приемнике может применяться к цифровому битовому потоку или при демодуляции несущей с цифровой модуляцией. Для последнего FEC является неотъемлемой частью начального аналого-цифрового преобразования в приемнике. Декодер Витерби реализует алгоритм мягкого решения для демодуляции цифровых данных из аналогового сигнала, искаженного шумом. Многие кодеры FEC могут также генерировать сигнал с коэффициентом ошибок по битам (BER), который можно использовать в качестве обратной связи для точной настройки аналоговой приемной электроники.

Максимальная доля ошибок или недостающих битов, которые могут быть исправлены, определяется конструкцией ECC, поэтому разные коды прямого исправления ошибок подходят для разных условий. Как правило, более сильный код вызывает большую избыточность, которую необходимо передавать с использованием доступной полосы пропускания, что снижает эффективную скорость передачи данных при одновременном улучшении принимаемого эффективного отношения сигнал / шум. Теорема кодирования канала с шумом Клода Шеннона отвечает на вопрос о том, какая полоса пропускания остается для передачи данных при использовании наиболее эффективного кода, который обращает вероятность ошибки декодирования в ноль. Это устанавливает границы теоретической максимальной скорости передачи информации канала с некоторым заданным базовым уровнем шума. Его доказательство неконструктивно и, следовательно, не дает понимания того, как создать код, обеспечивающий производительность. Однако после многих лет исследований некоторые передовые системы FEC, такие как полярный код, достигают пропускной способности канала Шеннона при гипотезе кадра бесконечной длины.

Как это работает

ECC достигается путем добавления избыточности к передаваемой информации с использованием алгоритма. Избыточный бит может быть сложной функцией многих исходных информационных битов. Исходная информация может появляться или не появляться буквально в закодированном выводе; коды, которые включают немодифицированный ввод в вывод, являются систематическими, тогда как те, которые не включают, являются несистематическими .

Упрощенный пример ECC — передача каждого бита данных 3 раза, что известно как код повторения (3,1) . Через шумный канал приемник может видеть 8 вариантов вывода, см. Таблицу ниже.

Получен триплет	Интерпретируется как
000	0 (без ошибок)
001	0
010	0
100	0
111	1 (без ошибок)
110	1
101	1
011	1

Это позволяет исправить ошибку в любой из трех выборок «большинством голосов» или «демократическим голосованием». Корректирующая способность этого ECC:

До 1 бита триплета с ошибкой или
до 2 битов триплета пропущены (случаи не показаны в таблице).

Хотя прост в реализации и Это широко используемое тройное модульное резервирование является относительно неэффективным ECC. Более совершенные коды ECC обычно проверяют несколько последних десятков или даже несколько последних сотен ранее принятых битов, чтобы определить, как декодировать текущую небольшую группу битов (обычно в группах от 2 до 8 бит).

Усреднение шума для уменьшения ошибок

Можно сказать, что ECC работает посредством «усреднения шума»; поскольку каждый бит данных влияет на многие передаваемые символы, искажение одних символов шумом обычно позволяет извлекать исходные пользовательские данные из других неповрежденных принятых символов, которые также зависят от тех же пользовательских данных.

Из-за этого эффекта «объединения рисков» цифровые системы связи, использующие ECC, как правило, работают значительно выше определенного минимального отношения сигнал / шум, а не ниже него.
Эта тенденция «все или ничего» — эффект обрыва — становится более выраженной по мере использования более сильных кодов, которые более близко подходят к теоретическому пределу Шеннона.
Чередование данных, закодированных с помощью ECC, может уменьшить все или ничего свойства переданных кодов ECC, когда ошибки канала имеют тенденцию возникать в пакетах. Однако у этого метода есть ограничения; его лучше всего использовать для узкополосных данных.

Большинство телекоммуникационных систем используют фиксированный канальный код, рассчитанный на ожидаемый наихудший случай частоты ошибок по битам, а затем вообще не работают если частота ошибок по битам станет еще хуже. Однако некоторые системы адаптируются к данным условиям ошибки канала: некоторые экземпляры гибридного автоматического запроса на повторение используют фиксированный метод ECC, пока ECC может обрабатывать частоту ошибок, затем переключаются на ARQ когда частота ошибок становится слишком высокой; адаптивная модуляция и кодирование использует различные скорости ECC, добавляя больше битов исправления ошибок на пакет, когда в канале более высокие частоты ошибок, или удаляя их, когда они не нужны.

Типы ECC

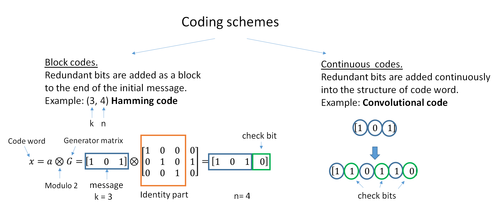
Краткая классификация кодов коррекции ошибок.

Двумя основными категориями кодов ECC являются блочные коды и сверточные коды.

Блочные коды работают с блоками фиксированного размера (пакетами) битов или символов заранее определенного размера. Практические блочные коды обычно могут быть жестко декодированы за полиномиальное время до их длины блока.
Сверточные коды работают с битовыми или символьными потоками произвольной длины. Чаще всего они программно декодируются с помощью алгоритма Витерби, хотя иногда используются и другие алгоритмы. Декодирование Витерби обеспечивает асимптотически оптимальную эффективность декодирования с увеличением длины ограничения сверточного кода, но за счет экспоненциально возрастающей сложности. Завершенный сверточный код также является «блочным кодом» в том смысле, что он кодирует блок входных данных, но размер блока сверточного кода, как правило, произвольный, в то время как блочные коды имеют фиксированный размер, определяемый их алгебраическими характеристиками. Типы завершения для сверточных кодов включают в себя «бит в конце» и «сброс битов».

Существует много типов блочных кодов; Кодирование Рида-Соломона примечательно тем, что оно широко используется в компакт-дисках, DVD и жестких дисках. Другие примеры классических блочных кодов включают Голея, BCH, многомерную четность и коды Хэмминга.

ECC Хэмминга обычно используются для исправления NAND flash ошибки памяти. Это обеспечивает исправление однобитовых ошибок и обнаружение двухбитовых ошибок. Коды Хэмминга подходят только для более надежной одноуровневой ячейки (SLC) NAND. Более плотная многоуровневая ячейка (MLC) NAND может использовать многобитовый корректирующий ECC, такой как BCH или Reed-Solomon. NOR Flash обычно не использует никакого исправления ошибок.

Классические блочные коды обычно декодируются с использованием алгоритмов жесткого решения, что означает, что для каждого входного и выходного сигнала принимается жесткое решение, будет ли он соответствует единице или нулю бит. Напротив, сверточные коды обычно декодируются с использованием алгоритмов мягкого решения, таких как алгоритмы Витерби, MAP или BCJR, которые обрабатывают (дискретизированные) аналоговые сигналы и которые допускают гораздо более высокие ошибки — производительность коррекции, чем декодирование с жестким решением.

Почти все классические блочные коды применяют алгебраические свойства конечных полей. Поэтому классические блочные коды часто называют алгебраическими кодами.

В отличие от классических блочных кодов, которые часто определяют способность обнаружения или исправления ошибок, многие современные блочные коды, такие как коды LDPC, не имеют таких гарантий. Вместо этого современные коды оцениваются с точки зрения их частоты ошибок по битам.

Большинство кодов прямого исправления ошибок исправляют только перевороты битов, но не вставки или удаления битов. В этой настройке расстояние Хэмминга является подходящим способом измерения коэффициента битовых ошибок. Несколько кодов прямого исправления ошибок предназначены для исправления вставки и удаления битов, например, коды маркеров и коды водяных знаков. Расстояние Левенштейна является более подходящим способом измерения частоты ошибок по битам при использовании таких кодов.

Кодовая скорость и компромисс между надежностью и скоростью передачи данных

Фундаментальный принцип ECC состоит в добавлении избыточных битов, чтобы помочь декодеру узнать истинное сообщение, которое было закодировано передатчик. Кодовая скорость данной системы ЕСС определяется как соотношение между количеством информационных битов и общим количеством битов (то есть информацией плюс биты избыточности) в данном коммуникационном пакете. Кодовая скорость, следовательно, является действительным числом. Низкая кодовая скорость, близкая к нулю, подразумевает сильный код, который использует много избыточных битов для достижения хорошей производительности, в то время как большая кодовая скорость, близкая к 1, подразумевает слабый код.

Избыточные биты, защищающие информацию, должны передаваться с использованием тех же коммуникационных ресурсов, которые они пытаются защитить. Это вызывает фундаментальный компромисс между надежностью и скоростью передачи данных. В одном крайнем случае сильный код (с низкой кодовой скоростью) может вызвать значительное увеличение SNR приемника (отношение сигнал / шум), уменьшая частоту ошибок по битам, за счет снижения эффективной скорости передачи данных. С другой стороны, без использования какого-либо ECC (то есть кодовой скорости, равной 1) используется полный канал для целей передачи информации за счет того, что биты остаются без какой-либо дополнительной защиты.

Один интересный вопрос заключается в следующем: насколько эффективным с точки зрения передачи информации может быть ECC, имеющий незначительную частоту ошибок декодирования? На этот вопрос ответил Клод Шеннон с его второй теоремой, которая гласит, что пропускная способность канала — это максимальная скорость передачи данных, достижимая для любого ECC, частота ошибок которого стремится к нулю: его доказательство основано на гауссовском случайном кодировании, которое не подходит для реального мира. Приложения. Верхняя граница, заданная работой Шеннона, вдохновила на долгий путь к разработке ECC, которые могут приблизиться к пределу конечных характеристик. Различные коды сегодня могут достигать почти предела Шеннона. Однако ECC, обеспечивающие пропускную способность, обычно чрезвычайно сложно реализовать.

Наиболее популярные ECC имеют компромисс между производительностью и вычислительной сложностью. Обычно их параметры дают диапазон возможных кодовых скоростей, которые можно оптимизировать в зависимости от сценария. Обычно эта оптимизация выполняется для достижения низкой вероятности ошибки декодирования при минимальном влиянии на скорость передачи данных. Другим критерием оптимизации кодовой скорости является уравновешивание низкой частоты ошибок и количества повторных передач с учетом энергетических затрат на связь.

Составные коды ECC для повышения производительности

Классические (алгебраические) блочные коды а сверточные коды часто комбинируются в схемах конкатенированного кодирования, в которых сверточный код, декодированный по Витерби с короткой ограниченной длиной, выполняет большую часть работы, а блочный код (обычно Рида-Соломона) с большим размером символа и длиной блока «стирает» любые ошибки, сделанные сверточным декодером. Однопроходное декодирование с использованием этого семейства кодов с исправлением ошибок может дать очень низкий уровень ошибок, но для условий передачи на большие расстояния (например, в глубоком космосе) рекомендуется итеративное декодирование.

Составные коды были стандартной практикой в спутниковой связи и связи в дальнем космосе с тех пор, как «Вояджер-2 » впервые применил эту технику во время встречи с Ураном в 1986 году. Аппарат Galileo использовал итеративные конкатенированные коды для компенсации условий очень высокой частоты ошибок, вызванных отказом антенны.

Проверка на четность с низкой плотностью (LDPC)

Коды с проверкой на четность с низкой плотностью (LDPC) — это класс высокоэффективных линейных блочных кодов, созданных из множества кодов одиночной проверки на четность (SPC). Они могут обеспечить производительность, очень близкую к пропускной способности канала (теоретический максимум), используя подход итеративного декодирования с мягким решением, при линейной временной сложности с точки зрения длины их блока. Практические реализации в значительной степени полагаются на параллельное декодирование составляющих кодов SPC.

Коды LDPC были впервые введены Робертом Г. Галлагером в его докторской диссертации в 1960 году, но из-за вычислительных усилий при реализации кодера и декодера и введения Рида-Соломона коды, они в основном игнорировались до 1990-х годов.

Коды LDPC теперь используются во многих недавних стандартах высокоскоростной связи, таких как DVB-S2 (цифровое видеовещание — спутниковое — второе поколение), WiMAX ( стандарт IEEE 802.16e для микроволновой связи), высокоскоростная беспроводная локальная сеть (IEEE 802.11n ), 10GBase-T Ethernet (802.3an) и G.hn/G.9960 (Стандарт ITU-T для организации сетей по линиям электропередач, телефонным линиям и коаксиальному кабелю). Другие коды LDPC стандартизированы для стандартов беспроводной связи в пределах 3GPP MBMS (см. исходные коды ).

Турбокоды

Турбокодирование — это схема повторяющегося мягкого декодирования, которая объединяет два или более относительно простых сверточных кода и перемежитель для создания блочного кода, который может работать с точностью до долей децибела. предела Шеннона. Предшествующие LDPC-коды с точки зрения практического применения, теперь они обеспечивают аналогичную производительность.

Одним из первых коммерческих приложений турбо-кодирования была технология цифровой сотовой связи CDMA2000 1x (TIA IS-2000), разработанная Qualcomm и продаваемая Verizon Беспроводная связь, Sprint и другие операторы связи. Он также используется для развития CDMA2000 1x специально для доступа в Интернет, 1xEV-DO (TIA IS-856). Как и 1x, EV-DO был разработан Qualcomm и продается Verizon Wireless, Sprint и другими операторами (маркетинговое название Verizon для 1xEV-DO — Широкополосный доступ, потребительские и бизнес-маркетинговые названия компании Sprint для 1xEV-DO — Power Vision и Mobile Broadband соответственно).

Локальное декодирование и тестирование кодов

Иногда необходимо декодировать только отдельные биты сообщения или проверить, является ли данный сигнал кодовым словом, и делать это, не глядя на все сигнал. Это может иметь смысл в настройке потоковой передачи, где кодовые слова слишком велики для того, чтобы их можно было классически декодировать достаточно быстро, и где на данный момент интересны только несколько битов сообщения. Также такие коды стали важным инструментом в теории сложности вычислений, например, для разработки вероятностно проверяемых доказательств.

Локально декодируемые коды являются кодами с исправлением ошибок, для которых отдельные биты сообщение может быть восстановлено вероятностно, если посмотреть только на небольшое (скажем, постоянное) количество позиций кодового слова, даже после того, как кодовое слово было искажено на некоторой постоянной доле позиций. Локально тестируемые коды — это коды с исправлением ошибок, для которых можно вероятностно проверить, близок ли сигнал к кодовому слову, посмотрев только на небольшое количество позиций сигнала.

Чередование

Краткая иллюстрация идеи чередования.

Чередование часто используется в системах цифровой связи и хранения для повышения производительности кодов прямого исправления ошибок. Многие каналы связи не лишены памяти: ошибки обычно возникают в пакетах, а не независимо друг от друга. Если количество ошибок в кодовом слове превышает возможности кода исправления ошибок, ему не удается восстановить исходное кодовое слово. Чередование облегчает эту проблему путем перетасовки исходных символов по нескольким кодовым словам, тем самым создавая более равномерное распределение ошибок. Поэтому перемежение широко используется для пакетной коррекции ошибок.

. Анализ современных повторяющихся кодов, таких как турбокоды и коды LDPC, обычно предполагает независимое распределение ошибок.. Поэтому системы, использующие коды LDPC, обычно используют дополнительное перемежение символов в кодовом слове.

Для турбокодов перемежитель является неотъемлемым компонентом, и его правильная конструкция имеет решающее значение для хорошей производительности. Алгоритм итеративного декодирования работает лучше всего, когда нет коротких циклов в графе коэффициентов, который представляет декодер; перемежитель выбран, чтобы избежать коротких циклов.

Конструкции перемежителя включают:

прямоугольные (или однородные) перемежители (аналогично методу с использованием коэффициентов пропуска, описанному выше)
сверточные перемежители
случайные перемежители (где перемежитель — известная случайная перестановка)
S-случайный перемежитель (где перемежитель — это известная случайная перестановка с ограничением, что никакие входные символы на расстоянии S не появляются на расстоянии S на выходе).
бесконфликтный квадратичный многочлен с перестановками (QPP). Пример использования — в стандарте мобильной связи 3GPP Long Term Evolution.

В системах связи с несколькими несущими может использоваться перемежение по несущим для обеспечения частотного разнесения., например, для уменьшения частотно-избирательного замирания или узкополосных помех.

Пример

Передача без перемежения :

Сообщение без ошибок: aaaabbbbccccddddeeeeffffgggg Передача с пакетной ошибкой: aaaabbbbccc____deeeeffffgggg

Здесь каждая группа одинаковых букв представляет 4-битное однобитовое кодовое слово с исправлением ошибок. Кодовое слово cccc изменяется в один бит и может быть исправлено, но кодовое слово dddd изменяется в трех битах, поэтому либо оно не может быть декодировано вообще, либо может быть декодировано неправильно.

С чередованием :

Ошибка- свободные кодовые слова: aaaabbbbccccddddeeeeffffgggg Interleaved: abcdefgabcdefgabcdefgabcdefg Передача с ошибкой пакета: abcdefgabcd____bcdefgabcdefg Полученные кодовые слова после деинтерлейвинга: "aa_abbb_gg2ccd_dd>,", ",", ",", ","

Передача без чередования :

Исходное переданное предложение: ThisIsAnExampleOfInterleaving Полученное предложение с пакетной ошибкой: ThisIs______pleOfInterleaving

Термин «AnExample» оказывается в основном неразборчивым и трудным для исправления.

С чередованием :

Переданное предложение: ThisIsAnExampleOfInterleaving... Безошибочная передача: TIEpfeaghsxlIrv.iAaenli.snmOten. Получено предложение с пакетной ошибкой: TIEpfe ______ Irv.iAaenli.snmOten. Полученное предложение после деинтерлейвинга: T_isI_AnE_amp_eOfInterle_vin _...

Ни одно слово не потеряно полностью, а недостающие буквы можно восстановить с минимальными догадками.

Недостатки чередования

Использование методов чередования увеличивает общую задержку. Это связано с тем, что весь чередующийся блок должен быть принят до того, как пакеты могут быть декодированы. Также перемежители скрывают структуру ошибок; Без перемежителя более совершенные алгоритмы декодирования могут использовать структуру ошибок и обеспечивать более надежную связь, чем более простой декодер, объединенный с перемежителем. Пример такого алгоритма основан на структурах нейронной сети .

Программное обеспечение для кодов с исправлением ошибок

Моделирование поведения кодов с исправлением ошибок (ECC) в программном обеспечении является обычной практикой для разработки, проверки и улучшения кодов ECC. Предстоящий стандарт беспроводной связи 5G поднимает новый диапазон приложений для программных ECC: Облачные сети радиодоступа (C-RAN) в контексте Программно-определяемого радио (SDR). Идея состоит в том, чтобы напрямую использовать программные ECC в коммуникациях. Например, в 5G программные ECC могут быть расположены в облаке, а антенны могут быть подключены к этим вычислительным ресурсам: таким образом повышается гибкость сети связи и, в конечном итоге, повышается энергоэффективность системы.

В этом контексте существует различное доступное программное обеспечение с открытым исходным кодом, перечисленное ниже (не является исчерпывающим).

AFF3CT (Панель инструментов быстрого исправления ошибок): полная цепочка связи на C ++ (многие поддерживаемые коды, такие как Turbo, LDPC, полярные коды и т. Д.), Очень быстрая и специализированная на канальном кодировании (может использоваться как программа для моделирования или как библиотека для SDR).
IT ++ : библиотека классов и функций C ++ для линейной алгебры, числовой оптимизации, обработки сигналов, связи и статистики.
OpenAir : реализация (на языке C) спецификаций 3GPP, касающихся Evolved Packet Core Networks.

Список кодов исправления ошибок

Расстояние	Код
2 (обнаружение единичной ошибки)	Четность
3 (исправление одиночной ошибки)	Тройное модульное резервирование
3 (исправление одиночной ошибки)	совершенное Хэмминга, такое как Хэмминга (7,4)
4 (SECDED )	Расширенный Хэмминга
5 (исправление двойной ошибки)
6 (исправление двойной ошибки / обнаружение тройной ошибки)
7 (исправление трех ошибок)	совершенный двоичный код Голея
8 (TECFED)	расширенный двоичный код Голея

коды AN
код BCH, который может быть разработан для исправления любого произвольного количества ошибок в кодовом блоке.
код Бергера
код постоянного веса
сверточный код
Расширительные коды
Групповые коды
коды Голея, из которых двоичный код Голея представляет практический интерес
код Гоппа, используемый в Криптосистема Мак-Элиса
Код Адамара
Код Хагельбаргера
Код Хэмминга
Код на основе латинского квадрата для небелого шума (преобладающий, например, в широкополосной связи по сравнению с линиями электропередач)
Лексикографический код
Линейное сетевое кодирование, тип кода с исправлением стирания в сетях вместо двухточечных ссылок
Длинный код
Код проверки четности с низкой плотностью, также известный как код Галлагера, как архетип для кодов разреженного графа
LT-кода, который является почти оптимальным бесскоростным кодом коррекции стирания (код Фонтана)
m из n кодов
Онлайн-код, почти оптимальный код бесскоростной коррекции стирания
Полярный код (codi ng теория)
Код Raptor, почти оптимальный код с бесскоростной коррекцией стирания
Исправление ошибок Рида – Соломона
Код Рида – Маллера
Код повторения-накопления
Коды повторения, например, Тройная модульная избыточность
Спинальный код, бесскоростной нелинейный код, основанный на псевдослучайных хэш-функциях
Код Торнадо, почти оптимальный код коррекции стирания, и предшественник кодов Фонтана
Турбо-код
код Уолша – Адамара
Циклические проверки избыточности (CRC) могут исправлять 1-битные ошибки для сообщений не более 2 n - 1 - 1 { displaystyle 2 ^ {n-1} -1} $2 ^ {n-1} -1$ бит длиной для оптимальных порождающих полиномов степени n { displaystyle n}, см. Математика циклических проверок избыточности # Битовые фильтры

См. Также

Ссылки

Дополнительная литература

Clark, Jr., George C.; Каин, Дж. Бибб (1981). Кодирование с коррекцией ошибок для цифровой связи. Нью-Йорк, США: Plenum Press. ISBN 0-306-40615-2. ISBN 978-0-306-40615-7.
Уикер, Стивен Б. (1995). Системы контроля ошибок для цифровой связи и хранения. Энглвуд Клиффс, Нью-Джерси, США: Прентис-Холл. ISBN 0-13-200809-2. ISBN 978-0-13-200809-9.
Уилсон, Стивен Г. (1996). Цифровая модуляция и кодирование. Энглвуд Клиффс, Нью-Джерси, США: Прентис-Холл. ISBN 0-13-210071-1. ISBN 978-0-13-210071-7.
"Код коррекции ошибок в одноуровневой ячейке NAND флэш-памяти « 16 февраля 2007 г.
« Код исправления ошибок во флэш-памяти NAND » 29 ноября 2004 г.
Наблюдения за ошибками, исправлениями и доверием зависимых систем, Джеймс Гамильтон, 26 февраля 2012 г.
Сферические упаковки, решетки и группы, Дж. Х. Конвей, NJA Sloane, Springer Science Business Media, 9 марта 2013 г. - Математика - 682 страницы.

Внешние ссылки

Источник

Шум или ошибка – основная проблема в сигнале, которая нарушает надежность системы связи. Кодирование с контролем ошибок – это процедура кодирования, выполняемая для контроля появления ошибок. Эти методы помогают в обнаружении ошибок и исправлении ошибок.

Существует много различных кодов, исправляющих ошибки, в зависимости от применяемых к ним математических принципов. Но исторически эти коды были классифицированы на линейные блочные коды и коды свертки .

Линейные Блочные Коды

В линейных блочных кодах биты четности и биты сообщения имеют линейную комбинацию, что означает, что результирующее кодовое слово является линейной комбинацией любых двух кодовых слов.

Рассмотрим некоторые блоки данных, которые содержат k битов в каждом блоке. Эти биты отображаются с блоками, которые имеют n битов в каждом блоке. Здесь n больше, чем k . Передатчик добавляет избыточные биты, которые являются (nk) битами. Отношение k / n является скоростью кода . Обозначается через r, а значение r равно r <1 .

Добавленные здесь биты (nk) являются битами четности . Биты четности помогают в обнаружении и исправлении ошибок, а также в поиске данных. В передаваемых данных самые левые биты кодового слова соответствуют битам сообщения, а самые правые биты кодового слова соответствуют битам четности.

Систематический код

Любой линейный блочный код может быть систематическим кодом, пока он не будет изменен. Следовательно, неизмененный блочный код называется систематическим кодом .

Ниже приведено представление структуры кодовых слов в соответствии с их распределением.

Если сообщение не изменено, оно называется систематическим кодом. Это означает, что шифрование данных не должно изменять данные.

Сверточные коды

До сих пор в линейных кодах мы обсуждали, что систематический неизмененный код является предпочтительным. Здесь данные из общего числа n битов, если переданы, k битов являются битами сообщения и (nk) битами являются биты четности.

В процессе кодирования биты четности вычитаются из целых данных, а биты сообщения кодируются. Теперь биты четности снова добавляются, и все данные снова кодируются.

На следующем рисунке приведены примеры блоков данных и потоков данных, используемых для передачи информации.

Весь процесс, изложенный выше, утомителен и имеет недостатки. Выделение буфера является основной проблемой, когда система занята.

Этот недостаток устраняется в сверточных кодах. Где весь поток данных назначается символам, а затем передается. Поскольку данные представляют собой поток битов, для хранения не требуется буфер.

Коды Хэмминга

Свойство линейности кодового слова состоит в том, что сумма двух кодовых слов также является кодовым словом. Коды Хэмминга – это тип линейных кодов, исправляющих ошибки , которые могут обнаруживать до двухбитовых ошибок или исправлять однобитовые ошибки без обнаружения неисправленных ошибок.

При использовании кодов Хэмминга дополнительные биты четности используются для идентификации ошибки одного бита. Чтобы перейти от одного бита к другому, в данных нужно изменить несколько битов. Такое количество битов можно назвать расстоянием Хэмминга . Если четность имеет расстояние 2, может быть обнаружен однобитовый переворот. Но это не может быть исправлено. Кроме того, любые два бита не могут быть обнаружены.

Тем не менее, код Хэмминга – лучшая процедура, чем обсуждаемые ранее при обнаружении и исправлении ошибок.

Коды BCH

Коды БЧХ названы в честь изобретателей B ose, C haudari и H ocquenghem. Во время разработки кода BCH существует контроль количества символов, которые должны быть исправлены, и, следовательно, возможна множественная битовая коррекция. Коды БЧХ – это мощный метод исправления ошибок.

Для любых натуральных чисел m ≥ 3 и t <2 ^m-1 существует двоичный код BCH. Ниже приведены параметры такого кода.

Длина блока n = 2 ^м -1

Количество проверочных цифр n – k ≤ mt

Минимальное расстояние d _min ≥ 2t + 1

Этот код может называться кодом BCH с коррекцией ошибок .

Циклические коды

Циклическое свойство кодовых слов заключается в том, что любой циклический сдвиг кодового слова также является кодовым словом. Циклические коды следуют этому циклическому свойству.

Для линейного кода C , если каждое кодовое слово, т. Е. C = (C1, C2, …… Cn) из C, имеет циклический сдвиг вправо компонентов, оно становится кодовым словом. Этот сдвиг вправо равен n-1 циклическим сдвигам влево. Следовательно, он инвариантен при любом сдвиге. Таким образом, линейный код C , поскольку он инвариантен при любом сдвиге, можно назвать циклическим кодом .

Циклические коды используются для исправления ошибок. Они в основном используются для исправления двойных ошибок и пакетных ошибок.

Следовательно, это несколько кодов с исправлением ошибок, которые должны быть обнаружены в приемнике. Эти коды предотвращают появление ошибок и нарушают связь. Они также предотвращают прослушивание сигнала нежелательными приемниками. Для этого существует класс методов сигнализации, которые обсуждаются в следующей главе.

Источник

Корректирующие коды «на пальцах»

Каналы с ошибкой

Код с утроением

Расстояния между кодами

Окрестности

Сколько ошибок может исправить код?

Интерлюдия: поле GF(2)

Проверяем корректность

Кодирование

Ошибка по синдрому

Что же дальше?

5.2.1. Основные принципы построения кодов Хэмминга с исправлением ошибок

4.1. Алгоритмы коррекции ошибок

Содержание

Прямое исправление ошибок

Как это работает

Усреднение шума для уменьшения ошибок

Типы ECC

Кодовая скорость и компромисс между надежностью и скоростью передачи данных

Составные коды ECC для повышения производительности

Проверка на четность с низкой плотностью (LDPC)

Турбокоды

Локальное декодирование и тестирование кодов

Чередование

Пример

Недостатки чередования

Программное обеспечение для кодов с исправлением ошибок

Список кодов исправления ошибок

См. Также

Ссылки

Дополнительная литература

Внешние ссылки

Линейные Блочные Коды

Систематический код

Сверточные коды

Коды Хэмминга

Коды BCH

Циклические коды

Возможно, вам также будет интересно: