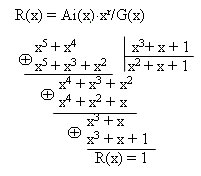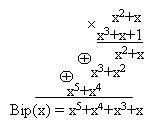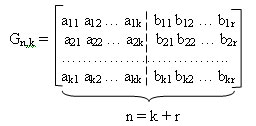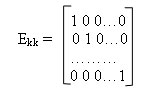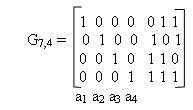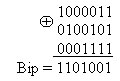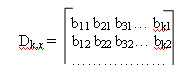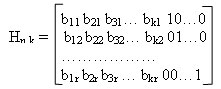Теория
кодирования занимается проблемами
построения разнообразных кодов. При
этом для конкретного класса кодов
решаются три основные задачи: 1) код
должен корректировать заданный класс
ошибок; 2) процедуры кодирования и
декодирования должны быть формализованы,
т. е. выполняться по определенным
правилам; 3) схемы кодирования и
декодирования должны быть простыми.
Рассмотрим
наиболее распространенные коды с
обнаружением ошибок. Каждый такой код
должен обнаруживать все одиночные
ошибки как наиболее вероятные. Кроме
того, он может и исправлять некоторые
ошибки.
Код
с контролем на четность.(1а) У
этого кода все разрешенные кодовые
слова содержат четное число единиц. Для
его формирования к обыкновенному
коду достаточно добавить один избыточный
контрольный разряд.
Пусть
надо передать S
= 4 сообщения. Тогда обыкновенный код
имеет два разряда, которые несут
информацию, а третий контрольный разряд
определяется исходя из четности числа
единиц в слове:
123
000 011 101
110 (столбик)
Такой
код, у которого разряды делятся на
информационные, служащие для передачи
сообщения, и контрольные (избыточные),
служащие для коррекции ошибок, называется
разделимым.

Равновесный
код (код с постоянным числом единиц). У
этого кода
все кодовые слова имеют постоянное
число единиц. Поэтому его еще называют
кодом «т
из
п»,
так
как каждое слово имеет т
единиц
из п
разрядов.
Число т
называют
весом
кода.
S=Cm,n
Корреляционные
коды. У этих кодов существует зависимость
(корреляция) между определенными
элементами кода. Примером является код
с повторением, у которого каждое слово
обыкновенного кода повторяется
дважды. Ниже приведен данный код для
передачи S
= 4 сообщений:
-
1
2
3
4
0
0
0
0
0
1
0
1
1
0
1
0
1
1 1 1
Он
является разделимым. Первый и второй
разряды можно считать информационными,
а третий и четвертый — контрольными.
34
Код
с суммированием (код Бергера). Этот
код позволяет обна руживать однонаправленные
ошибки любой кратности. Однонаправленным
назыв-ся кратные
Ошибки,
содержащие только искажения вида 1-0 или
0-1.код применяется в тех случаях,
Когда
в канале свзи возникают помехи,
длительность которых больше длительности
одного импульса тока.
35
11.5. Код Хемминга
Среди
кодов с исправлением ошибок наибольшее
распространение на практике имеет
код Хэмминга. Код
Хэмминга исправляет
ошибки кратности 1 и является разделимым.
Число информационных разрядов т
=
]log2N[,
где N
—
число сообщений, которые необходимо
передать. Длина кода определяется из
неравенства (11.14).
41
12.4.
Программируемые
распределители
Распределители,
работающие с использованием двоичного
кода,
имеют
2п
позиций.
Это число в системе ТУ — ТС обычно должно
быть равно длине используемого кода.
Поэтому возникает задача построения
распределителя (а фактически счетчика)
с модулем счета не равным 2″ Такие
распределители называют программируемыми.
42
Генераторы
в системах ТУ — ТС используются для
выполнения
двух
функций. Тактовые генераторы определяют
временное такты функционирования
системы. Они управляют работой счетчика
или распределителя и обеспечивают
синхронизацию. Генераторы качеств
формируют импульсы тока с определенным
качеством и воздействуют на линейные
устройства.
Генератором
называется
устройство, которое благодаря энергии
непериодического источника питания
создает периодически изменяющееся
электрическое напряжение или ток и
обеспечивает периодическое замыкание
и размыкание электрической цепи (1а).
В
зависимости от формы генерируемых
импульсов различают генераторы
синусоидальных колебаний (1 б) и
релаксационные генераторы. Последние
генерируют импульсы специальной
формы с наличием скачков — прямоугольные,
экспоненциальные, пилообразные (1 в,
г, д) и
др. При этом импульсные последовательности
характеризуются длительностями импульса
tи
и
паузы tn,
периодом
колебаний T
= tи
+tn,
частотой
следования f
= 1/Т
и
скважностью Q
=
T/tп.
Простейший
тактовый генератор (2 а)состоит из
источника питания ИП,
устройства
управления УУ,
накопителя
энергии Я и обратной связи ОС. В качестве
У
У используется
переключательный элемент (реле,
транзистор, тиристор и т. п.). Накопителем
энергии обычно служит конденсатор.
Пример
релейно-контактного генератора
(пульс-пара) рассмотрен в п. 5.3.
В
бесконтактной технике аналогами
пульс-пары являются мультивибраторы.
Простейшая схема мультивибратора
состоит из двух инверторов с емкостными
обратными связями (3а).
При
включении питания эта схема оказывается
в состоянии неустойчивого равновесия,
когда оба транзистора открыты с некоторой
степенью насыщения. Возрастание
коллекторного тока iК2
транзистора VT2
приводит
к увеличению тока заряда tc1
и увеличению падения напряжения на
резисторе Rb1.
В результате потенциал базы транзистора
VT1
становится более положительным и
уменьшается ток iK1.
Потенциал коллектора транзистора VT1
становится
более отрицательным и поэтому увеличивается
ток заряда ic2.
Так как последний является базовым
током транзистора VT2,
то
возрастает ток iK2
и
снова возрастает ток гс!
и т. д. Описанный процесс приводит к
тому, что транзистор VT2
полностью
открывается, а транзистор VT1
полностью
закрывается. Это состояние схемы также
неустойчиво, так как продолжается заряд
конденсатора С1 и ток icl
начинает уменьшаться. Снижается падение
напряжения на резисторе Rb1,
потенциал
базы транзистора VT1
становится
более отрицательным. При некотором
значении этого потенциала транзистор
VT1
начинает
открываться, возрастает его ток iK1
и
процесс протекает в обратную сторону.
На выходе схемы формируются импульсы
(3б), частота следования которых
определяется постоянной времени R6C.
44
Коды с обнаружением
ошибок
1.
Код с проверкой на четность.
Такой
код образуется путем добавления к
передаваемой комбинации, состоящей из k
информационных символов, одного
контрольного символа (0 или 1), так, чтобы
общее число единиц в передаваемой
комбинации было четным.
Пример
5.1.
Построим коды для проверки на четность, где k
—
исходные комбинации, r
—
контрольные символы.
| k |
r
|
n
|
| 11011 |
0 |
110110 |
| 11100 |
1 |
111001
|
Определим, каковы обнаруживающие свойства
этого кода. Вероятность Poo
обнаружения ошибок будет равна
Так как вероятность ошибок
является
весьма малой величиной, то можно
ограничится
Вероятность
появления всевозможных ошибок, как
обнаруживаемых так и не обнаруживаемых,
равна
,
где
—
вероятность отсутствия искажений в кодовой
комбинации. Тогда
.
При
передаче большого количества кодовых
комбинаций Nk
, число кодовых
комбинаций, в которых ошибки
обнаруживаются, равно:
Общее
количество комбинаций с обнаруживаемыми и
не обнаруживаемыми ошибками равно
Тогда
коэффициент обнаружения Kобн
для кода с четной защитой будет равен
Например,
для кода с k=5
и вероятностью ошибки
коэффициент
обнаружения составит
. То есть 90% ошибок
обнаруживаем, при этом избыточность будет
составлять
или
17%.
2.
Код с
постоянным весом.
Этот
код содержит постоянное число единиц и
нулей. Число кодовых комбинаций составит
Пример 5.2. Коды с двумя единицами из пяти и
тремя единицами из семи.
| 11000 10010 00101 |
0000111 1001001 1010100 |
Этот код позволяет обнаруживать любые
одиночные ошибки и часть многократных
ошибок. Не обнаруживаются этим кодом только
ошибки смещения, когда одновременно одна
единица переходит в ноль и один ноль
переходит в единицу, два ноля и две единицы
меняются на обратные символы и т.д.
Рассмотрим
код с тремя единицами из семи. Для этого
кода возможны смещения трех типов.
Вероятность появления
не обнаруживаемых ошибок смещения
, где
При
p<<1
, тогда
Вероятность
появления всевозможных ошибок как
обнаруживаемых, так и не обнаруживаемых
будет составлять
Вероятность
обнаруживаемых ошибок
. Тогда
коэффициент обнаружения будет равен
Например,
код
при
коэффициент обнаружения составит
,
избыточность L=27%.
3.
Корреляционный код
(Код с удвоением). Элементы
данного кода заменяются двумя символами,
единица ‘1’ преобразуется в 10, а ноль ‘0’ в
01.
Вместо комбинации 1010011
передается 10011001011010.
Ошибка обнаруживается в том случае, если в
парных элементах будут одинаковые символы
00 или 11 (вместо 01 и 10).
Например,
при k=5,
n=10
и вероятности ошибки
,
.
Но при этом избыточность будет
составлять 50%.
4.
Инверсный код. К
исходной комбинации добавляется такая же
комбинация по длине. В линию посылается
удвоенное число символов. Если в исходной
комбинации четное число единиц, то
добавляемая комбинация повторяет исходную
комбинацию, если нечетное, то добавляемая
комбинация является инверсной по отношению
к исходной.
| k |
r
|
n
|
| 11011 |
11011 |
1101111011 |
| 11100 |
00011 |
1110000011 |
Прием
инверсного кода осуществляется в два этапа.
На первом этапе суммируются единицы в
первой основной группе символов. Если число
единиц четное, то контрольные символы
принимаются без изменения, если нечетное,
то контрольные символы инвертируются. На
втором этапе контрольные символы
суммируются с информационными символами по
модулю два. Нулевая сумма говорит об
отсутствии ошибок. При ненулевой сумме,
принятая комбинация бракуется. Покажем
суммирование для принятых комбинаций без
ошибок (1,3) и с ошибками (2,4).
Обнаруживающие способности
данного кода достаточно велики. Данный код
обнаруживает практически любые ошибки,
кроме редких ошибок смещения, которые
одновременно происходят как среди
информационных символов, так и среди
соответствующих контрольных. Например, при k=5, n=10
и
. Коэффициент обнаружения будет
составлять
.
5.
Код Грея.
Код Грея используется для
преобразования угла поворота тела вращения
в код. Принцип
работы можно представить по рис.5.2. На
пластине, которая вращается на
валу, сделаны отверстия, через
которые может
проходить свет.
Причём, диск разбит
на сектора, в
которых и
сделаны эти
отверстия. При вращении, свет
проходит через
них, что приводит
к срабатыванию фотоприёмников. При
снятии информации в виде двоичных кодов
может произойти существенная ошибка.
Например, возьмем две соседние цифры 7 и 8.
Двоичные коды этих цифр отличаются во всех
разрядах.
7 0111
—> 1111
8 1000
—>
0000
Если ошибка произойдет в старшем разряде,
то это приведет к максимальной ошибке, на 3600.
А код Грея,
это такой код в котором все соседние
комбинации отличаются только одним
символом, поэтому при переходе от
изображения одного числа к изображению
соседнего происходит изменение только на
единицу младшего разряда. Ошибка будет
минимальной.
Рис.5.2. Схема съема
информации угла поворота вала в код
Код Грея
записывается следующим образом
| Номер |
Код Грея |
| 0 |
0 0 0 0 |
| 1 |
0 0 0 1 |
| 2 |
0 0 1 1 |
| 3 |
0 0 1 0 |
| 4 |
0 1 1 0 |
| 5 | 0 1 1 1 |
| 6 |
0 1 0 1 |
| 7 |
0 1 0 0 |
| 8 |
1 1 0 0 |
| 9 |
1 1 0 1 |
| 10 |
1 1 1 1 |
| 11 |
1 1 1 0 |
| 12 |
1 0 1 0 |
| 13 |
1 0 1 1 |
| 14 |
1 0 0 1 |
| 15 |
1 0 0 0 |
Разряды
в коде Грея не имеют постоянного веса. Вес k—разряда
определяется следующим образом
.
При этом все нечетные
единицы, считая слева направо, имеют
положительный вес, а все четные единицы
отрицательный.
Например,
Непостоянство
весов разрядов затрудняет выполнение
арифметических операций в коде Грея,
поэтому необходимо уметь делать перевод
кода Грея в обычный двоичный код и наоборот.
Алгоритм перевода чисел можно представить
следующим образом.
Пусть
— двоичный код,
— код Грея
Тогда
переход из двоичного кода
в код Грея выполнится
по следующему алгоритму
Например,
.
Обратный переход из кода Грея в
двоичный код
Например,
.
Аннотация[править]
Здесь мы рассмотрим основные принципы и методы надёжной и
эффективной передачи данных между двумя машинами, соединёнными
каналом. Под каналом следует понимать любую физическую среду
передачи данных. Посредством этой физической среды
нужно научиться передавать биты так, чтобы они безошибочно
принимались получателем точно в той последовательности,
в какой они были переданы.
Канальный уровень[править]
На уровне канала данных решается ряд проблем, присущих
только этому уровню:
- реализация сервиса для сетевого уровня,
- разбиение потока бит на кадры,
- управление потоком кадров,
- обработка ошибок передачи.
Основная задача канального уровня — обеспечить сервис сетевому уровню,
а это значит помочь передать данные с сетевого уровня одной машины на
сетевой уровень другой машины.
Разбиение на кадры[править]
Сервис, создаваемый канальным уровнем для сетевого, опирается на
сервис, создаваемый физическим уровнем. На физическом уровне
протекают потоки битов. Значение посланного бита не обязательно
равно принятому, и количество посланных битов не обязательно
равно количеству принятых. Всё это требует специальных усилий на
канальном уровне по обнаружению и исправлению ошибок.
Типовой подход к решению этой проблемы — разбиение потока битов
на кадры и подсчёт контрольной суммы для каждого кадра при
посылке данных.
Контрольная сумма — это, в общем смысле, функция от
содержательной части кадра (слова длины 
значений которой — слова фиксированной длины 
Эти r бит добавляются обычно в конец кадра. При приёме
контрольная сумма вычисляется заново и сравнивается с той, что
хранится в кадре. Если они различаются, то это признак ошибки
передачи. Канальный уровень должен принять меры к исправлению
ошибки, например, сбросить плохой кадр, послать сообщение об
ошибке тому кто прислал этот кадр. Разбиение потока битов на
кадры — задача не простая. Один из способов — делать
временную паузу между битами разных кадров. Однако, в сети, где
нет единого таймера, нет гарантии, что эта пауза сохранится или,
наоборот, не появятся новые. Так как временные методы ненадёжны,
то применяются другие. Здесь мы рассмотрим три основных:
- счетчик символов;
- вставка специальных стартовых и конечных символов или последовательностей бит;
- специальная кодировка на физическом уровне.
Первый метод очевиден. В начале каждого кадра указывается сколько
символов в кадре. При приёме число принятых символов
подсчитывается опять. Однако, этот метод имеет существенный
недостаток — счётчик символов может быть искажён при передаче.
Тогда принимающая сторона не сможет обнаружить границы кадра.
Даже обнаружив несовпадение контрольных сумм, принимающая
сторона не сможет сообщить передающей какой кадр надо переслать,
сколько символов пропало. Этот метод ныне используется редко.
Второй метод построен на вставке специальных символов.
Обычно для этого используют управляющие последовательности:
последовательность 
для конца кадра. 

TeXt, 
потеряна граница текущего кадра, надо просто искать
ближайшую последовательность 



нужно избегать появления этих комбинаций внутри самого тела
кадра. Это осуществляется дублированием комбинаций 
встречающихся внутри тела кадра, и удаление дублей после
получения кадра. Недостатком этого метода является
зависимость от кодировки (кодозависимость).
По мере развития сетей эта связь становилась все более и более
обременительной и был предложен новый очевидный кодонезависимый
метод — управляющие последовательности должны быть
бит-ориентированными. В частности, в протоколе 
начинается и заканчивается со специального флаг-байта: 01111110.
Посылающая сторона, встретив последовательно 5 единиц внутри тела
кадра, обязательно вставит 0. Принимающая сторона, приняв 5
последовательных единиц обязательно удалит следующий за ними 0,
если таковой будет. Это называется bit-stuffing. Если
принято шесть и за ними следует ноль, то это управляющий сигнал:
начало или конец кадра, а в случае, когда подряд идут более шести
единиц, — сигнал ожидания или аварийного завершения.
(а) 0 1 1 0 1 1 1 1 1 1 1 1 1 1 1 0 0 1 (б) 0 1 1 0 1 1 1 1 1 0 1 1 1 1 1 0 1 0 0 1
Bit Stuffing. (a) исходные данные (б) посылаемые данные. Жирным отмечены вставленные нули.
Таким образом, кадр легко может быть распознан по
флаг-байту. Если граница очередного кадра по какой-то
причине была потеряна, то все что надо делать — ловить
ближайший флаг-байт.
И наконец, последний метод используется там, где конкретизирована
физическая среда. Например, в случае проводной связи для передачи
одного бита используется два импульса. 1 кодируется как переход
высокое-низкое, 0 — как низкое-высокое. Сочетания низкое-низкое
или высокое-высокое не используются для передачи данных, и их
используют для границ кадра.
На практике используют, как правило, комбинацию этих методов.
Например, счётчик символов с флаг-байтами. Тогда, если число
символов в кадре соответствует кодировке границы кадра, кадр
считается переданным правильно.
Контроль ошибок[править]
Решив проблему разбиения на кадры, мы приходим к следующей
проблеме: как обеспечить, чтобы кадры, пройдя по физическому
каналу с помехами, попадали на сетевой уровень по назначению, в
надлежащей последовательности и в надлежащем виде?
Частичное решение этой проблемы осуществляется посредством
введения обратной связи между отправителем и получателем в
виде кадра подтверждения, а также специального кодирования,
позволяющего обнаруживать или даже исправлять ошибки
передачи конкретного кадра.
Если кадр-подтверждение несет положительную информацию, то
считается что переданные кадры прошли нормально, если там
сообщение об ошибке, то переданные кадры надо передать
заново.
Однако, возможны случаи когда из-за ошибок в канале
кадр исчезнет целиком. В этом случае получатель не будет
реагировать никак, а отправитель будет сколь угодно долго ждать
подтверждения. Для решения этой проблемы на канальном уровне
вводят таймеры. Когда передаётся очередной кадр, то одновременно
устанавливается таймер на определённое время. Этого времени должно
хватать на то, чтобы получатель получил кадр, а отправитель
получил подтверждение. Если отправитель не получит подтверждение
раньше, чем истечёт время, установленное на таймере то он будет
считать, что кадр потерян и повторит его еще раз.
Однако, если кадр-подтверждение был утерян, то вполне возможно, что один и
тот же кадр получатель получит дважды. Как быть? Для решения
этой проблемы каждому кадру присваивают порядковый номер. С
помощью этого номера получатель может обнаружить дубли.
Итак, таймеры, нумерация кадров, флаг-байты,
кодирование и обратная связь — вот основные средства на канальном уровне,
обеспечивающие надёжную доставку каждого кадра до сетевого
уровня в единственном экземпляре. Но и с помощью этих
средств невозможно достигнуть стопроцентной надёжности
передачи.
Управление потоком[править]
Другая важная проблема, которая решается на канальном уровне
— управление потоком. Вполне может
случиться, что отправитель будет слать кадры столь часто, что
получатель не будет успевать их обрабатывать(например, если
машина-отправитель более мощная или загружена слабее, чем
машина-получатель). Для борьбы с такими ситуациями вводят
управления потоком. Это управление предполагает обратную связь
между отправителем и получателем, которая позволяет им
урегулировать такие ситуации. Есть много схем управления потоком
и все они в основе своей имеют следующий сценарий: прежде, чем
отправитель начнёт передачу, он спрашивает у получателя сколько
кадров тот может принять. Получатель сообщает ему определённое
число кадров. Отправитель после того, как передаст это число
кадров, должен приостановить передачу и снова спросить получателя,
как много кадров тот может принять, и т.д.
Помехоустойчивое кодирование[править]
Характеристики ошибок[править]
Физическая среда, по которой передаются данные, не может быть
абсолютно надёжной. Более того, уровень шума бывает очень
высоким, например в беспроводных системах связи и телефонных
системах. Ошибки при передаче — это реальность, которую
надо обязательно учитывать.
В разных средах характер помех разный. Ошибки могут быть
одиночные, а могут возникать группами, сразу по несколько. В
результате помех могут исчезать биты или наоборот — появляться
лишние.
Основной характеристикой интенсивности помех в канале
является параметр шума — p. Это число от 0 до 1, равное
вероятности инвертирования бита, при условии, что он был
передан по каналу и получен на другом конце.
Следующий параметр — 
события, но при условии, что предыдущий бит также был
инвертирован.
Этими двумя параметрами вполне можно ограничиться при построении
теории. Но, в принципе, можно было бы учитывать аналогичные
вероятности для исчезновения бита, а также использовать полную
информацию о пространственной корреляции ошибок, — то есть
корреляции соседних ошибок, разделённых одним, двумя или более
битами.
У групповых ошибок есть свои плюсы и минусы. Плюсы
заключаются в следующем. Пусть данные передаются блоками по
1000 бит, а уровень ошибки 0,001 на бит. Если ошибки
изолированные и независимые, то 63 % (
возникают группами по 100 сразу, то ошибки будут содержать
1 % (
Зато, если ошибки не группируются, то в каждом кадре они невелики,
и есть возможность их исправить. Групповые ошибки портят
кадр безвозвратно. Требуется его повторная пересылка, но в
некоторых системах это в принципе невозможно, — например,
в телефонных системах, использующие цифровое кодирование,
возникает эффект пропадания слов/слогов.
Для надёжной передачи кодов было предложено два основных метода.
Первый — добавить в передаваемый блок данных нескольких «лишних» бит так, чтобы, анализируя
полученный блок, можно было бы сказать, есть в переданном
блоке ошибки или нет. Это так называемые коды с обнаружением ошибок.
Второй — внести избыточность настолько, чтобы,
анализируя полученные данные, можно не только замечать
ошибки, но и указать, где именно возникли искажения. Это
коды, исправляющие ошибки.
Такое деление условно. Более общий вариант — это коды,
обнаруживающие k ошибок и исправляющие l ошибок, где

* Элементы теории передачи информации[править]
Информационным каналом называется пара зависимых
случайных величин 
называется входом другая выходом канала. Если случайные величины
дискретны и конечны, то есть имеют конечные множества событий:
то канал определяется матрицей условных вероятностей


будет значение 
значение 
Входная случайная величина определяется распределением


выходе вычисляется по формуле
Объединённое распределение на

Информация 
канал, есть взаимная информация входа и выхода:
(eq:inf)
где
Если случайные величины 

есть 


((eq:inf)) можно из следующего соображения: энтропия случайной
величины равна информации, которую мы получаем при одном её
измерении. 

содержится по отдельности во входе и в выходе. Но часть этой
информации общая, её нам и нужно найти.
равна величине объединённой информации. В теории
меры[1] есть выражение
аналогичное ((eq:inf)):
Распределение входной случайной величины 
варьировать и получать различные значения I. Её максимум
называется пропускной способностью канала
(eq:cdef)
Эта функция есть решение задачи
Задача 1.
(task:shanon) Каково максимальное количество информации,
которое можно передать с одним битом по каналу

Конец задачи.
Итак, пропускная способность есть функция на множестве стохастических матриц[2].
Стандартный информационный канал это
(eq:sm)
То есть канал с бинарным алфавитом и вероятностью помехи p
(p — вероятность того, что бит будет случайно
инвертирован). Его пропускная способность равна
Эта функция является решением задачи на максимум ((eq:cdef))
для матрицы ((eq:sm)).
begin{figure}[t!]
centeringincludegraphics[clip=true,
width=0.75textwidth]{pictures/cideal.eps} caption{ 
Пропускная способность канала как функция вероятности
инвертирования бита.} (fig:cideal)
end{figure}
Эта функция 
помехоустойчивого кодирования — если мы хотим с абсолютной
надёжностью передать по каналу с пропускной способностью C
сообщение длиной m, то минимальное количество бит, которое нам
нужно будет передать 
помехоустойчивое кодирование, обеспечивающее вероятность
незамеченной ошибки в переданном слове меньше, чем 
раздувает данные в 
Кодирование, при котором в этом пределе достигается
равенство, называется эффективным. Отметим, что
абсолютно надёжного способа передачи конечного количества
данных по каналу с помехами не существует: то есть

Задача дуальная (task:shanon) формулируется следующим
образом
Задача 2.
(task:dual)
Мы хотим передавать информацию со скоростью V по каналу с
пропускной способностью C. Какова минимальная вероятность
ошибочной передачи одного бита?
Конец задачи.
Решением будет функция заданная неявно




Оказывается, вероятность ошибки растет не так уж и быстро.
Например, если по каналу передавать данных в два раза
больше, чем его пропускная способность, то лишь 11 бит из
ста будут переданы с ошибкой.
begin{figure}[t!]
psfrag{v}{v} psfrag{p}{ 
centeringincludegraphics[clip=true,
width=0.75textwidth]{pictures/pv.eps} caption{ 
минимальная вероятность ошибки в одном бите как функция от
отношения скорости передачи и пропускной способности 
(fig:pv)
end{figure}
Построение конкретных способов кодирования, приближающихся
по пропускной способности к теоретической границе —
сложная математическая задача.
Метод «чётности» и общая идея[править]
Простым примером
кода с обнаружением одной ошибки является код с битом чётности.
Конструкция его такова: к исходному слову добавляется бит
чётности. Если в исходном слове число единичек чётно, то значение
этого бита 0, если нечётно — 1. Таким образом допустимые слова
этого кода имеют чётное количество единичек. Если получено слово
с нечётным количеством единичек, то при передаче произошла ошибка.
В случае вероятных групповых ошибок эту технику можно
скорректировать. Разобъём передаваемые данные на n слов по k
бит и расположим их в виде матрицы 
каждого столбца вычислим бит чётности и разместим его в
дополнительной строке. Матрица затем передается по строкам. По
получению матрица восстанавливается, и если обнаруживется
несоответствие, то весь блок передается повторно. Этот метод
позволяет обнаружить групповые ошибки длины 
Задача 3.
Слово длиной n с чётным количеством единиц передано по каналу с
уровнем шума p. Покажите, что вероятность того, что при
передаче произошли ошибки и мы их не заметили равна
Что можно привести к виду
Например, при 


Конец задачи.
Следующая задача повышенной сложности.
Задача 4. (task:errmod) Пусть у нас есть возможность контролировать
сумму единичек по модулю d. Тогда вероятность нефиксируемых
ошибок в слове длиной n при передаче его по каналу с шумом p
равна 
Примечание. Интерес здесь представляет неявно
заданная функция 
содержания полезной информации

бит как функция от величины шума и вероятности незамеченных
ошибок. Чем выше желаемая надёжность передачи, то есть чем меньше
вероятность 
полезной информации.
Конец задачи.
Итак, с помощью одного бита чётности мы повышаем надёжность
передачи, и вероятность незамеченной ошибки равна

При 

дублированию каждого бита. Рассмотрим общую идею того, как с
помощью специального кодирования можно добиться сколь угодно
высокой надёжности передачи.
Общая идея На множестве слов длины n определена
метрика Хемминга: расстояние Хемминга между двумя словами
равно количеству несовпадающих бит. Например,
Задача 5.
Докажите, что 
Конец задачи.
Если два слова находятся на расстоянии r по Хеммингу,
это значит, что надо инвертировать ровно r разрядов, чтобы
преобразовать одно слово в другое. В описанном ниже
кодировании Хемминга любые два различных допустимых слова
находятся на расстоянии 
обнаруживать d ошибок, то надо, чтобы слова отстояли друг
от друга на расстояние 
исправлять ошибки, то надо чтобы кодослова отстояли друг от
друга на 
переданное слово содержит d ошибок, оно, как следует из
неравенства треугольника, все равно ближе к правильному
слову, чем к какому-либо еще, и следовательно можно
определить, исходное слово. Минимальное расстояние Хемминга
между двумя различными допустимыми кодовыми словами
называется расстоянием Хемминга данного кода.
Элементарный пример помехоустойчивого кода — это код, у
которого есть только четыре допустимых кодовых слова:
Расстояние по Хеммингу у этого кода 5, следовательно он может
исправлять двойные ошибки и замечать 4 ошибки. Если получатель
получит слово 0001010111, то ясно, что исходное слово имело
вид 0000011111. Коэффициент раздувания равен 5. То есть
исходное слово длины m будет кодироваться в слово длины 
Отметим что имеет смысл говорить о двух коэффициентах:
Первый есть функция от переменной n, а второй, обратный
ему, — от переменной m.
Здесь мы подошли к довольно трудной задаче —
минимизировать коэффициент раздувания для требуемой
надёжности передачи. Она рассматривается в разделе (theory).
Циклические коды[править]
На практике активно применяются полиномиальные коды
или циклические избыточные коды (Cyclic Redundancy Code
— CRC).
CRC коды построены на рассмотрении битовой строки как
строки коэффициентов полинома. k-битовая строка
соответствует полиному степени 
— коэффициент при старшей степени. Например, строка 110001
представляет полином 
принадлежат полю 
Основная идея заключена в том, чтобы пересылать только такие
сообщения, полиномы которых делятся на некоторый фиксированный
полином 
на 
ошибок, если они один допустимый полином (то есть полином
делящийся на 
Полином 
на парах допустимых полиномов.
Есть два очевидных способа кодирования сообщения в полином,
который делится на 
сообщения на 
количество бит так, чтобы результирующий полином делился на

Отправитель и получатель заранее договариваются
о конкретном полиноме-генераторе 

равна l.
Мы добавляем контрольные l бит в конец передаваемого
блоку так, чтобы получился полином кратный генератору

он проверяет его делимость на G. Если есть остаток 
Алгоритм кодирования CRC:
Дано слово W длины m. Ему соответствует полином 
- Добавить к исходному слову W справа r нулей. Получится слово длины
и полином :
- Разделить полином
на
и вычислить остаток от деления
:
- Вычесть остаток (вычитание в
то же самое, что и сложение) из полинома
:
Слово, которое соответствует полиному
, и есть результат.
Рис. (fig:crc) иллюстрирует этот алгоритм для блока
1101011011 и 
begin{figure}[h!]
psfrag{Remainder}{Остаток}
centeringparbox{0.66textwidth}{
begin{tabular}{lcl}
Слово&:&1101011011 \
Результат&:&11010110111110
end{tabular}}
centeringincludegraphics[clip=true,
width=0.75textwidth]{pictures/crc2.eps}
caption{CRC — полиномиальное кодирование}
(fig:crc)
end{figure}
Этот метод позволяет отлавливать одиночные ошибки и
групповые ошибки длины не более степени полинома.
Существует три международных стандарта на вид 

Два остальных — для 8 разрядных. 

одиночные, двойные ошибки, групповые ошибки длины не более 16 и
нечётное число изолированных ошибок с вероятностью 0.99997.
* Теоретический предел[править]
(theory) В примечании
к задаче (task:errmod) было указано как можно получить
значение коэффициента содержания полезной информации (КПС) на
один бит, если передавать данные по каналу с шумом p словами
длиной n бит, при условии, чтобы вероятность незамеченной
ошибки была меньше 
Но ясно, что указанная там функция дает лишь оценку снизу
оптимального значения КПС
— возможно, существует другие методы контролирования
ошибок, для которых он выше. Теория информации позволяет нам
найти точное значение этого коэффициента.
Сформулируем задачу о кодировании, обнаруживающем ошибки.
Для начала предположим, что наличие ошибки фиксируется с
абсолютной точностью.
Задача 6.
(task:err)
Мы хотим передавать информацию блоками, которые содержали
бы m бит полезной информации, так, чтобы
вероятность ошибки в одном бите равнялась p, а
правильность передачи «фиксировалось контрольной суммой». Найти
минимальный размер блока 

Конец задачи.
Решение.
Для передачи m бит с вероятностью ошибки в отдельном бите
p требуется передать 
(см. задачу (task:dual)). Кроме того мы хотим сообщать
об ошибке в передаче. Её вероятность равна 
значит информация, заложенная в этом сообщении,


Конец решения.
Заметим, что 
сообщение об ошибке в нём равносильно передаче самого бита.
Если передавать эти сообщения по каналу с уровнем помех p, то
количество бит на одно сообщение равно 
теоретическая оценка для количества лишних бит равна
Понятно, что данная теоретическая оценка занижена.
Коды Хэмминга[править]
Элементарный пример кода исправляющего ошибки был показан на
странице pageref{simplecode}. Его обобщение очевидно. Для
подобного кода, обнаруживающего одну ошибку, КПС равен 
единице с помощью кодов Хемминга. В частности, при кодировании
11 бит получается слово длинной 15 бит, то есть

Оценим минимальное количество контрольных
разрядов, необходимое для исправления одиночных ошибок. Пусть
содержательная часть составляет m бит, и мы добавляем ещё r
контрольных. Каждое из 
его неправильных вариантов с ошибкой в одном бите. Такими
образом, с каждым из 
слов и эти множества не должны пересекаться. Так как общее число
слов 
Этот теоретический предел достижим при использовании
метода, предложенного Хеммингом. Идея его в следующем: все
биты, номера которых есть степень 2, — контрольные,
остальные — биты сообщения. Каждый контрольный бит
отвечает за чётность суммы некоторой группы бит. Один и тот
же бит может относиться к разным группам. Чтобы определить
какие контрольные биты контролируют бит в позиции k надо
разложить k по степеням двойки: если 
бит относится к трём группам — к группе, чья чётность
подсчитывается в 1-ом бите, к группе 2-ого и к группе 8-ого
бита. Другими словами в контрольный бит с номером
заносится сумма (по модулю 2) бит с номерами, которые имеют
в разложении по степеням двойки степень 
(eq:hem)
Код Хемминга оптимален при 

![{displaystyle m=n-[log _{2}(n+1)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d24a7d287da182a9c3ab18a6fbd87ef3988a6b9)
![{displaystyle [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07548563c21e128890501e14eb7c80ee2d6fda4d)


n однозначно определяет m).
Пример для 
- Невозможно разобрать выражение (неизвестная функция «fbox»): {displaystyle fbox{10110100111}to fbox{fbox{0}fbox{0}1fbox{1}011fbox{0}0100111} }
- Невозможно разобрать выражение (неизвестная функция «fbox»): {displaystyle hphantom{fbox{10110100111}to};; lefteqn{,b_1}hphantom{fbox{0}} lefteqn{,b_2}hphantom{fbox{0}} lefteqn{b_3}hphantom{1} lefteqn{;b_4}hphantom{fbox{1}011} lefteqn{,b_8}hphantom{fbox{0}} lefteqn{b_9}hphantom{010011} lefteqn{b_{15}}hphantom{1} }
Получив слово,
получатель проверяет каждый контрольный бит на предмет
правильности чётности и складывая номера контрольных бит, в
которых нарушена чётность. Полученное число, есть XOR номеров
бит, где произошла ошибка. Если ошибка одна, то это число есть
просто номер ошибочного бита.
Например, если в контрольных разрядах 1, 2, 8 обнаружено
несовпадение чётности, то ошибка в 11 разряде, так как
только он связан одновременно с этими тремя контрольными
разрядами.
begin{figure}[h!]
psfrag{Check bits}{hspace{-12mm}Контрольные биты}
centeringincludegraphics[clip=true,
width=0.65textwidth]{pictures/hem.eps} caption{Кодирование
Хемминга} (fig:hem)
end{figure}
Задача 7.
Покажите, что 

Конец задачи.
Код Хемминга может исправлять только единичные ошибки. Однако,
есть приём, который позволяет распространить этот код на случай
групповых ошибок. Пусть нам надо передать k кодослов.
Расположим их в виде матрицы одно слово — строка. Обычно,
передают слово за словом. Но мы поступим иначе, передадим слово
длины k, из 1-ых разрядов всех слов, затем — вторых и т. д. По
приёме всех слов матрица восстанавливается. Если мы хотим
обнаруживать групповые ошибки размера k, то в каждой строке
восстановленной матрицы будет не более одной ошибки. А с
одиночными ошибками код Хемминга справится.
Анализ эффективности[править]
Начнём c небольшого примера. Пусть у нас есть канал с уровнем
ошибок 
передаче блоками по 
10 контрольных бит: 1, 2, dots, 
приходится 1013 бит полезной информации. При передаче 1000
таких блоков потребуется 
В тоже время для обнаружения единичной ошибки достаточно одного
бита чётности. И если мы применим технику повторной передачи, то
на передачу 1000 блоков надо будет потратить 1000 бит
дополнительно и примерно 
повторно. То есть на 1000 блоков приходится один попорченый, и
дополнительная нагрузка линии составляет 

Хемминга плох для такого канала. Надо правильно выбрать длину
блока — если 
Рассмотрим этот вопрос подробнее. Пусть нам нужно передать
информацию M бит. Разобьем её на L блоков по 
и будем передавать двумя способами
— с помощью кодов Хемминга и без них. При этом будем
считать, что в обоих случаях осуществлено предварительное
кодирование, позволяющее с вероятностью
определять ошибочность передачи. Это осуществляется путем
добавления «лишней» информации. Обозначим коэффициент
раздувания для этого кодирования 
этого кодирования каждый блок несёт информацию

1) Без кода Хемминга.
Если пересылать информацию
блоками по 
обнаружения ошибки, то получим, что в среднем нам придётся
переслать D бит:
Где 
повторной передачи равная вероятности ошибки умноженной на
вероятность того, что мы её заметим. Коэффициент раздувания
равен
2) С кодом Хемминга.
При кодировании методом Хемминга слова длины 
(eq:hnm)
Для отдельного блока вероятность
безошибочной передачи равна 
одинарной ошибки 
что произошло более чем одна ошибка, и мы это заметили
— в этом случае требуется повторная передача кадра.
Количество передаваемых данных:
И коэффициент раздувания
где 
функция. Удобно записать соответствующие коэффициенты
полезного содержания:
,
(eq:kps)
Легко обнаружить что при 

оказывается эффективнее, то есть 
begin{figure}[h!]
psfrag{knc}{кпс} psfrag{n}{n}
centeringincludegraphics[clip=true,
width=0.48textwidth]{pictures/kps.eps}
centeringincludegraphics[clip=true,
width=0.48textwidth]{pictures/kps2.eps} caption{

в канале с помехами как функция размера элементарного блока.}
parbox{0.85textwidth}{small Светлый график — без кодирования Хемминга;\
Темный график — с кодированием Хемминга;
\Параметры: 

(fig:kps)
end{figure}
begin{figure}[h!]
psfrag{C}{C} psfrag{p}{p}
centeringincludegraphics[clip=true,
width=0.75textwidth]{pictures/kpseff.eps}
caption{
содержания в канале с помехами как функция уровня помех.}
parbox{0.97textwidth}{ small Светлый график — без кодирования Хемминга;\ Темный график — с кодированием Хемминга;\Тонкий график — теоретический
предел, задаваемый функцией 

end{figure}
Значение 
формулах ((eq:kps)) можно оценить как
Напомним, что 
надёжности передачи
— чем меньше 
По определению 
ошибочной передачи блока при условии, что «контрольная сумма
сошлась» и кадр засчитан правильно переданным.
Такое выражение для
получается из формулы
Но это безусловно лишь оценочная формула. Оптимальное
значение 
зависит от p.
Из графика на рисунке (fig:kps) хорошо видно, что при
больших n код Хемминга начинает работать на пользу.
Но зависимость КПС от n не есть критерий эффективности
кода. Эффективность кода определяется функцией
На рисунке (fig:kpseff) показан график этой функции и из
него ясно, что код Хемминга можно использовать с пользой
всегда — при любых 
возможность выбирать подходящее n.
Коды как линейные операторы[править]
То, что на множестве {0,1} есть структура числового поля,
позволяет осуществлять алгебраические интерпретации кодирования.
Заметим, в частности, что как коды Хемминга, так и циклические
коды линейны:\ 1) отношения ((eq:hem)) на
с. pageref{eq:hem}, связывающие контрольные биты кода Хемминга с
другими линейны,\ 2) остаток от деления суммы многочленов на
третий равен сумме остатков.\ То есть кодирование в этих двух
случаях есть линейное отображение из 

матрица кода Хемминга 
соотношения ((eq:hem))). Исходное слово есть

(слова соответствуют столбцам).
Процесс выявления ошибок тоже линейная операция, она
осуществляется с помощью проверочной матрицы 
Пусть принято слово 

случае правильной передачи должно быть равно 000. Значение

слова 
((eq:hem)) и, таким образом, 
бит в которых произошла ошибка, как векторов в 
Заметим, что столбцы проверочной матрицы представляют собой
последовательно записанные в двоичной форме натуральные
числа от 1 до 7.
Вычиcление рабочей матрицы для циклических кодов
основывается на значениях 
её часть равна единичной, так m бит сообщения помещаются
без изменения в начало слова, а нижние r строчек есть m
столбцов высоты r состоящие из коэффициентов многочленов


dots, 




Рабочая и проверочная матрицы равны
то есть
Кроме рабочей и проверочной матриц есть ещё множество порождающих матриц 

слова образуют линейное подпространство 

которой образуют базис этого подпространства, называется
порождающей. В частности, рабочая матрица является порождающей.
Способность обнаруживать и исправлять ошибки однозначно
определяется подпространством L. Порождающих, рабочих и
проверочных матриц соответствующих L несколько.
Действительно, в порождающей и рабочей матрицах можно осуществлять
элементарные операции со столбцами, а в проверочной — со
строчками. Матрицы 

всегда удовлетворяют отношениям
где


Любая порождающая матрица может использоваться как
рабочая.
Декодирующая матрица 

таким свойством может быть несколько. Множество декодирующих
матриц определяется рабочей матрицей:
где 

подпространстве L все декодирующие матрицы действуют одинаково.
Они отличаются на подпространстве ортогональном L. Приведём
декодирующую матрицу для 

К каждой строчке декодирующей матрицы можно добавить любую
линейную комбинацию строчек из проверочной матрицы. Следует
отметить, что процесс исправления ошибок для кодов Хемминга
нелинеен и его нельзя «внедрить» в декодирующую матрицу.
Сформулируем теперь основные моменты, касающиеся линейных кодов.
- Процесс кодирования и декодирования — линейные операторы. :
- Обнаружение ошибок равносильно проверке принадлежности полученного слова подпространству L допустимых слов. Для этого необходимо найти проекцию
(синдром ошибки) полученного слова на
— тоже линейная операция. Для правильно переданного слова
. :
- В случае, когда векторы подпространства L достаточно удалены друг от друга в смысле метрики Хемминга, есть возможность обнаруживать и исправлять некоторые ошибки. В частности, значение синдрома ошибки в случае кода Хемминга равно векторной сумме номеров бит, где произошла ошибка.
- Комбинация (композиция) линейных кодов есть снова линейный код.
Практические методы помехоустойчивого кодирования все основаны на
линейных кодах. В основном это модифицированные CRC, коды
Хемминга и их композиции. Например 
чётность. Такой код может исправлять уже две ошибки. Построение
эффективных и удобных на практике задача сходная с творчеством
художника. На практике важны не только корректирующая способность
кода, но и вычислительная сложность процессов кодирования и
декодирования, а также спектральная характеристика
результирующего аналогового сигнала. Кроме того, важна
способность исправлять специфические для данного физического
уровня групповые ошибки.
Задача 8.
Для данной проверочной матрицы постройте рабочую и декодирующую
матрицу. Докажите, что кодовое расстояние равно 4.
Подсказка
- Это проверочная матрица
плюс условие на чётность числа единичек в закодированном слове вместе с дополнительным восьмым контрольным битом.
- Кодовое расстояние равно минимальному количеству линейно зависимых столбцов в
.
Конец задачи.
Задача 9.
Посторойте декодирующую и проверочную матрицу для циклического
кода с 

рабочей матрицы использовалась матрица
Конец задачи.
*Коды Рида-Соломона[править]
После перехода на язык линейной алгебры естественно возникает
желание изучить свойства линейных кодов над другими конечными
числовыми полями. С помощью такого обобщения появились коды
Рида-Соломона.
Коды Рида-Соломона являются циклическими кодами над
числовым полем отличным от 
Напомним, что существует бесконечное количество конечных полей, и
количество элементов в конечном поле всегда равно степени
простого числа. Если мы зафиксируем число элементов 
найдётся единственное с точностью до изоморфности конечное поле с
таким числом элементов, которое обозначается как

многочленов по модулю неприводимого[3] многочлена 
полем 
многочленов с действительными коэффициентами неприводимыми
многочленами являются только квадратные многочлены с
отрицательным дискриминантом. Поэтому существует только
квадратичное расширение действительного поля — комплексные
числа. А над конечным полем существуют неприводимые многочлены
любой степени. В частности, над 

модулю 

Примеры протоколов канала данных[править]
HDLC протокол[править]
Здесь мы познакомимся с группой протоколов давно известных, но
по-прежнему широко используемых. Все они имеют одного
предшественника — SDLC (Synchronous Data Link Control) —
протокол управления синхронным каналом, предложенным фирмой IBM
в рамках SNA. ISO модифицировала этот протокол и выпустила
под названием HDLC — High level Data Link Control. MKTT
модифицировала HDLC для X.25 и выпустила под именем LAP —
Link Access Procedure. Позднее он был модифицирован в LAPB.
Все эти протоколы построены на одних и тех же принципах. Все
используют технику вставки специальных последовательностей
битов. Различия между ними незначительные.
begin{figure}[h!]
centeringincludegraphics[clip=true,
width=0.88textwidth]{pictures/frame.eps} caption{Типовая
структура кадра} (fig:frame)
end{figure}
На рис. (fig:frame) показана типовая структура кадра.
Поле адреса используется для адресации терминала, если их
несколько на линии. Для линий точка-точка это поле
используется для различия команды от ответа.
- Поле Control используется для последовательных номеров кадров, подтверждений и других нужд.
- Поле Data может быть сколь угодно большим и используется для передачи данных. Надо только иметь ввиду, что чем оно длиннее тем, больше вероятность повреждения кадра на линии.
- Поле Checksum — это поле используется CRC кодом.
Флаговые последовательности 01111110 используются для
разделения кадров и постоянно передаются по незанятой линии
в ожидании кадра. Существуют три вида кадров: 

Организация поля Control для этих трех видов кадров показана на
рис. (fig:cfield). Как видно из размера поля Seq в окне
отправителя может быть до 7 неподтверждённых кадров. Поле
Next используется для посылки подтверждения вместе с
передаваемым кадром. Подтверждение может быть в форме номера
последнего правильно переданного кадра, а может быть в форме
первого не переданного кадра. Какой вариант будет использован —
это параметр.
begin{figure}[h!]
centeringincludegraphics[clip=true,
width=0.88textwidth]{pictures/cfield.eps} caption{Cтруктура поля
Control}
parbox{0.66textwidth}{small (а) Информационный кадр (
(б) Управляющий кадр (
кадр (Unnumbered) }
(fig:cfield)
end{figure}
Разряд 
Когда компьютер приглашает терминал к передаче он
устанавливает этот разряд в P. Все кадры, посылаемые
терминалами имеют здесь P. Если это последний кадр,
посылаемый терминалом, то здесь стоит F.

- Тип 0 — уведомление в ожидании следующего кадра (RECEIVE READY). Используется когда нет встречного трафика, чтобы передать уведомление в кадре с данными.
- Тип 1 — негативное уведомление (REJECT) — указывает на ошибку при передаче. Поле Next указывает номер кадра, начиная с которого надо перепослать кадры.
- Тип 2 — RECEIVE NOT READY. Подтверждает все кадры, кроме указанного в Next. Используется, чтобы сообщить источнику кадров об необходимости приостановить передачу в силу каких-то проблем у получателя. После устранения этих проблем получатель шлет RECEIVE REDAY, REJECT или другой надлежащий управляющий кадр.
- Тип 3 — SELECTIVE REJECT — указывает на необходимость перепослать только кадр, указанный в Next. LAPB и SDLC не используют этого типа кадров.
Третий класс кадров — Unnubered. Кадры этого класса иногда
используются для целей управления, но чаще для передачи данных
при ненадёжной передаче без соединения.
Все протоколы имеют команду DISConnect для указания о разрыве
соединения, SNRM и SABM — для установки счётчиков кадров в ноль,
сброса соединения в начальное состояние, установки
соподчинённости на линии. Команда FRMR — указывает на
повреждение управляющего кадра.
- ^ Идея рассмотрения информации как меры на множестве ещё не до конца исчерпала себя — такой меры ещё не построено. Однако доказано, что с помощью этой аналогии можно доказывать неравенства, например
.
- ^ Матрица называется стохастической, если все её элементы неотрицательны и сумма элементов в каждом столбце равна единице.
- ^ Многочлен называется неприводимым, если он не разлагается в произведение многочленов меньшей степени.
Принципы помехоустойчивого кодирования
Помехоустойчивым (корректирующим) кодированием называется кодирование при котором осуществляется обнаружение либо обнаружение и исправление ошибок в принятых кодовых комбинациях.
Возможность помехоустойчивого кодирования осуществляется на основании теоремы, сформулированной Шенноном, согласно ей:
если производительность источника (Hи’(A)) меньше пропускной способности канала связи (Ск), то существует по крайней мере одна процедура кодирования и декодирования при которой вероятность ошибочного декодирования сколь угодно мала, если же производительность источника больше пропускной способности канала, то такой процедуры не существует.
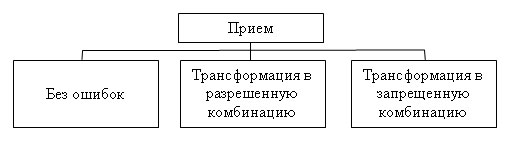
Основным принципом помехоустойчивого кодирования является использование избыточных кодов, причем если для кодирования сообщения используется простой код, то в него специально вводят избыточность. Необходимость избыточности объясняется тем, что в простых кодах все кодовые комбинации являются разрешенными, поэтому при ошибке в любом из разрядов приведет к появлению другой разрешенной комбинации, и обнаружить ошибку будет не возможно. В избыточных кодах для передачи сообщений используется лишь часть кодовых комбинаций (разрешенные комбинации). Прием запрещенной кодовой комбинации означает ошибку. Причем, в процессе приема закодированного сообщения возможны три случая (рисунок 3).
Рисунок 3 — Случаи приема закодированного сообщения
Прием сообщения без ошибок является оптимальным, но возможен только если канал связи идеальный. В этом случае помехоустойчивое декодирование не нужно.
В реальном канале из-за воздействия помех происходят ошибки в принимаемых кодовых комбинациях. Если принимаемая кодовая комбинация в результате воздействия помех перешла (трансформировалась) из одной разрешенной комбинации в другую, то определить ошибку не возможно, даже при использовании помехоустойчивого кодирования.
Если же передаваемая разрешенная кодовая комбинация, в результате воздействия помех, трансформируется в запрещенную комбинация, то в этом случае существует возможность обнаружить ошибку и исправить ее.
Помехоустойчивое кодирование может осуществляться двумя способами: с обнаружением ошибок либо с исправлением ошибок. Возможность кода обнаруживать или исправлять ошибки определяется кодовым расстоянием.
Если осуществляется кодирование с обнаружением ошибок, то кодовое расстояние должно быть хотя бы на единицу больше чем кратность обнаруживаемых ошибок, т. е.
d0? qо ош + 1.
Если данное условие не выполняется, то одни из ошибок обнаруживаются, а другие нет.
Если осуществляется кодирование с исправлением ошибок, то кодовое расстояние должно быть хотя бы на единицу больше удвоенного значения кратности исправляемых ошибок, т. е.
d0? 2qи ош + 1.
Если данное условие не выполняется, то одни из ошибок исправляются, а другие нет.
Следует отметить, что если код способен исправить одну ошибку (qи ош = 1), что соответствует кодовому расстоянию 3 (d0 = 1?2+1 = 3), то обнаружить он может две ошибки, т. к.
qо ош = d0 – 1 = 2.
Декодирование помехоустойчивых кодов
Декодирование — это процесс перехода от вторичного отображения сообщения к первичному алфавиту.
Декодирование помехоустойчивых кодов может осуществляться тремя способами: сравнения, синдромным и мажоритарным.
Способ сравнения основан на том, что, принятая кодовая комбинация сравнивается со всеми разрешенными комбинациями, которые заранее известны на приеме. Если принятая комбинация не совпадает ни с одной из разрешенных, выносится решение о принятии запрещенной комбинации. Недостатком данного способа является громоздкость и необходимость большого времени для декодирования в случае применения многоразрядных кодов. Данный способ используется в кодах с обнаружением ошибок.
Синдромный способ основан на вычислении определенным образом контрольного числа — синдрома ошибки (С). Если синдром ошибки равен нулю, то кодовая комбинация принята верно, если синдром не равен нулю, то комбинация принята не верно. Данный способ может быть использован в кодах с исправлением ошибок, в этом случае синдром указывает не только на наличие ошибки в кодовой комбинации, но и на место положение этой ошибки в кодовой комбинации. Для двоичного кода знание местоположения ошибки достаточно для ее исправления. Это объясняется тем, что любой символ кодовой комбинации может принимать всего два значения и если символ ошибочный, то его необходимо инвертировать. Следовательно, синдрома ошибки достаточно для исправления ошибок, если d0? 2qи ош + 1.
Мажоритарное декодирование основано на том, что каждый информационный символ кодовой комбинации определяется нескольким линейными выражениями через другие символы кодовой комбинации. Если принята комбинация без ошибок, то все соотношения остаются и все выражения дают одинаковые результаты (единицу или ноль). При ошибке в одном из разрядов эти соотношения нарушаются, в результате чего одни линейные выражения равны нулю, а другие единице. Решение о принятом символе определяется по большинству: если в результате вычислений выражений больше нулей, то принимается решение о принятии нуля, если больше единиц, то принимается решение о приеме единицы. Если, при декодировании, результаты вычисления выражений дают одинаковое число единиц и нулей, то при определении принятого символа приоритет имеет принятый символ, значение которого в данный момент определяется.
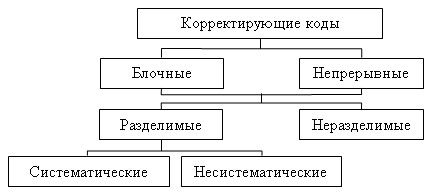
Классификация корректирующих кодов
Классификация корректирующих кодов представлена схемой (рисунок 4)
Блочные — это коды, в которых передаваемое сообщение разбивается на блоки и каждому блоку соответствует своя кодовая комбинация (например, в телеграфии каждой букве соответствует своя кодовая комбинация).
Рисунок 4 — Классификация корректирующих кодов
Непрерывные — коды, в которых сообщение не разбивается на блоки, а проверочные символы располагаются между информационными.
Неразделимые — это коды, в кодовых комбинациях которых нельзя выделить проверочные разряды.
Разделимые — это коды, в кодовых комбинациях которых можно указать положение проверочных разрядов, т. е. кодовые комбинации можно разделить на информационную и проверочную части.
Систематические (линейные) — это коды, в которых проверочные символы определяются как линейные комбинации информационных символов, в таких кодах суммирование по модулю два двух разрешенных кодовых комбинаций также дает разрешенную комбинацию. В несистематических кодах эти условия не выполняются.
Код с постоянным весом
Данный код относится к классу блочных не разделимых кодов. В нем все разрешенные кодовые комбинации имеют одинаковый вес. Примером кода с постоянным весом является Международный телеграфный код МТК-3. В этом коде все разрешенные кодовые комбинации имеют вес равный трем, разрядность же комбинаций n=7. Таким образом, из 128 комбинаций (N0 = 27 = 128) разрешенными являются Nа = 35 (именно столько комбинаций из всех имеют W=3). При декодировании кодовых комбинаций осуществляется вычисление веса кодовой комбинации и если W?3, то выносится решение об ошибке. Например, из принятых комбинаций 0110010, 1010010, 1000111 ошибочной является третья, т. к. W=4. Данный код способен обнаруживать все ошибки нечетной кратности и часть ошибок четной кратности. Не обнаруживаются только ошибки смещения, при которых вес комбинации не изменяется, например, передавалась комбинация 1001001, а принята 1010001 (вес комбинации не изменился W=3). Код МТК-3 способен только обнаруживать ошибки и не способен их исправлять. При обнаружении ошибки кодовая комбинация не используется для дальнейшей обработки, а на передающую сторону отправляется запрос о повторной передаче данной комбинации. Поэтому данный код используется в системах передачи информации с обратной связью.
Код с четным числом единиц
Данный код относится к классу блочных, разделимых, систематических кодов. В нем все разрешенные кодовые комбинации имеют четное число единиц. Это достигается введением в кодовую комбинацию одного проверочного символа, который равен единице если количество единиц в информационной комбинации нечетное и нулю ? если четное. Например:
При декодировании осуществляется поразрядное суммирование по модулю два всех элементов принятой кодовой комбинации и если результат равен единице, то принята комбинация с ошибкой, если результат равен нулю принята разрешенная комбинация. Например:
101101 = 1 + 0 + 1 + 1 + 0 + 1 = 0 — разрешенная комбинация
101111 = 1 + 0 + 1 + 1 + 1 + 1 = 1 — запрещенная комбинация.
Данный код способен обнаруживать как однократные ошибки, так и любые ошибки нечетной кратности, но не способен их исправлять. Данный код также используется в системах передачи информации с обратной связью.
Код Хэмминга
Код Хэмминга относится к классу блочных, разделимых, систематических кодов. Кодовое расстояние данного кода d0=3 или d0=4.
Блочные систематические коды характеризуются разрядностью кодовой комбинации n и количеством информационных разрядов в этой комбинации k остальные разряды являются проверочными (r):
r = n — k.
Данные коды обозначаются как (n,k).
Рассмотрим код Хэмминга (7,4). В данном коде каждая комбинация имеет 7 разрядов, из которых 4 являются информационными,
При кодировании формируется кодовая комбинация вида:
а1 а2 а3 а4 b1 b2 b
где аi — информационные символы;
bi — проверочные символы.
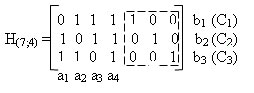
В данном коде проверочные элементы bi находятся через линейные комбинации информационных символов ai, причем, для каждого проверочного символа определяется свое правило. Для определения правил запишем таблицу синдромов кода (С) (таблица 3), в которой записываются все возможные синдромы, причем, синдромы имеющие в своем составе одну единицу соответствуют ошибкам в проверочных символах:
- синдром 100 соответствует ошибке в проверочном символе b1;
- синдром 010 соответствует ошибке в проверочном символе b2;
- синдром 001 соответствует ошибке в проверочном символе b3.
Синдромы с числом единиц больше 2 соответствуют ошибкам в информационных символах. Синдромы для различных элементов кодовой комбинации аi и bi должны быть различными.
Таблица 3 — Синдромы кода Хэмминга (7;4)
| Число | Элементы синдрома | Элементы кодовой | ||
| синдрома | С1 | С2 | С3 | комбинации |
| 1 | 0 | 0 | 1 | b3 |
| 2 | 0 | 1 | 0 | b2 |
| 3 | 0 | 1 | 1 | a1 |
| 4 | 1 | 0 | 0 | b1 |
| 5 | 1 | 0 | 1 | a2 |
| 6 | 1 | 1 | 0 | a3 |
| 7 | 1 | 1 | 1 | a4 |
Определим правило формирования элемента b3. Как следует из таблицы, ошибке в данном символе соответствует единица в младшем разряде синдрома С4. Поэтому, из таблицы, необходимо отобрать те элементы аi у которых, при возникновении ошибки, появляется единица в младшем разряде. Наличие единиц в младшем разряде, кроме b3,соответствует элементам a1, a2 и a4. Просуммировав эти информационные элементы получим правило формирования проверочного символа:
b3 = a1 + a2 + a4
Аналогично определяем правила для b2 и b1:
b2 = a1 + a3 + a4
b1 = a2 + a3 + a4
Пример 3, необходимо сформировать кодовую комбинацию кода Хэмминга (7,4) соответствующую информационным символам 1101.
В соответствии с проверочной матрицей определяем bi:
b1 = 1 + 0 + 1 = 0; b2 = 1 + 0 + 1=1; b3 = 1 + 1 + 1 = 1.
Добавляем проверочные символы к информационным и получаем кодовую комбинацию:
Biр = 1101001.
В теории циклических кодов все преобразования кодовых комбинаций производятся в виде математических операций над полиномами (степенными функциями). Поэтому двоичные комбинации преобразуют в полиномы согласно выражения:
Аi(х) = аn-1xn-1 + аn-2xn-2 +…+ а0x0
где an-1, … коэффициенты полинома принимающие значения 0 или 1. Например, комбинации 1001011 соответствует полином
Аi(х) = 1?x6 + 0?x5 + 0?x4 + 1?x3 + 0?x2 + 1?x+1?x0 ? x6 + x3 + x+1.
При формировании кодовых комбинаций над полиномами производят операции сложения, вычитания, умножения и деления. Операции умножения и деления производят по арифметическим правилам, сложение заменяется суммированием по модулю два, а вычитание заменяется суммированием.
Разрешенные кодовые комбинации циклических кодов обладают тем свойством, что все они делятся без остатка на образующий или порождающий полином G(х). Порождающий полином вычисляется с применением ЭВМ. В приложении приведена таблица синдромов.
Этапы формирования разрешенной кодовой комбинации разделимого циклического кода Biр(х).
1. Информационная кодовая комбинация Ai преобразуется из двоичной формы в полиномиальную (Ai(x)).
2. Полином Ai(x) умножается на хr,
Ai(x)?xr
где r количество проверочных разрядов:
r = n — k.
3. Вычисляется остаток от деления R(x) полученного произведения на порождающий полином:
R(x) = Ai(x)?xr/G(x).
4. Остаток от деления (проверочные разряды) прибавляется к информационным разрядам:
Biр(x) = Ai(x)?xr + R(x).
5. Кодовая комбинация Bip(x) преобразуется из полиномиальной формы в двоичную (Bip).
Пример 4. Необходимо сформировать кодовую комбинацию циклического кода (7,4) с порождающим полиномом G(x)=х3+х+1, соответствующую информационной комбинации 0110.
1. Преобразуем комбинацию в полиномиальную форму:
Ai = 0110 ? х2 + х = Ai(x).
2. Находим количество проверочных символов и умножаем полученный полином на xr:
r = n – k = 7 – 4 =3
Ai(x)?xr = (х2 + х)? x3 = х5 + х4
3. Определяем остаток от деления Ai(x)?xr на порождающий полином, деление осуществляется до тех пор пока наивысшая степень делимого не станет меньше наивысшей степени делителя:
R(x) = Ai(x)?xr/G(x)
4. Прибавляем остаток от деления к информационным разрядам и переводим в двоичную систему счисления:
Biр(x) = Ai(x)?xr+ R(x) = х5 + х4 + 1? 0110001.
5. Преобразуем кодовую комбинацию из полиномиальной формы в двоичную:
Biр(x) = х5 + х4 + 1 ? 0110001 = Biр
Как видно из комбинации четыре старших разряда соответствуют информационной комбинации, а три младших — проверочные.
Формирование разрешенной кодовой комбинации неразделимого циклического кода.
Формирование данных комбинаций осуществляется умножением информационной комбинации на порождающий полином:
Biр(x) = Ai(x)?G(x).
Причем умножение можно производить в двоичной форме.
Пример 5, необходимо сформировать кодовую комбинацию неразделимого циклического кода используя данные примера 2, т. е. G(x) = х3+х+1, Ai(x) = 0110, код (7,4).
1. Переводим комбинацию из двоичной формы в полиномиальную:
Ai = 0110? х2+х = Ai(x)
2. Осуществляем деление Ai(x)?G(x)
3. Переводим кодовую комбинацию из полиномиальной форы в двоичную:
Bip(x) = х5+х4+х3+х ? 0111010 = Bip
В этой комбинации невозможно выделить информационную и проверочную части.
Матричное представление систематических кодов
Систематические коды, рассмотренные выше (код Хэмминга и разделимый циклический код) удобно представить в виде матриц. Рассмотрим, как это осуществляется.
Поскольку систематические коды обладают тем свойством, что сумма двух разрешенных комбинаций по модулю два дают также разрешенную комбинацию, то для формирования комбинаций таких кодов используют производящую матрицу Gn,k. С помощью производящей матрицы можно получить любую кодовую комбинацию кода путем суммирования по модулю два строк матрицы в различных комбинациях. Для получения данной матрицы в нее заносятся исходные комбинации, которые полностью определяют систематический код. Исходные комбинации определяются исходя из условий:
1) все исходные комбинации должны быть различны;
2) нулевая комбинация не должна входить в число исходных комбинаций;
3) каждая исходная комбинация должна иметь вес не менее кодового расстояния, т. е. W?d0;
4) между любыми двумя исходными комбинациями расстояние Хэмминга должно быть не меньше кодового расстояния, т. е. dij?d0.
Производящая матрица имеет вид:
Производящая подматрица имеет k строк и n столбцов. Она образована двумя подматрицами: информационной (включает элементы аij) и проверочной (включает элементы bij). Информационная матрица имеет размеры k?k, а проверочная — r?k.
В качестве информационной подматрицы удобно брать единичную матрицу Ekk:
Проверочная подматрица Gr,k строится путем подбора различных r-разрядных комбинаций, удовлетворяющих следующим правилам:
1) в каждой строке подматрицы количество единиц должно быть не менее d0-1;
2) сумма по модулю два двух любых строк должна иметь не менее d0-2 единицы;
Полученная таким образом подматрица Gr,k приписывается справа к подматрице Ekk, в результате чего получается производящая матрица Gn,k. Затем, используя производящую матрицу, можно получить любую комбинацию кода путем суммирования двух и более строк по модулю два в различных комбинациях.
Пример 6. Необходимо построить производящую матрицу кода Хэмминга способного исправлять 1 ошибку и имеющего n=7. Закодировать с помощью полученной матрицы комбинацию Ai=1101.
Определяем кодовое расстояние:
d0=2qи ош+1= 2?1+1=3.
Для кодов с d0=3 количество проверочных разрядов определяется по формуле:
r=log2(n+1)= log28=3.
Определяем разрядность информационной части:
k = n — r = 7 — 4 =3.
Запишем все возможные комбинации проверочной подматрицы: 000, 001, 010, 011, 100, 101, 110, 111. Выберем из этих комбинаций те, что удовлетворяют правилам:
1) в каждой строке не менее d0-1, этому условию соответствуют комбинации 011, 101, 110, 111;
2) сумма двух любых комбинаций по модулю два содержит единиц не менее d0-2:
3) записываем проверочную подматрицу:
4) приписываем полученную подматрицу к единичной и получаем производящую матрицу:
Если произвести определение d0 для исходных комбинаций полученной матрицы (определив расстояние Хэмминга для всех пар комбинаций), то оно окажется равным 3.
Для кодирования заданной комбинации Ai, необходимо просуммировать те строки матрицы G, которые в информационной части имеют единицу на том месте, на котором они находятся в комбинации Аi. Для заданной комбинации 1101 единичными разрядами являются а1, а2, а4. В матрице G единицы на этих местах имеют строки: первая, вторая и четвертая. Просуммировав их получаем разрешенную комбинацию заданного кода.
Сравнивая полученную кодовую комбинацию Bip с комбинацией полученной примере 3, для которой также использована комбинация Ai=1101, видим что они одинаковы.
Для кода Хэмминга выше были определены правила формирования проверочных символов bk:
Эти правила можно отобразить в виде проверочной матрицы Нn,k. Она состоит из n столбцов (соответствует разрядности кодовой комбинации) и r столбцов (соответствует количеству проверочных разрядов кодовой комбинации). В правой части матрицы указываются синдромы, соответствующие ошибкам в проверочных символах, в левой части записываются элементы информационной части комбинации, причем, те элементы, которые участвуют в образовании определенного элемента bi равны единицы, а те которые не участвуют — нулю.
В данном случае обведенные пунктиром проверочные элементы образуют единичную матрицу. Проверочная матрица позволяет определить ошибочный разряд, поскольку каждый столбец данной матрицы представляет собой синдром соответствующего символа. При этом строки матрицы будут соответствовать разрядам синдрома Ck. Например, согласно приведенной проверочной матрице, синдром соответствующий ошибку в разряде а1 имеет вид 011, в разряде а2 — 101, в разряде а3 — 110, в разряде а4 — 111, в разряде b1 — 100, в разряде b2 — 010, в разряде b3 — 001. Также с помощью проверочной матрицы легко определить проверочные и символы и сформировать кодовую комбинацию. Например, необходимо сформировать кодовую комбинацию кода Хэмминга (7,4) соответствующую информационным символам 1101.
В соответствии с проверочной матрицей определяем bi:
b1 = 1 + 0 + 1 = 0; b2 = 1 + 0 + 1=0; b3 = 1 + 1 + 1 = 1.
Добавляем проверочные символы к информационным и получаем кодовую комбинацию:
Biр = 1101001.
Также проверочную матрицу можно построить и другим способом. Для этого сначала строится единичная матрица Еr. К которой слева приписывается подматрица Dk,r. Каждая строка этой подматрицы соответствует столбцу проверочных разрядов подматрицы Сr,k производящей матрицы Gn,k.
Такое преобразование строк матрицы в столбцы называется транспонированием.
В результате получаем
Декодирование циклических кодов
При декодировании таких кодов (разделимых и неразделимых) используется Синдромный способ. Вычисление синдрома осуществляется в три этапа:
1. принятая комбинация Bip’ преобразуется их двоичной формы в полиномиальную (Bip(x));
2. осуществляется деление Bip(x) на порождающий полином G(x) в результате чего определяется синдром ошибки C(x) (остаток от деления);
3. синдром ошибки преобразуется из полиномиальной формы в двоичную;
4. По проверочной матрице или таблице синдромов определяется ошибочный разряд;
5. Ошибочный разряд в Bip’(x) инвертируется;
6. Исправленная комбинация преобразуется из полиномиальной формы в двоичную Bip.
делением принятой кодовой комбинации Biр’(x) на порождающий полином G(x), который заранее известен на приеме. Остаток от деления и является синдромом ошибки С(х).
Мажоритарное декодирование циклических кодов
Мажоритарное декодирование может применятся только для декодирования систематических кодов (кода Хэмминга, циклического разделимого кода). Рассмотрим мажоритарное декодирование на примере циклического кода.
Корректирующие коды «на пальцах»
Время на прочтение
11 мин
Количество просмотров 63K

Как нетрудно догадаться, ко всему этому причастны корректирующие коды. Собственно, ECC так и расшифровывается — «error-correcting code», то есть «код, исправляющий ошибки». А CRC — это один из алгоритмов, обнаруживающих ошибки в данных. Исправить он их не может, но часто это и не требуется.
Давайте же разберёмся, что это такое.
Для понимания статьи не нужны никакие специальные знания. Достаточно лишь понимать, что такое вектор и матрица, как они перемножаются и как с их помощью записать систему линейных уравнений.
Внимание! Много текста и мало картинок. Я постарался всё объяснить, но без карандаша и бумаги текст может показаться немного запутанным.
Каналы с ошибкой
Разберёмся сперва, откуда вообще берутся ошибки, которые мы собираемся исправлять. Перед нами стоит следующая задача. Нужно передать несколько блоков данных, каждый из которых кодируется цепочкой двоичных цифр. Получившаяся последовательность нулей и единиц передаётся через канал связи. Но так сложилось, что реальные каналы связи часто подвержены ошибкам. Вообще говоря, ошибки могут быть разных видов — может появиться лишняя цифра или какая-то пропасть. Но мы будем рассматривать только ситуации, когда в канале возможны лишь замены нуля на единицу и наоборот. Причём опять же для простоты будем считать такие замены равновероятными.
Ошибка — это маловероятное событие (а иначе зачем нам такой канал вообще, где одни ошибки?), а значит, вероятность двух ошибок меньше, а трёх уже совсем мала. Мы можем выбрать для себя некоторую приемлемую величину вероятности, очертив границу «это уж точно невозможно». Это позволит нам сказать, что в канале возможно не более, чем ошибок. Это будет характеристикой канала связи.
Для простоты введём следующие обозначения. Пусть данные, которые мы хотим передавать, — это двоичные последовательности фиксированной длины. Чтобы не запутаться в нулях и единицах, будем иногда обозначать их заглавными латинскими буквами (,
,
, …). Что именно передавать, в общем-то неважно, просто с буквами в первое время будет проще работать.
Кодирование и декодирование будем обозначать прямой стрелкой (), а передачу по каналу связи — волнистой стрелкой (
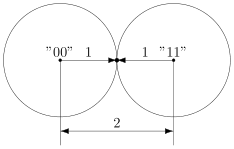
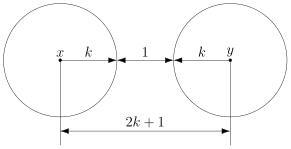
). Ошибки при передаче будем подчёркивать.
Например, пусть мы хотим передавать только сообщения и
. В простейшем случае их можно закодировать нулём и единицей (сюрприз!):
Передача по каналу, в котором возникла ошибка будет записана так:
Цепочки нулей и единиц, которыми мы кодируем буквы, будем называть кодовыми словами. В данном простом случае кодовые слова — это и
.
Код с утроением
Давайте попробуем построить какой-то корректирующий код. Что мы обычно делаем, когда кто-то нас не расслышал? Повторяем дважды:
Правда, это нам не очень поможет. В самом деле, рассмотрим канал с одной возможной ошибкой:
Какие выводы мы можем сделать, когда получили ? Понятно, что раз у нас не две одинаковые цифры, то была ошибка, но вот в каком разряде? Может, в первом, и была передана буква
. А может, во втором, и была передана
.
То есть, получившийся код обнаруживает, но не исправляет ошибки. Ну, тоже неплохо, в общем-то. Но мы пойдём дальше и будем теперь утраивать цифры.
Проверим в деле:
Получили . Тут у нас есть две возможности: либо это
и было две ошибки (в крайних цифрах), либо это
и была одна ошибка. Вообще, вероятность одной ошибки выше вероятности двух ошибок, так что самым правдоподобным будет предположение о том, что передавалась именно буква
. Хотя правдоподобное — не значит истинное, поэтому рядом и стоит вопросительный знак.
Если в канале связи возможна максимум одна ошибка, то первое предположение о двух ошибках становится невозможным и остаётся только один вариант — передавалась буква .
Про такой код говорят, что он исправляет одну ошибку. Две он тоже обнаружит, но исправит уже неверно.
Это, конечно, самый простой код. Кодировать легко, да и декодировать тоже. Ноликов больше — значит передавался ноль, единичек — значит единица.
Если немного подумать, то можно предложить код исправляющий две ошибки. Это будет код, в котором мы повторяем одиночный бит 5 раз.
Расстояния между кодами
Рассмотрим поподробнее код с утроением. Итак, мы получили работающий код, который исправляет одиночную ошибку. Но за всё хорошее надо платить: он кодирует один бит тремя. Не очень-то и эффективно.
И вообще, почему этот код работает? Почему нужно именно утраивать для устранения одной ошибки? Наверняка это всё неспроста.
Давайте подумаем, как этот код работает. Интуитивно всё понятно. Нолики и единички — это две непохожие последовательности. Так как они достаточно длинные, то одиночная ошибка не сильно портит их вид.
Пусть мы передавали , а получили
. Видно, что эта цепочка больше похожа на исходные
, чем на
. А так как других кодовых слов у нас нет, то и выбор очевиден.
Но что значит «больше похоже»? А всё просто! Чем больше символов у двух цепочек совпадает, тем больше их схожесть. Если почти все символы отличаются, то цепочки «далеки» друг от друга.
Можно ввести некоторую величину , равную количеству различающихся цифр в соответствующих разрядах цепочек
и
. Эту величину называют расстоянием Хэмминга. Чем больше это расстояние, тем меньше похожи две цепочки.
Например, , так как все цифры в соответствующих позициях равны, а вот
.
Расстояние Хэмминга называют расстоянием неспроста. Ведь в самом деле, что такое расстояние? Это какая-то характеристика, указывающая на близость двух точек, и для которой верны утверждения:
- Расстояние между точками неотрицательно и равно нулю только, если точки совпадают.
- Расстояние в обе стороны одинаково.
- Путь через третью точку не короче, чем прямой путь.
Достаточно разумные требования.
Математически это можно записать так (нам это не пригодится, просто ради интереса посмотрим):
.
Предлагаю читателю самому убедиться, что для расстояния Хэмминга эти свойства выполняются.
Окрестности
Таким образом, разные цепочки мы считаем точками в каком-то воображаемом пространстве, и теперь мы умеем находить расстояния между ними. Правда, если попытаться сколько нибудь длинные цепочки расставить на листе бумаги так, чтобы расстояния Хэмминга совпадали с расстояниями на плоскости, мы можем потерпеть неудачу. Но не нужно переживать. Всё же это особое пространство со своими законами. А слова вроде «расстояния» лишь помогают нам рассуждать.
Пойдём дальше. Раз мы заговорили о расстоянии, то можно ввести такое понятие как окрестность. Как известно, окрестность какой-то точки — это шар определённого радиуса с центром в ней. Шар? Какие ещё шары! Мы же о кодах говорим.
Но всё просто. Ведь что такое шар? Это множество всех точек, которые находятся от данной не дальше, чем некоторое расстояние, называемое радиусом. Точки у нас есть, расстояние у нас есть, теперь есть и шары.
Так, скажем, окрестность кодового слова радиуса 1 — это все коды, находящиеся на расстоянии не больше, чем 1 от него, то есть отличающиеся не больше, чем в одном разряде. То есть это коды:
Да, вот так странно выглядят шары в пространстве кодов.
А теперь посмотрите. Это же все возможные коды, которые мы получим в канале в одной ошибкой, если отправим ! Это следует прямо из определения окрестности. Ведь каждая ошибка заставляет цепочку измениться только в одном разряде, а значит удаляет её на расстояние 1 от исходного сообщения.
Аналогично, если в канале возможны две ошибки, то отправив некоторое сообщение , мы получим один из кодов, который принадлежит окрестности
радиусом 2.
Тогда всю нашу систему декодирования можно построить так. Мы получаем какую-то цепочку нулей и единиц (точку в нашей новой терминологии) и смотрим, в окрестность какого кодового слова она попадает.
Сколько ошибок может исправить код?
Чтобы код мог исправлять больше ошибок, окрестности должны быть как можно шире. С другой стороны, они не должны пересекаться. Иначе если точка попадёт в область пересечения, непонятно будет, к какой окрестности её отнести.
В коде с удвоением между кодовыми словами и
расстояние равно 2 (оба разряда различаются). А значит, если мы построим вокруг них шары радиуса 1, то они будут касаться. Это значит, точка касания будет принадлежать обоим шарам и непонятно будет, к какому из них её отнести.
Именно это мы и получали. Мы видели, что есть ошибка, но не могли её исправить.
Что интересно, точек касания в нашем странном пространстве у шаров две — это коды и
. Расстояния от них до центров равны единице. Конечно же, в обычно геометрии такое невозможно, поэтому рисунки — это просто условность для более удобного рассуждения.
В случае кода с утроением, между шарами будет зазор.
Минимальный зазор между шарами равен 1, так как у нас расстояния всегда целые (ну не могут же две цепочки отличаться в полутора разрядах).
В общем случае получаем следующее.
Этот очевидный результат на самом деле очень важен. Он означает, что код с минимальным кодовым расстоянием будет успешно работать в канале с
ошибками, если выполняется соотношение
Полученное равенство позволяет легко определить, сколько ошибок будет исправлять тот или иной код. А сколько код ошибок может обнаружить? Рассуждения такие же. Код обнаруживает ошибок, если в результате не получится другое кодовое слово. То есть, кодовые слова не должны находиться в окрестностях радиуса
других кодовых слов. Математически это записывается так:
Рассмотрим пример. Пусть мы кодируем 4 буквы следующим образом.
Чтобы найти минимальное расстояние между различными кодовыми словами, построим таблицу попарных расстояний.
| A | B | C | D | |
|---|---|---|---|---|
| A | — | 3 | 3 | 4 |
| B | 3 | — | 4 | 3 |
| C | 3 | 4 | — | 3 |
| D | 4 | 3 | 3 | — |
Минимальное расстояние , а значит
, откуда получаем, что такой код может исправить до
ошибок. Обнаруживает же он две ошибки.
Рассмотрим пример:
Чтобы декодировать полученное сообщение, посмотрим, к какому символу оно ближе всего.
Минимальное расстояние получилось для символа , значит вероятнее всего передавался именно он:
Итак, этот код исправляет одну ошибку, как и код с утроением. Но он более эффективен, так как в отличие от кода с утроением здесь кодируется уже 4 символа.
Таким образом, основная проблема при построении такого рода кодов — так расположить кодовые слова, чтобы они были как можно дальше друг от друга, и их было побольше.
Для декодирования можно было бы использовать таблицу, в которой указывались бы все возможные принимаемые сообщения, и кодовые слова, которым они соответствуют. Но такая таблица получилась бы очень большой. Даже для нашего маленького кода, который выдаёт 5 двоичных цифр, получилось бы варианта возможных принимаемых сообщений. Для более сложных кодов таблица будет значительно больше.
Попробуем придумать способ коррекции сообщения без таблиц. Мы всегда сможем найти полезное применение освободившейся памяти.
Интерлюдия: поле GF(2)
Для изложения дальнейшего материала нам потребуются матрицы. А при умножении матриц, как известно мы складываем и перемножаем числа. И тут есть проблема. Если с умножением всё более-менее хорошо, то как быть со сложением? Из-за того, что мы работаем только с одиночными двоичными цифрами, непонятно, как сложить 1 и 1, чтобы снова получилась одна двоичная цифра. Значит вместо классического сложения нужно использовать какое-то другое.
Введём операцию сложения как сложение по модулю 2 (хорошо известный программистам XOR):
Умножение будем выполнять как обычно. Эти операции на самом деле введены не абы как, а чтобы получилась система, которая в математике называется полем. Поле — это просто множество (в нашем случае из 0 и 1), на котором так определены сложение и умножение, чтобы основные алгебраические законы сохранялись. Например, чтобы основные идеи, касающиеся матриц и систем уравнений по-прежнему были верны. А вычитание и деление мы можем ввести как обратные операции.
Множество из двух элементов с операциями, введёнными так, как мы это сделали, называется полем Галуа GF(2). GF — это Galois field, а 2 — количество элементов.
У сложения есть несколько очень полезных свойств, которыми мы будем пользоваться в дальнейшем.
Это свойство прямо следует из определения.
А в этом можно убедиться, прибавив к обеим частям равенства. Это свойство, в частности означает, что мы можем переносить в уравнении слагаемые в другую сторону без смены знака.
Проверяем корректность
Вернёмся к коду с утроением.
Для начала просто решим задачу проверки, были ли вообще ошибки при передаче. Как видно, из самого кода, принятое сообщение будет кодовым словом только тогда, когда все три цифры равны между собой.
Пусть мы приняли вектор-строку из трёх цифр. (Стрелочки над векторами рисовать не будем, так как у нас почти всё — это вектора или матрицы.)
Математически равенство всех трёх цифр можно записать как систему:
Или, если воспользоваться свойствами сложения в GF(2), получаем
Или
В матричном виде эта система будет иметь вид
где
Транспонирование здесь нужно потому, что — это вектор-строка, а не вектор-столбец. Иначе мы не могли бы умножать его справа на матрицу.
Будем называть матрицу проверочной матрицей. Если полученное сообщение — это корректное кодовое слово (то есть, ошибки при передаче не было), то произведение проверочной матрицы на это сообщение будет равно нулевому вектору.
Умножение на матрицу — это гораздо более эффективно, чем поиск в таблице, но у нас на самом деле есть ещё одна таблица — это таблица кодирования. Попробуем от неё избавиться.
Кодирование
Итак, у нас есть система для проверки
Её решения — это кодовые слова. Собственно, мы систему и строили на основе кодовых слов. Попробуем теперь решить обратную задачу. По системе (или, что то же самое, по матрице ) найдём кодовые слова.
Правда, для нашей системы мы уже знаем ответ, поэтому, чтобы было интересно, возьмём другую матрицу:
Соответствующая система имеет вид:
Чтобы найти кодовые слова соответствующего кода нужно её решить.
В силу линейности сумма двух решений системы тоже будет решением системы. Это легко доказать. Если и
— решения системы, то для их суммы верно
что означает, что она тоже — решение.
Поэтому если мы найдём все линейно независимые решения, то с их помощью можно получить вообще все решения системы. Для этого просто нужно найти их всевозможные суммы.
Выразим сперва все зависимые слагаемые. Их столько же, сколько и уравнений. Выражать надо так, чтобы справа были только независимые. Проще всего выразить .
Если бы нам не так повезло с системой, то нужно было бы складывая уравнения между собой получить такую систему, чтобы какие-то три переменные встречались по одному разу. Ну, или воспользоваться методом Гаусса. Для GF(2) он тоже работает.
Итак, получаем:
Чтобы получить все линейно независимые решения, приравниваем каждую из зависимых переменных к единице по очереди.
Всевозможные суммы этих независимых решений (а именно они и будут кодовыми векторами) можно получить так:
где равны либо нулю или единице. Так как таких коэффициентов два, то всего возможно
сочетания.
Но посмотрите! Формула, которую мы только что получили — это же снова умножение матрицы на вектор.
Строчки здесь — линейно независимые решения, которые мы получили. Матрица называется порождающей. Теперь вместо того, чтобы сами составлять таблицу кодирования, мы можем получать кодовые слова простым умножением на матрицу:
Найдём кодовые слова для этого кода. (Не забываем, что длина исходных сообщений должна быть равна 2 — это количество найденных решений.)
Итак, у нас есть готовый код, обнаруживающий ошибки. Проверим его в деле. Пусть мы хотим отправить 01 и у нас произошла ошибка при передаче. Обнаружит ли её код?
А раз в результате не нулевой вектор, значит код заподозрил неладное. Провести его не удалось. Ура, код работает!
Для кода с утроением, кстати, порождающая матрица выглядит очень просто:
Подобные коды, которые можно порождать и проверять матрицей называются линейными (бывают и нелинейные), и они очень широко применяются на практике. Реализовать их довольно легко, так как тут требуется только умножение на константную матрицу.
Ошибка по синдрому
Ну хорошо, мы построили код обнаруживающий ошибки. Но мы же хотим их исправлять!
Для начала введём такое понятие, как вектор ошибки. Это вектор, на который отличается принятое сообщение от кодового слова. Пусть мы получили сообщение , а было отправлено кодовое слово
. Тогда вектор ошибки по определению
Но в странном мире GF(2), где сложение и вычитание одинаковы, будут верны и соотношения:
В силу особенностей сложения, как читатель сам может легко убедиться, в векторе ошибки на позициях, где произошла ошибка будет единица, а на остальных ноль.
Как мы уже говорили раньше, если мы получили сообщение с ошибкой, то
. Но ведь векторов, не равных нулю много! Быть может то, какой именно ненулевой вектор мы получили, подскажет нам характер ошибки?
Назовём результат умножения на проверочную матрицу синдромом:
И заметим следующее
Это означает, что для ошибки синдром будет таким же, как и для полученного сообщения.
Разложим все возможные сообщения, которые мы можем получить из канала связи, по кучкам в зависимости от синдрома. Тогда из последнего соотношения следует, что в каждой кучке будут вектора с одной и той же ошибкой. Причём вектор этой ошибки тоже будет в кучке. Вот только как его узнать?
А очень просто! Помните, мы говорили, что у нескольких ошибок вероятность ниже, чем у одной ошибки? Руководствуясь этим соображением, наиболее правдоподобным будет считать вектором ошибки тот вектор, у которого меньше всего единиц. Будем называть его лидером.
Давайте посмотрим, какие синдромы дают всевозможные 5-элементные векторы. Сразу сгруппируем их и подчеркнём лидеров — векторы с наименьшим числом единиц.
В принципе, для корректирования ошибки достаточно было бы хранить таблицу соответствия синдрома лидеру.
Обратите внимание, что в некоторых строчках два лидера. Это значит для для данного синдрома два паттерна ошибки равновероятны. Иными словами, код обнаружил две ошибки, но исправить их не может.
Лидеры для всех возможных одиночных ошибок находятся в отдельных строках, а значит код может исправить любую одиночную ошибку. Ну, что же… Попробуем в этом убедиться.
Вектор ошибки равен , а значит ошибка в третьем разряде. Как мы и загадали.
Ура, всё работает!
Что же дальше?
Чтобы попрактиковаться, попробуйте повторить рассуждения для разных проверочных матриц. Например, для кода с утроением.
Логическим продолжением изложенного был бы рассказ о циклических кодах — чрезвычайно интересном подклассе линейных кодов, обладающим замечательными свойствами. Но тогда, боюсь, статья уж очень бы разрослась.
Если вас заинтересовали подробности, то можете почитать замечательную книжку Аршинова и Садовского «Коды и математика». Там изложено гораздо больше, чем представлено в этой статье. Если интересует математика кодирования — то поищите «Теория и практика кодов, контролирующих ошибки» Блейхута. А вообще, материалов по этой теме довольно много.
Надеюсь, когда снова будет свободное время, напишу продолжение, в котором расскажу про циклические коды и покажу пример программы для кодирования и декодирования. Если, конечно, почтенной публике это интересно.