«Interleaver» redirects here. For the fiber-optic device, see optical interleaver.
In computing, telecommunication, information theory, and coding theory, forward error correction (FEC) or channel coding[1][2][3] is a technique used for controlling errors in data transmission over unreliable or noisy communication channels.
The central idea is that the sender encodes the message in a redundant way, most often by using an error correction code or error correcting code, (ECC).[4][5] The redundancy allows the receiver not only to detect errors that may occur anywhere in the message, but often to correct a limited number of errors. Therefore a reverse channel to request re-transmission may not be needed. The cost is a fixed, higher forward channel bandwidth.
The American mathematician Richard Hamming pioneered this field in the 1940s and invented the first error-correcting code in 1950: the Hamming (7,4) code.[5]
FEC can be applied in situations where re-transmissions are costly or impossible, such as one-way communication links or when transmitting to multiple receivers in multicast.
Long-latency connections also benefit; in the case of a satellite orbiting Uranus, retransmission due to errors can create a delay of five hours. FEC is widely used in modems and in cellular networks, as well.
FEC processing in a receiver may be applied to a digital bit stream or in the demodulation of a digitally modulated carrier. For the latter, FEC is an integral part of the initial analog-to-digital conversion in the receiver. The Viterbi decoder implements a soft-decision algorithm to demodulate digital data from an analog signal corrupted by noise. Many FEC decoders can also generate a bit-error rate (BER) signal which can be used as feedback to fine-tune the analog receiving electronics.
FEC information is added to mass storage (magnetic, optical and solid state/flash based) devices to enable recovery of corrupted data, and is used as ECC computer memory on systems that require special provisions for reliability.
The maximum proportion of errors or missing bits that can be corrected is determined by the design of the ECC, so different forward error correcting codes are suitable for different conditions. In general, a stronger code induces more redundancy that needs to be transmitted using the available bandwidth, which reduces the effective bit-rate while improving the received effective signal-to-noise ratio. The noisy-channel coding theorem of Claude Shannon can be used to compute the maximum achievable communication bandwidth for a given maximum acceptable error probability. This establishes bounds on the theoretical maximum information transfer rate of a channel with some given base noise level. However, the proof is not constructive, and hence gives no insight of how to build a capacity achieving code. After years of research, some advanced FEC systems like polar code[3] come very close to the theoretical maximum given by the Shannon channel capacity under the hypothesis of an infinite length frame.
How it works[edit]
ECC is accomplished by adding redundancy to the transmitted information using an algorithm. A redundant bit may be a complicated function of many original information bits. The original information may or may not appear literally in the encoded output; codes that include the unmodified input in the output are systematic, while those that do not are non-systematic.
A simplistic example of ECC is to transmit each data bit 3 times, which is known as a (3,1) repetition code. Through a noisy channel, a receiver might see 8 versions of the output, see table below.
| Triplet received | Interpreted as |
|---|---|
| 000 | 0 (error-free) |
| 001 | 0 |
| 010 | 0 |
| 100 | 0 |
| 111 | 1 (error-free) |
| 110 | 1 |
| 101 | 1 |
| 011 | 1 |
This allows an error in any one of the three samples to be corrected by «majority vote», or «democratic voting». The correcting ability of this ECC is:
- Up to 1 bit of triplet in error, or
- up to 2 bits of triplet omitted (cases not shown in table).
Though simple to implement and widely used, this triple modular redundancy is a relatively inefficient ECC. Better ECC codes typically examine the last several tens or even the last several hundreds of previously received bits to determine how to decode the current small handful of bits (typically in groups of 2 to 8 bits).
Averaging noise to reduce errors[edit]
ECC could be said to work by «averaging noise»; since each data bit affects many transmitted symbols, the corruption of some symbols by noise usually allows the original user data to be extracted from the other, uncorrupted received symbols that also depend on the same user data.
- Because of this «risk-pooling» effect, digital communication systems that use ECC tend to work well above a certain minimum signal-to-noise ratio and not at all below it.
- This all-or-nothing tendency – the cliff effect – becomes more pronounced as stronger codes are used that more closely approach the theoretical Shannon limit.
- Interleaving ECC coded data can reduce the all or nothing properties of transmitted ECC codes when the channel errors tend to occur in bursts. However, this method has limits; it is best used on narrowband data.
Most telecommunication systems use a fixed channel code designed to tolerate the expected worst-case bit error rate, and then fail to work at all if the bit error rate is ever worse.
However, some systems adapt to the given channel error conditions: some instances of hybrid automatic repeat-request use a fixed ECC method as long as the ECC can handle the error rate, then switch to ARQ when the error rate gets too high;
adaptive modulation and coding uses a variety of ECC rates, adding more error-correction bits per packet when there are higher error rates in the channel, or taking them out when they are not needed.
Types of ECC[edit]
A block code (specifically a Hamming code) where redundant bits are added as a block to the end of the initial message
A continuous code convolutional code where redundant bits are added continuously into the structure of the code word
The two main categories of ECC codes are block codes and convolutional codes.
- Block codes work on fixed-size blocks (packets) of bits or symbols of predetermined size. Practical block codes can generally be hard-decoded in polynomial time to their block length.
- Convolutional codes work on bit or symbol streams of arbitrary length. They are most often soft decoded with the Viterbi algorithm, though other algorithms are sometimes used. Viterbi decoding allows asymptotically optimal decoding efficiency with increasing constraint length of the convolutional code, but at the expense of exponentially increasing complexity. A convolutional code that is terminated is also a ‘block code’ in that it encodes a block of input data, but the block size of a convolutional code is generally arbitrary, while block codes have a fixed size dictated by their algebraic characteristics. Types of termination for convolutional codes include «tail-biting» and «bit-flushing».
There are many types of block codes; Reed–Solomon coding is noteworthy for its widespread use in compact discs, DVDs, and hard disk drives. Other examples of classical block codes include Golay, BCH, Multidimensional parity, and Hamming codes.
Hamming ECC is commonly used to correct NAND flash memory errors.[6]
This provides single-bit error correction and 2-bit error detection.
Hamming codes are only suitable for more reliable single-level cell (SLC) NAND.
Denser multi-level cell (MLC) NAND may use multi-bit correcting ECC such as BCH or Reed–Solomon.[7][8] NOR Flash typically does not use any error correction.[7]
Classical block codes are usually decoded using hard-decision algorithms,[9] which means that for every input and output signal a hard decision is made whether it corresponds to a one or a zero bit. In contrast, convolutional codes are typically decoded using soft-decision algorithms like the Viterbi, MAP or BCJR algorithms, which process (discretized) analog signals, and which allow for much higher error-correction performance than hard-decision decoding.
Nearly all classical block codes apply the algebraic properties of finite fields. Hence classical block codes are often referred to as algebraic codes.
In contrast to classical block codes that often specify an error-detecting or error-correcting ability, many modern block codes such as LDPC codes lack such guarantees. Instead, modern codes are evaluated in terms of their bit error rates.
Most forward error correction codes correct only bit-flips, but not bit-insertions or bit-deletions.
In this setting, the Hamming distance is the appropriate way to measure the bit error rate.
A few forward error correction codes are designed to correct bit-insertions and bit-deletions, such as Marker Codes and Watermark Codes.
The Levenshtein distance is a more appropriate way to measure the bit error rate when using such codes.
[10]
Code-rate and the tradeoff between reliability and data rate[edit]
The fundamental principle of ECC is to add redundant bits in order to help the decoder to find out the true message that was encoded by the transmitter. The code-rate of a given ECC system is defined as the ratio between the number of information bits and the total number of bits (i.e., information plus redundancy bits) in a given communication package. The code-rate is hence a real number. A low code-rate close to zero implies a strong code that uses many redundant bits to achieve a good performance, while a large code-rate close to 1 implies a weak code.
The redundant bits that protect the information have to be transferred using the same communication resources that they are trying to protect. This causes a fundamental tradeoff between reliability and data rate.[11] In one extreme, a strong code (with low code-rate) can induce an important increase in the receiver SNR (signal-to-noise-ratio) decreasing the bit error rate, at the cost of reducing the effective data rate. On the other extreme, not using any ECC (i.e., a code-rate equal to 1) uses the full channel for information transfer purposes, at the cost of leaving the bits without any additional protection.
One interesting question is the following: how efficient in terms of information transfer can an ECC be that has a negligible decoding error rate? This question was answered by Claude Shannon with his second theorem, which says that the channel capacity is the maximum bit rate achievable by any ECC whose error rate tends to zero:[12] His proof relies on Gaussian random coding, which is not suitable to real-world applications. The upper bound given by Shannon’s work inspired a long journey in designing ECCs that can come close to the ultimate performance boundary. Various codes today can attain almost the Shannon limit. However, capacity achieving ECCs are usually extremely complex to implement.
The most popular ECCs have a trade-off between performance and computational complexity. Usually, their parameters give a range of possible code rates, which can be optimized depending on the scenario. Usually, this optimization is done in order to achieve a low decoding error probability while minimizing the impact to the data rate. Another criterion for optimizing the code rate is to balance low error rate and retransmissions number in order to the energy cost of the communication.[13]
Concatenated ECC codes for improved performance[edit]
Classical (algebraic) block codes and convolutional codes are frequently combined in concatenated coding schemes in which a short constraint-length Viterbi-decoded convolutional code does most of the work and a block code (usually Reed–Solomon) with larger symbol size and block length «mops up» any errors made by the convolutional decoder. Single pass decoding with this family of error correction codes can yield very low error rates, but for long range transmission conditions (like deep space) iterative decoding is recommended.
Concatenated codes have been standard practice in satellite and deep space communications since Voyager 2 first used the technique in its 1986 encounter with Uranus. The Galileo craft used iterative concatenated codes to compensate for the very high error rate conditions caused by having a failed antenna.
Low-density parity-check (LDPC)[edit]
Low-density parity-check (LDPC) codes are a class of highly efficient linear block
codes made from many single parity check (SPC) codes. They can provide performance very close to the channel capacity (the theoretical maximum) using an iterated soft-decision decoding approach, at linear time complexity in terms of their block length. Practical implementations rely heavily on decoding the constituent SPC codes in parallel.
LDPC codes were first introduced by Robert G. Gallager in his PhD thesis in 1960,
but due to the computational effort in implementing encoder and decoder and the introduction of Reed–Solomon codes,
they were mostly ignored until the 1990s.
LDPC codes are now used in many recent high-speed communication standards, such as DVB-S2 (Digital Video Broadcasting – Satellite – Second Generation), WiMAX (IEEE 802.16e standard for microwave communications), High-Speed Wireless LAN (IEEE 802.11n),[14] 10GBase-T Ethernet (802.3an) and G.hn/G.9960 (ITU-T Standard for networking over power lines, phone lines and coaxial cable). Other LDPC codes are standardized for wireless communication standards within 3GPP MBMS (see fountain codes).
Turbo codes[edit]
Turbo coding is an iterated soft-decoding scheme that combines two or more relatively simple convolutional codes and an interleaver to produce a block code that can perform to within a fraction of a decibel of the Shannon limit. Predating LDPC codes in terms of practical application, they now provide similar performance.
One of the earliest commercial applications of turbo coding was the CDMA2000 1x (TIA IS-2000) digital cellular technology developed by Qualcomm and sold by Verizon Wireless, Sprint, and other carriers. It is also used for the evolution of CDMA2000 1x specifically for Internet access, 1xEV-DO (TIA IS-856). Like 1x, EV-DO was developed by Qualcomm, and is sold by Verizon Wireless, Sprint, and other carriers (Verizon’s marketing name for 1xEV-DO is Broadband Access, Sprint’s consumer and business marketing names for 1xEV-DO are Power Vision and Mobile Broadband, respectively).
Local decoding and testing of codes[edit]
Sometimes it is only necessary to decode single bits of the message, or to check whether a given signal is a codeword, and do so without looking at the entire signal. This can make sense in a streaming setting, where codewords are too large to be classically decoded fast enough and where only a few bits of the message are of interest for now. Also such codes have become an important tool in computational complexity theory, e.g., for the design of probabilistically checkable proofs.
Locally decodable codes are error-correcting codes for which single bits of the message can be probabilistically recovered by only looking at a small (say constant) number of positions of a codeword, even after the codeword has been corrupted at some constant fraction of positions. Locally testable codes are error-correcting codes for which it can be checked probabilistically whether a signal is close to a codeword by only looking at a small number of positions of the signal.
Interleaving[edit]
«Interleaver» redirects here. For the fiber-optic device, see optical interleaver.
A short illustration of interleaving idea
Interleaving is frequently used in digital communication and storage systems to improve the performance of forward error correcting codes. Many communication channels are not memoryless: errors typically occur in bursts rather than independently. If the number of errors within a code word exceeds the error-correcting code’s capability, it fails to recover the original code word. Interleaving alleviates this problem by shuffling source symbols across several code words, thereby creating a more uniform distribution of errors.[15] Therefore, interleaving is widely used for burst error-correction.
The analysis of modern iterated codes, like turbo codes and LDPC codes, typically assumes an independent distribution of errors.[16] Systems using LDPC codes therefore typically employ additional interleaving across the symbols within a code word.[17]
For turbo codes, an interleaver is an integral component and its proper design is crucial for good performance.[15][18] The iterative decoding algorithm works best when there are not short cycles in the factor graph that represents the decoder; the interleaver is chosen to avoid short cycles.
Interleaver designs include:
- rectangular (or uniform) interleavers (similar to the method using skip factors described above)
- convolutional interleavers
- random interleavers (where the interleaver is a known random permutation)
- S-random interleaver (where the interleaver is a known random permutation with the constraint that no input symbols within distance S appear within a distance of S in the output).[19]
- a contention-free quadratic permutation polynomial (QPP).[20] An example of use is in the 3GPP Long Term Evolution mobile telecommunication standard.[21]
In multi-carrier communication systems, interleaving across carriers may be employed to provide frequency diversity, e.g., to mitigate frequency-selective fading or narrowband interference.[22]
Example[edit]
Transmission without interleaving:
Error-free message: aaaabbbbccccddddeeeeffffgggg Transmission with a burst error: aaaabbbbccc____deeeeffffgggg
Here, each group of the same letter represents a 4-bit one-bit error-correcting codeword. The codeword cccc is altered in one bit and can be corrected, but the codeword dddd is altered in three bits, so either it cannot be decoded at all or it might be decoded incorrectly.
With interleaving:
Error-free code words: aaaabbbbccccddddeeeeffffgggg Interleaved: abcdefgabcdefgabcdefgabcdefg Transmission with a burst error: abcdefgabcd____bcdefgabcdefg Received code words after deinterleaving: aa_abbbbccccdddde_eef_ffg_gg
In each of the codewords «aaaa», «eeee», «ffff», and «gggg», only one bit is altered, so one-bit error-correcting code will decode everything correctly.
Transmission without interleaving:
Original transmitted sentence: ThisIsAnExampleOfInterleaving Received sentence with a burst error: ThisIs______pleOfInterleaving
The term «AnExample» ends up mostly unintelligible and difficult to correct.
With interleaving:
Transmitted sentence: ThisIsAnExampleOfInterleaving... Error-free transmission: TIEpfeaghsxlIrv.iAaenli.snmOten. Received sentence with a burst error: TIEpfe______Irv.iAaenli.snmOten. Received sentence after deinterleaving: T_isI_AnE_amp_eOfInterle_vin_...
No word is completely lost and the missing letters can be recovered with minimal guesswork.
Disadvantages of interleaving[edit]
Use of interleaving techniques increases total delay. This is because the entire interleaved block must be received before the packets can be decoded.[23] Also interleavers hide the structure of errors; without an interleaver, more advanced decoding algorithms can take advantage of the error structure and achieve more reliable communication than a simpler decoder combined with an interleaver[citation needed]. An example of such an algorithm is based on neural network[24] structures.
Software for error-correcting codes[edit]
Simulating the behaviour of error-correcting codes (ECCs) in software is a common practice to design, validate and improve ECCs. The upcoming wireless 5G standard raises a new range of applications for the software ECCs: the Cloud Radio Access Networks (C-RAN) in a Software-defined radio (SDR) context. The idea is to directly use software ECCs in the communications. For instance in the 5G, the software ECCs could be located in the cloud and the antennas connected to this computing resources: improving this way the flexibility of the communication network and eventually increasing the energy efficiency of the system.
In this context, there are various available Open-source software listed below (non exhaustive).
- AFF3CT(A Fast Forward Error Correction Toolbox): a full communication chain in C++ (many supported codes like Turbo, LDPC, Polar codes, etc.), very fast and specialized on channel coding (can be used as a program for simulations or as a library for the SDR).
- IT++: a C++ library of classes and functions for linear algebra, numerical optimization, signal processing, communications, and statistics.
- OpenAir: implementation (in C) of the 3GPP specifications concerning the Evolved Packet Core Networks.
List of error-correcting codes[edit]
| Distance | Code |
|---|---|
| 2 (single-error detecting) | Parity |
| 3 (single-error correcting) | Triple modular redundancy |
| 3 (single-error correcting) | perfect Hamming such as Hamming(7,4) |
| 4 (SECDED) | Extended Hamming |
| 5 (double-error correcting) | |
| 6 (double-error correct-/triple error detect) | Nordstrom-Robinson code |
| 7 (three-error correcting) | perfect binary Golay code |
| 8 (TECFED) | extended binary Golay code |
- AN codes
- Algebraic geometry code
- BCH code, which can be designed to correct any arbitrary number of errors per code block.
- Barker code used for radar, telemetry, ultra sound, Wifi, DSSS mobile phone networks, GPS etc.
- Berger code
- Constant-weight code
- Convolutional code
- Expander codes
- Group codes
- Golay codes, of which the Binary Golay code is of practical interest
- Goppa code, used in the McEliece cryptosystem
- Hadamard code
- Hagelbarger code
- Hamming code
- Latin square based code for non-white noise (prevalent for example in broadband over powerlines)
- Lexicographic code
- Linear Network Coding, a type of erasure correcting code across networks instead of point-to-point links
- Long code
- Low-density parity-check code, also known as Gallager code, as the archetype for sparse graph codes
- LT code, which is a near-optimal rateless erasure correcting code (Fountain code)
- m of n codes
- Nordstrom-Robinson code, used in Geometry and Group Theory[25]
- Online code, a near-optimal rateless erasure correcting code
- Polar code (coding theory)
- Raptor code, a near-optimal rateless erasure correcting code
- Reed–Solomon error correction
- Reed–Muller code
- Repeat-accumulate code
- Repetition codes, such as Triple modular redundancy
- Spinal code, a rateless, nonlinear code based on pseudo-random hash functions[26]
- Tornado code, a near-optimal erasure correcting code, and the precursor to Fountain codes
- Turbo code
- Walsh–Hadamard code
- Cyclic redundancy checks (CRCs) can correct 1-bit errors for messages at most
bits long for optimal generator polynomials of degree
, see Mathematics of cyclic redundancy checks#Bitfilters
See also[edit]
- Code rate
- Erasure codes
- Soft-decision decoder
- Burst error-correcting code
- Error detection and correction
- Error-correcting codes with feedback
- Linear code
- Quantum error correction
References[edit]
- ^ Charles Wang; Dean Sklar; Diana Johnson (Winter 2001–2002). «Forward Error-Correction Coding». Crosslink. The Aerospace Corporation. 3 (1). Archived from the original on 14 March 2012. Retrieved 5 March 2006.
- ^ Charles Wang; Dean Sklar; Diana Johnson (Winter 2001–2002). «Forward Error-Correction Coding». Crosslink. The Aerospace Corporation. 3 (1). Archived from the original on 14 March 2012. Retrieved 5 March 2006.
How Forward Error-Correcting Codes Work]
- ^ a b Maunder, Robert (2016). «Overview of Channel Coding».
- ^ Glover, Neal; Dudley, Trent (1990). Practical Error Correction Design For Engineers (Revision 1.1, 2nd ed.). CO, USA: Cirrus Logic. ISBN 0-927239-00-0.
- ^ a b Hamming, Richard Wesley (April 1950). «Error Detecting and Error Correcting Codes». Bell System Technical Journal. USA: AT&T. 29 (2): 147–160. doi:10.1002/j.1538-7305.1950.tb00463.x. S2CID 61141773.
- ^ «Hamming codes for NAND flash memory devices» Archived 21 August 2016 at the Wayback Machine. EE Times-Asia. Apparently based on «Micron Technical Note TN-29-08: Hamming Codes for NAND Flash Memory Devices». 2005. Both say: «The Hamming algorithm is an industry-accepted method for error detection and correction in many SLC NAND flash-based applications.»
- ^ a b «What Types of ECC Should Be Used on Flash Memory?» (Application note). Spansion. 2011.
Both Reed–Solomon algorithm and BCH algorithm are common ECC choices for MLC NAND flash. … Hamming based block codes are the most commonly used ECC for SLC…. both Reed–Solomon and BCH are able to handle multiple errors and are widely used on MLC flash.
- ^ Jim Cooke (August 2007). «The Inconvenient Truths of NAND Flash Memory» (PDF). p. 28.
For SLC, a code with a correction threshold of 1 is sufficient. t=4 required … for MLC.
- ^ Baldi, M.; Chiaraluce, F. (2008). «A Simple Scheme for Belief Propagation Decoding of BCH and RS Codes in Multimedia Transmissions». International Journal of Digital Multimedia Broadcasting. 2008: 1–12. doi:10.1155/2008/957846.
- ^ Shah, Gaurav; Molina, Andres; Blaze, Matt (2006). «Keyboards and covert channels». USENIX. Retrieved 20 December 2018.
- ^ Tse, David; Viswanath, Pramod (2005), Fundamentals of Wireless Communication, Cambridge University Press, UK
- ^ Shannon, C. E. (1948). «A mathematical theory of communication» (PDF). Bell System Technical Journal. 27 (3–4): 379–423 & 623–656. doi:10.1002/j.1538-7305.1948.tb01338.x. hdl:11858/00-001M-0000-002C-4314-2.
- ^ Rosas, F.; Brante, G.; Souza, R. D.; Oberli, C. (2014). «Optimizing the code rate for achieving energy-efficient wireless communications». Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC). pp. 775–780. doi:10.1109/WCNC.2014.6952166. ISBN 978-1-4799-3083-8.
- ^ IEEE Standard, section 20.3.11.6 «802.11n-2009» Archived 3 February 2013 at the Wayback Machine, IEEE, 29 October 2009, accessed 21 March 2011.
- ^ a b Vucetic, B.; Yuan, J. (2000). Turbo codes: principles and applications. Springer Verlag. ISBN 978-0-7923-7868-6.
- ^ Luby, Michael; Mitzenmacher, M.; Shokrollahi, A.; Spielman, D.; Stemann, V. (1997). «Practical Loss-Resilient Codes». Proc. 29th Annual Association for Computing Machinery (ACM) Symposium on Theory of Computation.
- ^ «Digital Video Broadcast (DVB); Second generation framing structure, channel coding and modulation systems for Broadcasting, Interactive Services, News Gathering and other satellite broadband applications (DVB-S2)». En 302 307. ETSI (V1.2.1). April 2009.
- ^ Andrews, K. S.; Divsalar, D.; Dolinar, S.; Hamkins, J.; Jones, C. R.; Pollara, F. (November 2007). «The Development of Turbo and LDPC Codes for Deep-Space Applications». Proceedings of the IEEE. 95 (11): 2142–2156. doi:10.1109/JPROC.2007.905132. S2CID 9289140.
- ^ Dolinar, S.; Divsalar, D. (15 August 1995). «Weight Distributions for Turbo Codes Using Random and Nonrandom Permutations». TDA Progress Report. 122: 42–122. Bibcode:1995TDAPR.122…56D. CiteSeerX 10.1.1.105.6640.
- ^ Takeshita, Oscar (2006). «Permutation Polynomial Interleavers: An Algebraic-Geometric Perspective». IEEE Transactions on Information Theory. 53 (6): 2116–2132. arXiv:cs/0601048. Bibcode:2006cs……..1048T. doi:10.1109/TIT.2007.896870. S2CID 660.
- ^ 3GPP TS 36.212, version 8.8.0, page 14
- ^ «Digital Video Broadcast (DVB); Frame structure, channel coding and modulation for a second generation digital terrestrial television broadcasting system (DVB-T2)». En 302 755. ETSI (V1.1.1). September 2009.
- ^ Techie (3 June 2010). «Explaining Interleaving». W3 Techie Blog. Retrieved 3 June 2010.
- ^ Krastanov, Stefan; Jiang, Liang (8 September 2017). «Deep Neural Network Probabilistic Decoder for Stabilizer Codes». Scientific Reports. 7 (1): 11003. arXiv:1705.09334. Bibcode:2017NatSR…711003K. doi:10.1038/s41598-017-11266-1. PMC 5591216. PMID 28887480.
- ^ Nordstrom, A.W.; Robinson, J.P. (1967), «An optimum nonlinear code», Information and Control, 11 (5–6): 613–616, doi:10.1016/S0019-9958(67)90835-2
- ^ Perry, Jonathan; Balakrishnan, Hari; Shah, Devavrat (2011). «Rateless Spinal Codes». Proceedings of the 10th ACM Workshop on Hot Topics in Networks. pp. 1–6. doi:10.1145/2070562.2070568. hdl:1721.1/79676. ISBN 9781450310598.
Further reading[edit]
- MacWilliams, Florence Jessiem; Sloane, Neil James Alexander (2007) [1977]. Written at AT&T Shannon Labs, Florham Park, New Jersey, USA. The Theory of Error-Correcting Codes. North-Holland Mathematical Library. Vol. 16 (digital print of 12th impression, 1st ed.). Amsterdam / London / New York / Tokyo: North-Holland / Elsevier BV. ISBN 978-0-444-85193-2. LCCN 76-41296. (xxii+762+6 pages)
- Clark, Jr., George C.; Cain, J. Bibb (1981). Error-Correction Coding for Digital Communications. New York, USA: Plenum Press. ISBN 0-306-40615-2.
- Arazi, Benjamin (1987). Swetman, Herb (ed.). A Commonsense Approach to the Theory of Error Correcting Codes. MIT Press Series in Computer Systems. Vol. 10 (1 ed.). Cambridge, Massachusetts, USA / London, UK: Massachusetts Institute of Technology. ISBN 0-262-01098-4. LCCN 87-21889. (x+2+208+4 pages)
- Wicker, Stephen B. (1995). Error Control Systems for Digital Communication and Storage. Englewood Cliffs, New Jersey, USA: Prentice-Hall. ISBN 0-13-200809-2.
- Wilson, Stephen G. (1996). Digital Modulation and Coding. Englewood Cliffs, New Jersey, USA: Prentice-Hall. ISBN 0-13-210071-1.
- «Error Correction Code in Single Level Cell NAND Flash memories» 2007-02-16
- «Error Correction Code in NAND Flash memories» 2004-11-29
- Observations on Errors, Corrections, & Trust of Dependent Systems, by James Hamilton, 2012-02-26
- Sphere Packings, Lattices and Groups, By J. H. Conway, Neil James Alexander Sloane, Springer Science & Business Media, 2013-03-09 – Mathematics – 682 pages.
External links[edit]
- Morelos-Zaragoza, Robert (2004). «The Correcting Codes (ECC) Page». Retrieved 5 March 2006.
- lpdec: library for LP decoding and related things (Python)
Корректирующие коды «на пальцах»
Время на прочтение
11 мин
Количество просмотров 63K

Как нетрудно догадаться, ко всему этому причастны корректирующие коды. Собственно, ECC так и расшифровывается — «error-correcting code», то есть «код, исправляющий ошибки». А CRC — это один из алгоритмов, обнаруживающих ошибки в данных. Исправить он их не может, но часто это и не требуется.
Давайте же разберёмся, что это такое.
Для понимания статьи не нужны никакие специальные знания. Достаточно лишь понимать, что такое вектор и матрица, как они перемножаются и как с их помощью записать систему линейных уравнений.
Внимание! Много текста и мало картинок. Я постарался всё объяснить, но без карандаша и бумаги текст может показаться немного запутанным.
Каналы с ошибкой
Разберёмся сперва, откуда вообще берутся ошибки, которые мы собираемся исправлять. Перед нами стоит следующая задача. Нужно передать несколько блоков данных, каждый из которых кодируется цепочкой двоичных цифр. Получившаяся последовательность нулей и единиц передаётся через канал связи. Но так сложилось, что реальные каналы связи часто подвержены ошибкам. Вообще говоря, ошибки могут быть разных видов — может появиться лишняя цифра или какая-то пропасть. Но мы будем рассматривать только ситуации, когда в канале возможны лишь замены нуля на единицу и наоборот. Причём опять же для простоты будем считать такие замены равновероятными.
Ошибка — это маловероятное событие (а иначе зачем нам такой канал вообще, где одни ошибки?), а значит, вероятность двух ошибок меньше, а трёх уже совсем мала. Мы можем выбрать для себя некоторую приемлемую величину вероятности, очертив границу «это уж точно невозможно». Это позволит нам сказать, что в канале возможно не более, чем ошибок. Это будет характеристикой канала связи.
Для простоты введём следующие обозначения. Пусть данные, которые мы хотим передавать, — это двоичные последовательности фиксированной длины. Чтобы не запутаться в нулях и единицах, будем иногда обозначать их заглавными латинскими буквами (,
,
, …). Что именно передавать, в общем-то неважно, просто с буквами в первое время будет проще работать.
Кодирование и декодирование будем обозначать прямой стрелкой (), а передачу по каналу связи — волнистой стрелкой (
). Ошибки при передаче будем подчёркивать.
Например, пусть мы хотим передавать только сообщения и
. В простейшем случае их можно закодировать нулём и единицей (сюрприз!):
Передача по каналу, в котором возникла ошибка будет записана так:
Цепочки нулей и единиц, которыми мы кодируем буквы, будем называть кодовыми словами. В данном простом случае кодовые слова — это и
.
Код с утроением
Давайте попробуем построить какой-то корректирующий код. Что мы обычно делаем, когда кто-то нас не расслышал? Повторяем дважды:
Правда, это нам не очень поможет. В самом деле, рассмотрим канал с одной возможной ошибкой:
Какие выводы мы можем сделать, когда получили ? Понятно, что раз у нас не две одинаковые цифры, то была ошибка, но вот в каком разряде? Может, в первом, и была передана буква
. А может, во втором, и была передана
.
То есть, получившийся код обнаруживает, но не исправляет ошибки. Ну, тоже неплохо, в общем-то. Но мы пойдём дальше и будем теперь утраивать цифры.
Проверим в деле:
Получили . Тут у нас есть две возможности: либо это
и было две ошибки (в крайних цифрах), либо это
и была одна ошибка. Вообще, вероятность одной ошибки выше вероятности двух ошибок, так что самым правдоподобным будет предположение о том, что передавалась именно буква
. Хотя правдоподобное — не значит истинное, поэтому рядом и стоит вопросительный знак.
Если в канале связи возможна максимум одна ошибка, то первое предположение о двух ошибках становится невозможным и остаётся только один вариант — передавалась буква .
Про такой код говорят, что он исправляет одну ошибку. Две он тоже обнаружит, но исправит уже неверно.
Это, конечно, самый простой код. Кодировать легко, да и декодировать тоже. Ноликов больше — значит передавался ноль, единичек — значит единица.
Если немного подумать, то можно предложить код исправляющий две ошибки. Это будет код, в котором мы повторяем одиночный бит 5 раз.
Расстояния между кодами
Рассмотрим поподробнее код с утроением. Итак, мы получили работающий код, который исправляет одиночную ошибку. Но за всё хорошее надо платить: он кодирует один бит тремя. Не очень-то и эффективно.
И вообще, почему этот код работает? Почему нужно именно утраивать для устранения одной ошибки? Наверняка это всё неспроста.
Давайте подумаем, как этот код работает. Интуитивно всё понятно. Нолики и единички — это две непохожие последовательности. Так как они достаточно длинные, то одиночная ошибка не сильно портит их вид.
Пусть мы передавали , а получили
. Видно, что эта цепочка больше похожа на исходные
, чем на
. А так как других кодовых слов у нас нет, то и выбор очевиден.
Но что значит «больше похоже»? А всё просто! Чем больше символов у двух цепочек совпадает, тем больше их схожесть. Если почти все символы отличаются, то цепочки «далеки» друг от друга.
Можно ввести некоторую величину , равную количеству различающихся цифр в соответствующих разрядах цепочек
и
. Эту величину называют расстоянием Хэмминга. Чем больше это расстояние, тем меньше похожи две цепочки.
Например, , так как все цифры в соответствующих позициях равны, а вот
.
Расстояние Хэмминга называют расстоянием неспроста. Ведь в самом деле, что такое расстояние? Это какая-то характеристика, указывающая на близость двух точек, и для которой верны утверждения:
- Расстояние между точками неотрицательно и равно нулю только, если точки совпадают.
- Расстояние в обе стороны одинаково.
- Путь через третью точку не короче, чем прямой путь.
Достаточно разумные требования.
Математически это можно записать так (нам это не пригодится, просто ради интереса посмотрим):
.
Предлагаю читателю самому убедиться, что для расстояния Хэмминга эти свойства выполняются.
Окрестности
Таким образом, разные цепочки мы считаем точками в каком-то воображаемом пространстве, и теперь мы умеем находить расстояния между ними. Правда, если попытаться сколько нибудь длинные цепочки расставить на листе бумаги так, чтобы расстояния Хэмминга совпадали с расстояниями на плоскости, мы можем потерпеть неудачу. Но не нужно переживать. Всё же это особое пространство со своими законами. А слова вроде «расстояния» лишь помогают нам рассуждать.
Пойдём дальше. Раз мы заговорили о расстоянии, то можно ввести такое понятие как окрестность. Как известно, окрестность какой-то точки — это шар определённого радиуса с центром в ней. Шар? Какие ещё шары! Мы же о кодах говорим.
Но всё просто. Ведь что такое шар? Это множество всех точек, которые находятся от данной не дальше, чем некоторое расстояние, называемое радиусом. Точки у нас есть, расстояние у нас есть, теперь есть и шары.
Так, скажем, окрестность кодового слова радиуса 1 — это все коды, находящиеся на расстоянии не больше, чем 1 от него, то есть отличающиеся не больше, чем в одном разряде. То есть это коды:
Да, вот так странно выглядят шары в пространстве кодов.
А теперь посмотрите. Это же все возможные коды, которые мы получим в канале в одной ошибкой, если отправим ! Это следует прямо из определения окрестности. Ведь каждая ошибка заставляет цепочку измениться только в одном разряде, а значит удаляет её на расстояние 1 от исходного сообщения.
Аналогично, если в канале возможны две ошибки, то отправив некоторое сообщение , мы получим один из кодов, который принадлежит окрестности
радиусом 2.
Тогда всю нашу систему декодирования можно построить так. Мы получаем какую-то цепочку нулей и единиц (точку в нашей новой терминологии) и смотрим, в окрестность какого кодового слова она попадает.
Сколько ошибок может исправить код?
Чтобы код мог исправлять больше ошибок, окрестности должны быть как можно шире. С другой стороны, они не должны пересекаться. Иначе если точка попадёт в область пересечения, непонятно будет, к какой окрестности её отнести.
В коде с удвоением между кодовыми словами и
расстояние равно 2 (оба разряда различаются). А значит, если мы построим вокруг них шары радиуса 1, то они будут касаться. Это значит, точка касания будет принадлежать обоим шарам и непонятно будет, к какому из них её отнести.
Именно это мы и получали. Мы видели, что есть ошибка, но не могли её исправить.
Что интересно, точек касания в нашем странном пространстве у шаров две — это коды и
. Расстояния от них до центров равны единице. Конечно же, в обычно геометрии такое невозможно, поэтому рисунки — это просто условность для более удобного рассуждения.
В случае кода с утроением, между шарами будет зазор.
Минимальный зазор между шарами равен 1, так как у нас расстояния всегда целые (ну не могут же две цепочки отличаться в полутора разрядах).
В общем случае получаем следующее.
Этот очевидный результат на самом деле очень важен. Он означает, что код с минимальным кодовым расстоянием будет успешно работать в канале с
ошибками, если выполняется соотношение
Полученное равенство позволяет легко определить, сколько ошибок будет исправлять тот или иной код. А сколько код ошибок может обнаружить? Рассуждения такие же. Код обнаруживает ошибок, если в результате не получится другое кодовое слово. То есть, кодовые слова не должны находиться в окрестностях радиуса
других кодовых слов. Математически это записывается так:
Рассмотрим пример. Пусть мы кодируем 4 буквы следующим образом.
Чтобы найти минимальное расстояние между различными кодовыми словами, построим таблицу попарных расстояний.
| A | B | C | D | |
|---|---|---|---|---|
| A | — | 3 | 3 | 4 |
| B | 3 | — | 4 | 3 |
| C | 3 | 4 | — | 3 |
| D | 4 | 3 | 3 | — |
Минимальное расстояние , а значит
, откуда получаем, что такой код может исправить до
ошибок. Обнаруживает же он две ошибки.
Рассмотрим пример:
Чтобы декодировать полученное сообщение, посмотрим, к какому символу оно ближе всего.
Минимальное расстояние получилось для символа , значит вероятнее всего передавался именно он:
Итак, этот код исправляет одну ошибку, как и код с утроением. Но он более эффективен, так как в отличие от кода с утроением здесь кодируется уже 4 символа.
Таким образом, основная проблема при построении такого рода кодов — так расположить кодовые слова, чтобы они были как можно дальше друг от друга, и их было побольше.
Для декодирования можно было бы использовать таблицу, в которой указывались бы все возможные принимаемые сообщения, и кодовые слова, которым они соответствуют. Но такая таблица получилась бы очень большой. Даже для нашего маленького кода, который выдаёт 5 двоичных цифр, получилось бы варианта возможных принимаемых сообщений. Для более сложных кодов таблица будет значительно больше.
Попробуем придумать способ коррекции сообщения без таблиц. Мы всегда сможем найти полезное применение освободившейся памяти.
Интерлюдия: поле GF(2)
Для изложения дальнейшего материала нам потребуются матрицы. А при умножении матриц, как известно мы складываем и перемножаем числа. И тут есть проблема. Если с умножением всё более-менее хорошо, то как быть со сложением? Из-за того, что мы работаем только с одиночными двоичными цифрами, непонятно, как сложить 1 и 1, чтобы снова получилась одна двоичная цифра. Значит вместо классического сложения нужно использовать какое-то другое.
Введём операцию сложения как сложение по модулю 2 (хорошо известный программистам XOR):
Умножение будем выполнять как обычно. Эти операции на самом деле введены не абы как, а чтобы получилась система, которая в математике называется полем. Поле — это просто множество (в нашем случае из 0 и 1), на котором так определены сложение и умножение, чтобы основные алгебраические законы сохранялись. Например, чтобы основные идеи, касающиеся матриц и систем уравнений по-прежнему были верны. А вычитание и деление мы можем ввести как обратные операции.
Множество из двух элементов с операциями, введёнными так, как мы это сделали, называется полем Галуа GF(2). GF — это Galois field, а 2 — количество элементов.
У сложения есть несколько очень полезных свойств, которыми мы будем пользоваться в дальнейшем.
Это свойство прямо следует из определения.
А в этом можно убедиться, прибавив к обеим частям равенства. Это свойство, в частности означает, что мы можем переносить в уравнении слагаемые в другую сторону без смены знака.
Проверяем корректность
Вернёмся к коду с утроением.
Для начала просто решим задачу проверки, были ли вообще ошибки при передаче. Как видно, из самого кода, принятое сообщение будет кодовым словом только тогда, когда все три цифры равны между собой.
Пусть мы приняли вектор-строку из трёх цифр. (Стрелочки над векторами рисовать не будем, так как у нас почти всё — это вектора или матрицы.)
Математически равенство всех трёх цифр можно записать как систему:
Или, если воспользоваться свойствами сложения в GF(2), получаем
Или
В матричном виде эта система будет иметь вид
где
Транспонирование здесь нужно потому, что — это вектор-строка, а не вектор-столбец. Иначе мы не могли бы умножать его справа на матрицу.
Будем называть матрицу проверочной матрицей. Если полученное сообщение — это корректное кодовое слово (то есть, ошибки при передаче не было), то произведение проверочной матрицы на это сообщение будет равно нулевому вектору.
Умножение на матрицу — это гораздо более эффективно, чем поиск в таблице, но у нас на самом деле есть ещё одна таблица — это таблица кодирования. Попробуем от неё избавиться.
Кодирование
Итак, у нас есть система для проверки
Её решения — это кодовые слова. Собственно, мы систему и строили на основе кодовых слов. Попробуем теперь решить обратную задачу. По системе (или, что то же самое, по матрице ) найдём кодовые слова.
Правда, для нашей системы мы уже знаем ответ, поэтому, чтобы было интересно, возьмём другую матрицу:
Соответствующая система имеет вид:
Чтобы найти кодовые слова соответствующего кода нужно её решить.
В силу линейности сумма двух решений системы тоже будет решением системы. Это легко доказать. Если и
— решения системы, то для их суммы верно
что означает, что она тоже — решение.
Поэтому если мы найдём все линейно независимые решения, то с их помощью можно получить вообще все решения системы. Для этого просто нужно найти их всевозможные суммы.
Выразим сперва все зависимые слагаемые. Их столько же, сколько и уравнений. Выражать надо так, чтобы справа были только независимые. Проще всего выразить .
Если бы нам не так повезло с системой, то нужно было бы складывая уравнения между собой получить такую систему, чтобы какие-то три переменные встречались по одному разу. Ну, или воспользоваться методом Гаусса. Для GF(2) он тоже работает.
Итак, получаем:
Чтобы получить все линейно независимые решения, приравниваем каждую из зависимых переменных к единице по очереди.
Всевозможные суммы этих независимых решений (а именно они и будут кодовыми векторами) можно получить так:
где равны либо нулю или единице. Так как таких коэффициентов два, то всего возможно
сочетания.
Но посмотрите! Формула, которую мы только что получили — это же снова умножение матрицы на вектор.
Строчки здесь — линейно независимые решения, которые мы получили. Матрица называется порождающей. Теперь вместо того, чтобы сами составлять таблицу кодирования, мы можем получать кодовые слова простым умножением на матрицу:
Найдём кодовые слова для этого кода. (Не забываем, что длина исходных сообщений должна быть равна 2 — это количество найденных решений.)
Итак, у нас есть готовый код, обнаруживающий ошибки. Проверим его в деле. Пусть мы хотим отправить 01 и у нас произошла ошибка при передаче. Обнаружит ли её код?
А раз в результате не нулевой вектор, значит код заподозрил неладное. Провести его не удалось. Ура, код работает!
Для кода с утроением, кстати, порождающая матрица выглядит очень просто:
Подобные коды, которые можно порождать и проверять матрицей называются линейными (бывают и нелинейные), и они очень широко применяются на практике. Реализовать их довольно легко, так как тут требуется только умножение на константную матрицу.
Ошибка по синдрому
Ну хорошо, мы построили код обнаруживающий ошибки. Но мы же хотим их исправлять!
Для начала введём такое понятие, как вектор ошибки. Это вектор, на который отличается принятое сообщение от кодового слова. Пусть мы получили сообщение , а было отправлено кодовое слово
. Тогда вектор ошибки по определению
Но в странном мире GF(2), где сложение и вычитание одинаковы, будут верны и соотношения:
В силу особенностей сложения, как читатель сам может легко убедиться, в векторе ошибки на позициях, где произошла ошибка будет единица, а на остальных ноль.
Как мы уже говорили раньше, если мы получили сообщение с ошибкой, то
. Но ведь векторов, не равных нулю много! Быть может то, какой именно ненулевой вектор мы получили, подскажет нам характер ошибки?
Назовём результат умножения на проверочную матрицу синдромом:
И заметим следующее
Это означает, что для ошибки синдром будет таким же, как и для полученного сообщения.
Разложим все возможные сообщения, которые мы можем получить из канала связи, по кучкам в зависимости от синдрома. Тогда из последнего соотношения следует, что в каждой кучке будут вектора с одной и той же ошибкой. Причём вектор этой ошибки тоже будет в кучке. Вот только как его узнать?
А очень просто! Помните, мы говорили, что у нескольких ошибок вероятность ниже, чем у одной ошибки? Руководствуясь этим соображением, наиболее правдоподобным будет считать вектором ошибки тот вектор, у которого меньше всего единиц. Будем называть его лидером.
Давайте посмотрим, какие синдромы дают всевозможные 5-элементные векторы. Сразу сгруппируем их и подчеркнём лидеров — векторы с наименьшим числом единиц.
В принципе, для корректирования ошибки достаточно было бы хранить таблицу соответствия синдрома лидеру.
Обратите внимание, что в некоторых строчках два лидера. Это значит для для данного синдрома два паттерна ошибки равновероятны. Иными словами, код обнаружил две ошибки, но исправить их не может.
Лидеры для всех возможных одиночных ошибок находятся в отдельных строках, а значит код может исправить любую одиночную ошибку. Ну, что же… Попробуем в этом убедиться.
Вектор ошибки равен , а значит ошибка в третьем разряде. Как мы и загадали.
Ура, всё работает!
Что же дальше?
Чтобы попрактиковаться, попробуйте повторить рассуждения для разных проверочных матриц. Например, для кода с утроением.
Логическим продолжением изложенного был бы рассказ о циклических кодах — чрезвычайно интересном подклассе линейных кодов, обладающим замечательными свойствами. Но тогда, боюсь, статья уж очень бы разрослась.
Если вас заинтересовали подробности, то можете почитать замечательную книжку Аршинова и Садовского «Коды и математика». Там изложено гораздо больше, чем представлено в этой статье. Если интересует математика кодирования — то поищите «Теория и практика кодов, контролирующих ошибки» Блейхута. А вообще, материалов по этой теме довольно много.
Надеюсь, когда снова будет свободное время, напишу продолжение, в котором расскажу про циклические коды и покажу пример программы для кодирования и декодирования. Если, конечно, почтенной публике это интересно.
схема управления ошибками в данных по зашумленным каналам связи
В вычислениях, телекоммуникации, теория информации и теория кодирования, код исправления ошибок, иногда код исправления ошибок, (ECC ) используется для контроля ошибок в данных по ненадежным или зашумленным каналам связи. Основная идея заключается в том, что отправитель кодирует сообщение с помощью избыточной информации в форме ECC. Избыточность позволяет получателю обнаруживать ограниченное количество ошибок, которые могут возникать в любом месте сообщения, и часто исправлять эти ошибки без повторной передачи. Американский математик Ричард Хэмминг был пионером в этой области в 1940-х годах и изобрел первый исправляющий ошибки код в 1950 году: код Хэмминга (7,4).
ECC контрастирует с обнаружением ошибок. в том, что обнаруженные ошибки можно исправить, а не просто обнаружить. Преимущество состоит в том, что системе, использующей ECC, не требуется обратный канал для запроса повторной передачи данных при возникновении ошибки. Обратной стороной является то, что к сообщению добавляются фиксированные накладные расходы, что требует более высокой полосы пропускания прямого канала. Таким образом, ECC применяется в ситуациях, когда повторные передачи являются дорогостоящими или невозможными, например, при односторонних каналах связи и при передаче на несколько приемников в многоадресной передаче. Соединения с длительной задержкой также выигрывают; в случае спутника, вращающегося вокруг Урана, повторная передача из-за ошибок может вызвать задержку в пять часов. Информация ECC обычно добавляется к запоминающим устройствам для восстановления поврежденных данных, широко используется в модемах и используется в системах, где основной памятью является память ECC.
Обработка ЕСС в приемнике может применяться к цифровому потоку битов или к демодуляции несущей с цифровой модуляцией. В последнем случае ECC является неотъемлемой частью начального аналого-цифрового преобразования в приемнике. Декодер Витерби реализует алгоритм мягкого решения для демодуляции цифровых данных из аналогового сигнала, искаженного шумом. Многие кодеры / декодеры ECC также могут генерировать сигнал с коэффициентом ошибок по битам (BER), который можно использовать в качестве обратной связи для точной настройки аналоговой приемной электроники.
Максимальная доля ошибок или отсутствующих битов, которые могут быть исправлены, определяется конструкцией кода ECC, поэтому разные коды исправления ошибок подходят для разных условий. Как правило, более сильный код вызывает большую избыточность, которую необходимо передавать с использованием доступной полосы пропускания, что снижает эффективную скорость передачи данных при одновременном улучшении принимаемого эффективного отношения сигнал / шум. Теорема кодирования с шумом канала из Клод Шеннон отвечает на вопрос о том, какая полоса пропускания остается для передачи данных при использовании наиболее эффективного кода, который сводит вероятность ошибки декодирования к нулю. Это устанавливает границы теоретической максимальной скорости передачи информации канала с некоторым заданным базовым уровнем шума. Однако это доказательство неконструктивно и, следовательно, не дает представления о том, как создать код, обеспечивающий производительность. После многих лет исследований некоторые современные системы ECC сегодня очень близки к теоретическому максимуму.
Содержание
- 1 Прямое исправление ошибок
- 2 Как это работает
- 3 Усреднение шума для уменьшения количества ошибок
- 4 Типы ECC
- 5 Кодовая скорость и компромисс между надежностью и скоростью передачи данных
- 6 Составные коды ECC для повышения производительности
- 7 Проверка четности с низкой плотностью (LDPC)
- 8 Турбо-коды
- 9 Локальное декодирование и тестирование кодов
- 10 Чередование
- 10.1 Пример
- 10.2 Недостатки чередования
- 11 Программное обеспечение для кодов исправления ошибок
- 12 Список кодов исправления ошибок
- 13 См. Также
- 14 Ссылки
- 15 Дополнительная литература
- 16 Внешние ссылки
Прямое исправление ошибок
В электросвязи, теории информации и теории кодирования, прямое исправление ошибок (FEC ) или канальное кодирование — это метод, используемый для контроля ошибок в передаче данных по ненадежным или зашумленным каналам связи. Основная идея заключается в том, что отправитель кодирует сообщение с помощью избыточного способа, чаще всего с помощью ECC.
Избыточность позволяет получателю обнаруживать ограниченное количество ошибок, которые могут возникнуть в любом месте сообщения, и часто исправлять эти ошибки без повторной передачи. FEC дает приемнику возможность исправлять ошибки без необходимости использования обратного канала для запроса повторной передачи данных, но за счет фиксированной более высокой полосы пропускания прямого канала. Поэтому FEC применяется в ситуациях, когда повторные передачи являются дорогостоящими или невозможными, например, при односторонних каналах связи и при передаче на несколько приемников в многоадресной передаче. Информация FEC обычно добавляется к запоминающим устройствам (магнитным, оптическим и твердотельным / флэш-накопителям) для восстановления поврежденных данных, широко используется в модемах, используется в системах, где первичной памятью является память ECC, и в ситуациях широковещательной передачи, когда приемник не имеет возможности запрашивать повторную передачу или это может вызвать значительную задержку. Например, в случае спутника, вращающегося вокруг Урана, повторная передача из-за ошибок декодирования может вызвать задержку не менее 5 часов.
Обработка FEC в приемнике может применяться к цифровому битовому потоку или при демодуляции несущей с цифровой модуляцией. Для последнего FEC является неотъемлемой частью начального аналого-цифрового преобразования в приемнике. Декодер Витерби реализует алгоритм мягкого решения для демодуляции цифровых данных из аналогового сигнала, искаженного шумом. Многие кодеры FEC могут также генерировать сигнал с коэффициентом ошибок по битам (BER), который можно использовать в качестве обратной связи для точной настройки аналоговой приемной электроники.
Максимальная доля ошибок или недостающих битов, которые могут быть исправлены, определяется конструкцией ECC, поэтому разные коды прямого исправления ошибок подходят для разных условий. Как правило, более сильный код вызывает большую избыточность, которую необходимо передавать с использованием доступной полосы пропускания, что снижает эффективную скорость передачи данных при одновременном улучшении принимаемого эффективного отношения сигнал / шум. Теорема кодирования канала с шумом Клода Шеннона отвечает на вопрос о том, какая полоса пропускания остается для передачи данных при использовании наиболее эффективного кода, который обращает вероятность ошибки декодирования в ноль. Это устанавливает границы теоретической максимальной скорости передачи информации канала с некоторым заданным базовым уровнем шума. Его доказательство неконструктивно и, следовательно, не дает понимания того, как создать код, обеспечивающий производительность. Однако после многих лет исследований некоторые передовые системы FEC, такие как полярный код, достигают пропускной способности канала Шеннона при гипотезе кадра бесконечной длины.
Как это работает
ECC достигается путем добавления избыточности к передаваемой информации с использованием алгоритма. Избыточный бит может быть сложной функцией многих исходных информационных битов. Исходная информация может появляться или не появляться буквально в закодированном выводе; коды, которые включают немодифицированный ввод в вывод, являются систематическими, тогда как те, которые не включают, являются несистематическими .
Упрощенный пример ECC — передача каждого бита данных 3 раза, что известно как код повторения (3,1) . Через шумный канал приемник может видеть 8 вариантов вывода, см. Таблицу ниже.
| Получен триплет | Интерпретируется как |
|---|---|
| 000 | 0 (без ошибок) |
| 001 | 0 |
| 010 | 0 |
| 100 | 0 |
| 111 | 1 (без ошибок) |
| 110 | 1 |
| 101 | 1 |
| 011 | 1 |
Это позволяет исправить ошибку в любой из трех выборок «большинством голосов» или «демократическим голосованием». Корректирующая способность этого ECC:
- До 1 бита триплета с ошибкой или
- до 2 битов триплета пропущены (случаи не показаны в таблице).
Хотя прост в реализации и Это широко используемое тройное модульное резервирование является относительно неэффективным ECC. Более совершенные коды ECC обычно проверяют несколько последних десятков или даже несколько последних сотен ранее принятых битов, чтобы определить, как декодировать текущую небольшую группу битов (обычно в группах от 2 до 8 бит).
Усреднение шума для уменьшения ошибок
Можно сказать, что ECC работает посредством «усреднения шума»; поскольку каждый бит данных влияет на многие передаваемые символы, искажение одних символов шумом обычно позволяет извлекать исходные пользовательские данные из других неповрежденных принятых символов, которые также зависят от тех же пользовательских данных.
- Из-за этого эффекта «объединения рисков» цифровые системы связи, использующие ECC, как правило, работают значительно выше определенного минимального отношения сигнал / шум, а не ниже него.
- Эта тенденция «все или ничего» — эффект обрыва — становится более выраженной по мере использования более сильных кодов, которые более близко подходят к теоретическому пределу Шеннона.
- Чередование данных, закодированных с помощью ECC, может уменьшить все или ничего свойства переданных кодов ECC, когда ошибки канала имеют тенденцию возникать в пакетах. Однако у этого метода есть ограничения; его лучше всего использовать для узкополосных данных.
Большинство телекоммуникационных систем используют фиксированный канальный код, рассчитанный на ожидаемый наихудший случай частоты ошибок по битам, а затем вообще не работают если частота ошибок по битам станет еще хуже. Однако некоторые системы адаптируются к данным условиям ошибки канала: некоторые экземпляры гибридного автоматического запроса на повторение используют фиксированный метод ECC, пока ECC может обрабатывать частоту ошибок, затем переключаются на ARQ когда частота ошибок становится слишком высокой; адаптивная модуляция и кодирование использует различные скорости ECC, добавляя больше битов исправления ошибок на пакет, когда в канале более высокие частоты ошибок, или удаляя их, когда они не нужны.
Типы ECC
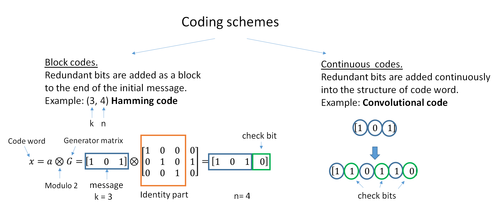
Двумя основными категориями кодов ECC являются блочные коды и сверточные коды.
- Блочные коды работают с блоками фиксированного размера (пакетами) битов или символов заранее определенного размера. Практические блочные коды обычно могут быть жестко декодированы за полиномиальное время до их длины блока.
- Сверточные коды работают с битовыми или символьными потоками произвольной длины. Чаще всего они программно декодируются с помощью алгоритма Витерби, хотя иногда используются и другие алгоритмы. Декодирование Витерби обеспечивает асимптотически оптимальную эффективность декодирования с увеличением длины ограничения сверточного кода, но за счет экспоненциально возрастающей сложности. Завершенный сверточный код также является «блочным кодом» в том смысле, что он кодирует блок входных данных, но размер блока сверточного кода, как правило, произвольный, в то время как блочные коды имеют фиксированный размер, определяемый их алгебраическими характеристиками. Типы завершения для сверточных кодов включают в себя «бит в конце» и «сброс битов».
Существует много типов блочных кодов; Кодирование Рида-Соломона примечательно тем, что оно широко используется в компакт-дисках, DVD и жестких дисках. Другие примеры классических блочных кодов включают Голея, BCH, многомерную четность и коды Хэмминга.
ECC Хэмминга обычно используются для исправления NAND flash ошибки памяти. Это обеспечивает исправление однобитовых ошибок и обнаружение двухбитовых ошибок. Коды Хэмминга подходят только для более надежной одноуровневой ячейки (SLC) NAND. Более плотная многоуровневая ячейка (MLC) NAND может использовать многобитовый корректирующий ECC, такой как BCH или Reed-Solomon. NOR Flash обычно не использует никакого исправления ошибок.
Классические блочные коды обычно декодируются с использованием алгоритмов жесткого решения, что означает, что для каждого входного и выходного сигнала принимается жесткое решение, будет ли он соответствует единице или нулю бит. Напротив, сверточные коды обычно декодируются с использованием алгоритмов мягкого решения, таких как алгоритмы Витерби, MAP или BCJR, которые обрабатывают (дискретизированные) аналоговые сигналы и которые допускают гораздо более высокие ошибки — производительность коррекции, чем декодирование с жестким решением.
Почти все классические блочные коды применяют алгебраические свойства конечных полей. Поэтому классические блочные коды часто называют алгебраическими кодами.
В отличие от классических блочных кодов, которые часто определяют способность обнаружения или исправления ошибок, многие современные блочные коды, такие как коды LDPC, не имеют таких гарантий. Вместо этого современные коды оцениваются с точки зрения их частоты ошибок по битам.
Большинство кодов прямого исправления ошибок исправляют только перевороты битов, но не вставки или удаления битов. В этой настройке расстояние Хэмминга является подходящим способом измерения коэффициента битовых ошибок. Несколько кодов прямого исправления ошибок предназначены для исправления вставки и удаления битов, например, коды маркеров и коды водяных знаков. Расстояние Левенштейна является более подходящим способом измерения частоты ошибок по битам при использовании таких кодов.
Кодовая скорость и компромисс между надежностью и скоростью передачи данных
Фундаментальный принцип ECC состоит в добавлении избыточных битов, чтобы помочь декодеру узнать истинное сообщение, которое было закодировано передатчик. Кодовая скорость данной системы ЕСС определяется как соотношение между количеством информационных битов и общим количеством битов (то есть информацией плюс биты избыточности) в данном коммуникационном пакете. Кодовая скорость, следовательно, является действительным числом. Низкая кодовая скорость, близкая к нулю, подразумевает сильный код, который использует много избыточных битов для достижения хорошей производительности, в то время как большая кодовая скорость, близкая к 1, подразумевает слабый код.
Избыточные биты, защищающие информацию, должны передаваться с использованием тех же коммуникационных ресурсов, которые они пытаются защитить. Это вызывает фундаментальный компромисс между надежностью и скоростью передачи данных. В одном крайнем случае сильный код (с низкой кодовой скоростью) может вызвать значительное увеличение SNR приемника (отношение сигнал / шум), уменьшая частоту ошибок по битам, за счет снижения эффективной скорости передачи данных. С другой стороны, без использования какого-либо ECC (то есть кодовой скорости, равной 1) используется полный канал для целей передачи информации за счет того, что биты остаются без какой-либо дополнительной защиты.
Один интересный вопрос заключается в следующем: насколько эффективным с точки зрения передачи информации может быть ECC, имеющий незначительную частоту ошибок декодирования? На этот вопрос ответил Клод Шеннон с его второй теоремой, которая гласит, что пропускная способность канала — это максимальная скорость передачи данных, достижимая для любого ECC, частота ошибок которого стремится к нулю: его доказательство основано на гауссовском случайном кодировании, которое не подходит для реального мира. Приложения. Верхняя граница, заданная работой Шеннона, вдохновила на долгий путь к разработке ECC, которые могут приблизиться к пределу конечных характеристик. Различные коды сегодня могут достигать почти предела Шеннона. Однако ECC, обеспечивающие пропускную способность, обычно чрезвычайно сложно реализовать.
Наиболее популярные ECC имеют компромисс между производительностью и вычислительной сложностью. Обычно их параметры дают диапазон возможных кодовых скоростей, которые можно оптимизировать в зависимости от сценария. Обычно эта оптимизация выполняется для достижения низкой вероятности ошибки декодирования при минимальном влиянии на скорость передачи данных. Другим критерием оптимизации кодовой скорости является уравновешивание низкой частоты ошибок и количества повторных передач с учетом энергетических затрат на связь.
Составные коды ECC для повышения производительности
Классические (алгебраические) блочные коды а сверточные коды часто комбинируются в схемах конкатенированного кодирования, в которых сверточный код, декодированный по Витерби с короткой ограниченной длиной, выполняет большую часть работы, а блочный код (обычно Рида-Соломона) с большим размером символа и длиной блока «стирает» любые ошибки, сделанные сверточным декодером. Однопроходное декодирование с использованием этого семейства кодов с исправлением ошибок может дать очень низкий уровень ошибок, но для условий передачи на большие расстояния (например, в глубоком космосе) рекомендуется итеративное декодирование.
Составные коды были стандартной практикой в спутниковой связи и связи в дальнем космосе с тех пор, как «Вояджер-2 » впервые применил эту технику во время встречи с Ураном в 1986 году. Аппарат Galileo использовал итеративные конкатенированные коды для компенсации условий очень высокой частоты ошибок, вызванных отказом антенны.
Проверка на четность с низкой плотностью (LDPC)
Коды с проверкой на четность с низкой плотностью (LDPC) — это класс высокоэффективных линейных блочных кодов, созданных из множества кодов одиночной проверки на четность (SPC). Они могут обеспечить производительность, очень близкую к пропускной способности канала (теоретический максимум), используя подход итеративного декодирования с мягким решением, при линейной временной сложности с точки зрения длины их блока. Практические реализации в значительной степени полагаются на параллельное декодирование составляющих кодов SPC.
Коды LDPC были впервые введены Робертом Г. Галлагером в его докторской диссертации в 1960 году, но из-за вычислительных усилий при реализации кодера и декодера и введения Рида-Соломона коды, они в основном игнорировались до 1990-х годов.
Коды LDPC теперь используются во многих недавних стандартах высокоскоростной связи, таких как DVB-S2 (цифровое видеовещание — спутниковое — второе поколение), WiMAX ( стандарт IEEE 802.16e для микроволновой связи), высокоскоростная беспроводная локальная сеть (IEEE 802.11n ), 10GBase-T Ethernet (802.3an) и G.hn/G.9960 (Стандарт ITU-T для организации сетей по линиям электропередач, телефонным линиям и коаксиальному кабелю). Другие коды LDPC стандартизированы для стандартов беспроводной связи в пределах 3GPP MBMS (см. исходные коды ).
Турбокоды
Турбокодирование — это схема повторяющегося мягкого декодирования, которая объединяет два или более относительно простых сверточных кода и перемежитель для создания блочного кода, который может работать с точностью до долей децибела. предела Шеннона. Предшествующие LDPC-коды с точки зрения практического применения, теперь они обеспечивают аналогичную производительность.
Одним из первых коммерческих приложений турбо-кодирования была технология цифровой сотовой связи CDMA2000 1x (TIA IS-2000), разработанная Qualcomm и продаваемая Verizon Беспроводная связь, Sprint и другие операторы связи. Он также используется для развития CDMA2000 1x специально для доступа в Интернет, 1xEV-DO (TIA IS-856). Как и 1x, EV-DO был разработан Qualcomm и продается Verizon Wireless, Sprint и другими операторами (маркетинговое название Verizon для 1xEV-DO — Широкополосный доступ, потребительские и бизнес-маркетинговые названия компании Sprint для 1xEV-DO — Power Vision и Mobile Broadband соответственно).
Локальное декодирование и тестирование кодов
Иногда необходимо декодировать только отдельные биты сообщения или проверить, является ли данный сигнал кодовым словом, и делать это, не глядя на все сигнал. Это может иметь смысл в настройке потоковой передачи, где кодовые слова слишком велики для того, чтобы их можно было классически декодировать достаточно быстро, и где на данный момент интересны только несколько битов сообщения. Также такие коды стали важным инструментом в теории сложности вычислений, например, для разработки вероятностно проверяемых доказательств.
Локально декодируемые коды являются кодами с исправлением ошибок, для которых отдельные биты сообщение может быть восстановлено вероятностно, если посмотреть только на небольшое (скажем, постоянное) количество позиций кодового слова, даже после того, как кодовое слово было искажено на некоторой постоянной доле позиций. Локально тестируемые коды — это коды с исправлением ошибок, для которых можно вероятностно проверить, близок ли сигнал к кодовому слову, посмотрев только на небольшое количество позиций сигнала.
Чередование

Чередование часто используется в системах цифровой связи и хранения для повышения производительности кодов прямого исправления ошибок. Многие каналы связи не лишены памяти: ошибки обычно возникают в пакетах, а не независимо друг от друга. Если количество ошибок в кодовом слове превышает возможности кода исправления ошибок, ему не удается восстановить исходное кодовое слово. Чередование облегчает эту проблему путем перетасовки исходных символов по нескольким кодовым словам, тем самым создавая более равномерное распределение ошибок. Поэтому перемежение широко используется для пакетной коррекции ошибок.
. Анализ современных повторяющихся кодов, таких как турбокоды и коды LDPC, обычно предполагает независимое распределение ошибок.. Поэтому системы, использующие коды LDPC, обычно используют дополнительное перемежение символов в кодовом слове.
Для турбокодов перемежитель является неотъемлемым компонентом, и его правильная конструкция имеет решающее значение для хорошей производительности. Алгоритм итеративного декодирования работает лучше всего, когда нет коротких циклов в графе коэффициентов, который представляет декодер; перемежитель выбран, чтобы избежать коротких циклов.
Конструкции перемежителя включают:
- прямоугольные (или однородные) перемежители (аналогично методу с использованием коэффициентов пропуска, описанному выше)
- сверточные перемежители
- случайные перемежители (где перемежитель — известная случайная перестановка)
- S-случайный перемежитель (где перемежитель — это известная случайная перестановка с ограничением, что никакие входные символы на расстоянии S не появляются на расстоянии S на выходе).
- бесконфликтный квадратичный многочлен с перестановками (QPP). Пример использования — в стандарте мобильной связи 3GPP Long Term Evolution.
В системах связи с несколькими несущими может использоваться перемежение по несущим для обеспечения частотного разнесения., например, для уменьшения частотно-избирательного замирания или узкополосных помех.
Пример
Передача без перемежения :
Сообщение без ошибок: aaaabbbbccccddddeeeeffffgggg Передача с пакетной ошибкой: aaaabbbbccc____deeeeffffgggg
Здесь каждая группа одинаковых букв представляет 4-битное однобитовое кодовое слово с исправлением ошибок. Кодовое слово cccc изменяется в один бит и может быть исправлено, но кодовое слово dddd изменяется в трех битах, поэтому либо оно не может быть декодировано вообще, либо может быть декодировано неправильно.
С чередованием :
Ошибка- свободные кодовые слова: aaaabbbbccccddddeeeeffffgggg Interleaved: abcdefgabcdefgabcdefgabcdefg Передача с ошибкой пакета: abcdefgabcd____bcdefgabcdefg Полученные кодовые слова после деинтерлейвинга: "aa_abbb_gg2ccd_dd>,", ",", ",", ","Передача без чередования :
Исходное переданное предложение: ThisIsAnExampleOfInterleaving Полученное предложение с пакетной ошибкой: ThisIs______pleOfInterleavingТермин «AnExample» оказывается в основном неразборчивым и трудным для исправления.
С чередованием :
Переданное предложение: ThisIsAnExampleOfInterleaving... Безошибочная передача: TIEpfeaghsxlIrv.iAaenli.snmOten. Получено предложение с пакетной ошибкой: TIEpfe ______ Irv.iAaenli.snmOten. Полученное предложение после деинтерлейвинга: T_isI_AnE_amp_eOfInterle_vin _...Ни одно слово не потеряно полностью, а недостающие буквы можно восстановить с минимальными догадками.
Недостатки чередования
Использование методов чередования увеличивает общую задержку. Это связано с тем, что весь чередующийся блок должен быть принят до того, как пакеты могут быть декодированы. Также перемежители скрывают структуру ошибок; Без перемежителя более совершенные алгоритмы декодирования могут использовать структуру ошибок и обеспечивать более надежную связь, чем более простой декодер, объединенный с перемежителем. Пример такого алгоритма основан на структурах нейронной сети .
Программное обеспечение для кодов с исправлением ошибок
Моделирование поведения кодов с исправлением ошибок (ECC) в программном обеспечении является обычной практикой для разработки, проверки и улучшения кодов ECC. Предстоящий стандарт беспроводной связи 5G поднимает новый диапазон приложений для программных ECC: Облачные сети радиодоступа (C-RAN) в контексте Программно-определяемого радио (SDR). Идея состоит в том, чтобы напрямую использовать программные ECC в коммуникациях. Например, в 5G программные ECC могут быть расположены в облаке, а антенны могут быть подключены к этим вычислительным ресурсам: таким образом повышается гибкость сети связи и, в конечном итоге, повышается энергоэффективность системы.
В этом контексте существует различное доступное программное обеспечение с открытым исходным кодом, перечисленное ниже (не является исчерпывающим).
- AFF3CT (Панель инструментов быстрого исправления ошибок): полная цепочка связи на C ++ (многие поддерживаемые коды, такие как Turbo, LDPC, полярные коды и т. Д.), Очень быстрая и специализированная на канальном кодировании (может использоваться как программа для моделирования или как библиотека для SDR).
- IT ++ : библиотека классов и функций C ++ для линейной алгебры, числовой оптимизации, обработки сигналов, связи и статистики.
- OpenAir : реализация (на языке C) спецификаций 3GPP, касающихся Evolved Packet Core Networks.
Список кодов исправления ошибок
| Расстояние | Код |
|---|---|
| 2 (обнаружение единичной ошибки) | Четность |
| 3 (исправление одиночной ошибки) | Тройное модульное резервирование |
| 3 (исправление одиночной ошибки) | совершенное Хэмминга, такое как Хэмминга (7,4) |
| 4 (SECDED ) | Расширенный Хэмминга |
| 5 (исправление двойной ошибки) | |
| 6 (исправление двойной ошибки / обнаружение тройной ошибки) | |
| 7 (исправление трех ошибок) | совершенный двоичный код Голея |
| 8 (TECFED) | расширенный двоичный код Голея |
- коды AN
- код BCH, который может быть разработан для исправления любого произвольного количества ошибок в кодовом блоке.
- код Бергера
- код постоянного веса
- сверточный код
- Расширительные коды
- Групповые коды
- коды Голея, из которых двоичный код Голея представляет практический интерес
- код Гоппа, используемый в Криптосистема Мак-Элиса
- Код Адамара
- Код Хагельбаргера
- Код Хэмминга
- Код на основе латинского квадрата для небелого шума (преобладающий, например, в широкополосной связи по сравнению с линиями электропередач)
- Лексикографический код
- Линейное сетевое кодирование, тип кода с исправлением стирания в сетях вместо двухточечных ссылок
- Длинный код
- Код проверки четности с низкой плотностью, также известный как код Галлагера, как архетип для кодов разреженного графа
- LT-кода, который является почти оптимальным бесскоростным кодом коррекции стирания (код Фонтана)
- m из n кодов
- Онлайн-код, почти оптимальный код бесскоростной коррекции стирания
- Полярный код (codi ng теория)
- Код Raptor, почти оптимальный код с бесскоростной коррекцией стирания
- Исправление ошибок Рида – Соломона
- Код Рида – Маллера
- Код повторения-накопления
- Коды повторения, например, Тройная модульная избыточность
- Спинальный код, бесскоростной нелинейный код, основанный на псевдослучайных хэш-функциях
- Код Торнадо, почти оптимальный код коррекции стирания, и предшественник кодов Фонтана
- Турбо-код
- код Уолша – Адамара
- Циклические проверки избыточности (CRC) могут исправлять 1-битные ошибки для сообщений не более 2 n - 1 - 1 { displaystyle 2 ^ {n-1} -1}
бит длиной для оптимальных порождающих полиномов степени n { displaystyle n}
, см. Математика циклических проверок избыточности # Битовые фильтры
См. Также
Ссылки
Дополнительная литература
- Clark, Jr., George C.; Каин, Дж. Бибб (1981). Кодирование с коррекцией ошибок для цифровой связи. Нью-Йорк, США: Plenum Press. ISBN 0-306-40615-2. ISBN 978-0-306-40615-7.
- Уикер, Стивен Б. (1995). Системы контроля ошибок для цифровой связи и хранения. Энглвуд Клиффс, Нью-Джерси, США: Прентис-Холл. ISBN 0-13-200809-2. ISBN 978-0-13-200809-9.
- Уилсон, Стивен Г. (1996). Цифровая модуляция и кодирование. Энглвуд Клиффс, Нью-Джерси, США: Прентис-Холл. ISBN 0-13-210071-1. ISBN 978-0-13-210071-7.
- "Код коррекции ошибок в одноуровневой ячейке NAND флэш-памяти « 16 февраля 2007 г.
- « Код исправления ошибок во флэш-памяти NAND » 29 ноября 2004 г.
- Наблюдения за ошибками, исправлениями и доверием зависимых систем, Джеймс Гамильтон, 26 февраля 2012 г.
- Сферические упаковки, решетки и группы, Дж. Х. Конвей, NJA Sloane, Springer Science Business Media, 9 марта 2013 г. - Математика - 682 страницы.
Внешние ссылки
Обнаружение ошибок в технике связи — действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) — процедура восстановления информации после чтения её из устройства хранения или канала связи.
Для обнаружения ошибок используют коды обнаружения ошибок, для исправления — корректирующие коды (коды, исправляющие ошибки, коды с коррекцией ошибок, помехоустойчивые коды).
Способы борьбы с ошибками[]
В процессе хранения данных и передачи информации по сетям связи неизбежно возникают ошибки. Контроль целостности данных и исправление ошибок — важные задачи на многих уровнях работы с информацией (в частности, физическом, канальном, транспортном уровнях модели OSI).
В системах связи возможны несколько стратегий борьбы с ошибками:
- обнаружение ошибок в блоках данных и автоматический запрос повторной передачи повреждённых блоков — этот подход применяется в основном на канальном и транспортном уровнях;
- обнаружение ошибок в блоках данных и отбрасывание повреждённых блоков — такой подход иногда применяется в системах потокового мультимедиа, где важна задержка передачи и нет времени на повторную передачу;
- исправление ошибок (forward error correction) применяется на физическом уровне.
Коды обнаружения и исправления ошибок[]
Корректирующие коды — коды, служащие для обнаружения или исправления ошибок, возникающих при передаче информации под влиянием помех, а также при её хранении.
Для этого при записи (передаче) в полезные данные добавляют специальным образом структурированную избыточную информацию (контрольное число), а при чтении (приёме) её используют для того, чтобы обнаружить или исправить ошибки. Естественно, что число ошибок, которое можно исправить, ограничено и зависит от конкретного применяемого кода.
С кодами, исправляющими ошибки, тесно связаны коды обнаружения ошибок. В отличие от первых, последние могут только установить факт наличия ошибки в переданных данных, но не исправить её.
В действительности, используемые коды обнаружения ошибок принадлежат к тем же классам кодов, что и коды, исправляющие ошибки. Фактически, любой код, исправляющий ошибки, может быть также использован для обнаружения ошибок (при этом он будет способен обнаружить большее число ошибок, чем был способен исправить).
По способу работы с данными коды, исправляющие ошибки делятся на блоковые, делящие информацию на фрагменты постоянной длины и обрабатывающие каждый из них в отдельности, и свёрточные, работающие с данными как с непрерывным потоком.
Блоковые коды[]
Пусть кодируемая информация делится на фрагменты длиной 



Если исходные 

Задать блоковый код можно по-разному, в том числе таблицей, где каждой совокупности из 

- способность исправлять как можно большее число ошибок,
- как можно меньшая избыточность,
- простота кодирования и декодирования.
Нетрудно видеть, что приведённые требования противоречат друг другу. Именно поэтому существует большое количество кодов, каждый из которых пригоден для своего круга задач.
Практически все используемые коды являются линейными. Это связано с тем, что нелинейные коды значительно сложнее исследовать, и для них трудно обеспечить приемлемую лёгкость кодирования и декодирования.
Линейные коды общего вида[]
Линейный блоковый код — такой код, что множество его кодовых слов образует 



Это значит, что операция кодирования соответствует умножению исходного 

Пусть 



Минимальное расстояние и корректирующая способность[]
-
Основная статья: Расстояние Хемминга
Расстоянием Хемминга (метрикой Хемминга) между двумя кодовыми словами 



Минимальное расстояние Хемминга 
, округляем «вниз», так чтобы
.
Корректирующая способность определяет, сколько ошибок передачи кода (типа 







Таким образом получив искажённый код из 


Поясним на примере. Предположим, что есть два кодовых слова 










Коды Хемминга[]
Коды Хемминга — простейшие линейные коды с минимальным расстоянием 3, то есть способные исправить одну ошибку. Код Хемминга может быть представлен в таком виде, что синдром
, где
— принятый вектор, будет равен номеру позиции, в которой произошла ошибка. Это свойство позволяет сделать декодирование очень простым.
Общий метод декодирования линейных кодов[]
Любой код (в том числе нелинейный) можно декодировать с помощью обычной таблицы, где каждому значению принятого слова 

Для линейных кодов этот метод можно существенно упростить. При этом для каждого принятого вектора 





Линейные циклические коды[]
Несмотря на то, что декодирование линейных кодов уже значительно проще декодирования большинства нелинейных, для большинства кодов этот процесс всё ещё достаточно сложен. Циклические коды, кроме более простого декодирования, обладают и другими важными свойствами.
Циклическим кодом является линейный код, обладающий следующим свойством: если 
Слова циклического кода удобно представлять в виде многочленов. Например, кодовое слово 



В дальнейшем, если не указано иное, мы будем считать, что циклический код является двоичным, то есть 
Порождающий (генераторный) полином[]
Можно показать, что все кодовые слова конкретного циклического кода кратны определённому порождающему полиному 

С помощью порождающего полинома осуществляется кодирование циклическим кодом. В частности:
Коды CRC[]
Коды CRC (cyclic redundancy check — циклическая избыточная проверка) являются систематическими кодами, предназначенными не для исправления ошибок, а для их обнаружения. Они используют способ систематического кодирования, изложенный выше: «контрольная сумма» вычисляется путем деления 

Таким образом, вид полинома 
| название кода | степень | полином |
|---|---|---|
| CRC-12 | 12 | 
|
| CRC-16 | 16 | 
|
| CRC-CCITT | 16 | 
|
| CRC-32 | 32 | 
|
Коды БЧХ[]
Коды Боуза — Чоудхури — Хоквингема (БЧХ) являются подклассом циклических кодов. Их отличительное свойство — возможность построения кода БЧХ с минимальным расстоянием не меньше заданного. Это важно, потому что, вообще говоря, определение минимального расстояния кода есть очень сложная задача.
Математически полинома 
Коды коррекции ошибок Рида — Соломона[]
Коды Рида — Соломона — недвоичные циклические коды, позволяющие исправлять ошибки в блоках данных. Элементами кодового вектора являются не биты, а группы битов (блоки). Очень распространены коды Рида-Соломона, работающие с байтами (октетами).
Математически коды Рида — Соломона являются кодами БЧХ.
Преимущества и недостатки блоковых кодов[]
Хотя блоковые коды, как правило, хорошо справляются с редкими, но большими пачками ошибок, их эффективность при частых, но небольших ошибках (например, в канале с АБГШ), менее высока.
Свёрточные коды[]
Файл:ECC NASA standard coder.png Свёрточный кодер (
Свёрточные коды, в отличие от блоковых, не делят информацию на фрагменты и работают с ней как со сплошным потоком данных.
Свёрточные коды, как правило, порождаются дискретной линейной инвариантной во времени системой. Поэтому, в отличие от большинства блоковых кодов, свёрточное кодирование — очень простая операция, чего нельзя сказать о декодировании.
Кодирование свёрточным кодом производится с помощью регистра сдвига, отводы от которого суммируются по модулю два. Таких сумм может быть две (чаще всего) или больше.
Декодирование свёрточных кодов, как правило, производится по алгоритму Витерби, который пытается восстановить переданную последовательность согласно критерию максимального правдоподобия.
Преимущества и недостатки свёрточных кодов[]
Свёрточные коды эффективно работают в канале с белым шумом, но плохо справляются с пакетами ошибок. Более того, если декодер ошибается, на его выходе всегда возникает пакет ошибок.
Каскадное кодирование. Итеративное декодирование[]
Преимущества разных способов кодирования можно объединить, применив каскадное кодирование. При этом информация сначала кодируется одним кодом, а затем другим, в результате получается код-произведение.
Например, популярной является следующая конструкция: данные кодируются кодом Рида-Соломона, затем перемежаются (при этом символы, расположенные близко, помещаются далеко друг от друга) и кодируются свёрточным кодом. На приёмнике сначала декодируется свёрточный код, затем осуществляется обратное перемежение (при этом пачки ошибок на выходе свёрточного декодера попадают в разные кодовые слова кода Рида — Соломона), и затем осуществляется декодирование кода Рида — Соломона.
Некоторые коды-произведения специально сконструированы для итеративного декодирования, при котором декодирование осуществляется в несколько проходов, каждый из которых использует информацию от предыдущего. Это позволяет добиться большой эффективности, однако, декодирование требует больших ресурсов. К таким кодам относят турбо-коды и LDPC-коды (коды Галлагера).
Оценка эффективности кодов[]
Эффективность кодов определяется количеством ошибок, которые тот может исправить, количеством избыточной информации, добавление которой требуется, а также сложностью реализации кодирования и декодирования (как аппаратной, так и в виде программы для ЭВМ).
Граница Хемминга и совершенные коды[]
-
Основная статья: Граница Хэмминга
Пусть имеется двоичный блоковый 

Коды, удовлетворяющие этой границе с равенством, называются совершенными. К совершенным кодам относятся, например, коды Хемминга. Часто применяемые на практике коды с большой корректирующей способностью (такие, как коды Рида — Соломона) не являются совершенными.
Энергетический выигрыш[]
При передаче информации по каналу связи вероятность ошибки зависит от отношения сигнал/шум на входе демодулятора, таким образом при постоянном уровне шума решающее значение имеет мощность передатчика. В системах спутниковой и мобильной, а также других типов связи остро стоит вопрос экономии энергии. Кроме того, в определённых системах связи (например, телефонной) неограниченно повышать мощность сигнала не дают технические ограничения.
Поскольку помехоустойчивое кодирование позволяет исправлять ошибки, при его применении мощность передатчика можно снизить, оставляя скорость передачи информации неизменной. Энергетический выигрыш определяется как разница отношений с/ш при наличии и отсутствии кодирования.
Применение кодов, исправляющих ошибки[]
Коды, исправляющие ошибки, применяются:
- в системах цифровой связи, в том числе: спутниковой, радиорелейной, сотовой, передаче данных по телефонным каналам.
- в системах хранения информации, в том числе магнитных и оптических.
Коды, обнаруживающие ошибки, применяются в сетевых протоколах различных уровней.
Автоматический запрос повторной передачи[]
Системы с автоматическим запросом повторной передачи (ARQ — Automatic Repeat reQuest) основаны на технологии обнаружения ошибок. Распространены следующие методы автоматического запроса:
Запрос ARQ с остановками (stop-and-wait ARQ)[]
Идея этого метода заключается в том, что передатчик ожидает от приемника подтверждения успешного приема предыдущего блока данных перед тем как начать передачу следующего. В случае, если блок данных был принят с ошибкой, приемник передает отрицательное подтверждение (negative acknowledgement, NAK), и передатчик повторяет передачу блока. Данный метод подходит для полудуплексного канала связи. Его недостатком является низкая скорость из-за высоких накладных расходов на ожидание.
Непрерывный запрос ARQ с возвратом (continuous ARQ with pullback)[]
Для этого метода необходим полнодуплексный канал. Передача данных от передатчика к приемнику производится одновременно. В случае ошибки передача возобновляется, начиная с ошибочного блока (то есть, передается ошибочный блок и все последующие).
Непрерывный запрос ARQ с выборочным повторением (continuous ARQ with selective repeat)[]
При этом подходе осуществляется передача только ошибочно принятых блоков данных.
См. также[]
- Цифровая связь
- Линейный код
- Циклический код
- Код Боуза — Чоудхури — Хоквингема
- Код Рида — Соломона
- LDPC
- Свёрточный код
- Турбо-код
Литература[]
- Мак-Вильямс Ф. Дж., Слоэн Н. Дж. А. Теория кодов, исправляющих ошибки. М.: Радио и связь, 1979.
- Блейхут Р. Теория и практика кодов, контролирующих ошибки. М.: Мир, 1986.
- Морелос-Сарагоса Р. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение. М.: Техносфера, 2005. — ISBN 5-94836-035-0
Ссылки[]
Имеется викиучебник по теме:
Обнаружение и исправление ошибок
- Помехоустойчивое кодирование (11 ноября 2001). — реферат по проблеме кодирования сообщений с исправлением ошибок. Проверено 25 декабря 2006.
Эта страница использует содержимое раздела Википедии на русском языке. Оригинальная статья находится по адресу: Обнаружение и исправление ошибок. Список первоначальных авторов статьи можно посмотреть в истории правок. Эта статья так же, как и статья, размещённая в Википедии, доступна на условиях CC-BY-SA .
Обнаружение ошибок в технике связи — действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) — процедура восстановления информации после чтения её из устройства хранения или канала связи.
Для обнаружения ошибок используют коды обнаружения ошибок, для исправления — корректирующие коды (коды, исправляющие ошибки, коды с коррекцией ошибок, помехоустойчивые коды).
Содержание
- 1 Способы борьбы с ошибками
- 2 Коды обнаружения и исправления ошибок
- 2.1 Блоковые коды
- 2.1.1 Линейные коды общего вида
- 2.1.1.1 Минимальное расстояние и корректирующая способность
- 2.1.1.2 Коды Хемминга
- 2.1.1.3 Общий метод декодирования линейных кодов
- 2.1.2 Линейные циклические коды
- 2.1.2.1 Порождающий (генераторный) полином
- 2.1.2.2 Коды CRC
- 2.1.2.3 Коды БЧХ
- 2.1.2.4 Коды коррекции ошибок Рида — Соломона
- 2.1.3 Преимущества и недостатки блоковых кодов
- 2.1.1 Линейные коды общего вида
- 2.2 Свёрточные коды
- 2.2.1 Преимущества и недостатки свёрточных кодов
- 2.3 Каскадное кодирование. Итеративное декодирование
- 2.4 Сетевое кодирование
- 2.5 Оценка эффективности кодов
- 2.5.1 Граница Хемминга и совершенные коды
- 2.5.2 Энергетический выигрыш
- 2.6 Применение кодов, исправляющих ошибки
- 2.1 Блоковые коды
- 3 Автоматический запрос повторной передачи
- 3.1 Запрос ARQ с остановками (stop-and-wait ARQ)
- 3.2 Непрерывный запрос ARQ с возвратом (continuous ARQ with pullback)
- 3.3 Непрерывный запрос ARQ с выборочным повторением (continuous ARQ with selective repeat)
- 4 См. также
- 5 Литература
- 6 Ссылки
[править] Способы борьбы с ошибками
В процессе хранения данных и передачи информации по сетям связи неизбежно возникают ошибки. Контроль целостности данных и исправление ошибок — важные задачи на многих уровнях работы с информацией (в частности, физическом, канальном, транспортном уровнях сетевой модели OSI).
В системах связи возможны несколько стратегий борьбы с ошибками:
- обнаружение ошибок в блоках данных и автоматический запрос повторной передачи повреждённых блоков — этот подход применяется, в основном, на канальном и транспортном уровнях;
- обнаружение ошибок в блоках данных и отбрасывание повреждённых блоков — такой подход иногда применяется в системах потокового мультимедиа, где важна задержка передачи и нет времени на повторную передачу;
- исправление ошибок (англ. forward error correction) применяется на физическом уровне.
[править] Коды обнаружения и исправления ошибок
Корректирующие коды — коды, служащие для обнаружения или исправления ошибок, возникающих при передаче информации под влиянием помех, а также при её хранении.
Для этого при записи (передаче) в полезные данные добавляют специальным образом структурированную избыточную информацию (контрольное число), а при чтении (приёме) её используют для того, чтобы обнаружить или исправить ошибки. Естественно, что число ошибок, которое можно исправить, ограничено и зависит от конкретного применяемого кода.
С кодами, исправляющими ошибки, тесно связаны коды обнаружения ошибок. В отличие от первых, последние могут только установить факт наличия ошибки в переданных данных, но не исправить её.
В действительности, используемые коды обнаружения ошибок принадлежат к тем же классам кодов, что и коды, исправляющие ошибки. Фактически любой код, исправляющий ошибки, может быть также использован для обнаружения ошибок (при этом он будет способен обнаружить большее число ошибок, чем был способен исправить).
По способу работы с данными коды, исправляющие ошибки, делятся на блоковые, делящие информацию на фрагменты постоянной длины и обрабатывающие каждый из них в отдельности, и свёрточные, работающие с данными как с непрерывным потоком.
[править] Блоковые коды
Пусть кодируемая информация делится на фрагменты длиной 



Если исходные 

Задать блоковый код можно по-разному, в том числе таблицей, где каждой совокупности из 

- способность исправлять как можно большее число ошибок,
- как можно меньшая избыточность,
- простота кодирования и декодирования.
Нетрудно видеть, что приведённые требования противоречат друг другу. Именно поэтому существует большое количество кодов, каждый из которых пригоден для своего круга задач.
Практически все используемые коды являются линейными. Это связано с тем, что нелинейные коды значительно сложнее исследовать, и для них трудно обеспечить приемлемую лёгкость кодирования и декодирования.
[править] Линейные коды общего вида
Линейный блоковый код — такой код, что множество его кодовых слов образует 



Это значит, что операция кодирования соответствует умножению исходного 

Пусть 



[править] Минимальное расстояние и корректирующая способность
Расстоянием Хемминга (метрикой Хемминга) между двумя кодовыми словами 

.
Минимальное расстояние Хемминга 
.
Корректирующая способность определяет, сколько ошибок передачи кода (типа 







Таким образом, получив искажённую кодовую комбинацию из 


Поясним на примере. Предположим, что есть два кодовых слова 










[править] Коды Хемминга
Коды Хемминга — простейшие линейные коды с минимальным расстоянием 3, то есть способные исправить одну ошибку. Код Хемминга может быть представлен в таком виде, что синдром
, где
— принятый вектор, будет равен номеру позиции, в которой произошла ошибка. Это свойство позволяет сделать декодирование очень простым.
[править] Общий метод декодирования линейных кодов
Любой код (в том числе нелинейный) можно декодировать с помощью обычной таблицы, где каждому значению принятого слова 

Для линейных кодов этот метод можно существенно упростить. При этом для каждого принятого вектора 





[править] Линейные циклические коды
Несмотря на то, что декодирование линейных кодов значительно проще декодирования большинства нелинейных, для большинства кодов этот процесс всё ещё достаточно сложен. Циклические коды, кроме более простого декодирования, обладают и другими важными свойствами.
Циклическим кодом является линейный код, обладающий следующим свойством: если 
Слова циклического кода удобно представлять в виде многочленов. Например, кодовое слово 



В дальнейшем, если не указано иное, мы будем считать, что циклический код является двоичным, то есть 
[править] Порождающий (генераторный) полином
Можно показать, что все кодовые слова конкретного циклического кода кратны определённому порождающему полиному 

С помощью порождающего полинома осуществляется кодирование циклическим кодом. В частности:
[править] Коды CRC
Коды CRC (англ. cyclic redundancy check — циклическая избыточная проверка) являются систематическими кодами, предназначенными не для исправления ошибок, а для их обнаружения. Они используют способ систематического кодирования, изложенный выше: «контрольная сумма» вычисляется путем деления 

Таким образом, вид полинома 
| название кода | степень | полином |
|---|---|---|
| CRC-12 | 12 |  |
| CRC-16 | 16 |  |
| CRC-CCITT | 16 |  |
| CRC-32 | 32 |  |
[править] Коды БЧХ
Коды Боуза — Чоудхури — Хоквингема (БЧХ) являются подклассом циклических кодов. Их отличительное свойство — возможность построения кода БЧХ с минимальным расстоянием не меньше заданного. Это важно, потому что, вообще говоря, определение минимального расстояния кода есть очень сложная задача.
Математически полинома 
[править] Коды коррекции ошибок Рида — Соломона
Коды Рида — Соломона — недвоичные циклические коды, позволяющие исправлять ошибки в блоках данных. Элементами кодового вектора являются не биты, а группы битов (блоки). Очень распространены коды Рида-Соломона, работающие с байтами (октетами).
Математически коды Рида — Соломона являются кодами БЧХ.
[править] Преимущества и недостатки блоковых кодов
Хотя блоковые коды, как правило, хорошо справляются с редкими, но большими пачками ошибок, их эффективность при частых, но небольших ошибках (например, в канале с АБГШ), менее высока.
[править] Свёрточные коды
Свёрточные коды, в отличие от блоковых, не делят информацию на фрагменты и работают с ней как со сплошным потоком данных.
Свёрточные коды, как правило, порождаются дискретной линейной инвариантной во времени системой. Поэтому, в отличие от большинства блоковых кодов, свёрточное кодирование — очень простая операция, чего нельзя сказать о декодировании.
Кодирование свёрточным кодом производится с помощью регистра сдвига, отводы от которого суммируются по модулю два. Таких сумм может быть две (чаще всего) или больше.
Декодирование свёрточных кодов, как правило, производится по алгоритму Витерби, который пытается восстановить переданную последовательность согласно критерию максимального правдоподобия.
[править] Преимущества и недостатки свёрточных кодов
Свёрточные коды эффективно работают в канале с белым шумом, но плохо справляются с пакетами ошибок. Более того, если декодер ошибается, на его выходе всегда возникает пакет ошибок.
[править] Каскадное кодирование. Итеративное декодирование
Преимущества разных способов кодирования можно объединить, применив каскадное кодирование. При этом информация сначала кодируется одним кодом, а затем другим, в результате получается код-произведение.
Например, популярной является следующая конструкция: данные кодируются кодом Рида-Соломона, затем перемежаются (при этом символы, расположенные близко, помещаются далеко друг от друга) и кодируются свёрточным кодом. На приёмнике сначала декодируется свёрточный код, затем осуществляется обратное перемежение (при этом пачки ошибок на выходе свёрточного декодера попадают в разные кодовые слова кода Рида — Соломона), и затем осуществляется декодирование кода Рида — Соломона.
Некоторые коды-произведения специально сконструированы для итеративного декодирования, при котором декодирование осуществляется в несколько проходов, каждый из которых использует информацию от предыдущего. Это позволяет добиться большой эффективности, однако декодирование требует больших ресурсов. К таким кодам относят турбо-коды и LDPC-коды (коды Галлагера).
[править] Сетевое кодирование
[править] Оценка эффективности кодов
Эффективность кодов определяется количеством ошибок, которые тот может исправить, количеством избыточной информации, добавление которой требуется, а также сложностью реализации кодирования и декодирования (как аппаратной, так и в виде программы для ЭВМ).
[править] Граница Хемминга и совершенные коды
Пусть имеется двоичный блоковый 

Коды, удовлетворяющие этой границе с равенством, называются совершенными. К совершенным кодам относятся, например, коды Хемминга. Часто применяемые на практике коды с большой корректирующей способностью (такие, как коды Рида — Соломона) не являются совершенными.
[править] Энергетический выигрыш
При передаче информации по каналу связи вероятность ошибки зависит от отношения сигнал/шум на входе демодулятора, таким образом, при постоянном уровне шума решающее значение имеет мощность передатчика. В системах спутниковой и мобильной, а также других типов связи остро стоит вопрос экономии энергии. Кроме того, в определённых системах связи (например, телефонной) неограниченно повышать мощность сигнала не дают технические ограничения.
Поскольку помехоустойчивое кодирование позволяет исправлять ошибки, при его применении мощность передатчика можно снизить, оставляя скорость передачи информации неизменной. Энергетический выигрыш определяется как разница отношений с/ш при наличии и отсутствии кодирования.
[править] Применение кодов, исправляющих ошибки
Коды, исправляющие ошибки, применяются:
- в системах цифровой связи, в том числе: спутниковой, радиорелейной, сотовой, передаче данных по телефонным каналам.
- в системах хранения информации, в том числе магнитных и оптических.
Коды, обнаруживающие ошибки, применяются в сетевых протоколах различных уровней.
[править] Автоматический запрос повторной передачи
Системы с автоматическим запросом повторной передачи (ARQ — Automatic Repeat reQuest) основаны на технологии обнаружения ошибок. Распространены следующие методы автоматического запроса:
[править] Запрос ARQ с остановками (stop-and-wait ARQ)
Идея этого метода заключается в том, что передатчик ожидает от приемника подтверждения успешного приема предыдущего блока данных перед тем, как начать передачу следующего. В случае, если блок данных был принят с ошибкой, приемник передает отрицательное подтверждение (negative acknowledgement, NAK), и передатчик повторяет передачу блока. Данный метод подходит для полудуплексного канала связи. Его недостатком является низкая скорость из-за высоких накладных расходов на ожидание.
[править] Непрерывный запрос ARQ с возвратом (continuous ARQ with pullback)
Для этого метода необходим полнодуплексный канал. Передача данных от передатчика к приемнику производится одновременно. В случае ошибки передача возобновляется, начиная с ошибочного блока (то есть передается ошибочный блок и все последующие).
[править] Непрерывный запрос ARQ с выборочным повторением (continuous ARQ with selective repeat)
При этом подходе осуществляется передача только ошибочно принятых блоков данных.
[править] См. также
- Цифровая связь
- Код ответа (Код причины завершения)
- Линейный код
- Циклический код
- Код Боуза — Чоудхури — Хоквингема
- Код Рида — Соломона
- LDPC
- Свёрточный код
- Турбо-код
[править] Литература
- Блейхут Р. Теория и практика кодов, контролирующих ошибки = Theory and Practice of Error Control Codes. — М.: Мир, 1986. — 576 с.
- Мак-Вильямс Ф. Дж., Слоэн Н. Дж. А. Теория кодов, исправляющих ошибки. М.: Радио и связь, 1979.
- Морелос-Сарагоса Р. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение / пер. с англ. В. Б. Афанасьева. — М.: Техносфера, 2006. — 320 с. — (Мир связи). — 2000 экз. — ISBN 5-94836-035-0
[править] Ссылки
- Помехоустойчивое кодирование (11 ноября 2001). — реферат по проблеме кодирования сообщений с исправлением ошибок. Архивировано из первоисточника 25 августа 2011. Проверено 25 декабря 2006.


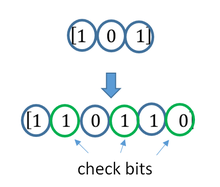

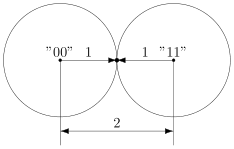

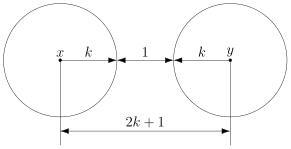







 .
. .
. , где
, где  — принятый вектор, будет равен номеру позиции, в которой произошла ошибка. Это свойство позволяет сделать декодирование очень простым.
— принятый вектор, будет равен номеру позиции, в которой произошла ошибка. Это свойство позволяет сделать декодирование очень простым.