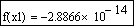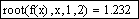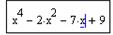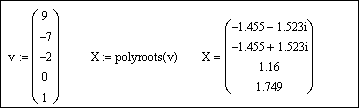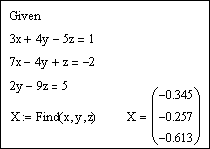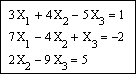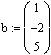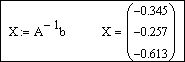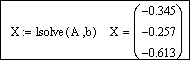|
0 / 0 / 0 Регистрация: 12.05.2015 Сообщений: 10 |
|
|
1 |
|
Ошибка — эта переменная не определена. Как исправить08.01.2017, 20:05. Показов 66894. Ответов 16
Добрый день.
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
08.01.2017, 20:05 |
|
16 |
|
Модератор 5104 / 3915 / 1349 Регистрация: 30.07.2012 Сообщений: 11,726 |
|
|
08.01.2017, 20:11 |
2 |
|
Nikon19, везде вместо = (символа эквивалентности) поставьте := (символ присваивания). И будет Вам счастье…
1 |
|
0 / 0 / 0 Регистрация: 12.05.2015 Сообщений: 10 |
|
|
08.01.2017, 20:17 [ТС] |
3 |
|
Менял на символ присваивания, после чего такая ошибка возникает внутри самой формулы(сначала пишет, что не определена M,например).
0 |
|
Модератор 5104 / 3915 / 1349 Регистрация: 30.07.2012 Сообщений: 11,726 |
|
|
08.01.2017, 20:18 |
4 |
|
Nikon19, файл в архив и сюда… (НЕ КАРТИНКУ)
0 |
|
0 / 0 / 0 Регистрация: 12.05.2015 Сообщений: 10 |
|
|
08.01.2017, 20:21 [ТС] |
5 |
|
Здесь уже поменял обратно на символ присваивания.
0 |
|
Модератор 5104 / 3915 / 1349 Регистрация: 30.07.2012 Сообщений: 11,726 |
|
|
08.01.2017, 20:36 |
6 |
|
РешениеNikon19, Вам надо объявить еще одну функцию, имя которой Вы используете в последней функции… (желтый фон). Как-то так…
1 |
|
0 / 0 / 0 Регистрация: 12.05.2015 Сообщений: 10 |
|
|
08.01.2017, 20:47 [ТС] |
7 |
|
Большое спасибо! Миниатюры
0 |
|
Модератор 5104 / 3915 / 1349 Регистрация: 30.07.2012 Сообщений: 11,726 |
|
|
08.01.2017, 20:56 |
8 |
|
Nikon19, так Вам надо просто построить график ОПРЕДЕЛЕННОГО вида ИЛИ решить какую-то конкретную задачу и посмотреть, какой график получится? Уточните, пожалуйста.
0 |
|
0 / 0 / 0 Регистрация: 12.05.2015 Сообщений: 10 |
|
|
08.01.2017, 21:08 [ТС] |
9 |
|
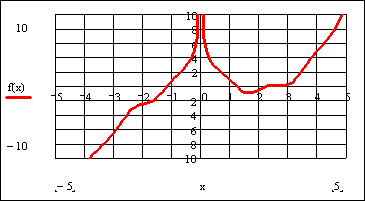
Есть пример, в рамках которого получено значение вероятности безотказной работы программы. Формула расчета в маткаде представлена. Необходимо построить график (вида как экспоненциальный) в зависимости от времени, но проблема в том, что t=20 в этом примере.
0 |
|
44 / 1 / 0 Регистрация: 14.06.2014 Сообщений: 150 |
|
|
12.09.2017, 15:43 |
10 |
|
Привет всем!
0 |
|
2154 / 1506 / 766 Регистрация: 25.12.2016 Сообщений: 4,285 |
|
|
12.09.2017, 16:02 |
11 |
|
Nikon19, экспонента так получается,аргумент надо поменять Миниатюры
0 |
|
0 / 0 / 0 Регистрация: 16.10.2021 Сообщений: 3 |
|
|
16.10.2021, 19:47 |
12 |
|
ошибка при построении графика (эта переменная не определена)
0 |
|
2154 / 1506 / 766 Регистрация: 25.12.2016 Сообщений: 4,285 |
|
|
16.10.2021, 20:01 |
13 |
|
wern, график ниже опустите.
1 |
|
0 / 0 / 0 Регистрация: 16.10.2021 Сообщений: 3 |
|
|
16.10.2021, 20:11 |
14 |
|
т.е проблема только в положении графика относительно матриц? я передвинул и все получилось, спасибо большое
0 |
|
2154 / 1506 / 766 Регистрация: 25.12.2016 Сообщений: 4,285 |
|
|
16.10.2021, 20:19 |
15 |
|
т.е проблема только в положении графика относительно матриц? да,так и есть.
1 |
|
0 / 0 / 0 Регистрация: 16.10.2021 Сообщений: 3 |
|
|
16.10.2021, 20:34 |
16 |
|
прошу прощения, а что делать когда появляется ошибка «формы этих значений должны совпадать. Это значение имеет форму Unitless а другие имеют форму: [] Unitless»
0 |
|
2154 / 1506 / 766 Регистрация: 25.12.2016 Сообщений: 4,285 |
|
|
16.10.2021, 20:40 |
17 |
|
wern, десятичная точка в маткаде применяется,а не запятая. Изображения
0 |
Перейти к контенту
|
0 / 0 / 0 Регистрация: 12.05.2015 Сообщений: 10 |
|
|
1 |
|
Ошибка — эта переменная не определена. Как исправить08.01.2017, 20:05. Показов 59554. Ответов 16
Добрый день.
__________________ 0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
08.01.2017, 20:05 |
|
16 |
|
Модератор 5033 / 3864 / 1327 Регистрация: 30.07.2012 Сообщений: 11,440 |
|
|
08.01.2017, 20:11 |
2 |
|
Nikon19, везде вместо = (символа эквивалентности) поставьте := (символ присваивания). И будет Вам счастье… 1 |
|
0 / 0 / 0 Регистрация: 12.05.2015 Сообщений: 10 |
|
|
08.01.2017, 20:17 [ТС] |
3 |
|
Менял на символ присваивания, после чего такая ошибка возникает внутри самой формулы(сначала пишет, что не определена M,например). 0 |
|
Модератор 5033 / 3864 / 1327 Регистрация: 30.07.2012 Сообщений: 11,440 |
|
|
08.01.2017, 20:18 |
4 |
|
Nikon19, файл в архив и сюда… (НЕ КАРТИНКУ) 0 |
|
0 / 0 / 0 Регистрация: 12.05.2015 Сообщений: 10 |
|
|
08.01.2017, 20:21 [ТС] |
5 |
|
Здесь уже поменял обратно на символ присваивания. 0 |
|
Модератор 5033 / 3864 / 1327 Регистрация: 30.07.2012 Сообщений: 11,440 |
|
|
08.01.2017, 20:36 |
6 |
|
РешениеNikon19, Вам надо объявить еще одну функцию, имя которой Вы используете в последней функции… (желтый фон). Как-то так… 1 |
|
0 / 0 / 0 Регистрация: 12.05.2015 Сообщений: 10 |
|
|
08.01.2017, 20:47 [ТС] |
7 |
|
Большое спасибо! Миниатюры
0 |
|
Модератор 5033 / 3864 / 1327 Регистрация: 30.07.2012 Сообщений: 11,440 |
|
|
08.01.2017, 20:56 |
8 |
|
Nikon19, так Вам надо просто построить график ОПРЕДЕЛЕННОГО вида ИЛИ решить какую-то конкретную задачу и посмотреть, какой график получится? Уточните, пожалуйста. 0 |
|
0 / 0 / 0 Регистрация: 12.05.2015 Сообщений: 10 |
|
|
08.01.2017, 21:08 [ТС] |
9 |
|
Есть пример, в рамках которого получено значение вероятности безотказной работы программы. Формула расчета в маткаде представлена. Необходимо построить график (вида как экспоненциальный) в зависимости от времени, но проблема в том, что t=20 в этом примере. 0 |
|
44 / 1 / 0 Регистрация: 14.06.2014 Сообщений: 150 |
|
|
12.09.2017, 15:43 |
10 |
|
Привет всем! 0 |
|
2049 / 1437 / 730 Регистрация: 25.12.2016 Сообщений: 4,039 |
|
|
12.09.2017, 16:02 |
11 |
|
Nikon19, экспонента так получается,аргумент надо поменять Миниатюры
0 |
|
0 / 0 / 0 Регистрация: 16.10.2021 Сообщений: 3 |
|
|
16.10.2021, 19:47 |
12 |
|
ошибка при построении графика (эта переменная не определена) 0 |
|
2049 / 1437 / 730 Регистрация: 25.12.2016 Сообщений: 4,039 |
|
|
16.10.2021, 20:01 |
13 |
|
wern, график ниже опустите. 1 |
|
0 / 0 / 0 Регистрация: 16.10.2021 Сообщений: 3 |
|
|
16.10.2021, 20:11 |
14 |
|
т.е проблема только в положении графика относительно матриц? я передвинул и все получилось, спасибо большое 0 |
|
2049 / 1437 / 730 Регистрация: 25.12.2016 Сообщений: 4,039 |
|
|
16.10.2021, 20:19 |
15 |
|
т.е проблема только в положении графика относительно матриц? да,так и есть. 1 |
|
0 / 0 / 0 Регистрация: 16.10.2021 Сообщений: 3 |
|
|
16.10.2021, 20:34 |
16 |
|
прошу прощения, а что делать когда появляется ошибка «формы этих значений должны совпадать. Это значение имеет форму Unitless а другие имеют форму: [] Unitless» 0 |
|
2049 / 1437 / 730 Регистрация: 25.12.2016 Сообщений: 4,039 |
|
|
16.10.2021, 20:40 |
17 |
|
wern, десятичная точка в маткаде применяется,а не запятая. Изображения
0 |
-
nikanto
- Сообщения: 6
- Зарегистрирован: Пт ноя 22, 2013 8:10 pm
Find эта переменная не определена
Всем доброго времени суток. Пытаюсь решить СЛУ при помощи given-find в mathcad 14.
Когда ввожу find, оператор выделяется красным с примечанием переменная не определена. Все переменные вроде как задал. Подскажите пожалуйста в чем проблема?
Заранее спасибо за помощь!
-
Korobov V I
- Сообщения: 1609
- Зарегистрирован: Вт янв 21, 2003 5:12 pm
Re: Find эта переменная не определена
Сообщение Korobov V I » Сб ноя 23, 2013 2:09 pm
nikanto писал(а):Всем доброго времени суток. Пытаюсь решить СЛУ при помощи given-find в mathcad 14.
Когда ввожу find, оператор выделяется красным с примечанием переменная не определена. Все переменные вроде как задал. Подскажите пожалуйста в чем проблема?
Заранее спасибо за помощь!
1. В девятом уравнении переменная «c» набрана в русской раскладке клавиатуры.
2. Вместо функции Find примените функцию Minerr.
-
nikanto
- Сообщения: 6
- Зарегистрирован: Пт ноя 22, 2013 8:10 pm
Re: Find эта переменная не определена
Сообщение nikanto » Сб ноя 23, 2013 7:11 pm
Korobov V I писал(а):1. В девятом уравнении переменная «c» набрана в русской раскладке клавиатуры.
2. Вместо функции Find примените функцию Minerr.
спасибо букву исправил, но minerr не помог. Ничего не происходит =( просто равно появляется и все…
-
nikanto
- Сообщения: 6
- Зарегистрирован: Пт ноя 22, 2013 8:10 pm
Сообщение nikanto » Вс ноя 24, 2013 1:34 am
а у меня после равно прямоугольничек черный. как место для цифры. Ладно, спасибо и на этом
-
Vladimir__
- Сообщения: 1660
- Зарегистрирован: Вс дек 21, 2003 8:52 am
Сообщение Vladimir__ » Вс ноя 24, 2013 2:36 pm
nikanto писал(а):а у меня после равно прямоугольничек черный. как место для цифры. Ладно, спасибо и на этом
А какую версию Mathcad вы используете?
-
nikanto
- Сообщения: 6
- Зарегистрирован: Пт ноя 22, 2013 8:10 pm
Сообщение nikanto » Вс ноя 24, 2013 2:49 pm
Mathcad 14. Еще я попробовал подставить полученные значения в систему и равенство не выполняется. Наверное, я не до конца понимаю способ работы этих операторов. Количество неизвестных равно количеству уравнений. Зачем я задаю в начале приближенные значения? Разве здесь нужны итерации? Хотел избежать решения на листочках и трехэтажных подстановок, но, видимо не удастся =(
-
Vladimir__
- Сообщения: 1660
- Зарегистрирован: Вс дек 21, 2003 8:52 am
Сообщение Vladimir__ » Пн ноя 25, 2013 8:59 am
nikanto писал(а):Mathcad 14. Еще я попробовал подставить полученные значения в систему и равенство не выполняется. Наверное, я не до конца понимаю способ работы этих операторов. Количество неизвестных равно количеству уравнений. Зачем я задаю в начале приближенные значения? Разве здесь нужны итерации? Хотел избежать решения на листочках и трехэтажных подстановок, но, видимо не удастся =(
1. Обновите версию до последнего сервис релиза Mathcad 15 M020.
2. Подробнее про работу функцию «Minerr«:
http://www.exponenta.ru/soft/mathcad/us … 5/15_3.asp
http://www.sistemair.ru/dok/mathcad/text/index5-10.html
-
nikanto
- Сообщения: 6
- Зарегистрирован: Пт ноя 22, 2013 8:10 pm
Сообщение nikanto » Вт ноя 26, 2013 2:12 am
Обновил. Minerr заработал. Только я так и не понял, как получить решение этой системы. То, что в табличке — это не корни.
-
VFO
- Сообщения: 4227
- Зарегистрирован: Ср фев 27, 2002 8:03 pm
Re: Find эта переменная не определена
Сообщение VFO » Вт ноя 26, 2013 8:11 am
[quote=»nikanto»]Всем доброго времени суток. Пытаюсь решить СЛУ при помощи given-find в mathcad 14.
quote]
А почему вы не используете функцию lsolve
-
nikanto
- Сообщения: 6
- Зарегистрирован: Пт ноя 22, 2013 8:10 pm
Re: Find эта переменная не определена
Сообщение nikanto » Ср ноя 27, 2013 11:03 am
VFO писал(а):quote]
А почему вы не используете функцию lsolve
Я до этого не пользовался Mathcad и на поисковый запрос «решение системы уравнений Mathcad» мне попалась функция Find. Хотел заставить комп решить мне уравнения, в итоге сижу решаю на листах, ибо так быстрее =)
MathCad 7.0 Professional – универсальный инструмент для работы с формулами, графиками и текстами. Он обладает мощными вычислительными функциями и возможностью аналитических преобразований.

Инструкция
MathCad обрабатывает документ слева направо и сверху вниз. Поэтому, задав значение переменной, можно будет использовать ее во всех дальнейших вычислениях. Чтобы определить переменную, введите ее имя. Символом присваивания является знак «двоеточия». После него укажите конкретное значение, которое вы хотите присвоить переменной.
К переменной можно приравнивать определенное число, числовое выражение, формулу из других переменных, заданных ранее. Пусть, например, необходимо определить переменную quantity, равную 50. Введите с клавиатуры текст: «quantity:50». На экране отобразится «quantity:=50». В арифметическом меню программы есть специальная кнопка присваивания := .
Если вы хотите изменить значение quantity, сотрите клавишей BackSpace 50 и введите нужное выражение или число. Нажмите Enter и переменная примет новое значение. Изменятся также значения всех переменных, каким-либо образом зависящих от quantity. Если MathCad обнаружит некорректную операцию (к примеру, деление на ноль), выражение окрасится в красный цвет, рядом с оператором появится сообщение-подсказка.
Пусть теперь нужно вычислить значение функции для переменной function. При этом сама функция зависит от переменной quantity: function=sin(1/2*quantity). Присвойте function данное выражение: function:=sin(1/2*quantity). После запуска программы на экране появится результат.
Все вычисления в MathCad можно сопровождать комментариями и пояснениями. Щелкните в свободном месте экрана мышкой, нажмите Insert и выберите Text Region в строке меню. В появившейся текстовой рамке начните ввод текста. Для ввода второй строки нажмите Enter и продолжите набирать текст. Так, операцию присваивания вы можете сопроводить комментарием типа «x равно 6». Комментировать можно любой шаг программы. В некоторых случаях это очень помогает человеку, работающему с кодом, понять суть происходящего и не запутаться в алгоритме.
Источники:
- по каким переменным for
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Что ж, хотя мы уже немало всего успели обсудить насчет программирования в такой замечательной математической среде, как MathCAD, еще немало весьма существенных тем осталось за кадром. И, пожалуй, самая существенная из них — это взаимодействие начинающего программиста, пишущего программы в MathCAD’е, и ошибок в его программах. Именно на ней мы с вами сейчас и остановимся.
В общем-то, если сказать, что ошибки никто не любит, это будет не так уж далеко от истины. Точнее, никто не любит собственные ошибки. Чужие любят все, а не только экзаменаторы и разнообразные инспекторы. Однако, к сожалению, при программировании (а написание небольших вспомогательных программок в MathCAD’е, как я уже когда-то давно тому назад говорил, это тоже программирование) ошибки попросту неизбежны. Даже самые лучшие программисты совершают ежедневно множество ошибок, и никто, в общем-то, за это не применяет к ним особых санкций. Существует даже такое мнение, что программа без ошибок совершенно бесполезна — если в ней нет ошибок, значит, в ней нет и никакой полезной функциональности, потому что не ошибается только тот, кто ничего не делает. Так что ошибки в программах — это вполне естественные спутники каждого, кто пишет даже самые маленькие программки, а потому и бояться их не следует. Тем не менее, с ошибками в программах можно и нужно бороться. И для этого существуют специальные средства, некоторые из которых доступны и тем, кто пишет программы в MathCAD’е. Однако, прежде чем рассказывать о том, что это за средства, и как ими нужно пользоваться, нужно, как мне лично кажется, поговорить еще немного о том, вокруг чего будет сосредоточена наша борьба — то есть о самих ошибках.
Классификация ошибок
Поскольку, как я уже говорил, ошибки довольно многочисленны, их имеет смысл классифицировать. Сделать это стоит, в общем-то, уже хотя бы попросту потому, что разные виды ошибок требуют различных к себе подходов, и их устранение требует вложения различного количества труда того, кто писал программу.
Самые простые ошибки — синтаксические. Как вы уже имели возможность воочию убедиться, при программировании очень важно придерживаться определенных правил в записи конструкций. Например, если вы вместо имени функции rkfixed напишете в программе tkfixed, ошибившись при вводе на одну букву и нажав на соседнюю с r клавишу t, то как раз и получите в свое распоряжение самую что ни на есть классическую синтаксическую ошибку. Ни к каким особенно страшным последствиям она (как, впрочем, и все другие ошибки аналогичного класса) не приведет: программа просто не сможет быть выполнена по той причине, что MathCAD не сможет найти функцию, которую вы ему указали. Искать такие ошибки тоже совсем не сложно — они всегда хорошо видны, поскольку даже сама среда подсвечивает их, чтобы можно было найти особенно быстро. Исправлять, соответственно, тоже очень просто: достаточно записать идентификатор правильно, и все в программе станет на положенные места. MathCAD, кстати, избавляет пользователя от множества таких ошибок благодаря необходимости вводить все операторы, управляющие ходом программы, с помощью специальных горячих клавиш или соответствующих кнопок на панели инструментов Программирование. Если бы их нужно было, напротив, набирать вручную с клавиатуры, то и возможности сделать синтаксическую ошибку были бы несравнимо шире.
Второй тип ошибок — ошибки алгоритмические. Это такие ошибки, которые, в принципе, не мешают выполнению программы, но делают результаты такого выполнения полностью лишенными всякого смысла. Многие из таких ошибок — банальные опечатки: там, где нужно было поставить плюс, вы, например, поставили в спешке минус или же сделали что-нибудь другое примерно в таком же духе. Конечно, сказать, что алгоритмические ошибки — это сплошь и рядом одни только опечатки, было бы, мягко говоря, не до конца верно. Потому что очень многие из них являются следствием недостаточности знаний писавшего программу — то есть если ошибочно составлена сама последовательность действий, которые должен сделать MathCAD для того, чтобы вы могли получить интересующий вас результат. Еще великое множество алгоритмических ошибок — результат банальной невнимательности: например, присвоение значения не той переменной, ее необнуление либо, например, вывод не той переменной в качестве результата выполнения вашей программы. В общем-то, именно об алгоритмических ошибках мы с вами сейчас и будем говорить более подробно. Однако есть еще один, особенно неприятный, тип ошибок.
Третий тип — это ошибки мистические. Да-да, именно мистические, я не оговорился. Какие именно это ошибки? Это ошибки, имеющие совершенно непонятную природу и столь же непонятный способ лечения — как правило, это проявления ошибок не в вашей программе, а в каком-то из внутренних компонентов MathCAD’а. К сожалению, эти ошибки, в «большом» программировании встречающиеся не так уж, в общем-то, и часто, в MathCAD’е не такие уж редкие гости. Отчасти это объясняется тем, что MathCAD — это все-таки средство расчетов, а не программирования, которое играет в этой среде второстепенную и вспомогательную роль, но, конечно, когда реально сталкиваешься с такими вот мистическими ошибками, это все не слишком успокаивает. Хотя поначалу почти все ошибки в программах кажутся мистическими, на самом деле большая их часть все-таки имеет рациональную природу. Если же природа появившейся ошибки вам совершенно непонятна, то вам следует коренным образом перестроить структуру программы или хотя бы тот ее фрагмент, в котором локализовалось проявление этой ошибки. Практически во всех случаях этот не слишком хитрый прием позволяет полностью избавить программу от досадной непонятной ошибки.
Что ж, о самих ошибках мы с вами, можно считать, побеседовали. Теперь давайте, пожалуй, перейдем к тому, какими именно способами можно бороться с самыми распространенными из них — то есть алгоритмическими. Об остальных, в общем-то, я уже довольно подробно все рассказал, а вот что касается алгоритмических ошибок, то здесь нужно будет в большинстве случаев прибегнуть к помощи специализированных встроенных в MathCAD инструментов.
Отладка в MathCAD’е
Процесс поиска и устранения алгоритмических ошибок называется по-русски отладкой. По-английски этот же самый процесс называется debugging, то есть, если дословно, «избавление от жучков». В общем-то, и по-русски довольно часто можно услышать термины «дебагинг» или «баг», однако во избежание путаницы мы будем использовать слово «отладка» (если, конечно, не возражаете). Кстати, история возникновения английского термина весьма любопытна, и, вполне возможно, вы ее слышали. Первые компьютеры были машинами весьма громоздкими и дорогостоящими, а потому и всевозможные поломки для них были делом далеко не просто устранимым. Когда выяснилось, что причиной очередной поломки стал жучок, забравшийся внутрь компьютера и вызвавший замыкание, в счете за ремонт записали: «debugging». Рука шутника оказалась легкой — термин, как видите, прижился и используется на протяжении уже многих десятилетий.
В чем же заключается процесс отладки? На самом деле ничего особенно таинственного и трудного для понимания здесь нет. Просто во время отладки у вас есть возможность выполнять программу не сразу «залпом», как это происходит обычно, а пошагово, то есть выполнять последовательно друг за другом каждую строчку программы, делая, когда нужно, паузы для осмысления работы программы и просмотра промежуточных значений каждой из переменных. Отладка используется при разработке любых программ, а потому и создатели MathCAD включили поддержку этого удобного и, в общем-то, достаточно универсального средства выявления ошибок в свой программный продукт. Доступ к инструментам, используемым при отладке программ в MathCAD’е, осуществляется через подпункт Debug меню Tools в главном рабочем окне MathCAD’а (см. соответствующий скриншот).
Стоит отметить, что, поскольку MathCAD — это среда, ориентированная не на программирование, а на различные вычислительные действия, то отладка в ней имеет более широкое применение, чем только отладка программ, которые пишет пользователь. Отлаживать можно и все вычисления даже в том случае, если они выполняются без применения какого-либо программирования с вашей стороны. В общем-то, поскольку такая возможность будет весьма полезной для большинства читателей не столько при программировании в MathCAD’е, сколько при обычных вычислениях, то именно с такой позиции мы с вами и станем рассматривать отладку в этой мощной математической среде. Нам также понадобится панель отладки. Ее включают так же, как все остальные панели инструментов, в меню View -> Toolbars. Конечно, эта панель, как вы могли уже заметить, дублирует отладочное меню в Tools -> Debug, однако, думаю, нажать на кнопку, расположенную на этой панели, будет все-таки проще и быстрее, чем искать соответствующий пункт в надежно спрятанном от пользователя меню.
При переходе в отладочный режим (кнопка либо пункт меню Toggle Debug Mode) внешний вид главного окна MathCAD’а меняется (см. скриншот): внизу появляется специальное окно, используемое для просмотра промежуточной отладочной информации. Оно называется Trace Window.
Однако о том, что именно отображается в этом самом окне, а также о том, что от нас требуется сделать с документом перед тем, как его можно будет уже полноценно отлаживать, мы с вами поговорим, пожалуй, в следующий раз, чтобы не перегружать вас разнообразной полезной информацией. Сейчас же подведем итоги разговора про ошибки, возникающие в процессе написания программ в математической среде MathCAD.
Выводы
Как видите, ошибок в программах действительно бояться не следует. Это вполне нормальная составляющая процесса программирования, неизбежно проявляющаяся в каждом из результатов этого процесса. Тем не менее, с ошибками можно и нужно бороться, и с большинством из них это можно производить с весьма высокой вероятностью достижения успеха. Хотя, конечно же, встречаются и такие ошибки, с которыми трудно будет разобраться даже тому, кто на программировании, что называется, собаку съел. Но все-таки они встречаются не так уж часто. Так что в программировании, если вы хотите избежать мучений, связанных с поиском ошибок, очень важна ваша внимательность. Если вы будете достаточно внимательны при написании программы, то риск допустить ошибку будет сравнительно невелик. Впрочем, это правило применимо не только к программированию.
SF, spaceflyer@tut.by
Компьютерная газета. Статья была опубликована в номере 42 за 2008 год в рубрике soft
Содержание
- MathCad | ANSYS CFX | MS Office
- Поиск по сайту
- Выбор языка
- Решение уравнений в MathCad
- Рекомендуем к прочтению
MathCad | ANSYS CFX | MS Office
Поиск по сайту
Выбор языка

Часто в курсовом проекте, либо в лабораторной работе встает вопрос о решении какого-либо сложного большого уравнения с одним неизвестным. Не всегда хочется тратить 10 — 20 минут на рутинные преобразования в процессе которых, велика вероятность допущения ошибки. Целесообразно воспользоваться математической программой (в данном случае MathCad), которая быстро и правильно сможет дать ответ. Мы рассмотрим пример использования 2-ух способов решения уравнений, причем как в числах так и в символьном виде.
Способ №1: использование вычислительного блока Given — Find:
Это наиболее распространенный способ решения обычных алгебраических уравнений. Он достаточно прост. В рабочем поле записываем первое слово Given. Это служебное слово. Оно «подключает» определенные программные модули mathcad, необходимые для решения уравнения. Эти модули в своем составе содержат основные численные методы решения: метод бисекции, простой итерации и пр. Далее пишется наше уравнение в любом — явном или неявном виде. Само уравнение набирается с клавиатуры с использованием логического символа «равно». На панельке Boolean (Булева алгебра) он выделен жирным шрифтом (см. рис. 1).

Далее пишется слово Find(x) (где х — переменная). Это функция, которая и получает ответ. Функцию Find(x) можно присвоить какой-либо переменной и использовать далее в расчетах. Для получения результата, после Find(x) следует поставить символ «→» либо «=» (см. рис. 2).

В зависимости от сложности уравнения через некоторое время MathCad выведет результат.
Возможности MathCad позволяют определить корень как в численном виде (т. е. результат решения уравнения представляет собой число) так и в символьном (результат — выражение). Для численного определения корня необходимо задать (определить) ВСЕ переменные входящие в уравнение и даже искомую переменную. MathCad воспринимает задание искомой переменной как начальное приближение корня. Крайне важно задаться начальным приближением, поскольку без него корень уравнения невозможно определить в силу особенностей используемых численных методов. Нужно отметить, что некорректное задание начального приближения часто становится причиной получения неверного результата либо его отсутствия вообще. Но не стоит забывать также и о том, что корня может не быть, потому что само уравнение его не имеет.
В том случае, если необходимо решить уравнение относительно какой-либо переменной в символьном виде, то нет необходимости задаваться значениями всех входящих в уравнение параметров и начальным приближением переменной. В этом случае достаточно ввести уравнение (также через «жирное равно») и после оператора Find(x) поставить «→». При этом будут работать уже другие функции MathCad, которые заточены под символьное преобразование и упрощение выражений. Результатом решения будет выражение. Стоит отметить, что MathCad сможет записать решение далеко не всякого уравнения. В этом смысле его возможности ограничены.
Для подтверждения и закрепления выше сказанного, Вам предлагается скачать и познакомиться с примерами решения уравнений как в численном так и в символьном виде.
Пример №1. Решение уравнения в MathCad с помощью блока Given Find численно: Скачать
Пример №2. Решение уравнения в MathCad с помощью блока Given Find символьно: Скачать
Способ №2: Применение метода solve:
Этот метод по существу не отличается от выше рассмотренного, поскольку процедура нахождения корня аналогична. Разница лишь в оформлении. В этом случае наше уравнение записывается без операторов Given и Find. После ввода уравнения на панели Symbolic нажимаем кнопку solve (см. рис. 3), определяем через запятую искомую переменную, жмем «→» и получаем ответ.

Иногда, то что не получается найти с помощью Given Find получается в solve.
Пример №3. Решение уравнения в MathCad с помощью solve: Скачать
РЕШЕНИЕ УРАВНЕНИЙ И СИСТЕМ УРАВНЕНИЙ
4 Решение уравнений и систем средствами Mathcad
Система Mathcad обладает широкими возможностями численного решения уравнений и систем уравнений.
Функция root, блоки Given…Find, Given…Minerr
В ходе численного решения обычно выделяют два этапа:
- отделение корней – определение интервала нахождения каждого корня или определение приблизительного значения корня. В системе Mathcad наиболее наглядным будет отделение корней уравнения графическим способом;
- уточнение корней – нахождение численного значения корня с указанной точностью.
Точность нахождения корня устанавливается с помощью системной переменной TOL (Convergence Tolerance – Допуск сходимости), которая по умолчанию равна 10 -3 . Чем меньше значение TOL, тем точнее, вообще говоря, находится корень уравнения. Однако оптимальным является TOL = 10 -5 . Переопределить значение TOL можно в окне математических свойств документа Math Options на вкладке Build-In Variables (Встроенные переменные) или присваиванием, например, TOL:=0.0001.
Для решения одного уравнения с одной неизвестной предназначена встроенная функция root, которая в общем виде задается
root(f(x), x, [a, b])
и возвращает значение переменной x, при котором функция f(x) обращается в ноль. Аргументы функции root:
- f(x) – функция левой части уравнения f(x) = 0;
- x – переменная, относительно которой требуется решить уравнение;
- a, b (необязательные) – действительные числа, такие что a -1 слева: A -1 Ax=A -1 b. Учитывая, что A -1 A, вектор-столбец решений системы можно искать в виде
Этот прием используется в Mathcad так:
- задается матрица коэффициентов при неизвестных системы A;
- задается столбец свободных членов b;
- вводится формула для нахождения решения системы X:=A -1 b;
- выводится вектор решений системы X=.
Кроме того, пакет Mathcad имеет встроенную функцию
lsolve(A, b),
возвращающую вектор-столбец решений системы линейных алгебраических уравнений. Аргументами функции lsolve являются матрица коэффициентов при неизвестных системы и столбец свободных членов. Порядок решения аналогичен рассмотренному, но вместо формулы X:=A -1 b используется X:=lsolve(A, b).
Реализовать широко известный метод Гаусса решения систем линейных уравнений позволяет встроенная функция rref(M), возвращающая ступенчатый вид матрицы M. Если в качестве аргумента взять расширенную матрицу системы, то в результате применения rref получится матрица, на диагонали которой – единицы, а последний столбец представляет собой столбец решений системы.
Решение системы линейных уравнений можно осуществить с помощью блоков Given…Find, Given…Minerr. При этом неизвестным системы задается произвольное начальное приближение, а проверка необязательна.
Порядок выполнения лабораторной работы
- Загрузить Mathcad Start / All Programs / Mathsoft Apps / Mathcad (Пуск / Все программы / Mathsoft Apps / Mathcad).
- Сохранить в личной папке на диске z: новый документ с именем ФИО1, лучше использовать латинские буквы. Производить сохранение регулярно в процессе работы (Ctrl + S).
- Вставить текстовую область Insert / Text Region (Вставка / Область текста) и ввести в поле документа текст:
Лабораторная работа № 4
Решение уравнений и систем в Mathcad.
- В новой текстовой области ввести фамилию, имя, отчество, учебный шифр и номер варианта.
- Выполнить задание 1.
Задание 1. Решить уравнение 
Решение.
Решение данного уравнения будем проводить в два этапа: отделение корней уравнения графически, уточнение корней уравнения.
Определим функцию f(x), равную левой части данного уравнения, когда правая равна нулю:
Зададим ранжированную переменную x на некотором диапазоне с мелким шагом, например:
Вставим в документ графическую область. Для этого выберем дважды пиктограмму с изображением графика 
Снизу по оси абсцисс наберем x, а сбоку по оси ординат введем f(x).
Для появления графика щелкнем левой клавишей мыши вне графической области.
Отформатируем график функции f(x). Для этого щелкнем правой клавишей мыши в области графика и выберем в контекстном меню команду Format (Формат). Установим пересечение осей графика (Crossed – Только оси), добавим вспомогательные линии по координатным осям (Grid Lines – Вспомогательные линии). Отменим при этом автосетку (Autogrid – Автосетка) и установим количество линий сетки, равное 10.
Для подтверждения внесенных изменений нажмем последовательно кнопки Apply (Применить) и ОК.
После указанных преобразований график функции f(x) будет выглядеть следующим образом:
Из графика функции f(x) видно, что уравнение 
Этап отделения корней завершен.
Уточним теперь корни уравнения с помощью функции root.
Присвоим начальное приближение переменной x и укажем точность поиска корня:
Уточним заданное приближение к значению корня с помощью функции root:
Выполним проверку, подтверждающую, что первый корень найден с заявленной точностью:
Начальное приближение можно не задавать при использовании в качестве аргументов root границ отрезка нахождения корня, например, второй корень можно уточнить:
Задание 2. Решить уравнение 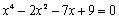
Решение.
Напечатаем левую часть уравнения, не приравнивая выражение к 0, и выделим синим курсором переменную x:
Выберем из главного меню Symbolics / Polynomial Coefficients (Символика / Коэффициенты полинома). Появившийся вектор коэффициентов полинома выделим целиком синим курсором и вырежем в буфер обмена, используя кнопку Вырезать 
Напечатаем v := и вставим вектор из буфера обмена, используя кнопку Вставить 
Для получения результата напечатаем polyroots(v) =:
Задание 3. Решить систему линейных уравнений 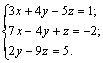
Решение.
1-й способ. Использование блока Given … Find.
Зададим всем неизвестным, входящим в систему уравнений, произвольные начальные приближения, например:
Напечатаем слово Given. Установим визир ниже и наберем уравнения системы, каждое в своем блоке. Используем при этом логический знак равенства (Ctrl + =).
После ввода уравнений системы напечатаем X := Find(x, y, z) и получим решение системы в виде вектора, состоящего из трех элементов:
Сделаем проверку, подставив полученные значения неизвестных в уравнения системы, например, следующим образом
После набора знака «=» в каждой строке должен быть получен результат, равный или приблизительно равный правой части системы. В данном примере системная переменная ORIGIN = 1.
2-й способ. Использование блока Given…Minerr.
Порядок решения системы этим способом аналогичен порядку использования блока Given … Find и представлен ниже вместе с проверкой:
3-й способ. Решение системы линейных уравнений матричным способом.
Создадим матрицу А, состоящую из коэффициентов при неизвестных системы. Для этого напечатаем A := , вызовем окно создания массивов (Ctrl + M). Число строк (Rows) и столбцов (Columns) матрицы данной системы равно 3. Заполним пустые места шаблона матрицы коэффициентами при неизвестных системы, как показано ниже:
Зададим вектор b свободных членов системы. Сначала напечатаем b :=, затем вставим шаблон матрицы(Ctrl + M), где количество строк (Rows) равно 3, а количество столбцов (Columns) равно 1. Заполним его:
Решим систему матричным способом по формуле
Решим систему с помощью функции lsolve:
Для проверки правильности решения системы, полученного матричным способом, достаточно вычислить произведение A·X, которое должно совпасть с вектором-столбцом свободных членов b:
программирование mathcad скалярный трехмерный
Функция Find (Найти) работает в ключевой связке с ключевым словом Given (Дано). Конструкция Given — Find использует расчетную методику, основанную на поиске корня вблизи точки начального приближения, заданной пользователем.
Если задано уравнение f(x) = 0, то его можно решить следующим образом с помощью блока Given — Find:
— задать начальное приближение
— ввести служебное слово
- — записать уравнение, используя знак боулево равно
- — написать функцию find с неизвестной переменной в качестве параметра
В результате после знака равно выведется найденный корень.
Если существует несколько корней, то их можно найти, меняя начальное приближение х0 на близкое к искомому корню.
В Mathcad можно писать программы двух видов
- 1)в виде скриптов(последовательность команд)
- 2)в виде настоящих программ с входными и выходными параметрами.
Mathcad — система компьютерной алгебры из класса систем автоматизированного проектирования, ориентированная на подготовку интерактивных документов с вы0числениями и визуальным сопровождением, отличается легкостью использования и применения для коллективной работы.
Mathcad был задуман и первоначально написан Алленом Раздовом из Массачусетского технологического института (MIT).
Mathcad имеет интуитивный и простой для использования интерфейс пользователя. Для ввода формул и данных можно использовать как клавиатуру, так и специальные панели инструментов.
Работа осуществляется в пределах рабочего листа, на котором уравнения и выражения отображаются графически, в противовес текстовой записи в языках программирования. При создании документов-приложений используется принцип WYSIWYG (What You See Is What You Get — «что видишь, то и получаешь»).
Несмотря на то, что эта программа в основном ориентирована на пользователей-непрограммистов, Mathcad также используется в сложных проектах, чтобы визуализировать результаты математического моделирования, путем использования распределённых вычислений и традиционных языков программирования. Также Mathcad часто используется в крупных инженерных проектах, где большое значение имеет трассируемость и соответствие стандартам.
Mathcad достаточно удобно использовать для обучения, вычислений и инженерных расчетов. Открытая архитектура приложения в сочетании с поддержкой технологий .NET и XML позволяют легко интегрировать Mathcad практически в любые ИТ-структуры и инженерные приложения. Есть возможность создания электронных книг (e-Book).
Программа содержит сотни операторов и встроенных функций для решения различных технических задач. Программа позволяет выполнять численные и символьные вычисления, производить операции с скалярными величинами, векторами и матрицами, автоматически переводить одни единицы измерения в другие.
Mathcad find переменная не определена
MathCad | ANSYS CFX | MS Office
Поиск по сайту
Выбор языка
Решение уравнений в MathCad
Часто в курсовом проекте, либо в лабораторной работе встает вопрос о решении какого-либо сложного большого уравнения с одним неизвестным. Не всегда хочется тратить 10 — 20 минут на рутинные преобразования в процессе которых, велика вероятность допущения ошибки. Целесообразно воспользоваться математической программой (в данном случае MathCad), которая быстро и правильно сможет дать ответ. Мы рассмотрим пример использования 2-ух способов решения уравнений, причем как в числах так и в символьном виде.
Способ №1: использование вычислительного блока Given — Find:
Это наиболее распространенный способ решения обычных алгебраических уравнений. Он достаточно прост. В рабочем поле записываем первое слово Given. Это служебное слово. Оно «подключает» определенные программные модули mathcad, необходимые для решения уравнения. Эти модули в своем составе содержат основные численные методы решения: метод бисекции, простой итерации и пр. Далее пишется наше уравнение в любом — явном или неявном виде. Само уравнение набирается с клавиатуры с использованием логического символа «равно». На панельке Boolean (Булева алгебра) он выделен жирным шрифтом (см. рис. 1).
Рис. 1. Панель «Булевая алгебра»
Далее пишется слово Find(x) (где х — переменная). Это функция, которая и получает ответ. Функцию Find(x) можно присвоить какой-либо переменной и использовать далее в расчетах. Для получения результата, после Find(x) следует поставить символ «→» либо «=» (см. рис. 2).
Рис. 2. Панель «Вычисления»
В зависимости от сложности уравнения через некоторое время MathCad выведет результат.
Возможности MathCad позволяют определить корень как в численном виде (т. е. результат решения уравнения представляет собой число) так и в символьном (результат — выражение). Для численного определения корня необходимо задать (определить) ВСЕ переменные входящие в уравнение и даже искомую переменную. MathCad воспринимает задание искомой переменной как начальное приближение корня. Крайне важно задаться начальным приближением, поскольку без него корень уравнения невозможно определить в силу особенностей используемых численных методов. Нужно отметить, что некорректное задание начального приближения часто становится причиной получения неверного результата либо его отсутствия вообще. Но не стоит забывать также и о том, что корня может не быть, потому что само уравнение его не имеет.
В том случае, если необходимо решить уравнение относительно какой-либо переменной в символьном виде, то нет необходимости задаваться значениями всех входящих в уравнение параметров и начальным приближением переменной. В этом случае достаточно ввести уравнение (также через «жирное равно») и после оператора Find(x) поставить «→». При этом будут работать уже другие функции MathCad, которые заточены под символьное преобразование и упрощение выражений. Результатом решения будет выражение. Стоит отметить, что MathCad сможет записать решение далеко не всякого уравнения. В этом смысле его возможности ограничены.
Для подтверждения и закрепления выше сказанного, Вам предлагается скачать и познакомиться с примерами решения уравнений как в численном так и в символьном виде.
Пример №1. Решение уравнения в MathCad с помощью блока Given Find численно: Скачать
Пример №2. Решение уравнения в MathCad с помощью блока Given Find символьно: Скачать
Способ №2: Применение метода solve:
Этот метод по существу не отличается от выше рассмотренного, поскольку процедура нахождения корня аналогична. Разница лишь в оформлении. В этом случае наше уравнение записывается без операторов Given и Find. После ввода уравнения на панели Symbolic нажимаем кнопку solve (см. рис. 3), определяем через запятую искомую переменную, жмем «→» и получаем ответ.
Рис. 3. Панель «Символьные»
Иногда, то что не получается найти с помощью Given Find получается в solve.
Пример №3. Решение уравнения в MathCad с помощью solve: Скачать
РЕШЕНИЕ УРАВНЕНИЙ И СИСТЕМ УРАВНЕНИЙ
4 Решение уравнений и систем средствами Mathcad
Система Mathcad обладает широкими возможностями численного решения уравнений и систем уравнений.
Функция root, блоки Given…Find, Given…Minerr
В ходе численного решения обычно выделяют два этапа:
- отделение корней – определение интервала нахождения каждого корня или определение приблизительного значения корня. В системе Mathcad наиболее наглядным будет отделение корней уравнения графическим способом;
- уточнение корней – нахождение численного значения корня с указанной точностью.
Точность нахождения корня устанавливается с помощью системной переменной TOL (Convergence Tolerance – Допуск сходимости), которая по умолчанию равна 10 -3 . Чем меньше значение TOL, тем точнее, вообще говоря, находится корень уравнения. Однако оптимальным является TOL = 10 -5 . Переопределить значение TOL можно в окне математических свойств документа Math Options на вкладке Build-In Variables (Встроенные переменные) или присваиванием, например, TOL:=0.0001.
Для решения одного уравнения с одной неизвестной предназначена встроенная функция root, которая в общем виде задается
root(f(x), x, [a, b])
и возвращает значение переменной x, при котором функция f(x) обращается в ноль. Аргументы функции root:
- f(x) – функция левой части уравнения f(x) = 0;
- x – переменная, относительно которой требуется решить уравнение;
- a, b (необязательные) – действительные числа, такие что a -1 слева: A -1 Ax=A -1 b. Учитывая, что A -1 A, вектор-столбец решений системы можно искать в виде
Этот прием используется в Mathcad так:
- задается матрица коэффициентов при неизвестных системы A;
- задается столбец свободных членов b;
- вводится формула для нахождения решения системы X:=A -1 b;
- выводится вектор решений системы X=.
Кроме того, пакет Mathcad имеет встроенную функцию
lsolve(A, b),
возвращающую вектор-столбец решений системы линейных алгебраических уравнений. Аргументами функции lsolve являются матрица коэффициентов при неизвестных системы и столбец свободных членов. Порядок решения аналогичен рассмотренному, но вместо формулы X:=A -1 b используется X:=lsolve(A, b).
Реализовать широко известный метод Гаусса решения систем линейных уравнений позволяет встроенная функция rref(M), возвращающая ступенчатый вид матрицы M. Если в качестве аргумента взять расширенную матрицу системы, то в результате применения rref получится матрица, на диагонали которой – единицы, а последний столбец представляет собой столбец решений системы.
Решение системы линейных уравнений можно осуществить с помощью блоков Given…Find, Given…Minerr. При этом неизвестным системы задается произвольное начальное приближение, а проверка необязательна.
Порядок выполнения лабораторной работы
- Загрузить Mathcad Start / All Programs / Mathsoft Apps / Mathcad (Пуск / Все программы / Mathsoft Apps / Mathcad).
- Сохранить в личной папке на диске z: новый документ с именем ФИО1, лучше использовать латинские буквы. Производить сохранение регулярно в процессе работы (Ctrl + S).
- Вставить текстовую область Insert / Text Region (Вставка / Область текста) и ввести в поле документа текст:
Лабораторная работа № 4
Решение уравнений и систем в Mathcad.
- В новой текстовой области ввести фамилию, имя, отчество, учебный шифр и номер варианта.
- Выполнить задание 1.
Задание 1. Решить уравнение .
Решение.
Решение данного уравнения будем проводить в два этапа: отделение корней уравнения графически, уточнение корней уравнения.
Определим функцию f(x), равную левой части данного уравнения, когда правая равна нулю:
Зададим ранжированную переменную x на некотором диапазоне с мелким шагом, например:
Вставим в документ графическую область. Для этого выберем дважды пиктограмму с изображением графика сначала на панели Math (Математика), затем на палитре графиков Graph или выполним из главного меню последовательность команд Insert / Graph / X-Y Plot (Вставка / График / X-Y Зависимость).
Снизу по оси абсцисс наберем x, а сбоку по оси ординат введем f(x).
Для появления графика щелкнем левой клавишей мыши вне графической области.
Отформатируем график функции f(x). Для этого щелкнем правой клавишей мыши в области графика и выберем в контекстном меню команду Format (Формат). Установим пересечение осей графика (Crossed – Только оси), добавим вспомогательные линии по координатным осям (Grid Lines – Вспомогательные линии). Отменим при этом автосетку (Autogrid – Автосетка) и установим количество линий сетки, равное 10.
Для подтверждения внесенных изменений нажмем последовательно кнопки Apply (Применить) и ОК.
После указанных преобразований график функции f(x) будет выглядеть следующим образом:
Из графика функции f(x) видно, что уравнение имеет три корня, которые приблизительно равны: x1 ≈ -1; x2 ≈ 1; x3 ≈ 2,5.
Этап отделения корней завершен.
Уточним теперь корни уравнения с помощью функции root.
Присвоим начальное приближение переменной x и укажем точность поиска корня:
Уточним заданное приближение к значению корня с помощью функции root:
Выполним проверку, подтверждающую, что первый корень найден с заявленной точностью:
Начальное приближение можно не задавать при использовании в качестве аргументов root границ отрезка нахождения корня, например, второй корень можно уточнить:
Задание 2. Решить уравнение .
Решение.
Напечатаем левую часть уравнения, не приравнивая выражение к 0, и выделим синим курсором переменную x:
Выберем из главного меню Symbolics / Polynomial Coefficients (Символика / Коэффициенты полинома). Появившийся вектор коэффициентов полинома выделим целиком синим курсором и вырежем в буфер обмена, используя кнопку Вырезать на панели инструментов Formatting (Форматирование) или комбинацию клавиш Ctrl + X.
Напечатаем v := и вставим вектор из буфера обмена, используя кнопку Вставить на панели инструментов или комбинацию клавиш Ctrl + V.
Для получения результата напечатаем polyroots(v) =:
Задание 3. Решить систему линейных уравнений Сделать проверку.
Решение.
1-й способ. Использование блока Given … Find.
Зададим всем неизвестным, входящим в систему уравнений, произвольные начальные приближения, например:
Напечатаем слово Given. Установим визир ниже и наберем уравнения системы, каждое в своем блоке. Используем при этом логический знак равенства (Ctrl + =).
После ввода уравнений системы напечатаем X := Find(x, y, z) и получим решение системы в виде вектора, состоящего из трех элементов:
Сделаем проверку, подставив полученные значения неизвестных в уравнения системы, например, следующим образом
После набора знака «=» в каждой строке должен быть получен результат, равный или приблизительно равный правой части системы. В данном примере системная переменная ORIGIN = 1.
2-й способ. Использование блока Given…Minerr.
Порядок решения системы этим способом аналогичен порядку использования блока Given … Find и представлен ниже вместе с проверкой:
3-й способ. Решение системы линейных уравнений матричным способом.
Создадим матрицу А, состоящую из коэффициентов при неизвестных системы. Для этого напечатаем A := , вызовем окно создания массивов (Ctrl + M). Число строк (Rows) и столбцов (Columns) матрицы данной системы равно 3. Заполним пустые места шаблона матрицы коэффициентами при неизвестных системы, как показано ниже:
Зададим вектор b свободных членов системы. Сначала напечатаем b :=, затем вставим шаблон матрицы(Ctrl + M), где количество строк (Rows) равно 3, а количество столбцов (Columns) равно 1. Заполним его:
Решим систему матричным способом по формуле
Решим систему с помощью функции lsolve:
Для проверки правильности решения системы, полученного матричным способом, достаточно вычислить произведение A·X, которое должно совпасть с вектором-столбцом свободных членов b:
программирование mathcad скалярный трехмерный
Функция Find (Найти) работает в ключевой связке с ключевым словом Given (Дано). Конструкция Given — Find использует расчетную методику, основанную на поиске корня вблизи точки начального приближения, заданной пользователем.
Если задано уравнение f(x) = 0, то его можно решить следующим образом с помощью блока Given — Find:
— задать начальное приближение
— ввести служебное слово
- — записать уравнение, используя знак боулево равно
- — написать функцию find с неизвестной переменной в качестве параметра
В результате после знака равно выведется найденный корень.
Если существует несколько корней, то их можно найти, меняя начальное приближение х0 на близкое к искомому корню.
В Mathcad можно писать программы двух видов
- 1)в виде скриптов(последовательность команд)
- 2)в виде настоящих программ с входными и выходными параметрами.
Mathcad — система компьютерной алгебры из класса систем автоматизированного проектирования, ориентированная на подготовку интерактивных документов с вы0числениями и визуальным сопровождением, отличается легкостью использования и применения для коллективной работы.
Mathcad был задуман и первоначально написан Алленом Раздовом из Массачусетского технологического института (MIT).
Mathcad имеет интуитивный и простой для использования интерфейс пользователя. Для ввода формул и данных можно использовать как клавиатуру, так и специальные панели инструментов.
Работа осуществляется в пределах рабочего листа, на котором уравнения и выражения отображаются графически, в противовес текстовой записи в языках программирования. При создании документов-приложений используется принцип WYSIWYG (What You See Is What You Get — «что видишь, то и получаешь»).
Несмотря на то, что эта программа в основном ориентирована на пользователей-непрограммистов, Mathcad также используется в сложных проектах, чтобы визуализировать результаты математического моделирования, путем использования распределённых вычислений и традиционных языков программирования. Также Mathcad часто используется в крупных инженерных проектах, где большое значение имеет трассируемость и соответствие стандартам.
Mathcad достаточно удобно использовать для обучения, вычислений и инженерных расчетов. Открытая архитектура приложения в сочетании с поддержкой технологий .NET и XML позволяют легко интегрировать Mathcad практически в любые ИТ-структуры и инженерные приложения. Есть возможность создания электронных книг (e-Book).
Программа содержит сотни операторов и встроенных функций для решения различных технических задач. Программа позволяет выполнять численные и символьные вычисления, производить операции с скалярными величинами, векторами и матрицами, автоматически переводить одни единицы измерения в другие.
Урок 5. Переменные и функции в Mathcad
Возможности Mathcad можно в полной мере оценить только при использовании переменных и функций.
Два знака равенства
В выражениях Вам необходимо использовать числа (константы), переменные, операторы и знаки равенства. В повседневной жизни мы используем знак равенства = для различных операций. Mathcad, однако, различает эти операции. Наиболее важные из них:
- определение (присвоить значение) – вводится через двоеточие [:]
- вычисление – вводится через знак равенства [=]
Оператор определения не менее важен, чем оператор вычисления. Значение выражения y можно отобразить только после присвоения ему какого-либо значения. x и y здесь являются переменными.
Введите следующие выражения:
Эти два знака равенства принципиально различны, поэтому их не следует путать.
Поместите курсор перед числом 4 в первом выражении:
Удалите число 4 с помощью клавиши [Delete] и введите 5. Щелкните по пустой области и убедитесь, что результат третьего выражения изменился на 25:
Попробуйте удалить число 25. Вы увидите, что при первом нажатии число станет красным, а при повторном нажатии удалится 25 и знак равенства:
Использование переменных
Введите следующие выражения:
Попробуйте изменить значение x на 100, 0.5, -4 и 0:
Первые два случая дадут в результате число. При -4 получится мнимое число. Да, Mathcadможет работать и с такими числами. При нуле программа выдаст ошибку, а результат будет обведен красным. Если Вы щелкните по неправильному выражению, то получите описание, что может быть не так:
Теперь о том, какие имена можно и нельзя использовать для переменных. Есть несколько правил: имя переменной не может начинаться с цифры и в имени переменной нельзя использовать пробелы и знаки операторов. Имена переменных могут начинаться:
- с любой строчной или прописной буквы
- другие символы, если они не являются операторами
- символы с вкладки Математика –> Операторы и символы –> Символы
- символы из Таблицы символов Windows
Вот несколько примеров:
Переменные можно использовать, только если они были определены ранее. «Ранее» означает, что объявление переменной должно располагать выше или левее выражения, где она используется. Если переменная не объявлена, появится сообщение об ошибке:
Подстрочные индексы
В Mathcad есть два различных вида подстрочных индекса для переменных:
- Описательный подстрочный индекс.
- Индекс массива (матрицы).
Чтобы набрать описательный подстрочный индекс, введите имя переменной, нажмите [Ctrl+-] и наберите подстрочный индекс:
Переменная с описательным подстрочным индексом – это обычная переменная, со своим именем. Индекс массива существенно отличается от него. Этот индекс можно ввести, нажав открывающую квадратную скобку [ после имени переменной. У переменной может быть один или два индекса массива:
Индекс массива должен быть числом. При этом не следует путать виды подстрочных индексов, т.к. они выглядят практически идентично:
Разница видна при щелчке мышью по выражению:
У переменной может быть сразу описательный индекс и индекс массива. Сначала всегда идет описательный индекс:
Функции
Переменные можно использовать, только если они были определены ранее. Однако есть одно важное исключение – определение функции. Можно определить собственную функцию, как на примере ниже:
Переменная a является локальной для функции. Она не определена за пределами функции:
Если Вы определили a до определения функции, значение a не будет изменено в процессе вычисления значения функции.
Внимание: если Вы дали переменной такое же имя, как и функции, Вы больше не сможете использовать эту функцию. У переменной и функции должны быть разные имена:
Этой проблемы можно избежать, задав для переменной и функции разные обозначения. Об этом мы поговорим в уроке 10 «Обозначения и единицы измерения».
Функции могут содержать две и более переменной:
Здесь значения переменных xи yтакже не изменяются при вычислении функции.
Встроенные функции
В Mathcad есть большое число встроенных функций. Зайдите на вкладку Функции:
Список всех функций можно увидеть, щелкнув по кнопке Все функции.
Заметьте, что тригонометрические функции принимаю в качестве аргумента угол в радианах, а не в градусах. Для использования градусов используйте символ с вкладки Математика –> Операторы и символы –> Символы:
Математика в тексте
В текст можно вставить математическую область. Таким образом, можно использовать над- и подстрочные символы в тексте. Для этого при редактировании текстовой области нажмите кнопку Математика с вкладки Математика –> Области:
Функции и переменные в MathСad
Mathcad раскрывается в полной мере при использовании переменных и функций.
Два знака равенства
В математических вычислениях мы используем множество различных констант, переменных, операторов и знаков равенства. Обычно в жизни мы используем знак равенства для многих разных операций, но Mathcad отличает их. Наиболее важными операциями являются:
- определение (присвоение значения) — используется двоеточие;
- вычисление — используется знак равенства.
Важность оператора определения не меньше, чем важность оператора вычисления. В приведенном ниже примере значение y можно вычислить лишь после присвоения ему определенного значения. х и у здесь являются переменными.
Два знака равенства, которые изображены выше, имеют совершенно разные значения, поэтому нужно очень внимательно относится к ним.
Поставьте курсор перед числом 4 в примере выше.
Удалите число 4 клавишей [Delete], и введите 5. Нажмите на пустой области, чтобы выйти из области вычисления и увидите, что результат вычислений поменялся на 25:
Теперь попробуйте провести операцию удаления с числом 25. Вы увидите, что при попытке удаления число подсвечивается красным, а при следующем нажатии удалиться и знак равно.
Использование переменных
Введите такие выражения в область вычисления
Проведите операции замены значения х на такие: 100, 0.5, -4 и 0.
В первых двух случаях вы получите число в качестве результата. В третьем случае у вас будет мнимое число. При значении х ноль программа выведет ошибку и обведет результат красным. Если вы нажмете на красное выделение, то увидите описание проблемы:
Дальше мы поговорим о том, какие имена можно использовать для переменных, а какие нельзя. Существуют такие правила: имя переменной не может начинаться с цифры и в ней нельзя использовать пробелы или знаки операторов. Имена могут начинаться:
- с любой буквы как большой, так и маленькой;
- с других символов, которые не являются операторами;
- с символов из вкладки Математика -> Операторы и символы -> Символы;
- с символов из таблицы символов ОС Windows.
Использование переменных доступно, только если вы определите их заранее. Термин «заранее» обозначает, что присвоение значения переменной должно производиться выше или левее выражения, где эта переменная используется. Если вы не объявили переменную заранее, то появится сообщение об ошибке:
Подстрочные индексы
Mathcad существует два типа подстрочных индексов:
- Описательный подстрочный индекс.
- Индекс массива (матрицы).
Для ввода описательного индекса сначала введите желаемое имя переменной, а потом нажмите комбинацию [Ctrl+-], далее вводите подстрочный индекс.
Переменная, которая имеет описательный индекс — это простая переменная, которой присвоено имя. Индекс массива сильно отличается от него. Такой индекс можно присвоить, если ввести квадратную скобку [ после имени переменной. Переменная может иметь один или два индекса массива:
Индекс массива может иметь только числовое значение. При этом не путайте разные типы индексов, так как они довольно схожи визуально.
Более четко разницу видно, если нажать мышкой на выражение
Любая переменная может иметь оба индекса одновременно: описательный и индекс массива. Сначала всегда будет прописан описательный.
Функции
Использование переменных возможно только при определении их заранее. Но есть исключение из этого правила — определение функции. Можно произвести определение своей функции. Пример ниже.
Переменная а имеет для функции локальное значение. Она не несет определения за пределами этой функции.
Если вы присвоили значение переменной а до определения функции, то значение этой переменной не будет меняться в процессе вычисления функции. Внимание: Если вы присвоили переменной такое же имя, как и функции, вы не сможете использовать эту функцию. Переменная и функции должны иметь разные имена.
Вы не будете сталкиваться с такой проблемой, если будете задавать переменной и функции различные имена. Об обозначениях мы поговорим в уроке 10.
Функции могут иметь более одной переменной.
Значения переменных х и у не изменяются и в этой функции.
Встроенные функции
Mathcad имеет очень много встроенных функций. Перейдите во вкладку Функции.
Все функции вы можете увидеть, если нажмете на кнопку Все функции.
Обратите внимание, что все тригонометрические функции в качестве аргумента получают угол не в градусах, а в радианах. Чтобы использовать градусы нужно выбрать их во вкладке Математика -> Операторы и символы -> Символы.
Математика в тексте
В текстовую область можно поместить область вычислений. Так вы сможете использовать в тексте подстрочные и надстрочные символы. Чтобы сделать это, при редактировании текстовой области нужно нажать на кнопку Математика во вкладке Математика -> Области.
Резюме
1. Mathcad использует два знака равенства отдельно для определения := и для вычисления =.
2. Имя переменной нельзя начинать с цифры. Можно использовать для этого только буквы или символы, отличные от символов операторов. Символы можно вводить с панели Математика -> Операторы и символы -> Символы, а также брать из панели символов Windows.
3. Для определения значения переменной нужно:
- щелкнуть на пустую область;
- ввести имя переменной;
- ввести оператор определения [:=];
- ввести значение переменной.
4. Для присвоения переменной подстрочного описательного индекса нужно:
- нажать мышкой в конце имени переменной;
- нажать [Ctrl+-];
- ввести подстрочный индекс.
5. Для присвоения переменной индекса массива:
- нажмите мышкой в конце имени переменной;
- нажмите на клавиатуре на открывающуюся квадратную скобку [;
- ввести нужный подстрочный индекс.
6. Определять переменную нужно только выше или левее места использования ее в вычислениях.
7. Имя функции вводится с теме же правилами, что и имя переменной, с той лишь разницей, что заканчивать имя функции нужно вводом открывающейся скобки [(]. В них будут размещаться аргументы функции.
8. Переменные в функциях имеют определение только в рамках этой функции.
9. В тексте можно размещать математическую область. Это можно применять при интеграции в текст надстрочных или подстрочных символов.
http://sapr-journal.ru/uroki-mathcad/urok-5-peremennye-i-funkcii/
http://stylingsoft.com/sapr/mathcad/uroki-mathcad/1124-funktsii-i-peremennye-v-mathsad


 Сообщение было отмечено Nikon19 как решение
Сообщение было отмечено Nikon19 как решение