Загрузить PDF
Загрузить PDF
В этой статье мы расскажем вам, как в Excel вычислить стандартную ошибку среднего. Для этого стандартное отклонение (σ) нужно разделить на квадратный корень (√) из размера выборки (N).
Шаги
-
1
Запустите Excel. Нажмите на значок в виде белой буквы «Х» на зеленом фоне.
-
2
Откройте или создайте таблицу Excel. Чтобы открыть готовую таблицу с данными, нажмите «Открыть» на левой панели. Чтобы создать таблицу, нажмите «Создать» и введите данные.
-
3
Вычислите стандартное отклонение. Чтобы сделать это, нужно выполнить несколько действий, но в Excel можно просто ввести следующую формулу: =СТАНДОТКЛОН.В(''диапазон ячеек'').
- Например, если данные находятся в ячейках с A1 по A20, в пустой ячейке введите =СТАНДОТКЛОН.В(A1:A20), чтобы вычислить стандартное отклонение.
-
4
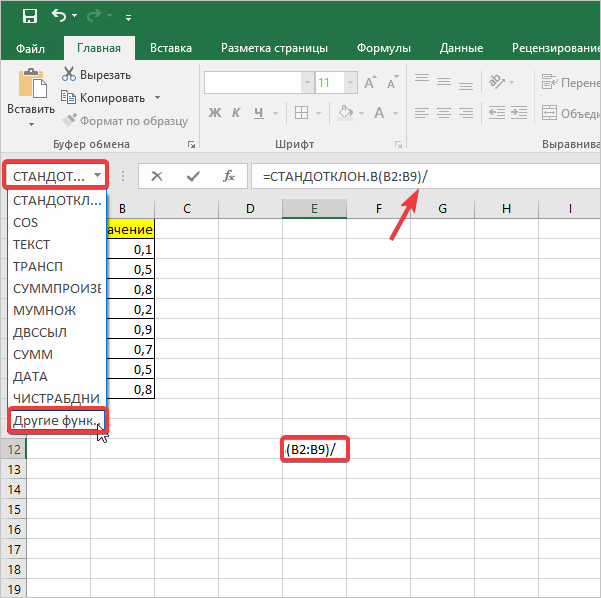
Введите формулу для вычисления стандартной ошибки среднего в пустой ячейке. Формула выглядит так:=СТАНДОТКЛОН.В(''диапазон ячеек'')/КОРЕНЬ(СЧЁТ("диапазон ячеек")).
- Например, если данные находятся в ячейках с A1 по A20, в пустой ячейке введите формулу =СТАНДОТКЛОН.В(A1:A20)/КОРЕНЬ(СЧЁТ(A1:A20)). Так вы вычислите стандартную ошибку среднего.
Реклама
Об этой статье
Эту страницу просматривали 33 679 раз.
Была ли эта статья полезной?
17 авг. 2022 г.
читать 2 мин
Стандартная ошибка среднего — это способ измерить, насколько разбросаны значения в наборе данных. Он рассчитывается как:
Стандартная ошибка = с / √n
куда:
- s : стандартное отклонение выборки
- n : размер выборки
Вы можете рассчитать стандартную ошибку среднего для любого набора данных в Excel, используя следующую формулу:
= СТАНДОТКЛОН (диапазон значений) / КОРЕНЬ ( СЧЁТ (диапазон значений))
В следующем примере показано, как использовать эту формулу.
Пример: Стандартная ошибка в Excel
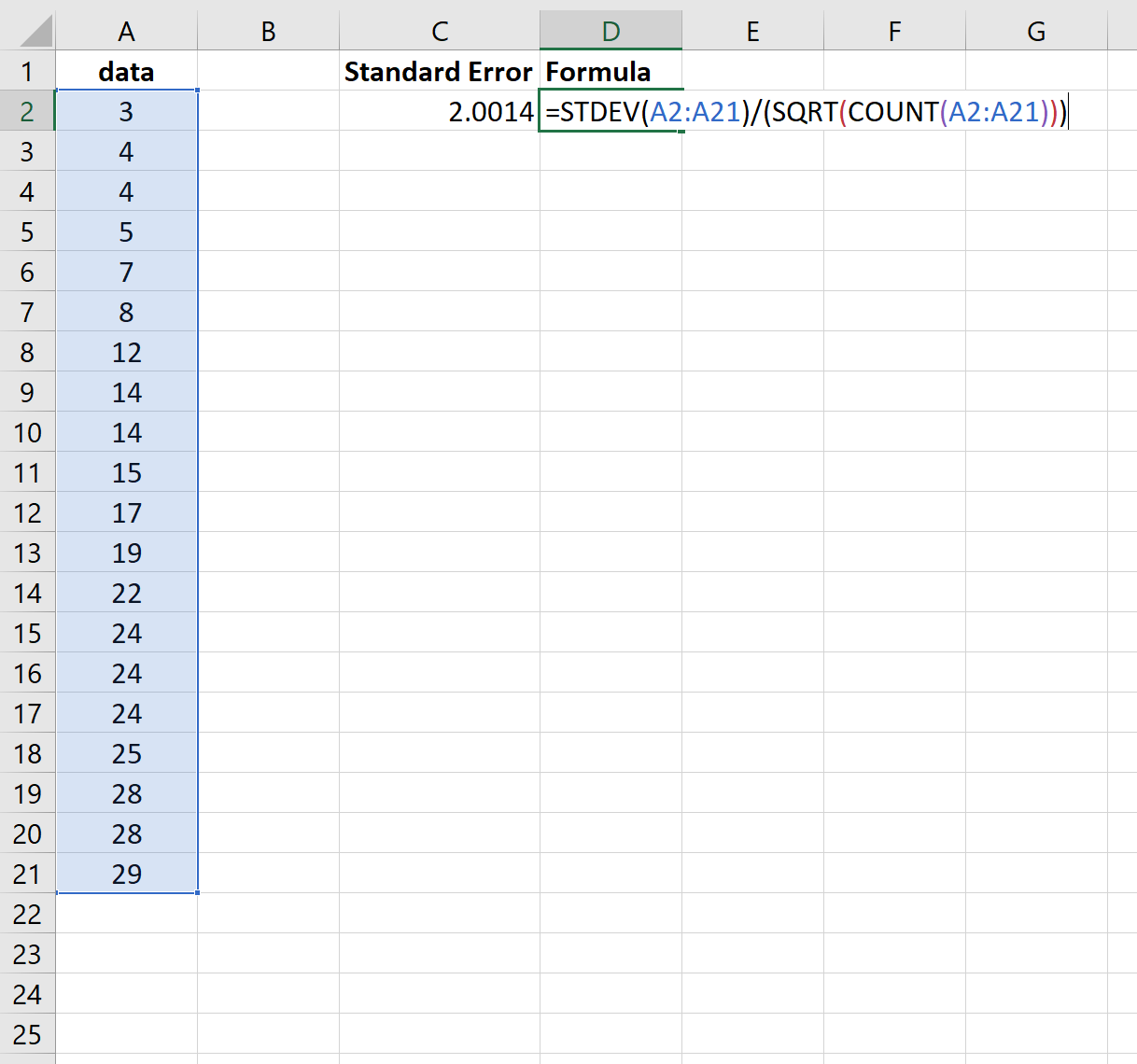
Предположим, у нас есть следующий набор данных:
На следующем снимке экрана показано, как рассчитать стандартную ошибку среднего значения для этого набора данных:
Стандартная ошибка оказывается равной 2,0014 .
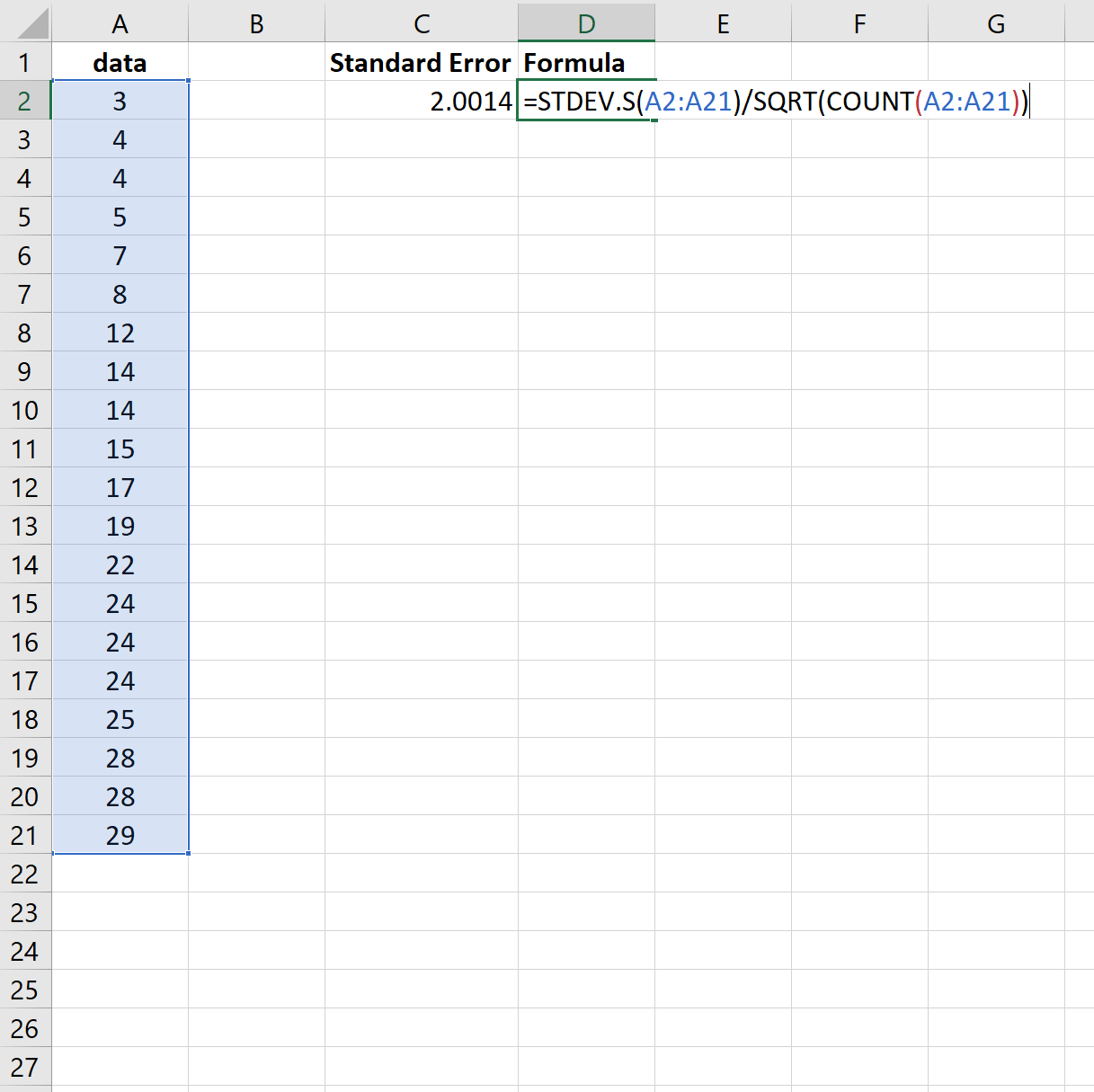
Обратите внимание, что функция =СТАНДОТКЛОН() вычисляет выборочное среднее, что эквивалентно функции =СТАНДОТКЛОН.С() в Excel.
Таким образом, мы могли бы использовать следующую формулу для получения тех же результатов:
И снова стандартная ошибка оказывается равной 2,0014 .
Как интерпретировать стандартную ошибку среднего
Стандартная ошибка среднего — это просто мера того, насколько разбросаны значения вокруг среднего. При интерпретации стандартной ошибки среднего следует помнить о двух вещах:
1. Чем больше стандартная ошибка среднего, тем более разбросаны значения вокруг среднего в наборе данных.
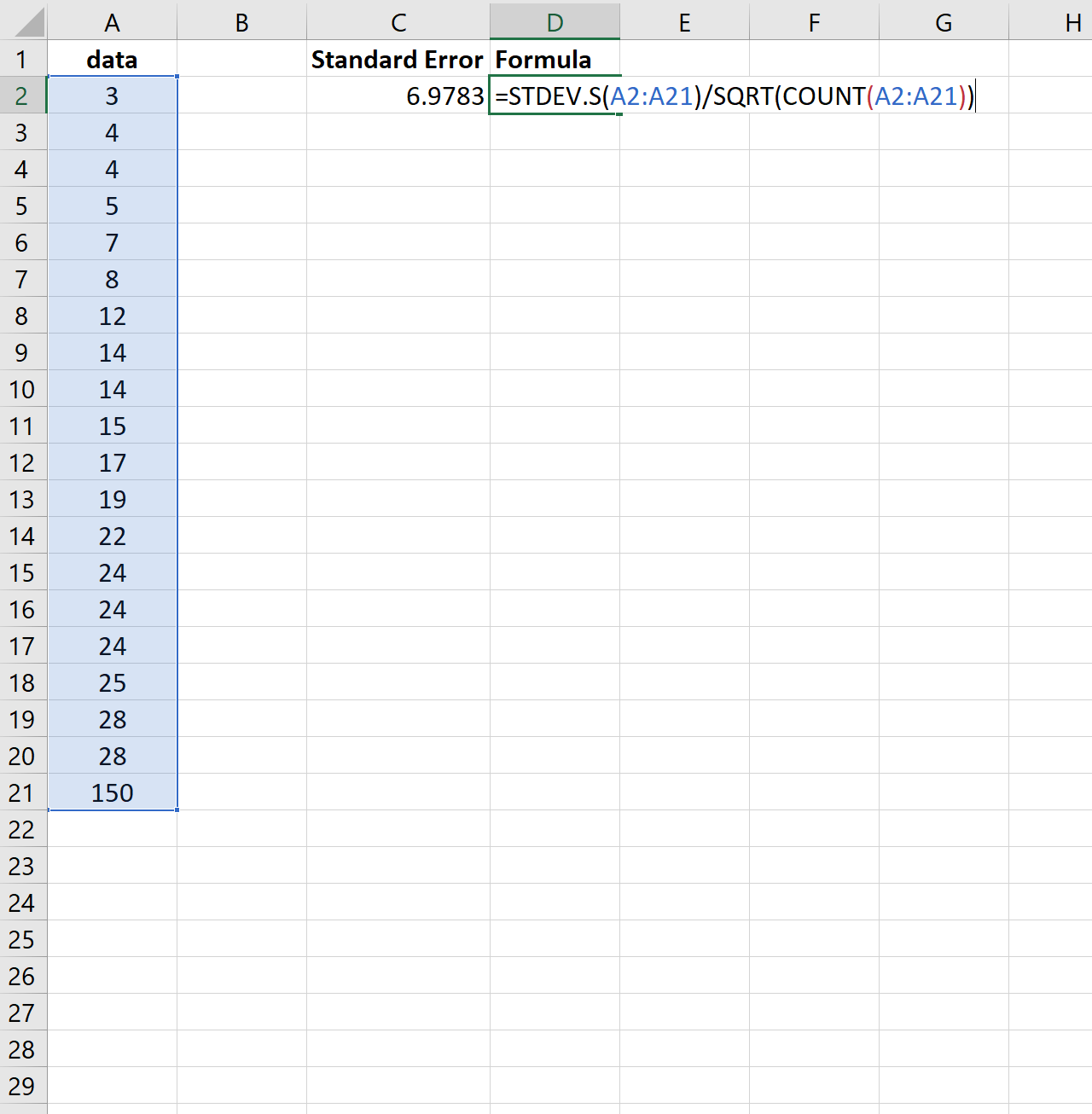
Чтобы проиллюстрировать это, рассмотрим, изменим ли мы последнее значение в предыдущем наборе данных на гораздо большее число:
Обратите внимание на скачок стандартной ошибки с 2,0014 до 6,9783.Это указывает на то, что значения в этом наборе данных более разбросаны вокруг среднего значения по сравнению с предыдущим набором данных.
2. По мере увеличения размера выборки стандартная ошибка среднего имеет тенденцию к уменьшению.
Чтобы проиллюстрировать это, рассмотрим стандартную ошибку среднего для следующих двух наборов данных:
Второй набор данных — это просто первый набор данных, повторенный дважды. Таким образом, два набора данных имеют одинаковое среднее значение, но второй набор данных имеет больший размер выборки, поэтому стандартная ошибка меньше.
Стандартная ошибка появляется при прогнозировании каких-либо данных или арифметических вычислениях, поэтому важно научиться находить этот параметр. В этой публикации разбираем, как найти и исправить стандартную ошибку путем использования инструментов Excel.
Расчет средней арифметической ошибки
В Microsoft Excel цельность и однородность выборки определяется при помощи стандартной ошибки. Стандартная ошибка — это квадратный корень из дисперсии. В приложении предусмотрено два варианта поиска стандартной ошибки: при помощи пакетного анализа и расширенных функций программы.
Чтобы найти значение средней арифметической, необходимо выполнить деление суммарной величины выборки на ее количество в электронной книге.
Расчет стандартной ошибки при помощи встроенных функций
Для того, чтобы правильно вычислять, необходимо изучить пошаговую инструкцию. В этом способе подбор результатов будет осуществляться с помощью комбинированных манипуляций.
- Для расчетов будем использовать таблицу с выборкой чисел. Кликаем на любой пустой ячейке на листе, где будет отображаться результат. Затем нажимаем кнопку «Вставить функцию.
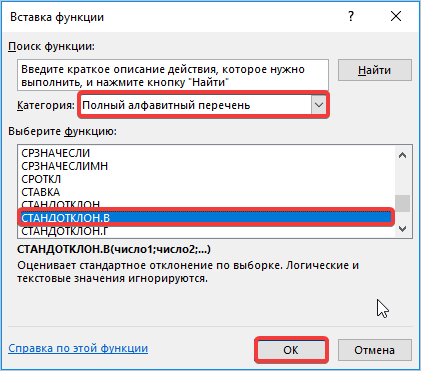
- Далее перед вами открывается диалоговое окно, в котором необходимо использовать «СТАНДОТКЛ.В», для этого в поле «Категория» необходимо выбрать «Полный алфавитный перечень». Затем нажмите кнопку «ОК».
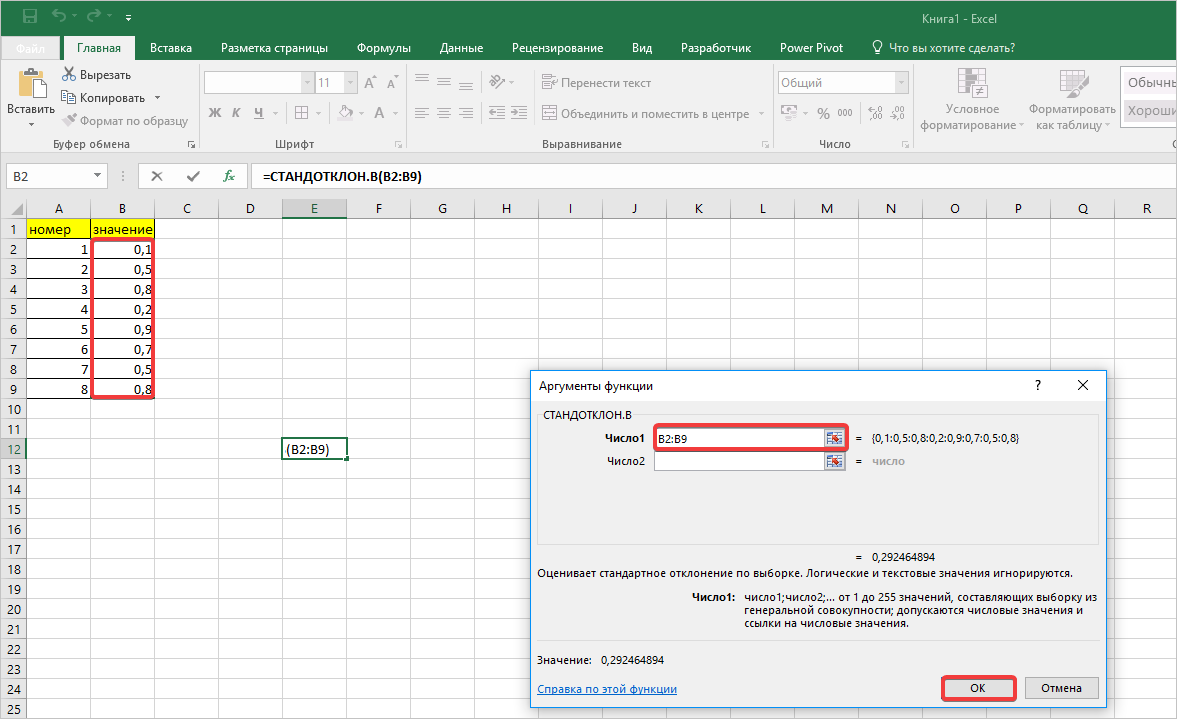
- В окне «Аргументы функции» кликаем в первом поле «Число 1», затем выполняем выделение мышью диапазона ячеек со значениями таблицы и нажимаем кнопку «ОК».
- Далее активируем ячейку с нашими значениями, переходим в строку формулы и ставим после значений наклонную линию. Переходим в поле наименования, кликаем на указывающий вниз флажок, где из списка выбираем «Другие функции».
- Снова активируется окно с перечнем функций, в котором необходимо выбрать категорию «Математические», затем функцию «Корень». Далее нажмите кнопку «ОК».
- Далее открывается окно, в котором необходимо заполнить поле с числом. Для этого переходим в поле «Имя», где спускаемся к пункту «Счет». Если его нет, ищите в дополнительных функциях.
После выполнения этих шагов, стандартная ошибка высчитывается автоматически, пользователю остается только сверить их и проверить значение на некорректное отображение.
Для малых и стандартных выборок необходимо использовать разные формулы. В первом случае (если находится до 30 значений), ее необходимо видоизменить.
Решение задачи с помощью опции «Описательная статистика»
Благодаря опции «Описательная статистика» удается выполнить вычисление по различным критериям. По этим правилам удается найти среднюю арифметическую ошибку. Для использования данного метода предварительно нужно запустить «Пакет анализа».
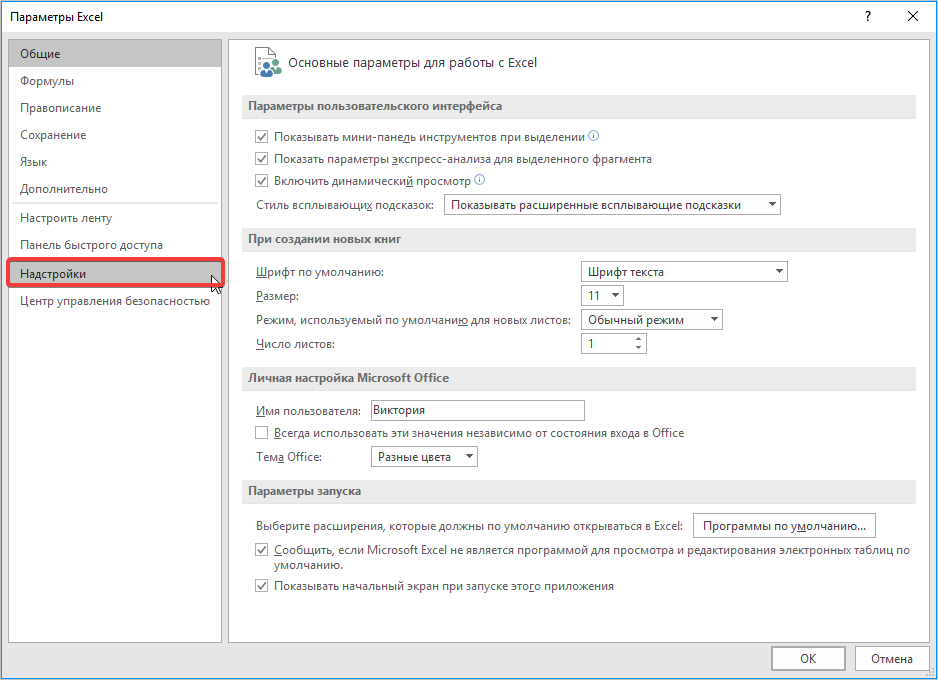
- Переходим во вкладку «Файл», где перемещаемся в пункт «Параметры». Далее нажимаем на запись «Надстройки».
- Открывается окошко, в нем в графе «Управление» должно быть прописано «Надстройки Excel», затем рядом нажимаем кнопку «Параметры».
- В появившемся окне находим «Пакет анализа» и нажимаем кнопку «ОК».
- Далее выбираем любую свободную ячейку, переходим во вкладку «Данные» и нажимаем «Анализ данных» в блоке «Анализ».
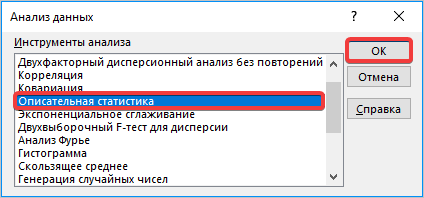
- Происходит запуск вспомогательного окошка, в котором необходимо выбрать из всех инструментов «Описательную статистику» и нажать кнопку «ОК».
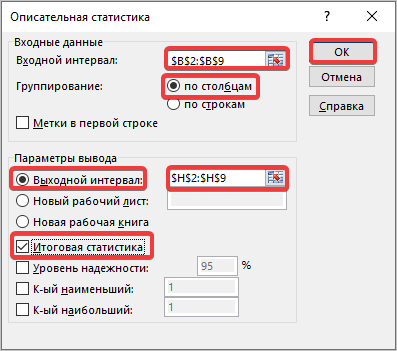
- Открывается новый мастер значений. Здесь нужно вводить данные предельно внимательно. В поле «Входной интервал» вносим адрес диапазона ячеек с выборкой. Затем указываем параметр «Группирование» «По столбцам». Затем выбираем место для «выходного интервала», его должно быть столько же, сколько и «входного». Ставим галочку напротив «Итоговая статистика» и нажимаем кнопку «ОК».
В результате вычислений вы получаете небольшую таблицу, в которой указаны все данные с определенной стандартной ошибкой.
Среднее арифметическое, как известно, используется для получения обобщающей характеристики некоторого набора данных. Если данные более-менее однородны и в них нет аномальных наблюдений (выбросов), то среднее хорошо обобщает данные, сведя к минимуму влияние случайных факторов (они взаимопогашаются при сложении).
Когда анализируемые данные представляют собой выборку (которая состоит из случайных значений), то среднее арифметическое часто (но не всегда) выступает в роли приближенной оценки математического ожидания. Почему приближенной? Потому что среднее арифметическое – это величина, которая зависит от набора случайных чисел, и, следовательно, сама является случайной величиной. При повторных экспериментах (даже в одних и тех же условиях) средние будут отличаться друг от друга.
Для того, чтобы на основе статистического анализа данных делать корректные выводы, необходимо оценить возможный разброс полученного результата. Для этого рассчитываются различные показатели вариации. Но то исходные данные. И как мы только что установили, среднее арифметическое также обладает разбросом, который необходимо оценить и учитывать в дальнейшем (в выводах, в выборе метода анализа и т.д.).
Интуитивно понятно, что разброс средней должен быть как-то связан с разбросом исходных данных. Основной характеристикой разброса средней выступает та же дисперсия.
Дисперсия выборочных данных – это средний квадрат отклонения от средней, и рассчитать ее по исходным данным не составляет труда, например, в Excel предусмотрены специальные функции. Однако, как же рассчитать дисперсию средней, если в распоряжении есть только одна выборка и одно среднее арифметическое?
Расчет дисперсии и стандартной ошибки средней арифметической
Чтобы получить дисперсию средней арифметической нет необходимости проводить множество экспериментов, достаточно иметь только одну выборку. Это легко доказать. Для начала вспомним, что средняя арифметическая (простая) рассчитывается по формуле:
где xi – значения переменной,
n – количество значений.
Теперь учтем два свойства дисперсии, согласно которым, 1) — постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат и 2) — дисперсия суммы независимых случайных величин равняется сумме соответствующих дисперсий. Предполагается, что каждое случайное значение xi обладает одинаковым разбросом, поэтому несложно вывести формулу дисперсии средней арифметической:
Используя более привычные обозначения, формулу записывают как:
где σ2 – это дисперсия, случайной величины, причем генеральная.
На практике же, генеральная дисперсия известна далеко не всегда, точнее совсем редко, поэтому в качестве оной используют выборочную дисперсию:
Стандартное отклонение средней арифметической называется стандартной ошибкой средней и рассчитывается, как квадратный корень из дисперсии.
Формула стандартной ошибки средней при использовании генеральной дисперсии
Формула стандартной ошибки средней при использовании выборочной дисперсии
Последняя формула на практике используется чаще всего, т.к. генеральная дисперсия обычно не известна. Чтобы не вводить новые обозначения, стандартную ошибку средней обычно записывают в виде соотношения стандартного отклонения выборки и корня объема выборки.
Назначение и свойство стандартной ошибки средней арифметической
Стандартная ошибка средней много, где используется. И очень полезно понимать ее свойства. Посмотрим еще раз на формулу стандартной ошибки средней:
Числитель – это стандартное отклонение выборки и здесь все понятно. Чем больше разброс данных, тем больше стандартная ошибка средней – прямо пропорциональная зависимость.
Посмотрим на знаменатель. Здесь находится квадратный корень из объема выборки. Соответственно, чем больше объем выборки, тем меньше стандартная ошибка средней. Для наглядности изобразим на одной диаграмме график нормально распределенной переменной со средней равной 10, сигмой – 3, и второй график – распределение средней арифметической этой же переменной, полученной по 16-ти наблюдениям (которое также будет нормальным).
Судя по формуле, разброс стандартной ошибки средней должен быть в 4 раза (корень из 16) меньше, чем разброс исходных данных, что и видно на рисунке выше. Чем больше наблюдений, тем меньше разброс средней.
Казалось бы, что для получения наиболее точной средней достаточно использовать максимально большую выборку и тогда стандартная ошибка средней будет стремиться к нулю, а сама средняя, соответственно, к математическому ожиданию. Однако квадратный корень объема выборки в знаменателе говорит о том, что связь между точностью выборочной средней и размером выборки не является линейной. Например, увеличение выборки с 20-ти до 50-ти наблюдений, то есть на 30 значений или в 2,5 раза, уменьшает стандартную ошибку средней только на 36%, а со 100-а до 130-ти наблюдений (на те же 30 значений), снижает разброс данных лишь на 12%.
Лучше всего изобразить эту мысль в виде графика зависимости стандартной ошибки средней от размера выборки. Пусть стандартное отклонение равно 10 (на форму графика это не влияет).
Видно, что примерно после 50-ти значений, уменьшение стандартной ошибки средней резко замедляется, после 100-а – наклон постепенно становится почти нулевым.
Таким образом, при достижении некоторого размера выборки ее дальнейшее увеличение уже почти не сказывается на точности средней. Этот факт имеет далеко идущие последствия. Например, при проведении выборочного обследования населения (опроса) чрезмерное увеличение выборки ведет к неоправданным затратам, т.к. точность почти не меняется. Именно поэтому количество опрошенных редко превышает 1,5 тысячи человек. Точность при таком размере выборки часто является достаточной, а дальнейшее увеличение выборки – нецелесообразным.
Подведем итог. Расчет дисперсии и стандартной ошибки средней имеет довольно простую формулу и обладает полезным свойством, связанным с тем, что относительно хорошая точность средней достигается уже при 100 наблюдениях (в этом случае стандартная ошибка средней становится в 10 раз меньше, чем стандартное отклонение выборки). Больше, конечно, лучше, но бесконечно увеличивать объем выборки не имеет практического смысла. Хотя, все зависит от поставленных задач и цены ошибки. В некоторых опросах участие принимают десятки тысяч людей.
Дисперсия и стандартная ошибка средней имеют большое практическое значение. Они используются в проверке гипотез и расчете доверительных интервалов.
Поделиться в социальных сетях:
Использование математических функций в Microsoft Excel может облегчить быстрое и точное выполнение сложных математических вычислений. Изучение того, как рассчитать стандартную ошибку в Excel, позволит вам получить точные результаты стандартной ошибки для набора данных. Автоматическое вычисление может снизить риск возможных ошибок и одновременно сэкономить ваше время. В этой статье мы обсудим, что такое расчет стандартной ошибки, почему он важен и как его выполнять в Excel, включая советы, как сделать это более эффективно.
Что такое расчет стандартной ошибки?
Расчет стандартной ошибки показывает, насколько далеко среднее значение выборочного набора данных может быть от общего среднего значения данных, которые вы оцениваете. Например, компания, изучающая рейтинги удовлетворенности клиентов в рамках популяции, может попытаться сделать это, собрав рейтинги от части своих клиентов. Расчет стандартной ошибки позволяет компании определить, насколько информация, которую они собирают с помощью этой выборки, вероятно, близка к общему мнению их клиентов, исходя из размера выборки.
Почему важен расчет стандартной ошибки?
Стандартная ошибка может быть ценным расчетом при использовании выборочных наборов данных, поскольку она позволяет оценить их надежность. По мере увеличения количества выборок, включенных в расчет стандартного отклонения, размер стандартной ошибки уменьшается. Это указывает на то, что вы можете в большей степени доверять точности выборки по отношению к генеральной совокупности, так как вы включили в выборку больший объем.
Как рассчитать стандартную ошибку в Excel
Выполните следующие шаги, чтобы создать формулу в Excel, которая вычисляет стандартную ошибку для набора данных:
1. Введите свои данные
Для того чтобы использовать Microsoft Excel для выполнения расчетов, вы должны сначала предоставить все необходимые данные. Введите каждую точку данных в отдельную ячейку. Хотя вам не обязательно группировать все данные вместе, это может облегчить создание формул на более поздних этапах процесса, если вы сделаете это. Расположение данных в виде вертикальной, горизонтальной или прямоугольной линии позволяет включить все данные в формулы, используя простые обозначения, вместо того, чтобы выбирать каждую ячейку по отдельности.
В этом примере компания использует Microsoft Excel для отслеживания ежедневных продаж за пять будних дней, чтобы найти стандартную ошибку в течение недели.
|
A |
B |
|
|
1 |
||
|
2 |
57 |
|
|
3 |
45 |
|
|
4 |
68 |
|
|
5 |
57 |
|
|
6 |
46 |
2. Создайте метки
Использование меток в документе Microsoft Excel может облегчить идентификацию информации на листе. Это не только облегчает понимание листа при просмотре результатов вычислений, но и позволяет правильно вводить формулы и избегать ошибок. Маркировка различных ячеек, в которые вы вводите ключевые фрагменты информации, служит ориентиром при выборе ячеек для включения в формулы.
Для расчета стандартной ошибки, помимо обозначения данных, вы можете включить обозначения для стандартного отклонения, количества оцениваемых элементов и стандартной ошибки.
|
A |
B |
|
|
1 |
Ежедневные продажи |
Стандартное отклонение |
|
2 |
57 |
|
|
3 |
45 |
Ежедневный подсчет |
|
4 |
68 |
|
|
5 |
57 |
Стандартная ошибка |
|
6 |
46 |
3. Рассчитайте стандартное отклонение
Стандартное отклонение является одной из двух важных переменных при расчете стандартной ошибки набора данных. Microsoft Excel упрощает вычисление стандартного отклонения, автоматически обрабатывая все математические уравнения с помощью функции STDEV() функция. Щелкните по ячейке, которую вы хотите использовать для хранения значения стандартного отклонения, и введите =STDEV([Ячейка 1]:[Ячейка 2]) где ячейка 1 — первая ячейка данных в введенном вами наборе, а ячейка 2 — последняя ячейка данных. Excel автоматически включает данные для всех ячеек между двумя введенными вами ячейками при расчете стандартного отклонения.
В примере пользователь вводит =STDEV(A2:A6) в ячейке под меткой стандартного отклонения. Excel не отображает эту формулу на листе. Вместо этого вычисляется значение стандартного отклонения и выводится результат. На этом и последующих этапах курсивом выделена формула, которую вводит пользователь, а текст без курсива показывает, как ячейки отображаются в электронной таблице.
|
A |
B |
|
|
1 |
Ежедневные продажи |
Стандартное отклонение |
|
2 |
57 |
=STDEV(A2:A6) |
|
3 |
45 |
Ежедневный подсчет |
|
4 |
68 |
|
|
5 |
57 |
Стандартная ошибка |
|
6 |
46 |
Похожие: Что такое стандартное отклонение? Как это работает и другие часто задаваемые вопросы
4. Подсчитайте ваши предметы
Второй важной переменной при расчете стандартной ошибки является общее количество элементов, включенных в расчет стандартного отклонения. Как и в случае со стандартным отклонением, Excel включает функцию, которая позволяет автоматически генерировать значение для этой переменной. Щелкните по ячейке, которую вы хотите использовать для хранения значения подсчета, и введите =COUNT([Ячейка 1]:[Ячейка 2]) где ячейка 1 — первая ячейка данных в наборе, который вы ввели, а ячейка 2 — последняя ячейка данных.
В примере пользователь вводит =COUNT(A2:A6) в ячейке под табличкой ежедневных подсчетов. Как и в случае с расчетом стандартного отклонения, хотя формула появляется в строке в верхней части экрана, как только пользователь нажимает клавишу Enter, на листе вместо формулы отображается значение подсчета.
|
A |
B |
|
|
1 |
Ежедневные продажи |
Стандартное отклонение |
|
2 |
57 |
9.449867 |
|
3 |
45 |
Ежедневный подсчет |
|
4 |
68 |
=COUNT(A2:A6) |
|
5 |
57 |
Стандартная ошибка |
|
6 |
46 |
Похожие: Основные формулы Excel и как их использовать
5. Рассчитать стандартную ошибку
Теперь, когда вы рассчитали для обеих переменных, вы можете использовать последнюю функцию Microsoft Excel, чтобы легко рассчитать стандартную ошибку для вашего набора данных. Щелкните на ячейке, в которой вы хотите сохранить значение стандартной ошибки, и введите =[Ячейка результата стандартного отклонения]SQRT([Ячейка результата подсчета]) как формула. Деление стандартного отклонения на квадратный корень из количества элементов в расчете отклонения дает стандартную ошибку, которую Excel вычисляет для вас автоматически.
В примере пользователь вводит =B2SQRT(B4) в ячейке под меткой стандартной ошибки. Если пользователь обнаружит ошибку в исходном наборе данных или захочет обновить набор данных с новой неделей чисел, он может изменить значения в ячейках набора данных, а все остальные значения обновятся автоматически.
|
A |
B |
|
|
1 |
Ежедневные продажи |
Стандартное отклонение |
|
2 |
57 |
9.449867 |
|
3 |
45 |
Ежедневный подсчет |
|
4 |
68 |
5 |
|
5 |
57 |
Стандартная ошибка |
|
6 |
46 |
=B2SQRT(B4) |
Советы по расчету стандартной ошибки в Excel
Если вы используете Microsoft Excel для расчета стандартной ошибки, запомните эти советы:
-
Сократите свои вычисления. Хотя отдельные вычисления для стандартного отклонения и подсчета могут сделать ваш лист более понятным, они не обязательны, и вы можете выбрать только одну формулу для всех вычислений. Для этого замените каждую отдельную ячейку в формуле стандартной ошибки на формулу, которую вы ввели в эти ячейки, например =STDEV(A2:A6)SQRT(COUNT(A2:A6)).
-
Планирование документа. Перед созданием макета документа электронной таблицы уделите время планированию своих потребностей, чтобы создать более эффективный дизайн. Понимание типа данных, которые вы собираетесь включить, включая количество записей и то, является ли ваш набор данных статичным или тем, который вы планируете пополнять в будущем, может помочь вам выбрать правильное расположение меток и расчетов.
-
Расширение диапазонов. При создании формул для стандартного отклонения и подсчета вы можете расширить диапазоны за пределы конечной точки данных, если собираетесь в будущем пополнять статистику. Функции, используемые для расчета стандартного отклонения и подсчета, игнорируют пустые ячейки, что означает, что вы можете расширить диапазон за пределы конечной точки и получить правильные результаты сейчас, а в будущем добавить дополнительные точки и попросить Excel рассчитать их без необходимости обновления формул.
Обратите внимание, что ни одна из компаний, упомянутых в этой статье, не связана с Indeed.