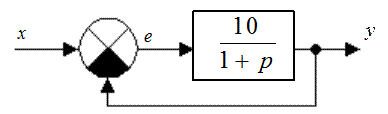
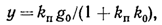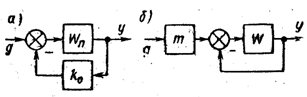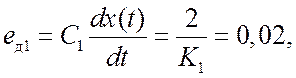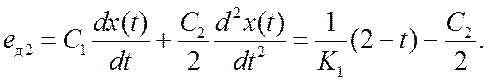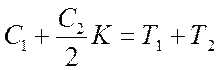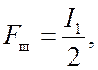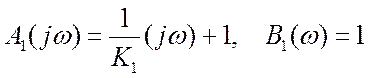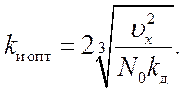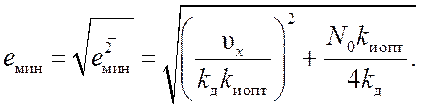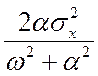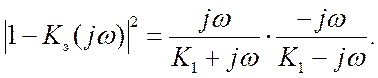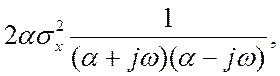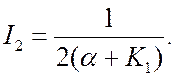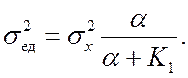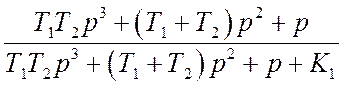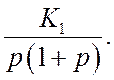Точность системы автоматического управления Статическая ошибка системы
В системах
автоматического управления часто
приходится решать задачу стабилизации
управляемой величины. Точность поддержания
требуемого значения управляемой величины
в такой системе можно оценить как разницу
между заданным значением управляемой
величины и её установившимся значением
в системе после окончания переходного
процесса:
.
Эта величина
получила название статической ошибки
системы. При вычислении статической
ошибки предполагается, что система
находится в статике и все сигналы в ней
имеют постоянные величины. Статическая
ошибка используется для оценки точности
установления в системе заданной
постоянной выходной величины после
окончания переходного процесса.
Используя
передаточную функцию замкнутой системы
по ошибке, для изображения ошибки в
системе можно записать
,
гдепередаточная
функция замкнутой системы по ошибке,изображение
задающего воздействия.
Для статики,
когда все сигналы в системе неизменны,
выражение для ошибки можно перенести
в область оригиналов
.
Поскольку
,
гдеW(p)
– передаточная функция разомкнутой
системы, то статическую ошибку системы
можно вычислить, зная передаточную
функцию разомкнутой системы:
,
где.
Вместо
абсолютного значения статической ошибки
часто используют относительную
статическую ошибку
.
Если система
статическая (т.е. не содержит интегрирующих
звеньев), то передаточную функцию
разомкнутой системы можно представить
в следующем нормированном виде:
,
гдеK– коэффициент
усиления системы,A*(p),B*(p)
– нормированные полиномыA(p)
иB(p).
При этоми
.
Тогдаи статическая ошибка в статической
системе
.
Статическая
ошибка в статической системе уменьшается
с увеличением коэффициента усиления
системы. Статическая система всегда
будет иметь некоторую ошибку. Физический
смысл такой ошибки заключается в
необходимости некоторого рассогласования
между задающей и выходной величинами
системы для получения сигнала управления.
Если в системе
управления имеются интегрирующие
звенья, то система будет астатической.
Для астатической системы первого порядка
(содержащей одно интегрирующее звено)
передаточная функция разомкнутой
системы
и передаточная функция замкнутой системы
по ошибке
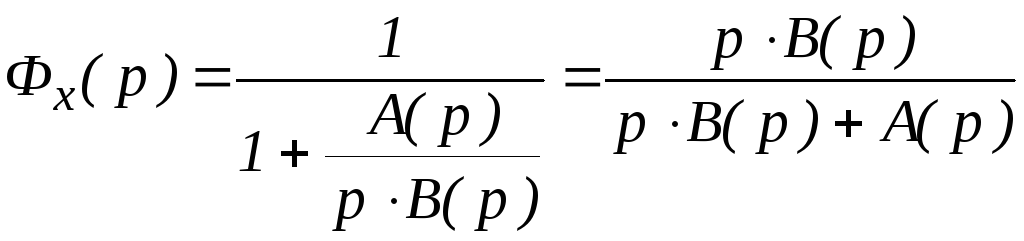
В этом случае всегда
и, следовательно, статическая ошибка
астатической системы будет равна нулю.
Таким образом, статическая ошибка в
астатической системе в принципе
отсутствует, что обуславливает более
высокую точность астатических систем,
по сравнению со статическими системами.
В астатической системе автоматического
управления установившееся значение
управляемой величины равно заданному
значению этой величины.
Вынужденная ошибка системы
Процесс в
системе складывается из свободного
процесса и вынужденного процесса:
.
Для
устойчивой системы свободный процесс
по истечении времениtпзатухает и в системе устанавливается
вынужденный процесс
Точность
поддержания заданного значения
управляемой величины в вынужденном
режиме характеризуется вынужденной
ошибкой системы
.
Вынужденная
ошибка хорошо характеризует работу
системы автоматического управления в
том случае, когда изменения управляющего
воздействия происходят существенно
медленнее собственных переходных
процессов в системе и последними можно
пренебречь.
Рассмотрим
вычисление вынужденной ошибки системы
автоматического управления. Изображение
для вынужденной ошибки
.
В общем случае
является дробно-рациональной функцией
отpи ее можно разложить
в ряд Тейлора по степенямрвблизи, тогда
и
выражение для вынужденной ошибки системы
примет вид
где
постоянные
коэффициенты.
Для полученного
изображения вынужденной ошибки на
основе свойств преобразования Лапласа
легко находится выражение для оригинала
ошибки
где
,
,
…коэффициенты
ошибок, полученные выше (C0– коэффициент статической ошибки,C1
– коэффициент скоростной ошибки и
т. д.).
Коэффициенты
ошибки могут быть также получены делением
числителя передаточной функции на ее
знаменатель. Полученное выражение для
вынужденной ошибки позволяет оценить
точность системы автоматического
управления в установившемся режиме.
Вынужденная ошибка, например, хорошо
характеризует точность работы следящих
систем автоматического управления.
Соседние файлы в папке ТАУ
- #
- #
- #
Щербаков В.С. и др. Элементы автоматики и системы автоматического управления — файл n1.doc
приобрести
Щербаков В.С. и др. Элементы автоматики и системы автоматического управления
скачать (618.5 kb.)
Доступные файлы (1):
- Смотрите также:
- Барышев Г.А., Муромцев Д.Ю. Основы автоматики и системы автоматического управления. Лабораторный практикум (Документ)
- Келим Ю.М. Основы автоматики предприятий почтовой связи (Документ)
- Красовский А.А., Вавилов Ю.А., Сучков А.И. Системы автоматического управления летательных аппаратов (Документ)
- Рубанов В.Г. Линейные системы автоматизированного управления (САУ) (Документ)
- Маругин А.П. Элементы систем автоматики (Документ)
- Маругин А.П. Элементы систем автоматики (Документ)
- Глазырин А.С. Элементы системы автоматики. Практикум (Документ)
- Нетушил А.В. Теория автоматического управления (Документ)
- Кузнецов В.П., Лукьянец С.В., Крупская М.А. Теория автоматического управления. Часть 1: Линейные непрерывные системы (Документ)
- Соломенцев Ю.М. Теория автоматического управления (Документ)
- Теория автоматического управления (Документ)
- Барашко О.Г. Автоматика, автоматизация и автоматизированные системы управления (Документ)
n1.doc
ИССЛЕДОВАНИЕ РАБОТЫ СЛЕДЯЩЕГО ПРИВОДА
Цель работы: изучение принципа действия электрической следящей системы и экспериментальное определение статической ошибки.
- Общие положения
Следящие системы – это устройства автоматического управления, предназначенные для воспроизведения величины, изменяющейся по произвольному закону.
Следящие системы можно разделить на две основные группы:
а) самосинхронизирующиеся следящие системы;
б) следящие системы с искусственной внешней синхронизацией при помощи обратных связей.
К самосинхронизирующимся следящим системам, в которых с определенной степенью точности осуществляется синхронное и синфазное перемещение двух или нескольких не связанных между собой механических валов, относятся следящие приводы. Следящим приводом называется устройство, при помощи которого объект регулирования с определенной точностью воспроизводит движение, задаваемое следящим органом.
Следящий привод, включающий элементы автоматического управления, позволяет воспроизводить требуемые перемещения в широких пределах по произвольному закону от устройства (датчика), задающего этот закон, что обуславливает его широкое применение. Следящий привод может использоваться для автоматического контроля за изменением различных физических величин, для автоматического управления поворотом массивных платформ на заданный угол, например, в экскаваторах, в системе автоматического вождения автомобиля, при автоматизации процессов управления землеройно-планировочными машинами.
В данной работе рассматривается синхронно следящий привод, который состоит из сельсина-датчика (задающий орган, сельсина-трансформатора (датчика угла поворота объекта), фазочувствительного электронного усилителя и исполнительного двигателя, перемещающего какой-либо объект. Структурная схема следящего привода приведена на рис.5.1.
ЭС
Рис. 5.1. Структурная схема следящего привода: ЗО – задающий орган; У – усилитель; ИО – исполнительный орган; О – объект регулирования; Д – датчик; ЭС – элемент сравнения
Элементы следящего привода соединены между собой так, что изменение в положении датчика воздействует через элемент сравнения и усилитель на исполнительный двигатель, который отрабатывает заданную величину перемещения. Процесс работы следящего привода сводится к автоматическому устранению возникающего рассогласования.
Синхронноследящие приводы с электронными усилителями обладают следующими достоинствами:
- быстрое протекание переходных процессов благодаря сравнительно малой инерционности системы управления;
- отсутствие вращающихся и трущихся частей в усилителе.
К недостаткам системы можно отнести:
- ограниченную мощность исполнительного двигателя;
- сравнительно большую ошибку в слежении при установившемся режиме;
- чувствительность работы системы к колебаниям напряжения сети.
Особенности работы системы синхронно следящего привода выявляются при анализе ее статических и динамических характеристик.
Под статическими характеристиками следящего привода понимают зависимость момента, тока и других параметров в схеме от величины угла рассогласования в установившемся режиме, когда отработка угла исполнительным двигателем происходит с неизменной скоростью. Однако только статические характеристики неполно характеризуют работу следящего привода. Необходимо, кроме статических характеристик, знать также и динамические свойства системы, определяющие устойчивость, величину угла рассогласования в переходном режиме, время переходного режима и т.п. Эти свойства системы анализируются на основании уравнений переходного режима. В данной работе изучаются только статические характеристики.
Важной характеристикой следящего привода является статическая ошибка, которая в данном случае представляет собой разность между углом поворота ротора сельсина-датчика (задающий орган) и углом поворота объекта (вала исполнительного двигателя). Статическая ошибка измеряется после прохождения всех переходных процессов, после полной остановки двигателя. Статическая ошибка зависит от состояния вращающихся частей: трения, момента сопротивления повороту двигателя, от колебаний напряжения сети и от инерционности вращаемого объекта.
- Вопросы допуска к лабораторной работе
- Что следует понимать под следящей системой и следящим приводом?
- Область применения следящего привода.
- Элементы следящего привода.
- Достоинства и недостатки синхронно-следящего привода с электронным усилителем.
- Характеристики, применяемые при анализе работы синхронно следящего привода.
- Описание лабораторного стенда
Синхронно следящий привод малой мощности с электронным усилителем смонтирован на лабораторном стенде. Электрическая схема стенда представлена на рис. 5.2. В его схему входят: сельсин-датчик СД со шкалой, сельсин-приемник (сельсин-трансформатор) СТ, электронный фазочувствительный усилитесь, исполнительный двигатель М. Исполнительным двигателем является двухфазный асинхронный двигатель, который обычно применяется для маломощных следящих приводов. На валу исполнительного двигателя находится стрелка, которая в данном случае является объектом регулирования. Стрелка перемещается по круговой шкале.
Принцип работы следящего привода заключается в следующем. При повороте ротора сельсина-датчика СД в однофазной обмотке сельсина-трансформатора СТ наводится ЭДС (напряжение ошибки) и поступает на вход усилителя. На выходе усилителя одна статорная (управляющая) обмотка ?1 исполнительного двигателя. Другая статорная обмотка ?2. включена в переменное напряжение сети через конденсатор, который создает между токами в статорных обмотках сдвиг фаз примерно в 90°.
Исполнительный двигатель М приходит во вращение и перемещает управляемый объект и ротор сельсина-трансформатора CТ. Вращение двигателя происходит до тех пор, пока не произойдет согласование углов поворота входного и выходного валов, при котором напряжение ошибки равно нулю. Для реверсирования исполнительного двигателя в системе необходимо изменить направление рассогласования, что осуществляют изменением направления вращения ротора сельсина-датчика. При этом изменяется фаза напряжения ошибки на 1800 и исполнительный двигатель реверсируется.
Рис. 5.2. Принципиальная схема следящего привода
4. Задание на выполнение работы
1. Сделать отсчет статической ошибки по круговой шкале измерений.
2. Построить график кривой статических ошибок n = ѓ(?).
3. Произвести расчет среднего значения статической ошибки.
- Порядок выполнения работы
- Собрать схему следящего привода (см. рис.5.2).
- Проверить работоспособность следящего привода. Для этого, поворачивая ротор сельсина-датчика по часовой стрелке и против, убедиться, что стрелка, связанная с исполнительным двигателем, поворачивается в ту же сторону.
- Установить ротор сельсина-датчика на нуль по его шкале и убедиться, что стрелка на валу двигателя останавливается в пределах 1. Если этого нет, то расстопорить стрелку и установить в соответствующее положение.
4. Последовательно вращая ротор сельсина-датчика против часовой стрелки и останавливая через 30°, определить установившиеся значения положения стрелки, связанной с двигателем.
5. Выполнить п.4 с поворотом в противоположную сторону.
- Результаты измерений занести в табл. 5.1, где ? – угол поворота задатчика, град; n1 и n2 – угол поворота стрелки исполнительного механизма, град, соответственно по и против часовой стрелки.
- Определить статические ошибки ? n1 и ? n2 по формулам:
?n1 =│? – n1│ , ?n2 = │? – n2│.
Таблица 5.1
| ? | 0 | 30 | 60 | 90 | 120 | 150 | 180 | 210 | 240 | 270 | 300 | 330 | 360 |
| n1 | |||||||||||||
| n2 | |||||||||||||
| ?n1 | |||||||||||||
| ?n2 |
- Содержание отчета
1. Название и цель работы.
2. Электрическая схема следящего привода.
3. Результаты измерений, представленные в виде таблицы, и расчет
средней статической ошибки.
7.Контрольные вопросы
- Принцип работы синхронно следящего привода.
- Объясните, что следует понимать под статической ошибкой следящей системы?
- Чем объяснить возникновение статической ошибки системы?
- Как определить статическую ошибку следящей системы?
- Каким образом можно изменить направление вращения исполнительного двигателя, не меняя направления вращения сельсина-датчика?
Библиографический список
- Бородин И. Ф. Технические средства автоматики: Учебник для вузов/ И.Ф. Бородин. – М.:Колос, 1982. – 303 с.
- Казаков А. А. Стационарные устройства автоматики и телемеханики: Учебник/А.А. Казаков, В.Д. Бубнов, Е.А. Казаков. – М.: Транспорт, 1990. – 431 с.
- Кузнецов Е.С. Управление техническими системами: Учеб. пособие/Е.С. Кузнецов; МАДИ(ТУ). – 3-е изд., перераб. и доп. М., 2001. – 262 с.
- Курсовое и дипломное проектирование по автоматизации технологических процессов: Учеб. пособие для вузов/Ф.Я. Изаков, В.Р. Казадаев, А.Х. Ройтман, Б.В. Шмаков. – М.:Агропромиздат, 1988.–183 с.
Учебное издание
ЭЛЕМЕНТЫ АВТОМАТИКИ
И СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Методические указания к лабораторным работам
Составители:
Виталий Сергеевич Щербаков
Алексей Александрович Руппель
Виталий Алексеевич Глушец
* * *
Редактор Н.И. Косенкова
Лицензия ИД № 00064 от 16.08.99
Подписано к печати 2003
Формат 60х90 1/16. Бумага писчая
Оперативный способ печати
Гарнитура Times New Roman
Усл. п. л. 2,75 , уч. — изд. л. 2,75
Тираж 300 экз. Изд. № 44. Заказ
Цена договорная
Издательство СибАДИ
644099, Омск, ул. П.Некрасова, 10
Отпечатано в ПЦ издательства СибАДИ
644099, Омск, ул. П.Некрасова, 10
ИССЛЕДОВАНИЕ РАБОТЫ СЛЕДЯЩЕГО ПРИВОДА
Лабораторная работа N 1
ИССЛЕДОВАНИЕ СЛЕДЯЩЕЙ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С РЕОСТАТНОЙ ОБРАТНОЙ СВЯЗЬЮ
Цель работы: Ознакомиться с принципом работы и устройством следящей САР с реостатной обратной связью на постоянном токе; исследовать статическую характеристику системы; определить качество процесса регулирования.
Инструмент и принадлежности к работе
1. Лабораторная установка 1 шт.
2. Цифровая измерительная установка Ф-5071/75 1 шт.
Основные положения
Следящей САР называется такая система, алгоритм функционирования которой содержит предписание изменять управляемую величину в зависимости от неизвестного заранее значения переменной величины на входе автоматической системы. Следящие системы являются частью семейства систем, известных как системы регулирования с обратной связью. Широко распространены дистанционные следящие системы воспроизведения угла и линейных перемещений. Дистанционные следящие системы применяются для управления станками, дистанционной передачи информации, управления антеннами, положением орудий, в управлении высотой и курсом самолёта с помощью автопилота, в счётно-решающих устройствах и др.
Функциональная схема следящей САР в общем виде приведена на рис. 1. Специфика работы систем, описанных выше, связана с требованиями получения необходимой точности передачи угловых и линейных перемещений.
Рис. 1. Функциональная схема следящей САР.
Существует большое множество следящих систем, отличающихся принципом действия, структурными элементами, принципом управления, исполнительным устройством, родом источников питания и пр.
По методу сравнения сигналов следящие системы могут быть аналоговыми, в которых сигнал рассогласования выделяется различными методами в аналоговой форме, цифровыми, в которых задающим устройством является ЭВМ, а сигнал рассогласования выделяется в цифровой форме в виде кода, и цифро-аналоговыми.
По структурной схеме следящие системы могут быть одно- и двухканальными, с одним или несколькими принимающими устройствами, с последовательными или параллельными корректирующими устройствами, простыми и взаимосвязанными сложными и т.п.
На практике наиболее распространёнными являются одноканальные следящие системы. Для повышения точности применяются двухканальные следящие системы, известные как системы с грубого и точного отсчётов.
В случае, когда суммарная погрешность исчисляется угловыми секундами при большом передаточном отношении электрической редукции, применяются трёхканальные следящие системы.
По типу измерительных элементов следящие системы могут иметь индуктивные, индукционные, потенциометрические, фотоэлектрические, ёмкостные, генераторные и другие датчики.
По типу исполнительных устройств следящие системы могут быть гидравлическими, пневматическими и комбинированными (с муфтами), с электродвигателями переменного и постоянного токов, шаговыми двигателями, моментными двигателями и т.п.
В зависимости от типа исполнительных устройств в маломощных системах применяются, главным образом, полупроводниковые усилители постоянного и переменного токов. В системах средней мощности возможно применение магнитных и тиристорных усилителей. В мощных системах применяются электромашинные усилители и тиристорные преобразователи.
По принципу управления исполнительным двигателем наибольшее распространение имеют следящие системы непрерывного действия с пропорциональным изменением сигнала. На обмотку управления двигателем подаётся напряжение, пропорциональное углу рассогласования, и, соответственно, частота вращения исполнительного двигателя пропорциональна сигналу рассогласования.
Применяется также управление релейного типа, при котором на обмотку управления двигателя при определённом угле рассогласования или при определённом значении управляющего сигнала подаётся максимальное напряжение. При частотном управлении двигателем на обмотку управления подаются импульсы определённой длительности во времени, но изменяется частота их следования или при постоянной частоте следования импульсов изменяется их длительность. При этом частота вращения двигателя пропорциональна частоте импульсов или соответственно длительности импульсов.
Возможны схемы управления, в которых при малом рассогласовании имеется линейный участок изменения сигнала, а при каком-то заданном угле рассогласования применяется релейное управление.
При создании следящих систем в технических требованиях задаются следующие параметры: точность, диапазон работы, максимальная скорость и ускорение входной оси, величина, и характер нагрузки, род источника, питания, габариты и надежность, а также условия эксплуатации систем – температура, влажность окружающей среды, вибрации и пр. В соответствии с этими требованиями предварительно выбирают измерительные элементы, отвечающие требованиям точности в заданном диапазоне работ.
Исходя из значений нагрузки, скорости и ускорения, а также из режима работы, выбирают исполнительное устройство и передаточное отношение редуктора привода. В маломощных следящих системах в качестве исполнительного элемента получили широкое распространение двухфазные асинхронные двигатели. При проектировании необходимы малые люфты и малый момент инерции редуктора. Момент инерции редуктора должен быть меньше момента инерции ротора двигателя, поэтому необходимо предельно уменьшать момент инерции трибки на валу двигателя. Для уменьшения диаметра шестерни, зацепляющейся с трибкой, передаточное отношение первой пары шестерён редуктора следует выбирать в пределах 2-3, передаточное отношение второй пары должно быть не более 4-6. Приведенный момент инерции последующих пар будет пренебрежимо малым. Тип усилителя и входящие в него преобразовательные элементы выбирают в соответствии с выходными параметрами измерительных элементов (выходным сопротивлением приемника, остаточным и максимальным выходными напряжениями приёмника и т. д.) и исполнительного элемента (сопротивлением нагрузки и максимальной выходной мощностью) с учётом принципа управления двигателем. В маломощных следящих системах используются полупроводниковые усилители. Постоянные времени всех цепей и элементов, коэффициенты усиления преобразователей и усилителей, передаточные отношения и прочие параметры элементов определяются расчётным или экспериментальным путем, а также по справочным данным. Далее выбирается структурная схема и составляются дифференциальные уравнения звеньев системы и передаточные функции звеньев для расчёта системы на устойчивость и выбора корректирующих цепей в целях обеспечения необходимого запаса устойчивости и необходимого качества переходного процесса.
При расчете погрешностей следящих систем учитывают, что суммарная погрешность состоит из статической Δφст динамической Δφдин погрешностей.
Статическая погрешность следящей системы представляет собой разность между угловыми наложениями входной и выходной осей после отработки двигателем системы заданного угла. Эта погрешность складывается из погрешностей измерительных элементов Δφиз датчика и приёмника системы, погрешностей преобразователей аналоговых сигналов в код в цифровых следящих системах Δφак, погрешности зоны нечувствительности Δφ3,.обусловленной моментом нагрузки, погрешности от дрейфа нулевого положения датчика и приемника, усилительно-преобразовательного устройства Δφз погрешности изготовления зубчатых колёс редуктора в системах грубого и точного отсчётов Δφзк погрешности люфта в них Δφл. Часто необходимо учитывать погрешности от температуры окружающей среды Δφt изменения напряжения и частоты питания и от каких-либо других факторов. Так как перечисленные источники погрешностей являются взаимно независимыми, суммарную погрешность можно определить как среднеквадратическую, т. е.:
.
Динамическая погрешность следящей системы Δφдин представляет собой разность между угловыми положениями входной и выходной осей при произвольном законе вращения входной оси. Слежение за положением входной оси осуществляется с определённой точностью в зависимости от выбранных параметров системы. Оценку динамической погрешности, как правило, производят либо при непрерывном вращении, либо при гармонических колебаниях входной оси. При допустимой динамической погрешности требуемый переходной процесс должен обеспечиваться выбором необходимых корректирующих устройств и их параметров. Погрешность в установившемся режиме при вращении входной оси с постоянной скоростью называют кинетической погрешностью. Она зависит от коэффициента усиления усилителя и параметров следящей системы. Отношение частоты вращения входного вала системы к установившемуся значению скоростной погрешности Δφск носит название добротности системы по скорости К: Δφск = Ωвх/К.
Перечисленные динамические погрешности должны быть либо одного порядка со значением основной погрешности – погрешности измерительных элементов, либо меньше её даже в тех случаях, когда погрешность измерительных элементов исчисляется угловыми секундами. Таким образом, суммарная погрешность всей системы ΔφΣ может быть определена как
.
На рисунке 2 представлена следящая система автоматического регулирования (САР), состоящая из потенциометра-датчика ПД и потенциометра-приёмника ПП, включенных параллельно к общему источнику питания Uп. Подвижные контакты потенциометров соответственно соединены механически с задающим и исполнительным рабочими органами. Напряжение Uс, снимаемое с подвижных контактов потенциометров, является напряжением сигнала рассогласования системы. При согласованном положении рабочих органов, когда φд = φп, напряжение сигнала равно нулю. Напряжение сигнала рассогласования Uс поступает на вход электронного усилителя У, а далее на исполнительный асинхронный двигатель Д. Вал двигателя через зубчатую передачу связан с подвижным контактом потенциометра приёмника. Система работает на устранение ошибки рассогласования. Для отсчёта углов поворота задающего и исполнительного органов применена цифровая измерительная установка Ф-5071/75, в качестве датчиков угла поворота используются сельсины СД1 и СД2, кинематически связанные c задающими и исполнительными рабочими органами. Отсчётным устройством служат блоки индикации Х и Z.
Рис. 2. Следящая САР угла поворота.
Порядок выполнения работы
- Включить установку в сеть 220 В.
- Включить питание установки и прогреть в течение 3 минут.
- Установить шкалу потенциометра-датчика на «НОЛЬ».
- Нажать на блоках индикации X, Z кнопку «СБРОС».
- Установить минимальный коэффициент усиления усилителя при помощи ручки регулятора «УСИЛЕНИЕ».
- Поворачивая движок потенциометра-датчика по часовой стрелке на углы кратные 20˚, снять показания значений угла поворота с блоков индикации Х и Z (Х – угол поворота потенциометра-датчика, Z – угол поворота потенциометра-приемника). После поворота на 360˚ измерения повторить, поворачивая рукоятку против часовой стрелки.
- Пункты 3-6 повторить для среднего и максимального значения коэффициента усиления усилителя.
- Полученные данные занести в таблицу.
|
№ |
По часовой стрелке |
Против часовой стрелки |
||||
|
Х |
Z |
σ |
Х |
Z |
σ |
|
- Определить для каждого направления вращения потенциометра-датчика и коэффициента усиления усилителя максимальную погрешность передачи угла в установившемся режиме σ = X – Z.
- Построить график зависимости z = f(x) для поворота по часовой и против часовой стрелки.
Содержание отчёта
- Результаты измерений в виде таблицы.
- Графики зависимости z = f(x) для различных коэффициентов усиления.
- Выводы по работе.
Контрольные вопросы к лабораторной работе
- Принцип действия и классификация следящих САР.
- Основные источники погрешностей следящих САР.
- Потенциометрические следящие САР угла поворота.
- Какие параметры задаются в технических требованиях при создании следящих систем?
- Как определить добротность следящей САР?
В
любой реальной CАУ
невозможно точное равенство задающего
воздействия g
и управляемой величины y.
Ошибку САУ при этом вычислим согласно
уравнению ошибки как разность этих
воздействий, т.е.:

Учитывая
историю переходных процессов, ошибку
можно представить в виде двух составляющих:
установившейся (статической) и переходной
(динамической):
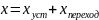
В
линейных САУ установившаяся (статическая)
ошибка определяется частным решением
её дифференциального уравнения, а
переходная (динамическая) ошибка –
решением однородного дифференциального
уравнения.
Таким
образом, установившуюся ошибку САУ в
неподвижном состоянии называют
статической, а ошибку при переходных
режимах – динамической.
Текущая
ошибка отработки переменного сигнала
называется динамической ошибкой САУ.
Динамическая ошибка системы изменяется
с течением времени. Она зависит от
структуры, параметров и характера
изменения воздействий САУ.
38 Повышение качества и синтез линейных сау
В
системе регулирования по отклонению
установившаяся [ошибка имеет три
составляющие:
(5—24)
|
где
—
ошибка воспроизведения задающего
воздействия
—
ошибка, вызываемая действием возмущений;
—
ошибка чувствительного элемента,
измеряющего рассогласование
Как
было показано в гл. 4, установившаяся
ошибка может [быть представлена в виде
ряда (4.3). При этом коэффициенты [ошибок
воспроизведения
вычисляют
по передаточной функции
замкнутой
системы для ошибки воспроизведения
Нужно,
заметить, что в статической системе
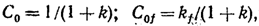
где
k
—
передаточный коэффициент разомкнутой
системна;
—
передаточный коэффициент прямой, цепи
от возмущения
до
выходной координаты у.
Следовательно,
уменьшение установившейся ошибки
постоянных значениях задающего
воздействия и возмущения достигается
увеличением передаточного коэффициента
разомкнутой системы. Однако с
увеличением статической точности в
большинстве случаев уменьшаются запасы
устойчивости I
и при значительном увеличении k
система
становится неустойчивой.
Противоречие
между статической точностью и
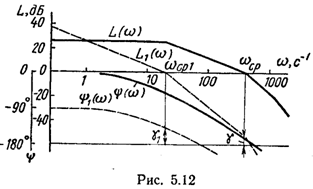
устойчивостью проиллюстрировано на
рис. 5.9, где сплошными линиями показаны
логарифмические частотные характеристики
разомкнутой системы с передаточной
функцией
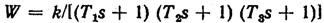
при
Если
передаточный коэффициент увеличить
до k
— 60,
то ЛАЧХ принимает положение, показанное
пунктиром. Частота среза увеличилась
и запас устойчивости по фазе уменьшился
с
до
Столь
малый запас по фазе совершенно недопустим.
При
повышении статической точности путем
увеличения передаточного коэффициента
k
разомкнутой
системы необходимы мероприятия для
обеспечения достаточного запаса
устойчивости. Они будут рассмотрены
в следующем параграфе. Возможно,
вообще говоря, создание такой структуры
системы, которая допускает неограниченное
увеличение передаточного коэффициента
k
разомкнутой
цепи 121.
Другой
путь повышения статической точности
— обеспечение астатизма. В астатической
системе младшие коэффициенты ошибки
имеют следующие значения:

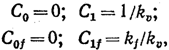
где
k0
—
передаточный коэффициент разомкнутой
системы называемый в данном случае
добротностью системы по скорости
(или коэффициентом добротности
по скорости). Таким образом, в астатической
системе отсутствует установившаяся
ошибка от постоянного задающего
воздействия и постоянных возмущений.
Для
астатизма относительно возмущения
интегрирующее звено должно быть введено
до точки, в которой приложено возмущение
(рис. 5.10).
Влияние
интегрирующего звена на динамические
свойства системы
где
сплошными линиями показаны
логарифмические частотные характеристики
системы с передаточной функцией
(5.26). При введении в разомкнутую цепь
этой системы интегрирующего звена
характеристики принимают положение,
показанное пунктиром. Фазочастотная
характеристика переместилась вниз
на —90°, а амплитудно-частотная
характеристика повернулась вокруг
точки а
по
направлению часовой стрелки . В
результате запас устойчивости по фазе
уменьшился с
до
недопустимо малого значения
Система
остается устойчивой, но переходный
процесс будет сильно колебательным.
Кроме того, уменьшилась частота среза
и переходные процессы будут более
продолжительными.
Однако
в других ситуациях введение интегрирующего
звена может не только не ухудшить, а
даже улучшить динамические свойства
системы. Пусть, например, постоянные
времени системы с передаточной функцией
(5.26) имеют следующие значения: Т1
=
= 0,05 с, Т2
=
0,0025 с и T3
= 0,001 с. Логарифмические частотные
характеристики разомкнутой системы
показаны
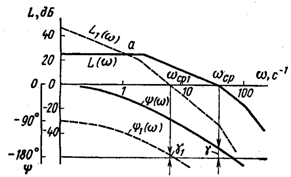
При
введении интегрирующего звена
характеристики принимают положение,
показанное пунктирными линиями. В
данном случае интегрирующее звено
уменьшило частоту среза, но запас
устойчивости по фазе увеличился с
|до
.
Хотя быстродействие системы
уменьшилось, но уменьшилась и
колебательность.
Таким
образом, при повышении статической
точности путем введения интегрирующего
звена могут оказаться необходимыми
мероприятия по сохранению запасов
устойчивости САУ.
Значительно
лучшие результаты получают при получении
астатизма с помощью изодромного звена,
т. е- звена с передаточной функцией
постоянная
времени изодрома.
Если
постоянная времени
достаточно
велика, то запас устойчивости может
быть сохранен неизменным. Уменьшение
передаточного коэффициента разомкнутой
системы должно быть скомпенсировано
увеличением коэффициента усиления
усилителя. Следует учитывать, что при
большом значении
могут
увеличиться старшие коэффициенты
ошибки.
Астатизм
САУ относительно задающего воздействия
можно обеспечить более простыми
способами: неединичной обратной
связью и масштабированием [3).
Структурная
схема системы с неединичной обратной
связью показана на рис. 5.13, а.
В
установившемся режиме регулируемая
координата связана с постоянным задающим
воздействием соотношением
(5.27)
где
kn
—
передаточный коэффициент прямой цепи
системы.
Если
выполнить основную обратную связь
системы с коэффициентом
и
система относительно задающего
воздействия будет астатической.Структурная
схема системы масштабированием входной
(величины показана на рис. 5.13, б.
Ее
особенность — наличие
усилительного
звена с передаточным коэффициентом
m
на входе. В установившемся режиме
где
k
—
передаточный коэффициент разомкнутой
системы.
При
/л = 1 -f-
УЬ
получаем
у
= g0
и
система является астатической
относительно задающего воздействия.
Недостаток
этих способов в том, что астатизм
обеспечивается только при сохранении
указанных соотношений между передаточными
коэффициентами. Неточное определение
передаточного коэффициента какого-либо
элемента системы и его изменение в
процессе эксплуатации ведут к появлению
статической ошибки. Астатизм,
достигнутый введением интегрирующего
или изодромного звена, сохраняется и
при изменении параметров системы.
Однако нужно иметь в виду, что введение
двух интегрирующих звеньев в систему,
состоящую из усилительных, апериодических
и колебательных звеньев, сделает ее
структурно-неустойчивой. Возможно
обеспечение астатизма и более высокого
порядка. При этом из-за введения большого
числа интегрирующих или изодромных
звеньев и мероприятий, обеспечивающих
требуемые динамические свойства,
структура САУ значительно усложняется.
Компенсация
внешнего воздействия (обеспечение
инвариантности). Рассмотренные выше
способы улучшения статических и
динамических свойств системы связаны
лишь с изменениями параметров
элементов САУ и структуры ее отдельных
участков, но при этом не затрагивают
принципа действия системы.
Помимо
принципа регулирования по отклонению
существует принцип регулирования
по внешнему воздействию. Значительный
эффект дает их одновременное использование.
В этом случае системы называются
комбинированными. Кроме замкнутого
контура они имеют дополнительную
цепь влияния внешнего воздействия —
возмущения или задающего.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Определить установившуюся ошибку следящей
системы при воздействиях: 1) x(t)=20+2tи 2) x(t)=20+2t–0,5t2, если известна передаточная функция
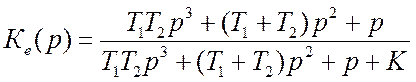
и заданы параметры: K=100 с–1; T1=0,1 c; T2=0,01
c.
Решение
Передаточную функцию Ke(p) преобразуем к виду
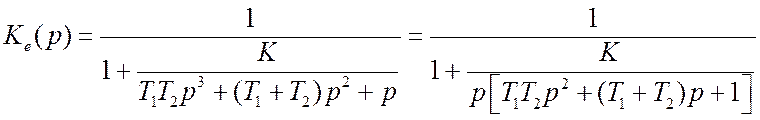
Отсюда находим передаточную функцию разомкнутой системы
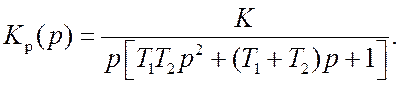
Рассматриваемая система имеет первый порядок астатизма и добротность
K1=K=100 с–1. Следовательно, установившаяся
динамическая ошибка в первом случае равна
а во втором случае
Для нахождения коэффициента С2/2 используем уравнение (11.8)
(лекция 11), которое в данном случае принимает вид
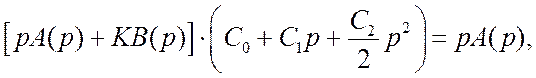
где
A(p)=T1T2p2+(T1+T2)p+1,
а B(p)=1.
Приравнивая
коэффициенты при p2
в обеих частях уравнения, находим
или
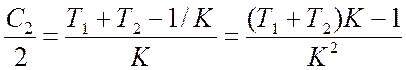
Подставив значения параметров K, Т1
и Т2, получим С2/2=0,001.
Окончательно для ошибки имеем
Первая
составляющая (0,019) определяет скоростную ошибку, а вторая (–0,01t) – ошибку по ускорению. Как видим, вклад составляющей – С2/2=–0,001
действительно мал, и можно полагать, что .
Пример 19
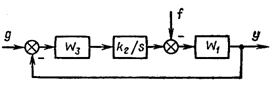
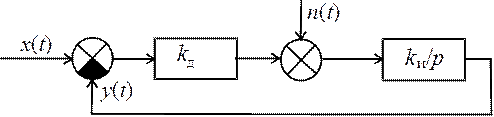
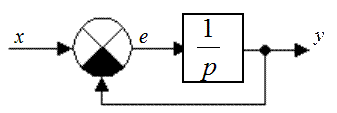
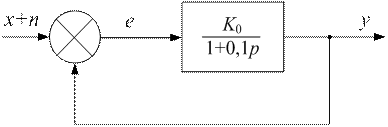
Провести оптимизацию системы (рис. 19.1)
по параметру kи при воздействии и помехе
– белом шуме с спектральной плотностью
N0 Bт /Гц.
Решение
Оптимизацию проводим в соответствии с критерием
(1.106), так как воздействие детерминированное.
Рис. 19.1
Используя результаты п.п. 1.5.2, 1.5.3, для среднего квадрата
ошибки (1.94) запишем
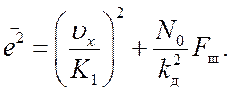
Шумовая полоса системы в
соответствии с (1.98) равна
где
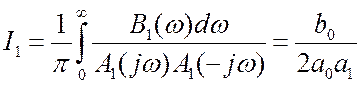
– табличный интеграл вида (1.100), а полиномы
соответствуют
передаточной функции замкнутой системы Kз(p)=1/[1+p(1/K1)].
Подставив значения параметров a0=1/K1, a1=1
и b0=1 в (19.2), находим I1=K1/2.
Шумовая полоса
определяется добротностью системы по скорости K1=kдkи:
(19.3)
Критерий оптимизации (1.106) в данном случае принимает
вид
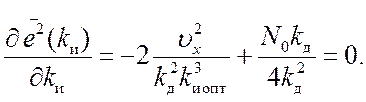
Решая уравнение (19.4), получаем
Оптимальное значение шумовой полосы и минимально достижимую ошибку
находим подстановкой в выражение для Fш (19.3) и
, (19.1):
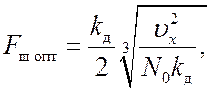
Анализ выражения (19.5) показывает, что оптимальное значение полосы
системы определяется скоростью изменения воздействия и
интенсивностью шума N0
(уменьшается с ростом N0).
Пример
20
Для системы, рассмотренной в примере 19, провести оптимизацию по
параметру kи при условия, что воздействие х(t) – стационарный
случайный процесс с нулевым средним значением и спектральной плотностью
Sx(w)=
(помеха n(t),
как и ранее, белый шум со спектральной плотностью N0).
Решение
В качестве
критерия оптимальности используем выражение (1.107), которое принимает вид
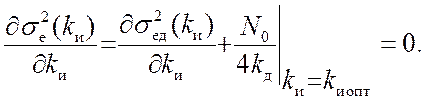
Дисперсию динамической ошибки находим из (12.10) (лекция 12) после
подстановки в него выражений для энергетического спектра воздействия и квадрата
АЧХ
Используя для Sx(w) представление в виде
Sx(w) =
дисперсию
динамической ошибки выражаем через табличный интеграл:
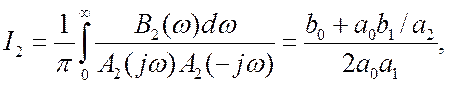
где
полиномы
A2(jw)=(jw)2+(a+K1)(jw)+aK1,
B2(w)=w2.
После
подстановки параметров a0=1, a1=a+K1, a2=aK1, b0=1 и b1=0 в
выражение (20.2), получаем
Дисперсия
динамической ошибки
С
учетом этого выражения после решения уравнения (20.1) относительно параметра kи опт имеем
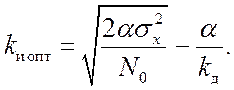
Значения оптимальной шумовой полосы и минимально достижимой ошибки
находим подстановкой k иопт в
соответствующие выражения для Fш опт и . Как видно из (20.3),
значение kиопт (а следовательно, Fшопт) определяется дисперсией и
шириной спектра a воздействия, а также интенсивностью шума N0.
Задача 40
Найти установившуюся ошибку в следящей системе (рис. 40.1),
полагая, что воздействие х(t) = 20+2t–0,5t2.
Рис.
40.1
Задача 41
Для системы с передаточной функцией
найти
статическую ошибку, ошибку по скорости и ошибку по ускорению.
Задача 42
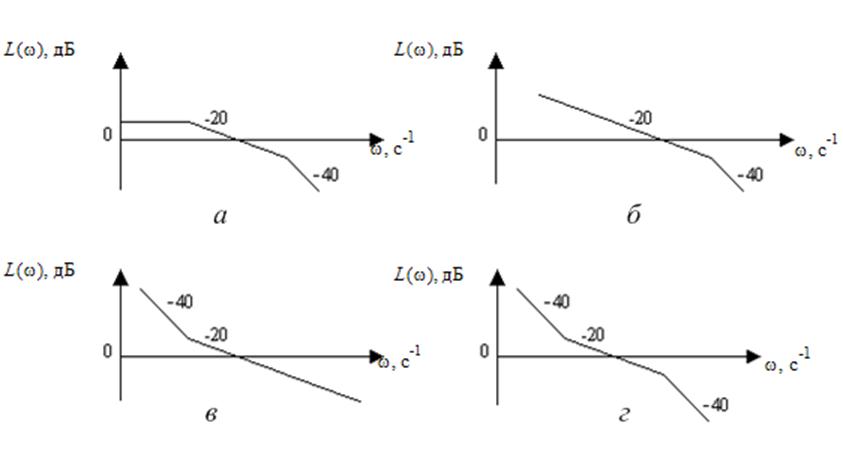
Для систем, ЛАХ которых представлены на рис. 42.1, а, б,
в, г, найти установившуюся ошибку слежения при задающем воздействии x(t)=x0+xt+0,5
xt2.
Рис.
42.1
Задача 43
Для замкнутой системы (рис. 43.1) найти шумовую
полосу, а также установившуюся ошибку при задающем воздействии х(t)
= 1+0,5t.
Рис.
43.1
Задача 44
Передаточная функция разомкнутой системы
Найти шумовую полосу замкнутой системы при условии, что запас устойчивости
по фазе Δφ = π/4 рад.
Задача 45
Передаточная функция разомкнутой системы
Найти шумовую полосу замкнутой системы при условии,
что скоростная ошибка слежения еск < 0,01% от скорости изменения параметра х.
Задача 46
Для замкнутой системы (рис. 46.1) найти шумовую
полосу, а также установившуюся ошибку при задающем воздействии х(t)
= 20 – t.
Рис.
46.1
Задача 47
Для замкнутой системы (рис. 47.1) определить значение
параметра K0, при
котором обеспечивается заданная точность: дисперсия шумовой ошибки равна
квадрату установившейся статической ошибки. Задающее воздействие х(t)
= 10, а спектральная плотность белого шума N0 = 0,1 Гц –1.
Рис.
47.1
Задача 48
ЛАХ разомкнутой системы имеет вид (рис. 48.1).
 |
Рис.
48.1
Определить параметры системы, при которых шумовая
полоса замкнутой системы равна 1Гц, а запас устойчивости по фазе Δφ >
π/6 рад.
Задача 49
Провести оптимизацию системы (рис. 49.1) по параметру K,
используя критерий минимума среднего квадрата ошибки. Воздействие х(t) = x0, а помеха – белый шум с
энергетическим спектром N0 Гц
–1.
Статическая ошибка
Cтраница 3
Статическая ошибка, равная AU, характеризует чувствительность блока сравнения. Оценка динамических свойств блока сравнения зависит от режима его работы.
[31]
Статическая ошибка ест х — ууст, где х — входная величина. Время достижения первого максимума tM определяется по графику. Время tp соответствует последней точке пересечения y ( t) с данной границей. То есть время, когда колебания регулируемой величины перестают превышать допустимого отклонения от установившегося значения. Обычно допустимое отклонение принимается равным 5 % от установившегося значения: А 5 % ууст.
[32]
Статическая ошибка равна статизму только при номинальной нагрузке.
[33]
Статическая ошибка САР с И-регулятором теоретически равна нулю. Использование их в объектах без самовыравнивания приводит к структурно неустойчивым системам.
[34]
Статическая ошибка едоо О, если система обладает астатиз-мом 1-го порядка ( у 1) относительно задающего воздействия.
[35]
Статическая ошибка привода, возникающая при отказе канала, не превышает текущего рассогласования между каналами.
[36]
Статическая ошибка сельсинов может быть разложена на несколько пространственных гармоник. Она вызывается главным образом эллиптичностью статора. Другой общей гармоникой магнитного потока в пространстве является шестая гармоника, обусловливаемая распределением трех фаз обмоток — неравными полными сопротивлениями обмоток и проводов, соединяющих сельсины. Следующая имеющаяся гармоника равна числу пазов в роторе или в статоре, или двойному числу пазов, и вызывается несинусоидальным распределением потока вследствие неравномерности магнитного сопротивления пазов, а также изменяющегося активного или магнитного сопротивлений самих обмоток.
[37]
Здесь статическая ошибка равна нулю, но максимум динамической ошибки, отнесенной к статической ошибке в однократнопнтегрпрующей системе, оказывается постоянно близким к единице.
[39]
Статическая ошибка следящей системы складывается из двух составляющих, обусловленных действием iWCT и Д1 / с. Каждая из этих составляющих должна равняться такой величине ошибки, при которой достигается компенсация соответствующего внешнего воздействия.
[40]
Статическая ошибка регулятора прямого действия существенно зависит от силы, возникающей со стороны регулирующего органа насоса, в частности, наклонной шайбы. Сила трения на регулирующем органе нассса приводит к петлевой статической характеристике регулятора прямого действия. Снизить влияние нагрузки на регулятор можно, увеличив эффективную площадь плунжера и соответственно жесткость пружинного блока. Однако из-за этого во многих случаях габаритные размеры регулятора мощности прямого действия значительно увеличиваются.
[42]
Статическую ошибку при постоянном возмущении у получают, предполагая, что на линейную систему при нулевых начальных условиях действует возмущающий момент в виде единичного скачка.
[43]
Статической ошибкой называется отклонение заданного значения регулируемой величины в установившемся режиме в связи с изменением величины нагрузки. Регуляторы, не устраняющие такой ошибки, называются статическими.
[44]
Статической ошибкой называют угол рассогласования оси ротора нагруженного ЩД в режиме фиксированного останова под током по отношению к направлению вектора МДС, который может быть в пределе равен отрицательной части зоны Эсу.
[45]
Страницы:
1
2
3
4