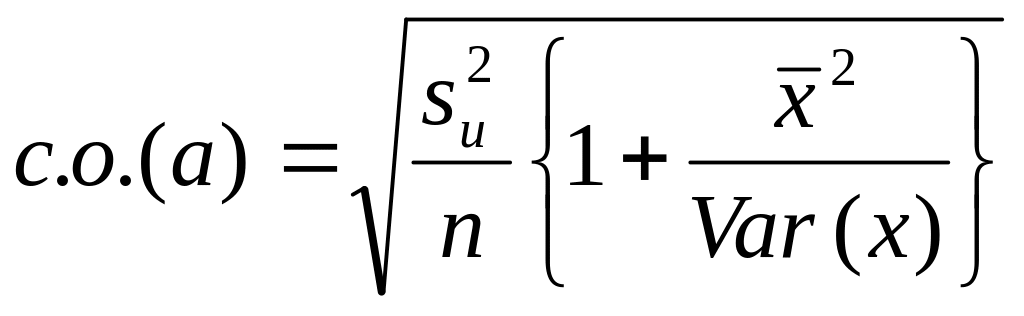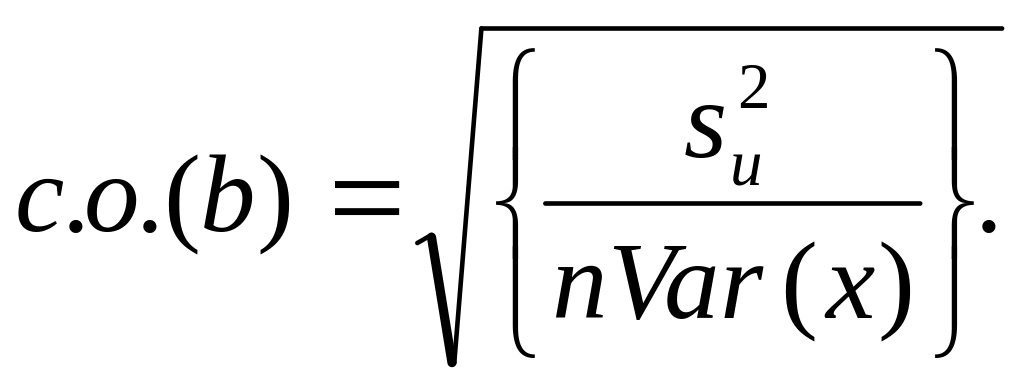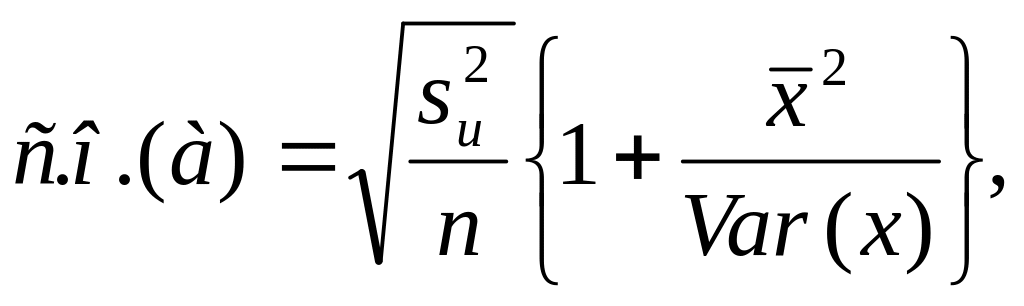Как определить стандартную ошибку регрессии - ErrorsMaster.ru - большая энциклопедия ошибок и их решений

Когда мы подгоняем регрессионную модель к набору данных, нас часто интересует, насколько хорошо регрессионная модель «подходит» к набору данных. Две метрики, обычно используемые для измерения согласия, включают R -квадрат (R2) и стандартную ошибку регрессии , часто обозначаемую как S.

В этом руководстве объясняется, как интерпретировать стандартную ошибку регрессии (S), а также почему она может предоставить более полезную информацию, чем R 2 .

Стандартная ошибка по сравнению с R-квадратом в регрессии

Предположим, у нас есть простой набор данных, который показывает, сколько часов 12 студентов занимались в день в течение месяца, предшествующего важному экзамену, а также их баллы за экзамен:

Если мы подгоним простую модель линейной регрессии к этому набору данных в Excel, мы получим следующий результат:

R-квадрат — это доля дисперсии переменной отклика, которая может быть объяснена предикторной переменной. При этом 65,76% дисперсии экзаменационных баллов можно объяснить количеством часов, потраченных на учебу.

Стандартная ошибка регрессии — это среднее расстояние, на которое наблюдаемые значения отклоняются от линии регрессии. В этом случае наблюдаемые значения отклоняются от линии регрессии в среднем на 4,89 единицы.

Если мы нанесем фактические точки данных вместе с линией регрессии, мы сможем увидеть это более четко:

Обратите внимание, что некоторые наблюдения попадают очень близко к линии регрессии, в то время как другие не так близки. Но в среднем наблюдаемые значения отклоняются от линии регрессии на 4,19 единицы .

Стандартная ошибка регрессии особенно полезна, поскольку ее можно использовать для оценки точности прогнозов. Примерно 95% наблюдений должны находиться в пределах +/- двух стандартных ошибок регрессии, что является быстрым приближением к 95% интервалу прогнозирования.

Если мы заинтересованы в прогнозировании с использованием модели регрессии, стандартная ошибка регрессии может быть более полезной метрикой, чем R-квадрат, потому что она дает нам представление о том, насколько точными будут наши прогнозы в единицах измерения.

Чтобы проиллюстрировать, почему стандартная ошибка регрессии может быть более полезной метрикой для оценки «соответствия» модели, рассмотрим другой пример набора данных, который показывает, сколько часов 12 студентов занимались в день в течение месяца, предшествующего важному экзамену, а также их экзаменационная оценка:

Обратите внимание, что это точно такой же набор данных, как и раньше, за исключением того, что все значения s сокращены вдвое.Таким образом, студенты из этого набора данных учились ровно в два раза дольше, чем студенты из предыдущего набора данных, и получили ровно половину экзаменационного балла.

Обратите внимание, что R-квадрат 65,76% точно такой же, как и в предыдущем примере.

Однако стандартная ошибка регрессии составляет 2,095 , что ровно вдвое меньше стандартной ошибки регрессии в предыдущем примере.

Если мы нанесем фактические точки данных вместе с линией регрессии, мы сможем увидеть это более четко:

Обратите внимание на то, что наблюдения располагаются гораздо плотнее вокруг линии регрессии. В среднем наблюдаемые значения отклоняются от линии регрессии на 2,095 единицы .

Таким образом, несмотря на то, что обе модели регрессии имеют R-квадрат 65,76% , мы знаем, что вторая модель будет давать более точные прогнозы, поскольку она имеет более низкую стандартную ошибку регрессии.

Преимущества использования стандартной ошибки

Стандартную ошибку регрессии (S) часто бывает полезнее знать, чем R-квадрат модели, потому что она дает нам фактические единицы измерения. Если мы заинтересованы в использовании регрессионной модели для получения прогнозов, S может очень легко сказать нам, достаточно ли точна модель для прогнозирования.

Например, предположим, что мы хотим создать 95-процентный интервал прогнозирования, в котором мы можем прогнозировать результаты экзаменов с точностью до 6 баллов от фактической оценки.

Наша первая модель имеет R-квадрат 65,76%, но это ничего не говорит нам о том, насколько точным будет наш интервал прогнозирования. К счастью, мы также знаем, что у первой модели показатель S равен 4,19. Это означает, что 95-процентный интервал прогнозирования будет иметь ширину примерно 2*4,19 = +/- 8,38 единиц, что слишком велико для нашего интервала прогнозирования.

Наша вторая модель также имеет R-квадрат 65,76%, но опять же это ничего не говорит нам о том, насколько точным будет наш интервал прогнозирования. Однако мы знаем, что вторая модель имеет S 2,095. Это означает, что 95-процентный интервал прогнозирования будет иметь ширину примерно 2*2,095= +/- 4,19 единиц, что меньше 6 и, следовательно, будет достаточно точным для использования для создания интервалов прогнозирования.

Дальнейшее чтение

Введение в простую линейную регрессию
Что такое хорошее значение R-квадрата?

Источник

Загрузить PDF

Стандартная ошибка оценки служит для того, чтобы выяснить, как линия регрессии соответствует набору данных. Если у вас есть набор данных, полученных в результате измерения, эксперимента, опроса или из другого источника, создайте линию регрессии, чтобы оценить дополнительные данные. Стандартная ошибка оценки характеризует, насколько верна линия регрессии.

1

Создайте таблицу с данными. Таблица должна состоять из пяти столбцов, и призвана облегчить вашу работу с данными. Чтобы вычислить стандартную ошибку оценки, понадобятся пять величин. Поэтому разделите таблицу на пять столбцов. Обозначьте эти столбцы так:^[1]
2
Введите данные в таблицу. Когда вы проведете эксперимент или опрос, вы получите пары данных — независимую переменную обозначим как , а зависимую или конечную переменную как . Введите эти значения в первые два столбца таблицы.
- Не перепутайте данные. Помните, что определенному значению независимой переменной должно соответствовать конкретное значение зависимой переменной.
- Например, рассмотрим следующий набор пар данных:
  - (1,2)
  - (2,4)
  - (3,5)
  - (4,4)
  - (5,5)
3
Вычислите линию регрессии. Сделайте это на основе представленных данных. Эта линия также называется линией наилучшего соответствия или линией наименьших квадратов. Расчет можно сделать вручную, но это довольно утомительно. Поэтому рекомендуем воспользоваться графическим калькулятором или онлайн-сервисом, которые быстро вычислят линию регрессии по вашим данным.^[2]
- В этой статье предполагается, что уравнение линии регрессии дано (известно).
- В нашем примере линия регрессии описывается уравнением $y^{{prime }}=0,6x+2,2$ .
4

Вычислите прогнозируемые значения по линии регрессии. С помощью уравнения линии регрессии можно вычислить прогнозируемые значения «y» для значений «x», которые есть и которых нет в наборе данных.

Реклама

1
Вычислите ошибку каждого прогнозируемого значения. В четвертом столбце таблицы запишите ошибку каждого прогнозируемого значения. В частности, вычтите прогнозируемое значение ( $y^{{prime }}$ ) из фактического (наблюдаемого) значения ().^[3]
- В нашем примере вычисления будут выглядеть так:
2
Вычислите квадраты ошибок. Возведите в квадрат каждое значение четвертого столбца, а результаты запишите в последнем (пятом) столбце таблицы.
- В нашем примере вычисления будут выглядеть так:
3
Найдите сумму квадратов ошибок. Она пригодится для вычисления стандартного отклонения, дисперсии и других величин. Чтобы найти сумму квадратов ошибок, сложите все значения пятого столбца. ^[4]
- В нашем примере вычисления будут выглядеть так:
4
Завершите расчеты. Стандартная ошибка оценки — это квадратный корень из среднего значения суммы квадратов ошибок. Обычно ошибка оценки обозначается греческой буквой . Поэтому сначала разделите сумму квадратов ошибок на число пар данных. А потом из полученного значения извлеките квадратный корень.^[5]
- Если рассматриваемые данные представляют всю совокупность, среднее значение находится так: сумму нужно разделить на N (количество пар данных). Если же рассматриваемые данные представляют некоторую выборку, вместо N подставьте N-2.
- В нашем примере, скорее всего, имеет место выборка, потому что мы рассматриваем всего 5 пар данных. Поэтому стандартную ошибку оценки вычислите следующим образом:
5
Интерпретируйте полученный результат. Стандартная ошибка оценки — это статистический показатель, которые оценивает, насколько близко измеренные данные лежат к линии регрессии. Ошибка оценка «0» означает, что каждая точка лежит непосредственно на линии. Чем выше ошибка оценки, тем дальше от линии регрессии лежат точки.^[6]
- В нашем примере выборка достаточно маленькая, поэтому стандартная оценка ошибки 0,894 является довольно низкой и характеризует близко расположенные данные.
Реклама

Об этой статье

Эту страницу просматривали 4772 раза.

Была ли эта статья полезной?

Источник

На
основании уравнения (3.20) можно показать,
что b
будет несмещенной оценкой

,
если выполняется 4-е условие Гаусса —
Маркова:

(3.21)

так
как

— константа. Если мы примем сильную форму
4-го условия Гаусса — Маркова и предположим,
что х — неслучайная величина, мы можем
также считать Var(x)
известной константой и, таким образом,

(3.22)

Далее,
если х — неслучайная величина, то
M{Cov(x,u)}
= 0 и, следовательно, M{b}
=

Таким
образом,

— несмещенная оценка

Можно получить тот же результат со
слабой формой 4-го условия Гаусса —
Маркова (которая допускает, что переменная
х имеет случайную ошибку, но предполагает,
что она распределена независимо от u
).

За
исключением того случая, когда случайные
факторы в n
наблюдениях в точности «гасят»
друг друга, что может произойти лишь
при случайном совпадении, b
будет отличаться от

в каждом конкретном эксперименте. Не
будет систематической ошибки, завышающей
или занижающей оценку. То же самое
справедливо и для коэффициента а.

Используем
уравнение (2.15):

(3.23)

Следовательно,

(3.24)

Поскольку
у определяется уравнением (3.1),

(3.25)

так
как M{u}=0,
если выполнено 1-е условие Гаусса —
Маркова. Следовательно

(3.26)

Подставив
это выражение в (3.24) и воспользовавшись
тем, что

получим:

(3.27)

Таким
образом, а
— это несмещенная оценка а при условии
выполнения 1-го и 4-го условий Гаусса —
Маркова. Безусловно, для любой конкретной
выборки фактор случайности приведет к
расхождению оценки и истинного значения.

Рассмотрим
теперь теоретические дисперсии оценок
а и Ь. Они задаются следующими выражениями
(доказательства для эквивалентных
выражений можно найти в работе Дж. Томаса
[Thomas,
1983, section
833]):

(3.28)

Из
уравнения 3.28 можно сделать три очевидных
заключения. Во-первых, дисперсии а
и b
прямо пропорциональны дисперсии
остаточного члена

.

Чем
больше фактор случайности, тем хуже
будут оценки при прочих равных условиях.
Это уже было проиллюстрировано в
экспериментах по методу Монте-Карло.
Оценки в серии II
были гораздо более неточными, чем в
серии I,
и это произошло потому, что в каждой
выборке мы удвоили случайный член.
Удвоив u,
мы удвоили его стандартное отклонение
и, следовательно, удвоили стандартные
отклонения a
и b.
Во вторых, чем больше число наблюдений,
тем меньше дисперсионных оценок. Это
также имеет определенный смысл. Чем
большей информацией вы располагаете,
тем более точными, вероятно, будут ваши
оценки. В третьих, чем больше дисперсия

,
тем меньше будет дисперсия коэффициентов
регрессии. В чем причина этого? Напомним,
что (I)
коэффициенты регрессии вычисляются на
основании предположения, что наблюдаемые
изменения

происходят вследствие изменений

,
но (2) в действительности они лишь отчасти
вызваны изменениями

,
а отчасти вариациями u.
Чем меньше дисперсия

,
тем больше, вероятно, будет относительное
влияние фактора случайности при
определении отклонений

и тем более вероятно, что регрессионный
анализ может оказаться неверным. В
действительности, как видно из уравнения
(3.28), важное значение имеет не абсолютная,
а относительная величина

и Var(x).

На
практике мы не можем вычислить
теоретические дисперсии

или

,
так как

неизвестно, однако мы можем получить
оценку

на основе остатков. Очевидно, что разброс
остатков относительно линии регрессии
будет отражать неизвестный разброс u
относительно линии

,
хотя в общем остаток и случайный член
в любом данном наблюдении не равны друг
другу. Следовательно, выборочная
дисперсия остатков Var(е),
которую мы можем измерить, сможет быть
использована для оценки

,
которую мы получить не можем.

Прежде
чем пойти дальше, задайте себе следующий
вопрос: какая прямая будет ближе к
точкам, представляющим собой выборку
наблюдений по

,
истинная прямая

или линия регрессии

?
Ответ будет таков: линия регрессии,
потому что по определению она строится
таким образом, чтобы свести к минимуму
сумму квадратов расстояний между ней
и значениями наблюдений. Следовательно,
разброс остатков у нее меньше, чем
разброс значений u,
и Var(e)
имеет тенденцию занижать оценку

.
Действительно, можно показать, что
математическое ожидание Var(e),
если имеется всего одна независимая
переменная, равно

.
Однако отсюда следует, что если определить

как

,
(3.29)

То

будет представлять собой несмещенную
оценку

Таким
образом, несмещенной оценкой параметра
регрессии

является оценка

.
(3.30)

Теперь
вспомним следующие определения:

стандартное
отклонение случайной величины
– корень квадратный из теоретической
дисперсии случайной величины; среднее
ожидаемое расстояние между наблюдениями
этой случайной величины и ее математическим
ожиданием,

стандартная
ошибка случайной величины
– оценка стандартного отклонения
случайной величины, полученная по данным
выборки.

Используя
уравнения (3.28) и (3.29), можно получить
оценки теоретических дисперсий для a
и b
и после извлечения квадратного корня
– оценки их стандартных отклонений.
Вместо слишком громоздкого термина
«оценка стандартного отклонения функции
плотности вероятости» коэффицинта
регрессии будем использовать термин
«стандартная ошибка» коэффициента
регрессии, которую в дальнейшем мы будем
обозначать в виде сокрашения «с.о.».
Таким образом, для парного регрессионного
анализа мы имеем:

(3.31)

Если
воспользоваться компьютерной программой
оценивания регрессии, то стандартные
ошибки будут подсчитаны автоматически
одновременно с оценками a
и b.

Подводя
итог сказанному о точности коэффициентов
регрессии, акценктируем внимание на
следующих выводах.

1.
Оценка a
для параметра

имеет нормальное распределение с
математическим ожиданием a
и стандартным отклонением

,
оценка b
для параметра

имеет
нормальное распределение с математическим
ожиданием b
и стандартным отклонением

.

2.
Для улучшения точности оценок по МНК
можно увеличивать количество наблюдений
в выборке n,
увеличивать диапазон наблюдений Var(x)
или уменьшать

,
(например, увеличивать точность
измерений).

3.
Стандартная ошибка оценки a
считается по формуле

а
стандартная ошибка оценки b
считается по формуле

.

В компьютерных программах именно эти
числа приводятся в круглых скобках под
значениями оценок.

Полученные
соотношения проиллюстрируем экспериментами
по методу Монте-Карло, описанными ранее.
В серии I
u
определялось на основе случайных чисел,
взятых из генеральной совокупности с
нулевым средним и единичной дисперсией

а x
представлял собой набор чисел от 1 до
20. Можно легко вычислить Var(x),
которая равна 33,25.

Следовательно,

(3.32)

.
(3.33)

Таким
образом, истинное стандартное отклонение
для b
равно

.
Какие же результаты получены вместо
этого компьютером в 10 экспериментах
серии I?
Он должен был вычислить стандартную
ошибку, используя уравнение (3.31).
Результаты этих расчетов для 10
экспериментов представлены в табл. 3.5.

Таблица 3.5

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
#
#
22.03.2016179.71 Кб71а1.doc
#
#
#
#
#
#
#

Источник