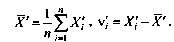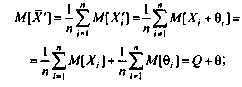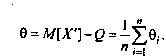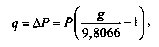При прямых измеренияхзначение
измеряемой величины отсчитывается
непосредственно по шкале измерительного
прибора. Ошибка в отсчете может достигать
нескольких десятых долей деления шкалы.
Обычно при таких измерениях величину
систематической погрешности считают
равной половине цены деления шкалы
измерительного прибора. Например, при
измерении штангенциркулем с ценой
деления 0,05 мм величина приборной
погрешности измерения принимают равной
0,025 мм.
Цифровые измерительные приборы дают
значение измеряемых ими величин с
погрешностью, равной значению одной
единицы последнего разряда на шкале
прибора. Так, если цифровой вольтметр
показывает значение20,45 мВ, то абсолютная
погрешность при измерении равна
мВ.
Систематические погрешности возникают
и при использовании постоянных величин,
определяемых из таблиц. В подобных
случаях погрешность принимается равной
половине последнего значащего разряда.
Например, если в таблице значение
плотности стали дается величиной, равной
7,9∙103кг/м3, то абсолютная
погрешность в этом случае равнакг/м3.
Некоторые особенности в расчете приборных
погрешностей электроизмерительных
приборов будут рассмотрены ниже.
При определении систематической
(приборной) погрешности косвенных
измеренийфункциональной величиныиспользуется
формула
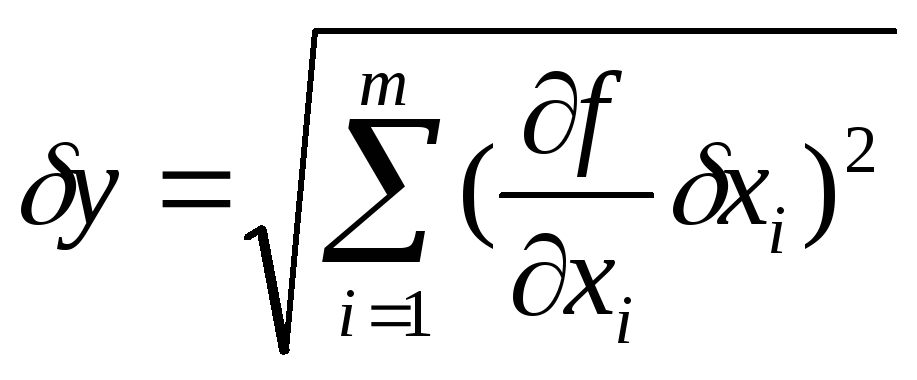
(1)
где
— приборные ошибки прямых измерений
величины,
—
частные производные функции по переменной.
В качестве примера, получим формулу для
расчета систематической погрешности
при измерении объема цилиндра. Формула
вычисления объема цилиндра имеет вид
.
Частные производные по переменным d
и hбудут равны
,
.
Таким образом, формула для определения
абсолютной систематической погрешности
при измерении объема цилиндра в
соответствии с (2. ..) имеет следующий вид
,
где
и
приборные
ошибки при измерении диаметра и высоты
цилиндра
3. Оценка случайной погрешности. Доверительный интервал и доверительная вероятность
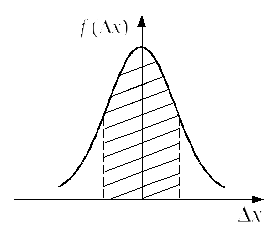
Д
Рис. 1
ля подавляющего большинства простых
измерений достаточно хорошо выполняется
так называемый нормальный закон случайных
погрешностей (закон Гаусса), выведенный
из следующих эмпирических положений.
-
погрешности измерений могут принимать
непрерывный ряд значений; -
при большом числе измерений погрешности
одинаковой величины, но разного знака
встречаются одинаково часто, -
чем больше величина случайной погрешности,
тем меньше вероятность ее появления.
График нормального закона распределения
Гаусса представлен на рис.1. Уравнение
кривой имеет вид
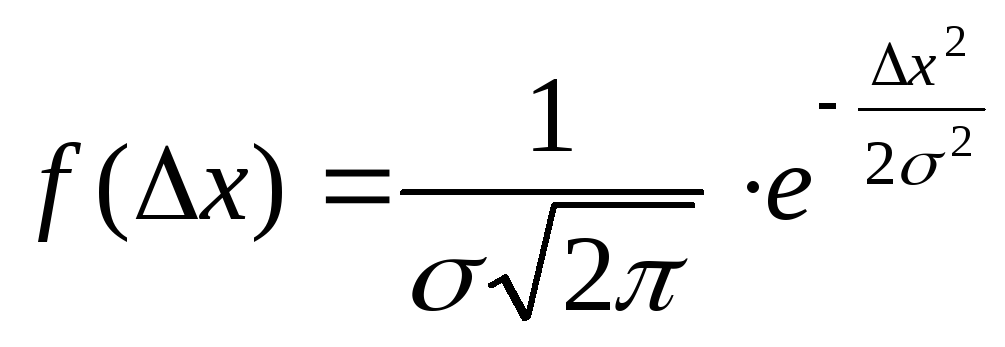
(2)
где
— функция распределения случайных ошибок
(погрешностей), характеризующая
вероятность появления ошибки,σ– средняя
квадратичная ошибка.
Величина σне
является случайной величиной и
характеризует процесс измерений. Если
условия измерений не изменяются, то σ
остается постоянной величиной. Квадрат
этой величины называютдисперсией
измерений.Чем меньше дисперсия, тем
меньше разброс отдельных значений и
тем выше точность измерений.
Точное значение средней квадратичной
ошибки σ, как
и истинное значение измеряемой величины,
неизвестно. Существует так называемая
статистическая оценка этого параметра,
в соответствии с которой средняя
квадратичная ошибка равняется средней
квадратичной ошибке среднего
арифметического.
Величина которой определяется по формуле

(3)
где
— результатi-го
измерения;—
среднее арифметическое полученных
значений;n – число
измерений.
Чем больше число измерений, тем меньше
и тем больше оно приближается кσ.
Если истинное значение измеряемой
величины μ, ее среднее арифметическое
значение, полученное в результате
измерений ,
а случайная абсолютная погрешность,
то результат измерений запишется в виде.
Интервал значений от
до
,
в который попадает истинное значение
измеряемой величины μ, называетсядоверительным интервалом.Посколькуявляется случайной величиной, то истинное
значение попадает в доверительный
интервал с вероятностью α, которая
называетсядоверительной вероятностью,илинадежностью измерений. Эта
величина численно равна площади
заштрихованной криволинейной трапеции.
(см. рис.)
Все это справедливо для достаточно
большого числа измерений, когда
близка к σ. Для отыскания доверительного
интервала и доверительной вероятности
при небольшом числе измерений, с которым
мы имеем дело в ходе выполнения
лабораторных работ, используетсяраспределение вероятностей Стьюдента.
Это распределение вероятностей
случайной величины,
называемойкоэффициентом Стьюдента,
дает значение доверительного интервалав долях средней квадратичной ошибки
среднего арифметического.
.
(4)
Распределение вероятностей этой величины
не зависит от σ2, а существенно
зависит от числа опытовn.С увеличением числа опытовnраспределение
Стьюдента стремится к распределению
Гаусса.
Функция распределения табулирована
(табл.1). Значение коэффициента Стьюдента
находится на пересечении строки,
соответствующей числу измерений n,
и столбца, соответствующего доверительной
вероятности α
Таблица 1.
|
n |
α |
n |
α |
||||||
|
0,8 |
0,9 |
0,95 |
0,98 |
0,8 |
0,9 |
0,95 |
0,98 |
||
|
3 |
1,9 |
2,9 |
4,3 |
7,0 |
6 |
1,5 |
2,0 |
2,6 |
3,4 |
|
4 |
1,6 |
2,4 |
3,2 |
4,5 |
7 |
1,4 |
1,9 |
2,4 |
3,1 |
|
5 |
1,5 |
2,1 |
2,8 |
3,7 |
8 |
1,4 |
1,9 |
2,4 |
3,9 |
Пользуясь данными таблицы, можно:
-
определить доверительный интервал,
задаваясь определенной вероятностью; -
выбрать доверительный интервал и
определить доверительную вероятность.
При косвенных измерениях среднюю
квадратичную ошибку среднего
арифметического значения функции
вычисляют по формуле
.
(5)
Доверительный интервал и доверительная
вероятность определяются так же, как и
в случае прямых измерений.
Оценка суммарной погрешности измерений.
Запись окончательного результата.
Суммарную погрешность результата
измерений величины Х будем определять
как среднее квадратичное значение
систематической и случайной погрешностей
,
(6)
где δх – приборная погрешность, Δх
– случайная погрешность.
В качестве Х может быть как непосредственно,
так и косвенно измеряемая величина.
Окончательный результат измерений
рекомендуется представлять в следующем
виде
,
α=…, Е=…(7)
Следует иметь в виду, что сами формулы
теории ошибок справедливы для большого
число измерений. Поэтому значение
случайной, а следовательно, и суммарной
погрешности определяется при малом nс большой ошибкой. При вычислении Δхпри числе измеренийрекомендуется
ограничиваться одной значащей цифрой,
если она больше 3 и двумя, если первая
значащая цифра меньше 3. Например, если
Δх= 0,042, то отбрасываем 2 и пишем
Δх=0,04, а если Δх=0,123, то пишем
Δх=0,12.
Число разрядов результата и суммарной
погрешности должно быть одинаковым.
Поэтому среднее арифметическое
погрешности должно быть одинаковым.
Поэтому среднее арифметическое
вычисляется вначале на один разряд
больше, чем измерение, а при записи
результата его значение уточняется до
числа разрядов суммарной ошибки.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Систематические погрешности при повторных измерениях остаются постоянными или изменяются по определенному закону.
Когда судят о погрешности, подразумевают не значение, а интервал значений, в котором с заданной вероятностью находится истинное значение. Поэтому говорят об оценке погрешности. Если бы погрешность оказалась измеренной, т.е. стали бы известны её знак и значение, то её можно было бы исключить из действительного значения измеряемой физической величины и получить истинное значение.
Для получения результатов, минимально отличающихся от истинного значения измеряемой физической величины, проводят многократные наблюдения и проводят математическую обработку полученного массива с целью определения и минимизации случайной составляющей погрешности.
Минимизация систематической погрешности в процессе наблюдений выполняется следующими методами: метод замещения (состоит в замещении измеряемой величины мерой), метод противопоставления (состоит в двух поочерёдных измерениях при замене местами меры и измеряемого объекта), метод компенсации погрешности по знаку (состоит в двух поочерёдных измерениях, при которых влияющая величина становится противоположной).
При многократных наблюдениях возможно апостериорное (после выполнения наблюдений) исключение систематической погрешности в результате анализа рядов наблюдений. Рассмотрим графический анализ. При этом результаты последовательных наблюдений представляются функцией времени либо ранжируются в порядке возрастания погрешности.
Рассмотрим временную зависимость. Будем проводить наблюдения через одинаковые интервалы времени. Результаты последовательных наблюдений являются случайной функцией времени. В серии экспериментов, состоящих из ряда последовательных наблюдений, получаем одну реализацию этой функции. При повторении серии получаем новую реализацию, отличающуюся от первой.
Реализации отличаются преимущественно из-за влияния факторов, определяющих случайную погрешность, а факторы, определяющие систематическую погрешность, одинаково проявляются для соответствующих моментов времени в каждой реализации. Значение, соответствующее каждому моменту времени, называется сечением случайной функции времени. Для каждого сечения можно найти среднее по всем реализациям значение. Очевидно, что эта составляющая и определяет систематическую погрешность. Если через значения систематической погрешности для всех моментов времени провести плавную кривую, то она будет характеризовать временную закономерность изменения погрешности. Зная закономерность изменения, можем определить поправку для исключения систематической погрешности. После исключения систематической погрешности получаем «исправленный ряд результатов наблюдений».
Известен ряд способов исключения систематических погрешностей, которые условно можно разделить па 4 основные группы:
- устранение источников погрешностей до начала измерений;
- исключение почетностей в процессе измерения способами замещения, компенсации погрешностей по знаку, противопоставления, симметричных наблюдений;
- внесение известных поправок в результат измерения (исключение погрешностей начислением);
- оценка границ систематических погрешностей, если их нельзя исключить.
По характеру проявления систематические погрешности подразделяют на постоянные, прогрессивные и периодические.
Постоянные систематические погрешности сохраняют свое значение в течение всего времени измерений (например, погрешность в градуировке шкалы прибора переносится на все результаты измерений).
Прогрессивные погрешности – погрешности, которые в процессе измерении подрастают или убывают (например, погрешности, возникающие вследствие износа контактирующих деталей средств измерения).
И группу систематических погрешностей можно отнести: инструментальные погрешности; погрешности из-за неправильной установки измерительного устройства; погрешности, возникающие вследствие внешних влияний; погрешности метода измерения (теоретические погрешности); субъективные погрешности.
Систематической погрешностью называется составляющая погрешности измерения, остающаяся постоянной или закономерно меняющаяся при повторных измерениях одной и той же величины. При этом предполагается, что систематические погрешности представляют собой определенную функцию неслучайных факторов, состав которых зависит от физических, конструкционных и технологических особенностей средств измерений, условий их применения, а также индивидуальных качеств наблюдателя. Сложные детерминированные закономерности, которым подчиняются систематические погрешности, определяются либо при создании средств измерений и комплектации измерительной аппаратуры, либо непосредственно при подготовке измерительного эксперимента и в процессе его проведения. Совершенствование методов измерения, использование высококачественных материалом, прогрессивная технология — все это позволяет на практике устранить систематические погрешности настолько, что при обработке результатов наблюдений с их наличием зачастую не приходится считаться.
Систематические погрешности принято классифицировать в зависимости от причин их возникновения и по характеру их проявления при измерениях.
В зависимости от причин возникновения рассматриваются четыре вида систематических погрешностей.
1. Погрешности метода, или теоретические погрешности, проистекающие от ошибочности или недостаточной разработки принятой теории метода измерений в целом или от допущенных упрощений при проведении измерений.
Погрешности метода возникают также при экстраполяции свойства, измеренного на ограниченной части некоторого объекта, на весь объект, если последний не обладает однородностью измеряемого свойства. Так, считая диаметр цилиндрического вала равным результату, полученному при измерении в одном сечении и в одном направлении, мы допускаем систематическую погрешность, полностью определяемую отклонениями формы исследуемого вала. При определении плотности вещества по измерениям массы и объема некоторой пробы возникает систематическая погрешность, если проба содержала некоторое количество примесей, а результат измерения принимается за характеристику данного вещества -вообще.
К погрешностям метода следует отнести также те погрешности, которые возникают вследствие влияния измерительной аппаратуры на измеряемые свойства объекта. Подобные явления возникают, например, при измерении длин, когда измерительное усилие используемых приборов достаточно велико, при регистрации быстропротекаюших процессов недостаточно быстродействующей аппаратурой, при измерениях температур жидкостными или газовыми термометрами и т.д.
2. Инструментальные погрешности, зависящие от погрешностей применяемых средств измерений.. Среди инструментальных погрешностей в отдельную группу выделяются погрешности схемы, не связанные с неточностью изготовления средств измерения и обязанные своим происхождением самой структурной схеме средств измерений. Исследование инструментальных погрешностей является предметом специальной дисциплины — теории точности измерительных устройств.
3. Погрешности, обусловленные неправильной установкой и взаимным расположением средств измерения, являющихся частью единого комплекса, несогласованностью их характеристик, влиянием внешних температурных, гравитационных, радиационных и других полей, нестабильностью источников питания, несогласованностью входных и выходных параметров электрических цепей приборов и т.д.
4. Личные погрешности, обусловленные индивидуальными особенностями наблюдателя. Такого рода погрешности вызываются, например, запаздыванием или опережением при регистрации сигнала, неправильным отсчетом десятых долей деления шкалы, асимметрией, возникающей при установке штриха посередине между двумя рисками.
По характеру своего поведения в процессе измерения систематические погрешности подразделяются на постоянные и переменные.
Постоянные систематические погрешности возникают, например, при неправильной установке начала отсчета, неправильной градуировке и юстировке средств измерения и остаются постоянными при всех повторных наблюдениях. Поэтому, если уж они возникли, их очень трудно обнаружить в результатах наблюдений.
Среди переменных систематических погрешностей принято выделять прогрессивные и периодические.
Прогрессивная погрешность возникает, например, при взвешивании, когда одно из коромысел весов находится ближе к источнику тепла, чем другое, поэтому быстрее нагревается и
удлиняется. Это приводит к систематическому сдвигу начала отсчета и к монотонному изменению показаний весов.
Периодическая погрешность присуща измерительным приборам с круговой шкалой, если ось вращения указателя не совпадает с осью шкалы.
Все остальные виды систематических погрешностей принято называть погрешностями, изменяющимися по сложному закону.
В тех случаях, когда при создании средств измерений, необходимых для данной измерительной установки, не удается устранить влияние систематических погрешностей, приходится специально организовывать измерительный процесс и осуществлять математическую обработку результатов. Методы борьбы с систематическими погрешностями заключаются в их обнаружении и последующем исключении путем полной или частичной компенсации. Основные трудности, часто непреодолимые, состоят именно в обнаружении систематических погрешностей, поэтому иногда приходится довольствоваться приближенным их анализом.
Способы обнаружения систематических погрешностей. Результаты наблюдений, полученные при наличии систематических погрешностей, будем называть неисправленными и в отличие от исправленных снабжать штрихами их обозначения (например, Х1, Х2 и т.д.). Вычисленные в этих условиях средние арифметические значения и отклонения от результатов наблюдений будем также называть неисправленными и ставить штрихи у символов этих величин. Таким образом,
Поскольку неисправленные результаты наблюдений включают в себя систематические погрешности, сумму которых для каждого /-го наблюдения будем обозначать через 8., то их математическое ожидание не совпадает с истинным значением измеряемой величины и отличается от него на некоторую величину 0, называемую систематической погрешностью неисправленного среднего арифметического. Действительно,
Если систематические погрешности постоянны, т.е. 0/ = 0, /=1,2, …, п, то неисправленные отклонения могут быть непосредственно использованы для оценки рассеивания ряда наблюдений. В противном случае необходимо предварительно исправить отдельные результаты измерений, введя в них так называемые поправки, равные систематическим погрешностям по величине и обратные им по знаку:
q = -Oi.
Таким образом, для нахождения исправленного среднего арифметического и оценки его рассеивания относительно истинного значения измеряемой величины необходимо обнаружить систематические погрешности и исключить их путем введения поправок или соответствующей каждому конкретному случаю организации самого измерения. Остановимся подробнее на некоторых способах обнаружения систематических погрешностей.
Постоянные систематические погрешности не влияют на значения случайных отклонений результатов наблюдений от средних арифметических, поэтому никакая математическая обработка результатов наблюдений не может привести к их обнаружению. Анализ таких погрешностей возможен только на основании некоторых априорных знаний об этих погрешностях, получаемых, например, при поверке средств измерений. Измеряемая величина при поверке обычно воспроизводится образцовой мерой, действительное значение которой известно. Поэтому разность между средним арифметическим результатов наблюдения и значением меры с точностью, определяемой погрешностью аттестации меры и случайными погрешностями измерения, равна искомой систематической погрешности.
Одним из наиболее действенных способов обнаружения систематических погрешностей в ряде результатов наблюдений является построение графика последовательности неисправленных значений случайных отклонений результатов наблюдений от средних арифметических.
Рассматриваемый способ обнаружения постоянных систематических погрешностей можно сформулировать следующим образом: если неисправленные отклонения результатов наблюдений резко изменяются при изменении условий наблюдений, то данные результаты содержат постоянную систематическую погрешность, зависящую от условий наблюдений.
Систематические погрешности являются детерминированными величинами, поэтому в принципе всегда могут быть вычислены и исключены из результатов измерений. После исключения систематических погрешностей получаем исправленные средние арифметические и исправленные отклонения результатов наблюдении, которые позволяют оценить степень рассеивания результатов.
Для исправления результатов наблюдений их складывают с поправками, равными систематическим погрешностям по величине и обратными им по знаку. Поправку определяют экспериментально при поверке приборов или в результате специальных исследований, обыкновенно с некоторой ограниченной точностью.
Поправки могут задаваться также в виде формул, по которым они вычисляются для каждого конкретного случая. Например, при измерениях и поверках с помощью образцовых манометров следует вводить поправки к их показаниям на местное значение ускорения свободного падения
где Р — измеряемое давление.
Введением поправки устраняется влияние только одной вполне определенной систематической погрешности, поэтому в результаты измерения зачастую приходится вводить очень большое число поправок. При этом вследствие ограниченной точности определения поправок накапливаются случайные погрешности и дисперсия результата измерения увеличивается.
Систематическая погрешность, остающаяся после введения поправок на ее наиболее существенные составляющие включает в себя ряд элементарных составляющих, называемых неисключенными остатками систематической погрешности. К их числу относятся погрешности:
• определения поправок;
• зависящие от точности измерения влияющих величин, входящих в формулы для определения поправок;
• связанные с колебаниями влияющих величин (температуры окружающей среды, напряжения питания и т.д.).
Перечисленные погрешности малы, и поправки на них не вводятся.
Систематические
погрешности не изменяются при увеличении
числа измерений, поскольку согласно
определению остаются постоянными или
изменяются по определенному закону в
процессе измерения. Систематические
погрешности могут быть выявлены на
основе теоретических оценок результатов,
путем сопоставления результатов,
полученных разными методами, на разных
приборах. Имеются возможности определить
систематические погрешности путем
тщательного исследования средства или
метода измерений путем построения
зависимости результатов от какого-либо
изменяющегося параметра, например
времени, климатических условий,
электромагнитных полей, напряжения
питания и т.д. В ряде случаев необходимо
выполнить большой объем исследовательской
работы для того, чтобы выявить условия,
создающие систематические погрешности
и, соответственно, представить либо
график, либо таблицу поправок, либо
определить аналитическую зависимость
систематической погрешности от
какого-либо параметра.
На
результат измерения влияют несколько
факторов, каждый из которых вызывает
свою систематическую погрешность. В
этом случае выявление аналитического
вида погрешности значительно усложняется,
приходится проводить трудоемкие
тщательные исследования, которые иногда
оканчиваются неудачей. Тем не менее,
необнаруженная систематическая
погрешность опаснее случайной, т.к.
последняя может быть минимизирована
соответствующей методикой измерения,
а систематическая невыявленная
погрешность исказит результат
непредсказуемо.
Особую
категорию систематических погрешностей
составляют измеренные с недостаточной
точностью фундаментальные и физические
константы, используемые в процессе
измерения. То же самое относится к
неточностям в стандартных справочных
данных, или к недостаточно точной
аттестации стандартных образцов.
Появление более точных справочных
данных требует пересчета результатов
всех измерений с их использованием, или
переградуировки шкал приборов. Например,
получение более точных данных о давлении
насыщающих паров индивидуальных веществ
может привести к необходимости
переградуировки термометров, манометров,
приборов для измерения концентраций и
т. д.
Уточнения
постоянной
Авогадро приводят к переградуировке
шкал всех приборов в физико-химических
измерениях. Новые исследования свойств
воды могут изменить результаты измерения
огромного числа приборов, т. к. на этих
постоянных строится температурная
шкала, шкала плотности, шкала вязкости.
Рассмотрим
группы систематических погрешностей,
отличающихся одна от другой причиной
возникновения. В основном различают
следующие группы:
-
Инструментальные
погрешности, связанные с несовершенством
конструкции прибора, неправильностью
технологии его изготовления. -
Погрешности
внешних влияний. Особенно часто в
измерительной практике приходится
сталкиваться с влиянием климатических
условий — температуры, давления,
влажности. Кроме того, весьма
распространенным источником такого
рода погрешностей является влияние
внешних электромагнитных полей и
изменения в напряжении сети питания
измерительных приборов. -
Погрешности
метода измерения. Этот вид погрешности
может быть связан как с неточностью
знания свойства объекта измерения, так
и с одинаковым влиянием разных факторов
на датчик измерительного прибора. Сюда
же можно отнести погрешности
пробоподготовки в определении состава
веществ и материалов. -
Субъективные
погрешности, связанные либо с недостаточным
вниманием, либо с невысокой квалификацией
персонала, обслуживающего прибор.
Особенно большое значение этот вид
погрешности имеет при пользовании
приборами с визуальным отсчетом. Большая
часть промахов также может быть связана
с субъективными погрешностями.
Инструментальная
погрешность
Инструментальная
погрешность — это составляющая погрешности,
зависящая от погрешности (класса
точности) средства измерения. Такие
погрешности могут быть выявлены либо
теоретически на основании механического,
электрического, теплового, оптического
расчета конструкции прибора, либо
опытным путем на основе контроля его
показаний по образцовым мерам, по
стандартным образцам, а также
компарированием показаний прибора с
аналогичными измерениями на других
приборах.
Инструментальные
погрешности, присущие конструкции
прибора, могут быть легко выявлены из
рассмотрения кинематической, электрической
или оптической схемы. Например, взвешивание
на весах с коромыслом обязательно
содержит погрешность, связанную с
неравенством длин коромысла от точек
подвеса чашек до средней точки опоры
коромысла. В электрических измерениях
на переменном токе обязательно будут
погрешности от сдвига фаз, который
появляется в любой электрической цепи.
В оптических приборах наиболее частыми
источниками систематической погрешности
являются аберрации оптических систем
и явления параллакса. Общим источником
погрешностей в большинстве приборов
является трение и связанные с ним наличие
люфтов, мертвого хода, свободного хода,
проскальзывания.
Способы
устранения или учета инструментальных
погрешностей достаточно хорошо известны
для каждого типа прибора. В метрологии
процедуры аттестации или испытаний
часто включают в себя исследования
инструментальных погрешностей. В ряде
случаев инструментальную погрешность
можно учесть и устранить за счет методики
измерений. Например, неравноплечесть
весов можно установить, поменяв местами
объект и гири. Аналогичные приемы
существуют практически во всех видах
измерения.
Инструментальные
погрешности, часто связанные с
несовершенством технологии изготовления
измерительного прибора. Особенно это
касается серийных приборов, выпускаемых
большими партиями. При сборке может
иметь место отличие в сигналах с датчиков,
отличие в установке шкал. Подвижные
части приборов могут собираться с разным
натягом, механические детали могут
иметь разные значения допусков и посадок
даже в пределах установленной нормы. В
оптических приборах огромное значение
имеет качество сборки или юстировка
оптической измерительной системы.
Современные оптические приборы могут
иметь десятки и сотни сборочных единиц,
а допуски при сборке составляют дол и
длины волны оптического излучения (λ =
0,4 — 0,7 мкм).
Методы
выявления таких погрешностей чаще всего
состоят в индивидуальной градуировке
измерительного прибора по образцовым
мерам или по образцовым приборам. В
современных приборах коррекция показаний
может быть выполнена не только
переградуировкой шкалы, но и коррекцией
электрического сигнала или компьютерной
обработкой результата. Естественно,
что во всех случаях коррекции должно
предшествовать исследование показаний
прибора.
Инструментальные
погрешности, связанные с износом или
старением средства измерения, имеют
определенные характерные особенности.
Процесс износа, как правило, проявляется
в погрешностях измерения постепенно.
Изменяются зазоры в сопрягаемых деталях,
соприкасающиеся поверхности покрываются
коррозией, изменяются упругости пружин
и т. д. Изменяется масса гирь, уменьшаются
размеры образцовых мер, изменяются
электрические и физико-химические
свойства узлов и деталей приборов, и
все это приводит к изменению показаний
приборов. Старение приборов — это, как
правило, следствие изменений структуры
материалов, из которых сделан прибор.
Изменяются не только механические
характеристики, но и электрические,
оптические, физико-химические. Стареют
металлы и сплавы, изменяя исходную
намагниченность, стареет оптика,
приобретая дополнительное светорассеяние
или центры окраски, стареют датчики
состава веществ. Последнее хорошо
известно тем, кто профессионально
работал с химреактивами, которые могут
сорбировать воду, реагировать с окружающей
средой и с примесями. Использование
химических веществ в измерительной
технике всегда необходимо с учетом
срока годности реактива.
Устранение
погрешностей приборов от старения или
износа, как правило, проводится по
результатам поверки, когда устанавливается
погрешность по истечении какого-либо
длительного времени хранения или
эксплуатации. В ряде случаев достаточно
почистить прибор, но иногда требуется
ремонт или перекалибровка шкалы.
Например, при появлении систематических
погрешностей во взвешивании на весах
удается вернуть им работоспособность
обычным техническим обслуживанием —
регулировкой и смазкой. При более
серьезном старении приходится
переполировывать трущиеся детали или
заменять сопрягаемые детали.
Особенно
важно выявить систематическую погрешность
у приборов, предназначенных для поверки
средств измерений — у образцовых приборов.
Как правило, на образцовых приборах
выполняется меньший объем работы, чем
на рабочих приборах, и по этой причине
систематический временной «уход»
показаний может не так наглядно
проявляться. Вместе с тем невыявленная
в образцовых приборах погрешность
передается другим приборам, которые по
данному образцовому прибору поверяются.
С
целью уменьшения влияния процессов
старения на измерительную технику в
ряде случаев прибегают к искусственному
старению наиболее ответственных узлов.
У оптических приборов — рефрактометров,
интерферометров, гониометров — старение
проявляется часто в том, что несущие
конструкции «ведет», т. е. они изменяют
форму, особенно в тех местах, где есть
сварка или обработка металла резанием.
Для того чтобы свести к минимуму влияние
такого старения, готовые узлы выдерживаются
какое-то время в жестких климатических
условиях или в специальных камерах, где
процесс старения можно ускорить, изменив
температуру, давление или влажность.
Отдельное
место в инструментальных погрешностях
занимает неправильная установка и
исходная регулировка средства измерения.
Многие приборы имеют встроенные указатели
уровня. Это значит, что перед измерением
нужно отгоризонтировать прибор. Причем,
такие требования предъявляются не
только к средствам измерений высокой
точности, но и к рутинным приборам
массового использования. Например,
неправильно установленные весы будут
систематически «обвешивать» покупателя,
на гониометре невозможно работать без
тщательного горизонтирования отсчетного
устройства. В приборах для измерения
магнитного поля весьма существенным
может оказаться ориентация его
относительно силовых линий поля Земли.
Озонометры нужно очень тщательно
ориентировать по Солнцу. Многие приборы
требуют установки по уровню или по
отвесу. Если двухплечие весы не установлены
горизонтально, нарушаются соотношения
длин между коромыслами. Если маятниковые
механизмы или грузопоршневые манометры
установлены не по отвесу, то показания
таких приборов будут сильно отличаться
от истинных.
Погрешности,
возникающие вследствие внешних влияний
Под
категорией
погрешностей,
возникающих вследствие внешних влияний,
обычно понимают изменение показаний
приборов под воздействием температуры,
влажности и давления. Тем не менее, это
лишь часть причин, приводящих к появлению
систематических погрешностей. Сюда же
следует отнести влияние вибраций,
постоянных и переменных ускорений,
влияние электромагнитного поля и
различных излучений: рентгеновского,
ультрафиолетового, ионизирующих
излучений, гамма-излучения. По мере
развития техники и науки появилась
возможность и необходимость проводить
измерения в нестандартных условиях,
например в Космосе или внутри подводной
лодки. Специфичность условий измерения
может доходить до высших категорий,
если ставить задачу измерения погодных
условий на Марсе или на Венере. Такие
же особенности могут иметь место в
реальных жизненно важных для нас
ситуациях. Если речь идет о контроле
параметров ядерного реактора, то условия,
в которых работает измерительный прибор,
могут значительно отличаться от
стандартных.
Влияние
температуры
— наиболее распространенный источник
погрешности при измерениях. Поскольку
от температуры зависит длина тел,
сопротивление проводников, объем
определенного количества газа, давление
насыщенного пара индивидуальных веществ,
то сигналы со всех видов датчиков, где
используются упомянутые физические
явления, будут изменяться с изменением
температуры. Существенно, что сигнал
сдатчика не только зависит от абсолютного
значения температуры, но от градиента
температуры в том месте, где расположен
датчик. Еще одна из причин появления
«температурной» систематической
погрешности — это изменение температуры
в процессе измерения. Указанные причины
существенны при косвенных измерениях,
т. е. в тех случаях, когда нет
необходимости измерять температуру
как физическую величину. Тем не менее
в собственно температурных измерениях
необходимо тщательно исследовать
показания приборов в различных
температурных интервалах. Например,
результаты измерения теплоемкости,
теплопроводности, теплотворной
способности топлива могут сильно
искажаться от различного рода температурных
воздействий.
Учитывая
большое влияние температуры на физические
свойства материалов и, соответственно,
на показания приборов, особое внимание
следует обращать на температурные
условия в тех комнатах, лабораториях и
зданиях, где проводятся градуировочнные
или поверочные работы. Здесь необходимо
тщательно следить за отсутствием
тепловых потоков, градиентов температуры,
однородностью температуры окружающей
среды и измерительного прибора. Для
того чтобы избежать влияния этих факторов
на измерения, приборы длительное время
выдерживают в термостатированном
помещении, прежде чем начинать какие-либо
работы. Для особо точных измерений
иногда используют дистанционные
манипуляторы, чтобы исключить тепловые
помехи, создаваемые операторами.
Для
большинства приборов при испытаниях
на право серийного выпуска программа
испытаний обязательно содержит
исследование показаний прибора (одного
или нескольких образцов) в зависимости
от температуры.
Влияние
магнитных или электрических полей
сказывается не только на средствах
измерения электромагнитных величин. В
зависимости от принципа действия прибора
наведенная ЭДС или токи Фуко могут
исказить показания любого датчика,
выходным сигналом которого служит
напряжение, ток, сопротивление или
электрическая емкость. Таких приборов
существует великое множество, особенно
в тех случаях, когда приборы имеют
цифровой выход. Аналогово-цифровые
преобразователи иногда начинают
регистрировать сигналы радиочастотных
или еще каких-либо электрических полей.
Очень часто электромагнитные помехи
попадают в прибор по сети питания.
Выяснить причины появления таких ложных
сигналов, научиться вводить поправки
в измерения при наличии электромагнитных
помех — это одна из важных проблем
метрологии и измерительной техники.
Особенно
важен рассматриваемый фактор появления
систематических погрешностей в больших
городах, где хорошо поставлена связь,
телевидение, радиовещание и т.п. Уровень
электромагнитного излучения бывает
настолько высоким, что, например, вблизи
мощного телецентра может загореться
низковольтная лампочка, если ее соединить
с проволочным контуром без источника
питания. Тот же эффект можно наблюдать
в зоне действия радиолокаторов вблизи
какого-либо аэропорта. О том, что этот
фактор может существенно влиять на
показания измерительных приборов,
свидетельствует тот факт, что буквально
за последние несколько лет появились
возможности уверенной радиотелефонной
связи, а также уверенного приема
спутникового телевидения. Это означает,
что уровень сигнала в окружающем нас
пространстве достаточно высок и легко
регистрируется соответствующей техникой.
Этот же сигнал будет накладываться на
сигналы, поступающие с датчиков
измерительных приборов.
Еще
один интересный случай появления
систематических погрешностей при
измерениях связан с измерительными
приборами на кораблях. Много лет назад
опытными мореплавателями было установлено,
что если корабль идет долгое время
курсом «норд» или «зюйд» некоторые
приборы начинают показывать неверные
результаты, т. е. приобретают какую-то
систематическую погрешность. Причина
этого была выяснена довольно точно:
корабль намагничивается от магнитного
поля Земли и при дальнейшем изменении
курса сохраняет остаточную намагниченность.
В наше время это хорошо исследованный
эффект. Во время мировой войны суда
специально размагничивали, чтобы
избежать срабатывания магнитных мин.
Сейчас в ряде стран, в том числе и у нас,
созданы корабли науки, которые либо
делаются из немагнитных материалов,
либо персонал тщательно следит за
намагниченностью корпуса. Такие суда
осуществляют дальнюю и космическую
связь, занимаются экологическими
измерениями, исследуют озоновый слой
Земли, исследуют прохождения радиоволн
и выполняют еще целый ряд необходимых
функций.
Влияние
второго климатического фактора — давления
— распространяется на несколько более
узкий круг измерений, чем температура,
но существует целый ряд очень важных
видов измерения, где данные об атмосферном
или внешнем давлении практически
определяют уровень точности измерений.
Так же, как в предыдущем случае, имеет
смысл отдельно рассматривать собственно
показания датчиков в других видах
измерения. Многие типы манометров по
сути своей являются дифференциальными,
т. е. измеряют разность давлений между
двумя различными точками какой-либо
системы. В этом случае любая погрешность
определения абсолютной величины давления
в той точке, относительно которой
измеряется давление, аддитивно
накладывается на результат измерения.
Влияние
давления на сигналы датчиков очень
существенны в рефрактометрии — измерении
показателя преломления — воздуха и
газов. Это относится собственно к
измерениям рефракции, а также к измерениям
с использованием соответствующих
датчиков, например при измерении
концентрации газов и газовых смесей.
От изменения давления меняется не только
показатель преломления газа, но и другие
характеристики, такие как диэлектрическая
постоянная. Соответственно, может
измениться сигнал с любого емкостного
датчика.
В
измерении массы информация о давлении
весьма существенна в связи с тем, что
при точных измерениях массы основной
вклад в систематическую погрешность
дает архимедова сила, выталкивающая
гирю. Силы Архимеда зависят от плотности
среды (плотности воздуха) и, следовательно,
непосредственно зависят от давления,
поскольку число молекул газа в единице
объема
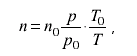
где
n0
— постоянная, называемая числом Лошмита;
р — давление; Т — температура; a p0
и T0
— нормальные значения давления и
температуры.

В
метрологических справочниках всегда
можно найти данные о поправках, которые
необходимо ввести при взвешивании для
учета
силы
Архимеда. Нетрудно показать, что
выталкивающая сила, действующая на
гирю, выражается формулой
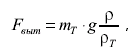
где
ρ — плотность воздуха; ρT
— плотность материала взвешиваемого
тела; mT
— масса тела. Масса взвешиваемого тела
будет равна:
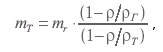
где
ρГ
— плотность материала гири. Если плотность
воздуха считать много меньшей плотности
материалов тела и гири, то массу
взвешиваемого тела можно выразить через
действительную массу гири плюс некоторая
поправка на силу Архимеда
(3.10)
Из
приведенныхформул следует, что при
взвешивании гирями из материала большой
плотности систематическая погрешность
от силы Архимеда меньше, чем при
взвешивании гирями из легкого материала.
В табл. 3.1 представлены поправки на силы
Архимеда, которые необходимо учитывать
при взвешивании для тела массой 100 г.
Таблица
3.1
Поправки
на силы Архимеда, которые нужно делать
при
взвешивании гирями для тела массой 100
г.
|
Плотность |
0,5 |
1 |
1,5 |
2 |
4 |
6 |
8 |
|
Поправка |
230 |
100 |
70 |
50 |
15 |
6 |
0,7 |
Отдельно
следует рассматривать систематические
погрешности при измерении давления в
условиях вакуума. Здесь наиболее
существенным источником погрешностей
является селективность процесса
откачивания воздуха насосами с различными
принципами действия. Этот вопрос очень
сложен с точки зрения анализа физической
сущности процесса вакуумирования.
Насосы ротационные, сорбционные,
магниторазрядные, турбо-молекулярные
создают совершенно разный состав
остаточных газов. В итоге в каждом
отдельном случае при оценке погрешностей
измерения
вакуума
нужно анализировать совместные искажения,
вносимые в состав остаточного газа
насосом, и искажения, вносимые тем или
иным датчиком давления. В ряде случаев
для прояснения картины недостаточна
даже дополнительная калибровка, т. к.
создать достаточно точно ту среду по
составу, в которой будет работать датчик,
очень трудно.
Проблема
создания вакуума и измерения давления
остаточного вакуума является одной из
ключевых проблем современной техники
и науки. Уверенно можно утверждать, что
уровень вакуумной техники определяет
уровень многих технологий, например
технологии изготовления микросхем и
микросборок.
То
же самое относится к наукоемким видам
измерения —
масс-спектометрии
или ЯМР спектометрии. Все метрологические
категории этих видов измерения напрямую
зависят от того, насколько «чистый»
вакуум удается создать и с какой точностью
удается этот вакуум измерить.
Третий
климатический фактор, вносящий
систематические погрешности во многие
измерения, — это влажность, т. е. содержание
молекул воды в том или ином месте
расположения измерительного прибора.
При оценке такой погрешности можно
рассматривать гигрометрию как вид
измерения, т. е. возможные систематические
погрешности в измерении влагосодержания
(абсолютная влажность) и Благосостояния
(относительная влажность). Можно также
оценивать погрешность как следствие
влияния влаги на показания других типов
приборов. Например, наличие влаги
изменяет проводимость или емкость
электрических элементов датчиков. Влага
ухудшает изоляционные свойства
материалов, вызывая токи утечки. Влага
изменяет структуру многих химических
соединений, трансформируясь из свободной
влаги в кристаллизационную и обратно.
С
учетом этого становится очевидным
всеобъемлющий характер учета влажности
при оценке систематических погрешностей.
На
эти трудности накладываются еще
неоднозначности в выражении измеряемых
в гигрометрии величин и единиц. По одной
из версий исходным моментом в гигрометрии
является упругость насыщенного водяного
пара при фиксированной температуре. В
этом случае любое уточнение термодинамических
свойств воды должно привести к пересчету
всех результатов измерений. По другой
версии исходным моментом в
гигрометрии
должно являться число молекул воды в
единице объема. Эти измерения наиболее
точно выполняются радиочастотными
методами, возможности которых и определяют
погрешности гигрометрии.
Вся
проблема влияния влажности на
систематические погрешности в измерениях
обозначена во многих странах и
международных организациях как одна
из наиболее существенных. По этой причине
влияние влажности на показания любого
прибора являются обязательным элементом
любых испытаний и исследований на
предмет выявления систематической
погрешности.
Погрешности
метода измерения или теоретические
погрешности
Любое
измерение имеет предел точности. Какой
бы мы не создали измерительный инструмент,
всегда будут существовать рамки возможной
точности, превзойти которые созданием
совершенных измерительных устройств
невозможно. Всегда при измерениях идут
на допущения, отклонения от идеальных
ситуаций, от функциональных зависимостей,
ограничивая трудоемкость процесса на
основании принципа достаточности
точности измерения для решения
практической задачи. Такие допущения
приходится делать во всех видах измерений.
В
механических измерениях на практике
постоянно присутствующей систематической
погрешностью является сила Архимеда,
по разному действующая на взвешиваемый
предмет и на гири. Учет
силы
Архимеда делается только при взвешивании
на высшем уровне точности при аттестации
мер высшего разряда. Во всех практических
измерениях массы такие поправки не
делаются, ограничивая тем самым точность
определения массы.
В
электрических измерениях постоянным
источником систематической погрешности
являются собственные сопротивления
приборов, собственная распределенная
емкость и индуктивность проводников.
При использовании законов для цепей
постоянного и переменного тока как
правило собственные электрические
параметры не учитываются. Не учитываются
в большинстве случаев и возможные
термоЭДС в цепи или образования
гальванических пар. Можно свести эти
погрешности к минимуму тщательным
исследованием цепей, но в реальных
случаях стремятся работать в таких
ситуациях, когда влияние перечисленных
причин ничтожно в сравнении с необходимой
и достаточной точностью измерений.
Измерения
физико-химических величин в каждой
конкретной задаче имеет определенные
систематические погрешности, специфические
для данного вида измерения. Прежде всего
это порог чувствительности датчика
концентрации какого-либо вещества.
Детектирование отдельных атомов, т. е.
отсутствие порога чувствительности,
имеет место только для весьма специфических
методов и для очень узкого класса
веществ. Второй фактор — вещество,
например вода, может входить как в виде
собственно молекул воды, так и в виде
кристаллизационной воды. Особенно
сложно выявить фактор многообразия
различных форм существования измеряемого
компонента в случае элементного анализа.
Так, водород может встречаться в газе
или в воздухе в виде молекул водорода
Н^, может входить в состав паров воды, в
состав углеводородов и т. д. Если при
измерениях используется метод с
предварительной атомизацией пробы, то
информацию о содержании водорода в
составе какого-либо соединения можно
получить только с использованием
дополнительных усилий, например с
использованием хроматографической
колонки, которая разделит компоненты
пробы по массам.
В
температурных измерениях всегда
существуют погрешности, связанные с
температурными
градиентами, т. е. с неоднородностью
температурного поля. Практически
невозможно реализовать такую ситуацию,
когда все части термометра будут
находиться в одинаковых температурных
условиях, а это приведет к тому, что в
жидкостных термометрах не весь объем
жидкости примет измеряемую температуру,
а термопарный термометр кроме полезного
сигнала зарегистрирует все влияния
температурных градиентов на ЭДС
термопары.
В
оптических измерениях, особенно в
измерении характеристик светового
потока — фотометрии, постоянный источник
систематических погрешностей — это
рассеянный свет в измерительных приборах.
Поскольку не существует идеально
отражающих и идеально поглощающих
поверхностей, в любой ситуации внутри
каждого прибора существует некий
постоянный фон паразитной подсветки.
В прецизионных оптических прибоpax
принимаются специальные меры борьбы с
рассеянным светом: устанавливаются
светофильтры, предварительные
монохроматизаторы излучения,
изготавливаются специфические
дифракционные решетки (голографические).Тем
не менее на каком-то уровне рассеянный
свет присутствует в оптических измерениях
всегда.
В
приборах для измерения показателей
преломления —
рефрактометрах
— систематическая погрешность обычно
связана с влиянием показателя преломления
воздуха. Чтобы исключить эту погрешность,
рефрактометры высокой точности иногда
вакуумируют, т. е. откачивают из объема
прибора воздух. Эта процедура делает
прибор громоздким и дорогим, поэтому
по такому пути идут только при крайней
необходимости. Чаще просто вносят
поправки на преломление воздуха,
используя таблицы показателя преломления
при различных температурах и давлениях.
В
магнитных измерениях источником
систематической погрешности служит,
как уже указывалось, магнитное поле
Земли, а также электромагнитные поля,
создаваемые теле- и радиопередатчиками,
системами связи, линиями электропередач.
В зависимости от расстояния между
измерительным прибором и источником
помех такого рода влияние может быть
очень сильным. Методы борьбы с такими
погрешностями достаточно хорошо освоены:
это либо защита измерительных приборов
экранами, либо измерение уровня помех
другими, более чувствительными и более
точными специальными приборами.
К
систематическим погрешностям метода
измерения относятся не только перечисленные
погрешности, которые можно назвать
инструментальными, поскольку они есть
следствие влияния каких-либо причин на
измерительный прибор, но и систематические
погрешности метода или процедуры
приготовления объекта к измерениям.
Особенно наглядно это видно в измерениях
состава веществ и материалов. Например,
существует распространенный метод
определения влажности зерна путем
взвешивания определенного его количества
до и после сушки. При этом полагается,
во-первых, что испаряется вся влага и,
во-вторых, что ничего, кроме воды, не
испаряется. Понятно, что и то и другое
справедливо только с какими-то допущениями.
Другой пример — измерение содержания
двуокиси серы в дымовых газах. Если в
пробозаборном тракте есть следы влаги,
а сам зонд находится при комнатной
температуре, то сернистый газ по пути
транспортировки от трубы до измерительного
прибора прореагирует с парами воды с
образованием серной кислоты. Естественно,
что прибор покажет неверное, заниженное
значение концентрации двуокиси серы.
Еще
один источник систематической погрешности,
связанный с несовершенством методов
измерения, имеет место в тех случаях,
когда приходится пользоваться при
измерениях какими-либо таблицами или
справочными данными. Любые данные в
справочниках получены с определенной
погрешностью, которая переносится на
объект измерения автоматически. Такого
же рода погрешности появляются при
использовании стандартных образцов.
Погрешности в аттестации стандартного
образца непосредственно ограничиваютточность
измерения в любом методе, когда
используются при калибровке и градуировке
стандартные образцы.
После
перечисления многочисленных причин
появления систематических погрешностей,
заключенных в методе измерения, может
показаться, что точно вообще ничего
измерить невозможно. На самом деле в
большинстве случаев обеспечивается
достаточный запас точности, или проводятся
специальные исследования по выявлению
причин систематических погрешностей.
После этого вносятся поправки либо в
показания шкал приборов, либо в методику
измерений.
Субъективные
систематические погрешности
На
результаты измерений непосредственное
влияние оказывает квалификация персонала
и индивидуальные особенности человека,
работающего на приборе. Для полной
реализации возможностей измерительного
прибора или метода предела для
совершенствования не существует. В
главе, посвященной эталонам, изложена
история совершенствования эталона
длины. На таком уровне обычных инженерных
знаний недостаточно, по этой причине
процесс измерения ставят рядом с
искусством. Понятно, что получить
информацию о результатах измерений
состава атмосферы на Венере, расшифровать
ее и оценить погрешность может только
очень квалифицированный человек. С
другой стороны, некоторые измерения,
например температуры тела человека,
может выполнить любой, даже неграмотный
человек.
На
субъективные погрешности измерений
влияют самые разнообразные особенности
человека. Известно, что время реакции
на звук, на свет, на запах, на тепло у
каждого человека разное. Хорошо известно,
что дискретные кадры в кино или в
телевизоре, следующие 25 раз в секунду,
воспринимаются наблюдателем как
непрерывная картина. Из этого следует,
что между откликом прибора и реакцией
человека временной интервал в 1/25 секунды
не может быть зарегистрирован.
Еще
одним наглядным примером влияния
оператора на результат измерения служат
измерения цвета. Человеческий глаз
имеет два аппарата зрения — дневной и
сумеречный. Дневной аппарат представляет
собой комбинацию из красных, зеленых и
синих рецепторов. У большой части людей
наблюдаются отклонения от средних
статистических характеристик — хорошо
известный дефект, называемый в обиходе
дальтонизмом. У человека может ненормально
функционировать либо какой-нибудь
рецептор, либо какой-нибудь аппарат
зрения. Принято проверять на правильность
цветовосприятия только водителей
транспорта. Обычный персонал, занимающийся
измерениями, никто на цветовосприятие
не проверяет. Это может привести к
неверным измерениям координат цвета
или температуры пирометром, т. е. в тех
случаях, когда используются визуальные
методы оценки яркости или цвета. Известно
также, что у человека цветовосприятие
может измениться с возрастом. Это связано
с тем, что стекловидное тело глаза с
возрастом желтеет, в результате чего
цвет одним и тем же человеком воспринимается
с годами по-разному. Некоторые художники,
восстанавливавшие свои собственные
картины через десятки лет, изображали
все в синих тонах.
Субъективное
восприятие человеком результата
измерения в большой степени определяется
также опытом работы. Например, при
измерении состава сплавов визуальным
стилометром опыт работы является
определяющим в получении достоверного
и точного результата. Опытный оператор
по появлению спектральных линий в поле
зрения прибора может определить не
только тип сплава, но и количественное
содержание в нем многих элементов.
From Wikipedia, the free encyclopedia
«Systematic bias» redirects here. For the sociological and organizational phenomenon, see Systemic bias.
Observational error (or measurement error) is the difference between a measured value of a quantity and its true value.[1] In statistics, an error is not necessarily a «mistake». Variability is an inherent part of the results of measurements and of the measurement process.
Measurement errors can be divided into two components: random and systematic.[2]
Random errors are errors in measurement that lead to measurable values being inconsistent when repeated measurements of a constant attribute or quantity are taken. Systematic errors are errors that are not determined by chance but are introduced by repeatable processes inherent to the system.[3] Systematic error may also refer to an error with a non-zero mean, the effect of which is not reduced when observations are averaged.[citation needed]
Measurement errors can be summarized in terms of accuracy and precision.
Measurement error should not be confused with measurement uncertainty.
Science and experiments[edit]
When either randomness or uncertainty modeled by probability theory is attributed to such errors, they are «errors» in the sense in which that term is used in statistics; see errors and residuals in statistics.
Every time we repeat a measurement with a sensitive instrument, we obtain slightly different results. The common statistical model used is that the error has two additive parts:
- Systematic error which always occurs, with the same value, when we use the instrument in the same way and in the same case.
- Random error which may vary from observation to another.
Systematic error is sometimes called statistical bias. It may often be reduced with standardized procedures. Part of the learning process in the various sciences is learning how to use standard instruments and protocols so as to minimize systematic error.
Random error (or random variation) is due to factors that cannot or will not be controlled. One possible reason to forgo controlling for these random errors is that it may be too expensive to control them each time the experiment is conducted or the measurements are made. Other reasons may be that whatever we are trying to measure is changing in time (see dynamic models), or is fundamentally probabilistic (as is the case in quantum mechanics — see Measurement in quantum mechanics). Random error often occurs when instruments are pushed to the extremes of their operating limits. For example, it is common for digital balances to exhibit random error in their least significant digit. Three measurements of a single object might read something like 0.9111g, 0.9110g, and 0.9112g.
Characterization[edit]
Measurement errors can be divided into two components: random error and systematic error.[2]
Random error is always present in a measurement. It is caused by inherently unpredictable fluctuations in the readings of a measurement apparatus or in the experimenter’s interpretation of the instrumental reading. Random errors show up as different results for ostensibly the same repeated measurement. They can be estimated by comparing multiple measurements and reduced by averaging multiple measurements.
Systematic error is predictable and typically constant or proportional to the true value. If the cause of the systematic error can be identified, then it usually can be eliminated. Systematic errors are caused by imperfect calibration of measurement instruments or imperfect methods of observation, or interference of the environment with the measurement process, and always affect the results of an experiment in a predictable direction. Incorrect zeroing of an instrument leading to a zero error is an example of systematic error in instrumentation.
The Performance Test Standard PTC 19.1-2005 “Test Uncertainty”, published by the American Society of Mechanical Engineers (ASME), discusses systematic and random errors in considerable detail. In fact, it conceptualizes its basic uncertainty categories in these terms.
Random error can be caused by unpredictable fluctuations in the readings of a measurement apparatus, or in the experimenter’s interpretation of the instrumental reading; these fluctuations may be in part due to interference of the environment with the measurement process. The concept of random error is closely related to the concept of precision. The higher the precision of a measurement instrument, the smaller the variability (standard deviation) of the fluctuations in its readings.
Sources[edit]
Sources of systematic error[edit]
Imperfect calibration[edit]
Sources of systematic error may be imperfect calibration of measurement instruments (zero error), changes in the environment which interfere with the measurement process and sometimes imperfect methods of observation can be either zero error or percentage error. If you consider an experimenter taking a reading of the time period of a pendulum swinging past a fiducial marker: If their stop-watch or timer starts with 1 second on the clock then all of their results will be off by 1 second (zero error). If the experimenter repeats this experiment twenty times (starting at 1 second each time), then there will be a percentage error in the calculated average of their results; the final result will be slightly larger than the true period.
Distance measured by radar will be systematically overestimated if the slight slowing down of the waves in air is not accounted for. Incorrect zeroing of an instrument leading to a zero error is an example of systematic error in instrumentation.
Systematic errors may also be present in the result of an estimate based upon a mathematical model or physical law. For instance, the estimated oscillation frequency of a pendulum will be systematically in error if slight movement of the support is not accounted for.
Quantity[edit]
Systematic errors can be either constant, or related (e.g. proportional or a percentage) to the actual value of the measured quantity, or even to the value of a different quantity (the reading of a ruler can be affected by environmental temperature). When it is constant, it is simply due to incorrect zeroing of the instrument. When it is not constant, it can change its sign. For instance, if a thermometer is affected by a proportional systematic error equal to 2% of the actual temperature, and the actual temperature is 200°, 0°, or −100°, the measured temperature will be 204° (systematic error = +4°), 0° (null systematic error) or −102° (systematic error = −2°), respectively. Thus the temperature will be overestimated when it will be above zero and underestimated when it will be below zero.
Drift[edit]
Systematic errors which change during an experiment (drift) are easier to detect. Measurements indicate trends with time rather than varying randomly about a mean. Drift is evident if a measurement of a constant quantity is repeated several times and the measurements drift one way during the experiment. If the next measurement is higher than the previous measurement as may occur if an instrument becomes warmer during the experiment then the measured quantity is variable and it is possible to detect a drift by checking the zero reading during the experiment as well as at the start of the experiment (indeed, the zero reading is a measurement of a constant quantity). If the zero reading is consistently above or below zero, a systematic error is present. If this cannot be eliminated, potentially by resetting the instrument immediately before the experiment then it needs to be allowed by subtracting its (possibly time-varying) value from the readings, and by taking it into account while assessing the accuracy of the measurement.
If no pattern in a series of repeated measurements is evident, the presence of fixed systematic errors can only be found if the measurements are checked, either by measuring a known quantity or by comparing the readings with readings made using a different apparatus, known to be more accurate. For example, if you think of the timing of a pendulum using an accurate stopwatch several times you are given readings randomly distributed about the mean. Hopings systematic error is present if the stopwatch is checked against the ‘speaking clock’ of the telephone system and found to be running slow or fast. Clearly, the pendulum timings need to be corrected according to how fast or slow the stopwatch was found to be running.
Measuring instruments such as ammeters and voltmeters need to be checked periodically against known standards.
Systematic errors can also be detected by measuring already known quantities. For example, a spectrometer fitted with a diffraction grating may be checked by using it to measure the wavelength of the D-lines of the sodium electromagnetic spectrum which are at 600 nm and 589.6 nm. The measurements may be used to determine the number of lines per millimetre of the diffraction grating, which can then be used to measure the wavelength of any other spectral line.
Constant systematic errors are very difficult to deal with as their effects are only observable if they can be removed. Such errors cannot be removed by repeating measurements or averaging large numbers of results. A common method to remove systematic error is through calibration of the measurement instrument.
Sources of random error[edit]
The random or stochastic error in a measurement is the error that is random from one measurement to the next. Stochastic errors tend to be normally distributed when the stochastic error is the sum of many independent random errors because of the central limit theorem. Stochastic errors added to a regression equation account for the variation in Y that cannot be explained by the included Xs.
Surveys[edit]
The term «observational error» is also sometimes used to refer to response errors and some other types of non-sampling error.[1] In survey-type situations, these errors can be mistakes in the collection of data, including both the incorrect recording of a response and the correct recording of a respondent’s inaccurate response. These sources of non-sampling error are discussed in Salant and Dillman (1994) and Bland and Altman (1996).[4][5]
These errors can be random or systematic. Random errors are caused by unintended mistakes by respondents, interviewers and/or coders. Systematic error can occur if there is a systematic reaction of the respondents to the method used to formulate the survey question. Thus, the exact formulation of a survey question is crucial, since it affects the level of measurement error.[6] Different tools are available for the researchers to help them decide about this exact formulation of their questions, for instance estimating the quality of a question using MTMM experiments. This information about the quality can also be used in order to correct for measurement error.[7][8]
Effect on regression analysis[edit]
If the dependent variable in a regression is measured with error, regression analysis and associated hypothesis testing are unaffected, except that the R2 will be lower than it would be with perfect measurement.
However, if one or more independent variables is measured with error, then the regression coefficients and standard hypothesis tests are invalid.[9]: p. 187 This is known as attenuation bias.[10]
See also[edit]
- Bias (statistics)
- Cognitive bias
- Correction for measurement error (for Pearson correlations)
- Errors and residuals in statistics
- Error
- Replication (statistics)
- Statistical theory
- Metrology
- Regression dilution
- Test method
- Propagation of uncertainty
- Instrument error
- Measurement uncertainty
- Errors-in-variables models
- Systemic bias
References[edit]
- ^ a b Dodge, Y. (2003) The Oxford Dictionary of Statistical Terms, OUP. ISBN 978-0-19-920613-1
- ^ a b John Robert Taylor (1999). An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements. University Science Books. p. 94, §4.1. ISBN 978-0-935702-75-0.
- ^ «Systematic error». Merriam-webster.com. Retrieved 2016-09-10.
- ^ Salant, P.; Dillman, D. A. (1994). How to conduct your survey. New York: John Wiley & Sons. ISBN 0-471-01273-4.
- ^ Bland, J. Martin; Altman, Douglas G. (1996). «Statistics Notes: Measurement Error». BMJ. 313 (7059): 744. doi:10.1136/bmj.313.7059.744. PMC 2352101. PMID 8819450.
- ^ Saris, W. E.; Gallhofer, I. N. (2014). Design, Evaluation and Analysis of Questionnaires for Survey Research (Second ed.). Hoboken: Wiley. ISBN 978-1-118-63461-5.
- ^ DeCastellarnau, A. and Saris, W. E. (2014). A simple procedure to correct for measurement errors in survey research. European Social Survey Education Net (ESS EduNet). Available at: http://essedunet.nsd.uib.no/cms/topics/measurement Archived 2019-09-15 at the Wayback Machine
- ^ Saris, W. E.; Revilla, M. (2015). «Correction for measurement errors in survey research: necessary and possible» (PDF). Social Indicators Research. 127 (3): 1005–1020. doi:10.1007/s11205-015-1002-x. hdl:10230/28341. S2CID 146550566.
- ^ Hayashi, Fumio (2000). Econometrics. Princeton University Press. ISBN 978-0-691-01018-2.
- ^ Angrist, Joshua David; Pischke, Jörn-Steffen (2015). Mastering ‘metrics : the path from cause to effect. Princeton, New Jersey. p. 221. ISBN 978-0-691-15283-7. OCLC 877846199.
The bias generated by this sort of measurement error in regressors is called attenuation bias.
Further reading[edit]
- Cochran, W. G. (1968). «Errors of Measurement in Statistics». Technometrics. 10 (4): 637–666. doi:10.2307/1267450. JSTOR 1267450.
From Wikipedia, the free encyclopedia
«Systematic bias» redirects here. For the sociological and organizational phenomenon, see Systemic bias.
Observational error (or measurement error) is the difference between a measured value of a quantity and its true value.[1] In statistics, an error is not necessarily a «mistake». Variability is an inherent part of the results of measurements and of the measurement process.
Measurement errors can be divided into two components: random and systematic.[2]
Random errors are errors in measurement that lead to measurable values being inconsistent when repeated measurements of a constant attribute or quantity are taken. Systematic errors are errors that are not determined by chance but are introduced by repeatable processes inherent to the system.[3] Systematic error may also refer to an error with a non-zero mean, the effect of which is not reduced when observations are averaged.[citation needed]
Measurement errors can be summarized in terms of accuracy and precision.
Measurement error should not be confused with measurement uncertainty.
Science and experiments[edit]
When either randomness or uncertainty modeled by probability theory is attributed to such errors, they are «errors» in the sense in which that term is used in statistics; see errors and residuals in statistics.
Every time we repeat a measurement with a sensitive instrument, we obtain slightly different results. The common statistical model used is that the error has two additive parts:
- Systematic error which always occurs, with the same value, when we use the instrument in the same way and in the same case.
- Random error which may vary from observation to another.
Systematic error is sometimes called statistical bias. It may often be reduced with standardized procedures. Part of the learning process in the various sciences is learning how to use standard instruments and protocols so as to minimize systematic error.
Random error (or random variation) is due to factors that cannot or will not be controlled. One possible reason to forgo controlling for these random errors is that it may be too expensive to control them each time the experiment is conducted or the measurements are made. Other reasons may be that whatever we are trying to measure is changing in time (see dynamic models), or is fundamentally probabilistic (as is the case in quantum mechanics — see Measurement in quantum mechanics). Random error often occurs when instruments are pushed to the extremes of their operating limits. For example, it is common for digital balances to exhibit random error in their least significant digit. Three measurements of a single object might read something like 0.9111g, 0.9110g, and 0.9112g.
Characterization[edit]
Measurement errors can be divided into two components: random error and systematic error.[2]
Random error is always present in a measurement. It is caused by inherently unpredictable fluctuations in the readings of a measurement apparatus or in the experimenter’s interpretation of the instrumental reading. Random errors show up as different results for ostensibly the same repeated measurement. They can be estimated by comparing multiple measurements and reduced by averaging multiple measurements.
Systematic error is predictable and typically constant or proportional to the true value. If the cause of the systematic error can be identified, then it usually can be eliminated. Systematic errors are caused by imperfect calibration of measurement instruments or imperfect methods of observation, or interference of the environment with the measurement process, and always affect the results of an experiment in a predictable direction. Incorrect zeroing of an instrument leading to a zero error is an example of systematic error in instrumentation.
The Performance Test Standard PTC 19.1-2005 “Test Uncertainty”, published by the American Society of Mechanical Engineers (ASME), discusses systematic and random errors in considerable detail. In fact, it conceptualizes its basic uncertainty categories in these terms.
Random error can be caused by unpredictable fluctuations in the readings of a measurement apparatus, or in the experimenter’s interpretation of the instrumental reading; these fluctuations may be in part due to interference of the environment with the measurement process. The concept of random error is closely related to the concept of precision. The higher the precision of a measurement instrument, the smaller the variability (standard deviation) of the fluctuations in its readings.
Sources[edit]
Sources of systematic error[edit]
Imperfect calibration[edit]
Sources of systematic error may be imperfect calibration of measurement instruments (zero error), changes in the environment which interfere with the measurement process and sometimes imperfect methods of observation can be either zero error or percentage error. If you consider an experimenter taking a reading of the time period of a pendulum swinging past a fiducial marker: If their stop-watch or timer starts with 1 second on the clock then all of their results will be off by 1 second (zero error). If the experimenter repeats this experiment twenty times (starting at 1 second each time), then there will be a percentage error in the calculated average of their results; the final result will be slightly larger than the true period.
Distance measured by radar will be systematically overestimated if the slight slowing down of the waves in air is not accounted for. Incorrect zeroing of an instrument leading to a zero error is an example of systematic error in instrumentation.
Systematic errors may also be present in the result of an estimate based upon a mathematical model or physical law. For instance, the estimated oscillation frequency of a pendulum will be systematically in error if slight movement of the support is not accounted for.
Quantity[edit]
Systematic errors can be either constant, or related (e.g. proportional or a percentage) to the actual value of the measured quantity, or even to the value of a different quantity (the reading of a ruler can be affected by environmental temperature). When it is constant, it is simply due to incorrect zeroing of the instrument. When it is not constant, it can change its sign. For instance, if a thermometer is affected by a proportional systematic error equal to 2% of the actual temperature, and the actual temperature is 200°, 0°, or −100°, the measured temperature will be 204° (systematic error = +4°), 0° (null systematic error) or −102° (systematic error = −2°), respectively. Thus the temperature will be overestimated when it will be above zero and underestimated when it will be below zero.
Drift[edit]
Systematic errors which change during an experiment (drift) are easier to detect. Measurements indicate trends with time rather than varying randomly about a mean. Drift is evident if a measurement of a constant quantity is repeated several times and the measurements drift one way during the experiment. If the next measurement is higher than the previous measurement as may occur if an instrument becomes warmer during the experiment then the measured quantity is variable and it is possible to detect a drift by checking the zero reading during the experiment as well as at the start of the experiment (indeed, the zero reading is a measurement of a constant quantity). If the zero reading is consistently above or below zero, a systematic error is present. If this cannot be eliminated, potentially by resetting the instrument immediately before the experiment then it needs to be allowed by subtracting its (possibly time-varying) value from the readings, and by taking it into account while assessing the accuracy of the measurement.
If no pattern in a series of repeated measurements is evident, the presence of fixed systematic errors can only be found if the measurements are checked, either by measuring a known quantity or by comparing the readings with readings made using a different apparatus, known to be more accurate. For example, if you think of the timing of a pendulum using an accurate stopwatch several times you are given readings randomly distributed about the mean. Hopings systematic error is present if the stopwatch is checked against the ‘speaking clock’ of the telephone system and found to be running slow or fast. Clearly, the pendulum timings need to be corrected according to how fast or slow the stopwatch was found to be running.
Measuring instruments such as ammeters and voltmeters need to be checked periodically against known standards.
Systematic errors can also be detected by measuring already known quantities. For example, a spectrometer fitted with a diffraction grating may be checked by using it to measure the wavelength of the D-lines of the sodium electromagnetic spectrum which are at 600 nm and 589.6 nm. The measurements may be used to determine the number of lines per millimetre of the diffraction grating, which can then be used to measure the wavelength of any other spectral line.
Constant systematic errors are very difficult to deal with as their effects are only observable if they can be removed. Such errors cannot be removed by repeating measurements or averaging large numbers of results. A common method to remove systematic error is through calibration of the measurement instrument.
Sources of random error[edit]
The random or stochastic error in a measurement is the error that is random from one measurement to the next. Stochastic errors tend to be normally distributed when the stochastic error is the sum of many independent random errors because of the central limit theorem. Stochastic errors added to a regression equation account for the variation in Y that cannot be explained by the included Xs.
Surveys[edit]
The term «observational error» is also sometimes used to refer to response errors and some other types of non-sampling error.[1] In survey-type situations, these errors can be mistakes in the collection of data, including both the incorrect recording of a response and the correct recording of a respondent’s inaccurate response. These sources of non-sampling error are discussed in Salant and Dillman (1994) and Bland and Altman (1996).[4][5]
These errors can be random or systematic. Random errors are caused by unintended mistakes by respondents, interviewers and/or coders. Systematic error can occur if there is a systematic reaction of the respondents to the method used to formulate the survey question. Thus, the exact formulation of a survey question is crucial, since it affects the level of measurement error.[6] Different tools are available for the researchers to help them decide about this exact formulation of their questions, for instance estimating the quality of a question using MTMM experiments. This information about the quality can also be used in order to correct for measurement error.[7][8]
Effect on regression analysis[edit]
If the dependent variable in a regression is measured with error, regression analysis and associated hypothesis testing are unaffected, except that the R2 will be lower than it would be with perfect measurement.
However, if one or more independent variables is measured with error, then the regression coefficients and standard hypothesis tests are invalid.[9]: p. 187 This is known as attenuation bias.[10]
See also[edit]
- Bias (statistics)
- Cognitive bias
- Correction for measurement error (for Pearson correlations)
- Errors and residuals in statistics
- Error
- Replication (statistics)
- Statistical theory
- Metrology
- Regression dilution
- Test method
- Propagation of uncertainty
- Instrument error
- Measurement uncertainty
- Errors-in-variables models
- Systemic bias
References[edit]
- ^ a b Dodge, Y. (2003) The Oxford Dictionary of Statistical Terms, OUP. ISBN 978-0-19-920613-1
- ^ a b John Robert Taylor (1999). An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements. University Science Books. p. 94, §4.1. ISBN 978-0-935702-75-0.
- ^ «Systematic error». Merriam-webster.com. Retrieved 2016-09-10.
- ^ Salant, P.; Dillman, D. A. (1994). How to conduct your survey. New York: John Wiley & Sons. ISBN 0-471-01273-4.
- ^ Bland, J. Martin; Altman, Douglas G. (1996). «Statistics Notes: Measurement Error». BMJ. 313 (7059): 744. doi:10.1136/bmj.313.7059.744. PMC 2352101. PMID 8819450.
- ^ Saris, W. E.; Gallhofer, I. N. (2014). Design, Evaluation and Analysis of Questionnaires for Survey Research (Second ed.). Hoboken: Wiley. ISBN 978-1-118-63461-5.
- ^ DeCastellarnau, A. and Saris, W. E. (2014). A simple procedure to correct for measurement errors in survey research. European Social Survey Education Net (ESS EduNet). Available at: http://essedunet.nsd.uib.no/cms/topics/measurement Archived 2019-09-15 at the Wayback Machine
- ^ Saris, W. E.; Revilla, M. (2015). «Correction for measurement errors in survey research: necessary and possible» (PDF). Social Indicators Research. 127 (3): 1005–1020. doi:10.1007/s11205-015-1002-x. hdl:10230/28341. S2CID 146550566.
- ^ Hayashi, Fumio (2000). Econometrics. Princeton University Press. ISBN 978-0-691-01018-2.
- ^ Angrist, Joshua David; Pischke, Jörn-Steffen (2015). Mastering ‘metrics : the path from cause to effect. Princeton, New Jersey. p. 221. ISBN 978-0-691-15283-7. OCLC 877846199.
The bias generated by this sort of measurement error in regressors is called attenuation bias.
Further reading[edit]
- Cochran, W. G. (1968). «Errors of Measurement in Statistics». Technometrics. 10 (4): 637–666. doi:10.2307/1267450. JSTOR 1267450.
Систематическая погрешность (или, на физическом жаргоне, систематика) характеризует неточность измерительного инструмента или метода обработки данных. Если точнее, то она показывает наше ограниченное знание этой неточности: ведь если инструмент «врет», но мы хорошо знаем, насколько именно, то мы сможем скорректировать его показания и устранить инструментальную неопределенность результата. Слово «систематическая» означает, что вы можете повторять какое-то измерение на этой установке миллионы раз, но если у нее «сбит прицел», то вы систематически будете получать значение, отличающееся от истинного.
Конечно, систематические погрешности хочется взять под контроль. Поскольку это чисто инструментальный эффект, ответственность за это целиком лежит на экспериментаторах, собиравших, настраивавших и работающих на этой установке. Они прилагают все усилия для того, чтобы, во-первых, корректно определить эти погрешности, а во-вторых, их минимизировать. Собственно, они этим начинают заниматься с самых первых дней работы установки, даже когда еще собственно научная программа исследований и не началась.
Возможные источники систематических погрешностей
Современный коллайдерный эксперимент очень сложен. В нём есть место огромному количеству источников систематических погрешностей на самых разных стадиях получения экспериментального результата. Вот некоторые из них.
Погрешности могут возникать на уровне «железа», при получении сырых данных:
- дефектные или неработающие отдельные регистрирующие компоненты или считывающие элементы. В детекторе миллионы отдельных компонентов, и даже если 1% из них оказался дефектным, это может ухудшить «зоркость» детектора и четкость регистрации сигналов. Надо подчеркнуть, что, даже если при запуске детектор работает на все 100%, постоянное детектирование частиц (это же жесткая радиация!) с течением времени выводит из строя отдельные компоненты, так что следить за поведением детектора абсолютно необходимо;
- наличие «слепых зон» детектора; например, если частица вылетает близко к оси пучков, то она улетит в трубу и детектор ее просто не заметит.
Погрешности могут возникать на этапе распознавания сырых данных и их превращение в физическое событие:
- погрешность при измерении энергии частиц в калориметре;
- погрешность при измерении траектории частиц в трековых детекторах, из-за которой неточно измеряется точка вылета и импульс частицы;
- неправильная идентификация типа частицы (например, система неудачно распознала след от π-мезона и приняла его за K-мезон). Более тонкий вариант: неправильное объединение адронов в одну адронную струю и неправильная оценка ее энергии;
- неправильный подсчет числа частиц (две частицы случайно вылетели так близко друг к другу, что детектор «увидел» только один след и посчитал их за одну).
Наконец, новые систематические погрешности добавляются на этапе позднего анализа события:
- неточность в измерении светимости пучков, которая влияет на пересчет числа событий в сечение процесса;
- наличие посторонних процессов рождения частиц, которые отличаются с физической точки зрения, но, к сожалению, выглядят для детектора одинаковыми. Такие процессы порождают неустранимый фон, который часто мешает разглядеть искомый эффект;
- необходимость моделировать процессы (в особенности, адронизацию, превращение кварков в адроны), опираясь частично на теорию, частично на прошлые эксперименты. Несовершенство того и другого привносит неточности и в новый экспериментальный результат. По этой причине теоретическую погрешность тоже часто относят к систематике.
В отдельных случаях встречаются источники систематических погрешностей, которые умудряются попасть сразу во все категории, они совмещают в себе и свойства детекторного «железа», и методы обработки и интерпретации данных. Например, если вы хотите сравнить друг с другом количество рожденных частиц и античастиц какого-то сорта (например, мюонов и антимюонов), то вам не стоит забывать, что ваш детектор состоит из вещества, а не из антивещества! Этот «перекос» в сторону вещества может привести к тому, что детектор будет видеть мюонов меньше, чем антимюонов, подробности см. в заметке Немножко про CP-нарушение, или Как жаль, что у нас нет детекторов из антивещества!.
Всю эту прорву источников потенциальных проблем надо распознать и оценить их влияние на выполняемый анализ. Здесь никаких абсолютно универсальных алгоритмов нет; исследователь должен сам понять, на какие погрешности надо обращать внимание и как грамотно их оценить. Конечно, тут на помощь приходят разные калибровочные измерения, выполненные в первые год-два работы детектора, и программы моделирования, которые позволяют виртуально протестировать поведение детектора в тех или иных условиях. Но главным в этом искусстве всё же является физическое чутье экспериментатора, его квалификация и накопленный опыт.
Почему важна грамотная оценка систематики
Беспечная оценка систематических погрешностей может привести к двум крайностям, причем обе очень нежелательны.
Заниженная погрешность — то есть неоправданная уверенность экспериментатора в том, что погрешности в его детекторе маленькие, хотя они на самом деле намного больше, — исключительно опасна, поскольку она может привести к совершенно неправильным научным выводам. Например, экспериментатор может на их основании решить, что измерения отличаются от теоретических предсказаний на уровне статистической значимости 10 стандартных отклонений (сенсация!), хотя истинная причина расхождения может просто состоять в том, что он проглядел источник ошибок, в 10 раз увеличивающий неопределенность измерения, и никакого расхождения на самом деле нет.
В борьбе с этой опасностью есть соблазн впасть в другую крайность: «А вдруг там есть еще какие-то погрешности? Может, я что-то не учел? Давай-ка я на всякий случай увеличу погрешности измерения в 10 раз для пущей безопасности.» Такая крайность плоха тем, что она обессмысливает измерение. Неоправданно завышая погрешность, вы рискуете получить результат, который будет, конечно, правильным, но очень неопределенным, ничем не лучше тех результатов, которые уже были получены до вас на гораздо более скромных установках. Такой подход, фактически, перечеркивает всю работу по разработке технологий, по изготовлению компонентов, по сборке детектора, все затраты на его работу и на анализ результатов.
Грамотный и ответственный анализ систематики должен удерживать оптимальный баланс (максимальная достоверность при максимальной научной ценности), не допуская таких крайностей. Это очень тонкая и сложная работа, и первые страницы в большинстве современных экспериментальных статей по физике частиц посвящены тщательному обсуждению систематических (а также статистических) погрешностей.
Мы не будем обсуждать подробности того, как обсчитывать систематические погрешности. Подчеркнем только, что это серьезная наука с множеством тонкостей и подводных камней. В качестве примера умеренно простого обсуждения некоторых вопросов см. статью Systematic Errors: facts and fictions.
Содержание
- Как рассчитать систематическую ошибку?
- Постоянство и соразмерность
- Систематическая ошибка в химии
- Систематическая ошибка в физический
- Примеры eсистематическая ошибка
- Ссылки
В систематическая ошибка Это одна из составляющих ошибок эксперимента или наблюдений (ошибок измерения), которая влияет на точность результатов. Это также известно как детерминированная ошибка, поскольку в большинстве случаев ее можно обнаружить и устранить, не повторяя эксперименты.
Важной характеристикой систематической ошибки является постоянство ее относительной величины; то есть он не зависит от размера выборки или толщины данных. Например, предполагая, что его относительное значение составляет 0,2%, если измерения повторяются в тех же условиях, ошибка всегда будет оставаться 0,2%, пока не будет исправлена.
Как правило, систематическая ошибка возникает из-за неправильного обращения с приборами или из-за технической неисправности аналитика или ученого. Его легко обнаружить, если сравнить экспериментальные значения со стандартным или сертифицированным значением.
Примеры экспериментальной ошибки этого типа возникают, когда аналитические весы, термометры и спектрофотометры не откалиброваны; или в случаях, когда не выполняется хорошее чтение правил, верньеров, градуированных цилиндров или бюреток.
Как рассчитать систематическую ошибку?
Систематическая ошибка влияет на точность, в результате чего экспериментальные значения могут быть выше или ниже фактических результатов. Под реальным результатом или значением понимается результат, который был исчерпывающе проверен многими аналитиками и лабораториями и зарекомендовал себя в качестве эталона сравнения.
Таким образом, сравнивая экспериментальное значение с реальным, получается разница. Чем больше эта разница, тем больше абсолютное значение систематической ошибки.
Например, предположим, что в аквариуме насчитывается 105 рыб, но известно заранее или из других источников, что истинное число составляет 108. Таким образом, систематическая ошибка составляет 3 (108-105). Мы сталкиваемся с систематической ошибкой, если, повторяя подсчет рыб, мы снова и снова получаем 105 рыб.
Однако более важным, чем вычисление абсолютного значения этой ошибки, является определение ее относительного значения:
Относительная погрешность = (108-105) ÷ 108
= 0,0277
Если выражать в процентах, то получается 2,77%. То есть ошибка подсчета имеет вес 2,77% от истинного количества рыбы. Если в аквариуме теперь есть 1000 рыб, и он будет считать их с той же систематической ошибкой, то будет на 28 рыб меньше, чем ожидалось, а не на 3, как это происходит с меньшим аквариумом.
Постоянство и соразмерность
Систематическая ошибка обычно постоянная, аддитивная и пропорциональная. В приведенном выше примере ошибка 2,77% останется постоянной до тех пор, пока измерения будут повторяться в одних и тех же условиях, независимо от размера аквариума (уже соприкасающегося с аквариумом).
Также обратите внимание на пропорциональность систематической ошибки: чем больше размер выборки или толщина данных (или объем аквариума и количество рыб в нем), тем больше систематическая ошибка. Если в аквариуме теперь 3500 рыб, ошибка будет 97 рыб (3500 x 0,0277); абсолютная погрешность увеличивается, но ее относительное значение неизменно, постоянно.
Если число удвоить, на этот раз с 7000 рыб, то ошибка будет 194 рыбы. Таким образом, систематическая ошибка постоянна и пропорциональна.
Это не означает, что необходимо повторить подсчет рыбы: достаточно знать, что определенное количество соответствует 97,23% от общего количества рыбы (100–2,77%). Отсюда истинное количество рыбы можно рассчитать, умножив на коэффициент 100 / 97,23.
Например, если было подсчитано 5200 рыб, то фактическое количество было бы 5 348 рыб (5200 x 100 / 97,23).
Систематическая ошибка в химии
В химии систематические ошибки обычно возникают из-за неправильного взвешивания из-за некалиброванных весов или из-за неправильного считывания объемов стеклянных материалов. Хотя они могут показаться не такими, как это, они влияют на точность результатов, потому что чем их больше, тем больше их негативных эффектов.
Например, если весы плохо откалиброваны, и при определенном анализе необходимо провести несколько взвешиваний, то окончательный результат будет все дальше и дальше от ожидаемого; это будет более неточно. То же самое происходит, если анализ постоянно измеряет объемы бюреткой, показания которой неверны.
Помимо весов и стеклянных материалов, химики также могут ошибаться в обращении с термометрами и pH-метрами, в скорости перемешивания, во времени, необходимом для протекания реакции, в калибровке весов. спектрофотометры, если предполагается высокая чистота образца или реагента и т. д.
Другие систематические ошибки в химии могут быть связаны с изменением порядка добавления реагентов, нагревом реакционной смеси до температуры выше, чем рекомендованная методом, или неправильной перекристаллизацией продукта синтеза.
Систематическая ошибка в физический
В физических лабораториях систематические ошибки носят еще более технический характер: любое оборудование или инструмент без надлежащей калибровки, неправильное поданное напряжение, неправильное расположение зеркал или деталей в эксперименте, добавление слишком большого момента к объекту, который должен упасть. из-за эффекта гравитации, среди других экспериментов.
Обратите внимание на то, что есть систематические ошибки, которые происходят из инструментального несовершенства, а другие, скорее, операционного типа, являются результатом ошибки со стороны аналитика, ученого или отдельного человека, который выполняет какое-либо действие.
Примеры eсистематическая ошибка
Ниже будут упомянуты другие примеры систематических ошибок, которые не обязательно должны происходить в лаборатории или в научной сфере:
— Поместите булочки в нижнюю часть духовки, поджаривая их больше, чем хотелось бы.
-Плохая осанка при сидении
-Закройте горшок для мокко только из-за недостатка прочности
-Не очищайте пароварки кофемашин сразу после текстурирования или нагрева молока.
-Используйте чашки разных размеров, когда вы следуете или хотите повторить определенный рецепт
-Хотите дозировать солнечную радиацию в тенистые дни
— Выполняйте подтягивания на перекладине, подняв плечи к ушам.
-Играйте несколько песен на гитаре без предварительной настройки струн
-Жарить оладьи с недостаточным количеством масла в казане
-Проведите последующее объемное титрование без повторной стандартизации раствора титранта
Ссылки
- Дэй Р. и Андервуд А. (1986). Количественная аналитическая химия. (Пятое изд.). ПИРСОН Прентис Холл.
- Хельменстин, Энн Мари, доктор философии (11 февраля 2020 г.). Случайная ошибка vs. Систематическая ошибка. Получено с: thinkco.com
- Bodner Research Web. (н.д.). Ошибки. Получено с: chemed.chem.purdue.edu
- Elsevier B.V. (2020). Систематическая ошибка. ScienceDirect. Получено с: sciencedirect.com
- Сепульведа, Э. (2016). Систематические ошибки. Получено из Physics Online: fisicaenlinea.com
- Мария Ирма Гарсиа Ордас. (н.д.). Проблемы с ошибкой измерения. Автономный университет штата Идальго. Получено с: uaeh.edu.mx
- Википедия. (2020). Ошибка наблюдения. Получено с: en.wikipedia.org
- Джон Спейси. (2018, 18 июля). 7 видов систематической ошибки. Получено с: simplicable.com
Систематические погрешности при повторных измерениях остаются постоянными или изменяются по определенному закону.
Когда судят о погрешности, подразумевают не значение, а интервал значений, в котором с заданной вероятностью находится истинное значение. Поэтому говорят об оценке погрешности. Если бы погрешность оказалась измеренной, т.е. стали бы известны её знак и значение, то её можно было бы исключить из действительного значения измеряемой физической величины и получить истинное значение.
Для получения результатов, минимально отличающихся от истинного значения измеряемой физической величины, проводят многократные наблюдения и проводят математическую обработку полученного массива с целью определения и минимизации случайной составляющей погрешности.
Минимизация систематической погрешности в процессе наблюдений выполняется следующими методами: метод замещения (состоит в замещении измеряемой величины мерой), метод противопоставления (состоит в двух поочерёдных измерениях при замене местами меры и измеряемого объекта), метод компенсации погрешности по знаку (состоит в двух поочерёдных измерениях, при которых влияющая величина становится противоположной).
При многократных наблюдениях возможно апостериорное (после выполнения наблюдений) исключение систематической погрешности в результате анализа рядов наблюдений. Рассмотрим графический анализ. При этом результаты последовательных наблюдений представляются функцией времени либо ранжируются в порядке возрастания погрешности.
Рассмотрим временную зависимость. Будем проводить наблюдения через одинаковые интервалы времени. Результаты последовательных наблюдений являются случайной функцией времени. В серии экспериментов, состоящих из ряда последовательных наблюдений, получаем одну реализацию этой функции. При повторении серии получаем новую реализацию, отличающуюся от первой.
Реализации отличаются преимущественно из-за влияния факторов, определяющих случайную погрешность, а факторы, определяющие систематическую погрешность, одинаково проявляются для соответствующих моментов времени в каждой реализации. Значение, соответствующее каждому моменту времени, называется сечением случайной функции времени. Для каждого сечения можно найти среднее по всем реализациям значение. Очевидно, что эта составляющая и определяет систематическую погрешность. Если через значения систематической погрешности для всех моментов времени провести плавную кривую, то она будет характеризовать временную закономерность изменения погрешности. Зная закономерность изменения, можем определить поправку для исключения систематической погрешности. После исключения систематической погрешности получаем «исправленный ряд результатов наблюдений».
Известен ряд способов исключения систематических погрешностей, которые условно можно разделить па 4 основные группы:
- устранение источников погрешностей до начала измерений;
- исключение почетностей в процессе измерения способами замещения, компенсации погрешностей по знаку, противопоставления, симметричных наблюдений;
- внесение известных поправок в результат измерения (исключение погрешностей начислением);
- оценка границ систематических погрешностей, если их нельзя исключить.
По характеру проявления систематические погрешности подразделяют на постоянные, прогрессивные и периодические.
Постоянные систематические погрешности сохраняют свое значение в течение всего времени измерений (например, погрешность в градуировке шкалы прибора переносится на все результаты измерений).
Прогрессивные погрешности – погрешности, которые в процессе измерении подрастают или убывают (например, погрешности, возникающие вследствие износа контактирующих деталей средств измерения).
И группу систематических погрешностей можно отнести: инструментальные погрешности; погрешности из-за неправильной установки измерительного устройства; погрешности, возникающие вследствие внешних влияний; погрешности метода измерения (теоретические погрешности); субъективные погрешности.
Абсолютная погрешность
- Причины возникновения погрешности измерения
- Систематическая и случайная погрешности
- Определение абсолютной погрешности
- Алгоритм оценки абсолютной погрешности в серии прямых измерений
- Значащие цифры и правила округления результатов измерений
- Примеры
Причины возникновения погрешности измерения
Погрешность измерения – это отклонение измеренного значения величины от её истинного (действительного) значения.
Обычно «истинное» значение неизвестно, и можно только оценить погрешность, приняв в качестве «истинного» среднее значение, полученное в серии измерений. Таким образом, процесс оценки проводится статистическими методами.
Виды погрешности измерений
Причины
Инструментальная погрешность
Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.)
Погрешность метода
Определяется несовершенством методов и допущениями в методике.
Теоретическая погрешность
Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.
Погрешность оператора
Определяется субъективным фактором, ошибками экспериментатора.
Систематическая и случайная погрешности
Систематической погрешностью называют погрешность, которая остаётся постоянной или изменяется закономерно во времени при повторных измерениях одной и той же величины.
Систематическая погрешность всегда имеет знак «+» или «-», т.е. говорят о систематическом завышении или занижении результатов измерений.
Систематическую погрешность можно легко определить, если известно эталонное (табличное) значение измеряемой величины. Для других случаев разработаны эффективные статистические методы выявления систематических погрешностей. Причиной систематической погрешности может быть неправильная настройка приборов или неправильная оценка параметров (завышенная или заниженная) в расчётных формулах.
Случайной погрешностью называют погрешность, которая не имеет постоянного значения при повторных измерениях одной и той же величины.
Случайные погрешности неизбежны и всегда присутствуют при измерениях.
Определение абсолютной погрешности
Абсолютная погрешность измерения – это модуль разности между измеренным и истинным значением измеряемой величины:
$$ Delta x = |x_{изм}-x_{ист} | $$
Например:
При пяти взвешиваниях гири с маркировкой 100 г были получены различные значения массы. Если принять маркировку за истинное значение, то получаем следующие значения абсолютной погрешности:
$m_i,г$
98,4
99,2
98,1
100,3
98,5
$Delta m_i, г$
1,6
0,8
1,9
0,3
1,5
Граница абсолютной погрешности – это величина h: $ |x-x_{ист}| le h $
Для оценки границы абсолютной погрешности на практике используются статистические методы.
Алгоритм оценки абсолютной погрешности в серии прямых измерений
Шаг 1. Проводим серию из N измерений, в каждом из которых получаем значение измеряемой величины $x_i, i = overline{1, N}$.
Шаг 2. Находим оценку истинного значения x как среднее арифметическое данной серии измерений:
$$ a = x_{cp} = frac{x_1+x_2+ cdots +x_N}{N} = frac{1}{N} sum_{i = 1}^N x_i $$
Шаг 3. Рассчитываем абсолютные погрешности для каждого измерения:
$$ Delta x_i = |x_i-a| $$
Шаг 4. Находим среднее арифметическое абсолютных погрешностей:
$$ Delta x_{cp} = frac{Delta x_1+ Delta x_2+ cdots + Delta x_N}{N} = frac{1}{N} sum_{i = 1}^N Delta x_i $$
Шаг 5. Определяем инструментальную погрешность при измерении как цену деления прибора (инструмента) d.
Шаг 6. Проводим оценку границы абсолютной погрешности серии измерений, выбирая большую из двух величин:
$$ h = max {d; Delta x_{cp} } $$
Шаг 7. Округляем и записываем результаты измерений в виде:
$$ a-h le x le a+h или x = a pm h $$
Значащие цифры и правила округления результатов измерений
Значащими цифрами – называют все верные цифры числа, кроме нулей слева. Результаты измерений записывают только значащими цифрами.
Например:
0,00501 — три значащие цифры 5,0 и 1.
5,01 — три значащие цифры.
5,0100 – пять значащих цифр; такая запись означает, что величина измерена с точностью 0,0001.
Внимание!
Правила округления.
Погрешность измерения округляют до первой значащей цифры, всегда увеличивая ее на единицу (округление по избытку, “ceiling”).
Округлять результаты измерений и вычислений нужно так, чтобы последняя значащая цифра находилась в том же десятичном разряде, что и абсолютная погрешность измеряемой величины.
Например: если при расчетах по результатам серии измерений получена оценка истинного значения a=1,725, а оценка абсолютной погрешности h = 0,11, то результат записывается так:
$$ a approx 1,7; h approx ↑0,2; 1,5 le x le 1,9 или x = 1,7 pm 0,2 $$
Примеры
Пример 1. При измерении температура воды оказалась в пределах от 11,55 ℃ до 11,63 ℃. Какова абсолютная погрешность этих измерений?
По условию $11,55 le t le 11,63$. Получаем систему уравнений:
$$ {left{ begin{array}{c} a-h = 11,55 \ a+h = 11,63 end{array} right.} Rightarrow {left{ begin{array}{c} 2a = 11,55+11,63 = 23,18 \ 2h = 11,63-11,55 = 0,08 end{array} right.} Rightarrow {left{ begin{array}{c} a = 11,59 \ h = 0,04end{array} right.} $$
$$ t = 11,59 pm 0,04 ℃ $$
Ответ: 0,04 ℃
Пример 2. По результатам измерений найдите границы измеряемой величины. Инструментальная погрешность d = 0,1.
$x_i$
15,3
16,4
15,3
15,8
15,7
16,2
15,9
Находим среднее арифметическое:
$$ a = x_{ср} = frac{15,3+16,4+ cdots +15,9}{7} = 15,8 $$
Находим абсолютные погрешности:
$$ Delta x_i = |x_i-a| $$
$ Delta x_i$
0,5
0,6
0,5
0
0,1
0,4
0,1
Находим среднее арифметическое:
$$ Delta x_{ср} = frac{0,5+0,6+ cdots + 0,1}{7} approx 0,31 gt d $$
Выбираем большую величину:
$$ h = max {d; Delta x_{ср} } = max {0,1; 0,31} = 0,31 $$
Округляем по правилам округления по избытку: $h approx ↑0,4$.
Получаем: x = 15, $8 pm 0,4$
Границы: $15,4 le x le 16,2$
Ответ: $15,4 le x le 16,2$
Пример 3*. В первой серии экспериментов было получено значение $x = a pm 0,3$. Во второй серии экспериментов было получено более точное значение $x = 5,631 pm 0,001$. Найдите оценку средней a согласно полученным значениям x.
Более точное значение определяет более узкий интервал для x. По условию:
$$ {left{ begin{array}{c} a-0,3 le x le a+0,3 \ 5,630 le x le 5,632 end{array} right.} Rightarrow a-0,3 le 5,630 le x le 5,632 le a+0,3 Rightarrow $$
$$ Rightarrow {left{ begin{array}{c} a-0,3 le 5,630 \ 5,632 le a+0,3 end{array} right.} Rightarrow {left{ begin{array}{c} a le 5,930 \ 5,332 le a end{array} right.} Rightarrow 5,332 le a le 5,930 $$
Т.к. a получено в серии экспериментов с погрешностью h=0,3, следует округлить полученные границы до десятых:
$$ 5,3 le a le 5,9 $$
Ответ: $ 5,3 le a le 5,9 $
Свойства физического объекта (явления, процесса) определяются набором
количественных характеристик — физических величин.
Как правило, результат измерения представляет
собой число, задающее отношение измеряемой величины к некоторому эталону.
Сравнение с эталоном может быть как
прямым (проводится непосредственно
экспериментатором), так и косвенным (проводится с помощью некоторого
прибора, которому экспериментатор доверяет).
Полученные таким образом величины имеют размерность, определяемую выбором эталона.
Замечание. Результатом измерения может также служить количество отсчётов некоторого
события, логическое утверждение (да/нет) или даже качественная оценка
(сильно/слабо/умеренно). Мы ограничимся наиболее типичным для физики случаем,
когда результат измерения может быть представлен в виде числа или набора чисел.
Взаимосвязь между различными физическими величинами может быть описана
физическими законами, представляющими собой идеализированную
модель действительности. Конечной целью любого физического
эксперимента (в том числе и учебного) является проверка адекватности или
уточнение параметров таких моделей.
1.1 Результат измерения
Рассмотрим простейший пример: измерение длины стержня
с помощью линейки. Линейка проградуирована производителем с помощью
некоторого эталона длины — таким образом, сравнивая длину
стержня с ценой деления линейки, мы выполняем косвенное сравнение с
общепринятым стандартным эталоном.
Допустим, мы приложили линейку к стержню и увидели на шкале некоторый результат
x=xизм. Можно ли утверждать, что xизм — это длина
стержня?
Во-первых, значение x не может быть задано точно, хотя бы
потому, что оно обязательно округлено до некоторой значащей
цифры: если линейка «обычная», то у неё
есть цена деления; а если линейка, к примеру, «лазерная»
— у неё высвечивается конечное число значащих цифр
на дисплее.
Во-вторых, мы никак не можем быть уверенны, что длина стержня на
самом деле такова хотя бы с точностью до ошибки округления. Действительно,
мы могли приложить линейку не вполне ровно; сама линейка могла быть
изготовлена не вполне точно; стержень может быть не идеально цилиндрическим
и т.п.
И, наконец, если пытаться хотя бы гипотетически переходить к бесконечной
точности измерения, теряет смысл само понятие «длины стержня». Ведь
на масштабах атомов у стержня нет чётких границ, а значит говорить о его
геометрических размерах в таком случае крайне затруднительно!
Итак, из нашего примера видно, что никакое физическое измерение не может быть
произведено абсолютно точно, то есть
у любого измерения есть погрешность.
Замечание. Также используют эквивалентный термин ошибка измерения
(от англ. error). Подчеркнём, что смысл этого термина отличается от
общеупотребительного бытового: если физик говорит «в измерении есть ошибка»,
— это не означает, что оно неправильно и его надо переделать.
Имеется ввиду лишь, что это измерение неточно, то есть имеет
погрешность.
Количественно погрешность можно было бы определить как разность между
измеренным и «истинным» значением длины стержня:
δx=xизм-xист. Однако на практике такое определение
использовать нельзя: во-первых, из-за неизбежного наличия
погрешностей «истинное» значение измерить невозможно, и во-вторых, само
«истинное» значение может отличаться в разных измерениях (например, стержень
неровный или изогнутый, его торцы дрожат из-за тепловых флуктуаций и т.д.).
Поэтому говорят обычно об оценке погрешности.
Об измеренной величине также часто говорят как об оценке, подчеркивая,
что эта величина не точна и зависит не только от физических свойств
исследуемого объекта, но и от процедуры измерения.
Замечание.
Термин оценка имеет и более формальное значение. Оценкой называют результат процедуры получения значения параметра или параметров физической модели, а также иногда саму процедуру. Теория оценок является подразделом математической статистики. Некоторые ее положения изложены в главе 3, но для более серьезного понимания следует обратиться к [5].
Для оценки значения физической величины корректно использовать
не просто некоторое фиксированное число xизм, а интервал (или
диапазон) значений, в пределах которого может лежать её
«истинное» значение. В простейшем случае этот интервал
может быть записан как
где δx — абсолютная величина погрешности.
Эта запись означает, что исследуемая величина лежит в интервале
x∈(xизм-δx;xизм+δx)
с некоторой достаточно большой долей вероятности (более подробно о
вероятностном содержании интервалов см. п. 2.2).
Для наглядной оценки точности измерения удобно также использовать
относительную величину погрешности:
Она показывает, насколько погрешность мала по сравнению с
самой измеряемой величиной (её также можно выразить в процентах:
ε=δxx⋅100%).
Пример. Штангенциркуль —
прибор для измерения длин с ценой деления 0,1мм. Пусть
диаметр некоторой проволоки равен 0,37 мм. Считая, что абсолютная
ошибка составляет половину цены деления прибора, результат измерения
можно будет записать как d=0,40±0,05мм (или
d=(40±5)⋅10-5м).
Относительная погрешность составляет ε≈13%, то
есть точность измерения весьма посредственная — поскольку
размер объекта близок к пределу точности прибора.
О необходимости оценки погрешностей.
Измерим длины двух стержней x1 и x2 и сравним результаты.
Можно ли сказать, что стержни одинаковы или различны?
Казалось бы,
достаточно проверить, справедливо ли x1=x2. Но никакие
два результата измерения не равны друг другу с абсолютной точностью! Таким
образом, без указания погрешности измерения ответ на этот вопрос дать
невозможно.
С другой стороны, если погрешность δx известна, то можно
утверждать, что если измеренные длины одинаковы
в пределах погрешности опыта, если |x2-x1|<δx
(и различны в противоположном случае).
Итак, без знания погрешностей невозможно сравнить между собой никакие
два измерения, и, следовательно, невозможно сделать никаких
значимых выводов по результатам эксперимента: ни о наличии зависимостей
между величинами, ни о практической применимости какой-либо теории,
и т. п. В связи с этим задача правильной оценки погрешностей является крайне
важной, поскольку существенное занижение или завышение значения погрешности
(по сравнению с реальной точностью измерений) ведёт к неправильным выводам.
В физическом эксперименте (в том числе лабораторном практикуме) оценка
погрешностей должна проводиться всегда
(даже когда составители задания забыли упомянуть об этом).
1.2 Многократные измерения
Проведём серию из n одинаковых (однотипных) измерений одной
и той же физической величины (например, многократно приложим линейку к стержню) и получим
ряд значений
Что можно сказать о данном наборе чисел и о длине стержня?
И можно ли увеличивая число измерений улучшить конечный результат?
Если цена деления самой линейки достаточно мала, то как нетрудно убедиться
на практике, величины {xi} почти наверняка окажутся
различными. Причиной тому могут быть
самые разные обстоятельства, например: у нас недостаточно остроты
зрения и точности рук, чтобы каждый раз прикладывать линейку одинаково;
стенки стержня могут быть слегка неровными; у стержня может и не быть
определённой длины, например, если в нём возбуждены звуковые волны,
из-за чего его торцы колеблются, и т. д.
В такой ситуации результат измерения интерпретируется как
случайная величина, описываемая некоторым вероятностным законом
(распределением).
Подробнее о случайных величинах и методах работы с ними см. гл. 2.
По набору результатов 𝐱 можно вычислить их среднее арифметическое:
| ⟨x⟩=x1+x2+…+xnn≡1n∑i=1nxi. | (1.1) |
Это значение, вычисленное по результатам конечного числа n измерений,
принято называть выборочным средним. Здесь и далее для обозначения
выборочных средних будем использовать угловые скобки.
Кроме среднего представляет интерес и то, насколько сильно варьируются
результаты от опыта к опыту. Определим отклонение каждого измерения от среднего как
Разброс данных относительно среднего принято характеризовать
среднеквадратичным отклонением:
| s=Δx12+Δx22+…+Δxn2n=1n∑i=1nΔxi2 | (1.2) |
или кратко
Значение среднего квадрата отклонения s2 называют
выборочной дисперсией.
Будем увеличивать число измерений n (n→∞). Если объект измерения и методика
достаточно стабильны, то отклонения от среднего Δxi будут, во-первых,
относительно малы, а во-вторых, положительные и отрицательные отклонения будут
встречаться примерно одинаково часто. Тогда при вычислении (1.1)
почти все отклонения Δxi скомпенсируются и можно ожидать,
что выборочное среднее при n≫1 будет стремиться к некоторому пределу:
Тогда предельное значение x¯ можно отождествить с «истинным» средним
для исследуемой величины.
Предельную величину среднеквадратичного отклонения при n→∞
обозначим как
Замечание. В общем случае указанные пределы могут и не существовать. Например, если измеряемый параметр
меняется во времени или в результате самого измерения, либо испытывает слишком большие
случайные скачки и т. п. Такие ситуации требуют особого рассмотрения и мы на них не
останавливаемся.
Замечание. Если n мало (n<10), для оценки среднеквадратичного отклонения
математическая статистика рекомендует вместо формулы (1.3) использовать
исправленную формулу (подробнее см. п. 5.2):
sn-12=1n-1∑i=1nΔxi2,
(1.4)
где произведена замена n→n-1. Величину sn-1
часто называют стандартным отклонением.
Итак, можно по крайней мере надеяться на то, что результаты небольшого числа
измерений имеют не слишком большой разброс, так что величина ⟨x⟩
может быть использована как приближенное значение (оценка) истинного значения
⟨x⟩≈x¯,
а увеличение числа измерений позволит уточнить результат.
Многие случайные величины подчиняются так называемому нормальному закону
распределения (подробнее см. Главу 2). Для таких величин
могут быть строго доказаны следующие свойства:
-
•
при многократном повторении эксперимента бо́льшая часть измерений
(∼68%) попадает в интервал x¯-σ<x<x¯+σ
(см. п. 2.2). -
•
выборочное среднее значение ⟨x⟩ оказывается с большей
вероятностью ближе к истинному значению x¯, чем каждое из измерений
{xi} в отдельности. При этом ошибка вычисления среднего
убывает пропорционально корню из числа опытов n
(см. п. 2.4).
Упражнение. Показать, что
s2=⟨x2⟩-⟨x⟩2.
(1.5)
то есть дисперсия равна разности среднего значения квадрата
⟨x2⟩=1n∑i=1nxi2
и квадрата среднего ⟨x⟩2=(1n∑i=1nxi)2.
1.3 Классификация погрешностей
Чтобы лучше разобраться в том, нужно ли многократно повторять измерения,
и в каком случае это позволит улучшить результаты опыта,
проанализируем источники и виды погрешностей.
В первую очередь, многократные измерения позволяют проверить
воспроизводимость результатов: повторные измерения в одинаковых
условиях, должны давать близкие результаты. В противном случае
исследование будет существенно затруднено, если вообще возможно.
Таким образом, многократные измерения необходимы для того,
чтобы убедиться как в надёжности методики, так и в существовании измеряемой
величины как таковой.
При любых измерениях возможны грубые ошибки — промахи
(англ. miss). Это «ошибки» в стандартном
понимании этого слова — возникающие по вине экспериментатора
или в силу других непредвиденных обстоятельств (например, из-за сбоя
аппаратуры). Промахов, конечно, нужно избегать, а результаты таких
измерений должны быть по возможности исключены из рассмотрения.
Как понять, является ли «аномальный» результат промахом? Вопрос этот весьма
непрост. В литературе существуют статистические
критерии отбора промахов, которыми мы, однако, настоятельно не рекомендуем
пользоваться (по крайней мере, без серьезного понимания последствий
такого отбора). Отбрасывание аномальных данных может, во-первых, привести
к тенденциозному искажению результата исследований, а во-вторых, так
можно упустить открытие неизвестного эффекта. Поэтому при научных
исследованиях необходимо максимально тщательно проанализировать причину
каждого промаха, в частности, многократно повторив эксперимент. Лишь
только если факт и причина промаха установлены вполне достоверно,
соответствующий результат можно отбросить.
Замечание. Часто причины аномальных отклонений невозможно установить на этапе
обработки данных, поскольку часть информации о проведении измерений к этому моменту
утеряна. Единственным способ борьбы с этим — это максимально подробное описание всего
процесса измерений в лабораторном журнале. Подробнее об этом
см. п. 4.1.1.
При многократном повторении измерении одной и той же физической величины
погрешности могут иметь систематический либо случайный
характер. Назовём погрешность систематической, если она повторяется
от опыта к опыту, сохраняя свой знак и величину, либо закономерно
меняется в процессе измерений. Случайные (или статистические)
погрешности меняются хаотично при повторении измерений как по величине,
так и по знаку, и в изменениях не прослеживается какой-либо закономерности.
Кроме того, удобно разделять погрешности по их происхождению. Можно
выделить
-
•
инструментальные (или приборные) погрешности,
связанные с несовершенством конструкции (неточности, допущенные при
изготовлении или вследствие старения), ошибками калибровки или ненормативными
условиями эксплуатации измерительных приборов; -
•
методические погрешности, связанные с несовершенством
теоретической модели явления (использование приближенных формул и
моделей явления) или с несовершенством методики измерения (например,
влиянием взаимодействия прибора и объекта измерения на результат измерения); -
•
естественные погрешности, связанные со случайным
характером
измеряемой физической величины — они являются не столько
«ошибками» измерения, сколько характеризуют
природу изучаемого объекта или явления.
Замечание. Разделение погрешностей на систематические и случайные
не является однозначным и зависит от постановки опыта. Например, производя
измерения не одним, а несколькими однотипными приборами, мы переводим
систематическую приборную ошибку, связанную с неточностью шкалы и
калибровки, в случайную. Разделение по происхождению также условно,
поскольку любой прибор подвержен воздействию «естественных»
случайных и систематических ошибок (шумы и наводки, тряска, атмосферные
условия и т. п.), а в основе работы прибора всегда лежит некоторое
физическое явление, описываемое не вполне совершенной теорией.
1.3.1 Случайные погрешности
Случайный характер присущ большому количеству различных физических
явлений, и в той или иной степени проявляется в работе всех без исключения
приборов. Случайные погрешности обнаруживаются просто при многократном
повторении опыта — в виде хаотичных изменений (флуктуаций)
значений {xi}.
Если случайные отклонения от среднего в большую или меньшую стороны
примерно равновероятны, можно рассчитывать, что при вычислении среднего
арифметического (1.1) эти отклонения скомпенсируются,
и погрешность результирующего значения ⟨x⟩ будем меньше,
чем погрешность отдельного измерения.
Случайные погрешности бывают связаны, например,
-
•
с особенностями используемых приборов: техническими
недостатками
(люфт в механических приспособлениях, сухое трение в креплении стрелки
прибора), с естественными (тепловой и дробовой шумы в электрических
цепях, тепловые флуктуации и колебания измерительных устройств из-за
хаотического движения молекул, космическое излучение) или техногенными
факторами (тряска, электромагнитные помехи и наводки); -
•
с особенностями и несовершенством методики измерения (ошибка
при отсчёте по шкале, ошибка времени реакции при измерениях с секундомером); -
•
с несовершенством объекта измерений (неровная поверхность,
неоднородность состава); -
•
со случайным характером исследуемого явления (радиоактивный
распад, броуновское движение).
Остановимся несколько подробнее на двух последних случаях. Они отличаются
тем, что случайный разброс данных в них порождён непосредственно объектом
измерения. Если при этом приборные погрешности малы, то «ошибка»
эксперимента возникает лишь в тот момент, когда мы по своей
воле совершаем замену ряда измеренных значений на некоторое среднее
{xi}→⟨x⟩. Разброс данных при этом
характеризует не точность измерения, а сам исследуемый объект или
явление. Однако с математической точки зрения приборные и
«естественные»
погрешности неразличимы — глядя на одни только
экспериментальные данные невозможно выяснить, что именно явилось причиной
их флуктуаций: сам объект исследования или иные, внешние причины.
Таким образом, для исследования естественных случайных процессов необходимо
сперва отдельно исследовать и оценить случайные инструментальные погрешности
и убедиться, что они достаточно малы.
1.3.2 Систематические погрешности
Систематические погрешности, в отличие от случайных, невозможно обнаружить,
исключить или уменьшить просто многократным повторением измерений.
Они могут быть обусловлены, во-первых, неправильной работой приборов
(инструментальная погрешность), например, сдвигом нуля отсчёта
по шкале, деформацией шкалы, неправильной калибровкой, искажениями
из-за не нормативных условий эксплуатации, искажениями из-за износа
или деформации деталей прибора, изменением параметров прибора во времени
из-за нагрева и т.п. Во-вторых, их причиной может быть ошибка в интерпретации
результатов (методическая погрешность), например, из-за использования
слишком идеализированной физической модели явления, которая не учитывает
некоторые значимые факторы (так, при взвешивании тел малой плотности
в атмосфере необходимо учитывать силу Архимеда; при измерениях в электрических
цепях может быть необходим учет неидеальности амперметров и вольтметров
и т. д.).
Систематические погрешности условно можно разделить на следующие категории.
-
1.
Известные погрешности, которые могут быть достаточно точно вычислены
или измерены. При необходимости они могут быть учтены непосредственно:
внесением поправок в расчётные формулы или в результаты измерений.
Если они малы, их можно отбросить, чтобы упростить вычисления. -
2.
Погрешности известной природы, конкретная величина которых неизвестна,
но максимальное значение вносимой ошибки может быть оценено теоретически
или экспериментально. Такие погрешности неизбежно присутствуют в любом
опыте, и задача экспериментатора — свести их к минимуму,
совершенствуя методики измерения и выбирая более совершенные приборы.Чтобы оценить величину систематических погрешностей опыта, необходимо
учесть паспортную точность приборов (производитель, как правило, гарантирует,
что погрешность прибора не превосходит некоторой величины), проанализировать
особенности методики измерения, и по возможности, провести контрольные
опыты. -
3.
Погрешности известной природы, оценка величины которых по каким-либо
причинам затруднена (например, сопротивление контактов при подключении
электронных приборов). Такие погрешности должны быть обязательно исключены
посредством модификации методики измерения или замены приборов. -
4.
Наконец, нельзя забывать о возможности существования ошибок, о
которых мы не подозреваем, но которые могут существенно искажать результаты
измерений. Такие погрешности самые опасные, а исключить их можно только
многократной независимой проверкой измерений, разными методами
и в разных условиях.
В учебном практикуме учёт систематических погрешностей ограничивается,
как правило, паспортными погрешностями приборов и теоретическими поправками
к упрощенной модели исследуемого явления.
Точный учет систематической ошибки возможен только при учете специфики конкретного эксперимента. Особенное внимание надо обратить на зависимость (корреляцию) систематических смещений при повторных измерениях. Одна и та же погрешность в разных случаях может быть интерпретирована и как случайная, и как систематическая.
Пример.
Калибровка электромагнита производится при помощи внесения в него датчика Холла или другого измерителя магнитного потока. При последовательных измерениях с разными токами (и соотственно полями в зазоре) калибровку можно учитыать двумя различными способами:
•
Измерить значение поля для разных токов, построить линейную калибровочную кривую и потом использовать значения, восстановленные по этой кривой для вычисления поля по току, используемому в измерениях.
•
Для каждого измерения проводить допольнительное измерения поля и вообще не испльзовать значения тока.
В первом случае погрешность полученного значения будет меньше, поскльку при проведении прямой, отдельные отклонения усреднятся. При этом погрешность измерения поля будет носить систематический харрактер и при обработке данных ее надо будет учитывать в последний момент. Во втором случае погрешность будет носить статистический (случайный) харрактер и ее надо будет добавить к погрешности каждой измеряемой точки. При этом сама погрешность будет больше. Выбор той или иной методики зависит от конретной ситуации. При большом количестве измерений, второй способ более надежный, поскольку статистическая ошибка при усреднении уменьшается пропорционально корню из количества измерений. Кроме того, такой способ повзоляет избежать методической ошибки, связанной с тем, что зависимость поля от тока не является линейной.
Пример.
Рассмотрим измерение напряжения по стрелочному вольтметру. В показаниях прибора будет присутствовать три типа погрешности:
1.
Статистическая погрешность, связанная с дрожанием стрелки и ошибкой визуального наблюдения, примерно равная половине цены деления.
2.
Систематическая погрешность, связанная с неправильной установкой нуля.
3.
Систематическая погрешность, связанная с неправильным коэффициентом пропорциональности между напряжением и отклонением стрелки. Как правило приборы сконструированы таким образом, чтобы максимальное значение этой погрешности было так же равно половине цены деления (хотя это и не гарантируется).