Чтобы найти погрешность косвенных измерений, надо воспользоваться формулами, приведенными в таблице. Эти формулы могут быть выведены «методом границ».
Сначала надо вспомнить основные понятия теории погрешности.
Абсолютная погрешность физической величины ΔА — это
разница между точным значением физической величины и ее приближенным значением и измеряется в тех же единицах, что и сама величина:
ΔА = А — Апр .
Так как мы никогда не знаем точного значения величины А, а лишь определяем из опыта ее приближенное значение, то и величину абсолютной
погрешности мы можем определить лишь приблизительно. Наиболее просто находится максимальная величина абсолютной погрешности, которая и используется нами в лабораторных работах.
Относительная погрешность измерения
εА равна:

При косвенных измерениях величину погрешности искомой величины вычисляют по формулам:

В случае, когда искомая величина находится по формуле, в которой в основном присутствуют произведение и частное, удобней находить сначала относительную погрешность. Если при этом один из
множителей представляет собой сумму или разность, нужно предварительно найти его абсолютную погрешность (сложением абсолютных погрешностей слагаемых), а затем относительную.
Зная относительную погрешность, найти абсолютную погрешность измерений можно так:
ΔА = εA· А.
«Правило ничтожных погрешностей»
при суммировании погрешностей любым из слагаемых можно пренебречь, если оно не превосходит ⅓ – ⅟4 от другого.
Запись результата с указанием погрешности.
Абсолютная погрешность измерений обычно округляется до 1 значащей цифры, а, если эта цифра 1, то до двух.
Пример:

Результат записывается в виде:
А = Аизм ± ΔА, например: ℓ = (13 ± 2) мм.
При этом в измеренном значении следует оставлять столько десятичных знаков, сколько их в значении
погрешности (последняя цифра погрешности «поправляет» последнюю цифру измеренного значения). Значение величины и погрешность следует
выражать в одних и тех же единицах!
Пример:

Пример оценки погрешностей косвенных измерений № 1

Пример оценки погрешностей косвенных измерений № 2

Задания для самостоятельного решения
Задание 1. Найдите плотность вещества, из которого сделан куб со стороной 7,00 ± 0,15 см, если его масса 847 ± 2 г. Что это за вещество?
Задание 2. Найдите удельную теплоту сгорания топлива, 2,10 ± 0,15 г которого хватило, чтобы нагреть 400 ± 10 мл воды на 35°С ± 2°С. Что это за
топливо?
Определение относительной погрешности косвенных измерений
Мы
уже отмечали, что часто бывает удобно
сначала определить относительную
погрешность косвенного измерения
,
а затем абсолютную. Покажем это на
примерах.
Пример.
Пусть x,
y
и z
– прямо измеренные величины, а f
– косвенно определяемая через них
величина. Вывести формулы для определения
относительной погрешности косвенных
измерений:
а)
f=(xy)z; б)
f=sin(x2+y2); в)
.
Значения
,
,
и
считать
известными.
Решение:
Напомним,
что
рассчитывается по формуле:
.
а)
Сначала прологарифмируем функцию
f=(xy)z
:
.
Теперь
найдем частные производные
,
и
:
;
;
.
Тогда:

.
Теперь,
зная
и
,
рассчитаем
:
.
б)
Прологарифмировав данную функцию
f=sin(x2+y2),
получим:
.
Мы видим, что выражение лишь усложнилось,
искать производную от исходной функции
проще, чем от ее логарифма. Поэтому
запишем частные производные функции:
;
.
Подставим
эти данные в формулу для определения
абсолютной погрешности косвенного
измерения. Напомним, что
рассчитывается
так:.Получим:
.
Теперь,
зная
и
,
можно рассчитать
:
.
в)
В этом примере исходную функцию удобно
прологарифмировать:
.
Теперь
будет проще искать частные производные.
Итак:
,
,
.
Подставим
полученные значения в формулу для
определения
.
Получим:

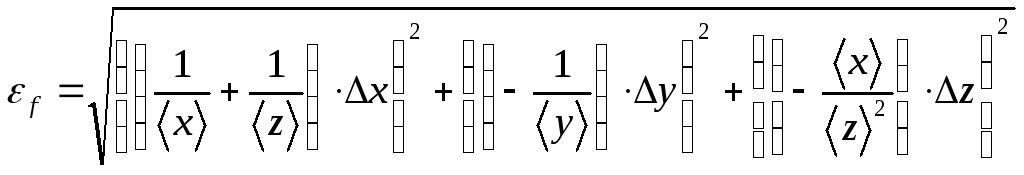
Теперь,
зная
и
,
рассчитаем
:
.
ПРИЛОЖЕНИЕ
5
Погрешности элементарных функций
Таблица 4
|
№ |
Вид функции
z |
Абсолютная z |
Относительная
|
|
1 |
ca, c = const |
ca |
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
|
6 |
|
|
|
|
7 |
|
|
|
|
8 |
|
|
|
|
9 |
|
|
|
|
10 |
|
|
|
|
11 |
|
|
|
|
12 |
|
|
|
Наиболее часто
встречаются следующие случаи определения
погрешностей:
1.
Погрешности в суммах и разностях.
Если а1
и а2
измерены с погрешностями Δа1
и Δа2
и измеренные значения используются для
вычисления суммы или разности А
= а1
± а2,
то суммируются абсолютные погрешности
(без учета знака):
ΔА
= Δа1
+ Δа2.
2.
Погрешности в произведениях и частных.
Если измеренные значения а1
и а2
используются для вычисления А
= а1
а2
или А =
а1
/ а2,
то суммируются относительные погрешности:
εА
= εа1
+ εа2,
где ε = Δа
/ а.
3.
Измеренная величина умножается на
точное число.
Если а
используется для вычисления произведения
А
= В
а,
в котором В
не имеет погрешности, то А
= | В
|
εа.
4.
Возведение в степень.
Если а
используется для вычисления степени А
= аn,
то А
= n
εа.
5.
Погрешности в произвольной функции
одной переменной.
Если а
используется для вычисления функции
А(а),
то:
.
Пример
1. Производится
косвенное измерение электрической
мощности, рассеиваемой на резисторе
сопротивлением R
при протекании по нему тока I.
Так как P
= I2
R,
то, применяя правила 2 и 4, получим εP
= εR
+ 2εI.
Пример
2. Измерением
найдено значение угла α = (20±3).
Необходимо найти cosα.
Наилучшая оценка для cos20
= 0,94. Погрешности Δα = 3
= 0,05 рад. Тогда по правилу 5 имеем εcosα
= (sin20)
0,05 = 0,34
0,05 = 0,02. Окончательно cosα
= 0,94 ± 0,02.
ПРИЛОЖЕНИЕ 6
В
приведенной таблице представлены
экспериментальные данные, с помощью
которых можно определить сопротивление
некоторого образца:
Таблица
5
-
I,
мАU,
ВI2,(
мА)2U2,
В2IU,
мАВ12,1
2,7
146,41
7,29
32,67
15,9
3,3
252,81
10,98
52,47
21,8
3,2
475,24
10,24
69,76
25,0
3,2
625,00
10,24
80,00
29,8
3,5
888,04
12,25
104,30
33,5
4,3
1122,25
18,49
144,05
38,3
4,0
1466,89
16,00
153,20
41,0
4,6
1681,00
21,16
188,60
46,6
5,1
2171,56
26,01
237,66
54,8
5,1
3003,04
26,01
279,48
1.
В качестве переменной x
выступает сила тока I,
переменной y
является напряжение U.
По формулам
и
вычисляют средние значения переменных:,
.
2.
По формулам
и
вычисляют средние квадраты:
,
3.
Рассчитывают <xy>
как
:
4.
Определить оптимальные значения
коэффициентов а
и b
по формулам:

,
.
5.
Определяют квадрат среднего квадратичного
отклонения σ2:
4.Определить
квадраты средних квадратичных отклонений
σа2
и σb2:

.
,
5.
Вычислить погрешности
и
:
,
.
ПРИЛОЖЕНИЕ 7
Значения
tα,n
для различных
значений доверительной вероятности
α
и числа
измерений n
(распределение Стьюдента)
Таблица 6
|
α n |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
0,95 |
0,98 |
0,99 |
0,999 |
|
2 |
1,000 |
1,376 |
1,963 |
3,08 |
6,31 |
12,71 |
31,8 |
63,7 |
636,6 |
|
3 |
0,816 |
1,061 |
1,336 |
1,886 |
2,92 |
4,30 |
6,96 |
9,92 |
31,6 |
|
4 |
0,765 |
0,978 |
1,250 |
1,638 |
2,35 |
3,18 |
4,54 |
5,84 |
12,94 |
|
5 |
0,741 |
0,941 |
1,190 |
1,533 |
2,13 |
2,77 |
3,75 |
4,60 |
8,61 |
|
6 |
0,727 |
0,920 |
1,156 |
1,476 |
2,02 |
2,57 |
3,36 |
4,03 |
6,86 |
|
7 |
0,718 |
0,906 |
1,134 |
1,440 |
1,943 |
2,45 |
3,14 |
4,71 |
5,96 |
|
8 |
0,711 |
0,896 |
1,119 |
1,415 |
1,895 |
2,36 |
3,00 |
3,50 |
5,40 |
|
9 |
0,706 |
0,889 |
1,108 |
1,397 |
1,860 |
2,31 |
2,90 |
3,36 |
5,04 |
|
10 |
0,703 |
0,883 |
1,110 |
1,383 |
1,833 |
2,26 |
2,82 |
3,25 |
4,78 |
|
11 |
0,700 |
0,879 |
1,093 |
1,372 |
1,812 |
2,23 |
2,76 |
3,17 |
4,59 |
|
12 |
0,697 |
0,876 |
1,088 |
1,363 |
1,796 |
2,20 |
2,72 |
3,11 |
4,49 |
|
13 |
0,695 |
0,873 |
1,083 |
1,356 |
1,782 |
2,18 |
2,68 |
3,06 |
4,32 |
|
14 |
0,694 |
0,870 |
1,079 |
1,350 |
1,771 |
2,16 |
2,65 |
3,01 |
4,22 |
|
15 |
0,692 |
0,868 |
1,076 |
1,345 |
1,761 |
2,14 |
2,62 |
2,98 |
4,14 |
|
16 |
0,691 |
0,866 |
1,074 |
1,341 |
1,753 |
2,13 |
2,60 |
2,95 |
4,07 |
|
17 |
0,690 |
0,868 |
1,071 |
1,337 |
1,746 |
2,12 |
2,58 |
2,92 |
4,02 |
|
18 |
0,689 |
0,863 |
1,069 |
1,333 |
1,740 |
2,11 |
2,57 |
2,92 |
3,96 |
|
19 |
0,688 |
0,862 |
1,067 |
1,330 |
1,734 |
2,10 |
2,55 |
2,88 |
3,92 |
|
20 |
0,688 |
0,861 |
1,066 |
1,328 |
1,729 |
2,09 |
2,54 |
2,86 |
3,88 |
|
|
0,674 |
0,842 |
1,036 |
1,282 |
1,645 |
1,960 |
2,33 |
2,58 |
3,29 |
1
Более подробно о классе точности прибора
см. Сысоев С.М. Лабораторный практикум
по электричеству и магнетизму:
Методические указания к лабораторным
работам по курсу общей физики. Для
студентов всех специальностей / Сысоев
С.М., Манина Е.А., Никонова Н.О.; Под ред.
С.М. Сысоева. – Сургут: Изд-во СурГУ,
2004.
52
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как определять погрешности измерений
Измерение – нахождение значения физической величины
опытным путем с помощью средств измерений.
Прямое
измерение
– определение значения физической
величины непосредственно средствами измерения.
Косвенное
измерение
– определение значения физической
величины по формуле, связывающей ее с другими физическими величинами, определяемыми
прямыми измерениями.
А, В, С, … — физические величины.
Апр. – приближенное значение физической величины.
А – абсолютная погрешность измерения физической
величины.
— относительная погрешность измерения
физической величины.
иА
– абсолютная
инструментальная погрешность, определяемая конструкцией прибора.
оА – абсолютная погрешность отсчета, она равна в
большинстве случаев
половине цены деления; при
измерении времени – цене деления секундомера или часов.
Абсолютную погрешность измерения
обычно округляют до одной значащей цифры:
Численное значение результата
измерений округляют так, чтобы его последняя цифра оказалась в том же разряде,
что и цифра погрешности:
Результат
измерения записывается так:
%
Определение погрешности методом среднего арифметического
При многократных
измерениях величины погрешность можно оценить следующим образом:
1.
Определить среднее
значение величины А:

измерениях).
2.Определить отклонение каждого значения от среднего:
3.Определить среднее значение отклонения,
его и принимают за абсолютную погрешность:
4.Определить
относительную погрешность и выразить ее в процентах:
|
|
|
|
|
|
|
1 |
|
|
||
|
2 |
|
|
||
|
3 |
|
|
Многократные измерения
предпочтительнее, так как при их проведении возможна компенсация случайных
факторов, влияющих на результат. Обычно многократные измерения проводят, слегка
изменяя условия опыта, но предполагая, что значение величины А не изменяются
Определение
погрешности косвенных измерений
При косвенных измерениях значение
физической величины находится путем расчетов по формуле.
Относительную погрешность
определяют так, как показано в таблице:
|
Формула величины |
Формула |
|
1. |
|
|
2. 3. |
|
|
4. |
|
Абсолютную погрешность определяют
по формуле:
( выражается десятичной дробью)
Пример: пусть измеряется сопротивление проводника. 
Результаты прямых измерений:
Тогда 


,
;
,
,
.
Графическое
представление результатов эксперимента
Правила построения
графиков
выберите соответствующую бумагу;
выберите масштаб по осям координат;
напишите обозначения измеряемых физических величин;
нанесите на график данные;
нанесите на график доверительные интервалы;
проведите кривую через нанесенные точки;
составьте заголовок графика.
Для построения графиков выпускают
специальную бумагу-миллиметровку.
При выборе масштабов по осям
координат следует руководствоваться следующими правилами:
— значение независимой переменной
откладывают вдоль оси абсцисс, функции – вдоль оси ординат;
— цена наименьшего деления масштабной
сетки должна быть сравнимой с величиной погрешности измерения;
— точка пересечения оси абсцисс и оси
ординат не обязательно должна иметь координаты (0,0).
При построении графиков следует
иметь в виду, что по результатам опытов мы получаем не точку, а прямоугольник
со сторонами и
.

В
|
|
|||||
|
|
|||||
0
А
При выполнении простых лабораторных
работ достаточно обвести экспериментальную точку кружком или пометить
крестиком, не указывая доверительных интервалов.
Этот кружок или крестик будут
обозначать, что данная точка получена с каким-то приближением и истинное
значение измеряемой величины лежит где-то в ее окрестности.
Правила
приближенных вычислений
1. Основное
правило округления.
Если первая
отброшенная цифра равна 5 или больше, то последнюю из сохраняемых цифр
увеличивают на единицу; если первая отброшенная цифра меньше 5, то последнюю из
сохраняемых цифр оставляют без изменения, например:
2. При сложении и
вычитании приближенных чисел
в полученном результате сохраняют столько десятичных знаков, сколько их в числе
с наименьшим количеством десятичных знаков, например:
3. При умножении
и делении приближенных чисел
в полученном результате нужно сохранить столько значащих цифр, сколько их имеет
приближенное число с наименьшим количеством значащих цифр, например:
4. При возведении
в квадрат приближенного числа
нужно в результате сохранять столько значащих цифр, сколько их имеет возводимое
в степень число, например:
5. При извлечении
квадратного корня в результате
нужно сохранять столько значащих цифр, сколько их имеет подкоренное число,
например:
6. При вычислении
промежуточных результатов в
них следует сохранять на одну цифру больше, чем требуют правила 2-5. Причем при
подсчете значащих цифр запасные цифры не учитываются. В окончательном
результате запасная цифра отбрасывается по основному правилу округления.
7. При нахождении
углов или тригонометрических функций значение соответствующего угла записывают с точностью до градуса, если
значение тригонометрической функции имеет две значащие цифры; если угол задан с
точностью до градусов, то в значении тригонометрической функции сохраняют две
значащие цифры, например:














