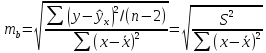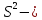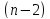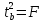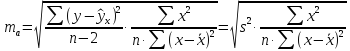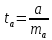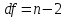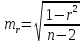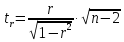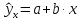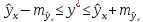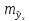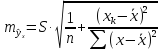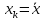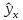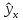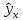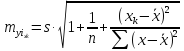Как найти стандартные ошибки параметров - ErrorsMaster.ru - большая энциклопедия ошибок и их решений

В
линейной регрессии обычно оценивается
значимость не только уравнения в целом,
но и отдельных его параметров. С этой
целью по каждому из параметров определяется
его стандартная ошибка: т_b
и
т_а.

Стандартная
ошибка коэффициента регрессии параметра
bрассчитывается
по формуле:

Где

остаточная дисперсия на одну степень
свободы.

Отношение
коэффициента регрессии к его стандартной
ошибке дает t-статистику,
которая подчиняется статистике Стьюдента
при

степенях
свободы. Эта статистика применяется
для проверки статистической значимости
коэффициента регрессии и для расчета
его доверительных интервалов.

Для
оценки значимости коэффициента регрессии
его величину сравнивают с его стандартной
ошибкой, т.е. определяют фактическое
значение t-критерия
Стьюдента:
,
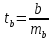
которое затем сравнивают с табличным
значением при определенном уровне
значимостиα
и
числе степеней свободы
.

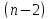
Справедливо
равенство

Доверительный
интервал для коэффициента регрессии
определяется как
.

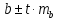
Стандартная
ошибка параметра а
определяется
по формуле

Процедура
оценивания значимости данного параметра
не отличается от рассмотренной выше
для коэффициента регрессии: вычисляется
t-критерий:

Его
величина сравнивается с табличным
значением при

степенях свободы.

Значимость
линейного коэффициента корреляции
проверяется на основе величины ошибки
коэффициента корреляции m_r:

Фактическое
значение t-критерия
Стьюдента определяется как

Данная
формула свидетельствует, что в парной
линейной регрессии
,
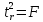
ибо как уже указывалось,
.
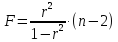
Кроме того,,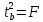
следовательно,.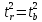

Таким
образом, проверка гипотез о значимости
коэффициентов регрессии и корреляции
равносильна проверке гипотезы о
значимости линейного уравнения регрессии.

Рассмотренную
формулу оценки коэффициента корреляции
рекомендуется применять при большом
числе наблюдений, а также если r
не близко к +1 или –1.

2.3 Интервальный прогноз на основе линейного уравнения регрессии

В
прогнозных расчетах по уравнению
регрессии определяется предсказываемое
y_р
значение
как точечный прогноз
_х
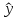
при
х_р
= х_k
т.
е. путем подстановки в линейное уравнение
регрессии

соответствующего
значения х.
Однако
точечный прогноз явно нереален, поэтому
он дополняется расчетом стандартной
ошибки
_х,
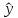
т.
е.
,
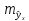
и
соответственно мы получаем интервальную
оценку прогнозного значения у*:

Считая,
что прогнозное значение фактора х_р
= х_k
получим
следующую формулу расчета стандартной
ошибки предсказываемого по линии
регрессии значения, т. е.

имеет выражение:

Рассмотренная
формула стандартной ошибки предсказываемого
среднего значения у
при
заданном значении х_k
характеризует
ошибку положения линии регрессии.
Величина стандартной ошибки
достигает
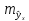
минимума при
и
возрастает по мере того, как «удаляется»
от
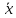
в любом направлении. Иными словами, чем
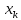
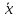
больше разность междуи,
тем больше ошибка,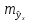
с
которой предсказывается среднее значение
у
для
заданного значения
.
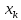
Можно ожидать наилучшие результаты
прогноза, если признак-фактор х находится
в центре области наблюдений х, и нельзя
ожидать хороших результатов прогноза
при удалении.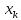
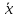
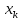
от. Если же значение.
оказывается за пределами наблюдаемых
значенийх,
используемых при построении линейной
регрессии, то результаты прогноза
ухудшаются в зависимости от того,
насколько
.
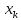
отклоняется от области наблюдаемых
значений факторах.

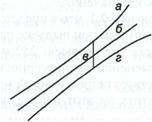
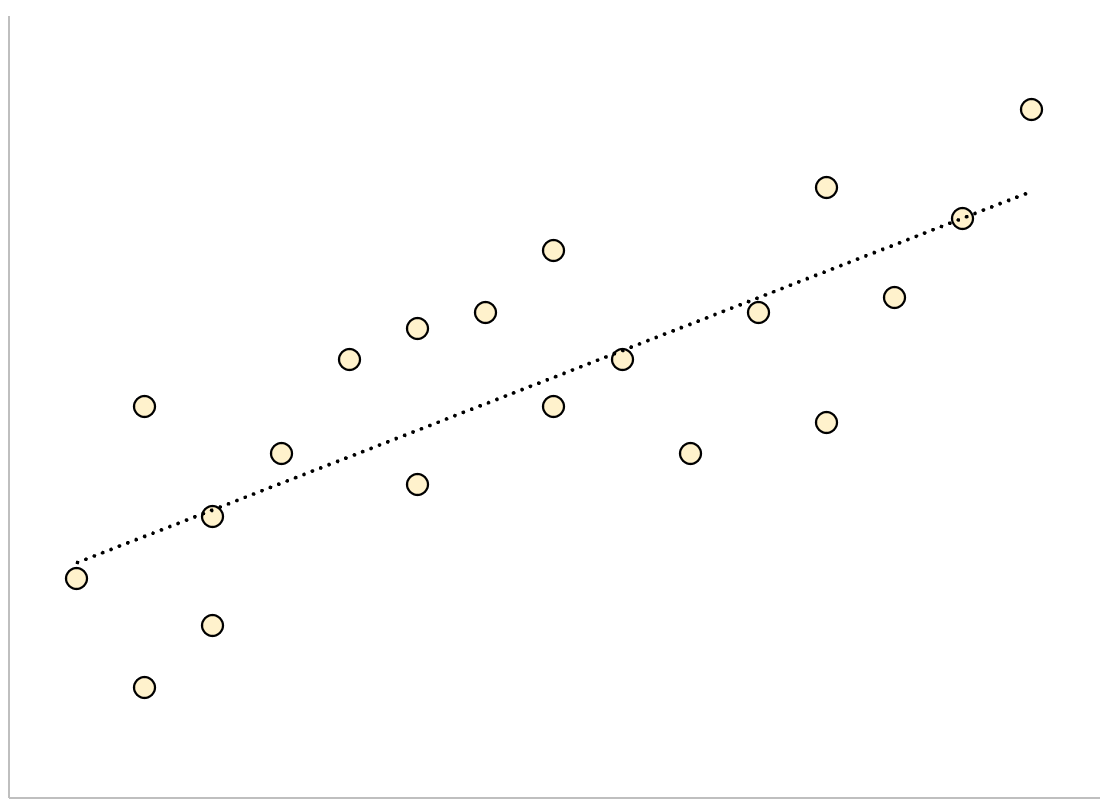
На
графике, приведенном на рис. 1, доверительные
границы для

представляют
собой гиперболы, расположенные по обе
стороны от линии регрессии. Рис. 1
показывает, как изменяются пределы в
зависимости от изменения
.:
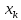
две гиперболы по обе стороны от линии
регрессии определяют 95 %-ные доверительные
интервалы для среднего значенияу
при
заданном значении х.

Однако
фактические значения у
варьируют
около среднего значения
.
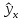
Индивидуальные
значения у
могут
отклоняться от

на
величину случайной ошибки ε, дисперсия
которой оценивается как остаточная
дисперсия на одну степень свободы
.
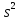
Поэтому ошибка предсказываемого
индивидуального значенияу
должна включать не только стандартную
ошибку
,
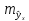
но и случайную ошибкуs.

Рис.
1. Доверительный интервал линии регрессии:

а
— верхняя
доверительная граница; б
— линия
регрессии;

в
— доверительный
интервал для

при
;

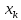
г
— нижняя
доверительная граница.

Средняя
ошибка прогнозируемого индивидуального
значения у
составит:

При
прогнозировании на основе уравнения
регрессии следует помнить, что величина
прогноза зависит не только от стандартной
ошибки индивидуального значения у,
но
и от точности прогноза значения фактора
х.
Его
величина может задаваться на основе
анализа других моделей исходя из
конкретной ситуации, а также анализа
динамики данного фактора.

Рассмотренная
формула средней ошибки индивидуального
значения признака у
может
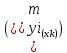
быть использована также для оценки
существенности различия предсказываемого
значения и некоторого гипотетического
значения.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Загрузить PDF

Стандартная ошибка оценки служит для того, чтобы выяснить, как линия регрессии соответствует набору данных. Если у вас есть набор данных, полученных в результате измерения, эксперимента, опроса или из другого источника, создайте линию регрессии, чтобы оценить дополнительные данные. Стандартная ошибка оценки характеризует, насколько верна линия регрессии.

1

Создайте таблицу с данными. Таблица должна состоять из пяти столбцов, и призвана облегчить вашу работу с данными. Чтобы вычислить стандартную ошибку оценки, понадобятся пять величин. Поэтому разделите таблицу на пять столбцов. Обозначьте эти столбцы так:^[1]
2
Введите данные в таблицу. Когда вы проведете эксперимент или опрос, вы получите пары данных — независимую переменную обозначим как , а зависимую или конечную переменную как . Введите эти значения в первые два столбца таблицы.
- Не перепутайте данные. Помните, что определенному значению независимой переменной должно соответствовать конкретное значение зависимой переменной.
- Например, рассмотрим следующий набор пар данных:
  - (1,2)
  - (2,4)
  - (3,5)
  - (4,4)
  - (5,5)
3
Вычислите линию регрессии. Сделайте это на основе представленных данных. Эта линия также называется линией наилучшего соответствия или линией наименьших квадратов. Расчет можно сделать вручную, но это довольно утомительно. Поэтому рекомендуем воспользоваться графическим калькулятором или онлайн-сервисом, которые быстро вычислят линию регрессии по вашим данным.^[2]
- В этой статье предполагается, что уравнение линии регрессии дано (известно).
- В нашем примере линия регрессии описывается уравнением $y^{{prime }}=0,6x+2,2$ .
4

Вычислите прогнозируемые значения по линии регрессии. С помощью уравнения линии регрессии можно вычислить прогнозируемые значения «y» для значений «x», которые есть и которых нет в наборе данных.

Реклама

1
Вычислите ошибку каждого прогнозируемого значения. В четвертом столбце таблицы запишите ошибку каждого прогнозируемого значения. В частности, вычтите прогнозируемое значение ( $y^{{prime }}$ ) из фактического (наблюдаемого) значения ().^[3]
- В нашем примере вычисления будут выглядеть так:
2
Вычислите квадраты ошибок. Возведите в квадрат каждое значение четвертого столбца, а результаты запишите в последнем (пятом) столбце таблицы.
- В нашем примере вычисления будут выглядеть так:
3
Найдите сумму квадратов ошибок. Она пригодится для вычисления стандартного отклонения, дисперсии и других величин. Чтобы найти сумму квадратов ошибок, сложите все значения пятого столбца. ^[4]
- В нашем примере вычисления будут выглядеть так:
4
Завершите расчеты. Стандартная ошибка оценки — это квадратный корень из среднего значения суммы квадратов ошибок. Обычно ошибка оценки обозначается греческой буквой . Поэтому сначала разделите сумму квадратов ошибок на число пар данных. А потом из полученного значения извлеките квадратный корень.^[5]
- Если рассматриваемые данные представляют всю совокупность, среднее значение находится так: сумму нужно разделить на N (количество пар данных). Если же рассматриваемые данные представляют некоторую выборку, вместо N подставьте N-2.
- В нашем примере, скорее всего, имеет место выборка, потому что мы рассматриваем всего 5 пар данных. Поэтому стандартную ошибку оценки вычислите следующим образом:
5
Интерпретируйте полученный результат. Стандартная ошибка оценки — это статистический показатель, которые оценивает, насколько близко измеренные данные лежат к линии регрессии. Ошибка оценка «0» означает, что каждая точка лежит непосредственно на линии. Чем выше ошибка оценки, тем дальше от линии регрессии лежат точки.^[6]
- В нашем примере выборка достаточно маленькая, поэтому стандартная оценка ошибки 0,894 является довольно низкой и характеризует близко расположенные данные.
Реклама

Об этой статье

Эту страницу просматривали 4719 раз.

Была ли эта статья полезной?

Источник

Что такое стандартная ошибка оценки? (Определение и пример)

17 авг. 2022 г.
читать 3 мин

Стандартная ошибка оценки — это способ измерения точности прогнозов, сделанных регрессионной моделью.

Часто обозначаемый σ est , он рассчитывается как:

σ est = √ Σ(y – ŷ) 2 /n

куда:

y: наблюдаемое значение
ŷ: Прогнозируемое значение
n: общее количество наблюдений

Стандартная ошибка оценки дает нам представление о том, насколько хорошо регрессионная модель соответствует набору данных. Особенно:

Чем меньше значение, тем лучше соответствие.
Чем больше значение, тем хуже соответствие.

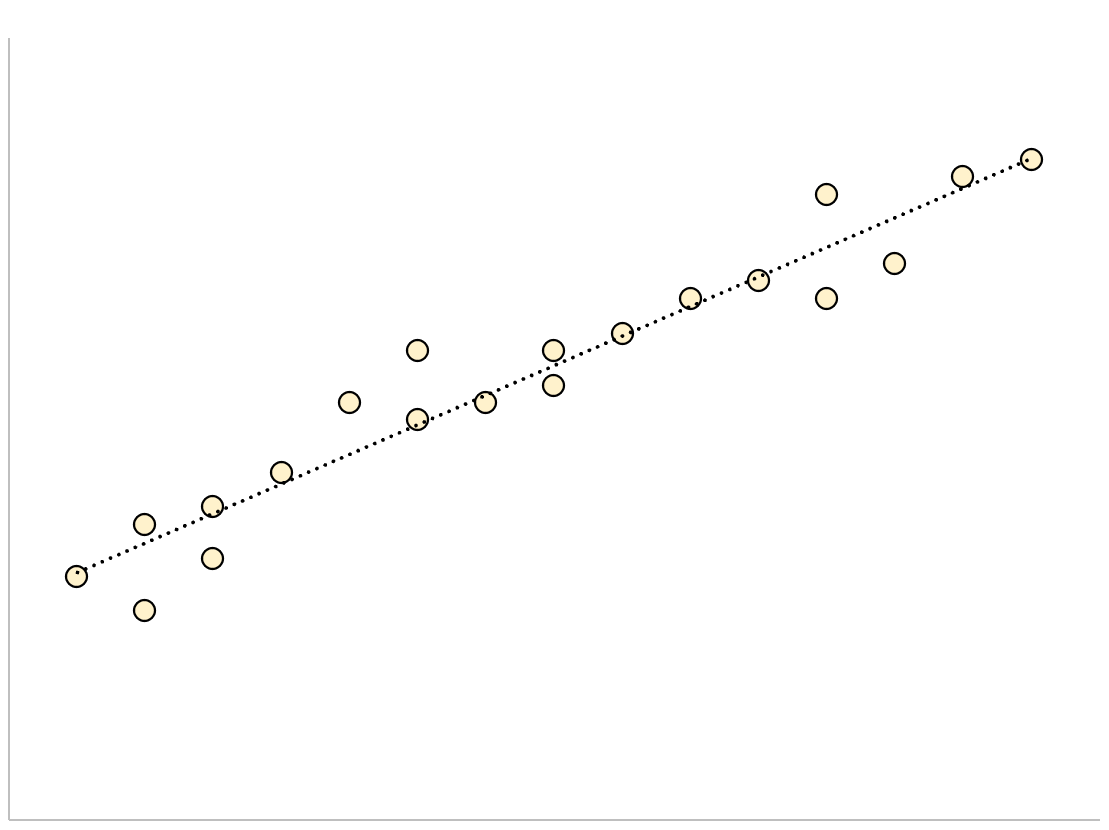
Для регрессионной модели с небольшой стандартной ошибкой оценки точки данных будут плотно сгруппированы вокруг предполагаемой линии регрессии:

И наоборот, для регрессионной модели с большой стандартной ошибкой оценки точки данных будут более свободно разбросаны по линии регрессии:

В следующем примере показано, как рассчитать и интерпретировать стандартную ошибку оценки для регрессионной модели в Excel.

Пример: стандартная ошибка оценки в Excel

Используйте следующие шаги, чтобы вычислить стандартную ошибку оценки для регрессионной модели в Excel.

Шаг 1: введите данные

Сначала введите значения для набора данных:

Шаг 2: выполните линейную регрессию

Затем щелкните вкладку « Данные » на верхней ленте. Затем выберите параметр « Анализ данных» в группе « Анализ ».

Если вы не видите эту опцию, вам нужно сначала загрузить пакет инструментов анализа .

В появившемся новом окне нажмите « Регрессия », а затем нажмите « ОК ».

В появившемся новом окне заполните следующую информацию:

Как только вы нажмете OK , появится вывод регрессии:

Мы можем использовать коэффициенты из таблицы регрессии для построения оценочного уравнения регрессии:

ŷ = 13,367 + 1,693 (х)

И мы видим, что стандартная ошибка оценки для этой регрессионной модели оказывается равной 6,006.Проще говоря, это говорит нам о том, что средняя точка данных отклоняется от линии регрессии на 6,006 единицы.

Мы можем использовать оценочное уравнение регрессии и стандартную ошибку оценки, чтобы построить 95% доверительный интервал для прогнозируемого значения определенной точки данных.

Например, предположим, что x равно 10. Используя оценочное уравнение регрессии, мы можем предсказать, что y будет равно:

ŷ = 13,367 + 1,693 * (10) = 30,297

И мы можем получить 95% доверительный интервал для этой оценки, используя следующую формулу:

95% ДИ = [ŷ – 1,96*σ расч ., ŷ + 1,96*σ расч .]

Для нашего примера доверительный интервал 95% будет рассчитываться как:

95% ДИ = [ŷ – 1,96*σ расч ., ŷ + 1,96*σ расч .]
95% ДИ = [30,297 – 1,96*6,006, 30,297 + 1,96*6,006]
95% ДИ = [18,525, 42,069]

Дополнительные ресурсы

Как выполнить простую линейную регрессию в Excel
Как выполнить множественную линейную регрессию в Excel
Как создать остаточный график в Excel

Источник

When we fit a regression model to a dataset, we’re often interested in how well the regression model “fits” the dataset. Two metrics commonly used to measure goodness-of-fit include R-squared (R²) and the standard error of the regression, often denoted S.

This tutorial explains how to interpret the standard error of the regression (S) as well as why it may provide more useful information than R².

Standard Error vs. R-Squared in Regression

Suppose we have a simple dataset that shows how many hours 12 students studied per day for a month leading up to an important exam along with their exam score:

If we fit a simple linear regression model to this dataset in Excel, we receive the following output:

R-squared is the proportion of the variance in the response variable that can be explained by the predictor variable. In this case, 65.76% of the variance in the exam scores can be explained by the number of hours spent studying.

The standard error of the regression is the average distance that the observed values fall from the regression line. In this case, the observed values fall an average of 4.89 units from the regression line.

If we plot the actual data points along with the regression line, we can see this more clearly:

Notice that some observations fall very close to the regression line, while others are not quite as close. But on average, the observed values fall 4.19 units from the regression line.

The standard error of the regression is particularly useful because it can be used to assess the precision of predictions. Roughly 95% of the observation should fall within +/- two standard error of the regression, which is a quick approximation of a 95% prediction interval.

If we’re interested in making predictions using the regression model, the standard error of the regression can be a more useful metric to know than R-squared because it gives us an idea of how precise our predictions will be in terms of units.

To illustrate why the standard error of the regression can be a more useful metric in assessing the “fit” of a model, consider another example dataset that shows how many hours 12 students studied per day for a month leading up to an important exam along with their exam score:

Notice that this is the exact same dataset as before, except all of the values are cut in half. Thus, the students in this dataset studied for exactly half as long as the students in the previous dataset and received exactly half the exam score.

If we fit a simple linear regression model to this dataset in Excel, we receive the following output:

Notice that the R-squared of 65.76% is the exact same as the previous example.

However, the standard error of the regression is 2.095, which is exactly half as large as the standard error of the regression in the previous example.

If we plot the actual data points along with the regression line, we can see this more clearly:

Notice how the observations are packed much more closely around the regression line. On average, the observed values fall 2.095 units from the regression line.

So, even though both regression models have an R-squared of 65.76%, we know that the second model would provide more precise predictions because it has a lower standard error of the regression.

The Advantages of Using the Standard Error

The standard error of the regression (S) is often more useful to know than the R-squared of the model because it provides us with actual units. If we’re interested in using a regression model to produce predictions, S can tell us very easily if a model is precise enough to use for prediction.

For example, suppose we want to produce a 95% prediction interval in which we can predict exam scores within 6 points of the actual score.

Our first model has an R-squared of 65.76%, but this doesn’t tell us anything about how precise our prediction interval will be. Luckily we also know that the first model has an S of 4.19. This means a 95% prediction interval would be roughly 2*4.19 = +/- 8.38 units wide, which is too wide for our prediction interval.

Our second model also has an R-squared of 65.76%, but again this doesn’t tell us anything about how precise our prediction interval will be. However, we know that the second model has an S of 2.095. This means a 95% prediction interval would be roughly 2*2.095= +/- 4.19 units wide, which is less than 6 and thus sufficiently precise to use for producing prediction intervals.

Further Reading

Introduction to Simple Linear Regression
What is a Good R-squared Value?

Источник