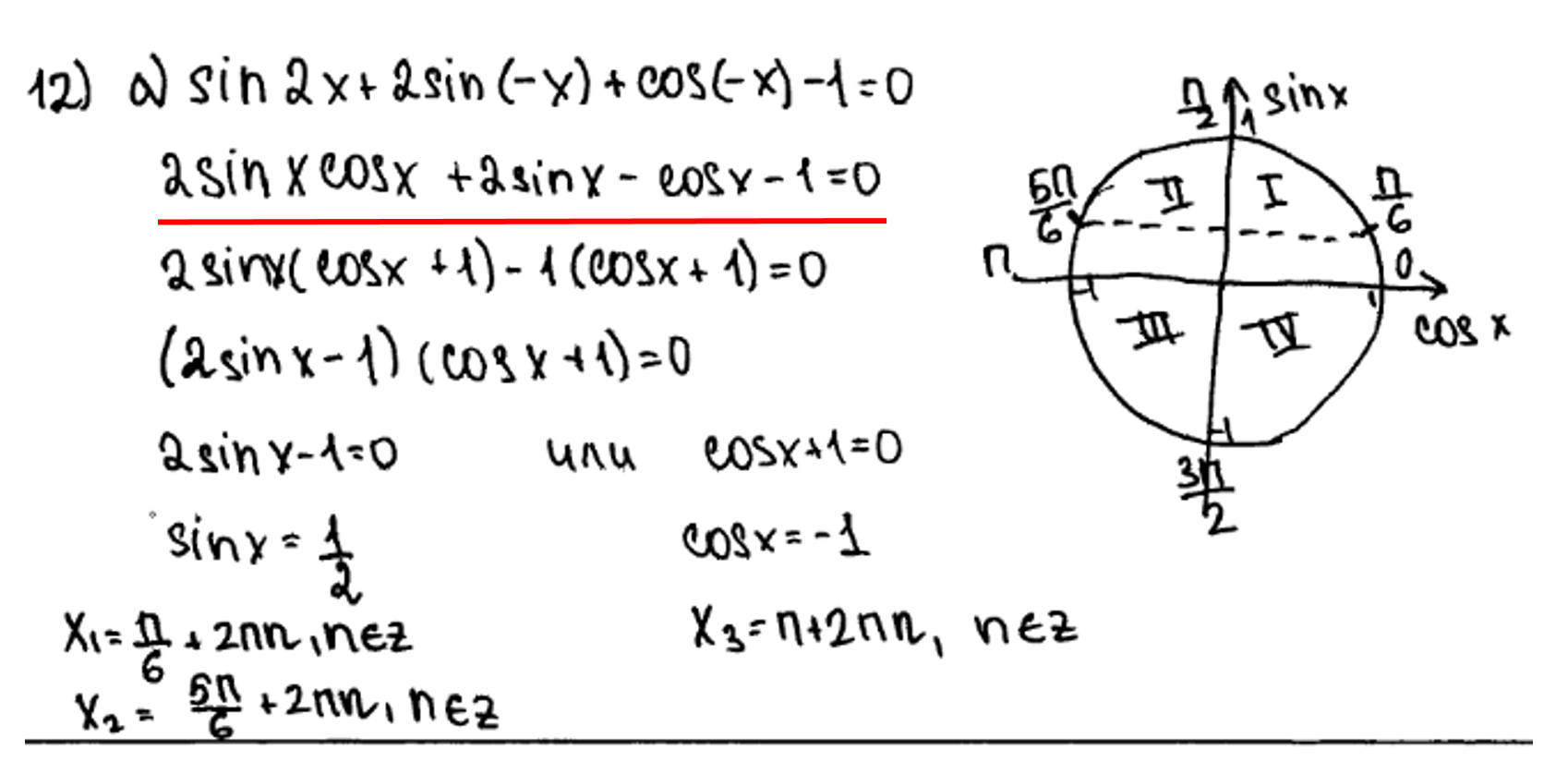
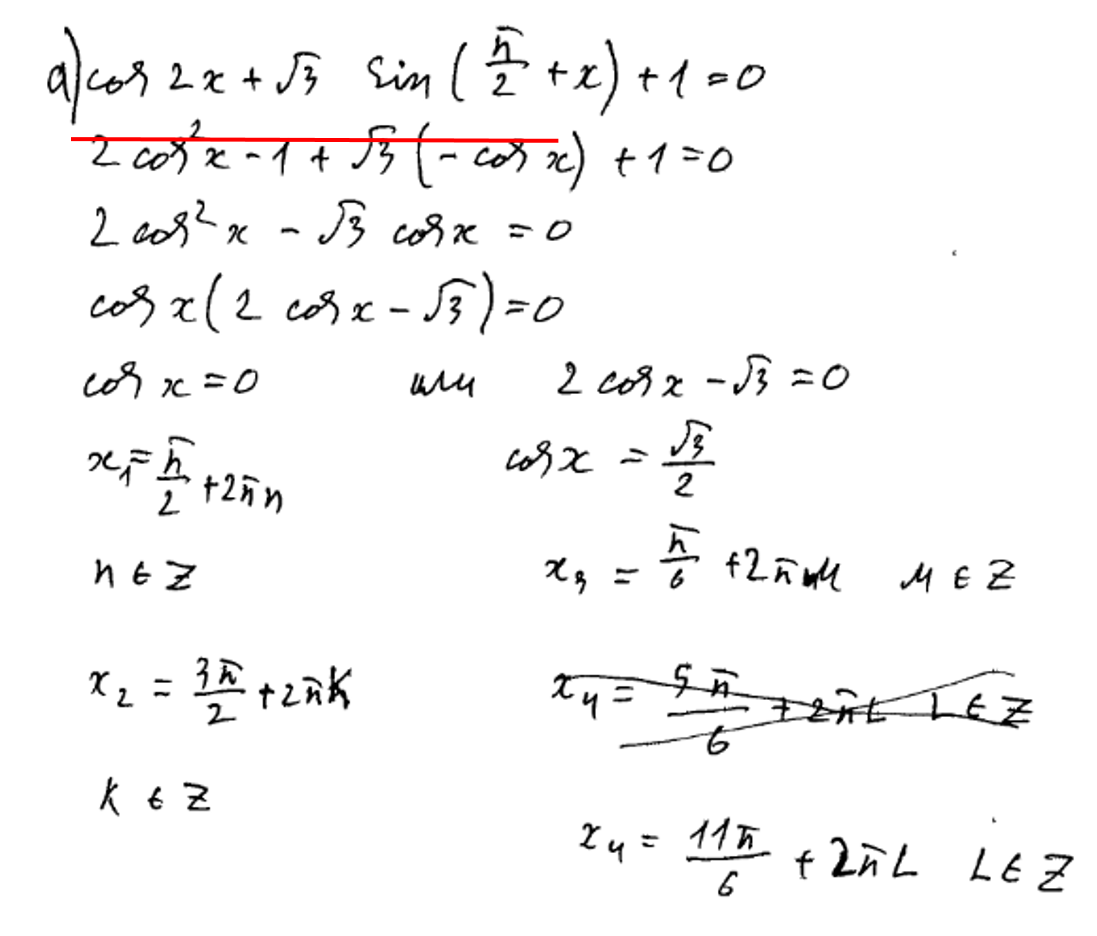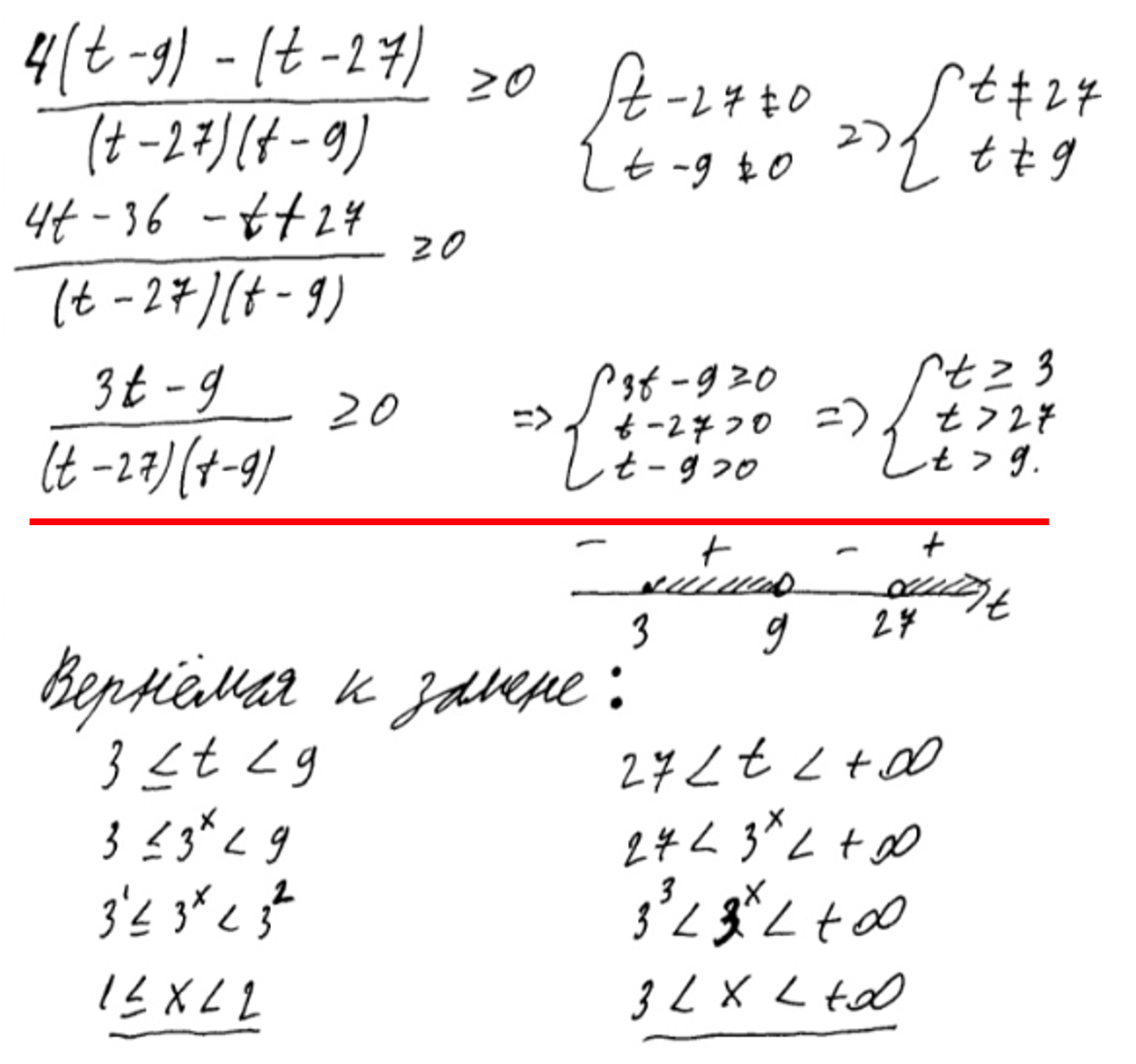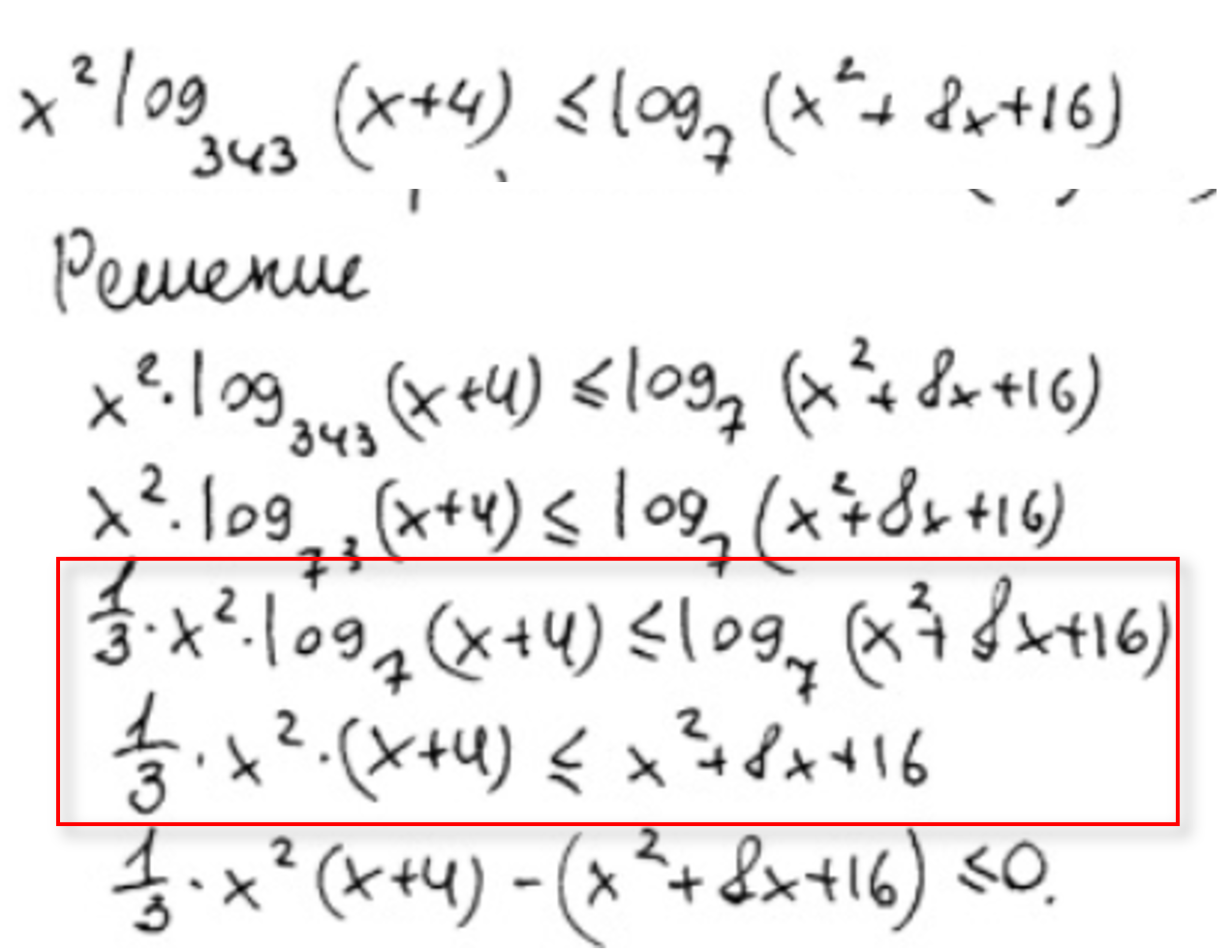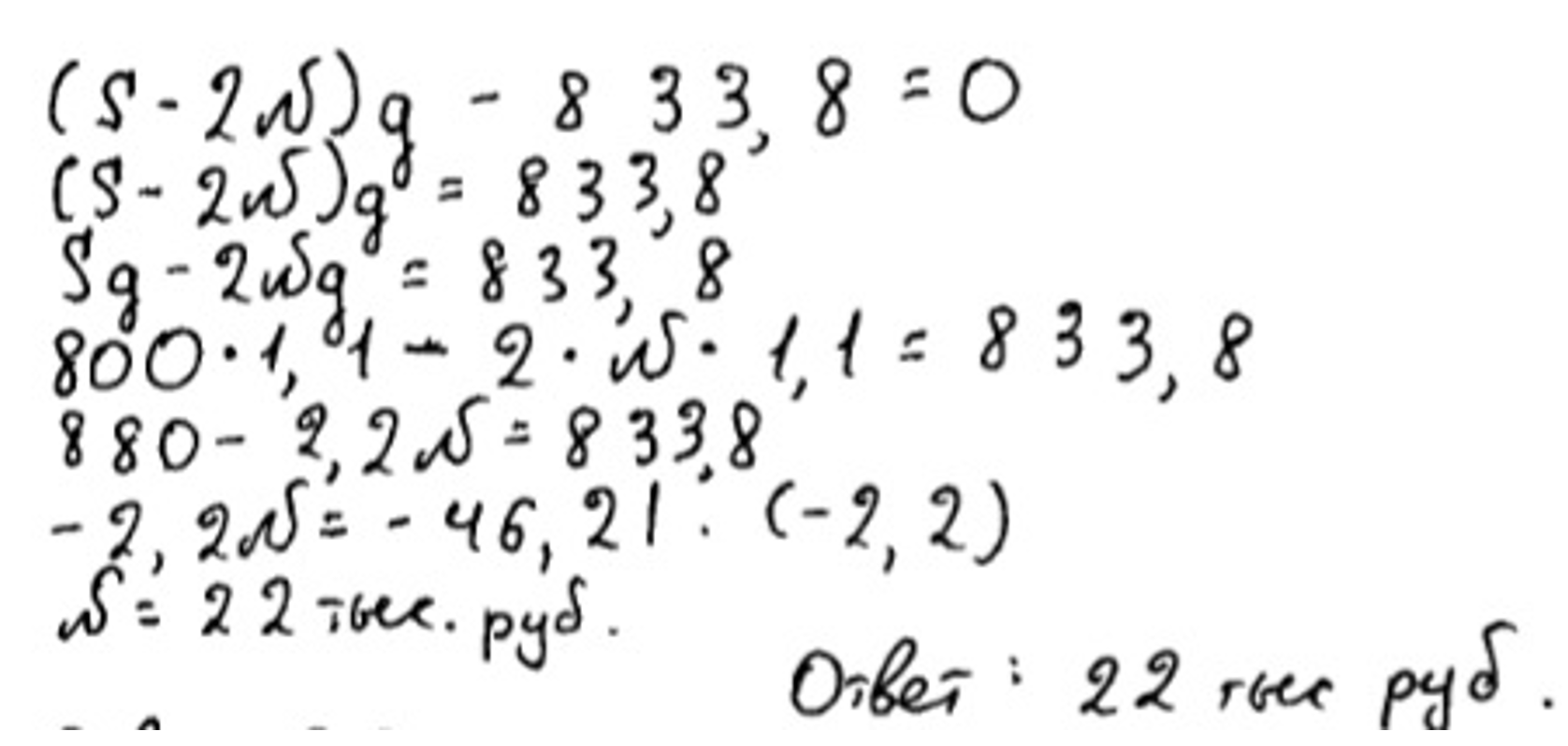Как найти ошибку в математике - ErrorsMaster.ru - большая энциклопедия ошибок и их решений

Ошибки учащихся при изучении математики,

их предупреждение и объяснение

Автор работы:

Дука Наталья Ивановна

учитель математики МОУ «СОШ №4 г. Ртищево Саратовской обл.» ____________________________

Аннотация

В данной работе рассматриваются типичные ошибки, которые допускают учащиеся при выполнении математических заданий. Здесь разобраны причины, способы исправления и предупреждения ошибок, разобраны конкретные ошибки из курса алгебры и начал анализа и способы их объяснения и устранения, указаны ошибки в работах государственной итоговой аттестации учащихся 9 и 11 классов. Рассмотрены ошибки по математике в учебниках и методической литературе. Материал, представленный в работе, может заинтересовать учителей математики.

Тезисы

В математике приходится учиться, в основном, на собственных ошибках. Если ученик не ошибается, то он не учится. Ошибка – вещь необходимая и полезная.

Цель исследования: рассмотреть методику предупреждения типичных ошибок учащихся в процессе обучения математике.

Объект исследования: процесс обучения математике в основной общеобразовательной школе.

Предмет исследования: процесс возникновения типичных ошибок и средства их предупреждения.

Гипотеза исследования заключается в следующем: если в процессе обучения математике целенаправленно и систематически организовывать работу учащихся над типичными ошибками, то это будет способствовать повышению качества математической подготовки учащихся.

Необходимо осуществлять процесс обучения правилам с помощью специальной модели с использованием приема, активизирующего рефлексивную деятельность учащихся по предупреждению и исправлению ошибок, которые возникают в результате формального усвоения правил.

Самостоятельная работа учащихся над ошибками обеспечивает более осознанный их анализ и анализ собственных действий по решению конкретной задачи, что оказывает благоприятное влияние на качество получаемых знаний и стимулирует развитие логического мышления.

Пример неосознанного применения алгоритма: получив уравнение sin x = 1,2, ученик автоматически ищет его корни по хорошо известной формуле, не обращая внимания на недопустимые значения sin x.

Для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля. Выработке навыков самоконтроля помогает и приём приближённой оценки ожидаемого результата.

Каждый учитель знает, что планомерное и систематическое повторение и есть основной помощник в ликвидации пробелов, а, следовательно, и ошибок.

Некоторые учащиеся считают, что arcsin(sink)= k при любом k и дают такой ответ: arcsin(sin) =. Это очень грубая ошибка. Аналогичное задание «вычислить arctg(tg130о)» вызывает у учащихся неверный ответ 130о.

Иногда ученики используют неверную формулу, не задумываясь над ней.

Например, определяя, является ли число рациональным, ученик пишет: = и получает неверный ответ,

При работе с «многоэтажными дробями» ученики делают много ошибок. Например: . Должна появиться верная запись .

При выполнении преобразований со степенями учащиеся не только допускают ошибки, но просто забывают формулы, например формулу

an am = an+m.

Пример ошибки на свойство степени: . Если при этом объяснить ученику, что дробь только в показателе степени, он это объяснение забудет и следующий раз опять ошибется. Необходимо в результате записать формулу .

Встречаются ошибки от непонимания. Большинство учащихся, решая впервые неравенство х24, приводят неверное решение х2.

Выполняя тригонометрические задания, ученик часто «изобретает формулы», например: «sin 2 х = 2 sin x».

Систематические проверки чужих записей формируют у ученика привычку критически относиться к своему решению. Для этого подходят задания типа «найди ошибку в решении». Процесс отыскания и исправления ошибок самими учащимися под руководством учителя можно сделать поучительным для учащихся.

Учебный год в 9-х и 11-х классах должен заканчиваться повторением и систематизацией учебного материала. повторение нужно нацелить на закрепление опорных знаний.

В учебнике Л. С. Атанасяна и других «Геометрия 7-9» была приведена некорректно составленная задача № 536: «Отрезок BD является биссектрисой треугольника АВС. Найдите DС, если АВ = 30, АD = 20, ВD = 16 и ∠ВDС = ∠С». Треугольник, описанный в условии задачи, не существует.

Объяснение деления с остатком круглых чисел в теме «Деление круглых чисел» ( урок 66) учебника математики для 4 –ого класса (Т. Е. Демидова, С. А. Козлова, А. П. Тонких) дается с ошибкой.

В газете «Математика» предлагается уравнение и к нему ответ:1. Приведенное решение неверное, так как приводит к потере корней.

Вступление

Вспоминается расхожая истина – умные люди учатся на чужих ошибках. В математике приходится учиться, в основном, на собственных ошибках. Если ученик не ошибается, то он не учится. Ошибка – вещь необходимая и полезная. Нужно лишь правильно относиться к ошибке, правильно ее использовать.

Обидно получать плохие оценки из-за ошибок «на ровном месте». Глупые ошибки – проблема многих учеников: случайная потеря знака, скобки, необоснованное изменение чисел, пропуски переменных и всевозможные ляпы. Сами ученики не могут объяснить, чем вызваны эти ошибки.

Причины ошибок, допускаемых учащимися при изучении математики

Проблема исследования состоит в теоретическом обосновании и разработке такой методики обучения математике, которая создавала бы условия для развития рефлексивной деятельности учащихся, способствующей предупреждению типичных ошибок.

Объект исследования: процесс обучения математике в основной общеобразовательной школе.

Предмет исследования: процесс возникновения типичных ошибок и средства их предупреждения.

Большинство ошибок напрямую не связаны с наличием или отсутствием знаний, хотя доведение некоторых вычислительных операций до автоматизма несколько снижает вероятность их появления. Снижает, но не исключает. Можно ли избавиться от таких ошибок? Ученик знает, что нужно решать внимательно, но ничего не может с собой поделать.

Известно, что осознание правила или определяет действия, или, по крайней мере, их контролирует. Знание правила необходимо и для того, чтобы осуществить проверку решения и дать его обоснование. Но большинство учащихся воспринимают курс алгебры как набор несвязанных между собой правил, которые заучиваются (иногда формально) для применения их к решению задач. Поэтому необходимо осуществлять процесс обучения правилам с помощью специальной модели с использованием приема, активизирующего рефлексивную деятельность учащихся по предупреждению и исправлению ошибок, которые возникают в результате формального усвоения правил.

Процесс отыскания и исправления ошибок самими учащимися под руководством учителя можно сделать поучительным для учащихся, в результате чего изучение и анализ ошибок становится эффективным средством в развитии познавательного интереса к изучению математики.

Выполняя математические задания, учащиеся допускают типичные ошибки:

Незнание правил, определений, формул.
Непонимание правил, определений, формул.
Неумение применять правила, определения, формулы.
Неверное применение формул.
Невнимательное чтение условия и вопроса задания.
Вычислительные ошибки.
Не использование свойств фигур при решении геометрических задач.
Логические ошибки при решении текстовых задач.
Раскрытие скобок и применение формул сокращенного умножения.

Какие причины ошибок по математике?

Пропуски занятий приводят к незнанию материала, пробелам в знаниях.
Поверхностное, невдумчивое восприятие нового материала приводят к непониманию его.
Недостаточная мозговая деятельность приводит к неумению применять правила, определения и формулы .
Неряшливый, неаккуратный почерк ученика приводит к досадным ошибкам. Учащиеся не всегда сами понимают, что именно они написали.
Усталость. Чрезмерная нагрузка и недостаточный сон приводит к снижению внимания, скорости мышления и, как следствие, к многочисленным ошибкам.
Кратковременное или полное переключение внимания с одной деятельности на другую (учебную или внеучебную) приводит к утрате только что воспринятого материала, приходится все начинать сначала.
Скорость работы. Низкая скорость выполнения мыслительных операций часто мешает ученику контролировать себя и это может стать еще одной причиной ошибки. «Зависание» с какой-нибудь одной частью задания удаляет из «оперативной памяти» информацию о другой, в которой допускается не вынужденная ошибка. Скорость работы определяется физиологией конкретного школьника и навыками выполнения тех или иных операций.
Мотивация. Следствие низкой мотивации – потеря внимания и ошибка.

Работа над ошибками

В приемах работы над ошибками отсутствует диагностика причин ошибок. Не уделяется должного внимания работе по формированию рефлексивной деятельности учащихся и ее использованию в работе по предупреждению и исправлению математических ошибок. При отсутствии должной доли самостоятельности при работе над ошибками, совершаемые учеником действия никак не контролируются, допущенные ошибки не замечаются, причины их появления остаются невыясненными, что приводит к их повторению. Напротив, самостоятельная работа учащихся над ошибками обеспечивает более осознанный их анализ и анализ собственных действий по решению конкретной задачи, что оказывает благоприятное влияние на качество получаемых знаний и стимулирует развитие логического мышления. При этом у школьников постепенно развиваются стремление и умение разобраться в задаче, планировать ее решение, продумывать возможные варианты действий и прогнозировать их результаты. Например, ученик многократно применяет к преобразованию алгебраических выражений формулы квадрата суммы и разности двух чисел, но получив задание представить в виде многочлена

(–х–5)2, теряется. Следует предложить учащемуся ответить на вопрос что вызывает затруднение? И как преобразовать выражение, чтобы можно было применить одну из формул в том виде, в каком они предложены в учебнике. Другой пример неосознанного применения алгоритма: получив уравнение

sin x = 1,2, ученик автоматически ищет его корни по хорошо известной формуле, не обращая внимания на недопустимые значения sin x. Полезно предложить ученику представить наглядное решение на тригонометрическом круге.

Самоконтроль

Для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля. Эти навыки состоят из двух частей: а) умения обнаружить ошибку; б) умения её объяснить и исправить. В процессе обучения применяются несколько приёмов самоконтроля, которые помогают обнаружить допущенные ошибки и своевременно их исправить. К ним относятся:

проверка вычисления и тождественного преобразования путём выполнения обратного действия или преобразования;
проверка правильности решения задач путём составления и решения задач, обратных к данной;
оценка результата решения задачи с точки зрения здравого смысла;
проверка аналитического решения графическим способом.

Выработке навыков самоконтроля помогает и приём приближённой оценки ожидаемого результата. Установление возможных пределов ожидаемого ответа предупреждает недочёты типа описок, пропуска цифр.

Например, рассмотрим задачу: “За неделю завод выпустил 130 холодильников, выполнив месячный план на 25%. Сколько холодильников должен выпустить завод за месяц по плану”.

Ученик написал = 52, ошибка становится очевидной, если перед решением ученик прикинет в уме: “За неделю завод выпустил 130 холодильников. Следовательно, за месяц он выпустит больше. Значит, ответ должен быть больше, чем 130” .

Объяснение и предупреждение ошибок

Свести ошибки к минимуму способствуют следующие профилактические меры.

Тексты письменных заданий должны быть удобными для восприятия: грамотно сформулированными, хорошо читаемыми.
Активная устная отработка основных ЗУН, регулярный разбор типичных ошибок.
При объяснении нового материала предугадать ошибку и подобрать систему заданий на отработку правильного усвоения понятия. Акцентировать внимание на каждом элементе формулы, выполнение разнотипных заданий позволит свести ошибочность к минимуму.
Подбирать задания, вызывающие интерес, формирующие устойчивое внимание.
Прочному усвоению (а значит, отсутствию ошибок) способствуют правила, удобные для запоминания, четкие алгоритмы, следуя которым заведомо придешь к намеченной цели.

Каждый учитель знает, что планомерное и систематическое повторение и есть основной помощник в ликвидации пробелов, а, следовательно, и ошибок. В математике, как ни в какой другой науке, особенно сильна взаимосвязь материала. Изучение и понимание последующего невозможно без знания предыдущего, отсюда неизбежность повторения на каждом уроке. При объяснении нового материала следует использовать ряд определений и теорем, которые были изучены ранее.

Например, перед изучением темы «Теоремы сложения» следует повторить следующие теоретические вопросы:

1. Четные и нечетные функции.
2. Изменение тригонометрических функций при возрастании и убывании аргумента.
3. Знаки тригонометрических функций.
4. Таблицы значений тригонометрических функций.

А также выполнить задания:

1. Определите четность и нечетность тригонометрической функции:

а) y = – cos x + x2; б) y = sin2 x; в) y = .
2. Найдите область определения функции y = x2 – 6x + 10.

3. При каких значениях x функции y = sin x и y = cos x принимают одинаковые значения?

Перед прохождением темы «Первообразная и интеграл» повторяем все формулы дифференцирования. Затем предлагается самостоятельная работа (на 10–15 мин), на которой ученики получают карточки-задания, в которых «опущены» один–два компонента из формулы дифференцирования и приведены две функции, производные которых необходимо найти. После проверки самостоятельной работы анализируем допущенные ошибки, определяем пробелы в знаниях и проводим работу по их устранению.

Рассмотрим ошибки, допускаемые в курсе алгебры и начал анализа. Задание. Найти точное значение arcsin (sin).

Некоторые учащиеся считают, что arcsin(sink)= k при любом k и дают такой ответ: arcsin(sin) =. Это очень грубая ошибка. По определению . Следовательно, число arcsin(sin) должно принадлежать промежутку , число этому промежутку не принадлежит. Имеем: arcsin (sin) = arcsin (sin)) = arcsin (sin ) = arcsin =

Аналогичное задание «вычислить arctg(tg130о)» вызывает у учащихся неверный ответ 130о. Можно исправить ошибку следующим образом: учитывая, что 90о 90о для любого и arctg (tgх) = х при

х arctg (tg130о) = arctg (tg180о 50о) = arctg (tg( 50о)) = 50о. Существует второй способ решения. Пусть arctg (tg130о) = х, получаем tg х = tg (arctg (tg130о)), откуда tg х = tg 130о. По условию равенства тангенсов имеем х = 130о + k, где kZ. Учитывая область определения функции у = arctg х, где х(90О; 90О), при k = 1 х = 130о 180о = 50о.

Рассмотрим еще один пример правильного решения аналогичного задания вычислить arcsin(sin2) при неверном ответе учащихся «2». Решение: arcsin (sink) = k, если , arcsin (sin2) = arcsin (sin() = 2, т. к. 2.

Иногда ученики используют неверную формулу, не задумываясь над ней. Например, определяя, является ли число рациональным, ученик пишет: = и получает неверный ответ, выполняя преобразование иррационального выражения, учащийся получил = х+2. Во-первых, учащиеся забывают, что , во-вторых, опять ошибочная аналогия с формулой = , где Применение «формулы =» в классе обязательно происходит независимо от того, повторяются свойства радикалов на уроках или нет. Ученик проводит аналогию с формулой = , где и не понимает, почему он неправ. Если заставить ученика написать правильно по свойству, то долговременного эффекта не получится. Необходимо, чтобы ученик понял и осознал свою ошибку. Для этой цели пригоден совет: вычислите по тому алгоритму, который только что применили, имеем = и по действиям 2 = 1 и определите, какое решение верное. Ученик задумывается и находит ошибку.

Можно предложить учащимся проверить себя, взяв, например, значение х = 2 но ;

при х = –2 но .

Делаем вывод: преобразование выполнено неверно, формула «=» не существует и

При работе с «многоэтажными дробями» ученики делают много ошибок. Например: . Нужно посоветовать ученику проверить написанное при конкретных значениях переменных. Так, при a = b = 1, c = 2, получим , с другой стороны , тогда 2= В результате ученик должен сделать вывод, что при работе с «трехэтажными дробями» лучше ставить скобки, чем сравнивать длины дробных «черточек»: . И, разумеется, должна появиться верная запись .

an am = an+m. Полезно учащимся показать, как они могут вспомнить формулу, пользуясь определением степени, например a3a4=aaa=a 7=a 3+4. Применяя определение степени в подобных ситуациях, учащиеся могут вывести любую формулу действий со степенями. Аналогично можно показать ошибки в действиях со степенями.

Ещё пример ошибки: . Если при этом объяснить ученику, что дробь только в показателе степени, он это объяснение забудет и следующий раз опять ошибется. Следует привести конкретный пример с удобным вычислением

=. Здесь же можно предложить другой способ

Необходимо в результате записать формулу .

Встречаются ошибки от непонимания. Большинство учащихся, решая впервые неравенство х24, приводят неверное решение х2. Полезно в этом случае предложить учащимся проверить число, например. -3, при этом учащиеся убеждаются в неверности ответа. Можно показать три способа решения этого неравенства. 1 способ тот, которым и пользовались учащиеся «», но допустили следующую ошибку «=х». Верное решение Этот способ решения содержит опасный момент – необходимо обратить внимание на возрастание функции у = при х0, иначе в дальнейшем будут еще ошибки при решении неравенств. Второй способ основан на методе интервалов х24, х2,

(х-2)(х+2)0, . Третий способ графический.

х24 при .

Выполняя тригонометрические задания, ученик часто «изобретает формулы», например: «sin 2 х = 2 sin x». В этом случае можно поступить двумя способами: подставить х =/6 и получить неверное равенство sin 2sin , /2 = 21/2 или вспомнить определение sin х на тригонометрическом круге. Наглядно хорошо видно, что sin 2х 2sinх. Обращение к тригонометрическому кругу всегда полезно повторением определения тригонометрических функций и наглядностью определений.

Не нужно специально исправлять каждое ошибочное утверждение ученика и предупреждать его об ошибках. Лучше поставить это утверждение на обсуждение всего класса и добиться осознанного исправления ошибки. Практика показывает, что систематические проверки чужих записей формируют у ученика привычку критически относиться к своему решению. Для этого подходят задания типа «найди ошибку в решении»:

Анализ работ ГИА и ЕГЭ

Анализ работ государственной итоговой аттестации учащихся 11-х классов показал, что типичные ошибки допущены при:

преобразовании дробно-рациональных выражений, содержащих корень

n-ой степени

исследовании функций на наибольшее и наименьшее значения;
решении показательных и логарифмических неравенств (отсутствует ссылка на соответствующие свойства функций);
вычислении площади криволинейной трапеции;
построении графика функции с модулем;
изображении тел вращения в геометрической задаче;
теоретическом обосновании используемых формул и фактов при решении задачи по стереометрии;
построении множества точек плоскости, удовлетворяющего заданному условию;
решении задач с параметром.

Для повышения уровня учебных достижений учащихся на ГИА за курс старшей школы рекомендуется обратить внимание на следующие темы и разделы курса алгебры и начал анализа и геометрии:

комбинация тел;
углы в пространстве;
производная и её применение к исследованию функции на отрезке;
построение ГМТ, удовлетворяющего заданным условиям;
логарифмические и показательные неравенства;
тригонометрические функции и их свойства;
тождественные преобразования дробно-рациональных выражений, содержащих корень n-ой степени.

Учебный год в 9-х и 11-х классах должен заканчиваться повторением и систематизацией учебного материала. повторение нужно нацелить на закрепление опорных знаний, построение и развитие межпредметных связей и осознание взаимосвязи с ранее выученными темами, на подготовку к итоговому оцениванию знаний, установлению формально-логических подходов к построению курса школьной математики, закрепление необходимости обосновывать и доказывать математические факты.

Ошибки в учебниках и методической литературе

В учебнике Л. С. Атанасяна и других «Геометрия 7-9» была приведена задача № 536: «Отрезок BD является биссектрисой треугольника АВС. Найдите DС, если АВ = 30, АD = 20, ВD = 16 и ∠ВDС = ∠С».

Решение.

ВD – биссектриса АВС =

∠ВDС = ∠С ВDС равнобедренный ВD = DС =

Отсюда СD =

Ответ:

Решим задачу вторым способом.

ВЕ – высота АВС. Пусть DЕ = х. Из прямоугольных треугольников АВЕ и DВЕ получаем:

АВ2 – АЕ2 = ВD2 – DЕ2,

302 – (20 + х)2 = 162 – х2,

900 – 400 – 40х – х2 = 256 – х2,

40х = 244,

х = 6,1.

ВЕ высота и медиана DЕ = СЕ СD = 2х = 12,2. Получили несоответствие с ответом первого способа решения.

Проверим, существует ли треугольник, у которого выполнены условия: ∠ВDС = ∠С и ∠АВD = ∠DВС. Найдем величины ∠DВС, ∠ВDС, ∠С.

АD2 = АВ2 + ВD2 – 2 cos ∠AВD

cos ∠AВD =

Тогда ∠АВD 38,5о. ∠DВС = ∠АВD 38,5о.

Аналогично cos ∠ADВ =

Тогда ∠АDВ = 180о – 67,59о ∠ВDС 67,59о. Из ВDС

∠С = 180о – 38,05о – 67,59о = 74,36о,

Отсюда следует, что ∠ВDС ∠С и треугольник DВС неравнобедренный.

Значит, задача составлена некорректно: треугольник, описанный в условии задачи, не существует.

Возможны два корректных варианта задачи:

Дан треугольник АВС, точка D лежит на стороне ВС. Найдите DС, если АВ = 30, АD = 20, ВD = 16 и ∠ВDС = ∠С.

В этом случае ВD не является медианой. По второму способу получаем СD = 12,2.

Отрезок BD является биссектрисой треугольника АВС. Найдите DС, если АВ = 30. АD = 20, ВD = 16.

∠ВDС ∠С, в этом случае из треугольника DВС по теореме синусов получаем

В действующем учебнике задача № 536 имеет вид:

Отрезок BD является биссектрисой треугольника АВС. а) Найдите АВ, если ВС = 9 см, АD = 7,5 см, DС = 4,5 см. б) Найдите DС, если АВ = 30. АD = 20, ВD = 16.

Посмотрим объяснение деления с остатком круглых чисел в теме «Деление круглых чисел» ( урок 66) учебника математики для 4 –ого класса (Т. Е. Демидова, С. А. Козлова, А. П. Тонких).

Цитируем: «Прочитай, объясни и проверь записи.

190 : 20 = 190 : 10 : 2 = 9 ( 1 остаток)

190 : 20 = 19 д. : 2 д. = 9 ( 1 остаток)

4700 : 500 = 4700 : 100 : 5 = 9 ( 2 остаток)

4700 : 500 = 47 с. : 5 с. = 9 ( 2 остаток)»

Проверяем 20 ∙ 9 + 1 = 190 – равенство неверное, делаем вывод: ошибка при выполнении деления с остатком. В чем ошибка? Анализируем 1-ое равенство 190 : 20 = 190 : 10 : 2 = 19 : 2, получаем деление числа 19 на число 2 и соответственно остаток от деления 19 на 2, но не от деления 190 на 20, действительно 19 : 2 = 9 ( 1 остаток). В этом случае 19 показывает, сколько десятков содержится в числе 190, поэтому остаток так же получаем в десятках, но не в единицах.

Анализируем 2-ое равенство 190 : 20 = 19 д. : 2 д. здесь мы делим десятки, поэтому остаток также будет в десятках 9 о чем сказано ранее), т, е. получаем 19 д. : 2 д. = 9 (1 д. остаток), проверкой убеждаемся в истинности деления 9 ∙ 2 д. + 1 д. = 19 д. = 190.

Предлагаем верные записи:

190 : 20 = 190 : 10 : 2 = 9 ( 1 д. остаток)

190 : 20 = 19 д. : 2 д. = 9 ( 1 д. остаток)

4700 : 500 = 4700 : 100 : 5 = 9 ( 2 с. остаток)

4700 : 500 = 47 с. : 5 с. = 9 ( 2 с. остаток).

В газете «Математика» предлагается уравнение и к нему ответ:1. Предложено решение уравнения по следующей схеме:

af(x)bg(x) = apbp

Приведенное решение неверное, так как приводит к потере корней. данное уравнение следует решать по схеме:

a f(x) b g(x) = a p b p a f(x)– р b q – g(x)

Вернемся к данном уравнению.

= 40 2 3

Заключение

Хотя проблемы формирования и развития рефлексивной деятельности в процессе обучения и поиск новых форм работы над математическими ошибками школьников и не являются абсолютно новыми, изучение такого аспекта, как использование рефлексивной деятельности учащихся при работе над типичными ошибками всегда актуальны. В данной работе рассмотрены некоторые типичные ошибки, допускаемые учащимися при изучении математики, их объяснение, меры их предупреждения. Хорошо организованная учителем работа учащихся над типичными ошибками посредством исследовательского приема приводит к улучшению результата обучению математики и развитию рядя показателей логического мышления. К тому же предмет «математика» настолько сложен, что даже методисты допускают ошибки.

Литература

Далингер В. А. «Анализ типичных ошибок, допускаемых в курсе алгебры и начала анализа» «Математика в школе» 6-98
2-98 Ярский А. С, «Что делать с ошибками»
Хэкало С. П. «Корни терять нельзя» 5-98
Игнатенко В. З. «Сюрпризы биссектрисы» 5-98

Интернет-ресурсы

http://mat.1september.ru/view_article.php?ID=200900304
http://www.distedu.ru/mirror/_fiz/archive.1september.ru/mat/1998/no38.htm
http://www.ankolpakov.ru/2011/10/03/repetitor-po-matematike-o-durackix-oshibkax/
http://www.referun.com/n/preduprezhdenie-tipichnyh-oshibok-uchaschihsya-v-protsesse-obucheniya-algebre-posredstvom-formirovaniya-i-ispolzovaniya-r#ixzz2PJHLl9cJ
http://www.referun.com/n/preduprezhdenie-tipichnyh-oshibok-uchaschihsya-v-protsesse-obucheniya-algebre-posredstvom-formirovaniya-i-ispolzovaniya-r

Источник

Математические софизмы и задания «Найди ошибку»

Авторы
Руководители
Файлы работы
Наградные документы

Сафарова А.Г. 1

1IT лицей № 9 имени О.А.Жолдасбекова

Ильина Светлана Владимировна 1

1IT лицей № 9 имени О.А.Жолдасбекова

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

«Правильно понятая ошибка – это путь к открытию»

И. П. Павлов

ВВЕДЕНИЕ

Бесконечно разнообразны ошибки, которые совершались и совершаются в различных математических рассуждениях. Рассмотреть такие ошибки полезно по двум причинам: во-первых, хорошо ознакомившись с какой-нибудь такой ошибкой, мы защитим себя от повторения такой ошибки в будущем; во- вторых, сам процесс разыскания ошибки легко сделать весьма увлекательным, и изучение ошибок становится средством поднять интерес к изучению математики.

Рассуждение, в котором допущена та или иная ошибка, в большинстве случаев легко довести до получения явно неверного вывода. Получается видимость доказательства какой-нибудь нелепости, или так называемый софизм.

Разбор и решение любого рода математических задач, а в особенности нестандартных, помогает развивать смекалку и логику.

Цель исследования софизмов заключается в приобщении к критическому мышлению, умению не только воспроизводить определенные логические мыслительные процессы, но и критически осмысливать каждый этап рассуждений в соответствии с усвоенными принципами математического мышления.

Наверняка, каждый человек слышал хоть раз в жизни подобную фразу:

«Дважды два равно пяти» или «Два равно трем». На самом деле таких примеров очень много. Что они обозначают? Имеют ли какое-то логическое объяснение или это вымысел?

Именно это я хочу рассмотреть в этой работе, название которой «Математические софизмы и задания «Найди ошибку». Целью моей работы является исследование разнообразных математических софизмов для формирования критического мышления, приобретения необходимых в жизни навыков правильного мышления и разбор собственных заданий «Найди ошибку» по различным темам курса алгебры и геометрии. 1

СОФИЗМЫ

Софизм (в переводе с греческого sophisma — уловка, выдумка, головоломка), формально кажущийся правильным, но по существу ложное умозаключение, основанное на преднамеренном неправильном подборе исходных положений. Каков бы не был софизм, он обязательно содержит одну или несколько замаскированных ошибок. Особенно часто в математических софизмах выполняются «запрещенные» действия или не учитываются условия применимости теорем, форму и правил. Иногда рассуждения ведутся с использованием ошибочного чертежа или опираются на приводящие к ошибочным заключениям «очевидности». Встречаются софизмы, содержащие и другие ошибки.

ИСТОРИЯ СОФИЗМОВ

В истории развития математики софизмы играли существенную роль. Они способствовали повышению строгости математических рассуждений и содействовали более глубокому уяснению понятий методов математики. Роль софизмов в развитии математики сходно с той ролью, какую играют непреднамеренные ошибки математических исследований, допускаемые выдающимися математиками. Именно уяснение ошибок математических рассуждение часто содействовало развитию математики. Пожалуй, особенно поучительна в этом отношении история аксиомы Евклида о параллельных прямых. Сформировать эту аксиому можно так: через данную точку лежащую вне данной прямой, можно провести не более одной прямой, параллельной данной. Это утверждение на протяжении более двух тысяч лет пытались доказать, но все попытки не увенчались успехом. Полученные «доказательства» оказались ошибочными. И все же, несмотря на ошибочность этих «доказательств», они принесли большую пользу развитию геометрии. Они подготовили одно из величайших достижений в области геометрии и всей математики – создание неевклидовой геометрии. Честь разработки новой геометрии принадлежит Н.И. Лобачевскому и венгерскому математику Яношу Бойяи.

Понятие софизмов включает в себя несколько видов софизмов: арифметические, алгебраические и геометрические.

АРИФМЕТИЧЕСКИЕ СОФИЗМЫ

Арифметические софизмы — это числовые выражения, имеющие неточность или ошибку, незаметную с первого взгляда. Рассмотрим такие примеры.

Пример 1

« 5 = 6 »

Решение:

Попытаемся доказать, что 5 = 6. С этой целью возьмем числовое тождество:

35 + 10 – 45 = 42 + 12 – 54.

Вынесем общие множители левой и правой частей за скобки. Получим:

5 (7 + 2 – 9) = 6 (7 + 2 – 9).

Разделим обе части этого равенства на общий множитель

Получаем 5 = 6.

Где ошибка?

Ответ: общий множитель (7 + 2 – 9) = 0, а делить на 0 нельзя.

Пример 2

« 2 * 2 = 5 »

Решение:

Имеем числовое равенство (верное): 4 : 4 = 5 : 5.

Вынесем за скобки в каждой части его общий множитель. Получим:

4 (1 : 1) = 5 (1 : 1).

Числа в скобках равны, поэтому

4 = 5 или 2 * 2 = 5.

Где ошибка?

Ответ: допущена ошибка в вынесении общего множителя за скобки в левой и правой частях тождества 4 : 4 = 5 : 5. Общий множитель нельзя вынести.

АЛГЕБРАИЧЕСКИЕ СОФИЗМЫ

Алгебра — один из больших разделов математики, принадлежащий наряду с арифметикой и геометрией, к числу старейших ветвей этой науки. Задачи, а также методы, отличающие ее от других отраслей математики, создавались постепенно, начиная с древности. Алгебра возникла под влиянием нужд общественной практики, в результате поисков общих приемов для решения однотипных арифметических задач. Приемы эти заключаются обычно в составлении и решении уравнений, т.е. алгебраические софизмы – намеренно скрытые ошибки в уравнениях и числовых выражениях.

Пример 1

«Любое число равно его половине»

Возьмем два равных числа а и b, а =b обе части этого равенства умножим на а и затем вычтем из произведений по b². Получим: а² – b² = ab — b² или (а + b)(a — b)=b(a — b).

Отсюда а + b = b, или а + а = а, так как b = a.

Значит, 2а = а, .

Где ошибка?

Ответ: нельзя делить на (а – b), так как ( a – b) = 0.

Пример 2

«Любое число равно нулю»

Возьмем произвольное положительное число а и рассмотрим сумму х и бесконечного числа слагаемых, равных а:

х = а + а + а + а + … . (1)

Очевидно, что мы можем представить эту сумму как

х = а + (а + а + а +…), (2)

в которой сумма, стоящая в скобках, так же ровна х, как сумма бесконечного числа слагаемых, равных а. Так что можем записать, что х = а + х, откуда заключаем, что а=0

Где ошибка?

Ответ: ошибка допущена в равенстве (1), в котором бесконечная сумма чисел а обозначена конечным числом х.

Пример 3

«Всякое число равно своему удвоенному значению»

Запишем очевидное для любого числа а тождество:

а² – а² = а² – а².

Вынесем множитель а в левой части за скобку, а правую часть разложим на множители по формуле разности квадратов, получим:

а (а — а) = ( а + а) ( а – а ). (1)

Разделив обе части на ( а – а ), получим:

а = а + а , а = 2а.

Где ошибка?

Ответ: используется распространенная ошибка, а именно деление на 0 в неравенстве (1) (а—а=0).

Пример 4

«Все числа равны между собой»

Возьмем любые два числа х , у.

Рассмотрим тождество:

х²— 2ху + у²= у²— 2ху + х². Имеем: ( х – у )²= ( у – х )².

отсюда: х – у = у – х или 2х = 2у, а значит, х = у.

Где ошибка?

Ответ: ошибка заключается в том, что из равенства ( х – у )² = (у – х )² следует, что х = у, а это равенство справедливо для любых чисел х, у.

Пример 5

Если «а» больше «b», в тогда «а» всегда больше, чем «2b».

Возьмем два произвольных положительных числа а и b, такие, что а > b. Умножив это неравенство на b, получим новое неравенство аb > bb, а отняв от обеих его частей аа, получим неравенства аb – аа > bb – аа, которое равносильно следующему: а ( b – a ) > ( b + a ) ( b — a ). (1)

После деления обеих частей неравенства (1) на (b – а), получим а > b + a (2).

А прибавив к этому неравенству почленно исходное неравенство а > b, имеем 2а > 2b + a, откуда а > 2b. Итак, если а > b, то а > 2b.

Где ошибка?

Ответ: ошибка совершена при переходе от равенства (1) к (2). Так как а > b, то b – a < 0, следовательно, при делении неравенства (1) на b – а, мы должны

поменять знак неравенства на противоположный.

Пример 6

« 8 = 6 »

Решим систему уравнений:

Решим подстановкой у из второго уравнения в первое, получаем

х + 8 – х = 6, откуда 8 = 6.

Где ошибка?

Ответ: второе уравнение системы можно записать как х + 2у = 8, так что исходная система запишется в виде:

В этой системе уравнений коэффициенты при переменных одинаковы, а правые части не равны между собой, из этого следует, что система не имеет ни одного решения.

Графически это означает, что прямые у = 3 — и у = 4 — параллельны и не совпадают. Перед тем, как решать систему линейных уравнений, полезно проанализировать, имеет ли система единственное решение, бесконечно много решений или не имеет решений вообще.

Пример 7

«Неравные числа равны»

Возьмем два неравных между собой произвольных числа а и b.

Пусть их разность равна с, то есть а – b = с. Умножив обе части этого равенства на ( а – b ), получим ( а – b )² = с ( а – b ). Раскрыв скобки, придем к равенству а²– 2аb + b²= ca – cb. После преобразования получаем а²– аb — ас= аb – b² – bc. Выносим общий множитель а слева и общий множитель b справа, получим: а ( а – b – c ) = b ( a – b – c ).

Разделив последнее равенство на ( а – b – c ), получаем : а = b.

Где ошибка?

Ответ: здесь ошибка совершена при переходе от равенства а ( а – b – c ) = b ( a – b – c ) к равенству а = b. Действительно, согласно условию разность двух произвольных чисел а и b равна с, то есть а – b = с, откуда а – b — c = 0. Можно записать равенство а ( а – b – c ) = b ( a – b – c ) в виде: а*0 = b*0. Переход от этого равенства к равенству, а=b осуществляется путем деления обеих частей на равное нулю число а – b – с = 0.Следовательно, здесь мы имеем деление нуля на нуль, которое не имеет смысла, поскольку равенство, а*0=b*0 выполняется при любых а и b. Поэтому, вывод о том, что числа а и b равны, неверен.

Пример 8

« 7 = 13 »

Рассмотрим уравнение: . (1)

Оно может быть решено следующим образом. Приведя левую часть уравнения к общему знаменателю, получим

= , откуда – = , или

= . (2)

Поскольку числители дробей в левой и в правой частях уравнения равны, то для того чтобы имело место равенство обеих частей уравнения, необходимо, чтобы были равны и знаменатели дробей. Таким образом, приходим к равенству

7 = 13.

Где ошибка? Ответ: область допустимых значений исходного уравнения (1) состоит из всех значений переменой х, кроме х=7, х=13. В этом софизме неявно подразумевается, что равенство (2) является не уравнением, а тождеством, равным при любых значениях х, что неверно. Поэтому, утверждение софизма неверно.

ГЕОМЕТРИЧЕСКИЕ СОФИЗМЫ

Геометрические софизмы – это умозаключение или рассуждение, обосновывающее какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, связанное с геометрическими фигурами и действиями над ними.

Пример 1

«Катет равен гипотенузе»

Доказательство

Угол С равен 90°, ВД — биссектриса угла СВА, СК = КА, ОК перпендикулярно СА, О – точка пересечения прямых ОК и ВД, ОМ перпендикулярно АВ, ОL перпендикулярно ВС. Имеем: ∆LВО равен ∆МВО, ВL=ВМ, ОМ = ОL = СК = КА, ∆КОА = ∆ОМА (ОА- общая сторона, КА = ОМ, ∠ОКА и ∠ОМА- прямые), ∠ОАК= ∠МОА, ОК=МА=СL, ВА= ВМ+МА, ВС=ВL+LС, но ВМ=ВL, МА=СL, и потому ВА=ВС.

С К D A

К D

Где ошибка?

Ответ: ошибка заключается в том, что рассуждения, о том, что катет равен гипотенузе, опирались на ошибочный чертеж. Точка пересечения прямой, определяемой биссектрисой ВD и серединного перпендикуляра к катету АС, находится вне треугольника АВС.

Пример 2

«Отрезки параллельных прямых, заключенные между сторонами угла, равны»

Рассмотрим произвольный угол с вершиной в точке Е и пересечем их стороны двумя параллельными прямыми, отрезки которых АВ и СD заключены между сторонами этого угла.

Как известно параллельные прямые отсекают от сторон угла пропорциональные отрезки, следовательно, откуда АЕ · DE = BE · CE.

Умножив обе части последнего равенства на отличную от нуля разность

АВ – СD , запишем AE · DE · AB – AE · DE · CD = AE · DE · CD – BE · CE · CD,

ИлиАВ (AE · DE – BE · CE) = CD (AE · DE – BE · CE).

Разделив обе части последнего равенства на (AE · DE – BE · CE) получим равенство АВ = СD.

D А

B С

Где ошибка?

Ответ: так как АЕ · DE = BE · CE, то АЕ · DE – ВЕ · СЕ = 0, то ошибка в делении на 0.

Пример 3

«Катет прямоугольного треугольника равен его гипотенузе»

Пусть BO (рис.1) – биссектриса угла B, D – середина катета AC, DO ┴ AC, OE ┴ BC, OF ┴ BA.

Так как О — на биссектрисе угла B,

то Δ BFO = Δ BEO (по гипотенузе и острому углу). Поэтому

BF = BE. (1)

Далее, OA = OC, ибо каждая точка перпендикулярна к отрезку AC,

9проходящего через середину AC, равноудалена от А и С. Так как ОF = OE,

то Δ AOF = Δ СОЕ, и поэтому АF = СЕ. (2)

n DD D

кладывая почленно (1) и (2), получим AB = CB, то есть катет равен гипотенузе, что и требовалось доказать.

n O

O O

В В

E A C

F F О Е

А D С Рис. 2

Рис. 1

Где ошибка? Ответ: точка О не может быть внутри Δ ABC. Тогда можно показать, что если точка О лежит вне Δ ABC или на его стороне, то опять AB = CB (рис.2). Именно, показываем, что BF = BE, АF = СЕ. Отсюда AB = CB.

Пример 4

«Прямой угол равен тупому!»

Пусть угол АDC — прямой, угол DCВ — тупой, СВ=DА, СМ=DМ, АF=ВА, МО ┴ СD, FО ┴ АВ. Следовательно, ∆DMO = ∆СМО (по двум катетам). Поэтому, ∠ МDО= ∠ МСО. (1) OD=ОС, ∆ AFO =∆ ВFО (по двум катетам).

Следовательно, АО=ОВ и ∆ АDО= ∆ ВСО (по трем сторонам).

Значит, ∠АDО = ∠ВСО. (2)

A F B

D M C

∠АDO –∠ МDО =∠ ВСО – ∠МСО, то есть ∠АDC=∠ BCD.

Таким образом, прямой угол равен тупому углу. Что и требовалось доказать.

ЗАДАНИЯ «НАЙДИ ОШИБКУ»

В процессе изучения и исследования математических софизмов мне стало интересно, а как можно предупредить ошибки учеников моего класса в решении примеров на уроках. Ведь часто при неправильном решении получается явно неверный результат, который не могут увидеть сами ученики. Поэтому, я заинтересовалась заданиями с ошибками в решении. Используя учебную литературу, я попробовала самостоятельно составить задания, в которых есть ошибка.

Пример 1

Решить неравенство:

( 4 — х²)³ ( х – 3 )²≥ 0.

( х²-4)³ ( х – 3 )²≤ 0,

( х – 2 )³( х + 2 )³( х – 3 )²≤ 0.

Найдем нули выражения

х – 2 =0, х + 2 =0, х – 3 = 0,

х = 2, х = -2, х = 3.

— + — +

-2 2 3

х (-∞; -2] υ [2; 3]

Где ошибка?

Ответ: в выражении второй множитель в квадрате. Поэтому, при переходе через точку х=3 знак выражения не должен измениться.

+ — + +

-2 2 3

х [-2; 2] Ответ: [-2; 2]

Пример 2

Найти производную функции f(х) = sin⁶ .

f‘ꞌ(х) = (sin⁶)’ =6sin⁵ · · · (5х²-6х) = =6sin⁵ = 3sin⁵ .

Где ошибка?

Ответ: ошибка заключается в нахождении производной степенной функции.

f‘ꞌ(х) = (sin⁶)’ =6sin⁵ · · · (5х²-6х) = =6sin⁵ =sin⁵ .

Пример 3 Решить биквадратное уравнение:

9х⁴– 2х²— 7 = 0.

Введем замену х²=z, решаем квадратное уравнение:

9z²— 2z – 7 = 0, k=

Д₁ = k²— ac = (-1)²— 9 · (-7) = 1 +63 = 64 > 0, имеет 2 корня

z_1,2= =

z₁₌-1, z₂= ,

х²= — 1, х²= ,

не имеет решения, х = ± .

Где ошибка? Ответ: при нахождении корней уравнения допущена ошибка: k=-1, а в формуле корней знак не изменен. Правильное решение:

z_1,2 = = ,

z₁= 1,z₂=- ,

х²= 1 , х²= — ,

х = ± 1, не имеет решения. Ответ: ± 1

Пример 4

Решить тригонометрические уравнения:

а) 2соsх = 1.

соsх = ,

х = аrccos + 2n, n Z,

x = + 2n, n Z.

Где ошибка?

Ответ: ошибка заключается в неправильном определении табличного значения косинуса.

х = аrccos + 2 n, n Z

x = + 2 n, n Z

б) 3sin²x — 2sinx -1 = 0.

Введем замену sinx=t , тогда получим и решим квадратное уравнение:

3t²-2t -1 = 0.

По свойству коэффициентов a+ b +c = 0 получаем:

t₁ = 1, t₂ = — ,

sinx= 1, sinx= — ,

х =(-1)ⁿ + n, n Z. х= (-1)ⁿarcsin(- ) + n, n Z,

х= — (-1)ⁿarcsin + n, n Z.

Где ошибка?

Ответ: 1) ошибка заключается в нахождении корня тригонометрического уравнения sinx= 1. Это частный случай. Поэтому, х = + 2n, n Z.

2) ошибка при определении корня уравнения sinx= — . Отрицательное значение синуса увеличивает степень числа (-1) на единицу.

Правильный ответ: х= (-1)ⁿ⁺¹arcsin + n, n Z

Пример 5. Задача.

Стороны параллелограмма АВСD относятся как 2:3, а его периметр равен 20 см, угол между сторонами равен 60°. Найдите его площадь.

А В

С D

Решение.

АВ : АD = 2 : 3.

х – коэффициент пропорциональности,

тогда АВ = 2х (см), АD = 3х (см)., Р_АВ_CD = 2(АВ + АD), получим

(2х + 3х) · 2 = 20,

5х = 10,

х = 2 (см).

АВ = 2 · 2 = 4 (см), АD = 2 · 3 = 6 (см).

S_АВ_CD = аbsinα = АВ · АD · sin60°,

S_АВ_CD = 4 · 6 · = 12 (cм²).

Где ошибка?

Ответ: ошибка в определении значения синуса. Правильно sin60° = .

Поэтому, S_АВ_CD = 4 · 6 · = 12 (cм²).

ЗАКЛЮЧЕНИЕ

Исследовать софизмы очень интересно и необычно. Перед тобой открывается какой-то особый мир рассуждений, которые поистине кажутся верными.

Изучая и исследуя математические софизмы, я научилась контролировать логические рассуждения при решении задач и примеров.. Поэтому, я могу найти ошибку в своем решении и увидеть ошибку в решении других учеников во время урока.

Мне было очень интересно изучать и исследовать математические софизмы, а особенно придумывать новые задания, содержащие ошибку и анализировать их.

Такие задания помогут мне еще лучше подготовиться к государственному экзамену по математике и сдаче ЕНТ.

Литература

1. М. Б. Балк, Г. Д. Балк, «Математика после уроков», «Просвещение», Москва, 1971

2. сайт ppt4.web.rumatematisheskie—sofizmy.htlm

3. А. Н. Шыныбеков, учебник «Геометрия 8», «Атамура», Алматы, 2004

4. А. Н. Шыныбеков, учебник «Алгебра 8», «Атамура», Алматы, 2004

5. А. Е. Абылкасомова, З .А Жумагулова, К. Д. Шойынбеков,

6. В. Е. Корчевский, учебник «Алгебра и начала анализа 10», «Мектеп», Алматы, 2014

7. И. П. Рустюмова, С. Т. Рустюмова, «Тренажер по математике для подготовки к Единому Национальному Тестированию (ЕНТ)», Алматы,2011

Просмотров работы: 108

Источник

И снова здравствуйте, уважаемые одиннадцатиклассники! Полагаю, что Вы хорошо отдохнули и готовы к работе для достижения своих высоких целей.

В этом году июнь месяц выдался очень продуктивным. Моя работа не закончилась 6 июня, когда мои ученики написали ЕГЭ по физике. После публикации результатов ЕГЭ (сначала по математике, а потом и по физике) стало поступать множество сообщений от учеников, даже тех, с кем я не занималась, с просьбой помочь разобраться, за что сняли баллы. А в некоторых случаях даже была необходима помощь с составлением апелляции. Бесценный опыт, если честно…..Только вот от этого опыта седых волос становится больше. И желание сжечь критерии не отпускает меня.

Сразу замечу, что апелляция возможна только по заданиям второй части. По первой части апелляция производится только тогда, когда компьютер неверно считал знак, записанный Вами в бланке ответов.

Уважаемые одиннадцатиклассники, вы должны понимать, что недостаточно просто получить верный ответ, недостаточно записать решение в стиле «я художник, я так вижу». Ваше решение будут оценивать по вполне определенным критериям. И даже абсолютно верный ответ не гарантирует полный балл за выполненное задание.

Анализ ошибок мы начнем с разбора сканов работ по профильной математике. Эти сканы я собирала не один год. К сожалению, в математике, просто за идею решения, за набор формул, не дадут ни одного балла. А снимают баллы за наличие вычислительных ошибок, недостаточную обоснованность, наличие лишних записей. Не указали необходимые признаки, свойства, теоремы – все, полный балл Вам не дадут.

Основной упор будет сделан на задачи 12, 14, 15 (уравнения, неравенства, задачи с экономическим содержанием). Это так называемый джентельменский набор, который старается выполнить большая часть выпускников. Погнали…

Для удобства статья представлена в двух форматах. Текст и видео. Вот ролик:

Уравнения

Основные ошибки:

1) неправильное использование формул приведения.

При преобразовании допущена ошибка. Минуса перед косинусом быть не должно. Задание оценивается в 0 баллов.

2) незнание свойств четных и нечетных функций. Также ребята забывают, что косинус функция честная, а вот синус, тангенс и котангенс нечетные.

допущена ошибка. Минуса перед косинусом быть не должно. Задание оценивается в 0 баллов.

Классическая ошибка! – нечетная функция, следовательно знак минус выносится вперед, а не пропадает. Если бы функция была четная, то мы смело могли бы убрать знак минус. Задание оценивается в 0 баллов.

3) неправильное или некорректное использование тригонометрических формул.

Пару лет назад мне написал ученик, которому на экзамене досталось уравнение вида – нечетная функция, следовательно знак минус выносится вперед, а не пропадает. Если бы функция была четная, то мы смело могли бы убрать знак минус. Задание оценивается в 0 баллов.

3) неправильное или некорректное использование тригонометрических формул.

Пару лет назад мне написал ученик, которому на экзамене досталось уравнение вида .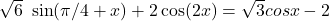

Скан он мне не отправил, но в процессе обсуждений выяснилось, что в первой скобке для он использовал не формулу синуса суммы, а формулы приведения. Чего делать категорически нельзя! Как Вы понимаете, задание оценили в 0 баллов.

4) Самое банальное. Неверное решение простейших тригонометрических уравнений.

он использовал не формулу синуса суммы, а формулы приведения. Чего делать категорически нельзя! Как Вы понимаете, задание оценили в 0 баллов.

4) Самое банальное. Неверное решение простейших тригонометрических уравнений.

При решении простейшего тригонометрического уравнения допущена ошибка. Третий и четвертый корень записаны неверно. Задание оценивается в 0 баллов.

Неравенства

С неравенствами у ребят дела идут посложнее, чем с уравнениями. Тут ваша фантазия разыгрывается по полной. Какие только ошибки не встречались(( Постараюсь выделить основные.

1)Пожалуй, самая распространенная ошибка – ошибка в расстановке знаков на координатной прямой. В идеале, если выпускник умеет определять – перед ним корень четного или нечетного порядка, меняется знак или дублируется.

Нули найдены верно. Но при расстановке знаков на координатной прямой допущена ошибка. Мы видим, что единица – нуль числителя второго порядка, следовательно знак сохраняется, и в крайнем левом интервале должен быть плюс. Эта ошибка уже позволяет эксперту поставить за данное задание 0 баллов.

2)Отбрасывание знаменателя и, как следствие, потеря части корней. В примере, приведенном ниже, выпускник отбросил знаменатель и находил нули только числителя.

Это привело к тому, что на координатной прямой не хватает нулей двух скобок: .

Такая грубая ошибка на экзамене не прощается.

Оценка эксперта – 0 баллов.

Такая грубая ошибка на экзамене не прощается.

Оценка эксперта – 0 баллов.

3) Неравносильный переход от неравенства к системе неравенств.

Я думаю, эта ошибка даже не нуждается в комментариях. Даже несмотря на то, что ученик верно нашел нули, верно расставил знаки на координатной прямой, это задание оценили в 0 баллов. Если бы системы с тремя неравенствами не было, ученик имел бы возможность взять полный балл.

4) Ошибки при использовании свойств логарифмов.

Стоит заметить, что для снятия логарифмов в правой и левой части, необходимо, чтобы перед логарифмом не было никаких цифр или букв. Выпускник снял логарифмы, хотя по задумке нужно было в правой части свернуть в полный квадрат подлогарифмическое выражение и вынести общий множитель. Как Вы понимаете, эксперт оценил это задание в 0 баллов.

Из моего текста у Вас, возможно, сложилось впечатление, что эксперты по всем поводам снимают сразу два балла. К счастью, это не так. Один балл Вам могут поставить, если Вы допустили ошибку в скобке (вместо круглой написали квадратную или наоборот) или допустили вычислительную ошибку, но при этом присутствует верная последовательность всех шагов решения.

Экономические задачи

В решении задач с экономическим содержанием ребятам в первую очередь нужно определить, какая форма кредитования – с дифференцированными платежами, аннуитентными или иная форма кредитования.

Могу выделить несколько основных ошибок.

1)Неверное построение математической модели, связанное с неверным определением формы кредитования.

Для лучшего понимания начну с условия задачи.

В июле 2026 года будет взят кредит на три года в размере 800 тыс рублей. Условия возврата таковы:

– каждый январь долг возрастает на 10 процентов по сравнению с концом прошлого года

– размер платежей в 2027 и 2028 годах одинаковый

– к июлю 2029 года долг выплачивается полностью.

Также известно, что в 2029 году платеж составит 833,8 тыс рублей. Сколько рублей будет составлять платеж в 2027 году?

Согласно записям таблицы, ученик решил, что перед ним дифференцированная форма кредитования и остаток уменьшается у него равномерно, ровно на N рублей каждый год. Но это совсем не так. Из условия задачи, мы видим, что выплаты одинаковые первые два года. Но при этом остаток не будет уменьшаться равномерно. Правильная запись остатка во второй строчке должна выглядеть так: .

Основываясь на критериях оценивания данного задания, математическая модель построена неверно, задание оценивается в 0 баллов.

Идем дальше. Наверняка Вы встречали задачи вида:

15 января 2020 года был выдан кредит на сумму 900 тыс. рублей на 31 месяц. Условия возврата таковы:

– 1 -го числа каждого месяца долг увеличивается на 2 по сравнению с концом предыдущего месяца.

– со 2 по 14 число необходимо выплатить часть долга;

– 15 -го числа каждого месяца с 1-го по 30-й долг должен быть на одну и ту же величину меньше долго на 15 число предыдущего месяца;

– 15 июля 2027 года долг составит 300 тыс рублей.

– 15 августа 2027 года долг должен быть выплачен полностью.

Найдите общую сумму выплат после полного погашения кредита.

Идем дальше. Наверняка Вы встречали задачи вида:

15 января 2020 года был выдан кредит на сумму 900 тыс. рублей на 31 месяц. Условия возврата таковы:

– 1 -го числа каждого месяца долг увеличивается на 2 по сравнению с концом предыдущего месяца.

– со 2 по 14 число необходимо выплатить часть долга;

– 15 июля 2027 года долг составит 300 тыс рублей.

– 15 августа 2027 года долг должен быть выплачен полностью.

Найдите общую сумму выплат после полного погашения кредита.

В этой таблице полностью неправильно записаны столбцы с остатками и выплатами. Согласно условию задачи, первые 30 месяцев долг уменьшается равномерно, на меньше чем, прошлом месяце. Но не забываем, что первоначальный долг – это S, а не Sk рублей. То есть остаток в первые 30 месяцев должен выглядеть так: меньше чем, прошлом месяце. Но не забываем, что первоначальный долг – это S, а не Sk рублей. То есть остаток в первые 30 месяцев должен выглядеть так: . Как Вы понимаете, и выплаты будет принимать совсем другой вид, так как они получаются путем вычитания из долга после начисления процентов самого остатка. Для примера запишем первую выплату: .

С учетом полностью неправильно построенной математической модели, задание оценивается в 0 баллов.

2)Ошибки при применении формул арифметической прогрессии и расчета общей суммы выплат.

Год назад ребятам на экзамене попалась задача, где в процессе кредитования менялась процентная ставка. Приведу пример:

25 августа 2020 года был дан кредит на 12 лет в размере 300 тыс рублей.

— 25 января с 2021 по 2026 года долг возрастает на 10 процентов;

— 25 января с 2027 по 2032 года долг возрастает на 15 процентов;

– с февраля по июль необходимо выплатить часть долга;

– в августе каждого года долг должен быть на одну и туже величину меньше по сравнению с августом прошлого года;

– к августу 2032 года кредит должен быть полностью погашен.

Найдите общую сумму выплат после полного погашения кредита.

Я уверена, что для многих ребят покажется очевидным, что нельзя складывать первую и последнюю (двенадцатую) выплату. Но я все же поясню.

Действительно, это задача на дифференцированные платежи. И можно заметить, что выплаты подчиняются арифметической прогрессии. Но так как у вас меняется процентная ставка, у Вас меняется и так называемый коэффициент или разность арифметической прогрессии. Поэтому правильно будет сначала просуммировать по формуле арифметической прогрессии первые шесть выплат, потом вторые шесть и полученные выражения сложить. Таким образом Вы получите верный ответ.

В каком же случае Вы можете получить 1 балл – если Вы верно построили математическую модель, но допустили вычислительную ошибку при получении численного значения.

PS: в подавляющем большинстве работ, которые поступали на проверку, ребята просили пояснить, почему за параметр (17 задание) и за задание на числа и их свойства так сильно срезали баллы. В большинстве случаев ребята получали по одному баллу за параметр, а в задаче на числа им засчитывали только пункт а), который также дает только один балл. Ребята, эти задачи считаются олимпиадными, не зря за их полное выполнение дается целых 4 балла. Критерии оценивания данных номеров очень жесткие. Должно быть и максимальное подробное объяснение, и разбор всех случаев и вариантов. В 17 задании это и правильно построенный график (если это необходимо), и рассчитаные все точки, и правильно раскрытый модуль, и расписанные все значения параметра и т.д и т.д.

В погоне за «легкими «баллами ребята даже не трогают планиметрию и стереометрию. А они, напомню, оцениваются в три балла каждый. Даже если Вы испытываете трудности в геометрии, пункт а (доказательство) не пропускайте мимо, как правило он значительно легче пункта б), где нужно найти численное значение той или иной величины. Но по одному первичному баллу за каждый номер Вы спокойно можете получить.

На этом мой краткий обзор подошел к концу. Я желаю удачи и сил всем одиннадцатиклассникам в этом году. Не бойтесь ЕГЭ, настраивайтесь на работу, идите к своей цели. У Вас все получится!

Все, что не убивает, делает нас сильнее!

P.S.: Вот моя группа ВКонтакте, где я выкладываю подобные тексты, ролики и полезности для ЕГЭ по физике и математике: https://vk.com/public185877660 Подписывайтесь!

Источник

ВЫСТУПЛЕНИЕ

на РМО математиков

«Диагностика типичных ошибок

при решении задач»

Учитель математики

МБОУ «Ливенская СОШ №1»

Чебакова Галина Владимировна

Одним из вопросов методики преподавания математики является вопрос формирования у учащихся умений и навыков решения текстовых задач.

Задачи являются материалом для ознакомления учащихся с новыми понятиями, для развития логического мышления, формирования межпредметных связей. Задачи позволяют применять знания, полученные при изучении математики, при решении вопросов, которые возникают в жизни человека. Этапы решения задач являются формами развития мыслительной деятельности.

«На ошибках учатся», — гласит народная мудрость. Но для того, чтобы извлечь урок из негативного опыта, в первую очередь, необходимо увидеть ошибку. К сожалению, школьник зачастую не способен ее обнаружить при решении той или иной задачи.

Целенаправленная работа над ошибками требует их систематизации. При этом главную роль должны сыграть группы ошибок, которые объединены общими причинами их появления, общей методикой работы над ними. Такая систематизация ошибок позволяет наметить пути их исправления и предупреждения этих ошибок в дальнейшем.

Широко известны серьезные трудности, которые испытывают учащиеся при решении задач.

1. Ошибки и недочёты, которые обусловлены невниманием к формированию теоретико-множественных представлений учащихся:

ошибки, связанные с недостаточно чётким владением понятиями множества, элемента множества, отношения принадлежности, равенства множеств;
ошибки, которые возникают в результате недостаточно чёткого владения операциями пересечения и объединения множеств.

2. Ошибки, которые связаны с недостаточной логической подготовкой учащихся:

ошибки, связанные с непониманием структуры теоремы;
ошибки, которые обусловлены непониманием зависимости между прямой и обратной теоремами;
ошибки, связанные с непониманием метода доказательства от противного.

3. Ошибки, которые допускают учащиеся из-за отсутствия и неустойчивости самоконтроля.

Первая трудность состоит в математизации предложенного текста, т.е. в составлении математической модели, которая может представлять собой уравнение, неравенство или их систему, диаграмму, график, таблицу, функцию и т.д.
Для того, чтобы перевести содержание задачи на математический язык, учащемуся необходимо тщательно изучить и правильно истолковать его, формализовать вопрос задачи, выразив искомые величины через известные величины и введенные переменные.
Вторая трудность — составление уравнений и неравенств, связывающих данные величины и переменные, которые вводит учащийся.
Третья трудность — это решение полученной системы уравнений или неравенств желательно наиболее рациональным способом.

Проанализируем некоторые типичные ошибки учащихся, допускаемых при решении тренировочных заданий для подготовки к ГИА

Зачастую при решении задач на движение учащиеся не обращают внимание на то, что скорость дана в одних единицах измерения, а время или расстояние в других, поэтому логически рассуждение строится верно, но в результате задача не решена. Что очень важно при ГИА, ЕГЭ – 1 части.
При сопоставлении текста задачи и уравнения для её решения уч-ся обозначают за х не ту величину, которая предложена им в задании.

(Скорость первого велосипедиста на 3 км/ч больше скорости второго, поэтому на путь длинной 20 км ему потребовалось на 20 мин. Меньше, чем второму. Чему равны скорости велосипедистов? Пусть х км/ч скорость первого велосипедиста.)

Типичные ошибки:

20: (х+3)-20:х=20

При решении задач на проценты ( подорожание , скидки) учащиеся повторное изменение величины находят, не применяя правила нахождения части от предыдущей цены, путём сложения и вычитания процентов.

(Магазин закупил на складе футболки и стал продавать их по цене, приносящей доход в 40 % . В конце года цена была снижена на 50 %. Какая цена меньше: та, по которой магазин закупил футболки, или цена в конце года – и на сколько процентов .

Типичные ошибки: 100+40-50=90% Разница на 10 %.))

Рассмотренные ошибки и недочёты типичны на всех ступенях обучения.

Рассмотренные ошибки свидетельствуют о том, что ученики, не справившиеся с решением задач, не смогли представить себе жизненной ситуации, отраженной в задаче, не уяснили отношений между величинами в ней, зависимости между данными и искомым, а поэтому просто механически манипулировали числами.

Почему учащиеся допустили много ошибок при повторном решении знакомых задач? Анализ результатов позволяет сделать вывод о том, что одна из основных причин допускаемых детьми ошибок в решении текстовых задач – неправильная организация первичного восприятия учащимися условия задачи и ее анализа, которые проводятся без должной опоры на жизненную ситуацию, отраженную в задаче, без ее предметного или графического моделирования. Как правило, в процессе анализа используются лишь различные виды краткой записи условия или готовые схемы, а создание модели на глазах у детей или самими детьми в процессе разбора задачи применяется крайне редко. К тому же при фронтальном анализе и решении задачи учитель нередко ограничивается правильными ответами двух-трех учеников, а остальные записывают за ними готовые решения без глубокого их понимания, т.е. не проводятся все этапы работы над задачей.

Для устранения этих недостатков необходимо прежде всего улучшить методику организации первичного восприятия и анализа задачи, чтобы обеспечить осознанный и доказательный выбор арифметического действия всеми учащимися.

Типичные методические ошибки учителя при работе с текстовыми задачами

Ошибка 1. Пропуск этапа анализа условия задачи.

«Прочитайте условие задачи. Кто пойдет к доске?» – такое часто можно видеть на уроке. И сразу начинается оформление решения. Этап анализа отсутствует и в некоторых учебниках, и в решебниках. Может быть, проведение этого этапа обязательно не для всех учащихся. В классе найдутся такие ученики, у которых этап анализа свернут. Они его проходят очень быстро, поэтому сразу видят решение и переходят к его оформлению. Задача педагога – помогать тем, у которых не получается. Решение задачи основывается на тех связях, которые существуют между данными и искомыми величинами. На выделение этих связей и направлен анализ условия задачи. Чтобы помочь учащимся самостоятельно осуществлять анализ условия, преподаватель может предложить им специальные памятки.

Ошибка 2. Пропуск этапа поиска решения.

Пропуск этого этапа ведет к недопониманию учащимися сущности эвристической деятельности, и как результат, к возникновению трудностей при самостоятельном решении задач. В практике обучения традиционной является ситуация, когда учитель вызывает к доске учащегося, который знает, как решить задачу. Однако при личностно ориентированном обучении основная забота учителя должна быть связана с теми, кто испытывает затруднения при самостоятельном решении задач.

Тем же учащимся, которые без учителя могут решать задачи, необходимо подбирать задания, усиливающие их умения и способствующие их развитию (составить задачи на основе справочных данных; рассмотреть другие способы решения предложенной задачи; составить граф-схемы других уравнений по задаче и др.)

Ошибка 3. Пропуск этапа исследования решения.

Зачем нужен этот этап? На этапе исследования выясняем, соответствует ли полученный ответ условию задачи (правдоподобность результата); есть ли другие способы решения; что полезного можно извлечь на будущее из решенной задачи. Последний вопрос позволяет рассматривать каждую задачу как звено в общем умении решать задачи, что ведет к накоплению опыта по решению задач.

Ошибка 4. Смешение этапов анализа и поиска решения.

Чтобы этого избежать, надо точно знать, какую цель мы преследуем на каждом этапе. Цель этапа анализа условия – выявить все имеющиеся связи между данными и искомыми величинами, чему помогает составление таблицы (схемы, рисунка). Цель этапа поиска решения – выбрать метод решения (алгебраический или арифметический) и составить план решения. Цели этапов разные, значит, и смешивать эти этапы никак нельзя.

Если для решения задачи выбран алгебраический метод, то поиск ведем по следующим этапам:

определяем условия, которые могут быть основанием для составления уравнения, и выбираем одно из них;

составляем схему уравнения, соответствующего выбранному условию;

определяем, какие величины можно обозначить за х; выбираем одну из них;

определяем, какие величины нужно выразить через х, и находим условия, которые позволяют это сделать.

Завершается этап поиска составлением плана решения задачи.

Ошибка 5. На этапе анализа условия фиксируются не все связи между величинами.

Надо стараться зафиксировать как можно больше таких связей. Почему это важно? Упустив какую-нибудь связь, мы можем потерять:

условие для составления уравнения;

возможность одну величину выразить через другие;

предусмотреть несколько способов решения.

Ошибка 6. Поиск решения задачи алгебраическим методом начинается с выбора переменной.

Обратим внимание на то, что при перечислении этапов, которые мы проходим при поиске решения задачи алгебраическим методом, сначала был назван выбор условия для составления уравнения, затем составление схемы уравнения, и только тогда мы вводим переменную. На практике мы почти везде видим иное: сначала вводят переменную, затем выражают остальные величины через нее и затем составляют уравнение. Вот этот момент настолько «закостенел» в нашем сознании, что от него отказаться очень трудно.

На самом деле, лучше делать «по-новому». Представьте себя на месте ученика в классе. Рассмотрим ситуацию, когда не были проведены этапы анализа и поиска решения, к доске вызван ученик, который знает, как решить задачу, и он начинает: «За х обозначим…» И что же наш ученик, который затрудняется в самостоятельном решении? Мы из решения сделали тайну непостижимую. «Как он угадал, что обозначить за х?» И когда он будет пробовать дома решать задачу, у него сразу закрадывается сомнение: «А вдруг я не угадаю?»

И насколько спокойнее и увереннее чувствует себя наш ученик, если у него есть карточка по проведению анализа и поиска решения задач; он смог составить по условию задачи таблицу; найти несколько условий для составления уравнений; записать схему уравнения для выбранного условия. Ученик знает, что за х можно обозначить любую из неизвестных величин, и, если не получится уравнение по одной схеме, то можно попробовать составить его по другой схеме.

Ошибка 7. Постановка частных, подсказывающих вопросов учащимся.

Очень много зависит от умения ставить (задавать) вопросы учащимся. Вопросы не должны нести в себе подсказку, а подталкивать учащихся к размышлению. Вместо вопросов: «Во сколько туров проходила олимпиада?», «Как распределились посевные площади?», «Какое время находились туристы в пути?», «Какие машины находятся в автопарке?» лучше задавать общие вопросы: «Что происходит по условию задачи?», «Какие объекты участвуют в задаче?», «Какие части можно выделить в задаче?». Вместо вопроса «Можно ли найти такую-то величину?» лучше задать вопрос: «Что можно найти по данным задачи?», поскольку он может вывести на несколько вариантов решения.

Задавая вопросы, учитель не должен вести учащихся к своему решению; нужно рассмотреть все пути решения, выслушать и обсудить все варианты.

2.Для осуществления целенаправленных мер по исправлению и предупреждению ошибок учителю необходимо систематически изучать ошибки учащихся, выявлять наиболее устойчивые и типичные из них, вести учёт распространённых и индивидуальных ошибок учащихся. Знание учителем типичных ученических ошибок, а также причин их возникновения и проявления даёт ему возможность предвидеть и предупреждать их появление. Достичь этого можно путём подбора таких упражнений, которые препятствуют образованию односторонних ассоциаций и неправильных обобщений.

Ошибки учащихся, которые регистрирует и учитывает учитель, помогают ему установить, что не понимают учащиеся, что ими плохо усвоено; это даёт возможность учителю своевременно ликвидировать пробелы в знаниях учащихся и внести соответствующие коррективы в дальнейшее преподавание с целью предупреждения повторения аналогичных ошибок.

Чтобы определить сущность допускаемых учащимися ошибок, необходимо проследить ход рассуждений, который приводит к такому ошибочному решению, установить этап, на котором зарождаются такие ошибки. Как показывает опыт, часто учащемуся непонятен не весь материал, а лишь какая-то его часть. Выявив, что именно непонятно ученику, можно сосредоточить на этом материале всё внимание, не отвлекаясь на те моменты, которые уже усвоены.

Допускаемые учеником ошибки свидетельствуют не только о недостатках его знаний, но и о потенциальных возможностях. Ошибки служат также показателем проблем, которые могут быть поставлены перед учеником, а иногда они приводят к созданию проблемных ситуаций, которые необходимы в данный момент для развития действий.

Ни в коем случае нельзя снижать оценок ученикам за ошибки в процессе поиска. Очень важно приучить их не бояться допускаемых ошибок. Ошибки, допускаемые учениками, надо исправлять тактично, обоснованно, привлекая к этой работе самих учащихся.

Боязнь допустить ошибку сковывает инициативу ученика. Боясь ошибиться, он не будет сам решать поставленную проблему, а станет ждать помощи от учителя. Он будет решать только лёгкие проблемы. Но без такого самостоятельного решения задач с последовательно нарастающей сложностью не может происходить интеллектуальное развитие. Во многих случаях по этой причине учащиеся проявляют робость и интеллектуальную пассивность, что в дальнейшем приводит к неуспеваемости.

Очень оживлённо воспринимаются учащимися “Задачи на выявление ошибки”. Речь идёт не только о софизмах, но и об ошибках, которые допускают сами школьники. Не нужно специально исправлять каждое ошибочное утверждение школьника. Лучше поставить это утверждение на обсуждение всего класса и добиться осознанного исправления ошибки. Если они и не допускают ошибок, то всё же нередко целесообразно проверить, насколько они “устойчивы” против типичных ошибок.

Например: Найти ошибки:

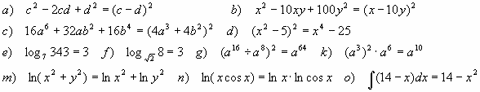
С учетом полностью неправильно построенной математической модели, задание оценивается в 0 баллов.

2)Ошибки при применении формул арифметической прогрессии и расчета общей суммы выплат.

25 августа 2020 года был дан кредит на 12 лет в размере 300 тыс рублей.

— 25 января с 2021 по 2026 года долг возрастает на 10 процентов;

— 25 января с 2027 по 2032 года долг возрастает на 15 процентов;

– с февраля по июль необходимо выплатить часть долга;

– к августу 2032 года кредит должен быть полностью погашен.

Найдите общую сумму выплат после полного погашения кредита.

Все, что не убивает, делает нас сильнее!

Источник

ВЫСТУПЛЕНИЕ

на РМО математиков

«Диагностика типичных ошибок

при решении задач»

Учитель математики

МБОУ «Ливенская СОШ №1»

Чебакова Галина Владимировна

Широко известны серьезные трудности, которые испытывают учащиеся при решении задач.

ошибки, связанные с недостаточно чётким владением понятиями множества, элемента множества, отношения принадлежности, равенства множеств;
ошибки, которые возникают в результате недостаточно чёткого владения операциями пересечения и объединения множеств.

2. Ошибки, которые связаны с недостаточной логической подготовкой учащихся:

ошибки, связанные с непониманием структуры теоремы;
ошибки, которые обусловлены непониманием зависимости между прямой и обратной теоремами;
ошибки, связанные с непониманием метода доказательства от противного.

3. Ошибки, которые допускают учащиеся из-за отсутствия и неустойчивости самоконтроля.

Первая трудность состоит в математизации предложенного текста, т.е. в составлении математической модели, которая может представлять собой уравнение, неравенство или их систему, диаграмму, график, таблицу, функцию и т.д.
Для того, чтобы перевести содержание задачи на математический язык, учащемуся необходимо тщательно изучить и правильно истолковать его, формализовать вопрос задачи, выразив искомые величины через известные величины и введенные переменные.
Вторая трудность — составление уравнений и неравенств, связывающих данные величины и переменные, которые вводит учащийся.
Третья трудность — это решение полученной системы уравнений или неравенств желательно наиболее рациональным способом.

Зачастую при решении задач на движение учащиеся не обращают внимание на то, что скорость дана в одних единицах измерения, а время или расстояние в других, поэтому логически рассуждение строится верно, но в результате задача не решена. Что очень важно при ГИА, ЕГЭ – 1 части.
При сопоставлении текста задачи и уравнения для её решения уч-ся обозначают за х не ту величину, которая предложена им в задании.

Типичные ошибки:

20: (х+3)-20:х=20

При решении задач на проценты ( подорожание , скидки) учащиеся повторное изменение величины находят, не применяя правила нахождения части от предыдущей цены, путём сложения и вычитания процентов.

Типичные ошибки: 100+40-50=90% Разница на 10 %.))

Рассмотренные ошибки и недочёты типичны на всех ступенях обучения.

Типичные методические ошибки учителя при работе с текстовыми задачами

Ошибка 1. Пропуск этапа анализа условия задачи.

Ошибка 2. Пропуск этапа поиска решения.

Ошибка 3. Пропуск этапа исследования решения.

Ошибка 4. Смешение этапов анализа и поиска решения.

Если для решения задачи выбран алгебраический метод, то поиск ведем по следующим этапам:

определяем условия, которые могут быть основанием для составления уравнения, и выбираем одно из них;

составляем схему уравнения, соответствующего выбранному условию;

определяем, какие величины можно обозначить за х; выбираем одну из них;

определяем, какие величины нужно выразить через х, и находим условия, которые позволяют это сделать.

Завершается этап поиска составлением плана решения задачи.

Ошибка 5. На этапе анализа условия фиксируются не все связи между величинами.

условие для составления уравнения;

возможность одну величину выразить через другие;

предусмотреть несколько способов решения.

Ошибка 6. Поиск решения задачи алгебраическим методом начинается с выбора переменной.

Ошибка 7. Постановка частных, подсказывающих вопросов учащимся.

Например: Найти ошибки:

Для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля. Эти навыки состоят из двух частей: а) умения обнаружить ошибку; в) умения её объяснить и исправить.

В процессе обучения применяются несколько приёмов самоконтроля, которые помогают обнаружить допущенные ошибки и своевременно их исправить. К ним относятся:

проверка вычисления и тождественного преобразования путём выполнения обратного действия или преобразования;
проверка правильности решения задач путём составления и решения задач, обратных к данной;
оценка результата решения задачи с точки зрения здравого смысла;
проверка аналитического решения графическим .

Пусть решение ученика выглядит так: . Ошибка становится очевидной, если перед решением ученик прикинет в уме: “За неделю завод выпустил 130 холодильников. Следовательно, за месяц он выпустит больше. Значит, ответ должен быть больше, чем 130”. Такая прикидка в уме полезна при решении задач с дробными числами и процентами.

В жизненной практике в чертежах, схемах, расчётах, с которыми ребята будут встречаться, могут быть и ошибки. Если не научить их критически относиться к данным, то могут быть и аварии, и брак, и серьёзные упущения в работе. Чтобы этого избежать, необходимо формировать у учащихся умение анализировать данные, способность обнаруживать встречающиеся ошибки и обосновывать ошибочность положения.

Польский математик Г. Штейнгауз, отмечая большое значение работы над математическими ошибками для активизации мыслительной деятельности учащихся, пишет:

“Если учащегося заверить, что в предложенном ему доказательстве есть ошибка, то можно быть уверенным даже без специальной проверки, что материал будет изучен полностью и очень тщательно”. Поэтому составление списка математических ошибок и использование его в учебных целях является одним из важных факторов повышения эффективности обучения.

Таким образом, важную роль в предупреждении ошибок играет продуманная организация изучения нового материала. Изучение нового материала надо строить так, чтобы ученик был активным участником этого процесса. Не надо бояться, если при первом изложении материала им будут допускаться ошибки, высказываться необоснованные выводы. Важно, чтобы те или иные ошибки в понимании материала исправлялись в зародыше, чтобы ученики воспринимали материал осознанно.

Такому подходу к изучению нового материала способствует создание проблемной ситуации и решение её учащимися под руководством учителя. На таких уроках ученики проходят через следующие стадии: поиск нового, возможное появление ошибок в процессе поиска нового, обоснованное опровержение этих ошибок, снова поиски, в результате которых приходят к правильной догадке, и, наконец, доказательство составленного в поисках предложения. Всё это способствует развитию математического мышления.

Текстовые задача — это способ стимулирования мыслительной активности. Считаю необходимым сформировать такой подход к задаче, при котором задача выступает как объект тщательного изучения, а ее решение — как объект конструирования и изобретения. Необходимо построить процесс обучения математике так, чтобы обеспечить успешное овладение учащимися методами и приемами решения задач и создать условия для формирования у них ряда общенаучных умений — таких, как анализ, синтез, обобщение, сравнение, аналогия.

Необходимо организовать деятельность учащихся на учебном занятии таким образом, чтобы она способствовала формированию исследовательской культуры.

Предлагаю на занятии несколько приемов организации интенсивной мыслительной деятельности, которые используются мною на различных этапах процесса обучения: при актуализации знаний, первичном усвоении материала, его осмыслении, применении и обобщении.

Это можно сделать на следующем содержании материала:

Правоцирующие задачи.

Это задачи, условия которых содержат упоминания, указания, намеки или другие побудители, подталкивающие учащихся к выбору ошибочного пути решения или неверного ответа. Попадая в заранее подготовленную ловушку, ученик испытывает досаду, сожаление оттого, что не придал особого значения тем нюансам условия, из-за которых он угодил в неловкое положение. Простое сообщение о том, что учащиеся, как правило, допускают в заданиях такого-то рода ошибки, несравнимо менее действенно. Ибо оно, несмотря на общность, не является для конкретно взятого ученика личностно значимым, поскольку, во-первых, события, о которых сообщается, происходили когда-то давно, в прошлом, не сейчас, а во-вторых, каждый из учащихся наивно полагает, что в число неудачников сам он не попадает.

Дидактическая ценность этих задач в том, что они служат предупреждением от различного рода ошибок и заблуждений.

Провоцирующие задачи обладают высоким развивающим потенциалом, они способствуют воспитанию одного из важнейших качеств мышления- критичности, приучают к анализу воспринимаемой информации, ее разносторонней оценке, повышают интерес школьников к занятиям математикой.

Я использую такие разновидности провоцирующих задач:

условия, в которых навязывают неверный ответ;
условия, которые подсказывают неверный путь решения;
условия, вводящие в заблуждение из-за неоднозначности трактовки и т.д.

В качестве примера приведу задачи, побуждающие выбор неверного способа решения.

Тройка лошадей проскакала 15 км. Сколько километров проскакала каждая лошадь?

Или, на уроке в 6 классе по теме «Простые и составные числа» предлагаю задание: «Какие из чисел 205, 206, 207, 208, 209, 210 являются простыми?»

2.Задачи стандартные с нестандартным решением.

Это задачи, при предъявлении которых учащиеся не знают заранее ни способа их решений, ни того, на какой учебный материал опирается решение. Иными словами, учащиеся в ходе решения таких задач должны провести поиск плана решения задачи, установить, какой теоретический материал дает ключ к тому или иному решению. Незначительная обработка условий той или иной задачи из учебника, изменение места и времени ее постановки существенно меняют ее дидактическую значимость, оставляя неизменным практическое содержание.

Проиллюстрирую сказанное примером. Стандартная задача для учащихся 7 класса: «В клетке находится неизвестное число фазанов и кроликов. Известно, что вся клетка содержит 35 голов и 94 ноги. Сколько фазанов и кроликов в клетке?». Данную задачу предлагаю решить не алгебраическим способом, приводя к стандартному уравнению, а арифметическим. Таким образом, по существу, данную задачу превращаем в нестандартную для шестиклассников и даже семиклассников.

Задачи такого плана всегда органически связаны с изучаемым материалом. Допуская нестандартное решение, приучаю школьников не довольствоваться шаблоном, а нацеливаю на вдумчивый подход, воспитываю стремление как можно лучше выполнить порученное дело. Они развивают гибкость, рациональность, целенаправленность математического мышления и ценны тем, что дается возможность каждому ученику с любой структурой мышления проявить себя.

3. Проблемные задачи.

Это задачи, алгоритм решения которых неизвестен до начала решения. Главное в том, чтобы открыть способ решения и убедиться в его пригодности. Следует иметь в виду, что определить, является данная задача проблемной или нет, можно только относительно конкретного школьника, только с учетом его знаний и умений в момент постановки задачи.

Задачи такого плана решаются исследовательским методом и этим очень интересны для учащихся. Ведь исследование предполагает творчество. Проблемы, которые ставятся перед учащимися, могут иметь разнообразный характер: введение в новую тему, решение задачи новым более эффективным способом, связь известного учебного материала с новым и т.д.

При подборе проблемных задач учитываю знания учащихся и уровень развития их логического мышления, поскольку непосильная задача порождает неуверенность в своих силах и в дальнейшем отвращение от решения любых задач, а излишне простая вводит в заблуждение относительно уровня собственных знаний и умений, не стимулирует поисковую деятельность.

Самое главное- это суметь правильно поставить вопрос, заинтриговать учащихся, создать проблему, а не дать ответ, решив ее. Учащиеся познают понятия, закономерности, теории в ходе поиска, наблюдения, анализа фактов, мыслительной деятельности, результатом чего является знание.

Приведу пример задачи из темы «Смежные углы» (геометрия 7 класс).

Найти два смежных угла, один из которых больше другого на прямой угол.

Возможны различные варианты решения, в частности, алгебраический и геометрический. Здесь проблемный характер проявляется в неявной форме, но ученики понимают непригодность геометрического способа решения.

Другой пример. В 5 классе в ходе изучения темы «Сравнение десятичных дробей» предлагаю вариант решения задания на сравнение дробей 0,31 и 0,6 ученика Петрова. Если целые части дробей равны, сравним дробные части: 316, значит, 0,310,6. Согласны ли вы с таким решением? Начинается обсуждение, поиск, анализ решения.

Логические задачи.(задачи-шутки, таблицы, верные и неверные утверждения, здравый смысл)

Это задачи, ведущие к формированию важнейших характеристик творческих способностей: беглость мысли, гибкость ума, оригинальность, любознательность, умение выдвигать и разрабатывать гипотезы.

Опыт работы показывает, что глубокие, прочные и, главное, осознанные знания могут получить все школьники, если развивать у них не столько память, сколько логическое мышление. Логика учит, как нужно рассуждать, чтобы наше мышление было определенным, связанным, последовательным, доказательным и непротиворечивым. В математике приходится путем рассуждений выводить разнообразные формулы, числовые закономерности, правила, доказывать теоремы.

Основные методы решения логических задач:

метод рассуждения;
метод таблицы;
метод граф;
метод кругов Эйлера;
комбинированный метод.

Метод рассуждений сопровождаю схемами, чертежами, краткими записями, вырабатывая умения выбирать информацию, пользоваться правилом перебора.

Так, при изучении темы «Степень» в 7 классе, я даю задание: запишите степени x, x², x³, x⁴, x⁵, x⁶, x⁷, x⁸, x⁹ в пустые клетки квадрата так, чтобы произведение их по любой горизонтали, вертикали и диагонали было равно x в 15 степени. Можно рассказать о магическом квадрате, тогда задача станет еще интереснее для учеников.


	X⁵

Таблицы хорошо применять тогда, когда устанавливается соответствие между двумя множествами (можно и между тремя множествами), когда количество элементов во множествах одинаково и неодинаково. Перед составлением таблиц отрабатываю правила их заполнения.

Например, в 5 классе знакомлю детей с задачей Пуассона (на переливание). Некто имеет 12 пинт сока (пинта- 0,57л) и желает подарить половину своему другу, но у него нет сосуда в 6 пинт, а есть два сосуда в 8 и 5 пинт. Каким образом можно налить 6 пинт сока в сосуд емкостью 8 пинт?

Решение.

Ходы	0	1	2	3	4	5	6	7
12 пинт	12	4	4	9	9	1	1	6
8 пинт	—	8	3	3	—	8	6	6
5 пинт	—	—	5	—	3	3	5	—

Логические связи, при помощи которых была выстроена общая схема решения задачи, помогут учащимся без труда решить подобного рода задачу.

Введение серии таких задач в содержание урока считаю необходимым. Это позволит стереть явную границу между занимательным и учебным материалом. Особенно целесообразно использовать задачи тогда, когда есть опасность неприятия учащимися какого-либо учебного задания; при прохождении сложных тем; при выработке умений и навыков учащихся, когда требуется выполнить значительное количество однотипных упражнений; при изучении материала, подлежащего прочному запоминанию.

Для каждой задачи, которую предполагаю использовать на уроке, прежде выясняю: будет ли она интересна классу, органично ли войдет в структуру урока, будет ли ее использование эффективным. Практика показала: учебный навык, на формирование которого направлена та или иная задача, вырабатывается быстрее, ибо он связан с продуктивной мыслительной деятельностью ученика.

При работе над провоцирующими, проблемными, логическими и стандартными с нестандартным решением задачами наиболее эффективной считаю групповую, парную, индивидуальную, фронтальную работу.

Приведу пример. Расстояние от реки до турбазы туристы рассчитывали пройти за 6 часов. Однако после 2 часов пути они уменьшили скорость на 0,5 км/ч и в результате опоздали на турбазу на 30 мин. С какой скоростью шли туристы первоначально?

Работа над задачей предполагает следующие действия учителя:

Предъявление задачи (читает учитель).
Определение вида задачи (творческая группа).
Выделение гипотез (индивидуальная самостоятельная работа).
Обмен мнениями (в творческой группе).
Формулировка предположительного ответа (в паре).
Проверка ответа на достоверность (фронтальная работа).

Или, задача. Определить площадь равнобедренной трапеции, у которой основания равны 12см и 20см, а диагонали взаимно перпендикулярны.

Предъявление задачи (творческие группы составляют задачи по готовому чертежу).
Выделение гипотез (работа в парах).
Обмен мнениями (фронтальная работа).
Формулировка предположительного ответа (индивидуальная работа).
Проверка ответа на достоверность (индивидуальная работа).

Обязательным этапом на уроке является устный и письменный счет. Целями устного счета являются, во-первых, совершенствование в вычислительных навыков, во-вторых, развитие творческого мышления учащихся.

На своих уроках я стараюсь разнообразить формы и методы устной работы:

— устный счет в начале, в середине, в конце урока;

устная форма проверки домашнего задания;
устная форма творческой работы;
устные самостоятельная и контрольная работы;
уроки устной работы.

Работая устно, воспитываю у учащихся навыки сознательного усвоения изучаемого материала, приучаю ценить и экономить время, развиваю желание поиска рациональных путей решения задачи. В этих целях использую такие приемы, развивающие творческие способности, как «Зашифрованные задания», «Найди ошибку», «Восстановление»,

«Выбор», «Задачи- сказки», детские презентации на устный счёт, математические листы с задачами, изготовленные самими учащимися, ребусы, кроссворды, которые учащиеся составляют самостоятельно.

Обязательно провожу подробный анализ результатов работы и коррекцию знаний. Объявляя количество набранных баллов, полученных за олимпиадное задание, называю ребят, которые представили самые «красивые» решения. При этом опираюсь на формулу «красивой» задачи по В.Г. Болтянскому: красивая задача = непредсказуемость + непредполагаемость +неожиданность + удивительная простота + простота + фантазия + революционный шаг + удивление + оптимизм + труд + …

Таким образом, решение текстовых задач не случайно всегда волновало учителей, методистов, да и самих учащихся и их родителей.

Во-первых, нельзя решить задачу, не поняв ее содержание. Следовательно, умение решать текстовые задачи свидетельствует об одной из самых важных способностей человека — способности понимать текст. Правы те учителя, которые добиваются понимания текста не только на уроках чтения, но и на уроках математики. Критерием понимания задачи является факт решения задачи.

Поэтому решение текстовых задач — это деятельность, весьма важная для общего развития. Обучая решать текстовые задачи, мы приучаем ориентироваться в ситуациях, делаем человека более компетентным. Конечно, для этого нужно резко расширить тематику задач, давать детям задачи, разнообразные по тематике, а не только «на скорость», «на работу», «на покупки».

Решение текстовых задач способствует, с одной стороны, закреплению на практике приобретённых умений и навыков, с другой стороны, развитию логического мышления учащихся.

Наблюдается активизация их мыслительной деятельности. При правильной организации работы у учащихся развивается активность, наблюдательность, находчивость, сообразительность, смекалка, развивается абстрактное мышление, умение применять теорию к решению конкретных задач.

Источник

Задания на поиск ошибки, как инструмент формирования
регулятивных УУД

Задания на поиск ошибки активизируют внимание учащихся, формируют умение анализировать информацию, умение применять знания в нестандартной ситуации, умение критически оценивать полученную информацию.
С целью формирования регулятивных универсальных действий учителем предлагается проверить работу виртуального ученика с последующим выставлением оценки, согласно критериям, предложенным учителем (I). После обсуждения правильности выполнения задания, ученик выставляет оценку за проверку работы себе (II). Итоговая оценка выставляется учителем с учетом самооценки ученика.
Таким образом происходит формирование самооценки, возрастает ответственность за оценку, выставленную товарищу. А ответы на вопросы анкеты в конце задания позволят учителю более адекватно планировать дальнейшую работу с данным учеником.
Ниже приведены примеры карточек с заданиями на поиск ошибки из различных тем курса математики.

Проверь работу ученика 5 Екласса Иванова Вани.		I	II
1) 185х+272х=457х	1
2) 230у-175у=55у	2
3) 156а+79а+21а+44а=300а	3
4) 35х+17х+65+33х=150х	4
5) 55а+а=56а	5
6) 1307у-500у+93=807у+93	6
7) 14+17с-8с=14+9с	7
Отметка

Задание на поиск ошибки по теме: «Упрощение выражений» (5 класс)
Критерии оценивания
менее 4 верных заданий — отметка «2»
4-5 верных заданий – отметка «3»
6 верных заданий — отметка «4»
7 верных заданий — отметка «5»

— Мне было все понятно
— Я испытывал небольшие затруднения, которые сумел преодолеть
— Мне нужно еще поработать над этой темой
— Мне не понятно, без помощи учителя я не справлюсь

Задание на поиск ошибки по теме: « Законы арифметических действий»
(5 класс)

Проверь работу ученика 5 Екласса Иванова Вани.		I	II
1) 2	1
2) 72	2
3) 9 =90+972=1062	3
4) 321+266+134=321+300=621	4
5)	5
6) 3 =621-27=594	6
7)	7
Отметка

Критерии оценивания
менее 4 верных заданий — отметка «2»
4-5 верных заданий – отметка «3»
6 верных заданий — отметка «4»
7 верных заданий — отметка «5»

Задание на поиск ошибки по теме: « Разложение многочленов на множители» (7 класс)

Проверь работу ученика 7 Д класса Иванова Вани.		I	II
1) 15ас – 7с — ас = с ( 15а -7-а )	1
2) 2х ²у + ху = 2ху( х )	2
3) 16а³с²х — 2ас² =2 ас²( 8ас – 1 )	3
4) 6х²у( х –у) + ( у – х )= (х-у)(6х²у -1)	4
5) 35ас – 14 ас² + 4 = а ( 35с – 14с² + 4 )	5
6) 49 – а²= ( 7 – а )( 7 + а )	6
7) 16х⁴у² – 64 =( 4х²у – 8 )( 4х²у + 8 )	7
Отметка

Задание на поиск ошибки по теме: «Признаки равенства треугольников и равнобедренный треугольник» (7 класс)

Проверь работу ученика 7 Д класса Иванова Вани.		I	II
1)Треугольники равны по стороне и двум прилежащим углам	1
2) Если треугольник равносторонний, то все его углы равны	2
3) Треугольники равны по двум сторонам и углу между ними	3
4) Медиана в равнобедренном треугольнике всегда является биссектрисой и высотой.	4
5) Треугольники равны по стороне и двум прилежащим углам	5
6) Треугольники равны по трем сторонам	6
7) Если треугольник равносторонний, то он равнобедренный.	7
Отметка

В конце урока заполни анкету:

Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/245757-zadanija-na-poisk-oshibki-kak-instrument-form

Источник