Percent deviation measures the degree to which individual data points in a statistic deviate from the average measurement of that statistic. To calculate percent deviation, first determine the mean of the data and the average deviation of data points from that mean.
Calculate the Mean
Calculate the average, or mean of your data points. To do this, add the values of all data points, then divide by the number of data points. Say you have four melons, with weights of 2 pounds, 5 pounds, 6 pounds and 7 pounds. Find the sum: 2 + 5 + 6 + 7 = 20, then divide by four, since there are four data points: 20 / 4 = 5. So your potatoes have a mean weight of 5 pounds.
Calculate Average Deviation
Once you know the mean of your data, calculate the average deviation. Average deviation measures the average distance of your data points from the mean.
First, calculate the distance of each data point from the mean: the distance, D, of a data point equal to the absolute value of the data point’s value, d, minus the mean, m: D = |d — m| Absolute value, represented by the | |, signifies that if the result of the subtraction is a negative number, convert it into a positive number. For example, the 2-pound melon has a deviation of 3, since 2 minus the mean, 5, is -3, and the absolute value of -3 is 3. Using this formula, you can find that the deviation of the 6-pound melon is 1, and the 7-pound melon is 2. The 5-pound melon’s deviation is zero, since its weight is equal to the mean.
Once you know the deviations of all your data points, find their average by adding them, and dividing by the number of data points. The deviations are 3, 2, 1 and zero, which have a sum of 6. If you divide 6 by the number of data points, 4, you get an average deviation of 1.5.
Percent Deviation from Mean and Average
The mean and average deviation are used to find the percent deviation. Divide the average deviation by the mean, then multiply by 100. The number you get will show the average percentage that a data point differs from the mean. Your melons have a mean weight of 5 pounds, and an average deviation of 1.5 pounds, so:
percent deviation = 1.5 / 5 x 100 = 30 percent
So on average, your data points are distant from your mean by 30 percent of the mean’s value.
Percent Deviation From a Known Standard
Percent deviation can also refer to how much the mean of a set of data differs from a known or theoretical value. This can be useful, for instance, when comparing data gathered from a lab experiment to a known weight or density of a substance. To find this type of percent deviation, subtract the known value from the mean, divide the result by the known value and multiply by 100.
Suppose you did an experiment to determine the density of aluminum, and came up with a mean density of 2,500 kilograms per meter squared. The known density of aluminum is 2,700 kilogram per meter squared, so you can use these two numbers to calculate by how much your experimental mean differs from the known mean. Subtract 2,700 from 2,500, divide the result by 2,700, then multiply by 100:
percent deviation = (2,500 — 2,700) / 2,700 x 100 = -200 / 2,700 x 100 = -7.41 percent
The negative sign in your answer signifies that your mean is lower than the expected mean. If the percent deviation is positive, it signifies your mean is higher than expected. So your mean density is 7.41 percent lower than the known density.
Абсолютная и относительная погрешности (ошибки).
Пусть некоторая
величина x
измерена n
раз. В результате получен ряд значений
этой величины: x1,
x2,
x3,
…, xn
Величиной, наиболее
близкой к действительному значению,
является среднее арифметическое этих
результатов:
Отсюда следует,
что каждое физическое измерение должно
быть повторено несколько раз.
Разность между
средним значением
измеряемой
величины и значением отдельного измерения
называется абсолютной
погрешностью отдельного измерения:
(13)
Абсолютная
погрешность может быть как положительной,
так и отрицательной и измеряется в тех
же единицах, что и измеряемая величина.
Средняя абсолютная
ошибка результата — это среднее
арифметическое значений абсолютных
погрешностей отдельных измерений,
взятых по абсолютной величине (модулю):
(14)
Отношения
называются относительными погрешностями
(ошибками) отдельных измерений.
Отношение средней
абсолютной погрешности результата
к среднему арифметическому значению
измеряемой величины называют относительной
ошибкой результата и выражают в процентах:
Относительная
ошибка характеризует точность измерения.
Законы распределения случайных величин.
Результат измерения
физической величины зависит от многих
факторов, влияние которых заранее учесть
невозможно. Поэтому значения, полученные
в результате прямых измерений какого
— либо параметра, являются случайными,
обычно не совпадающие между собой.
Следовательно, случайные
величины —
это такие величины, которые в зависимости
от обстоятельств могут принимать те
или иные значения. Если случайная
величина принимает только определенные
числовые значения, то она называется
дискретной.
Например,
количество заболеваний в данном регионе
за год, оценка, полученная студентом на
экзамене, энергия электрона в атоме и
т.д.
Непрерывная
случайная величина принимает любые
значения в данном интервале.
Например: температура
тела человека, мгновенные скорости
теплового движения молекул, содержание
кислорода в воздухе и т.д.
Под событием
понимается всякий результат или исход
испытания. В теории вероятностей
рассматриваются события, которые при
выполнение некоторых условий могут
произойти, а могут не произойти. Такие
события называются
случайными.
Например, событие, состоящее в появлении
цифры 1 при выполнении условия — бросания
игральной кости, может произойти, а
может не произойти.
Если событие
неизбежно происходит в результате
каждого испытания, то оно называется
достоверным.
Событие называется невозможным,
если оно вообще не происходит ни при
каких условиях.
Два события,
одновременное появление которых
невозможно, называются несовместными.
Пусть случайное
событие А в серии из n
независимых испытаний произошло m
раз, тогда отношение:
называется
относительной частотой события А. Для
каждой относительной частоты выполняется
неравенство:
При небольшом
числе опытов относительная частота
событий в значительной мере имеет
случайный характер и может заметно
изменяться от одной группы опытов к
другой. Однако при увеличении числа
опытов частота событий все более теряет
свой случайный характер и приближается
к некоторому постоянному положительному
числу, которое является количественной
мерой возможности реализации случайного
события А. Предел, к которому стремится
относительная частота событий при
неограниченном увеличении числа
испытаний, называется статистической
вероятностью события:
Например, при
многократном бросании монеты частота
выпадения герба будет лишь незначительно
отличаться от ½. Для достоверного события
вероятность Р(А) равна единице. Если
Р=0, то событие невозможно.
Математическим
ожиданием
дискретной случайной величины называется
сумма произведений всех ее возможных
значений хi
на вероятность этих значений рi:
Статистическим
аналогом математического ожидания
является среднее арифметическое значений
:
,
где mi
— число дискретных случайных величин,
имеющих значение хi.
Для непрерывной
случайной величины математическим
ожиданием служит интеграл:
,
где р(х) — плотность
вероятности.
Отдельные значения
случайной величины группируются около
математического ожидания. Отклонение
случайной величины от ее математического
ожидания (среднего значения) характеризуется
дисперсией,
которая для дискретной случайной
величины определяется формулой:
(15)
(16)
Дисперсия имеет
размерность случайной величины. Для
того, чтобы оценивать рассеяние
(отклонение) случайной величины в
единицах той же размерности, введено
понятие среднего
квадратичного отклонения
σ(Х), которое
равно корню квадратному из дисперсии:
(17)
Вместо среднего
квадратичного отклонения иногда
используется термин «стандартное
отклонение».
Всякое отношение,
устанавливающее связь между всеми
возможными значениями случайной величины
и соответствующими им вероятностями,
называется законом
распределения случайной величины.
Формы задания закона распределения
могут быть разными:
а) ряд распределения
(для дискретных величин);
б) функция
распределения;
в) кривая распределения
(для непрерывных величин).
Существует
относительно много законов распределения
случайных величин.
Нормальный
закон распределения случайных
величин (закон
Гаусса).
Случайная величина
распределена по
нормальному закону, если ее плотность
вероятности f(x)
определяется формулой:
(18),
где <x>
— математическое ожидание (среднее
значение) случайной величины <x>
= M
(X);
—
среднее квадратичное отклонение;
—
основание натурального логарифма
(неперово число);
f
(x)
– плотность вероятности (функция
распределения вероятностей).
Многие случайные
величины (в том числе все случайные
погрешности) подчиняются нормальному
закону распределения (закону Гаусса).
Для этого распределения наиболее
вероятным значением
измеряемой
величины
является
её среднее
арифметическое
значение.
График нормального
закона распределения изображен на
рисунке (колоколообразная кривая).
Кривая симметрична
относительно прямой х=<x>=α,
следовательно, отклонения случайной
величины вправо и влево от <x>=α
равновероятны. При х=<x>±
кривая асимптотически приближается к
оси абсцисс. Если х=<x>,
то функция распределения вероятностей
f(x)
максимальна и принимает вид:
(19)
Таким образом,
максимальное значение функции fmax(x)
зависит от величины среднего квадратичного
отклонения. На рисунке изображены 3
кривые распределения. Для кривых 1 и 2
<x>
= α = 0 соответствующие значения среднего
квадратичного отклонения различны, при
этом 2>1.
(При увеличении
кривая распределения становится более
пологой, а при уменьшении
– вытягивается вверх). Для кривой 3 <x>
= α ≠ 0 и 3
= 2.
Закон
распределения
молекул в газах по скоростям называется
распределением
Максвелла.
Функция плотности вероятности попадания
скоростей молекул в определенный
интервал
теоретически была определена в 1860 году
английским физиком Максвеллом
. На рисунке
распределение Максвелла представлено
графически. Распределение движется
вправо или влево в зависимости от
температуры газа (на рисунке Т1
< Т2).
Закон распределения Максвелла определяется
формулой:
(20),
где mо
– масса молекулы, k
– постоянная Больцмана, Т – абсолютная
температура газа,
—
скорость молекулы.
Распределение
концентрации молекул газа в атмосфере
Земли (т.е.
в силовом поле) в зависимости от высоты
было дано австрийским физиком Больцманом
и называется
распределением
Больцмана:
(21)
Где n(h)
– концентрация молекул газа на высоте
h,
n0
– концентрация у поверхности Земли, g
– ускорение свободного падения, m
– масса молекулы.
Распределение
Больцмана.
Совокупность всех
значений случайной величины называется
простым
статистическим рядом.
Так как простой статистический ряд
оказывается большим, то его преобразуют
в вариационный
статистический
ряд или интервальный
статистический ряд. По интервальному
статистическому ряду для оценки вида
функции распределения вероятностей по
экспериментальным данным строят
гистограмму
– столбчатую
диаграмму. (Гистограмма – от греческих
слов “histos”–
столб и “gramma”–
запись).
n
-
h
Гистограмма
распределения Больцмана.
Для построения
гистограммы интервал, содержащий
полученные значения случайной величины
делят на несколько интервалов xi
одинаковой ширины. Для каждого интервала
подсчитывают число mi
значений случайной величины, попавших
в этот интервал. После этого вычисляют
плотность частоты случайной величины
для каждого интервала xi
и среднее значение случайной величины
<xi
> в каждом интервале.
Затем по оси абсцисс
откладывают интервалы xi,
являющиеся основаниями прямоугольников,
высота которых равна
(или
высотой
– плотностью относительной частоты
).
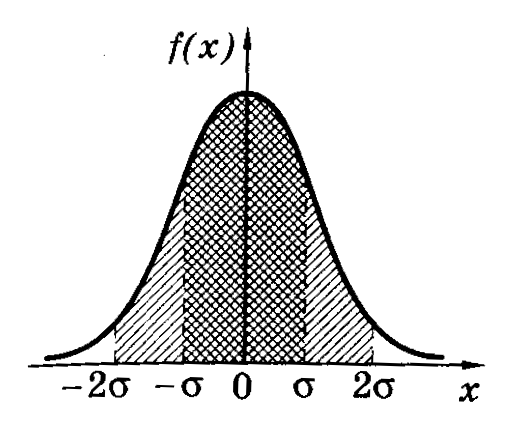
Расчетами показано,
что вероятность попадания нормально
распределенной случайной величины в
интервале значений от <x>–
до <x>+
в среднем равна 68%. В границах вдвое
более широких (<x>–2;
<x>+2)
размещается в среднем 95% всех значений
измерений, а в интервале (<x>–3;<x>+3)
– уже 99,7%. Таким образом, вероятность
того, что отклонение значений нормально
распределенной случайной величины
превысит 3
(
– среднее квадратичное отклонение)
чрезвычайно мала (~0,003). Такое событие
можно считать практически невозможным.
Поэтому границы <x>–3
и <x>+3
принимаются за границы практически
возможных значений нормально распределенной
случайной величины («правило трех
сигм»).
Если число измерений
(объем выборки) невелико (n<30),
дисперсия вычисляется по формуле:
(22)
Уточненное среднее
квадратичное отклонение отдельного
измерения вычисляется по формуле:
(23)
Напомним, что для
эмпирического распределения по выборке
аналогом математического ожидания
является среднее арифметическое значение
<x>
измеряемой величины.
Чтобы дать
представление о точности и надежности
оценки измеряемой величины, используют
понятия доверительного интервала и
доверительной вероятности.
Доверительным
интервалом
называется интервал (<x>–x,
<x>+x),
в который по определению попадает с
заданной вероятностью действительное
(истинное) значение измеряемой величины.
Доверительный интервал характеризует
точность полученного результата: чем
уже доверительный интервал, тем меньше
погрешность.
Доверительной
вероятностью
(надежностью)
результата серии измерений называется
вероятность того, что истинное значение
измеряемой величины попадает в данный
доверительный интервал (<x>±x).
Чем больше величина доверительного
интервала, т.е. чем больше x,
тем с большей надежностью величина <x>
попадает в этот интервал. Надежность
выбирается самим исследователем
самостоятельно, например, =0,95;
0,98. В медицинских и биологических
исследованиях, как правило, доверительную
вероятность (надежность) принимают
равной 0,95.
Если величина х
подчиняется нормальному закону
распределения Гаусса, а <x>
и <>
оцениваются по выборке (числу измерений)
и если объем выборки невелик (n<30),
то интервал (<x>
– t,n<>,
<x>
+ t,n<>)
будет доверительным интервалом для
известного параметра х с доверительной
вероятностью .
Коэффициент t,n
называется коэффициентом
Стьюдента
(этот коэффициент был предложен в 1908 г.
английским математиком и химиком В.С.
Госсетом, публиковавшим свои работы
под псевдонимом «Стьюдент» – студент).
Значении коэффициента
Стьюдента t,n
зависит от доверительной вероятности
и числа измерений n
(объема выборки). Некоторые значения
коэффициента Стьюдента приведены в
таблице 1.
Таблица 1
|
n |
|
||||||
|
0,6 |
0,7 |
0,8 |
0,9 |
0,95 |
0,98 |
0,99 |
|
|
2 |
1,38 |
2,0 |
3,1 |
6,3 |
12,7 |
31,8 |
63,7 |
|
3 |
1,06 |
1,3 |
1,9 |
2,9 |
4,3 |
7,0 |
9,9 |
|
4 |
0,98 |
1,3 |
1,6 |
2,4 |
3,2 |
4,5 |
5,8 |
|
5 |
0,94 |
1,2 |
1,5 |
2,1 |
2,8 |
3,7 |
4,6 |
|
6 |
0,92 |
1,2 |
1,5 |
2,0 |
2,6 |
3,4 |
4,0 |
|
7 |
0,90 |
1,1 |
1,4 |
1,9 |
2,4 |
3,1 |
3,7 |
|
8 |
0,90 |
1,1 |
1,4 |
1,9 |
2,4 |
3,0 |
3,5 |
|
9 |
0,90 |
1,1 |
1,4 |
1,9 |
2,3 |
2,9 |
3,4 |
|
10 |
0,88 |
1,1 |
1,4 |
1,9 |
2,3 |
2,8 |
3,3 |
В таблице 1 в верхней
строке заданы значения доверительной
вероятности
от 0,6 до 0,99, в левом столбце – значение
n.
Коэффициент Стьюдента следует искать
на пересечении соответствующих строки
и столбца.
Окончательный
результат измерений записывается в
виде:
(25)
Где
– полуширина доверительного интервала.
Результат серии
измерений оценивается относительной
погрешностью:
(26)
Загрузить PDF
Загрузить PDF
Стандартной ошибкой называется величина, которая характеризует стандартное (среднеквадратическое) отклонение выборочного среднего. Другими словами, эту величину можно использовать для оценки точности выборочного среднего. Множество областей применения стандартной ошибки по умолчанию предполагают нормальное распределение. Если вам нужно рассчитать стандартную ошибку, перейдите к шагу 1.
-
1
Запомните определение среднеквадратического отклонения. Среднеквадратическое отклонение выборки – это мера рассеянности значения. Среднеквадратическое отклонение выборки обычно обозначается буквой s. Математическая формула среднеквадратического отклонения приведена выше.
-
2
Узнайте, что такое истинное среднее значение. Истинное среднее является средним группы чисел, включающим все числа всей группы – другими словами, это среднее всей группы чисел, а не выборки.
-
3
Научитесь рассчитывать среднеарифметическое значение. Среднеаримфетическое означает попросту среднее: сумму значений собранных данных, разделенную на количество значений этих данных.
-
4
Узнайте, что такое выборочное среднее. Когда среднеарифметическое значение основано на серии наблюдений, полученных в результате выборок из статистической совокупности, оно называется “выборочным средним”. Это среднее выборки чисел, которое описывает среднее значение лишь части чисел из всей группы. Его обозначают как:
-
5
Усвойте понятие нормального распределения. Нормальные распределения, которые используются чаще других распределений, являются симметричными, с единичным максимумом в центре – на среднем значении данных. Форма кривой подобна очертаниям колокола, при этом график равномерно опускается по обе стороны от среднего. Пятьдесят процентов распределения лежит слева от среднего, а другие пятьдесят процентов – справа от него. Рассеянность значений нормального распределения описывается стандартным отклонением.
-
6
Запомните основную формулу. Формула для вычисления стандартной ошибки приведена выше.
Реклама
-
1
Рассчитайте выборочное среднее. Чтобы найти стандартную ошибку, сначала нужно определить среднеквадратическое отклонение (поскольку среднеквадратическое отклонение s входит в формулу для вычисления стандартной ошибки). Начните с нахождения средних значений. Выборочное среднее выражается как среднее арифметическое измерений x1, x2, . . . , xn. Его рассчитывают по формуле, приведенной выше.
- Допустим, например, что вам нужно рассчитать стандартную ошибку выборочного среднего результатов измерения массы пяти монет, указанных в таблице:
Вы сможете рассчитать выборочное среднее, подставив значения массы в формулу:
- Допустим, например, что вам нужно рассчитать стандартную ошибку выборочного среднего результатов измерения массы пяти монет, указанных в таблице:
-
2
Вычтите выборочное среднее из каждого измерения и возведите полученное значение в квадрат. Как только вы получите выборочное среднее, вы можете расширить вашу таблицу, вычтя его из каждого измерения и возведя результат в квадрат.
- Для нашего примера расширенная таблица будет иметь следующий вид:
-
3
Найдите суммарное отклонение ваших измерений от выборочного среднего. Общее отклонение – это сумма возведенных в квадрат разностей от выборочного среднего. Чтобы определить его, сложите ваши новые значения.
- В нашем примере нужно будет выполнить следующий расчет:
Это уравнение дает сумму квадратов отклонений измерений от выборочного среднего.
- В нашем примере нужно будет выполнить следующий расчет:
-
4
Рассчитайте среднеквадратическое отклонение ваших измерений от выборочного среднего. Как только вы будете знать суммарное отклонение, вы сможете найти среднее отклонение, разделив ответ на n -1. Обратите внимание, что n равно числу измерений.
- В нашем примере было сделано 5 измерений, следовательно n – 1 будет равно 4. Расчет нужно вести следующим образом:
-
5
Найдите среднеквадратичное отклонение. Сейчас у вас есть все необходимые значения для того, чтобы воспользоваться формулой для нахождения среднеквадратичного отклонения s.
- В нашем примере вы будете рассчитывать среднеквадратичное отклонение следующим образом:
Следовательно, среднеквадратичное отклонение равно 0,0071624.
Реклама
- В нашем примере вы будете рассчитывать среднеквадратичное отклонение следующим образом:
-
1
Чтобы вычислить стандартную ошибку, воспользуйтесь базовой формулой со среднеквадратическим отклонением.
- В нашем примере вы сможете рассчитать стандартную ошибку следующим образом:
Таким образом в нашем примере стандартная ошибка (среднеквадратическое отклонение выборочного среднего) составляет 0,0032031 грамма.
- В нашем примере вы сможете рассчитать стандартную ошибку следующим образом:
Советы
- Стандартную ошибку и среднеквадратическое отклонение часто путают. Обратите внимание, что стандартная ошибка описывает среднеквадратическое отклонение выборочного распределения статистических данных, а не распределения отдельных значений
- В научных журналах понятия стандартной ошибки и среднеквадратического отклонения несколько размыты. Для объединения двух величин используется знак ±.
Реклама
Об этой статье
Эту страницу просматривали 49 566 раз.
Была ли эта статья полезной?
Бизнес-профессионалы, специалисты по данным и финансовым аналитикам, а также бухгалтеры используют модели прогнозирования, чтобы предсказать, как все изменится в течение определенного периода. Чтобы обеспечить точность своих моделей, эти специалисты измеряют, насколько модель похожа на фактические данные. Для этого они могут использовать средневзвешенную абсолютную процентную ошибку или WMAPE. Знание того, что такое WMAPE и как его рассчитать, может помочь вам делать более точные прогнозы будущих данных и финансовых тенденций. В этой статье мы обсудим, что такое WMAPE, рассмотрим способы его использования и рассмотрим, как рассчитать WMAPE для выборки данных.
Что такое средневзвешенная абсолютная ошибка в процентах?
Средневзвешенная абсолютная процентная ошибка, обычно называемая WMAPE, представляет собой способ измерения точности финансовых и статистических прогнозов по сравнению с фактическими или реальными результатами для выборки. Например, если вы предсказали, что продадите пять автомобилей, и действительно продали пять автомобилей в этот день, то ваш WMAPE будет равен 0 %, поскольку в вашем прогнозе не было ошибок. Если бы вы продали три автомобиля, то ваш WMAPE составил бы 66,6%, потому что в прогнозе был указан один результат, а реальный результат был другим. Различные части WMAPE:
-
Взвешенный: это означает, что есть компонент, по которому вы измеряете результат расчета.
-
Среднее: это означает, что ваш результат для этого расчета является средним показателем точности ваших прогнозов.
-
Абсолют: это означает, что независимо от того, был ли реальный результат больше или меньше прогноза, ваш расчет даст положительное число.
-
Процент: это означает, что результат вашего расчета представлен в процентном формате для простоты использования.
-
Ошибка: это означает, что результат вашего расчета является мерой разницы между вашим прогнозом и вашим реальным результатом.
Как используется средневзвешенная абсолютная процентная ошибка?
Вы можете использовать WMAPE для исследования средней ошибки ваших прогнозов с течением времени по сравнению с тем, что происходит на самом деле. Как правило, вы используете WMAPE для сравнения прогнозов за более длительный период, потому что это показывает общую тенденцию правильности ваших прогнозов, а не конкретный день или час. Вы также можете использовать WMAPE в сочетании с другими измерениями прогнозирования, чтобы получить представление о точности и скорости отклика ваших моделей данных.
Как рассчитывается средневзвешенная абсолютная ошибка в процентах?
Формула для расчета WMAPE:
(1/n) x Σ(|Факт. — Прогноз|) x 100 / |Факт.| = WMAPE
Где части формулы:
-
n = размер выборки
-
Σ = сумма всех значений в скобках
-
|х| = символы, представляющие абсолютное значение чисел между ними
-
Факт = реальная стоимость за данный период
-
Прогноз = ожидаемое значение для данного периода
Например, если у вас есть следующие прогнозируемые и фактические значения:
Прогноз**Фактический**53101555Следующие шаги могут помочь вам найти WMAPE для вашего набора данных:
1. Найдите все значения для |Факт — Прогноз|
Чтобы найти эти значения, вы можете ввести каждое значение прогнозируемого и фактического в уравнение. Например:
|3 — 5| = 2
|15 -10| = 5
|5 — 5| = 0
Это удовлетворяет части формулы |Факт — Прогноз| и может помочь вам рассчитать вес каждого значения. Примечательно, что в первом уравнении используются символы абсолютных значений |x| и преобразует отрицательное число два в значение положительного числа два. Это связано с тем, что символы абсолютного значения заботятся о расстоянии числа от нуля, а не о его реальном значении. Здесь минус два — это два от нуля.
2. Разделите каждое значение на фактическое значение.
После того как вы рассчитали абсолютные значения фактических и прогнозируемых данных, вы можете разделить эти данные на фактическое значение. Например:
2/3 = 0,66
5/15 = 0,33
0 / 5 = 0
Это удовлетворяет части уравнения /|Actual|. Каждый из результатов вычислений является положительным числом из-за использования символов абсолютного значения. Это может помочь вам рассчитать вес для каждого значения в вашем наборе данных.
3. Умножить на 100 и разделить на фактическое значение
После того, как вы нашли результаты своих предыдущих расчетов, вы можете умножить каждый из них на 100. Это гарантирует, что все ваши значения находятся в той же шкале, что и фактические значения, удовлетворяет части уравнения x 100 и может помочь вам определить каждое значение. масса. Например:
0,66 х 100 = 66
0,33 х 100 = 33
0 х 100 = 0
После того, как вы завершили приведенные выше расчеты, вы можете разделить каждый результат на исходное фактическое значение. Например:
66/3 = 22
33/15 = 2,2
0 / 5 = 0
Эти числа представляют веса каждого вычисления, которые используются в следующих шагах. Для этого шага вы также можете присвоить веса на основе важных моментов в вашем наборе данных. Например, если понедельник — лучший день продаж на неделе, а все остальные дни равны, то понедельнику можно присвоить вес, равный шести, а другим дням — один. Это означает, что понедельник имеет 60% веса, а все остальные дни имеют 10% веса.
4. Рассчитать сумму фактических значений и сумму весов
Теперь, когда вы вычислили веса каждого набора значений, вы можете вычислить сумму фактических значений. Вы можете сделать это, добавив каждое фактическое значение к другим. Например:
3 + 15 + 0 = 18
После того, как вы подсчитали сумму фактических значений, вы можете сложить свои веса. Например:
22 + 2,2 = 24,2
5. Рассчитайте средневзвешенную абсолютную процентную ошибку.
Наконец, вы можете рассчитать средневзвешенную абсолютную процентную ошибку, разделив сумму весов на сумму фактических значений. Например:
24,2/18 = 1,34
Преобразованное в проценты, это значение составляет 1,34%, что равно средневзвешенной абсолютной процентной ошибке значений. Это относительно низкая процентная ошибка, означающая, что модели прогнозирования были почти на 100% точными.
Содержание
- Примеры расчета процентной ошибки
- 1 — Измерение двух полей
- 2 — Измерение алюминия
- 3 — Участники мероприятия
- 4 — падение мяча
- 5 — Время, необходимое для прибытия машины
- 6 — Измерение длины
- 7 — Длина моста
- 8 — Диаметр винта
- 9 — Вес объекта
- 10 — Измерение стали
- Ссылки
В процентная ошибка это проявление относительной погрешности в процентном отношении. Другими словами, это числовая ошибка, выраженная значением, которое дает относительную ошибку, впоследствии умноженную на 100.
Чтобы понять, что такое процентная ошибка, в первую очередь необходимо понять, что такое числовая ошибка, абсолютная ошибка и относительная ошибка, поскольку процентная ошибка выводится из этих двух членов.
Числовая ошибка — это ошибка, которая появляется, когда измерение проводится двусмысленным образом при использовании устройства (прямое измерение) или когда математическая формула применяется неправильно (косвенное измерение).
Все числовые ошибки могут быть выражены в абсолютном или процентном выражении. Со своей стороны, абсолютная ошибка — это ошибка, которая получается при приближении к математической величине, полученной в результате измерения элемента или ошибочного применения формулы.
Таким образом, точное математическое значение изменяется приближением. Расчет абсолютной ошибки выполняется путем вычитания приближения из точного математического значения, например:
Абсолютная ошибка = точный результат — приближение.
Единицы измерения, используемые для выражения относительной ошибки, те же, что и для числовой ошибки. Точно так же эта ошибка может давать положительное или отрицательное значение.
Относительная ошибка — это частное, полученное путем деления абсолютной ошибки на точное математическое значение.
Таким образом, процентная ошибка — это ошибка, полученная путем умножения результата относительной ошибки на 100. Другими словами, процентная ошибка — это выражение в процентах (%) относительной ошибки.
Относительная ошибка = (Абсолютная ошибка / точный результат)
Процентное значение, которое может быть отрицательным или положительным, т. Е. Может быть чрезмерно или заниженным. Это значение, в отличие от абсолютной ошибки, не представляет единиц, кроме процента (%).
Относительная ошибка = (абсолютная ошибка / точный результат) x 100%
Задача относительных и процентных ошибок — указать качество чего-либо или предоставить сравнительную ценность.
Примеры расчета процентной ошибки
1 — Измерение двух полей
При измерении двух партий или партий считается, что погрешность измерения составляет около 1 м. Один участок 300 метров, другой 2000.
В этом случае относительная погрешность первого измерения будет больше, чем у второго, поскольку пропорция 1 м в этом случае представляет более высокий процент.
300 м участок:
Ep = (1/300) x 100%
Ep = 0,33%
2000 м участок:
Ep = (1/2000) x 100%
Ep = 0,05%
2 — Измерение алюминия
Алюминиевый блок доставлен в лабораторию. Путем измерения размеров блока и расчета его массы и объема определяется плотность блока (2,68 г / см3).
Однако при просмотре числовой таблицы для материала указано, что плотность алюминия составляет 2,7 г / см3. Таким образом, абсолютная и процентная погрешность будут рассчитываться следующим образом:
Ea = 2,7 — 2,68
Ea = 0,02 г / см3.
Ер = (0,02 / 2,7) х 100%
Ep = 0,74%
3 — Участники мероприятия
Предполагалось, что на какое-то мероприятие приедет 1 000 000 человек. Однако точное количество человек, посетивших мероприятие, составило 88 тысяч. Абсолютная и процентная ошибка будет следующей:
Ea = 1 000 000–88 000
Ea = 912 000
Ep = (912 000/1 000 000) x 100
Ep = 91,2%
4 — падение мяча
Расчетное время, за которое мяч должен достичь земли после броска с расстояния 4 метра, составляет 3 секунды.
Однако во время экспериментов выяснилось, что мяч достиг земли за 2,1 секунды.
Ea = 3 — 2,1
Ea = 0,9 секунды
Ер = (0,9 / 2,1) х 100
Ep = 42,8%
5 — Время, необходимое для прибытия машины
Приблизительно, если автомобиль проехал 60 км, он доберется до места назначения за 1 час. Однако в реальной жизни автомобиль добирался до места назначения за 1,2 часа. Процентная погрешность этого вычисления времени будет выражена следующим образом:
Ea = 1 — 1,2
Ea = -0,2
Ер = (-0,2 / 1,2) х 100
Ep = -16%
6 — Измерение длины
Любая длина измеряется величиной 30 см. При проверке измерения этой длины очевидно, что была ошибка 0,2 см. Процентная ошибка в этом случае будет проявляться следующим образом:
Ер = (0,2 / 30) х 100
Ep = 0,67%
7 — Длина моста
Расчет длины моста по планам — 100 м. Однако при подтверждении этой длины после постройки становится очевидным, что на самом деле она составляет 99,8 м. Таким образом будет подтверждена процентная ошибка.
Ea = 100 — 99,8
Ea = 0,2 м
Ер = (0,2 / 99,8) х 100
Ep = 0,2%
8 — Диаметр винта
Головка стандартного винта должна быть диаметром 1 см.
Однако при измерении этого диаметра видно, что головка винта на самом деле составляет 0,85 см. Процентная ошибка будет следующей:
Ea = 1 — 0,85
Ea = 0,15 см
Ер = (0,15 / 0,85) х 100
Ep = 17,64%
9 — Вес объекта
Исходя из его объема и материалов, вес данного объекта составляет 30 кг. После анализа объекта выясняется, что его реальный вес составляет 32 кг.
В этом случае значение процентной ошибки описывается следующим образом:
Ea = 30–32
Ea = -2 кг
Ep = (2/32) x 100
Ep = 6,25%
В лаборатории изучается стальной лист. Путем измерения размеров листа и расчета его массы и объема определяется плотность листа (3,51 г / см3).
Однако при просмотре числовой таблицы для материала указано, что плотность стали составляет 2,85 г / см3. Таким образом, абсолютная и процентная погрешность будут рассчитываться следующим образом:
Ea = 3,51 — 2,85
Ea = 0,66 г / см3.
Ep = (0,66 / 2,85) x 100%
Ep = 23,15%
Ссылки
- Веселье, М. и. (2014). Математика — это весело. Получено из процентной ошибки: mathsisfun.com
- Хельменстин, А. М. (8 февраля 2017 г.). ThoughtCo. Получено из раздела «Как рассчитать процент ошибки»: thinkco.com
- Уртадо, А. Н., и Санчес, Ф. К. (н.э.). Технологический институт Тустла Гутьеррес. Получено из 1.2. Типы ошибок: абсолютная ошибка, относительная ошибка, процентная ошибка, ошибки округления и усечения.: Sites.google.com
- Айова, штат Юта. (2017). Визуализация Вселенной. Получено по формуле процента ошибок: astro.physics.uiowa.edu
- Леферс, М. (26 июля 2004 г.). Процент ошибки. Получено из определения: groups.molbiosci.northwestern.edu.