Коэффициент
вариации,
или изменчивости, годового
стока служит мерой оценки колебания
годовых величин стока относительно его
нормы и численно равен относительному
среднему
квадратическому отклонению
.
Он служит также
для сравнения отдельных статистических
рядов, например годовых
величин стока разных рек, в отношении
их изменчивости
или рассеяния точек на кривой.
При
наличии длительных наблюдений Указаниями
СН 371-67 предусматриваются
два метода определения
в зависимости от
изменчивости годового стока.
Если
изменчивость годового стока невелика
и характеризуется коэффициентом вариации
,
рекомендуется следующая
формула
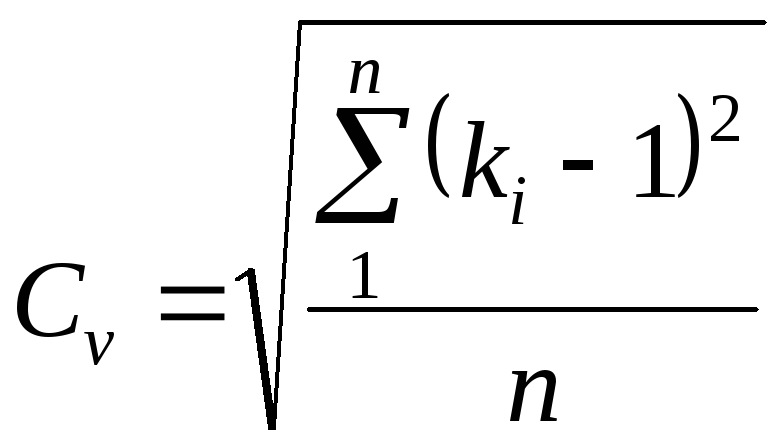
где
ki
– модульный
коэффициент стока каждого года; n
– число лет
наблюдений (число членов статистического
ряда).
При
n<30
формула (3.1) используется в виде
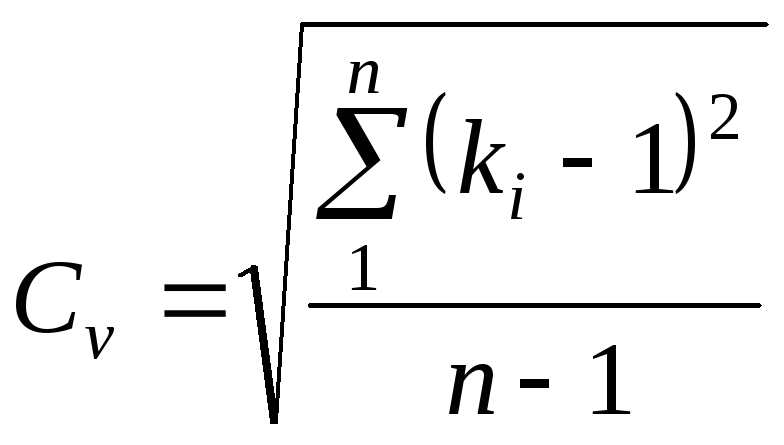
Формула
(3.1) представляет собой выражение второго
момента
площади кривой распределения относительно
центральной ординаты,
а метод определения
и
по
формулам (3.1 ) и
(3.6) называется методом моментов.
Относительная
средняя квадратическая ошибка коэффициента
вариации, вычисленная по этим формулам,
равна
(3.2)
Формула
(4.2) предложена Е. Г. Блохиновым и
рекомендована Указаниями СН 371-67.
Для
нормального распределения параметра
или близкого к нему более обоснованной
формулой определения
является:
(3.3)
Значения
в зависимости
от п и
вычисленные по формулам (3.2) и (3.3),
приводятся в таблицах 3.1 и 3.2.
Таблица
3.1
Относительные
средние квадратические ошибки (%)
коэффициента вариации, вычисленные по
формуле (3.2)
|
|
Число |
|||||||||
|
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
|
|
0,20 |
23 |
16 |
13 |
11 |
10 |
9,3 |
8,6 |
8,1 |
7,6 |
7,2 |
|
0,30 |
23 |
17 |
14 |
12 |
10 |
9,6 |
8,8 |
8,3 |
7,8 |
7,4 |
|
0,40 |
24 |
17 |
14 |
12 |
11 |
9,8 |
9,1 |
8,5 |
8,0 |
7,6 |
Примечание.
При
промежуточных значениях Cv
и
п
определяется
по
интерполяции.
Таблица
3.2
Относительные
средние квадратические ошибки (%)
коэффициента вариации, вычисленные по
формуле (3.3)
|
n |
|
||||
|
0,20 |
0,40 |
0,60 |
0,80 |
1,00 |
|
|
10 |
23,2 |
25 7 |
29,4 |
33,7 |
38,6 |
|
20 |
16,5 |
18,2 |
20,7 |
23,9 |
27,4 |
|
30 |
13,4 |
14,8 |
16,9 |
19,5 |
22,3 |
|
50 |
10,4 |
11,5 |
13,1 |
15,1 |
17,3 |
|
100 |
7,4 |
8,2 |
9,3 |
10,7 |
12,3 |
Из
этих таблиц видно, что для определения
<0,50
с точ-ностью ±10% необходимо иметь ряд
наблюдений продолжительностью 50—60
лет, а вычисления по формулам (3.2) и (3.3)
дают малую разницу, которая практически
не сказывается на конечных результатах
расчетов.
При
большой изменчивости годового стока
(>0,50),
что характерно для рек засушливых
районов, коэффициент вариации определяется
методом наибольшего правдоподобия. По
этому методу значение Cv
устанавливается
в зависимости от параметра ,
который представляет собой среднее
значение логарифмов модульных
коэффициентов lg
k
и вычисляется по равенству
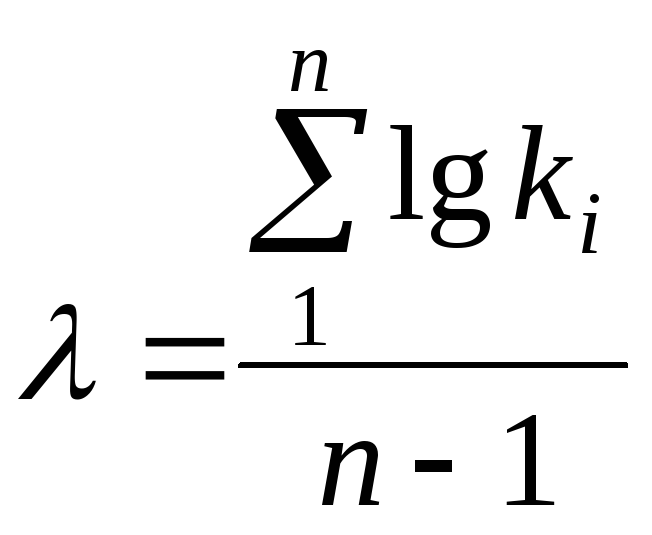
Имея
значение ,
по таблице 3.3 легко установить величину
Cv.
Относительная
средняя квадратическая ошибка Cv,
установленного
с помощью параметра ,
приближенно
равна
(3.5)
Более
точные значения
,
вычисленные
методом наибольшего
правдоподобия, приводятся в таблице
3.4.
Значения
коэффициентов вариации, определенные
методом моментов
и методом наибольшего правдоподобия
при Сv
>0,5,
различаются
не более чем на 2–3% (таблица 3.4). В то же
время метод
наибольшего правдоподобия отличается
сложностью и громоздкостью
вычислений. Поэтому можно считать, что
метод наибольшего
правдоподобия для определения Cv
не
имеет преимущества перед методом
моментов и при массовых расчетах Cv
лучше пользоваться последним, т.е.
формулой (3.1),
который
оправдал себя при многочисленном
практическом применении.
Коэффициенты
вариации, установленные по формуле
(4.1)
и по
табл. 3.4 с помощью параметра ,
принимаются
в качестве расчетных,
когда их средняя квадратическая ошибка,
вычисленная
по формуле (3.2), не превышает следующие
пределы:
Интервалы
значений Cv
0,2—0,3
0,4—0,8 больше 0,8
Допустимая средняя
квадратическая
ошибка, %
20 10 5
Таблица
3.3
Относительная
средняя квадратическая ошибка (%)
коэффициента изменчивости
|
Cv |
Число |
|||||||||
|
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
|
|
0 50 |
21,5 |
15,2 |
12,4 |
10,8 |
9,6 |
8,8 |
8,1 |
7,6 |
7,2 |
6,8 |
|
0,75 |
20,5 |
14,5 |
11,8 |
10,3 |
9,2 |
8,4 |
7,7 |
7,2 |
6,9 |
6,5 |
|
1,00 |
19,4 |
13,7 |
11,2 |
9,7 |
8,7 |
7,9 |
7,3 |
6,8 |
6,5. |
6,1 |
|
1,25 |
18,2 |
12,8 |
10,5 |
9,1 |
8,1 |
7,5 |
6,9 |
6,4 |
6,1 |
5,8 |
|
1,50 |
16,9 |
12,0 |
9,8 |
8,5 |
7,6 |
6,9 |
6,4 |
6,0 |
5,7 |
5,4 |
|
1,75 |
15,8 |
11,2 |
9,1 |
7,9 |
7,0 |
6,4 |
6,0 |
5,6 |
5,3 |
5,0 |
|
2,00 |
14,6 |
10,4 |
8,4 |
7,3 |
6,6 |
6,0 |
5,5 |
5,2 |
4,9 |
4,6 |
Примечание.
При промежуточных значениях
Cv
и п средняя
квадра. тическая
ошибка определяется по интерполяции.
Таблица
3.4
Средние
значения Cv,
определенные
методами моментов и наибольшего
правдоподобия
-
Истинное
значение CvОбъем
выборки
иЗначение
Cvпо методу
моментовпо
методу наибольшего
правдоподобия0,25
0,50
1,00
25
50
25
50
25
50
0,25
0,24
0,49
0,50
0,97
0,98
0,25
0,25
0,49
0,50
0,99
1,00
Максимальные
ошибки Cv
значительно
превышают среднее квадратическос
значение. Они возможны тогда, когда в
короткий
ряд наблюдений, по которому определяются
Cv
, входит очень многоводный
или маловодный год, повторяемость
которого значительно
реже чем один раз в п
лет.
Однако вероятность больших
ошибок Cv,
в два-три раза превышающих ее среднюю
квадратическую
величину, очень мала.
Коэффициент
асимметрии
Cs
характеризует
несимметричность ряда
величин стока относительно его среднего
значения.
Это менее устойчивый параметр кривой
распределения
или обеспеченности и для надежного его
определения требуется
ряд наблюдений над стоком более 100—150
лет. По
имеющимся рядам наблюдений можно
установить лишь приближенное
значение коэффициента асимметрии. Для
этой цели используется формула третьего
момента
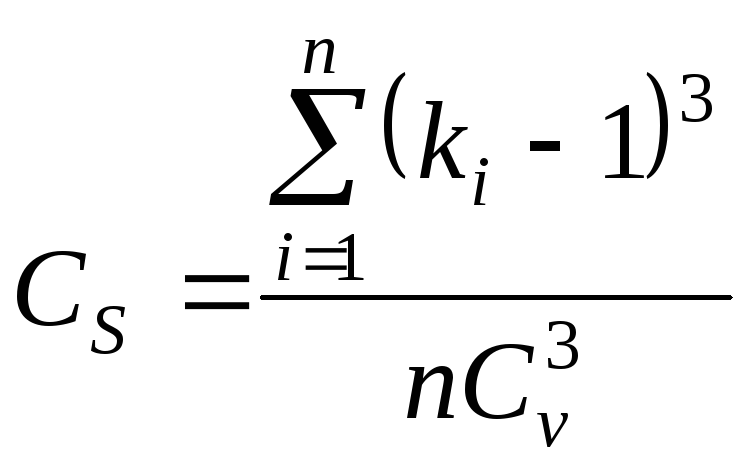
Относительная
средняя квадратическая ошибка Cs
зависит от
коэффициента вариации Сv
и числа лет наблюдений п.
Ее значение
при Cs
= 2Cv
с учетом
асимметричного распределения годовых
величин стока может быть определена по
формуле С. Н. Крицкого и М. Ф. Менкеля.
Так
при обычных значениях CV=0,20—0,40
средняя квадратичная ошибка
при
n=20—30
составляет около 14—16% от значения
коэффициента, а при n
= 50 уменьшается до 10—12%. Относительная
среднеквадратичная ошибка определения
коэффициента Cs
вычисляется
по формуле
(3.7)
Величины
этих ошибок коэффициентов Cv
и
Cs,
определенных
по формулам (3.2-3.3) и (3.7), даны в таблицах
3.2–3.3 и 3.6.
Для
наиболее распространенных величин
годового стока рек лесной и лесостепной
зон Cv=0,20÷0,50.
Средняя ошибка его определения при
n=20-30
лет находится в пределах 15,5-19,5%.
Для
надежного подсчета коэффициента Сs
необходимо иметь, длительный ряд
(порядка
100
и
более), что практически бывает крайне
редко. Коэффициент обладaeт
более значительной устойчивостью во
времени и для надежного его подсчета
достаточен более короткий ряд наблюдении.
Поэтому обычно величину Сs
принимают
кратно значению Сv
т.е.
Сs=а
Сv (3.8)
Таблица
3.5
Относительные
средние квадратические ошибки определения
коэффициента асимметрии
в % приСs
=2Cv
|
п |
Коэффициент |
|||||
|
0,10 |
0,20 |
0,40 |
126 |
0,80 |
1,00 |
|
|
10 |
399 |
216 |
140 |
126 |
126 |
134 |
|
20 |
281 |
153 |
99 |
85 |
89 |
95 |
|
30 |
234 |
125 |
80 |
72 |
74 |
78 |
|
40 |
199 |
108 |
70 |
63 |
64 |
67 |
|
50 |
178 |
96 |
63 |
56 |
57 |
60 |
|
100 |
125 |
69 |
44 |
39 |
41 |
42 |
Величина
а для
различных гидрологических характеристик
принимается различной. Так, для
биноминальной асимметричной кривой
пределом этой величины могут быть от
а=2 до
;Кмин
– отношение
наинизшего расхода к среднему данного
ряда). Для среднегодового стока равенство
коэффициентов CS=Cv
справедливо
только при малых величинах Cv.
При больших
величинах
Cv
следует
применять
,
что дает, как правило, величинуCS>2CV.
Для других
гидрологических величин соотношение
между Cv
и CS,
будет указано ниже.
При
наличии ряда наблюдений порядка 20 и
более построение кривой обеспеченности
выполняется с помощью таблицы
вспомогательных величин, образец которой
приведен в таблице. 3.6.
В
графе 12 подсчитывается обеспеченность
точек (модульных коэффициентов)
эмпирической кривой р
% определяется
по формуле
(3.9)
где
m
– порядковый номер члена ряда при
расположении их в убывающем порядке; n
– число членов в ряду.
Таблица
3.6
Вспомогательные
величины для построения кривой
обеспеченности
|
№ пп |
Год |
Q м3/сек |
в убывающ ем |
|
(k |
(k |
(k |
р, % |
|||
|
+ |
|
+ |
|
||||||||
|
годы |
Q, |
||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
1 |
1894 |
1938 |
|||||||||
|
2 |
1895 |
1941 |
|||||||||
|
… |
… |
||||||||||
|
… |
1941 |
||||||||||
|
Сумма |
|
|
|
|
|
На
график (рис. 3.1) наносят точки ряда
наблюдений (полые кружки) и получают
кривую обеспеченности. Пользуясь табл.
3.6.можно построить на этом же графике
теоретическую кривую обеспеченности.
Для этого из графы 5 надо получить
величину откуда
можно получить
Для
контроля правильности подсчета сумма
модульных коэффициентов должна
удовлетворять равенству
,
а
в графах 7, 8 .Используя
сумму ,
из графы 9 можно получить значение
значение Cv
по
формуле (3.1-3.1′). В первом приближении
применяем CS=2CV.
Для
получения теоретических точек кривой
обеспеченности следует пользоваться
таблицей Фостера – Рыбкина, в которой
приведены отклонения ординат кривой
обеспеченности от середины Ф
при Хср
= 1 и Cv=1
(см. табл. 3.9).
Пользуясь
табл. 3.7, можно подсчитать значения
модульных коэффициентов по формуле
(3.10)
Затем
по формуле (4.5) определить значения
расходов разной обеспеченности:
(3.11)
|
р, |
0,1 |
1 |
5 |
10 |
25 |
50 |
75 |
80 |
90 |
95 |
97 |
99 |
99,9 |
|
Сs=0,57 |
|||||||||||||
|
Фр |
|||||||||||||
|
Фр |
|||||||||||||
|
kp |
|||||||||||||
|
Qp |
|||||||||||||
|
kp |
|||||||||||||
|
Qp |
Результаты заносятся
в табл. 3.7.
Таблица 3.7
Полученные
значения Qр
– наносят
на график, приведенный на рис. 3.1 (на
рисунке значения Qр.
обозначены сплошными кружками). Если
проведенная по этим кружкам кривая
обеспеченности (пунктирная) не совпадает
с кривой, построенной по наблюденным
данным, то это обозначает, что принятое
значение Cs
для построения
теоретической кривой не соответствует
значению Cs
соответствующего
фактическим данным. Это значение
необходимо изменять до
тех
пор, пока теоретическая кривая не
совпадет с кривой натурных наблюдений.
Биноминальная
кривая обеспеченности хорошо согласуется
с натурными данными. Однако она имеет
ряд недостатков, одним из которых
является то, что при соотношении Cs
< 2 Cv
встречающемся на практике при расчетах
годового стока рек засушливых районов,
ординаты кривой обеспеченности в нижней
части имеют отрицательные значения.
Для исключения этого недостатка С. Н.
Крицкий и М. Ф. Менкель предложили новые
кривые обеспеченности [35]. По этим кривым
при любом соотношении Cs
и Cv
нулевая
ордината получается только при
обеспеченности в 100%. При CS=2CV
кривая
обеспеченности совпадает с биномальной
ассиметричной кривой.
Ассиметричные
кривые на
клетчатке вероятности спрямляются не
полностью и имеют выпуклость тем большую
, чем больше коэффициент асимметрии.
При положительной асимметрии выпуклость
обращена вниз, при отрицательной –
вверх.
Характеристика
связи между обеспеченностью и
повторяемостью расходов приведена в
табл. 3.8.
Применение
методов теории вероятности и математической
статистики
в решении гидрологических задач получило
широкое распространение как у нас, так
и за границей. Однако следует отметить
несовершенство
и условность этих методов. Кривые
обеспеченности, построенные теоретическим
путем, необходимо каждый раз анализировать
и проверять, используя фактические
наблюдения.
Рис.
3.1. Кривая обеспеченности средних годовых
расходов на клетчатке вероятности
Дальнейшее
развитие гидрологии должно идти по пути
все большего
развития генетических методов. Под ними
следует подразумевать
исследование закономерностей развития
гидрологических явлений и процессов
на основе обобщения данных наблюдений
и их физического анализа.
Таблица
3.8
Характеристики
лет
разной
обеспеченности
-
Обеспеченность,
%Повторяется
1
раз в n
летХарактеристика
года0,1
1000
Катастрофически
многоводный1
100
Очень многоводный
5
20
Многоводный
10
10
Средней
многоводности25
4
Средней
многоводности50
2
Медианный
75
4
Средней
маловодности90
10
Средней
маловодности95
20
Маловодный
97
33
Маловодный
99
100
Очень маловодный
99,9
1000
Катастрофически
маловодный
Таблица 3.9
Отклонение
ординат биноминальной асимметрической
кривой обеспеченности от середины (от
1,0) при Cv=1
|
CS |
Обеспеченность |
CS |
|||||||||||||||||||
|
0,01 |
0,1 |
1 |
3 |
5 |
10 |
20 |
25 |
30 |
40 |
50 |
60 |
70 |
75 |
80 |
90 |
95 |
97 |
99 |
99,9 |
||
|
0,00 |
3,72 |
3,09 |
2,33 |
1,88 |
1,64 |
1,28 |
0,84 |
0,67 |
0,52 |
0,25 |
0,00 |
-0,25 |
-0,52 |
-0,67 |
-0,84 |
-1,28 |
-1,64 |
-1,88 |
-2,33 |
-3,09 |
0,00 |
|
0,05 |
3,83 |
3,16 |
2,36 |
1,90 |
1,65 |
1,28 |
0,84 |
0,66 |
0,52 |
0,24 |
-0,01 |
-0,26 |
-0,52 |
-0,68 |
-0,84 |
-1,28 |
-1,62 |
-1,86 |
-2,29 |
-3,02 |
0,05 |
|
0,10 |
3,94 |
3,23 |
2,40 |
1,92 |
1,67 |
1,29 |
0,84 |
0,66 |
0,51 |
0,24 |
-0,02 |
-0,27 |
-0,53 |
-0,68 |
-0,85 |
-1,27 |
-1,61 |
-1,81 |
-2,25 |
-2,95 |
0,10 |
|
0,15 |
4,05 |
3,31 |
2,44 |
194 |
1,68 |
1,30 |
0,84 |
0,66 |
0,50 |
0,23 |
-0,02 |
-0,28 |
-0,54 |
-0,68 |
-0,85 |
-1,26 |
-1,60 |
-1,82 |
-2,22 |
-2,88 |
0,15 |
|
0,20 |
4,16 |
3,38 |
2,47 |
1,96 |
1,70 |
1,30 |
0,83 |
0,65 |
050 |
0,22 |
-0,03 |
-0,28 |
-0,55 |
-0,69 |
-0,85 |
-1,26 |
-1,58 |
-1,79 |
-2,18 |
-2,81 |
0,20 |
|
0,25 |
4,27 |
3,45 |
2,50 |
1,98 |
1,71 |
1,30 |
0,82 |
0,64 |
0,49 |
0,21 |
-0,04 |
-0,29 |
-0,56 |
-0,70 |
-0,85 |
-1,25 |
-1,56 |
-1,77 |
-2,14 |
-2,74 |
0,25 |
|
0,30 |
4,38 |
3,52 |
2,54 |
2,00 |
1,72 |
1,31 |
0,82 |
0,64 |
0,48 |
0,20 |
-0,05 |
-0,30 |
-0,56 |
-0,70 |
-0,85 |
-1,24 |
-1,55 |
-1,75 |
-2,10 |
-2,67 |
0,30 |
|
0,35 |
4,50 |
3,59 |
2,58 |
2,02 |
1,73 |
1,32 |
0,82 |
0,64 |
0,48 |
0,20 |
-0,06 |
-0,30 |
0,56 |
-0,70 |
-0,85 |
-1,24 |
-1,53 |
-1,72 |
-2,06 |
-2,60 |
0,35 |
|
0,40 |
4,61 |
3,66 |
2,61 |
2,04 |
1,75 |
1,32 |
0,82 |
0,63 |
0,47 |
0,19 |
-0,07 |
-0,31 |
-0,57 |
-0,71 |
-0,85 |
-1,23 |
-1,52 |
-1,70 |
-2,03 |
-2,54 |
0,40 |
|
0,45 |
4,72 |
3,74 |
2,64 |
2,06 |
1,76 |
1,32 |
0,82 |
0,62 |
0,46 |
0,18 |
-0,08 |
-0,32 |
-0,58 |
-0,71 |
-0,85 |
-1,22 |
-1,51 |
-1,68 |
-2,00 |
-2,47 |
0,45 |
|
0,50 |
4,83 |
3,81 |
2,68 |
2,08 |
1,77 |
1,32 |
0,81 |
0,62 |
0,46 |
0,17 |
-0,08 |
-0,33 |
-0,58 |
-0,71 |
-0,85 |
-1,22 |
-1,49 |
-1,66 |
-1,99 |
-2,40 |
0,50 |
|
0,55 |
4,94 |
3,88 |
2,72 |
2,10 |
1,78 |
1,32 |
0,80 |
0,62 |
0,45 |
0,16 |
-0,09 |
-0,34 |
-0,58 |
-0,72 |
-0,85 |
-1,21 |
-1,47 |
-1,64 |
-1,92 |
-2,32 |
0,55 |
|
0,60 |
5,05 |
3,96 |
2,75 |
2,12 |
1,80 |
1,33 |
0,80 |
0,61 |
0,44 |
0,16 |
-0,10 |
-0,34 |
-0,59 |
0,72 |
-0,85 |
-1,20 |
-1,45 |
-1,61 |
-1,88 |
-2,27 |
0,60 |
|
0,65 |
5,16 |
4,03 |
2,78 |
2,14 |
1,81 |
1,33 |
0,80 |
0,60 |
0,44 |
0,15 |
-0,11 |
-0,35 |
-0,60 |
-0,72 |
-0,85 |
-1,44 |
1,19- |
1,59 |
-1,84 |
-2,20 |
0,65 |
|
0,70 |
5,28 |
4,10 |
2,82 |
2,15 |
1,82 |
1,33 |
0,79 |
0,59 |
0,43 |
0,14 |
-0,12 |
-0,36 |
-0,60 |
-0,72 |
-0,85 |
-1,18 |
-1,42 |
-1,57 |
-1,81 |
-2,14 |
0,70 |
|
0,75 |
5,39 |
4,17 |
2,86 |
2,16 |
1,83 |
1,34 |
0,78 |
0,58 |
0,42 |
0,13 |
-0,12 |
-0,36 |
-0,60 |
-0,72 |
-0,86 |
-1,18 |
-1,40 |
-1,54 |
-1,78 |
-2,08 |
0,75 |
|
0,80 |
5,50 |
4,24 |
2,89 |
2,18 |
1,84 |
1,34 |
0,78 |
0,58 |
0,41 |
0,12 |
-0,13 |
-0,37 |
-0,60 |
-0,73 |
-0,86 |
-1,17 |
-1,38 |
-1,52 |
-1,74 |
-2,02 |
0,80 |
|
0,85 |
5,62 |
4,31 |
2,92 |
2,20 |
1,85 |
1,34 |
0,78 |
0,58 |
0,40 |
0,12 |
-0,14 |
-0,38 |
-0,60 |
-0,73 |
-0,86 |
-1,16 |
-1,35 |
-,49 |
-1,70 |
-1,96 |
0,85 |
|
0,90 |
5,73 |
4,38 |
2,96 |
2,22 |
1,86 |
1,34 |
0,77 |
0,57 |
0,40 |
0,11 |
-0,15 |
-0,38 |
-0,61 |
-0,73 |
-0,85 |
-1,15 |
-1,35 |
-1,47 |
-1,66 |
-1,90 |
0,90 |
|
0,95 |
5,84 |
4,46 |
2,99 |
2,24 |
1,87 |
1,34 |
0,76 |
0,56 |
0,39 |
0,10 |
-0,16 |
-0,38 |
-0,62 |
-0,73 |
-0,85 |
-1,14 |
-1,34 |
-1,44 |
-1,62 |
-1,84 |
0,95 |
|
1,00 |
5,96 |
4,53 |
3,02 |
2,25 |
1,88 |
1,34 |
0,76 |
0,55 |
0,38 |
0,09 |
-0,16 |
-0,39 |
-0,62 |
-0,73 |
-0,85 |
-1,13 |
-1,32 |
-1,42 |
-1,59 |
-1,79 |
1,00 |
|
1,05 |
6,07 |
4,60 |
3,06 |
2,26 |
1,88 |
1,84 |
0,75 |
0,54 |
0,37 |
0,08 |
-0,17 |
-0,40 |
-0,62 |
-0,74 |
-0,85 |
-1,12 |
-1,30 |
-1,40 |
-1,56 |
-1,74 |
1,05 |
|
1,10 |
6,18 |
4,67 |
3,09 |
2,28 |
1,89 |
1,34 |
0,74 |
0,54 |
0,36 |
0,07 |
-0,18 |
-0,41 |
-0,62 |
-0,74 |
-0,85 |
-1,10 |
-1,28 |
-1,38 |
-1,52 |
-1,68 |
1,10 |
|
1,15 |
6,30 |
4,74 |
3,12 |
2,30 |
1,90 |
1,34 |
0,74 |
0,53 |
0,36 |
0,06 |
-0,18 |
-0,42 |
-0,62 |
-0,74 |
-0,84 |
-1,09 |
-1,26 |
-1,36 |
-1,48 |
-1,63 |
1,15 |
|
1,20 |
6,41 |
4,81 |
3,15 |
2,31 |
1,91 |
1,34 |
0,73 |
0,52 |
0,35 |
0,05 |
-0,19 |
-0,42 |
-0,63 |
-0,74 |
-0,84 |
-1,08 |
-1,24 |
-1,33 |
-1,45 |
-1,58 |
1,20 |
|
1,25 |
6,52 |
4,88 |
3,18 |
2,32 |
1,92 |
1,34 |
0,72 |
0,52 |
0,34 |
0,04 |
-0,20 |
-0,42 |
-0,63 |
-0,74 |
-0,84 |
-1,07 |
-1,22 |
-1,30 |
-1,42 |
-1,53 |
1,25 |
|
1,30 |
6,64 |
4,95 |
3,21 |
2,34 |
1,92 |
1,34 |
0,72 |
0,51 |
0,33 |
0,04 |
-0,21 |
-0,43 |
-0,63 |
-0,74 |
-0,84 |
-1,06 |
-1,20 |
-1,28 |
-1,38 |
-1,48 |
1,30 |
|
1,35 |
6,76 |
5,02 |
3,24 |
2,36 |
1,93 |
1,34 |
0,72 |
0,50 |
0,32 |
0,03 |
-0,22 |
-0,44 |
-0,64 |
-0,74 |
-0,84 |
-1,05 |
-1,18 |
-1,26 |
-1,35 |
-1,44 |
1,35 |
|
1,40 |
6,87 |
5,09 |
3,27 |
2,37 |
1,94 |
1,34 |
0,71 |
0,49 |
0,31 |
0,02 |
-0,22 |
-0,44 |
-0,64 |
-0,73 |
-0,83 |
-1,04 |
-1,17 |
-1,23 |
-1,32 |
-1,39 |
1,40 |
|
1,45 |
6,98 |
5,16 |
3,30 |
2,38 |
1,94 |
1,34 |
0,70 |
0,48 |
0,30 |
0,01 |
-0,23 |
-0,44 |
-0,64 |
-0,73 |
-0,82 |
-1,03 |
-1,15 |
-1,21 |
-1,29 |
-1,35 |
1,45 |
|
1,50 |
7,09 |
5,23 |
3,33 |
2,39 |
1,95 |
1,33 |
0,69 |
0,47 |
0,30 |
0,00 |
-0,24 |
-0,45 |
-0,64 |
-0,73 |
-0,82 |
-1,02 |
-1,13 |
-1,19 |
-1,26 |
-1,31 |
1,50 |
|
1,60 |
7,31 |
5,37 |
3,39 |
2,42 |
1,96 |
1,33 |
0,68 |
1,46 |
0,28 |
-0,02 |
-0,25 |
-0,46 |
-0,64 |
-0,73 |
-0,81 |
-0,99 |
-1,10 |
-1,14 |
-1,20 |
-1,24 |
1,60 |
Окончание
3.9
|
CS |
Обеспеченность |
CS |
|||||||||||||||||||
|
0,01 |
0,1 |
1 |
3 |
5 |
10 |
20 |
25 |
30 |
40 |
50 |
60 |
70 |
75 |
80 |
90 |
95 |
97 |
99 |
99,9 |
||
|
1,70 |
7,54 |
5,50 |
3,44 |
2,44 |
1,97 |
1,32 |
0,66 |
0,44 |
0,26 |
-0,03 |
-0,27 |
-0,47 |
-0,64 |
-0,72 |
-0,81 |
-0,97 |
-1,06 |
-1,10 |
-1,14 |
-1,17 |
1,70 |
|
1,80 |
7,76 |
5,64 |
3,50 |
2,46 |
1,98 |
1,32 |
0,64 |
0,42 |
0,24 |
-0,05 |
-0,28 |
-0,48 |
-0,64 |
-0,72 |
-0,80 |
-0,94 |
-1,02 |
-1,06 |
-1,09 |
-1,11 |
1,80 |
|
1,90 |
7,98 |
5,77 |
3,55 |
2,49 |
1,99 |
1,31 |
0,63 |
0,40 |
0,22 |
-0,07 |
-0,29 |
-0,48 |
-0,64 |
-0,72 |
-0,79 |
-0,92 |
-0,98 |
-1,01 |
-1,04 |
-1,05 |
1,90 |
|
2,0 |
8,21 |
5,91 |
3,60 |
2,51 |
2,00 |
1,30 |
0,61 |
0,39 |
0,20 |
-0,08 |
-0,31 |
-0,49 |
-0,64 |
-0,71 |
-0,78 |
-0,90 |
-,095 |
-0,97 |
-0,99 |
-1,00 |
2,0 |
|
2,10 |
— |
6,06 |
3,65 |
2,53 |
2,00 |
1,29 |
0,60 |
0,38 |
0,19 |
-0,01 |
-0,32 |
-0,49 |
-0,64 |
-0,70 |
-0,77 |
-0,87 |
-0,92 |
-0,94 |
-0,95 |
-0,95 |
2,10 |
|
2,20 |
— |
6,20 |
3,70 |
2,55 |
2,01 |
1,28 |
0,58 |
0,37 |
017 |
-0,11 |
-0,33 |
-0,49 |
-0,63 |
-0,69 |
-0,75 |
-0,85 |
-0,89 |
-0,90 |
-0,90 |
-0,91 |
2,20 |
|
2,30 |
— |
6,34 |
3,75 |
2,56 |
2,01 |
1,27 |
0,56 |
0,35 |
0,15 |
-0,12 |
-0,34 |
-0,49 |
-0,62 |
-0,68 |
-0,73 |
-0,82 |
-0,85 |
-0,86 |
-0,87 |
-0,87 |
2,30 |
|
2,40 |
— |
6,47 |
3,79 |
2,57 |
2,01 |
1,25 |
0,54 |
0,33 |
0,13 |
-0,14 |
-0,35 |
-0,50 |
-0,62 |
-0,66 |
-0,72 |
-0,79 |
-0,82 |
-0,83 |
-0,83 |
-0,83 |
2,40 |
|
2,50 |
— |
6,60 |
3,83 |
2,58 |
2,01 |
1,24 |
0,53 |
0,32 |
0,12 |
-0,15 |
-0,36 |
-0,50 |
-0,61 |
-0,65 |
-0,70 |
-0,77 |
-0,79 |
-0,80 |
-0,80 |
-0,80 |
2,50 |
|
2,60 |
— |
6,73 |
3,87 |
2,59 |
2,01 |
1,23 |
0,51 |
0,30 |
0,10 |
-0,17 |
-0,37 |
-0,50 |
-0,60 |
-0,64 |
-0,68 |
-0,74 |
-0,76 |
-0,76 |
-0,77 |
-0,77 |
2,60 |
|
2,70 |
— |
6,86 |
3,91 |
2,60 |
2,01 |
1,21 |
0,49 |
0,28 |
0,08 |
-0,18 |
-0,38 |
-0,50 |
-0,60 |
-0,63 |
-0,67 |
-0,72 |
-0,73 |
-0,74 |
-0,74 |
-0,74 |
2,70 |
|
2,80 |
— |
6,99 |
3,95 |
2,61 |
2,02 |
1,20 |
0,47 |
0,27 |
0,06 |
-0,20 |
-0,38 |
-0,50 |
-0,59 |
-0,62 |
-0,65 |
-0,70 |
-0,71 |
-0,71 |
-0,71 |
-0,71 |
2,80 |
|
2,90 |
— |
7,12 |
3,99 |
2,62 |
2,02 |
1,19 |
0,45 |
0,26 |
0,04 |
-0,21 |
-0,39 |
-0,50 |
-0,58 |
-0,61 |
-0,64 |
-0,67 |
-0,68 |
-0,69 |
-0,69 |
-0,69 |
2,90 |
|
3,00 |
— |
7,25 |
4,02 |
2,63 |
2,02 |
1,18 |
0,42 |
0,25 |
0,03 |
-0,23 |
-0,40 |
-0,50 |
-0,57 |
-0,61 |
-0,62 |
-0,65 |
-0,66 |
-0,66 |
-0,67 |
-0,67 |
3,00 |
|
3,10 |
— |
7,23 |
4,09 |
2,66 |
1,97 |
1,11 |
0,37 |
0,17 |
0,010 |
-0,23 |
-0,40 |
-0,51 |
-0,58 |
-0,60 |
-0,62 |
-0641 |
-0,645 |
-0,646 |
-0,646 |
-0,646 |
3,10 |
|
3,20 |
— |
7,35 |
4,11 |
2,66 |
1,96 |
1,09 |
0,35 |
0,15 |
-0,0006 |
-0,25 |
-0,41 |
-0,51 |
-0,57 |
-0,59 |
-0,61 |
-0,621 |
-0,625 |
-0,625 |
-0,625 |
-0,625 |
3,20 |
|
3,30 |
— |
7,44 |
4,15 |
2,66 |
1,95 |
1,08 |
0,33 |
0,13 |
-0,022 |
-0,26 |
-0,41 |
-0,50 |
-0,56 |
-0,58 |
-0,59 |
-0,605 |
-0,606 |
-0,606 |
-0,606 |
-0,606 |
3,30 |
|
3,40 |
— |
7,54 |
4,18 |
2,66 |
1,94 |
1,06 |
0,31 |
0,11 |
-0,036 |
-0,27 |
-0,41 |
-0,50 |
-0,55 |
-0,57 |
-0,58 |
-0,586 |
-0,587 |
-0,589 |
-0,589 |
-0,589 |
3,40 |
|
3,50 |
— |
7,64 |
4,21 |
2,66 |
1,93 |
1,04 |
0,29 |
0,085 |
-0,049 |
-0,28 |
-0,41 |
-0,50 |
-0,54 |
-0,55 |
-0,56 |
-0,57 |
-0,571 |
-0,571 |
-0,571 |
-0,571 |
3,50 |
|
3,60 |
— |
7,72 |
4,24 |
2,65 |
1,93 |
1,03 |
0,28 |
0,064 |
-0,072 |
-0,28 |
-0,42 |
-0,49 |
-0,54 |
-0,54 |
-0,55 |
-0,555 |
-0,556 |
-0,566 |
-0,556 |
0,552 |
3,60 |
|
3,70 |
— |
7,86 |
4,26 |
2,66 |
1,91 |
1,01 |
0,26 |
0,048 |
-0,084 |
-0,29 |
-0,42 |
-0,48 |
-0,52 |
-0,53 |
-0,54 |
-0,541 |
-0,541 |
-0,541 |
-0541 |
-0,541 |
3,70 |
|
3,80 |
— |
7,97 |
4,29 |
2,65 |
1,90 |
1,00 |
0,24 |
0,032 |
-0,095 |
-0,30 |
-0,42 |
-0,48 |
-0,51 |
-0,52 |
-0,52 |
-0,526 |
-0,526 |
-0,526 |
-0,526 |
-0,526 |
3,80 |
|
3,90 |
— |
8,08 |
4,32 |
2,65 |
1,90 |
0,98 |
0,23 |
0,020 |
-0,11 |
-0,30 |
-0,41 |
-0,47 |
-0,50 |
-0,51 |
-0,51 |
-0,513 |
-0,513 |
-0,513 |
-0,513 |
-0,513 |
3,90 |
|
4,00 |
— |
8,17 |
4,34 |
2,65 |
1,90 |
0,96 |
0,21 |
0,010 |
-0,12 |
-0,31 |
-0,41 |
-0,46 |
-0,49 |
-0,49 |
-0,50 |
-0,50 |
-0,50 |
-0,50 |
-0,50 |
-0,50 |
4,00 |
|
4,10 |
— |
8,29 |
4,36 |
2,65 |
1,89 |
0,95 |
0,20 |
0,000 |
-0,13 |
-0,31 |
-0,41 |
-0,46 |
-0,48 |
-0,484 |
-0,486 |
-0,487 |
-0,487 |
-0,487 |
-0,487 |
-0,487 |
4,10 |
|
4,20 |
— |
8,38 |
4,39 |
2,64 |
1,88 |
0,93 |
0,19 |
0,010 |
-0,13 |
-0,31 |
-0,41 |
-0,45 |
-0,47 |
-0,473 |
-0,476 |
-0,476 |
-0,476 |
-0,476 |
-0,476 |
-0,476 |
4,20 |
|
4,30 |
— |
8,49 |
4,40 |
2,64 |
1,87 |
0,92 |
0,17 |
0,021 |
-0,14 |
-0,32 |
-0,40 |
-0,44 |
-0,46 |
-0,462 |
-0,465 |
-0,465 |
-0,465 |
-0,465 |
-0,465 |
-0,465 |
4,30 |
|
4,40 |
— |
8,60 |
4,42 |
2,63 |
1,86 |
0,91 |
0,15 |
0,032 |
-0,15 |
-0,32 |
-0,40 |
-0,44 |
-0,451 |
-0,454 |
-0,455 |
-0,455 |
-0,455 |
-0,455 |
-0,455 |
-0,455 |
4,40 |
|
4,50 |
— |
8,69 |
4,44 |
2,62 |
1,85 |
0,89 |
0,14 |
0,042 |
-0,16 |
-0,32 |
-0,40 |
-0,43 |
-0,441 |
-0,444 |
-0,445 |
-0,445 |
-0,445 |
-0,445 |
-0,445 |
-0,445 |
4,50 |
|
4,60 |
— |
8,79 |
4,46 |
2,62 |
1,84 |
0,87 |
0,13 |
0,052 |
-0,17 |
-0,32 |
-0,40 |
-0,42 |
-0,432 |
-0,434 |
-0,435 |
-0,435 |
-0,435 |
-0,435 |
-0,435 |
-0,435 |
4,60 |
|
4,70 |
— |
8,89 |
4,49 |
2,61 |
1,83 |
0,85 |
0,11 |
0,064 |
-0,18 |
-0,32 |
-0,40 |
-0,42 |
-0,424 |
-0,425 |
-0,426 |
-0,426 |
-0,426 |
-0,426 |
-0,426 |
-0,426 |
4,70 |
|
4,80 |
— |
8,96 |
4,50 |
2,60 |
1,81 |
0,82 |
0,10 |
0,075 |
-0,19 |
-0,32 |
-0,39 |
-0,41 |
-0,416 |
-0,416 |
-0,416 |
-0,416 |
-0,416 |
-0,416 |
-0,416 |
-0,416 |
4,80 |
|
4,90 |
— |
9,04 |
4,51 |
2,60 |
1,80 |
0,80 |
0,084 |
0,087 |
-0,19 |
-0,33 |
-0,386 |
-0,401 |
-0,407 |
-0,408 |
-0,409 |
-0,409 |
-0,409 |
-0,409 |
-0,409 |
-0,409 |
4,90 |
|
5,00 |
— |
9,12 |
4,54 |
2,60 |
1,78 |
0,78 |
0,068 |
0,099 |
-0,20 |
-0,33 |
-0,380 |
-0,395 |
-0,399 |
-0,400 |
-0,400 |
-0,400 |
-0,400 |
-0,400 |
-0,400 |
-0,400 |
5,00 |
|
5,10 |
— |
9,20 |
4,57 |
2,60 |
1,76 |
0,76 |
0,051 |
0,11 |
-0,21 |
-0,33 |
-0,376 |
-0,388 |
-0,391 |
-0,392 |
-0,392 |
-0,392 |
-0,392 |
-0,392 |
-0,392 |
-0,392 |
5,10 |
|
5,20 |
— |
9,27 |
4,59 |
2,60 |
1,74 |
0,73 |
0,035 |
0,12 |
-0,21 |
-0,33 |
-0,370 |
-0,382 |
-0,384 |
-0,385 |
-0,385 |
-0,385 |
-0,385 |
-0,385 |
-0,385 |
-0,385 |
5,20 |
Таблица 3.10
Ординаты
биноминальной асимметрической кривой
обеспеченности kp
при CS
=2Cv
|
Cv |
Обеспеченность |
Cv |
|||||||||||||||||||
|
0,01 |
0,1 |
1 |
3 |
5 |
10 |
20 |
25 |
30 |
40 |
50 |
60 |
70 |
75 |
80 |
90 |
95 |
97 |
99 |
99,9 |
||
|
0,05 |
1,197 |
1,162 |
1,120 |
1,096 |
1,084 |
1,064 |
1,042 |
1,033 |
1,026 |
1,012 |
0,999 |
0,986 |
0,974 |
0,966 |
0,958 |
0,936 |
0,920 |
0,908 |
0,888 |
0,852 |
0,05 |
|
0,06 |
1,241 |
1,197 |
1,145 |
1,116 |
1,101 |
1,077 |
1,050 |
1,039 |
1,031 |
1,014 |
0,999 |
0,983 |
0,968 |
0,959 |
0,949 |
0,924 |
0,904 |
0,890 |
0,867 |
0,825 |
0,06 |
|
0,07 |
1,285 |
1,232 |
1,171 |
1,135 |
1,118 |
1,090 |
1,058 |
1,046 |
1,036 |
1,016 |
0,998 |
0,980 |
0,962 |
0,952 |
0,941 |
0,911 |
0,889 |
0,873 |
0,846 |
0,779 |
0,07 |
|
0,08 |
1,328 |
1,268 |
1,196 |
1,155 |
1,136 |
1,104 |
1,067 |
1,052 |
1,040 |
1,018 |
0,998 |
0,978 |
0,956 |
0,945 |
0,932 |
0,899 |
0,873 |
0,856 |
0,824 |
0,772 |
0,08 |
|
0,09 |
1,372 |
1,303 |
1,221 |
1,176 |
1,153 |
1,117 |
1,074 |
1,058 |
1,045 |
1,020 |
0,997 |
0,975 |
0,951 |
0,938 |
0,924 |
0,886 |
0,858 |
0,838 |
0,803 |
0,746 |
0,09 |
|
0,10 |
1,416 |
1,338 |
1,247 |
1,196 |
1,170 |
1,130 |
1,083 |
1,065 |
1,050 |
1,022 |
0,997 |
0,972 |
0,945 |
0,931 |
0,915 |
0,874 |
0,842 |
0,821 |
0,782 |
0,719 |
0,10 |
|
0,11 |
1,467 |
1,377 |
1,274 |
1,217 |
1,188 |
1,143 |
1,091 |
1,071 |
1,054 |
1,024 |
0,996 |
0,969 |
0,939 |
0,924 |
0,906 |
0,862 |
0,827 |
0,805 |
0,763 |
0,696 |
0,11 |
|
0,12 |
1,517 |
1,417 |
1,302 |
1,238 |
1,206 |
1,157 |
1,090 |
1,077 |
1,059 |
1,025 |
0,995 |
0,965 |
0,933 |
0,916 |
0,898 |
0,850 |
0,813 |
0,789 |
0,744 |
0,674 |
0,12 |
|
0,13 |
1,568 |
1,456 |
1,330 |
1,260 |
1,224 |
1,170 |
1,107 |
1,083 |
1,063 |
1,027 |
0,994 |
0,962 |
0,927 |
0,909 |
0,890 |
0,838 |
0,798 |
0,783 |
0,726 |
0,651 |
0,13 |
|
0,14 |
1,618 |
1,496 |
1,357 |
1,281 |
1,242 |
1,184 |
1,115 |
1,089 |
1,068 |
1,028 |
0,993 |
0,958 |
0,921 |
0,902 |
0,881 |
0,826 |
0,784 |
0,757 |
0,707 |
0,628 |
0,14 |
|
0,15 |
1,669 |
1,535 |
1,384 |
1,302 |
1,260 |
1,197 |
1,124 |
1,096 |
1,072 |
1,030 |
0,992 |
0,955 |
0,916 |
0,894 |
0,872 |
0,814 |
0,769 |
0,740 |
0,688 |
0,606 |
0,15 |
|
0,16 |
1,720 |
1,574 |
1,412 |
1,323 |
1,278 |
1,210 |
1,132 |
1,101 |
1,076 |
1,032 |
0,990 |
0,952 |
0,910 |
0,887 |
0,864 |
0,802 |
0,754 |
0,724 |
0,669 |
0,583 |
0,16 |
|
0,17 |
1,770 |
1,614 |
1,440 |
1,344 |
1,296 |
1,224 |
1,140 |
1,108 |
1,081 |
1,033 |
0,989 |
0,948 |
0,904 |
0,880 |
0,856 |
0,790 |
0,740 |
0,708 |
0,650 |
0,560 |
0,17 |
|
0,18 |
1,821 |
1,653 |
1,467 |
1,366 |
1,314 |
1,237 |
1,148 |
1,114 |
1,085 |
1,035 |
0,988 |
0,945 |
0,898 |
0,873 |
0,847 |
0,778 |
0,725 |
0,692 |
0,632 |
0,537 |
0,18 |
|
0,19 |
1,871 |
1,693 |
1,494 |
1,387 |
1,332 |
1,251 |
1,156 |
1,120 |
1,090 |
1,036 |
0,987 |
0,941 |
0,892 |
0,865 |
0,838 |
0,766 |
0,711 |
0,676 |
0,613 |
0,515 |
0,19 |
|
0,20 |
1,922 |
1,732 |
1,522 |
1,408 |
1,350 |
1,264 |
1,164 |
1,126 |
1,094 |
1,038 |
0,986 |
0,938 |
0,886 |
0,858 |
0,830 |
0,754 |
0,696 |
0,660 |
0,594 |
0,492 |
0,20 |
|
0,21 |
1,981 |
1,778 |
1,552 |
1,431 |
1,369 |
1,278 |
1,172 |
1,132 |
1,098 |
1,039 |
0,984 |
0,934 |
0,880 |
0,851 |
0,822 |
0,743 |
0,683 |
0,646 |
0,578 |
0,475 |
0,21 |
|
0,22 |
2,041 |
1,823 |
1,582 |
1,454 |
1,388 |
1,291 |
1,179 |
1,137 |
1,102 |
1,040 |
0,983 |
0,930 |
0,873 |
0,843 |
0,813 |
0,731 |
0,670 |
0,631 |
0,562 |
1,457 |
0,22 |
|
0,23 |
2,100 |
1,869 |
1,613 |
1,476 |
1,407 |
1,304 |
1,187 |
1,142 |
1,105 |
1,041 |
0,981 |
0,926 |
0,867 |
0,836 |
0,804 |
0,720 |
0,657 |
0,617 |
0,547 |
0,440 |
0,23 |
|
0,24 |
2,159 |
1,914 |
1,643 |
1,499 |
1,426 |
1,318 |
1,194 |
1,149 |
1,109 |
1,042 |
0,980 |
0,922 |
0,861 |
0828 |
0,796 |
0,708 |
0,644 |
0,603 |
0,531 |
0,423 |
0,24 |
|
0,25 |
2,218 |
1,960 |
1,674 |
1,522 |
1,445 |
1,332 |
1,202 |
1,154 |
1,113 |
1,043 |
0,978 |
0,918 |
0,854 |
0,821 |
0,788 |
0,697 |
0,630 |
0,588 |
0,515 |
0,406 |
0,25 |
|
0,26 |
2,278 |
2,006 |
1,704 |
1,545 |
1,464 |
1,345 |
1,210 |
1,160 |
1,117 |
1,044 |
0,976 |
0,914 |
0,848 |
0,814 |
0,779 |
0,686 |
0,617 |
0,574 |
0,499 |
0,388 |
0,26 |
|
0,27 |
2,337 |
2,051 |
1,734 |
1,568 |
1,483 |
1,358 |
1,217 |
1,166 |
1,121 |
1,045 |
0,975 |
0,910 |
0,842 |
0,806 |
0,770 |
0,674 |
0,604 |
0,560 |
0,483 |
0,371 |
0,27 |
|
0,28 |
2,396 |
2,097 |
1,764 |
1,590 |
1,502 |
1,372 |
1,225 |
1,172 |
1,124 |
1,046 |
0,973 |
0,906 |
0,836 |
0,799 |
0,762 |
0,663 |
0,591 |
0,546 |
0,468 |
0,354 |
0,28 |
|
0,29 |
2,456 |
2,142 |
1,795 |
1,613 |
1,521 |
1,386 |
1,232 |
1,177 |
1,128 |
1,047 |
0,972 |
0,902 |
0,829 |
0,791 |
0,754 |
0,651 |
0,578 |
0,531 |
0,452 |
0,336 |
0,29 |
|
0,30 |
2,515 |
2,188 |
1,825 |
1,636 |
1,540 |
1,399 |
1,240 |
1,183 |
1,132 |
1,048 |
0,970 |
0,898 |
0,823 |
0,784 |
0,745 |
0,640 |
0,564 |
0,517 |
0,436 |
0,319 |
0,30 |
|
0,31 |
2,584 |
2,239 |
1,858 |
1,660 |
1,560 |
1,413 |
1,247 |
1,188 |
1,135 |
1,048 |
0,968 |
0,893 |
0,817 |
0,776 |
0,736 |
0,629 |
0,553 |
0,504 |
0,423 |
0,306 |
0,31 |
|
0,32 |
2,662 |
2,290 |
1,891 |
1,683 |
1,579 |
1,426 |
1,254 |
1,193 |
1,138 |
1,048 |
0,966 |
0,889 |
0,810 |
0,769 |
0,727 |
0,618 |
0,542 |
0,492 |
0,410 |
0,294 |
0,32 |
|
0,33 |
2,721 |
2,340 |
1,924 |
1,707 |
1,599 |
1,440 |
1,262 |
1,198 |
1,142 |
1,048 |
0,963 |
0,884 |
0,804 |
0,761 |
0,718 |
0,608 |
0,530 |
0,480 |
0,396 |
0,281 |
0,33 |
|
0,34 |
2,789 |
2,391 |
1,957 |
1,730 |
1,618 |
1,454 |
1,269 |
1,203 |
1,145 |
1,048 |
0,961 |
0,880 |
0,798 |
0,754 |
0,709 |
0,597 |
0,518 |
0,467 |
0,383 |
0,268 |
0,34 |
|
0,35 |
2,858 |
2,442 |
1,990 |
1,754 |
1,638 |
1,468 |
1,276 |
1,208 |
1,148 |
1,048 |
0,959 |
0,875 |
0,792 |
0,746 |
0,700 |
0,586 |
0,506 |
0,454 |
0,370 |
0,256 |
0,35 |
|
0,36 |
2,926 |
2,493 |
2,024 |
1,778 |
1,658 |
1,481 |
1,283 |
1,212 |
1,151 |
1,048 |
0,957 |
0,870 |
0,785 |
0,738 |
0,692 |
0,575 |
0,495 |
0,442 |
0,357 |
0,243 |
0,36 |
Продолжение
табл.3.10
|
Cv |
Обеспеченность |
Cv |
|||||||||||||||||||
|
0,01 |
0,1 |
1 |
3 |
5 |
10 |
20 |
25 |
30 |
40 |
50 |
60 |
70 |
75 |
80 |
90 |
95 |
97 |
99 |
99,9 |
||
|
0,37 |
2,994 |
2,544 |
2,057 |
1,801 |
1,677 |
1,495 |
1,290 |
1,217 |
1,154 |
1,048 |
0,955 |
0,866 |
0,779 |
0,731 |
0,683 |
0,564 |
0,483 |
0,430 |
0,344 |
0,230 |
0,37 |
|
0,38 |
30,063 |
2,594 |
2,090 |
1,825 |
1,697 |
1,509 |
1,298 |
1,222 |
1,158 |
1,048 |
0,952 |
0,861 |
0,773 |
0,723 |
0,674 |
0,554 |
0,471 |
0,417 |
0,330 |
0,217 |
0,38 |
|
0,39 |
3,132 |
2,645 |
2,123 |
1,848 |
1,716 |
1,522 |
1,305 |
1,227 |
1,161 |
1,048 |
0,950 |
0,857 |
0,769 |
0,716 |
0,665 |
0,543 |
0,460 |
0,404 |
0,317 |
0,205 |
0,39 |
|
0,40 |
3,200 |
2,696 |
2,156 |
1,872 |
1,736 |
1,536 |
1,312 |
1,232 |
1,164 |
1,048 |
0,948 |
0,852 |
0,766 |
0,708 |
0,656 |
0,533 |
0,448 |
0,392 |
0,304 |
0,192 |
0,40 |
|
0,41 |
3,278 |
2,753 |
2,192 |
1,897 |
1,756 |
1,549 |
1,319 |
1,236 |
1,167 |
1,048 |
0,945 |
0,847 |
0,753 |
0,701 |
0,648 |
0,522 |
0,437 |
0,382 |
0,294 |
0,184 |
0,41 |
|
0,42 |
3,356 |
2,810 |
2,227 |
1,923 |
1,776 |
1,563 |
1,325 |
1,241 |
1,169 |
1,047 |
0,942 |
0,842 |
0,746 |
0,693 |
0,640 |
0,513 |
0,427 |
0,371 |
0,284 |
0,175 |
0,42 |
|
0,43 |
3,433 |
2,867 |
2,262 |
1,948 |
1,797 |
1,576 |
1,332 |
1,246 |
1,172 |
1,047 |
0,939 |
0,837 |
0,739 |
0,686 |
0,631 |
0,503 |
0,416 |
0,361 |
0,275 |
0,166 |
0,43 |
|
0,44 |
3,511 |
2,924 |
2,298 |
1,974 |
1,817 |
1,590 |
1,338 |
1,250 |
1,174 |
1,046 |
0,936 |
0,832 |
0,732 |
0,678 |
0,623 |
0,494 |
0,406 |
0,350 |
0,265 |
0,158 |
0,44 |
|
0,45 |
3,589 |
2,981 |
2,334 |
1,999 |
1,837 |
1,603 |
1,345 |
1,254 |
1,177 |
1,046 |
0,933 |
0,828 |
0,726 |
0,671 |
0,615 |
0,484 |
0,395 |
0,340 |
0,255 |
0,150 |
0,45 |
|
0,46 |
3,667 |
3,038 |
2,369 |
2,024 |
1,857 |
1,616 |
1,352 |
1,259 |
1,180 |
1,046 |
0,930 |
0,823 |
0,719 |
0,664 |
0,607 |
0,474 |
0,384 |
0,330 |
0,245 |
0,141 |
0,46 |
|
0,47 |
3,745 |
3,095 |
2,404 |
2,050 |
1,877 |
1,630 |
1,358 |
1,264 |
1,182 |
1,045 |
0,927 |
0,818 |
0,712 |
0,656 |
0,599 |
0,465 |
0,374 |
0,319 |
0,236 |
0,132 |
0,47 |
|
0,48 |
3,822 |
3,152 |
2,440 |
2,075 |
1,898 |
1,643 |
1,365 |
1,268 |
1,185 |
1,045 |
0,924 |
0,813 |
0,705 |
0,649 |
0,590 |
0,455 |
0,363 |
0,309 |
0,226 |
0,126 |
0,48 |
|
0,49 |
3,900 |
3,209 |
2,476 |
2,101 |
1,918 |
1,657 |
1,371 |
1,272 |
1,187 |
1,044 |
0,921 |
0,808 |
0,698 |
0,641 |
0,582 |
0,446 |
0,353 |
0,298 |
0,216 |
0,116 |
0,49 |
|
0,50 |
3,978 |
3,226 |
2,511 |
2,126 |
1,938 |
1,670 |
1,378 |
1,277 |
1,190 |
1,044 |
0,918 |
0,803 |
0,691 |
0,634 |
0,574 |
0,436 |
0,342 |
0,288 |
0,206 |
0,107 |
0,50 |
|
0,51 |
4,065 |
3,328 |
2,549 |
2,152 |
1,959 |
1,683 |
1,384 |
1,280 |
1,192 |
1,043 |
0,915 |
0,798 |
0,684 |
0,626 |
0,566 |
0,428 |
0,333 |
0,279 |
0,198 |
0,102 |
0,51 |
|
0,52 |
4,152 |
3,390 |
2,587 |
2,178 |
1,980 |
1,697 |
1,390 |
1,284 |
1,191 |
1,041 |
0,912 |
0,792 |
0,677 |
0,618 |
0,558 |
0,419 |
0,325 |
0,271 |
0,191 |
0,096 |
0,52 |
|
0,53 |
4,238 |
3,452 |
2,625 |
2,204 |
2,000 |
1,710 |
1,396 |
1,288 |
1,196 |
1,040 |
0,908 |
0,786 |
0,670 |
0,611 |
0,551 |
0,411 |
0,316 |
0,262 |
0,0183 |
0,090 |
0,53 |
|
0,54 |
4,325 |
3,514 |
2,663 |
2,230 |
2,0021 |
1,724 |
1,402 |
1,291 |
1,198 |
1,038 |
0,905 |
0,781 |
0,663 |
0,603 |
0,543 |
0,402 |
0,308 |
0,254 |
0,176 |
0,085 |
0,54 |
|
0,55 |
4,412 |
3,576 |
2,700 |
2,256 |
2,042 |
1,737 |
1,408 |
1,294 |
1,200 |
1,037 |
0,902 |
0,776 |
0,656 |
0,595 |
0,535 |
0,394 |
0,299 |
0,245 |
0,168 |
0,080 |
0,55 |
|
0,56 |
4,499 |
3,638 |
2,738 |
2,282 |
2,063 |
1,750 |
1,414 |
1,298 |
1,202 |
1,036 |
0,899 |
0,770 |
0,650 |
0,587 |
0,527 |
0,386 |
0,290 |
0,236 |
0,160 |
0,074 |
0,56 |
|
0,57 |
4,586 |
3,700 |
2,776 |
2,308 |
2,084 |
1,764 |
1,420 |
1,302 |
1,204 |
1,034 |
0,896 |
0,765 |
0,643 |
0,579 |
0,519 |
0,377 |
0,282 |
0,228 |
0,153 |
0,068 |
0,57 |
|
0,58 |
4,672 |
3,762 |
2,814 |
2,334 |
2,104 |
1,777 |
1,426 |
1,305 |
1,206 |
1,033 |
0,892 |
0,759 |
0,636 |
0,572 |
0,512 |
0,369 |
0,273 |
0,219 |
0,145 |
0,063 |
0,58 |
|
0,59 |
4,759 |
3,824 |
2,852 |
2,360 |
2,125 |
1,791 |
1,432 |
1,308 |
1,208 |
1,031 |
0,889 |
0,754 |
0,629 |
0,564 |
0,504 |
0,360 |
0,265 |
0,211 |
0,0138 |
0,058 |
0,59 |
|
0,60 |
4,846 |
3,886 |
2,890 |
2,386 |
2,146 |
1,804 |
1,438 |
1,312 |
1,210 |
1,030 |
0,886 |
0,748 |
0,622 |
0,556 |
0,496 |
0,352 |
0,256 |
0,202 |
0,130 |
0,052 |
0,60 |
|
0,61 |
4,942 |
3,954 |
2,930 |
2,413 |
2,167 |
1,817 |
1,444 |
1,315 |
1,211 |
1,028 |
0,882 |
0,742 |
0,615 |
0,549 |
0,488 |
0,344 |
0,248 |
0,196 |
0,125 |
0,050 |
0,61 |
|
0,62 |
5,039 |
4,021 |
2,970 |
2,441 |
2,188 |
1,831 |
1,450 |
1,318 |
1,211 |
1,027 |
0,878 |
0,737 |
0,608 |
0,543 |
0,481 |
0,336 |
0,241 |
0,189 |
0,119 |
0,047 |
0,62 |
|
0,63 |
5,135 |
4,089 |
3,010 |
2,468 |
2,210 |
1,844 |
1,456 |
1,321 |
1,212 |
10,25 |
0,874 |
0,731 |
0,601 |
0,536 |
0,473 |
0,328 |
0,234 |
0,183 |
0,114 |
0,044 |
0,63 |
|
0,64 |
5,231 |
4,157 |
3,050 |
2,495 |
2,231 |
1,858 |
1,462 |
1,324 |
1,213 |
1,024 |
0,870 |
0,726 |
0,594 |
0,529 |
0,465 |
0,320 |
0,226 |
0,177 |
0,108 |
0,042 |
0,64 |
|
0,65 |
5,328 |
4,224 |
3,090 |
2,522 |
2,252 |
1,871 |
1,468 |
1,328 |
1,214 |
1,022 |
0,866 |
0,720 |
0,587 |
0,522 |
0,458 |
0,312 |
0,218 |
0,170 |
0,103 |
0,040 |
0,65 |
|
0,66 |
5,424 |
4,292 |
3,129 |
2,550 |
2,273 |
1,884 |
1,473 |
1,331 |
1,214 |
1,020 |
0,862 |
0,714 |
0,580 |
0,516 |
0,450 |
0,304 |
0,211 |
0,164 |
0,098 |
0,037 |
0,66 |
|
0,67 |
5,520 |
4,360 |
3,169 |
2,577 |
2,294 |
1,898 |
1,479 |
1,334 |
1,215 |
1,019 |
0,858 |
0,709 |
0,573 |
0,509 |
0,442 |
0,296 |
0,204 |
0,158 |
0,092 |
0,034 |
0,67 |
|
0,68 |
5,616 |
4,428 |
30,209 |
2,604 |
2,316 |
1,911 |
1,485 |
1,337 |
1,216 |
1,017 |
0,854 |
0,703 |
0,566 |
0,502 |
0,434 |
0,288 |
0,196 |
0,152 |
0,087 |
0,032 |
0,68 |
|
0,69 |
5,713 |
4,495 |
3,249 |
2,632 |
2,337 |
1,925 |
1,491 |
1,339 |
1,216 |
1,016 |
0,850 |
0,698 |
0,559 |
0,496 |
0,427 |
0,280 |
0,188 |
0,145 |
0,081 |
0,030 |
0,69 |
|
0,70 |
5,809 |
4,563 |
3,289 |
2,659 |
2,358 |
1,938 |
1,497 |
1,343 |
1,217 |
1,014 |
0,846 |
0,692 |
0,552 |
0,489 |
0,419 |
0,272 |
0,181 |
0,139 |
0,076 |
0,027 |
0,70 |
|
0,71 |
5,913 |
4,636 |
3,331 |
2,687 |
2,379 |
1,951 |
1,502 |
1,346 |
1,218 |
1,011 |
0,841 |
0,686 |
0,546 |
0,482 |
0,412 |
0,266 |
0,175 |
0,134 |
0,072 |
0,025 |
0,71 |
Продолжение
табл.3.10
|
Cv |
Обеспеченность |
Cv |
|||||||||||||||||||
|
0,01 |
0,1 |
1 |
3 |
5 |
10 |
20 |
25 |
30 |
40 |
50 |
60 |
70 |
75 |
80 |
90 |
95 |
97 |
99 |
99,9 |
||
|
0,72 |
6,017 |
4,710 |
3,374 |
2,714 |
2,400 |
1,963 |
1,506 |
1,348 |
1,218 |
1,008 |
0,837 |
0,680 |
0,539 |
0,474 |
0,406 |
0,259 |
0,168 |
0,129 |
0,069 |
0,023 |
0,72 |
|
0,73 |
6,121 |
4,783 |
3,416 |
2,742 |
2,421 |
1,976 |
1,511 |
1,350 |
1,219 |
1,005 |
0,832 |
0,674 |
0,533 |
0,467 |
0,399 |
0,253 |
0,163 |
0,124 |
0,065 |
0,021 |
0,73 |
|
0,74 |
6,225 |
4,856 |
3,458 |
2,770 |
2,442 |
1,988 |
1,516 |
1,353 |
1,220 |
1,002 |
0,828 |
0,668 |
0,526 |
0,460 |
0,392 |
0,246 |
0,157 |
0,119 |
0,062 |
0,019 |
0,74 |
|
0,75 |
6,328 |
4,930 |
3,500 |
2,798 |
2,463 |
2,001 |
1,520 |
1,356 |
1,220 |
0,999 |
0,823 |
0,662 |
0,520 |
0,452 |
0,386 |
0,240 |
0,150 |
0,113 |
0,058 |
0,018 |
0,75 |
|
0,76 |
6,432 |
5,003 |
3,543 |
2,825 |
2,484 |
2,014 |
1,525 |
1,358 |
1,221 |
0,996 |
0,818 |
0,656 |
0,514 |
0,445 |
0,379 |
0,234 |
0,144 |
0,108 |
0,054 |
0,016 |
0,76 |
|
0,77 |
6,536 |
5,076 |
3,585 |
2,853 |
2,505 |
2,026 |
1,530 |
1,360 |
1,222 |
0,993 |
0,814 |
0,650 |
0,507 |
0,438 |
0,372 |
0,227 |
0,138 |
0,103 |
0,051 |
0,014 |
0,77 |
|
0,78 |
6,640 |
5,149 |
3,627 |
2,881 |
2,526 |
2,039 |
1,535 |
1,363 |
1,223 |
0,990 |
0,809 |
0,644 |
0,501 |
0,431 |
0,365 |
0,221 |
0,132 |
0,098 |
0,047 |
0,012 |
0,78 |
|
0,79 |
6,744 |
5,223 |
3,670 |
2,908 |
2,547 |
2,051 |
1,539 |
1,366 |
1,223 |
0,987 |
0,805 |
0,638 |
0,494 |
0,423 |
0,359 |
0,214 |
0,126 |
0,093 |
0,044 |
0,010 |
0,79 |
|
0,80 |
6,848 |
5,296 |
3,712 |
2,936 |
2,568 |
2,064 |
1,544 |
1,368 |
1,224 |
0,984 |
0,800 |
0,632 |
0,488 |
0,416 |
0,352 |
0,208 |
0,120 |
0,088 |
0,040 |
0,008 |
0,80 |
|
0,81 |
6,962 |
5,374 |
3,756 |
2,964 |
2,589 |
2,076 |
1,547 |
1,369 |
1,223 |
0,981 |
0,795 |
0,626 |
0,482 |
0,410 |
0,345 |
0,203 |
0,116 |
0,084 |
0,038 |
0,007 |
0,81 |
|
0,82 |
7,075 |
5,452 |
3,800 |
2,992 |
2,611 |
2,089 |
1,550 |
1,370 |
1,222 |
0,978 |
0,790 |
0,619 |
0,475 |
0,403 |
0,338 |
0,197 |
0,112 |
0,080 |
0,036 |
0,007 |
0,82 |
|
0,83 |
0,189 |
5,530 |
3,843 |
3,019 |
2,632 |
2,101 |
1,554 |
1,371 |
1,222 |
0,975 |
0,784 |
0,613 |
0,469 |
0,397 |
0,330 |
0,192 |
0,109 |
0,075 |
0,034 |
0,006 |
0,83 |
|
0,84 |
7,302 |
5,608 |
3,887 |
2,047 |
2,654 |
2,114 |
1,557 |
1,372 |
1,221 |
0,972 |
0,779 |
0,606 |
0,462 |
0,390 |
0,323 |
0,186 |
0,105 |
0,071 |
0,032 |
0,006 |
0,84 |
|
0,85 |
7,416 |
5,686 |
3,931 |
3,075 |
2,675 |
2,126 |
1,546 |
1,373 |
1,220 |
0,970 |
0,774 |
0,600 |
0,456 |
0,384 |
0,316 |
0,181 |
0,0101 |
0,067 |
0,030 |
0,005 |
0,85 |
|
0,86 |
7,530 |
5,764 |
3,975 |
3,103 |
2,696 |
2,138 |
1,563 |
1,374 |
1,219 |
0,967 |
0,769 |
0,594 |
0,450 |
0,378 |
0,309 |
0,176 |
0,097 |
0,063 |
0,027 |
0,004 |
0,86 |
|
0,87 |
7,643 |
5,542 |
4,019 |
3,131 |
2,718 |
2,151 |
1,566 |
1,375 |
1,218 |
0,964 |
0,764 |
0,587 |
0,443 |
0,371 |
0,302 |
0,170 |
0,093 |
0,058 |
0,025 |
0,004 |
0,87 |
|
0,88 |
7,757 |
5,920 |
4,062 |
3,158 |
2,739 |
2,163 |
1,570 |
1,376 |
1,218 |
0,961 |
0,758 |
0,581 |
0,437 |
0,365 |
0,294 |
0,165 |
0,090 |
0,054 |
0,023 |
0,003 |
0,88 |
|
0,89 |
7,870 |
5,998 |
4,106 |
3,186 |
2,761 |
2,176 |
1,573 |
1,377 |
1,217 |
0,958 |
0,753 |
0,574 |
0,430 |
0,358 |
0,287 |
0,0,159 |
0,086 |
0,050 |
0,021 |
0,003 |
0,89 |
|
0,90 |
7,984 |
6,076 |
4,150 |
3,214 |
2,782 |
2,188 |
1,576 |
1,378 |
1,216 |
0,955 |
0,748 |
0,568 |
0,424 |
0,352 |
0,280 |
0,154 |
0,082 |
0,046 |
0,019 |
0,002 |
0,90 |
|
0,91 |
8,107 |
6,159 |
4,196 |
3,243 |
2,803 |
2,200 |
1,579 |
1,379 |
1,215 |
0,951 |
0,742 |
0,562 |
0,417 |
0,346 |
0,274 |
0,149 |
0,079 |
0,044 |
0,018 |
0,002 |
0,91 |
|
0,92 |
8,229 |
6,242 |
4,241 |
3,273 |
2,825 |
2,211 |
1,583 |
1,380 |
1,214 |
0,947 |
0,737 |
0,557 |
0,411 |
0,339 |
0,269 |
0,144 |
0,076 |
0,043 |
0,017 |
0,002 |
0,92 |
|
0,93 |
8,352 |
6,326 |
4,286 |
3,302 |
2,846 |
2,222 |
1,586 |
1,380 |
1,212 |
0,943 |
0,732 |
0,551 |
0,404 |
0,333 |
0,263 |
0,139 |
0,073 |
0,041 |
0,016 |
0,002 |
0,93 |
|
0,94 |
8,474 |
6,409 |
4,332 |
3,331 |
2,868 |
2,234 |
1,590 |
1,381 |
1,211 |
0,939 |
0,726 |
0,545 |
0,397 |
0,326 |
0,257 |
0,134 |
0,070 |
0,040 |
0,015 |
0,002 |
0,94 |
|
0,95 |
8,597 |
6,492 |
4,378 |
3,360 |
2,889 |
2,246 |
1,593 |
1,382 |
1,210 |
0,936 |
0,720 |
0,540 |
0,390 |
0,320 |
0,252 |
0,129 |
0,066 |
0,038 |
0,014 |
0,001 |
0,95 |
|
0,96 |
8,720 |
6,575 |
4,423 |
3,390 |
2,910 |
2,257 |
1,596 |
1,383 |
1,209 |
0,932 |
0,715 |
0,534 |
0,384 |
0,314 |
0,246 |
0,125 |
0,063 |
0,036 |
0,014 |
0,001 |
0,96 |
|
0,97 |
8,842 |
6,658 |
7,468 |
3,419 |
2,932 |
2,268 |
1,600 |
1,384 |
1,208 |
0,928 |
0,710 |
0,528 |
0,377 |
0,307 |
0,240 |
0,120 |
0,060 |
0,035 |
0,013 |
0,001 |
0,97 |
|
0,98 |
8,965 |
6,742 |
4,514 |
3,448 |
2,953 |
2,280 |
1,603 |
1,384 |
1,206 |
0,924 |
0,704 |
0,522 |
0,370 |
0,301 |
0,234 |
0,115 |
0,057 |
0,033 |
0,012 |
0,001 |
0,98 |
|
0,99 |
9,087 |
6,825 |
4,560 |
3,478 |
2,975 |
2,292 |
1,607 |
1,385 |
1,205 |
0,920 |
0,698 |
0,517 |
0,364 |
0,294 |
0,229 |
0,110 |
0,054 |
0,032 |
0,011 |
0,001 |
0,99 |
|
1,00 |
9,210 |
6,908 |
4,605 |
3,507 |
2,996 |
2,303 |
1,610 |
1,386 |
1,204 |
0,916 |
0,693 |
0,511 |
0,357 |
0,288 |
0,223 |
0,105 |
0,051 |
0,030 |
0,010 |
0,001 |
1,00 |
|
1,05 |
7,329 |
4,828 |
3,654 |
3,108 |
2,352 |
1,618 |
1,388 |
1,190 |
0,893 |
0,666 |
0,480 |
0,328 |
0,264 |
0,190 |
0,090 |
0,040 |
0,023 |
0,0074 |
0,000 |
1,05 |
|
|
1,10 |
7,750 |
5,050 |
3,800 |
3,220 |
2,400 |
1,625 |
1,380 |
1,175 |
0,870 |
0,640 |
0,450 |
0,300 |
0,241 |
0,175 |
0,074 |
0,030 |
0,016 |
0,0047 |
0,000 |
1,10 |
|
|
1,15 |
8,200 |
5,290 |
3,960 |
3,310 |
2,450 |
1,628 |
1,370 |
1,160 |
0,850 |
0,610 |
0,420 |
0,275 |
0,217 |
0,152 |
0,062 |
0,023 |
0,012 |
0,0031 |
0,000 |
1,15 |
|
|
1,20 |
8,650 |
5,530 |
4,120 |
3,400 |
2,500 |
1,630 |
1,350 |
1,145 |
0,830 |
0,580 |
0,390 |
0,250 |
0,198 |
0,130 |
0,049 |
0,016 |
0,008 |
0,0015 |
0,000 |
1,20 |
|
|
1,25 |
9,125 |
5,775 |
4,270 |
3,500 |
2,535 |
1,626 |
1340 |
1,128 |
0,805 |
0,550 |
0,362 |
0,226 |
0,170 |
0,112 |
0,040 |
0,012 |
0,0059 |
0,0010 |
0,000 |
1,25 |
|
|
1,30 |
9,600 |
6,020 |
4,420 |
3,600 |
2,570 |
1,621 |
1,330 |
1,110 |
0,780 |
0,520 |
0,334 |
0,203 |
0,146 |
0,094 |
0,030 |
0,0086 |
0,0038 |
0,0005 |
0,000 |
1,30 |
Окончание
табл. 3.10
|
Cv |
Обеспеченность |
Cv |
|||||||||||||||||||
|
0,01 |
0,1 |
1 |
3 |
5 |
10 |
20 |
25 |
30 |
40 |
50 |
60 |
70 |
75 |
80 |
90 |
95 |
97 |
99 |
99,9 |
||
|
1,35 |
10,10 |
6,285 |
4,565 |
3,700 |
2,605 |
1,616 |
1,320 |
1,095 |
0,752 |
0,490 |
0,308 |
0,179 |
0,126 |
0,080 |
0,023 |
0,0063 |
0,0025 |
0,0002 |
0,000 |
1,35 |
|
|
1,40 |
10,60 |
6,550 |
4,710 |
3,800 |
2,640 |
1,610 |
1,310 |
1,080 |
0,725 |
0,460 |
0,283 |
0,155 |
0,106 |
0,065 |
0,016 |
0,0040 |
0,0012 |
0,000 |
0,000 |
1,40 |
|
|
1,45 |
11,12 |
6,815 |
4,845 |
3,880 |
2,670 |
1,600 |
1,295 |
1,060 |
0,698 |
0,432 |
0,258 |
0,138 |
0,092 |
0,056 |
0,012 |
0,0030 |
0,0006 |
0,000 |
0,000 |
1,45 |
|
|
1,50 |
11,65 |
7,080 |
4,980 |
3,960 |
2,700 |
590 |
1,280 |
1,040 |
0,670 |
0,405 |
0,234 |
0,120 |
0,077 |
0,046 |
0,009 |
0,0020 |
0,000 |
0,000 |
0,000 |
1,50 |
|
|
1,55 |
12,20 |
7,330 |
5,115 |
4,045 |
2,725 |
1,575 |
1,260 |
1,015 |
0,638 |
0,378 |
0,212 |
0,105 |
0,066 |
0,038 |
0,007 |
0,001 |
0,000 |
0,000 |
0,000 |
1,55 |
|
|
1,60 |
12,75 |
7,580 |
5,250 |
4,130 |
2,750 |
1,560 |
1,240 |
0990 |
0,605 |
0,350 |
0,190 |
0,090 |
0,056 |
0,030 |
0,005 |
0,000 |
0,000 |
0,000 |
0,000 |
1,60 |
|
|
1,65 |
13,28 |
7,840 |
5,385 |
4,215 |
2,775 |
1,545 |
1,210 |
0964 |
0,575 |
0,325 |
0,170 |
0,078 |
0,048 |
0,024 |
0,0035 |
0,000 |
0,000 |
0,000 |
0,000 |
1,65 |
|
|
1,70 |
13,80 |
8,100 |
5,520 |
4,300 |
2,800 |
1,530 |
1,180 |
0938 |
0,545 |
0,300 |
0,150 |
0,067 |
0,039 |
0,019 |
0,002 |
0,000 |
0,000 |
0,000 |
0,000 |
1,70 |
|
|
1,75 |
14,35 |
8,360 |
5,650 |
4,385 |
2,825 |
1,512 |
1,148 |
0,904 |
0,518 |
0,275 |
0,134 |
0,058 |
0,033 |
0,016 |
0,0012 |
0,000 |
0,000 |
0,000 |
0,000 |
1,75 |
|
|
1,80 |
14,90 |
8,620 |
5,780 |
4,470 |
8,850 |
1,495 |
1,115 |
0,870 |
0,490 |
0,250 |
0,117 |
0,048 |
0,027 |
0,012 |
0,0005 |
0,000 |
0,000 |
0,000 |
0,000 |
1,80 |
|
|
1,85 |
15,52 |
8,885 |
5,905 |
4,540 |
8,875 |
1,478 |
1,088 |
0,845 |
0,462 |
0,231 |
0,104 |
0,040 |
0,022 |
0,0094 |
0,0002 |
0,000 |
0,000 |
0,000 |
0,000 |
1,85 |
|
|
1,90 |
16,15 |
9,150 |
6,030 |
4,620 |
8,900 |
1,460 |
1,060 |
0,820 |
0,435 |
0,212 |
0,090 |
0,033 |
0,017 |
0,0068 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
1,90 |
|
|
1,95 |
16,75 |
9,415 |
6,165 |
4,705 |
8,915 |
1,441 |
1,040 |
0,791 |
0,408 |
0,194 |
0,080 |
0,028 |
0,014 |
0,0053 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
1,95 |
|
|
2,00 |
17,35 |
9,680 |
6,300 |
4,790 |
8,930 |
1,422 |
1,020 |
0,762 |
0,380 |
0,175 |
0,070 |
0,022 |
0,011 |
0,0038 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
2,00 |
|
|
2,05 |
17,98 |
9,940 |
6,425 |
7,870 |
2,940 |
1,404 |
1,000 |
0,740 |
0,360 |
0,158 |
0,062 |
0,018 |
0,009 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
2,05 |
|
|
2,10 |
18,60 |
10,200 |
6,550 |
4,950 |
2,950 |
1,385 |
0,979 |
0,719 |
0,340 |
0,140 |
0,053 |
0,014 |
0,007 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
2,10 |
|
|
2,15 |
19,25 |
10,465 |
6,665 |
5,025 |
2,975 |
1,362 |
0,954 |
0,690 |
0,318 |
0,124 |
0,045 |
0,012 |
0,0054 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
2,15 |
|
|
2,20 |
19,90 |
10,730 |
6,780 |
5,100 |
3,000 |
1,340 |
0,930 |
0,660 |
0,295 |
0,108 |
0,037 |
0,009 |
0,0038 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
2,20 |
|
|
2,25 |
20,55 |
11,00 |
6,900 |
5,165 |
3,000 |
1,318 |
0,905 |
0,635 |
0,278 |
0,095 |
0,032 |
0,0072 |
0,0029 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
2,25 |
|
|
2,30 |
21,20 |
11,28 |
7,020 |
5,230 |
3,000 |
1,295 |
0,880 |
0,610 |
0,260 |
0,082 |
0,027 |
0,0055 |
0,0020 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
2,30 |
|
|
2,35 |
21,85 |
11,54 |
7,135 |
5,290 |
2,990 |
1,286 |
0,850 |
0,582 |
0,240 |
0,071 |
0,023 |
0,0043 |
0,0015 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
2,35 |
|
|
2,40 |
22,50 |
11,80 |
7,250 |
5,350 |
2,980 |
1,240 |
0,820 |
0,555 |
0,220 |
0,060 |
0,019 |
0,0031 |
0,0010 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
2,40 |
|
|
2,45 |
23,15 |
12,08 |
7,375 |
5,400 |
2,965 |
1,205 |
0,786 |
0,528 |
0,200 |
0,055 |
0,016 |
0,0026 |
0,0006 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
2,45 |
|
|
2,50 |
23,80 |
12,36 |
7,500 |
5,450 |
2,950 |
1,170 |
0,752 |
0,500 |
0,180 |
0,050 |
0,012 |
0,0020 |
0,0002 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
2,50 |
|
|
2,55 |
24,45 |
12,64 |
7,625 |
5,485 |
2,925 |
1,130 |
0,716 |
0,475 |
0,165 |
0,040 |
0,010 |
0,0015 |
0,0001 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
2,55 |
|
|
2,60 |
25,10 |
12,92 |
7,750 |
5,520 |
2,900 |
1,090 |
0,680 |
0,450 |
0,150 |
0,040 |
0,008 |
0,0010 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
2,60 |
Пример 3.1.
Определить
расходы воды р. Енисея у г. Енисейска
заданных обеспеченностей:
р = 5, 10, 25, 50, 75, 95, 97 и 99%. Для
решения поставленной задачи необходимо:
-
вычислить
параметры кривой обеспеченности Q0,
Cv
и
Cs; -
построить кривые
обеспеченности — эмпирическую и
теоретическую;
-
по
принятой теоретической кривой
обеспеченности вычислить расходы воды
заданной обеспеченности.
Продолжительность
наблюдений над стоком Енисея у г.
Енисейска 60
лет — с 1903 по 1966 г. за исключением 1906,
1922, 1923 и 1924 гг., когда имелись
перерывы в наблюдениях. Вычисления Qo,
Cv
и
Cs
сводятся в стандартную
таблицу (табл. 3.11);
Cv
и
Са
вычисляются
методом моментов.
В
графе 1 таблицы выписывается порядковый
номер, который используется
в формуле при определении эмпирической
обеспеченности, в графах
2 — 3 — годы и средние годовые расходы
или модули в хронологическом порядке.
В графе 4 годовые расходы расположены
в убывающем порядке от наибольшего,
который имеет первый номер убывающего
ряда, до наименьшего с
порядковым номером 60.
Затем
определяются
,
модульные коэффициенты расходов
убывающего ряда(гр. 5) и значения (k
-1), (k -1)2,
(k -1)3 (гр. 6 —
9). Вычисления выполняются с точностьюk – два знака после
запятой,
(k
-1)2, (k -1)3– четыре знака после запятой.
Контроль
вычислений
(числу членов ряда);
.Погрешности
за счет округления k
при
вычислении его с помощью логарифмической
линейки обычно не велики, и если невязка
не превышает 0,2—0,4, то она разбрасывается
в ряд k.
Грубые
ошибки вычисления k
и
(k—1)2
скажутся на
точности Cv
и
кривой обеспеченности, и поэтому значения
k
должны
быть исправлены.
Значения
Cv
и
Ся
вычисляются по алгебраическим суммам
и
.
Таблица
3.11.
Подсчет коэффициента
вариации и асимметрии годового стока
р. Енисея
у г. Енисейска
F=
1420 000 км2
|
№ пп |
Год |
Q м3/сек |
Q,
в убывающем |
k |
(k |
(k |
(k-1)3 |
р, % |
||
|
+ |
|
+ |
|
|||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
1 |
1903 |
6560 |
10200 |
1,34 |
0,34 |
0,1156 |
0,0393 |
1,64 |
||
|
2 |
1904 |
8100 |
9350 |
1,22 |
0,22 |
0,0484 |
0,0106 |
3,28 |
||
|
3 |
1905 |
7350 |
9260 |
1,21 |
0,21 |
0,0441 |
0,0093 |
4,92 |
||
|
… |
||||||||||
|
56 |
1962 |
6680 |
6610 |
0,86 |
0,14 |
0,0196 |
0,0027 |
91,8 |
||
|
57 |
1963 |
6950 |
6660 |
0,86 |
0,14 |
0,0196 |
0,0027 |
93,5 |
||
|
58 |
1964 |
6400 |
6420 |
0,84 |
0,16 |
0,0256 |
0,0041 |
95,1 |
||
|
59 |
1965 |
7360 |
6400 |
0,84 |
0,16 |
0,0256 |
0,0041 |
96,9 |
||
|
60 |
1966 |
8480 |
6180 |
0,81 |
0,19 |
0,0361 |
0,0069 |
98,5 |
||
|
Сумма |
59,96 |
0 |
0,6944 |
0,0458 |
Q0=7640
м3/сек
;
%
;
%
Параметры кривой
обеспеченности годового стока р. Енисея
у г. Енисейска, вычисленные по 60-летнему
ряду наблюдений, и их средние квадратические
ошибки , Q0= 7640 м3/сек,%,Cv
= 0,11,%,Сs=0,57,
%.
Ошибки определения
Q0
и Cv
незначительны, и вычисленные значения
Qo
и Си могут быть приняты
для дальнейших расчетов. Ошибка Cs
при n
= 60 годам получилась
большой. Поэтому расчетную кривую
обеспеченности выбираем из двух
теоретических кривых, построенных при
Cs
вычисленном и Cs
= 2 Cv.
Кривые обеспеченности построим для
расходов.
Сначала
строим эмпирическую кривую обеспеченности.
Для этого пользуемся графами 5 и 11 табл.
3.11.
Построение выполняем на специальной
клетчатке (см. рис. 3.1).
Затем вычисляем ординаты теоретических
кривых обеспеченности. Так как Cv
=0,11, то для построения теоретических
кривых обеспеченности пользуемся
таблицами биномиальной кривой (приложение
6 и 7). Вычисления ординат кривой при Cs
= 0,57 сводятся в табл. 3.12.
Значения ФР
выписываем из строчки
приложения 6, соответствующей Cs=0,57.
Значения kp
и Qp.
При
CS=2CV
пользуемся таблицей ординат кривой
обеспеченности (приложение 7), где
приводятся значения kp,
соответствующие Cv
(значения kp
выписываем из строки
Cv
= 0,11). По вычисленным QP
построены две теоретические кривые
обеспеченности, совмещенные с эмпирической
кривой (рис. 1).
Сопоставление
совмещенных кривых позволяет сделать
вывод, что теоретическая кривая
обеспеченности, построенная при Cs=0,57,
лучше соответствует эмпирической кривой
(наблюденным точкам) во всем диапазоне
и поэтому она принимается в качестве
расчетной (табл. 3.13).
Таблица
3.12.
Вычисление
ординат кривой обеспеченности годовых
расходов воды р. Енисея у г. Енисейска
N= 60,Q0= 7640 м3/сек,Cv
= 0,11
|
р, |
0,1 |
1 |
5 |
10 |
25 |
50 |
75 |
80 |
90 |
95 |
97 |
99 |
99,9 |
|
Сs=0,57 |
|||||||||||||
|
Фр |
3,92 |
2,73 |
1,79 |
1,32 |
0,62 |
-0,1 |
-0,72 |
-1,85 |
-1,2 |
-1,46 |
-1,63 |
-1,9 |
-2,3 |
|
Фр |
0,43 |
0,3 |
0,2 |
0,14 |
0,07 |
-0,01 |
-0,08 |
-0,09 |
-0,13 |
-0,16 |
-0,18 |
-0,21 |
-0,25 |
|
kp |
1,43 |
1,3 |
1,2 |
1,14 |
1,07 |
0,99 |
0,92 |
0,91 |
0,87 |
0,84 |
0,82 |
0,79 |
0,75 |
|
Qp |
10900 |
9940 |
9140 |
8640 |
8170 |
7560 |
7020 |
6950 |
6630 |
6420 |
6250 |
6020 |
5720 |
|
Сs |
|||||||||||||
|
kp |
1,37 |
1,27 |
1,19 |
1,14 |
1,07 |
1,0 |
0,92 |
0,91 |
0,86 |
0,83 |
0,80 |
0,76 |
0,70 |
|
Qp |
10530 |
9700 |
9090 |
8700 |
8170 |
7640 |
7020 |
6950 |
6560 |
6340 |
6100 |
5800 |
5340 |
Таблица
3.13.
Годовые расходы
воды р. Енисея у г. Енисейска заданных
обеспеченностей
Qo
= 7640 м3/сек,
и Cv
= 0,11, Cs=0,57.
|
Обеспеченность |
5 |
10 |
50 |
75 |
90 |
95 |
97 |
99 |
|
Qp |
9140 |
8640 |
7560 |
7020 |
6630 |
6420 |
6250 |
6020 |
Рис.3.1.
Кривые обеспеченности средних годовых
расходов воды р. Енисея у г. Енисейска,
n
=60, Q0=7640
м*/сек, Cv
= 0,11, Cs=0,57.
Пример
3.2.
Определить
параметры кривой обеспеченностей
и значения годового стока разной
обеспеченности р. Илека (F=
11 000 км2)
р=5, 10, 25, 50, 75, 95, 97 и 99%.
Для решения
поставленной задачи необходимо:
-
вычислить
параметры кривой обеспеченности Q0,
Cv
и
Cs; -
построить кривые
обеспеченности – эмпирическую и
теоретическую;
-
по
принятой теоретической кривой
обеспеченности вычислить расходы воды
заданной обеспеченности.
Cv
и
Са
вычисляются
методом моментов.
-
№
Год
Мср, л/сек
с 1 км21
1940
0,72
2
1941
3,39
3
1942
5,19
4
1944
0,43
5
1946
4,04
6
1947
1,23
7
1948
3,75
8
1949
2,54
9
1950
0,70
10
1951
0,68
11
1952
2,74
12
1953
0,95
13
1954
1,25
14
1955
0,78
15
1956
1,16
16
1957
3,74
17
1958
1,64
18
1959
1,50
19
1960
1,79
20
1961
0,82
21
1962
1,06
При проведении диагностики нижнего пояса резервуара на внутренней поверхности не было обнаружено видимых локальных повреждений металла типа язв и питтингов. По-видимому, в данном случае имела место равномерная коррозия, и предварительный коэффициент вариации глубин коррозионного разрушения V был принят равным 0,2. С учетом условий эксплуатации величины доверительной вероятности оценки у и допустимой относительной ошибки расчета 5 считали равными 0,95 и 0,1 соответственно. По параметрам у, б, V с помощью [c.213]
Проведенные исследования показывают, что при коэффициенте вариации сроков службы, меньшем 0,35, вполне возможна замена распределения Вейбулла нормальным с теми же математическим ожиданием и дисперсией, Ошибка в вычислении числа восстановлений или интенсивности их при такой замене практически отсутствует. Кроме того, как показывают наблюдения, сроки службы многих машин (автомобилей, тракторов, комбайнов и др,) имеют распределения, близкие к нормальному. [c.31]
Во второй группе источников неточностей эксперимента столь же незакономерно могут вносить погрешности и влиять па коэффициент вариации распределения ошибки при отборе проб картерного масла и расчета износа. Эти ошибки устраняются системой контроля. Например, наибольшая ошибка в определении износа, связанная с отбором пробы объемом 20 мл, заключается в том, что промывка отборного трубопровода и крана проводится недостаточно, в результате чего в пробу попадает масло, наполнившее трубопровод в предшествующий проводимому отбору пробы. Для устранения этой ошибки проводится операция отбора последовательно двух проб, первая (нечетная) из которых ложная . Регистрацию обеих проб осуществляет оператор, выполнивший отбор, а взвешивание и последующие операции — другой (обычно следующей смены), который выполняет операцию упаковки, регистрирует отправку на анализ действительной пробы и слив ложной в картер двигателя. Для осуществления отбора проб масла двигатель был оборудован пробоотборным краном в масляной магистрали, скорость перемещения в которой смазывающей жидкости составляла около 2—2,5 м/с. [c.51]
В технических задачах критерием пренебрежимой малости отбрасываемой величины обычно считается значение последней, меньшее 1—2% результата. В некоторых задачах ошибками измерения пренебрегают, если полное поле практического рассеяния результатов измерения, т. е. 6а, меньше чем 5—10% значения измеряемой величины (коэффициент вариации порядка 1—2%). [c.212]
Относительная величина средней квадратичной ошибки w, выраженная в процентах, называется коэффициентом вариации [c.29]
Так как выборочный коэффициент вариации оказался больше первоначально принятого Уш то при п = 11 фактическая ошибка будет больше = 0,02. [c.45]
Пусть далее по результатам испытания п = 11 -1- 9 = 20 образцов выборочный коэффициент вариации а = 0,045. Определяем по формуле (2.76) ожидаемую с вероятностью Р = 0,9 максимальную относительную ошибку оценки среднего значения предела прочности [c.45]
Коэффициент вариации разрушающ,его напряжения, вычисленный по средней квадратической ошибке, равен ш = 18%, а средняя арифметическая ошибка р=18,3%. [c.98]
При статистической обработке остальных результатов вычислялись средние арифметические значения измеряемых величин Жср, средние квадратичные ошибки отдельных измерений Ох, квадратичные ошибки средних арифметических tq, коэффициент вариации V. Окончательный результат измерений полагали А = = (Та + Хер, а предельные отклонения — равными 3Wx- В табл. 6.1 приведены результаты обработки при определении коэффициента к , модуля El и коэффициента Ui. [c.239]
Результаты статистической обработки числа Fo/Fo p при Кр = = 0,5 и числе измерений п = 10 таковы среднее арифметическое значение = 0,444 средняя квадратичная ошибка отдельного измерения = 0,058, квадратичная ошибка среднего арифметического tq = 0,0184 коэффициент вариации V = 13%. [c.247]
Тип образца V, кг-см/см Коэффициент вариации, % Относи- тельная ошибка, % [c.130]
Выполненные авторами методики исследования показали, что наибольшее влияние на функцию интенсивности ремонтов оказывает величина М. Влияние второго параметра распределения сроков службы а на функцию интенсивности ремонтов зависит от его относительной величины — коэффициента вариации V, и может быть заметным только на начальном участке вычисляемых функций для отдельных элементов. Что же. касается такой многоэлементной системы, какой является парк автомобилей, то, как выяснилось, изменение величины V в пределах от 0,1 до 0,3 в вычисление функции интенсивности ремонтов заметной ошибки не вносит. Исследованиями установлено также, что при одних и тех же значениях М п V вид закона распределения сроков службы мало влияет на величину искомых функций. Так, при коэффициенте вариации, меньшем 0,35, вполне допустима замена закона Вейбулла нормальным законом. Ошибка при вычислениях интенсивности ремонтов при такой замене практически отсутствует. На этом основании в перспективных расчетах вполне допустимо обходиться такими распределениями, которые более удобны для вычислений. Настоящей методикой предусмотрено, выполнение расчетов с использованием данных о функции [c.385]
Часто величины и называются соответственно генеральной и выборочной дисперсиями, а а и S — стандартной или среднеквадратичной ошибкой (сокращенно стандартом). Относительную величину стандарта называют иногда коэффициентом вариации ф, %, [c.34]
В качестве примера можно указать, что при надежности у=0,01 и относительной ошибке 6=0,05 в определении среднего логарифма долговечности потребное число образцов в зависимости от коэффициента вариации составляет [c.77]
Поправка (1 -Ь дИ) учитывает также и возможные ошибки при определении средней интенсивности изнашивания а, вызванные ограниченным количеством наблюдений, и рассеивание его результатов, так как на величину среднеквадратического отклонения < , а следовательно, и коэффициент вариации V оказывает влияние число опытов (наблюдений) п. [c.168]
Нередко представляется желательным определить, каково должно быть число образцов К, чтобы средний параметр X был найден с заданной относительной ошибкой 5 при известном коэффициенте вариации V для вероятности а. Для [c.585]
При доверительной вероятности р = 0,95, относительной ошибке в определении средней наработки до отказа б =0,10 и коэффициенте вариации V = 0,462 число объектов наблюдения для закона распределения Вейбулла необходимо не менее N — 64. [c.243]
При 14 интервалах, 11 степенях свободы и 1—р = 0,050, критерий х = 4,570 число объектов наблюдения при р = 0,95 и ошибке б = 0,1 составляет N = 51 коэффициент вариации v = 0,417. [c.251]
Обработка полученных данных проводится по ГОСТ 14359-69, действие которого продлено до 1983 г. Она состоит в расчете основных статистических характеристик достоверности полученных результатов-среднего арифметического (или логарифмического), стандартного отклонения и стандартного отклонения среднего значения, вероятного отклонения искомого, коэффициента вариации и относительной ошибки. [c.66]
Выбирая доверительный интервал при измерении данного параметра, следует руководствоваться, с одной стороны, средней квадратичной ошибкой (или коэффициентом вариации У ), а с другой стороны — точностью самого метода измерений (аппаратуры, датчиков, способа расшифровки). Если систематическую погрешность измерений, определяемую лишь классом точности аппаратуры (а не вариацией самой измеряемой величины), обозначить б, то доверительный интервал будет [c.64]
Число объектов наблюдения N определяют в зависимости от относительной ошибки А среднего значения / р исследуемой случайной величины (наработка до первого отказа, ресурс, срок службы и т. п.) с доверительной вероятностью р и ожидаемой величины коэффициента вариации Уа. Значения А, взаимосвязаны. [c.158]
Исходные данные предельная относительная ошибка 8 доверительная вероятность д предполагаемый коэффициент вариации V распределения наработок между отказами предполагаемый коэффициент вариации Kg распределения времени восстановления. [c.570]
Оценка разности между коэффициентами вариации. Разность между коэффициентами вариации сравниваемых групп, извлеченных из нормально распределяющихся совокупностей, можно оценить с помощью критерия Стьюдента. Приближенной оценкой разности Сю —Си2 = с со служит ее отношение к своей ошибке, которая равна корню квадратному из суммы ошибок коэффициентов вариации сравниваемых групп, т. е. [c.126]
На основании уравнений (2) и (3) и с учетом того, что для нормального закона распределения и распределения Вейбулла параметры распределения и коэффициент вариации связаны однозначно [26], составлены [8, 9] графики (рис. 3, а и б), позволяющие приближенно рассчитать объем партии N для первичных испытаний при малом объеме предварительной информации о надежности. Ошибка при планировании испытаний по предлагаемо- [c.14]
Определить количество клиновых вентиляторных ремней, которые необходимо испытать для определения их среднего ресурса с доверительной вероятностью р=0,9 и предельной относительной ошибкой 6=0,1. Для клиновых ремней характерны отказы из-за трещин резины слоя сжатия, расслоения, остаточной деформации (удлинения). По табл. 4 и уравнению (1) определяем наиболее вероятное значение параметра Вейбулла й=2,74-3,2 и коэффициента вариации 11=0,35- 0,4. По графику на рис. 3 находим iV=33-b38. [c.17]
На рис. 7.5 а приведен средний вертикальный профиль оптической толщины т для Х==10,6 мкм до высоты 30 км. Здесь же приведено среднее значение коэффициента поглощения на уровне земли (/1 = 0). На рис. 7.6 6 дан профиль стандартного отклонения ат. Величина сгх характеризует ошибку в определении т, связанную с вариациями температуры и влажности. Из рис. 7.5 6 следует, что на высоте 22 км сгт достигает значения 0,15 и далее с высотой не изменяется. Ошибка в определении пропускания слоя О— 30 км составляет 15 %. [c.221]
Систематические ошибки возникают за счет погрешностей априорного расчета профиля дифференциального коэффициента поглощения Ах(Я), которые зависят от многих факторов, таких как вариаций давления, температуры и влажности по трассе зондирования, нестабильности длины волны и ширины спектра излучения, поглощения другими газами, доплеровского уширения спектра эхо-сигнала за счет хаотического движения молекул воздуха, флуоресценции. К перечисленным факторам следует отнести и сдвиг центра линии поглощения Н2О давлением воздуха. Оценим его влияние при решении обратной задачи зондирования. [c.199]
Максимальные ошибки определения профиля коэффициента Даэ(Уе, г)/аэ(Уо, г) в процентах, вызванные вариациями частоты лазерного излучения Ve около центральной частоты го линии поглощения Н2О 694,38 нм. Модель атмосферы — [c.145]
Относительная величина среднеквадратичной ошибки-в процентах называется коэффициентом вариации, а интервал значений от х—Ал до х+Дж —доверительным интервалом. Знание доверительной вероятности позволяет оценить степень надежности полученного результата. Обычно ограничиваются доверительной вероятностью, )авной 0,9 или 0,95. Она рассчитывается по формуле «аусса для разных значений доверительного интервала. Эти значения приводятся в виде таблиц, помещенных, например, в [Л. 30]. Среднеквадратичной ошибке соответствует доверительная вероятность 0,69, удвоенной ошибке 0,95 и утроенной ошибке 0,997. [c.42]
Если после дополнительных испытаний девяти образцов выборочный коэффициент вариации оказался бы существенно выше 0,051, а величина максимальной ошибки, подсчитанная по формуле (2.76), была бы неприемлемо высокой, то следовало бы вновь йкйрректировать объем испытаний с учетом полученного значения после дополнительных испытаний коэффициента вариации н т. д. [c.45]
Наиболее полно сопротивление усталости характеризуется кривыми усталости, получаемыми для различных вероятностей разрушения с заданной точностью и принятым значением уровня значимости (надежности). Такие характеристики требуют испытания большого числа образцов (или деталей) на нескольких уровнях напряжений. Число испытуемых образцов п на каждом уровне напряжений зависит от величины рассеяния, характеризуемого коэффициентом вариации F=SIgJv/lgЛ (отношение среднего квадратического отклонения логарифма долговечности к среднему значению) и принятыми односторонними значениями урорня значимости у (характеризует надежность), и точности, характеризуемой величиной относительной ошибки б, равной отношению абсолютной ошибки Д к среднему значению 1 N. [c.76]
В связи с этим Лайн для получения достоверных данных рекомендует производить до 10 испытаний манжет в одинаковых условиях. Шнюрле и Уппер проводили по 4—10 испытаний манжет для получения каждой точки на графике изучаемой зависимости [141]. Статистический анализ показывает [43], что при коэффициенте вариации 0,1—0,2 и допустимой относительной ошибке измеряемого параметра 0,1, при доверительной вероятности 0,95 необходимо проводить 6—18 испытаний резинотехнических деталей. [c.57]
Число объектов наблюдения опредляется по заданной величине относительной ошибки 6, доверительной вероятности р и коэффициенту вариации V = 1 (по табл. 12). При б = 0,15, Р = 0,80 и V = 1 число объектов наблюдения N = 45. [c.248]
При диагностировании нижнего пояса резервуара, выполненном изнутри, не было обнаружено видимых локальных повреждений металла поверхности в виде явных язв и питтингов. Па этом основании было признано, что в данном случае имела место слабая неравномерность коррозионного повреждения, и был принят предварительный коэффициент вариации глубин коррозионного разрушения V = 0,2. Исходя из условий эксплуатации, в данном случае приняты следующие величины доверительной вероятности оценки (у) и допустимой относительной ошибки расчета (б) у = 0,95 и б = 0,1. По трем принятым параметрам — у, б, V — из табл. 4.6 было выбрано минимальное число необходимых измерений — = 13. Измерения ульт- [c.211]
Методы численного решения систем типа (3.39) будут подробно нами рассматриваться в п. 4.2, а сейчас лишь напомним, что в основе этой системы лежат предположения о сферичности рассеивающих частиц и априорное задание показателя преломления аэрозольного вещества т = т —т»1 в пределах зондируемого слоя [ЯьЯг]. В силу этого изложенная выше теория многочастотного касательного зондирования приводит к вычислительным схемам обращения оптических данных, применимых при тех же исходных допущениях, что и в методе многочастотного лазерного зондирования. Это обусловлено единством методологического подхода к теории оптического зондирования рассеивающей компоненты атмосферы. Вместе с тем необходимо обратить внимание на то обстоятельство, что требования к выполнению указанных выше допущений существенно различны для указанных двух методов. Действительно, уравнения теории касательного зондирования относительно локальных оптических характеристик светорассеяния являются интегральными, причем первого рода, и поэтому вариации бРех (то же самое бт и б/)ц), обусловленные ошибками Ат в задании подходящих значений т, слабо сказываются на значении интегралов (3.24). В силу этого схемы обращения в методе касательного зондирования более устойчивы к неопределенностям при априорном задании соответствующих оптических операторов в (3.39). В локационных задачах оптические сигналы Р %1,г) прямо пропорциональны значениям аэрозольных коэффициентов обратного рассеяния (Зя(Я/, г), и поэтому вариации бРяг связанные с Дт, непосредственно сказываются на точности интерпретации оптических данных. [c.166]
Производные в ЭТИХ формулах являются функциями координат и могут быть получены на основании формул (22.37) и (22.38). Они должны быть вычислены для невозмущепной траектории снаряда. Однако этот метод приводит к дифференциальным уравнениям с переменными коэффициентами, которые не могут быть проинтегрированы в замкнутой форме. При полетах в области пространства шириной порядка нескольких сотен миль коэффициенты могут быть вычислены в точках самой траектории с точностью, достаточной для наших целей. Это дает следующие уравнения для определения возмущений в положении снаряда, вызываемых вариациями ускорения силы тяги и ошибками акселерометров [c.668]
Коэффициент вариации и стандартное отклонение: разница
17 авг. 2022 г.
читать 2 мин
Стандартное отклонение набора данных — это способ измерить, насколько среднее значение отличается от среднего.
Чтобы найти стандартное отклонение данного образца , мы можем использовать следующую формулу:
s = √(Σ(x i – x ) 2 / (n-1))
куда:
- Σ: символ, означающий «сумма».
- x i : значение i -го наблюдения в выборке
- x : среднее значение выборки
- n: размер выборки
Чем выше значение стандартного отклонения, тем более разбросаны значения в выборке. Однако трудно сказать, является ли заданное значение стандартного отклонения «высоким» или «низким», потому что это зависит от типа данных, с которыми мы работаем.
Например, стандартное отклонение 500 можно считать низким, если речь идет о годовом доходе жителей определенного города. И наоборот, стандартное отклонение 50 можно считать высоким, если мы говорим об экзаменационных баллах студентов по определенному тесту.
Один из способов понять, является ли определенное значение стандартного отклонения высоким или низким, состоит в том, чтобы найти коэффициент вариации , который рассчитывается как:
CV = с / х
куда:
- s: Стандартное отклонение выборки
- x : Среднее значение выборки
Проще говоря, коэффициент вариации — это отношение между стандартным отклонением и средним значением.
Чем выше коэффициент вариации, тем выше стандартное отклонение выборки относительно среднего значения.
Пример: расчет стандартного отклонения и коэффициента вариации
Предположим, у нас есть следующий набор данных:
Набор данных: 1, 4, 8, 11, 13, 17, 19, 19, 20, 23, 24, 24, 25, 28, 29, 31, 32
Используя калькулятор, мы можем найти следующие показатели для этого набора данных:
- Среднее значение выборки ( x ): 19,29
- Стандартное отклонение выборки (с): 9,25
Затем мы можем использовать эти значения для расчета коэффициента вариации:
- CV = с / х
- КВ = 9,25/19,29
- КВ = 0,48
Для этого набора данных полезно знать как стандартное отклонение, так и коэффициент вариации.
Стандартное отклонение говорит нам о том, что типичное значение в этом наборе данных отличается от среднего на 9,25 единицы. Затем коэффициент вариации говорит нам, что стандартное отклонение составляет примерно половину среднего значения выборки.
Стандартное отклонение против коэффициента вариации: когда использовать каждый
Стандартное отклонение чаще всего используется, когда мы хотим узнать разброс значений в одном наборе данных.
Однако коэффициент вариации чаще используется, когда мы хотим сравнить вариацию между двумя наборами данных.
Например, в финансах коэффициент вариации используется для сравнения среднего ожидаемого дохода от инвестиций с ожидаемым стандартным отклонением инвестиций.
Например, предположим, что инвестор рассматривает возможность инвестирования в следующие два взаимных фонда:
Взаимный фонд A: среднее = 9%, стандартное отклонение = 12,4%
Взаимный фонд B: среднее = 5%, стандартное отклонение = 8,2%
Инвестор может рассчитать коэффициент вариации для каждого фонда:
- CV для взаимного фонда A = 12,4% / 9% = 1,38
- CV для взаимного фонда B = 8,2% / 5% = 1,64
Поскольку взаимный фонд А имеет более низкий коэффициент вариации, он предлагает лучшую среднюю доходность по сравнению со стандартным отклонением.
Резюме
Вот краткое изложение основных моментов в этой статье:
- И стандартное отклонение, и коэффициент вариации измеряют разброс значений в наборе данных.
- Стандартное отклонение измеряет, насколько далеко среднее значение от среднего.
- Коэффициент вариации измеряет отношение стандартного отклонения к среднему значению.
- Стандартное отклонение используется чаще, когда мы хотим измерить разброс значений в одном наборе данных.
- Коэффициент вариации чаще используется, когда мы хотим сравнить вариацию между двумя разными наборами данных.
Дополнительные ресурсы
Как рассчитать среднее и стандартное отклонение в Excel
Как рассчитать коэффициент вариации в Excel
Корреляция и регрессия
Линейное уравнение регрессии имеет вид y=bx+a+ε
Здесь ε — случайная ошибка (отклонение, возмущение).
Причины существования случайной ошибки:
1. Невключение в регрессионную модель значимых объясняющих переменных;
2. Агрегирование переменных. Например, функция суммарного потребления – это попытка общего выражения совокупности решений отдельных индивидов о расходах. Это лишь аппроксимация отдельных соотношений, которые имеют разные параметры.
3. Неправильное описание структуры модели;
4. Неправильная функциональная спецификация;
5. Ошибки измерения.
Так как отклонения εi для каждого конкретного наблюдения i – случайны и их значения в выборке неизвестны, то:
1) по наблюдениям xi и yi можно получить только оценки параметров α и β
2) Оценками параметров α и β регрессионной модели являются соответственно величины а и b, которые носят случайный характер, т.к. соответствуют случайной выборке;
Тогда оценочное уравнение регрессии (построенное по выборочным данным) будет иметь вид y = bx + a + ε, где ei – наблюдаемые значения (оценки) ошибок εi, а и b соответственно оценки параметров α и β регрессионной модели, которые следует найти.
Для оценки параметров α и β — используют МНК (метод наименьших квадратов).
Система нормальных уравнений.
Для наших данных система уравнений имеет вид:
10a + 356b = 49
356a + 2135b = 9485
Из первого уравнения выражаем а и подставим во второе уравнение
Получаем b = 68.16, a = 11.17
Уравнение регрессии:
y = 68.16 x — 11.17
1. Параметры уравнения регрессии.
Выборочные средние.
1.1. Коэффициент корреляции
Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:
Линейный коэффициент корреляции принимает значения от –1 до +1.
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 Y фактором X весьма высокая и прямая.
1.2. Уравнение регрессии (оценка уравнения регрессии).
Линейное уравнение регрессии имеет вид y = 68.16 x -11.17
Коэффициентам уравнения линейной регрессии можно придать экономический смысл. Коэффициент уравнения регрессии показывает, на сколько ед. изменится результат при изменении фактора на 1 ед.
Коэффициент b = 68.16 показывает среднее изменение результативного показателя (в единицах измерения у ) с повышением или понижением величины фактора х на единицу его измерения. В данном примере с увеличением на 1 единицу y повышается в среднем на 68.16.
Коэффициент a = -11.17 формально показывает прогнозируемый уровень у , но только в том случае, если х=0 находится близко с выборочными значениями.
Но если х=0 находится далеко от выборочных значений x , то буквальная интерпретация может привести к неверным результатам, и даже если линия регрессии довольно точно описывает значения наблюдаемой выборки, нет гарантий, что также будет при экстраполяции влево или вправо.
Подставив в уравнение регрессии соответствующие значения x , можно определить выровненные (предсказанные) значения результативного показателя y(x) для каждого наблюдения.
Связь между у и x определяет знак коэффициента регрессии b (если > 0 – прямая связь, иначе — обратная). В нашем примере связь прямая.
1.3. Коэффициент эластичности.
Коэффициенты регрессии (в примере b) нежелательно использовать для непосредственной оценки влияния факторов на результативный признак в том случае, если существует различие единиц измерения результативного показателя у и факторного признака х.
Для этих целей вычисляются коэффициенты эластичности и бета — коэффициенты. Коэффициент эластичности находится по формуле:
Он показывает, на сколько процентов в среднем изменяется результативный признак у при изменении факторного признака х на 1%. Он не учитывает степень колеблемости факторов.
В нашем примере коэффициент эластичности больше 1. Следовательно, при изменении Х на 1%, Y изменится более чем на 1%. Другими словами — Х существенно влияет на Y.
Бета – коэффициент показывает, на какую часть величины своего среднего квадратичного отклонения изменится в среднем значение результативного признака при изменении факторного признака на величину его среднеквадратического отклонения при фиксированном на постоянном уровне значении остальных независимых переменных:
Т.е. увеличение x на величину среднеквадратического отклонения этого показателя приведет к увеличению среднего Y на 0.9796 среднеквадратичного отклонения этого показателя.
1.4. Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации.
Поскольку ошибка больше 15%, то данное уравнение не желательно использовать в качестве регрессии.
1.6. Коэффициент детерминации.
Квадрат (множественного) коэффициента корреляции называется коэффициентом детерминации, который показывает долю вариации результативного признака, объясненную вариацией факторного признака.
Чаще всего, давая интерпретацию коэффициента детерминации, его выражают в процентах.
R 2 = 0.98 2 = 0.9596, т.е. в 95.96 % случаев изменения x приводят к изменению у . Другими словами — точность подбора уравнения регрессии — высокая. Остальные 4.04 % изменения Y объясняются факторами, не учтенными в модели.
| x | y | x 2 | y 2 | x·y | y(x) | (yi— y ) 2 | (y-y(x)) 2 | (xi— x ) 2 | |y — yx|:y |
| 0.371 | 15.6 | 0.1376 | 243.36 | 5.79 | 14.11 | 780.89 | 2.21 | 0.1864 | 0.0953 |
| 0.399 | 19.9 | 0.1592 | 396.01 | 7.94 | 16.02 | 559.06 | 15.04 | 0.163 | 0.1949 |
| 0.502 | 22.7 | 0.252 | 515.29 | 11.4 | 23.04 | 434.49 | 0.1176 | 0.0905 | 0.0151 |
| 0.572 | 34.2 | 0.3272 | 1169.64 | 19.56 | 27.81 | 87.32 | 40.78 | 0.0533 | 0.1867 |
| 0.607 | 44.5 | .3684 | 1980.25 | 27.01 | 30.2 | 0.9131 | 204.49 | 0.0383 | 0.3214 |
| 0.655 | 26.8 | 0.429 | 718.24 | 17.55 | 33.47 | 280.38 | 44.51 | 0.0218 | 0.2489 |
| 0.763 | 35.7 | 0.5822 | 1274.49 | 27.24 | 40.83 | 61.54 | 26.35 | 0.0016 | 0.1438 |
| 0.873 | 30.6 | 0.7621 | 936.36 | 26.71 | 48.33 | 167.56 | 314.39 | 0.0049 | 0.5794 |
| 2.48 | 161.9 | 6.17 | 26211.61 | 402 | 158.07 | 14008.04 | 14.66 | 2.82 | 0.0236 |
| 7.23 | 391.9 | 9.18 | 33445.25 | 545.2 | 391.9 | 16380.18 | 662.54 | 3.38 | 1.81 |
2. Оценка параметров уравнения регрессии.
2.1. Значимость коэффициента корреляции.
По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=7 находим tкрит:
tкрит = (7;0.05) = 1.895
где m = 1 — количество объясняющих переменных.
Если tнабл > tкритич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически — значим
В парной линейной регрессии t 2 r = t 2 b и тогда проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.
2.3. Анализ точности определения оценок коэффициентов регрессии.
Несмещенной оценкой дисперсии возмущений является величина:
S 2 y = 94.6484 — необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии).
Sy = 9.7287 — стандартная ошибка оценки (стандартная ошибка регрессии).
S a — стандартное отклонение случайной величины a.
Sb — стандартное отклонение случайной величины b.
2.4. Доверительные интервалы для зависимой переменной.
Экономическое прогнозирование на основе построенной модели предполагает, что сохраняются ранее существовавшие взаимосвязи переменных и на период упреждения.
Для прогнозирования зависимой переменной результативного признака необходимо знать прогнозные значения всех входящих в модель факторов.
Прогнозные значения факторов подставляют в модель и получают точечные прогнозные оценки изучаемого показателя. (a + bxp ± ε) где
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X p = 1 (-11.17 + 68.16*1 ± 6.4554)
(50.53;63.44)
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.
Индивидуальные доверительные интервалы для Y при данном значении X.
(a + bx i ± ε)
где
| xi | y = -11.17 + 68.16xi | εi | ymin | ymax |
| 0.371 | 14.11 | 19.91 | -5.8 | 34.02 |
| 0.399 | 16.02 | 19.85 | -3.83 | 35.87 |
| 0.502 | 23.04 | 19.67 | 3.38 | 42.71 |
| 0.572 | 27.81 | 19.57 | 8.24 | 47.38 |
| 0.607 | 30.2 | 19.53 | 10.67 | 49.73 |
| 0.655 | 33.47 | 19.49 | 13.98 | 52.96 |
| 0.763 | 40.83 | 19.44 | 21.4 | 60.27 |
| 0.873 | 48.33 | 19.45 | 28.88 | 67.78 |
| 2.48 | 158.07 | 25.72 | 132.36 | 183.79 |
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.
2.5. Проверка гипотез относительно коэффициентов линейного уравнения регрессии.
1) t-статистика. Критерий Стьюдента.
Проверим гипотезу H0 о равенстве отдельных коэффициентов регрессии нулю (при альтернативе H1 не равно) на уровне значимости α=0.05.
tкрит = (7;0.05) = 1.895
Поскольку 12.8866 > 1.895, то статистическая значимость коэффициента регрессии b подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
Поскольку 2.0914 > 1.895, то статистическая значимость коэффициента регрессии a подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
Доверительный интервал для коэффициентов уравнения регрессии.
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими:
(b — tкрит Sb; b + tкрит Sb)
(68.1618 — 1.895 • 5.2894; 68.1618 + 1.895 • 5.2894)
(58.1385;78.1852)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
(a — ta)
(-11.1744 — 1.895 • 5.3429; -11.1744 + 1.895 • 5.3429)
(-21.2992;-1.0496)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
2) F-статистики. Критерий Фишера.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с lang=EN-US>n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.
где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R 2 =0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:
где m=1 для парной регрессии.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=1 и k2=7, Fkp = 5.59
Поскольку фактическое значение F > Fkp, то коэффициент детерминации статистически значим (Найденная оценка уравнения регрессии статистически надежна).
Проверка на наличие автокорреляции остатков.
Важной предпосылкой построения качественной регрессионной модели по МНК является независимость значений случайных отклонений от значений отклонений во всех других наблюдениях. Это гарантирует отсутствие коррелированности между любыми отклонениями и, в частности, между соседними отклонениями.
Автокорреляция (последовательная корреляция) определяется как корреляция между наблюдаемыми показателями, упорядоченными во времени (временные ряды) или в пространстве (перекрестные ряды). Автокорреляция остатков (отклонений) обычно встречается в регрессионном анализе при использовании данных временных рядов и очень редко при использовании перекрестных данных.
В экономических задачах значительно чаще встречается положительная автокорреляция, нежели отрицательная автокорреляция. В большинстве случаев положительная автокорреляция вызывается направленным постоянным воздействием некоторых неучтенных в модели факторов.
Отрицательная автокорреляция фактически означает, что за положительным отклонением следует отрицательное и наоборот. Такая ситуация может иметь место, если ту же зависимость между спросом на прохладительные напитки и доходами рассматривать по сезонным данным (зима-лето).
Среди основных причин, вызывающих автокорреляцию, можно выделить следующие:
1. Ошибки спецификации. Неучет в модели какой-либо важной объясняющей переменной либо неправильный выбор формы зависимости обычно приводят к системным отклонениям точек наблюдения от линии регрессии, что может обусловить автокорреляцию.
2. Инерция. Многие экономические показатели (инфляция, безработица, ВНП и т.д.) обладают определенной цикличностью, связанной с волнообразностью деловой активности. Поэтому изменение показателей происходит не мгновенно, а обладает определенной инертностью.
3. Эффект паутины. Во многих производственных и других сферах экономические показатели реагируют на изменение экономических условий с запаздыванием (временным лагом).
4. Сглаживание данных. Зачастую данные по некоторому продолжительному временному периоду получают усреднением данных по составляющим его интервалам. Это может привести к определенному сглаживанию колебаний, которые имелись внутри рассматриваемого периода, что в свою очередь может служить причиной автокорреляции.
Последствия автокорреляции схожи с последствиями гетероскедастичности: выводы по t- и F-статистикам, определяющие значимость коэффициента регрессии и коэффициента детерминации, возможно, будут неверными.
Обнаружение автокорреляции
1. Графический метод
Есть ряд вариантов графического определения автокорреляции. Один из них увязывает отклонения ei с моментами их получения i. При этом по оси абсцисс откладывают либо время получения статистических данных, либо порядковый номер наблюдения, а по оси ординат – отклонения ei (либо оценки отклонений).
Естественно предположить, что если имеется определенная связь между отклонениями, то автокорреляция имеет место. Отсутствие зависимости скоре всего будет свидетельствовать об отсутствии автокорреляции.
Автокорреляция становится более наглядной, если построить график зависимости ei от ei-1.
Расчет линейной регрессии онлайн
Быстрая навигация по странице:
Общая характеристика линейной регрессии
Под линейной регрессией понимается функция вида Y = a0 + a1X1 + a2X2 + … anXn, объясняющая изменение величины зависимой (или эндогенной) переменной Y от изменения величин объясняющих (независимых) переменных X1, X2, … Xn. В том случае, когда в построенной функции объясняющая переменная (или фактор) X только одна, то тогда такую регрессию называют парной, если же в модели используется несколько факторных переменных X – то множественной регрессией. Особенностью линейной регрессии является то, что изменение (приращение) зависимой переменной Y пропорционально изменению объясняющих факторов X, а графиком такой регрессии является прямая линия. Расчет параметров линейной регрессии выполняется, как правило, при помощи метода наименьших квадратов (МНК). Качество построенной модели во многом зависит от количества значений наблюдений, используемых для построения уравнения линейной регрессии.
Размещено на www.rnz.ru
Формулы уравнения и коэффициентов линейной регрессии
Общая формула парной линейной регрессии следующая:
Y^ = a + b*x + ε
где: Y^ — теоретические (расчетные) значения зависимого показателя (зависимой переменной), получаемые по построенному уравнению;
a — свободный член уравнения регрессии;
b — коэффициент уравнения регрессии
Для нахождения параметров (коэффициентов) линейной регрессии существует множество формул. Приведем некоторые из них:
— формулы для нахождения свободного члена уравнения регрессии a:
— формулы для нахождения коэффициента регрессии b:
Для расчета параметров уравнения регрессии также можно решить следующую систему уравнений:
Пример расчета уравнения регрессии
Приведем пример расчета параметров уравнения регрессии для значений, приведенных в следующей таблице (пример условный):
По семи территориям Уральского региона известны значения двух признаков за 201_ год:
| Район | Расходы на покупку продовольственных товаров в общих расходах, %, y | Среднедневная заработная плата одного работающего, руб., х |
|---|---|---|
| Удмуртская республика | 66.3 | 41.5 |
| Свердловская область | 59.9 | 57.7 |
| Республика Башкортостан | 57.3 | 55.8 |
| Челябинская область | 53.1 | 59.4 |
| Пермский край | 51.7 | 56.7 |
| Курганская область | 50.7 | 44.6 |
| Оренбургская область | 48 | 52.7 |
1. Для характеристики зависимости y от x рассчитать параметры уравнения парной линейной регрессии;
2. Рассчитать линейный коэффициент парной корреляции и дать его интерпретацию;
3. Рассчитать коэффициент детерминации и дать его интерпретацию;
4. Рассчитать коэффициент эластичности для линейной парной регрессии и дать его интерпретацию.
Для построения уравнения парной линейной регрессии составим таблицу вспомогательных расчетов, где будут произведены необходимые промежуточные вычисления:
| № района | Расходы на покупку продовольственных товаров в общих расходах, %, y | Среднедневная заработная плата одного работающего, руб., х | yx |
|---|---|---|---|
| 1 | 66.3 | 41.5 | 2751.45 |
| 2 | 59.9 | 57.7 | 3456.23 |
| 3 | 57.3 | 55.8 | 3197.34 |
| 4 | 53.1 | 59.4 | 3154.14 |
| 5 | 51.7 | 56.7 | 2931.39 |
| 6 | 50.7 | 44.6 | 2261.22 |
| 7 | 48 | 52.7 | 2529.6 |
| Итого | 387 | 368.4 | 20281.37 |
| Среднее значение | 55.29 | 52.63 | 2897.34 |
| σ | 5.84 | 6.4 | — |
| σ 2 | 34.06 | 40.93 | — |
Далее рассчитаем коэффициенты уравнения парной линейной регрессии.
Коэффициент b вычислим по формуле:
Формула расчета коэффициента b уравнения парной линейной регрессии
Пример расчета коэффициента b уравнения парной линейной регрессии: b = (2897.34-55.29*52.63)/40.93 = -0.31
Коэффициент a вычислим по формуле:
Формула расчета коэффициента a уравнения парной линейной регрессии
Пример расчета коэффициента a уравнения парной линейной регрессии: a = 55.29 — -0.31*52.63 = 71.61
Получим следующее уравнение парной линейной регрессии:
Линейный коэффициент парной корреляции рассчитаем по формуле:
Формула расчета линейного коэффициента парной корреляции
Пример расчета линейного коэффициента парной корреляции:
ryx = -0.31*6.4 / 5.84 = -0.3397
Далее вычислим коэффициент детерминации по формуле:
Формула расчета коэффициента детерминации
Пример расчета значения коэффициента детерминации:
r 2 yx = -0.3397*-0.3397 = 0.1154 или 11.54%
Интерпретация значения коэффициента детерминации: согласно полученному значению коэффициента детерминации вариация расходов на покупку продовольственных товаров в общих расходах только на 11.54% определяется вариацией среднедневной заработной платой одного работающего, что является низким показателем.
Далее рассчитаем коэффициент эластичности для линейной регресии по формуле:
Формула расчета коэффициента эластичности для линейной регрессии
Пример расчета величины коэффициента эластичности для линейной регрессии:
Интерпретация значения коэффициента эластичности для линейной регрессии: полученное значение коэффициента эластичности показывает, что с изменением среднедневной заработной платы одного работающего на 1% от своего среднего значения величина расходов на покупку продовольственных товаров изменится на -0.295% в среднем по совокупности.
Далее рассчитаем значение F-критерия Фишера для построенного уравнения парной линейной регрессии. Расчет F-критерия Фишера выполним по формуле:
Формула расчета F-критерия Фишера
Пример расчета F-критерия Фишера: F = 0.1154 / 0.8846*5 = 0.65.
Интерпретация значения F-критерия Фишера. Так как полученное значение F-критерия Фишера меньше табличного критерия, то полученное уравнение парной линейной регрессии является статистически незначимым и не пригодным для описания зависимости доли расходов на покупку продовольственных товаров в общих расходах только от величины среднедневной заработной платой одного работающего. Показатель тесноты связи также признается статистически незначимым.
Онлайн калькулятор расчета уравнения регрессии
В заключении приводим небольшой онлайн калькулятор расчета параметров уравнения линейной регрессии, используя который, Вы можете самостоятельно определить значения соответствующих коэффициентов и построить линейную регрессии онлайн. При заполнении приведенной формы калькулятора внимательно соблюдайте размерность полей, что позволит выполнить построить уравнение регрессии онлайн быстро и точно. В приведенной форме онлайн калькулятора уже содержатся данные условного примера, чтобы пользователь мог посмотреть, как это работает. Для определения значений соответствующих показателей по своим данным просто внесите их в соответствующие поля формы онлайн калькулятора и нажмите кнопку «Выполнить вычисления». При заполнении формы соблюдайте размерность показателей! Дробные числа записываются с точной, а не запятой!
Приведенная форма рассчитана на ввод максимум 10 значений. Если у вас их меньше, то обязательно оставьте «лишние» поля формы пустыми!
Онлайн-калькулятор расчета коэффициента корреляции:
Заказать решение задач на построение уравнения регрессии
Мы можем помочь Вам выполнить построение различных уравнений регрессии, как линейных, так и нелинейных:
Как найти коэффициенты линейного уравнения регрессии
Регрессионный анализ позволяет приближенно определить форму связи между результативным и факторными признаками, а также решить вопрос о том, значима ли эта связь. Вид функции, с помощью которой приближенно выражается форма связи, выбирают заранее, исходя из содержательных соображений или визуального анализа данных. Математическое решение задачи основано на методе наименьших квадратов.
Суть метода наименьших квадратов. Рассмотрим содержание метода на конкретном примере. Пусть имеются данные о сборе хлеба на душу населения по совокупности черноземных губерний. От каких факторов зависит величина этого сбора? Вероятно, определяющее влияние на величину сбора хлеба оказывает величина посева и уровень урожайности. Рассмотрим сначала зависимость величины сбора хлеба на душу населения от размера посева на душу ( столбцы 1 и 2 табл .4 ) Попытаемся представить интересующую нас зависимость с помощью прямой линии. Разумеется, такая линия может дать только приближенное представление о форме реальной статистической связи. Постараемся сделать это приближение наилучшим. Оно будет тем лучше, чем меньше исходные данные будут отличаться от соответствующих точек, лежащих на линии. Степень близости может быть выражена величиной суммы квадратов отклонении, реальных значений от, расположенных на прямой. Использование именно квадратов отклонений (не просто отклонений) позволяет суммировать отклонения различных знаков без их взаимного погашения и дополнительно обеспечивает сравнительно большее внимание, уделяемое большим отклонениям. Именно этот критерий (минимизация суммы квадратов отклонений) положен в основу метода наименьших квадратов.
В вычислительном аспекте метод наименьших квадратов сводится к составлению и решению системы так называемых нормальных уравнений. Исходным этапом для этого является подбор вида функции, отображающей статистическую связь.
Тип функции в каждом конкретном случае можно подобрать путем прикидки на графике исходных данных подходящей, т. е. достаточно хорошо приближающей эти данные, линии. В нашем случае связь между сбором хлеба на душу и величиной посева на душу может быть изображена с помощью прямой линии ( рис. 14 ) и записана в виде
где у—величина сбора хлеба на душу (результативный признак или зависимая переменная); x—величина посева на душу (факторный признак или независимая переменная); a o и a 1 — параметры уравнения, которые могут быть найдены методом наименьших квадратов.
Для нахождения искомых параметров нужно составить систему уравнений, которая в данном случае будет иметь вид
Полученная система может быть решена известным из школьного курса методом Гаусса. Искомые параметры системы из двух нормальных уравнений можно вычислить и непосредственно с помощью последовательного использования нижеприведенных формул:
где y i — i-e значение результативного признака; x i — i-e значение факторного признака; и — средние арифметические результативного и факторного признаков соответственно; n— число значений признака y i , или, что то же самое, число значений признака x i .
Пример 9. Найдем уравнение линейной связи между величиной сбора хлеба (у) и размером посева (х) по данным табл. 4. Проделав необходимые вычисления, получим из (6.17):
Таким образом, уравнение связи, или, как принято говорить, уравнение регрессии, выглядит следующим образом:
Интерпретация коэффициента регрессии. Уравнение регрессии не только определяет форму анализируемой связи, но и показывает, в какой степени изменение одного признака сопровождается изменением другого признака.
Коэффициент при х, называемый коэффициентом регрессии, показывает, на какую величину в среднем изменяется результативный признак у при изменении факторного признака х на единицу.
В примере 9 коэффициент регрессии получился равным 24,58. Следовательно, с увеличением посева, приходящегося на душу, на одну десятину сбор хлеба на душу населения в среднем увеличивается на 24,58 пуда.
Средняя и предельная ошибки коэффициента регрессии. Поскольку уравнения регрессии рассчитываются, как правило, для выборочных данных, обязательно встают вопросы точности и надежности полученных результатов. Вычисленный коэффициент регрессии, будучи выборочным, с некоторой точностью оценивает соответствующий коэффициент регрессии генеральной совокупности. Представление об этой точности дает средняя ошибка коэффициента регрессии ( ), рассчитываемая по формуле
у i , — i-e значение результативного признака; ŷ i — i-e выравненное значение, полученное из уравнения (6.15); x i —i-e значение факторного признака; σ x —среднее квадратическое отклонение х; n — число значений х или, что то же самое, значений у; m—число факгорных признаков (независимых переменных).
В формуле (6.18), в частности, формализовано очевидное положение: чем больше фактические значения отклоняются от выравненных, тем большую ошибку следует ожидать; чем меньше число наблюдений, на основе которых строится уравнение, тем больше будет ошибка.
Средняя ошибка коэффициента регрессии является основой для расчета предельной ошибки. Последняя показывает, в каких пределах находится истинное значение коэффициента регрессии при заданной надежности результатов. Предельная ошибка коэффициента регрессии вычисляется аналогично предельной ошибке средней арифметической (см. гл. 5), т. е. как t где t—величина, числовое значение которой определяется в зависимости от принятого уровня надежности.
Пример 10. Найти среднюю и предельную ошибки коэффициента регрессии, полученного в примере 9.
Для расчета прежде всего подсчитаем выравненные значения ŷ i для чего в уравнение регрессии, полученное в примере 9, подставим конкретные значения x i :
ŷ i = 17,6681 +24,5762*0,91 = 40,04 и т. д.
Затем вычислим отклонения фактических значений у i , от выравненных и их квадраты
Далее, подсчитав средний по черноземным губерниям посев на душу ( =0,98), отклонения фактических значений x i от этой средней, квадраты отклонений и среднее квадратическое отклонение , получим все необходимые составляющие формул (618) и (619):
Таким образом, средняя ошибка коэффициента регрессии равна 2,89, что составляет 12% от вычисленного коэффициента
Задавшись уровнем надежности, равным 0,95, найдем по табл. 1 приложения соответствующее ему значение t=1,96, рассчитаем предельную ошибку 1,96*2,89=5,66 и пределы коэффициента регрессии для принятого уровня надежности ( В случае малых выборок величина t находится из табл. 2 приложения. ). Нижняя граница коэффициента регрессии равна 24,58-5,66=18,92, а верхняя граница 24,58+5,66=30,24
Средняя квадратическая ошибка линии регрессии. Уравнение регрессии представляет собой функциональную связь, при которой по любому значению х можно однозначно определить значение у. Функциональная связь лишь приближенно отражает связь реальную, причем степень этого приближения может быть различной и зависит она как от свойств исходных данных, так и от выбора вида функции, по которой производится выравнивание.
На рис. 15 представлены два различных случая взаимоотношения между двумя признаками. В обоих случаях предполагаемая связь описывается одним и тем же уравнением, но во втором случае соотношение между признаками х и у достаточно четко выражено и уравнение, по-видимому, довольно хорошо описывает это соотношение, тогда как в первом случае сомнительно само наличие сколько-нибудь закономерного соотношения между признаками. И в том, и в другом случаях, несмотря на их существенное различие, метод наименьших квадратов дает одинаковое уравнение, поскольку этот метод нечувствителен к потенциальным возможностям исходного материала вписаться в ту или иную схему. Кроме того, метод наименьших квадратов применяется для расчета неизвестных параметров заранее выбранного вида функции, и вопрос о выборе наиболее подходящего для конкретных данных вида функции в рамках этого метода не ставится и не решается. Таким образом, при пользовании методом наименьших квадратов открытыми остаются два важных вопроса, а именно: существует ли связь и верен ли выбор вида функции, с помощью которой делается попытка описать форму связи.
Чтобы оценить, насколько точно уравнение регрессии описывает реальные соотношения между переменными, нужно ввести меру рассеяния фактических значений относительно вычисленных с помощью уравнения. Такой мерой служит средняя квадратическая ошибка регрессионного уравнения, вычисляемая по приведенной выше формуле (6.19).
Пример 11. Определить среднюю квадратическую ошибку уравнения, полученного в примере 9.
Промежуточные расчеты примера 10 дают нам среднюю квадратическую ошибку уравнения. Она равна 4,6 пуда.
Этот показатель аналогичен среднему квадратическому отклонению для средней. Подобно тому, как по величине среднего квадратического отклонения можно судить о представительности средней арифметической (см. гл. 5), по величине средней квадратической ошибки регрессионного уравнения можно сделать вывод о том, насколько показательна для соотношения между признаками та связь, которая выявлена уравнением. В каждом конкретном случае фактическая ошибка может оказаться либо больше, либо меньше средней. Средняя квадратическая ошибка уравнения показывает, насколько в среднем мы ошибемся, если будем пользоваться уравнением, и тем самым дает представление о точности уравнения. Чем меньше σ y.x , тем точнее предсказание линии регрессии, тем лучше уравнение регрессии описывает существующую связь. Показатель σ y.x позволяет различать случаи, представленные на рис. 15. В случае б) он окажется значительно меньше, чем в случае а). Величина σ y.x зависит как от выбора функции, так и от степени описываемой связи.
Варьируя виды функций для выравнивания и оценивая результаты с помощью средней квадратической ошибки, можно среди рассматриваемых выбрать лучшую функцию, функцию с наименьшей средней ошибкой. Но существует ли связь? Значимо ли уравнение регрессии, используемое для отображения предполагаемой связи? На эти вопросы отвечает определяемый ниже критерий значи-мости регрессии.
Мерой значимости линии регрессии может служить следующее соотношение:
где ŷ i —i-e выравненное значение; —средняя арифметическая значений y i ; σ y.x —средняя квадратическая ошибка регрессионного уравнения, вычисляемая по формуле (6.19); n—число сравниваемых пар значений признаков; m—число факторных признаков.
Действительно, связь тем больше, чем значительнее мера рассеяния признака, обусловленная регрессией, превосходит меру рассеяния отклонений фактических значений от выравненных.
Соотношение (6.20) позволяет решить вопрос о значимости регрессии. Регрессия значима, т. е. между признаками существует линейная связь, если для данного уровня значимости вычисленное значение F ф [m,n-(m+1)] превышает критическое значение F кр [m,n-(m+1)], стоящее на пересечении m-го столбца и [n—(m+1)]-й строки специальной таблицы ( см. табл. 4 приложения ).
Пример 12. Выясним, связаны ли сбор хлеба на душу населения и посев на душу населения линейной зависимостью.
Воспользуемся F-критерием значимости регрессии. Подставив в формулу (6.20) данные табл. 4 и результат примера 10, получим
Обращаясь к таблице F-распределения для Р=0,95 (α=1—Р=0,5) и учитывая, что n=23, m =1, в табл. 4А приложения на пересечения 1-го столбца и 21-й строки находим критическое значение F кр , равное 4,32 при степени надежности Р=0,95. Поскольку вычисленное значение F ф существенно превосходит по величине F кр , то обнаруженная линейная связь существенна, т. е. априорная гипотеза о наличии линейной связи подтвердилась. Вывод сделан при степени надежности P=0,95. Между прочим, вывод в данном случае останется прежним, если надежность повысить до Р=0,99 (соответствующее значение F кр =8,02 по табл. 4Б приложения для уровня значимости α=0,01).
Коэффициент детерминации. С помощью F-критерия мы Установили, что существует линейная зависимость между величиной сбора хлеба и величиной посева на душу. Следовательно, можно утверждать, что величина сбора хлеба, приходящегося на душу, линейно зависит от величины посева на душу. Теперь уместно поставить уточняющий вопрос — в какой степени величина посева на душу определяет величину сбора хлеба на душу? На этот вопрос можно ответить, рассчитав, какая часть вариации результативного признака может быть объяснена влиянием факторного признака.
Оно показывает долю разброса, учитываемого регрессией, в общем разбросе результативного признака и носит название коэффициента детерминации. Этот показатель, равный отношению факторной вариации к полной вариации признака, позволяет судить о том, насколько «удачно» выбран вид функции ( Отметим, что по смыслу коэффициент детерминации в регрессионном анализе соответствует квадрату корреляционного отношения для корреляционной таблицы (см. § 2). ). Проведя расчеты, основанные на одних и тех же исходных данных, для нескольких типов функций, мы можем из них выбрать такую, которая дает наибольшее значение R 2 и, следовательно, в большей степени, чем другие функции, объясняет вариацию результативного признака. Действительно, при расчете R 2 для одних и тех же данных, но разных функций знаменатель выражения (6.21) остается неизменным, а числитель показывает ту часть вариации результативного признака, которая учитывается выбранной функцией. Чем больше R 2 , т. е. чем больше числитель, тем больше изменение факторного признака объясняет изменение результативного признака и тем, следовательно, лучше уравнение регрессии, лучше выбор функции.
Наконец, отметим, что введенный ранее, при изложении методов корреляционного анализа, коэффициент детерминации совпадает с определенным здесь показателем, если выравнивание производится По прямой линии. Но последний показатель (R 2 ) имеет более широкий спектр применения и может использоваться в случае связи, отличной от линейной ( см. § 4 данной главы ).
Пример 13. Рассчитать коэффициент детерминации для уравнения, полученного в примере 9.
Вычислим R 2 , воспользовавшись формулой (6.21) и данными табл. 4:
Итак, уравнение регрессии почти на 78% объясняет колебания сбора хлеба на душу. Это немало, но, По-видимому, можно улучшить модель введением в нее еще одного фактора.
Случай двух независимых переменных. Простейший случай множественной регрессии. В предыдущем изложении регрессионного анализа мы имели дело с двумя признаками — результативным и факторным. Но на результат действует обычно не один фактор, а несколько, что необходимо учитывать для достаточно полного анализа связей.
В математической статистике разработаны методы множественной регрессии ( Регрессия называется множественной, если число независимых переменных, учтенных в ней, больше или равно двум. ), позволяющие анализировать влияние на результативный признак нескольких факторных. К рассмотрению этих методов мы и переходим.
Возвратимся к примеру 9. В нем была определена форма связи между величиной сбора хлеба на душу и размером посева на душу. Введем в анализ еще один фактор — уровень урожайности (см. столбец З табл. 4). Без сомнения, эта переменная влияет на сбор хлеба на душу. Но в какой степени влияет? Насколько обе независимые переменные определяют сбор хлеба на душу в черноземных губерниях? Какая из переменных — посев на душу или урожайность — оказывает определяющее влияние на сбор хлеба? Попытаемся ответить на эти вопросы.
После добавления второй независимой переменной уравнение регрессии будет выглядеть так:
где у—сбор хлеба на душу; х 1 —размер посева на душу; x 2 —урожай с десятины (в пудах); а 0 , а 1 , а 2 —параметры, подлежащие определению.
Для нахождения числовых значений искомых параметров, как и в случае одной независимой переменной, пользуются методом наименьших квадратов. Он сводится к составлению и решению системы нормальных уравнений, которая имеет вид
Когда система состоит из трех и более нормальных уравнений, решение ее усложняется. Существуют стандартные программы расчета неизвестных параметров регрессионного уравнения на ЭВМ. При ручном счете можно воспользоваться известным из школьного курса методом Гаусса.
Пример 14. По данным табл. 4 описанным способом найдем параметры a 0 , а 1 , а 2 уравнения (6.22). Получены следующие результаты: a 2 =0,3288, a 1 =28,7536, a 0 =-0,2495.
Таким образом, уравнение множественной регрессии между величиной сбора хлеба на душу населения (у), размером посева на душу (x 1 ) и уровнем урожайности (х 2 ) имеет вид:
у=-0,2495+28,7536x 1 +0,3288x 2 .
Интерпретация коэффициентов уравнения множественной регрессии. Коэффициент при х 1 в полученном уравнении отличается от аналогичного коэффициента в уравнении примера 9.
Коэффициент при независимой переменной в уравнении простой регрессии отличается от коэффициента при соответствующей переменной в уравнении множественной регрессии тем, что в последнем элиминировано влияние всех учтенных в данном уравнении признаков.
Коэффициенты уравнения множественной регрессии поэтому называются частными или чистыми коэффициентами регрессии.
Частный коэффициент множественной регрессии при х 1 показывает, что с увеличением посева на душу на 1 дес. и при фиксированной урожайности сбор хлеба на душу населения вырастает в среднем на 28,8 пуда. Частный коэффициент при x 2 показывает, что при фиксированном посеве на душу увеличение урожая на единицу, т. е. на 1 пуд с десятины, вызывает в среднем увеличение сбора хлеба на душу на 0,33 пуда. Отсюда можно сделать вывод, что увеличение сбора хлеба в черноземных губерниях России идет, в основном, за счет расширения посева и в значительно меньшей степени—за счет повышения урожайности, т. е. экстенсивная форма развития зернового хозяйства является господствующей.
Введение переменной х 2 в уравнение позволяет уточнить коэффициент при х 1 . Конкретно, коэффициент оказался выше (28,8 против 24,6), когда в изучаемой связи вычленилось влияние урожайности на сбор хлеба.
Однако выводы, полученные в результате анализа коэффициентов регрессии, не являются пока корректными, поскольку, во-первых, не учтена разная масштабность факторов, во-вторых, не выяснен вопрос о значимости коэффициента a 2 .
Величина коэффициентов регрессии изменяется в зависимости от единиц измерения, в которых представлены переменные. Если переменные выражены в разном масштабе измерения, то соответствующие им коэффициенты становятся несравнимыми. Для достижения сопоставимости коэффициенты регрессии исходного уравнения стандартизуют, взяв вместо исходных переменных их отношения к собственным средним квадратическим отклонениям. Тогда уравнение (6.22) приобретает вид
Сравнивая полученное уравнение с уравнением (6.22), определяем стандартизованные частные коэффициенты уравнения, так называемые бета-коэффициенты, по формулам:
где β 1 и β 2 —бета-коэффициенты; а 1 и а 2 —коэффициенты регрессии исходного уравнения; σ у , , и — средние квадратические отклонения переменных у, х 1 и х 2 соответственно.
Вычислив бета-коэффициенты для уравнения, полученного в примере 14:
видим, что вывод о преобладании в черноземной полосе россии экстенсивной формы развития хозяйства над интенсивной остается в силе, так как β 1 значительно больше, чем β 2 .
Оценка точности уравнения множественной регрессии.
Точность уравнения множественной регрессии, как и в случае уравнения с одной независимой переменной, оценивается средней квадратической ошибкой уравнения. Обозначим ее , где подстрочные индексы указывают, что результативным признаком в уравнении является у, а факторными признаками х 1 и x 2 . Для расчета средней квадратической ошибки уравнения множественной регрессии применяется приведенная выше формула (6.19).
Пример 15. Оценим точность полученного в примере 14 уравнения регрессии.
Воспользовавшись формулой (6.19) и данными табл. 4, вычислим среднюю квадратическую ошибку уравнения:
Оценка полезности введения дополнительной переменной. Точность уравнения регрессии тесно связана с вопросом ценности включения дополнительных членов в это уравнение.
Сравним средние квадратические ошибки, рассчитанные для уравнения с одной переменной х 1 (пример 11) и для уравнения с двумя независимыми переменными х 1 и х 2 . Включение в уравнение новой переменной (урожайности) уменьшило среднюю квадратическую ошибку почти вдвое.
Можно провести сравнение ошибок с помощью коэффициентов вариации
где σ f —средняя квадратическая ошибка регрессионного уравнения; —средняя арифметическая результативного признака.
Для уравнения, содержащего одну независимую переменную:
Для уравнения, содержащего две независимые переменные:
Итак, введение независимой переменной «урожайность» уменьшило среднюю квадратическую ошибку до величины порядка 7,95% среднего значения зависимой переменной.
Наконец, по формуле (6.21) рассчитаем коэффициент детерминации
Он показывает, что уравнение регрессии на 81,9% объясняет колебания сбора хлеба на душу населения. Сравнивая полученный результат (81,9%) с величиной R 2 для однофакторного уравнения (77,9%), видим, что включение переменной «урожайность» заметно увеличило точность уравнения.
Таким образом, сравнение средних квадратических ошибок уравнения, коэффициентов вариации, коэффициентов детерминации, рассчитанных до и после введения независимой переменной, позволяет судить о полезности включения этой переменной в уравнение. Однако следует быть осторожными в выводах при подобных сравнениях, поскольку увеличение R 2 или уменьшение σ и V σ не всегда имеют приписываемый им здесь смысл. Так, увеличение R 2 может объясняться тем фактом, что число рассматриваемых параметров в уравнении приближается к числу объектов наблюдения. Скажем, весьма сомнительными будут ссылки на увеличение R 2 или уменьшение σ, если в уравнение вводится третья или четвертая независимая переменная и уравнение строится на данных по шести, семи объектам.
Полезность включения дополнительного фактора можно оценить с помощью F-критерия.
Частный F-критерий показывает степень влияния дополнительной независимой переменной на результативный признак и может использоваться при решении вопроса о добавлении в уравнение или исключении из него этой независимой переменной.
Разброс признака, объясняемый уравнением регрессии (6.22), можно разложить на два вида: 1) разброс признака, обусловленный независимой переменной х 1 , и 2) разброс признака, обусловленный независимой переменной x 2 , когда х 1 уже включена в уравнение. Первой составляющей соответствует разброс признака, объясняемый уравнением (6.15), включающим только переменную х 1 . Разность между разбросом признака, обусловленным уравнением (6.22), и разбросом признака, обусловленным уравнением (6.15), определит ту часть разброса, которая объясняется дополнительной независимой переменной x 2 . Отношение указанной разности к разбросу признака, регрессией не объясняемому, представляет собой значение частного критерия. Частный F-критерий называется также последовательным, если статистические характеристики строятся при последовательном добавлении переменных в регрессионное уравнение.
Пример 16. Оценить полезность включения в уравнение регрессии дополнительной переменной «урожайность» (по данным и результатам примеров 12 и 15).
Разброс признака, объясняемый уравнением множественной регрессии и рассчитываемый как сумма квадратов разностей выравненных значений и их средней, равен 1623,8815. Разброс признака, объясняемый уравнением простой регрессии, составляет 1545,1331.
Разброс признака, регрессией не объясняемый, определяется квадратом средней квадратической ошибки уравнения и равен 10,9948 (см. пример 15).
Воспользовавшись этими характеристиками, рассчитаем частный F-критерий
С уровнем надежности 0,95 (α=0,05) табличное значение F (1,20), т. е. значение, стоящее на пересечении 1-го столбца и 20-й строки табл. 4А приложения, равно 4,35. Рассчитанное значение F ф значительно превосходит табличное, и, следовательно, включение в уравнение переменной «урожайность» имеет смысл.
Таким образом, выводы, сделанные ранее относительно коэффициентов регрессии, вполне правомерны.
Важным условием применения к обработке данных метода множественной регрессии является отсутствие сколько-нибудь значительной взаимосвязи между факторными признаками. При практическом использовании метода множественной регрессии, прежде чем включать факторы в уравнение, необходимо убедиться в том, что они независимы.
Если один из факторов зависит линейно от другого, то система нормальных уравнений, используемая для нахождения параметров уравнения, не разрешима. Содержательно этот факт можно толковать так: если факторы х 1 и x 2 связаны между собой, то они действуют на результативный признак у практически как один фактор, т. е. сливаются воедино и их влияние на изменение у разделить невозможно. Когда между независимыми переменными уравнения множественной регрессии имеется линейная связь, следствием которой является неразрешимость системы нормальных уравнений, то говорят о наличии мультиколлинеарности.
На практике вопрос о наличии или об отсутствии мультиколлинеарности решается с помощью показателей взаимосвязи. В случае двух факторных признаков используется парный коэффициент корреляции между ними: если этот коэффициент по абсолютной величине превышает 0,8, то признаки относят к числу мультиколлинеарных. Если число факторных признаков больше двух, то рассчитываются множественные коэффициенты корреляции. Фактор признается мультиколлинеарным, если множественный коэффициент корреляции, характеризующий совместное влияние на этот фактор остальных факторных признаков, превзойдет по величине коэффициент множественной корреляции между результативным признаком и совокупностью всех независимых переменных.
Самый естественный способ устранения мультиколлинеарности — исключение одного из двух линейно связанных факторных признаков. Этот способ прост, но не всегда приемлем, так как подлежащий исключению фактор может оказывать на зависимую переменную особое влияние. В такой ситуации применяются более сложные методы избавления от мультиколлинеарности ( См.: Мот Ж. Статистические предвидения и решения на предприятии. М., 1966; Ковалева Л. Н. Многофакторное прогнозирование на основе рядов динамики. М., 1980. ).
Выбор «наилучшего» уравнения регрессии. Эта проблема связана с двойственным отношением к вопросу о включении в регрессионное уравнение независимых переменных. С одной стороны, естественно стремление учесть все возможные влияния на результативный признак и, следовательно, включить в модель полный набор выявленных переменных. С другой стороны, возрастает сложность расчетов и затраты, связанные с получением максимума информации, могут оказаться неоправданными. Нельзя забывать и о том, что для построения уравнения регрессии число объектов должно в несколько раз превышать число независимых переменных. Эти противоречивые требования приводят к необходимости компромисса, результатом которого и является «наилучшее» уравнение регрессии. Существует несколько методов, приводящих к цели: метод всех возможных регрессий, метод исключения, метод включения, шаговый регрессионный и ступенчатый регрессионный методы.
Метод всех возможных регрессий заключается в переборе и сравнении всех потенциально возможных уравнений. В качестве критерия сравнения используется коэффициент детерминации R 2 . «Наилучшим» признается уравнение с наибольшей величиной R 2 . Метод весьма трудоемок и предполагает использование вычислительных машин.
Методы исключения и включения являются усовершенствованными вариантами предыдущего метода. В методе исключения в качестве исходного рассматривается регрессионное уравнение, включающее все возможные переменные. Рассчитывается частный F-критерий для каждой из переменных, как будто бы она была последней переменной, введенной в регрессионное уравнение. Минимальная величина частного F-критерия (F min ) сравнивается с критической величиной (F кр ), основанной на заданном исследователем уровне значимости. Если F min >F кр , то уравнение остается без изменения. Если F min кр , то переменная, для которой рассчитывался этот частный F-критерий, исключается. Производится перерасчет уравнения регрессии для оставшихся переменных, и процедура повторяется для нового уравнения регрессии. Исключение из рассмотрения уравнений с незначимыми переменными уменьшает объем вычислений, что является достоинством этого метода по сравнению с предыдущим.
Метод включения состоит в том, что в уравнение включаются переменные по степени их важности до тех пор, пока уравнение не станет достаточно «хорошим». Степень важности определяется линейным коэффициентом корреляции, показывающим тесноту связи между анализируемой независимой переменной и результативным признаком: чем теснее связь, тем больше информации о результирующем признаке содержит данный факторный признак и тем важнее, следовательно, введение этого признака в уравнение.
Процедура начинается с отбора факторного признака, наиболее тесно связанного с результативным признаком, т. е. такого факторного признака, которому соответствует максимальный по величине парный линейный коэффициент корреляции. Далее строится линейное уравнение регрессии, содержащее отобранную независимую переменную. Выбор следующих переменных осуществляется с помощью частных коэффициентов корреляции, в которых исключается влияние вошедших в модель факторов. Для каждой введенной переменной рассчитывается частный F-критерий, по величине которого судят о том, значим ли вклад этой переменной. Как только величина частного F-критерия, относящаяся к очередной переменной, оказывается незначимой, т. е. эффект от введения этой переменной становится малозаметным, процесс включения переменных заканчивается. Метод включения связан с меньшим объемом вычислений, чем предыдущие методы. Но при введении новой переменной нередко значимость включенных ранее переменных изменяется. Метод включения этого не учитывает, что является его недостатком. Модификацией метода включения, исправляющей этот недостаток, является шаговый регрессионный метод.
Шаговый регрессионный метод кроме процедуры метода включения содержит анализ переменных, включенных в уравнение на предыдущей стадии. Потребность в таком анализе возникает в связи с тем, что переменная, обоснованно введенная в уравнение на ранней стадии, может оказаться лишней из-за взаимосвязи ее с переменными, позднее включенными в уравнение. Анализ заключается в расчете на каждом этапе частных F-критериев для каждой переменной уравнения и сравнении их с величиной F кр , точкой F-распределения, соответствующей заданному исследователем уровню значимости. Частный F-критерий показывает вклад переменной в вариацию результативного признака в предположении, что она вошла в модель последней, а сравнение его с F кр позволяет судить о значимости рассматриваемой переменной с учетом влияния позднее включенных факторов. Незначимые переменные из уравнения исключаются.
Рассмотренные методы предполагают довольно большой объем вычислений и практически неосуществимы без ЭВМ. Для реализации ступенчатого регрессионного метода вполне достаточно малой вычислительной техники.
Ступенчатый регрессионный метод включает в себя такую последовательность действий. Сначала выбирается наиболее тесно связанная с результативным признаком переменная и составляется уравнение регрессии. Затем находят разности фактических и выравненных значений и эти разности (остатки) рассматриваются как значения результативной переменной. Для остатков подбирается одна из оставшихся независимых переменных и т. д. На каждой стадии проверяется значимость регрессии. Как только обнаружится незначимость, процесс прекращается и окончательное уравнение получается суммированием уравнений, полученных на каждой стадии за исключением последней.
Ступенчатый регрессионный метод менее точен, чем предыдущие, но не столь громоздок. Он оказывается полезным в случаях, когда необходимо внести содержательные правки в уравнение. Так, для изучения факторов, влияющих на цены угля в Санкт-Петербурге в конце XIX— начале XX в., было получено уравнение множественной регрессии. В него вошли следующие переменные: цены угля в Лондоне, добыча угля в России и экспорт из России. Здесь не обосновано появление в модели такого фактора, как добыча угля, поскольку Санкт-Петербург работал исключительно на импортном угле. Модели легко придать экономический смысл, если независимую переменную «добыча» заменить независимой переменной «импорт». Формально такая замена возможна, поскольку между импортом и добычей существует тесная связь. Пользуясь ступенчатым методом, исследователь может совершить эту замену, если предпочтет содержательно интерпретируемый фактор.
§ 4. Нелинейная регрессия и нелинейная корреляция
Построение уравнений нелинейной регрессии. До сих пор мы, в основном, изучали связи, предполагая их линейность. Но не всегда связь между признаками может быть достаточно хорошо представлена линейной функцией. Иногда для описания существующей связи более пригодными, а порой и единственно возможными являются более сложные нелинейные функции. Ограничимся рассмотрением наиболее простых из них.
Одним из простейших видов нелинейной зависимости является парабола, которая в общем виде может быть представлена функцией (6.2):
Неизвестные параметры а 0 , а 1 , а 2 находятся в результате решения следующей системы уравнений:
Дает ли преимущества описание связи с помощью параболы по сравнению с описанием, построенным по гипотезе линейности? Ответ на этот вопрос можно получить, рассчитав последовательный F-критерий, как это делалось в случае множественной регрессии (см. пример 16).
На практике для изучения связей используются полиномы более высоких порядков (3-го и 4-го порядков). Составление системы, ее решение, а также решение вопроса о полезности повышения порядка функции для этих случаев аналогичны описанным. При этом никаких принципиально новых моментов не возникает, но существенно увеличивается объем расчетов.
Кроме класса парабол для анализа нелинейных связей можно применять и другие виды функций. Для расчета неизвестных параметров этих функций рекомендуется использовать метод наименьших квадратов, как наиболее мощный и широко применяемый.
Однако метод наименьших квадратов не универсален, поскольку он может использоваться только при условии, что выбранные для выравнивания функции линейны по отношению к своим параметрам. Не все функции удовлетворяют этому условию, но большинство применяемых на практике с помощью специальных преобразований могут быть приведены к стандартной форме функции с линейными параметрами.
Рассмотрим некоторые простейшие способы приведения функций с нелинейными параметрами к виду, который позволяет применять к ним метод наименьших квадратов.
Функция не является линейной относительно своих параметров.
Прологарифмировав обе части приведенного равенства
получим функцию, линейную относительно своих новых параметров:
Кроме логарифмирования для приведения функций к нужному виду используют обратные величины.
с помощью следующих переобозначений:
может быть приведена к виду
Подобные преобразования расширяют возможности использования метода наименьших квадратов, увеличивая число функций, к которым этот метод применим.
Измерение тесноты связи при криволинейной зависимости. Рассмотренные ранее линейные коэффициенты корреляции оценивают тесноту взаимосвязи при линейной связи между признаками. При наличии криволинейной связи указанные меры связи не всегда приемлемы. Разберем подобную ситуацию на примере.
Пример 17. В 1-м и 2-м столбцах табл. 5 приведены значения результативного признака у и факторного признака х (данные условные). Поставив вопрос о тесноте связи между ними, рассчитаем парный линейный коэффициент корреляции по формуле (6.3). Он оказался равным нулю, что свидетельствует об отсутствии линейной связи. Тем не менее связь между признаками существует, более того, она является функциональной и имеет вид
Для измерения тесноты связи при криволинейной зависимости используется индекс корреляции, вычисляемый по формуле
где у i —i-e значение результативного признака; ŷ i —i-e выравненное значение этого признака; —среднее арифметическое значение результативного признака.
Числитель формулы (6.27) характеризует разброс выравненных значений результативного признака. Поскольку изменения выравненных, т. е. вычисленных по уравнению регрессии, значений признака происходят только в результате изменения факторного признака х. то числитель измеряет разброс результативного признака, обусловленный влиянием на него факторного признака. Знаменатель же измеряет разброс признака-результата, который определен влиянием на него всех факторов, в том числе и учтенного. Таким образом, индекс корреляции оценивает участие данного факторного признака в общем действии всего комплекса факторов, вызывающих колеблемость результативного признака, тем самым определяя тесноту зависимости признака у от признака х. При этом, если признак х не вызывает никаких изменений признака у, то числитель и, следовательно, индекс корреляции равны 0. Если же линия регрессии полностью совпадает с фактическими данными, т. е. признаки связаны функционально, как в примере 17, то индекс корреляции равен 1. В случае линейной зависимости между х и у индекс корреляции численно равен линейному коэффициенту корреляции г. Квадрат индекса корреляции совпадает с введенным ранее (6.21) коэффициентом детерминации. Если же вопрос о форме связи не ставится, то роль коэффициента детерминации играет квадрат корреляционного отношения η 2 y/x (6.12).
Таковы основные принципы и условия, методика и техника применения корреляционного и регрессионного анализа. Их подробное рассмотрение обусловлено тем, что они являются высокоэффективными и потому очень широко применяемыми методами анализа взаимосвязей в объективном мире природы и общества. Корреляционный и регрессионный анализ широко и успешно применяются и в исторических исследованиях.
http://www.rnz.ru/econometrica/regressija.php
http://masters.donntu.org/2005/kita/tokarev/library/linreg.htm



