Как минимизировать ошибки первого и второго рода

Всякий раз, когда кто-то начинает изучать машинное обучение/статистику, первая концепция, с которой он сталкивается, — это проверка гипотез, которая, конечно же, является наиболее фундаментальной концепцией, от которой зависят все концепции машинного обучения. Я знаю, что это очень сбивает с толку, если только вы не видели болливудский фильм.😊. Кто не любит фильмы Болливуда?

Я понял эту идею проверки гипотез и ее различных ошибок, основанных на сценарии «Судья и преступник». В этой статье говорится о различных сценариях в этой ситуации, является ли обвиняемый преступником или нет, применительно к проверке гипотез.

Прежде чем вы продолжите читать эту статью, я должен сказать вам, что вам нужно иметь немного предварительных знаний о статистической проверке гипотез.

Теперь всегда говорят, что

«Обвиняемый не является преступником, если нет достаточных доказательств, доказывающих его вину (осуждения)». Теперь представьте, что вы судья, назначенный для слушания дела. Можно надеть судейскую фуражку. Все нормально. 😊

Теперь ваша задача собрать достаточно улик, чтобы доказать, что этот парень не преступник. Теперь вопрос, почему вы как судья должны это делать? Я приду к этому ответу сейчас, как показано ниже. Теперь есть 4 возможности. Вы, должно быть, угадали правильно.

Возможно, что обвиняемый может быть преступником или не быть преступником в действительности. Также решение, принятое вами как судьей, может быть в пользу обвиняемого или против обвиняемого.

Теперь справедливость восторжествует, если: (Ситуация I)

1.1. Обвиняемый преступник, и вы осудили его.

1.2. Обвиняемый не преступник, и вы сделали его невиновным.

Но другой плохой вывод, если: (Ситуация II)

2.1. Обвиняемый преступник, но вы освободили его. (Плохая ситуация I)

2.2. Обвиняемый не преступник, но вы осудили его. (Плохая ситуация 2)

Теперь, как судья, вы можете погладить себя, если попадете в ситуацию I. Но, к сожалению, допустим, вы попали в ситуацию II; Как вы думаете, вы сделали ошибку/ошибку? Если да, то какой из двух более опасен, 2.1 или 2.2.

Ситуация 2.2 более опасна. Не так ли?

Более несправедливо осуждать невиновного (2.2), чем освобождать преступника (2.1). Любая судебная система работает на этом понятии, по крайней мере индийская судебная система.😊. Основная идея, по крайней мере, невиновный парень не должен быть осужден. Вы так не думаете?

Теперь мы доведем эту идею до статистической гипотезы и ее ошибок. Сравните картинку выше с картинкой ниже. Это просто обобщение любой случайной ситуации (не то что в сценарии «Судья и преступник»).

В настоящее время,

α означает ошибку, которую вы допустили, отвергнув H0 (нулевую гипотезу/статус-кво), когда в действительности она должна была быть правдой или должна была быть принята.

ß означает ошибку, которую вы допустили, приняв H0 (нулевая гипотеза/статус-кво), хотя на самом деле она должна была быть ложной или должна была быть отвергнута.

Как указывалось ранее, бета более опасна, чем альфа. Не так ли?

Теперь, поскольку статус-кво был отвергнут, поскольку у вас есть достаточно доказательств, чтобы доказать это, хотя на самом деле это правда. Вы говорите это как «уровень значимости». Как правило, он установлен на 0,05, что означает, насколько важно для вас отказаться от статус-кво на основе доказательств. Теперь очевидно, что он должен быть как можно ниже, чтобы отказаться от статус-кво.

Хм… Стоп здесь… Думайте об этом какое-то время, пока это не проникнет в ваш разум.

Помните, что обвиняемый не является преступником (статус-кво), если его не отвергают, он не является преступником. (доказанная судимость)

Теперь возникает вопрос; Как уменьшить количество ошибок α?

Очень простой. Максимально уменьшите уровень α, чтобы быть уверенным, что вы не совершаете ошибок. Посмотрите на нормальное распределение ниже:

Если вы стремитесь уменьшить область отклонения, вы увеличиваете вероятность принятия H0 (нулевая гипотеза/статус-кво). Другими словами, вы увеличиваете вероятность принятия H0. Вы должны делать это, когда хотите быть увереннее, чем просто 95% (95% — общепринятая норма).

Теперь спросите себя, что представляет собой ß?

Что вы думаете? Думайте, что судья осуждает невиновного парня. Вам не кажется, что судья недостаточно все изучил, прежде чем вынести решение?

Если да, не думаете ли вы, что это отражает уровень выступления (в данном случае судьи). На самом деле он недостаточно изучил, вероятно, потому, что не встречал достаточного количества подобных случаев. Возможно, это уникальный для него случай. Если бы он был разоблачен в достаточном количестве подобных случаев, он, возможно, не осудил бы невиновного парня.

Хммм… Стоп здесь… Подумайте об этом какое-то время, пока оно не проникнет в ваш разум.

Теперь возникает вопрос; Как уменьшить число ß-ошибок?

Простой ответ — увеличение пространства выборки. Я еще раз повторю: «Если судья будет сталкиваться с достаточным количеством подобных дел, его работа улучшится».

Так так так…

Возможно, вас ввело в заблуждение мое заявление, когда я сказал, что ß более опасен, чем α. Как я могу это сказать? Ты прав.

Фактический ответ: «Это зависит от того, с каким делом вы имеете дело».

В этом случае «Судья и преступник» опаснее ß, чем α.

Можете ли вы представить себе ситуацию, когда иначе, т. е. α более опасен, чем ß? Ваши мысли приветствуются.

Перенос знаний от выборочной
совокупности к генеральной может быть
осуществлен лишь с некоторой вероятностью
P{Θ},
т.е. суждение о генеральной совокупности
носит вероятностный характер и содержит
элемент риска (1-P{Θ}).
Суждения о свойствах генеральной
совокупности называются статистическими
гипотезами. Их
проверка осуществляется с помощью
статистических
критериев, назначаемых
в зависимости от формулировки гипотезы
H.

Основная выдвинутая
гипотеза называется нуль-гипотеза
(H₀).
Противоречащие ей
гипотезы H_i
называют альтернативными,
или конкурирующими.

Нуль-гипотеза
Н₀:
между обеими
выборками нет существенной разницы,
обе они принадлежат одной генеральной
совокупности, а имеющиеся различия
обусловлены случайным характером
выборок, например, влиянием случайных
ошибок. В этом случае любые оценки,
рассчитанные по этим двум выборкам,
будут оценками одних и тех же генеральных
(истинных) значений; тогда в большинстве
случаев имеет смысл объединить обе
выборки в одну, увеличив тем самым число
степеней свободы.

Противоположная, или
альтернативная
гипотеза H₁
различия объясняются не случайностью,
а существом дела. Выборки относятся к
разным генеральным совокупностям.

Поскольку проверка гипотез
ведется по выборке, то могут возникнуть
ошибки двух родов. Если будет отвергнута
правильная гипотеза,
то совершается ошибка
первого рода, если
будет допущена
неправильная гипотеза,
то совершается ошибка
второго рода.

Вероятность допустить
ошибку первого рода называется уровнем
значимости и
обозначается α.
Область, отвечающая вероятности α,
называется критической, а дополняющая
ее область, вероятность попадания в
некоторую P{Θ_α}=1-α,
называется областью
правдоподобных
статистических
критериев Cr.

Вероятность ошибки второго
рода обозначается β, а величина P{Θ_β}=1-β
называется мощностью
критерия. Чем больше
эта мощность, тем меньше вероятность
совершить ошибку второго рода.

В задачах статистического
моделирования обычно устанавливают
некоторое значение α, и статистический
критерий Cr
выбирают так, чтобы минимизировать β.

Обычная процедура проверки
гипотез заключается в следующем:

1) по выборочным данным
рассчитывается критерий проверки;

2) полученное значение
критерия сравнивают с критическим
значением, находимым из таблиц. Критическое
значение каждого конкретного критерия
определяется уровнем значимости и
числом степеней свободы, по которому
были рассчитаны величины, входящие в
критерий.

Критерий Пирсона χ².
Для проверки гипотезы о соответствии
эмпирического распределения СВ
теоретическому наиболее часто применяют
критерий Пирсона
χ².
Суть этой проверки сводится к следующему.
Предположим, что за время испытаний t
выборки объемом n
отказало d
изделий, причем отказы фиксировались
в различные моменты времени испытаний.

Требуется проверить,
согласуются ли экспериментальные данные
с гипотезой о том, что СВ d
имеет данный закон распределения
заданный функцией F(d)
или плотностью вероятности f(d).
Назовем этот закон распределения
«теоретическим».

Зная этот закон, можно
вычислить ожидаемое число отказов
изделия в определенных интервалах, на
которые разбить время испытания.

В результате получим
теоретический ряд
частот в k
интервалах времени
испытаний:

Подсчитаем также число
отказавших изделий в этих же интервалах
в нашем опыте и получим экспериментальный
ряд частот

Для проверки согласованности
теоретического и экспериментального
распределений подсчитывается мера
расхождения χ².

и число степеней свободы
v=k–f,
где f
– число ограничений. Число ограничений
равно числу параметров распределения,
увеличенному на единицу. Так, например,
для нормального закона распределения
имеет места два параметра распределения
(математическое ожидание и среднеквадратичное
отклонение). Для распределения Пирсона
составлены специальные таблицы. Пользуясь
этими таблицами, можно для каждого
значения критерия Пирсона и числа
степеней свободы v
определить вероятность
P
того, что за счет
случайных причин мера расхождения
теоретического и эмпирического
распределений будет не меньше, чем
фактически наблюдаемое в данной серии
опытов значение χ².

Если эта вероятность
сравнительно велика (P≥0,05),
то можно признать гипотезу о соответствии
эмпирического распределения теоретическому
правильно.

Если вероятность весьма
мала (P<0,05),
т.е. событие с такой вероятностью можно
считать практически невозможным, то
результат опыта следует считать
противоречащим гипотезе о том, что закон
распределения величины x
(в нашем случае x=d)
есть F(x).

Следовательно, гипотеза
отвергается и следует подобрать другую
теоретическую кривую.

Критерий Колмогорова
λ.
Критерий Пирсона применяют только в
тех случаях, когда число наблюдений
(n≥25).
Если теоретические значения параметров
распределения известны, то лучшим
критерием является критерий Колмогорова.

Для расчета критерия
Колмогорова, как и для критерия Пирсона
определяют теоретический m_i
и экспериментальный ряд частот m_i^/.
Затем рассчитывают накопленные суммы,
которые образуются путем прибавления
последующих частот к сумме предыдущих.
Составляют разность между накопленными
теоретическими и эмпирическими суммами
и находят максимальное значение этой
разности, вычисляя величину D
по формуле:

Где

,

– разность функций экспериментального
и теоретического распределения СВ.

Коэффициент λ
находят по формуле:

_.Пользуясь
табличными данными для вычисленного
значения λ, определяют вероятность P(λ)
– вероятность того, что гипотетическая
функция выбрана правильно.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Проверка корректности А/Б тестов

Хабр, привет! Сегодня поговорим о том, что такое корректность статистических критериев в контексте А/Б тестирования. Узнаем, как проверить, является критерий корректным или нет. Разберём пример, в котором тест Стьюдента не работает.

Меня зовут Коля, я работаю аналитиком данных в X5 Tech. Мы с Сашей продолжаем писать серию статей по А/Б тестированию, это наша третья статья. Первые две можно посмотреть тут:

• Стратификация. Как разбиение выборки повышает чувствительность A/Б теста

• Бутстреп и А/Б тестирование

Корректный статистический критерий

В А/Б тестировании при проверке гипотез с помощью статистических критериев можно совершить одну из двух ошибок:

• ошибку первого рода – отклонить нулевую гипотезу, когда на самом деле она верна. То есть сказать, что эффект есть, хотя на самом деле его нет;

• ошибку второго рода – не отклонить нулевую гипотезу, когда на самом деле она неверна. То есть сказать, что эффекта нет, хотя на самом деле он есть.

Совсем не ошибаться нельзя. Чтобы получить на 100% достоверные результаты, нужно бесконечно много данных. На практике получить столько данных затруднительно. Если совсем не ошибаться нельзя, то хотелось бы ошибаться не слишком часто и контролировать вероятности ошибок.

В статистике ошибка первого рода считается более важной. Поэтому обычно фиксируют допустимую вероятность ошибки первого рода, а затем пытаются минимизировать вероятность ошибки второго рода.

Предположим, мы решили, что допустимые вероятности ошибок первого и второго рода равны 0.1 и 0.2 соответственно. Будем называть статистический критерий корректным, если его вероятности ошибок первого и второго рода равны допустимым вероятностям ошибок первого и второго рода соответственно.

Как сделать критерий, в котором вероятности ошибок будут равны допустимым вероятностям ошибок?

Вероятность ошибки первого рода по определению равна уровню значимости критерия. Если уровень значимости положить равным допустимой вероятности ошибки первого рода, то вероятность ошибки первого рода должна стать равной допустимой вероятности ошибки первого рода.

Вероятность ошибки второго рода можно подогнать под желаемое значение, меняя размер групп или снижая дисперсию в данных. Чем больше размер групп и чем ниже дисперсия, тем меньше вероятность ошибки второго рода. Для некоторых гипотез есть готовые формулы оценки размера групп, при которых достигаются заданные вероятности ошибок.

Например, формула оценки необходимого размера групп для гипотезы о равенстве средних:

где и – допустимые вероятности ошибок первого и второго рода, – ожидаемый эффект (на сколько изменится среднее), и – стандартные отклонения случайных величин в контрольной и экспериментальной группах.

Проверка корректности

Допустим, мы работаем в онлайн-магазине с доставкой. Хотим исследовать, как новый алгоритм ранжирования товаров на сайте влияет на среднюю выручку с покупателя за неделю. Продолжительность эксперимента – одна неделя. Ожидаемый эффект равен +100 рублей. Допустимая вероятность ошибки первого рода равна 0.1, второго рода – 0.2.

Оценим необходимый размер групп по формуле:

import numpy as np
from scipy import stats

alpha = 0.1                     # допустимая вероятность ошибки I рода
beta = 0.2                      # допустимая вероятность ошибки II рода
mu_control = 2500               # средняя выручка с пользователя в контрольной группе
effect = 100                    # ожидаемый размер эффекта
mu_pilot = mu_control + effect  # средняя выручка с пользователя в экспериментальной группе
std = 800                       # стандартное отклонение

# исторические данные выручки для 10000 клиентов
values = np.random.normal(mu_control, std, 10000)

def estimate_sample_size(effect, std, alpha, beta):
    """Оценка необходимого размер групп."""
    t_alpha = stats.norm.ppf(1 - alpha / 2, loc=0, scale=1)
    t_beta = stats.norm.ppf(1 - beta, loc=0, scale=1)
    var = 2 * std ** 2
    sample_size = int((t_alpha + t_beta) ** 2 * var / (effect ** 2))
    return sample_size

estimated_std = np.std(values)
sample_size = estimate_sample_size(effect, estimated_std, alpha, beta)
print(f'оценка необходимого размера групп = {sample_size}')

оценка необходимого размера групп = 784

Чтобы проверить корректность, нужно знать природу случайных величин, с которыми мы работаем. В этом нам помогут исторические данные. Представьте, что мы перенеслись в прошлое на несколько недель назад и запустили эксперимент с таким же дизайном, как мы планировали запустить его сейчас. Дизайн – это совокупность параметров эксперимента, таких как: целевая метрика, допустимые вероятности ошибок первого и второго рода, размеры групп и продолжительность эксперимента, техники снижения дисперсии и т.д.

Так как это было в прошлом, мы знаем, какие покупки совершили пользователи, можем вычислить метрики и оценить значимость отличий. Кроме того, мы знаем, что эффекта на самом деле не было, так как в то время эксперимент на самом деле не запускался. Если значимые отличия были найдены, то мы совершили ошибку первого рода. Иначе получили правильный результат.

Далее нужно повторить эту процедуру с мысленным запуском эксперимента в прошлом на разных группах и временных интервалах много раз, например, 1000.

После этого можно посчитать долю экспериментов, в которых была совершена ошибка. Это будет точечная оценка вероятности ошибки первого рода.

Оценку вероятности ошибки второго рода можно получить аналогичным способом. Единственное отличие состоит в том, что каждый раз нужно искусственно добавлять ожидаемый эффект в данные экспериментальной группы. В этих экспериментах эффект на самом деле есть, так как мы сами его добавили. Если значимых отличий не будет найдено – это ошибка второго рода. Проведя 1000 экспериментов и посчитав долю ошибок второго рода, получим точечную оценку вероятности ошибки второго рода.

Посмотрим, как оценить вероятности ошибок в коде. С помощью численных синтетических А/А и А/Б экспериментов оценим вероятности ошибок и построим доверительные интервалы:

def run_synthetic_experiments(values, sample_size, effect=0, n_iter=10000):
    """Проводим синтетические эксперименты, возвращаем список p-value."""
    pvalues = []
    for _ in range(n_iter):
        a, b = np.random.choice(values, size=(2, sample_size,), replace=False)
        b += effect
        pvalue = stats.ttest_ind(a, b).pvalue
        pvalues.append(pvalue)
    return np.array(pvalues)

def print_estimated_errors(pvalues_aa, pvalues_ab, alpha):
    """Оценивает вероятности ошибок."""
    estimated_first_type_error = np.mean(pvalues_aa < alpha)
    estimated_second_type_error = np.mean(pvalues_ab >= alpha)
    ci_first = estimate_ci_bernoulli(estimated_first_type_error, len(pvalues_aa))
    ci_second = estimate_ci_bernoulli(estimated_second_type_error, len(pvalues_ab))
    print(f'оценка вероятности ошибки I рода = {estimated_first_type_error:0.4f}')
    print(f'  доверительный интервал = [{ci_first[0]:0.4f}, {ci_first[1]:0.4f}]')
    print(f'оценка вероятности ошибки II рода = {estimated_second_type_error:0.4f}')
    print(f'  доверительный интервал = [{ci_second[0]:0.4f}, {ci_second[1]:0.4f}]')

def estimate_ci_bernoulli(p, n, alpha=0.05):
    """Доверительный интервал для Бернуллиевской случайной величины."""
    t = stats.norm.ppf(1 - alpha / 2, loc=0, scale=1)
    std_n = np.sqrt(p * (1 - p) / n)
    return p - t * std_n, p + t * std_n

pvalues_aa = run_synthetic_experiments(values, sample_size, effect=0)
pvalues_ab = run_synthetic_experiments(values, sample_size, effect=effect)
print_estimated_errors(pvalues_aa, pvalues_ab, alpha)

оценка вероятности ошибки I рода = 0.0991
  доверительный интервал = [0.0932, 0.1050]
оценка вероятности ошибки II рода = 0.1978
  доверительный интервал = [0.1900, 0.2056]

Оценки вероятностей ошибок примерно равны 0.1 и 0.2, как и должно быть. Всё верно, тест Стьюдента на этих данных работает корректно.

Распределение p-value

Выше рассмотрели случай, когда тест контролирует вероятность ошибки первого рода при фиксированном уровне значимости. Если решим изменить уровень значимости с 0.1 на 0.01, будет ли тест контролировать вероятность ошибки первого рода? Было бы хорошо, если тест контролировал вероятность ошибки первого рода при любом заданном уровне значимости. Формально это можно записать так:

Для любого выполняется .

Заметим, что в левой части равенства записано выражение для функции распределения p-value. Из равенства следует, что функция распределения p-value в точке X равна X для любого X от 0 до 1. Эта функция распределения является функцией распределения равномерного распределения от 0 до 1. Мы только что показали, что статистический критерий контролирует вероятность ошибки первого рода на заданном уровне для любого уровня значимости тогда и только тогда, когда при верности нулевой гипотезы p-value распределено равномерно от 0 до 1.

При верности нулевой гипотезы p-value должно быть распределено равномерно. А как должно быть распределено p-value при верности альтернативной гипотезы? Из условия для вероятности ошибки второго рода следует, что .

Получается, график функции распределения p-value при верности альтернативной гипотезы должен проходить через точку , где и – допустимые вероятности ошибок конкретного эксперимента.

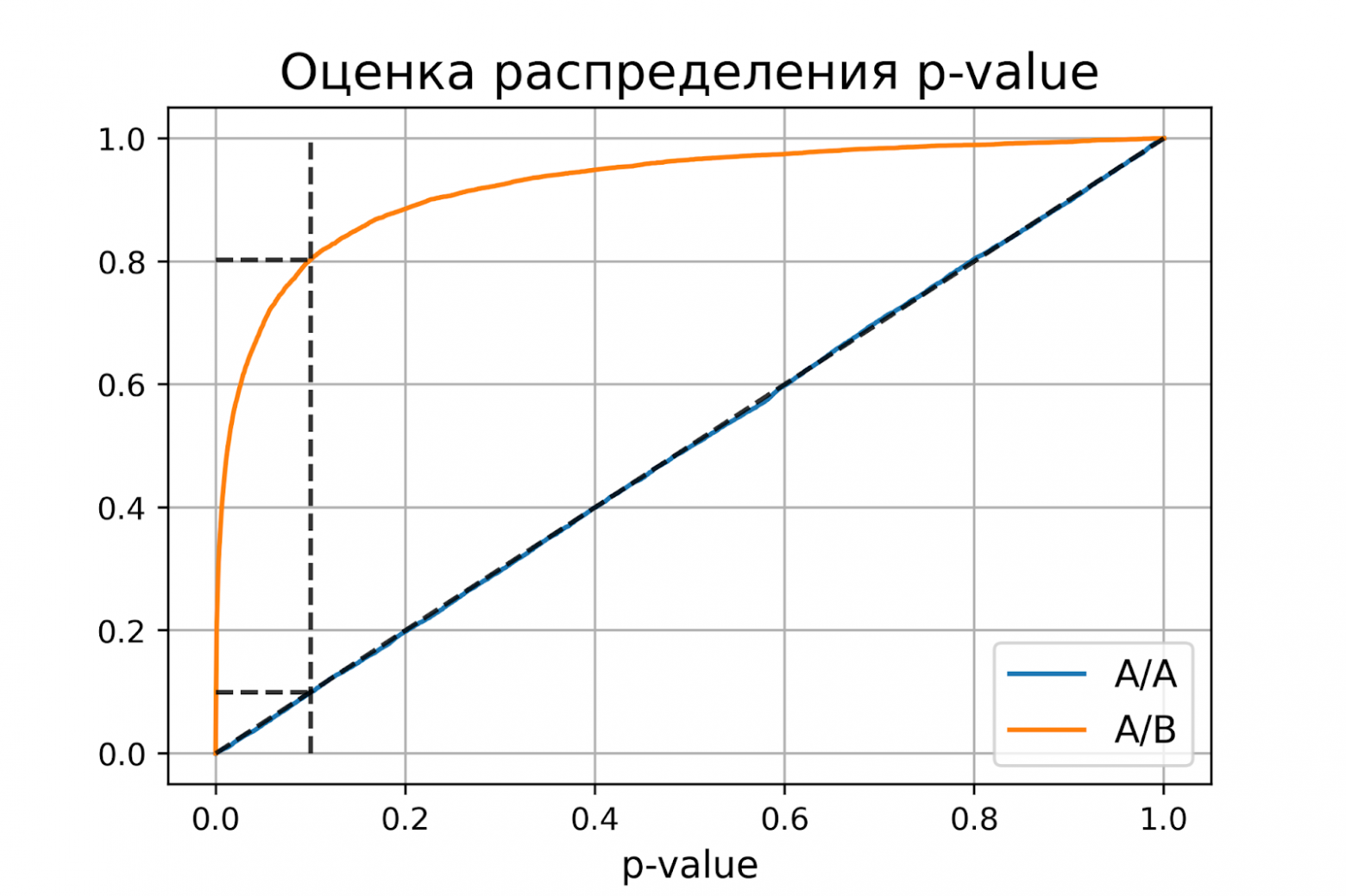
Проверим, как распределено p-value в численном эксперименте. Построим эмпирические функции распределения p-value:

import matplotlib.pyplot as plt

def plot_pvalue_distribution(pvalues_aa, pvalues_ab, alpha, beta):
    """Рисует графики распределения p-value."""
    estimated_first_type_error = np.mean(pvalues_aa < alpha)
    estimated_second_type_error = np.mean(pvalues_ab >= alpha)
    y_one = estimated_first_type_error
    y_two = 1 - estimated_second_type_error
    X = np.linspace(0, 1, 1000)
    Y_aa = [np.mean(pvalues_aa < x) for x in X]
    Y_ab = [np.mean(pvalues_ab < x) for x in X]

    plt.plot(X, Y_aa, label='A/A')
    plt.plot(X, Y_ab, label='A/B')
    plt.plot([alpha, alpha], [0, 1], '--k', alpha=0.8)
    plt.plot([0, alpha], [y_one, y_one], '--k', alpha=0.8)
    plt.plot([0, alpha], [y_two, y_two], '--k', alpha=0.8)
    plt.plot([0, 1], [0, 1], '--k', alpha=0.8)

    plt.title('Оценка распределения p-value', size=16)
    plt.xlabel('p-value', size=12)
    plt.legend(fontsize=12)
    plt.grid()
    plt.show()

plot_pvalue_distribution(pvalues_aa, pvalues_ab, alpha, beta)

P-value для синтетических А/А тестах действительно оказалось распределено равномерно от 0 до 1, а для синтетических А/Б тестов проходит через точку .

Кроме оценок распределений на графике дополнительно построены четыре пунктирные линии:

• диагональная из точки [0, 0] в точку [1, 1] – это функция распределения равномерного распределения на отрезке от 0 до 1, по ней можно визуально оценивать равномерность распределения p-value;

• вертикальная линия с – пороговое значение p-value, по которому определяем отвергать нулевую гипотезу или нет. Проекция на ось ординат точки пересечения вертикальной линии с функцией распределения p-value для А/А тестов – это вероятность ошибки первого рода. Проекция точки пересечения вертикальной линии с функцией распределения p-value для А/Б тестов – это мощность теста (мощность = 1 — ). 

• две горизонтальные линии – проекции на ось ординат точки пересечения вертикальной линии с функцией распределения p-value для А/А и А/Б тестов.

График с оценками распределения p-value для синтетических А/А и А/Б тестов позволяет проверить корректность теста для любого значения уровня значимости.

Некорректный критерий

Выше рассмотрели пример, когда тест Стьюдента оказался корректным критерием для случайных данных из нормального распределения. Может быть, все критерии всегда работаю корректно, и нет смысла каждый раз проверять вероятности ошибок?

Покажем, что это не так. Немного изменим рассмотренный ранее пример, чтобы продемонстрировать некорректную работу критерия. Допустим, мы решили увеличить продолжительность эксперимента до 2-х недель. Для каждого пользователя будем вычислять стоимость покупок за первую неделю и стоимость покупок за второю неделю. Полученные стоимости будем передавать в тест Стьюдента для проверки значимости отличий. Положим, что поведение пользователей повторяется от недели к неделе, и стоимости покупок одного пользователя совпадают.

def run_synthetic_experiments_two(values, sample_size, effect=0, n_iter=10000):
    """Проводим синтетические эксперименты на двух неделях."""
    pvalues = []
    for _ in range(n_iter):
        a, b = np.random.choice(values, size=(2, sample_size,), replace=False)
        b += effect
        # дублируем данные
        a = np.hstack((a, a,))
        b = np.hstack((b, b,))
        pvalue = stats.ttest_ind(a, b).pvalue
        pvalues.append(pvalue)
    return np.array(pvalues)

pvalues_aa = run_synthetic_experiments_two(values, sample_size)
pvalues_ab = run_synthetic_experiments_two(values, sample_size, effect=effect)
print_estimated_errors(pvalues_aa, pvalues_ab, alpha)
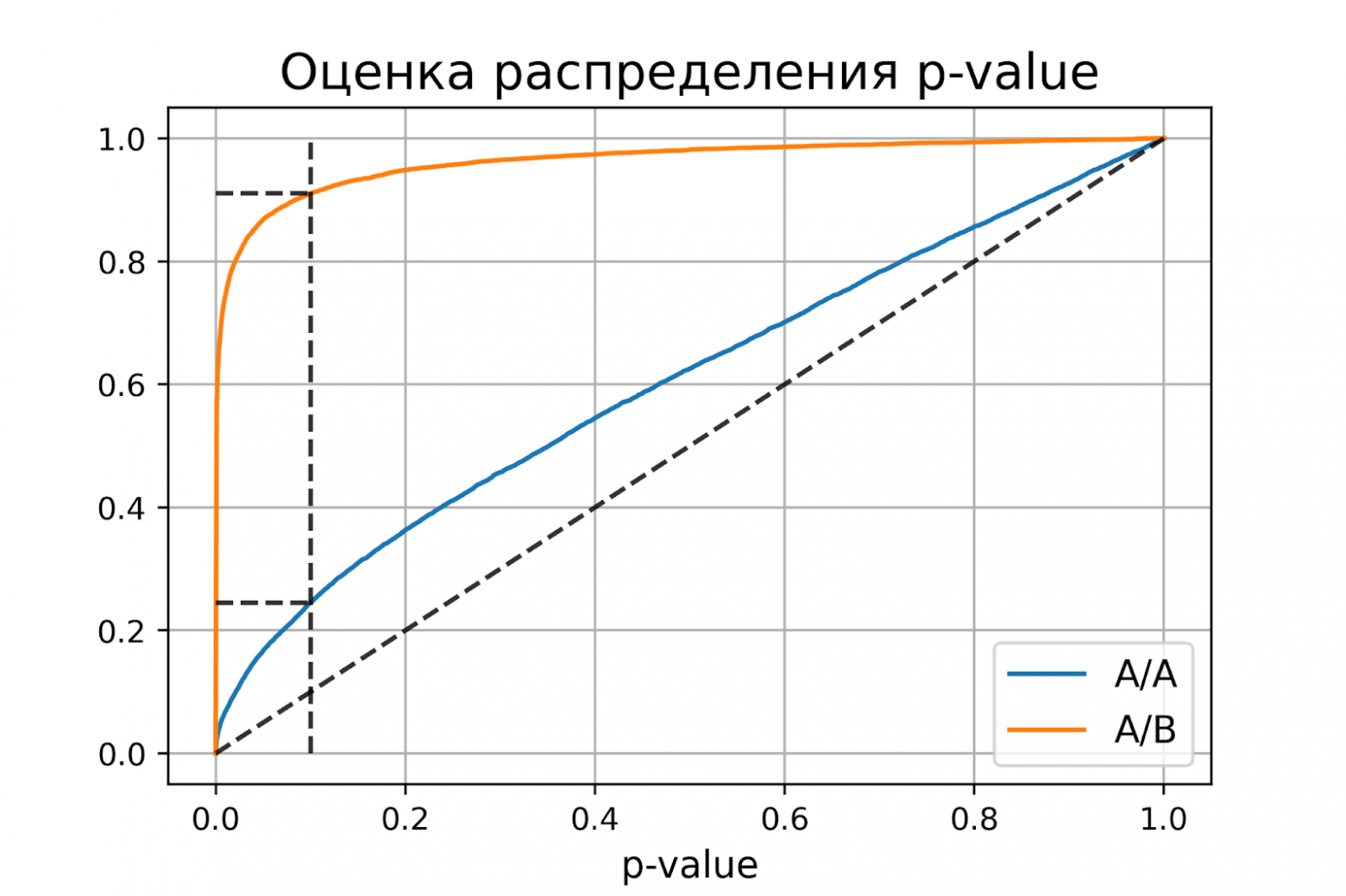
plot_pvalue_distribution(pvalues_aa, pvalues_ab, alpha, beta)

оценка вероятности ошибки I рода = 0.2451
  доверительный интервал = [0.2367, 0.2535]
оценка вероятности ошибки II рода = 0.0894
  доверительный интервал = [0.0838, 0.0950]

Получили оценку вероятности ошибки первого рода около 0.25, что сильно больше уровня значимости 0.1. На графике видно, что распределение p-value для синтетических А/А тестов не равномерно, оно отклоняется от диагонали. В этом примере тест Стьюдента работает некорректно, так как данные зависимые (стоимости покупок одного человека зависимы). Если бы мы сразу не догадались про зависимость данных, то оценка вероятностей ошибок помогла бы нам понять, что такой тест некорректен.

Итоги

Мы обсудили, что такое корректность статистического теста, посмотрели, как оценить вероятности ошибок на исторических данных и привели пример некорректной работы критерия.

Таким образом:

• корректный критерий – это критерий, у которого вероятности ошибок первого и второго рода равны допустимым вероятностям ошибок первого и второго рода соответственно;

• чтобы критерий контролировал вероятность ошибки первого рода для любого уровня значимости, необходимо и достаточно, чтобы p-value при верности нулевой гипотезы было распределено равномерно от 0 до 1.