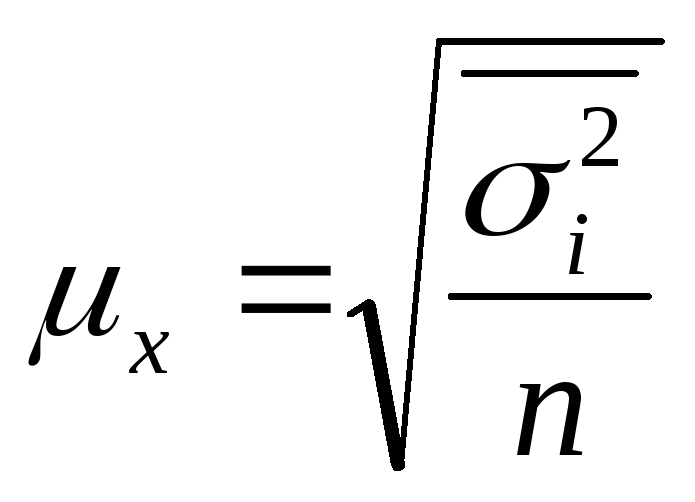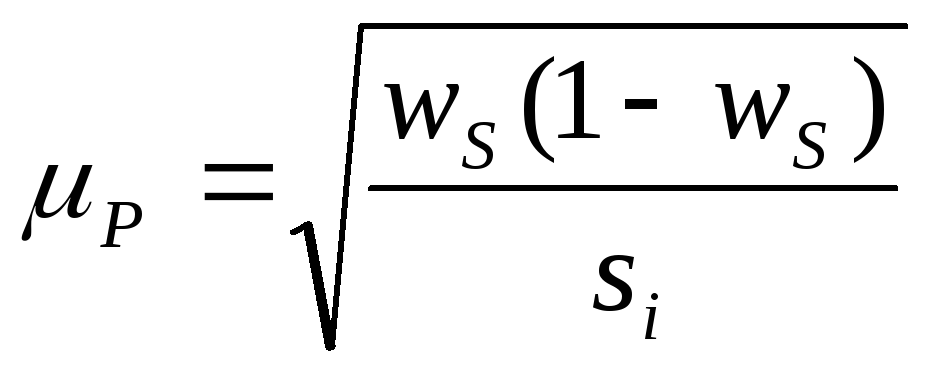Чтобы получить решение, напишите мне в WhatsApp, оплатите, и я Вам вышлю файлы.
Кстати, если эта работа не по вашей теме или не по вашим данным, не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу, я смогу выполнить её в срок 1-3 дня!
Описание и исходные данные задания, 50% решения + фотография:
Определить:
1) как изменится средняя ошибка повторной выборки, если объем наблюдения: а) увеличить в 4 раза, в 2,5 раза, на 50%; б) уменьшить в 2 раза, на 20 %?
2) каким образом надо изменить объем выборки, чтобы ошибка уменьшилась в 3 раза, на 50%, на 20%?
Решение:
1) Средняя ошибка повторной выборки определяется следующей формулой:
где σ2 – выборочная дисперсия;
n – объем выборки.
Если объем наблюдения увеличить в 4 раза (n1=4n0):
Средняя ошибка повторной выборки уменьшится в 2 раза.
Если объем наблюдения увеличить в 2,5 раза (n1=2,5n0):
Средняя ошибка повторной выборки сократится на 36,8% (63,2-100).
- Строительная организация с сезонным характером работы работала с мая по сентябрь, а среднее списочное число промышленно-производственного персонала составляло в мае 650 чел.
- Имеются данные по двум предприятиям (табл. 57). Определить уровень и динамику фондоотдачи по двум предприятиям в целом с использованием: среднего индекса фондоотдачи переменного состава.
- Какая экономическая школа считает инструменты денежно-кредитной политики наиболее эффективными средствами государственного регулирования: а) институционализм; б) кейнсианство; в) монетаризм.
- По плану предприятия объем производства продукции в отчетном году должен возрасти по сравнению с прошлым годом на 2,5%. План по объему производства продукции перевыполнен в отчетном году на 3,0 %.
Целью
выборочного наблюдения является
определение характеристик генеральной
совокупности – генеральной средней
()
и генеральной доли (р).
Характеристики выборочной совокупности
— выборочная средняя () и выборочная доля (
)
отличаются от генеральных характеристик
на величину ошибки выборки ().
Расчет
ошибок при проведении отбора позволяет
решить одну из главных проблем организации
выборочного наблюдения – оценить
репрезентативность (представительность)
выборочной совокупности. Различают
среднюю и предельную ошибки выборки.
Эти два вида ошибок связаны между собой
следующим образом:
,
где
—
предельная ошибка выборки;—
средняя ошибка выборки;— коэффициент доверия, связанный с
вероятностью (P)
и определяемый по таблице значений
интегральной функции Лапласа.
Так
как вероятность, с которой гарантируется
ошибка выборки, должна быть близка к 1
(в связи с этим ошибка называется
предельно возможной, т.е. наивероятной),
величина коэффициента доверия при-нимает
определенные значения. Для целых значений
коэффициента уровни вероятности,
наиболее часто используемые в экономических
и социологических исследованиях,
следующие:
-
P
1
0,683
2
0,954
3
0,997
Величина
средней ошибки выборки рассчитывается
дифференцировано в зависимости от
способа и вида отбора (таблица 6.1).
Расчет
средней и предельной ошибок выборки
позволяет определять возможные пределы,
в которых будут находиться характеристики
генеральной совокупности:
Таблица 6.1
Формулы для
определения средней ошибки выборки
|
Способы отбора |
Виды |
|
|
повторный отбор |
бесповторный |
|
|
Собственно-cлучайный
а) при изучении
б) при изучении |
|
|
а) при изучении
б) при изучении |
— — |
|
а) при изучении
б) при изучении |
|
|
|
где |
||
а) при изучении
б) при изучении |
|
|
|
где
si |
Формулы необходимого объема выборки для различных способов формирования выборочной совокупности выводятся из соответствующих соотношений, используются при расчете предельных ошибок выборки.
Таблица 6.2
Формулы для
определения численности выборочной
совокупности
|
Способы |
Виды отбора |
|
|
повторный отбор |
бесповторный |
|
|
1.Собственно-случайный
а) при изучении
б) при изучении |
|
|
|
2. Механический
а) при изучении
б) при изучении |
— — |
|
|
3. Типический
а) при изучении
б) при изучении |
|
|
а) при изучении
б) при изучении |
|
|
Тесты
1. По
какой формуле определяются пределы
генеральной средней?
1);
2)
;
3)
;
4).
2.
По какой формуле определяются пределы
генеральной доли?
1);
2)
;
3)
;
4).
3.
Какие ошибки не специфичны для выборочного
наблюдения?
1)
ошибки регистрации
преднамеренные; 2) ошибки регистрации
не-преднамеренные; 3) случайные ошибки
репрезентативности; 4) пре-дельная ошибка
выборки.
4. Как изменится
средняя ошибка выборки при повторном
отборе, если объем выборки увеличить в
четыре раза?
1) уменьшится в 4
раза; 3) увеличится в 2 раза;
2) уменьшится в 2
раза; 4) увеличится в 4 раза.
5.
Какой способ отбора является наиболее
точным?
1) собственно-случайный;
3) типический;
2) механический;
4) серийный.
6. Чему равна
средняя ошибка выборочной доли при
случайном бесповторном отборе?
1)
2)
3)

4)

7. По какой формуле
определяется предельная ошибка выборки
для признака при механическом отборе?
1)

2)

3)
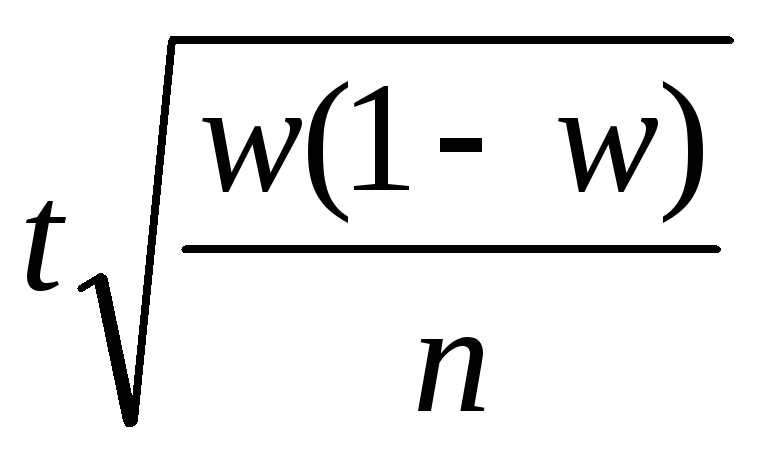
4)

8. Какая формула
положена в основу определения необходимого
объема выборочной совокупности при
собственно-случайном повторном отборе?
1)

2)

3)

4)

9. Как
определяется предельная ошибка доли
при типическом отборе?
1)
2)

3)

4)

10. По какой формуле
определяется предельная ошибка выборки
для признака при серийном повторном
отборе?
1)

2)

3)

4)

Решение типовых
задач
Пример
1. Для изучения
оснащения заводов основными
производственными фондами было проведено
10%-ное собственно-слу-чайное обследование,
в результате которого получены следующие
данные о распределении заводов по
стоимости фондов:
|
Средняя годовая |
До 4 |
4 — 6 |
6 — 8 |
Свыше 8 |
Итого |
|
Количество |
7 |
12 |
21 |
10 |
50 |
Определите:
1) с вероятностью 0,997 границы, в которых
будет находиться средняя годовая
стоимость основных фондов заводов в
генеральной совокупности; 2) с вероятностью
0,954 границы, в которых будет находиться
удельный вес заводов со стоимостью
фондов выше 6 млн.грн. в генеральной
совокупности.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Калькулятор для расчета достаточного объема выборки
Калькулятор ошибки выборки для доли признака
Калькулятор ошибки выборки для среднего значения
Калькулятор значимости различий долей
Калькулятор значимости различий средних
1. Формула (даже две)
Бытует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с размером генеральной совокупности. Например, при опросах организаций (B2B).
Если речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная.
На рис.1. пример выборки 15000 человек (!) при опросе в муниципальном районе. Возможно, от численности населения взяли 10%?
Размер выборки никогда не рассчитывается как процент от генеральной совокупности!
Рис.1. Размер выборки 15000 человек, как реальный пример некомпетентности (или хуже).
В таких случаях для расчета объема выборки используется следующая формула:

где
n – объем выборки,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует,
∆ – предельная ошибка выборки.
Доверительный уровень – это вероятность того, что реальная доля лежит в границах полученного доверительного интервала: выборочная доля (p) ± ошибка выборки (Δ). Доверительный уровень устанавливает сам исследователь в соответствии со своими требованиями к надежности полученных результатов. Чаще всего применяются доверительные уровни, равные 0,95 или 0,99. В маркетинговых исследованиях, как правило, выбирается доверительный уровень, равный 0,95. При этом уровне коэффициент Z равен 1,96.
Значения p и q чаще всего неизвестны до проведения исследования и принимаются за 0,5. При этом значении размер ошибки выборки максимален.
Допустимая предельная ошибка выборки выбирается исследователем в зависимости от целей исследования. Считается, что для принятия бизнес-решений ошибка выборки должна быть не больше 4%. Этому значению соответствует объем выборки 500-600 респондентов. Для важных стратегических решений целесообразно минимизировать ошибку выборки.
Рассмотрим кривую зависимости ошибки выборки от ее объема (Рис.2).

Рис.2. Зависимость ошибки выборки от ее объема при 95% доверительном уровне
Как видно из диаграммы, с ростом объема выборки значение ошибки уменьшается все медленнее. Так, при объеме выборки 1500 человек предельная ошибка выборки составит ±2,5%, а при объеме 2000 человек – ±2,2%. То есть, при определенном объеме выборки дальнейшее его увеличение не дает значительного выигрыша в ее точности.
ШПАРГАЛКА (скопируйте ссылку или текст)
Подходы к решению проблемы:
Случай 1. Генеральная совокупность значительно больше выборки:

Случай 2. Генеральная совокупность сопоставима с объемом выборки: (см. раздел исследований B2B)

где
n – объем выборки,
N – объем генеральной совокупности,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует, (значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования)
∆ – предельная ошибка выборки.
Например,
рассчитаем ошибку выборки объемом 1000 человек при 95% доверительном уровне, если генеральная совокупность значительно больше объема выборки:
Ошибка выборки = 1,96 * КОРЕНЬ(0,5*0,5/1000) = 0,031 = ±3,1%
При расчете объема выборки следует также учитывать стоимость проведения исследования. Например, при цене за 1 анкету 200 рублей стоимость опроса 1000 человек составит 200 000 рублей, а опрос 1500 человек будет стоить 300 000 рублей. Увеличение затрат в полтора раза сократит ошибку выборки всего на 0,6%, что обычно неоправданно экономически.
2. Причины «раздувать» выборку
Анализ полученных данных обычно включает в себя и анализ подвыборок, объемы которых меньше основной выборки. Поэтому ошибка для выводов по подвыборкам больше, чем ошибка по выборке в целом. Если планируется анализ подгрупп / сегментов, объем выборки должен быть увеличен (в разумных пределах).
Рис.3 демонстрирует данную ситуацию. Если для исследования авиапассажиров используется выборка численностью 500 человек, то для выводов по выборке в целом ошибка составляет 4,4%, что вполне приемлемо для принятия бизнес-решений. Но при делении выборки на подгруппы в зависимости от цели поездки, выводы по каждой подгруппе уже недостаточно точны. Если мы захотим узнать какие-либо количественные характеристики группы пассажиров, совершающих бизнес-поездку и покупавших билет самостоятельно, ошибка полученных показателей будет достаточно велика. Даже увеличение выборки до 2000 человек не обеспечит приемлемой точности выводов по этой подвыборке.

Рис.3. Проектирование объема выборки с учетом необходимости анализа подвыборок
Другой пример – анализ подгрупп потребителей услуг торгово-развлекательного центра (Рис.4).

Рис.4. Потенциальный спрос на услуги торгово-развлекательного центра
При объеме выборки в 1000 человек выводы по каждой отдельной услуге (например, социально-демографический профиль, частота пользования, средний чек и др.) будут недостаточно точными для использования в бизнес планировании. Особенно это касается наименее популярных услуг (Таблица 1).
Таблица 1. Ошибка по подвыборкам потенциальных потребителей услуг торгово-развлекательного центра при выборке 1000 чел.

Чтобы ошибка в самой малочисленной подвыборке «Ночной клуб» составила меньше 5%, объем выборки исследования должен составлять около 4000 человек. Но это будет означать 4-кратное удорожание проекта. В таких случаях возможно компромиссное решение:
- увеличение выборки до 1800 человек, что даст достаточную точность для 6 самых популярных видов услуг (от кинотеатра до парка аттракционов);
- добор 200-300 пользователей менее популярных услуг с опросом по укороченной анкете (см. Таблицу 2).
Таблица 2. Разница в ошибке выборки по подвыборкам при разных объемах выборки.

При обсуждении с исследовательским агентством точности результатов планируемого исследования рекомендуется принимать во внимание бюджет, требования к точности результатов в целом по выборке и в разрезе подгрупп. Если бюджет не позволяет получить информацию с приемлемой ошибкой, лучше пока отложить проект (или поторговаться).
КАЛЬКУЛЯТОРЫ ДЛЯ РАСЧЕТА СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ И ОПРЕДЕЛЕНИЯ ЗНАЧИМОСТИ РАЗЛИЧИЙ:
КАЛЬКУЛЯТОР ДЛЯ РАСЧЕТА
ДОСТАТОЧНОГО ОБЪЁМА ВЫБОРКИ
Доверительный уровень:
Ошибка выборки (?):
%
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
РЕЗУЛЬТАТ
Один из важных вопросов, на которые нужно ответить при планировании исследования, — это оптимальный объем выборки. Слишком маленькая выборка не сможет обеспечить приемлемую точность результатов опроса, а слишком большая приведет к лишним расходам.
Онлайн-калькулятор объема выборки поможет рассчитать оптимальный размер выборки, исходя из максимально приемлемого для исследователя размера ошибки выборки.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке!
Формулы для других типов выборки отличаются.
Объем выборки рассчитывается по следующим формулам
1) если объем выборки значительно меньше генеральной совокупности:

2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели соков и нектаров, постоянно проживающие в Москве и Московской области). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
q = 1 — p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален. В данном калькуляторе значения p и q по умолчанию равны 0,5.
Δ– предельная ошибка выборки (для доли признака), приемлемая для исследователя. Считается, что для принятия бизнес-решений ошибка выборки не должна превышать 4%.
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании.
ПРИМЕР РАСЧЕТА ОБЪЕМА ВЫБОРКИ:
Допустим, мы хотим рассчитать объем выборки, предельная ошибка которой составит 4%. Мы принимаем доверительный уровень, равный 95%. Генеральная совокупность значительно больше выборки. Тогда объем выборки составит:
n = 1,96 * 1,96 * 0,5 * 0,5 / (0,04 * 0,04) = 600,25 ≈ 600 человек
Таким образом, если мы хотим получить результаты с предельной ошибкой 4%, нам нужно опросить 600 человек.
КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА
Доверительный уровень:
Объём выборки (n):
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
Доля признака (p):
%
РЕЗУЛЬТАТ
Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).
Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.
Ошибка выборки для доли признака рассчитывается по следующим формулам.
1) если объем выборки значительно меньше генеральной совокупности:
(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели шоколада, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.
p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
q = 1 — p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален.
Δ– предельная ошибка выборки.
Таким образом, зная объем выборки исследования, мы можем заранее оценить показатель ее ошибки.
А получив значение p, мы можем рассчитать доверительный интервал для доли признака: (p — ∆; p + ∆)
ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА:
Например, в ходе исследования были опрошены 1000 человек (n=1000). 20% из них заинтересовались новым продуктом (p=0,2). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):
∆ = 1,96 * КОРЕНЬ (0,2*0,8/1000) = 0,0248 = ±2,48%
Рассчитаем доверительный интервал:
(p — ∆; p + ∆) = (20% — 2,48%; 20% + 2,48%) = (17,52%; 22,48%)
Таким образом, с вероятностью 95% мы можем быть уверены, что реальная доля заинтересованных в новом продукте (среди всей генеральной совокупности) находится в пределах полученного диапазона (17,52%; 22,48%).
Если бы мы выбрали доверительный уровень, равный 99%, то для тех же значений p и n ошибка выборки была бы больше, а доверительный интервал – шире. Это логично, поскольку, если мы хотим быть более уверены в том, что наш доверительный интервал «накроет» реальное значение признака, то интервал должен быть более широким.
КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ
Доверительный уровень:
Объём выборки (n):
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
Среднее значение (x̄):
Стандартное отклонение (s):
РЕЗУЛЬТАТ
Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).
Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.
Ошибка выборки для среднего значения рассчитывается по следующим формулам.
1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели мороженого, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.
s — выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:
где, x ̅ – среднее арифметическое показателя, xi– значение i-го показателя, n – объем выборки
Δ– предельная ошибка выборки.
Зная среднее значение показателя x ̅ и ошибку ∆, мы можем рассчитать доверительный интервал для среднего значения:(x ̅ — ∆; x ̅ + ∆)
ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ:
Например, в ходе исследования были опрошены 1000 человек (n=1000). Каждого из них попросили указать их примерную среднюю сумму покупки (средний чек) в известной сети магазинов. Среднее арифметическое всех ответов составило 500 руб. (x ̅=500), а стандартное отклонение составило 120 руб. (s=120). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):
∆ = 1,96 * 120 / КОРЕНЬ (1000) = 7,44
Рассчитаем доверительный интервал:
(x ̅ — ∆; x ̅ + ∆) = (500 – 7,44; 500 + 7,44) = (492,56; 507,44)
Таким образом, с вероятностью 95% мы можем быть уверены, что значение среднего чека по всей генеральной совокупности находится в границах полученного диапазона: от 492,56 руб. до 507,44 руб.
КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ ДОЛЕЙ
Доверительный уровень:
| Измерение 1 | Измерение 2 | |
| Доля признака (p): | % | % |
| Объём выборки (n): |
РЕЗУЛЬТАТ
Если в прошлогоднем исследовании вашу марку вспомнили 10% респондентов, а в исследовании текущего года – 15%, не спешите открывать шампанское, пока не воспользуетесь нашим онлайн-калькулятором для оценки статистической значимости различий.
Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.
Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.
В приведенном здесь калькуляторе используется двухвыборочный z-тест для долей. Для его применения должны соблюдаться следующие условия:
- Обе выборки – простые случайные
- Выборки независимы (между значениями двух выборок нет закономерной связи)
- Генеральные совокупности значительно больше выборок
- Произведения n*p и n*(1-p), где n=размер выборки а p=доля признака, – не меньше 5.
В калькуляторе используются следующие вводные данные:
Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.
Доля признака (p) – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.
Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.
КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ СРЕДНИХ
Доверительный уровень:
| Измерение 1 | Измерение 2 | |
| Среднее значение (x̄): | ||
| Стандартное отклонение (s): | ||
| Объём выборки (n): |
РЕЗУЛЬТАТ
Допустим, выборочный опрос посетителей двух разных ТРЦ показал, что средний чек в одном из них равен 1000 рублей, а в другом – 1200 рублей. Следует ли отсюда вывод, что суммы среднего чека в двух этих ТРЦ действительно отличаются?
Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.
Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.
В приведенном здесь калькуляторе используется двухвыборочный z-тест для средних значений. Для его применения должны соблюдаться следующие условия:
- Обе выборки – простые случайные
- Выборки независимы (между значениями двух выборок нет закономерной связи)
- Генеральные совокупности значительно больше выборок
- Распределения значений в выборках близки к нормальному распределению.
В калькуляторе используются следующие вводные данные:
Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.
Среднее значение ( ̅x) – среднее арифметическое показателя.
Стандартное отклонение (s) – выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:
где, x ̅ – среднее арифметическое показателя, xi– значение i-го показателя, n – объем выборки
Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.
Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.
Вы можете подписаться на уведомления о новых материалах СканМаркет
Размер
выборки
– это количество элементов, которые
необходимо отобрать из генеральной
совокупности для проведения выборочного
исследования.
Определение
размера выборки для вероятностного
метода отбора представляет собой сложный
процесс, включающий ряд этапов: 1) оценка
факторов, влияющих на объем выборки; 2)
выбор метода расчета размера выборки;
3) расчет размера выборки; 4) оценка
стандартного отклонения среднего в
выборочной совокупности; 5) расчет
предельной ошибки выборки; 6) оценка
среднего значения признака в генеральной
совокупности (см. рис. 4.8).
В
случае применения детерминированного
метода отбора используются только
приблизительные методы расчета размера
выборки и оценить объективно точность
результатов исследования не представляется
возможным.
1.
Оценка факторов, влияющих на размер
выборки.
К наиболее важным факторам, определяющим
объем выборки, относятся следующие:
важность принимаемого решения, характер
исследования, бюджет исследования,
стоимость сбора информации, число групп
и подгрупп в генеральной совокупности,
коэффициенты охвата и завершенности,
размер генеральной совокупности и
требуемая точность исследования (см.
рис. 4.9). На размер ошибки выборки и,
соответственно, точность результатов
исследования влияют применяемая
процедура отбора и степень вариации
признака в совокупности.
Как
правило, для
принятия важных решений
необходима детальная, максимально
точная информация. Ее получение
предусматривает создание больших
выборок, но при увеличении объема выборки
возрастает и стоимость каждой
дополнительной единицы информации.
На
величину объема выборки влияет также
характер
исследования.
В поисковых исследованиях, изучающих
качественные характеристики, объем
выборки, как правило, невелик. Для
исследований, предусматривающих
статистическое заключение, таких как
дескриптивные, необходим больший объем
выборки. Кроме того, большие выборки
нужны, когда информация собирается
с учетом большого количества переменных.
Большой объем выборки позволяет снизить
общий эффект от ошибок выборки по всем
переменным.
Принимая
решения об объеме выборки, нужно учитывать
фактор ограниченности ресурсов или
располагаемый
бюджет исследования.
В любом исследовательском проекте
существуют временные и финансовые
ограничения. При жестких бюджетных
ограничениях исследователь будет стоять
перед выбором: использовать более
дешевые методы сбора информации или
ограничить размер выборки, допуская
снижение точности результатов.
Р
исунок
4.8.
Этапы расчета необходимого размера
выборки и оценки значения признака в
генеральной совокупности
Р
исунок
4.9.
Факторы, учитываемые при определении
размера выборки и взаимосвязи между
ними
Чем
больше размер выборки
(чем
он ближе к размерам генеральной
совокупности в целом), тем надежнее и
достовернее полученные данные, однако
стоимость
сбора информации
(включающая в себя расходы на размножение
инструментария, оплату труда интервьюеров,
супервайзеров и операторов компьютерного
набора данных) при этом значительно
возрастает;
При
проведении углубленного анализа данных
с использованием разнообразных
методов многомерного статистического
анализа необходим большой объем выборки.
Это же касается данных, которые
анализируются с особой точностью. Таким
образом, для
анализа данных на уровне группы или
подгруппы
потребуется больший объем выборки, чем
для анализа общей или генеральной
совокупности.
К примеру, мы хотим
исследовать потребительское поведение
населения города. Перед нами – структура
генеральной совокупности, которая
представляет распределение в целом
населения города и по трем квотным
признакам: район города, пол, возраст.
Совершенно очевидно, что если в
исследовании ставится задача изучить
мнения населения города в целом — это
одна ситуация; если в том числе и по
возрастным группам – это другая (здесь
мы имеем 3 группы); если необходимо
выявить распределения мнений по
возрастным и половым группам — это третья
ситуация (здесь мы имеем уже шесть
групп); наконец, если в исследовании нас
интересует распределение информации
по возрастным, половым группам и районам
города (к примеру, мы хотим определить,
как к покупкам того или иного товара
относятся молодые женщины, проживающие
во Фрунзенском районе г. Минска), то
здесь мы имеем дело уже с четвертой
ситуацией (54 группы). Для получения
репрезентативной информации в последним
случае необходимо обеспечить
представительство в минимальной из
этих пятидесяти четырех групп 25-30 чел.
Следовательно, минимальный объем
выборочной совокупности здесь будет
находиться в пределах 1600 чел.
Статистически
определенный объем выборки представляет
собой конечный, или чистый объем выборки,
который необходимо получить, чтобы
обеспечить расчет параметров с желательной
степенью точности и заданным уровнем
достоверности. При проведении опросов
он выражается в количестве завершенных
интервью. Для получения конечного объема
выборки необходимо связаться с большим
количеством потенциальных респондентов.
Другими словами, начальный объем выборки
должен намного превышать конечный,
поскольку коэффициенты охвата и
завершенности обычно составляют меньше
100%.
Коэффициентом
охвата
называется степень наличия или процент
людей, подходящих для участия в
исследовании. Коэффициент охвата
определяет, какое количество контактов
с людьми необходимо осуществить, чтобы
в итоге получить объем выборки,
соответствующий заданным критериям.
Предположим,
что для исследования характеристик
моющих средств необходимо создать
выборку из женщин – глав семьи в возрасте
от 25 до 55 лет. Приблизительно 75% женщин
в возрасте от 20 до 60 лет, к которым можно
обратиться, – это женщины – главы семьи
в возрасте от 25 до 55 лет. Это означает,
что, в среднем, необходимо обратиться
к 1,33 женщин, чтобы получить одного
подходящего респондента. Дополнительные
критерии для отбора респондентов
(например, каким образом использовался
продукт) увеличивают необходимое
количество контактов. Предположим, что
дополнительным критерием является
использование женщиной моющего средства
для пола в течение последних двух
месяцев. Предполагается, что 60% женщин,
к которым обратятся исследователи,
будут соответствовать этому критерию.
Тогда коэффициент охвата составит 0,75
х 0,60 = 0,45. Таким образом, конечный объем
выборки следует увеличить на 2,22 (1/0,45).
Точно
так же при определении объема выборки
необходимо учитывать ожидаемые отказы
людей, соответствующих критериям
исследования. Коэффициент
завершенности
указывает на процент респондентов,
соответствующих критериям отбора,
которые полностью прошли интервью.
Например, если исследователь предполагает,
что коэффициент завершенности интервью
составит 80% от числа подходящих
респондентов, необходимое количество
контактов следует умножить на коэффициент
1,25. Применение коэффициентов охвата и
завершенности означает, что число
контактов с потенциальными респондентами,
т.е. начальный объем выборки, должно
быть в 2,22 х 1,25 (или 2,77) раз больше
необходимого объема выборки.
Заранее
заданная точность
результатов исследования или допустимая
ошибка выборки
позволяют рассчитать необходимый размер
выборочной совокупности, используя
статистические методы, которые будут
рассмотрены далее.
Ошибкой
выборочного исследования
называется
любая ошибка, возникающая в результате
опроса или наблюдения и являющаяся
следствием использования выборки, а не
всей генеральной совокупности. Ошибки
выборочного исследования обусловлены
процедурой формирования выборки и
объемом выборки. Крупные выборки
порождают меньшую ошибку выборочного
исследования, чем малые.
Чтобы
извлечь выборку, как уже отмечалось в
предыдущем параграфе, сначала необходимо
определит: основу
выборки,
представляющую собой сводный список
все членов генеральной совокупности.
Как известно, списки не всегда полно
представляют генеральную совокупность,
поскольку в ней постоянно происходят
изменения: одни члены появляются, другие
– уходят. Кроме того, списки не застрахованы
от ошибок и опечаток. Таким образом,
ошибка
основы выборки
выражается
в неправильном описании всей генеральной
совокупности. Независимо от способа
формирования выборки, исследователь
должен учитывать ошибку основы. Иногда
в распоряжении исследователя оказывается
основа, лишь приблизительно описывающая
всю генеральную совокупность, однако,
если альтернативы нет, приходится
использовать и такие списки. Исследователь
должен тщательно выбирать основу
выборки, стремясь минимизировать
ошибки. Кроме того, исследователь должен
предупредить клиента о том, что
используемая основа выборки может
содержать ошибки.
Далее
будет идти речь только о случайных
ошибках выборочного
исследования, которые не связанны с
основой выборки и могут быть оценены
статистически. Иначе говоря, будем
предполагать, что основа выборки является
достаточно качественной и обеспечивает
низкий уровень ошибок, так что мы можем
извлечь из нее репрезентативную выборку.
Ошибка
выборки
зависит
не
только от ее величины, но и от
степени различий между отдельными
единицами внутри данной генеральной
совокупности.
Например, если нужно узнать, средний
размер потребления пива молодежью г.
Минска в возрасте 18-25 лет, то обнаружится,
что внутри имеющейся генеральной
совокупности нормы потребления у
различных людей существенно различны
(гетерогенная
генеральная
совокупность). Если же необходимо узнать
размер потребления хлеба в той же
генеральной совокупности, то он будет
различаться значительно меньше
(гомогенная
генеральная
совокупность). Чем больше различия
(гетерогенность) внутри генеральной
совокупности, тем больше возможная
ошибка выборки.
Некоторые
методы выборочного исследования
минимизируют ошибку выборки, другие –
никак на нее не влияют.
Например, использование стратифицированного
отбора может дать выигрыш в точности
при оценивании характеристик всей
совокупности. Часто неоднородную
совокупность удается расслоить на
подсовокупности (страты), каждая из
которых внутренне однородна. Если каждая
страта однородна в том смысле, что
результаты измерений в ней мало изменяются
от единицы к единице, то можно получить
точную оценку среднего значения для
любой страты по небольшой выборке в
этой страте. Затем эти оценки можно
объединить в одну точную оценку для
всей совокупности.
2. Выбор метода
расчета размера выборки.
Если специалист из опыта знает, какой
размер выборки следует использовать,
или же существуют различные ограничения
(например, связанные с бюджетом),
используют приблизительные
методы расчета размера выборки,
к которым относятся следующие:
— произвольный
метод расчета.
В этом случае объем выборки определяется
на уровне 5-10 % от генеральной совокупности.
— по
эмпирическим правилам.
Рекомендуется
выбирать размер выборки таким образом,
чтобы при ее разделении на группы в
каждой группе было не меньше 100 элементов.
Кроме сопоставления основных групп
анализ часто может потребовать
использования подгрупп. Размеры таких
подгрупп должны составлять от 20 до 50
человек. Это основано на том, что для
подгрупп требуется меньшая точность.
Если
одна из групп или подгрупп составляет
сравнительно небольшой процент
совокупности, то будет разумно использовать
непропорциональную выборку. Допустим,
что только 10% совокупности смотрит
образовательные телепередачи, и мнения
представителей этой группы требуется
сопоставить с мнениями других членов
совокупности. Если используются
телефонные интервью, контакты с жителями
могут устанавливаться случайно до тех
пор, пока не будут набраны 100 человек,
которые не смотрят образовательные
телепередачи. Далее опрос продолжается,
однако уже опрашиваются лишь те
респонденты, кто образовательные
телепередачи смотрит. В результате
будет получена выборка из 200 человек,
половина из которых смотрят образовательные
телепередачи.
— традиционный
метод расчета
связан с проведением периодических
ежегодных исследований, охватывающих,
например, 500, 1000 или 1500 респондентов.
— на
основе опыта сопоставимых исследований.
Таблица
4.7 дает представление об объемах выборок,
используемых в различных маркетинговых
исследованиях. Эти величины установлены
опытным путем и могут использоваться
в качестве ориентировочных данных,
особенно при детерминированных методах
формирования выборки.
— затратный
метод основан
на размере расходов, которые допустимо
затратить на проведение исследования.
Статистический
метод определения объема выборки
основан на традиционном статистическом
заключении. В соответствии с этим методом
заранее определяется уровень (степень)
точности.
Рассмотрение
данного метода начнем с краткой
характеристики базовых
понятий математической статистики.
Наиболее
важным понятием, позволяющим делать
заключения о свойствах генеральной
совокупности на основе выборочных
методов является кривая нормального
распределения.
Таблица
4.7.
Объемы выборок, используемых в
маркетинговых исследованиях
|
Вид исследования |
Минимальный объем |
Обычный диапазон |
|
Исследование, цель которого |
500 |
1000-2500 |
|
Исследование, цель которого |
200 |
300-500 |
|
Тестирование товара |
200 |
300-500 |
|
Пробный маркетинг |
200 |
300-500 |
|
Теле- радио- и печатная |
150 |
200-300 |
|
Аудит на пробном рынке |
10 магазинов |
10-20 магазинов |
|
Фокус-группы |
2 группы |
10-15 групп |
Кривая нормального
распределения
– это теоретическая модель, представляющая
собой абсолютно симметричный и гладкий
вид полигона частот. Она имеет форму
колокола и одну вершину, а ее концы
уходят в бесконечность в обоих
направлениях. Важнейшим свойством,
которым обладает кривая нормального
распределения, является то, что расстояние
по абсциссе (горизонтальная ось)
распределения, измеренное в единицах
стандартного отклонения от среднего
арифметического распределения, всегда
дает одинаковую общую площадь под
кривой: между ±1 стандартным отклонением
находится 68,3% площади; между ±2 стандартными
отклонениями – 95,4% площади; между ±3
стандартными отклонениями – 99,7% площади
(см. рис. 4.10).

Рисунок
4.10. Области
под теоретической кривой нормального
распределения
C
понятием кривой нормального распределения
связана центральная
предельная теорема, которая
гласит:
«Если
из генеральной совокупности, имеющей
любое распределение со средним μ
и
стандартным отклонением σ,
многократно извлекать случайные выборки
объема n,
то
при большом n
распределение всех возможных выборочных
средних будет стремиться к нормальному
распределению со средним μ
и
стандартным
отклонением σ
/
».
Таким
образом, центральная предельная теорема
позволяет распространять данные,
полученные в результате выборочного
исследования на всю генеральную
совокупность с определенной степенью
допущения при условии достаточно
большого объема выборки.
Конечно,
остается вопрос о том, что же такое
большой объем выборки. Полезное
эмпирическое правило гласит: если объем
выборки (n)
равен
100 или более, то применима центральная
предельная теорема и вы можете принять
допущение о нормальности распределения
всех возможных выборочных средних. Если
же n
меньше
100, то вы должны иметь веские доказательства
нормальности распределения генеральной
совокупности, и только после этого вы
можете полагать, что распределение,
которому подчиняются выборочные
статистики, является нормальным.
Следовательно, нормальность распределения
выборочных статистик гарантируется
путем использования довольно больших
выборок.
3.
Выбор требуемой степени точности и
достоверности результатов исследования.
При проведении любого выборочного
опроса или наблюдения перед исследователем
ставится задача оценить, каково истинное
значение во всей генеральной совокупности
либо среднего
значения
абсолютного
признака (доход
потребителей, размер потребления
конкретного товара), либо доли
единиц в совокупности, обладающих
каким-либо
признаком
(доля постоянных потребителей конкретного
товара; доля потребителей, удовлетворенных
уровнем обслуживания). Точность
выборки
в первом случае будет представлена в
виде абсолютной величины со знаком ±
(например, ±100 тыс. руб.; ±1 кг), или в виде
процента, во втором случае – только в
виде процента с тем же знаком (например,
±1% или ±5%).
Интерпретация
точности выборки подчиняется следующей
логике: если объем выборки обеспечивает
точность ±5%, то результаты опроса или
наблюдения, полученные с помощью выборки,
отличаются от результатов полной
переписи не более чем на 5%.
Еще одним фактором,
влияющим на объем выборки является
заданная исследователем степень
достоверности
(надежности)
оценки,
то есть степень
уверенности в том, что оценка близка к
истинному значению.
Для выборки
фиксированного объема степень точности
и степень достоверности являются
связанными величинами. На деле определение
объема выборки предполагает достижение
известного баланса между двумя этими
принципами.
Зависимость
точности выборки от ее объема для 95,4% и
99,7% уровня надежности представлена на
рисунке 4.11. Объем выборок на графике
колеблется от 50 до 2000. График демонстрирует,
что при увеличении объема выборки
ее ошибка уменьшается. Однако, как видим,
зависимость ошибки выборки от ее объема
не является прямолинейной. Иначе говоря,
удвоение объема выборки, не приводит к
существенному уменьшению ошибки.
Р
исунок
4.11. Зависимость
точности и достоверности от объема
выборки
Если
объем выборки превышает 500, ошибка
выборки для 95,4% надежности падает ниже
±4% и продолжает очень медленно снижаться.
С другой стороны, анализ графика в
области малых выборок показывает, что
относительно небольшое изменение объема
выборки позволяет значительно повысить
их точность. Например, если объем выборки
равен 50, то ее уровень точности равен
±13,9%, а увеличение их объема до 250 позволяет
уменьшить ошибку выборки до ±6,2%. Иными
словами, точность выборки, объем которой
равен 25 примерно вдвое выше, чем точность
выборки, объем которой равен 50. Однако
в области крупных выборок это правило
не выполняется.
4. Определение
t
параметра, связанного с уровнем
надежности.
Определить значение t,
связанное с уровнем надежности можно
воспользовавшись таблицей 1 приложения.
Как видно по данным таблицы, при объеме
выборки больше 100 для 95,4% надежности
t≈2,
для 99,7% надежности t≈3.
5. Поиск информации
об уровне стандартного отклонения
среднего значения признака в генеральной
совокупности.
Здесь возможны
две различные ситуации: 1) стандартное
отклонение среднего значения признака
(σ)
в генеральной совокупности известно и
2) стандартное отклонение среднего
значения признака в генеральной
совокупности неизвестно.
В
первом случае можно приступить к расчету
объема
выборки с помощью формулы стандартной
ошибки выборки.
6.
Определение
объема выборки с помощью формулы
стандартной ошибки с учетом корректировки
на охват и завершенность.
Принято различать
среднюю и предельную ошибки выборки.
Предельная ошибка выборки определяется
следующим образом:
где
∆
— предельная ошибка выборки;
t
– параметр, связанный с уровнем
надежности;
μ
– средняя ошибка выборки.
Формулы расчета
средней ошибки
выборки для средней и для доли с учетом
способа отбора приведены в таблице 4.8.
Доверительные
интервалы для генеральной средней
можно установить на основе соотношений
Доверительные
интервалы для генеральной доли
устанавливаются на основе соотношений
Далее
для вычисления объема выборки применяется
формула
вычисление объема выборки по заданному
доверительному интервалу.
Формулы
расчета численности выборки
для определения средней и доли с учетом
способа отбора приведены в таблице 4.9.
Например,
для обследования, преследующего цель
выявить мнение потребителей о новом
товаре, в регионе, насчитывающем 10 тыс.
семей, необходимо провести анкетирование.
Условно принимается, что в каждой
квартире проживает одна семья и на нее
будет выделена одна анкета. Предварительные
исследования установили, что дисперсия
среднего размера покупки составляет
24 тыс. руб.; σ2
= 2; предельная ошибка не должна превышать
0,5 тыс. руб. Отсюда численность выборки
(п)
составит:
Эта
величина округляется до 400 семей
(квартир), т.е. установлена 4%-я выборка.
Однако практика показывает, что некоторая
часть анкет не возвращается (предположим
каждая пятая), поэтому увеличиваем число
анкет до 500. Следовательно, необходимо
включить в выборку каждую 20-ю квартиру
(10000 : 500).
Все
вышеприведенные формулы применимы для
большой выборки.
Кроме большой выборки используются так
называемые малые
выборки (n
< 30), которые могут иметь место в случаях
нецелесообразности использования
больших выборок.
При
расчете ошибок малой
выборки
необходимо учесть два момента:
1) формула средней
ошибки имеет вид
2)
при определении доверительных интервалов
исследуемого показателя в генеральной
совокупности или при нахождении
вероятности допуска той или иной ошибки
необходимо использовать таблицы
вероятности Стьюдента. При этом
вероятность
определяется
в зависимости от объема выборки и t
(см. табл.
прил. 1).
Таблица 4.8.
Формулы определения стандартной ошибки
выборки при различных способах отбора
|
Виды выборки Способы отбора |
Повторная выборка |
Бесповторная выборка |
|
Для средней |
||
|
Простая случайная выборка |
|
|
|
Стратифицированная |
|
|
|
Кластерная, |
— |
|
|
Для доли |
||
|
Простая случайная выборка |
|
|
|
Стратифицированная |
|
|
|
Кластерная, |
— |
— |
В
таблице используются следующие условные
обозначения:
N
– объем генеральной совокупности;
п
– объем выборочной совокупности;
– средняя в
генеральной совокупности;
–
средняя в выборочной
совокупности;
р
– доля единиц в генеральной совокупности;
w
– доля единиц в выборочной совокупности;
– генеральная
дисперсия (заменяется на выборочную
(S2) в случае, если она
не известна);
– межсерийная
дисперсия
;
r
— число отобранных серий;
R—
число серий в генеральной совокупности.
Таблица 4.9.
Формулы определения численности выборки
(n)
при различных способах отбора
|
Виды выборки Способы отбора |
Повторная выборка |
Бесповторная выборка |
|
Для средней |
||
|
Простая случайная выборка |
|
|
|
Стратифицированная |
|
|
|
Кластерная, |
— |
|
|
Для доли |
||
|
Простая случайная выборка |
|
|
|
Стратифицированная |
|
|
|
Кластерная, |
— |
— |
Например, для
разработки бизнес-плана нового ресторана,
который открывается в центральной части
г. Минска необходимо узнать ожидаемый
диапазон расходов одного посетителя в
вечернее время. Удалось получить
информацию о том, что стандартное
отклонение расходов посетителей близкого
по уровню и месту расположения ресторана
составляет 30$. Существует возможность
опросить около 26 посетителей ресторана.
С какой достоверностью можно получить
результат при заданной точности ±10$?
Рассчитаем среднюю
ошибку выборки:
Тогда
Из
таблицы приложения 1 для n=26
и t=1,66
можно определить, что при допуске ошибки
±10$ достоверность
результатов составит менее 90%. Более
точное значение достоверности для тех
же параметров можно получить, например,
при помощи функции СТЬЮДРАСП в Microsoft
Excel
— 89,2%.
С 95,4% надежностью
будет обеспечена меньшая точность:
7. Отбор
произвольной пробной выборки.
В случае если стандартное
отклонение среднего значения признака
в генеральной совокупности неизвестно,
необходимо сформировать произвольную
пробную выборку.
8. Расчет
стандартного отклонения средней в
выборочной совокупности.
На основе полученных данных рассчитывается
стандартное отклонение признака в
выборочной совокупности и, затем –
необходимый размер выборки по приведенным
выше формулам.
9. Расчет точности
полученных результатов по формуле
предельной ошибки выборки.По
данным, собранным в ходе проведенного
выборочного исследования, рассчитывается
точность результатов. Если полученная
точность не устраивает исследователя,
может возникнуть необходимость увеличить
размер выборки с учетом рассчитанного
стандартного отклонения и коэффициентов
отклика и завершенности.
Предположим, что
в предыдущем примере не было возможности
узнать стандартное отклонение расходов
посетителей ресторана. По данным опроса
30 случайно отобранных респондентов
получены следующие данные: 25$ – 2 чел.;
30$ – 3 чел.; 45$ – 7 чел.; 55$ – 6 чел.; 70$ – 3
чел.; 85$ – 5 чел.; 110$ – 2 чел.; 150$ – 2 чел.
Определяем среднее
значение по формуле средней взвешенной:

Далее
рассчитываем дисперсию (квадрат
стандартного отклонения) расходов
посетителей ресторана по выборочной
совокупности.

Тогда
точность полученных результатов с
достоверностью 95,4%:
Для
того, чтобы обеспечить заданную точность
(±10$) рассчитываем
необходимый размер выборки:
В
целом, для принятия взвешенного решения
по размеру выборки наряду со статистическими
методами расчета следует применить
рассмотренные ранее приблизительные
методы и сравнить полученные результаты.
10. Оценка значения
признака в генеральной совокупности.
Основными
методами распространения выборочного
наблюдения на генеральную совокупность
являются прямой пересчет и способ
коэффициентов.
Прямой
пересчет есть
произведение среднего значения признака
на объем генеральной совокупности.
Однако большое число факторов не
позволяет в полной мере использовать
точечную оценку прямого пересчета при
распространении результатов выборки
на генеральную совокупность. На практике
чаще пользуются интервальной оценкой,
которая дает возможность учитывать
размер предельной ошибки выборки,
которая рассчитана для средней или для
доли признака.
Оценка
среднего по совокупности при использовании
стратифицированной выборки является
взвешенным средним средних значений
по каждой страте выборки.
Например,
производителю пива для оценки емкости
внутреннего рынка в частности необходимо
определить долю потребителей пива в
общей численности населения региона в
возрасте от 20 до 60 лет с точностью ±5%.
Можно предположить, что данный показатель
будет варьировать по полу и возрасту.
В таблице 4.10 представлена информация
о численности и структуре населения
региона в возрасте от 20 до 60 лет.
Таблица
4.10. Численность
населения региона в возрасте от 20 до 60
лет
|
Возрастные категории населения |
Всего, тыс. чел. |
В том числе |
|
|
мужчины |
женщины |
||
|
20-29 |
1576,0 |
802,0 |
774,0 |
|
30-39 |
1357,3 |
671,4 |
685,9 |
|
40-49 |
1559,6 |
751,9 |
807,7 |
|
50-59 |
1276,1 |
582,7 |
693,4 |
|
Всего |
5769,0 |
2807,9 |
2961,1 |
Ранее
проведенный опрос 200 респондентов в
возрасте от 20 до 60 лет показал, что доля
потребителей пива в общей численности
населения региона составляет 83%. По
имеющейся информации был рассчитан
необходимый объем выборки:
С
учетом необходимости обеспечить
необходимый минимальный размер подгрупп
округляем полученный результат до 300
человек и рассчитываем объем выборки
для каждой из страт по полу и возрасту
пропорционально соответствующей
численности населения. Результаты
расчета представлены в таблице 4.11.
Таблица
4.11. Структура
населения региона в возрасте от 20 до 60
лет и численность выборки.
|
Возрастные категории населения |
В % к общей численности населения |
Численность выборки |
|||
|
всего |
мужчины |
женщины |
мужчины |
женщины |
|
|
20-29 |
27,3 |
13,9 |
13,4 |
42 |
40 |
|
30-39 |
23,6 |
11,7 |
11,9 |
35 |
36 |
|
40-49 |
27,0 |
13,0 |
14,0 |
39 |
42 |
|
50-59 |
22,1 |
10,1 |
12,0 |
30 |
36 |
|
Всего |
100,0 |
48,7 |
51,3 |
146 |
154 |
В
результате опроса получены данные,
представленные в таблице 4.12.
Таблица
4.12. Доля
потребителей пива в общей численности
населения в разрезе возрастных категорий
по данным выборочного опроса.
|
Возрастные категории населения |
Доля потребителей пива |
|
|
мужчины |
женщины |
|
|
20-29 |
0,812 |
0,795 |
|
30-39 |
0,855 |
0,743 |
|
40-49 |
0,848 |
0,683 |
|
50-59 |
0,867 |
0,542 |
Определяем долю
потребителей пива по формуле средней
взвешенной:
Средняя
ошибка выборки:
Предельная ошибка
выборки для 95,4% надежности составит:
Таким
образом, с 95,4% надежностью можно
утверждать, что доля потребителей пива
в общей численности населения региона
в возрасте от 20 до 60 лет находится в
интервале от 71,8% (76,6% — 4,8%) до 81,4% (76,6% +
4,8%).
Опрос
обычно не ограничивается одним вопросом
–
иногда их сотни. Поэтому повторять
подобный процесс для каждого вопроса
смысла не имеет. Разумный подход –
выбрать несколько репрезентативных
вопросов и по ним определить размер. В
этот набор следует включить наиболее
критичные вопросы с максимальным уровнем
ожидаемой дисперсии.
В таком случае
может оказаться полезным подход
к расчету объема выборки, основанный
на сценарии максимально возможной
вариации признака в совокупности. Как
видно на рисунке 6, вариант,
когда w=
0,5 (50%) является наиболее консервативным,
поскольку он порождает максимальный
размер ошибки и, соответственно,
максимальный объем выборки. Следовательно,
его следует выбирать, когда изменчивость
не известна. Тогда формула размера
выборки упрощается:
Для 95% уровня
надежности и 5% уровня точности:
Р
исунок
4.12.
График
Использование
номограмм для
расчета
объема выборки. Стремление
упростить процедуру расчета объема
выборки приводит к созданию таблиц,
шкал или программ, которые ориентированы
на обеспечение статистической
надежности информации, но при этом не
обременяют пользователя знаниями
специальных формул из области статистики.
Например, существует калькулятор выборки
(www.
shortway.
to/few/calculator,
htm).
Номограмма является
графическим способом определения
размера выборки. Номограмма включает
три шкалы (рис. 7). На шкале слева
устанавливается разметка показателя
среднеквадратического отклонения
или распределения доли признака. На
правой шкале наносится разметка точности
измерения в виде допустимой ошибки при
заданной доверительной вероятности
95,4% или 99,7%. На средней шкале делается
разметка, соответствующая требуемому
объему выборки. На правой и левой
шкалах делаются отметки на уровне
желаемых значений показателей (доли
признака и допустимой ошибки). Линейкой
эти две отметки соединяются, на пересечении
линейки со средней шкалой делается
отметка, соответствующая тому объему
выборки, который отвечает пожеланиям
исследователя.
Калькулятор для расчета достаточного объема выборки
Калькулятор ошибки выборки для доли признака
Калькулятор ошибки выборки для среднего значения
Калькулятор значимости различий долей
Калькулятор значимости различий средних
1. Формула (даже две)
Бытует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с размером генеральной совокупности. Например, при опросах организаций (B2B).
Если речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная.
На рис.1. пример выборки 15000 человек (!) при опросе в муниципальном районе. Возможно, от численности населения взяли 10%?
Размер выборки никогда не рассчитывается как процент от генеральной совокупности!
Рис.1. Размер выборки 15000 человек, как реальный пример некомпетентности (или хуже).
В таких случаях для расчета объема выборки используется следующая формула:

где
n – объем выборки,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует,
∆ – предельная ошибка выборки.
Доверительный уровень – это вероятность того, что реальная доля лежит в границах полученного доверительного интервала: выборочная доля (p) ± ошибка выборки (Δ). Доверительный уровень устанавливает сам исследователь в соответствии со своими требованиями к надежности полученных результатов. Чаще всего применяются доверительные уровни, равные 0,95 или 0,99. В маркетинговых исследованиях, как правило, выбирается доверительный уровень, равный 0,95. При этом уровне коэффициент Z равен 1,96.
Значения p и q чаще всего неизвестны до проведения исследования и принимаются за 0,5. При этом значении размер ошибки выборки максимален.
Допустимая предельная ошибка выборки выбирается исследователем в зависимости от целей исследования. Считается, что для принятия бизнес-решений ошибка выборки должна быть не больше 4%. Этому значению соответствует объем выборки 500-600 респондентов. Для важных стратегических решений целесообразно минимизировать ошибку выборки.
Рассмотрим кривую зависимости ошибки выборки от ее объема (Рис.2).

Рис.2. Зависимость ошибки выборки от ее объема при 95% доверительном уровне
Как видно из диаграммы, с ростом объема выборки значение ошибки уменьшается все медленнее. Так, при объеме выборки 1500 человек предельная ошибка выборки составит ±2,5%, а при объеме 2000 человек – ±2,2%. То есть, при определенном объеме выборки дальнейшее его увеличение не дает значительного выигрыша в ее точности.
Подходы к решению проблемы:
Случай 1. Генеральная совокупность значительно больше выборки:

Случай 2. Генеральная совокупность сопоставима с объемом выборки: (см. раздел исследований B2B)

где
n – объем выборки,
N – объем генеральной совокупности,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует, (значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования)
∆ – предельная ошибка выборки.
Например,
рассчитаем ошибку выборки объемом 1000 человек при 95% доверительном уровне, если генеральная совокупность значительно больше объема выборки:
Ошибка выборки = 1,96 * КОРЕНЬ(0,5*0,5/1000) = 0,031 = ±3,1%
При расчете объема выборки следует также учитывать стоимость проведения исследования. Например, при цене за 1 анкету 200 рублей стоимость опроса 1000 человек составит 200 000 рублей, а опрос 1500 человек будет стоить 300 000 рублей. Увеличение затрат в полтора раза сократит ошибку выборки всего на 0,6%, что обычно неоправданно экономически.
2. Причины «раздувать» выборку
Анализ полученных данных обычно включает в себя и анализ подвыборок, объемы которых меньше основной выборки. Поэтому ошибка для выводов по подвыборкам больше, чем ошибка по выборке в целом. Если планируется анализ подгрупп / сегментов, объем выборки должен быть увеличен (в разумных пределах).
Рис.3 демонстрирует данную ситуацию. Если для исследования авиапассажиров используется выборка численностью 500 человек, то для выводов по выборке в целом ошибка составляет 4,4%, что вполне приемлемо для принятия бизнес-решений. Но при делении выборки на подгруппы в зависимости от цели поездки, выводы по каждой подгруппе уже недостаточно точны. Если мы захотим узнать какие-либо количественные характеристики группы пассажиров, совершающих бизнес-поездку и покупавших билет самостоятельно, ошибка полученных показателей будет достаточно велика. Даже увеличение выборки до 2000 человек не обеспечит приемлемой точности выводов по этой подвыборке.

Рис.3. Проектирование объема выборки с учетом необходимости анализа подвыборок
Другой пример – анализ подгрупп потребителей услуг торгово-развлекательного центра (Рис.4).

Рис.4. Потенциальный спрос на услуги торгово-развлекательного центра
При объеме выборки в 1000 человек выводы по каждой отдельной услуге (например, социально-демографический профиль, частота пользования, средний чек и др.) будут недостаточно точными для использования в бизнес планировании. Особенно это касается наименее популярных услуг (Таблица 1).
Таблица 1. Ошибка по подвыборкам потенциальных потребителей услуг торгово-развлекательного центра при выборке 1000 чел.

Чтобы ошибка в самой малочисленной подвыборке «Ночной клуб» составила меньше 5%, объем выборки исследования должен составлять около 4000 человек. Но это будет означать 4-кратное удорожание проекта. В таких случаях возможно компромиссное решение:
- увеличение выборки до 1800 человек, что даст достаточную точность для 6 самых популярных видов услуг (от кинотеатра до парка аттракционов);
- добор 200-300 пользователей менее популярных услуг с опросом по укороченной анкете (см. Таблицу 2).
Таблица 2. Разница в ошибке выборки по подвыборкам при разных объемах выборки.

При обсуждении с исследовательским агентством точности результатов планируемого исследования рекомендуется принимать во внимание бюджет, требования к точности результатов в целом по выборке и в разрезе подгрупп. Если бюджет не позволяет получить информацию с приемлемой ошибкой, лучше пока отложить проект (или поторговаться).
КАЛЬКУЛЯТОРЫ ДЛЯ РАСЧЕТА СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ И ОПРЕДЕЛЕНИЯ ЗНАЧИМОСТИ РАЗЛИЧИЙ:
КАЛЬКУЛЯТОР ДЛЯ РАСЧЕТА
ДОСТАТОЧНОГО ОБЪЁМА ВЫБОРКИ
Доверительный уровень:
Ошибка выборки (?):
%
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
РЕЗУЛЬТАТ
Один из важных вопросов, на которые нужно ответить при планировании исследования, — это оптимальный объем выборки. Слишком маленькая выборка не сможет обеспечить приемлемую точность результатов опроса, а слишком большая приведет к лишним расходам.
Онлайн-калькулятор объема выборки поможет рассчитать оптимальный размер выборки, исходя из максимально приемлемого для исследователя размера ошибки выборки.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке!
Формулы для других типов выборки отличаются.
Объем выборки рассчитывается по следующим формулам
1) если объем выборки значительно меньше генеральной совокупности:

2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели соков и нектаров, постоянно проживающие в Москве и Московской области). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
q = 1 — p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален. В данном калькуляторе значения p и q по умолчанию равны 0,5.
Δ– предельная ошибка выборки (для доли признака), приемлемая для исследователя. Считается, что для принятия бизнес-решений ошибка выборки не должна превышать 4%.
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании.
ПРИМЕР РАСЧЕТА ОБЪЕМА ВЫБОРКИ:
Допустим, мы хотим рассчитать объем выборки, предельная ошибка которой составит 4%. Мы принимаем доверительный уровень, равный 95%. Генеральная совокупность значительно больше выборки. Тогда объем выборки составит:
n = 1,96 * 1,96 * 0,5 * 0,5 / (0,04 * 0,04) = 600,25 ≈ 600 человек
Таким образом, если мы хотим получить результаты с предельной ошибкой 4%, нам нужно опросить 600 человек.
КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА
Доверительный уровень:
Объём выборки (n):
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
Доля признака (p):
%
РЕЗУЛЬТАТ
Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).
Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.
Ошибка выборки для доли признака рассчитывается по следующим формулам.
1) если объем выборки значительно меньше генеральной совокупности:
(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели шоколада, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.
p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
q = 1 — p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален.
Δ– предельная ошибка выборки.
Таким образом, зная объем выборки исследования, мы можем заранее оценить показатель ее ошибки.
А получив значение p, мы можем рассчитать доверительный интервал для доли признака: (p — ∆; p + ∆)
ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА:
Например, в ходе исследования были опрошены 1000 человек (n=1000). 20% из них заинтересовались новым продуктом (p=0,2). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):
∆ = 1,96 * КОРЕНЬ (0,2*0,8/1000) = 0,0248 = ±2,48%
Рассчитаем доверительный интервал:
(p — ∆; p + ∆) = (20% — 2,48%; 20% + 2,48%) = (17,52%; 22,48%)
Таким образом, с вероятностью 95% мы можем быть уверены, что реальная доля заинтересованных в новом продукте (среди всей генеральной совокупности) находится в пределах полученного диапазона (17,52%; 22,48%).
Если бы мы выбрали доверительный уровень, равный 99%, то для тех же значений p и n ошибка выборки была бы больше, а доверительный интервал – шире. Это логично, поскольку, если мы хотим быть более уверены в том, что наш доверительный интервал «накроет» реальное значение признака, то интервал должен быть более широким.
КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ
Доверительный уровень:
Объём выборки (n):
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
Среднее значение (x̄):
Стандартное отклонение (s):
РЕЗУЛЬТАТ
Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).
Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.
Ошибка выборки для среднего значения рассчитывается по следующим формулам.
1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели мороженого, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.
s — выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:
где, x ̅ – среднее арифметическое показателя, xi– значение i-го показателя, n – объем выборки
Δ– предельная ошибка выборки.
Зная среднее значение показателя x ̅ и ошибку ∆, мы можем рассчитать доверительный интервал для среднего значения:(x ̅ — ∆; x ̅ + ∆)
ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ:
Например, в ходе исследования были опрошены 1000 человек (n=1000). Каждого из них попросили указать их примерную среднюю сумму покупки (средний чек) в известной сети магазинов. Среднее арифметическое всех ответов составило 500 руб. (x ̅=500), а стандартное отклонение составило 120 руб. (s=120). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):
∆ = 1,96 * 120 / КОРЕНЬ (1000) = 7,44
Рассчитаем доверительный интервал:
(x ̅ — ∆; x ̅ + ∆) = (500 – 7,44; 500 + 7,44) = (492,56; 507,44)
Таким образом, с вероятностью 95% мы можем быть уверены, что значение среднего чека по всей генеральной совокупности находится в границах полученного диапазона: от 492,56 руб. до 507,44 руб.
КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ ДОЛЕЙ
Доверительный уровень:
| Измерение 1 | Измерение 2 | |
| Доля признака (p): | % | % |
| Объём выборки (n): |
РЕЗУЛЬТАТ
Если в прошлогоднем исследовании вашу марку вспомнили 10% респондентов, а в исследовании текущего года – 15%, не спешите открывать шампанское, пока не воспользуетесь нашим онлайн-калькулятором для оценки статистической значимости различий.
Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.
Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.
В приведенном здесь калькуляторе используется двухвыборочный z-тест для долей. Для его применения должны соблюдаться следующие условия:
- Обе выборки – простые случайные
- Выборки независимы (между значениями двух выборок нет закономерной связи)
- Генеральные совокупности значительно больше выборок
- Произведения n*p и n*(1-p), где n=размер выборки а p=доля признака, – не меньше 5.
В калькуляторе используются следующие вводные данные:
Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.
Доля признака (p) – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.
Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.
КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ СРЕДНИХ
Доверительный уровень:
| Измерение 1 | Измерение 2 | |
| Среднее значение (x̄): | ||
| Стандартное отклонение (s): | ||
| Объём выборки (n): |
РЕЗУЛЬТАТ
Допустим, выборочный опрос посетителей двух разных ТРЦ показал, что средний чек в одном из них равен 1000 рублей, а в другом – 1200 рублей. Следует ли отсюда вывод, что суммы среднего чека в двух этих ТРЦ действительно отличаются?
Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.
Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.
В приведенном здесь калькуляторе используется двухвыборочный z-тест для средних значений. Для его применения должны соблюдаться следующие условия:
- Обе выборки – простые случайные
- Выборки независимы (между значениями двух выборок нет закономерной связи)
- Генеральные совокупности значительно больше выборок
- Распределения значений в выборках близки к нормальному распределению.
В калькуляторе используются следующие вводные данные:
Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.
Среднее значение ( ̅x) – среднее арифметическое показателя.
Стандартное отклонение (s) – выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:
где, x ̅ – среднее арифметическое показателя, xi– значение i-го показателя, n – объем выборки
Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.
Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.
Вы можете подписаться на уведомления о новых материалах СканМаркет