Перейти к содержанию

На чтение 1 мин Просмотров 4.7к.
Отклонение результата измерения от истинного значения
измеряемой величины называется погрешностью измерения. Это сумма составляющих,
каждая из которых имеет свою причину возникновения. Далее более подробно
рассмотрим основные причины возникновения погрешности измерения.
Причины возникновения погрешности измерения
1. Неправильная настройка инструментов измерения или
смещение уровня настройки во время эксплуатации является первой причиной
возникновения погрешности измерения.
2. Низкий уровень квалификации или профессионализма
оператора, который проводил измерения. Сюда также относится его плохое
настроение или ухудшения состояния здоровья. Все это влияет на возникновение
погрешности.
3. Определенные особенности или характеристики
измерительного объекта, которые влияют на процесс исследования.
4. Негативное влияние факторов внешней среды на
инструмент или измерительный объект. Это может быть резкий перепад температур
или давления, влияние магнитного или электрического поля, вибрации.
5. Возникновение ошибок при получении, переработке и
выдачи информации в измерительной цепи измерительных инструментов.
6. Неправильная установка измерительного объекта на
плоскость может привести к возникновению погрешности.
7. Несоблюдение последовательности проведения анализа исследуемого объекта.
проголосуй за пост!
Загрузка…
Свойства физического объекта (явления, процесса) определяются набором
количественных характеристик — физических величин.
Как правило, результат измерения представляет
собой число, задающее отношение измеряемой величины к некоторому эталону.
Сравнение с эталоном может быть как
прямым (проводится непосредственно
экспериментатором), так и косвенным (проводится с помощью некоторого
прибора, которому экспериментатор доверяет).
Полученные таким образом величины имеют размерность, определяемую выбором эталона.
Замечание. Результатом измерения может также служить количество отсчётов некоторого
события, логическое утверждение (да/нет) или даже качественная оценка
(сильно/слабо/умеренно). Мы ограничимся наиболее типичным для физики случаем,
когда результат измерения может быть представлен в виде числа или набора чисел.
Взаимосвязь между различными физическими величинами может быть описана
физическими законами, представляющими собой идеализированную
модель действительности. Конечной целью любого физического
эксперимента (в том числе и учебного) является проверка адекватности или
уточнение параметров таких моделей.
1.1 Результат измерения
Рассмотрим простейший пример: измерение длины стержня
с помощью линейки. Линейка проградуирована производителем с помощью
некоторого эталона длины — таким образом, сравнивая длину
стержня с ценой деления линейки, мы выполняем косвенное сравнение с
общепринятым стандартным эталоном.
Допустим, мы приложили линейку к стержню и увидели на шкале некоторый результат
x=xизм. Можно ли утверждать, что xизм — это длина
стержня?
Во-первых, значение x не может быть задано точно, хотя бы
потому, что оно обязательно округлено до некоторой значащей
цифры: если линейка «обычная», то у неё
есть цена деления; а если линейка, к примеру, «лазерная»
— у неё высвечивается конечное число значащих цифр
на дисплее.
Во-вторых, мы никак не можем быть уверенны, что длина стержня на
самом деле такова хотя бы с точностью до ошибки округления. Действительно,
мы могли приложить линейку не вполне ровно; сама линейка могла быть
изготовлена не вполне точно; стержень может быть не идеально цилиндрическим
и т.п.
И, наконец, если пытаться хотя бы гипотетически переходить к бесконечной
точности измерения, теряет смысл само понятие «длины стержня». Ведь
на масштабах атомов у стержня нет чётких границ, а значит говорить о его
геометрических размерах в таком случае крайне затруднительно!
Итак, из нашего примера видно, что никакое физическое измерение не может быть
произведено абсолютно точно, то есть
у любого измерения есть погрешность.
Замечание. Также используют эквивалентный термин ошибка измерения
(от англ. error). Подчеркнём, что смысл этого термина отличается от
общеупотребительного бытового: если физик говорит «в измерении есть ошибка»,
— это не означает, что оно неправильно и его надо переделать.
Имеется ввиду лишь, что это измерение неточно, то есть имеет
погрешность.
Количественно погрешность можно было бы определить как разность между
измеренным и «истинным» значением длины стержня:
δx=xизм-xист. Однако на практике такое определение
использовать нельзя: во-первых, из-за неизбежного наличия
погрешностей «истинное» значение измерить невозможно, и во-вторых, само
«истинное» значение может отличаться в разных измерениях (например, стержень
неровный или изогнутый, его торцы дрожат из-за тепловых флуктуаций и т.д.).
Поэтому говорят обычно об оценке погрешности.
Об измеренной величине также часто говорят как об оценке, подчеркивая,
что эта величина не точна и зависит не только от физических свойств
исследуемого объекта, но и от процедуры измерения.
Замечание.
Термин оценка имеет и более формальное значение. Оценкой называют результат процедуры получения значения параметра или параметров физической модели, а также иногда саму процедуру. Теория оценок является подразделом математической статистики. Некоторые ее положения изложены в главе 3, но для более серьезного понимания следует обратиться к [5].
Для оценки значения физической величины корректно использовать
не просто некоторое фиксированное число xизм, а интервал (или
диапазон) значений, в пределах которого может лежать её
«истинное» значение. В простейшем случае этот интервал
может быть записан как
где δx — абсолютная величина погрешности.
Эта запись означает, что исследуемая величина лежит в интервале
x∈(xизм-δx;xизм+δx)
с некоторой достаточно большой долей вероятности (более подробно о
вероятностном содержании интервалов см. п. 2.2).
Для наглядной оценки точности измерения удобно также использовать
относительную величину погрешности:
Она показывает, насколько погрешность мала по сравнению с
самой измеряемой величиной (её также можно выразить в процентах:
ε=δxx⋅100%).
Пример. Штангенциркуль —
прибор для измерения длин с ценой деления 0,1мм. Пусть
диаметр некоторой проволоки равен 0,37 мм. Считая, что абсолютная
ошибка составляет половину цены деления прибора, результат измерения
можно будет записать как d=0,40±0,05мм (или
d=(40±5)⋅10-5м).
Относительная погрешность составляет ε≈13%, то
есть точность измерения весьма посредственная — поскольку
размер объекта близок к пределу точности прибора.
О необходимости оценки погрешностей.
Измерим длины двух стержней x1 и x2 и сравним результаты.
Можно ли сказать, что стержни одинаковы или различны?
Казалось бы,
достаточно проверить, справедливо ли x1=x2. Но никакие
два результата измерения не равны друг другу с абсолютной точностью! Таким
образом, без указания погрешности измерения ответ на этот вопрос дать
невозможно.
С другой стороны, если погрешность δx известна, то можно
утверждать, что если измеренные длины одинаковы
в пределах погрешности опыта, если |x2-x1|<δx
(и различны в противоположном случае).
Итак, без знания погрешностей невозможно сравнить между собой никакие
два измерения, и, следовательно, невозможно сделать никаких
значимых выводов по результатам эксперимента: ни о наличии зависимостей
между величинами, ни о практической применимости какой-либо теории,
и т. п. В связи с этим задача правильной оценки погрешностей является крайне
важной, поскольку существенное занижение или завышение значения погрешности
(по сравнению с реальной точностью измерений) ведёт к неправильным выводам.
В физическом эксперименте (в том числе лабораторном практикуме) оценка
погрешностей должна проводиться всегда
(даже когда составители задания забыли упомянуть об этом).
1.2 Многократные измерения
Проведём серию из n одинаковых (однотипных) измерений одной
и той же физической величины (например, многократно приложим линейку к стержню) и получим
ряд значений
Что можно сказать о данном наборе чисел и о длине стержня?
И можно ли увеличивая число измерений улучшить конечный результат?
Если цена деления самой линейки достаточно мала, то как нетрудно убедиться
на практике, величины {xi} почти наверняка окажутся
различными. Причиной тому могут быть
самые разные обстоятельства, например: у нас недостаточно остроты
зрения и точности рук, чтобы каждый раз прикладывать линейку одинаково;
стенки стержня могут быть слегка неровными; у стержня может и не быть
определённой длины, например, если в нём возбуждены звуковые волны,
из-за чего его торцы колеблются, и т. д.
В такой ситуации результат измерения интерпретируется как
случайная величина, описываемая некоторым вероятностным законом
(распределением).
Подробнее о случайных величинах и методах работы с ними см. гл. 2.
По набору результатов 𝐱 можно вычислить их среднее арифметическое:
| ⟨x⟩=x1+x2+…+xnn≡1n∑i=1nxi. | (1.1) |
Это значение, вычисленное по результатам конечного числа n измерений,
принято называть выборочным средним. Здесь и далее для обозначения
выборочных средних будем использовать угловые скобки.
Кроме среднего представляет интерес и то, насколько сильно варьируются
результаты от опыта к опыту. Определим отклонение каждого измерения от среднего как
Разброс данных относительно среднего принято характеризовать
среднеквадратичным отклонением:
| s=Δx12+Δx22+…+Δxn2n=1n∑i=1nΔxi2 | (1.2) |
или кратко
Значение среднего квадрата отклонения s2 называют
выборочной дисперсией.
Будем увеличивать число измерений n (n→∞). Если объект измерения и методика
достаточно стабильны, то отклонения от среднего Δxi будут, во-первых,
относительно малы, а во-вторых, положительные и отрицательные отклонения будут
встречаться примерно одинаково часто. Тогда при вычислении (1.1)
почти все отклонения Δxi скомпенсируются и можно ожидать,
что выборочное среднее при n≫1 будет стремиться к некоторому пределу:
Тогда предельное значение x¯ можно отождествить с «истинным» средним
для исследуемой величины.
Предельную величину среднеквадратичного отклонения при n→∞
обозначим как
Замечание. В общем случае указанные пределы могут и не существовать. Например, если измеряемый параметр
меняется во времени или в результате самого измерения, либо испытывает слишком большие
случайные скачки и т. п. Такие ситуации требуют особого рассмотрения и мы на них не
останавливаемся.
Замечание. Если n мало (n<10), для оценки среднеквадратичного отклонения
математическая статистика рекомендует вместо формулы (1.3) использовать
исправленную формулу (подробнее см. п. 5.2):
sn-12=1n-1∑i=1nΔxi2,
(1.4)
где произведена замена n→n-1. Величину sn-1
часто называют стандартным отклонением.
Итак, можно по крайней мере надеяться на то, что результаты небольшого числа
измерений имеют не слишком большой разброс, так что величина ⟨x⟩
может быть использована как приближенное значение (оценка) истинного значения
⟨x⟩≈x¯,
а увеличение числа измерений позволит уточнить результат.
Многие случайные величины подчиняются так называемому нормальному закону
распределения (подробнее см. Главу 2). Для таких величин
могут быть строго доказаны следующие свойства:
- •
при многократном повторении эксперимента бо́льшая часть измерений
(∼68%) попадает в интервал x¯-σ<x<x¯+σ
(см. п. 2.2). - •
выборочное среднее значение ⟨x⟩ оказывается с большей
вероятностью ближе к истинному значению x¯, чем каждое из измерений
{xi} в отдельности. При этом ошибка вычисления среднего
убывает пропорционально корню из числа опытов n
(см. п. 2.4).
Упражнение. Показать, что
s2=⟨x2⟩-⟨x⟩2.
(1.5)
то есть дисперсия равна разности среднего значения квадрата
⟨x2⟩=1n∑i=1nxi2
и квадрата среднего ⟨x⟩2=(1n∑i=1nxi)2.
1.3 Классификация погрешностей
Чтобы лучше разобраться в том, нужно ли многократно повторять измерения,
и в каком случае это позволит улучшить результаты опыта,
проанализируем источники и виды погрешностей.
В первую очередь, многократные измерения позволяют проверить
воспроизводимость результатов: повторные измерения в одинаковых
условиях, должны давать близкие результаты. В противном случае
исследование будет существенно затруднено, если вообще возможно.
Таким образом, многократные измерения необходимы для того,
чтобы убедиться как в надёжности методики, так и в существовании измеряемой
величины как таковой.
При любых измерениях возможны грубые ошибки — промахи
(англ. miss). Это «ошибки» в стандартном
понимании этого слова — возникающие по вине экспериментатора
или в силу других непредвиденных обстоятельств (например, из-за сбоя
аппаратуры). Промахов, конечно, нужно избегать, а результаты таких
измерений должны быть по возможности исключены из рассмотрения.
Как понять, является ли «аномальный» результат промахом? Вопрос этот весьма
непрост. В литературе существуют статистические
критерии отбора промахов, которыми мы, однако, настоятельно не рекомендуем
пользоваться (по крайней мере, без серьезного понимания последствий
такого отбора). Отбрасывание аномальных данных может, во-первых, привести
к тенденциозному искажению результата исследований, а во-вторых, так
можно упустить открытие неизвестного эффекта. Поэтому при научных
исследованиях необходимо максимально тщательно проанализировать причину
каждого промаха, в частности, многократно повторив эксперимент. Лишь
только если факт и причина промаха установлены вполне достоверно,
соответствующий результат можно отбросить.
Замечание. Часто причины аномальных отклонений невозможно установить на этапе
обработки данных, поскольку часть информации о проведении измерений к этому моменту
утеряна. Единственным способ борьбы с этим — это максимально подробное описание всего
процесса измерений в лабораторном журнале. Подробнее об этом
см. п. 4.1.1.
При многократном повторении измерении одной и той же физической величины
погрешности могут иметь систематический либо случайный
характер. Назовём погрешность систематической, если она повторяется
от опыта к опыту, сохраняя свой знак и величину, либо закономерно
меняется в процессе измерений. Случайные (или статистические)
погрешности меняются хаотично при повторении измерений как по величине,
так и по знаку, и в изменениях не прослеживается какой-либо закономерности.
Кроме того, удобно разделять погрешности по их происхождению. Можно
выделить
- •
инструментальные (или приборные) погрешности,
связанные с несовершенством конструкции (неточности, допущенные при
изготовлении или вследствие старения), ошибками калибровки или ненормативными
условиями эксплуатации измерительных приборов; - •
методические погрешности, связанные с несовершенством
теоретической модели явления (использование приближенных формул и
моделей явления) или с несовершенством методики измерения (например,
влиянием взаимодействия прибора и объекта измерения на результат измерения); - •
естественные погрешности, связанные со случайным
характером
измеряемой физической величины — они являются не столько
«ошибками» измерения, сколько характеризуют
природу изучаемого объекта или явления.
Замечание. Разделение погрешностей на систематические и случайные
не является однозначным и зависит от постановки опыта. Например, производя
измерения не одним, а несколькими однотипными приборами, мы переводим
систематическую приборную ошибку, связанную с неточностью шкалы и
калибровки, в случайную. Разделение по происхождению также условно,
поскольку любой прибор подвержен воздействию «естественных»
случайных и систематических ошибок (шумы и наводки, тряска, атмосферные
условия и т. п.), а в основе работы прибора всегда лежит некоторое
физическое явление, описываемое не вполне совершенной теорией.
1.3.1 Случайные погрешности
Случайный характер присущ большому количеству различных физических
явлений, и в той или иной степени проявляется в работе всех без исключения
приборов. Случайные погрешности обнаруживаются просто при многократном
повторении опыта — в виде хаотичных изменений (флуктуаций)
значений {xi}.
Если случайные отклонения от среднего в большую или меньшую стороны
примерно равновероятны, можно рассчитывать, что при вычислении среднего
арифметического (1.1) эти отклонения скомпенсируются,
и погрешность результирующего значения ⟨x⟩ будем меньше,
чем погрешность отдельного измерения.
Случайные погрешности бывают связаны, например,
- •
с особенностями используемых приборов: техническими
недостатками
(люфт в механических приспособлениях, сухое трение в креплении стрелки
прибора), с естественными (тепловой и дробовой шумы в электрических
цепях, тепловые флуктуации и колебания измерительных устройств из-за
хаотического движения молекул, космическое излучение) или техногенными
факторами (тряска, электромагнитные помехи и наводки); - •
с особенностями и несовершенством методики измерения (ошибка
при отсчёте по шкале, ошибка времени реакции при измерениях с секундомером); - •
с несовершенством объекта измерений (неровная поверхность,
неоднородность состава); - •
со случайным характером исследуемого явления (радиоактивный
распад, броуновское движение).
Остановимся несколько подробнее на двух последних случаях. Они отличаются
тем, что случайный разброс данных в них порождён непосредственно объектом
измерения. Если при этом приборные погрешности малы, то «ошибка»
эксперимента возникает лишь в тот момент, когда мы по своей
воле совершаем замену ряда измеренных значений на некоторое среднее
{xi}→⟨x⟩. Разброс данных при этом
характеризует не точность измерения, а сам исследуемый объект или
явление. Однако с математической точки зрения приборные и
«естественные»
погрешности неразличимы — глядя на одни только
экспериментальные данные невозможно выяснить, что именно явилось причиной
их флуктуаций: сам объект исследования или иные, внешние причины.
Таким образом, для исследования естественных случайных процессов необходимо
сперва отдельно исследовать и оценить случайные инструментальные погрешности
и убедиться, что они достаточно малы.
1.3.2 Систематические погрешности
Систематические погрешности, в отличие от случайных, невозможно обнаружить,
исключить или уменьшить просто многократным повторением измерений.
Они могут быть обусловлены, во-первых, неправильной работой приборов
(инструментальная погрешность), например, сдвигом нуля отсчёта
по шкале, деформацией шкалы, неправильной калибровкой, искажениями
из-за не нормативных условий эксплуатации, искажениями из-за износа
или деформации деталей прибора, изменением параметров прибора во времени
из-за нагрева и т.п. Во-вторых, их причиной может быть ошибка в интерпретации
результатов (методическая погрешность), например, из-за использования
слишком идеализированной физической модели явления, которая не учитывает
некоторые значимые факторы (так, при взвешивании тел малой плотности
в атмосфере необходимо учитывать силу Архимеда; при измерениях в электрических
цепях может быть необходим учет неидеальности амперметров и вольтметров
и т. д.).
Систематические погрешности условно можно разделить на следующие категории.
- 1.
Известные погрешности, которые могут быть достаточно точно вычислены
или измерены. При необходимости они могут быть учтены непосредственно:
внесением поправок в расчётные формулы или в результаты измерений.
Если они малы, их можно отбросить, чтобы упростить вычисления. - 2.
Погрешности известной природы, конкретная величина которых неизвестна,
но максимальное значение вносимой ошибки может быть оценено теоретически
или экспериментально. Такие погрешности неизбежно присутствуют в любом
опыте, и задача экспериментатора — свести их к минимуму,
совершенствуя методики измерения и выбирая более совершенные приборы.Чтобы оценить величину систематических погрешностей опыта, необходимо
учесть паспортную точность приборов (производитель, как правило, гарантирует,
что погрешность прибора не превосходит некоторой величины), проанализировать
особенности методики измерения, и по возможности, провести контрольные
опыты. - 3.
Погрешности известной природы, оценка величины которых по каким-либо
причинам затруднена (например, сопротивление контактов при подключении
электронных приборов). Такие погрешности должны быть обязательно исключены
посредством модификации методики измерения или замены приборов. - 4.
Наконец, нельзя забывать о возможности существования ошибок, о
которых мы не подозреваем, но которые могут существенно искажать результаты
измерений. Такие погрешности самые опасные, а исключить их можно только
многократной независимой проверкой измерений, разными методами
и в разных условиях.
В учебном практикуме учёт систематических погрешностей ограничивается,
как правило, паспортными погрешностями приборов и теоретическими поправками
к упрощенной модели исследуемого явления.
Точный учет систематической ошибки возможен только при учете специфики конкретного эксперимента. Особенное внимание надо обратить на зависимость (корреляцию) систематических смещений при повторных измерениях. Одна и та же погрешность в разных случаях может быть интерпретирована и как случайная, и как систематическая.
Пример.
Калибровка электромагнита производится при помощи внесения в него датчика Холла или другого измерителя магнитного потока. При последовательных измерениях с разными токами (и соотственно полями в зазоре) калибровку можно учитыать двумя различными способами:
•
Измерить значение поля для разных токов, построить линейную калибровочную кривую и потом использовать значения, восстановленные по этой кривой для вычисления поля по току, используемому в измерениях.
•
Для каждого измерения проводить допольнительное измерения поля и вообще не испльзовать значения тока.
В первом случае погрешность полученного значения будет меньше, поскльку при проведении прямой, отдельные отклонения усреднятся. При этом погрешность измерения поля будет носить систематический харрактер и при обработке данных ее надо будет учитывать в последний момент. Во втором случае погрешность будет носить статистический (случайный) харрактер и ее надо будет добавить к погрешности каждой измеряемой точки. При этом сама погрешность будет больше. Выбор той или иной методики зависит от конретной ситуации. При большом количестве измерений, второй способ более надежный, поскольку статистическая ошибка при усреднении уменьшается пропорционально корню из количества измерений. Кроме того, такой способ повзоляет избежать методической ошибки, связанной с тем, что зависимость поля от тока не является линейной.
Пример.
Рассмотрим измерение напряжения по стрелочному вольтметру. В показаниях прибора будет присутствовать три типа погрешности:
1.
Статистическая погрешность, связанная с дрожанием стрелки и ошибкой визуального наблюдения, примерно равная половине цены деления.
2.
Систематическая погрешность, связанная с неправильной установкой нуля.
3.
Систематическая погрешность, связанная с неправильным коэффициентом пропорциональности между напряжением и отклонением стрелки. Как правило приборы сконструированы таким образом, чтобы максимальное значение этой погрешности было так же равно половине цены деления (хотя это и не гарантируется).
Случайная погрешность — это ошибка в измерениях, которая носит неконтролируемый характер и очень труднопредсказуема. Так происходит из-за того, что существует огромное количество параметров, находящихся вне контроля экспериментатора, которые влияют на итоговые показатели. Случайные погрешности с абсолютной точностью вычислить невозможно. Они вызваны не сразу очевидными источниками и требуют много времени на выяснение причины их возникновения.
Как определить наличие случайной погрешности
Непредсказуемые ошибки присутствует не во всех измерениях. Но для того чтобы полностью исключить ее возможное влияние на результаты измерений, необходимо повторить эту процедуру несколько раз. Если итог не меняется от эксперимента к эксперименту либо изменяется, но на определенное относительное число — величина этой случайной погрешности равна нулю, и о ней можно не думать. И, наоборот, если полученный результат измерений каждый раз другой (близкий к какому-то среднему значению, но отличный), и отличия носят неопределенный характер, следовательно, на него влияет непредсказуемая ошибка.
Люди часто сталкиваются с нахождением какой-либо физической величины. В этом случае говорят об…
Пример возникновения
Случайная составляющая погрешности возникает вследствие действия различных факторов. Например, при измерении сопротивления проводника, необходимо собрать электрическую цепь, состоящую из вольтметра, амперметра и источника тока, которым служит выпрямитель, подключенный в осветительную сеть. Первым делом нужно измерить напряжение, записав показания с вольтметра. Затем перенести взгляд на амперметр, чтобы зафиксировать его данные о силе тока. После использовать формулу, где R = U / I.
Но может случиться так, что в момент снятия показаний с вольтметра в соседней комнате включили кондиционер. Это довольно мощный прибор. В результате этого напряжение сети немного уменьшилось. Если бы не пришлось отводить взгляд на амперметр, можно было заметить, что показания вольтметра изменились. Поэтому данные первого прибора уже не соответствуют записанным ранее значениям. Из-за непредсказуемого включения кондиционера в соседней комнате получается результат уже со случайной погрешностью. Сквозняки, трения в осях измерительных приборов — потенциальные источники ошибок в измерениях.
Как проявляется
Допустим, необходимо рассчитать сопротивление круглого проводника. Для этого нужно знать его длину и диаметр. Помимо этого, учитывается удельное сопротивление материала, из которого он изготовлен. При измерении длины проводника случайная погрешность себя проявлять не будет. Ведь этот параметр всегда один и тот же. Но вот при измерении диаметра штангенциркулем или микрометром окажется, что данные разняться. Так происходит потому, что идеально круглый проводник невозможно изготовить в принципе. Поэтому, если измерить диаметр в нескольких местах изделия, то он может оказаться разным вследствие действия непредсказуемых факторов в момент его изготовления. Это случайная погрешность.
Иногда она также называется статистической погрешностью, поскольку эту величину можно уменьшить, увеличив количество экспериментов при одинаковых условиях их проведения.
Природа возникновения
В отличие от систематической ошибки, простое усреднение нескольких итоговых показателей одной и той же величины компенсирует случайные погрешности результатов измерений. Природа их возникновения определяется очень редко, и поэтому никогда не фиксируется, как постоянная величина. Случайная погрешность — это отсутствие каких-либо природных закономерностей. Например, она не пропорциональна измеряемой величине или никогда не остается постоянной при проведении нескольких измерений.
Проблема алкоголя в России была всегда. Борьба с пьянством и некачественным алкоголем в разные…
Может существовать ряд возможных источников случайных ошибок в экспериментах, и он полностью зависит от типа эксперимента и используемых приборов.
Например, биолог, изучающий размножение конкретного штамма бактерии, может столкнуться с непредсказуемой ошибкой из-за небольшого изменения температуры или освещения в помещении. Однако когда эксперимент будет повторяться в течение определенного периода времени, он избавится от этих различий в результатах путем их усреднения.
Формула случайной погрешности
Допустим, нужно определить какую-то физическую величину x. Чтобы исключить случайную погрешность необходимо провести несколько измерений, итогом которых будет серия результатов N количества измерений — x1, x2,…, xn.
Чтобы обработать эти данные следует:
- За результат измерений х0 принять среднее арифметическое х̅. Иными словами, х0 = (x1 + x2 +… + xn) / N.
- Найти стандартное отклонение. Обозначается оно греческой буквой σ и вычисляется следующим образом: σ = √((х1 — х̅ )2 + (х2-х̅ )2 + … + (хn — х̅ )2 / N — 1). Физический смысл σ состоит в том, что если провести еще одно измерение (N+1), то оно с вероятностью 997 шансов из 1000 ляжет в интервал х̅ -3σ < хn+1 < с + 3σ.
- Найти границу абсолютной погрешности среднего арифметического х̅. Находится она по следующей формуле: Δх = 3σ / √N.
- Ответ: х = х̅ + (-Δх).
Относительная погрешность будет равна ε = Δх /х̅.
Пример вычисления
Формулы расчета случайной погрешности достаточно громоздкие, поэтому, чтобы не запутаться в вычислениях, лучше использовать табличный способ.
Пример:
При измерении длины l, были получены следующие значения: 250 см, 245 см, 262 см, 248 см, 260 см. Количество измерений N = 5.
|
N п/п |
l, см |
I ср. арифм., см |
|l-l ср. арифм.| |
(l-l ср. арифм.)2 |
σ, см |
Δ l, см |
|
1 |
250 |
253,0 |
3 |
9 |
7,55 |
10,13 |
|
2 |
245 |
8 |
64 |
|||
|
3 |
262 |
9 |
81 |
|||
|
4 |
248 |
5 |
25 |
|||
|
5 |
260 |
7 |
49 |
|||
|
Σ = 1265 |
Σ = 228 |
Относительная погрешность равна ε = 10,13 см / 253,0 см = 0,0400 см.
Ответ: l = (253 + (-10)) см, ε = 4 %.
Практическая польза высокой точности измерений
Следует учитывать, что достоверность результатов тем выше, чем большее количество измерений проводится. Чтобы повысить точность в 10 раз, необходимо провести в 100 раз больше измерений. Это достаточно трудоемкое занятие. Однако оно может привести к очень важным результатам. Иногда приходится иметь дело со слабыми сигналами.
Например, в астрономических наблюдениях. Допустим, необходимо изучить звезду, блеск которой изменяется периодически. Но это небесное тело настолько далеко, что шум электронной аппаратуры или датчиков, принимающих излучения, может быть во много раз больше, чем сигнал, который необходимо обработать. Что же делать? Оказывается, если проводить миллионы измерений, то возможно среди этого шума выделить необходимый сигнал с очень большой достоверностью. Однако для этого потребуется совершать огромное количество измерений. Такая методика используется, чтобы различать слабые сигналы, которые едва заметны на фоне различных шумов.
Причина, по которой случайные погрешности могут быть решены путем усреднения, заключается в том, что они имеют нулевое ожидаемое значение. Они действительно непредсказуемы и разбросаны по среднему значению. Исходя из этого, среднее арифметическое ошибок ожидается равным нулю.
Случайная погрешность присутствуют в большинстве экспериментов. Поэтому исследователь должен быть подготовлен к ним. В отличие от систематических, случайные погрешности не предсказуемы. Это затрудняет их обнаружение, но от них легче избавиться, поскольку они являются статистическими и удаляются математическим методом, таким как усреднение.
Статья обновлена 10.07.2022
Что такое погрешность измерения
Любой расчет состоит из истинного и вычисляемого значения. При этом всегда должны учитываться значения ошибки или погрешности. Погрешность — это расхождение между истинным значением и вычисляемым. В маркетинге выделяют следующие виды погрешностей.
- Математическая погрешность. Она описывается алгебраической формулой и бывает абсолютной, относительной и приведенной. Абсолютная погрешность измерения — это разница между вычисляемым и истинным значением. Относительная погрешность вычисляется в процентном соотношении истинного значения и полученного. Вычисление погрешности приведенной схоже с относительной, указывается она также в процентах, но дает разницу между нормирующей шкалой и полученными данными, то есть между эталонными и полученными значениями.
- Оценочная погрешность. В маркетинге она бывает случайной и систематической. Случайная погрешность возникает из-за любых факторов, которые случайным образом влияют на измерение переменной в выборке. Систематическая погрешность вызывается факторами, которые систематически влияют на измерение переменной в выборке.
Математическая погрешность: формула для каждого типа
Если определение погрешности можно провести точным путем, она считается математической. Зачем нужно вычисление этого значения в маркетинге?
Погрешности возникают настолько часто, что популярной практикой в исследованиях является включение значения погрешности в окончательные результаты. Для этого используются формулы. Математическая погрешность — это значение, которое отражает разницу между выборкой и фактическим результатом. Если при расчетах учитывалась погрешность, в тексте исследования указывается что-то вроде: «Абсолютная погрешность для этих данных составляет 3,25%». Погрешность можно вычислить с любыми цифрами: количество человек, участвующих в опросе, погрешность суммы, затраченной на маркетинговый бюджет, и так далее.
Формулы погрешностей вычисляются следующим образом.
Абсолютная погрешность измерений: формула
Формула дает разницу между измеренным и реальным значением.
Относительная погрешность: формула
Формула использует значение абсолютной погрешности и вычисляется в процентах по отношению к фактическому значению.
Приведенная погрешность: формула
Формула также использует значение абсолютной погрешности. В чем измеряется приведенная погрешность? Тоже в процентах, но в качестве «эталона» используется не реальное значение, а единица измерения любой нормирующей шкалы. Например, для обычной линейки это значение равно 1 мм.
Классификация оценочной погрешности
Определение погрешности в оценках — это всегда методическая погрешность, то есть допустимое значение ошибки, основанное на методах проведения исследования. Погрешность метода вызывает два типа погрешностей — случайные и систематические. Таблица погрешностей в графической форме покажет все возможные типы.
Что такое случайная погрешность
Случайная погрешность бывает статической и динамической. Динамическая погрешность возникает, когда мы имеем дело с меняющимися значениями — например, количество человек в выборке при маркетинговом исследовании. Статическая погрешность описывает ошибки при вычислении неизменных величин — вроде количества вопросов в вопроснике. Все они относятся к случайным погрешностям.
Типичный пример возникновения случайной погрешности — настроение участников маркетингового опроса. Как известно, эмоциональный настрой человека всегда влияет на его производительность. В ходе тестирования одни люди могут быть в хорошем расположении духа, а другие — в «миноре». Если настроение влияет на их ответы по заданному критерию выборки, это может искусственно завышать или занижать наблюдаемые оценки. Например, в случае с истинным значением 1 случайная погрешность может дать как -0,8, так и +0,5 к этому числу. Очень часто это случается при оценке времени ответа, например.
Случайная погрешность добавляет изменчивости данным, но не оказывает постоянного влияния на всю выборку. Вместо этого она произвольно изменяет измеряемые значения в диапазоне. В маркетинговой практике считается, что все случайные погрешности в распределении перекрывают друг друга и практически не влияют на конечный результат. Поэтому случайная погрешность считается «шумом» и в расчет не принимается. Эту погрешность нельзя устранить совсем, но можно уменьшить, просто увеличив размер выборки.
Что такое систематическая погрешность
Систематическая погрешность существует в результатах исследования, если эти результаты показывают устойчивую тенденцию к отклонению от истинных значений. Иными словами, если полученные цифры постоянно выше или ниже расчетных, речь идет о том, что в данных имеется систематическая погрешность.
В маркетинговых исследованиях есть два основных типа систематической погрешности: погрешность выборки и погрешность измерения.
Погрешность выборки
Погрешность выборки возникает, когда выборка, используемая в исследовании, не репрезентативна для всей совокупности данных. Типы такой погрешности включают погрешность структуры, погрешность аудитории и погрешность отбора.
Погрешность структуры
Погрешность структуры возникает из-за использования неполной или неточной основы для выборки. Распространенным источником такой погрешности в рамках маркетинговых исследований является проведение какого-либо опроса по телефону на основе существующего телефонного справочника или базы данных абонентов. Многие данные там указаны неполно или неточно — например, если люди недавно переехали или изменили свой номер телефона. Также такие данные часто указывают неполную или неверную демографию.
Если в качестве основы для исследования взят телефонный справочник, оно подвержено погрешности структуры, так как не учитывает всех возможных респондентов.
Погрешность аудитории
Погрешность аудитории возникает, если исследователь не знает, как определить аудиторию для исследования. Пример — оценка результатов исследования, проведенного среди клиентов крупного банка. Доля ответов на анкету составила чуть менее 1%. Анализ профессий всех опрошенных показал, что процент пенсионеров среди них в 20 раз выше, чем в целом по городу. Если эта группа значительно различается по интересующим переменным, то результаты будут неверными из-за погрешности аудитории.
Погрешность отбора
Даже если маркетологи правильно определили структуру и аудиторию, они не застрахованы от погрешности отбора. Она возникает, когда процедуры отбора являются неполными, неправильными или не соблюдаются должным образом. Например, интервьюеры при полевом исследовании могут избегать людей, которые живут в муниципальных домах. Потому что, по их мнению, жители вряд ли согласятся пройти такой опрос. Если жители муниципальных домов отличаются от тех, кто проживает в домах бизнес-класса, в результаты опроса будет внесена погрешность отбора.
Как минимизировать погрешность выборки
- Знайте свою аудиторию.
Знайте, кто покупает ваш продукт, использует его, работает с вами и так далее. Имея базовую социально-экономическую информацию, можно составить стабильную выборку целевой аудитории. Маркетинговые исследования часто касаются одной конкретной группы населения — например, пользователей Facebook или молодых мам. - Разделите аудиторию на группы.
Вместо случайной выборки разбейте аудиторию на группы в соответствии с их численностью в общей совокупности данных. Например, если люди с определенной демографией составляют 35% населения, убедитесь, что 35% респондентов исследования отвечают этому условию. - Увеличьте размер выборки.
Больший размер выборки приводит к более точному результату.
Погрешность измерения
Погрешность измерения представляет собой серьезную угрозу точности исследования. Она возникает, когда существует разница между искомой информацией — то есть истинным значением, и информацией, фактически полученной в процессе измерения. К таким погрешностям приводят различные недостатки процесса исследования. Погрешность измерения, в основном, вызывается человеческим фактором — например, формулировкой вопросника, ошибками ввода данных и необъективными выводами.
К погрешностям измерения приводят следующие виды ошибок.
Ошибка цели
Ошибка цели возникает, когда существует несоответствие между информацией, фактически необходимой для решения проблемы, и данными , которые собирает исследование. Например, компания Kellogg впустую потратила миллионы на разработку завтраков для снижения уровня холестерина. Реальный вопрос, который нужно было бы задать в исследовании, заключался в том, купят ли люди овсяные хлопья для решения своей проблемы. Ответ «Нет» обошелся бы компании дешевле.
Предвзятость ответов
Некоторые люди склонны отвечать на конкретный вопрос определенным образом. Тогда возникает предвзятость ответа. Предвзятость ответа может быть результатом умышленной фальсификации или неосознанного искажения фактов.
Умышленная фальсификация происходит, когда респонденты целенаправленно дают неверные ответы на вопросы. Есть много причин, по которым люди могут сознательно искажать информацию. Например, они хотят скрыть или хотят казаться лучше, чем есть на самом деле.
Бессознательное искажение информации происходит, когда респондент пытается быть правдивым, но дает неточный ответ. Этот тип предвзятости может возникать из-за формата вопроса, его содержания или по другим причинам.
Предвзятость интервьюера
Интервьюер оказывает влияние на респондента — сознательно или бессознательно. Одежда, возраст, пол, выражение лица, язык тела или тон голоса могут повлиять на ответы некоторых или всех респондентов.
Ошибка обработки
Примеры включают наводящие вопросы или элементы дизайна анкеты, которые затрудняют запись ответов или приводят к ошибкам в них.
Ошибка ввода
Это ошибки, возникающие при вводе информации. Например, документ может быть отсканирован неправильно, и его данные по ошибке перенесутся неверно. Или люди, заполняющие опросы на смартфоне или ноутбуке, могут нажимать не те клавиши.
Виды проводимых маркетинговых исследований различны, поэтому универсальных рецептов не существует. Мы дадим несколько общих советов, используемых для минимизации систематических погрешностей разного типа.
Как минимизировать погрешность измерения
- Предварительно протестируйте.
Погрешностей обработки и предвзятости можно избежать, если проводить предварительные тесты вопросника до начала основных интервью. - Проводите выборку случайным образом.
Чтобы устранить предвзятость, при выборке респондентов можно включать каждого четвертого человека из общего списка. - Тренируйте команду интервьюеров и наблюдателей.
Отбор и обучение тех, кто проводит исследования, должен быть тщательным. Особое внимание нужно уделять соблюдению инструкций в ходе каждого исследования. - Всегда выполняйте проверку сделанных записей.
Чтобы исключить ошибки ввода, все данные, вводимые для компьютерного анализа, должны быть перепроверены как минимум дважды.
Мир без ошибок не может существовать. Но понимание факторов, влияющих на маркетинговые исследования и измеряемые погрешности, имеет важное значение для сбора качественных данных.
Основные причины возникновения погрешностей :
- неверная настройка средства измерений или смещение уровня настройки во время эксплуатации;
- неверная установка объекта измерения на измерительную позицию;
- ошбки в процессе получения, преобразования и выдачи информации в измерительной цепи средства измерений ;
Meer items
В чем причина погрешностей выполненных измерений?
Они возникают из-за разности температур объекта измерения и средства измерения. Существуют два основных источника, обуславливающих погрешность от температурных деформаций: отклонение температуры воздуха от 20 °C и кратковременные колебания температуры воздуха в процессе измерения.
Какие факторы влияют на погрешность измерения?
Измерение физических величин основано на том, что физика исследует объективные закономерности, которые происходят в природе. Найти значение физической величины — умножить конкретное число на единицу измерения данной величины, которая стандартизирована ( эталоны ).
расположение наблюдателя относительно измерительного прибора: если на линейку смотреть сбоку, погрешность измерений произойдёт по причине неточного определения полученного значения;деформация измерительного прибора: металлические и пластиковые линейки могут изогнуться, сантиметровая лента растягивается со временем;несоответствие шкалы прибора эталонным значениям: при множественном копировании эталонов может произойти ошибка, которая будет множиться;физический износ шкалы измерений, что приводит к невозможности распознавания значений.
Рассмотрим на примере измерения длины бруска линейкой с сантиметровой шкалой. Рис. (1). Линейка и брусок Внимательно рассмотрим шкалу. Расстояние между двумя соседними метками составляет (1) см. Если этой линейкой измерять брусок, который изображён на рисунке, то правый конец бруска будет находиться между (9) и (10) метками.
- У нас есть два варианта определения длины этого бруска. (1).
- Если мы заявим, что длина бруска — (9) сантиметров, то недостаток длины от истинной составит более половины сантиметра ((0,5) см (= 5) мм). (2).
- Если мы заявим, что длина бруска — (10) сантиметров, то избыток длины от истинной составит менее половины сантиметра ((0,5) см (= 5) мм).
Погрешность измерений — это отклонение полученного значения измерения от истинного. Погрешность измерительного прибора равна цене деления прибора. Для первой линейки цена деления составляет (1) сантиметр. Значит, погрешность этой линейки (1) см. Если нам необходимо произвести более точные измерения, то следует поменять линейку на другую, например, с миллиметровыми делениями. Рис. (2). Деревянная линейка Если же необходимы ещё более точные измерения, то нужно найти прибор с меньшей ценой деления, например, штангенциркуль. Существуют штангенциркули с ценой деления (0,1) мм и (0,05) мм, Рис. (3). Штангенциркуль На процесс измерения влияют следующие факторы: масштаб шкалы прибора, который определяет значения делений и расстояние между ними; уровень экспериментальных умений. Считается, что погрешность прибора превосходит по величине погрешность метода вычисления, поэтому за абсолютную погрешность принимают погрешность прибора.
Каковы причины возникновения грубой погрешности?
Грубые погрешности (промахи) обычно обусловлены неправильным отсчетом по шкале прибора, ошибкой при записи наблюдений, наличием сильно влияющей величины, неисправностью средств измерений и другими причинами.
Какие виды измерений вы знаете?
По видам измерений — Согласно РМГ 29-99 «Метрология. Основные термины и определения» выделяют следующие виды измерений:
- Прямое измерение — измерение, при котором искомое значение физической величины получают непосредственно.
- Косвенное измерение — определение искомого значения физической величины на основании результатов прямых измерений других физических величин, функционально связанных с искомой величиной.
- Совместные измерения — проводимые одновременно измерения двух или нескольких не одноимённых величин для определения зависимости между ними.
- Совокупные измерения — проводимые одновременно измерения нескольких одноимённых величин, при которых искомые значения величин определяют путём решения системы уравнений, получаемых при измерениях этих величин в различных сочетаниях.
- Равноточные измерения — ряд измерений какой-либо величины, выполненных одинаковыми по точности средствами измерений в одних и тех же условиях с одинаковой тщательностью.
- Неравноточные измерения — ряд измерений какой-либо величины, выполненных различающимися по точности средствами измерений и (или) в разных условиях.
- Однократное измерение — измерение, выполненное один раз.
- Многократное измерение — измерение физической величины одного и того же размера, результат которого получен из нескольких следующих друг за другом измерений, то есть состоящее из ряда однократных измерений
- Статическое измерение — измерение физической величины, принимаемой в соответствии с конкретной измерительной задачей за неизменную на протяжении времени измерения.
- Динамическое измерение — измерение изменяющейся по размеру физической величины.
- Абсолютное измерение — измерение, основанное на прямых измерениях одной или нескольких основных величин и (или) использовании значений физических констант.
- Относительное измерение — измерение отношения величины к одноимённой величине, играющей роль единицы, или измерение изменения величины по отношению к одноимённой величине, принимаемой за исходную (см. ниже нулевой метод ).
Также стоит отметить, что в различных источниках дополнительно выделяют такие виды измерений: метрологические и технические, необходимые и избыточные и др.
Какие бывают погрешности в химии?
Погрешности (иногда их же называют ошибками, что не совсем правильно) подразделяют на грубые, систематические и случайные. Грубые, систематические и случайные погрешности.
Почему получается погрешность?
Систематические погрешности порождаются: несовершенством приборов; неточной установкой прибора; смещением шкалы прибора; неточной установкой стрелки прибора в нулевом положении; недостаточной чувствительностью прибора; неучетом тепловых, электрических и магнитных полей, давлений, влажности и других внешних факторов,
Что понимается под погрешностью измерений?
Погре́шность измере́ния — отклонение измеренного значения величины от её истинного (действительного) значения. Погрешность измерения является характеристикой точности измерения. Выяснить с абсолютной точностью истинное значение измеряемой величины, как правило, невозможно, поэтому невозможно и указать величину отклонения измеренного значения от истинного.
Это отклонение принято называть ошибкой измерения, Возможно лишь оценить величину этого отклонения, например, при помощи статистических методов, На практике вместо истинного значения используют действительное значение величины х д, то есть значение физической величины, полученное экспериментальным путём и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него,
Такое значение обычно вычисляется как среднестатистическое значение, полученное при статистической обработке результатов серии измерений. Это полученное значение не является точным, а лишь наиболее вероятным. Поэтому при записи результатов измерений необходимо указывать их точность,
- Например, запись T = 2,8 ± 0,1 с; P = 0,95 означает, что истинное значение величины T лежит в интервале от 2,7 с до 2,9 с с доверительной вероятностью 95 %.
- Количественная оценка величины погрешности измерения — мера «сомнения в измеряемой величине» — приводит к такому понятию, как « неопределённость измерения ».
В то же время иногда, особенно в физике, термин «погрешность измерения» ( англ. measurement error ) используется как синоним термина «неопределённость измерения» ( англ. measurement uncertainty ),
Какие бывают погрешности В физике?
Какие бывают погрешности — Любое число, которое выдает нам эксперимент, это результат измерения. Измерение производится прибором, и это либо непосредственные показания прибора, либо результат обработки этих показаний. И в том, и в другом случае полученный результат измерения неидеален, он содержит погрешности,
- И потому любой грамотный физик должен не только предъявить численный результат измерения, но и обязан указать все сопутствующие погрешности.
- Не будет преувеличением сказать, что численный экспериментальный результат, предъявленный без указания каких-либо погрешностей, бессмыслен.
- В физике элементарных частиц к указанию погрешностей относятся исключительно ответственно.
Экспериментаторы не только сообщают погрешности, но и разделяют их на разные группы. Три основных погрешности, которые встречаются чаще всего, это статистическая, систематическая и теоретическая (или модельная) погрешности. Цель такого разделения — дать четкое понимание того, что именно ограничивает точность этого конкретного измерения, а значит, за счет чего эту точность можно улучшить в будущем.
Статистическая погрешность связана с разбросом значений, которые выдает эксперимент после каждой попытки измерить величину. ( Подробнее о статистической погрешности ) Систематическая погрешность характеризует несовершенство самого измерительного инструмента или методики обработки данных, а точнее, недостаточное знание того, насколько «сбоит» инструмент или методика.
( Подробнее о систематической погрешности ) Теоретическая/модельная погрешность — это неопределенность результата измерения, которая возникла потому, что методика обработки данных была сложная и в чем-то опиралась на теоретические предположения или результаты моделирования, которые тоже несовершенны.
- Впрочем, иногда эту погрешность считают просто разновидностью систематических погрешностей.
- Подробнее о погрешности теории и моделирования ) Наконец, в отдельный класс, видимо, можно отнести возможные человеческие ошибки, прежде всего психологического свойства (предвзятость при анализе данных, ленность при проверке того, как результаты зависят от методики анализа).
Строго говоря, они не являются погрешностью измерения, поскольку могут и должны быть устранены. Зачастую это избавление от человеческих ошибок может быть вполне формализовано. Так называемый дважды слепой эксперимент в биомедицинских науках — один тому пример.
В чем причина возникновения ошибок при измерениях?
Основные причины возникновения погрешностей: ошбки в процессе получения, преобразования и выдачи информации в измерительной цепи средства измерений ; внешние воздействия на средтво и объект измерений (изменение температуры и давления, влияние электрического и магнитного полей, вибрация и т.
В чем измеряется погрешность измерений?
Погрешность средств измерения и результатов измерения. Погрешности средств измерений – отклонения метрологических свойств или параметров средств измерений от номинальных, влияющие на погрешности результатов измерений (создающие так называемые инструментальные ошибки измерений).
Погрешность результата измерения – отклонение результата измерения от действительного (истинного) значения измеряемой величины. Инструментальные и методические погрешности. Методическая погрешность обусловлена несовершенством метода измерений или упрощениями, допущенными при измерениях. Так, она возникает из-за использования приближенных формул при расчете результата или неправильной методики измерений.
Выбор ошибочной методики возможен из-за несоответствия (неадекватности) измеряемой физической величины и ее модели. Причиной методической погрешности может быть не учитываемое взаимное влияние объекта измерений и измерительных приборов или недостаточная точность такого учета.
Например, методическая погрешность возникает при измерениях падения напряжения на участке цепи с помощью вольтметра, так как из-за шунтирующего действия вольтметра измеряемое напряжение уменьшается. Механизм взаимного влияния может быть изучен, а погрешности рассчитаны и учтены. Инструментальная погрешность обусловлена несовершенством применяемых средств измерений.
Причинами ее возникновения являются неточности, допущенные при изготовлении и регулировке приборов, изменение параметров элементов конструкции и схемы вследствие старения. В высокочувствительных приборах могут сильно проявляться их внутренние шумы. Статическая и динамическая погрешности.
Статическая погрешность измерений – погрешность результата измерений, свойственная условиям статического измерения, то есть при измерении постоянных величин после завершения переходных процессов в элементах приборов и преобразователей. Статическая погрешность средства измерений возникает при измерении с его помощью постоянной величины. Если в паспорте на средства измерений указывают предельные погрешности измерений, определенные в статических условиях, то они не могут характеризовать точность его работы в динамических условиях. Динамическая погрешность измерений – погрешность результата измерений, свойственная условиям динамического измерения. Динамическая погрешность появляется при измерении переменных величин и обусловлена инерционными свойствами средств измерений. Динамической погрешностью средства измерений является разность между погрешностью средсва измерений в динамических условиях и его статической погрешностью, соответствующей значению величины в данный момент времени. При разработке или проектировании средства измерений следует учитывать, что увеличение погрешности измерений и запаздывание появления выходного сигнала связаны с изменением условий.
Статические и динамические погрешности относятся к погрешностям результата измерений. В большей части приборов статическая и динамическая погрешности оказываются связаны между собой, поскольку соотношение между этими видами погрешностей зависит от характеристик прибора и характерного времени изменения величины.
Как оценить погрешность измерения?
1.1 Результат измерения — Рассмотрим простейший пример: измерение длины стержня с помощью линейки. Линейка проградуирована производителем с помощью некоторого эталона длины — таким образом, сравнивая длину стержня с ценой деления линейки, мы выполняем косвенное сравнение с общепринятым стандартным эталоном.
Допустим, мы приложили линейку к стержню и увидели на шкале некоторый результат x = x изм, Можно ли утверждать, что x изм — это длина стержня? Во-первых, значение x не может быть задано точно, хотя бы потому, что оно обязательно округлено до некоторой значащей цифры: если линейка «обычная», то у неё есть цена деления ; а если линейка, к примеру, «лазерная» — у неё высвечивается конечное число значащих цифр на дисплее.
Во-вторых, мы никак не можем быть уверенны, что длина стержня на самом деле такова хотя бы с точностью до ошибки округления. Действительно, мы могли приложить линейку не вполне ровно; сама линейка могла быть изготовлена не вполне точно; стержень может быть не идеально цилиндрическим и т.п.
- И, наконец, если пытаться хотя бы гипотетически переходить к бесконечной точности измерения, теряет смысл само понятие «длины стержня».
- Ведь на масштабах атомов у стержня нет чётких границ, а значит говорить о его геометрических размерах в таком случае крайне затруднительно! Итак, из нашего примера видно, что никакое физическое измерение не может быть произведено абсолютно точно, то есть у любого измерения есть погрешность,
Замечание. Также используют эквивалентный термин ошибка измерения (от англ. error). Подчеркнём, что смысл этого термина отличается от общеупотребительного бытового: если физик говорит «в измерении есть ошибка», — это не означает, что оно неправильно и его надо переделать.
- Имеется ввиду лишь, что это измерение неточно, то есть имеет погрешность,
- Количественно погрешность можно было бы определить как разность между измеренным и «истинным» значением длины стержня: δ x = x изм — x ист,
- Однако на практике такое определение использовать нельзя: во-первых, из-за неизбежного наличия погрешностей «истинное» значение измерить невозможно, и во-вторых, само «истинное» значение может отличаться в разных измерениях (например, стержень неровный или изогнутый, его торцы дрожат из-за тепловых флуктуаций и т.д.).
Поэтому говорят обычно об оценке погрешности. Об измеренной величине также часто говорят как об оценке, подчеркивая, что эта величина не точна и зависит не только от физических свойств исследуемого объекта, но и от процедуры измерения. Замечание. Термин оценка имеет и более формальное значение.
Что такое грубые погрешности измерений?
Грубая погрешность измерения – погрешность измерения, существенно превышающая ожидаемую при данных условиях измерения. Источник – монография Е.Ф. Кретова «Ультразвуковая дефектоскопия в энергомашиностроении» Грубая погрешность измерения: погрешность измерения, существенно превышающая зависящие от объективных условий измерений значения систематической и случайной погрешностей.
Как определить грубую погрешность?
Секция «Метрология, стандартизация и сертификация» УДК 519.254 МЕТОДЫ ИСКЛЮЧЕНИЯ ГРУБОЙ ПОГРЕШНОСТИ Ю.А. Петровская, Е.А. Петровская Научный руководитель — М.С. Эльберг Сибирский государственный аэрокосмический университет имени академика М.Ф. Решетнева Российская Федерация, 660037, г. Красноярск, просп. им. газ. «Красноярский рабочий», 31 Е-mail: timeswallower0@gmail.com Рассматриваются методы исключения грубой погрешности, использующие нулевую гипотезу о том, что генеральная совокупность не содержит промаха, а также приводится пример расчета с использованием некоторых методов. Ключевые слова: исключения грубой погрешности, критерий Диксона, критерий «трех сигм». ELIMINATION OF GROSS ERRORS’ METHODS Y.А. Petrovskaya, Е.А. Petrovskaya Scientific supervisor — M.S. Elberg Reshetnev Siberian State Aerospace University 31, Krasnoyarsky Rabochy Av., Krasnoyarsk, 660037, Russian Federation E-mail: timeswallower0@gmail.com There are elimination of gross errors’ methods in the article. The methods commonly based on hypothesis testing. In a gross error detection case, the null hypothesis is that no gross error is present. Also, there is an example for calculation including some of these methods. Keywords: elimination of gross error, Dickson’s criterion, «three sigma» criterion. На сегодня очень важно обеспечивать высокое качество выпускаемой продукции для поддержания конкурентоспособности. Одним из методов контроля обеспечения качества является выборка. При статистической обработке результатов наблюдения первым шагом является выявление грубых погрешностей. Эта задача позволяет исключить промахи из результатов наблюдений для последующих методов математической статистики. Существует несколько методов обнаружения и исключения грубой погрешности: критерий «трех сигм», критерий Романовского, вариационный критерий Диксона и критерий Шовине. Во всех этих методах проверяется гипотеза о том, что результаты наблюдения не содержат грубой погрешности. Пользуясь конкретными критериями, эту гипотезу пытаются опровергнуть. Если это удается, то результат наблюдений рассматривают как содержащий грубую погрешность и его исключают. Обычно проверяются наибольшее и наименьшее значения результатов наблюдений. Например, перед нами поставлена задача проведения проверки на наличие промахов для приведенного ряда измерений, указанных в таблице: Ряд измерений 25 25 23 22 25 25 23 24 26 24 23 26 25 25 23 25 28 25 23 24 25 23 23 25 24 24 25 24 23 24 Данную задачу можно решить используя критерий «трех сигм» и вариационный критерий Диксона. Так как число измерений п = 30, то мы исключаем возможность использования критерия Романовского, для которого число измерений должно быть не больше 20, и критерия Шовине, для которого число измерений должно быть не больше 10, Актуальные проблемы авиации и космонавтики — 2015. Том 2 По критерию «трех сигм» считается, что результат является промахом, если выполняется следующее условие: |х — хп| > 3 □, где х — среднее арифметическое результатов измерения, не учитывающий проверяемые значения измерений; хп — результат измерения, вызывающий подозрение; □ — среднее квадратичное отклонение.
Что такое погрешность средств измерений?
Погрешность средства измерений — это разность между показаниями СИ и истинным (действительным) значением измеряемой величины.
Можно ли устранить прогрессирующие погрешности?
Прогрессирующая (дрейфовая) погрешность – это непредсказуемая погрешность, медленно меняющаяся во времени. Они могут быть скорректированы поправками только в данный момент времени.
Статья обновлена 10.07.2022
Что такое погрешность измерения
Любой расчет состоит из истинного и вычисляемого значения. При этом всегда должны учитываться значения ошибки или погрешности. Погрешность — это расхождение между истинным значением и вычисляемым. В маркетинге выделяют следующие виды погрешностей.
- Математическая погрешность. Она описывается алгебраической формулой и бывает абсолютной, относительной и приведенной. Абсолютная погрешность измерения — это разница между вычисляемым и истинным значением. Относительная погрешность вычисляется в процентном соотношении истинного значения и полученного. Вычисление погрешности приведенной схоже с относительной, указывается она также в процентах, но дает разницу между нормирующей шкалой и полученными данными, то есть между эталонными и полученными значениями.
- Оценочная погрешность. В маркетинге она бывает случайной и систематической. Случайная погрешность возникает из-за любых факторов, которые случайным образом влияют на измерение переменной в выборке. Систематическая погрешность вызывается факторами, которые систематически влияют на измерение переменной в выборке.
Математическая погрешность: формула для каждого типа
Если определение погрешности можно провести точным путем, она считается математической. Зачем нужно вычисление этого значения в маркетинге?
Погрешности возникают настолько часто, что популярной практикой в исследованиях является включение значения погрешности в окончательные результаты. Для этого используются формулы. Математическая погрешность — это значение, которое отражает разницу между выборкой и фактическим результатом. Если при расчетах учитывалась погрешность, в тексте исследования указывается что-то вроде: «Абсолютная погрешность для этих данных составляет 3,25%». Погрешность можно вычислить с любыми цифрами: количество человек, участвующих в опросе, погрешность суммы, затраченной на маркетинговый бюджет, и так далее.
Формулы погрешностей вычисляются следующим образом.
Абсолютная погрешность измерений: формула
Формула дает разницу между измеренным и реальным значением.

Относительная погрешность: формула
Формула использует значение абсолютной погрешности и вычисляется в процентах по отношению к фактическому значению.

Приведенная погрешность: формула
Формула также использует значение абсолютной погрешности. В чем измеряется приведенная погрешность? Тоже в процентах, но в качестве «эталона» используется не реальное значение, а единица измерения любой нормирующей шкалы. Например, для обычной линейки это значение равно 1 мм.

Классификация оценочной погрешности
Определение погрешности в оценках — это всегда методическая погрешность, то есть допустимое значение ошибки, основанное на методах проведения исследования. Погрешность метода вызывает два типа погрешностей — случайные и систематические. Таблица погрешностей в графической форме покажет все возможные типы.
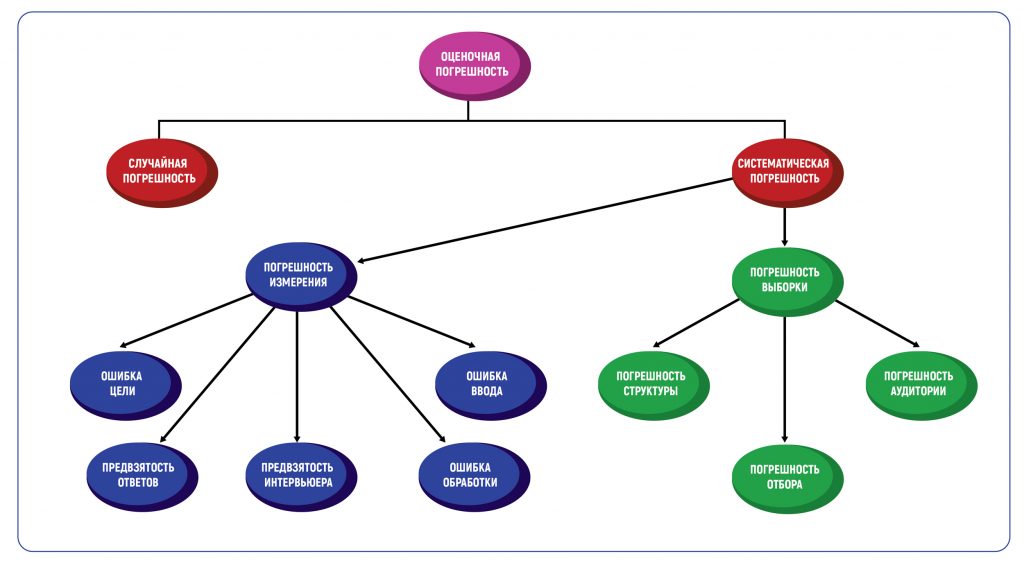
Что такое случайная погрешность
Случайная погрешность бывает статической и динамической. Динамическая погрешность возникает, когда мы имеем дело с меняющимися значениями — например, количество человек в выборке при маркетинговом исследовании. Статическая погрешность описывает ошибки при вычислении неизменных величин — вроде количества вопросов в вопроснике. Все они относятся к случайным погрешностям.
Типичный пример возникновения случайной погрешности — настроение участников маркетингового опроса. Как известно, эмоциональный настрой человека всегда влияет на его производительность. В ходе тестирования одни люди могут быть в хорошем расположении духа, а другие — в «миноре». Если настроение влияет на их ответы по заданному критерию выборки, это может искусственно завышать или занижать наблюдаемые оценки. Например, в случае с истинным значением 1 случайная погрешность может дать как -0,8, так и +0,5 к этому числу. Очень часто это случается при оценке времени ответа, например.
Случайная погрешность добавляет изменчивости данным, но не оказывает постоянного влияния на всю выборку. Вместо этого она произвольно изменяет измеряемые значения в диапазоне. В маркетинговой практике считается, что все случайные погрешности в распределении перекрывают друг друга и практически не влияют на конечный результат. Поэтому случайная погрешность считается «шумом» и в расчет не принимается. Эту погрешность нельзя устранить совсем, но можно уменьшить, просто увеличив размер выборки.
Что такое систематическая погрешность
Систематическая погрешность существует в результатах исследования, если эти результаты показывают устойчивую тенденцию к отклонению от истинных значений. Иными словами, если полученные цифры постоянно выше или ниже расчетных, речь идет о том, что в данных имеется систематическая погрешность.
В маркетинговых исследованиях есть два основных типа систематической погрешности: погрешность выборки и погрешность измерения.
Погрешность выборки
Погрешность выборки возникает, когда выборка, используемая в исследовании, не репрезентативна для всей совокупности данных. Типы такой погрешности включают погрешность структуры, погрешность аудитории и погрешность отбора.
Погрешность структуры
Погрешность структуры возникает из-за использования неполной или неточной основы для выборки. Распространенным источником такой погрешности в рамках маркетинговых исследований является проведение какого-либо опроса по телефону на основе существующего телефонного справочника или базы данных абонентов. Многие данные там указаны неполно или неточно — например, если люди недавно переехали или изменили свой номер телефона. Также такие данные часто указывают неполную или неверную демографию.
Если в качестве основы для исследования взят телефонный справочник, оно подвержено погрешности структуры, так как не учитывает всех возможных респондентов.
Погрешность аудитории
Погрешность аудитории возникает, если исследователь не знает, как определить аудиторию для исследования. Пример — оценка результатов исследования, проведенного среди клиентов крупного банка. Доля ответов на анкету составила чуть менее 1%. Анализ профессий всех опрошенных показал, что процент пенсионеров среди них в 20 раз выше, чем в целом по городу. Если эта группа значительно различается по интересующим переменным, то результаты будут неверными из-за погрешности аудитории.
Погрешность отбора
Даже если маркетологи правильно определили структуру и аудиторию, они не застрахованы от погрешности отбора. Она возникает, когда процедуры отбора являются неполными, неправильными или не соблюдаются должным образом. Например, интервьюеры при полевом исследовании могут избегать людей, которые живут в муниципальных домах. Потому что, по их мнению, жители вряд ли согласятся пройти такой опрос. Если жители муниципальных домов отличаются от тех, кто проживает в домах бизнес-класса, в результаты опроса будет внесена погрешность отбора.
Как минимизировать погрешность выборки
- Знайте свою аудиторию.
Знайте, кто покупает ваш продукт, использует его, работает с вами и так далее. Имея базовую социально-экономическую информацию, можно составить стабильную выборку целевой аудитории. Маркетинговые исследования часто касаются одной конкретной группы населения — например, пользователей Facebook или молодых мам. - Разделите аудиторию на группы.
Вместо случайной выборки разбейте аудиторию на группы в соответствии с их численностью в общей совокупности данных. Например, если люди с определенной демографией составляют 35% населения, убедитесь, что 35% респондентов исследования отвечают этому условию. - Увеличьте размер выборки.
Больший размер выборки приводит к более точному результату.
Погрешность измерения
Погрешность измерения представляет собой серьезную угрозу точности исследования. Она возникает, когда существует разница между искомой информацией — то есть истинным значением, и информацией, фактически полученной в процессе измерения. К таким погрешностям приводят различные недостатки процесса исследования. Погрешность измерения, в основном, вызывается человеческим фактором — например, формулировкой вопросника, ошибками ввода данных и необъективными выводами.
К погрешностям измерения приводят следующие виды ошибок.
Ошибка цели
Ошибка цели возникает, когда существует несоответствие между информацией, фактически необходимой для решения проблемы, и данными , которые собирает исследование. Например, компания Kellogg впустую потратила миллионы на разработку завтраков для снижения уровня холестерина. Реальный вопрос, который нужно было бы задать в исследовании, заключался в том, купят ли люди овсяные хлопья для решения своей проблемы. Ответ «Нет» обошелся бы компании дешевле.
Предвзятость ответов
Некоторые люди склонны отвечать на конкретный вопрос определенным образом. Тогда возникает предвзятость ответа. Предвзятость ответа может быть результатом умышленной фальсификации или неосознанного искажения фактов.
Умышленная фальсификация происходит, когда респонденты целенаправленно дают неверные ответы на вопросы. Есть много причин, по которым люди могут сознательно искажать информацию. Например, они хотят скрыть или хотят казаться лучше, чем есть на самом деле.
Бессознательное искажение информации происходит, когда респондент пытается быть правдивым, но дает неточный ответ. Этот тип предвзятости может возникать из-за формата вопроса, его содержания или по другим причинам.
Предвзятость интервьюера
Интервьюер оказывает влияние на респондента — сознательно или бессознательно. Одежда, возраст, пол, выражение лица, язык тела или тон голоса могут повлиять на ответы некоторых или всех респондентов.
Ошибка обработки
Примеры включают наводящие вопросы или элементы дизайна анкеты, которые затрудняют запись ответов или приводят к ошибкам в них.
Ошибка ввода
Это ошибки, возникающие при вводе информации. Например, документ может быть отсканирован неправильно, и его данные по ошибке перенесутся неверно. Или люди, заполняющие опросы на смартфоне или ноутбуке, могут нажимать не те клавиши.
Виды проводимых маркетинговых исследований различны, поэтому универсальных рецептов не существует. Мы дадим несколько общих советов, используемых для минимизации систематических погрешностей разного типа.
Как минимизировать погрешность измерения
- Предварительно протестируйте.
Погрешностей обработки и предвзятости можно избежать, если проводить предварительные тесты вопросника до начала основных интервью. - Проводите выборку случайным образом.
Чтобы устранить предвзятость, при выборке респондентов можно включать каждого четвертого человека из общего списка. - Тренируйте команду интервьюеров и наблюдателей.
Отбор и обучение тех, кто проводит исследования, должен быть тщательным. Особое внимание нужно уделять соблюдению инструкций в ходе каждого исследования. - Всегда выполняйте проверку сделанных записей.
Чтобы исключить ошибки ввода, все данные, вводимые для компьютерного анализа, должны быть перепроверены как минимум дважды.
Мир без ошибок не может существовать. Но понимание факторов, влияющих на маркетинговые исследования и измеряемые погрешности, имеет важное значение для сбора качественных данных.
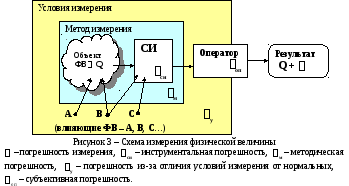
Погрешности измерений
Погрешность
результата измерения
(погрешность измерения) – отклонение
результата измерения от истинного
(действительного) значения измеряемой
величины.
Формально погрешность
можно представить выражением
= X
– Q, (1)
где
– абсолютная погрешность измерения;
X
– результат измерения физической
величины;
Q
– истинное значение измеряемой физической
величины.
В РМГ 29 отмечается,
что истинное значение величины всегда
остается неизвестным, на практике
вместо него используют действительное
значение величины хд
и погрешность
измерения Δxизм
определяют
по формуле
Δxизм
= xизм–
хд
где
xизм
—
измеренное значение величины.
Классификация
погрешностей измерений может осуществляться
по разным классификационным признакам
(основаниям), например:
-
по источникам
возникновения (например, инструментальные
погрешности, субъективные погрешности), -
по степени
интегративности (интегральная погрешность
и составляющие погрешности); -
по характеру
проявления или изменения от измерения
к измерению (случайные, систематические
и грубые), -
по значимости
(значимые, пренебрежимо малые), -
по причинам,
связанным с режимом измерения (статические
и динамические).
Рассмотрим более
подробно некоторые из классификаций.
Поскольку
деление погрешностей по источникам их
возникновения не является самоцелью,
а используется для выявления составляющих,
представляется достаточно логичной
следующая классификация:
-
погрешности
средств измерений
(они же
«аппаратурные погрешности» или
«инструментальные
погрешности»); -
методические
погрешности
или «погрешности
метода измерения»; -
погрешности из-за
отличия условий измерения от нормальных
(«погрешности
условий»); -
субъективные
погрешности измерения
(«погрешности
оператора»,
или же «личные»
либо «личностные» погрешности).
Инструментальная
погрешность измерения
– составляющая погрешности измерения,
обусловленная погрешностью применяемого
средства измерений. Фактически
к инструментальным погрешностям
относятся
погрешности всех
применяемых в данных измерениях
технических средств и вспомогательных
устройств, влияющих на результат
измерений, включая погрешности прибора,
мер для его настройки, дополнительных
сопротивлений, шунтов, установочных
узлов или соединительных проводов и
т.д. Например, при измерении массы на
весах методом сравнения с мерой к
погрешности весов добавляются погрешности
гирь.
Для измерения
длины достаточно часто используют
узкодиапазонные приборы, которые
настраивают по концевым мерам длины.
Так при измерении диаметра d
детали индикатором часового типа на
стойке (рисунок 1), инструментальные
погрешности складываются из погрешностей
самой измерительной головки 1, погрешностей
стойки 2 и погрешностей блока
плоскопараллельных концевых мер длины
3, на который настраивался прибор. В свою
очередь каждую из приведенных
инструментальных составляющих погрешности
измерения можно разбить на элементарные
составляющие. Например, погрешность
измерительной головки 1 включает в себя
множество составляющих, которые зависят
от ее конструкции; погрешности элементов
стойки 2 (колонка, кронштейн, рабочая
поверхность стола) приводят к неправильному
ориентированию прибора и детали;
погрешности блока плоскопараллельных
концевых мер длины 3, на который
настраивался прибор, определяются
погрешностями каждой из мер блока и
погрешностями их притирки.
Погрешность
метода измерений
(погрешность
метода)
–.В.
Чтобы
не связывать «метод измерений» и
«погрешность метода», поскольку прямой
связи здесь нет, предпочтительно
рассматриваемый класс погрешностей
называть «методическими
погрешностями». Методические
погрешности
могут возникать из-за несоответствий
реальной методики выполнения измерений
идеальным теоретическим положениям,
на которых основаны измерения. Эти
погрешности делятся на две
группы. К первой
можно отнести погрешности
из-за
допущений,
принятых при измерении или обработке
результатов, а также используемых в
ходе измерительного преобразования
приближений
и упрощений
(погрешности
из-за несоответствия процесса
измерительного преобразования его
идеальной модели).
Другой возможной
причиной погрешностей метода является
некорректная
идеализация реального объекта измерений
(несоответствие объекта измерения и
модели, положенной в основу процесса
измерения).
Рассмотрим примеры
погрешностей первой группы. При косвенных
измерениях диаметров больших деталей
часто рулеткой измеряют длину окружности,
а затем рассчитывают диаметр. Здесь в
любом случае будет присутствовать
погрешность из-за округления
трансцендентного числа .
По той же причине образуются методические
погрешности при измерении площади
круглых сечений, объема тел с такими
сечениями и плотности их материала.
При измерении
азимута по магнитному компасу методическая
погрешность возникает из-за несовпадения
магнитных и географических полюсов
Земли.
Измерение параметров
электрической цепи специально подключаемым
прибором приводит к изменению структуры
цепи из-за подключения дополнительной
нагрузки. Результаты измерений
электрических параметров объектов
также могут искажаться из-за наличия
присоединительных проводов, меняющихся
переходных сопротивлений в местах
присоединения чувствительных элементов
(щупов или клемм) измерительных приборов.
Измерение массы
взвешиванием на весах с гирями в воздушной
среде, как правило, осуществляют без
учета воздействия на меры и объект
выталкивающей архимедовой силы, которой
бы не было при взвешивании в вакууме.
В большинстве
случаев погрешности из-за принятых
допущений пренебрежимо малы, но в случае
прецизионных измерений их
приходится оценивать и учитывать или
компенсировать.
Появление
методической погрешности второй
группы
(погрешности из-за некорректной
идеализации реального объекта измерений)
можно рассмотреть на примере измерения
диаметра номинально цилиндрической
детали станковым средством измерений
(измерительной головкой на стойке). В
частности, измерение детали с седлообразной
поверхностью приведет к появлению
методической погрешности, примерно
равной отклонению образующей от
прямолинейности (рисунок 2).
Анализ приведенного
примера показывает, что некорректная
идеализация формы объекта при линейных
измерениях может привести к возникновению
методических погрешностей, которые
могут существенно превышать инструментальную
составляющую.
При измерении
плотности номинально компактного и
однородного твердого тела неидеальность
объекта может быть связана с наличием
необнаруженных полостей или инородных
включений.
Перечень видов
неидеальности объектов может быть
значительно расширен. Например, значения
параметров твердости и шероховатости
поверхностей деталей, химический состав
материала детали, определяемые на
конкретном участке, могут отличаться
от параметров на других участках той
же поверхности. Температура в объеме
жидкости или газа практически всегда
различается по слоям (температурные
градиенты), скорость жидкости или газа
в потоке в разных сечениях неодинакова
(градиенты скорости) и т.д.
Погрешность
(измерения) из-за изменений условий
измерения
– составляющая
систематической погрешности измерения,
являющаяся следствием неучтенного
влияния отклонения в одну сторону
какого-либо из параметров, характеризующих
условия измерений, от установленного
значения.
Примечание
— Этот термин применяют в случае
неучтенного или недостаточно учтенного
действия той или иной влияющей величины
(температуры, атмосферного давления,
влажности воздуха, напряженности
магнитного поля, вибрации и др.); и др.
Как
и в предыдущем случае, определение
содержит неправомочное указание на
систематический
характер погрешности. Погрешность
связывают с отклонением влияющей
величины в одну сторону (а как быть с ее
колебанием при многократных измерениях?).
«Неучтенное или недостаточно учтенное
влияние»
не имеет никакого смысла в определении
источника погрешности – это проблема
обнаружения и оценки погрешности.
Наиболее
логичным представляется термин
«погрешности
из-за отличия условий измерения от
идеальных (от нормальных)».
Обычно такие погрешности называют
«погрешностями условий», что не совсем
корректно, но подразумевает то же
содержание. Фактически эти погрешности
имеют место тогда, когда не удается
выдержать нормальные условия измерений.
Нормальные
условия связаны с понятием влияющих
физических величин.
Влияющая
физическая величина
– физическая
величина, оказывающая влияние на размер
измеряемой величины и (или) результат
измерений.
Определение
требует
расшифровки: фактически под влияющими
физическими величинами понимают те,
которые не
являются измеряемыми, но влияют на
результаты измерений, воздействуя на
объект и/или средства измерений
Пределы
допустимых изменений таких величин или
их отклонений от номинальных значений
нормируют либо нормальной областью
значений (нормальные
условия измерений)
или рабочей областью значений (рабочие
условия измерений).
Поскольку при нормальных условиях
измерений влияющие величины отличаются
от номинальных значений, погрешности
обязательно возникают. Однако нормальные
условия назначают таким образом, чтобы
«погрешности условий» оказались
пренебрежимо малыми, например, по
сравнению с инструментальными
составляющими. В таком случае «погрешности
условий» можно считать практически
равными нулю.
К погрешностям
из-за несоблюдения нормальных условий
измерений следует отнести все составляющие
погрешности измерения, которые вызваны
воздействием на измеряемый объект и
средства измерений любой
влияющей
физической величины, выходящей за
пределы нормальной области значений.
Влияющие величины обычно обусловлены
температурными, электромагнитными и
другими полями в рабочей зоне (измерительная
позиция и ближайшее окружение), давлением
воздуха, его избыточной влажностью,
наличием вибраций на рабочем месте, где
выполняются измерения.
Есть множество
факторов, которые могут привести к
искажению самой измеряемой величины и
(или) измерительной информации о ней.
Например, изменение температуры тела
не приводит к изменению его массы, но
вызывает изменения линейных размеров,
сопротивления прохождению электрического
тока. Повышенная влажность не влияет
на размеры металлических деталей, но
может привести к изменению размеров и
массы изделий из гидрофильных материалов,
которые впитывают влагу из окружающей
атмосферы.
Поиск влияющих
величин осуществляется при анализе
конкретной методики выполнения измерений.
В процессе проведения анализа следует
внимательно относиться к «дополнительным
погрешностям средств измерений»,
возникающим из-за действия влияющих
величин, поскольку учет только
этих составляющих может привести к
«потере» результатов воздействия тех
же влияющих величин на объект измерения.
«Погрешности
условий» могут возникать либо из-за
закономерно изменяющегося отличия
влияющей величины от ее номинального
значения, либо из-за стохастических
колебаний около него. Например, если
рассматривать температурные погрешности,
то они могут возникать из-за стабильного
отличия температуры от нормальной (при
измерениях длины температура детали
25 оС,
а не 20 оС
вызовет постоянную температурную
погрешность), а постепенный рост
температуры в помещении от начала к
концу рабочей смены приведет к переменной
температурной погрешности.
Как
бы мы ни старались поддерживать постоянную
температуру в помещении, никакие
технические устройства не обеспечат
ее абсолютной стабильности. Невозможно
полностью компенсировать воздействия
ряда случайных факторов (изменение
теплового баланса при движении воздушных
масс в помещении, при воздействии
солнечных лучей, при вносе и выносе
деталей, перемещении операторов,
включении и выключении приборов и т.д.).
В результате возникают стохастические
колебания температуры и случайно
изменяющаяся составляющая температурной
погрешности.
Субъективная
погрешность измерения
– составляющая
систематической погрешности измерений,
обусловленная индивидуальными
особенностями оператора.
Иногда
субъективную погрешность называют
личной
погрешностью или
личной
разностью.
Понятно, что определять характер этой
погрешности как систематический
нет никаких оснований
Субъективные
погрешности
включают погрешности
отсчитывания
и погрешности
манипулирования
средствами измерений и измеряемым
объектом.
Погрешности
отсчитывания
возникают при использовании аналоговых
средств измерений с устройством выдачи
измерительной информации типа
«шкала-указатель». При положении
указателя между отметками шкалы
отсчитывание осуществляется либо с
округлением
до ближайшего деления, либо с
интерполированием
доли деления
на глаз. Погрешность округления результата
до целого деления составляет не более
половины цены деления отсчетного
устройства, а при интерполировании
опытным оператором и удачной эргономике
отсчетного устройства погрешность
отсчитывания еще меньше и составляет
не более 1/10 части цены интерполируемого
деления.
В случае, если
плоскости шкалы и указателя не совпадают,
возможно возникновение погрешности
отсчитывания из-за
параллакса
при «косом» направлении взгляда
оператора. Для уменьшения погрешностей
от параллакса используют методы сближения
указателя со шкалой (скошенные кромки
нониуса штангенциркуля и барабана
микрометра, расположенный в плоскости
шкалы световой указатель) или искусственные
приемы получения нормального угла
зрения (специальные наглазники и
налобники в оптических приборах,
зеркальная полоска под шкалой прецизионных
приборов и др.).
Очевидно, что
погрешности отсчитывания при округлении
или интерполировании и погрешности
из-за параллакса не возникают при
использовании приборов с дискретной
выдачей информации на цифровых табло.
При измерениях
часто приходится оперировать устройствами
совмещения, настройки и корректировки
нуля, арретирования, базирования средства
измерений или измеряемого объекта,
чувствительными элементами средства
измерений. Эти манипуляции часто приводят
к погрешностям, особенно существенным
у операторов с недостаточно высокой
квалификацией.
Распределение
источников погрешностей можно
проиллюстрировать на схеме измерения
физической величины (рисунок 3).
В трактовке данной
схемы взаимодействие средства измерений
с измеряемым объектом определяет «метод
измерения», следовательно, и методические
погрешности. «Условия измерений» на
схеме взяты в широком смысле и включают
в себя не только влияющие величины, но
и факторы, оказывающие отрицательное
воздействие на оператора (недостаточная
освещенность, шумовое загрязнение среды
и др.). Тем не менее, оценивать «погрешность
условий» предлагается только как
результат действия влияющих величин
(величина А воздействует только на
измеряемый объект, В – на измеряемый
объект и на средство измерений, С –
только на средство измерений).
Погрешность
измерения ,
которая всегда являетсяинтегральной
погрешностью,образуется в результате
объединениясоставляющих погрешностейот разных источников:
= си*
м
*у
*оп
,
где
*– знак объединения (комплексирования
а не алгебраического сложения), поскольку
погрешности разного характера объединяют
с использованием разных математических
операций.
Каждый из источников
может дать одну, либо несколько
элементарных составляющих. В последнем
случае составляющая погрешность сама
является интегральной. В качестве
примеров, иллюстрирующих множество
составляющих в одном источнике, можно
представить представленные выше
результаты рассмотрения субъективной
и инструментальной погрешностей.
В метрологической
литературе встречаются разные
классификации погрешностей измерений
по характеру их проявления (изменения).
Традиционным является деление погрешностей
на случайные, систематические и грубые,
и этот же подход принят в стандартах.
Однозначно
распределить погрешности в соответствии
с принятым в стандарте делением на
систематические и случайные в ряде
случаев не удается из-за возможности
произвольной трактовки их определений.
Результаты нечеткого деления погрешностей
приводят к явно нелепым ситуациям.
Например, в некоторых источниках, включая
РМГ 29 – 99, погрешности методические,
«условий» и субъективные относят к
систематическим. Такая позиция
способствует образованию неправильного
стереотипа, увязывающего характер
погрешности с источником ее появления.
Очевидно, что одни и те же погрешности
в некоторых случаях могут проявляться
либо как систематические, либо как
случайные.
В литературе
встречается подход, который трактует
распределение погрешностей на
систематические и случайные как один
из приемов анализа. Принятие этой
концепции равноценно признанию
возможности приписывания
погрешностям произвольно выбранного
характера проявления.
Реальное положение
характеризуется фактическим наличием
как детерминированных,
так и случайных (стохастических) явлений,
которые вызывают появление
соответствующих
погрешностей.
Например, наряду с закономерным изменением
длины стержня при повышении или понижении
температуры широко известно броуновское
движение, которое следует рассматривать
как проявление стохастических (случайных)
явлений, проходящих на молекулярном
уровне. Надо признать также возможность
объединенного воздействия множества
явлений, которые по отдельности имеют
функциональную природу, но в итоге
комплексирования при измерениях приводят
к появлению случайных результатов из-за
неопределенности действующих факторов,
малости воздействия каждого из них и
неоднозначности объединения воздействий
отдельных факторов. При большом числе
действующих факторов такой механизм
приводит к стохастическому характеру
комплексных воздействий. Подобные
механизмы действуют при бросании
игральных костей, игре в рулетку,
выбрасывании «лототроном» шара с
определенным номером. Описанные системы
используют как генераторы случайных
чисел.
Поскольку механизмы
образования значительной части
составляющих погрешности измерений
сходны с механизмами формирования
случайных величин, можно ожидать наличия
в результатах измерений случайных
погрешностей.
Если это допущение справедливо, то после
исключения систематических погрешностей
для обработки результатов измерений
можно использовать аппарат теории
вероятностей и математической статистики.
С другой стороны,
очевидно наличие детерминированных
механизмов образования погрешностей.
И средства измерений, и измеряемые
объекты, и окружающая среда подчиняются
физическим законам. Поэтому при
взвешивании груза на пружинных весах
надо считаться с широтой и высотой над
уровнем моря, учитывать температурные
изменения объема тел, диэлектрические
свойства воздуха при использовании
емкостных преобразователей и его
оптические свойства при измерении длины
лазерным интерферометром.
К систематическим
погрешностям
измерений можно отнести те составляющие,
для которых можно считать доказанным
наличие функциональных связей с
вызывающими их аргументами. Для них
можно предложить формальную запись в
виде
s
= F (,
…),
где ,
– аргументы, вызывающие систематическую
погрешность.
Главной особенностью
систематической погрешности является
принципиальная
возможность ее выявления, прогнозирования
и однозначной оценки,
если
удается узнать вид функции и значения
аргументов.
В
зависимости от характера измерения
систематические погрешности подразделяют
на элементарные и изменяющиеся
по сложному закону.
Элементарные
погрешности можно условно разделить
на постоянные,
прогрессирующие
(прогрессивные)
и периодические.
Прогрессирующими
называют монотонно возрастающие или
монотонно убывающие погрешности.
Периодические погрешности – погрешности,
изменение которых можно описать
периодической функцией. Погрешности,
изменяющиеся по сложному закону,
образуются при объединении нескольких
систематических погрешностей.
Постоянные
систематические погрешности представлены
в графической форме на рисунке 4а (s
= a,
или s
= const), а переменные – на рисунке 4б – е.
Простейшие переменные систематические
погрешности, которые аппроксимируют
графиками без перегибов (фактически
это монотонно
изменяющиеся
или прогрессирующие погрешности)
показаны на рисунке 4б – г, а периодические
или гармонические
погрешности – на рисунке 4е.
Всем известны
«спешащие» и «отстающие» часы, погрешности
которых прогрессируют во времени, но
мало кто анализирует показания часов
за полный оборот стрелки. Если оценивать
погрешности, то можно утверждать, что
в результате многократного повторения
вращения стрелки часов должны проявляться
периодические погрешности, обусловленные
эксцентриситетом и превращающиеся в
нуль при завершении каждого полного
оборота.
Обычно для описания
и для аппроксимации систематической
погрешности подбирают наиболее простую
функцию, например линейную для
прогрессирующей погрешности. Такой же
упрощенный подход применяют и для
аппроксимации гармонической систематической
погрешности, которая может быть описана
как синусоида, косинусоида, пилообразная
либо другая периодическая функция.
Систематическая
погрешность может иметь не только
элементарный, но и более сложный характер,
который можно аппроксимировать функцией,
включающей приведенные простые
составляющие. Сложная систематическая
погрешность, включающая постоянную,
прогрессирующую
и периодическую
составляющие, в общем виде может быть
описана выражением
s
= a
+ b
+ dsin,
где a
– постоянная составляющая сложной
систематической погрешности;
,
– соответственно аргументы прогрессирующей
и периодической составляющих сложной
систематической погрешности.
Стандартное
определение случайной погрешностиизмерения в строгом смысле не является
определением, поскольку содержит
«порочный круг»:составляющая
погрешности результата
измерения, изменяющаяся случайным
образом (по знаку и
значению) при повторных измерениях,
проведенных с одинаковой тщательностью,
одной и той же физической
величины. Здесь опять
использовано некорректное упоминание
измерений одной и той же величины, а,
кроме того, содержится бессмысленная
характеристика качества выполнения
измерений («проведенных с
одинаковой тщательностью»).
Случайными
погрешностямив строгом смысле
термина можно считать только те, которые
обладают статистической устойчивостью
(ведут себя как центрированная случайная
величина). Причиной появления таких
погрешностей чаще всего является
совокупное действие ряда слабо влияющих
дестабилизирующих факторов, связанных
с любыми источниками погрешностей,
причем функциональные связи аргументов
с погрешностями либо отсутствуют (в
наличии только стохастические
зависимости), либо не могут быть выявлены
из-за неопределенности факторов и
большого их числа.
Погрешности,
которые нельзя отнести ни к случайным,
ни к систематическим из-за совершенно
иного механизма образования и принципиально
отличного от ожидаемого значения,
называют грубыми
погрешностями измерений
или промахами.
Промах – погрешность
результата отдельного измерения,
входящего в ряд измерений, которая для
данных условий резко отличается от
остальных результатов этого ряда.
Определение промаха
сформулировано весьма неудачно, в первую
очередь некорректным является упоминание
«данных условий». Очевидно, что причинами
возникновения грубой погрешности могут
быть промах оператора при снятии отсчета
или его записи, ошибка в реализации
методики измерений, сбой в измерительной
цепи прибора или незамеченное импульсное
изменение влияющей физической величины.
Причины появления результатов с грубыми
погрешностями резко выпадают из ряда
механизмов, формирующих систематические
или случайные составляющие погрешности
измерений. Однако «резкое отличие» не
является критерием и оставляет
значительные возможности для произвола.
«Результат измерения
с грубой погрешностью» фактически
вызван ошибкой, допущенной при измерении,
поэтому результаты с грубыми погрешностями
следует признать ошибочными и подлежащими
устранению.
Грубые погрешности
в принципе непредсказуемы, а их значения
невозможно прогнозировать с учетом
вероятности как это делают для случайных
погрешностей. Фактически к результатам
с грубыми погрешностями относят либо
такие, которые явно не соответствуют
ожидаемому результату измерений (нелепые
результаты), либо экстремальные значения,
отличия которых от средних значений
массива выражены не столь откровенно,
но принадлежность которых к данному
массиву результатов имеет весьма малую
вероятность.
Отбрасывание
(элиминация) результатов с грубыми
погрешностями предупреждает возможность
значительного искажения оценки
результатов измерений. Исключение
результатов может осуществляться либо
цензурированием явно нелепых значений,
либо статистическим отбраковыванием
экстремальных результатов (подозрительных
на наличие грубых погрешностей), которое
основано на принципе практической
уверенности. Применение этого принципа
позволяет отбрасывать те значения,
вероятность появления которых в
исследуемом массиве данных меньше
некоторой заранее выбранной.
По значимости все
погрешности (составляющие и интегральные)
можно делить на значимыеипренебрежимо
малые. Кпренебрежимо малым
составляющим относят погрешности,
которые значительно меньше доминирующих
составляющих. Соотношение между
пренебрежимо малойminи доминирующейmaxсоставляющими можно записать в виде
min
<< max.
Практика показывает,
что случайную или систематическую
составляющую можно отнести к пренебрежимо
малым погрешностям, если она на порядок
меньше доминирующей составляющей той
же интегральной погрешности. Столь
малые погрешности при объединении всех
составляющих i
в комплексную
оценку интегральной погрешности
практически не оказывают влияния на
окончательный результат, что формально
после ранжирования составляющих в
порядке увеличения можно записать как
=
1*
2
*… *i
*… *n
2
*…*i
*… *n,
где
1
=
min<<
max.
Пренебрежимо малой
погрешностью измерения (интегральной)
можно считать такую, которая не является
препятствием для замены истинного
значения физической величины полученным
результатом. В соответствии со стандартом
за действительное
значение физической величины принимают
такое значение, которое получено
экспериментально (в результате измерений)
и настолько близко к истинному, что для
данной задачи
измерений
может заменить истинное
X
дQ
Q,
где X
дQ
– действительное значение физической
величины;
Q
– истинное значение физической величины.
Если различие
между истинным значением величины Q
и результатом ее измерения XдQ
мы считаем пренебрежимо малым, можно
записать
дQ
0,
где дQ
– погрешность измерения действительного
значения величины.
Для одной и той же
физической величины могут рассматриваться
разные действительные значения. Близость
этих значений к истинному зависит от
задачи измерения. Очевидно, что для
некоторой физической величины точность
измерения при установлении годности
детали по заданному параметру может
быть значительно ниже, чем при сортировке
деталей по этому параметру на группы
для последующей селективной сборки или
при исследовании точности технологического
процесса обработки детали. Для установления
действительного значения измеряемой
величины следует выбрать значение
допустимой
погрешности измерений,
которая будет представлять собой предел
пренебрежимо
малого значения
погрешности
измерений. Допустимая погрешность –
это норма, которую не должна превысить
реализуемая погрешность измерений.
В зависимости от
режима измерения погрешности принято
делить на статические и динамические.
Статическая
погрешность измерений
– погрешность результата измерений,
свойственная условиям статического
измерения. Динамическая
погрешность измерений
– погрешность результата измерений,
свойственная условиям динамического
измерения.
Стандартные
«определения» фактически только именуют,
но не определяют статическую и динамическую
погрешности измерений. Динамическая
погрешность средства измерений–погрешность средства измерений,
возникающая при измерении изменяющейся
(в процессе измерений)физической
величины. Статическая
погрешность средства измерений –погрешность средства измерений,
применяемого при измерении физической
величины, принимаемой за неизменную.
Эти определения непригодны для
идентификации динамической погрешности,
поэтому метрологи вынуждены искать
выход из сложившейся ситуации
самостоятельно.
В соответствии с
ранее действовавшим стандартом
динамической погрешностьюсредства
измерений называлась составляющая
погрешности, дополнительная к статической,
ивозникающая при измерении в
динамическом режиме. В соответствии
с этим определением
дин
= д.р
– ст.р
,
где дин
– динамическая погрешность средства
измерения;
д.р
– погрешность средства измерения при
использовании его в динамическом режиме;
ст.р
– статическая погрешность средства
измерения (погрешность при использовании
средства измерений в статическом
режиме).
Динамический режим
измерений встречается не только при
измерении изменяющейся величины, но и
при измерении величины постоянной. И в
том и в другом случаях (рисунок 5) возможна
слишком высокая скорость «подачи
информации» на средство измерений VQ
(скорость изменения сигнала измерительной
информации на входе средства измерений)
которая оказывается соизмерима со
скоростью преобразования измерительной
информации VQ
X
и/или даже выше ее.
Например, в
контрольно-сортировочных автоматах
для измерения диаметров тел качения
подшипников измеряется постоянная
физическая величина – длина. Но из-за
необходимости обеспечить высокую
производительность автомата скорость
изменения входного сигнала измерительной
информации может оказаться выше скорости
преобразования измерительной информации
средством измерения. В таком случае
из-за «запаздывания» с преобразованием
сигнала возникают динамические
погрешности.
Поскольку речь
идет не столько о средствах измерений,
сколько об их работе в специфическим
режиме, динамическую
погрешность не следует считать
инструментальной.
Эту погрешность нужно рассматривать
более широко – как составляющую итоговой
(интегральной) погрешности, обусловленную
динамическим режимом измерений.
В тех случаях,
когда удается определить значение
погрешности, в результат измерений
может быть внесена поправка
– значение величины, вводимое в
неисправленный результат измерения с
целью исключения погрешности.
Знак поправки противоположен знаку
погрешности.
Исключение
систематических погрешностей измерения
не только из отдельных результатов
измерений, но из целых серий, полученных
при многократных измерениях одной и
той же физической величины, в метрологии
принято называть «исправлением
результатов», а полученные при этом
результаты – исправленными.
Статистическая обработка массивов
результатов измерений, образующих
серии, недопустима без предварительного
«исправления результатов», т.е. исключения
результатов воздействия, по крайней
мере,переменных систематических
составляющих погрешностей.
Неисключенная
систематическая погрешность
– составляющая погрешности результата
измерений, обусловленная погрешностями
вычисления и введения поправок на
влияние систематических погрешностей
или систематической погрешностью,
поправка на действие которой не введена
вследствие ее малости. (Иногда этот вид
погрешности называют неисключенный
остаток систематической погрешности).
Неисключенные
систематические погрешности могут быть
либо значимыми, либо пренебрежимо
малыми. К значимымотносятся те
невыявленные систематические погрешности
и неисключенные остатки систематических
погрешностей, которые соизмеримы со
случайными составляющими погрешности
измерений.
Невыявленные
систематические погрешности, превосходящие
случайные составляющие, могут привести
к существенному искажению результатов
измерений, что особенно опасно при
выполнении прецизионных измерений со
сравнительно малыми случайными
погрешностями. В грамотно организованных
измерениях значимые невыявленныесистематические погрешности не имеют
права на существование, они подлежат
обязательному выявлению и оценке либо
исключению.
Неисключенные
остатки
имеют место при любом, даже самом
тщательном выявлении и исключении
систематических составляющих. В принципе
они могут быть выявлены и исключены
(как систематические), однако иногда
остаются невыявленными из-за сложности
технического решения такой задачи. В
подобных случаях необходимо оценивать
предельные значения этих погрешностей
или их порядок. Если измерения
характеризуются наличием нескольких
неисключенных остатков систематических
погрешностей, для расчета результирующего
(«суммарного») значения применяют
аппарат теории вероятностей и
математической статистики, в силу
сходства механизмов формирования
ансамбля этих погрешностей и случайных
величин.
Применение такого
математического аппарата тем более
оправдано в случаях, когда систематическая
погрешность отдельной реализации
является случайной величиной в ансамбле
однородных событий. Например,
систематическая погрешность конкретной
меры массы (гири) является случайной
для партии гирь одного номинала и класса
точности. Граница такой погрешности
может быть определена как граница поля
допуска меры.
Статистическая
обработка ансамбля неисключенных
систематических составляющих приводит
к появлению таких парадоксальных оценок,
как значение
среднего квадратического отклонения
систематической составляющей погрешности
и связанные с ним предельные значения
или доверительные границы неисключенных
остатков систематической погрешности
с указанием доверительной вероятности,
а также качественные оценки (принятая
аппроксимация) закона распределения.
Если полученные оценки значений
неисключенных систематических
погрешностей соизмеримы со случайными
составляющими, расчет «суммарного
значения» неисключенных остатков
систематических погрешностей и учет
их совместного со случайными составляющими
влияния на результаты измерений должен
осуществляться с применением специального
аппарата математической обработки,
который приведен в ГОСТ 8.207.
Общеприняты и
практически непротиворечивы классификации
погрешностей измерений по формам
выражения.
Абсолютные
погрешности
выражают в единицах измеряемой величины,
а относительные,
которые представляют собой отношение
абсолютной погрешности
к значению измеряемой величины, могут
быть рассчитаны в неименованных
относительных единицах (или в именованных
относительных единицах, например в
процентах или в промилле). Формальное
выражение относительной погрешности
(отн)
может быть представлено в виде:
отн
= /Q,
а при использовании
относительной погрешности, выраженной
в процентах
отн
= (/Q)
100 %.
где
– абсолютная погрешность измерения;
Q
– истинное значение физической величины.
Либо, принимая во
внимание незначительное для данного
выражения различие между истинным
значением физической величины Q
и результатом ее измерения X,
можно записать
отн
/X,
а также
отн
(/X)
100 %.
Для характеристики
средств измерений иногда используют
такой специфический класс относительных
погрешностей, какприведенные
погрешностисредств измерений(прив),
то есть отношение абсолютной погрешности
к некоторой нормирующей величине (Qнорм)
прив
= /Qнорм,
В качестве
нормирующей величины могут использоваться
верхний предел измерений, больший из
модулей пределов измерений, если нулевое
значение находится внутри диапазона
измерений, а верхний и нижний пределы
не одинаковы по модулю, и другие величины,
оговоренные ГОСТ 8.401.
Формы оценок
погрешностей, используемые в метрологии
и в технических измерениях, весьма
разнообразны. Они включают качественные
характеристикииколичественные
оценки погрешностей измерений.
Качественные
характеристикипогрешностей в
простейшем случае ограничиваются
указанием их детерминированного или
стохастического характера. Для
систематических погрешностей дополнительно
может быть указана тенденция (постоянная,
прогрессирующая, периодическая), а при
более полной информации – функция,
описывающая изменение погрешности.
Для случайных
погрешностей качественной характеристикой
может быть аппроксимация функции
распределения вероятностей. В метрологии
приняты и наиболее часто применяются
нормальное распределение (распределение
Гаусса), равновероятное, трапециевидное
и распределение Релея. При необходимости
используют и другие аппроксимации.
Случайная
составляющая погрешности вызывает
рассеяние результатов измерений, которое
носит вероятностный характер. Рассеяние
результатов в ряду измерений
– несовпадение результатов измерений
одной и той же величины в ряду равноточных
измерений, как правило, обусловленное
действием случайных погрешностей.
Количественными оценками рассеяния
результатов в ряду измерений могут
быть:
-
размах
результатов измерений, -
среднее
арифметическое значение погрешности
(по модулю), -
среднее
квадратическое значение погрешности
или стандартное отклонение результатов
измерений (среднее квадратическое
отклонение, экспериментальное среднее
квадратическое отклонение), -
доверительные
границы погрешности (доверительная
граница или доверительная погрешность).
Размах результатов
измерений
– оценка Rn
рассеяния результатов единичных
измерений физической величины, образующих
ряд (или выборку из п измерений). Размах
результатов измерений Rn определяют из
зависимости
Rn
= Xmax
– Xmin,
где Xmax
и
Xmin
– наибольшее и наименьшее значения
результатов в серии.
Размах отклонений
Re
от среднего
или произвольно выбранного значения
(равен размаху результатов измерений)
определяют из зависимости
Re
= emax
– emin,
где
emax
и
emin
– наибольшее и наименьшее отклонения
результатов от некоторого фиксированного
значения.
Более строгими в
математическом смысле оценками
погрешностей можно считать среднее
арифметическое значение погрешности
в серии результатов, среднее квадратическое
отклонение погрешности от точечного
значения результата измерения, границы
погрешности.
Средняя
квадратическая погрешность результатов
единичных измерений в ряду измерений
– оценка рассеяния единичных результатов
измерений в ряду равноточных измерений
одной и той же физической величины около
среднего их значения.
В метрологической практике широко
распространен термин среднее
квадратическое отклонение (СКО)
единичных результатов в ряду измерений
от их среднего арифметического значения.
Это отклонение иногда называют стандартной
погрешностью измерений. Если в результаты
измерений введены поправки для устранения
систематических погрешностей, то
отклонения от среднего арифметического
значения можно рассматривать как
случайные погрешности. В РМГ 29 – 99
предлагается для упорядочения совокупности
терминов, родовым среди которых является
термин «погрешность
измерения»,
применять термин «средняя
квадратическая погрешность».
При обработке ряда результатов измерений,
свободных от систематических погрешностей,
СКП и СКО представляют собой одну и ту
же оценку рассеяния результатов единичных
измерений.
Границы погрешности
могут быть определены как предельные
значения или как доверительные границы
с указанием вероятности попадания
погрешности в указанный интервал. В
качестве предельных значений или границ
могут рассматриваться нижняя и верхняя
границы (н
и в
либо –
и
+),
значение модуля погрешности
(в случае если –
= +)
или значение модуля, равное большему
из абсолютных значений –
и +.
Доверительные
границы погрешности результата измерений
(доверительные
границы погрешности; доверительные
границы) –
наибольшее и наименьшее значения
погрешности измерений, ограничивающие
интервал, внутри которого с заданной
вероятностью находится искомое значение
погрешности результата измерений.
Доверительные
границы результата
измерений при симметричном
распределении вычисляются как
,
,
где
,
–
средние
квадратические погрешности, соответственно,
единичного и среднего арифметического
результатов измерений;
t
–
коэффициент, зависящий от доверительной
вероятности Р
и
числа измерений п.
При
симметричных границах термин может
применяться в единственном числе –
доверительная
граница.
Иногда
вместо термина
доверительная
граница
применяют
термин доверительная
погрешность
или
погрешность
при данной доверительной вероятности.