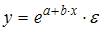Вопрос № 201326
Относительно формы зависимости различают …
линейную и множественную регрессии
положительную и отрицательную регрессии
простую и множественную регрессии
линейную и нелинейную регрессии
Вопрос № 201327
Относительно количества факторов, включенных в уравнение регрессии различают …
линейную и множественную регрессии
множественную и многофакторную регрессии
парную и линейную регрессии
простую и множественную регрессии
Вопрос № 201328
Простая линейная регрессия предполагает …
наличие двух и более факторов и нелинейность уравнения регрессии
наличие двух и более факторов и линейность уравнения регрессии
наличие одного фактора и нелинейность уравнения регрессии
наличие одного фактора и линейность уравнения регрессии
Вопрос № 201329
Объем выборки определяется числом параметров при…
зависимых переменных
случайных факторах
независимых и зависимых переменных
независимых переменных
1.
«Белым
шумом»
называется
___________ процесс
чисто
случайный
2.
Автокорреляционной
функцией временного ряда называется
последовательность
значений коэффициентов автокорреляции
различных порядков
3.
В
исходном соотношении МНК сумма квадратов
отклонений фактических значений
результативного признака от его
теоретических значений
минимизируется
4.
В
качестве показателя тесноты связи для
линейного уравнения парной регрессии
используется
линейный
коэффициент корреляции
5.
В
качестве фиктивных переменных в модель
множественной регрессии включаются
факторы
не
имеющие количественных значений
6.
В
левой части системы взаимозависимых
переменных, как правило, находится
одна
зависимая переменная
7.
В
левой части системы независимых уравнений
находится
совокупность
зависимых переменных
8.
В
линейном уравнении парной регрессии
коэффициентом регрессии является
значение
параметра
b
9.
В
матрице парных коэффициентов корреляции
отображены значения парных коэффициентов
линейной корреляции между
переменными
10.
В
нелинейной модели парной регрессии
функция является
нелинейной
11.
В
общем случае каждый уровень временного
ряда формируется под воздействием
тенденции,
сезонных колебаний и случайных факторов
12.
В
основе метода наименьших квадратов
лежит
минимизация
суммы квадратов отклонений фактических
значений результативного признака от
его теоретических значений
13.
В
приведенной форме модели в правой части
уравнений находятся
только
независимые переменные
14.
В
системах рекурсивных уравнений количество
переменных в правой части каждого
уравнения определяется как ______________
уравнений и количества независимых
факторов
сумма
количества зависимых переменных
предыдущих
15.
В
системе независимых уравнений каждое
уравнение представлено
изолированным
уравнением регрессии
16.
В
стандартизованном уравнении множественной
регрессии ;. Определите, какой из факторов
х1
или
х2
оказывает
более сильное влияние на
,так
как 2,1>0,3
17.
В
стандартизованном уравнении множественной
регрессии переменными являются
стандартизованные
переменные
18.
В
стандартизованном уравнении свободный
член
отсутствует
19.
Величина
коэффициента детерминации при включении
существенного фактора в эконометрическую
модель
будет
увеличиваться
20.
Величина
остаточной дисперсии при включении
существенного фактора в модель
будет
уменьшаться
21.
Величина
отклонений фактических значений
результативного признака от его
теоретических значений представляет
собой
ошибку
аппроксимации
22.
Величина
параметра в уравнении парной линейной
регрессии характеризует значение
результирующей
переменной при нулевом значении фактора
23.
Взаимодействие
факторов эконометрической модели
означает, что
влияние
одного из факторов на результирующий
признак не зависит от значений другого
фактора
24.
Включение
фактора в модель целесообразно, если
коэффициент регрессии при этом факторе
является
существенным
25.
Временной
ряд – это совокупность значений
экономического показателя
за
несколько последовательных моментов
(периодов) времени
26.
Временной
ряд называется стационарным, если он
является реализацией _____________ процесса
стационарного
стохастического
27.
Временной
ряд характеризует
данные,
описывающие один объект за ряд
последовательных моментов (периодов)
времени
28.
Выбор
формы зависимости экономических
показателей и определение количества
факторов в модели называется
________________ эконометрической модели
спецификацией
29.
Выделяют
три класса систем эконометрических
уравнений
независимые,
взаимозависимые и рекурсивные
30.
Гетероскедастичность
остатков подразумевает _____________ от
значения фактора
зависимость
дисперсии остатков
31.
Гетероскедастичность
подразумевает ________________________ от значения
фактора
зависимость
дисперсии остатков
32.
Графическое
изображение наблюдений на декартовой
плоскости координат называется полем
корреляции
33.
Дано
уравнение регрессии . Определите
спецификацию модели
линейное
уравнение множественной регрессии
34.
Двухшаговый
метод наименьших квадратов предполагает
______ использование обычного МНК
однократное
35.
Двухшаговый
метод наименьших квадратов применим
для решения
только
сверхидентифицируемой системы
одновременных уравнений
36.
Двухшаговый
метод наименьших квадратов применяется
для оценки параметров
систем
эконометрических уравнений
37.
Для
модели зависимости среднедушевого (в
расчете на одного человека) месячного
дохода населения (р.) от объема производства
(млн р.) получено уравнение . При изменении
объема производства на 1
млн
р. доход в среднем изменится на
0,003
млн
р.
38.
Для
моделирования зависимости предложения
от цены не может быть использовано
уравнение регрессии
39.
Для
моделирования сложных экономических
систем целесообразно использовать
систему
эконометрических уравнений
40.
Для
нелинейных уравнений метод наименьших
квадратов применяется к
преобразованным
линеаризованным уравнениям
41.
Для
оценки коэффициентов структурной формы
модели не применяют _____ метод наименьших
квадратов
обычный
42.
Для
существенного параметра расчетное
значение критерия Стьюдента
больше
табличного значения критерия
43.
Для
уравнения зависимости выручки от
величины оборотных средств получено
значение коэффициента детерминации,
равное 0,7.
Следовательно,
_% дисперсии обусловлено случайными
факторами
30
44.
Для
уравнения у = 3,14
+ 2х
+e
значение
коэффициента корреляции составило 2.
Следовательно
значение
коэффициента корреляции рассчитано с
ошибкой
45.
Если
доверительный интервал для параметра
проходит через точку ноль, следовательно
параметр
является несущественным
46.
Если
значение индекса корреляции для
нелинейного уравнения регрессии
стремится к 1,
следовательно
нелинейная
связь достаточно тесная
47.
Если
значение коэффициента корреляции равно
единице, то связь между результатом и
фактором
функциональная
48.
Если
коэффициент регрессии является
несущественным, то его значения
приравниваются к
нулю
и соответствующий фактор не включается
в модель
49.
Если
между экономическими показателями
существует нелинейная связь, то
целесообразно
использовать спецификацию нелинейного
уравнения регрессии
50.
Если
наиболее высоким оказался коэффициент
автокорреляции первого порядка, то
исследуемый ряд содержит только
тенденцию
51.
Если
наиболее высоким оказался коэффициент
автокорреляции третьего порядка, то
исследуемый ряд содержит
случайную
величину, влияющую на каждый третий
уровень ряда
52.
Если
оценка параметра эффективна, то это
означает
наименьшую
дисперсию остатков
53.
Если
предпосылки метода наименьших квадратов
нарушены, то
оценки
параметров могут не обладать свойствами
эффективности, состоятельности и
несмещенности
54.
Если
расчетное значение критерия Фишера
меньше табличного значения, то гипотеза
о статистической незначимости уравнения
принимается
55.
Если
спецификация модели нелинейное уравнение
регрессии, то нелинейной является
функция
56.
Если
спецификация модели отображает нелинейную
форму зависимости между экономическими
показателями, то нелинейно уравнение
регрессии
57.
Если
факторы входят в модель как произведение,
то модель называется
мультипликативной
58.
Если
факторы входят в модель как сумма, то
модель называется
аддитивной
59.
Значение
индекса корреляции, рассчитанное для
нелинейного уравнения регрессии
характеризует тесноту ______ связи
нелинейной
60.
Значение
коэффициента автокорреляции второго
порядка характеризует связь между
исходными
уровнями и уровнями этого же ряда,
сдвинутыми на 2
момента
времени
61.
Значение
коэффициента автокорреляции первого
порядка равно 0,9
следовательно
линейная
связь между последующим и предыдущим
уровнями тесная
62.
Значение
коэффициента автокорреляции рассчитывается
по аналогии с
линейным
коэффициентом корреляции
63.
Значение
коэффициента детерминации рассчитывается
как отношение дисперсии результативного
признака, объясненной регрессией, к
___________ дисперсии результативного
признака
общей
64.
Значение
коэффициента детерминации составило
0,9,
следовательно
уравнение
регрессии объяснено 90%
дисперсии
результативного признака
65.
Значение
коэффициента корреляции не характеризует
статистическую
значимость уравнения
66.
Значение
коэффициента корреляции равно 0,9.
Следовательно,
значение коэффициента детерминации
составит
0,81
67.
Значение
коэффициента корреляции равно 1.
Следовательно
связь
функциональная
68.
Значение
линейного коэффициента корреляции
характеризует тесноту ________ связи
линейной
69.
Значения
коэффициента автокорреляции первого
порядка равно 0,9.
Следовательно
линейная
связь между последующим и предыдущим
уровнями тесная
70.
Значения
коэффициента корреляции может находиться
в отрезке
[-1;1]
71.
Из
пары коллинеарных факторов в
эконометрическую модель включается
тот фактор, который при
достаточно
тесной связи с результатом имеет меньшую
связь с другими факторами
72.
Известны
значения аддитивной модели временного
ряда: Yt
— значение
уровня ряда, Yt
= 30,
Т-
— значение тренда, Т+15,
Е-
значение случайной компоненты случайных
факторов Е=2.
Определите
значение сезонной компоненты S
13
73.
Изолированное
уравнение множественной регрессии
может быть использовано для моделирования
взаимосвязи экономических показателей,
если
факторы
не взаимодействуют друг с другом
74.
Исследуется
зависимость, которая характеризуется
линейным уравнением множественной
регрессии. Для уравнения рассчитано
значение тесноты связи результативной
переменной с набором факторов. В качестве
этого показателя был использован
множественный коэффициент
корреляции
75.
Исходные
значения фиктивных переменных предполагают
значения
качественные
76.
К
линейному виду нельзя привести:
нелинейную
модель внутренне нелинейную
77.
К
ошибкам спецификации относится
неправильный
выбор той или иной математической
функции
78.
Качество
подбора уравнения оценивает коэффициент
детерминации
79.
Коррелограммой
называется ______________________________ функции
графическое
отображение автокорреляционной
80.
Косвенный
метод наименьших квадратов требует
преобразования
структурной формы модели в приведенную
81.
Критерий
Стьюдента предназначен для определения
значимости
каждого
коэффициента регрессии
82.
Критерий
Фишера используется для оценки значимости
построенного
уравнения
83.
Критические
значения критерия Фишера определяются
по
уровню
значимости и степеням свободы факторной
и остаточной дисперсий
84.
Критическое
значение критерия Стьюдента определяет
максимально
возможную величину, допускающую принятие
гипотезы о несущественности параметра
85.
Критическое
значение критерия Стьюдента определяет
минимально возможную величину, допускающую
принятие гипотезы о
существенности
параметра
86.
Линеаризация
не подразумевает процедуру
включение
в модель дополнительных существенных
факторов
87.
Линеаризация
подразумевает процедуру приведения
нелинейного
уравнения к линейному виду
88.
Линейное
уравнение множественной регрессии
имеет вид . Определите какой из факторов
или оказывает более сильное влияние на
y
так
как 2,5<-3,7
89.
Математическое
ожидание остатков равно нулю, если
оценки параметров обладают свойством
несмещенности
90.
Матрица
парных коэффициентов корреляции строится
для выявления коллинеарных и
мультиколлинеарных
существенных
факторов
91.
Метод
наименьших квадратов не применим для
уравнений,
нелинейных по оцениваемым параметрам
92.
Метод
наименьших квадратов позволяет оценить
_______ уравнений регрессии
параметры
93.
Метод
оценки параметров моделей с
гетероскедастичными остатками называется
____________ методом наименьших квадратов
обобщенным
94.
Методом
присвоения числовых значений фиктивным
переменным не является
нахождения
среднего значения
95.
Минимальная
дисперсия остатков характерна для
оценок, обладающих свойством
эффективности
96.
Множественная
регрессия не является результатом
преобразования уравнения
97.
Моделирование
тенденции осуществляется на основе
построения уравнения регрессии
зависимости
уровня
ряда от времени
98.
Модель
временного ряда не предполагает
независимость
значений экономического показателя от
времени
99.
Модель
временного ряда предполагает
зависимость
значений экономического показателя от
времени
100.
Модель
идентифицируема, если число параметров
структурной формы модели
равно
числу параметров приведенной формы
модели
101.
Может
ли ряд содержать только одну из компонент?
может,
если другие две компоненты не участвуют
в формировании уровня ряда
102.
Мультиколлинеарность
факторов эконометрической модели
подразумевает
наличие
линейной зависимости между более чем
двумя факторами
103.
Мультипликативная
модель содержит исследуемые факторы в
виде
сомножителей
104.
На
основании преобразования переменных
при помощи обобщенного метода наименьших
квадратов получаем новое уравнение
регрессии, которое представляет собой
взвешенную
регрессию, в которой переменные взяты
с весами
105.
На
первом этапе применения косвенного
метода наименьших квадратов
структурная
форма преобразуется в приведенную
106.
Назовите
показатель корреляции для нелинейных
моделей регрессии
индекс
корреляции
107.
Назовите
показатель тесноты связи для нелинейных
моделей регрессии
индекс
детерминации
108.
Нелинейное
уравнение регрессии означает нелинейную
форму зависимости между
результатом
и факторами
109.
Нелинейную
модель зависимостей экономических
показателей нельзя привести к линейному
виду, если
нелинейная
модель является внутренне нелинейной
110.
Нелинейным
называется уравнение регрессии, если
независимые
переменные входят в уравнение нелинейным
образом
111.
Нелинейным
не является уравнение
112.
Нелинейным
является уравнение
113.
Несмещенность
оценки на практике означает
что
при большом числе выборочных оцениваний
остатки не будут накапливаться
114.
Обобщенный
метод наименьших квадратов используется
для корректировки
гетероскедастичности
остатков в уравнении регрессии
115.
Обобщенный
метод наименьших квадратов не используется
для моделей с _______ остатками
гомоскедастичными
116.
Обобщенный
метод наименьших квадратов отличается
от обычного МНК тем, что при применении
ОМНК
преобразуются
исходные уровни переменных
117.
Обобщенный
метод наименьших квадратов подразумевает
преобразование
переменных
118.
Обобщенный
метод наименьших квадратов рекомендуется
применять в случае
автокорреляции
остатков
119.
Общая
дисперсия служит для оценки влияния
как
учтенных факторов, так и случайных
воздействий
120.
Объем
выборки должен превышать число
рассчитываемых параметров при исследуемых
факторах в
5-6
раз
121.
Объем
выборки определяется
числом
параметров при независимых переменных
122.
Одним
из методов присвоения числовых значений
фиктивным переменным является
ранжирование
123.
Основной
задачей моделирования временных рядов
является
выявление
и придание количественного значения
каждой из трех компонент
124.
Основной
задачей построения систем эконометрических
уравнений является описание
структуры
связей реальной экономической системы
125.
Основной
задачей эконометрики является
исследование
взаимосвязей экономических явлений и
процессов
126.
Основной
целью линеаризации уравнения регрессии
является
возможность
применения метода наименьших квадратов
для оценки параметров
127.
Основным
преимуществом использования систем
эконометрических уравнений является
возможность
описания сложных систем
128.
Основным
требованием к факторам, включаемым в
модель множественной регрессии, является
отсутствие
линейной взаимосвязи между факторами
129.
Остаточная
дисперсия служит для оценки влияния
случайных
воздействий
130.
Отбор
факторов в модель множественной регрессии
при помощи метода включения основан на
сравнении значений
остаточной
дисперсии до и после включения фактора
модель
131.
Относительно
количества факторов, включенных в
уравнение регрессии, различают
простую
и множественную регрессию
132.
Относительно
формы зависимости различают
_________________ регрессии
линейную
и нелинейную
133.
Отсутствие
автокорреляции в остатках предполагает,
что значения ____ не зависят друг от друга
остатков
134.
Оценить
статистическую значимость нелинейного
уравнения регрессии можно с помощью
критерия
Фишера
135.
Оценка
значимости параметров уравнения
регрессии осуществляется по критерию
Стьюдента
136.
Оценка
значимости уравнения в целом осуществляется
по критерию
Фишера
137.
Оценки
параметров линейного уравнения
множественной регрессии можно найти
при помощи метода
наименьших
квадратов
138.
Оценки
параметров уравнений регрессии при
помощи метода наименьших квадратов
находятся на основании решения
системы
нормальных уравнений
139.
Оценки
параметров, найденных при помощи метода
наименьших квадратов, обладают свойствами
эффективности, состоятельности и
несмещенности, если предпосылки метода
наименьших квадратов
выполняются
140.
Парабола
второй степени может быть использована
для зависимостей экономических
показателей
если
для определенного интервала значений
фактора меняется скорость изменений
значений результата, то есть возрастает
динамика роста или спада
141.
Параметр
является существенным, если
доверительный
интервал не проходит через ноль
142.
Параметры
уравнения тренда определяются ________
методом наименьших квадратов
обычным
143.
Первопричиной
использования систем эконометрических
уравнений является то, что
изолированное
уравнение не отображает истинные влияния
факторов на вариацию результативных
переменных
144.
Переход
от точечного оценивания к интервальному
возможен, если оценки являются
эффективными
и несмещенными
145.
По
результатам исследования было выявлено,
что рентабельность производства падает
с увеличением трудоемкости. Какую
спецификацию уравнения регрессии можно
использовать для построения модели
такой зависимости?
146.
Под
идентификационной моделью подразумевается
единственность
соответствия между приведенной и
структурной формами моделей
147.
Под
лагом подразумевается число
периодов,
по которым рассчитывается коэффициент
автокорреляции
148.
Под
стационарным процессом можно понимать
стохастический
процесс, для которого среднее и дисперсия
независимо от рассматриваемого периода
имеют постоянные значения
149.
Показатель,
характеризующий на сколько сигм изменится
в среднем результат при изменении
соответствующего фактора на одну сигму,
при неизменном уровне других факторов,
называется ____________ коэффициентом
регрессии
стандартизованным
150.
После
применения обобщенного метода наименьших
квадратов удается избежать ______ остатков
гетероскедастичности
151.
Построена
аддитивная модель временного ряда, где
Yt
– значение
уровня ряда, Yt
= 10,
T
– значение
тренда, S
– значение
сезонной компоненты, E
– значений
случайной компоненты. Определите вариант
правильно найденных значений компонент
уровня ряда.
T=5,
S=2,
E=3
152.
Построена
модель парной регрессии зависимости
предложения от цены . Влияние случайных
факторов на величину предложения в этой
модели учтено посредством
случайной
величины ε
153.
Предпосылки
метода наименьших квадратов исследуют
поведение
остаточных
величин
154.
Предпосылкой
метода наименьших квадратов не является
условие
неслучайный
характер остатков
155.
Предпосылкой
метода наименьших квадратов является
отсутствие
автокорреляции в остатках
156.
Предпосылкой
метода наименьших квадратов является
то, что
остаточные
величины имеют случайный характер
157.
Предпосылкой
метода наименьших квадратов является
то, что остатки
подчиняются
закону нормального распределения
158.
При
включении фиктивных переменных в модель
им присваиваются
числовые
метки
159.
При
выборе спецификации модели парная
регрессия используется в случае, когда
среди множества факторов, влияющих на
результат
можно
выделить доминирующий фактор
160.
При
выборе спецификации нелинейная регрессия
используется, если
между
экономическими показателями обнаруживается
нелинейная зависимость
161.
При
изучении взаимодействия спроса и
предложения целесообразно использовать
систему
эконометрических уравнений
162.
При
моделировании временных рядов
экономических показателей необходимо
учитывать
стохастический
характер уровней исследуемых показателей
163.
При
оценке параметров приведенной формы
модели косвенный метод наименьших
квадратов использует алгоритм
обычного
метода наименьших квадратов
164.
При
оценке параметров систем одновременных
уравнений не производят
линеаризацию
уравнений системы
165.
При
оценке статистической значимости
уравнения и существенности связи
осуществляется проверка
существенности
коэффициента детерминации
166.
При
помощи модели степенного уравнения
регрессии вида (b>1,
то
есть x
возрастает
и y
тоже
возрастает) не может быть описана
зависимость
выработки
от трудоемкости
167.
При
построении модели временного ряда
проводится расчет
каждого
уровня временного ряда
168.
При
построении систем независимых уравнений
набор факторов в каждом уравнении
определяется числом факторов, оказывающих
________ на моделируемый показатель
существенное
влияние
169.
При
построении системы эконометрических
уравнений необходимо учитывать
структуру
связей реальной экономической системы
170.
При
применении метода наименьших квадратов
исследуются свойства
оценок
параметров уравнения регрессии
171.
При
применении метода наименьших квадратов
исследуются свойства оценок
параметров
уравнения регрессии
172.
При
применении метода наименьших квадратов
уменьшить гетероскедастичность остатков
удается путем
преобразования
переменных
173.
При
расчете значения коэффициента детерминации
используется отношение
дисперсий
174.
При
хорошем качестве модели допустимым
значением средней ошибки аппроксимации
является ___%
5-7
175.
Приведенная
форма модели получена из _________формы
модели
структурной
176.
Приведенная
форма модели представляет собой систему
________ функций эндогенных переменных от
экзогенных
линейных
177.
Приведенная
форма модели является результатом
преобразования
структурной
формы модели
178.
Проверка
является ли временной ряд «белым шумом»
осуществляется
с помощью
статистики
Бокса-Пирса
179.
Проводится
исследование зависимости выработки
работника предприятия от ряда факторов.
Примером фиктивной переменной в данной
модели будет являться ______ работника
уровень
образования
180.
Простая
линейная регрессия предполагает наличие
одного
фактора и линейность уравнения регрессии
181.
Расчет
значения коэффициента детерминации не
позволяет оценить
существенность
коэффициента регрессии
182.
Расчет
средней ошибки аппроксимации для
нелинейных уравнений регрессии связан
с расчетом разности между
____________________________ переменной
фактическим
и теоретическим значениями результативной
183.
Расчетное
значение критерия Фишера определяется
как
отношение
факторной дисперсии к остаточной,
рассчитанных на одну степень свободы
184.
Расчетное
значение критерия Фишера определяется
как ___________ факторной дисперсии и
остаточной, рассчитанных на одну степень
свободы
отношение
185.
Расчетное
значение критерия Фишера определяется
как отношение
дисперсий
186.
Результатом
линеаризации полиномиальных уравнений
является ______________ регрессии
линейные
уравнения множественной
187.
Свойствами
оценок МНК являются: эффективность, а
также
состоятельность
и несмещенность
188.
Система
взаимозависимых уравнений в ее
классическом виде называется также
системой ______ уравнений
одновременных
189.
Система
независимых уравнений предполагает
совокупность
независимых уравнений регрессии
190.
Система
нормальных уравнений метода наименьших
квадратов строится на основании
таблицы
исходных данных
191.
Система
рекурсивных уравнений включает в каждое
предыдущее
(должно быть последующее) уравнение в
качестве факторов все зависимые
переменные предшествующих уравнений
с набором собственно факторов
192.
Система
эконометрических уравнений не используется
при моделировании
взаимосвязей
временных рядов данных
193.
Система
эконометрических уравнений предполагает
наличие _________ независимых признаков
нескольких
зависимых и нескольких
194.
Система
эконометрических уравнений представляет
систему
уравнений
регрессии
195.
Систему
МНК, построенную для оценки параметров
линейного уравнения множественной
регрессии можно решить
методом
определителей
196.
Системы
эконометрических уравнений классифицируются
по
способу
вхождения зависимых и независимых
переменных в уравнение регрессии
197.
Случайный
характер остатков предполагает
независимость
остатков от величины предсказанных по
модели значений результативного признака
198.
Смысл
расчета средней ошибки аппроксимации
состоит в определении среднего
арифметического значения
отклонений,
выраженных в процентах от фактических
значений результативного признака
199.
Совокупность
значений критерия, при которых принимается
нулевая гипотеза, называется областью
_____________ гипотезы
принятия
200.
Состоятельность
оценки характеризуется
увеличением
ее точности с увеличением объема выборки
201.
Спецификацию
нелинейного уравнения парной регрессии
целесообразно использовать, если
значение
индекса
детерминации, рассчитанного для данной
модели достаточно близко к 1
202.
Спецификация
модели нелинейная парная (простая)
регрессия подразумевает нелинейную
зависимость и
независимую
переменную
203.
Стандартная
ошибка рассчитывается для проверки
существенности
параметра
204.
Статистические
гипотезы используются для оценки
значимости
уравнения регрессии в целом
205.
Стационарность
временного ряда не подразумевает
отсутствие
стационарного
стохастического процесса
206.
Стационарность
временного ряда означает отсутствие
тренда
207.
Стационарность
характерна для временного ряда
типа
«белый шум»
208.
Стохастическим
процессом называется
Эконометрика
Известны значения аддитивной модели временного ряда: Yt — значение уровня ряда, Yt = 30, Т- — значение тренда, Т+15, Е- значение случайной компоненты случайных факторов Е=2. Определите значение сезонной компоненты S
Эконометрика
Состоятельность оценки характеризуется
зависимостью от объема выборки значения математического ожидания остатков
увеличением ее точности с увеличением объема выборки
уменьшением ее точности с увеличением объема выборки
независимостью от объема выборки значения математического ожидания остатков
Эконометрика
Двухшаговый метод наименьших квадратов применим для решения
только идентифицируемой системы одновременных уравнений
неидентифицируемой системы одновременных уравнений
системы одновременных уравнений в качестве наиболее общего метода решения
только сверхидентифицируемой системы одновременных уравнений
Эконометрика
При изучении взаимодействия спроса и предложения целесообразно использовать
уравнение зависимости спроса от цены
систему эконометрических уравнений
уравнение зависимости предложения от цены
Эконометрика
К ошибкам спецификации относится
однородность выбранной совокупности
неправильный выбор той или иной математической функции
учет в модели существенных факторов
учет в модели случайных факторов
Эконометрика
После применения обобщенного метода наименьших квадратов удается избежать ______ остатков
нормального распределения
Эконометрика
При хорошем качестве модели допустимым значением средней ошибки аппроксимации является ___%
Эконометрика
Гетероскедастичность остатков подразумевает _____________ от значения фактора
зависимость дисперсии остатков
независимость математического ожидания остатков
постоянство дисперсий остатков независимо
зависимость математического ожидания остатков
Эконометрика
При построении модели временного ряда проводится расчет
последующих и предыдущих значений уровней временного ряда
значений компонент для каждого уровня временного ряда
каждого уровня временного ряда
средних значений компонент для временного ряда в целом
Эконометрика
Для уравнения зависимости выручки от величины оборотных средств получено значение коэффициента детерминации, равное 0,7. Следовательно, _% дисперсии обусловлено случайными факторами
Эконометрика
Взаимодействие факторов эконометрической модели означает, что
влияние факторов на результирующий признак усиливается, начиная с определенного уровня значений факторов
факторы дублируют влияние друг друга на результат
влияние факторов на результирующий признак зависит от значений другого неколлинеарного им фактора
влияние одного из факторов на результирующий признак не зависит от значений другого фактора
Эконометрика
Для нелинейных уравнений метод наименьших квадратов применяется к
преобразованным линеаризованным уравнениям
не преобразованным линейным уравнениям
Эконометрика
Если доверительный интервал для параметра проходит через точку ноль, следовательно
параметр является существенным
параметр является несущественным
значение параметра может принимать как отрицательные, так и положительные значения
параметр признается статистически значимым
Эконометрика
Оценки параметров уравнений регрессии при помощи метода наименьших квадратов находятся на основании решения
системы нормальных неравенств
системы нормальных уравнений
Эконометрика
Если между экономическими показателями существует нелинейная связь, то
нецелесообразно использовать спецификацию нелинейного уравнения регрессии
целесообразно использовать спецификацию линейного уравнение парной регрессии
целесообразно использовать спецификацию нелинейного уравнения регрессии
необходимо включить в модель другие факторы и использовать линейное уравнение множественной регрессии
Эконометрика
Случайный характер остатков предполагает
зависимость предсказанных по модели значений результативного признака от значений факторного признака
независимость остатков от величины предсказанных по модели значений результативного признака
зависимость остатков от величины предсказанных по модели значений результативного признака
независимость предсказанных по модели значений результативного признака от значений факторного признака
Эконометрика
Если факторы входят в модель как сумма, то модель называется
Эконометрика
Метод наименьших квадратов позволяет оценить _______ уравнений регрессии
переменные и случайные величины
Эконометрика
Модель идентифицируема, если число параметров структурной формы модели
равно числу уравнений модели
равно числу параметров приведенной формы модели
больше числа параметров приведенной формы модели
меньше числа параметров приведенной формы модели
Эконометрика
Включение фактора в модель целесообразно, если коэффициент регрессии при этом факторе является
Эконометрика
Стационарность временного ряда означает отсутствие
наблюдений по уровням временного ряда
Эконометрика
Построена аддитивная модель временного ряда, где Yt – значение уровня ряда, Yt = 10, T – значение тренда, S – значение сезонной компоненты, E – значений случайной компоненты. Определите вариант правильно найденных значений компонент уровня ряда.
Эконометрика
Строится модель зависимости спроса от ряда факторов. Фиктивной переменной в данном уравнении множественной регрессии не является _________ потребителя
Эконометрика
Проверка является ли временной ряд «белым шумом» осуществляется с помощью
коэффициента автокорреляции
Эконометрика
Фиктивные переменные включаются в уравнение множественной регрессии для учета действия на результат признаков ____________ характера
Эконометрика
Экономические временные ряды, представляющие собой данные наблюдений за ряд лет, как правило, являются _______________________ временными рядами
функционально зависящими от времени
Эконометрика
Парабола второй степени может быть использована для зависимостей экономических показателей
если исходные данные не обнаруживают изменения направленности
если для определенного интервала значений фактора меняется характер связи рассматриваемых показателей: прямая связь изменяется на обратную или обратная на прямую
если для определенного интервала значений фактора меняется скорость изменений значений результата, то есть возрастает динамика роста или спада
если характер связи зависит от случайных факторов
Эконометрика
Эндогенными переменными не являются:
переменные в уравнениях системы вида
переменные, значения которых определяется внутри системы
Эконометрика
Нелинейным называется уравнение регрессии, если
параметры и зависимые переменные входят в уравнение нелинейным образом
независимые переменные входят в уравнение нелинейным образом
зависимые переменные входят в уравнение нелинейным образом
параметры входят нелинейным образом, а переменные линейны
Эконометрика
Система эконометрических уравнений предполагает наличие _________ независимых признаков
нескольких зависимых и одного
одного зависимого и совокупности
одного зависимого и нескольких
нескольких зависимых и нескольких
Эконометрика
Для существенного параметра расчетное значение критерия Стьюдента
не больше табличного значения критерия
больше табличного значения критерия
меньше табличного значения критерия
Эконометрика
При оценке параметров систем одновременных уравнений не производят
преобразование структурной формы модели в приведенную
линеаризацию уравнений системы
идентификацию системы одновременных уравнений
расчет коэффициентов приведенной формы
Эконометрика
Для существенного параметра расчетное значение критерия Стьюдента
больше табличного значения критерия
не больше табличного значения критерия Стьюдента
меньше табличного значения критерия
Эконометрика
При применении метода наименьших квадратов исследуются свойства оценок
переменных и параметров уравнения регрессии
случайных величин уравнения регрессии
переменных уравнения регрессии
параметров уравнения регрессии
Эконометрика
Автокорреляционной функцией временного ряда называется
последовательность приращений коэффициентов автокорреляции уровней различных порядков
последовательность отношений коэффициентов автокорреляции к величинам соответствующих лагов
зависимость коэффициентов автокорреляции первого порядка от числа уровней временного ряда
последовательность значений коэффициентов автокорреляции различных порядков
Эконометрика
Основной задачей моделирования временных рядов является
добавление новых уравнений к совокупности значений временного ряда
исключение значений каждой из трех компонент из уровней ряда
исключение уровней из совокупности значений временного ряда
выявление и придание количественного значения каждой из трех компонент
Эконометрика
Значение коэффициента корреляции не характеризует
корень из значения коэффициента детерминации
статистическую значимость уравнения
Эконометрика
Одним из методов присвоения числовых значений фиктивным переменным является
нахождение среднего значения
выравнивание числовых значений по возрастанию
выравнивание числовых значений по убыванию
Эконометрика
Критическое значение критерия Стьюдента определяет минимально возможную величину, допускающую принятие гипотезы о
статистической незначимости значения параметра
равенства нулю значения параметра
несущественности параметра
Эконометрика
Модель временного ряда не предполагает
учет временных характеристик
зависимость значений экономического показателя от времени
независимость значений экономического показателя от времени
последовательность моментов (периодов) времени, в течении которых рассматривается поведение экономического показателя
Эконометрика
Если между экономическими показателями существует нелинейная связь, то
нецелесообразно использовать спецификацию нелинейного уравнения регрессии
целесообразно использовать спецификацию нелинейного уравнения регрессии
необходимо включить в модель другие факторы и использовать линейное уравнение множественной регрессии
целесообразно использовать линейное уравнение парной регрессии
Эконометрика
Может ли ряд содержать только одну из компонент?
не может, так как уровень ряда должен формироваться под воздействием всех трех компонент
может, если он представлен данными, описывающими совокупность различных объектов в определенный момент (период) времени
не может, так как временной ряд не содержит компонент, влияющих на его уровни
может, если другие две компоненты не участвуют в формировании уровня ряда
Эконометрика
Объем выборки определяется
числовыми значением переменных, отбираемых в выборку
числом результативных переменных
числом параметров при независимых переменных
объемом генеральной совокупности
Эконометрика
Основной целью линеаризации уравнения регрессии является
улучшение качества модели
повышения существенности связи между рассматриваемыми переменными
возможность применения метода наименьших квадратов для оценки параметров
получение новых нелинейных зависимостей
Эконометрика
Предпосылкой метода наименьших квадратов является то, что остатки
не подчиняются закону больших чисел
подчиняются закону больших чисел
подчиняются закону нормального распределения
не подчиняются закону нормального распределения
Эконометрика
Назовите показатель корреляции для нелинейных моделей регрессии
линейный коэффициент корреляции
парный коэффициент линейной корреляции
Эконометрика
Критерий Стьюдента предназначен для определения значимости
каждого коэффициента корреляции
каждого коэффициента регрессии
построенного уравнения в целом
Эконометрика
Расчет значения коэффициента детерминации не позволяет оценить
качество подбора уравнения регрессии
долю остаточной дисперсии результативного признака в общей дисперсии результативного признака
долю факторной дисперсии результативного признака в общей дисперсии результативного признака
существенность коэффициента регрессии
Эконометрика
В системах рекурсивных уравнений количество переменных в правой части каждого уравнения определяется как ______________ уравнений и количества независимых факторов
сумма количества зависимых переменных предыдущих
сумма количества зависимых переменных последующих
разность количества зависимых переменных предыдущих
разность количества зависимых переменных последующих
Эконометрика
В матрице парных коэффициентов корреляции отображены значения парных коэффициентов линейной корреляции между
переменными и случайными факторами
параметрами и переменными
1. Ошибки спецификации эконометрической модели имеют место вследствие …
неправильного
выбора математической функции или
недоучета в уравнении регрессии какого-то
существенного фактора
недостоверности
или недостаточности исходной информации
неоднородности
данных в исходной статистической
совокупности
недостаточного
количества данных
Решение:
Спецификацией
модели называется отбор факторов,
включаемых в модель, и выбор математической
функции для
.
Поэтому к ошибкам спецификации относятся
не только неправильный выбор той или
иной математической функции для,
но и недоучет в уравнении регрессии
какого-то существенного фактора, то
есть использование парной регрессии
вместо множественной.
2. Для регрессионной модели вида необходим минимальный объем наблюдений, содержащий _____ объектов наблюдения.
15
30
9
5
Решение:
Считается, на
каждый оцениваемый коэффициент регрессии
необходимо не менее 5–7 объектов
статистических наблюдений. Так как
представленная модель содержит 3
независимые переменные, то на каждый
из параметров регрессии при независимой
переменной необходимо по 5–7 наблюдений,
то есть в совокупности не менее 15–21
наблюдения. Берем нижнюю границу
интервала, тогда правильный вариант
ответа – «15».
3. Нелинейным по объясняющим переменным, но линейным по параметрам уравнением регрессии является …
Решение:
Из приведенных
функций только в функции параметры
имеют степень 1, а объясняющая переменнаях
имеет степень, отличную от 1.
4. В модели вида количество объясняющих переменных равно …
3
4
2
1
Решение:
Эконометрическая
модель уравнения регрессии может быть
представлена линейным уравнением
множественной регрессии в виде выражения
,
гдеy
– зависимая переменная; xj
– объясняющая независимая переменная
(j =
1,…, k;
k
– количество независимых переменных);
a,
bj
– параметры (a
– свободный член уравнения, bj
– коэффициент регрессии);
–
случайные факторы. Независимые переменныеxj
называются
также факторами, объясняющими переменными.
На количество объясняющих переменных
в линейном уравнении указывает также
количество коэффициентов регрессии
bj.
Поэтому количество объясняющих переменных
в модели равно 3.
5. При идентификации модели множественной регрессии количество оцениваемых параметров равно …
5
4
6
3
Решение:
При оценке модели
множественной регрессии
рассчитываются
следующие параметры: свободный членa
и четыре параметра при независимых
переменных х.
Итого 5 параметров.
Тема 2: Отбор факторов, включаемых в модель множественной регрессии
1. В модели множественной регрессии определитель матрицы парных коэффициентов корреляции между факторами,иблизок к единице. Это означает, что факторы,и…
независимы
мультиколлинеарны
количественно
измеримы
значимы
Решение:
Для оценки
мультиколлинеарности факторов может
использоваться определитель матрицы
парных коэффициентов корреляции между
факторами. Если факторы не коррелированы
между собой, то матрица парных коэффициентов
корреляции между факторами была бы
единичной. Поскольку все недиагональные
элементы
были
бы равны нулю.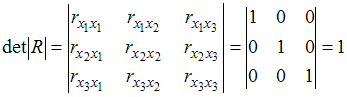
поскольку=
=
и
=
=
=0.
Если
между факторами существует полная
линейная зависимость и все коэффициенты
парной корреляции равны единице, то
определитель такой матрицы равен
нулю.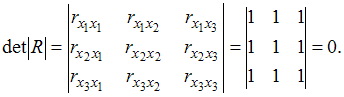
ближе к нулю определитель матрицы
межфакторной корреляции, тем сильнее
мультиколлинеарность факторов и
ненадежнее результаты множественной
регрессии. И, наоборот, чем ближе к
единице определитель матрицы межфакторной
корреляции, тем меньше мультиколлинеарность
факторов.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Подборка по базе: Задание Тема 10.docx, Задание к темам 6-7.docx, 3D моделирование.pdf, Реферат ПСО. Тема 27 Дударева Е.Г. ПСО-19С.docx, Выбор модели информационной системы.pptx, 02 Самостоятельная работа тема 2.docx, 01 Самостоятельная работа тема 1.docx, ОВУ тема1 занятие 1-2.docx, Итоговое задание математическое моделирование.docx, Практическая работа по дисциплине экономическое моделирование.do
Тема 1: Спецификация эконометрической модели
1. Ошибки спецификации эконометрической модели имеют место вследствие …
неправильного выбора математической функции или недоучета в уравнении регрессии какого-то существенного фактора
2. Для регрессионной модели вида необходим минимальный объем наблюдений, содержащий _____ объектов наблюдения.
15
3. Нелинейным по объясняющим переменным, но линейным по параметрам уравнением регрессии является …
4. В модели вида количество объясняющих переменных равно …
3
5. При идентификации модели множественной регрессии количество оцениваемых параметров равно …
5
Тема 2: Отбор факторов, включаемых в модель множественной регрессии
1. В модели множественной регрессии определитель матрицы парных коэффициентов корреляции между факторами , и близок к единице. Это означает, что факторы , и …
Мультиколлинеарны
2. При моделировании линейного уравнения множественной регрессии вида необходимо, чтобы выполнялось требование отсутствия взаимосвязи между …
x1 и x2
3. Дана матрица парных коэффициентов корреляции.
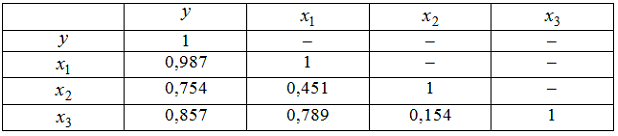
и
4. В модели множественной регрессии определитель матрицы парных коэффициентов корреляции между факторами , и близок к нулю. Это означает, что факторы , и …
мультиколлинеарны
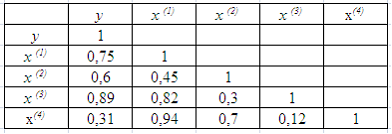
5. Для эконометрической модели линейного уравнения множественной регрессии вида построена матрица парных коэффициентов линейной корреляции (y – зависимая переменная; х(1), х(2), х(3), x(4)– независимые переменные):
Коллинеарными (тесно связанными) независимыми (объясняющими) переменными не являются …
x(2) и x(3)
Тема 3: Фиктивные переменные
1. Дана таблица исходных данных для построения эконометрической регрессионной модели:
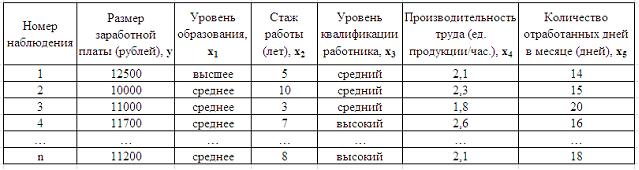
стаж работы
производительность труда
2. При исследовании зависимости потребления мяса от уровня дохода и пола потребителя можно рекомендовать …
использовать фиктивную переменную – пол потребителя
разделить совокупность на две: для потребителей женского пола и для потребителей мужского пола
3. Изучается зависимость цены квартиры (у) от ее жилой площади (х) и типа дома. В модель включены фиктивные переменные, отражающие рассматриваемые типы домов: монолитный, панельный, кирпичный. Получено уравнение регрессии: ,
где ,
Частными уравнениями регрессии для кирпичного и монолитного являются …
для типа дома кирпичный
для типа дома монолитный
для типа дома кирпичный
для типа дома монолитный
Решение:
Требуется узнать частное уравнение регрессии для кирпичного и монолитного домов. Для кирпичного дома значения фиктивных переменных следующие , . Уравнение примет вид: или
для типа дома кирпичный.
Для монолитного дома значения фиктивных переменных следующие , . Уравнение примет вид
или для типа дома монолитный.
4. При анализе промышленных предприятий в трех регионах (Республика Марий Эл, Республика Чувашия, Республика Татарстан) были построены три частных уравнения регрессии:
для Республики Марий Эл;
для Республики Чувашия;
для Республики Татарстан.
Укажите вид фиктивных переменных и уравнение с фиктивными переменными, обобщающее три частных уравнения регрессии.
Итоговое уравнение будет
5. В эконометрике фиктивной переменной принято считать …
переменную, принимающую значения 0 и 1
Тема 4: Линейное уравнение множественной регрессии
1. Для регрессионной модели зависимости среднедушевого денежного дохода населения (руб., у) от объема валового регионального продукта (тыс. р., х1) и уровня безработицы в субъекте (%, х2) получено уравнение . Величина коэффициента регрессии при переменной х2 свидетельствует о том, что при изменении уровня безработицы на 1% среднедушевой денежный доход ______ рубля при неизменной величине валового регионального продукта.
изменится на (-1,67)
2. В уравнении линейной множественной регрессии: , где – стоимость основных фондов (тыс. руб.); – численность занятых (тыс. чел.); y – объем промышленного производства (тыс. руб.) параметр при переменной х1, равный 10,8, означает, что при увеличении объема основных фондов на _____ объем промышленного производства _____ при постоянной численности занятых.
на 1 тыс. руб. … увеличится на 10,8 тыс. руб.
3. Известно, что доля остаточной дисперсии зависимой переменной в ее общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет …
0,8
4. Построена эконометрическая модель для зависимости прибыли от реализации единицы продукции (руб., у) от величины оборотных средств предприятия (тыс. р., х1): . Следовательно, средний размер прибыли от реализации, не зависящий от объема оборотных средств предприятия, составляет _____ рубля.
10,75
5. F-статистика рассчитывается как отношение ______ дисперсии к ________ дисперсии, рассчитанных на одну степень свободы.
факторной … остаточной
Тема 5: Оценка параметров линейных уравнений регрессии
1. Для эконометрической модели уравнения регрессии ошибка модели определяется как ______ между фактическим значением зависимой переменной и ее расчетным значением.
разность
2. Величина называется …
случайной составляющей
3. В эконометрической модели уравнения регрессии величина отклонения фактического значения зависимой переменной от ее расчетного значения характеризует …
ошибку модели
4. Известно, что доля объясненной дисперсии в общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет …
0,2
5. При методе наименьших квадратов параметры уравнения парной линейной регрессии определяются из условия ______ остатков .
минимизации суммы квадратов
Тема 6: Предпосылки МНК, методы их проверки
1. Для обнаружения автокорреляции в остатках используется …
статистика Дарбина – Уотсона
тест Уайта
критерий Гольдфельда – Квандта
2. Известно, что коэффициент автокорреляции остатков первого порядка равен –0,3. Также даны критические значения статистики Дарбина – Уотсона для заданного количества параметров при неизвестном и количестве наблюдений , . По данным характеристикам можно сделать вывод о том, что …
автокорреляция остатков отсутствует
3. Значение критерия Дарбина – Уотсона можно приблизительно рассчитать по формуле , где – значение коэффициента автокорреляции остатков модели. Минимальная величина значения будет наблюдаться при ________ автокорреляции остатков.
положительной
4. Из перечисленного условием выполнения предпосылок метода наименьших квадратов не является ____ остатков.
Гетероскедатичность
5. Значение критерия Дарбина – Уотсона можно приблизительно рассчитать по формуле , где – значение коэффициента автокорреляции остатков модели. Максимальная величина значения будет наблюдаться при ________ автокорреляции остатков.
отрицательной
Тема 7: Свойства оценок параметров эконометрической модели, получаемых при помощи МНК
1. Пусть – оценка параметра регрессионной модели, полученная с помощью метода наименьших квадратов; – математическое ожидание оценки . В том случае если , то оценка обладает свойством …
несмещенности
2. Из несмещенности оценки параметра следует, что среднее значение остатков равно …
0
3. Несмещенность оценок параметров регрессии означает, что …
математическое ожидание остатков равно нулю
4. Если оценка параметра является смещенной, то нарушается предпосылка метода наименьших квадратов о _________ остатков.
нулевой средней величине
5. Состоятельность оценок параметров регрессии означает, что …
точность оценок выборки увеличивается с увеличением объема выборки
Тема 8: Обобщенный метод наименьших квадратов (ОМНК)
1. В случае нарушений предпосылок метода наименьших квадратов применяют обобщенный метод наименьших квадратов, который используется для оценки параметров линейных регрессионных моделей с __________ остатками.
автокоррелированными и/или гетероскедастичными
2. При нарушении гомоскедастичности остатков и наличии автокорреляции остатков рекомендуется применять _____________ метод наименьших квадратов.
обобщенный
3. Пусть y – издержки производства, – объем продукции, – основные производственные фонды, – численность работников. Известно, что в уравнении дисперсии остатков пропорциональны квадрату численности работников
.После применения обобщенного метода наименьших квадратов новая модель приняла вид
. Тогда параметр в новом уравнении характеризует среднее изменение затрат …
на работника при увеличении производительности труда на единицу при неизменном уровне фондовооруженности труда
4. Обобщенный метод наименьших квадратов не может применяться для оценки параметров линейных регрессионных моделей в случае, если …
средняя величина остатков не равна нулю
5. Пусть y – издержки производства, – объем продукции, – основные производственные фонды, – численность работников. Известно, что в уравнении дисперсии остатков пропорциональны квадрату объема продукции
.Применим обобщенный метод наименьших квадратов, поделив обе части уравнения на После применения обобщенного метода наименьших квадратов новая модель приняла вид
. Тогда параметр в новом уравнении характеризует среднее изменение затрат на единицу продукции при увеличении …
фондоемкости продукции при неизменном уровне трудоемкости продукции
Тема 9: Оценка тесноты связи
1. Для эконометрической модели вида показателем тесноты связи между переменными и является парный коэффициент линейной …
Регрессии
2. Самым коротким интервалом изменения коэффициента корреляции для уравнения парной линейной регрессии является …
[–1; 0]
3. Самым коротким интервалом изменения показателя множественной корреляции для уравнения множественной линейной регрессии , если известны парные коэффициенты корреляции , является интервал …
[0,7; 1]
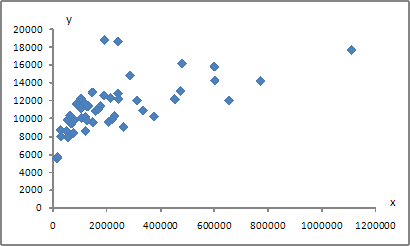
4. Для регрессионной модели вида получена диаграмма
Такое графическое отображение называется …
полем корреляции
Тема 10: Оценка качества подбора уравнения
1. Известно, что доля остаточной регрессии в общей составила 0,19. Тогда значение коэффициента корреляции равно …
0,9
2. Известно, что общая сумма квадратов отклонений , а остаточная сумма квадратов отклонений,
. Тогда значение коэффициента детерминации равно …
0,8
3. Для регрессионной модели вида , где рассчитаны дисперсии:
;
;
. Тогда величина
характеризует долю …
остаточной дисперсии
4. Если общая сумма квадратов отклонений , и остаточная сумма квадратов отклонений
, то сумма квадратов отклонений, объясненная регрессией, равна …
90
Главная / Ответы на новые тесты / Эконометрика / Страница 2
Упражнение 41830:
Номер
Левая часть системы эконометрических уравнений представлена совокупностью _________ переменных.
Ответ:
зависимых
эндогенных
экзогенных
независимых
Упражнение 41831:
Номер
Линия регрессии _______ через точку ( , ) :
Ответ:
_ __
x y
1) может пройти
2) всегда проходит
3) несколько раз проходит
4) никогда не проходит
5) может пройти или не пройти
Упражнение 41832:
Номер
МНК автоматически дает ___________ для данной выборки значение коэффициента де-
Ответ:
терминации R2:
1) минимальное
2) максимальное
3) среднее
4) средневзвешенное
5) случайное
Упражнение 41833:
Номер
Множественный регрессионный анализ является ________ парного регрессионного анализа:
Ответ:
1) развитием
2) противоположностью
3) частным случаем
4) подобием
5) эквивалентностью
Упражнение 41834:
Номер
Наблюдение зависимой переменной регрессии в предшествующий момент, используемое как объясняющая переменная, называется:
Ответ:
1) временной
2) замещающей
3) лаговой
4) лишней
5) сезонной
Упражнение 41835:
Номер
Наиболее частая причина положительной автокорреляции заключается в положительной направленности воздействия ________ переменных:
Ответ:
1) не включенных в уравнение
2) сезонных
3) фиктивных
4) лишних
5) циклических
Упражнение 41836:
Номер
Наиболее частая причина положительной автокорреляции заключается в постоянной направленности воздействия _____________ переменных:
Ответ:
1) не включенных в уравнение
2) лишних
3) сезонных
4) фиктивных
5) циклических
Упражнение 41837:
Номер
Наилучший способ устранения автокорреляции – установление ответственного за нее
Ответ:
фактора и включение соответствующей ___________ переменной в регрессию:
1) фиктивной
2) объясняющей
3) сезонной
4) зависимой
5) циклической
Упражнение 41838:
Номер
Обобщенный метод наименьших квадратов не может применяться для оценки параметров линейных регрессионных моделей в случае, если ...
Ответ:
средняя величина остатков не равна нулю
остатки гетероскедастичны
остатки автокоррелированны
дисперсия остатков не является постоянной величиной
Упражнение 41839:
Номер
Определение отдельного вклада каждой из независимых переменных в объясненную
Ответ:
дисперсию в случае их коррелированности является ___________ задачей:
1) достаточно простой
2) невыполнимой
3) достаточно сложной
4) первостепенной
5) выполнимой
Упражнение 41840:
Номер
Оценка параметра для модели множественной регрессии в случае двух независимых пе-
Ответ:
ременных вычисляется по формуле: а =
1) 1 1 2 2 b x ? b x
2) 1 1 2 2 y + b x + b x
3) ( ) 1 1 2 2 y + b x ? b x
4) 1 1 2 2 y ? b x ? b x
5) 1 1 2 2 y ?b x + b x
Упражнение 41841:
Номер
Ошибки спецификации эконометрической модели имеют место вследствие ...
Ответ:
неправильного выбора математической функции или недоучета в уравнении регрессии какого-то существенного фактора
недостоверности или недостаточности исходной информации
неоднородности данных в исходной статистической совокупности
недостаточного количества данных
Упражнение 41842:
Номер
Параметры множественной регрессии ?1 , ?2 ,...?м показывают _________ соответствующих экономических факторов:
Ответ:
1) степень влияния
2) случайность
3) уровень независимости
4) непостоянство
5) цикличность
Упражнение 41843:
Номер
Положительная автокорреляция –ситуация, когда случайный член регрессии в сле-
Ответ:
дующем наблюдении ожидается:
1) противоположного знака по сравнению с настоящим наблюдением
2) того же знака, что и в первом наблюдении
3) того же знака, что и в настоящем наблюдении
4) противоположного знака по сравнению с первым наблюдением
5) равным 0
Упражнение 41844:
Номер
При автокорреляции оценка коэффициентов регрессии становится:
Ответ:
1) смещенной
2) невозможной
3) неэффективной
4) равной 0
5) равной максимальному значению
Упражнение 41845:
Номер
При добавлении еще одной переменной в уравнение регрессии коэффициент детерминации:
Ответ:
1) остается неизменным
2) уменьшается
3) не уменьшается
4) не увеличивается
5) увеличивается
Упражнение 41846:
Номер
При исследовании зависимости потребления мяса от уровня дохода и пола потребителя можно рекомендовать ...
Ответ:
использовать фиктивную переменную – пол потребителя
разделить совокупность на две: для потребителей женского пола и для потребителей мужского пола
использовать фиктивную переменную – уровень дохода
исключить из рассмотрения пол потребителя, так как данный фактор нельзя измерить количественным образом
Упражнение 41847:
Номер
При нарушении гомоскедастичности остатков и наличии автокорреляции остатков рекомендуется применять _____________ метод наименьших квадратов.
Ответ:
обобщенный
косвенный
двухшаговый
трехшаговый
Упражнение 41848:
Номер
При отрицательной автокорреляции DW:
Ответ:
1) = 0
2) < 2
3) > 2
4) > 1
5) = 1
Упражнение 41849:
Номер
При проверке счетного правила выяснилось, что для всех уравнений системы одновременных уравнений выполняется необходимое условие идентификации и все уравнения по счетному правилу сверхидентифицируемы. Чтобы получить структурные коэффициенты системы, действия нужно выполнить в следующем порядке:
Ответ:
для каждого уравнения проверить условие неравенства нулю определителя матрицы коэффициентов, присутствующих в других уравнениях, но отсутствующих в данном уравнении
преобразовать структурную форму модели в приведенную форму модели
для каждого уравнения приведенной формы модели обычным методом наименьших квадратов оценить приведенные коэффициенты
на основе коэффициентов приведенной формы модели получить теоретические значения эндогенных переменных, содержащихся в правой части сверхидентифицированных уравнений
применить обычный метод наименьших квадратов, подставив вместо фактических значений эндогенных переменных, стоящих в правой части уравнения, рассчитанные теоретические значения, и получить структурные коэффициенты модели
Упражнение 41850:
Номер
При проверке счетного правила выяснилось, что для всех уравнений системы одновременных уравнений выполняется необходимое условие идентификации и все уравнения по счетному правилу точно идентифицируемы. Чтобы получить структурные коэффициенты системы, действия нужно выполнить в следующем порядке:
Ответ:
для каждого уравнения проверить условие неравенства нулю определителя матрицы коэффициентов, присутствующих в других уравнениях, но отсутствующих в данном уравнении
преобразовать структурную форму модели в приведенную форму модели
для каждого уравнения приведенной формы модели обычным методом наименьших квадратов оценить приведенные коэффициенты
коэффициенты приведенной формы модели преобразовать в параметры структурной модели
Упражнение 41851:
Номер
Процесс выбора необходимых переменных для регрессии переменных и отбрасывание
Ответ:
лишних переменных называется:
1) унификацией переменных
2) моделированием
3) спецификацией переменных
4) прогнозированием
5) подгонкой
Упражнение 41852:
Номер
Система независимых эконометрических уравнений может быть идентифицирована с помощью обычного метода наименьших квадратов. Определите последовательность этапов алгоритма оценки параметров для такой модели.
Ответ:
оценка возможности идентификации модели как системы независимых уравнений
разделение системы независимых уравнений на отдельные уравнения регрессии
построение общего вида системы нормальных уравнений для каждого уравнения системы и расчет необходимых значений сумм
решение системы нормальных уравнений для каждого уравнения системы
подстановка найденных значений оценок параметров в уравнения системы
Упражнение 41853:
Номер
Системой эконометрических уравнений не является система линейных _____ уравнений.
Ответ:
нормальных
стандартизованных
рекурсивных
одновременных
Упражнение 41854:
Номер
Совокупность значений экономического показателя за несколько последовательных моментов (периодов) времени называется ...
Ответ:
временным рядом
тенденцией
коррелограммой
автокорреляционной функцией
Упражнение 41855:
Номер
Стандартные отклонения коэффициентов регрессии обратно пропорциональны величи-
Ответ:
не _________, где n – число наблюдений:
1) n
2) n2
3) n3
4) n
5) n4
Упражнение 41856:
Номер
Стандартные ошибки, вычисленные при гетероскедастичности:
Ответ:
1) завышены по сравнению с истинными значениями
2) занижены по сравнению с истинными значениями
3) соответствуют истинным значениям
4) не имеют математического смысла
5) являются случайными
Упражнение 41857:
Номер
Строгая линейная зависимость между переменными – ситуация, когда ________ двух
Ответ:
переменных равна 1 или -1:
1) выборочная корреляция
2) разность
3) сумма
4) теоретическая корреляция
5) произведение
Упражнение 41858:
Номер
Сумма квадратов отклонений величины y от своего выборочного значения ? _____ сумма квадратов отклонений:
Ответ:
__
y
1) объясняющая
2) случайная
3) необъясняющая
4) общая
5) результирующая
Упражнение 41859:
Номер
Тест Фишера является:
Ответ:
1) двусторонним
2) односторонним
3) многосторонним
4) многокритериальным
5) трехшаговым
Упражнение 41860:
Номер
Уровень временного ряда (yt) формируется под воздействием различных факторов – компонент: Т (тенденция), S (циклические и/или сезонные колебания), Е (случайные факторы). Для аддитивной модели временного ряда для уровня y3 получено уравнение тренда T = 3,14 + 2,07t. Известны значения компонент: S3 = 1,6; E3 = –0,3. Тогда значение уровня временного ряда y3 будет равно ...
Ответ:
10,65
9,35
1,3
6,51
Упражнение 41861:
Номер
Уровень временного ряда (yt) формируется под воздействием различных факторов – компонент: Т (тенденция), S (циклические и/или сезонные колебания), Е (случайные факторы). Для мультипликативной модели временного ряда, содержащего периодические колебания в 4 момента, получены значения сезонных компонент: S1 = 2,087; S2 = 0,632; S3 = 0,931; S4 = 3,256. Известны значения компонент: T5 = 20,6 и E5 = 0,4. Рассчитайте значение уровня временного ряда y5.
Ответ:
17,2
23,1
33
0,83
Упражнение 41862:
Номер
Условие гетероскедастичности означает, что вероятность того, что случайный член при-
Ответ:
мет какое-либо конкретное значение ________ наблюдений:
1) зависит от числа
2) зависит от времени проведения
3) зависит от номера
4) одинакова для всех
5) не зависит от времени проведения
Упражнение 41863:
Номер
Условие гомоскедастичности означает, что вероятность того, что случайный член при-
Ответ:
мет какое-либо конкретное значение _________ наблюдений:
1) зависит от времени проведения
2) одинакова для всех
3) зависит от номера
4) зависит от числа
5) от характера
Упражнение 41864:
Номер
Фиктивная переменная – переменная, принимающая в каждом наблюдении:
Ответ:
1) ряд значений от 0 до 1
2) только отрицательные значения
3) только два значения 0 или 1
4) только положительные значения
5) случайные
Упражнение 41865:
Номер
Фиктивная переменная взаимодействия – фиктивная переменная, предназначенная для
Ответ:
установления влияния на регрессию __________событий:
1) одновременного наступления нескольких независимых
2) степени взаимосвязи возможных
3) наступления одного из нескольких взаимосвязанных
4) наступления одного из нескольких независимых
5) циклических
Упражнение 41866:
Номер
Фиктивная переменная взаимодействия – это __________ фиктивных переменных:
Ответ:
1) произведение
2) среднее
3) разность
4) сумма
5) отношение
Упражнение 41867:
Номер
Фиктивные переменные включаются в модель множественной регрессии, если необходимо установить влияние каких-либо ___________ факторов:
Ответ:
1) непрерывных
2) дискретных
3) трудноизмеримых
4) случайных
5) циклических
Упражнение 41868:
Номер
Чем больше число наблюдений, тем __________ зона неопределенности для критерия Дарбина-Уотсона:
Ответ:
1) левее расположена
2) уже
3) шире
4) правее расположена
5) неизменна
Упражнение 41869:
Номер
Число степеней свободы для уравнения m-мерной регрессии при достаточном числе
Ответ:
наблюдений n составляет:
1) n/m
2) n-m
3) n-m+1
4) n-m-1
5) m-1
Упражнение 41870:
Номер
Число степеней свободы для уравнения множественной (m-мерной) регрессии при достаточном числе наблюдений n составляет:
Ответ:
1) n-m-1
2) n-m+1
3) n-m
4)m/n
5) n+m+1
Тема 2: Отбор факторов, включаемых в модель множественной регрессии
Тема 1: Спецификация эконометрической модели
1. Ошибки спецификации эконометрической модели имеют место вследствие …
неправильного выбора математической функции или недоучета в уравнении регрессии какого-то существенного фактора
недостоверности или недостаточности исходной информации
неоднородности данных в исходной статистической совокупности
недостаточного количества данных
Решение:
Спецификацией модели называется отбор факторов, включаемых в модель, и выбор математической функции для 

2. Для регрессионной модели вида 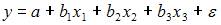
Решение:
Считается, на каждый оцениваемый коэффициент регрессии необходимо не менее 5–7 объектов статистических наблюдений. Так как представленная модель содержит 3 независимые переменные, то на каждый из параметров регрессии при независимой переменной необходимо по 5–7 наблюдений, то есть в совокупности не менее 15–21 наблюдения. Берем нижнюю границу интервала, тогда правильный вариант ответа – «15».
3. Нелинейным по объясняющим переменным, но линейным по параметрам уравнением регрессии является …
Решение:
Из приведенных функций только в функции 
4. В модели вида 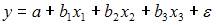
Решение:
Эконометрическая модель уравнения регрессии может быть представлена линейным уравнением множественной регрессии в виде выражения 

5. При идентификации модели множественной регрессии 
Решение:
При оценке модели множественной регрессии 
Тема 2: Отбор факторов, включаемых в модель множественной регрессии
1. В модели множественной регрессии 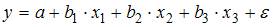






Решение:
Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами. Если факторы не коррелированы между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной. Поскольку все недиагональные элементы 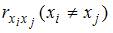

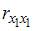
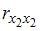
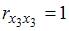
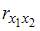
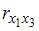
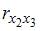
Если между факторами существует полная линейная зависимость и все коэффициенты парной корреляции равны единице, то определитель такой матрицы равен нулю.
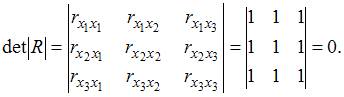
Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.
2. При моделировании линейного уравнения множественной регрессии вида 
Решение:
Эконометрическая модель уравнения регрессии может быть представлена линейным уравнением множественной регрессии в виде выражения 

Линейная множественная регрессия
Тесты по эконометрике
Введение
1. Эконометрическая модель имеет вид
2. Установите соответствие
| а) регрессионная модель | 1) x-1=0, x=0x-1, x>0 |
| b) система одновременных уравнений | 2) R=a1+b11M+b12Y+ε1,Y=a2+b21R+ε2, |
| c) модель временного ряда | 1. 3) y=a+b1x1+b2x2+ε |
| 4) yt=Tt+St+Et |
3. Регрессия – это
a. зависимость значений результативной переменной от значений объясняющих переменных (факторов)
b. правило, согласно которому каждому значению одной переменной ставится в соответствие единственное значение другой переменной
c. правило, согласно которому каждому значению независимой переменной ставится в соответствие значение зависимой переменной
d. зависимость среднего значения результативной переменной от значений объясняющих переменных (факторов)
4. Метод наименьших квадратов …
a. Позволяет получить оценки параметров линейной регрессии, исходя из условия i=1nyi-yi2→min
b. Позволяет получить оценки параметров регрессии, исходя из условия ln(i=1nf(yi,)→max
c. Позволяет проверить статистическую значимость параметров регрессии
d. Позволяет получить оценки параметров нелинейной регрессии, исходя из условия i=1ny-yi2→min
Линейная множественная регрессия
5. Уравнение линейной множественной регрессии
6. Для линейного уравнения множественной регрессии установите соответствие
| 5. а) Факторные переменные | 6. 1) y |
| 7. b) Результативная переменная | 8. 2) a |
| 9. c) Параметры | 10. 3) a, ε |
| 11. d) Случайная компонента | 12. 4) x1, x2 |
| 13. | 14. 5) ε |
| 15. | 16. 6) a, b1, b2 |
17. Ответ: a-4, b-1, c-6, d-5
7. Проблема спецификации регрессионной модели включает в себя
a. Отбор факторов, включаемых в уравнение регрессии
b. Оценка параметров уравнения регрессии
c. Оценка надежности результатов регрессионного анализа
d. Выбор вида уравнения регрессии
19. Требования к факторам, включаемым в модель линейной множественной регрессии…
a. Число факторов должно быть в 6 раз меньше объема совокупности
b. Факторы должны представлять временные ряды
c. Факторы должны иметь одинаковую размерность
d. Между факторами не должно быть высокой корреляции
21. Верные утверждения относительно мультиколлинеарности факторов
e. В модель линейной множественной регрессии рекомендуется включать мультиколлинеарные факторы
f. Мультиколлинеарность факторов приводит к снижению надежности оценок параметров уравнения регрессии
g. Мультиколинеарность факторов проявляется в наличии парных коэффициентов межфакторной корреляции со значениями, большими 0,7
h. Мультиколинеарность факторов проявляется в наличии парных коэффициентов межфакторной корреляции со значениями, меньшими 0,3
23. Верные утверждения о включении в уравнение линейной множественной регрессии факторов
i. Включение фактора в модель приводит к заметному возрастанию коэффициента множественной детерминации
j. Коэффициент парной корреляции для фактора и результативной переменной меньше 0,3
k. Значение t-критерия Стьюдента для коэффициента регрессии при факторе меньше табличного значения
l. Фактор должен объяснять поведение изучаемого показателя согласно принятым положениям экономической теории
25. При построении модели множественной регрессии методом пошагового включения переменных на первом этапе рассматривается модель с …
m. Одной объясняющей переменной, которая имеет с зависимой переменной наименьший коэффициент корреляции
n. Одной объясняющей переменной, которая имеет с зависимой переменной наибольший коэффициент корреляции
o. Несколькими объясняющими переменными, которые имеют с зависимой переменной коэффициенты корреляции по модулю больше 0,5
p. Полным перечнем объясняющих переменных
8. Параметры при факторах в линейной множественной регрессии
y=a+b1x1+b2x2+…+bpxp характеризуют
a. Долю дисперсии результативной переменной, объясненную регрессией в его общей дисперсии
b. Тесноту связи между результативной переменной и соответствующим фактором, при устранении влияния других факторов, включенных в модель
c. Среднее изменение результативной переменной с изменением соответствующего фактора на единицу, при неизменном значении других факторов, закрепленных на среднем уровне
d. На сколько процентов в среднем изменяется результативная переменная с изменением соответствующего фактора на 1%
28. Стандартизация переменных проводится по формуле
9. Уравнение множественной регрессии в стандартизованном масштабе имеет вид ty=20+0,9tx1+0,5tx2+ε. На результативный признак оказывает большое влияние:
x. нельзя сделать вывод
10. Уравнение множественной регрессии в естественной форме имеет вид
y=20+0,7×1+0,5×2+ε. На результативный признак оказывает большое влияние:
bb. нельзя сделать вывод
30. К свойствам уравнения регрессии в стандартизированном виде относятся …
cc. Коэффициенты регрессии при объясняющих переменных равны между собой
dd. Постоянный параметр (свободный член уравнения) регрессии отсутствует
ee. Стандартизированные коэффициенты регрессии несравнимы между собой
ff. Входящие в состав уравнения переменные являются безразмерными
32. Тесноту совместного влияния факторов на результат в уравнении линейной множественной регрессии оценивает
gg. Коэффициент парной корреляции
hh. Коэффициент частной корреляции
ii. Коэффициент множественной корреляции
jj. Коэффициент множественной детерминации
34. Установите соответствие
| 35. а) общая сумма квадратов отклонений TSS | 36. 1) y-y2 |
| 37. b) регрессионная сумма квадратов отклонений RSS | 38. 2) y-x2 |
| 39. c) остаточная сумма квадратов отклонений ЕSS | 40. 3) y-y2 |
| 41. | 42. 4) y-y2 |
43. Коэффициент множественной корреляции для линейной зависимости можно рассчитать по формуле
mm.
45. Верные утверждения относительно коэффициента множественной корреляции
oo. Чем ближе значение к единице Ryx1…xp, тем теснее связь результативного признака со всеми факторами
pp. Чем ближе значение к нулю Ryx1…xp, тем теснее связь результативного признака со всеми факторами
qq. Ryx1…xp принимает значения из промежутка [0, 1]
rr. Ryx1…xp принимает значения из промежутка [– 1, 1]
47. Коэффициент множественной детерминации характеризует
ss. Тесноту совместного влияния факторов на результат в уравнении линейной множественной регрессии
tt. Тесноту связи между результатом и соответствующим фактором, при устранении влияния других факторов, включенных в модель
uu. Долю дисперсии результативного признака, объясненную регрессией в его общей дисперсии
vv. Среднее изменение результативной переменной с изменением соответствующего фактора на единицу, при неизменном значении других факторов, закрепленных на среднем уровне
49. Для общей (TSS), регрессионной (RSS) и остаточной (ESS) суммы квадратов отклонений и коэффициента детерминации R2 выполняется равенство …
51. Отношение остаточной дисперсии к общей дисперсии равно 0,05. Это означает …
bbb. Коэффициент детерминации R2=0,95
ccc. Коэффициент детерминации R2=0,05
ddd. Разность (1-R2)=0,95, где R2 – коэффициент детерминации
eee. Разность (1-R2)=0,05, где R2 – коэффициент детерминации
53. Для устранения систематической ошибки остаточной дисперсии для оценки качества модели линейной множественной регрессии используется
fff. Коэффициент множественной детерминации
ggg. Коэффициент множественной корреляции
hhh. Скорректированный коэффициент множественной детерминации
iii. Скорректированный коэффициент частной корреляции
55. Оценка статистической значимости уравнения линейной множественной регрессии в целом осуществляется с помощью
jjj. Критерия Стьюдента
kkk. Критерия Фишера
lll. Критерия Дарбина-Уотсона
56. Оценка статистической значимости коэффициентов линейной множественной регрессии осуществляется с помощью
nnn. Критерия Стьюдента
ooo. Критерия Фишера
ppp. Критерия Дарбина-Уотсона
qqq. Критерия Фостера-Стюарта
57. Если коэффициент регрессии является существенным, то для него выполняются условия
rrr. Фактическое значение t-критерия Стьюдента меньше критического
sss. Фактическое значение t-критерия Стьюдента больше критического
ttt. Доверительный интервал проходит через ноль
uuu. Стандартная ошибка не превышает половины значения параметра
59. Если уравнение регрессии является существенным, то фактическое значение F-критерия …
vvv. больше критического
www. меньше критического
xxx. близко к единице
yyy. близко к нулю
61. Предпосылками МНК являются…
zzz. Дисперсия случайных отклонений постоянна для всех наблюдений
aaaa. Дисперсия случайных отклонений не постоянна для всех наблюдений
bbbb. Случайные отклонения коррелируют друг с другом
cccc. Случайные отклонения являются независимыми друг от друга
63. Укажите выводы, которые соответствуют графику зависимости остатков
dddd. Нарушена предпосылка МНК о независимости остатков друг от друга
eeee. Имеет место автокорреляция остатков
ffff. Отсутствует закономерность в поведении остатков
gggg. Отсутствует автокорреляция остатков
66. При выполнении предпосылок метода наименьших квадратов (МНК) остатки уравнения регрессии, как правило, характеризуются…
hhhh. Нулевой средней величиной
jjjj. Случайным характером
kkkk. Высокой степенью автокорреляции
68. К методам обнаружения гетероскедастичности остатков относятся
llll. Критерий Дарбина-Уотсона
mmmm. Тест Голдфелда-Квандта
nnnn. Графический анализ остатков
oooo. Метод наименьших квадратов
70. Фиктивными переменными в уравнении множественной регрессии являются …
pppp. Качественные переменные, преобразованные в количественные
qqqq. Переменные, представляющие простейшие функции от уже включенных в модель переменных
rrrr. Дополнительные количественные переменные, улучшающие решение
ssss. Комбинации из включенных в уравнение регрессии факторов, повышающие адекватность модели
71. Для отражения влияния качественной сопутствующей переменной, имеющей m состояний, обычно включают в модель … фиктивную переменную
Нелинейная регрессия
72. Регрессии, нелинейные по объясняющим переменным, но линейные по оцениваемым параметрам
73. Регрессии, нелинейные по оцениваемым параметрам
74. Укажите верные утверждения по поводу модели
jjjjj. Относится к типу моделей нелинейных по объясняющим переменным, но линейных по оцениваемым параметрам
kkkkk. Относится к типу моделей, нелинейных по оцениваемым параметрам
lllll. Относится к типу линейных моделей
mmmmm. Нельзя привести к линейному виду
nnnnn. Можно привести к линейному виду
76. Укажите верные утверждения по поводу модели
ooooo. Линеаризуется линейную модель множественной регрессии
ppppp. Линеаризуется линейную модель парной регрессии
qqqqq. Относится к классу нелинейных моделей по объясняющим переменным, но линейных по оцениваемым параметрам
rrrrr. Относится к классу линейных моделей
79. Модель y=a∙bx∙ε относится к классу … эконометрических моделей нелинейной регрессии
81. Модель y=a∙xb∙ε относится к классу … эконометрических моделей нелинейной регрессии
83. Модель y=a+bx+cx2+ε относится к классу … эконометрических моделей нелинейной регрессии
85. Было замечено, что при увеличении количества вносимых удобрений урожайность также возрастает, однако, по достижении определенного значения фактора моделируемый показатель начинает убывать. Для исследования данной зависимости можно использовать спецификацию уравнения регрессии…
87. Для получения оценок параметров степенной регрессионной модели y=a∙xb …
iiiiii. Метод наименьших квадратов неприменим
jjjjjj. Требуется подобрать соответствующую подстановку
kkkkkk. Необходимо выполнить логарифмическое преобразование
llllll. Необходимо выполнить тригонометрическое преобразование
89. С помощью метода наименьших квадратов нельзя оценить значения параметров уравнения регрессии …
Уравнение множественной регрессии
Назначение сервиса . С помощью онлайн-калькулятора можно найти следующие показатели:
- уравнение множественной регрессии, матрица парных коэффициентов корреляции, средние коэффициенты эластичности для линейной регрессии;
- множественный коэффициент детерминации, доверительные интервалы для индивидуального и среднего значения результативного признака;
Кроме этого проводится проверка на автокорреляцию остатков и гетероскедастичность.
- Шаг №1
- Шаг №2
- Видеоинструкция
- Оформление Word
Отбор факторов обычно осуществляется в два этапа:
- теоретический анализ взаимосвязи результата и круга факторов, которые оказывают на него существенное влияние;
- количественная оценка взаимосвязи факторов с результатом. При линейной форме связи между признаками данный этап сводится к анализу корреляционной матрицы (матрицы парных линейных коэффициентов корреляции). Научно обоснованное решение задач подобного вида также осуществляется с помощью дисперсионного анализа — однофакторного, если проверяется существенность влияния того или иного фактора на рассматриваемый признак, или многофакторного в случае изучения влияния на него комбинации факторов.
Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:
- Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность.
- Каждый фактор должен быть достаточно тесно связан с результатом (т.е. коэффициент парной линейной корреляции между фактором и результатом должен быть существенным).
- Факторы не должны быть сильно коррелированы друг с другом, тем более находиться в строгой функциональной связи (т.е. они не должны быть интеркоррелированы). Разновидностью интеркоррелированности факторов является мультиколлинеарность — тесная линейная связь между факторами.
Пример . Постройте регрессионную модель с 2-мя объясняющими переменными (множественная регрессия). Определите теоретическое уравнение множественной регрессии. Оцените адекватность построенной модели.
Решение.
К исходной матрице X добавим единичный столбец, получив новую матрицу X
| 1 | 5 | 14.5 |
| 1 | 12 | 18 |
| 1 | 6 | 12 |
| 1 | 7 | 13 |
| 1 | 8 | 14 |
Матрица Y
Транспонируем матрицу X, получаем X T :
| 1 | 1 | 1 | 1 | 1 |
| 5 | 12 | 6 | 7 | 8 |
| 14.5 | 18 | 12 | 13 | 14 |
| Умножаем матрицы, X T X = |
|
В матрице, (X T X) число 5, лежащее на пересечении 1-й строки и 1-го столбца, получено как сумма произведений элементов 1-й строки матрицы X T и 1-го столбца матрицы X
| Умножаем матрицы, X T Y = |
Находим обратную матрицу (X T X) -1
| 13.99 | 0.64 | -1.3 |
| 0.64 | 0.1 | -0.0988 |
| -1.3 | -0.0988 | 0.14 |
Вектор оценок коэффициентов регрессии равен
| (X T X) -1 X T Y = y(x) = |
|
* | = |
Получили оценку уравнения регрессии: Y = 34.66 + 1.97X1-2.45X2
Оценка значимости уравнения множественной регрессии осуществляется путем проверки гипотезы о равенстве нулю коэффициент детерминации рассчитанного по данным генеральной совокупности. Для ее проверки используют F-критерий Фишера.
R 2 = 1 — s 2 e/∑(yi — yср) 2 = 1 — 33.18/77.2 = 0.57
F = R 2 /(1 — R 2 )*(n — m -1)/m = 0.57/(1 — 0.57)*(5-2-1)/2 = 1.33
Табличное значение при степенях свободы k1 = 2 и k2 = n-m-1 = 5 — 2 -1 = 2, Fkp(2;2) = 19
Поскольку фактическое значение F = 1.33 Пример №2 . Приведены данные за 15 лет по темпам прироста заработной платы Y (%), производительности труда X1 (%), а также по уровню инфляции X2 (%).
| Год | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| X1 | 3,5 | 2,8 | 6,3 | 4,5 | 3,1 | 1,5 | 7,6 | 6,7 | 4,2 | 2,7 | 4,5 | 3,5 | 5,0 | 2,3 | 2,8 |
| X2 | 4,5 | 3,0 | 3,1 | 3,8 | 3,8 | 1,1 | 2,3 | 3,6 | 7,5 | 8,0 | 3,9 | 4,7 | 6,1 | 6,9 | 3,5 |
| Y | 9,0 | 6,0 | 8,9 | 9,0 | 7,1 | 3,2 | 6,5 | 9,1 | 14,6 | 11,9 | 9,2 | 8,8 | 12,0 | 12,5 | 5,7 |
Решение. Подготовим данные для вставки из MS Excel (как транспонировать таблицу для сервиса см. Задание №2) .
Включаем в отчет: Проверка общего качества уравнения множественной регрессии (F-статистика. Критерий Фишера, Проверка на наличие автокорреляции),
После нажатия на кнопку Дале получаем готовое решение.
Уравнение регрессии (оценка уравнения регрессии):
Y = 0.2706 + 0.5257X1 + 1.4798X2
Скачать.
Качество построенного уравнения регрессии проверяется с помощью критерия Фишера (п. 6 отчета).
Пример №3 .
В таблице представлены данные о ВВП, объемах потребления и инвестициях некоторых стран.
| ВВП | 16331,97 | 16763,35 | 17492,22 | 18473,83 | 19187,64 | 20066,25 | 21281,78 | 22326,86 | 23125,90 |
| Потребление в текущих ценах | 771,92 | 814,28 | 735,60 | 788,54 | 853,62 | 900,39 | 999,55 | 1076,37 | 1117,51 |
| Инвестиции в текущих ценах | 176,64 | 173,15 | 151,96 | 171,62 | 192,26 | 198,71 | 227,17 | 259,07 | 259,85 |
Решение:
Для проверки полученных расчетов используем инструменты Microsoft Excel «Анализ данных» (см. пример).
Пример №4 . На основе данных, приведенных в Приложении и соответствующих Вашему варианту (таблица 2), требуется:
- Построить уравнение множественной регрессии. При этом признак-результат и один из факторов остаются теми же, что и в первом задании. Выберите дополнительно еще один фактор из приложения 1 (границы наблюдения должны совпадать с границами наблюдения признака-результата, соответствующего Вашему варианту). При выборе фактора нужно руководствоваться его экономическим содержанием или другими подходами. Пояснить смысл параметров уравнения.
- Рассчитать частные коэффициенты эластичности. Сделать вывод.
- Определить стандартизованные коэффициенты регрессии (b-коэффициенты). Сделать вывод.
- Определить парные и частные коэффициенты корреляции, а также множественный коэффициент корреляции; сделать выводы.
- Оценить значимость параметров уравнения регрессии с помощью t-критерия Стьюдента, а также значимость уравнения регрессии в целом с помощью общего F-критерия Фишера. Предложить окончательную модель (уравнение регрессии). Сделать выводы.
Решение. Определим вектор оценок коэффициентов регрессии. Согласно методу наименьших квадратов, вектор получается из выражения:
s = (X T X) -1 X T Y
Матрица X
| 1 | 3.9 | 10 |
| 1 | 3.9 | 14 |
| 1 | 3.7 | 15 |
| 1 | 4 | 16 |
| 1 | 3.8 | 17 |
| 1 | 4.8 | 19 |
| 1 | 5.4 | 19 |
| 1 | 4.4 | 20 |
| 1 | 5.3 | 20 |
| 1 | 6.8 | 20 |
| 1 | 6 | 21 |
| 1 | 6.4 | 22 |
| 1 | 6.8 | 22 |
| 1 | 7.2 | 25 |
| 1 | 8 | 28 |
| 1 | 8.2 | 29 |
| 1 | 8.1 | 30 |
| 1 | 8.5 | 31 |
| 1 | 9.6 | 32 |
| 1 | 9 | 36 |
Матрица Y
| 7 |
| 7 |
| 7 |
| 7 |
| 7 |
| 7 |
| 8 |
| 8 |
| 8 |
| 10 |
| 9 |
| 11 |
| 9 |
| 11 |
| 12 |
| 12 |
| 12 |
| 12 |
| 14 |
| 14 |
Матрица X T
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 3.9 | 3.9 | 3.7 | 4 | 3.8 | 4.8 | 5.4 | 4.4 | 5.3 | 6.8 | 6 | 6.4 | 6.8 | 7.2 | 8 | 8.2 | 8.1 | 8.5 | 9.6 | 9 |
| 10 | 14 | 15 | 16 | 17 | 19 | 19 | 20 | 20 | 20 | 21 | 22 | 22 | 25 | 28 | 29 | 30 | 31 | 32 | 36 |
Умножаем матрицы, (X T X)
Умножаем матрицы, (X T Y)
Находим определитель det(X T X) T = 139940.08
Находим обратную матрицу (X T X) -1
Уравнение регрессии
Y = 1.8353 + 0.9459X 1 + 0.0856X 2
Для несмещенной оценки дисперсии проделаем следующие вычисления:
Несмещенная ошибка e = Y — X*s
| 0.62 |
| 0.28 |
| 0.38 |
| 0.01 |
| 0.11 |
| -1 |
| -0.57 |
| 0.29 |
| -0.56 |
| 0.02 |
| -0.31 |
| 1.23 |
| -1.15 |
| 0.21 |
| 0.2 |
| -0.07 |
| -0.07 |
| -0.53 |
| 0.34 |
| 0.57 |
se 2 = (Y — X*s) T (Y — X*s)
Несмещенная оценка дисперсии равна
Оценка среднеквадратичного отклонения равна
Найдем оценку ковариационной матрицы вектора k = σ*(X T X) -1
| k(x) = 0.36 |
|
= |
|
Дисперсии параметров модели определяются соотношением S 2 i = Kii, т.е. это элементы, лежащие на главной диагонали
С целью расширения возможностей содержательного анализа модели регрессии используются частные коэффициенты эластичности, которые определяются по формуле
Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции (от 0 до 1)
Связь между признаком Y факторами X сильная
Частные коэффициенты (или индексы) корреляции, измеряющие влияние на у фактора хi при неизменном уровне других факторов определяются по стандартной формуле линейного коэффициента корреляции — последовательно берутся пары yx1,yx2. , x1x2, x1x3.. и так далее и для каждой пары находится коэффициент корреляции
Коэффициент детерминации
R 2 = 0.97 2 = 0.95, т.е. в 95% случаев изменения х приводят к изменению y. Другими словами — точность подбора уравнения регрессии — высокая
Значимость коэффициента корреляции
По таблице Стьюдента находим Tтабл: Tтабл (n-m-1;a) = (17;0.05) = 1.74
Поскольку Tнабл Fkp, то коэффициент детерминации статистически значим и уравнение регрессии статистически надежно
Построение парной регрессионной модели
Рекомендации к решению контрольной работы.
Статистические данные по экономике можно получить на странице Россия в цифрах.
После определения зависимой и объясняющих переменных можно воспользоваться сервисом Множественная регрессия. Регрессионную модель с 2-мя объясняющими переменными можно построить используя матричный метод нахождения параметров уравнения регрессии или метод Крамера для нахождения параметров уравнения регрессии.
Пример №3 . Исследуется зависимость размера дивидендов y акций группы компаний от доходности акций x1, дохода компании x2 и объема инвестиций в расширение и модернизацию производства x3. Исходные данные представлены выборкой объема n=50.
Тема I. Парная линейная регрессия
Постройте парные линейные регрессии — зависимости признака y от факторов x1, x2, x3 взятых по отдельности. Для каждой объясняющей переменной:
- Постройте диаграмму рассеяния (поле корреляции). При построении выберите тип диаграммы «Точечная» (без отрезков, соединяющих точки).
- Вычислите коэффициенты уравнения выборочной парной линейной регрессии (для вычисления коэффициентов регрессии воспользуйтесь встроенной функцией ЛИНЕЙН (функция находится в категории «Статистические») или надстройкой Пакет Анализа), коэффициент детерминации, коэффициент корреляции (функция КОРЕЛЛ), среднюю ошибку аппроксимации
.
- Запишите полученное уравнение выборочной регрессии. Дайте интерпретацию найденным в предыдущем пункте значениям.
- Постройте на поле корреляции прямую линию выборочной регрессии по точкам
.
- Постройте диаграмму остатков.
- Проверьте статистическую значимость коэффициентов регрессии по критерию Стьюдента (табличное значение определите с помощью функции СТЬЮДРАСПОБР) и всего уравнения в целом по критерию Фишера (табличное значение Fтабл определите с помощью функции FРАСПОБР).
- Постройте доверительные интервалы для коэффициентов регрессии. Дайте им интерпретацию.
- Постройте прогноз для значения фактора, на 50% превышающего его среднее значение.
- Постройте доверительный интервал прогноза. Дайте ему экономическую интерпретацию.
- Оцените полученные результаты — сделайте выводы о качестве построенной модели, влиянии рассматриваемого фактора на показатель.
Тема II. Множественная линейная регрессия
1. Постройте выборочную множественную линейную регрессию показателя на все указанные факторы. Запишите полученное уравнение, дайте ему экономическую интерпретацию.
2. Определите коэффициент детерминации, дайте ему интерпретацию. Вычислите среднюю абсолютную ошибку аппроксимации 
3. Проверьте статистическую значимость каждого из коэффициентов и всего уравнения в целом.
4. Постройте диаграмму остатков.
5. Постройте доверительные интервалы коэффициентов. Для статистически значимых коэффициентов дайте интерпретации доверительных интервалов.
6. Постройте точечный прогноз значения показателя y при значениях факторов, на 50% превышающих их средние значения.
7. Постройте доверительный интервал прогноза, дайте ему экономическую интерпретацию.
8. Постройте матрицу коэффициентов выборочной корреляции между показателем и факторами. Сделайте вывод о наличии проблемы мультиколлинеарности.
9. Оцените полученные результаты — сделайте выводы о качестве построенной модели, влиянии рассматриваемых факторов на показатель.
источники:
http://megaobuchalka.ru/4/7472.html
http://math.semestr.ru/regress/corel.php
Для автокорреляции характерным является соотношение (u u ) __ 0: k i COV
1) ?
2) >
3) ?
4) =
Процесс выбора необходимых переменных для регрессии переменных и отбрасывание лишних переменных называется:
1) прогнозированием
2) подгонкой
3) унификацией переменных
4) моделированием
5) спецификацией переменных
В авторегрессионной схеме первого порядка предполагается, что значение ? в каждом
наблюдении:
1) зависит от его значения в предыдущих наблюдениях
2) зависит от его значения в первом наблюдении
3) зависит от его значения во всех других наблюдениях
4) не зависит от его значения во всех других наблюдениях
5) равны 0
Множественный регрессионный анализ является ________ парного регрессионного анализа:
1) эквивалентностью
2) противоположностью
3) развитием
4) подобием
5) частным случаем
Для мультипликативной модели временного ряда Y = T · S · E сумма скорректированных сезонных компонент равна …
0
1
лагу
половине лага
Гетероскедастичность заключается в том, что дисперсия случайного члена регрессии _______ наблюдений:
1) зависит от номера наблюдений
2) зависит от характера
3) зависит от числа
4) одинакова для всех
5) зависит от времени проведения
Наиболее частая причина положительной автокорреляции заключается в постоянной направленности воздействия _____________ переменных:
1) фиктивных
2) циклических
3) сезонных
4) не включенных в уравнение
5) лишних
Сумма квадратов отклонений величины y от своего выборочного значения ? _____ сумма квадратов отклонений:
1) результирующая
2) необъясняющая
3) общая
4) случайная
5) объясняющая
Известно, что дисперсия временного ряда Y увеличивается с течением времени. Значит, ряд Y …
сбалансированным
стационарным
автокорреляционным
нестационарным
К зоне неопределенности в тесте Дарбина-Уотсона относится случай, при котором ________ (d1, d2 – нижняя и верхняя границы):
1) DW
2) DW = 0
3) DW > d2
4) DW ? 0
5) d1
Значение статистики DW находится между значениями:
1) 0 и 6
2) 0 и 4
3) -1 и 1
4) -2 и 2
5) -3 и 3
Если предположение о природе гетероскедастичности верно, то дисперсия случайного
члена для первых наблюдений в упорядоченном ряду будет ________ для последних:
1) ниже, чем
2) равно 0
3) больше, чем
4) такая же, как
5) равно 1
Условие гетероскедастичности означает, что вероятность того, что случайный член при-
мет какое-либо конкретное значение ________ наблюдений:
1) зависит от числа
2) зависит от времени проведения
3) зависит от номера
4) одинакова для всех
5) не зависит от времени проведения
Ошибки спецификации эконометрической модели имеют место вследствие …
недостоверности или недостаточности исходной информации
неоднородности данных в исходной статистической совокупности
неправильного выбора математической функции или недоучета в уравнении регрессии какого-то существенного фактора
недостаточного количества данных
В состав любого временного ряда, построенного по реальным данным, обязательно входит _____ компонента.
сезонная
циклическая
случайная
трендовая