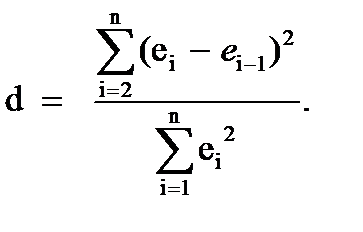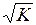Вопрос № 201326
Относительно формы зависимости различают …
линейную и множественную регрессии
положительную и отрицательную регрессии
простую и множественную регрессии
линейную и нелинейную регрессии
Вопрос № 201327
Относительно количества факторов, включенных в уравнение регрессии различают …
линейную и множественную регрессии
множественную и многофакторную регрессии
парную и линейную регрессии
простую и множественную регрессии
Вопрос № 201328
Простая линейная регрессия предполагает …
наличие двух и более факторов и нелинейность уравнения регрессии
наличие двух и более факторов и линейность уравнения регрессии
наличие одного фактора и нелинейность уравнения регрессии
наличие одного фактора и линейность уравнения регрессии
Вопрос № 201329
Объем выборки определяется числом параметров при…
зависимых переменных
случайных факторах
независимых и зависимых переменных
независимых переменных
Эконометрика
Известны значения аддитивной модели временного ряда: Yt — значение уровня ряда, Yt = 30, Т- — значение тренда, Т+15, Е- значение случайной компоненты случайных факторов Е=2. Определите значение сезонной компоненты S
Эконометрика
Состоятельность оценки характеризуется
зависимостью от объема выборки значения математического ожидания остатков
увеличением ее точности с увеличением объема выборки
уменьшением ее точности с увеличением объема выборки
независимостью от объема выборки значения математического ожидания остатков
Эконометрика
Двухшаговый метод наименьших квадратов применим для решения
только идентифицируемой системы одновременных уравнений
неидентифицируемой системы одновременных уравнений
системы одновременных уравнений в качестве наиболее общего метода решения
только сверхидентифицируемой системы одновременных уравнений
Эконометрика
При изучении взаимодействия спроса и предложения целесообразно использовать
уравнение зависимости спроса от цены
систему эконометрических уравнений
уравнение зависимости предложения от цены
Эконометрика
К ошибкам спецификации относится
однородность выбранной совокупности
неправильный выбор той или иной математической функции
учет в модели существенных факторов
учет в модели случайных факторов
Эконометрика
После применения обобщенного метода наименьших квадратов удается избежать ______ остатков
нормального распределения
Эконометрика
При хорошем качестве модели допустимым значением средней ошибки аппроксимации является ___%
Эконометрика
Гетероскедастичность остатков подразумевает _____________ от значения фактора
зависимость дисперсии остатков
независимость математического ожидания остатков
постоянство дисперсий остатков независимо
зависимость математического ожидания остатков
Эконометрика
При построении модели временного ряда проводится расчет
последующих и предыдущих значений уровней временного ряда
значений компонент для каждого уровня временного ряда
каждого уровня временного ряда
средних значений компонент для временного ряда в целом
Эконометрика
Для уравнения зависимости выручки от величины оборотных средств получено значение коэффициента детерминации, равное 0,7. Следовательно, _% дисперсии обусловлено случайными факторами
Эконометрика
Взаимодействие факторов эконометрической модели означает, что
влияние факторов на результирующий признак усиливается, начиная с определенного уровня значений факторов
факторы дублируют влияние друг друга на результат
влияние факторов на результирующий признак зависит от значений другого неколлинеарного им фактора
влияние одного из факторов на результирующий признак не зависит от значений другого фактора
Эконометрика
Для нелинейных уравнений метод наименьших квадратов применяется к
преобразованным линеаризованным уравнениям
не преобразованным линейным уравнениям
Эконометрика
Если доверительный интервал для параметра проходит через точку ноль, следовательно
параметр является существенным
параметр является несущественным
значение параметра может принимать как отрицательные, так и положительные значения
параметр признается статистически значимым
Эконометрика
Оценки параметров уравнений регрессии при помощи метода наименьших квадратов находятся на основании решения
системы нормальных неравенств
системы нормальных уравнений
Эконометрика
Если между экономическими показателями существует нелинейная связь, то
нецелесообразно использовать спецификацию нелинейного уравнения регрессии
целесообразно использовать спецификацию линейного уравнение парной регрессии
целесообразно использовать спецификацию нелинейного уравнения регрессии
необходимо включить в модель другие факторы и использовать линейное уравнение множественной регрессии
Эконометрика
Случайный характер остатков предполагает
зависимость предсказанных по модели значений результативного признака от значений факторного признака
независимость остатков от величины предсказанных по модели значений результативного признака
зависимость остатков от величины предсказанных по модели значений результативного признака
независимость предсказанных по модели значений результативного признака от значений факторного признака
Эконометрика
Если факторы входят в модель как сумма, то модель называется
Эконометрика
Метод наименьших квадратов позволяет оценить _______ уравнений регрессии
переменные и случайные величины
Эконометрика
Модель идентифицируема, если число параметров структурной формы модели
равно числу уравнений модели
равно числу параметров приведенной формы модели
больше числа параметров приведенной формы модели
меньше числа параметров приведенной формы модели
Эконометрика
Включение фактора в модель целесообразно, если коэффициент регрессии при этом факторе является
Эконометрика
Стационарность временного ряда означает отсутствие
наблюдений по уровням временного ряда
Эконометрика
Построена аддитивная модель временного ряда, где Yt – значение уровня ряда, Yt = 10, T – значение тренда, S – значение сезонной компоненты, E – значений случайной компоненты. Определите вариант правильно найденных значений компонент уровня ряда.
Эконометрика
Строится модель зависимости спроса от ряда факторов. Фиктивной переменной в данном уравнении множественной регрессии не является _________ потребителя
Эконометрика
Проверка является ли временной ряд «белым шумом» осуществляется с помощью
коэффициента автокорреляции
Эконометрика
Фиктивные переменные включаются в уравнение множественной регрессии для учета действия на результат признаков ____________ характера
Эконометрика
Экономические временные ряды, представляющие собой данные наблюдений за ряд лет, как правило, являются _______________________ временными рядами
функционально зависящими от времени
Эконометрика
Парабола второй степени может быть использована для зависимостей экономических показателей
если исходные данные не обнаруживают изменения направленности
если для определенного интервала значений фактора меняется характер связи рассматриваемых показателей: прямая связь изменяется на обратную или обратная на прямую
если для определенного интервала значений фактора меняется скорость изменений значений результата, то есть возрастает динамика роста или спада
если характер связи зависит от случайных факторов
Эконометрика
Эндогенными переменными не являются:
переменные в уравнениях системы вида
переменные, значения которых определяется внутри системы
Эконометрика
Нелинейным называется уравнение регрессии, если
параметры и зависимые переменные входят в уравнение нелинейным образом
независимые переменные входят в уравнение нелинейным образом
зависимые переменные входят в уравнение нелинейным образом
параметры входят нелинейным образом, а переменные линейны
Эконометрика
Система эконометрических уравнений предполагает наличие _________ независимых признаков
нескольких зависимых и одного
одного зависимого и совокупности
одного зависимого и нескольких
нескольких зависимых и нескольких
Эконометрика
Для существенного параметра расчетное значение критерия Стьюдента
не больше табличного значения критерия
больше табличного значения критерия
меньше табличного значения критерия
Эконометрика
При оценке параметров систем одновременных уравнений не производят
преобразование структурной формы модели в приведенную
линеаризацию уравнений системы
идентификацию системы одновременных уравнений
расчет коэффициентов приведенной формы
Эконометрика
Для существенного параметра расчетное значение критерия Стьюдента
больше табличного значения критерия
не больше табличного значения критерия Стьюдента
меньше табличного значения критерия
Эконометрика
При применении метода наименьших квадратов исследуются свойства оценок
переменных и параметров уравнения регрессии
случайных величин уравнения регрессии
переменных уравнения регрессии
параметров уравнения регрессии
Эконометрика
Автокорреляционной функцией временного ряда называется
последовательность приращений коэффициентов автокорреляции уровней различных порядков
последовательность отношений коэффициентов автокорреляции к величинам соответствующих лагов
зависимость коэффициентов автокорреляции первого порядка от числа уровней временного ряда
последовательность значений коэффициентов автокорреляции различных порядков
Эконометрика
Основной задачей моделирования временных рядов является
добавление новых уравнений к совокупности значений временного ряда
исключение значений каждой из трех компонент из уровней ряда
исключение уровней из совокупности значений временного ряда
выявление и придание количественного значения каждой из трех компонент
Эконометрика
Значение коэффициента корреляции не характеризует
корень из значения коэффициента детерминации
статистическую значимость уравнения
Эконометрика
Одним из методов присвоения числовых значений фиктивным переменным является
нахождение среднего значения
выравнивание числовых значений по возрастанию
выравнивание числовых значений по убыванию
Эконометрика
Критическое значение критерия Стьюдента определяет минимально возможную величину, допускающую принятие гипотезы о
статистической незначимости значения параметра
равенства нулю значения параметра
несущественности параметра
Эконометрика
Модель временного ряда не предполагает
учет временных характеристик
зависимость значений экономического показателя от времени
независимость значений экономического показателя от времени
последовательность моментов (периодов) времени, в течении которых рассматривается поведение экономического показателя
Эконометрика
Если между экономическими показателями существует нелинейная связь, то
нецелесообразно использовать спецификацию нелинейного уравнения регрессии
целесообразно использовать спецификацию нелинейного уравнения регрессии
необходимо включить в модель другие факторы и использовать линейное уравнение множественной регрессии
целесообразно использовать линейное уравнение парной регрессии
Эконометрика
Может ли ряд содержать только одну из компонент?
не может, так как уровень ряда должен формироваться под воздействием всех трех компонент
может, если он представлен данными, описывающими совокупность различных объектов в определенный момент (период) времени
не может, так как временной ряд не содержит компонент, влияющих на его уровни
может, если другие две компоненты не участвуют в формировании уровня ряда
Эконометрика
Объем выборки определяется
числовыми значением переменных, отбираемых в выборку
числом результативных переменных
числом параметров при независимых переменных
объемом генеральной совокупности
Эконометрика
Основной целью линеаризации уравнения регрессии является
улучшение качества модели
повышения существенности связи между рассматриваемыми переменными
возможность применения метода наименьших квадратов для оценки параметров
получение новых нелинейных зависимостей
Эконометрика
Предпосылкой метода наименьших квадратов является то, что остатки
не подчиняются закону больших чисел
подчиняются закону больших чисел
подчиняются закону нормального распределения
не подчиняются закону нормального распределения
Эконометрика
Назовите показатель корреляции для нелинейных моделей регрессии
линейный коэффициент корреляции
парный коэффициент линейной корреляции
Эконометрика
Критерий Стьюдента предназначен для определения значимости
каждого коэффициента корреляции
каждого коэффициента регрессии
построенного уравнения в целом
Эконометрика
Расчет значения коэффициента детерминации не позволяет оценить
качество подбора уравнения регрессии
долю остаточной дисперсии результативного признака в общей дисперсии результативного признака
долю факторной дисперсии результативного признака в общей дисперсии результативного признака
существенность коэффициента регрессии
Эконометрика
В системах рекурсивных уравнений количество переменных в правой части каждого уравнения определяется как ______________ уравнений и количества независимых факторов
сумма количества зависимых переменных предыдущих
сумма количества зависимых переменных последующих
разность количества зависимых переменных предыдущих
разность количества зависимых переменных последующих
Эконометрика
В матрице парных коэффициентов корреляции отображены значения парных коэффициентов линейной корреляции между
переменными и случайными факторами
параметрами и переменными
На первом этапе применения косвенного метода наименьших квадратов структурная форма преобразуется в приведенную
Вопрос посетителя
К ошибкам спецификации относится
(*ответ*) неправильный выбор той или иной математической функции
учет в модели существенных факторов
учет в модели случайных факторов
однородность выбранной совокупности
Коррелограммой называется _ функции
(*ответ*) графическое отображение автокорреляционной
процесс экспериментального нахождения значений автокорреляционной
графическое отображение регрессионной
аналитическое выражение для автокорреляционной
Косвенный метод наименьших квадратов требует
(*ответ*) преобразования структурной формы модели в приведенную
нормализации уравнений структурной формы
линеаризации уравнений структурной формы модели
линеаризации уравнений приведенной формы
Моделирование тенденции осуществляется на основе построения уравнения регрессии зависимости
(*ответ*) уровня ряда от времени
случайной компоненты от времени
сезонной компоненты от времени
трендовой компоненты от времени
Модель временного ряда не предполагает
(*ответ*) учет временных характеристик
зависимость значений экономического показателя от времени
последовательность моментов (периодов) времени, в течение которых рассматривается поведение экономического показателя
рассмотрение значений экономического показателя в привязке ко времени
Модель временного ряда не предполагает
(*ответ*) независимость значений экономического показателя от времени
зависимость значений экономического показателя от времени
последовательность моментов (периодов) времени, в течении которых рассматривается поведение экономического показателя
учет временных характеристик
Модель временного ряда предполагает
(*ответ*) зависимость значений экономического показателя от времени
независимость значений экономического показателя от времени
пренебрежение временными характеристиками ряда
отсутствие последовательности моментов (периодов) времени, в течение которых рассматривается поведение экономического показателя
Модель идентифицируема, если число параметров структурной формы модели
(*ответ*) равно числу параметров приведенной формы модели
больше числа параметров приведенной формы модели
меньше числа параметров приведенной формы модели
равно числу уравнений модели
Может ли ряд содержать только одну из компонент?
(*ответ*) может, если другие две компоненты не участвуют в формировании уровня ряда
не может, так как временной ряд не содержит компонент, влияющих на его уровни
может, если он представлен данными, описывающими совокупность различных объектов в определенный момент (период) времени
не может, так как уровень ряда должен формироваться под воздействием всех трех компонент
Мультипликативная модель содержит исследуемые факторы в виде
(*ответ*) сомножителей
их отношений
слагаемых
комбинации слагаемых и сомножителей
На первом этапе применения косвенного метода наименьших квадратов
(*ответ*) структурная форма преобразуется в приведенную
проводят процедуру линеаризации приведенной формы модели
проводят процедуру линеаризации структурной формы модели
приведенную форму преобразуют в структурную
Ответ эксперта
К ошибкам спецификации относится
(*ответ*) неправильный выбор той или иной математической функции
учет в модели существенных факторов
учет в модели случайных факторов
однородность выбранной совокупности
Коррелограммой называется _ функции
(*ответ*) графическое отображение автокорреляционной
процесс экспериментального нахождения значений автокорреляционной
графическое отображение регрессионной
аналитическое выражение для автокорреляционной
Косвенный метод наименьших квадратов требует
(*ответ*) преобразования структурной формы модели в приведенную
нормализации уравнений структурной формы
линеаризации уравнений структурной формы модели
линеаризации уравнений приведенной формы
Моделирование тенденции осуществляется на основе построения уравнения регрессии зависимости
(*ответ*) уровня ряда от времени
случайной компоненты от времени
сезонной компоненты от времени
трендовой компоненты от времени
Модель временного ряда не предполагает
(*ответ*) учет временных характеристик
зависимость значений экономического показателя от времени
последовательность моментов (периодов) времени, в течение которых рассматривается поведение экономического показателя
рассмотрение значений экономического показателя в привязке ко времени
Модель временного ряда не предполагает
(*ответ*) независимость значений экономического показателя от времени
зависимость значений экономического показателя от времени
последовательность моментов (периодов) времени, в течении которых рассматривается поведение экономического показателя
учет временных характеристик
Модель временного ряда предполагает
(*ответ*) зависимость значений экономического показателя от времени
независимость значений экономического показателя от времени
пренебрежение временными характеристиками ряда
отсутствие последовательности моментов (периодов) времени, в течение которых рассматривается поведение экономического показателя
Модель идентифицируема, если число параметров структурной формы модели
(*ответ*) равно числу параметров приведенной формы модели
больше числа параметров приведенной формы модели
меньше числа параметров приведенной формы модели
равно числу уравнений модели
Может ли ряд содержать только одну из компонент?
(*ответ*) может, если другие две компоненты не участвуют в формировании уровня ряда
не может, так как временной ряд не содержит компонент, влияющих на его уровни
может, если он представлен данными, описывающими совокупность различных объектов в определенный момент (период) времени
не может, так как уровень ряда должен формироваться под воздействием всех трех компонент
Мультипликативная модель содержит исследуемые факторы в виде
(*ответ*) сомножителей
их отношений
слагаемых
комбинации слагаемых и сомножителей
На первом этапе применения косвенного метода наименьших квадратов
(*ответ*) структурная форма преобразуется в приведенную
проводят процедуру линеаризации приведенной формы модели
проводят процедуру линеаризации структурной формы модели
приведенную форму преобразуют в структурную
Спецификация переменных в уравнение регрессии. Ошибки спецификации.
Построение математической модели — это скорее искусство, чем наука, и, прежде всего, требует глубоких знаний предметной области. Социально-экономические системы имеют чрезвычайно сложную структуру, со многими явными и неявными взаимосвязями между элементами системы, подвержены влиянию многих скрытых факторов, относятся к классу так называемых больших систем. Стечением времени меняются не только их характеристики, учитываемые в модели в виде отдельных параметров, но и структура самих уравнений, которые описывают процесс. Для их адекватного описания требуется соответствующий математический аппарат. Однако, даже самые сложные математические методы не в состоянии описать реальную систему во всех ее деталях, да это и не нужно. Модель не должна быть слишком сложной. Излишняя детализация и учет второстепенных факторов затрудняет
исследование и не дает существенной информации об изучаемой системе. Если модель слишком сложна, то ее трудно использовать и интерпретировать на практике. Относительная простота — важная характеристика удачно построенной модели. С другой стороны, слишком упрощенная модель не будет адекватно описывать реальную систему. Таким образом, сложность модели должна соответствовать сложности изучаемого экономического объекта.
В связи с этим возникает необходимость формулировки некоторых разумных упрощающих гипотез (предположений), исключения из анализа второстепенных факторов и т. п., с тем, чтобы была возможность описать процесс математически. При этом существенные для данного социально-экономического процесса характерные черты должны быть учтены в модели в соответствии с поставленной целью исследования.
Другой характерной проблемой, с которой сталкивается эконометрист, является то, что часто приходится довольствоваться неточными данными, которые имеются в наличии и быстро устаревают. Этих данных не всегда хватает, а провести управляемый эксперимент с целью получения дополнительной информации невозможно. В подобном случае целесообразно сочетание количественных методов с привлечением экспертных знаний и суждений.
Таким образом, при создании эконометрической модели возникают следующие вопросы.
1. Какую модель желательно построить — статическую или динамическую (с учетом фактора времени), нелинейную или линеаризованную? Как учесть влияние внешней среды (возмущений)? (Ответ на эти вопросы определяет желаемую точность и сложность модели, выбор адекватного математического аппарата и т. д.)
2.Достаточно ли имеющихся данных, необходимых для построения адекватной модели, насколько они достоверны? Существует ли возможность получения дополнительной информации, если это необходимо? Следует ли привлечь экспертную информацию?
3. Как оценить качество модели, т. е. определить, насколько адекватно (правильно) она описывает поведение реального объекта?
В рамках эконометрического подхода существует мощный арсенал средств, который включает многие современные эффективные математические методы, такие, например, как аппарат нейронных сетей, и разработанные на их основе компьютерные технологии, в известной степени помогающие справиться с этими проблемами. Но решающая роль принадлежит специалисту — эконометристу. Окончательный успех зависит от его способности к неформальному анализу проблемной ситуации, адекватной оценке возможностей современных эконометрических методов, от их правильного применения и интерпретации полученных результатов.
Построив удачную математическую модель и оценив ее количественно с использованием эконометрических методов, экономист-аналитик получает в распоряжение эффективнейшее средство анализа и прогноза, а управляющий-практик — инструмент для обоснования управленческих решений. Такие модели широко применяются на практике.
Практически величина y складывается из двух слагаемых:
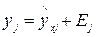

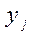
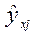
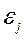
СВ 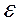
1) спецификацией модели;
2) выборочным характером исходных данных;
3) особенностями измерения.
От правильно выбранной спецификации модели зависит величина случайных ошибок: они тем меньше, чем больше теоретические значения результативного признака 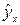
К ошибкам спецификации будут относиться не только неправильный выбор той или иной математической функции для 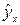
Наряду с ошибками спецификации могут иметь место ошибки выборки (неоднородность данных в исходной статистической совокупности). Если совокупность неоднородна, то УР не имеет практического смысла.
Для получения хорошего результата обычно исключают из совокупности единицы с аномальными значениями исследуемых признаков, то есть результаты регрессии представляют собой выборочные характеристики.
Наибольшую опасность в практическом использовании методов регрессии представляют ошибки измерения. Если ошибки спецификации можно уменьшить, изменяя форму модели, а ошибки выборки – увеличивая объём исходных данных, то ошибки измерения практически сводят на нет все усилия по количественной оценке связи между признаками. Особенно велика роль ошибок измерения при исследовании на макроуровне.
Дата добавления: 2016-05-16 ; просмотров: 667 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Спецификация уравнения регрессии
Под спецификацией уравнения регрессии понимают выбор объясняющих переменных и установление вида связи между изучаемыми явлениями. В случае парной регрессии эта задача сводится к выбору независимой переменной и вида связи. Решение этих вопросов должна давать теория, описывающая взаимосвязи изучаемых процессов.
К ошибкам спецификации в случае парной регрессии можно отнести неправильный выбор доминирующего фактора, влияющего на изменение изучаемого показателя, или неправильный выбор вида зависимости между изучаемыми показателями. И в том и в другом случае будут нарушены предпосылки МНК, особенно 3-я и 4-я, т.е. остатки регрессии будут гетероскедастичными и автокоррелироваными.
Гетероскедастичность и автокорреляция остатков уравнения регрессии могут сказаться на эффективности оценок, полученных на основе МНК и на смещённости оценки их дисперсии. Поэтому интервальные оценки и статистические выводы о значимости оценок в этом случае могут быть ненадёжными.
Разработаны специальные статистические методы проверки остатков на гомоскедастичность и автокорреляцию. Рассмотрим сначала наиболее простые из них.
1.3.1. Проверка остатков регрессии на гетероскедастичность (тест Голдфелда–Квандта)
Этот тест применяется в предположении нормально распределённых остатков и в предположении их пропорциональности величинам объясняющей переменной х. Для применения рассматриваемого теста пары наблюдений упорядочиваются в порядке роста значений независимой переменной х. Затем выбираются первые и последние наблюдения в количестве не менее n/3. По выбранным наблюдениям строятся уравнения регрессии (отдельно по каждому набору) и сравниваются их остаточные суммы квадратов. Гипотеза о гомоскедастичности в этом случае будет равносильна гипотезе о том, что остатки в этих уравнениях представляют собой выборочные наблюдения нормально распределённых случайных величин с одинаковыми дисперсиями. Сравнивая эти дисперсии по критерию Фишера (число степеней свободы числителя и знаменателя здесь совпадают, т. к. слева и справа берётся одинаковое число наблюдений) принимаем или отклоняем гипотезу о гомоскедастичности остатков.
Несмотря на ограниченность применения этого критерия (пропорциональность величин остатков значениям независимой переменной), данный тест работает с элементами выборки и не требует больших объёмов выборки как асимптотические тесты.
1.3.2. Проверка остатков регрессии на автокорреляцию (статистика Дарбина–Уотсона)
При анализе остатков на автокорреляцию в случае пространственной выборки надо меть в виду, что последовательную зависимость остатков друг от друга необходимо рассматривать не для случайного набора пар наблюдений, а для пар наблюдений, упорядоченных по величине значений независимой переменной. И только в этом случае поведение остатков будет соответствовать ситуации, проверяемой по описываемому ниже критерию.
Проверку остатков регрессии на автокорреляцию можно осуществить на основе статистики Дарбина-Уотсона. Этот критерий основан на гипотезе о существовании автокорреляции между соседними членами ряда остатков и использует статистику
Здесь ei = yi – 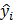


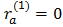

Для d-статистики найдены критические границы (du – верхняя и dl – нижняя), на основе которых можно определить области, позволяющие принять или отклонить нулевую гипотезу об отсутствии автокорреляции при фиксированном уровне значимости 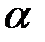
Таблица 1.3 – Механизм проверки гипотезы об автокорреляции в остатках по критерию Дарбина – Уотсона
| Автокорреляция есть | Область неопределённости | Автокорреляция отсутствует | Область неопределённости | Автокорреляция есть |
Если вычисленное значение d-статистики попало в область неопределенности критерия, то это означает, что нет статистических оснований ни принять, ни отклонить нулевую гипотезу об отсутствии автокорреляции в остатках. В этом случае нужно использовать какой-либо иной критерий или для большей точности увеличить объём выборки. Учитывая наличие области неопределённости, в литературе по эконометрике можно встретить такую рекомендацию: считать приближённо, что автокорреляции в остатках нет, если значение критерия находится в интервале (1,5 – 2,5), в противном случае признаётся наличие автокорреляции.
В некоторых статистических пакетах программ при проверке гипотезы об отсутствии автокорреляции в остатках совместно со статистикой Дарбина – Уотсона рассчитывается р-value, например в Statgraphics. В этом случае проверяется гипотеза H0: 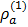
Как уже отмечалось, статистика Дарбина-Уотсона в большей мере используется при анализе временных рядов, поскольку именно для них актуально понятие автокорреляции. Однако она может быть использована для проверки правильной спецификации уравнения парной (простой) регрессии, но при этом необходимо случайную выборку упорядочить по степени возрастания независимой переменной. Тогда появится смысл в понятии «последовательные остатки». Если при этом с помощью критерия Дарбина-Уотсона обнаружена существенная автокорреляция остатков, то необходимо признать наличие проблемы в спецификации уравнения регрессии и либо вернуться к выбору объясняющей переменной, либо к форме регрессионной зависимости, либо попытаться избавиться от автокорреляции другими методами.
Следует иметь в виду, что статистика Дарбина-Уотсона обладает рядом недостатков: проверяет автокорреляцию только первого порядка, имеет области неопределённости и не может использоваться, если в качестве независимой переменной выступает лаговое значение зависимой переменной и если в уравнении регрессии отсутствует константа.
Несмотря на указанные недостатки, данная статистика используется наиболее часто и работает с выборочными наблюдениями, не требуя жёстких требований к выборке в отличие от асимптотических критериев.
Пример 1. Анализ функции потребления.
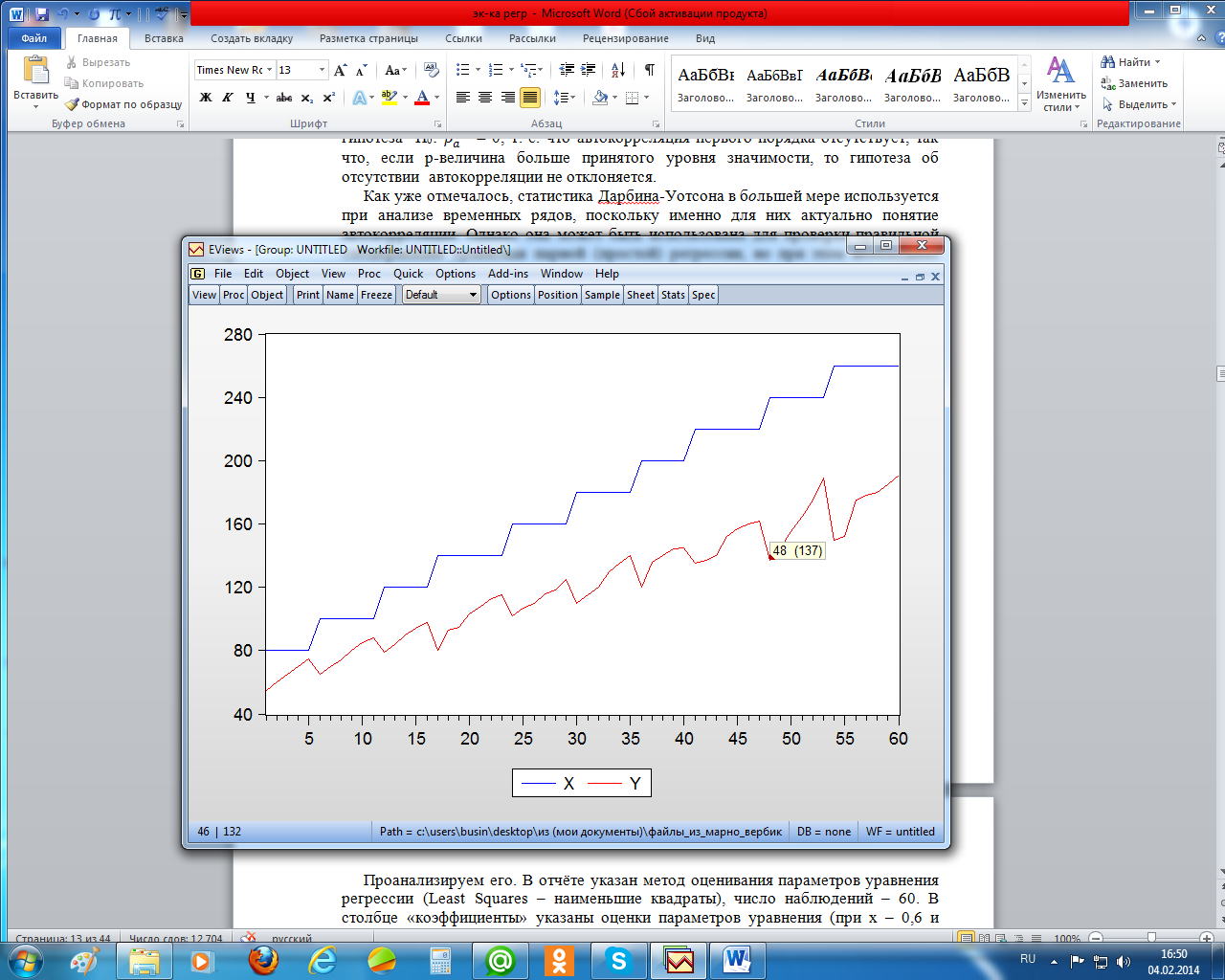
Приведём пример использования рассмотренных положений теории по простой регрессии, анализируя зависимость расхода 60 семей от их доходов. Эта информация представлена на графике (рисунок 1.1).
Рисунок 1.1 – График исходных данных
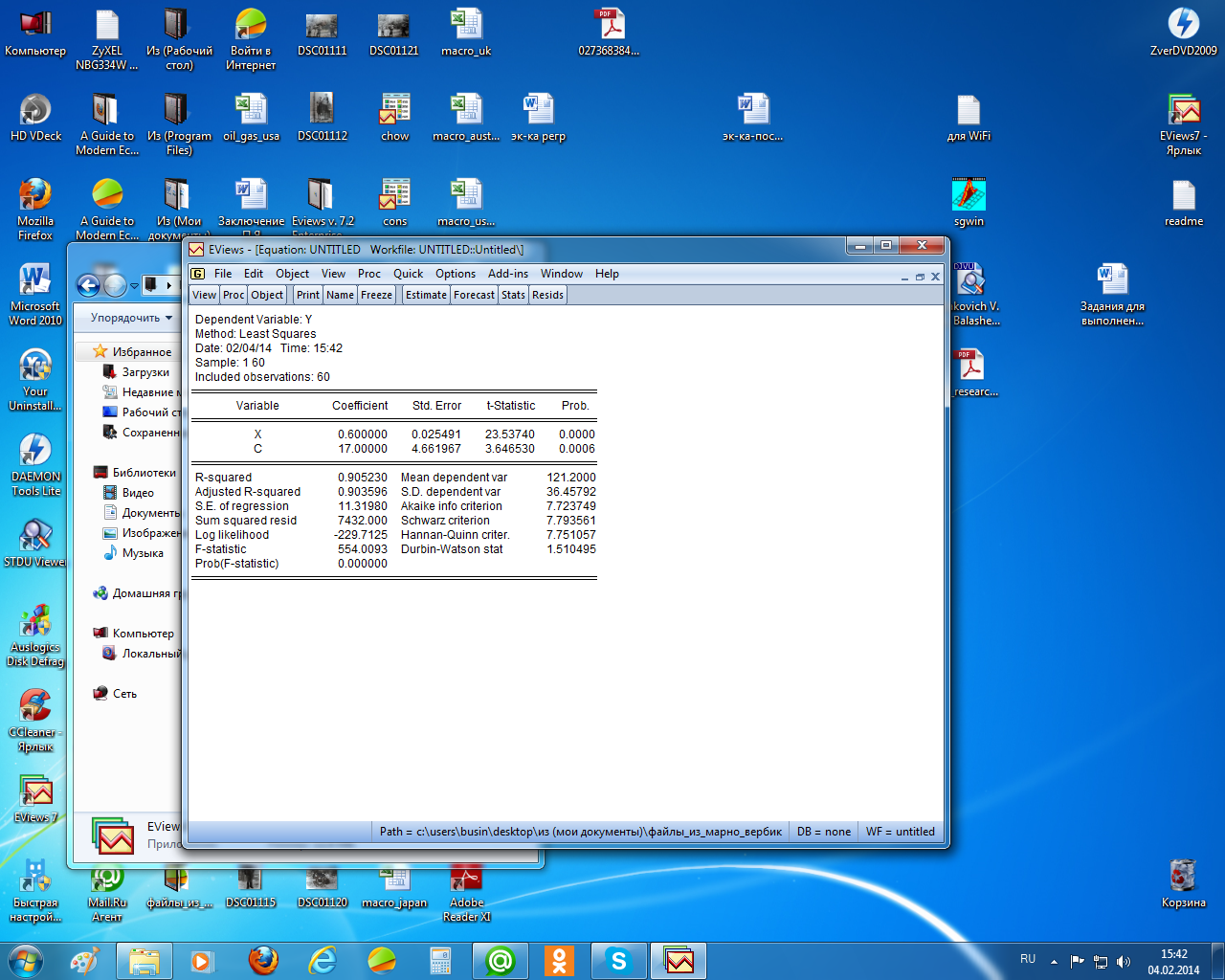
Уравнение регрессии зависимости расходов (y) от доходов (х) раcсчитано в EViews и отчёт о регрессии приведён ниже (рисунок 1.2).
Проанализируем его. В отчёте указан метод оценивания параметров уравнения регрессии (Least Squares – наименьшие квадраты), число наблюдений – 60. В столбце «коэффициенты» указаны оценки параметров уравнения регрессии (коэффициент при х равен 0,6 и свободный член (с) равен 17). Следовательно, можно выписать уравнение регрессии: 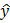
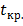


Рисунок 1.2 – Отчёт о регрессии
Проанализируем показатели точности уравнения регрессии. Начнём с анализа значимости уравнения регрессии. F-satstistic = 544, а вероятность для неё (Prob(F-statistic)) равна нулю. Это – результат дисперсионного анализа уравнения регрессии. Здесь проверяется гипотеза о значимости уравнения регрессии, т. е., что коэффициент уравнения регрессии равен нулю. Поскольку расчётный уровень значимости здесь меньше принятого (0,05), то гипотеза о равенстве коэффициента регрессии отклоняется и считается, что уравнение регрессии значимо.
Коэффициент детерминации (R-squared) равен 0,9. Следовательно, изменение расходов в нашем примере на 90% зависит от изменения доходов. Показатель Adjusted R-squared (исправленный коэффициент детерминации) в простой регрессии не анализируется. Затем указана стандартная ошибка регрессии (S.E. of regression). Она равна 11.32. Затем показана сумма квадратов остатков регрессии (Sum squared resid – 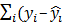
Далее (в правом столбце нижней части отчёта) указано среднее значение зависимой переменной (Mean dependent var) – средний уровень доходов этих 60 семей (он равен 121,2). Стандартную ошибку регрессии (11,32) можно сравнить с этим средним доходом и определить, насколько точно в среднем прогнозируются расходы семьи по этому уравнению регрессии.
Далее указаны три информационных критерия (Akaike, Schwarz, Hannan), которые в парной регрессии не анализируются.
Статистика Дарбина – Уотсона (d) рассчитана для проверки гипотезы о наличии в остатках регрессии автокорреляции первого порядка. Как отмечалось, эта информация более полезна при анализе временных рядов. Для пространственной информации надо данные упорядочить, чтобы понятие «соседние» остатки приняло какой-то смысл. В случае случайной выборки это понятие теряет смысл. В нашем случае данные упорядочены по росту доходов (см. рисунок1.1), следовательно, можно анализировать эту статистику без предварительного упорядочения. Как видно из отчёта, d = 1,51. Табличные значения нижней (dl) и верхней (du) границ соответственно равны 1,55 и 1,62. Построим области принятия решения о наличия или отсутствия автокорреляции в остатках в соответствии с приведённой схемой в таблице 1.3.
| Автокорреляция есть | Область неопределённости | Автокорреляция отсутствует | Область неопределённости | Автокорреляция есть |
0 1,55 1,62 2,38 3,45 4
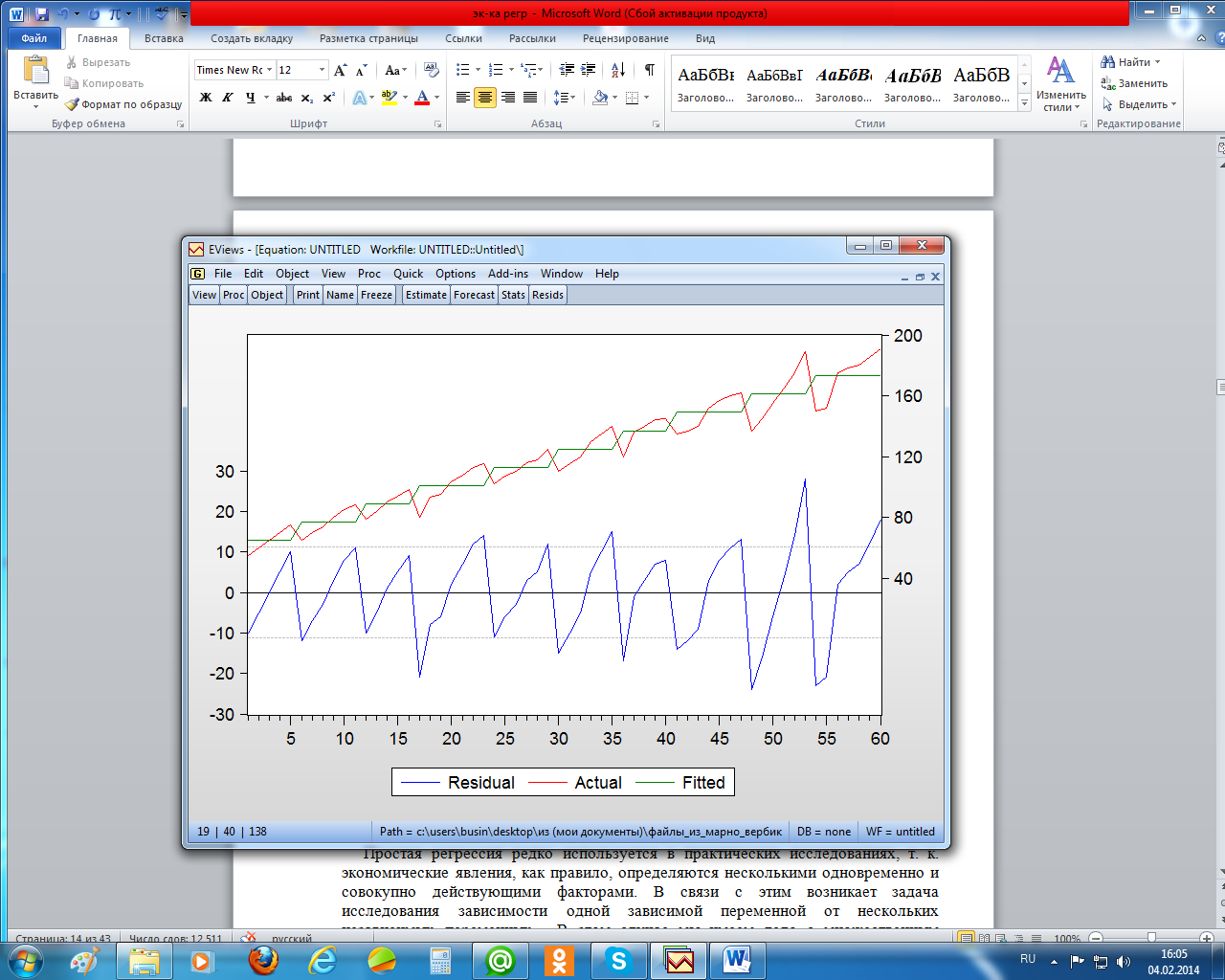
Как видим, расчётное значение попало в область, где автокорреляция есть. Да и по графику (рисунок 1.3) видно, что остатки не являются случайным процессом. Видна закономерность их изменения – регулярная смена отрицательных остатков на положительные. На этом рисунке изображены реальные (Actual) и расчётные (Fitted – подобранные) значения моделируемой переменной (расходов) и остатки (Residual). Причём, правая вертикальная ось – для моделируемого показателя, левая – для остатков.
Рисунок 1.3 – Графики остатков, выборочных и расчётных значений
Гомоскедастичность остатков проверим тестом Голдфелда – Квандта. Для этого всю выборку разобьём на три части по 20 наблюдений, рассчитаем уравнения регрессии поотдельности для первых 20 наблюдений и для последних 20 наблюдений и выпишем остаточные суммы квадратов этих уравнений (Sum squared resid). Получим для первой части выборки 1 246,276, а для третьей – 4 164,0 (рисунок 1.4 и рисунок 1.5). Обратите внимание на позицию Sample – выборка. В первом случае в окне спецификации было установлено «1 20» (т. е. первых 20 наблюдений), а во втором – «41 60» (последних 20 наблюдений).
Рисунок 1.4 – Регрессия для первых 20 наблюдений
Рисунок 1.5 – Регрессия для последних 20 наблюдений
Вычислим F-статистику как отношение этих двух дисперсий и сравним с критическим значением. Получим F = 3,34, а табличное значение F(20;20;0,05) = 2,1. Поскольку выборочное значение F-статистики оказалось больше табличного, то гипотеза о равенстве дисперсий отклоняется, и делаем вывод, что дисперсии различаются значимо, а значит, остатки анализируемого уравнения гетероскедастичны (растут с ростом доходов).
Тестирование предпосылки о нормальном законе распределения остатков проведём тестом Jarque – Bera, который сравнивает асимметрию и эксцесс остатков с асимметрией и эксцессом нормального закона распределения.
Чтобы провести это тестирование, необходимо после оценки уравнения регрессии сначала создать остатки, выбрав Proc/Make Residual Series…/OK. Затем выбрать View/Descriptive Statistics&Tests/Histogram and Stats. Получим рисунок 1.6. Здесь кроме гистограммы остатков приведены описательные статистики остатков, а также асимметрия (Skewness) и эксцесс (Kurtosis). Известно, что для нормального закона распределения эти характеристики равны соответственно 0 и 3. Статистика Jarque – Bera рассчитывается из соотношения
JB = (n–k) 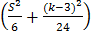
где n – объём выборки, k – число оцениваемых параметров, S – асимметрия, K – эксцесс. Поскольку в нашем случае вероятность больше 0,05, то гипотезе о нормальном законе распределения остатков не отклоняется.
Рисунок 1.6 – Гистограмма остатков и тест Jarque – Bera
Как поступить, если установлены наличие автокорреляции и гетероскедастичность остатков, а также тестирование второй предпосылки МНК – рассмотрим далее, при анализе уравнения множественной регрессии.
Оценка параметров линейных уравнений регрессии
Спецификация модели
+наука, которая дает количественное выражение взаимосвязей экономических явлений и процессов
-раздел экономической теории, связанный с анализом статистической информации
-специальный раздел математики, посвященный анализу экономической информации
-наука, которая осуществляет качественный анализ взаимосвязей экономических явлений и процессов
#Основной задачей эконометрики является…
+исследование взаимосвязей экономических явлений и процессов
-отражение особенностей социального развития общества
-установление связей между различными процессами в обществе и технических процессом
— анализ технического прогресса на примере социально–экономических показателей
#При выборе спецификации модели парная регрессия используется в случае, когда …
+среди множества факторов, влияющих на результат можно выделить доминирующий фактор
-среди множества факторов, влияющих на результат нельзя выделить доминирующий фактор
-среди множества факторов, влияющих на результат можно выделить несколько факторов
-среди множества факторов, влияющих на результат можно выделить лишь случайные факторы
#Объем выборки должен превышать число рассчитываемых параметров при исследуемых факторах …
#К ошибкам спецификации относится …
+неправильный выбор той или иной математической функции
-однородность выбранной совокупности
-учет в модели случайных факторов
— учет в модели существенных факторов
#Относительно формы зависимости различают …
+линейную и нелинейную регрессии
-простую и множественную регрессии
-непосредственную и косвенную регрессии
-положительную и отрицательную регрессии
#Относительно количества факторов, включенных в уравнение регрессии различают …
+простую и множественную регрессии
-линейную и нелинейную регрессии
-непосредственную и косвенную регрессии
— множественную и многофакторную регрессии
#Простая линейная регрессия предполагает …
+наличие одного фактора и линейность уравнения регрессии
-наличие двух и более факторов и линейность уравнения регрессии
-наличие одного фактора и нелинейность уравнения регрессии
-наличие двух и более факторов и нелинейность уравнения регрессии
#Объем выборки определяется …
+числом параметров при независимых переменных
-числом результативных переменных
-объемом генеральной совокупности
-числовыми значениями переменных отбираемых в выборку
#Дано уравнение регрессии 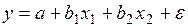
+линейное уравнение множественной регрессии
-линейное уравнение простой регрессии
-полиномиальное уравнение множественной регрессии
— полиномиальное уравнение парной регрессии
#Выбор формы зависимости экономических показателей и определение количества факторов в модели называется _____________ эконометрической модели.
#Коэффициент парной корреляции характеризует …
+тесноту линейной связи между двумя переменными
-тесноту нелинейной связи между двумя переменными
-тесноту линейной связи между несколькими переменными
-тесноту нелинейной связи между несколькими переменными
#Мультиколлинеарность факторов эконометрической модели подразумевает …
+наличие линейной зависимости между более чем двумя факторами
-наличие линейной зависимости между двумя факторами
-отсутствие зависимости между факторами
-наличие нелинейной зависимости между двумя факторами
#Взаимодействие факторов эконометрической модели означает, что …
+факторы дублируют влияние друг друга на результат
-влияние одного из факторов на результирующий признак не зависит от значений другого фактора
-влияние факторов на результирующий признак усиливается, начиная с определенного уровня значений факторов
— влияние факторов на результирующий признак зависит от значений другого неколлинеарного им фактора
#Отбор факторов в модель множественной регрессии при помощи метода включения основан на сравнении значений …
+остаточной дисперсии до и после включения фактора в модель
-общей дисперсии до и после включения фактора в модель
-дисперсии до и после включения результата в модель
-остаточной дисперсии до и после включения случайных факторов в модель
#Величина остаточной дисперсии при включении существенного фактора в модель …
— будет равна нулю
#В матрице парных коэффициентов корреляции отображены значения парных коэффициентов линейной корреляции между …
-параметрами и переменными
-переменными и случайными факторами
#Матрица парных коэффициентов корреляции строится для выявления коллинеарных и мультиколлинеарных …
#Факторы эконометрической модели являются коллинеарными, если коэффициент …
+корреляции между ними по модулю больше 0,7
-детерминации между ними по модулю больше 0,7
-корреляции между ними по модулю меньше 0,7
-детерминации между ними по модулю меньше 0,7
#Из пары коллинеарных факторов в эконометрическую модель включается тот фактор …
+который при достаточно тесной связи с результатом имеет меньшую связь с другими факторами
-который при который при отсутствии связи с результатом имеет меньшую связь с другими факторами
-который при отсутствии связи с результатом имеет максимальную связь с другими факторами
-который при достаточно тесной связи с результатом имеет наибольшую связь с другими факторами
#Величина коэффициента детерминации при включении существенного фактора в эконометрическую модель …
-существенно не изменится
— будет равна нулю
#Основным требованием к факторам, включаемым в модель множественной регрессии, является …
+отсутствие взаимосвязи между факторами
-наличие тесной взаимосвязи между факторами
-отсутствие взаимосвязи между результатом и фактором
-отсутствие линейной взаимосвязи между факторами
#Фиктивными переменными в уравнении множественной регрессии являются …
+качественные переменные, преобразованные в количественные
-дополнительные количественные переменные, улучшающие решение
-комбинации из включенных в уравнение регрессии факторов, повышающие адекватность модели
-переменные, представляющие простейшие функции от уже включенных в модель переменных
#В качестве фиктивных переменных в модель множественной регрессии включаются факторы, …
+не имеющие количественных значений
-имеющие количественные значения
-не имеющие качественных значений
— имеющие вероятностные значения
#При включении фиктивных переменных в модель им присваиваются …
#Исходные значения фиктивных переменных предполагают значения …
#Проводится исследование зависимости выработки работника предприятия от ряда факторов. Примером фиктивной переменной в данной модели будет являться ____________ работника
#Строится модель зависимости спроса от ряда факторов. Фиктивной переменной в данном уравнении множественной регрессии не является __________ потребителя
#Факторные переменные уравнения множественной регрессии, преобразованные из качественных в количественные называются …
#Фиктивные переменные включаются в уравнение множественной регрессии для учета действия на результат признаков …
#Фиктивные переменные включаются в уравнения __________ регрессии
#Одним из методов присвоения числовых значений фиктивным переменным является …
-нахождение среднего значения
-выравнивание числовых значений по убыванию
-выравнивание числовых значений по возрастанию
#Методом присвоения числовых значений фиктивным переменным не является …
+нахождение среднего значения
-присвоение цифровых меток
-присвоение количественных значений
#Величина коэффициента регрессии показывает …
+среднее изменение результата при изменении фактора на одну единицу
-характер связи между фактором и результатом
-тесноту связи между фактором и результатом
-тесноту связи между исследуемыми факторами
#Величина параметра a в уравнении парной линейной регрессии 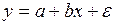
+результирующей переменной при нулевом значении фактора
-факторной переменной при нулевом значении результата
-результирующей переменной при нулевом значении случайной величины
-факторной переменной при нулевом значении случайного фактора
#Уравнение регрессии, которое связывает результирующий признак с одним из факторов при зафиксированном на среднем уровне значении других переменных называется …
#В линейном уравнении парной регрессии 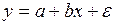
#Линейное уравнение множественной регрессии имеет вид 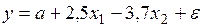
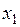
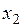
+по этому уравнению нельзя ответить на поставленный вопрос, так как коэффициенты регрессии несравнимы между собой
— 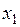
— 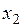
-оказывают одинаковое влияние
#В стандартизованном уравнении множественной регрессии 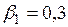
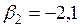
+ 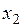
— 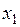
-по этому уравнению нельзя ответить на поставленный вопрос, так как стандартизованные коэффициенты регрессии несравнимы между собой
-по этому уравнению нельзя ответить на поставленный вопрос, так как неизвестны значения «чистых» коэффициентов регрессии
#Построена модель парной регрессии зависимости предложения от цены 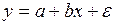
+случайной величины ε
-посредством константы ε
-случайной величины x
-посредством параметра b
#Для модели зависимости дохода населения (р.) от объема производства (млн. р.) получено уравнение у = 0,003х + 1200 + ε. При изменении объема производства на 1 млн. р. доход в среднем изменится на …
#В стандартизованном уравнении множественной регрессии переменными являются …
-средние значения исходных переменных
#Показатель, характеризующий на сколько сигм изменится в среднем результат при изменении соответствующего фактора на одну сигму, при неизменном уровне других факторов называется __________ коэффициентом регрессии
#В стандартизованном уравнении свободный член …
-равен коэффициенту множественной корреляции
-равен коэффициенту множественной детерминации
Оценка параметров линейных уравнений регрессии
#Метод наименьших квадратов используется для оценивания …
+параметров линейной регрессии
-величины коэффициента корреляции
-величины коэффициента детерминации
-средней ошибки аппроксимации
#Метод наименьших квадратов не применимдля …
+уравнений нелинейных по оцениваемым параметрам
-линейных уравнений множественной регрессии
-линейных уравнений парной регрессии
-полиномиальных уравнений множественной регрессии
#В основе метода наименьших квадратов лежит …
+минимизация суммы квадратов отклонений фактических значений результативного признака от его теоретических значений
-равенство нулю суммы квадратов отклонений фактических значений результативного признака от его теоретических значений
-максимизация суммы квадратов отклонений фактических значений результативного признака от его теоретических значений
-минимизация суммы квадратов отклонений фактических значений результативного признака от его средних значений
#Систему МНК, построенную для оценки параметров линейного уравнения множественной регрессии можно решить …
-методом первых разностей
-методом скользящего среднего
#В исходном соотношении МНК сумма квадратов отклонений фактических значений результативного признака от его теоретических значений …
-приравнивается к нулю
-приравнивается к системе нормальных уравнений
#Метод наименьших квадратов позволяет оценить _____________ уравнений регрессии
-параметры и переменные
-переменные и случайные величины
#Оценки параметров уравнений регрессии при помощи метода наименьших квадратов находятся на основании решения …
+решения системы нормальных уравнений
-решения двойственной задачи
-решения уравнения регрессии
-решения системы нормальных неравенств
#Оценки параметров линейного уравнения множественной регрессии можно найти при помощи метода …
+метода наименьших квадратов
-метода наибольших квадратов
-метода средних квадратов
-метода нормальных квадратов
#Метод наименьших квадратов применяется для оценки …
+параметров линейных уравнений регрессии
-качества линейных уравнений регрессии
-уравнений регрессии, нелинейных по параметрам
-качества уравнений, нелинейных по параметрам
#Система нормальных уравнений метода наименьших квадратов строится на основании …
+таблицы исходных данных
-предсказанных значений результативного признака
-отклонений фактических значений результативного признака от его теоретических значений
-отклонений фактических значений объясняющей переменной от ее теоретических значений
#Требованием к уравнениям регрессии, параметры которых можно найти при помощи МНК является …
-равенство нулю средних значений результативной переменной
-равенство нулю средних значений факторного признака
#Несмещенность оценки характеризует …
+равенство нулю математического ожидания остатков
-наименьшую дисперсию остатков
-увеличение точности ее вычисления с увеличением объема выборки
-ее зависимость от объема выборки
#Если оценка параметра эффективна, то это означает …
+наименьшую дисперсию остатков
-равенство нулю математического ожидания остатков
-максимальную дисперсию остатков
-уменьшение точности с увеличением объема выборки
#Состоятельность оценки характеризуется .
+увеличением ее точности с увеличением объема выборки
-независимостью от объема выборки значения математического ожидания остатков
-уменьшением ее точности с увеличением объема выборки
-зависимостью от объема выборки значения математического ожидания остатков
#Несмещенность оценки на практике означает …
+что при большом числе выборочных оцениваний остатки не будут накапливаться
-что найденное значение коэффициента регрессии нельзя рассматривать как среднее значение из возможного большого количества несмещенных оценок
-невозможность перехода от точечного оценивания к интервальному
-уменьшение точности с увеличением объема выборки
#Эффективность оценки на практике характеризуется …
+возможностью перехода от точечного оценивания к интервальному
-отсутствием накапливания значений остатков при большом числе выборочных оцениваний
-невозможностью перехода от точечного оценивания к интервальному
-уменьшением точности с увеличением объема выборки
#Свойствами оценок МНК являются …
+эффективность, состоятельность и несмещенность
-эффективность, состоятельность и смещенность
-эффективность, несостоятельность и смещенность
-эффективность, несостоятельность и несмещенность
#Увеличение точности оценок с увеличением объема выборки описывает свойство _______ оценки.
#Математическое ожидание остатков равно нулю, если оценки параметров обладают свойством …
#Минимальная дисперсия остатков характерна для оценок, обладающих свойством …
#Переход от точечного оценивания к интервальному возможен, если оценки являются …
+ эффективными и несмещенными
-эффективными и несостоятельными
-неэффективными и состоятельными
-состоятельными и смещенными
#При примени метода наименьших квадратов исследуются свойства …
+оценок параметров уравнения регрессии
-оценок переменных уравнения регрессии
-оценок случайных величин уравнения регрессии
-оценок переменных и параметров уравнения регрессии
+одинаковую дисперсию остатков при каждом значении фактора
-рост дисперсии остатков с увеличением значения фактора
-уменьшение дисперсии остаток с уменьшением значения фактора
-максимальную дисперсию остатков при средних значениях фактора
#Предпосылкой метода наименьших квадратов является то, что…
+остаточные величины имеют случайный характер
-остаточные величины имеют неслучайный характер
-при увеличении моделируемых значений результативного признака значение остатка увеличивается
-при уменьшении моделируемых значений результативного признака значение остатка уменьшается
+зависимость дисперсии остатков от значения фактора
-постоянство дисперсии остатков независимо от значения фактора
-независимость математического ожидания остатков от значения фактора
-зависимость математического ожидания остатков от значения фактора
#Предпосылкой метода наименьших квадратов является то, что остатки…
+подчиняются закону нормального распределения
-не подчиняются закону нормального распределения
-подчиняются закону больших чисел
-не подчиняются закону больших чисел
#Предпосылки метода наименьших квадратов исследуют поведение …
-параметров уравнения регрессии
-переменных уравнения регрессии
#Предпосылкой метода наименьших квадратов является …
+отсутствие автокорреляции в остатках
-присутствие автокорреляции в остатках
-отсутствие корреляции между результатом и фактором
-присутствие автокорреляции между результатом и фактором
#Предпосылкой метода наименьших квадратов не является условие …
+неслучайного характера остатков
-отсутствия автокорреляции в остатках
-случайного характера остатков
#Случайный характер остатков предполагает …
+независимость остатков от величины предсказанных по модели значений результативного признака
-зависимость остатков от величины предсказанных по модели значений результативного признака
-зависимость предсказанных по модели значений результативного признака от значений факторного признака
-независимость предсказанных по модели значений результативного признака от значений факторного признака
#Отсутствие автокорреляции в остатках предполагает, что значения ______ не зависят друг от друга
#Оценки параметров, найденные при помощи метода наименьших квадратов обладают свойствами эффективности, состоятельности и несмещенности, если предпосылки метода наименьших квадратов …
-можно не учитывать
#Если предпосылки метода наименьших квадратов нарушены, то …
+оценки параметров могут не обладать свойствами эффективности, состоятельности и несмещенности
-коэффициент регрессии является несущественным
-коэффициент корреляции является несущественным
-полученное уравнение статистически незначимо
#Обобщенный метод наименьших квадратов применяется в случае…
#Обобщенный метод наименьших квадратов используется для корректировки…
+гетероскедастичности остатков в уравнении регрессии
-автокорреляции между независимыми переменными
-параметров нелинейного уравнения регрессии
-точности определения коэффициента множественной корреляции
#Обобщенный метод наименьших квадратов подразумевает …
-линеаризацию уравнения регрессии
-двухэтапное применение метода наименьших квадратов
-переход от множественной регрессии к парной
#Обобщенный метод наименьших квадратов рекомендуется применять в случае …
-нормально распределенных остатков
-автокорреляции результативного признака
#При применении метода наименьших остатков уменьшить гетероскедастичность остатков удается путем …
-введения дополнительных факторов в модель
-введения дополнительных результатов в модель
#На основании преобразования переменных при помощи обобщенного метода наименьших квадратов получаем новое уравнение регрессии, которое представляет собой …
+взвешенную регрессию, в которой переменные взяты с весами
-нелинейную регрессию, в которой переменные взяты с весами
-взвешенную регрессию, в которой переменные взяты с весами
-нелинейную регрессию, в которой переменные взяты с весами
#Обобщенный метод наименьших квадратов не используется для моделей с _______ остатками
-автокоррелярованными и гетероскедастичными
#Что преобразуется при применении обобщенного метода наименьших квадратов?
+исходные уровни переменных
-дисперсия результативного признака
-дисперсия факторного признака
-стандартизованные коэффициенты регрессии
#Обобщенный метод наименьших квадратов отличается от обычного МНК тем, что при применении ОМНК…
+преобразуются исходные уровни переменных
-уменьшается количество наблюдений
-остатки приравниваются к нулю
-остатки не изменяются
#После применения обобщенного метода наименьших квадратов удается избежать ______ остатков
-равенства нулю суммы
#Метод оценки параметров моделей с гетероскедастичными остатками называется …методом наименьших квадратов
источники:
http://megalektsii.ru/s9786t1.html
http://poisk-ru.ru/s54891t1.html
Построение
математической модели — это скорее
искусство, чем наука, и, прежде всего,
требует глубоких знаний предметной
области. Социально-экономические системы
имеют чрезвычайно сложную структуру,
со многими явными и неявными взаимосвязями
между элементами системы, подвержены
влиянию многих скрытых факторов,
относятся к классу так называемых
больших систем. Стечением
времени меняются не только их
характеристики, учитываемые в модели
в виде отдельных параметров, но и
структура самих уравнений, которые
описывают процесс. Для их адекватного
описания требуется соответствующий
математический аппарат. Однако, даже
самые сложные математические методы
не в состоянии описать реальную систему
во всех ее деталях, да это и не нужно.
Модель не должна быть слишком сложной.
Излишняя детализация и учет второстепенных
факторов затрудняет
исследование
и не дает существенной информации об
изучаемой системе. Если модель слишком
сложна, то ее трудно использовать и
интерпретировать на практике.
Относительная
простота — важная характеристика
удачно построенной модели.
С другой стороны, слишком упрощенная
модель не будет адекватно описывать
реальную систему. Таким образом, сложность
модели должна соответствовать сложности
изучаемого экономического объекта.
В связи
с этим возникает необходимость
формулировки некоторых разумных
упрощающих гипотез (предположений),
исключения из анализа второстепенных
факторов и т. п., с тем, чтобы была
возможность описать процесс математически.
При этом существенные для
данного
социально-экономического процесса
характерные черты
должны
быть учтены в модели в соответствии с
поставленной целью исследования.
Другой
характерной проблемой, с которой
сталкивается эконометрист, является
то, что часто приходится довольствоваться
неточными
данными,
которые имеются в наличии и быстро
устаревают. Этих данных не всегда
хватает, а провести управляемый
эксперимент с целью получения
дополнительной информации невозможно.
В подобном случае целесообразно сочетание
количественных методов с привлечением
экспертных знаний и суждений.
Таким
образом, при создании эконометрической
модели возникают следующие вопросы.
1.
Какую модель желательно построить —
статическую или динамическую (с
учетом фактора времени), нелинейную или
линеаризованную? Как учесть влияние
внешней среды (возмущений)? (Ответ на
эти вопросы определяет желаемую точность
и сложность модели, выбор адекватного
математического аппарата и т. д.)
2.
Достаточно
ли имеющихся данных, необходимых для
построения адекватной модели,
насколько они достоверны? Существует
ли возможность получения дополнительной
информации, если это необходимо? Следует
ли привлечь экспертную информацию?
3. Как
оценить качество модели, т. е. определить,
насколько адекватно (правильно) она
описывает поведение реального объекта?
В
рамках эконометрического подхода
существует мощный арсенал средств,
который включает многие современные
эффективные
математические методы,
такие, например, как аппарат
нейронных сетей,
и разработанные на их основе компьютерные
технологии, в известной степени помогающие
справиться с этими проблемами. Но
решающая
роль принадлежит специалисту —
эконометристу.
Окончательный успех зависит от его
способности к неформальному анализу
проблемной ситуации, адекватной оценке
возможностей современных эконометрических
методов, от их правильного применения
и интерпретации полученных результатов.
Построив
удачную математическую модель и оценив
ее количественно с использованием
эконометрических методов, экономист-аналитик
получает в распоряжение эффективнейшее
средство анализа и прогноза, а
управляющий-практик — инструмент для
обоснования управленческих решений.
Такие модели широко применяются на
практике.
Практически
величина y
складывается из двух слагаемых:
,
где
— фактическое
значение, результат признака;
— теоретическое
значение результата признака, найденное
из математической модели или уравнения
регрессии;
— СВ, характерное
отклонение реального значения результата
признака от теоретического.
СВ
называется
возмущением. Она включает влияние
неучтённых в модели факторов, случайных
ошибок и особенно измерения. Её присутствие
в модели порождено тремя источниками:
-
спецификацией
модели; -
выборочным
характером исходных данных; -
особенностями
измерения.
От правильно
выбранной спецификации модели зависит
величина случайных ошибок: они тем
меньше, чем больше теоретические
значения результативного признака
подходит к фактическим данным y.
К ошибкам спецификации
будут относиться не только неправильный
выбор той или иной математической
функции для
,
но и недоучет в УР какого-либо существенного
фактора (например, использование парной
регрессии вместо множественной).
Наряду с ошибками
спецификации могут иметь место ошибки
выборки (неоднородность данных в исходной
статистической совокупности). Если
совокупность неоднородна, то УР не имеет
практического смысла.
Для получения
хорошего результата обычно исключают
из совокупности единицы с аномальными
значениями исследуемых признаков, то
есть результаты регрессии представляют
собой выборочные характеристики.
Наибольшую опасность
в практическом использовании методов
регрессии представляют ошибки
измерения.
Если ошибки спецификации можно уменьшить,
изменяя форму модели, а ошибки выборки
– увеличивая объём исходных данных, то
ошибки измерения практически сводят
на нет все усилия по количественной
оценке связи между признаками. Особенно
велика роль ошибок измерения при
исследовании на макроуровне.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
04.08.2019218.11 Кб0kv.doc
- #
- #
- #
Методам простой или парной регрессии и корреляции, возможностям их применения в эконометрике посвящен данный раздел.
Любое эконометрическое исследование начинается со Спецификации модели, т. е. с формулировки вида модели исходя из соответствующей теории связи между переменными.
Парная регрессия достаточна, если имеется доминирующий фактор, который и используется в качестве объясняющей переменной.
Уравнение простой регрессии характеризует связь между двумя переменными, которая проявляется как некоторая закономерность лишь в среднем по совокупности наблюдений. Например, если зависимость спроса у от цены х будет характеризоваться уравнением , то это означает, что с ростом цены на 1 д. е. спрос в среднем уменьшается на 2 д. е. В уравнении регрессии корреляционная по сути связь признаков представляется в виде функциональной связи, выраженной соответствующей математической функцией. Практически в каждом отдельном случае величина у складывается из двух слагаемых:
, (1.1)
Где – фактическое значение результативного признака;
– теоретическое значение результативного признака, найденное исходя из соответствующей математической функции связи у и х, т. е. их уравнения регрессии;
– случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии.
Случайная величина ε, или Возмущение, Включает влияние неучтенных в модели факторов, случайных ошибок и особенностей измерения. Ее присутствие в модели обусловлено тремя источниками: спецификацией модели, выборочным характером исходных данных и особенностями измерения переменных.
При правильно выбранной спецификации модели зависит величина случайных ошибок, поэтому, чем они меньше, тем в большей мере теоретические значения результативного признака подходят к фактическим данным
.
К ошибкам спецификации будет относится не только неправильный выбор той или иной математической функции для , но и недоучет в уравнении регрессии какого-либо существенного фактора, т. е. использование парной регрессии вместо множественной.
Наряду с ошибками спецификации могут иметь место ошибки выборки, поскольку исследователь чаще всего работает с выборочными данными при установлении закономерной связи между признаками. Ошибки выборки имеют место и в силу неоднородности данных в исходной статистической совокупности, что, как правило, бывает при изучении эконометрических процессов. Если совокупность неоднородна, то уравнение регрессии не имеет практического смысла.
Наибольшую опасность в практическом использовании методов регрессии представляют ошибки измерения. Если ошибки спецификации можно уменьшить, изменяя форму модели (вид математической формулы), а ошибки выборки – увеличивая объем исходных данных, то ошибки измерения практически сводят на нет все усилия по количественной оценке связи между признаками.
Предполагая, что ошибки измерения сведены к минимуму, основное внимание в эконометрических исследованиях уделяется ошибкам спецификации модели.
В парной регрессии выбор вида математической функции может быть осуществлен тремя методами:
— графическим;
— аналитическим, т. е. исходя из теории изучаемой взаимосвязи;
— экспериментальным.
При изучении зависимости между двумя признаками Графический метод подбора вида уравнения регрессии достаточно нагляден. Он базируется на поле корреляции.
Класс математических функций для описания связи двух переменных достаточно широк. Кроме уже указанных используются и другие типы кривых:
;
;
;
;
;
.
Значительный интерес представляет Аналитический метод выбора типа уравнения регрессии. Он основан на изучении материальной природы связи исследуемых признаков.
При обработке информации на компьютере выбор вида уравнения регрессии обычно проводится экспериментальным методом, т. е. путем сравнения величины остаточной дисперсии Dост, рассчитанной при разных моделях.
Если уравнение регрессии проходит через все точки корреляционного поля, что возможно только при функциональной связи, когда все точки лежат на линии регрессии , то фактические значения результативного признака совпадают с теоретическими
, т. е. они полностью обусловлены влиянием фактора х. в этом случае остаточная дисперсия Dост=0. В практических исследованиях, как правило, имеет место некоторое рассеяние точек относительно линии регрессии. Оно обусловлено влиянием прочих не учитываемых в уравнении регрессии факторов. Иными словами, имеют место отклонения фактических данных от теоретических (у-
). Величина этих отклонений и лежит в основе расчета остаточной дисперсии:

Чем меньше величина остаточной дисперсии, тем в меньшей мере наблюдается влияние прочих не учитываемых в уравнении регрессии факторов и тем лучше уравнение регрессии подходит к исходным данным.
Линейная регрессия находит широкое применение в эконометрике ввиду четкой экономической интерпретацией ее параметров.
Линейная регрессия сводится к нахождению уравнения вида
или
. (1.3)
Построение линейной регрессии сводится к оценке ее параметров – а и b. Классический подход к оцениванию параметров линейной регрессии основан на Методе наименьших квадратов (МНК).
МНК позволяет получить такие оценки параметров а и b, при которых сумма квадратов отклонений фактических значений результативного признака у от расчетных (теоретических) минимальна:

Иными словами, из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была минимальной.
Для того чтобы найти минимум функции 1.4, надо вычислить частные производные по каждому из параметров а и b и приравнять их к нулю. Обозначим через S, тогда:



Преобразуя формулу 1.5, получим следующую систему нормальных уравнений для оценки параметров а и b:

Решая систему нормальных уравнений 1.6 либо методом последовательного исключения переменных, либо методом определителей, найдем искомые оценки параметров а и b. Можно воспользоваться следующими формулами для а и b:
. (1.7)
Формула 1.7. получена из первого уравнения системы 1.6, если все его члены разделить на n:

Где — ковариация признаков;
— дисперсия признака х.
Поскольку , а
, получим следующую формулу расчета оценки параметра b:

Формула 1.8 получается также при решении системы 1.6 методом определителей, если все элементы расчета разделить на n2.
Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. Знак при коэффициенте регрессии b показывает направление связи: при b>0 – связь прямая, а при b<0 – связь обратная.
Формально а – значение у при х=0. Если признак-фактор х не имеет и не может иметь нулевого значения, то трактовка свободного члена а не имеет смысла. Параметр а может не иметь экономического содержания. Попытки интерпретировать экономически параметр а могут привести к абсурду, особенно при a<0. Интерпретировать можно лишь знак при параметре а. Если a>0, то относительное изменение результата происходит медленнее, чем изменение фактора.
Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции rxy. Имеются разные модификации формулы линейного коэффициента корреляции, например:


Значение линейного коэффициента корреляции находится в границах . Если коэффициент регрессии b>0, то 0
, и, наоборот, при b<0 —
. Следует отметить, что величина линейного коэффициента корреляции оценивает тесноту связи рассматриваемых признаков в ее линейной форме. Чем ближе значение данного коэффициента к 1, тем связь между показателями сильнее, чем ближе к нулю, тем связь слабее.
Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции , называемый Коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака у, объясняемую регрессией, в общей дисперсии результативного признака:

Соответственно величина 1-r2 характеризует долю дисперсии у, вызванную влиянием остальных не учтенных в модели факторов. Величина коэффициента детерминации является одним из критериев оценки качества линейной модели. Чем больше доля объясненной вариации, тем соответственно меньше роль прочих факторов и, следовательно, линейная модель хорошо объясняет исходные данные, и ею можно воспользоваться для прогноза значений результативного признака.
Коэффициенты регрессии – величины именованные, и потому несравнимы для разных признаков. Так, коэффициент регрессии по модели прибыли предприятия от состава выпускаемой продукции несопоставим с коэффициентом регрессии прибыли предприятия от затрат на рекламу.
Сделать коэффициенты регрессии сопоставимыми по разным признакам позволяет определение аналогичного показателя в стандартизованной системе единиц, где в качестве единицы измерения признака используется его среднее квадратическое отклонение (σ). Поскольку коэффициент регрессии b имеет единицы измерения дробные (результат/фактор), то умножив его на среднее квадратическое отклонение фактора х (σх) и разделив на среднее квадратическое отклонение результата (σу), получим показатель, пригодный для сравнения интенсивности изменения результата под влиянием разных факторов. Иными словами, мы вернулись к формуле линейного коэффициента корреляции. Его величина выступает в качестве стандартизованного коэффициента регрессии и характеризует среднее в сигмах (σу) изменение результата с изменением фактора на одну σх.
Линейный коэффициент корреляции как измеритель тесноты линейной связи признаков логически связан не только с коэффициентом регрессии b, но и с коэффициентом эластичности, который является показателем силы связи, выраженным в процентах. При линейной связи признаков х и у средний коэффициент эластичности в целом по совокупности определяется как и характеризует, на сколько % в среднем изменится у при увеличении фактора x на 1%.
Несмотря на схожесть этих показателей, измерителем тесноты связи выступает линейный коэффициент корреляции (rxy), а коэффициент регрессии (b) и коэффициент эластичности (Э) – показатели силы связи; коэффициент регрессии является абсолютной мерой, ибо имеет единицы измерения, присущие изучаемым признакам у и х, а коэффициент эластичности — относительным показателем силы связи, потому что выражен в процентах.
После того как уравнение линейной регрессии найдено, проводится оценка значимости как уравнения в целом, так и отдельных его параметров.
Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера. При этом выдвигается нулевая гипотеза, что коэффициент регрессии равен нулю, т. е. b=0, и, следовательно, фактор х не оказывает влияния на результат у.
Непосредственному расчету F-критерия предшествует анализ дисперсии. Центральное место в нем занимает разложение общей суммы квадратов отклонений переменной у от среднего значения на две части – «объясненную» и «остаточную» («необъясненную»):

|
Общая сумма квадратов отклонений |
= |
Сумма квадратов отклонений, объясненная регрессией |
+ |
Остаточная сумма квадратов отклонений |
Любая сумма квадратов отклонений связана с числом степеней свободы df, т. е. с числом свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности n и с числом определяемых по ней констант.
Так, для общей суммы квадратов необходимо (n-1) независимых отклонений, ибо из совокупности из n единиц после расчета среднего уровня свободно варьируют лишь (n-1) число отклонений. Например, имеем ряд значений у: 1,2,3,4,5. Среднее из них равно 3, и тогда n отклонений от среднего составят: -2, -1, 0, 1, 2. Видим, что свободно варьируют только четыре отклонения, а пятое может быть определено, если четыре предыдущие известны.
При расчете объясненной, или факторной, суммы квадратов используются теоретические (расчетные) значения результативного признака
, найденные по линии регрессии:
. Вследствие чего факторная сумма квадратов отклонений имеет число степеней свободы, равное 1.
Существует равенство между числом степеней свободы общей, факторной и остаточной суммами квадратов. Число степеней свободы остаточной суммы квадратов при линейной регрессии составляет n-2.
Итак, имеем два равенства:
Разделив каждую сумму квадратов на соответствующее ей число степеней свободы, получим Средний квадрат отклонений или Дисперсию на одну степень свободы D.



Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F-отношения, т. е. критерия F:

Если нулевая гипотеза Н0 справедлива, то факторная и остаточная дисперсия не отличаются друг от друга. Если Н0 несправедлива, то факторная дисперсия превышает остаточную в несколько раз. Кроме расчетных значений F-критерия существуют также и табличные. Табличные значения F-критерия – это максимальная величина отношений дисперсий, которая может быть иметь место при случайном расхождении их для данного уровня вероятности наличия нулевой гипотезы. Вычисленное значение F-отношения признается достоверным (отличным от единицы), если оно больше табличного. В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи: Fфакт>Fтабл, Н0 отклоняется. Если же величина F окажется меньше табличной, то вероятность нулевой гипотезы выше заданного уровня (например, 0,05) и она не может быть отклонена без риска сделать неправильный вывод о наличии связи. В этом случае уравнение регрессии считается статистически незначимым: Fфакт<Fтабл, Н0 не отклоняется.
Величина F-критерия связана с коэффициентом детерминации r2. Факторную сумму квадратов отклонений можно представить как

А остаточную сумму квадратов – как

Тогда значение F-критерия можно выразить следующим образом:

Для измерения точности построенной модели используется Средняя относительная ошибка аппроксимации

Для экономических исследований применяются следующие уровни ошибки аппроксимации: если до 10%, то построенное уравнение регрессии достаточно точно выражает закон изменения исследуемого показателя под действием факторов и приемлемо для целей анализа; в случае построения модели для прогнозирования, допустимое значение
до 4%.
В линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров определяется его стандартная ошибка: mb и ma.
Стандартная ошибка коэффициента регрессии параметра mb рассчитывается по формуле:

Отношение коэффициента регрессии к его стандартной ошибке дает t-статистику, которая подчиняется статистике Стьюдента при (n-2) степенях свободы. Эта статистика применяется для проверки статистической значимости коэффициента регрессии и для расчета его доверительных интервалов.
Для оценки значимости коэффициента регрессии его величину сравнивают с его стандартной ошибкой, т. е. определяют фактическое значение t-критерия Стьюдента:

Которое затем сравнивают с табличным значением при определенном уровне значимости α и числе степеней свободы (n-2).
Если фактическое значение t-критерия превышает табличное, гипотезу о несущественности коэффициента регрессии можно отклонить. Доверительный интервал для коэффициента регрессии определяется как .
Стандартная ошибка параметра а определяется по формуле

Процедура оценивания значимости данного параметра не отличается от рассмотренной выше для коэффициента регрессии: вычисляется t-критерий:

Его величина сравнивается с табличным значением при (n-2) степенях свободы.
Значимость линейного коэффициента корреляции проверяется на основе величины ошибки коэффициента корреляции mr:

Фактическое значение t-критерия Стьюдента определяется как

Рассмотренную формулу оценки коэффициента корреляции рекомендуется применять при большом числе наблюдений, а также, если r не близко к +1 или -1.
В прогнозных расчетах по уравнению регрессии определяется предсказываемое ур значение как точечный прогноз при хр=хк, т. е. путем подстановки в линейное уравнение регрессии
соответствующего значения х. Однако точечный прогноз явно нереален, поэтому он дополняется расчетом стандартной ошибки
, т. е.
, и соответственно мы получаем интервальную оценку прогнозного значения у*:
. (1.22)
Для того чтобы понять, как строится формула для определения величин стандартной ошибки , подставим в уравнение линейной регрессии выражение параметра а:
, тогда уравнение регрессии примет вид:
.
Отсюда следует, что стандартная ошибка зависит от ошибки
и ошибки коэффициента регрессии b, т. е.
. (1.23)
Из теории выборки известно, что . Используя в качестве оценки
остаточную дисперсию на одну степень свободы Dост, получим формулу расчета ошибки среднего значения переменной у:

Ошибка коэффициента регрессии определяется формулой 
:

Соответственно имеет выражение:

Рассмотренная формула стандартной ошибки предсказываемого среднего значения у при заданном значении хк характеризует ошибку положения линии регрессии. Величина стандартной ошибки достигает минимума при
и возрастает по мере того, как «удаляется» от
в любом направлении.
Графически доверительные интервалы для будут выглядеть как гиперболы, расположенные по обе стороны от линии регрессии, см. рис. 2.
Средняя ошибка прогнозируемого индивидуального значения у составит: 
При прогнозировании на основе уравнения регрессии следует помнить, что величина прогноза зависит не только от стандартной ошибки индивидуального значения у, но и от точности прогноза значения фактора х. рассмотренная формула средней ошибки индивидуального значения признака может быть использована также для оценки существенности различия предсказываемого значения и некоторого гипотетического значения.
Вопросы для самопроверки
1. В чем состоят ошибки спецификации модели?
2. Поясните смысл коэффициента регрессии, назовите способы его оценивания.
3. Что такое число степеней свободы и как оно определяется для факторной и остаточной сумм квадратов?
4. Какова концепция F-критерия Фишера?
5. Как оценивается значимость параметров уравнения регрессии?
6. Как определяется коэффициент эластичности и что он показывает?
7. В чем смысл средней ошибки аппроксимации и как она определяется?
| < Предыдущая | Следующая > |
|---|