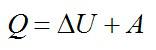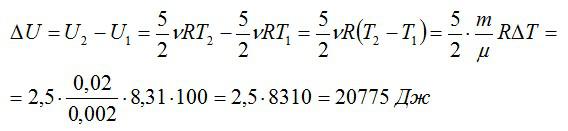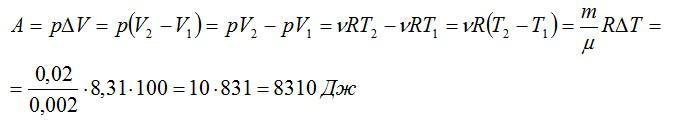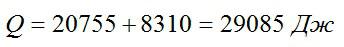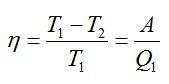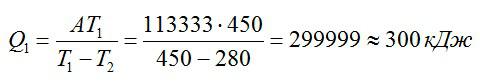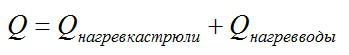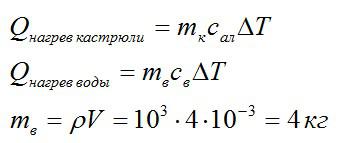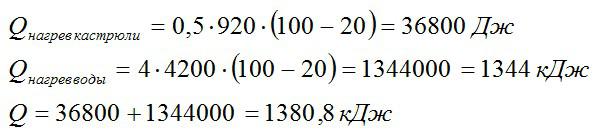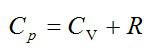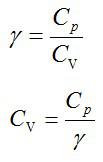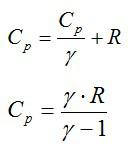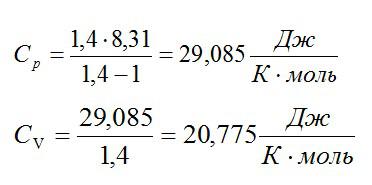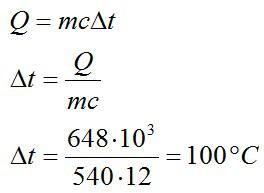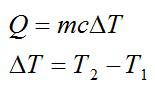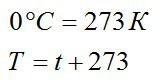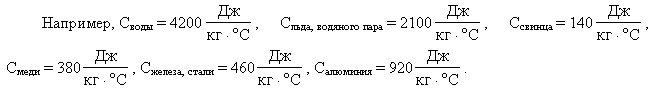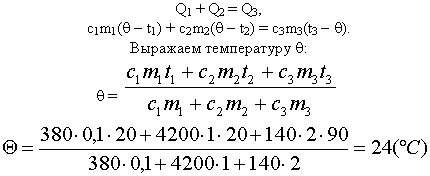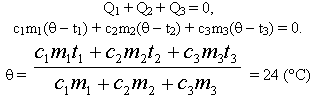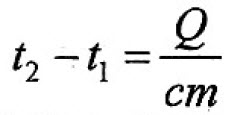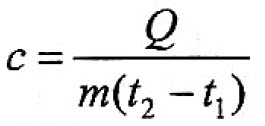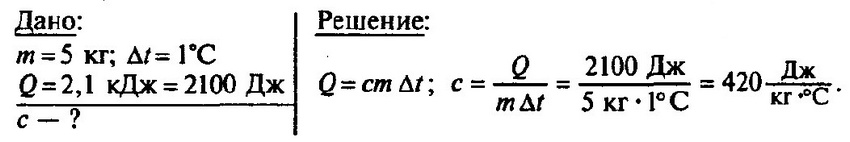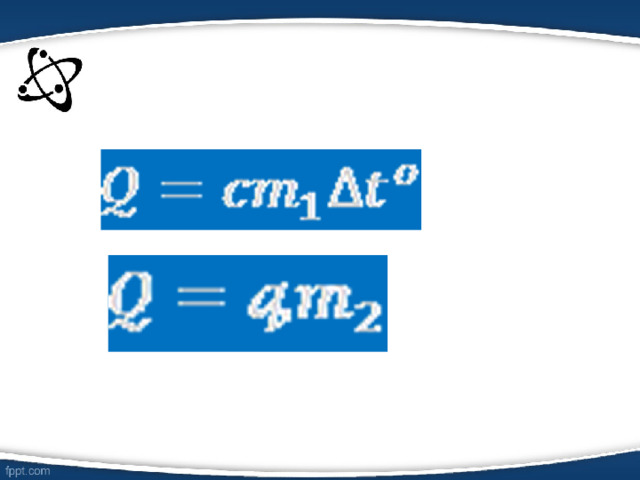Обучайтесь и развивайтесь всесторонне вместе с нами, делитесь знаниями и накопленным опытом, расширяйте границы знаний и ваших умений.
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,667 -
гуманитарные
33,655 -
юридические
17,917 -
школьный раздел
612,004 -
разное
16,907
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Найди верный ответ на вопрос ✅ «При кипении вода в сосуде получила некоторое количество теплоты, в результате чего ее масса уменьшилась на 42 г. Определите массу воды, …» по предмету 📙 Физика, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Правильный ответ на вопрос 👍 «Тело получило некоторое количество теплоты Q и совершило работу A. Чему равно изменение внутренней энергии ΔU тела? …» по предмету 📗 Физика. Развернутая система поиска нашего сайта обязательно приведёт вас к нужной информации. Как вариант — оцените ответы на похожие вопросы. Но если вдруг и это не помогло — задавайте свой вопрос знающим оппонентам, которые быстро дадут на него ответ!
Искать готовые ответы
Главная » Физика » Тело получило некоторое количество теплоты Q и совершило работу A. Чему равно изменение внутренней энергии ΔU тела?
Каталог заданий
Версия для печати и копирования в MS Word
1
Задания Д6 B9 № 3635
У порции идеального газа отняли некоторое количество теплоты. При этом над газом совершили положительную работу. В результате внутренняя энергия порции газа
1) увеличилась
2) уменьшилась
3) не изменилась
4) могла и увеличиться, и уменьшиться и остаться неизменной
Решение
·
Помощь
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
Найди верный ответ на вопрос ✅ «При кипении вода в сосуде получила некоторое количество теплоты, в результате чего ее масса уменьшилась на 42 г. Определите массу воды, …» по предмету 📙 Физика, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Методическое пособие для решения задач по
разделу «Тепловые явления. Количество теплоты. Изменения агрегатных
состояний веществ.»
Эта
статья, надеюсь, будет полезна преподавателям физики в средней школе, а также
ученикам, проявляющим интерес к физике и желающим научиться решать физические
задачи. Точнее, цель не столько научить решать задачи, сколько правильно
анализировать условия, что является залогом правильного решения. Речь пойдет о
решении задач среднего и высокого уровня сложности по разделу «Тепловая физика»
8 класса, в которых описываются теплообменные процессы между телами,
сопряженные с фазовыми переходами (изменением агрегатных состояний) веществ,
либо без них. Невзирая на сравнительно несложный математический аппарат и
небольшое количество формул, применяемых при решении задач, этому разделу в
программе физики 8 класса отведен значительный объем учебных часов.
При всём многообразии задач по данному разделу, различаются они лишь постановкой
вопросов. При этом практически все указанные задачи имеют один общий момент,
лежащий в основе их условий – это теплообмен между двумя и более
телами (далее буду их называть «телами-участниками» теплообмена), заканчивающийся
установлением состояния теплового равновесия. Из этого и
будем исходить, приступая к анализу, казалось бы, разных по содержанию условий
задач.
Общими моментами в решениях этих задач являются:
—
необходимость
расчета количества теплоты Q, передаваемого
друг-другу «телами–участниками»;
—
обязательное применение уравнения теплового баланса (Закон сохранения
энергии, применительно к теплообменным процессам), так как подавляющее
большинство задач предполагают теплопередачу в замкнутых (теплоизолированных)
системах. При
этом, даже если в условии задачи описывается неизолированный процесс, то
уравнение теплового баланса можно применить с учетом потерь энергии.
Непременным условием успешного решения задач по данному (как, впрочем, и по
любому другому) разделу, в первую очередь, является знание учениками формул и
соответствующих физических величин, набор которых в нашем случае относительно
не велик. В частности:
|
Процесс |
Соответствующие формулы |
|
Нагревание |
|
|
Плавление |
Q = |
|
Парообразование |
Q = Lm, где L – удельная |
|
Сгорание |
Q = qm, где q – |
|
Изолированный |
Q1+Q2+…+Qn=0 или Qполуч=|Qотд| Уравнение |
|
Неизолированный |
η |
Анализ наиболее характерных ошибок, допускаемых при решении задач по
рассматриваемому разделу, показывает, что ученики зачастую «не видят» скрытые
тепловые процессы, которые прямо не описываются в условии. Как правило, это
происходит в основном из-за того, что учащиеся не подвергают тщательному
анализу ситуацию, описанную в задаче, применительно к каждому «телу-участнику»
теплообмена в отдельности, а стараются охватить все физические процессы,
протекающие со всеми «телами-участниками» одновременно.
В этой связи, предлагаю следующий алгоритм решения задач на теплообмен: составление
«Дано» к задаче;
1.
из
условия задачи, определить количество «тел-участников» теплообмена, при этом
учитывать только те тела, о которых открыто говорится в условии;
2.
распределить
«тела» на 2 категории: отдающие тепло — «доноры», получающие — «получатели»;
3.
составить
таблицу, из двух основных колонок и озаглавить их в шапке таблицы «Доноры»
и «Получатели». При необходимости, если в теплообмене участвуют 3 и
более «тел-участников», каждую колонку дополнительно разбить на подколонки, по
количеству тел в каждой из вышеуказанных категорий. Каждую подколонку
обозначить названием соответствующего тела. [Замечание: в колонке
доноры, процессы охлаждения тел (t1>t2) описывать
формулой Q = cm(t1—t2)];
4.
пошагово
описать все процессы, произошедшие с каждым «телом-участником» в отдельности.
Очерёдность при этом значения не имеет. Описание каждого процесса завершать
написанием соответствующей формулы расчёта количества теплоты. Важно
(!): Не приступать к описанию процессов, произошедших со следующим
телом, до тех пор, пока не «разберётесь» с предыдущим;
5.
после
математического описания физических процессов, произошедших с каждым из
«тел-участников», под каждой из основных колонок в отдельности написать
выражения суммы количеств теплоты отданных «телами – донорами» и полученных
«телами-получателями».
6.
подставить
полученные в п.5 выражения сумм в уравнение теплового баланса в виде: Qполуч=Qотд.
7.
Решить
уравнение относительно искомой величины.
Решение задач по вышеуказанному алгоритму позволяет с большей вероятностью
рассчитывать на то, ученик на основе тщательного анализа условия задачи, к
которому он будет обращаться неоднократно в ходе составления таблицы, проследит
и математически опишет всю цепочку физических «превращений», не упуская в том
числе и скрытые, происходящие с каждым «телом-участником» теплообмена до
установления теплового равновесия. Это достигается за счет того, что учащийся
не распыляет внимание одновременно на все «тела-участники», а сосредотачивается
на каждом теле в отдельности.
Рассмотрим
несколько примеров:
Задача
1:
Кусок льда массой 500 г при начальной температуре -15°С положили в сосуд с
водой, начальная температура которой 10°С. После установления теплового
равновесия, температура системы стала равна 5°С. Найти массу воды, в сосуде
после установления теплового равновесия. Процесс считать теплоизолированным,
теплоемкость сосуда не учитывать.
Применим наш алгоритм.
Дано: m1=0,5 кг; t1= -15°C; t2= 10°C; t=5°C; св
= 4200 Дж/(кг °C);
сл = 2100 Дж/(кг °C); λл= 330 кДж/кг. Найти m.
Решение: Ясно,
что искомая масса воды в сосуде будет равна сумме начальной массы воды m0 и массы
льда m1. То есть m= m0+ m1. Следовательно
вся задача сводится к тому, чтобы найти m0.
Из условия видно, что «телами-участниками» здесь являются кусок льда
и вода в сосуде начальной массы m0, при этом
вода – донор, лёд – получатель тепла. Так как других тел нет, то
наша таблица будет состоять из двух колонок.
Составим
нашу таблицу:
|
Донор |
Получатель |
|
1.охлаждение |
1.нагревание Q2 = cлm1(tпл — t1) 2.Плавление 3.Нагревание |
|
Итак, |
|
|
Qотд =|Q1| |
Qполуч=Q2+Q3+Q4 |
|
|Q1|=Q2+Q3+Q4 Так как m0 входит в Отсюда искомая Вычисляем |
Задача
2.
Медный
чайник, в котором находится 2 литра воды при температуре 20С, поставили на керосиновый нагреватель.
Через некоторое время четверть объема воды выпарилось. Сколько керосина было
израсходовано, если КПД нагревателя 20%, а теплоемкость чайника 600 Дж/°С.
Решение:
Дано:
V1=2 л = 0,002
м3; t1=20°C; V2=0,25V1;
t2=100 °C; св
= 4200 Дж/(кг °C); ρв
= 1000 кг/м3; L = 2,3 МДж/кг;
Сч=600
Дж/°С, qк=46 МДж/кг
η = 20%. Найти mк -?
В
данной задаче «донором» тепла является керосин, выделяющий энергию при
сжигании, а «получателями» – чайник и вода.
Получаем
следующую таблицу:
|
Донор |
получатель |
|
|
керосин |
вода |
чайник |
|
1. Сгорание Q1 = qкmк |
1.нагревание
= 2.Кипение Q3 = Lmпара=LρвV2 |
1.
|
|
Учитывая, что |
Qполуч= Q2+Q3+Q4 |
|
|
Уравнение
Так как
Вычисляем |
Во всех рассмотренных задачах была известна температура
теплового равновесия (tобщ). Если же
она не известна, то в таких задачах необходимо понимать, что tобщ будет
иметь значение между минимальной (tmin) и максимальной (tmax) начальными
температурами «тел-участников» (tmin<tобщ
<tmax). Исходя
из этого, следует:
—
определить
– содержит ли температурный интервал от tmin до tmax «критические»
температуры (плавления (кристаллизации), кипения (конденсации))
«тел-участников»;
—
рассчитать
количества теплоты, которые «тела-участники»
могут получить (выделить) при нагревании (охлаждении) от начального состояния
до своих «критических температур»;
—
сравнить
эти количества теплоты и определить – какое из тел будет плавиться
(кристаллизоваться) или кипеть (конденсироваться).
—
по
вышеуказанному алгоритму решить задачу.
Например: если тело с большей начальной
температурой при охлаждении до своей «критической» температуры выделит количество
теплоты |Q1| больше теплоты Q2, необходимой
для нагревания тела с меньшей начальной температурой до своей «критической»
температуры, то, очевидно, второе тело будет плавиться (кипеть). Далее, следует
рассчитать количество теплоты Q3, необходимое
для полного плавления (превращения в пар) второго тела и снова сравнить |Q1| с Q1+Q3. Если |Q1| >
Q1+Q3 , то
второе тело полностью перейдёт в другое агрегатное состояние и продолжит
нагревание. Если же |Q1|<Q1+ Q3, то
изменять агрегатные состояния будут оба тела. Рассуждая
таким образом необходимо установить все цепочки тепловых процессов «тел-участников»
и определить tобщ.
21.11.2019
«Использование графического приема при решении задач на составление уравнения теплового баланса»
В работе описан приём, который использую в своей практической деятельности, при изучении тепловых явлений в 8-м и 10-м классах. Примеры и иллюстрации, приведённые в данном материале, позволяют продемонстрировать образцы решения задач на составление теплового баланса.
Оценить
465
Содержимое разработки
«Использование графического приема при решении задач на составление уравнения теплового баланса»
При решении задач на составление уравнения теплового баланса учащиеся нередко испытывают трудности и допускают ошибки. Даже простые задачи оказываются нерешенными.
При поиске решения данных проблем нужно учитывать два важных параметра:
Методы решения должны быть наглядными и универсальными;
Доступными для понимания и применения большинству учащихся непрофильных классов.
Данный прием позволяет научить различать процессы, сопровождающиеся выделением или поглощением теплоты, правильно записывать уравнение теплового баланса.
Как правило, учащиеся забывают учесть процессы, связанные с фазовыми переходами, происходящими при постоянной температуре.
Чтобы избежать подобных ошибок, по мере изучения материала вместе с учениками мы заполняем таблицу (таблица1), решаем пробные задачи и составляем алгоритм решения задач.
Название игры «ЧТО? ГДЕ? КОГДА?» превратилось в алгоритм решения задач:
«ЧТО ОТДАЕТ? ЧЕМУ ОТДАЕТ? СКОЛЬКО ОТДАЕТ?»
Анализируя задачу, учащиеся отвечают на три вопроса:
«Что» отдает тепло?
«Чему» отдается тепло?
Сколько» отдается тепла? (этот вопрос необходим при решении задач с учетом КПД установки)
Примерный алгоритм решения задач на расчет количества теплоты и составление уравнения теплового баланса
Внимательно прочитайте условие задачи. Выясните, какие тела участвуют в теплообмене; какие тела получают или отдают тепло.
Запишите условие задачи; используя справочные материалы найдите удельную теплоемкость, удельную теплоту плавления, удельную теплоту парообразования, температуру плавления, температуру кипения. Перейдите при необходимости в систему СИ.
Выясните, какие фазовые изменения происходят с телами (плавление или кристаллизация; кипение или конденсация) увеличивается температура тел или уменьшается.
На графике зависимости t(τ) на оси температур отметьте начальные и конечные температуры тел, а также температуру плавления(кристаллизации) или кипения (конденсации). В результате теплообмена у тел устанавливается общая температура. Укажите на графике температуру смеси.
Проведите пунктиром линию, соответствующую Θ– температуре смеси.
Постройте графики зависимости t(τ)для тел, помня о том, что температура охлаждающегося тела уменьшается и стремится к Θ, а температура нагревающегося тела увеличивается и тоже стремится кΘ.
Составьте уравнение теплового баланса. В одной части уравнения должна быть сумма количеств теплоты, которые тела отдают. Это процессы, расположенные выше пунктирной
линии, соответствующей температуре смеси. В другой части – сумма
количеств теплоты, которые тела получают в процессе теплообмена; эти процессы, находятся ниже пунктирной линии.
Решите данное уравнение. Запишите полученный ответ.
Таблица 1
Используя таблицу, учащиеся легко ориентируются в тепловых процессах, происходящих с телами. Красным цветом выделяем процессы, связанные с увеличением температуры тела и его внутренней энергии. Синим цветом – уменьшение температуры и внутренней энергии тела.
Решая задачу, учащиеся строят график изменения температуры тела с течением времени, указывая начальные и конечные температуры тел, а также называя процессы, происходящие с телами.
Приведу примеры решения следующих задач.
Задача № 1
Какое количество теплоты потребуется для плавления 1,5 кг цинка, взятого при температуре 20 ОС? (рисунок 1)
Задача №2
Какое количество теплоты выделится при охлаждении 200 г водяного пара, взятого при температуре 100оС до температуры 20оС? (рисунок 2)
Задача № 3
В сосуд, содержащий 500г воды при 16оС, впускают 75 г водяного пара при температуре 100оС, который обращается в воду. Какая температура установится в сосуде? Теплоемкостью сосуда пренебречь. Ответ дать по шкале Цельсия с точностью до десятых. (рисунок 3)
Задача №4
Расплавленный алюминий массой 1,2 кг, взятый при температуре плавления, влили в воду, масса которой 2,1 кг и температура 16оС. Определите, какое количество воды при этом выкипит. (рисунок 4)
Задача №5.
Для охлаждения лимонада массой 200г в него бросают кубики льда при температуре 0оС. Масса каждого кубика 8 г. Чему равна первоначальная температура лимонада, если установилась температура 15оС после того, как в него бросили 4 кубика? Удельная теплоемкость лимонада равна удельной теплоемкости воды. Тепловыми потерями пренебречь.
(рисунок 5)
Задачи для самостоятельного решения
Какое количество теплоты потребуется для того, чтобы вскипятить в алюминиевом чайнике массой 700 г 2 л воды? Начальная температура воды 20оС. (723,5 кДж)
В кокиль залили 50 кг расплавленного железа при температуре плавления. Какое количество теплоты выделится при его охлаждении до 39оС. (48 МДж)
В холодильнике изготовили 750 см3 льда при температуре (– 5оС). Сколько энергии было отведено от воды и льда при этом, если начальная температура воды 15оС? (≈ 279 кДж)
Кусок свинца, имеющий начальную температуру 27оС, нагревают до температуры плавления за 10 мин. Через какое время он весь расплавится? (6 мин)
Смешали 39 л воды при 20оС и 21 л при 60оС. Определите температуру смеси. (34оС)
Чтобы охладить выточенную из меди деталь, имеющую температуру 100оС, ее погрузили в воду массой 420 г с температурой 15оС. Определите массу детали, если известно, что в процессе теплообмена вода нагрелась до 18оС. (160 г)
Для приготовления ванны вместимостью 200 л смешали холодную воду при температуре 10оС с горячей водой при температуре 60оС. Какие объемы той и другой воды надо взять, чтобы температура воды установилась 40оС? (80 л, 120 л)
После опускания в воду, имеющую температуру 10оС, тела, нагретого до 100оС, через некоторое время установилась общая температура 40оС. Какой станет температура воды, если, не вынимая первого тела, в нее опустить еще одно такое же тело, нагретое до 100оС. (55оС)
В углубление, сделанное во льду, взятом при температуре 0оС, положили кусок олова массой 66 г при температуре 110оС. Какая масса льда растает? (5 г)
Требуется пропусканием пара нагреть 80 л воды, взятой при температуре 6оС, до 35оС. Какое количество 100-градусного пара потребуется для этого? (3,8 кг)
Девочка налила в чайник 3 л воды, начальная температура которой 20оС, и поставила его на газовую горелку. Через некоторое время она обнаружила, что вода в чайнике уже кипит, причем треть воды выкипела. Во сколько раз израсходованное количество теплоты больше того, что необходимо было для доведения воды до кипения? (≈3,3 раза)
В сосуде, из которого быстро откачивают воздух, находится небольшое количество воды при температуре 0оС. В результате интенсивного испарения происходит замораживание воды. Какая часть первоначального количества воды обратилось в лед? Удельная теплота парообразования воды при 0оС равна 2,5 МДж/кг. (0,88)
Литература
Л.А. Кирик. Физика 8, самостоятельные и контрольные работы. М: «Илекса», 2010.
Ю.С. Куперштейн, Е.А. Марон. Контрольные работы по физике, 7-9 класс. С-П: «Специальная литература»,1998.
В.И. Лукашик, Е.В. Иванова. Сборник задач по физике, 7-9 класс. М: «Просвещение»,2017
А.П. Рымкевич. Сборник задач по физике, 10-11 класс. М: «Дрофа», 2019.
Г.Н. Степанова. Сборник вопросов и задач по физике, 7-8 класс. С-П: «Специальная литература»,2003.
Материалы ЕГЭ, ФИПИ
8
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/383308-ispolzovanie-graficheskogo-priema-pri-resheni

«Свидетельство участника экспертной комиссии»
Оставляйте комментарии к работам коллег и получите документ
БЕСПЛАТНО!
Технологическая карта урока физики в 8 классе.
Урок:
Решение задач по теме:
«Способы расчета количества теплоты, необходимого для плавления вещества».
Тип урока: урок рефлексии и развивающего контроля.
Используемые технологии: здоровьесбережения, информационно—
коммуникационные, уровневой дифференциации, игрового обучения, развития
критического мышления.
Цель урока: закрепить знания учащихся о способах расчета количества теплоты,
необходимого для плавления вещества, о методах решения графических задач.
Формируемые УУД: предметные: научиться выполнять расчеты для
нахождения удельной теплоты плавления, количества теплоты, необходимого для
плавления тела или выделяемого им при отвердевании; описывать тепловые
характеристики веществ на основе графических данных; пользоваться справочными
таблицами;
метапредметные: выполнять действия по образцу,
оценивать и корректировать их; создавать, анализировать и перерабатывать
информацию, представленную в виде таблиц, набора символов; искать информацию;
применять полученные знания для решения задач; овладеть навыками организации
учебной деятельности, самоконтроля и оценки результатов;
личностные: формирование целостного
мировоззрения, соответствующего современному уровню развития науки и
общественной практики; развитие интеллектуальных способностей учащихся.
Приборы и материалы: справочные таблицы «Удельная теплоемкость»,
«Удельная теплота сгорания топлива», «Температура плавления и кристаллизации»,
«Удельная теплота плавления».
Что должен знать обучающийся:
— Знать обозначения физических величин: количества теплоты, удельная теплоёмкость,
удельная теплота плавления, удельная теплота сгорания топлива.
— Знать единицы измерения физических величин: количества теплоты, удельная
теплоёмкость, удельная теплота плавления, удельная теплота сгорания топлива.
— Знать формулы расчёта количества теплоты в процессах: плавления, сгорания
топлива, нагревания.
Что должен уметь обучающийся:
— уметь выделять составные части задачи, дополнять условие задачи, ставить вопросы
к условию задачи;
— уметь при решении задач находить величины.
Развитие УУД познавательные: уметь формулировать проблемы;
самостоятельно создавать способы решения заданий;
коммуникативные: уметь слушать и вступать в
диалог; участвовать в коллективном обсуждении; осуществлять взаимопроверку;
регулятивные: уметь организовывать свое
рабочее место и приводить его в порядок по окончании работы.
Есть тут те, кто хочет научиться решать задачи и щелкать их, как орешки? Наш совет: практикуйтесь с различными заданиями побольше! А мы поможем и в этой статье дадим вам несколько примеров решения задач на тему «расчет количества теплоты».
Подписывайтесь на наш телеграм-канал, чтобы не только решать задачи, но и просто быть в курсе актуальных новостей студенческой жизни.
Задачи на количество теплоты
Для начала, запомним, что количество теплоты обозначается буквой Q. Кроме того, не забываем держать под рукой общую памятку по решению физических задач и список полезных формул. Но сначала, конечно же, читаем теорию в старых советских учебниках или в нашем отдельном материале по термодинамике.
Задача №1. Нахождение количества теплоты
Условие
Водород массой 20 г был нагрет на 100 градусов Цельсия при постоянном давлении. Найти количество теплоты, переданное газу.
Решение
Будем использовать первое начало термодинамики, согласно которому:
Изменение внутренней энергии дельта U вычисляется по формуле (газ считаем двухатомным):
Работа газа при изобарном процессе равна:
Теперь можно вычислить количество теплоты:
Ответ: 29085 Дж.
Задача №2. Количество теплоты, пример цикла Карно
Условие
В ходе цикла Карно рабочее вещество совершает работу, равную 113333 Дж. Температуры нагревателя и холодильника соответственно равны 450 К и 280 К. Какое количество теплоты рабочее тело получает от нагревателя в ходе цикла?
Решение
По определению, КПД цикла Карно:
Можно записать:
Ответ: 300 кДж.
Задача №3. Расчет количества теплоты, теплоемкость
Условие
Определить количество теплоты, необходимое для нагревания 4 литров воды в алюминиевой кастрюле массой 500 г от 30 градусов Цельсия до кипения.
Решение
Это типичная задача на вычисление количества теплоты. Искомое количество теплоты складывается из количества теплоты для нагревания кастрюли и количества теплоты, которое пойдет на нагревание воды. Запишем уравнение теплового баланса:
Запишем выражения для количества теплоты и массы воды:
Вычислим, пользуясь табличными значениями для теплоемкостей:
Ответ: 1380,8 кДж
Задача №4. Молярная теплоемкость вещества
Условие
Вычислить молярные теплоёмкости газа, масса киломоля которого равна M = 30 г/моль, а отношение теплоёмкостей (Cp/Cv) = γ = 1,4.
Решение
Молярная теплоёмкость газа при p = const находится из уравнения Майера:
Молярная теплоёмкость газа при V = const находится из выражения:
Первое выражение можно переписать в виде:
Здесь R – универсальная газовая постоянная, R=8,31 Дж/(К* моль).
Ответ: 29,085 Дж/(К*моль); 20,775 Дж/(К*моль).
Задача №5. Количество теплоты
Условие
На сколько градусов изменилась температура чугунной детали массой 12 кг, если при остывании она отдала 648 кДж теплоты?
Решение
Это простая задача, которая решается в одно действие:
Ответ: 100 градусов Цельсия.
Кстати! Для всех наших читателей действует скидка 10% на решение задач по физике на количество теплоты и любые другие виды работ.
Вопросы по теме «количество теплоты»
Вопрос 1. В чем измеряется количество теплоты?
Ответ. В системе СИ единицей измерения количества теплоты является 1 Джоуль.
Теплота – это мера энергии, которая передается при теплообмене, поэтому она измеряется в тех же единицах.
Существуют также внесистемные и широко применяемые единицы измерения количества теплоты:
- калория;
- килокалория.
1 калория равна 4,19 Дж.
Объясним на примере, как рассчитывают количество теплоты. Допустим, есть брусок из какого-то вещества, который нагревают от температуры Т1 до температуры Т2. Количество теплоты, которое для этого нужно, можно определить по формуле:
Здесь с – удельная теплоемкость вещества
Вопрос 2. Что такое теплоемкость?
Ответ. По определению:
Теплоемкость – это скалярная физическая величина, которая показывает, какое количество теплоты нужно сообщить телу, чтобы нагреть его на один градус.
Удельная теплоемкость – это теплоемкость, отнесенная к единице массы. Именно значения удельной теплоемкости указаны в таблицах. Например, удельная теплоемкость воды равна 4200 Дж/(К*кг). Это значит, что для нагрева одного килограмма воды на один градус понадобится 4200 Джоулей.
Вопрос 3. Какие есть единицы измерения температуры?
Ответ. В системе СИ температура измеряется в Кельвинах. В быту мы привыкли к шкале Цельсия, которая наряду со шкалой Кельвина применяется в системе СИ. Также широко известна температурная шкала Фаренгейта, используемая в Англии и США.
Связь между температурой в Кельвинах и Цельсиях можно выразить формулой:
Температура кипения воды по шкале Фаренгейта равна 212 градусам, а лед тает при 32 градусах по Фаренгейту. Один градус Фаренгейта равен 1/180 разности этих температур.
Вопрос 4. Дайте определение температуры:
Ответ. Температура – это физическая величина, характеристика термодинамической системы, описывающая степень нагретости тел.
Вопрос 5. Какие виды теплопередачи вы знаете?
Ответ. Есть следующие виды теплопередачи:
- Теплопроводность – переход теплоты от более нагретых участков твердых тел к более холодным.
- Конвекция – передача теплоты потоками газа или жидкости.
- Излучение – теплота передается посредством электромагнитных волн.
Кстати, если у вас есть какой-то вопрос, вы всегда можете задать его в комментариях или обратиться за помощью к специалистам профессионального студенческого сервиса, которые всегда смогут вычислить удельную теплоемкость и рассчитать количество теплоты при теплообмене.
Пособие рекомендовано учащимся, желающим
получить практические навыки в решении задач на
теплообмен, и может быть полезным для учителей и
абитуриентов.
При соприкосновении тел, имеющих разные
температуры, между этими телами происходит
теплообмен. С точки зрения
молекулярно-кинетической теории, это
объясняется так: молекулы более нагретого тела
имеют большую кинетическую энергию, чем молекулы
тела, менее нагретого. При “столкновениях”
молекул соприкасающихся тел происходит процесс
выравнивания их средних кинетических энергий.
Молекулы более нагретого тела теряют часть своей
кинетической энергии, при этом нагретое тело
будет остывать. Кинетическая энергия молекул
холодного тела возрастает, поэтому температура
этого тела будет увеличиваться. В конечном итоге
кинетические энергии молекул обоих тел
сравняются, и температуры тел станут
одинаковыми. На этом теплообмен прекращается.
Энергию, которую тело получает или отдаёт в
процессе теплообмена, называют количеством
теплоты (Q).
Количество теплоты, как и все другие виды
энергии, измеряется в системе СИ в Джоулях: [Q] = Дж.
(Здесь и в дальнейшем единицы измеряются в
системе СИ.)
Нагревание или охлаждение
При нагревании или охлаждении тела количество
теплоты, поглощаемое или выделяемое им,
рассчитывается по формуле:
Q = сm(t2 – t1), (1)
где m – масса тела, кг;
(t2 – t1) – разность температур
тела,° С (или К);с – удельная теплоёмкость вещества, из
которого состоит тело,
Удельная теплоёмкость вещества – это
количество теплоты, которое нужно сообщить
одному килограмму данного вещества, чтобы
увеличить его температуру на 1° С (или это
количество теплоты, которое выделяет один
килограмм данного вещества, остывая на 1° С).
Значения удельных теплоемкостей других
веществ можно найти в справочниках, а также в
школьном учебнике или задачнике.
При нагревании тела его внутренняя энергия
увеличивается. Это требует притока энергии к
телу от других тел. Значит, оно поглощает
некоторое количество теплоты, принимая его от
других тел, участвующих в теплообмене.
При охлаждении тела его внутренняя энергия
уменьшается. Поэтому остывающее тело отдаёт
кому-либо некоторое количество теплоты.
Обычно конечную температуру, установившуюся в
результате теплообмена, обозначают греческой
буквой (тэта).
В формуле (1) произведение cm для каждого
конкретного тела есть величина постоянная. Её
называют теплоёмкостью тела и обозначают С:
C = c m.(2)
Размерность теплоемкости: Теплоемкость тела показывает,
сколько энергии нужно подвести к данному телу,
чтобы нагреть его на 1° С (или сколько энергии
выделяет это тело, остывая на 1° С).
Теплообмен между телами, имеющими одинаковые
температуры, не происходит, даже если
контактируют вещества, находящиеся в разных
агрегатных состояниях. Например, при температуре
плавления (0° С) лёд и вода могут находиться
бесконечно долго, при этом количество льда и
количество воды останутся неизменными.
Аналогично ведут себя пар и жидкость,
находящиеся при температуре кипения. Теплообмен
между ними не происходит.
Плавление или кристаллизация
Если при нагревании тела его температура
достигнет температуры плавления, то начинает
происходить процесс перехода этого вещества из
твердого состояния в жидкое. При этом идут
изменения в расположении и характере
взаимодействия молекул. Температура при
плавлении не изменяется. Это означает, что
средние кинетические энергии молекул жидкости и
твердого тела при температуре плавления
одинаковы. Однако внутренняя энергия тела при
плавлении возрастает за счет увеличения энергии
взаимодействия молекул. Количество теплоты,
поглощаемое телом при плавлении, рассчитывается
по формуле
(3)
где m – масса тела, кг;
–
удельная теплота плавления,
При кристаллизации, наоборот, внутренняя
энергия тела уменьшается на величину и эта теплота данным
телом выделяется. Она поглощается другими
телами, участвующими в теплообмене.
Удельная теплота плавления показывает,
сколько энергии нужно сообщить одному
килограмму данного вещества, взятого при
температуре плавления, чтобы полностью
превратить его при этой температуре в жидкость
(или сколько энергии выделяет 1 кг жидкости,
взятой при температуре кристаллизации, если вся
она при этой температуре полностью превратится в
твёрдое тело).
Удельную теплоту плавления любого вещества
можно найти в справочниках. Для льда же
Температура плавления у каждого вещества своя.
Её также можно найти в справочниках. Важно
подчеркнуть, что температура плавления вещества
равна температуре кристаллизации этого же
вещества. У льда tпл = 0° С.
Кипение или конденсация
При достижении жидкостью температуры кипения
начинает происходить другой фазовый переход –
кипение, при котором расстояния между молекулами
значительно увеличиваются, а силы
взаимодействия молекул уменьшаются. Вся
подводимая к жидкости теплота идет на разрыв
связей между молекулами. При конденсации пара в
жидкость, наоборот, расстояния между молекулами
значительно сокращаются, а силы взаимодействия
молекул увеличиваются. Для кипения жидкости
энергию к жидкости нужно подводить, при
конденсации пара энергия выделяется. Количество
теплоты, поглощаемое при кипении или выделяемое
при конденсации, рассчитывается по формуле:
где m – масса тела, кг; L – удельная
теплота парообразования,
Удельная теплота парообразования
показывает, сколько энергии нужно сообщить
одному килограмму жидкости, взятой при
температуре кипения, чтобы при этой температуре
полностью превратить её в пар (для конденсации:
сколько энергии выделяет один килограмм пара,
взятого при температуре конденсации, полностью
превращаясь в жидкость).
При одинаковом давлении температура кипения и
температура конденсации одного и того же
вещества одинаковы.
Температуры кипения и удельные теплоты
парообразования также можно найти в
справочниках. Для воды же они соответственно
равны: рис. 9 (при нормальном атмосферном
давлении).
Уравнение теплового баланса
Тела, участвующие в теплообмене, представляют
собой термодинамическую систему.
Термодинамическая система называется теплоизолированной,
если она не получает энергию извне и не отдаёт её;
теплообмен происходит только между телами,
входящими в эту систему. Для любой
теплоизолированной системы тел справедливо
следующее утверждение: количество теплоты,
отданное одними телами, равно количеству
теплоты, принимаемому другими телами.
Qотд. = Qполуч. (5)
Это утверждение описывает частный случай
закона сохранения и превращения энергии в
применении к процессу теплообмена. А формула (5)
является одним из видов уравнения теплового
баланса.
При решении задач с помощью данного вида
уравнения теплового баланса в формуле (1) в
качестве t2 следует брать большую
температуру, а в качестве t1 – меньшую.
Тогда разность (t2 – t1) будет
положительна и всё произведение cm(t2–t1)
также будет положительным. Все теплоты, отданные
и полученные, будут положительными.
Уравнение теплового баланса можно записать и в
таком виде:
Q1+ Q2+…+ Qn= 0, (6)
где n – количество тел системы.
Алгебраическая сумма всех количеств теплоты
(поглощенных и выделенных) в теплоизолированной
системе равна нулю.
Q1, Q2, …, Qn – это теплоты,
поглощаемые или выделяемые участниками
теплообмена. Очевидно, что в этом случае какие-то
теплоты должны быть положительны, а какие-то –
отрицательны. При записи уравнения теплового
баланса в виде (6) всегда t2 – конечная
температура, а t1 – начальная.
Если тело нагревается, то разность (t2 – t1)
положительна и все произведение cm(t2 – t1)
положительно. То есть Q > 0 тогда, когда теплота к
данному телу подводится.
А если t2 < t1 (тело остывает), то
разность (t2 – t1) отрицательна, то есть
Q < 0. В этом случае тело энергию выделяет.
Если при фазовом переходе энергия к телу
подводится (плавление, кипение), то Q > 0; если
тело выделяет энергию (кристаллизация,
конденсация), то Q < 0.
В принципе уравнения (5) и (6) равносильны.
Результат решения задачи не зависит от того,
каким видом уравнения пользуемся. Выбор способа
решения – за читателем.
Применим уравнение теплового баланса для
решения ряда задач (здесь приводим лишь одну
задачу, остальные материалы можно найти по
адресу http:// kirov-festival.nm.ru).
Задача 1
В медном калориметре массой 100 г находится 1 кг
воды при температуре 20° С. В воду опускают
свинцовую деталь массой 2 кг, имеющую температуру
90° С. До какой температуры нагреется вода? (В этой
и последующих задачах потерями теплоты в
калориметре пренебречь.)
Решение
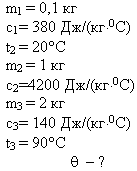 |
Проведём анализ:
Вода и калориметр При опускании в воду с температурой 20° С |
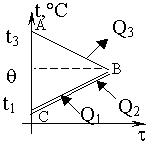 |
Изменение температур тел с течением времени удобно изображать на графике зависимости t(t ). Отрезок АВ соответствует |
| Два параллельных отрезка СВ соответствуют графикам изменения температур калориметра и воды. Стрелки, идущие к ним, показывают, что для нагревания калориметра и воды требуется энергия Q1 и Q2, которую они поглощают. |
|
| Решим задачу с использованием уравнения теплового баланса в виде (5): |
Решим задачу с использованием уравнения
теплового баланса в виде (6):
Ответ: Вода нагреется до 24° С.
Предлагаю читателю самостоятельно сделать
проверку размерности.
Напомним, остальной материал (полноценную
версию пособия) можно найти по адресу http:// kirov-festival.nm.ru.
Вы познакомились с понятиями количества теплоты и удельной теплоемкости. В уроке «Расчет количества теплоты, необходимого для нагревании тела или выделяемого им при охлаждении» вы познакомились с основной формулой, которую мы будем использовать и в этом уроке:
$Q = cm(t_2 — t_1)$
В данном уроке мы рассмотрим задачи на нахождение различных величин, связанных с нагреванием и охлаждением тел. При их решении вам может понадобиться таблица значений удельной теплоемкости различных веществ из прошлого урока.
Задача №1 на расчет количества теплоты
Рассчитайте количество теплоты, необходимое для нагрева $15 space кг$ меди на $80 degree C$.
Дано:
$m = 15 space кг$
$c = 400 frac{Дж}{кг cdot degree C}$
$Delta t = 80 degree C$
$Q — ?$
Показать решение и ответ
Скрыть
Решение:
Для решения этой задачи мы будем использовать формулу для расчета количества теплоты, необходимого для нагревания тела:
$Q = cm(t_2 — t_1)$.
В данном случае нам не известны начальная и конечная температуры тела ($t_2$ и $t_1$). Нам известно изменение этой температуры: $Delta t = t_2 — t_1$. Тогда формула для расчета количества теплоты примет вид:
$Q = cm Delta t$.
Подставим значения всех величин и рассчитаем количество теплоты:
$Q = 400 frac{Дж}{кг cdot degree C} cdot 15 space кг cdot 80 degree C = 480 space 000 space Дж = 480 space кДж$.
Ответ: $Q = 480 space кДж$.
Задача №2 на расчет количества теплоты
Рассчитайте количество теплоты, необходимое, чтобы нагреть бассейн объемом $300 space м^3$ на $10 degree C$.
В задаче идет речь о бассейне, а значит, о пресной воде. Она имеет плотность, равную $1000 frac{кг}{м^3}$. Запишем условия задачи и решим ее.
Дано:
$V = 300 space м^3$
$Delta t = 10 degree C$
$c = 4200 frac{Дж}{кг cdot degree C}$
$rho = 1000 frac{кг}{м^3}$
$c = 4200 frac{Дж}{кг cdot degree C}$
$Q — ?$
Показать решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела:
$Q = cm(t_2 — t_1)$.
Нам неизвестна масса воды в бассейне, но известен ее объем и плотность. Плотность по определению:
$rho = frac{m}{V}$.
Тогда масса будет равна:
$m = rho V$.
Также нам неизвестны начальная и конечная температуры тела ($t_2$ и $t_1$). Нам известно изменение этой температуры: $Delta t = t_2 — t_1$. Тогда формула для расчета количества теплоты примет вид:
$Q = c rho V Delta t$.
Рассчитаем количество теплоты:
$Q = 4200 frac{Дж}{кг cdot degree C} cdot 1000 frac{кг}{м^3} cdot 300 space м^3 cdot 10 degree C = 12.6 cdot 10^9 space Дж = 12.6 space ГДж$.
Ответ: $Q = 12.6 space ГДж$.
Задача №3 на расчет массы
Найдите массу глицерина, если при нагревании от $10 degree C$ до $15 degree C$ он поглотил $12 space кДж$ теплоты. Удельная теплоемкость глицерина равна $2430 frac{Дж}{кг cdot degree C}$.
Дано:
$Q = 12 space кДж$
$t_1 = 10 degree C$
$t_2 = 15 degree C$
$c = 2430 frac{Дж}{кг cdot degree C}$
СИ:
$Q = 12 cdot 10^3 space Дж$
$m — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела:
$Q = cm(t_2 — t_1)$.
Выразим отсюда массу глицерина:
$m = frac{Q}{c(t_2 — t_1)}$.
Рассчитаем:
$m = frac{12 cdot 10^3 space Дж}{2430 frac{Дж}{кг cdot degree C} cdot (15 degree C — 10 degree C)} approx 1 space кг$.
Ответ: $m approx 1 space кг$.
Задача №4 на расчет плотности
Определите плотность машинного масла объемом $1 space л$, если известно, что для увеличения температуры на $30 degree C$ ему требуется передать $45 space кДж$ теплоты. Удельная теплоемкость масла равна $1.67 frac{кДж}{кг cdot degree C}$.
Дано:
$V = 1 space л$
$Q = 45 space кДж$
$c = 1.67 frac{кДж}{кг cdot degree C}$
$Delta t = 30 degree C$
СИ:
$V = 10^{-3} space м^3$
$Q = 45 cdot 10^3 space Дж$
$c = 1.67 cdot 10^3 frac{Дж}{кг cdot degree C}$
$rho — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела:
$Q = cm(t_2 — t_1)$.
Нам известны изменение температуры ($Delta t = t_2 — t_1$), количество теплоты и удельная теплоемкость машинного масла. Выразим массу и рассчитаем ее:
$m = frac{Q}{c Delta t} = frac{45 cdot 10^3 space Дж}{1.67 cdot 10^3 frac{Дж}{кг cdot degree C} cdot 30 degree C} approx 0.9 space кг$.
По определению плотности:
$rho = frac{m}{V}$.
Рассчитаем плотность машинного масла:
$rho = frac{0.9 space кг}{10^{-3} space м^3} = 0.9 cdot 10^3 frac{кг}{м^3} = 900 frac{кг}{м^3}$.
Ответ: $rho = 900 frac{кг}{м^3}$.
Задача №5 на расчет удельной теплоемкости
В калориметр было налито $450 space г$ воды, температура которой $20 degree C$. Когда в эту воду погрузили $200 space г$ железных опилок, нагретых до $100 degree C$, температура воды стала равна $24 degree C$. Определите удельную теплоемкость опилок.
Записывая условия задачи, используем индекс “в” для обозначения величин, связанных с водой, и индекс “ж” для обозначения величин, связанных с железными опилками.
Дано:
$m_в = 450 space г$
$m_ж = 200 space г$
$t_{в1} = 20 degree C$
$t_{в2} = 24 degree C$
$c_в = 4200 frac{Дж}{кг cdot degree C}$
$t_{ж1} = 100 degree C$
СИ:
$m_в = 0.45 space кг$
$m_ж = 0.2 space кг$
$с_ж — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела и выделяемого при его охлаждении:
$Q = cm(t_2 — t_1)$.
Запишем эту формулу для воды:
$Q_в = c_в m_в (t_{в2} — t_{в1})$.
Запишем формулу количества теплоты для железных опилок:
$Q_ж = c_ж m_ж (t_{ж2} — t_{ж1})$.
Нагретые железные опилки помещают в воду для их охлаждения. Значит, вода будет нагреваться и поглотит некоторое количество теплоты, а опилки будут охлаждаться и выделят некоторое количество теплоты. Т.е., между этими телами будет происходить теплообмен, для которого действует уже известное вам правило:
Если между телами происходит теплообмен, то внутренняя энергия всех нагревающихся тел увеличивается на столько, на сколько уменьшается внутренняя энергия остывающих тел.
Это значит, что количество теплоты $Q_в$, полученное водой, будет равно количеству теплоту $Q_ж$, которое выделится при охлаждении железных опилок, но с обратным знаком: $Q_в = — Q_ж$.
Подставим выражения, которые дает формула для расчета количества теплоты:
$c_в m_в (t_{в2} — t_{в1}) = — c_ж m_ж (t_{ж2} — t_{ж1})$.
После завершения теплообмена температура воды и температура железных опилок будут равны друг другу: $t_в2 = t_ж2 = t_2$.
Подставим в наше равенство и выразим $c_ж$:
$c_ж = — frac{c_в m_в (t_2 — t_{в1})}{m_ж (t_2 — t_{ж1})}$.
Рассчитаем удельную теплоемкость железных опилок:
$c_ж = — frac{4200 frac{Дж}{кг cdot degree C} cdot 0.45 space кг cdot (24 degree C — 20 degree C)}{0.2 space кг cdot (24 degree C — 100 degree C)} = — frac{7560 space Дж}{- 15.2 space кг cdot degree C} approx 497 frac{Дж}{кг cdot degree C} approx 0.5 frac{кДж}{кг cdot degree C}$.
Ответ: $c_ж approx 0.5 frac{кДж}{кг cdot degree C}$.
Задача №6 на использование графика
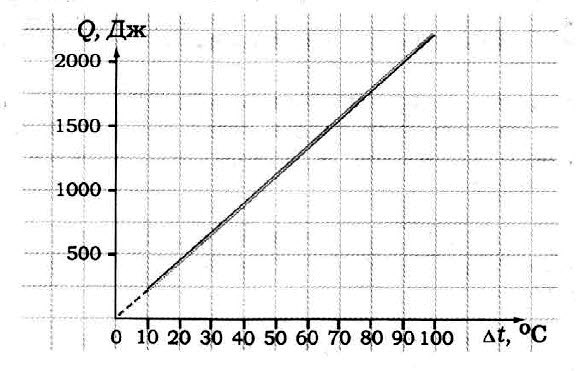
Используя график зависимости температуры керосина от сообщенного ему количества теплоты (рисунок 1), определите массу керосина.
Для начала нам нужно записать условия задачи. Из графика мы видим, что начальная температура керосина $t_1$ была равна $0 degree C$. Теперь выберем удобную нам точку на графике. Например, когда керосину сообщили количество теплоты $Q$, равное $2 space кДж$, его температура $t_2$ стала равной $10 degree C$. Теперь мы можем записать условия задачи и решить ее. Удельная теплоемкость керосина известна нам из таблицы.
Дано:
$Q = 2 space кДж$
$t_1 = 0 degree C$
$t_2 = 10 degree C$
$c = 2100 frac{Дж}{кг cdot degree C}$
СИ:
$Q = 2 cdot 10^3 space Дж$
$m — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела:
$Q = cm(t_2 — t_1)$.
Выразим отсюда массу:
$m = frac{Q}{c (t_2 — t_1)}$.
Рассчитаем ее:
$m = frac{2 cdot 10^3 space Дж}{2100 frac{Дж}{кг cdot degree C} cdot (10 degree C — 0 degree C)} approx 0.095 space кг approx 100 space г$.
Ответ: $m approx 100 space г$.
Задача №7 на расчет температуры нагрева
Стальной резец массой $2 space кг$ был нагрет до температуры $800 degree C$ и затем опущен в сосуд, содержащий $15 space л$ воды при температуре $10 degree C$. До какой температуры нагреется вода в сосуде?
Записывая условия задачи, используем индекс “в” для обозначения величин, связанных с водой, и индекс “р” для обозначения величин, связанных со стальным резцом.
Дано:
$V_в = 15 space л$
$m_р = 2 space кг$
$t_{р1} = 800 degree C$
$c_р = 500 frac{Дж}{кг cdot degree C}$
$rho_в = 1000 frac{кг}{м^3}$
$c_в = 4200 frac{Дж}{кг cdot degree C}$
$t_{в1} = 10 degree C$
СИ:
$V_в = 15 cdot 10^3 м^3$
$t_{в2} — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Когда нагретый резец опускают в холодную воду, между этими двумя телами происходит теплообмен. Резец остывает и выделяет энергию, а вода получает эту энергию и нагревается. Соответственно, количество теплоты, которое выделится при остывании стального резца, численно будет равно количеству теплоту, которое получит вода.
Когда теплообмен завершится,температуры стального резца и воды будут одинаковы: $t_{в2} = t_{р2} = t_2$.
Запишем формулу для расчета количества теплоты, которое выделится при остывании резца:
$Q_р = с_р m_р (t_2 — t_{р1})$.
Запишем формулу для расчета количества теплоты, которое получила вода:
$Q_в = с_в m_в (t_2 — t_{в1})$.
Приравняем правые части этих уравнений, не забыв про знак “минус”, которые указывает на выделение энергии при охлаждении тела:
$с_р m_р (t_2 — t_{р1}) = — с_в m_в (t_2 — t_{в1})$.
Раскроем скобки:
$с_р m_р t_2 — с_р m_р t_{р1} = — с_в m_в t_2 + с_в m_в t_{в1}$.
Перенесем множители с $t_2$ на одну сторону уравнения и выразим эту температуру, до которой нагреется вода:
$с_р m_р t_2 + с_в m_в t_2 = с_в m_в t_{в1} + с_р m_р t_{р1}$,
$t_2 (с_р m_р + с_в m_в) = с_в m_в t_{в1} + с_р m_р t_{р1}$,
$t_2 = frac{с_в m_в t_{в1} + с_р m_р t_{р1}}{с_р m_р + с_в m_в}$.
Нам неизвестна масса воды, но известны ее плотность и объем. Выразим и рассчитаем массу через эти величины:
$m_в = rho_в V_в = 1000 frac{кг}{м^3} cdot 15 cdot 10^3 м^3 = 15 space кг$.
Теперь мы можем рассчитать температуру $t_2$:
$t_2 = frac{4200 frac{Дж}{кг cdot degree C} cdot 15 space кг cdot 10 degree C + 500 frac{Дж}{кг cdot degree C} cdot 2 space кг cdot 800 degree C}{500 frac{Дж}{кг cdot degree C} cdot 2 space кг + 4200 frac{Дж}{кг cdot degree C} cdot 15 space кг} = frac{630 cdot 10^3 space Дж + 800 cdot 10^3 space Дж}{1 cdot 10^3 frac{Дж}{degree C} + 63 cdot 10^3 frac{Дж}{degree C}} = frac{1430 cdot 10^3 space Дж}{64 cdot 10^3 frac{Дж}{degree C}} approx 22.3 degree C$.
Ответ: $t_2 approx 22.3 degree C$.
Какой температуры получится вода, если смешать $0.02 space кг$ воды при $15 degree C$, $0.03 space кг$ воды при $25 degree C$ и $0.01 space кг$ воды при $60 degree C$?
Дано:
$m_1 = 0.02 space кг$
$t_1 = 15 degree C$
$m_2 = 0.03 space кг$
$t_2 = 25 degree C$
$m_3 = 0.01 space кг$
$t_3 = 60 degree C$
$t — ?$
Посмотреть решение и ответ
Скрыть
Решение:
При смешивании жидкостей разных температур, мы знаем, что внутренняя энергия всех нагревающихся тел увеличивается на столько, на сколько уменьшается внутренняя энергия остывающих тел.
Для смешивания двух жидкостей мы можем записать, что $Q_1 = — Q_2$ или $Q_1 + Q_2 = 0$.
Сначала рассмотрим смешивание первых двух порций воды. Первая порция с температурой $15 degree C$ будет нагреваться (получать энергию), а вторая порция с температурой $25 degree C$ будет охлаждаться (выделять энергию). Эти энергии будут численно равны друг другу, но противоположны по знаку:
$cm_1(t_{1+2} — t_1) = — cm_2(t_{1+2} — t_2)$.
Найдем конечную температуру этой смеси:
$m_1(t_{1+2} — t_1) = — m_2 (t_{1+2} — t_2)$,
$m_1 t_{1+2} — m_1 t_1 = -m_2 t_{1+2} + m_2 t_2$,
$t_{1+2} (m_1 + m_2) = m_1 t_1 + m_2 t_2$,
$t_{1+2} = frac{m_1 t_1 + m_2 t_2}{m_1 + m_2} = frac{0.02 space кг cdot 15 degree C + 0.03 space кг cdot 25 degree }{0.02 space кг + 0.03 space кг} = frac{0.3 space кг cdot degree + 0.75 space кг cdot degree C}{0.05 space кг} = 21 degree C$.
Так мы получили смесь первой и второй порций воды массой $m_{1+2} = 0.05 space кг$ и температурой $t_{1+2} = 21 degree C$.
Теперь добавим третью порцию воды в полученную смесь. Смесь будет нагреваться (получать энергию), а третья порция воды будет охлаждаться (выделять энергию):
$Q_{1+2} = — Q_3$.
$cm_{1+2} (t — t_{1+2}) = — cm_3 (t — t_3)$,
$m_{1+2} (t — t_{1+2}) = — m_3 (t — t_3)$.
Выразим отсюда конечную температуру смеси из трех порций воды $t$:
$m_{1+2} t — m_{1+2} t_{1+2} = -m_3 t + m_3 t_3$,
$t (m_{1+2} + m_3) = m_{1+2} t_{1+2} + m_3 t_3$,
$t = frac{m_{1+2} t_{1+2} + m_3 t_3}{m_{1+2} + m_3}$.
Рассчитаем ее:
$t = frac{0.05 space кг cdot 21 degree C + 0.01 space кг cdot 60 degree}{0.05 space кг + 0.01 space кг} = frac{1.05 space кг cdot degree C + 0.6 space кг cdot degree C}{0.06 space кг} = 27.5 degree C$.
Ответ: $t = 27.5 degree C$.
Задача №9 на расчет количества теплоты, рассеиваемого в окружающую среду
Электрочайник с водой нагревается от температуры $70 degree C$ до температуры $80 degree C$ за $3 space мин$, а остывает от температуры $80 degree C$ до температуры $70 degree C$ за $9 space мин$. Какая часть количества теплоты, выделяемой спиралью чайника при нагревании воды, рассеивается в окружающую среду? Тепловые потери считать постоянными.
Внесем необходимые пояснения. Спираль чайника передает воде определенное количество теплоты $Q_2$. Часть ее ($Q_1$) рассеивается в окружающую среду. Т.е., количество теплоты $Q_2$, выделяемое спиралью, больше количества теплоты $Q$, необходимого для нагрева воды.
Дано:
$t_1 = 70 degree C$
$t_2 = 80 degree C$
$T_1 = 3 space мин$
$T_2 = 9 space мин$
$frac{Q_1}{Q_2} — ?$
Показать решение и ответ
Скрыть
Решение:
Сначала рассчитаем количество теплоты, которое необходимо сообщить воде в чайнике, чтобы ее температура увеличилась с $70 degree C$ до $80 degree C$:
$Q = cm(t_2 — t_1)$.
Масса воды в чайнике нам неизвестна, поэтому примем ее, равной $1 space кг$. Тогда,
$Q = 4200 frac{Дж}{кг cdot degree C} cdot 1 space кг cdot (80 degree C — 70 degree C) = 42 space 000 space Дж = 42 space кДж$.
Когда вода в чайнике остывает с температуры $80 degree C$ до температуры $70 degree C$, она выделяет в окружающую среду точно такое же количество энергии $Q$. Остывание происходит за $9 space мин$. Значит, количество теплоты, которое выделяется в окружающую среду за $1 space мин$ будет равно:
$Q_0 = frac{42 space кДж}{9 space мин} approx 4.7 frac{кДж}{мин}$.
В условиях задачи сказано, что тепловые потери постоянны. Это означает, что вода массой $1 space кг$ отдает $4.7 space кДж$ каждую минуту, в том числе, и при ее нагревании.
Нагревается вода за 3 минуты. За это время она отдает в окружающую среду следующее количество теплоты:
$Q_1 = 4.7 space кДж cdot 3 = 14.1 space кДж$.
Тем не менее, чайник нагрел воду до нужной температуры. Значит, он сообщил воде количество энергии, равное $Q_2 = Q + Q_1$.
$Q_2 = 42 space кДж + 14.1 space кДж = 56.1 space кДж$.
Теперь мы можем рассчитать отношение $frac{Q_1}{Q_2}$, и узнать какая часть теплоты, выделяемая спиралью чайника, рассеивается в окружающую среду:
$frac{Q_1}{Q_2} = frac{14.1 space кДж}{56.1 space кДж} approx 0.25$.
Т.е., в окружающую среду рассеивается $frac{1}{4}$ часть энергии, сообщаемая воде в чайнике.
Можно доказать, что это соотношение останется постоянным для воды любой массы в этой задаче. Чем больше будет масса воды, тем больше энергии ей будет нужно, чтобы нагреться до определенной температуры. Больше будут и тепловые потери. Искомое соотношение же останется неизменным.
Ответ: $frac{Q_1}{Q_2} approx 0.25$.
Задачи на количество теплоты с решениями
Формулы, используемые на уроках «Задачи на количество теплоты,
удельную теплоемкость».
Название величины |
Обозначение |
Единица измерения |
Формула |
Масса |
m |
кг |
|
Температура |
t |
°С |
|
Удельная теплоемкость |
c |
Дж/кг•°С |
|
Количество теплоты |
Q |
Дж |
|
1 г = 0,001 кг; 1 т = 1000 кг; 1 кДж = 1000 Дж; 1 МДж = 1000000 Дж
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
В железный котёл массой 5 кг налита вода массой 10 кг. Какое количество теплоты нужно передать котлу с водой для изменения их температуры от 10 до 100 °С?
При решении задачи нужно учесть, что оба тела — и котёл, и вода — будут нагреваться вместе. Между ними происходит теплообмен. Их температуры можно считать одинаковыми, т. е. температура котла и воды изменяется на 100 °С — 10 °С = 90 °С. Но количества теплоты, полученные котлом и водой, не будут одинаковыми. Ведь их массы и удельные теплоёмкости различны.
Задача № 2.
Смешали воду массой 0,8 кг, имеющую температуру 25 °С, и воду при температуре 100 °С массой 0,2 кг. Температуру полученной смеси измерили, и она оказалась равной 40 °С. Вычислите, какое количество теплоты отдала горячая вода при остывании и получила холодная вода при нагревании. Сравните эти количества теплоты.
Задача № 3.
Стальная деталь массой 3 кг нагрелась от 25 до 45 °С. Какое количество теплоты было израсходовано?
Задача № 4.
В сосуде содержится 3 л воды при температуре 20 °С. Сколько воды при температуре 45 °С надо добавить в сосуд, чтобы в нём установилась температура 30 °С? Необходимый свободный объём в сосуде имеется. Теплообменом с окружающей средой пренебречь
Задача № 5.
На сколько градусов изменилась температура чугунной детали массой 12 кг, если при остывании она отдала 648000 Дж теплоты?
Задача № 6.
По графику определите удельную теплоёмкость образца, если его масса 50 г.
Задача № 7.
Для нагревания медного бруска массой 3 кг от 20 до 30 °С потребовалось 12000 Дж теплоты. Какова удельная теплоемкость меди?
Задача № 8.
Нагретый камень массой 5 кг, охлаждаясь в воде на 1 °С, передает ей 2,1 кДж энергии. Чему равна удельная теплоемкость камня?
Задача № 9.
Какое количество теплоты потребуется для нагревания на 1 °С воды объемом 0,5 л; олова массой 500 г; серебра объемом 2 см3; стали объемом 0,5 м3; латуни массой 0,2 т?
Задача № 10.
Какое количество теплоты получили алюминиевая кастрюля массой 200 г и находящаяся в ней вода объемом 1,5 л при нагревании от 20 °С до кипения при температуре 100 °С?
Задача № 11.
а) Воздух, заполняющий объем 0,5 л в цилиндре с легким поршнем, нагрели от 0 до 30 °С при постоянном атмосферном давлении. Какое количество теплоты получил воздух?
б) В порожнем закрытом металлическом баке вместимостью 60 м3 под действием солнечного излучения воздух нагрелся от 0 до 20 °С. Как и на сколько изменилась внутренняя энергия воздуха в баке? (Удельная теплоемкость воздуха при постоянном объеме равна 720 Дж/кг-°С.)
Задача № 12.
ОГЭ
Металлический цилиндр массой m = 60 г нагрели в кипятке до температуры t = 100 °С и опустили в воду, масса которой mв = 300 г, а температура tв = 24 °С. Температура воды и цилиндра стала равной Θ = 27 °С. Найти удельную теплоёмкость металла, из которого изготовлен цилиндр. Удельная теплоёмкость воды св = 4200 Дж/(кг К).
Задача № 13.
В теплоизолированном сосуде сначала смешивают три порции воды 100 г, 200 г и 300 г с начальными температурами 20 °C, 70 °C и 50 °C соответственно. После установления теплового равновесия в сосуд добавляют новую порцию воды массой 400 г при температуре 20 °C. Определите конечную температуру в сосуде. Ответ дайте в °C, округлив до целого числа. Теплоёмкостью калориметра пренебрегите.
Решение.
Ответ: 39 °С.
Задача № 14. (повышенной сложности)
Стальной шарик радиусом 5 см, нагретый до температуры 500 ˚С, положили на лед, температура которого 0 ˚С. На какую глубину погрузится шарик в лед? (Считать, что шарик погрузился в лед полностью. Теплопроводностью шарика и нагреванием воды пренебречь.)
Дано: R = 0,05 м; t1 = 500 ˚С; t2 = 0 ˚С;
ρ1 (плотность стали) = 7800 кг/м3.;
ρ2 (плотность льда) = 900 кг/м3.
c (удельная теплоемкость стали) = 460 Дж/кг •˚С,
λ (удельная теплота плавления льда) = 3,3 • 105 Дж/кг,
Найти: h – ?
Краткая теория для решения Задачи на количество теплоты.
Конспект урока «Задачи на количество теплоты».
Посмотреть конспект урока по теме «Количество теплоты. Удельная теплоемкость»
Следующая тема: «ЗАДАЧИ на сгорание топлива с решениями».
Тема урока :
« Решение задач на расчет количества теплоты и энергии топлива »
Этапы урока
- Организационный .
- Повторение пройденного материала.
- Самопроверка знаний.
- Закрепление полученных навыков.
- Решение практической задачи
- Рефлексия.
- Домашнее задание .
«Все в твоих руках»
В чем физический смысл записи?
Назовите формулы:
— количество теплоты, которое идет на нагревание тела
— количество теплоты, которое выделяется при сгорании топлива
— коэффицент полезного действия
— формула кинетической энергии тела
— удельная теплота сгорания топлива
http://ppt4web.ru/uploads/ppt/1194/b2035b32c272ce46e4df7f3d6c732599.ppt
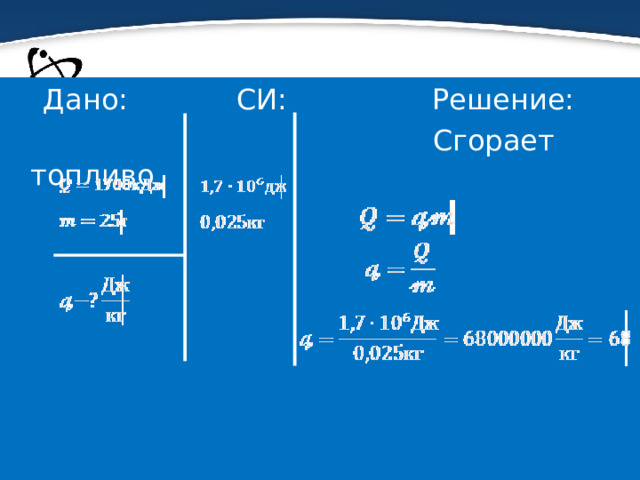
Задача
- Чему равна удельная теплота сгорания авиационного керосина, если при полном сгорании 25г этого топлива выделяется 1700 кДж теплоты?
Дано: СИ: Решение:
Сгорает топливо
Задача
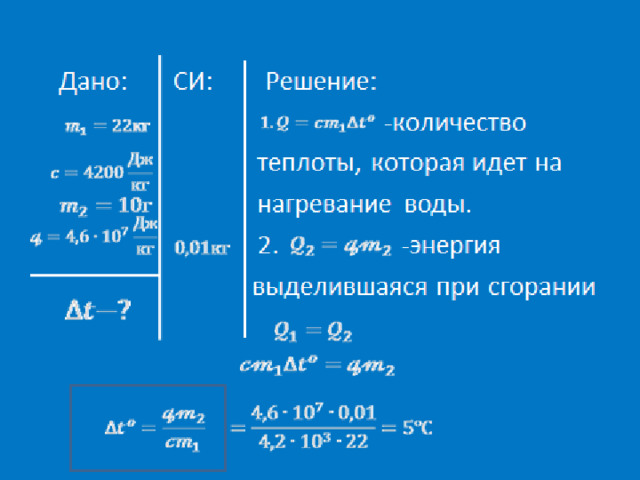
- На сколько изменится температура воды 22 кг, если ей передать всю энергию, выделившуюся при сгорании керосина массой 10 кг?
Дано: СИ: Решение:
Сгорает топливо
Задача
- Сколько килограммов сухих дров нужно сжечь, чтобы нагреть 10 кг воды от 30 0 С до кипения. Потерями энергии пренебречь. Ответ представьте целым числом граммов.
И наконец:
- Является ли человек источником энергии?
- Домашнее задание
Домашнее задание.
- Решить задачи.
- 1. Какое количество теплоты выделяется при охлаждении 200 г алюминия на 50 0 С?
- 2. Тело массой 0.05 кг нагревается на 20 0 С при сообщении ему 3,8 кДж теплоты. Из какого вещества изготовлено тело?
По желанию
- ОПРЕДЕЛИТЬ КОЛИЧЕСТВО ТЕПЛОТЫ, ОТДАВАЕМОГО ОРГАНИЗМОМ ЧЕЛОВЕКА В ОКРУЖАЮЩУЮ СРЕДУ.
- Приборы и оборудование :
- термометр, напольные весы