-
Обнаружение и исправление ошибок
-
Общие понятия
-
Для
защиты полезной информации от помех
необходимо в том или ином виде вводить
избыточность: увеличивать число символов
и время их передачи, повторять целые
сообщения, повышать мощность сигнала
— все это ведет к усложнению и удорожанию
аппаратуры. В качестве исследуемой
модели достаточно рассмотреть канал
связи с помехами, потому что к этому
случаю легко сводятся остальные.
Например, запись на диск можно рассматривать
как передачу данных в канал, а чтение с
диска – как прием данных из канала.
Коды
без избыточности обнаружить, а тем более
исправлять
ошибки не могут.
Количество символов, в которых любые
две комбинации кода отличаются друг от
друга, называется кодовым
расстоянием.
Минимальное
количество символов, в которых все
комбинации кода отличаются друг от
друга, называется минимальным
кодовым расстоянием.
Минимальное кодовое расстояние —
параметр, определяющий помехоустойчивость
кода и заложенную в коде избыточность,
т.е. корректирующие свойства кода.
В
общем случае для обнаружения t
ошибок минимальное кодовое расстояние
d0
= t
+ 1.
Минимальное
кодовое расстояние, необходимое для
одновременного обнаружения t
и исправления
ошибок,
d0
= t
+
+ 1.,
Для
кодов, только исправляющих
ошибок,
d0
= 2
+ 1.
Для
того чтобы определить кодовое расстояние
между двумя комбинациями двоичного
кода, достаточно просуммировать эти
комбинации по модулю 2 и подсчитать
число единиц полученной комбинации.
Для
обнаружения и исправления одиночной
ошибки соотношение между числом
информационных разрядив k
и числом корректирующих разрядов
должно удовлетворять следующим условиям:
,
,
при
этом подразумевается, что общая длина
кодовой комбинации
n
= k + ρ
Для
практических расчетов при определении
числа контрольных разрядов кодов с
минимальным кодовым расстоянием d0
= 3 удобно
пользоваться выражениями
ρ1(2)
= [ log2
( n + 1
) ],
если
известна длина полной кодовой комбинации
n,
и
ρ
1(2) =
[log2 {
( k
+ 1 ) + [ log2
(
k + 1) ] } ],
если
при расчетах удобнее исходить из
заданного числа информационных символов
k
.
Для
кодов, обнаруживающих все трехкратные
ошибки (d0
= 4),
ρ
1(3)
1
+ log2
(
n + 1
),
или
ρ
1(3)
1 + log2
[ (
k + 1
) + log2
(
k + 1
) ].
Для
кодов длиной в n
символов, исправляющих одну или две
ошибки (d0
= 5),
ρ
2
log2
(Cn2
+ Cn1
+ 1).
Для практических
расчетов можно пользоваться выражением:
.
Для
кодов, исправляющих 3 ошибки (d0
= 7),
.
-
Линейные групповые коды
Линейными
называются коды, в которых проверочные
символы представляют собой линейные
комбинации информационных символов.
Для
двоичных кодов в качестве линейной
операции используется сложение по
модулю 2.
Последовательность
нулей и единиц, принадлежащих данному
коду, будем называть кодовым
вектором.
Свойство
линейных кодов:
сумма
(разность) кодовых векторов линейного
кода дает вектор, принадлежащий данному
коду.
Линейные
коды образуют алгебраическую группу
по отношению к операции сложения по
модулю 2. В этом смысле они являются
групповыми
кодами.
Свойство
группового кода:
минимальное кодовое
расстояние между кодовыми векторами
группового кода равно минимальному
весу ненулевых кодовых векторов.
Вес
кодового вектора
(кодовой комбинации) равен числу его
ненулевых компонент.
Расстояние
между двумя кодовыми векторами
равно весу вектора, полученного в
результате сложения исходных векторов
по модулю 2. Таким образом, для данного
группового кода
Wmin
=d0.
Групповые
коды удобно задавать матрицами,
размерность которых определяется
параметрами кода k
и .
Число строк матрицы равно k,
число столбцов равно
n
= k +
:
Коды,
порождаемые этими матрицами, известны
как (n,k)-коды,
соответствующие им матрицы называют
порождающими
(производящими, образующими).
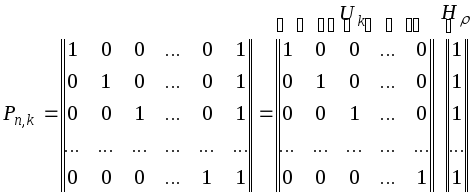
Порождающая
матрица P
может быть представлена двумя матрицами
Uk
и H
(информационной и проверочной). Число
столбцов матрицы H
равно ,
число столбцов матрицы Uk
равно k
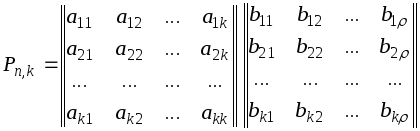
Теорией
и практикой установлено, что в качестве
матрицы Uk
удобно брать единичную матрицу в
канонической форме
Для
кодов с d0
= 2
производящая матрица P
имеет вид
Во всех комбинациях
кода построенного при помощи такой
матрицы, четное число единиц.
Для
кодов с d0
3 порождающая
матрица не может быть представлена в
форме, общей для всех кодов с данным
d0.
Вид матрицы
зависит от конкретных требований к
порождающему коду. Этими требованиями
могут быть либо минимум корректирующих
разрядов, либо максимальная простота
аппаратуры.
Корректирующие
коды с минимальным количеством избыточных
разрядов называют плотно
упакованными
или
совершенными
кодами.
Для
кодов d0
= 3
соотношения n
и k
следующие: (3; 1), (7; 4),
(15; 11), (31; 26), (63; 57)
и так далее.
Строчки
образующей матрицы P
представляют собой k
комбинаций искомого кода. Остальные
комбинации кода строятся при помощи
образующей матрицы по следующему
правилу: корректирующие символы,
предназначенные для обнаружения и
исправления ошибки в информационной
части кода, находятся путем суммирования
по модулю 2 тех строк матрицы H,
номера которых совпадают с номерами
разрядов, содержащих единицы в кодовом
векторе, представляющем информационную
часть кода. Полученную комбинацию
приписывают справа к информационной
части кода и получают полный вектор
корректирующего кода. Аналогичную
процедуру проделывают со второй, третьей
и последующими информационными кодовыми
комбинациями, пока не будет построен
корректирующий код для передачи всех
символов первичного алфавита.
Алгоритм
образования проверочных символов по
известной информационной части кода
может быть записан следующим образом
или
.
В процессе
декодирования осуществляются проверки,
идея которых в общем виде может быть
представлена следующим образом
Для
каждой конкретной матрицы существует
своя, одна-единственная система проверок.
Проверки производятся по следующему
правилу : в первую проверку вместе с
проверочным рядом b1
входят информационные разряды, которые
соответствуют единицам первого столбца
проверочной матрицы H;
во вторую проверку входит второй
проверочный разряд b2
и информационные
разряды, и т. д. Число проверок равно
числу проверочных разрядов корректирующего
кода .
В
результате осуществления проверок
образуется проверочный
вектор
S1,
S2,
…, S,
который называется синдромом.
Если вес синдрома равен нулю, то принятая
комбинация считается безошибочной.
Если хотя бы один разряд проверочного
вектора содержит единицу, то принятая
комбинация содержит ошибку. Исправление
ошибки производится по виду синдрома,
так как каждому ошибочному разряду
соответствует один единственный
проверочный вектор.
Вид
синдрома для каждой конкретной матрицы
может быть определен при помощи
проверочной матрицы Н’,
которая представляет собой транспонированную
матрицу H,
дополненной единичной матрицей I,
число столбцов которой равно число
проверочных разрядов кода
Н’
= HТI.
Столбцы
такой матрицы представляют собой
значение синдрома для разряда,
соответствующего номеру столбца матрицы
Н’.
Процедура исправления
ошибок в процессе декодирования групповых
кодов сводится к следующему.
Строится
кодовая таблица. В первой строке таблицы
располагаются все кодовые векторы Ai.
В первом столбце второй строки размещается
вектор a1,
вес которого равен 1.
Остальные
позиции второй строки заполняются
векторами, полученными в результате
суммирования по модулю 2 вектора a1
с Аi,
расположенным в соответствующем столбце
первой строки. В первом столбце третьей
строки записывается вектор a2,
вес которого также равен 1, однако , если
вектор a1
содержит единицу в первом разряде, то
a2
— во втором. В остальные позиции третьей
строки записывают суммы Аi
и a2
.
Аналогично
поступают до тех пор, пока не будут
просуммированы с векторами Аi
все векторы
aj
весом 1, с единицей в каждом из n
разрядов. Затем суммируются по модулю
2 векторы aj,
весом 2, с последовательным перекрытием
всех возможных разрядов. Вес вектора
aj
определяет число исправляемых ошибок.
Число векторов aj
определяется возможным числом
неповторяющихся синдромов и равно 2-1
(нулевая комбинация говорит об отсутствии
ошибки). Условие неповторяемости синдрома
позволяет по его виду определять
один-единственный соответствующий ему
вектор aj.
Векторы aj
есть векторы
ошибок, которые могут быть исправлены
данным групповым кодом.
По
виду синдрома принятая комбинация может
быть отнесена к тому или иному смежному
классу, образованному сложением по
модулю 2 кодовой комбинации Аi
с вектором ошибки aj,
т. е. к определенной строке кодовой
таблицы 3.2.1.
Таблица 3.2.1-
Кодовая таблица групповых кодов
|
a |
A1 |
A2 |
… |
A(2k-1) |
|
a1 |
a1A1 |
a2A2 |
… |
a1A(2k-1) |
|
a2 |
a2A1 |
a2A2 |
… |
a2A(2k-1) |
|
… |
… |
… |
… |
… |
|
a(2-1) |
a(2 |
a(2-1)A2 |
… |
a(2-1)A(2k-1) |
Принятая
кодовая комбинация Axn
сравнивается
с векторами, записанными в строке,
соответствующей полученному в результате
проверок синдрому. Истинный код будет
расположен в строке той же колонки
таблицы. Процесс исправления ошибки
заключается в замене на обратное значение
разрядов.
Векторы
a1,
a2,
…,a(2-1)
не должны
быть равными ни одному из векторов А1,
А2,
…, А(2-1),
в противном случае в таблице появились
бы нулевые векторы.
Пример.
Построить
кодовую таблицу, при помощи которой
обнаруживаются и исправляются все
одиночные ошибки и некоторые ошибки
кратностью r
+ 1,
в информационной
части кода (11,7), построенного по матрице
Решение.
Используя
таблицу 3.2.1, строим кодовую таблицу
3.2.2 для кодов, построенных по данной
матрице P,
кодовые комбинации строятся путем
добавления к четырехразрядным комбинациям
натурального двоичного кода корректирующих
разрядов по правилу, описанному выше.
Определяем
систему проверок исходя из матрицы H
Находим
вид синдрома для каждой строки таблицы.
Для этого достаточно произвести проверки
для кодовых комбинаций любого столбца
кодовой таблицы.
Для
нашего примера возьмем столбец A3
.
Таблица 3.2.1 – Пример таблицы
для столбца А3
|
№ |
e |
A1 1000111 |
A2 0100011 |
A3 1100100 |
A4 0010110 |
A5 1010001 |
A6 0110101 |
A7 1110010 |
|
1 2 3 4 5 6 7 |
1000000 0100000 0010000 0001000 1100000 1001000 1010000 |
0000111 1100111 1010111 1001111 0100111 0001111 0010111 |
1100011 0000011 0110011 0101011 1000011 1101011 1110011 |
0100100 1000100 1110100 1101100 0000100 0101100 0110100 |
1010110 0110110 0000110 0011110 1110110 1011110 1000110 |
0010001 1110001 1000001 1011001 0110001 0011001 0000001 |
1110101 0010101 0100101 0111101 1010101 1111101 1100101 |
0110010 1010010 1100010 1111010 0010010 0111010 0100010 |
|
№ |
A8 0001101 |
A9 1001010 |
A10 0101110 |
A11 1101001 |
A12 0011011 |
A13 1011100 |
A14 0111000 |
A15 1111111 |
|
1 2 3 4 5 6 7 |
1001101 0101101 0011101 0000101 1101101 1000101 1011101 |
0001010 1101010 1011010 1000010 0101010 0000010 0011010 |
1101110 0001110 0111110 0100110 1001110 1100110 1111110 |
0101001 1001001 1111001 1100001 0001001 0100001 0111001 |
1011011 0111011 0001011 0010011 1111011 1010011 1001011 |
0011100 1111100 1001100 1010100 0111100 0010100 0001100 |
1111000 0011000 0101000 0110000 1011000 1110000 1101000 |
0111111 1011111 1101111 1110111 0011111 0110111 0101111 |
-
0
1 0 0 1 0 0 -
1
0 0 0 1 0 0 -
1
1 1 0 1 0 0 -
1
1 0 1 1 0 0 -
0
0 0 0 1 0 0 -
0
1 0 1 1 0 0 -
0
1 1 0 1 0 0
Таким
образом вектору ошибки a1
соответствует синдром 1 1 1
“ a2 “ 0
1 1
“ a3 “ 1
1 0
“ a4 “ 1
0 1
“ a5 “ 1
0 0
“ a6 “ 0
1 0
“ a7 “ 0
0 1
Предположим,
приняты комбинации 1011001, 1000101, 0001100,
0000001 и 1010001. Производим проверки
Синдром
первой принятой комбинации — 101, значит
вектор ошибки а4
= 0001000, исправление ошибки производится
заменой символа в четвертом разряде
принятой комбинации на обратный. Истинная
комбинация — А5,
так как принятая комбинация находится
в шестом столбце таблицы в строке,
соответствующей синдрому 101.
Синдром
второй принятой комбинации — 010, находим
ее в шестой строке (010 соответствует а6)
и в девятом столбце. Истинная комбинация
А8
= 0001101, т.е. исправлена двойная ошибка.
Синдром
третьей принятой комбинации — 001
соответствует а7,
истинная комбинация А13.
Синдром
четвертой из принятых комбинаций — 001
также соответствует а7,
но принятую комбинацию мы находим в
шестом столбце таблицы , следовательно,
истинная комбинация — А5.
Синдром шестой
принятой комбинации — 000. Ошибки нет.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Систематические корректирующие коды. Линейно групповой код
Время на прочтение
6 мин
Количество просмотров 8.3K
В данной публикации будет рассматриваться линейно групповой код, как один из представителей систематических корректирующих кодов и предложена его реализация на C++.
Что из себя представляет корректирующий код. Корректирующий код – это код направленный на обнаружение и исправление ошибок. А систематические коды — Это коды, в которых контрольные и информационные разряды размещаются по определенной системе. Одним из таких примеров может служить Код Хэмминга или собственно линейно групповые коды.
Линейно групповой код состоит из информационных бит и контрольных. Например, для исходной комбинации в 4 символа, линейно групповой код будет выглядеть вот так:
|1100|110|Где первые 4 символа это наша исходная комбинация, а последние 3 символа это контрольные биты.
Общая длина линейно группового кода составляет 7 символов. Если число бит исходной комбинации нам известно, то чтобы вычислить число проверочных бит, необходимо воспользоваться формулой:
Где n — это число информационных бит, то есть длина исходной комбинации, и log по основанию 2. И общая длина N кода будет вычисляться по формуле:
Допустим исходная комбинация будет составлять 10 бит.
d всегда округляется в
большую сторону
, и d=4.
И полная длина кода будет составлять
14
бит.
Разобравшись с длиной кода, нам необходимо составить производящую и проверочную матрицу.
Производящая матрица, размерностью N на n, где N — это длина линейно группового кода, а n — это длина информационной части линейно группового кода. По факту производящая матрица представляет из себя две матрицы: единичную размерностью m на m, и матрицу контрольных бит размерностью d на n. Если единичная матрица составляется путём расставления единиц по главной диагонали, то составление «контрольной» части матрицы имеет некоторые правила. Проще объяснить на примере. Мы возьмем уже известную нам комбинацию из 10 информационных битов, но добавим коду избыточность, и добавим ему 5-ый контрольный бит. Матрица будет иметь размерность 15 на 10.
1 0 0 0 0 0 0 0 0 0 1 1 1 1 1
0 1 0 0 0 0 0 0 0 0 1 1 1 1 0
0 0 1 0 0 0 0 0 0 0 1 1 1 0 1
0 0 0 1 0 0 0 0 0 0 1 1 0 1 1
0 0 0 0 1 0 0 0 0 0 1 0 1 1 1
0 0 0 0 0 1 0 0 0 0 0 1 1 1 1
0 0 0 0 0 0 1 0 0 0 1 1 1 0 0
0 0 0 0 0 0 0 1 0 0 1 1 0 0 1
0 0 0 0 0 0 0 0 1 0 1 0 0 1 1
0 0 0 0 0 0 0 0 0 1 0 1 0 1 1«Контрольная» часть составляется по схеме уменьшения двоичного числа и соблюдения минимального кодового расстояния между строками: в нашем случае это 11111, 11110, 11101…
Минимальное кодовое расстояние для комбинации будет вычисляться по формуле:
Wp=r+s
Где r – это ранг обнаруживаемой ошибки, а s – ранг исправляемой ошибки.
В нашем случае ранг исправляемой и обнаруживаемой ошибки 1.
Также необходимо составить проверочную матрицу. Она составляется путём транспонирования «контрольной» части и после неё добавляется единичная матрица размерности d на d.
1 1 1 1 1 0 1 1 1 0 1 0 0 0 0
1 1 1 1 0 1 1 1 0 1 0 1 0 0 0
1 1 1 0 1 1 1 0 0 0 0 0 1 0 0
1 1 0 1 1 1 0 0 1 1 0 0 0 1 0
1 0 1 1 1 1 0 1 1 1 0 0 0 0 1Составив матрицы, мы уже можем написать линейно групповой код, путём суммирования строк производящей матрицы под номерами ненулевых бит исходного сообщения.
Рассмотрим этот этап на примере исходного сообщения 1001101010.
Линейно групповой код: 100110101011100
Сразу обозначим, что контрольные разряды в ЛГК определяются по правилам чётности суммы соответствующих индексов, в нашем случае, эти суммы составляют: 5,3,3,4,4. Следовательно, контрольная часть кода выглядит: 11100.
В результате мы составили линейно групповой код. Однако, как уже говорилось ранее, линейно групповой код имеет исправляющую способность, в нашем случае, он способен обнаружить и исправить одиночную ошибку.
Допустим, наш код был отправлен с ошибкой в 6-ом разряде. Для определения ошибок в коде служит, уже ранее составленная проверочная матрица
Для того, чтобы определить, в каком конкретно разряде произошла ошибка, нам необходимо узнать «синдром ошибки». Синдром ошибки вычисляется методом проверок по ненулевым позициям проверочной матрицы на чётность. В нашем случае этих проверок пять, и мы проводим наше полученное сообщение через все эти проверки.
Получив двоичное число, мы сверяем его со столбцами проверочной матрицы. Как только находим соответствующий «синдром», определяем его индекс, и выполняем инверсию бита по полученному индексу.
В нашем случае синдром равен: 01111, что соответствует 6-му разряду в ЛГК. Мы инвертируем бит и получаем корректный линейно групповой код.
Декодирование скорректированного ЛГК происходит путём простого удаления контрольных бит. После удаления контрольных разрядов ЛГК мы получаем исходную комбинацию, которая была отправлена на кодировку.
В заключение можно сказать, что такие корректирующие коды как линейно групповые коды, Код Хэмминга уже достаточно устарели, и в своей эффективности однозначно уступят своим современным альтернативам. Однако они вполне справляются с задачей познакомиться с процессом кодирования двоичных кодов и методом исправления ошибок в результате воздействия помех на канал связи.
Реализация работы с ЛГК на C++:
#include <iostream>
#include <vector>
#include <string>
#include <cstdlib>
#include <ctime>
#include <algorithm>
#include <iterator>
#include <cctype>
#include <cmath>
using namespace std;
int main()
{
setlocale(LC_ALL, "Russian");
cout<<"Производящая матрица:"<<endl;
int matr [10][15]={{1,0,0,0,0,0,0,0,0,0,1,1,1,1,1},{0,1,0,0,0,0,0,0,0,0,1,1,1,1,0},{0,0,1,0,0,0,0,0,0,0,1,1,1,0,1},{0,0,0,1,0,0,0,0,0,0,1,1,0,1,1},{0,0,0,0,1,0,0,0,0,0,1,0,1,1,1},
{0,0,0,0,0,1,0,0,0,0,0,1,1,1,1},{0,0,0,0,0,0,1,0,0,0,1,1,1,0,0},{0,0,0,0,0,0,0,1,0,0,1,1,0,0,1},{0,0,0,0,0,0,0,0,1,0,1,0,0,1,1},{0,0,0,0,0,0,0,0,0,1,0,1,0,1,1}};
for(int i=0;i<10;i++)
{
for(int j=0;j<15;j++)
{
cout<<matr[i][j]<<' ';
}
cout<<endl;
}
cout<<"Проверочная матрица:"<<endl;
int matr_2 [5][15]={{1,1,1,1,1,0,1,1,1,0,1,0,0,0,0},{1,1,1,1,0,1,1,1,0,1,0,1,0,0,0},{1,1,1,0,1,1,1,0,0,0,0,0,1,0,0},{1,1,0,1,1,1,0,0,1,1,0,0,0,1,0},{1,0,1,1,1,1,0,1,1,1,0,0,0,0,1}};
for(int i=0;i<5;i++)
{
for(int j=0;j<15;j++)
{
cout<<matr_2[i][j]<<' ';
}
cout<<endl;
}
cout<<"Введите комбинацию: "<<endl;
string str;
bool flag=false;
while(flag!=true)
{
cin>>str;
if(str.size()!=10)
{
cout<<"Недопустимая размерность строки!"<<endl;
flag=false;
}
else
flag=true;
}
vector <int> arr;
for(int i=0;i<str.size();i++)
{
if(str[i]=='1')
arr.push_back(1);
else if(str[i]=='0')
arr.push_back(0);
}
cout<<"Ваша комбинация: ";
for(int i=0;i<arr.size();i++)
cout<<arr[i];
cout<<endl;
vector <int> S;
vector <vector<int>> R;
for(int i=0;i<10;i++)
{
if(arr[i]==1)
{
vector <int> T;
for(int j=0;j<15;j++)
{
T.push_back(matr[i][j]);
}
R.push_back(T);
}
}
cout<<endl;
cout<<"Суммиирвоание строк для построения группового кода: "<<endl;
for(vector <vector<int>>::iterator it=R.begin();it!=R.end();it++)
{
copy((*it).begin(),(*it).end(),ostream_iterator<int>(cout,"t"));
cout<<"n";
}
cout<<endl;
vector <int> P;
for(int i=0; i<15;i++)
{
int PT=0;
for(int j=0; j<R.size();j++)
{
PT+=R[j][i];
}
P.push_back(PT);
}
for(int i=10; i<15;i++)
{
if(P[i]%2==0)
P[i]=0;
else if(P[i]%2!=0)
P[i]=1;
}
cout<<endl<<"Групповой линейный код: "<<endl;
for(int i=0; i<P.size();i++)
{
cout<<P[i]<<' ';
}
int rand_i;
rand_i=5;
cout<<endl<<"В сообщении сгенерирована ошибка: ";
if(P[rand_i]==0)
P[rand_i]=1;
else if(P[rand_i]==1)
P[rand_i]=0;
for(int i=0; i<P.size();i++)
{
cout<<P[i]<<' ';
}
int S1, S2, S3, S4, S5;
//Проверки на чётность
S1=P[0]+P[1]+P[2]+P[3]+P[4]+P[6]+P[7]+P[8]+P[10];
S2=P[0]+P[1]+P[2]+P[3]+P[5]+P[6]+P[7]+P[9]+P[11];
S3=P[0]+P[1]+P[2]+P[4]+P[5]+P[6]+P[12];
S4=P[0]+P[1]+P[3]+P[4]+P[5]+P[8]+P[9]+P[13];
S5=P[0]+P[2]+P[3]+P[4]+P[5]+P[7]+P[8]+P[9]+P[14];
//Составление синдрома
if(S1%2==0)
{
S1=0;
}
else if(S1%2!=0)
{
S1=1;
}
if(S2%2==0)
{
S2=0;
}
else if(S2%2!=0)
{
S2=1;
}
if(S3%2==0)
{
S3=0;
}
else if(S3%2!=0)
{
S3=1;
}
if(S4%2==0)
{
S4=0;
}
else if(S4%2!=0)
{
S4=1;
}
if(S5%2==0)
{
S5=0;
}
else if(S5%2!=0)
{
S5=1;
}
cout<<endl<<"Синдром ошибки: "<<S1<<S2<<S3<<S4<<S5<<endl;
int mas_s[5]={S1,S2,S3,S4,S5};
int index_j=0;
bool flag_s=false;
for(int i=0;i<15;i++)
{
if((matr_2[0][i]==mas_s[0])&&(matr_2[1][i]==mas_s[1])&&(matr_2[2][i]==mas_s[2])&&(matr_2[3][i]==mas_s[3])&&(matr_2[4][i]==mas_s[4]))
{
index_j=i;
}
}
cout<<endl<<"Разряд ошибки: "<<index_j+1<<endl;
if(P[index_j]==0)
P[index_j]=1;
else if(P[index_j]==1)
P[index_j]=0;
cout<<"Исправленный код: ";
for(int i=0; i<P.size();i++)
{
cout<<P[i]<<' ';
}
cout<<endl;
P.erase(P.begin()+14);
P.erase(P.begin()+13);
P.erase(P.begin()+12);
P.erase(P.begin()+11);
P.erase(P.begin()+10);
cout<<"Исходный код: ";
for(int i=0; i<P.size();i++)
{
cout<<P[i]<<' ';
}
cout<<endl;
return 0;
}Источники:
1. StudFiles – файловый архив студентов [Электронный ресурс] studfiles.net/preview/4514583/page:2/.
2. Задачник по теории информации и кодированию [Текст] / В.П. Цымбал. – Изд. объед. «Вища школа», 1976. – 276 с.
3. Тенников, Ф.Е. Теоретические основы информационной техники / Ф.Е. Тенников. – М.: Энергия, 1971. – 424 с.
В теории кодирования линейный код является исправляющим ошибки код, для которого любая линейная комбинация из кодовых слов также является кодовым словом. Линейные коды традиционно делятся на блочные коды и сверточные коды, хотя турбокоды можно рассматривать как гибрид этих двух типов. Линейные коды позволяют использовать более эффективные алгоритмы кодирования и декодирования, чем другие коды (см. синдромное декодирование ).
Линейные коды используются в прямом исправлении ошибок и применяются в методах передачи символов (например, биты ) на канале связи, так что в случае возникновения ошибок при обмене данными некоторые ошибки могут быть исправлены или обнаружены получателем блока сообщения. Кодовые слова в линейном блочном коде являются блоки символов, которые закодированы с использованием большего количества символов, чем исходное значение, которое должно быть отправлено. Линейный код длины n передает блоки, содержащие n символов. Например, [7,4,3] код Хэмминга является линейный двоичный код, который представляет 4-битные сообщения с использованием 7-битных кодовых слов. Два отдельных кодовых слова отличаются по крайней мере тремя битами. Как следствие, может быть обнаружено до двух ошибок на каждое кодовое слово, в то время как одна ошибка может быть исправлено. Этот код содержит 2 = 16 кодовых слов.
Содержание
- 1 Определение и параметры
- 2 Генератор и c чертовы матрицы
- 3 Пример: коды Хэмминга
- 4 Пример: коды Адамара
- 5 Алгоритм ближайшего соседа
- 6 Популярные обозначения
- 7 Граница синглтона
- 8 Теорема Бонизоли
- 9 Примеры
- 10 Обобщение
- 11 См. Также
- 12 Ссылки
- 12.1 Библиография
- 13 Внешние ссылки
Определение и параметры
A линейный код длины n и ранга k является линейное подпространство C с размером k векторного пространства F qn { displaystyle mathbb {F} _ {q} ^ {n}}

Вес кодового слова — это количество его элементов, которые не равны нулю, а расстояние между двумя кодовыми словами — это расстояние Хэмминга между ними., то есть количество элементов, в которых они различаются. Расстояние d линейного кода — это минимальный вес его ненулевых кодовых слов или, что эквивалентно, минимальное расстояние между различными кодовыми словами. Линейный код длины n, размерности k и расстояния d называется кодом [n, k, d].
Мы хотим дать F qn { displaystyle mathbb {F} _ {q} ^ {n}}
Генератор и проверка матриц
Как линейное подпространство из F qn { displaystyle mathbb {F} _ {q} ^ {n}}

![{ displaystyle { boldsymbol {G}} = [I_ {k} | P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92a00d2764ceb53abed846d99a766b918f10902a)



Матрица H, представляющая линейную функцию ϕ: F qn → F qn — k { displaystyle phi: mathbb {F} _ {q} ^ {n} to mathbb {F} _ {q} ^ {nk}}
![{ displaystyle { boldsymbol {G}} = [I_ {k} | P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92a00d2764ceb53abed846d99a766b918f10902a)
![{ displaystyle { boldsymbol {H}} = [- P ^ {T} | I_ {nk}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf073820dfea39e704650fee6958cf29c59f03c7)


Линейность гарантирует, что минимальное расстояние Хэмминга d между кодовым словом c 0 и любым другим кодовым словом c ≠ c 0 не зависит от c 0. Это следует из того свойства, что разность c — c 0 двух кодовых слов в C также является кодовым словом (т. Е. элементом подпространства C), и свойством, что d ( c, c 0) = d (c — c 0, 0). Из этих свойств следует, что
- min c ∈ C, c ≠ c 0 d (c, c 0) = min c ∈ C, c ≠ c 0 d (c — c 0, 0) = min c ∈ C, c ≠ 0 d (c, 0) = d. { displaystyle min _ {c in C, c neq c_ {0}} d (c, c_ {0}) = min _ {c in C, c neq c_ {0}} d ( c-c_ {0}, 0) = min _ {c in C, c neq 0} d (c, 0) = d.}
Другими словами, чтобы узнать минимальное расстояние между кодовые слова линейного кода, нужно будет только смотреть на ненулевые кодовые слова. Ненулевое кодовое слово с наименьшим весом тогда имеет минимальное расстояние до нулевого кодового слова и, следовательно, определяет минимальное расстояние кода.
Расстояние d линейного кода C также равно минимальному количеству линейно зависимых столбцов проверочной матрицы H.
Доказательство: поскольку H ⋅ c T = 0 { displaystyle { boldsymbol {H}} cdot { boldsymbol {c}} ^ {T} = { boldsymbol {0}}}


















Пример: коды Хэмминга
В качестве первого класса линейных кодов, разработанных для исправления ошибок, коды Хэмминга широко используются в цифровых системах связи. Для любого положительного целого числа r ≥ 2 { displaystyle r geq 2}
![[2 ^ {r} -1,2 ^ {r} -r-1,3] _ {2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4b7099796302beb1cea00796f3d9a67b448e08c)

Пример: Код линейного блока со следующей образующей матрицей и матрицей проверки на четность: [7, 4, 3] 2 { displaystyle [7,4,3] _ {2}}![[7,4,3] _ {2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/499457f6464e18a49d7e72d66681299c4862829a)
- G = (1 0 0 0 1 1 0 0 1 0 0 0 1 1 0 0 1 0 1 1 1 0 0 0 1 1 0 1), { displaystyle { boldsymbol {G}} = { begin {pmatrix} 1 0 0 0 1 1 0 \ 0 1 0 0 0 1 1 \ 0 0 1 0 1 1 1 \ 0 0 0 1 1 0 1 конец {pmatrix}},}
H = (1 0 1 1 1 0 0 1 1 1 0 0 1 0 0 1 1 1 0 0 1) { displaystyle { boldsymbol {H}} = { begin {pmatrix} 1 0 1 1 1 0 0 \ 1 1 1 0 0 1 0 \ 0 1 1 1 0 0 1 end {pmatrix}}}
Пример: коды Адамара
код Адамара — это [2 r, r, 2 r — 1] 2 { displaystyle [ 2 ^ {r}, r, 2 ^ {r-1}] _ {2}}![[2 ^ {r}, r, 2 ^ {r-1}] _ {2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e698d84a6a5cfe250e1e1831a36917bc5f6dbc60)




Пример: Код линейного блока со следующей образующей матрицей: [8, 3, 4] 2 { displaystyle [8,3,4] _ {2}}![[8,3,4] _ {2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25e2abe070a736c1d85fc3d68f41ad9d65cc9a85)

Код Адамара является частным случаем кода Рида – Маллера. Если мы возьмем первый столбец (столбец со всеми нулями) из GH ad { displaystyle { boldsymbol {G}} _ {Had}}
![[7,3,4] _ {2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61062d9e8384323c74a528929abb584e5c30caba)
Алгоритм ближайшего соседа
Параметр d тесно связан со способностью кода исправлять ошибки. Следующая конструкция / алгоритм иллюстрирует это (так называемый алгоритм декодирования ближайшего соседа):
Вход: полученный вектор v в F qn { displaystyle mathbb {F} _ {q} ^ {n} }
Вывод: кодовое слово w { displaystyle w}


Мы говорим, что линейная C { displaystyle C}




Популярные обозначения
Коды обычно обозначаются буквой C и кодом длины n и rank k (т. е., имеющий k кодовых слов в своей основе и k строк в своей порождающей матрице) обычно называют (n, k) кодом. Линейные блочные коды часто обозначаются как коды [n, k, d], где d относится к минимальное расстояние Хэмминга между любыми двумя кодовыми словами.
([n, k, d] n Нотацию не следует путать с обозначением (n, M, d), используемым для обозначения нелинейного кода длины n, размера M (т.е. имеющего M кодовых слов) и минимального расстояния Хэмминга d.)
Граница синглтона
Лемма (Граница синглтона ): каждый линейный [n, k, d] код C удовлетворяет k + d ≤ n + 1 { displaystyle k + d leq n + 1}
Код C, параметры которого удовлетворяют k + d = n + 1, называется максимальное разделимое расстояние или MDS . Такие коды, если они существуют, в некотором смысле являются наилучшими из возможных.
Если C 1 и C 2 — два кода длины n, и если в симметричной группе Snесть перестановка p, для которой ( c 1,…, c n) в C 1 тогда и только тогда, когда (c p (1),…, c p (n)) в C 2, тогда мы говорим, что C 1 и C 2 являются эквивалентными перестановками . В более общем смысле, если существует n × n { displaystyle n times n}

Лемма: Любой линейный код является перестановочным эквивалентом кода, который находится в стандартной форме.
Теорема Бонисоли
Код определяется как равноудаленный тогда и только тогда, когда существует некоторая константа d такая, что расстояние между любыми двумя различными кодовыми словами кода равно к д. В 1984 году Арриго Бонисоли определил структуру линейных одновесовых кодов над конечными полями и доказал, что каждый эквидистантный линейный код представляет собой последовательность двойных кодов Хэмминга.
Примеры
Некоторые примеры линейных кодов включают:
Обобщение
Пространства Хэмминга над алфавитами без полей также были рассмотрены, особенно над конечными кольцами (особенно над Z4 ), что приводит к появлению модулей вместо векторных пространств и (идентифицируемых с помощью подмодулей ) вместо линейных кодов. Типичная метрика, используемая в этом случае, — расстояние Ли. Существует изометрия серого между Z 2 2 m { displaystyle mathbb {Z} _ {2} ^ {2m}}



В последнее время некоторые авторы называют такие коды над кольцами просто линейными кодами
См. также
Ссылки
- ^Уильям Э. Райан и Шу Линь (2009). Коды каналов: классический и современный. Издательство Кембриджского университета. п. 4. ISBN 978-0-521-84868-8.
- ^Маккей, Дэвид, Дж. К. (2003). Теория информации, логические выводы и алгоритмы обучения (PDF). Издательство Кембриджского университета. п. 9. Bibcode : 2003itil.book….. M. ISBN 9780521642989.
В линейном блочном коде дополнительные биты N — K { displaystyle NK}
являются линейными функциями исходного K { displaystyle K}
биты; эти дополнительные биты называются битами проверки четности
- ^Thomas M. Cover и Joy A. Thomas (1991). Элементы теории информации. John Wiley Sons, Inc., стр. 210–211. ISBN 978-0-471-06259-2.
- ^Эцион, Туви; Равив, Нетанель (2013). «Эквидистантные коды в грассманиане». arXiv : 1308.6231 [math.CO ].
- ^Бонисоли, А. (1984). «Каждый эквидистантный линейный код представляет собой последовательность дуальных кодов Хэмминга». Ars Combinatoria. 18 : 181–186.
- ^Маркус Греферат (2009). «Введение в теорию линейного кодирования». В Массимилиано Сала; Тео Мора; Людовик Перре; Сёдзиро Саката; Карло Траверсо (ред.). Основы Грёбнера, кодирование и криптография. Springer Science Business Media. ISBN 978-3-540-93806-4.
- ^«Энциклопедия математики». www.encyclopediaofmath.org.
- ^Дж. Х. ван Линт (1999). Введение в теорию кодирования (3-е изд.). Springer. Глава 8: Коды ℤ 4. ISBN 978-3-540-64133-9.
- ^S.T. Догерти; Ж.-Л. Ким; П. Соле (2015). «Открытые проблемы теории кодирования». В Стивене Догерти; Альберто Факкини; Андре Жерар Лерой; Эдмунд Пучиловски; Патрик Соул (ред.). Некоммутативные кольца и их приложения. American Mathematical Soc. п. 80. ISBN 978-1-4704-1032-2.
Библиография
- J. Ф. Хамфрис; М. Ю. Перст (2004). Числа, группы и коды (2-е изд.). Издательство Кембриджского университета. ISBN 978-0-511-19420-7.Глава 5 содержит более мягкое введение (чем эта статья) в предмет линейных кодов.
Внешние ссылки
- q программа-генератор кода
- Таблицы кодов: границы параметров различных типов кодов, IAKS, Fakultät für Informatik, Universität Karlsruhe (TH)]. Обновленная онлайн-таблица оптимальных двоичных кодов включает недвоичные коды.
- База данных кодов Z4 Онлайн, обновленная база данных оптимальных кодов Z4.
From Wikipedia, the free encyclopedia
In coding theory, a linear code is an error-correcting code for which any linear combination of codewords is also a codeword. Linear codes are traditionally partitioned into block codes and convolutional codes, although turbo codes can be seen as a hybrid of these two types.[1] Linear codes allow for more efficient encoding and decoding algorithms than other codes (cf. syndrome decoding).[citation needed]
Linear codes are used in forward error correction and are applied in methods for transmitting symbols (e.g., bits) on a communications channel so that, if errors occur in the communication, some errors can be corrected or detected by the recipient of a message block. The codewords in a linear block code are blocks of symbols that are encoded using more symbols than the original value to be sent.[2] A linear code of length n transmits blocks containing n symbols. For example, the [7,4,3] Hamming code is a linear binary code which represents 4-bit messages using 7-bit codewords. Two distinct codewords differ in at least three bits. As a consequence, up to two errors per codeword can be detected while a single error can be corrected.[3] This code contains 24=16 codewords.
Definition and parameters[edit]
A linear code of length n and dimension k is a linear subspace C with dimension k of the vector space 

The weight of a codeword is the number of its elements that are nonzero and the distance between two codewords is the Hamming distance between them, that is, the number of elements in which they differ. The distance d of the linear code is the minimum weight of its nonzero codewords, or equivalently, the minimum distance between distinct codewords. A linear code of length n, dimension k, and distance d is called an [n,k,d] code (or, more precisely, ![[n,k,d]_{q}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5eef76e1d6b74cc535236a6249e75afeea540ee3)
We want to give 
Generator and check matrices[edit]
As a linear subspace of 

![{displaystyle {boldsymbol {G}}=[I_{k}|P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92a00d2764ceb53abed846d99a766b918f10902a)



A matrix H representing a linear function 
![{displaystyle {boldsymbol {G}}=[I_{k}|P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92a00d2764ceb53abed846d99a766b918f10902a)
![{displaystyle {boldsymbol {H}}=[-P^{T}|I_{n-k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf073820dfea39e704650fee6958cf29c59f03c7)


Linearity guarantees that the minimum Hamming distance d between a codeword c0 and any of the other codewords c ≠ c0 is independent of c0. This follows from the property that the difference c − c0 of two codewords in C is also a codeword (i.e., an element of the subspace C), and the property that d(c, c0) = d(c − c0, 0). These properties imply that
In other words, in order to find out the minimum distance between the codewords of a linear code, one would only need to look at the non-zero codewords. The non-zero codeword with the smallest weight has then the minimum distance to the zero codeword, and hence determines the minimum distance of the code.
The distance d of a linear code C also equals the minimum number of linearly dependent columns of the check matrix H.
Proof: Because 


















Example: Hamming codes[edit]
As the first class of linear codes developed for error correction purpose, Hamming codes have been widely used in digital communication systems. For any positive integer 
![[2^{r}-1,2^{r}-r-1,3]_{2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4b7099796302beb1cea00796f3d9a67b448e08c)

Example : The linear block code with the following generator matrix and parity check matrix is a ![[7,4,3]_{2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/499457f6464e18a49d7e72d66681299c4862829a)
Example: Hadamard codes[edit]
Hadamard code is a ![[2^{r},r,2^{r-1}]_{2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e698d84a6a5cfe250e1e1831a36917bc5f6dbc60)




Example: The linear block code with the following generator matrix is a ![[8,3,4]_{2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25e2abe070a736c1d85fc3d68f41ad9d65cc9a85)

Hadamard code is a special case of Reed–Muller code. If we take the first column (the all-zero column) out from 
![[7,3,4]_{2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61062d9e8384323c74a528929abb584e5c30caba)
Nearest neighbor algorithm[edit]
The parameter d is closely related to the error correcting ability of the code. The following construction/algorithm illustrates this (called the nearest neighbor decoding algorithm):
Input: A received vector v in 
Output: A codeword 


We say that a linear 




Popular notation[edit]
Codes in general are often denoted by the letter C, and a code of length n and of rank k (i.e., having k code words in its basis and k rows in its generating matrix) is generally referred to as an (n, k) code. Linear block codes are frequently denoted as [n, k, d] codes, where d refers to the code’s minimum Hamming distance between any two code words.
(The [n, k, d] notation should not be confused with the (n, M, d) notation used to denote a non-linear code of length n, size M (i.e., having M code words), and minimum Hamming distance d.)
Singleton bound[edit]
Lemma (Singleton bound): Every linear [n,k,d] code C satisfies 
A code C whose parameters satisfy k+d=n+1 is called maximum distance separable or MDS. Such codes, when they exist, are in some sense best possible.
If C1 and C2 are two codes of length n and if there is a permutation p in the symmetric group Sn for which (c1,…,cn) in C1 if and only if (cp(1),…,cp(n)) in C2, then we say C1 and C2 are permutation equivalent. In more generality, if there is an 

Lemma: Any linear code is permutation equivalent to a code which is in standard form.
Bonisoli’s theorem[edit]
A code is defined to be equidistant if and only if there exists some constant d such that the distance between any two of the code’s distinct codewords is equal to d.[4] In 1984 Arrigo Bonisoli determined the structure of linear one-weight codes over finite fields and proved that every equidistant linear code is a sequence of dual Hamming codes.[5]
Examples[edit]
Some examples of linear codes include:
- Repetition codes
- Parity codes
- Cyclic codes
- Hamming codes
- Golay code, both the binary and ternary versions
- Polynomial codes, of which BCH codes are an example
- Reed–Solomon codes
- Reed–Muller codes
- Algebraic geometry codes
- Binary Goppa codes
- Low-density parity-check codes
- Expander codes
- Multidimensional parity-check codes
- Toric codes
- Turbo codes
Generalization[edit]
Hamming spaces over non-field alphabets have also been considered, especially over finite rings, most notably Galois rings over Z4. This gives rise to modules instead of vector spaces and ring-linear codes (identified with submodules) instead of linear codes. The typical metric used in this case the Lee distance. There exist a Gray isometry between 



More recently,[when?] some authors have referred to such codes over rings simply as linear codes as well.[9]
See also[edit]
- Decoding methods
References[edit]
- ^ William E. Ryan and Shu Lin (2009). Channel Codes: Classical and Modern. Cambridge University Press. p. 4. ISBN 978-0-521-84868-8.
- ^ MacKay, David, J.C. (2003). Information Theory, Inference, and Learning Algorithms (PDF). Cambridge University Press. p. 9. Bibcode:2003itil.book…..M. ISBN 9780521642989.
In a linear block code, the extra
bits are linear functions of the original
bits; these extra bits are called parity-check bits
- ^ Thomas M. Cover and Joy A. Thomas (1991). Elements of Information Theory. John Wiley & Sons, Inc. pp. 210–211. ISBN 978-0-471-06259-2.
- ^ Etzion, Tuvi; Raviv, Netanel (2013). «Equidistant codes in the Grassmannian». arXiv:1308.6231 [math.CO].
- ^ Bonisoli, A. (1984). «Every equidistant linear code is a sequence of dual Hamming codes». Ars Combinatoria. 18: 181–186.
- ^ Marcus Greferath (2009). «An Introduction to Ring-Linear Coding Theory». In Massimiliano Sala; Teo Mora; Ludovic Perret; Shojiro Sakata; Carlo Traverso (eds.). Gröbner Bases, Coding, and Cryptography. Springer Science & Business Media. ISBN 978-3-540-93806-4.
- ^ «Encyclopedia of Mathematics». www.encyclopediaofmath.org.
- ^ J.H. van Lint (1999). Introduction to Coding Theory (3rd ed.). Springer. Chapter 8: Codes over ℤ4. ISBN 978-3-540-64133-9.
- ^ S.T. Dougherty; J.-L. Kim; P. Sole (2015). «Open Problems in Coding Theory». In Steven Dougherty; Alberto Facchini; Andre Gerard Leroy; Edmund Puczylowski; Patrick Sole (eds.). Noncommutative Rings and Their Applications. American Mathematical Soc. p. 80. ISBN 978-1-4704-1032-2.
Bibliography[edit]
- J. F. Humphreys; M. Y. Prest (2004). Numbers, Groups and Codes (2nd ed.). Cambridge University Press. ISBN 978-0-511-19420-7. Chapter 5 contains a more gentle introduction (than this article) to the subject of linear codes.
External links[edit]
- q-ary code generator program
- Code Tables: Bounds on the parameters of various types of codes, IAKS, Fakultät für Informatik, Universität Karlsruhe (TH)]. Online, up to date table of the optimal binary codes, includes non-binary codes.
- The database of Z4 codes Online, up to date database of optimal Z4 codes.
| Определение: |
| Линейный код (англ. Linear code) — код фиксированной длины (блоковый код), исправляющий ошибки, для которого любая линейная комбинация кодовых слов также является кодовым словом. |
Линейные коды обычно делят на блоковые коды и свёрточные коды. Также можно рассматривать турбо-коды, как гибрид двух предыдущих.[1]
По сравнению с другими кодами, линейные коды позволяют реализовывать более эффективные алгоритмы кодирования и декодирования информации (см. синдромы ошибок).
Содержание
- 1 Формальное определение
- 2 Порождающая матрица
- 3 Проверочная матрица
- 4 Кодирование и декодирование, примеры
- 4.1 Пример
- 5 Минимальное расстояние и корректирующая способность
- 6 Синдромы и метод обнаружения ошибок в линейном коде
- 7 Преимущества и недостатки линейных кодов
- 8 Примечания
- 9 Источники информации
Формальное определение
| Определение: |
| Линейный код длины и ранга является линейным подпространством размерности векторного пространства , где — конечное поле (поле Галуа) из элементов. Такой код с параметром называется -арным кодом (напр. если — то это 5-арный код). Если или , то код представляет собой двоичный код, или тернарный соответственно. |
Векторы в называют кодовыми словами. Размер кода — это количество кодовых слов, т.е. .
Весом кодового слова называют число его ненулевых элементов. Расстояние между двумя кодовыми словами определяется как расстояние Хэмминга. Расстояние линейного кода — это минимальный вес его ненулевых кодовых слов или равным образом минимальное расстояние между всеми парами различных кодовых слов.
Линейный код длины , ранга и с расстоянием называют -кодом (англ. [n,k,d] code). Параметр d в обозначении кода часто опускается, потому что через него не задается структура кода. В таком случае пишут просто -код. В литературе встречается обозначение как в квадратных, так и в круглых скобках.[2][3]
Порождающая матрица
| Определение: |
| Порождающая матрица — это матрица, столбцы которой задают базис линейного кода. |
Так как линейный код является линейным подпространством , целиком код (может быть очень большим) может быть представлен как линейная оболочка набора из кодовых слов (т.е. базис). Этот базис часто объединяют в столбцы матрицы и называют такую матрицу порождающей матрицей кода .
В случае, если , где — это единичная матрица размера , а — это матрица размера говорят, что матрица находится в каноническом виде.
Имея матрицу можно получить из некоторого входного вектора кодовое слово линейного кода
- ,
где и — векторы-строки. Порождающая матрица линейного -кода имеет вид . Число избыточных бит тогда определяется как .
Проверочная матрица
| Определение: |
| Проверочная матрица линейного кода — это порождающая матрица ортогонального дополнения . Другими словами, это матрица, которая описывает правила, которым должны удовлетворять части кодового слова. |
Используется, чтобы определить, является ли некий вектор кодовым словом, а также в алгоритмах декодирования (напр. syndrome decoding).
Кодовое слово принадлежит коду тогда и только тогда, когда или, что то же самое, .
Проверочную матрицу можно получить из порождающей и наоборот: пусть дана порождающая матрица в каноническом виде , тогда проверочную матрицу можно получить по формуле
- ,
так как .
Кодирование и декодирование, примеры
Предположим, что имеется линия связи, по которой мы можем пересылать и принимать биты. В среднем какой-то известный процент переданных битов будет поврежден, ошибочен. Такая модель называется двоичным симметричным каналом.
Блок из символов сообщения будет кодироваться в кодовое слово , где ; эти кодовые слова образуют код.
Первая часть кодового слова состоит из информационных битов сообщения:
- ,
за которым следуют проверочных битов . Проверочные биты выбраны так, чтобы кодовые слова удовлетворяли уравнению
- ,
где — проверочная матрица.
Пример
Проверочная матрица
определяет код с и . Для этого кода
.
Сообщение кодируется в кодовое слово , которое начинается с самого сообщения:
- ,
а последующих три проверочных символа выбираются так, чтобы выполнялось уравнение .
Если сообщение , то , и проверочные биты легко определяются: , так что кодовое слово .
Минимальное расстояние и корректирующая способность
Линейность гарантирует, что расстояние Хэмминга между кодовым словом и любым другим кодовым словом не зависит от . Так как — тоже кодовое слово, а , то
Иными словами, чтобы найти минимальное расстояние между кодовыми словами линейного кода, необходимо рассмотреть ненулевые кодовые слова. Тогда ненулевое кодовое слово с минимальным весом будет иметь минимальное расстояние до нулевого кодового слова, таким образом показывая минимальное расстояние линейного кода.
Минимальное расстояние кода однозначно определяет количество ошибок, которое способен обнаружить () и исправить () данный код.
Синдромы и метод обнаружения ошибок в линейном коде
Любой код (в том числе нелинейный) можно декодировать с помощью обычной таблицы, где каждому значению принятого слова соответствует наиболее вероятное переданное слово . Однако, данный метод требует применения огромных таблиц уже для кодовых слов сравнительно небольшой длины.
Для линейных кодов этот метод можно существенно упростить. При этом для каждого принятого вектора вычисляется синдром . Поскольку , где — кодовое слово, а — вектор ошибки, то . Затем с помощью таблицы по синдрому определяется вектор ошибки, с помощью которого определяется переданное кодовое слово. При этом таблица получается гораздо меньше, чем при использовании предыдущего метода.
Преимущества и недостатки линейных кодов
+ Благодаря линейности для запоминания или перечисления всех кодовых слов достаточно хранить в памяти кодера или декодера существенно меньшую их часть, а именно только те слова, которые образуют базис соответствующего линейного пространства. Это существенно упрощает реализацию устройств кодирования и декодирования и делает линейные коды весьма привлекательными с точки зрения практических приложений.
— Хотя линейные коды, как правило, хорошо справляются с редкими, но большими пачками ошибок, их эффективность при частых, но небольших ошибках (например, в канале с АБГШ), менее высока.
Примечания
- ↑ William E. Ryan and Shu Lin (2009). Channel Codes: Classical and Modern. Cambridge University Press. p. 4. ISBN 978-0-521-84868-8.
- ↑ В. А. Липницкий, Н. В. Чесалин — Линейные коды и кодовые последовательности: учеб.-метод. пособие для студентов мех.-мат. фак. БГУ. Минск: БГУ, 2008. — 41 с., стр. 6
- ↑ Мак-Вильямс Ф. Дж., Слоэн Н. Дж. А. Теория кодов, исправляющих ошибки: Пер. с англ. — М: Связь, 1979. — 744 с., стр. 17
Источники информации
- wikipedia.org — Линейный код
- wikipedia.org — Linear code
- Мак-Вильямс Ф. Дж., Слоэн Н. Дж. А. Теория кодов, исправляющих ошибки: Пер. с англ. — М: Связь, 1979. — 744 с., стр. 12-33
- Ф.И. Соловьева — Введение в теорию кодирования
- В. А. Липницкий, Н. В. Чесалин — Линейные коды и кодовые последовательности: учеб.-метод. пособие для студентов мех.-мат. фак. БГУ. Минск: БГУ, 2008. — 41 с.

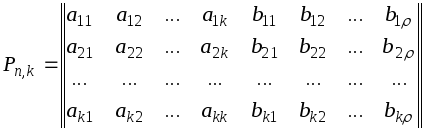
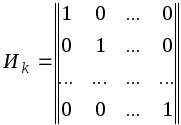


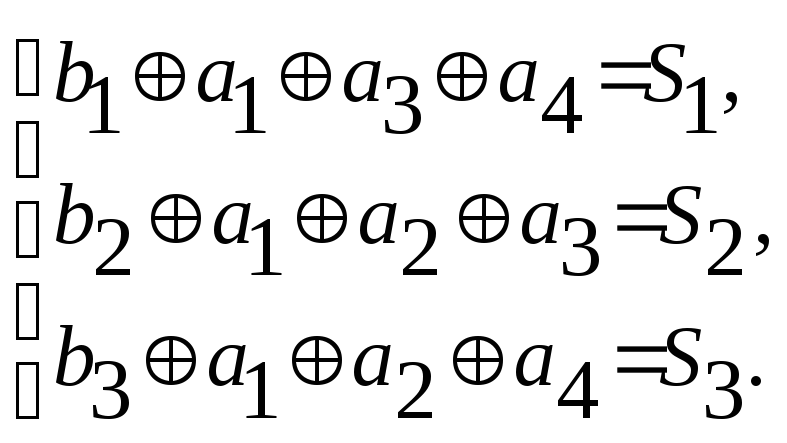













 H = (1 0 1 1 1 0 0 1 1 1 0 0 1 0 0 1 1 1 0 0 1) { displaystyle { boldsymbol {H}} = { begin {pmatrix} 1 0 1 1 1 0 0 \ 1 1 1 0 0 1 0 \ 0 1 1 1 0 0 1 end {pmatrix}}}
H = (1 0 1 1 1 0 0 1 1 1 0 0 1 0 0 1 1 1 0 0 1) { displaystyle { boldsymbol {H}} = { begin {pmatrix} 1 0 1 1 1 0 0 \ 1 1 1 0 0 1 0 \ 0 1 1 1 0 0 1 end {pmatrix}}}
 являются линейными функциями исходного K { displaystyle K}
являются линейными функциями исходного K { displaystyle K} биты; эти дополнительные биты называются битами проверки четности
биты; эти дополнительные биты называются битами проверки четности