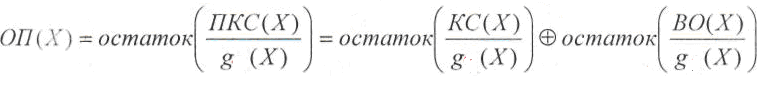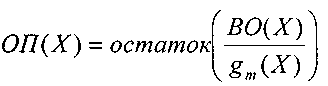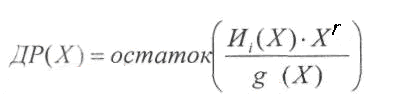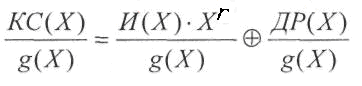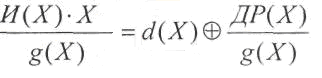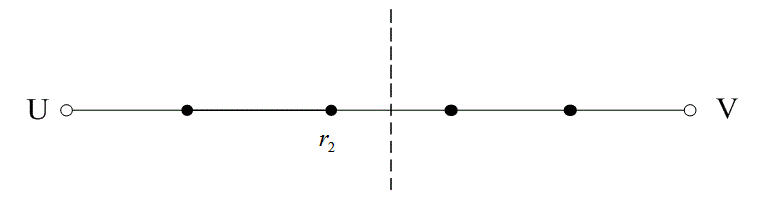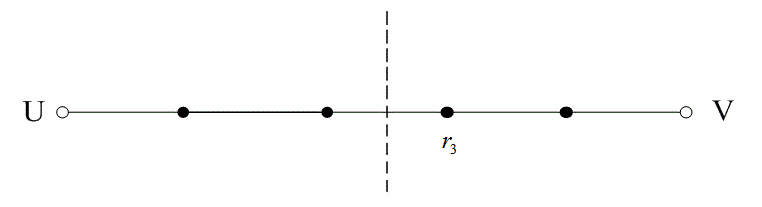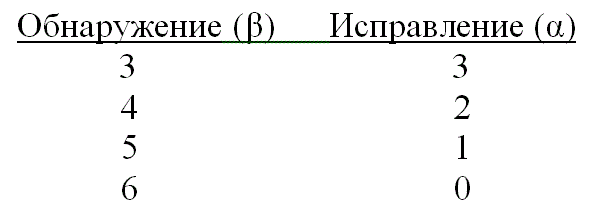Коды, исправляющие ошибки. Варианты программной реализации
Время на прочтение
2 мин
Количество просмотров 7.7K
Сразу прошу не «прогонять пинками», я старался, и это может быть полезно для таких же школьников как я.
Коды, исправляющие ошибки.
Существует множество кодов, исправляющих ошибки в двоичном коде. Это очень полезно, потому что множество информации портиться при хранении или передачи информации. Одним из примеров данных кодов можно привести «код Хемминга»(Подробно о нём уже написал другой автор http://habrahabr.ru/post/140611/). Они добавляют к бинарному тексту дополнительные, кодовые биты, при помощи которых мы сможем исправить полученные ошибки.
Каждый такой код имеет две характеристики – k и n. Такой код называется (n,k)-кодом. Здесь “n” обозначает общее количество символов в блоке закодированного текста, а “k” – число значимых символов.
Например, простейшим кодом является код с повторениями. В этом коде к каждому символу двоичного кода добавляется по n-1 кодовых битов, которые дублируют, значимый символ и в последствие мы сможем исправить ошибку. Например (3,1)-код дописывает к каждому символу в двоичной системе два таких же и при зашумлении, если меняется один символ из блока, то остаётся 2 одинаковых и по ним мы возвращаем исходный символ.
Описание проекта
В моей программе мы использовали 2 вида таких кодов, это (3,1)-код с повторением и (7,4)-код, который является одним из так называемых «кодов Хэмминга». Однако моя программа написана так, что в неё без особых усилий и затрат времени можно добавить любой другой код типа (n,k).
Для того чтобы осуществить свою цель, мне потребовалось переводить обычный текст в бинарный вид, затем добавлять кодовые биты, помогающие мне восстановить текст. И для того, чтобы с эмитировать ошибки в бинарном коде, я написал процедуру, зашумляющую текст (совершающую ошибки в бинарном коде).
Затем я переводил в обычный текст зашумлённый код, чтобы продемонстрировать пользователю действенность зашумления. Следующим действием я исправлял оставшийся у мой зашумленный код и переводили его в обычный текст.
Для создания своей программы я использовал справку программы Pascal, мои собственные знания и «великий» Google.com.
Выводы и перспективы.
Я создал программу, реализующую два кода исправляющих ошибки в тексте, полученные при переносе или длительном хранении файла с информацией. А так же улучшил свои навыки в языке программирования Pascal.
Исходные коды
Прошу прощения за «еврейский код» и за турбо паскаль тоже(нормальный компьютер сломался, писал на пеньтиуме втором). Код может помочь школьникам на уроках информатике и олимпиадникам.
Пример
. Предположим, в канале связи под действием
помех произошло искажение и вместо
0100101 было принято 01001(1)1.
Решение:
Для обнаружения ошибки производят уже
знакомые нам проверки на четность.
Первая
проверка:
сумма П1+П3+П5+П7
= 0+0+1+1 четна.
В младший разряд номера ошибочной
позиции запишем 0.
Вторая
проверка:
сумма П2+П3+П6+П7
= 1+0+1+1 нечетна.
Во второй разряд номера ошибочной
позиции запишем 1
Третья
проверка:
сумма П4+П5+П6+П7
= 0+1+1+1 нечетна.
В третий разряд номера ошибочной позиции
запишем 1. Номер ошибочной позиции 110=
6. Следовательно,
символ шестой позиции следует изменить
на обратный, и получим правильную кодовую
комбинацию.
Код, исправляющий
одиночную и обнаруживающий двойную
ошибки
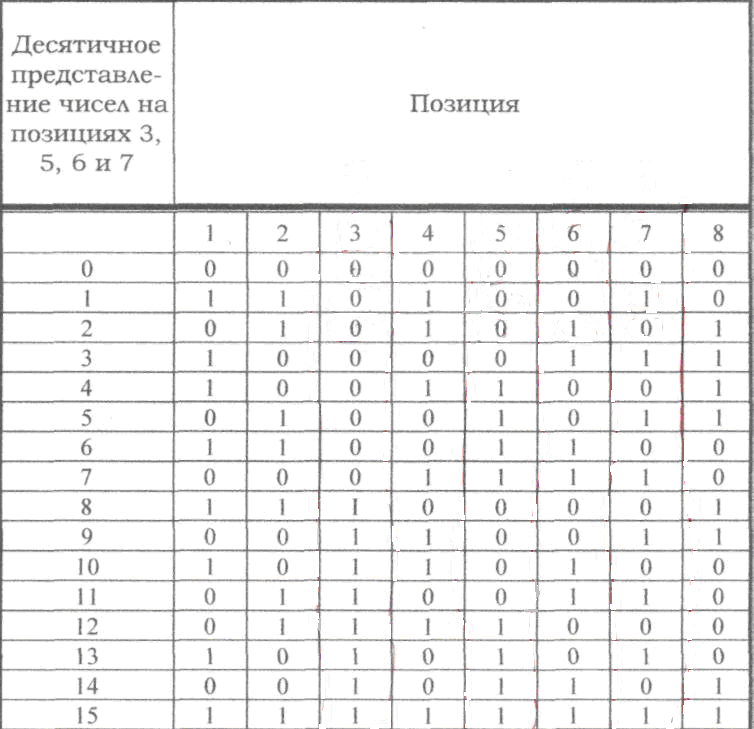
Если по изложенным
выше правилам строить корректирующий
код с обнаружением и исправлением
одиночной ошибки для равномерного
двоичного кода, то первые 16 кодовых
комбинаций будут иметь вид, показанный
в таблице. Такой код может быть использован
для построения кода с исправлением
одиночной ошибки и обнаружением двойной.
Для
этого, кроме указанных выше проверок
по контрольным позициям, следует провести
еще одну проверку на четность для всей
строки в целом. Чтобы осуществить такую
проверку, следует к каждой строке кода
добавить контрольные символы, записанные
в дополнительной колонке (таблица,
колонка 8). Тогда в случае одной ошибки
проверки по позициям укажут номер
ошибочной позиции, а проверка на четность
— на наличие ошибки. Если проверки позиций
укажут на наличие ошибки, а проверка на
четность не фиксирует ее, значит в
кодовой комбинации две ошибки.
Лекция 8
8.1 Двоичные циклические коды
Вышеприведенная
процедура построения линейного кода
матричным методом имеет ряд недостатков.
Она неоднозначна (МДР можно задать
различным образом) и неудобна
в реализации в виде технических устройств.
Этих недостатков лишены
линейные корректирующие коды, принадлежащие
к классу циклических.
Циклическими
называют
линейные (n,k)-коды,
обладающие
следующим свойством:
для любого кодового слова:
существует другое
кодовое слово:
полученное
циклическим сдвигом элементов исходного
кодового слова ||КС||
вправо
или влево, которое также принадлежит
этому коду.
Для
описания циклических кодов используют
полиномы с фиктивной переменной
X.
Например,
пусть кодовое слово ||КС||
=
||011010||.
Его
можно описать полиномом
Таким
образом, разряды кодового слова в
описывающем его полиноме используются
в качестве коэффициентов при степенях
фиктивной переменной
X.
Наибольшая
степень фиктивной переменной X
в
слагаемом с ненулевым
коэффициентом называется степенью
полинома. В вышеприведенном примере
получился полином 4-й степени.
Теперь
действия над кодовыми словами сводятся
к действиям над полиномами.
Вместо алгебры матриц здесь используется
алгебра полиномов.
Рассмотрим
алгебраические действия над полиномами,
используемые в теории
циклических кодов. Суммирование
полиномов разберем на примере
С(Х)=А(Х)+В(Х).
Пусть
||A||
= ||011010||,
||В|| =
||110111|.
Тогда
—————————————————————
Таким
образом, при суммировании коэффициентов
при X
в одинаковой степени
результат берется по модулю 2. При таком
правиле вычитание эквивалентно
суммированию.
Умножение
выполняется как обычно, но с использованием
суммирования
по модулю 2.
Рассмотрим
умножение на примере умножения полинома
(X3+X1+X0)
на
полином X1+X0
X3
+ 0*X2+X1+X0
*
X1+X0
—————————————————
X3+
0*X2+X1+Х0
X4+0*Х3+
X2+Х1
____________________________________
Х4+
X3+
X2+0*X1+X0
Операция
— обратная умножению -деление. Деление
полиномов выполняется как обычно, за
исключением того, что вычитание
выполняется по модулю 2. Вспомним, что
вычитание по модулю 2 эквивалентно
сложению по модулю 2
Пример
деления полинома X6+X4+X3
на полином
X3+X2+1
X6+0*X5+X4
+ X3+0*X2+0*X1+0
| X3+X2+1
X6+X5+0*X4+X3 результат== |X3+X2
————————————
X5
+X4
+ 0*X3+0*X2
X5
+X4
+ 0*X3+
X2
—————————————-
остаток==
X2
=
100
Циклический
сдвиг влево на одну позицию коэффициентов
полинома степени n-1
получается
путем его умножения на X
с
последующим вычитанием из
результата полинома Xn+1,
если его порядок >
п.
Проверим это на
примере.
Пусть требуется
выполнить циклический сдвиг влево на
одну позицию
коэффициентов
полинома
C(X)=X5+Х3+X2+1
→ (101101)
В результате должен
получиться полином
C1(X)=X4+Х3+X1+1
→ (011011)
Это легко
доказывается:
C1(X)=C(X)*X-(X6+1)=(X6+Х4+X3+X)+(
X6+1)=X4+Х3+X1+1
В
основе циклического кода лежит образующий
полином r-го
порядка
(напомним, что r—
число дополнительных разрядов). Будем
обозначать
его gr(X).
Образование
кодовых слов (кодирование) КС
выполняется
путем умножения
информационного полинома с коэффициентами,
являющимися информационной
последовательностью
И(Х)
порядка
i<k
на
образующий полином gr(X)
КСr+k(Х)=gr(X)+ИСk(Х).
Принятое кодовое
слово может отличаться от переданного
искаженными разрядами в результате
воздействия помех.
ПКС(Х)=КС(Х)+ВО(Х).
где
ВО(Х)
— полином
вектора ошибки, а суммирование, как
обычно, ведется
по модулю 2.
Декодирование,
как и раньше начинается с нахождения
опознавателя,
в данном случае в виде полинома ОП(Х).
Этот
полином вычисляется как
остаток от деления полинома принятого
кодового слова ПКС(Х)
на
образующий
полином g(Х):
Первое
слагаемое остатка не имеет, т.к. кодовое
слово было образовано путем умножения
полинома информационной последовательности
на
образующий полином. Следовательно, и в
данном случае опознаватель
полностью зависит от вектора ошибки.
Образующий
полином выбирается таким, чтобы при
данном r
как
можно
большее число отношений ВО(Х)/g(Х)
давало
различные остатки.
Такому
требованию отвечают так называемые
неприводимые
полиномы,
которые
не делятся без остатка ни на один полином
степени r
и ниже, а
делятся только сами на себя и на 1.
Приведенная
здесь процедура образования кодового
слова неудобна тем,
что такой код получается несистематическим,
т.е. таким, в кодовых словах
которого нельзя выделить информационные
и дополнительные разряды.
Этот недостаток
был устранен следующим образом.
Способ
кодирования, приводящий к получению
систематического линейного циклического
кода, состоит в приписывании к
информационной
последовательности И
дополнительных разрядов ДР.
Эти
дополнительные разряды предлагается
находить по следующей формуле:
Порядок
полинома ДР(Х)
гарантировано
меньше r
(поскольку
это остаток).
Приписывание
дополнительных разрядов к информационной
последовательности,
используя алгебру полиномов, можно
описать формулой:
Одним
из свойств циклических линейных кодов
является то, что результат
деления любого разрешенного кодового
слова КС
на
образующий полином также, является
разрешенным кодовым словом.
Покажем,
что получаемые по вышеприведенному
алгоритму кодовые
слова являются кодовыми словами
циклического линейного кода. Для
этого нужно убедиться в том, что
произвольное разрешенное кодовое
слово делится на образующий полином
g(X)
без остатка:
Рассмотрим первое
слагаемое:
где
d(Х)
— целая
часть результата деления.
Подставим полученную
сумму на место первого слагаемого:
Суммирование
последних двух слагаемых дает нулевой
результат (напомним,
что суммирование выполняется по модулю
2).
Значит
—
целая часть деления. Остатка нет. Это
означает,
что описанный выше способ кодирования
соответствует циклическому
коду.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Мы знаем, что биты 0 и 1 соответствуют двум разным диапазонам аналоговых напряжений. Таким образом, во время передачи двоичных данных из одной системы в другую, шум также может быть добавлен. Из-за этого могут быть ошибки в полученных данных в другой системе.
Это означает, что бит 0 может измениться на 1 или бит 1 может измениться на 0. Мы не можем избежать помех от шума. Но мы можем сначала получить исходные данные, обнаружив, присутствуют ли какие-либо ошибки, а затем исправив эти ошибки. Для этой цели мы можем использовать следующие коды.
- Коды обнаружения ошибок
- Коды исправления ошибок
Коды обнаружения ошибок – используются для обнаружения ошибок, присутствующих в принятых данных (битовом потоке). Эти коды содержат некоторые биты, которые включены (добавлены) в исходный поток битов. Эти коды обнаруживают ошибку, если она произошла во время передачи исходных данных (потока битов). Пример – код четности, код Хэмминга.
Коды исправления ошибок – используются для исправления ошибок, присутствующих в полученных данных (битовом потоке), чтобы мы получили исходные данные. Коды исправления ошибок также используют аналогичную стратегию кодов обнаружения ошибок. Пример – код Хэмминга.
Поэтому, чтобы обнаружить и исправить ошибки, дополнительные биты добавляются к битам данных во время передачи.
Код паритета
Легко включить (добавить) один бит четности либо слева от MSB, либо справа от LSB исходного битового потока. Существует два типа кодов четности, а именно четный код четности и нечетный код четности, в зависимости от типа выбранной четности.
Четный код
Значение четного бита должно быть равно нулю, если в двоичном коде присутствует четное количество единиц. В противном случае он должен быть один. Таким образом, четное число единиц присутствует в четном коде четности . Четный код четности содержит биты данных и четный бит четности.
В следующей таблице приведены коды четности, соответствующие каждому 3-битному двоичному коду. Здесь бит четности включен справа от LSB двоичного кода.
| Бинарный код | Четный бит | Четный код |
|---|---|---|
| 000 | 0 | 0000 |
| 001 | 1 | 0011 |
| 010 | 1 | 0101 |
| 011 | 0 | 0110 |
| 100 | 1 | 1001 |
| 101 | 0 | 1010 |
| 110 | 0 | 1100 |
| 111 | 1 | 1111 |
Здесь число битов, присутствующих в четных кодах четности, равно 4. Таким образом, возможное четное число единиц в этих четных кодах четности равно 0, 2 и 4.
-
Если другая система получает один из этих четных кодов четности, то в полученных данных нет ошибки. Биты, отличные от четного бита, совпадают с битами двоичного кода.
-
Если другая система получит коды, отличные от четных, то в полученных данных возникнет ошибка (и). В этом случае мы не можем предсказать исходный двоичный код, потому что мы не знаем битовую позицию (ы) ошибки.
Если другая система получает один из этих четных кодов четности, то в полученных данных нет ошибки. Биты, отличные от четного бита, совпадают с битами двоичного кода.
Если другая система получит коды, отличные от четных, то в полученных данных возникнет ошибка (и). В этом случае мы не можем предсказать исходный двоичный код, потому что мы не знаем битовую позицию (ы) ошибки.
Поэтому четный бит четности полезен только для обнаружения ошибки в принятом коде четности. Но недостаточно исправить ошибку.
Код нечетного паритета
Значение нечетного бита четности должно быть нулевым, если в двоичном коде присутствует нечетное число единиц. В противном случае, он должен быть один. Так что нечетное количество единиц присутствует в нечетном коде четности . Нечетный код четности содержит биты данных и нечетный бит четности.
В следующей таблице показаны нечетные коды четности, соответствующие каждому 3-битному двоичному коду. Здесь нечетный бит четности включен справа от LSB двоичного кода.
| Бинарный код | Нечетный бит четности | Код нечетного паритета |
|---|---|---|
| 000 | 1 | 0001 |
| 001 | 0 | 0010 |
| 010 | 0 | 0100 |
| 011 | 1 | 0111 |
| 100 | 0 | 1000 |
| 101 | 1 | 1011 |
| 110 | 1 | 1101 |
| 111 | 0 | 1110 |
Здесь число битов, присутствующих в нечетных кодах четности, равно 4. Таким образом, возможное нечетное число единиц в этих нечетных кодах четности равно 1 и 3.
-
Если другая система получает один из этих нечетных кодов четности, то в полученных данных нет ошибки. Биты, отличные от нечетного бита четности, совпадают с битами двоичного кода.
-
Если другая система получает не четные коды четности, то в полученных данных есть ошибка (и). В этом случае мы не можем предсказать исходный двоичный код, потому что мы не знаем битовую позицию (ы) ошибки.
Если другая система получает один из этих нечетных кодов четности, то в полученных данных нет ошибки. Биты, отличные от нечетного бита четности, совпадают с битами двоичного кода.
Если другая система получает не четные коды четности, то в полученных данных есть ошибка (и). В этом случае мы не можем предсказать исходный двоичный код, потому что мы не знаем битовую позицию (ы) ошибки.
Следовательно, нечетный бит четности полезен только для обнаружения ошибки в принятом коде четности. Но недостаточно исправить ошибку.
Код Хэмминга
Код Хэмминга полезен как для обнаружения, так и для исправления ошибок, присутствующих в полученных данных. Этот код использует несколько битов четности, и мы должны поместить эти биты четности в позиции степеней 2.
Минимальное значение «k», для которого следующее соотношение является правильным (действительным), является не чем иным, как требуемым количеством битов четности.
2k geqn+k+1
Куда,
«n» – количество бит в двоичном коде (информация)
‘k’ – количество бит четности
Следовательно, количество битов в коде Хэмминга равно n + k.
Пусть код Хэмминга равен bn+kbn+k−1.....b3b2b1 и битам четности pk,pk−1,....p1. Мы можем поместить биты четности ‘k’ только в степени 2 позиции. В оставшихся битовых позициях мы можем разместить n бит двоичного кода.
Исходя из требований, мы можем использовать четную или нечетную четность при формировании кода Хемминга. Но тот же метод контроля четности следует использовать для того, чтобы определить, присутствует ли какая-либо ошибка в полученных данных.
Выполните эту процедуру для поиска битов четности .
-
Найдите значение p 1 , основанное на количестве единиц, присутствующих в позициях битов b 3 , b 5 , b 7 и так далее. Все эти битовые позиции (суффиксы) в их эквивалентном двоичном файле имеют «1» в значении места 2 0 .
-
Найдите значение p 2 , основанное на количестве единиц, присутствующих в позициях битов b 3 , b 6 , b 7 и так далее. Все эти битовые позиции (суффиксы) в их эквивалентном двоичном файле имеют «1» в значении места 2 1 .
-
Найдите значение p 3 , основанное на количестве единиц, присутствующих в позициях битов b 5 , b 6 , b 7 и так далее. Все эти битовые позиции (суффиксы) в их эквивалентном двоичном файле имеют «1» в значении места 2 2 .
-
Аналогично найдите другие значения битов четности.
Найдите значение p 1 , основанное на количестве единиц, присутствующих в позициях битов b 3 , b 5 , b 7 и так далее. Все эти битовые позиции (суффиксы) в их эквивалентном двоичном файле имеют «1» в значении места 2 0 .
Найдите значение p 2 , основанное на количестве единиц, присутствующих в позициях битов b 3 , b 6 , b 7 и так далее. Все эти битовые позиции (суффиксы) в их эквивалентном двоичном файле имеют «1» в значении места 2 1 .
Найдите значение p 3 , основанное на количестве единиц, присутствующих в позициях битов b 5 , b 6 , b 7 и так далее. Все эти битовые позиции (суффиксы) в их эквивалентном двоичном файле имеют «1» в значении места 2 2 .
Аналогично найдите другие значения битов четности.
Выполните эту процедуру для поиска контрольных битов .
-
Найдите значение c 1 , основанное на количестве единиц, присутствующих в битовых позициях b 1 , b 3 , b 5 , b 7 и так далее. Все эти битовые позиции (суффиксы) в их эквивалентном двоичном файле имеют «1» в значении места 2 0 .
-
Найдите значение c 2 , основанное на количестве единиц, присутствующих в позициях битов b 2 , b 3 , b 6 , b 7 и так далее. Все эти битовые позиции (суффиксы) в их эквивалентном двоичном файле имеют «1» в значении места 2 1 .
-
Найдите значение c 3 , основанное на количестве единиц, присутствующих в позициях битов b 4 , b 5 , b 6 , b 7 и так далее. Все эти битовые позиции (суффиксы) в их эквивалентном двоичном файле имеют «1» в значении места 2 2 .
-
Аналогично найдите другие значения контрольных битов.
Найдите значение c 1 , основанное на количестве единиц, присутствующих в битовых позициях b 1 , b 3 , b 5 , b 7 и так далее. Все эти битовые позиции (суффиксы) в их эквивалентном двоичном файле имеют «1» в значении места 2 0 .
Найдите значение c 2 , основанное на количестве единиц, присутствующих в позициях битов b 2 , b 3 , b 6 , b 7 и так далее. Все эти битовые позиции (суффиксы) в их эквивалентном двоичном файле имеют «1» в значении места 2 1 .
Найдите значение c 3 , основанное на количестве единиц, присутствующих в позициях битов b 4 , b 5 , b 6 , b 7 и так далее. Все эти битовые позиции (суффиксы) в их эквивалентном двоичном файле имеют «1» в значении места 2 2 .
Аналогично найдите другие значения контрольных битов.
Десятичный эквивалент контрольных битов в полученных данных дает значение позиции бита, где присутствует ошибка. Просто добавьте значение, присутствующее в этой позиции бита. Поэтому мы получим оригинальный двоичный код после удаления битов четности.
Пример 1
Найдем код Хемминга для двоичного кода: d 4 d 3 d 2 d 1 = 1000. Рассмотрим четные биты четности.
Количество битов в данном двоичном коде равно n = 4.
Мы можем найти необходимое количество бит четности, используя следующее математическое соотношение.
2k geqn+k+1
Подставим n = 4 в вышеприведенном математическом соотношении.
Rightarrow2k geq4+k+1
Rightarrow2k geq5+k
Минимальное значение k, удовлетворяющее указанному выше соотношению, равно 3. Следовательно, нам требуется 3 бита четности p 1 , p 2 и p 3 . Следовательно, количество битов в коде Хэмминга будет равно 7, поскольку в двоичном коде 4 бита и 3 бита четности. Мы должны поместить биты четности и биты двоичного кода в код Хэмминга, как показано ниже.
7-битный код Хэмминга : b7b6b5b4b3b2b1=d4d3d2p3D1р−2bp1
Подставляя биты двоичного кода, код Хэмминга будет b7b6b5b4b3b2b1=100p3Op2p1. Теперь давайте найдем биты четности.
p1=b7 oplusb5 oplusb3=1 oplus0 oplus0=1
p2=b7 oplusb6 oplusb3=1 oplus0 oplus0=1
p3=b7 oplusb6 oplusb5=1 oplus0 oplus0=1
Подставляя эти биты четности, код Хэмминга будет иметь значение b7b6b5b4b3b2b1=1001011.
Пример 2
В приведенном выше примере мы получили код Хэмминга в виде b7b6b5b4b3b2b1=1001011. Теперь давайте найдем позицию ошибки, когда полученный код равен b7b6b5b4b3b2b1=1001111.
Теперь давайте найдем контрольные биты.
c1=b7 oplusb5 oplusb3 oplusb1=1 oplus0 oplus1 oplus1=1
c2=b7 oplusb6 oplusb3 oplusb2=1 oplus0 oplus1 oplus1=1
c3=b7 oplusb6 oplusb5 oplusb4=1 oplus0 oplus0 oplus1=0
Десятичное значение контрольных битов дает позицию ошибки в полученном коде Хэмминга.
c3c2c1= left(011 right)2= left(3 right)10
Следовательно, ошибка присутствует в третьем бите (b 3 ) кода Хэмминга. Просто добавьте значение, присутствующее в этом бите, и удалите биты четности, чтобы получить исходный двоичный код.
6.5.1. Весовой коэффициент двоичных векторов и расстояние между ними
6.5.2. Минимальное расстояние для линейного кода
6.5.3. Обнаружение и исправление ошибок
6.5.3.1. Распределение весовых коэффициентов кодовых слов
6.5.3.2.Одновременное обнаружение и исправление ошибок
6.5.4. Визуализация пространства 6-кортежей
6.5.5. Коррекция со стиранием ошибок
6.5.1. Весовой коэффициент двоичных векторов и расстояние между ними
Конечно же, понятно, что правильно декодировать можно не все ошибочные комбинации. Возможности кода для исправления ошибок в первую очередь определяются его структурой. Весовой коэффициент Хэмминга (Hamming weight) w(U) кодового слова U определяется как число ненулевых элементов в U. Для двоичного вектора это эквивалентно числу единиц в векторе. Например, если U=100101101, то w(U) = 5. Расстояние Хэмминга (Hamming distance) между двумя кодовыми словами U и V, обозначаемое как d(U, V), определяется как количество элементов, которыми они отличаются.
U=100101101
V=011110100
d(U,V)=6
Согласно свойствам сложения по модулю 2, можно отметить, что сумма двух двоичных векторов является другим двоичным вектором, двоичные единицы которого расположены на тех позициях, которыми эти векторы отличаются.
U + V=111011001
Таким образом, можно видеть, что расстояние Хэмминга между двумя векторами равно весовому коэффициенту Хэмминга их суммы, т.е. d(U, V) = w(U + V). Также видно, что весовой коэффициент Хэмминга кодового слова равен его расстоянию Хэмминга до нулевого вектора.
6.5.2. Минимальное расстояние для линейного кода
Рассмотрим множество расстояний между всеми парами кодовых слой в пространстве Vn. Наименьший элемент этого множества называется минимальным расстоянием кода и обозначается dmin. Как вы думаете, почему нас интересует именно минимальное расстояние, а не максимальное? Минимальное расстояние подобно наиболее слабому звену в цепи, оно дает нам меру минимальных возможностей кода и, следовательно, характеризует его мощность.
Как обсуждалось ранее, сумма двух произвольных кодовых слов дает другой элемент пространства кодовых слов. Это свойство линейных кодов формулируется просто: если U и V — кодовые слова, то и W = U + V тоже должно быть кодовым словом. Следовательно, расстояние между двумя кодовыми словами равно весовому коэффициенту третьего кодового слова, т.е. d(U, V) = w(U + V) = w(W). Таким образом, минимальное расстояние линейного кода можно определить, не прибегая к изучению расстояний между всеми комбинациями пар кодовых слов. Нам нужно лишь определить вес каждого кодового слова (за исключением нулевого вектора) в подпространстве; минимальный вес соответствует минимальному расстоянию dmin. Иными словами, dmin соответствует наименьшему из множества расстояний между нулевым кодовым словом и всеми остальными кодовыми словами.
6.5.3. Обнаружение и исправление ошибок
Задача декодера после приема вектора r заключается в оценке переданного кодового слова Ui. Оптимальная стратегия декодирования может быть выражена в терминах алгоритма максимального правдоподобия (см. приложение Б); считается, что передано было слово Ui, если
(6.41)
Поскольку для двоичного симметричного канала (binary symmetric channel — BSC) правдоподобие Ui относительно r обратно пропорционально расстоянию между r и U, можно сказать, что передано было слово Ui, если
(6.42)
Другими словами, декодер определяет расстояние между r и всеми возможными переданными кодовыми словами Uj, после чего выбирает наиболее правдоподобное Uj, для которого
(6.43)
где М = 2k — это размер множества кодовых слов. Если минимум не один, выбор между минимальными расстояниями является произвольным. Наше обсуждение метрики расстояний будет продолжено в главе 7.
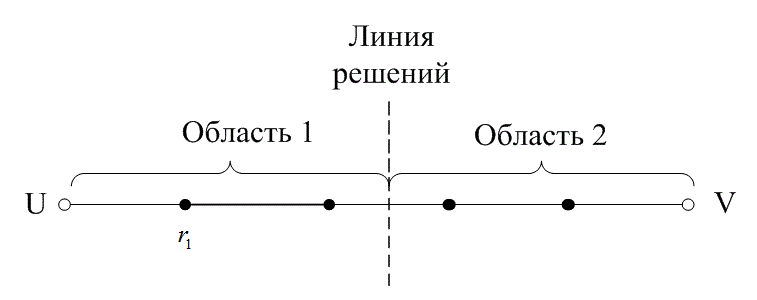
На рис. 6.13 расстояние между двумя кодовыми словами U и V показано как расстояние Хэмминга. Каждая черная точка обозначает искаженное кодовое слово. На рис. 6.13, а проиллюстрирован прием вектора r1 находящегося на расстоянии 1 от кодового слова U и на расстоянии 4 от кодового слова V. Декодер с коррекцией ошибок, следуя стратегии максимального правдоподобия, выберет при принятом векторе r1 кодовое слово U. Если r1 получился в результате появления одного ошибочного бита в переданном векторе кода U, декодер успешно исправит ошибку. Но если же это произошло в результате 4-битовой ошибки в векторе кода V, декодирование будет ошибочным. Точно так же, как показано на рис. 6.13, б, двойная ошибка при передаче U может привести к тому, что в качестве переданного вектора будет ошибочно определен вектор r2, находящийся на расстоянии 2 от вектора U и на расстоянии 3 от вектора кода V. На рис. 6.13 показана ситуация, когда в качестве переданного вектора ошибочно определен вектор r3, который находится на расстоянии 3 от вектора кода U и на расстоянии 2 от вектора V. Из рис. 6.13 видно, что если задача состоит только в обнаружении ошибок, а не в их исправлении, то можно определить искаженный вектор — изображенный черной точкой и представляющий одно-, двух-, трех- и четырехбитовую ошибку. В то же время пять ошибок при передаче могут привести к приему кодового слова V, когда в действительности было передано кодовое слово U; такую ошибку невозможно будет обнаружить.
Из рис. 6.13 можно видеть, что способность кода к обнаружению и исправлению ошибок связана с минимальным расстоянием между кодовыми словами. Линия решения на рисунке служит той же цели, что и в процессе демодуляции, — для разграничения областей решения.
а)
б)
в)
Рис. 6.13. Возможности определения и исправления ошибок: а) принятый вектор r1; б) принятый вектор r2; в) принятый вектор r3
В примере, приведенном на рис. 6.13, критерий принятия решения может быть следующим: выбрать U, если r попадает в область 1, и выбрать V, если r попадает в область 2. Выше показывалось, что такой код (при dmin = 5) может исправить две ошибки. Вообще, способность кода к исправлению ошибок t определяется, как максимальное число гарантированно исправимых ошибок на кодовое слово, и записывается следующим образом [4].
(6.44)
Здесь означает наибольшее целое, не превышающее х. Часто код, который исправляет все искаженные символы, содержащие ошибку в t или меньшем числе бит, также может исправлять символы, содержащие t +1 ошибочных бит. Это можно увидеть на рис. 6.11. В этом случае dmin = 3, поэтому из уравнения (6.44) можно видеть, что исправимы все ошибочные комбинации из t = 1 бит. Также исправима одна ошибочная комбинация, содержащая / +1 (т.е. 2) ошибочных бит. Вообще, линейный код (n, k), способный исправлять все символы, содержащие t ошибочных бит, может исправить всего 2n—k ошибочных комбинаций. Если блочный код с возможностью исправления символов, имеющих ошибки в t бит, применяется для исправления ошибок в двоичном симметричном канале с вероятностью перехода р, то вероятность ошибки сообщения Рм(вероятность того, что декодер совершит неправильное декодирование и п-битовый блок содержит ошибку) можно оценить сверху, используя уравнение (6.18).
(6.45)
Оценка переходит в равенство, если декодер исправляет все ошибочные комбинации, содержащие до t ошибочных бит включительно, но не комбинации с числом ошибочных бит, большим t. Такие декодеры называются декодерами с ограниченным расстоянием. Вероятность ошибки в декодированном бите РB зависит от конкретного кода и декодера. Приближенно ее можно выразить следующим образом [5].
(6.46)
В блочном коде, прежде чем исправлять ошибки, необходимо их обнаружить. (Или же код может использоваться только для определения наличия ошибок.) Из рис. 6.13 видно, что любой полученный вектор, который изображается черной точкой (искаженное кодовое слово), можно определить как ошибку. Следовательно, возможность определения наличия ошибки дается следующим выражением.
(6.47)
Блочный код с минимальным расстоянием dmin гарантирует обнаружение всех ошибочных комбинаций, содержащих dmin — 1 или меньшее число ошибочных бит. Такой код также способен обнаружить и большую ошибочную комбинацию, содержащую dmin или более ошибок. Фактически код (n, k) может обнаружить 2n – 2k ошибочных комбинаций длины п. Объясняется это следующим образом. Всего в пространстве 2n n-кортежей существует 2n -1 возможных ненулевых ошибочных комбинаций. Даже правильное кодовое слово — это потенциальная ошибочная комбинация. Поэтому всего существует 2k -1 ошибочных комбинаций, которые идентичны 2k -1 ненулевым кодовым словам. При появлении любая из этих 2k — 1 ошибочных комбинаций изменяет передаваемое кодовое слово Uj на другое кодовое слово Uj. Таким образом, принимается кодовое слово Uj и его синдром равен нулю. Декодер принимает Uj за переданное кодовое слово, и поэтому декодирование дает неверный результат. Следовательно, существует 2k -1 необнаружимых ошибочных комбинаций. Если ошибочная комбинация не совпадает с одним из 2k кодовых слов, проверка вектора r с помощью синдромов дает ненулевой синдром и ошибка успешно обнаруживается. Отсюда следует, что существует ровно 2n-2k выявляемых ошибочных комбинаций. При больших n, когда 2k<<2n, необнаружимой будет только незначительная часть ошибочных комбинаций.
6.5.3.1. Распределение весовых коэффициентов кодовых слов
Пусть Aj — количество кодовых слов с весовым коэффициентом j в линейном коде (п, k). Числа A0,A1,…,An называются распределением весовых коэффициентов этого кода. Если код применяется только для обнаружения ошибок в двоичном симметричном канале, то вероятность того, что декодер не сможет определить ошибку, можно рассчитать, исходя из распределения весовых коэффициентов кода [5].
(6.48)
где р — вероятность перехода в двоичном симметричном канале. Если минимальное расстояние кода равно dmin значения от А1 до , равны нулю.
Пример 6.5. Вероятность необнаруженной ошибки в коде
Пусть код (6,3), введенный в разделе 6.4.3, используется только для обнаружения наличия ошибок. Рассчитайте вероятность необнаруженной ошибки, если применяется двоичный симметричный канал, а вероятность перехода равна 10-2.
Решение
Распределение весовых коэффициентов этого кода выглядит следующим образом: A0=1, А1= А2 = 0, A3 = 4, A5 = 0, A6 = 0. Следовательно, используя уравнение (6.48), можно записать следующее.
Для р = 10-2 вероятность необнаруженной ошибки будет равна 3,9 х 10-6.
6.5.3.2. Одновременное обнаружение и исправление ошибок
Возможностями исправления ошибок с максимальным гарантированным (t), где t определяется уравнением (6.44), можно пожертвовать в пользу определения класса ошибок. Код можно использовать для одновременного исправления α и обнаружения β ошибок, причем , а минимальное расстояние кода дается следующим выражением [4].
(6.49)
При появлении t или меньшего числа ошибок код способен обнаруживать и исправлять их. Если ошибок больше t, но меньше е+1, где е определяется уравнением (6.47), код может определять наличие ошибок, но исправить может только некоторые из них. Например, используя код с dmin = 7. можно выполнить обнаружение и исправление со следующими значениями α и β.
Заметим, что исправление ошибки подразумевает ее предварительное обнаружение. В приведенном выше примере (с тремя ошибками) все ошибки можно обнаружить и исправить. Если имеется пять ошибок, их можно обнаружить, но исправить можно только одну из них.
6.5.4. Визуализация пространства 6-кортежей
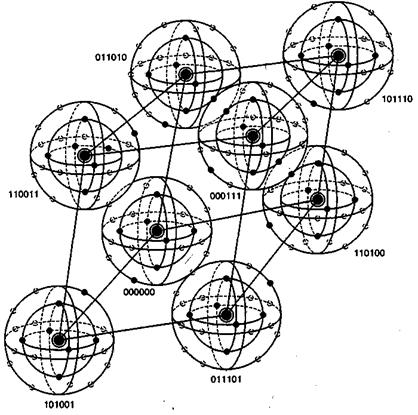
На рис. 6.14 визуально представлено восемь кодовых слов, фигурирующих в примере из раздела 6.4.3. Кодовые слова образованы посредством линейных комбинаций из трех независимых 6-кортежей, приведенных в уравнении (6.26); сами кодовые слова образуют трехмерное подпространство. На рисунке показано, что такое подпространство полностью занято восемью кодовыми словами (большие черные круги); координаты подпространства умышленно выбраны неортогональными. На рис. 6.14 предпринята попытка изобразить все пространство, содержащее шестьдесят четыре 6-кортежей, хотя точно нарисовать или составить такую модель невозможно. Каждое кодовое слово окружают сферические слои или оболочки. Радиус внутренних непересекающихся слоев — это расстояние Хэмминга, равное 1; радиус внешнего слоя — это расстояние Хэмминга, равное 2. Большие расстояния в этом примере не рассматриваются. Для каждого кодового слова два показанных слоя заняты искаженными кодовыми словами. На каждой внутренней сфере существует шесть таких точек (всего 48 точек), представляющих шесть возможных однобитовых ошибок в векторах, соответствующих каждому кодовому слову. Эти кодовые слова с однобитовыми возмущениями могут быть соотнесены только с одним кодовым словом; следовательно, такие ошибки могут быть исправлены. Как видно из нормальной матрицы, приведенной на рис. 6.11, существует также одна двухбитовая ошибочная комбинация, которая также поддается исправлению. Всего существует
Заметим, что исправление ошибки подразумевает ее предварительное обнаружение. В приведенном выше примере (с тремя ошибками) все ошибки можно обнаружить и исправить. Если имеется пять ошибок, их можно обнаружить, но исправить можно только одну из них.
6.5.4. Визуализация пространства 6-кортежей
На рис. 6.14 визуально представлено восемь кодовых слов, фигурирующих в примере из раздела 6.4.3. Кодовые слова образованы посредством линейных комбинаций из трех независимых 6-кортежей, приведенных в уравнении (6.26); сами кодовые слова образуют трехмерное подпространство. На рисунке показано, что такое подпространство полностью занято восемью кодовыми словами (большие черные круги); координаты подпространства умышленно выбраны неортогональными. На рис. 6.14 предпринята попытка изобразить все пространство, содержащее шестьдесят четыре 6-кортежей, хотя точно нарисовать или составить такую модель невозможно. Каждое кодовое слово окружают сферические слои или оболочки. Радиус внутренних непересекающихся слоев — это расстояние Хэмминга, равное 1; радиус внешнего слоя — это расстояние Хэмминга, равное 2. Большие расстояния в этом примере не рассматриваются. Для каждого кодового слова два показанных слоя заняты искаженными кодовыми словами. На каждой внутренней сфере существует шесть таких точек (всего 48 точек), представляющих шесть возможных однобитовых ошибок в векторах, соответствующих каждому кодовому слову. Эти кодовые слова с однобитовыми возмущениями могут быть соотнесены только с одним кодовым словом; следовательно, такие ошибки могут быть исправлены. Как видно из нормальной матрицы, приведенной на рис. 6.11, существует также одна двухбитовая ошибочная комбинация, которая также поддается исправлению. Всего существует 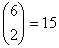
Рис, 6.14. Пример восьми кодовых слов в пространстве 6-кортежей
При представлении свойств класса кодов, известных как совершенные коды (perfect code), рис. 6.14 весьма полезен. Код, исправляющий ошибки в t битах, называется совершенным, если нормальная матрица содержит все ошибочные комбинации из t или меньшего числа ошибок и не содержит иных образующих элементов классов смежности (отсутствует возможность исправления остаточных ошибок). В контексте рис. 6.14 совершенный код с коррекцией ошибок в t битах — это такой код, который (при использовании обнаружения по принципу максимального правдоподобия) может исправить все искаженные кодовые слова, находящиеся на расстоянии Хэмминга t (или ближе) от исходного кодового слова, и не способен исправить ни одну из ошибок, находящихся на расстоянии, превышающем t.
Кроме того, рис. 6.14 способствует пониманию основной цели поиска хороших кодов. Предпочтительным является пространство, максимально заполненное кодовыми словами (эффективное использование введенной избыточности), а также желательно, чтобы кодовые слова были по возможности максимально удалены друг от друга. Очевидно, что эти цели противоречивы.
6.5.5. Коррекция со стиранием ошибок
Приемник можно сконструировать так, чтобы он объявлял символ стертым, если последний принят неоднозначно либо обнаружено наличие помех или кратковременных сбоев. Размер входного алфавита такого канала равен Q, а выходного —Q + 1; лишний выходной символ называется меткой стирания (erasure flag), или просто стиранием (erasure). Если демодулятор допускает символьную ошибку, то для ее исправления необходимы два параметра, определяющие ее расположение и правильное значение символа. В случае двоичных символов эти требования упрощаются — нам необходимо только расположение ошибки. В то же время, если демодулятор объявляет символ стертым (при этом правильное значение символа неизвестно), расположение этого символа известно, поэтому декодирование стертого кодового слова может оказаться проще исправления ошибки. Код защиты от ошибок можно использовать для исправления стертых символов или одновременного исправления ошибок и стертых символов. Если минимальное расстояние кода равно dmin, любая комбинация из ρ или меньшего числа стертых символов может быть исправлена при следующем условии [6].
(6.50)
Предположим, что ошибки появляются вне позиций стирания. Преимущество исправления посредством стираний качественно можно выразить так: если минимальное расстояние кода равно dmin, согласно уравнению (6.50), можно восстановить dmin-1 стирание. Поскольку число ошибок, которые можно исправить без стирания информации, не превышает (dmin-1)/2, то преимущество исправления ошибок посредством стираний очевидно. Далее, любую комбинацию из α ошибок и γ стираний можно исправить одновременно, если, как показано в работе [6],
(6.51)
Одновременное исправление ошибок и стираний можно осуществить следующим образом. Сначала позиции из у стираний замещаются нулями, и получаемое кодовое слово декодируется обычным образом. Затем позиции из у стираний замещаются единицами, и декодирование повторяется для этого варианта кодового слова. После обработки обоих кодовых слов (одно с подставленными нулями, другое — с подставленными единицами) выбирается то из них, которое соответствует наименьшему числу ошибок, исправленных вне позиций стирания. Если удовлетворяется неравенство (6.51), то описанный метод всегда дает верное декодирование.
Пример 6.6. Коррекция со стиранием ошибок
Рассмотрим набор кодовых слов, представленный в разделе 6.4.3.
000000 110100 011010 101110 101001 011101 110011 000111
Пусть передано кодовое слово 110011, в котором два крайних слева разряда приемник объявил стертыми. Проверьте, что поврежденную последовательность хx0011 можно исправить.
Решение
Поскольку , код может исправить
= 2 стирания. В этом легко убедиться из рис. 6.11 или приведенного выше перечня кодовых слов, сравнивая 4 крайних правых разряда xx00l1 с каждым из допустимых кодовых слов. Действительно переданное кодовое слово — это ближайшее (с точки зрения расстояния Хэмминга) к искаженной последовательности.
| Обноружение ошибок | Обноружение ошибок |  |
||||
| Исправление ошибок | Исправление ошибок |  |
||||
| Коррекция ошибок | Коррекция ошибок |  |
||||
| Назад | Назад |  |
||||
Методы обнаружения ошибок
В обычном равномерном непомехоустойчивом коде число разрядов n в кодовых
комбинациях определяется числом сообщений и основанием кода.
Коды, у которых все кодовые комбинации разрешены, называются простыми или
равнодоступными и являются полностью безызбыточными. Безызбыточные коды обладают
большой «чувствительностью» к помехам. Внесение избыточности при использовании
помехоустойчивых кодов связано с увеличением n – числа разрядов кодовой комбинации. Таким
образом, все множество

подмножество разрешенных комбинаций, обладающих определенными признаками, и
подмножество запрещенных комбинаций, этими признаками не обладающих.
Помехоустойчивый код отличается от обычного кода тем, что в канал передаются не все
кодовые комбинации N, которые можно сформировать из имеющегося числа разрядов n, а только
их часть Nk , которая составляет подмножество разрешенных комбинаций. Если при приеме
выясняется, что кодовая комбинация принадлежит к запрещенным, то это свидетельствует о
наличии ошибок в комбинации, т.е. таким образом решается задача обнаружения ошибок. При
этом принятая комбинация не декодируется (не принимается решение о переданном
сообщении). В связи с этим помехоустойчивые коды называют корректирующими кодами.
Корректирующие свойства избыточных кодов зависят от правила их построения, определяющего
структуру кода, и параметров кода (длительности символов, числа разрядов, избыточности и т. п.).
Первые работы по корректирующим кодам принадлежат Хеммингу, который ввел понятие
минимального кодового расстояния dmin и предложил код, позволяющий однозначно указать ту
позицию в кодовой комбинации, где произошла ошибка. К информационным элементам k в коде
Хемминга добавляется m проверочных элементов для автоматического определения
местоположения ошибочного символа. Таким образом, общая длина кодовой комбинации
составляет: n = k + m.
Метричное представление n,k-кодов
В настоящее время наибольшее внимание с точки зрения технических приложений
уделяется двоичным блочным корректирующим кодам. При использовании блочных кодов
цифровая информация передается в виде отдельных кодовых комбинаций (блоков) равной
длины. Кодирование и декодирование каждого блока осуществляется независимо друг от друга.
Почти все блочные коды относятся к разделимым кодам, кодовые комбинации которых
состоят из двух частей: информационной и проверочной. При общем числе n символов в блоке
число информационных символов равно k, а число проверочных символов:
К основным характеристикам корректирующих кодов относятся:
|
— число разрешенных и запрещенных кодовых комбинаций; |
Для блочных двоичных кодов, с числом символов в блоках, равным n, общее число
возможных кодовых комбинаций определяется значением
Число разрешенных кодовых комбинаций при наличии k информационных разрядов в
первичном коде:
Очевидно, что число запрещенных комбинаций:
а с учетом отношение будет
где m – число избыточных (проверочных) разрядов в блочном коде.
Избыточностью корректирующего кода называют величину
откуда следует:
Эта величина показывает, какую часть общего числа символов кодовой комбинации
составляют информационные символы. В теории кодирования величину Bk называют
относительной скоростью кода. Если производительность источника информации равна H
символов в секунду, то скорость передачи после кодирования этой информации будет
поскольку в закодированной последовательности из каждых n символов только k символов
являются информационными.
Если число ошибок, которые нужно обнаружить или исправить, значительно, то необходимо
иметь код с большим числом проверочных символов. Чтобы при этом скорость передачи
оставалась достаточно высокой, необходимо в каждом кодовом блоке одновременно
увеличивать как общее число символов, так и число информационных символов.
При этом длительность кодовых блоков будет существенно возрастать, что приведет к
задержке информации при передаче и приеме. Чем сложнее кодирование, тем длительнее
временная задержка информации.
Минимальное кодовое расстояние – dmin. Для того чтобы можно было обнаружить и
исправлять ошибки, разрешенная комбинация должна как можно больше отличаться от
запрещенной. Если ошибки в канале связи действуют независимо, то вероятность преобразования
одной кодовой комбинации в другую будет тем меньше, чем большим числом символов они
различаются.
Если интерпретировать кодовые комбинации как точки в пространстве, то отличие
выражается в близости этих точек, т. е. в расстоянии между ними.
Количество разрядов (символов), которыми отличаются две кодовые комбинации, можно
принять за кодовое расстояние между ними. Для определения этого расстояния нужно сложить
две кодовые комбинации «по модулю 2» и подсчитать число единиц в полученной сумме.
Например, две кодовые комбинации xi = 01011 и xj = 10010 имеют расстояние d(xi,xj) , равное 3,
так как:
Здесь под операцией ⊕ понимается сложение «по модулю 2».
Заметим, что кодовое расстояние d(xi,x0) между комбинацией xi и нулевой x0 = 00…0
называют весом W комбинации xi, т.е. вес xi равен числу «1» в ней.
Расстояние между различными комбинациями некоторого конкретного кода могут
существенно отличаться. Так, в частности, в безызбыточном первичном натуральном коде n = k это
расстояние для различных комбинаций может изменяться от единицы до величины n, равной
разрядности кода. Особую важность для характеристики корректирующих свойств кода имеет
минимальное кодовое расстояние dmin, определяемое при попарном сравнении всех кодовых
комбинаций, которое называют расстоянием Хемминга.
В безызбыточном коде все комбинации являются разрешенными и его минимальное
кодовое расстояние равно единице – dmin=1. Поэтому достаточно исказиться одному символу,
чтобы вместо переданной комбинации была принята другая разрешенная комбинация. Чтобы код
обладал корректирующими свойствами, необходимо ввести в него некоторую избыточность,
которая обеспечивала бы минимальное расстояние между любыми двумя разрешенными
комбинациями не менее двух – dmin ≥ 2..
Минимальное кодовое расстояние является важнейшей характеристикой помехоустойчивых
кодов, указывающей на гарантируемое число обнаруживаемых или исправляемых заданным
кодом ошибок.
Число обнаруживаемых или исправляемых ошибок
При применении двоичных кодов учитывают только дискретные искажения, при которых
единица переходит в нуль («1» → «0») или нуль переходит в единицу («0» → «1»). Переход «1» →
«0» или «0» → «1» только в одном элементе кодовой комбинации называют единичной ошибкой
(единичным искажением). В общем случае под кратностью ошибки подразумевают число
позиций кодовой комбинации, на которых под действием помехи одни символы оказались
замененными на другие. Возможны двукратные (g = 2) и многократные (g > 2) искажения
элементов в кодовой комбинации в пределах 0 ≤ g ≤ n.
Минимальное кодовое расстояние является основным параметром, характеризующим
корректирующие способности данного кода. Если код используется только для обнаружения
ошибок кратностью g0, то необходимо и достаточно, чтобы минимальное кодовое расстояние
было равно dmin ≥ g0 + 1.
В этом случае никакая комбинация из go ошибок не может перевести одну разрешенную
кодовую комбинацию в другую разрешенную. Таким образом, условие обнаружения всех ошибок
кратностью g0 можно записать
Чтобы можно было исправить все ошибки кратностью gu и менее, необходимо иметь
минимальное расстояние, удовлетворяющее условию dmin ≥ 2gu
В этом случае любая кодовая комбинация с числом ошибок gu отличается от каждой
разрешенной комбинации не менее чем в gu+1 позициях. Если условие не выполнено,
возможен случай, когда ошибки кратности g исказят переданную комбинацию так, что она станет
ближе к одной из разрешенных комбинаций, чем к переданной или даже перейдет в другую
разрешенную комбинацию. В соответствии с этим, условие исправления всех ошибок кратностью
не более gи можно записать:
Из и
следует, что если код исправляет все ошибки кратностью gu, то число
ошибок, которые он может обнаружить, равно go = 2gu. Следует отметить, что эти соотношения
устанавливают лишь гарантированное минимальное число обнаруживаемых или
исправляемых ошибок при заданном dmin и не ограничивают возможность обнаружения ошибок
большей кратности. Например, простейший код с проверкой на четность с dmin = 2 позволяет
обнаруживать не только одиночные ошибки, но и любое нечетное число ошибок в пределах go < n.
Корректирующие возможности кодов
Вопрос о минимально необходимой избыточности, при которой код обладает нужными
корректирующими свойствами, является одним из важнейших в теории кодирования. Этот вопрос
до сих пор не получил полного решения. В настоящее время получен лишь ряд верхних и нижних
оценок (границ), которые устанавливают связь между максимально возможным минимальным
расстоянием корректирующего кода и его избыточностью.
Коды Хэмминга
Построение кодов Хемминга базируется на принципе проверки на четность веса W (числа
единичных символов «1») в информационной группе кодового блока.
Поясним идею проверки на четность на примере простейшего корректирующего кода,
который так и называется кодом с проверкой на четность или кодом с проверкой по паритету
(равенству).
В таком коде к кодовым комбинациям безызбыточного первичного двоичного k-разрядного
кода добавляется один дополнительный разряд (символ проверки на четность, называемый
проверочным, или контрольным). Если число символов «1» исходной кодовой комбинации
четное, то в дополнительном разряде формируют контрольный символ «0», а если число
символов «1» нечетное, то в дополнительном разряде формируют символ «1». В результате
общее число символов «1» в любой передаваемой кодовой комбинации всегда будет четным.
Таким образом, правило формирования проверочного символа сводится к следующему:
где i – соответствующий информационный символ («0» или «1»); k – общее их число а, под
операцией ⊕ здесь и далее понимается сложение «по модулю 2». Очевидно, что добавление
дополнительного разряда увеличивает общее число возможных комбинаций вдвое по сравнению
с числом комбинаций исходного первичного кода, а условие четности разделяет все комбинации
на разрешенные и неразрешенные. Код с проверкой на четность позволяет обнаруживать
одиночную ошибку при приеме кодовой комбинации, так как такая ошибка нарушает условие
четности, переводя разрешенную комбинацию в запрещенную.
Критерием правильности принятой комбинации является равенство нулю результата S
суммирования «по модулю 2» всех n символов кода, включая проверочный символ m1. При
наличии одиночной ошибки S принимает значение 1:
— ошибок нет,
— однократная ошибка
Этот код является (k+1,k)-кодом, или (n,n–1)-кодом. Минимальное расстояние кода равно
двум (dmin = 2), и, следовательно, никакие ошибки не могут быть исправлены. Простой код с
проверкой на четность может использоваться только для обнаружения (но не исправления)
однократных ошибок.
Увеличивая число дополнительных проверочных разрядов, и формируя по определенным
правилам проверочные символы m, равные «0» или «1», можно усилить корректирующие
свойства кода так, чтобы он позволял не только обнаруживать, но и исправлять ошибки. На этом и
основано построение кодов Хемминга.
Коды Хемминга позволяют исправлять одиночную ошибку, с помощью непосредственного
описания. Для каждого числа проверочных символов m =3, 4, 5… существует классический код
Хемминга с маркировкой
т.е. (7,4), (15,11) (31,26) …
При других значениях числа информационных символов k получаются так называемые
усеченные (укороченные) коды Хемминга. Так для кода имеющего 5 информационных символов,
потребуется использование корректирующего кода (9,5), являющегося усеченным от
классического кода Хемминга (15,11), так как число символов в этом коде уменьшается
(укорачивается) на 6.
Для примера рассмотрим классический код Хемминга (7,4), который можно сформировать и
описать с помощью кодера, представленного на рис. 1 В простейшем варианте при заданных
четырех информационных символах: i1, i2, i3, i4 (k = 4), будем полагать, что они сгруппированы в
начале кодового слова, хотя это и не обязательно. Дополним эти информационные символы
тремя проверочными символами (m = 3), задавая их следующими равенствами проверки на
четность, которые определяются соответствующими алгоритмами, где знак ⊕ означает
сложение «по модулю 2»: r1 = i1 ⊕ i2 ⊕ i3, r2 = i2 ⊕ i3 ⊕ i4, r3 = i1 ⊕ i2 ⊕ i4.
В соответствии с этим алгоритмом определения значений проверочных символов mi, в табл.
1 выписаны все возможные 16 кодовых слов (7,4)-кода Хемминга.
Таблица 1 Кодовые слова (7,4)-кода Хэмминга
|
k=4 |
m=4 |
|
i1 i2 i3 i4 |
r1 r2 r3 |
|
0 0 0 0 |
0 0 0 |
|
0 0 0 1 |
0 1 1 |
|
0 0 1 0 |
1 1 0 |
|
0 0 1 1 |
1 0 1 |
|
0 1 0 0 |
1 1 1 |
|
0 1 0 1 |
1 0 0 |
|
0 1 1 0 |
0 0 1 |
|
0 1 1 1 |
0 1 0 |
|
1 0 0 0 |
1 0 1 |
|
1 0 0 1 |
1 0 0 |
|
1 0 1 0 |
0 1 1 |
|
1 0 1 1 |
0 0 0 |
|
1 1 0 0 |
0 1 0 |
|
1 1 0 1 |
0 0 1 |
|
1 1 1 0 |
1 0 0 |
|
1 1 1 1 |
1 1 1 |
На рис.1 приведена блок-схема кодера – устройства автоматически кодирующего
информационные разряды в кодовые комбинации в соответствии с табл.1

Рис. 1 Кодер для (7,4)-кода Хемминга
На рис. 1.4 приведена схема декодера для (7,4) – кода Хемминга, на вход которого
поступает кодовое слово
. Апостроф означает, что любой символ слова может
быть искажен помехой в телекоммуникационном канале.
В декодере в режиме исправления ошибок строится последовательность:
Трехсимвольная последовательность (s1, s2, s3) называется синдромом. Термин «синдром»
используется и в медицине, где он обозначает сочетание признаков, характерных для
определенного заболевания. В данном случае синдром S = (s1, s2, s3) представляет собой
сочетание результатов проверки на четность соответствующих символов кодовой группы и
характеризует определенную конфигурацию ошибок (шумовой вектор).
Число возможных синдромов определяется выражением:
При числе проверочных символов m =3 имеется восемь возможных синдромов (23 = 
Нулевой синдром (000) указывает на то, что ошибки при приеме отсутствуют или не обнаружены.
Всякому ненулевому синдрому соответствует определенная конфигурация ошибок, которая и
исправляется. Классические коды Хемминга имеют число синдромов, точно равное их
необходимому числу (что позволяет исправить все однократные ошибки в любом информативном
и проверочном символах) и включают один нулевой синдром. Такие коды называются
плотноупакованными.
Усеченные коды являются неплотноупакованными, так как число синдромов у них
превышает необходимое. Так, в коде (9,5) при четырех проверочных символах число синдромов
будет равно 24 =16, в то время как необходимо всего 10. Лишние 6 синдромов свидетельствуют о
неполной упаковке кода (9,5).

Рис. 2 Декодер для (7, 4)-кода Хемминга
Для рассматриваемого кода (7,4) в табл. 2 представлены ненулевые синдромы и
соответствующие конфигурации ошибок.
Таблица 2 Синдромы (7, 4)-кода Хемминга
|
Синдром |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
|
Конфигурация ошибок |
0000001 |
0000010 |
0000100 |
0001000 |
0010000 |
0100000 |
1000000 |
|
Ошибка в символе |
m1 |
m2 |
i4 |
m1 |
i1 |
i3 |
i2 |
Таким образом, (7,4)-код позволяет исправить все одиночные ошибки. Простая проверка
показывает, что каждая из ошибок имеет свой единственный синдром. При этом возможно
создание такого цифрового корректора ошибок (дешифратора синдрома), который по
соответствующему синдрому исправляет соответствующий символ в принятой кодовой группе.
После внесения исправления проверочные символы ri можно на выход декодера (рис. 2) не
выводить. Две или более ошибок превышают возможности корректирующего кода Хемминга, и
декодер будет ошибаться. Это означает, что он будет вносить неправильные исправления и
выдавать искаженные информационные символы.
Идея построения подобного корректирующего кода, естественно, не меняется при
перестановке позиций символов в кодовых словах. Все такие варианты также называются (7,4)-
кодами Хемминга.
Циклические коды
Своим названием эти коды обязаны такому факту, что для них часть комбинаций, либо все
комбинации могут быть получены путем циклическою сдвига одной или нескольких базовых
комбинаций кода.
Построение такого кода основывается на использовании неприводимых многочленов в поле
двоичных чисел. Такие многочлены не могут быть представлены в виде произведения
многочленов низших степеней подобно тому, как простые числа не могут быть представлены
произведением других чисел. Они делятся без остатка только на себя или на единицу.
Для определения неприводимых многочленов раскладывают на простые множители бином
хn -1. Так, для n = 7 это разложение имеет вид:
(x7)=(x-1)(x3+x2)(x3+x-1)
Каждый из полученных множителей разложения может применяться для построения
корректирующего кода.
Неприводимый полином g(x) называют задающим, образующим или порождающим
для корректирующего кода. Длина n (число разрядов) создаваемого кода произвольна.
Кодовая последовательность (комбинация) корректирующего кода состоит из к информационных
разрядов и n — к контрольных (проверочных) разрядов. Степень порождающего полинома
r = n — к равна количеству неинформационных контрольных разрядов.
Если из сделанного выше разложения (при n = 7) взять полипом (х — 1), для которого
r=1, то k=n-r=7-1=6. Соответствующий этому полиному код используется для контроля
на чет/нечет (обнаружение ошибок). Для него минимальное кодовое расстояние D0 = 2
(одна единица от D0 — для исходного двоичного кода, вторая единица — за счет контрольного разряда).
Если же взять полином (x3+x2+1) из указанного разложения, то степень полинома
r=3, а k=n-r=7-3=4.
Контрольным разрядам в комбинации для некоторого кода могут быть четко определено место (номера разрядов).
Тогда код называют систематическим или разделимым. В противном случае код является неразделимым.
Способы построения циклических кодов по заданному полиному.
1) На основе порождающей (задающей) матрицы G, которая имеет n столбцов, k строк, то есть параметры которой
связаны с параметрами комбинаций кода. Порождающую матрицу строят, взяв в качестве ее строк порождающий
полином g(x) и (k — 1) его циклических сдвигов:

Пример; Определить порождающую матрицу, если известно, что n=7, k=4, задающий полином g(x)=x3+х+1.
Решение: Кодовая комбинация, соответствующая задающему полиному g(x)=x3+х+1, имеет вид 1011.
Тогда порождающая матрица G7,4 для кода при n=7, к=4 с учетом того, что k-1=3, имеет вид:

Порождающая матрица содержит k разрешенных кодовых комбинаций. Остальные комбинации кода,
количество которых (2k — k) можно определить суммированием по модулю 2 всевозможных сочетаний
строк матрицы Gn,k. Для матрицы, полученной в приведенном выше примере, суммирование по модулю 2
четырех строк 1-2, 1-3, 1-4, 2-3, 2-4, 3-4 дает следующие кодовые комбинации циклического кода:
001110101001111010011011101010011101110100
Другие комбинации искомого корректирующего кода могут быть получены сложением трех комбинаций, например,
из сочетания строк 1-3-4, что дает комбинацию 1111111, а также сложением четырех строк 1-2-3-4, что
дает комбинацию 1101001 и т.д.
Ряд комбинаций искомого кода может быть получено путем дальнейшего циклического сдвига комбинаций
порождающей матрицы, например, 0110001, 1100010, 1000101. Всего для образования искомого циклического
кода требуется 2k=24=16 комбинаций.
2) Умножение исходных двоичных кодовых комбинаций на задающий полином.
Исходными комбинациями являются все k-разрядные двоичные комбинации. Так, например, для исходной
комбинации 1111 (при k = 4) умножение ее на задающий полином g(x)=x3+х+1=1011 дает 1101001.
Полученные на основе двух рассмотренных способов циклические коды не являются разделимыми.
3) Деление на задающий полином.
Для получения разделимого (систематического) циклического кода необходимо разделить многочлен
xn-k*h(x), где h(x) — исходная двоичная комбинация, на задающий полином g(x) и прибавить полученный
остаток от деления к многочлену xn-k*h(x).
Заметим, что умножение исходной комбинации h(x) на xn-k эквивалентно сдвигу h(x) на (n-к) разрядов влево.
Пример: Требуется определить комбинации циклического разделимого кода, заданного полиномом g(x)=x3+х+1=1011 и
имеющего общее число разрядов 7, число информационных разрядов 4, число контрольных разрядов (n-k)=3.
Решение: Пусть исходная комбинация h(x)=1100. Умножение ее на xn-k=x3=1000 дает
x3*(x3+x2)=1100000, то есть эквивалентно
сдвигу исходной комбинации на 3 разряда влево. Деление комбинации 1100000 на комбинацию 1011, эквивалентно задающему полиному, дает:

Полученный остаток от деления, содержащий xn-k=3 разряда, прибавляем к полиному, в результате чего получаем искомую комбинацию
разделимого циклического кода: 1100010. В ней 4 старших разряда (слева) соответствуют исходной двоичной комбинации, а три младших
разряда являются контрольными.
Следует сделать ряд указаний относительно процедуры деления:
1) При делении задающий полином совмещается старшим разрядом со старшим «единичными разрядом делимого.
2) Вместо вычитания по модулю 2 выполняется эквивалентная ему процедура сложения по модулю 2.
3) Деление продолжается до тех пор, пока степень очередного остатка не будет меньше степени делителя (задающего полинома). При достижении
этого полученный остаток соответствует искомому содержанию контрольных разрядов для данной искомой двоичной комбинации.
Для проверки правильности выполнения процедуры определения комбинации циклического кода необходимо разделить полученную комб1шацию на задающий полином с
учетом сделанных выше замечаний. Получение нулевого остатка от такого деления свидетельствует о правильности определения комбинации.
Логический код 4В/5В
Логический код 4В/5В заменяет исходные символы длиной в 4 бита на символы длиной в 5 бит. Так как результирующие символы содержат избыточные биты, то
общее количество битовых комбинаций в них больше, чем в исходных. Таким образом, пяти-битовая схема дает 32 (25) двухразрядных буквенно-цифровых символа,
имеющих значение в десятичном коде от 00 до 31. В то время как исходные данные могут содержать только четыре бита или 16 (24) символов.
Поэтому в результирующем коде можно подобрать 16 таких комбинаций, которые не содержат большого количества нулей, а остальные считать запрещенными кодами
(code violation). В этом случае длинные последовательности нулей прерываются, и код становится самосинхронизирующимся для любых передаваемых данных.
Исчезает также постоянная составляющая, а значит, еще более сужается спектр сигнала. Но этот метод снижает полезную пропускную способность линии,
так как избыточные единицы пользовательской информации не несут, и только «занимают эфирное время». Избыточные коды позволяют приемнику распознавать
искаженные биты. Если приемник принимает запрещенный код, значит, на линии произошло искажение сигнала.
Итак, рассмотрим работу логического кода 4В/5В. Преобразованный сигнал имеет 16 значений для передачи информации и 16 избыточных значений. В декодере
приемника пять битов расшифровываются как информационные и служебные сигналы.
Для служебных сигналов отведены девять символов, семь символов — исключены.
Исключены комбинации, имеющие более трех нулей (01 — 00001, 02 — 00010, 03 — 00011, 08 — 01000, 16 — 10000). Такие сигналы интерпретируются символом
V и командой приемника VIOLATION — сбой. Команда означает наличие ошибки из-за высокого уровня помех или сбоя передатчика. Единственная
комбинация из пяти нулей (00 — 00000) относится к служебным сигналам, означает символ Q и имеет статус QUIET — отсутствие сигнала в линии.
Такое кодирование данных решает две задачи — синхронизации и улучшения помехоустойчивости. Синхронизация происходит за счет исключения
последовательности более трех нулей, а высокая помехоустойчивость достигается приемником данных на пяти-битовом интервале.
Цена за эти достоинства при таком способе кодирования данных — снижение скорости передачи полезной информации.
К примеру, В результате добавления одного избыточного бита на четыре информационных, эффективность использования полосы
частот в протоколах с кодом MLT-3 и кодированием данных 4B/5B уменьшается соответственно на 25%.
Схема кодирования 4В/5В представлена в таблице.
|
Двоичный код 4В |
Результирующий код 5В |
|
0 0 0 0 |
1 1 1 1 0 |
|
0 0 0 1 |
0 1 0 0 1 |
|
0 0 1 0 |
1 0 1 0 0 |
|
0 0 1 1 |
1 0 1 0 1 |
|
0 1 0 0 |
0 1 0 1 0 |
|
0 1 0 1 |
0 1 0 1 1 |
|
0 1 1 0 |
0 1 1 1 0 |
|
0 1 1 1 |
0 1 1 1 1 |
|
1 0 0 0 |
1 0 0 1 0 |
|
1 0 0 1 |
1 0 0 1 1 |
|
1 0 1 0 |
1 0 1 1 0 |
|
1 0 1 1 |
1 0 1 1 1 |
|
1 1 0 0 |
1 1 0 1 0 |
|
1 1 0 1 |
1 1 0 1 1 |
|
1 1 1 0 |
1 1 1 0 0 |
|
1 1 1 1 |
1 1 1 0 1 |
Итак, соответственно этой таблице формируется код 4В/5В, затем передается по линии с помощью физического кодирования по
одному из методов потенциального кодирования, чувствительному только к длинным последовательностям нулей — например, в помощью
цифрового кода NRZI.
Символы кода 4В/5В длиной 5 бит гарантируют, что при любом их сочетании на линии не могут встретиться более трех нулей подряд.
Буква ^ В в названии кода означает, что элементарный сигнал имеет 2 состояния — от английского binary — двоичный. Имеются
также коды и с тремя состояниями сигнала, например, в коде 8В/6Т для кодирования 8 бит исходной информации используется
код из 6 сигналов, каждый из которых имеет три состояния. Избыточность кода 8В/6Т выше, чем кода 4В/5В, так как на 256
исходных кодов приходится 36=729 результирующих символов.
Как мы говорили, логическое кодирование происходит до физического, следовательно, его осуществляют оборудование канального
уровня сети: сетевые адаптеры и интерфейсные блоки коммутаторов и маршрутизаторов. Поскольку, как вы сами убедились,
использование таблицы перекодировки является очень простой операцией, поэтому метод логического кодирования избыточными
кодами не усложняет функциональные требования к этому оборудованию.
Единственное требование — для обеспечения заданной пропускной способности линии передатчик, использующий избыточный код,
должен работать с повышенной тактовой частотой. Так, для передачи кодов 4В/5В со скоростью 100 Мб/с передатчик должен
работать с тактовой частотой 125 МГц. При этом спектр сигнала на линии расширяется по сравнению со случаем, когда по
линии передается чистый, не избыточный код. Тем не менее, спектр избыточного потенциального кода оказывается уже
спектра манчестерского кода, что оправдывает дополнительный этап логического кодирования, а также работу приемника
и передатчика на повышенной тактовой частоте.
В основном для локальных сетей проще, надежней, качественней, быстрей — использовать логическое кодирование данных
с помощью избыточных кодов, которое устранит длительные последовательности нулей и обеспечит синхронизацию
сигнала, потом на физическом уровне использовать для передачи быстрый цифровой код NRZI, нежели без предварительного
логического кодирования использовать для передачи данных медленный, но самосинхронизирующийся манчестерский код.
Например, для передачи данных по линии с пропускной способностью 100М бит/с и полосой пропускания 100 МГц,
кодом NRZI необходимы частоты 25 — 50 МГц, это без кодирования 4В/5В. А если применить для NRZI еще и
кодирование 4В/5В, то теперь полоса частот расширится от 31,25 до 62,5 МГц. Но тем не менее, этот диапазон
еще «влазит» в полосу пропускания линии. А для манчестерского кода без применения всякого дополнительного
кодирования необходимы частоты от 50 до 100 МГц, и это частоты основного сигнала, но они уже не будут пропускаться
линией на 100 МГц.
Скрэмблирование
Другой метод логического кодирования основан на предварительном «перемешивании» исходной информации таким
образом, чтобы вероятность появления единиц и нулей на линии становилась близкой.
Устройства, или блоки, выполняющие такую операцию, называются скрэмблерами (scramble — свалка, беспорядочная сборка) .
При скремблировании данные перемешиваються по определенному алгоритму и приемник, получив двоичные данные, передает
их на дескрэмблер, который восстанавливает исходную последовательность бит.
Избыточные биты при этом по линии не передаются.
Суть скремблирования заключается просто в побитном изменении проходящего через систему потока данных. Практически
единственной операцией, используемой в скремблерах является XOR — «побитное исключающее ИЛИ», или еще говорят —
сложение по модулю 2. При сложении двух единиц исключающим ИЛИ отбрасывается старшая единица и результат записывается — 0.
Метод скрэмблирования очень прост. Сначала придумывают скрэмблер. Другими словами придумывают по какому соотношению
перемешивать биты в исходной последовательности с помощью «исключающего ИЛИ». Затем согласно этому соотношению из текущей
последовательности бит выбираются значения определенных разрядов и складываются по XOR между собой. При этом все разряды
сдвигаются на 1 бит, а только что полученное значение («0» или «1») помещается в освободившийся самый младший разряд.
Значение, находившееся в самом старшем разряде до сдвига, добавляется в кодирующую последовательность, становясь очередным
ее битом. Затем эта последовательность выдается в линию, где с помощью методов физического кодирования передается к
узлу-получателю, на входе которого эта последовательность дескрэмблируется на основе обратного отношения.
Например, скрэмблер может реализовывать следующее соотношение:
где Bi — двоичная цифра результирующего кода, полученная на i-м такте работы скрэмблера, Ai — двоичная цифра исходного
кода, поступающая на i-м такте на вход скрэмблера, Bi-3 и Bi-5 — двоичные цифры результирующего кода, полученные на
предыдущих тактах работы скрэмблера, соответственно на 3 и на 5 тактов ранее текущего такта, ⊕ — операция исключающего
ИЛИ (сложение по модулю 2).
Теперь давайте, определим закодированную последовательность, например, для такой исходной последовательности 110110000001.
Скрэмблер, определенный выше даст следующий результирующий код:
B1=А1=1 (первые три цифры результирующего кода будут совпадать с исходным, так как еще нет нужных предыдущих цифр)

Таким образом, на выходе скрэмблера появится последовательность 110001101111. В которой нет последовательности из шести нулей, п
рисутствовавшей в исходном коде.
После получения результирующей последовательности приемник передает ее дескрэмблеру, который восстанавливает исходную
последовательность на основании обратного соотношения.
Существуют другие различные алгоритмы скрэмблирования, они отличаются количеством слагаемых, дающих цифру
результирующего кода, и сдвигом между слагаемыми.
Главная проблема кодирования на основе скремблеров — синхронизация передающего (кодирующего) и принимающего
(декодирующего) устройств. При пропуске или ошибочном вставлении хотя бы одного бита вся передаваемая информация
необратимо теряется. Поэтому, в системах кодирования на основе скремблеров очень большое внимание уделяется методам синхронизации.
На практике для этих целей обычно применяется комбинация двух методов:
а) добавление в поток информации синхронизирующих битов, заранее известных приемной стороне, что позволяет ей при ненахождении
такого бита активно начать поиск синхронизации с отправителем,
б) использование высокоточных генераторов временных импульсов, что позволяет в моменты потери синхронизации производить
декодирование принимаемых битов информации «по памяти» без синхронизации.
Существуют и более простые методы борьбы с последовательностями единиц, также относимые к классу скрэмблирования.
Для улучшения кода ^ Bipolar AMI используются два метода, основанные на искусственном искажении последовательности нулей запрещенными символами.

Рис. 3 Коды B8ZS и HDB3
На этом рисунке показано использование метода ^ B8ZS (Bipolar with 8-Zeros Substitution) и метода HDB3 (High-Density Bipolar 3-Zeros) для корректировки
кода AMI. Исходный код состоит из двух длинных последовательностей нулей (8- в первом случае и 5 во втором).
Код B8ZS исправляет только последовательности, состоящие из 8 нулей. Для этого он после первых трех нулей вместо оставшихся пяти нулей вставляет пять
цифр: V-1*-0-V-1*. V здесь обозначает сигнал единицы, запрещенной для данного такта полярности, то есть сигнал, не изменяющий полярность предыдущей
единицы, 1* — сигнал единицы корректной полярности, а знак звездочки отмечает тот факт, что в исходном коде в этом такте была не единица, а ноль. В
результате на 8 тактах приемник наблюдает 2 искажения — очень маловероятно, что это случилось из-за шума на линии или других сбоев передачи. Поэтому
приемник считает такие нарушения кодировкой 8 последовательных нулей и после приема заменяет их на исходные 8 нулей.
Код B8ZS построен так, что его постоянная составляющая равна нулю при любых последовательностях двоичных цифр.
Код HDB3 исправляет любые 4 подряд идущих нуля в исходной последовательности. Правила формирования кода HDB3 более сложные, чем кода B8ZS.
Каждые четыре нуля заменяются четырьмя сигналами, в которых имеется один сигнал V. Для подавления постоянной составляющей полярность сигнала
V чередуется при последовательных заменах.
Кроме того, для замены используются два образца четырехтактовых кодов. Если перед заменой исходный код содержал нечетное число единиц, то
используется последовательность 000V, а если число единиц было четным — последовательность 1*00V.
Таким образом, применение логическое кодирование совместно с потенциальным кодированием дает следующие преимущества:
Улучшенные потенциальные коды обладают достаточно узкой полосой пропускания для любых последовательностей единиц и нулей,
которые встречаются в передаваемых данных. В результате коды, полученные из потенциального путем логического кодирования,
обладают более узким спектром, чем манчестерский, даже при повышенной тактовой частоте.
Линейные блочные коды
При передаче информации по каналам связи возможны ошибки вследствие помех и искажений сигналов. Для обнаружения и
исправления возникающих ошибок используются помехоустойчивые коды. Упрощенная схема системы передачи информации
при помехоустойчивом кодировании показана на рис. 4
Кодер служит для преобразования поступающей от источника сообщений последовательности из k информационных
символов в последовательность из n cимволов кодовых комбинаций (или кодовых слов). Совокупность кодовых слов образует код.
Множество символов, из которых составляется кодовое слово, называется алфавитом кода, а число различных символов в
алфавите – основанием кода. В дальнейшем вследствие их простоты и наибольшего распространения рассматриваются главным
образом двоичные коды, алфавит которых содержит два символа: 0 и 1.

Рис. 4 Система передачи дискретных сообщений
Правило, по которому информационной последовательности сопоставляется кодовое слово, называется правилом кодирования.
Если при кодировании каждый раз формируется блок А из k информационных символов, превращаемый затем в n-символьную
кодовую комбинацию S, то код называется блочным. При другом способе кодирования информационная последовательность на
блоки не разбивается, и код называется непрерывным.
С математической точки зрения кодер осуществляет отображение множества из 2k элементов (двоичных информационных
последовательностей) в множество, состоящее из 2n элементов (двоичных последовательностей длины n). Для практики
интересны такие отображения, в результате которых получаются коды, обладающие способностью исправлять часть ошибок
и допускающие простую техническую реализацию кодирующих и декодирующих устройств.
Дискретный канал связи – это совокупность технических средств вместе со средой распространения радиосигналов, включенных
между кодером и декодером для передачи сигналов, принимающих конечное число разных видов. Для описания реальных каналов
предложено много математических моделей, с разной степенью детализации отражающих реальные процессы. Ограничимся рассмотрением
простейшей модели двоичного канала, входные и выходные сигналы которого могут принимать значения 0 и 1.
Наиболее распространено предположение о действии в канале аддитивной помехи. Пусть S=(s1,s2,…,sn)
и Y=(y1,y2,…,yn) соответственно входная и выходная последовательности двоичных символов.
Помехой или вектором ошибки называется последовательность из n символов E=(e1,e2,…,en), которую
надо поразрядно сложить с переданной последовательностью, чтобы получить принятую:
Y=S+E
Таким образом, компонента вектора ошибки ei=0 указывает на то, что 2-й символ принят правильно (yi=si),
а компонента ei=1 указывает на ошибку при приеме (yi≠si).Поэтому важной характеристикой вектора ошибки
является число q ненулевых компонентов, которое называется весом или кратностью ошибки. Кратность ошибки – дискретная случайная величина,
принимающая целочисленные значения от 0 до n.
Классификация двоичных каналов ведется по виду распределения случайного вектора E. Основные результаты теории кодирования получены в
предположении, что вероятность ошибки в одном символе не зависит ни от его номера в последовательности, ни от его значения. Такой
канал называется стационарным и симметричным. В этом канале передаваемые символы искажаются с одинаковой вероятностью
P, т.е. P(ei=1)=P, i=1,2,…,n.
Для симметричного стационарного канала распределение вероятностей векторов ошибки кратности q является биноминальным:
P(Ei)=Pq(1-P)n-q
которая показывает, что при P<0,5 вероятность β2=αj является убывающей функцией q,
т.е. в симметричном стационарном канале более вероятны ошибки меньшей кратности. Этот важный факт используется при построении
помехоустойчивых кодов, т.к. позволяет обосновать тактику обнаружения и исправления в первую очередь ошибок малой кратности.
Конечно, для других моделей канала такая тактика может и не быть оптимальной.
Декодирующее устройство (декодер) предназначено оценить по принятой последовательности Y=(y1,y2,…,yn)
значения информационных символов A‘=(a‘1,a‘2,…,a‘k,).
Из-за действия помех возможны неправильные решения. Процедура декодирования включает решение двух задач: оценивание переданного кодового
слова и формирование оценок информационных символов.
Вторая задача решается относительно просто. При наиболее часто используемых систематических кодах, кодовые слова которых содержат информационные
символы на известных позициях, все сводится к простому их стробированию. Очевидно также, что расположение информационных символов внутри кодового
слова не имеет существенного значения. Удобно считать, что они занимают первые k позиций кодового слова.
Наибольшую трудность представляет первая задача декодирования. При равновероятных информационных последовательностях ее оптимальное решение
дает метод максимального правдоподобия. Функция правдоподобия как вероятность получения данного вектора Y при передаче кодовых слов
Si, i=1,2,…,2k на основании Y=S+E определяется вероятностями появления векторов ошибок:
P(Y/Si)=P(Ei)=Pqi(1-P)n-qi
где qi – вес вектора Ei=Y+Si
Очевидно, вероятность P(Y/Si) максимальна при минимальном qi. На основании принципа максимального правдоподобия оценкой S‘ является кодовое слово,
искажение которого для превращения его в принятое слово Y имеет минимальный вес, т. е. в симметричном канале является наиболее вероятным (НВ):
S‘=Y+EHB
Если несколько векторов ошибок Ei имеют равные минимальные веса, то наивероятнейшая ошибка EHB определяется случайным выбором среди них.
В качестве расстояния между двумя кодовыми комбинациями принимают так называемое расстояние Хэмминга, которое численно равно количеству символов, в которых одна
комбинация отлична от другой, т.е. весу (числу ненулевых компонентов) разностного вектора. Расстояние Хэмминга между принятой последовательностью Y и всеми
возможными кодовыми словами 5, есть функция весов векторов ошибок Ei:

Поэтому декодирование по минимуму расстояния, когда в качестве оценки берется слово, ближайшее к принятой
последовательности, является декодированием по максимуму правдоподобия.
Таким образом, оптимальная процедура декодирования для симметричного канала может быть описана следующей последовательностью операций. По принятому
вектору Y определяется вектор ошибки с минимальным весом EHB, который затем вычитается (в двоичном канале — складывается по модулю 2) из Y:
Y→EHB→S‘=Y+EHB
Наиболее трудоемкой операцией в этой схеме является определение наи-вероятнейшего вектора ошибки, сложность которой
существенно возрастает при увеличении длины кодовых комбинаций. Правила кодирования, которые нацелены на упрощение
процедур декодирования, предполагают придание всем кодовым словам технически легко проверяемых признаков.
Широко распространены линейные коды, называемые так потому, что их кодовые слова образуют линейное
подпространство над конечным полем. Для двоичных кодов естественно использовать поле характеристики p=2.
Принадлежность принятой комбинации Y известному подпространству является тем признаком, по которому
выносится решение об отсутствии ошибок (EHB=0).
Так как по данному коду все пространство последовательностей длины n разбивается на смежные классы,
то для каждого смежного класса можно заранее определить вектор ошибки минимального веса,
называемый лидером смежного класса. Тогда задача декодера состоит в определении номера смежного класса,
которому принадлежит Y, и формировании лидера этого класса.