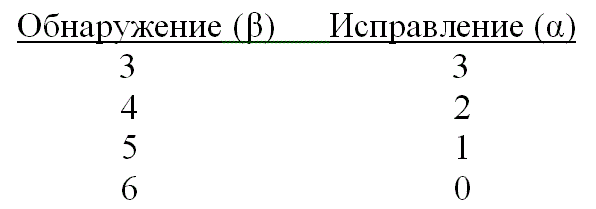Корректирующие коды «на пальцах»
Время на прочтение
11 мин
Количество просмотров 63K

Как нетрудно догадаться, ко всему этому причастны корректирующие коды. Собственно, ECC так и расшифровывается — «error-correcting code», то есть «код, исправляющий ошибки». А CRC — это один из алгоритмов, обнаруживающих ошибки в данных. Исправить он их не может, но часто это и не требуется.
Давайте же разберёмся, что это такое.
Для понимания статьи не нужны никакие специальные знания. Достаточно лишь понимать, что такое вектор и матрица, как они перемножаются и как с их помощью записать систему линейных уравнений.
Внимание! Много текста и мало картинок. Я постарался всё объяснить, но без карандаша и бумаги текст может показаться немного запутанным.
Каналы с ошибкой
Разберёмся сперва, откуда вообще берутся ошибки, которые мы собираемся исправлять. Перед нами стоит следующая задача. Нужно передать несколько блоков данных, каждый из которых кодируется цепочкой двоичных цифр. Получившаяся последовательность нулей и единиц передаётся через канал связи. Но так сложилось, что реальные каналы связи часто подвержены ошибкам. Вообще говоря, ошибки могут быть разных видов — может появиться лишняя цифра или какая-то пропасть. Но мы будем рассматривать только ситуации, когда в канале возможны лишь замены нуля на единицу и наоборот. Причём опять же для простоты будем считать такие замены равновероятными.
Ошибка — это маловероятное событие (а иначе зачем нам такой канал вообще, где одни ошибки?), а значит, вероятность двух ошибок меньше, а трёх уже совсем мала. Мы можем выбрать для себя некоторую приемлемую величину вероятности, очертив границу «это уж точно невозможно». Это позволит нам сказать, что в канале возможно не более, чем ошибок. Это будет характеристикой канала связи.
Для простоты введём следующие обозначения. Пусть данные, которые мы хотим передавать, — это двоичные последовательности фиксированной длины. Чтобы не запутаться в нулях и единицах, будем иногда обозначать их заглавными латинскими буквами (,
,
, …). Что именно передавать, в общем-то неважно, просто с буквами в первое время будет проще работать.
Кодирование и декодирование будем обозначать прямой стрелкой (), а передачу по каналу связи — волнистой стрелкой (
). Ошибки при передаче будем подчёркивать.
Например, пусть мы хотим передавать только сообщения и
. В простейшем случае их можно закодировать нулём и единицей (сюрприз!):
Передача по каналу, в котором возникла ошибка будет записана так:
Цепочки нулей и единиц, которыми мы кодируем буквы, будем называть кодовыми словами. В данном простом случае кодовые слова — это и
.
Код с утроением
Давайте попробуем построить какой-то корректирующий код. Что мы обычно делаем, когда кто-то нас не расслышал? Повторяем дважды:
Правда, это нам не очень поможет. В самом деле, рассмотрим канал с одной возможной ошибкой:
Какие выводы мы можем сделать, когда получили ? Понятно, что раз у нас не две одинаковые цифры, то была ошибка, но вот в каком разряде? Может, в первом, и была передана буква
. А может, во втором, и была передана
.
То есть, получившийся код обнаруживает, но не исправляет ошибки. Ну, тоже неплохо, в общем-то. Но мы пойдём дальше и будем теперь утраивать цифры.
Проверим в деле:
Получили . Тут у нас есть две возможности: либо это
и было две ошибки (в крайних цифрах), либо это
и была одна ошибка. Вообще, вероятность одной ошибки выше вероятности двух ошибок, так что самым правдоподобным будет предположение о том, что передавалась именно буква
. Хотя правдоподобное — не значит истинное, поэтому рядом и стоит вопросительный знак.
Если в канале связи возможна максимум одна ошибка, то первое предположение о двух ошибках становится невозможным и остаётся только один вариант — передавалась буква .
Про такой код говорят, что он исправляет одну ошибку. Две он тоже обнаружит, но исправит уже неверно.
Это, конечно, самый простой код. Кодировать легко, да и декодировать тоже. Ноликов больше — значит передавался ноль, единичек — значит единица.
Если немного подумать, то можно предложить код исправляющий две ошибки. Это будет код, в котором мы повторяем одиночный бит 5 раз.
Расстояния между кодами
Рассмотрим поподробнее код с утроением. Итак, мы получили работающий код, который исправляет одиночную ошибку. Но за всё хорошее надо платить: он кодирует один бит тремя. Не очень-то и эффективно.
И вообще, почему этот код работает? Почему нужно именно утраивать для устранения одной ошибки? Наверняка это всё неспроста.
Давайте подумаем, как этот код работает. Интуитивно всё понятно. Нолики и единички — это две непохожие последовательности. Так как они достаточно длинные, то одиночная ошибка не сильно портит их вид.
Пусть мы передавали , а получили
. Видно, что эта цепочка больше похожа на исходные
, чем на
. А так как других кодовых слов у нас нет, то и выбор очевиден.
Но что значит «больше похоже»? А всё просто! Чем больше символов у двух цепочек совпадает, тем больше их схожесть. Если почти все символы отличаются, то цепочки «далеки» друг от друга.
Можно ввести некоторую величину , равную количеству различающихся цифр в соответствующих разрядах цепочек
и
. Эту величину называют расстоянием Хэмминга. Чем больше это расстояние, тем меньше похожи две цепочки.
Например, , так как все цифры в соответствующих позициях равны, а вот
.
Расстояние Хэмминга называют расстоянием неспроста. Ведь в самом деле, что такое расстояние? Это какая-то характеристика, указывающая на близость двух точек, и для которой верны утверждения:
- Расстояние между точками неотрицательно и равно нулю только, если точки совпадают.
- Расстояние в обе стороны одинаково.
- Путь через третью точку не короче, чем прямой путь.
Достаточно разумные требования.
Математически это можно записать так (нам это не пригодится, просто ради интереса посмотрим):
.
Предлагаю читателю самому убедиться, что для расстояния Хэмминга эти свойства выполняются.
Окрестности
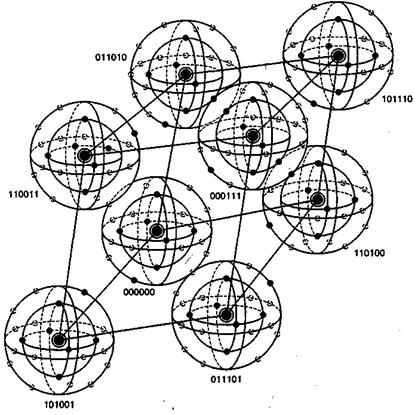
Таким образом, разные цепочки мы считаем точками в каком-то воображаемом пространстве, и теперь мы умеем находить расстояния между ними. Правда, если попытаться сколько нибудь длинные цепочки расставить на листе бумаги так, чтобы расстояния Хэмминга совпадали с расстояниями на плоскости, мы можем потерпеть неудачу. Но не нужно переживать. Всё же это особое пространство со своими законами. А слова вроде «расстояния» лишь помогают нам рассуждать.
Пойдём дальше. Раз мы заговорили о расстоянии, то можно ввести такое понятие как окрестность. Как известно, окрестность какой-то точки — это шар определённого радиуса с центром в ней. Шар? Какие ещё шары! Мы же о кодах говорим.
Но всё просто. Ведь что такое шар? Это множество всех точек, которые находятся от данной не дальше, чем некоторое расстояние, называемое радиусом. Точки у нас есть, расстояние у нас есть, теперь есть и шары.
Так, скажем, окрестность кодового слова радиуса 1 — это все коды, находящиеся на расстоянии не больше, чем 1 от него, то есть отличающиеся не больше, чем в одном разряде. То есть это коды:
Да, вот так странно выглядят шары в пространстве кодов.
А теперь посмотрите. Это же все возможные коды, которые мы получим в канале в одной ошибкой, если отправим ! Это следует прямо из определения окрестности. Ведь каждая ошибка заставляет цепочку измениться только в одном разряде, а значит удаляет её на расстояние 1 от исходного сообщения.
Аналогично, если в канале возможны две ошибки, то отправив некоторое сообщение , мы получим один из кодов, который принадлежит окрестности
радиусом 2.
Тогда всю нашу систему декодирования можно построить так. Мы получаем какую-то цепочку нулей и единиц (точку в нашей новой терминологии) и смотрим, в окрестность какого кодового слова она попадает.
Сколько ошибок может исправить код?
Чтобы код мог исправлять больше ошибок, окрестности должны быть как можно шире. С другой стороны, они не должны пересекаться. Иначе если точка попадёт в область пересечения, непонятно будет, к какой окрестности её отнести.
В коде с удвоением между кодовыми словами и
расстояние равно 2 (оба разряда различаются). А значит, если мы построим вокруг них шары радиуса 1, то они будут касаться. Это значит, точка касания будет принадлежать обоим шарам и непонятно будет, к какому из них её отнести.
Именно это мы и получали. Мы видели, что есть ошибка, но не могли её исправить.
Что интересно, точек касания в нашем странном пространстве у шаров две — это коды и
. Расстояния от них до центров равны единице. Конечно же, в обычно геометрии такое невозможно, поэтому рисунки — это просто условность для более удобного рассуждения.
В случае кода с утроением, между шарами будет зазор.
Минимальный зазор между шарами равен 1, так как у нас расстояния всегда целые (ну не могут же две цепочки отличаться в полутора разрядах).
В общем случае получаем следующее.
Этот очевидный результат на самом деле очень важен. Он означает, что код с минимальным кодовым расстоянием будет успешно работать в канале с
ошибками, если выполняется соотношение
Полученное равенство позволяет легко определить, сколько ошибок будет исправлять тот или иной код. А сколько код ошибок может обнаружить? Рассуждения такие же. Код обнаруживает ошибок, если в результате не получится другое кодовое слово. То есть, кодовые слова не должны находиться в окрестностях радиуса
других кодовых слов. Математически это записывается так:
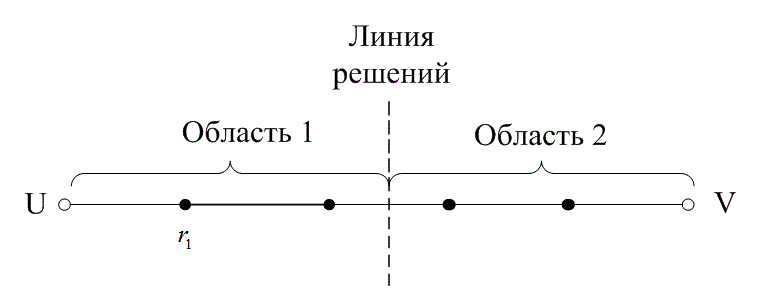
Рассмотрим пример. Пусть мы кодируем 4 буквы следующим образом.
Чтобы найти минимальное расстояние между различными кодовыми словами, построим таблицу попарных расстояний.
| A | B | C | D | |
|---|---|---|---|---|
| A | — | 3 | 3 | 4 |
| B | 3 | — | 4 | 3 |
| C | 3 | 4 | — | 3 |
| D | 4 | 3 | 3 | — |
Минимальное расстояние , а значит
, откуда получаем, что такой код может исправить до
ошибок. Обнаруживает же он две ошибки.
Рассмотрим пример:
Чтобы декодировать полученное сообщение, посмотрим, к какому символу оно ближе всего.
Минимальное расстояние получилось для символа , значит вероятнее всего передавался именно он:
Итак, этот код исправляет одну ошибку, как и код с утроением. Но он более эффективен, так как в отличие от кода с утроением здесь кодируется уже 4 символа.
Таким образом, основная проблема при построении такого рода кодов — так расположить кодовые слова, чтобы они были как можно дальше друг от друга, и их было побольше.
Для декодирования можно было бы использовать таблицу, в которой указывались бы все возможные принимаемые сообщения, и кодовые слова, которым они соответствуют. Но такая таблица получилась бы очень большой. Даже для нашего маленького кода, который выдаёт 5 двоичных цифр, получилось бы варианта возможных принимаемых сообщений. Для более сложных кодов таблица будет значительно больше.
Попробуем придумать способ коррекции сообщения без таблиц. Мы всегда сможем найти полезное применение освободившейся памяти.
Интерлюдия: поле GF(2)
Для изложения дальнейшего материала нам потребуются матрицы. А при умножении матриц, как известно мы складываем и перемножаем числа. И тут есть проблема. Если с умножением всё более-менее хорошо, то как быть со сложением? Из-за того, что мы работаем только с одиночными двоичными цифрами, непонятно, как сложить 1 и 1, чтобы снова получилась одна двоичная цифра. Значит вместо классического сложения нужно использовать какое-то другое.
Введём операцию сложения как сложение по модулю 2 (хорошо известный программистам XOR):
Умножение будем выполнять как обычно. Эти операции на самом деле введены не абы как, а чтобы получилась система, которая в математике называется полем. Поле — это просто множество (в нашем случае из 0 и 1), на котором так определены сложение и умножение, чтобы основные алгебраические законы сохранялись. Например, чтобы основные идеи, касающиеся матриц и систем уравнений по-прежнему были верны. А вычитание и деление мы можем ввести как обратные операции.
Множество из двух элементов с операциями, введёнными так, как мы это сделали, называется полем Галуа GF(2). GF — это Galois field, а 2 — количество элементов.
У сложения есть несколько очень полезных свойств, которыми мы будем пользоваться в дальнейшем.
Это свойство прямо следует из определения.
А в этом можно убедиться, прибавив к обеим частям равенства. Это свойство, в частности означает, что мы можем переносить в уравнении слагаемые в другую сторону без смены знака.
Проверяем корректность
Вернёмся к коду с утроением.
Для начала просто решим задачу проверки, были ли вообще ошибки при передаче. Как видно, из самого кода, принятое сообщение будет кодовым словом только тогда, когда все три цифры равны между собой.
Пусть мы приняли вектор-строку из трёх цифр. (Стрелочки над векторами рисовать не будем, так как у нас почти всё — это вектора или матрицы.)
Математически равенство всех трёх цифр можно записать как систему:
Или, если воспользоваться свойствами сложения в GF(2), получаем
Или
В матричном виде эта система будет иметь вид
где
Транспонирование здесь нужно потому, что — это вектор-строка, а не вектор-столбец. Иначе мы не могли бы умножать его справа на матрицу.
Будем называть матрицу проверочной матрицей. Если полученное сообщение — это корректное кодовое слово (то есть, ошибки при передаче не было), то произведение проверочной матрицы на это сообщение будет равно нулевому вектору.
Умножение на матрицу — это гораздо более эффективно, чем поиск в таблице, но у нас на самом деле есть ещё одна таблица — это таблица кодирования. Попробуем от неё избавиться.
Кодирование
Итак, у нас есть система для проверки
Её решения — это кодовые слова. Собственно, мы систему и строили на основе кодовых слов. Попробуем теперь решить обратную задачу. По системе (или, что то же самое, по матрице ) найдём кодовые слова.
Правда, для нашей системы мы уже знаем ответ, поэтому, чтобы было интересно, возьмём другую матрицу:
Соответствующая система имеет вид:
Чтобы найти кодовые слова соответствующего кода нужно её решить.
В силу линейности сумма двух решений системы тоже будет решением системы. Это легко доказать. Если и
— решения системы, то для их суммы верно
что означает, что она тоже — решение.
Поэтому если мы найдём все линейно независимые решения, то с их помощью можно получить вообще все решения системы. Для этого просто нужно найти их всевозможные суммы.
Выразим сперва все зависимые слагаемые. Их столько же, сколько и уравнений. Выражать надо так, чтобы справа были только независимые. Проще всего выразить .
Если бы нам не так повезло с системой, то нужно было бы складывая уравнения между собой получить такую систему, чтобы какие-то три переменные встречались по одному разу. Ну, или воспользоваться методом Гаусса. Для GF(2) он тоже работает.
Итак, получаем:
Чтобы получить все линейно независимые решения, приравниваем каждую из зависимых переменных к единице по очереди.
Всевозможные суммы этих независимых решений (а именно они и будут кодовыми векторами) можно получить так:
где равны либо нулю или единице. Так как таких коэффициентов два, то всего возможно
сочетания.
Но посмотрите! Формула, которую мы только что получили — это же снова умножение матрицы на вектор.
Строчки здесь — линейно независимые решения, которые мы получили. Матрица называется порождающей. Теперь вместо того, чтобы сами составлять таблицу кодирования, мы можем получать кодовые слова простым умножением на матрицу:
Найдём кодовые слова для этого кода. (Не забываем, что длина исходных сообщений должна быть равна 2 — это количество найденных решений.)
Итак, у нас есть готовый код, обнаруживающий ошибки. Проверим его в деле. Пусть мы хотим отправить 01 и у нас произошла ошибка при передаче. Обнаружит ли её код?
А раз в результате не нулевой вектор, значит код заподозрил неладное. Провести его не удалось. Ура, код работает!
Для кода с утроением, кстати, порождающая матрица выглядит очень просто:
Подобные коды, которые можно порождать и проверять матрицей называются линейными (бывают и нелинейные), и они очень широко применяются на практике. Реализовать их довольно легко, так как тут требуется только умножение на константную матрицу.
Ошибка по синдрому
Ну хорошо, мы построили код обнаруживающий ошибки. Но мы же хотим их исправлять!
Для начала введём такое понятие, как вектор ошибки. Это вектор, на который отличается принятое сообщение от кодового слова. Пусть мы получили сообщение , а было отправлено кодовое слово
. Тогда вектор ошибки по определению
Но в странном мире GF(2), где сложение и вычитание одинаковы, будут верны и соотношения:
В силу особенностей сложения, как читатель сам может легко убедиться, в векторе ошибки на позициях, где произошла ошибка будет единица, а на остальных ноль.
Как мы уже говорили раньше, если мы получили сообщение с ошибкой, то
. Но ведь векторов, не равных нулю много! Быть может то, какой именно ненулевой вектор мы получили, подскажет нам характер ошибки?
Назовём результат умножения на проверочную матрицу синдромом:
И заметим следующее
Это означает, что для ошибки синдром будет таким же, как и для полученного сообщения.
Разложим все возможные сообщения, которые мы можем получить из канала связи, по кучкам в зависимости от синдрома. Тогда из последнего соотношения следует, что в каждой кучке будут вектора с одной и той же ошибкой. Причём вектор этой ошибки тоже будет в кучке. Вот только как его узнать?
А очень просто! Помните, мы говорили, что у нескольких ошибок вероятность ниже, чем у одной ошибки? Руководствуясь этим соображением, наиболее правдоподобным будет считать вектором ошибки тот вектор, у которого меньше всего единиц. Будем называть его лидером.
Давайте посмотрим, какие синдромы дают всевозможные 5-элементные векторы. Сразу сгруппируем их и подчеркнём лидеров — векторы с наименьшим числом единиц.
В принципе, для корректирования ошибки достаточно было бы хранить таблицу соответствия синдрома лидеру.
Обратите внимание, что в некоторых строчках два лидера. Это значит для для данного синдрома два паттерна ошибки равновероятны. Иными словами, код обнаружил две ошибки, но исправить их не может.
Лидеры для всех возможных одиночных ошибок находятся в отдельных строках, а значит код может исправить любую одиночную ошибку. Ну, что же… Попробуем в этом убедиться.
Вектор ошибки равен , а значит ошибка в третьем разряде. Как мы и загадали.
Ура, всё работает!
Что же дальше?
Чтобы попрактиковаться, попробуйте повторить рассуждения для разных проверочных матриц. Например, для кода с утроением.
Логическим продолжением изложенного был бы рассказ о циклических кодах — чрезвычайно интересном подклассе линейных кодов, обладающим замечательными свойствами. Но тогда, боюсь, статья уж очень бы разрослась.
Если вас заинтересовали подробности, то можете почитать замечательную книжку Аршинова и Садовского «Коды и математика». Там изложено гораздо больше, чем представлено в этой статье. Если интересует математика кодирования — то поищите «Теория и практика кодов, контролирующих ошибки» Блейхута. А вообще, материалов по этой теме довольно много.
Надеюсь, когда снова будет свободное время, напишу продолжение, в котором расскажу про циклические коды и покажу пример программы для кодирования и декодирования. Если, конечно, почтенной публике это интересно.
Для
того, чтобы код исправлял ошибки,
необходимо увеличить его минимальное
кодовое расстояние.
Пример.
Трёхразрядный код состоит из двух
допустимых комбинаций 000 и 111. В случае
одиночной ошибки для первого кодового
набора возможные кодовые наборы
001,010,100, для второго – 011,101,110. У каждого
допустимого кодового набора “свои”
недопустимые кодовые наборы. Его
минимальное кодовое расстояние dmin
равно 3.
Если
ошибка одиночная, то удается определить
её местоположение и исправить её, так
как каждая ошибка приводит к недопустимому
кодовому набору, соответствующему
только одному из допустимых кодовых
наборов.
Определение.
Код называется
кодом с исправлением ошибок, если всегда
из неправильного кодового набора можно
получить правильный кодовый набор
(например, коды Хэмминга).
Если
dmin
= 3, то любая
одиночная ошибка переводит допустимый
кодовый набор в недопустимый, находящийся
на расстоянии, равном 1, от исходного
кодового набора, и на расстоянии, равном
2, от любого другого допустимого кодового
набора. Поэтому в коде с dmin
= 3 можно
исправить любую одиночную ошибку или
обнаружить любую двойную ошибку. Если
dmin
= 4, то можно
исправить любую одиночную ошибку и
обнаружить любую двойную или обнаружить
тройную ошибку.
Основное
свойство кода – возможность обнаруживать
и выделять местоположение ошибочных
разрядов. Когда местоположение ошибки
определено, то осуществляют замену
ошибочного разряда на его дополнение.
5.2.1. Основные принципы построения кодов Хэмминга с исправлением ошибок
-
К
каждому набору из m
информационных разрядов (сообщению)
присоединяются k
разрядов p1,
p2,
…pk
проверки на чётность. -
Каждому
из (m+k)
присваивается десятичное значение
позиции, начиная со значения 1 для
старшего разряда и кончая значением
(m+k)
для младшего разряда. -
Производится
k
проверок на чётность числа единиц в
выбранных разрядах каждого кодового
набора. Результат каждой проверки на
чётность записывается как 1 или 0 в
зависимости от того, обнаружена ошибка
или нет. -
По
результатам проверок строится двоичное
число ck
…
c2c1,
равное десятичному значению, присвоенному
местоположению ошибочного разряда,
если произошла ошибка, и нулю при её
отсутствии. Это число называется номером
позиции ошибочного разряда.
Число
разрядов k
должно быть достаточно большим для
указания положения любой из (m+k)
возможных одиночных ошибок. Так как
m+k+1-количество
возможных событий, 2k
– максимальное количество кодовых
комбинаций, то k
должно удовлетворять неравенству 2k
m+k+1.
Определим
максимальное значение m
для заданного количества k.Обозначим
количество разрядов в коде n=
m+k.
Таблица 15
|
n |
1 |
2…3 |
4…7 |
8…15 |
16…31 |
32…63 |
|
m |
0 |
0…1 |
1…4 |
4…11 |
11…26 |
26…57 |
|
k |
1 |
2…2 |
3…3 |
4…4 |
5…5 |
6…6 |
Определим
теперь позиции, которые необходимо
проверить в каждой из k
проверок. Если в кодовой комбинации
ошибок нет, то контрольное число двоичное
ck…
c2c1
содержит
только 0. Если в первом разряде контрольного
числа стоит 1, то в результате первой
проверки обнаружена ошибка.
Таблица 16
|
№ позиции возможной |
Двоичный |
|
0 |
00000 |
|
1 |
00001 |
|
2 |
00010 |
|
3 |
00011 |
|
4 |
00100 |
|
5 |
00101 |
|
6 |
00110 |
|
7 |
00111 |
|
8 |
01000 |
|
9 |
01001 |
Окончание
таблицы 16
|
№ позиции возможной |
Двоичный |
|
10 |
01010 |
|
11 |
01011 |
|
12 |
01100 |
|
13 |
01101 |
|
14 |
01110 |
|
15 |
01111 |
|
16 |
10000 |
|
17 |
10001 |
|
18 |
10010 |
|
… |
… |
Из
табл. 16 двоичных эквивалентов для номера
позиции возможной ошибки видно, что в
первую проверяемую группу разрядов
входят 1,3,5,7,9, 11,13,15, 17 и т.д., во вторую –
2,3,6,7,10,11,14,15,18 и т.д.
Таблица
17
|
Проверка |
Проверяемые |
|
1 |
1,3,5,7,9, |
|
2 |
2,3,6,7,10,11,14,15,18 |
|
3 |
4,5,6,7, |
|
4 |
8,9,10,11, |
|
… |
… |
Разряды,
номера которых кратны степеням 2:
1,2,4,8,16…, встречаются в каждой проверяемой
группе один раз. Удобно использовать
эти разряды в качестве контрольных, а
остальные – информационных разрядов.
Пример.
Пусть исходное сообщение 00111. Количество
информационных разрядов m=5.
Количество контрольных разрядов k=4.
Длина кода Хэмминга равна 9. Построим
код Хэмминга для исходного сообщения.
|
Номер |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Исходное |
0 |
0 |
1 |
1 |
1 |
||||
|
1-я |
0 |
0 |
0 |
1 |
1 |
||||
|
2-я |
0 |
0 |
1 |
1 |
|||||
|
3-я |
0 |
0 |
1 |
1 |
|||||
|
4-я |
1 |
1 |
|||||||
|
Код |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
Код
Хэмминга для десятичных цифр в
двоично-десятичном коде 8421 приведен в
табл. 18.
Таблица
18
|
Десятичная |
p1 |
p2 |
m1 |
p3 |
m2 |
m3 |
m4 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
|
2 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
|
3 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
|
4 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
|
5 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
|
6 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
|
7 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
8 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
|
9 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
Рассмотрим
способ выявления положения ошибки и её
исправления.
Пример.
Пусть передана последовательность
1000011. Из-за ошибки в третьем разряде
принято сообщение 1010011. Положение ошибки
можно определить, выполняя 3 проверки
на четность.
|
Номер |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
ci |
|
Сообщение |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
|
|
1-я |
1 |
1 |
0 |
1 |
1 |
|||
|
2-я |
0 |
1 |
1 |
1 |
1 |
|||
|
3-я |
0 |
0 |
1 |
1 |
0 |
|||
|
Исправленное |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
Полученный
номер позиции c3c2c1=
011, т.е. ошибка в третьем разряде.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
| Reed–Solomon codes | |
|---|---|
| Named after | Irving S. Reed and Gustave Solomon |
| Classification | |
| Hierarchy | Linear block code Polynomial code Reed–Solomon code |
| Block length | n |
| Message length | k |
| Distance | n − k + 1 |
| Alphabet size | q = pm ≥ n (p prime) Often n = q − 1. |
| Notation | [n, k, n − k + 1]q-code |
| Algorithms | |
| Berlekamp–Massey Euclidean et al. |
|
| Properties | |
| Maximum-distance separable code | |
|
Reed–Solomon codes are a group of error-correcting codes that were introduced by Irving S. Reed and Gustave Solomon in 1960.[1]
They have many applications, the most prominent of which include consumer technologies such as MiniDiscs, CDs, DVDs, Blu-ray discs, QR codes, data transmission technologies such as DSL and WiMAX, broadcast systems such as satellite communications, DVB and ATSC, and storage systems such as RAID 6.
Reed–Solomon codes operate on a block of data treated as a set of finite-field elements called symbols. Reed–Solomon codes are able to detect and correct multiple symbol errors. By adding t = n − k check symbols to the data, a Reed–Solomon code can detect (but not correct) any combination of up to t erroneous symbols, or locate and correct up to ⌊t/2⌋ erroneous symbols at unknown locations. As an erasure code, it can correct up to t erasures at locations that are known and provided to the algorithm, or it can detect and correct combinations of errors and erasures. Reed–Solomon codes are also suitable as multiple-burst bit-error correcting codes, since a sequence of b + 1 consecutive bit errors can affect at most two symbols of size b. The choice of t is up to the designer of the code and may be selected within wide limits.
There are two basic types of Reed–Solomon codes – original view and BCH view – with BCH view being the most common, as BCH view decoders are faster and require less working storage than original view decoders.
History[edit]
Reed–Solomon codes were developed in 1960 by Irving S. Reed and Gustave Solomon, who were then staff members of MIT Lincoln Laboratory. Their seminal article was titled «Polynomial Codes over Certain Finite Fields». (Reed & Solomon 1960). The original encoding scheme described in the Reed & Solomon article used a variable polynomial based on the message to be encoded where only a fixed set of values (evaluation points) to be encoded are known to encoder and decoder. The original theoretical decoder generated potential polynomials based on subsets of k (unencoded message length) out of n (encoded message length) values of a received message, choosing the most popular polynomial as the correct one, which was impractical for all but the simplest of cases. This was initially resolved by changing the original scheme to a BCH code like scheme based on a fixed polynomial known to both encoder and decoder, but later, practical decoders based on the original scheme were developed, although slower than the BCH schemes. The result of this is that there are two main types of Reed Solomon codes, ones that use the original encoding scheme, and ones that use the BCH encoding scheme.
Also in 1960, a practical fixed polynomial decoder for BCH codes developed by Daniel Gorenstein and Neal Zierler was described in an MIT Lincoln Laboratory report by Zierler in January 1960 and later in a paper in June 1961.[2] The Gorenstein–Zierler decoder and the related work on BCH codes are described in a book Error Correcting Codes by W. Wesley Peterson (1961).[3] By 1963 (or possibly earlier), J. J. Stone (and others) recognized that Reed Solomon codes could use the BCH scheme of using a fixed generator polynomial, making such codes a special class of BCH codes,[4] but Reed Solomon codes based on the original encoding scheme, are not a class of BCH codes, and depending on the set of evaluation points, they are not even cyclic codes.
In 1969, an improved BCH scheme decoder was developed by Elwyn Berlekamp and James Massey, and has since been known as the Berlekamp–Massey decoding algorithm.
In 1975, another improved BCH scheme decoder was developed by Yasuo Sugiyama, based on the extended Euclidean algorithm.[5]
In 1977, Reed–Solomon codes were implemented in the Voyager program in the form of concatenated error correction codes. The first commercial application in mass-produced consumer products appeared in 1982 with the compact disc, where two interleaved Reed–Solomon codes are used. Today, Reed–Solomon codes are widely implemented in digital storage devices and digital communication standards, though they are being slowly replaced by Bose–Chaudhuri–Hocquenghem (BCH) codes. For example, Reed–Solomon codes are used in the Digital Video Broadcasting (DVB) standard DVB-S, in conjunction with a convolutional inner code, but BCH codes are used with LDPC in its successor, DVB-S2.
In 1986, an original scheme decoder known as the Berlekamp–Welch algorithm was developed.
In 1996, variations of original scheme decoders called list decoders or soft decoders were developed by Madhu Sudan and others, and work continues on these types of decoders – see Guruswami–Sudan list decoding algorithm.
In 2002, another original scheme decoder was developed by Shuhong Gao, based on the extended Euclidean algorithm.[6]
Applications[edit]
Data storage[edit]
Reed–Solomon coding is very widely used in mass storage systems to correct
the burst errors associated with media defects.
Reed–Solomon coding is a key component of the compact disc. It was the first use of strong error correction coding in a mass-produced consumer product, and DAT and DVD use similar schemes. In the CD, two layers of Reed–Solomon coding separated by a 28-way convolutional interleaver yields a scheme called Cross-Interleaved Reed–Solomon Coding (CIRC). The first element of a CIRC decoder is a relatively weak inner (32,28) Reed–Solomon code, shortened from a (255,251) code with 8-bit symbols. This code can correct up to 2 byte errors per 32-byte block. More importantly, it flags as erasures any uncorrectable blocks, i.e., blocks with more than 2 byte errors. The decoded 28-byte blocks, with erasure indications, are then spread by the deinterleaver to different blocks of the (28,24) outer code. Thanks to the deinterleaving, an erased 28-byte block from the inner code becomes a single erased byte in each of 28 outer code blocks. The outer code easily corrects this, since it can handle up to 4 such erasures per block.
The result is a CIRC that can completely correct error bursts up to 4000 bits, or about 2.5 mm on the disc surface. This code is so strong that most CD playback errors are almost certainly caused by tracking errors that cause the laser to jump track, not by uncorrectable error bursts.[7]
DVDs use a similar scheme, but with much larger blocks, a (208,192) inner code, and a (182,172) outer code.
Reed–Solomon error correction is also used in parchive files which are commonly posted accompanying multimedia files on USENET. The distributed online storage service Wuala (discontinued in 2015) also used Reed–Solomon when breaking up files.
Bar code[edit]
Almost all two-dimensional bar codes such as PDF-417, MaxiCode, Datamatrix, QR Code, and Aztec Code use Reed–Solomon error correction to allow correct reading even if a portion of the bar code is damaged. When the bar code scanner cannot recognize a bar code symbol, it will treat it as an erasure.
Reed–Solomon coding is less common in one-dimensional bar codes, but is used by the PostBar symbology.
Data transmission[edit]
Specialized forms of Reed–Solomon codes, specifically Cauchy-RS and Vandermonde-RS, can be used to overcome the unreliable nature of data transmission over erasure channels. The encoding process assumes a code of RS(N, K) which results in N codewords of length N symbols each storing K symbols of data, being generated, that are then sent over an erasure channel.
Any combination of K codewords received at the other end is enough to reconstruct all of the N codewords. The code rate is generally set to 1/2 unless the channel’s erasure likelihood can be adequately modelled and is seen to be less. In conclusion, N is usually 2K, meaning that at least half of all the codewords sent must be received in order to reconstruct all of the codewords sent.
Reed–Solomon codes are also used in xDSL systems and CCSDS’s Space Communications Protocol Specifications as a form of forward error correction.
Space transmission[edit]
Deep-space concatenated coding system.[8] Notation: RS(255, 223) + CC («constraint length» = 7, code rate = 1/2).
One significant application of Reed–Solomon coding was to encode the digital pictures sent back by the Voyager program.
Voyager introduced Reed–Solomon coding concatenated with convolutional codes, a practice that has since become very widespread in deep space and satellite (e.g., direct digital broadcasting) communications.
Viterbi decoders tend to produce errors in short bursts. Correcting these burst errors is a job best done by short or simplified Reed–Solomon codes.
Modern versions of concatenated Reed–Solomon/Viterbi-decoded convolutional coding were and are used on the Mars Pathfinder, Galileo, Mars Exploration Rover and Cassini missions, where they perform within about 1–1.5 dB of the ultimate limit, the Shannon capacity.
These concatenated codes are now being replaced by more powerful turbo codes:
| Years | Code | Mission(s) |
|---|---|---|
| 1958–present | Uncoded | Explorer, Mariner, many others |
| 1968–1978 | convolutional codes (CC) (25, 1/2) | Pioneer, Venus |
| 1969–1975 | Reed-Muller code (32, 6) | Mariner, Viking |
| 1977–present | Binary Golay code | Voyager |
| 1977–present | RS(255, 223) + CC(7, 1/2) | Voyager, Galileo, many others |
| 1989–2003 | RS(255, 223) + CC(7, 1/3) | Voyager |
| 1989–2003 | RS(255, 223) + CC(14, 1/4) | Galileo |
| 1996–present | RS + CC (15, 1/6) | Cassini, Mars Pathfinder, others |
| 2004–present | Turbo codes[nb 1] | Messenger, Stereo, MRO, others |
| est. 2009 | LDPC codes | Constellation, MSL |
Constructions (encoding)[edit]
The Reed–Solomon code is actually a family of codes, where every code is characterised by three parameters: an alphabet size q, a block length n, and a message length k, with k < n ≤ q. The set of alphabet symbols is interpreted as the finite field of order q, and thus, q must be a prime power. In the most useful parameterizations of the Reed–Solomon code, the block length is usually some constant multiple of the message length, that is, the rate R = k/n is some constant, and furthermore, the block length is equal to or one less than the alphabet size, that is, n = q or n = q − 1.[citation needed]
Reed & Solomon’s original view: The codeword as a sequence of values[edit]
There are different encoding procedures for the Reed–Solomon code, and thus, there are different ways to describe the set of all codewords.
In the original view of Reed & Solomon (1960), every codeword of the Reed–Solomon code is a sequence of function values of a polynomial of degree less than k. In order to obtain a codeword of the Reed–Solomon code, the message symbols (each within the q-sized alphabet) are treated as the coefficients of a polynomial p of degree less than k, over the finite field F with q elements.
In turn, the polynomial p is evaluated at n ≤ q distinct points 
Formally, the set 
Since any two distinct polynomials of degree less than 







Being a code that achieves this optimal trade-off, the Reed–Solomon code belongs to the class of maximum distance separable codes.
While the number of different polynomials of degree less than k and the number of different messages are both equal to 

Simple encoding procedure: The message as a sequence of coefficients[edit]
In the original construction of Reed & Solomon (1960), the message 

The codeword of 





This function 




This matrix is the transpose of a Vandermonde matrix over 

Systematic encoding procedure: The message as an initial sequence of values[edit]
There is an alternative encoding procedure that also produces the Reed–Solomon code, but that does so in a systematic way. Here, the mapping from the message 



To compute this polynomial 

Once it has been found, it is evaluated at the other points 
The alternative encoding function 
Since the first 


Since Lagrange interpolation is a linear transformation, 

Discrete Fourier transform and its inverse[edit]
A discrete Fourier transform is essentially the same as the encoding procedure; it uses the generator polynomial p(x) to map a set of evaluation points into the message values as shown above:
The inverse Fourier transform could be used to convert an error free set of n < q message values back into the encoding polynomial of k coefficients, with the constraint that in order for this to work, the set of evaluation points used to encode the message must be a set of increasing powers of α:
However, Lagrange interpolation performs the same conversion without the constraint on the set of evaluation points or the requirement of an error free set of message values and is used for systematic encoding, and in one of the steps of the Gao decoder.
The BCH view: The codeword as a sequence of coefficients[edit]
In this view, the message is interpreted as the coefficients of a polynomial 











For a «narrow sense code», 
Systematic encoding procedure[edit]
The encoding procedure for the BCH view of Reed–Solomon codes can be modified to yield a systematic encoding procedure, in which each codeword contains the message as a prefix, and simply appends error correcting symbols as a suffix. Here, instead of sending 









Formally, the construction is done by multiplying 





The remainder has degree at most 





As a result, the codewords 


Properties[edit]
The Reed–Solomon code is a [n, k, n − k + 1] code; in other words, it is a linear block code of length n (over F) with dimension k and minimum Hamming distance 
The error-correcting ability of a Reed–Solomon code is determined by its minimum distance, or equivalently, by 



Theoretical BER performance of the Reed-Solomon code (N=255, K=233, QPSK, AWGN). Step-like characteristic.
The theoretical error bound can be described via the following formula for the AWGN channel for FSK:[11]
and for other modulation schemes:
where 




For practical uses of Reed–Solomon codes, it is common to use a finite field 


The sender sends the data points as encoded blocks, and the number of symbols in the encoded block is 






The Reed–Solomon code properties discussed above make them especially well-suited to applications where errors occur in bursts. This is because it does not matter to the code how many bits in a symbol are in error — if multiple bits in a symbol are corrupted it only counts as a single error. Conversely, if a data stream is not characterized by error bursts or drop-outs but by random single bit errors, a Reed–Solomon code is usually a poor choice compared to a binary code.
The Reed–Solomon code, like the convolutional code, is a transparent code. This means that if the channel symbols have been inverted somewhere along the line, the decoders will still operate. The result will be the inversion of the original data. However, the Reed–Solomon code loses its transparency when the code is shortened. The «missing» bits in a shortened code need to be filled by either zeros or ones, depending on whether the data is complemented or not. (To put it another way, if the symbols are inverted, then the zero-fill needs to be inverted to a one-fill.) For this reason it is mandatory that the sense of the data (i.e., true or complemented) be resolved before Reed–Solomon decoding.
Whether the Reed–Solomon code is cyclic or not depends on subtle details of the construction. In the original view of Reed and Solomon, where the codewords are the values of a polynomial, one can choose the sequence of evaluation points in such a way as to make the code cyclic. In particular, if 












[edit]
Designers are not required to use the «natural» sizes of Reed–Solomon code blocks. A technique known as «shortening» can produce a smaller code of any desired size from a larger code. For example, the widely used (255,223) code can be converted to a (160,128) code by padding the unused portion of the source block with 95 binary zeroes and not transmitting them. At the decoder, the same portion of the block is loaded locally with binary zeroes. The Delsarte–Goethals–Seidel[12] theorem illustrates an example of an application of shortened Reed–Solomon codes. In parallel to shortening, a technique known as puncturing allows omitting some of the encoded parity symbols.
BCH view decoders[edit]
The decoders described in this section use the BCH view of a codeword as a sequence of coefficients. They use a fixed generator polynomial known to both encoder and decoder.
Peterson–Gorenstein–Zierler decoder[edit]
Daniel Gorenstein and Neal Zierler developed a decoder that was described in a MIT Lincoln Laboratory report by Zierler in January 1960 and later in a paper in June 1961.[13] The Gorenstein–Zierler decoder and the related work on BCH codes are described in a book Error Correcting Codes by W. Wesley Peterson (1961).[14]
Formulation[edit]
The transmitted message, 
As a result of the Reed-Solomon encoding procedure, s(x) is divisible by the generator polynomial g(x):
where α is a primitive element.
Since s(x) is a multiple of the generator g(x), it follows that it «inherits» all its roots.
Therefore,
The transmitted polynomial is corrupted in transit by an error polynomial e(x) to produce the received polynomial r(x).
Coefficient ei will be zero if there is no error at that power of x and nonzero if there is an error. If there are ν errors at distinct powers ik of x, then
The goal of the decoder is to find the number of errors (ν), the positions of the errors (ik), and the error values at those positions (eik). From those, e(x) can be calculated and subtracted from r(x) to get the originally sent message s(x).
Syndrome decoding[edit]
The decoder starts by evaluating the polynomial as received at points 
Note that 


The advantage of looking at the syndromes is that the message polynomial drops out. In other words, the syndromes only relate to the error, and are unaffected by the actual contents of the message being transmitted. If the syndromes are all zero, the algorithm stops here and reports that the message was not corrupted in transit.
Error locators and error values[edit]
For convenience, define the error locators Xk and error values Yk as:
Then the syndromes can be written in terms of these error locators and error values as
This definition of the syndrome values is equivalent to the previous since 
The syndromes give a system of n − k ≥ 2ν equations in 2ν unknowns, but that system of equations is nonlinear in the Xk and does not have an obvious solution. However, if the Xk were known (see below), then the syndrome equations provide a linear system of equations that can easily be solved for the Yk error values.
Consequently, the problem is finding the Xk, because then the leftmost matrix would be known, and both sides of the equation could be multiplied by its inverse, yielding Yk
In the variant of this algorithm where the locations of the errors are already known (when it is being used as an erasure code), this is the end. The error locations (Xk) are already known by some other method (for example, in an FM transmission, the sections where the bitstream was unclear or overcome with interference are probabilistically determinable from frequency analysis). In this scenario, up to 
The rest of the algorithm serves to locate the errors, and will require syndrome values up to 

Error locator polynomial[edit]
There is a linear recurrence relation that gives rise to a system of linear equations. Solving those equations identifies those error locations Xk.
Define the error locator polynomial Λ(x) as
The zeros of Λ(x) are the reciprocals 


Let 


Sum for k = 1 to ν and it will still be zero.
Collect each term into its own sum.
Extract the constant values of 
These summations are now equivalent to the syndrome values, which we know and can substitute in! This therefore reduces to
Subtracting 
Recall that j was chosen to be any integer between 1 and v inclusive, and this equivalence is true for any and all such values. Therefore, we have v linear equations, not just one. This system of linear equations can therefore be solved for the coefficients Λi of the error location polynomial:
The above assumes the decoder knows the number of errors ν, but that number has not been determined yet. The PGZ decoder does not determine ν directly but rather searches for it by trying successive values. The decoder first assumes the largest value for a trial ν and sets up the linear system for that value. If the equations can be solved (i.e., the matrix determinant is nonzero), then that trial value is the number of errors. If the linear system cannot be solved, then the trial ν is reduced by one and the next smaller system is examined. (Gill n.d., p. 35)
Find the roots of the error locator polynomial[edit]
Use the coefficients Λi found in the last step to build the error location polynomial. The roots of the error location polynomial can be found by exhaustive search. The error locators Xk are the reciprocals of those roots. The order of coefficients of the error location polynomial can be reversed, in which case the roots of that reversed polynomial are the error locators 

Calculate the error values[edit]
Once the error locators Xk are known, the error values can be determined. This can be done by direct solution for Yk in the error equations matrix given above, or using the Forney algorithm.
Calculate the error locations[edit]
Calculate ik by taking the log base 
Fix the errors[edit]
Finally, e(x) is generated from ik and eik and then is subtracted from r(x) to get the originally sent message s(x), with errors corrected.
Example[edit]
Consider the Reed–Solomon code defined in GF(929) with α = 3 and t = 4 (this is used in PDF417 barcodes) for a RS(7,3) code. The generator polynomial is
If the message polynomial is p(x) = 3 x2 + 2 x + 1, then a systematic codeword is encoded as follows.
Errors in transmission might cause this to be received instead.
The syndromes are calculated by evaluating r at powers of α.
Using Gaussian elimination:
Λ(x) = 329 x2 + 821 x + 001, with roots x1 = 757 = 3−3 and x2 = 562 = 3−4
The coefficients can be reversed to produce roots with positive exponents, but typically this isn’t used:
R(x) = 001 x2 + 821 x + 329, with roots 27 = 33 and 81 = 34
with the log of the roots corresponding to the error locations (right to left, location 0 is the last term in the codeword).
To calculate the error values, apply the Forney algorithm.
Ω(x) = S(x) Λ(x) mod x4 = 546 x + 732
Λ'(x) = 658 x + 821
e1 = −Ω(x1)/Λ'(x1) = 074
e2 = −Ω(x2)/Λ'(x2) = 122
Subtracting 
Berlekamp–Massey decoder[edit]
The Berlekamp–Massey algorithm is an alternate iterative procedure for finding the error locator polynomial. During each iteration, it calculates a discrepancy based on a current instance of Λ(x) with an assumed number of errors e:
and then adjusts Λ(x) and e so that a recalculated Δ would be zero. The article Berlekamp–Massey algorithm has a detailed description of the procedure. In the following example, C(x) is used to represent Λ(x).
Example[edit]
Using the same data as the Peterson Gorenstein Zierler example above:
| n | Sn+1 | d | C | B | b | m |
|---|---|---|---|---|---|---|
| 0 | 732 | 732 | 197 x + 1 | 1 | 732 | 1 |
| 1 | 637 | 846 | 173 x + 1 | 1 | 732 | 2 |
| 2 | 762 | 412 | 634 x2 + 173 x + 1 | 173 x + 1 | 412 | 1 |
| 3 | 925 | 576 | 329 x2 + 821 x + 1 | 173 x + 1 | 412 | 2 |
The final value of C is the error locator polynomial, Λ(x).
Euclidean decoder[edit]
Another iterative method for calculating both the error locator polynomial and the error value polynomial is based on Sugiyama’s adaptation of the extended Euclidean algorithm .
Define S(x), Λ(x), and Ω(x) for t syndromes and e errors:
The key equation is:
For t = 6 and e = 3:
The middle terms are zero due to the relationship between Λ and syndromes.
The extended Euclidean algorithm can find a series of polynomials of the form
Ai(x) S(x) + Bi(x) xt = Ri(x)
where the degree of R decreases as i increases. Once the degree of Ri(x) < t/2, then
Ai(x) = Λ(x)
Bi(x) = −Q(x)
Ri(x) = Ω(x).
B(x) and Q(x) don’t need to be saved, so the algorithm becomes:
R−1 := xt R0 := S(x) A−1 := 0 A0 := 1 i := 0 while degree of Ri ≥ t/2 i := i + 1 Q := Ri-2 / Ri-1 Ri := Ri-2 - Q Ri-1 Ai := Ai-2 - Q Ai-1
to set low order term of Λ(x) to 1, divide Λ(x) and Ω(x) by Ai(0):
Λ(x) = Ai / Ai(0)
Ω(x) = Ri / Ai(0)
Ai(0) is the constant (low order) term of Ai.
Example[edit]
Using the same data as the Peterson–Gorenstein–Zierler example above:
| i | Ri | Ai |
|---|---|---|
| −1 | 001 x4 + 000 x3 + 000 x2 + 000 x + 000 | 000 |
| 0 | 925 x3 + 762 x2 + 637 x + 732 | 001 |
| 1 | 683 x2 + 676 x + 024 | 697 x + 396 |
| 2 | 673 x + 596 | 608 x2 + 704 x + 544 |
Λ(x) = A2 / 544 = 329 x2 + 821 x + 001
Ω(x) = R2 / 544 = 546 x + 732
Decoder using discrete Fourier transform[edit]
A discrete Fourier transform can be used for decoding.[15] To avoid conflict with syndrome names, let c(x) = s(x) the encoded codeword. r(x) and e(x) are the same as above. Define C(x), E(x), and R(x) as the discrete Fourier transforms of c(x), e(x), and r(x). Since r(x) = c(x) + e(x), and since a discrete Fourier transform is a linear operator, R(x) = C(x) + E(x).
Transform r(x) to R(x) using discrete Fourier transform. Since the calculation for a discrete Fourier transform is the same as the calculation for syndromes, t coefficients of R(x) and E(x) are the same as the syndromes:
Use 

Let v = number of errors. Generate E(x) using the known coefficients 

Then calculate C(x) = R(x) − E(x) and take the inverse transform (polynomial interpolation) of C(x) to produce c(x).
Decoding beyond the error-correction bound[edit]
The Singleton bound states that the minimum distance d of a linear block code of size (n,k) is upper-bounded by n − k + 1. The distance d was usually understood to limit the error-correction capability to ⌊(d−1) / 2⌋. The Reed–Solomon code achieves this bound with equality, and can thus correct up to ⌊(n−k) / 2⌋ errors. However, this error-correction bound is not exact.
In 1999, Madhu Sudan and Venkatesan Guruswami at MIT published «Improved Decoding of Reed–Solomon and Algebraic-Geometry Codes» introducing an algorithm that allowed for the correction of errors beyond half the minimum distance of the code.[16] It applies to Reed–Solomon codes and more generally to algebraic geometric codes. This algorithm produces a list of codewords (it is a list-decoding algorithm) and is based on interpolation and factorization of polynomials over 
Soft-decoding[edit]
The algebraic decoding methods described above are hard-decision methods, which means that for every symbol a hard decision is made about its value. For example, a decoder could associate with each symbol an additional value corresponding to the channel demodulator’s confidence in the correctness of the symbol. The advent of LDPC and turbo codes, which employ iterated soft-decision belief propagation decoding methods to achieve error-correction performance close to the theoretical limit, has spurred interest in applying soft-decision decoding to conventional algebraic codes. In 2003, Ralf Koetter and Alexander Vardy presented a polynomial-time soft-decision algebraic list-decoding algorithm for Reed–Solomon codes, which was based upon the work by Sudan and Guruswami.[17]
In 2016, Steven J. Franke and Joseph H. Taylor published a novel soft-decision decoder.[18]
MATLAB example[edit]
Encoder[edit]
Here we present a simple MATLAB implementation for an encoder.
function encoded = rsEncoder(msg, m, prim_poly, n, k) % RSENCODER Encode message with the Reed-Solomon algorithm % m is the number of bits per symbol % prim_poly: Primitive polynomial p(x). Ie for DM is 301 % k is the size of the message % n is the total size (k+redundant) % Example: msg = uint8('Test') % enc_msg = rsEncoder(msg, 8, 301, 12, numel(msg)); % Get the alpha alpha = gf(2, m, prim_poly); % Get the Reed-Solomon generating polynomial g(x) g_x = genpoly(k, n, alpha); % Multiply the information by X^(n-k), or just pad with zeros at the end to % get space to add the redundant information msg_padded = gf([msg zeros(1, n - k)], m, prim_poly); % Get the remainder of the division of the extended message by the % Reed-Solomon generating polynomial g(x) [~, remainder] = deconv(msg_padded, g_x); % Now return the message with the redundant information encoded = msg_padded - remainder; end % Find the Reed-Solomon generating polynomial g(x), by the way this is the % same as the rsgenpoly function on matlab function g = genpoly(k, n, alpha) g = 1; % A multiplication on the galois field is just a convolution for k = mod(1 : n - k, n) g = conv(g, [1 alpha .^ (k)]); end end
Decoder[edit]
Now the decoding part:
function [decoded, error_pos, error_mag, g, S] = rsDecoder(encoded, m, prim_poly, n, k) % RSDECODER Decode a Reed-Solomon encoded message % Example: % [dec, ~, ~, ~, ~] = rsDecoder(enc_msg, 8, 301, 12, numel(msg)) max_errors = floor((n - k) / 2); orig_vals = encoded.x; % Initialize the error vector errors = zeros(1, n); g = []; S = []; % Get the alpha alpha = gf(2, m, prim_poly); % Find the syndromes (Check if dividing the message by the generator % polynomial the result is zero) Synd = polyval(encoded, alpha .^ (1:n - k)); Syndromes = trim(Synd); % If all syndromes are zeros (perfectly divisible) there are no errors if isempty(Syndromes.x) decoded = orig_vals(1:k); error_pos = []; error_mag = []; g = []; S = Synd; return; end % Prepare for the euclidean algorithm (Used to find the error locating % polynomials) r0 = [1, zeros(1, 2 * max_errors)]; r0 = gf(r0, m, prim_poly); r0 = trim(r0); size_r0 = length(r0); r1 = Syndromes; f0 = gf([zeros(1, size_r0 - 1) 1], m, prim_poly); f1 = gf(zeros(1, size_r0), m, prim_poly); g0 = f1; g1 = f0; % Do the euclidean algorithm on the polynomials r0(x) and Syndromes(x) in % order to find the error locating polynomial while true % Do a long division [quotient, remainder] = deconv(r0, r1); % Add some zeros quotient = pad(quotient, length(g1)); % Find quotient*g1 and pad c = conv(quotient, g1); c = trim(c); c = pad(c, length(g0)); % Update g as g0-quotient*g1 g = g0 - c; % Check if the degree of remainder(x) is less than max_errors if all(remainder(1:end - max_errors) == 0) break; end % Update r0, r1, g0, g1 and remove leading zeros r0 = trim(r1); r1 = trim(remainder); g0 = g1; g1 = g; end % Remove leading zeros g = trim(g); % Find the zeros of the error polynomial on this galois field evalPoly = polyval(g, alpha .^ (n - 1 : - 1 : 0)); error_pos = gf(find(evalPoly == 0), m); % If no error position is found we return the received work, because % basically is nothing that we could do and we return the received message if isempty(error_pos) decoded = orig_vals(1:k); error_mag = []; return; end % Prepare a linear system to solve the error polynomial and find the error % magnitudes size_error = length(error_pos); Syndrome_Vals = Syndromes.x; b(:, 1) = Syndrome_Vals(1:size_error); for idx = 1 : size_error e = alpha .^ (idx * (n - error_pos.x)); err = e.x; er(idx, :) = err; end % Solve the linear system error_mag = (gf(er, m, prim_poly) gf(b, m, prim_poly))'; % Put the error magnitude on the error vector errors(error_pos.x) = error_mag.x; % Bring this vector to the galois field errors_gf = gf(errors, m, prim_poly); % Now to fix the errors just add with the encoded code decoded_gf = encoded(1:k) + errors_gf(1:k); decoded = decoded_gf.x; end % Remove leading zeros from Galois array function gt = trim(g) gx = g.x; gt = gf(gx(find(gx, 1) : end), g.m, g.prim_poly); end % Add leading zeros function xpad = pad(x, k) len = length(x); if len < k xpad = [zeros(1, k - len) x]; end end
Reed Solomon original view decoders[edit]
The decoders described in this section use the Reed Solomon original view of a codeword as a sequence of polynomial values where the polynomial is based on the message to be encoded. The same set of fixed values are used by the encoder and decoder, and the decoder recovers the encoding polynomial (and optionally an error locating polynomial) from the received message.
Theoretical decoder[edit]
Reed & Solomon (1960) described a theoretical decoder that corrected errors by finding the most popular message polynomial. The decoder only knows the set of values 



Berlekamp Welch decoder[edit]
In 1986, a decoder known as the Berlekamp–Welch algorithm was developed as a decoder that is able to recover the original message polynomial as well as an error «locator» polynomial that produces zeroes for the input values that correspond to errors, with time complexity 

Example[edit]
Using RS(7,3), GF(929), and the set of evaluation points ai = i − 1
a = {0, 1, 2, 3, 4, 5, 6}
If the message polynomial is
p(x) = 003 x2 + 002 x + 001
The codeword is
c = {001, 006, 017, 034, 057, 086, 121}
Errors in transmission might cause this to be received instead.
b = c + e = {001, 006, 123, 456, 057, 086, 121}
The key equations are:
Assume maximum number of errors: e = 2. The key equations become:
Using Gaussian elimination:
Q(x) = 003 x4 + 916 x3 + 009 x2 + 007 x + 006
E(x) = 001 x2 + 924 x + 006
Q(x) / E(x) = P(x) = 003 x2 + 002 x + 001
Recalculate P(x) where E(x) = 0 : {2, 3} to correct b resulting in the corrected codeword:
c = {001, 006, 017, 034, 057, 086, 121}
Gao decoder[edit]
In 2002, an improved decoder was developed by Shuhong Gao, based on the extended Euclid algorithm.[6]
Example[edit]
Using the same data as the Berlekamp Welch example above:
| i | Ri | Ai |
|---|---|---|
| −1 | 001 x7 + 908 x6 + 175 x5 + 194 x4 + 695 x3 + 094 x2 + 720 x + 000 | 000 |
| 0 | 055 x6 + 440 x5 + 497 x4 + 904 x3 + 424 x2 + 472 x + 001 | 001 |
| 1 | 702 x5 + 845 x4 + 691 x3 + 461 x2 + 327 x + 237 | 152 x + 237 |
| 2 | 266 x4 + 086 x3 + 798 x2 + 311 x + 532 | 708 x2 + 176 x + 532 |
Q(x) = R2 = 266 x4 + 086 x3 + 798 x2 + 311 x + 532
E(x) = A2 = 708 x2 + 176 x + 532
divide Q(x) and E(x) by most significant coefficient of E(x) = 708. (Optional)
Q(x) = 003 x4 + 916 x3 + 009 x2 + 007 x + 006
E(x) = 001 x2 + 924 x + 006
Q(x) / E(x) = P(x) = 003 x2 + 002 x + 001
Recalculate P(x) where E(x) = 0 : {2, 3} to correct b resulting in the corrected codeword:
c = {001, 006, 017, 034, 057, 086, 121}
See also[edit]
- BCH code
- Cyclic code
- Chien search
- Berlekamp–Massey algorithm
- Forward error correction
- Berlekamp–Welch algorithm
- Folded Reed–Solomon code
Notes[edit]
- ^ Authors in Andrews et al. (2007), provide simulation results which show that for the same code rate (1/6) turbo codes outperform Reed-Solomon concatenated codes up to 2 dB (bit error rate).[9]
References[edit]
- ^ Reed & Solomon (1960)
- ^ D. Gorenstein and N. Zierler, «A class of cyclic linear error-correcting codes in p^m symbols», J. SIAM, vol. 9, pp. 207–214, June 1961
- ^ Error Correcting Codes by W_Wesley_Peterson, 1961
- ^ Error Correcting Codes by W_Wesley_Peterson, second edition, 1972
- ^ Yasuo Sugiyama, Masao Kasahara, Shigeichi Hirasawa, and Toshihiko Namekawa. A method for solving key equation for decoding Goppa codes. Information and Control, 27:87–99, 1975.
- ^ a b Gao, Shuhong (January 2002), New Algorithm For Decoding Reed-Solomon Codes (PDF), Clemson
- ^ Immink, K. A. S. (1994), «Reed–Solomon Codes and the Compact Disc», in Wicker, Stephen B.; Bhargava, Vijay K. (eds.), Reed–Solomon Codes and Their Applications, IEEE Press, ISBN 978-0-7803-1025-4
- ^ J. Hagenauer, E. Offer, and L. Papke, Reed Solomon Codes and Their Applications. New York IEEE Press, 1994 — p. 433
- ^ a b Andrews, Kenneth S., et al. «The development of turbo and LDPC codes for deep-space applications.» Proceedings of the IEEE 95.11 (2007): 2142-2156.
- ^ See Lin & Costello (1983, p. 171), for example.
- ^ «Analytical Expressions Used in bercoding and BERTool». Archived from the original on 2019-02-01. Retrieved 2019-02-01.
- ^ Pfender, Florian; Ziegler, Günter M. (September 2004), «Kissing Numbers, Sphere Packings, and Some Unexpected Proofs» (PDF), Notices of the American Mathematical Society, 51 (8): 873–883, archived (PDF) from the original on 2008-05-09, retrieved 2009-09-28. Explains the Delsarte-Goethals-Seidel theorem as used in the context of the error correcting code for compact disc.
- ^ D. Gorenstein and N. Zierler, «A class of cyclic linear error-correcting codes in p^m symbols,» J. SIAM, vol. 9, pp. 207–214, June 1961
- ^ Error Correcting Codes by W Wesley Peterson, 1961
- ^ Shu Lin and Daniel J. Costello Jr, «Error Control Coding» second edition, pp. 255–262, 1982, 2004
- ^ Guruswami, V.; Sudan, M. (September 1999), «Improved decoding of Reed–Solomon codes and algebraic geometry codes», IEEE Transactions on Information Theory, 45 (6): 1757–1767, CiteSeerX 10.1.1.115.292, doi:10.1109/18.782097
- ^ Koetter, Ralf; Vardy, Alexander (2003). «Algebraic soft-decision decoding of Reed–Solomon codes». IEEE Transactions on Information Theory. 49 (11): 2809–2825. CiteSeerX 10.1.1.13.2021. doi:10.1109/TIT.2003.819332.
- ^ Franke, Steven J.; Taylor, Joseph H. (2016). «Open Source Soft-Decision Decoder for the JT65 (63,12) Reed–Solomon Code» (PDF). QEX (May/June): 8–17. Archived (PDF) from the original on 2017-03-09. Retrieved 2017-06-07.
Further reading[edit]
- Gill, John (n.d.), EE387 Notes #7, Handout #28 (PDF), Stanford University, archived from the original (PDF) on June 30, 2014, retrieved April 21, 2010
- Hong, Jonathan; Vetterli, Martin (August 1995), «Simple Algorithms for BCH Decoding» (PDF), IEEE Transactions on Communications, 43 (8): 2324–2333, doi:10.1109/26.403765
- Lin, Shu; Costello, Jr., Daniel J. (1983), Error Control Coding: Fundamentals and Applications, New Jersey, NJ: Prentice-Hall, ISBN 978-0-13-283796-5
- Massey, J. L. (1969), «Shift-register synthesis and BCH decoding» (PDF), IEEE Transactions on Information Theory, IT-15 (1): 122–127, doi:10.1109/tit.1969.1054260
- Peterson, Wesley W. (1960), «Encoding and Error Correction Procedures for the Bose-Chaudhuri Codes», IRE Transactions on Information Theory, IT-6 (4): 459–470, doi:10.1109/TIT.1960.1057586
- Reed, Irving S.; Solomon, Gustave (1960), «Polynomial Codes over Certain Finite Fields», Journal of the Society for Industrial and Applied Mathematics, 8 (2): 300–304, doi:10.1137/0108018
- Welch, L. R. (1997), The Original View of Reed–Solomon Codes (PDF), Lecture Notes
- Berlekamp, Elwyn R. (1967), Nonbinary BCH decoding, International Symposium on Information Theory, San Remo, Italy
- Berlekamp, Elwyn R. (1984) [1968], Algebraic Coding Theory (Revised ed.), Laguna Hills, CA: Aegean Park Press, ISBN 978-0-89412-063-3
- Cipra, Barry Arthur (1993), «The Ubiquitous Reed–Solomon Codes», SIAM News, 26 (1)
- Forney, Jr., G. (October 1965), «On Decoding BCH Codes», IEEE Transactions on Information Theory, 11 (4): 549–557, doi:10.1109/TIT.1965.1053825
- Koetter, Ralf (2005), Reed–Solomon Codes, MIT Lecture Notes 6.451 (Video), archived from the original on 2013-03-13
- MacWilliams, F. J.; Sloane, N. J. A. (1977), The Theory of Error-Correcting Codes, New York, NY: North-Holland Publishing Company
- Reed, Irving S.; Chen, Xuemin (1999), Error-Control Coding for Data Networks, Boston, MA: Kluwer Academic Publishers
External links[edit]
Information and tutorials[edit]
- Introduction to Reed–Solomon codes: principles, architecture and implementation (CMU)
- A Tutorial on Reed–Solomon Coding for Fault-Tolerance in RAID-like Systems
- Algebraic soft-decoding of Reed–Solomon codes
- Wikiversity:Reed–Solomon codes for coders
- BBC R&D White Paper WHP031
- Geisel, William A. (August 1990), Tutorial on Reed–Solomon Error Correction Coding, Technical Memorandum, NASA, TM-102162
- Concatenated codes by Dr. Dave Forney (scholarpedia.org).
- Reid, Jeff A. (April 1995), CRC and Reed Solomon ECC (PDF)
Implementations[edit]
- FEC library in C by Phil Karn (aka KA9Q) includes Reed–Solomon codec, both arbitrary and optimized (223,255) version
- Schifra Open Source C++ Reed–Solomon Codec
- Henry Minsky’s RSCode library, Reed–Solomon encoder/decoder
- Open Source C++ Reed–Solomon Soft Decoding library
- Matlab implementation of errors and-erasures Reed–Solomon decoding
- Octave implementation in communications package
- Pure-Python implementation of a Reed–Solomon codec
| Обноружение ошибок | Обноружение ошибок |  |
||||
| Исправление ошибок | Исправление ошибок |  |
||||
| Коррекция ошибок | Коррекция ошибок |  |
||||
| Назад | Назад |  |
||||
Методы обнаружения ошибок
В обычном равномерном непомехоустойчивом коде число разрядов n в кодовых
комбинациях определяется числом сообщений и основанием кода.
Коды, у которых все кодовые комбинации разрешены, называются простыми или
равнодоступными и являются полностью безызбыточными. Безызбыточные коды обладают
большой «чувствительностью» к помехам. Внесение избыточности при использовании
помехоустойчивых кодов связано с увеличением n – числа разрядов кодовой комбинации. Таким
образом, все множество

подмножество разрешенных комбинаций, обладающих определенными признаками, и
подмножество запрещенных комбинаций, этими признаками не обладающих.
Помехоустойчивый код отличается от обычного кода тем, что в канал передаются не все
кодовые комбинации N, которые можно сформировать из имеющегося числа разрядов n, а только
их часть Nk , которая составляет подмножество разрешенных комбинаций. Если при приеме
выясняется, что кодовая комбинация принадлежит к запрещенным, то это свидетельствует о
наличии ошибок в комбинации, т.е. таким образом решается задача обнаружения ошибок. При
этом принятая комбинация не декодируется (не принимается решение о переданном
сообщении). В связи с этим помехоустойчивые коды называют корректирующими кодами.
Корректирующие свойства избыточных кодов зависят от правила их построения, определяющего
структуру кода, и параметров кода (длительности символов, числа разрядов, избыточности и т. п.).
Первые работы по корректирующим кодам принадлежат Хеммингу, который ввел понятие
минимального кодового расстояния dmin и предложил код, позволяющий однозначно указать ту
позицию в кодовой комбинации, где произошла ошибка. К информационным элементам k в коде
Хемминга добавляется m проверочных элементов для автоматического определения
местоположения ошибочного символа. Таким образом, общая длина кодовой комбинации
составляет: n = k + m.
Метричное представление n,k-кодов
В настоящее время наибольшее внимание с точки зрения технических приложений
уделяется двоичным блочным корректирующим кодам. При использовании блочных кодов
цифровая информация передается в виде отдельных кодовых комбинаций (блоков) равной
длины. Кодирование и декодирование каждого блока осуществляется независимо друг от друга.
Почти все блочные коды относятся к разделимым кодам, кодовые комбинации которых
состоят из двух частей: информационной и проверочной. При общем числе n символов в блоке
число информационных символов равно k, а число проверочных символов:
К основным характеристикам корректирующих кодов относятся:
|
— число разрешенных и запрещенных кодовых комбинаций; |
Для блочных двоичных кодов, с числом символов в блоках, равным n, общее число
возможных кодовых комбинаций определяется значением
Число разрешенных кодовых комбинаций при наличии k информационных разрядов в
первичном коде:
Очевидно, что число запрещенных комбинаций:
а с учетом отношение будет
где m – число избыточных (проверочных) разрядов в блочном коде.
Избыточностью корректирующего кода называют величину
откуда следует:
Эта величина показывает, какую часть общего числа символов кодовой комбинации
составляют информационные символы. В теории кодирования величину Bk называют
относительной скоростью кода. Если производительность источника информации равна H
символов в секунду, то скорость передачи после кодирования этой информации будет
поскольку в закодированной последовательности из каждых n символов только k символов
являются информационными.
Если число ошибок, которые нужно обнаружить или исправить, значительно, то необходимо
иметь код с большим числом проверочных символов. Чтобы при этом скорость передачи
оставалась достаточно высокой, необходимо в каждом кодовом блоке одновременно
увеличивать как общее число символов, так и число информационных символов.
При этом длительность кодовых блоков будет существенно возрастать, что приведет к
задержке информации при передаче и приеме. Чем сложнее кодирование, тем длительнее
временная задержка информации.
Минимальное кодовое расстояние – dmin. Для того чтобы можно было обнаружить и
исправлять ошибки, разрешенная комбинация должна как можно больше отличаться от
запрещенной. Если ошибки в канале связи действуют независимо, то вероятность преобразования
одной кодовой комбинации в другую будет тем меньше, чем большим числом символов они
различаются.
Если интерпретировать кодовые комбинации как точки в пространстве, то отличие
выражается в близости этих точек, т. е. в расстоянии между ними.
Количество разрядов (символов), которыми отличаются две кодовые комбинации, можно
принять за кодовое расстояние между ними. Для определения этого расстояния нужно сложить
две кодовые комбинации «по модулю 2» и подсчитать число единиц в полученной сумме.
Например, две кодовые комбинации xi = 01011 и xj = 10010 имеют расстояние d(xi,xj) , равное 3,
так как:
Здесь под операцией ⊕ понимается сложение «по модулю 2».
Заметим, что кодовое расстояние d(xi,x0) между комбинацией xi и нулевой x0 = 00…0
называют весом W комбинации xi, т.е. вес xi равен числу «1» в ней.
Расстояние между различными комбинациями некоторого конкретного кода могут
существенно отличаться. Так, в частности, в безызбыточном первичном натуральном коде n = k это
расстояние для различных комбинаций может изменяться от единицы до величины n, равной
разрядности кода. Особую важность для характеристики корректирующих свойств кода имеет
минимальное кодовое расстояние dmin, определяемое при попарном сравнении всех кодовых
комбинаций, которое называют расстоянием Хемминга.
В безызбыточном коде все комбинации являются разрешенными и его минимальное
кодовое расстояние равно единице – dmin=1. Поэтому достаточно исказиться одному символу,
чтобы вместо переданной комбинации была принята другая разрешенная комбинация. Чтобы код
обладал корректирующими свойствами, необходимо ввести в него некоторую избыточность,
которая обеспечивала бы минимальное расстояние между любыми двумя разрешенными
комбинациями не менее двух – dmin ≥ 2..
Минимальное кодовое расстояние является важнейшей характеристикой помехоустойчивых
кодов, указывающей на гарантируемое число обнаруживаемых или исправляемых заданным
кодом ошибок.
Число обнаруживаемых или исправляемых ошибок
При применении двоичных кодов учитывают только дискретные искажения, при которых
единица переходит в нуль («1» → «0») или нуль переходит в единицу («0» → «1»). Переход «1» →
«0» или «0» → «1» только в одном элементе кодовой комбинации называют единичной ошибкой
(единичным искажением). В общем случае под кратностью ошибки подразумевают число
позиций кодовой комбинации, на которых под действием помехи одни символы оказались
замененными на другие. Возможны двукратные (g = 2) и многократные (g > 2) искажения
элементов в кодовой комбинации в пределах 0 ≤ g ≤ n.
Минимальное кодовое расстояние является основным параметром, характеризующим
корректирующие способности данного кода. Если код используется только для обнаружения
ошибок кратностью g0, то необходимо и достаточно, чтобы минимальное кодовое расстояние
было равно dmin ≥ g0 + 1.
В этом случае никакая комбинация из go ошибок не может перевести одну разрешенную
кодовую комбинацию в другую разрешенную. Таким образом, условие обнаружения всех ошибок
кратностью g0 можно записать
Чтобы можно было исправить все ошибки кратностью gu и менее, необходимо иметь
минимальное расстояние, удовлетворяющее условию dmin ≥ 2gu
В этом случае любая кодовая комбинация с числом ошибок gu отличается от каждой
разрешенной комбинации не менее чем в gu+1 позициях. Если условие не выполнено,
возможен случай, когда ошибки кратности g исказят переданную комбинацию так, что она станет
ближе к одной из разрешенных комбинаций, чем к переданной или даже перейдет в другую
разрешенную комбинацию. В соответствии с этим, условие исправления всех ошибок кратностью
не более gи можно записать:
Из и
следует, что если код исправляет все ошибки кратностью gu, то число
ошибок, которые он может обнаружить, равно go = 2gu. Следует отметить, что эти соотношения
устанавливают лишь гарантированное минимальное число обнаруживаемых или
исправляемых ошибок при заданном dmin и не ограничивают возможность обнаружения ошибок
большей кратности. Например, простейший код с проверкой на четность с dmin = 2 позволяет
обнаруживать не только одиночные ошибки, но и любое нечетное число ошибок в пределах go < n.
Корректирующие возможности кодов
Вопрос о минимально необходимой избыточности, при которой код обладает нужными
корректирующими свойствами, является одним из важнейших в теории кодирования. Этот вопрос
до сих пор не получил полного решения. В настоящее время получен лишь ряд верхних и нижних
оценок (границ), которые устанавливают связь между максимально возможным минимальным
расстоянием корректирующего кода и его избыточностью.
Коды Хэмминга
Построение кодов Хемминга базируется на принципе проверки на четность веса W (числа
единичных символов «1») в информационной группе кодового блока.
Поясним идею проверки на четность на примере простейшего корректирующего кода,
который так и называется кодом с проверкой на четность или кодом с проверкой по паритету
(равенству).
В таком коде к кодовым комбинациям безызбыточного первичного двоичного k-разрядного
кода добавляется один дополнительный разряд (символ проверки на четность, называемый
проверочным, или контрольным). Если число символов «1» исходной кодовой комбинации
четное, то в дополнительном разряде формируют контрольный символ «0», а если число
символов «1» нечетное, то в дополнительном разряде формируют символ «1». В результате
общее число символов «1» в любой передаваемой кодовой комбинации всегда будет четным.
Таким образом, правило формирования проверочного символа сводится к следующему:
где i – соответствующий информационный символ («0» или «1»); k – общее их число а, под
операцией ⊕ здесь и далее понимается сложение «по модулю 2». Очевидно, что добавление
дополнительного разряда увеличивает общее число возможных комбинаций вдвое по сравнению
с числом комбинаций исходного первичного кода, а условие четности разделяет все комбинации
на разрешенные и неразрешенные. Код с проверкой на четность позволяет обнаруживать
одиночную ошибку при приеме кодовой комбинации, так как такая ошибка нарушает условие
четности, переводя разрешенную комбинацию в запрещенную.
Критерием правильности принятой комбинации является равенство нулю результата S
суммирования «по модулю 2» всех n символов кода, включая проверочный символ m1. При
наличии одиночной ошибки S принимает значение 1:
— ошибок нет,
— однократная ошибка
Этот код является (k+1,k)-кодом, или (n,n–1)-кодом. Минимальное расстояние кода равно
двум (dmin = 2), и, следовательно, никакие ошибки не могут быть исправлены. Простой код с
проверкой на четность может использоваться только для обнаружения (но не исправления)
однократных ошибок.
Увеличивая число дополнительных проверочных разрядов, и формируя по определенным
правилам проверочные символы m, равные «0» или «1», можно усилить корректирующие
свойства кода так, чтобы он позволял не только обнаруживать, но и исправлять ошибки. На этом и
основано построение кодов Хемминга.
Коды Хемминга позволяют исправлять одиночную ошибку, с помощью непосредственного
описания. Для каждого числа проверочных символов m =3, 4, 5… существует классический код
Хемминга с маркировкой
т.е. (7,4), (15,11) (31,26) …
При других значениях числа информационных символов k получаются так называемые
усеченные (укороченные) коды Хемминга. Так для кода имеющего 5 информационных символов,
потребуется использование корректирующего кода (9,5), являющегося усеченным от
классического кода Хемминга (15,11), так как число символов в этом коде уменьшается
(укорачивается) на 6.
Для примера рассмотрим классический код Хемминга (7,4), который можно сформировать и
описать с помощью кодера, представленного на рис. 1 В простейшем варианте при заданных
четырех информационных символах: i1, i2, i3, i4 (k = 4), будем полагать, что они сгруппированы в
начале кодового слова, хотя это и не обязательно. Дополним эти информационные символы
тремя проверочными символами (m = 3), задавая их следующими равенствами проверки на
четность, которые определяются соответствующими алгоритмами, где знак ⊕ означает
сложение «по модулю 2»: r1 = i1 ⊕ i2 ⊕ i3, r2 = i2 ⊕ i3 ⊕ i4, r3 = i1 ⊕ i2 ⊕ i4.
В соответствии с этим алгоритмом определения значений проверочных символов mi, в табл.
1 выписаны все возможные 16 кодовых слов (7,4)-кода Хемминга.
Таблица 1 Кодовые слова (7,4)-кода Хэмминга
|
k=4 |
m=4 |
|
i1 i2 i3 i4 |
r1 r2 r3 |
|
0 0 0 0 |
0 0 0 |
|
0 0 0 1 |
0 1 1 |
|
0 0 1 0 |
1 1 0 |
|
0 0 1 1 |
1 0 1 |
|
0 1 0 0 |
1 1 1 |
|
0 1 0 1 |
1 0 0 |
|
0 1 1 0 |
0 0 1 |
|
0 1 1 1 |
0 1 0 |
|
1 0 0 0 |
1 0 1 |
|
1 0 0 1 |
1 0 0 |
|
1 0 1 0 |
0 1 1 |
|
1 0 1 1 |
0 0 0 |
|
1 1 0 0 |
0 1 0 |
|
1 1 0 1 |
0 0 1 |
|
1 1 1 0 |
1 0 0 |
|
1 1 1 1 |
1 1 1 |
На рис.1 приведена блок-схема кодера – устройства автоматически кодирующего
информационные разряды в кодовые комбинации в соответствии с табл.1

Рис. 1 Кодер для (7,4)-кода Хемминга
На рис. 1.4 приведена схема декодера для (7,4) – кода Хемминга, на вход которого
поступает кодовое слово
. Апостроф означает, что любой символ слова может
быть искажен помехой в телекоммуникационном канале.
В декодере в режиме исправления ошибок строится последовательность:
Трехсимвольная последовательность (s1, s2, s3) называется синдромом. Термин «синдром»
используется и в медицине, где он обозначает сочетание признаков, характерных для
определенного заболевания. В данном случае синдром S = (s1, s2, s3) представляет собой
сочетание результатов проверки на четность соответствующих символов кодовой группы и
характеризует определенную конфигурацию ошибок (шумовой вектор).
Число возможных синдромов определяется выражением:
При числе проверочных символов m =3 имеется восемь возможных синдромов (23 = 
Нулевой синдром (000) указывает на то, что ошибки при приеме отсутствуют или не обнаружены.
Всякому ненулевому синдрому соответствует определенная конфигурация ошибок, которая и
исправляется. Классические коды Хемминга имеют число синдромов, точно равное их
необходимому числу (что позволяет исправить все однократные ошибки в любом информативном
и проверочном символах) и включают один нулевой синдром. Такие коды называются
плотноупакованными.
Усеченные коды являются неплотноупакованными, так как число синдромов у них
превышает необходимое. Так, в коде (9,5) при четырех проверочных символах число синдромов
будет равно 24 =16, в то время как необходимо всего 10. Лишние 6 синдромов свидетельствуют о
неполной упаковке кода (9,5).

Рис. 2 Декодер для (7, 4)-кода Хемминга
Для рассматриваемого кода (7,4) в табл. 2 представлены ненулевые синдромы и
соответствующие конфигурации ошибок.
Таблица 2 Синдромы (7, 4)-кода Хемминга
|
Синдром |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
|
Конфигурация ошибок |
0000001 |
0000010 |
0000100 |
0001000 |
0010000 |
0100000 |
1000000 |
|
Ошибка в символе |
m1 |
m2 |
i4 |
m1 |
i1 |
i3 |
i2 |
Таким образом, (7,4)-код позволяет исправить все одиночные ошибки. Простая проверка
показывает, что каждая из ошибок имеет свой единственный синдром. При этом возможно
создание такого цифрового корректора ошибок (дешифратора синдрома), который по
соответствующему синдрому исправляет соответствующий символ в принятой кодовой группе.
После внесения исправления проверочные символы ri можно на выход декодера (рис. 2) не
выводить. Две или более ошибок превышают возможности корректирующего кода Хемминга, и
декодер будет ошибаться. Это означает, что он будет вносить неправильные исправления и
выдавать искаженные информационные символы.
Идея построения подобного корректирующего кода, естественно, не меняется при
перестановке позиций символов в кодовых словах. Все такие варианты также называются (7,4)-
кодами Хемминга.
Циклические коды
Своим названием эти коды обязаны такому факту, что для них часть комбинаций, либо все
комбинации могут быть получены путем циклическою сдвига одной или нескольких базовых
комбинаций кода.
Построение такого кода основывается на использовании неприводимых многочленов в поле
двоичных чисел. Такие многочлены не могут быть представлены в виде произведения
многочленов низших степеней подобно тому, как простые числа не могут быть представлены
произведением других чисел. Они делятся без остатка только на себя или на единицу.
Для определения неприводимых многочленов раскладывают на простые множители бином
хn -1. Так, для n = 7 это разложение имеет вид:
(x7)=(x-1)(x3+x2)(x3+x-1)
Каждый из полученных множителей разложения может применяться для построения
корректирующего кода.
Неприводимый полином g(x) называют задающим, образующим или порождающим
для корректирующего кода. Длина n (число разрядов) создаваемого кода произвольна.
Кодовая последовательность (комбинация) корректирующего кода состоит из к информационных
разрядов и n — к контрольных (проверочных) разрядов. Степень порождающего полинома
r = n — к равна количеству неинформационных контрольных разрядов.
Если из сделанного выше разложения (при n = 7) взять полипом (х — 1), для которого
r=1, то k=n-r=7-1=6. Соответствующий этому полиному код используется для контроля
на чет/нечет (обнаружение ошибок). Для него минимальное кодовое расстояние D0 = 2
(одна единица от D0 — для исходного двоичного кода, вторая единица — за счет контрольного разряда).
Если же взять полином (x3+x2+1) из указанного разложения, то степень полинома
r=3, а k=n-r=7-3=4.
Контрольным разрядам в комбинации для некоторого кода могут быть четко определено место (номера разрядов).
Тогда код называют систематическим или разделимым. В противном случае код является неразделимым.
Способы построения циклических кодов по заданному полиному.
1) На основе порождающей (задающей) матрицы G, которая имеет n столбцов, k строк, то есть параметры которой
связаны с параметрами комбинаций кода. Порождающую матрицу строят, взяв в качестве ее строк порождающий
полином g(x) и (k — 1) его циклических сдвигов:

Пример; Определить порождающую матрицу, если известно, что n=7, k=4, задающий полином g(x)=x3+х+1.
Решение: Кодовая комбинация, соответствующая задающему полиному g(x)=x3+х+1, имеет вид 1011.
Тогда порождающая матрица G7,4 для кода при n=7, к=4 с учетом того, что k-1=3, имеет вид:

Порождающая матрица содержит k разрешенных кодовых комбинаций. Остальные комбинации кода,
количество которых (2k — k) можно определить суммированием по модулю 2 всевозможных сочетаний
строк матрицы Gn,k. Для матрицы, полученной в приведенном выше примере, суммирование по модулю 2
четырех строк 1-2, 1-3, 1-4, 2-3, 2-4, 3-4 дает следующие кодовые комбинации циклического кода:
001110101001111010011011101010011101110100
Другие комбинации искомого корректирующего кода могут быть получены сложением трех комбинаций, например,
из сочетания строк 1-3-4, что дает комбинацию 1111111, а также сложением четырех строк 1-2-3-4, что
дает комбинацию 1101001 и т.д.
Ряд комбинаций искомого кода может быть получено путем дальнейшего циклического сдвига комбинаций
порождающей матрицы, например, 0110001, 1100010, 1000101. Всего для образования искомого циклического
кода требуется 2k=24=16 комбинаций.
2) Умножение исходных двоичных кодовых комбинаций на задающий полином.
Исходными комбинациями являются все k-разрядные двоичные комбинации. Так, например, для исходной
комбинации 1111 (при k = 4) умножение ее на задающий полином g(x)=x3+х+1=1011 дает 1101001.
Полученные на основе двух рассмотренных способов циклические коды не являются разделимыми.
3) Деление на задающий полином.
Для получения разделимого (систематического) циклического кода необходимо разделить многочлен
xn-k*h(x), где h(x) — исходная двоичная комбинация, на задающий полином g(x) и прибавить полученный
остаток от деления к многочлену xn-k*h(x).
Заметим, что умножение исходной комбинации h(x) на xn-k эквивалентно сдвигу h(x) на (n-к) разрядов влево.
Пример: Требуется определить комбинации циклического разделимого кода, заданного полиномом g(x)=x3+х+1=1011 и
имеющего общее число разрядов 7, число информационных разрядов 4, число контрольных разрядов (n-k)=3.
Решение: Пусть исходная комбинация h(x)=1100. Умножение ее на xn-k=x3=1000 дает
x3*(x3+x2)=1100000, то есть эквивалентно
сдвигу исходной комбинации на 3 разряда влево. Деление комбинации 1100000 на комбинацию 1011, эквивалентно задающему полиному, дает:

Полученный остаток от деления, содержащий xn-k=3 разряда, прибавляем к полиному, в результате чего получаем искомую комбинацию
разделимого циклического кода: 1100010. В ней 4 старших разряда (слева) соответствуют исходной двоичной комбинации, а три младших
разряда являются контрольными.
Следует сделать ряд указаний относительно процедуры деления:
1) При делении задающий полином совмещается старшим разрядом со старшим «единичными разрядом делимого.
2) Вместо вычитания по модулю 2 выполняется эквивалентная ему процедура сложения по модулю 2.
3) Деление продолжается до тех пор, пока степень очередного остатка не будет меньше степени делителя (задающего полинома). При достижении
этого полученный остаток соответствует искомому содержанию контрольных разрядов для данной искомой двоичной комбинации.
Для проверки правильности выполнения процедуры определения комбинации циклического кода необходимо разделить полученную комб1шацию на задающий полином с
учетом сделанных выше замечаний. Получение нулевого остатка от такого деления свидетельствует о правильности определения комбинации.
Логический код 4В/5В
Логический код 4В/5В заменяет исходные символы длиной в 4 бита на символы длиной в 5 бит. Так как результирующие символы содержат избыточные биты, то
общее количество битовых комбинаций в них больше, чем в исходных. Таким образом, пяти-битовая схема дает 32 (25) двухразрядных буквенно-цифровых символа,
имеющих значение в десятичном коде от 00 до 31. В то время как исходные данные могут содержать только четыре бита или 16 (24) символов.
Поэтому в результирующем коде можно подобрать 16 таких комбинаций, которые не содержат большого количества нулей, а остальные считать запрещенными кодами
(code violation). В этом случае длинные последовательности нулей прерываются, и код становится самосинхронизирующимся для любых передаваемых данных.
Исчезает также постоянная составляющая, а значит, еще более сужается спектр сигнала. Но этот метод снижает полезную пропускную способность линии,
так как избыточные единицы пользовательской информации не несут, и только «занимают эфирное время». Избыточные коды позволяют приемнику распознавать
искаженные биты. Если приемник принимает запрещенный код, значит, на линии произошло искажение сигнала.
Итак, рассмотрим работу логического кода 4В/5В. Преобразованный сигнал имеет 16 значений для передачи информации и 16 избыточных значений. В декодере
приемника пять битов расшифровываются как информационные и служебные сигналы.
Для служебных сигналов отведены девять символов, семь символов — исключены.
Исключены комбинации, имеющие более трех нулей (01 — 00001, 02 — 00010, 03 — 00011, 08 — 01000, 16 — 10000). Такие сигналы интерпретируются символом
V и командой приемника VIOLATION — сбой. Команда означает наличие ошибки из-за высокого уровня помех или сбоя передатчика. Единственная
комбинация из пяти нулей (00 — 00000) относится к служебным сигналам, означает символ Q и имеет статус QUIET — отсутствие сигнала в линии.
Такое кодирование данных решает две задачи — синхронизации и улучшения помехоустойчивости. Синхронизация происходит за счет исключения
последовательности более трех нулей, а высокая помехоустойчивость достигается приемником данных на пяти-битовом интервале.
Цена за эти достоинства при таком способе кодирования данных — снижение скорости передачи полезной информации.
К примеру, В результате добавления одного избыточного бита на четыре информационных, эффективность использования полосы
частот в протоколах с кодом MLT-3 и кодированием данных 4B/5B уменьшается соответственно на 25%.
Схема кодирования 4В/5В представлена в таблице.
|
Двоичный код 4В |
Результирующий код 5В |
|
0 0 0 0 |
1 1 1 1 0 |
|
0 0 0 1 |
0 1 0 0 1 |
|
0 0 1 0 |
1 0 1 0 0 |
|
0 0 1 1 |
1 0 1 0 1 |
|
0 1 0 0 |
0 1 0 1 0 |
|
0 1 0 1 |
0 1 0 1 1 |
|
0 1 1 0 |
0 1 1 1 0 |
|
0 1 1 1 |
0 1 1 1 1 |
|
1 0 0 0 |
1 0 0 1 0 |
|
1 0 0 1 |
1 0 0 1 1 |
|
1 0 1 0 |
1 0 1 1 0 |
|
1 0 1 1 |
1 0 1 1 1 |
|
1 1 0 0 |
1 1 0 1 0 |
|
1 1 0 1 |
1 1 0 1 1 |
|
1 1 1 0 |
1 1 1 0 0 |
|
1 1 1 1 |
1 1 1 0 1 |
Итак, соответственно этой таблице формируется код 4В/5В, затем передается по линии с помощью физического кодирования по
одному из методов потенциального кодирования, чувствительному только к длинным последовательностям нулей — например, в помощью
цифрового кода NRZI.
Символы кода 4В/5В длиной 5 бит гарантируют, что при любом их сочетании на линии не могут встретиться более трех нулей подряд.
Буква ^ В в названии кода означает, что элементарный сигнал имеет 2 состояния — от английского binary — двоичный. Имеются
также коды и с тремя состояниями сигнала, например, в коде 8В/6Т для кодирования 8 бит исходной информации используется
код из 6 сигналов, каждый из которых имеет три состояния. Избыточность кода 8В/6Т выше, чем кода 4В/5В, так как на 256
исходных кодов приходится 36=729 результирующих символов.
Как мы говорили, логическое кодирование происходит до физического, следовательно, его осуществляют оборудование канального
уровня сети: сетевые адаптеры и интерфейсные блоки коммутаторов и маршрутизаторов. Поскольку, как вы сами убедились,
использование таблицы перекодировки является очень простой операцией, поэтому метод логического кодирования избыточными
кодами не усложняет функциональные требования к этому оборудованию.
Единственное требование — для обеспечения заданной пропускной способности линии передатчик, использующий избыточный код,
должен работать с повышенной тактовой частотой. Так, для передачи кодов 4В/5В со скоростью 100 Мб/с передатчик должен
работать с тактовой частотой 125 МГц. При этом спектр сигнала на линии расширяется по сравнению со случаем, когда по
линии передается чистый, не избыточный код. Тем не менее, спектр избыточного потенциального кода оказывается уже
спектра манчестерского кода, что оправдывает дополнительный этап логического кодирования, а также работу приемника
и передатчика на повышенной тактовой частоте.
В основном для локальных сетей проще, надежней, качественней, быстрей — использовать логическое кодирование данных
с помощью избыточных кодов, которое устранит длительные последовательности нулей и обеспечит синхронизацию
сигнала, потом на физическом уровне использовать для передачи быстрый цифровой код NRZI, нежели без предварительного
логического кодирования использовать для передачи данных медленный, но самосинхронизирующийся манчестерский код.
Например, для передачи данных по линии с пропускной способностью 100М бит/с и полосой пропускания 100 МГц,
кодом NRZI необходимы частоты 25 — 50 МГц, это без кодирования 4В/5В. А если применить для NRZI еще и
кодирование 4В/5В, то теперь полоса частот расширится от 31,25 до 62,5 МГц. Но тем не менее, этот диапазон
еще «влазит» в полосу пропускания линии. А для манчестерского кода без применения всякого дополнительного
кодирования необходимы частоты от 50 до 100 МГц, и это частоты основного сигнала, но они уже не будут пропускаться
линией на 100 МГц.
Скрэмблирование
Другой метод логического кодирования основан на предварительном «перемешивании» исходной информации таким
образом, чтобы вероятность появления единиц и нулей на линии становилась близкой.
Устройства, или блоки, выполняющие такую операцию, называются скрэмблерами (scramble — свалка, беспорядочная сборка) .
При скремблировании данные перемешиваються по определенному алгоритму и приемник, получив двоичные данные, передает
их на дескрэмблер, который восстанавливает исходную последовательность бит.
Избыточные биты при этом по линии не передаются.
Суть скремблирования заключается просто в побитном изменении проходящего через систему потока данных. Практически
единственной операцией, используемой в скремблерах является XOR — «побитное исключающее ИЛИ», или еще говорят —
сложение по модулю 2. При сложении двух единиц исключающим ИЛИ отбрасывается старшая единица и результат записывается — 0.
Метод скрэмблирования очень прост. Сначала придумывают скрэмблер. Другими словами придумывают по какому соотношению
перемешивать биты в исходной последовательности с помощью «исключающего ИЛИ». Затем согласно этому соотношению из текущей
последовательности бит выбираются значения определенных разрядов и складываются по XOR между собой. При этом все разряды
сдвигаются на 1 бит, а только что полученное значение («0» или «1») помещается в освободившийся самый младший разряд.
Значение, находившееся в самом старшем разряде до сдвига, добавляется в кодирующую последовательность, становясь очередным
ее битом. Затем эта последовательность выдается в линию, где с помощью методов физического кодирования передается к
узлу-получателю, на входе которого эта последовательность дескрэмблируется на основе обратного отношения.
Например, скрэмблер может реализовывать следующее соотношение:
где Bi — двоичная цифра результирующего кода, полученная на i-м такте работы скрэмблера, Ai — двоичная цифра исходного
кода, поступающая на i-м такте на вход скрэмблера, Bi-3 и Bi-5 — двоичные цифры результирующего кода, полученные на
предыдущих тактах работы скрэмблера, соответственно на 3 и на 5 тактов ранее текущего такта, ⊕ — операция исключающего
ИЛИ (сложение по модулю 2).
Теперь давайте, определим закодированную последовательность, например, для такой исходной последовательности 110110000001.
Скрэмблер, определенный выше даст следующий результирующий код:
B1=А1=1 (первые три цифры результирующего кода будут совпадать с исходным, так как еще нет нужных предыдущих цифр)

Таким образом, на выходе скрэмблера появится последовательность 110001101111. В которой нет последовательности из шести нулей, п
рисутствовавшей в исходном коде.
После получения результирующей последовательности приемник передает ее дескрэмблеру, который восстанавливает исходную
последовательность на основании обратного соотношения.
Существуют другие различные алгоритмы скрэмблирования, они отличаются количеством слагаемых, дающих цифру
результирующего кода, и сдвигом между слагаемыми.
Главная проблема кодирования на основе скремблеров — синхронизация передающего (кодирующего) и принимающего
(декодирующего) устройств. При пропуске или ошибочном вставлении хотя бы одного бита вся передаваемая информация
необратимо теряется. Поэтому, в системах кодирования на основе скремблеров очень большое внимание уделяется методам синхронизации.
На практике для этих целей обычно применяется комбинация двух методов:
а) добавление в поток информации синхронизирующих битов, заранее известных приемной стороне, что позволяет ей при ненахождении
такого бита активно начать поиск синхронизации с отправителем,
б) использование высокоточных генераторов временных импульсов, что позволяет в моменты потери синхронизации производить
декодирование принимаемых битов информации «по памяти» без синхронизации.
Существуют и более простые методы борьбы с последовательностями единиц, также относимые к классу скрэмблирования.
Для улучшения кода ^ Bipolar AMI используются два метода, основанные на искусственном искажении последовательности нулей запрещенными символами.

Рис. 3 Коды B8ZS и HDB3
На этом рисунке показано использование метода ^ B8ZS (Bipolar with 8-Zeros Substitution) и метода HDB3 (High-Density Bipolar 3-Zeros) для корректировки
кода AMI. Исходный код состоит из двух длинных последовательностей нулей (8- в первом случае и 5 во втором).
Код B8ZS исправляет только последовательности, состоящие из 8 нулей. Для этого он после первых трех нулей вместо оставшихся пяти нулей вставляет пять
цифр: V-1*-0-V-1*. V здесь обозначает сигнал единицы, запрещенной для данного такта полярности, то есть сигнал, не изменяющий полярность предыдущей
единицы, 1* — сигнал единицы корректной полярности, а знак звездочки отмечает тот факт, что в исходном коде в этом такте была не единица, а ноль. В
результате на 8 тактах приемник наблюдает 2 искажения — очень маловероятно, что это случилось из-за шума на линии или других сбоев передачи. Поэтому
приемник считает такие нарушения кодировкой 8 последовательных нулей и после приема заменяет их на исходные 8 нулей.
Код B8ZS построен так, что его постоянная составляющая равна нулю при любых последовательностях двоичных цифр.
Код HDB3 исправляет любые 4 подряд идущих нуля в исходной последовательности. Правила формирования кода HDB3 более сложные, чем кода B8ZS.
Каждые четыре нуля заменяются четырьмя сигналами, в которых имеется один сигнал V. Для подавления постоянной составляющей полярность сигнала
V чередуется при последовательных заменах.
Кроме того, для замены используются два образца четырехтактовых кодов. Если перед заменой исходный код содержал нечетное число единиц, то
используется последовательность 000V, а если число единиц было четным — последовательность 1*00V.
Таким образом, применение логическое кодирование совместно с потенциальным кодированием дает следующие преимущества:
Улучшенные потенциальные коды обладают достаточно узкой полосой пропускания для любых последовательностей единиц и нулей,
которые встречаются в передаваемых данных. В результате коды, полученные из потенциального путем логического кодирования,
обладают более узким спектром, чем манчестерский, даже при повышенной тактовой частоте.
Линейные блочные коды
При передаче информации по каналам связи возможны ошибки вследствие помех и искажений сигналов. Для обнаружения и
исправления возникающих ошибок используются помехоустойчивые коды. Упрощенная схема системы передачи информации
при помехоустойчивом кодировании показана на рис. 4
Кодер служит для преобразования поступающей от источника сообщений последовательности из k информационных
символов в последовательность из n cимволов кодовых комбинаций (или кодовых слов). Совокупность кодовых слов образует код.
Множество символов, из которых составляется кодовое слово, называется алфавитом кода, а число различных символов в
алфавите – основанием кода. В дальнейшем вследствие их простоты и наибольшего распространения рассматриваются главным
образом двоичные коды, алфавит которых содержит два символа: 0 и 1.

Рис. 4 Система передачи дискретных сообщений
Правило, по которому информационной последовательности сопоставляется кодовое слово, называется правилом кодирования.
Если при кодировании каждый раз формируется блок А из k информационных символов, превращаемый затем в n-символьную
кодовую комбинацию S, то код называется блочным. При другом способе кодирования информационная последовательность на
блоки не разбивается, и код называется непрерывным.
С математической точки зрения кодер осуществляет отображение множества из 2k элементов (двоичных информационных
последовательностей) в множество, состоящее из 2n элементов (двоичных последовательностей длины n). Для практики
интересны такие отображения, в результате которых получаются коды, обладающие способностью исправлять часть ошибок
и допускающие простую техническую реализацию кодирующих и декодирующих устройств.
Дискретный канал связи – это совокупность технических средств вместе со средой распространения радиосигналов, включенных
между кодером и декодером для передачи сигналов, принимающих конечное число разных видов. Для описания реальных каналов
предложено много математических моделей, с разной степенью детализации отражающих реальные процессы. Ограничимся рассмотрением
простейшей модели двоичного канала, входные и выходные сигналы которого могут принимать значения 0 и 1.
Наиболее распространено предположение о действии в канале аддитивной помехи. Пусть S=(s1,s2,…,sn)
и Y=(y1,y2,…,yn) соответственно входная и выходная последовательности двоичных символов.
Помехой или вектором ошибки называется последовательность из n символов E=(e1,e2,…,en), которую
надо поразрядно сложить с переданной последовательностью, чтобы получить принятую:
Y=S+E
Таким образом, компонента вектора ошибки ei=0 указывает на то, что 2-й символ принят правильно (yi=si),
а компонента ei=1 указывает на ошибку при приеме (yi≠si).Поэтому важной характеристикой вектора ошибки
является число q ненулевых компонентов, которое называется весом или кратностью ошибки. Кратность ошибки – дискретная случайная величина,
принимающая целочисленные значения от 0 до n.
Классификация двоичных каналов ведется по виду распределения случайного вектора E. Основные результаты теории кодирования получены в
предположении, что вероятность ошибки в одном символе не зависит ни от его номера в последовательности, ни от его значения. Такой
канал называется стационарным и симметричным. В этом канале передаваемые символы искажаются с одинаковой вероятностью
P, т.е. P(ei=1)=P, i=1,2,…,n.
Для симметричного стационарного канала распределение вероятностей векторов ошибки кратности q является биноминальным:
P(Ei)=Pq(1-P)n-q
которая показывает, что при P<0,5 вероятность β2=αj является убывающей функцией q,
т.е. в симметричном стационарном канале более вероятны ошибки меньшей кратности. Этот важный факт используется при построении
помехоустойчивых кодов, т.к. позволяет обосновать тактику обнаружения и исправления в первую очередь ошибок малой кратности.
Конечно, для других моделей канала такая тактика может и не быть оптимальной.
Декодирующее устройство (декодер) предназначено оценить по принятой последовательности Y=(y1,y2,…,yn)
значения информационных символов A‘=(a‘1,a‘2,…,a‘k,).
Из-за действия помех возможны неправильные решения. Процедура декодирования включает решение двух задач: оценивание переданного кодового
слова и формирование оценок информационных символов.
Вторая задача решается относительно просто. При наиболее часто используемых систематических кодах, кодовые слова которых содержат информационные
символы на известных позициях, все сводится к простому их стробированию. Очевидно также, что расположение информационных символов внутри кодового
слова не имеет существенного значения. Удобно считать, что они занимают первые k позиций кодового слова.
Наибольшую трудность представляет первая задача декодирования. При равновероятных информационных последовательностях ее оптимальное решение
дает метод максимального правдоподобия. Функция правдоподобия как вероятность получения данного вектора Y при передаче кодовых слов
Si, i=1,2,…,2k на основании Y=S+E определяется вероятностями появления векторов ошибок:
P(Y/Si)=P(Ei)=Pqi(1-P)n-qi
где qi – вес вектора Ei=Y+Si
Очевидно, вероятность P(Y/Si) максимальна при минимальном qi. На основании принципа максимального правдоподобия оценкой S‘ является кодовое слово,
искажение которого для превращения его в принятое слово Y имеет минимальный вес, т. е. в симметричном канале является наиболее вероятным (НВ):
S‘=Y+EHB
Если несколько векторов ошибок Ei имеют равные минимальные веса, то наивероятнейшая ошибка EHB определяется случайным выбором среди них.
В качестве расстояния между двумя кодовыми комбинациями принимают так называемое расстояние Хэмминга, которое численно равно количеству символов, в которых одна
комбинация отлична от другой, т.е. весу (числу ненулевых компонентов) разностного вектора. Расстояние Хэмминга между принятой последовательностью Y и всеми
возможными кодовыми словами 5, есть функция весов векторов ошибок Ei:

Поэтому декодирование по минимуму расстояния, когда в качестве оценки берется слово, ближайшее к принятой
последовательности, является декодированием по максимуму правдоподобия.
Таким образом, оптимальная процедура декодирования для симметричного канала может быть описана следующей последовательностью операций. По принятому
вектору Y определяется вектор ошибки с минимальным весом EHB, который затем вычитается (в двоичном канале — складывается по модулю 2) из Y:
Y→EHB→S‘=Y+EHB
Наиболее трудоемкой операцией в этой схеме является определение наи-вероятнейшего вектора ошибки, сложность которой
существенно возрастает при увеличении длины кодовых комбинаций. Правила кодирования, которые нацелены на упрощение
процедур декодирования, предполагают придание всем кодовым словам технически легко проверяемых признаков.
Широко распространены линейные коды, называемые так потому, что их кодовые слова образуют линейное
подпространство над конечным полем. Для двоичных кодов естественно использовать поле характеристики p=2.
Принадлежность принятой комбинации Y известному подпространству является тем признаком, по которому
выносится решение об отсутствии ошибок (EHB=0).
Так как по данному коду все пространство последовательностей длины n разбивается на смежные классы,
то для каждого смежного класса можно заранее определить вектор ошибки минимального веса,
называемый лидером смежного класса. Тогда задача декодера состоит в определении номера смежного класса,
которому принадлежит Y, и формировании лидера этого класса.
6.5.1. Весовой коэффициент двоичных векторов и расстояние между ними
6.5.2. Минимальное расстояние для линейного кода
6.5.3. Обнаружение и исправление ошибок
6.5.3.1. Распределение весовых коэффициентов кодовых слов
6.5.3.2.Одновременное обнаружение и исправление ошибок
6.5.4. Визуализация пространства 6-кортежей
6.5.5. Коррекция со стиранием ошибок
6.5.1. Весовой коэффициент двоичных векторов и расстояние между ними
Конечно же, понятно, что правильно декодировать можно не все ошибочные комбинации. Возможности кода для исправления ошибок в первую очередь определяются его структурой. Весовой коэффициент Хэмминга (Hamming weight) w(U) кодового слова U определяется как число ненулевых элементов в U. Для двоичного вектора это эквивалентно числу единиц в векторе. Например, если U=100101101, то w(U) = 5. Расстояние Хэмминга (Hamming distance) между двумя кодовыми словами U и V, обозначаемое как d(U, V), определяется как количество элементов, которыми они отличаются.
U=100101101
V=011110100
d(U,V)=6
Согласно свойствам сложения по модулю 2, можно отметить, что сумма двух двоичных векторов является другим двоичным вектором, двоичные единицы которого расположены на тех позициях, которыми эти векторы отличаются.
U + V=111011001
Таким образом, можно видеть, что расстояние Хэмминга между двумя векторами равно весовому коэффициенту Хэмминга их суммы, т.е. d(U, V) = w(U + V). Также видно, что весовой коэффициент Хэмминга кодового слова равен его расстоянию Хэмминга до нулевого вектора.
6.5.2. Минимальное расстояние для линейного кода
Рассмотрим множество расстояний между всеми парами кодовых слой в пространстве Vn. Наименьший элемент этого множества называется минимальным расстоянием кода и обозначается dmin. Как вы думаете, почему нас интересует именно минимальное расстояние, а не максимальное? Минимальное расстояние подобно наиболее слабому звену в цепи, оно дает нам меру минимальных возможностей кода и, следовательно, характеризует его мощность.
Как обсуждалось ранее, сумма двух произвольных кодовых слов дает другой элемент пространства кодовых слов. Это свойство линейных кодов формулируется просто: если U и V — кодовые слова, то и W = U + V тоже должно быть кодовым словом. Следовательно, расстояние между двумя кодовыми словами равно весовому коэффициенту третьего кодового слова, т.е. d(U, V) = w(U + V) = w(W). Таким образом, минимальное расстояние линейного кода можно определить, не прибегая к изучению расстояний между всеми комбинациями пар кодовых слов. Нам нужно лишь определить вес каждого кодового слова (за исключением нулевого вектора) в подпространстве; минимальный вес соответствует минимальному расстоянию dmin. Иными словами, dmin соответствует наименьшему из множества расстояний между нулевым кодовым словом и всеми остальными кодовыми словами.
6.5.3. Обнаружение и исправление ошибок
Задача декодера после приема вектора r заключается в оценке переданного кодового слова Ui. Оптимальная стратегия декодирования может быть выражена в терминах алгоритма максимального правдоподобия (см. приложение Б); считается, что передано было слово Ui, если
(6.41)
Поскольку для двоичного симметричного канала (binary symmetric channel — BSC) правдоподобие Ui относительно r обратно пропорционально расстоянию между r и U, можно сказать, что передано было слово Ui, если
(6.42)
Другими словами, декодер определяет расстояние между r и всеми возможными переданными кодовыми словами Uj, после чего выбирает наиболее правдоподобное Uj, для которого
(6.43)
где М = 2k — это размер множества кодовых слов. Если минимум не один, выбор между минимальными расстояниями является произвольным. Наше обсуждение метрики расстояний будет продолжено в главе 7.
На рис. 6.13 расстояние между двумя кодовыми словами U и V показано как расстояние Хэмминга. Каждая черная точка обозначает искаженное кодовое слово. На рис. 6.13, а проиллюстрирован прием вектора r1 находящегося на расстоянии 1 от кодового слова U и на расстоянии 4 от кодового слова V. Декодер с коррекцией ошибок, следуя стратегии максимального правдоподобия, выберет при принятом векторе r1 кодовое слово U. Если r1 получился в результате появления одного ошибочного бита в переданном векторе кода U, декодер успешно исправит ошибку. Но если же это произошло в результате 4-битовой ошибки в векторе кода V, декодирование будет ошибочным. Точно так же, как показано на рис. 6.13, б, двойная ошибка при передаче U может привести к тому, что в качестве переданного вектора будет ошибочно определен вектор r2, находящийся на расстоянии 2 от вектора U и на расстоянии 3 от вектора кода V. На рис. 6.13 показана ситуация, когда в качестве переданного вектора ошибочно определен вектор r3, который находится на расстоянии 3 от вектора кода U и на расстоянии 2 от вектора V. Из рис. 6.13 видно, что если задача состоит только в обнаружении ошибок, а не в их исправлении, то можно определить искаженный вектор — изображенный черной точкой и представляющий одно-, двух-, трех- и четырехбитовую ошибку. В то же время пять ошибок при передаче могут привести к приему кодового слова V, когда в действительности было передано кодовое слово U; такую ошибку невозможно будет обнаружить.
Из рис. 6.13 можно видеть, что способность кода к обнаружению и исправлению ошибок связана с минимальным расстоянием между кодовыми словами. Линия решения на рисунке служит той же цели, что и в процессе демодуляции, — для разграничения областей решения.
а)
б)
в)
Рис. 6.13. Возможности определения и исправления ошибок: а) принятый вектор r1; б) принятый вектор r2; в) принятый вектор r3
В примере, приведенном на рис. 6.13, критерий принятия решения может быть следующим: выбрать U, если r попадает в область 1, и выбрать V, если r попадает в область 2. Выше показывалось, что такой код (при dmin = 5) может исправить две ошибки. Вообще, способность кода к исправлению ошибок t определяется, как максимальное число гарантированно исправимых ошибок на кодовое слово, и записывается следующим образом [4].
(6.44)
Здесь означает наибольшее целое, не превышающее х. Часто код, который исправляет все искаженные символы, содержащие ошибку в t или меньшем числе бит, также может исправлять символы, содержащие t +1 ошибочных бит. Это можно увидеть на рис. 6.11. В этом случае dmin = 3, поэтому из уравнения (6.44) можно видеть, что исправимы все ошибочные комбинации из t = 1 бит. Также исправима одна ошибочная комбинация, содержащая / +1 (т.е. 2) ошибочных бит. Вообще, линейный код (n, k), способный исправлять все символы, содержащие t ошибочных бит, может исправить всего 2n—k ошибочных комбинаций. Если блочный код с возможностью исправления символов, имеющих ошибки в t бит, применяется для исправления ошибок в двоичном симметричном канале с вероятностью перехода р, то вероятность ошибки сообщения Рм(вероятность того, что декодер совершит неправильное декодирование и п-битовый блок содержит ошибку) можно оценить сверху, используя уравнение (6.18).
(6.45)
Оценка переходит в равенство, если декодер исправляет все ошибочные комбинации, содержащие до t ошибочных бит включительно, но не комбинации с числом ошибочных бит, большим t. Такие декодеры называются декодерами с ограниченным расстоянием. Вероятность ошибки в декодированном бите РB зависит от конкретного кода и декодера. Приближенно ее можно выразить следующим образом [5].
(6.46)
В блочном коде, прежде чем исправлять ошибки, необходимо их обнаружить. (Или же код может использоваться только для определения наличия ошибок.) Из рис. 6.13 видно, что любой полученный вектор, который изображается черной точкой (искаженное кодовое слово), можно определить как ошибку. Следовательно, возможность определения наличия ошибки дается следующим выражением.
(6.47)
Блочный код с минимальным расстоянием dmin гарантирует обнаружение всех ошибочных комбинаций, содержащих dmin — 1 или меньшее число ошибочных бит. Такой код также способен обнаружить и большую ошибочную комбинацию, содержащую dmin или более ошибок. Фактически код (n, k) может обнаружить 2n – 2k ошибочных комбинаций длины п. Объясняется это следующим образом. Всего в пространстве 2n n-кортежей существует 2n -1 возможных ненулевых ошибочных комбинаций. Даже правильное кодовое слово — это потенциальная ошибочная комбинация. Поэтому всего существует 2k -1 ошибочных комбинаций, которые идентичны 2k -1 ненулевым кодовым словам. При появлении любая из этих 2k — 1 ошибочных комбинаций изменяет передаваемое кодовое слово Uj на другое кодовое слово Uj. Таким образом, принимается кодовое слово Uj и его синдром равен нулю. Декодер принимает Uj за переданное кодовое слово, и поэтому декодирование дает неверный результат. Следовательно, существует 2k -1 необнаружимых ошибочных комбинаций. Если ошибочная комбинация не совпадает с одним из 2k кодовых слов, проверка вектора r с помощью синдромов дает ненулевой синдром и ошибка успешно обнаруживается. Отсюда следует, что существует ровно 2n-2k выявляемых ошибочных комбинаций. При больших n, когда 2k<<2n, необнаружимой будет только незначительная часть ошибочных комбинаций.
6.5.3.1. Распределение весовых коэффициентов кодовых слов
Пусть Aj — количество кодовых слов с весовым коэффициентом j в линейном коде (п, k). Числа A0,A1,…,An называются распределением весовых коэффициентов этого кода. Если код применяется только для обнаружения ошибок в двоичном симметричном канале, то вероятность того, что декодер не сможет определить ошибку, можно рассчитать, исходя из распределения весовых коэффициентов кода [5].
(6.48)
где р — вероятность перехода в двоичном симметричном канале. Если минимальное расстояние кода равно dmin значения от А1 до , равны нулю.
Пример 6.5. Вероятность необнаруженной ошибки в коде
Пусть код (6,3), введенный в разделе 6.4.3, используется только для обнаружения наличия ошибок. Рассчитайте вероятность необнаруженной ошибки, если применяется двоичный симметричный канал, а вероятность перехода равна 10-2.
Решение
Распределение весовых коэффициентов этого кода выглядит следующим образом: A0=1, А1= А2 = 0, A3 = 4, A5 = 0, A6 = 0. Следовательно, используя уравнение (6.48), можно записать следующее.
Для р = 10-2 вероятность необнаруженной ошибки будет равна 3,9 х 10-6.
6.5.3.2. Одновременное обнаружение и исправление ошибок
Возможностями исправления ошибок с максимальным гарантированным (t), где t определяется уравнением (6.44), можно пожертвовать в пользу определения класса ошибок. Код можно использовать для одновременного исправления α и обнаружения β ошибок, причем , а минимальное расстояние кода дается следующим выражением [4].
(6.49)
При появлении t или меньшего числа ошибок код способен обнаруживать и исправлять их. Если ошибок больше t, но меньше е+1, где е определяется уравнением (6.47), код может определять наличие ошибок, но исправить может только некоторые из них. Например, используя код с dmin = 7. можно выполнить обнаружение и исправление со следующими значениями α и β.
Заметим, что исправление ошибки подразумевает ее предварительное обнаружение. В приведенном выше примере (с тремя ошибками) все ошибки можно обнаружить и исправить. Если имеется пять ошибок, их можно обнаружить, но исправить можно только одну из них.
6.5.4. Визуализация пространства 6-кортежей
На рис. 6.14 визуально представлено восемь кодовых слов, фигурирующих в примере из раздела 6.4.3. Кодовые слова образованы посредством линейных комбинаций из трех независимых 6-кортежей, приведенных в уравнении (6.26); сами кодовые слова образуют трехмерное подпространство. На рисунке показано, что такое подпространство полностью занято восемью кодовыми словами (большие черные круги); координаты подпространства умышленно выбраны неортогональными. На рис. 6.14 предпринята попытка изобразить все пространство, содержащее шестьдесят четыре 6-кортежей, хотя точно нарисовать или составить такую модель невозможно. Каждое кодовое слово окружают сферические слои или оболочки. Радиус внутренних непересекающихся слоев — это расстояние Хэмминга, равное 1; радиус внешнего слоя — это расстояние Хэмминга, равное 2. Большие расстояния в этом примере не рассматриваются. Для каждого кодового слова два показанных слоя заняты искаженными кодовыми словами. На каждой внутренней сфере существует шесть таких точек (всего 48 точек), представляющих шесть возможных однобитовых ошибок в векторах, соответствующих каждому кодовому слову. Эти кодовые слова с однобитовыми возмущениями могут быть соотнесены только с одним кодовым словом; следовательно, такие ошибки могут быть исправлены. Как видно из нормальной матрицы, приведенной на рис. 6.11, существует также одна двухбитовая ошибочная комбинация, которая также поддается исправлению. Всего существует
Заметим, что исправление ошибки подразумевает ее предварительное обнаружение. В приведенном выше примере (с тремя ошибками) все ошибки можно обнаружить и исправить. Если имеется пять ошибок, их можно обнаружить, но исправить можно только одну из них.
6.5.4. Визуализация пространства 6-кортежей
На рис. 6.14 визуально представлено восемь кодовых слов, фигурирующих в примере из раздела 6.4.3. Кодовые слова образованы посредством линейных комбинаций из трех независимых 6-кортежей, приведенных в уравнении (6.26); сами кодовые слова образуют трехмерное подпространство. На рисунке показано, что такое подпространство полностью занято восемью кодовыми словами (большие черные круги); координаты подпространства умышленно выбраны неортогональными. На рис. 6.14 предпринята попытка изобразить все пространство, содержащее шестьдесят четыре 6-кортежей, хотя точно нарисовать или составить такую модель невозможно. Каждое кодовое слово окружают сферические слои или оболочки. Радиус внутренних непересекающихся слоев — это расстояние Хэмминга, равное 1; радиус внешнего слоя — это расстояние Хэмминга, равное 2. Большие расстояния в этом примере не рассматриваются. Для каждого кодового слова два показанных слоя заняты искаженными кодовыми словами. На каждой внутренней сфере существует шесть таких точек (всего 48 точек), представляющих шесть возможных однобитовых ошибок в векторах, соответствующих каждому кодовому слову. Эти кодовые слова с однобитовыми возмущениями могут быть соотнесены только с одним кодовым словом; следовательно, такие ошибки могут быть исправлены. Как видно из нормальной матрицы, приведенной на рис. 6.11, существует также одна двухбитовая ошибочная комбинация, которая также поддается исправлению. Всего существует 
Рис, 6.14. Пример восьми кодовых слов в пространстве 6-кортежей
При представлении свойств класса кодов, известных как совершенные коды (perfect code), рис. 6.14 весьма полезен. Код, исправляющий ошибки в t битах, называется совершенным, если нормальная матрица содержит все ошибочные комбинации из t или меньшего числа ошибок и не содержит иных образующих элементов классов смежности (отсутствует возможность исправления остаточных ошибок). В контексте рис. 6.14 совершенный код с коррекцией ошибок в t битах — это такой код, который (при использовании обнаружения по принципу максимального правдоподобия) может исправить все искаженные кодовые слова, находящиеся на расстоянии Хэмминга t (или ближе) от исходного кодового слова, и не способен исправить ни одну из ошибок, находящихся на расстоянии, превышающем t.
Кроме того, рис. 6.14 способствует пониманию основной цели поиска хороших кодов. Предпочтительным является пространство, максимально заполненное кодовыми словами (эффективное использование введенной избыточности), а также желательно, чтобы кодовые слова были по возможности максимально удалены друг от друга. Очевидно, что эти цели противоречивы.
6.5.5. Коррекция со стиранием ошибок
Приемник можно сконструировать так, чтобы он объявлял символ стертым, если последний принят неоднозначно либо обнаружено наличие помех или кратковременных сбоев. Размер входного алфавита такого канала равен Q, а выходного —Q + 1; лишний выходной символ называется меткой стирания (erasure flag), или просто стиранием (erasure). Если демодулятор допускает символьную ошибку, то для ее исправления необходимы два параметра, определяющие ее расположение и правильное значение символа. В случае двоичных символов эти требования упрощаются — нам необходимо только расположение ошибки. В то же время, если демодулятор объявляет символ стертым (при этом правильное значение символа неизвестно), расположение этого символа известно, поэтому декодирование стертого кодового слова может оказаться проще исправления ошибки. Код защиты от ошибок можно использовать для исправления стертых символов или одновременного исправления ошибок и стертых символов. Если минимальное расстояние кода равно dmin, любая комбинация из ρ или меньшего числа стертых символов может быть исправлена при следующем условии [6].
(6.50)
Предположим, что ошибки появляются вне позиций стирания. Преимущество исправления посредством стираний качественно можно выразить так: если минимальное расстояние кода равно dmin, согласно уравнению (6.50), можно восстановить dmin-1 стирание. Поскольку число ошибок, которые можно исправить без стирания информации, не превышает (dmin-1)/2, то преимущество исправления ошибок посредством стираний очевидно. Далее, любую комбинацию из α ошибок и γ стираний можно исправить одновременно, если, как показано в работе [6],
(6.51)
Одновременное исправление ошибок и стираний можно осуществить следующим образом. Сначала позиции из у стираний замещаются нулями, и получаемое кодовое слово декодируется обычным образом. Затем позиции из у стираний замещаются единицами, и декодирование повторяется для этого варианта кодового слова. После обработки обоих кодовых слов (одно с подставленными нулями, другое — с подставленными единицами) выбирается то из них, которое соответствует наименьшему числу ошибок, исправленных вне позиций стирания. Если удовлетворяется неравенство (6.51), то описанный метод всегда дает верное декодирование.
Пример 6.6. Коррекция со стиранием ошибок
Рассмотрим набор кодовых слов, представленный в разделе 6.4.3.
000000 110100 011010 101110 101001 011101 110011 000111
Пусть передано кодовое слово 110011, в котором два крайних слева разряда приемник объявил стертыми. Проверьте, что поврежденную последовательность хx0011 можно исправить.
Решение
Поскольку , код может исправить
= 2 стирания. В этом легко убедиться из рис. 6.11 или приведенного выше перечня кодовых слов, сравнивая 4 крайних правых разряда xx00l1 с каждым из допустимых кодовых слов. Действительно переданное кодовое слово — это ближайшее (с точки зрения расстояния Хэмминга) к искаженной последовательности.

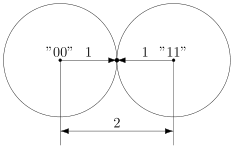

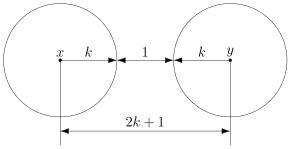

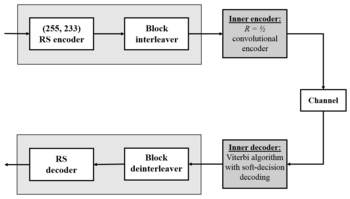





























![{displaystyle {begin{aligned}&Y_{k}X_{k}^{j+nu }Lambda (X_{k}^{-1})=0.\[1ex]&Y_{k}X_{k}^{j+nu }left(1+Lambda _{1}X_{k}^{-1}+Lambda _{2}X_{k}^{-2}+cdots +Lambda _{nu }X_{k}^{-nu }right)=0.\[1ex]&Y_{k}X_{k}^{j+nu }+Lambda _{1}Y_{k}X_{k}^{j+nu }X_{k}^{-1}+Lambda _{2}Y_{k}X_{k}^{j+nu }X_{k}^{-2}+cdots +Lambda _{nu }Y_{k}X_{k}^{j+nu }X_{k}^{-nu }=0.\[1ex]&Y_{k}X_{k}^{j+nu }+Lambda _{1}Y_{k}X_{k}^{j+nu -1}+Lambda _{2}Y_{k}X_{k}^{j+nu -2}+cdots +Lambda _{nu }Y_{k}X_{k}^{j}=0.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6573fa0f429ac4349f5da794df9c4fb7831e8cbf)















![{displaystyle {begin{aligned}S(x)&=S_{t}x^{t-1}+S_{t-1}x^{t-2}+cdots +S_{2}x+S_{1}\[1ex]Lambda (x)&=Lambda _{e}x^{e}+Lambda _{e-1}x^{e-1}+cdots +Lambda _{1}x+1\[1ex]Omega (x)&=Omega _{e}x^{e}+Omega _{e-1}x^{e-1}+cdots +Omega _{1}x+Omega _{0}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a84cd05dee4a72d23c59b3f95c4efdf3c8703600)