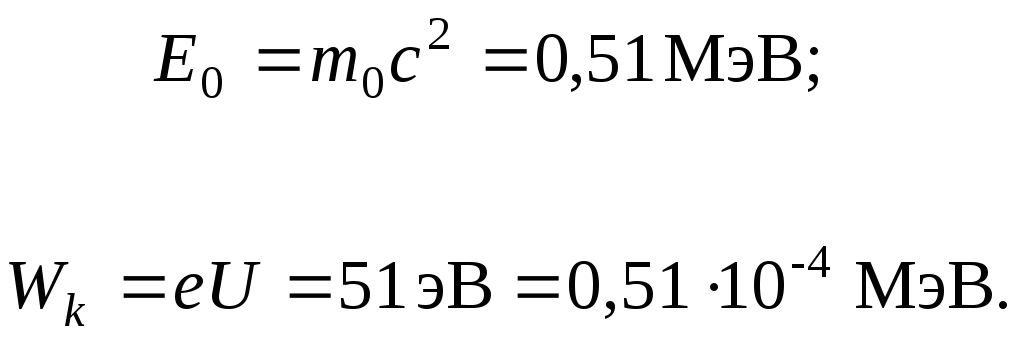Используя соотношение неопределенностей оценить наименьшие ошибки в определении скорости - ErrorsMaster.ru

Задача 622, Чертов А.Г., Воробьев А.А

622. Используя соотношение неопределенностей, оценить наименьшие ошибки Δp в определении импульса электрона и протона, если координаты центра масс частиц могут быть установлены с неопределенностью 1 мкм.

Download (PDF, 177KB)

Максим 14 декабря, 2013

Posted In: Задача, Квантовая механика, Квантовая физика, Физика, Физика. Воробьев А.А, Чертов А.Г., 1987

Метки: Вариант 1

Источник

Примеры решения задач

Задача 1.
Определить энергию фотона, соответствующего
второй линии в первой инфракрасной
серии (серии Пашена) атома водорода.

Решение

Энергия кванта
света, излучаемого атомом водорода при
переходе электрона с одной орбиты на
другую,

где E_i
– энергия ионизации атома водорода (
E_i
=13,6 эВ); n₁
= 1, 2, 3,…- номер орбиты, на которую переходит
электрон;
—
номер орбиты, с которой переходит
электрон (т
— номер спектральной линии в данной
серии).

Для серии Пашена
n₁= 3, m
= 2, n₂
= n₁
+ m
= 3 + 2 = 5.

Подставив числовые
значения, найдем энергию фотона:

Ответ: 
= 0,97 эВ.

Задача 2.
Электрон, начальной скоростью которого
можно пренебречь, прошел ускоряющую
разность потенциалов U
= 51 В. Найти длину волны де Бройля.

Решение

Длина волны де
Бройля

Дано:

U
= 51 B

m_o
= 9,1 ^.
10^-31
кг

Кл


-?

где h
– постоянная Планка, т
– масса электрона, V
– скорость. Кинетическая энергия
электрона, прошедшего ускоряющее поле,
равна работе этого поля, т.е.

откуда

Тогда

Ответ: 
= 1,71 ^.
10^-10
м.

Примечание.
Для решения задачи необходимо сравнить
кинетическую энергию электрона с его
энергией покоя Е_о.

Таким образом, W_к
<< E_o,
и для решения задачи можно использовать
формулы классической механики.

Если
,
то необходимо учитывать зависимость
массы от скорости и пользоваться
формулами релятивистской механики.

Задача 3.
Кинетическая энергия W_к
электрона в атоме водорода составляет
величину порядка 10 эВ. Используя
соотношение неопределенности, оценить
минимальные линейные размеры атома.

Решение

Соотношение
неопределенности для координаты и
импульса имеет вид

где х
– неопределенность координаты частицы
(в данном случае электрона); р
– неопределенность импульса частицы
(электрона);

— постоянная Планка, деленная на 2.

Из соотношения
неопределенности следует, что чем точнее
определяется положение частицы в
пространстве, тем более неопределенным
становится импульс, а следовательно, и
энергия частицы. Пусть атом имеет
линейные размеры l,
тогда электрон атома будет находиться
где-то в пределах области с неопределенностью

х
= l.

(1)

Соотношение
неопределенности (1) можно записать в
этом случае в виде

Откуда

Физически разумная
неопределенность импульса р,
во всяком случае, не должна превышать
значения самого импульса р,
т.е.

Импульс р
связан с кинетической энергией W_к
соотношением

Заменим р
значением

( такая замена не увеличит l).
Переходя от неравенства к равенству,
получим

Подставим числовые
значения и произведем вычисления:

Ответ: l_min
= 6,2 ^.
10^-11
м.

Задачи для самостоятельного решения

Задача 1.
Исходя из первого постулата Бора, вывести
формулу, определяющую радиус n-й
орбиты электрона в атоме водорода.
Вычислить радиусы первых трех орбит.

Ответ: r₁
= 0,529 ^.
10^-10
м; r₂
= 2,12 ^.
10^-10
м; r₃
= 4,77 ^.
10^-10
м.

Задача 2. Зная
заряд электрона и радиус орбиты,
определить потенциальную, кинетическую
и полную энергии электрона, находящегося
на первой орбите в атоме водорода.

Ответ: W_п
= -27,2 эВ; W_k
= 13,6 эВ; W
= -13,6 эВ.

Задача 3. Определить
длину волны, соответствующую третьей
спектральной линии в серии Бальмера.

Ответ: 
= 4,34 ^.
10^-7
м.

Задача 4. Найти
наибольшую и наименьшую длины волн в
первой инфракрасной серии спектра
водорода (серии Пашена).

Ответ: ₁
= 1,87 ^.
10^-6
м; ₂
= 8,2 ^.
10^-7
м.

Задача 5.
Вычислить энергию фотона, испускаемого
при переходе электрона в атоме водорода
с третьего энергетического уровня на
первый.

Ответ: W
= 12,1 эВ.

Задача 6.
Определить наименьшее и наибольшее
значения энергии фотона в ультрафиолетовой
части спектра водорода (серии Лаймана).

Ответ: W₁
= 10,2 эВ; W₂
= 13,6 эВ.

Задача 7. Атомарный
водород, возбужденный светом с определенной
длиной волны, при переходе в основное
состояние испускает только три
спектральные линии. Определить длины
волн этих линий и указать, каким сериям
они принадлежат.

Ответ: серия Лаймана
₁
= 1,216 ^.
10^-7
м; ₂
= 1,026^.
10^-7
м; серия Бальмера 
= 6,563 ^.
10^-7
м.

Задача 8. Фотон
с энергией 16,5 эВ выбил электрон из
невозбужденного атома водорода. Какую
скорость будет иметь электрон вдали от
ядра атома?

Ответ: V
= 10⁶
.

Задача 9.
Вычислить длину волны, которую испускает
ион гелия Не⁺
при переходе со второго энергетического
уровня на первый. Сделать такой же
подсчет для иона лития Li⁺⁺.

Ответ: ₁
= 0,3 ^.
10^-7
м; ₂
= 0,135^.
10^-7
м.

Задача 10. Найти
энергию E_i
и потенциал U_i
ионизации ионов Не⁺
и Li⁺⁺.

Ответ: гелий E_i
= 8,64 ^.
10^-18
Дж = 54 эВ; U_i
= 54 В; литий E_i
= = 1,95 ^.
10^-17
Дж = 122 эВ; U_i
= 122 В.

Задача 11.
Вычислить частоты обращения электрона
в атоме водорода на второй и третьей
орбитах. Сравнить эти частоты с частотой
излучения при переходе электрона с
третьей на вторую орбиту.

Ответ: частота
обращения 8,3 ^.
10¹⁴

и 2,4 ^.
10¹⁴
;
частота излучения 4,6 ^.10¹⁴
.

Задача 12. Атом
водорода в основном состоянии поглотил
квант света с длиной волны 
= 1215
.
Определить радиус электронной орбиты
возбужденного атома водорода.

Ответ: r
= 2,12 ^.
10^-10м.

Задача
13.
Определить первый потенциал возбуждения
атома водорода.

Ответ: U₁
= 10,2 В.

Задача 14.
Найти: 1) радиусы первых трех боровских
электронных орбит в атоме водорода; 2)
скорость электрона на них.

Ответ: r₁
= 0,53 ^.10^-10
м; r₂
= 2,12 ^.
10^-10
м; r₃
= 4,77 ^.
10^-10
м; V₁
= = 2,19 ^.
10⁶
;
V₂
= 1,1 ^.
10 ⁶
;
V₃
= 7,3 ^.
10⁶
.

Задача 15.
Вычислить кинетическую энергию электрона,
находящегося на п-й
орбите атома водорода. Задачу решить
для п
= 1, 2, 3 и .

Ответ: W₁
= 2,18 ^.
10 ^–18
Дж = 13,6 эВ; W₂
= 5,44 ^.
10^-19
Дж = 3,4 эВ; W₃
= 2,42 ^.
10 ^-19
Дж = 1,51 эВ; W₄
= 0.

Задача 16. Найти:
1) период обращения электрона на первой
боровской орбите в атоме водорода; 2)
его угловую скорость.

Ответ: Т
= 1,43 ^.
10^–16с;

= 4,4 ^.
10¹⁶
.

Задача 17.
Найти наименьшую и наибольшую длины
волн спектральных линий водорода в
видимой области спектра.

Ответ: ₁
= 3,65 ^.
10^–7
м; ₂
= 6,56 ^.
10^–7
м.

Задача 18.
1) Найти наибольшую длину волны в
ультрафиолетовой серии спектра водорода.
2) Какую наименьшую скорость должны
иметь электроны, чтобы при возбуждении
атомов водорода ударами электронов
появилась эта линия?

Ответ: 
= 1,21 ^.10^–7 м; V
= 1,9 ^.
10⁶
.

Задача 19. Определить
потенциал ионизации атома водорода.

Ответ: U_i
=13,6 В.

Задача 20. 1)
Какую наименьшую энергию (в электрон-вольтах)
должны иметь электроны, чтобы при
возбуждении атомов водорода ударами
этих электронов появились все линии
всех серий спектра водорода? 2) Какую
наименьшую скорость должны иметь эти
электроны?

Ответ: V
= 2,2 ^.
10⁶
;
W
= 13,6 эВ.

Задача 21.
В каких пределах должна лежать энергия
бомбардирующих электронов, чтобы при
возбуждении атомов водорода ударами
этих электронов спектр водорода имел
только одну спектральную линию?

Ответ:
.

Задача 22.
Какую наименьшую энергию (в электрон-вольтах)
должны иметь электроны, чтобы при
возбуждении атомов водорода ударами
этих электронов спектр водорода имел
три спектральные линии? Найти длины
волн этих линий.

Ответ: W
= 12,1 эВ; ₁
= 1,21 ^.10^–7 м; ₂
= 1,03 ^.10^–7 м; ₃
= 6,56^.10^–7 м.

Задача 23. В
каких пределах должны лежать длины волн
монохроматического света, чтобы при
возбуждении атомов водорода квантами
этого света наблюдались три спектральные
линии?

Ответ:
.

Задача 24.
На сколько изменилась кинетическая
энергия электрона в атоме водорода при
излучении атомом фотона с длиной волны
?

Ответ: на 2,56 эВ.

Задача 25.
В каких пределах должны лежать длины
волн монохроматического света, чтобы
при возбуждении атомов водорода квантами
этого света радиус орбиты электрона
увеличился в 9 раз?

Ответ:

Задача 26. Определить
максимальную энергию _max
фотона серии Бальмера в спектре излучения
атомарного водорода.

Ответ: _max
= 3,4 эВ.

Задача 27.
В каких пределах должны лежать длины
волн монохроматического света, чтобы
при возбуждении атома водорода квантами
этого света наблюдались три спектральные
линии?

Ответ:
.

Задача 28.
Определить наибольшее и наименьшее
значения энергии фотона в ультрафиолетовой
серии спектра водорода (серия Лаймана).

Ответ: _min
= 10,2 эВ; _max
= 13,6 эВ.

Задача 29.
Невозбужденный атом водорода поглощает
квант излучения с длиной волны 
= 102,6 нм. Вычислить, пользуясь теорией
Бора, радиус электронной орбиты
возбужденного атома водорода.

Ответ: r
= 4,75 ^.
10^–10
м.

Задача 30.
Электрон в атоме водорода перешел с
четвертого энергетического уровня на
второй. Определить энергию испущенного
при этом фотона.

Ответ: 
= 2,55 эВ.

Задача 31. Определить
энергию фотона, испускаемого при переходе
электрона в атоме водорода с третьего
энергетического уровня на основной.

Ответ: 
= 12,1 эВ.

Задача 32.
Определить длину волны де Бройля,
характеризующую волновые свойства
электрона, если его скорость равна 1000
.
Сделать такой же подсчет для протона.

Ответ: ₁
= 7,3 ^.
10^–10
м; ₂
= 4 ^.
10^–13
м.

Задача 33. Электрон
движется со скоростью 200000
.
Определить длину волны де Бройля,
учитывая изменение массы в зависимости
от скорости.

Ответ: 
= 2,7 ^.
10^–12
м.

Задача 34. Какую
ускоряющую разность потенциалов должен
пройти электрон, чтобы длина волны де
Бройля была равна 1?

Ответ: U
= 150 В.

Задача 35.
Определить длину волны де бройля
электрона, если его кинетическая энергия
равна 1кэВ.

Ответ: 
= 0,38 ^.
10^–10
м.

Задача 36.
Найти длину волны де Бройля для протона,
прошедшего ускоряющую разность
потенциалов в 1 кВ и 1 МВ.

Ответ: ₁=
9,07 ^.
10^–13
м; ₂
= 2,86 ^.
10^-14
м.

Задача 37.
Вычислить длину волны де Бройля для
электрона, движущегося по круговой
орбите атома водорода, находящегося в
основном состоянии.

Ответ: 
= 3,3 ^.
10^–10
м.

Задача 38. Определить
длину дебройлевской волны электрона,
находящегося на второй орбите в атоме
водорода.

Ответ: 
= 6,7 ^.
10 ^–10
м.

Задача 39.
С какой скоростью движется электрон,
если дебройлевская длина волны электрона
численно равна его комптоновской длине
волны?

Ответ: V
= 2,12 ^.
10⁸
.

Задача 40.
Определить длину дебройлевской волны
электронов, бомбардирующих антикатод
рентгеновской трубки, если граница
сплошного спектра рентгеновских лучей
приходится на длину волны
.

Ответ: 
= 0,6 ^.
10^–10 м.

Задача 41.
Электрон движется по окружности радиусом
0,5 см в однородном магнитном поле с
индукцией 8^. 10 ^–3
Тл. Определить длину волны де Бройля
электрона.

Ответ: 
= 10 ^–10
м.

Задача 42.
Вычислить длину волны де Бройля для
электрона, прошедшего ускоряющую
разность потенциалов U
= 22,5 В.

Ответ: 
= 2,58 ^.10^–10 м.

Задача 43. Вычислить
длину волны де Бройля для протона,
движущегося со скоростью V
= 0,6 с
(с
— скорость света в вакууме).

Ответ: 
= 1,76 ^.
10^–15
м.

Задача 44.
На узкую щель шириной 1 мкм направлен
параллельный пучок электронов, имеющих
скорость 3,65 ^.
10 ⁸
.
Учитывая волновые свойства электронов,
определить расстояние между двумя
максимумами первого порядка в дифракционной
картине, полученной на экране, отстоящем
на L
= 10 cм
от щели.

Ответ: х
= 6 ^.10^–5м.

Задача 45.
Рассчитать длину волны де Бройля для:
а) электрона, прошедшего ускоряющее
поле с разностью потенциалов 100 В; б)
камня массой 100 г, летящего со скоростью
1
;
в) Земли на своей орбите (М_з
= 6 ^.
10²⁷кг).
R_з-с
= 1,510¹¹
м. v
=
.

Ответ: а) 
= 10 ^–10
м; б) 
= 6,6 ^.
10^–33 м; в) 
= 3,6^.
10^–63
м.

Задача 46.
Получить в общем виде формулу, выражающую
зависимость волны де Бройля от ускоряющего
потенциала для релятивистской частицы.

Задача 47. Какую
ускоряющую разность потенциалов U
должен пройти протон, чтобы дебройлевская
длина волны 
была равна: 1) 1 нм; 2) 1 пм?

Ответ: 1) U
= 8,2 ^.
10^-4
В; 2) U
= 820 В.

Задача 48. Определить
длины волн де Бройля -частицы
и протона, прошедших одинаковую ускоряющую
разность потенциалов U
= 1 кВ.

Ответ: ₁
= 3,2 ^.10^–13 м; ₂
= 9 ^.
10^–13
м.

Задача 49.
Протон обладает кинетической энергией
W_k
= 1 кэВ. Определить величину дополнительной
энергии W
, которую необходимо ему сообщить для
того, чтобы дебройлевская длина волны
уменьшилась в три раза.

Ответ: W
= 8 кэВ.

Задача 50. Определить
длину волны де Бройля для частицы массой
т
= 1 г, движущейся со скоростью V
= 10
.
Нужно ли учитывать в этом случае волновые
свойства частицы? Почему?

Ответ: 
= 6,62 ^.
10^–32м.

Задача 51.
Вычислить длину волны 
де Бройля для электрона, обладающего
кинетической энергией W_k
= 13,6 эВ (энергия ионизации атома водорода).
Сравнить полученное значение 
с диаметром d
атома водорода (найти отношение
).
Нужно ли учитывать волновые свойства
электрона при изучении движения электрона
в атоме водорода? Диаметр атома водорода
принять равным удвоенному значению
боровского радиуса.

Ответ: 
= 3,3 ^.
10^–10
м.

Задача
52.
Вычислить длину волны 
де Бройля для тепловых (Т
= 300 К) нейтронов. Следует ли учитывать
волновые свойства нейтронов при анализе
их взаимодействия с кристаллом? Расстояние
между атомами в кристалле принять равным
0,5 нм (масса нейтрона т_n
= 1,67 ^.10^–27
кг).

Ответ: 
= 1,78 ^.
10 ^–10
м.

Задача 53.
Определить неточность в определении
координаты электрона, движущегося в
атоме водорода со скоростью V
= 1,5 ^.
10⁶
,
если допускаемая неточность в определении
скорости V
составляет 10 % от ее величины. Сравнить
с диаметром атома водорода и указать,
применимо ли понятие траектории в данном
случае (d

10^–10м).

Ответ: х
= 7,7 ^.
10 ^–10
м.

Задача 54.
Определить с помощью соотношения
неопределенностей минимальную
кинетическую энергию W_min
электрона, движущегося внутри сферической
области диаметром d
= 0,1 нм.

Ответ: W_min
= 3,8
эВ.

Задача 55.
Электрон находится в бесконечно глубокой
одномерной потенциальной «яме» шириной
l
= 0,1 нм. Определить в электрон-вольтах
наименьшую разность энергетических
уровней электрона.

Ответ: W_min
= 112,5 эВ.

Задача 56*.
Показать, используя соотношение
неопределенностей, что в ядре не могут
находиться электроны. Линейные размеры
ядра принять равными 5 ^.
10^–15
м.

Задача 57. Электрон,
неопределенность импульса которого не
превышает 1 %, движется в электронно-лучевой
трубке со скоростью 10 ⁸

.
Можно ли в данном случае рассматривать
электрон как материальную частицу, т.е.
не учитывать его волновые свойства?

Ответ: х
= 0,7 ^.
10^–7
м.

Задача 58.
Используя соотношение неопределенностей,
оценить наименьшие ошибки в определении
скорости электрона и протона, если
координаты центра масс этих частиц
могут быть установлены с неопределенностью
1 мкм.

Задача 59.
Электрон с кинетической энергией W
= 15 эВ находится в металлической пылинке
диаметром d
= 1 мкм. Оценить (в процентах) относительную
неточность, с которой может быть
определена скорость электрона.

Ответ: 5 ^.
10^–3
%.

Задача 60.
Используя соотношение неопределенностей

,
оценить низший энергетический уровень
электрона в атоме водорода. Принять
линейные размеры атома l

1 ^.10^–10 м.

Ответ: 
= 4 эВ.

Задача 61.
Приняв, что минимальная энергия нуклона
в ядре W_min
= 10 МэВ, оценить, исходя из соотношения
неопределенностей, размеры ядра.

Ответ: d
= 1,44
^.
10^–15
м.

Задача 62.
Рассмотрим следующий мысленный
эксперимент. Пусть моноэнергетический
(W
= 10 эВ) пучок электронов падает на щель
шириной а.
Можно считать, что если электрон прошел
через щель, то его координата известна
с неточностью х
= а.
Оценить получаемую при этом относительную
неточность в определении импульса

электрона в двух случаях: а) а
= 1 ^.
10^–8
м; б) а
= 1^.
10^–10
м.

Ответ: а) 0,6 %; б) 60
%.

Задача 63*.
При какой скорости электрона его
дебройлевская длина волны будет равна:
а) 5^.
10^–7
м; б) 1^.
10^–10
м? Каким областям спектра электромагнитных
волн соответствуют эти длины волн?

Задача 64. При
движении вдоль оси х
скорость оказывается определенной с
точностью V_x
= 10^–2

.
Оценить неопределенность координаты
х:
а) для электрона; б) для броуновской
частицы массой т

10 ^–15
кг; в) для дробинки массой т

10 ^–4
кг.

Задача 65.
Исходя из того, что радиус атома имеет
величину порядка 10 ^–10м, оценить
скорость движения электрона в атоме
водорода.

Ответ: V

2 ^.
10⁶

Задача
66.
Положение пылинки массой т

10^–15
г определено с точностью до 10 ^–6
м. Определить неточность в определении
скорости пылинки.

Задача 67*.
Во сколько раз дебройлевская длина
волны -частицы
меньше неопределенности ее координаты
х,
которая соответствует неопределенности
импульса в 1 %?

Ответ: 16 раз.

Задача 68.
Если допустить, что неопределенность
координаты движущейся частицы равна
дебройлевской длине волны, то какова
будет относительная неточность

импульса этой частицы?

Ответ: 16 %.

Задача 69.
Используя соотношение неопределенностей

,
найти выражение, позволяющее оценить
минимальную энергию W_min
электрона, находящегося в одномерном
потенциальном ящике шириной l
.

Ответ:
.

Задача 70.
Используя соотношение неопределенностей
,
оценить низший энергетический уровень
электрона в атоме водорода. Принять
линейные размеры атома l

.

Ответ: W
= 4 эВ.

Задача 71.
Электронный
пучок ускоряется в электронно-лучевой
трубке разностью потенциалов U
= 1кВ. Известно, что неопределенность
скорости составляет 0,1% от ее числового
значения. Определите неопределенность
координаты электрона. Являются ли
электроны в данных условиях квантовой
или классической частицей?

Ответ: х
= 38,8 нм.

Задача 72. Определите
отношение неопределенности скорости
элктрона, если его координата установлена
с точностью до 10^-5
м, и пылинки массой m
= 10^-12
кг, если ее координата установлена с
такой же точностью.

Ответ:
.

Задача 73. Протон
движется в однородном магнитном поле
с индукцией
В = 15 мТл по
окружности радиусом R
= 1,4 м. Определите длину волны де Бройля
для протона.

Ответ: 
= 0,197 пм.

Задача 74.
Определите,
какую ускоряющую разность потенциалов
должен пройти протон, чтобы длина волны
де Бройля 
для него была равна 1 нм.

Ответ: U
= 0,822 мВ.

Задача 75. Определите
длину волны де Бройля для электрона,
находящегося в атоме водорода на третьей
боровской орбите.

Ответ: 
= 1 нм.

Задача 76. Заряженная
частица, ускоренная разностью потенциалов
U
= 500 В, имеет длину волны де Бройля 
= 1,282 пм. Принимая заряд этой частицы
равным заряду электрона, определите ее
массу.

Ответ: m
= 1,67210^-27
кг.

Источник

Решебник по физике Чертова А.Г. 1987г — вариант 2 контрольная 6

Решенные задачи из учебника ФИЗИКА. Методические указания и контрольные задания. Под редакцией А. Г. Чертова

Ниже приведены условия задач и отсканированные листы с решениями. Загрузка страницы может занять некоторое время.

602. Вычислить по теории Бора радиус r2 второй стационарной орбиты и скорость v2 электрона на этой орбите для атома водорода.
612. Определить энергию ΔE, которую необходимо дополнительно сообщить электрону, чтобы его дебройлевская длина волны уменьшилась от λ1 = 0,2нм до λ2=0,1 нм.
622. Используя соотношение неопределенностей, оценить наименьшие ошибки ΔV в определении скорости электрона и протона, если координаты центра масс этих частиц могут быть установлены с неопределенностью 1 мкм.
632. Электрон находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной l=0,1 нм. Определить в электрон-вольтах наименьшую разность энергетических уровней электрона.
642. Определить, какая доля радиоактивного изотопа 225Aс распадается в течение времени t= 6 сут.
652. Масса m = 1 г урана 238U в равновесии с продуктами его распада выделяет мощность Р=1.07×10-7 Вт. Найти молярную теплоту Qm, выделяемую ураном за среднее время жизни атомов урана.
662. Вычислить характеристическую температуру θD Дебая для железа, если при температуре Т = 20 К молярная теплоемкость железа Сm = 0,226 Дж/К×моль. Условие Т<<θD считать выполненным.
672. Германиевый кристалл, ширина Δε запрещенной зоны в котором равна 0,72 эВ, нагревают от температуры T1 = 0°С до температуры T2 = 15°С. Во сколько раз возрастет его удельная проводимость?

Источник

Готовое решение: Заказ №8389

Тип работы: Задача

Статус: Выполнен (Зачтена преподавателем ВУЗа)

Предмет: Физика

Дата выполнения: 28.09.2020

Цена: 227 руб.

Чтобы получить решение, напишите мне в WhatsApp, оплатите, и я Вам вышлю файлы.

Кстати, если эта работа не по вашей теме или не по вашим данным, не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу, я смогу выполнить её в срок 1-3 дня!

Описание и исходные данные задания, 50% решения + фотография:

№1 Условие 1 612. Используя соотношение неопределённостей, оценить наименьшие ошибки Dv в определении скорости электрона и протона, если координаты центра масс этих частиц могут быть установлены с точностью Dx = 1 мкм. Условие 2 622. Используя соотношение неопределённостей, оценить наименьшие ошибки Dv в определении скорости электрона и протона, если координаты центра масс этих частиц могут быть установлены с точностью 1 мкм.

Решение.

Соотношение неопределённостей Гейзенберга для координаты и импульса имеет вид: , где Дж∙с – постоянная Планка; – неопределённость импульса частицы; – неопределённость координаты частицы. Импульс классической частицы равен: , где – масса частицы; – скорость частицы. Масса классической частицы остаётся неизменной, поэтому для неопределённостей импульса и скорости можем записать:

Оценить наименьшую ошибку DV в определении скорости элек¬трона, если координата его центра масс установлена с неопределён¬ностью Dx = 1 мкм.
Оцените с помощью соотношения неопределённостей скорость электрона в атоме водорода, полагая размер атома d = 0,1 нм. Сравните полученную величину со скоростью электрона на первой боровской орбите данного атома.
Положения электрона можно измерить с точностью 1,6·10^-8 м. С какой точностью можно определить его скорость?
Моноэнергетический пучок электронов, прошедших ускоряющую разность потенциалов U = 20 кВ, высвечивает в центре экрана электроннолучевой трубки, длина которой l = 0,5 м, пятно радиусом r = 10-3 см. Пользуясь соотношением неопределённостей, определить, во сколько раз неопределённость Dx координаты электрона на экране в направлении, перпендикулярном оси трубки, меньше радиуса r пятна. Условие 2 628. Моноэнергетический пучок электронов высвечивает в центре экрана электронно-лучевой трубки пятно радиусом r = 10-3 см. Пользуясь соотношением неопределённостей, найти, во сколько раз неопределённость Dx координаты электрона на экране в направлении, перпендикулярном оси трубки, меньше размера r пятна. Длину L электронно-лучевой трубки принять равной 0,50 м, а ускоряющее электрон напряжение U – равным 20 кВ.

Источник

|
Библиотека решений
|
Задача 622 из сборника Чертова Используя соотношение неопределенностей, оценить наименьшие ошибки ΔV в определении скорости электрона и протона, если координаты центра масс этих частиц могут быть установлены с неопределенностью 1 мкм

Ирина Эланс

Автор который поможет с любыми образовательными и учебными заданиями

Заказ: 1013248

Задача 622 из сборника Чертова Используя соотношение неопределенностей, оценить наименьшие ошибки ΔV в определении скорости электрона и протона, если координаты центра масс этих частиц могут быть установлены с неопределенностью 1 мкм

Описание

Аккуратное решение в WORD

Неопределенность Гейзенберга, Задачник Чертова для заочников

Задача 623 из сборника Чертова Какова должна быть кинетическая энергия Т протона в моноэнергетическом пучке, используемого для исследования структуры с линейными размерами l≈10-13 см?
Задача 624 из сборника Чертова Используя соотношение неопределенностей, оценить ширину L одномерного потенциального ящика, в котором минимальная энергия электрона T = 10 эВ
Задача 6.24 Исходные данные: Е = 100 B, L = 1 Гн, C = 10-3 Ф, R1 = R2 = 10 Ом. Определить ток i2(t) после коммутации и построить его график
Задача 6.24 Исходные данные: Е = 100 B, L = 1 Гн, C = 10-3 Ф, R1 = R2 = 10 Ом. Определить ток i2(t) после коммутации и построить его график
Задача 6.24. Переходный процесс в RL-цепи
Задача 6.24. Переходный процесс в RL-цепи
Задача 625 из сборника Чертова Альфа-частица находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике. Используя соотношение неопределенностей, оценить ширину L ящика, если известно, что минимальная энергия α-частицы T = 8 МэВ
Задача 61) Определить тип данного контура – последовательный или параллельный; 2) Записать комплексные выражения для входного сопротивления Z(jω) и коэффициента передачи по напряжению; 3) Найти выражения для АЧХ Ku(ω) и ФЧХ φk(ω) коэффициента передачи по напряжению; 4) Получить формулы для определения резонансной частоты контура ω0 полосы пропускания Δω , добротности Q; 5) Определить численные значения ω0, Δω, Q. 6) Построить численно графики АЧХ и ФЧХ передаточной функции Ku(jω). Групповой вариант 2 схема 7
Задача 61) Определить тип данного контура – последовательный или параллельный; 2) Записать комплексные выражения для входного сопротивления Z(jω) и коэффициента передачи по напряжению; 3) Найти выражения для АЧХ Ku(ω) и ФЧХ φk(ω) коэффициента передачи по напряжению; 4) Получить формулы для определения резонансной частоты контура ω0 полосы пропускания Δω , добротности Q; 5) Определить численные значения ω0, Δω, Q. 6) Построить численно графики АЧХ и ФЧХ передаточной функции Ku(jω). Групповой вариант 2 схема 8
Задача 61) Определить тип данного контура – последовательный или параллельный; 2) Записать комплексные выражения для входного сопротивления Z(jω) и коэффициента передачи по напряжению; 3) Найти выражения для АЧХ Ku(ω) и ФЧХ φk(ω) коэффициента передачи по напряжению; 4) Получить формулы для определения резонансной частоты контура ω0 полосы пропускания Δω , добротности Q; 5) Определить численные значения ω0, Δω, Q. 6) Построить численно графики АЧХ и ФЧХ передаточной функции Ku(jω). Групповой вариант 2 схема 8
Задача 6.1.Сборник Бессонова. Ламповая нагрузка питается от сети, система линейных напряжений которой симметрична (Uл=220 В). В каждую фразу включено по одной лампе на номинальную мощность 50 Вт и номинальное напряжение 220 В (рис.6.1,а).Определить фазные и линейные токи, напряжение на каждой лампе и показания ваттметров P1 и P2, если нагрузка соединена: а) звездой, как показано на рисунке; б) звездой, обрыв фазы С в точке М; в) треугольником. По найденным показаниям ваттметров найти мощность, потребляемую трёхфазной нагрузкой в каждом случае. Для всех случаев построить топографические диаграммы и векторные диаграммы токов.
Задача 6.1.Сборник Бессонова. Ламповая нагрузка питается от сети, система линейных напряжений которой симметрична (Uл=220 В). В каждую фразу включено по одной лампе на номинальную мощность 50 Вт и номинальное напряжение 220 В (рис.6.1,а).Определить фазные и линейные токи, напряжение на каждой лампе и показания ваттметров P1 и P2, если нагрузка соединена: а) звездой, как показано на рисунке; б) звездой, обрыв фазы С в точке М; в) треугольником. По найденным показаниям ваттметров найти мощность, потребляемую трёхфазной нагрузкой в каждом случае. Для всех случаев построить топографические диаграммы и векторные диаграммы токов.
Задача 620 из сборника Чертова Кинетическая энергия Ek электрона равна удвоенному значению его энергии покоя (2m0с ). Вычислить длину волны λ, де Бройля для такого электрона
Задача 621 из сборника Чертова Оценить с помощью соотношения неопределенностей минимальную кинетическую энергию электрона, движущегося внутри сферы радиусом R = 0,05 нм.

Источник