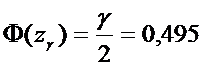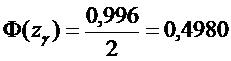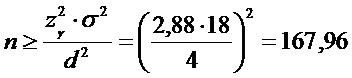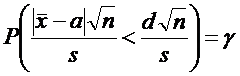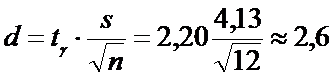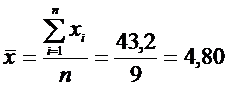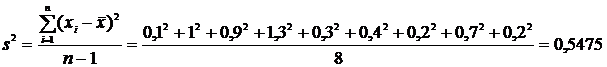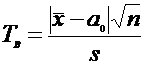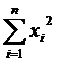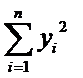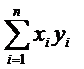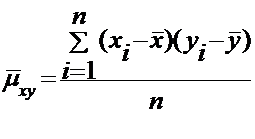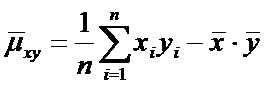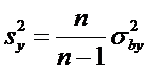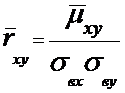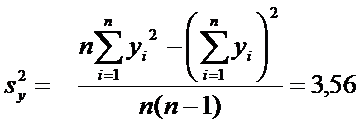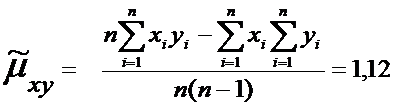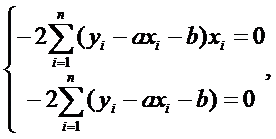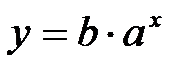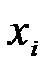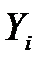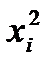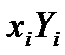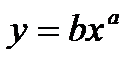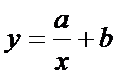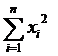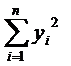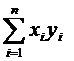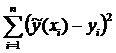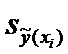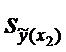Глубина моря измеряется прибором систематическая ошибка которого равна

Теория вероятностей и математическая статистика Лекция № 12 1

Элементы теории оценок Точечные и интервальные оценки параметров 2

Оценка неизвестных параметров Пусть изучается случайная величина X с законом распределения, зависящим от одного или нескольких параметров. Например, это параметр а в распределении Пуассона ( ) или параметры а и σ для нормаль- ного закона распределения. Требуется по выборке X 1, Х 2, . . . , Хn , полученной в результате n наблюдений (опытов), оценить неизвестный параметр θ. Напомним, что X 1, Х 2, . . . , Хn — случайные величины: Х 1 — результат первого наблюдения, Х 2 — второго и т. д. , причем СВ Хi, i = 1, 2, . . . , n, имеют такое же распределение, что и СВ X; конкретная выборка х1, х2, . . . , хn — это значения (реализация) независимых СВ X 1, Х 2, . . . , Хn. 3

Оценка неизвестных параметров Статистической оценкой (далее просто – оценкой ) параметра θ теоретического распределения называют его приближенное значение, зависящее от данных выбора. Очевидно, что оценка есть значение некоторой функции результатов наблюдений над случайной величиной, т. е. Функцию результатов наблюдений (т. е. функцию выборки) называют статистикой. Можно сказать, что оценка параметра θ есть статистика, которая в определенном смысле близка к истинному значению θ. Так, F*(x) есть оценка Fx(x), гистограмма — плотности f(x). 4

Оценка неизвестных параметров Оценка является случайной величиной, так как является функцией независимых СВ X 1, Х 2, . . . , Хn , если произвести другую выборку, то функция примет, вообще говоря, другое значение. Если число опытов (наблюдений) невелико, то замена неизвестного параметра θ его оценкой , например математического ожидания средним арифметическим, приводит к ошибке. Это ошибка в среднем тем больше, чем меньше число опытов. К оценке любого параметра предъявляется ряд требований, которым она должна удовлетворять, чтобы быть «близкой» к истинному значению параметра, т. е. быть в каком-то смысле «доброкачественной» оценкой. 5

Свойства статистических оценок Качество оценки определяют, проверяя, обладает ли она свойствами несмещенности, состоятельности, эффективности. Оценка параметра θ называется несмещенной, если М = θ. Если М θ, то оценка называется смещенной. Чтобы оценка не давала систематической ошибки (ошибки одного знака) в сторону завышения (М > θ) или занижения (М < θ) надо потребовать, чтобы «математическое ожидание оценки было равно оцениваемому параметру» . Если М → θ то оценка называется асимптотически несмещенной. Требование несмещенности особенно важно при малом числе наблюдений (опытов). 6

Свойства статистических оценок Оценка параметра θ называется состоятельной, если она сходится по вероятности к оцениваемому параметру: р т. е. для любого ε > 0 выполнено Это означает, что с увеличением объема выборки мы все ближе приближаемся к истинному значению параметра θ, т. е. практически достоверно. Свойство состоятельности обязательно для любого правила оценивания (несостоятельные оценки не используются). Состоятельность оценки часто может быть установлена с помощью следующей теоремы. Теорема 1. Если оценка параметра θ является несмещенной и при n→∞, то — состоятельная оценка. 7

Свойства статистических оценок Несмещенная оценка параметра θ называется эффективной, если она имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра θ, т. е. оценка эффективна, если ее дисперсия минимальна. Эффективную оценку в ряде случаев можно найти, используя неравенство Рао-Крамера: где I = I(θ) — информация Фишера. Отметим, что на практике не всегда удается удовлетворить всем перечисленным выше требованиям (несмещенность, состоятельность, эффективность), и поэтому приходится довольствоваться оценками, не обладающими сразу всеми тремя свойствами. Все же три свойства, как правило, выделяют оценку однозначно. 8

Точечные оценки математического ожидания и дисперсии Пусть изучается СВ X с математическим ожиданием а = MX и дисперсией DX, оба параметра неизвестны. Статистика, используемая в качестве приближенного значения неизвестного параметра генеральной совокупности, называется ее точечной оценкой. Т. е. точечная оценка характеристики генеральной совокупности — это число, определяемое по выборке. Пусть х1, х2, . . . , хn— выборка, полученная в результате проведения n независимых наблюдений за СВ X. Чтобы подчерк -нуть случайный характер величин х1, х2, . . . , хn, перепишем их в виде X 1, X 2, . . . , Хn, т. е. под Xi будем понимать значение СВ X в i-м опыте. Случайные величины X 1, X 2, . . . , Хn можно рас-сматривать как n независимых «экземпляров» величины X. Поэтому МХ 1 = МХ 2 =…= МХn = MX = a, DX 1 = DX 2 =…= DXn = 9 DX.

Точечные оценки математического ожидания и дисперсии Теорема 2. Пусть X 1, X 2, . . . , Хn — выборка из генеральной совокупности и МХi = MX = a, Dxi = DX (i = 1, …, n). Тогда выборочное среднее — несмещенная и состоятельная оценка математического ожидания MX. Можно показать, что при нормальном распределении СВ X эта оценка, т. е. , будет и эффективной. На практике во всех случаях в качестве оценки математического ожидания используется среднее арифметическое, т. е. . В статистике оценку математического ожидания принято обозначать через или , а не. 10

Точечные оценки математического ожидания и дисперсии Для выборочной дисперсии справедлива формула Из этого равенства следует, что MDB ≠ DX, т. е. выборочная дисперсия является смещенной оценкой дисперсии DX. Поэтому выборочную дисперсию исправляют, умножив ее на n/(n – 1), получая формулу S 2 = n/(n – 1)*Dв Теорема 3. Пусть X 1, X 2, . . . , Хn — выборка из генеральной совокупности и МХi = MX = a, Dxi = DX (i = 1, …, n). Тогда выборочное среднее Тогда исправленная выборочная дисперсия — несмещенная состоятельная оценка дисперсии DX. Замечание: при больших значениях n разница между DB и S 2 очень мала и они практически равны, поэтому оценку S 2 используют для оценки дисперсии при малых выборках, 11

Точечные оценки математического ожидания и дисперсии Имеют место следующие теоремы. Теорема 4. Относительная частота n. A /n появления события А в n независимых испытаниях является несмещенной состоятельной и эффективной оценкой неизвестной вероятности р = Р(А) этого события (р — вероятность наступления события А в каждом испытании). Теорема 5. Эмпирическая функция распределения выборки F*(x) является несмещенной состоятельной оценкой функции распределения F(x) случайной величины X. Пример 1. Монету подбрасывают n раз. Вероятность выпадения герба при каждом подбрасывания равна р. В ходе опыта монета выпала гербом n. A раз. Показать несмещенность оценки вероятности θ = р выпадения герба в каждом опыте. 12

Методы нахождения точечных оценок Рассмотрим наиболее распространенные методы получения точечных оценок параметров распределения: q метод моментов (кратко: ММ), q метод максимального правдоподобия (кратко: ММП), q метод наименьших квадратов (кратко: МНК). 13

Метод моментов для нахождения точечных оценок неизвестных параметров заданного распределения состоит в приравнивании теоретических моментов распределения соответствующим эмпирическим моментам, найденных по выборке. Так, если распределение зависит от одного параметра θ (например, задан вид плотности распределения f(х, θ)), то для нахождения его оценки надо решить относительно θ одно уравнение: 14

Метод моментов Если распределение зависит от двух параметров (например, вид плотности распределения f(x, θ 1, θ 2)) — надо решить относительно θ 1 и θ 2 систему уравнений: И, наконец, если надо оценить n параметров θ 1, θ 2, …, θn решить одну из систем вида: или 15

Метод моментов является наиболее простым методом оценки параметров. Он был предложен в 1894 г. Пирсоном. Оценки метода моментов обычно состоятельны, однако их эффективность часто значительно меньше единицы. Пример 2. Найти оценки параметров нормального распределения СВ X методом моментов. 16

Метод максимального правдоподобия Пусть х1, х2, . . . , хn — выборка, полученная в результате проведения n независимых наблюдений за СВ X. И пусть вид закона распределения величины X, например, вид плотности f(x, θ), известен, но неизвестен параметр θ, которым определяется этот закон. Требуется по выборке оценить параметр θ. В основе метода максимального правдоподобия (ММП), предложенного Р. Фишером, лежит понятие функции правдоподобия. Функцией правдоподобия, построенной по выборке х1, х2, . . . , хn, называется функция аргумента θ вида или где f(x, θ) — плотность распределения непрерывной СВ 17 X

Метод максимального правдоподобия Если X — дискретная СВ, то функция правдоподобия имеет вид Где Из определения следует, что чем больше значение функции L(x, θ), тем более вероятно (правдоподобнее) появление (при фиксированном θ) в результате наблюдений чисел х1, х2, . . . , хn. За точечную оценку параметра θ, согласно ММП, берут такое его значение , при котором функция правдоподо-бия достигает максимума. Эта оценка, называемая оценкой максимального правдоподобия, является решением уравнения 18

Метод максимального правдоподобия Так как функции L(x, θ) и In L(x, θ) достигают максимума при одном и том же значении θ, то вместо отыскания максимума функции L(x, θ) ищут (что проще) максимум функции In L(x, θ). Таким образом, для нахождения оценки максимального правдоподобия надо: • решить уравнение правдоподобия 2. отобрать то решение, которое обращает функцию In L(x, θ) в максимум (удобно использовать вторую производную: если то — точка максимума). 19

Метод максимального правдоподобия Если оценке подлежат несколько параметров θ 1, θ 2, . . . , θn распределения, то оценки определяются решением системы уравнений правдоподобия: Пример 3. Найти оценку параметра а распределения Пуассона методом максимального правдоподобия. 20

Метод наименьших квадратов Метод нахождения оценки неизвестного параметра θ, основанный на минимизации суммы квадратов отклонений выборочных данных от определяемой (искомой) оценки θ, называется методом наименьших квадратов (коротко: МНК). Другими словами, в МНК требуется найти такое значение , которое минимизировало бы сумму Отметим, что МНК является наиболее простым методом нахождения оценок параметра θ. Пример 4. Найти оценку параметра а распределения Пуассона методом наименьших квадратов. 21

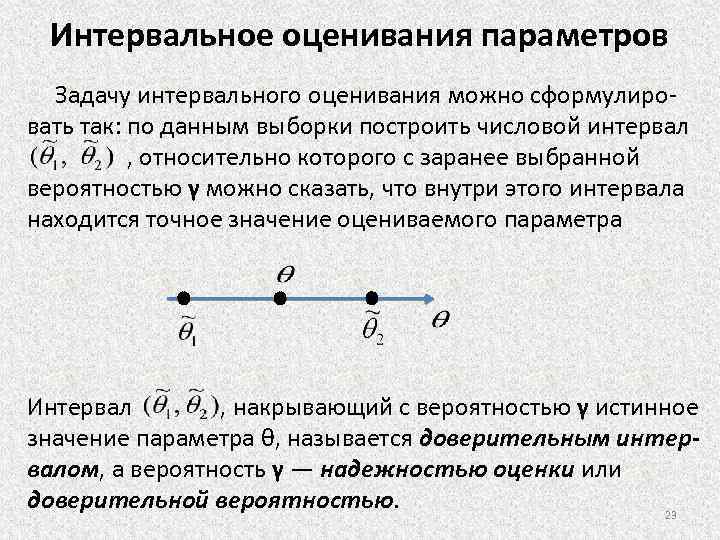
Интервальное оценивания параметров Точечные оценки неизвестного параметра θ хороши в качестве первоначальных результатов обработки наблюдений. Их недостаток в том, что неизвестно, с какой точностью они дают оцениваемый параметр. Для выборок небольшого объема вопрос о точности оценок очень существенен, так как между θ и может быть большое расхождение в этом случае. Кроме того, при решении практических задач часто требуется определить и надежность этих оценок. Тогда и возникает задача о прибли -жении параметра θ не одним числом, а целым интервалом. Оценка неизвестного параметра называется интервальной, если она определяется двумя числами — концами интервала. 22

Интервальное оценивания параметров Задачу интервального оценивания можно сформулировать так: по данным выборки построить числовой интервал , относительно которого с заранее выбранной вероятностью γ можно сказать, что внутри этого интервала находится точное значение оцениваемого параметра Интервал , накрывающий с вероятностью γ истинное значение параметра θ, называется доверительным интервалом, а вероятность γ — надежностью оценки или доверительной вероятностью. 23

Интервальное оценивания параметров Очень часто (но не всегда) доверительный интервал выбирается симметричным относительно несмещенной точечной оценки θ, т. е. выбирается интервал вида такой, что Число ε > 0 характеризует точность оценки: чем меньше разность , тем точнее оценка. Величина γ выбирается заранее, ее выбор зависит от конкретно решаемой задачи. Так, степень доверия авиапассажира к надежности самолета, очевидно, должна быть выше степени доверия покупателя к надежности телевизора, лампочки, игрушки. . . Надежность γ принято выбирать равной 0, 9; 0, 95; 0, 99 или 0, 999. Тогда практически достоверно нахождение параметра 0 в доверительном интервале 24.

Доверительные интервалы для параметров нормального распределения Построим доверительные интервалы для параметров нормального распределения, т. е. когда выборка производится из генеральной совокупности, имеющей нормальное распределение с параметрами а и σ. 25

Доверительный интервал для математического ожидания при известной дисперсии Пусть СВ X ~ N(a, σ); σ — известна, доверительная вероятность (надежность) γ — задана. Пусть х1, х2, . . . , хn — выборка, полученная в результате проведения n независимых наблюдений за СВ X. Чтобы подчеркнуть случайный характер величин х1, х2, . . . , хn , перепишем их в виде Х 1, Х 2, . . . , Хn, т. е. под Xi будем понимать зна -чение СВ X в i-м опыте. Случайные величины Х 1, Х 2, . . . , Хn – независимы, закон распределения любой из них совпадает с законом распределения СВ X (т. е. Xi ~ N(a, σ)). А это зна-чит, что МХ 1 = МХ 2 =. . . = МХn = MX = a, DX 1 = DX 2 =. . . = DXn = DX. 26

Доверительный интервал для математического ожидания при известной дисперсии Выборочное среднее также будет распределено по нормальному закону (примем без доказательства). Параметры распределения X таковы: М( ) = a, D( ) = Действительно, Таким образом, 27

Доверительный интервал для математического ожидания при известной дисперсии Следовательно, пользуясь формулой можно записать где поэтому Из последнего равенства находим или 28

Доверительный интервал для математического ожидания при известной дисперсии В соответствии с определением доверительного интервала получаем, что доверительный интервал для а = MX есть где t определяется из уравнения (или ) при заданном γ по таблице функции Лапласа находим аргумент t. Заметим, что из равенства следует: с возрастанием объема выборки n число ε убывает и, значит, точность оценки увеличивается; увеличение надежности γ влечет уменьшение точности оценки. 29

Доверительный интервал для математического ожидания при известной дисперсии Пример 5. Произведено 5 независимых наблюдений над СВ X ~ N(a, 20). Результаты наблюдений таковы: х1 = — 25, х2 = 34, х3 = — 20, х4 = 10, х5 = 21. Найти оценку для а = MX, а также построить для него 95%-й доверительный интервал. Решение: Находим сначала (-25 + 34 — 20 + 10 + 21) = 4, т. е. =4. Учитывая, что γ = 0, 95 и , получаем Ф 0(t) = 0, 475. По таблице (см. Приложение) выясняем, что t = tγ = 1, 96. Тогда ε = (1, 96 · 20)/√ 5 ≈ 17, 5. Доверительный интервал для а = MX таков: (4 — 17, 5; 4 + 17, 5), т. е. (-13, 5; 21, 5). 30

Доверительный интервал для математического ожидания при неизвестной дисперсии Пусть СВ X ~ N(a, σ); σ — известна, доверительная вероятность (надежность) γ — задана. Найдем такое число ε, чтобы выполнялось соотношение Выполнив ряд преобразований, получим доверительный интервал (для неизвестного математического ожидания СВ X), который покрывает a = MX с вероятностью γ: где S — исправленное среднее квадратическое отклонение СВ X, вычисленное по выборке, находим по таблице квантилей распределения Стьюдента. 31

Доверительный интервал для математического ожидания при неизвестной дисперсии Пример 6. Произведено 5 независимых наблюдений над СВ X ~ N(a, σ). Результаты наблюдений таковы: х1 = — 25, х2 = 34, х3 = — 20, х4 = 10, х5 = 21. Найти оценку для а = MX, а также построить для него 95%-й доверительный интервал. Решение: Из примера 5 находим = 4. Затем определим значение S: S 2 = 1/4·((-25 – 4)2 + (34 – 4)2 + (-20 – 4)2 + (10 – 4)2 + (21 – 4)2) = = 660, 5; S = 25, 7. Учитывая, что γ = 0, 95 и n – 1 =4, получаем по таблице (см. Приложение) tγ = 2, 78. Тогда ε = (2, 78 · 25, 7)/√ 5 ≈ 31, 9. Доверительный интервал для а = MX таков: 32 (4 — 31, 9; 4 + 31, 9), т. е. (-27, 9; 35, 9).

Доверительный интервал для среднего квадратического отклонения нормального распределения Пусть СВ X ~ N(a, σ); σ — неизвестна, доверительная вероятность γ — задана. Можно показать, что если MX = а известно, то доверительный интервал для среднего квадратического отклонения σ имеет вид: Если а = MX неизвестно, то доверительный интервал для неизвестного σ имеет вид: где n — объем выборки, являются квантилями деления, определяемые по таблице квантилей -распре 33

Пример 7. Глубина моря измеряется прибором, систематическая ошибка которого равна нулю, а случайные ошибки распределены нормально с а = 15 м. Сколько надо сделать независимых измерений, чтобы определить глубину моря с ошибкой не более 5 м при надежности 7 = 0, 9? Решение: 34

Я мечтал собрать в одно целое 2 моих основных страстей: Математику, Информатику и Обучение, c самого истока своей карьеры, когда еще обучался в аспирантуре.

Профессиональный математик для школьников и студентов, PhD, педагогический стаж более 19 лет, без промедления   подготовит без посредников контрольной работе по математике на 5 курс с помощью современных методик по улучшению памяти и   мышления. Помощь в оформлении конспектов.

Консультирование по математическим пакетам Maple, Sage и SPSS . Участвует в международных научных конференциях ICML, ICCV и CIKM . Некоторое время поработал директором в стартапе по Machine Learning и Information Retrieval. Без усилий «кодит» на Perl, Node и Erlang.

Занятия проводятся Локально в Москве м. Китай-город и дистанционно по TeamViewer. Более 320 учащихся  поступили «на бюджет» в ВУЗы Москвы: МАИ, ФИ, МЭИ и ВШЭ и т.д.. Опыт репетитора по математике для студентов более 20 лет. Speaks to English.

Котрольная работа по математике

1.
Статистические ряды

Х – изучаемый признак  – случайной величиной.

Произведено
 наблюдений.

Полученные
наблюдения образуют выборку объемом :

.

Значения — варианты.

Результаты наблюдений, записанные в порядке
возрастания вариант:

называются вариационным рядом.

Пример 1. При исследовании состояния лесного массива выявлено на одном гектаре
следующее число пораженных деревьев:

4   12   11  13   15   7   15   6   4   9   10   15.

Расположив
полученные данные в порядке возрастания, получим вариационный ряд:

4   4   6   7   9   10   11   12   13   15   15   15.

Количество
исследованных гектаров – объем выборки .

Если значение  встречается
в наблюдениях   раз, то число  называется частотой величины , а отношение частоты к общему числу
опытов называется относительной частотой  или частостью:

.

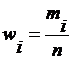
В
примере 1 для варианты        и       .

Важное свойство частот и частостей:

        и ,                        (1)

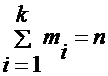
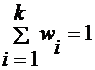
где
 — число различных вариант в
выборке.

В
примере 1 .

Последовательность чисел называется
статистическим рядом и записывается в виде таблицы.

			.  .  .
			.  .  .

Пример 2.  Количество ежедневных нарушений техники безопасности в цехе,
сделанных за месяц, представлено следующими данными:

5     6       5       6       6       4       9       6       4       5

1     4       5       10     10     5       2       2       5       7

4     0       6       5       7       6       9       1       9       4.

Статистический
ряд распределения частот будет иметь вид:

	0	1	2	4	5	6	7	9	10
	1	2	2	5	7	6	2	3	2

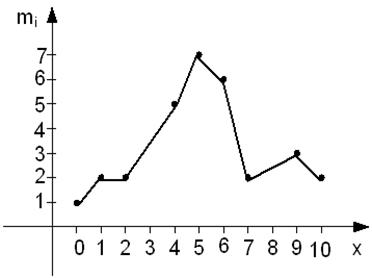
Ломаная линия, соединяющая точки , называется полигоном частот.
Для примера 2 полигон частот имеет вид:

Полигон частот распределения ежедневных нарушений ТБ.

Замечание. Если
вместо значений частот взять значения относительных частот, то  ломаная линия,
соединяющая точки , называется полигоном
относительных частот.

Для непрерывных признаков и при большом объеме выборки
данные группируются, и результаты представляются в виде интервального
статистического ряда.

2.
Оценки
математического ожидания

Статистической оценкой математического ожидания  называется среднее арифметическое
элементов выборки, которая называется выборочное среднее и обозначается .

Для выборки объемом n, заданной
вариационным рядом :

.                                   (2)

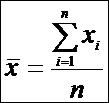
Пример.
В контрольной точке на морской акватории из придонного слоя отобрали 5 проб
воды и определили в них содержание растворенного кислорода, получив следующие
значения (мл/л): 5,07      5,16     
5,19     5,23      5,25.

 Тогда содержание растворённого кислорода в придонном
слое оценим значением

.

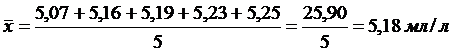
Если учитывается повтор значений вариант, то данные
представляются статистическим рядом

			.  .  .
			.  .  .

и
выборочное среднее рассчитывается по формуле:

                                    (3)

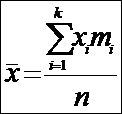
3.
Доверительный
интервал для математического ожидания нормального распределения с известной
дисперсией

Условие (1) для математического ожидания принимает вид

                             (2)

Для
нормального распределения

.         (3)

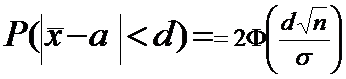
Из
(2) и (3) имеем уравнение для определения d

.                                   (4)

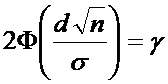
Введем
обозначение: .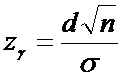

Тогда

.

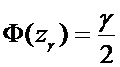
Значение
 определяется по таблице 2 значений
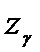
функции Лапласа.

Например,
для     и
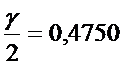
в таблице 2 находим:

1,96	0,4750

Следовательно,.

После определения  определяем
точность оценки по формуле:

                                           (5)

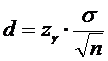
и
границы доверительного интервала:

    и              (6)

Таким образом, с надежностью  доверительный
интервал  содержит в себе генеральное среднее
(математическое ожидание) а или в %
случаев построенный интервал накроет истинное значение параметра а.

Задача. 1. Пусть имеется
генеральная совокупность с некоторой характеристикой, распределенной по
нормальному закону с дисперсией, равной .
Произведена выборка объема  n = 27 и получено выборочное среднее характеристики
. Найти доверительный интервал,
покрывающий неизвестное математическое ожидание исследуемой характеристики
генеральной совокупности с надежностью .

Дано: n = 27, ,
, .

Решение.

1)
По таблице 2 для функции
Лапласа из уравнения

найдем значение .

2) Определим точность оценки d:

.

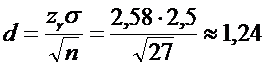
3)Находим границы доверительного интервала:

Отсюда
получаем искомый доверительный интервал:

(10,76; 13,24).

Случай
больших выборок. Приведенные выше
расчеты доверительного интервала применяются и в случаях с неизвестной
дисперсии, но только если объем выборок ,
т.е. в случаях больших выборок.

В
этом случае в формулах (3) и (4) вместо  используется
его вычисленная по выборке несмещенная оценка .

Для примера (из лекций) о концентрации нитратов в
огурцах найдем доверительный интервал генерального среднего с надежностью . При этом мы предполагаем нормальное
распределение концентрации нитратов.

 Имеем ,   .

1)Для   находим по таблице 2 ,

2)Тогда .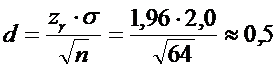

3)       и .

Отсюда
получаем искомый доверительный интервал: (7,0; 8,0).

Минимальный
объем выборки. Если требуется оценить
математическое ожидание с наперед заданной точностью оценки d
и надежностью , то из формулы (3) получим
формулу для минимального объема выборки, который обеспечит эту точность:

.                        

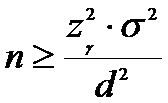
Задача
2. Морская глубина измеряется
прибором, систематическая ошибка измерения которого равна нулю, а случайная ошибка измерения распределена нормально со
среднеквадратическим отклонением 18м. Сколько надо сделать независимых
измерений, чтобы определить глубину моря с точностью 4 м при надежности 0,996?

Решение. Согласно условию задачи . По
таблице 2 для функции Лапласа из уравнения

найдем
значение        .

откуда

.

Поскольку
n – число целое, то .

Доверительный
интервал для математического ожидания нормального распределения с неизвестной
дисперсией

Обычно дисперсия распределения неизвестна и мы можем
только по выборке получить оценки

                    и               
.

По данным выборки построим случайную величину

.

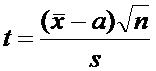
Условие определения доверительного интервала (2)
перепишем в виде

Введем
обозначение: .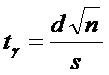

Тогда
последнее уравнение примет вид

.                                          (7)

Значения
, удовлетворяющие уравнению (7)  при
различных значениях  и n,
определяются по таблице 3.

После определения  алгоритм
построения доверительного интервала аналогичен случаю известной дисперсии.

Случайная величина t имеет t-распределение
Стьюдента, вид которого, сильно зависит от объема выборки .

При  распределение
Стьюдента близко к нормальному распределению и можно пользоваться таблицей 2
для нормального распределения.

При  — случай малых
выборок — распределение Стьюдента далеко от нормального. Поэтому в этом
случае использование таблиц распределения Стьюдента необходимо.

Алгоритм построения
доверительного интервала:

1)
Значения ,
удовлетворяющие уравнению (7)  при различных значениях  и
n, определяются по таблице 3

2)
Точность оценки находим по
формуле:

.                                        (8)

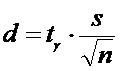
      3)
Находим границы доверительного интервала :

 

.

Пример
1лекции 1 (продолжение).

 Дано:
,

1)По
таблице 3

.

2)Точность

3)
Границы интервала:

.

Получим доверительный интервал (7,5;  12,7).

Оценка
достоверных различий между результатами измерений и фиксированной величиной с
помощью доверительного интервала

В практической деятельности по контролю состояния
окружающей среды нередко возникает необходимость сравнить результаты измерений
с какой-либо заданной фиксированной величиной.

 Наиболее типичный случай – сравнение с величиной
предельно допустимой концентрации (ПДК) загрязняющего вещества в объектах
окружающей среды.

Пусть фиксированная величина – ПДК, тогда

если  >
ПДК  ПДК превышена (с надежностью ):

если  <
ПДК  ПДК не превышена (с надежностью ):

если  <ПДК <  различия
недостоверны (с надежностью ):

.

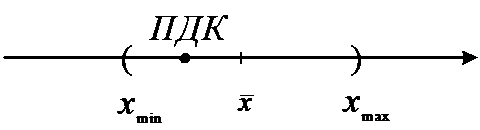
В % случаев наши выводы
могут оказаться неверными.

Задача
3. Произведено девять проб почвы с целью определения,
превышает ли концентрация загрязняющего вещества уровень ПДК, равный 4,2 мг/кг.
Получены следующие результаты в мг/кг:

4.7; 5.8; 3.9; 6.1; 5.1; 4.4; 4.6; 4.1; 4.5

Можно ли с надежностью 0.95 утверждать, что ПДК в
среднем превышена?

Решение.
1)  Вычисляем выборочное среднее:

2)
Вычисляем дисперсию:

и
выборочное среднее отклонение .

3)
Так как   то по таблице 3

.

4) Точность оценки

,

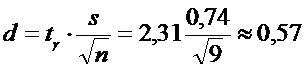
5) Границы интервала:

.

 Получим доверительный интервал
(4,23;5,37) мг/кг.

6)Так как  >
ПДК=4,2, то можно утверждать, что ПДК превышена.

Ответ: Можно с заданной доверительной
вероятностью.

4. Задача.
4.
Пусть имеется генеральная совокупность с некоторой характеристикой,
распределенной по нормальному закону с дисперсией, равной . Произведена выборка объема  n = 27 и
получено выборочное среднее характеристики .
Найти доверительный интервал, покрывающий неизвестное математическое ожидание
исследуемой характеристики генеральной совокупности с надежностью .

Дано: n = 27, , , .

Решение.

2) По таблице 2 для функции Лапласа из
уравнения

найдем значение .

2) Определим точность
оценки d:

.

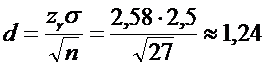
3)Находим границы
доверительного интервала:

Отсюда получаем искомый доверительный
интервал:

(10,76; 13,24).

Случай больших выборок. Приведенные выше расчеты
доверительного интервала применяются и в случаях с неизвестной дисперсии, но
только если объем выборок , т.е. в случаях
больших выборок.

В этом случае в формулах (3) и (4)
вместо  используется его вычисленная по выборке
несмещенная оценка .

Для примера (из
лекций) о концентрации нитратов в огурцах найдем доверительный интервал
генерального среднего с надежностью . При этом мы
предполагаем нормальное распределение концентрации нитратов.

 Имеем ,   .

1)Для   находим
по таблице 2 ,

2)Тогда .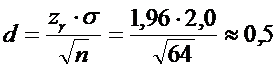

3)       и .

Отсюда получаем искомый доверительный
интервал: (7,0; 8,0).

Минимальный объем выборки. Если требуется оценить
математическое ожидание с наперед заданной точностью оценки d и надежностью , то из формулы (3) получим формулу для
минимального объема выборки, который обеспечит эту точность:

.                        

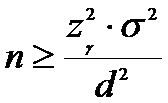
Задача 5. Морская глубина измеряется
прибором, систематическая ошибка измерения которого равна нулю, а случайная ошибка измерения распределена нормально со
среднеквадратическим отклонением 18м. Сколько надо сделать независимых
измерений, чтобы определить глубину моря с точностью 4 м при надежности 0,996?

Решение. Согласно условию задачи . По таблице 2 для функции Лапласа из
уравнения

найдем значение        .

откуда

.

Поскольку n – число целое, то .

5.
Понятие статистической гипотезы

Статистической гипотезой называется предположение о виде распределения или о
параметрах известных распределений.

Гипотезы
о значениях параметров  распределения или о сравнительной величине параметров
двух распределений называются параметрическими гипотезами.

Гипотезы
о виде распределения называются непараметрическими гипотезами.

Проверить статистическую гипотезу – это значит проверить, согласуются ли данные,
полученные из выборки с этой гипотезой.

Гипотезу, выдвинутую для проверки ее согласия с
выборочными данными, называют нулевой гипотезой и обозначают H₀.
Вместе с гипотезой H₀ выдвигается альтернативная
или конкурирующая гипотеза, которая противоречит основной и которая
обозначается H₁.

ПРИМЕРЫ

Гипотеза 1. При исследовании местности было
произведено несколько проб древесины и вычислено, что среднее число пораженных
деревьев на 1 га равно . Через некоторое время
произведено повторное исследование, и среднее число пораженных деревьев стало , причем .

Встает вопрос, расхождение случайно и связано с
недостаточным числом измерений или закономерно и связано с изменением течения
болезни?

Пусть случайная величина Х
−первоначальное состояние всех деревьев;

случайная
величина Y − состояние через некоторое время.

Тогда

.

Гипотеза
2. На акватории в контрольной точке ниже выпуска сточных вод предприятия взяты
пробы воды для определения содержания в воде некоторого загрязняющего вещества.
Полученная средняя концентрация равна ,
причем , где  —
фоновая концентрация загрязняющего вещества, полученная до начала работы
предприятия.

Если
полученное превышение значимо, то предприятие может быть подвергнуто
экономическим санкциям. Поэтому утверждение о превышении фоновой концентрации
должно быть подвергнуто статистической проверки.

Пусть
Х – фоновая концентрация вещества,

    Y – концентрация вещества после начала работы
предприятия.

Задача
проверки гипотез имеет вид:

.

Принятие гипотезы в результате проверки
не означает утверждения, что гипотеза верна. Это лишь означает, что  результаты
наблюдений не дают оснований её отвергнуть. 

Если основная гипотеза отвергается, то
принимается альтернативная гипотеза.

Ошибки принятия
гипотез

Ошибка 1 рода
состоит в том, что будет отвергнута правильная гипотеза.

Ошибка 2 рода
состоит в том, что будет принята неправильная гипотеза.

	принимается	отвергается
верна	Решение правильное	Ошибка 1 рода
неверна	Ошибка 2 рода	Решение правльн

Вероятность  допустить ошибку 1
рода называют уровнем значимости.

6. Проверка гипотезы о равенстве дисперсий

На практике задача сравнения дисперсий возникает, если
требуется сравнить точность приборов, инструментов, методов измерений,
технологий.

Очевидно, предпочтительнее взять тот прибор,
инструмент и т.п., который обеспечивает наименьшее рассеяние результатов
измерений, т.е. наименьшую дисперсию.

Проведем
измерения на двух приборах.

Пусть все возможные измерения первым прибором − Х 
и этим прибором проведено  измерений, и по ним
вычислена  − оценка .

Пусть все возможные измерения первым прибором − Y 
и этим прибором проведено  измерений, и по ним
вычислена  − оценка ,
причем  .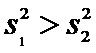

Требуется по выборочным средним и заданном  проверить значимость этого различия.

Краткое
условие:

Х:                   ,

Y:                   , причем                        .

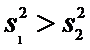
Сформулируем
гипотезу:

Зададим
 или  в
зависимости от конкретной задачи.

Вычислим

,                                    

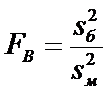
где 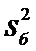 — большая дисперсия,
а  — меньшая дисперсия.

Соответствующая
случайная величина F − статистический критерий данной задачи
−  имеет распределение Фишера – Снедекора.

Если
, то выборочное значение критерия

.

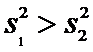
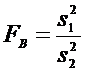
Критическая
область  — правосторонняя.

Для
определения  найдем степени свободы:

,         

где
 — объем выборки с большей дисперсией  

 — объем выборки с меньшей дисперсией .

По
таблице 7 определим

.

Сравниваем
 с :

—
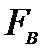
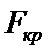
если   , принимаем, (различие в оценках дисперсии
незначимо и точности обоих приборов одинаковы);

—
если   , принимаем
. (отклоняем гипотезу . Второй прибор точнее.)

Задача
6.
Для проверки точности дозировки двух автоматов по упаковке химического вещества
отобраны от первого автомата 12 проб, от второго – 15 проб. По отобранным
пробам рассчитаны оценки дисперсии: 11,41 и 6,52 соответственно. Можно ли на
основе сделанных измерений и по уровню значимости 0,05 сделать вывод, что
второй прибор точнее.

Краткое 
условие:

 Х: 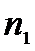   =12              =11,41

Y:     =15       =6,52,

Согласно
условию                       .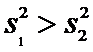

Решение.

.

Так
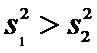
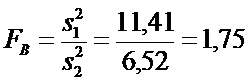
как  вычисляем

.

Для
определения  определим

.

По
таблице 7

.

Так
как

   принимаем.

Это
означает, что точности автоматов по упаковке химического вещества одинаковы.

Схема
решения:

Ho	H1	Статистика критерия	Критические точки	Условие принятия Ho
			таблица 7

7. Проверка
гипотезы о числовом значении среднего нормального распределения

Рассмотрим производство, при котором автоматически
должен соблюдаться некоторый параметр производимых изделий.

Значение параметра для каждого отдельного изделия
может, естественно, как отклоняться от заданного номинала.

Очевидно, что для того, чтобы проверить правильность
настройки станка, надо убедиться в том, что среднее значение параметра у
производимых на нем изделий будет соответствовать номиналу, т.е. проверить
гипотезу

.

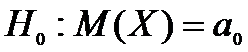
Здесь Х – нормально распределенная генеральная
совокупность значений этого параметра.

Гипотезы о
числовом значении среднего нормального распределения

(случай известной дисперсии)

Предположение о том, что дисперсия известна, оправдано
для случай большой выборки. Так же это оправдано, если данным методом ранее уже
было произведено множество измерений и дисперсия определена.

Пусть из совокупности Х с известной
дисперсией  сделана выборка объемом , и по наблюдениям вычислено . Пусть  —
предполагаемое значение для М(Х) и .
Требуется по выборочным средним и заданном уровне значимости проверить
значимость этого различия.

Кратко:

Х:              известна.

Для
поставленной задачи выдвинем гипотезу

.

Альтернативная
гипотеза может иметь  вид:

а)  или ,

б) .

Случайная величина N имеет
нормальное распределение N(O,1),

По
выборке вычисляем

.

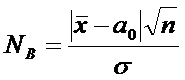
Случайная величина N имеет
нормальное распределение N(O,1),

Схема
решения:

Ho	H1	Статистика критерия	Критические точки	Условие принятия Ho
		таблица 2

Задача
7. Установлено, что средний вес таблетки лекарства
сильного действия должен быть равен мг. Выборочная
проверка 121 таблетки полученной партии лекарства показала, что средний вес
таблетки этой партии  мг. Требуется проверить
значимость этого превышения нормы при уровне значимости 0,01. Многократными
предварительными опытами по взвешиванию таблеток, поставляемых фармацевтическим
заводом, было установлено, что вес таблеток распределен нормально со средним
квадратичным отклонением мг.

Решение.
Кратко:

Х:     =121    =0,53   .

Для
поставленной задачи выдвинем гипотезы

.

По
выборке вычисляем

.

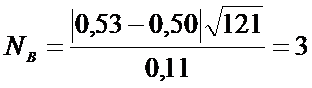
Критическая
точка  является решением уравнения

,

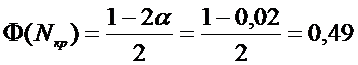
и 
по таблице 2 находим =2,34.

Так
как

 

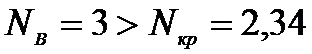
отвергаем
гипотезу   и принимаем гипотезу , что означает, различие в весе таблетки
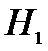
значимо.

А
это значит, что партия таблеток не может быть пущена в продажу.
Фармацевтическая фирма терпит убытки.

Если
бы эти таблетки были пущены в продажу, то была бы совершена ошибка 2 рода, и
она могла бы иметь очень серьезные последствия для здоровья людей.

Гипотезы о
числовом значении среднего нормального распределения

 (случай неизвестной дисперсии)

Схема
решения:

Ho	H1	Статистика критерия	Критические точки	Условие принятия Ho
			таблица 6

9. Проверка гипотезы
о равенстве средних двух нормальных совокупностей

(зависимые выборки)

Ранее при сравнении средних двух серий измерений
предполагалось, что эти измерения проводятся независимо друг от друга.

Такое условие не выполняется, если следим за развитием
болезни у одних и тех же больных.

Пусть, например, группа объектов подвергается какому-то
воздействию. Измеряется некоторый признак до и после воздействия.

Требуется проверить влияние воздействия на данный
признак. 

В этом случае задачу сравнения средних двух
совокупностей можно переформулировать.

Будем рассматривать разность значений признака до и
после лечения у одних и тех же объектов.

Тогда это значение предположительно равно нулю
(нулевая гипотеза) и можно применить весь аппарат проверки гипотезы о равенстве
среднего предполагаемому значению.

Пусть значение признака в первой серии взяты из
генеральной совокупности Х, а во второй – Y. 

Из этих совокупностей произведены выборки одинакового
объема , варианты которых равны  и .
Рассмотрим случайную величину

 D= Y
—X,

варианты
которой имеют значения

.

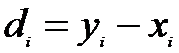
Тогда условие задачи сводится к проверке гипотезы

.

Задача
8. Пусть 10 пациентов получали изучаемый метод лечения,
и у каждого пациента измерялось значение признака до после лечения:

до	0,8	0,9	2,5	1,2	1,3	1,5	1,6	2,1	2,0	1,0
после	4,8	5,9	6,5	4,7	6,3	6,5	5,1	6,1	4,0	6,0

Требуется,
при  проверить оказало ли лечение влияние на
изучаемый признак.

Решение. 
Вычислим значения разностей :

di

4,0

5,0

4,0

3,5

5,0

5,0

3,5

4,0

2,0

5,0

и
рассчитаем требуемые числовые характеристики:

        .

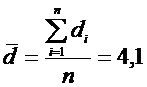
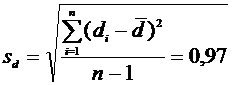
По
полученным данным рассчитаем

.

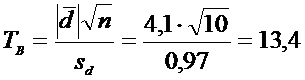
Определим границы
двусторонней критической области:

,

.

Так как    , то принимаем гипотезу . Следовательно, лечение оказало влияние
на изучаемый признак.

Аналогичные задачи возникают,
если одни и те же пробы почвы анализируются разными  методами.

10. Точечные статистические оценки
параметров двумерных совокупностей

Пусть требуется обработать результаты наблюдений двух
величин X и Y.

Таблицы наблюдений

Если число наблюдений n небольшое,
то результаты наблюдений  представляются в
виде таблицы наблюдений

			.  .  .
			.  .  .

Для вычисления числовых характеристик в этом случае
таблицу наблюдений удобно дополнить до следующей таблицы:

№	1	2		n	суммы
xi	x1	x2	…	xn
yi	y1	y2	…	yn
xi2	x12	x22	…	xk2
yi2	y12	y22	…	yn2
xi yi	x1y1	x2y2	…	xnyn

Используя последний столбец таблицы, находим оценки
числовых характеристик.

Оценками математических ожиданий являются выборочные
средние значения

                                  ,            (4)

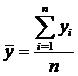
Несмещенные
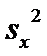
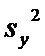
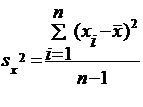
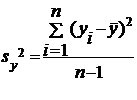
оценки дисперсий  и :

                                      (5)

Расчетные
формулы:

,         (6)

.                (7)

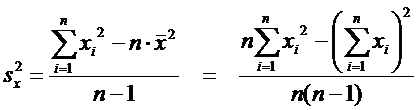
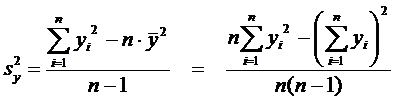
Несмещенная оценка корреляционного момента называется эмпирический
корреляционный момент:

                             (8)

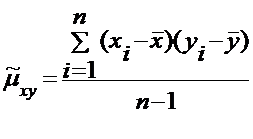
Оценка
коэффициента корреляции:

,                                                      (9)

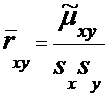
и

                                           (10)

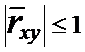
Расчетные
формулы:

                

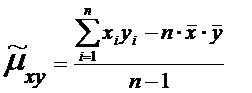
или

              (11)

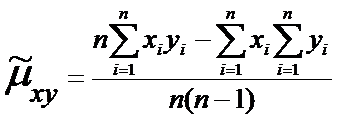
и

       (12)

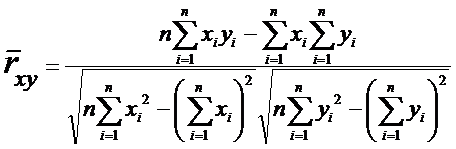
Замечание. Применяются также выборочные оценки дисперсий:

             .

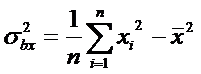
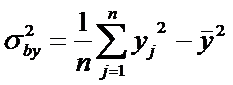
и выборочный
корреляционный момент

или

При
этом

          

                           

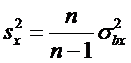
Выборочный корреляционный момент и выборочные
дисперсии  являются смещенными оценками корреляционного момента и дисперсий.

Пример. Дана таблица наблюдений

номер наблюдения	x	y
1	1	3,3
2	1,4	2,0
3	1,8	5,8
4	2,2	4,1
5	2,6	5,2
6	3	7,3

Решение:

Для вычисления оценок
числовых характеристик заполним следующую таблицу

номер наблюдения	1	2	3	4	5	6	суммы
xi	1,0	1,4	1,8	2,2	2,6	3,0	12,0
yi	3,3	2,0	5,8	4,1	5,2	7,3	27,7
xi2	1,00	1,96	3,24	4,84	6,76	9,00	26,8
yi2	10,89	4,00	33,64	16,81	27,04	53,29	145,67
xi yi	3,30	2,80	10,44	9,02	13,52	21,90	60,98

По суммам в последнем столбце
рассчитаем числовые характеристики

                                  ,       

,    

     

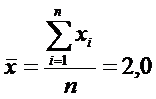
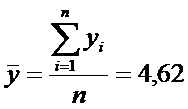
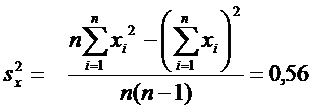
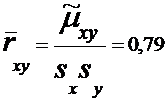
Проверка значимости коэффициента корреляции

Пусть известно, что проведены наблюдения для  нормально
распределенной двумерной характеристики (X; Y).

При  между переменами
отсутствует линейная корреляция. Если оценка , то,
так как число наблюдений ограничено, нельзя заключить, что коэффициент
корреляции 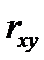 также отличен от нуля.

Тем самым требуется проверить, действительно ли
величины X и Y линейно коррелированны или это вызвано случайными
факторами.

Для этого при заданном уровне значимости  проводится проверка гипотезы

,

.

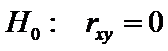
При
справедливости гипотезы  статистический
критерий

                                  (13)

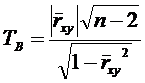
имеет
распределение Стьюдента с  степенями свободы.

Поэтому
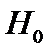
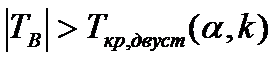
гипотеза  отвергается, если

,                              (14)

а
значения  определяется по таблице 6.

11. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ

Пусть исходная информация
задана таблицей наблюдений

			.  .  .
			.  .  .

Тогда

                (2)

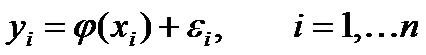
         В основе метода
наименьших квадратов (метод МНК) лежит критерий    минимизации суммы
квадратов ошибок ., т.е.

              (3)

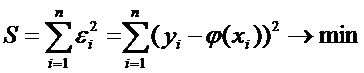
1)  
Линейная регрессия.

Пусть

                                                     (4)

где и
  — некоторые параметры. Тогда задача
(2) имеет вид

          (5)

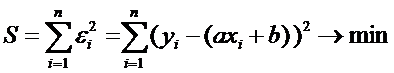
Нахождение минимума функции
двух переменных  сводится к решению системы
уравнений

                                                 (6)

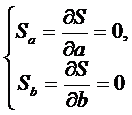
или

Раскрыв скобки, и проведя
преобразования, получим

систему

.                                           (7)

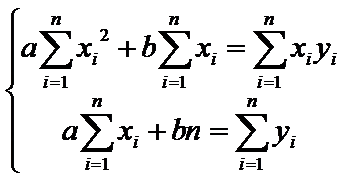
Решая эту систему, найдем,
что

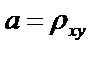
, а                                         (8)

т.е. получим коэффициенты выборочного
уравнения линейной регрессии. тем самым прямая, построенная по методу МНК
совпадает с выборочным уравнением линейной регрессии.

2) Квадратичная регрессия

Пусть

                                         (9)

где ,
 и  —
некоторые параметры. Тогда задача (2) имеет вид

       (10)

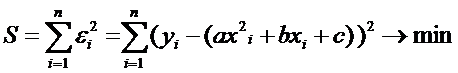
Нахождение минимума функции
двух переменных  сводится к решению системы
уравнений

                                                 (11)

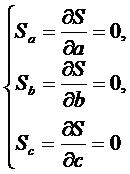
или

                (12)

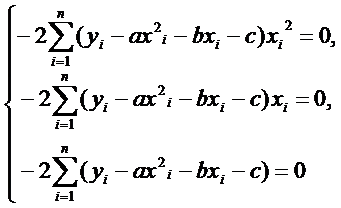
3)
Другие виды функции регрессии.

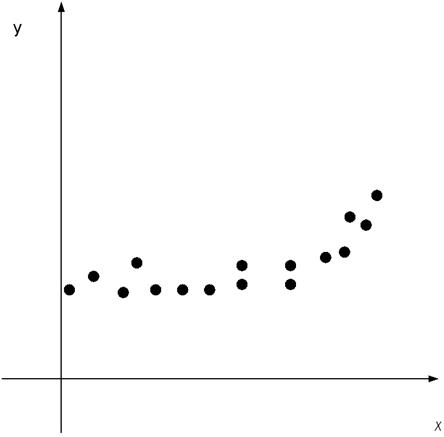
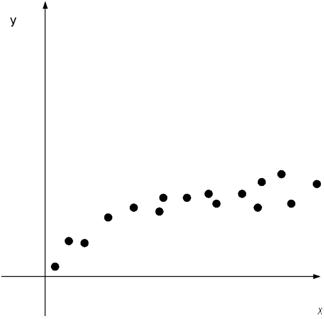
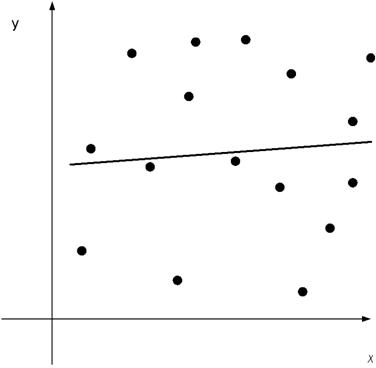
Если диаграмма рассеяния
имеет вид

то
функцию регрессии ищут в виде

Поиск
неизвестных коэффициентов и  производится путем логарифмирования
уравнения:

Обозначим
,  и . Тогда в новых переменных уравнение
регрессии примет линейный вид:

,

и
коэффициенты А и В ищем методом МНК для линейной регрессии.

Пример.
В результате многолетних исследований толщины слоя ила после разлива на
пойменных лугах в зависимости от толщины снежного покрова получены следующие
данные

толщина снежного покрова , см	1	2	3	4	5	6	7
толщина слоя ила, см	0,5	1,0	1,4	1,7	1,8	1,9	2,0

Требуется
найти зависимость между толщиной снежного покрова и толщиной слоя ила.

Решение. Пусть x – толщина слоя снега, а y – толщина
слоя ила. Предполагаем, что зависимость между ними имеет вид

Введя обозначения  ,  и , для линейной регрессии:

,

Система (7) имеет вид

                                          (13)

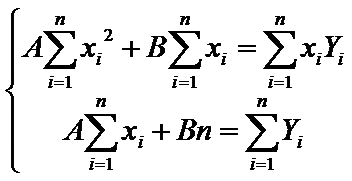
составим таблицу

					0,5	-0,3010	1	-0,3010
2	1,0	0	4	0
3	1,4	0,1461	9	0,4383
4	1,7	0,2304	16	0,9216
5	1,8	0,2553	25	1,2765
6	1,9	0,2788	36	1,6728
7	2,0	0,3010	49	2,1070
28	10,3	0,9106	140	6,1152

Система (13) тогда имеет вид

,

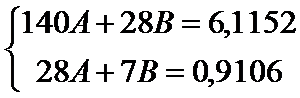
Решив систему, и сделав
преобразование ,  получим:

.

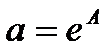
Следовательно,
уравнение регрессии для зависимости толщины слоя ила от толщины снежного
покрова имеет вид:

.

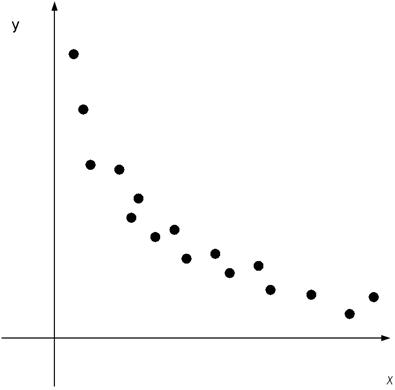
Если диаграмма рассеяния
имеет вид

то функцию регрессии ищем в
виде

Это уравнение также может
быть линеаризовано путем перехода к переменным

,

в которых уравнение имеет вид

.

Если диаграмма рассеяния
имеет вид

то зависимость между
переменными можно искать в виде

которое может быть
линеаризовано, положив 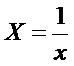. Тогда уравнение
имеет вид

.

            12.            Выборочная линейная
регрессия

Определение. Выборочным уравнением линейной регрессии Y на X называется уравнение

                               (1)

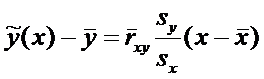
где
 — значения линии регрессии, причем
величина

                          (2)

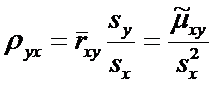
называется
коэффициентом линейной регрессии Y на X.

Выборочное уравнение линейной регрессии (1) может быть
приведено к виду

,                                   (3)

в
котором

        и       .                       (4)

Рассмотрим положение точек наблюдения  относительно выборочной линейной
регрессии.

Если
, то

Если
, то

Если
, то

Если
, то

Если
, то

Чем ближе к единице, тем
«теснее» расположены точки наблюдений относительно выборочного уравнения
линейной регрессии.

Тогда выборочное уравнение линейной регрессии может
приближенно описывать функцию регрессии ,
т.е. считаться её оценкой.

Чем меньше , тем расплывчатее
«облако» наблюдений, тем в меньшей степени уравнение линейной регрессии
отражает связь между наблюдениями.

Коэффициент корреляции  является
показателем тесноты линейной зависимости между переменными.

13. Доверительный
интервал для линейной регрессии

Пусть  — измерения величины
y при различных значениях  независимой
величины x.

Считаем, что Y –
случайная величина, а X – неслучайная.

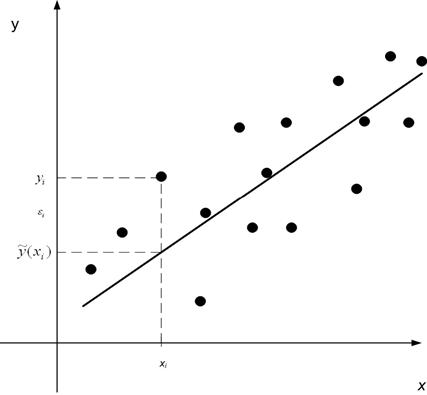
По этим измерениям ищем функцию регрессии , предполагая, что она линейная.

Оценим функцию регрессии с помощью выборочной линейной
функцией регрессии:

Для любых пар наблюдений  можно
записать соотношение

,    (5)

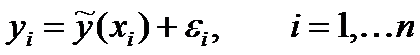
где
 — случайные ошибки измерений, а

.

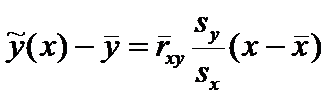
Пусть случайные ошибки измерений удовлетворяют
условиям:

1)
 они независимы;

2)
,
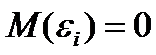
что означает отсутствие систематической ошибки измерений;

3)
,
что означает, что разброс ошибок измерений не зависит от значения x.

4)
 Случайные ошибки измерений
распределены по нормальному закону.

Воздействие
случайных ошибок определяется с помощью остаточной дисперсии

.              (6)

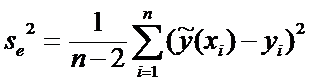
Выборочное линейное уравнение регрессии приближенно
описывает зависимость у от x:

.

ЗАДАЧА: определить область на плоскости, в которой с
заданной вероятностью  находится функция регрессии .

Данная область называется доверительный интервал
для условного математического ожидания  и
определяется неравенством

,(7)

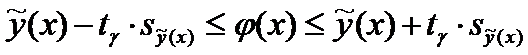
где

                                    (8)

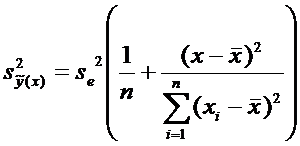
и  определяется по таблице 3 по формуле

                               (9)

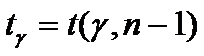
или
по формуле

     ,        (10)

используя
таблицу 6.

Используя
уже полученные оценки, формулу (8) можно преобразовать к виду

            (11)

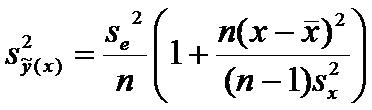
откуда
находим 

.                            (12)

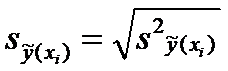
Величина доверительного интервала зависит от значения .

Построение доверительного интервала

Введем
обозначения для значений  нижней и верхней границ доверительного интервала при
значениях :

                             (13)

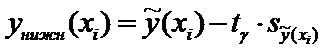
                               (14)

Для построения доверительного интервала добавим строки
в таблицу для вычисления точечных оценок:

Таблица

№	1	2		n	суммы
xi	x1	x2	…	xn
yi	y1	y2	…	yn
xi2	x12	x22	…	xk2
yi2	y12	y22	…	yn2
xi yi	x1y1	x2y2	…	xnyn
			…
			…
			…
			…
			…

График линейной регрессии строится по двум точкам,
причем точка 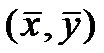 лежит на этой прямой. Границы
доверительного интервала имеют форму гиперболы, причем наименьшее расстояние
между ветвями имеет место в точке .

Ошибка! Ошибка связи.

Заметим, что отдельные наблюдения могут выходить за
пределы построенной области.

         По
мере удаления x от  величина
доверительного интервала увеличивается.

Таким
образом, прогноз значений зависимой переменной y по
уравнению регрессии оправдан, если значение независимой переменной x
не выходит за диапазон ее значений по выборке.

14.
Проверка гипотез об однородности выборок с помощью
критерия «хи-квадрат» (задача с последнего семинара).

16. Критерий Вилкоксона проверки однородности двух
выборок (лекция 12).

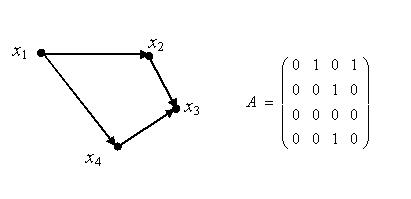
23. Ориентированные графы. Матрица смежности вершин.

Если
в графе G все элементы множества U — дуги, то граф называется ориентированным
(орграфом).

Матрицей
смежности обыкновенного графа
(орграфа), содержащего n вершин, называется квадратная матрица A_n´n , каждый
элемент которой  a_ij ,     i,j=1,…,n,      
определяется следующим образом:

, если существует ребро (дуга),
соединяющее вершины x_i  и  x_j ;

,  в противном случае.

Матрица
смежности ориентированного графа.

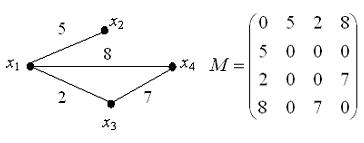
24. Знаковый и взвешенный
орграф.

Взвешенный граф можно задать с
помощью специальной матрицы смежности, в которой при наличии ребра (дуги), 
соединяющего вершины x_i и  x_j в качестве соответствующего
элемента указывается вес этого ребра (дуги).

При изображении графа его вершины можно располагать
произвольно и по своему усмотрению выбирать форму соединяющих их линий. В тех
случаях, если имена вершин несущественны. естественно не различать графы,
отличающиеся лишь именами (порядком) вершин. О таких графах говорят, что они изоморфны.

                   

Матрица
смежности взвешенного неориентированного графа

Знаковый
орграф и его матрица.

…,Х„, т.е. под Х, будем понимать значение с.в. Х в г-м опыте. Случайные величины Хыхз,…,Մ— независимы, закон распределения любой из них совпадает с законом распределения с.в. Х (т.е. Х, М(а, н)). А это значит, что Мхг = Мхз = … = МХ„= МХ = а, вх =вх =…=вх„=вх. Выборочное среднее я Х =Х=~1~ Х; также будет распределено по нормальному закону (примем без доказательства). Параметры распределения Х таковы: М(Х) = а, В(Х) = (72 = —.

Действительно, н(х)=м(„-‘~х,) =„-‘ ~мх, а(х) = а(„-‘~х,) = — ‘, ~ах, = 1=1 ,=1 — „’ ~мх= 1=1 ~вх = „— ‘. МХ = а, н вх = —. и ‘ Таким образом, Х М а, Следовательно, пользуясь формулой Р()Х вЂ” а( < Ц = 2Фо (о) 2Ф® — 1 Доверительный интервал для математического ожидания при известной дисперсии Глава 7. Элементы теории оценок и проверки гипотез ‘ 205 (формула (2.47)), можно записать ‘у = р(~Х вЂ” а~ < е) = 2Фо ~, ~ = 2Фо(1) /Е Ъ/й~ е,/и где ~ = . Из последнего равенства находим (7.3) поэтому у = р /Х вЂ” а/ < — ‘~ = 2Фо(1) или ,Я) р Х вЂ” 1 < а < Х+1 ° = 2Фо(1) = у. (7.4) т/и /ч В соответствии с определением доверительного интервала получаем,что доверительный интервал для а = МХ есть Х вЂ” ~ ~,Х+1 (7.5) где 1 определяется из равенства (7.4), т.е. из уравнения Ф~(~) = 7 (7.б) 1+ у (или Ф(1) = ); при заданном у по таблице функции Лапласа находим аргумент 8.

Заметим, что из равенства (7.3) следует: с возрастанием объема выборки тт число е убывает и, значит, точность оценки увеличивается; увеличение надежности у влечет уменьшение точности оценки. Находим сначала х,: х = — ( — 25+ 34 — 20 + 10+ 21) = 4, т.е. — — 1 7 х = 4. Учитывая, что у = 0,95 и Фо(1) = —, получаем Фо(1) = 0,475. По таблице (см. Приложение) выясняем, что 1 = 1т — — 1,9б. Тогда е = 1,9б 20 17,5 (формула (7.3)). Доверительный интервал для а = тг’5 = МХ (согласно (7.б)) таков: (4 — 17,5;4+ 17,5), т.е.

( — 13,5; 21,5). ° Пример 7.5. Произведено 5 независимых наблюдений над с.в. Х 1У(а,20). Результаты наблюдений таковы: х1 = — 25, хт = 34, хз = = — 20, х4 = 10, хз = 21. Найти оценку для а = МХ, а также построить для него 95%-й доверительный интервал. 206 ° Раздел второй. Основы математической статистики Доверительный интервал для математического ожидания при неизвестной дисперсии Пусть с. в.

Х М(а, и), и — неизвестна, т — задана. Найдем такое число е, чтобы выполнялось соотношение р(Х вЂ” е < а < Х + е1 = т или р()Х вЂ” а) < е) = т. (7.7) Введем случайную величину где Я вЂ” исправленное среднее квадратическое отклонение с. в. Х, вычисленное по выборке: Доказывается, что с.в. Т имеет распределение Стьюдента (см. п. 4.3) с и — 1 степенью свободы. Плотность этого распределения имеет вид: где Г(р) = ог е «Ии — гамма-функция; ~т(~, и — 1) — четная о функция.

Перейдем в левой части равенства (7.7) от с. в. Х к с. в. Т: ~~/й ) или р )Т) < — ) = т или р()Т! < Й,,1 = у, где (7.8) Глава 7. Элементытеорииоценоки проверки гипотез ‘ 207 Величина 8т находится из условия -гт т.е. из равенства 2 /7(1,п — 1) й =.~. о Пользуясь таблицей квантилей распределения Стьюдента (см. приложение 4 на с.

252), находим значение 1 в зависимости от доверительной вероятности 7 и числа степеней свободы и — 1 (1т — квантиль уровня 1 — 7). Определив значение 1 из равенства (7.8), находим значение е: (7.9) Следовательно, равенство (7.7) принимает вид р Х вЂ” Ст < а < Х+~7. ;/т~ тг’и ) А это значит, что интервал Х -47 ~,Х+~т покрывает а = МХ с вероятностью 7, т.е.

является доверительным интервалом для неизвестного математического ожидания с. в. Х. Пример 7.6. По условию примера 7.5, считая, что с.в. Х М(а,~т), П построить для неизвестного МХ = а доверительный интервал. Считать .у = 0,95. О Оценку З для МХ уже знаем: х = 4. Находим значение Я: У = — (( — 25 — 4)з 1+ (34 — 4)~+ ( — 20 — 4)з + (10 — 4)з+ (21 — 4)з) = = бб0,5; Я 25,7. По таблицедля у = 0,95 ип — 1 = 4 находим 17 = 2,78. 25,7 Слецовательно, г = 2,78 — 4 = 31,9. Доверительный интервал таков: (-27,9; 35,9). 208 ° Раздел второй. Основы математической статистики Доверительный интервал для среднего квадратического отклонения нормального распределения < 1Н. Я> 1Н ~0~ Хг Х1 ) г 1 где и — объем выборки, оог = — 2 <Х; — а)г, а г г, г г Х1 = Х1ет ‘ Хг = Х1 —.„ ,и г —;ь г являются квантилями Хг-распределения с и степенями свободы <см. п.

4.3), определяемые по таблице квантилей Хг„„распределения Хг <см. приложение 3 на с. 251). Если а = МХ неизвестпно, то доверительный интервал для неизвестного о имеет вид: с ъ/и — 1 Я 1/и — 1 Я’1 Хг ‘ Х1 /’ в где и — объем выборки, Я г 1 х р <Х, — Х) — исправленное — 1 2 и=1 среднее квадратическое отклонение, квайтили г г Х1 = Х1~-т —;0-1 г г г Хг =Х1-„ в;л-1 г 1+т 1 — 7 определяются по таблице Хг ь при Й = и — 1 и г1 = 2 2 И Г1 = соответственно. Пример 7.7. Для оценки параметра нормально распределенной слу- чайной величины была сделана выборка объема в 30 единиц и вычи- слено Я = 1,5.

Найти доверительный интервал, покрывающий ц с ве- роятностью 7 = 0,90. Имеем и = 30, 7 = 0,9. По таблице Хг ь находим Х1 = Х1 + 0,0 = Х <0,95; 29) = 17,7, ;30 — 1 Пусть с.в. Х 111<а,ц), ц — неизвестно, 7 задано. Можно показать, что если МХ = а известно, то доверительный интервал для среднего квадратического отклонения о имеет вид: Глава 7. Элементы теории оценок и проверки гипотез ° 209 / ° ‘1~ъгм 0 д: ~~ (О 05~ 29): 42 б. ;30-1 Доверительный интервал имеет вид: ~/42,6 ‘ т/17,7 или 1,238 < о < 1,920. Скажем несколько слов о доверительном интервале для оценки вероятности успеха при большом числе испытаний Бернулли. Доверительный интервал, который с надежностью 7 покрывает оцениваемый параметр р при больших значениях и (порядка сотен), имеет вид (рмрд), где Р1 =р* — 1 и и Рг =Р» +1 и, (7.10) Р*(1 — Р*) „ Р*(1 — Р*) где р = — — относительная частота события А; 1 определяется из пА равенства 2Ф0(~) = ~.

Для оценки приближенного равенства р р» можно использовать / е ~/й’1 равенство р(~р* — р( < е) = 2Ф0 ( ) (см. п. 4.1). Упражнения 1. Глубина моря измеряется прибором, систематическая ошибка которого равна нулю, а случайные ошибки распределены нормально с о = 15 м. Сколько надо сделать независимых измерений, чтобы определить глубину моря с ошибкой не более 5 м при надежности 7 = О 9? 2. По условию примера 6.3 найти точечную оценку и доверительный интервал для среднего роста студентов, считать у = 0,95. 3. Производятся независимые испытания с одинаковой, но с неизвестной вероятностью р появления события А в каждом испытании.

Найти доверительный интервал для оценки р с надежностью 0,95, если в 400 испытаниях события А появилось 80 раз. 210 ° Раздел второй. Основы математической статистики 7.5. Проверка статистических гипотез Задачи статистической проверки гипотез Одна из часто встречающихся на практике задач, связанных с применением статистических методов, состоит в решении вопроса о том, должно ли на основании данной выборки быть принято или, напротив, отвергнуто некоторое предположение (гипотеза) относительно генеральной совокупности (случайной величины).

Например, новое лекарство испытано на определенном числе людей. Можно ли сделать по данным результатам лечения обоснованный вывод о том, что новое лекарство более эффективно, чем применявшиеся ранее методы лечения? Аналогичный вопрос логично задать, говоря о новом правиле поступления в вуз, о новом методе обучения, о пользе быстрой ходьбы, о преимуществах новой модели автомобиля или технологического процесса и т. д. Процедура сопоставления высказанного предположения (гипотезы) с выборочными данными называется проверкой гипотез. Задачи статистической проверки гипотез ставятся в следующем виде: относительно некоторой генеральной совокупности высказываечся та или иная гипотеза Н.

Из этой генеральной совокупности извлекается выборка. Требуется указать правило, при помощи которого можно было бы по выборке решить вопрос о том, следует ли отклонить гипотезу Н или принять ее. Следует отметить, что статистическими методами гипотезу можно только опровергнуть или не опровергнуть, но не доказать. Например, для проверки утверждения (гипотеза Н) автора, что «в рукописи нет ошибок», рецензент прочел (изучил) несколько страниц рукописи. Если он обнаружил хотя бы одну ошибку, то гипотеза Н отвергается, в противном случае — не отвергается, говорят, что «результат проверки с гипотезой согласуется».