Вглядываясь в зеркала или еще раз о проблеме гетероскедастичности
Время на прочтение
2 мин
Количество просмотров 1.3K
Секунда теории
Гетероскедастичность – это ситуация, когда ошибка регрессии не удовлетворяет условию гомоскедастичности, т.е. дисперсия этой самой ошибки непостоянно. Это приводит при использовании метода наименьших квадратов к разным неприятным эффектам смещения значений оценок, что ставит под сомнение смысл всей проделанной на основании данного уравнения регрессии работы.
В странствиях по CRAN-у попался пакет skedastic, в котором реализованы 25 разных тестов гомоскедастичности – о нем и поговорим.
О тестах
Вдумчивый разбор математического основания всех реализованных тестов – это дело статьи в специализированном журнале, дело данной заметки – посмотреть, как они работают.
Возьмем из пакета UsingR данные о бриллиантах diamond и посмотрим уравнение регрессии (цена зависит от веса)
library(tidyverse)
library(ggplot2)
library(skedastic)
library(AER)
library(gvlma)
library(UsingR)
data(diamond)
ggplot(data = diamond, aes(x=carat, y=price)) + geom_point()
model_1 <- lm(price~carat, data=diamond)
summary(model_1)
gvlma(model_1)
ggplot(data = diamond, aes(x=carat, y=model_1$residuals)) + geom_point() + ylab("Error of model")На графике видна классическая линейная зависимость. Соответствующая модель значима и даже (по версии пакета gvlma) все условия Гаусса-Маркова выполняются
График ошибок говорит о том же самом:
Есть значительные основания полагать, что гетероскедастичности тут нет. Теперь посмотрим на результаты применения пакета skedastic (во всех тестах нулевая гипотеза: есть гомоскедастичность; при уровне значимости меньше заданного, допустим, 0.05, она будет отвергнута):
Собственно, тесты почти единодушны: 24 из 25 (кроме теста Хонды) указали, что нулевая гипотеза не может быть отвергнута, значит, можно смело говорить про гомоскедастичность.
Эксперимент
Самое интересное, правда, другое – вопрос о том, насколько эти тесты определяют гетероскедастичность, когда у нас она есть. Создадим искусственный датафрейм по формуле y = ax+b+e(1+s|x|) при разных значениях s. При s=0 у нас классическая гомоскедастичность (ошибки происходят из нормального распределения), при s=1 – классическая гетероскедастичность (когда дисперсия ошибок растет при увеличении х по модулю). Логично предположить, что нормальное поведение теста в этих случаях – обратная пропорциональность p-значения от значения s. Каждый тест проводился 100 раз на разных значениях a и b, его результаты потом усреднялись. Соответствующие графики представлены ниже:
Собственно, тестов, определяющий данный вид гетероскедастичности, всего 4 (из 25): Диблази-Боуманна, Уайта, Юса и Чжоу. Это говорит о том, что даже если вам тесты показали, что у вас все хорошо, это не значит, что оно так и есть. И это также повод внимательно посмотреть и определить области эффективности этих тестов.
Все материалы, в т.ч. статьи авторов-изобретателей тестов, есть на https://github.com/acheremuhin/Heteroscedacity
Понимание гетероскедастичности в регрессионном анализе
17 авг. 2022 г.
читать 3 мин
В регрессионном анализе гетероскедастичность (иногда пишется как гетероскедастичность) относится к неравномерному разбросу остатков или ошибок. В частности, это относится к случаю, когда имеет место систематическое изменение разброса невязок по диапазону измеренных значений.
Гетероскедастичность является проблемой, потому что обычная регрессия методом наименьших квадратов (OLS) предполагает, что остатки поступают из совокупности с гомоскедастичностью , что означает постоянную дисперсию.
Когда в регрессионном анализе присутствует гетероскедастичность, его результатам становится трудно доверять. В частности, гетероскедастичность увеличивает дисперсию оценок коэффициента регрессии, но регрессионная модель этого не учитывает.
Это повышает вероятность того, что регрессионная модель объявит термин в модели статистически значимым, хотя на самом деле это не так.
В этом руководстве объясняется, как обнаружить гетероскедастичность, причины гетероскедастичности и потенциальные способы решения проблемы гетероскедастичности.
Как обнаружить гетероскедастичность
Самый простой способ обнаружить гетероскедастичность — использовать график сопоставления значения и остатка .
После того, как вы подгоните линию регрессии к набору данных, вы можете создать диаграмму рассеяния, которая показывает подобранные значения модели в сравнении с остатками этих подобранных значений.
На приведенной ниже диаграмме рассеяния показано типичное подобранное значение по сравнению с остаточным графиком , на котором присутствует гетероскедастичность.
Обратите внимание, как остатки становятся намного более разбросанными по мере того, как подобранные значения становятся больше. Эта форма «конуса» является явным признаком гетероскедастичности.
Что вызывает гетероскедастичность?
Гетероскедастичность возникает естественным образом в наборах данных с большим диапазоном наблюдаемых значений данных. Например:
- Рассмотрим набор данных, который включает годовой доход и расходы 100 000 человек в Соединенных Штатах. Для лиц с более низкими доходами изменчивость соответствующих расходов будет ниже, поскольку у этих людей, вероятно, достаточно денег только для оплаты самого необходимого. Для людей с более высокими доходами будет более высокая изменчивость соответствующих расходов, поскольку у этих людей есть больше денег, которые они могут потратить, если захотят. Некоторые люди с более высоким доходом предпочтут тратить большую часть своего дохода, в то время как некоторые могут предпочесть быть бережливыми и тратить только часть своего дохода, поэтому изменчивость расходов среди этих людей с более высоким доходом по своей сути будет выше.
- Рассмотрим набор данных, включающий население и количество цветочных магазинов в 1000 различных городах США. Для городов с небольшим населением может быть обычным наличие только одного или двух цветочных магазинов. Но в городах с большим населением будет гораздо большая вариабельность количества цветочных магазинов. В этих городах может быть от 10 до 100 магазинов. Это означает, что когда мы создаем регрессионный анализ и используем население для прогнозирования количества цветочных магазинов, по своей сути будет большая изменчивость остатков для городов с более высоким населением.
Некоторые наборы данных просто более склонны к гетероскедастичности, чем другие.
Как исправить гетероскедастичность
Существует три распространенных способа исправить гетероскедастичность:
1. Преобразуйте зависимую переменную
Один из способов исправить гетероскедастичность — каким-то образом преобразовать зависимую переменную. Одним из распространенных преобразований является просто получение журнала зависимой переменной.
Например, если мы используем численность населения (независимая переменная) для прогнозирования количества цветочных магазинов в городе (зависимая переменная), вместо этого мы можем попытаться использовать численность населения для прогнозирования логарифма количества цветочных магазинов в городе.
Использование журнала зависимой переменной, а не исходной зависимой переменной, часто приводит к исчезновению гетероскедастичности.
2. Переопределите зависимую переменную
Другой способ исправить гетероскедастичность — переопределить зависимую переменную. Один из распространенных способов сделать это — использовать скорость для зависимой переменной, а не необработанное значение.
Например, вместо использования численности населения для прогнозирования количества цветочных магазинов в городе мы можем вместо этого использовать численность населения для прогнозирования количества цветочных магазинов на душу населения.
В большинстве случаев это снижает изменчивость, которая естественным образом возникает среди больших групп населения, поскольку мы измеряем количество цветочных магазинов на человека, а не простое количество цветочных магазинов.
3. Используйте взвешенную регрессию
Другой способ исправить гетероскедастичность — использовать взвешенную регрессию. Этот тип регрессии присваивает вес каждой точке данных на основе дисперсии ее подобранного значения.
По сути, это дает небольшие веса точкам данных с более высокой дисперсией, что уменьшает их квадраты невязок. Когда используются правильные веса, это может устранить проблему гетероскедастичности.
Вывод
Гетероскедастичность — довольно распространенная проблема, когда дело доходит до регрессионного анализа, потому что многие наборы данных по своей природе склонны к непостоянной дисперсии.
Однако, используя график сравнения подобранного значения с остатком , можно довольно легко обнаружить гетероскедастичность.
А путем преобразования зависимой переменной, переопределения зависимой переменной или использования взвешенной регрессии проблему гетероскедастичности часто можно устранить.
При проведении регрессионного анализа, основанного на методе наименьших квадратов, на практике следует обратить серьезное внимание на проблемы, связанные с выполнимостью свойств случайных отклонений моделей. Как мы отмечали ранее, свойства оценок коэффициентов регрессии напрямую зависят от свойств случайного члена в уравнении регрессии. Для получения качественных оценок необходимо следить за выполнимостью предпосылок МНК (условий Гаусса− Маркова), т. к. при их нарушении МНК может давать оценки с плохими статистическими свойствами. При этом существуют другие методы определения более точных оценок. Одной из ключевых предпосылок МНК является условие постоянства дисперсий случайных отклонений (см. параграф 5.1, предпосылка 20):
дисперсия случайных отклонений εi постоянна. D(εi)=D(εj) = σ2 для любых наблюдений i и j.
Выполнимость данной предпосылки называется гомоскедастич-
ностью (постоянством дисперсии отклонений). Невыполнимость данной предпосылки называется гетероскедастичностью (непостоянством дисперсий отклонений).
В данной главе мы подробно проанализируем суть гетероскедастичности, ее причины и последствия, а также приведем несколько способов смягчения этих последствий.
8.1. Суть гетероскедастичности
При рассмотрении выборочных данных требование постоянства дисперсии случайных отклонений может вызвать определенное недоумение в силу того, что при каждом i-м наблюдении имеется единственное значение εi. Откуда же появляется разброс? Дело в том, что при рассмотрении выборочных данных мы имеем дело с конкретными реализациями зависимой переменной yi и соответственно c определенными случайными отклонениями εi, i = 1, 2, …, n. Но до осуществления выборки эти показатели априори могли принимать произвольные значения на основе некоторых вероятностных распределений. Одним из требований к этим распределениям является равенство дисперсий. Данное условие подразумевает, что несмотря на то что при каждом конкретном наблюдении случайное отклонение может быть большим либо маленьким, положительным либо отрицательным, не должно быть некой априорной причины, вызывающей большую
209
ошибку (отклонение) при одних наблюдениях и меньшую − при других.
Однако на практике гетероскедастичность не так уж и редка. Зачастую есть основания считать, что вероятностные распределения случайных отклонений εi при различных наблюдениях будут различными. Это не означает, что случайные отклонения обязательно будут большими при определенных наблюдениях и малыми − при других, но это означает, что априорная вероятность этого велика. Поэтому важно понимать суть этого явления и его последствия.
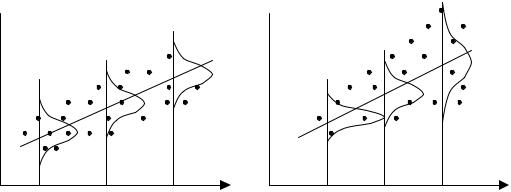
На рис. 8.1 приведены два примера линейной регрессии − зависимости потребления С от дохода I: C = β0 + β1I + ε.
C
|
I1 |
Ik |
In |
I |
I1 |
Ik |
In |
I |
|
а |
б |
Рис. 8.1
В обоих случаях с ростом дохода растет среднее значение потребления. Но если на рис. 8.1, а дисперсия потребления остается одной и той же для различных уровней дохода, то на рис. 8.1, б при аналогичной зависимости среднего потребления от дохода дисперсия потребления не остается постоянной, а увеличивается с ростом дохода. Фактически это означает, что во втором случае субъекты с большим доходом в среднем потребляют больше, чем субъекты с меньшим доходом, и, кроме того, разброс в их потреблении более существенен для большего уровня дохода. Фактически люди с большими доходами имеют больший простор для распределения своего дохода. Реалистичность данной ситуации не вызывает сомнений. Разброс значений потребления вызывает разброс точек наблюдения относительно линии регрессии, что и определяет дисперсию случайных отклонений. Динамика изменения дисперсий (распределений) отклонений для данного примера проиллюстрирована на рис. 8.2. При гомоскедастичности
210
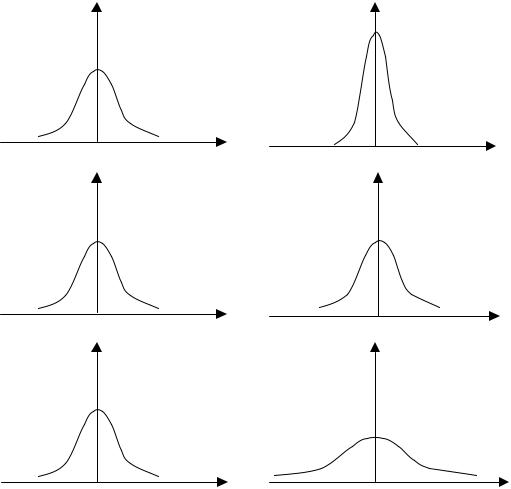
(рис. 8.2, а) дисперсии εi постоянны, а при гетероскедастичности (рис. 8.2, б) дисперсии εi изменяются (в нашем примере − увеличиваются).
|
а − гомоскедастичность |
б − гетероскедастичность |
|
Рис. 8.2 |
Проблема гетероскедастичности в большей степени характерна для перекрестных данных и довольно редко встречается при рассмотрении временных рядов. Это можно объяснить следующим образом. При перекрестных данных учитываются экономические субъекты (потребители, домохозяйства, фирмы, отрасли, страны и т. п.), имеющие различные доходы, размеры, потребности и т. д. Но в этом случае возможны проблемы, связанные с эффектом масштаба. Во временных рядах обычно рассматриваются одни и те же показатели в различные моменты времени (например, ВНП, чистый экспорт, темпы инфляции
211
и т. д. в определенном регионе за определенный период времени). Однако при увеличении (уменьшении) рассматриваемых показателей с течением времени может возникнуть проблема гетероскедастичности.
8.2. Последствия гетероскедастичности
Как отмечалось в разделе 5.1, при рассмотрении классической линейной регрессионной модели МНК дает наилучшие линейные несмещенные оценки (BLUE-оценки) лишь при выполнении ряда предпосылок, одной из которых является постоянство дисперсии отклонений (гомоскедастичность): σ2(εi) = σ2 для всех наблюдений i, i = 1, 2, …, n.
При невыполнимости данной предпосылки (при гетероскедастичности) последствия применения МНК будут следующими.
1.Оценки коэффициентов по-прежнему остаются несмещенными и линейными.
2.Оценки не будут эффективными (т. е. они не будут иметь наименьшую дисперсию по сравнению с другими оценками данного параметра). Они не будут даже асимптотически эффективными. Увеличение дисперсии оценок снижает вероятность получения максимально точных оценок.
3.Дисперсии оценок будут рассчитываться со смещением. Смещенность появляется вследствие того, что необъясненная уравнением
|
2 |
∑ ei2 |
|||
|
регрессии дисперсия S |
= |
(m − число объясняющих пере- |
||
|
n − m − 1 |
менных), которая используется при вычислении оценок дисперсий всех коэффициентов (см. параграф 6.2, (6.23)), не является более несмещенной.
4.Вследствие вышесказанного все выводы, получаемые на основе соответствующих t- и F-статистик, а также интервальные оценки будут ненадежными. Следовательно, статистические выводы, получаемые при стандартных проверках качества оценок, могут быть ошибочными и приводить к неверным заключениям по построенной модели. Вполне вероятно, что стандартные ошибки коэффициентов будут занижены, а следовательно, t-статистики будут завышены. Это может привести к признанию статистически значимыми коэффициентов, таковыми на самом деле не являющимися.
Причину неэффективности оценок МНК при гетероскедастичности легко пояснить следующим примером парной регрессии.
212
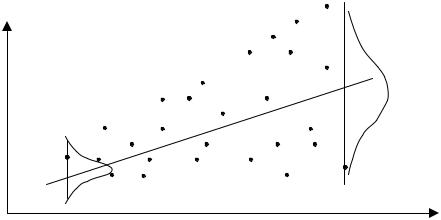
y
Из рис. 8.3 видно, что для каждого конкретного значения хi СВ Х переменная Y принимает значение уi из некоторого множества, имеющего свое распределение, отличное одно от другого в силу непостоянства дисперсий (сравните распределения для значений у1 и уn).
По МНК минимизируется сумма квадратов отклонений
∑ei2 = ∑(yi − b0 − b1xi )2.
Но в этом случае каждое конкретное значение ei2 в данной сумме имеет одинаковый “вес” вне зависимости от того, получено оно из распределения с маленькой дисперсией (например, e12 ) или с большой (например, e2n ). Но это противоречит логике, т. к. точка, полученная
из распределения с меньшей дисперсией, более точно определяет направление линии регрессии. Поэтому она должна иметь больший “вес”, чем точка из распределения с большей дисперсией. Следовательно, методы оценивания, учитывающие “веса” точек наблюдений, позволяют получать более точные (эффективные) оценки. Учет “весов” точек характерен, например, для метода взвешенных наименьших квадратов, рассмотренного ниже.
8.3.Обнаружение гетероскедастичности
Вряде случаев на базе знаний характера данных появление проблемы гетероскедастичности можно предвидеть и попытаться устранить этот недостаток еще на этапе спецификации. Однако значительно чаще эту проблему приходится решать после построения уравнения регрессии.
213
Обнаружение гетероскедастичности в каждом конкретном случае является довольно сложной задачей, т. к. для знания дисперсий отклонений σ2(еi) необходимо знать распределение СВ Y, соответствующее выбранному значению хi СВ Х. На практике зачастую для каждого конкретного значения хi определяется единственное значение уi , что не позволяет оценить дисперсию СВ Y для данного хi .
Естественно, не существует какого-либо однозначного метода определения гетероскедастичности. Однако к настоящему времени для такой проверки разработано довольно большое число тестов и критериев для них. Рассмотрим наиболее популярные и наглядные: графический анализ отклонений, тест ранговой корреляции Спирмена, тест Парка, тест Глейзера, тест Голдфелда−Квандта.
8.3.1. Графический анализ остатков
Использование графического представления отклонений позволяет определиться с наличием гетероскедастичности. В этом случае по оси абсцисс откладывается объясняющая переменная Х (либо линейная комбинация объясняющих переменных Y = b0 + b1X1 + … +
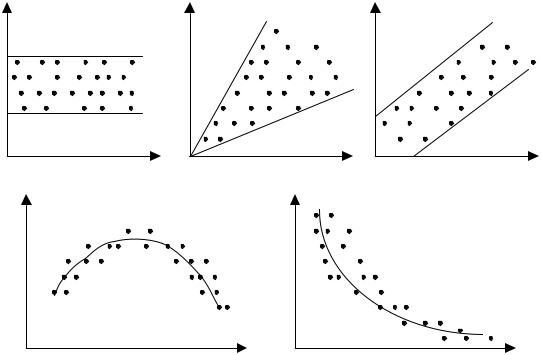
+ bmXm), а по оси ординат либо отклонения еi, либо их квадраты ei2 . Примеры таких графиков приведены на рис. 8.4.
|
а |
xi |
б |
xi |
xi |
|
в |
||||
|
ei2 |
ei2 |
214
На рис. 8.4, а все отклонения ei2 находятся внутри полуполосы постоянной ширины, параллельной оси абсцисс. Это говорит о независимости дисперсий ei2 от значений переменной Х и их постоянстве, т.е. в этом случае мы находимся в условиях гомоскедастичности.
На рис. 8.4, б − г наблюдаются некие систематические изменения в соотношениях между значениями xi переменной Х и квадратами от-
клонений ei2 . Рис. 8.4, б соответствует примеру из параграфа 8.1. На
рис. 8.4, в отражена линейная; 8.4, г − квадратичная; 8.4, д − гиперболическая зависимости между квадратами отклонений и значениями объясняющей переменной Х. Другими словами, ситуации, представленные на рис. 8.4, б − д, отражают большую вероятность наличия гетероскедастичности для рассматриваемых статистических данных.
Отметим, что графический анализ отклонений является удобным и достаточно надежным в случае парной регрессии. При множественной регрессии графический анализ возможен для каждой из объясняющих переменных Хj , j = 1, 2, …, m отдельно. Чаще же вместо объясняющих переменных Хj по оси абсцисс откладывают значения yi ,
получаемые из эмпирического уравнения регрессии. Поскольку по уравнению множественной линейной регрессии yi является линейной
комбинацией хij , j = 1, 2, … , m, то график, отражающий зависимость ei2 от yi , может указать на наличие гетероскедастичности аналогично
ситуациям на рис. 8.4, б − д. Такой анализ наиболее целесообразен при большом количестве объясняющих переменных.
8.3.2. Тест ранговой корреляции Спирмена
При использовании данного теста предполагается, что дисперсия отклонения будет либо увеличиваться, либо уменьшаться с увеличением значения Х. Поэтому для регрессии, построенной по МНК, абсолютные величины отклонений еi и значения хi СВ Х будут коррелированы. Значения хi и еi ранжируются (упорядочиваются по величинам). Затем определяется коэффициент ранговой корреляции:
|
rx,e = 1− 6 |
∑di2 |
, |
(8.1) |
|
|
n(n2 |
−1) |
|||
где di − разность между рангами хi и ei , i = 1, 2, … , n; n − число наблюдений.
Например, если х20 является 25-м по величине среди всех наблюдений Х; а е20 − является 32-м, то di = 25 − 32= −7.
215
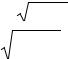
Доказано, что если коэффициент корреляции ρх,е для генеральной совокупности равен нулю, то статистика
|
t = |
rx,e n − 2 |
(8.2) |
|
|
1 − r2 |
|||
|
x,e |
имеет распределение Стьюдента с числом степеней свободы ν = n − 2. Следовательно, если наблюдаемое значение t-статистики, вычисленное по формуле (8.2), превышает tкр. = tα,n−2 (определяемое по таблице критических точек распределения Стьюдента), то необходимо отклонить гипотезу о равенстве нулю коэффициента корреляции ρх,е, а следовательно, и об отсутствии гетероскедастичности. В противном
случае гипотеза об отсутствии гетероскедастичности принимается. Если в модели регрессии больше чем одна объясняющая пере-
менная, то проверка гипотезы может осуществляться с помощью t- статистики для каждой из них отдельно.
8.3.3. Тест Парка
Р. Парк предложил критерий определения гетероскедастичности, дополняющий графический метод некоторыми формальными зависимостями. Предполагается, что дисперсия σi2 = σ2(ei ) является функцией i-го значения хi объясняющей переменной. Парк предложил следующую функциональную зависимость
|
уi2 = у2xвi ev i . |
(8.3) |
|
Прологарифмировав (8.4), получим: |
|
|
lnуi2 = lnу2 + вlnxi + vi . |
(8.4) |
Так как дисперсии уi2 обычно неизвестны, то их заменяют оценками квадратов отклонений ei2 .
|
Критерий Парка включает следующие этапы: |
||
|
1. |
Строится уравнение регрессии yi = b0 + b1xi + еi. |
|
|
2. |
Для каждого наблюдения определяются lnei2 |
) |
|
= ln(yi − yi )2 . |
||
|
3. |
Строится регрессия |
|
|
ln ei2 = α + βlnxi + vi , |
(8.5) |
|
|
где α = lnσ2. |
В случае множественной регрессии зависимость (8.5) строится для каждой объясняющей переменной.
216

4. Проверяется статистическая значимость коэффициента β уравнения
(8.5) на основе t-статистики t = в . Если коэффициент β статисти- Sв
чески значим, то это означает наличие связи между lnei2 и lnxi, т. е. гетероскедастичности в статистических данных.
Отметим, что использование в критерии Парка конкретной функциональной зависимости (8.5) может привести к необоснованным выводам (например, коэффициент β статистически незначим, а гетероскедастичность имеет место). Возможна еще одна проблема. Для случайного отклонения vi в свою очередь может иметь место гетероскедастичность. Поэтому критерий Парка дополняется другими тестами.
8.3.4. Тест Глейзера
Тест Глейзера по своей сути аналогичен тесту Парка и дополняет его анализом других (возможно, более подходящих) зависимостей между дисперсиями отклонений σi и значениями переменной хi. По данному методу оценивается регрессионная зависимость модулей отклонений ei (тесно связанных с σi2) от хi. При этом рассматриваемая зависимость моделируется следующим уравнением регрессии:
|
| ei |= α + βхik + vi . |
(8.6) |
Изменяя значения k, можно построить различные регрессии. Обычно k = …, −1, −0.5, 0.5, 1, … Статистическая значимость коэффициента β в каждом конкретном случае фактически означает наличие гетероскедастичности. Если для нескольких регрессий (8.6) коэффициент β оказывается статистически значимым, то при определении характера зависимости обычно ориентируются на лучшую из них.
Отметим, что так же, как и в тесте Парка, в тесте Глейзера для отклонений vi может нарушаться условие гомоскедастичности. Однако во многих случаях предложенные модели являются достаточно хорошими для определения гетероскедастичности.
8.3.5.Тест Голдфелда−Квандта
Вданном случае также предполагается, что стандартное отклонение σi = σ(εi) пропорционально значению хi переменной Х в этом
наблюдении, т. е. уi2 = у2 xi2 . Предполагается, что εi имеет нормальное распределение и отсутствует автокорреляция остатков.
Тест Голдфелда−Квандта состоит в следующем:
217
1.Все n наблюдений упорядочиваются по величине Х.
2.Вся упорядоченная выборка после этого разбивается на три подвыборки размерностей k, (n − 2k), k соответственно.
3.Оцениваются отдельные регрессии для первой подвыборки (k первых наблюдений) и для третьей подвыборки (k последних наблюдений). Если предположение о пропорциональности дисперсий от-
клонений значениям Х верно, то дисперсия регрессии (сумма квад-
k
ратов отклонений S1 = ∑ei2 ) по первой подвыборке будет сущест-
i=1
венно меньше дисперсии регрессии (суммы квадратов отклонений
n
S3 = ∑ei2 ) по третьей подвыборке.
i=n-k
4.Для сравнения соответствующих дисперсий строится следующая F-статистика:
|
F = |
S3/(k − m − 1) |
= |
S3 . |
(8.7) |
|
S /(k − m − 1) |
S |
|||
|
1 |
1 |
Здесь (k − m − 1) − число степеней свободы соответствующих выборочных дисперсий (m − количество объясняющих переменных в уравнении регрессии).
При сделанных предположениях относительно случайных отклонений построенная F-статистика имеет распределение Фишера с числами степеней свободы ν1 = ν2 = k − m − 1.
|
5. Если Fнабл.= |
S3 |
> Fкр.= F |
, то гипотеза об отсутствии гетероскеда- |
|
|
S1 |
б;н ;н |
|||
|
1 |
2 |
|||
стичности отклоняется (здесь α − выбранный уровень значимости).
Естественным является вопрос, какими должны быть размеры подвыборок для принятия обоснованных решений. Для парной регрессии Голфелд и Квандт предлагают следующие пропорции: n = 30, k = 11; n = 60, k = 22.
Для множественной регрессии данный тест обычно проводится для той объясняющей переменной, которая в наибольшей степени связана с σi. При этом k должно быть больше, чем (m + 1). Если нет уверенности относительно выбора переменной Xj, то данный тест может осуществляться для каждой из объясняющих переменных.
Этот же тест может быть использован при предположении об обратной пропорциональности между σi и значениями объясняющей переменной. При этом статистика Фишера примет вид: F = S1/S3.
218
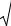
8.4. Методы смягчения проблемы гетероскедастичности
Как отмечалось в разделе 8.2, гетероскедастичность приводит к неэффективности оценок, несмотря на их несмещенность. Это может привести к необоснованным выводам по качеству модели. Поэтому при установлении гетероскедастичности возникает необходимость преобразования модели с целью устранения данного недостатка. Вид преобразования зависит от того, известны или нет дисперсии σi2 отклонений εi .
8.4.1. Метод взвешенных наименьших квадратов (ВНК)
Данный метод применяется при известных для каждого наблюдения значениях σi2. В этом случае можно устранить гетероскедастичность, разделив каждое наблюдаемое значение на соответствующее ему значение дисперсии. В этом суть метода взвешенных наименьших квадратов.
Для простоты изложения опишем ВНК на примере парной ре-
|
грессии: |
||||||||||||||||
|
yi = β0 + β1xi + εi . |
(8.8) |
|||||||||||||||
|
Разделим обе части (9.7) на известное σi |
= |
уi2 |
: |
|||||||||||||
|
yi |
= в0 |
1 |
+ в1 |
xi + |
еi |
. |
(8.9) |
|||||||||
|
уi |
уi |
уi |
||||||||||||||
|
уi |
||||||||||||||||
|
Положив |
yi |
= уi* , |
xi |
= |
xi*, |
ei |
= vi, |
1 |
= zi, получим уравнение |
|||||||
|
уi |
||||||||||||||||
|
уi |
уi |
уi |
регрессии без свободного члена, но с дополнительной объясняющей переменной Z и с “преобразованным” отклонением v:
|
уi* =β0zi + β1xi* + vi. |
(8.10) |
При этом для vi выполняется условие гомоскедастичности. Действительно,
уi2 (vi ) = M(vi − M(vi ))2 = M(vi2 ) − M2 (vi ) .
|
Так как по предпосылке 10 МНК M(ei) = 0, то M(vi ) = |
1 |
M(ei ) = 0, и |
||||||||
|
уi2 |
||||||||||
|
тогда уi2 (vi ) = M(vi2 ) = |
||||||||||
|
= M( |
ei2 |
) = |
1 |
M(ei2 ) = |
1 |
M(ei − M(ei ))2 = |
1 |
уi2 = 1 = const. |
||
|
уi2 |
уi2 |
|||||||||
|
уi2 |
уi2 |
219
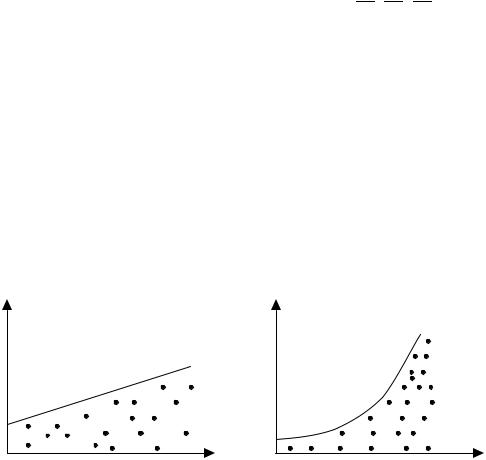
Следовательно, для преобразованной модели (8.10) выполняются предпосылки 10 − 50 МНК. В этом случае оценки, полученные по МНК, будут наилучшими линейными несмещенными оценками.
Таким образом, метод взвешенных наименьших квадратов включает следующие этапы:
1.Каждую из пар наблюдений (хi , уi) делят на известную величину σi . Тем самым наблюдениям с наименьшими дисперсиями придаются наибольшие “веса”, а с максимальными дисперсиями − наименьшие “веса”. Действительно, наблюдения с меньшими дисперсиями отклонений будут более значимыми при оценке коэффициентов регрессии, чем наблюдения с большими дисперсиями. Учет этого факта увеличивает вероятность получения более точных оценок.
1 2. По МНК для преобразованных значений
уi
уравнение регрессии без свободного члена с гарантированными качествами оценок.
8.4.2. Дисперсии отклонений не известны
Для применения ВНК необходимо знать фактические значения дисперсий уi2 отклонений. На практике такие значения известны крайне редко. Следовательно, чтобы применить ВНК, необходимо сделать реалистические предположения о значениях уi2 .
Например, может оказаться целесообразным предположить, что дисперсии уi2 отклонений εi пропорциональны значениям хi (рис.8.5, а) или значениям хi2 (рис. 8.5, б).
Рис. 8.5
1. Дисперсии σ i2 пропорциональны хi (рис. 8.5, а).
уi2 = σ2 хi (σ2 − коэффициент пропорциональности).
220
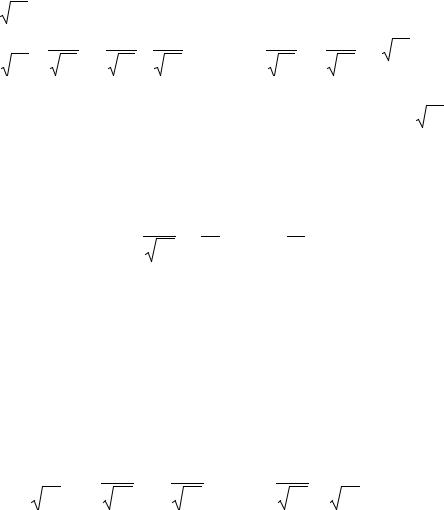
Тогда уравнение (8.9) преобразуется делением его левой и правой частей на xi :
|
yi |
= |
a |
+ b |
xi |
+ |
ei |
yi = a |
1 + b xi + vi . |
(8.11) |
|||
|
xi |
||||||||||||
|
xi |
xi |
xi |
xi |
xi |
||||||||
|
Несложно показать, что для случайных отклонений vi = |
ei |
выпол- |
||||||||||
|
xi |
||||||||||||
няется условие гомоскедастичности. Следовательно, для регрессии (8.11) применим обычный МНК. Действительно, в силу выполнимо-
сти предпосылки уi2 = σ2 (εi) = σ2 хi имеем:
|
у2 (vi ) = у2 ( |
еi |
) = |
1 у2 (еi ) = |
1 у2 xi = у2 = const. |
|
xi |
xi |
xi |
Таким образом, оценив для (8.11) по МНК коэффициенты β0 и β1, затем возвращаются к исходному уравнению регрессии (8.8).
Если в уравнении регрессии присутствует несколько объясняющих переменных, можно поступить следующим образом. Вместо кон-
кретной объясняющей переменной Xj используетсяY исходного уравнения множественной линейной регрессии Y = b0 + b1X1 + … + bmXm ,
т. е. фактически линейная комбинация объясняющих переменных. В этом случае получают следующую регрессию:
|
yi |
1 |
xi1 |
xim |
еi |
||||||
|
= в0 |
) |
+ в1 |
) |
+ … + вm |
) |
+ |
. |
(8.12) |
||
|
) |
) |
|||||||||
|
yi |
yi |
yi |
yi |
yi |
Иногда из всех объясняющих переменных выбирается наиболее подходящая, исходя из графического представления (рис. 8.4).
2. Дисперсия σi2 пропорциональна хi2 (рис. 8.4, б).
В случае, если зависимость σi2 от хi целесообразнее выразить не линейной функцией, а квадратичной, то соответствующим преобразованием будет деление уравнения регрессии (8.8) на хi:
|
yi |
= в0 |
1 |
+ в1 + |
еi |
yi |
= в0 |
1 |
+ в1 + vi |
, где vi = |
еi |
. (8.13) |
|
|
xi |
xi |
|||||||||||
|
xi |
xi |
xi |
xi |
По аналогии с вышеизложенным несложно показать, что для отклонений vi будет выполняться условие гомоскедастичности. После определения по МНК оценок коэффициентов β0 и β1 для уравнения (8.13) возвращаются к исходному уравнению (8.8).
221
Отметим, что для применения описанных выше преобразований существенную роль играют знания об истинных значениях дисперсий отклонений σi2, либо предположения, какими эти дисперсии могут быть. Во многих случаях дисперсии отклонений зависят не от включенных в уравнение регрессии объясняющих переменных, а от тех, которые не включены в модель, но играют существенную роль в исследуемой зависимости. В этом случае они должны быть включены в модель. В ряде случаев для устранения гетероскедастичности необходимо изменить спецификацию модели (например, линейную на логлинейную, мультипликативную на аддитивную и т. п.).
В заключение отметим, что наличие гетероскедастичности не позволяет получить эффективные оценки, что зачастую приводит к необоснованным выводам по их качеству. Обнаружение гетероскедастичности — достаточно трудоемкая проблема и для ее решения разработано несколько методов (тестов). В случае установления наличия гетероскедастичности ее корректировка также представляет довольно серьезную проблему. Одним из возможных решений является метод взвешенных наименьших квадратов (при этом необходима определенная информация либо обоснованные предположения о величинах дисперсий отклонений). На практике имеет смысл попробовать несколько методов определения гетероскедастичности и способов ее корректировки (преобразований, стабилизирующих дисперсию).
Вопросы для самопроверки
1.В чем суть гетероскедастичности?
2.Какое из следующих утверждений верно, ложно или не определено:
а) вследствие гетероскедастичности оценки перестают быть эффективными и состоятельными; б) оценки и дисперсии оценок остаются несмещенными;
в) выводы по t- и F-статистикам являются ненадежными;
г) при наличии гетероскедастичности стандартные ошибки оценок будут заниженными; д) гетероскедастичность проявляется через низкое значение статистики Дар-
бина−Уотсона DW;
е) не существует общего теста для анализа гетероскедастичности;
ж) тест ранговой корреляции Спирмена основан на использовании t- статистики; з) тест Парка является частным случаем теста Глейзера;
и) использование метода взвешенных наименьших квадратов носит ограниченный характер, т. к. для его использования необходимо знать дисперсии отклонений;
222
к) если в парной регрессии дисперсия случайных отклонений пропорциональна величине объясняющей переменной (х), то для получения эффективных оценок необходимо все наблюдаемые значения поделить на х.
3.Приведите аргументы в пользу графического теста, теста Парка и теста Глейзера.
4.Приведите схему теста Голдфелда−Квандта.
5.В чем суть метода взвешенных наименьших квадратов (ВНК)?
6.Объясните кратко, почему при наличии гетероскедастичности ВНК позволяет получить более эффективные оценки, чем обычный МНК.
7.Есть основание считать, что в регрессии, построенной по квартальным данным, случайные отклонения в первых кварталах больше, нежели отклонения в других кварталах. Как это можно проверить?
Упражнения и задачи
1.Пусть зависимость заработной платы (Y) от стажа работы (X) сотрудника выражена следующим уравнением регрессии:
Y = β0 + β1X + γD + ε,
где D − фиктивная переменная, отражающая пол сотрудника. Как можно проверить предположение о том, что пол сотрудника не влияет на дисперсию случайных отклонений εi?
2.Приведены данные в условных единицах по доходам (Х) и расходам на непродовольственные товары (Y) для тридцати домохозяйств:
|
X |
26.2 |
33.1 |
42.5 |
47.0 |
48.5 |
49.0 |
49.1 |
50.9 |
52.4 |
53.2 |
|
|
Y |
10.0 |
11.2 |
15.0 |
20.5 |
21.2 |
19.5 |
23.0 |
19.0 |
19.5 |
18.0 |
|
|
Х |
54.0 |
54.8 |
59.0 |
61.3 |
62.5 |
63.1 |
64.0 |
66.2 |
70.0 |
71.5 |
|
|
Y |
24.5 |
21.5 |
35.4 |
25.0 |
17.3 |
21.6 |
15.3 |
32.6 |
34.0 |
23.8 |
|
|
Х |
73.2 |
75.4 |
76.0 |
80.6 |
81.2 |
83.3 |
92.0 |
95.5 |
103.2 |
110.4 |
|
|
Y |
22.5 |
27.4 |
40.0 |
23.5 |
20.0 |
40.1 |
15.5 |
39.0 |
47.4 |
21.3 |
а) Определите по МНК оценки парного уравнения регрессии yi = b0+ b1xi+ ei. б) Оцените качество построенного уравнения.
в) Проведите графический анализ остатков.
г) Примените для указанных статистических данных ВНК предположение,
что σ2(ei) = σ2xi2.
д) Примените к полученным в п. а) результатам тест ранговой корреляции Спирмена и тест Парка.
е) Определите, существенно ли повлияла гетероскедастичность на качество оценок в уравнении, построенном по МНК.
223
|
3. |
Для предприятий некоторой отрасли анализируют зависимость заработной |
||||||||
|
платы (Y) сотрудников в зависимости от масштаба (от количества сотрудни- |
|||||||||
|
ков) предприятия (Х). Наблюдения по тридцати случайно отобранным пред- |
|||||||||
|
приятиям представлены следующей таблицей: |
|||||||||
|
Y |
X |
||||||||
|
75.5 |
75.5 |
77.5 |
78.5 |
80.0 |
81.0 |
100 |
|||
|
80.5 |
82.0 |
84.5 |
85.0 |
85.5 |
86.5 |
200 |
|||
|
85.5 |
88.5 |
90.0 |
91.0 |
95.0 |
96.0 |
300 |
|||
|
93.0 |
93.5 |
97.5 |
99.0 |
102.5 |
105.0 |
400 |
|||
|
102.0 |
105.5 |
107.0 |
110.5 |
115.0 |
118.5 |
500 |
а) Постройте уравнение регрессии Y на Х и оцените его качество.
б) Можно ли ожидать наличие гетероскедастичности в данном случае. Ответ поясните.
в) Проверьте наличие гетероскедастичности, используя тест Голдфелда− Квандта. Рекомендуется использовать разбиение, при котором k = 12.
г) Если предположить, что гетероскедастичность имеет место, и дисперсии отклонений пропорциональны значениям Х, то какое преобразование вы предложите, чтобы получить несмещенные, эффективные и состоятельные оценки.
д) Постройте новое уравнение регрессии на основе преобразования, осуществленного в предыдущем пункте, и оцените его качество.
е) Сравните результаты, полученные в пунктах а) и д).
4. Пусть для эмпирического уравнения парной регрессии Y = b0 + b1X + e име-
ет место следующее соотношение M(ei2) = σ2xi. Какое преобразование можно предложить, чтобы устранить проблему гетероскедастичности. Опишите поэтапно предложенную схему.
5. Пусть для регрессии Y = b0 + b1X1 + b2X2 + e, оцениваемой по ежегодным данным (1971−1998), получены следующие результаты: сумма квадратов от-
клонений для данных 1971−1980 гг. равна S1 = ∑ei2 = 15, для данных 1981−
1998 гг. эта сумма равна S2 = ∑ei2 = 50. С помощью теста Голдфелда−Квандта проверьте предположение о том, что дисперсия отклонений не постоянна (в частности, что дисперсия претерпела изменение где-то в 1981 г.).
6. Анализируется объем инвестиций для вымышленной страны. По данным с 1961 по 1990 г. построены два уравнения регрессии:
|
1) |
it = |
52.5 + 0.275gnpt |
− 0.63ct , |
R2 = 0.98. |
|||||||
|
(t) = (12.5) (10.2) |
(6.4) |
||||||||||
|
2) |
it |
= 50.7 |
1 |
+ |
0.27 − |
0.62 |
ct |
, |
|||
|
gnpt |
gnpt |
gnpt |
|||||||||
|
R2 = 0.87, |
|||||||||||
|
(t) |
(13.3) |
(9.3) |
(6.9) |
224
где GNP − валовой национальный продукт; С − совокупное частное потребление; I − объем инвестиций; gnpt, ct, it − значения соответствующих показателей в момент времени t.
а) Что могло послужить причиной преобразования первого уравнения во второе?
б) Если причиной преобразования являлась гетероскедастичность, то какое предположение о дисперсии отклонений являлось основанием для данного преобразования?
в) Можно ли сравнить качества обоих уравнений на основе коэффициентов детерминации? Ответ поясните.
г) Должно ли преобразованное уравнение проходить через начало координат?
7.Выдвигается предположение, что средняя заработная плата наемных рабочих пропорциональна их стажу. Для анализа данного утверждения обследуются по 20 рабочих восьми категорий стажа. Получены следующие статистические данные:
|
Стаж |
[0, 5) [5, 10) [10, 15) [15, 20) [20, 25) [25, 30) [30, 35) [35, 40] |
|
З/п |
10000 12500 14300 18700 25400 29000 32000 34300 |
а) Постройте эмпирическое уравнение регрессии, в котором заработная плата является зависимой переменной, а стаж работы − объясняющей переменной (уравнение строится в предположение, что дисперсии отклонений постоянны).
б) Оцените качество построенной регрессии.
в) Есть ли основания считать, что для данной регрессионной модели весьма вероятна гетероскедастичность? Если да, то почему?
г) Предполагая, что дисперсия отклонений пропорциональна трудовому стажу, постройте на основании тех же данных уравнение по методу взвешенных наименьших квадратов (ВНК).
д) Предполагая, что дисперсия отклонений пропорциональна квадрату величины трудового стажа, постройте по ВНК соответствующее уравнение регрессии.
е) Какое из трех предположений относительно дисперсии отклонений наиболее реалистично с вашей точки зрения?
8.Исследуется зависимость между доходом (Х) домохозяйства и его расходом
(Y) на продукты питания. Выборочные данные по 40 домохозяйствам представлены ниже.
|
X |
25.5 |
26.5 |
27.2 |
29.6 |
35.7 |
38.6 |
39.0 |
39.3 |
40.0 |
41.9 |
42.5 |
44.2 |
44.8 |
45.5 |
|
Y |
14.5 |
11.3 |
14.7 |
10.2 |
13.5 |
9.9 |
12.4 |
8.6 |
10.3 |
13.9 |
14.9 |
11.6 |
21.5 |
10.8 |
|
Х |
45.5 |
48.3 |
49.5 |
52.3 |
55.7 |
59.0 |
61.0 |
61.7 |
62.5 |
64.7 |
69.7 |
71.2 |
73.8 |
74.7 |
|
Y |
13.8 |
16.0 |
18.2 |
19.1 16.3 |
17.5 |
10.9 |
16.1 |
10.5 |
10.6 |
29.0 |
8.2 |
14.3 |
21.8 |
225

Х 75.8 76.9 79.2 81.5 82.4 82.8 83.0 85.9 86.4 86.9 88.3 89.0
Y 26.1 20.0 19.8 21.2 29.0 17.3 23.5 22.0 18.3 13.7 14.5 27.3
а) Постройте эмпирическое уравнение регрессии Y на Х. б) Вычислите отклонения ei.
в) Проведите анализ модели на гетероскедастичность по тесту ранговой корреляции Спирмена.
г) Проведите графический анализ отклонений и выдвиньте предположение о зависимости дисперсии отклонений от значений Х.
д) На основании предыдущего пункта постройте новое уравнение регрессии, используя для этого ВНК.
9.Проводится анализ зависимости средней заработной платы от средней производительности на предприятиях различного масштаба. Проведенное обследование нашло отражение в следующей таблице.
|
Количество сотрудников |
Средняя |
Средняя |
Стандартное |
|
|
предприятия, |
производительность, |
з/п, |
отклонение з/п, |
|
|
n |
X ($) |
Y ($) |
σi ($) |
|
|
1 |
− 4 |
9320 |
3320 |
740 |
|
4 |
− 9 |
8630 |
3640 |
850 |
|
10 |
− 19 |
8050 |
3900 |
730 |
|
20 |
− 49 |
8320 |
4120 |
820 |
|
50 |
− 99 |
8600 |
4090 |
950 |
|
100 |
− 199 |
9120 |
4200 |
1100 |
|
200 |
− 499 |
9540 |
4380 |
1250 |
|
500 |
− 999 |
9730 |
4500 |
1290 |
|
1000 |
− 1999 |
10120 |
4610 |
1350 |
|
2000 |
− 4999 |
10740 |
4800 |
1100 |
|
> 5000 |
11200 |
5000 |
1520 |
а) Постройте уравнение регрессии yi МНК.
б) Постройте уравнение регрессии yi
уi
= b0 + b1xi + ei, используя обычный
|
= b |
1 |
+ b xi |
+ |
ei |
. |
|
|
уi |
||||||
|
0 |
1 уi |
уi |
в) Сравните полученные результаты. Какое из уравнений вы предпочтете и почему?
226
Соседние файлы в папке ЭКОНОМЕТРИКА и математическая экономика
- #
- #
- #
- #
- #
- #
20.04.20152.55 Mб68Кобелев Н.Б. Практика применения экономико-математических методов и моделей. 2000.djvu
- #
- #
Гетероскедастичность (англ. Heterosсedasticity) — понятие, используемое в эконометрике, означающее неоднородность наблюдений, выражающуюся в неодинаковой (непостоянной) дисперсии случайной ошибки регрессионной (эконометрической) модели. Гетероскедастичность противоположна понятию гомоскедастичность, которое означает однородность наблюдений, то есть постоянство дисперсии случайных ошибок модели.
Наличие гетероскедастичности случайных ошибок приводит к неэффективности оценок, полученных с помощью метода наименьших квадратов. Кроме того, в этом случае оказывается смещённой и несостоятельной классическая оценка ковариационной матрицы МНК-оценок параметров. Следовательно статистические выводы о качестве полученных оценок могут быть неадекватными. В связи с этим тестирование моделей на гетероскедастичность является одной из необходимых процедур при построении регрессионных моделей.
Содержание
- 1 Тестирование гетероскедастичности
- 2 Оценка модели при гетероскедастичности
- 3 Пример
- 4 См. также
- 5 Литература
Тестирование гетероскедастичности
В первом приближении наличие гетероскедастичности можно заметить на графиках остатков регрессии (или их квадратов) по некоторым переменным, по оцененной зависимой переменной или по номеру наблюдения. На этих графиках разброс точек может меняться в зависимости от значения этих переменных.
Для более строгой проверки применяют, например, следующие статистические тесты
- Тест Уайта
- Тест Голдфелда-Куандта
- Тест Бройша — Пагана
- Тест Парка
- Тест Глейзера
- Тест ранговой корреляции Спирмэна
Оценка модели при гетероскедастичности
Поскольку МНК-оценки параметров моделей остаются несмещёнными состоятельными даже при гетероскедастичности, то при достаточном количестве наблюдений возможно применение обычного МНК. Однако, для более точных и правильных статистических выводов необходимо использовать стандартные ошибки в форме Уайта.
Альтернативный подход — использование взвешенного метода наименьших квадратов (ВМНК, WLS). В этом методе каждое наблюдение взвешивается обратно пропорционально предполагаемому стандартному отклонению случайной ошибки в этом наблюдении. Такой подход позволяет сделать случайные ошибки модели гомоскедастичными.
В частности, если предполагается, что стандартное отклонение ошибок пропорционально некоторой переменной Z, то данные делятся на эту переменную, включая константу.
Пример
Пусть рассматривается, например, зависимость прибыли от размера активов:
Однако, скорее всего не только прибыль зависит от активов, но и «колеблемость» прибыли не одинакова для той или иной величины активов. То есть скорее всего стандартное отклонение случайной ошибки модели следует полагать пропорциональным стоимости активов:
В этом случае разумнее рассматривать не исходную модель, а следующую:
предполагая что в этой модели случайные ошибки гомоскедастичны. Можно использовать эту преобразованную модель непосредственно, а можно использовать полученные оценки параметров как оценки параметров исходной модели (взвешенный МНК). Теоретически полученные таким образом оценки должны быть лучше.
См. также
- Скедастичность
Литература
- Магнус Я. Р., Катышев П. К., Пересецкий А. А. Эконометрика. — М.: Дело, 2004. — 576 с.
- William H. Greene Econometric analysis. — New York: Pearson Education, Inc., 2003. — 1026 с.
Что такое Гетероскедастичность?
В статистике гетероскедастичность (или гетероскедастичность) возникает, когда стандартные отклонения прогнозируемой переменной, отслеживаемые по различным значениям независимой переменной или относящиеся к предыдущим периодам времени, непостоянны. В случае гетероскедастичности контрольным признаком при визуальном осмотре остаточных ошибок является то, что они будут иметь тенденцию со временем расширяться, как показано на изображении ниже.
Гетероскедастичность часто возникает в двух формах: условной и безусловной. Условная гетероскедастичность определяет непостоянную волатильность, связанную с волатильностью предыдущего периода (например, дневной). Безусловная гетероскедастичность относится к общим структурным изменениям волатильности, которые не связаны с волатильностью предыдущего периода. Безусловная гетероскедастичность используется, когда можно определить будущие периоды высокой и низкой волатильности.
Ключевые моменты
- В статистике гетероскедастичность (или гетероскедастичность) возникает, когда стандартные ошибки переменной, отслеживаемые в течение определенного времени, непостоянны.
- В случае гетероскедастичности контрольным признаком при визуальном осмотре остаточных ошибок является то, что они будут иметь тенденцию со временем расширяться, как показано на изображении выше.
- Гетероскедастичность — это нарушение допущений для моделирования линейной регрессии, поэтому она может повлиять на достоверность эконометрического анализа или финансовых моделей, таких как CAPM.
Краткая справка
Хотя гетероскедастичность не вызывает смещения оценок коэффициентов, она делает их менее точными; более низкая точность увеличивает вероятность того, что оценки коэффициентов дальше от правильного значения генеральной совокупности.
Основы гетероскедастичности
В финансах условная гетероскедастичность часто наблюдается в ценах акций и облигаций. Уровень волатильности этих акций невозможно предсказать ни на какой период. Безусловная гетероскедастичность может использоваться при обсуждении переменных, которые имеют идентифицируемую сезонную изменчивость, таких как потребление электроэнергии.
Что касается статистики, гетероскедастичность (также обозначаемая как гетероскедастичность) относится к дисперсии ошибок или зависимости рассеяния в пределах как минимум одной независимой переменной в пределах конкретной выборки. Эти вариации можно использовать для расчета погрешности между наборами данных, такими как ожидаемые результаты и фактические результаты, поскольку они обеспечивают меру отклонения точек данных от среднего значения.
Чтобы набор данных считался релевантным, большинство точек данных должно находиться в пределах определенного числа стандартных отклонений от среднего, как описано в теореме Чебышева, также известной как неравенство Чебышева. Это дает рекомендации относительно вероятности того, что случайная величина отличается от среднего.
В зависимости от количества указанных стандартных отклонений случайная величина имеет определенную вероятность присутствия в этих точках. Например, может потребоваться, чтобы диапазон двух стандартных отклонений содержал не менее 75% точек данных, которые будут считаться действительными. Распространенная причина отклонений, выходящих за рамки минимальных требований, часто связана с проблемами качества данных.
Противоположность гетероскедастичности — гомоскедастика . Гомоскедастичность относится к состоянию, при котором дисперсия остаточного члена является постоянной или почти постоянной. Гомоскедастичность — одно из предположений линейного регрессионного моделирования. Это необходимо для обеспечения точности оценок, достоверности пределов прогноза для зависимой переменной и достоверности доверительных интервалов и значений p для параметров.
Типы гетероскедастичности
Безусловный
Безусловная гетероскедастичность предсказуема и может относиться к переменным, имеющим циклический характер. Это может включать более высокие розничные продажи, зарегистрированные в период традиционных праздничных покупок, или увеличение количества обращений в ремонт кондиционеров в теплые месяцы.
Изменения в пределах дисперсии могут быть напрямую связаны с возникновением определенных событий или прогнозных маркеров, если сдвиги традиционно не являются сезонными. Это может быть связано с увеличением продаж смартфонов с выпуском новой модели, так как активность является циклической в зависимости от события, но не обязательно определяется сезоном.
Гетероскедастичность также может относиться к случаям, когда данные приближаются к границе; где дисперсия обязательно должна быть меньше, так как граница ограничивает диапазон данных.
Условный
Условная гетероскедастичность непредсказуема по своей природе. Нет явных признаков, которые заставляли бы аналитиков полагать, что данные станут более или менее разбросанными в любой момент времени. Часто считается, что финансовые продукты подвержены условной гетероскедастичности, поскольку не все изменения можно отнести к конкретным событиям или сезонным изменениям.
Условная гетероскедастичность обычно применяется к фондовым рынкам, где сегодняшняя волатильность во многом связана с волатильностью вчера. Эта модель объясняет периоды постоянной высокой и низкой волатильности.
Особые соображения
Гетероскедастичность и финансовое моделирование
Гетероскедастичность — важное понятие в регрессионном моделировании, а в инвестиционном мире регрессионные модели используются для объяснения эффективности ценных бумаг и инвестиционных портфелей. Наиболее известной из них является Модель ценообразования капитальных активов (CAPM), которая объясняет эффективность акций с точки зрения их волатильности по отношению к рынку в целом. Расширения этой модели добавили другие переменные-предикторы, такие как размер, импульс, качество и стиль (ценность против роста).
Эти переменные-предикторы были добавлены, поскольку они объясняют или учитывают дисперсию зависимой переменной. Эффективность портфеля объясняется CAPM. Например, разработчики модели CAPM знали, что их модель не может объяснить интересную аномалию: высококачественные акции, которые были менее волатильными, чем акции низкого качества, имели тенденцию работать лучше, чем предсказывала модель CAPM. CAPM утверждает, что акции с более высоким риском должны превосходить акции с более низким риском. Другими словами, акции с высокой волатильностью должны превосходить акции с низкой волатильностью. Но качественные акции, которые менее волатильны, имели тенденцию работать лучше, чем прогнозирует CAPM.
Позже другие исследователи расширили модель CAPM (которая уже была расширена за счет включения других переменных-предикторов, таких как размер, стиль и импульс), включив качество в качестве дополнительной переменной-предиктора, также известной как «фактор». Теперь, когда этот фактор включен в модель, была учтена аномалия производительности акций с низкой волатильностью. Эти модели, известные как многофакторные модели , составляют основу факторного инвестирования и интеллектуального бета-тестирования.




































