Найдем вероятность попадания случайной величины, распределенной по нормальному закону, в заданный интервал.
Обозначим
Тогда
Т. к. интеграл не выражается через элементарные функции, то вводится в рассмотрение функция
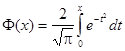
Которая называется Функцией Лапласа Или Интегралом вероятностей.
Значения этой функции при различных значениях Х посчитаны и приводятся в специальных таблицах.
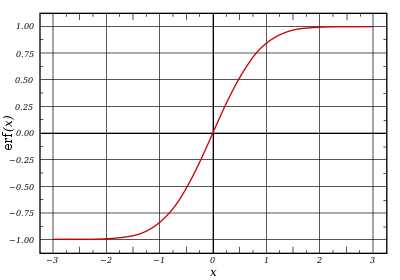
Ниже показан график функции Лапласа.
Функция Лапласа обладает следующими свойствами:
1) Ф(0) = 0;
2) Ф(-Х) = — Ф(Х);
3) Ф(¥) = 1.
Функцию Лапласа также называют Функцией ошибок и обозначают erf X.
Еще используется Нормированная Функция Лапласа, которая связана с функцией Лапласа соотношением:
Ниже показан график нормированной функции Лапласа.
При рассмотрении нормального закона распределения выделяется важный частный случай, известный как Правило трех сигм.
Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины D:
Если принять D = 3s, то получаем с использованием таблиц значений функции Лапласа:
Т. е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую чем утроенное среднее квадратичное отклонение, практически равна нулю.
Это правило называется Правилом трех сигм.
Не практике считается, что если для какой – либо случайной величины выполняется правило трех сигм, то эта случайная величина имеет нормальное распределение.
Пример. Поезд состоит из 100 вагонов. Масса каждого вагона – случайная величина, распределенная по нормальному закону с математическим ожидание А = 65 т и средним квадратичным отклонением s = 0,9 т. Локомотив может везти состав массой не более 6600 т, в противном случае необходимо прицеплять второй локомотив. Найти вероятность того, что второй локомотив не потребуется.
Второй локомотив не потребуется, если отклонение массы состава от ожидаемого (100×65 = 6500) не превосходит 6600 – 6500 = 100 т.
Т. к. масса каждого вагона имеет нормальное распределение, то и масса всего состава тоже будет распределена нормально.
Получаем:
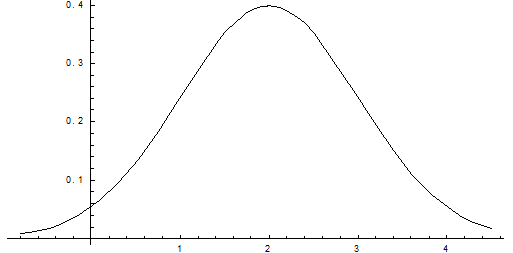
Пример. Нормально распределенная случайная величина Х задана своими параметрами – А =2 – Математическое ожидание и s = 1 – среднее квадратическое отклонение. Требуется написать плотность вероятности и построить ее график, найти вероятность того, Х примет значение из интервала (1; 3), найти вероятность того, что Х отклонится (по модулю) от математического ожидания не более чем на 2.
Плотность распределения имеет вид:
Построим график:
Найдем вероятность попадания случайной величины в интервал (1; 3).
Найдем вероятность отклонение случайной величины от математического ожидания на величину, не большую чем 2.
Тот же результат может быть получен с использованием нормированной функции Лапласа.
| < Предыдущая | Следующая > |
|---|
Нормальным называется
распределение вероятностей непрерывной
случайной величины, которое описывается
плотностью вероятности
Найдем
вероятность попадания случайной
величины, распределенной по нормальному
закону, в заданный интервал.
Обозначим
Тогда
Т.к.
интеграл не
выражается через элементарные функции,
то вводится в рассмотрение функция
которая
называется функцией
Лапласа или интегралом
вероятностей.
Значения
этой функции при различных
значениях х посчитаны
и приводятся в специальных таблицах.
Ниже
показан график функции Лапласа.
Функция
Лапласа обладает следующими свойствами:
1)
Ф(0) = 0;
2)
Ф(-х)
= — Ф(х);
3)
Ф(¥) = 1.
Функцию
Лапласа также называют функцией
ошибок и
обозначают erf x.
Еще
используется нормированная функция
Лапласа, которая связана с функцией
Лапласа соотношением:
Ниже
показан график нормированной функции
Лапласа.
25. Функция распределения двумерной случайной величины.
Определение 8.1. Функцией распределения
F(x,
y) двумерной
случайной величины (X,
Y) называется
вероятность того, чтоX
< x, a
Y < y:
F(х,
у) =p(X
< x, Y
< y ).
(8.1)
y
Рис.1.
Это означает, что точка (X,
Y) попадет в область,
заштрихованную на рис. 1, если вершина
прямого угла располагается в точке (х,
у).
Замечание. Определение функции
распределения справедливо как для
непрерывной, так и для дискретной
двумерной случайной величины.
Свойства функции
распределения.
-
0 ≤ F(x,
y) ≤ 1 (так какF(x,
y) является
вероятностью). -
F(x,
y) есть неубывающая
функция по каждому аргументу:
F(x2,y) ≥F(x1,y), еслиx2>x1;
F(x,
y2) ≥F(x,
y1), еслиy2>y1.
Доказательство. F(x2,y) =p(X
< x2,Y
< y) =p(X
< x1,Y
< y) +p(x1≤X < x2,Y < y)
≥
≥ p(X
< x1,Y
< y) =F(x1,y). Аналогично
доказывается и второе утверждение.
-
Имеют место предельные соотношения:
а) F(-∞,y)
= 0;b)F(x,
—∞) = 0;c)F(-
∞, -∞) = 0;d)F(
∞, ∞) = 1.
Доказательство. События а), b)
и с) невозможны ( так как невозможно
событиеХ<-∞ илиY
<-∞), а событиеd)
достоверно, откуда следует справедливость
приведенных равенств.
-
При у = ∞ функция распределения
двумерной случайной величины становится
функцией распределения составляющейХ:
F(x,
∞) =F1(x).
При х = ∞ функция распределения
двумерной случайной величины становится
функцией распределения составляющейY:
F(
∞,y) =F2(y).
Доказательство. Так как событие Y
< ∞ достоверно, тоF(x,
∞) =р(Х < x)
=F1(x).
Аналогично доказывается второе
утверждение.
26. Плотность распределения вероятностей двумерной случайной величины и её свойства.
.Плотностью совместного распределения
вероятностей (двумерной плотностью
вероятности) непрерывной двумерной
случайной величины называется смешанная
частная производная 2-го порядка от
функции распределения:
.
(8.2)
Замечание. Двумерная плотность
вероятности представляет собой предел
отношения вероятности попадания
случайной точки в прямоугольник со
сторонами Δхи Δук площади этого
прямоугольника при
Свойства двумерной плотности
вероятности.
-
f(x,
y) ≥ 0 (см. предыдущее
замечание: вероятность попадания точки
в прямоуголь-ник неотрицательна, площадь
этого прямоугольника положительна,
следовательно, предел их отношения
неотрицателен). -
(cледует из определения
двумерной плотности вероятно-сти). -
(поскольку это вероятность того, что
точка попадет на плос-кость Оху, то
есть достоверного события).
Вероятность попадания случайной точки
в произвольную область.
Пусть в плоскости Охузадана
произвольная областьD.
Найдем вероятность того, что точка,
координаты которой представляют собой
систему двух случайных величин (двумерную
случайную величину) с плотностью
распределенияf(x,
y), попадет в областьD. Разобьем эту область
прямыми, параллельными осям координат,
на прямоугольники со сторонами Δхи Δу.Вероятность попадания в каждый
такой прямоугольник равна,
где— координаты точки, принадлежащей
прямоугольнику. Тогда вероятность
попадания точки в областьD
есть предел интегральной суммы,
то есть
(8.3)
Отыскание плотностей
вероятности составляющих
двумерной случайной
величины.
Выше было сказано, как найти функцию
распределения каждой составляющей,
зная двумерную функцию распределения.
Тогда по определению плотности
распределения

Аналогично находится
(8.4′)
Соседние файлы в предмете Теория вероятностей и математическая статистика
- #
- #
- #
- #
- #
- #
- #
- #
- #
03.10.201339.94 Кб57Практикум по теор веру и мат стат.xls
- #
- #
График функции ошибок
В математике функция ошибок — это неэлементарная функция, возникающая в теории вероятностей, статистике и теории дифференциальных уравнений в частных производных. Она определяется как
.
Дополнительная функция ошибок, обозначаемая 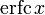
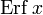
.
Комплексная функция ошибок, обозначаемая w(x), также определяется через функцию ошибок:
.
Содержание
- 1 Свойства
- 2 Применение
- 3 Асимптотическое разложение
- 4 Родственные функции
- 4.1 Обобщённые функции ошибок
- 4.2 Итерированные интегралы дополнительной функции ошибок
- 5 Реализация
- 6 См. также
- 7 Литература
- 8 Внешние ссылки
Свойства
- Функция ошибок нечётна:
- Для любого комплексного x выполняется
где черта обозначает комплексное сопряжение числа x.
- Функция ошибок не может быть представлена через элементарные функции, но, разлагая интегрируемое выражение в ряд Тейлора и интегрируя почленно, мы можем получить её представление в виде ряда:
Это равенство выполняется (и ряд сходится) как для любого вещественного x, так и на всей комплексной плоскости. Последовательность знаменателей образует последовательность A007680 в OEIS.
- Для итеративного вычисления элементов ряда полезно представить его в альтернативном виде:
поскольку 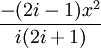
- Функция ошибок на бесконечности равна единице; однако это справедливо только при приближении к бесконечности по вещественной оси, так как:
- При рассмотрении функции ошибок в комплексной плоскости точка
будет для неё существенно особой.
- Производная функции ошибок выводится непосредственно из определения функции:
- Обратная функция ошибок представляет собой ряд
где c0 = 1 и
Поэтому ряд можно представить в следующем виде (заметим, что дроби сокращены):
[1]
Последовательности числителей и знаменателей после сокращения — A092676 и A132467 в OEIS; последовательность числителей до сокращения — A002067 в OEIS.
Дополнительная функция ошибок
Применение
Если набор случайных чисел подчиняется нормальному распределению со стандартным отклонением σ, то вероятность, что число отклонится от среднего не более чем на a, равна 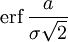
Функция ошибок и дополнительная функция ошибок встречаются в решении некоторых дифференциальных уравнений, например, уравнения теплопроводности с граничными условиями описываемыми функцией Хевисайда («ступенькой»).
В системах цифровой оптической коммуникации, вероятность ошибки на бит также выражается формулой, использующей функцию ошибок.
Асимптотическое разложение
При больших x полезно асимптотическое разложение для дополнительной функции ошибок:
Хотя для любого конечного x этот ряд расходится, на практике первых нескольких членов достаточно для вычисления 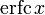
Другое приближение даётся формулой
где
Родственные функции
С точностью до масштаба и сдвига, функция ошибок совпадает с нормальным интегральным распределением, обозначаемым Φ(x)
Обратная функция к Φ, известная как нормальная квантильная функция, иногда обозначается 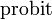
Нормальное интегральное распределение чаще применяется в теории вероятностей и математической статистике, в то время как функция ошибок чаще применяется в других разделах математики.
Функция ошибок является частным случаем функции Миттаг-Леффлера, а также может быть представлена как вырожденная гипергеометрическая функция (функция Куммера):
Функция ошибок выражается также через интеграл Френеля. В терминах регуляризованной неполной гамма-функции P и неполной гамма-функции,
Обобщённые функции ошибок
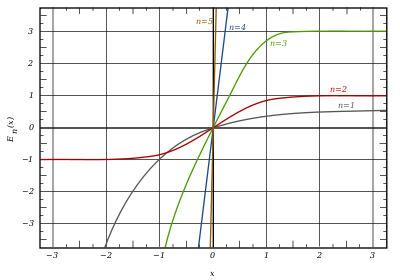
График обобщённых функций ошибок En(x):
серая линия:
красная линия:
зелёная линия: E3(x)
синяя линия: E4(x)
жёлтая линия: E5(x).
Некоторые авторы обсуждают более общие функции
Примечательными частными случаями являются:
После деления на n! все En с нечётными n выглядят похоже (но не идентично). Все En с чётными n тоже выглядят похоже, но не идентично, после деления на n!. Все обощённые функции ошибок с n > 0 выглядят похоже на полуоси x > 0.
На полуоси x > 0 все обобщённые функции могут быть выражены через гамма-функцию:
Следовательно, мы можем выразить функцию ошибок через гамма-функцию:
Итерированные интегралы дополнительной функции ошибок
Итерированные интегралы дополнительной функции ошибок определяются как
Их можно разложить в ряд:
откуда следуют свойства симметрии
и
Реализация
В стандартах языков Си и C++ функция ошибок 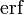
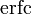
double erf(double x) и double erfc(double x). Функции находятся в заголовочных файлах math.h или cmath. Там же есть пары функций erff(),erfcf() и erfl(),erfcl(). Первая пара получает и возвращает значения типа float, а вторая — значения типа long double. Соответствующие функции также содержатся в библиотеке Math проекта Boost.
В языке [2]. Класс Erf есть в пакете org.apache.commons.math.special от [3]. Однако эта библиотека не является одной из стандартных библиотек Java 6.
Matlab[4] и
В языке Special проекта scipy [5].
См. также
- Функция Гаусса
Литература
- Milton Abramowitz and Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972. (См. часть 7)
Внешние ссылки
- MathWorld — Erf
- Онлайновый калькулятор Erf и много других специальных функций (до 6 знаков)
- Онлайновый калькулятор, вычисляющий в том числе Erf
Wikimedia Foundation.
2010.
Таблица значений функции Лапласа
В таблице даны значения функции
для положительных значений
и для
;
для
пользуются той же таблицей, так как функция
нечетна, то есть
.
В таблице приведены значения интеграла лишь до
,
так как для
можно принять
.
Эту функцию называют функцией Лапласа.
Таблица значений функции Лапласа в теории вероятностей и математической статистике используется довольно часто. На сайте можно посмотреть примеры ее использования в следующих задачах:
-
Отклонение относительной частоты от постоянной вероятности в независимых испытаниях
-
Интегральная теорема Муавра – Лапласа
-
Доверительные интервалы для среднего и дисперсии
-
Проверка гипотезы о равенстве средних
Цветом в таблице подсвечены аргументы функции Лапласа, рядом, в соседнем столбце — значения функции Лапласа.
| x | Ф(x) | x | Ф(x) | x | Ф(x) | x | Ф(x) |
| 0,00 | 0,0000 | 0,32 | 0,1255 | 0,64 | 0,2389 | 0,96 | 0,3315 |
| 0,01 | 0,0040 | 0,33 | 0,1293 | 0,65 | 0,2422 | 0,97 | 0,3340 |
| 0,02 | 0,0080 | 0,34 | 0,1331 | 0,66 | 0,2454 | 0,98 | 0,3365 |
| 0,03 | 0,0120 | 0,35 | 0,1368 | 0,67 | 0,2486 | 0,99 | 0,3389 |
| 0,04 | 0,0160 | 0,36 | 0,1406 | 0,68 | 0,2517 | 1,00 | 0,3413 |
| 0,05 | 0,0199 | 0,37 | 0,1443 | 0,69 | 0,2549 | 1,01 | 0,3438 |
| 0,06 | 0,0239 | 0,38 | 0,1480 | 0,70 | 0,2580 | 1,02 | 0,3461 |
| 0,07 | 0,0279 | 0,39 | 0,1517 | 0,71 | 0,2611 | 1,03 | 0,3485 |
| 0,08 | 0,0319 | 0,40 | 0,1554 | 0,72 | 0,2642 | 1,04 | 0,3508 |
| 0,09 | 0,0359 | 0,41 | 0,1591 | 0,73 | 0,2673 | 1,05 | 0,3531 |
| 0,10 | 0,0398 | 0,42 | 0,1628 | 0,74 | 0,2703 | 1,06 | 0,3554 |
| 0,11 | 0,0438 | 0,43 | 0,1664 | 0,75 | 0,2734 | 1,07 | 0,3577 |
| 0,12 | 0,0478 | 0,44 | 0,1700 | 0,76 | 0,2764 | 1,08 | 0,3599 |
| 0,13 | 0,0517 | 0,45 | 0,1736 | 0,77 | 0,2794 | 1,09 | 0,3621 |
| 0,14 | 0,0557 | 0,46 | 0,1772 | 0,78 | 0,2823 | 1,10 | 0,3643 |
| 0,15 | 0,0596 | 0,47 | 0,1808 | 0,79 | 0,2852 | 1,11 | 0,3665 |
| 0,16 | 0,0636 | 0,48 | 0,1844 | 0,80 | 0,2881 | 1,12 | 0,3686 |
| 0,17 | 0,0675 | 0,49 | 0,1879 | 0,81 | 0,2910 | 1,13 | 0,3708 |
| 0,18 | 0,0714 | 0,50 | 0,1915 | 0,82 | 0,2939 | 1,14 | 0,3729 |
| 0,19 | 0,0753 | 0,51 | 0,1950 | 0,83 | 0,2967 | 1,15 | 0,3749 |
| 0,20 | 0,0793 | 0,52 | 0,1985 | 0,84 | 0,2995 | 1,16 | 0,3770 |
| 0,21 | 0,0832 | 0,53 | 0,2019 | 0,85 | 0,3023 | 1,17 | 0,3790 |
| 0,22 | 0,0871 | 0,54 | 0,2054 | 0,86 | 0,3051 | 1,18 | 0,3810 |
| 0,23 | 0,0910 | 0,55 | 0,2088 | 0,87 | 0,3078 | 1,19 | 0,3830 |
| 0,24 | 0,0948 | 0,56 | 0,2123 | 0,88 | 0,3106 | 1,20 | 0,3849 |
| 0,25 | 0,0987 | 0,57 | 0,2157 | 0,89 | 0,3133 | 1,21 | 0,3869 |
| 0,26 | 0,1026 | 0,58 | 0,2190 | 0,90 | 0,3159 | 1,22 | 0,3883 |
| 0,27 | 0,1064 | 0,59 | 0,2224 | 0,91 | 0,3186 | 1,23 | 0,3907 |
| 0,28 | 0,1103 | 0,60 | 0,2257 | 0,92 | 0,3212 | 1,24 | 0,3925 |
| 0,29 | 0,1141 | 0,61 | 0,2291 | 0,93 | 0,3238 | 1,25 | 0,3944 |
| 0,30 | 0,1179 | 0,62 | 0,2324 | 0,94 | 0,3264 | ||
| 0,31 | 0,1217 | 0,63 | 0,2357 | 0,95 | 0,3289 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Продолжение таблицы
| x | Ф(x) | x | Ф(x) | x | Ф(x) | x | Ф(x) |
| 1,26 | 0,3962 | 1,59 | 0,4441 | 1,92 | 0,4726 | 2,50 | 0,4938 |
| 1,27 | 0,3980 | 1,60 | 0,4452 | 1,93 | 0,4732 | 2,52 | 0,4941 |
| 1,28 | 0,3997 | 1,61 | 0,4463 | 1,94 | 0,4738 | 2,54 | 0,4945 |
| 1,29 | 0,4015 | 1,62 | 0,4474 | 1,95 | 0,4744 | 2,56 | 0,4948 |
| 1,30 | 0,4032 | 1,63 | 0,4484 | 1,96 | 0,4750 | 2,58 | 0,4951 |
| 1,31 | 0,4049 | 1,64 | 0,4495 | 1,97 | 0,4756 | 2,60 | 0,4953 |
| 1,32 | 0,4066 | 1,65 | 0,4505 | 1,98 | 0,4761 | 2,62 | 0,4956 |
| 1,33 | 0,4082 | 1,66 | 0,4515 | 1,99 | 0,4767 | 2,64 | 0,4959 |
| 1,34 | 0,4099 | 1,67 | 0,4525 | 2,00 | 0,4772 | 2,66 | 0,4961 |
| 1,35 | 0,4115 | 1,68 | 0,4535 | 2,02 | 0,4783 | 2,68 | 0,4963 |
| 1,36 | 0,4131 | 1,69 | 0,4545 | 2,04 | 0,4793 | 2,70 | 0,4965 |
| 1,37 | 0,4147 | 1,70 | 0,4554 | 2,06 | 0,4803 | 2,72 | 0,4967 |
| 1,38 | 0,4162 | 1,71 | 0,4564 | 2,08 | 0,4812 | -2,74 | 0,4969 |
| 1,39 | 0,4177 | 1,72 | 0,4573 | 2,10 | 0,4821 | 2,76 | 0,4971 |
| 1,40 | 0,4192 | 1,73 | 0,4582 | 2,12 | 0,4830 | 2,78 | 0,4973 |
| 1,41 | 0,4207 | 1,74 | 0,4591 | 2,14 | 0,4838 | 2,80 | 0,4974 |
| 1,42 | 0,4222 | 1,75 | 0,4599 | 2,16 | 0,4846 | 2,82 | 0,4976 |
| 1,43 | 0,4236 | 1,76 | 0,4608 | 2,18 | 0,4854 | 2,84 | 0,4977 |
| 1,44 | 0,4251 | 1,77 | 0,4616 | 2,20 | 0,4861 | 2,86 | 0,4979 |
| 1,45 | 0,4265 | 1,78 | 0,4625 | 2,22 | 0,4868 | 2,88 | 0,4980 |
| 1,46 | 0,4279 | 1,79 | 0,4633 | 2,24 | 0,4875 | 2,90 | 0,4981 |
| 1,47 | 0,4292 | 1,80 | 0,4641 | 2,26 | 0,4881 | 2,92 | 0,4982 |
| 1,48 | 0,4306 | 1,81 | 0,4649 | 2,28 | 0,4887 | 2,94 | 0,4984 |
| 1,49 | 0,4319 | 1,82 | 0,4656 | 2,30 | 0,4893 | 2,96 | 0,4985 |
| 1,50 | 0,4332 | 1,83 | 0,4664 | 2,32 | 0,4898 | 2,98 | 0,4986 |
| 1,51 | 0,4345 | 1,84 | 0,4671 | 2,34 | 0,4904 | 3,00 | 0,49865 |
| 1,52 | 0,4357 | 1,85 | 0,4678 | 2,36 | 0,4909 | 3,20 | 0,49931 |
| 1,53 | 0,4370 | 1,86 | 0,4686 | 2,38 | 0,4913 | 3,40 | 0,49966 |
| 1,54 | 0,4382 | 1,87 | 0,4693 | 2,40 | 0,4918 | 3,60 | 0,499841 |
| 1,55 | 0,4394 | 1,88 | 0,4699 | 2,42 | 0,4922 | 3,80 | 0,499928 |
| 1,56 | 0,4406 | 1,89 | 0,4706 | 2,44 | 0,4927 | 4,00 | 0,499968 |
| 1,57 | 0,4418 | 1,90 | 0,4713 | 2,46 | 0,4931 | 4,50 | 0,499997 |
| 1,58 | 0,4429 | 1,91 | 0,4719 | 2,48 | 0,4934 | 5,00 | 0,499997 |
Пример решения задачи
Задача
Вероятность того, что
желание, загаданное на Новый год, сбудется, равна 0,7. Найти вероятность того,
что из 100 загаданных желаний сбудется от 60 до 85 желаний.
Решение
Вероятность того, что
событие
появится в
независимых
испытаниях от
до
раз:
В нашем случае
По таблице функции
Лапласа:
Искомая вероятность:
Функция ошибок
| Аргумент функции ошибок erf(x) |
| Функция ошибок |
| Дополнительная функция ошибок |
Функция ошибок, она же функция Лапласа, он же интеграл вероятности — все это одна и та же сущность, которая выражается функцией
и используется в статистике и теории вероятностей.
Функция неэлементарная, то есть её нельзя представить в виде элементарных (тригонометрических и алгебраических) функций.
Для расчета в нашем калькуляторе, мы используем связь с неполной гамма функцией
Кроме этого мы сможем здесь же вычислить, дополнительную функцию ошибок, обозначаемую 

В приницпе это все, что можно сказать о ней.
Калькулятор высчитывает результат как в вещественном так и комплексном поле.
Замечание: Функция прекрасно работает на всем поле комплексных чисел при условии если аргумент ( фаза) меньше 180 градусов. Это связано с особенностью вычисления этой функции, неполной гамма функции, интегральной показательной функцией через непрерывные дроби.
Отсюда следует вывод, что при отрицательных вещественных аргументах, функция будет выдавать неверные решения. Но при всех положительных, а также отрицательных комплексных аргументах функция ошибок выдает верный ответ.
Несколько примеров:

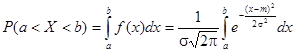
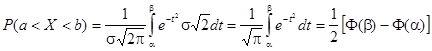
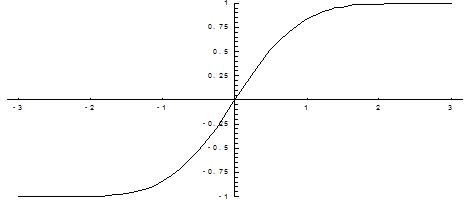
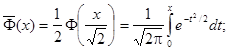
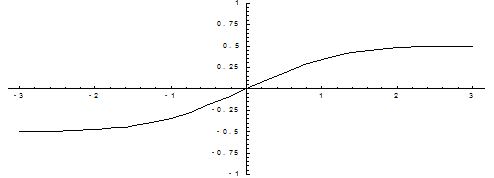
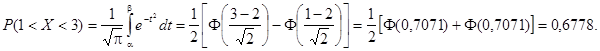









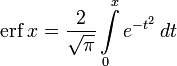 .
.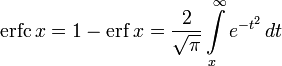 .
.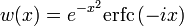 .
.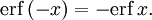
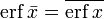
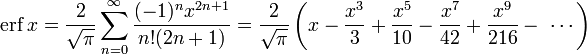
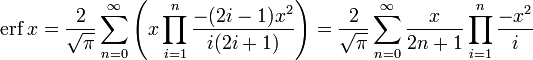
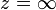 будет для неё существенно особой.
будет для неё существенно особой.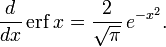
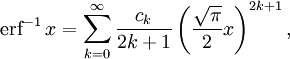
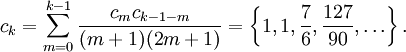
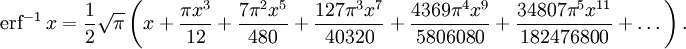 [1]
[1]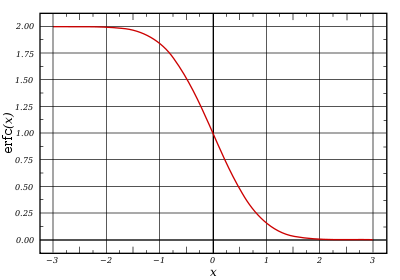
![operatorname{erfc},x = frac{e^{-x^2}}{xsqrt{pi}}left [1+sum_{n=1}^infty (-1)^n frac{1cdot3cdot5cdots(2n-1)}{(2x^2)^n}right ]=frac{e^{-x^2}}{xsqrt{pi}}sum_{n=0}^infty (-1)^n frac{(2n)!}{n!(2x)^{2n}}.,](https://dic.academic.ru/pictures/wiki/files/50/2d5fe0b0f05b66753a4dc4d68612c2e1.png)
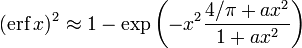
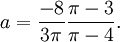
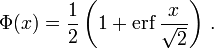
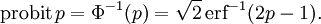
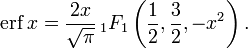
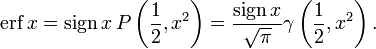
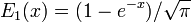
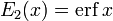
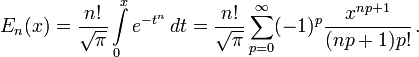
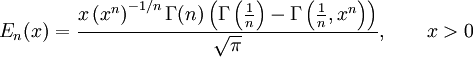
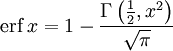
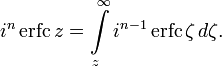
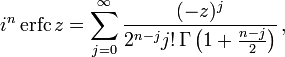
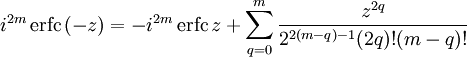
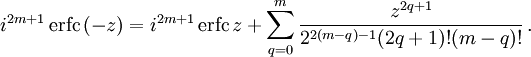

}{{sqrt%20%20pi%20}}})
