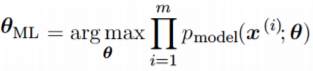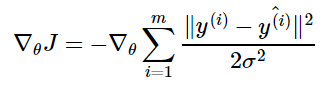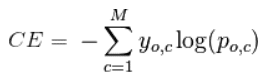Адаптированный перевод прекрасной статьи энтузиаста технологий машинного обучения Javaid Nabi.
Чтобы понимать как алгоритм машинного обучения учится предсказывать результаты на основе данных, важно разобраться в основных концепциях и понятиях, используемых при обучении алгоритма.
Функции оценки
В контексте технологии машинного обучения, оценка – это
статистический термин для нахождения некоторого приближения неизвестного
параметра на основе некоторых данных. Точечная
оценка – это попытка найти единственное лучшее приближение некоторого
количества интересующих нас параметров. Или на более формальном языке математической статистики — точечная оценка это число, оцениваемое на основе наблюдений,
предположительно близкое к оцениваемому параметру.
Под количеством
интересующих параметров обычно подразумевается:
• Один параметр
• Вектор параметров – например, веса в линейной
регрессии
• Целая функция
Точечная оценка
Чтобы отличать оценки параметров от их истинного значения, представим точечную оценку параметра θ как θˆ. Пусть {x(1), x(2), .. x(m)} будут m независимыми и одинаково распределенными величинами. Тогда точечная оценка может быть записана как некоторая функция этих величин:
Такое определение точечной оценки является очень общим и предоставляет разработчику большую свободу действий. Почти любая функция, таким образом, может рассматриваться как оценщик, но хороший оценщик – это функция, значения которой близки к истинному базовому значению θ, которое сгенерированно обучающими данными.
Точечная оценка также может относиться к оценке взаимосвязи между
входными и целевыми переменными, в этом случае чаще называемой функцией оценки.
Функция оценки
Задача, решаемая машинным обучением, заключается в попытке
предсказать переменную y по
заданному входному вектору x. Мы
предполагаем, что существует функция f(x), которая описывает приблизительную
связь между y и x. Например, можно предположить, что y = f(x) + ε, где ε обозначает
часть y, которая явно не
предсказывается входным вектором x.
При оценке функций нас интересует приближение f с помощью модели или оценки fˆ.
Функция оценки в действительности это тоже самое, что оценка параметра θ; функция оценки f это просто точечная
оценка в функциональном пространстве. Пример: в полиномиальной регрессии мы
либо оцениваем параметр w, либо оцениваем функцию отображения из x в y.
Смещение и дисперсия
Смещение и дисперсия измеряют два разных источника ошибки функции оценки.
Смещение измеряет ожидаемое отклонение от истинного значения функции или
параметра. Дисперсия, с другой стороны, показывает меру отклонения от
ожидаемого значения оценки, которую может вызвать любая конкретная выборка
данных.
Смещение
Смещение определяется следующим
образом:
где ожидаемое значение E(θˆm) для данных (рассматриваемых как выборки из случайной величины) и
θ является истинным базовым значением, используемым для определения
распределения, генерирующего данные.
Оценщик θˆm называется несмещенным, если bias(θˆm)=0, что подразумевает что E(θˆm) = θ.
Дисперсия и Стандартная ошибка
Дисперсия оценки обозначается как Var(θˆ), где случайная величина
является обучающим множеством. Альтернативно, квадратный корень дисперсии
называется стандартной ошибкой, обозначаемой как SE(θˆ). Дисперсия или стандартная ошибка
оценщика показывает меру ожидания того, как оценка, которую мы вычисляем, будет
изменяться по мере того, как мы меняем выборки из базового набора данных,
генерирующих процесс.
Точно так же, как мы хотели бы, чтобы функция оценки имела малое
смещение, мы также стремимся, чтобы у нее была относительно низкая дисперсия.
Давайте теперь рассмотрим некоторые обычно используемые функции оценки.
Оценка Максимального Правдоподобия (MLE)
Оценка максимального правдоподобия может быть определена как метод
оценки параметров (таких как среднее значение или дисперсия) из выборки данных,
так что вероятность получения наблюдаемых данных максимальна.
Рассмотрим набор из m примеров X={x(1),… , x(m)} взятых независимо из неизвестного набора данных,
генерирующих распределение Pdata(x). Пусть Pmodel(x;θ) –
параметрическое семейство распределений вероятностей над тем же пространством,
индексированное параметром θ.
Другими словами, Pmodel(x;θ) отображает любую конфигурацию x в значение, оценивающее истинную
вероятность Pdata(x).
Оценка максимального правдоподобия для θ определяется как:
Поскольку мы предположили, что примеры являются независимыми выборками, приведенное выше
уравнение можно записать в виде:
Эта произведение многих вероятностей может быть неудобным по ряду
причин. В частности, оно склонно к числовой недооценке. Кроме того, чтобы найти
максимумы/минимумы этой функции, мы должны взять производную этой функции от θ и приравнять ее к 0. Поскольку это
произведение членов, нам нужно применить правило цепочки, которое довольно
громоздко. Чтобы получить более удобную, но эквивалентную задачу оптимизации,
можно использовать логарифм вероятности, который не меняет его argmax, но
удобно превращает произведение в сумму, и поскольку логарифм – строго
возрастающая функция (функция натурального логарифма – монотонное
преобразование), это не повлияет на итоговое значение θ.
В итоге, получаем:
Два важных свойства: сходимость и
эффективность
Сходимость. По мере того, как число обучающих выборок приближается к
бесконечности, оценка максимального правдоподобия сходится к истинному значению
параметра.
Эффективность. Способ измерения того, насколько мы близки к истинному
параметру, – это ожидаемая средняя квадратичная ошибка, вычисление квадратичной
разницы между оценочными и истинными значениями параметров, где математическое
ожидание вычисляется над m обучающими выборками из данных, генерирующих
распределение. Эта параметрическая среднеквадратичная ошибка уменьшается с
увеличением m, и для
больших m нижняя
граница неравенства Крамера-Рао показывает, что ни у одной сходящейся функции оценки нет
среднеквадратичной ошибки меньше, чем у оценки максимального правдоподобия.
Именно по причине
сходимости и эффективности, оценка максимального правдоподобия часто считается
предпочтительным оценщиком для машинного обучения.
Когда количество примеров достаточно мало, чтобы привести к
переобучению, стратегии регуляризации, такие как понижающие веса, могут
использоваться для получения смещенной версии оценки максимального
правдоподобия, которая имеет меньшую дисперсию, когда данные обучения
ограничены.
Максимальная апостериорная (MAP) оценка
Согласно байесовскому подходу, можно учесть влияние предварительных
данных на выбор точечной оценки. MAP может использоваться для получения
точечной оценки ненаблюдаемой величины на основе эмпирических данных. Оценка
MAP выбирает точку максимальной апостериорной вероятности (или максимальной
плотности вероятности в более распространенном случае непрерывного θ):
где с правой стороны, log(p(x|θ)) – стандартный член
логарифмической вероятности и log(p(θ)) соответствует изначальному
распределению.
Как и при полном байесовском методе, байесовский MAP имеет преимущество
использования изначальной информации, которой нет
в обучающих данных. Эта дополнительная информация помогает уменьшить дисперсию
для точечной оценки MAP (по сравнению с оценкой MLE). Однако, это происходит ценой повышенного смещения.
Функции потерь
В большинстве обучающих сетей ошибка рассчитывается как разница
между фактическим выходным значением y и прогнозируемым выходным значением ŷ.
Функция, используемая для вычисления этой ошибки, известна как функция потерь,
также часто называемая функцией ошибки или затрат.
До сих пор наше основное внимание уделялось оценке параметров с
помощью MLE или MAP. Причина, по которой мы обсуждали это раньше, заключается в
том, что и MLE, и MAP предоставляют механизм для получения функции потерь.
Давайте рассмотрим некоторые часто используемые функции потерь.
Средняя
квадратичная ошибка (MSE): средняя
квадратичная ошибка является наиболее распространенной функцией потерь. Функция
потерь MSE широко используется в линейной регрессии в качестве показателя
эффективности. Чтобы рассчитать MSE, надо взять разницу между предсказанными
значениями и истинными, возвести ее в квадрат и усреднить по всему набору
данных.
где y(i) – фактический ожидаемый результат, а ŷ(i) – прогноз модели.
Многие функции потерь (затрат), используемые в машинном обучении,
включая MSE, могут быть получены из метода максимального правдоподобия.
Чтобы увидеть, как мы можем вывести функции потерь из MLE или MAP,
требуется некоторая математика. Вы можете пропустить ее и перейти к следующему
разделу.
Получение MSE из MLE
Алгоритм линейной регрессии учится принимать входные данные x и получать выходные значения ŷ. Отображение x в ŷ делается так,
чтобы минимизировать среднеквадратичную ошибку. Но как мы выбрали MSE в
качестве критерия для линейной регрессии? Придем к этому решению с точки зрения
оценки максимального правдоподобия. Вместо того, чтобы производить одно
предсказание ŷ , давайте рассмотрим
модель условного распределения p(y|x).
Можно смоделировать модель
линейной регрессии следующим образом:
мы предполагаем, что у имеет
нормальное распределение с ŷ в качестве
среднего значения распределения и некоторой постоянной σ² в качестве дисперсии, выбранной пользователем. Нормальное
распределения являются разумным выбором во многих случаях. В отсутствие
предварительных данных о том, какое распределение в действительности
соответствует рассматриваемым данным, нормальное распределение является хорошим
выбором по умолчанию.
Вернемся к логарифмической вероятности, определенной ранее:
где ŷ(i) – результат
линейной регрессии на i-м входе, а m – количество обучающих примеров. Мы видим,
что две первые величины являются постоянными, поэтому максимизация
логарифмической вероятности сводится к минимизации MSE:
Таким образом, максимизация логарифмического правдоподобия
относительно θ дает такую же оценку параметров θ, что и минимизация
среднеквадратичной ошибки. Два критерия имеют разные значения, но одинаковое
расположение оптимума. Это оправдывает использование MSE в качестве функции
оценки максимального правдоподобия.
Кросс-энтропия
(или логарифмическая функция потерь – log loss): Кросс-энтропия измеряет расхождение между двумя вероятностными
распределениями. Если кросс-энтропия велика, это означает, что разница между
двумя распределениями велика, а если кросс-энтропия мала, то распределения
похожи друг на друга.
Кросс-энтропия определяется как:
где P – распределение истинных ответов, а Q – распределение
вероятностей прогнозов модели. Можно
показать, что функция кросс-энтропии также получается из MLE, но я не буду
утомлять вас большим количеством математики.
Давайте еще
упростим это для нашей модели с:
• N – количество наблюдений
• M – количество возможных меток класса (собака,
кошка, рыба)
• y – двоичный индикатор (0 или 1) того, является
ли метка класса C правильной классификацией для наблюдения O
• p – прогнозируемая вероятность модели
Бинарная классификация
В случае бинарной классификации (M=2),
формула имеет вид:
При двоичной классификации каждая предсказанная вероятность
сравнивается с фактическим значением класса (0 или 1), и вычисляется оценка,
которая штрафует вероятность на основе расстояния от ожидаемого значения.
Визуализация
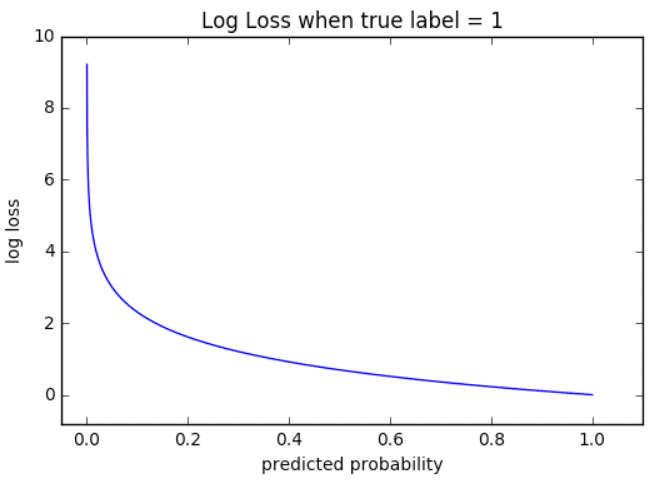
На приведенном ниже графике показан диапазон возможных значений
логистической функции потерь с учетом истинного наблюдения (y = 1). Когда
прогнозируемая вероятность приближается к 1, логистическая функция потерь
медленно уменьшается. Однако при уменьшении прогнозируемой вероятности она быстро возрастает.
Логистическая функция потерь наказывает оба типа ошибок, но
особенно те прогнозы, которые являются достоверными и ошибочными!
Мульти-классовая классификация
В случае мульти-классовой классификации (M>2) мы берем сумму значений логарифмических функций потерь для
каждого прогноза наблюдаемых классов.
Кросс-энтропия для бинарной или двух-классовой задачи
прогнозирования фактически рассчитывается как средняя кросс-энтропия среди всех
примеров. Log loss использует отрицательные
значения логарифма, чтобы обеспечить удобную метрику для сравнения. Этот подход
основан на том, что логарифм чисел <1 возвращает отрицательные значения, что
затрудняет работу при сравнении производительности двух моделей. Вы можете
почитать эту статью, где детально обсуждается функция кросс-энтропии потерь.
Задачи ML и соответствующие функции потерь
Давайте посмотрим, какие обычно используются выходные слои и
функции потерь в задачах машинного обучения:
Задача регрессии
Задача, когда
вы прогнозируете вещественное число.
• Конфигурация выходного уровня: один
узел с линейной единицей активации.
• Функция
потерь: средняя квадратическая ошибка (MSE).
Задача бинарной классификации
Задача состоит в том, чтобы классифицировать пример как
принадлежащий одному из двух классов. Или более точно, задача сформулирована
как предсказание вероятности того, что пример принадлежит первому классу,
например, классу, которому вы присваиваете целочисленное значение 1, тогда как
другому классу присваивается значение 0.
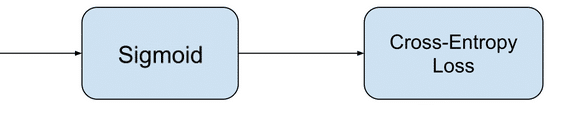
• Конфигурация выходного
уровня: один узел с сигмовидной активационной функцией.
• Функция
потерь: кросс-энтропия, также называемая логарифмической функцией потерь.
Задача мульти-классовой классификации
Эта задача состоит в том, чтобы классифицировать пример как
принадлежащий одному из нескольких классов. Задача сформулирована как
предсказание вероятности того, что пример принадлежит каждому классу.
• Конфигурация выходного уровня: один
узел для каждого класса, использующий функцию активации softmax.
• Функция потерь: кросс-энтропия, также называемая логарифмической функцией потерь.
Рассмотрев оценку и различные функции потерь, давайте перейдем к
роли оптимизаторов в алгоритмах ML.
Оптимизаторы
Чтобы свести к минимуму ошибку или потерю в прогнозировании,
модель, используя примеры из обучающей выборки, обновляет параметры модели W. Расчеты
ошибок строятся в зависимости от W и также описываются графиком функции затрат
J(w), поскольку она определяет затраты/наказание модели. Таким образом, минимизация
ошибки также часто называется минимизацией функции затрат.
Но как именно это делается? Используя оптимизаторы.
Оптимизаторы используются для обновления весов и смещений, то есть
внутренних параметров модели, чтобы уменьшить ошибку.
Самым важным методом и основой того, как мы обучаем и оптимизируем
нашу модель, является метод Градиентного Спуска.
Градиентный Спуск
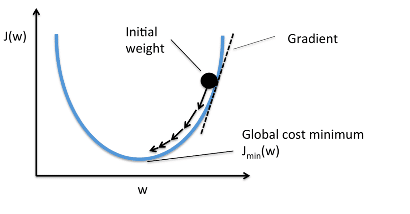
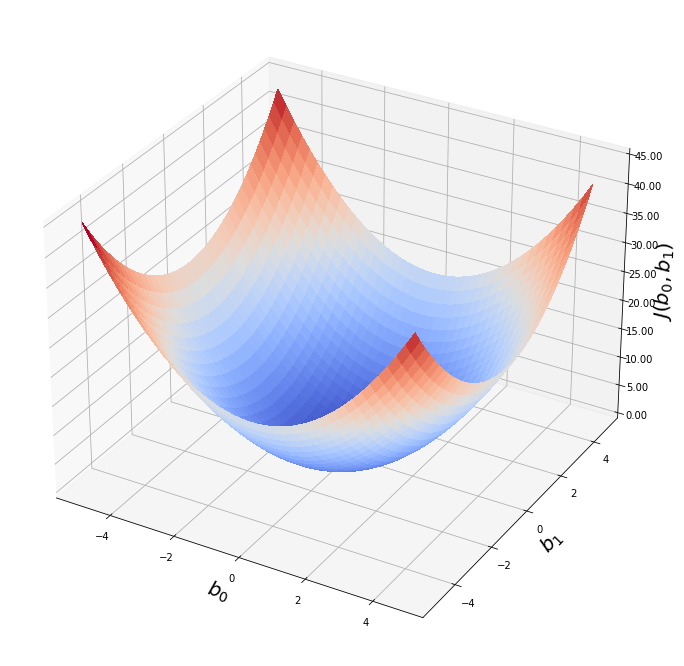
Когда мы строим функцию затрат J(w), это можно представить следующим
образом:
Как видно из кривой, существует значение параметров W, которое
имеет минимальное значение Jmin. Нам нужно найти способ достичь
этого минимального значения.
В алгоритме градиентного спуска мы начинаем со случайных
параметров модели и вычисляем ошибку для каждой итерации обучения, продолжая
обновлять параметры, чтобы приблизиться к минимальным значениям.
Повторяем до достижения минимума:
{
}
В приведенном выше уравнении мы обновляем параметры модели после
каждой итерации. Второй член уравнения вычисляет наклон или градиент кривой на
каждой итерации.
Градиент функции затрат вычисляется как частная производная
функции затрат J по каждому параметру модели Wj, где j принимает
значение числа признаков [1, n]. α – альфа, это скорость обучения, определяющий
как быстро мы хотим двигаться к минимуму. Если α слишком велико, мы можем
проскочить минимум. Если α слишком мало, это приведет к небольшим этапам обучения,
поэтому общее время, затрачиваемое моделью для достижения минимума, будет
больше.
Есть три способа сделать градиентный спуск:
Пакетный
градиентный спуск: использует
все обучающие данные для обновления параметров модели в каждой итерации.
Мини-пакетный градиентный спуск: вместо использования всех данных, мини-пакетный градиентный спуск делит тренировочный набор на меньший размер, называемый партией, и обозначаемый буквой «b». Таким образом, мини-пакет «b» используется для обновления параметров модели на каждой итерации.
Вот некоторые другие часто
используемые Оптимизаторы:
Стохастический
Градиентный Спуск (SGD): обновляет
параметры, используя только один обучающий параметр на каждой итерации. Такой
параметр обычно выбирается случайным образом. Стохастический градиентный спуск
часто предпочтителен для оптимизации функций затрат, когда есть сотни тысяч
обучающих или более параметров, поскольку он будет сходиться быстрее, чем
пакетный градиентный спуск.
Адаград
Адаград адаптирует скорость обучения конкретно к индивидуальным
особенностям: это означает, что некоторые веса в вашем наборе данных будут
отличаться от других. Это работает очень хорошо для разреженных наборов данных,
где пропущено много входных значений. Однако, у Адаграда есть одна серьезная
проблема: адаптивная скорость обучения со временем становится очень маленькой.
Некоторые другие оптимизаторы, описанные ниже, пытаются справиться
с этой проблемой.
RMSprop
RMSprop – это специальная версия Adagrad,
разработанная профессором Джеффри Хинтоном в его
классе нейронных сетей. Вместо того,
чтобы вычислять все градиенты, он вычисляет градиенты только в фиксированном
окне. RMSprop похож на Adaprop, это еще один оптимизатор, который пытается
решить некоторые проблемы, которые Адаград оставляет открытыми.
Адам
Адам означает адаптивную оценку момента и является еще одним способом использования
предыдущих градиентов для вычисления текущих градиентов. Адам также использует
концепцию импульса,
добавляя доли предыдущих градиентов к текущему. Этот оптимизатор получил
довольно широкое распространение и практически принят для использования в
обучающих нейронных сетях.
Вы только что ознакомились с кратким обзором
оптимизаторов. Более подробно об этом можно прочитать здесь.
Я надеюсь,
что после прочтения этой статьи, вы будете лучше понимать что происходит, когда
Вы пишите следующий код:
# loss function: Binary Cross-entropy and optimizer: Adam
model.compile(loss='binary_crossentropy', optimizer='adam')или
# loss function: MSE and optimizer: stochastic gradient descent
model.compile(loss='mean_squared_error', optimizer='sgd')Спасибо за проявленный интерес!
Ссылки:
[1] https://www.deeplearningbook.org/contents/ml.html
[2] https://machinelearningmastery.com/loss-and-loss-functions-for-training-deep-learning-neural-networks/
[3] https://blog.algorithmia.com/introduction-to-optimizers/
[4] https://jhui.github.io/2017/01/05/Deep-learning-Information-theory/
[5] https://blog.algorithmia.com/introduction-to-loss-functions/
[6] https://gombru.github.io/2018/05/23/cross_entropy_loss/
[7] https://www.kdnuggets.com/2018/04/right-metric-evaluating-machine-learning-models-1.html
[8] https://rohanvarma.me/Loss-Functions/
[9] http://blog.christianperone.com/2019/01/mle/
Основной сложностью при выборе функций ошибок для работы с 3D данными является неевклидовость рассматриваемых структур, из-за которой задача определения расстояния в пространстве 3D моделей становится совсем нетривиальной.
В этой заметке мы поговорим о том, какие функции ошибки (Loss functions) алгоритмов используются в 3D ML, какие из них можно использовать в качеств метрик качества (metrics), а какие — в качестве регуляризаторов (regularizers).
Про то, чем евклидовы данные отличаются от неевклидовых, можно узнать здесь.
Серия 3D ML на Хабре:
- Формы представления 3D данных
- Функции потерь в 3D ML
- Датасеты и фреймворки в 3D ML
- Дифференциальный рендеринг
- Сверточные операторы на графах
Заметка от партнера IT-центра МАИ и организатора магистерской программы “VR/AR & AI” — компании PHYGITALISM.
Формальная постановка задачи. Предварительные сведения.
В предыдущей части, мы обозначили, что работа с 3D структурами с привлечением методов машинного обучения приводит нас к новой обширной науке 3D ML. Среди всех задач этой области можно выделить класс подзадач, который мы назовём 2D-to-3D (также эта задача часто в англоязычной литературе имеет название “3D reconstruction from 2D image”). Эти задачи характеризуются тем, что на входе у алгоритма как правило одно или несколько изображений, а на выходе мы хотим получить какую-либо трехмерную структуру.
Например, можно восстанавливать карту глубины для произвольного изображения [2] (RGB-to-RGBD, или же можно было бы назвать такую задачу 2D-to-2.5D).
Рис.1 Архитектура автокодировщика, восстанавливающая depth слой изображения при помощи специализированных сверточных операторов [3].
Другой пример схожего класса задач — восстановление облака точек объекта по его единственному RGB-D изображению [3] (2.5D-to-3D или “3D Shape completion”).
Рис.2 Архитектура Voxlets [3] восстанавливает пространственную информацию для одного RGBD изображения: a — исходное RGB изображение;
b — воксельная модель, полученная с помощью depth слоя исходного снимка;
c — настоящая пространственная модель объектов; d — пространственная модель, полученная с помощью Voxlets.
В дальнейшем мы подробнее рассмотрим задачу 3D model reconstruction from single RGB image.
Рис.3 Пример подготовленного входного изображения (слева) и полигональной модели, полученной с помощью Occupancy Net [1] (справа).
Поскольку результатом работы описанных выше алгоритмов являются трехмерные структуры, нам бы хотелось в первую очередь научится понимать, насколько результирующая модель близка к исходной модели из обучающей выборки.
Решение задачи машинного обучения, какая бы она не была (классификация, кластеризация, порождения новых объектов и т.д.) — это зачастую решение оптимизационной задачи. Для фиксированной параметризованной архитектуры алгоритма машинного обучения необходимо найти множество параметров, при которых функция ошибки (при выборе которой во многом отталкиваются от типа конкретной задачи) принимает наименьшее значение. При этом, необходимо следить, чтобы в процессе поиска минимума, обобщающая способность алгоритма возрастала. Подробнее про постановку задач машинного обучения и про классификацию задач можно прочесть здесь.
Оптимизируемые функции в задачах машинного обучения делятся на три категории:
- Функции потерь (Loss functions/objectives) — позволяют вычислить ошибку алгоритма на каждом конкретном объекте. Выбираются обычно непрерывными и почти всюду дифференцируемыми для того чтобы применять градиентные методы. Среднее значение функции потерь на датасете (функционал качества алгоритма) оптимизируется в процессе обучения.
-
Регуляризаторы (Regularizers) — вводятся в функционал качества для того чтобы сделать оптимизационную задачу обучения корректной, процесс обучения устойчивым и получить более качественное решение. Зачастую регуляризация помогает избежать переобучения. В отличие от функции потерь, для вычисления значения регуляризатора зачастую не требуется использование информации об объектах из датасета.
-
Метрики качества (Metrics) — функции по которым определяется (валидируется) качество обученной модели (как на всем датасете в целом, так и на отдельных моделях), но не происходит непосредственной оптимизации. Используются для контроля переобучения и для сравнения различных моделей.
Далее мы подробнее поговорим про конкретные функции потерь и регуляризаторы, а для большей наглядности будем рассматривать примеры с кодом. Код с примерами к заметке доступен в нашем GitHub репозитории.
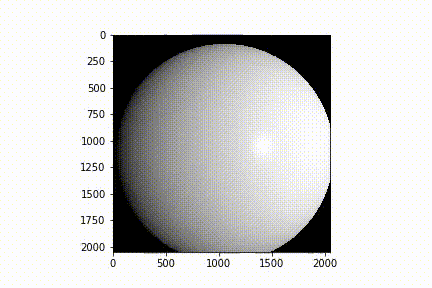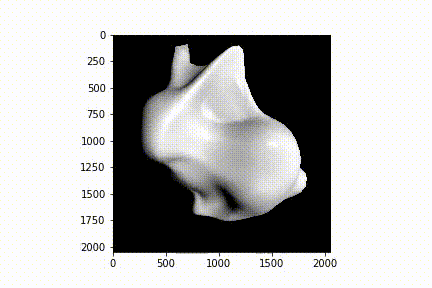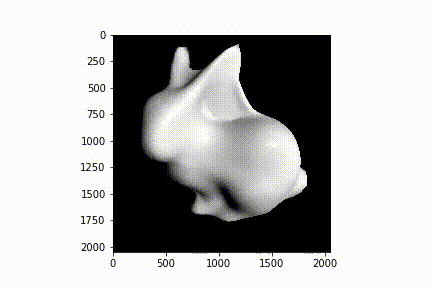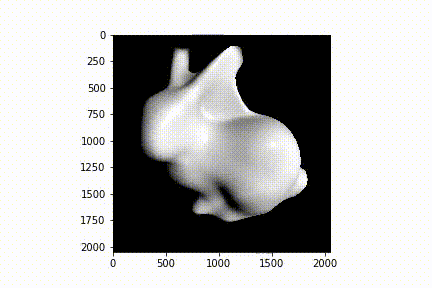
Как и в предыдущей части, в качестве тестовых моделей будем рассматривать модель икосферы и кролика, а в качестве рабочего инструмента будем использовать библиотеку pytorch3d.
Загрузка моделей и установка рабочего устройства
import os
import pathlib
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
%matplotlib inline
# You should work in Jupyter.
from tqdm import tqdm_notebook
from celluloid import Camera
import torch
# untilitis
from pytorch3d.utils import ico_sphere
# loss functions and regulaziers
from pytorch3d.loss import (
chamfer_distance,
mesh_edge_loss,
mesh_laplacian_smoothing,
mesh_normal_consistency
)
# io utils
from pytorch3d.io import load_obj
# operations with data
from pytorch3d.ops import sample_points_from_meshes
# datastructures
from pytorch3d.structures import Meshes, Textures
# render
from pytorch3d.renderer import (
look_at_view_transform,
OpenGLPerspectiveCameras,
DirectionalLights,
RasterizationSettings,
MeshRenderer,
MeshRasterizer,
HardPhongShader
)
import trimesh
from trimesh import registration
from trimesh import visual
# If you have got a CUDA device, you can use GPU mode
if torch.cuda.is_available():
device = torch.device('cuda:0')
torch.cuda.set_device(device)
else:
device = torch.device('cpu')Подготовка моделей
# Bunny mesh in pytorch3d
verts, faces_idx, _ = load_obj(path_to_model)
faces = faces_idx.verts_idx
center = verts.mean(0)
verts = verts - center
scale = max(verts.abs().max(0)[0])
verts = verts / scale
# Initialize each vertex to be white in color.
verts_rgb = torch.ones_like(verts)[None] # (1, V, 3)
textures = Textures(verts_rgb=verts_rgb.to(device))
# Create a Meshes object for the bunny.
bunny_mesh = Meshes(
verts=[verts.to(device)],
faces=[faces.to(device)],
textures=textures
)
# Sphere mesh in pytorch3d
sphere_mesh = ico_sphere(4, device)
verts_rgb = torch.ones_like(sphere_mesh.verts_list()[0])[None]
sphere_mesh.textures = Textures(verts_rgb=verts_rgb.to(device))
# Mesh to pointcloud with normals in pytorch3d
num_points_to_sample = 25000
bunny_vert, bunny_norm = sample_points_from_meshes(
bunny_mesh,
num_points_to_sample ,
return_normals=True
)
sphere_vert, sphere_norm = sample_points_from_meshes(
sphere_mesh,
num_points_to_sample,
return_normals=True
)
def convert_to_mesh(mesh):
"""Trimesh может загружать сцены вместо монолитного объекта
"""
if isinstance(mesh, trimesh.Scene):
return mesh.dump(concatenate=True)
else:
return mesh
def scale_to_unit(mesh: trimesh.Trimesh):
length, weight, height = mesh.extents
scale = 1 / max(length, weight, height)
mesh.apply_scale((scale, scale, scale))
mesh_target = convert_to_mesh(trimesh.load_mesh(str(path_to_orig)))
mesh_source = convert_to_mesh(trimesh.load_mesh(str(path_to_rot)))
mesh_target.rezero()
mesh_source.rezero()
scale_to_unit(mesh_target)
scale_to_unit(mesh_source)
mesh_source.visual = visual.ColorVisuals(mesh_source, vertex_colors=(255, 0, 0, 255))
mesh_target.visual = visual.ColorVisuals(mesh_target, vertex_colors=(0, 255, 0, 255))
scene = trimesh.Scene([mesh_source, mesh_target])Подготовка визуализации моделей
# Initialize an OpenGL perspective camera.
cameras = OpenGLPerspectiveCameras(device=device)
# We will also create a phong renderer. This is simpler and only needs to render one face per pixel.
raster_settings = RasterizationSettings(
image_size=1024,
blur_radius=0,
faces_per_pixel=1,
)
# We can add a directional light in the scene.
ambient_color = torch.FloatTensor([[0.0, 0.0, 0.0]]).to(device)
diffuse_color = torch.FloatTensor([[1.0, 1.0, 1.0]]).to(device)
specular_color = torch.FloatTensor([[0.1, 0.1, 0.1]]).to(device)
direction = torch.FloatTensor([[1, 1, 1]]).to(device)
lights = DirectionalLights(ambient_color=ambient_color,
diffuse_color=diffuse_color,
specular_color=specular_color,
direction=direction,
device=device)
phong_renderer = MeshRenderer(
rasterizer=MeshRasterizer(
cameras=cameras,
raster_settings=raster_settings
),
shader=HardPhongShader(
device=device,
cameras=cameras,
lights=lights
)
)
# Select the viewpoint using spherical angles
distance = 2.0 # distance from camera to the object`
elevation = 40.0 # angle of elevation in degrees
azimuth = 0.0 # No rotation so the camera is positioned on the +Z axis.
# Get the position of the camera based on the spherical angles
R, T = look_at_view_transform(distance, elevation, azimuth, device=device,at=((-0.02,0.1,0.0),))
# Render the bunny providing the values of R and T.
image_bunny = phong_renderer(meshes_world=bunny_mesh, R=R, T=T)
image_sphere = phong_renderer(meshes_world=sphere_mesh, R=R, T=T)
image_sphere = image_sphere.cpu().numpy()
image_bunny = image_bunny.cpu().numpy()Визуализация моделей
# Source mesh of sphere
plt.figure(figsize=(13, 13))
plt.imshow(image_sphere.squeeze())
plt.grid(False)
# Target mesh of bunny
plt.figure(figsize=(13, 13))
plt.imshow(image_bunny.squeeze())
plt.grid(False)Функции потерь, регуляризаторы и метрики качества в задачах 3D ML
Прежде чем ввести в рассмотрение конкретные функции потерь, отметим, что две сравниваемые модели должны быть предварительно приведены к одинаковому масштабу и ориентированы друг относительно друга таким образом, чтобы функция потерь принимала свое наименьшее значение из всех возможных при различных взаимных ориентациях. Решением задачи по совмещению друг с другом двух трехмерных объектов занимаются алгоритмы регистрации облаков точек, реализации которых можно найти в библиотеках trimesh или pcl.
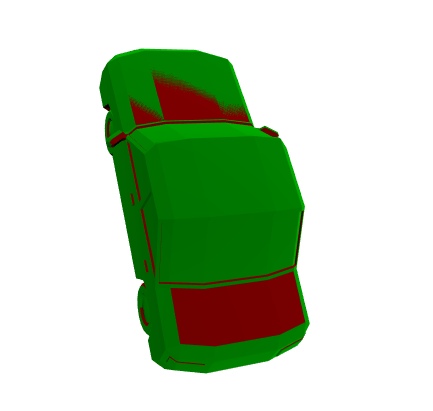
В качестве примера задачи регистрации рассмотрим совмещение двух полигональных моделей автомобилей ( mesh_source.obj и mesh_target.obj из директории data ).
scene.show()В качестве метода регистрации можно взять метод главных осей инерции (principal axes of inertia) — разновидности метода ICP.
transform, cost = registration.mesh_other(mesh_source, mesh_target, samples=2_000, scale=True)
new_scene = scene.copy()
new_scene.geometry["geometry_0"].apply_transform(transform)
print("Величина ошибки регистрации: ", cost)
print("Матрица преобразования модели:")
print(transform)Out:
>>Величина ошибки регистрации: 2.5801412889832494e-10
>>Матрица преобразования модели:
>>[[-0.97327281 0.33386218 -0.23301026 0.65454393]
[-0.07505283 0.44631862 0.95298713 -0.01844067]
[ 0.40015598 0.89574184 -0.38799414 0.28013195]
[ 0. 0. 0. 1. ]]После применения алгоритма можно увидеть, что модели совместились:
new_scene.show()Помимо рассмотренного метода регистрации в библиотеке trimesh также содержится классический алгоритм icp и метод Procrustes analysis. Пример применения другого метода к данным моделям можно найти в jupyter notebook 3dml_habr_phygitalism_part_2.ipynb.
Заметим, что для практических приложений скорость работы рассматриваемых алгоритмов может быть недостаточно, в силу того, что их реализации написана на языке Python. В случае, если есть необходимость в имплементации более быстрых версий алгоритмов регистрации или иных алгоритмов из trimesh, можно воспользоваться библиотекой trimesh2, написанной на языке C++.
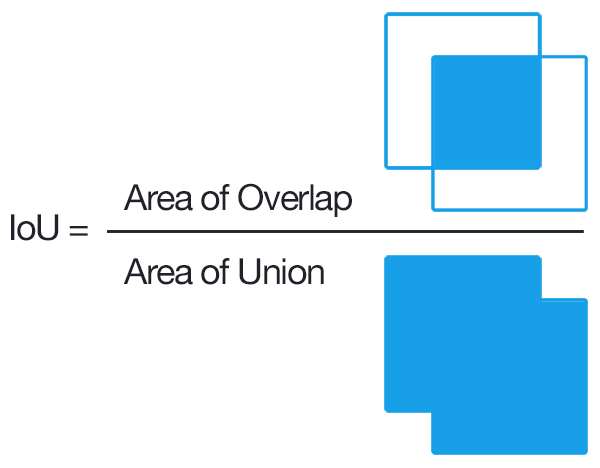
1. IoU metric
Метрика Intersection over Union (), также известная как Jaccard index, — число от 0 до 1, показывающее, насколько у двух объектов (эталонного (ground true) и текущего) совпадает внутренний “объем”.
Формально, для двух непустых множеств A и B, функция IoU определяется как:
Для того чтобы подсчитать необходимо уметь вычислять внутренний объем рассматриваемых объектов. В случаи с полигональными моделями чаще всего прибегают к оценке объема методом Монте-Карло.
В задачах компьютерного зрения и 3D ML часто используют при оценке того, насколько корректно найден ограничивающий прямоугольник или ограничивающий параллелепипед (bounding box), т.е. в качестве метрики качества алгоритма, но в последнее время появились различные модификации
, которые могут использованы и в качестве функции потерь [9].
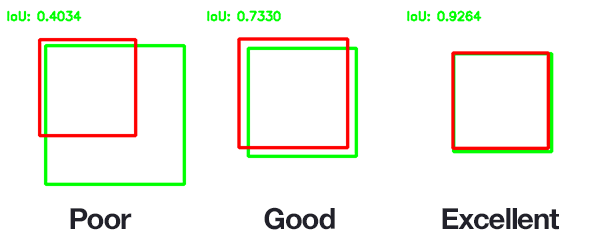
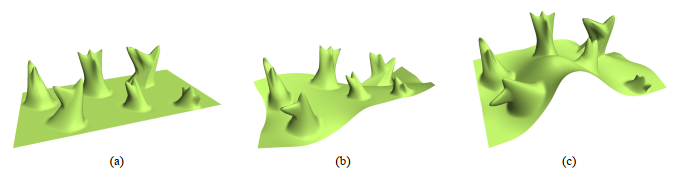
В случае с трехмерными объектами обычно используется в качестве метрики, однако данная метрика не всегда корректна. Действительно, большая часть информации об объекте определяется его поверхностью. На рисунке ниже продемонстрировано, что две модели могут иметь существенно отличные поверхности, при этом значение
будет высоко.
Для воксельных моделей значение данной метрики может быть некорректным ещё и по той причине, что “внутренность” моделей может отличаться, даже если у них схожие поверхности. На изображении ниже, из статьи [1], авторы продемонстрировали то, как при увеличении разрешения воксельной сетки растет качество метрики, но в тоже время растет и количество затрачиваемой памяти, времени обучения и параметров воксельной архитектуры. Для функциональной же модели (в данном случае Occupancy Net) качество не зависит от разрешения, а количество параметров неизменно.
Для работы с облаками точек данная функция обычно не применяется из-за того, что определить понятие объёма пересечения облаков точек достаточно затруднительно, однако такая возможность все равно имеется, так например в [8] авторы преобразуют выходное облако точек для их архитектуры в воксельную модель и сравнивают качество работы полученной модели по метрике. Для оценки качества работы модели на всем датасете обычно подсчитывают средние значения данной функции —
(mean intersection over union) для всего датасета и для отдельных категорий. Метрика
в процессе обучения максимизируется.
2. Chamfer loss/distance
Данная функция используется для работы как с полигональными моделями, так и с облаками точек. Она показывает, насколько вершины одной полигональной модели (облака точек) близки к вершинам другой полигональной модели (облаку точек), и следовательно, подлежит минимизации. Обычно сравнивают полигональную модель, полученную в результате работы алгоритма, и аналогичную модель из датасета.
Пусть мы имеем два множества вершин (точек) в трехмерном пространстве и
. Введем в рассмотрение множество пар
, такое, что для
точка
будет ближайшим соседом, т.е.:
тогда chamfer loss для данных точечных множеств определяется как:
Зачастую для вычисления chamfer loss имеющихся вершин полигональной модели недостаточно, поэтому дополнительно сэмплируют точки на гранях моделей, например так, как это делают авторы в недавно вышедшей работе [5]. Chamfer loss используется в качестве функции потерь. В [17] предложена модификация chamfer loss, использующая семплирования дополнительных точек на полигонах для вычисления значения функции потерь.
3. Normal loss / distance
Пусть аналогично предыдущему пункту мы рассматриваем два точечных множества и
, но помимо информации о вершинах мы можем также использовать информацию о нормалях, в частности, можем восстанавливать единичную нормаль
к произвольной точке
—
, тогда normal loss для данных точечных множеств определяется как:
Normal loss используется в качестве функции потерь и показывает, насколько сильно различаются поля нормалей у двух полигональных моделей, т.е. по сути, минимизируя данный критерий, мы стараемся сделать углы между соответствующими нормалями как можно меньше.
Вычислим значение chamfer loss и normal loss для наших тестовых моделей:
# Chamfer loss and normal loss
loss_chamfer, loss_normals_chamfer = chamfer_distance(
bunny_vert,
sphere_vert,
x_normals=bunny_norm,
y_normals=sphere_norm
)
print("Chamfer loss =", loss_chamfer.item())
print("Normal loss =", loss_normals_chamfer.item())Out:
>>Chamfer loss = 0.2609584927558899
>>Normal loss = 0.473361194133758544. Edge loss / regularizer
Недостатком chamfer и normal loss является чувствительность к выбросам. На рисунки ниже продемонстрирована ситуация, когда значение chamfer distance (CD) для двух в равной степени непохожих на оригинал объектов может значительно отличаться.
Помимо чувствительности к выбросам, на практике часто наблюдается эффект перекрытия полигонов. Чтобы избежать появления данного эффекта, вместе с chamfer и normal loss используют специальные регуляризаторы формы итогового меша (shape regularizers). Пусть — множество вершин полигональной модели, а
— множество ребер модели, тогда в качестве регуляризатора формы меша можно использовать среднее значение длины ребер:
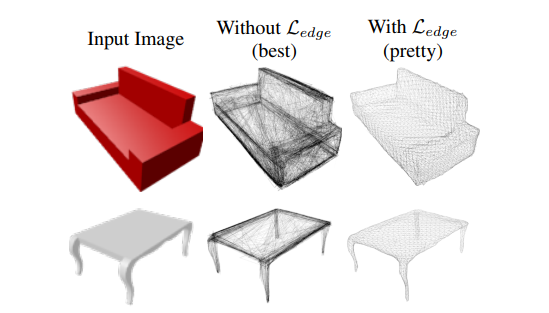
Авторы в [5], используя данный регуляризатор, улучшили качество итоговых моделей, что можно увидеть на изображениях ниже. Edge normalizer вводится дополнительным слагаемым к основной функции потерь с положительным коэффициентом.
Рис.4 Пример из статьи [5]: восстановление меша из изображения без использования регуляризатора формы (лучший результат) и с использованием регуляризатора формы (средний результат).
Рис.5 Пример из статьи [5]: сравнение результатов восстановления меша сетью, использовавшей регуляризатор при обучении (Mesh R-CNN), с сетью, в которой регуляризатор не использовался (Pixel2Mesh+).
Сравним значение данного регуляризатора для наших моделей:
print("Edge loss for bunny.obj:", mesh_edge_loss(bunny_mesh).item())
print("Edge loss for sphere.obj:", mesh_edge_loss(sphere_mesh).item())Out:
>>Edge loss for bunny.obj: 0.004127349238842726
>>Edge loss for sphere.obj: 0.0057241991162300115. Smooth loss / regularizer
Для того, чтобы итоговые модели имели более гладкие поверхности без выбросов и шума, часто прибегают к сглаживающим регуляризаторам. Простейшим сглаживающим регуляризатором является Smooth loss. Для его вычисления необходимо провести суммирование по всем “внутренним” двугранным углам между полигонами меша :
Введенная таким образом функция регуляризатора как бы стремится “распрямить” меш так, чтобы минимизировать поверхностное натяжение.
Рис.6 Пример из статьи [10]: сравнение работы алгоритма 2D-to-3D без использования smooth regularizer и с использованием данного регуляризатора. Слева направо: входное изображение, восстановленная полигональная модель без использования smooth regularizer, восстановленная полигональная модель c использования smooth regularizer.
Сравним значение данного регуляризатора для наших моделей:
print("Smooth regularizer for bunny.obj:", mesh_normal_consistency(bunny_mesh).item())
print("Smooth regularizer for sphere.obj:", mesh_normal_consistency(sphere_mesh).item())Out:
>>Smooth regularizer for bunny.obj: 0.03854169696569443
>>Smooth regularizer for sphere.obj: 0.00097806937992572786. Hausdorff losses
Проблема определения функции расстояния между двумя поверхностями в пространстве (которая используется для построения функции ошибки) стояла задолго до появления компьютерной графики. Вопрос о том, как находить расстояние между двумя вложенными в некоторое пространство многообразиями, был поставлен в функциональном анализе, и сегодня многие исследователи, при определении функции ошибки в задачах 3D ML, пользуются результатами из этой области. Так, в частности, существуют подходы, основанные на понятии метрики Хаусдорфа. Рассмотрим два таких подхода.
Оба подхода базируются на одинаковых математических понятиях, поэтому сначала опишем их. Во-первых, будем считать, что расстояние между некоторой точкой пространства и поверхностью
в этом пространстве определяется с помощью Евклидовой нормы следующим образом:
тогда “одностороннее” расстояние между двумя поверхностями и
можно определить как:
Под “односторонностью” здесь имеется в виду несимметричность данной функции. Чтобы определить симметричную функцию расстояния между двумя множествами, Хаусдорф предложил следующую конструкцию (называемую сегодня метрикой Хаусдорфа):
В качестве функции потерь, впрочем, используют не саму метрику, а средние значения расстояний от точки до поверхности. Введем в рассмотрении две функции. Средняя ошибка (mean distance error) между двумя поверхностями определяется как:
где — означает площадь поверхности
, а среднеквадратичная ошибка (root mean square distance error) между двумя поверхностями определяется как:
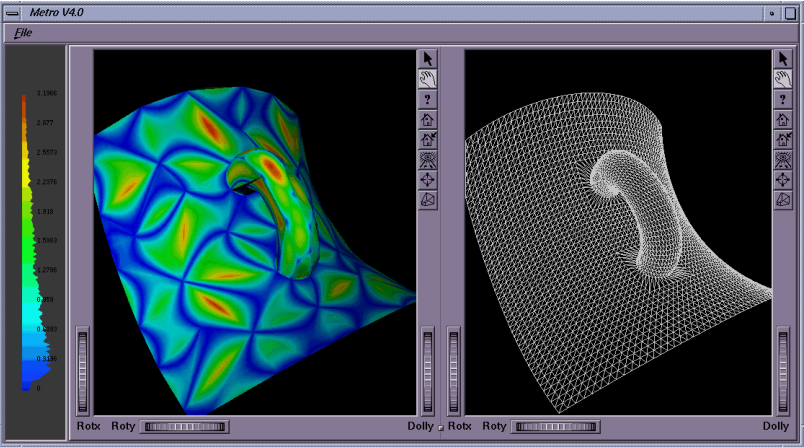
Существуют различные подходы к тому, как вычислять средние ошибки по Хаусдорфу на полигональном меше. Так, например, в [13] предложено вычислять значения средней ошибки на основании подсчета “ориентированных расстояний” между точкой и поверхностью. Такой подход авторы назвали Metro distance.
Рис.7 Пример из статьи [13]: сравнение двух мешей одного объекта: высокополигональная исходная модель (слева), оптимизированная низкополигональная модель.
В статье [14] авторы предлагают вычислять среднеквадратичную ошибку и конструируют оптимизированный численный метод для интегрирования по поверхности меша. Такой подход авторы называют Mesh distance.
Рис.8 Пример из статьи [13]: средняя ошибка, вычисленная по расстоянию Metro, для низкополигональной модели по сравнению с исходной высокополигональной моделью.
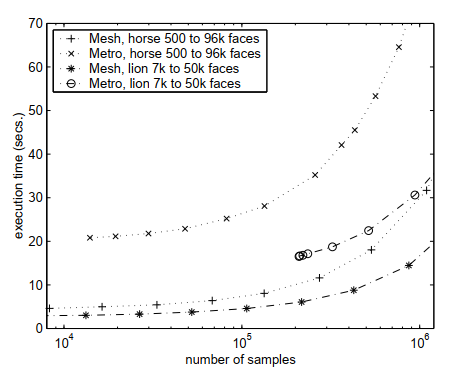
Также в статье [14] приведено сравнение этих двух подходов: Mesh distance оказывается более быстрым и экономным с точки зрения затраченной памяти способом вычисления Хаусдорфова расстояния. Данные функции можно использовать в качестве регуляризатора, если на каждой итерации алгоритма обучения хранить меш объекта с предыдущей итерации, и высчитывать значение ошибки приближения текущего меша предыдущим.
Рис.9 Пример из статьи [14]: сравнение вычислительной эффективности Mesh distance и Metro distance.
7. Laplacian loss / regularizer
Еще одним примером сглаживающего регуляризатора является Laplacian loss. Для того, чтобы сконструировать этот регуляризатор, используют часто возникающий в 3D ML и в компьютерной графике т.н. umbrella operator [15] — дискретизацию оператора Лапласа, вычисленного в вершинах полигонального меша:
Суммирование производится по вершинам, которые связаны с данной вершиной. В дальнейшем будем использовать обозначение для множества вершин, которые связаны с данным ребром. Можно рассматривать применение данного оператора как перевод вершин в новую систему координат. Такие координаты называют Лапласовыми. В [12] и [16] идея использования данного оператора применяется к задачам сглаживания, деформирования и конкатенации меша.
Рис.10 Пример из статьи [12]: сглаживание меша с помощью применения Laplacian smooth. (а) — исходный меш, (b) — после многократного применения Laplacian smooth.
Если оператор преобразования вершины меша в Лапласовы координаты будет иметь вид:
тогда Лапласов регуляризатор определяется как:
где суммирование производится по всем вершинам меша, а штриховая Лапласова координата обозначает меш на предыдущей итерации. Применительно к решению задачи 2D-to-3D данный регуляризатор применяется, например, в [11].
Рис.11 Пример из статьи [16]: деформирование меша с помощью применения Laplacian smooth.
Рис.12 Пример из статьи [16]: конкатенация меша с помощью применения Laplacian smooth. (а), (b) — исходные меши, (с) — конкатенированный меш, полученный с помощью применения Laplacian smooth.
Сравним значение данного регуляризатора для наших моделей:
print("Laplacian smoothing objective for bunny.obj:", mesh_laplacian_smoothing(bunny_mesh).item())
print("Laplacian smoothing objective for sphere.obj:", mesh_laplacian_smoothing(sphere_mesh).item())Out:
>>Laplacian smoothing objective for bunny.obj: 0.014459558762609959
>>Laplacian smoothing objective for sphere.obj: 0.0040009506046772Хорошую видеолекцию на тему применения оператора Лапласа в компьютерной графике можно найти здесь.
8. F1 score
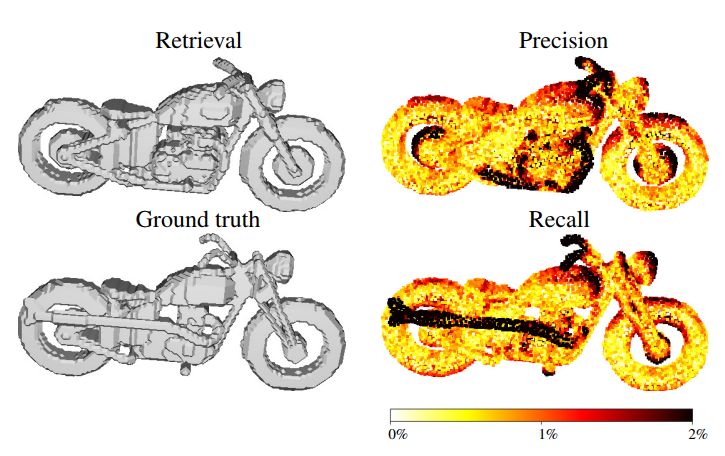
Если считать, что количество вершин в восстановленном меше (retrieval) равно количеству вершин в целевом меше (ground true), то каждую вершину восстановленного меша можно отнести либо к правильно восстановленой, либо к неправильно восстановленной. Для этого вводится пороговое значение расстояния между вершинами восстановленного и исходного объектов: если расстояние между соответствующими вершинами меньше порогового, то данную вершину восстановленного меша относят к верно восстановленной. Таким образом, для каждой вершины восстановленного меша можно определить два класса и использовать для всего объекта метрики качества задач классификации. В частности, как это продемонстрировано в работах [5,6], можно использовать F1 метрику, являющуюся средним гармоническим между точностью (precision) и полнотой (recall). Точность в данном случае определяется как отношение количества вершин восстановленного меша, находящихся в пределах порогового расстояния от соответствующих вершин исходного меша. Полнота определяется симметрично, как отношение количества точек исходного меша, лежащих не более чем на пороговом расстоянии от соответствующих точек восстановленного меша.
F1 устойчива к выбросам и лучше отражает качество восстановления формы объекта. F1 метрика максимизируется. Реализацию данной метрики и некоторых других можно найти в библиотеке pytorch geometric — фреймворке для работы с пространственными графами.
Рис.13 Пример из статьи [6]: слева сверху — восстановленный меш, слева снизу — исходный меш, справа сверху для восстановленного меша показано, насколько его вершины отличаются от исходного (в % длины ограничивающего параллелепипеда (bounding box)), справа снизу — для исходного меша показано, насколько его вершины отличаются от восстановленного (в % длины ограничивающего параллелепипеда (bounding box)).
9. Earth mover’s distance
Еще одной часто применяемой метрикой, в основном для облаков точек, является Earth mover’s distance (EMD), также известной в более общем виде как Wasserstein metric. Данная метрика возникает в задачах кластеризации изображений. До наступления эпохи глубокого обучения эта метрика часто применялась в области анализа изображений. Вычисление метрики тесно связано с решением оптимизационной транспортной задачи (подробнее про это и про то, как использовать эту метрику для различных типов данных, можно прочитать здесь).
Формально EMD определяется как минимальное значение функционала расстояния в следующей вариационной задаче:
Самое оптимальное биективное отображение в каждой конкретной задаче отличается, но преимуществом данной метрики является то, что оно инвариантно к произвольным инфиниматезиальным преобразованиям облака точек. Честное решение данной оптимизационной задачи обычно очень вычислительно затратно в задачах глубокого обучения, даже при использовании видеокарт, поэтому часто используют аппроксимированное вычисление этой метрики [7], как например это сделали авторы в [8]. Критерий EMD минимизируется в процессе обучения.
Рис.14 Пример из статьи [8]: сравнение восстановления средней формы (в смысле распределения исходных облаков точек) с помощью расстояний chamfer distance (CD) и Earth mover’s distance (EMD) для различных синтетических двумерных облаков точек (a-d).
Эксперимент с деформацией моделей
Чтобы лучше понять, как изменяются рассмотренные выше функции потерь и регуляризаторы в процессе обучения, рассмотрим модельный пример. Предположим, что модель сферы это исходное приближение, которое может генерировать наша модель машинного обучения, а в качестве целевой модели выступает модель кролика.
В качестве параметров модели машинного обучения возьмем координаты генерируемого меша (в данном случае сферы) и зададим оптимизатор, который будет минимизировать рассогласование между source (sphere) и target (bunny):
deform_verts = torch.full(sphere_mesh.verts_packed().shape, 0.0, device=device, requires_grad=True)
optimizer = torch.optim.SGD([deform_verts], lr=1.0, momentum=0.9)Зафиксируем параметры оптимизационного процесса:
# Number of optimization steps
Niter = 3000
# Weight for the chamfer loss
w_chamfer = 1.0
# Weight for mesh edge loss
w_edge = 1.0
# Weight for mesh normal consistency
w_normal = 0.01
# Weight for mesh laplacian smoothing
w_laplacian = 0.1
# Plot period for the losses
plot_period = 50
chamfer_losses = []
laplacian_losses = []
edge_losses = []
normal_losses = []В цикле будем делать градиентный спуск по функции потерь, представляющей из себя взвешенную сумму функций ошибок и регуляризаторов:
loop = tqdm_notebook(range(Niter))
fig = plt.figure()
camera = Camera(fig)
for i in loop:
# Initialize optimizer
optimizer.zero_grad()
# Deform the mesh
new_src_mesh = sphere_mesh.offset_verts(deform_verts)
# We sample 5k points from the surface of each mesh
sample_trg = sample_points_from_meshes(bunny_mesh, 5000)
sample_src = sample_points_from_meshes(new_src_mesh, 5000)
# We compare the two sets of pointclouds by computing (a) the chamfer loss
loss_chamfer, _ = chamfer_distance(sample_trg, sample_src)
# and (b) the edge length of the predicted mesh
loss_edge = mesh_edge_loss(new_src_mesh)
# mesh normal consistency
loss_normal = mesh_normal_consistency(new_src_mesh)
# mesh laplacian smoothing
loss_laplacian = mesh_laplacian_smoothing(new_src_mesh, method="uniform")
# Weighted sum of the losses
loss = loss_chamfer * w_chamfer + loss_edge * w_edge + loss_normal * w_normal + loss_laplacian * w_laplacian
# Print the losses
loop.set_description('total_loss = %.6f' % loss)
# Save the losses for plotting
chamfer_losses.append(loss_chamfer)
edge_losses.append(loss_edge)
normal_losses.append(loss_normal)
laplacian_losses.append(loss_laplacian)
# Plot mesh
if i % plot_period == 0 or i==0:
# Render the bunny providing the values of R and T.
image_bunny = phong_renderer(meshes_world=new_src_mesh, R=R, T=T)
image_bunny = image_bunny.detach().cpu().numpy()
plt.imshow(image_bunny.squeeze())
plt.grid(False)
camera.snap()
# Optimization step
loss.backward()
optimizer.step()
Для того, чтобы лучше понять динамику процесса оптимизации, мы использовали библиотеку celluloid для создании анимации.
Посмотрим, как изменялись функции потерь и регуляризаторы в процессе обучения:
# Losses evaluation
fig = plt.figure(figsize=(13, 5))
ax = fig.gca()
ax.plot(chamfer_losses, label="chamfer loss")
ax.plot(edge_losses, label="edge loss")
ax.plot(normal_losses, label="normal loss")
ax.plot(laplacian_losses, label="laplacian loss")
ax.legend(fontsize="16")
ax.set_xlabel("Iteration", fontsize="16")
ax.set_ylabel("Loss", fontsize="16")
ax.set_title("Loss vs iterations", fontsize="16")Заключение
Помимо перечисленных выше метрик используются и другие. Так, например, для воксельного представления моделей, воксели часто “вытягивают” в обычные числовые вектора и пользуются метриками и функциями потерь для векторов [4], например косинусной мерой.
После того, как модель обучена и показывает приемлемый результат по метрикам качества, ее нужно встраивать в общий pipeline обработки данных в конкретном проекте. На этом этапе появляются другие показатели качества используемой модели, такие как: размер памяти, которая занимает модель; размер памяти, необходимой для обработки данных моделью; скорость обработки данных моделью; время, необходимое для пере/дообучения модели. Все эти характеристики относят к внешним метрикам качества, в то время как рассмотренные выше метрики относят к внутренним метрикам качества решаемой задачи. Так же немаловажно, чтобы полученная архитектура и способ ее обучения были воспроизводимы. Обычно в статьях, описывающих новую архитектуру, указывается только алгоритм обучения, его параметры, и на каком датасете производилось обучение. Пример того, как измеряется производительность моделей глубокого обучения и некоторые связанные с этим аспекты, можно посмотреть здесь.
Понять, как отличать сложные трехмерные структуры друг от друга, и на основе этого судить о том, как хорошо справляется алгоритм машинного обучения с поставленной задачей — чрезвычайно важная задача. В зависимости от выбранной функции ошибки, качество результата и даже цель процесса обучения разнятся, поэтому важно понимать, как устроены такие функции. В современных библиотеках, использующихся для решения задач Geometrical Deep Learning, обычно такие функции уже имеют готовую реализацию, и исследователь имеет возможность просто выбрать необходимую функцию ошибки для его задачи. Например, такая возможность реализована в библиотеке Kaolin [18] от NVidia или в библиотеке pytorch3d [19] от Facebook, как мы убедились на примерах в данной заметке.
Про хороший и интересный пример того как корректно подобранная функция ошибки может улучшить качество работы алгоритмов в 3D ML вы можете узнать из лекции Алексея Артемова прошедшей в рамках Phygital Days.
О том, какие еще существуют библиотеки для работы в области 3D ML, как они устроены, какие есть датасеты с трехмерными данными, в чем заключается их специфика, мы поговорим в следующей заметке.
Источники
-
Mescheder, Lars & Oechsle, Michael & Niemeyer, Michael & Nowozin, Sebastian & Geiger, Andreas. (2018). Occupancy Networks: Learning 3D Reconstruction in Function Space. [code]
-
Facil, Jose & Ummenhofer, Benjamin & Zhou, Huizhong & Montesano, Luis & Brox, Thomas & Civera, Javier. (2019). CAM-Convs: Camera-Aware Multi-Scale Convolutions for Single-View Depth. [code]
-
Firman, Michael and Mac Aodha, Oisin and Julier, Simon and Brostow, Gabriel J. (2016). Structured Prediction of Unobserved Voxels From a Single Depth Image / Firman CVPR 2016 [code]
-
Richter, Stephan & Roth, Stefan. (2018). Matryoshka Networks: Predicting 3D Geometry via Nested Shape Layers.
-
Gkioxari, G., Malik, J., & Johnson, J. (2019). Mesh R-CNN. ArXiv, abs/1906.02739.
-
Tatarchenko, Maxim & Richter, Stephan & Ranftl, Rene & Li, Zhuwen & Koltun, Vladlen & Brox, Thomas. (2019). What Do Single-view 3D Reconstruction Networks Learn? [code]
-
D. P. Bertsekas. A distributed asynchronous relaxation algorithm for the assignment problem. In Decision and Control, 1985 24th IEEE Conference on, pages 1703–1704. IEEE, 1985
-
H. Fan, H. Su, and L. J. Guibas. A point set generation network for 3D object reconstruction from a single image. In Proc. IEEE Conf. on Computer Vision and Pattern Recognition (CVPR), 2017. [code]
-
Rezatofighi, Hamid & Tsoi, Nathan & Gwak, JunYoung & Sadeghian, Amir & Reid, Ian & Savarese, Silvio. (2019). Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression.
-
Hiroharu Kato, Yoshitaka Ushiku, and Tatsuya Harada. Neural 3d mesh renderer. In The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2018.
-
Nanyang Wang, Yinda Zhang, Zhuwen Li, Yanwei Fu, Wei Liu, and Yu-Gang Jiang. Pixel2mesh: Generating 3d mesh models from single rgb images. In ECCV, 2018.
-
M. Desbrun, M. Meyer, P. Schroder, and A. H. Barr. Implicit fairing of irregular meshes using diffusion and curvature flow. In SIGGRAPH, 1999.
-
P. Cignoni, C. Rocchini, and R. Scopigno, “Metro: measuring error on simplified surfaces,” Computer Graphics Forum, vol. 17, no. 2, pp. 167–174, June 1998.
-
Aspert, Nicolas & Santa-cruz, Diego & Ebrahimi, Touradj. (2002). MESH: Measuring Errors between Surfaces Using the Hausdorff Distance. Proceedings of the IEEE International Conference in Multimedia and Expo (ICME). 1. 705 — 708 vol.1. 10.1109/ICME.2002.1035879.
-
KOBBELT, L. Iterative Erzeugung glatter Interpolanten. Shaker Verlag, ISBN
3-8265-0540-9, 1995. -
O. Sorkine, Y. Lipman, D. Cohen-Or, M. Alexa, C. R¨ossl and H.P. Seidel: “Laplacian surface editing,” In Symposium on Geometry Processing, Vol. 71(2004), p. 175
-
Edward Smith, Scott Fujimoto, Adriana Romero, and David Meger. GEOMetrics: Exploiting geometric structure for graph-encoded objects. In Kamalika Chaudhuri and Ruslan Salakhutdinov, editors, Proceedings of the 36th International Conference on Machine Learning, volume 97 of Proceedings of Machine Learning Research, pages 5866–5876, Long Beach, California, USA, 09–15 Jun 2019. PMLR.
-
Jatavallabhula, Krishna Murthy, Edward Smith, Jean-Francois Lafleche, Clement Fuji Tsang, Artem Rozantsev, Wenzheng Chen, Tommy Xiang, Rev Lebaredian and Sanja Fidler. “Kaolin: A PyTorch Library for Accelerating 3D Deep Learning Research.” ArXivabs/1911.05063 (2019): n. pag. [project page]
-
Nikhila Ravi and Jeremy Reizenstein and David Novotny and Taylor Gordon and Wan-Yen Lo and Justin Johnson and Georgia Gkioxari. “PyTorch3D”, 2020 [project page]
“Мир полон волшебных вещей, терпеливо ожидающих того момента, когда наши чувства станут острее”. — У.Б. Йейтс
Что стоит за #(хэштегом)?
Совсем недавно я начала новую серию статей, смысл которых выражен хэштегом: #TheNotSoToughML (#НисколькоНеСложноеМО).
Предыдущие части: Часть 1, Часть 2.
Мне хотелось бы дать вам упрощенные решения некоторых проблем, возникающих в связи с алгоритмами/концепциями. Вместо того, чтобы сразу вдаваться в математику, я обращаюсь к вашей интуиции. Поверьте: машинное обучение вовсе не сложно. Оно больше похоже на интуитивное постижение, проверяемое алгоритмически.
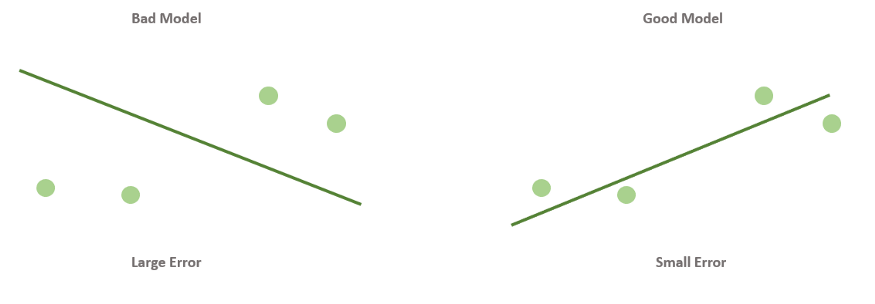
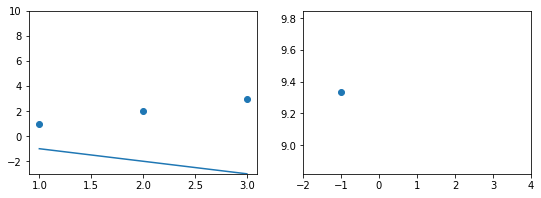
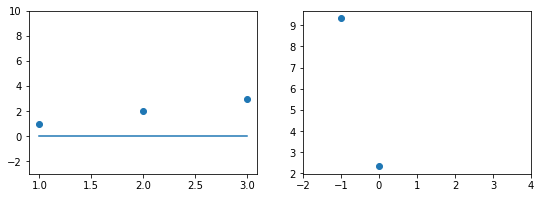
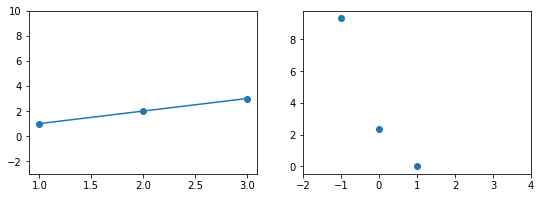
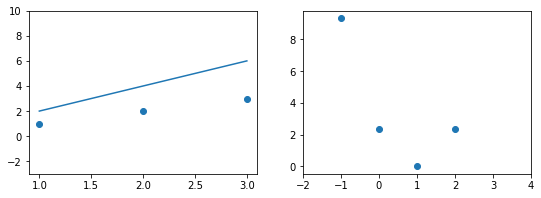
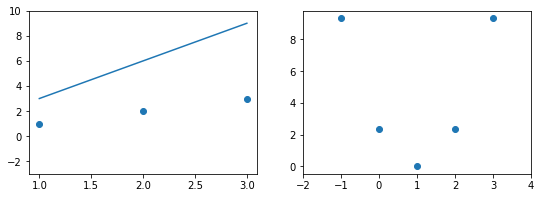
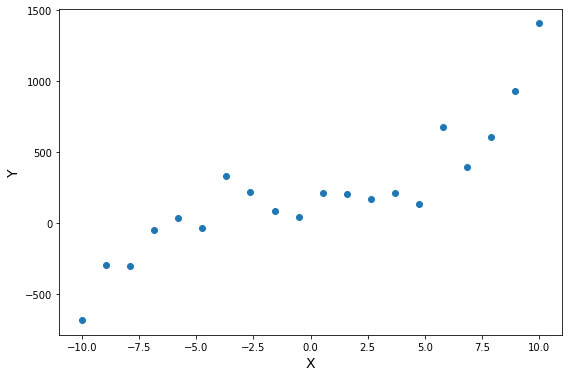
Концепция 1: Функция ошибки. Измерение результатов
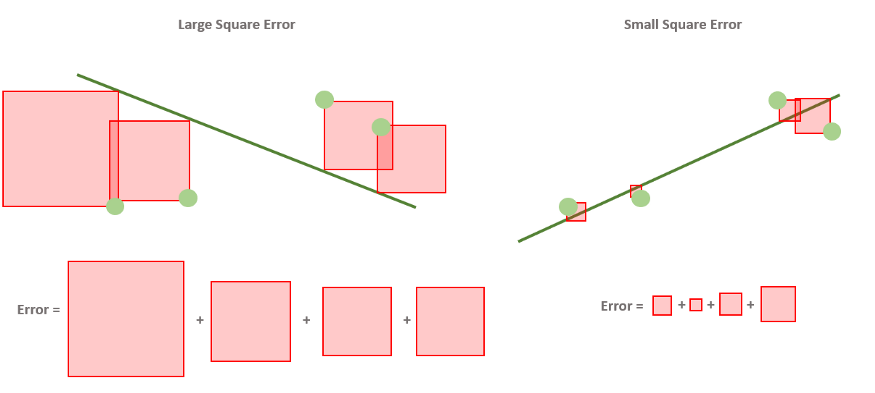
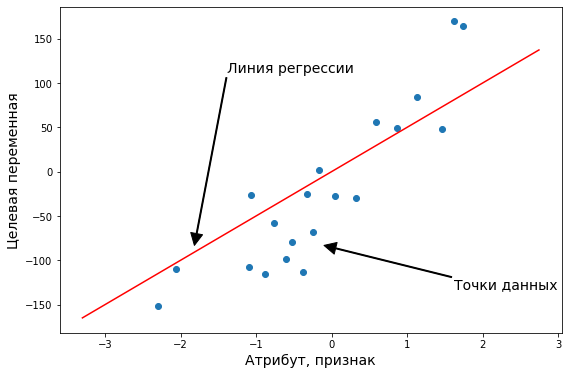
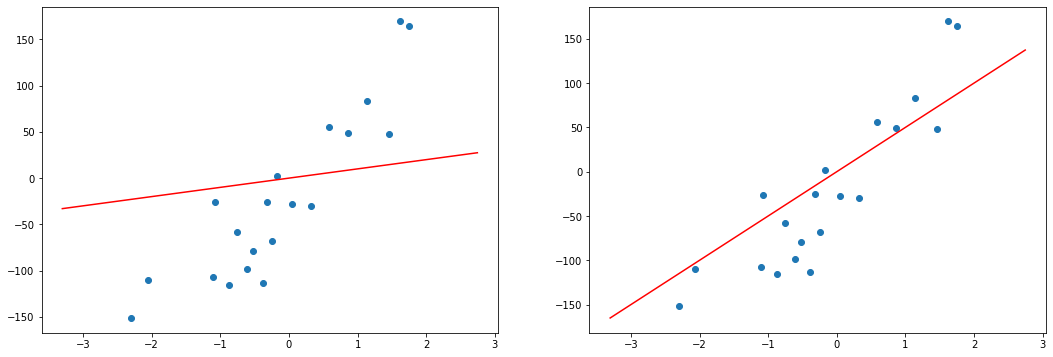
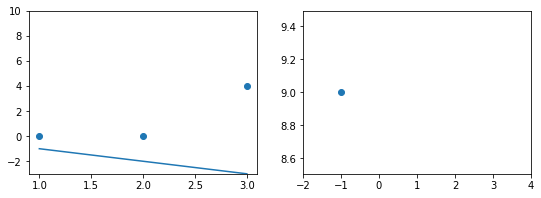
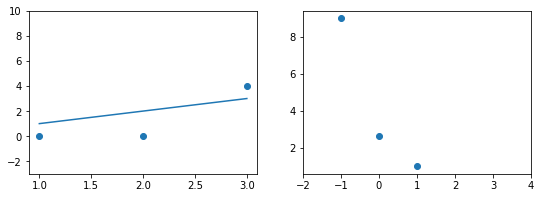
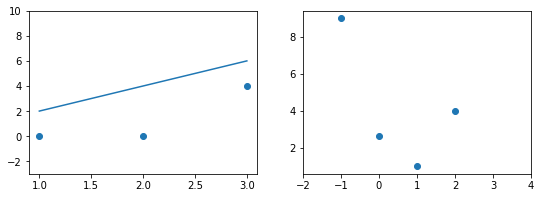
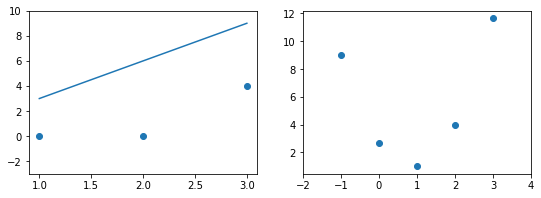
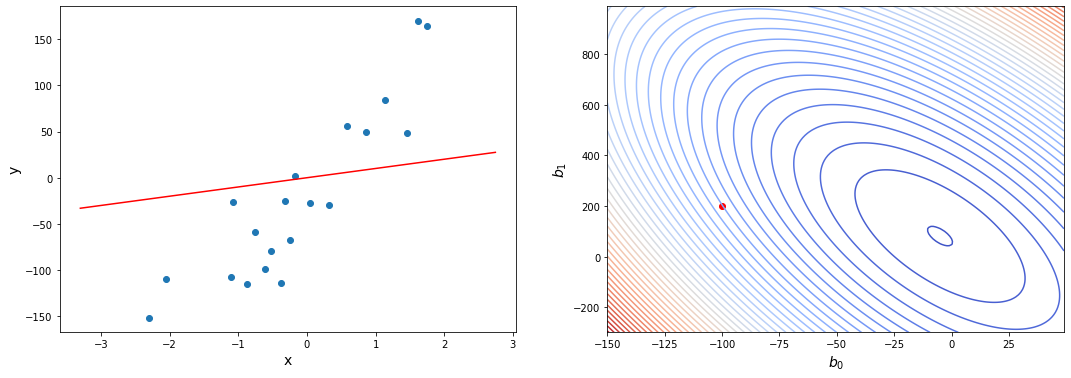
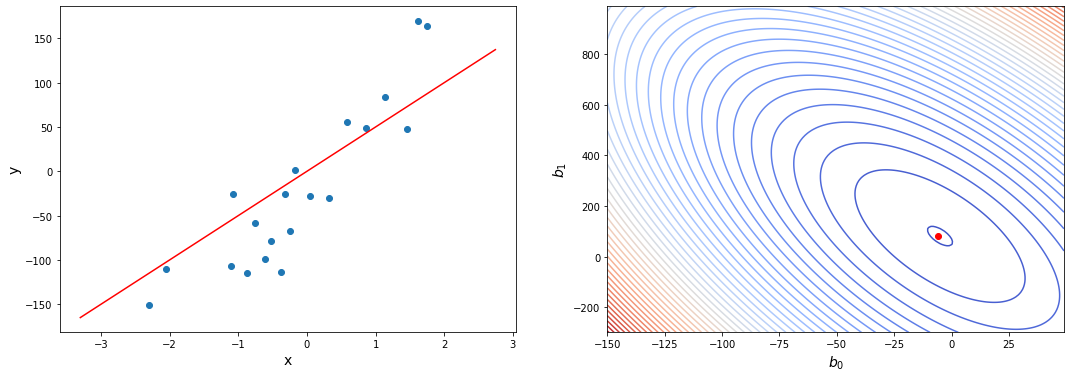
Когда вы смотрите на две модели выше и сравниваете их, приходите ли вы к тому же выводу, что и я? Как по-вашему, является ли плохая модель действительно “плохой” по сравнению с моделью справа? Если да, это значит, что вы сконцентрировали внимание на “зазоре” или расстоянии линии от каждой точки данных; таким образом, в среднем (или по совокупности признаков) вам показалось, что модель слева имеет большее расстояние между точками и линией по сравнению с моделью справа.
Функция ошибки помогает нам понять то же самое! Это метрика, показывающая то, как работает наша модель.
Функция ошибки будет присваивать большее значение модели слева и меньшее — модели справа. В специальной литературе такие функции также называют функциями потерь или функциями затрат.
Теперь перейдем к более важному вопросу.
Как определить, насколько точно работает функция ошибки для моделей линейной регрессии?
Сейчас мы поговорим об абсолютной ошибке и квадратичной ошибке.
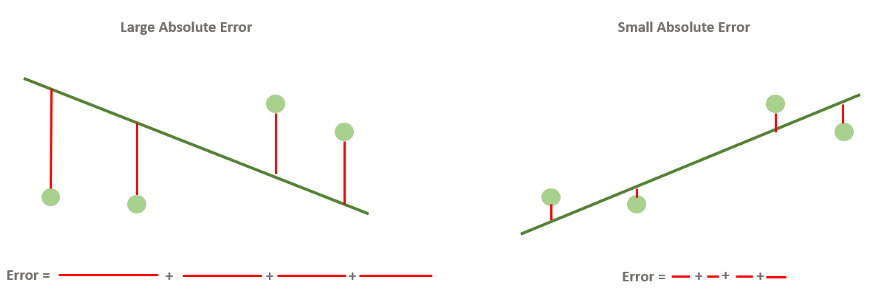
Абсолютная ошибка — метрика, которая складывает расстояния и показывает, насколько хороша наша модель.
Это самый простой для понимания и интерпретации показатель.
Это просто суммирование расстояний между точками данных и линией. Оно называется “абсолютным”, потому что расстояние может быть положительным или отрицательным в зависимости от расположения точек данных по отношению к линии. Следовательно, чтобы не упустить ни одного нюанса в поведении модели, мы принимаем абсолютное значение ошибок.
Итак, мы знаем, что хорошая модель линейной регрессии — это та модель, в которой линия близка к точкам данных.
Но что значит “близка”?
Выбираем ли мы линию, которая близка к некоторым точкам и далека от других? Или мы выбираем линию, которая близка ко всем точкам?
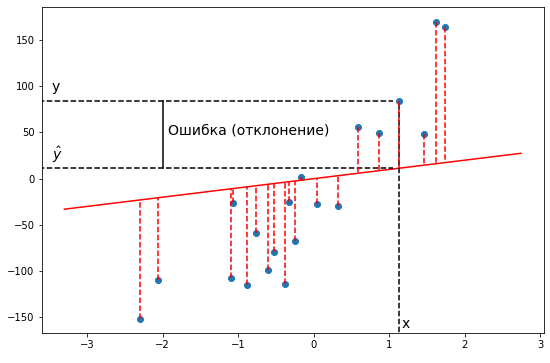
Вот тут-то и пригодится функция абсолютной ошибки. Мы выбираем линию, которая минимизирует абсолютную ошибку, т.е. ту, для которой сумма вертикальных расстояний от каждой точки до линии минимальна.
На рисунке ниже показаны разные абсолютные ошибки.
Теперь перейдем к следующему приему, связанному с ошибками.
Квадратичная ошибка — метрика, которая складывает квадраты расстояний и показывает, насколько хороша наша модель.
Квадратичная ошибка очень похожа на абсолютную ошибку. Но теперь, вместо того, чтобы брать абсолютное значение разницы между меткой и прогнозированной меткой, мы используем квадрат, что снова превращает число в положительное.
Давайте попробуем представить это так же, как мы это делали для абсолютной ошибки!
Квадратичная ошибка используется на практике чаще, чем абсолютная. Почему? Одна из причин заключается в том, что у квадрата гораздо более наглядная производная, чем у абсолютного значения, что очень удобно в процессе обучения.
Мы убедимся в этом чуть ниже.
Средняя абсолютная ошибка и (корневая) средняя квадратичная ошибка — самые распространенные и наиболее полезные ошибки для нашей модели
Абсолютная и квадратичная ошибки, показанные выше, служили простыми примерами того, что такое ошибки и как они могут выглядеть. Однако наиболее часто используемыми ошибками в проектах машинного обучения, особенно когда мы имеем дело с регрессионными моделями, являются средняя абсолютная ошибка (MAE) и средняя квадратичная ошибка (MSE).
Они определяются практически так же, только вместо вычисления сумм мы вычисляем средние значения.
Итак, MAE — это среднее значение вертикальных расстояний от точек до линии, а MSE — среднее значение квадратов этих же расстояний.
Эти ошибки более полезны, чем абсолютная и квадратичная ошибка, которые мы вычисляли в предыдущем разделе, и вот почему. Допустим, мы пытаемся подогнать одну и ту же модель к двум разным наборам данных, в одном из которых всего 10 точек данных, а в другом — миллион. Если ошибка является суммой величин (как в случае абсолютной или квадратичной ошибки), то она, вероятно, будет намного выше в наборе данных, состоящем из миллиона точек, потому что мы будем складывать гораздо больше чисел. Но эта проблема решается с помощью средних значений.
Еще один полезный показатель — среднеквадратичная ошибка (RMSE). Как следует из названия, это корень из средней квадратичной ошибки. Этот показатель используется для сопоставления единиц в задаче, а также для того, чтобы дать нам лучшее представление о том, насколько сильно модель ошибается при прогнозировании.
Концепция 2: Градиентный спуск. Уменьшение функции ошибки путем медленного “спуска с горы”
Теперь поговорим о перемещении линий на некоторое расстояние в контексте МО.
Поскольку цель этого цикла — объяснить интуитивный подход, а математические понятия использовать только там, где это абсолютно необходимо, мы воздержимся от того, чтобы углубляться в технические аспекты в этом разделе. Но если вы хотите разобраться в расчетах, которые проводятся при градиентном спуске, можете зайти на этот сайт и ознакомиться с ними.
Пока же мы попробуем понять, как градиентный спуск помогает нам уменьшить ошибку модели. При этом постараемся не погружаться в высшую математику. Скромная попытка, но все же.
Давайте решим вышеуказанную задачу в следующем порядке:
- Кратко разберем, как работает градиентный спуск.
- Расскажем, как он может решить задачу уменьшения ошибки
- Выясним, как с помощью полученных знаний мы узнаем, когда нужно останавливать работу алгоритма.
Как работает градиентный спуск
Представьте, что вы находитесь на вершине высокой горы — скажем, горы “Эррорест”.
Вы хотите спуститься с нее, но стоит очень туманная погода и вы видите только на расстоянии около 1 метра от себя. Что же делать? Вот вам дельный совет — оглянитесь вокруг себя и определите, в каком направлении можно сделать один единственный шаг так, чтобы спуститься максимально низко.
Нашли это направление? Теперь сделайте маленький шаг. Поскольку этот шаг был сделан в направлении максимального спуска, то, скорее всего, вы спуститесь на небольшое расстояние.
Теперь вам нужно повторять это действие много раз до тех пор, пока вы не достигнете подножия горы (хотелось бы надеяться на это).
Я написал “хотелось бы надеяться”, потому что в этом примере слишком много нюансов, которые мы разбирать не будем, чтобы не вдаваться в сложные математические понятия. Вы можете достичь подножия горы, а можете очутиться в долине, и вам больше некуда будет идти. Сейчас мы не станем разбирать все эти варианты.
Суть в том, что при градиентном спуске мы делаем один шаг за раз в направлении самой низкой точки (в нашем примере — подножия горы).
Как градиентный спуск помогает решить задачу уменьшения ошибки
Напомню, что мы определяем алгоритм линейной регрессии по следующей схеме:
- Начинаем с любой линии.
- Находим наилучшее направление, в котором можно немного сдвинуть нашу линию, используя прием из сферы абсолютных или квадратичных значений.
- Перемещаем линию в этом направлении.
- Повторяем эти шаги 2, 3 и более раз.
В предыдущем разделе мы говорили о градиентном спуске. Чтобы закрепить принцип его работы с помощью примера с горой, пройдем описанные этапы еще раз:
- Мы находимся на вершине горы.
- Находим оптимальное направление для первого маленького шага.
- Делаем маленький шаг в этом направлении.
- Повторяем эти шаги 2, 3 и более раз.
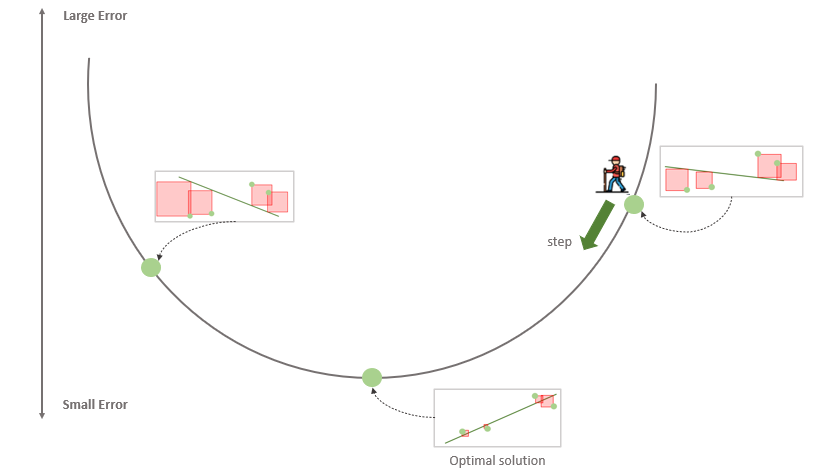
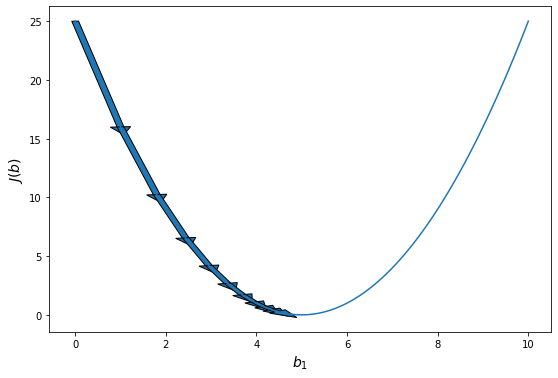
Знакомая схема, не так ли? Посмотрим на рисунок ниже.
Единственное отличие от нашего прежнего понимания линейной регрессии заключается в том, что эта функция ошибки больше напоминает долину, чем гору. Наша цель — спуститься в самую низкую точку. Каждая точка в этой долине соответствует некоторой модели (линии), которая пытается подогнать наши данные. Высота точки — это ошибка, которую выдает данная модель. Таким образом, плохие модели располагаются сверху, а хорошие — снизу. Мы стараемся опуститься как можно ниже. Каждый шаг ведет нас от худшей модели к чуть лучшей. Если мы будем делать такие шаги много раз, то в конце концов дойдем до лучшей модели (или, по крайней мере, довольно хорошей!).
Подытожим: что же нам нужно делать?
Мы хотим найти линию, которая лучше всего соответствует нашим данным. У нас есть метрика “функция ошибки”, которая показывает, насколько линия далека от данных. Таким образом, если мы сможем уменьшить это число как можно больше, мы найдем наиболее подходящую линию.
Этот процесс часто используется во многих областях математики и называется минимизацией функций (т.е. нахождение наименьшего возможного значения, которое может вернуть функция). В данном случае функция, которую мы пытаемся минимизировать, — это ошибка (абсолютная или квадратичная) нашей модели. Для минимизации этой функции мы используем градиентный спуск.
Как узнать, когда нужно останавливать работу алгоритма?
Давайте рассчитаем RMSE для любого набора данных, где мы пытаемся предсказать неизвестные значения (“метки”) и получить новые метки после запуска нашей модели (“прогнозы”):
def rmse(labels, predictions):
n = len(labels)
differences = np.subtract(labels, predictions)
return np.sqrt(1.0/n * (np.dot(differences, differences)))
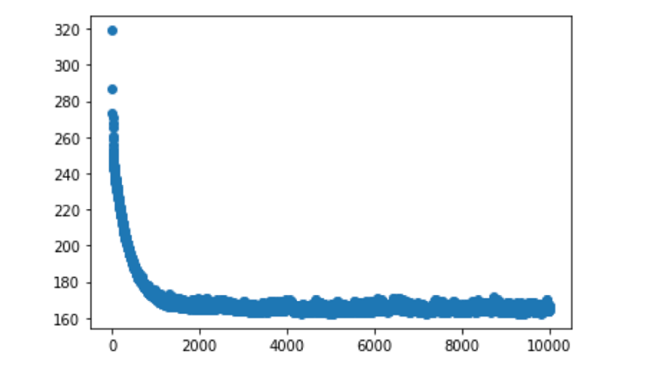
Теперь построим график, отобразив на нем, помимо прочего, количество эпох (итераций), в течение которых работает ваша модель. В итоге вы получите результат, похожий на тот, который вышел у меня, когда я тестировал таким образом свой образец набора данных:
Мы видим стремительное падение примерно после 1000 итераций, и после этого изменений на графике практически не наблюдается. Это говорит нам о том, что для данной конкретной модели мы можем запустить алгоритм обучения не на 10 000, а всего на 1000 или 2000 итераций. Тем не менее, мы все равно получим схожие результаты.
В целом, функция ошибки предоставляет надежную информацию, помогающую определиться с тем, когда следует прекращать выполнение алгоритма. Очень часто такое решение основывается на доступном нам времени и вычислительной мощности. Однако есть и другие полезные факторы, на которые часто ориентируются специалисты в сфере данных. Выполнение алгоритма также прекращают в следующих случаях:
- когда функция потерь достигает определенного значения, которое мы заранее установили;
- когда функция потерь не уменьшается в течение нескольких эпох.
Что дальше?
Это был краткий обзор работы функции ошибки и того, как градиентный спуск помогает нам уменьшить ее. Но, думаю, вы уже поняли, что есть масса других моментов, которые я не стал затрагивать в этой статье, чтобы не перегружать вас. Если у вас возникли дополнительные вопросы, можете заняться самообразованием и продолжать “копать” в этом направлении дальше.
Тем не менее, представленный в этой статье материал должен дать вам базовое представление о том, как работает большинство моделей. Наверняка вы убедились в том, что вам не нужны глубинные познания в математике, чтобы понять принципы машинного обучения!
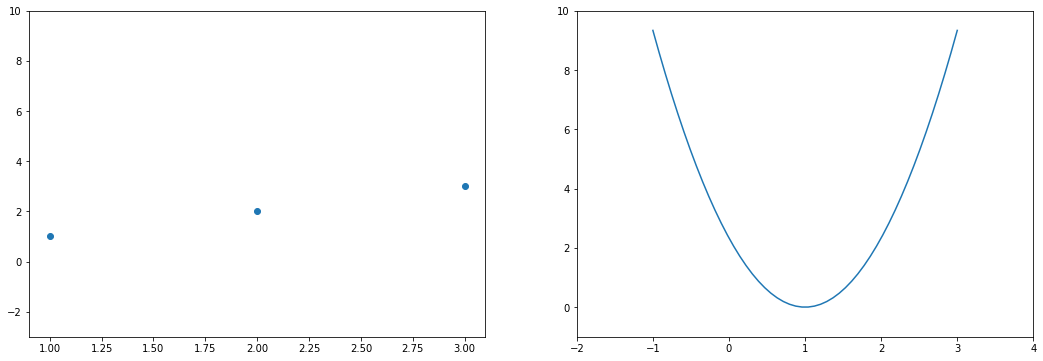
В следующей статье мы рассмотрим другую форму подгонки, а именно полиномиальную подгонку к данным (а не линейную) и будем использовать ее в дальнейшем, чтобы понять, как можно спасти наши модели от “недо/переподгонки”.
Самое главное, мы поймем, как функции ошибок и концепция градиентного спуска помогают регулировать веса, находить лучшее решение при оптимальном завершении процесса, и узнаем, как определить, что наша модель действительно работает!
Эта статья, как и многие другие, была написана под впечатлением от книги, которую я сейчас читаю — “Grokking Machine Learning” Луиса Серрано. Книга еще не вышла, но я приобрела ранний доступ к ней и думаю, что поступила правильно. Я считаю, что книги/материалы этого автора определенно заслуживают того, чтобы их прочитал каждый, кто хочет получить полное представление об алгоритмах и о том, как работают модели МО.
Читайте также:
- Создание модели машинного обучения с помощью Google Colab без дополнительных настроек
- 6 концептов книги Эндрю Ына «Жажда машинного обучения»
- Самая лучшая идея в науке о данных
Читайте нас в Telegram, VK и Яндекс.Дзен
Перевод статьи Anushree Chatterjee, #03TheNotSoToughML | Regression: Errors → Descending from a Mountain Top
Постановка задачи регрессии
Задача регрессии — это один из основных типов моделей машинного обучения. И хотя, большинство задач на практике относятся к другому типу — классификации, мы начнем знакомство с машинным обучением именно с регрессии. Регрессионные модели были известны задолго до появления машинного обучения как отрасли и активно применяются в статистике, эконометрике, математическом моделировании. Машинное обучение предлагает новый взгляд на уже известные в математике модели. И этот новый взгляд позволит строить более сложные и мощные модели, чем классические математические дисциплины.
Задача регрессии относится к категории задач обучения с учителем. Это значит, что набор данных, который используется для обучения, должен иметь определенную структуру. Обычно, датасеты для машинного обучения представляют собой таблицу, в которой по строкам перечислены разные объекты наблюдений или измерений. В столбцах — различные характеристики, или атрибуты, объектов. А на пересечении строк и столбцов — значение данной характеристики у данного объекта. Обычно один атрибут (или переменная) имеет особый характер — именно ее значение мы и хотим научиться предсказывать с помощью модели машинного обучения. Эта характеристика объекта называется целевая переменная. И если эта целевая переменная выражена числом (а точнее, некоторой непрерывной величиной) — то мы говорим о задаче регрессии.
Задача регрессии в машинном обучении — это задача предсказания какой-то численной характеристики объекта предметной области по определенному набору его параметров (атрибутов).
Задачи регрессии на практике встречаются довольно часто. Например, предсказание цены объекта недвижимости — классическая регрессионная задача. В таких проблемах атрибутами выступают разные характеристики квартир или домов — площадь, этажность, расположение, расстояние до центра города, количество комнат, год постройки. В разных наборах данных собрана разная информация И, соответственно, модели тоже должны быть разные. Другой пример — предсказание цены акций или других финансовых активов. Или предсказание температуры завтрашним днем.
Во всех таких задачах нам нужно иметь данные, которые позволят осуществить такое предсказание. Да, “предсказание” — это условный термин, не всегда мы говорим о будущих событиях. Зачастую говорят именно о “моделировании” значения целевой переменной. Регрессионные модели используют информацию об объектах в обучающем наборе данных, чтобы сделать вывод о возможном значении целевой переменной. И для этого нужно, чтобы ее значение имело какую-то зависимость от имеющихся у нас атрибутов. Если построить модель предсказания цены акции, но на вход подать информацию о футбольных матчах — ничего не получится. Мы предполагаем, что в наборе данных собраны именно те атрибуты объектов, которые имеют влияние на на значение целевой переменной. И чем больше это предположение выполняется, тем точнее будет потенциально наша модель.
Немного поговорим о терминах. Набор данных который мы используем для обучения модели называют датасетом (dataset) или обучающей выборкой (training set). Объекты, которые описываются в датасете еще называют точками данных (data points). Целевую переменную еще называют на статистический манер зависимой переменной (dependent variable) или результативной, выходной (output), а остальные атрибуты — независимыми переменными (independent variables), или признаками (features), или факторами, или входными переменными (input). Значения одного конкретного атрибута для всех объектов обучающей выборки часто представляют как вектор этого признака (feature vector). А всю таблицу всех атрибутов называют матрицей атрибутов (feature matrix). Соответственно, еще есть вектор целевой переменной, он не входит в матрицу атрибутов.
Датасет, набор данных — совокупность информации в определенной структурированной форме, которая используется для построения модели машинного обучения для решения определенной задачи. Датасет обычно представляется в табличной форме. Датасет описывает некоторое множество объектов предметной области — точек данных.
С точки зрения информатики, регрессионная модель — это функция, которая принимает на вход значения атрибутов какого-то конкретного объекта и выдает на выходе предполагаемое значение целевой переменной. В большинстве случаев мы предполагаем, что целевая переменная у нас одна. Если стоит задача предсказания нескольких характеристик, то их чаще воспринимают как несколько независимых задач регрессии на одних и тех же атрибутах.
Мы пока ничего не говорили о том, как изнутри устроена регрессионная модель. Это потому, что она может быть какой угодно. Это может быть математическое выражение, условный алгоритм, сложная программа со множеством ветвлений и циклов, нейронная сеть — все это можно представить регрессионной моделью. Единственное требование к модели машинного обучения — она должна быть параметрической. То есть иметь какие-то внутренние параметры, от которых тоже зависит результат вычисления. В простых случаях, чаще всего в качестве регрессионной модели используют аналитические функции. Таких функций бесконечное количество, но чаще всего используется самая простая функция, с которой мы и начнем изучение регрессии — линейная функция.
Регрессионные модели подразделяют на парную и множественную регрессии. Парная регрессия — это когда у нас всего один атрибут. Множественная — когда больше одного. Конечно, на практике парная регрессия не встречается, но на примере такой простой модели мы поймем основные концепции машинного обучения. Плюс, парную регрессию очень удобно и наглядно можно изобразить на графике. Когда у нас больше двух переменных, графики уже не особо построишь, и модели приходится визуализировать иначе, более косвенно.
Выводы:
- Регрессия — это задача машинного обучения с учителем, которая заключается в предсказании некоторой непрерывной величины.
- Для использования регрессионных моделей нужно, чтобы в датасете были характеристики объектов и “правильные” значения целевой переменной.
- Примеры регрессионных задач — предсказание цены акции, оценка цены объекта недвижимости.
- Задача регрессии основывается на предположении, что значение целевой переменной зависит от значения признаков.
- Регрессионная модель принимает набор значений и выдает предсказание значения целевой переменной.
- В качестве регрессионных моделей часто берут аналитические функции, например, линейную.
Парная линейная регрессия
Функция гипотезы
Напомним, что в задачах регрессии мы принимаем входные переменные и пытаемся получить более-менее достоверное значение целевой переменной. Любая функция, даже самая простая линейная может выдавать совершенно разные значения для одних и тех же входных данных, если в функции будут разные параметры. Поэтому, любая регрессионная модель — это не какая-то конкретная математическая функция, а целое семейство функций. И задача алгоритма обучения — подобрать значения параметров таким образом, чтобы для объектов обучающей выборки, для которых мы уже знаем правильные ответы, предсказанные (или теоретические, вычисленные из модели) значения были как можно ближе к тем, которые есть в датасете (эмпирические, истинные значения).
Функция гипотезы — преобразование, которое принимает на вход набор значений признаков определенного объекта и выдает оценку значения целевой переменной данного объекта. Она лежит в основе модели машинного обучения.
Парная, или одномерная (univariate) регрессия используется, когда вы хотите предсказать одно выходное значение (чаще всего обозначаемое $y$), зависящее от одного входного значения (обычно обозначается $x$). Сама функция называется функцией гипотезы или моделью. В качестве функции гипотезы для парной регрессии можно выбрать любую функцию, но мы пока потренируемся с самой простой функцией одной переменной — линейной функцией. Тогда нашу модель можно назвать парной линейной регрессией.
В случае парной линейной регрессии функция гипотезы имеет следующий общий вид:
[hat{y} = h_b (x) = b_0 + b_1 x]
Обратите внимание, что это похоже на уравнение прямой. Эта модель соответствует множеству всех возможных прямых на плоскости. Когда мы конкретизируем модель значениями параметров (в данном случае — $b_0$ и $b_1$), мы получаем конкретную прямую. И наша задача состоит в том, чтобы выбрать такую прямую, которая бы лучше всего “легла” в точки из нашей обучающей выборки.
В данном случае, мы пытаемся подобрать функцию h(x) таким образом, чтобы отобразить данные нам значения x в данные значения y. Допустим, мы имеем следующий обучающий набор данных:
| входная переменная x | выходная переменная y |
| 0 | 4 |
| 1 | 7 |
| 2 | 7 |
| 3 | 8 |
Мы можем составить случайную гипотезу с параметрами $ b_0 = 2, b_1 = 2 $. Тогда для входного значения $ x=1 $ модель выдаст предсказание, что $ y=4 $, что на 3 меньше данного. Значение $y$, которое посчитала модель будем называть теоретическим или предсказанным (predicted), а значение, которое дано в наборе данных — эмпирическим или истинным (true). Задача регрессии состоит в нахождении таких параметров функции гипотезы, чтобы она отображала входные значения в выходные как можно более точно (чтобы теоретические значения были как можно ближе к эмпирическим), или, другими словами, описывала линию, наиболее точно ложащуюся в данные точки на плоскости $(x, y)$.
Выводы:
- Модель машинного обучения — это параметрическая функция.
- Задача обучения состоит в том, чтобы подобрать параметры модели таким образом, чтобы она лучше всего описывала обучающие данные.
- Парная линейная регрессия работает, если есть всего одна входящая переменная.
- Парная линейная регрессия — одна из самых простых моделей машинного обучения.
- Парная линейная регрессия соответствует множеству всех прямых на плоскости. Из них мы выбираем одну, наиболее подходящую.
Функция ошибки
Как мы уже говорили, разные значения параметров дают разные конкретные модели. Для того, чтобы подобрать наилучшую модель, нам нужно средство измерения “точности” модели, некоторая функция, которая показывает, насколько модель хорошо или плохо соответствует имеющимся данным.
В простых случаях мы можем отличить хорошие модели от плохих, только взглянув на график. Но это затруднительно, если количество признаков очень велико, или если модели лишь немного отличаются друг от друга. Да и для автоматизации процесса нужен способ формализовать наше общее представление о том, что модель “ложится” в точки данных.
Такая функция называется функцией ошибки (cost function). Она измеряет отклонения теоретических значений (то есть тех, которые предсказывает модель) от эмпирических (то есть тех, которые есть в данных). Чем выше значение функции ошибки, тем хуже модель соответствует имеющимся данным, хуже описывает их. Если модель полностью соответствует данным, то значение функции ошибки будет нулевым.
В задачах регрессии в качестве функции ошибки чаще всего берут среднеквадратичное отклонение теоретических значений от эмпирических. То есть сумму квадратов отклонений, деленную на удвоенное количество измерений. Казалось бы, что это довольно произвольный выбор. Но он вполне обоснован и логичен. Давайте порассуждаем. Чтобы оценить, насколько хороша модель, мы должны оценить, насколько отклоняются эмпирические значения, то есть (y_i) от теоретических, предсказанных моделью, то есть (h_b(x_i)). Проще всего это отклонение выразить в виде разницы между этими двумя значениями. Но эта разница будет характеризовать отклонение только в одной точке данных, а в датасете может быть их произвольное количество. Поэтому имеет смысл взять сумму этих разностей для всех точек данных:
[J = sum_{i=1}^{m} (h_b(x_i) — y_i)]
Но с этим подходом есть одна проблема. Дело в том, что отклонения реальных значений от предсказанных могут быть как положительные, так и отрицательные. И если мы просто их все сложим, то положительные как бы скомпенсируют отрицательные. И в итоге даже очень плохие модели могут выглядеть, как имеющие маленькие ошибки. Фактически, для любого набора данных, если модель проходит через геометрический центр распределения, то такая ошибка будет равна нулю. То есть для достижения нулевой ошибки линии регрессии достаточно проходить через одну определенную точку. Таких моделей, очевидно, бесконечное количество, и все они будут иметь нулевую сумму отклонений. Конечно, так не пойдет и нужно придумать такую формулу, чтобы положительные и отрицательные отклонения не взаимоуничтожались, а складывались без учета знака.
Можно было бы взять отклонения по модулю. Но у такого подхода есть один большой недостаток: Функция абсолютного значения не везде дифференцируема. В одной точке у нее не существует производной. А чуть позже нам очень понадобится брать производную от функции ошибки. Поэтому модуль нам не подходит. Но в математике есть и другие функции, которые позволяют “избавиться” от знака числа. Например, возведение в квадрат. Его как раз и применяют в функции ошибки:
[J = sum_{i=1}^{m} (h_b(x_i) — y_i)^2]
У этого подхода есть еще одно неочевидное достоинство. Квадратичная функция дополнительно сильно увеличивает размер больших чисел. То есть, если среди наших отклонений будет какое-то очень большое, то после возведения в квадрат оно станет еще непропорционально больше. Таким образом квадратичная функция ошибки как бы сильнее “штрафует” сильные отклонения предсказанных значений от реальных.
Но есть еще одна проблема. Дело в том, что в разных наборах данных может быть разное количество точек. Если мы просто будем считать сумму отклонений, то чем больше точек будем суммировать, тем больше итоговое отклонение будет только из-за количества слагаемых. Поэтому модели, обученные на маленьких объемах данных будут иметь преимущество. Это тоже неправильно и поэтому берут не сумму, а среднее из отклонений. Для этого достаточно лишь поделить эту сумму на количество точек данных:
[J = frac{1}{2m} sum_{i=1}^{m} (h_b(x_i) — y_i)^2]
В итоге мы как раз получаем среднеквадратичное отклонение реальных значений от предсказанных. Эта функция дает хорошее представление о том, какая конкретная модель хорошо соответствует имеющимся данным, а какая — хуже или еще лучше.
[J(b_0, b_1)
= frac{1}{2m} sum_{i=1}^{m} (hat{y_i} — y_i)^2
= frac{1}{2m} sum_{i=1}^{m} (h_b(x_i) — y_i)^2]
Эту функцию называют «функцией квадрата ошибки» или «среднеквадратичной ошибкой» (mean squared error, MSE). Среднее значение уменьшено вдвое для удобства вычисления градиентного спуска, так как производная квадратичной функции будет отменять множитель 1/2. Вообще, функцию ошибки можно свободно домножить или разделить на любое число (положительное), ведь нам не важна конкретная величина этой функции. Нам важно, что какие-то модели (то есть наборы значений параметров модели) имеют низкую ошибку, они нам подходят больше, а какие-то — высокую ошибку, они подходят нам меньше.
Обратите внимание, что в качестве аргументов у функции ошибки выступают параметры нашей функции гипотезы. Ведь функция ошибки оценивает отклонение конкретной функции гипотезы (то есть набора значений параметров этой функции) от эмпирических значений, то есть ставит в соответствие каждому набору параметров модели число, характеризующее ошибку этого набора.
Давайте проследим формирование функции ошибки на еще более простом примере. Возьмем упрощенную форму линейной модели — прямую пропорциональность. Она выражается формулой:
[hat{y} = h_b (x) = b_1 x]
Эта модель поможет нам, так как у нее всего один параметр. И функцию ошибки можно будет изобразить на плоскости. Возьмем фиксированный набор точек и попробуем несколько значений параметра для вычисления функции ошибки. Слева на графике изображены точки данных и текущая функция гипотезы, а на правом графике бы будем отмечать значение использованного параметра (по горизонтали) и получившуюся величину функции ошибки (по вертикали):
При значении $b_1 = -1$ линия существенно отклоняется от точек. Отметим уровень ошибки (примерно 10) на правом графике.
Если взять значение $b_1 = 0$ линия гораздо ближе к точкам, но ошибка все еще есть. Отметим новое значение на правом графике в точке 0.
При значении $b_1 = 1$ график точно ложится в точки, таким образом ошибка становится равной нулю. Отмечаем ее так же.
При дальнейшем увеличении $b_1$ линия становится выше точек. Но функция ошибки все равно будет положительной. Теперь она опять станет расти.
На этом примере мы видим еще одно преимущество возведения в квадрат — это то, что такая функция в простых случаях имеет один глобальный минимум. На правом графике формируется точка за точкой некоторая функция, которая похожа очертаниями на параболу. Но мы не знаем аналитического вида этой параболы, мы можем лишь строить ее точка за точкой.
В нашем примере, в определенной точке функция ошибки обращается в ноль. Это соответствует “идеальной” функции гипотезы. То есть такой, когда она проходит четко через все точки. В нашем примере это стало возможно благодаря тому, что точки данных и так располагаются на одной прямой. В общем случае это не выполняется и функция ошибки, вообще говоря, не обязана иметь нули. Но она должна иметь глобальный минимум. Рассмотрим такой неидеальный случай:
Какое бы значение параметра мы не использовали, линейная функция неспособна идеально пройти через такие три точки, которые не лежат на одной прямой. Эта ситуация называется “недообучение”, об этом мы еще будем говорить дальше. Это значит, что наша модель слишком простая, чтобы идеально описать данные. Но зачастую, идеальная модель и не требуется. Важно лишь найти наилучшую модель из данного класса (например, линейных функций).
Выше мы рассмотрели упрощенный пример с функцией гипотезы с одним параметром. Но у парной линейной регрессии же два параметра. В таком случае, функция ошибки будет описывать не параболу, а параболоид:
Теперь мы можем конкретно измерить точность нашей предсказывающей функции по сравнению с правильными результатами, которые мы имеем, чтобы мы могли предсказать новые результаты, которых у нас нет.
Если мы попытаемся представить это наглядно, наш набор данных обучения будет разбросан по плоскости x-y. Мы пытаемся подобрать прямую линию, которая проходит через этот разбросанный набор данных. Наша цель — получить наилучшую возможную линию. Лучшая линия будет такой, чтобы средние квадраты вертикальных расстояний точек от линии были наименьшими. В лучшем случае линия должна проходить через все точки нашего набора данных обучения. В таком случае значение J будет равно 0.
В более сложных моделях параметров может быть еще больше, но это не важно, ведь нам не нужно строить функцию ошибки, нам нужно лишь оптимизировать ее.
Выводы:
- Функция ошибки нужна для того, чтобы отличать хорошие модели от плохих.
- Функция ошибки показывает численно, насколько модель хорошо описывает данные.
- Аргументами функции ошибки являются параметры модели, ошибка зависит от них.
- Само значение функции ошибки не несет никакого смысла, оно используется только в сравнении.
- Цель алгоритма машинного обучения — минимизировать функцию ошибки, то есть найти такой набор параметров модели, при которых ошибка минимальна.
- Чаще всего используется так называемая L2-ошибка — средний квадрат отклонений теоретических значений от эмпирических (метрика MSE).
Метод градиентного спуска
Таким образом, у нас есть функция гипотезы, и способ оценить, насколько хорошо конкретная гипотеза вписывается в данные. Теперь нам нужно подобрать параметры функции гипотезы. Вот где приходит на помощь метод градиентного спуска. Идея этого метода достаточно проста, но потребует для детального знакомства вспомнить основы математического анализа и дифференциального исчисления.
Несмотря на то, что мы настоятельно советуем разобраться в основах функционирования метода градиентного спуска шаг за шагом для более полного понимания того, как модели машинного обучения подбирают свои параметры, если читатель совсем не владеет матанализом, данные объяснения можно пропустить, они не являются критичными для повседневного понимания сути моделей машинного обучения.
Это происходит при помощи производной функции ошибки. Напомним, что производная функции показывает направление роста этой функции с ростом аргумента. Необходимое условие минимума функции — обращение в ноль ее производной. А так как мы знаем, что квадратичная функция имеет один глобальный экстремум — минимум, то наша задача очень проста — вычислить производную функции ошибки и найти, где она равна нулю.
Давайте найдем производную среднеквадратической функции ошибки. Так как эта функция зависит от двух аргументов — (b_0) и (b_1), то нам понадобится взять частные производные этой функции по всем ее аргументам. Для начала вспомним формулу самой функции ошибки:
[J(b_0, b_1) = frac{1}{2 m} sum_{i=1}^{m} (h_b(x_i) — y_i)^2]
Частная производная обозначается (frac{partial f}{partial x}) или (frac{partial}{partial x} f) и является обобщением обычной (полной) производной для функций нескольких аргументов. Частая производная показывает наклон функции в направлении изменения определенного аргумента, то есть как бы “в разрезе” этого аргумента. Градиент — это вектор частных производных функции по всем ее аргументам. Вектор градиента показывает направление максимального роста функции.
Что бы посчитать производную по какому-то из аргументов нам понадобятся обычные правила вычисления производной. Во-первых, общий множитель можно вынести из-под производной, Во-вторых, производная суммы равна сумме производных, поэтому знак суммы тоже можно вынести из-под производной. Поэтому получаем:
[frac{partial}{partial b_i} J =
frac{1}{2 m} sum_{i=1}^{m} frac{partial}{partial b_i} (h_b(x_i) — y^{(i)})^2]
Теперь самое сложное — производная сложной функции. По правилу она равна производной внешней функции, умноженной на производную внутренней. Внешняя функция — это квадратическая, ее производная равна удвоенному подквадратному выражению ((frac{d}{dt} t^2 = 2 t)). Подставляем (t = h_b(x_i) — y^{(i)}) и получаем:
[frac{partial}{partial b_i} J =
frac{1}{m} sum_{i=1}^{m} (h_b(x_i) — y^{(i)}) cdot frac{partial}{partial b_i} h_b(x_i)]
Обратите внимание, что эта самая двойка прекрасно сократилась со знаменателем в постоянном множителе функции ошибки. Именно за этим он и был нужен.
Чтобы продолжить вычисление производной дальше, нужно представить функцию гипотезы как линейную функцию:
[J(b_0, b_1) = frac{1}{2m} sum_{i=1}^{m} (b_0 + b_1 x_i — y_i)^2]
И теперь мы уже не можем говорить о какой-то частной производной в общем, нужно отдельно посчитать производные по разным значениям параметров. Но тут все как раз очень просто, так как нам осталось посчитать производные линейной функции. Они равны просто коэффициентам при соответствующих аргументах. Для свободного коэффициента аргумент равен, очевидно, 1:
[frac{partial J}{partial b_0} =
frac{1}{m} sum (b_0 + b_1 x_i — y_i) =
frac{1}{m} sum (h_b(x_i) — y_i)]
А для коэффициента при $x_i$ производная равна самому значению $x_i$:
[frac{partial J}{partial b_1} =
frac{1}{m} sum (b_0 + b_1 x_i — y_i) cdot x_i =
frac{1}{m} sum (h_b(x_i) — y_i) cdot x_i]
Теперь для нахождения минимального значения функции ошибки нам нужно только приравнять эти производные к нулю, то есть решить для $b_0, b_1$ следующую систему уравнений:
[frac{partial J}{partial b_0} =
frac{1}{m} sum (h_b(x_i) — y_i) = 0]
[frac{partial J}{partial b_1} =
frac{1}{m} sum (h_b(x_i) — y_i) cdot x_i = 0]
Проблема в том, что мы не можем просто решить эти уравнения аналитически. Ведь мы не знаем общий вид функции ошибки, не то, что ее производной. Ведь он зависит от всех точек данных. Но мы можем вычислить эту функцию (и ее производную) в любой точке. А точка на этой функции — это конкретный набор значений параметров модели. Поэтому пришлось изобрести численный алгоритм. Он работает следующим образом.
Сначала, мы выбираем произвольное значение параметров модели. То есть, произвольную точку в области определения функции. Мы не знаем, является ли эта точка оптимальной (скорее нет), не знаем, насколько она далека от оптимума. Но мы можем вычислить направление к оптимуму. Ведь мы знаем наклон касательной к графику функции ошибки.
Наклон касательной является производной в этой точке, и это даст нам направление движения в сторону самого крутого уменьшения значения функции. Если представить себе функцию одной переменной (параболу), то там все очень просто. Если производная в точке отрицательна, значит функция убывает, значит, что оптимум находится справа от данной точки. То есть, чтобы приблизиться к оптимуму надо увеличить аргумент функции. Если же производная положительна, то все наоборот — функция возрастает, оптимум находится слева и нам нужно уменьшить значение аргумента. Причем, чем дальше от оптимума, тем быстрее возрастает или убывает функция. То есть значение производной дает нам не только направление, но и величину нужного шага. Сделав шаг, пропорциональный величине производной и в направлении, противоположном ей, можно повторить процесс и еще больше приблизиться к оптимуму. С каждой итерацией мы будем приближаться к минимуму ошибки и математически доказано, что мы можем приблизиться к ней произвольно близко. То есть, данный метод сходится в пределе.
В случае с функцией нескольких переменных все немного сложнее, но принцип остается прежним. Только мы оперируем не полной производной функции, а вектором частных производных по каждому параметру. Он задает нам направление максимального увеличения функции. Чтобы получить направление максимального спада функции нужно просто домножить этот вектор на -1. После этого нужно обновить значения каждого компонента вектора параметров модели на величину, пропорциональную соответствующему компоненту вектора градиента. Таким образом мы делаем шаги вниз по функции ошибки в направлении с самым крутым спуском, а размер каждого шага пропорционален определяется параметром $alpha$, который называется скоростью обучения.
Алгоритм градиентного спуска:
повторяйте до сходимости:
[b_j := b_j — alpha frac{partial}{partial b_j} J(b_0, b_1)]
где j=0,1 — представляет собой индекс номера признака.
Это общий алгоритм градиентного спуска. Она работает для любых моделей и для любых функций ошибки. Это итеративный алгоритм, который сходится в пределе. То есть, мы никогда не придем в сам оптимум, но можем приблизиться к нему сколь угодно близко. На практике нам не так уж важно получить точное решение, достаточно решения с определенной точностью.
Алгоритм градиентного спуска имеет один параметр — скорость обучения. Он влияет на то, как быстро мы будем приближаться к оптимуму. Кажется, что чем быстрее, тем лучше, но оказывается, что если значение данного параметра слишком велико, то мы буем постоянно промахиваться и алгоритм будет расходиться.
Алгоритм градиентного спуска для парной линейной регрессии:
повторяйте до сходимости:
[b_0 := b_0 — alpha frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)} )- y^{(i)})]
[b_1 := b_1 — alpha frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)}) cdot x^{(i)}]
На практике “повторяйте до сходимости” означает, что мы повторяем алгоритм градиентного спуска до тех пор, пока значение функции ошибки не перестанет значимо изменяться. Это будет означать, что мы уже достаточно близко к минимуму и дальнейшие шаги градиентного спуска слишком малы, чтобы быть целесообразными. Конечно, это оценочное суждение, но на практике обычно, нескольких значащих цифр достаточно для практического применения моделей машинного обучения.
Алгоритм градиентного спуска имеет одну особенность, про которую нужно помнить. Он в состоянии находить только локальный минимум функции. Он в принципе, по своей природе, локален. Поэтому, если функция ошибки будет очень сложна и иметь несколько локальных оптимумов, то результат работы градиентного спуска будет зависеть от выбора начальной точки.
На практике эту проблему решают методом семплирования — запускают градиентный спуск из множества случайных точек и выбирают то минимум, который оказался меньше по значению функции ошибки. Но этот подход понадобится нам при рассмотрении более сложных и глубоких моделей машинного обучения. Для простых линейных, полиномиальных и других моделей метод градиентного спуска работает прекрасно. В настоящее время этот алгоритм — это основная рабочая лошадка классических моделей машинного обучения.
Выводы:
- Метод градиентного спуска нужен, чтобы найти минимум функции, если мы не можем ее вычислить аналитически.
- Это численный итеративный алгоритм локальной оптимизации.
- Для запуска градиентного спуска нужно знать частную производную функции ошибки.
- Для начала мы берем произвольные значения параметров, затем обновляем их по данной формуле.
- Доказано, что этот метод сходится к локальному минимуму.
- Если функция ошибки достаточно сложная, то разные начальные точки дадут разный результат.
- Метод градиентного спуска имеет свой параметр — скорость обучения. Обычно его подстаивают автоматически.
- Метод градиентного спуска повторяют много раз до тех пор, пока функция ошибки не перестанет значимо изменяться.
Регрессия с несколькими переменными
Множественная линейная регрессия
Парная регрессия, как мы увидели выше, имеет дело с объектами, которые характеризуются одним числовым признаком ($x$). На практике, конечно, объекты характеризуются несколькими признаками, а значит в модели должна быть не одна входящая переменная, а несколько (или, что то же самое, вектор). Линейная регрессия с несколькими переменными также известна как «множественная линейная регрессия». Введем обозначения для уравнений, где мы можем иметь любое количество входных переменных:
$ x^{(i)} $- вектор-столбец всех значений признаков i-го обучающего примера;
$ x_j^{(i)} $ — значение j-го признака i-го обучающего примера;
$ x_j $ — вектор j-го признака всех обучающих примеров;
m — количество примеров в обучающей выборке;
n — количество признаков;
X — матрица признаков;
b — вектор параметров регрессии.
Задачи множественной регрессии уже очень сложно представить на графике, ведь количество параметров каждого объекта обучающей выборки соответствует измерению, в котором находятся точки данных. Плюс нужно еще одно измерение для целевой переменной. И вместо того, чтобы подбирать оптимальную прямую, мы будем подбирать оптимальную гиперплоскость. Но в целом идея линейной регрессии остается неизменной.
Для удобства примем, что $ x_0^{(i)} = 1 $ для всех $i$. Другими словами, мы ведем некий суррогатный признак, для всех объектов равный единице. Это никак не сказывается на самой функции гипотезы, это лишь условность обозначения, но это сильно упростит математические выкладки, особенно в матричной форме.
Вообще, уравнения для алгоритмов машинного обучения, зависящие от нескольких параметров часто записываются в матричной форме. Это лишь способ сделать запись уравнений более компактной, а не какое-то новое знание. Если вы не владеете линейной алгеброй, то можете просто безболезненно пропустить эти формы записи уравнений. Однако, лучше, конечно, разобраться. Особенно это пригодится при изучении нейронных сетей.
Теперь определим множественную форму функции гипотезы следующим образом, используя несколько признаков. Она очень похожа на парную, но имеет больше входных переменных и, как следствие, больше параметров.
Общий вид модели множественной линейной регрессии:
[h_b(x) = b_0 + b_1 x_1 + b_2 x_2 + … + b_n x_n]
Или в матричной форме:
[h_b(x) = X cdot vec{b}]
Используя определение матричного умножения, наша многопараметрическая функция гипотезы может быть кратко представлена в виде: $h(x) = B X$.
Обратите внимание, что в любой модели линейной регрессии количество параметров на единицу больше количества входных переменных. Это верно для любой линейной модели машинного обучения. Вообще, всегда чем больше признаков, тем больше параметров. Это будет важно для нас позже, когда мы будем говорить о сложности моделей.
Теперь, когда мы знаем виды функции гипотезы, то есть нашей модели, мы можем переходить к следующему шагу: функции ошибки. Мы построим ее по аналогии с функцией ошибки для парной модели. Для множественной регрессии функция ошибки от вектора параметров b выглядит следующим образом:
Функция ошибки для множественной линейной регрессии:
[J(b) = frac{1}{2m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)})^2]
Или в матричной форме:
[J(b) = frac{1}{2m} (X b — vec{y})^T (X b — vec{y})]
Обратите внимание, что мы специально не раскрываем выражение (h_b(x^{(i)})). Это нужно, чтобы подчеркнуть, что форма функции ошибки не зависит от функции гипотезы, она выражается через нее.
Теперь нам нужно взять производную этой функции ошибки. Здесь уже нужно знать производную самой функции гипотезы, так как:
[frac{partial}{partial b_i} J =
frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)}) cdot frac{partial}{partial b_i} h_b(x^{(i)})]
В такой формулировке мы представляем частные производные функции ошибки (градиент) через частную производную функции гипотезы. Это так называемое моделенезависимое представление градиента. Ведь для этой формулы совершенно неважно, какой функцией будет наша гипотеза. Пока она является дифференцируемой, мы можем использовать градиент ее функции ошибки. Именно поэтому метод градиентного спуска работает с любыми аналитическими моделями, и нам не нужно каждый раз заново “переизобретать” математику градиентного спуска, адаптировать ее к каждой конкретной модели машинного обучения. Достаточно изучить этот метод один раз, в общей форме.
Метод градиентного спуска для множественной регрессии определяется следующими уравнениями:
повторять до сходимости:
[b_0 := b_0 — alpha frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)}) cdot x_0^{(i)}]
[b_1 := b_1 — alpha frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)}) cdot x_1^{(i)}]
[b_2 := b_2 — alpha frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)}) cdot x_2^{(i)}]
[…]
Или в матричной форме:
[b := b — frac{alpha}{m} X^T (X b — vec{y})]
Выводы:
- Множественная регрессия очень похожа на парную, но с большим количеством признаков.
- Для удобства и однообразия, почти всегда обозначают $x_0 = 1$.
- Признаки образуют матрицу, поэтому уравнения множественной регрессии часто приводят в матричной форме, так короче.
- Алгоритм градиентного спуска для множественной регрессии точно такой же, как и для парной.
Нормализация признаков
Мы можем ускорить сходимость метода градиентного спуска, преобразовав входные данные таким образом, чтобы все атрибуты имели значения примерно в том же диапазоне. Это называется нормализация данных — приведение всех признаков к одной шкале. Это ускоряет сходимость градиентного спуска за счет эффекта масштаба. Дело в том, что зачастую значения разных признаков измеряются по шкалам с очень разным порядком величины. Например, $x_1$ измеряется в миллионах, а $x_2$ — в долях единицы.
В таком случае форма функции ошибки будет очень вытянутой. Это не проблема для математической формализации градиентного спуска — при достаточно малых $alpha$ метод все равно рано или поздно сходится. Проблема в практической реализации. Получается, что если выбрать скорость обучения выше определенного предела по самому компактному признаку, спуск разойдется. Значит, скорость обучения надо делать меньше. Но тогда в направлении второго признака спуск будет проходить слишком медленно. И получается, что градиентный спуск потребует гораздо больше итераций для завершения.
Эту проблему можно решить если изменить диапазоны входных данных, чтобы они выражались величинами примерно одного порядка. Это не позволит одному измерению численно доминировать над другим. На практике применяют несколько алгоритмов нормализации, самые распространенные из которых — минимаксная нормализация и стандартизация или z-оценки.
Минимаксная нормализация — это изменение входных данных по следующей формуле:
[x’ = frac{x — x_{min}}{x_{max} — x_{min}}]
После преобразования все значения будут лежать в диапазоне $x in [0; 1]$.
Z-оценки или стандартизация производится по формуле:
[x’ = frac{x — M[x]}{sigma_x}]
В таком случае данный признак приводится к стандартному распределению, то есть такому, у которого среднее 0, а дисперсия — 1.
У каждого из этих двух методов нормализации есть по два параметра. У минимаксной — минимальное и максимальное значение признака. У стандартизации — выборочные среднее и дисперсия. Параметры нормализации, конечно, вычисляются по каждому признаку (столбцу данных) отдельно. Причем, эти параметры надо запомнить, чтобы при использовании модели для предсказании использовать именно их (вычисленные по обучающей выборке). Даже если вы используете тестовую выборку, ее надо нормировать с использованием параметров, вычисленных по обучающей. Да, при этом может получиться, что при применении модели на данных, которых не было в обучающей выборке, могут получиться значения, например, меньше нуля или больше единицы (при использовании минимаксной нормализации). Это не страшно, главное, что будет соблюдена последовательность вычисления нормированных значений.
Про использование обучающей и тестовой выборок мы будем говорить значительно позже, при рассмотрении диагностики моделей машинного обучения.
Целевая переменная не нормируется. Это просто не нужно, а если ее нормировать, это сильно усложнит все математические расчеты и преобразования.
При использовании библиотечных моделей машинного обучения беспокоиться о нормализации входных данных вручную, как правило, не нужно. Большинство готовых реализаций моделей уже включают нормализацию как неотъемлемый этап подготовки данных. Более того, некоторые типы моделей обучения с учителем вовсе не нуждаются в нормализации. Но об этом пойдет речь в следующих главах.
Выводы:
- Нормализация нужна для ускорения метода градиентного спуска.
- Есть два основных метода нормализации — минимаксная и стандартизация.
- Параметры нормализации высчитываются по обучающей выборке.
- Нормализация встроена в большинство библиотечных методов.
- Некоторые методы более чувствительны к нормализации, чем другие.
- Нормализацию лучше сделать, чем не делать.
Полиномиальная регрессия
Функция гипотезы не обязательно должна быть линейной, если это не соответствует данным. На практике вы не всегда будете иметь данные, которые можно хорошо аппроксимировать линейной функцией. Наглядный пример вы видите на иллюстрации. Вполне очевидно, что в среднем увеличение целевой переменной замедляется с ростом входной переменной. Это значит, что данные демонстрируют нелинейную динамику. И это так же значит, что мы никак не сможем их хорошо приблизить линейной моделью.
Надо подчеркнуть, что это не свидетельствует о несовершенстве наших методов оптимизации. Мы действительно можем найти самую лучшую линейную функцию для данных точек, но проблема в том, что мы всегда выбираем лучшую функцию из некоторого класса функций, в данном случае — линейных. То есть проблема не в алгоритмах оптимизации, а в ограничении самого вида модели.
вполне логично предположить, что для описания таких нелинейных наборов данных следует использовать нелинейные же функции моделей. Но очень бы не хотелось, для каждого нового класса функций изобретать собственный метод оптимизации, поэтому мы постараемся максимально “переиспользовать” те подходы, которые описали выше. И механизм множественной регрессии в этом сильно поможет.
Мы можем изменить поведение или кривую нашей функции гипотезы, сделав ее квадратичной, кубической или любой другой формой.
Например, если наша функция гипотезы
$ hat{y} = h_b (x) = b_0 + b_1 x $,
то мы можем добавить еще один признак, основанный на $ x_1 $, получив квадратичную функцию
[hat{y} = h_b (x) = b_0 + b_1 x + b_2 x^2]
или кубическую функцию
[hat{y} = h_b (x) = b_0 + b_1 x + b_2 x^2 + b_3 x^3]
В кубической функции мы по сути ввели два новых признака:
$ x_2 = x^2, x_3 = x^3 $.
Точно таким же образом, мы можем создать, например, такую функцию:
[hat{y} = h_b (x) = b_0 + b_1 x + b_2 sqrt{x}]
В любом случае, мы из парной линейной функции сделали какую-то другую функцию. И к этой нелинейной функции можно относиться по разному. С одной стороны, это другой класс функций, который обладает нелинейным поведением, а следовательно, может описывать более сложные зависимости в данных. С другой стороны, это линейна функция от нескольких переменных. Только сами эти переменные оказываются в функциональной зависимости друг от друга. Но никто не говорил, что признаки должны быть независимы.
И вот такое представление нелинейной функции как множественной линейной позволяет нам без изменений воспользоваться алгоритмом градиентного спуска для множественной линейной регрессии. Только вместо $ x_2, x_3, … , x_n $ нам нужно будет подставить соответствующие функции от $ x_1 $.
Очевидно, что нелинейных функций можно придумать бесконечное количество. Поэтому встает вопрос, как выбрать нужный класс функций для решения конкретной задачи. В случае парной регрессии мы можем взглянув на график точек обучающей выборки сделать предположение о том, какой вид нелинейной зависимости связывает входную и целевую переменные. Но если у нас множество признаков, просто так проанализировать график нам не удастся. Поэтому по умолчанию используют полиномиальную регрессию, когда в модель добавляют входные переменные второго, третьего, четвертого и так далее порядков.
Порядок полиномиальной регрессии подбирается в качестве компромисса между качеством получаемой регрессии, и вычислительной сложностью. Ведь чем выше порядок полинома, тем более сложные зависимости он может аппроксимировать. И вообще, чем выше степень полинома, тем меньше будет ошибка при прочих равных. Если степень полинома на единицу меньше количества точек — ошибка будет нулевая. Но одновременно с этим, чем выше степень полинома, тем больше в модели параметров, тем она сложнее и занимает больше времени на обучение. Есть еще вопросы переобучения, но про это мы поговорим позднее.
А что делать, если изначально в модели было несколько признаков? Тогда обычно для определенной степени полинома берутся все возможные комбинации признаком соответствующей степени и ниже. Например:
Для регрессии с двумя признаками.
Линейная модель (полином степени 1):
[h_b (x) = b_0 + b_1 x_1 + b_2 x_2]
Квадратичная модель (полином степени 2):
[h_b (x) = b_0 + b_1 x + b_2 x_2 + b_3 x_1^2 + b_4 x_2^2 + b_5 x_1 x_2]
Кубическая модель (полином степени 3):
[hat{y} = h_b (x) = b_0 + b_1 x_1 + b_2 x_2 + b_3 x_1^2 + b_4 x_2^2 + b_5 x_1 x_2 + b_6 x_1^3 + b_7 x_2^3 + b_7 x_1^2 x_2 + b_8 x_1 x_2^2]
При этом количество признаков и, соответственно, количество параметров растет экспоненциально с ростом степени полинома. Поэтому полиномиальные модели обычно очень затратные в обучении при больших степенях. Но полиномы высоких степеней более универсальны и могут аппроксимировать более сложные данные лучше и точнее.
Выводы:
- Данные в датасете не всегда располагаются так, что их хорошо может описывать линейная функция.
- Для описания нелинейных зависимостей нужна более сложная, нелинейная модель.
- Чтобы не изобретать алгоритм обучения заново, можно просто ввести в модель суррогатные признаки.
- Суррогатный признак — это новый признак, который считается из существующих атрибутов.
- Чаще всего используют полиномиальную регрессию — это когда в модель вводят полиномиальные признаки — степени существующих атрибутов.
- Обычно берут все комбинации факторов до какой-то определенной степени полинома.
- Полиномиальная регрессия может аппроксимировать любую функцию, нужно только подобрать степень полинома.
- Чем больше степень полиномиальной регрессии, тем она сложнее и универсальнее, но вычислительно сложнее (экспоненциально).
Практическое построение регрессии
В данной главе мы посмотрим, как можно реализовать методы линейной регрессии на практике. Сначала мы попробуем создать алгоритм регрессии с нуля, а затем воспользуемся библиотечной функцией. Это поможет нам более полно понять, как работают модели машинного обучения в целом и в библиотеке sckikit-learn (самом популярном инструменте для создания и обучения моделей на языке программирования Python) в частности.
Для понимания данной главы предполагаем, что читатель знаком с основами языка программирования Python. Нам понадобится знание его базового синтаксиса, немного — объектно-ориентированного программирования, немного — использования стандартных библиотек и модулей. Никаких продвинутых возможностей языка (типа метапрограммирования или декораторов) мы использовать не будем.
Как должны быть представлены данные для машинного обучения?
Применение любых моделей машинного обучения начинается с подготовки данных в необходимом формате. Для этого очень удобными для нас будут библиотеки numpy и pandas. Они практически всегда используются совместно с библиотекой sckikit-learn и другими инструментами машинного обучения. В первую очередь мы будем использовать numpy для создания массивов и операций с векторами и матрицами. Pandas нам понадобится для работы с табличными структурами — датасетами.
Если вы хотите самостоятельно задать в явном виде данные обучающей выборки, то нет ничего лучше использования обычных массивов ndarray. Обычно в одном массиве хранятся значения атрибутов — x, а в другом — значения целевой переменной — y.
1
2
3
4
5
6
7
8
9
10
11
import numpy as np
x = np.array([1.46, 1.13, -2.30, 1.74, 0.04,
-0.61, 0.32, -0.76, 0.58, -1.10,
0.87, 1.62, -0.53, -0.25, -1.07,
-0.38, -0.17, -0.32, -2.06, -0.88, ])
y = np.array([101.16, 78.44, -159.24, 120.72, 2.92,
-42.33, 22.07, -52.67, 40.32, -76.10,
59.88, 112.38, -36.54, -17.25, -74.24,
-26.57, -11.93, -22.31, -142.54, -60.74,])
Если мы имеем дело с задачей множественной регрессии, то в массиве атрибутов будет уже двумерный массив, состоящий из нескольких векторов атрибутов, вот так:
1
2
3
4
5
x = np.array([
[0, 1, 2, 3, 4],
[5, 4, 9, 6, 3],
[7.8, -0.1, 0.0, -2.14, 10.7],
])
Важно следить за тем, чтобы в массиве атрибутов в каждом вложенном массиве количество элементов было одинаковым и в свою очередь совпадало с количеством элементов в массиве целевой переменной. Это называется соблюдение размерности задачи. Если размерность не соблюдается, то модели машинного обучения будут работать неправильно. А библиотечные функции чаще всего будут выдавать ошибку, связанную с формой массива (shape).
Но чаще всего вы не будете задавать исходные данные явно. Практически всегда их приходится читать из каких-либо входных файлов. Удобнее всего это сделать при помощи библиотеки pandas вот так:
1
2
3
4
import pandas as pd
x = pd.read_csv('x.csv', index_col=0)
y = pd.read_csv('y.csv', index_col=0)
Или, если данные лежат в одном файле в общей таблице (что происходит чаще всего), тогда его читают в один датафрейм, а затем выделяют целевую переменную, и факторные переменные:
1
2
3
4
5
6
7
8
import pandas as pd
data = pd.read_csv('data.csv', index_col=0)
y = data.Y
y = data["Y"]
x = data.drop(["Y"])
Обратите внимание, что матрицу атрибутов проще всего сформировать, удалив из полной таблицы целевую переменную. Но, если вы хотите выбрать только конкретные столбцы, тогда можно использовать более явный вид, через перечисление выбранных колонок.
Если вы используете pandas или numpy для формирования массивов данных, то получившиеся переменные будут разных типов — DataFrame или ndarray, соответственно. Но на дальнейшую работу это не повлияет, так как интерфейс работы с этими структурами данных очень похож. Например, неважно, какие именно массивы мы используем, их можно изобразить на графике вот так:
1
2
3
4
5
import maiplotlib.pyplot as plt
plt.figure()
plt.scatter(x, y)
plt.show()
Конечно, такая визуализация будет работать только в случае задачи парной регрессии. Если x многомерно, то простой график использовать не получится.
Давайте соберем весь наш код вместе:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import numpy as np
import pandas as pd
import maiplotlib.pyplot as plt
# x = pd.read_csv('x.csv', index_col=0)
x = np.array([1.46, 1.13, -2.30, 1.74, 0.04,
-0.61, 0.32, -0.76, 0.58, -1.10,
0.87, 1.62, -0.53, -0.25, -1.07,
-0.38, -0.17, -0.32, -2.06, -0.88, ])
# y = pd.read_csv('y.csv', index_col=0)
y = np.array([101.16, 78.44, -159.24, 120.72, 2.92,
-42.33, 22.07, -52.67, 40.32, -76.10,
59.88, 112.38, -36.54, -17.25, -74.24,
-26.57, -11.93, -22.31, -142.54, -60.74,])
plt.figure()
plt.scatter(x, y)
plt.show()
Это код генерирует вот такой вот график:
Как работает метод машинного обучения “на пальцах”?
Для того, чтобы более полно понимать, как работает метод градиентного спуска для линейной регрессии, давайте реализуем его самостоятельно, не обращаясь к библиотечным методам. На этом примере мы проследим все шаги обучения модели.
Мы будем использовать объектно-ориентированный подход, так как именно он используется в современных библиотеках. Начнем строить класс, который будет реализовывать метод парной линейной регрессии:
1
2
3
4
5
class hypothesis(object):
"""Модель парной линейной регрессии"""
def __init__(self):
self.b0 = 0
self.b1 = 0
Здесь мы определили конструктор класса, который запоминает в полях экземпляра параметры регрессии. Начальные значения этих параметров не очень важны, так как градиентный спуск сойдется из любой точки. В данном случае мы выбрали нулевые, но можно задать любые другие начальные значения.
Реализуем метод, который принимает значение входной переменной и возвращает теоретическое значение выходной — это прямое действие нашей регрессии — метод предсказания результата по факторам (в случае парной регрессии — по одному фактору):
1
2
def predict(self, x):
return self.b0 + self.b1 * x
Название выбрано не случайно, именно так этот метод называется и работает в большинстве библиотечных классов.
Теперь зададим функцию ошибки:
1
2
def error(self, X, Y):
return sum((self.predict(X) - Y)**2) / (2 * len(X))
В данном случае мы используем простую функцию ошибки — среднеквадратическое отклонение (mean squared error, MSE). Можно использовать и другие функции ошибки. Именно вид функции ошибки будет определять то, какой вид регрессии мы реализуем. Существует много разных вариаций простого алгоритма регрессии. О большинстве распространенных методах регрессии можно почитать в официальной документации sklearn.
Теперь реализуем метод градиентного спуска. Он должен принимать массив X и массив Y и обновлять параметры регрессии в соответствии в формулами градиентного спуска:
1
2
3
4
5
6
def BGD(self, X, Y):
alpha = 0.5
dJ0 = sum(self.predict(X) - Y) /len(X)
dJ1 = sum((self.predict(X) - Y) * X) /len(X)
self.b0 -= alpha * dJ0
self.b1 -= alpha * dJ1
О выборе конкретного значения alpha мы говорить пока не будем,на практике его довольно просто подбирают, мы же возьмем нейтральное значение.
Давайте создадим объект регрессии и проверим начальное значение ошибки. В примерах приведены значения на модельном наборе данных, но этот метод можно использовать на любых данных, которые подходят по формату — x и y должны быть одномерными массивами чисел.
1
2
3
4
5
6
7
8
hyp = hypothesis()
print(hyp.predict(0))
print(hyp.predict(100))
J = hyp.error(x, y)
print("initial error:", J)
0
0
initial error: 36271.58344889084
Как мы видим, для начала оба параметра регрессии равны нулю. Конечно, такая модель не дает надежных предсказаний, но в этом и состоит суть метода градиентного спуска: начиная с любого решения мы постепенно его улучшаем и приходим к оптимальному решению.
Теперь все готово к запуску градиентного спуска.
1
2
3
4
5
6
7
8
9
10
hyp.BGD(x, y)
J = hyp.error(x, y)
print("error after gradient descent:", J)
error after gradient descent: 6734.135540194945
X0 = np.linspace(60, 180, 100)
Y0 = hyp.predict(X0)
plt.figure()
plt.scatter(x, y)
plt.plot(X0, Y0, 'r')
plt.show()
Как мы видим, численное значение ошибки значительно уменьшилось. Да и линия на графике существенно приблизилась к точкам. Конечно, наша модель еще далека от совершенства. Мы прошли всего лишь одну итерацию градиентного спуска. Модифицируем метод так, чтобы он запускался в цикле пока ошибка не перестанет меняться существенно:
1
2
3
4
5
6
7
8
9
10
11
12
13
def BGD(self, X, Y, alpha=0.5, accuracy=0.01, max_steps=5000):
step = 0
old_err = hyp.error(X, Y)
new_err = hyp.error(X, Y)
dJ = 1
while (dJ > accuracy) and (step < max_steps):
dJ0 = sum(self.predict(X) - Y) /len(X)
dJ1 = sum((self.predict(X) - Y) * X) /len(X)
self.b0 -= alpha * dJ0
self.b1 -= alpha * dJ1
old_err = new_err
new_err = hyp.error(X, Y)
dJ = abs(old_err - new_err)
Заодно мы проверяем, насколько изменилось значение функции ошибки. Если оно изменилось на величину, меньшую, чем заранее заданная точность, мы завершаем спуск. Таким образом, мы реализовали два стоп-механизма — по количеству итераций и по стабилизации ошибки. Вы можете выбрать любой или использовать оба в связке.
Запустим наш градиентный спуск:
1
2
3
4
5
hyp = hypothesis()
hyp.BGD(x, y)
J = hyp.error(x, y)
print("error after gradient descent:", J)
error after gradient descent: 298.76881676471504
Как мы видим, теперь ошибка снизилась гораздо больше. Однако, она все еще не достигла нуля. Заметим, что нулевая ошибка не всегда возможна в принципе из-за того, что точки данных не всегда будут располагаться на одной линии. Нужно стремиться не к нулевой, а к минимально возможной ошибке.
Посмотрим, как теперь наша регрессия выглядит на графике:
1
2
3
4
5
6
X0 = np.linspace(60, 180, 100)
Y0 = hyp.predict(X0)
plt.figure()
plt.scatter(x, y)
plt.plot(X0, Y0, 'r')
plt.show()
Уже значительно лучше. Линия регрессии довольно похожа на оптимальную. Так ли это на самом деле, глядя на график, сказать сложно, для этого нужно проанализировать, как ошибка регрессии менялась со временем:
Как оценить качество регрессионной модели?
В простых случаях качество модели можно оценить визуально на графике. Но если у вас многомерная задача, это уже не представляется возможным. Кроме того, если ошибка и сама модель меняется незначительно, то очень сложно определить, стало хуже или лучше. Поэтому для диагностики моделей машинного обучения используют кривые.
Самая простая кривая обучения — зависимость ошибки от времени (итерации градиентного спуска). Для того, чтобы построить эту кривую, нам нужно немного модифицировать наш метод обучения так, чтобы он возвращал нужную нам информацию:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def BGD(self, X, Y, alpha=0.1, accuracy=0.01, max_steps=1000):
steps, errors = [], []
step = 0
old_err = hyp.error(X, Y)
new_err = hyp.error(X, Y) - 1
dJ = 1
while (dJ > accuracy) and (step < max_steps):
dJ0 = sum(self.predict(X) - Y) /len(X)
dJ1 = sum((self.predict(X) - Y) * X) /len(X)
self.b0 -= alpha * dJ0
self.b1 -= alpha * dJ1
old_err = new_err
new_err = hyp.error(X, Y)
dJ = abs(old_err - new_err)
step += 1
steps.append(step)
errors.append(new_err)
return steps, errors
Мы просто запоминаем в массивах на номер шаа и ошибку на каждом шаге. Получив эти данные можно легко построить их на графике:
1
2
3
4
5
6
hyp = hypothesis()
steps, errors = hyp.BGD(x, y)
plt.figure()
plt.plot(steps, errors, 'g')
plt.show()
На этом графике наглядно видно, что в начале обучения ошибка падала быстро, но в ходе градиентного спуска она вышла на плато. Учитывая, что мы используем гладкую функцию ошибки второго порядка, это свидетельствует о том, что мы достигли локального оптимума и дальнейшее повторение алгоритма не принесет улучшения модели.
Если бы мы наблюдали на графике обучения ситуацию, когда по достижении конца обучения ошибка все еще заметно снижалась, это значит, что мы рано прекратили обучение, и нужно продолжить его еще на какое-то количество итераций.
При анализе графиков с библиотечными моделями не получится таких гладких графиков, они больше напоминают случайные колебания. Это из-за того, что в готовых реализациях используется очень оптимизированный вариант метода градиентного спуска. А он может работать с произвольными флуктуациями. В любом случае, нас интересует общий вид этой кривой.
Как подбирать скорость обучения?
В нашей реализации метода градиентного спуска есть один параметр — скорость обучения — который нам приходится так же подбирать руками. Какой смысл автоматизировать подбор параметров линейной регрессии, если все равно приходится вручную подбирать какой-то другой параметр?
На самом деле подобрать скорость обучения гораздо легче. Нужно использовать тот факт, что при превышении определенного порогового значения ошибка начинает возрастать. Кроме того, мы знаем, что скорость обучения должна быть положительна, но меньше единицы. Вся проблема в этом пороговом значении, которое сильно зависит от размерности задачи. При одних данных хорошо работает $ alpha = 0.5 $, а при каких-то приходится уменьшать ее на несколько порядков, например, $ alpha = 0.00000001 $.
Мы еще не говорили о нормализации данных, которая тоже практически всегда применяется при обучении. Она “благотворно” влияет на возможный диапазон значений скорости обучения. При использовании нормализации меньше вероятность, что скорость обучения нужно будет уменьшать очень сильно.
Подбирать скорость обучения можно по следующему алгоритму. Сначала мы выбираем $ alpha $ близкое к 1, скажем, $ alpha = 0.7 $. Производим одну итерацию градиентного спуска и оцениваем, как изменилась ошибка. Если она уменьшилась, то ничего не надо менять, продолжаем спуск как обычно. Если же ошибка увеличилась, то скорость обучения нужно уменьшить. Например, раа в два. После чего мы повторяем первый шаг градиентного спуска. Таким образом мы не начинаем спуск, пока скорость обучения не снизится настолько, чтобы он начал сходиться.
Как применять регрессию с использованием scikit-learn?
Для серьезной работы, все-таки рекомендуется использовать готовые библиотечные решения. Они работаю гораздо быстрее, надежнее и гораздо проще, чем написанные самостоятельно. Мы будем использовать библиотеку scikit-learn для языка программирования Python как наш основной инструмент реализации простых моделей. Сегодня это одна их самых популярных библиотек для машинного обучения. Мы не будем повторять официальную документацию этой библиотеки, которая на редкость подробная и понятная. Наша задача — на примере этих инструментов понять, как работают и как применяются модели машинного обучения.
В библиотеке scikit-learn существует огромное количество моделей машинного обучения и других функций, которые могут понадобиться для их работы. Поэтому внутри самой библиотеки есть много разных пакетов. Все простые модели, например, модель линейной регрессии, собраны в пакете linear_models. Подключить его можно так:
1
from sklearn import linear_model
Надо помнить, что все модели машинного обучения из это библиотеки имеют одинаковый интерфейс. Это очень удобно и универсально. Но это значит, в частности, что все модели предполагают, что массив входных переменных — двумерный, а массивы целевых переменных — одномерный. Отдельного класса для парной регрессии не существует. Поэтому надо убедиться, что наш массив имеет нужную форму. Проще всего для преобразования формы массива использовать метод reshape, например, вот так:
Если вы используете DataFrame, то они обычно всегда настроены правильно, поэтому этого шага может не потребоваться. Важно запомнить, что все методы библиотечных моделей машинного обучения предполагают, что в x будет двумерный массив или DataFrame, а в y, соответственно, одномерный массив или Series.
Эта строка преобразует любой массив в вектор-столбец. Это если у вас один признак, то есть парная регрессия. Если признаков несколько, то вместо 1 следует указать число признаков. -1 на первой позиции означает, что по нулевому измерению будет столько элементов, сколько останется в массиве.
Само использование модели машинного обучения в этой библиотеке очень просто и сводится к трем действиям: создание экземпляра модели, обучение модели методом fit(), получение предсказаний методом predict(). Это общее поведение для любых моделей библиотеки. Для модели парной линейной регрессии нам понадобится класс LinearRegression.
1
2
3
4
5
6
reg = linear_model.LinearRegression()
reg.fit(x, y)
y_pred = reg.predict(x)
print(reg.score(x, y))
print("Коэффициенты: n", reg.coef_)
В этом классе кроме уже упомянутых методов fit() и predict(), которые есть в любой модели, есть большое количество методов и полей для получения дополнительной информации о моделях. Так, практически в каждой модели есть встроенный метод score(), который оценивает качество полученной модели. А поле coef_ содержит коэффициенты модели.
Обратите внимание, что в большинстве моделей коэффициентами считаются именно параметры при входящих переменных, то есть $ b_1, b_2, …, b_n $. Коэффициент $b_0$ считается особым и хранится отдельно в поле intercept_
Так как мы работаем с парной линейной регрессией, результат можно нарисовать на графике:
1
2
3
4
plt.figure(figsize=(12, 9))
plt.scatter(x, y, color="black")
plt.plot(x, y_pred, color="blue", linewidth=3)
plt.show()
Как мы видим, результат ничем не отличается от модели, которую мы обучили сами, вручную:
Соберем код вместе и получим пример довольно реалистичного фрагмента работы с моделью машинного обучение. Примерно такой код можно встретить и в промышленных проектах по интеллектуальному анализу данных:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from sklearn.linear_model import LinearRegression
x = x.reshape((-1, 1))
reg = LinearRegression()
reg.fit(x, y)
print(reg.score(x, y))
from sklearn.metrics import mean_squared_error, r2_score
y_pred = reg.predict(x)
print("Коэффициенты: n", reg.coef_)
print("Среднеквадратичная ошибка: %.2f" % mean_squared_error(y, y_pred))
print("Коэффициент детерминации: %.2f" % r2_score(y, y_pred))
plt.figure(figsize=(12, 9))
plt.scatter(x, y, color="black")
plt.plot(x, y_pred, color="blue", linewidth=3)
plt.show()
Вы спрашиваете об этом, потому что начали следить за темами машинного обучения и много раз сталкивались с термином «минимизация функции ошибки» в статьях, блогах или технических документах. Что ж, в этой статье мы познакомимся с основами функции ошибки.
Давайте возьмем общий простой пример в ML (машинное обучение) только с двумя переменными x и одной переменной y.
+----+----+----+ | X1 | X2 | Y | +----+----+----+ | 0 | 2 | 6 | | 1 | 3 | 10 | | 4 | 2 | 10 | | 2 | 4 | 14 | +----+----+----+
Здесь X1, X2 — входные переменные, а Y — выходная переменная. В реальном мире могут быть тысячи входных переменных для работы. Каждая строка называется экземпляром, а каждый входной столбец называется функцией (или измерением). Теперь, что будут представлять эти входные переменные? Что ж, эти (входные переменные) могут быть продуктами компании CocaCola, проданными через 500 брендов напитков в более чем 200 странах, а переменная Y может быть общим объемом продаж.
Или входные переменные могут быть пиксельным представлением изображения, а переменные Y могут быть именем этого изображения. См. пример ниже,
Это похоже на изображение Авраама Линкольна. Как мы видим, столбцов и строк больше, чем в нашем крошечном наборе данных.
В любом случае, давайте продолжим с нашим крошечным набором данных для примера. Этот набор данных можно понимать немного по-другому. Если (0,2)=6, (1,3)=10 и (2,4)=14, то чему равно (4,5) = ? . Мы видели такие вопросы в переадресации WhatsApp, верно?
Мы можем использовать ручку и бумагу, чтобы легко научиться и понять решение этой проблемы.
First Term + 3 * (Second Term) = Answer.
Это уже известный нам формат y=mx+c.
Теперь попробуйте узнать решение для изображения, показанного выше (Авраам Линкольн). Это сложно!! Нам нужны решения Machines to Learning для таких сложных проблем, поэтому это называется Machine Learning.
Машины ничему не учатся сами по себе; мы должны написать алгоритмы, чтобы заставить их учиться. Давайте попробуем написать алгоритм для нашего крошечного набора данных. Нам нужно определить идеальное «m» в уравнении (y=mx+c), которое соответствует всем экземплярам данных.
Не заблуждайтесь, в крошечном примере, приведенном выше, простое линейное уравнение (y=mx+c) решит проблему, но решение не всегда должно быть линейным. Он также может быть полиномиальным (y=ax²+bx+c или y=ax³+ bx²+cx+d)
y m x c ---- --- --- --- 6 ? 2 0 10 ? 3 1 10 ? 2 4
Давайте возьмем первый экземпляр данных ( 6 = (2,0)) и попробуем идентифицировать «m».
+---+-------+---+--------------------+ | m | m*x+c | y | difference(y-mx+c) | +---+-------+---+--------------------+ | 1 | 2 | 6 | 4 | | 5 | 10 | 6 | -4 | +---+-------+---+--------------------+
Мы случайным образом выбираем число m = 1, и значение (m * x + c) становится равным 2, но фактическое значение, которое вы хотите получить, равно 6. Таким образом, мы не можем использовать m = 1. Чтобы продолжить, мы должны выбрать другое значение m. Теперь, должны ли мы выбрать другое случайное число или мы должны принять подсказку из нашего открытия?
Мы видим, что существует разница +4 между фактическим значением и значением, которое мы получили (прогнозируемое значение). Это дает нам подсказку, что нам нужно взять значение m>1, а не M‹1, потому что если мы возьмем значение m‹1, то разница будет увеличиваться в положительном направлении. Теперь давайте выберем значение m = 5, тогда разница между фактическим значением и прогнозируемым значением составит -4. Мы получаем еще один намек на то, что значение m должно быть меньше 5, потому что если мы возьмем значение m > 5 (m = 6), то разница (-6) продолжит увеличиваться в отрицательном направлении. См. числовую шкалу ниже,
-6 | -4 | -2 | 0 | +2 | +4 | +6
<----|----|----|---|----|----|---->
^ ^
| |
Наша цель — найти такое значение m, при котором разность (y-mx+c) становится равной нулю. Эта разница называется функцией ошибки.
У нас есть внешние границы «m», поэтому мы можем продолжать проверять значение между 1 и 5.
+-----+------+---+--------------------+ | m | mx+c | y | Difference(y-mx+c) | +-----+------+---+--------------------+ | 1 | 2 | 6 | 4 | | 1.5 | 3 | 6 | 3 | | 2 | 4 | 6 | 2 | | 2.5 | 5 | 6 | 1 | | 3 | 6 | 6 | 0 | | 3.5 | 7 | 6 | -1 | | 4 | 8 | 6 | -2 | | 4.5 | 9 | 6 | -3 | | 5 | 10 | 6 | -4 | +-----+------+---+--------------------+
Таким образом, идеальное значение m равно 3, потому что разница (Функция ошибки) равна нулю. Теперь мы предсказали значение ‘m’ для нашего первого экземпляра ((0,2) =6). Нам нужно повторить упражнение для других случаев, чтобы с уверенностью сказать, что значение m равно 3 для всех уравнений.
+----+----+---------+-----------+---------------------+ | x1 | x2 | y(mx+c) | y(actual) | difference(y-mx+c) | +----+----+---------+-----------+---------------------+ | 0 | 2 | 6 | 6 | 0 | | 1 | 3 | 10 | 10 | 0 | | 4 | 2 | 10 | 10 | 0 | | 2 | 4 | 14 | 14 | 0 | +----+----+---------+-----------+---------------------+
Похоже, что m=3 подходит для всех экземпляров данных. Опять же, в нашем крошечном наборе данных значение m таково, что разность (y-mx+c) всегда равна нулю, но в реальных наборах данных вы можете не найти значение ‘m ‘ с нулевой разницей. В таких случаях мы пытаемся найти такое значение m, чтобы разница была близка к нулю для всех случаев. Это называется Функция минимизации ошибок.
Подводя итог, можно сказать, что любая проблема машинного обучения будет иметь форму набора данных с входными переменными (X) и выходными переменными (Y), и ваша первая задача — найти связь между ними. Эта связь называется функцией. Для разработки функции необходимо определить зависимость между переменными (линейная/нелинейная), а затем доработать функцию ошибки. Затем вы можете обучить свой алгоритм, минимизируя функцию ошибок.