Суть
МНК состоит в:
—минимизации
суммы квадратов коэффициентов регрессии
—минимизации
суммы квадратов значений зависимой
переменной
+—минимизации
суммы квадратов отклонений точек
наблюдений от уравнения регрессии
—минимизации
суммы квадратов отклонений точек
эмпирического уравнения регрессии от
точек теоретического уравнения регрессии
Коэффициент
уравнения регрессии показывает
—на
сколько % изменится результат при
изменении фактора на 1%
—на
сколько % изменится фактор при изменении
результата на 1%
+—на
сколько единиц изменится результат при
изменении фактора на 1 единицу
—на
сколько единиц изменится фактор при
изменении результата на 1 единицу
—во
сколько раз изменится результат при
изменении фактора на 1 единицу
Коэффициент
эластичности показывает
—на
сколько единиц изменится фактор при
изменении результата на 1 единицу
—на
сколько единиц изменится результат при
изменении фактора на 1 единицу
—во
сколько раз изменится результат при
изменении фактора на одну единицу
+—на
сколько % изменится результат при
изменении фактора на 1 %
—на
сколько %изменится фактор при изменении
результата на 1%
Не
является предпосылкой классической
модели предположение:
—факторы
экзогенны
—длина
исходного ряда данных больше, чем
количество факторов
—матрица
факторов содержит все важные факторы,
влияющие на результат
+—факторы
являются случайными величинами
На
основании наблюдений за 100 домохозяйствами
построено эмпирическое уравнение
регрессии, у- потребление, х -доход:
У=145,65+0,825*х
Соответствуют
ли знаки и значения коэффициентов
регрессии теоретическим представлениям
+—да
—нет
—частично
соответствуют
В
производственной функции Кобба-Дугласа
параметр
соответствует коэффициенту:
—корреляции
—вариации
+—эластичности
—детерминации
Найдите
предположение, не являющееся предпосылкой
классической модели
—Случайное
отклонение имеет нулевое математическое
ожидание
—Случайное
отклонение имеет постоянную дисперсию
—Отсутствует
автокорреляция случайных отклонений
—Случайное
отклонение независимо от объясняющих
переменных
+—Случайное
отклонение не обладает нормальным
распределением
По
месячным данным за 6 лет построена
следующая регрессия:
Y=-12,23+0,91*x1-2,1*x2,
R2=0,976,
DW=1,79
t
(-3,38) (123,7) (3,2)
y-
потребление, х1 –располагаемый доход,
х2 – процентная банковская ставка по
вкладам
Оцените
качество построенной модели, не прибегая
к таблицам, совпадает ли направление
влияния объясняющих переменных с
теоретическим?
+—качество
модели высокое, направление влияния
совпадает
—качество
модели низкое, направление влияния
совпадает
—качество
модели высокое, но направление влияния
не совпадает
—качество
модели низкое, направление влияния
совпадает
Критерий
Стьюдента предназначен для:
—Определения
экономической значимости каждого
коэффициента уравнения
+—Определения
статистической значимости каждого
коэффициента уравнения
—Проверки
модели на автокорреляцию остатков
—Определения
экономической значимости модели в целом
—Проверки
на гомоскедастичность
Если
коэффициент уравнения регрессии (k)
статистически значим, то
—k
>
1
—|k
|
>
1
+—k
0
—k
>
0
—0
<
k
<
1
Табличное
значение критерия Стьюдента зависит
—Только
от уровня доверительной вероятности
—Только
от числа факторов в модели
—Только
от длины исходного ряда
—Только
от уровня доверительной вероятности и
длины исходного ряда
+—И
от доверительной вероятности, и от числа
факторов, и от длины исходного ряда
Имеется
уравнение, полученное МНК:
Зная,
что регрессионная сумма квадратов
составила 110,32, остаточная сумма квадратов
21,43, найдите коэффициент детерминации:
+—0,837
—0,999
—1,000
—0,736
Суть
коэффициента детерминации
состоит
в следующем:
+—коэффициент
определяет долю общего разброса значений
,
объясненного уравнением регрессии
—коэффициент
свидетельствует о значимости коэффициентов
регрессии
—коэффициент
определяет тесноту связи между признаками
—коэффициент
свидетельствует о наличии / отсутствии
автокорреляции
Какое
из уравнений регрессии нельзя свести
к линейному виду?
+—
—
—
—
—
Какое
из уравнений регрессии является
степенным?
—
+—
—
—
—
Парная
регрессия представляет собой модель
вида:
+—y=f(x)
—y=f(x1,x2,…xm)
—y=f(y
t-1)
Уравнение
парной регрессии характеризует связь
между:
+—двумя
переменными
—несколькими
переменными
Согласно
содержанию регрессии, наблюдаемая
величина зависимой переменной складывается
из:
+—теоретического
значения зависимой переменной, найденного
из уравнения регрессии, и случайного
отклонения
—теоретического
значения зависимой переменной, найденного
из уравнения регрессии, скорректированного
на величину стандартной ошибки
—теоретического
значения зависимой переменной, найденного
из уравнения регрессии и остаточной
дисперсии
Использование
парной регрессии вместо множественной
является примером:
+—ошибки
спецификации
—ошибки
выборки
—ошибки
измерения
Включение
в совокупность единиц с “выбросами”
данных является примером:
+—ошибки
выборки
—ошибки
спецификации
—ошибки
измерения
Заниженная
балансовая прибыль в отчетности является
примером:
+—ошибки
измерения
—ошибки
спецификации
—ошибки
выборки
Аналитический
метод подбора вида уравнения регрессии
основан на:
+—изучении
природы связи признаков
—изучении
поля корреляции
—сравнении
величины остаточной дисперсии при
разных моделях
Графический
метод подбора вида уравнения регрессии
основан на:
+—изучении
поля корреляции
—изучении
природы связи признаков
—сравнении
величины остаточной дисперсии при
разных моделях
Экспериментальный
метод подбора вида уравнения регрессии
основан на:
+—сравнении
величины остаточной дисперсии при
разных моделях
—изучении
поля корреляции
—изучении
природы связи признаков
Классический
подход к оцениванию коэффициентов
регрессии основан на:
+—методе
наименьших квадратов
—графической
оценке
—методе
максимального правдоподобия
Величина
коэффициента регрессии показывает:
+—среднее
изменение результата с изменением
фактора на одну единицу
—среднее
изменение результата с изменением
фактора на один процент
—изменение
результата в процентах с изменением
фактора на один процент
Уравнение
парной регрессии дополняется коэффициентом
парной корреляции потому, что:
+—необходимо
знать тесноту связи в линейной форме
—это
требуется для получения оценок
коэффициентов регрессии
—это
необходимо для расчета величины
остаточной дисперсии
Коэффициент
детерминации характеризует:
+—долю
факторной дисперсии в общей дисперсии
результативного признака
—соотношение
факторной и остаточной дисперсий
—долю
остаточной дисперсии в общей дисперсии
результативного признака
F-критерий
характеризует:
+—соотношение
факторной и остаточной дисперсий
—долю
факторной дисперсии в общей дисперсии
результативного признака
—долю
остаточной дисперсии в общей дисперсии
результативного признака
Оценка
значимости уравнения регрессии в целом
дается с помощью:
+—F-критерия
Фишера
—коэффициента
детерминации
—стандартной
ошибки регрессии
«Объясненная»
сумма квадратов отклонений отражает
влияние на разброс y:
+—изучаемого
фактора х
—прочих
факторов
—изучаемого
фактора х и прочих факторов
Остаточная
сумма квадратов отклонений отражает
влияние на разброс у:
—изучаемого
фактора х
+—прочих
факторов
—изучаемого
фактора х и прочих факторов
Если
фактор не оказывает влияния на результат,
то линия регрессии на графике:
+—параллельна
оси ох
—параллельна
оси оу
—является
биссектрисой первой четверти декартовой
системы координат
Остаточная
сумма квадратов равна нулю в том случае,
когда:
+—у
связан с х функционально
—значения
у, рассчитанные по уравнению регрессии,
равны среднему значению у
—вся
общая дисперсия у обусловлена влиянием
прочих факторов
Общая
сумма квадратов отклонений совпадает
с остаточной, когда:
+—фактор
х не оказывает влияния на результат
—прочие
факторы не влияют на результат
—фактор
х и прочие факторы в равной степени
влияют на результат
Уравнение
регрессии статистически значимо, если
+—«объясненная»
сумма квадратов отклонений значимо
больше остаточной суммы квадратов
отклонений
—остаточная
сумма квадратов отклонений значимо
больше «объясненной» суммы квадратов
отклонений
—«объясненная»
и остаточная суммы квадратов отклонений
равны
Число
степеней свободы связано с:
+—числом
единиц совокупности n
и числом определяемых по совокупности
констант
—числом
определяемых по совокупности констант
—числом
единиц совокупности n
“Объясненная”
(факторная) сумма квадратов отклонений
в парной регрессии имеет число степеней
свободы, равное:
+—1
—n-1
—n-2
Остаточная
сумма квадратов отклонений в парной
регрессии имеет число степеней свободы,
равное:
+—n-2
—n-1
—1
Общая
сумма квадратов отклонений в парной
регрессии имеет число степеней свободы,
равное:
+—n-1
—1
—n-2
Какое
из утверждений истинно:
+—оценки
коэффициентов регрессии будут иметь
нормальное распределение, если случайные
отклонения распределены нормально
—чем
больше стандартная ошибка регрессии
(остаточная дисперсия), тем точнее оценки
коэффициентов
—90%-й
доверительный интервал для условного
математического ожидания зависимой
переменной определяет область возможных
значений для 90 % -ов наблюдений за
зависимой переменной при соответствующем
уровне объясняющей переменной
Для
оценки значимости коэффициентов
регрессии рассчитывают:
+—t-статистику
Стьюдента
—F-критерий
Фишера
—коэффициент
детерминации
Какой
нелинейной функцией можно заменить
параболу, если не наблюдается смена
направленности связи признаков:
+—степенной
функцией
—гиперболой
—логистической
функцией
В
большинстве случаев зависимости между
экономическими переменными являются:
+—стохастическими
—функциональными
—строгими
Компонента
в уравнении линейной регрессии отражает:
+—связь
в генеральной совокупности
—случайность
—связь
в генеральной совокупности и случайность
Коэффициент
а в уравнении линейной регрессии
измеряет:
+—сдвиг
по оси ординат
—наклон
прямой
—среднее
значение y
Коэффициент
b
в уравнении линейной регрессии измеряет:
+—наклон
прямой
—сдвиг
по оси ординат
—среднее
значение у
По
выборке данных можно построить так
называемое:
+—эмпирическое
уравнение регрессии
—теоретическое
уравнение регрессии
—любое
уравнение регрессии
Эмпирические
коэффициенты регрессии а и b
являются точечными оценками:
+—теоретических
коэффициентов регрессии
—условного
математического ожидания у
—теоретического
случайного отклонения
есть точечная
оценка:
+—
—
—
Коэффициент
регрессии b
пропорционален:
+—коэффициенту
корреляции
—стандартному
отклонению х
—стандартному
отклонению у
Эмпирическая
прямая регрессии обязательно проходит
через точку:
+—
—
—
Эмпирическое
уравнение регрессии построено таким
образом, что:
+—
—
—
Коэффициент
b
регрессии Y
на X
имеет тот же знак, что и:
+—
—
—
Если
по одной и той же выборке рассчитаны
регрессии У на Х и Х на У, то совпадут ли
в этом случае линии регрессии:
+—нет
—да
Если
переменная Х принимает среднее по
выборке значение х, то:
+—наблюдаемая
величина зависимой переменной У равна
среднему значению у
—регрессионная
величина Ух
в среднем
равна среднему значению у, но не
обязательно в каждом конкретном случае
—регрессионная
величина Ух
равна
среднему значению у
—регрессионный
остаток минимален среди всех других
отклонений
Выберите
истинное утверждение:
+—коэффициенты
эмпирического уравнения регрессии
являются по сути случайными величинами
—коэффициент
b
эмпирического парного линейного
уравнения регрессии показывает процентное
изменение зависимой переменной у при
однопроцентном изменении х
—коэффициент
a
эмпирического парного линейного
уравнения регрессии показывает значение
переменной y
при среднем значении переменной x
Случайное
отклонение в среднем не оказывает
влияние на зависимую переменную, если:
—
+—
—
Случайное
отклонение приведет к увеличению
дисперсии оценок, если
+—
—
—
Гомоскедастичность
подразумевает:
+—
—
—
Отсутствие
автокорреляции случайных отклонений
влечет соотношение:
+—
—
—
Эмпирический
коэффициент регрессии b
является несмещенной оценкой
если:
+—
—
—
Эмпирический
коэффициент регрессии b
является состоятельной оценкой
если:
+—
—
—
Эмпирический
коэффициент регрессии b
является эффективной оценкой
если:
+—
—
—
С
увеличением числа наблюдений n
дисперсии оценок а и b:
+—уменьшаются
—увеличиваются
—не
изменяются
С
увеличением дисперсии х дисперсия
оценок a
и b:
+—уменьшается
—увеличивается
—не
изменяется
С
увеличением наклона прямой регрессии
(b)
разброс значений свободного члена а:
+—увеличивается
—уменьшается
—не
изменяется
Разброс
значений свободного члена а:
+—тем
больше, чем больше среднее значение
квадрата х
—тем
больше, чем меньше среднее значение
квадрата х
—не
зависит от величины х
Свободным
членом уравнения парной линейной
регрессии (а) можно пренебречь, когда:
+—
—
—
Значимая
линейная связь между х и у имеет место,
когда:
+—
—
—
С
увеличением объема выборки:
+—увеличивается
точность оценок
—увеличивается
точность прогноза по модели
—уменьшается
коэффициент детерминации
При
оценке парной линейной регрессии
получена завышенная оценка b1
теоретического коэффициента
.
Какая оценка наиболее вероятна для
коэффициента
+—заниженная
—завышенная
—несмещенная
Доверительный
интервал для среднего значения У при
Х=хр
будет:
+—уже,
чем таковой для индивидуальных значений
у
—шире,
чем таковой для индивидуальных значений
у
Дополнительные
вопросы
Для
уравнения
значение коэффициента корреляции
составило 2. Следовательно . . . .
+
значение коэффициента корреляции
рассчитано с ошибкой;
—
теснота связи в 2 раза сильнее, чем для
функциональной связи;
—
связь функциональная;
—
при увеличении фактора на единицу
значение результата увеличивается в 2
раза.
Графическое
изображение наблюдений на декартовой
плоскости координат называется полем
…
—
регрессии;
+
корреляции;
—
случайных воздействий;
—
автокорреляции.
Факторная
дисперсия служит для оценки влияния:
—
как учтенных факторов, так и случайные
воздействия;
+
учтенных явно в модели факторов;
—
величины постоянной составляющей в
уравнении;
—
случайных воздействий.
Спецификацию
нелинейного уравнения парной регрессии
целесообразно использовать, если
значение …
—
линейного коэффициента корреляции для
исследуемой зависимости близко к 1;
—
индекса корреляции для исследуемой
зависимости близко к 0;
+
индекса детерминации, рассчитанного
для данной модели достаточно близко к
1;
—
доля остаточной дисперсии результативного
признака в его общей дисперсии стремится
к 1.
Система
нормальных уравнений метода наименьших
квадратов строится на основании:
+
таблицы исходных данных;
—
отклонений фактических значений
результативного признака от его
теоретических значений;
—
предсказанных значений результативного
признака;
—
отклонений фактических значений
объясняющей переменной от ее теоретических
значений.
Общая
дисперсия служит для оценки влияния …
—
учтенных явно в модели факторов;
+
как учтенных факторов, так и случайных
воздействий;
—
величины постоянной составляющей в
уравнении;
—
случайных воздействий.
Экспоненциальным
не является
уравнение регрессии:
—
;
—
;
+
;
—
.
Объем
выборки определяется …
—
числовыми значениями переменных,
отбираемых в выборку;
—
объемом генеральной совокупности;
+
числом параметров при независимых
переменных;
—
числом результативных переменных.
При
расчете значения коэффициента детерминации
используется отношение:
—
математических ожиданий;
—
остаточных величин;
—
параметров уравнения регрессии;
+
дисперсий.
Предпосылкой
метода наименьших квадратов является
…
—
присутствие автокорреляции между
результатом и фактором;
—
отсутствие корреляции между результатом
и фактором;
—
присутствие автокорреляции в остатках;
+
отсутствие автокорреляции в остатках.
Смысл
расчета средней ошибки аппроксимации
состоит в определении среднего
арифметического значения . . . .
—
теоретических значений результативного
признака, выраженных в процентах от его
фактических значений;
+
отклонений
,
выраженных в процентах от фактических
значений результативного признака;
—
теоретических значений результативного
признака, выраженных в процентах от его
фактических значений признака;
—
отклонений
,
выраженных в процентах от фактических
значений независимой переменной.
Для
моделирования зависимости предложения
от цены не
может быть
использовано уравнение регрессии:
—
;
—
;
+
;
—
.
Основной
целью линеаризации уравнения регрессии
является. . . .
—
повышения существенности связи между
рассматриваемыми переменными;
—
получение новых нелинейных зависимостей;
+
возможность применения метода наименьших
квадратов для оценки параметров;
—
улучшение качества модели.
Требованием
к уравнениям регрессии, параметры
которых можно найти при помощи МНК
является:
+
линейность параметров;
—
равенство нулю средних значений
результативной переменной;
—
нелинейность параметров;
—
равенство нулю средних значений
факторного признака.
Совокупность
значений критерия, при которых принимается
нулевая гипотеза, называется областью
_____________ гипотезы:
+
принятия;
—
нулевых значений;
—
допустимых значений;
—
отрицания.
Качество
подбора уравнения оценивает коэффициент
. . . .
—
корреляции;
+
детерминации;
—
эластичности;
—
регрессии.
Увеличение точности
оценок с увеличением объема выборки
описывает свойство ___________ оценки
—
несмещенности;
—
смещенности;
+
состоятельности;
—
эффективности.
Оценки
параметров, найденных при помощи метода
наименьших квадратов, обладают свойствами
эффективности, состоятельности и
несмещенности, если предпосылки метода
наименьших квадратов . . .
+
выполняются;
—
не выполняются;
—
можно не учитывать;
—
можно исключить.
Нелинейным
не является уравнение . . . .
+
;
—
;
—
;
—
.
Критерий
Стьюдента предназначен для определения
значимости . . .
—
построенного уравнения в целом;
—
каждого коэффициента корреляции;
—
уравнения;
+
каждого коэффициента регрессии.
Для
моделирования зависимости предложения
от цены не
может быть
использовано уравнение регрессии:
—
;
—
;
+
;
—
.
Для
уравнения
значение коэффициента корреляции
составило 2. Следовательно . . . .
+
значение коэффициента корреляции
рассчитано с ошибкой;
—
теснота связи в 2 раза сильнее, чем для
функциональной связи;
—
связь функциональная;
—
при увеличении фактора на единицу
значение результата увеличивается в 2
раза.
Назовите
показатель корреляции для нелинейных
моделей регрессии:
—
парный коэффициент линейной корреляции;
—
индекс детерминации;
—
линейный коэффициент корреляции;
+
индекс корреляции.
Если
спецификация модели
нелинейного уравнения регрессии, то
нелинейной является функция:
—
;
—
;
+
;
—
.
Значение
коэффициента корреляции не характеризует
…
+
статистическую значимость уравнения;
—
корень из значения коэффициента
детерминации;
—
тесноту связи;
—
силу связи.
Расчетное
значение критерия Фишера определяется
как отношение ….
+
дисперсий;
—
результата к фактору;
—
математических ожиданий;
—
случайных величин.
Парабола
второй степени может быть использована
для зависимостей экономических
показателей,
—
если исходные данные не обнаруживают
изменения направленности;
—
если для определенного интервала
значений фактора меняется скорость
изменений значений результата, то есть
возрастает динамика роста или спада;
—
если характер связи зависит от случайных
факторов;
+
если для определенного интервала
значений фактора меняется характер
связи рассматриваемых показателей:
прямая связь изменяется на обратную
или обратная на прямую.
Оценки
параметров уравнений регрессии при
помощи метода наименьших квадратов
находятся на основании:
—
решения уравнения регрессии;
—
решения системы нормальных неравенств;
—
решения двойственной задачи;
+
решения системы нормальных уравнений.
Для
уравнения зависимости выручки от
величины оборотных средств получено
значение коэффициента детерминации,
равное 0,7. Следовательно, _______ процентов
дисперсии обусловлено случайными
факторами.
+
30%;
—
100%;
—
70%;
—
0%.
Если
доверительный интервал для параметра
проходит через точку ноль, следовательно
…
—
значение параметра может принимать как
отрицательные, так и положительные
значения;
+
параметр является несущественным;
—
параметр является существенным;
—
параметр признается статистически
значимым.
Уравнение
регрессии
характеризует ________ зависимость.
+
обратно пропорциональную;
—
линейную;
—
функциональную;
—
прямо пропорциональную
Значения
коэффициента корреляции может находиться
в отрезке:
—
[-1;0];
—
[0;1];
+
[-1;1];
—
[-2;2].
Оценка
значимости уравнения в целом осуществляется
по критерию:
+
Фишера;
—
Дарбина-Уотсона;
—
Пирсона;
—
Стьюдента.
Метод
наименьших квадратов позволяет оценить
_______ уравнений регрессии
—
переменные и случайные величины;
+
параметры;
—
переменные;
—
параметры и переменные
Расчет
средней ошибки аппроксимации для
нелинейных уравнений регрессии связан
с расчетом разности между …
+
фактическим и теоретическим значениями
результативной переменной;
—
фактическим и теоретическим значениями
независимой переменной;
—
прогнозным и теоретическим значениями
результативной переменной;
—
прогнозным и теоретическим значениями
независимой переменной.
Предпосылкой
метода наименьших квадратов является
то, что …
—
при увеличении моделируемых значений
результативного признака значение
остатка увеличивается;
+
остаточные величины имеют случайный
характер;
—
при уменьшении моделируемых значений
результативного признака значение
остатка уменьшается;
—
остаточные величины имеют неслучайный
характер.
Проводится
исследование финансовых результатов
деятельности предприятий, среди которых
обнаруживаются как прибыльные, так и
убыточные. Среди факторов, влияющих на
прибыль, был выделен доминирующий. При
этом нельзя
использовать
спецификацию:
—
;
—
;
+
;
—
.
Значение
коэффициента детерминации рассчитывается
как отношение дисперсии результативного
признака, объясненной регрессией, к
___________ дисперсии результативного
признака.
—
средней;
—
факторной;
—
остаточной;
+
общей
Расчет
значения коэффициента детерминации не
позволяет
оценить:
—
качество подбора уравнения регрессии;
—
долю факторной дисперсии результативного
признака в общей дисперсии результативного
признака;
+
существенность коэффициента регрессии;
—
долю остаточной дисперсии результативного
признака в общей дисперсии результативного
признака.
Предпосылкой
метода наименьших квадратов является
то, что остатки …
—
не подчиняются закону больших чисел;
+
подчиняются закону нормального
распределения;
—
не подчиняются закону нормального
распределения;
—
подчиняются закону больших чисел.
Критическое
значение критерия Стьюдента определяет:
—
максимально возможную величину,
допускающую принятие гипотезы о
существенности параметра;
+
максимально возможную величину,
допускающую принятие гипотезы о
несущественности параметра;
—
минимально возможную величину, допускающую
принятие гипотезы о равенстве нулю
значения параметра;
—
минимально возможную величину, допускающую
принятие гипотезы о несущественности
параметра.
Графическое
изображение наблюдений на декартовой
плоскости координат называется полем
…
—
регрессии;
+
корреляции;
—
случайных воздействий;
—
автокорреляции.
В
линейном уравнении парной регрессии
коэффициентом регрессии является
значение …
—
параметров
и
;
—
параметра
;
—
переменной
;
+
параметра
.
Линеаризация
подразумевает процедуру …
—
приведения уравнения множественной
регрессии к парной;
+
приведения нелинейного уравнения к
линейному виду;
—
приведения линейного уравнения к
нелинейному виду;
—
приведения нелинейного уравнения
относительно параметров к уравнению,
линейному относительно результата.
Система
нормальных уравнений метода наименьших
квадратов строится на основании:
—
таблицы исходных данных;
+
отклонений фактических значений
результативного признака от его
теоретических значений;
—
предсказанных значений результативного
признака;
—
отклонений фактических значений
объясняющей переменной от ее теоретических
значений.
При
помощи модели степенного уравнения
регрессии вида
не может быть
описана
зависимость …
—
выработки от уровня квалификации;
—
заработной платы от выработки;
—
объема предложения от цены;
+
выработки от трудоемкости.
Замена
не подходит
для уравнения …
—
;
—
;
—
;
+
.
При
хорошем качестве модели допустимым
значением средней ошибки аппроксимации
является …
+
5-7%;
—
50%;
—
90-95%;
—
20-25%.
Простая
линейная регрессия предполагает …
—
наличие двух и более факторов и
нелинейность уравнения регрессии;
+
наличие одного фактора и линейность
уравнения регрессии;
—
наличие одного фактора и нелинейность
уравнения регрессии;
—
наличие двух и более факторов и линейность
уравнения регрессии.
Минимальная
дисперсия остатков характерна для
оценок, обладающих свойством …
+
эффективности;
—
несостоятельности;
—
состоятельности;
—
несмещенности.
Нелинейным
является уравнение:
+
;
—
;
+
;
—
.
Построена
модель парной регрессии зависимости
предложения от цены
.
Влияние случайных факторов на величину
предложения в этой модели учтено
посредством …
—
константы
;
—
параметра
;
—
случайной величины
;
+
случайной величины
.
При
расчете значения коэффициента детерминации
используется отношение:
—
математических ожиданий;
—
остаточных величин;
—
параметров уравнения регрессии;
+
дисперсий.
Случайными
воздействиями обусловлено 12% дисперсии
результативного признака, следовательно,
значение коэффициента детерминации
составило:
—
88;
—
0,12;
+
0,88;
—
12.
Свойствами
оценок МНК являются:
—
эффективность, состоятельность и
смещенность;
—
эффективность, несостоятельность и
несмещенность;
—
эффективность, несостоятельность и
смещенность;
+
эффективность, состоятельность и
несмещенность.
Спецификация
модели нелинейная парная (простая)
регрессия подразумевает нелинейную
зависимость и …
+
независимую переменную;
—
пару существенных переменных;
—
пару независимых переменных;
—
пару зависимых переменных.
Значение
линейного коэффициента корреляции
характеризует тесноту ________ связи.
-нелинейной;
+
линейной;
-случайной;
—
множественной линейной.
Для
нелинейных уравнений метод наименьших
квадратов применяется к …
—
не преобразованным линейным уравнениям;
—
обратным уравнениям;
+
преобразованным линеаризованным
уравнениям;
—
нелинейным уравнениям.
Величина
коэффициента детерминации при включении
существенного фактора в эконометрическую
модель …
+
будет увеличиваться;
—
будет равно нулю;
—
существенно не изменится;
—
будет уменьшаться.
К
линейному виду нельзя
привести:
—
линейную модель внутренне линейную;
+
нелинейную модель внутренне нелинейную;
—
линейную модель внутренне нелинейную;
—
нелинейную модель внутренне линейную.
Математическое
ожидание остатков равно нулю, если
оценки параметров обладают свойством…
—
смещенности;
+
несмещенности;
—
состоятельности;
—
эффективности.
В
нелинейной модели парной регрессии
функция
является:
—
равной нулю;
—
несущественной;
—
линейной;
+
нелинейной.
Критические
значения критерия Фишера определяются
по:
+
уровню значимости и степеням свободы
факторной и остаточной дисперсий;
—
уровню значимости и степени свободы
общей дисперсии;
—
уровню значимости;
—
степени свободы факторной и остаточной
дисперсий.
В
качестве показателя тесноты связи для
линейного уравнения парной регрессии
используется:
—
множественный коэффициент линейной
корреляции;
+
линейный коэффициент корреляции;
—
линейный коэффициент регрессии;
—
линейный коэффициент детерминации.
Предпосылки
метода наименьших квадратов исследуют
поведение …
—
параметров уравнения регрессии;
—
неслучайных величин;
+
остаточных величин;
—
переменных уравнения регрессии.
Величина
параметра
в уравнении парной линейной регрессии
характеризует значение …
—
факторной переменной при нулевом
значении результата;
—
результирующей переменной при нулевом
значении случайной величины;
—
факторной переменной при нулевом
значении случайного фактора;
+
результирующей переменной при нулевом
значении фактора.
Если
значение индекса корреляции для
нелинейного уравнения регрессии
стремится к 1, следовательно, …
—
нелинейная связь недостаточно тесная;
—
линейная связь достаточно тесная;
+
нелинейная связь достаточно тесная;
—
нелинейная связь отсутствует.
Состоятельность
оценки характеризуется …
—
независимостью от объема выборки
значения математического ожидания
остатков;
+
увеличением ее точности с увеличением
объема выборки;
—
уменьшением ее точности с увеличением
объема выборки;
—
зависимостью от объема выборки значения
математического ожидания остатков.
Если
предпосылки метода наименьших квадратов
нарушены, то …
—
полученное уравнение статистически
незначимо;
+
оценки параметров могут не обладать
свойствами эффективности, состоятельности
и несмещенности;
—
коэффициент регрессии является
несущественным;
—
коэффициент корреляции является
несущественным.
Общая
дисперсия служит для оценки влияния …
—
учтенных явно в модели факторов;
+
как учтенных факторов, так и случайных
воздействий;
—
величины постоянной составляющей в
уравнении;
—
случайных воздействий.
Значение
коэффициента корреляции равно -1.
Следовательно …
—
связь отсутствует;
—
связь слабая;
+
связь функциональная;
—
ситуация неопределенна.
Нелинейным
называется уравнение регрессии, если
…
—
параметры входят нелинейным образом,
а переменные линейны;
+
независимые переменные входят в уравнение
нелинейным образом;
—
параметры и зависимые переменные входят
в уравнение нелинейным образом;
—
зависимые переменные входят в уравнение
нелинейным образом.
Если
коэффициент регрессии является
несущественным, то его значения
приравниваются к …
—
табличному значению и соответствующий
фактор не включается в модель;
+
нулю и соответствующий фактор не
включается в модель;
—
единице и не влияет на результат;
—
нулю и соответствующий фактор включается
в модель.
Величина
отклонений фактических значений
результативного признака от его
теоретических значений представляет
собой …
—
ошибку корреляции;
—
значение критерия Фишера;
+
ошибку аппроксимации;
—
показатель эластичности.
Объем
выборки должен превышать число
рассчитываемых параметров при исследуемых
факторах ..
—
в 2-3 раза;
—
в 20-25 раз;
—
в 10-12 раз;
+
в 5-6 раз.
Остаточная
дисперсия служит для оценки влияния …
+
случайных воздействий;
—
величины постоянной составляющей в
уравнении;
—
учтенных явно в модели факторов;
—
как учтенных факторов, так и случайных
воздействий.
Значение
коэффициента корреляции равно 0,9.
Следовательно, значение коэффициента
детерминации составит …
—
0,3;
+
0,81;
—
0,95;
—
0,1.
По
результатам исследования было выявлено,
что рентабельность производства падает
с увеличением трудоемкости. Какую
спецификацию уравнения регрессии можно
использовать для построения модели
такой зависимости?
—
;
+
;
—
;
—
.
Случайный
характер остатков предполагает …
—
независимость предсказанных по модели
значений результативного признака от
значений факторного признака;
+
независимость остатков от величины
предсказанных по модели значений
результативного признака;
—
зависимость остатков от величины
предсказанных по модели значений
результативного признака;
—
зависимость предсказанных по модели
значений результативного признака от
значений факторного признака.
Статистические
гипотезы используются для оценки:
—
тесноты связи между результатом и
фактором;
—
тесноты связи между результатом и
случайными факторами;
—
автокорреляции в остатках;
+
значимости уравнения регрессии в целом.
Параметр
является существенным, если …
+
доверительный интервал не проходит
через ноль;
—
доверительный интервал проходит через
ноль;
—
расчетное значение критерия Стьюдента
меньше табличного значения;
—
стандартная ошибка превышает половину
значения самого параметра.
Замена
,
подходит
для уравнения:
—
;
—
;
—
;
+
.
В
исходном соотношении МНК сумма квадратов
отклонений фактических значений
результативного признака от его
теоретических значений …
—
приравнивается к нулю;
+
минимизируется;
—
максимизируется;
—
приравнивается к системе нормальных
уравнений.
При
выборе спецификации нелинейная регрессия
используется, если …
—
нелинейная зависимость для исследуемых
экономических показателей является
несущественной;
+
между экономическими показателями
обнаруживается нелинейная зависимость;
—
между экономическими показателями не
обнаруживается нелинейная зависимость;
—
между экономическими показателями
обнаруживается линейная зависимость.
Табличное
значение критерия Фишера служит для …
+
проверки статистической гипотезы о
равенстве факторной и остаточной
дисперсий;
—
проверки статистической гипотезы о
равенстве дисперсии некоторой
гипотетической величины;
—
проверки статистической гипотезы о
равенстве двух математических ожиданий;
—
проверки статистической гипотезы о
равенстве математического ожидания
некоторой гипотетической величины.
Предпосылкой
метода наименьших квадратов является
то, что остатки …
—
не подчиняются закону больших чисел;
+
подчиняются закону нормального
распределения;
—
не подчиняются закону нормального
распределения;
—
подчиняются закону больших чисел.
Расчетное
значение критерия Фишера определяется
как …
—
разность факторной дисперсии и остаточной,
рассчитанных на одну степень свободы;
—
отношение факторной дисперсии к
остаточной;
+
отношение факторной дисперсии к
остаточной, рассчитанных на одну степень
свободы;
—
суммы факторной дисперсии к остаточной,
рассчитанных на одну степень свободы.
Предпосылкой
метода наименьших квадратов не
является
условие …
—
гомоскедастичности остатков;
—
случайный характер остатков;
—
отсутствие автокорреляции в остатках;
+
неслучайный характер остатков.
Нелинейное
уравнение регрессии означает нелинейную
форму зависимости между:
—
фактором и результатом;
—
фактором и случайной величиной;
+
результатом и факторами;
—
результатом и параметрами.
Несмещенность
оценки на практике означает …
—
уменьшение точности с увеличением
объема выборки;
—
невозможность перехода от точечного
оценивания к интервальному;
—
что найденное значение коэффициента
регрессии нельзя рассматривать как
среднее значение из возможного большого
количества несмещенных оценок;
+
что при большом числе выборочных
оцениваний остатки не будут накапливаться.
Стандартная
ошибка рассчитывается для проверки
существенности …
+
параметра;
—
коэффициента детерминации;
—
случайной величины;
—
коэффициента корреляции.
Факторная
дисперсия служит для оценки влияния:
—
как учтенных факторов, так и случайные
воздействия;
+
учтенных явно в модели факторов;
—
величины постоянной составляющей в
уравнении;
—
случайных воздействий.
Экспоненциальным
не является
уравнение регрессии:
—
;
—
;
+
;
—
.
Известно,
что с увеличением объема производства
себестоимость единицы продукции
уменьшается за счет того, что происходит
перераспределение постоянных издержек.
Пусть
— совокупная величина постоянных
издержек, а
—
величина переменных издержек в расчете
на 1 изделие. Тогда зависимость
себестоимости единицы продукции от
объема производства можно описать с
помощью модели:
—
;
—
;
+
;
—
.
В
основе метода наименьших квадратов
лежит …
—
равенство нулю суммы квадратов отклонений
фактических значений результативного
признака от его теоретических значений;
—
минимизация суммы квадратов отклонений
фактических значений результативного
признака от его средних значений;
+
минимизация суммы квадратов отклонений
фактических значений результативного
признака от его теоретических значений;
—
максимизация суммы квадратов отклонений
фактических значений результативного
признака от его теоретических значений.
Объем
выборки определяется …
—
числовыми значениями переменных,
отбираемых в выборку;
—
объемом генеральной совокупности;
+
числом параметров при независимых
переменных;
—
числом результативных переменных.
При
оценке статистической значимости
уравнения и существенности связи
осуществляется проверка …
—
существенности параметров;
—
существенности коэффициента корреляции;
+
существенности коэффициента детерминации;
—
нулевой гипотезы.
Для
модели зависимости дохода населения
(р.) от объема производства (млн р.)
получено уравнение
.
При изменении объема производства на
1 млн р. доход в среднем изменится на …
+
0,003 млн р.;
—
1200 млн р.;
—
1200 р.;
—
0,003 р.
Относительно
формы зависимости различают …
—
простую и множественную регрессию;
—
положительную и отрицательную регрессию;
—
непосредственную и косвенную регрессию;
+
линейную и нелинейную регрессию.
В
матрице парных коэффициентов корреляции
отображены значения парных коэффициентов
линейной корреляции между …
—
переменными и случайными факторами;
+
переменными;
—
параметрами;
—
параметрами и переменными.
Уравнение
регрессии
может быть реализовано при помощи
подстановки:
—
;
—
;
+
;
—
.
Спецификацию
нелинейного уравнения парной регрессии
целесообразно использовать, если
значение …
—
линейного коэффициента корреляции для
исследуемой зависимости близко к 1;
—
индекса корреляции для исследуемой
зависимости близко к 0;
+
индекса детерминации, рассчитанного
для данной модели достаточно близко к
1;
—
доля остаточной дисперсии результативного
признака в его общей дисперсии стремится
к 1.
Если
значение коэффициента корреляции равно
единице, то связь между результатом и
фактором …
—
стохастическая;
—
вероятностная;
+
функциональная;
—
отсутствует.
Эффективность
оценки на практике характеризуется …
—
невозможностью перехода от точечного
оценивания к интервальному;
—
отсутствием накапливания значений
остатков при большом числе выборочных
оцениваний;
—
уменьшением точности с увеличением
объема выборки;
+
возможность перехода от точечного
оценивания к интервальному
.
Линеаризация
не подразумевает
процедуру …
+
включение в модель дополнительных
существенных факторов;
—
приведение нелинейного уравнения к
линейному;
—
замены переменных;
—
преобразования уравнения.
Основной
задачей эконометрики является …
—
установление связей между различными
процессами в обществе и техническим
процессом;
—
анализ технического процесса на примере
социально-экономических показателей;
—
отражение особенности социального
развития общества;
+
исследование взаимосвязей экономических
явлений и процессов.
При
применении метода наименьших остатков
уменьшить гетероскедастичность остатков
удается путем …
+
преобразования переменных;
—
преобразования параметров;
—
введения дополнительных результатов
в модель;
—
введения дополнительных факторов в
модель.
Значение
индекса детерминации, рассчитанное для
нелинейного уравнения регрессии
характеризует …
+
долю дисперсии результативного признака,
объясненную нелинейной регрессией в
общей дисперсии результативного
признака;
—
долю дисперсии результативного признака,
объясненную линейной корреляцией в
общей дисперсии результативного
признака;
Предпосылкой
метода наименьших квадратов является
…
—
присутствие автокорреляции между
результатом и фактором;
—
отсутствие корреляции между результатом
и фактором;
—
присутствие автокорреляции в остатках;
+
отсутствие автокорреляции в остатках.
Было
замечено, что при увеличении количества
вносимых удобрений урожайность также
возрастает, однако, по достижении
определенного значения фактора
моделируемый показатель начинает
убывать. Для исследования данной
зависимости можно использовать
спецификацию уравнения регрессии …
—
;
—
;
—
;
+
.
Если
оценка параметра эффективна, то это
означает …
—
максимальную дисперсию остатков;
—
уменьшение точности с увеличением
объема выборки;
—
равенство нулю математического ожидания
остатков;
+
наименьшую дисперсию остатков.
При
выборе спецификации модели парная
регрессия используется в случае, когда
…
—
среди множества факторов, влияющих на
результат, можно выделить лишь случайные
факторы;
—
среди множества факторов, влияющих на
результат, можно выделить несколько
факторов;
+
среди множества факторов, влияющих на
результат, можно выделить доминирующий
фактор;
—
среди множества факторов, влияющих на
результат, нельзя выделить доминирующий
фактор.
Нелинейную
модель зависимостей экономических
показателей нельзя привести к линейному
виду, если …
+
нелинейная модель является внутренне
нелинейной;
—
нелинейная модель является внутренне
линейной;
—
линейная модель является внутренне
нелинейной;
—
линейная модель является внутренне
линейной.
Для
существенного параметра расчетное
значение критерия Стьюдента …
—
равно нулю;
+
больше табличного значения критерия;
—
не больше табличного значения критерия;
—
меньше табличного значения критерия.
Оценить
статистическую значимость нелинейного
уравнения регрессии можно с помощью …
—
средней ошибки аппроксимации;
+
критерия Фишера;
—
линейного коэффициента корреляции;
—
показателя эластичности.
Расчетное
значение критерия Фишера определяется
как ___________факторной дисперсии и
остаточной, рассчитанных на одну степень
свободы
—
произведение;
—
разность;
—
сумма;
+
отношение.
Критическое
значение критерия Стьюдента определяет
минимально возможную величину, допускающую
принятие гипотезы о …
—
несущественности параметра;
+
существенности параметра;
—
статистической незначимости значения
параметра;
—
равенства нулю значения параметра.
Если
между экономическими показателями
существует нелинейная связь, то …
—
нецелесообразно использовать спецификацию
нелинейного уравнения регрессии;
+
целесообразно использовать спецификацию
нелинейного уравнения регрессии;
—
целесообразно использовать линейное
уравнение парной регрессии;
—
необходимо включить в модель другие
факторы и использовать линейное уравнение
множественной регрессии.
Оценка
значимости параметров уравнения
регрессии осуществляется по критерию
…
—
Ингла-Гренджера (Энгеля-Грангера);
+
Стьюдента;
—
Фишера;
—
Дарбина-Уотсона.
Назовите
показатель тесноты связи для нелинейных
моделей регрессии:
+
индекс корреляции;
—
индекс детерминации;
—
линейный коэффициент корреляции;
—
парный коэффициент линейной корреляции.
Объем
выборки определяется числом параметров
при …
—
зависимых переменных;
+
независимых переменных;
—
случайных факторах;
—
независимых и зависимых переменных.
Значение
индекса корреляции, рассчитанное для
нелинейного уравнения регрессии
характеризует …
—
тесноту случайной связи;
—
тесноту линейной связи;
+
тесноту нелинейной связи;
—
тесноту обратной связи.
Тема
Парная регрессия (Задачи)
Зависимость
спроса на кухонные комбайны y
от цены x
по 12 торговым точкам компании имеет
вид:
В
скобках – фактическое значение t
– критерия. Ранее предполагалось, что
увеличение цены на 1 % приводит к уменьшению
спроса на 1,4 %. Можно ли утверждать, что
приведенное уравнение регрессии
подтверждает это предположение?
+—Нет,
на любом уровне (0,1; 0,05 и 0,1)
—Да,
на любом уровне (0,1; 0,05 и 0,1)
—Нет,
только на уровнях 0,05 и 0,1
—Нет,
только на уровне 0,1
Зависимость
спроса на кухонные комбайны y
от цены x
по 18 торговым точкам компании имеет
вид:
В
скобках – фактическое значение t
– критерия. Ранее предполагалось, что
увеличение цены на 1 % приводит к уменьшению
спроса на 1,5 %. Можно ли утверждать, что
приведенное уравнение регрессии
подтверждает это предположение?
+—Да,
только на уровне значимости 0,01
—Нет,
на любом уровне (0,01, 0,05 и 0,1)
—Да,
только на уровнях 0,01 и 0,05
—Да,
на любом уровне (0,1, 0,05 и 0,01)
Зависимость
спроса на кухонные комбайны y
от цены x
по 15 торговым точкам компании имеет
вид:
В
скобках – фактическое значение t
– критерия. Ранее предполагалось, что
увеличение цены на 1 % приводит к уменьшению
спроса на 1,3 %. Можно ли утверждать, что
приведенное уравнение регрессии
подтверждает это предположение?
+—Да,
на любом уровне (0,1, 0,05 и 0,01)
—Нет,
на любом уровне (0,01, 0,05 и 0,1)
—Да,
только на уровнях 0,01 и 0,05
—Да,
только на уровне значимости 0,01
Зависимость
спроса на кухонные комбайны y
от цены x
по 12 торговым точкам компании имеет
вид:
В
скобках – фактическое значение t
– критерия. Ранее предполагалось, что
увеличение цены на 1 % приводит к уменьшению
спроса на 1,3 %. Можно ли утверждать, что
приведенное уравнение регрессии
подтверждает это предположение?
+—Да,
только на уровнях 0,01 и 0,05
—Нет,
на любом уровне (0,01, 0,05 и 0,1)
—Да,
только на уровне значимости 0,01
—Да,
на любом уровне (0,1, 0,05 и 0,01)
Зависимость
спроса на кухонные комбайны y
от цены x
по 14 торговым точкам компании имеет
вид:
В
скобках – фактическое значение t
– критерия. Ранее предполагалось, что
увеличение цены на 1 % приводит к уменьшению
спроса на 1,2%. Можно ли утверждать, что
приведенное уравнение регрессии
подтверждает это предположение?
+—Нет,
на любом уровне (0,01, 0,05 и 0,1)
—Да,
только на уровне значимости 0,01
—Да,
только на уровнях 0,01 и 0,05
—Да,
на любом уровне (0,1, 0,05 и 0,01)
Зависимость
спроса на кухонные комбайны y
от цены x
по 15 торговым точкам компании имеет
вид:
В
скобках – фактическое значение t
– критерия. Ранее предполагалось, что
увеличение цены на 1 % приводит к уменьшению
спроса на 1,1 %. Можно ли утверждать, что
приведенное уравнение регрессии
подтверждает это предположение?
+—Да,
только на уровнях 0,01 и 0,05
—Нет,
на любом уровне (0,01, 0,05 и 0,1)
—Да,
только на уровне значимости 0,01
—Да,
на любом уровне (0,1, 0,05 и 0,01)
Зависимость
спроса на кухонные комбайны y
от цены x
по 20 торговым точкам компании имеет
вид:
В
скобках – фактическое значение t
– критерия. Ранее предполагалось, что
увеличение цены на 1 % приводит к уменьшению
спроса на 1,3 %. Можно ли утверждать, что
приведенное уравнение регрессии
подтверждает это предположение?
+—Да,
только на уровне значимости 0,01
—Нет,
на любом уровне (0,01, 0,05 и 0,1)
—Да,
только на уровнях 0,01 и 0,05
—Да,
на любом уровне (0,1, 0,05 и 0,01)
Для
двух видов продукции А и Б зависимость
удельных постоянных расходов от объема
выпускаемой продукции выглядят следующим
образом:
Сравнить
эластичности затрат по каждому виду
продукции при x=50
и определить объем выпускаемой продукции
обоих видов, при котором их эластичность
будут одинаковы
+—
—
—
—
Для
двух видов продукции А и Б зависимость
удельных постоянных расходов от объема
выпускаемой продукции выглядят следующим
образом:
Сравнить
эластичности затрат по каждому виду
продукции при x=60
и определить объем выпускаемой продукции
обоих видов, при котором их эластичность
будут одинаковы
+—
—
—
—
Для
двух видов продукции А и Б зависимость
удельных постоянных расходов от объема
выпускаемой продукции выглядят следующим
образом:
Сравнить
эластичности затрат по каждому виду
продукции при x=80
и определить объем выпускаемой продукции
обоих видов, при котором их эластичность
будут одинаковы
+—
—
—
—
Для
двух видов продукции А и Б зависимость
удельных постоянных расходов от объема
выпускаемой продукции выглядят следующим
образом:
Сравнить
эластичности затрат по каждому виду
продукции при x=40
и определить объем выпускаемой продукции
обоих видов, при котором их эластичность
будут одинаковы
+—
—
—
—
Для
двух видов продукции А и Б зависимость
удельных постоянных расходов от объема
выпускаемой продукции выглядят следующим
образом:
Сравнить
эластичности затрат по каждому виду
продукции при x=25
и определить объем выпускаемой продукции
обоих видов, при котором их эластичность
будут одинаковы
+—
—
—
—
Для
двух видов продукции А и Б зависимость
удельных постоянных расходов от объема
выпускаемой продукции выглядят следующим
образом:
Сравнить
эластичности затрат по каждому виду
продукции при x=30
и определить объем выпускаемой продукции
обоих видов, при котором их эластичность
будут одинаковы
+—
—
—
—
Для
двух видов продукции А и Б зависимость
удельных постоянных расходов от объема
выпускаемой продукции выглядят следующим
образом:
Сравнить
эластичности затрат по каждому виду
продукции при x=40
и определить объем выпускаемой продукции
обоих видов, при котором их эластичность
будут одинаковы
+—
—
—
—
Для
двух видов продукции А и Б зависимость
удельных постоянных расходов от объема
выпускаемой продукции выглядят следующим
образом:
Сравнить
эластичности затрат по каждому виду
продукции при x=45
и определить объем выпускаемой продукции
обоих видов, при котором их эластичность
будут одинаковы
+—
—
—
—
Для
двух видов продукции А и Б зависимость
удельных постоянных расходов от объема
выпускаемой продукции выглядят следующим
образом:
Сравнить
эластичности затрат по каждому виду
продукции при x=40
и определить объем выпускаемой продукции
обоих видов, при котором их эластичность
будут одинаковы
—
—
—
+—
Для
двух видов продукции А и Б зависимость
удельных постоянных расходов от объема
выпускаемой продукции выглядят следующим
образом:
Сравнить
эластичности затрат по каждому виду
продукции при x=55
и определить объем выпускаемой продукции
обоих видов, при котором их эластичность
будут одинаковы
+—
—
—
—
Пусть
имеется уравнение парной регрессии:
построенное
по 15 наблюдениям. При этом r=-0.7.
Доверительный интервал для коэффициента
регрессии в этой модели имеет вид:
+—(-11,11;
-0,89) с вероятностью 0,99
—(-9,67;-2,33)
с вероятностью 0,99
—(-9,01;
-2,99) с вероятностью 0,95
—(-8,53;
-2,32) с вероятностью 0,9
Пусть
имеется уравнение парной регрессии:
построенное
по 18 наблюдениям. При этом r=-0.75.
Доверительный интервал для коэффициента
регрессии в этой модели имеет вид:
+—(-6,92;
-3,08) с вероятностью 0,9
—(-6,92;-3,08)
с вероятностью 0,95
—(-8,22;
-1,78) с вероятностью 0,95
—(-7,34;
-2,66) с вероятностью 0,99
Пусть
имеется уравнение парной регрессии:
построенное
по 20 наблюдениям. При этом r=-0.65.
Доверительный интервал для коэффициента
регрессии в этой модели имеет вид:
+—(-6,32;-1,68)
с вероятностью 0,95
—(-5,91;-2,09)
с вероятностью 0,99
—(-6,32;
-1,68) с вероятностью 0,99
—(-5,91;
-2,09) с вероятностью 0,95
Пусть
имеется уравнение парной регрессии:
построенное
по 22 наблюдениям. При этом r=0.73.
Доверительный интервал для коэффициента
регрессии в этой модели имеет вид:
+—(1,69;
4,31) с вероятностью 0,95
—(-0,49;6,49)
с вероятностью 0,95
—(-1,76;
7,76) с вероятностью 0,99
—(1,23;
4,77) с вероятностью 0,99
Пусть
имеется уравнение парной регрессии:
построенное
по 24 наблюдениям. При этом r=0.68.
Доверительный интервал для коэффициента
регрессии в этой модели имеет вид:
+—(2,46;11,54)
с вероятностью 0,99
—(2,50;
11,50) с вероятностью 0,99
—(6,36;
7,64) с вероятностью 0,90
—(3,68;
10,32) с вероятностью 0,95
Пусть
имеется уравнение парной регрессии:
построенное
по 20 наблюдениям. При этом r=0.86.
Доверительный интервал для коэффициента
регрессии в этой модели имеет вид:
+—(2,27;3,73)
с вероятностью 0,90
—(2,14;3,86)
с вероятностью 0,95
—(2,28;
3,72) с вероятностью 0,99
—(1,85;
4,15) с вероятностью 0,99
Пусть
имеется уравнение парной регрессии:
построенное
по 15 наблюдениям. При этом r=0,53.
Доверительный интервал для коэффициента
регрессии в этой модели имеет вид:
+—(0,20;9,80)
с вероятностью 0,95
—(0,05;9,95)
с вероятностью 0,99
—(1,17;
8,83) с вероятностью 0,90
—(0,35;
9,65) с вероятностью 0,95
Пусть
имеется уравнение парной регрессии:
построенное
по 18 наблюдениям. При этом r=-0,6.
Доверительный интервал для коэффициента
регрессии в этой модели имеет вид:
+—(-3,42;-0,58)
с вероятностью 0,95
—(-3,7;-0,3)
с вероятностью 0,99
—(-3,21;
-0,79) с вероятностью 0,90
—(-3,56;
-0,44) с вероятностью 0,95
Пусть
имеется уравнение парной регрессии:
построенное
по 16 наблюдениям. При этом r=
.
Доверительный интервал для коэффициента
регрессии в этой модели имеет вид:
+—(-4,80;-1,2)
с вероятностью 0,99
—(-4,36;-1,64)
с вероятностью 0,95
—(-3,98;
-2,02) с вероятностью 0,90
—(-4,96;
-1,04) с вероятностью 0,99
Пусть
имеется уравнение парной регрессии:
построенное
по 14 наблюдениям. При этом
.
Доверительный интервал для коэффициента
регрессии в этой модели имеет вид:
+—(-16,72;
0,72) с вероятностью 0,95
—(-17,32;
1,32) с вероятностью 0,99
—(-16,13;
0,13) с вероятностью 0,90
—(-15,76;
-0,24) с вероятностью 0,90
Уравнение
регрессии потребления материалов
от объема производства
,
построенное по 18 наблюдениям, имеет
вид:
В
скобках – фактическое значение t
– критерия. Коэффициент детерминации
для этого уравнения равен:
+—0,360
—0,384
—0,247
—0,456
Уравнение
регрессии потребления материалов
от объема производства
,
построенное по 20 наблюдениям, имеет
вид:
В
скобках – фактическое значение t
– критерия. Коэффициент детерминации
для этого уравнения равен:
+—0,405
—0,428
—0,292
—0,501
Уравнение
регрессии потребления материалов
от объема производства
,
построенное по 15 наблюдениям, имеет
вид:
В
скобках – фактическое значение t
– критерия. Коэффициент детерминации
для этого уравнения равен:
+—0,448
—0,564
—0,356
—0,621
Уравнение
регрессии потребления материалов
от объема производства
,
построенное по 20 наблюдениям, имеет
вид:
В
скобках – фактическое значение t
– критерия. Коэффициент детерминации
для этого уравнения равен:
+—0,491
—0,425
—0,379
—0,531
Уравнение
регрессии потребления материалов
от объема производства
,
построенное по 18 наблюдениям, имеет
вид:
В
скобках – фактическое значение t
– критерия. Коэффициент детерминации
для этого уравнения равен:
+—0,327
—0,425
—0,517
—0,369
Уравнение
регрессии потребления материалов
от объема производства
,
построенное по 25 наблюдениям, имеет
вид:
В
скобках – фактическое значение t
– критерия. Коэффициент детерминации
для этого уравнения равен:
+—0,373
—0,321
—0,415
—0,512
Уравнение
регрессии потребления материалов
от объема производства
,
построенное по 15 наблюдениям, имеет
вид:
В
скобках – фактическое значение t
– критерия. Коэффициент детерминации
для этого уравнения равен:
+—0,675
—0,519
—0,631
—0,620
Уравнение
регрессии потребления материалов
от объема производства
,
построенное по 18 наблюдениям, имеет
вид:
В
скобках – фактическое значение t
– критерия. Коэффициент детерминации
для этого уравнения равен:
+—0,461
—0,395
—0,423
—0,522
Уравнение
регрессии потребления материалов
от объема производства
,
построенное по 20 наблюдениям, имеет
вид:
В
скобках – фактическое значение t
– критерия. Коэффициент детерминации
для этого уравнения равен:
+—0,495
—0,517
—0,444
—0,396
По
совокупности 15 предприятий торговли
изучается зависимость между ценой
на товар А и прибылью
торгового предприятия. При оценке
регрессионной модели были получены
следующие результаты:
Индекс
корреляции, фактическое значение F-
критерия значимость уравнения регрессии
следующие:
+—
уравнение статистически не значимо на
уровнях 0,01 и 0,05
—
уравнение
статистически значимо только на уровне
0,1
—
уравнение
статистически значимо только на уровнях
0,1 и 0,05
—
уравнение
статистически значимо на всех уровнях
По
совокупности 18 предприятий торговли
изучается зависимость между ценой
на товар А и прибылью
торгового предприятия. При оценке
регрессионной модели были получены
следующие результаты:
Определить
индекс корреляции и фактическое значение
F-
критерия, а также статистическую
значимость уравнения регрессии
+—
уравнение статистически значимо на
уровнях 0,05 и 0,1
—
уравнение
статистически не значимо на уровне 0,01
—
уравнение
статистически значимо на всех уровнях
—
уравнение
статистически не значимо на всех уровнях
По
совокупности 25 предприятий торговли
изучается зависимость между ценой
на товар А и прибылью
торгового предприятия. При оценке
регрессионной модели были получены
следующие результаты:
Определить
индекс корреляции и фактическое значение
F-
критерия, а также статистическую
значимость уравнения регрессии
+—
уравнение статистически значимо на
уровнях 0,1 и 0,05
—
уравнение
статистически не значимо на уровне 0,01
—
уравнение
статистически значимо на всех уровнях
—
уравнение
статистически не значимо на всех уровнях
По
совокупности 20 предприятий торговли
изучается зависимость между ценой
на товар А и прибылью
торгового предприятия. При оценке
регрессионной модели были получены
следующие результаты:
Определить
индекс корреляции и фактическое значение
F-
критерия, а также статистическую
значимость уравнения регрессии
+—
уравнение статистически значимо на
всех уровнях
—
уравнение
статистически значимо на уровне 0,1
—
уравнение
статистически значимо на уровнях 0,1 и
0,05
—
уравнение
статистически не значимо на уровнях
0,05 и 0,01
По
совокупности 30 предприятий торговли
изучается зависимость между ценой
на товар А и прибылью
торгового предприятия. При оценке
регрессионной модели были получены
следующие результаты:
Определить
индекс корреляции и фактическое значение
F-
критерия, а также статистическую
значимость уравнения регрессии
+—
уравнение статистически значимо на
всех уровнях
—
уравнение
статистически значимо на уровнях 0,1 и
0,05
—
уравнение
статистически не значимо на уровнях
0,05 и 0,01
—
уравнение
статистически значимо на уровне 0,10
По
совокупности 20 предприятий торговли
изучается зависимость между ценой
на товар А и прибылью
торгового предприятия. При оценке
регрессионной модели были получены
следующие результаты:
Определить
индекс корреляции и фактическое значение
F-
критерия, а также статистическую
значимость уравнения регрессии
+—
уравнение статистически значимо на
уровнях 0,1 и 0,05
—
уравнение
статистически значимо на всех уровнях
—
уравнение
статистически значимо на уровнях 0,1 и
0,05
—
уравнение
статистически не значимо на уровне 0,01
По
совокупности 22 предприятий торговли
изучается зависимость между ценой
на товар А и прибылью
торгового предприятия. При оценке
регрессионной модели были получены
следующие результаты:
Определить
индекс корреляции и фактическое значение
F-
критерия, а также статистическую
значимость уравнения регрессии
+—
уравнение статистически значимо на
уровне 0,1
—
уравнение
статистически значимо на уровнях 0,1 и
0,05
—
уравнение
статистически значимо на всех уровнях
—
уравнение
статистически не значимо на уровне 0,1
По
совокупности 28 предприятий торговли
изучается зависимость между ценой
на товар А и прибылью
торгового предприятия. При оценке
регрессионной модели были получены
следующие результаты:
Определить
индекс корреляции и фактическое значение
F-
критерия, а также статистическую
значимость уравнения регрессии
+—
уравнение статистически значимо на
уровнях 0,1 и 0,05
—
уравнение
статистически не значимо на уровне 0,01
—
уравнение
статистически значимо на всех уровнях
—
уравнение
статистически значимо на уровне 0,1
По
совокупности 30 предприятий торговли
изучается зависимость между ценой
на товар А и прибылью
торгового предприятия. При оценке
регрессионной модели были получены
следующие результаты:
Определить
индекс корреляции и фактическое значение
F-
критерия, а также статистическую
значимость уравнения регрессии
+—
уравнение статистически значимо на
всех уровнях
—
уравнение
статистически значимо на уровнях 0,1 и
0,05
—
уравнение
статистически значимо на уровне 0,1
—
уравнение
статистически не значимо на уровне 0,01
По
совокупности 20 предприятий торговли
изучается зависимость между ценой
на товар А и прибылью
торгового предприятия. При оценке
регрессионной модели были получены
следующие результаты:
Определить
индекс корреляции и фактическое значение
F-
критерия, а также статистическую
значимость уравнения регрессии
+—
уравнение статистически значимо уровне
0,1
—
уравнение
статистически значимо на уровнях 0,1 и
0,05
—
уравнение
статистически значимо на всех уровнях
—
уравнение
статистически не значимо на уровне 0,01
И
зучалась
зависимость вида y=a*xb.
Для преобразованных в логарифмах
переменных получены следующие данные:
Найдите
параметр b
+—0,4
—0,7
—0,6
—0,5
Изучалась
зависимость вида y=a*xb.
Для преобразованных в логарифмах
переменных получены следующие данные:

Найдите
параметр b
+—0,6
—0,5
—0,7
—0,4
Изучалась
зависимость вида y=a*xb.
Для преобразованных в логарифмах
переменных получены следующие данные:

Найдите
параметр b
+—0,6
—0,7
—0,5
—0,4
Изучалась
зависимость вида y=a*xb.
Для преобразованных в логарифмах
переменных получены следующие данные:
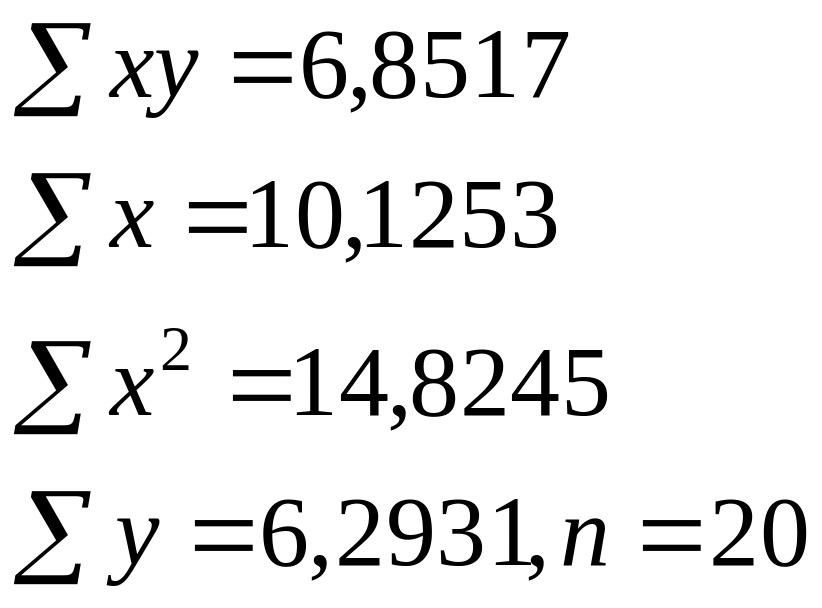
Найдите
параметр b
+—0,4
—0,7
—0,6
—0,5
Изучалась
зависимость вида y=a*xb.
Для преобразованных в логарифмах
переменных получены следующие данные:
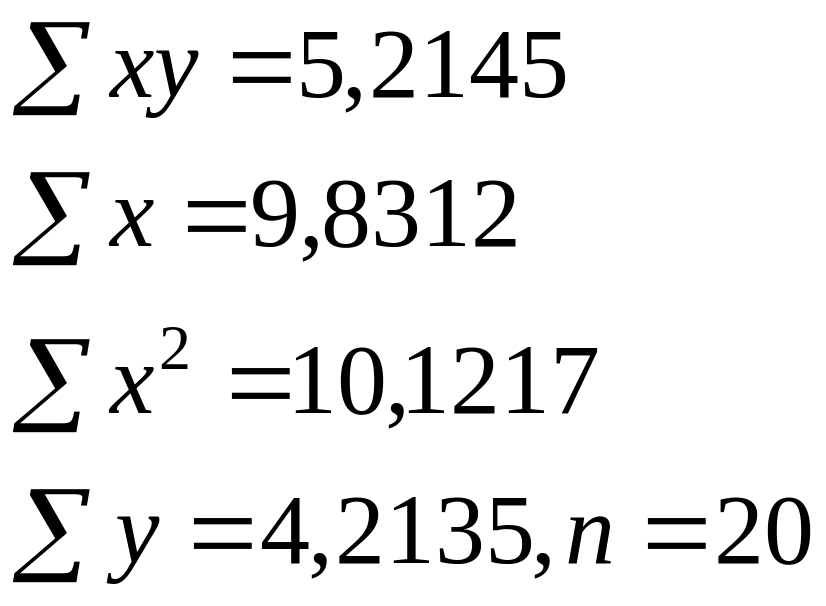
Найдите
параметр b
+—0,6
—0,4
—0,7
—0,5
Изучалась
зависимость вида y=a*xb.
Для преобразованных в логарифмах
переменных получены следующие данные:

Найдите
параметр b
+—0,9
—0,7
—0,6
—0,8
Изучалась
зависимость вида y=a*xb.
Для преобразованных в логарифмах
переменных получены следующие данные:

Найдите
параметр b
+—0,4
—0,7
—0,6
—0,5
Изучалась
зависимость вида y=a*xb.
Для преобразованных в логарифмах
переменных получены следующие данные:
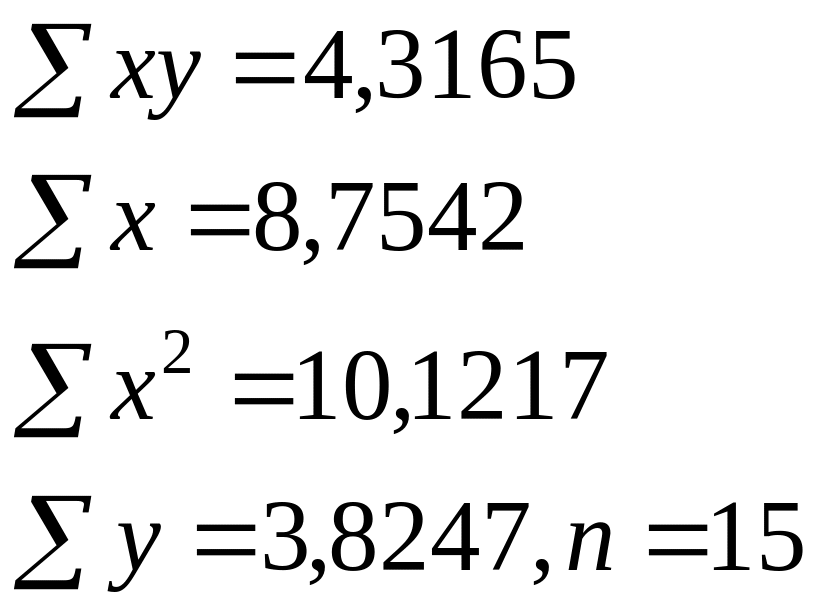
Найдите
параметр b
+—0,4
—0,7
—0,6
—0,5
Изучалась
зависимость вида y=a*xb.
Для преобразованных в логарифмах
переменных получены следующие данные:

Найдите
параметр b
+—0,3
—0,4
—0,6
—0,5
Изучалась
зависимость вида y=a*xb.
Для преобразованных в логарифмах
переменных получены следующие данные:

Найдите
параметр b
+—0,5
—0,7
—0,6
—0,4
Зависимость
объема продаж y от расходов на рекламу
х характеризуется по 12 предприятиям
концерна следующим образом:

Определите
коэффициент корреляции, регрессионную
сумму квадратов отклонений, t-статистику
коэффициента регрессии, F-статистику
+—Rxy=0,83;
S2регр=7,95;
F=22,04,tb=4,69
—Rxy=0,83;
S2регр=5,35;
F=12,tb=3,9
—Rxy=0,43;
S2регр=3,74;
F=5,tb=2,4
—Rxy=0,43;
S2регр=3,48;
F=7,tb=2,5
Зависимость
объема продаж y от расходов на рекламу
х характеризуется по 15 предприятиям
концерна следующим образом:
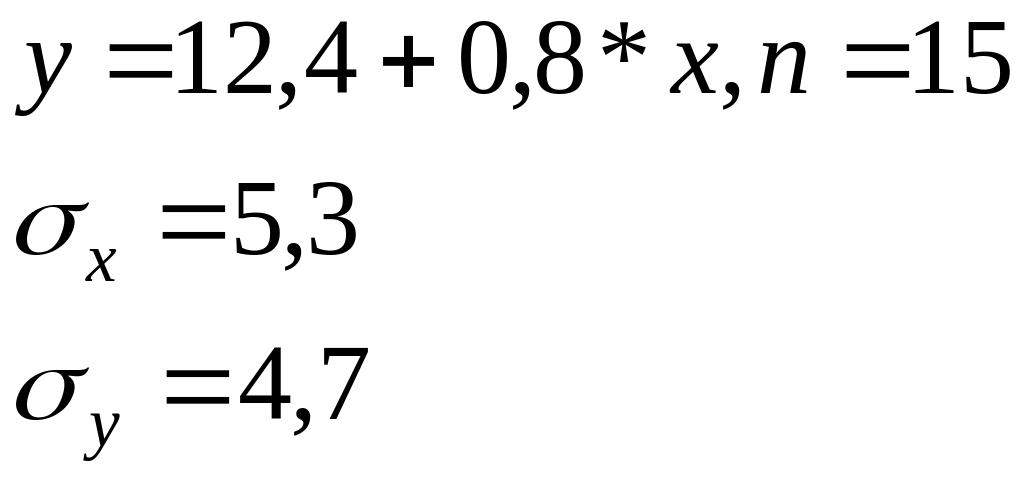
Определите
коэффициент корреляции, регрессионную
сумму квадратов отклонений, t-статистику
коэффициента регрессии, F-статистику
+—Rxy=0,90;
S2регр=17,98;
F=56,83,tb=7,54
—Rxy=0,90;
S2регр=15,35;
F=32,0, tb=6,9
—Rxy=0,71;
S2регр=13,74;
F=5,0, tb=2,4
—Rxy=0,71;
S2регр=9,48;
F=7,0, tb=2,5
Зависимость
объема продаж y от расходов на рекламу
х характеризуется по 18 предприятиям
концерна следующим образом:
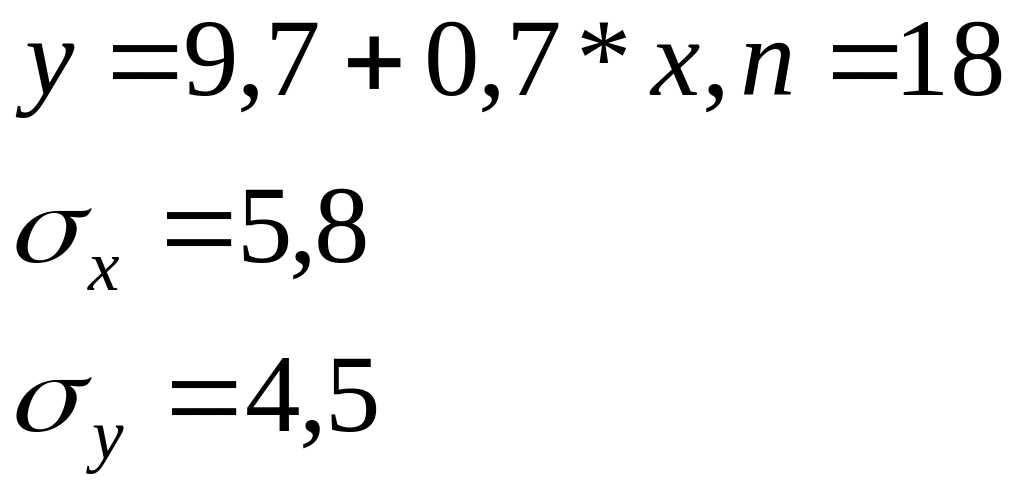
Определите
коэффициент корреляции, регрессионную
сумму квадратов отклонений, t-статистику
коэффициента регрессии, F-статистику
+—Rxy=0,90;
S2регр=16,48;
F=70,02, tb=8,37
—Rxy=0,90;
S2регр=15,35;
F=50,01, tb=5,2
—Rxy=0,54;
S2регр=9,82;
F=40,2, tb=4,8
—Rxy=0,54;
S2регр=8,32;
F=38,9, tb=4,5
Зависимость
объема продаж y от расходов на рекламу
х характеризуется по 15 предприятиям
концерна следующим образом:
О
пределите
коэффициент корреляции, регрессионную
сумму квадратов отклонений, t-статистику
коэффициента регрессии, F-статистику
+—Rxy=0,91;
S2регр=14,75;
F=66,24, tb=8,14
—Rxy=0,91;
S2регр=12,32;
F=50,1, tb=7,12
—Rxy=0,39;
S2регр=5,42;
F=10,31, tb=3,49
—Rxy=0,39;
S2регр=6,17;
F=11,32, tb=4,21
Зависимость
объема продаж y от расходов на рекламу
х характеризуется по 12 предприятиям
концерна следующим образом:

Определите
коэффициент корреляции, регрессионную
сумму квадратов отклонений, t-статистику
коэффициента регрессии, F-статистику
+—Rxy=0,82;
S2регр=14,75;
F=20,08, tb=4,48
—Rxy=0,82;
S2регр=12,82;
F=18,42, tb=3,37
—Rxy=0,76;
S2регр=9,28;
F=10,12, tb=4,21
—Rxy=0,76;
S2регр=8,32;
F=12,05, tb=4,75
Зависимость
объема продаж y от расходов на рекламу
х характеризуется по 18 предприятиям
концерна следующим образом:

Определите
коэффициент корреляции, регрессионную
сумму квадратов отклонений, t-статистику
коэффициента регрессии, F-статистику
+—Rxy=0,88;
S2регр=39,31;
F=56,68, tb=7,53
—Rxy=0,88;
S2регр=25,12;
F=40,12, tb=6,32
—Rxy=0,37;
S2регр=13,10;
F=16,17, tb=5,21
—Rxy=0,37;
S2регр=6,12;
F=4,31, tb=1,18
Зависимость
объема продаж y от расходов на рекламу
х характеризуется по 20 предприятиям
концерна следующим образом:
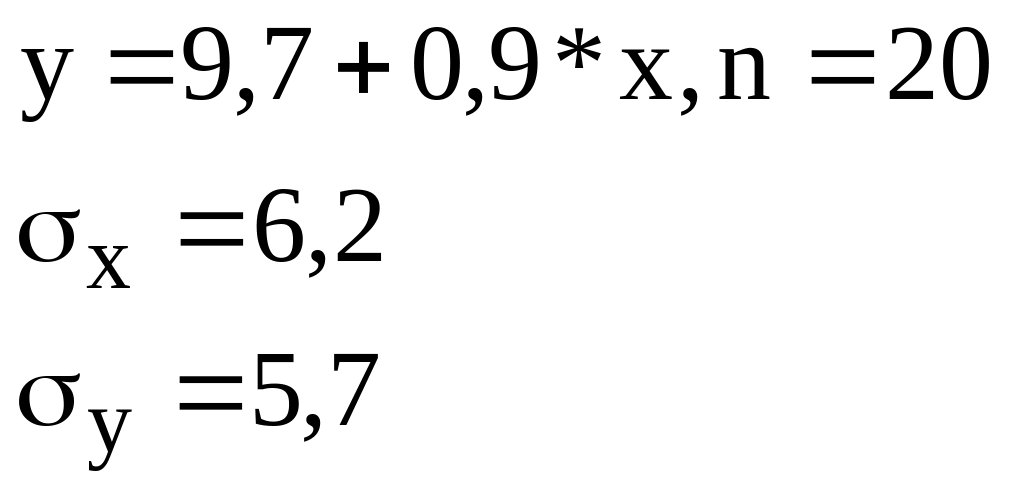
Определите
коэффициент корреляции, регрессионную
сумму квадратов отклонений, t-статистику
коэффициента регрессии, F-статистику
+—Rxy=0,9789;
S2регр=31,14;
F=413,116, tb=20,33
—Rxy=0,9789;
S2регр=41,17;
F=420,08, tb=21,17
—Rxy=0,83;
S2регр=25,12;
F=57,2, tb=8,3
—Rxy=0,83;
S2регр=20,18;
F=48,1, tb=7,8
Зависимость
объема продаж y от расходов на рекламу
х характеризуется по 16 предприятиям
концерна следующим образом:

Определите
коэффициент корреляции, регрессионную
сумму квадратов отклонений, t-статистику
коэффициента регрессии, F-статистику
+—Rxy=0,84;
S2регр=43,03;
F=33,83, tb=5,82
—Rxy=0,84;
S2регр=38,07;
F=25,71, tb=4,72
—Rxy=0,76;
S2регр=17,05;
F=8,3, tb=2,78
—Rxy=0,76;
S2регр=15,32;
F=6,8, tb=2,12
Зависимость
объема продаж y от расходов на рекламу
х характеризуется по 18 предприятиям
концерна следующим образом:

Определите
коэффициент корреляции, регрессионную
сумму квадратов отклонений, t-статистику
коэффициента регрессии, F-статистику
+—Rxy=0,74;
S2регр=15,21;
F=18,89, tb=4,35
—Rxy=0,74;
S2регр=12,32;
F=16,05, tb=3,15
—Rxy=0,50;
S2регр=8,32;
F=12,47, tb=2,32
—Rxy=0,50;
S2регр=6,15;
F=10,16, tb=1,78
Зависимость
объема продаж y от расходов на рекламу
х характеризуется по 20 предприятиям
концерна следующим образом:

Определите
коэффициент корреляции, регрессионную
сумму квадратов отклонений, t-статистику
коэффициента регрессии, F-статистику
+—Rxy=0,89;
S2регр=53,58;
F=70,62, tb=8,4
—Rxy=0,89;
S2регр=49,12;
F=51,2, tb=7,8
—Rxy=0,61;
S2регр=15,2;
F=12,3, tb=3,2
—Rxy=0,61;
S2регр=12,9;
F=5,7, tb=2,3
Уравнение регрессии
имеет вид: ln
y
= 4,5 + 0,003x
+ ln
e.
При значении фактора, равном 85, коэффициент
эластичности y
по х
составит:
+—0,255
—0,003
—0,00066
—0,0536
—0,00063
Уравнение регрессии
имеет вид: ln
y
= 4,5 + 0,003 ln
x
+ ln
e.
При значении фактора, равном 85, коэффициент
эластичности y
по х
составит:
+—0,003
—0,255
—0,00066
—0,0536
—0,00071
Уравнение регрессии
имеет вид: y
= 4,5 + 0,003 ln
x
+ e.
При значении фактора, равном 85, коэффициент
эластичности y
по х
составит:
+—0,00066
—0,255
—0,003
—0,0536
—0,00063
Уравнение регрессии
имеет вид: y
= 4,5 + 0,003x
+ e.
При значении фактора, равном 85, коэффициент
эластичности y
по х
составит:
+—0,0536
—0,255
—0,003
—0,00063
—0,0582
Уравнение регрессии
имеет вид: ln
y
= 2,3 + 0,0043x
+ ln
e.
При значении фактора, равном 108, коэффициент
эластичности y
по х
составит:
+—0,4644
—0,0043
—0,00185
—0,168
—0,4218
Уравнение регрессии
имеет вид: ln
y
= 2,3 + 0,0043 ln
x
+ ln
e.
При значении фактора, равном 108, коэффициент
эластичности y
по х
составит:
+—0,0043
—0,4644
—0,00185
—0,168
—0,00129
Уравнение регрессии
имеет вид: y
= 2,3 + 0,0043 ln
x
+ e.
При значении фактора, равном 108, коэффициент
эластичности y
по х
составит:
+—0,00185
—0,0043
—0,4644
—0,168
—0,4215
Уравнение регрессии
имеет вид: y
= 2,3 + 0,0043x
+ e.
При значении фактора, равном 108, коэффициент
эластичности y
по х
составит:
+—0,168
—0,00185
—0,0043
—0,4644
—0,00129
Уравнение регрессии
имеет вид: ln
y
= 2,2 + 0,0037x
+ ln
e.
При значении фактора, равном 95, коэффициент
эластичности y
по х
составит:
+—0,3515
—0,0037
—0,00167
—0,137
—0,167
Уравнение регрессии
имеет вид: ln
y
= 2,2 + 0,0037 ln
x
+ ln
e.
При значении фактора, равном 95, коэффициент
эластичности y
по х
составит:
+—0,0037
—0,3515
—0,00167
—0,137
—0,4644
Уравнение регрессии
имеет вид: y
= 2,2 + 0,0037 ln
x
+ e.
При значении фактора, равном 95, коэффициент
эластичности y
по х
составит:
+—0,00167
—0,0037
—0,3515
—0,137
—0,00137
Уравнение регрессии
имеет вид: y
= 2,2 + 0,0037x
+ e.
При значении фактора, равном 95, коэффициент
эластичности y
по х
составит:
+—0,137
—0,00167
—0,0037
—0,3515
—0,3218
Уравнение регрессии
имеет вид: ln
y
= 1,8 + 0,0027x
+ ln
e.
При значении фактора, равном 125, коэффициент
эластичности y
по х
составит:
+—0,3375
—0,0015
—0,0027
—0,158
—0,3916
Уравнение регрессии
имеет вид: ln
y
= 1,8 + 0,0027 ln
x
+ ln
e.
При значении фактора, равном 125, коэффициент
эластичности y
по х
составит:
+—0,0027
—0,3375
—0,0015
—0,158
—0,00158
Уравнение регрессии
имеет вид: y
= 1,8 + 0,0027 ln
x
+ e.
При значении фактора, равном 125, коэффициент
эластичности y
по х
составит:
+—0,0015
—0,0027
—0,3375
—0,158
—0,00158
Уравнение регрессии
имеет вид: y
= 1,8 + 0,0027x
+ e.
При значении фактора, равном 125, коэффициент
эластичности y
по х
составит:
+—0,158
—0,0015
—0,0027
—0,3375
—0,4218
Несмещённость, эффективность и состоятельность оценок параметров регрессии
Оценки параметров регрессии должны отвечать определенным критериям. Они должны быть несмещенными, состоятельными и эффективными. Эти свойства оценок, полученных по МНК, имеют чрезвычайно важное практическое значение в использовании результатов регрессии и корреляции.
Несмещенность оценки означает, что математическое ожидание остатков равно нулю. Если оценки обладают свойством несмещенности, то их можно сравнивать по разным исследованиям.
Оценки считаются эффективными, если они характеризуются наименьшей дисперсией. В практических исследованиях это означает возможность перехода от точечного оценивания к интервальному.
Состоятельность оценок характеризует увеличение их точности с увеличением объема выборки. Большой практический интерес представляют те результаты регрессии, для которых доверительный интервал ожидаемого значения параметра регрессии bi имеет предел значений вероятности, равный единице. Иными словами, вероятность получения оценки на заданном расстоянии от истинного значения параметра близка к единице.
Указанные критерии оценок (несмещенность, состоятельность и эффективность) обязательно учитываются при разных способах оценивания.
тест . Оценка тесноты связи
Значение линейного коэффициента корреляции не может характеризовать тесноту связи для уравнения …
В случае стохастической зависимости множественный коэффициент корреляции R не может принимать значения …R=100 % R=1,2
Значение коэффициента детерминации, рассчитанное для линейного уравнения парной регрессии составило . Следовательно, значение линейного коэффициента парной корреляции может быть равно …- 0,9; если b. 0,9; если b > 0
В качестве показателя тесноты связи для построенного уравнения регрессии может использоваться …коэффициент множественной корреляции, если исследуется связь между зависимой переменной и несколькими независимыми переменными. коэффициент парной корреляции, если исследуется связь между зависимой переменной и одной независимой переменной
Значение коэффициента корреляции может находится в отрезке …[0; 1] [-1; 0]
Значение коэффициента корреляции может находится в отрезке …[0; 1][-1; 0]
Пусть для множественной линейной регрессии оценки параметров теоретической регрессии таковы, что гипотеза отвергается, а гипотезы принимаются. Это означает, что… добавление переменной значимо улучшает регрессионную модель по сравнению с регрессией только по переменным и. совместное добавление переменных и не приведет к значимому улучшению предсказания по сравнению с регрессией только по
Если значение коэффициента корреляции, рассчитанное для линейного уравнения регрессии равно единице, то … величина не оказывает влияния на переменную у. связь между переменными у и х функциональная
Пусть и — случайные величины, — эмпирическое корреляционное отношение. Свойствами эмпирического корреляционного отношения являются: корреляционное отношение есть неотрицательная величина, не превосходящая единицы: …. если , то между переменными корреляционная связь отсутствует
Выберите значение коэффициента корреляции, которое характеризует функциональную связь между переменными у и х.
Тест 10.
Коэффициент детерминации …является безразмерной величиной
Пусть , где y – фактическое значение зависимой переменной, — теоретическое , рассчитанное по уравнению значение зависимой переменной (объясненное уравнением регрессии), – ошибка модели. Тогда значение характеризует дисперсию …фактических значений зависимой переменной, где m– число факторных признаков. Приведена формула подсчета ______.объясненной дисперсии
Рассматривается регрессионная модель , где — линейная функция. Количество наблюдений =25. Остаточная сумма квадратов равна 440. Тогда остаточная дисперсия на одну степень свободы равна … 440/25-4-1
Значение коэффициента детерминации не является статистически значимым. Это означает, что построенное уравнение регрессии не объясняет разброс наблюдаемых значений результирующего признака относительно величины …Y
Значение коэффициента детерминации составило 0,9, следовательно …уравнением регрессии объяснено 90% дисперсии результативного признака y
Значение коэффициента детерминации составило 0,81, следовательно уравнением регрессии объяснено _____ дисперсии зависимой переменной. 81 %
Для множественной линейной регрессии с числом факторов вычисляют коэффициент детерминации с учетом величины дисперсии на одну степень свободы. В этом случае скорректированный коэффициент детерминации находят по формуле …22 н-м-1н-1
Случайными воздействиями обусловлено 12% дисперсии результативного признака, следовательно, значение коэффициента детерминации составило …0,88
Пусть исследуется линейная зависимость вида и оценена регрессия , – фактические значения, а – расчетные значения зависимой переменной, . Тогда общую дисперсию можно оценить по формуле …н-1
Тест 11.
Если расчетное значение F–критерия Фишера меньше табличного, то можно сделать вывод о …незначимости (несущественности) моделируемой зависимости…статистической незначимости построенной модели
В таблице представлены результаты дисперсионного анализа. Значение остаточной дисперсии на одну степень свободы можно определить, как …отношение чисел, определенных на пересечении строки «Остаток» и столбцов «SS» и «df»…число на пересечении строки «Остаток» и столбца «MS»
В таблице представлены результаты дисперсионного анализа. Значение остаточной суммы квадратов можно определить, как …число на пересечении строки «Остаток» и столбца «SS»…разность чисел, определенных на пересечении столбца «SS» и строк «Итого» и «Регрессия»
Статистические гипотезы используются для оценки статистической значимости …уравнения…оцениваемых параметров
В таблице представлены результаты дисперсионного анализа. Значение общей суммы квадратов можно определить, как …число на пересечении строки «Итого» и столбца «SS»…сумму чисел, определенных на пересечении столбца «SS» и строк «Регрессия» и «Остаток»
В таблице представлены результаты дисперсионного анализа. Расчетное значение F-критерия можно определить, как …отношение чисел, определенных на пересечении столбца «MS» и строк «Регрессия» и «Остаток»…число на пересечении строки «Регрессия» и столбца «F»
Какие статистические гипотезы выдвигаются при проверке статистической значимости построенной модели. нулевая о статистической незначимости….альтернативная о статистической значимости
При проверке статистической значимости построенной модели проводят сравнение …расчетного значения критерия Фишера…табличного значения критерия Фишера
В таблице представлены результаты дисперсионного анализа. Значение объясненной (факторной) дисперсии на одну степень свободы можно определить, как …отношение чисел, определенных на пересечении строки «Регрессия» и столбцов «SS» и «df»…число на пересечении строки «Регрессия» и столбца «MS»
В таблице представлены результаты дисперсионного анализа. Значение объясненной (факторной) суммы квадратов можно определить, как …разность чисел, определенных на пересечении столбца «SS» и строк «Итого» и «Остаток»…число на пересечении строки «Регрессия» и столбца «SS»
Тест 12.
Пусть t – рассчитанная для коэффициента регрессии статистика Стьюдента, а t крит — критическое значение этой статистики. Коэффициент регрессии считается статистически значимым, если выполняются следующие неравенства: t > t крит…t крит
Выберите пропущенное в таблице значение(. 4,3) – ..12
Если коэффициент регрессии является несущественным, то для него выполняются условия …доверительный интервал проходит через ноль…расчетное значение t–критерия Стьюдента по модулю меньше табличного
Какое условие не выполняется, если коэффициент регрессии является незначимым (несущественным)? его значение признается отличным от нуля
С помощью частного -критерия можно проверить значимость -го коэффициента чистой регрессии в предположении, что -й фактор в уравнение множественной регрессии …был включен последним
Если -критерий, вычисленный для оценки параметра регрессии меньше значения , вычисленного по таблицам распределения Стьюдента, то на данном уровне значимости …не отвергается гипотеза о равенстве нулю параметра для генеральной совокупности
Для парной линейной регрессии y=a+bx+e проверка гипотезы о значимости коэффициента регрессии b равносильна проверкам гипотез о значимости: коэффициента детерминации…линейной связи между x и y
Если доверительный интервал для коэффициента регрессии содержит 0, то справедливы следующие утверждения: фактическое значение статистики Стьюдента для этого коэффициента по модулю меньше критического (табличного).. коэффициент регрессии статистически незначим
Коэффициент регрессии считается статистически значимым, если справедливы следующие утверждения: доверительный интервал для этого коэффициента не содержит 0…фактическое значение статистики Стьюдента для этого коэффициента по модулю больше критического (табличного)
Критическое значение критерия Стьюдента определяет минимально возможную величину, допускающую принятие гипотезы о …статистической значимости (существенности) параметра.
Гипотеза о значимости в целом уравнения нелинейной регрессии проверяется с помощью критерия…
Нелинейная связь между рассматриваемыми признаками тем теснее, чем значение индекса корреляции ближе к …
Выражение 
Уравнение нелинейной регрессии 





Квадрат индекса корреляции для нелинейных форм называется …
Коэффициент детерминации для нелинейной модели часто называют…
Значение индекса корреляции находится в пределах …
Для степенной функции 


Индекс корреляции для нелинейных форм связи находят по формуле …
Значение индекса детерминации, рассчитанное для нелинейного уравнения регрессии характеризует долю дисперсии результативного признака, _____, в общей дисперсии результативного признака.
объясненную нелинейной регрессией
Тест
1. Вопрос: Если оценка параметра эффективна, то это означает …
Выберите несколько ответов: наименьшую дисперсию остатков
возможность перехода от точечного оценивания к интервальному
2. Вопрос: Минимальная дисперсия остатков характерна для оценок, обладающих свойством …
Укажите ответ: эффективности
3. Вопрос: Несмещенная оценка параметра имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра , вычисленных по выборкам одного и того же объема . Такая оценка называется .
4. Вопрос: Если предпосылки метода наименьших квадратов не выполняются, то оценки параметров уравнения регрессии могут не обладать свойствами …
Выберите несколько ответов: эффективности несмещенности
5. Вопрос: Если оценки параметров линейного уравнения регрессии обладают свойством несмещенности, то математическое ожидание остатков …
6. Вопрос: Если оценки параметров линейного уравнения регрессии обладают свойством эффективности, то дисперсия остатков характеризуется …
7. Вопрос: Если оценки параметров уравнения регрессии обладают свойствами состоятельности, эффективности и несмещенности, то …
Выберите несколько ответов:
при большом числе выборочных оцениваний остатки не будут накапливаться
возможен переход от точечного оценивания к интервальному
8. Вопрос: Укажите условия, которые выполняются, если оценки параметров уравнения регрессии обладают свойствами состоятельности, эффективности и несмещенности.
Выберите несколько ответов: наименьшая дисперсия остатков
равенство нулю математического ожидания остатков
9. Вопрос: Переход от точечного оценивания к интервальному возможен, если оценки являются …
Укажите ответ: эффективными и несмещенными
10. Вопрос: Если оценки параметров уравнения регрессии, полученных при помощи метода наименьших квадратов обладают свойствами несмещенности, эффективности и состоятельности, то …
Выберите несколько ответов: возможен переход от точечного оценивания к интервальному
математическое ожидание остатков равно нулю и они характеризуются минимальной дисперсией
Тест
1. Вопрос: Обобщенный метод наименьших квадратов не используется в случае ______ остатков.
2. Вопрос: Обобщенный метод наименьших квадратов применяется в случае…
3. Вопрос: После применения обобщенного метода наименьших квадратов удается избежать ______ остатков.
4. Вопрос: Проявление гетероскедастичности в остатках удается устранить при помощи метода обобщенного метода наименьших квадратов путем …
Выберите несколько ответов:
введения в выражение для дисперсии остатков коэффициента пропорциональности
5. Вопрос: Обобщенный метод наименьших квадратов может использоваться для корректировки _______ остатков.
Выберите несколько ответов:
6. Вопрос: Для преодоления проблемы автокорреляции служит …
обобщенный метод наименьших квадратов
7. Вопрос: Обобщенный метод наименьших квадратов применяется, когда случайные отклонения…
не имеют постоянной дисперсии и коррелированны между собой
8. Вопрос: Обобщенный метод наименьших квадратов используется для корректировки…
Укажите ответ: гетероскедастичности остатков в уравнении регрессии
9. Вопрос: Обобщенный метод наименьших квадратов применяется в случае ______ остатков.
гетероскедастичности или автокорреляции
Замена 

Все нижеприведенные нелинейные модели можно свести к модели множественной линейной регрессии W = b0 + b1·U + b2·V. Установите соответствие между видом нелинейной модели и соотношениями между исходными переменными Y, X, Z и новыми переменными W, U, V линеаризованной модели.
Соотношение хрен знает как делать.
Соотношение №2 хрен знает как делать.
Включение случайного отклонения мультипликативным способом позволяет линеаризовать регрессионную модель вида .
Эконометрической моделью, приводимой к линейной регрессионной модели при логарифмировании и соответствующей подстановке, является .
Эконометрическую модель, линейную по параметрам и нелинейную по переменным с аддитивным включением случайного возмущения .
всегда можно свести к классической регрессионной модели с помощью соответствующей подстановки
Соотношение №3 хрен знает как делать.
Соотношение №4 хрен знает как делать.
Эконометрическая модель 
нелинейной по параметрам и нелинейной по переменным
Соотношение №5 хрен знает как делать.
1.Зависимость спроса 




2. Нелинейную модель зависимостей экономических показателей нельзя привести к линейному виду, если …нелинейная модель является внутренне нелинейной
3. Зависимость 




4. Зависимость объема производства 




5. Функции Торнквиста относятся к классу _________ моделей…обратных
6. При выборе спецификации нелинейная регрессия используется, если …между экономическими показателями обнаруживается нелинейная зависимость
7. Зависимость спроса на товары первой необходимости от дохода (функция Торнквиста, 


8. Производственная функция Кобба-Дугласа относится к классу _________ моделей…степенных
9. В модели вида 





10. Зависимости 





1. Установите соответствие между названием модели и видом ее уравнения:
Читайте также:
- II. Оценка эффективности инвестиционного менеджмента.
- IV.Оценка эффективности деятельности структурного подразделения организации
- Анализ и оценка состояния управления инвестиционным процессом в ОАО «Дашковка»
- АНАЛИЗ ЛИКВИДНОСТИ БАЛАНСА (ОЦЕНКА ТЕКУЩЕЙ И ПЕРСПЕКТИВНОЙ ЛИКВИДНОСТИ)
- Ассортимент шерстяных и шелковых тканей. Оценка качества.
- Вживленная оценка
- Вопрос 42: оценка эффективности монетарной политики и влияние их изменений на равновесие.
- Вопрос – 130 Доказывание в ПАП. Предмет доказывания. Доказательства в производстве по делам об административных правонарушениях: понятие, виды и оценка.
- Выбор вида модели и оценка ее параметров
- Вычисление коэффициентов корреляции количественных признаков и оценка его достоверности
- ГЛАВА 3. КОЛИЧЕСТВЕННАЯ ОЦЕНКА ИНФОРМАЦИИ 1 страница
- ГЛАВА 3. КОЛИЧЕСТВЕННАЯ ОЦЕНКА ИНФОРМАЦИИ 10 страница
Пишет что не правильно( не знаю как по другому.
2. Установите соответствие между названием модели и видом ее уравнения.
3. Установите соответствие между названием модели и видом ее уравнения:
4. Установите соответствие между названием модели и видом ее уравнения:
5. Установите соответствие между характером модели и видом уравнения:
6. Установите соответствие между названием модели и видом ее уравнения:
7. Установите соответствие между характером модели и видом уравнения:
8. Установите соответствие между видом нелинейной зависимости и величинами остатков модели, к которым предъявляются предпосылки метода наименьших квадратов при оценке параметров линеаризованной модели.
9. Установите соответствие между видом уравнения и характером модели:
10. Установите соответствие между названием модели и видом ее уравнения:
При отборе факторов в модель множественной регрессии проводят анализ …
1. значений матрицы парных коэффициентов корреляции
2. остаточной дисперсии до и после включения факторов в модель
Матрица парных коэффициентов корреляции строится для …
1. отбора факторов в модель множественной регрессии
2. определения коллинеарных факторов
Матрица парных коэффициентов линейной корреляции может служить для решения следующих задач:
1. выявления мультиколлинеарных факторов
2. определения тесноты линейной связи между переменными
только
Взаимодействие коллинеарных факторов эконометрической модели означает, что …
1. факторы дублируют влияние друг друга на результат
2. теснота связи между ними превышает по абсолютной величине 0,7
При построении модели множественной регрессии методом пошагового включения переменных на первом этапе рассматривается…
модель с одной объясняющей переменной, которая имеет с зависимой переменной наибольший коэффициент корреляции
Отбор факторов в модель множественной регрессии с использованием метода включения может быть основан на сравнении ….
Из двух коллинеарных факторов из модели множественной регрессии исключается тот, для которого абсолютное значение стандартизованного коэффициента … Меньше В исходное уравнение множественной регрессии 







ТЕСТ 3 ФИКТИВНЫЕ ПЕРЕМЕННЫЕ
Для оценки заработной платы некоторого работника используется следующая модель 






Фиктивная переменная может принимать значения:
Исследуется зависимость потребления кофе от ряда факторов: х1 – марки кофе, х2 – уровня крепости кофе (крепкий, средней крепости, слабой крепости), х3 – дохода потребителя, х4 – цены на кофе. Фиктивными переменными в модели не являются …
В страховой компании решили оценить влияние знака зодиака (всего 12), под которым рожден работник, на производительность его труда. Тогда максимальное количество фиктивных переменных, необходимых для проведения анализа и построения оценок равно…
Фиктивными переменными в уравнении множественной регрессии могут быть …
1. качественные переменные, преобразованные в количественные
2. переменные, исходные значения которых не имеют количественного значения
В модели необходимо учесть влияние возраста на производительность труда работника. На предприятии работают пенсионеры и лица, не достигшие пенсионного возраста (всего 2 категории). Тогда максимальное количество фиктивных переменных, необходимых для проведения анализа и построения оценок равно…
Укажите уравнения регрессии, в которых фиктивная переменная D используется только в аддитивной форме:
В модели необходимо учесть влияние уровня образования на заработную плату работника. На предприятии работают люди со средним специальным, высшим и незаконченным высшим образованием (всего 3 категории). Тогда максимальное количество фиктивных переменных, необходимых для проведения анализа и построения оценок равно…
Проводится эконометрическое моделирование зависимости объема продаж компании от ряда факторов: х1 – цены на товар, х2 – степени известности торговой марки фирмы, х3 – дохода потребителя, х4 – уровня интенсивности рекламной деятельности (высокий уровень – массированная реклама; средний уровень – регулярно повторяющаяся; низкий уровень – время от времени повторяющаяся). Фиктивными переменными в модели не являются …
Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.034 сек.)
Учебные материалы для студентов
Методические указания, конспекты, лекции, контрольные, лабораторные работы, курсовые.
Тесты по эконометрике
1. «Белым шумом» называется ___________ процесс
чисто случайный
2. Автокорреляционной функцией временного ряда называется
последовательность значений коэффициентов автокорреляции различных порядков
3. В исходном соотношении МНК сумма квадратов отклонений фактических значений результативного признака от его теоретических значений
минимизируется
4. В качестве показателя тесноты связи для линейного уравнения парной регрессии используется
линейный коэффициент корреляции
5. В качестве фиктивных переменных в модель множественной регрессии включаются факторы
не имеющие количественных значений
6. В левой части системы взаимозависимых переменных, как правило, находится
одна зависимая переменная
7. В левой части системы независимых уравнений находится
совокупность зависимых переменных
8. В линейном уравнении парной регрессии коэффициентом регрессии является значение
параметра b
9. В матрице парных коэффициентов корреляции отображены значения парных коэффициентов линейной корреляции между
переменными
10. В нелинейной модели парной регрессии функция является
нелинейной
11. В общем случае каждый уровень временного ряда формируется под воздействием
тенденции, сезонных колебаний и случайных факторов
12. В основе метода наименьших квадратов лежит
минимизация суммы квадратов отклонений фактических значений результативного признака от его теоретических значений
13. В приведенной форме модели в правой части уравнений находятся
только независимые переменные
14. В системах рекурсивных уравнений количество переменных в правой части каждого уравнения определяется как ______________ уравнений и количества независимых факторов
сумма количества зависимых переменных предыдущих
15. В системе независимых уравнений каждое уравнение представлено
изолированным уравнением регрессии
16. В стандартизованном уравнении множественной регрессии ;. Определите, какой из факторов х1 или х2 оказывает более сильное влияние на
,так как 2,1>0,3
17. В стандартизованном уравнении множественной регрессии переменными являются
стандартизованные переменные
18. В стандартизованном уравнении свободный член
отсутствует
19. Величина коэффициента детерминации при включении существенного фактора в эконометрическую модель
будет увеличиваться
20. Величина остаточной дисперсии при включении существенного фактора в модель
будет уменьшаться
21. Величина отклонений фактических значений результативного признака от его теоретических значений представляет собой
ошибку аппроксимации
22. Величина параметра в уравнении парной линейной регрессии характеризует значение
результирующей переменной при нулевом значении фактора
23. Взаимодействие факторов эконометрической модели означает, что
влияние одного из факторов на результирующий признак не зависит от значений другого фактора
24. Включение фактора в модель целесообразно, если коэффициент регрессии при этом факторе является
существенным
25. Временной ряд – это совокупность значений экономического показателя
за несколько последовательных моментов (периодов) времени
26. Временной ряд называется стационарным, если он является реализацией _____________ процесса
стационарного стохастического
27. Временной ряд характеризует
данные, описывающие один объект за ряд последовательных моментов (периодов) времени
28. Выбор формы зависимости экономических показателей и определение количества факторов в модели называется ________________ эконометрической модели
спецификацией
29. Выделяют три класса систем эконометрических уравнений
независимые, взаимозависимые и рекурсивные
30. Гетероскедастичность остатков подразумевает _____________ от значения фактора
зависимость дисперсии остатков
31. Гетероскедастичность подразумевает ________________________ от значения фактора
зависимость дисперсии остатков
32. Графическое изображение наблюдений на декартовой плоскости координат называется полем
корреляции
33. Дано уравнение регрессии . Определите спецификацию модели
линейное уравнение множественной регрессии
34. Двухшаговый метод наименьших квадратов предполагает ______ использование обычного МНК
однократное
35. Двухшаговый метод наименьших квадратов применим для решения
только сверхидентифицируемой системы одновременных уравнений
36. Двухшаговый метод наименьших квадратов применяется для оценки параметров
систем эконометрических уравнений
37. Для модели зависимости среднедушевого (в расчете на одного человека) месячного дохода населения (р.) от объема производства (млн р.) получено уравнение . При изменении объема производства на 1 млн р. доход в среднем изменится на
0,003 млн р.
38. Для моделирования зависимости предложения от цены не может быть использовано уравнение регрессии
39. Для моделирования сложных экономических систем целесообразно использовать
систему эконометрических уравнений
40. Для нелинейных уравнений метод наименьших квадратов применяется к
преобразованным линеаризованным уравнениям
41. Для оценки коэффициентов структурной формы модели не применяют _____ метод наименьших квадратов
обычный
42. Для существенного параметра расчетное значение критерия Стьюдента
больше табличного значения критерия
43. Для уравнения зависимости выручки от величины оборотных средств получено значение коэффициента детерминации, равное 0,7. Следовательно, _% дисперсии обусловлено случайными факторами
30
44. Для уравнения у = 3,14 + 2х +e значение коэффициента корреляции составило 2. Следовательно
значение коэффициента корреляции рассчитано с ошибкой
45. Если доверительный интервал для параметра проходит через точку ноль, следовательно
параметр является несущественным
46. Если значение индекса корреляции для нелинейного уравнения регрессии стремится к 1, следовательно
нелинейная связь достаточно тесная
47. Если значение коэффициента корреляции равно единице, то связь между результатом и фактором
функциональная
48. Если коэффициент регрессии является несущественным, то его значения приравниваются к
нулю и соответствующий фактор не включается в модель
49. Если между экономическими показателями существует нелинейная связь, то
целесообразно использовать спецификацию нелинейного уравнения регрессии
50. Если наиболее высоким оказался коэффициент автокорреляции первого порядка, то исследуемый ряд содержит только
тенденцию
51. Если наиболее высоким оказался коэффициент автокорреляции третьего порядка, то исследуемый ряд содержит
случайную величину, влияющую на каждый третий уровень ряда
52. Если оценка параметра эффективна, то это означает
наименьшую дисперсию остатков
53. Если предпосылки метода наименьших квадратов нарушены, то
оценки параметров могут не обладать свойствами эффективности, состоятельности и несмещенности
54. Если расчетное значение критерия Фишера меньше табличного значения, то гипотеза о статистической незначимости уравнения
принимается
55. Если спецификация модели нелинейное уравнение регрессии, то нелинейной является функция
56. Если спецификация модели отображает нелинейную форму зависимости между экономическими показателями, то нелинейно уравнение
регрессии
57. Если факторы входят в модель как произведение, то модель называется
мультипликативной
58. Если факторы входят в модель как сумма, то модель называется
аддитивной
59. Значение индекса корреляции, рассчитанное для нелинейного уравнения регрессии характеризует тесноту ______ связи
нелинейной
60. Значение коэффициента автокорреляции второго порядка характеризует связь между
исходными уровнями и уровнями этого же ряда, сдвинутыми на 2 момента времени
61. Значение коэффициента автокорреляции первого порядка равно 0,9 следовательно
линейная связь между последующим и предыдущим уровнями тесная
62. Значение коэффициента автокорреляции рассчитывается по аналогии с
линейным коэффициентом корреляции
63. Значение коэффициента детерминации рассчитывается как отношение дисперсии результативного признака, объясненной регрессией, к ___________ дисперсии результативного признака
общей
64. Значение коэффициента детерминации составило 0,9, следовательно
уравнение регрессии объяснено 90% дисперсии результативного признака
65. Значение коэффициента корреляции не характеризует
статистическую значимость уравнения
66. Значение коэффициента корреляции равно 0,9. Следовательно, значение коэффициента детерминации составит
0,81
67. Значение коэффициента корреляции равно 1. Следовательно
связь функциональная
68. Значение линейного коэффициента корреляции характеризует тесноту ________ связи
линейной
69. Значения коэффициента автокорреляции первого порядка равно 0,9. Следовательно
линейная связь между последующим и предыдущим уровнями тесная
70. Значения коэффициента корреляции может находиться в отрезке
[-1;1]
71. Из пары коллинеарных факторов в эконометрическую модель включается тот фактор, который при
достаточно тесной связи с результатом имеет меньшую связь с другими факторами
72. Известны значения аддитивной модели временного ряда: Yt — значение уровня ряда, Yt = 30, Т- — значение тренда, Т+15, Е- значение случайной компоненты случайных факторов Е=2. Определите значение сезонной компоненты S
13
73. Изолированное уравнение множественной регрессии может быть использовано для моделирования взаимосвязи экономических показателей, если
факторы не взаимодействуют друг с другом
74. Исследуется зависимость, которая характеризуется линейным уравнением множественной регрессии. Для уравнения рассчитано значение тесноты связи результативной переменной с набором факторов. В качестве этого показателя был использован множественный коэффициент
корреляции
75. Исходные значения фиктивных переменных предполагают значения
качественные
76. К линейному виду нельзя привести:
нелинейную модель внутренне нелинейную
77. К ошибкам спецификации относится
неправильный выбор той или иной математической функции
78. Качество подбора уравнения оценивает коэффициент
детерминации
79. Коррелограммой называется ______________________________ функции
графическое отображение автокорреляционной
80. Косвенный метод наименьших квадратов требует
преобразования структурной формы модели в приведенную
81. Критерий Стьюдента предназначен для определения значимости
каждого коэффициента регрессии
82. Критерий Фишера используется для оценки значимости
построенного уравнения
83. Критические значения критерия Фишера определяются по
уровню значимости и степеням свободы факторной и остаточной дисперсий
84. Критическое значение критерия Стьюдента определяет
максимально возможную величину, допускающую принятие гипотезы о несущественности параметра
85. Критическое значение критерия Стьюдента определяет минимально возможную величину, допускающую принятие гипотезы о
существенности параметра
86. Линеаризация не подразумевает процедуру
включение в модель дополнительных существенных факторов
87. Линеаризация подразумевает процедуру приведения
нелинейного уравнения к линейному виду
88. Линейное уравнение множественной регрессии имеет вид . Определите какой из факторов или оказывает более сильное влияние на y
так как 2,5 1, то есть x возрастает и y тоже возрастает) не может быть описана зависимость
выработки от трудоемкости
167. При построении модели временного ряда проводится расчет
каждого уровня временного ряда
168. При построении систем независимых уравнений набор факторов в каждом уравнении определяется числом факторов, оказывающих ________ на моделируемый показатель
существенное влияние
169. При построении системы эконометрических уравнений необходимо учитывать
структуру связей реальной экономической системы
170. При применении метода наименьших квадратов исследуются свойства
оценок параметров уравнения регрессии
171. При применении метода наименьших квадратов исследуются свойства оценок
параметров уравнения регрессии
172. При применении метода наименьших квадратов уменьшить гетероскедастичность остатков удается путем
преобразования переменных
173. При расчете значения коэффициента детерминации используется отношение
дисперсий
174. При хорошем качестве модели допустимым значением средней ошибки аппроксимации является ___%
5-7
175. Приведенная форма модели получена из _________формы модели
структурной
176. Приведенная форма модели представляет собой систему ________ функций эндогенных переменных от экзогенных
линейных
177. Приведенная форма модели является результатом преобразования
структурной формы модели
178. Проверка является ли временной ряд «белым шумом» осуществляется с помощью
статистики Бокса-Пирса
179. Проводится исследование зависимости выработки работника предприятия от ряда факторов. Примером фиктивной переменной в данной модели будет являться ______ работника
уровень образования
180. Простая линейная регрессия предполагает наличие
одного фактора и линейность уравнения регрессии
181. Расчет значения коэффициента детерминации не позволяет оценить
существенность коэффициента регрессии
182. Расчет средней ошибки аппроксимации для нелинейных уравнений регрессии связан с расчетом разности между ____________________________ переменной
фактическим и теоретическим значениями результативной
183. Расчетное значение критерия Фишера определяется как
отношение факторной дисперсии к остаточной, рассчитанных на одну степень свободы
184. Расчетное значение критерия Фишера определяется как ___________ факторной дисперсии и остаточной, рассчитанных на одну степень свободы
отношение
185. Расчетное значение критерия Фишера определяется как отношение
дисперсий
186. Результатом линеаризации полиномиальных уравнений является ______________ регрессии
линейные уравнения множественной
187. Свойствами оценок МНК являются: эффективность, а также
состоятельность и несмещенность
188. Система взаимозависимых уравнений в ее классическом виде называется также системой ______ уравнений
одновременных
189. Система независимых уравнений предполагает
совокупность независимых уравнений регрессии
190. Система нормальных уравнений метода наименьших квадратов строится на основании
таблицы исходных данных
191. Система рекурсивных уравнений включает в каждое
предыдущее (должно быть последующее) уравнение в качестве факторов все зависимые переменные предшествующих уравнений с набором собственно факторов
192. Система эконометрических уравнений не используется при моделировании
взаимосвязей временных рядов данных
193. Система эконометрических уравнений предполагает наличие _________ независимых признаков
нескольких зависимых и нескольких
194. Система эконометрических уравнений представляет систему
уравнений регрессии
195. Систему МНК, построенную для оценки параметров линейного уравнения множественной регрессии можно решить
методом определителей
196. Системы эконометрических уравнений классифицируются по
способу вхождения зависимых и независимых переменных в уравнение регрессии
197. Случайный характер остатков предполагает
независимость остатков от величины предсказанных по модели значений результативного признака
198. Смысл расчета средней ошибки аппроксимации состоит в определении среднего арифметического значения
отклонений, выраженных в процентах от фактических значений результативного признака
199. Совокупность значений критерия, при которых принимается нулевая гипотеза, называется областью _____________ гипотезы
принятия
200. Состоятельность оценки характеризуется
увеличением ее точности с увеличением объема выборки
201. Спецификацию нелинейного уравнения парной регрессии целесообразно использовать, если значение
индекса детерминации, рассчитанного для данной модели достаточно близко к 1
202. Спецификация модели нелинейная парная (простая) регрессия подразумевает нелинейную зависимость и
независимую переменную
203. Стандартная ошибка рассчитывается для проверки существенности
параметра
204. Статистические гипотезы используются для оценки
значимости уравнения регрессии в целом
205. Стационарность временного ряда не подразумевает отсутствие
стационарного стохастического процесса
206. Стационарность временного ряда означает отсутствие
тренда
207. Стационарность характерна для временного ряда
типа «белый шум»
208. Стохастическим процессом называется
набор случайных переменных X(t), где t – вещественные числа
209. Строится модель зависимости спроса от ряда факторов. Фиктивной переменной в данном уравнении множественной регрессии не является _________ потребителя
доход
210. Структурной формой модели называется система _______ уравнений
взаимосвязанных
211. Структурными коэффициентами модели называются коэффициенты ___________ в структурной форме модели
при экзогенных и эндогенных переменных
212. Структуру временного ряда можно выявить с помощью коэффициента __________ уровней ряда
автокорреляции
213. Табличное значение критерия Фишера служит для проверки статистической гипотезы о равенстве
факторной и остаточной дисперсий
214. Требованием к уравнениям регрессии, параметры которых можно найти при помощи МНК является
линейность параметров
215. Требованием к уравнениям регрессии, параметры которых можно найти при помощи МНК является:
линейность параметров
216. Увеличение точности оценок с увеличением объема выборки описывает свойство _______ оценки
состоятельности
217. Уравнение может быть линеаризовано при помощи подстановки
218. Уравнение регрессии характеризует зависимость
обратно пропорциональную
219. Уравнение регрессии, которое связывает результирующий признак с одним из факторов при зафиксированных на среднем уровне значении других переменных, называется
частным
220. Уровнем временного ряда является
значение временного ряда в конкретный момент (период) времени
221. Факторная дисперсия служит для оценки влияния
учтенных явно в модели факторов
222. Факторные переменные уравнения множественной регрессии, преобразованные из качественных в количественные называются
фиктивными
223. Факторы эконометрической модели являются коллинеарными, если коэффициент
корреляции между ними по модулю больше 0,7
224. Фиктивные переменные включаются в уравнение множественной регрессии для учета действия на результат признаков ____________ характера
качественного
225. Фиктивные переменные включаются в уравнения ____________ регрессии
множественной
226. Циклические колебания связаны с
общей динамикой конъюнктуры рынка
227. Экзогенными переменными не являются
зависимые переменные
228. Экзогенными переменными являются
независимые переменные
229. Экономические временные ряды, представляющие собой данные наблюдений за ряд лет, как правило, являются _______________________ временными рядами
нестационарными
230. Экспоненциальным не является уравнение регрессии
231. Эндогенными переменными не являются:
независимые переменные
232. Эндогенными переменными являются
зависимые переменные
233. Эффективность оценки на практике характеризуется
возможность перехода от точечного оценивания к интервальному
также в рубрике Контрольные, тесты:
источники:
http://studall.org/all4-12208.html
http://studystuff.ru/controlnaya/testyi-po-ekonometrike
Парная регрессия
и корреляция
Контрольные вопросы
- Сформулируйте задачи, решаемые эконометрикой.
Эконометрика — наука,в которой
на базе реальных статистичеких данных
строятся,анализируются и совершенствуются
модели реальных экономических явлений.
Задачи эконометрики можно
классифицировать по 3 признакам:
1. по конечным прикладным
целям
2. по уровню иерархии
3. по профилю анализируемой
экономической системы.
1. Прогноз экономических
и социальных показателей,характеризующих
состояние и развитие системы. Имитация
возможных сценариев социально-экономического
развития системы для выявления того,как
это скажется на выходных характеристиках.
2.
- макроуровень (страна в целом)
- мезоуровень (отрасль,регион,корпорация)
- микроуровень (предприятие)
3. Задачи,направленные на решение
проблем:
- рынка
- инвестиционной финансовой деятельности
- ценообразования (большая доля государственного регулирования)
- распределительных отношений
- спроса и потребления
- Дайте определение парной регрессии.
Парная регрессия –
это уравнение связи двух переменных
у и х: y=f(х),
где
— независимая переменная, объясняющая,
входная, предсказывающая,
экзогенная, фактор, регрессор, факторный
признак.
— зависимая переменная, функция
отклика, объясняемая, выходная, результирующая,
эндогенная переменная, результативный
признак
Что такое
линия регрессии?
Вычисляемая с помощью
метода наименьших квадратов прямая
линия называется линией регрессии
. Она характеризуется тем, что сумма квадратов
расстояний от точек на диаграмме до этой
линии минимальна (по сравнению со всеми
возможными линиями). Линия регрессии
дает наилучшее приближенное описание
линейной зависимости между двумя переменными.
- Поясните экономическую сущность параметров уравнения парной регрессии.
В общем случае коэффициент
регрессии показывает, как в среднем изменится
результативный признак y, если факторный
признак x увеличится
на единицу . Коэффициент a может не иметь
экономического содержания, интерпретировать
можно только знак, он показывает направления
связи. Параметр а = у, когда х = 0. Если х
не может быть равен 0, то а не имеет экономического
смысла. Интерпретировать можно только
знак при а: если а > 0. то относительное
изменение результата происходит медленнее,
чем изменение фактора, т. е. вариация результата
меньше вариации фактора: V < V. и наоборот.
- Как производится оценка параметров уравнения парной регрессии.
Построение линейной регрессии
сводится к оценке ее параметров –
a и b. Классический подход к оцениванию
параметров линейной регрессии основан
на методе наименьших квадратов (МНК).
МНК позволяет получить такие
оценки параметров a и b, при которых
сумма квадратов отклонений фактических
значений результативного признака
y от теоретических минимальна.
- Что является показателем тесноты связи в парной линейной регрессии?
Тесноту связи изучаемых
явлений оценивает линейный коэффициент
парной корреляции rxy
для линейной регрессии.
- В каких пределах находится значение коэффициента корреляции?
Коэффициент корреляции принимает
значения в интервале от -1 до +1. Теснота
линейной связи между переменными
может быть оценена на основании
шкалы Чеддока:
Положительное значение коэффициента
корреляции говорит о положительной связи
между х и у, когда с ростом одной из переменных
другая тоже растет. Отрицательное значение
коэффициента корреляции означает, с ростом
одной из переменных другая убывает, с
убыванием одной из переменной другая
растет.
- Для чего рассчитывают коэффициент детерминации и что он характеризует?
Оценку качества построенной
модели дает коэффициент (индекс) детерминации
R2.
Для оценки качества подбора
линейной функции рассчитывается квадрат
линейного коэффициента корреляции, называемый
коэффициентом детерминации. Коэффициент
детерминации показывает, сколько процентов
приходится на долю учтенных в модели
факторов:
Соответственно величина
1-R2 характеризует долю дисперсии
y, вызванную влиянием остальных, не учтенных
в модели, факторов. Коэффициентом детерминации, или долей
объясненной дисперсии называется:
.
В силу определения
.
Что такое
число степеней свободы и как
оно определяется для факторной
и остаточной суммы квадратов?
Любая сумма квадратов
отклонений связана с числом степеней
свободы, т.е. с числом свободы независимого
варьирования признака. Значит число
степеней свободы связано с числом
единиц совокупности
и с числом определяемых по ней констант.
Применительно к исследуемой проблеме
число степеней свободы должно показывать,
сколько независимых отклонений из
возможных
требуется для образования данной
суммы квадратов. Так для общей суммы квадратов
требуется
независимое отклонение, ибо по совокупности
из
единиц после расчета среднего уровня
, свободно варьируют лишь
числом отклонений. Число степеней
свободы в левой и правой частях соотношения
(*) должно совпадать, то число степеней
свободы второго слагаемого должно быть
равно (n — 2).
То есть
.
При расчете факторной
суммы квадратов — 1 степень свободы,
и при расчете остаточной суммы
квадратов — (n-2) степени свободы.
- Какова концепция F-критерия Фишера?
Разделив каждую сумму
квадратов на соответствующее ей
число степеней свободы, получим средний квадрат
отклонений, или, что тоже самое, дисперсию на
одну степень свободы D
.
Это приводит дисперсии к
сравнимому виду. Сопоставляя факторную
и остаточные дисперсии в расчете
на одну степень свободы, получим
величину F — отношения (F- критерия):
, где F- критерий для проверки нулевой
гипотезы
:
.
Если нулевая гипотеза
справедлива, то
и
не отличаются друг от друга. Для
необходимо опровержение,
то есть, чтобы факторная дисперсия превышала
остаточную в несколько раз.
— это максимальная величина
отношения дисперсий, которая
может иметь место при случайном
их расхождении для данного
уровня вероятности.
F-критерий — это оценивание качества
уравнения регрессии, которое состоит
в проверке гипотезы
о статистической незначимости
уравнения регрессии и показателя
тесноты связи. Для этого производится
сравнение фактического
и
значений F критерия Фишера-Снедекора.
определяется из соотношения значений
факторной и остаточной дисперсий, рассчитанных
на одну степень свободы
.
— это максимально возможное
значение критерия под влиянием
случайных факторов при данных
степенях свободы и уровне
значимости
. Уровень значимости
— это вероятность отвергнуть правильную
гипотезу при условии, что она верна. Обычно
.
Если
<
, то
— гипотеза о случайной природе оцениваемых
характеристик отклоняется и признается
их статистическая значимость и надежность.
Если
>
, то
— гипотеза не отклоняется и признается
статистическая незначимость, ненадежность
уравнения регрессии.
- В чем смысл средней ошибки аппроксимации и как она определяется?
Cредняя ошибка аппроксимации
дает оценку качества построенной модели.
Средняя ошибка аппроксимации — среднее
отклонение расчетных значений от фактических
в процентах:
.
Предел значений
считаем допустимым при построении
модели.
- Как оценивается значимость параметров уравнения регрессии?
Оценку статистической значимости
коэффициента корреляции проводят с помощью
t-критерия Стьюдента. Выдвигают гипотезу
Н0 о статистически незначимом отличии
коэффициента от нуля. Величина стандартной
ошибки совместно с t-распределением Стьюдента
при n-2 степенях свободы применяется для
проверки значимости коэффициента регрессии
и для расчета его доверительного интервала.
Для оценки значимости коэффициента регрессии
его величина сравнивается с его стандартной
ошибкой, т.е. определяется фактическое
значение t-критерия Стьюдента:
, причем
,причем
,т.е
.
которое затем сравнивается
с табличным значением при определенном
уровне значимости a и числе степеней свободы
n-2. Если tфакт>tтабл, то делается вывод
о значимости параметра.
От чего зависит
точность предсказания значения зависимой
переменной на основе уравнения парной
регрессии?
- Запишите все виды моделей, нелинейных относительно включаемых переменных и оцениваемых параметров.
Если между экономическими
явлениями существуют нелинейные соотношения,
то они выражаются с помощью соответствующих
нелинейных функций.
Различают два класса нелинейных
регрессий:
- Нелинейные по объясняющим параметрам:
Полиномы различных
степеней
Равносторонняя
гипербола
Полулогарифмическая
функция
- Регрессии, нелинейные по оцениваемым параметрам:
Степенная:
Показательная:
Экспоненциальная:
Логарифмическая:
Полулогарифмическая:
Обратная:
- Как осуществляется линеаризация модели?
Для нахождения параметров
регрессии необходимо провести
ее линеаризацию:Y=A+bX
Регрессии нелинейные по включенным
переменным приводятся к линейному виду
простой заменой переменных, а дальнейшая
оценка параметров производится с помощью
метода наименьших квадратов.
Несколько иначе обстоит
дело с регрессиями нелинейными по оцениваемым
параметрам, которые делятся на два типа:
нелинейные модели внутренне линейные
(приводятся к линейному виду с помощью
соответствующих преобразований, например,
логарифмированием) и нелинейные модели
внутренне нелинейные (к линейному виду
не
приводятся).
- Назовите показатели корреляции, используемые при нелинейных соотношениях рассматриваемых признаков.
Уравнение нелинейной регрессии,
так же как и в линейной зависимости,
дополняется показателем корреляции,
а именно индексом корреляции (R):
где
Так как
то индекс корреляции можно
выразить как
Величина данного показателя
находится в границах
чем ближе к единице, тем теснее связь
рассматриваемых признаков, тем более
надежно найденное уравнение регрессии.
- Как определяются коэффициенты эластичности по разным видам регрессионных моделей?
Средний коэффициент эластичности
показывает, на сколько % в среднем
по совокупности изменится результат
от своей средней величины при изменении
фактора
на 1% от своего среднего значения
— характеризует соотношение
прироста результата и фактора
для соответствующей формы связи.
Т.к., коэффициент Э не
всегда const, то используем среднее значение
—
.
В таблице представлены формулы
эластичности для наиболее употребительных
функций.
|
|
||
Иногда коэффициент Э экономического
смысла не имеет. Это происходит тогда,
когда для рассматриваемых признаков
бессмысленно определение изменения значений
в процентах. Например, изменение роста
заработной платы с ростом стажа работы
на 1%.
Тест 1
1. Графическое
изображение наблюдений на декартовой
плоскости координат называется
полем …
1. регрессии;
2. корреляции;
3. случайных воздействий;
4. автокорреляции.
2. В линейном
уравнении парной регрессии у=а+bx коэффициентом
регрессии является значение
1. параметров а и b;
2. параметра a;
3. переменной x;
4. параметра b.
3. Величина параметра а в уравнении
парной линейной регрессии у=а+bx характеризует
значение …
1. факторной переменной
при нулевом значении результата;
2. результирующей переменной
при нулевом значении случайной
величины;
3. факторной переменной
при нулевом значении случайного
фактора;
4. результирующей
переменной при нулевом значении фактора.
4. Объем выборки
должен превышать число рассчитываемых
параметров при исследуемых факторах
1. в 2-3 раза;
2. в 20-25 раз;
3. в 10-12 раз;
4. в 7-8 раз.
5. Объем выборки
определяется …
1. числовыми значениями
переменных, отбираемых в выборку;
2. объёмом генеральной
совокупности;
3. числом параметров при
независимых переменных;
4. числом результативных
переменных.
6. Основной задачей
эконометрики является …
1. установление связей
между различными процессами
в обществе и техническим процессом;
2. анализ технического
процесса на примере социально-экономических
показателей;
3. отражение особенности
социального развития общества;
4. исследование
взаимосвязей экономических явлений и
процессов.
7. Наиболее наглядным
видом выбора уравнения парной
регрессии является:
1. аналитический;
2. графический;
3. экспериментальный (табличный).
8. Суть метода
наименьших квадратов состоит
в:
1. минимизации суммы остаточных
величин;
2. минимизации дисперсии
результативного признака;
3. минимизации
суммы квадратов остаточных величин.
9. Коэффициент
линейного парного уравнения
регрессии:
1. показывает среднее
изменение результата с изменением фактора
на одну единицу;
2. оценивает статистическую
значимость уравнения регрессии;
3. показывает, на сколько
процентов изменится в среднем
результат, если фактор изменится
на 1%.
10. Классический
метод к оцениванию параметров
регрессии основан на:
1. методе наименьших
квадратов;
2. методе максимального
правдоподобия;
3. шаговом регрессионном
анализе.
11. Простая линейная
регрессия предполагает …
1. наличие двух и более
факторов и нелинейность уравнения
регрессии;
2. наличие одного
фактора и линейность уравнения регрессии;
3. наличие одного фактора
и нелинейность уравнения регрессии;
4. наличие двух и более
факторов и линейность уравнения
регрессии.
12. Метод наименьших
квадратов позволяет оценить
уравнений регрессии:
1. переменные и случайные
величины;
2. параметры;
3. переменные;
4. параметры и переменные.
13. Коэффициент
регрессии в линейной регрессии
совокупного спроса на мобильные
телефоны (тыс. руб.) по цене (руб.)
оказался равным -1 Это означает:
1. увеличение цены на 1%
снижает спрос на мобильные
телефоны на 1%;
2. увеличение цена на 1
рубль снижает спрос на мобильные
телефоны на 1%;
3. увеличение цены на 1%
снижает спрос на мобильные
телефоны на 1 тысячу рублей;
4. увеличение цены на 1
рубль снижает спрос на мобильные
телефоны на 1 тысячу рублей;
5. полученное число
никак не интерпретируется.
Тест 2
1. Значение коэффициента
корреляции составило 2, следовательно
1. значение коэффициента
корреляции рассчитано с ошибкой;
2. теснота связи в 2
раза сильнее, чем для функциональной
связи;
3. связь функциональная;
4. при увеличении фактора
на единицу значение результата
увеличивается в 2 раза.
2. Значение коэффициента
корреляции не характеризует
…
1. статистическую
значимость уравнения;
2. корень из значения
коэффициента детерминации;
3. тесноту связи;
4. силу связи.
3. Для уравнения зависимости
выручки от величины оборотных
средств получено значение коэффициента
детерминации, равное 0,7.
Следовательно, _______ процентов
дисперсии обусловлено случайными
факторами.
1. 30%;
2. 100%;
3. 70%;
4. 0%.
4. Значения коэффициента
корреляции может находиться
в отрезке:
1. [-1;0];
2. [0;1];
3. [-1;1];
4. [-2;2].
5. Качество подбора
уравнения оценивает коэффициент
1. корреляции;
2. детерминации;
3. эластичности;
4. регрессии.
6. Расчётное значение
критерия Фишера определяется
как отношение
1. дисперсий;
2. результата к фактору;
3. математических ожиданий;
4. случайных величин.
7. При хорошем
качестве модели допустимым значением
средней ошибки аппроксимации
является
1. 5-7%;
2. 50%;
3. 90-95%;
4. 20-25%.
8. Случайными воздействиями
обусловлено 12% дисперсии результативного
признака, следовательно, значение
коэффициента детерминации составило:
1. 88;
2. 0,12;
3. 0,88;
4. 12.
9. Значение линейного
коэффициента корреляции характеризует
тесноту … связи.
1. нелинейной;
2. линейной;
3. случайной;
4. множественной линейной.
10. В качестве
показателя тесноты связи для
линейного уравнения парной регрессии
используется:
1. множественный коэффициент
линейной корреляции;
2. линейный коэффициент
корреляции;
03. линейный коэффициент регрессии;
4. линейный коэффициент
детерминации.
11. Значение коэффициента
корреляции равно 0,9. Следовательно,
значение коэффициента детерминации
составит …
1. 0,3;
2. 0,81;
3. 0,95;
4. 0,1.
12. Если средняя
ошибка аппроксимации равна 12%,
то говорят, что
1. качество построенной
модели плохое;
2. связь между признаком
и фактором слабая;
3. качество построенной
модели хорошее;
4. связь между признаком
и фактором сильная.
13. Если 0≤ │rxy│≤ 0,3, то о связи между
фактором и признаком можно сказать, что
она
1. умеренная;
2. сильная;
3. отсутствует;
4. слабая.
14. О сильной
связи между фактором и признаком
говорит то, что
Правильный
ответ: 2
15. «Необъяснённую»
сумму квадратов отклонений иначе
называют:
1. остаточной суммой
квадратов отклонений;
2. факторной суммой квадратов
отклонений;
3. общей суммой квадратов
отклонений;
4. средней суммой квадратов
отклонений.
16. О слабой
связи между фактором и признаком
говорит то, что
Правильный
ответ: 3
17. «Объяснённую»
сумму квадратов отклонений иначе
называют:
1. общей суммой квадратов
отклонений;
2. факторной суммой
квадратов отклонений;
3. остаточной суммой квадратов
отклонений;
4. средней суммой квадратов
отклонений.
18. Коэффициент
уравнения парной регрессии показывает:
1. тесноту связи между
зависимой и независимой переменными;
2. на сколько процентов
изменится зависимая переменная,
если независимая переменная
изменится на единицу;
3. на сколько процентов
изменится зависимая переменная,
если независимая переменная
изменится на 1%;
4. на сколько
единиц изменится зависимая переменная,
если независимая переменная изменится
на 1 ед.
19. Степень влияния
неучтённых факторов в рассматриваемой
модели можно определить на
основе:
- парного линейного коэффициента корреляции;
2. частного коэффициента
корреляции;
3. индекса корреляции;
4. коэффициента
детерминации
5. коэффициента регрессии.
20. Дисперсионный
анализ уравнения парной регрессии
проверяет:
1. значимость коэффициента
корреляции;
2. значимость уравнения
регрессии;
3. значимость коэффициента
регрессии;
4. значимость свободного
члена уравнения регрессии.
21. Коэффициент
корреляции больше нуля, это означает,
что
1. связь между
переменными тесная;
2. связь между переменными
прямая;
3. связь между переменными
обратная;
4. связь между переменными
отсутствует.
22. Оценка значимости
уравнения в целом осуществляется
по критерию:
1. Фишера;
2. Дарбина-Уотсона;
3. Пирсона;
4. Стьюдента.
23. Если расчётное
значение критерия Фишера меньше
табличного значения, то гипотеза
о статистической незначимости уравнения
1. незначима;
2. несущественна;
3. отвергается;
4. принимается.
24. Табличное значение
критерия Фишера определяется
по:
1. уровню значимости
и степеням свободы факторной и остаточной
дисперсий;
2. уровню значимости и
степени свободы общей дисперсии;
3. уровню значимости;
4. степени свободы факторной
и остаточной дисперсий.
25. Общая дисперсия
служит для оценки влияния
1. учтённых явно в модели
факторов;
2. как учтённых
факторов, так и случайных воздействий;
3. величины постоянной
составляющей в уравнении;
4. случайных воздействий.
26. Остаточная дисперсия
служит для оценки влияния
1. случайных воздействий;
2. величины постоянной
составляющей в уравнении;
3. учтённых явно в модели
факторов;
4. как учтённых факторов,
так и случайных воздействий.
27. Расчётное значение
критерия Фишера определяется
как
1. разность факторной
дисперсии и остаточной, рассчитанных
на одну степень свободы;
2. отношение факторной
дисперсии к остаточной;
3. отношение факторной
дисперсии к остаточной, рассчитанных
на одну степень свободы;
4. суммы факторной дисперсии
к остаточной, рассчитанных на одну
степень свободы.
28. Факторная дисперсия
служит для оценки влияния:
1. как учтённых факторов,
так и случайные воздействия;
2. учтённых явно
в модели факторов;
3. величины постоянной
составляющей в уравнении;
4. случайных воздействий.
29. Расчётное значение
критерия Фишера определяется
как …факторной дисперсии и
остаточной, рассчитанных на одну степень
свободы
1. произведение;
2. разность;
3. сумма;
4. отношение.
30. Парный линейный коэффициент
корреляции характеризует наличие
слабой обратной связи, значит
он принимает следующее значение:
1. 1,2;
2. –0,82;
3. 0,23;
4. 0,92;
5. –0,24.
31. Коэффициент
корреляции равен нулю, это означает,
что
1. связь между переменными
тесная;
2. связь между переменными
прямая;
3. связь между переменными
обратная;
4. связь между
переменными отсутствует.
32. Коэффициент
корреляции меньше нуля, это означает,
что
1. связь между переменными
тесная;
2. связь между переменными
прямая;
3. связь между
переменными обратная;
4. связь между переменными
отсутствует.
33. Остаточная
сумма квадратов равна нулю:
1. когда правильно подобрана
регрессионная модель;
2. когда между признаками
существует точная функциональная
связь;
3. никогда.
34. Табличное значение F-критерия Фишера
меньше расчётного F-критерия Фишера.
Это значит:
1. уравнение регрессии
значимо;
2. уравнение регрессии
незначимо;
3. все коэффициенты уравнения
регрессии равны нулю;
4. не все коэффициенты
уравнения регрессии равны нулю.
35. Остаточная
сумма квадратов отклонений вычисляется
по формуле:1
Тест 3
1. Критерий Стьюдента
предназначен для определения
значимости
1. построенного уравнения
в целом;
2. коэффициента детерминации;
3. уравнения;
4. параметров регрессии.
2. Если доверительный
интервал для параметра проходит
через точку ноль, то
1. значение параметра
может принимать как отрицательные,
так и положительные значения;
2. параметр является
несущественным;
3. параметр является существенным;
4. параметр признается
статистически значимым.
3. Параметр является
существенным, если
1. доверительный
интервал не проходит через ноль;
2. доверительный интервал
проходит через ноль;
3. расчётное значение
критерия Стьюдента меньше табличного
значения;
4. стандартная ошибка
превышает половину значения
самого параметра.
4. Стандартная
ошибка рассчитывается для проверки
существенности
1. параметра;
2. коэффициента детерминации;
3. случайной величины;
4. коэффициента эластичности.
5. Для существенного
параметра расчётное значение
критерия Стьюдента
1. равно нулю;
2. больше табличного
значения критерия;
3. не больше табличного
значения критерия;
4. меньше табличного значения
критерия.
6. Назовите показатель
корреляции для нелинейных моделей
регрессии:
1. парный коэффициент
линейной корреляции;
2. индекс детерминации;
3. линейный коэффициент
корреляции;
4. индекс корреляции.
7. Линеаризация
подразумевает процедуру …
1. приведения уравнения
множественной регрессии к парной;
2. приведения нелинейного
уравнения к линейному виду;
3. приведения линейного
уравнения к нелинейному виду;
4. приведения нелинейного
уравнения относительно параметров к
уравнению, линейному относительно результата.
8. К линейному
виду нельзя привести:
Градация значений средней ошибки аппроксимации
|
Значение |
Менее |
10% – |
20% – |
Более 50% |
|
Уровень |
высокая |
хорошая |
удовлетворительная |
неудовлетворительная |
Как
видно из таблицы, чем меньше ошибка
аппроксимации, тем ближе расчетные
уровни признака, полученные из уравнения
регрессии, к их фактическим значениям.
Коэффициент
регрессии применяют для расчета
коэффициента
эластичности,
который показывает на сколько процентов
изменится величина результативного Y
при изменении признак-фактора Х на 1%.
Для
определения коэффициента эластичности
используется формула:
.
(11.14)
4. Измерение тесноты связей в корреляционно-регрессионном анализе: определение линейного коэффициента корреляции и детерминации
В
случае линейной зависимости между Х и
Y
тесноту связи между признаками
устанавливают с помощью коэффициента
линейной корреляции (
):
.
(11.15)
Значение
коэффициента линейной корреляции
изменяется в пределах от
.
Если
знак с положительным коэффициентом, то
связь прямая, а если с отрицательным,
то связь обратная. Чем ближе он к 1, тем
теснее связь.
Показатели
тесноты связи характеризуют зависимость
вариации результативного признака от
вариации факторного признака.
К
этим показателям относятся:
-
индекс
корреляции; -
индекс
детерминации.
Для
расчета этих индексов необходимы
сведения о различных видах дисперсий:
-
общей;
-
факторной;
-
остаточной.
Используем
условные обозначения:
– фактические
значения результативного признака;
–
расчетные значения результативного
признака;
–
среднее значение результативного
признака.
Общая
дисперсия
– характеризует общую вариацию
результативного признака у, объясняемую
влиянием всех факторов, действующих в
данной совокупности.
Общая
дисперсия
для несгруппированных данных:
.
(11.16)
Общая
взвешенная дисперсия (по сгруппированным
данным):
.
(11.17)
Общая
дисперсия раскладывается на 2 части:
Факторная
дисперсия (
):
,
(11.18)
где
–
расчетное значение признака из уравнения
регрессии.
Она
объясняется фактором Х и характеризует
меру колеблемости расчетных значений
признака около их средней величины.
Остаточная
дисперсия:
.
(11.19)
Остаточная
дисперсия объясняется другими кроме Х
факторами и показывает меру колеблемости
фактических значений результативного
признака (
)
около теоретической линии регрессии
(
).
Эти
дисперсии связаны по правилу сложения
дисперсий, т.е.
.
(11.20)
Общая
дисперсия равна сумме факторной и
остаточной дисперсий.
На
основе правила сложения дисперсий
рассчитаем показатели тесноты связи:
-
Индекс
детерминации
(причинности), который выражает долю
факторной дисперсии в общей и показывает,
какая часть колеблемости результативного
признака Y
объясняется изучаемым фактором X.
Расчет производится по формуле:
.
(11.21)
Изменяется
в пределах
.
Долю
случайной вариации результативного
признака (под влиянием всех прочих
факторов, кроме Х) показывает отношение:
.
-
R
– индекс корреляции
(теоретическое корреляционное отношение):
(11.22)
или
.
(11.23)
Он
характеризует тесноту связи между
результативным и факторным признаками
и изменяется в пределах
.
При
функциональной зависимости значения
Yx
полностью совпадают с соответствующими
индивидуальными значениями Yij
. Тогда:
,
а
.
При
отсутствии связи вариация Х не отражается
на изменении Y.
В этом случае:
,
а
.
При
наличии корреляционной (соотносительной)
связи
.
При этом величина
изменяется
в пределах
.
Для
получения выводов о практической
значимости полученных в анализе моделей,
показаниям тесноты связи дается
качественная оценка (табл. 11.2).
Таблица
11.2
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
Рисунок 4 Результат вычисления функции ЛИНЕЙН
Получили уровнение регрессии:
Делаем вывод: С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.
Означает, что 52% вариации заработной платы (у) объясняется вариацией фактора х — среднедушевого прожиточного минимума, а 48% — действием других факторов, не включённых в модель.
По вычисленному коэффициенту детерминации можно рассчитать коэффициент корреляции: 
Связь оценивается как тесная.
4. С помощью среднего (общего) коэффициента эластичности определим силу влияния фактора на результат.
Для уравнения прямой средний (общий) коэффициент эластичности определим по формуле:
Средние значения найдём, выделив область ячеек со значениями х, и выберем Формулы / Автосумма / Среднее , и то же самое произведём со значениями у.
Рисунок 5 Расчёт средних значений функции и аргумент
Таким образом, при изменении среднедушевого прожиточного минимума на 1% от своего среднего значения среднедневная заработная плата изменится в среднем на 0,51%.
С помощью инструмента анализа данных Регрессия можно получить:
— результаты регрессионной статистики,
— результаты дисперсионного анализа,
— результаты доверительных интервалов,
— остатки и графики подбора линии регрессии,
— остатки и нормальную вероятность.
Порядок действий следующий:
1) проверьте доступ к Пакету анализа . В главном меню последовательно выберите: Файл/Параметры/Надстройки .
2) В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.
3) В окне Надстройки установите флажок Пакет анализа , а затем нажмите кнопку ОК .
Если Пакет анализа отсутствует в списке поля Доступные надстройки , нажмите кнопку Обзор , чтобы выполнить поиск.
Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да , чтобы установить его.
4) В главном меню последовательно выберите: Данные / Анализ данных / Инструменты анализа / Регрессия , а затем нажмите кнопку ОК .
5) Заполните диалоговое окно ввода данных и параметров вывода:
Входной интервал Y — диапазон, содержащий данные результативного признака;
Входной интервал X — диапазон, содержащий данные факторного признака;
Метки — флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа — ноль — флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал — достаточно указать левую верхнюю ячейку будущего диапазона;
6) Новый рабочий лист — можно задать произвольное имя нового листа.
Затем нажмите кнопку ОК .
Рисунок 6 Диалоговое окно ввода параметров инструмента Регрессия
Результаты регрессионного анализа для данных задачи представлены на рисунке 7.
Рисунок 7 Результат применения инструмента регрессия
5. Оценим с помощью средней ошибки аппроксимации качество уравнений. Воспользуемся результатами регрессионного анализа представленного на Рисунке 8.
Рисунок 8 Результат применения инструмента регрессия «Вывод остатка»
Составим новую таблицу как показано на рисунке 9. В графе С рассчитаем относительную ошибку аппроксимации по формуле:
Рисунок 9 Расчёт средней ошибки аппроксимации
Средняя ошибка аппроксимации рассчитывается по формуле:
Качество построенной модели оценивается как хорошее, так как не превышает 8 — 10%.
6. Из таблицы с регрессионной статистикой (Рисунок 4) выпишем фактическое значение F-критерия Фишера:
Поскольку 
8. Оценку статистической значимости параметров регрессии проведём с помощью t-статистики Стьюдента и путём расчёта доверительного интервала каждого из показателей.
Выдвигаем гипотезу Н 0 о статистически незначимом отличии показателей от нуля:


На рисунке 7 имеются фактические значения t-статистики:
t-критерий для коэффициента корреляции можно рассчитать двумя способами:
где 
Данные для расчёта возьмём из таблицы на Рисунке 7.
Фактические значения t-статистики превосходят табличные значения:
Поэтому гипотеза Н 0 отклоняется, то есть параметры регрессии и коэффициент корреляции не случайно отличаются от нуля, а статистически значимы.
Доверительный интервал для параметра a определяется как
Для параметра a 95%-ные границы как показано на рисунке 7 составили:
Доверительный интервал для коэффициента регрессии определяется как
Для коэффициента регрессии b 95%-ные границы как показано на рисунке 7 составили:
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью 
7. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:
Тогда прогнозное значение прожиточного минимума составит:
Ошибку прогноза рассчитаем по формуле:
где
Дисперсию посчитаем также с помощью ППП Excel. Для этого:
1) Активизируйте Мастер функций : в главном меню выберете Формулы / Вставить функцию .
3) Заполните диапазон, содержащий числовые данные факторного признака. Нажмите ОК .
Рисунок 10 Расчёт дисперсии
Получили значение дисперсии
Для подсчёта остаточной дисперсии на одну степень свободы воспользуемся результатами дисперсионного анализа как показано на Рисунке 7.
Доверительные интервалы прогноза индивидуальных значений у при с вероятностью 0,95 определяются выражением:
Интервал достаточно широк, прежде всего, за счёт малого объёма наблюдений. В целом выполненный прогноз среднемесячной заработной платы оказался надёжным.
Условие задачи взято из: Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. — М.: Финансы и статистика, 2003. — 192 с.: ил.
Для общей оценки качества построенной эконометрической определяются такие характеристики как коэффициент детерминации, индекс корреляции, средняя относительная ошибка аппроксимации, а также проверяется значимость уравнения регрессии с помощью F -критерия Фишера. Перечисленные характеристики являются достаточно универсальными и могут применяться как для линейных, так и для нелинейных моделей, а также моделей с двумя и более факторными переменными. Определяющее значение при вычислении всех перечисленных характеристик качества играет ряд остатков ε i , который вычисляется путем вычитания из фактических (полученных по наблюдениям) значений исследуемого признака y i значений, рассчитанных по уравнению модели y рi .
показывает, какая доля изменения исследуемого признака учтена в модели. Другими словами коэффициент детерминации показывает, какая часть изменения исследуемой переменной может быть вычислена, исходя из изменений включённых в модель факторных переменных с помощью выбранного типа функции, связывающей факторные переменные и исследуемый признак в уравнении модели.
Коэффициент детерминации R 2 может принимать значения от 0 до 1. Чем ближе коэффициент детерминации R 2 к единице, тем лучше качество модели.
Индекс корреляции можно легко вычислить, зная коэффициент детерминации:
Индекс корреляции R характеризует тесноту выбранного при построении модели типа связи между учтёнными в модели факторами и исследуемой переменной. В случае линейной парной регрессии его значение по абсолютной величине совпадает с коэффициентом парной корреляции r (x, y) , который мы рассмотрели ранее, и характеризует тесноту линейной связи между x и y . Значения индекса корреляции, очевидно, также лежат в интервале от 0 до 1. Чем ближе величина R к единице, тем теснее выбранный вид функции связывает между собой факторные переменные и исследуемый признак, тем лучше качество модели.

выражается в процентах и характеризует точность модели. Приемлимая точность модели при решении практических задач может определяться, исходя из соображений экономической целесообразности с учётом конкретной ситуации. Широко применяется критерий, в соответствии с которым точность считается удовлетворительной, если средняя относительная погрешность меньше 15%. Если E отн.ср. меньше 5%, то говорят, что модель имеет высокую точность. Не рекомендуется применять для анализа и прогноза модели с неудовлетворительной точностью, то есть, когда E отн.ср. больше 15%.
F-критерий Фишера используется для оценки значимости уравнения регрессии. Расчётное значение F-критерия определяется из соотношения:

Критическое значение F -критерия определяется по таблицам при заданном уровне значимости α и степенях свободы (можно использовать функцию FРАСПОБР в Excel). Здесь, по-прежнему, m – число факторов, учтённых в модели, n – количество наблюдений. Если расчётное значение больше критического, то уравнение модели признаётся значимым. Чем больше расчётное значение F -критерия, тем лучше качество модели.
Определим характеристики качества построенной нами линейной модели для Примера 1 . Воспользуемся данными Таблицы 2. Коэффициент детерминации :
Следовательно, в рамках линейной модели изменение объёма продаж на 90,1% объясняется изменением температуры воздуха.

Значение индекса корреляции в случае парной линейной модели как мы видим, действительно по модулю равно коэффициенту корреляции между соответствующими переменными (объём продаж и температура). Поскольку полученное значение достаточно близко к единице, то можно сделать вывод о наличии тесной линейной связи между исследуемой переменной (объём продаж) и факторной переменноё (температура).
Критическое значение F кр при α = 0,1; ν 1 =1; ν 2 =7-1-1=5 равно 4,06. Расчётное значение F -критерия больше табличного, следовательно, уравнение модели является значимым.
Средняя относительная ошибка аппроксимации
Построенная линейная модель парной регрессии имеет неудовлетворительную точность (>15%), и её не рекомендуется использовать для анализа и прогнозирования.
В итоге, несмотря на то, что большинство статистических характеристик удовлетворяют предъявляемым к ним критериям, линейная модель парной регрессии непригодна для прогнозирования объёма продаж в зависимости от температуры воздуха. Нелинейный характер зависимости между указанными переменными по данным наблюдений достаточно хорошо виден на Рис.1. Проведённый анализ это подтвердил.
Среди различных методов прогнозирования нельзя не выделить аппроксимацию. С её помощью можно производить приблизительные подсчеты и вычислять планируемые показатели, путем замены исходных объектов на более простые. В Экселе тоже существует возможность использования данного метода для прогнозирования и анализа. Давайте рассмотрим, как этот метод можно применить в указанной программе встроенными инструментами.
Наименование данного метода происходит от латинского слова proxima – «ближайшая» Именно приближение путем упрощения и сглаживания известных показателей, выстраивание их в тенденцию и является его основой. Но данный метод можно использовать не только для прогнозирования, но и для исследования уже имеющихся результатов. Ведь аппроксимация является, по сути, упрощением исходных данных, а упрощенный вариант исследовать легче.
Главный инструмент, с помощью которого проводится сглаживания в Excel – это построение линии тренда. Суть состоит в том, что на основе уже имеющихся показателей достраивается график функции на будущие периоды. Основное предназначение линии тренда, как не трудно догадаться, это составление прогнозов или выявление общей тенденции.
Но она может быть построена с применением одного из пяти видов аппроксимации:
- Линейной;
- Экспоненциальной;
- Логарифмической;
- Полиномиальной;
- Степенной.
Рассмотрим каждый из вариантов более подробно в отдельности.
Способ 1: линейное сглаживание
Прежде всего, давайте рассмотрим самый простой вариант аппроксимации, а именно с помощью линейной функции. На нем мы остановимся подробнее всего, так как изложим общие моменты характерные и для других способов, а именно построение графика и некоторые другие нюансы, на которых при рассмотрении последующих вариантов уже останавливаться не будем.
Прежде всего, построим график, на основании которого будем проводить процедуру сглаживания. Для построения графика возьмем таблицу, в которой помесячно указана себестоимость единицы продукции, производимой предприятием, и соответствующая прибыль в данном периоде. Графическая функция, которую мы построим, будет отображать зависимость увеличения прибыли от уменьшения себестоимости продукции.
Сглаживание, которое используется в данном случае, описывается следующей формулой:
В конкретно нашем случае формула принимает такой вид:
Величина достоверности аппроксимации у нас равна 0,9418 , что является довольно приемлемым итогом, характеризующим сглаживание, как достоверное.
Способ 2: экспоненциальная аппроксимация
Теперь давайте рассмотрим экспоненциальный тип аппроксимации в Эксель.
Общий вид функции сглаживания при этом такой:
где e – это основание натурального логарифма.
В конкретно нашем случае формула приняла следующую форму:
Способ 3: логарифмическое сглаживание
Теперь настала очередь рассмотреть метод логарифмической аппроксимации.
В общем виде формула сглаживания выглядит так:
где ln – это величина натурального логарифма. Отсюда и наименование метода.
В нашем случае формула принимает следующий вид:
Способ 4: полиномиальное сглаживание
Настал черед рассмотреть метод полиномиального сглаживания.
Формула, которая описывает данный тип сглаживания, приняла следующий вид:
Способ 5: степенное сглаживание
В завершении рассмотрим метод степенной аппроксимации в Excel.
Данный способ эффективно используется в случаях интенсивного изменения данных функции. Важно учесть, что этот вариант применим только при условии, что функция и аргумент не принимают отрицательных или нулевых значений.
Общая формула, описывающая данный метод имеет такой вид:
В конкретно нашем случае она выглядит так:
Как видим, при использовании конкретных данных, которые мы применяли для примера, наибольший уровень достоверности показал метод полиномиальной аппроксимации с полиномом в шестой степени (0,9844 ), наименьший уровень достоверности у линейного метода (0,9418 ). Но это совсем не значит, что такая же тенденция будет при использовании других примеров. Нет, уровень эффективности у приведенных выше методов может значительно отличаться, в зависимости от конкретного вида функции, для которой будет строиться линия тренда. Поэтому, если для этой функции выбранный метод наиболее эффективен, то это совсем не означает, что он также будет оптимальным и в другой ситуации.
Если вы пока не можете сразу определить, основываясь на вышеприведенных рекомендациях, какой вид аппроксимации подойдет конкретно в вашем случае, то есть смысл попробовать все методы. После построения линии тренда и просмотра её уровня достоверности можно будет выбрать оптимальный вариант.
Контрольная работа: Парная регрессия
Смысл регрессионного анализа – построение функциональных зависимостей между двумя группами переменных величин Х1 , Х2 , … Хр и Y. При этом речь идет о влиянии переменных Х (это будут аргументы функций) на значения переменной Y (значение функции). Переменные Х мы будем называть факторами, а Y – откликом.
Наиболее простой случай – установление зависимости одного отклика y от одного фактора х. Такой случай называется парной (простой) регрессией.
Парная регрессия – уравнение связи двух переменных у иx :
,
где у – зависимая переменная (результативный признак);
х – независимая, объясняющая переменная (признак-фактор).
Различают линейные и нелинейные регрессии.
Линейная регрессия:.
Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам.
Регрессии, нелинейные по объясняющим переменным:
• полиномы разных степеней
•равносторонняя гипербола
Регрессии, нелинейные по оцениваемым параметрам:
• степенная ;
• показательная
• экспоненциальная
Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессий, линейных по параметрам, используют метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических минимальна, т.е.
Для линейных и нелинейных уравнений, приводимых к линейным, решается следующая система относительно а и b :
Можно воспользоваться готовыми формулами, которые вытекают из этой системы:
Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции для линейной регрессии
и индекс корреляции — для нелинейной регрессии ():
Оценку качества построенной модели даст коэффициент (индекс) детерминации, а также средняя ошибка аппроксимации.
Средняя ошибка аппроксимации – среднее отклонение расчетных значений от фактических:
Допустимый предел значений – не более 8 – 10%.
Средний коэффициент эластичности показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора x на 1% от своего среднего значения:
Задача дисперсионного анализа состоит в анализе дисперсии зависимой переменной:
где – общая сумма квадратов отклонений;
– сумма квадратов отклонений, обусловленная регрессией («объясненная» или «факторная»);
–остаточная сумма квадратов отклонений.
Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака у характеризует коэффициент (индекс) детерминации R 2 :
Коэффициент детерминации – квадрат коэффициента или индекса корреляции.
F -тест – оценивание качества уравнения регрессии – состоит в проверке гипотезы Но о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт и критического (табличного) Fтабл значений F -критерия Фишера. F факт определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:
п – число единиц совокупности;
т – число параметров при переменных х.
Fтабл – это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости а. Уровень значимости а – вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно а принимается равной 0,05 или 0,01.
Если Fтабл Fфакт , то гипотеза Н0 не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.
Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t -критерий Стьюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза Н0 о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью f-критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки:
Случайные ошибки параметров линейной регрессии и коэффициента корреляции определяются по формулам:
Сравнивая фактическое и критическое (табличное) значения t-статистики – tтабл и tфакт – принимаем или отвергаем гипотезу Hо .
Связь между F-критерием Фишера и t-статистикой Стьюдента выражается равенством
Если tтабл tфакт , то гипотеза Но не отклоняется и признается случайная природа формирования a , b или .
Для расчета доверительного интервала определяем предельную ошибку ∆ для каждого показателя:
Формулы для расчета доверительных интервалов имеют следующий вид:
Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значения.
Прогнозное значение определяется путем подстановки в уравнение регрессии соответствующего (прогнозного) значения . Вычисляется средняя стандартная ошибка прогноза :
где
и строится доверительный интервал прогноза:
где
По 22 регионам страны изучается зависимость розничной продажи телевизоров, y от среднедушевых денежных доходов в месяц, x (табл. 1):
| Название: Парная регрессия Раздел: Рефераты по математике Тип: контрольная работа Добавлен 13:41:57 15 апреля 2011 Похожие работы Просмотров: 3780 Комментариев: 22 Оценило: 4 человек Средний балл: 4.5 Оценка: неизвестно Скачать |
| № региона | X | Y |
| 1,000 | 2,800 | 28,000 |
| 2,000 | 2,400 | 21,300 |
| 3,000 | 2,100 | 21,000 |
| 4,000 | 2,600 | 23,300 |
| 5,000 | 1,700 | 15,800 |
| 6,000 | 2,500 | 21,900 |
| 7,000 | 2,400 | 20,000 |
| 8,000 | 2,600 | 22,000 |
| 9,000 | 2,800 | 23,900 |
| 10,000 | 2,600 | 26,000 |
| 11,000 | 2,600 | 24,600 |
| 12,000 | 2,500 | 21,000 |
| 13,000 | 2,900 | 27,000 |
| 14,000 | 2,600 | 21,000 |
| 15,000 | 2,200 | 24,000 |
| 16,000 | 2,600 | 34,000 |
| 17,000 | 3,300 | 31,900 |
| 19,000 | 3,900 | 33,000 |
| 20,000 | 4,600 | 35,400 |
| 21,000 | 3,700 | 34,000 |
| 22,000 | 3,400 | 31,000 |
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Рассчитайте параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессий.
3. Оцените тесноту связи с помощью показателей корреляции и детерминации.
4. С помощью среднего (общего) коэффициента эластичности дайте сравнительную оценку силы связи фактора с результатом.
5. Качество уравнений оцените с помощью средней ошибки аппроксимации.
6. С помощью F-критерия Фишера определите статистическую надежность результатов регрессионного моделирования. Выберите лучшее уравнение регрессии и дайте его обоснование.
7. Рассчитайте прогнозное значение результата по линейному уравнению регрессии, если прогнозное значение фактора увеличится на 7% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости α=0,05.
8. Оцените полученные результаты, выводы оформите в аналитической записке.
1. Поле корреляции для:
· Линейной регрессии y=a+b*x:
Гипотеза о форме связи: чем больше размер среднедушевого денежного дохода в месяц (факторный признак), тем больше при прочих равных условиях розничная продажа телевизоров (результативный признак). В данной модели параметр b называется коэффициентом регрессии и показывает, насколько в среднем отклоняется величина результативного признака у при отклонении величины факторного признаках на одну единицу.
· Степенной регрессии :
Гипотеза о форме связи : степенная функция имеет вид Y=ax b .
Параметр b степенного уравнения называется показателем эластичности и указывает, на сколько процентов изменится у при возрастании х на 1%. При х = 1 a = Y.
· Экспоненциальная регрессия :
· Равносторонняя гипербола :
Гипотеза о форме связи: В ряде случаев обратная связь между факторным и результативным признаками может быть выражена уравнением гиперболы: Y=a+b/x.
· Обратная гипербола :
· Полулогарифмическая регрессия :
2. Рассчитайте параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессий.
· Рассчитаем параметры уравнений линейной парной регрессии. Для расчета параметров a и b линейной регрессии y=a+b*x решаем систему нормальных уравнений относительно a и b:
По исходным данным рассчитываем ∑y, ∑x, ∑yx, ∑x 2 , ∑y 2 (табл. 2):
| № региона | X | Y | XY | X^2 | Y^2 | Y^cp | Y-Y^cp | Ai |
| 1 | 2,800 | 28,000 | 78,400 | 7,840 | 784,000 | 25,719 | 2,281 | 0,081 |
| 2 | 2,400 | 21,300 | 51,120 | 5,760 | 453,690 | 22,870 | -1,570 | 0,074 |
| 3 | 2,100 | 21,000 | 44,100 | 4,410 | 441,000 | 20,734 | 0,266 | 0,013 |
| 4 | 2,600 | 23,300 | 60,580 | 6,760 | 542,890 | 24,295 | -0,995 | 0,043 |
| 5 | 1,700 | 15,800 | 26,860 | 2,890 | 249,640 | 17,885 | -2,085 | 0,132 |
| 6 | 2,500 | 21,900 | 54,750 | 6,250 | 479,610 | 23,582 | -1,682 | 0,077 |
| 7 | 2,400 | 20,000 | 48,000 | 5,760 | 400,000 | 22,870 | -2,870 | 0,144 |
| 8 | 2,600 | 22,000 | 57,200 | 6,760 | 484,000 | 24,295 | -2,295 | 0,104 |
| 9 | 2,800 | 23,900 | 66,920 | 7,840 | 571,210 | 25,719 | -1,819 | 0,076 |
| 10 | 2,600 | 26,000 | 67,600 | 6,760 | 676,000 | 24,295 | 1,705 | 0,066 |
| 11 | 2,600 | 24,600 | 63,960 | 6,760 | 605,160 | 24,295 | 0,305 | 0,012 |
| 12 | 2,500 | 21,000 | 52,500 | 6,250 | 441,000 | 23,582 | -2,582 | 0,123 |
| 13 | 2,900 | 27,000 | 78,300 | 8,410 | 729,000 | 26,431 | 0,569 | 0,021 |
| 14 | 2,600 | 21,000 | 54,600 | 6,760 | 441,000 | 24,295 | -3,295 | 0,157 |
| 15 | 2,200 | 24,000 | 52,800 | 4,840 | 576,000 | 21,446 | 2,554 | 0,106 |
| 16 | 2,600 | 34,000 | 88,400 | 6,760 | 1156,000 | 24,295 | 9,705 | 0,285 |
| 17 | 3,300 | 31,900 | 105,270 | 10,890 | 1017,610 | 29,280 | 2,620 | 0,082 |
| 19 | 3,900 | 33,000 | 128,700 | 15,210 | 1089,000 | 33,553 | -0,553 | 0,017 |
| 20 | 4,600 | 35,400 | 162,840 | 21,160 | 1253,160 | 38,539 | -3,139 | 0,089 |
| 21 | 3,700 | 34,000 | 125,800 | 13,690 | 1156,000 | 32,129 | 1,871 | 0,055 |
| 22 | 3,400 | 31,000 | 105,400 | 11,560 | 961,000 | 29,992 | 1,008 | 0,033 |
| Итого | 58,800 | 540,100 | 1574,100 | 173,320 | 14506,970 | 540,100 | 0,000 | |
| сред значение | 2,800 | 25,719 | 74,957 | 8,253 | 690,808 | 0,085 | ||
| станд. откл | 0,643 | 5,417 |
Система нормальных уравнений составит:
Ур-ие регрессии: = 5,777+7,122∙x. Данное уравнение показывает, что с увеличением среднедушевого денежного дохода в месяц на 1 тыс. руб. доля розничных продаж телевизоров повышается в среднем на 7,12%.
· Рассчитаем параметры уравнений степенной парной регрессии. Построению степенной модели предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения:
где
Для расчетов используем данные табл. 3:
| № рег | X | Y | XY | X^2 | Y^2 | Yp^cp | y^cp |
| 1 | 1,030 | 3,332 | 3,431 | 1,060 | 11,104 | 3,245 | 25,67072 |
| 2 | 0,875 | 3,059 | 2,678 | 0,766 | 9,356 | 3,116 | 22,56102 |
| 3 | 0,742 | 3,045 | 2,259 | 0,550 | 9,269 | 3,004 | 20,17348 |
| 4 | 0,956 | 3,148 | 3,008 | 0,913 | 9,913 | 3,183 | 24,12559 |
| 5 | 0,531 | 2,760 | 1,465 | 0,282 | 7,618 | 2,827 | 16,90081 |
| 6 | 0,916 | 3,086 | 2,828 | 0,840 | 9,526 | 3,150 | 23,34585 |
| 7 | 0,875 | 2,996 | 2,623 | 0,766 | 8,974 | 3,116 | 22,56102 |
| 8 | 0,956 | 3,091 | 2,954 | 0,913 | 9,555 | 3,183 | 24,12559 |
| 9 | 1,030 | 3,174 | 3,268 | 1,060 | 10,074 | 3,245 | 25,67072 |
| 10 | 0,956 | 3,258 | 3,113 | 0,913 | 10,615 | 3,183 | 24,12559 |
| 11 | 0,956 | 3,203 | 3,060 | 0,913 | 10,258 | 3,183 | 24,12559 |
| 12 | 0,916 | 3,045 | 2,790 | 0,840 | 9,269 | 3,150 | 23,34585 |
| 13 | 1,065 | 3,296 | 3,509 | 1,134 | 10,863 | 3,275 | 26,4365 |
| 14 | 0,956 | 3,045 | 2,909 | 0,913 | 9,269 | 3,183 | 24,12559 |
| 15 | 0,788 | 3,178 | 2,506 | 0,622 | 10,100 | 3,043 | 20,97512 |
| 16 | 0,956 | 3,526 | 3,369 | 0,913 | 12,435 | 3,183 | 24,12559 |
| 17 | 1,194 | 3,463 | 4,134 | 1,425 | 11,990 | 3,383 | 29,4585 |
| 19 | 1,361 | 3,497 | 4,759 | 1,852 | 12,226 | 3,523 | 33,88317 |
| 20 | 1,526 | 3,567 | 5,443 | 2,329 | 12,721 | 3,661 | 38,90802 |
| 21 | 1,308 | 3,526 | 4,614 | 1,712 | 12,435 | 3,479 | 32,42145 |
| 22 | 1,224 | 3,434 | 4,202 | 1,498 | 11,792 | 3,408 | 30,20445 |
| итого | 21,115 | 67,727 | 68,921 | 22,214 | 219,361 | 67,727 | 537,270 |
| сред зн | 1,005 | 3,225 | 3,282 | 1,058 | 10,446 | 3,225 | |
| стан откл | 0,216 | 0,211 |
Рассчитаем С и b:
Получим линейное уравнение: . Выполнив его потенцирование, получим:
Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата y .
· Рассчитаем параметры уравнений экспоненциальной парной регрессии. Построению экспоненциальной модели предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения:
где
Для расчетов используем данные табл. 4:
| № региона | X | Y | XY | X^2 | Y^2 | Yp | y^cp |
| 1 | 2,800 | 3,332 | 9,330 | 7,840 | 11,104 | 3,225 | 25,156 |
| 2 | 2,400 | 3,059 | 7,341 | 5,760 | 9,356 | 3,116 | 22,552 |
| 3 | 2,100 | 3,045 | 6,393 | 4,410 | 9,269 | 3,034 | 20,777 |
| 4 | 2,600 | 3,148 | 8,186 | 6,760 | 9,913 | 3,170 | 23,818 |
| 5 | 1,700 | 2,760 | 4,692 | 2,890 | 7,618 | 2,925 | 18,625 |
| 6 | 2,500 | 3,086 | 7,716 | 6,250 | 9,526 | 3,143 | 23,176 |
| 7 | 2,400 | 2,996 | 7,190 | 5,760 | 8,974 | 3,116 | 22,552 |
| 8 | 2,600 | 3,091 | 8,037 | 6,760 | 9,555 | 3,170 | 23,818 |
| 9 | 2,800 | 3,174 | 8,887 | 7,840 | 10,074 | 3,225 | 25,156 |
| 10 | 2,600 | 3,258 | 8,471 | 6,760 | 10,615 | 3,170 | 23,818 |
| 11 | 2,600 | 3,203 | 8,327 | 6,760 | 10,258 | 3,170 | 23,818 |
| 12 | 2,500 | 3,045 | 7,611 | 6,250 | 9,269 | 3,143 | 23,176 |
| 13 | 2,900 | 3,296 | 9,558 | 8,410 | 10,863 | 3,252 | 25,853 |
| 14 | 2,600 | 3,045 | 7,916 | 6,760 | 9,269 | 3,170 | 23,818 |
| 15 | 2,200 | 3,178 | 6,992 | 4,840 | 10,100 | 3,061 | 21,352 |
| 16 | 2,600 | 3,526 | 9,169 | 6,760 | 12,435 | 3,170 | 23,818 |
| 17 | 3,300 | 3,463 | 11,427 | 10,890 | 11,990 | 3,362 | 28,839 |
| 19 | 3,900 | 3,497 | 13,636 | 15,210 | 12,226 | 3,526 | 33,978 |
| 20 | 4,600 | 3,567 | 16,407 | 21,160 | 12,721 | 3,717 | 41,140 |
| 21 | 3,700 | 3,526 | 13,048 | 13,690 | 12,435 | 3,471 | 32,170 |
| 22 | 3,400 | 3,434 | 11,676 | 11,560 | 11,792 | 3,389 | 29,638 |
| Итого | 58,800 | 67,727 | 192,008 | 173,320 | 219,361 | 67,727 | 537,053 |
| сред зн | 2,800 | 3,225 | 9,143 | 8,253 | 10,446 | ||
| стан откл | 0,643 | 0,211 |
Рассчитаем С и b:
Получим линейное уравнение: . Выполнив его потенцирование, получим:
Для расчета теоретических значений y подставим в уравнение значения x .
· Рассчитаем параметры уравнений полулогарифмической парной регрессии. Построению полулогарифмической модели предшествует процедура линеаризации переменных. В примере линеаризация производится путем замены:
где
Для расчетов используем данные табл. 5:
| № региона | X | Y | XY | X^2 | Y^2 | y^cp |
| 1 | 1,030 | 28,000 | 28,829 | 1,060 | 784,000 | 26,238 |
| 2 | 0,875 | 21,300 | 18,647 | 0,766 | 453,690 | 22,928 |
| 3 | 0,742 | 21,000 | 15,581 | 0,550 | 441,000 | 20,062 |
| 4 | 0,956 | 23,300 | 22,263 | 0,913 | 542,890 | 24,647 |
| 5 | 0,531 | 15,800 | 8,384 | 0,282 | 249,640 | 15,525 |
| 6 | 0,916 | 21,900 | 20,067 | 0,840 | 479,610 | 23,805 |
| 7 | 0,875 | 20,000 | 17,509 | 0,766 | 400,000 | 22,928 |
| 8 | 0,956 | 22,000 | 21,021 | 0,913 | 484,000 | 24,647 |
| 9 | 1,030 | 23,900 | 24,608 | 1,060 | 571,210 | 26,238 |
| 10 | 0,956 | 26,000 | 24,843 | 0,913 | 676,000 | 24,647 |
| 11 | 0,956 | 24,600 | 23,506 | 0,913 | 605,160 | 24,647 |
| 12 | 0,916 | 21,000 | 19,242 | 0,840 | 441,000 | 23,805 |
| 13 | 1,065 | 27,000 | 28,747 | 1,134 | 729,000 | 26,991 |
| 14 | 0,956 | 21,000 | 20,066 | 0,913 | 441,000 | 24,647 |
| 15 | 0,788 | 24,000 | 18,923 | 0,622 | 576,000 | 21,060 |
| 16 | 0,956 | 34,000 | 32,487 | 0,913 | 1156,000 | 24,647 |
| 17 | 1,194 | 31,900 | 38,086 | 1,425 | 1017,610 | 29,765 |
| 19 | 1,361 | 33,000 | 44,912 | 1,852 | 1089,000 | 33,351 |
| 20 | 1,526 | 35,400 | 54,022 | 2,329 | 1253,160 | 36,895 |
| 21 | 1,308 | 34,000 | 44,483 | 1,712 | 1156,000 | 32,221 |
| 22 | 1,224 | 31,000 | 37,937 | 1,498 | 961,000 | 30,406 |
| Итого | 21,115 | 540,100 | 564,166 | 22,214 | 14506,970 | 540,100 |
| сред зн | 1,005 | 25,719 | 26,865 | 1,058 | 690,808 | |
| стан откл | 0,216 | 5,417 |
Рассчитаем a и b:
Получим линейное уравнение: .
· Рассчитаем параметры уравнений обратной парной регрессии. Для оценки параметров приведем обратную модель к линейному виду, заменив , тогда
Для расчетов используем данные табл. 6:
| № региона | X | Y | XY | X^2 | Y^2 | Y^cp |
| 1 | 2,800 | 0,036 | 0,100 | 7,840 | 0,001 | 24,605 |
| 2 | 2,400 | 0,047 | 0,113 | 5,760 | 0,002 | 22,230 |
| 3 | 2,100 | 0,048 | 0,100 | 4,410 | 0,002 | 20,729 |
| 4 | 2,600 | 0,043 | 0,112 | 6,760 | 0,002 | 23,357 |
| 5 | 1,700 | 0,063 | 0,108 | 2,890 | 0,004 | 19,017 |
| 6 | 2,500 | 0,046 | 0,114 | 6,250 | 0,002 | 22,780 |
| 7 | 2,400 | 0,050 | 0,120 | 5,760 | 0,003 | 22,230 |
| 8 | 2,600 | 0,045 | 0,118 | 6,760 | 0,002 | 23,357 |
| 9 | 2,800 | 0,042 | 0,117 | 7,840 | 0,002 | 24,605 |
| 10 | 2,600 | 0,038 | 0,100 | 6,760 | 0,001 | 23,357 |
| 11 | 2,600 | 0,041 | 0,106 | 6,760 | 0,002 | 23,357 |
| 12 | 2,500 | 0,048 | 0,119 | 6,250 | 0,002 | 22,780 |
| 13 | 2,900 | 0,037 | 0,107 | 8,410 | 0,001 | 25,280 |
| 14 | 2,600 | 0,048 | 0,124 | 6,760 | 0,002 | 23,357 |
| 15 | 2,200 | 0,042 | 0,092 | 4,840 | 0,002 | 21,206 |
| 16 | 2,600 | 0,029 | 0,076 | 6,760 | 0,001 | 23,357 |
| 17 | 3,300 | 0,031 | 0,103 | 10,890 | 0,001 | 28,398 |
| 19 | 3,900 | 0,030 | 0,118 | 15,210 | 0,001 | 34,844 |
| 20 | 4,600 | 0,028 | 0,130 | 21,160 | 0,001 | 47,393 |
| 21 | 3,700 | 0,029 | 0,109 | 13,690 | 0,001 | 32,393 |
| 22 | 3,400 | 0,032 | 0,110 | 11,560 | 0,001 | 29,301 |
| Итого | 58,800 | 0,853 | 2,296 | 173,320 | 0,036 | 537,933 |
| сред знач | 2,800 | 0,041 | 0,109 | 8,253 | 0,002 | |
| стан отклон | 0,643 | 0,009 |
Рассчитаем a и b:
Получим линейное уравнение: . Выполнив его потенцирование, получим:
Для расчета теоретических значений y подставим в уравнение значения x .
· Рассчитаем параметры уравнений равносторонней гиперболы парной регрессии. Для оценки параметров приведем модель равносторонней гиперболы к линейному виду, заменив , тогда
Для расчетов используем данные табл. 7:
| № региона | X=1/z | Y | XY | X^2 | Y^2 | Y^cp |
| 1 | 0,357 | 28,000 | 10,000 | 0,128 | 784,000 | 26,715 |
| 2 | 0,417 | 21,300 | 8,875 | 0,174 | 453,690 | 23,259 |
| 3 | 0,476 | 21,000 | 10,000 | 0,227 | 441,000 | 19,804 |
| 4 | 0,385 | 23,300 | 8,962 | 0,148 | 542,890 | 25,120 |
| 5 | 0,588 | 15,800 | 9,294 | 0,346 | 249,640 | 13,298 |
| 6 | 0,400 | 21,900 | 8,760 | 0,160 | 479,610 | 24,227 |
| 7 | 0,417 | 20,000 | 8,333 | 0,174 | 400,000 | 23,259 |
| 8 | 0,385 | 22,000 | 8,462 | 0,148 | 484,000 | 25,120 |
| 9 | 0,357 | 23,900 | 8,536 | 0,128 | 571,210 | 26,715 |
| 10 | 0,385 | 26,000 | 10,000 | 0,148 | 676,000 | 25,120 |
| 11 | 0,385 | 24,600 | 9,462 | 0,148 | 605,160 | 25,120 |
| 12 | 0,400 | 21,000 | 8,400 | 0,160 | 441,000 | 24,227 |
| 13 | 0,345 | 27,000 | 9,310 | 0,119 | 729,000 | 27,430 |
| 14 | 0,385 | 21,000 | 8,077 | 0,148 | 441,000 | 25,120 |
| 15 | 0,455 | 24,000 | 10,909 | 0,207 | 576,000 | 21,060 |
| 16 | 0,385 | 34,000 | 13,077 | 0,148 | 1156,000 | 25,120 |
| 17 | 0,303 | 31,900 | 9,667 | 0,092 | 1017,610 | 29,857 |
| 19 | 0,256 | 33,000 | 8,462 | 0,066 | 1089,000 | 32,564 |
| 20 | 0,217 | 35,400 | 7,696 | 0,047 | 1253,160 | 34,829 |
| 21 | 0,270 | 34,000 | 9,189 | 0,073 | 1156,000 | 31,759 |
| 22 | 0,294 | 31,000 | 9,118 | 0,087 | 961,000 | 30,374 |
| Итого | 7,860 | 540,100 | 194,587 | 3,073 | 14506,970 | 540,100 |
| сред знач | 0,374 | 25,719 | 9,266 | 0,146 | 1318,815 | |
| стан отклон | 0,079 | 25,639 |
Рассчитаем a и b:
Получим линейное уравнение: . Получим уравнение регрессии: .
3. Оценка тесноты связи с помощью показателей корреляции и детерминации :
· Линейная модель. Тесноту линейной связи оценит коэффициент корреляции. Был получен следующий коэффициент корреляции rxy =b=7,122*, что говорит о прямой сильной связи фактора и результата. Коэффициент детерминации r²xy =(0,845)²=0,715. Это означает, что 71,5% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
· Степенная модель. Тесноту нелинейной связи оценит индекс корреляции. Был получен следующий индекс корреляции =, что говорит о очень сильной тесной связи, но немного больше чем в линейной модели. Коэффициент детерминации r²xy =0,7175. Это означает, что 71,75% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
· Экспоненциальная модель. Был получен следующий индекс корреляции ρxy =0,8124, что говорит о том, что связь прямая и очень сильная, но немного слабее, чем в линейной и степенной моделях. Коэффициент детерминации r²xy =0,66. Это означает, что 66% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
· Полулогарифмическая модель. Был получен следующий индекс корреляции ρxy =0,8578, что говорит о том, что связь прямая и очень сильная, но немного больше чем в предыдущих моделях. Коэффициент детерминации r²xy =0,7358. Это означает, что 73,58% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
· Гиперболическая модель. Был получен следующий индекс корреляции ρxy =0,8448 и коэффициент корреляции rxy =-0,1784 что говорит о том, что связь обратная очень сильная. Коэффициент детерминации r²xy =0,7358. Это означает, что 73,5% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
· Обратная модель. Был получен следующий индекс корреляции ρxy =0,8114 и коэффициент корреляции rxy =-0,8120, что говорит о том, что связь обратная очень сильная. Коэффициент детерминации r²xy =0,6584. Это означает, что 65,84% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
Вывод: по полулогарифмическому уравнению получена наибольшая оценка тесноты связи: ρxy =0,8578 (по сравнению с линейной, степенной, экспоненциальной, гиперболической, обратной регрессиями).
4. С помощью среднего (общего) коэффициента эластичности дайте сравнительную оценку силы связи фактора с результатом.
Рассчитаем коэффициент эластичности для линейной модели:
· Для уравнения прямой:y = 5,777+7,122∙x
· Для уравнениястепенноймодели :
· Для уравненияэкспоненциальноймодели :
Для уравненияполулогарифмическоймодели :
· Для уравнения обратной гиперболической модели :
· Для уравнения равносторонней гиперболической модели :
Сравнивая значения , характеризуем оценку силы связи фактора с результатом:
·
·
·
·
·
·
Известно, что коэффициент эластичности показывает связь между фактором и результатом, т.е. на сколько% изменится результат y от своей средней величины при изменении фактора х на 1% от своего среднего значения. В данном примере получилось, что самая большая сила связи между фактором и результатом в полулогарифмической модели, слабая сила связи в обратной гиперболической модели.
5. Оценка качества уравнений с помощью средней ошибки аппроксимации.
Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчетные) значения . Найдем величину средней ошибки аппроксимации :
В среднем расчетные значения отклоняются от фактических на:
· Линейная регрессия. =*100%= 8,5%, что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.
Качество построенной модели оценивается как хорошее, так как не превышает 8 -10%.
· Степенная регрессия. =*100%= 8,2%, что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.
Качество построенной модели оценивается как хорошее, так как не превышает 8 -10%.
· Экспоненциальная регрессия. =*100%= 9%, что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.
Качество построенной модели оценивается как хорошее, так как не превышает 8 -10%.
· Полулогарифмическая регрессия. =*100%= 7,9 что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.
Качество построенной модели оценивается как хорошее, так как не превышает 8 -10%.
· Гиперболическая регрессия. =*100%= 9,3 что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.
Качество построенной модели оценивается как хорошее, так как не превышает 8 -10%.
· Обратная регрессия. =*100%= 9,9 3 что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.
Качество построенной модели оценивается как хорошее, так как не превышает 8 -10%.
6. Рассчитаем F-критерий:
· Линейная регрессия. = *19= 47,579
http://welom.ru/srednyaya-oshibka-approksimacii-v-excel-ocenka-kachestva-uravneniya/
http://www.bestreferat.ru/referat-268496.html
















































