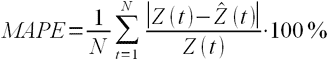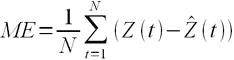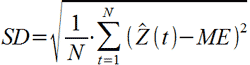Ошибка прогнозирования: виды, формулы, примеры
Ошибка прогнозирования — это такая величина, которая показывает, как сильно прогнозное значение отклонилось от фактического. Она используется для расчета точности прогнозирования, что в свою очередь помогает нам оценивать как точно и корректно мы сформировали прогноз. В данной статье я расскажу про основные процентные «ошибки прогнозирования» с кратким описанием и формулой для расчета. А в конце статьи я приведу общий пример расчётов в Excel. Напомню, что в своих расчетах я в основном использую ошибку WAPE или MAD-Mean Ratio, о которой подробно я рассказал в статье про точность прогнозирования, здесь она также будет упомянута.
В каждой формуле буквой Ф обозначено фактическое значение, а буквой П — прогнозное. Каждая ошибка прогнозирования (кроме последней!), может использоваться для нахождения общей точности прогнозирования некоторого списка позиций, по типу того, что изображен ниже (либо для любого другого подобной детализации):
Алгоритм для нахождения любой из ошибок прогнозирования для такого списка примерно одинаковый: сначала находим ошибку прогнозирования по одной позиции, а затем рассчитываем общую. Итак, основные ошибки прогнозирования!
MPE — Mean Percent Error
MPE — средняя процентная ошибка прогнозирования. Основная проблема данной ошибки заключается в том, что в нестабильном числовом ряду с большими выбросами любое незначительное колебание факта или прогноза может значительно поменять показатель ошибки и, как следствие, точности прогнозирования. Помимо этого, ошибка является несимметричной: одинаковые отклонения в плюс и в минус по-разному влияют на показатель ошибки.
- Для каждой позиции рассчитывается ошибка прогноза (из факта вычитается прогноз) — Error
- Для каждой позиции рассчитывается процентная ошибка прогноза (ошибка прогноза делится на фактический показатель) — Percent Error
- Находится среднее арифметическое всех процентных ошибок прогноза (процентные ошибки суммируются и делятся на количество) — Mean Percent Error
MAPE — Mean Absolute Percent Error
MAPE — средняя абсолютная процентная ошибка прогнозирования. Основная проблема данной ошибки такая же, как и у MPE — нестабильность.
- Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта по модулю) — Absolute Error
- Для каждой позиции рассчитывается абсолютная процентная ошибка прогноза (абсолютная ошибка прогноза делится на фактический показатель) — Absolute Percent Error
- Находится среднее арифметическое всех абсолютных процентных ошибок прогноза (абсолютные процентные ошибки суммируются и делятся на количество) — Mean Absolute Percent Error
Вместо среднего арифметического всех абсолютных процентных ошибок прогноза можно использовать медиану числового ряда (MdAPE — Median Absolute Percent Error), она наиболее устойчива к выбросам.
WMAPE / MAD-Mean Ratio / WAPE — Weighted Absolute Percent Error
WAPE — взвешенная абсолютная процентная ошибка прогнозирования. Одна из «лучших ошибок» для расчета точности прогнозирования. Часто называется как MAD-Mean Ratio, то есть отношение MAD (Mean Absolute Deviation — среднее абсолютное отклонение/ошибка) к Mean (среднее арифметическое). После упрощения дроби получается искомая формула WAPE, которая очень проста в понимании:
- Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта, по модулю) — Absolute Error
- Находится сумма всех фактов по всем позициям (общий фактический объем)
- Сумма всех абсолютных ошибок делится на сумму всех фактов — WAPE
Данная ошибка прогнозирования является симметричной и наименее чувствительна к искажениям числового ряда.
Рекомендуется к использованию при расчете точности прогнозирования. Более подробно читать здесь.
RMSE (as %) / nRMSE — Root Mean Square Error
RMSE — среднеквадратичная ошибка прогнозирования. Примерно такая же проблема, как и в MPE и MAPE: так как каждое отклонение возводится в квадрат, любое небольшое отклонение может значительно повлиять на показатель ошибки. Стоит отметить, что существует также ошибка MSE, из которой RMSE как раз и получается путем извлечения корня. Но так как MSE дает расчетные единицы измерения в квадрате, то использовать данную ошибку будет немного неправильно.
- Для каждой позиции рассчитывается квадрат отклонений (разница между фактом и прогнозом, возведенная в квадрат) — Square Error
- Затем рассчитывается среднее арифметическое (сумма квадратов отклонений, деленное на количество) — MSE — Mean Square Error
- Извлекаем корень из полученного результат — RMSE
- Для перевода в процентную или в «нормализованную» среднеквадратичную ошибку необходимо:
- Разделить на разницу между максимальным и минимальным значением показателей
- Разделить на разницу между третьим и первым квартилем значений показателей
- Разделить на среднее арифметическое значений показателей (наиболее часто встречающийся вариант)
MASE — Mean Absolute Scaled Error
MASE — средняя абсолютная масштабированная ошибка прогнозирования. Согласно Википедии, является очень хорошим вариантом для расчета точности, так как сама ошибка не зависит от масштабов данных и является симметричной: то есть положительные и отрицательные отклонения от факта рассматриваются в равной степени.
Важно! Если предыдущие ошибки прогнозирования мы могли использовать для нахождения точности прогнозирования некого списка номенклатур, где каждой из которых соответствует фактическое и прогнозное значение (как было в примере в начале статьи), то данная ошибка для этого не предназначена: MASE используется для расчета точности прогнозирования одной единственной позиции, основываясь на предыдущих показателях факта и прогноза, и чем больше этих показателей, тем более точно мы сможем рассчитать показатель точности. Вероятно, из-за этого ошибка не получила широкого распространения.
Здесь данная формула представлена исключительно для ознакомления и не рекомендуется к использованию.
Суть формулы заключается в нахождении среднего арифметического всех масштабированных ошибок, что при упрощении даст нам следующую конечную формулу:
Также, хочу отметить, что существует ошибка RMMSE (Root Mean Square Scaled Error — Среднеквадратичная масштабированная ошибка), которая примерно похожа на MASE, с теми же преимуществами и недостатками.
Это основные ошибки прогнозирования, которые могут использоваться для расчета точности прогнозирования. Но не все! Их очень много и, возможно, чуть позже я добавлю еще немного информации о некоторых из них. А примеры расчетов уже описанных ошибок прогнозирования будут выложены через некоторое время, пока что я подготавливаю пример, ожидайте.
Об авторе
HeinzBr
Автор статей и создатель сайта SHTEM.RU
Ошибка прогнозирования
Поскольку
будущее никогда нельзя в точности
предугадать по прошлому, то прогноз
будущего спроса всегда будет содержать
в себе ошибки в той или иной степени.
Модель экспоненциального сглаживания
прогнозирует средний уровень спроса.
Поэтому следует построить модель так,
чтобы уменьшить разность между прогнозом
и фактическим уровнем спроса. Эта
разность называется ошибкой прогнозирования.
Ошибка
прогнозирования выражается такими
показателями, как среднеквадратическое
отклонение, вариация или среднее
абсолютное отклонение. Раньше среднее
абсолютное отклонение использовалось
в качестве основного измерителя ошибки
прогнозирования при использовании
модели экспоненциального сглаживания.
Среднеквадратическое отклонение
отвергли из-за того, что рассчитывать
его сложнее, чем среднее абсолютное
отклонение, и у компьютеров на это просто
не хватало памяти. Сейчас у компьютеров
достаточно памяти, и теперь
среднеквадратическое отклонение
используется чаще.
Ошибку
прогнозирования можно определить с
помощью следующей формулы:
ОШИБКА
ПРОГНОЗА = ФАКТИЧЕСКИЙ СПРОС – ПРОГНОЗ
СПРОСА
Е
Рис. 3а. Нормальное
распределение ошибок прогноза
HeinzBr
Автор статей и создатель сайта SHTEM.RU
Ошибка прогнозирования
Поскольку
будущее никогда нельзя в точности
предугадать по прошлому, то прогноз
будущего спроса всегда будет содержать
в себе ошибки в той или иной степени.
Модель экспоненциального сглаживания
прогнозирует средний уровень спроса.
Поэтому следует построить модель так,
чтобы уменьшить разность между прогнозом
и фактическим уровнем спроса. Эта
разность называется ошибкой прогнозирования.
Ошибка
прогнозирования выражается такими
показателями, как среднеквадратическое
отклонение, вариация или среднее
абсолютное отклонение. Раньше среднее
абсолютное отклонение использовалось
в качестве основного измерителя ошибки
прогнозирования при использовании
модели экспоненциального сглаживания.
Среднеквадратическое отклонение
отвергли из-за того, что рассчитывать
его сложнее, чем среднее абсолютное
отклонение, и у компьютеров на это просто
не хватало памяти. Сейчас у компьютеров
достаточно памяти, и теперь
среднеквадратическое отклонение
используется чаще.
Ошибку
прогнозирования можно определить с
помощью следующей формулы:
ОШИБКА
ПРОГНОЗА = ФАКТИЧЕСКИЙ СПРОС – ПРОГНОЗ
СПРОСА
Е
Рис. 3а. Нормальное
распределение ошибок прогноза

прогноз спроса представляет собой
среднее арифметическое фактического
спроса, то сумма ошибок прогнозирования
за определенное количество временных
периодов будет равна нулю. Следовательно,
значение ошибки можно отыскать путем
суммирования квадратов ошибок
прогнозирования, что позволяет избежать
взаимного устранения положительных и
отрицательных ошибок прогнозирования.
Эта сумма делится на количество наблюдений
и затем из нее извлекается квадратный
корень. Показатель корректируется с
уменьшением одной степени свободы,
которая теряется при составлении
прогноза. В результате, уравнение
среднеквадратического отклонения имеет
вид:

г
SE
– средняя ошибка прогнозирования; Ai
– фактический спрос в период i;
Fi
– прогноз на период i;
N
– размер временного ряда.
Ф
Рис. 3б. Скошенное
распределение ошибок прогноза
орма распределения ошибок
прогнозирования является важной, когда
формулируются вероятностные утверждения
о степени надежности прогноза. Две
типовые формы распределения ошибок
прогнозирования показаны на рисунке
3.
Полагая,
что модель прогнозирования отражает
средние значения фактического спроса
достаточно хорошо и отклонения фактических
продаж от прогноза относительно невелики
по сравнению с абсолютной величиной
продаж, то вполне вероятно предположить
нормальное распределение ошибок
прогнозирования. В тех же случаях, когда
ошибка прогнозирования сопоставима по
величине с величиной спроса, имеет место
скошенное, или усеченное нормальное
распределение ошибок прогноза.
Определить
тип распределения в конкретной ситуации
можно с помощью теста на соответствие
критерию согласия хи-квадрат. В качестве
альтернативы можно использовать другой
тест, с помощью которого можно определить,
является ли распределение симметричным
(нормальным) или экспоненциальным
(разновидность скошенного распределения):
При
нормальном распределении около 2%
наблюдаемых значений превышают значение,
равное сумме среднего и удвоенного
значения среднеквадратического
отклонения. При экспоненциальном
распределении около 2% наблюдаемых
значений превышают среднее на величину
среднеквадратического отклонения,
умноженного на коэффициент 2,75.
Следовательно, в первом случае используется
нормальное распределение, а во втором
случае – экспоненциальное.
Пример.
Снова вернемся к нашему примеру. В
базовой модели экспоненциального
сглаживания были получены следующие
результаты:
-
Квартал
I
II
III
IV
Прошлый
год1
200700
900
1
100Текущий
год1
4001
000F3
= ?Прогноз
1
200779
1
005
Оценим
стандартную ошибку прогнозирования по
данным за первый и второй кварталы
текущего года, по которым нам известны
фактические и прогнозные значения.
Допустим, что спрос имеет нормальное
распределение относительно прогноза.
Рассчитаем границы доверительного
интервала с вероятностью 95% для третьего
квартала.
Стандартная
ошибка прогнозирования:
Используя
таблицу А (см. Приложение I), определяем
коэффициент z95%
= 1,96 и получаем границы доверительного
интервала по формуле:
Y
= F3
z(SE)
=1005
1,96298
= 1064
584,2
Следовательно,
с 95%-й вероятностью границы доверительного
интервала прогноза спроса на третий
квартал текущего года составляют
значения:
420,8
< Y
< 1589,2
Основной задачей при управлении запасами является определение объема пополнения, то есть, сколько необходимо заказать поставщику. При расчете этого объема используется несколько параметров — сколько будет продано в будущем, за какое время происходит пополнение, какие остатки у нас на складе и какое количество уже заказано у поставщика. То, насколько правильно мы определим эти параметры, будет влиять на то, будет ли достаточно товара на складе или его будет слишком много. Но наибольшее влияние на эффективность управления запасами влияет то, насколько точен будет прогноз. Многие считают, что это вообще основной вопрос в управлении запасами. Действительно, точность прогнозирования очень важный параметр. Поэтому важно понимать, как его оценивать. Это важно и для выявления причин дефицитов или неликвидов, и при выборе программных продуктов для прогнозирования продаж и управления запасами.
В данной статье я представила несколько формул для расчета точности прогноза и ошибки прогнозирования. Кроме этого, вы сможете скачать файлы с примерами расчетов этого показателя.
Статистические методы
Для оценки прогноза продаж используются статистические оценки Оценка ошибки прогнозирования временного ряда. Самый простой показатель – отклонение факта от прогноза в количественном выражении.
В практике рассчитывают ошибку прогнозирования по каждой отдельной позиции, а также рассчитывают среднюю ошибку прогнозирования. Следующие распространенные показатели ошибки относятся именно к показателям средних ошибок прогнозирования.
К ним относятся:
MAPE – средняя абсолютная ошибка в процентах
где Z(t) – фактическое значение временного ряда, а 
Данная оценка применяется для временных рядов, фактические значения которых значительно больше 1. Например, оценки ошибки прогнозирования энергопотребления почти во всех статьях приводятся как значения MAPE.
Если же фактические значения временного ряда близки к 0, то в знаменателе окажется очень маленькое число, что сделает значение MAPE близким к бесконечности – это не совсем корректно. Например, фактическая цена РСВ = 0.01 руб/МВт.ч, a прогнозная = 10 руб/МВт.ч, тогда MAPE = (0.01 – 10)/0.01 = 999%, хотя в действительности мы не так уж сильно ошиблись, всего на 10 руб/МВт.ч. Для рядов, содержащих значения близкие к нулю, применяют следующую оценку ошибки прогноза.
MAE – средняя абсолютная ошибка

Для оценки ошибки прогнозирования цен РСВ и индикатора БР корректнее использовать MAE.
После того, как получены значения для MAPE и/или MAE, то в работах обычно пишут: «Прогнозирование временного ряда энергопотребления с часовым разрешение проводилось на интервале с 01.01.2001 до 31.12.2001 (общее количество отсчетов N ~ 8500). Для данного прогноза значение MAPE = 1.5%». При этом, просматривая статьи, можно сложить общее впечатление об ошибки прогнозирования энергопотребления, для которого MAPE обычно колеблется от 1 до 5%; или ошибки прогнозирования цен на электроэнергию, для которого MAPE колеблется от 5 до 15% в зависимости от периода и рынка. Получив значение MAPE для собственного прогноза, вы можете оценить, насколько здорово у вас получается прогнозировать.
Кроме указанных методов иногда используют другие оценки ошибки, менее популярные, но также применимые. Подробнее об этих оценках ошибки прогноза читайте указанные статьи в Википедии.
ME – средняя ошибка
Встречается еще другое название этого показателя — Bias (англ. – смещение) демонстрирует величину отклонения, а также — в какую сторону прогноз продаж отклоняется от фактической потребности. Этот индикатор показывает, был ли прогноз оптимистичным или пессимистичным. То есть, отрицательное значение Bias говорит о том, что прогноз был завышен (реальная потребность оказалась ниже), и, наоборот, положительное значение о том, что прогноз был занижен. Цифровое значение показателя определяет величину отклонения (смещения).
MSE – среднеквадратичная ошибка

RMSE – квадратный корень из среднеквадратичной ошибки

.
SD – стандартное отклонение
где ME – есть средняя ошибка, определенная по формуле выше.
Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме ниже. Скачать пример расчета в Excel >>>
Связь точности и ошибки прогнозирования
В начале этого обсуждения разберемся с определениями.
Ошибка прогноза — апостериорная величина отклонения прогноза от действительного состояния объекта. Если говорить о прогнозе продаж, то это показатель отклонения фактических продаж от прогноза.
Точность прогнозирования есть понятие прямо противоположное ошибке прогнозирования. Если ошибка прогнозирования велика, то точность мала и наоборот, если ошибка прогнозирования мала, то точность велика. По сути дела оценка ошибки прогноза MAPE есть обратная величина для точности прогнозирования — зависимость здесь простая.
Точность прогноза в % = 100% – MAPE, встречается еще название этого показателя Forecast Accuracy. Вы практически не найдете материалов о прогнозировании, в которых приведены оценки именно точности прогноза, хотя с точки зрения здравого маркетинга корректней говорить именно о высокой точности. В рекламных статьях всегда будет написано о высокой точности. Показатель точности прогноза выражается в процентах:
- Если точность прогноза равна 100%, то выбранная модель описывает фактические значения на 100%, т.е. очень точно. Нужно сразу оговориться, что такого показателя никогда не будет, основное свойство прогноза в том, что он всегда ошибочен.
- Если 0% или отрицательное число, то совсем не описывает, и данной модели доверять не стоит.
Выбрать подходящую модель прогноза можно с помощью расчета показателя точность прогноза. Модель прогноза, у которой показатель точность прогноза будет ближе к 100%, с большей вероятностью сделает более точный прогноз. Такую модель можно назвать оптимальной для выбранного временного ряда. Говоря о высокой точности, мы говорим о низкой ошибки прогноза и в этой области недопонимания быть не должно. Не имеет значения, что именно вы будете отслеживать, но важно, чтобы вы сравнивали модели прогнозирования или целевые показатели по одному показателю – ошибка прогноза или точность прогнозирования.
Ранее я использовала оценку MAPE, до тех пор пока не встретила формулу, которую рекомендует Валерий Разгуляев.
Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме. Скачать пример расчета в Excel >>>
Оценка ошибки прогноза – формула Валерия Разгуляева (сайт http://upravlenie-zapasami.ru/)
Одной из самых используемых формул оценки ошибки прогнозирования является следующая формула:
где: P – это прогноз, а S – факт за тот же месяц. Однако у этой формулы есть серьезное ограничение — как оценить ошибку, если факт равен нулю? Возможный ответ, что в таком случае D = 100% – который означает, что мы полностью ошиблись. Однако простой пример показывает, что такой ответ — не верен:
|
вариант |
прогноз |
факт |
ошибка прогноза |
|
№1 |
4 |
0 |
100% |
|
№2 |
4 |
1 |
300% |
|
№3 |
1 |
4 |
75% |
Оказывается, что в варианте развития событий №2, когда мы лучше угадали спрос, чем в варианте №1, ошибка по данной формуле оказалась – больше. То есть ошиблась уже сама формула. Есть и другая проблема, если мы посмотрим на варианты №2 и №3, то увидим, что имеем дело с зеркальной ситуацией в прогнозе и факте, а ошибка при этом отличается – в разы!.. То есть при такой оценке ошибки прогноза нам лучше его заведомо делать менее точным, занижая показатель – тогда ошибка будет меньше!.. Хотя понятно, что чем точнее будет прогноз – тем лучше будет и закупка. Поэтому для расчёта ошибки Валерий Разгуляев рекомендует использовать следующую формулу:
В таком случае для тех же примеров ошибка рассчитается иначе:
|
вариант |
прогноз |
факт |
ошибка прогноза |
|
№1 |
4 |
0 |
100% |
|
№2 |
4 |
1 |
75% |
|
№3 |
1 |
4 |
75% |
Как мы видим, в варианте №1 ошибка становится равной 100%, причём это уже – не наше предположение, а чистый расчёт, который можно доверить машине. Зеркальные же варианты №2 и №3 – имеют и одинаковую ошибку, причём эта ошибка меньше ошибки самого плохого варианта №1. Единственная ситуация, когда данная формула не сможет дать однозначный ответ – это равенство знаменателя нулю. Но максимум из прогноза и факта равен нулю, только когда они оба равны нулю. В таком случае получается, что мы спрогнозировали отсутствие спроса, и его, действительно, не было – то есть ошибка тоже равна нулю – мы сделали совершенно точное предсказание.
Визуальный метод – графический
Визуальный метод состоит в том, что мы на график выводим значение прогнозной модели и факта продаж по тем моделям, которые хотим сравнить. Далее сравниваем визуально, насколько прогнозная модель близка к фактическим продажам. Давайте рассмотрим на примере. В таблице представлены две прогнозные модели, а также фактические продажи по этому товару за тот же период. Для наглядности мы также рассчитали ошибку прогнозирования по обеим моделям.
По графикам очевидно, что модель 2 описывает лучше продажи этого товара. Оценка ошибки прогнозирования тоже это показывает – 65% и 31% ошибка прогнозирования по модели 1 и модели 2 соответственно.


Недостатком данного метода является то, что небольшую разницу между моделями сложно выявить — разницу в несколько процентов сложно оценить по диаграмме. Однако эти несколько процентов могут существенно улучшить качество прогнозирования и планирования пополнения запасов в целом.
Использование формул ошибки прогнозирования на практике
Практический аспект оценки ошибки прогнозирования я вывела отдельным пунктом. Это связано с тем, что все статистические методы расчета показателя ошибки прогнозирования рассчитывают то, насколько мы ошиблись в прогнозе в количественных показателях. Давайте теперь обсудим, насколько такой показатель будет полезен в вопросах управления запасами. Дело в том, что основная цель управления запасами — обеспечить продажи, спрос наших клиентов. И, в конечном счете, максимизировать доход и прибыль компании. А эти показатели оцениваются как раз в стоимостном выражении. Таким образом, нам важно при оценке ошибки прогнозирования понимать какой вклад каждая позиция внесла в объем продаж в стоимостном выражении. Когда мы оцениваем ошибку прогнозирования в количественном выражении мы предполагаем, что каждый товар имеет одинаковый вес в общем объеме продаж, но на самом деле это не так – есть очень дорогие товары, есть товары, которые продаются в большом количестве, наша группа А, а есть не очень дорогие товары, есть товары которые вносят небольшой вклад в объем продаж. Другими словами большая ошибка прогнозирования по товарам группы А будет нам «стоить» дороже, чем низкая ошибка прогнозирования по товарам группы С, например. Для того, чтобы наша оценка ошибки прогнозирования была корректной, релевантной целям управления запасами, нам необходимо оценивать ошибку прогнозирования по всем товарам или по отдельной группе не по средними показателями, а средневзвешенными с учетом прогноза и факта в стоимостном выражении.
Пример расчета такой оценки Вы сможете увидеть в файле Excel.
Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме. Скачать пример расчета в Excel >>>
При этом нужно помнить, что для оценки ошибки прогнозирования по отдельным позициям мы рассчитываем по количеству, но вот если нам важно понять в целом ошибку прогнозирования по компании, например, для оценки модели, которую используем, то нам нужно рассчитывать не среднюю оценку по всем товарам, а средневзвешенную с учетом стоимостной оценки. Оценку можно брать по ценам себестоимости или ценам продажи, это не играет большой роли, главное, эти же цены (тип цен) использовать при всех расчетах.
Для чего используется ошибка прогнозирования
В первую очередь, оценка ошибки прогнозирования нам необходима для оценки того, насколько мы ошибаемся при планировании продаж, а значит при планировании поставок товаров. Если мы все время прогнозируем продажи значительно больше, чем потом фактически продаем, то вероятнее всего у нас будет излишки товаров, и это невыгодно компании. В случае, когда мы ошибаемся в обратную сторону – прогнозируем продажи меньше чем фактические продажи, с большой вероятностью у нас будут дефициты и компания не дополучит прибыль. В этом случае ошибка прогнозирования служит индикатором качества планирования и качества управления запасами.
Индикатором того, что повышение эффективности возможно за счет улучшения качества прогнозирования. За счет чего можно улучшить качество прогнозирования мы не будем здесь рассматривать, но одним из вариантов является поиск другой модели прогнозирования, изменения параметров расчета, но вот насколько новая модель будет лучше, как раз поможет показатель ошибки прогнозирования или точности прогноза. Сравнение этих показателей по нескольким моделям поможет определить ту модель, которая дает лучше результат.
В идеальном случае, мы можем так подбирать модель для каждой отдельной позиции. В этом случае мы будем рассчитывать прогноз по разным товарам по разным моделям, по тем, которые дают наилучший вариант именно для конкретного товара.
Также этот показатель можно использовать при выборе автоматизированного инструмента для прогнозирования спроса и управления запасами. Вы можете сделать тестовые расчеты прогноза в предлагаемой программе и сравнить ошибку прогнозирования полученного прогноза с той, которая есть у вашей существующей модели. Если у предлагаемого инструмента ошибка прогнозирования меньше. Значит, этот инструмент можно рассматривать для применения в компании. Кроме этого, показатель точности прогноза или ошибки прогнозирования можно использовать как KPI сотрудников, которые отвечают за подготовку прогноза продаж или менеджеров по закупкам, в том случае, если они рассчитывают прогноз будущих продаж при расчете заказа.
Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме. Скачать пример расчета в Excel >>>
Если вы хотите повысить эффективность управления запасами и увеличить оборачиваемость товарных запасов, предлагаю изучить мастер-класс «Как увеличить оборачиваемость товарных запасов».
Источник: сайт http://uppravuk.net/
Что такое ошибка прогноза в статистике? (Определение и примеры)
17 авг. 2022 г.
читать 2 мин
В статистике ошибка прогнозирования относится к разнице между прогнозируемыми значениями, сделанными некоторой моделью, и фактическими значениями.
Ошибка прогноза часто используется в двух случаях:
1. Линейная регрессия: используется для прогнозирования значения некоторой переменной непрерывного отклика.
Обычно мы измеряем ошибку прогноза модели линейной регрессии с помощью метрики, известной как RMSE , что означает среднеквадратичную ошибку.
Он рассчитывается как:
СКО = √ Σ(ŷ i – y i ) 2 / n
куда:
- Σ — это символ, который означает «сумма»
- ŷ i — прогнозируемое значение для i -го наблюдения
- y i — наблюдаемое значение для i -го наблюдения
- n — размер выборки
2. Логистическая регрессия: используется для прогнозирования значения некоторой бинарной переменной отклика.
Одним из распространенных способов измерения ошибки прогнозирования модели логистической регрессии является метрика, известная как общий коэффициент ошибочной классификации.
Он рассчитывается как:
Общий коэффициент ошибочной классификации = (# неверных прогнозов / # всего прогнозов)
Чем ниже значение коэффициента ошибочной классификации, тем лучше модель способна предсказать результаты переменной отклика.
В следующих примерах показано, как на практике рассчитать ошибку прогнозирования как для модели линейной регрессии, так и для модели логистической регрессии.
Пример 1: Расчет ошибки прогноза в линейной регрессии
Предположим, мы используем регрессионную модель, чтобы предсказать количество очков, которое 10 игроков наберут в баскетбольном матче.
В следующей таблице показаны прогнозируемые очки по модели и фактические очки, набранные игроками:
Мы рассчитали бы среднеквадратичную ошибку (RMSE) как:
- СКО = √ Σ(ŷ i – y i ) 2 / n
- СКО = √(((14-12) 2 +(15-15) 2 +(18-20) 2 +(19-16) 2 +(25-20) 2 +(18-19) 2 +(12- 16) 2 +(12-20) 2 +(15-16) 2 +(22-16) 2 ) / 10)
- СКО = 4
Среднеквадратическая ошибка равна 4. Это говорит нам о том, что среднее отклонение между прогнозируемыми набранными баллами и фактическими набранными баллами равно 4.
Связанный: Что считается хорошим значением RMSE?
Пример 2: Расчет ошибки прогноза в логистической регрессии
Предположим, мы используем модель логистической регрессии, чтобы предсказать, попадут ли 10 баскетболистов из колледжа в НБА.
В следующей таблице показан прогнозируемый результат для каждого игрока по сравнению с фактическим результатом (1 = выбран на драфте, 0 = не выбран на драфте):
Мы рассчитали бы общий коэффициент ошибочной классификации как:
- Общий коэффициент ошибочной классификации = (# неверных прогнозов / # всего прогнозов)
- Общий коэффициент ошибочной классификации = 4/10
- Общий коэффициент ошибочной классификации = 40%
Общий уровень ошибочной классификации составляет 40% .
Это значение довольно велико, что указывает на то, что модель не очень хорошо предсказывает, будет ли игрок выбран на драфте.
Дополнительные ресурсы
Следующие руководства содержат введение в различные типы методов регрессии:
Введение в простую линейную регрессию
Введение в множественную линейную регрессию
Введение в логистическую регрессию
Для анализа результатов расчета прогноза, в продолжение ряда вы можете рассчитать следующие ошибки:
- MAPE – средняя абсолютная ошибка в % . Ошибка оценивает на сколько велики ошибки в сравнении со значением ряда и с ошибками в соседних рядах.
Подробнее читайте в статье на нашем сайте: http://4analytics.ru/metodi-analiza/mape-%E2%80%93-srednyaya-absolyutnaya-oshibka-praktika-primeneniya.html - MRPE – средняя относительная ошибка в %, оценивает на сколько велика дельта между фактом и прогнозом. Чем ближе к 100%, тем больше ошибка, чем ближе к нулю, тем ошибка меньше.
- MSE – средняя квадратическая ошибка, подчеркивает большие ошибки за счет возведения каждой ошибки в квадрат.
Подробнее читайте в статье на нашем сайте:
http://4analytics.ru/metodi-analiza/mse-%E2%80%93-srednekvadraticheskaya-oshibka-v-excel.html - MPE – средняя процентная ошибка – показывает завышен или занижен прогноз относительно факта. Если ошибка меньше нулю, то прогноз последовательно завышен, если ошибка больше нуля, то прогноз последовательно занижен.
Подробнее читайте в статье на нашем сайте:
http://4analytics.ru/metodi-analiza/mpe-%E2%80%93-srednyaya-procentnaya-oshibka-v-excel.html - MAD – среднее абсолютное отклонение. Используется, когда важно измерить ошибку в тех же единицах, что и исходный ряд.
Подробнее читайте в статье на нашем сайте:
http://4analytics.ru/planirovanie-i-prognozirovanie-praktika/dopolnitelnie-oborotnie-sredstva-za-schet-povisheniya-tochnosti-prognoza.html - A MAPE – ошибка, которая показывает отклонение средних значений ряда к средним значениям модели прогноза. Имеет значение при неравномерном перераспределении значений ряда по периодам.
- S MAPE – ошибка, которая показывает отклонение суммы значения ряда к сумме значений модели прогноза. Имеет значение при неравномерном перераспределении значений ряда по периодам.
А также 2 показателя «Точность прогноза»:
- Точность прогноза = 1 – МАРЕ
- Точность прогноза 2 = 1 – MRPE
Для расчета ошибок одновременно с прогнозом, нажимаем кнопку «Расчет ошибок» в меню «FORECAST»
В открывшемся окне выбираем нужные для расчета ошибки:
Теперь при расчете прогноза, в продолжение ряда, программа автоматически сделает расчет отмеченных Вами ошибок:
Когда перед компанией встают задачи прогнозирования спроса для управления товарными запасами, обычно появляется вопрос, связанный с выбором метода прогнозирования. Но как определить, какой метод лучше? Однозначного ответа на этот вопрос нет. Однако, исходя из нашей практики, самым распространенным методам оценки точности прогноза является средняя абсолютная процентная ошибка (MAPE). Также используются средняя абсолютная ошибка (MAE) и средняя квадратичная ошибка прогнозирования (RMSE).
Ошибка прогноза в данном случае – это разница между фактическим значением спроса и его прогнозным значением. Т.е, чем больше будет ошибка прогнозирования, тем менее точен прогноз. Например, при ошибке прогнозирования 5%, точность прогноза будет составлять 95%. Изначально MAPE использовалась для прогнозирования временных рядов, которые имеют регулярное нормальное распределение, такие как, например, потребление электроэнергии. И только после ее стали применять для оценки прогноза спроса. На практике ошибку могут рассчитывать по каждой позиции товара, а также среднюю оценку по всем товарным группам.
Несмотря на то, что большинство компаний до сих пор используют вышеописанные методы для оценки, мы считаем, что они не достаточно корректны и не подходят для применения в реальном бизнесе. Для простоты изложения, выделим три ключевых момента, которые приводят к некорректным выводам при использовании вышеописанных методов оценки. Назовем их ошибка №1, №2 и №3. Сначала мы подробно опишем эти ошибки, а потом расскажем, как наши методы сравнения помогаю их ликвидировать.
О некорректности использования MAPE, RMSE и других распространенных ошибок
Ошибка № 1 заключается в том, что используемые методы больше относятся к математике, нежели к бизнесу, по той причине, что это обезличенные цифры (или проценты), которые ничего не говорят про деньги. Бизнесу же нужно принимать решения на основе выгоды, которую он получит в деньгах. Например, ошибка в 80% на первый взгляд звучит устрашающие. Но в реальности за ней могут скрываться совершенно разные вещи. Ошибка по гвоздям со стоимостью одного гвоздя в 0,5 рублей – это одни потери. Но они совершенно несопоставимы с потерями от продажи промышленного оборудования стоимостью 700 000 рублей с той же величиной ошибки прогнозирования. Ко всему прочему также больше значение имеет объем продукции, что тоже никак не учитывается данными ошибками прогнозирования.
Второй важный момент (ошибка №2), который не учитывают данные оценки прогнозирования – это заморозка денежных средств в запасах и недополученная прибыль от дефицита продукции на складе. Например, если мы прогнозируем продажу 20 колесных дисков, а по факту продали 15. То это одна цена ошибки – 5 колесных дисков, которые потребуют затраты на хранение на определенное время, и как следствие стоимость замороженных оборотных средств под определенный процент. Если рассмотреть обратную ситуацию – прогнозируем продажу 20 дисков, спрос составляет 25 штук. Это уже упущенная прибыль, которая составляет разницу сумм закупки и реализации продукции. По сути мы имеет одну и ту же ошибку прогнозирования, но результат от нее может быть совершенно разным.
Третий ключевой момент (ошибка №3) – описанные ошибки распространяются только на точечный прогноз спроса и не описывают страховой запас. А он в некоторых случаях может составлять от 20% до 70% от общих товарных запасов на складе. Поэтому, какой бы точный не был прогноз с точки зрения описанных выше методов, мы все равно не оцениваем точность страхового запаса, а значит реальные данные могут быть значительно искажены.
Критерии, привязанные к прибыльности бизнеса
Учитывая описанные выше недостатки ошибок прогнозирования, такой подход не является корректным и надежным для сравнения алгоритмов. Ко всему прочему он зачастую оторван от реального бизнеса. Используемый же нами подход позволяет оценить точность алгоритмов в деньгах, рассчитать стоимость ошибки прогнозирования на понятном для бизнеса языке финансов. Таким образом это позволяет нам ликвидировать ошибку №1.
В случае с ошибкой № 2, мы рассчитываем два различных значения. Если прогноз окажется меньше реального спроса, то он приведет к дефициту, экономический урон от которого рассчитывается, как количество недопроданных товаров, умноженное на разность цен закупки и реализации. Например, вы закупаете колесные диски по 3000 рублей за штуку и продаете по 4000. Прогноз на месяц составил 1000 дисков, реальный спрос оказался 1200 штук. Экономический урон будет равен:
(1200-1000)*(4000-3000)=200 000 рублей.
В случае превышения прогноза над реальным спросом компания понесет убытки по хранению продукции. Экономический урон будет равен сумме затрат на нереализованную продукцию, помноженную на ставку альтернативных вложений за этот период. Предположим, что реальный спрос в предыдущем примере оказался 800 дисков и вам пришлось хранить диски еще один месяц. Пусть ставка альтернативных вложений составляет 20% в год. Тогда экономический урон будет равен
(1000-800)*3000*0,2/12=10 000 рублей.
Соответственно, в каждом конкретном случае, мы будет учитывать одно из этих значений.
Для того, чтобы ликвидировать ошибку № 3, мы сравниваем алгоритмы с использованием понятия уровень сервиса. Уровень сервиса (здесь и далее — уровень сервиса II рода, fill rate) – это доля спроса, которую мы гарантировано покроем с использованием имеющихся на складе запасов в течении периода их пополнения. Например, уровень сервиса 90% означает, что мы удовлетворим 90% спроса. На первый взгляд может показаться логичным, что уровень сервиса всегда должен составлять 100%. Тогда и прибыль будет максимальна. Но в реальных ситуациях зачастую дело обстоит иначе: удовлетворение 100% уровня сервиса приводит к сильному перезатариванию склада, а для товаров с ограниченными сроками годности еще и к списанию. И убытки от затрат на хранение, списания просроченной продукции и недополученной прибыли от вложения свободных денег в итоге снизят прибыть от реализации, в случае если бы мы поддерживали уровень сервиса 95%. Нужно заметить, что для каждой отдельной позиции товаров будет свой оптимальный уровень сервиса.
Подробнее о уровне сервиса, его видах и примерах расчета читайте в статье «Что такое уровень сервиса и почему он важен.»
Так как страховой запас может составлять значительную долю, его нельзя игнорировать при сравнении алгоритмов (как это делается при расчете ошибок MAPE, RMSE и т.д.). Поэтому мы делаем сравнение не прогноза, а оптимального запаса с заданным уровнем сервиса. Оптимальный запас для заданного уровня сервиса – это такое количество товаров, которое нужно хранить на складе, чтобы получить максимум прибыли от реализации товаров и одновременно сократить издержки на хранение до минимума.
В качестве основного критерия (критерий №1) качества прогнозирования мы используем суммарное значение потерь для заданного уровня сервиса, о котором писали выше (исправление ошибки №2). Таким образом мы оцениваем потери в денежном выражении при использовании данного конкретного алгоритма. Чем меньше потери — тем точнее работает алгоритм.
Здесь нужно заметить, что для разных уровней сервиса оптимальный запас тоже может различаться. И в одном случае прогноз будет точно в него попадать, а в другом возможны перекосы в большую, либо меньшую сторону. Так как многие компании не рассчитывают оптимальный уровень сервиса, а используют заданный заранее, значение основного критерия мы вычисляем для всех самых распространенных уровней сервиса: 70%, 75%, 80%, 85%, 90%, 95%, 98%, 99% и суммируем потери. Таким образом мы можем проверить, насколько хорошо в целом работает модель.
Для компаний, которые, считают оптимальный уровень сервиса мы используем дополнительный критерий (критерий №2) для оценки. В общем виде он выглядит как соотношение потерь на оптимальном уровне сервиса по ожидаемому (модельному) распределению продаж и по реальному распределению продаж (по факту). Прогнозируемое значение оптимального уровня сервиса не всегда соответствует оптимальному значению уже на реальном распределении продаж. Поэтому мы должны сравнивать ошибку между прогнозом объема продаж на оптимальном (по модели) уровне сервиса и реальным объемом продаж, обеспечивающим оптимальное значение уровня сервиса по реальным данным.
Что проиллюстрировать применение данного критерия, вернемся к нашему примеру с дисками. Предположим, что прогнозное значение оптимального уровня сервиса для него составляет 90%, а оптимальный объем запаса для этого случая примем равным 3000 колесных дисков. Пусть в первом случае реальный уровень сервиса оказался выше прогнозного и составил 92%. Соответственно объем заказов также вырос и составил 3300 дисков. Ошибка прогнозирования будет рассчитываться как разность между реальным и фактическим объемом продаж, умноженная на разность цен реализации. Итого, мы имеем:
(3300-3000)*(4000-3000)=300 000 рублей.
Теперь представим обратную ситуацию: реальный уровень сервиса оказался меньше прогнозного и составил 87%. Реальный объем продаж при этом составил 2850 дисков. Ошибка прогнозирования будет рассчитана, как сумма затрат на нереализованную продукцию, умноженную на ставку альтернативных вложений за этот период (в качестве примера берем период сроком месяц и ставку равную 20% годовых). Итоговое значение критерия будет равно:
(3000-2850)*3000*0,2/12 = 7500 рублей
Конечно, в идеальном случае, мы должны рассчитывать ошибку только при оптимальном уровне сервиса, между прогнозным и реальным значениями. Но так как не все компании еще перешли на оптимальный уровень сервиса, мы вынуждены использовать два критерия.
Используемые нами критерии в отличие от классических математических ошибок, показывают суммарные потери в деньгах при применении той или иной модели. Соответственно, наилучшей будет модель, которая обеспечивает минимальные потери. Такой подход позволят бизнес-пользователям оценить работу различных алгоритмов на понятном им языке.
Пример сравнения точности прогнозирования системы Forecast NOW c методом ARIMA (на базе номенклатуры бытовой химии):
|
Критерий (потери в рублях) |
Forecast NOW! |
ARIMA |
Разность |
|
Критерий №1 (потери на оптимальном уровне сервиса) |
92 997 114 |
169 916 601 |
82,71% |
|
Критерий №2 |
4 188 749 |
7 611 365 |
81,71% |
|
Критерий №1 (суммарное значение по распространенным уровням сервиса) |
820 099 299 |
1 550 434 475 |
89,05% |
Пример сравнения точности прогнозирования системы Forecast NOW c методом Кростона (на базе номенклатуры бытовой химии):
|
Критерий (потери в рублях) |
Forecast NOW! |
Метод Кростона |
Разность |
|
Критерий №1 (потери на оптимальном уровне сервиса) |
6 379 616 |
8 328 509 |
30,55% |
|
Критерий №2 |
1 076 984 |
1 341 537 |
24,56% |
|
Критерий №1 (суммарное значение по распространенным уровням сервиса) |
128 690 989 |
161 891 666 |
20,51% |
Оценка ошибки прогнозирования временного ряда
Работая с научными публикациями, сталкиваюсь с различными показателями ошибок прогнозирования временных рядов. Среди всех встречающихся оценок ошибки прогнозирования стоит отметить две, которые в настоящее время, являются самыми популярными: MAE и MAPE.
Пусть ошибка есть разность:
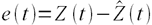
где Z(t) – фактическое значение временного ряда, а 
Тогда формулы для оценок ошибки прогнозирования временных рядов для N отчетов можно записать в следующем виде.
MAPE – средняя абсолютная ошибка в процентах
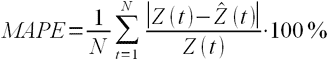
Данная оценка применяется для временных рядов, фактические значения которых значительно больше 1. Например, оценки ошибки прогнозирования энергопотребления почти во всех статьях приводятся как значения MAPE.
Если же фактические значения временного ряда близки к 0, то в знаменателе окажется очень маленькое число, что сделает значение MAPE близким к бесконечности – это не совсем корректно. Например, фактическая цена РСВ = 0.01 руб/МВт.ч, a прогнозная = 10 руб/МВт.ч, тогда MAPE = (0.01 – 10)/0.01 = 999%, хотя в действительности мы не так уж сильно ошиблись, всего на 10 руб/МВт.ч. Для рядов, содержащих значения близкие к нулю, применяют следующую оценку ошибки прогноза.
MAE – средняя абсолютная ошибка

Для оценки ошибки прогнозирования цен РСВ и индикатора БР корректнее использовать MAE.
После того, как получены значения для MAPE и/или MAE, то в работах обычно пишут: «Прогнозирование временного ряда энергопотребления с часовым разрешение проводилось на интервале с 01.01.2001 до 31.12.2001 (общее количество отсчетов N ~ 8500). Для данного прогноза значение MAPE = 1.5%». При этом, просматривая статьи, можно сложить общее впечатление об ошибки прогнозирования энергопотребления, для которого MAPE обычно колеблется от 1 до 5%; или ошибки прогнозирования цен на электроэнергию, для которого MAPE колеблется от 5 до 15% в зависимости от периода и рынка. Получив значение MAPE для собственного прогноза, вы можете оценить, насколько здорово у вас получается прогнозировать.
Кроме указанных иногда используют другие оценки ошибки, менее популярные, но также применимые. Подробнее об этих оценках ошибки прогноза читайте указанные статьи в Википедии.
MSE – среднеквадратичная ошибка

RMSE – квадратный корень из среднеквадратичной ошибки

ME – средняя ошибка
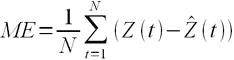
SD – стандартное отклонение
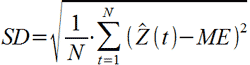
Связь точности и ошибки прогнозирования
Точность прогнозирования есть понятие прямо противоположное ошибке прогнозирования. Если ошибка прогнозирования велика, то точность мала и наоборот, если ошибка прогнозирования мала, то точность велика. По сути дела оценка ошибки прогноза MAPE есть обратная величина для точности прогнозирования — зависимость здесь простая.
Точность прогноза в % = 100% – MAPE
Величину точности оценивать не принято, говоря о прогнозировании всегда оценивают, то есть определяют значение именно ошибки прогноза, то есть величину MAPE и/или MAE. Однако нужно понимать, что если MAPE = 5%, то точность прогнозирования = 95%. Говоря о высокой точности, мы всегда говорим о низкой ошибки прогноза и в этой области недопонимания быть не должно. Вы практически не найдете материалов о прогнозировании, в которых приведены оценки именно точности прогноза, хотя с точки зрения здравого маркетинга корректней говорить именно о высокой точности. В рекламных статьях всегда будет написано о высокой точности.
При этом величина MAPE является количественной оценкой именно ошибки, и эта величина нам ясно говорит и о точности прогнозирования, исходя из приведенной выше простой формулы. Таким образом, оценивая ошибку, мы всегда оцениваем точность прогнозирования.
Перевод
Ссылка на автора
Показатели эффективности прогнозирования по временным рядам дают сводку об умениях и возможностях модели прогноза, которая сделала прогнозы.
Есть много разных показателей производительности на выбор. Может быть непонятно, какую меру использовать и как интерпретировать результаты.
В этом руководстве вы узнаете показатели производительности для оценки прогнозов временных рядов с помощью Python.
Временные ряды, как правило, фокусируются на прогнозировании реальных значений, называемых проблемами регрессии. Поэтому показатели эффективности в этом руководстве будут сосредоточены на методах оценки реальных прогнозов.
После завершения этого урока вы узнаете:
- Основные показатели выполнения прогноза, включая остаточную ошибку прогноза и смещение прогноза.
- Вычисления ошибок прогноза временного ряда, которые имеют те же единицы, что и ожидаемые результаты, такие как средняя абсолютная ошибка.
- Широко используются вычисления ошибок, которые наказывают большие ошибки, такие как среднеквадратическая ошибка и среднеквадратичная ошибка.
Давайте начнем.
Ошибка прогноза (или остаточная ошибка прогноза)
ошибка прогноза рассчитывается как ожидаемое значение минус прогнозируемое значение.
Это называется остаточной ошибкой прогноза.
forecast_error = expected_value - predicted_valueОшибка прогноза может быть рассчитана для каждого прогноза, предоставляя временной ряд ошибок прогноза.
В приведенном ниже примере показано, как можно рассчитать ошибку прогноза для серии из 5 прогнозов по сравнению с 5 ожидаемыми значениями. Пример был придуман для демонстрационных целей.
expected = [0.0, 0.5, 0.0, 0.5, 0.0]
predictions = [0.2, 0.4, 0.1, 0.6, 0.2]
forecast_errors = [expected[i]-predictions[i] for i in range(len(expected))]
print('Forecast Errors: %s' % forecast_errors)При выполнении примера вычисляется ошибка прогноза для каждого из 5 прогнозов. Список ошибок прогноза затем печатается.
Forecast Errors: [-0.2, 0.09999999999999998, -0.1, -0.09999999999999998, -0.2]Единицы ошибки прогноза совпадают с единицами прогноза. Ошибка прогноза, равная нулю, означает отсутствие ошибки или совершенный навык для этого прогноза.
Средняя ошибка прогноза (или ошибка прогноза)
Средняя ошибка прогноза рассчитывается как среднее значение ошибки прогноза.
mean_forecast_error = mean(forecast_error)Ошибки прогноза могут быть положительными и отрицательными. Это означает, что при вычислении среднего из этих значений идеальная средняя ошибка прогноза будет равна нулю.
Среднее значение ошибки прогноза, отличное от нуля, указывает на склонность модели к превышению прогноза (положительная ошибка) или занижению прогноза (отрицательная ошибка). Таким образом, средняя ошибка прогноза также называется прогноз смещения,
Ошибка прогноза может быть рассчитана непосредственно как среднее значение прогноза. В приведенном ниже примере показано, как среднее значение ошибок прогноза может быть рассчитано вручную.
expected = [0.0, 0.5, 0.0, 0.5, 0.0]
predictions = [0.2, 0.4, 0.1, 0.6, 0.2]
forecast_errors = [expected[i]-predictions[i] for i in range(len(expected))]
bias = sum(forecast_errors) * 1.0/len(expected)
print('Bias: %f' % bias)При выполнении примера выводится средняя ошибка прогноза, также известная как смещение прогноза.
Bias: -0.100000Единицы смещения прогноза совпадают с единицами прогнозов. Прогнозируемое смещение нуля или очень маленькое число около нуля показывает несмещенную модель.
Средняя абсолютная ошибка
средняя абсолютная ошибка или MAE, рассчитывается как среднее значение ошибок прогноза, где все значения прогноза вынуждены быть положительными.
Заставить ценности быть положительными называется сделать их абсолютными. Это обозначено абсолютной функциейабс ()или математически показано как два символа канала вокруг значения:| Значение |,
mean_absolute_error = mean( abs(forecast_error) )кудаабс ()делает ценности позитивными,forecast_errorодна или последовательность ошибок прогноза, иимею в виду()рассчитывает среднее значение.
Мы можем использовать mean_absolute_error () функция из библиотеки scikit-learn для вычисления средней абсолютной ошибки для списка прогнозов. Пример ниже демонстрирует эту функцию.
from sklearn.metrics import mean_absolute_error
expected = [0.0, 0.5, 0.0, 0.5, 0.0]
predictions = [0.2, 0.4, 0.1, 0.6, 0.2]
mae = mean_absolute_error(expected, predictions)
print('MAE: %f' % mae)При выполнении примера вычисляется и выводится средняя абсолютная ошибка для списка из 5 ожидаемых и прогнозируемых значений.
MAE: 0.140000Эти значения ошибок приведены в исходных единицах прогнозируемых значений. Средняя абсолютная ошибка, равная нулю, означает отсутствие ошибки.
Средняя квадратическая ошибка
средняя квадратическая ошибка или MSE, рассчитывается как среднее значение квадратов ошибок прогноза. Возведение в квадрат значений ошибки прогноза заставляет их быть положительными; это также приводит к большему количеству ошибок.
Квадратные ошибки прогноза с очень большими или выбросами возводятся в квадрат, что, в свою очередь, приводит к вытягиванию среднего значения квадратов ошибок прогноза, что приводит к увеличению среднего квадрата ошибки. По сути, оценка дает худшую производительность тем моделям, которые делают большие неверные прогнозы.
mean_squared_error = mean(forecast_error^2)Мы можем использовать mean_squared_error () функция из scikit-learn для вычисления среднеквадратичной ошибки для списка прогнозов. Пример ниже демонстрирует эту функцию.
from sklearn.metrics import mean_squared_error
expected = [0.0, 0.5, 0.0, 0.5, 0.0]
predictions = [0.2, 0.4, 0.1, 0.6, 0.2]
mse = mean_squared_error(expected, predictions)
print('MSE: %f' % mse)При выполнении примера вычисляется и выводится среднеквадратическая ошибка для списка ожидаемых и прогнозируемых значений.
MSE: 0.022000Значения ошибок приведены в квадратах от предсказанных значений. Среднеквадратичная ошибка, равная нулю, указывает на совершенное умение или на отсутствие ошибки.
Среднеквадратическая ошибка
Средняя квадратичная ошибка, описанная выше, выражается в квадратах единиц прогнозов.
Его можно преобразовать обратно в исходные единицы прогнозов, взяв квадратный корень из среднего квадрата ошибки Это называется среднеквадратичная ошибка или RMSE.
rmse = sqrt(mean_squared_error)Это можно рассчитать с помощьюSQRT ()математическая функция среднего квадрата ошибки, рассчитанная с использованиемmean_squared_error ()функция scikit-learn.
from sklearn.metrics import mean_squared_error
from math import sqrt
expected = [0.0, 0.5, 0.0, 0.5, 0.0]
predictions = [0.2, 0.4, 0.1, 0.6, 0.2]
mse = mean_squared_error(expected, predictions)
rmse = sqrt(mse)
print('RMSE: %f' % rmse)При выполнении примера вычисляется среднеквадратичная ошибка.
RMSE: 0.148324Значения ошибок RMES приведены в тех же единицах, что и прогнозы. Как и в случае среднеквадратичной ошибки, среднеквадратическое отклонение, равное нулю, означает отсутствие ошибки.
Дальнейшее чтение
Ниже приведены некоторые ссылки для дальнейшего изучения показателей ошибки прогноза временных рядов.
- Раздел 3.3 Измерение прогнозирующей точности, Практическое прогнозирование временных рядов с помощью R: практическое руководство,
- Раздел 2.5 Оценка точности прогноза, Прогнозирование: принципы и практика
- scikit-Learn Metrics API
- Раздел 3.3.4. Метрики регрессии, scikit-learn API Guide
Резюме
В этом руководстве вы обнаружили набор из 5 стандартных показателей производительности временных рядов в Python.
В частности, вы узнали:
- Как рассчитать остаточную ошибку прогноза и как оценить смещение в списке прогнозов.
- Как рассчитать среднюю абсолютную ошибку прогноза, чтобы описать ошибку в тех же единицах, что и прогнозы.
- Как рассчитать широко используемые среднеквадратические ошибки и среднеквадратичные ошибки для прогнозов.
Есть ли у вас какие-либо вопросы о показателях эффективности прогнозирования временных рядов или об этом руководстве?
Задайте свои вопросы в комментариях ниже, и я сделаю все возможное, чтобы ответить.
Когда перед компанией встают задачи прогнозирования спроса для управления товарными запасами, обычно появляется вопрос, связанный с выбором метода прогнозирования. Но как определить, какой метод лучше?
Однозначного ответа на этот вопрос нет. Однако, исходя из нашей практики, самым распространенным методам оценки точности прогноза является средняя абсолютная процентная ошибка (MAPE) . Также используются средняя абсолютная ошибка (MAE) и средняя квадратичная ошибка прогнозирования (RMSE).
Ошибка прогноза в данном случае – это разница между фактическим значением спроса и его прогнозным значением. Т. е, чем больше будет ошибка прогнозирования, тем менее точен прогноз. Например, при ошибке прогнозирования 5%, точность прогноза будет составлять 95%. Изначально MAPE использовалась для прогнозирования временных рядов, которые имеют регулярное нормальное распределение, такие как, например, потребление электроэнергии. И только после ее стали применять для оценки прогноза спроса. На практике ошибку могут рассчитывать по каждой позиции товара, а также среднюю оценку по всем товарным группам.
Несмотря на то, что большинство компаний до сих пор используют вышеописанные методы для оценки, мы считаем, что они не достаточно корректны и не подходят для применения в реальном бизнесе. Для простоты изложения, выделим три ключевых момента, которые приводят к некорректным выводам при использовании вышеописанных методов оценки. Назовем их ошибка № 1, № 2 и № 3. Сначала мы подробно опишем эти ошибки, а потом расскажем, как наши методы сравнения помогаю их ликвидировать.
О некорректности использования MAPE, RMSE и других распространенных ошибок
Ошибка № 1 заключается в том, что используемые методы больше относятся к математике, нежели к бизнесу, по той причине, что это обезличенные цифры (или проценты) , которые ничего не говорят про деньги. Бизнесу же нужно принимать решения на основе выгоды, которую он получит в деньгах. Например, ошибка в 80% на первый взгляд звучит устрашающие. Но в реальности за ней могут скрываться совершенно разные вещи. Ошибка по гвоздям со стоимостью одного гвоздя в 0,5 рублей – это одни потери. Но они совершенно несопоставимы с потерями от продажи промышленного оборудования стоимостью 700 000 рублей с той же величиной ошибки прогнозирования. Ко всему прочему также больше значение имеет объем продукции, что тоже никак не учитывается данными ошибками прогнозирования.
Второй важный момент (ошибка №2), который не учитывают данные оценки прогнозирования – это заморозка денежных средств в запасах и недополученная прибыль от дефицита продукции на складе. Например, если мы прогнозируем продажу 20 колесных дисков, а по факту продали 15. То это одна цена ошибки – 5 колесных дисков, которые потребуют затраты на хранение на определенное время, и как следствие стоимость замороженных оборотных средств под определенный процент. Если рассмотреть обратную ситуацию – прогнозируем продажу 20 дисков, спрос составляет 25 штук. Это уже упущенная прибыль, которая составляет разницу сумм закупки и реализации продукции. По сути мы имеет одну и ту же ошибку прогнозирования, но результат от нее может быть совершенно разным.
Третий ключевой момент (ошибка №3) – описанные ошибки распространяются только на точечный прогноз спроса и не описывают страховой запас. А он в некоторых случаях может составлять от 20% до 70% от общих товарных запасов на складе. Поэтому, какой бы точный не был прогноз с точки зрения описанных выше методов, мы все равно не оцениваем точность страхового запаса, а значит реальные данные могут быть значительно искажены.
Критерии, привязанные к прибыльности бизнеса
Учитывая описанные выше недостатки ошибок прогнозирования, такой подход не является корректным и надежным для сравнения алгоритмов. Ко всему прочему он зачастую оторван от реального бизнеса. Используемый же нами подход позволяет оценить точность алгоритмов в деньгах, рассчитать стоимость ошибки прогнозирования на понятном для бизнеса языке финансов. Таким образом это позволяет нам ликвидировать ошибку №1.
В случае с ошибкой № 2, мы рассчитываем два различных значения. Если прогноз окажется меньше реального спроса, то он приведет к дефициту, экономический урон от которого рассчитывается, как количество недопроданных товаров, умноженное на разность цен закупки и реализации. Например, вы закупаете колесные диски по 3000 рублей за штуку и продаете по 4000. Прогноз на месяц составил 1000 дисков, реальный спрос оказался 1200 штук. Экономический урон будет равен:
(1200-1000)*(4000-3000)=200 000 рублей.
В случае превышения прогноза над реальным спросом компания понесет убытки по хранению продукции. Экономический урон будет равен сумме затрат на нереализованную продукцию, помноженную на ставку альтернативных вложений за этот период. Предположим, что реальный спрос в предыдущем примере оказался 800 дисков и вам пришлось хранить диски еще один месяц. Пусть ставка альтернативных вложений составляет 20% в год. Тогда экономический урон будет равен
(1000-800)*3000*0,2/12=10 000 рублей.
Соответственно, в каждом конкретном случае, мы будет учитывать одно из этих значений.
Для того, чтобы ликвидировать ошибку № 3, мы сравниваем алгоритмы с использованием понятия уровень сервиса. Уровень сервиса (здесь и далее — уровень сервиса II рода, fill rate) – это доля спроса, которую мы гарантировано покроем с использованием имеющихся на складе запасов в течении периода их пополнения. Например, уровень сервиса 90% означает, что мы удовлетворим 90% спроса. На первый взгляд может показаться логичным, что уровень сервиса всегда должен составлять 100%. Тогда и прибыль будет максимальна. Но в реальных ситуациях зачастую дело обстоит иначе: удовлетворение 100% уровня сервиса приводит к сильному перезатариванию склада, а для товаров с ограниченными сроками годности еще и к списанию. И убытки от затрат на хранение, списания просроченной продукции и недополученной прибыли от вложения свободных денег в итоге снизят прибыть от реализации, в случае если бы мы поддерживали уровень сервиса 95%. Нужно заметить, что для каждой отдельной позиции товаров будет свой оптимальный уровень сервиса.
Так как страховой запас может составлять значительную долю, его нельзя игнорировать при сравнении алгоритмов (как это делается при расчете ошибок MAPE, RMSE и т. д.) . Поэтому мы делаем сравнение не прогноза, а оптимального запаса с заданным уровнем сервиса. Оптимальный запас для заданного уровня сервиса – это такое количество товаров, которое нужно хранить на складе, чтобы получить максимум прибыли от реализации товаров и одновременно сократить издержки на хранение до минимума.
В качестве основного критерия (критерий №1) качества прогнозирования мы используем суммарное значение потерь для заданного уровня сервиса, о котором писали выше (исправление ошибки №2). Таким образом мы оцениваем потери в денежном выражении при использовании данного конкретного алгоритма. Чем меньше потери — тем точнее работает алгоритм.
Здесь нужно заметить, что для разных уровней сервиса оптимальный запас тоже может различаться. И в одном случае прогноз будет точно в него попадать, а в другом возможны перекосы в большую, либо меньшую сторону. Так как многие компании не рассчитывают оптимальный уровень сервиса, а используют заданный заранее, значение основного критерия мы вычисляем для всех самых распространенных уровней сервиса: 70%, 75%, 80%, 85%, 90%, 95%, 98%, 99% и суммируем потери. Таким образом мы можем проверить, насколько хорошо в целом работает модель.
Для компаний, которые, считают оптимальный уровень сервиса мы используем дополнительный критерий (критерий №2) для оценки. В общем виде он выглядит как соотношение потерь на оптимальном уровне сервиса по ожидаемому (модельному) распределению продаж и по реальному распределению продаж (по факту) . Прогнозируемое значение оптимального уровня сервиса не всегда соответствует оптимальному значению уже на реальном распределении продаж. Поэтому мы должны сравнивать ошибку между прогнозом объема продаж на оптимальном (по модели) уровне сервиса и реальным объемом продаж, обеспечивающим оптимальное значение уровня сервиса по реальным данным.
Что проиллюстрировать применение данного критерия, вернемся к нашему примеру с дисками. Предположим, что прогнозное значение оптимального уровня сервиса для него составляет 90%, а оптимальный объем запаса для этого случая примем равным 3000 колесных дисков. Пусть в первом случае реальный уровень сервиса оказался выше прогнозного и составил 92%. Соответственно объем заказов также вырос и составил 3300 дисков. Ошибка прогнозирования будет рассчитываться как разность между реальным и фактическим объемом продаж, умноженная на разность цен реализации. Итого, мы имеем:
(3300-3000)*(4000-3000)=300 000 рублей.
Теперь представим обратную ситуацию: реальный уровень сервиса оказался меньше прогнозного и составил 87%. Реальный объем продаж при этом составил 2850 дисков. Ошибка прогнозирования будет рассчитана, как сумма затрат на нереализованную продукцию, умноженную на ставку альтернативных вложений за этот период (в качестве примера берем период сроком месяц и ставку равную 20% годовых) . Итоговое значение критерия будет равно:
(3000-2850)*3000*0,2/12 = 7500 рублей
Конечно, в идеальном случае, мы должны рассчитывать ошибку только при оптимальном уровне сервиса, между прогнозным и реальным значениями. Но так как не все компании еще перешли на оптимальный уровень сервиса, мы вынуждены использовать два критерия.
Используемые нами критерии в отличие от классических математических ошибок, показывают суммарные потери в деньгах при применении той или иной модели. Соответственно, наилучшей будет модель, которая обеспечивает минимальные потери. Такой подход позволят бизнес-пользователям оценить работу различных алгоритмов на понятном им языке.
Пример сравнения точности прогнозирования системы Forecast NOW c методом ARIMA (на базе номенклатуры бытовой химии) :
Пример сравнения точности прогнозирования системы Forecast NOW c методом Кростона (на базе номенклатуры бытовой химии) :
Насколько корректно на ваш взгляд считать ошибки, а не деньги? Предлагаем порассуждать на эту тему в комментариях!