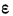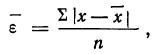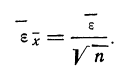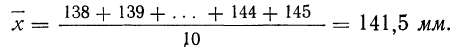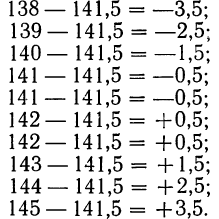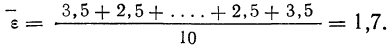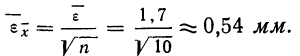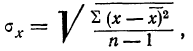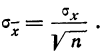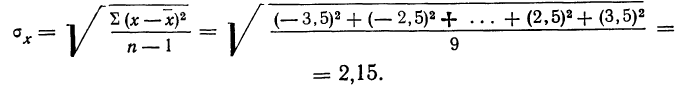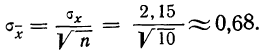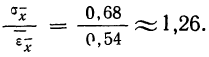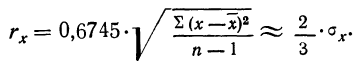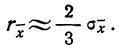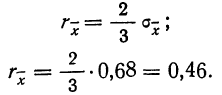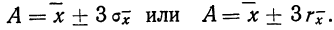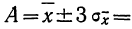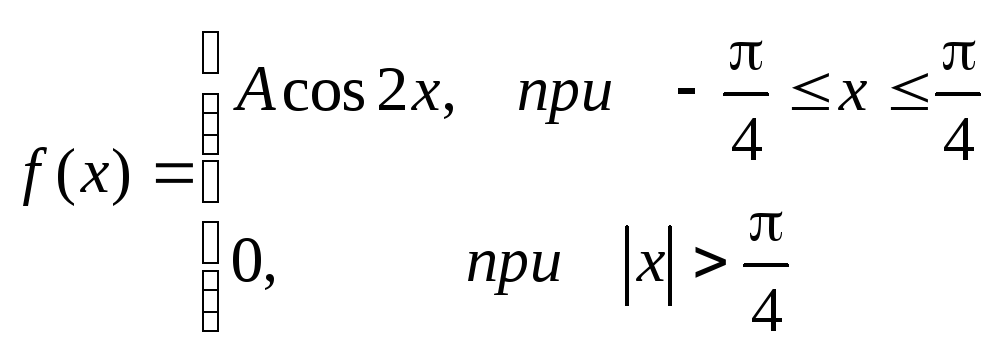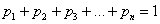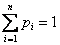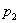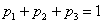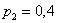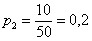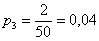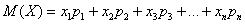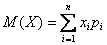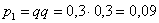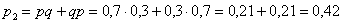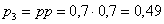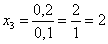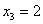Математическое ожидание — ошибка
Cтраница 1
Математическое ожидание ошибки называется систематической ошибкой, ее среднее квадратическое отклонение — среднеквадра-тической ошибкой. Анализ качества систем управления сводится к определению указанных ошибок по вероятностным характеристикам случайных внешних воздействий.
[2]
Математическое ожидание ошибки слежения равно ее среднеарифметическому значению.
[3]
Система имеет математическое ожидание ошибки тст 0 и центрированную составляющую С, подчиненную нормальному закону распределения.
[4]
Известно, что математическое ожидание ошибки уменьшается с увеличением частоты замеров и с уменьшением скорости линейного изменения коэффициентом.
[5]
В этом случае математическое ожидание ошибки равно нулю.
[6]
Учитывая, что при усечении математическое ожидание ошибки квантования отлично от нуля, более целесообразно использовать округление.
[7]
При совпадении ПФ с видом г математическое ожидание ошибки прогноза будет равно нулю.
[9]
Получаемые вероятностные оценки поступают на сумматор 2, который определяет величину математического ожидания ошибок Мп для каждой из сравниваемых кодовых комбинаций.
[10]
Формулы (5.5.12) и (5.5.14) характеризуют собой общие выражения соответственно корреляционной функции и математического ожидания ошибки положения для партии механизмов.
[11]
При приеме в целом принятая кодовая комбинация будет ошибочной, если при математическом ожидании ошибок на ее длине Мл Мп mln и зафиксированное значение кодовой комбинации содержит любые варианты ошибок.
[12]
Согласно соотношению ( 11) каждому из возможных состояний канала связи соответствует случайная величина математического ожидания ошибок Мс, которая через финальные вероятности состояний принятой модели может указать на наличие того или иного состояния с некоторой вероятностью правдоподобия рс.
[13]
Чтобы упростить сравнение указанных методов, будем полагать, что первичные параметры взаимонезависимы, а математическое ожидание ошибок ( допусков) равно нулю.
[14]
Функция потерь) в общем случае является функционалом от выходных сигналов объекта и модели или от математического ожидания ошибок оценок параметров.
[15]
Страницы:
1
2
30 ₽
Количество товара Вопрос №9 Если математическое ожидание ошибки равно нулю, то ее называют
Описание
Если математическое ожидание ошибки равно нулю, то ее называют
- Вариант №1: случайной
- Вариант №2: истинной
- Вариант №3: средней квадратической
- Вариант №4: систематической
- Вариант №5: предельной
Формат файла — JPG
Количество товара Вопрос №9 Если математическое ожидание ошибки равно нулю, то ее называют
Содержание:
Ошибки измерения: Опыт убеждает, что измерения объектов не могут быть произведены абсолютно точно и каждое конкретное измерение дает лишь, как правило, приближенное значение величины явления, истинное значение которой (A) нам неизвестно. Ошибки измерения (
Рассмотрим такие измерения, которые производятся одним наблюдателем, одним и тем же инструментом, в одинаковых условиях, т. е. равноточные измерения.
Различают два вида ошибок измерения:
- систематические ошибки, т. е. такие, которые при данных условиях проведения измерения имеют вполне определенное значение (например, ошибка измерительного прибора);
- случайные — такие, которые являются результатом взаимодействия большого числа незначительных в отдельности факторов и имеют в каждом отдельном случае различные значения.
Задача математической статистики — предусмотреть возможность возникновения систематических ошибок и добиться их ликвидации или сведения к минимуму.
Случайные ошибки измерения обладают рядом свойств: при большом числе измерений крупные ошибки встречаются реже мелких и число положительных ошибок примерно равно числу отрицательных, вследствие чего сумма всех ошибок близка к нулю.
Если ошибки получаются весьма малыми по сравнению с величиной явления, то ими просто пренебрегают или считаются с наибольшей возможной ошибкой, чтобы обезопасить себя от влияния случайной неточности.
В теории ошибок изучаются те ошибки, которые, являясь, с одной стороны, ошибками случайного характера, по своему абсолютному значению настолько велики, что ими пренебречь нельзя, а с другой стороны, для них существует закон, позволяющий установить зависимость между величиной ошибки и вероятностью ее появления. Закон случайных ошибок, полученный Гауссом, состоит в том, что случайные ошибки подчиняются закону нормального распределения.
Средняя ошибка сводного результата измерения
Принимая за действительное значение измеряемой величины при равноточном измерении среднюю арифметическую из всех результатов n измерений, можно охарактеризовать точность одного измерения с помощью средней арифметической из абсолютных величин значений ошибок:
где n — число измерений, х — численное значение отдельных измерений, 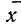
За меру точности соответствия принятой средней арифметической 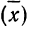
Пример 1. Произведено 10-кратное измерение размера детали (в мм), давшее следующие, расположенные в возрастающем порядке результаты: 138; 139; 140; 141; 141; 142; 142; 143; 144; 145.
Охарактеризуем сначала точность одного измерения, т. е. вычислим среднюю арифметическую из абсолютных значений ошибок. Для этой цели вычислим среднюю арифметическую из результатов измерений:
Найдем ошибки измерения:
Следовательно:
Теперь можно вычислить среднюю ошибку сводного результата измерения:
Значит, мерой точности соответствия 141,5 мм истинной величине размера детали является средняя ошибка, равная 0,54 мм.
Средняя квадратическая ошибка
Если в качестве меры точности одного измерения принять не среднюю арифметическую из абсолютных значений ошибок (средняя ошибка), а среднюю квадратическую из ошибок измерений, т. е.
то средняя квадратическая ошибка найденной средней арифметической из ошибок измерения вычисляется по формуле:
Между средней -квадратической ошибкой и средней ошибкой сводного результата измерения существует связь: 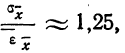
Пример 2. Используя данные предыдущего примера, находим меру точности одного измерения, т. е. среднюю квадратическую ошибку:
Затем исчисляем среднюю квадратическую ошибку найденной средней арифметической, равной 141,5 мм:
Сопоставляя среднюю квадратическую ошибку сводного результата измерения со средней ошибкой, получаем:
Вероятная ошибка
За меру точности одного измерения иногда принимают вероятную ошибку:
Тогда в качестве вероятной ошибки сводного результата измерения используют соотношение:
Пример 3. Используя данные предыдущих примеров, находим вероятную ошибку сводного результата измерения:
Наиболее вероятные границы сводных результатов измерения
Математическое ожидание случайной ошибки равно нулю. В качестве значения измеряемой величины применяется средняя арифметическая всех измерений (если они равноточны). Использование отклонений результатов измерений (х) от средней из них 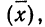
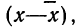
Для этой цели используют удвоенную или утроенную среднюю квадратическую ошибку сводного результата измерения или его вероятную ошибку и получают:
Найденные границы неизвестной истинной величины в случае, если ошибки подчинены нормальному закону распределения Гаусса (чаще всего так и бывает), соблюдаются с большой вероятностью (0,997 и 0,954).
Пример 4. По данным предыдущих примеров находим границы истинного значения размера детали 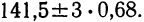
- Методы математической статистики
- Комбинаторика — правила, формулы и примеры
- Классическое определение вероятности
- Геометрические вероятности
- Законы распределения случайных величин
- Дисперсионный анализ
- Математическая обработка динамических рядов
- Корреляция — определение и вычисление
Математическое ожидание, дисперсия, среднее квадратичное отклонение
Эти величины определяют некоторое
среднее значение, вокруг которого
группируются значения случайной
величины, и степень их разбросанности
вокруг этого среднего значения.
Математическое ожидание Mдискретной случайной величины — это
среднее значение случайной величины,
равное сумме произведений всех возможных
значений случайной величины на их
вероятности.
Свойства математического ожидания:
-
Математическое ожидание постоянной
величины равно самой постоянной . -
Постоянный множитель можно выносить
за знак математического ожидания . -
Математическое ожидание произведения
двух независимых случайных величин
равно произведению их математических
ожиданий . -
Математическое ожидание суммы двух
случайных величин равно сумме
математических ожиданий слагаемых
Для описания многих практически важных
свойств случайной величины необходимо
знание не только ее математического
ожидания, но и отклонения возможных ее
значений от среднего значения.
Дисперсия случайной величины— мера разброса случайной величины,
равная математическому ожиданию квадрата
отклонения случайной величины от ее
математического ожидания.
.
Принимая во внимание свойства
математического ожидания, легко показать
что
Казалось бы естественным рассматривать
не квадрат отклонения случайной величины
от ее математического ожидания, а просто
отклонение. Однако математическое
ожидание этого отклонения равно нулю.
Это объясняется тем, что одни возможные
отклонения положительны, другие
отрицательны, и в результате их взаимного
погашения получается ноль. Можно было
бы принять за меру рассеяния математическое
ожидание модуля отклонения случайной
величины от ее математического ожидания,
но как правило, действия связанные с
абсолютными величинами, приводят к
громоздким вычислениям.
Свойства дисперсии:
-
Дисперсия постоянной равна нулю.
-
Постоянный множитель можно выносить
за знак дисперсии, возводя его в квадрат. -
Если x и y независимые случайные величины
, то дисперсия суммы этих величин равна
сумме их дисперсий.
Средним квадратическим отклонением
случайной величины(иногда применяется
термин «стандартное отклонение случайной
величины») называется число равное.
Среднее квадратическое отклонение,
является, как и дисперсия, мерой рассеяния
распределения, но измеряется, в отличие
от дисперсии, в тех же единицах, которые
используют для измерения значений
случайной величины.
Решение задач:
1)Дана случайная величина Х:
-
xi
-3
-2
0
1
2
pi
0,1
0,2
0,05
0,3
0,35
Найти М(х), D(X).
Решение:
.
=9
=2,31.
.
2) Известно, что М(Х)=5, М(Y)=2.
Найти математическое ожидание случайной
величиныZ=6X-2Y+9-XY.
Решение:М(Z)=6М(Х)-2М(Y)+9-M(X)M(Y)=30-4+9-10=25.
Пример:Известно, чтоD(Х)=5,D(Y)=2. Найти
математическое ожидание случайной
величиныZ=6X-2Y+9.
Решение:D(Z)=62D(Х)-22D(Y)+0=180-8=172.
Тема 7. Непрерывные случайные величины
Задача 14
Случайная
величина, значения которой заполняют
некоторый промежуток, называется
непрерывной.
Плотностью распределениявероятностей непрерывной случайной
величины Х называется функцияf(x)– первая производная от функции
распределенияF(x).
Плотность
распределения также называют
дифференциальной
функцией.
Для описания дискретной случайной
величины плотность распределения
неприемлема.
Зная плотность распределения, можно
вычислить вероятность того, что некоторая
случайная величина Х примет значение,
принадлежащее заданному интервалу.
Вероятность того, что непрерывная
случайная величина Х примет значение,
принадлежащее интервалу (a,
b), равна определенному
интегралу от плотности распределения,
взятому в пределах от a
до b.
Функция распределения может быть легко
найдена, если известна плотность
распределения, по формуле:
Свойства плотности распределения.
1) Плотность распределения – неотрицательная
функция.
2) Несобственный интеграл
от плотности распределения в пределах
от -доравен единице.
Решение задач.
1.Случайная величина подчинена
закону распределения с плотностью:
Требуется найти коэффициент а,
определить вероятность того, что
случайная величина попадет в интервал
от 0 до.
Решение:
Для нахождения коэффициента авоспользуемся свойством.
2 .Задана непрерывная случайная
величинахсвоей функцией распределенияf(x).
Требуется определить
коэффициент А, найти функцию распределения,
определить вероятность того, что
случайная величинахпопадет в
интервал.
Решение:
Найдем коэффициент А.
Найдем функцию распределения:
1) На участке
:
2) На участке
3) На участке
Итого:
Найдем вероятность попадания случайной
величины в интервал
.
Ту же самую вероятность можно искать
и другим способом:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
- 11. Свойства математического ожидания
- Как найти математическое ожидание?
- Формула среднего случайной величины
- Пример нахождения математического ожидания
- Вычисление математического ожидания онлайн
- Видео. Полезные ссылки
- Видеоролики: что такое среднее (математическое ожидание)
- Полезные ссылки
- Случайные величины. Дискретная случайная величина. Математическое ожидание
- Закон распределения дискретной случайной величины
- Математическое ожидание дискретной случайной величины
11. Свойства математического ожидания
1) Математическое ожидание постоянной величины равно самой постоянной.
2) Постоянный множитель можно выносить за знак математического ожидания.
3) Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.
Это свойство справедливо для произвольного числа случайных величин.
4) Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых.
Это свойство также справедливо для произвольного числа случайных величин.
Пусть производится П независимых испытаний, вероятность появления события А в которых равна Р.
Теорема. Математическое ожидание М(Х) числа появления события А в п независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании.
Однако, математическое ожидание не может полностью характеризовать случайный процесс. Кроме математического ожидания надо ввести величину, которая характеризует отклонение значений случайной величины от математического ожидания.
Это отклонение равно разности между случайной величиной и ее математическим ожиданием. При этом математическое ожидание отклонения равно нулю. Это объясняется тем, что одни возможные отклонения положительны, другие отрицательны, и в результате их взаимного погашения получается ноль.
Определение. Дисперсией (рассеиванием) дискретной случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.
Пример. Для рассмотренного выше примера закон распределения случайной величины имеет вид:
Источник
Как найти математическое ожидание?
Математическое ожидание случайной величины $X$ (обозначается $M(X)$ или реже $E(X)$) характеризует среднее значение случайной величины (дискретной или непрерывной). Мат. ожидание — это первый начальный момент заданной СВ.
Математическое ожидание относят к так называемым характеристикам положения распределения (к которым также принадлежат мода и медиана). Эта характеристика описывает некое усредненное положение случайной величины на числовой оси. Скажем, если матожидание случайной величины — срока службы лампы, равно 100 часов, то считается, что значения срока службы сосредоточены (с обеих сторон) от этого значения (с тем или иным разбросом, о котором уже говорит дисперсия).
Формула среднего случайной величины
Математическое ожидание дискретной случайной величины Х вычисляется как сумма произведений значений $x_i$ , которые принимает СВ Х, на соответствующие вероятности $p_i$: $$ M(X)=sum_^. $$ Для непрерывной случайной величины (заданной плотностью вероятностей $f(x)$), формула вычисления математического ожидания Х выглядит следующим образом: $$ M(X)=int_<-infty>^ <+infty>f(x) cdot x dx. $$
Пример нахождения математического ожидания
Рассмотрим простые примеры, показывающие как найти M(X) по формулам, введеным выше.
Пример 1. Вычислить математическое ожидание дискретной случайной величины Х, заданной рядом: $$ x_i quad -1 quad 2 quad 5 quad 10 quad 20 \ p_i quad 0.1 quad 0.2 quad 0.3 quad 0.3 quad 0.1 $$
Используем формулу для м.о. дискретной случайной величины: $$ M(X)=sum_^. $$ Получаем: $$ M(X)=sum_^ =-1cdot 0.1 + 2 cdot 0.2 +5cdot 0.3 +10cdot 0.3+20cdot 0.1=6.8. $$ Вот в этом примере 2 описано также нахождение дисперсии Х.
Пример 2. Найти математическое ожидание для величины Х, распределенной непрерывно с плотностью $f(x)=12(x^2-x^3)$ при $x in(0,1)$ и $f(x)=0$ в остальных точках.
Используем для нахождения мат. ожидания формулу: $$ M(X)=int_<-infty>^ <+infty>f(x) cdot x dx. $$ Подставляем из условия плотность вероятности и вычисляем значение интеграла: $$ M(X)=int_<-infty>^ <+infty>f(x) cdot x dx = int_<0>^ <1>12(x^2-x^3) cdot x dx = int_<0>^ <1>12(x^3-x^4) dx = \ =left.(3x^4-frac<12><5>x^5) right|_0^1=3-frac<12> <5>= frac<3><5>=0.6. $$
Вычисление математического ожидания онлайн
Как найти математическое ожидание онлайн для произвольной дискретной случайной величины? Используйте калькулятор ниже.
- Введите число значений случайной величины К.
- Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -10.3 или 0.5). Введите нужные значения (проверьте, что сумма вероятностей равна 1, то есть закон распределения корректный).
- Нажмите на кнопку «Вычислить».
- Калькулятор покажет вычисленное математическое ожидание $M(X)$.
Видео. Полезные ссылки
Видеоролики: что такое среднее (математическое ожидание)
Если вам нужно более подробное объяснение того, что такое мат.ожидание, как она вычисляется и какими свойствами обладает, рекомендую два видео (для дискретной и непрерывной случайной величины соответственно).
Полезные ссылки
Что еще может пригодиться? Например, для изучения основ теории вероятностей — онлайн учебник по терверу. Для закрепления материала — еще примеры решений по теории вероятностей.
А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:
Источник
Случайные величины. Дискретная случайная величина.
Математическое ожидание
Второй раздел по теории вероятностей посвящён случайным величинам, которые незримо сопровождали нас буквально в каждой статье по теме. И настал момент чётко сформулировать, что же это такое:
Случайной называют величину, которая в результате испытания примет одно и только одно числовое значение, зависящее от случайных факторов и заранее непредсказуемое.
Случайные величины, как правило, обозначают через 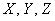
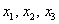
* Иногда используют 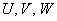
Пример встретился нам на первом же уроке по теории вероятностей, где мы фактически рассмотрели следующую случайную величину:
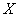
В результате данного испытания выпадет одна и только грань, какая именно – не предсказать (фокусы не рассматриваем); при этом случайная величина 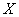
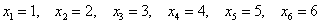
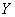
Совершенно понятно, что это количество заранее не известно, и в очередном десятке родившихся детей может оказаться:
И, дабы соблюсти форму, немного физкультуры:
Её не в состоянии предугадать даже мастер спорта 🙂
Тем не менее, ваши гипотезы?
Коль скоро речь идёт о множестве действительных чисел, то случайная величина 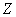
Таким образом, случайные величины целесообразно разделить на 2 большие группы:
1) Дискретная (прерывная) случайная величина – принимает отдельно взятые, изолированные значения. Количество этих значений конечно либо бесконечно, но счётно.
…нарисовались непонятные термины? Срочно повторяем основы алгебры!
2) Непрерывная случайная величина – принимает все числовые значения из некоторого конечного или бесконечного промежутка.
Примечание: в учебной литературе популярны аббревиатуры ДСВ и НСВ
Сначала разберём дискретную случайную величину, затем – непрерывную.
Закон распределения дискретной случайной величины
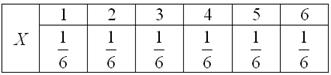
– это соответствие между возможными значениями этой величины и их вероятностями. Чаще всего закон записывают таблицей: 
Довольно часто встречается термин ряд распределения, но в некоторых ситуациях он звучит двусмысленно, и поэтому я буду придерживаться «закона».
А теперь очень важный момент: поскольку случайная величина 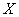
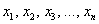
или, если записать свёрнуто:
Так, например, закон распределения вероятностей выпавших на кубике очков имеет следующий вид:
Возможно, у вас сложилось впечатление, что дискретная случайная величина может принимать только «хорошие» целые значения. Развеем иллюзию – они могут быть любыми:
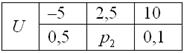
Некоторая игра имеет следующий закон распределения выигрыша:
Найти
…наверное, вы давно мечтали о таких задачах 🙂 Открою секрет – я тоже. В особенности после того, как завершил работу над теорией поля.
Решение: так как случайная величина 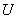
Разоблачаем «партизана»: 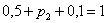
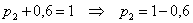
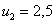
Контроль: 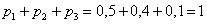
Ответ:
Не редкость, когда закон распределения требуется составить самостоятельно. Для этого используют классическое определение вероятности, теоремы умножения / сложения вероятностей событий и другие фишки тервера:
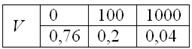
В коробке находятся 50 лотерейных билетов, среди которых 12 выигрышных, причём 2 из них выигрывают по 1000 рублей, а остальные – по 100 рублей. Составить закон распределения случайной величины 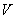
Решение: как вы заметили, значения случайной величины принято располагать в порядке их возрастания. Поэтому мы начинаем с самого маленького выигрыша, и именно 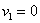
Всего таковых билетов 50 – 12 = 38, и по классическому определению:
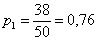
С остальными случаями всё просто. Вероятность выигрыша 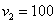
И для 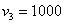
Проверка: 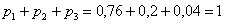
Ответ: искомый закон распределения выигрыша:
Следующее задание для самостоятельного решения:
Вероятность того, что стрелок поразит мишень, равна 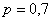
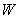
…я знал, что вы по нему соскучились 🙂 Вспоминаем теоремы умножения и сложения. Решение и ответ в конце урока.
Закон распределения полностью описывает случайную величину, однако на практике бывает полезно (а иногда и полезнее) знать лишь некоторые её числовые характеристики.
Математическое ожидание дискретной случайной величины
Говоря простым языком, это среднеожидаемое значение при многократном повторении испытаний. Пусть случайная величина 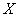
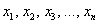
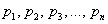
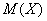
или в свёрнутом виде:
Вычислим, например, математическое ожидание случайной величины 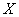
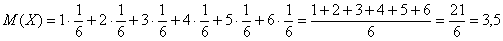
В чём состоит вероятностный смысл полученного результата? Если подбросить кубик достаточно много раз, то среднее значение выпавших очков будет близкО к 3,5 – и чем больше провести испытаний, тем ближе. Собственно, об этом эффекте я уже подробно рассказывал на уроке о статистической вероятности.
Теперь вспомним нашу гипотетическую игру:
Возникает вопрос: а выгодно ли вообще играть в эту игру? …у кого какие впечатления? Так ведь «навскидку» и не скажешь! Но на этот вопрос можно легко ответить, вычислив математическое ожидание, по сути – средневзвешенный по вероятностям выигрыш:
Не верь впечатлениям – верь цифрам!
Да, здесь можно выиграть 10 и даже 20-30 раз подряд, но на длинной дистанции нас ждёт неминуемое разорение. И я бы не советовал вам играть в такие игры 🙂 Ну, может, только ради развлечения.
Из всего вышесказанного следует, что математическое ожидание – это уже НЕ СЛУЧАЙНАЯ величина.
Творческое задание для самостоятельного исследования:
Мистер Х играет в европейскую рулетку по следующей системе: постоянно ставит 100 рублей на «красное». Составить закон распределения случайной величины 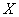
Справка: европейская рулетка содержит 18 красных, 18 чёрных и 1 зелёный сектор («зеро»). В случае выпадения «красного» игроку выплачивается удвоенная ставка, в противном случае она уходит в доход казино
Существует много других систем игры в рулетку, для которых можно составить свои таблицы вероятностей. Но это тот случай, когда нам не нужны никакие законы распределения и таблицы, ибо доподлинно установлено, что математическое ожидание игрока будет точно таким же. От системы к системе меняется лишь дисперсия, о которой мы узнаем во 2-й части урока.
Но прежде будет полезно размять пальцы на клавишах калькулятора:
Случайная величина 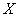
Найти 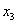
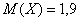
Тогда переходим к изучению дисперсии дискретной случайной величины, и по возможности, ПРЯМО СЕЙЧАС!! – чтобы не потерять нить темы.
Решения и ответы:
Пример 3. Решение: по условию 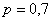
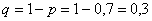
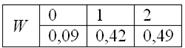
Составим 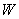
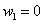
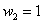
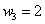
Проверка: 0,09 + 0,42 + 0,49 = 1
Ответ:
Примечание: можно было использовать обозначения 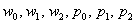
Пример 4. Решение: игрок выигрывает 100 рублей в 18 случаях из 37, и поэтому закон распределения его выигрыша имеет следующий вид: 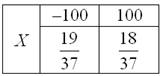
Вычислим математическое ожидание: 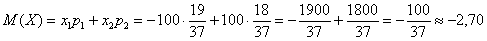
Таким образом, с каждой поставленной сотни игрок в среднем проигрывает 2,7 рубля.
Пример 5. Решение: по определению математического ожидания: 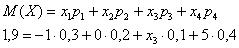
поменяем части местами и проведём упрощения: 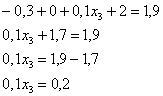
таким образом:
Выполним проверку: 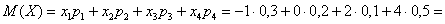
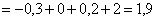
Ответ:
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Источник