Что такое стандартная ошибка оценки в статистике - ErrorsMaster.ru - большая энциклопедия ошибок и их решений

Стандартное отклонение и стандартная ошибка: в чем разница?

17 авг. 2022 г.
читать 2 мин

В статистике студенты часто путают два термина: стандартное отклонение и стандартная ошибка .

Стандартное отклонение измеряет, насколько разбросаны значения в наборе данных.

Стандартная ошибка — это стандартное отклонение среднего значения в повторных выборках из совокупности.

Давайте рассмотрим пример, чтобы ясно проиллюстрировать эту идею.

Пример: стандартное отклонение против стандартной ошибки

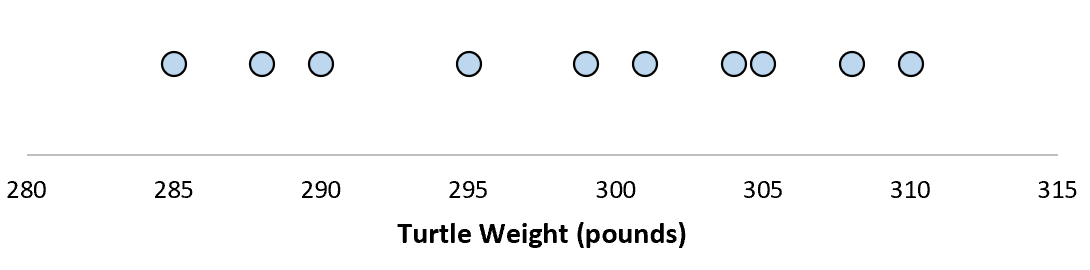
Предположим, мы измеряем вес 10 разных черепах.

Для этой выборки из 10 черепах мы можем вычислить среднее значение выборки и стандартное отклонение выборки:

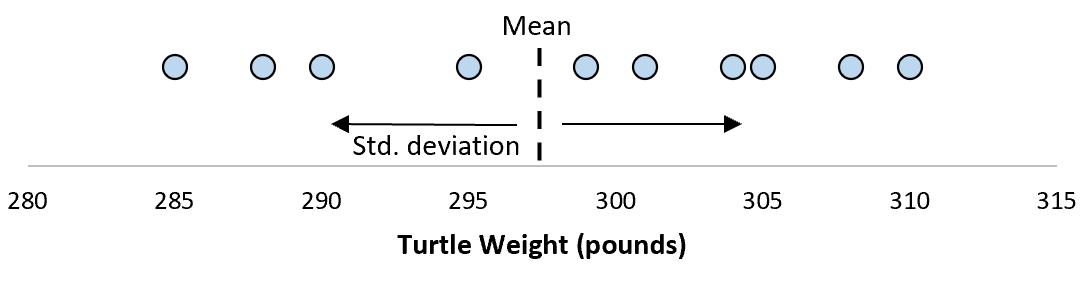
Предположим, что стандартное отклонение оказалось равным 8,68. Это дает нам представление о том, насколько распределен вес этих черепах.

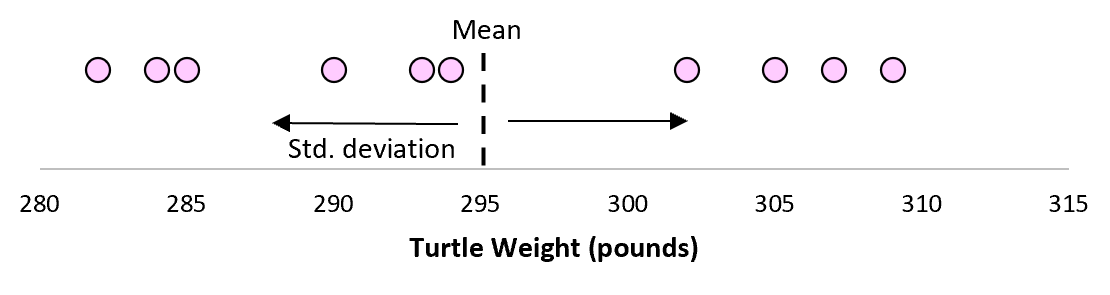
Но предположим, что мы собираем еще одну простую случайную выборку из 10 черепах и также проводим их измерения. Более чем вероятно, что эта выборка из 10 черепах будет иметь немного другое среднее значение и стандартное отклонение, даже если они взяты из одной и той же популяции:

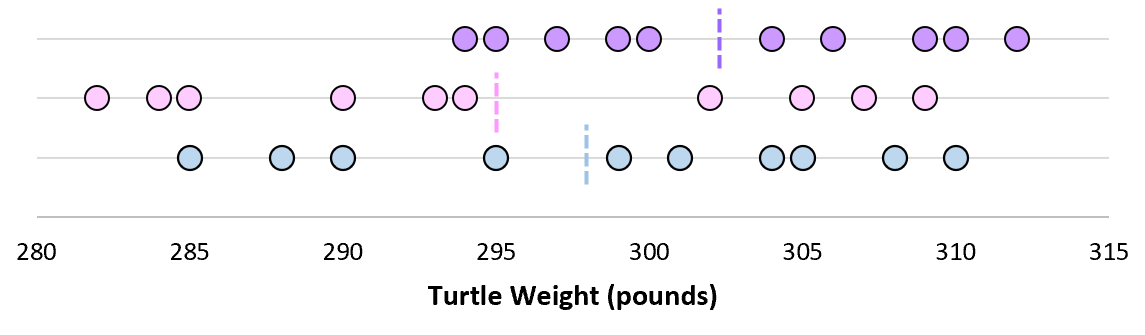
Теперь, если мы представим, что мы берем повторные выборки из одной и той же совокупности и записываем выборочное среднее и выборочное стандартное отклонение для каждой выборки:

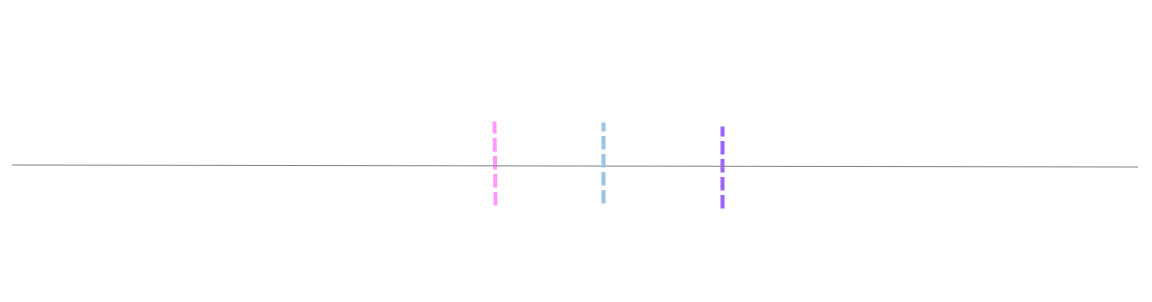
Теперь представьте, что мы наносим каждое среднее значение выборки на одну и ту же строку:

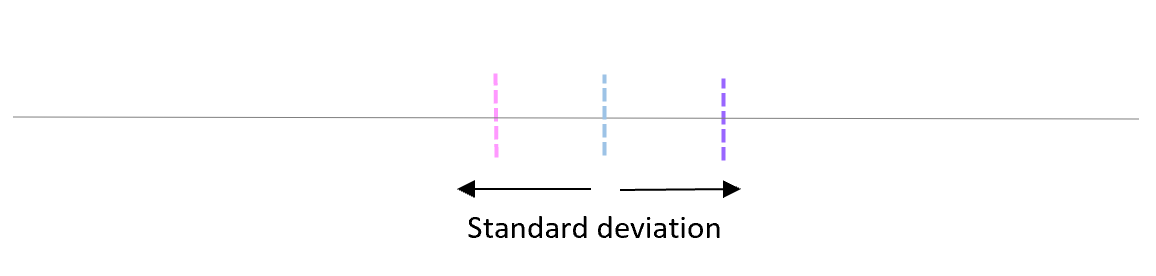
Стандартное отклонение этих средних значений известно как стандартная ошибка.

Формула для фактического расчета стандартной ошибки:

Стандартная ошибка = s/ √n

куда:

s: стандартное отклонение выборки
n: размер выборки

Какой смысл использовать стандартную ошибку?

Когда мы вычисляем среднее значение данной выборки, нас на самом деле интересует не среднее значение этой конкретной выборки, а скорее среднее значение большей совокупности, из которой взята выборка.

Однако мы используем выборки, потому что для них гораздо проще собирать данные, чем для всего населения. И, конечно же, среднее значение выборки будет варьироваться от выборки к выборке, поэтому мы используем стандартную ошибку среднего значения как способ измерить, насколько точна наша оценка среднего значения.

Вы заметите из формулы для расчета стандартной ошибки, что по мере увеличения размера выборки (n) стандартная ошибка уменьшается:

Стандартная ошибка = s/ √n

Это должно иметь смысл, поскольку большие размеры выборки уменьшают изменчивость и увеличивают вероятность того, что среднее значение нашей выборки ближе к фактическому среднему значению генеральной совокупности.

Когда использовать стандартное отклонение против стандартной ошибки

Если мы просто заинтересованы в измерении того, насколько разбросаны значения в наборе данных, мы можем использовать стандартное отклонение .

Однако, если мы заинтересованы в количественной оценке неопределенности оценки среднего значения, мы можем использовать стандартную ошибку среднего значения .

В зависимости от вашего конкретного сценария и того, чего вы пытаетесь достичь, вы можете использовать либо стандартное отклонение, либо стандартную ошибку.

Источник

What Is the Standard Error?

The standard error (SE) of a statistic is the approximate standard deviation of a statistical sample population.

The standard error is a statistical term that measures the accuracy with which a sample distribution represents a population by using standard deviation. In statistics, a sample mean deviates from the actual mean of a population; this deviation is the standard error of the mean.

Key Takeaways

The standard error (SE) is the approximate standard deviation of a statistical sample population.
The standard error describes the variation between the calculated mean of the population and one which is considered known, or accepted as accurate.
The more data points involved in the calculations of the mean, the smaller the standard error tends to be.

Standard Error

Understanding Standard Error

The term «standard error» is used to refer to the standard deviation of various sample statistics, such as the mean or median. For example, the «standard error of the mean» refers to the standard deviation of the distribution of sample means taken from a population. The smaller the standard error, the more representative the sample will be of the overall population.

The relationship between the standard error and the standard deviation is such that, for a given sample size, the standard error equals the standard deviation divided by the square root of the sample size. The standard error is also inversely proportional to the sample size; the larger the sample size, the smaller the standard error because the statistic will approach the actual value.

The standard error is considered part of inferential statistics. It represents the standard deviation of the mean within a dataset. This serves as a measure of variation for random variables, providing a measurement for the spread. The smaller the spread, the more accurate the dataset.

Standard error and standard deviation are measures of variability, while central tendency measures include mean, median, etc.

Formula and Calculation of Standard Error

The standard error of an estimate can be calculated as the standard deviation divided by the square root of the sample size:

SE = σ / √n

where

σ = the population standard deviation
√n = the square root of the sample size

If the population standard deviation is not known, you can substitute the sample standard deviation, s, in the numerator to approximate the standard error.

Requirements for Standard Error

When a population is sampled, the mean, or average, is generally calculated. The standard error can include the variation between the calculated mean of the population and one which is considered known, or accepted as accurate. This helps compensate for any incidental inaccuracies related to the gathering of the sample.

In cases where multiple samples are collected, the mean of each sample may vary slightly from the others, creating a spread among the variables. This spread is most often measured as the standard error, accounting for the differences between the means across the datasets.

The more data points involved in the calculations of the mean, the smaller the standard error tends to be. When the standard error is small, the data is said to be more representative of the true mean. In cases where the standard error is large, the data may have some notable irregularities.

The standard deviation is a representation of the spread of each of the data points. The standard deviation is used to help determine the validity of the data based on the number of data points displayed at each level of standard deviation. Standard errors function more as a way to determine the accuracy of the sample or the accuracy of multiple samples by analyzing deviation within the means.

Standard Error vs. Standard Deviation

The standard error normalizes the standard deviation relative to the sample size used in an analysis. Standard deviation measures the amount of variance or dispersion of the data spread around the mean. The standard error can be thought of as the dispersion of the sample mean estimations around the true population mean. As the sample size becomes larger, the standard error will become smaller, indicating that the estimated sample mean value better approximates the population mean.

Example of Standard Error

Say that an analyst has looked at a random sample of 50 companies in the S&P 500 to understand the association between a stock’s P/E ratio and subsequent 12-month performance in the market. Assume that the resulting estimate is -0.20, indicating that for every 1.0 point in the P/E ratio, stocks return 0.2% poorer relative performance. In the sample of 50, the standard deviation was found to be 1.0.

The standard error is thus:

SE = 1.0/√50 = 1/7.07 = 0.141

Therefore, we would report the estimate as -0.20% ± 0.14, giving us a confidence interval of (-0.34 — -0.06). The true mean value of the association of the P/E on returns of the S&P 500 would therefore fall within that range with a high degree of probability.

Say now that we increase the sample of stocks to 100 and find that the estimate changes slightly from -0.20 to -0.25, and the standard deviation falls to 0.90. The new standard error would thus be:

SE = 0.90/√100 = 0.90/10 = 0.09.

The resulting confidence interval becomes -0.25 ± 0.09 = (-0.34 — -0.16), which is a tighter range of values.

What Is Meant by Standard Error?

Standard error is intuitively the standard deviation of the sampling distribution. In other words, it depicts how much disparity there is likely to be in a point estimate obtained from a sample relative to the true population mean.

What Is a Good Standard Error?

Standard error measures the amount of discrepancy that can be expected in a sample estimate compared to the true value in the population. Therefore, the smaller the standard error the better. In fact, a standard error of zero (or close to it) would indicate that the estimated value is exactly the true value.

How Do You Find the Standard Error?

The standard error takes the standard deviation and divides it by the square root of the sample size. Many statistical software packages automatically compute standard errors.

The Bottom Line

The standard error (SE) measures the dispersion of estimated values obtained from a sample around the true value to be found in the population. Statistical analysis and inference often involves drawing samples and running statistical tests to determine associations and correlations between variables. The standard error thus tells us with what degree of confidence we can expect the estimated value to approximate the population value.

Источник

Загрузить PDF

Стандартная ошибка оценки служит для того, чтобы выяснить, как линия регрессии соответствует набору данных. Если у вас есть набор данных, полученных в результате измерения, эксперимента, опроса или из другого источника, создайте линию регрессии, чтобы оценить дополнительные данные. Стандартная ошибка оценки характеризует, насколько верна линия регрессии.

1

Создайте таблицу с данными. Таблица должна состоять из пяти столбцов, и призвана облегчить вашу работу с данными. Чтобы вычислить стандартную ошибку оценки, понадобятся пять величин. Поэтому разделите таблицу на пять столбцов. Обозначьте эти столбцы так:^[1]
2
Введите данные в таблицу. Когда вы проведете эксперимент или опрос, вы получите пары данных — независимую переменную обозначим как , а зависимую или конечную переменную как . Введите эти значения в первые два столбца таблицы.
- Не перепутайте данные. Помните, что определенному значению независимой переменной должно соответствовать конкретное значение зависимой переменной.
- Например, рассмотрим следующий набор пар данных:
  - (1,2)
  - (2,4)
  - (3,5)
  - (4,4)
  - (5,5)
3
Вычислите линию регрессии. Сделайте это на основе представленных данных. Эта линия также называется линией наилучшего соответствия или линией наименьших квадратов. Расчет можно сделать вручную, но это довольно утомительно. Поэтому рекомендуем воспользоваться графическим калькулятором или онлайн-сервисом, которые быстро вычислят линию регрессии по вашим данным.^[2]
- В этой статье предполагается, что уравнение линии регрессии дано (известно).
- В нашем примере линия регрессии описывается уравнением $y^{{prime }}=0,6x+2,2$ .
4

Вычислите прогнозируемые значения по линии регрессии. С помощью уравнения линии регрессии можно вычислить прогнозируемые значения «y» для значений «x», которые есть и которых нет в наборе данных.

Реклама

1
Вычислите ошибку каждого прогнозируемого значения. В четвертом столбце таблицы запишите ошибку каждого прогнозируемого значения. В частности, вычтите прогнозируемое значение ( $y^{{prime }}$ ) из фактического (наблюдаемого) значения ().^[3]
- В нашем примере вычисления будут выглядеть так:
2
Вычислите квадраты ошибок. Возведите в квадрат каждое значение четвертого столбца, а результаты запишите в последнем (пятом) столбце таблицы.
- В нашем примере вычисления будут выглядеть так:
3
Найдите сумму квадратов ошибок. Она пригодится для вычисления стандартного отклонения, дисперсии и других величин. Чтобы найти сумму квадратов ошибок, сложите все значения пятого столбца. ^[4]
- В нашем примере вычисления будут выглядеть так:
4
Завершите расчеты. Стандартная ошибка оценки — это квадратный корень из среднего значения суммы квадратов ошибок. Обычно ошибка оценки обозначается греческой буквой . Поэтому сначала разделите сумму квадратов ошибок на число пар данных. А потом из полученного значения извлеките квадратный корень.^[5]
- Если рассматриваемые данные представляют всю совокупность, среднее значение находится так: сумму нужно разделить на N (количество пар данных). Если же рассматриваемые данные представляют некоторую выборку, вместо N подставьте N-2.
- В нашем примере, скорее всего, имеет место выборка, потому что мы рассматриваем всего 5 пар данных. Поэтому стандартную ошибку оценки вычислите следующим образом:
5
Интерпретируйте полученный результат. Стандартная ошибка оценки — это статистический показатель, которые оценивает, насколько близко измеренные данные лежат к линии регрессии. Ошибка оценка «0» означает, что каждая точка лежит непосредственно на линии. Чем выше ошибка оценки, тем дальше от линии регрессии лежат точки.^[6]
- В нашем примере выборка достаточно маленькая, поэтому стандартная оценка ошибки 0,894 является довольно низкой и характеризует близко расположенные данные.
Реклама

Об этой статье

Эту страницу просматривали 4741 раз.

Была ли эта статья полезной?

Источник

Имея
прямую регрессии, необходимо оценить
насколько сильно точки исходных данных
отклоняются от прямой регрессии. Можно
выполнить оценку разброса, аналогичную
стандартному отклонению выборки. Этот
показатель, называемый стандартной
ошибкой оценки, демонстрирует величину
отклонения точек исходных данных от
прямой регрессии в направлении оси Y.
Стандартная ошибка оценки ()
вычисляется по следующей формуле.

Стандартная
ошибка оценки измеряет степень отличия
реальных значений Y от оцененной величины.
Для сравнительно больших выборок следует
ожидать, что около 67% разностей по модулю
не будет превышать

и около 95% модулей разностей будет не
больше 2.

Стандартная
ошибка оценки подобна стандартному
отклонению. Ее можно использовать для
оценки стандартного отклонения
совокупности. Фактически

оценивает стандартное отклонение

слагаемого ошибки

в статистической модели простой линейной
регрессии. Другими словами,

оценивает общее стандартное отклонение

нормального распределения значений Y,
имеющих математические ожидания

для каждого X.

Малая
стандартная ошибка оценки, полученная
при регрессионном анализе, свидетельствует,
что все точки данных находятся очень
близко к прямой регрессии. Если стандартная
ошибка оценки велика, точки данных могут
значительно удаляться от прямой.

2.3 Прогнозирование величины y

Регрессионную
прямую можно использовать для оценки
величины переменной Y
при данных значениях переменной X. Чтобы
получить точечный прогноз, или предсказание
для данного значения X, просто вычисляется
значение найденной функции регрессии
в точке X.

Конечно
реальные значения величины Y,
соответствующие рассматриваемым
значениям величины X, к сожалению, не
лежат в точности на регрессионной
прямой. Фактически они разбросаны
относительно прямой в соответствии с
величиной
.
Более того, выборочная регрессионная
прямая является оценкой регрессионной
прямой генеральной совокупности,
основанной на выборке из определенных
пар данных. Другая случайная выборка
даст иную выборочную прямую регрессии;
это аналогично ситуации, когда различные
выборки из одной и той же генеральной
совокупности дают различные значения
выборочного среднего.

Есть
два источника неопределенности в
точечном прогнозе, использующем уравнение
регрессии.

Неопределенность,
обусловленная отклонением точек данных
от выборочной прямой регрессии.
Неопределенность,
обусловленная отклонением выборочной
прямой регрессии от регрессионной
прямой генеральной совокупности.

Интервальный
прогноз значений переменной Y
можно построить так, что при этом будут
учтены оба источника неопределенности.

Стандартная
ошибка прогноза

дает меру вариативности предсказанного
значения Y
около истинной величины Y
для данного значения X.
Стандартная ошибка прогноза равна:

Стандартная
ошибка прогноза зависит от значения X,
для которого прогнозируется величина
Y.

минимально, когда
,
поскольку тогда числитель в третьем
слагаемом под корнем в уравнении будет
0. При прочих неизменных величинах
большему отличию соответствует большее
значение стандартной ошибки прогноза.

Если
статистическая модель простой линейной
регрессии соответствует действительности,
границы интервала прогноза величины Y
равны:

где

— квантиль распределения Стьюдента с
n-2 степенями свободы ().
Если выборка велика (),
этот квантиль можно заменить соответствующим
квантилем нормального распределения.
Например, для большой выборки 95%-ный
интервал прогноза задается следующими
значениями:

Завершим
раздел обзором предположений, положенных
в основу статистической модели линейной
регрессии.

Для
заданного значения X генеральная
совокупность значений Y имеет нормальное
распределение относительно регрессионной
прямой совокупности. На практике
приемлемые результаты получаются
и
тогда, когда значения Y имеют
нормальное распределение лишь
приблизительно.
Разброс
генеральной совокупности точек данных
относительно регрессионной прямой
совокупности остается постоянным всюду
вдоль этой прямой. Иными словами, при
возрастании значений X в точках данных
дисперсия генеральной совокупности
не увеличивается и не уменьшается.
Нарушение этого предположения называется
гетероскедастичностью.
Слагаемые
ошибок

независимы между собой. Это предположение
определяет случайность выборки точек
Х-Y.
Если точки данных X-Y
записывались в течение некоторого
времени, данное предположение часто
нарушается. Вместо независимых данных,
такие последовательные наблюдения
будут давать серийно коррелированные
значения.
В
генеральной совокупности существует
линейная зависимость между X и Y.
По аналогии с простой линейной регрессией
может рассматриваться и нелинейная
зависимость между X и У. Некоторые такие
случаи будут обсуждаться ниже.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Для значения, которое выбирается с несмещенной ошибкой с нормальным распределением , приведенное выше показывает долю выборок, которая будет находиться между 0, 1, 2 и 3 стандартными отклонениями выше и ниже фактического значения.

Стандартная ошибка ( SE ) из статистики (обычно подсчет параметра ) является стандартным отклонением ее выборочного распределения или оценка этого стандартного отклонения. Если статистика является выборочным средним, это называется стандартной ошибкой среднего ( SEM ).

Распределение выборки из среднего генерируется путем повторного отбора образцов из того же населения и записи средств , полученных образцов. Это формирует распределение различных средних, и это распределение имеет собственное среднее значение и дисперсию . Математически дисперсия полученного распределения выборки равна дисперсии генеральной совокупности, деленной на размер выборки. Это связано с тем, что по мере увеличения размера выборки средние значения выборки сгруппируются более близко к среднему значению генеральной совокупности.

Следовательно, соотношение между стандартной ошибкой среднего и стандартным отклонением таково, что для данного размера выборки стандартная ошибка среднего равна стандартному отклонению, деленному на квадратный корень из размера выборки. Другими словами, стандартная ошибка среднего — это мера разброса выборочных средних вокруг среднего по генеральной совокупности.

В регрессионном анализе термин «стандартная ошибка» относится либо к квадратному корню из приведенной статистики хи-квадрат , либо к стандартной ошибке для конкретного коэффициента регрессии (который используется, например, в доверительных интервалах ).

Стандартная ошибка среднего

Точное значение

Если статистически независимые выборки наблюдений берется из статистической совокупности с стандартным отклонением от , то среднее значение , рассчитанное из образца будет иметь ассоциированную стандартную ошибку среднего значения на заданном с помощью:
${ Displaystyle x_ {1}, x_ {2}, ldots, x_ {n}}$ ${ displaystyle { sigma} _ { bar {x}}}$

${ displaystyle { sigma} _ { bar {x}} = { frac { sigma} { sqrt {n}}}}$

На практике это говорит нам о том, что при попытке оценить значение среднего по совокупности из-за фактора уменьшение ошибки оценки в два раза требует получения в четыре раза большего количества наблюдений в выборке; уменьшение его в десять раз требует в сто раз больше наблюдений.

Оценивать

Стандартное отклонение отобранной совокупности известно редко. Таким образом, стандартная ошибка среднего обычно оцениваются путем замены с стандартным отклонением выборки вместо:
$sigma _ {x}$

${ displaystyle { sigma} _ { bar {x}} приблизительно { frac { sigma _ {x}} { sqrt {n}}}}$

Поскольку это только оценка истинной «стандартной ошибки», здесь часто встречаются другие обозначения, такие как:

${ displaystyle { widehat { sigma}} _ { bar {x}} = { frac { sigma _ {x}} { sqrt {n}}}}$

или поочередно . ${ displaystyle {s} _ { bar {x}} = { frac {s} { sqrt {n}}}}$

Общим источником путаницы возникает при отсутствии четко различать между стандартным отклонением населения ( ), стандартное отклонение выборки ( ), стандартное отклонение среднего само по себе ( , который является стандартная ошибка), а оценка из стандартное отклонение среднего ( которое является наиболее часто вычисляемой величиной и также часто в просторечии называется стандартной ошибкой ).
$sigma _ {x}$ ${ displaystyle sigma _ { bar {x}}}$ ${ displaystyle { widehat { sigma}} _ { bar {x}}}$

Точность оценщика

Когда размер выборки невелик, использование стандартного отклонения выборки вместо истинного стандартного отклонения генеральной совокупности будет иметь тенденцию к систематическому занижению стандартного отклонения генеральной совокупности, а, следовательно, и стандартной ошибки. При n = 2 занижение составляет около 25%, но для n = 6 занижение составляет всего 5%. Гурланд и Трипати (1971) предлагают поправку и уравнение для этого эффекта. Сокал и Рольф (1981) приводят уравнение поправочного коэффициента для малых выборок n <20. См. Несмещенную оценку стандартного отклонения для дальнейшего обсуждения.

Вывод

Стандартная ошибка среднего может быть получена из дисперсии суммы независимых случайных величин с учетом определения дисперсии и некоторых ее простых свойств . Если это независимые наблюдения от совокупности со средним значением и стандартным отклонением , то мы можем определить общую
${ Displaystyle x_ {1}, x_ {2}, ldots, x_ {n}}$

${ Displaystyle T = (x_ {1} + x_ {2} + cdots + x_ {n})}$

которые по формуле Биенайме будут иметь дисперсию

${ displaystyle operatorname {Var} (T) = { big (} operatorname {Var} (x_ {1}) + operatorname {Var} (x_ {2}) + cdots + operatorname {Var} ( x_ {n}) { big)} = n sigma ^ {2}.}$

Среднее значение этих измерений просто дается выражением

Тогда дисперсия среднего составляет

${ displaystyle operatorname {Var} ({ bar {x}}) = operatorname {Var} left ({ frac {T} {n}} right) = { frac {1} {n ^ { 2}}} operatorname {Var} (T) = { frac {1} {n ^ {2}}} n sigma ^ {2} = { frac { sigma ^ {2}} {n}} .}$

Стандартная ошибка — это, по определению, стандартное отклонение, которое представляет собой квадратный корень из дисперсии:

${ displaystyle sigma _ { bar {x}} = { sqrt { frac { sigma ^ {2}} {n}}} = { frac { sigma} { sqrt {n}}}}$

Для коррелированных случайных величин дисперсия выборки должна быть вычислена в соответствии с центральной предельной теоремой Маркова .

Независимые и одинаково распределенные случайные величины со случайным размером выборки

Бывают случаи, когда образец берут, не зная заранее, сколько наблюдений будет приемлемым по какому-либо критерию. В таких случаях размер выборки является случайной величиной, вариация которой добавляется к вариации , так что,
Икс

${ Displaystyle OperatorName {Var} (T) = OperatorName {E} (N) OperatorName {Var} (X) + Operatorname {Var} (N) { big (} Operatorname {E} (X) { big)} ^ {2}}$

Если имеет распределение Пуассона , то с оценкой . Следовательно, оценка становится , приводя к следующей формуле для стандартной ошибки:
${ displaystyle nS_ {X} ^ {2} + n { bar {X}} ^ {2}}$

${ displaystyle operatorname {Standard ~ Error} ({ bar {X}}) = { sqrt { frac {S_ {X} ^ {2} + { bar {X}} ^ {2}} {n }}}}$

(поскольку стандартное отклонение — это квадратный корень из дисперсии)

Приближение Стьюдента при неизвестном значении σ

Во многих практических приложениях истинное значение σ неизвестно. В результате нам нужно использовать распределение, которое учитывает этот разброс возможных σ . Когда известно, что истинное базовое распределение является гауссовым, хотя и с неизвестным σ, тогда полученное оцененное распределение следует t-распределению Стьюдента. Стандартная ошибка — это стандартное отклонение t-распределения Стьюдента. Т-распределения немного отличаются от гауссовых и меняются в зависимости от размера выборки. Небольшие выборки с большей вероятностью недооценивают стандартное отклонение совокупности и имеют среднее значение, которое отличается от истинного среднего значения совокупности, а t-распределение Стьюдента учитывает вероятность этих событий с несколько более тяжелыми хвостами по сравнению с гауссовым. Для оценки стандартной ошибки t-распределения Стьюдента достаточно использовать выборочное стандартное отклонение «s» вместо σ , и мы могли бы использовать это значение для вычисления доверительных интервалов.

Примечание. Распределение вероятностей Стьюдента хорошо аппроксимируется распределением Гаусса, когда размер выборки превышает 100. Для таких выборок можно использовать последнее распределение, которое намного проще.

Предположения и использование

Пример того, как это используется, — это сделать доверительные интервалы для неизвестного среднего значения генеральной совокупности. Если распределение выборки имеет нормальное распределение , среднее значение выборки, стандартная ошибка и квантили нормального распределения могут использоваться для расчета доверительных интервалов для истинного среднего значения генеральной совокупности. Следующие выражения могут быть использованы для расчета верхнего и нижнего 95% доверительных интервалов, где равно среднему значению выборки, равно стандартной ошибке для среднего значения выборки, а 1,96 является приблизительным значением точки процентиля 97,5 нормального распространение :

Верхний предел 95% и

{ displaystyle = { bar {x}} + ( operatorname {SE} times 1,96),}

Нижний предел 95%

В частности, стандартная ошибка выборочной статистики (например, выборочное среднее ) — это фактическое или расчетное стандартное отклонение выборочного среднего в процессе, в котором оно было создано. Другими словами, это фактическое или оценочное стандартное отклонение выборочного распределения статистической выборки. Обозначение для стандартной ошибки может быть любым из SE, SEM (для стандартной ошибки измерения или среднего ), или S _E .

Стандартные ошибки обеспечивают простые меры неопределенности значения и часто используются, потому что:

во многих случаях, если известна стандартная ошибка нескольких отдельных величин, то стандартную ошибку некоторой функции величин можно легко вычислить;
когда распределение вероятностей значения известно, его можно использовать для вычисления точного доверительного интервала ;
когда распределение вероятностей неизвестно, для расчета консервативного доверительного интервала можно использовать неравенства Чебышева или Высочанского – Петунина ; а также
поскольку размер выборки стремится к бесконечности, центральная предельная теорема гарантирует, что выборочное распределение среднего является асимптотически нормальным .

Стандартная ошибка среднего значения по сравнению со стандартным отклонением

В научно-технической литературе экспериментальные данные часто обобщаются либо с использованием среднего значения и стандартного отклонения выборочных данных, либо среднего значения со стандартной ошибкой. Это часто приводит к путанице в отношении их взаимозаменяемости. Однако среднее значение и стандартное отклонение являются описательной статистикой , тогда как стандартная ошибка среднего описывает процесс случайной выборки. Стандартное отклонение данных выборки — это описание вариации в измерениях, в то время как стандартная ошибка среднего — это вероятностное утверждение о том, как размер выборки обеспечит лучшую границу оценок среднего для генеральной совокупности в свете центрального предела. теорема.

Проще говоря, стандартная ошибка выборочного среднего — это оценка того, насколько далеко среднее значение выборки может быть от среднего значения по совокупности, тогда как стандартное отклонение выборки — это степень, в которой отдельные лица в выборке отличаются от выборочного среднего. Если стандартное отклонение генеральной совокупности конечно, стандартная ошибка среднего значения выборки будет стремиться к нулю с увеличением размера выборки, потому что оценка генерального среднего будет улучшаться, в то время как стандартное отклонение выборки будет иметь тенденцию приближаться к стандарту генеральной совокупности. отклонение по мере увеличения размера выборки.

Расширения

Поправка на конечную популяцию (FPC)

Приведенная выше формула для стандартной ошибки предполагает, что размер выборки намного меньше, чем размер генеральной совокупности, так что совокупность может считаться фактически бесконечной по размеру. Обычно это имеет место даже в случае конечных популяций, потому что большую часть времени люди в первую очередь заинтересованы в управлении процессами, которые создали существующую конечную популяцию; это называется аналитическим исследованием вслед за У. Эдвардсом Демингом . Если люди заинтересованы в управлении существующей конечной совокупностью, которая не будет меняться с течением времени, то необходимо сделать поправку на размер популяции; это называется перечислительным исследованием .

Когда доля выборки (часто называемая f ) велика (примерно 5% или более) в переписном исследовании , оценка стандартной ошибки должна быть скорректирована путем умножения на «поправку на конечную совокупность» (также известную как fpc ):

${ displaystyle operatorname {FPC} = { sqrt { frac {Nn} {N-1}}}}$

что для больших N :

${ displaystyle operatorname {FPC} приблизительно { sqrt {1 - { frac {n} {N}}}} = { sqrt {1-f}}}$

чтобы учесть дополнительную точность, полученную за счет выборки, близкой к большему проценту населения. Эффект FPC является то , что ошибка становится равной нулю , когда размер выборки п равен размеру популяции N .

Это происходит в методологии обследования при выборке без замены . Если выборка с заменой, то FPC не играет роли.

Поправка на корреляцию в выборке

Ожидаемая ошибка среднего значения A для выборки из n точек данных с коэффициентом смещения выборки ρ . Несмещенная стандартная ошибка строится как диагональная линия ρ = 0 с логарифмическим наклоном −½.

Если значения измеренной величины A не являются статистически независимыми, но были получены из известных мест в пространстве параметров x , несмещенная оценка истинной стандартной ошибки среднего (фактически поправка на часть стандартного отклонения) может быть получена путем умножения рассчитанная стандартная ошибка выборки по коэффициенту f :

$f = { sqrt { frac {1+ rho} {1- rho}}},$

где коэффициент смещения выборки ρ представляет собой широко используемую оценку Прайса – Винстена коэффициента автокорреляции (величина от -1 до +1) для всех пар точек выборки. Эта приблизительная формула предназначена для выборки среднего и большого размера; Справочник дает точные формулы для любого размера выборки и может применяться к сильно автокоррелированным временным рядам, таким как котировки акций Уолл-стрит. Более того, эта формула работает как для положительного, так и для отрицательного значения ρ. См. Также объективную оценку стандартного отклонения для более подробного обсуждения.

Смотрите также

Иллюстрация центральной предельной теоремы
Допустимая погрешность
Вероятная ошибка
Стандартная ошибка средневзвешенного значения
Среднее значение выборки и ковариация выборки
Стандартная ошибка медианы
Дисперсия

использованная литература

Источник