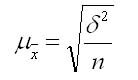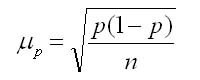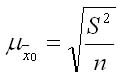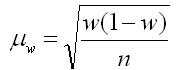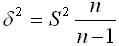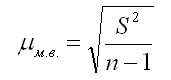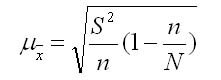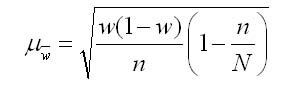|
n t |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
15 |
20 |
|
|
0.5 |
0.348 |
0.356 |
0.362 |
0.366 |
0.368 |
0.370 |
0.372 |
0.376 |
0.378 |
0.383 |
|
1.0 |
0.608 |
0.626 |
0.636 |
0.644 |
0.650 |
0.654 |
0.656 |
0.666 |
0.670 |
0.683 |
|
1.5 |
0.770 |
0.792 |
0.806 |
0.816 |
0.832 |
0.828 |
0.832 |
0.846 |
0.850 |
0.865 |
|
2.0 |
0.860 |
0.884 |
0.908 |
0.908 |
0.914 |
0.920 |
0.924 |
0.936 |
0.940 |
0.954 |
|
2.5 |
0.933 |
0.946 |
0.955 |
0.959 |
0.963 |
0.966 |
0.968 |
0.975 |
0.978 |
0.988 |
|
3.0 |
0.942 |
0.960 |
0.970 |
0.976 |
0.980 |
0.938 |
0.984 |
0.992 |
0.992 |
0.997 |
Примечание
При
оценке результатов малой
выборки
(численность которой не превышает 30
единиц), величина генеральной дисперсии
в расчетах не используется. Величина
и предельная ошибка малой выборки
вычисляются на основе данных выборочного
наблюдения:
и
,
где
мера случайных колебаний выборочной
средней в малой выборке, а
.
На
заключительном этапе на основе предельной
ошибки выборки определяют доверительные
интервалы, в
которых может находиться генеральная
средняя или генеральная доля. Выход за
пределы этой области имеет весьма малую
вероятность. Доверительные интервалы
определяются по формулам:
-
для
среднего значения:;
-
для
доли:.
Типовая задача 1
Для
анализа выполнения норм выработки
предприятия было проведено 10%-ное
механическое повторное выборочное
обследование, результаты которого
показали следующее распределение
рабочих по выполнению норм выработки:
|
Группы |
Число |
|
1. 2. 3. 4. 5. |
5 19 25 36 15 |
|
Итого |
100 |
Определить:
1)
с вероятностью 0,954 возможные пределы,
в которых ожидается средний процент
выполнения норм выработки по предприятию;
2)
с вероятностью 0.997 возможные пределы
доли рабочих, выполняющих нормы выработки
на 100% и более, в общей численности
предприятия.
Решение
1)
Определим возможные пределы среднего
выполнения норм выработки по предприятию,
т.е. доверительный интервал
.
Сначала
определим выборочную среднюю:
.
Т.к.
отбор единиц в выборку по условию
бесповторный, то определим величину
предельной ошибки выборки по формуле:
,
где
t
= 2 (при p
= 0,954);
n
= 100 (чел.);
,
т.к. по условию выборка 10%-ная, т.е. n
составляет 10% от общей численности
рабочих;

.
Следовательно,
определим границы доверительного
интервала:
(98,7-2,1;
98,7+2,1)
(96,6;
100,8).
Таким
образом, с вероятностью 0.954 можно
утверждать, что среднее выполнение норм
выработки по всему предприятию изменяется
от 96,6 до 100,8%.
2)
Определим возможные пределы доли
рабочих, выполняющих нормы выработки
сверх плана, т.е. доверительный интервал:
.
Рассчитаем
долю рабочих, выполняющих план на 100% и
более. По условию таких рабочих 51 человек,
значит:
или
51%.
Т.к.
отбор единиц в выборку по условию
бесповторный, то определим величину
предельной ошибки выборки по формуле:
,
где t
= 3 (при p
= 0,997), тогда получим
или
14%.
Определим
границы доверительного интервала:
(51-14;
51+14)
(37;
65)
Таким
образом, с вероятностью 0.997 можно
утверждать, что доля рабочих, выполняющих
план на 100% и более, в общей численности
предприятия изменяется от 37 до 65%.
При
проектировании выборочного наблюдения
с заранее заданным значением допустимой
ошибки выборки важно правильно определить
численность
(объем) выборочной совокупности,
которая с определенной вероятностью
обеспечит заданную точность результатов
наблюдения. Для этого используют
следующие формулы расчета (табл. 4.3).
Таблица
4.3
|
Вид |
Методы |
|
|
Повторный |
Бесповторный |
|
|
Собственно-случайная |
||
|
для |
|
|
|
для |
|
|
|
Типическая |
||
|
для |
|
|
|
для |
|
|
|
Серийная |
||
|
для |
|
|
|
для |
|
|
Отметим,
что с увеличением предельной ошибки
уменьшается необходимый объем выборки,
и наоборот.
Соседние файлы в папке статистика
- #
- #
- #
- #
- #
- #
- #
Средние ошибки повторной и бесповторной выборки
Средняя ошибка выборки
Средняя ошибка выборки представляет из себя такое расхождение между средними выборочной и генеральной совокупностями, которое не превышает ±б (дельта).
На основании теоремы Чебышева П. Л. величина средней ошибки при случайном повторном отборе в контрольных работах по статистике рассчитывается по формуле (для среднего количественного признака):
где числитель — дисперсия признака х в выборочной совокупности;
n — численность выборочной совокупности.
Для альтернативного признака формула средней ошибки выборки для доли по теореме Я. Бернулли рассчитывается по формуле:
где р(1- р) — дисперсия доли признака в генеральной совокупности;
n — объем выборки.
Вследствие, того что дисперсия признака в генеральной совокупности точно не известна, на практике используют значение дисперсии, которое рассчитано для выборочной совокупности на основании закона больших чисел. Согласно данному закону выборочная совокупность при большом объеме выборки достаточно точно воспроизводит характеристики генеральной совокупности.
Поэтому расчетные формулы средней ошибки при случайном повторном отборе будут выглядеть таким образом:
1. Для среднего количественного признака:
где S^2 — дисперсия признака х в выборочной совокупности;
n — объем выборки.
2. Для доли (альтернативного признака):
где w (1 — w) — дисперсия доли изучаемого признака в выборочной совокупности.
В теории вероятностей было показано, что генеральная дисперсия выражается через выборочную согласно формуле:
В случаях малой выборки, когда её объем меньше 30, необходимо учитывать коэффициент n/(n-1). Тогда среднюю ошибку малой выборки рассчитывают по формуле:
Так как в процессе бесповторной выборки сокращается численность единиц генеральной совокупности, то в представленных выше формулах расчета средних ошибок выборки нужно подкоренное выражение умножить на 1- (n/N).
Расчетные формулы для такого вида выборки будут выглядеть так:
1. Для средней количественного признака:
где N — объем генеральной совокупности; n — объем выборки.
2. Для доли (альтернативного признака):
где 1- (n/N) — доля единиц генеральной совокупности, не попавших в выборку.
Поскольку n всегда меньше N, то дополнительный множитель 1 — (n/N) всегда будет меньше единицы. Это означает, что средняя ошибка при бесповторном отборе всегда будет меньше, чем при повторном. Когда доля единиц генеральной совокупности, которые не попали в выборку, существенная, то величина 1 — (n/N) близка к единице и тогда расчет средней ошибки производится по общей формуле.
Средняя ошибка зависит от следующих факторов:
1. При выполнении принципа случайного отбора средняя ошибка выборки определяется во-первых объемом выборки: чем больше численность, тем меньше величины средней ошибки выборки. Генеральная совокупность характеризуется точнее тогда, когда больше единиц данной совокупности охватывает выборочное наблюдение
2. Средняя ошибка также зависит от степени варьирования признака. Степень варьирования характеризуется дисперсией. Чем меньше вариация признака (дисперсия), тем меньше средняя ошибка выборки. При нулевой дисперсии (признак не варьируется) средняя ошибка выборки равна нулю, таким образом, любая единица генеральной совокупности будет характеризовать всю совокупность по этому признаку.
Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.
Среднее арифметическое, как известно, используется для получения обобщающей характеристики некоторого набора данных. Если данные более-менее однородны и в них нет аномальных наблюдений (выбросов), то среднее хорошо обобщает данные, сведя к минимуму влияние случайных факторов (они взаимопогашаются при сложении).
Когда анализируемые данные представляют собой выборку (которая состоит из случайных значений), то среднее арифметическое часто (но не всегда) выступает в роли приближенной оценки математического ожидания. Почему приближенной? Потому что среднее арифметическое – это величина, которая зависит от набора случайных чисел, и, следовательно, сама является случайной величиной. При повторных экспериментах (даже в одних и тех же условиях) средние будут отличаться друг от друга.
Для того, чтобы на основе статистического анализа данных делать корректные выводы, необходимо оценить возможный разброс полученного результата. Для этого рассчитываются различные показатели вариации. Но то исходные данные. И как мы только что установили, среднее арифметическое также обладает разбросом, который необходимо оценить и учитывать в дальнейшем (в выводах, в выборе метода анализа и т.д.).
Интуитивно понятно, что разброс средней должен быть как-то связан с разбросом исходных данных. Основной характеристикой разброса средней выступает та же дисперсия.
Дисперсия выборочных данных – это средний квадрат отклонения от средней, и рассчитать ее по исходным данным не составляет труда, например, в Excel предусмотрены специальные функции. Однако, как же рассчитать дисперсию средней, если в распоряжении есть только одна выборка и одно среднее арифметическое?
Расчет дисперсии и стандартной ошибки средней арифметической
Чтобы получить дисперсию средней арифметической нет необходимости проводить множество экспериментов, достаточно иметь только одну выборку. Это легко доказать. Для начала вспомним, что средняя арифметическая (простая) рассчитывается по формуле:
где xi – значения переменной,
n – количество значений.
Теперь учтем два свойства дисперсии, согласно которым, 1) — постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат и 2) — дисперсия суммы независимых случайных величин равняется сумме соответствующих дисперсий. Предполагается, что каждое случайное значение xi обладает одинаковым разбросом, поэтому несложно вывести формулу дисперсии средней арифметической:
Используя более привычные обозначения, формулу записывают как:
где σ2 – это дисперсия, случайной величины, причем генеральная.
На практике же, генеральная дисперсия известна далеко не всегда, точнее совсем редко, поэтому в качестве оной используют выборочную дисперсию:
Стандартное отклонение средней арифметической называется стандартной ошибкой средней и рассчитывается, как квадратный корень из дисперсии.
Формула стандартной ошибки средней при использовании генеральной дисперсии
Формула стандартной ошибки средней при использовании выборочной дисперсии
Последняя формула на практике используется чаще всего, т.к. генеральная дисперсия обычно не известна. Чтобы не вводить новые обозначения, стандартную ошибку средней обычно записывают в виде соотношения стандартного отклонения выборки и корня объема выборки.
Назначение и свойство стандартной ошибки средней арифметической
Стандартная ошибка средней много, где используется. И очень полезно понимать ее свойства. Посмотрим еще раз на формулу стандартной ошибки средней:
Числитель – это стандартное отклонение выборки и здесь все понятно. Чем больше разброс данных, тем больше стандартная ошибка средней – прямо пропорциональная зависимость.
Посмотрим на знаменатель. Здесь находится квадратный корень из объема выборки. Соответственно, чем больше объем выборки, тем меньше стандартная ошибка средней. Для наглядности изобразим на одной диаграмме график нормально распределенной переменной со средней равной 10, сигмой – 3, и второй график – распределение средней арифметической этой же переменной, полученной по 16-ти наблюдениям (которое также будет нормальным).
Судя по формуле, разброс стандартной ошибки средней должен быть в 4 раза (корень из 16) меньше, чем разброс исходных данных, что и видно на рисунке выше. Чем больше наблюдений, тем меньше разброс средней.
Казалось бы, что для получения наиболее точной средней достаточно использовать максимально большую выборку и тогда стандартная ошибка средней будет стремиться к нулю, а сама средняя, соответственно, к математическому ожиданию. Однако квадратный корень объема выборки в знаменателе говорит о том, что связь между точностью выборочной средней и размером выборки не является линейной. Например, увеличение выборки с 20-ти до 50-ти наблюдений, то есть на 30 значений или в 2,5 раза, уменьшает стандартную ошибку средней только на 36%, а со 100-а до 130-ти наблюдений (на те же 30 значений), снижает разброс данных лишь на 12%.
Лучше всего изобразить эту мысль в виде графика зависимости стандартной ошибки средней от размера выборки. Пусть стандартное отклонение равно 10 (на форму графика это не влияет).
Видно, что примерно после 50-ти значений, уменьшение стандартной ошибки средней резко замедляется, после 100-а – наклон постепенно становится почти нулевым.
Таким образом, при достижении некоторого размера выборки ее дальнейшее увеличение уже почти не сказывается на точности средней. Этот факт имеет далеко идущие последствия. Например, при проведении выборочного обследования населения (опроса) чрезмерное увеличение выборки ведет к неоправданным затратам, т.к. точность почти не меняется. Именно поэтому количество опрошенных редко превышает 1,5 тысячи человек. Точность при таком размере выборки часто является достаточной, а дальнейшее увеличение выборки – нецелесообразным.
Подведем итог. Расчет дисперсии и стандартной ошибки средней имеет довольно простую формулу и обладает полезным свойством, связанным с тем, что относительно хорошая точность средней достигается уже при 100 наблюдениях (в этом случае стандартная ошибка средней становится в 10 раз меньше, чем стандартное отклонение выборки). Больше, конечно, лучше, но бесконечно увеличивать объем выборки не имеет практического смысла. Хотя, все зависит от поставленных задач и цены ошибки. В некоторых опросах участие принимают десятки тысяч людей.
Дисперсия и стандартная ошибка средней имеют большое практическое значение. Они используются в проверке гипотез и расчете доверительных интервалов.
Поделиться в социальных сетях: