В
практике большое распространение
получил так называемый допусковый
контроль,
суть которого состоит в определении
путем измерения или испытания значения
контролируемого параметра объекта и
сравнение полученного результата с
заданными граничными допустимыми
значениями. Частным случаем допускового
контроля является поверка средств
измерений, в процессе которой исследуется
попадание погрешностей средства
измерений в допустимые пределы. По
расположению зоны контролируемого
состояния различают допусковый контроль
состояний:
• ниже
допускаемого значения Х
< Хдн;
• выше
допускаемого значения Х
> Хдв;
• между
верхним и нижним допускаемыми значениями
Хдн< Х
< Хдв.
Результатом
контроля является не число, а одно из
взаимоисключающих утверждений:
• «контролируемая
характеристика (параметр) находится в
пределах допускаемых значений»,
результат контроля
— «годен»;
• «контролируемая
характеристика (параметр) находится за
пределами допускаемых значений»,
результат контроля
—»не
годен » или «брак».
Для
определенности примем, что решение
«годен» должно приниматься, если
выполняется условие Хдн
Х
Xвд,
где
X, Хдн, Xдв
— истинное значение и допускаемые
верхнее и нижнее значения контролируемого
параметра. На самом же деле с допускаемыми
значениями Хд и Хд сравнивается не
истинное значение Х (поскольку оно
неизвестно), а его оценка Хо, полученная
в результате измерений. Значение Х
отличается от Х на величину погрешности
измерения: Хо
= Хо+ А.
Решение «годен» при проведении
контроля принимается в случае выполнения
неравенства ХднХоХдв.
Отсюда следует, что при допусковом
контроле возможны четыре исхода.
-
Принято
решение «годен», когда значение
контролируемого параметра находится
в допускаемых пределах, т.е. имели место
события ХднХХдв
, ХднХоХдв.
Если известны плотности вероятностей
законов распределения f(X)
контролируемого параметра Х и погрешности
его измерения f(А),
то при взаимной независимости тих
законов и заданных допустимых верхнем
и нижнем значениях параметра вероятность
события «годен» .
2.
Принято решение «брак», когда
значение контролируемого параметра
находится вне пределов допускаемых
значений, т.е. имели место события Х
< Хдн или
Х >
Хдв и Хо< Хдн или Хо> Хдв. При оговоренных
допущениях вероятность события «негоден»
или «брак»
-
Принято
решение «брак», когда истинное
значение контролируемого параметра
лежит в пределах допускаемых значений,
т.е. Хо<Хдн или Хо>Хдв и Хдн
Х Хдв
и забракован исправный объект. В этом
случае принято говорить, что имеет
место ошибка
I рода. Ее
вероятность
4.
Принято решение «годен», когда
истинное значение контролируемого
параметра лежит вне пределов допускаемых
значений, т.е. имели место события Х
< Хдн или
Х>Хдв и ХднХо<Хдв
и неисправный объект признан годным. В
этом случае говорят, что произошла
ошибка
II рода,
вероятность которой
Очевидно,
что ошибки I
и
II родов
имеют разное значение для изготовителей
и потребителей (заказчиков) контролируемой
продукции
[26]. Ошибки
I рода ведут
к прямым потерям изготовителя, так как
ошибочное признание негодным в
действительности годного изделия
приводит к дополнительным затратам на
исследование, доработку и регулировку
изделия. Ошибки
II рода
непосредственно сказываются на
потребителе, который получает
некачественное изделие. При нормальной
организации отношений между потребителем
и производителем брак, обнаруженный
первым из них, приводит к рекламациям
и ущербу для изготовителя.
Рассмотренные
вероятности Рг, Рнг, Р1, и Р2 при массовом
контроле партии изделий характеризуют
средние доли годных, негодных,
неправильно забракованных и неправильно
пропущенных изделий среди всей
контролируемой их совокупности. Очевидно,
что Рг+Ргн+Р1+Р2=
1.
Достоверность
результатов допускового контроля
описывается различными показателями,
среди которых наибольшее распространение
получили вероятности ошибок
I (Р1
) и
II (Р2
) родов
и риски изготовителя и заказчика
(потребителя):
Одна
из важнейших задач планирования контроля
— выбор
оптимальной точности измерения
контролируемых параметров. При завышении
допускаемых погрешностей измерения
уменьшается стоимость средств измерений,
но увеличиваются вероятности ошибок
при контроле, что в конечном итоге
приводит к потерям. При занижении
допускаемых погрешностей стоимость
средств измерений возрастает,
вероятность ошибок контроля уменьшается,
увеличивает себестоимости выпускаемой
продукции. Очевидно, что существует
некоторая оптимальная точность,
соответствующая минимуму суммы потерь
от брака и стоимости контроля.
Приведенные
формулы позволяют осуществить
целенаправленный поиск таких значений
погрешности измерения, которые бы при
заданных верхнем и нижнем значениях
контролируемого параметра обеспечили
бы допускаемые значения вероятностей
ошибок
I и
II родов
(Р1д и Р2д
) или
соответствующих рисков. Этот поиск
производится путем численного или
графического интегрирования. Следовательно,
для рационального выбора точностных
характеристик средств измерений,
используемых при проведении контроля,
каждом конкретном случае должны быть
заданы допускаемые значения Р1д и Р2д.
3.7.
Метод импульсной рефлектометрии для
контроля протяженных объектов.
Метод
импульсной рефлектометрии, называемый
также методом
отраженных импульсов
или локационным
методом, базируется на распространении
импульсных сигналов в двух- и многопроводных
системах.
Сущность
метода импульсной рефлектометрии
заключается в следующих операциях:
-
Зондировании
трубопроводной системы импульсами
напряжения. -
Приеме импульсов,
отраженных от места повреждения и
неоднородностей волнового сопротивления. -
Выделении отражений
от места повреждений на фоне помех
(случайных и отражений от неоднородностей
трубопроводов). -
Определении
расстояния до повреждения по временной
задержке отраженного импульса
относительно зондирующего.
Упрощенная
структурная схема измерений с помощью
импульсного рефлектометра приведена
на рисунке 3.
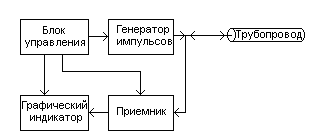
Рис.3. Упрощенная
структурная схема измерений.
С
генератора импульсов зондирующие
импульсы подаются в трубопровод.
Отраженные импульсы поступают с
трубопровода в приемник, в котором
производятся необходимые преобразования
над ними. С выхода приемника преобразованные
сигналы поступают на графический
индикатор. Все блоки импульсного
рефлектометра функционируют по сигналам
блока управления. На графическом
индикаторе рефлектометра воспроизводится
рефлектограмма трубопровода — реакция
трубопровода на зондирующий импульс.
Образование
рефлектограммы трубопровода легко
проследить по диаграмме, приведенной
на рисунке 4. Здесь осью ординат является
ось расстояния, а осью абсцисс — ось
времени.
В левой
части рисунка показан трубопровод из
двух секций с согласующим устройством
и коротким замыканием, а в нижней части
— рефлектограмма этого трубопровода.
Анализируя рефлектограмму трубопровода,
оператор получает информацию о наличии
или отсутствии в ней повреждений и
неоднородностей.

Рис.4. Пример
рефлектограммы с двумя неоднородностями
в трубопроводе.
Например, по
приведенной рефлектограмме можно
сделать несколько выводов:
-
На рефлектограмме,
кроме зондирующего импульса, есть
только два отражения: отражение от
согласующего устройства и отражение
от короткого замыкания. Это свидетельствует
о хорошей однородности трубопровода
от начала до согласующего устройства
и от согласующего устройства до короткого
замыкания. -
Выходное
сопротивление рефлектометра согласовано
с волновым сопротивлением трубопровода,
так как переотраженные сигналы, которые
при отсутствии согласования располагаются
на двойном расстоянии, отсутствуют. -
Повреждение имеет
вид короткого замыкания, так как
отраженный от него сигнал изменил
полярность. -
Короткое замыкание
полное, так как после отражения от него
других отражений нет. -
Линия имеет большое
затухание, так как амплитуда отражения
от короткого замыкания много меньше,
чем амплитуда зондирующего сигнала.
Если
выходное сопротивление рефлектометра
не согласовано с волновым сопротивлением
трубопровода, то в моменты времени 2*
tм,
4* tм
и т.д. будут наблюдаться переотраженные
сигналы от согласующего устройства,
убывающие по амплитуде, а в моменты
времени 2*
tх,
4*tх
и т.д. — переотражения от места короткого
замыкания.
Основную
сложность и трудоемкость при методе
отраженных импульсов представляет
выделение отражения от места повреждения
на фоне помех.
Важное
значение для метода импульсной
рефлектометрии имеет отношение между
напряжением и током введенной в систему
электромагнитной волны, которое одинаково
в любой точке трубопровода. Это
соотношение:
Z
= U/I
имеет размерность
сопротивления и называется волновым
сопротивлением трубопровода.
При использовании метода импульсной
рефлектометрии в трубопроводную систему
контроля посылают зондирующий импульс
и измеряют интервал tх — время двойного
пробега этого импульса до места
повреждения (неоднородности волнового
сопротивления). Расстояние до места
повреждения рассчитывают по выражению:
Lx
= tx*V/2
,
где
V
— скорость распространения импульса в
трубопровода.
Отношение
амплитуды отраженного импульса Uо к
амплитуде зондирующего импульса Uз
обозначают коэффициентом отражения p:
p
= Uo/Uз = (Z1
— Z)
/ (Z1
+ Z),
где:
Z
— волновое сопротивление трубопровода
до места повреждения (неоднородности),
Z1
— волновое сопротивление трубопровода
в месте повреждения (неоднородности).
Отраженный
сигнал появляется в тех местах
трубопровода, где волновое сопротивление
отклоняется от своего среднего значения:
согласующие устройства, изгибах
трубопроводов, в месте обрыва, короткого
замыкания и т.д.
Если
выходное сопротивление импульсного
рефлектометра отличается от волнового
сопротивления измеряемого трубопровода,
то в месте подключения рефлектометра
к трубопровода возникают переотражения.
Переотражения
— это отражения от входного сопротивления
рефлектометра отраженных сигналов,
которые пришли к месту подключения
рефлектометра из трубопровода.
В
зависимости от соотношения входного
сопротивления рефлектометра и волнового
сопротивления трубопровода изменяется
полярность и амплитуда переотражений,
которая может оказаться соизмеримой с
амплитудой отражений. Поэтому перед
измерением рефлектометром обязательно
нужно выполнить операцию согласования
выходного сопротивления рефлектометра
с волновым сопротивлением трубопровода.
Примеры
рефлектограммы трубопровода с
переотражением без согласования
выходного сопротивления с трубопроводом
и с согласованием приведены на рис. 5 и
6:
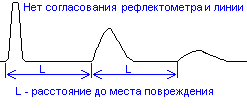
Рис.5. Рефлектограмма
трубопровода в отсутствие согласования.
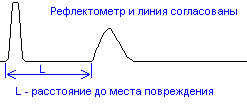
Рис.6. Рефлектограмма
трубопровода при согласовании.
При
распространении вдоль трубопровода
импульсный сигнал затухает. Затухание
трубопровода определяется ее геометрической
конструкцией и выбором материалов для
проводников и изоляции и является
частотно-зависимым. Следствием
частотной зависимости является изменение
зондирующих импульсов при их распространении
по трубопроводу: изменяется не только
амплитуда, но и форма импульса —
длительности фронта и среза импульса
увеличиваются («расплывание”
импульса). Чем длиннее трубопроводная
система, тем больше “расплывание” и
меньше амплитуда импульса. Это затрудняет
точное определение расстояния до
повреждения.
Примеры
рефлектограмм трубопроводов без
затухания и с затуханием показаны на
рисунке 7.


Рис.7. Влияние
затухания трубопровода на вид
рефлектограммы в отсутствие согласования.
Для
более точного измерения необходимо
правильно, в соответствии с длиной и
частотной характеристикой затухания
трубопровода, выбирать параметры
зондирующего импульса в рефлектометре.
Критерием правильного выбора является
минимальное «расплывание» и
максимальная амплитуда отраженного
сигнала.
Если при подключенном
трубопроводе на рефлектограмме
наблюдается только зондирующий импульс,
а отраженные сигналы отсутствуют, то
это свидетельствует о точном согласовании
выходного сопротивления рефлектометра
с волновым сопротивлением трубопровода,
отсутствии повреждений и наличии на
конце трубопровода нагрузки равной
волновому сопротивлению трубопровода
(Рис.8).

Рис.8. Рефлектограмма
при идеальном согласовании.
Вид
отраженного сигнала зависит от характера
повреждения или неоднородности. Например,
при обрыве отраженный импульс имеет ту
же полярность, что и зондирующий, а при
коротком замыкании отраженный импульс
меняет полярность (Рис.9).

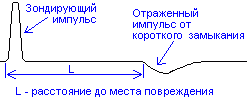
Рис.9. Рефлектограммы
при обрыве и коротком замыкании.
В
идеальном случае, когда отражение от
повреждения полное и затухание
отсутствует, амплитуда отраженного
сигнала равна амплитуде зондирующего
импульса.
Рассмотрим два
случая эквивалентных схем повреждений,
которые наиболее часто встречаются на
практике: шунтирующая
утечка
и продольное
сопротивление.
Пусть
место повреждения трубопровода
представляет собой
шунтирующую утечку
Rш:
С изменением
сопротивления утечки от нуля (соответствует
короткому замыканию) до бесконечности
(соответствует исправности трубопровода),
при положительном зондирующем импульсе
отраженный импульс имеет отрицательную
полярность и изменяется по амплитуде
от максимального значения до нулевого,
в соответствии с выражением:
p=
(Z1
— Z)
/ (Z1
+ Z)
= — Z
/ (Z+2*Rш),
где:
Rш
— сопротивление шунтирующей утечки,
Z1
— волновое сопротивление трубопровода
в месте повреждения, определяется
выражением:
Z1
= (Z*R
ш) / (Z
+ Rш)
Так,
например, при коротком замыкании (Rш=0)
получаем:
p
= -1
В
этом случае сигнал отражается полностью
с изменением полярности.
При отсутствии
шунтирующей нагрузки (Rш=
)
имеем:
p
= 0
Сигнал
не отражается вообще.
При
изменении Rш
от 0 до
амплитуда отраженного сигнала уменьшается
от максимального значения до нулевого,
сохраняя отрицательную полярность (см.
рисунок).
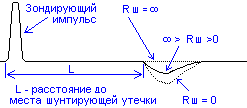
Рис.10. Рефлектограмма
при наличии шунта.
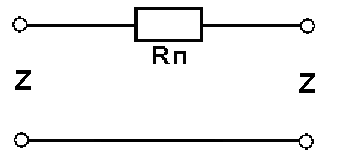
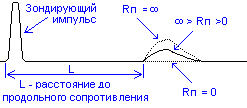
Если
эквивалентная схема места повреждения
трубопровода имеет вид включения
продольного сопротивления (например,
нарушение спайки), то с изменением
величины продольного сопротивления
отраженный импульс изменяется по
амплитуде, оставаясь той же полярности
что и зондирующий импульс.
Выражение для коэффициента отражения
при наличии включения продольного
сопротивления
будет иметь вид:
p
= (Z1
— Z)
/ (Z1
+ Z)
= 1 / (1+2*Z/Rп),
где:
Rп
— продольное сопротивление,
Z1
— волновое сопротивление трубопровода
в месте включения продольного повреждения,
определяемое выражением:
Z1
= Rп + Z
В
случае обрыва жилы (Rп=
)
получаем
коэффициент отражения:
р = 1.
Это
означает, что сигнал отражается полностью
без изменения полярности.
При нулевом
значении продольного сопротивления
(Rп=0)
имеем:
р = 0
С
игнал
не отражается вообще.
При
изменении Rп
от
до
0 отраженный сигнал уменьшается по
амплитуде от максимального значения
до нулевого, без изменения полярности.
Рис.11. Рефлектограмма
— влияние продольного сопротивления.
Разрешающая
способность —
это минимальное расстояние между двумя
неоднородностями волнового сопротивления
при котором отраженные от них сигналы
еще наблюдаются как отдельные сигналы.
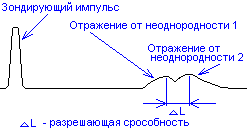
Рис.12. Рефлектограмма
— отражение от двух близких неоднородностей.
На рисунке 11
отраженные от двух неоднородностей
импульсы еще наблюдаются раздельно.
Зондирующие импульсы
распространяются в кабельных линиях
по определенным волновым каналам.
Импульсный
сигнал распространяется в трубопроводе
с определенной скоростью, которая
зависит от типа диэлектрика и определяется
выражением:
где
с
— скорость света,
g
— коэффициент укорочения электромагнитной
волны в трубопровода,
ε
— диэлектрическая проницаемость материала
изоляции трубопровода.
Коэффициент
укорочения
показывает, во сколько раз скорость
распространения импульса в трубопроводе
меньше скорости распространения в
воздухе.
В любом рефлектометре
перед измерением расстояния нужно
установить коэффициент укорочения.
Точность измерения расстояния до места
повреждения зависит от правильной
установки коэффициента укорочения.
По соотношению величин
отражения от повреждения и напряжения
помех все отражения можно разделить на
простые
и сложные.
Простое
повреждение — это такое повреждение
кабельной трубопровода, при котором
амплитуда отражения от места повреждения
больше амплитуды помех.
Сложное
повреждение — это такое повреждение,
для которого амплитуда отражения от
места повреждения меньше или равна
амплитуде помех.
По
источникам возникновения помехи бывают
асинхронные
(аддитивные)
и синхронные.
Асинхронные
помехи
не связаны с зондирующим сигналом и
неоднородностями кабельной трубопровода
и вызваны наводками от соседних кабельных
трубопроводов, от оборудования, транспорта
и различной аппаратуры.
Пример рефлектограммы трубопровода с
асинхронными помехами показан на рисунке
13.
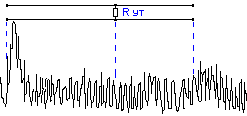
Рис.13. Рефлектограмма
трубопровода с асинхронными помехами.
На рефлектограмме
асинхронные помехи полностью закрывают
отражение от повреждения. Это отражение
невозможно рассмотреть на фоне помех.
Эффективными
методами отстройки от асинхронных помех
являются аналоговая
фильтрация
и цифровое
накопление сигнала.
Сущность цифрового
накопления
заключается в том, что одну и туже
рефлектограмму считывают несколько
раз и вычисляют среднее значение. В
связи с тем, что асинхронные помехи
носят случайный характер, после цифрового
накопления их уровень значительно
снижается.
Пример
предыдущей рефлектограммы трубопровода,
«очищенной» в результате цифрового
накопления рефлектометром, приведен
на рисунке.

Рис.14. Рефлектограмма
с асинхронными помехами после цифровой
очистки.
На
этой рефлектограмме можно легко выделить
сигнал, отраженный от места утечки.
Синхронные
помехи связаны с зондирующим сигналом
и являются отражениями зондирующего
сигнала от неоднородностей волнового
сопротивления трубопровода (отражения
от согласующих устройств, неоднородностей
трубопроводов технологического характера
и др.).
В принципе трубопроводы
не предназначены для передачи коротких
импульсных сигналов, используемых при
методе импульсной рефлектометрии.
Поэтому этим системам контроля
трубопроводов присуще большое количество
синхронных помех. Пример рефлектограммы
трубопровода с синхронными помехами
показан на рисунке.
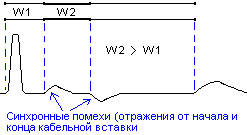
Рис.11. Рефлектограмма
трубопровода с синхронными помехами.
Синхронные
помехи можно существенно уменьшить
посредством сравнения
или
дифференциального
анализа.
При сравнении
накладывают
рефлектограммы двух трубопроводов
(неповрежденного и поврежденного),
проложенных по одной трассе.
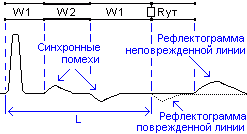
Наложение
двух рефлектограмм позволяет быстро
обнаружить начальную точку их различия,
по которой и определяют расстояние L до
повреждения.
При
дифференциальном
анализе рефлектограммы поврежденного
и неповрежденного трубопроводов
вычитают, как показано на рисунке ниже
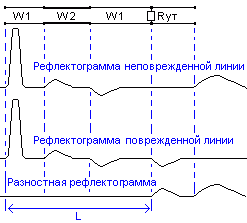
Из
рисунка видно, что при вычитании все
синхронные помехи компенсируются. По
разностной рефлектограмме легко
обнаружить отражение от места повреждения
и определить расстояние L
до него.
При
измерении качества трубопровода методом
импульсной рефлектометрии асинхронные
и синхронные помехи присутствуют на
рефлектограмме одновременно.
Асинхронные
помехи (кроме помех импульсного
характера), как правило, имеют одинаковые
величины, независимо от того, с какого
конца кабельной трубопровода ведется
измерение рефлектометром.
Синхронные
помехи при измерении с разных концов
кабеля имеют различную величину, в
зависимости от многих факторов: длины
кабельной трубопровода, затухания
импульсных сигналов, удаленности места
повреждения и мест неоднородностей
волнового сопротивления трубопровода,
точности согласования выходного
сопротивления импульсного рефлектометра
с волновым сопротивлением трубопровода
и других факторов. Поэтому отраженный
сигнал от одной и той же неоднородности
может иметь различные величины при
измерении с разных концов трубопровода.
Если
хотя бы предположительно известно, к
какому концу кабельной трубопровода
ближе может быть расположено место
повреждения, то для измерений нужно
выбирать именно этот конец кабельной
трубопровода. В других случаях желательно
проводить измерения последовательно
с двух концов трубопровода.
Следует учитывать, что даже такие
повреждения как «короткое замыкание»
и «обрыв», дающие максимальные
отражения зондирующего сигнала, не
всегда можно легко обнаружить на фоне
помех. Например, при большом затухании
и больших неоднородностях волнового
сопротивления трубопровода амплитуда
отражения от удаленного повреждений
типа “короткое замыкание” или “обрыв”
зачастую бывает меньше, чем отражения
от близко расположенных неоднородностей
волнового сопротивления. Поэтому такие
повреждения являются сложным для
обнаружения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Ошибки первого рода (англ. type I errors, α errors, false positives) и ошибки второго рода (англ. type II errors, β errors, false negatives) в математической статистике — это ключевые понятия задач проверки статистических гипотез. Тем не менее, данные понятия часто используются и в других областях, когда речь идёт о принятии «бинарного» решения (да/нет) на основе некоего критерия (теста, проверки, измерения), который с некоторой вероятностью может давать ложный результат.
Содержание
- 1 Определения
- 2 О смысле ошибок первого и второго рода
- 3 Вероятности ошибок (уровень значимости и мощность)
- 4 Примеры использования
- 4.1 Радиолокация
- 4.2 Компьютеры
- 4.2.1 Компьютерная безопасность
- 4.2.2 Фильтрация спама
- 4.2.3 Вредоносное программное обеспечение
- 4.2.4 Поиск в компьютерных базах данных
- 4.2.5 Оптическое распознавание текстов (OCR)
- 4.2.6 Досмотр пассажиров и багажа
- 4.2.7 Биометрия
- 4.3 Массовая медицинская диагностика (скрининг)
- 4.4 Медицинское тестирование
- 4.5 Исследования сверхъестественных явлений
- 5 См. также
- 6 Примечания
Определения
Пусть дана выборка 

где 

,
сопоставляющий каждой реализации выборки 
- Распределение
выборки
соответствует гипотезе
, и она точно определена статистическим критерием, то есть
.
- Распределение
выборки
соответствует гипотезе
, но она неверно отвергнута статистическим критерием, то есть
.
- Распределение
выборки
соответствует гипотезе
, и она точно определена статистическим критерием, то есть
.
- Распределение
выборки
соответствует гипотезе
, но она неверно отвергнута статистическим критерием, то есть
.
Во втором и четвертом случае говорят, что произошла статистическая ошибка, и её называют ошибкой первого и второго рода соответственно. [1][2]
| Верная гипотеза | |||
|---|---|---|---|
 |
 |
||
| Результат применения критерия |
 |
 верно принята верно принята |
 неверно принята неверно принята (Ошибка второго рода) |
 |
 неверно отвергнута неверно отвергнута (Ошибка первого рода) |
 верно отвергнута верно отвергнута |
О смысле ошибок первого и второго рода
Как видно из вышеприведённого определения, ошибки первого и второго рода являются взаимно-симметричными, то есть если поменять местами гипотезы 



С учётом этого ошибку первого рода часто называют ложной тревогой, ложным срабатыванием или ложноположительным срабатыванием — например, анализ крови показал наличие заболевания, хотя на самом деле человек здоров, или металлодетектор выдал сигнал тревоги, сработав на металлическую пряжку ремня. Слово «положительный» в данном случае не имеет отношения к желательности или нежелательности самого события.
Термин широко используется в медицине. Например, тесты, предназначенные для диагностики заболеваний, иногда дают положительный результат (т.е. показывают наличие заболевания у пациента), когда на самом деле пациент этим заболеванием не страдает. Такой результат называется ложноположительным.
В других областях обычно используют словосочетания со схожим смыслом, например, «ложное срабатывание», «ложная тревога» и т.п. В информационных технологиях часто используют английский термин false positive без перевода.
Из-за возможности ложных срабатываний не удаётся полностью автоматизировать борьбу со многими видами угроз. Как правило, вероятность ложного срабатывания коррелирует с вероятностью пропуска события (ошибки второго рода). То есть: чем более чувствительна система, тем больше опасных событий она детектирует и, следовательно, предотвращает. Но при повышении чувствительности неизбежно вырастает и вероятность ложных срабатываний. Поэтому чересчур чувствительно (параноидально) настроенная система защиты может выродиться в свою противоположность и привести к тому, что побочный вред от неё будет превышать пользу.
Соответственно, ошибку второго рода иногда называют пропуском события или ложноотрицательным срабатыванием — человек болен, но анализ крови этого не показал, или у пассажира имеется холодное оружие, но рамка металлодетектора его не обнаружила (например, из-за того, что чувствительность рамки отрегулирована на обнаружение только очень массивных металлических предметов).
Слово «отрицательный» в данном случае не имеет отношения к желательности или нежелательности самого события.
Термин широко используется в медицине. Например, тесты, предназначенные для диагностики заболеваний, иногда дают отрицательный результат (т.е. показывают отсутствие заболевания у пациента), когда на самом деле пациент страдает этим заболеванием. Такой результат называется ложноотрицательным.
В других областях обычно используют словосочетания со схожим смыслом, например, «пропуск события», и т.п. В информационных технологиях часто используют английский термин false negative без перевода.
Степень чувствительности системы защиты должна представлять собой компромисс между вероятностью ошибок первого и второго рода. Где именно находится точка баланса, зависит от оценки рисков обоих видов ошибок.
Вероятности ошибок (уровень значимости и мощность)
Вероятность ошибки первого рода при проверке статистических гипотез называют уровнем значимости и обычно обозначают греческой буквой 

Вероятность ошибки второго рода не имеет какого-то особого общепринятого названия, на письме обозначается греческой буквой 


Обе эти характеристики обычно вычисляются с помощью так называемой функции мощности критерия. В частности, вероятность ошибки первого рода есть функция мощности, вычисленная при нулевой гипотезе. Для критериев, основанных на выборке фиксированного объема, вероятность ошибки второго рода есть единица минус функция мощности, вычисленная в предположении, что распределение наблюдений соответствует альтернативной гипотезе. Для последовательных критериев это также верно, если критерий останавливается с вероятностью единица (при данном распределении из альтернативы).
В статистических тестах обычно приходится идти на компромисс между приемлемым уровнем ошибок первого и второго рода. Зачастую для принятия решения используется пороговое значение, которое может варьироваться с целью сделать тест более строгим или, наоборот, более мягким. Этим пороговым значением является уровень значимости, которым задаются при проверке статистических гипотез. Например, в случае металлодетектора повышение чувствительности прибора приведёт к увеличению риска ошибки первого рода (ложная тревога), а понижение чувствительности — к увеличению риска ошибки второго рода (пропуск запрещённого предмета).
Примеры использования
Радиолокация
В задаче радиолокационного обнаружения воздушных целей, прежде всего, в системе ПВО ошибки первого и второго рода, с формулировкой «ложная тревога» и «пропуск цели» являются одним из основных элементов как теории, так и практики построения радиолокационных станций. Вероятно, это первый пример последовательного применения статистических методов в целой технической области.
Компьютеры
Понятия ошибок первого и второго рода широко используются в области компьютеров и программного обеспечения.
Компьютерная безопасность
Наличие уязвимостей в вычислительных системах приводит к тому, что приходится, с одной стороны, решать задачу сохранения целостности компьютерных данных, а с другой стороны — обеспечивать нормальный доступ легальных пользователей к этим данным (см. компьютерная безопасность). Moulton (1983, с.125) отмечает, что в данном контексте возможны следующие нежелательные ситуации:
- когда нарушители классифицируются как авторизованные пользователи (ошибки первого рода)
- когда авторизованные пользователи классифицируются как нарушители (ошибки второго рода)
Фильтрация спама
Ошибка первого рода происходит, когда механизм блокировки/фильтрации спама ошибочно классифицирует легитимное email-сообщение как спам и препятствует его нормальной доставке. В то время как большинство «антиспам»-алгоритмов способны блокировать/фильтровать большой процент нежелательных email-сообщений, гораздо более важной задачей является минимизировать число «ложных тревог» (ошибочных блокировок нужных сообщений).
Ошибка второго рода происходит, когда антиспам-система ошибочно пропускает нежелательное сообщение, классифицируя его как «не спам». Низкий уровень таких ошибок является индикатором эффективности антиспам-алгоритма.
Пока не удалось создать антиспамовую систему без корреляции между вероятностью ошибок первого и второго рода. Вероятность пропустить спам у современных систем колеблется в пределах от 1% до 30%. Вероятность ошибочно отвергнуть валидное сообщение — от 0,001 % до 3 %. Выбор системы и её настроек зависит от условий конкретного получателя: для одних получателей риск потерять 1% хорошей почты оценивается как незначительный, для других же потеря даже 0,1% является недопустимой.
Вредоносное программное обеспечение
Понятие ошибки первого рода также используется, когда антивирусное программное обеспечение ошибочно классифицирует безвредный файл как вирус. Неверное обнаружение может быть вызвано особенностями эвристики, либо неправильной сигнатурой вируса в базе данных. Подобные проблемы могут происходить также и с антитроянскими и антишпионскими программами.
Поиск в компьютерных базах данных
При поиске в базе данных к ошибкам первого рода можно отнести документы, которые выдаются поиском, несмотря на их иррелевантность (несоответствие) поисковому запросу. Ошибочные срабатывания характерны для полнотекстового поиска, когда поисковый алгоритм анализирует полные тексты всех хранимых в базе данных документов и пытается найти соответствия одному или нескольким терминам, заданным пользователем в запросе.
Большинство ложных срабатываний обусловлены сложностью естественных языков, многозначностью слов: например, «home» может обозначать как «место проживания человека», так и «корневую страницу веб-сайта». Число подобных ошибок может быть снижено за счёт использования специального словаря. Однако это решение относительно дорогое, поскольку подобный словарь и разметка документов (индексирование) должны создаваться экспертом.
Оптическое распознавание текстов (OCR)
Разнообразные детектирующие алгоритмы нередко выдают ошибки первого рода. Программное обеспечение оптического распознавания текстов может распознать букву «a» в ситуации, когда на самом деле изображены несколько точек, которые используемый алгоритм расценил как «a».
Досмотр пассажиров и багажа
Ошибки первого рода регулярно встречаются каждый день в компьютерных системах предварительного досмотра пассажиров в аэропортах. Установленные в них детекторы предназначены для предотвращения проноса оружия на борт самолёта; тем не менее, уровень чувствительности в них зачастую настраивается настолько высоко, что много раз за день они срабатывают на незначительные предметы, такие как ключи, пряжки ремней, монеты, мобильные телефоны, гвозди в подошвах обуви и т.п. (см. обнаружение взрывчатых веществ, металлодетекторы).
Таким образом, соотношение числа ложных тревог (идентифицикация благопристойного пассажира как правонарушителя) к числу правильных срабатываний (обнаружение действительно запрещённых предметов) очень велико.
Биометрия
Ошибки первого и второго рода являются большой проблемой в системах биометрического сканирования, использующих распознавание радужной оболочки или сетчатки глаза, черт лица и т.д. Такие сканирующие системы могут ошибочно отождествить кого-то с другим, «известным» системе человеком, информация о котором хранится в базе данных (к примеру, это может быть лицо, имеющее право входа в систему, или подозреваемый преступник и т.п.). Противоположной ошибкой будет неспособность системы распознать легитимного зарегистрированного пользователя, или опознать подозреваемого в преступлении.[3]
Массовая медицинская диагностика (скрининг)
В медицинской практике есть существенное различие между скринингом и тестированием:
- Скрининг включает в себя относительно дешёвые тесты, которые проводятся для большой группы людей при отсутствии каких-либо клинических признаков болезни (например, мазок Папаниколау).
- Тестирование подразумевает гораздо более дорогие, зачастую инвазивные, процедуры, которые проводятся только для тех, у кого проявляются клинические признаки заболевания, и которые, в основном, применяются для подтверждения предполагаемого диагноза.
К примеру, в большинстве штатов в США обязательно прохождение новорожденными процедуры скрининга на оксифенилкетонурию и гипотиреоз, помимо других врождённых аномалий. Несмотря на высокий уровень ошибок первого рода, эти процедуры скрининга считаются целесообразными, поскольку они существенно увеличивают вероятность обнаружения этих расстройств на самой ранней стадии.[4]
Простые анализы крови, используемые для скрининга потенциальных доноров на ВИЧ и гепатит, имеют существенный уровень ошибок первого рода; однако в арсенале врачей есть гораздо более точные (и, соответственно, дорогие) тесты для проверки, действительно ли человек инфицирован каким-либо из этих вирусов.
Возможно, наиболее широкие дискуссии вызывают ошибки первого рода в процедурах скрининга на рак груди (маммография). В США уровень ошибок первого рода в маммограммах достигает 15%, это самый высокий показатель в мире.[5] Самый низкий уровень наблюдается в Нидерландах, 1%.[6]
Медицинское тестирование
Ошибки второго рода являются существенной проблемой в медицинском тестировании. Они дают пациенту и врачу ложное убеждение, что заболевание отсутствует, в то время как в действительности оно есть. Это зачастую приводит к неуместному или неадекватному лечению. Типичным примером является доверие результатам кардиотестирования при выявлении коронарного атеросклероза, хотя известно, что кардиотестирование выявляет только те затруднения кровотока в коронарной артерии, которые вызваны стенозом.
Ошибки второго рода вызывают серьёзные и трудные для понимания проблемы, особенно когда искомое условие является широкораспространённым. Если тест с 10%-ным уровнем ошибок второго рода используется для обследования группы, где вероятность «истинно-положительных» случаев составляет 70%, то многие отрицательные результаты теста окажутся ложными. (См. Теорему Байеса).
Ошибки первого рода также могут вызывать серьёзные и трудные для понимания проблемы. Это происходит, когда искомое условие является редким. Если уровень ошибок первого рода у теста составляет один случай на десять тысяч, но в тестируемой группе образцов (или людей) вероятность «истинно-положительных» случаев составляет в среднем один случай на миллион, то большинство положительных результатов этого теста будут ложными.[7]
Исследования сверхъестественных явлений
Термин ошибка первого рода был взят на вооружение исследователями в области паранормальных явлений и привидений для описания фотографии или записи или какого-либо другого свидетельства, которое ошибочно трактуется как имеющее паранормальное происхождение — в данном контексте ошибка первого рода — это какое-либо несостоятельное «медиасвидетельство» (изображение, видеозапись, аудиозапись и т.д.), которое имеет обычное объяснение.[8]
См. также
- Статистическая значимость
- Ложноположительный
- Атака второго рода
- Случаи ложного срабатывания систем предупреждения о ракетном нападении
- Receiver_operating_characteristic
Примечания
- ↑ ГОСТ Р 50779.10-2000. «Статистические методы. Вероятность и основы статистики. Термины и определения.». Стр. 26
- ↑ Valerie J. Easton, John H. McColl. Statistics Glossary: Hypothesis Testing.
- ↑ Данный пример как раз характеризует случай, когда классификация ошибок будет зависеть от назначения системы: если биометрическое сканирование используется для допуска сотрудников (нулевая гипотеза: «проходящий сканирование человек действительно является сотрудником»), то ошибочное отождествление будет ошибкой второго рода, а «неузнавание» — ошибкой первого рода; если же сканирование используется для опознания преступников (нулевая гипотеза: «проходящий сканирование человек не является преступником»), то ошибочное отождествление будет ошибкой первого рода, а «неузнавание» — ошибкой второго рода.
- ↑ Относительно скрининга новорожденных, последние исследования показали, что количество ошибок первого рода в 12 раз больше, чем количество верных обнаружений (Gambrill, 2006. [1])
- ↑ Одним из последствий такого высокого уровня ошибок первого рода в США является то, что за произвольный 10-летний период половина обследуемых американских женщин получают как минимум одну ложноположительную маммограмму. Такие ошибочные маммограммы обходятся дорого, приводя к ежегодным расходам в 100 миллионов долларов на последующее (ненужное) лечение. Кроме того, они вызывают излишнюю тревогу у женщин. В результате высокого уровня подобных ошибок первого рода в США, примерно у 90-95% женщин, получивших хотя бы раз в жизни положительную маммограмму, на самом деле заболевание отсутствует.
- ↑ Наиболее низкие уровни этих ошибок наблюдаются в северной Европе, где маммографические плёнки считываются дважды, и для дополнительного тестирования устанавливается повышенное пороговое значение (высокий порог снижает статистическую эффективность теста).
- ↑ Вероятность того, что выдаваемый тестом результат окажется ошибкой первого рода, может быть вычислена при помощи Теоремы Байеса.
- ↑ На некоторых сайтах приведены примеры ошибок первого рода, например: Атлантическое Сообщество Паранормальных явлений (The Atlantic Paranormal Society, TAPS) и Морстаунская организация по Исследованию Привидений (Moorestown Ghost Research).
Ошибка первого рода — ситуация, когда отвергнута правильная нулевая гипотеза (англ. type I errors, α errors, false positive, ошибочное отвержение) и ошибка второго рода — ситуация, когда принята неправильная нулевая гипотеза (англ. type II errors, β errors, false negative, ошибочное принятие). В математической статистике это ключевые понятия задач проверки статистических гипотез.
Данные понятия часто используются и в других областях, когда речь идёт о принятии «бинарного» решения (да/нет) на основе некоего критерия (теста, проверки, измерения), который с некоторой вероятностью может давать ложный результат.
Определения
Пусть дана выборка X = ( X 1 , … , X n ) ⊤ {displaystyle mathbf {X} =(X_{1},ldots ,X_{n})^{ op }} из неизвестного совместного распределения P X {displaystyle mathbb {P} ^{mathbf {X} }} , и поставлена бинарная задача проверки статистических гипотез:
H 0 H 1 , {displaystyle {egin{matrix}H_{0}H_{1},end{matrix}}}
где H 0 {displaystyle H_{0}} — нулевая гипотеза, а H 1 {displaystyle H_{1}} — альтернативная гипотеза. Предположим, что задан статистический критерий
f : R n → { H 0 , H 1 } {displaystyle f:mathbb {R} ^{n} o {H_{0},H_{1}}} ,
сопоставляющий каждой реализации выборки X = x {displaystyle mathbf {X} =mathbf {x} } одну из имеющихся гипотез. Тогда возможны следующие четыре ситуации:
Во втором и четвёртом случае говорят, что произошла статистическая ошибка, и её называют ошибкой первого и второго рода соответственно.
О смысле ошибок первого и второго рода
Из определения выше видно, что ошибки первого и второго рода являются взаимно-симметричными, то есть если поменять местами гипотезы H 0 {displaystyle H_{0}} и H 1 {displaystyle H_{1}} , то ошибки первого рода превратятся в ошибки второго рода и наоборот. Тем не менее, в большинстве практических ситуаций путаницы не происходит, поскольку принято считать, что нулевая гипотеза H 0 {displaystyle H_{0}} соответствует состоянию «по умолчанию» (естественному, наиболее ожидаемому положению вещей) — например, что обследуемый человек здоров, или что проходящий через рамку металлодетектора пассажир не имеет запрещённых металлических предметов. Соответственно, альтернативная гипотеза H 1 {displaystyle H_{1}} обозначает противоположную ситуацию, которая обычно трактуется как менее вероятная, неординарная, требующая какой-либо реакции.
С учётом вышесказанного, ошибку первого рода часто называют ложной тревогой, ложным срабатыванием или ложноположительным срабатыванием. Если, например, анализ крови показал наличие заболевания, хотя на самом деле человек здоров, или металлодетектор выдал сигнал тревоги, сработав на металлическую пряжку ремня, то принятая гипотеза не верна, а следовательно совершена ошибка первого рода. Слово «ложноположительный» в данном случае не имеет отношения к желательности или нежелательности самого события.
Термин широко используется в медицине. Например, тесты, предназначенные для диагностики заболеваний, иногда дают положительный результат (то есть показывают наличие заболевания у пациента), когда на самом деле пациент этим заболеванием не страдает. Такой результат называется ложноположительным.
В других областях обычно используют словосочетания со схожим смыслом, например, «ложное срабатывание», «ложная тревога» и т. п. В информационных технологиях часто используют английский термин false positive без перевода.
Из-за возможности ложных срабатываний не удаётся полностью автоматизировать борьбу со многими видами угроз. Как правило, вероятность ложного срабатывания коррелирует с вероятностью пропуска события (ошибки второго рода). То есть: чем более чувствительна система, тем больше опасных событий она детектирует и, следовательно, предотвращает. Но при повышении чувствительности неизбежно вырастает и вероятность ложных срабатываний. Поэтому чересчур чувствительно (параноидально) настроенная система защиты может выродиться в свою противоположность и привести к тому, что побочный вред от неё будет превышать пользу.
Соответственно, ошибку второго рода иногда называют пропуском события или ложноотрицательным срабатыванием. Человек болен, но анализ крови этого не показал, или у пассажира имеется холодное оружие, но рамка металлодетектора его не обнаружила (например, из-за того, что чувствительность рамки отрегулирована на обнаружение только очень массивных металлических предметов). Данные примеры указывают на совершение ошибки второго рода. Слово «ложноотрицательный» в данном случае не имеет отношения к желательности или нежелательности самого события.
Термин широко используется в медицине. Например, тесты, предназначенные для диагностики заболеваний, иногда дают отрицательный результат (то есть показывают отсутствие заболевания у пациента), когда на самом деле пациент страдает этим заболеванием. Такой результат называется ложноотрицательным.
В других областях обычно используют словосочетания со схожим смыслом, например, «пропуск события», и т. п.
Так как с ростом вероятности ошибки первого рода обычно уменьшается вероятность ошибки второго рода, и наоборот, настройка принимающей решение системы должна представлять собой компромисс. Где именно находится точка получаемого такой настройкой баланса, зависит от оценки последствий при совершении обоих видов ошибок.
Вероятности ошибок (уровень значимости и мощность)
Вероятность ошибки первого рода при проверке статистических гипотез называют уровнем значимости и обычно обозначают греческой буквой α {displaystyle alpha } (отсюда название α {displaystyle alpha } -errors).
Вероятность ошибки второго рода не имеет какого-то особого общепринятого названия, на письме обозначается греческой буквой β {displaystyle eta } (отсюда β {displaystyle eta } -errors). Однако с этой величиной тесно связана другая, имеющая большое статистическое значение — мощность критерия. Она вычисляется по формуле ( 1 − β ) {displaystyle (1-eta )} . Таким образом, чем выше мощность, тем меньше вероятность совершить ошибку второго рода.
Обе эти характеристики обычно вычисляются с помощью так называемой функции мощности критерия. В частности, вероятность ошибки первого рода есть функция мощности, вычисленная при нулевой гипотезе. Для критериев, основанных на выборке фиксированного объёма, вероятность ошибки второго рода есть единица минус функция мощности, вычисленная в предположении, что распределение наблюдений соответствует альтернативной гипотезе. Для последовательных критериев это также верно, если критерий останавливается с вероятностью единица (при данном распределении из альтернативы).
В статистических тестах обычно приходится идти на компромисс между приемлемым уровнем ошибок первого и второго рода. Зачастую для принятия решения используется пороговое значение, которое может варьироваться с целью сделать тест более строгим или, наоборот, более мягким. Этим пороговым значением является уровень значимости, которым задаются при проверке статистических гипотез. Например, в случае металлодетектора повышение чувствительности прибора приведёт к увеличению риска ошибки первого рода (ложная тревога), а понижение чувствительности — к увеличению риска ошибки второго рода (пропуск запрещённого предмета).
Примеры использования
Радиолокация
В задаче радиолокационного обнаружения воздушных целей, прежде всего, в системе ПВО ошибки первого и второго рода, с формулировкой «ложная тревога» и «пропуск цели» являются одним из основных элементов как теории, так и практики построения радиолокационных станций. Вероятно, это первый пример последовательного применения статистических методов в целой технической области.
Компьютеры
Понятия ошибок первого и второго рода широко используются в области компьютеров и программного обеспечения.
Компьютерная безопасность
Наличие уязвимостей в вычислительных системах приводит к тому, что приходится, с одной стороны, решать задачу сохранения целостности компьютерных данных, а с другой стороны — обеспечивать нормальный доступ легальных пользователей к этим данным (см. компьютерная безопасность). В данном контексте возможны следующие нежелательные ситуации:
- когда авторизованные пользователи классифицируются как нарушители (ошибки первого рода)
- когда нарушители классифицируются как авторизованные пользователи (ошибки второго рода)
Фильтрация спама
Ошибка первого рода происходит, когда механизм блокировки/фильтрации спама ошибочно классифицирует легитимное email-сообщение как спам и препятствует его нормальной доставке. В то время как большинство «антиспам»-алгоритмов способны блокировать/фильтровать большой процент нежелательных email-сообщений, гораздо более важной задачей является минимизировать число «ложных тревог» (ошибочных блокировок нужных сообщений).
Ошибка второго рода происходит, когда антиспам-система ошибочно пропускает нежелательное сообщение, классифицируя его как «не спам». Низкий уровень таких ошибок является индикатором эффективности антиспам-алгоритма.
Пока не удалось создать антиспамовую систему без корреляции между вероятностью ошибок первого и второго рода. Вероятность пропустить спам у современных систем колеблется в пределах от 1 % до 30 %. Вероятность ошибочно отвергнуть валидное сообщение — от 0,001 % до 3 %. Выбор системы и её настроек зависит от условий конкретного получателя: для одних получателей риск потерять 1 % хорошей почты оценивается как незначительный, для других же потеря даже 0,1 % является недопустимой.
Вредоносное программное обеспечение
Понятие ошибки первого рода также используется, когда антивирусное программное обеспечение ошибочно классифицирует безвредный файл как вирус. Неверное обнаружение может быть вызвано особенностями эвристики, либо неправильной сигнатурой вируса в базе данных. Подобные проблемы могут происходить также и с антитроянскими и антишпионскими программами.
Поиск в компьютерных базах данных
При поиске в базе данных к ошибкам первого рода можно отнести документы, которые выдаются поиском, несмотря на их иррелевантность (несоответствие) поисковому запросу. Ошибочные срабатывания характерны для полнотекстового поиска, когда поисковый алгоритм анализирует полные тексты всех хранимых в базе данных документов и пытается найти соответствия одному или нескольким терминам, заданным пользователем в запросе.
Большинство ложных срабатываний обусловлены сложностью естественных языков, многозначностью слов: например, «home» может обозначать как «место проживания человека», так и «корневую страницу веб-сайта». Число подобных ошибок может быть снижено за счёт использования специального словаря. Однако это решение относительно дорогое, поскольку подобный словарь и разметка документов (индексирование) должны создаваться экспертом.
Оптическое распознавание текстов (OCR)
Разнообразные детектирующие алгоритмы нередко выдают ошибки первого рода. Программное обеспечение оптического распознавания текстов может распознать букву «a» в ситуации, когда на самом деле изображены несколько точек.
Досмотр пассажиров и багажа
Ошибки первого рода регулярно встречаются каждый день в компьютерных системах предварительного досмотра пассажиров в аэропортах. Установленные в них детекторы предназначены для предотвращения проноса оружия на борт самолёта; тем не менее, уровень чувствительности в них зачастую настраивается настолько высоко, что много раз за день они срабатывают на незначительные предметы, такие как ключи, пряжки ремней, монеты, мобильные телефоны, гвозди в подошвах обуви и т. п. (см. обнаружение взрывчатых веществ, металлодетекторы).
Таким образом, соотношение числа ложных тревог (идентифицикация благопристойного пассажира как правонарушителя) к числу правильных срабатываний (обнаружение действительно запрещённых предметов) очень велико.
Биометрия
Ошибки первого и второго рода являются большой проблемой в системах биометрического сканирования, использующих распознавание радужной оболочки или сетчатки глаза, черт лица и т. д. Такие сканирующие системы могут ошибочно отождествить кого-то с другим, «известным» системе человеком, информация о котором хранится в базе данных (к примеру, это может быть лицо, имеющее право входа в систему, или подозреваемый преступник и т. п.). Противоположной ошибкой будет неспособность системы распознать легитимного зарегистрированного пользователя, или опознать подозреваемого в преступлении.
Массовая медицинская диагностика (скрининг)
В медицинской практике есть существенное различие между скринингом и тестированием:
- Скрининг включает в себя относительно дешёвые тесты, которые проводятся для большой группы людей при отсутствии каких-либо клинических признаков болезни (например, мазок Папаниколау).
- Тестирование подразумевает гораздо более дорогие, зачастую инвазивные, процедуры, которые проводятся только для тех, у кого проявляются клинические признаки заболевания, и которые, в основном, применяются для подтверждения предполагаемого диагноза.
К примеру, в большинстве штатов в США обязательно прохождение новорожденными процедуры скрининга на оксифенилкетонурию и гипотиреоз, помимо других врождённых аномалий. Несмотря на высокий уровень ошибок первого рода, эти процедуры скрининга считаются целесообразными, поскольку они существенно увеличивают вероятность обнаружения этих расстройств на самой ранней стадии.
Простые анализы крови, используемые для скрининга потенциальных доноров на ВИЧ и гепатит, имеют существенный уровень ошибок первого рода; однако в арсенале врачей есть гораздо более точные (и, соответственно, дорогие) тесты для проверки, действительно ли человек инфицирован каким-либо из этих вирусов.
Возможно, наиболее широкие дискуссии вызывают ошибки первого рода в процедурах скрининга на рак груди (маммография). В США уровень ошибок первого рода в маммограммах достигает 15 %, это самый высокий показатель в мире. Самый низкий уровень наблюдается в Нидерландах, 1 %.
Медицинское тестирование
Ошибки второго рода являются существенной проблемой в медицинском тестировании. Они дают пациенту и врачу ложное убеждение, что заболевание отсутствует, в то время как в действительности оно есть. Это зачастую приводит к неуместному или неадекватному лечению. Типичным примером является доверие результатам велоэргометрии при выявлении коронарного атеросклероза, хотя известно, что велоэргометрия выявляет только те затруднения кровотока в коронарной артерии, которые вызваны стенозом.
Ошибки второго рода вызывают серьёзные и трудные для понимания проблемы, особенно когда искомое условие является широкораспространённым. Если тест с 10%-ным уровнем ошибок второго рода используется для обследования группы, где вероятность «истинно-положительных» случаев составляет 70 %, то многие отрицательные результаты теста окажутся ложными. (См. Теорему Байеса).
Ошибки первого рода также могут вызывать серьёзные и трудные для понимания проблемы. Это происходит, когда искомое условие является редким. Если уровень ошибок первого рода у теста составляет один случай на десять тысяч, но в тестируемой группе образцов (или людей) вероятность «истинно-положительных» случаев составляет в среднем один случай на миллион, то большинство положительных результатов этого теста будут ложными.
Исследования сверхъестественных явлений
Термин ошибка первого рода был взят на вооружение исследователями в области паранормальных явлений и привидений для описания фотографии или записи или какого-либо другого свидетельства, которое ошибочно трактуется как имеющее паранормальное происхождение — в данном контексте ошибка первого рода — это какое-либо несостоятельное «медиасвидетельство» (изображение, видеозапись, аудиозапись и т. д.), которое имеет обычное объяснение.



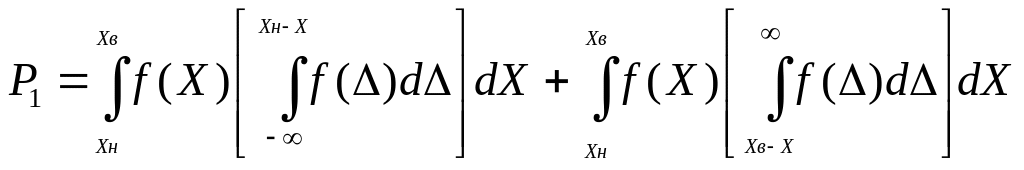



 ,
, соответствует гипотезе
соответствует гипотезе  .
. .
.