Что такое ошибка отсчета нуля

Министерство образования и науки Российской Федерации Ярославский государственный университет

им. П. Г. Демидова

В.П. Алексеев, Е. О. Неменко,

В.А. Папорков, Е. В. Рыбникова

Лабораторная работа № 3

Измерение линейных размеров тел.

Ярославль 2013

Лабораторная работа № 3.

Измерение линейных размеров тел

Цель работы:

1)изучить линейный нониус;

2)научиться пользоваться измерительной линейкой, штангенциркулем, микрометром и измерительным микроскопом;

3)научиться определять погрешности измерений.

Оборудование:

•измерительная линейка,

•штангенциркуль,

•микрометр,

•измерительный микроскоп,

•набор измеряемых тел: прямоугольное, цилиндрическое, проволока, волос.

3.1. Краткая теория

В экспериментальной практике, как правило, для сопоставления линейных размеров тел их просто прикладывают друг к другу, причём одно из тел является эталоном. Приложив эталон к предмету, можно узнать, во сколько раз он больше или меньше эталона.

Операция сравнения с эталоном носит название измерения.

Эталоны мер хранятся при строго определенных условиях и охраняются государством. Для проведения повседневных измерений пользуются приборами, которые тем или иным способом сверены с эталонами. Такими измерительными инструментами являются, например, масштабная линейка, штангенциркуль, микрометр и многие другие. Причем выбор способа и средств для измерений зависит от изучаемых задач, наличия приборов и требуемой погрешности измерений.

Прикладывая линейку к измеряемому телу многократно, мы можем получать величину, несколько отличающуюся от ранее найденной. К этому же результату придем, измеряя физическую величину (длину) разными способами.

Для любой физической величины можно указать интервал, в пределах которого лежит измеренное её значение. Его величина определяется точностью измерительного прибора. Когда говорят о значении какой-либо физической величины x, его необходимо описывать в виде:

x1 < x < x2,

где x1 и x2 – границы этого интервала.

Точно так же любое измерение значения физической величины должно давать интервал, в котором значение этой величины с определенной вероятностью содержится.

Ошибки прямых измерений. Прямым называется такое измерение, в котором значение интересующей нас величины получается непосредственно из отсчета по прибору.

Оценивая ошибки прямых измерений, необходимо учитывать систематическую, случайную ошибки и погрешность отсчета. В любом измерении можно указать главный источник ошибок, определяющий наибольший вклад в погрешность. Именно ошибку этого типа и следует уменьшить в первую очередь.

Во всех случаях, когда погрешность измерительного прибора явно не указана, её значение принимают равным половине точности.

3.1.1. Измерительная линейка

Линейка позволяет получать результаты с точностью примерно до 0.5 мм. Но чтобы добиться такой точности, важно избежать следующих ошибок.

Ошибка, обусловленная неправильно приложенной линейкой

Во избежание неправильного измерения, линейку следует прикладывать ровно, а не наискось,

кпримеру вдоль одной из граней измеряемого тела.

Вслучае необходимости измерить линейкой размер, меньший, чем её цена деления, например диаметр проволоки, поступают следующим образом: на какой-либо предмет (стержень, карандаш и т. п.) проволоку наматывают плотно, виток к витку, не менее 10 витков. Очевидно, что диаметр D проволоки будет равен отношению длины намотки L к числу витков n

D = Ln .

Ошибка, обусловленная параллаксом

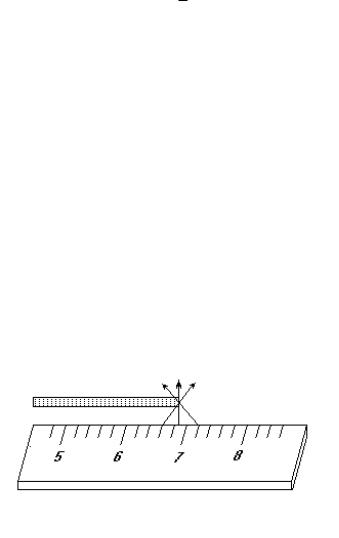
Если измеряемый предмет находится на некотором расстоянии от шкалы и если мы смотрим не под прямым углом к шкале, то отсчет будет неверным (см. рис. 3.1).

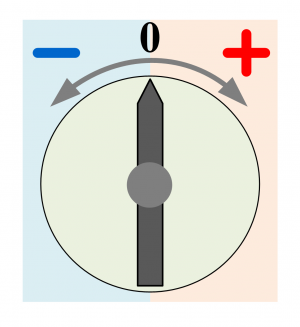
Такая ошибка называется ошибкой параллакса. Ее удается уменьшить, по возможности приближая к шкале измеряемый предмет, а также используя зеркало, расположенное рядом со шкалой (см. рис 3.2). Совмещая предмет с его отражением в зеркале, мы обеспечиваем прямой угол между линией зрения и шкалой. Аналогичная ситуация наблюдатеся при пользовании любым стрелочным прибором. В этом случае зеркало располагается на шкале и при отсчёте необходимо совместить стрелку и её изображение.

Ошибка отсчета нуля

Если располагать линейку так, чтобы ее край совпадал с одним концом предмета и отсчитывал показания с другого конца – такой способ годится только для грубых измерений длины. Вместо этого предмет следует располагать таким образом, чтобы можно было снимать показания у обоих концов. Дело в том, что нулевая отметка может быть поставлена неверно или край линейки может оказаться испорченным. Вообще всегда в любом приборе следует с некоторым подозрением относиться к нулевому делению шкалы. Ошибки удается избежать, если брать разность двух отсчетов.

Рис. 3.1. Ошибка, обусловленная параллаксом

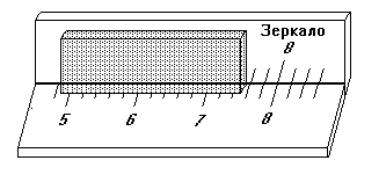
Рис. 3.2. Измерение с помощью зеркала

Калибровка

Шкала линейки может быть неправильной. Поэтому линейку следует проверять и откалибровывать. Сделать это можно, совмещая ее с более точной эталонной линейкой и сличая их показания. Наиболее точными считаются стальные линейки, изготовленные согласно ГОСТ 427-75. Они обязаны иметь отклонение не более 0.1 мм на длине до 300 мм. Хорошей точностью обладают также

чертёжные линейки, выполненные из твёрдых пород дерева (у них есть белая полоса, на которую и наносится шкала). Линейки, выполненные из пластика, с делениями, образованными путём вдавливания штампа являются наименее точными, т. к. при их изготовлении материал испытывает деформацию и подвергается температурным воздействиям. Обычные деревянные “школьные” линейки бывают различного качества, в зависимости от производителя. Среди них встречаются как очень хорошие, так и никуда не годные экземпляры, имеющие погрешность порядка 1 мм на расстоянии 100 ÷ 150 мм.

3.1.2.Измерения с применением нониуса. Штангенциркуль

Нониус

В обычных условиях невозможно создать линейку с ценой деления, меньшей чем 0.5 мм. Деле-

ния, расположенные более часто, человеческий глаз не способен различить. Однако при измерении длины какого-либо тела она редко укладывается в целое число делений масштаба. Для того чтобы можно было поручиться при линейных измерениях и за десятые доли целого деления масштаба (а иногда и за меньшие), пользуются нониусом. Это же необходимо делать и при измерении углов.

Нониус – вспомогательная шкала, при помощи которой отсчитываются доли деления основной шкалы измерительного прибора. Прототип современного нониуса предложен французским математиком П. Вернье, поэтому его иногда называют верньером. Название ¾нониус¿ это приспособление

получило в честь португальского учёного П. Нуниша (в латинизированной форме его фамилия как раз и произносится как Нониус), предложившего для отсчета долей делений шкалы сходный прибор.

Различают линейный, угловой (угломерный), спиральный, трансверсальный и др. виды нониусов. Принцип деиствия линейного нониуса виден из диаграммы, изображенной на рис. 3.3 и основан на геометрической теореме Фалеса о делении отрезка на произвольное равное число частей. На рис. 3.4 приведён пример деления отрезка AB на 5 равных частей.

Нониус позволяет повысить точность измерения в 10 – 20 раз. Нониусы с точностью большей, чем 1/20 деления основной шкалы, применяются редко, т. к. в этом случае не один, а сразу несколь-

ко штрихов выглядят совпадающими (рис. 3.5). Обычно подобные нониусы используют вместе с оптической системой, позволяющей рассматривать шкалы под сильным увеличением.

Обычный линейный нониус представляет собой маленькую шкалу, скользящую вдоль основной линейки (рис. 3.6). Эта шкала состоит из m делений. Суммарная длина всех m делений нониуса равна (m − 1) наименьшим делениям основной линейки, т. е.

mx = (m − 1)y,

где x — длина деления нониуса, а y — длина наименьшего деления линейки.

Рис. 3.3. Принцип действия линейного нониуса

Таким образом, одно целое деление нониуса короче одного целого деления линейки на x

x = y − x =

или на 1/m долю его. Эта величина y/m, являющаяся разностью длин делений линейки и нониуса,

называется точностью нониуса и используется при измерении.

Рассмотрим процесс измерения при помощи линейного нониуса. Пусть L — измеряемый отрезок (рис. 3.7). Совместим его с началом нулевого деления линейки. Пусть при этом конец его окажется между k и (k + 1)-м её делениями. Тогда можно записать

где L — неизвестная пока еще доля деления линейки. Приложим теперь к концу отрезка наш

нониус так, чтобы нуль нониуса совпал с концом этого отрезка. При этом обязательно найдется такое деление нониуса n, которое ближе подходит к соответствующему (k +n)-му делению линейки,

так как деления нониуса и линейки не равны. Как видно из рис. 3.7,

L = ny − nx = n(y − x) = n x,

(3.2)

и вся длина, следовательно, будет равна

L = ky + n x.

Это можно записать и сформулировать следующим образом:

L = ky + n	y	,	(3.3)

m

Рис. 3.4. Теорема Фалеса

Рис. 3.5. Нониус 1/10, 1/20 и 1/50.

т. е. длина отрезка, измеряемого при помощи нониуса, равна числу целых делений линейки плюс точность нониуса, умноженная на номер деления нониуса, совпадающего с некоторым делением линейки.

На практике делают нониусы растянутыми (см. обычный штангенциркуль), чтобы легче было определить, какое деление нониуса совпадает с каким-либо делением основной шкалы. Растянутый нониус (имеется в виду линейный) получится, если длина одного деления нониуса x будет короче

не одного наименьшего деления основного масштаба (как полагалось до сих пор), а двух или трех. При этом y соответственно увеличивают в два или три раза.

Допустим, необходимо построить нониус с точностью 0, 1. Для обычного нониуса следует взять

дополнительную шкалу, общая длина которой равна 9 делениям основной шкалы, и разделить ее на 10 частей. Действительно, x = 0.1y. Если же строить растянутый нониус с той точностью 0.1

так, чтобы одно деление нониуса было короче двух делений основного масштаба, то общая длина нониуса в делениях основной шкалы определится из формулы

mx = (2m − 1)y; m(2y − x) = y;	x =	y	;	(3.4)
m

(2y − x) =	y				(3.5)
m

и (m − 1) = 19, т. е. длина нониуса должна быть равна 19 делениям основной шкалы и разбита на 10 частей.

Штангенциркуль

Штангенциркуль – это измерительный прибор (см. рис. 3.8), состоящий из массивной линейки (штанги) 1 с основной миллиметровой шкалой 2 и подвижной рамки 3 с нониусом 4 и закрепляющим винтом 7. На штанге и рамке имеются две пары ножек (губок) 5 и 6. С внутренней стороны ножки 5 имеют плоские поверхности. При сомкнутых ножках 5 нули нониуса и основной шкалы должны совпадать. Часто штангенциркуль имеет выдвигающийся стержень 8 для определения глубины отверстий, называемый колумбик.

Рис. 3.6. Линейный нониус

Рис. 3.7. Измерение с помощью нониуса

Для определения линейных размеров с помощью штангенциркуля измеряемое тело зажимается между ножками 5. При этом нуль нониуса смещается вдоль основной шкалы на отрезок L, равный

длине измеряемого тела, величина которого определяется по формуле 3.3.

На нониусе с достаточно крупными делениями указывается непосредственное значение точности, выраженное в соответствующих долях миллиметра.

В штангенциркулях обычно используются нониусы с постоянным k = 0.1 мм. Также встречаются штангенциркули повышенной точности с k = 0.05 мм.

Совместим нули нониуса и основной шкалы, легко определить (по основной шкале) длину m

делений нониуса (m − 1), а затем найти
xm = (m − 1); x =	(m − 1)y	.	(3.6)

	m

При измерениях внутренних размеров используются ножки 6 штангенциркуля. Их рабочие поверхности расположены на внешней стороне.

Основными характеристиками штангенциркуля являются: цена деления основной шкалы y; цена деления нониуса x; постоянная нониуса k = (x − y); инструментальная ошибка D.

Инструментальная ошибка, вызываемая износом инструмента или неточностью его изготовления, определяется следующим образом. Ножки штангенциркуля сдвигают до легкого соприкосновения и делают отсчет показаний. Взятый с обратным знаком отсчет показаний и равен инструментальной ошибке D.

Штангенциркули подразделяются на измерительные и измерительно-разметочные. Губки измерительно-разметочного штангенциркуля выполнены из твёрдого сплава и остро заточены. Современные варианты штангенциркулей могут в качестве отсчётного приспособления иметь не только нониус, но и часовой индикатор, и электронное устройство с цифровым отсчётом. Различные виды штангенциркулей приведены на рис. 3.9.

3.1.3. Микрометр

Микр´ометром (с ударением на “о”, не путать с микром´етром – 1/1000 миллиметра) называют прибор, позволяющий измерять линейные размеры тел с точностью 0.01 мм. Микрометр для изме-

рения внешних размеров изображен на рис. 3.10. Основные части микрометра – стальная скоба 1 и втулка 2, внутри которой находится бронзовая вставка с микрометрической резьбой. На поверхности втулки нанесены две шкалы с делениями и продольная черта.

Рис. 3.8. Устройство штангенциркуля

Рис. 3.9. Различные виды штангенциркулей

Во втулку ввёрнут стержень 3 с микрометрическим винтом и подвижной губкой. На правый конец стержня надет барабан 5 с круговой шкалой, имеющей 50 делений. Барабан укреплен на

стержне с помощью стопорного винта или накидной гайки и вращается вместе с ним. На его торце установлена трещётка 6, которая обеспечивает постоянное усилие затяжки микровинта, что позволяет получить более точные результаты измерений.

На противоположном конце скобы находится упорная губка – наковаленка 4. Для фиксации стержня микрометра в определённом положении используется фиксатор 7 в виде стопорного винта или рычажка. На торцы подвижной и неподвижной губок обычно напаиваются твёрдосплавные наконечники для снижения износа рабочих поверхностей.

Шаг винта микрометра равен 0.5 мм. За два оборота шкала барабана проходит 100 делений, а стержень смещается на 1 мм. Соответственно, цена деления шкалы составляет 0.01 мм.

Цена деления круговой шкалы αK , число делений N и шаг винта h связаны очевидным соотно-

шением:

αK =	h	.	(3.7)

	N

Величины h и N всегда подбираются так, что αK = 0.01 мм:

h1 = 1мм при N1 = 100,

h2 = 0.5мм при N2 = 50.

Таким образом, линейная шкала служит для отсчета миллиметров, а круговая – сотых долей миллиметра.

При h = 0.5 мм на корпусе микрометра наносятся 2 линейные шкалы, разделённые продольной

чертой: нижняя – для отсчета целых значений миллиметров, а верхняя – их половинных долей. Так, в случае, изображенном на рис. 3.10(а), суммарный отсчет по всем шкалам микрометра равен: 5 мм + 0.5 мм + 0.35 мм = 5.85 мм. В случае, показанном на рис. 3.10(б), край барабана не перешел половинную метку, разделяющую деления 5 мм и 6 мм, поэтому суммарный отсчет равен 5 мм + 0.35 мм = 5.35 мм.

Во избежание грубых ошибок при снятии отсчета по микрометру внимательно следите за положением края барабана относительно штрихов верхней шкалы!

При измерениях микрометром основным источником ошибок является непостоянство давления микровинта на измеряемую деталь. Для устранения этого недостатка микрометр снабжен особым приспособлением – трещеткой 6 (рис. 3.10), связанной силами трения с микрометрическим винтом. Зажатие измеряемого предмета с помощью трещетки обеспечивает малость измерительного давления и достаточное для практических целей постоянство его. На практике для обеспечения наиболее стабильного усилия затяжки микровинта используют плавный доворот трещётки на три щелчка.

Рис. 3.10. Устройство микрометра

Правила пользования микрометром

Категорически запрещается затягивать микрометр, держась за барабан. Даже прилагая не слишком большие усилия, с помощью микрометрического винта можно развить усилие до тонны и более, что неминуемо приведёт к выходу прибора из строя. При измерениях микрометром обязательно пользуйтесь трещеткой.

Перед тем как пользоваться микрометром, проверьте, освобожден ли его микрометрический винт!

После этого необходимо привести в соприкосновение измерительные стержни микрометра и снять отсчет N0 нулевого значения. Длина измеряемого предмета Z = N − N0, где N – отсчет

по микрометру при зажатом предмете.

3.1.4. Измерительный микроскоп

Микроскоп представляет собой комбинацию двух оптических систем – объектива и окуляра. При практическом измерении размеров рассматриваемого в микроскоп предмета нужно непо-

средственно сравнить его с некоторым масштабом. Лучше всего расположить этот масштаб в плоскости самого измеряемого предмета, но во многих случаях это оказывается невозможным. Измерительный масштаб можно расположить и в одной из плоскостей изображения предмета. В обоих случаях предмет и масштаб будут видны одновременно и могут быть, следовательно, сопоставлены друг с другом. Однако при таком измерении с измерительным масштабом сравнивается не сам предмет, а его увеличенное изображение, и для получения правильного результата нужно в другом опыте, не перестраивая микроскопа, сравнить с ним эталонный масштаб, помещенный вместо предмета.

Обычно измерительный масштаб располагается в фокальной плоскости окуляра и имеет вид шкалы или сетки.

Правильное сравнение с масштабом возможно только в том случае, если изображение предмета и масштаб не только четко видны в микроскоп одновременно, но и с хорошей точностью совмещены друг с другом.

Измерения микроскопом

Прежде всего необходимо отъюстировать микроскоп. Это делается в следующем порядке:

1)Перед началом работы тубус микроскопа перемещается почти до упора в объект (за расстоянием между предметом и тубусом удобно следить, наблюдая сбоку в плоскости рассматриваемого предмета).

3.2. Порядок выполнения работы	9

Рис. 3.11. Градуировка окулярной шкалы микроскопа

2)Перемещая окуляр относительно окулярной шкалы, получают резкое изображение шкалы.

3)Наблюдая в окуляр, медленно поднимают тубус винтом грубой наводки до тех пор, пока в поле зрения не мелькнет изображение предмета. Винтом точной наводки регулируют микроскоп до получения резкого изображения. Таким образом, в поле зрения микроскопа одновременно и одинаково резко видны объект и окулярная шкала.

Обращаем особое внимание студентов на то, что при отсутствии контроля сбоку тубус микроскопа можно передвигать только вверх! При движении вниз нетрудно проскочить правильное расстояние и упереть объектив в рассматриваемый предмет – объектив при этом может быть испорчен.

Чтобы определить размеры объекта по окулярной шкале, ее необходимо проградуировать. Для градуировки окулярной шкалы служит объективная шкала, нанесенная на стекле, называемая объект-микрометр. Цена деления такой шкалы обычно составляет 0.01 мм. Помещая объект-

микрометр под микроскоп и совмещая первичное изображение его шкалы с окулярной шкалой, можно определить цену деления последней. При градуировке совмещают произвольные деления шкалы объектива и окулярной шкалы (рис. 3.11).

Так как видимые расстояния между штрихами окулярной шкалы и изображением объективной шкалы не равны друг другу, то всегда находится такое n-е деление объект-микрометра, которое совпадает с k-м делением окулярной шкалы. Цена деления окулярной шкалы (приведенное к объективу и выраженное в миллиметрах расстояние между штрихами) iок равна при этом

iок =	n	γоб,	(3.8)
k

где γоб – цена деления объект-микрометра. (В случае, если микроскоп имеет небольшое увеличение,

в качестве объективной шкалы можно использовать точную линейку, например основную шкалу штангенциркуля.)

Следует заметить, что определение цены деления окулярной шкалы имеет смысл для данного окуляра, данного объектива и данной длины тубуса микроскопа.

Вместо окулярной шкалы для определения размеров предмета можно воспользоваться винтовым окулярным микрометром.

Нити, видимые в поле зрения окулярного микрометра, передвигаются с помощью микрометрического винта, так, чтобы скрещение нитей совместилось сначала с одной границей изображения измеряемого объекта, а затем с другой. Микровинт барабаном со шкалами, аналогично обычному микрометру. Сначала, рассматривая в микроскоп шкалу объект-микрометра, определяют цену деления шкалы окулярного микрометра (градуируют его). Затем, помещают под микроскоп объект и определяют по шкале микрометра его размер.

После этого линейный размер объекта d можно вычислить в миллиметрах по формуле

d = (NZ + δn) [мм],

(3.9)

где N – число полных оборотов винта окулярного микрометра; z – шаг винта за один полный оборот винта микрометра; δ – цена деления шкалы (на барабане) окулярного микрометра; n –

номер деления на шкале барабана.

3.2. Порядок выполнения работы

3.2.1. Измерения линейкой

1)Измерить с помощью масштабной линейки длину А, ширину В и высоту С прямоугольной пластинки.

Соседние файлы в предмете Механика

Источник

Ошибка нуля микрометрического калибра для винта возникает, когда плоский конец винта касается шпильки или упора, и показания калибра отличаются от нуля. Если есть ошибка, это приводит к положительный или отрицательный расчет. Однако хорошо откалиброванные микрометры, находящиеся в хорошем состоянии, измеряют значение, близкое к нулю; и они не вносят заметной ошибки.

Машинисты проверяют точность микрометров, используя калибровочные блоки или стержни точной толщины. Если они обнаруживают ошибку, они повторно калибруют устройство. Они устраняют нулевую ошибку, заставляя микрометр показывать ноль при закрытии губок. Правильная калибровка требует тщательного внимания и чистоты прибора и эталона. Большинство микрометров имеют конструкцию, которая позволяет гаечному ключу поворачивать ствол по отношению к раме, и это регулирует нулевую линию.

В коммерческих магазинах контракты часто требуют ежегодной калибровки микрометров. Даже с такой осторожностью машинистам следует каждые два-три месяца проверять нулевую погрешность, используя стандарты. В большинстве случаев такие проверки не выявляют ошибок.

Стандартные дюймовые микрометры имеют деление отсчета 0,001 дюйма с точностью 0,0001 дюйма. Для обеспечения точности и калибр, и измеряемый материал должны храниться при комнатной температуре. Грязь, неправильное обращение и ошибки оператора вносят наибольшую погрешность в использование микрометров.

Источник

Свойства физического объекта (явления, процесса) определяются набором
количественных характеристик — физических величин.
Как правило, результат измерения представляет
собой число, задающее отношение измеряемой величины к некоторому эталону.
Сравнение с эталоном может быть как
прямым (проводится непосредственно
экспериментатором), так и косвенным (проводится с помощью некоторого
прибора, которому экспериментатор доверяет).
Полученные таким образом величины имеют размерность, определяемую выбором эталона.

Замечание. Результатом измерения может также служить количество отсчётов некоторого
события, логическое утверждение (да/нет) или даже качественная оценка
(сильно/слабо/умеренно). Мы ограничимся наиболее типичным для физики случаем,
когда результат измерения может быть представлен в виде числа или набора чисел.

Взаимосвязь между различными физическими величинами может быть описана
физическими законами, представляющими собой идеализированную
модель действительности. Конечной целью любого физического
эксперимента (в том числе и учебного) является проверка адекватности или
уточнение параметров таких моделей.

1.1 Результат измерения

Рассмотрим простейший пример: измерение длины стержня
с помощью линейки. Линейка проградуирована производителем с помощью
некоторого эталона длины — таким образом, сравнивая длину
стержня с ценой деления линейки, мы выполняем косвенное сравнение с
общепринятым стандартным эталоном.

Допустим, мы приложили линейку к стержню и увидели на шкале некоторый результат
x=xизм. Можно ли утверждать, что xизм — это длина
стержня?

Во-первых, значение x не может быть задано точно, хотя бы
потому, что оно обязательно округлено до некоторой значащей
цифры: если линейка «обычная», то у неё
есть цена деления; а если линейка, к примеру, «лазерная»
— у неё высвечивается конечное число значащих цифр
на дисплее.

Во-вторых, мы никак не можем быть уверенны, что длина стержня на
самом деле такова хотя бы с точностью до ошибки округления. Действительно,
мы могли приложить линейку не вполне ровно; сама линейка могла быть
изготовлена не вполне точно; стержень может быть не идеально цилиндрическим
и т.п.

И, наконец, если пытаться хотя бы гипотетически переходить к бесконечной
точности измерения, теряет смысл само понятие «длины стержня». Ведь
на масштабах атомов у стержня нет чётких границ, а значит говорить о его
геометрических размерах в таком случае крайне затруднительно!

Итак, из нашего примера видно, что никакое физическое измерение не может быть
произведено абсолютно точно, то есть
у любого измерения есть погрешность.

Замечание. Также используют эквивалентный термин ошибка измерения
(от англ. error). Подчеркнём, что смысл этого термина отличается от
общеупотребительного бытового: если физик говорит «в измерении есть ошибка»,
— это не означает, что оно неправильно и его надо переделать.
Имеется ввиду лишь, что это измерение неточно, то есть имеет
погрешность.

Количественно погрешность можно было бы определить как разность между
измеренным и «истинным» значением длины стержня:
δ⁢x=xизм-xист. Однако на практике такое определение
использовать нельзя: во-первых, из-за неизбежного наличия
погрешностей «истинное» значение измерить невозможно, и во-вторых, само
«истинное» значение может отличаться в разных измерениях (например, стержень
неровный или изогнутый, его торцы дрожат из-за тепловых флуктуаций и т.д.).
Поэтому говорят обычно об оценке погрешности.

Об измеренной величине также часто говорят как об оценке, подчеркивая,
что эта величина не точна и зависит не только от физических свойств
исследуемого объекта, но и от процедуры измерения.

Замечание.
Термин оценка имеет и более формальное значение. Оценкой называют результат процедуры получения значения параметра или параметров физической модели, а также иногда саму процедуру. Теория оценок является подразделом математической статистики. Некоторые ее положения изложены в главе 3, но для более серьезного понимания следует обратиться к [5].

Для оценки значения физической величины корректно использовать
не просто некоторое фиксированное число xизм, а интервал (или
диапазон) значений, в пределах которого может лежать её
«истинное» значение. В простейшем случае этот интервал
может быть записан как

где δ⁢x — абсолютная величина погрешности.
Эта запись означает, что исследуемая величина лежит в интервале
x∈(xизм-δ⁢x;xизм+δ⁢x)
с некоторой достаточно большой долей вероятности (более подробно о
вероятностном содержании интервалов см. п. 2.2).
Для наглядной оценки точности измерения удобно также использовать
относительную величину погрешности:

Она показывает, насколько погрешность мала по сравнению с
самой измеряемой величиной (её также можно выразить в процентах:
ε=δ⁢xx⋅100%).

Пример. Штангенциркуль —
прибор для измерения длин с ценой деления 0,1⁢мм. Пусть
диаметр некоторой проволоки равен 0,37 мм. Считая, что абсолютная
ошибка составляет половину цены деления прибора, результат измерения
можно будет записать как d=0,40±0,05⁢мм (или
d=(40±5)⋅10-5⁢м).
Относительная погрешность составляет ε≈13%, то
есть точность измерения весьма посредственная — поскольку
размер объекта близок к пределу точности прибора.

О необходимости оценки погрешностей.

Измерим длины двух стержней x1 и x2 и сравним результаты.
Можно ли сказать, что стержни одинаковы или различны?

Казалось бы,
достаточно проверить, справедливо ли x1=x2. Но никакие
два результата измерения не равны друг другу с абсолютной точностью! Таким
образом, без указания погрешности измерения ответ на этот вопрос дать
невозможно.

С другой стороны, если погрешность δ⁢x известна, то можно
утверждать, что если измеренные длины одинаковы
в пределах погрешности опыта, если |x2-x1|<δ⁢x
(и различны в противоположном случае).

Итак, без знания погрешностей невозможно сравнить между собой никакие
два измерения, и, следовательно, невозможно сделать никаких
значимых выводов по результатам эксперимента: ни о наличии зависимостей
между величинами, ни о практической применимости какой-либо теории,
и т. п. В связи с этим задача правильной оценки погрешностей является крайне
важной, поскольку существенное занижение или завышение значения погрешности
(по сравнению с реальной точностью измерений) ведёт к неправильным выводам.

В физическом эксперименте (в том числе лабораторном практикуме) оценка
погрешностей должна проводиться всегда
(даже когда составители задания забыли упомянуть об этом).

1.2 Многократные измерения

Проведём серию из n одинаковых (однотипных) измерений одной
и той же физической величины (например, многократно приложим линейку к стержню) и получим
ряд значений

Что можно сказать о данном наборе чисел и о длине стержня?
И можно ли увеличивая число измерений улучшить конечный результат?

Если цена деления самой линейки достаточно мала, то как нетрудно убедиться
на практике, величины {xi} почти наверняка окажутся
различными. Причиной тому могут быть
самые разные обстоятельства, например: у нас недостаточно остроты
зрения и точности рук, чтобы каждый раз прикладывать линейку одинаково;
стенки стержня могут быть слегка неровными; у стержня может и не быть
определённой длины, например, если в нём возбуждены звуковые волны,
из-за чего его торцы колеблются, и т. д.

В такой ситуации результат измерения интерпретируется как
случайная величина, описываемая некоторым вероятностным законом
(распределением).
Подробнее о случайных величинах и методах работы с ними см. гл. 2.

По набору результатов 𝐱 можно вычислить их среднее арифметическое:

⟨x⟩=x1+x2+…+xnn≡1n⁢∑i=1nxi.

(1.1)

Это значение, вычисленное по результатам конечного числа n измерений,
принято называть выборочным средним. Здесь и далее для обозначения
выборочных средних будем использовать угловые скобки.

Кроме среднего представляет интерес и то, насколько сильно варьируются
результаты от опыта к опыту. Определим отклонение каждого измерения от среднего как

Разброс данных относительно среднего принято характеризовать
среднеквадратичным отклонением:

s=Δ⁢x12+Δ⁢x22+…+Δ⁢xn2n=1n⁢∑i=1nΔ⁢xi2

(1.2)

или кратко

Значение среднего квадрата отклонения s2 называют
выборочной дисперсией.

Будем увеличивать число измерений n (n→∞). Если объект измерения и методика
достаточно стабильны, то отклонения от среднего Δ⁢xi будут, во-первых,
относительно малы, а во-вторых, положительные и отрицательные отклонения будут
встречаться примерно одинаково часто. Тогда при вычислении (1.1)
почти все отклонения Δ⁢xi скомпенсируются и можно ожидать,
что выборочное среднее при n≫1 будет стремиться к некоторому пределу:

Тогда предельное значение x¯ можно отождествить с «истинным» средним
для исследуемой величины.

Предельную величину среднеквадратичного отклонения при n→∞
обозначим как

Замечание. В общем случае указанные пределы могут и не существовать. Например, если измеряемый параметр
меняется во времени или в результате самого измерения, либо испытывает слишком большие
случайные скачки и т. п. Такие ситуации требуют особого рассмотрения и мы на них не
останавливаемся.

Замечание. Если n мало (n<10), для оценки среднеквадратичного отклонения
математическая статистика рекомендует вместо формулы (1.3) использовать
исправленную формулу (подробнее см. п. 5.2):

sn-12=1n-1⁢∑i=1nΔ⁢xi2,

(1.4)

где произведена замена n→n-1. Величину sn-1
часто называют стандартным отклонением.

Итак, можно по крайней мере надеяться на то, что результаты небольшого числа
измерений имеют не слишком большой разброс, так что величина ⟨x⟩
может быть использована как приближенное значение (оценка) истинного значения
⟨x⟩≈x¯,
а увеличение числа измерений позволит уточнить результат.

Многие случайные величины подчиняются так называемому нормальному закону
распределения (подробнее см. Главу 2). Для таких величин
могут быть строго доказаны следующие свойства:

•
при многократном повторении эксперимента бо́льшая часть измерений
(∼68%) попадает в интервал x¯-σ<x<x¯+σ
(см. п. 2.2).
•
выборочное среднее значение ⟨x⟩ оказывается с большей
вероятностью ближе к истинному значению x¯, чем каждое из измерений
{xi} в отдельности. При этом ошибка вычисления среднего
убывает пропорционально корню из числа опытов n
(см. п. 2.4).

Упражнение. Показать, что

s2=⟨x2⟩-⟨x⟩2.

(1.5)

то есть дисперсия равна разности среднего значения квадрата
⟨x2⟩=1n⁢∑i=1nxi2
и квадрата среднего ⟨x⟩2=(1n⁢∑i=1nxi)2.

1.3 Классификация погрешностей

Чтобы лучше разобраться в том, нужно ли многократно повторять измерения,
и в каком случае это позволит улучшить результаты опыта,
проанализируем источники и виды погрешностей.

В первую очередь, многократные измерения позволяют проверить
воспроизводимость результатов: повторные измерения в одинаковых
условиях, должны давать близкие результаты. В противном случае
исследование будет существенно затруднено, если вообще возможно.
Таким образом, многократные измерения необходимы для того,
чтобы убедиться как в надёжности методики, так и в существовании измеряемой
величины как таковой.

При любых измерениях возможны грубые ошибки — промахи
(англ. miss). Это «ошибки» в стандартном
понимании этого слова — возникающие по вине экспериментатора
или в силу других непредвиденных обстоятельств (например, из-за сбоя
аппаратуры). Промахов, конечно, нужно избегать, а результаты таких
измерений должны быть по возможности исключены из рассмотрения.

Как понять, является ли «аномальный» результат промахом? Вопрос этот весьма
непрост. В литературе существуют статистические
критерии отбора промахов, которыми мы, однако, настоятельно не рекомендуем
пользоваться (по крайней мере, без серьезного понимания последствий
такого отбора). Отбрасывание аномальных данных может, во-первых, привести
к тенденциозному искажению результата исследований, а во-вторых, так
можно упустить открытие неизвестного эффекта. Поэтому при научных
исследованиях необходимо максимально тщательно проанализировать причину
каждого промаха, в частности, многократно повторив эксперимент. Лишь
только если факт и причина промаха установлены вполне достоверно,
соответствующий результат можно отбросить.

Замечание. Часто причины аномальных отклонений невозможно установить на этапе
обработки данных, поскольку часть информации о проведении измерений к этому моменту
утеряна. Единственным способ борьбы с этим — это максимально подробное описание всего
процесса измерений в лабораторном журнале. Подробнее об этом
см. п. 4.1.1.

При многократном повторении измерении одной и той же физической величины
погрешности могут иметь систематический либо случайный
характер. Назовём погрешность систематической, если она повторяется
от опыта к опыту, сохраняя свой знак и величину, либо закономерно
меняется в процессе измерений. Случайные (или статистические)
погрешности меняются хаотично при повторении измерений как по величине,
так и по знаку, и в изменениях не прослеживается какой-либо закономерности.

Кроме того, удобно разделять погрешности по их происхождению. Можно
выделить

•
инструментальные (или приборные) погрешности,
связанные с несовершенством конструкции (неточности, допущенные при
изготовлении или вследствие старения), ошибками калибровки или ненормативными
условиями эксплуатации измерительных приборов;
•
методические погрешности, связанные с несовершенством
теоретической модели явления (использование приближенных формул и
моделей явления) или с несовершенством методики измерения (например,
влиянием взаимодействия прибора и объекта измерения на результат измерения);
•
естественные погрешности, связанные со случайным
характером
измеряемой физической величины — они являются не столько
«ошибками» измерения, сколько характеризуют
природу изучаемого объекта или явления.

Замечание. Разделение погрешностей на систематические и случайные
не является однозначным и зависит от постановки опыта. Например, производя
измерения не одним, а несколькими однотипными приборами, мы переводим
систематическую приборную ошибку, связанную с неточностью шкалы и
калибровки, в случайную. Разделение по происхождению также условно,
поскольку любой прибор подвержен воздействию «естественных»
случайных и систематических ошибок (шумы и наводки, тряска, атмосферные
условия и т. п.), а в основе работы прибора всегда лежит некоторое
физическое явление, описываемое не вполне совершенной теорией.

1.3.1 Случайные погрешности

Случайный характер присущ большому количеству различных физических
явлений, и в той или иной степени проявляется в работе всех без исключения
приборов. Случайные погрешности обнаруживаются просто при многократном
повторении опыта — в виде хаотичных изменений (флуктуаций)
значений {xi}.

Если случайные отклонения от среднего в большую или меньшую стороны
примерно равновероятны, можно рассчитывать, что при вычислении среднего
арифметического (1.1) эти отклонения скомпенсируются,
и погрешность результирующего значения ⟨x⟩ будем меньше,
чем погрешность отдельного измерения.

Случайные погрешности бывают связаны, например,

•
с особенностями используемых приборов: техническими
недостатками
(люфт в механических приспособлениях, сухое трение в креплении стрелки
прибора), с естественными (тепловой и дробовой шумы в электрических
цепях, тепловые флуктуации и колебания измерительных устройств из-за
хаотического движения молекул, космическое излучение) или техногенными
факторами (тряска, электромагнитные помехи и наводки);
•
с особенностями и несовершенством методики измерения (ошибка
при отсчёте по шкале, ошибка времени реакции при измерениях с секундомером);
•
с несовершенством объекта измерений (неровная поверхность,
неоднородность состава);
•
со случайным характером исследуемого явления (радиоактивный
распад, броуновское движение).

Остановимся несколько подробнее на двух последних случаях. Они отличаются
тем, что случайный разброс данных в них порождён непосредственно объектом
измерения. Если при этом приборные погрешности малы, то «ошибка»
эксперимента возникает лишь в тот момент, когда мы по своей
воле совершаем замену ряда измеренных значений на некоторое среднее
{xi}→⟨x⟩. Разброс данных при этом
характеризует не точность измерения, а сам исследуемый объект или
явление. Однако с математической точки зрения приборные и
«естественные»
погрешности неразличимы — глядя на одни только
экспериментальные данные невозможно выяснить, что именно явилось причиной
их флуктуаций: сам объект исследования или иные, внешние причины.
Таким образом, для исследования естественных случайных процессов необходимо
сперва отдельно исследовать и оценить случайные инструментальные погрешности
и убедиться, что они достаточно малы.

1.3.2 Систематические погрешности

Систематические погрешности, в отличие от случайных, невозможно обнаружить,
исключить или уменьшить просто многократным повторением измерений.
Они могут быть обусловлены, во-первых, неправильной работой приборов
(инструментальная погрешность), например, сдвигом нуля отсчёта
по шкале, деформацией шкалы, неправильной калибровкой, искажениями
из-за не нормативных условий эксплуатации, искажениями из-за износа
или деформации деталей прибора, изменением параметров прибора во времени
из-за нагрева и т.п. Во-вторых, их причиной может быть ошибка в интерпретации
результатов (методическая погрешность), например, из-за использования
слишком идеализированной физической модели явления, которая не учитывает
некоторые значимые факторы (так, при взвешивании тел малой плотности
в атмосфере необходимо учитывать силу Архимеда; при измерениях в электрических
цепях может быть необходим учет неидеальности амперметров и вольтметров
и т. д.).

Систематические погрешности условно можно разделить на следующие категории.

1.
Известные погрешности, которые могут быть достаточно точно вычислены
или измерены. При необходимости они могут быть учтены непосредственно:
внесением поправок в расчётные формулы или в результаты измерений.
Если они малы, их можно отбросить, чтобы упростить вычисления.
2.
Погрешности известной природы, конкретная величина которых неизвестна,
но максимальное значение вносимой ошибки может быть оценено теоретически
или экспериментально. Такие погрешности неизбежно присутствуют в любом
опыте, и задача экспериментатора — свести их к минимуму,
совершенствуя методики измерения и выбирая более совершенные приборы.

Чтобы оценить величину систематических погрешностей опыта, необходимо
учесть паспортную точность приборов (производитель, как правило, гарантирует,
что погрешность прибора не превосходит некоторой величины), проанализировать
особенности методики измерения, и по возможности, провести контрольные
опыты.
3.
Погрешности известной природы, оценка величины которых по каким-либо
причинам затруднена (например, сопротивление контактов при подключении
электронных приборов). Такие погрешности должны быть обязательно исключены
посредством модификации методики измерения или замены приборов.
4.
Наконец, нельзя забывать о возможности существования ошибок, о
которых мы не подозреваем, но которые могут существенно искажать результаты
измерений. Такие погрешности самые опасные, а исключить их можно только
многократной независимой проверкой измерений, разными методами
и в разных условиях.

В учебном практикуме учёт систематических погрешностей ограничивается,
как правило, паспортными погрешностями приборов и теоретическими поправками
к упрощенной модели исследуемого явления.

Точный учет систематической ошибки возможен только при учете специфики конкретного эксперимента. Особенное внимание надо обратить на зависимость (корреляцию) систематических смещений при повторных измерениях. Одна и та же погрешность в разных случаях может быть интерпретирована и как случайная, и как систематическая.

Пример.
Калибровка электромагнита производится при помощи внесения в него датчика Холла или другого измерителя магнитного потока. При последовательных измерениях с разными токами (и соотственно полями в зазоре) калибровку можно учитыать двумя различными способами:

•

Измерить значение поля для разных токов, построить линейную калибровочную кривую и потом использовать значения, восстановленные по этой кривой для вычисления поля по току, используемому в измерениях.

•

Для каждого измерения проводить допольнительное измерения поля и вообще не испльзовать значения тока.

В первом случае погрешность полученного значения будет меньше, поскльку при проведении прямой, отдельные отклонения усреднятся. При этом погрешность измерения поля будет носить систематический харрактер и при обработке данных ее надо будет учитывать в последний момент. Во втором случае погрешность будет носить статистический (случайный) харрактер и ее надо будет добавить к погрешности каждой измеряемой точки. При этом сама погрешность будет больше. Выбор той или иной методики зависит от конретной ситуации. При большом количестве измерений, второй способ более надежный, поскольку статистическая ошибка при усреднении уменьшается пропорционально корню из количества измерений. Кроме того, такой способ повзоляет избежать методической ошибки, связанной с тем, что зависимость поля от тока не является линейной.

Пример.
Рассмотрим измерение напряжения по стрелочному вольтметру. В показаниях прибора будет присутствовать три типа погрешности:

1.

Статистическая погрешность, связанная с дрожанием стрелки и ошибкой визуального наблюдения, примерно равная половине цены деления.

2.

Систематическая погрешность, связанная с неправильной установкой нуля.

3.

Систематическая погрешность, связанная с неправильным коэффициентом пропорциональности между напряжением и отклонением стрелки. Как правило приборы сконструированы таким образом, чтобы максимальное значение этой погрешности было так же равно половине цены деления (хотя это и не гарантируется).

Неотъемлемой частью любого измерения является погрешность измерений. С развитием приборостроения и методик измерений человечество стремиться снизить влияние данного явления на конечный результат измерений. Предлагаю более детально разобраться в вопросе, что же это такое погрешность измерений.

Погрешность измерения – это отклонение результата измерения от истинного значения измеряемой величины. Погрешность измерений представляет собой сумму погрешностей, каждая из которых имеет свою причину.

По форме числового выражения погрешности измерений подразделяются на абсолютные и относительные

Абсолютная погрешность – это погрешность, выраженная в единицах измеряемой величины. Она определяется выражением.

(1.2), где X — результат измерения; Х₀ — истинное значение этой величины.

Поскольку истинное значение измеряемой величины остается неизвестным, на практике пользуются лишь приближенной оценкой абсолютной погрешности измерения, определяемой выражением

(1.3), где Х_д — действительное значение этой измеряемой величины, которое с погрешностью ее определения принимают за истинное значение.

Относительная погрешность – это отношение абсолютной погрешности измерения к действительному значению измеряемой величины:

(1.4)

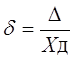
По закономерности появления погрешности измерения подразделяются на систематические, прогрессирующие, и случайные.

Систематическая погрешность – это погрешность измерения, остающаяся постоянной или закономерно изменяющейся при повторных измерениях одной и той же величины.

Прогрессирующая погрешность – это непредсказуемая погрешность, медленно меняющаяся во времени.

Систематические и прогрессирующие погрешности средств измерений вызываются:

первые — погрешностью градуировки шкалы или ее небольшим сдвигом;
вторые — старением элементов средства измерения.

Систематическая погрешность остается постоянной или закономерно изменяющейся при многократных измерениях одной и той же величины. Особенность систематической погрешности состоит в том, что она может быть полностью устранена введением поправок. Особенностью прогрессирующих погрешностей является то, что они могут быть скорректированы только в данный момент времени. Они требуют непрерывной коррекции.

Случайная погрешность – это погрешность измерения изменяется случайным образом. При повторных измерениях одной и той же величины. Случайные погрешности можно обнаружить только при многократных измерениях. В отличии от систематических погрешностей случайные нельзя устранить из результатов измерений.

По происхождению различают инструментальные и методические погрешности средств измерений.

Инструментальные погрешности — это погрешности, вызываемые особенностями свойств средств измерений. Они возникают вследствие недостаточно высокого качества элементов средств измерений. К данным погрешностям можно отнести изготовление и сборку элементов средств измерений; погрешности из-за трения в механизме прибора, недостаточной жесткости его элементов и деталей и др. Подчеркнем, что инструментальная погрешность индивидуальна для каждого средства измерений.

Методическая погрешность — это погрешность средства измерения, возникающая из-за несовершенства метода измерения, неточности соотношения, используемого для оценки измеряемой величины.

Погрешности средств измерений.

Абсолютная погрешность меры – это разность между номинальным ее значением и истинным (действительным) значением воспроизводимой ею величины:

(1.5), где X_н – номинальное значение меры; Х_д – действительное значение меры

Абсолютная погрешность измерительного прибора – это разность между показанием прибора и истинным (действительным) значением измеряемой величины:

(1.6), где X_п – показания прибора; Х_д – действительное значение измеряемой величины.

Относительная погрешность меры или измерительного прибора – это отношение абсолютной погрешности меры или измерительного прибора к истинному

(действительному) значению воспроизводимой или измеряемой величины. Относительная погрешность меры или измерительного прибора может быть выражена в ( % ).

(1.7)

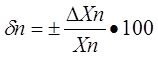
Приведенная погрешность измерительного прибора – отношение погрешности измерительного прибора к нормирующему значению. Нормирующие значение XN – это условно принятое значение, равное или верхнему пределу измерений, или диапазону измерений, или длине шкалы. Приведенная погрешность обычно выражается в ( % ).

(1.8)

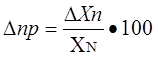
Предел допускаемой погрешности средств измерений – наибольшая без учета знака погрешность средства измерений, при которой оно может быть признано и допущено к применению. Данное определение применяют к основной и дополнительной погрешности, а также к вариации показаний. Поскольку свойства средств измерений зависят от внешних условий, их погрешности также зависят от этих условий, поэтому погрешности средств измерений принято делить на основные и дополнительные.

Основная – это погрешность средства измерений, используемого в нормальных условиях, которые обычно определены в нормативно-технических документах на данное средство измерений.

Дополнительная – это изменение погрешности средства измерений вследствии отклонения влияющих величин от нормальных значений.

Погрешности средств измерений подразделяются также на статические и динамические.

Статическая – это погрешность средства измерений, используемого для измерения постоянной величины. Если измеряемая величина является функцией времени, то вследствие инерционности средств измерений возникает составляющая общей погрешности, называется динамической погрешностью средств измерений.

Также существуют систематические и случайные погрешности средств измерений они аналогичны с такими же погрешностями измерений.

Факторы влияющие на погрешность измерений.

Погрешности возникают по разным причинам: это могут быть ошибки экспериментатора или ошибки из-за применения прибора не по назначению и т.д. Существует ряд понятий которые определяют факторы влияющие на погрешность измерений

Вариация показаний прибора – это наибольшая разность показаний полученных при прямом и обратном ходе при одном и том же действительном значении измеряемой величины и неизменных внешних условиях.

Класс точности прибора – это обобщенная характеристика средств измерений (прибора), определяемая пределами допускаемых основной и дополнительных погрешностей, а также другими свойствами средств измерений, влияющих на точность, значение которой устанавливаются на отдельные виды средств измерений.

Классы точности прибора устанавливают при выпуске, градуируя его по образцовому прибору в нормальных условиях.

Прецизионность — показывает, как точно или отчетливо можно произвести отсчет. Она определяется, тем насколько близки друг к другу результаты двух идентичных измерений.

Разрешение прибора — это наименьшее изменение измеряемого значения, на которое прибор будет реагировать.

Диапазон прибора — определяется минимальным и максимальным значением входного сигнала, для которого он предназначен.

Полоса пропускания прибора — это разность между минимальной и максимальной частотой, для которых он предназначен.

Чувствительность прибора — определяется, как отношение выходного сигнала или показания прибора к входному сигналу или измеряемой величине.

Шумы — любой сигнал не несущий полезной информации.

Инструментальные погрешности

Инструментальными называют погрешности, причина которых заключается в свойствах применяемых средств измерений. Эти свойства могут вызывать погрешности различного характера.

В общем случае инструментальные погрешности можно разделить на: инструментальные погрешности, являющиеся следствием несовершенства или неправильности технологии изготовления средств измерений; инструментальные погрешности, присущие данной конструкции; инструментальные погрешности, являющиеся следствием износа, старения или неисправности средств измерений.

Инструментальные погрешности, присущие данной конструкции

Одним из характерных источников погрешностей рассматриваемого вида, присущих почти всем средствам измерений, которые имеют подвижные части, является некоторая свобода перемещения этих частей, помимо движения, соответствующего принципу действия устройства. В зависимости от конструкции узла, в котором возникает такая свобода перемещения, а также от традиций той или иной отрасли приборостроения говорят о наличие «люфта», «зазора», «мертвого», «свободного» или «холостого хода» и т. д.

Еще одной причиной инструментальных погрешностей является трение в сочленениях подвижных деталей приборов.

Так, в средствах измерений, в которых при измерении приходится вращать или перемещать отдельные детали (например, в микрометрах), большое трение затрудняет правильную установку вращаемой детали и может привести к возникновению чрезмерно большого или чрезмерно малого давления на измеряемый объект.

Инструментальные погрешности, являющиеся следствием несовершенства или неправильности технологии изготовления средств измерений

Всем средствам измерений, имеющим шкалу, в большей или меньшей степени присущи погрешности, возникшие в результате неточности нанесения отметок шкалы, так называемые погрешности градуировки. В тех случаях, когда деления шкалы строго равномерны, как, например, в устройствах для измерения длины, отметки на шкалы наносятся механически при помощи соответствующих приспособлений. Несовершенство конструкции, износ или неисправности этих приспособлений могут привести к тому, что некоторые или все отметки окажутся смещенными в ту или иную сторону. При этом в процессе измерения результаты всегда будут содержать одну и ту же погрешность.

Более или менее точные измерительные приборы, шкалы которых неравномерны, градуируют нередко вручную. Процесс градуировки осуществляется следующим образом. Градуируемый измерительный прибор с основанием, подготовленным для нанесения шкалы, и образцовый измерительный прибор, погрешности которого значительно меньше предельно допускаемых для градуируемо, подключают к регулируемому источнику измеряемой величины. Устанавливая различные значения измеряемой величины показаниям образцового измерительного прибора, одновременно наносят отметки на шкалу градуируемого измерительного прибора. Уже на этом этапе возможно появление погрешностей, например, вследствие того, что исполнитель при нанесении отметки дет смотреть не строго перпендикулярно к плоскости шкалы, результате нанесенная им отметка окажется смещенной влево :и вправо от правильного положения (погрешность от параллакса). При градуировке на шкалу наносят только основные отметки, т. е. отметки, против которых ставят числовые значения (называть их «оцифрованными» не рекомендуется).

Промежуточные отметки в соответствии с характером шкалы наносят на глаз или при помощи приспособлений различной степени сложности. На этом этапе возможно появление погрешностей градуировки вследствие глазомерных ошибок или несовершенства приспособления, недостаточно точно воспроизводящего малых делениях характер неравномерности шкалы. Эти погрешности опасны тем, что при поверке средств измерений, как правило, ограничиваются сличением их показаний с показаниями образцового измерительного устройства также только на числовых метках.

Таким образом, систематические погрешности на промежуточных отметках могут остаться незамеченными.

Числовые, а иногда и промежуточные отметки при описанном особе градуировки наносят предварительно «вчерне», например виде карандашных точек, после чего вычерчивают шкалу тушью или иным способом. На этом этапе может возникнуть дополни-льная градуировочная погрешность, например, от того, что при нанесении штриха определенной ширины (а не толщины, как иногда говорят) его середина может оказаться смещенной по отношению к точке, поставленной при градуировке.

Таким образом, возможность появления инструментальных погрешностей в результате градуировки весьма значительна. Принимаются меры к тому, чтобы погрешности градуировки были меньше погрешностей, допускаемых для данного средства измерения, однако в какой-то степени они все же остаются. Их отрицательное влияние становится особенно заметно в процессе эксплуатации средств измерений, когда возрастают другие погрешности, например, вследствие износа деталей, старения материала, нарушения регулировки. Тогда суммарная погрешность может выйти за допускаемые пределы раньше срока естественного износа.

В последнее время стремятся изготовлять печатные шкалы (типографским, фотографическим и другими способами) не только для средств измерений массового выпуска, но и для более точных. В этом случае при конструировании предусматривают способы регулирования средств измерений, позволяющие «подогнать» их показания к шкале. Разумеется, и при этом способе неизбежны градуировочные погрешности.

Инструментальные погрешности, являющиеся следствием износа, старения или неисправности средств измерений.

Износ и старение материалов могут быть причиной появления погрешностей, имеющих некоторые характерные особенности. Так, совершенно очевидно, что средства измерений изнашиваются непрерывно и постепенно в процессе эксплуатации со скоростью, зависящей от интенсивности эксплуатации. Следовательно, и погрешности, появляющиеся в результате износа, как правило, возрастают постепенно. Однако рост этот происходит настолько медленно, что в определенный отрезок времени мы можем принимать погрешности, явившиеся следствием износа, постоянными и даже пользоваться соответствующими поправками. Только тогда, когда эти погрешности достигнут установленного предела, дальнейшее применение данного средства измерений считается недопустимым.

Типичным примером в этом отношении являются гири. Их износ всегда идет в одном направлении — постепенно уменьшается их масса. Характер износа гирь заставляет изготовлять их с положительным запасом массы. Масса новой гири всегда больше номинальной в пределах, допускаемых для данного класса гирь.

Другим примером являются концевые меры длины — плитки. В процессе эксплуатации и при ремонтах их размер постепенно уменьшается. Плитками пользуются до тех пор, пока их размер не достигнет установленного для них предела, после чего их или переводят в другой класс, или переаттестовывают, или, наконец, изымают из применения в качестве мер.

Несколько иначе обстоит дело со старением. Под старением понимают изменение каких-либо свойств материалов с течением времени, а иногда и в зависимости от условий применения или хранения.

Процесс старения может протекать различно. Старение может привести к потере каких-либо свойств, имеющих значение для средства измерений, или к постепенной их стабилизации. Одним из характерных примеров старения второго вида является старение манганина. Манганин—это сплав меди, марганца, никеля и некоторых других компонентов, добавляемых иногда в небольших количествах. Обладая сравнительно большим удельным электрическим сопротивлением, манганин в то же время имеет незначительный температурный коэффициент сопротивления. Термоэлектродвижущая сила (т. э. д. с), которая возникает в спае манганина с медью при его нагревании, относительно невелика. Благодаря этим качествам манганин широко применяется в электроприборостроении. Однако манганин имеет одно отрицательное свойство — с течением времени его сопротивление хотя и медленно, но изменяется. По истечении двух-трех лет процесс этот практически прекращается и сопротивление изделия из манганина стабилизируется.

Были разработаны приемы искусственного ускорения процесса старения манганина, стабилизации его свойств. Так как полной стабилизации все же достичь не удается, то для более точных приборов, в которых эта остаточная нестабильность влияет на показания, в первые годы эксплуатации проводят более частые поверки.

В особо ответственных случаях готовое изделие выдерживают годами без применения — до полной стабилизации его свойств, например, катушки сопротивления высшей точности. Во время выдержки ведутся периодические наблюдения за изменением их сопротивления.

Как видим, в данном случае процесс старения обратен процессу износа — с течением времени качество и надежность измерительного устройства улучшаются.

Манганин — не единственный пример старения материала в области измерительной техники. Так, в некоторых концевых мерах длины, изготовляемых из стали, также была обнаружена тенденция к изменению с течением времени их размеров, причем в сторону увеличения. Это явление назвали «ростом» плиток. Меры борьбы с этим явлением те же, что и в отношении манганина — искусственная стабилизация и более частая поверка до наступления надежной естественной стабилизации.

Неисправностей, которые являются или точнее могут являться причиной появления систематических погрешностей, множество. Перечислить их нет никакой возможности. Можно указать на деформации или коррозию деталей измерительного механизма, не прекращающих, но изменяющих характер взаимодействия отдельных его частей. Часто неисправность измерительного устройства является следствием его перегрузки. Перегрузка — механическая, электрическая, тепловая или какая-либо иная — может вызвать устойчивое «остаточное» изменение в материале или в механизме средства измерений и явиться причиной появления или изменения систематической погрешности.

Неисправности, ведущие к появлению небольших систематических погрешностей, гораздо опаснее тех, которые вызывают большие погрешности. Большие систематические погрешности сравнительно быстро обнаруживаются «на глаз», например, по значительному несоответствию результатов измерения ожидаемым. Небольшие систематические погрешности, в два — четыре раза превышающие допускаемые, могут в течение более или менее длительного времени оставаться незамеченными. Такие незамеченные погрешности могут принести огромный вред, особенно при большом числе измерений.

Особую опасность представляет появление или изменение систематических погрешностей в образцовых средствах измерений, применяемых для поверки других средств измерений. Мало того, что каждое средство измерений, поверенное или отградуированное по такому образцовому средству измерений, с самого начала будет нести в себе скрытую погрешность, оно будет передавать эту погрешность всем объектам, которые с его помощью будут измеряться или поверяться. Если вред, приносимый скрытой систематической погрешностью рабочего средства измерений, можно было бы выразить математически, то для выражения вреда, приносимого скрытой систематической погрешностью образцового средства измерений, это выражение следовало бы возвести в квадрат или даже в четвертую степень для случая поверки образцового средства измерений следующего, более низкого, разряда.

Из этого сопоставления роли систематических погрешностей рабочих и образцовых средств измерений наглядно видна важность особой тщательности проведения поверки образцовых средств измерений.

Данный обзор инструментальных погрешностей не является исчерпывающим. Его цель — подсказать читателю необходимость и пути анализа возможных систематических погрешностей, которые могут внести в результаты измерения применяемые измерительные устройства.

Использование термина

Термин особенно актуален для тензометрических и термометрических задач измерения.

Измерительная система LTR

Модуль АЦП тензометрический
4/8 каналов, 24 бит, 7,6 кГц

LTR212M

Модуль АЦП универсальный
16 каналов, 24 бит, 4 кГц

LTR114

Модуль АЦП тензометрический
16 каналов, 24 бит, 50 кГц

LTR216

Источник

1.1 Результат измерения

О необходимости оценки погрешностей.

1.2 Многократные измерения

1.3 Классификация погрешностей

1.3.1 Случайные погрешности

1.3.2 Систематические погрешности

Погрешности средств измерений.

Факторы влияющие на погрешность измерений.

Инструментальные погрешности

Инструментальные погрешности, присущие данной конструкции

Инструментальные погрешности, являющиеся следствием несовершенства или неправильности технологии изготовления средств измерений

Инструментальные погрешности, являющиеся следствием износа, старения или неисправности средств измерений.

Похожие материалы

Использование термина

Измерительная система LTR

LTR212M

LTR114

LTR216

Возможно, вам также будет интересно: