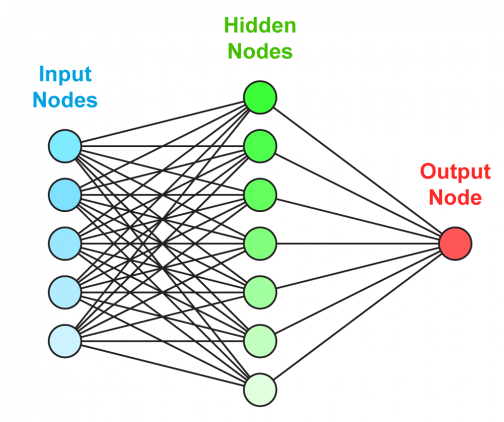
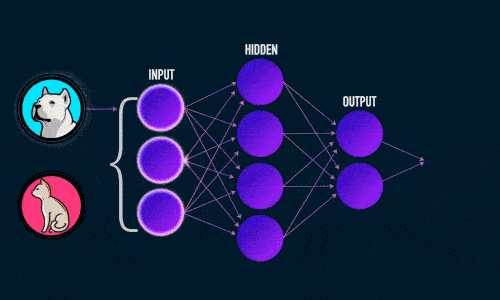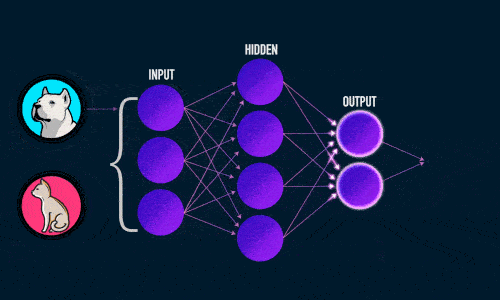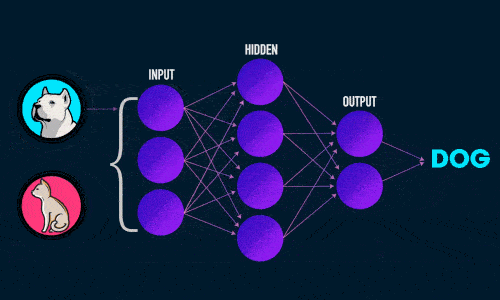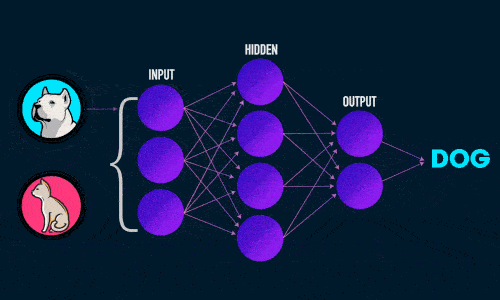
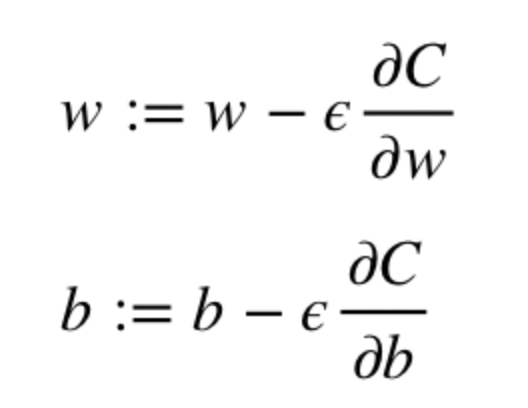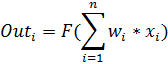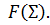Нейронная сеть — попытка с помощью математических моделей воспроизвести работу человеческого мозга для создания машин, обладающих искусственным интеллектом.
Искусственная нейронная сеть обычно обучается с учителем. Это означает наличие обучающего набора (датасета), который содержит примеры с истинными значениями: тегами, классами, показателями.
Неразмеченные наборы также используют для обучения нейронных сетей, но мы не будем здесь это рассматривать.
Например, если вы хотите создать нейросеть для оценки тональности текста, датасетом будет список предложений с соответствующими каждому эмоциональными оценками. Тональность текста определяют признаки (слова, фразы, структура предложения), которые придают негативную или позитивную окраску. Веса признаков в итоговой оценке тональности текста (позитивный, негативный, нейтральный) зависят от математической функции, которая вычисляется во время обучения нейронной сети.
Раньше люди генерировали признаки вручную. Чем больше признаков и точнее подобраны веса, тем точнее ответ. Нейронная сеть автоматизировала этот процесс.
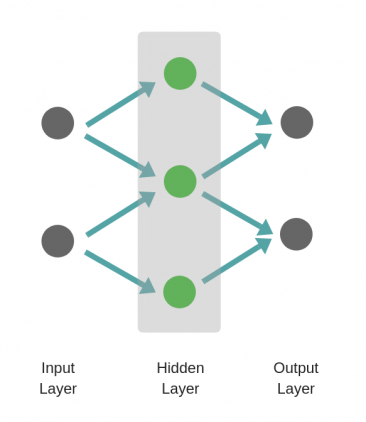
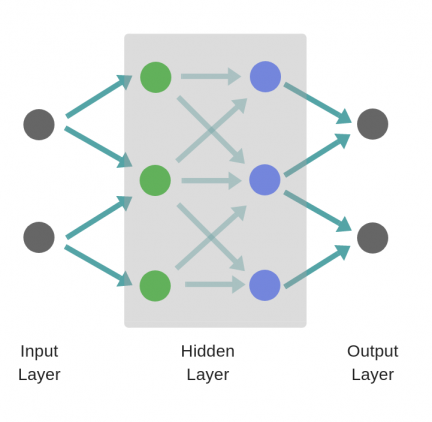
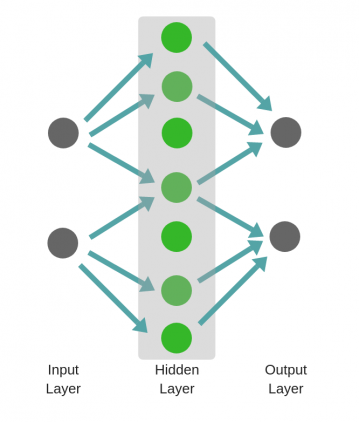
Искусственная нейронная сеть состоит из трех компонентов:
- Входной слой;
- Скрытые (вычислительные) слои;
- Выходной слой.
Обучение нейросетей происходит в два этапа:
- Прямое распространение ошибки;
- Обратное распространение ошибки.
Во время прямого распространения ошибки делается предсказание ответа. При обратном распространении ошибка между фактическим ответом и предсказанным минимизируется.
Прямое распространение ошибки
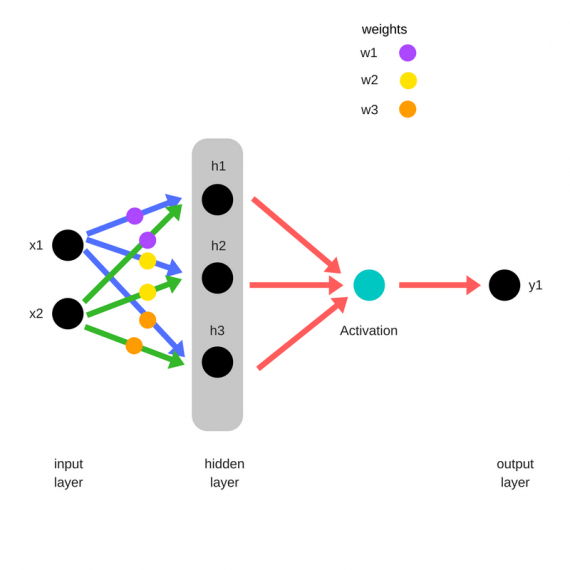
Зададим начальные веса случайным образом:
- w1
- w2
- w3
Умножим входные данные на веса для формирования скрытого слоя:
- h1 = (x1 * w1) + (x2 * w1)
- h2 = (x1 * w2) + (x2 * w2)
- h3 = (x1 * w3) + (x2 * w3)
Выходные данные из скрытого слоя передается через нелинейную функцию (функцию активации), для получения выхода сети:
- y_ = fn(h1 , h2, h3)
Обратное распространение
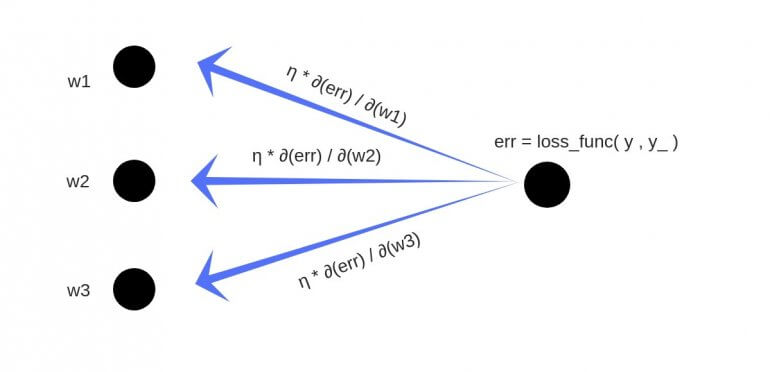
- Суммарная ошибка (total_error) вычисляется как разность между ожидаемым значением «y» (из обучающего набора) и полученным значением «y_» (посчитанное на этапе прямого распространения ошибки), проходящих через функцию потерь (cost function).
- Частная производная ошибки вычисляется по каждому весу (эти частные дифференциалы отражают вклад каждого веса в общую ошибку (total_loss)).
- Затем эти дифференциалы умножаются на число, называемое скорость обучения или learning rate (η).
Полученный результат затем вычитается из соответствующих весов.
В результате получатся следующие обновленные веса:
- w1 = w1 — (η * ∂(err) / ∂(w1))
- w2 = w2 — (η * ∂(err) / ∂(w2))
- w3 = w3 — (η * ∂(err) / ∂(w3))
То, что мы предполагаем и инициализируем веса случайным образом, и они будут давать точные ответы, звучит не вполне обоснованно, тем не менее, работает хорошо.
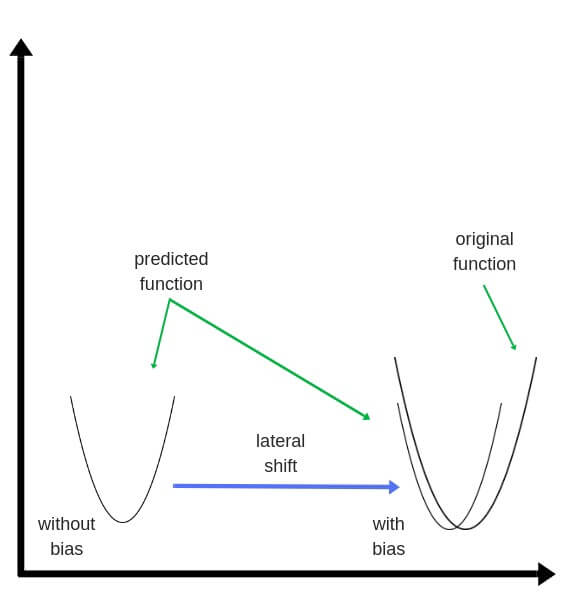
Смещения – это веса, добавленные к скрытым слоям. Они тоже случайным образом инициализируются и обновляются так же, как скрытый слой. Роль скрытого слоя заключается в том, чтобы определить форму базовой функции в данных, в то время как роль смещения – сдвинуть найденную функцию в сторону так, чтобы она частично совпала с исходной функцией.
Частные производные
Частные производные можно вычислить, поэтому известно, какой был вклад в ошибку по каждому весу. Необходимость производных очевидна. Представьте нейронную сеть, пытающуюся найти оптимальную скорость беспилотного автомобиля. Eсли машина обнаружит, что она едет быстрее или медленнее требуемой скорости, нейронная сеть будет менять скорость, ускоряя или замедляя автомобиль. Что при этом ускоряется/замедляется? Производные скорости.
Разберем необходимость частных производных на примере.
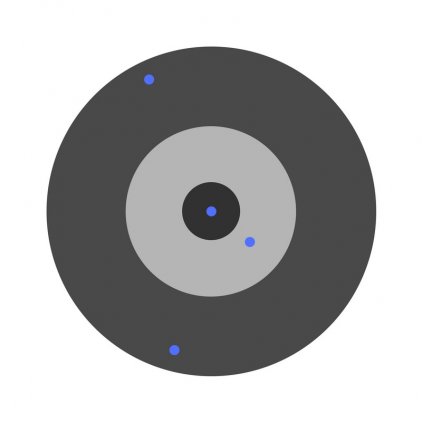
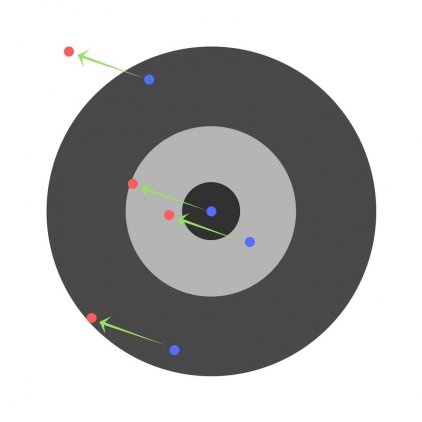
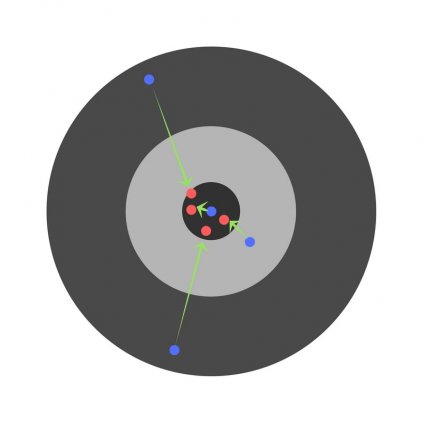
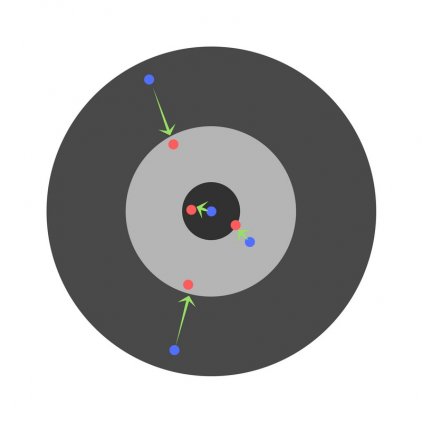
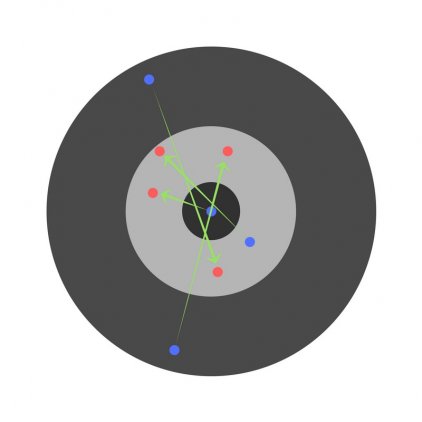
Предположим, детей попросили бросить дротик в мишень, целясь в центр. Вот результаты:
Теперь, если мы найдем общую ошибку и просто вычтем ее из всех весов, мы обобщим ошибки, допущенные каждым. Итак, скажем, ребенок попал слишком низко, но мы просим всех детей стремиться попадать в цель, тогда это приведет к следующей картине:
Ошибка нескольких детей может уменьшиться, но общая ошибка все еще увеличивается.
Найдя частные производные, мы узнаем ошибки, соответствующие каждому весу в отдельности. Если выборочно исправить веса, можно получить следующее:
Гиперпараметры
Нейронная сеть используется для автоматизации отбора признаков, но некоторые параметры настраиваются вручную.
Скорость обучения (learning rate)
Скорость обучения является очень важным гиперпараметром. Если скорость обучения слишком мала, то даже после обучения нейронной сети в течение длительного времени она будет далека от оптимальных результатов. Результаты будут выглядеть примерно так:
С другой стороны, если скорость обучения слишком высока, то сеть очень быстро выдаст ответы. Получится следующее:
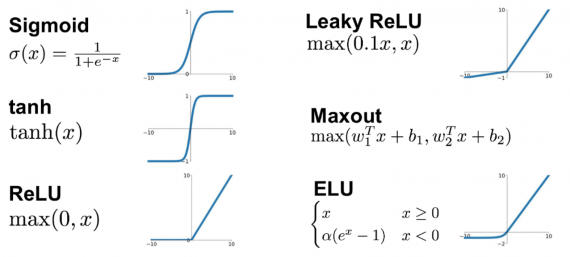
Функция активации (activation function)
Функция активации — это один из самых мощных инструментов, который влияет на силу, приписываемую нейронным сетям. Отчасти, она определяет, какие нейроны будут активированы, другими словами и какая информация будет передаваться последующим слоям.
Без функций активации глубокие сети теряют значительную часть своей способности к обучению. Нелинейность этих функций отвечает за повышение степени свободы, что позволяет обобщать проблемы высокой размерности в более низких измерениях. Ниже приведены примеры распространенных функций активации:
Функция потери (loss function)
Функция потерь находится в центре нейронной сети. Она используется для расчета ошибки между реальными и полученными ответами. Наша глобальная цель — минимизировать эту ошибку. Таким образом, функция потерь эффективно приближает обучение нейронной сети к этой цели.
Функция потерь измеряет «насколько хороша» нейронная сеть в отношении данной обучающей выборки и ожидаемых ответов. Она также может зависеть от таких переменных, как веса и смещения.
Функция потерь одномерна и не является вектором, поскольку она оценивает, насколько хорошо нейронная сеть работает в целом.
Некоторые известные функции потерь:
- Квадратичная (среднеквадратичное отклонение);
- Кросс-энтропия;
- Экспоненциальная (AdaBoost);
- Расстояние Кульбака — Лейблера или прирост информации.
Cреднеквадратичное отклонение – самая простая фукция потерь и наиболее часто используемая. Она задается следующим образом:
Функция потерь в нейронной сети должна удовлетворять двум условиям:
- Функция потерь должна быть записана как среднее;
- Функция потерь не должна зависеть от каких-либо активационных значений нейронной сети, кроме значений, выдаваемых на выходе.
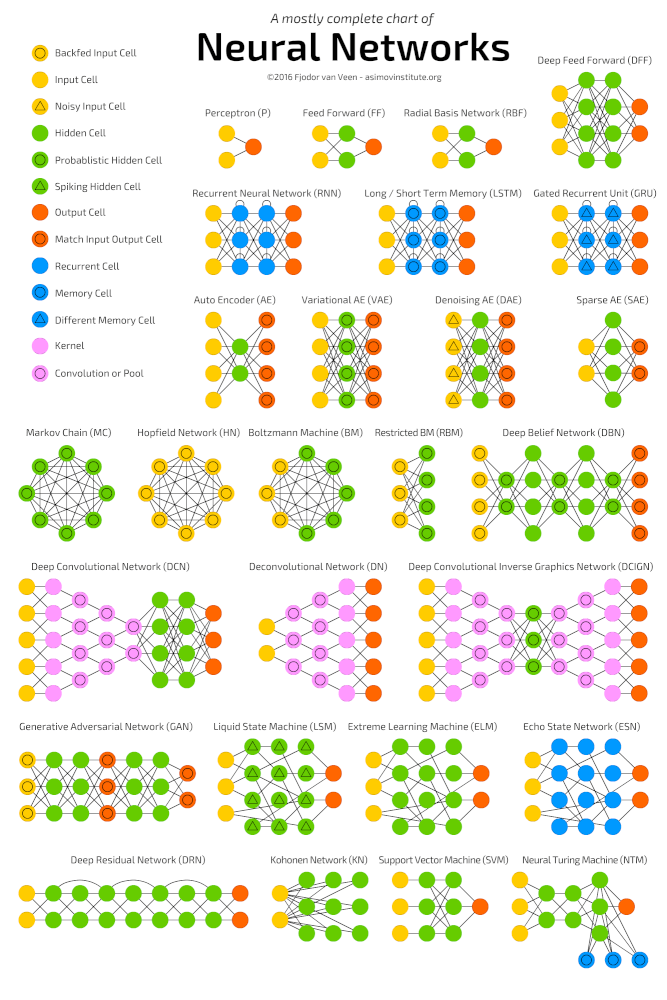
Глубокие нейронные сети
Глубокое обучение (deep learning) – это класс алгоритмов машинного обучения, которые учатся глубже (более абстрактно) понимать данные. Популярные алгоритмы нейронных сетей глубокого обучения представлены на схеме ниже.
Более формально в deep learning:
- Используется каскад (пайплайн, как последовательно передаваемый поток) из множества обрабатывающих слоев (нелинейных) для извлечения и преобразования признаков;
- Основывается на изучении признаков (представлении информации) в данных без обучения с учителем. Функции более высокого уровня (которые находятся в последних слоях) получаются из функций нижнего уровня (которые находятся в слоях начальных слоях);
- Изучает многоуровневые представления, которые соответствуют разным уровням абстракции; уровни образуют иерархию представления.
Пример
Рассмотрим однослойную нейронную сеть:
Здесь, обучается первый слой (зеленые нейроны), он просто передается на выход.
В то время как в случае двухслойной нейронной сети, независимо от того, как обучается зеленый скрытый слой, он затем передается на синий скрытый слой, где продолжает обучаться:
Следовательно, чем больше число скрытых слоев, тем больше возможности обучения сети.
Не следует путать с широкой нейронной сетью.
В этом случае большое число нейронов в одном слое не приводит к глубокому пониманию данных. Но это приводит к изучению большего числа признаков.
Пример:
Изучая английскую грамматику, требуется знать огромное число понятий. В этом случае однослойная широкая нейронная сеть работает намного лучше, чем глубокая нейронная сеть, которая значительно меньше.
Но
В случае изучения преобразования Фурье, ученик (нейронная сеть) должен быть глубоким, потому что не так много понятий, которые нужно знать, но каждое из них достаточно сложное и требует глубокого понимания.
Главное — баланс
Очень заманчиво использовать глубокие и широкие нейронные сети для каждой задачи. Но это может быть плохой идеей, потому что:
- Обе требуют значительно большего количества данных для обучения, чтобы достичь минимальной желаемой точности;
- Обе имеют экспоненциальную сложность;
- Слишком глубокая нейронная сеть попытается сломать фундаментальные представления, но при этом она будет делать ошибочные предположения и пытаться найти псевдо-зависимости, которые не существуют;
- Слишком широкая нейронная сеть будет пытаться найти больше признаков, чем есть. Таким образом, подобно предыдущей, она начнет делать неправильные предположения о данных.
Проклятье размерности
Проклятие размерности относится к различным явлениям, возникающим при анализе и организации данных в многомерных пространствах (часто с сотнями или тысячами измерений), и не встречается в ситуациях с низкой размерностью.
Грамматика английского языка имеет огромное количество аттрибутов, влияющих на нее. В машинном обучении мы должны представить их признаками в виде массива/матрицы конечной и существенно меньшей длины (чем количество существующих признаков). Для этого сети обобщают эти признаки. Это порождает две проблемы:
- Из-за неправильных предположений появляется смещение. Высокое смещение может привести к тому, что алгоритм пропустит существенную взаимосвязь между признаками и целевыми переменными. Это явление называют недообучение.
- От небольших отклонений в обучающем множестве из-за недостаточного изучения признаков увеличивается дисперсия. Высокая дисперсия ведет к переобучению, ошибки воспринимаются в качестве надежной информации.
Компромисс
На ранней стадии обучения смещение велико, потому что выход из сети далек от желаемого. А дисперсия очень мала, поскольку данные имеет пока малое влияние.
В конце обучения смещение невелико, потому что сеть выявила основную функцию в данных. Однако, если обучение слишком продолжительное, сеть также изучит шум, характерный для этого набора данных. Это приводит к большому разбросу результатов при тестировании на разных множествах, поскольку шум меняется от одного набора данных к другому.
Действительно,
алгоритмы с большим смещением обычно в основе более простых моделей, которые не склонны к переобучению, но могут недообучиться и не выявить важные закономерности или свойства признаков. Модели с маленьким смещением и большой дисперсией обычно более сложны с точки зрения их структуры, что позволяет им более точно представлять обучающий набор. Однако они могут отображать много шума из обучающего набора, что делает их прогнозы менее точными, несмотря на их дополнительную сложность.
Следовательно, как правило, невозможно иметь маленькое смещение и маленькую дисперсию одновременно.
Сейчас есть множество инструментов, с помощью которых можно легко создать сложные модели машинного обучения, переобучение занимает центральное место. Поскольку смещение появляется, когда сеть не получает достаточно информации. Но чем больше примеров, тем больше появляется вариантов зависимостей и изменчивостей в этих корреляциях.
Знакомимся с методом обратного распространения ошибки
Время на прочтение
6 мин
Количество просмотров 45K
Всем привет! Новогодние праздники подошли к концу, а это значит, что мы вновь готовы делиться с вами полезным материалом. Перевод данной статьи подготовлен в преддверии запуска нового потока по курсу «Алгоритмы для разработчиков».
Поехали!
Метод обратного распространения ошибки – вероятно самая фундаментальная составляющая нейронной сети. Впервые он был описан в 1960-е и почти 30 лет спустя его популяризировали Румельхарт, Хинтон и Уильямс в статье под названием «Learning representations by back-propagating errors».
Метод используется для эффективного обучения нейронной сети с помощью так называемого цепного правила (правила дифференцирования сложной функции). Проще говоря, после каждого прохода по сети обратное распространение выполняет проход в обратную сторону и регулирует параметры модели (веса и смещения).
В этой статья я хотел бы подробно рассмотреть с точки зрения математики процесс обучения и оптимизации простой 4-х слойной нейронной сети. Я считаю, что это поможет читателю понять, как работает обратное распространение, а также осознать его значимость.
Определяем модель нейронной сети
Четырехслойная нейронная сеть состоит из четырех нейронов входного слоя, четырех нейронов на скрытых слоях и 1 нейрона на выходном слое.
Простое изображение четырехслойной нейронной сети.
Входной слой
На рисунке нейроны фиолетового цвета представляют собой входные данные. Они могут быть простыми скалярными величинами или более сложными – векторами или многомерными матрицами.
Уравнение, описывающее входы xi.
Первый набор активаций (а) равен входным значениям. «Активация» — это значение нейрона после применения функции активации. Подробнее смотрите ниже.
Скрытые слои
Конечные значения в скрытых нейронах (на рисунке зеленого цвета) вычисляются с использованием zl – взвешенных входов в слое I и aI активаций в слое L. Для слоев 2 и 3 уравнения будут следующими:
Для l = 2:
Для l = 3:
W2 и W3 – это веса на слоях 2 и 3, а b2 и b3 – смещения на этих слоях.
Активации a2 и a3 вычисляются с помощью функции активации f. Например, эта функция f является нелинейной (как сигмоид, ReLU и гиперболический тангенс) и позволяет сети изучать сложные паттерны в данных. Мы не будем подробно останавливаться на том, как работают функции активации, но, если вам интересно, я настоятельно рекомендую прочитать эту замечательную статью.
Присмотревшись внимательно, вы увидите, что все x, z2, a2, z3, a3, W1, W2, b1 и b2 не имеют нижних индексов, представленных на рисунке четырехслойной нейронной сети. Дело в том, что мы объединили все значения параметров в матрицы, сгруппированные по слоям. Это стандартный способ работы с нейронными сетями, и он довольно комфортный. Однако я пройдусь по уравнениям, чтобы не возникло путаницы.
Давайте возьмем слой 2 и его параметры в качестве примера. Те же самые операции можно применить к любому слою нейронной сети.
W1 – это матрица весов размерности (n, m), где n – это количество выходных нейронов (нейронов на следующем слое), а m – число входных нейронов (нейронов в предыдущем слое). В нашем случае n = 2 и m = 4.
Здесь первое число в нижнем индексе любого из весов соответствует индексу нейрона в следующем слое (в нашем случае – это второй скрытый слой), а второе число соответствует индексу нейрона в предыдущем слое (в нашем случае – это входной слой).
x – входной вектор размерностью (m, 1), где m – число входных нейронов. В нашем случае m = 4.
b1 – это вектор смещения размерности (n, 1), где n – число нейронов на текущем слое. В нашем случае n = 2.
Следуя уравнению для z2 мы можем использовать приведенные выше определения W1, x и b1 для получения уравнения z2:
Теперь внимательно посмотрите на иллюстрацию нейронной сети выше:
Как видите, z2 можно выразить через z12 и z22, где z12 и z22 – суммы произведений каждого входного значения xi на соответствующий вес Wij1.
Это приводит к тому же самому уравнению для z2 и доказывает, что матричные представления z2, a2, z3 и a3 – верны.
Выходной слой
Последняя часть нейронной сети – это выходной слой, который выдает прогнозируемое значение. В нашем простом примере он представлен в виде одного нейрона, окрашенного в синий цвет и рассчитываемого следующим образом:
И снова мы используем матричное представление для упрощения уравнения. Можно использовать вышеприведенные методы, чтобы понять лежащую в их основе логику.
Прямое распространение и оценка
Приведенные выше уравнения формируют прямое распространение по нейронной сети. Вот краткий обзор:
(1) – входной слой
(2) – значение нейрона на первом скрытом слое
(3) – значение активации на первом скрытом слое
(4) – значение нейрона на втором скрытом слое
(5) – значение активации на втором скрытом уровне
(6) – выходной слой
Заключительным шагом в прямом проходе является оценка прогнозируемого выходного значения s относительно ожидаемого выходного значения y.
Выходные данные y являются частью обучающего набора данных (x, y), где x – входные данные (как мы помним из предыдущего раздела).
Оценка между s и y происходит через функцию потерь. Она может быть простой как среднеквадратичная ошибка или более сложной как перекрестная энтропия.
Мы назовем эту функцию потерь С и обозначим ее следующим образом:
Где cost может равняться среднеквадратичной ошибке, перекрестной энтропии или любой другой функции потерь.
Основываясь на значении С, модель «знает», насколько нужно скорректировать ее параметры, чтобы приблизиться к ожидаемому выходному значению y. Это происходит с помощью метода обратного распространения ошибки.
Обратное распространение ошибки и вычисление градиентов
Опираясь на статью 1989 года, метод обратного распространения ошибки:
Постоянно настраивает веса соединений в сети, чтобы минимизировать меру разности между фактическим выходным вектором сети и желаемым выходным вектором.
и
…дает возможность создавать полезные новые функции, что отличает обратное распространение от более ранних и простых методов…
Другими словами, обратное распространение направлено на минимизацию функции потерь путем корректировки весов и смещений сети. Степень корректировки определяется градиентами функции потерь по отношению к этим параметрам.
Возникает один вопрос: Зачем вычислять градиенты?
Чтобы ответить на этот вопрос, нам сначала нужно пересмотреть некоторые понятия вычислений:
Градиентом функции С(x1, x2, …, xm) в точке x называется вектор частных производных С по x.
Производная функции С отражает чувствительность к изменению значения функции (выходного значения) относительно изменения ее аргумента х (входного значения). Другими словами, производная говорит нам в каком направлении движется С.
Градиент показывает, насколько необходимо изменить параметр x (в положительную или отрицательную сторону), чтобы минимизировать С.
Вычисление этих градиентов происходит с помощью метода, называемого цепным правилом.
Для одного веса (wjk)l градиент равен:
(1) Цепное правило
(2) По определению m – количество нейронов на l – 1 слое
(3) Вычисление производной
(4) Окончательное значение
Аналогичный набор уравнений можно применить к (bj)l:
(1) Цепное правило
(2) Вычисление производной
(3) Окончательное значение
Общая часть в обоих уравнениях часто называется «локальным градиентом» и выражается следующим образом:
«Локальный градиент» можно легко определить с помощью правила цепи. Этот процесс я не буду сейчас расписывать.
Градиенты позволяют оптимизировать параметры модели:
Пока не будет достигнут критерий остановки выполняется следующее:
Алгоритм оптимизации весов и смещений (также называемый градиентным спуском)
- Начальные значения w и b выбираются случайным образом.
- Эпсилон (e) – это скорость обучения. Он определяет влияние градиента.
- w и b – матричные представления весов и смещений.
- Производная C по w или b может быть вычислена с использованием частных производных С по отдельным весам или смещениям.
- Условие завершение выполняется, как только функция потерь минимизируется.
Заключительную часть этого раздела я хочу посвятить простому примеру, в котором мы рассчитаем градиент С относительно одного веса (w22)2.
Давайте увеличим масштаб нижней части вышеупомянутой нейронной сети:
Визуальное представление обратного распространения в нейронной сети
Вес (w22)2 соединяет (a2)2 и (z2)2, поэтому вычисление градиента требует применения цепного правила на (z3)2 и (a3)2:
Вычисление конечного значения производной С по (a2)3 требует знания функции С. Поскольку С зависит от (a2)3, вычисление производной должно быть простым.
Я надеюсь, что этот пример сумел пролить немного света на математику, стоящую за вычислением градиентов. Если захотите узнать больше, я настоятельно рекомендую вам посмотреть Стэндфордскую серию статей по NLP, где Ричард Сочер дает 4 замечательных объяснения обратного распространения.
Заключительное замечание
В этой статье я подробно объяснил, как обратное распространение ошибки работает под капотом с помощью математических методов, таких как вычисление градиентов, цепное правило и т.д. Знание механизмов этого алгоритма укрепит ваши знания о нейронных сетях и позволит вам чувствовать себя комфортно при работе с более сложными моделями. Удачи вам в путешествии по глубокому обучению!
На этом все. Приглашаем всех на бесплатный вебинар по теме «Дерево отрезков: просто и быстро».
Обучение нейронных сетей
Перед использованием нейронной сети ее необходимо обучить.
Процесс обучения нейронной сети заключается в подстройке ее внутренних параметров под конкретную задачу.
Алгоритм работы нейронной сети является итеративным, его шаги называют эпохами или циклами.
Эпоха — одна итерация в процессе обучения, включающая предъявление всех примеров из обучающего множества и, возможно, проверку качества обучения на контрольном множестве.
Процесс обучения осуществляется на обучающей выборке.
Обучающая выборка включает входные значения и соответствующие им выходные значения набора данных. В ходе обучения нейронная сеть находит некие зависимости выходных полей от входных.
Таким образом, перед нами ставится вопрос — какие входные поля (признаки) нам необходимо использовать. Первоначально выбор осуществляется эвристически, далее количество входов может быть изменено.
Сложность может вызвать вопрос о количестве наблюдений в наборе данных. И хотя существуют некие правила, описывающие связь между необходимым количеством наблюдений и размером сети, их верность не доказана.
Количество необходимых наблюдений зависит от сложности решаемой задачи. При увеличении количества признаков количество наблюдений возрастает нелинейно, эта проблема носит название «проклятие размерности». При недостаточном количестве данных рекомендуется использовать линейную модель.
Аналитик должен определить количество слоев в сети и количество нейронов в каждом слое.
Далее необходимо назначить такие значения весов и смещений, которые смогут минимизировать ошибку решения. Веса и смещения автоматически настраиваются таким образом, чтобы минимизировать разность между желаемым и полученным на выходе сигналами, которая называется ошибка обучения.
Ошибка обучения для построенной нейронной сети вычисляется путем сравнения выходных и целевых (желаемых) значений. Из полученных разностей формируется функция ошибок.
Функция ошибок — это целевая функция, требующая минимизации в процессе управляемого обучения нейронной сети.
С помощью функции ошибок можно оценить качество работы нейронной сети во время обучения. Например, часто используется сумма квадратов ошибок.
От качества обучения нейронной сети зависит ее способность решать поставленные перед ней задачи.
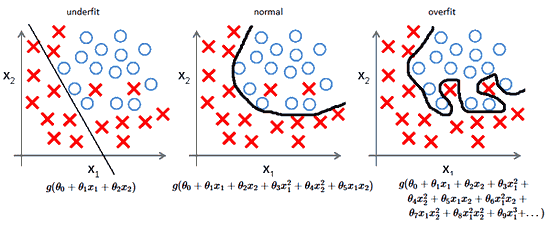
Переобучение нейронной сети
При обучении нейронных сетей часто возникает серьезная трудность, называемая проблемой переобучения (overfitting).
Переобучение, или чрезмерно близкая подгонка — излишне точное соответствие нейронной сети конкретному набору обучающих примеров, при котором сеть теряет способность к обобщению.
Переобучение возникает в случае слишком долгого обучения, недостаточного числа обучающих примеров или переусложненной структуры нейронной сети.
Переобучение связано с тем, что выбор обучающего (тренировочного) множества является случайным. С первых шагов обучения происходит уменьшение ошибки. На последующих шагах с целью уменьшения ошибки (целевой функции) параметры подстраиваются под особенности обучающего множества. Однако при этом происходит «подстройка» не под общие закономерности ряда, а под особенности его части — обучающего подмножества. При этом точность прогноза уменьшается.
Один из вариантов борьбы с переобучением сети — деление обучающей выборки на два множества (обучающее и тестовое).
На обучающем множестве происходит обучение нейронной сети. На тестовом множестве осуществляется проверка построенной модели. Эти множества не должны пересекаться.
С каждым шагом параметры модели изменяются, однако постоянное уменьшение значения целевой функции происходит именно на обучающем множестве. При разбиении множества на два мы можем наблюдать изменение ошибки прогноза на тестовом множестве параллельно с наблюдениями над обучающим множеством. Какое-то количество шагов ошибки прогноза уменьшается на обоих множествах. Однако на определенном шаге ошибка на тестовом множестве начинает возрастать, при этом ошибка на обучающем множестве продолжает уменьшаться. Этот момент считается концом реального или настоящего обучения, с него и начинается переобучение.
Описанный процесс проиллюстрирован на рис. 11.2.
Рис.
11.2.
Процесс обучений сети. Явление переобучения
На первом шаге ошибки прогноза для обучающего и тестового множества одинаковы. На последующих шагах значения обеих ошибок уменьшаются, однако с семидесятого шага ошибка на тестовом множестве начинает возрастать, т.е. начинается процесс переобучения сети.
Прогноз на тестовом множестве является проверкой работоспособности построенной модели. Ошибка на тестовом множестве может являться ошибкой прогноза, если тестовое множество максимально приближено к текущему моменту.
Рад снова всех приветствовать, и сегодня продолжим планомерно двигаться в выбранном направлении. Речь, конечно, о масштабном разборе искусственных нейронных сетей для решения широкого спектра задач. Продолжим ровно с того момента, на котором остановились в предыдущей части, и это означает, что героем данного поста будет ключевой процесс — обучение нейронных сетей.
- Градиентный спуск
- Функция ошибки
- Метод обратного распространения ошибки
- Пример расчета
Тема эта крайне важна, поскольку именно процесс обучения позволяет сети начать выполнять задачу, для которой она, собственно, и предназначена. То есть нейронная сеть функционирует не по какому-либо жестко заданному на этапе проектирования алгоритму, она совершенствуется в процессе анализа имеющихся данных. Этот процесс и называется обучением нейронной сети. Математически суть процесса обучения заключается в корректировке значений весов синапсов (связей между имеющимися нейронами). Изначально значения весов задаются случайно, затем производится обучение, результатом которого будут новые значения синаптических весов. Это все мы максимально подробно разберем как раз в этой статье.
На своем сайте я всегда придерживаюсь концепции, при которой теоретические выкладки по максимуму сопровождаются практическими примерами для максимальной наглядности. Так мы поступим и сейчас 👍
Итак, суть заключается в следующем. Пусть у нас есть простейшая нейронная сеть, которую мы хотим обучить (продолжаем рассматривать сети прямого распространения):

То есть на входы нейронов I1 и I2 мы подаем какие-либо числа, а на выходе сети получаем соответственно новое значение. При этом нам необходима некая выборка данных, включающая в себя значения входов и соответствующее им, правильное, значение на выходе:
| bold{I_1} | bold{I_2} | bold{O_{net}} |
|---|---|---|
| x_{11} | x_{12} | y_{1} |
| x_{21} | x_{22} | y_{2} |
| x_{31} | x_{32} | y_{3} |
| … | … | … |
| x_{N1} | x_{N2} | y_{N} |
Допустим, сеть выполняет суммирование значений на входе, тогда данный набор данных может быть таким:
| bold{I_1} | bold{I_2} | bold{O_{net}} |
|---|---|---|
| 1 | 4 | 5 |
| 2 | 7 | 9 |
| 3 | 5 | 8 |
| … | … | … |
| 1000 | 1500 | 2500 |
Эти значения и используются для обучения сети. Как именно — рассмотрим чуть ниже, пока сконцентрируемся на идее процесса в целом. Для того, чтобы иметь возможность тестировать работу сети в процессе обучения, исходную выборку данных делят на две части — обучающую и тестовую. Пусть имеется 1000 образцов, тогда можно 900 использовать для обучения, а оставшиеся 100 — для тестирования. Эти величины взяты исключительно ради наглядности и демонстрации логики выполнения операций, на практике все зависит от задачи, размер обучающей выборки может спокойно достигать и сотен тысяч образцов.
Итак, итог имеем следующий — обучающая выборка прогоняется через сеть, в результате чего происходит настройка значений синаптических весов. Один полный проход по всей выборке называется эпохой. И опять же, обучение нейронной сети — это процесс, требующий многократных экспериментов, анализа результатов и творческого подхода. Все перечисленные параметры (размер выборки, количество эпох обучения) могут иметь абсолютно разные значения для разных задач и сетей. Четкого правила тут просто нет, в этом и кроется дополнительный шарм и изящность )
Возвращаемся к разбору, и в результате прохода обучающей выборки через сеть мы получаем сеть с новыми значениями весов синапсов.
Далее мы через эту, уже обученную в той или иной степени, сеть прогоняем тестовую выборку, которая не участвовала в обучении. При этом сеть выдает нам выходные значения для каждого образца, которые мы сравниваем с теми верными значениями, которые имеем.
Анализируем нашу гипотетическую выборку:

Таким образом, для тестирования подаем на вход сети значения x_{(M+1)1}, x_{(M+1)2} и проверяем, чему равен выход, ожидаем очевидно значение y_{(M+1)}. Аналогично поступаем и для оставшихся тестовых образцов. После чего мы можем сделать вывод, успешно или нет работает сеть. Например, сеть дает правильный ответ для 90% тестовых данных, дальше уже встает вопрос — устраивает ли нас данная точность или процесс обучения необходимо повторить, либо провести заново, изменив какие-либо параметры сети.
В этом и заключается суть обучения нейронных сетей, теперь перейдем к деталям и конкретным действиям, которые необходимо осуществить для выполнения данного процесса. Двигаться снова будем поэтапно, чтобы сформировать максимально четкую и полную картину. Поэтому начнем с понятия градиентного спуска, который используется при обучении по методу обратного распространения ошибки. Обо всем этом далее…
Обучение нейронных сетей. Градиентный спуск.
Рассмотрев идею процесса обучения в целом, на данном этапе мы можем однозначно сформулировать текущую цель — необходимо определить математический алгоритм, который позволит рассчитать значения весовых коэффициентов таким образом, чтобы ошибка сети была минимальна. То есть грубо говоря нам необходима конкретная формула для вычисления:
Здесь Delta w_{ij} — величина, на которую необходимо изменить вес синапса, связывающего нейроны i и j нашей сети. Соответственно, зная это, необходимо на каждом этапе обучения производить корректировку весов связей между всеми элементами нейронной сети. Задача ясна, переходим к делу.
Пусть функция ошибки от веса имеет следующий вид:
Для удобства рассмотрим зависимость функции ошибки от одного конкретного веса:

В начальный момент мы находимся в некоторой точке кривой, а для минимизации ошибки попасть мы хотим в точку глобального минимума функции:
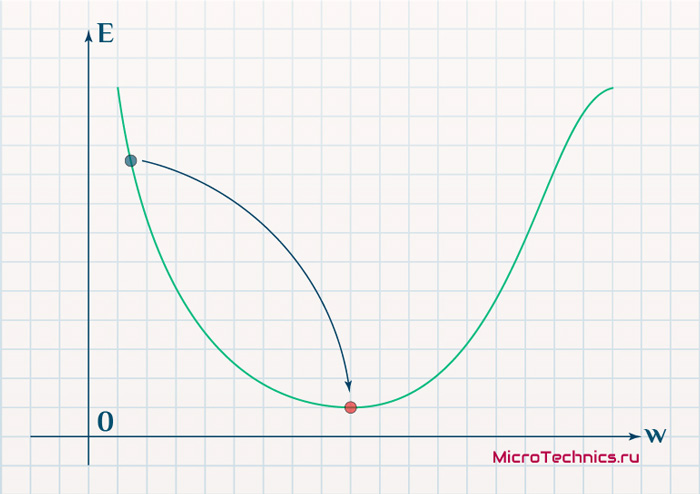
Нанесем на график вектора градиентов в разных точках. Длина векторов численно равна скорости роста функции в данной точке, что в свою очередь соответствует значению производной функции по данной точке. Исходя из этого, делаем вывод, что длина вектора градиента определяется крутизной функции в данной точке:
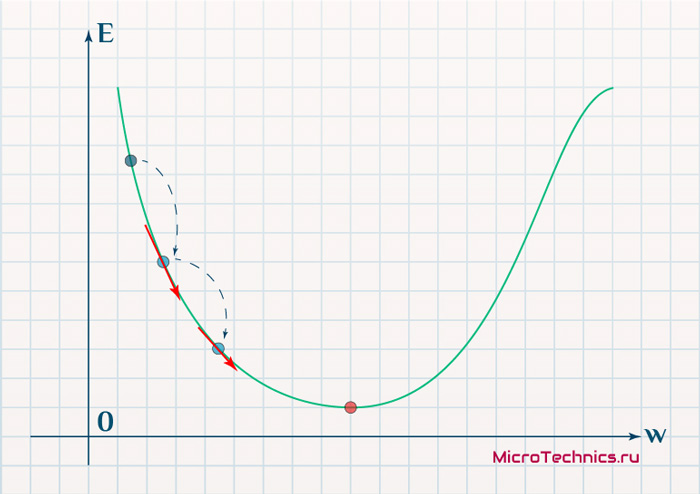
Вывод прост — величина градиента будет уменьшаться по мере приближения к минимуму функции. Это важный вывод, к которому мы еще вернемся. А тем временем разберемся с направлением вектора, для чего рассмотрим еще несколько возможных точек:
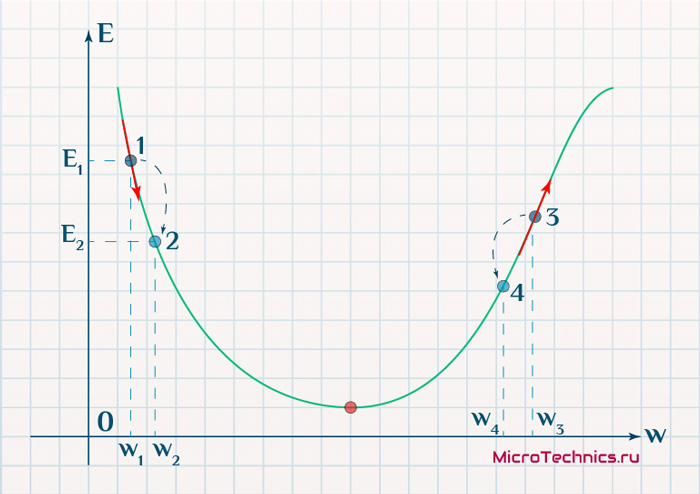
Находясь в точке 1, целью является перейти в точку 2, поскольку в ней значение ошибки меньше (E_2 < E_1), а глобальная задача по-прежнему заключается в ее минимизации. Для этого необходимо изменить величину w на некое значение Delta w (Delta w = w_2 — w_1 > 0). При всем при этом в точке 1 градиент отрицательный. Фиксируем данные факты и переходим к точке 3, предположим, что мы находимся именно в ней.
Тогда для уменьшения ошибки наш путь лежит в точку 4, а необходимое изменение значения: Delta w = w_4 — w_3 < 0. Градиент же в точке 3 положителен. Этот факт также фиксируем.
А теперь соберем воедино эту информацию в виде следующей иллюстрации:
| Переход | bold{Delta w} | Знак bold{Delta w} | Градиент |
|---|---|---|---|
| 1 rArr 2 | w_2 — w_1 | + | — |
| 3 rArr 4 | w_4 — w_3 | — | + |
Вывод напрашивается сам собой — величина, на которую необходимо изменить значение w, в любой точке противоположна по знаку градиенту. И, таким образом, представим эту самую величину в виде:
Delta w = -alpha cdot frac{dE}{dw}
Имеем в наличии:
- Delta w — величина, на которую необходимо изменить значение w.
- frac{dE}{dw} — градиент в этой точке.
- alpha — скорость обучения.
Собственно, логика метода градиентного спуска и заключается в данном математическом выражении, а именно в том, что для минимизации ошибки необходимо изменять w в направлении противоположном градиенту. В контексте нейронных сетей имеем искомый закон для корректировки весов синаптических связей (для синапса между нейронами i и j):
Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}}
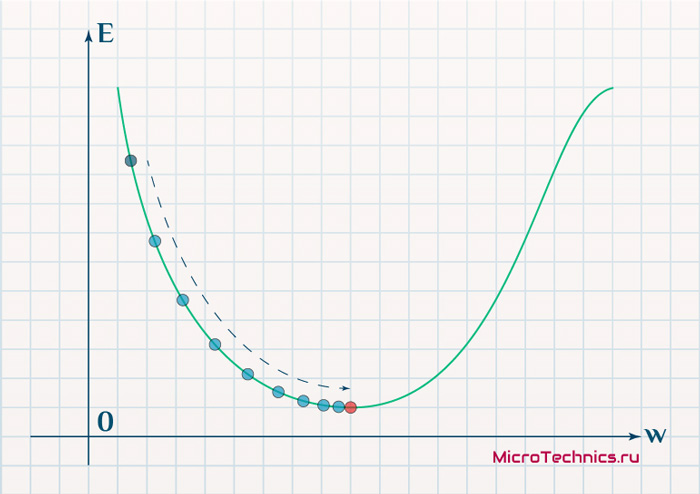
Более того, вспомним о важном свойстве, которое мы отдельно пометили. И заключается оно в том, что величина градиента будет уменьшаться по мере приближения к минимуму функции. Что это нам дает? А то, что в том случае, если наша текущая дислокация далека от места назначения, то величина, корректирующая вес связи, будет больше. А это обеспечит скорейшее приближение к цели. При приближении к целевому пункту, величина frac{dE}{dw_{ij}} будет уменьшаться, что поможет нам точнее попасть в нужную точку, а кроме того, не позволит нам ее проскочить. Визуализируем вышеописанное:
Скорость же обучения несет в себе следующий смысл. Она определяет величину каждого шага при поиске минимума ошибки. Слишком большое значение приводит к тому, что точка может «перепрыгнуть» через нужное значение и оказаться по другую сторону от цели:
Если же величина будет мала, то это приведет к тому, что спуск будет осуществляться очень медленно, что также является нежелательным эффектом. Поэтому скорость обучения, как и многие другие параметры нейронной сети, является очень важной величиной, для которой нет единственно верного значения. Все снова зависит от конкретного случая и оптимальная величина определяется исключительно исходя из текущих условий.
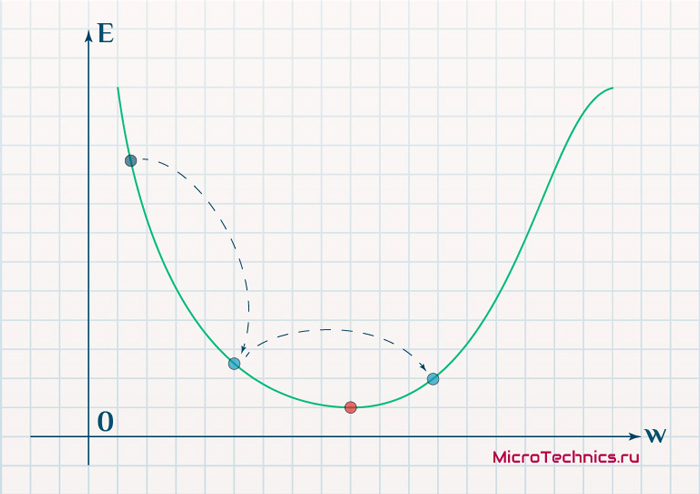
И даже на этом еще не все, здесь присутствует один важный нюанс, который в большинстве статей опускается, либо вовсе не упоминается. Реальная зависимость может иметь совсем другой вид:
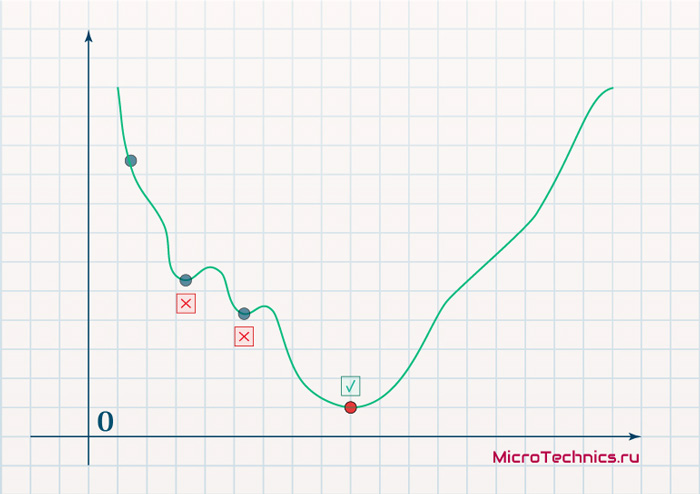
Из чего вытекает потенциальная возможность попадания в локальный минимум, вместо глобального, что является большой проблемой. Для предотвращения данного эффекта вводится понятие момента обучения и формула принимает следующий вид:
Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t - 1}
То есть добавляется второе слагаемое, которое представляет из себя произведение момента на величину корректировки веса на предыдущем шаге.
Итого, резюмируем продвижение к цели:
- Нашей задачей было найти закон, по которому необходимо изменять величину весов связей между нейронами.
- Наш результат — Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t — 1} — именно то, что и требовалось 👍
И опять же, полученный результат логичным образом перенаправляет нас на следующий этап, ставя вопросы — что из себя представляет функция ошибки, и как определить ее градиент.
Обучение нейронных сетей. Функция ошибки.
Начнем с того, что определимся с тем, что у нас в наличии, для этого вернемся к конкретной нейронной сети. Пусть вид ее таков:
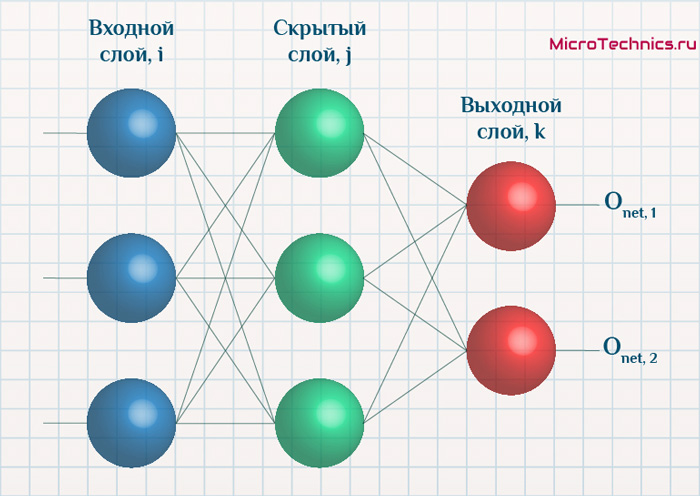
Интересует нас, в первую очередь, часть, относящаяся к нейронам выходного слоя. Подав на вход определенные значения, получаем значения на выходе сети: O_{net, 1} и O_{net, 2}. Кроме того, поскольку мы ведем речь о процессе обучения нейронной сети, то нам известны целевые значения: O_{correct, 1} и O_{correct, 2}. И именно этот набор данных на этом этапе является для нас исходным:
- Известно: O_{net, 1}, O_{net, 2}, O_{correct, 1} и O_{correct, 2}.
- Необходимо определить величины Delta w_{ij} для корректировки весов, для этого нужно вычислить градиенты (frac{dE}{dw_{ij}}) для каждого из синапсов.
Полдела сделано — задача четко сформулирована, начинаем деятельность по поиску решения.
В плане того, как определять ошибку, первым и самым очевидным вариантом кажется простая алгебраическая разность. Для каждого из выходных нейронов:
E_k = O_{correct, k} - O_{net, k}
Дополним пример числовыми значениями:
| Нейрон | bold{O_{net}} | bold{O_{correct}} | bold{E} |
|---|---|---|---|
| 1 | 0.9 | 0.5 | -0.4 |
| 2 | 0.2 | 0.6 | 0.4 |
Недостатком данного варианта является то, что в том случае, если мы попытаемся просуммировать ошибки нейронов, то получим:
E_{sum} = e_1 + e_2 = -0.4 + 0.4 = 0
Что не соответствует действительности (нулевая ошибка, говорит об идеальной работе нейронной сети, по факту оба нейрона дали неверный результат). Так что вариант с разностью откидываем за несостоятельностью.
Вторым, традиционно упоминаемым, методом вычисления ошибки является использование модуля разности:
E_k = | O_{correct, k} - O_{net, k} |
Тут в действие вступает уже проблема иного рода:
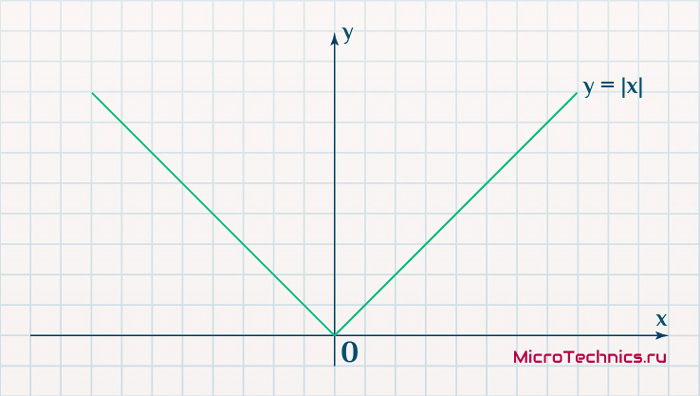
Функция, бесспорно, симпатична, но при приближении к минимуму ее градиент является постоянной величиной, скачкообразно меняясь при переходе через точку минимума. Это нас также не устраивает, поскольку, как мы обсуждали, концепция заключалась в том числе в том, чтобы по мере приближения к минимуму значение градиента уменьшалось.
В итоге хороший результат дает зависимость (для выходного нейрона под номером k):
E_k = (O_{correct, k} - O_{net, k})^2
Функция по многим своим свойствам идеально удовлетворяет нуждам обучения нейронной сети, так что выбор сделан, остановимся на ней. Хотя, как и во многих аспектах, качающихся нейронных сетей, данное решение не является единственно и неоспоримо верным. В каких-то случаях лучше себя могут проявить другие зависимости, возможно, что какой-то вариант даст большую точность, но неоправданно высокие затраты производительности при обучении. В общем, непаханное поле для экспериментов и исследований, это и привлекательно.
Краткий вывод промежуточного шага, на который мы вышли:
- Имеющееся: frac{dE}{dw_{jk}} = frac{d}{d w_{jk}}(O_{correct, k} — O_{net, k})^2.
- Искомое по-прежнему: Delta w_{jk}.
Несложные диффернциально-математические изыскания выводят на следующий результат:
frac{dE}{d w_{jk}} = -(O_{correct, k} - O_{net, k}) cdot f{Large{prime}}(sum_{j}w_{jk}O_j) cdot O_j
Здесь эти самые изыскания я все-таки решил не вставлять, дабы не перегружать статью, которая и так выходит объемной. Но в случае необходимости и интереса, отпишите в комментарии, я добавлю вычисления и закину их под спойлер, как вариант.
Освежим в памяти структуру сети:
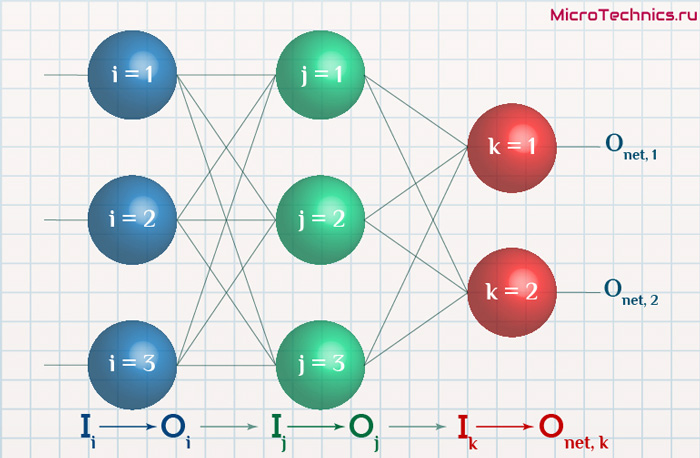
Формулу можно упростить, сгруппировав отдельные ее части:
- (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(sum_{j}w_{jk}O_j) — ошибка нейрона k.
- O_j — тут все понятно, выходной сигнал нейрона j.
f{Large{prime}}(sum_{j}w_{jk}O_j) — значение производной функции активации. Причем, обратите внимание, что sum_{j}w_{jk}O_j — это не что иное, как сигнал на входе нейрона k (I_{k}). Тогда для расчета ошибки выходного нейрона: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k).
Итог: frac{dE}{d w_{jk}} = -delta_k cdot O_j.
Одной из причин популярности сигмоидальной функции активности является то, что ее производная очень просто выражается через саму функцию:
f{'}(x) = f(x)medspace (1medspace-medspace f(x))
Данные алгебраические вычисления справедливы для корректировки весов между скрытым и выходным слоем, поскольку для расчета ошибки мы используем просто разность между целевым и полученным результатом, умноженную на производную.
Для других слоев будут незначительные изменения, касающиеся исключительно первого множителя в формуле:
frac{dE}{d w_{ij}} = -delta_j cdot O_i
Который примет следующий вид:
delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
То есть ошибка для элемента слоя j получается путем взвешенного суммирования ошибок, «приходящих» к нему от нейронов следующего слоя и умножения на производную функции активации. В результате:
frac{dE}{d w_{ij}} = -(sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j) cdot O_i
Снова подводим промежуточный итог, чтобы иметь максимально полную и структурированную картину происходящего. Вот результаты, полученные нами на двух этапах, которые мы успешно миновали:
- Ошибка:
- выходной слой: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k)
- скрытые слои: delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
- Градиент: frac{dE}{d w_{ij}} = -delta_j cdot O_i
- Корректировка весовых коэффициентов: Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t — 1}
Преобразуем последнюю формулу:
Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t - 1}
Из этого мы делаем вывод, что на данный момент у нас есть все, что необходимо для того, чтобы произвести обучение нейронной сети. И героем следующего подраздела будет алгоритм обратного распространения ошибки.
Метод обратного распространения ошибки.
Данный метод является одним из наиболее распространенных и популярных, чем и продиктован его выбор для анализа и разбора. Алгоритм обратного распространения ошибки относится к методам обучение с учителем, что на деле означает необходимость наличия целевых значений в обучающих сетах.
Суть же метода подразумевает наличие двух этапов:
- Прямой проход — входные сигналы двигаются в прямом направлении, в результате чего мы получаем выходной сигнал, из которого в дальнейшем рассчитываем значение ошибки.
- Обратный проход — обратное распространение ошибки — величина ошибки двигается в обратном направлении, в результате происходит корректировка весовых коэффициентов связей сети.
Начальные значения весов (перед обучением) задаются случайными, есть ряд методик для выбора этих значений, я опишу в отдельном материале максимально подробно. Пока вот можно полистать — ссылка.
Вернемся к конкретному примеру для явной демонстрации этих принципов:
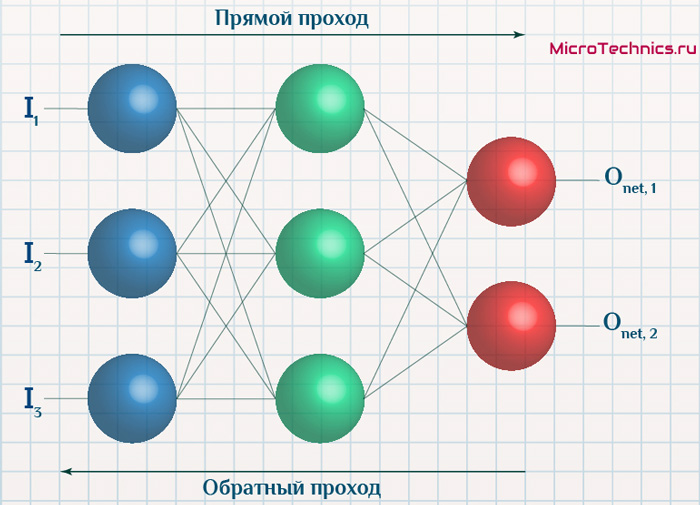
Итак, имеется нейронная сеть, также имеется набор данных обучающей выборки. Как уже обсудили в начале статьи — обучающая выборка представляет из себя набор образцов (сетов), каждый из которых состоит из значений входных сигналов и соответствующих им «правильных» значений выходных величин.
Процесс обучения нейронной сети для алгоритма обратного распространения ошибки будет таким:
- Прямой проход. Подаем на вход значения I_1, I_2, I_3 из обучающей выборки. В результате работы сети получаем выходные значения O_{net, 1}, O_{net, 2}. Этому целиком и полностью был посвящен предыдущий манускрипт.
- Рассчитываем величины ошибок для всех слоев:
- для выходного: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k)
- для скрытых: delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
- Далее используем полученные значения для расчета Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t — 1}
- И финишируем, рассчитывая новые значения весов: w_{ij medspace new} = w_{ij} + Delta w_{ij}
- На этом один цикл обучения закончен, данные шаги 1 — 4 повторяются для других образцов из обучающей выборки.
Обратный проход завершен, а вместе с ним и одна итерация процесса обучения нейронной сети по данному методу. Собственно, обучение в целом заключается в многократном повторении этих шагов для разных образцов из обучающей выборки. Логику мы полностью разобрали, при повторном проведении операций она остается в точности такой же.
Таким образом, максимально подробно концентрируясь именно на сути и логике процессов, мы в деталях разобрали метод обратного распространения ошибки. Поэтому переходим к завершающей части статьи, в которой разберем практический пример, произведя полностью все вычисления для конкретных числовых величин. Все в рамках продвигаемой мной концепции, что любая теоретическая информация на порядок лучше может быть осознана при применении ее на практике.
Пример расчетов для метода обратного распространения ошибки.
Возьмем нейронную сеть и зададим начальные значения весов:
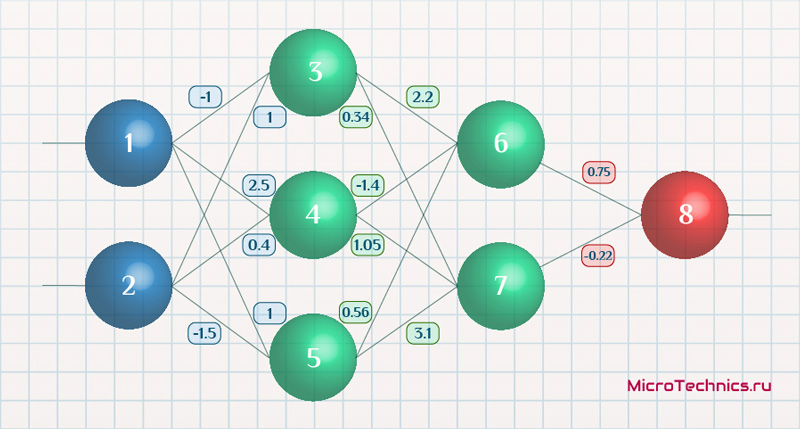
Здесь я задал значения не в соответствии с существующими на сегодняшний день методами, а просто случайным образом для наглядности примера.
В качестве функции активации используем сигмоиду:
f(x) = frac{1}{1 + e^{-x}}
И ее производная:
f{Large{prime}}(x) = f(x)medspace (1medspace-medspace f(x))
Берем один образец из обучающей выборки, пусть будут такие значения:
- Входные: I_1 = 0.6, I_1 = 0.7.
- Выходное: O_{correct} = 0.9.
Скорость обучения alpha пусть будет равна 0.3, момент — gamma = 0.1. Все готово, теперь проведем полный цикл для метода обратного распространения ошибки, то есть прямой проход и обратный.
Прямой проход.
Начинаем с выходных значений нейронов 1 и 2, поскольку они являются входными, то:
O_1 = I_1 = 0.6 \ O_2 = I_2 = 0.7
Значения на входе нейронов 3, 4 и 5:
I_3 = O_1 cdot w_{13} + O_2 cdot w_{23} = 0.6 cdot (-1medspace) + 0.7 cdot 1 = 0.1 \
I_4 = 0.6 cdot 2.5 + 0.7 cdot 0.4 = 1.78 \
I_5 = 0.6 cdot 1 + 0.7 cdot (-1.5medspace) = -0.45
На выходе этих же нейронов первого скрытого слоя:
O_3 = f(I3medspace) = 0.52 \ O_4 = 0.86\ O_5 = 0.39
Продолжаем аналогично для следующего скрытого слоя:
I_6 = O_3 cdot w_{36} + O_4 cdot w_{46} + O_5 cdot w_{56} = 0.52 cdot 2.2 + 0.86 cdot (-1.4medspace) + 0.39 cdot 0.56 = 0.158 \
I_7 = 0.52 cdot 0.34 + 0.86 cdot 1.05 + 0.39 cdot 3.1 = 2.288 \
O_6 = f(I_6) = 0.54 \
O_7 = 0.908
Добрались до выходного нейрона:
I_8 = O_6 cdot w_{68} + O_7 cdot w_{78} = 0.54 cdot 0.75 + 0.908 cdot (-0.22medspace) = 0.205 \
O_8 = O_{net} = f(I_8) = 0.551
Получили значение на выходе сети, кроме того, у нас есть целевое значение O_{correct} = 0.9. То есть все, что необходимо для обратного прохода, имеется.
Обратный проход.
Как мы и обсуждали, первым этапом будет вычисление ошибок всех нейронов, действуем:
delta_8 = (O_{correct} - O_{net}) cdot f{Large{prime}}(I_8) = (O_{correct} - O_{net}) cdot f(I_8) cdot (1-f(I_8)) = (0.9 - 0.551medspace) cdot 0.551 cdot (1-0.551medspace) = 0.0863 \
delta_7 = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_7) = (delta_8 cdot w_{78}) cdot f{Large{prime}}(I_7) = 0.0863 cdot (-0.22medspace) cdot 0.908 cdot (1 - 0.908medspace) = -0.0016 \
delta_6 = 0.086 cdot 0.75 cdot 0.54 cdot (1 - 0.54medspace) = 0.016 \
delta_5 = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_5) = (delta_7 cdot w_{57} + delta_6 cdot w_{56}) cdot f{Large{prime}}(I_7) = (-0.0016 cdot 3.1 + 0.016 cdot 0.56) cdot 0.39 cdot (1 - 0.39medspace) = 0.001 \
delta_4 = (-0.0016 cdot 1.05 + 0.016 cdot (-1.4)) cdot 0.86 cdot (1 - 0.86medspace) = -0.003 \
delta_3 = (-0.0016 cdot 0.34 + 0.016 cdot 2.2) cdot 0.52 cdot (1 - 0.52medspace) = -0.0087
С расчетом ошибок закончили, следующий этап — расчет корректировочных величин для весов всех связей. Для этого мы вывели формулу:
Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t - 1}
Как вы помните, Delta w_{ij}^{t — 1} — это величина поправки для данного веса на предыдущей итерации. Но поскольку у нас это первый проход, то данное значение будет нулевым, соответственно, в данном случае второе слагаемое отпадает. Но забывать о нем нельзя. Продолжаем калькулировать:
Delta w_{78} = alpha cdot delta_8 cdot O_7 = 0.3 cdot 0.0863 cdot 0.908 = 0.0235 \
Delta w_{68} = 0.3 cdot 0.0863 cdot 0.54= 0.014 \
Delta w_{57} = alpha cdot delta_7 cdot O_5 = 0.3 cdot (−0.0016medspace) cdot 0.39= -0.00019 \
Delta w_{47} = 0.3 cdot (−0.0016medspace) cdot 0.86= -0.0004 \
Delta w_{37} = 0.3 cdot (−0.0016medspace) cdot 0.52= -0.00025 \
Delta w_{56} = alpha cdot delta_6 cdot O_5 = 0.3 cdot 0.016 cdot 0.39= 0.0019 \
Delta w_{46} = 0.3 cdot 0.016 cdot 0.86= 0.0041 \
Delta w_{36} = 0.3 cdot 0.016 cdot 0.52= 0.0025 \
Delta w_{25} = alpha cdot delta_5 cdot O_2 = 0.3 cdot 0.001 cdot 0.7= 0.00021 \
Delta w_{15} = 0.3 cdot 0.001 cdot 0.6= 0.00018 \
Delta w_{24} = alpha cdot delta_4 cdot O_2 = 0.3 cdot (-0.003medspace) cdot 0.7= -0.00063 \
Delta w_{14} = 0.3 cdot (-0.003medspace) cdot 0.6= -0.00054 \
Delta w_{23} = alpha cdot delta_3 cdot O_2 = 0.3 cdot (−0.0087medspace) cdot 0.7= -0.00183 \
Delta w_{13} = 0.3 cdot (−0.0087medspace) cdot 0.6= -0.00157
И самый что ни на есть заключительный этап — непосредственно изменение значений весовых коэффициентов:
w_{78 medspace new} = w_{78} + Delta w_{78} = -0.22 + 0.0235 = -0.1965 \
w_{68 medspace new} = 0.75+ 0.014 = 0.764 \
w_{57 medspace new} = 3.1 + (−0.00019medspace) = 3.0998\
w_{47 medspace new} = 1.05 + (−0.0004medspace) = 1.0496\
w_{37 medspace new} = 0.34 + (−0.00025medspace) = 0.3398\
w_{56 medspace new} = 0.56 + 0.0019 = 0.5619 \
w_{46 medspace new} = -1.4 + 0.0041 = -1.3959 \
w_{36 medspace new} = 2.2 + 0.0025 = 2.2025 \
w_{25 medspace new} = -1.5 + 0.00021 = -1.4998 \
w_{15 medspace new} = 1 + 0.00018 = 1.00018 \
w_{24 medspace new} = 0.4 + (−0.00063medspace) = 0.39937 \
w_{14 medspace new} = 2.5 + (−0.00054medspace) = 2.49946 \
w_{23 medspace new} = 1 + (−0.00183medspace) = 0.99817 \
w_{13 medspace new} = -1 + (−0.00157medspace) = -1.00157\
И на этом данную масштабную статью завершаем, конечно же, не завершая на этом деятельность по использованию нейронных сетей. Так что всем спасибо за прочтение, любые вопросы пишите в комментариях и на форуме, ну и обязательно следите за обновлениями и новыми материалами, до встречи!
Привет, Вы узнаете про анализ алгоритма обратного распространения ошибки нейронной сети , Разберем основные ее виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое
анализ алгоритма обратного распространения ошибки нейронной сети , настоятельно рекомендую прочитать все из категории Computational Neuroscience (вычислительная нейронаука) Теория и приложения искусственных нейронных сетей.
В статье изложены основы нейронной сети, а также проведен анализ функционирования алгоритма обратного распространения ошибки.
На сегодняшний день, нейронная сеть является одним из способов интеллектуального анализа данных. Интеллектуальный анализ данных позволяет решить такие проблемы, как: классификация и кластеризация, прогнозирования, распознавание образов, сжатия данных и ассоциативная память, диагностика заболеваний и т. д.
Нейронные сети — это одно из направлений исследований в области искусственного интеллекта, основанное на попытках воспроизвести нервную систему человека. А именно, способность нейронной сети обучаться и исправлять ошибки, что должно позволить смоделировать, хотя и достаточно грубо, работу человеческого мозга [1].
Нейронная сеть — это математическая модель человеческого мозга, состоящая из многих простых вычислительных элементов (нейронов) рисунок 1, работающих параллельно, функция которых определяется структурой сети, а вычисления производятся в самих элементах. Считается, что способность мозга к обработке информации в основном обусловлена функционированием сетей, состоящих из таких нейронов [1; 2].
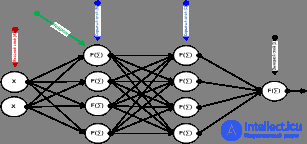
Рисунок 1. Многослойная нейронная сеть
Рассмотрим нейронную сеть стандартной архитектуры (рисунок 1), которая обычно имеет несколько слоев: А — рецепторный слой, на который подаются входные данные; B,C — скрытые слои, нейроны которых интерпретируют полученную информацию; D — выходной слой, предоставляющий реакцию нейронной сети.
Каждый слой сети состоит из нейронов. Нейрон — это основной элемент вычисления, нейронной сети. На рисунке 2 показана его структура.
В состав нейрона входит умножители, сумматоры и нелинейный преобразователь. Синапсы осуществляют связь между нейронами и умножают входной сигнал на число, характеризующее силу связи – веса синапсов.
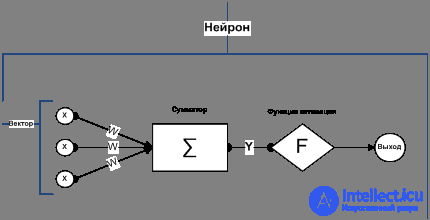
Рисунок. 2. Структура искусственного нейрона
Сумматор выполняет сложение сигналов, поступающих по синоптическим связям от других нейронов или внешних входных сигналов. Нелинейный преобразователь реализует нелинейную функцию одного аргумента — выход сумматора. Это функция называется «функцией активации» или «передаточной функцией» нейрона. Нейрон в целом реализует скалярную функцию векторного аргумента.
Математическая модель нейрона описывает соотношениями
где — 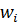
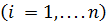
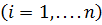
y — выходной сигнал нейрона; n — число входов нейрона; F— функция активации;
Главная задача в процессе разработки нейронной сети, является этап обучения, т. е . Об этом говорит сайт https://intellect.icu . корректировки весов сети, для минимизации ошибки на выходе нейронной сети.
Стандартная нейронная сеть прямого распространения приведена на рисунке 3, также известна как многослойный персептрон(MLP). Обратите внимание, что узлы входного уровня отличаются от узлов в других слоях, это означает, что никакая обработка не происходит в этих узлах, они служат только в качестве входов сети.
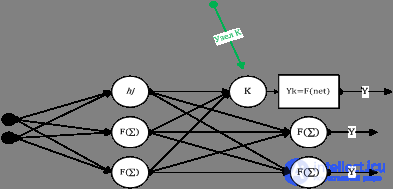
Рисунок 3. Стандартная сеть с прямым распространением
Каждый узел вычисляет взвешенную сумму его входов, и использует его как входные данные функции преобразования
В классическом многослойном персептроне, функция преобразования — сигмоид.
Сигмоида — это гладкая монотонная нелинейная S — образная функция, которая часто применяется для «сглаживания» значений некоторой величины.
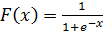
Рассмотрим узел k в скрытом слое. Его выход yk представляет 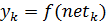
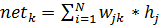
аналогично, выход каждого узла в каждом слое.
Для удобства, мы можем рассмотреть входы сети, как входной вектор X , где 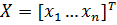
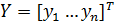
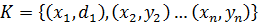
Каждый раз, когда входной вектор от учебного набора 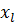
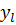
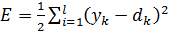
Главная задача, как уже было сказано в обучение нейронной сети, это минимизировать квадратичную ошибку E. Мы можем также определить полную квадратичную ошибку , суммирую все пары входа — выхода в учебном наборе:
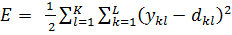
Для минимизации квадратичной ошибки, будем использовать алгоритм градиентного спуска. Определим какое направление является «скоростным спуском» на поверхности ошибок и изменим каждый вес так, чтобы мы двигались в этом направление. Математически это означает, что каждый вес будет изменен на небольшое значение в направлении уменьшения :

Здесь 

Для корректировки весов, между скрытым и выходным слоем, нужно найти частную производную, для каждого узла выходного слоя.
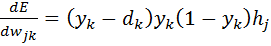
Таким образом, была найдена частная производная ошибки E по весам 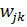
Теперь рассмотрим веса, между входным слоем и скрытым слоем.
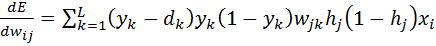
Была получена частная производная ошибки E по весу на основе известных величин (многие из которых мы уже вычислили при получении 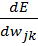
Рассмотрим алгоритм обратного распространения ошибки в виде блок-схемы (рисунок 4).

Рисунок 4. Алгоритм обучения нейронной сети прямого распространения
Принцип функционирования алгоритма обратного распространения ошибки, заключается в использование метода градиентного спуска и корректировки весов, для минимизации ошибки нейронной сети.
В процессе разработки нейронной сети, одним из основных этапов является обучения нейронной сети. В данной статье был проведен анализ алгоритма обратного распространения ошибки, которая использует метод градиентного спуска, для корректировки весов.
Список литературы:
1. Рассел С., Норвиг П. Искусственный интеллект. Современный подход. — М.: Изд-во «Вильямс», 2006. — 1408 с.
2. Хайкин С. Нейронные сети: полный курс. — М.: Изд-во «Вильямс», 2006. — 1104 с.
3. Алгоритм обратного распространения ошибки. — [Электронный ресурс] — Режим доступа. — URL:http://www.aiportal.ru/articles/neural-networks/back-propagation.
4. Алгоритм обратного распространения ошибки. — [Электронный ресурс] — Режим доступа. — URL:http://masters.donntu.edu.ua/2006/kita/kornev/library/l10.htm.
На этом все! Теперь вы знаете все про анализ алгоритма обратного распространения ошибки нейронной сети , Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое анализ алгоритма обратного распространения ошибки нейронной сети
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Computational Neuroscience (вычислительная нейронаука) Теория и приложения искусственных нейронных сетей