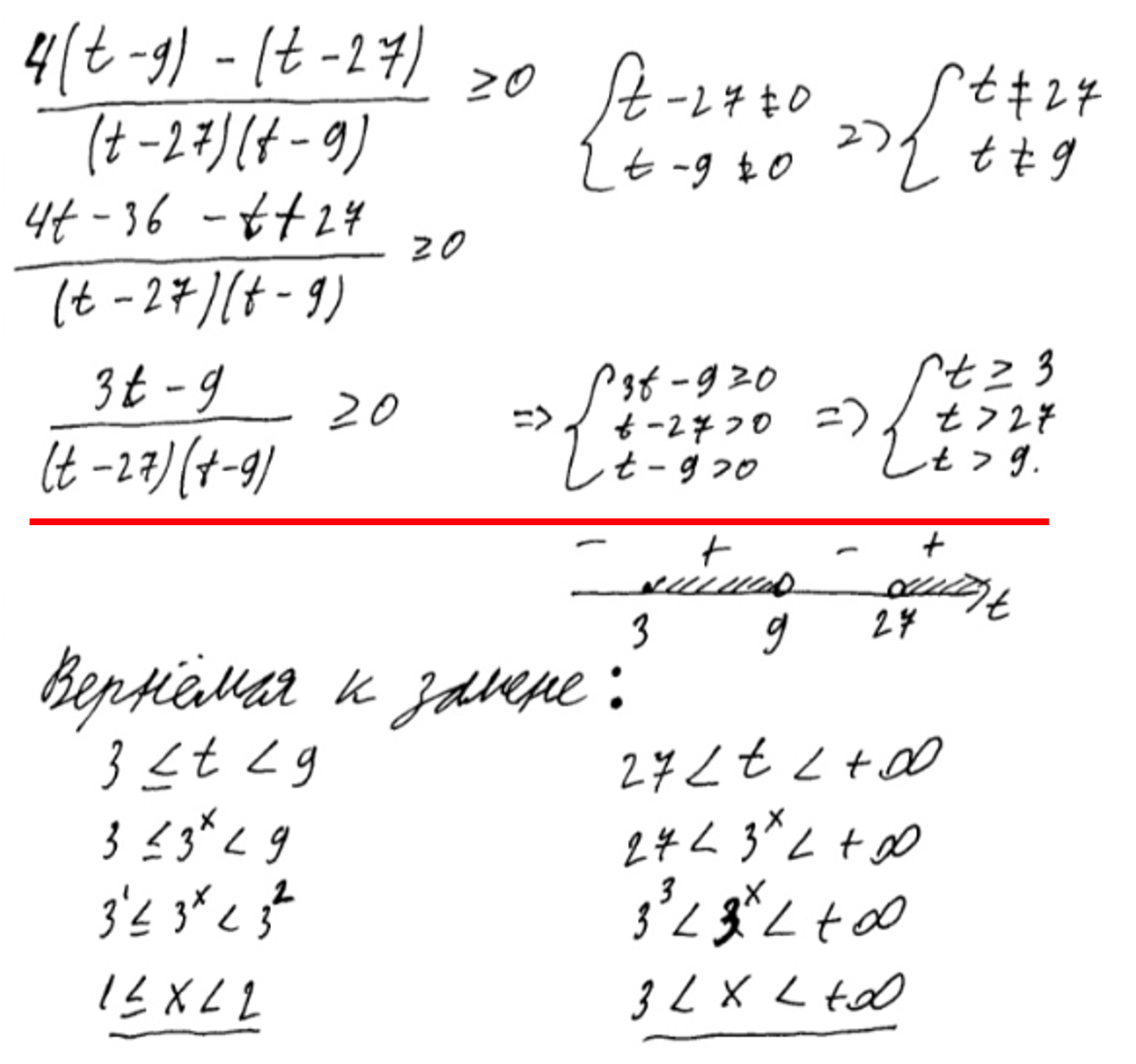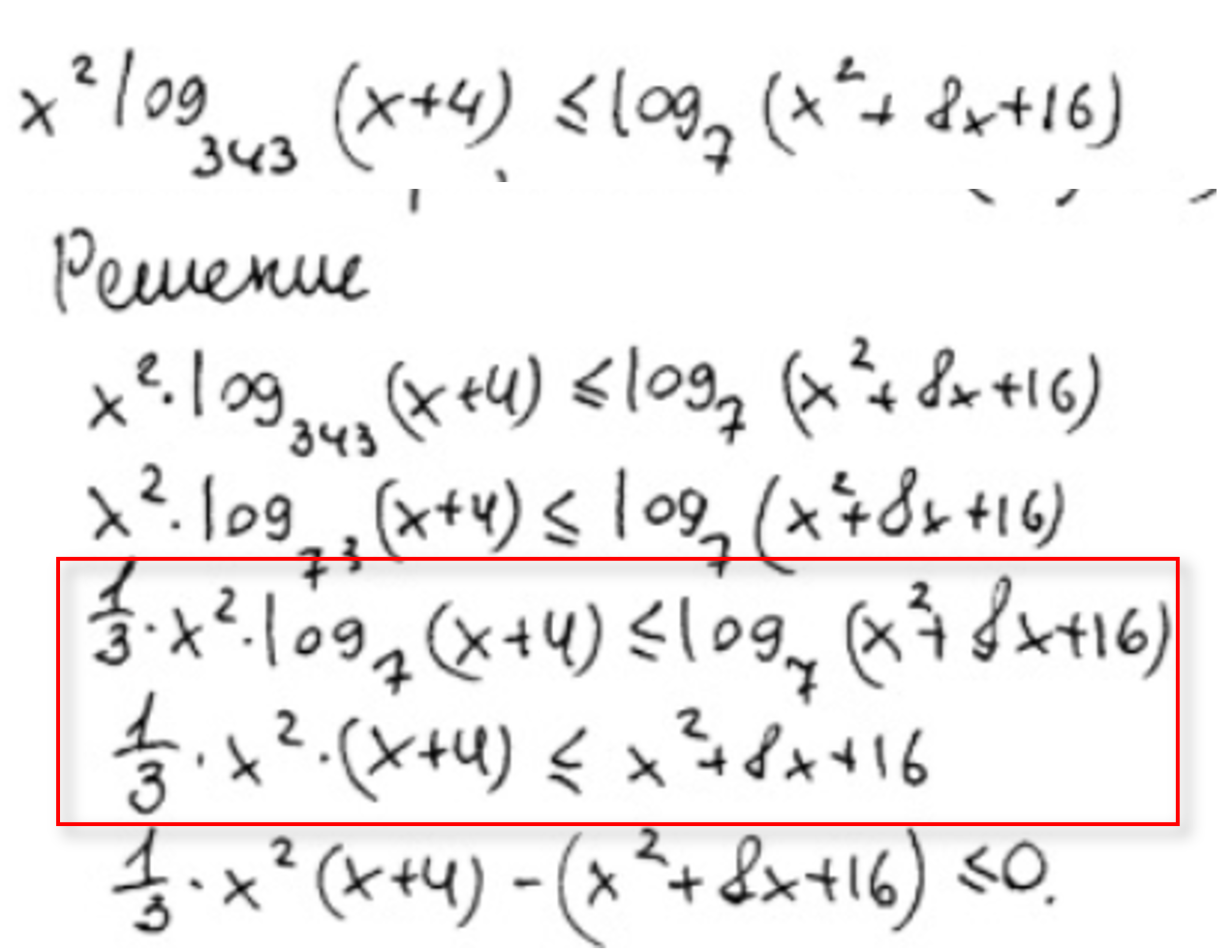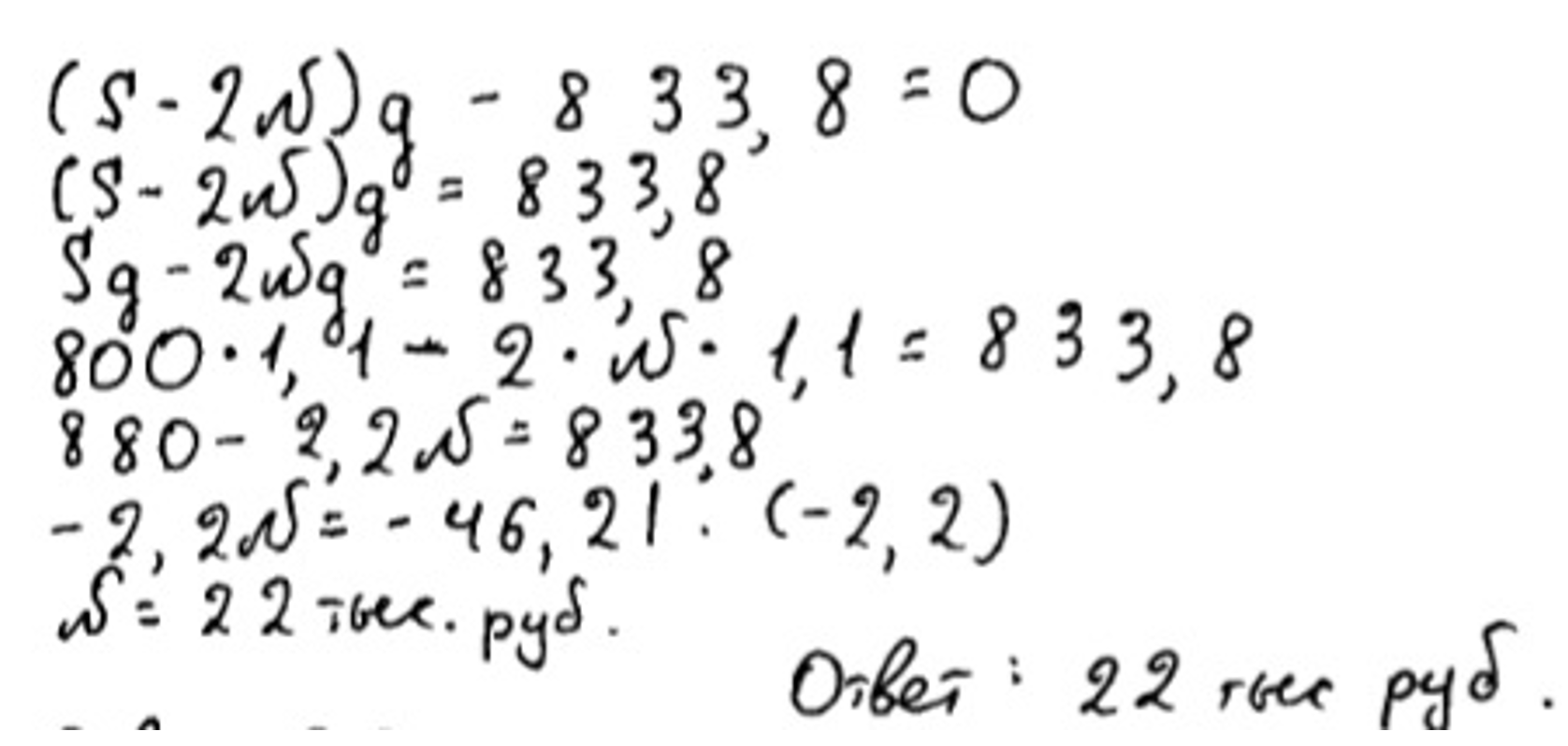И снова здравствуйте, уважаемые одиннадцатиклассники! Полагаю, что Вы хорошо отдохнули и готовы к работе для достижения своих высоких целей.
В этом году июнь месяц выдался очень продуктивным. Моя работа не закончилась 6 июня, когда мои ученики написали ЕГЭ по физике. После публикации результатов ЕГЭ (сначала по математике, а потом и по физике) стало поступать множество сообщений от учеников, даже тех, с кем я не занималась, с просьбой помочь разобраться, за что сняли баллы. А в некоторых случаях даже была необходима помощь с составлением апелляции. Бесценный опыт, если честно…..Только вот от этого опыта седых волос становится больше. И желание сжечь критерии не отпускает меня.
Сразу замечу, что апелляция возможна только по заданиям второй части. По первой части апелляция производится только тогда, когда компьютер неверно считал знак, записанный Вами в бланке ответов.
Уважаемые одиннадцатиклассники, вы должны понимать, что недостаточно просто получить верный ответ, недостаточно записать решение в стиле «я художник, я так вижу». Ваше решение будут оценивать по вполне определенным критериям. И даже абсолютно верный ответ не гарантирует полный балл за выполненное задание.
Анализ ошибок мы начнем с разбора сканов работ по профильной математике. Эти сканы я собирала не один год. К сожалению, в математике, просто за идею решения, за набор формул, не дадут ни одного балла. А снимают баллы за наличие вычислительных ошибок, недостаточную обоснованность, наличие лишних записей. Не указали необходимые признаки, свойства, теоремы – все, полный балл Вам не дадут.
Основной упор будет сделан на задачи 12, 14, 15 (уравнения, неравенства, задачи с экономическим содержанием). Это так называемый джентельменский набор, который старается выполнить большая часть выпускников. Погнали…
Для удобства статья представлена в двух форматах. Текст и видео. Вот ролик:
Уравнения
Основные ошибки:
1) неправильное использование формул приведения.
При преобразовании допущена ошибка. Минуса перед косинусом быть не должно. Задание оценивается в 0 баллов.
2) незнание свойств четных и нечетных функций. Также ребята забывают, что косинус функция честная, а вот синус, тангенс и котангенс нечетные.
2) незнание свойств четных и нечетных функций. Также ребята забывают, что косинус функция честная, а вот синус, тангенс и котангенс нечетные.
Классическая ошибка! – нечетная функция, следовательно знак минус выносится вперед, а не пропадает. Если бы функция была четная, то мы смело могли бы убрать знак минус. Задание оценивается в 0 баллов.
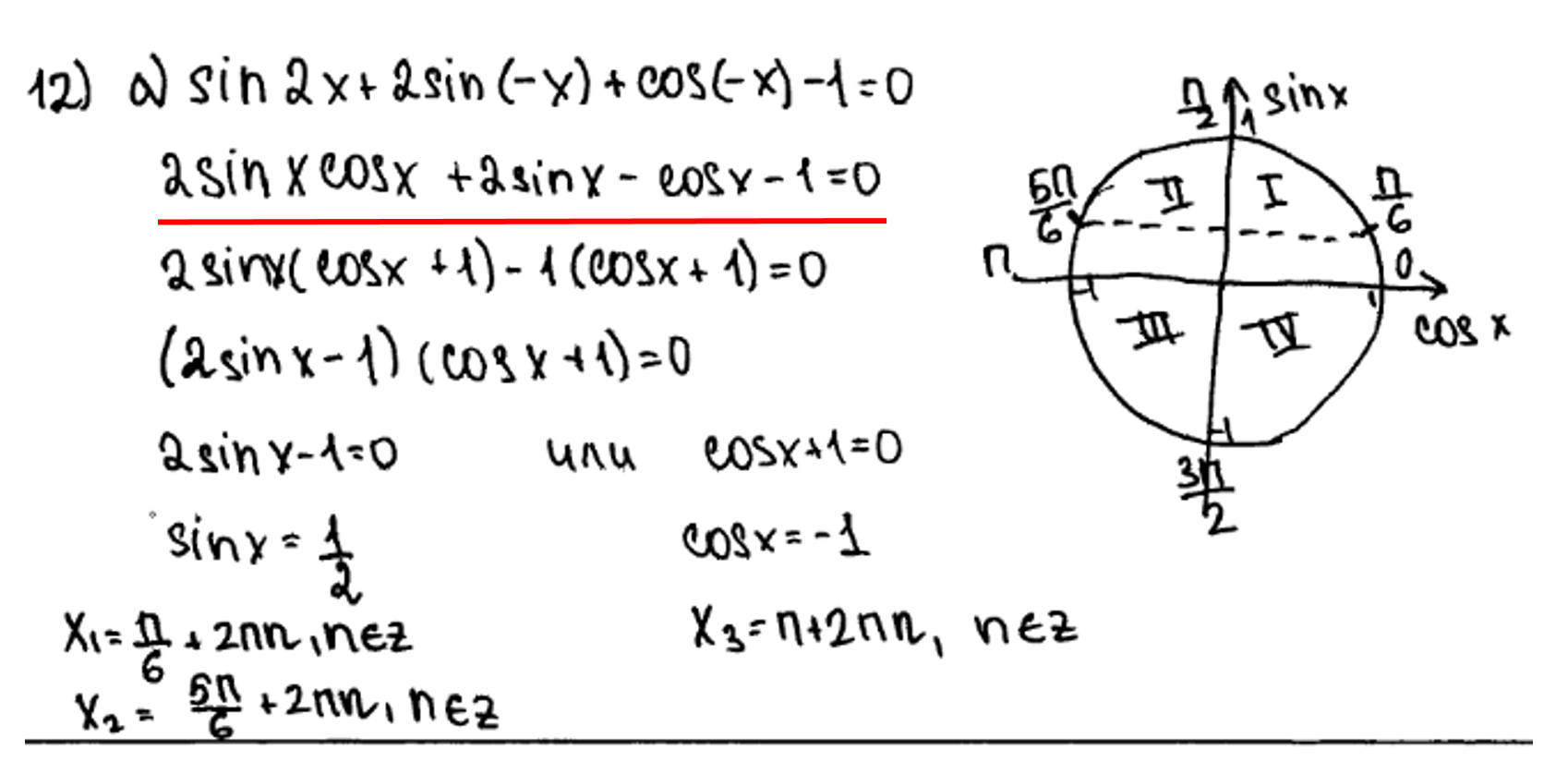
3) неправильное или некорректное использование тригонометрических формул.
Пару лет назад мне написал ученик, которому на экзамене досталось уравнение вида – нечетная функция, следовательно знак минус выносится вперед, а не пропадает. Если бы функция была четная, то мы смело могли бы убрать знак минус. Задание оценивается в 0 баллов.
3) неправильное или некорректное использование тригонометрических формул.
Пару лет назад мне написал ученик, которому на экзамене досталось уравнение вида 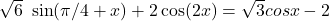
Скан он мне не отправил, но в процессе обсуждений выяснилось, что в первой скобке для он использовал не формулу синуса суммы, а формулы приведения. Чего делать категорически нельзя! Как Вы понимаете, задание оценили в 0 баллов.
4) Самое банальное. Неверное решение простейших тригонометрических уравнений.

4) Самое банальное. Неверное решение простейших тригонометрических уравнений.
При решении простейшего тригонометрического уравнения допущена ошибка. Третий и четвертый корень записаны неверно. Задание оценивается в 0 баллов.
Неравенства
С неравенствами у ребят дела идут посложнее, чем с уравнениями. Тут ваша фантазия разыгрывается по полной. Какие только ошибки не встречались(( Постараюсь выделить основные.
1)Пожалуй, самая распространенная ошибка – ошибка в расстановке знаков на координатной прямой. В идеале, если выпускник умеет определять – перед ним корень четного или нечетного порядка, меняется знак или дублируется.
Нули найдены верно. Но при расстановке знаков на координатной прямой допущена ошибка. Мы видим, что единица – нуль числителя второго порядка, следовательно знак сохраняется, и в крайнем левом интервале должен быть плюс. Эта ошибка уже позволяет эксперту поставить за данное задание 0 баллов.
2)Отбрасывание знаменателя и, как следствие, потеря части корней. В примере, приведенном ниже, выпускник отбросил знаменатель и находил нули только числителя.
Это привело к тому, что на координатной прямой не хватает нулей двух скобок: .
Такая грубая ошибка на экзамене не прощается.
Оценка эксперта – 0 баллов.

Такая грубая ошибка на экзамене не прощается.
Оценка эксперта – 0 баллов.
3) Неравносильный переход от неравенства к системе неравенств.
Я думаю, эта ошибка даже не нуждается в комментариях. Даже несмотря на то, что ученик верно нашел нули, верно расставил знаки на координатной прямой, это задание оценили в 0 баллов. Если бы системы с тремя неравенствами не было, ученик имел бы возможность взять полный балл.
4) Ошибки при использовании свойств логарифмов.
Стоит заметить, что для снятия логарифмов в правой и левой части, необходимо, чтобы перед логарифмом не было никаких цифр или букв. Выпускник снял логарифмы, хотя по задумке нужно было в правой части свернуть в полный квадрат подлогарифмическое выражение и вынести общий множитель. Как Вы понимаете, эксперт оценил это задание в 0 баллов.
Из моего текста у Вас, возможно, сложилось впечатление, что эксперты по всем поводам снимают сразу два балла. К счастью, это не так. Один балл Вам могут поставить, если Вы допустили ошибку в скобке (вместо круглой написали квадратную или наоборот) или допустили вычислительную ошибку, но при этом присутствует верная последовательность всех шагов решения.
Экономические задачи
В решении задач с экономическим содержанием ребятам в первую очередь нужно определить, какая форма кредитования – с дифференцированными платежами, аннуитентными или иная форма кредитования.
Могу выделить несколько основных ошибок.
1)Неверное построение математической модели, связанное с неверным определением формы кредитования.
Для лучшего понимания начну с условия задачи.
В июле 2026 года будет взят кредит на три года в размере 800 тыс рублей. Условия возврата таковы:
– каждый январь долг возрастает на 10 процентов по сравнению с концом прошлого года
– размер платежей в 2027 и 2028 годах одинаковый
– к июлю 2029 года долг выплачивается полностью.
Также известно, что в 2029 году платеж составит 833,8 тыс рублей. Сколько рублей будет составлять платеж в 2027 году?
Согласно записям таблицы, ученик решил, что перед ним дифференцированная форма кредитования и остаток уменьшается у него равномерно, ровно на N рублей каждый год. Но это совсем не так. Из условия задачи, мы видим, что выплаты одинаковые первые два года. Но при этом остаток не будет уменьшаться равномерно. Правильная запись остатка во второй строчке должна выглядеть так: .
Основываясь на критериях оценивания данного задания, математическая модель построена неверно, задание оценивается в 0 баллов.
Идем дальше. Наверняка Вы встречали задачи вида:
15 января 2020 года был выдан кредит на сумму 900 тыс. рублей на 31 месяц. Условия возврата таковы:
– 1 -го числа каждого месяца долг увеличивается на 2 по сравнению с концом предыдущего месяца.
– со 2 по 14 число необходимо выплатить часть долга;
– 15 -го числа каждого месяца с 1-го по 30-й долг должен быть на одну и ту же величину меньше долго на 15 число предыдущего месяца;
– 15 июля 2027 года долг составит 300 тыс рублей.
– 15 августа 2027 года долг должен быть выплачен полностью.
Найдите общую сумму выплат после полного погашения кредита.

Основываясь на критериях оценивания данного задания, математическая модель построена неверно, задание оценивается в 0 баллов.
Идем дальше. Наверняка Вы встречали задачи вида:
15 января 2020 года был выдан кредит на сумму 900 тыс. рублей на 31 месяц. Условия возврата таковы:
– 1 -го числа каждого месяца долг увеличивается на 2 по сравнению с концом предыдущего месяца.
– со 2 по 14 число необходимо выплатить часть долга;
– 15 -го числа каждого месяца с 1-го по 30-й долг должен быть на одну и ту же величину меньше долго на 15 число предыдущего месяца;
– 15 июля 2027 года долг составит 300 тыс рублей.
– 15 августа 2027 года долг должен быть выплачен полностью.
Найдите общую сумму выплат после полного погашения кредита.
В этой таблице полностью неправильно записаны столбцы с остатками и выплатами. Согласно условию задачи, первые 30 месяцев долг уменьшается равномерно, на меньше чем, прошлом месяце. Но не забываем, что первоначальный долг – это S, а не Sk рублей. То есть остаток в первые 30 месяцев должен выглядеть так:
меньше чем, прошлом месяце. Но не забываем, что первоначальный долг – это S, а не Sk рублей. То есть остаток в первые 30 месяцев должен выглядеть так:
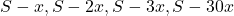
.
С учетом полностью неправильно построенной математической модели, задание оценивается в 0 баллов.
2)Ошибки при применении формул арифметической прогрессии и расчета общей суммы выплат.
Год назад ребятам на экзамене попалась задача, где в процессе кредитования менялась процентная ставка. Приведу пример:
25 августа 2020 года был дан кредит на 12 лет в размере 300 тыс рублей.
— 25 января с 2021 по 2026 года долг возрастает на 10 процентов;
— 25 января с 2027 по 2032 года долг возрастает на 15 процентов;
– с февраля по июль необходимо выплатить часть долга;
– в августе каждого года долг должен быть на одну и туже величину меньше по сравнению с августом прошлого года;
– к августу 2032 года кредит должен быть полностью погашен.
Найдите общую сумму выплат после полного погашения кредита.
Я уверена, что для многих ребят покажется очевидным, что нельзя складывать первую и последнюю (двенадцатую) выплату. Но я все же поясню.
Действительно, это задача на дифференцированные платежи. И можно заметить, что выплаты подчиняются арифметической прогрессии. Но так как у вас меняется процентная ставка, у Вас меняется и так называемый коэффициент или разность арифметической прогрессии. Поэтому правильно будет сначала просуммировать по формуле арифметической прогрессии первые шесть выплат, потом вторые шесть и полученные выражения сложить. Таким образом Вы получите верный ответ.
В каком же случае Вы можете получить 1 балл – если Вы верно построили математическую модель, но допустили вычислительную ошибку при получении численного значения.
PS: в подавляющем большинстве работ, которые поступали на проверку, ребята просили пояснить, почему за параметр (17 задание) и за задание на числа и их свойства так сильно срезали баллы. В большинстве случаев ребята получали по одному баллу за параметр, а в задаче на числа им засчитывали только пункт а), который также дает только один балл. Ребята, эти задачи считаются олимпиадными, не зря за их полное выполнение дается целых 4 балла. Критерии оценивания данных номеров очень жесткие. Должно быть и максимальное подробное объяснение, и разбор всех случаев и вариантов. В 17 задании это и правильно построенный график (если это необходимо), и рассчитаные все точки, и правильно раскрытый модуль, и расписанные все значения параметра и т.д и т.д.
В погоне за «легкими «баллами ребята даже не трогают планиметрию и стереометрию. А они, напомню, оцениваются в три балла каждый. Даже если Вы испытываете трудности в геометрии, пункт а (доказательство) не пропускайте мимо, как правило он значительно легче пункта б), где нужно найти численное значение той или иной величины. Но по одному первичному баллу за каждый номер Вы спокойно можете получить.
На этом мой краткий обзор подошел к концу. Я желаю удачи и сил всем одиннадцатиклассникам в этом году. Не бойтесь ЕГЭ, настраивайтесь на работу, идите к своей цели. У Вас все получится!
Все, что не убивает, делает нас сильнее!
P.S.: Вот моя группа ВКонтакте, где я выкладываю подобные тексты, ролики и полезности для ЕГЭ по физике и математике: https://vk.com/public185877660 Подписывайтесь!
Глава 1. Вебинар по оформлению задач второй части ЕГЭ по математике (3 часа, 10 минут)
Почему важно начать учиться оформлять задачи второй части за 30 дней до ЕГЭ? Потому что вам нужно выработать привычку это делать.
Привычка формируется 30 дней (есть исследования). Если вы узнаете о том, как оформлять задачи за неделю до экзамена, будет поздно.
Поэтому читайте материал первой главы, смотрите наше первый вебинар и потом применяйте на практике то, что вы узнаете при решении задач постоянно в течение 30 ДНЕЙ!
И прекратите терять баллы на ровном месте!
Научиться правильно оформлять задачи 2 части ЕГЭ по математике намного проще, чем научиться их решать!
Но тем не менее, каждый год огромное количество людей теряют десятки баллов из-за неправильного оформления.
Если вы посмотрите видео, вы научитесь оформлять задачи так, что гарантированно 100% экспертов ЕГЭ поставят вам полный балл (если вы правильно решите задачу, конечно же;)
На этом видео мы очень подробно разберем все задачи второй части профильного ЕГЭ по математике, и вы узнаете все нюансы оформления:
- Что такое критерии, как их понимать?
- Что считается опиской, что – арифметической ошибкой, а что – грубой «смысловой» ошибкой?
- Нужно ли делать проверку ответов (да), и как её делать?
- Тригонометрия: нужно ли писать разные буквы (n, m, k) в ответах или можно использовать одну для всех формул?
- Какие способы отбора корней лучше использовать в задаче 13 б), а какие лучше не трогать?
- Как правильно показывать отбор на единичной окружности и не потерять при этом балл?
- В каких случаях предпочтительно пользоваться окружностью, а в каких – двойным неравенством?
- Насколько подробно нужно расписывать решения уравнений и неравенств?
- Нужно ли на чистовике полностью прописывать дискриминант и поиск корней, или достаточно вычислить их устно «по теореме Виета»?
- Как не запутаться в «значках»: где использовать равносильность, а где следствие, как не перепутать систему и совокупность и прочее?
- Можно ли использовать метод рационализации: мифы и реальность Вспомним, что такое ОДЗ, и всегда ли его нужно писать, и как его правильно писать?
- Экономическая задача – это вообще отдельная история. Как могут давать аж 3 первичных балла за простую задачу на проценты? А оказывается, что их за саму задачу и не дают: их дают за правильное оформление! И снимают за каждую мелочь. Многие получают 0 баллов, даже получив правильный ответ. Я очень подробно разберу, что же именно от нас нужно, и как не упустить халявные 3 балла.
- Задачи с параметром чаще всего тоже требуют довольно подробных объяснений, особенно, если мы выбираем графический метод решения. Геометрия.
- Можно ли не решать пункт а, но пользоваться им в решении пункта б? Обязательно ли делать рисунок?
- Как в стереометрии показывать построение сечений? Какими теоремами можно пользоваться без доказательства?
- Обязательно ли писать название каждой теоремы? Задача 19 – в каких случаях достаточно примера, а в каких – обязательно писать полное доказательство?
- И много других нюансов, которые уже не помещаются в этот длинный список!
Если вам понравилось видео, подписывайтесь, ставьте лайки — это поможет тому, чтобы его увидели другие:
Тайм-коды для просмотра этого видео на YouTube:
Для тех, кто предпочитает смотреть видео на YouTube, вы можете перейти по этим тайм-кодам на наш канал на YouTube.
- 0:00 Вступление
- 2:52 Как выглядят критерии
- 4:09 Задача 13
- 5:59 ОДЗ
- 7:37 Можно ли не писать ОДЗ для логарифма?
- 9:00 Записали ОДЗ, но получили 0 баллов – как же так:(
- 12:23 Задача 13 (а)
- 14:00 Подписи осей единичной окружности
- 17:46 Разные или одинаковые буквы использовать в сериях корней (тригонометрия)?
- 26:30 Задача 13 (б) – первый способ, через двойное неравенство
- 32:35 Второй способ, через окружность
- 35:32 Система, совокупность – что это и что делать, если вы их путаете
- 37:11 Лайфхак – как быстро расставить корни на окружности
- 41:06 Третий способ – подбором
- 50:38 Замена переменных – как описывать
- 51:10 Квадратные уравнения – дискриминант или Виет?
- 58:13 Задача 15
- 1:02:26 Упрощаем себе вычисления ОДЗ
- 1:03:50 Пользуемся ОДЗ — упрощаем себе решение неравенства
- 1:04:55 Смешанное неравенство — первый способ (как лучше не делать)
- 1:07:47 Второй способ – обобщённый метод интервалов (и его подводные камни)
- 1:13:32 Метод рационализации – можно ли пользоваться и нужно ли доказывать?
- 1:18:50 Вывод по 15 задаче, критерии
- 1:21:35 Ответ, отличающийся на конечное число точек
- 1:25:42 Проверка ответов в неравенствах – как?
- 1:29:00 значок равносильности
- 1:40:30 Задача 17
- 1:49:50 Критерии; что такое мат. модель?
- 1:52:00 Четыре фразы, которые нужно обязательно написать
- 1:56:00 Умножать на проценты можно? А складывать?
- 2:03:28 Задача 18
- 2:09:46 Обязательно ли нужен красивый рисунок? Как потерять баллы из-за рисунка
- 2:14:05 Полностью обоснованное решение
- 2:15:40 Разбор критериев на 4, 3, 2 и 1 балл
- 2:20:11 Можно ли решать не через окружности, а аналитически?
- 2:21:13 Задача 19: подбор в пункте (а) и «оценка + пример» в пункте (в)
- 2:27:00 Задача 14
- 2:27:40 Координатный метод
- 2:30:33 Можно ли брать числа из пункта (б), когда решаем пункт (а)?
- 2:35:13 Построение сечения (с обоснованием)
- 2:39:05 Значки «лежит», «принадлежит» – в чём отличие и важно ли не перепутать?
- 2:44:35 В пункте (б) пользуемся недоказанным пунктом (а) – в задачах 14 и 16
- 2:48:15 Использование «необычных» теорем – можно ли без доказательства?
- 2:51:30 Если забыл название теоремы
- 2:53:54 Элементарные вещи можно не выводить
- 2:57:05 Теорема Фалеса или обратная теорем Фалеса?
- 2:58:35 Что будет на Марафоне и кому он нужен
- 3:00:16 Призы

Содержание
- Самые распространенные ошибки на ЕГЭ
- Задачи на проценты
- Невнимательное прочтение условий задачи
- Арифметические ошибки
- Неверное прочтение и построение чертежа
- Неумение дать развернутый ответ
- Как избежать ошибок по невнимательности
Для
успешной сдачи экзаменов важно начать подготовку заблаговременно. Если
самостоятельно не получается выявить свои слабые места и пробелы, стоит
разобраться, какие типичные ошибки чаще всего допускают выпускники. Ответ на
этот вопрос могут дать эксперты ФИПИ.
Самые
распространенные ошибки на ЕГЭ
Как
известно, математика делится на
базовую и профильную. Первую необходимо сдавать всем 11-классникам. А
профильный уровень относится к предметам по выбору. В нем содержатся
практико-ориентированные задания.
Нередко старшеклассники допускают ошибки теоретического характера из-за незнания определенных тем по
алгебре и геометрии. Также выпускники получают нулевые баллы, вычисляя
логарифмы и неравенства. Помимо этого, следует заняться изучением свойств и
графиков производных.
К
решению некоторых типов заданий придется готовиться с особым усилием. Рекомендуется
начинать с самой простой задачки, постепенно повышая уровень сложности. Помимо
этого, часть ошибок вызвана незнанием терминологии. Поэтому стоит обратить
внимание на изучение тригонометрических функций.
Задачи
на проценты
В
большинстве случаев ошибки связаны с тем, что школьники не понимают суть
процента. Например, если в задаче требуется сперва понизить цену на 20%, а
затем поднять на 20%.
Одной
из распространенных ошибок является то, что участники ЕГЭ думают, что проценты
равняются одной сумме. Однако считать нужно от старой цены. Поэтому
рекомендуется уделить внимание повторению основ подсчета процентов и
взаимосвязи величин.
Невнимательное
прочтение условий задачи
Из-за
волнения и напряженной обстановки многие ученики неверно понимают условие
математической задачи. В результате школьникам снижают итоговые баллы. Поэтому
желательно несколько раз вдумчиво и медленно прочесть задание. Перед тем как
записать ответ в бланк, стоит проверить единицу измерения.
Арифметические
ошибки
На
ЕГЭ по математике запрещено
пользоваться калькулятором. Поэтому при сдаче экзамена легкие вычисления вызывают у школьников затруднения. Если
не получается считать в столбик, то при прохождении тестирования есть риск
допустить глупую ошибку в простых примерах.
При этом выпускник может успешно справиться с задачами
второй части. Больше всего у участников единого госэкзамена возникают проблемы
с дробями и отрицательными числами. Это обычно копится на с пятого класса.
Также
следует внимательно смотреть за наличием минуса при вычислении. Если не удается
безошибочно решать определенные виды задач, следует тщательно изучить сложную
тему. Поскольку она может попасться в тестовой части ЕГЭ, что повлияет на
результат.
Неверное
прочтение и построение чертежа
Нередки
случаи, когда выпускник не может уловить взаимосвязь элементов геометрических
конструкций. Либо не владеет пространственными представлениями. Стоит научиться
правильно читать буквенные записи на чертежах.
В
частности, немало школьников допускали ошибки, путая расположение вершин углов.
Если с этим возникают сложности, рекомендуется потренироваться в решении
подобных задач. Так что стоит сперва решить задание на черновике для
визуализации.
Неумение
дать развернутый ответ
Задания
№14 и 16 обладают повышенной степенью сложности. В них требуется давать
развернутый ответ на отдельном бланке. Каждая задача делится на 2 пункта:
сначала понадобится доказать, а потом – сделать вычисления.
Зачастую
школьники сталкиваются с проблемой приведения доказательств. Поэтому в 1-ом
пункте многие участники неправильно оформляют ответ. Так что рекомендуется тренироваться
в доказательной базе и научиться обосновать методы решения.
Как
избежать ошибок по невнимательности
Существует
несколько советов, которые помогут не ошибиться из-за невнимательного прочтения
задачи. Для этого стоит придерживаться такой последовательности действий:
- Прочесть условие.
- Выписать данные величины. Также требуется
сделать чертеж в задаче по геометрии. - Установить взаимосвязи между известными
величинами. - Выписать, что нужно необходимо найти, и на
какие вопросы ответить. - Определить тип задачи.
- Сформулировать содержание и порядок
действий.
Это поможет не совершить обидных ошибок, потеряв
баллы. Данные условия необходимо выписывать на листок. Если просто
зафиксировать их в уме, можно в итоге получить неверный ответ.
Кроме того, важно не приступать к решению задачи
сразу, лишь прочитав ее. Психологи советуют выдерживать паузы перед записью
ответа, чтобы добиться успешных результатов.
Компания «РосДиплом» на протяжении 20 лет занимается студенческими работами и предлагает помощь студентам во всех областях и темах. Наши преимущества: огромный опыт работы, лучшие авторы, собранные со
всех уголков России, гарантии успешной сдачи и оптимальной цены, а также индивидуальный подход к каждому клиенту.
До начала ЕГЭ осталось совсем мало времени. Многие школьники в этому году выбрали математику в качестве профильного предмета. Но у выпускников нередко возникают затруднения при решении экзаменационных задач. Эксперты проанализировали популярные ошибки школьников при сдаче ЕГЭ по математике. В статье мы расскажем о том, как их избежать.
Самые частые ошибки
Эксперты отмечают, что с каждым годом растет число ошибок при решении геометрических задач. Многие школьники испытывают трудности при построении и чтении чертежей.
Немало выпускников ошибается при решении сложных неравенств с логарифмами и тригонометрическими функциями. Большой процент ошибок связан с заданиями на вычисление производных.
Однако первое место занимают арифметические ошибки. Они считаются самыми нелепыми и обидными, так как чаще всего допускаются по невнимательности. Бывают случаи, когда школьник отлично справился со сложным заданием, но при решении простой задачи случайно ошибся в вычислениях.
Далее мы рассмотрим самые частые ошибки и поговорим о том, как их избежать.
Вычисление процентов
Часто школьники делают ошибки в таких заданиях. Проценты изучают еще в 5 классе. Но нередко выпускники затрудняются при выполнении подобных задач. Причиной этого становятся пробелы в знаниях и непонимание сути процента.
Чтобы не допустить подобных ошибок, нужно повторить пройденный в 5 классе материал и вспомнить основы расчета процентов.
Невнимательность при чтении заданий
Сдача ЕГЭ часто связана с волнением и стрессом. В некоторых случаях это приводит к рассеянности. Многие школьники ошибаются не из-за слабого знания предмета, а по невнимательности.
Это самый досадный тип ошибок. Чтобы их избежать, необходимо сконцентрироваться, а затем не спеша, несколько раз прочитать текст задания. При этом нужно хорошо вдуматься в условия задачи.
Непонимание текста задачи
Нередки случаи, когда участники ЕГЭ не понимают условия задания. Это чаще всего происходит при решении практико-ориентированных задач. Многие школьники и вовсе пропускают такие нестандартные задания, что отрицательно сказывается на результате тестирования.
К практико-ориентированным заданиям можно отнести задачи на движение. Они требуют навыков математического моделирования. Часто школьники не понимают принципы движения и взаимосвязь величин, что приводит к ошибкам.
Иногда непонимание условий задач связано с плохим знанием величин и формул. В этом случае необходимо повторить теоретический материал. Следует также потренироваться в решении разнообразных задач с нестандартными условиями.
Ошибки при расчетах
В наши дни немало школьников постоянно пользуется калькулятором. Они разучиваются считать в уме и на бумаге. В результате на ЕГЭ многие выпускники допускают ошибки при элементарных вычислениях.
Чаще всего выпускники ошибаются при действиях с дробями и отрицательными числами, а также при преобразовании выражений. Эти пробелы в знаниях идут еще с 5 класса.
Если вы заметили у себя подобные проблемы, то подробно изучите ту тему, которую вы плохо знаете. Помните, что такие задания обязательно встретятся вам на экзамене.
Слабое знание теории
Плохое знание теоретических основ алгебры и геометрии — частая причина ошибок на ЕГЭ. Перед тестированием следует не только восстановить в памяти пройденный материал, но и потренироваться в решении заданий базового и профильного уровня.
В интернете вы можете найти реальные варианты ЕГЭ по математике прошлых лет. Попробуйте решить эти задачи и сравните результаты с правильными ответами. Если вы не понимаете, где ошиблись, то обратитесь за помощью к учителю или репетитору.
Неправильный алгоритм решения
Нередко школьники выполняют математические действия в неправильной последовательности и получают неверный результат задачи. Такие ошибки встречаются при решении рациональных дробных уравнений и логарифмических неравенств.
Научитесь правильному алгоритму решения таких задач. Всегда проверяйте полученный результат, подставив его в уравнение.
Неумение строить доказательство
В геометрии часто встречаются такие задачи, которые нужно не только решить, но и доказать полученный результат. Если вы испытываете затруднения при выполнении таких заданий, то потренируйтесь в логическом построении доказательств. Учитесь обосновывать метод решения задачи и полученные данные.
Ошибки в задачах по стереометрии
Многие выпускники испытывают трудности в чтении и построении чертежей. Далеко не все школьники обладают хорошими пространственными представлениями. В таких случаях нужно нарисовать конструкцию на черновике. Визуализация задачи облегчит ее решение.
Задания по тригонометрии
Тригонометрия — один из самых сложных разделов математики. Задания с тригонометрическими функциями часто вызывают затруднения.
Задачи по тригонометрии требуют хороших знаний теоретических фактов и умения применять их на практике. При их решении нужна внимательность и аккуратность.
Как правильно читать и решать задачу
Чтобы избежать ошибок, придерживайтесь следующего алгоритма при выполнении заданий:
- Медленно и вдумчиво изучите условие задачи. Прочитайте его несколько раз.
- Запишите на черновик все величины. Если вы выполняете задание по геометрии, то сделайте чертеж.
- Выявите взаимосвязи между данными и запишите их.
- Выпишите вопрос задачи.
- Определите, к какому типу относится задание.
- Составьте план решения задачи. Напишите в черновике последовательность ваших действий.
Обязательно записывайте все на бумаге, а не держите в уме. Не спешите сразу приступать к решению, сделайте небольшую паузу. Психологи считают, что это помогает получить наилучшие результаты.
Всегда начинайте с самых простых задач, а затем переходите к сложным. Это сбережет ваши силы и энергию, а также поможет избежать ошибок из-за невнимательности и усталости.
Заключение
ЕГЭ по математике требует серьезной подготовки. Перед тестированием следует восстановить в памяти теорию, восполнить все пробелы в знаниях и потренироваться в решении разнообразных заданий. Во время экзамена очень важно сконцентрироваться на задаче и вдумчиво изучать ее условия.
Нашли нарушение? Пожаловаться на содержание
И снова здравствуйте, уважаемые одиннадцатиклассники! Полагаю, что Вы хорошо отдохнули и готовы к работе для достижения своих высоких целей.
В этом году июнь месяц выдался очень продуктивным. Моя работа не закончилась 6 июня, когда мои ученики написали ЕГЭ по физике. После публикации результатов ЕГЭ (сначала по математике, а потом и по физике) стало поступать множество сообщений от учеников, даже тех, с кем я не занималась, с просьбой помочь разобраться, за что сняли баллы. А в некоторых случаях даже была необходима помощь с составлением апелляции. Бесценный опыт, если честно…..Только вот от этого опыта седых волос становится больше. И желание сжечь критерии не отпускает меня.
Сразу замечу, что апелляция возможна только по заданиям второй части. По первой части апелляция производится только тогда, когда компьютер неверно считал знак, записанный Вами в бланке ответов.
Уважаемые одиннадцатиклассники, вы должны понимать, что недостаточно просто получить верный ответ, недостаточно записать решение в стиле «я художник, я так вижу». Ваше решение будут оценивать по вполне определенным критериям. И даже абсолютно верный ответ не гарантирует полный балл за выполненное задание.
Анализ ошибок мы начнем с разбора сканов работ по профильной математике. Эти сканы я собирала не один год. К сожалению, в математике, просто за идею решения, за набор формул, не дадут ни одного балла. А снимают баллы за наличие вычислительных ошибок, недостаточную обоснованность, наличие лишних записей. Не указали необходимые признаки, свойства, теоремы – все, полный балл Вам не дадут.
Основной упор будет сделан на задачи 12, 14, 15 (уравнения, неравенства, задачи с экономическим содержанием). Это так называемый джентельменский набор, который старается выполнить большая часть выпускников. Погнали…
Для удобства статья представлена в двух форматах. Текст и видео. Вот ролик:
Уравнения
Основные ошибки:
1) неправильное использование формул приведения.
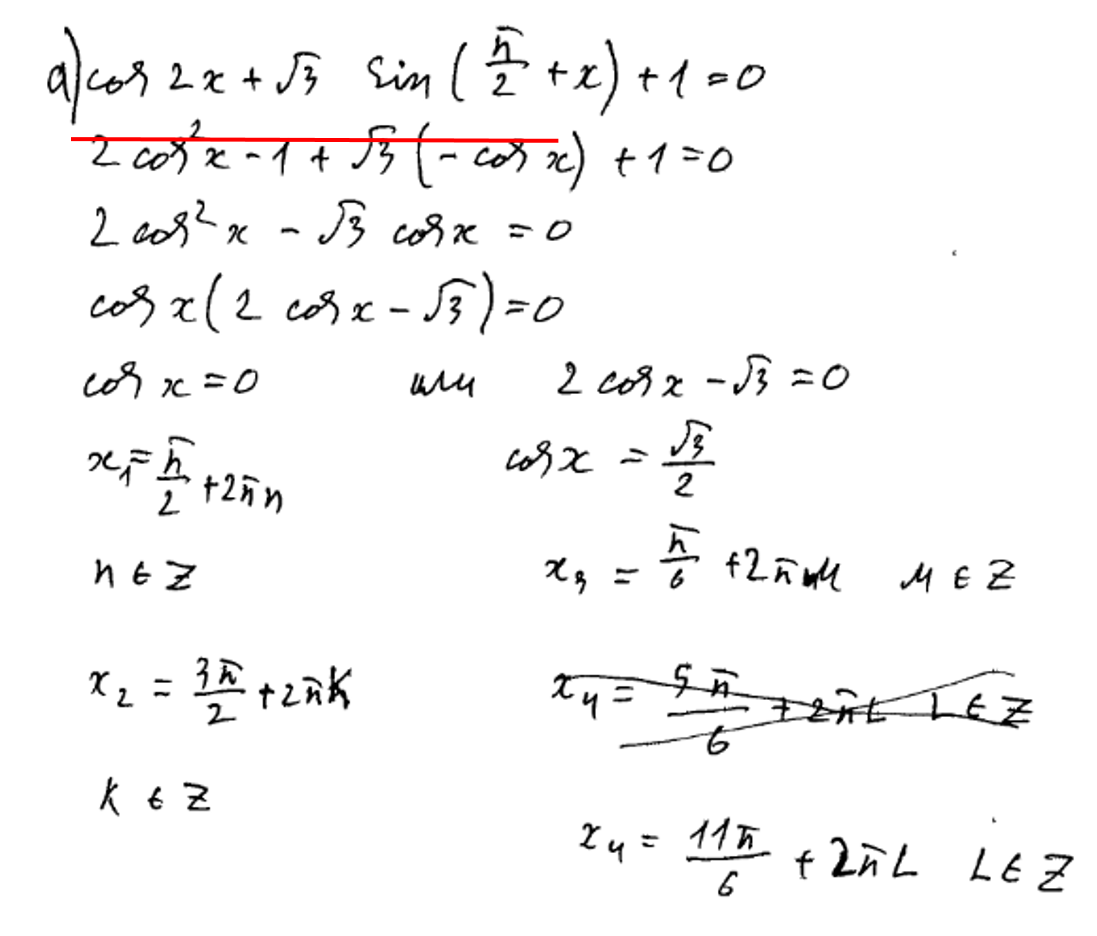
С учетом полностью неправильно построенной математической модели, задание оценивается в 0 баллов.
2)Ошибки при применении формул арифметической прогрессии и расчета общей суммы выплат.
Год назад ребятам на экзамене попалась задача, где в процессе кредитования менялась процентная ставка. Приведу пример:
25 августа 2020 года был дан кредит на 12 лет в размере 300 тыс рублей.
— 25 января с 2021 по 2026 года долг возрастает на 10 процентов;
— 25 января с 2027 по 2032 года долг возрастает на 15 процентов;
– с февраля по июль необходимо выплатить часть долга;
– в августе каждого года долг должен быть на одну и туже величину меньше по сравнению с августом прошлого года;
– к августу 2032 года кредит должен быть полностью погашен.
Найдите общую сумму выплат после полного погашения кредита.
Я уверена, что для многих ребят покажется очевидным, что нельзя складывать первую и последнюю (двенадцатую) выплату. Но я все же поясню.
Действительно, это задача на дифференцированные платежи. И можно заметить, что выплаты подчиняются арифметической прогрессии. Но так как у вас меняется процентная ставка, у Вас меняется и так называемый коэффициент или разность арифметической прогрессии. Поэтому правильно будет сначала просуммировать по формуле арифметической прогрессии первые шесть выплат, потом вторые шесть и полученные выражения сложить. Таким образом Вы получите верный ответ.
В каком же случае Вы можете получить 1 балл – если Вы верно построили математическую модель, но допустили вычислительную ошибку при получении численного значения.
PS: в подавляющем большинстве работ, которые поступали на проверку, ребята просили пояснить, почему за параметр (17 задание) и за задание на числа и их свойства так сильно срезали баллы. В большинстве случаев ребята получали по одному баллу за параметр, а в задаче на числа им засчитывали только пункт а), который также дает только один балл. Ребята, эти задачи считаются олимпиадными, не зря за их полное выполнение дается целых 4 балла. Критерии оценивания данных номеров очень жесткие. Должно быть и максимальное подробное объяснение, и разбор всех случаев и вариантов. В 17 задании это и правильно построенный график (если это необходимо), и рассчитаные все точки, и правильно раскрытый модуль, и расписанные все значения параметра и т.д и т.д.
В погоне за «легкими «баллами ребята даже не трогают планиметрию и стереометрию. А они, напомню, оцениваются в три балла каждый. Даже если Вы испытываете трудности в геометрии, пункт а (доказательство) не пропускайте мимо, как правило он значительно легче пункта б), где нужно найти численное значение той или иной величины. Но по одному первичному баллу за каждый номер Вы спокойно можете получить.
На этом мой краткий обзор подошел к концу. Я желаю удачи и сил всем одиннадцатиклассникам в этом году. Не бойтесь ЕГЭ, настраивайтесь на работу, идите к своей цели. У Вас все получится!
Все, что не убивает, делает нас сильнее!
P.S.: Вот моя группа ВКонтакте, где я выкладываю подобные тексты, ролики и полезности для ЕГЭ по физике и математике: https://vk.com/public185877660 Подписывайтесь!
Глава 1. Вебинар по оформлению задач второй части ЕГЭ по математике (3 часа, 10 минут)
Почему важно начать учиться оформлять задачи второй части за 30 дней до ЕГЭ? Потому что вам нужно выработать привычку это делать.
Привычка формируется 30 дней (есть исследования). Если вы узнаете о том, как оформлять задачи за неделю до экзамена, будет поздно.
Поэтому читайте материал первой главы, смотрите наше первый вебинар и потом применяйте на практике то, что вы узнаете при решении задач постоянно в течение 30 ДНЕЙ!
И прекратите терять баллы на ровном месте!
Научиться правильно оформлять задачи 2 части ЕГЭ по математике намного проще, чем научиться их решать!
Но тем не менее, каждый год огромное количество людей теряют десятки баллов из-за неправильного оформления.
Если вы посмотрите видео, вы научитесь оформлять задачи так, что гарантированно 100% экспертов ЕГЭ поставят вам полный балл (если вы правильно решите задачу, конечно же;)
На этом видео мы очень подробно разберем все задачи второй части профильного ЕГЭ по математике, и вы узнаете все нюансы оформления:
- Что такое критерии, как их понимать?
- Что считается опиской, что – арифметической ошибкой, а что – грубой «смысловой» ошибкой?
- Нужно ли делать проверку ответов (да), и как её делать?
- Тригонометрия: нужно ли писать разные буквы (n, m, k) в ответах или можно использовать одну для всех формул?
- Какие способы отбора корней лучше использовать в задаче 13 б), а какие лучше не трогать?
- Как правильно показывать отбор на единичной окружности и не потерять при этом балл?
- В каких случаях предпочтительно пользоваться окружностью, а в каких – двойным неравенством?
- Насколько подробно нужно расписывать решения уравнений и неравенств?
- Нужно ли на чистовике полностью прописывать дискриминант и поиск корней, или достаточно вычислить их устно «по теореме Виета»?
- Как не запутаться в «значках»: где использовать равносильность, а где следствие, как не перепутать систему и совокупность и прочее?
- Можно ли использовать метод рационализации: мифы и реальность Вспомним, что такое ОДЗ, и всегда ли его нужно писать, и как его правильно писать?
- Экономическая задача – это вообще отдельная история. Как могут давать аж 3 первичных балла за простую задачу на проценты? А оказывается, что их за саму задачу и не дают: их дают за правильное оформление! И снимают за каждую мелочь. Многие получают 0 баллов, даже получив правильный ответ. Я очень подробно разберу, что же именно от нас нужно, и как не упустить халявные 3 балла.
- Задачи с параметром чаще всего тоже требуют довольно подробных объяснений, особенно, если мы выбираем графический метод решения. Геометрия.
- Можно ли не решать пункт а, но пользоваться им в решении пункта б? Обязательно ли делать рисунок?
- Как в стереометрии показывать построение сечений? Какими теоремами можно пользоваться без доказательства?
- Обязательно ли писать название каждой теоремы? Задача 19 – в каких случаях достаточно примера, а в каких – обязательно писать полное доказательство?
- И много других нюансов, которые уже не помещаются в этот длинный список!
Если вам понравилось видео, подписывайтесь, ставьте лайки — это поможет тому, чтобы его увидели другие:
Тайм-коды для просмотра этого видео на YouTube:
Для тех, кто предпочитает смотреть видео на YouTube, вы можете перейти по этим тайм-кодам на наш канал на YouTube.
- 0:00 Вступление
- 2:52 Как выглядят критерии
- 4:09 Задача 13
- 5:59 ОДЗ
- 7:37 Можно ли не писать ОДЗ для логарифма?
- 9:00 Записали ОДЗ, но получили 0 баллов – как же так:(
- 12:23 Задача 13 (а)
- 14:00 Подписи осей единичной окружности
- 17:46 Разные или одинаковые буквы использовать в сериях корней (тригонометрия)?
- 26:30 Задача 13 (б) – первый способ, через двойное неравенство
- 32:35 Второй способ, через окружность
- 35:32 Система, совокупность – что это и что делать, если вы их путаете
- 37:11 Лайфхак – как быстро расставить корни на окружности
- 41:06 Третий способ – подбором
- 50:38 Замена переменных – как описывать
- 51:10 Квадратные уравнения – дискриминант или Виет?
- 58:13 Задача 15
- 1:02:26 Упрощаем себе вычисления ОДЗ
- 1:03:50 Пользуемся ОДЗ — упрощаем себе решение неравенства
- 1:04:55 Смешанное неравенство — первый способ (как лучше не делать)
- 1:07:47 Второй способ – обобщённый метод интервалов (и его подводные камни)
- 1:13:32 Метод рационализации – можно ли пользоваться и нужно ли доказывать?
- 1:18:50 Вывод по 15 задаче, критерии
- 1:21:35 Ответ, отличающийся на конечное число точек
- 1:25:42 Проверка ответов в неравенствах – как?
- 1:29:00 значок равносильности
- 1:40:30 Задача 17
- 1:49:50 Критерии; что такое мат. модель?
- 1:52:00 Четыре фразы, которые нужно обязательно написать
- 1:56:00 Умножать на проценты можно? А складывать?
- 2:03:28 Задача 18
- 2:09:46 Обязательно ли нужен красивый рисунок? Как потерять баллы из-за рисунка
- 2:14:05 Полностью обоснованное решение
- 2:15:40 Разбор критериев на 4, 3, 2 и 1 балл
- 2:20:11 Можно ли решать не через окружности, а аналитически?
- 2:21:13 Задача 19: подбор в пункте (а) и «оценка + пример» в пункте (в)
- 2:27:00 Задача 14
- 2:27:40 Координатный метод
- 2:30:33 Можно ли брать числа из пункта (б), когда решаем пункт (а)?
- 2:35:13 Построение сечения (с обоснованием)
- 2:39:05 Значки «лежит», «принадлежит» – в чём отличие и важно ли не перепутать?
- 2:44:35 В пункте (б) пользуемся недоказанным пунктом (а) – в задачах 14 и 16
- 2:48:15 Использование «необычных» теорем – можно ли без доказательства?
- 2:51:30 Если забыл название теоремы
- 2:53:54 Элементарные вещи можно не выводить
- 2:57:05 Теорема Фалеса или обратная теорем Фалеса?
- 2:58:35 Что будет на Марафоне и кому он нужен
- 3:00:16 Призы

Содержание
- Самые распространенные ошибки на ЕГЭ
- Задачи на проценты
- Невнимательное прочтение условий задачи
- Арифметические ошибки
- Неверное прочтение и построение чертежа
- Неумение дать развернутый ответ
- Как избежать ошибок по невнимательности
Для
успешной сдачи экзаменов важно начать подготовку заблаговременно. Если
самостоятельно не получается выявить свои слабые места и пробелы, стоит
разобраться, какие типичные ошибки чаще всего допускают выпускники. Ответ на
этот вопрос могут дать эксперты ФИПИ.
Самые
распространенные ошибки на ЕГЭ
Как
известно, математика делится на
базовую и профильную. Первую необходимо сдавать всем 11-классникам. А
профильный уровень относится к предметам по выбору. В нем содержатся
практико-ориентированные задания.
Нередко старшеклассники допускают ошибки теоретического характера из-за незнания определенных тем по
алгебре и геометрии. Также выпускники получают нулевые баллы, вычисляя
логарифмы и неравенства. Помимо этого, следует заняться изучением свойств и
графиков производных.
К
решению некоторых типов заданий придется готовиться с особым усилием. Рекомендуется
начинать с самой простой задачки, постепенно повышая уровень сложности. Помимо
этого, часть ошибок вызвана незнанием терминологии. Поэтому стоит обратить
внимание на изучение тригонометрических функций.
Задачи
на проценты
В
большинстве случаев ошибки связаны с тем, что школьники не понимают суть
процента. Например, если в задаче требуется сперва понизить цену на 20%, а
затем поднять на 20%.
Одной
из распространенных ошибок является то, что участники ЕГЭ думают, что проценты
равняются одной сумме. Однако считать нужно от старой цены. Поэтому
рекомендуется уделить внимание повторению основ подсчета процентов и
взаимосвязи величин.
Невнимательное
прочтение условий задачи
Из-за
волнения и напряженной обстановки многие ученики неверно понимают условие
математической задачи. В результате школьникам снижают итоговые баллы. Поэтому
желательно несколько раз вдумчиво и медленно прочесть задание. Перед тем как
записать ответ в бланк, стоит проверить единицу измерения.
Арифметические
ошибки
На
ЕГЭ по математике запрещено
пользоваться калькулятором. Поэтому при сдаче экзамена легкие вычисления вызывают у школьников затруднения. Если
не получается считать в столбик, то при прохождении тестирования есть риск
допустить глупую ошибку в простых примерах.
При этом выпускник может успешно справиться с задачами
второй части. Больше всего у участников единого госэкзамена возникают проблемы
с дробями и отрицательными числами. Это обычно копится на с пятого класса.
Также
следует внимательно смотреть за наличием минуса при вычислении. Если не удается
безошибочно решать определенные виды задач, следует тщательно изучить сложную
тему. Поскольку она может попасться в тестовой части ЕГЭ, что повлияет на
результат.
Неверное
прочтение и построение чертежа
Нередки
случаи, когда выпускник не может уловить взаимосвязь элементов геометрических
конструкций. Либо не владеет пространственными представлениями. Стоит научиться
правильно читать буквенные записи на чертежах.
В
частности, немало школьников допускали ошибки, путая расположение вершин углов.
Если с этим возникают сложности, рекомендуется потренироваться в решении
подобных задач. Так что стоит сперва решить задание на черновике для
визуализации.
Неумение
дать развернутый ответ
Задания
№14 и 16 обладают повышенной степенью сложности. В них требуется давать
развернутый ответ на отдельном бланке. Каждая задача делится на 2 пункта:
сначала понадобится доказать, а потом – сделать вычисления.
Зачастую
школьники сталкиваются с проблемой приведения доказательств. Поэтому в 1-ом
пункте многие участники неправильно оформляют ответ. Так что рекомендуется тренироваться
в доказательной базе и научиться обосновать методы решения.
Как
избежать ошибок по невнимательности
Существует
несколько советов, которые помогут не ошибиться из-за невнимательного прочтения
задачи. Для этого стоит придерживаться такой последовательности действий:
- Прочесть условие.
- Выписать данные величины. Также требуется
сделать чертеж в задаче по геометрии. - Установить взаимосвязи между известными
величинами. - Выписать, что нужно необходимо найти, и на
какие вопросы ответить. - Определить тип задачи.
- Сформулировать содержание и порядок
действий.
Это поможет не совершить обидных ошибок, потеряв
баллы. Данные условия необходимо выписывать на листок. Если просто
зафиксировать их в уме, можно в итоге получить неверный ответ.
Кроме того, важно не приступать к решению задачи
сразу, лишь прочитав ее. Психологи советуют выдерживать паузы перед записью
ответа, чтобы добиться успешных результатов.
Компания «РосДиплом» на протяжении 20 лет занимается студенческими работами и предлагает помощь студентам во всех областях и темах. Наши преимущества: огромный опыт работы, лучшие авторы, собранные со
всех уголков России, гарантии успешной сдачи и оптимальной цены, а также индивидуальный подход к каждому клиенту.
До начала ЕГЭ осталось совсем мало времени. Многие школьники в этому году выбрали математику в качестве профильного предмета. Но у выпускников нередко возникают затруднения при решении экзаменационных задач. Эксперты проанализировали популярные ошибки школьников при сдаче ЕГЭ по математике. В статье мы расскажем о том, как их избежать.
Самые частые ошибки
Эксперты отмечают, что с каждым годом растет число ошибок при решении геометрических задач. Многие школьники испытывают трудности при построении и чтении чертежей.
Немало выпускников ошибается при решении сложных неравенств с логарифмами и тригонометрическими функциями. Большой процент ошибок связан с заданиями на вычисление производных.
Однако первое место занимают арифметические ошибки. Они считаются самыми нелепыми и обидными, так как чаще всего допускаются по невнимательности. Бывают случаи, когда школьник отлично справился со сложным заданием, но при решении простой задачи случайно ошибся в вычислениях.
Далее мы рассмотрим самые частые ошибки и поговорим о том, как их избежать.
Вычисление процентов
Часто школьники делают ошибки в таких заданиях. Проценты изучают еще в 5 классе. Но нередко выпускники затрудняются при выполнении подобных задач. Причиной этого становятся пробелы в знаниях и непонимание сути процента.
Чтобы не допустить подобных ошибок, нужно повторить пройденный в 5 классе материал и вспомнить основы расчета процентов.
Невнимательность при чтении заданий
Сдача ЕГЭ часто связана с волнением и стрессом. В некоторых случаях это приводит к рассеянности. Многие школьники ошибаются не из-за слабого знания предмета, а по невнимательности.
Это самый досадный тип ошибок. Чтобы их избежать, необходимо сконцентрироваться, а затем не спеша, несколько раз прочитать текст задания. При этом нужно хорошо вдуматься в условия задачи.
Непонимание текста задачи
Нередки случаи, когда участники ЕГЭ не понимают условия задания. Это чаще всего происходит при решении практико-ориентированных задач. Многие школьники и вовсе пропускают такие нестандартные задания, что отрицательно сказывается на результате тестирования.
К практико-ориентированным заданиям можно отнести задачи на движение. Они требуют навыков математического моделирования. Часто школьники не понимают принципы движения и взаимосвязь величин, что приводит к ошибкам.
Иногда непонимание условий задач связано с плохим знанием величин и формул. В этом случае необходимо повторить теоретический материал. Следует также потренироваться в решении разнообразных задач с нестандартными условиями.
Ошибки при расчетах
В наши дни немало школьников постоянно пользуется калькулятором. Они разучиваются считать в уме и на бумаге. В результате на ЕГЭ многие выпускники допускают ошибки при элементарных вычислениях.
Чаще всего выпускники ошибаются при действиях с дробями и отрицательными числами, а также при преобразовании выражений. Эти пробелы в знаниях идут еще с 5 класса.
Если вы заметили у себя подобные проблемы, то подробно изучите ту тему, которую вы плохо знаете. Помните, что такие задания обязательно встретятся вам на экзамене.
Слабое знание теории
Плохое знание теоретических основ алгебры и геометрии — частая причина ошибок на ЕГЭ. Перед тестированием следует не только восстановить в памяти пройденный материал, но и потренироваться в решении заданий базового и профильного уровня.
В интернете вы можете найти реальные варианты ЕГЭ по математике прошлых лет. Попробуйте решить эти задачи и сравните результаты с правильными ответами. Если вы не понимаете, где ошиблись, то обратитесь за помощью к учителю или репетитору.
Неправильный алгоритм решения
Нередко школьники выполняют математические действия в неправильной последовательности и получают неверный результат задачи. Такие ошибки встречаются при решении рациональных дробных уравнений и логарифмических неравенств.
Научитесь правильному алгоритму решения таких задач. Всегда проверяйте полученный результат, подставив его в уравнение.
Неумение строить доказательство
В геометрии часто встречаются такие задачи, которые нужно не только решить, но и доказать полученный результат. Если вы испытываете затруднения при выполнении таких заданий, то потренируйтесь в логическом построении доказательств. Учитесь обосновывать метод решения задачи и полученные данные.
Ошибки в задачах по стереометрии
Многие выпускники испытывают трудности в чтении и построении чертежей. Далеко не все школьники обладают хорошими пространственными представлениями. В таких случаях нужно нарисовать конструкцию на черновике. Визуализация задачи облегчит ее решение.
Задания по тригонометрии
Тригонометрия — один из самых сложных разделов математики. Задания с тригонометрическими функциями часто вызывают затруднения.
Задачи по тригонометрии требуют хороших знаний теоретических фактов и умения применять их на практике. При их решении нужна внимательность и аккуратность.
Как правильно читать и решать задачу
Чтобы избежать ошибок, придерживайтесь следующего алгоритма при выполнении заданий:
- Медленно и вдумчиво изучите условие задачи. Прочитайте его несколько раз.
- Запишите на черновик все величины. Если вы выполняете задание по геометрии, то сделайте чертеж.
- Выявите взаимосвязи между данными и запишите их.
- Выпишите вопрос задачи.
- Определите, к какому типу относится задание.
- Составьте план решения задачи. Напишите в черновике последовательность ваших действий.
Обязательно записывайте все на бумаге, а не держите в уме. Не спешите сразу приступать к решению, сделайте небольшую паузу. Психологи считают, что это помогает получить наилучшие результаты.
Всегда начинайте с самых простых задач, а затем переходите к сложным. Это сбережет ваши силы и энергию, а также поможет избежать ошибок из-за невнимательности и усталости.
Заключение
ЕГЭ по математике требует серьезной подготовки. Перед тестированием следует восстановить в памяти теорию, восполнить все пробелы в знаниях и потренироваться в решении разнообразных заданий. Во время экзамена очень важно сконцентрироваться на задаче и вдумчиво изучать ее условия.
Нашли нарушение? Пожаловаться на содержание
И снова здравствуйте, уважаемые одиннадцатиклассники! Полагаю, что Вы хорошо отдохнули и готовы к работе для достижения своих высоких целей.
В этом году июнь месяц выдался очень продуктивным. Моя работа не закончилась 6 июня, когда мои ученики написали ЕГЭ по физике. После публикации результатов ЕГЭ (сначала по математике, а потом и по физике) стало поступать множество сообщений от учеников, даже тех, с кем я не занималась, с просьбой помочь разобраться, за что сняли баллы. А в некоторых случаях даже была необходима помощь с составлением апелляции. Бесценный опыт, если честно…..Только вот от этого опыта седых волос становится больше. И желание сжечь критерии не отпускает меня.
Сразу замечу, что апелляция возможна только по заданиям второй части. По первой части апелляция производится только тогда, когда компьютер неверно считал знак, записанный Вами в бланке ответов.
Уважаемые одиннадцатиклассники, вы должны понимать, что недостаточно просто получить верный ответ, недостаточно записать решение в стиле «я художник, я так вижу». Ваше решение будут оценивать по вполне определенным критериям. И даже абсолютно верный ответ не гарантирует полный балл за выполненное задание.
Анализ ошибок мы начнем с разбора сканов работ по профильной математике. Эти сканы я собирала не один год. К сожалению, в математике, просто за идею решения, за набор формул, не дадут ни одного балла. А снимают баллы за наличие вычислительных ошибок, недостаточную обоснованность, наличие лишних записей. Не указали необходимые признаки, свойства, теоремы – все, полный балл Вам не дадут.
Основной упор будет сделан на задачи 12, 14, 15 (уравнения, неравенства, задачи с экономическим содержанием). Это так называемый джентельменский набор, который старается выполнить большая часть выпускников. Погнали…
Для удобства статья представлена в двух форматах. Текст и видео. Вот ролик:
Уравнения
Основные ошибки:
1) неправильное использование формул приведения.
При преобразовании допущена ошибка. Минуса перед косинусом быть не должно. Задание оценивается в 0 баллов.
2) незнание свойств четных и нечетных функций. Также ребята забывают, что косинус функция честная, а вот синус, тангенс и котангенс нечетные.

2) незнание свойств четных и нечетных функций. Также ребята забывают, что косинус функция честная, а вот синус, тангенс и котангенс нечетные.
Классическая ошибка! – нечетная функция, следовательно знак минус выносится вперед, а не пропадает. Если бы функция была четная, то мы смело могли бы убрать знак минус. Задание оценивается в 0 баллов.
3) неправильное или некорректное использование тригонометрических формул.
Пару лет назад мне написал ученик, которому на экзамене досталось уравнение вида – нечетная функция, следовательно знак минус выносится вперед, а не пропадает. Если бы функция была четная, то мы смело могли бы убрать знак минус. Задание оценивается в 0 баллов.
3) неправильное или некорректное использование тригонометрических формул.
Пару лет назад мне написал ученик, которому на экзамене досталось уравнение вида 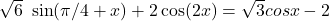
Скан он мне не отправил, но в процессе обсуждений выяснилось, что в первой скобке для он использовал не формулу синуса суммы, а формулы приведения. Чего делать категорически нельзя! Как Вы понимаете, задание оценили в 0 баллов.
4) Самое банальное. Неверное решение простейших тригонометрических уравнений.

4) Самое банальное. Неверное решение простейших тригонометрических уравнений.
При решении простейшего тригонометрического уравнения допущена ошибка. Третий и четвертый корень записаны неверно. Задание оценивается в 0 баллов.
Неравенства
С неравенствами у ребят дела идут посложнее, чем с уравнениями. Тут ваша фантазия разыгрывается по полной. Какие только ошибки не встречались(( Постараюсь выделить основные.
1)Пожалуй, самая распространенная ошибка – ошибка в расстановке знаков на координатной прямой. В идеале, если выпускник умеет определять – перед ним корень четного или нечетного порядка, меняется знак или дублируется.
Нули найдены верно. Но при расстановке знаков на координатной прямой допущена ошибка. Мы видим, что единица – нуль числителя второго порядка, следовательно знак сохраняется, и в крайнем левом интервале должен быть плюс. Эта ошибка уже позволяет эксперту поставить за данное задание 0 баллов.
2)Отбрасывание знаменателя и, как следствие, потеря части корней. В примере, приведенном ниже, выпускник отбросил знаменатель и находил нули только числителя.
Это привело к тому, что на координатной прямой не хватает нулей двух скобок: .
Такая грубая ошибка на экзамене не прощается.
Оценка эксперта – 0 баллов.

Такая грубая ошибка на экзамене не прощается.
Оценка эксперта – 0 баллов.
3) Неравносильный переход от неравенства к системе неравенств.
Я думаю, эта ошибка даже не нуждается в комментариях. Даже несмотря на то, что ученик верно нашел нули, верно расставил знаки на координатной прямой, это задание оценили в 0 баллов. Если бы системы с тремя неравенствами не было, ученик имел бы возможность взять полный балл.
4) Ошибки при использовании свойств логарифмов.
Стоит заметить, что для снятия логарифмов в правой и левой части, необходимо, чтобы перед логарифмом не было никаких цифр или букв. Выпускник снял логарифмы, хотя по задумке нужно было в правой части свернуть в полный квадрат подлогарифмическое выражение и вынести общий множитель. Как Вы понимаете, эксперт оценил это задание в 0 баллов.
Из моего текста у Вас, возможно, сложилось впечатление, что эксперты по всем поводам снимают сразу два балла. К счастью, это не так. Один балл Вам могут поставить, если Вы допустили ошибку в скобке (вместо круглой написали квадратную или наоборот) или допустили вычислительную ошибку, но при этом присутствует верная последовательность всех шагов решения.
Экономические задачи
В решении задач с экономическим содержанием ребятам в первую очередь нужно определить, какая форма кредитования – с дифференцированными платежами, аннуитентными или иная форма кредитования.
Могу выделить несколько основных ошибок.
1)Неверное построение математической модели, связанное с неверным определением формы кредитования.
Для лучшего понимания начну с условия задачи.
В июле 2026 года будет взят кредит на три года в размере 800 тыс рублей. Условия возврата таковы:
– каждый январь долг возрастает на 10 процентов по сравнению с концом прошлого года
– размер платежей в 2027 и 2028 годах одинаковый
– к июлю 2029 года долг выплачивается полностью.
Также известно, что в 2029 году платеж составит 833,8 тыс рублей. Сколько рублей будет составлять платеж в 2027 году?
Согласно записям таблицы, ученик решил, что перед ним дифференцированная форма кредитования и остаток уменьшается у него равномерно, ровно на N рублей каждый год. Но это совсем не так. Из условия задачи, мы видим, что выплаты одинаковые первые два года. Но при этом остаток не будет уменьшаться равномерно. Правильная запись остатка во второй строчке должна выглядеть так: .
Основываясь на критериях оценивания данного задания, математическая модель построена неверно, задание оценивается в 0 баллов.
Идем дальше. Наверняка Вы встречали задачи вида:
15 января 2020 года был выдан кредит на сумму 900 тыс. рублей на 31 месяц. Условия возврата таковы:
– 1 -го числа каждого месяца долг увеличивается на 2 по сравнению с концом предыдущего месяца.
– со 2 по 14 число необходимо выплатить часть долга;
– 15 -го числа каждого месяца с 1-го по 30-й долг должен быть на одну и ту же величину меньше долго на 15 число предыдущего месяца;
– 15 июля 2027 года долг составит 300 тыс рублей.
– 15 августа 2027 года долг должен быть выплачен полностью.
Найдите общую сумму выплат после полного погашения кредита.

Основываясь на критериях оценивания данного задания, математическая модель построена неверно, задание оценивается в 0 баллов.
Идем дальше. Наверняка Вы встречали задачи вида:
15 января 2020 года был выдан кредит на сумму 900 тыс. рублей на 31 месяц. Условия возврата таковы:
– 1 -го числа каждого месяца долг увеличивается на 2 по сравнению с концом предыдущего месяца.
– со 2 по 14 число необходимо выплатить часть долга;
– 15 -го числа каждого месяца с 1-го по 30-й долг должен быть на одну и ту же величину меньше долго на 15 число предыдущего месяца;
– 15 июля 2027 года долг составит 300 тыс рублей.
– 15 августа 2027 года долг должен быть выплачен полностью.
Найдите общую сумму выплат после полного погашения кредита.
В этой таблице полностью неправильно записаны столбцы с остатками и выплатами. Согласно условию задачи, первые 30 месяцев долг уменьшается равномерно, на меньше чем, прошлом месяце. Но не забываем, что первоначальный долг – это S, а не Sk рублей. То есть остаток в первые 30 месяцев должен выглядеть так:
меньше чем, прошлом месяце. Но не забываем, что первоначальный долг – это S, а не Sk рублей. То есть остаток в первые 30 месяцев должен выглядеть так:
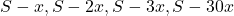
.
С учетом полностью неправильно построенной математической модели, задание оценивается в 0 баллов.
2)Ошибки при применении формул арифметической прогрессии и расчета общей суммы выплат.
Год назад ребятам на экзамене попалась задача, где в процессе кредитования менялась процентная ставка. Приведу пример:
25 августа 2020 года был дан кредит на 12 лет в размере 300 тыс рублей.
— 25 января с 2021 по 2026 года долг возрастает на 10 процентов;
— 25 января с 2027 по 2032 года долг возрастает на 15 процентов;
– с февраля по июль необходимо выплатить часть долга;
– в августе каждого года долг должен быть на одну и туже величину меньше по сравнению с августом прошлого года;
– к августу 2032 года кредит должен быть полностью погашен.
Найдите общую сумму выплат после полного погашения кредита.
Я уверена, что для многих ребят покажется очевидным, что нельзя складывать первую и последнюю (двенадцатую) выплату. Но я все же поясню.
Действительно, это задача на дифференцированные платежи. И можно заметить, что выплаты подчиняются арифметической прогрессии. Но так как у вас меняется процентная ставка, у Вас меняется и так называемый коэффициент или разность арифметической прогрессии. Поэтому правильно будет сначала просуммировать по формуле арифметической прогрессии первые шесть выплат, потом вторые шесть и полученные выражения сложить. Таким образом Вы получите верный ответ.
В каком же случае Вы можете получить 1 балл – если Вы верно построили математическую модель, но допустили вычислительную ошибку при получении численного значения.
PS: в подавляющем большинстве работ, которые поступали на проверку, ребята просили пояснить, почему за параметр (17 задание) и за задание на числа и их свойства так сильно срезали баллы. В большинстве случаев ребята получали по одному баллу за параметр, а в задаче на числа им засчитывали только пункт а), который также дает только один балл. Ребята, эти задачи считаются олимпиадными, не зря за их полное выполнение дается целых 4 балла. Критерии оценивания данных номеров очень жесткие. Должно быть и максимальное подробное объяснение, и разбор всех случаев и вариантов. В 17 задании это и правильно построенный график (если это необходимо), и рассчитаные все точки, и правильно раскрытый модуль, и расписанные все значения параметра и т.д и т.д.
В погоне за «легкими «баллами ребята даже не трогают планиметрию и стереометрию. А они, напомню, оцениваются в три балла каждый. Даже если Вы испытываете трудности в геометрии, пункт а (доказательство) не пропускайте мимо, как правило он значительно легче пункта б), где нужно найти численное значение той или иной величины. Но по одному первичному баллу за каждый номер Вы спокойно можете получить.
На этом мой краткий обзор подошел к концу. Я желаю удачи и сил всем одиннадцатиклассникам в этом году. Не бойтесь ЕГЭ, настраивайтесь на работу, идите к своей цели. У Вас все получится!
Все, что не убивает, делает нас сильнее!
P.S.: Вот моя группа ВКонтакте, где я выкладываю подобные тексты, ролики и полезности для ЕГЭ по физике и математике: https://vk.com/public185877660 Подписывайтесь!

Содержание
- Самые распространенные ошибки на ЕГЭ
- Задачи на проценты
- Невнимательное прочтение условий задачи
- Арифметические ошибки
- Неверное прочтение и построение чертежа
- Неумение дать развернутый ответ
- Как избежать ошибок по невнимательности
Для
успешной сдачи экзаменов важно начать подготовку заблаговременно. Если
самостоятельно не получается выявить свои слабые места и пробелы, стоит
разобраться, какие типичные ошибки чаще всего допускают выпускники. Ответ на
этот вопрос могут дать эксперты ФИПИ.
Самые
распространенные ошибки на ЕГЭ
Как
известно, математика делится на
базовую и профильную. Первую необходимо сдавать всем 11-классникам. А
профильный уровень относится к предметам по выбору. В нем содержатся
практико-ориентированные задания.
Нередко старшеклассники допускают ошибки теоретического характера из-за незнания определенных тем по
алгебре и геометрии. Также выпускники получают нулевые баллы, вычисляя
логарифмы и неравенства. Помимо этого, следует заняться изучением свойств и
графиков производных.
К
решению некоторых типов заданий придется готовиться с особым усилием. Рекомендуется
начинать с самой простой задачки, постепенно повышая уровень сложности. Помимо
этого, часть ошибок вызвана незнанием терминологии. Поэтому стоит обратить
внимание на изучение тригонометрических функций.
Задачи
на проценты
В
большинстве случаев ошибки связаны с тем, что школьники не понимают суть
процента. Например, если в задаче требуется сперва понизить цену на 20%, а
затем поднять на 20%.
Одной
из распространенных ошибок является то, что участники ЕГЭ думают, что проценты
равняются одной сумме. Однако считать нужно от старой цены. Поэтому
рекомендуется уделить внимание повторению основ подсчета процентов и
взаимосвязи величин.
Невнимательное
прочтение условий задачи
Из-за
волнения и напряженной обстановки многие ученики неверно понимают условие
математической задачи. В результате школьникам снижают итоговые баллы. Поэтому
желательно несколько раз вдумчиво и медленно прочесть задание. Перед тем как
записать ответ в бланк, стоит проверить единицу измерения.
Арифметические
ошибки
На
ЕГЭ по математике запрещено
пользоваться калькулятором. Поэтому при сдаче экзамена легкие вычисления вызывают у школьников затруднения. Если
не получается считать в столбик, то при прохождении тестирования есть риск
допустить глупую ошибку в простых примерах.
При этом выпускник может успешно справиться с задачами
второй части. Больше всего у участников единого госэкзамена возникают проблемы
с дробями и отрицательными числами. Это обычно копится на с пятого класса.
Также
следует внимательно смотреть за наличием минуса при вычислении. Если не удается
безошибочно решать определенные виды задач, следует тщательно изучить сложную
тему. Поскольку она может попасться в тестовой части ЕГЭ, что повлияет на
результат.
Неверное
прочтение и построение чертежа
Нередки
случаи, когда выпускник не может уловить взаимосвязь элементов геометрических
конструкций. Либо не владеет пространственными представлениями. Стоит научиться
правильно читать буквенные записи на чертежах.
В
частности, немало школьников допускали ошибки, путая расположение вершин углов.
Если с этим возникают сложности, рекомендуется потренироваться в решении
подобных задач. Так что стоит сперва решить задание на черновике для
визуализации.
Неумение
дать развернутый ответ
Задания
№14 и 16 обладают повышенной степенью сложности. В них требуется давать
развернутый ответ на отдельном бланке. Каждая задача делится на 2 пункта:
сначала понадобится доказать, а потом – сделать вычисления.
Зачастую
школьники сталкиваются с проблемой приведения доказательств. Поэтому в 1-ом
пункте многие участники неправильно оформляют ответ. Так что рекомендуется тренироваться
в доказательной базе и научиться обосновать методы решения.
Как
избежать ошибок по невнимательности
Существует
несколько советов, которые помогут не ошибиться из-за невнимательного прочтения
задачи. Для этого стоит придерживаться такой последовательности действий:
- Прочесть условие.
- Выписать данные величины. Также требуется
сделать чертеж в задаче по геометрии. - Установить взаимосвязи между известными
величинами. - Выписать, что нужно необходимо найти, и на
какие вопросы ответить. - Определить тип задачи.
- Сформулировать содержание и порядок
действий.
Это поможет не совершить обидных ошибок, потеряв
баллы. Данные условия необходимо выписывать на листок. Если просто
зафиксировать их в уме, можно в итоге получить неверный ответ.
Кроме того, важно не приступать к решению задачи
сразу, лишь прочитав ее. Психологи советуют выдерживать паузы перед записью
ответа, чтобы добиться успешных результатов.
Компания «РосДиплом» на протяжении 20 лет занимается студенческими работами и предлагает помощь студентам во всех областях и темах. Наши преимущества: огромный опыт работы, лучшие авторы, собранные со
всех уголков России, гарантии успешной сдачи и оптимальной цены, а также индивидуальный подход к каждому клиенту.
До начала ЕГЭ осталось совсем мало времени. Многие школьники в этому году выбрали математику в качестве профильного предмета. Но у выпускников нередко возникают затруднения при решении экзаменационных задач. Эксперты проанализировали популярные ошибки школьников при сдаче ЕГЭ по математике. В статье мы расскажем о том, как их избежать.
Самые частые ошибки
Эксперты отмечают, что с каждым годом растет число ошибок при решении геометрических задач. Многие школьники испытывают трудности при построении и чтении чертежей.
Немало выпускников ошибается при решении сложных неравенств с логарифмами и тригонометрическими функциями. Большой процент ошибок связан с заданиями на вычисление производных.
Однако первое место занимают арифметические ошибки. Они считаются самыми нелепыми и обидными, так как чаще всего допускаются по невнимательности. Бывают случаи, когда школьник отлично справился со сложным заданием, но при решении простой задачи случайно ошибся в вычислениях.
Далее мы рассмотрим самые частые ошибки и поговорим о том, как их избежать.
Вычисление процентов
Часто школьники делают ошибки в таких заданиях. Проценты изучают еще в 5 классе. Но нередко выпускники затрудняются при выполнении подобных задач. Причиной этого становятся пробелы в знаниях и непонимание сути процента.
Чтобы не допустить подобных ошибок, нужно повторить пройденный в 5 классе материал и вспомнить основы расчета процентов.
Невнимательность при чтении заданий
Сдача ЕГЭ часто связана с волнением и стрессом. В некоторых случаях это приводит к рассеянности. Многие школьники ошибаются не из-за слабого знания предмета, а по невнимательности.
Это самый досадный тип ошибок. Чтобы их избежать, необходимо сконцентрироваться, а затем не спеша, несколько раз прочитать текст задания. При этом нужно хорошо вдуматься в условия задачи.
Непонимание текста задачи
Нередки случаи, когда участники ЕГЭ не понимают условия задания. Это чаще всего происходит при решении практико-ориентированных задач. Многие школьники и вовсе пропускают такие нестандартные задания, что отрицательно сказывается на результате тестирования.
К практико-ориентированным заданиям можно отнести задачи на движение. Они требуют навыков математического моделирования. Часто школьники не понимают принципы движения и взаимосвязь величин, что приводит к ошибкам.
Иногда непонимание условий задач связано с плохим знанием величин и формул. В этом случае необходимо повторить теоретический материал. Следует также потренироваться в решении разнообразных задач с нестандартными условиями.
Ошибки при расчетах
В наши дни немало школьников постоянно пользуется калькулятором. Они разучиваются считать в уме и на бумаге. В результате на ЕГЭ многие выпускники допускают ошибки при элементарных вычислениях.
Чаще всего выпускники ошибаются при действиях с дробями и отрицательными числами, а также при преобразовании выражений. Эти пробелы в знаниях идут еще с 5 класса.
Если вы заметили у себя подобные проблемы, то подробно изучите ту тему, которую вы плохо знаете. Помните, что такие задания обязательно встретятся вам на экзамене.
Слабое знание теории
Плохое знание теоретических основ алгебры и геометрии — частая причина ошибок на ЕГЭ. Перед тестированием следует не только восстановить в памяти пройденный материал, но и потренироваться в решении заданий базового и профильного уровня.
В интернете вы можете найти реальные варианты ЕГЭ по математике прошлых лет. Попробуйте решить эти задачи и сравните результаты с правильными ответами. Если вы не понимаете, где ошиблись, то обратитесь за помощью к учителю или репетитору.
Неправильный алгоритм решения
Нередко школьники выполняют математические действия в неправильной последовательности и получают неверный результат задачи. Такие ошибки встречаются при решении рациональных дробных уравнений и логарифмических неравенств.
Научитесь правильному алгоритму решения таких задач. Всегда проверяйте полученный результат, подставив его в уравнение.
Неумение строить доказательство
В геометрии часто встречаются такие задачи, которые нужно не только решить, но и доказать полученный результат. Если вы испытываете затруднения при выполнении таких заданий, то потренируйтесь в логическом построении доказательств. Учитесь обосновывать метод решения задачи и полученные данные.
Ошибки в задачах по стереометрии
Многие выпускники испытывают трудности в чтении и построении чертежей. Далеко не все школьники обладают хорошими пространственными представлениями. В таких случаях нужно нарисовать конструкцию на черновике. Визуализация задачи облегчит ее решение.
Задания по тригонометрии
Тригонометрия — один из самых сложных разделов математики. Задания с тригонометрическими функциями часто вызывают затруднения.
Задачи по тригонометрии требуют хороших знаний теоретических фактов и умения применять их на практике. При их решении нужна внимательность и аккуратность.
Как правильно читать и решать задачу
Чтобы избежать ошибок, придерживайтесь следующего алгоритма при выполнении заданий:
- Медленно и вдумчиво изучите условие задачи. Прочитайте его несколько раз.
- Запишите на черновик все величины. Если вы выполняете задание по геометрии, то сделайте чертеж.
- Выявите взаимосвязи между данными и запишите их.
- Выпишите вопрос задачи.
- Определите, к какому типу относится задание.
- Составьте план решения задачи. Напишите в черновике последовательность ваших действий.
Обязательно записывайте все на бумаге, а не держите в уме. Не спешите сразу приступать к решению, сделайте небольшую паузу. Психологи считают, что это помогает получить наилучшие результаты.
Всегда начинайте с самых простых задач, а затем переходите к сложным. Это сбережет ваши силы и энергию, а также поможет избежать ошибок из-за невнимательности и усталости.
Заключение
ЕГЭ по математике требует серьезной подготовки. Перед тестированием следует восстановить в памяти теорию, восполнить все пробелы в знаниях и потренироваться в решении разнообразных заданий. Во время экзамена очень важно сконцентрироваться на задаче и вдумчиво изучать ее условия.
Нашли нарушение? Пожаловаться на содержание
Скачать материал

Скачать материал

С учетом полностью неправильно построенной математической модели, задание оценивается в 0 баллов.
2)Ошибки при применении формул арифметической прогрессии и расчета общей суммы выплат.
Год назад ребятам на экзамене попалась задача, где в процессе кредитования менялась процентная ставка. Приведу пример:
25 августа 2020 года был дан кредит на 12 лет в размере 300 тыс рублей.
— 25 января с 2021 по 2026 года долг возрастает на 10 процентов;
— 25 января с 2027 по 2032 года долг возрастает на 15 процентов;
– с февраля по июль необходимо выплатить часть долга;
– в августе каждого года долг должен быть на одну и туже величину меньше по сравнению с августом прошлого года;
– к августу 2032 года кредит должен быть полностью погашен.
Найдите общую сумму выплат после полного погашения кредита.
Я уверена, что для многих ребят покажется очевидным, что нельзя складывать первую и последнюю (двенадцатую) выплату. Но я все же поясню.
Действительно, это задача на дифференцированные платежи. И можно заметить, что выплаты подчиняются арифметической прогрессии. Но так как у вас меняется процентная ставка, у Вас меняется и так называемый коэффициент или разность арифметической прогрессии. Поэтому правильно будет сначала просуммировать по формуле арифметической прогрессии первые шесть выплат, потом вторые шесть и полученные выражения сложить. Таким образом Вы получите верный ответ.
В каком же случае Вы можете получить 1 балл – если Вы верно построили математическую модель, но допустили вычислительную ошибку при получении численного значения.
PS: в подавляющем большинстве работ, которые поступали на проверку, ребята просили пояснить, почему за параметр (17 задание) и за задание на числа и их свойства так сильно срезали баллы. В большинстве случаев ребята получали по одному баллу за параметр, а в задаче на числа им засчитывали только пункт а), который также дает только один балл. Ребята, эти задачи считаются олимпиадными, не зря за их полное выполнение дается целых 4 балла. Критерии оценивания данных номеров очень жесткие. Должно быть и максимальное подробное объяснение, и разбор всех случаев и вариантов. В 17 задании это и правильно построенный график (если это необходимо), и рассчитаные все точки, и правильно раскрытый модуль, и расписанные все значения параметра и т.д и т.д.
В погоне за «легкими «баллами ребята даже не трогают планиметрию и стереометрию. А они, напомню, оцениваются в три балла каждый. Даже если Вы испытываете трудности в геометрии, пункт а (доказательство) не пропускайте мимо, как правило он значительно легче пункта б), где нужно найти численное значение той или иной величины. Но по одному первичному баллу за каждый номер Вы спокойно можете получить.
На этом мой краткий обзор подошел к концу. Я желаю удачи и сил всем одиннадцатиклассникам в этом году. Не бойтесь ЕГЭ, настраивайтесь на работу, идите к своей цели. У Вас все получится!
Все, что не убивает, делает нас сильнее!
P.S.: Вот моя группа ВКонтакте, где я выкладываю подобные тексты, ролики и полезности для ЕГЭ по физике и математике: https://vk.com/public185877660 Подписывайтесь!

Содержание
- Самые распространенные ошибки на ЕГЭ
- Задачи на проценты
- Невнимательное прочтение условий задачи
- Арифметические ошибки
- Неверное прочтение и построение чертежа
- Неумение дать развернутый ответ
- Как избежать ошибок по невнимательности
Для
успешной сдачи экзаменов важно начать подготовку заблаговременно. Если
самостоятельно не получается выявить свои слабые места и пробелы, стоит
разобраться, какие типичные ошибки чаще всего допускают выпускники. Ответ на
этот вопрос могут дать эксперты ФИПИ.
Самые
распространенные ошибки на ЕГЭ
Как
известно, математика делится на
базовую и профильную. Первую необходимо сдавать всем 11-классникам. А
профильный уровень относится к предметам по выбору. В нем содержатся
практико-ориентированные задания.
Нередко старшеклассники допускают ошибки теоретического характера из-за незнания определенных тем по
алгебре и геометрии. Также выпускники получают нулевые баллы, вычисляя
логарифмы и неравенства. Помимо этого, следует заняться изучением свойств и
графиков производных.
К
решению некоторых типов заданий придется готовиться с особым усилием. Рекомендуется
начинать с самой простой задачки, постепенно повышая уровень сложности. Помимо
этого, часть ошибок вызвана незнанием терминологии. Поэтому стоит обратить
внимание на изучение тригонометрических функций.
Задачи
на проценты
В
большинстве случаев ошибки связаны с тем, что школьники не понимают суть
процента. Например, если в задаче требуется сперва понизить цену на 20%, а
затем поднять на 20%.
Одной
из распространенных ошибок является то, что участники ЕГЭ думают, что проценты
равняются одной сумме. Однако считать нужно от старой цены. Поэтому
рекомендуется уделить внимание повторению основ подсчета процентов и
взаимосвязи величин.
Невнимательное
прочтение условий задачи
Из-за
волнения и напряженной обстановки многие ученики неверно понимают условие
математической задачи. В результате школьникам снижают итоговые баллы. Поэтому
желательно несколько раз вдумчиво и медленно прочесть задание. Перед тем как
записать ответ в бланк, стоит проверить единицу измерения.
Арифметические
ошибки
На
ЕГЭ по математике запрещено
пользоваться калькулятором. Поэтому при сдаче экзамена легкие вычисления вызывают у школьников затруднения. Если
не получается считать в столбик, то при прохождении тестирования есть риск
допустить глупую ошибку в простых примерах.
При этом выпускник может успешно справиться с задачами
второй части. Больше всего у участников единого госэкзамена возникают проблемы
с дробями и отрицательными числами. Это обычно копится на с пятого класса.
Также
следует внимательно смотреть за наличием минуса при вычислении. Если не удается
безошибочно решать определенные виды задач, следует тщательно изучить сложную
тему. Поскольку она может попасться в тестовой части ЕГЭ, что повлияет на
результат.
Неверное
прочтение и построение чертежа
Нередки
случаи, когда выпускник не может уловить взаимосвязь элементов геометрических
конструкций. Либо не владеет пространственными представлениями. Стоит научиться
правильно читать буквенные записи на чертежах.
В
частности, немало школьников допускали ошибки, путая расположение вершин углов.
Если с этим возникают сложности, рекомендуется потренироваться в решении
подобных задач. Так что стоит сперва решить задание на черновике для
визуализации.
Неумение
дать развернутый ответ
Задания
№14 и 16 обладают повышенной степенью сложности. В них требуется давать
развернутый ответ на отдельном бланке. Каждая задача делится на 2 пункта:
сначала понадобится доказать, а потом – сделать вычисления.
Зачастую
школьники сталкиваются с проблемой приведения доказательств. Поэтому в 1-ом
пункте многие участники неправильно оформляют ответ. Так что рекомендуется тренироваться
в доказательной базе и научиться обосновать методы решения.
Как
избежать ошибок по невнимательности
Существует
несколько советов, которые помогут не ошибиться из-за невнимательного прочтения
задачи. Для этого стоит придерживаться такой последовательности действий:
- Прочесть условие.
- Выписать данные величины. Также требуется
сделать чертеж в задаче по геометрии. - Установить взаимосвязи между известными
величинами. - Выписать, что нужно необходимо найти, и на
какие вопросы ответить. - Определить тип задачи.
- Сформулировать содержание и порядок
действий.
Это поможет не совершить обидных ошибок, потеряв
баллы. Данные условия необходимо выписывать на листок. Если просто
зафиксировать их в уме, можно в итоге получить неверный ответ.
Кроме того, важно не приступать к решению задачи
сразу, лишь прочитав ее. Психологи советуют выдерживать паузы перед записью
ответа, чтобы добиться успешных результатов.
Компания «РосДиплом» на протяжении 20 лет занимается студенческими работами и предлагает помощь студентам во всех областях и темах. Наши преимущества: огромный опыт работы, лучшие авторы, собранные со
всех уголков России, гарантии успешной сдачи и оптимальной цены, а также индивидуальный подход к каждому клиенту.
До начала ЕГЭ осталось совсем мало времени. Многие школьники в этому году выбрали математику в качестве профильного предмета. Но у выпускников нередко возникают затруднения при решении экзаменационных задач. Эксперты проанализировали популярные ошибки школьников при сдаче ЕГЭ по математике. В статье мы расскажем о том, как их избежать.
Самые частые ошибки
Эксперты отмечают, что с каждым годом растет число ошибок при решении геометрических задач. Многие школьники испытывают трудности при построении и чтении чертежей.
Немало выпускников ошибается при решении сложных неравенств с логарифмами и тригонометрическими функциями. Большой процент ошибок связан с заданиями на вычисление производных.
Однако первое место занимают арифметические ошибки. Они считаются самыми нелепыми и обидными, так как чаще всего допускаются по невнимательности. Бывают случаи, когда школьник отлично справился со сложным заданием, но при решении простой задачи случайно ошибся в вычислениях.
Далее мы рассмотрим самые частые ошибки и поговорим о том, как их избежать.
Вычисление процентов
Часто школьники делают ошибки в таких заданиях. Проценты изучают еще в 5 классе. Но нередко выпускники затрудняются при выполнении подобных задач. Причиной этого становятся пробелы в знаниях и непонимание сути процента.
Чтобы не допустить подобных ошибок, нужно повторить пройденный в 5 классе материал и вспомнить основы расчета процентов.
Невнимательность при чтении заданий
Сдача ЕГЭ часто связана с волнением и стрессом. В некоторых случаях это приводит к рассеянности. Многие школьники ошибаются не из-за слабого знания предмета, а по невнимательности.
Это самый досадный тип ошибок. Чтобы их избежать, необходимо сконцентрироваться, а затем не спеша, несколько раз прочитать текст задания. При этом нужно хорошо вдуматься в условия задачи.
Непонимание текста задачи
Нередки случаи, когда участники ЕГЭ не понимают условия задания. Это чаще всего происходит при решении практико-ориентированных задач. Многие школьники и вовсе пропускают такие нестандартные задания, что отрицательно сказывается на результате тестирования.
К практико-ориентированным заданиям можно отнести задачи на движение. Они требуют навыков математического моделирования. Часто школьники не понимают принципы движения и взаимосвязь величин, что приводит к ошибкам.
Иногда непонимание условий задач связано с плохим знанием величин и формул. В этом случае необходимо повторить теоретический материал. Следует также потренироваться в решении разнообразных задач с нестандартными условиями.
Ошибки при расчетах
В наши дни немало школьников постоянно пользуется калькулятором. Они разучиваются считать в уме и на бумаге. В результате на ЕГЭ многие выпускники допускают ошибки при элементарных вычислениях.
Чаще всего выпускники ошибаются при действиях с дробями и отрицательными числами, а также при преобразовании выражений. Эти пробелы в знаниях идут еще с 5 класса.
Если вы заметили у себя подобные проблемы, то подробно изучите ту тему, которую вы плохо знаете. Помните, что такие задания обязательно встретятся вам на экзамене.
Слабое знание теории
Плохое знание теоретических основ алгебры и геометрии — частая причина ошибок на ЕГЭ. Перед тестированием следует не только восстановить в памяти пройденный материал, но и потренироваться в решении заданий базового и профильного уровня.
В интернете вы можете найти реальные варианты ЕГЭ по математике прошлых лет. Попробуйте решить эти задачи и сравните результаты с правильными ответами. Если вы не понимаете, где ошиблись, то обратитесь за помощью к учителю или репетитору.
Неправильный алгоритм решения
Нередко школьники выполняют математические действия в неправильной последовательности и получают неверный результат задачи. Такие ошибки встречаются при решении рациональных дробных уравнений и логарифмических неравенств.
Научитесь правильному алгоритму решения таких задач. Всегда проверяйте полученный результат, подставив его в уравнение.
Неумение строить доказательство
В геометрии часто встречаются такие задачи, которые нужно не только решить, но и доказать полученный результат. Если вы испытываете затруднения при выполнении таких заданий, то потренируйтесь в логическом построении доказательств. Учитесь обосновывать метод решения задачи и полученные данные.
Ошибки в задачах по стереометрии
Многие выпускники испытывают трудности в чтении и построении чертежей. Далеко не все школьники обладают хорошими пространственными представлениями. В таких случаях нужно нарисовать конструкцию на черновике. Визуализация задачи облегчит ее решение.
Задания по тригонометрии
Тригонометрия — один из самых сложных разделов математики. Задания с тригонометрическими функциями часто вызывают затруднения.
Задачи по тригонометрии требуют хороших знаний теоретических фактов и умения применять их на практике. При их решении нужна внимательность и аккуратность.
Как правильно читать и решать задачу
Чтобы избежать ошибок, придерживайтесь следующего алгоритма при выполнении заданий:
- Медленно и вдумчиво изучите условие задачи. Прочитайте его несколько раз.
- Запишите на черновик все величины. Если вы выполняете задание по геометрии, то сделайте чертеж.
- Выявите взаимосвязи между данными и запишите их.
- Выпишите вопрос задачи.
- Определите, к какому типу относится задание.
- Составьте план решения задачи. Напишите в черновике последовательность ваших действий.
Обязательно записывайте все на бумаге, а не держите в уме. Не спешите сразу приступать к решению, сделайте небольшую паузу. Психологи считают, что это помогает получить наилучшие результаты.
Всегда начинайте с самых простых задач, а затем переходите к сложным. Это сбережет ваши силы и энергию, а также поможет избежать ошибок из-за невнимательности и усталости.
Заключение
ЕГЭ по математике требует серьезной подготовки. Перед тестированием следует восстановить в памяти теорию, восполнить все пробелы в знаниях и потренироваться в решении разнообразных заданий. Во время экзамена очень важно сконцентрироваться на задаче и вдумчиво изучать ее условия.
Нашли нарушение? Пожаловаться на содержание
Скачать материал

Скачать материал




- Сейчас обучается 396 человек из 63 регионов




Описание презентации по отдельным слайдам:
-
1 слайд
Типичные ошибки в ЕГЭ по математике
Советы по подготовке -
2 слайд
1 часть:
8 заданий с кратким ответом базового уровня
2 часть:
4 задания с кратким ответом повышенного уровня сложности
7 заданий с развернутым ответом повышенного и высокого уровня сложности
Полученные баллы суммируются
Структура работы -
3 слайд
Выполняем внимательно
Не пишем в бланке ответов после числа единицы измерений
Не пишем карандашом (после сканирования записи исчезнут)
Исключаем возможность арифметической ошибки (делаем обязательную проверку)
Для экономии времени пропускаем задание, которое не удается решить сразу, а переходим к следующему
К выполнению пропущенных заданий можно вернуться, если останется время
Основное количество баллов можно и нужно получить за 12 первых заданий -
4 слайд
Минимум записей, но достаточный для того, чтобы контролировать решение, выполняя обратное действие, найти ошибку.
Устный счет создает лишь видимость экономии времени, при этом возникает риск допустить неустранимую ошибку. Даже если возникает подозрение в неправильности полученного ответа, как обнаружить ошибку в незаписанных выкладках? Все вычисления следует проводить на бумаге аккуратно и неторопливо, четко оформляя решение и ответ задачи.
Если вы будете решать устно, то каждый раз будете безуспешно ловить ускользающие от вас мысли «за хвост».
Вред от пристрастия к устному счету -
5 слайд
Знание приемов решения разных задач
Знание алгоритмов решения различных уравнений:
Линейные уравнения
Квадратные уравнения
Рациональные уравнения
Дробно-рациональные уравнения
Показательные уравнения
Логарифмические уравнения
Иррациональные уравнения
Тригонометрические уравненияЗнание общих методов решения уравнений
Замена уравнения h(f(x))=h(g(x)) уравнением f(x)=g(x)
Метод разложения на множители
Метод введения новой переменной
Функционально- графический метод
Знание общих методов решения неравенств
Знание специальных методов решения уравнений и неравенств. -
6 слайд
О потере корней
-деление обеих частей уравнения на одно и то же выражение
-сужение ОДЗ в процессе решения уравнения
Замена уравнения h(f(x))=h(g(x)) уравнением f(x)=g(x) в случае . если у=h(x) –немонотонная функцияРекомендуется следить за равносильностью уравнений и неравенств, полученных в результате преобразований
Правильное определение области допустимых значений – необходимое условие получения верного решения
ОДЗ, как правило, громоздка, ее вовсе не обязательно решать, лучше проверить решение подстановкой в ОДЗ -
7 слайд
Уметь задать себе вопрос «Что не нравится?»,
– думать на шаг вперед
Помечтать:
А что бы было, если…
На что похоже?
Примеры:
Вычислить 108 cos 2 23π /12 — 27
Знать формулы -
8 слайд
8−7𝑥 =𝑥
Если уравнение имеет несколько корней, в ответ запишите меньший
Ответ: 1
log 2 (−х) = log 2 ( х 2 −12)
Если уравнение имеет несколько корней, в ответ запишите больший
Ответ: -4
log х (4х) = 3
Если корней несколько, то в ответ запишите их произведение
Ответ: -4Задачи-ловушки
-
9 слайд
Правило за 100% брать ту величину, с которой мы сравниваем
Пример. Шесть одинаковых рубашек дешевле куртки на 2%. На сколько процентов девять таких рубашек дороже куртки?
Стоимость куртки возьмем за 100%
1) 100 – 2 = 98 (%) — 3 рубашки
2) 98 : 6 х 9 = 147 (%) — 9 рубашек
3) 147 – 100 = 47 (%)
Ответ: 47
Много ошибок при решении задач на проценты -
10 слайд
Быстрее по формуле:
А = А 0 1+ р 100 увеличение на р%
А = А 0 ( 1− р 100 ) уменьшение на р%
Пример решения задачи:
Телевизор стоил 11400 руб. На распродаже скидка на телевизор составила р% (р — целое число). Оказалось, что для покупки телевизора достаточно было 10000 руб. Найти наименьшее значение р.
А= А 0 1− р 100 ; А= 11400 1− р 100 ; А≤10000;
11400 1− р 100 ≤ 10000 ; р = 13
Формулы для решения задач на проценты -
11 слайд
Решаем 1 часть максимально быстро.
На чем можно сэкономить?
При решении задачи на движение
720 х − 720 х+10 =1
Х=10z
720 10𝑧 − 720 10𝑧+10 =1
72 𝑧 − 72 𝑧+1 =1
Ответ подбираем z=8
При решении задачи на смеси 0,3х+0.6у+5=0,41(х+у+10);
0,3х+0,6у=0,36(х+у+10)30х+60у+500=41(х+у+10);
30х+60у=36(х+у+10) -
12 слайд
Задание №13
ОТНОСИТЕЛЬНО НЕТРУДНОЕ УРАВНЕНИЕ
Может содержать тригонометрические функции, логарифмы, степени, корни, показательную функцию
Как правило, требует замены переменной, позволяющей свести уравнение к квадратному, и отбора корней на заданном отрезке, обусловленного ограниченностью новой переменной, наличием выражений с переменной в знаменателях дробей, а также под знаками корней четной степени и логарифмов -
13 слайд
Типичные ошибки в задании №13
Использование формулы корней для простейшего тригонометрического уравнения относительно синуса – к уравнению относительно косинуса и, наоборот, неверная периодичность корней, описки и другие ошибки в записи корня -
14 слайд
Типичные ошибки в задании № 13
По-прежнему, как и в прошлых годах, учащиеся теряют баллы в пункте б) решения задачи 13 по причине отсутствия обоснования отбора корней из промежутка
1 балл за решение пункта б) выставляется при условии присутствия «следов» отбора корней
Много ошибок связано с незнанием множества значений тригонометрических функций синус и косинус. В работах учащихся довольно часто в формуле корней тригонометрического уравнения встречались несуществующие значения обратных тригонометрических функций: -
15 слайд
Различные способы отбора корней
1. Арифметический способ:
а) непосредственная подстановка полученных корней в уравнение и имеющиеся ограничения;
б) перебор значений целочисленного параметра и вычисление корней.
2. Алгебраический способ:
а) решение неравенства относительно неизвестного целочисленного параметра и вычисление корней;
б) исследование уравнения с двумя целочисленными параметрами.
3. Геометрический способ:
а) изображение корней на тригонометрической окружности с последующим отбором и учетом имеющихся ограничений;
б) изображение корней на числовой прямой с последующим отбором и учетом имеющихся ограничений.
4. Функционально-графический способ:
выбор корней с помощью графика простейшей тригонометрической функции. -
16 слайд
Задания №14 и №16
Проверяют умения выполнять действия с геометрическими фигурами
В первом пункте – доказать
Во втором пункте – вычислить
Затруднения в оформлении доказательства
Неверное применение теоретического материала
Большое количество вычислительных ошибок -
17 слайд
Задание №15
Неравенство, содержащее степени, дроби, корни, логарифмы (в том числе, с переменным основанием).
Традиционно выполняемые задания
Основные проблемы:
Неумение решать логарифмические неравенства
Арифметические ошибки
Незнание свойств логарифмов
Неумение использовать замену переменных -
18 слайд
Задание №17
Задача с экономическим содержанием
Проблемы
Неумение работать с процентами
Неумение правильно считывать условие
Неумение составлять математическую модель по условию задачи
Вычислительные ошибки -
19 слайд
Задание №18
Задача с параметром
Нужно постараться решить эту задачу или хотя бы продвинуться в ее решении как можно дальше
Для успешного решения важно умение анализировать условие и находить возможные пути решения
Владеть функционально-графическими способами решения
Наибольшие проблемы:
Понимание логики задачи и анализ условия
Неумение искать ключевые факты и делать необходимые обоснования -
20 слайд
Задание №19
Задание олимпиадного типа
Для ее решения не требуется никаких специальных знаний, выходящих за рамки стандарта математического образования. Однако нужно проявить определенный уровень математической культуры, логического мышления.
Наибольшие проблемы:
Непонимание логики задачи
Неверный анализ условия
Неумение делать необходимые обоснования и выводы -
21 слайд
ЕГЭ 2017 (досрочный)
19. На доске написано несколько различных чисел, произведение любых двух из которых
больше 40 и меньше 100.
А) Может ли на доске быть 5 чисел?
Б) Может ли на доске быть 6 чисел?
В)Какое наибольшее значение может принимать сумма чисел на доске, если их четыре?А) Да
Например, 6;7;8;9; 10
Б) нет
В) 35 -
22 слайд
О проверке работ и об апелляции
Каждая работа проверяется
2 независимыми экспертами
При расхождении оценки двух экспертов по конкретному заданию на 1 балл выпускнику этот балл засчитывается
Если расхождение в оценке более 1 балла, то работу проверяет третий эксперт
При подаче апелляции вся ваша работа будет перепроверяться (а не только тот номер, с оценкой которого вы не согласны) -
23 слайд
Успешнее сдают ЕГЭ
— кто оказывается более внимательным и собранным;
— меньше делает ошибок в первой части;
— внимательно читает задания;
— не теряется увидев незнакомый или не типичный текст, а пытается соотнести его со своими знаниями;— использует рациональные приемы решений, счёта.
Умеет четко планировать своё время, расставлять приоритеты;
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 207 213 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 12.11.2020
- 395
- 1
- 13.09.2020
- 397
- 3
- 11.09.2020
- 478
- 1
- 10.09.2020
- 233
- 0
- 27.07.2020
- 306
- 19
- 15.06.2020
- 169
- 0
- 08.06.2020
- 441
- 0
- 01.06.2020
- 139
- 1
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Подростковый возраст — важнейшая фаза становления личности»
-
Курс повышения квалификации «Правовое обеспечение деятельности коммерческой организации и индивидуальных предпринимателей»
-
Курс повышения квалификации «Основы туризма и гостеприимства»
-
Курс повышения квалификации «Методика написания учебной и научно-исследовательской работы в школе (доклад, реферат, эссе, статья) в процессе реализации метапредметных задач ФГОС ОО»
-
Курс повышения квалификации «Управление финансами: как уйти от банкротства»
-
Курс повышения квалификации «Источники финансов»
-
Курс профессиональной переподготовки «Риск-менеджмент организации: организация эффективной работы системы управления рисками»
-
Курс профессиональной переподготовки «Политология: взаимодействие с органами государственной власти и управления, негосударственными и международными организациями»
-
Курс профессиональной переподготовки «Уголовно-правовые дисциплины: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Методика организации, руководства и координации музейной деятельности»
-
Курс профессиональной переподготовки «Техническая диагностика и контроль технического состояния автотранспортных средств»
-
Курс профессиональной переподготовки «Управление качеством»