Что понимают под ошибкой опыта

Изучение
всех влияющих на исследуемый объект
факторов одновременно провести
невозможно, поэтому в эксперименте
рассматривается их ограниченное число.
Остальные активные факторы стабилизируются,
т.е. устанавливаются на каких-то одинаковых
для всех опытов уровнях.

Некоторые
факторы не могут быть обеспечены
системами стабилизации (например,
погодные условия, самочувствие оператора
и т.д.), другие же стабилизируются с
какой-то погрешностью (например,
содержание какого-либо компонента в
среде зависит от ошибки при взятии
навески и приготовления раствора).
Учитывая также, что измерение параметра
у
осуществляется
прибором, обладающим какой-то погрешностью,
зависящей от класса точности прибора,
можно прийти к выводу, что результаты
повторностей одного и того же опыта у_к
будут
приближенными и должны отличаться один
от другого и от истинного значения
выхода процесса. Неконтролируемое,
случайное изменение и множества других
влияющих на процесс факторов вызывает
случайные
отклонения
измеряемой величины у_к
от
ее истинного значения – ошибку опыта.

Каждый
эксперимент содержит элемент
неопределенности вследствие ограниченности
экспериментального материала. Постановка
повторных (или параллельных) опытов не
дает полностью совпадающих результатов,
потому что всегда существует ошибка
опыта (ошибка воспроизводимости). Эту
ошибку и нужно оценить по параллельным
опытам. Для этого опыт воспроизводится
по возможности в одинаковых условиях
несколько раз и затем берется среднее
арифметическое всех результатов. Среднее
арифметическое у равно сумме всех n
отдельных результатов, деленной на
количество параллельных опытов n:

Отклонение
результата любого опыта от среднего
арифметического можно представить как
разность y_q–

,
где y_q
– результат отдельного опыта. Наличие
отклонения свидетельствует об
изменчивости, вариации значений повторных
опытов. Для измерения этой изменчивости
чаще всего используют дисперсию.

Дисперсией
называется среднее значение квадрата
отклонений величины от ее среднего
значения. Дисперсия обозначается s²
и выражается формулой:

где
(n-1)
– число степеней свободы, равное
количеству опытов минус единица. Одна
степень свободы использована для
вычисления среднего.

Корень
квадратный из дисперсии, взятый с
положительным знаком, называется средним
квадратическим отклонением, стандартом
или квадратичной ошибкой:

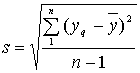
Ошибка
опыта является суммарной величиной,
результатом многих ошибок: ошибок
измерений факторов, ошибок измерений
параметра оптимизации и др. Каждую из
этих ошибок можно, в свою очередь,
разделить на составляющие.

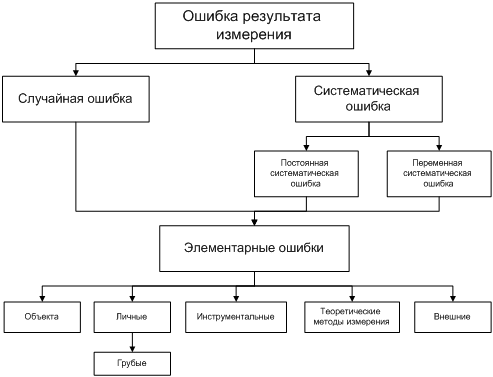
Все
ошибки принято разделять на два класса:
систематические и случайные (рисунок
1).

Систематические
ошибки порождаются причинами, действующими
регулярно, в определенном направлении.
Чаще всего эти ошибки можно изучить и
определить количественно. Систематическая
ошибка –
это ошибка, которая остаётся постоянно
или закономерно изменяется при повторных
измерениях одной и той же величины. Эти
ошибки появляются вследствие неисправности
приборов, неточности метода измерения,
какого либо упущения экспериментатора,
либо использования для вычисления
неточных данных. Обнаружить систематические
ошибки, а также устранить их во многих
случаях нелегко. Требуется тщательный
разбор методов анализа, строгая проверка
всех измерительных приборов и безусловное
выполнение выработанных практикой
правил экспериментальных работ. Если
систематические ошибки вызваны известными
причинами, то их можно определить.
Подобные погрешности можно устранить
введением поправок.

Систематические
ошибки находят, калибруя измерительные
приборы и сопоставляя опытные данные
с изменяющимися внешними условиями
(например, при градуировке термопары
по реперным точкам, при сравнении с
эталонным прибором). Если систематические
ошибки вызываются внешними условиями
(переменной температуры, сырья и т.д.),
следует компенсировать их влияние.

Случайными
ошибками называются те, которые появляются
нерегулярно, причины, возникновения
которых неизвестны и которые невозможно
учесть заранее. Случайные ошибки
вызываются и объективными причинами и
субъективными. Например, несовершенством
приборов, их освещением, расположением,
изменением температуры в процессе
измерений, загрязнением реактивов,
изменением электрического тока в цепи.
Когда случайная ошибка больше величины
погрешности прибора, необходимо
многократно повторить одно и тоже
измерение. Это позволяет сделать
случайную ошибку сравнимой с погрешностью
вносимой прибором. Если же она меньше
погрешности прибора, то уменьшать её
нет смысла. Такие ошибки имеют значение,
которое отличается в отдельных измерениях.
Т.е. их значения могут быть неодинаковыми
для измерений сделанных даже в одинаковых
условиях. Поскольку причины, приводящие
к случайным ошибкам неодинаковы в каждом
эксперименте, и не могут быть учтены,
поэтому исключить случайные ошибки
нельзя, можно лишь оценить их значения.
При многократном определении какого-либо
показателя могут встречаться результаты,
которые значительно отличаются от
других результатов той же серии. Они
могут быть следствием грубой ошибки,
которая вызвана невнимательностью
экспериментатора.

Систематические
и случайные ошибки состоят из множества
элементарных ошибок. Для того чтобы
исключать инструментальные ошибки,
следует проверять приборы перед опытом,
иногда в течение опыта и обязательно
после опыта. Ошибки при проведении
самого опыта возникают вследствие
неравномерного нагрева реакционной
среды, разного способа перемешивания
и т.п.

При
повторении опытов такие ошибки могут
вызвать большой разброс экспериментальных
результатов.

Очень
важно исключить из экспериментальных
данных грубые ошибки, так называемый
брак при повторных опытах. Грубые
ошибки легко
обнаружить. Для выявления ошибок
необходимо произвести измерения в
других условиях или повторить измерения
через некоторое время. Для предотвращения
грубых ошибок нужно соблюдать аккуратность
в записях, тщательность в работе и записи
результатов эксперимента. Грубая ошибка
должна быть исключена из экспериментальных
данных. Для отброса ошибочных данных
существуют определённые правила.

Например,
используют критерий Стьюдента t
(Р; f):
Опыт считается бракованным, если
экспериментальное значение критерия
t по модулю больше табличного значения
t
(Р; f).

Если
в распоряжении исследователя имеется
экспериментальная оценка дисперсии
S²(y_k)
с небольшим конечным числом степеней
свободы, то доверительные ошибки
рассчитываются с помощью критерий
Стьюдента t
(Р; f):

ε(
)
= t (Р;
f)* S(y_k)/
=
t (Р;
f)* S(
)

ε(y_k)
= t
(Р; f)*
S(y_k)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Ошибка опыта

Абсолютная и относительная погрешности (ошибки).

Пусть некоторая
величина x
измерена n
раз. В результате получен ряд значений
этой величины: x₁,
x₂,
x₃,
…, x_n

Величиной, наиболее
близкой к действительному значению,
является среднее арифметическое этих
результатов:

Отсюда следует,
что каждое физическое измерение должно
быть повторено несколько раз.

Разность между
средним значением
измеряемой
величины и значением отдельного измерения
называется абсолютной
погрешностью отдельного измерения:

(13)

Абсолютная
погрешность может быть как положительной,
так и отрицательной и измеряется в тех
же единицах, что и измеряемая величина.

Средняя абсолютная
ошибка результата — это среднее
арифметическое значений абсолютных
погрешностей отдельных измерений,
взятых по абсолютной величине (модулю):

(14)

Отношения

называются относительными погрешностями
(ошибками) отдельных измерений.

Отношение средней
абсолютной погрешности результата

к среднему арифметическому значению

измеряемой величины называют относительной
ошибкой результата и выражают в процентах:

Относительная
ошибка характеризует точность измерения.

Законы распределения случайных величин.

Результат измерения
физической величины зависит от многих
факторов, влияние которых заранее учесть
невозможно. Поэтому значения, полученные
в результате прямых измерений какого
— либо параметра, являются случайными,
обычно не совпадающие между собой.
Следовательно, случайные
величины —
это такие величины, которые в зависимости
от обстоятельств могут принимать те
или иные значения. Если случайная
величина принимает только определенные
числовые значения, то она называется
дискретной.

Например,
количество заболеваний в данном регионе
за год, оценка, полученная студентом на
экзамене, энергия электрона в атоме и
т.д.

Непрерывная
случайная величина принимает любые
значения в данном интервале.

Например: температура
тела человека, мгновенные скорости
теплового движения молекул, содержание
кислорода в воздухе и т.д.

Под событием
понимается всякий результат или исход
испытания. В теории вероятностей
рассматриваются события, которые при
выполнение некоторых условий могут
произойти, а могут не произойти. Такие
события называются
случайными.
Например, событие, состоящее в появлении
цифры 1 при выполнении условия — бросания
игральной кости, может произойти, а
может не произойти.

Если событие
неизбежно происходит в результате
каждого испытания, то оно называется
достоверным.
Событие называется невозможным,
если оно вообще не происходит ни при
каких условиях.

Два события,
одновременное появление которых
невозможно, называются несовместными.

Пусть случайное
событие А в серии из n
независимых испытаний произошло m
раз, тогда отношение:

называется
относительной частотой события А. Для
каждой относительной частоты выполняется
неравенство:

При небольшом
числе опытов относительная частота
событий в значительной мере имеет
случайный характер и может заметно
изменяться от одной группы опытов к
другой. Однако при увеличении числа
опытов частота событий все более теряет
свой случайный характер и приближается
к некоторому постоянному положительному
числу, которое является количественной
мерой возможности реализации случайного
события А. Предел, к которому стремится
относительная частота событий при
неограниченном увеличении числа
испытаний, называется статистической
вероятностью события:

Например, при
многократном бросании монеты частота
выпадения герба будет лишь незначительно
отличаться от ½. Для достоверного события
вероятность Р(А) равна единице. Если
Р=0, то событие невозможно.

Математическим
ожиданием
дискретной случайной величины называется
сумма произведений всех ее возможных
значений х_i
на вероятность этих значений р_i:

Статистическим
аналогом математического ожидания
является среднее арифметическое значений
:

,

где m_i
— число дискретных случайных величин,
имеющих значение х_i.

Для непрерывной
случайной величины математическим
ожиданием служит интеграл:

,

где р(х) — плотность
вероятности.

Отдельные значения
случайной величины группируются около
математического ожидания. Отклонение
случайной величины от ее математического
ожидания (среднего значения) характеризуется
дисперсией,
которая для дискретной случайной
величины определяется формулой:

(15)

(16)

Дисперсия имеет
размерность случайной величины. Для
того, чтобы оценивать рассеяние
(отклонение) случайной величины в
единицах той же размерности, введено
понятие среднего
квадратичного отклонения
σ(Х), которое
равно корню квадратному из дисперсии:

(17)

Вместо среднего
квадратичного отклонения иногда
используется термин «стандартное
отклонение».

Всякое отношение,
устанавливающее связь между всеми
возможными значениями случайной величины
и соответствующими им вероятностями,
называется законом
распределения случайной величины.
Формы задания закона распределения
могут быть разными:

а) ряд распределения
(для дискретных величин);

б) функция
распределения;

в) кривая распределения
(для непрерывных величин).

Существует
относительно много законов распределения
случайных величин.

Нормальный
закон распределения случайных
величин (закон
Гаусса).
Случайная величина

распределена по
нормальному закону, если ее плотность
вероятности f(x)
определяется формулой:

(18),

где <x>
— математическое ожидание (среднее
значение) случайной величины <x>
= M
(X);

—
среднее квадратичное отклонение;

—
основание натурального логарифма
(неперово число);

f
(x)
– плотность вероятности (функция
распределения вероятностей).

Многие случайные
величины (в том числе все случайные
погрешности) подчиняются нормальному
закону распределения (закону Гаусса).
Для этого распределения наиболее
вероятным значением
измеряемой
величины
является
её среднее
арифметическое
значение.

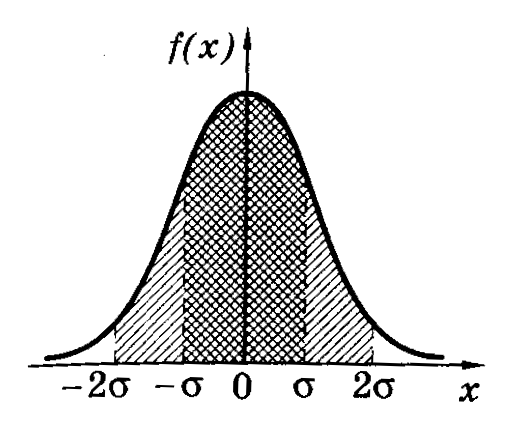
График нормального
закона распределения изображен на
рисунке (колоколообразная кривая).

Кривая симметрична
относительно прямой х=<x>=α,
следовательно, отклонения случайной
величины вправо и влево от <x>=α
равновероятны. При х=<x>±
кривая асимптотически приближается к
оси абсцисс. Если х=<x>,
то функция распределения вероятностей
f(x)
максимальна и принимает вид:

(19)

Таким образом,
максимальное значение функции f_max(x)
зависит от величины среднего квадратичного
отклонения. На рисунке изображены 3
кривые распределения. Для кривых 1 и 2
<x>
= α = 0 соответствующие значения среднего
квадратичного отклонения различны, при
этом ₂>₁.
(При увеличении 
кривая распределения становится более
пологой, а при уменьшении 
– вытягивается вверх). Для кривой 3 <x>
= α ≠ 0 и ₃
= ₂.

Закон
распределения
молекул в газах по скоростям называется
распределением
Максвелла.
Функция плотности вероятности попадания
скоростей молекул в определенный
интервал

теоретически была определена в 1860 году
английским физиком Максвеллом

. На рисунке
распределение Максвелла представлено
графически. Распределение движется
вправо или влево в зависимости от
температуры газа (на рисунке Т₁
< Т₂).
Закон распределения Максвелла определяется
формулой:

(20),

где m_о
– масса молекулы, k
– постоянная Больцмана, Т – абсолютная
температура газа,
—
скорость молекулы.

Распределение
концентрации молекул газа в атмосфере
Земли (т.е.
в силовом поле) в зависимости от высоты
было дано австрийским физиком Больцманом
и называется
распределением
Больцмана:

(21)

Где n(h)
– концентрация молекул газа на высоте
h,
n₀
– концентрация у поверхности Земли, g
– ускорение свободного падения, m
– масса молекулы.

Распределение
Больцмана.

Совокупность всех
значений случайной величины называется
простым
статистическим рядом.
Так как простой статистический ряд
оказывается большим, то его преобразуют
в вариационный
статистический
ряд или интервальный
статистический ряд. По интервальному

статистическому ряду для оценки вида
функции распределения вероятностей по
экспериментальным данным строят
гистограмму
– столбчатую
диаграмму. (Гистограмма – от греческих
слов “histos”–
столб и “gramma”–
запись).

n

1. h

Гистограмма
распределения Больцмана.

Для построения
гистограммы интервал, содержащий
полученные значения случайной величины
делят на несколько интервалов x_i
одинаковой ширины. Для каждого интервала
подсчитывают число m_i
значений случайной величины, попавших
в этот интервал. После этого вычисляют
плотность частоты случайной величины

для каждого интервала x_i
и среднее значение случайной величины
<x_i
> в каждом интервале.

Затем по оси абсцисс
откладывают интервалы x_i,
являющиеся основаниями прямоугольников,
высота которых равна
(или
высотой

– плотностью относительной частоты
).

Расчетами показано,
что вероятность попадания нормально
распределенной случайной величины в
интервале значений от <x>–
до <x>+
в среднем равна 68%. В границах вдвое
более широких (<x>–2;
<x>+2)
размещается в среднем 95% всех значений
измерений, а в интервале (<x>–3;<x>+3)
– уже 99,7%. Таким образом, вероятность
того, что отклонение значений нормально
распределенной случайной величины
превысит 3
(
– среднее квадратичное отклонение)
чрезвычайно мала (~0,003). Такое событие
можно считать практически невозможным.
Поэтому границы <x>–3
и <x>+3
принимаются за границы практически
возможных значений нормально распределенной
случайной величины («правило трех
сигм»).

Если число измерений
(объем выборки) невелико (n<30),
дисперсия вычисляется по формуле:

(22)

Уточненное среднее
квадратичное отклонение отдельного
измерения вычисляется по формуле:

(23)

Напомним, что для
эмпирического распределения по выборке
аналогом математического ожидания
является среднее арифметическое значение
<x>
измеряемой величины.

Чтобы дать
представление о точности и надежности
оценки измеряемой величины, используют
понятия доверительного интервала и
доверительной вероятности.

Доверительным
интервалом
называется интервал (<x>–x,
<x>+x),
в который по определению попадает с
заданной вероятностью действительное
(истинное) значение измеряемой величины.
Доверительный интервал характеризует
точность полученного результата: чем
уже доверительный интервал, тем меньше
погрешность.

Доверительной
вероятностью
(надежностью)

результата серии измерений называется
вероятность того, что истинное значение
измеряемой величины попадает в данный
доверительный интервал (<x>±x).
Чем больше величина доверительного
интервала, т.е. чем больше x,
тем с большей надежностью величина <x>
попадает в этот интервал. Надежность 
выбирается самим исследователем
самостоятельно, например, =0,95;
0,98. В медицинских и биологических
исследованиях, как правило, доверительную
вероятность (надежность) принимают
равной 0,95.

Если величина х
подчиняется нормальному закону
распределения Гаусса, а <x>
и <>
оцениваются по выборке (числу измерений)
и если объем выборки невелик (n<30),
то интервал (<x>
– t_,n<>,
<x>
+ t_,n<>)
будет доверительным интервалом для
известного параметра х с доверительной
вероятностью .

Коэффициент t_,n
называется коэффициентом
Стьюдента
(этот коэффициент был предложен в 1908 г.
английским математиком и химиком В.С.
Госсетом, публиковавшим свои работы
под псевдонимом «Стьюдент» – студент).

Значении коэффициента
Стьюдента t_,n
зависит от доверительной вероятности

и числа измерений n
(объема выборки). Некоторые значения
коэффициента Стьюдента приведены в
таблице 1.

Таблица 1

В таблице 1 в верхней
строке заданы значения доверительной
вероятности 
от 0,6 до 0,99, в левом столбце – значение
n.
Коэффициент Стьюдента следует искать
на пересечении соответствующих строки
и столбца.

Окончательный
результат измерений записывается в
виде:

(25)

Где

– полуширина доверительного интервала.

Результат серии
измерений оценивается относительной
погрешностью:

(26)

Проведение
эксперимента

Познакомимся с
вычислением ошибки опыта, или, как ее часто называют, ошибки воспроизводимости.

Ошибки параллельных
опытов

Каждый
эксперимент содержит элемент неопределен­ности вследствие ограниченности
экспериментального ма­териала. Постановка повторных (или параллельных) опытов
не дает полностью совпадающих результатов, потому что всегда существует ошибка
опыта (ошибка воспроиз­водимости). Эту ошибку и нужно оценить по параллель­ным
опытам. Для этого опыт воспроизводится по возмож­ности в одинаковых условиях
несколько раз и затем бе­рется среднее арифметическое всех результатов. Среднее
арифметическое  равно сумме всех п отдельных резуль­татов, деленной на количество
параллельных опытов п

.

Отклонение
результата любого опыта от среднего арифметического можно представить как
разность  где  – результат отдельного опыта. Наличие
откло­нения свидетельствует об изменчивости, вариации значе­ний повторных
опытов. Для измерения этой изменчи­вости чаще всего используют дисперсию.
Диспер­сией называется среднее значение квадрата отклонений величины от ее
среднего значения. Дисперсия обозна­чается s² и
выражается формулой

.

где (n – 1) – число
степеней свободы, равное количе­ству опытов минус единица. Одна степень свободы
исполь­зована для вычисления среднего.

Корень квадратный из
дисперсии, взятый с положи­тельным знаком, называется средним квадратическим от­клонением,
стандартом или квадратичной ошибкой

Стандарт имеет
размерность той величины, для кото­рой он вычислен. Дисперсия и стандарт – это
меры рассеяния, изменчивости. Чем больше дисперсия и стан­дарт, тем больше
рассеяны значения параллельных опы­тов около среднего значения.

Ошибка опыта являемся
суммарной величиной, результатом многих ошибок: ошибок измерений факторов,
ошибок измерений параметра оптимизации и др. Каждую из этих ошибок можно, в свою
очередь, разделить на состав­ляющие.

Вопрос о классификации ошибок
довольно сложный и вызывает много дискуссий. В качестве примера одной из
возможных схем классификации мы приведем схему из книги Ю. В. Кельница «Теория
ошибок измере­ний» (М., изд-во «Недра», 1967).

Все ошибки принято разделять
на два класса: система­тические и случайные.

Систематические ошибки
порождаются причинами, действующими регулярно, в определенном направлении. Чаще
всего эти ошибки можно изучить и определить количественно.

Систематические ошибки
находят, калибруя измери­тельные приборы и сопоставляя опытные данные с изме­няющимися
внешними условиями (например, при градуи­ровке термопары по реперным точкам,
при сравнении с эта­лонным прибором).

Если систематические ошибки
вызываются внешними условиями (переменной температуры, сырья и т. д.), следу­ет
компенсировать их влияние. Как это делать, будет показано ниже.

Случайными ошибками называются
те, которые появ­ляются нерегулярно, причины возникновения которых неизвестны и
которые невозможно учесть заранее.

Систематические и случайные
ошибки состоят из мно­жества элементарных ошибок. Для того, чтобы исключать инструментальные
ошибки, следует проверять приборы перед опытом, иногда в течение опыта и обязательно
после опыта. Ошибки при проведении самого опыта возникают вследствие неравномерного
нагрева реакционной среды, раз­ного способа перемешивания и т.п. При повторении
опытов такие ошибки могут вызвать большой разброс эксперимен­тальных
результатов.

Очень важно исключить из экспе­риментальных
данных грубые ошибки, так называемый брак при повторных опытах. Для отброса оши­бочных
опытов существуют правила. Для определения брака используют, например, кри­терий
Стьюдента

.

Значение t берут из таблицы t-распределения Стьюдента. Опыт считается
бракованным, если эксперименталь­ное значение критерия t по модулю больше табличного значения.

Дисперсия параметра
оптимизации

Дисперсия всего эксперимента
получается в результате усреднения дисперсий всех опытов. По терми­нологии,
принятой в планировании эксперимента, речь идет о подсчете дисперсии параметра
оптимизации  или, что то же самое, дисперсии воспроизводимости эксперимента

При подсчете дисперсии
параметра оптимизации квад­рат разности между значением y_q в каждом опыте и средним значением из n повторных наблюдений y нужно просумми­ровать по числу опытов в
матрице N, а затем разделить на N(n — 1):

,

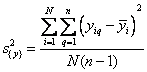
Где i = 1, 2, …, N;      q = 1, 2, …, n.

Такой формулой можно
пользоваться в случаях, когда число повторных опытов одинаково во всей матрице.

Дисперсию воспроизводимости
проще всего рассчиты­вать, когда соблюдается равенство числа повторных опы­тов
во всех экспериментальных точках. На практике весь­ма часто приходится
сталкиваться со случаями, когда число повторных опытов различно. Это происходит
вследствие отброса грубых наблюдений, неуверенности экспе­риментатора в
правильности некоторых результатов (в таких случаях возникает желание еще и еще
раз повторить опыт) и т.п.

Тогда при усреднении
дисперсий приходится пользо­ваться средним взвешенным значением дисперсий,
взятым с учетом числа степеней свободы

,

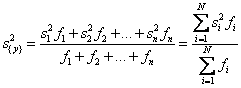
где

– дисперсия i-го опыта;

 – число степеней свободы i-м опыте, равное числу параллельных опытов
n_i минус 1.

Число степеней
свободы средней дисперсии принима­ется равным сумме чисел степеней свободы
дисперсий, из которых она вычислена.

Случай с неравным числом
наблюдений, который мы рассмотрели выше, связан с нарушением ортогональности
матрицы. Поэтому здесь нельзя использовать расчетные формулы для коэффициентов,
приведенные ранее. Этот вопрос будет рассмотрен ниже.

Экспериментатору не следует
забывать о про­верке однородности дисперсий, неоднородные дисперсии усреднять
нельзя. Прежде чем пользоваться приведёнными выше формулами, нужно убедиться в
однородности суммируемых дисперсий.

Проверка
однородности дисперсий

Проверка однородности
дисперсий производится с помощью различных статистических критериев. Простей­шим
из них является критерий Фишера, предназначенный для сравнения двух дисперсий.
Критерий Фишера (F—критерий)
представляет собою отношение большей дисперсии к меньшей. Полученная величина
сравнивается с таблич­ной величиной F-критерия.

Если полученное значение
дисперсионного отно­шения больше приведенного в таблице для соответствую­щих
степеней свободы и выбранного уровня значимости, это означает, что дисперсии
значимо отличаются друг от друга, т. е. что они неоднородны.

Если сравниваемое количество
дисперсий больше двух и одна дисперсия значительно превышает остальные, можно воспользоваться
критерием Кохрена. Этот критерий пригоден для случаев, когда во всех точках
имеется одина­ковое число повторных опытов. При этом подсчитывается дисперсия в
каждой горизонтальной строке матрицы

,

а затем из
всех дисперсий находится наибольшая  ко­торая делится на сумму всех дисперсий. Критерий Кохрена – это
отношение максимальной дисперсии к сумме всех дисперсий

.

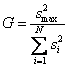
Гипотеза
об однородности дисперсий подтверждается, если экспериментальное значение
критерия Кохрена не превы­шает табличного значения. Тогда можно усреднять дис­персии
и пользоваться формулой

.

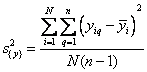
Если возникает предположение
о наличии неодно­родности дисперсий для случая, когда число повторных опытов неодина­ково
во всех точках, можно воспользоваться критерием Бартлета. По уже знакомой
формуле подсчитывается дисперсия воспроизводимости

.

Далее
находится величина

,

где

.

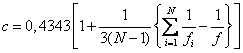
Здесь число
степеней свободы равно N–1, где N – число сравниваемых дисперсий. При планировании экспе­римента типа
2^k это число равно числу опытов в матрице.

Бартлет показал, что величина
 приближенно подчиняется  – распределению с (N–1) степенями свободы. Значимость критерия
Бартлета проверяется обычным способом.

Критерий Бартлета базируется
на нормальном распре­делении. Если имеются отклонения от нормального распре­деления,
то проверка неоднородности дисперсий может привести к ошибочным результатам.

Можно предложить
использование F-критерия даже в тех случаях, когда число
дисперсий больше двух. Делается это следующим образом. Из всех дисперсий
выделяются наибольшая и наименьшая. По F-критерию производится проверка, значимо ли они различаются между
собой. Ясно, что если наибольшая и наименьшая дисперсии не отличаются значимо,
то диспер­сии, имеющие промежуточные значения, также не могут значимо
отличаться друг от друга. Тогда всю группу дис­персий можно считать
принадлежащей к единой совокуп­ности. В таких случаях нет надобности применять
кри­терий Бартлета.

Рандомизация

Чтобы исключить влияние
систематических ошибок, вызванных внешними условиями (переменой температуры,
сырья, лаборанта и т. д.), рекомендуется случайная пос­ледовательность при
постановке опытов, запланированных матрицей. Опыты необходимо рандомизировать
во времени. Термин «рандомизация» происходит от английского слова random – случайный.

Если экспериментатор
располагает сведениями о пред­стоящих изменениях внешней среды, сырья,
аппаратуры и т. п., то целесообразно планировать эксперимент таким образом,
чтобы эффект влияния внешних условий был сме­шан с определенным
взаимодействием, которое не жалко потерять. Так, при наличии двух партий сырья
матрицу 2³ можно разбить на два блока таким образом, чтобы эффект
сырья сказался на величине трехфакторного взаимодейст­вия. Тогда все линейные
коэффициенты и парные взаимо­действия будут освобождены от влияния
неоднородности сырья.

В этой матрице при
составлении блока 1 отобраны все строки, для которых , а при составления бло­ка 2 – все строки,
для которых . Различие в сырье можно рассматривать как
новый фактор . Тогда матрица 2³, разбитая на
два блока, представляет собой полуреплику 2^4-1 с определяющим
контрастом .

,                 ;

,                ;

,               ;

,                  ;

,                 ;

,              ;

,              ;

,                ;

Эффект сырья
отразился на подсчете свободного члена b₀ и
эффекта взаимодействия второго порядка b₁₂₃.

Аналогично можно разбить на
два блока любой экспе­римент типа 2³. Главное – правильно выбрать
взаимодей­ствие, которым можно безболезненно пожертвовать. При отсутствии
априорных сведений выбирают взаимодействие самого высокого порядка: x₁x₂x₃ для 2³, x₁x₂x₃х₄ для 2⁴, x₁x₂x₃x₄x₅ 2⁵ и т. д. Но если
экспериментатору известно, что одно из парных взаимодействий лишено, например,
физико-химического смысла, то можно пожертвовать парным взаимодействием.

Матрицу типа 2^k можно разбить на количество блоков 2ⁿ (n – степень
двойки) при . Так, матрица 2³
разбивается на два блока по четыре опыта в каждом и на четыре блока по
два опыта в каждом. Матрица 2⁴ – на два блока по 8 опытов в каждом,
на четыре блока по четыре опыта и на восемь блоков по два опыта и т.д.