Что показывают статистические ошибки в генетике

Статистические ошибки

Использование
методов биометрии позволяет исследователю
на ограниченном по численности материале
делать заключения о проявлении признака,
его изменчивости и других параметрах
в генеральной совокупности. Но так
как выборочная совокупность — часть
генеральной и ее формируют методом
случайного отбора, то в выборку могут
попасть животные с более низкими
продуктивными качествами, или несколько
лучшие особи. В этом случае вычисленные
значения M, б, C_v и
других биометрических величин будут
отличаться от значений этих величин в
генеральной совокупности, то есть
выборка отражает генеральную совокупность
с ошибкой. Эти ошибки, связанные с
методом выборочности, называются
статистическими и устранить их нельзя.
Ошибки не будет лишь в том случае, когда
в обработку включаются все члены
генеральной совокупности. Величины
статистических ошибок зависят от
изменчивости признаков и объема выборки:
чем более изменчив признак, тем больше
ошибка, и чем больше объем выборки, тем
она меньше. Ошибки статистических
величин в биометрии принято обозначать
буквой m.

Ошибки
имеют все статистические величины.
Вычисляют их по формулам:

Все
ошибки измеряют в тех же единицах, что
и сами показатели, и записывают обычно
рядом с ними.

Статистические
ошибки указывают интервал, в котором
находится величина того или иного
статистического показателя в генеральной
совокупности. Зная среднее значение
признака (М) и его ошибку (m), можно
установить доверительные границы
средней величины в генеральной
совокупности по формуле: М_ген.=М_в. 
tm, где t — нормированное отклонение,
которое зависит от уровня вероятности
и объема выборки. Цифровое значение t
для каждого конкретного случая находят
с помощью специальной таблицы. Например,
нас интересует средняя частота пульса
у овец породы прекос. Для изучения этого
показателя была сформирована выборка
в количестве 50 голов и определена у
этих животных средняя частота пульса.
Оказалось, что этот показатель равен
75 ударов в минуту, изменчивость его б =
12 ударов. Ошибка средней арифметической
величины в этом случае составит:

б
12

m
= ──── = ──── = 1,7 (уд./мин).

n
50

Итоговая
запись будет иметь вид: М  
m или 75  
1,7, то есть частота пульса 75 ударов в
минуту — среднее значение для 50 голов.
Чтобы определить среднюю частоту пульса
в генеральной совокупности животных,
возьмем в качестве доверительной
вероятности P = 0,95. В этом случае, исходя
из таблицы, t = 2,01. Определим доверительные
границы частоты пульса в генеральной
совокупности M  
tm.

75,0
+ 2,01 x 1,7 = 75,0 + 3,4 = 78,4 (уд./мин)

75,0
— 2,01 x 1,7 = 75,0 — 3,4 = 71,6 (уд./мин)

Таким
образом, средняя частота пульса для
генеральной совокупности будет в
пределах от 71,6 до 78,4 ударов в минуту.

Зная
величину статистических ошибок,
устанавливают также, правильно ли
выборочная совокупность отражает тот
или иной параметр генеральной, то есть
устанавливают критерий доверительности
выборочных величин.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Применение статистического метода в генетическом анализе позволило Менделю установить основные законы наследования.

Для того чтобы при скрещивании у животных и высших растений все фенотипические классы проявились в расщеплении, необходимо равновероятное образование разных сортов гамет и осуществление всех возможных их сочетаний при оплодотворении. Например, гибридное мужское растение Аа производит равное число пыльцевых зерен А и а, а женское, гомозиготное по а, производит одинаковые яйцеклетки. Однако при опылении на каждую яйцеклетку с аллелью а может приходиться как малое, так и большое число пыльцевых зерен. При малом их числе нет гарантии, что оба сорта пыльцы (А и а) окажутся в равном соотношении, так как одних пыльцевых зерен в силу случайности может быть больше, а других меньше. При большом же их числе вероятность того, что они будут с одинаковой частотой соединяться с яйцеклетками данного типа, возрастает.

Следовательно, важным условием реализации расщепления является размер, или объем, выборки, оцениваемой в опыте. Чем меньше количество особей в анализируемом потомстве, тем более вероятно случайное отклонение от нормального расщепления. Значение объема выборки еще более возрастает, если при оплодотворении сочетаются два сорта яйцеклеток — А и а и два сорта спермиев — А и а, так как здесь возрастает момент случайности. Чем больше элементов (сортов гамет) участвует в сочетании при прочих равных условиях, тем большего объема необходима выборка для наилучшего совпадения эмпирического расщепления с теоретически ожидаемым.

В гаплофазе расщепление учитывается на гаметах, а в диплофазе на зиготах и организмах. В последнем случае от мейоза до проявления признака протекают сложные процессы, которые могут маскировать результаты расщепления, при этом часть зигот может погибнуть; кроме того, признаки, определяемые генами, могут измениться под влиянием различных негенетических факторов.

Само явление расщепления является биологическим, а проявление его носит статистический характер. Поэтому в экспериментальной работе каждый раз необходимо убедиться в том, является ли обнаруженное отклонение от теоретически ожидаемого расщепления (1 : 1; 3 : 1; 9 : 3 : 3 : 1) отклонением, вызванным закономерным влиянием каких-то факторов, нарушающих расщепление, или оно случайно, обусловлено, например, недостаточной величиной выборки.

В статистике принята считать, что если отклонение встречается чаще, чем 1 на 20 проб, то оно не случайно. Для оценки соответствия фактического расщепления теоретически ожидаемому необходимо определять значение отклонения.

Для статистической оценки отклонения применяют метод χ² (хи-квадрат). Расчеты с помощью этого метода производят следующим образом. Сначала составляют таблицу по классам расщепления на основании опытных числовых данных. Затем из суммы частот всех классов, составляющей объем выборки, вычисляются теоретически ожидаемые величины (q) для каждого класса соответственно предполагаемой формуле расщепления (1:1, 3:1, 9 : 3 : 3 : 1 и т. п.). Далее определяют отклонение (d) полученных данных от теоретически ожидаемых для каждого класса.

Каждое отклонение d возводят в квадрат, и квадрат отклонений (d²) делят на теоретически ожидаемое число (q) для данного класса:

d²/q

Все частные суммируют и получают величину χ²:

χ² = Σ (d²/q)

Чтобы убедиться в том, что одинаковые отклонения могут иметь разное значение в зависимости от объема выборки, разберем пример расщепления по одной паре аллелей — черная и серая окраска мух при анализирующем скрещивании в опытах с дрозофилой. Теоретически ожидаемое отношение в данном скрещивании 1:1. Допустим, что один студент ограничивается в опыте 60 особями, другой получает больше — 300 особей. Как показывают данные, абсолютов отклонения одинаковы как для большой, так и для малой выборки, но величина χ² гораздо больше для малой.

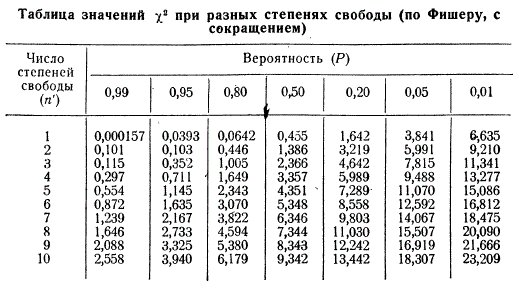
По методу χ² можно определить вероятность того, насколько данное отклонение является случайным или, наоборот, закономерным. Производится это с помощью специальной таблицы Фишера.

Чтобы определить вероятность соответствия опытных и теоретически ожидаемых данных (Р) по данной величине χ², необходимо сначала выяснить число степеней свободы. Отношения 1 : 1 и 3 : 1, т. е. в каждом по два класса, можно представить в виде суммы двух слагаемых, одно из которых устанавливается свободно, а второе — в зависимости от первого. В данном случае степень свободы может быть только одна. Чтобы было ясно, что такое степень свободы, приведем примеры.

В группе из 60 особей встречаются только два класса мух (черные и серые). Известно, что 40 из них серые. Если правильно отобрать 40 серых мух, то во втором классе автоматически будут только черные, и их должно быть 20, т. е. из суммы двух слагаемых одно взято свободно, а второе определилось автоматически. Если в F₂ имеет место расщепление на три фенотипических класса (АА : Аа : аа), то после учета одного из них останется еще возможность выбора второго класса, а третий класс будет определен автоматически; из суммы трех слагаемых два берутся свободно, а третье имеет зависимое значение и т. д. Таким образом, число степеней свободы при анализе классов расщепления всегда будет на единицу меньше числа последних, т. е. если n — числа, классов, то число степеней свободы и будет равно n′ = n — 1.

В приведенном выше примере при двух классах расщепления степень свободы будет только одна. Вычислив величины χ² отыскиваем соответствующие им вероятности для одной степени свободы по таблице Фишера. Так, для выборки в 60 особей, где χ² = 6,6, вероятность Р будет меньше 0,01 т. е. соответствие теоретических и фактически полученных данных будет наблюдаться реже чем раз на 100. Однако, как мы уже говорили, в статистике считают явление случайным, если оно встречается реже, чем 1 раз на 20 проб (0,05). Иначе говоря, расщепление 40 : 20 не соответствует 1:1. Во второй выборке в 300 особей χ² = 1,34. Находя соответствующее ему значение вероятности по той же таблице, мы убеждаемся в совпадении опытных данных с теоретически ожидаемыми: 0,50 > Р > 0,20, т. е. Р = 0,2 ~ 0,5, что указывает на соответствие получаемых и ожидаемых частот примерно в 1 случае из каждых 2.

Тем же путем можно высчитать достоверность различий при дигибридном расщеплении по признакам семян гороха, полученном в опытах Менделя.

Метод χ² дает возможность сравнивать различные численные отклонения при разных объемах выборок в одном масштабе, что очень важно для оценки опытных данных. Но следует иметь в виду, что этот метод неприменим, во-первых, к значениям, выраженным в процентах и относительных числах, и, во-вторых, к выборкам с числом особей в каком-либо из теоретически рассчитанных классов, меньшем, чем 5.

Предмет: 
биология                                   Учитель МБОУ Гвардейская школа
Хасанова Ф.Д.

10   класс

Дата
________

Урок
№ 70: «Статистическая природа генетических
закономерностей. Отклонения от теоретически ожидаемых расщеплений»

Цель:  способствовать развитию умений и навыков
групповой работы; содействовать осознанию практической значимости изучаемого
материала; продолжить формирование ответственного отношения к учебной
деятельности; способствовать развитию умений и навыков работы с биологическими
объектами; продолжить формирование общеучебных умений: анализировать,
сравнивать, делать выводы, работать с текстом.

Оборудование: мультимедийный проектор,
компьютер, интерактивная доска, электронное приложение учебника (презентация,
видеоролик).

УУД:

Личностные
УУД: смыслообразование (каков смысл изучения данной темы);  
нравственно-этическое оценивание  усваиваемого  содержания

Регулятивные
УУД (организация  учащимися  своей
 учебной деятельности):  целеполагание, планирование, прогнозирование,
 контроль, коррекция,  оценка, волевая  саморегуляция в ситуации
затруднения.

Познавательные
УУД: поиск  и выделение необходимой
информации, структурирование  знаний, смысловое чтение, умение
 осознанно строить  речевое высказывание, логические действия
(анализ, синтез, сравнение, обобщение).

Коммуникативные УУД:
учебное сотрудничество с учителем и учениками, постановка вопросов, оценка и
коррекция действий партнера

Планируемые
результаты:

– Учащиеся должны
знать: виды

– Учащиеся должны
уметь: определять

– Учащиеся должны
владеть: работа с парой, учебным материалом.

Тип урока: изучение
нового материала.

Ход работы:

1.                 
Организационный
момент.

2.                 
Проверка
отсутствующих

3.                 
Проверка
готовности к уроку.

4.                 
Изучение
нового материала.

5.                 
Ознакомление
с целью и задачами сегодняшнего занятия. Постановка цели урока.

Статистическая
природа генетических закономерностей. Рассмотрев закономерности расщепления при моно — и дигибридном
скрещиваниях, можно сделать вывод, что одним из условий их выполнения является
случайное и равновероятное сочетание аллелей при слиянии мужской и женской
гамет (образовании зиготы). Этот процесс можно смоделировать в эксперименте.
Перед учеником стоят две коробки. В каждой из них 50% черных и 50% белых шаров.
Ученик, не глядя в коробки, одновременно извлекает два шара один из левой,
другой из правой коробки и кладет их попарно в ячейки перед собой. После того
как все ячейки будут заполнены, можно убедиться, что примерно четверть ячеек
будет содержать только белые шары, четверть — только черные и половина — черные
и белые. Используя изложенные выше правила теории вероятности, можно получить
именно такие числовые отношения. Распределение пар шаров разного цвета
совпадает с расщеплением в F2 при моногибридном скрещивании 1/4: 2/4 : ¼. Это
закономерно, поскольку по своей сути модельный эксперимент и процесс
образования зиготы подобны.

К случайному сочетанию аллелей в зиготе приводит
цепь других случайностей — случайная встреча родителей с разными генотипами,
случайная встреча определенных гамет в процессе оплодотворения, независимое
расхождение хромосом во время мейоза и т. д. Таким образом, случайность
сочетания аллелей в зиготе является общебиологической закономерностью.

Теория
вероятности в генетике. Прежде
чем описывать статистическую природу генетических закономерностей, необходимо
сформулировать несколько простейших правил теории вероятности.

1. Вероятность (Р) случайного события А — Р(А) —
есть число, заключенное между 0 и 1;

0≤ Р(А) ≤1

2. Вероятность случайного события равна отношению
числа случаев М благоприятствующих этому событию, к общему числу N всех
случаев: Р(А)= М/N. Например, при скрещивании Аа х Аа вероятность появления
гомозигот АА равна Р(А) = 0,25, поскольку благоприятствующее событие —
попадание в зиготу двух доминантных аллелей А — будет происходить в среднем в
одном случае из четырех возможных.

3. Рассмотрим правило сложения вероятностей. Если
событие возникает как результат двух несовместимых событий А и В, То
вероятность события С равна сумме вероятностей событий А и В: Р(С)=Р(А) + Р(В).
(Несовместимыми событиями называют такие, совместное наступление которых в
одном испытании невозможно. Например, потомок не может одновременно иметь
генотип Аа и аа.) При моногибридном скрещивании Аа х Аа вероятность появления
АА, т. е. Р(А), равна 0,25 и вероятность появления аа, т. е. Р(В), тоже равна
0,25. Следовательно, вероятность появления гомозигот обоих типов равна Р(С) =
0,25 + 0,25 = = 0,5.

4. Если событие возникает как результат двух
независимых, полностью совместимых событий А и В, то вероятность такого события
Р(А×В) равна произведению вероятностей событий А и В: Р(А×В)=Р(А)×Р(В).
Вероятность рождения потомка с генотипом АаВb в F2 при дигибридном скрещивании
равна P(A×B) = ½ +1/2 = 0,25, поскольку вероятность рождения гетерозигот по
гену А и по гену В равна 1/2.

Статистический
характер расщепления. Пусть в
скрещивании Аа х Аа получено только четыре потомка. Можно ли точно предсказать
генотип каждого из них? Вероятность того, что соотношение генотипов будет равно
1АА:2Аа:1аа, мала. Может случиться, что все четыре потомка будут иметь генотип
АА или Аа. Возможно и любое другое соотношение, например три особи будут иметь
генотип Аа и одна — аа. Значит ли это, что закон расщепления в данном случае
нарушается. Нет, закон расщепления не может быть поколеблен результатами
скрещивания, в которых обнаружено отклонение от ожидаемого соотношения, в нашем
случае 1:2:1. Это объясняется тем, что законы генетики носят статистический
характер, что не отрицает их биологической сущности. Это означает, что
соотношение фенотипов потомков, ожидаемых в любом скрещивании, будет
выполняться тем точнее, чем больше потомков.

В опыте по скрещиванию растений гороха с желтыми и
зелеными семенами Г. Мендель получил в F2 большое количество семян, и поэтому
расщепление оказалось 3,01 : 1, т. е. близким к статистическому. Таким образом,
для того чтобы в каком-либо скрещивании получить расщепление, близкое к
теоретически ожидаемому, необходимо иметь достаточно большую выборку потомков.
Существуют различные статистические методы для того, чтобы оценить,
соответствует или нет отклонение, наблюдающееся в данной выборке, теоретически
ожидаемому.

Отклонения
от теоретически ожидаемых расщеплений. Такие отклонения возникают, когда нарушаются условия
выполнения теоретически ожидаемого расщепления — случайность и равновероятность
участия аллелей в формировании генотипа будущего организма. Например, если при
полигибридном скрещивании анализируемые неаллельные гены находятся в одной
хромосоме (а это случается часто), то в ходе мейоза эти гены не могут
расходиться в разные гаметы независимо. (Явление совместного наследования генов
будет подробнее рассмотрено в следующей лекции.)

К отклонениям от классических схем расщепления
потомства по фенотипу приводят и случаи нарушения мейотического процесса,
приводящие к образованию гамет, зигот или эмбрионов со сниженной
жизнеспособностью. Например, у самцов мышей в природе достаточно часто
встречается хромосома, несущая аллель t. Гетерозиготные самцы (знаком «+» часто
обозначают нормальный, не мутантный аллель гена) способны передавать 80-90%
своих потомков именно аллель t: 

Исследования показали, что причина такого резко
отличающегося от ожидаемого расщепления (1 :1) состоит в более низкой
оплодотворяющей способности гамет, несущих нормальный аллель, т. е. нарушается
условие равной вероятности участия обоих аллелей в образовании зиготы.

Рис. 1. Лисица платиновой окраски (гетерозиготная
самка WрW)

Другим примером может служить наследование
платиновой окраски у лисиц. При скрещивании гетерозиготных лисиц с платиновой
окраской (рис. 1) в потомстве наблюдают расщепление: две платиновые, одна
серебристо-черная. Изучение этого и других подобных случаев показало, что
гомозиготные по гену платиновой окраски эмбрионы гибнут задолго рождения. По
этой причине вместо соотношения 1:2:1 наблюдают соотношение 2:1. В этом случае среди
потомков отсутствует целый генотипическии класс — гомозиготы Wр Wр.

Необычные количественные соотношения фенотипов
потомков (9:7, 13:3, 15:1 И Т. П.) в случае взаимодействия неаллельных генов
является не отклонением от менделевских расщеплений, а следствием объединения
нескольких генотипических классов в один фенотипический.

Все эти явления не отрицают основных генетических
закономерностей

6.                 
Закрепление
нового материала.  Работа с учебником.

7.                 
Рефлексия. Выставление оценок.

8.                 
Д/з §     , вопросы.